金兰组织2013学年第二学期期中考试进度
2013—2014学年度第二学期七年级数学期中测试卷及答案
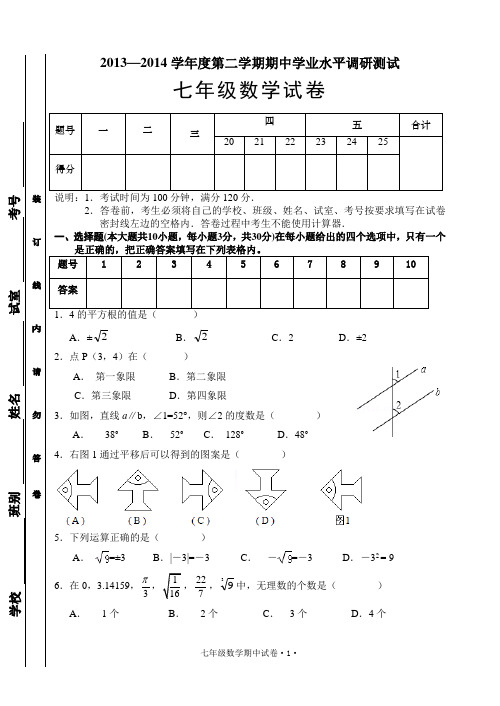
2013—2014学年度第二学期期中学业水平调研测试七年级数学试卷2.答卷前,考生必须将自己的学校、班级、姓名、试室、考号按要求填写在试卷密封线左边的空格内.答卷过程中考生不能使用计算器.一、选择题(本大题共10小题,每小题3分,共30分)在每小题给出的四个选项中,只有一个A .±2B .2C .2D .±22.点P (3,4)在( ) A . 第一象限B .第二象限C .第三象限D .第四象限3.如图,直线a ∥b ,∠1=52°,则∠2的度数是( ) A . 38°B . 52°C . 128°D .48°4.右图1通过平移后可以得到的图案是( )5.下列运算正确的是( ) A .=±3B . |-3|=-3C . -=-3D . -32 = 96.在0,3.14159,3 ,227,39中,无理数的个数是( )A . 1个B . 2个C . 3个D . 4个7.点A 的坐标为(﹣2,﹣3),现将点A 向下平移2个单位,则经过平移后的对应点A′的坐标是( ) A .(﹣2,﹣1)B .(﹣2,﹣5)C .(0,﹣3)D .(﹣4,﹣3)8.点到直线的距离是指( ) A .从直线外一点到这条直线的垂线 B .从直线外一点到这条直线的垂线段 C .从直线外一点到这条直线的垂线的长 D .从直线外一点到这条直线的垂线段的长9.有下列四个命题:(1)相等的角是对顶角;(2)两条直线被第三条直线所截,同位角相等;(3)如果两条直线都和第三条直线平行,那么这两条直线也互相平行;(4)垂直于同一条直线的两条直线互相垂直。
其中是假命题...的有( ) A .1个 B .2个 C . 3个 D .4个 10.如图2,直线a ∥b ,则|x ﹣y |=( ) A . 20 B . 80 C . 120D . 180二、填空题(本大题共6小题,每小题4分,共24分)请将下列各题的正确答案填写在相应位置上。
浙江省宁波市金兰教育合作组织2023-2024学年高二上学期期中联考英语答案

2023学年第一学期宁波金兰教育合作组织期中联考高二年级英语学科参考答案命题:龙赛中学曹素敏审稿:第一部分:听力(共20小题;每小题1.5分,满分30分)1-5. CACAB 6-10. ABABA 11-15. CCBBC 16-20. BABAC第二部分:阅读理解(共两节,满分50分)第一节:(共15小题;每小题2.5分,满分37.5分)21-23 ADB 24-27 BBDD 28-31 DBAB 32-35CADA第二节:(共5小题;每小题2.5分,满分12.5分)36-40 CDEFG第三部分:语言运用(共两节,满分30分)第一节:完形填空(共15小题;每小题1分,满分15分)41-45 ADDCD 46-50 ABBCC 51-55 BABAD第二节:语法填空(共10小题;每小题1.5分,满分15分)56 which 57 after 58 previously 59 was sent 60 valuable61 deepening 62 taken 63 a 64 has travelled / has traveled 65 mysteries第四部分:写作一、应用文写作(满分15分)Dear Jack,Knowing that you’re keen on the photos I posted on the WeChat Moments last week, I’m writing to share some relevant details.This year, the three-day sports meeting started last Friday on the playground, involving almost 20 events. Among them , what I participated in was the 100-meter dash, which required me to speed up to the extreme in a short time. Unfortunately, I ultimately failed to perform well in the race, making me determined to grasp the opportunity next time through continuing efforts.That’s all my experience of the event. Would you please share your school life with me? Looking forward to your reply.Yours,Li Hua 二、读后续写(满分25分)【参考范文】Then the two-hundred-metre breaststroke was announced. My heart pounded fiercely ,as I strode to my assigned place. Leaping into the water, I tried my best to lift up my chin and stretched my limps.“ It is time to face it.”I followed Morgan’s advice -- focus on your own route and don’t distract any attention toany other swimmers. Soon, my arms became sore and my legs were weak. I was on the verge of giving up. Exhausted and weary as I was, I kept moving and gradually felt my rhythm and managed to control my strokes. Without realizing , I had already accomplished one and a half hundred meters.There was only 50 meters to go. The shortness of breath made my body sink and my movement was more and more sluggish. I was going to give up when coach Cafferty’s smile flashed over my mind. I gritted my teeth and pushed myself forward,stroking my arms with water splashing around .When my hand touched the finishing bar, I felt both tired and a sense of achievement. When I pulled myself out of the water with shaking arms, Morgan hugged me tightly, crying, “You did it!” Coach Cafferty thumbed up to me, and the smile on her face seemed even more radiant, as if to say,” You see, girl. You finally go out of your comfort zone and managed to embrace the success.”听力原文第一节(Text 1)W: Hey, Warren. Would you like to go to the park today?M: I am sorry, Fatima. Since it’s so hot, I’m thinking about going to the shopping center instead.W: That sounds good! Can I join you?M: Sure. Let me go home first to have a shower. Then, let’s hit the center!(Text 2)M: What can you do in the sports club?W: Oh, the usual things, tennis, swimming, indoor golf, and yoga … but basically I just use the swimming pool.(Text 3)M: Would you like a drink of something? Cola, a beer, or water?W: You know, I’m on a diet, so I don’t drink cola. And I never drink beer.M: OK. I see.(Text 4)W: Brad, we’ve been here in the cafe for nearly two hours. I need my book now! No more waiting!M: Let’s wait for Tim a little longer. He’ll be here with your book any minute now.W: You told me that an hour ago. It’s already noon!(Text 5)M: Hi! I’m Paul. You’re new here, aren’t you?W: Oh, hi! My name is Jenny.M: Where are you from?W: I am from Canada. My dad got a new job here, so we moved and my brother and I will both study here.第二节(Text 6)M: How about the class size in your hometown?W: Well, in Brazil, we usually have lecture classes with about forty or fifty students and sometimes you’d find it hard to control the classes. Here, my English classes are much smaller, around fifteen students. M: Which do you like better?W: Well, I prefer smaller classes because it’s better for my English. I have a chance to talk more and discuss things in class, so my English has improved a lot.(Text 7)W: Hello, Tim. What’s up?M: I had a real disaster last night.W: Oh no. What happened?M: Well, I was preparing my presentation for today’s sales conference and my computer crashed. I’d nearly finished my PowerPoint slides, and my computer just closed down. It went completely dead. I’d lost my whole presentation.W: That’s terrible, Tim! So what did you do?M: Well, I explained the problem to my boss this morning, and he canceled the meeting. But he’s really not happy. I’ve got to see him now.W: I’m so sorry. Good luck.(Text 8)M: Ella, about the advertisement in the student magazine, have you found a suitable photo?W: I’ve got three possible photos here.M: Nice photos. Well, to my mind the one with the girls is better. It’s more modern. But teenagers these days are so different from when I was young. Can you tell me how modern teenagers have fun?W: Well, the way I see it, teenagers do the same things that they’ve always done. Maybe they use technology — you know, mobiles — but they still hang out with their friends, watch films, just like in the past.M: So what sort of advertisements do they like?W: Well, you have to bear in mind that they don’t like things that are childish.M: Yes, I see.W: So I think the black and white photo is the best. The main reason is that it appeals to teenagers.M: Well, in my opinion you’re right. Teenagers see thousands of images every day and this photo stands out.You don’t often see old-fashioned black and white photos of teenagers.(Text 9)W: Hello?M: Hello. I’m ringing about the advertisement for the bookcases. Are they still available?W: We still have two.M: Right. I’m looking for something to fit in my study. Can you tell me how wide each of them is?W: Yes, they’re both 75 cm wide and 180 cm high.M: OK ... And I don’t want anything that looks too serious … not metal or stone, for example. I was really looking for something made of wood.W: They are, both of them.M: So, are they the same price?W: No, the first bookcase is a bit cheaper. It’s just 15 dollars. We paid 60 dollars for it just five years ago.It’s yellow now, but you could easily change it.M: Yes, I’d probably paint it white if I got it. What about the second one?W: It’s light brown and 30 dollars.M: OK. I want both.(Text 10)Today, I’d like to tell you about a novel called Bend It Like Beckham. You may have watched the film which is a light-hearted comedy. The novel Bend It Like Beckham was written by Narinder Dhami after the release of the film in the previous year. It tells the story of Jess, the 18-year-old student, the daughter of Punjabi Sikhs living in London. Jess loves football and is a fan of David Beckham, but her parents forbid her to play because she is a girl and she can’t do that kind of thing. In spite of this, she secretly joins a local team, where she makes friends with Jules and falls in love with her coach, Joe. While Jess’s parents pay more attention to her sister’s wedding, Jess travels to Hamburg to take part in a tournament.Back in the U.K., the team reaches the final of the league but the match is due to take place on the same day as the wedding.Eventually, Jess persuades her father to let her play and she scores the winning goal. After the match, both Jess and Jules are offered football scholarships at universities in the U.S.The film, starring Parminder Nagra as Jess, Keira Knightley as Jules and Jonathan Rhys Meyers as Joe, was a surprise success.。
2022-2023学年浙江省金兰合作组织高一下学期期中物理试题

2022-2023学年浙江省金兰合作组织高一下学期期中物理试题1.下列物理量的单位属于能量单位的是()A.kg·m/s B.N s C.kg·m/s 2D.kg·m 2 /s 22.物理学科核心素养包括“物理观念、科学思维、科学探究和科学态度与责任”四个方面,下列关于物理观念和科学思维的认识,正确的是()A.驾驶员通过操作方向盘能使汽车在光滑的水平面上转弯B.加速度和功率的定义都运用了比值法C.地球使树上苹果下落的力,与太阳、地球之间的吸引力不是同一种力D.解决变力做功问题中提出的平均作用力体现了等效思想3.如图所示,转笔深受广大中学生的喜爱,其中也包含了许多的物理知识,假设小李同学是转笔高手,能让笔绕其手上的某一点O做匀速圆周运动,下列叙述正确的是()A.笔杆上各点的线速度方向沿着笔杆指向O点B.除了O点,笔杆上其他点的角速度大小都一样C.笔杆上各点的线速度大小与到O点的距离成反比D.笔杆上的点离O点越近,做圆周运动的向心加速度越大4.如图所示,光滑水平面上,小球m在拉力F的作用下做匀速圆周运动。
若小球运动到P点时,拉力F发生变化,下列关于小球运动情况的说法不正确的是()A.若拉力突然消失,小球将沿轨迹做离心运动B.若拉力突然变小,小球可能沿轨迹做离心运动C.若拉力突然变小,小球可能沿轨迹做离心运动D.若拉力突然变大,小球可能沿轨迹做向心运动5.有一辆私家车在前挡风玻璃内悬挂了一个挂件。
当汽车在水平公路上转弯时,驾驶员发现挂件向右倾斜并且倾斜程度在缓慢增加,已知汽车的转弯半径一定,则下列说法正确的是()A.汽车正在向右加速转弯B.汽车正在向右减速转弯C.汽车正在向左加速转弯D.汽车正在向左减速转弯6.天启星座是我国首个正在建设的低轨卫星物联网星座。
它由38颗低轨道卫星组成,这些低轨道卫星的周期大约为100分钟。
则关于这些做圆周运动的低轨道卫星,下列说法正确的是()A.线速度可能大于7.9km/sB.角速度一定大于地球同步卫星的角速度C.加速度可能小于地球同步卫星的加速度D.所需的向心力一定大于地球同步卫星所需的向心力7.把行星绕太阳的运动看成匀速圆周运动,关于太阳对行星的引力,下列说法中正确的是()A.太阳对行星的引力大于行星做匀速圆周运动的向心力B.太阳对行星的引力大小与行星的质量成正比,与行星和太阳间的距离成反比C.太阳对行星的引力规律是由实验得出的D.太阳对行星的引力规律是由开普勒定律和行星绕太阳做匀速圆周运动的规律等推导出来的8.某行星有两颗绕其做匀速圆周运动的卫星A和B,A的运行周期大于B的运行周期.设卫星与行星中心的连线在单位时间内扫过的面积为S,则下列图象中能大致描述S与两卫星的线速度v之间关系的是A.B.C.D.9.如图所示,携带月壤的嫦娥五号轨道器和返回器组合体经历了约6天环月等待后,于2020年12月12日在近月点A点火加速,从近圆轨道Ⅰ进入近月椭圆轨道Ⅱ,13日在点A再次加速,从轨道Ⅱ进入月地转移轨道Ⅲ,经过多次姿态调整后,16日在轨道Ⅲ的远月点B附近,实施轨道器和返回器分离,返回器进入预定返回轨道已知地球质量约为月球质量的81倍,则嫦娥五号轨道器和返回器组合体()A.在轨道Ⅰ上A点的速度大于在轨道Ⅱ上A点的速度B.在轨道Ⅰ上的运行周期大于在轨道Ⅱ上的运行周期C.在轨道Ⅲ上A点的加速度大于在轨道Ⅱ上A点的加速度D.在轨道Ⅲ上B点附近时,受到的地球引力大于月球引力10.如图所示,将3个木板1、2、3固定在墙角,现将一个可以视为质点的物块分别从3个木板的顶端由静止释放,物块沿木板下滑到底端,物块与木板之间的动摩擦因数均为μ。
2023—2024学年浙江省宁波金兰教有合作组织高二上学期期中联考物理试卷

2023—2024学年浙江省宁波金兰教有合作组织高二上学期期中联考物理试卷一、单题1. 下列哪一组物理量都是矢量且在国际单位制中的单位是相同的()A.功与能B.动能与动量C.动量变化量与冲量D.动量变化率与冲量2. 下列说法正确的是()A.赫兹预言了电磁波的存在B.奥斯特发现了电流的磁效应C.安培力的方向用安培定则判断D.麦克斯韦认为变化的磁场一定会产生恒定的电场3. 如图所示,直导线AB、螺线管E、电磁铁D三者相距较远,其磁场互不影响,当开关S闭合后,则小磁针北极N(黑色端)指示磁场方向正确的是()A.a B.b C.c D.d4. 如图所示,绕在铁芯上的线圈与电源、滑动变阻器和电键组成闭合回路,在铁芯的右端套有一个表面绝缘的铜环A,下列各种情况中铜环A中没有感应电流的是()A .将电键突然断开的瞬间B .通电时,保持变阻器的滑片P 位置不变C .通电时,使变阻器的滑片P 做匀速移动D .通电时,使变阻器的滑片P 做加速移动5. 一质量为的物块在合外力 F 的作用下从静止开始沿直线运动。
F 随时间t 变化的图线如图所示,则( )A .1秒末物块的速率为B .3秒末时物块的动量大小为C .前4秒内物块的运动方向不发生改变D .4秒末物块的速度为零6. 如图所示为某型号手机的一块电池板,则下列描述错误的是( )BT10锂离子高密度电池标准电压:充电限制电压执行标准:GB/T 18287-2000A.是电荷量的单位B.该电池充满电后能储存的电能C.电池对外供电时每通过1C的电荷量能产生的电能D.若该手机的移动待机功率为,则该电池充满电后能使该手机待机大约200小时7. 在如图所示的电路中,电源电压恒定不变,内阻不计,为定值电阻,闭合电键S,调节滑动变阻器R的阻值到r或4 r时,变阻器的电功率相等,要使R上消耗的功率最大,须调节滑动变阻器R的阻值到()A.r B.2r C.3r D.4r8. 某学校为了创建绿色校园,新装了一批节能灯。
浙江省宁波市金兰教育合作组织2023-2024学年高二上学期期中联考英语试题

浙江省宁波市金兰教育合作组织2023-2024学年高二上学期期中联考英语试题学校:___________姓名:___________班级:___________考号:___________一、短对话1.Where will the speakers go together?A.To the park.B.To the man’s house.C.To the shopping center. 2.What does the woman basically do in the sports club?A.Have a swim.B.Play tennis.C.Play indoor golf. 3.What does the woman want to drink?A.Cola.B.Beer.C.Water.4.When did the speakers arrive at the cafe?A.At about 10:00.B.At about 11:00.C.At about 12:00. 5.What is the probable relationship between the speakers?A.Workmates.B.Schoolmates.C.Brother and sister.二、长对话听下面一段较长对话,回答以下小题。
6.How many students are there in the woman’s English class?A.About 15.B.About 40.C.About 50.7.What does the woman say about her English class?A.It is large in size.B.It is beneficial for studying.C.It is hard to control.听下面一段较长对话,回答以下小题。
浙江省宁波市金兰教育合作组织2023-2024学年高二上学期期中联考技术试题含解析

2023学年第一学期宁波金兰教育合作组织期中联考高二年级技术学科试题(答案在最后)考生须知:1.本卷共10页满分100分,考试时间90分钟。
2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字。
3.所有答案必须写在答题纸上,写在试卷上无效。
4.考试结束后,只需上交答题纸。
第一部分信息技术(共50分)一、选择题(本大题共12小题,每小题2分,共24分。
每小题列出的四个选项中只有一个是符合题目要求的,不选、多选、错选均不给分)1.下列关于数据、信息的说法,正确的是()A.出土契刻文字的商代殷墟甲骨是数据B.计算机只能处理数字化后的信息C.数字是数据的唯一表现形式D.移动手机发明以后,信息不再需要载体【答案】B【解析】【详解】本题考查数据、信息的描述。
出土契刻文字的商代殷墟甲骨是数据的载体;计算机只能处理数字化后的信息;数字是数据的表现形式之一;移动手机发明以后,信息仍需要载体。
故选B。
2.有一个五位二进制数1□□10,其中两位数字不明,对应的十进制数为n,则下列说法正确的是()A.转化后的十进制数一定是偶数B.去掉最低位的“0”后,其对应的十进制数缩小10倍C.该十进制n的最小值可能是10D.该二进制数加1后可能变为六位二进制【答案】A【解析】【详解】本题考查二进制数的描述。
该二进制数末尾是0,因此转化后的十进制数一定是偶数;去掉最低位的“0”后,其对应的十进制数缩小2倍;十进制数10对应的二进制数是1010,因此十进制n的最小值不可能是10;该二进制数加1后不可能变为六位二进制。
故选A。
3.小明录制了一段运动会的宣传词音频文件,时长1分钟,采样频率为44.1KHZ,量化位数为16bit,2个声道,保存为不压缩的Wave格式,数据容量约为()A.80KBB.172KBC.656KBD.10MB【答案】D【解析】【详解】本题考查音频文件容量计算。
音频文件容量=采样频率*量化位数*声道数*时长/8=44.1*1000*16*2*1*60/8/1024/1024≈10MB。
七年级2012——2013学年度第一学期教学质量检测成绩统计表七年级
76 73 80 69 80 72 80 80 86 67 68 60 77 72 66 72 62 55 74 71 62 51 82 62 60 66 76 64 67 61 58 69 82 70 69 68 80 72 62 54 66 62 44 49 71 63 46
454 452 452 449 448 448 442 438 435 435 4315 415 414 413 413 413 412 409 405 405 402 399 396 395 394 393 393 393 393 390 390 389 387 387 380 376 375 374 372 369 367
2012370830120220006 2012370830120220284 2012370830120220078 2012370830120220096 2012370830120220239 2012370830120220241 2012370830120220093 2012370830120220036 2012370830120220131 2012370830120220223 2012370830120220260 2012370830120220145 2012370830120220058 2012370830120220282 2012370830120220190 2012370830120220046 2012370830120220070 2012370830120220229 2012370830120220293 2012370830120220095 2012370830120220136 2012370830120220177 2012370830120220265 2012370830120220037 2012370830120220263 2012370830120220059 2012370830120220017 2012370830120220285 2012370830120220148 2012370830120220294 2012370830120220068 2012370830120220181 2012370830120220117 2012370830120220182 2012370830120220171 2012370830120220159 2012370830120220247 2012370830120220115 2012370830120220062 2012370830120220292 2012370830120220153 2012370830120220016 2012370830120220235 2012370830120220297 2012370830120220217 2012370830120220318 2012370830120220246
浙江省宁波市金兰教育合作组织2023-2024学年高一上学期期中联考数学试题含解析

2023学年第一学期宁波金兰教育合作组织期中联考高一年级数学学科试题(答案在最后)考生须知:1.本卷共4页满分150分,考试时间120分钟.2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字.3.所有答案必须写在答题纸上,写在试卷上无效.4.考试结束后,只需上交答题纸.选择题部分一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}230P x x x =-≥,{}13Q x x =<≤,则()RP Q ð等于()A.[)0,1 B.(]0,3 C.()1,3 D.[]1,3【答案】C 【解析】【分析】利用一元二次不等式解法可得{3P x x =≥或}0x ≤,再由补集、交集的运算法则即可求得结果.【详解】解不等式230x x -≥可得3x ≥或0x ≤,即{3P x x =≥或}0x ≤,则{}R 03P x x =<<ð,又{}13Q x x =<≤,所以(){}()R 131,3P Q x x ⋂=<<=ð.故选:C2.命题“25,23x x x ∀<-+≥"的否定是()A.25,23x x x ∀<-+<B.25,23x x x ∃≥-+<C.25,23x x x ∃<-+<D.25,23x x x ∃<-+≤【答案】C 【解析】【分析】全称量词命题的否定是存在量词命题,把任意改为存在,把结论否定.【详解】命题“25,23x x x ∀<-+≥"的否定是“25,23x x x ∃<-+<".3.已知函数222,1(),22,1x xf xx x x⎧-≤=⎨+->⎩则2()(2)ff的值为()A.7136 B.6 C.74 D.179【答案】D 【解析】【分析】根据题意,由函数的解析式可得f(2)=6,进而可得2()(2)ff=f(13),由解析式计算可得答案.【详解】根据题意,函数222,1(),22,1x xf xx x x⎧-≤=⎨+->⎩,则f(2)=22+2×2﹣2=6,则2()(2)ff=f(13)=2﹣(13)2=179.故选D.【点睛】本题考查分段函数的求值,涉及分段函数的解析式,属于基础题.4.下图中可以表示以x为自变量的函数图象是()A. B.C. D.【答案】C【解析】【分析】根据函数的定义,对于自变量中的任意一个x,都有唯一确定的数y与之对应.【详解】根据函数的定义,对于自变量中的任意一个x,都有唯一确定的数y与之对应,所以ABD选项的图象不是函数图象,故排除,5.函数y =的定义域是()A.[]22-, B.()2,2- C.()()2,11,2- D.[)(]2,11,2- 【答案】B 【解析】【分析】根据函数的解析式有意义,列出不等式,即可求解.【详解】由函数y =有意义,则满足240x ->,即22x -<<,所以函数的定义域为()2,2-,故选:B.6.设1465a ⎛⎫= ⎪⎝⎭,1556b -⎛⎫= ⎪⎝⎭,1345c -⎛⎫= ⎪⎝⎭,则()A.c b a <<B.a c b<< C.b a c<< D.b c a<<【答案】C 【解析】【分析】对1556b -⎛⎫= ⎪⎝⎭,1345c -⎛⎫= ⎪⎝⎭,分别化简放缩,利用指数函数()65xf x ⎛⎫= ⎪⎝⎭单调性,即可求出.【详解】由题1465a ⎛⎫= ⎪⎝⎭,11555665b -⎛⎫⎛⎫== ⎪⎪⎝⎭⎝⎭,设函数()65xf x ⎛⎫= ⎪⎝⎭,因为615>,所以()f x 单调递增,因为1145>,所以a b >.因为1111333445665455c a -⎛⎫⎛⎫⎛⎫⎛⎫==>>= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,所以c a >,所以b a c <<,故选:C7.某家医院成为病毒检测定点医院,在开展检测工作的第n 天,每个检测对象从接受检测到检测报告生成平均耗时()t n (单位:小时)大致服从的关系为()00n N t n n N <=≥(0t ,0N 为常数).已知第16天检测过程平均耗时为10小时,第65天和第68天检测过程平均耗时均为5小时,那么可得到第36天检测过程平均耗时约为()A.6小时B.7小时C.9小时D.5小时【答案】B 【解析】【分析】按照题目所给的条件,算出0t ,0N ,再代入计算即可.【详解】因为第65天和第68天检测过程平均耗时均为5小时,所以016N <,10=,即040t =,5=,解得064N =,所以()645,64n t n n <=≥⎩所以第36天检测过程平均耗时()203673t ==≈小时,故选:B.8.已知函数()()121x mf x x x +=+≤≤,函数()()()112g m x x x =-≤≤,若任意的[]11,2x ∈,存在[]21,2x ∈,使得()()12f x g x =,则m 的取值范围是()A.51,3⎛⎤ ⎥⎝⎦B.()1,+∞ C.52,2⎡⎤⎢⎥⎣⎦D.55,32⎡⎤⎢⎥⎣⎦【答案】D 【解析】【分析】对()f x 分离变量化简,结合单调性,求出()f x 和()g x 的值域,由题意可得()f x 的值域为()g x 值域的子集,解不等式可得所求范围.【详解】()()111112111x m x m m f x x x x x +++--===+≤≤+++,()()()112g m x x x =-≤≤,①当1m >时,函数()f x 在区间[]1,2上单调递减,函数()g x 在区间[]1,2上单调递增,可得()21,32m m f x ++⎡⎤∈⎢⎥⎣⎦,()[]1,22g x m m ∈--,由题意,得2112232m m m m ++-≤<≤-,解得5532m ≤≤;②当1m <时,函数()f x 在区间[]1,2上单调递增,函数()g x 在区间[]1,2上单调递减,可得()12,23m m f x ++⎡⎤∈⎢⎥⎣⎦,()[]22,1g x m m ∈--,由题意,得1222123m m m m ++-≤<≤-,解得m ∈∅;③当1m =时,()1f x =,()0g x =,显然不满足,故实数m 的取值范围为55,32⎡⎤⎢⎥⎣⎦,故选:D.二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.设()f x 是定义在R 上的奇函数且在()0,∞+上单调递减,()40f -=,则()A.()f x 在(),0∞-上单调递减B.()80f >C.不等式()0f x >的解集为()(),40,4-∞- D.()f x 的图象与x 轴只有2个公共点【答案】AC 【解析】【分析】根据奇函数特征,画出()f x 的大致图象,结合图象分析四个选项.【详解】对于A,因为()f x 是定义在R 上的奇函数且在()0,∞+上单调递减,()40f -=,根据奇函数特征,所以()f x 在(),0∞-上单调递减,()()440f f =--=,()00f =,故A 正确;对于B,画出大致图象如图,根据图象可知()80f <,故B 错误;对于C,如图可知,不等式()0f x >的解集为()(),40,4-∞- ,故C 正确;对于D ,()f x 的图象与x 轴只有3个公共点,分别是()4,0-,()0,0,()4,0,故D 错误,故选:AC.10.下列命题中正确的是()A.B.已知,R a b ∈,则“0a ≠”是“0ab ≠”的必要不充分条件C.已知()f x 为定义在R 上的奇函数,且当0x >时,()2f x x x =-+,则0x <时,()2f x x x=+D.()f x x =与()g x =【答案】BCD 【解析】【分析】对于A ,由基本不等式即可判断;对于B ,利用充分必要条件的概念判断即可;对于C ,利用函数的奇偶性求解析式即可;对于D ,判断两个函数的定义域,对应关系是否一致即可.【详解】对于A+≥=当且仅当242x +=时取“=”,显然不成立,所以A 错误;对于B ,由00a ab ≠⇒≠,而00ab a ≠⇒≠,所以“0a ≠”是“0ab ≠”的必要不充分条件,所以B 正确;对于C ,()f x 为定义在R 上的奇函数,0x >时,()2f x x x =-+,0x <时,0x ->,则()()()2f x x x f x -=---=-,所以()2f x x x =--,则C 正确;对于D ,()f x x =,()g x x ==,两个函数的定义域,对应关系都一样,所以是两个相同的函数,则D 正确;故选:BCD11.已知函数()1y f x =-的图象关于1x =对称,当(]12,,0x x ∈-∞,且12x x ≠时,()()21210f x f x x x -<-成立,若()()2421f bx f x <+对任意x ∈R 恒成立,则实数b 的可能取值为()A .B.12-C.1- D.12【答案】ABD 【解析】【分析】由函数()1y f x =-的图象关于1x =对称,得到()y f x =的图象关于y 轴对称,即()f x 为偶函数,再根据当(]12,,0x x ∈-∞,且12x x ≠时,()()21210f x f x x x -<-成立,得到()f x 在(],0-∞上递减,在[0,)+∞上递增,然后将()()2421f bx f x <+对任意x ∈R 恒成立,转化为2421bx x <+对任意x ∈R 恒成立求解.【详解】解:因为函数()1y f x =-的图象关于1x =对称,所以函数()y f x =的图象关于y 轴对称,则()f x 为偶函数,又因为当(]12,,0x x ∈-∞,且12x x ≠时,()()21210f x f x x x -<-成立,所以()f x 在(],0-∞上递减,在[0,)+∞上递增,则()()2421f bx f x <+对任意x ∈R 恒成立,即()()2421fbx f x<+对任意x ∈R 恒成立,即2421bx x <+对任意x ∈R 恒成立,当0x =时,01<成立;当0x ≠时,即142b x x<+对任意x ∈R 恒成立,而12x x +≥=,当且仅当12x x =,即22x =时,等号成立,所以4b <,即2b <,故选:ABD12.德国著名数学家狄利克雷在数学领域成就显著,是解析数论的创始人之一,以其名命名的函数1,()0x f x x ⎧=⎨⎩为有理数,为无理数称为狄利克雷函数,则关于()f x 下列说法正确的是()A.函数()f x 的值域是[0,1]B.,(())1x R f f x ∀∈=C.(2)()f x f x +=对任意x R ∈恒成立D.存在三个点11(,())A x f x ,22(,())B x f x ,33(,())C x f x ,使得ABC 为等腰直角三角形【答案】BC 【解析】【分析】根据新定义函数得函数的值域为{0,1};无论x 为有理数还是无理数,()f x 均为有理数,故,(())1x R f f x ∀∈=;由于x 与2x +均属于有理数或均属于无理数,故(2)()f x f x +=对任意x R ∈恒成立;假设存在,则根据函数推出矛盾即可否定结论.【详解】解:对于A 选项,函数的值域为{0,1},故A 选项错误.对于B 选项,.当x 为有理数时,()1f x =,(())()1f f x f x ==当x 为无理数时,()0f x =,()()()01ff x f ==所以R ∀∈,(())1f f x =,故B 选项正确.对于C 选项,x 为有理数时,2x +为有理数,(2)()1f x f x +==当x 为无理数时,2x +为无理数,(2)()0f x f x +==所以(2)()f x f x +=恒成立,故C 选项正确.对于D 选项,若ABC 为等腰直角三角形,不妨设角B 为直角,则()()()123,,f x f x f x 的值得可能性只能为()()()1230,1,0f x f x f x ===或()()()1231,0,1f x f x f x ===,由等腰直角三角形的性质得211x x -=,所以12()()f x f x =,这与()()12f x f x ≠矛盾,故D 选项错误.故选:BC.【点睛】本题考查函数新定义问题,考查数学知识的迁移与应用能力,是中档题.本题解题的关键在于根据函数的定义,把握函数的值只有两种取值{0,1},再结合题意讨论各选项即可得答案.非选择题部分三、填空题:本题共4小题,每小题5分,共20分.13.已知幂函数()()222mf x m m x =--在第一象限单调递减,则()f m =__________.【答案】1-【解析】【分析】利用幂函数定义及单调性可得1m =-,代入解析式即可求得()1f m =-.【详解】由幂函数定义可得2221m m --=,即2230m m --=,解得3m =或1m =-,又函数()f x 在第一象限单调递减,所以1m =-,即()1f x x -=,即可得()()1111f m f -===--.故答案为:1-14.()31622390.12528-⎛⎫⎡⎤-+-+= ⎪⎣⎦⎝⎭____________.【答案】81【解析】【分析】利用指数幂运算法则化简即可求得答案.【详解】()31622390.12528-⎛⎫⎡⎤-+-+ ⎪⎣⎦⎝⎭161313322114238-⎛⎫⎛⎫=-++⨯ ⎪⎪⎝⎭⎝⎭1332381223=-++⨯21889=-++⨯81=故答案为:81.15.函数()()231f x ax a x =-++在(),a -∞上是减函数,则实数a 的取值范围是_________.【答案】30,2⎡⎤⎢⎥⎣⎦【解析】【分析】根据题意,分0a =和0a ≠两种情况讨论,结合函数特点,求出实数a 的取值范围.【详解】当0a =时,()31f x x =-+在(),0∞-上是减函数,符合题意;当0a ≠时,()()231f x ax a x =-++为一元二次函数,对称轴为32ax a+=,因为函数()()231f x ax a x =-++在(),a -∞上是减函数,所以032a a a a>⎧⎪+⎨≥⎪⎩,解得302<≤a ,综上,302a ≤≤,所以实数a 的取值范围是30,2⎡⎤⎢⎥⎣⎦,故答案为:30,2⎡⎤⎢⎥⎣⎦.16.已知函数()()()224100f x x a x a a a =-++++>,且()()2332f a f a +=-,则()()61f n a n N n *+∈+的最小值为______.【答案】145##2.8【解析】【分析】首先根据题中条件()()2332f a f a +=-,结合二次函数的图象求出实数a 的值;从而结合对号函数的单调性即可求出最小值.【详解】二次函数()()22410f x x a x a a =-++++的对称轴为42a x +=,因为()()2332f a f a +=-,所以2332a a +=-或23324222a a a +-++=,因为0a >,所以解得1a =.所以()2512f x x x =-+,所以()()()221712451262417111n n n n n n n n +-++-++==++-+++,因为()247g x x x =+-在(0,内单调递减,在()+∞单调递增,又()2444734g =+-=,()2414557355g =+-=<,所以()()61f n n N n *+∈+的最小值为145.故答案为:145.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.已知集合{4A x x =≤-或}3x ≥,{}15B x x =<≤,{}12C x m x m =-≤≤.(1)求A B ⋂,()R A B ð;(2)若B C C = ,求实数m 的取值范围.【答案】(1){}35A B x x ⋂=≤≤,(){}R 45A B x x ⋃=-<≤ð(2)()5,12,2⎛⎤-∞-⋃ ⎥⎝⎦【解析】【分析】(1)根据集合的交并补运算公式计算即可.(2)根据集合的包含关系,分C =∅与C ≠∅两类讨论即可求出m 的取值范围.【小问1详解】因为集合{4A x x =≤-或}3x ≥,{}15B x x =<≤,所以{}35A B x x ⋂=≤≤,{}R 43A x x =-<<ð所以(){}R 45A B x x ⋃=-<≤ð【小问2详解】∵B C C = ,∴C B⊆①当C =∅时,∴12m m ->,解得1m <-②当C ≠∅时,则121125m m m m -≤⎧⎪->⎨⎪≤⎩,解得522m <≤综上所述:m 的取值范围是()5,12,2⎛⎤-∞-⋃ ⎥⎝⎦18.已知正数a 、b 满足122a b+=.(1)求a b +的最小值;(2)求42211a b a b +--的最小值.【答案】(1)32+(2)8【解析】【分析】(1)由已知()1122a b a b a b ⎛⎫+=++ ⎪⎝⎭,展开后结合基本不等式求解.(2)对已知式子变形,结合已知条件求出()()2111a b -⋅-=,然后再利用基本不等式求解.【小问1详解】因为a 、b 是正数,所以()1121233222b a a b a b a b a b ⎛⎫⎛⎫+=++=+++ ⎪ ⎪⎝⎭⎝⎭≥当且仅当12a +=,22b +=时等号成立,所以a b +的最小值为32+.【小问2详解】因为122a b +=,所以12a >,1b >,所以210a ->,10b ->,()()2111a b -⋅-=则4222448211211a b a b a b +=+++----≥当且仅当1a =,2b =时等号成立,所以42211a b a b +--的最小值为8.19.已知函数()412x f x a a =-+(0a >且1a ≠)的定义域为R ,且()00f =.(1)求函数()f x 的解析式,并判断其奇偶性;(2)判断函数()f x 在R 上的单调性,并利用单调性定义法证明.【答案】(1)()2121x f x =-+,奇函数(2)单调递增,证明见解析【解析】【分析】(1)根据()00f =求出a 的值,然后根据奇偶函数的定义判断其奇偶性.(2)定义法判断函数的单调性.【小问1详解】∵函数()412x f x a a=-+(0a >且1a ≠)的定义域为R ,()40102f a =-=+,解得:2a =,∴()2121x f x =-+,()2121x x f x -=+,()21122121x x x x f x -----==++∴()()f x f x -=-∴()f x 是奇函数.【小问2详解】设12,R x x ∈且12x x <,∴()()()()()()()()121212121212221212222211212121212121x x x x x x x x x x f x f x +----=--+==++++++∵1210x +>,2210x +>,12220x x -<,∴()()120f x f x -<,即当12x x <时,()()12f x f x <,∴()f x 在R 上单调递增.20.已知二次函数()()2214f x x t x =--+.(1)若1t =,求()f x 在[]1,3-上的值域;(2)若存在[]4,10x ∈,使得不等式()f x tx <有解,求实数t 的取值范围.【答案】(1)[]4,13(2)73t >【解析】【分析】(1)将1t =代入,转换成二次函数求值域问题,求解即可..(2)分离参数,转换成不等式能成立问题,求解即可.【小问1详解】根据题意,函数()()2214f x x t x =--+,∵1t =,则()24f x x =+,又由13x -≤≤,当0x =时,()f x 有最小值4,当3x =时,()f x 有最大值13,则有()413f x ≤≤,即函数()f x 的值域为[]4,13【小问2详解】()()2214f x x t x tx =--+<整理得2243x x tx++<∵[]4,10x ∈,∴224432x x t x x x++>=++令()4g x x x=+,设[]12,4,10x x ∈,且12x x >,则()()()()121212*********x x x x g x g x x x x x x x --⎛⎫-=+-+= ⎪⎝⎭,因为1240x x ->,120x x ->,所以()()120g x g x ->,即()()12g x g x >,所以()4g x x x=+在[]4,10单调递增,所以当4x =时,min 427x x ⎛⎫++= ⎪⎝⎭,∴73t >.21.2020年初新冠肺炎袭击全球,严重影响人民生产生活.为应对疫情,某厂家拟加大生产力度.已知该厂家生产某种产品的年固定成本为200万元,每生产x 千件,需另投入成本()C x .当年产量不足50千件时,21()202C x x x =+(万元);年产量不小于50千件时,3600()51600C x x x=+-(万元).每千件商品售价为50万元.通过市场分析,该厂生产的商品能全部售完.(1)写出年利润()L x (万元)关于年产量x (千件)的函数解析式;(2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?最大利润是多少?【答案】(1)2130200,0502()3600400,50x x x L x x x x ⎧-+-<<⎪⎪=⎨⎛⎫⎪-+ ⎪⎪⎝⎭⎩;(2)60,280万元【解析】【分析】(1)可得销售额为0.051000x ⨯万元,分050<<x 和50x ≥即可求出;(2)当050<<x 时,利用二次函数性质求出最大值,当50x ≥,利用基本不等式求出最值,再比较即可得出.【详解】(1)∵每千件商品售价为50万元.则x 千件商品销售额50x 万元当050<<x 时,2211()50202003020022L x x x x x x ⎛⎫=-+-=-+- ⎪⎝⎭当50x 时,36003600()5051600200400⎛⎫⎛⎫=-+--=-+ ⎪ ⎪⎝⎭⎝⎭L x x x x x x 2130200,0502()3600400,50x x x L x x x x ⎧-+-<<⎪⎪=⎨⎛⎫⎪-+ ⎪⎪⎝⎭⎩(2)当050<<x 时,21()(30)2502L x x =--+此时,当30x =时,即()(30)250L x L = 万元当50x时,3600()400400⎛⎫=-+≤- ⎪⎝⎭L x x x 400120280=-=此时3600=x x,即60x =,则()(60)280=L x L 万元由于280250>所以当年产量为60千件时,该厂在这一商品生产中所获利润最大,最大利润为280万元.【点睛】关键点睛:本题考查函数模型的应用,解题的关键是理解清楚题意,正确的建立函数关系,再求最值时,需要利用函数性质分段讨论比较得出.22.已知函数()9f x x a a x=--+,a ∈R .(1)若0a =,求()f x 的单调递增区间;(2)若函数()f x 在[]1,a 上单调,且对任意[]1,x a ∈,()2f x <-恒成立,求a 的取值范围;(3)当()3,6a ∈时,函数()f x 在区间[]1,6上的最大值为()M a ,求()M a 的函数解析式.【答案】(1)单调增区间为()0,∞+,()3,0-(2)11a <<(3)()921,3,242126,,64a M a a a ⎧⎛⎫∈ ⎪⎪⎪⎝⎭=⎨⎡⎫⎪-∈⎪⎢⎪⎣⎭⎩【解析】【分析】(1)根据题意,分0x >与0x <讨论,即可得到结果;(2)根据题意,求得函数()f x 的最大值,即可得到()max 92f x a a=-+<-,从而求得结果;(3)根据题意,由条件可得()f x 在[)1,3上单调递增,在[]3,a 上单调递减,(],6a 上单调递增,即可得到结果.【小问1详解】当0a =时,()()90f x x x x=-≠,0x >时,()9f x x x =-,由y x =与9y x =-在()0,∞+单调递增可知,此时()f x 的单调增区间为()0,∞+,0x <时,()9f x x x=--,此时()f x 的单调增区间为()3,0-,由对勾函数的性质可知,∴此时()f x 的单调增区间为()0,∞+,()3,0-.【小问2详解】当[]1,x a ∈时,()92f x x a x=--+,因为函数()f x 在[]1,a 上单调,所以13a <£,此时()f x 在[]1,a 上单调递增,()()max 9f x f a a a==-+,由题意:()max 92f x a a =-+<-恒成立,即2290a a +-<,所以11a <<,又13a <£,∴a的取值范围为11a <<.【小问3详解】当[]1,6x ∈时,()[](]92,1,9,,6x a x a x f x x a a x ⎧--+∈⎪⎪=⎨⎪-∈⎪⎩,又()3,6a ∈,由上式知,()f x 在区间(],6a 单调递增,当()3,6a ∈时,()f x 在[)1,3上单调递增,在[]3,a 上单调递减,所以,()f x 在[)1,3上单调递增,在[]3,a 上单调递减,(],6a 上单调递增,则()()()()max 921,3,249max 3,6max 26,22126,,64a f x f f a a a ⎧⎛⎫∈ ⎪⎪⎪⎝⎭⎛⎫==-=⎨ ⎪⎝⎭⎡⎫⎪-∈⎪⎢⎪⎣⎭⎩,。
浙江省宁波金兰教育合作组织2023-2024学年高一年级上学期期中联考英语试题

浙江省宁波金兰教育合作组织2023-2024学年高一年级上学期期中联考英语试题一、短对话1.Which flower does Eric want to grow in the future?A.The daisy.B.The rose.C.The sunflower.2.What is the probable relationship between the speakers?A.Co-workers.B.Classmates.C.Friends.3.What are the speakers mainly talking about?A.A weekend plan.B.A college.C.Neighbors.4.How does the woman sound in the end?A.Excited.B.Indifferent.C.Interested.5.What does the woman mean?A.The man should be careful.B.The man should pay €500 first.C.The man should call back to make sure.二、长对话听下面一段较长对话,回答以下小题。
6.What happened to the old man in the shopping center?A.He lost his dog.B.He made his clothes dirty.C.He forgot what he was doing there.7.Who saved the little girl?A.Her dog.B.A former athlete.C.Her sister.听下面一段较长对话,回答以下小题。
8.Who is probably Jack?A.The woman’s neighbor.B.The woman’s husband.C.The woman’s brother.9.Where did the woman go this morning?A.To the grocery.B.To the backyard.C.To the police station. 10.What do we know about the woman?A.She didn’t lock the front door.B.She forgot to turn off the TV.C.Her window was broken.听下面一段较长对话,回答以下小题。
2023-2024学年浙江省金兰教育合作组织高一下学期期中考试数学试题

2023-2024学年浙江省金兰教育合作组织高一下学期期中考试数学试题1.已知向量,,若,则()A.2B.C.3D.2.下列四个命题中正确的是()A.每个面都是等腰三角形的三棱锥是正三棱锥B.所有棱长都相等的四棱柱是正方体C.以矩形的一边所在直线为旋转轴,其余三边旋转一周形成的面所围成的旋转体叫做圆柱D.以直角三角形的一边所在直线为旋转轴,其余两边旋转一周形成的面所围成的旋转体叫做圆锥3.已知复数,其中是虚数单位,则的虚部是()A.B.C.D.14.已知,为非零向量,且满足,则在上的投影向量为()A.B.C.D.5.已知的三条边长分别为a,b,c,且,则此三角形的最大角与最小角之和为()A.B.C.D.6.已知平面直角坐标系下,的三个顶点坐标为:,,,若斜二侧画法下的直观图是,则的面积为()A.B.C.D.7.如图所示,在中,点E为线段上的中点,点F为线段上靠近点C的三等分点,,分别与交于R,T两点.则()A.B.C.D.8.在中,角A,B,C所对的边分别为a,b,c,边上的中线、高线、角平分线长分别是,,,则下列结论中错误..的是()A.B.C.D.9.已知复数,均不为0,复数的共轭复数为,则()A.B.C.D.10.在中,角A,B,C所对的边分别为a,b,c,下列说法中正确的是()A.若,则是直角三角形B.若,则是锐角三角形C.若,则是等腰三角形D.若,则是等边三角形11.已知,为非零向量,且满足,,则()A.,夹角的取位范围是B.的取值范围是C.的取值范围是D.的取值范围是12.已知(是虚数单位),则__________13.已知球O的体积为,则球O的表面积为___________,球O的内接正四面体的体积为_________.14.勒洛三角形,也称圆弧三角形,是一种特殊三角形,在建筑、工业上应用广泛.如图所示,分别以正三角形的顶点为圆心,以边长为半径作圆弧,由这三段圆弧组成的曲边三角形即为勒洛三角形.已知正三角形边长为2,点P为圆弧上的一点,且满足:,则的值为__________.15.已知复数(1)若复数是方程的一个复数根,求实数a,b的值;(2)若复数满足,求.16.如图所示,已知三棱柱的所有棱长都为1,,点P为线段上的动点.(1)若点恰为线段上靠近点的三等分点,求三棱锥和三棱柱的体积之比;(2)求的最小值及此时的值.17.设向量,满足,,.(1)求的值;(2)已知与的夹角的余弦值为,求的值.18.已知a,b,c分别为三个内角A,B,C的对边,且满足,.(1)求B;(2)若D,E为线段上的两个动点,且满足,,求的取值范围.19.对于平面向量,定义“变换”:,(1)若向量,,求;(2)已知,,且与不平行,,,证明:;(3)若向量,求.。
2023-2024学年浙江省宁波市金兰教育合作组织高二上学期期中联考语文试题(解析版)

D.香雪不言不语地点着头……但她也很快就发现了别的。“皮书包!”她指着行李架上一只普通的棕色人造革学生书包。(《哦,香雪》)
浙江省宁波市金兰教育合作组织2023-2024学年高二
上学期期中联考语文试题
一、现代文阅读(35分)
(一)现代文阅读Ⅰ(本题共5小题,19分)
阅读下面的文字,完成小题。
材料一:
①小说由叙述和聚焦两部分组成。叙述与聚焦,是两种不同的叙事方式。叙述是“讲”,聚焦是“看”。叙述出自叙述者,聚焦或者出自叙述者,或者出自小说中的人物。叙述与聚焦,既相矛盾又相依存,当然主要是依存关系。
⑧根据《红楼梦》内部编年,黛玉初进荣国府时只有六岁,尚处于儿童时代,一个六岁的儿童怎么会辨认那么繁缛的服饰与质地呢?黛玉的所见,她的聚焦发生了偏离。作为聚焦者,黛玉是准确的,但聚焦对象是不准确的——不可能出于六岁儿童,这就使人怀疑黛玉的背后站着另外的聚焦者,这个背后的聚焦者当然也是叙述者。
⑨这就触及到叙述者与聚焦者的根本区别。在前者是讲,将后者的聚焦用话语传达出来,这样,总是聚焦在前而叙述在后,讲的人永远落后于看的人,因为讲的人在后,必然可以对聚焦者的感知进行总结与〖解 析〗,这种〖解 析〗可以是简捷的,也可以是繁复的,可以是模糊的,也可以是清晰的,既可以高于聚焦者,也可以低于聚焦者,十分繁缛复杂。为了制造现场感,叙述者有时要对当时的聚焦者保持模拟的姿态。比如,成年人讲述未成年人所看到的东西,大人是叙述者,儿童是聚焦者。这类叙述与聚焦的矛盾几乎存在于一切虚构性叙事作品之中。而且有时候,艺术水准越是高超的作品,二者之间的矛盾越是凸显。
3.根据材料一第⑨节,下列小说片段中属于叙述者高于聚焦者的一项是( )
【高考必做卷】浙江省宁波市金兰组织2013-2014学年高二下学期期中考试数学(理科)试题

【高考必做卷】宁波市金兰合作组织高二第二学期期中考试数学(理)试题(2014年4月)选择题部分 (共50分)一、选择题:本大题共10小题,每小题5分,共50分。
1.集合{}0,2,A a =,{}21,B a=,若{}0,1,2,4,16A B = ,则a 的值为 ( )A. 0B. 1C. 2D. 42.已知),2(ππα∈,53sin =α,则αtan 等于( )A . 43B . 34C . 43-D .34-3.在平行四边形ABCD 中, AC 为一条对角线,(2,4),(1,3),AB AC ==则AD = ( )A .)1,1(B .()1,1--C .)4,2(D .)4,2(--4. 已知b a ,都是实数,那么“22-->b a ”是“b a >”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件5. 函数⎪⎩⎪⎨⎧>+-≤-+=0,ln 20,32)(22x x x x x x f 的图像与x 轴的交点个数为( ) A . 0 B . 1 C . 2 D. 36.已知平面内三点AC BA x C B A ⊥满足),7(),3,1(),2,2(,则x 的值为( ) A . 3 B . 6 C . 7 D. 97.已知函数()f x 对任意的实数x ,满足()()f x f x π=-,且当(,)22x ππ∈-时,()sin f x x x =+,则( )A.(3)(1)(2)f f f <<B. )2()3()1(f f f <<C.(3)(2)(1)f f f <<D. (1)(2)(3)f f f << 8. 要得到函数πsin (2)3y x =-的图象,只需将函数cos2y x =的图象( ) A .向左平移π6个单位 B .向左平移5π12个单位C .向右平移5π12个单位 D .向右平移π3个单位 9.在ABC ∆中,若AD 是边BC 上的高,且BC AD =,则ACABAB AC +的最大值是( ) A .2B .5C .6D .310.已知函数x x a x f +-=)((a 为常数,且*N a ∈),对于定义域内的任意两个实数1x 、2x ,恒有1|)()(|21<-x f x f 成立,则正整数a 可以取的值有( )A .4个B .5个C .6 个D .7个非选择题部分 (共100分)二、 填空题 本大题共7小题, 每小题4分, 共28分。
浙江省金兰教育合作组织2023-2024学年高二下学期4月期中考试物理试题

浙江省金兰教育合作组织2023-2024学年高二下学期4月期中考试物理试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.关于教材中出现的以下四张图片,下列说法错误的是( )A.图1所示是利用多普勒测速仪来测量水在海底的流速B.图2所示竖直的肥㿝膜看起来常常是水平彩色横纹,是由于光的衍射产生的C.图3所示“洗”,用手摩擦盆耳会溅起层层水花是共振现象D.图4所示水流导光由于光的全反射引起的2.用扁担挑水时,有时桶里的水会荡得厉害,甚至从桶中溅出来。
如图,农夫肩上的扁担与木桶(含水)的固有频率是2Hz,下列说法正确的是( )A.农夫走路的步频越慢,桶里的水晃动得越剧烈B.农夫走路的步频越快,桶里的水晃动得越剧烈C.农夫走路时扁担与木桶(含水)上下振动的频率与农夫的步频无关D.当发现桶里的水晃得很厉害时,适当的把步频加快可减小水的晃动3.在我国北方部分地区经常出现低温雨雪冰冻天气,高压输电线因结冰而造成严重损毁,如图所示。
为消除高压输电线上的冰凌,有人设计了这样的融冰思路:利用电流的热效应除冰。
在正常供电时,高压线上送电电压为U,电流为I,热耗功率为PD;若输电功率和A.沿x轴正方向B.沿y轴正方向C.沿z轴正方向D.沿悬线向上6.安检门原理图如图所示,左边门框中有一通电线圈,右边门框中有一接收线圈。
若工作过程中某段时间内通电线圈中存在顺时针方向(从左向右看)均匀增大的电流,则下列说法正确的是(描述电流方向时均从左向右观察)( )A.无金属片通过时,接收线圈中感应电流的方向为逆时针方向B.无金属片通过时,接收线圈中感应电流逐渐增大C.有金属片通过时,接收线圈中感应电流的方向为顺时针方向D.有金属片通过时,接收线圈中没有感应电流7.如图所示为某品牌汽车的减震系统装置示意图,强磁体固定在汽车底盘上,阻尼线圈固定在轮轴上,轮轴与底盘通过弹簧主减震系统相连,在振动过程中磁体可在线圈内上下移动。
金兰合作组织2010学年第二学期期中考试进度

金兰合作组织2010学年第二学期期中考试进度地理学科模拟试题时间 100分钟分值 100分一.单项选择题(本大题共30小题,每小题2分,共60分。
在每小题给出的四个选项中,只有一项符合题目要求)北京时间2011年3月11日13点46分,日本发生了150年以来最大的9.0级强烈地震。
引发了海啸、核泄漏等次生灾害,成为全世界关注的中心。
请完成1—2题。
1.从地理角度看,影响核泄漏物质扩散的主要因素有A.风、地表径流、洋流 B.风、气温、太阳辐射C.气温、地表径流、植被覆盖率 D.植被覆盖率、洋流、大气能见度2.不属于日本主要农业地域类型的特点是A. 单产高B.机械化水平高C. 科技水平高D.商品率高读工业区位选择模式示意图,完成3—4题。
3.下列工业部门与工业模式二对应的是A.时装设计 B.炼铝厂C.电视机装配 D.水果罐头厂4.关于工业模式三的叙述,正确的是A.产品运输成本较高,布局宜靠近市场B.因大气污染严重,宜布局在郊外C.目前该产业在我国由沿海向内陆转移D.该模式的工业在布局时受科技影响较大在田纳西河的早期开发中,由于发展炼铜业,对环境造成了污染,并使植被遭到破坏。
据此回答5--6题。
5.造成田纳西河流域植被破坏的原因不包括A.扩大耕地面积 B.修建水库C.获取炼铜用的木炭 D.矿山开采6.田纳西河流域早期由于炼铜业所造成的环境污染主要表现为A.光化学污染 B.酸雨C.噪声污染 D.固体废弃物污染读右图,回答7--9题。
7.可持续发展的核心内容是A.人类与环境和谐共处B.人类尽可能地索取自然资源C.人类不要向环境释放废弃物D.环境无条件为人类服务8.下列人类活动中,具有可持续发展意义的是A.20世纪30年代美国开垦中西部大草原,引起“黑风暴”B.大力发展热带雨林迁移农业C.在长江河床大力挖沙出售,既有经济效益,又疏浚了航道D.我国在中西部一些地区实施“退耕还林”工程9.我国古人的行为或主张蕴含了可持续发展思想的是A.烧草为灰,取灰肥田 B.以人为本,人定胜天C. 竭泽而渔,焚薮而田D. 封山育林,定期开禁为了可持续发展,我国对水土资源进行了初步普查,得出下表资料。
2023学年第一学期宁波金兰教育合作组织期中联考-物理答案(高一)

2023 学年第一学期宁波金兰教育合作组织期中联考高一年级物理学科参考答案二、不定项选题(本题共 4 小题,共 16 分,每题至少有一个正确答案,全部选对得 4 分,三、实验题(本大题共 2 小题,每空 2分,共 12 分)19. (1)匀变(加)速(2)3.90(3)12.6(4)B20. (1)乙(2)AC四、计算题(本大题共 3 小题,共 30 分,21 题8分, 22 题各10分,23 题 12 分)21.(1)规定竖直向上为正方向v1=−√2gℎ1=√2×10×1.25=−5m/s(1分)v2=√2gℎ2=√2×10×5=10m/s(1分)∆v=v2−v1=15m/s(1分)方向:竖直向上(1分)(2)以地面为原点,竖直向上为正方向建立坐标轴x=x2−x1=5−1.25=3.75m(1分)t=t1+t2+∆t=v1g +v2g+∆t=0.5s+1s+0.5s=2s(1分)v̅=xt=1.875m/s(1分)方向竖直向上(1分)23.(1)由题意知,对物块A 受力分析,受拉力T 、重力、支持力,根据平衡条件,沿斜面方向,有:T cos 30°=mg sin 30° (1分)解得:T=√33mg (1分)对重物B 和动滑轮整体分析,受两个拉力和重力,根据平衡条件,有: m'g=T=√33mg (1分) 故m'=√33m (1分)(2) 对物块A 和斜面体整体受力分析,受重力、拉力、支持力和静摩擦力,根据平衡条件,有: f=T sin 30°=√36mg (3分)(3)如果物块A恰好不上滑,则对A,有:平行斜面方向:T1 cos 30°-mg sin 30°-f'=0其中f'=μN垂直斜面方向:N+T1 sin 30°-mg cos 30°=0 (两个式子1分)解得:T1=√3μ√3+μ; (1分)如果物块A恰好不下滑,则对A,有:平行斜面方向:T2 cos 30°-mg sin 30°+f″=0其中f″=μN'垂直斜面方向:N'+T2 sin 30°-mg cos 30°=0 (两个式子1分)解得:T2=√3μ√3-μ; (1分)由于绳子的拉力大小等于重物B的重力大小,故重物B的质量范围为:√3μ√3-μ≤m B≤√3μ√3+μ。
2023-2024学年浙江省宁波市金兰教育合作组织高二(上)期中数学试卷【答案版】

2023-2024学年浙江省宁波市金兰教育合作组织高二(上)期中数学试卷一、选择题:(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.直线x +√3y +1=0的倾斜角是( ) A .π6B .π3C .2π3D .5π62.如图所示,空间四边形OABC 中,OA →=a →,OB →=b →,OC →=c →,点M 在OA 上,且M 为OA 中点,N 为BC 中点,则MN →等于( )A .−12a →+12b →+12c →B .12a →+12b →+12c → C .12a →+12b →−12c → D .12a →−12b →+12c →3.抛物线y =ax 2(a ≠0)的焦点坐标是( ) A .(a 4,0) B .(−a 4,0)C .(0,−14a) D .(0,14a) 4.P 是椭圆x 25+y 24=1上在第一象限的点,已知以点P 及椭圆焦点F 1、F 2为顶点的三角形的面积等于1,则点P 的坐标为( ) A .(√152,1) B .(1,√152) C .(5√76,13) D .(13,5√76) 5.已知空间向量a →=(3,0,4),b →=(﹣3,2,5),则向量b →在向量a →上的投影向量是( ) A .1125(﹣3,2,5) B .1138(﹣3,2,5)C .1125(3,0,4)D .1138(3,0,4)6.若方程x 2−p+y 2q =1表示双曲线,则下列方程所表示的椭圆中,与此双曲线一定有共同焦点的是( ) A .x 22q+p +y 2p =−1 B .x 22q+p +y 2q =1 C .x 22p+q+y 2p=−1D .x 22p+q+y 2p=17.定义:两条异面直线之间的距离是指其中一条直线上任意一点到另一条直线距离的最小值.在棱长为2的正方体ABCD ﹣A 1B 1C 1D 1中,直线A 1C 1与AD 1之间的距离是( ) A .√2B .2√33C .1D .2√238.如图1,用一个平面去截圆锥,得到的截口曲线是椭圆.许多人从纯几何的角度对这个问题进行研究,其中比利时数学家Germinaldandelion (1794﹣1847)的方法非常巧妙,极具创造性.在圆锥内放两个大小不同的球,使得它们分别与圆锥的侧面、截面相切,两个球分别与截面切于E 、F ,在截口曲线上任取一点A ,过A 作圆锥的母线,分别与两个球切于C 、B ,由球和圆的几何性质,可以知道,AE =AC ,AF =AB ,于是AE +AF =AB +AC =BC ,由B 、C 的产生方法可知,它们之间的距离BC 是定值,由椭圆定义可知,截口曲线是以E 、F 为焦点的椭圆.如图2,一个半径为1的球放在桌面上,桌面上方有一点光源P ,则球在桌面上的投影是椭圆,已知A 1A 2是椭圆的长轴,P A 1垂直于桌面且与球相切,P A 1=3,则椭圆的离心率为( )A .12B .√32C .23D .35二、选择题:(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分)9.如图,过焦点F 的直线与抛物线y 2=2px (p >0)交于A (x 1,y 1),B (x 2,y 2)两点,则下列说法正确的是( )A .|AB |=x 1+x 2+p B .∠MON =90°C .以弦AB 为直径的圆与准线相切D .A ,O ,N 三点共线10.已知直线l 1:ax ﹣(a +2)y ﹣2=0,l 2:(a ﹣2)x +3ay +2=0,则下列说法正确的是( ) A .l 1恒过点(﹣1,﹣1)B .若l 1∥l 2,则a =±1C .若l 1⊥l 2,则a =0或a =﹣4D .若l 2不经过第三象限,则a <011.若点P (x ,y )是圆C :(x ﹣2)2+(y ﹣1)2=1上的动点,则下列说法正确的是( ) A .(yx)max =43B .(y −x)min =−1−√2C .[x 2+(y ﹣1)2]max =3D .若点Q 是直线3x +4y +5=0上的动点,则|PQ |min =212.如图,AB 是底面圆O 的直径,点C 是圆O 上异于A 、B 的点,PO 垂直于圆O 所在的平面且PO =OB =1,BC =√2,点E 在线段PB 上,则下列说法正确的是( )A .当E 为PB 中点时,PB ⊥平面CEOB .记直线CE 与平面BOP 所成角为θ,则tanθ∈[1,√2]C .存在点E ,使得平面CEO 与平面BEC 夹角为π6D .CE +OE 的最小值为√6+√22三、填空题:(本大题共4小题,每小题5分,共20分)13.已知双曲线的方程是16x 2﹣9y 2=﹣144,则该双曲线的渐近线方程为 .14.已知点A (﹣3,4),B (2,2),直线mx +y +m +2=0与线段AB 相交,则m 的范围为 . 15.如图,为保护河上古桥OA ,规划建一座新桥BC ,同时设立一个圆形保护区.规划要求:新桥BC 与河岸AB 垂直;保护区的边界为圆心M 在线段OA 上,并与BC 相切的圆,且古桥两端O 和A 到该圆上任意一点的距离均不少于80m .经测量,点A 位于点O 正北方向60m 处,点C 位于点O 正东方向170m 处(OC 为河岸),tan ∠BCO =43,则新桥BC 的长度为 .16.已知椭圆x 26+y 24=1,过点E (0,1)且斜率为k 的直线l 与x 轴相交于点M ,与椭圆相交于A ,B两点.若MA →=BE →,则k 的值为 .四、解答题:(本题共6个小题,其中17题10分,18至22题每题12分,共70分.解答应写出文字说明、证明过程或演算步骤)17.(10分)已知△ABC 的顶点A (5,1),边AB 上的中线CM 所在直线方程为2x ﹣y ﹣5=0,边AC 上的高BH 所在直线过点(1,﹣2),且直线BH 的一个方向向量为(﹣2,﹣1). (1)求顶点C 的坐标; (2)求直线BC 的方程.18.(12分)如图,在平行六面体ABCD ﹣A 'B 'C 'D '中,底面ABCD 是边长为a 的正方形,侧棱AA '的长为b ,且∠A 'AB =∠A 'AD =120°.求: (1)AC '的长;(2)直线BD '与AC 所成角的余弦值.19.(12分)已知圆C 的圆心为(﹣2,1),且圆C _____.在下列所给的三个条件中任选一个,填在直线上,并完成解答(注:若选择多个条件分别解答,按第一个解答计分) ①与直线3x +4y +17=0相切;②与圆M :(x ﹣2)2+(y ﹣4)2=4相外切; ③经过直线3x +y +2=0与直线x ﹣3y +14=0的交点.(1)求圆C 的方程;(2)圆N :(x ﹣m )2+y 2=m 2(m >0),是否存在实数m ,使得圆N 与圆C 公共弦的长度为2,若存在,求出实数m 的值;若不存在,请说明理由.20.(12分)如图,已知在四棱锥P ﹣ABCD 中,P A ⊥平面ABCD ,点Q 在棱P A 上,且P A =4PQ =4,底面为直角梯形,∠CDA =∠BAD =90°,AB =2,CD =1,AD =√2,M ,N 分别是PD ,PB 的中点. (1)求证:MQ ∥平面PCB ;(2)求直线BC 与平面MCN 所成角的正弦值.21.(12分)直线y =kx +b 与椭圆x 24+y 2=1交于A ,B 两点,记△AOB 的面积为S .(1)当k =0,12<b <√32时,求S 的取值范围; (2)当|AB|=43,S =2√23时,求直线AB 的方程. 22.(12分)已知双曲线x 2a 2−y 2b 2=1(a >0,b >0)与直线l :y =kx +m(k ≠±ba )有唯一的公共点M ,过点M 且与l 垂直的直线分别交x 轴、y 轴与A (x ,0),B (0,y )两点.点P 的坐标为(x ,y ),当M 点的坐标为(−2√2,−4)时,P 点坐标为(−10√2,−5). (1)求双曲线的标准方程;(2)当点M 运动时,求P 点的轨迹方程,并说明轨迹是什么曲线.2023-2024学年浙江省宁波市金兰教育合作组织高二(上)期中数学试卷参考答案与试题解析一、选择题:(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.直线x +√3y +1=0的倾斜角是( ) A .π6B .π3C .2π3D .5π6解:设直线的倾斜角为α,由题意直线的斜率为−√33,即tan α=−√33,所以α=5π6故选:D .2.如图所示,空间四边形OABC 中,OA →=a →,OB →=b →,OC →=c →,点M 在OA 上,且M 为OA 中点,N 为BC 中点,则MN →等于( )A .−12a →+12b →+12c →B .12a →+12b →+12c → C .12a →+12b →−12c → D .12a →−12b →+12c →解:∵M 为OA 中点,N 为BC 中点,∴OM →=12OA →=12a →,ON →=12(OB →+OC →)=12b →+12c →, ∴MN →=ON →−OM →=12b →+12c →−12a →,故选:A .3.抛物线y =ax 2(a ≠0)的焦点坐标是( ) A .(a 4,0)B .(−a 4,0)C .(0,−14a) D .(0,14a) 解:由抛物线y =ax 2(a ≠0)化为x 2=1a y .可得焦点坐标是(0,14a ). 故选:D . 4.P 是椭圆x 25+y 24=1上在第一象限的点,已知以点P 及椭圆焦点F 1、F 2为顶点的三角形的面积等于1,则点P 的坐标为( )A .(√152,1) B .(1,√152) C .(5√76,13) D .(13,5√76) 解:F 1、F 2是椭圆 x 25+y 24=1的左、右焦点,则F 1(﹣1,0),F 2(1,0),设P (x ,y )是椭圆上第一象限的点,则12×2×y =1,y =1,将y =1代入椭圆方程得:x 25+14=1,∴x =√152,则点P 的坐标为(√152,1).故选:A .5.已知空间向量a →=(3,0,4),b →=(﹣3,2,5),则向量b →在向量a →上的投影向量是( ) A .1125(﹣3,2,5) B .1138(﹣3,2,5)C .1125(3,0,4)D .1138(3,0,4)解:向量a →=(3,0,4),b →=(﹣3,2,5), 则|a →|=5,|b →|=√38,a →⋅b →=11, 所以向量b →在向量a →上的投影向量为|b →|cos <a →,b →>a→|a →|=|b →|a →⋅b →|a →||b →|a →|a →|=√38×5×√38×a→5=1125a →=1125(3,0,4).故选:C . 6.若方程x 2−p+y 2q =1表示双曲线,则下列方程所表示的椭圆中,与此双曲线一定有共同焦点的是( ) A .x 22q+p+y 2p =−1 B .x 22q+p +y 2q =1 C .x 22p+q+y 2p=−1 D .x 22p+q+y 2p=1解:若方程x 2−p+y 2q=1表示双曲线则﹣pq <0即pq >0①当p >0,q >0时,曲线y 2q−x 2p=1表示焦点在y 轴的双曲线,A ,C 的方程没有意义B :由于2q +p >q >0,表示焦点在x 轴上的椭圆, D :由于2p +q >p >0,表示焦点在x 轴上的椭圆 则此情况不符合题意,舍去②当p <0,q <0时,曲线y 2q−x 2p=1表示焦点在x 轴的双曲线A :由于﹣(2q +p )>﹣p >0,表示曲线是焦点在x 轴上的椭圆,B :由于2q +p <q <0,方程没有意义,C :由于﹣2p ﹣q >﹣p >0,表示焦点在x 轴上的椭圆,D :由于2p +q <p <0,方程没有意义, 综合可得C 符合题意. 故选:C .7.定义:两条异面直线之间的距离是指其中一条直线上任意一点到另一条直线距离的最小值.在棱长为2的正方体ABCD ﹣A 1B 1C 1D 1中,直线A 1C 1与AD 1之间的距离是( ) A .√2B .2√33C .1D .2√23解:以D 为坐标原点,建立空间直角坐标系,如图,则A (2,0,0),D 1(0,0,2),A 1(2,0,2),C 1(0,2,2), AD 1→=(﹣2,0,2),A 1C 1→=(﹣2,2,0),设AM →=λAD 1→,A 1N →=μA 1C 1→,M (x 0,y 0,z 0),N (x 1,y 1,z 1), 则AM →=(x 0﹣2,0,z 0),∴{x 0−2=−2λy 0=0z 0=2λ,即{x 0=2−2λy 0=0z 0=2λ, ∴M (2﹣2λ,0,2λ), 同理得N (2﹣2μ,2μ,2),则|MN |=√(2λ−2μ)2+4μ2+(2λ−2)2=2√2μ2−2λμ+λ2+(λ−1)2=2√2(μ−λ2)2+λ22+(λ−1)2≥2√λ22+(λ−1)2,当且仅当μ=λ2时,等号成立,对√λ22+(λ−1)2=√32λ2−2λ+1=√32(λ−23)2+13≥√33,当且仅当λ=23,等号成立,∴|MN |≥2√33,当且仅当λ=2μ=23,即AM →=23AD 1→,A 1N →=13A 1C 1→时取等号,即直线A 1C 1与AD 1之间的距离是2√33.故选:B .8.如图1,用一个平面去截圆锥,得到的截口曲线是椭圆.许多人从纯几何的角度对这个问题进行研究,其中比利时数学家Germinaldandelion (1794﹣1847)的方法非常巧妙,极具创造性.在圆锥内放两个大小不同的球,使得它们分别与圆锥的侧面、截面相切,两个球分别与截面切于E 、F ,在截口曲线上任取一点A ,过A 作圆锥的母线,分别与两个球切于C 、B ,由球和圆的几何性质,可以知道,AE =AC ,AF =AB ,于是AE +AF =AB +AC =BC ,由B 、C 的产生方法可知,它们之间的距离BC 是定值,由椭圆定义可知,截口曲线是以E 、F 为焦点的椭圆.如图2,一个半径为1的球放在桌面上,桌面上方有一点光源P ,则球在桌面上的投影是椭圆,已知A 1A 2是椭圆的长轴,P A 1垂直于桌面且与球相切,P A 1=3,则椭圆的离心率为( )A .12B .√32C .23D .35解:设椭圆的长半轴长=a ,半焦距为c , 由题意可得:P A 1⊥A 1A 2,∴P A 2=√PA 12+(A 1A 2)2,设切点分别为E ,F ,则四边形OEA 1F 为正方形. ∴1=r =PA 1+A 1A 2−PA 22,A 1F =a ﹣c =r ,c =r ,∴1+2a =√32+(2a)2,化为a =2,c =1, ∴e =c a =12. 故选:A .二、选择题:(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分)9.如图,过焦点F 的直线与抛物线y 2=2px (p >0)交于A (x 1,y 1),B (x 2,y 2)两点,则下列说法正确的是( )A .|AB |=x 1+x 2+pB .∠MON =90°C .以弦AB 为直径的圆与准线相切D .A ,O ,N 三点共线解:不妨设过焦点F 的直线方程为x =ty +p2,A (x 1,y 1) B (x 2,y 2), 联立{x =ty +p2y 2=2px ,消去x 并整理得y 2﹣2pty ﹣p 2=0,由韦达定理得y 1+y 2=2pt ,y 1⋅y 2=−p 2, 所以x 1+x 2=2pt 2+p ,此时以AB 为直径的圆的圆心为(pt 2+p 2,pt),易知|AB|=|AM|+|BN|=x 1+p 2+x 2+p2=x 1+x 2+p ,故选项A 正确; 而半径r =12|AB|=12(x 1+x 2+P)=pt 2+p , 圆心到准线的距离d =|pt 2+p 2−(−p2)|=pt 2+p , 所以以弦AB 为直径的圆与准线相切,故选项C 正确;不妨设l OA :y =y 1x 1x =2p y 1x ,N(−p2,y 2), 因为y 1⋅y 2=−p 2,所以点N(−p2,y 2)在直线OA 上, 则A ,O ,N 三点共线,故选项D 正确; 易知|AF |=|AM |,|BF |=|BN |,此时∠AFM =∠AMF =∠MFO ,∠BFN =∠BNF =∠NFO ,∠MFO +∠NFO =∠MFN =90°, 所以∠MON >90°,故选项B 错误. 故选:ACD .10.已知直线l 1:ax ﹣(a +2)y ﹣2=0,l 2:(a ﹣2)x +3ay +2=0,则下列说法正确的是( ) A .l 1恒过点(﹣1,﹣1)B .若l 1∥l 2,则a =±1C .若l 1⊥l 2,则a =0或a =﹣4D .若l 2不经过第三象限,则a <0解:A .直线l 1:ax ﹣(a +2)y ﹣2=0,化为a (x ﹣y )﹣2y ﹣2=0,令x ﹣y =0,则﹣2y ﹣2=0,解得y =﹣1=x ,∴直线l 1恒过点(﹣1,﹣1),因此A 正确;B .由a •3a ﹣[﹣(a +2)]•(a ﹣2)=0,化为a 2=1,解得a =±1,经过验证可得a =1时两条直线重合,舍去,a =﹣1时l 1∥l 2,因此B 不正确;C .由a •(a ﹣2)+[﹣(a +2)]•3a =0,化为a (a +4)=0,解得a =0或﹣4,满足l 1⊥l 2,因此C 正确;D .l 2:(a ﹣2)x +3ay +2=0,化为a (x +3y )﹣2x +2=0,令x +3y =0,则﹣2x +2=0,解得x =1,y =−13,∴直线l 2恒过点P (1,−13),k OP =−13,a =0时,直线化为x =1,此时直线l 2⊥x 轴,不经过第三象限,满足题意;a ≠0时,若l 2不经过第三象限,则k l 2=−a−23a ≤−13,解得a <0,综上可得a ≤0时l 2不经过第三象限,因此D 不正确. 故选:AC .11.若点P (x ,y )是圆C :(x ﹣2)2+(y ﹣1)2=1上的动点,则下列说法正确的是( ) A .(yx )max =43B .(y −x)min =−1−√2C .[x 2+(y ﹣1)2]max =3D .若点Q 是直线3x +4y +5=0上的动点,则|PQ |min =2解:圆C :(x ﹣2)2+(y ﹣1)2=1,圆心C (2,1),半径r =1, 对于A 选项,令yx =k ,则kx ﹣y =0,因为点P 在圆上,所以圆C :(x ﹣2)2+(y ﹣1)2=1与直线kx ﹣y =0相交或相切, 故圆心C 到直线的距离d 1≤r ,即√k 2≤1,解得0≤k ≤43,故A 正确;对于B 选项,令y ﹣x =b ,则x ﹣y +b =0,因为点P 在圆上, 所以圆C :(x ﹣2)2+(y ﹣1)2=1与直线x ﹣y +b =0相交或相切, 故圆心C 到直线的距离d 2<r ,即√2≤1,解得−√2−1≤b ≤√2−1,故B 正确;对于C 选项,x 2+(y ﹣1)2的几何意义是点P 到点M (0,1)的距离的平方, 又|PM |max =|CM |+r =3,所以|PM |2max =9,故C 错误; 对于D 选项,圆心C 到直线3x +4y +5=0的距离d 4=|6+4+5|25=3, 当PQ 与直线3x +4y +5=0垂直时,|PQ |能取得最小值, |PQ |min =d 4﹣r =2,故D 正确. 故选:ABD .12.如图,AB 是底面圆O 的直径,点C 是圆O 上异于A 、B 的点,PO 垂直于圆O 所在的平面且PO =OB =1,BC =√2,点E 在线段PB 上,则下列说法正确的是( )A .当E 为PB 中点时,PB ⊥平面CEOB .记直线CE 与平面BOP 所成角为θ,则tanθ∈[1,√2]C .存在点E ,使得平面CEO 与平面BEC 夹角为π6D .CE +OE 的最小值为√6+√22解:对于A :当E 为PB 中点时,由OP =PB ,可得OE ⊥PB , ∵OB =OC =1,BC =√2,∴OB 2+OC 2=1+1=2=BC 2, ∴OB ⊥OC ,∵PO 垂直于圆O 所在的平面,∴PO ⊥OC , ∵OP ∩OB =O ,∴OC ⊥平面POB ,∵PB ⊂平面POB ,∴OC ⊥BP ,又OE ∩OC =O ,∴PB ⊥平面CEO ,故A 正确; 对于B :∵OC ⊥平面POB ,∴∠CEO 是直线CE 与平面BOP 所成的角,即∠CEO =θ, ∴tan θ=OCOE =1OE ,又∵E 在线段PB 上,∴OE ∈[√22,1],∴tan θ∈[1,√2],故B 正确;对于C :以O 为坐标原点,OC ,OB ,OP 所在直线为坐标轴建立如图所示的空间直角坐标系,则O (0,0,0),C (1,0,0),B (0,1,0),P (0,0,1), 则BC →=(1,﹣1,0),BP →=(0,﹣1,1),OC →=(1,0,0),设BE →=λBP →=(0,﹣λ,λ),∴OE →=OB →+BE →=OB →+λBP →=(0,1,0)+(0,﹣λ,λ)=(0,1﹣λ,λ),设平面PBC 的一个法向量为n →=(x ,y ,z ), 则{n →⋅BP →=−y +z =0n →⋅BC →=x −y =0,令x =1,则y =1,z =1, ∴平面PBC 的一个法向量为n →=(1,1,1), 设平面OEC 的一个法向量为m →=(a ,b ,c ),则{m →⋅OC →=a =0m →⋅OE →=(1−λ)a +λc =0,令b =1,则c =λ−1λ,a =0,∴平面OEC 的一个法向量为m →=(0,1,λ−1λ),∴|cos <n →,m →>|=|n →⋅m →||n →|⋅|m →|=|1+λ−1λ|√3×√1+(λ−1λ)2,若平面CEO 与平面BEC 夹角为π6,则可得|cos <n →,m →>|=cos π6,即|1+λ−1λ|√3×√1+(λ)2=√32,整理得2λ2﹣2λ=5,Δ=(﹣2)2﹣4×2×5<0, 方程无解,故不存在点E ,使得平面CEO 与平面BEC 夹角为π6,故C 错误;对于D :如图,PO ⊥底面OCB ,则PO ⊥OB ,PO ⊥OC ,由PO =OB =1,得PB =√2,由PO =OC ,得PC =√2,又BC =√2,∴△PBC 为等边三角形,则∠PBC =60° 又∠PBO =45°, 沿PB 翻折平面PBC ,使平面PBC 与平面P AB 重合,则∠OBC '=105°,CE +OE 的最小值OC '在△OBC '中,由余弦定理可得:OC ′=√12+(√2)2−2×1×√2×cos105°=√3+2√2×√6−√24=√3+√3−1=√2+√3=√2+2⋅√34=√(√32+√12)2=√6+√22,故D 正确.故选:ABD .三、填空题:(本大题共4小题,每小题5分,共20分)13.已知双曲线的方程是16x 2﹣9y 2=﹣144,则该双曲线的渐近线方程为 y =±43x . 解:双曲线的方程是16x 2﹣9y 2=﹣144, 化为标准方程为y 216−x 29=1,则其渐近线方程为y =±43x . 故答案为:y =±43x .14.已知点A (﹣3,4),B (2,2),直线mx +y +m +2=0与线段AB 相交,则m 的范围为 (﹣∞,−43]∪[3,+∞). .解:直线mx +y +m +2=0,即m (x +1)+y +2=0,它经过定点P (﹣1,﹣2),斜率为﹣m , P A 的斜率为4+2−3+1=−3,PB 的斜率为2+22+1=43,∵直线mx +y +m +2=0与线段AB 相交,∴﹣m ≤﹣3 或﹣m ≥43,求得m ≥3 或m ≤−43, 故答案为:(﹣∞,−43]∪[3,+∞).15.如图,为保护河上古桥OA ,规划建一座新桥BC ,同时设立一个圆形保护区.规划要求:新桥BC 与河岸AB 垂直;保护区的边界为圆心M 在线段OA 上,并与BC 相切的圆,且古桥两端O 和A 到该圆上任意一点的距离均不少于80m .经测量,点A 位于点O 正北方向60m 处,点C 位于点O 正东方向170m 处(OC 为河岸),tan ∠BCO =43,则新桥BC 的长度为 150m .解:过点A 作AD ∥BC ,交x 轴于点D ,过点D 作DE ∥AB ,交BC 于点E ,因为AB ⊥BC ,所以DE ⊥BC ,AD ⊥AB , 所以四边形ABED 是矩形, 所以AD =BE ,∠ADO =∠BCO , 在Rt △ADO 中,tan ∠ADO =OA OD =tan ∠BCO =43, 所以OD =3OA 4=34×60=45,BE =AD =√OA 2+OD 2=√602+452=75, 所以CD =OC ﹣OD =170﹣45=125,由tan ∠BCO =43,且∠BCO 为锐角,所以cos ∠BCO =35, 在Rt △CDE 中,cos ∠BCO =CECD =35, 所以CE =35CD =75,所以BC =BE +CE =75+75=150m . 故答案为:150m . 16.已知椭圆x 26+y 24=1,过点E (0,1)且斜率为k 的直线l 与x 轴相交于点M ,与椭圆相交于A ,B两点.若MA →=BE →,则k 的值为 ±√63 .解:如图所示,由题意可得k =0时不符合条件.设直线l 的方为:m (y ﹣1)=x ,其中m =1k ,A (x 1,y 1),B (x 2,y 2). 联立{m(y −1)=x x 26+y 24=1,化为:(2m 2+3)y 2﹣4m 2y +2m 2﹣12=0,Δ>0, y 1+y 2=4m 22m 2+3, ∵MA →=BE →,∴(x 1+m ,y 1)=(﹣x 2,1﹣y 2), ∴y 1=1﹣y 2,即y 1+y 2=1, ∴4m 22m 2+3=1,解得m 2=32, ∵m =1k ,∴k 2=23, 解得k =±√63. 故答案为:±√63.四、解答题:(本题共6个小题,其中17题10分,18至22题每题12分,共70分.解答应写出文字说明、证明过程或演算步骤)17.(10分)已知△ABC 的顶点A (5,1),边AB 上的中线CM 所在直线方程为2x ﹣y ﹣5=0,边AC 上的高BH 所在直线过点(1,﹣2),且直线BH 的一个方向向量为(﹣2,﹣1). (1)求顶点C 的坐标; (2)求直线BC 的方程.解:(1)由直线BH 的方向向量可得直线BH 的斜率,即k BH =12,由AC ⊥BH ,则k AC =﹣2,直线AC 的方程为y ﹣1=﹣2(x ﹣5),即2x +y ﹣11=0, 则{2x +y −11=02x −y −5=0,得顶点C 的坐标为(4,3); (2)设点B (x ,y ),则AB 的中点M(x+52,y+12),M 在CM 上, 即2×x+52−y+12−5=0,即2x ﹣y ﹣1=0, BH 的方程为y +2=12(x −1),即x ﹣2y ﹣5=0, 则{2x −y −1=0x −2y −5=0,得B 的坐标为(﹣1,﹣3), 又C (4,3),所以直线BC 的方程为6x ﹣5y ﹣9=0.18.(12分)如图,在平行六面体ABCD ﹣A 'B 'C 'D '中,底面ABCD 是边长为a 的正方形,侧棱AA '的长为b ,且∠A 'AB =∠A 'AD =120°.求: (1)AC '的长;(2)直线BD '与AC 所成角的余弦值.解:(1)AC ′→=AB →+AD →+AA′→, 所以|AC′→|=√(AB →+AD →+AA′→)2=√AB →2+AD →2+AA′→2+2(AB →⋅AD →+AB →⋅AA′→+AD →⋅AA′→)=√2a 2+b 2−2ab , (2)BD ′→=BA →+BC →+BB′→,所以|BD′→|=√(BA →+BC →+BB′→)2 =√BA →2+BC →2+BB′→2+2(BA →⋅BC →+BA →⋅BB′→+BC →⋅BB′→) =√2a 2+b 2,AC →=AB →+BC →,|AC →|=√2a ,BD ′→⋅AC →=(BA →+BC →+BB′→)•(AB →+BC →)=﹣ab , cos <BD′,AC →>=BD′→⋅AC →|BD′→|⋅|AC →|=√2a 2+b √2a=√4a 2+2b ,所以直线BD '与AC 所成角的余弦值为√4a 2+2b 2.19.(12分)已知圆C 的圆心为(﹣2,1),且圆C _____.在下列所给的三个条件中任选一个,填在直线上,并完成解答(注:若选择多个条件分别解答,按第一个解答计分) ①与直线3x +4y +17=0相切;②与圆M :(x ﹣2)2+(y ﹣4)2=4相外切; ③经过直线3x +y +2=0与直线x ﹣3y +14=0的交点. (1)求圆C 的方程;(2)圆N :(x ﹣m )2+y 2=m 2(m >0),是否存在实数m ,使得圆N 与圆C 公共弦的长度为2,若存在,求出实数m 的值;若不存在,请说明理由. 解:(1)设圆C 的半径为r ,若选条件①,圆C 与直线3x +4y +17=0相切,所以圆心C 到直线3x +4y +17=0的距离是圆C 的半径, 即r =|−6+4+17|5=3, 所以圆C 的方程为(x +2)2+(y ﹣1)2=9;若选条件②,与圆M :(x ﹣2)2+(y ﹣4)2=4相外切,圆M 的圆心为(2,4),半径为2, 所以r +2=√(2+2)2+(4−1)2=5,所以r =3, 所以圆C 的方程为(x +2)2+(y ﹣1)2=9;若选条件③,经过直线3x +y +2=0与直线x ﹣3y +14=0的交点, 由{3x +y +2=0x −3y +14=0,得{x =−2y =4,所以r =4﹣1=3,所以圆C 的方程为(x +2)2+(y ﹣1)2=9;(2)圆N :(x ﹣m )2+y 2=m 2(m >0)的圆心为(m ,0),半径为m ,两个圆有公共弦,则|m ﹣3|<|CN |<m +3,即|m −3|<√(m +2)2+1<m +3,解得m >25,由{(x +2)2+(y −1)2=9(x −m)2+y 2=m 2得两圆公共弦所在直线方程为(m +2)x ﹣y ﹣2=0, 又两圆的公共弦长为2,则圆心C 到公共弦所在直线的距离为d =|−2m−4−1−2|√(m+2)+1=|2m+7|√m 2+4m+5,且2√9−d 2=2, 解得m =√10−12或m =−√10−12, 又m >25,所以m =√10−12,经检验符合题意,故存在实数m =√10−12,使得圆N 与圆C 公共弦的长度为2.20.(12分)如图,已知在四棱锥P ﹣ABCD 中,P A ⊥平面ABCD ,点Q 在棱P A 上,且P A =4PQ =4,底面为直角梯形,∠CDA =∠BAD =90°,AB =2,CD =1,AD =√2,M ,N 分别是PD ,PB 的中点. (1)求证:MQ ∥平面PCB ;(2)求直线BC 与平面MCN 所成角的正弦值.(1)证明:如图,以A 为原点,以AD ,AB ,AP 所在直线分别为x ,y ,z 轴建立空间直角坐标系O ﹣xyz , 由题意可得:A(0,0,0),B(0,2,0),C(√2,1,0),D(√2,0,0),P(0,0,4),Q(0,0,3),M(√22,0,2),N (0,1,2),∴BC →=(√2,−1,0),PB →=(0,2,−4),MQ →=(−√22,0,1),设n 0→=(x 1,y 1,z 1)为平面PBC 的法向量,则有:{n 0→⋅BC →=0n 0→⋅PB →=0⇒{√2x 1−y 1=02y 1−4z 1=0,令z 1=1,则平面PBC 的法向量n 0→=(√2,2,1), ∴MQ →⋅n 0→=(−√22,0,1)⋅(√2,2,1)=0,又MQ ⊄平面PCB ,∴MQ ∥平面PCB .(2)设n →=(x ,y ,z )为平面MCN 的法向量, 又CM →=(−√22,−1,2),CN →=(−√2,0,2)则有:{n →⋅CM →=0n →⋅CN →=0⇒{−√22x −y +2z =0−√2x +2z =0, 令z =1,则平面MCN 的法向量n →=(√2,1,1), 又BC →=(√2,−1,0),设直线BC 与平面MCN 所成角为θ,∴sin θ=|cos <n →,BC →>|=n →⋅BC→|n →|⋅|BC →|=12×3=√36, ∴直线BC 与平面MCN 所成的角的正弦值为√36.21.(12分)直线y =kx +b 与椭圆x 24+y 2=1交于A ,B 两点,记△AOB 的面积为S .(1)当k =0,12<b <√32时,求S 的取值范围; (2)当|AB|=43,S =2√23时,求直线AB 的方程. 解:(1)因为直线y =kx +b 与椭圆x 24+y 2=1交于A ,B 两点,当k =0,12<b <√32时, 不妨设A (x 1,b ),B (x 2,b ),且x 1>x 2,联立{x 24+y 2=1y =b,解得x 1=2√1−b 2,x 2=﹣2√1−b 2, 此时|AB|=|x 1−x 2|=4√1−b 2,所以S =12b ×4√1−b 2=2b√1−b 2=2√b 2−b 4, 因为12<b <√32, 所以14<b 2<34,易得当b 2=12时,S 取得最大值,最大值为1, 则S ∈(√32,1];(2)A (x 1,y 1),B (x 2,y 2),联立{y =kx +b x 24+y 2=1,消去y 并整理得(1+4k 2)x 2+8kbx +4(b 2﹣1)=0, 此时Δ=16(1+4k 2﹣b 2)>0,由韦达定理得x 1+x 2=−8kb1+4k 2,x 1x 2=4(b 2−1)1+4k 2,所以|AB|=√1+k 2|x 1−x 2|=√1+k 2√16(1+4k 2−b 2)1+4k 2, 易知点O 到直线AB 的距离d =|b|√1+k , 因为|AB|=43,S =2√23, 解得d =√2,所以b 2=2(1+k 2),而|AB|=√1+k 2√16(1+4k 2−b 2)1+4k 2=43, 所以k 2=2, 解得k =±√2,b =±√6所以AB 的方程为y =√2x +√6或y =−√2x +√6或y =√2x −√6或y =−√2x −√6.22.(12分)已知双曲线x 2a 2−y 2b 2=1(a >0,b >0)与直线l :y =kx +m(k ≠±ba)有唯一的公共点M ,过点M 且与l 垂直的直线分别交x 轴、y 轴与A (x ,0),B (0,y )两点.点P 的坐标为(x ,y ),当M 点的坐标为(−2√2,−4)时,P 点坐标为(−10√2,−5).(1)求双曲线的标准方程;(2)当点M 运动时,求P 点的轨迹方程,并说明轨迹是什么曲线.解:(1)不妨设AB :y +4=−1k (x +2√2),此时A(−4k −2√2,0),B(0,−4−2√2k ), 此时P(−4k −2√2,−4−2√2k ), 联立{−4k −2√2=−10√2−4−2√2k =−5, 解得k =2√2,因为直线l :y =kx +m 经过点M ,所以m =4,此时直线l 的方程为y =2√2x +4,联立{y =2√2x +4x 2a 2−y 2b2=1,消去y 并整理得(b 2−8a 2)x 2−16√2a 2x −16a 2−a 2b 2=0,因为直线l 与椭圆相切,所b 2﹣8a 2≠0,且Δ=0,即(−16√2a 2)2+4(b 2−8a 2)(16a 2+a 2b 2)=0整理得8b 2﹣16a 2=a 2b 2,①又因为点M 在双曲线上,所以8a 2−16b 2=1,②联立①②,解得a 2=4,b 2=16,则双曲线的标准方程为x 24−y 216=1; (2)联立{y =kx +mx 24−y 216=1,消去y 并整理得(4﹣k 2)x 2﹣2kmx ﹣(m 2+16)=0(k ≠±2) 因为点M 是双曲线与直线l 的唯一公共点,所以Δ=(﹣2km )2+4(4﹣k 2)(m 2+16)=0,即m 2=4(k 2﹣4),③解得M(km4−k 2,4m4−k 2),此时M(−4k m ,−16m ),其中km ≠0则经过点M 且与l 垂直的直线为y +16m =−1k (x +4k m ),可得A(−20k m ,0),B(0,−20m ),P(−20k m ,−20m ),所以{x =−20k m y =−20m,④ 联立③④,可得x 2=400k 2m 2=400m 2(m 24+4)=100+1600m 2=100+4y 2, 即x 2100−y 225=1,其中y ≠0,所以,点P 的轨迹方程为x 2100−y 225=1(y ≠0),轨迹是焦点在x 轴上,实轴长为20,虚轴长为10的双曲线(去掉两个顶点).。
浙江省宁波市金兰教育合作组织2022-2023学年高二下学期信息技术4月期中试卷含解析

浙江省宁波市金兰教育合作组织2022-2023学年高二下学期信息技术4月期中试卷(答案在最后)一、选择题(本大题共12小题,每小题2分,共24分。
每小题列出的四个备选项中只有一个是符合题目要求的,不选、错选、多选均不得分)1.关于数据、信息与知识,下列说法错误的是()A.数据是信息的载体,单纯的数据没有意义B.信息经过人为的解读和经验充实可以转化成知识C.计算机只能处理数字化后的信息D.不同的人接受同样的信息后,所构建的知识是相同的【答案】D【解析】【详解】本题考查的是数据、信息与知识。
由于信息的价值相对性,故不同的人接受同样的信息后,所构建的知识也不相同,选项D说法错误。
2.下列研究领域中,不属于人工智能范畴的是()A.机器学习B.专家系统C.编译原理D.人工神经网络【答案】C【解析】【详解】本题主要考查人工智能技术的描述。
人工智能研究包括机器人、语言识别、图像识别、自然语言处理和专家系统等。
机器学习、专家系统、人工神经网络均属于人工智能范畴,故本题选C选项。
3.宁波公共自行车是宁波市推出的公共自行车服务,用于解决公共交通中的“最后一公里”问题。
市民可通过具有租车功能的甬城通卡借还公共自行车。
租车时,在公共自行车锁止器的刷卡区域刷卡,听到“滴”声后,锁止器打开,市民就能轻松取车。
另外还推出了宁波公共自行车app,市民通过该app加手机验证码就可以安全租赁公共自行车,免去办卡等辅助的手续,更好的保障个人信息安全,并且提供宁波公共自行车网点信息查询,以及相关资讯服务。
关于宁波公共自行车系统,下列说法正确的是()A.该系统是一个人机交互系统,是一个工作系统B.市民通过甬城通卡借还自行车时,无需通信网络的支持C.借还自行车的市民是该系统的用户,但网点维护人员不是D.租赁公共自行车的手机验证码是该系统的软件【答案】A【解析】【详解】本题考查的是信息系统相关知识。
市民通过甬城通卡借还自行车时,需要通信网络的支持;用户包括系统的使用者、维护人员、开发人员等;租赁公共自行车的手机验证码是该系统的数据。
低年级组小学期末各学科学生综合考试成绩(3年级二班语文)

郑生康 蒋兴蕊 范青云 范云霞 刘鹏程
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
夏合扎提·帕塔
王丽欣 周宇俊楠 武世杰 董博 李新豫 祁正海
伊尔夏提·热素力
候美娜 裴静雯 张海涛 张婉怡 钱晓彤 李帅阳 郭佳庆 张陶哲 杨庆林 张家浩 张靖怡 史浩娟 魏雨婷 王建鹏 夏晶玉 吴敏敏 赵雪 岳双喜 杨程程
萨基丹姆·吾布力
马苏热·库都斯
刘靖葵 陈诗雷 王朝伟 何营东
艾米努尔·阿里根
A C A B A B A A A C C A A A A A A A A C A A A A A A C A B B C A A A A A B A A B A A A B B A B
A C A B A C A A A C B A A A A A A A A B A A A A A B B A B A C A A A A A B A A B A A A B A A B
B A B A B C B A A C A C B A A A A A A A A A A C A A A B A A C A A B A A A A C C A A A A C A B
A A B A B B A A A B A C B A A B A A A A A A A B A A A A A B C B A B B A A A C C B A A A B A B
2022-2023学年浙江省宁波市金兰教育合作组织高一(上)期中数学试卷【答案版】

2022-2023学年浙江省宁波市金兰教育合作组织高一(上)期中数学试卷一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合M={2022,2023},则M的子集有()A.1个B.2个C.3个D.4个2.函数f(x)=1√5−x(x+1)0的定义域为()A.(﹣∞,5)∪(5,+∞)B.(﹣∞,﹣1)∪(﹣1,5)C.(﹣∞,5)D.(﹣1,5)3.下列各图形中,不可能是函数图象的是()A.B.C.D.4.设x∈R,则“x≤3”是“﹣1≤x﹣1≤1”成立的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5.把物体放在冷空气中冷却,如果物体原来的温度是θ1℃,空气的温度是θ0℃,那么t分钟后物体的温度θ℃可由公式θ=θ0+(θ1﹣θ0)e﹣kt求得,其中k是一个随着物体与空气的接触状况而定的正常数.现有一个60℃的物体,放在10℃的空气中冷却,2分钟后物体的温度是50℃,那么4分钟后该物体的温度是()A.42℃B.45℃C.46℃D.47℃6.16世纪英国数学家哈利奥特首次使用“<”和“>”符号,并逐渐被数学界接受,不等号的引入对不等式的发展影响深远.若a=(13)23,b=(14)13,c=(12)−12,则a,b、c的大小关系为()A.c>a>b B.a>b>c C.c>b>a D.a>c>b7.为了保护水资源,提倡节约用水,某城市对居民生活用水实行“阶梯水价”,计费方法如下表:若某户居民本月缴纳的水费为99元,则此户居民本月的用水量为( ) A .21m 3B .20m 3C .19m 3D .18m 38.已知函数f(x)={3√x +2,x ≥0ax +b ,x <0满足条件:对于∀x 1≠0,∃唯一的x 2∈R ,x 2≠x 1,使得f (x 1)=f (x 2),当f (3a )=f (2b )成立时,则实数2a +3b 的值为( ) A .−6−2√2B .−6+2√2C .6−2√2D .6+2√2二、选择题:本题共4小题,每小题5分,共20分在每小题给出的选项中,有多项符合题目要求全部选对的得5分,部分选对的得2分,有选错的得0分. 9.下列说法正确的有( )A .函数f(x)=1x在其定义域内是减函数B .命题“∃x ∈R ,e x +2x >1”的否定是“∀x ∈R ,e x +2x ≤1”C .函数f (x )=x 与g(x)=(√x)2是同一个函数D .a ,b ,c 为任意的实数,若a +c >b +c ,则a >b10.已知函数f (x )是定义在R 上的偶函数,当x ≤0时f (x )=﹣x 2﹣2x ,则( ) A .f (x )的最大值为1B .f (x )在区间(1,+∞)上单调递减C .f (x )≥0的解集为[﹣2,2]D .当x >0时,f (x )=x 2﹣2x11.设正实数x ,y ,满足x +2y =2,则( ) A .y ∈(0,1) B .xy 的最大值为14C .x 2+y 2的最小值为45D .2x +4y 的最小值为412.把定义域为[0,+∞)且同时满足以下两个条件的函数f (x )称为“类增函数”:(1)对任意的x ∈[0,+∞),总有f (x )≥0;(2)若x ≥0,y ≥0,则有f (x +y )≥f (x )+f (y )成立.下列说法错误的是( ) A .若f (x )为“类增函数”,则f (0)=0B .若f (x )为“类增函数”,则f (x )不一定是增函数C .函数g(x)={0,x ∈Q 1,x ∉Q在[0,+∞)上是“类增函数”D .函数g (x )=[x ]在[0,+∞)上不是“类增函数”([x ]表示不大于x 的最大整数) 三、填空题:本题共4小题,每小题5分,共20分13.已知幂函数f(x)=x α(α∈{−2,−1,12,1,3})为奇函数,且在(0,+∞)上单调递减,则f(−12)= .14.若“∃x ∈(0,+∞),λx >2x 2+1”是假命题,则实数λ的取值范围是 .15.已知函数f (x )=ax 2+(b ﹣1)x +c (a ≠0)的图象关于y 轴对称,且关于x 的方程f (x )=x 有两个相等的实根,写出满足上述条件的一个函数f (x )= .16.某地方政府为鼓励全民创业,拟对本地年产值x ∈[50,500](单位:万元)的小微企业进行奖励,奖励方案为:奖金y (单位:万元)随企业年产值x 的增加而增加,且奖金不低于7万元,同时奖金不超过企业年产值的15%.若函数y =mx−15x+5,则m 的取值范围为 . 四、解答题:本题共6小题,共70分解答应写出文字说明、证明过程或演算步骤. 17.(10分)化简下列各式:(Ⅰ)√(π−4)2+2√3×3√1.53×√126; (Ⅱ)若10x =3,10y =5.求10x−3y2.18.(12分)设全集为R ,集合A ={x |x 2﹣7x ﹣8>0},B ={x |a +1<x <2a ﹣3}. (Ⅰ)若a =6,求A ∩∁R B ;(Ⅱ)在①A ∪B =A ;②A ∩B =B ;③(∁R A )∩B =∅,这三个条件中任选一个作为已知条件,求实数a 的取值范围.(注:如果选择多个条件分别解答,则按第一个解答计分) 19.(12分)设函数f (x )=ax 2+(2b ﹣3)x +4(a ≠0). (Ⅰ)若不等式f (x )>0的解集(﹣1,2),求a +b 的值; (Ⅱ)当a =﹣1时,设g(x)={f(x)−4,x ≤1(5−b)x +4,x >1,满足是对任意x 1≠x 2,都有g(x 1)−g(x 2)x 1−x 2>0成.求实数b 的取值范围.20.(12分)自2020新冠疫情爆发以来,直播电商迅猛发展,以信息流为代表的各大社交平台也相继入场,平台用短视频和直播的形式,激发起用户情感与场景的共鸣,让用户在大脑中不知不觉间自我说服,然后引起消费行动.某厂家往年不与直播平台合作时,每年都举行多次大型线下促销活动,经测算,只进行线下促销活动时总促销费用为20万元.为响应当地政府防疫政策,决定采用线上(直播促销)线下同时进行的促销模式,与某直播平台达成一个为期4年的合作协议,直播费用(单位:万元)只与4年的总直播时长x(单位:小时)成正比,比例系数为0.1.已知与直播平台合作后该厂家每年所需的线下促销费C(单位:万元)与总直播时长x(单位:小时)之间的关系为C=kx+50(x≥0,k为常数).记该厂家线上促销费用与4年线下促销费用之和为y(单位:万元).(Ⅰ)写出y关于x的函数关系式;(Ⅱ)该厂家直播时长x为多少时,可使y最小?并求出y的最小值.21.(12分)已知函数f(x)=3x+m3x−1.若f(x)为奇函数.(Ⅰ)求实数m的值;(Ⅱ)判断函数y=f(x)在(0,+∞)上的单调性,并给予证明;(Ⅲ)若∃x∈R,|f(x)|<2t﹣1成立,求实数t的取值范围.22.(12分)已知函数f(x)=x2﹣2|x﹣a|.(Ⅰ)当a=0时,求f(﹣2023)﹣f(2023)的值;(Ⅱ)当a=1时,求不等式f(x)<3的解集;(Ⅲ)当a>0时,若对任意的x∈[0,+∞),不等式f(x﹣1)≤2f(x)+1恒成立,求实数a的取值范围.2022-2023学年浙江省宁波市金兰教育合作组织高一(上)期中数学试卷参考答案与试题解析一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合M={2022,2023},则M的子集有()A.1个B.2个C.3个D.4个解:集合M={2022,2023},集合M的元素个数为2个,则M的子集有22=4.故选:D.2.函数f(x)=5−x(x+1)0的定义域为()A.(﹣∞,5)∪(5,+∞)B.(﹣∞,﹣1)∪(﹣1,5)C.(﹣∞,5)D.(﹣1,5)解:要使原函数有意义,则{5−x>0x+1≠0,解得x<5且x≠﹣1.∴函数f(x)=15−x(x+1)0的定义域为(﹣∞,﹣1)∪(﹣1,5).故选:B.3.下列各图形中,不可能是函数图象的是()A.B.C.D.解:∵根据函数的概念得出:y=f(x),直线x=a与f(x)的图象交点有1,或0个,∴B图象中当x=a>0时,有2个交点了,故答案B不可能是函数图象,故选:B.4.设x∈R,则“x≤3”是“﹣1≤x﹣1≤1”成立的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解:∵﹣1≤x﹣1≤1,∴0≤x≤2,∵[0,2]⫋(﹣∞,3],∴x≤3是﹣1≤x﹣1≤1成立的必要不充分条件,故选:B.5.把物体放在冷空气中冷却,如果物体原来的温度是θ1℃,空气的温度是θ0℃,那么t分钟后物体的温度θ℃可由公式θ=θ0+(θ1﹣θ0)e﹣kt求得,其中k是一个随着物体与空气的接触状况而定的正常数.现有一个60℃的物体,放在10℃的空气中冷却,2分钟后物体的温度是50℃,那么4分钟后该物体的温度是()A.42℃B.45℃C.46℃D.47℃解:将θ0=10,t=2,θ1=60,θ=50代入θ=θ0+(θ1﹣θ0)e﹣kt,可得50=10+(60﹣10)e﹣2k,解得e﹣2k=4 5,当t=4时,e﹣4k=(e﹣2k)2=16 25,所以θ=10+(60﹣10)e﹣4k=10+50×1625=42.故选:A.6.16世纪英国数学家哈利奥特首次使用“<”和“>”符号,并逐渐被数学界接受,不等号的引入对不等式的发展影响深远.若a=(13)23,b=(14)13,c=(12)−12,则a,b、c的大小关系为()A.c>a>b B.a>b>c C.c>b>a D.a>c>b解:b=(14)13=(12)23,由于幂函数f(x)=x23在(0,+∞)上单调递增,则f(13)<f(12),即a<b,根据指数函数的性质知a<b<1,而c=(12)−12=√2>1,故a<b<1<c,故选:C.7.为了保护水资源,提倡节约用水,某城市对居民生活用水实行“阶梯水价”,计费方法如下表:若某户居民本月缴纳的水费为99元,则此户居民本月的用水量为( ) A .21m 3B .20m 3C .19m 3D .18m 3解:依题意,设此户居民月用水量为x ,月缴纳的水费为y 元,则y ={3x ,0≤x ≤1236+6(x −12),12<x ≤1836+36+9(x −18),x >18,即:y ={3x ,0≤x ≤126x −36,12<x ≤189x −90,x >18,当y =99时,x ∉[0,12], 当12<x ≤18时,令6x ﹣36=99,解得x =22.5,与12<x ≤18相矛盾,故舍去; 当x >18时,令9x ﹣90=99, 解得x =21,满足x >18.所以此户居民本月的用水量为21m 3. 故选:A .8.已知函数f(x)={3√x +2,x ≥0ax +b ,x <0满足条件:对于∀x 1≠0,∃唯一的x 2∈R ,x 2≠x 1,使得f (x 1)=f (x 2),当f (3a )=f (2b )成立时,则实数2a +3b 的值为( ) A .−6−2√2B .−6+2√2C .6−2√2D .6+2√2解:因为当x >0时,f (x )=3√x +2>2,且单调递增,设此时f (x )的值域为A ,则A =(2,+∞); 当x <0时,f (x )=ax +b ,设此时f (x )的值域为B . 则根据题意可得A =B =(2,+∞), 所以{a <0b =2,又因为f (3a )=f (2b )=f (4), 即3a 2+2=8且a <0, 则a =−√2,所以2a +3b =﹣2√2+6. 故选:C .二、选择题:本题共4小题,每小题5分,共20分在每小题给出的选项中,有多项符合题目要求全部选对的得5分,部分选对的得2分,有选错的得0分.9.下列说法正确的有()A.函数f(x)=1x在其定义域内是减函数B.命题“∃x∈R,e x+2x>1”的否定是“∀x∈R,e x+2x≤1”C.函数f(x)=x与g(x)=(√x)2是同一个函数D.a,b,c为任意的实数,若a+c>b+c,则a>b解:对于A:由于f(﹣1)=﹣1<f(1)=1,不符合单调递减的定义,A错误;对于B:特称命题的否定是:将存在量词替换成全称量词,最后的语句变成对立面,B正确;对于C:f(x)=x定义域为R,g(x)=(√x)2定义域为:[0,+∞),定义域不同,C错误;对于D:若a+c>b+c,则两边同时加上﹣c,有a>b,D正确.故选:BD.10.已知函数f(x)是定义在R上的偶函数,当x≤0时f(x)=﹣x2﹣2x,则()A.f(x)的最大值为1B.f(x)在区间(1,+∞)上单调递减C.f(x)≥0的解集为[﹣2,2]D.当x>0时,f(x)=x2﹣2x解:设x>0,则﹣x<0,所以f(﹣x)=﹣(﹣x)2﹣2(﹣x)=﹣x2+2x,因为f(x)是偶函数,即f(﹣x)=f(x),所以f(x)=﹣x2+2x,所以f(x)={−x2−2x,x≤0−x2+2x,x>0,函数图象如图所示:由图可得:f (x )的最大值为1,f (x )在区间(1,+∞)上单调递减,f (x )≥0的解集为[﹣2,2], 故选:ABC .11.设正实数x ,y ,满足x +2y =2,则( ) A .y ∈(0,1) B .xy 的最大值为14C .x 2+y 2的最小值为45D .2x +4y 的最小值为4解:因为正实数x ,y ,满足x +2y =2, 所以x =2﹣2y >0, 所以0<y <1,A 正确,由基本不等式可得2=x +2y ≥2√2xy ,当且仅当x =2y 时取等号, 解得xy ≤12,B 错误;x 2+y 2=(2﹣2y )2+y 2=5y 2﹣8y +4在x =0.8时取最小值45,C 正确;2x +4y ≥2√2x ⋅4y =2√2x+2y =4,当且仅当x =2y =1时取等号,D 正确. 故选:ACD .12.把定义域为[0,+∞)且同时满足以下两个条件的函数f (x )称为“类增函数”:(1)对任意的x ∈[0,+∞),总有f (x )≥0;(2)若x ≥0,y ≥0,则有f (x +y )≥f (x )+f (y )成立.下列说法错误的是( ) A .若f (x )为“类增函数”,则f (0)=0B .若f (x )为“类增函数”,则f (x )不一定是增函数C .函数g(x)={0,x ∈Q 1,x ∉Q在[0,+∞)上是“类增函数”D .函数g (x )=[x ]在[0,+∞)上不是“类增函数”([x ]表示不大于x 的最大整数)解:对于A ,由“类增函数”的定义可知,f (0)≥0,再令x =y =0,则有f (0)≥f (0)+f (0),即f (0)≤0,∴f (0)=0,故A 正确,对于B ,对任意x ≥0,y ≥0,且x <y ,则y ﹣x >0, ∴f (y )=f [(y ﹣x )+x ]≥f (y ﹣x )+f (x ), ∴f (y )﹣f (x )≥f (y ﹣x )≥0,即f (y )≥f (x ) ∴f (x )在[0,+∞)上单调递增,故B 错误,对于C ,易知g (x )在[0,+∞)上不是增函数,由选项B 可知,g (x )不是“类增函数”,故C 错误, 对于D ,函数g (x )=[x ]在[0,+∞)上是“类增函数”,证明如下:(1)对任意的x∈[0,+∞),总有g(x)≥0成立,(2)若x≥0,y≥0,设x=m+p,y=n+p,(m∈N,n∈N,p∈[0,1),q∈[0,1)),则x+y=m+n+(p+q),∴g(x+y)≥m+n=g(x)+g(y)成立,∴g(x)=[x]在[0,+∞)上是“类增函数”,故D错误,故选:BCD.三、填空题:本题共4小题,每小题5分,共20分13.已知幂函数f(x)=xα(α∈{−2,−1,12,1,3})为奇函数,且在(0,+∞)上单调递减,则f(−12)=﹣2.解:若幂函数f(x)为奇函数,则α=﹣1或α=1或α=3,因为函数在(0,+∞)上单调递减,所以α=﹣1,f(x)=x﹣1则f(−12)=−2.故答案为:﹣2.14.若“∃x∈(0,+∞),λx>2x2+1”是假命题,则实数λ的取值范围是(−∞,2√2].解:若“∃x∈(0,+∞),λx>2x2+1”是假命题,则命题的否定即:∀x∈(0,+∞),λx≤2x2+1是真命题,即λ≤2x+1x在x>0时恒成立,只需λ≤(2x+1x)min,又2x+1x≥2√2x⋅1x=2√2,当且仅当2x=1x,即x=√22时取等号,则λ≤2√2,所以实数λ的取值范围为(−∞,2√2],故答案为:(−∞,2√2].15.已知函数f(x)=ax2+(b﹣1)x+c(a≠0)的图象关于y轴对称,且关于x的方程f(x)=x有两个相等的实根,写出满足上述条件的一个函数f(x)=x2+14.解:函数f(x)=ax2+(b﹣1)x+c(a≠0)的图象关于y轴对称,则b﹣1=0,b=1,又关于x的方程f(x)=x有两个相等的实根,则ax2+(b﹣1)x+c=x,即ax2+(b﹣2)x+c=0,Δ=(b﹣2)2﹣4ac=0,将b =1代入上式,有4ac =1,取a =1,则c =14,此时f (x )=x 2+14.答案为:f (x )=x 2+14.(答案不唯一)16.某地方政府为鼓励全民创业,拟对本地年产值x ∈[50,500](单位:万元)的小微企业进行奖励,奖励方案为:奖金y (单位:万元)随企业年产值x 的增加而增加,且奖金不低于7万元,同时奖金不超过企业年产值的15%.若函数y =mx−15x+5,则m 的取值范围为 [8,8.55] .解:y =f (x )=mx−15x+5=m −5m+15x+5, 函数在[50,500]递增,则f (x )min =f (50)≥7,即m −5m+1555≥7,解得m ≥8; 要使y =mx−15x+5≤0.15x 对x ∈[50,500]恒成立,即m ≤0.75+0.15x +15x对x ∈[50,500]恒成立, ∵0.75+0.15x +15x 在[50,500]上单调递增,∴(0.75+0.15x +15x )min =8.55, ∴m ≤8.55.综上可知,m 的取值范围为[8,8.55].故答案为:[8,8.55].四、解答题:本题共6小题,共70分解答应写出文字说明、证明过程或演算步骤.17.(10分)化简下列各式:(Ⅰ)√(π−4)2+2√3×3√1.53×√126;(Ⅱ)若10x =3,10y =5.求10x−3y 2.解:(Ⅰ)原式=4﹣π+2×312×3×(32)13×1216=4−π+2×312+1+13+16×2−13+13=4﹣π+2×9=22﹣π;(Ⅱ)由已知可得x =lg 3,y =lg 5,所以10x−3y 2=10lg3−3lg52=10lg3−lg532=1012lg 3125=(3125)12=√1525. 18.(12分)设全集为R ,集合A ={x |x 2﹣7x ﹣8>0},B ={x |a +1<x <2a ﹣3}.(Ⅰ)若a =6,求A ∩∁R B ;(Ⅱ)在①A ∪B =A ;②A ∩B =B ;③(∁R A )∩B =∅,这三个条件中任选一个作为已知条件,求实数a 的取值范围.(注:如果选择多个条件分别解答,则按第一个解答计分)解:(Ⅰ)全集为R ,集合A ={x |x 2﹣7x ﹣8>0}={x |x <﹣1或x >8},a =6时,B ={x |a +1<x <2a ﹣3}={x |7<x <9},∴∁R B ={x |x ≤7或x ≥9},∴A ∩∁R B ={x |x <﹣1或x ≥9}.(Ⅱ)①A ∪B =A ;②A ∩B =B ;③(∁R A )∩B =∅,选择①②③均得到B ⊆A ,当B =∅时,a +1≥2a ﹣3,解得a ≤4;当B ≠∅时,{a +1<2a −32a −3≤−1或{a +1<2a −3a +1≥8, 解得{a >4a ≤1或{a >4a ≥7,∴a ≥7, 综上,实数a 的取值范围是(﹣∞,4]∪[7,+∞).19.(12分)设函数f (x )=ax 2+(2b ﹣3)x +4(a ≠0).(Ⅰ)若不等式f (x )>0的解集(﹣1,2),求a +b 的值;(Ⅱ)当a =﹣1时,设g(x)={f(x)−4,x ≤1(5−b)x +4,x >1,满足是对任意x 1≠x 2,都有g(x 1)−g(x 2)x 1−x 2>0成.求实数b 的取值范围.解:(Ⅰ)∵不等式f (x )>0的解集(﹣1,2),∴﹣1和2是方程ax 2+(2b ﹣3)x +4=0的两个根,∴{−2b−3a =−1+24a=−1×2,解得{a =−2b =52, ∴a +b =12.(Ⅱ)当a =﹣1时,f (x )=﹣x 2+(2b ﹣3)x +4,∴g(x)={−x 2+(2b −3)x ,x ≤1(5−b)x +4,x >1, ∵对任意x 1≠x 2,都有g(x 1)−g(x 2)x 1−x 2>0成立,∴函数g (x )在R 上单调递增,∴{2b−32≥15−b >0−1+(2b −3)≤5−b +4,解得52≤b ≤133,即实数b 的取值范围为[52,133].20.(12分)自2020新冠疫情爆发以来,直播电商迅猛发展,以信息流为代表的各大社交平台也相继入场,平台用短视频和直播的形式,激发起用户情感与场景的共鸣,让用户在大脑中不知不觉间自我说服,然后引起消费行动.某厂家往年不与直播平台合作时,每年都举行多次大型线下促销活动,经测算,只进行线下促销活动时总促销费用为20万元.为响应当地政府防疫政策,决定采用线上(直播促销)线下同时进行的促销模式,与某直播平台达成一个为期4年的合作协议,直播费用(单位:万元)只与4年的总直播时长x (单位:小时)成正比,比例系数为0.1.已知与直播平台合作后该厂家每年所需的线下促销费C (单位:万元)与总直播时长x (单位:小时)之间的关系为C =k x+50(x ≥0,k 为常数).记该厂家线上促销费用与4年线下促销费用之和为y (单位:万元).(Ⅰ)写出y 关于x 的函数关系式;(Ⅱ)该厂家直播时长x 为多少时,可使y 最小?并求出y 的最小值.解:(Ⅰ)由题得,当x =0时,C =k 50=20,则k =1000,故该厂家4年促销费用与线上直播费用之和为y =4×1000x+50+0.1x =4000x+50+110x ,(x ≥0). (Ⅱ)由(Ⅰ)知y =4000x+50+110(x +50)−5≥2√4000x+50⋅110(x +50)−5=35,当且仅当4000x+50=110(x +50),即x =150时等号成立,即线上直播150小时可使y 最小为35万元.21.(12分)已知函数f(x)=3x +m 3x −1.若f (x )为奇函数. (Ⅰ)求实数m 的值;(Ⅱ)判断函数y =f (x )在(0,+∞)上的单调性,并给予证明;(Ⅲ)若∃x ∈R ,|f (x )|<2t ﹣1成立,求实数t 的取值范围.解:(Ⅰ)因为f (x )为奇函数,且由3x ﹣1≠0得x ≠0,所以f (﹣x )=﹣f (x ),即3−x +m 3−x −1=−3x +m 3x −1, ∴1+m⋅3x1−3x =−3x +m3x −1,∴1+m ⋅3x =3x +m ,∴m =1;(Ⅱ)由(Ⅰ)得f(x)=3x+13x −1=1+23x −1,在(0,+∞)上为递减的函数. 证明:设对∀x 1,x 2∈(0,+∞),且x 1<x 2,则f(x 1)−f(x 2)=1+23x 1−1−(1+23x 2−1)=23x 1−1−23x 2−1 =2[(3x 2−1)−(3x 1−1)](3x 2−1)(3x 1−1)=2(3x 2−3x 1)(3x 2−1)(3x 1−1), ∵x 1,x 2∈(0,+∞),且x 1<x 2,∴3x 1,3x 2>1,∴3x 2−3x 1>0,(3x 2−1)(3x 1−1)>0,∴3x 2−3x 1>0,(3x 2−1)(3x 1−1)>0,∴f (x 1)﹣f (x 2)>0,即f (x 1)>f (x 2),所以f (x )在(0,+∞)上单调递减;(Ⅲ)由题意得2t ﹣1>|f (x )|min ,因为f(x)=3x +13x −1=1+23x −1而:3x ﹣1>﹣1,∴23x −1∈(−∞,−2)∪(0,+∞),∴f (x )∈(﹣∞,﹣1)∪(1,+∞),(令y =3x+13x −1,则3x =1+y y−1>0,y >1或y <﹣1), ∴|f (x )|∈(1,+∞),所以2t ﹣1>1,∴t >1.22.(12分)已知函数f (x )=x 2﹣2|x ﹣a |.(Ⅰ)当a =0时,求f (﹣2023)﹣f (2023)的值;(Ⅱ)当a =1时,求不等式f (x )<3的解集;(Ⅲ)当a >0时,若对任意的x ∈[0,+∞),不等式f (x ﹣1)≤2f (x )+1恒成立,求实数a 的取值范围.解:(Ⅰ)当a =0时,f (x )=x 2﹣2|x |,所以任取x ∈R ,则有f (﹣x )=f (x )恒成立,即f (x )为偶函数,∴f (﹣2023)﹣f (2023)=f (2023)﹣f (2023)=0;(Ⅱ)当a =1时,f (x )=x 2﹣2|x ﹣1|<3,∴{x ≥1x 2−2x +2<3或{x <1x 2+2x −2<3, ∴{x ≥11−√2<x <1+√2或{x <1−1−√6<x <−1+√6,∴1≤x <1+√2或−1−√6<x <1, 所以不等式f (x )<3的解集为{x|−1−√6<x <1+√2};(Ⅲ)不等式f (x ﹣1)≤2f (x )+1化为(x ﹣1)2﹣2|x ﹣1﹣a |≤2x 2﹣4|x ﹣a |+1,即:4|x ﹣a |﹣2|x ﹣(1+a )|≤x 2+2x (*)对任意的x ∈[0,+∞)恒成立,因为a >0,所以分如下情况讨论:①当0≤x ≤a 时,不等式(*)化为﹣4(x ﹣a )+2[x ﹣(1+a )]≤x 2+2x 恒成立,即x 2+4x +2﹣2a ≥0对∀x ∈[0,a ]恒成立,∵g (x )=x 2+4x +2﹣2a 的对称轴为x =﹣2,故其在[0,a ]上单调递增,只需g (x )min =g (0)=2﹣2a ≥0,∴0<a ≤1;②当a <x ≤a +1时,不等式(*)化为4(x ﹣a )+2[x ﹣(1+a )]≤x 2+2x 恒成立,即x 2﹣4x +2+6a ≥0对∀x ∈(a ,a +1)恒成立,由①知0<a ≤1,∴h (x )=x 2﹣4x +2+6a 在(a ,a +1)上单调递减,∴只需ℎ(x)min =ℎ(1+a)=a 2+4a −1≥0,∴a ≤−2−√5或a ≥√5−2,∵√5−2<1,∴√5−2≤a≤1;③当x>a+1时,不等式(*)化为4(x﹣a)﹣2[x﹣(1+a)]≤x2+2x恒成立,即x2+2a﹣2≥0对∀x∈(a+1,+∞)恒成立,所以φ(x)=x2+2a﹣2≥0在(a+1,+∞)上单调递增,只需φ(a+1)=a2+4a﹣1≥0,∴a≤−2−√5或a≥√5−2,由②得√5−2≤a≤1,综上所述,a的取值范围是:[√5−2,1].。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
100
地理
必修三第一章第四节区域差异(会考难度)(宁二中文科不考)
《中国地理概况》加《中国地理分区》(北方地区和南方地区)
90
100
注:(1)注意控制试题难度系数,一般控制在0.7左右,会考难度的控制在0.75左右。
(2)试题要反映现阶段学生水平,无偏题怪题;要注意落实教材内容;不能直接引入近几年高考题,要改编。
科目
化学
物理
地理
时间
3:10~4:40
3:10~4:40
科目
政治
历史
高二
日期
4月16日(周三)
4月17日(周四)
4月18日(周五)
上午
时间
8:30—11:00
9:00—11:00
9:00—11:00
科目
语文
数学
英语
下午
时间
1:20~2:50
1:20~2:50
1:20~2:50
科目
化学(理)/政治(文)
金兰组织2013学年第二学期期中考试进度
一、考试范围
年级
学科
高一
高二
时间
分值
语文
必修三
1、《外国小说欣赏》全册(浒山龙赛)
2《论语》(姜中、宁二中、柴桥、余二中)
150
150
数学
必修四的第三章、必修五第一、二章
高考复习:
第一章集合与常用逻辑用语(必修1,选修2-1)
第二章函数(必修1)
第三章三角函数,解三角形(必修4,5)
第四章平面向量(必修5)
文理一样(IB不考)
120
150
外语
必修三第二单元
选修5第三单元至英语选修6第一单元
120
120+30(听力)
物理
必修2第五章和第七章前7节
选修3-4
ห้องสมุดไป่ตู้90
100
化学
必修一专题四、必修二专题一、选修《化学反应原理》专题一中的第一单元《化学反应热效应》
有机化学基础(余二中自己命题)
物理(理)/历史(文)
生物(理)/地理(文)
时间
3:10~4:40
3:10~4:10
科目
政治(理)/生物(文)
通用技术
注:政治(理)/生物(文),通用技术各校自己命题
90
100
生物
必修2第四章至必修3第二章
第二节(文科自己命题)
90
100
政治
必修2第一课至第五课(会考难度)
必须三
90
100
历史
必修三专题四(会考难度)(宁二中文科不考)
1《战争与和平》20%、必修一专题1-5 80%(浒中、姜中、柴桥、龙赛)
2《战争与和平》60%、选修四第一到四单元40%(宁二中、余二中)
(4)试卷不能有差错。
(5)参考答案的分值必须细化(注明每个得分点的分值)。
二、考试时间及科目
高一
日期
4月16日(周三)
4月17日(周四)
4月18日(周五)
上午
时间
8:30—11:00
9:00—11:00
9:00—11:00
科目
语文
数学
英语
下午
时间
1:20~2:50
1:20~2:50
1:20~2:50
