2015年历年浙江省丽水市初三数学中考试题真题及答案
浙江省丽水市2015学年九上小中考试卷及答案

2015学年第一学期初中学科教学质量监测科学试题卷考生须知:1.全卷共四大题,36小题,满分为180分。
考试时间为120分钟。
2.全卷分为卷Ⅰ(选择题)和卷Ⅱ(非选择题)两部分,全部在“答题纸”上作答。
卷Ⅰ的答案必须用2B铅笔填涂;卷Ⅱ的答案必须用黑色字迹钢笔或签字笔写在“答题纸”的相应位置上。
3.请用黑色字迹钢笔或签字笔在“答题纸”上先填写姓名和准考证号。
4.本卷可能用到的相对原子质量:O—16Na—23S—32Cl—35.5Fe—56Cu—645.本卷g取10牛/千克。
卷Ⅰ一、选择题(本大题共有15小题,1-5小题每题4分,6-15小题每题3分,共50分。
请选出一个符合题意的正确选项,不选、多选、错选均不得分)1.某校食堂设计的一份营养餐食谱:米饭、鸡汤、红烧肉、清蒸鲫鱼。
从膳食平衡的角度分析,还需添加A.炒青菜B.水煮虾C.面包D.蒸蛋2.下列都是日常生活中的常见物质,其中属于溶液的是A.食盐水B.牛奶C.米粥D.豆浆3.泥石流是我市多发的一种自然灾害,2015年11月13日在莲都区雅溪镇里东村发生重大泥石流灾害,人民生命财产遭受了极大的损失。
根据泥石流形成的条件,下列方法不.能.减少..泥石流发生的是A.修建水库、调蓄水流B.退耕还林、封山育林C.建立预测、预报、救灾体系D.优先抢救贵重物品、保护生命财产4.2015年11月26日下午,秀丽的南明湖中出现了11只天鹅。
关于天鹅看到自己在水中的像,下列说法正确的是A.是实像B.比它自己小C.是由光的反射形成的第4题图D.是由光的折射形成的5.某同学将稀盐酸滴在鸡蛋壳上,发现有气体产生,该气体能使澄清的石灰水变浑浊。
则下列哪种物质最有可能是鸡蛋壳主要成分A.氢氧化钙B.氧化钙C.氯化钙D .碳酸钙6.某同学在观看了《动物世界》后,记录了自己喜欢的4种动物E 、F 、G 和H ,并设计以下的二歧式检索表来分辨这些动物:1a 体外有毛皮,胎生………………………………………………………………………E 1b 体外无毛皮,卵生 (2)2a 体外长有羽毛,体温恒定……………………………………………………………F 2b 体外无羽毛,体温不恒定………………………………………………………………33a 表皮干燥,在陆地上产卵……………………………………………………………G 3b 表皮湿润,在水中产卵………………………………………………………………H这些动物中有一条鳄鱼,它是A .EB .FC .GD .H7.某同学在探究“酸与碱能否发生反应”时,用稀氢氧化钠溶液、稀盐酸和酸碱指示剂进行如图的实验过程,所加试剂①②③依次是A .稀氢氧化钠溶液、石蕊试液、稀盐酸B .稀盐酸、石蕊试液、稀氢氧化钠溶液C .稀氢氧化钠溶液、酚酞试液、稀盐酸D .稀盐酸、酚酞试液、稀氢氧化钠溶液8.如图是某化学反应过程的微观示意图,“”、“”分别代表两种不同的原子。
丽水2015中考数学试题(解析版)

2015年浙江省丽水市中考数学试卷解析(本试卷满分120分,考试时间120分钟)参考公式:抛物线2y ax bx c =++的顶点坐标为24,24b b ac a a ⎛⎫-- ⎪⎝⎭.一、选择题(本题有10小题,每小题3分,共30分)1. (2015年浙江丽水3分) 在数-3,-2,0,3中,大小在-1和2之间的数是【 】A. -3B. -2C. 0D. 3 【答案】C.【考点】有理数大小比较.【分析】在-1和2之间的数必然大于-1,小于2,四个答案中只有0符合条件. 故选C. 2. (2015年浙江丽水3分) 计算32)(a 结果正确的是【 】A. 23a B. 6a C. 5a D. a 6 【答案】B. 【考点】幂的乘方.【分析】根据幂的乘方运算法则计算作出判断:23236()a a a ⨯==.故选B.3. (2015年浙江丽水3分) 由4个相同小立方体搭成的几何体如图所示,则它的主视图是【 】A.B. C. D.【答案】A.【考点】简单组合体的三视图.【分析】找到从正面看所得到的图形即可,从正面看易得有两层,下层有2个正方形,上层左边有一个正方形.故选A .4. (2015年浙江丽水3分)分式x--11可变形为【 】 A. 11--x B. x +11 C. x +-11 D. 11-x【答案】D.【考点】分式的基本性质.【分析】根据分式的性质,分子分母都乘以﹣1,分式的值不变,可得答案:分式11x--的分子分母都乘以﹣1,得11x-.故选D.5. (2015年浙江丽水3分)一个多边形的每个内角均为120°,则这个多边形是【】A. 四边形B. 五边形C. 六边形D. 七边形【答案】C.【考点】多边形的外角性质.【分析】∵多边形的每个内角均为120°,∴外角的度数是:180°﹣120°=60°.∵多边形的外角和是360°,∴这个多边形的边数是:360÷60=6.故选C.6. (2015年浙江丽水3分)如图,数轴上所表示关于x的不等式组的解集是【】A. x≥2B. x>2C. x>-1D. -1<x≤2【答案】A.【考点】在数轴上表示不等式的解。
浙江省丽水市中考数学真题试题(带解析)

丽水市中考数学试题解析卷一、选择题(共10小题,每小题3分,满分30分)1.(•丽水)如果零上2℃记作+2℃,那么零下3℃记作( )A.-3℃B.-2℃C.+3℃D.+2℃考点:正数和负数。
专题:计算题。
分析:一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.解答:解:“正”和“负”相对,∴如果零上2℃记作+2℃,那么零下3℃记作-3℃,故选A.点评:此题考查了正数和负数,解题关键是理解“正”和“负”的相对性,确定一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.2.(•丽水)计算3a•(2b)的结果是( )A.3ab B.6a C.6ab D.5ab考点:单项式乘单项式。
分析:根据单项式与单项式相乘,把他们的系数分别相乘,相同字母的幂分别相加,其余字母连同他的指数不变,作为积的因式,计算即可.解答:解:3a•(2b)=3×2a•b=6ab.故选C.点评:本题考查了单项式与单项式相乘,熟练掌握运算法则是解题的关键.3.(•丽水)如图,数轴的单位长度为1,如果点A,B表示的数的绝对值相等,那么点A表示的数是( ) A.-4 B.-2 C.0 D.4考点:绝对值;数轴。
专题:计算题。
分析:如果点A,B表示的数的绝对值相等,那么AB的中点即为坐标原点.解答:解:如图,AC的中点即数轴的原点O.根据数轴可以得到点A表示的数是-2.故选B.点评:此题考查了数轴有关内容,用几何方法借助数轴来求解,非常直观,体现了数形结合的优点.确定数轴的原点是解决本题的关键.4.(•丽水)把分式方程转化为一元一次方程时,方程两边需同乘以( )A.x B.2x C.x+4 D.x(x+4)考点:解分式方程。
分析:根据各分母寻找公分母x(x+4),方程两边乘最简公分母,可以把分式方程转化为整式方程.解答:解:由两个分母(x+4)和x可得最简公分母为x(x+4),所以方程两边应同时乘以x(x+4).故选D.点评:本题考查解分式方程去分母的能力,确定最简公分母应根据所给分式的分母来决定.5.(•丽水)在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中阴影部分构成中心对称图形.该小正方形的序号是( )A.①B.②C.③D.④考点:利用旋转设计图案。
浙江省丽水市中考数学真题及答案

浙江省丽水市中考数学真题及答案(满分为120分,考试时间为120分钟)卷 Ⅰ一、选择题(本题有10小题,每小题3分,共30分) 1.实数3的相反数是( )A .3-B .3C .13-D .132.分式52x x +-的值是零,则x 的值为( ) A .2 B .5 C .2- D .5-3.下列多项式中,能运用平方差公式分解因式的是( ) A .22a b + B .22a b - C .22a b - D .22a b -- 4.下列四个图形中,是中心对称图形的是( )A .B .C .D .5.如图,有一些写有号码的卡片,它们的背面都相同,现将它们背面朝上,从中任意摸出一张,摸到1号卡片的概率是( )A .12 B .13 C .23 D .166.如图,工人师傅用角尺画出工件边缘AB 的垂线a 和b ,得到//a b .理由是( )A .连结直线外一点与直线上各点的所有线段中,垂线段最短B .在同一平面内,垂直于同一条直线的两条直线互相平行C .在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线D .经过直线外一点,有且只有一条直线与这条直线平行7.已知点(2-,)(2a ,)(3b ,)c 在函数(0)ky k x=>的图象上,则下列判断正确的是( )A .a b c <<B .b a c <<C .a c b <<D .c b a <<8.如图,O 是等边ABC ∆的内切圆,分别切AB ,BC ,AC 于点E ,F ,D ,P 是DF 上一点,则EPF ∠的度数是( )A .65︒B .60︒C .58︒D .50︒9.如图,在编写数学谜题时,“□”内要求填写同一个数字,若设“□”内数字为x .则列出方程正确的是( )A .3252x x ⨯+=B .3205102x x ⨯+=⨯C .320520x x ⨯++=D .3(20)5102x x ⨯++=+10.如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD 与正方形EFGH .连结EG ,BD 相交于点O 、BD 与HC 相交于点P .若GO GP =,则ABCD EFGHS S 正方形正方形的值是( )A.1+.2.5- D .154卷 Ⅱ二、填空题(本题有6小题,每小题4分,共24分)11.点(,2)P m 在第二象限内,则m 的值可以是(写出一个即可) .12.数据1,2,4,5,3的中位数是.13.如图为一个长方体,则该几何体主视图的面积为2cm.14.如图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数是︒.15.如图是小明画的卡通图形,每个正六边形的边长都相等,相邻两正六边形的边重合,点A, B,C均为正六边形的顶点,AB与地面BC所成的锐角为β.则tanβ的值是.16.图1是一个闭合时的夹子,图2是该夹子的主视示意图,夹子两边为AC,BD(点A与点B重合),点O是夹子转轴位置,OE ACOE OF cm==,⊥于点F,1⊥于点E,OF BD=,:2:3==,CE DFCE AE=.按图示方式用手指按夹子,夹子两边绕点O转AC BD cm6动.(1)当E,F两点的距离最大时,以点A,B,C,D为顶点的四边形的周长是cm.(2)当夹子的开口最大(即点C与点D重合)时,A,B两点的距离为cm.三、解答题(本题有8小题,共66分,各小题都必须写出解答过程)17.(6分)计算:0(2020)4tan 45|3|-+-︒+-. 18.(6分)解不等式:552(2)x x -<+.19.(6分)某市在开展线上教学活动期间,为更好地组织初中学生居家体育锻炼,随机抽取了部分初中学生对“最喜爱的体育锻炼项目”进行线上问卷调查(每人必须且只选其中一项),得到如图两幅不完整的统计图表.请根据图表信息回答下列问题: 抽取的学生最喜爱体育锻炼项目的统计表(1)求参与问卷调查的学生总人数.(2)在参与问卷调查的学生中,最喜爱“开合跳”的学生有多少人?(3)该市共有初中学生约8000人,估算该市初中学生中最喜爱“健身操”的人数. 20.(8分)如图,AB 的半径2OA =,OC AB ⊥于点C ,60AOC ∠=︒. (1)求弦AB 的长. (2)求AB 的长.21.(8分)某地区山峰的高度每增加1百米,气温大约降低0.6C ︒,气温(C)T ︒和高度h (百米)的函数关系如图所示.类别 项目 人数(人)A 跳绳 59B 健身操 ▲C 俯卧撑 31D 开合跳 ▲E 其它22请根据图象解决下列问题: (1)求高度为5百米时的气温; (2)求T 关于h 的函数表达式;(3)测得山顶的气温为6C ︒,求该山峰的高度.22.(10分)如图,在ABC ∆中,AB =45B ∠=︒,60C ∠=︒. (1)求BC 边上的高线长.(2)点E 为线段AB 的中点,点F 在边AC 上,连结EF ,沿EF 将AEF ∆折叠得到PEF ∆. ①如图2,当点P 落在BC 上时,求AEP ∠的度数. ②如图3,连结AP ,当PF AC ⊥时,求AP 的长.23.(10分)如图,在平面直角坐标系中,已知二次函数21()42y x m =--+图象的顶点为A ,与y 轴交于点B ,异于顶点A 的点(1,)C n 在该函数图象上. (1)当5m =时,求n 的值.(2)当2n =时,若点A 在第一象限内,结合图象,求当2y 时,自变量x 的取值范围. (3)作直线AC 与y 轴相交于点D .当点B 在x 轴上方,且在线段OD 上时,求m 的取值范围.24.(12分)如图,在平面直角坐标系中,正方形ABOC的两直角边分别在坐标轴的正半轴上,分别过OB,OC的中点D,E作AE,AD的平行线,相交于点F,已知8OB=.(1)求证:四边形AEFD为菱形.(2)求四边形AEFD的面积.(3)若点P在x轴正半轴上(异于点)D,点Q在y轴上,平面内是否存在点G,使得以点A, P,Q,G为顶点的四边形与四边形AEFD相似?若存在,求点P的坐标;若不存在,试说明理由.答案与解析卷Ⅰ一、选择题(本题有10小题,每小题3分,共30分)1.实数3的相反数是()A.3- B.3 C.13- D.13【知识考点】相反数;实数的性质【思路分析】直接利用相反数的定义分析得出答案.【解题过程】解:实数3的相反数是:3-.故选:A.【总结归纳】此题主要考查了实数的性质,正确掌握相反数的定义是解题关键.2.分式52xx+-的值是零,则x的值为()A.2 B.5 C.2- D.5-【知识考点】分式的值为零的条件【思路分析】利用分式值为零的条件可得50x+=,且20x-≠,再解即可.【解题过程】解:由题意得:50x+=,且20x-≠,解得:5x=-,故选:D.【总结归纳】此题主要考查了分式值为零的条件,关键是掌握分式值为零的条件是分子等于零且分母不等于零.注意:“分母不为零”这个条件不能少. 3.下列多项式中,能运用平方差公式分解因式的是( ) A .22a b + B .22a b - C .22a b - D .22a b -- 【知识考点】因式分解-运用公式法【思路分析】根据能够运用平方差公式分解因式的多项式必须是二项式,两项都能写成平方的形式,且符号相反进行分析即可.【解题过程】解:A 、22a b +不能运用平方差公式分解,故此选项错误;B 、22a b -不能运用平方差公式分解,故此选项错误;C 、22a b -能运用平方差公式分解,故此选项正确;D 、22a b --不能运用平方差公式分解,故此选项错误;故选:C .【总结归纳】此题考查了平方差公式,熟练掌握平方差公式是解本题的关键. 4.下列四个图形中,是中心对称图形的是( )A .B .C .D .【知识考点】中心对称图形【思路分析】根据中心对称图形的概念对各图形分析判断即可得解. 【解题过程】解:A 、该图形不是中心对称图形,故本选项不合题意;B 、该图形不是中心对称图形,故本选项不合题意;C 、该图形是中心对称图形,故本选项符合题意;D 、该图形不是中心对称图形,故本选项不合题意;故选:C .【总结归纳】本题考查了中心对称图形的概念,中心对称图形是要寻找对称中心,旋转180度后两部分重合.5.如图,有一些写有号码的卡片,它们的背面都相同,现将它们背面朝上,从中任意摸出一张,摸到1号卡片的概率是( )A .12 B .13 C .23 D .16【知识考点】概率公式【思路分析】根据概率公式直接求解即可.【解题过程】解:共有6张卡片,其中写有1号的有3张,∴从中任意摸出一张,摸到1号卡片的概率是3162=; 故选:A .【总结归纳】此题考查了概率的求法,用到的知识点为:可能性等于所求情况数与总情况数之比.6.如图,工人师傅用角尺画出工件边缘AB 的垂线a 和b ,得到//a b .理由是( )A .连结直线外一点与直线上各点的所有线段中,垂线段最短B .在同一平面内,垂直于同一条直线的两条直线互相平行C .在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线D .经过直线外一点,有且只有一条直线与这条直线平行 【知识考点】平行公理及推论;平行线的判定与性质【思路分析】根据垂直于同一条直线的两条直线平行判断即可. 【解题过程】解:由题意a AB ⊥,b AB ⊥, //a b ∴(垂直于同一条直线的两条直线平行),故选:B .【总结归纳】本题考查平行线的判定,平行公理等知识,解题的关键是理解题意,灵活运用所学知识解决问题.7.已知点(2-,)(2a ,)(3b ,)c 在函数(0)ky k x=>的图象上,则下列判断正确的是( )A .a b c <<B .b a c <<C .a c b <<D .c b a << 【知识考点】反比例函数图象上点的坐标特征【思路分析】根据反比例函数的性质得到函数(0)ky k x=>的图象分布在第一、三象限,在每一象限,y 随x 的增大而减小,则0b c >>,0a <. 【解题过程】解:0k >,∴函数(0)ky k x=>的图象分布在第一、三象限,在每一象限,y 随x 的增大而减小, 2023-<<<, 0b c ∴>>,0a <,a cb ∴<<.故选:C .【总结归纳】本题考查了反比例函数图象上点的坐标特征,熟练掌握反比例函数的性质是解题的关键.8.如图,O 是等边ABC ∆的内切圆,分别切AB ,BC ,AC 于点E ,F ,D ,P 是DF 上一点,则EPF ∠的度数是( )A .65︒B .60︒C .58︒D .50︒【知识考点】三角形的内切圆与内心;圆周角定理;等边三角形的性质;切线的性质 【思路分析】如图,连接OE ,OF .求出EOF ∠的度数即可解决问题. 【解题过程】解:如图,连接OE ,OF .O 是ABC ∆的内切圆,E ,F 是切点, OE AB ∴⊥,OF BC ⊥,90OEB OFB ∴∠=∠=︒, ABC ∆是等边三角形,60B ∴∠=︒, 120EOF ∴∠=︒,1602EPF EOF ∴∠=∠=︒,故选:B .【总结归纳】本题考查三角形的内切圆与内心,切线的性质,圆周角定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.9.如图,在编写数学谜题时,“□”内要求填写同一个数字,若设“□”内数字为x .则列出方程正确的是( )A .3252x x ⨯+=B .3205102x x ⨯+=⨯C .320520x x ⨯++=D .3(20)5102x x ⨯++=+【知识考点】由实际问题抽象出一元一次方程【思路分析】直接利用表示十位数的方法进而得出等式即可. 【解题过程】解:设“□”内数字为x ,根据题意可得: 3(20)5102x x ⨯++=+.故选:D .【总结归纳】此题主要考查了由实际问题抽象出一元一次方程,正确表示十位数是解题关键. 10.如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD 与正方形EFGH .连结EG ,BD 相交于点O 、BD 与HC 相交于点P .若GO GP =,则ABCD EFGHS S 正方形正方形的值是( )A.1+.2.5- D .154【知识考点】勾股定理的证明【思路分析】证明()BPG BCG ASA ∆≅∆,得出PG CG =.设OG PG CG x ===,则2EG x =,FG =,由勾股定理得出22(4BC x =+,则可得出答案.【解题过程】解:四边形EFGH 为正方形, 45EGH ∴∠=︒,90FGH ∠=︒, OG GP =,67.5GOP OPG ∴∠=∠=︒, 22.5PBG ∴∠=︒,又45DBC ∠=︒, 22.5GBC ∴∠=︒, PBG GBC ∴∠=∠,90BGP BG ∠=∠=︒,BG BG =,()BPG BCG ASA ∴∆≅∆,PG CG ∴=.设OG PG CG x ===, O 为EG ,BD 的交点,2EG x ∴=,FG =,四个全等的直角三角形拼成“赵爽弦图”, BF CG x ∴==, BG x ∴=,22222221)(4BC BG CG x x x ∴=+=+=+,∴(22422ABCD EFGHx S S x+==+正方形正方形.故选:B .【总结归纳】本题考查了正方形的性质,全等三角形的判定与性质,勾股定理,直角三角形的性质等知识,熟练掌握勾股定理的应用是解题的关键.卷 Ⅱ说明:本卷共有2大题,14小题,共90分。
浙江省丽水市中考数学真题及答案F

浙江省丽水市中考数学真题及答案F参考公式:二次函数)0(2≠++=a c bx ax y 图象的顶点坐标是(ab 2-,a b ac 442-);一组数据1x ,2x ,3x ,…,n x 的方差:])()()()[(122322212x x x x x x x x nS n -++-+-+-= (其中x 是这组数据的平均数)。
一、选择题(本题有10小题,每小题3分,共30分) 1. 在数32,1,-3,0中,最大的数....是 A.32B. 1C. -3D. 0 2. 下列四个几何体中,主视图为圆的是3. 下列式子运算正确的是A. 628a a a =÷B. 532a a a =+C. 1)1(22+=+a a D. 12322=-a a4. 如图,直线a ∥b ,AC ⊥AB,AC 交直线b 于点C,∠1=60°,则∠2的度数是A. 50°B. 45°C. 35°D. 30°5. 如图,河坝横断面迎水坡AB 的坡比是3:1(坡比是坡面的铅直高度BC 与水平宽度AC之比),坝高BC=3m,则坡面AB 的长度是A. 9mB. 6mC. 36mD. 33m6. 某地区5月3日至5月9日这7天的日气温最高值统计图如图所示。
从统计图看,该地区这7天日气温最高值的众数与中位数分别是A. 23,25B. 24,23C. 23,23D. 23,247. 如图,小红在作线段AB 的垂直平分线时,是这样操作的:分别以点A,B 为圆心,大于线段AB 长度一半的长为半径画弧,相交于点C,D,则直线CD 即为所求。
连结AC,BC,AD,BD,根据她的作图方法可知,四边形ADBC 一定是...A. 矩形B. 菱形C. 正方形D. 等腰梯形8. 在同一平面直角坐标系内,将函数3422-+=x x y 的图象向右平移2个单位,再向下平移1个单位得到图象的顶点坐标是A.(-3,-6)B. (1,-4)C. (1,-6)D. (-3,-4) 9. 如图,半径为5的⊙A 中,弦BC,ED 所对的圆心角分别是∠BAC,∠EAD 。
历年中考数学试卷62.浙江丽水

2015年浙江省丽水市中考数学试卷一、选择题,共10小题,每小题3分,共30分1.在数﹣3,﹣2,0,3中,大小在﹣1和2之间的数是()A .﹣3 B.﹣2 C.0 D.32.计算(a2)3的正确结果是()A .3a2B.a6C.a5D.6a3.由4个相同的小立方体搭成的几何体如图所示,则它的主视图是()A .B.C.D.4.分式﹣可变形为()A .﹣B.C.﹣D.5.一个多边形的每个内角均为120°,则这个多边形是()A .四边形B.五边形C.六边形D.七边形6.如图,数轴上所表示关于x的不等式组的解集是()A .x≥2B.x>2 C.x>﹣1 D.﹣1<x≤27.某小组7位学生的中考体育测试成绩(满分30分)依次为27,30,29,27,30,28,30.则这组数据的众数与中位数分别是()A .30,27 B.30,29 C.29,30 D.30,288.如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是()A .B.C.D.9.在平面直角坐标系中,过点(﹣2,3)的直线l经过一、二、三象限,若点(0,a),(﹣1,b),(c,﹣1)都在直线l上,则下列判断正确的是()A .a<b B.a<3 C.b<3 D.c<﹣210.如图,在方格纸中,线段a,b,c,d的端点在格点上,通过平移其中两条线段,使得和第三条线段首尾相接组成三角形,则能组成三角形的不同平移方法有()A .3种B.6种C.8种D.12种二、填空题(本题有6小题,每小题4分,共24分)11.分解因式:9﹣x2=.12.有6张卡片,每张卡片上分别写有不同的从1到6的一个自然数.从中任意抽出一张卡片,卡片上的数是3的倍数的概率是.13.如图,圆心角∠AOB=20°,将旋转n°得到,则的度数是度.14.解一元二次方程x2+2x﹣3=0时,可转化为解两个一元一次方程,请写出其中的一个一元一次方程.15.如图,四边形ABCD与四边形AECF都是菱形,点E、F在BD上.已知∠BAD=120°,∠EAF=30°,则=.16.如图,反比例函数y=的图象经过点(﹣1,﹣2),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C 在第四象限,AC与x轴交于点P,连结BP.(1)k的值为.(2)在点A运动过程中,当BP平分∠ABC时,点C的坐标是.三、解答题(本题有8个小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分,各小题都必须写出解答过程)17.计算:|﹣4|+(﹣)0﹣()﹣1.18.先化简,再求值:a(a﹣3)+(1﹣a)(1+a),其中a=.19.如图,已知△ABC,∠C=Rt∠,AC<BC.D为BC上一点,且到A,B两点的距离相等.(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);(2)连结AD,若∠B=37°,求∠CAD的度数.20.某运动品牌店对第一季度A、B两款运动鞋的销售情况进行统计.两款运动鞋的销售量及总销售额如图所示:(1)一月份B款运动鞋的销售量是A款的,则一月份B款运动鞋销售了多少双?(2)第一节度这两款款运动鞋的销售单价保持不变,求三月份的总销售额(销售额=销售单价×销售量);(3)综合第一季度的销售情况,请你对这两款运动鞋的进货、销售等方面提出一条建议.21.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.(1)求证:DF⊥AC;(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.22.甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象的一部分如图所示.(1)求甲行走的速度;(2)在坐标系中,补画s关于t的函数图象的其余部分;(3)问甲、乙两人何时相距360米?23.如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB 于点M,MN⊥CM交射线AD于点N.(1)当F为BE中点时,求证:AM=CE;(2)若==2,求的值;(3)若==n ,当n 为何值时,MN ∥BE ?24.某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A 处的正上方,假设每次出发的乒乓球的运动路线固定不变,且落在中线上.在乒乓球运行时,设乒乓球与端点A 的水平距离为x (米),与桌面的高度为y (米),运行时间为t (秒),经多次测试后,得到如下部分数据: t (秒) 0 0.16 0.2 0.4 0.6 0.64 0.8 6 X (米) 0 0.4 0.5 1 1.5 1.6 2 … y (米) 0.25 0.378 0.4 0.45 0.4 0.378 0.25 … (1)当t 为何值时,乒乓球达到最大高度?(2)乒乓球落在桌面时,与端点A 的水平距离是多少?(3)乒乓球落在桌面上弹起后,y 与x 满足y=a (x ﹣3)2+k . ①y 用含α的代数式表示k ;②球网高度为0.14米,球桌长(1.4×2)米.若球弹起后,恰好有唯一的击球点,可以将球沿直线扣杀到点A ,求α的值.参考答案一、选择题(本大题共10小题) 1. C解析:先将数-3,2,0,3按从小到大的顺序排列为-3,0,2,3,其中大小在-1和2之间的数只有0,故选择C .点评:本题考查了有理数的大小比较,解题的关键是熟练掌握有理数大小的比较方法. 2. B解析:23236()a a a ⨯==,故选择B.点评:本题考查了整式的幂的运算,幂的运算主要包括:同底数幂的运算、幂的乘方,积的乘方等,解题的关键是正确区分运算的类型,再按照运算法则计算.3.A解析:从正面看,第一列有2个正方体,第二列有1个正方体,故选择A .点评:本题考查了简单组合体的三视图,解题的关键是熟练掌握三种视图的概念.4. D解析:1111(1)1x x x-=-=----,故选择D .点评:本题考查了分式的基本性质的简单运用,解题的关键是理解分式符号变化的规律.5. C解析:因为多边形的每个内角均为120°,所以多边形的每个外角度数为180°-120°=60°,这个多边形的边数=360°÷60°=6,即这个多边形是六边形,故选择C.点评:本题考查了多边形的边数,解题的关键是理解并掌握多边形的内角和及外角和定理.6.A解析:由数轴可以获取各个不等式的解集分别x≥-1、x≥2,则两个一元一次不等式解集的公共部分为x≥2,故选择A.点评:本题考查了考查不等式组的解集,解题的关键是正确地从数轴上获取不等式组中各个不等式解集的公共部分.7. B解析:将题中的7个数据按照从小到大的顺序排列为:27,27,28,29,30,30,30,其中最中间位置上的数值是29,即中位数是29,出现次数最多的数据是30,即众数30,故选择B.点评:本题考查了数据的中位数和众数的求法,解题的关键是掌握中位数和众数的概念.8. jC解析:因为AC⊥BC,CD⊥AB,所以∠B+∠BAC=∠ACD+∠BAC=90°,所以∠B=∠ACD=α,即cosα=BDBC=BCAB=CDAC,故选择C.点评:本题考查了锐角三角形函数的概念,解题的关键是理解掌握正弦、余弦、正切等概念.9. jD解析:因为直线l经过点(-2,3),(0,a),(-1,b),(c,-1),如图所示,根据“y 随x的增大而增大”可以得出b<a,a>3,b>3,c<-2,所以选项A、B、C是错误的,故选择D.点评:本题考查了一次函数的图象性质,解题的关键是掌握一次函数的图象分布与增减性变化之间的关系.10. jB解析:根据题意得25255a b c d ====,,,,其中能组成三角形的三边是255a b d ===,,,要得到这三边组成的三角形,只要同时移动其中任意两边——ab 、ac 、bc ,如图所示,能组成三角形的不同平移方法有6种,故选择B.点评:本题考查了勾股定理及其三角形三边关系,解题的关键是灵活运用勾股定理和三角形三边关系定理.二、填空题(本大题共6小题) 11. (3)(3)x x +-解析:29x -=(3+x )(3-x ),故答案为(3+x )(3-x ).点评:本题考查了多项式的因式分解,解题的关键是会用公式法进行因式分解.12. 13解析:总共有6种情况,其中卡片上的数是3的倍数有2种可能,所以其概率21(3)63P ==卡片上的数是的倍数,故答案为13.点评:本题考查了等可能条件下的概率的计算,解题的关键是依据概率的意义,列举出所有等可能的结果数. 13.20解析:因为圆心角∠AOB =20°,所以»AB 的度数为20度,因为»CD =»AB ,所以»CD的度数是20°,故答案为20.点评:本题考查了圆心角、旋转的有关性质,解题的关键是理解圆心角与所对弧的度数的关系定理.14. 3x +=0(或1x -=0)解析:因为x 2+2x -3=0,所以(x -1)(x +3) =0,所以 x -1=0或x +3=0,故答案为3x +=0(或1x -=0). 点评:本题考查了因式分解法解一元二次方程,解题的关键是理解掌握因式分解法的方法步骤. 62+ 解析:因为四边形ABCD 是菱形,∠BAD =120°,所以AB=AD ,∠ABD=∠ADB=30°,因为四边形AECF 都是菱形,所以AE=AF ,所以△ABE ≌△ADF ,因为∠EAF =30°,即∠BAE=∠DAF=45°,过点E 作EM ⊥AB 于M ,所以∠MAE =∠MEA =45°,即MA =ME ,所以AE 22ME MA +2ME ,在Rt △BME 中,∠ABE =30°,tan MEMBE MB=∠,所以BM =tan MEMBE∠=3ME ,即AB =AM +MB =(31)ME ,所以AB AE =312ME ME+()=622+.故答案为622+.点评:本题考查了菱形的性质与等腰三角形的性质,解题的关键是熟练领会菱形和等腰三角形的性质.16.(1)22;(2)(2,22-) 解析:(1)∵反比例函数ky x=的图象经过点(-1,22-), ∴221k-=-,即22k =.(2)解析:如答图1,过点P 作PM ⊥AB 于点M ,过B 点作BN ⊥x 轴于点N ,设22,A x ⎛ ⎝⎭ ,则22,B x ⎛- ⎝⎭. ∴22222222328242AB x x x x x x=+=+=+()() ∵△ABC 是等腰直角三角形,∴2282BC AC x x ⎛⎫==+ ⎪⎝⎭BAC =45°. ∵BP 平分∠ABC ,∴()BPM BPC AAS ∆∆≌.∴2282BM BC x x ⎛⎫==+ ⎪⎝⎭∴(22822AM AB BM x x =-=+. ∵BP 平分∠ABC , PM ⊥AB ,∠C=90°, ∴(22822PM AM x x ==+又∵22182OB AB x x==+,∴()22821OM BM OB x x =-=-+. ∵∠BNO =∠PMO =90°,∠BON =∠POM , ∴OBN OPM ∆∆∽,∴ON BN OBOM PM OP ==. 由ON BNOM PM=得,即()()222222882122x x x x ⎛⎫-- ⎪⎝⎭=-+-+,解得2x =.∴点A 、B 的坐标分别为()2,2 ,()2,2- -..故答案为(22,2,2.点评:本题考查了待定系数法求反比例函数的解析式、正比例函数与反比例函数的交点坐标、等腰直角三角形的性质,解题的关键是从数形结合的角度理解正比例函数与反比例函数的图象性质.三、解答题(本大题共8小题)17. 解析:先分别利用绝对值性质求得4-=4,零指数幂性质求得0(2)-=1,负整数指数幂的运算性质求得11()22-=,然后加减运算.解:原式=4+1-2=3.点评:本题考查了实数的运算,解题的关键是掌握绝对值、零指数幂、负整数指数幂的运算性质.18.解析:根据乘法公式、单项式乘以多项式化简,再合并同类项,代入求值. 解:原式=2231a a a -+-=13a -.当a 3时,原式=13a -=13-点评:本题考查了乘法公式的应用,解题的关键是正确地利用乘法公式和运算法则进行化简代入求值.19. 解析:(1)先根据线段垂直平分线的作法找到点D ;(2)利用垂直平分线的性质和三角形内角和定理求解即可.解:(1)点D 的位置如图所示(D 为AB 中垂线与BC 的交点).(2)∵在Rt △ABC 中,∠B =37°, ∴∠CAB =53°. 又∵AD =BD , ∴∠BAD =∠B =37°. ∴∠CAD =53°-37°=16°.点评:本题考查了尺规作图及线段的垂直平分线,解题的关键是准确准确掌握线段垂直平分线的作图方法.20.解析:(1)依据“B 款运动鞋的销售量=A 款运动鞋的销售量×45”来求解;(2)要求三月份的总销售额必须先求出A ,B 两款运动鞋的销售单价,可以依据等量关系“一月份A 款运动鞋的销售+B 款运动鞋的销售=40000”与“二月份A 款运动鞋的销售+B 款运动鞋的销售=50000”来列方程组求解;(3)依据A 、B 款运动鞋1—3的销售情况来提建议.解:(1)50×45=40(双).∴一月份B 款运动鞋销售了40双. (2)设A ,B 两款运动鞋的销售单价分别为x 元,y 元. 由题意可得504040000605250000x y x y +=⎧⎨+=⎩.解方程组得400500x y =⎧⎨=⎩.∴三月份的总销售额为400×65+500×26=39000=3.9(万元). (3)答案不唯一,只要学生结合数据分析,言之有理即可.例如:从销售量来看,A 款运动鞋销售量逐月增加,比B 款运动鞋销售量大,建议多进A 款运动鞋,少进或不进B 款鞋.从总销售额来看,由于B 款运动鞋销售量减少,导致总销售额减少,建议店里采取一些促销手段,增加B 款运动鞋的销售量.点评:本题考查了条形统计图、折线统计图的知识,解题的关键是读懂统计图,从统计图中得到必要的信息. 21.解析:(1)连结OD ,因为DF 是⊙O 的切线,所以DF ⊥OD ,要证明DF ⊥AC ,只要证明OD ∥AC .由AB =AC ,OB =OD 可以证明∠ODB =∠ACB ;(2)连接OE ,先分别求出△ABCDAOE 和扇形AOE 的面积,依据AOC OAE S S S ∆=-阴影扇形求出阴影部分的面积.解:(1)证明:连结OD .∵OB =OD ,∴∠ABC =∠ODB .∵AB =AC ,∴∠ABC =∠ACB .∴∠ODB =∠ACB .∴OD ∥AC .∵DF 是⊙O 的切线,∴DF ⊥OD .∴DF ⊥AC .(2)连结OE .∵DF ⊥AC ,∠CDF =22.5°,∴∠ABC =∠ACB =67.5°.∴∠BAC =45°.∵OA =OE ,∴∠AOE =90°.∴⊙O 的半径为4,∴S 扇形AOE =4π,S △AOE =8.∴S 阴影=S 扇形AOE -S △AOE =4π-8.点评:本题考查了圆的切线的性质、等腰三角形的性质、三角形与扇形的面积公式等,解题的关键是根据圆的切线的性质正确作出相应的辅助线.22.解析:(1)根据图象,知甲出发5分钟行走了150米,据此求出甲行走的速度;(2)(2)因为乙走完全程要15005030÷=分钟,甲走完全程要15003050÷=分钟,所以两人最后相遇在50分钟处,据此补画s 关于t 函数图象.(3)甲、乙出发第一次相遇时,属于行程问题中的追击问题,依据等量关系“150+甲的速度×相遇时间+乙的行程甲的速度×相遇时间=1500”求出相遇时间,从而求出一次函数图象与x 轴的一个交点坐标为(12.5,0),一次函数图象与x 轴的另一个交点坐标为(50,0),利用待定系数法分别求出12.535t ≤≤和35<50t ≤时的函数解析式,再列方程求解即可.解:(1)甲行走的速度:150÷5=30(米/分);(2)补画的图象如图所示(横轴上对应的时间为50);(3)由函数图象可知,当t =12.5进,s =0.当12.5≤t ≤35时,s =20250t -.当35<t ≤50时,s =301500t -+.∵甲、乙两人相距360米,即s =360,解得1t =30.5,2t =38.∴当甲行走30.5分钟或38分钟时,甲、乙两人相距360米.点评:本题考查了题考查了待定系数法求一次函数表达式、一次函数实际应用,解题的关键是准确读取图象信息,求出一次函数的解析式.23.解析:(1)先利用AAS 证明△BMF ≌△ECF 得MB =CE ,结合AB =CD ,DE =CE 即可得到结论.(2)设MB =a ,先证明△BMF ∽△ECF ,利用相似三角形的性质求出CE 的长,再证明△AMN ∽△BCM ,利用相似三角形的性质求出AN 、ND 的长即可求解.(3)类比(2)问中的解法证明△AMN ∽△BCM ,利用平行四边形的性质进行求解.解:(1)∵F 为BE 的中点,∴BF =EF .∵AB ∥CD ,∴∠MBF =∠CEF ,∠BMF =∠ECF .∴△BMF ≌△ECF .∴MB =CE .∵AB =CD ,CE =DE ,∴MB =AM .∴AM =CE ;(2)设MB =a .∵AB ∥CD ,∴△BMF ∽△ECF . ∵EF BF =2, ∴CE MB=2.∴AB =CD =2CE =4a ,AM =AB -MB =3a . ∵AB BC=2, ∴BC =AD =2a .∵MN ⊥MC ,∠A =∠ABC =90°,∵∠AMN+∠BMC=∠BCM+∠BMC=90°,∴∠AMN=∠BCM ,∴△AMN ∽△BCM . ∴AN MB =AM BC ,即AN a =23a a. ∴AN =32a ,ND =322a a -=12a . ∴AN ND =32a ︰12a =3.(3)方法一:∵AB BC =EF BF=n ,设MB =a ,由(2)可得BC =2a ,CE =na ,AM =(21)n a -. 由△AMN ∽△BCM ,AN =1(21)2n a -,DN =(25)2n a -. ∵DH ∥AM ,DN AN =DH AM,DH =(25)n a -, ∴HE =(5)n a -.∵MBEH 是平行四边形,∴(5)n a -=a .A B C D EF HMN方法二:∵AB BC =EF BF=n ,设MB =a ,由(2)可得BC =2a ,CE =na . 当MN ∥BE 时,CM ⊥BE ,可证△MBC ∽△BCE . ∴MB BC =BC CE . ∴2a a =2a na. ∴n =4.点评:本题考查了矩形的性质,全等三角形、相似三角形的性质和判定,解题的关键是从复杂的图形中抽象出相似三角形,灵活运用相似三角形的性质构造方程求解.24. 解析:(1)观察表格中数据x 、y 与t 之间的变化规律直接求解;(2)通过在直角坐标系中列表、描点、连线的方法判定出y 是x 的二次函数,用顶点式设二次函数解析式,运用待定系数得出y 关于x 的解析式,求得0y =时的x 值即为所求;(3)①求出乒乓球落在桌面时的坐标代入2(3)y a x k =-+即可得结果;②球网高度为0.14米,球桌长(1.4×2)米,所以扣杀路线在直线110y x =上,将110y x =代入21(3)4y a x a =--,得()22012021750ax a x a -++=,由于球弹起后,恰好有唯一的击球点,所以方程根的判别式等于0,求出此时的a ,符合题意的即为所求.解:以点A 为原点,以桌面中线为x 轴,乒乓球运动方向为正方向,建立平面直角坐标系. (1)由表格中的数据,可得t =0.4(秒).答:当t 为0.4秒时,乒乓球达到最大高度.(2)由表格中数据,可画出y 关于x 的图象,根据图象的形状,可判断y 是x 的二次函数.可设y =2(1)0.45a x -+.将(0,0.25)代入,可得a =15-. ∴y =21(1)0.455x --+. 当y =0时,1x =52,2x =12-(舍去),即乒乓球与端点A 的水平距离是52米. (3)①由(2)得乒乓球落在桌面上时,对应的点为(52,0). 代入y =2(3)a x k -+,得25(3)2a k ⨯-+=0,化简整理,得k =14a -. ②由题意可知,扣杀路线在直线y =110x 上. 由①,得y =21(3)4a x a --. 令21(3)4a x a --=110x ,整理,得220(1202)175ax a x a -++=0.当∆=2(1202)420175a a a +-⨯⨯=0时符合题意.解方程,得1a 2a当1a x =,不符合题意,舍去.当2a x答:当a A . 点评:本题考查了考查了用待定系数法确定二次函数的解析式、函数值的求法、二次函数与一元二次方程的关系以及二次函数的图象及应用,解题的关键是通过建立二次函数模型,把实际问题转化为二次函数问题,运用二次函数图象性质来求解.。
中考丽水数学试题及答案

中考丽水数学试题及答案一、选择题(每题3分,共30分)1. 若a、b、c是三角形的三边长,且a^2 + b^2 = c^2,则该三角形是直角三角形。
A. 正确B. 错误答案:A2. 函数y = 2x + 3的图象经过第一、二、三象限。
A. 正确B. 错误答案:A3. 已知x = 2是方程x^2 - 5x + 6 = 0的解,则另一个解是x = 3。
A. 正确B. 错误答案:B4. 一个数的相反数是它本身,则这个数是0。
A. 正确B. 错误答案:A5. 圆的周长与它的半径成正比例。
A. 正确B. 错误答案:A6. 一个正数的算术平方根一定大于这个数。
A. 正确B. 错误答案:B7. 一个数的立方根与它本身相等的数是±1和0。
A. 正确B. 错误答案:A8. 一组数据的平均数是5,中位数是4,众数是6,则这组数据可能的中位数是4。
A. 正确B. 错误答案:A9. 一个等腰三角形的两边长分别是3和5,则它的周长是13。
A. 正确B. 错误答案:B10. 一个多边形的内角和是外角和的3倍,则这个多边形是八边形。
A. 正确B. 错误答案:A二、填空题(每题3分,共30分)11. 已知一个等腰三角形的底边长为6,腰长为5,则其周长为16。
12. 一个数的绝对值是5,则这个数是±5。
13. 一个数的平方是25,则这个数是±5。
14. 一个数的立方是-8,则这个数是-2。
15. 一个数的倒数是2,则这个数是1/2。
16. 一个数的相反数是-3,则这个数是3。
17. 一个数的算术平方根是3,则这个数是9。
18. 一个数的立方根是2,则这个数是8。
19. 一个数的平方根是±2,则这个数是4。
20. 一个数的平方是16,则这个数是±4。
三、解答题(共40分)21. 计算:(2x^2 - 3x + 1) - (x^2 - 4x + 5) = x^2 + x - 4。
22. 解方程:2x^2 - 5x - 3 = 0,解得x1 = -1/2,x2 = 3。
北师大版九年级下册数学J0028--2015丽水市中考数学试卷
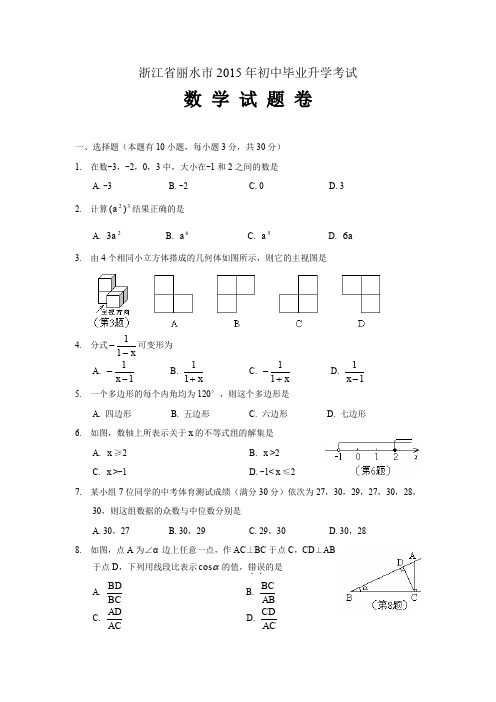
浙江省丽水市2015年初中毕业升学考试数 学 试 题 卷一、选择题(本题有10小题,每小题3分,共30分)1. 在数-3,-2,0,3中,大小在-1和2之间的数是A. -3B. -2C. 0D. 32. 计算32)(a 结果正确的是A. 23aB. 6aC. 5aD. a 63. 由4个相同小立方体搭成的几何体如图所示,则它的主视图是4. 分式x--11可变形为 A. 11--x B. x +11 C. x +-11 D. 11-x 5. 一个多边形的每个内角均为120°,则这个多边形是A. 四边形B. 五边形C. 六边形D. 七边形 6. 如图,数轴上所表示关于x 的不等式组的解集是A. x ≥2B. x >2C. x >-1D. -1<x ≤27. 某小组7位同学的中考体育测试成绩(满分30分)依次为27,30,29,27,30,28,30,则这组数据的众数与中位数分别是A. 30,27B. 30,29C. 29,30D. 30,288. 如图,点A 为∠α边上任意一点,作AC ⊥BC 于点C ,CD ⊥AB于点D ,下列用线段比表示αcos 的值,错误..的是 A. BCBD B. AB BC C. AC AD D. ACCD9. 平面直角坐标系中,过点(-2,3)的直线l 经过一、二、三象限,若点(0,a ),(-1,b ),(c ,-1)都在直线l 上,则下列判断正确的是A. b a <B. 3<aC. 3<bD. 2-<c10. 如图,在方格纸中,线段a ,b ,c ,d 的端点在格点上,通过平移其中两条线段,使得和第三条线段首尾相接组成三角形,则能组成三角形的不同平移方法有A. 3种B. 6种C. 8种D. 12种二、填空题(本题有6小题,每小题4分,共24分)11. 分解因式:=-29x ▲12. 有6张卡片,每张卡片上分别写有不同的从1到6的一个自然数,从中任意抽出一张卡片,卡片上的数是3的倍数的概率是 ▲13. 如图,圆心角∠AOB=20°,将旋转︒n 得到,则的度数是 ▲ 度14. 解一元二次方程0322=-+x x 时,可转化为两个一元一次方程,请写出其中的一个一元一次方程 ▲15. 如图,四边形ABCD 与四边形AECF 都是菱形,点E ,F在BD 上,已知∠BAD=120°,∠EAF=30°,则AE AB = ▲16. 如图,反比例函数xk y =的图象经过点(-1,22-),点A 是该图象第一象限分支上的动点,连结AO 并延长交另一支于点B ,以AB 为斜边作等腰直角三角形ABC ,顶点C 在第四象限,AC与x 轴交于点P ,连结BP 。
【2015中考真题】浙江省丽水市中考数学试题及解析

2015年浙江省丽水市中考数学试卷一、选择题,共10小题,每小题3分,共30分233.(3分)(2015•丽水)由4个相同的小立方体搭成的几何体如图所示,则它的主视图是( )C4.(3分)(2015•丽水)分式﹣可变形为( )C6.(3分)(2015•丽水)如图,数轴上所表示关于x 的不等式组的解集是( )7.(3分)(2015•丽水)某小组7位学生的中考体育测试成绩(满分30分)依次为27,30,29,27,30,8.(3分)(2015•丽水)如图,点A 为∠α边上的任意一点,作AC ⊥BC 于点C ,CD ⊥AB 于点D ,下列用线段比表示cos α的值,错误的是( )C9.(3分)(2015•丽水)在平面直角坐标系中,过点(﹣2,3)的直线l 经过一、二、三象限,若点(0,10.(3分)(2015•丽水)如图,在方格纸中,线段a,b,c,d的端点在格点上,通过平移其中两条线段,使得和第三条线段首尾相接组成三角形,则能组成三角形的不同平移方法有()A.3种B.6种C.8种D.12种二、填空题(本题有6小题,每小题4分,共24分)11.(4分)(2015•丽水)分解因式:9﹣x2=.12.(4分)(2015•丽水)有6张卡片,每张卡片上分别写有不同的从1到6的一个自然数.从中任意抽出一张卡片,卡片上的数是3的倍数的概率是.13.(4分)(2015•丽水)如图,圆心角∠AOB=20°,将旋转n°得到,则的度数是度.14.(4分)(2015•丽水)解一元二次方程x2+2x﹣3=0时,可转化为解两个一元一次方程,请写出其中的一个一元一次方程.15.(4分)(2015•丽水)如图,四边形ABCD与四边形AECF都是菱形,点E、F在BD上.已知∠BAD=120°,∠EAF=30°,则=.16.(4分)(2015•丽水)如图,反比例函数y=的图象经过点(﹣1,﹣2),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点P,连结BP.(1)k的值为.(2)在点A运动过程中,当BP平分∠ABC时,点C的坐标是.三、解答题(本题有8个小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分,各小题都必须写出解答过程)17.(6分)(2015•丽水)计算:|﹣4|+(﹣)0﹣()﹣1.18.(6分)(2015•丽水)先化简,再求值:a(a﹣3)+(1﹣a)(1+a),其中a=.19.(6分)(2015•丽水)如图,已知△ABC,∠C=Rt∠,AC<BC.D为BC上一点,且到A,B两点的距离相等.(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);(2)连结AD,若∠B=37°,求∠CAD的度数.20.(8分)(2015•丽水)某运动品牌店对第一季度A、B两款运动鞋的销售情况进行统计.两款运动鞋的销售量及总销售额如图所示:(1)一月份B款运动鞋的销售量是A款的,则一月份B款运动鞋销售了多少双?(2)第一节度这两款款运动鞋的销售单价保持不变,求三月份的总销售额(销售额=销售单价×销售量);(3)综合第一季度的销售情况,请你对这两款运动鞋的进货、销售等方面提出一条建议.21.(8分)(2015•丽水)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.(1)求证:DF⊥AC;(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.22.(10分)(2015•丽水)甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象的一部分如图所示.(1)求甲行走的速度;(2)在坐标系中,补画s关于t的函数图象的其余部分;(3)问甲、乙两人何时相距360米?23.(10分)(2015•丽水)如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB于点M,MN⊥CM交射线AD于点N.(1)当F为BE中点时,求证:AM=CE;(2)若==2,求的值;(3)若==n,当n为何值时,MN∥BE?24.(12分)(2015•丽水)某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次出发的乒乓球的运动路线固定不变,且落在中线上.在乒乓球运行时,设乒乓球与端点A的水平t(秒)0 0.16 0.2 0.4 0.6 0.64 0.8 6X(米)0 0.4 0.5 1 1.5 1.6 2 …y(米)0.25 0.378 0.4 0.45 0.4 0.378 0.25 …(2)乒乓球落在桌面时,与端点A的水平距离是多少?(3)乒乓球落在桌面上弹起后,y与x满足y=a(x﹣3)2+k.①y用含α的代数式表示k;②球网高度为0.14米,球桌长(1.4×2)米.若球弹起后,恰好有唯一的击球点,可以将球沿直线扣杀到点A,求α的值.2015年浙江省丽水市中考数学试卷参考答案与试题解析一、选择题,共10小题,每小题3分,共30分233.(3分)(2015•丽水)由4个相同的小立方体搭成的几何体如图所示,则它的主视图是()C4.(3分)(2015•丽水)分式﹣可变形为()C=﹣,6.(3分)(2015•丽水)如图,数轴上所表示关于x的不等式组的解集是()7.(3分)(2015•丽水)某小组7位学生的中考体育测试成绩(满分30分)依次为27,30,29,27,30,8.(3分)(2015•丽水)如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是()CACD===,9.(3分)(2015•丽水)在平面直角坐标系中,过点(﹣2,3)的直线l经过一、二、三象限,若点(0,k===,即=b3=,10.(3分)(2015•丽水)如图,在方格纸中,线段a,b,c,d的端点在格点上,通过平移其中两条线段,使得和第三条线段首尾相接组成三角形,则能组成三角形的不同平移方法有(),二、填空题(本题有6小题,每小题4分,共24分)11.(4分)(2015•丽水)分解因式:9﹣x2=(3+x)(3﹣x).12.(4分)(2015•丽水)有6张卡片,每张卡片上分别写有不同的从1到6的一个自然数.从中任意抽出一张卡片,卡片上的数是3的倍数的概率是.分析:分别求出从1到6的数中3的倍数的个数,再根据概率公式解答即可.∴从中任取一张卡片,P(卡片上的数是3的倍数)==.故答案为:.13.(4分)(2015•丽水)如图,圆心角∠AOB=20°,将旋转n°得到,则的度数是20度.先根据旋转的性质得=,的度数.解:∵将旋转得到=,的度数为14.(4分)(2015•丽水)解一元二次方程x2+2x﹣3=0时,可转化为解两个一元一次方程,请写出其中的一个一元一次方程x﹣1=0或x+3=0.15.(4分)(2015•丽水)如图,四边形ABCD与四边形AECF都是菱形,点E、F在BD上.已知∠BAD=120°,∠EAF=30°,则=.=∴==.故答案为:.题关键.16.(4分)(2015•丽水)如图,反比例函数y=的图象经过点(﹣1,﹣2),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点P,连结BP.(1)k的值为2.(2)在点A运动过程中,当BP平分∠ABC时,点C的坐标是(2,﹣).考点:反比例函数综合题.分析:(1)把点(﹣1,﹣2)代入反比例函数y=,求出k即可;(2)连接OC,作AM⊥x轴于M,CN⊥x轴于N,则AM∥CN,∠AMO=∠ONC=90°,先由AAS证明△OAM≌△CON,得出OM=CN,AM=ON,再由三角形的角平分线性质得出=,根据平行线的性质得出比例式:=,设CN=OM=x,则AM=ON=x,根据题意得出方程:x•x=2,解方程求出CN、ON,即可得出点C的坐标.解答:解:(1)把点(﹣1,﹣2)代入反比例函数y=得:k=﹣1×(﹣2)=2,故答案为:2;(2)连接OC,作AM⊥x轴于M,CN⊥x轴于N,如图所示:则AM∥CN,∠AMO=∠ONC=90°,∴∠AOM+∠OAM=90°,根据题意得:点A和点B关于原点对称,∴OA=OB,∵△ABC是等腰直角三角形,AB为斜边,∴OC⊥AB(三线合一),OC=AB=OA,AC=BC,AB=BC,∴∠AOC=90°,即∠AOM+∠CON=90°,∴∠OAM=∠CON,在△OAM和△CON中,,∴△OAM≌△CON(AAS),∴OM=CN,AM=ON,∵BP平分∠ABC,∴=,,AM=ON=y=AM=2x=2,x=,,﹣,﹣三、解答题(本题有8个小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分,各小题都必须写出解答过程)17.(6分)(2015•丽水)计算:|﹣4|+(﹣)0﹣()﹣1.18.(6分)(2015•丽水)先化简,再求值:a(a﹣3)+(1﹣a)(1+a),其中a=.时,原式.19.(6分)(2015•丽水)如图,已知△ABC,∠C=Rt∠,AC<BC.D为BC上一点,且到A,B两点的距离相等.(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);(2)连结AD,若∠B=37°,求∠CAD的度数.考点:作图—复杂作图;线段垂直平分线的性质.分析:(1)利用线段垂直平分线的作法得出D点坐标即可;(2)利用线段垂直平分线的性质得出,∠BAD=∠B=37°,进而求出即可.解答:解:(1)如图所示:点D即为所求;(2)在Rt△ABC中,∠B=37°,∴∠CAB=53°,又∵AD=BD,∴∠BAD=∠B=37°,∴∠CAD=53°﹣37°=16°.点评:此题主要考查了复杂作图以及线段垂直平分线的性质,正确利用线段垂直平分线的性质得出∠BAD=∠B=37°是解题关键.20.(8分)(2015•丽水)某运动品牌店对第一季度A、B两款运动鞋的销售情况进行统计.两款运动鞋的销售量及总销售额如图所示:(1)一月份B款运动鞋的销售量是A款的,则一月份B款运动鞋销售了多少双?(2)第一节度这两款款运动鞋的销售单价保持不变,求三月份的总销售额(销售额=销售单价×销售量);(3)综合第一季度的销售情况,请你对这两款运动鞋的进货、销售等方面提出一条建议.考点:折线统计图;条形统计图.分析:(1)用一月份A款的数量乘以,即可得出一月份B款运动鞋销售量;(2)设A,B两款运动鞋的销量单价分别为x元,y元,根据图形中给出的数据,列出算式,再进行计算即可;(3)根据条形统计图和折线统计图所给出的数据,提出合理的建议即可.解答:解:(1)根据题意得:50×=40(双).答:一月份B款运动鞋销售了40双;,.21.(8分)(2015•丽水)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.(1)求证:DF⊥AC;(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.22.(10分)(2015•丽水)甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象的一部分如图所示.(1)求甲行走的速度;(2)在坐标系中,补画s关于t的函数图象的其余部分;(3)问甲、乙两人何时相距360米?设乙出发经过x分和甲第一次相遇,根据题意得:150+30x=50x,解得:x=7.5,7.5+5=12.5(分),由函数图象可知,当t=12.5时,s=0,∴点B的坐标为(12.5,0),当12.5≤t≤35时,设BC的解析式为:s=kt+b,把C(35,450),B(12.5,0)代入可得:解得:,∴s=20t﹣250,当35<t≤50时,设CD的解析式为y=k1x+b1,把D(50,0),C(35,450)代入得:解得:∴s=﹣30t+1500,∵甲、乙两人相距360米,即s=360,解得:t1=30.5,t2=38,∴当甲行走30.5分钟或38分钟时,甲、乙两人何时相距360米.点评:本题考查了行程问题的数量关系的运用,一次函数的解析式的运用,解答时求出函数的解析式是关键.23.(10分)(2015•丽水)如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB于点M,MN⊥CM交射线AD于点N.(1)当F为BE中点时,求证:AM=CE;(2)若==2,求的值;(3)若==n,当n为何值时,MN∥BE?考点:相似形综合题;全等三角形的判定与性质;矩形的性质.专题:综合题.分析:(1)如图1,易证△BMF≌△ECF,则有BM=EC,然后根据E为CD的中点及AB=DC性质即可得到AN=a,从而可得ND=AD﹣AN=a,就可求出的值;EC=DC∴BM=EC=DC=AB,∴==2,=2∴=,=,∴AN=a,ND=AD﹣AN=2a﹣a=a,=)当==,∴=,24.(12分)(2015•丽水)某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次出发的乒乓球的运动路线固定不变,且落在中线上.在乒乓球运行时,设乒乓球与端点A的水平(2)乒乓球落在桌面时,与端点A的水平距离是多少?(3)乒乓球落在桌面上弹起后,y与x满足y=a(x﹣3)2+k.①y用含α的代数式表示k;②球网高度为0.14米,球桌长(1.4×2)米.若球弹起后,恰好有唯一的击球点,可以将球沿直线扣杀到点A,求α的值.x﹣a+0.45,将(0,0.25)代入,可得:a=﹣,﹣当y=0时,0=﹣(x﹣1)2+0.45,,(舍去)的水平距离是(代入y=a(x﹣3)2+k,得(﹣3)2a+k=0,ax a a=x解方程得:a1=,a2=,时,求得,不符合题意,舍去;x=。
中考复习数学真题汇编15:统计图表(含答案)

一、选择题1. (2015福建省福州市,5,3分)下列选项中,显示部分在总体中所占百分比的统计图是( ) A.扇形图 B.条形图 C.折线图 D.直方图 【答案】A2. (2015浙江省温州市,3,4分)某校学生参加体育兴趣小组情况的统计图如图所示,若参加人数最少的小组有25人,则参加人数最多的小组有( )A.25人B.35人C.40人D.100人【答案】C3. (2015内蒙古呼和浩特,8,3分)以下是某手机店1~4月份的两个统计图,分析统计图,对3、4月份三星手机的销售情况四个同学得出的以下四个结论,其中正确的为( )A. 4月份三星手机销售额为65万元B. 4月份三星手机销售额比3月份有所上升C. 4月份三星手机销售额比3月份有所下降D. 3月份与4月份的三星手机销售额无法比较,只能比较该店销售总额 【答案】B4. (2015年江苏扬州市)如图是某校学生参加课外兴趣小组的人数占总人数比例的统计图,则参加人数最多的课外兴趣小组是 ( )各月手机销售总额统计图三星手机销售额占该手机店 当月手机销售总额的百分比统计图A 、音乐组B 、美术组C 、体育组D 、科技组二、填空题 1.2. (2015四川省凉山州市,15,4分)小明同学根据全班同学的血型绘制了如图所示的扇形统计图,已知A 型血的有20人,则O 型血的有 人 【答案】10. 【解析】总人数为20÷40%=50人,O 型血的有50×(1﹣40%﹣30%﹣10%)=10人,故答案是10.3. (2015广东省广州市,12,3分)根据环保局公布的广州市2013年至2014年PM 2.5的主要来源的数据,制成扇形统计图(如图4),其中所占百分比最大的主要来源是 .(填主要来源的名称)【答案】机动车尾气【解析】用一个圆代表总体,圆中的各个扇形分别代表总体中的不同部分,扇形的大小反映部分在总体中所占百分比的大小,这样的统计图叫做扇形统计图.所以一看数据就知道是机动车尾气.4. (2015四川资阳,13,3分)某学校为了解本校学生课外阅读的情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成右图统计表.已知该校全体学生人数为1200人,由此可以估计每周课外阅读时间在1~2(不含1)小时的学生有_________人.每周课外阅读时间(小时)0~11~2(不含1) 2~3(不含2)超过3 人 数 7 10 14 19【答案】240.21.7%11.5%20.6%19%8.2%8.6%10.4% 机动车尾气 工业工艺源 燃煤 其他 生物质燃烧 生活面源扬尘图41296301518181312b 3课时数 组)与 不等式(组)A一次方程 B 一次方程组C 不等式与不等式组 D二次方程 E分式方程图数与代数(内容) 课时数数与式 67 方程(组)与 不等式(组) a图实践与综合应用统计与概率空间与图形 数与代数 40%45%5%图5. (2014江苏省苏州市,13,3分)某学校在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如图所示的扇形统计图.已知其中最喜欢羽毛球的人数比最喜欢乒乓球的人数少6人,则该校被调查的学生总人数为 ▲ 名.【答案】60【解析】最喜欢羽毛球的人数所占百分率比最喜欢乒乓球的人数所占百分率少10%,故被调查总人数为6÷105=60(人).6. (2015年湖南衡阳,22,6分)为了进一步了解义务教育阶段学生体质健康状况,教育部对我市某中学九年级的部分学生进行了体质抽测,体质抽测的结果分别为四个等级:优秀、良好、合格、不合格,根据调查结果绘制了下列两幅不完整的统计图,请你根据统计图提供的信息回答以下问题:(1)在扇形统计图中,“合格”的百分比为 ;(2)本次体质抽测中,抽测结果为“不合格”等级的学生有 人;(3)若该校九年级有400名学生,估计该校九年级体质为“不合格”等级的学生约有 人. 【答案】(1)40%;(2)16;(3)128【解析】解:(1)总人数=8÷16%=50人,合格百分比:20100%50=40%; (2)不合格的人数=50×32%=16人; (3)九年级不合格为数=400×32%=128人.三、解答题1. (2015浙江省丽水市,20,8分)某运动品牌店对第一季度A ,B 两款运动鞋的销售情况进行统计,两款运动鞋的销售量及总销售额如图所示:(第13题)20%30%40%乒乓球篮球羽毛球50606552销售量(双)A ,B 两款运动鞋销售量统计图6总销售额(万元)5A ,B 两款运动鞋总销售额统计图A B(1)一月份B款运动鞋的销售量是A款的45,则一月份B款运动鞋销售了多少双?(2)第一季度这两款运动鞋的销售单价保持不变,求三月份的总销售额(销售额=销售单价×销售量);(3)结合第一季度的销售情况,请你对这两款运动鞋的进货、销售等方面提出一条建议.【答案】解:(1)50×45=40(双).∴一月份B款运动鞋销售了40双.(2)设A,B两款运动鞋的销售单价分别为x元,y元.由题意可得504040000 605250000x yx y+⎧⎨+⎩==.解方程组得400500xy⎧⎨⎩==.∴三月份的总销售额为400×65+500×26=39000=3.9(万元).(3)答案不唯一,只要学生结合数据分析,言之有理即可.例如:从销售量来看,A款运动鞋销售量逐月增加,比B款运动鞋销售量大,建议多进A款运动鞋,少进或不进B款鞋.从总销售额来看,由于B款运动鞋销售量减少,导致总销售额减少,建议店里采取一些促销手段,增加B 款运动鞋的销售量.2.(2015四川省巴中市,26,10分)“中国梦”关系每个人的幸福生活,为展现巴中人追梦的风采,我市某中学举行“中国梦·我的梦”的演讲比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整.请你根据统计图解答下列问题.(1)参加比赛的学生人数共有名,在扇形统计图中,表示“D等级”的扇形的圆心角为度,图中m的值为;(2)补全条形统计图;(3)组委会决定从本次比赛中获得A等级的学生中,选出2名去参加市中学生演讲比赛.已知A等级中男生有1名,请用“列表”或“画树状图”的方法求出所选2名学生中恰好是一名男生和一名女生的概率.【答案】解:(1)根据统计图,可知A等级的有3人,占15%,∴参加比赛的共有3÷15%=20(人).∴C等级所占百分比为8=40%20,D等级所占百分比为4=20%20.∴m=40,D等级所占百分比为360°×20%=72°.(2)由题意,B等级所占百分比为1-15%-40%-20%=25%,∴B等级人数为20×25%=5(人),补全统计图如下所示.3.(2015山东省青岛市,17,6分)某中学为了了解学生每天完成家庭作业所用时间的情况,从每班抽取相同数量的学生进行调查,并将所得数据进行整理,制成条形统计图和扇形统计图如下:(1)补全条形统计图;(2)求扇形统计图中扇形D的圆心角的度数;(3)若该中学有2000名学生,请估计其中有多少名学生能在1.5小时内完成家庭作业?【答案】解:(1)∵10÷25%=40,∴B的人数为40-10-14-3-1=12.补全条形统计图如下:(2)∵1-25%-30%-35%-2.5%=7.5%,∴360°×7.5%=27°.∴扇形统计图中扇形D 的圆心角的度数为27°. (3)∵2000×35%=700,∴该中学有2000名学生中有700名学生能在1.5小时内完成家庭作业.4. (2015重庆B 卷,22,10分)某校七年级(1)班班主任对本班学生进行了“我最喜欢的课外活动”的调查,并将调查结果分为书法和绘画类(记为A )、音乐类(记为B )、球类(记为C )、其他类(记为D ).根据调查结果发现该班每个学生都进行了登记且只登记了一种自己最喜欢的课外活动.班主任根据调查情况把学生都进行了归类,并制作了如下两幅统计图,请你结合图中所给信息解答下列问题:(1)七年级(1)班学生总人数为_______人,扇形统计图中D 类所对应扇形的圆心角为_____度,请补全条形统计图;(2)学校将举行书法和绘画比赛,每班需派两名学生参加,A 类4名学生中有两名学生擅长书法,另两名擅长绘画.班主任现从A 类4名学生中随机抽取两名学生参加比赛,请你用列表或画树状图的方法求出抽到的两名学生恰好是一名擅长书法,另一名擅长绘画的概率.类别人数22题图”我最喜欢的课外活动“各类别人数占全班总人数的百分比的扇形统计图DCB25%A“我最喜欢的课外活动”各类别人数条形统计图141242018161412108642【答案】(1)48,105;(2)23【解析】解:(1)总人数=12÷25%=48人;D 类对应的圆心角的度数=360°×1448=105°. 类别人数18“我最喜欢的课外活动”各类别人数条形统计图141242018161412108642,则可列下表: A 1 A 1 A 2 A 2A 1 √ √ A 1 √ √ A 2 √ √ A 2√√∴由上表可得:82(123P =一名擅长书法一名擅长绘画)=5. 小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t ),并绘制了样本的频数分布表和频数分布直方图(如图). 月均用水量(单位:t )频数 百分比23x ≤<2 4% 34x ≤< 12 24% 45x ≤< 56x ≤< 10 20% 67x ≤< 12% 78x ≤<3 6% 89x ≤<24%(1)请根据题中已有的信息补全频数分布表和频数分布直方图;(2)如果家庭月均用水量“大于或等于4t 且小于7t ”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户?(3)从月均用水量在23x ≤<,89x ≤<这两个范围内的样本家庭中任意抽取2个,求抽取出的2个家庭来自不同范围的概率。
2015年浙江省丽水市初三上学期期末数学试卷[解析版]
![2015年浙江省丽水市初三上学期期末数学试卷[解析版]](https://img.taocdn.com/s3/m/4c451870f01dc281e53af0bb.png)
2014-2015学年浙江省丽水市初三上学期期末数学试卷一、选择题(本题有6小题,每小题4分,共24分)1.(4分)已知,则a﹣b的值是()A.2B.±2C.6D.±62.(4分)已知,则的值是()A.4B.C.8D.3.(4分)自然数n满足等式,这样n的个数是()A.3B.4C.5D.74.(4分)如果△ABC的两边长分别为a、b,那么△ABC的面积不可能等于()A.(a2+b2)B.(a2+b2)C.(a+b)2D.ab5.(4分)如图,平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE 折叠,使点A恰好落在CD上的点F,若△BCF的周长为14,CF的长为3,则△DEF的周长为()A.8B.7C.6D.56.(4分)如图,在△ABC中,AD=DC,BE=EF=FC,AE、AF与BD相交于点G、H.已知,则S的值是()四边形GEFHA.B.C.D.二、填空题(本题有4小题,每小题5分,共20分)7.(5分)因式分解:x2﹣4xy﹣2x+4y2+4y﹣3=.8.(5分)将三粒均匀的分别标有1,2,3,4,5,6的正六面体骰子同时掷出,出现的数字分别为a,b,c,则a,b,c正好是直角三角形三边长的概率是.9.(5分)如图,已知△ABC中,∠A=60°,D为AB上一点,且AC=2AD+BD,∠B=4∠ACD,则∠DCB的度数是.10.(5分)如图,直线y=﹣2x+b与双曲线y=(x>0)交于A,B两点,与x轴、y轴分别交于E,F两点,连结OA,OB,若S△OBF +S△OAE=4S△AOB,则b的值是.三、解答题(本题有3小题,共36分)11.(10分)已知a,b,c均为非负实数,且满足2a+3b﹣c=2,3a+b+2c=1,记S=3a+b﹣7c.求S的取值范围.12.(12分)如图,在⊙O中,AB为直径,Rt△OBC的直角边OC=BC=1,过点C 作直线DE∥AB交圆于D、E两点,BD与OC交于点F.(1)求∠BDE的度数;(2)证明:△CDF的面积小于.13.(14分)已知:关于x的方程x2﹣(m+1)x+m﹣2=0有两异号实数根x1,x2,且x1>|x2|,若x12+x22=8.(1)求m的值;(2)若函数y=x2+bx+c的图象与x轴的两个交点的横坐标为﹣x1+1,﹣x2+1.求当1≤x≤2时,函数y=|x2+bx+c|的最大值.2014-2015学年浙江省丽水市初三上学期期末数学试卷参考答案与试题解析一、选择题(本题有6小题,每小题4分,共24分)1.(4分)已知,则a﹣b的值是()A.2B.±2C.6D.±6【解答】解:∵,∴a2﹣4=0,a=±2,;∴2a+b=0,∴b=±4,∴a﹣b=6,a+b=﹣6,故选:D.2.(4分)已知,则的值是()A.4B.C.8D.【解答】解:﹣==2,即x﹣y=﹣2xy,则原式====8.故选:C.3.(4分)自然数n满足等式,这样n的个数是()A.3B.4C.5D.7【解答】解:①当n2﹣2n=1 时,无论指数为何值等式成立.解方程得n=(不合题意,舍去);②当n2﹣2n=﹣1 时,解得:n=1;③当n2﹣2n≠±1 时,当n为自然数,则n2﹣2n≠0,所以n2+47=16n﹣16等式成立.解方程得n1=7,n2=9.④当n=2时,左边=051=0,右边=016=0,所以左边=右边,n=2成立,⑤当n=0,左边=右边=0,成立,综上所述,满足条件的n值有5个.故选:C.4.(4分)如果△ABC的两边长分别为a、b,那么△ABC的面积不可能等于()A.(a2+b2)B.(a2+b2)C.(a+b)2D.ab【解答】解:∵△ABC的两边长时a、b,=absinC,∴S△ABC=ab,当∠C=90°时,△ABC的面积最大,且S△ABC又∵(a﹣b)2≥0,即ab≤(a2+b2),A、∵S=(a2+b2),故此选项可能;B、∵(a2+b2)>(a2+b2),故此选项不可能;C、∵(a+b)2=[(a2+b2)+ab]≥ab,故此选项可能;D、∵ab<ab,故此选项可能.故选:B.5.(4分)如图,平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE 折叠,使点A恰好落在CD上的点F,若△BCF的周长为14,CF的长为3,则△DEF的周长为()A.8B.7C.6D.5【解答】解:由折叠的性质得:△FBE≌△ABE,∴BF=AB,EF=AE,∵四边形ABCD是平行四边形,∴AB=DC,AD=BC,∵△BCF的周长为14,∴BC+BF+CF=14,∴BC+DC=14﹣3=11,∴△DEF的周长=DE+EF+DF=DE+AE+DC﹣CF=AD+DC﹣CF=11﹣3=8;故选:A.6.(4分)如图,在△ABC中,AD=DC,BE=EF=FC,AE、AF与BD相交于点G、H.已的值是()知,则S四边形GEFHA.B.C.D.【解答】解:连接DF,如图.∵AD=DC,EF=FC,∴DF∥AE,DF=AE∵GE∥DF,∴△BGE∽△BDF,∴==.∵BE=EF,∴BF=2BE,∴BD=2BG,DF=2EG,∴AE=2DF=4EG,∴AG=3EG=DF.∵AG∥DF,∴△AHG∽△FHD,∴==.设HD=2k,则HG=3k,DG=5k,BD=2BG=2GD=10k.∵==,==,∴==,=S△ABC.∴S△AGH∵===,=S△ABC,∴S△AEF∴S=S△AEF﹣S△AGH=S△ABC﹣S△ABC=S△ABC.四边形EFHG∵==,==,∴=×=.=,∵S△AHD∴S=3,△ABC=×3=.∴S四边形EFHG故选:D.二、填空题(本题有4小题,每小题5分,共20分)7.(5分)因式分解:x2﹣4xy﹣2x+4y2+4y﹣3=(x﹣2y﹣3)(x﹣2y+1).【解答】解:x2﹣4xy﹣2x+4y2+4y﹣3=(x﹣2y)2﹣2(x﹣2y)﹣3=(x﹣2y﹣3)(x﹣2y+1).故答案为:(x﹣2y﹣3)(x﹣2y+1).8.(5分)将三粒均匀的分别标有1,2,3,4,5,6的正六面体骰子同时掷出,出现的数字分别为a,b,c,则a,b,c正好是直角三角形三边长的概率是.【解答】解:因为将三粒均匀的分别标有1,2,3,4,5,6的正六面体骰子同时掷出,按出现数字的不同共6×6×6=216种情况,其中数字分别为3,4,5,是直角三角形三边长时,有6种情况,所以其概率为.故本题答案为:.9.(5分)如图,已知△ABC中,∠A=60°,D为AB上一点,且AC=2AD+BD,∠B=4∠ACD,则∠DCB的度数是20°.【解答】解:如图延长AB到E使BE=AD,连接CE,∴AE=AD+DB+BE=2AD+BD,∵AC=2AD+BD,∴AE=AC,∵∠A=60°,∴△AEC是等边三角形,∴∠E=∠ACE=60°,∵∠B=4∠ACD,设∠ACD=x,则∠ABC=4x,在△ADC与△EBC中,,∴△ADC≌△EBC,∠ACD=∠ECB=x,∴∠ABC=∠E+∠BCE,∴4x=60°+x,∴x=20°,∴∠BCD=60°﹣20°﹣20°=20°,故答案为:20°10.(5分)如图,直线y=﹣2x+b与双曲线y=(x>0)交于A,B两点,与x轴、y轴分别交于E,F两点,连结OA,OB,若S△OBF +S△OAE=4S△AOB,则b的值是5.【解答】解:在y=﹣2x+b中,令y=0,则x=,令x=0,则y=b,∴E(,0),F(0,b),∴OE=,OF=b,过点A作AN⊥OE于N,∴△AEN∽△EFO,∴==,设A(x1,y1),B(x2,y2),由得2x2﹣bx+3=0,∴x1•x2=,∴y1•y2=6,∴y1=2x2,y2=2x1,∵S△OBF=•OF•x2=•bx2,S△AOE=OE•y1=•2x2,∴S△BOF=S△AOE,∴AE=BF,∵S△OBF+S△OAE=4S△AOB,∴AE=BF=2AB,∴=,∴NA=,EN=,∴ON=,∴A(,),∴=3,∴b=5,故答案为:5.三、解答题(本题有3小题,共36分)11.(10分)已知a,b,c均为非负实数,且满足2a+3b﹣c=2,3a+b+2c=1,记S=3a+b﹣7c.求S的取值范围.【解答】解:解方程组得,∵a,b,c均为非负实数,∴,解得0≤c≤,∴S=3a+b﹣7c=1﹣2c﹣7c当c=0时,S=1,当c=时,S=﹣,∴﹣≤S≤1.12.(12分)如图,在⊙O中,AB为直径,Rt△OBC的直角边OC=BC=1,过点C 作直线DE∥AB交圆于D、E两点,BD与OC交于点F.(1)求∠BDE的度数;(2)证明:△CDF的面积小于.【解答】解:(1)如图,作CM⊥AB于M,DN⊥AB于N,连接OD.在Rt△OCB中,∵∠OCB=90°,OC=BC=1,∴OB=OD===,∵CM⊥OB,∴OM=MB,∴CM=OM=BM=,∵DE∥AB,DN⊥AB,CM⊥AB,∴DN=CM=,∴sin∠DON==,∴∠DON=30°=∠ODC,∵OD=OB,∴∠ODB=∠OBD=∠CDB,∴∠BDE=∠CDO=15°.(2)在Rt△BCF中,∵∠CBF=30°,BC=1,∴CF=,OF=1﹣,∴DC:OB=CF:OF,∴CD==,=••=,=,∵S△DOC=•S△DOC=,∴S△CDF∵≈1.7,<.∴S△CDF13.(14分)已知:关于x的方程x2﹣(m+1)x+m﹣2=0有两异号实数根x1,x2,且x1>|x2|,若x12+x22=8.(1)求m的值;(2)若函数y=x2+bx+c的图象与x轴的两个交点的横坐标为﹣x1+1,﹣x2+1.求当1≤x≤2时,函数y=|x2+bx+c|的最大值.【解答】解:(1)根据题意得x1+x2=m+1>0,x1x2=m﹣2<0,∵x12+x22=(x1+x2)2﹣2x1x2=8,∴(m+1)2﹣2(m﹣2)=8,整理得m2=3,解得m1=,m2=﹣.∴m=,∵△=(m+1)2﹣4(m﹣2)=(m﹣1)2+8>0,∴m的值为.(2)∵(﹣x1+1)+(﹣x2+1)=﹣b,(﹣x1+1)(﹣x2+1)=c,∴b=x1+x2﹣2=m+1﹣2=m﹣1=﹣1,c=x1x2﹣(x1+x2)+1=m﹣2﹣m﹣1+1=﹣2,∴y=|x2+bx+c|变形为y=|x2+(﹣1)x﹣2|,当1≤x≤2时,x=2,y有最大值2.附赠模型一:手拉手模型—全等等边三角形条件:△OAB,△OCD均为等边三角形结论:①△OAC≌△OBD;②∠AEB=60°;③OE平分∠AED(易忘)等腰RT△条件:△OAB,△OCD均为等腰直角三角形结论:①△OAC≌△OBD;②∠AEB=90°;③OE平分∠AED(易忘)导角核心图形任意等腰三角形条件:△OAB,△OCD均为等腰三角形,且∠AOB=∠COD结论:①△OAC≌△OBD;②∠AEB=∠AOB;③OE平分∠AED(易忘)模型总结:核心图形如右图,核心条件如下:①OA=OB,OC=OD;②∠AOB=∠COD模型二:手拉手模型—相似条件:CD ∥AB ,将△OCD 旋转至右图位置结论:右图 △OCD ∽△OAB ⇔△OAC ∽△OBD ;且延长AC 交BD 于点E 必有∠BEC=∠BOA 非常重要的结论:必须会熟练证明手拉手相似(特殊情况)当∠AOB =90°时,除△OCD ∽△OAB ⇔△OAC ∽△OBD 之外还会隐藏OCD OAOBOC OD AC BD ∠===tan ,满足BD ⊥AC ,若连接AD 、BC ,则必有 2222CD AB BC AD +=+;BD AC S ABCD ⨯=21(对角线互相垂直四边形)。
2015年浙江省丽水市中考数学试题及参考答案(word解析版)

2015年浙江省丽水市中考数学试题及参考答案一、选择题(本大题共10小题,每小题3分,共30分)1.在数﹣3,﹣2,0,3中,大小在﹣1和2之间的数是()A.﹣3 B.﹣2 C.0 D.32.计算(a2)3的正确结果是()A.3a2B.a6C.a5D.6a3.由4个相同的小立方体搭成的几何体如图所示,则它的主视图是()A.B.C.D.4.分式11x--可变形为()A.11x--B.11x+C.11x-+D.11x-5.一个多边形的每个内角均为120°,则这个多边形是()A.四边形B.五边形C.六边形D.七边形6.如图,数轴上所表示关于x的不等式组的解集是()A.x≥2B.x>2 C.x>﹣1 D.﹣1<x≤27.某小组7位学生的中考体育测试成绩(满分30分)依次为27,30,29,27,30,28,30.则这组数据的众数与中位数分别是()A.30,27 B.30,29 C.29,30 D.30,288.如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是()A.BDBCB.BCABC.ADACD.CDAC9.在平面直角坐标系中,过点(﹣2,3)的直线l 经过一、二、三象限,若点(0,a ),(﹣1,b ),(c ,﹣1)都在直线l 上,则下列判断正确的是( ) A .a <b B .a <3 C .b <3 D .c <﹣210.如图,在方格纸中,线段a ,b ,c ,d 的端点在格点上,通过平移其中两条线段,使得和第三条线段首尾相接组成三角形,则能组成三角形的不同平移方法有( )A .3种B .6种C .8种D .12种 二、填空题(本大题6小题,每小题4分,共24分) 11.分解因式:9﹣x 2= .12.有6张卡片,每张卡片上分别写有不同的从1到6的一个自然数.从中任意抽出一张卡片,卡片上的数是3的倍数的概率是 .13.如图,圆心角∠AOB=20°,将AB 旋转n°得到CD ,则CD 的度数是 度.14.解一元二次方程x 2+2x ﹣3=0时,可转化为解两个一元一次方程,请写出其中的一个一元一次方程 .15.如图,四边形ABCD 与四边形AECF 都是菱形,点E 、F 在BD 上.已知∠BAD=120°,∠EAF=30°,则ABAE= .16.如图,反比例函数ky x=的图象经过点(﹣1,-),点A 是该图象第一象限分支上的动点,连结AO 并延长交另一分支于点B ,以AB 为斜边作等腰直角三角形ABC ,顶点C 在第四象限,AC 与x 轴交于点P ,连结BP . (1)k 的值为 .(2)在点A 运动过程中,当BP 平分∠ABC 时,点C 的坐标是 .三、解答题(本大题共8个小题,共66分)17.(6分)计算:(11|4|2-⎛⎫-+- ⎪⎝⎭.18.(6分)先化简,再求值:a (a ﹣3)+(1﹣a )(1+a ),其中a =. 19.(6分)如图,已知△ABC ,∠C=Rt ∠,AC <BC .D 为BC 上一点,且到A ,B 两点的距离相等.(1)用直尺和圆规,作出点D 的位置(不写作法,保留作图痕迹); (2)连结AD ,若∠B=37°,求∠CAD 的度数.20.(8分)某运动品牌店对第一季度A 、B 两款运动鞋的销售情况进行统计.两款运动鞋的销售量及总销售额如图所示:(1)一月份B 款运动鞋的销售量是A 款的45,则一月份B 款运动鞋销售了多少双? (2)第一节度这两款款运动鞋的销售单价保持不变,求三月份的总销售额(销售额=销售单价×销售量);(3)综合第一季度的销售情况,请你对这两款运动鞋的进货、销售等方面提出一条建议. 21.(8分)如图,在△ABC 中,AB=AC ,以AB 为直径的⊙O 分别与BC ,AC 交于点D ,E ,过点D 作⊙O 的切线DF ,交AC 于点F . (1)求证:DF ⊥AC ;(2)若⊙O 的半径为4,∠CDF=22.5°,求阴影部分的面积.22.(10分)甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲、乙两人相距s (米),甲行走的时间为t (分),s 关于t 的函数图象的一部分如图所示. (1)求甲行走的速度;(2)在坐标系中,补画s 关于t 的函数图象的其余部分; (3)问甲、乙两人何时相距360米?23.(10分)如图,在矩形ABCD 中,E 为CD 的中点,F 为BE 上的一点,连结CF 并延长交AB 于点M ,MN ⊥CM 交射线AD 于点N . (1)当F 为BE 中点时,求证:AM=CE ;(2)若2AB EF BC BF ==,求ANND 的值; (3)若AB EFn BC BF==,当n 为何值时,MN ∥BE ?24.(12分)某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A 处的正上方,假设每次出发的乒乓球的运动路线固定不变,且落在中线上.在乒乓球运行时,设乒乓球与端点A 的水平距离为x (米),与桌面的高度为y (米),运行时间为t (秒),经多次测试后,得到如下部分数据:(1)当t 为何值时,乒乓球达到最大高度?(2)乒乓球落在桌面时,与端点A的水平距离是多少?(3)乒乓球落在桌面上弹起后,y与x满足y=a(x﹣3)2+k.①y用含α的代数式表示k;②球网高度为0.14米,球桌长(1.4×2)米.若球弹起后,恰好有唯一的击球点,可以将球沿直线扣杀到点A,求α的值.参考答案与解析一、选择题(本大题共10小题,每小题3分,共30分)1.在数﹣3,﹣2,0,3中,大小在﹣1和2之间的数是()A.﹣3 B.﹣2 C.0 D.3【知识考点】有理数大小比较.【思路分析】根据有理数的大小比较法则比较即可.【解答过程】解:根据0大于负数,小于正数,可得0在﹣1和2之间,故选:C.【总结归纳】本题考查了有理数的大小比较的应用,注意:正数都大于0,负数都小于0,正数都大于负数,两个负数比较大小,其绝对值大的反而小.2.计算(a2)3的正确结果是()A.3a2B.a6C.a5D.6a【知识考点】幂的乘方与积的乘方.【思路分析】根据幂的乘方,即可解答.【解答过程】解:(a2)3=a6,故选:B.【总结归纳】本题考查了幂的乘方,理清指数的变化是解题的关键.3.由4个相同的小立方体搭成的几何体如图所示,则它的主视图是()。
J0028--2015丽水市中考数学试卷 (2)
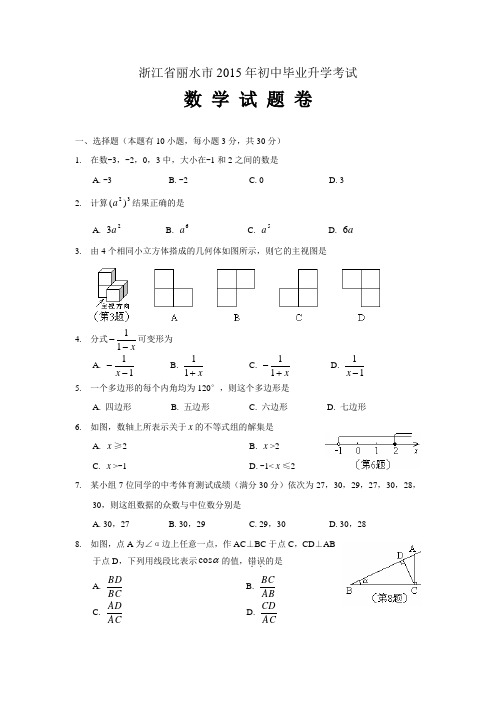
浙江省丽水市2015年初中毕业升学考试数 学 试 题 卷一、选择题(本题有10小题,每小题3分,共30分)1. 在数-3,-2,0,3中,大小在-1和2之间的数是A. -3B. -2C. 0D. 32. 计算32)(a 结果正确的是A. 23aB. 6aC. 5aD. a 63. 由4个相同小立方体搭成的几何体如图所示,则它的主视图是4. 分式x--11可变形为 A. 11--x B. x +11 C. x +-11 D. 11-x 5. 一个多边形的每个内角均为120°,则这个多边形是A. 四边形B. 五边形C. 六边形D. 七边形 6. 如图,数轴上所表示关于x 的不等式组的解集是A. x ≥2B. x >2C. x >-1D. -1<x ≤27. 某小组7位同学的中考体育测试成绩(满分30分)依次为27,30,29,27,30,28,30,则这组数据的众数与中位数分别是A. 30,27B. 30,29C. 29,30D. 30,288. 如图,点A 为∠α边上任意一点,作AC ⊥BC 于点C ,CD ⊥AB于点D ,下列用线段比表示αcos 的值,错误..的是 A.BCBD B. AB BC C. AC AD D. ACCD9. 平面直角坐标系中,过点(-2,3)的直线l 经过一、二、三象限,若点(0,a ),(-1,b ),(c ,-1)都在直线l 上,则下列判断正确的是A. b a <B. 3<aC. 3<bD. 2-<c10. 如图,在方格纸中,线段a ,b ,c ,d 的端点在格点上,通过平移其中两条线段,使得和第三条线段首尾相接组成三角形,则能组成三角形的不同平移方法有A. 3种B. 6种C. 8种D. 12种二、填空题(本题有6小题,每小题4分,共24分)11. 分解因式:=-29x ▲12. 有6张卡片,每张卡片上分别写有不同的从1到6的一个自然数,从中任意抽出一张卡片,卡片上的数是3的倍数的概率是 ▲13. 如图,圆心角∠AOB=20°,将旋转︒n 得到,则的度数是 ▲ 度14. 解一元二次方程0322=-+x x 时,可转化为两个一元一次方程,请写出其中的一个一元一次方程 ▲15. 如图,四边形ABCD 与四边形AECF 都是菱形,点E ,F在BD 上,已知∠BAD=120°,∠EAF=30°,则AE AB = ▲16. 如图,反比例函数xk y =的图象经过点(-1,22-),点A 是该图象第一象限分支上的动点,连结AO 并延长交另一支于点B ,以AB 为斜边作等腰直角三角形ABC ,顶点C 在第四象限,AC与x 轴交于点P ,连结BP 。
