201806高一第16周周测试题8K题多
苏教版数学高一周练习第16周练习与作业

第十六周第1次当堂训练 1.在平行四边形ABCD 中,向量→--AB 与→--CD ,→--AB 与−→−DC 有什么关系?2.已知A ={}与共线的向量a ,B ={}与长度相等的向量a , C ={}与长度相等,方向相反的向量a ,其中a 为非零向量,则A ,B ,C 的关系是什么? .下列说法正确的是 ①→--AB 与→--BA 是同一向量;②所有单位向量的大小是相等的; ③所有的单位向量都相等;④0与是一个意思。
第十六周第1次课后作业 判断下列命题是否正确,若不正确,请简述理由①向量→--AB 与→--CD 是共线向量,则D C B A ,,,四点必在一直线上;②单位向量都相等;③任一向量与它的相反向量不相等;④四边形ABCD 是平行四边形当且仅当→--AB =−→−DC⑤一个向量方向不确定当且仅当模为;⑥共线的向量,若起点不同,则终点一定不同. 2.命题“若∥,∥,则∥” ( )A.总成立,B.当≠时成立,C.当≠时成立,D.当≠时成立第十六周第2次当堂训练1.在平行四边形ABCD 中,++等于( )A.BCB.C.D.AC2.用下图证明 (a +b ) +c =a +(b +c )第十六周第2次课后作业1. 一架飞机向北飞行200千米后,改变航向向东飞行200千米,则飞行的路程为 ;两次位移的和的方向为 ,大小为 千米.2.一艘船距对岸,以h km /32的速度向垂直于对岸的方向行驶,到达对岸时,船的实际航程为8km ,求河水的流速。
3.在三角形ABC 中,求证:−→−AB +−→−AC +−→−BC ≠0第十六周第3次当堂训练1.已知正方形ABCD 的边长等于1,=→--AB a ,=→--BC b ,=→--AC c ,求作向量:(1)a b c ++(2)a b c -+;2.下列四个式子不能化简为的是 ( )A.(+)+B.(+)+(+CM )C. +-D. -+3.在△ABC 中,D 、E 、F 分别是AB 、BC 、CA 的中点,则AF —DB =第十六周第3次课后作业1.已知向量|a |=2,|b |=8,则|a +b |的最大值是 ,|a b -|的最小值是2.化简以下各式:①AB BC CA ++;②AB AC BD CD -+-;③OA OD AD -+;④NQ QP MN MP ++-.其中结果为0的是3.已知向量a ,b 的模分别是3,4,求||a b -的取值范围第十六周第4次当堂训练1.计算:(1)(3)4a -⨯;(2)3()2()a b a b a +---;(3)(23)(32)a b c a b c +---+2.已知向量a 和向量b ,作出向量a +2ba b3.已知为与的和向量,且=,则=____ __,=____ ____。
高一数学上学期第十六次周练试题及答案

河北省保定市高阳中学2018-2019学年高一数学上学期第十六次周练试题新人教A 版1.已知0a b >>,则2,,3a b a b 的关系为………………………………………………………( )A .23abab >> B .322aab>> C .232aab>> D .232baa>> 2.若指数函数()21xy a =-在x R ∈上是减函数,则a 的取值范围是………………………( )A .1a >或1a <- B.a <<C.a >a <.1a <<1a <<-3.下列函数值域是R +的是……………………………………………………………………( )A . 113xy -⎛⎫= ⎪⎝⎭B .125x y -= C.y =.y =4.函数()210,1x y a a a -=+>≠的图像必经过点……………………………………………( )A .(0,1)B .(2,3)C . (2, 1)D .(2,2)5.若函数()0,1x y a a a =>≠与()0,1x y b b b =>≠的图像关于y 轴对称,则有………( )A . a b >B .a b <C .1ab =D .,a b 无确定关系 6.下列说法正确的是:①任取x R ∈,都有32xx>;②当1a >,任取x R ∈,都有xxa a ->;③xy -=是增函数;④2x y =的最小值是1;⑤在同一坐标系中,2x y =与2xy -=的图像关于y 轴对称……………………………………………………………………………………( ) A .①②④ B .④⑤ C .②③④ D .①⑤7.若函数()1()0,1x f x a a a -=>≠,当1x >时,恒有()1f x <,则()f x 在R 上的单调性是( )A .增函数B .减函数C .非单调函数D .不能确定8.若集合2{2,},{,},x M y y x R N y y x x R ==∈==∈则………………………………( ) A .{2,4}MN = B .M N = C . N M Ø D .M N Ø9.函数()()0,1x f x a a a =>≠满足(2)81f =,则1()2f 的值为……………………………( )A .13±B .3±C .13D .3 10.设01a <<,则下列不等式正确的是………………………………………………………( )A .32(1)(1)a a ->+ B .1(1)1aa +-> C . 1(1)1aa -+> D . 1132(1)(1)a a ->+11.函数21x y k =+-的图像不经过第四象限的条件是 12.函数y =的定义域是[,0]-∞,则a 的取值范围是13.函数121x y =+的值域为 14.若函数()2()2x x b f x x e e -=+-,且()f a b =,则()f a -=15.求函数2233x x y -++=的单调区间和最值16.求函数[]111,3,242x xy x ⎛⎫⎛⎫=-+∈- ⎪ ⎪⎝⎭⎝⎭的单调区间,并求它的值域17.已知2231()xx f x a -+=,225()xx g x a +-=,(0,1)a a >≠试确定x 的取值范围,使得()()f x g x ≥18.已知函数2())21xf x a a R =-∈+,(是奇函数 (1)求a 的值(2)求证()f x 是R 上的增函数 (3)求证()0xf x ≥恒成立19.比较下列各组数的大小(1)10.332,2; (2)()()10.330.3,0.3; (3)()20.32,0.3。
高一数学上学期第16周周练试题

卜人入州八九几市潮王学校第五二零二零—二零二壹高一数学上学期第16周周练试题一、填空题〔每一小题5分,一共50分〕20 cm的圆中,165°圆心角所对应的弧长为()A.cmB.cmC.cmD.cm,那么扇形内切圆的圆面积与扇形面积之比为()A.1∶3B.2∶3 C.4∶3D.4∶9θ=-5,那么角θ的终边在()A.第四象限B.第三象限C.第二象限D.第一象限A={α|2kπ≤α≤(2k+1)π,k∈Z},B={α|-4≤α≤4},那么A∩B等于()A.∅B.{α|-4≤α≤π}C.{α|0≤α≤π}D.{α|-4≤α≤-π或者0≤α≤π}α的终边经过点(-4,3),那么cosα等于()A.B.C.-D.-α是第二象限角,那么点P(sinα,cosα)在()A.第一象限B.第二象限C.第三象限D.第四象限7.的化简结果为()A.sin3-cos3B.cos3-sin3 C.±(sin3-cos3)D.以上都不对8.假设sin(3π+α)=-,那么cos等于()A.-B.C.D.-9.cos(π+α)=-,那么sin等于()A.-B.C.D.±=,那么sin的值是()A.B.-C.D.-二、填空题(一共5小题,每一小题5分,一共25分)y=的定义域为________.12.sinαcosα=,且π<α<,那么cosα-sinα=________.13.化简=________.α=2,求值:(1)=________;(2)2sin2α-3cos2α=________.21°+sin22°+…+sin288°+sin289°=________.三、解答题〔每一小题每一小题10分,一共20分〕AOB的圆心角α为,半径长R为6,求:(1)弧AB的长;(2)扇形所含弓形的面积.α的终边上有一点P(24k,7k),k≠0,求sinα,cosα,tanα的值.2021年秋高一数学第16周周周清答题卡班级:__________考号:_________分数;__________一、填空题〔每一小题5分,一共50分〕题号 1 2 3 4 5 6 7 8 9 10 答案二、填空题〔每一小题5分、一共30分〕11、_______________________12、_______________________13、_______________________14、________________________15、________________________三、解答题〔每一小题10分,一共20分〕16、17、。
人教版高中英语必修一高一第十六周周考

高中英语学习材料madeofjingetieji南安一中2018届高一第十六周周考英语试卷组卷:黄锡龙DEC. 20, 2015(满分150分; 考试时间120分钟)第一部分:听力(满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话或独白。
每段对话后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. Where is the woman going?A. To the airportB. To a parkC. To a hotel2. What is the weather like now?A. CloudyB. WindyC. Rainy3. In which department is the man working?A. The Sales DepartmentB. The Planning DepartmentC. The Technology Department4. What will the man need to do in 15 minutes?A. Meet someoneB. Make a complaintC. Catch a train5. What did the girl do?A. She hurt herselfB. She broke a vaseC. She damaged the table by accident第二节(共15小题;每题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C 三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,每小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答第6至8题。
高一数学第十六周测试题(解析版) (同步滚动训练)

高一数学第十六周测试题(解析版)(同步滚动训练)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合A ={}10,,B ={}12=x x ,则A ∪B 的子集个数为( c )A. 2B. 4C. 8D.162.若幂函数()22231m m y m m x--=--在区间()0,+∞上是减函数,则实数m 的值为( A )A .2m =B .1m =-C .1m =-或2D .2m =-或13.已经,72log ,51log ,5152731==⎪⎭⎫ ⎝⎛=c b a 则( B )A. c b a <<B.c a b <<C. a c b <<D.a b c << 4. 240tan 750sin +的值是( c ) A.233 B.23 C.321+ D .321+-5.我国著名数学家华岁庚先生曾说:“数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万休.”在数学的学习和研究中,常用函数的图象来研究函数的性质,也常用函数的解析式来琢磨函数的图象的特征,如函数23()1xf x x=-的图象大致是( c ) A. B . C. D .6.不等式[)π2,0,01sin 2∈≥-x x ]的解集为( D )A.⎥⎦⎤⎢⎣⎡6,0πB.⎥⎦⎤⎢⎣⎡4,0πC.⎥⎦⎤⎢⎣⎡ππ,6D.⎥⎦⎤⎢⎣⎡65,6ππ 7.若函数224(1)()42(1)xa x f x x ax a x ⎧+≤⎪=⎨-+>⎪⎩在R 上单调,则a 的取值范围是( B )A. (]1,4B.[3,4]C (]1,3D . [)4,+∞8.设函数()||=++f x ax x bx c ,给出如下命题, (1).0,0ca 时,()y f x =是奇函数 (2).()y f x =的图像关于点(0,)c 对称(3).0b =,0>ac 时,方程()0=f x 只有一个实数根 (4).方程()f x =0最多有两个实根 则上述命题正确的个数是( C )A .1B .2C .3D .4二、选择题:本小题4小题,每小题5分,共20分。
高一数学16周周测试题
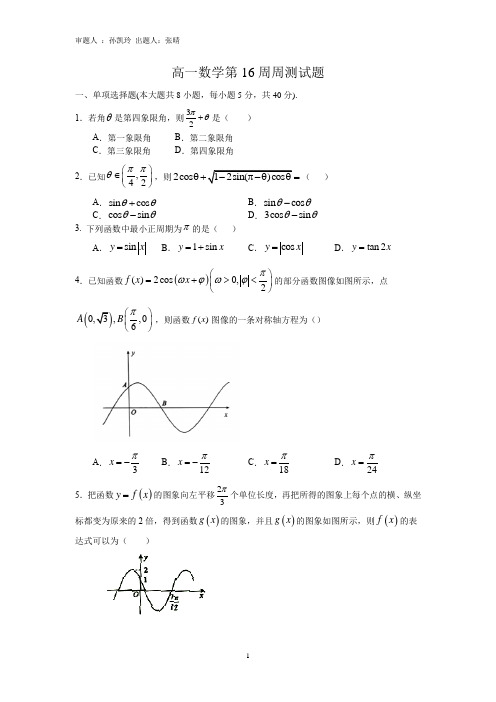
高一数学第16周周测试题一、单项选择题(本大题共8小题,每小题5分,共40分). 1.若角是第四象限角,则是( ) A .第一象限角 B .第二象限角C .第三象限角D .第四象限角2.已知,则( ) A . B .C .D .3. 下列函数中最小正周期为的是( )A .B .C .D .4.已知函数的部分函数图像如图所示,点,则函数图像的一条对称轴方程为()A .B .C .D .5.把函数的图象向左平移个单位长度,再把所得的图象上每个点的横、纵坐标都变为原来的2倍,得到函数的图象,并且的图象如图所示,则的表达式可以为( )θ32πθ+,42ππθ⎛⎫∈⎪⎝⎭2cos =sin cos θθ+sin cos θθ-cos sin θθ-3cos sin θθ-πsin y x =1sin y x =+cos y x =tan 2y x =()()2cos 0,2f x x πωϕωϕ⎛⎫=+><⎪⎝⎭(,,06A B π⎛⎫⎪⎝⎭()fx 3x π=-12x π=-18x π=24x π=()y f x =23π()g x ()g x ()fxA .B .C .D . 6. 将函数的图象向右平移个的单位长度,再将所得到的函数图象上所有点的横坐标变为原来的倍(纵坐标不变),则所得到的图象的函数解析式为( ).A .B .C .D .7. 最小正周期为,且图象关于直线对称的一个函数是A .B .C .D . 8.已知函数, 则的值等于( )A .B .C .D .二、多项选择题(本大题共4小题,每小题5分,共20分).9.函数(其中,)的部分图象如图所示,将函数的图象向左平移个单位长度,得到的图象,则下列说法错误的是( )A .函数为奇函数B .函数为偶函数()2sin 6f x x π⎛⎫=+ ⎪⎝⎭()sin 46f x x π⎛⎫=+ ⎪⎝⎭()sin 46f x x π⎛⎫=-⎪⎝⎭()2sin 46f x x π⎛⎫=-⎪⎝⎭sin 3y x π⎛⎫=+⎪⎝⎭6π2sin 26y x π⎛⎫=+⎪⎝⎭1sin 26y x π⎛⎫=+⎪⎝⎭sin 22y x π⎛⎫=+ ⎪⎝⎭1sin 22y x π⎛⎫=+ ⎪⎝⎭π3x π=()sin 26x y π⎛⎫=+⎪⎝⎭sin 26y x π⎛⎫=+⎪⎝⎭sin 26y x π⎛⎫=-⎪⎝⎭cos 26y x π⎛⎫=-⎪⎝⎭1()2sin()2f x x x =+-122018()()()201920192019f f f ++⋅⋅⋅⋅⋅+20192018201921009()sin()f x A x ωϕ=+0A >0>ω()f x 3π()y g x=()g x ()g xC .函数的图象的对称轴为直线D .函数的单调递增区间为 10.函数(其中,)的部分图象如图所示、将函数的图象向左平移个单位长度,得到的图象,则下列说法错误的是( )A .函数为奇函数B .函数的单调递增区间为C .函数为偶函数D .函数的图象的对称轴为直线11. 若1sin()22πα-=-,则tan(2)πα-=(). A .3 B .33C .3-D .33-12.设函数f (x )=cos ⎝⎛⎭⎫x +π3,则下列结论正确的是( ) A.f (x )的一个周期为-2π B.y =f (x )的图象关于直线x =8π3对称 C.f (x +π)的一个零点为x =π6D.f (x )在⎝⎛⎭⎫π2,π单调递减三、填空题(本大题共4小题,每小题5分,共20分)13.一个半径为r 的扇形,若它的周长等于弧所在的半圆的长,那么该扇形的圆心角是__________________弧度。
高中化学第16周限时训练新人教版必修220170724247.doc

第十六周限时训练(文科)一、单项选择题:(每小题10分)1.Co 6027是γ放射源,可用于农作物诱变育种,我国用该方法培育出了许多农作物新品种,对Co 6027 原子 的叙述不正确...的是 A .质量数是60 B .中子数是33 C .质子数是27 D .电子数是33 2、下列各组物质性质比较的表示中,正确的是 ( )A .还原性:HF>HCl>HBr>HIB .稳定性:HF<HCl<HBr<HIC .与水反应由易到难:Cl 2>Br 2>I 2>F 2D .得电子能力:F 2>Cl 2>Br 2>I 23. 下列各个装置中能组成原电池的是( )A. B .C. D .4. X 元素最高氧化物对应的水化物为H 2XO 3,则它对应的气态氢化物为:( ) A . HX B .H 2X C .XH 3 D .XH 45. 下列物质中,含离子键和非极性共价键的是( )A .H 2O 2B .Na 2O 2C .H 2SD .Mg(NO 3)2 6. 反应4NH 3(g)+5O 2 (g)4NO(g)+6H 2O(g)在2L 密闭容器中进行1分钟后,NH 3减少了0.12 mol ,则反应速率表示正确的是 ( )A .NO 0.001 mol·L -1·s -1B .H 2O 0.002 mol·L -1·s -1C .NH 3 0.002 mol·L -1·s -1D .O 2 0.0025 mol·L -1·s -17. 下列过程一定释放能量的是:( )A .原子组成分子B .分解反应C .分子拆成原子D .化合反应8、银锌钮扣电池广泛用作各种电子仪器的电源,它的充电和放电过程可以表示为( ) Ag 2O+Zn 2Ag+ZnO ,在此电池放电时,则下列说法正确的是 A. 氧化银为正极,被还原 B. 银为负极,被氧化 C. Zn 为负极,被还原D. 该装置中的电解质为酸性物质姓名 班级 成绩充电 放电一、选择题答题处:二、填空题:9.(8分)对下列物质进行分类(均填序号....)。
高一物理上学期第十六次周练试卷高一全册物理试题

应对市爱护阳光实验学校高一〔上〕第十六次周练物理试卷一、选择题1.〔3分〕〔2021秋•校级期末〕探究力的平行四边形那么的原理是效原理,其效性是指〔〕A.使两分力与合力满足平行四边形那么B.使两次橡皮筋与细绳套的结点都与某点O重合C.使两次橡皮筋伸长的长度相D.使弹簧秤在两种情况下发生相同的形变2.〔3分〕〔2021秋•北林区校级期末〕F1、F2是力F的两个分力.假设F=10N,那么以下不可能是F的两个分力的是〔〕A.F1=10 N,F2=10 N B.F1=20 N,F2=20 NC.F1=2 N,F2=6 N D.F1=20 N,F2=30 N3.〔3分〕〔2021秋•区期末〕小东在体育课上做单杠练习时,两臂伸直,双手平行握住单杠,之后逐渐增加双手间距,此过程中手臂上的拉力变化情况为〔〕A.逐渐变小B.逐渐变大C.先变大后变小D.先变小后变大4.〔3分〕〔2021秋•寿校级期末〕如下图,两个共点力F1、F2的大小一,夹角θ是变化的,合力为F.在θ角从0逐渐增大到180°的过程中,合力F的大小变化情况〔〕A.从最小逐渐增加B.从最大逐渐减小到零C.从最大逐渐减小D.先增大后减小5.〔3分〕〔2021秋•期末〕平面内作用于同一点的四个力假设以力的作用点为坐标原点,有F1=5N,方向沿x轴的正向;F2=6N,沿y轴正向;F3=4N,沿x轴负向;F4=8N,沿y轴负向,以上四个力的合力方向指向〔〕A.第一象限B.第二象限C.第三象限D.第四象限6.〔3分〕〔2021秋•区校级期末〕一个重为20N的物体置于光滑的水平面上,当用一个F=5N的力竖直向上拉该物体时,如下图,物体受到的合力为〔〕A.15 N B.25 N C.20 N D.0 N7.〔3分〕〔2007秋•期末〕一根轻质细绳能承受的最大拉力是G,现把一重为G的物体系在绳的中点,两手先并拢分别握住绳的两端,然后缓慢地左右对称分开,假设想绳不断,两绳间的夹角不能超过〔〕A.45°B.60° C.120° D.135°8.〔3分〕两个大小相的共点力F1、F2,当它们间的夹角为90°时,合力大小为20N,那么当它们之间的夹角为120°时,合力的大小为〔〕A.40 N B.10 N C.20 N D.10 N9.〔3分〕〔2021秋•校级月考〕设有三个力同时作用在质点P上,它们的大小和方向相当于正六边形两条边和一条对角线,如下图,这三个力中最小的力的大小为F,那么这三个力的合力于〔〕A.3F B.4F C.5F D.6F10.〔3分〕〔2021秋•区校级期中〕物体同时受到同一平面内三个力的作用,以下几组力的合力不可能为零的是〔〕A. 5 N,7 N,8 N B. 5 N,2 N,3 NC. 5 N,1 N,10 N D.10 N,10 N,10 N 11.〔3分〕〔2021•〕用一根长1m的轻质细绳将一副质量为1kg的画框对称悬挂在墙壁上,绳能承受的最大张力为10N,为使绳不断裂,画框上两个挂钉的间距最大为〔g取10m/s2〕〔〕A.B.C. D.二、填空题12.〔3分〕〔2021•一模〕图甲为“探究求合力的方法〞的装置.〔1〕以下说法中正确的选项是A.在测量同一组数据F1、F2和合力F的过程中,橡皮条结点O的位置不能变化B.弹簧测力计拉细线时,拉力方向必须竖直向下C.F1、F2和合力F的大小都不能超过弹簧测力计的量程D.为减小测量误差,F1、F2方向间夹角为90°〔2〕弹簧测力计的指针如图乙所示,由图可知拉力的大小为N.高一〔上〕第十六次周练物理试卷参考答案与试题解析一、选择题1.〔3分〕〔2021秋•校级期末〕探究力的平行四边形那么的原理是效原理,其效性是指〔〕A.使两分力与合力满足平行四边形那么B.使两次橡皮筋与细绳套的结点都与某点O重合C.使两次橡皮筋伸长的长度相D.使弹簧秤在两种情况下发生相同的形变考点:验证力的平行四边形那么.专题:题;平行四边形法那么图解法专题.分析:本中采用了两个力合力与一个力效果相同来验证的平行四边形那么,效果的相同是通过拉橡皮筋产生大小和方向相同的形变量来实现的.解答:解:在“探究力的平行四边形那么〞的中,采用了“效法〞,即要求两次拉橡皮筋到同一点O,从而是橡皮筋产生的形变大小和方向都相同,故ACD错误,B正确;应选:B.点评:在“验证力的平行四边形那么〞中,我们要知道分力和合力的效果是同的,这要求同学们对于根底知识要熟练掌握并能正确用,理解“效替换〞的含义,对根底理解.2.〔3分〕〔2021秋•北林区校级期末〕F1、F2是力F的两个分力.假设F=10N,那么以下不可能是F的两个分力的是〔〕A.F1=10 N,F2=10 N B.F1=20 N,F2=20 NC.F1=2 N,F2=6 N D.F1=20 N,F2=30 N考点:合力的大小与分力间夹角的关系.专题:平行四边形法那么图解法专题.分析:根据合力F和两分力F1、F2之间的关系|F1﹣F2|≤F≤|F1+F2|,求出两个力的合力范围,判断哪一组合力不可能为10N.解答:解:A、根据|F1﹣F2|≤F≤|F1+F2|,10N和10N的合力范围为[0N,20N],可能为10N.故A正确.B、根据|F1﹣F2|≤F≤|F1+F2|,20N和20N的合力范围为[0N,40N],可能为10N.故B正确.C、根据|F1﹣F2|≤F≤|F1+F2|,2N和6N的合力范围为[4N, 8N],不可能为10N.故C错误.D、根据|F1﹣F2|≤F≤|F1+F2|,20N30N的合力范围为[10N,50N],可能为10N.故D正确.此题选不可能的,应选:C.点评:此题考查合力和分力之间的关系.合力F和两分力F1、F2之间的关系为|F1﹣F2|≤F≤|F1+F2|.3.〔3分〕〔2021秋•区期末〕小东在体育课上做单杠练习时,两臂伸直,双手平行握住单杠,之后逐渐增加双手间距,此过程中手臂上的拉力变化情况为〔〕A.逐渐变小B.逐渐变大C.先变大后变小D.先变小后变大考点:合力的大小与分力间夹角的关系.分析:两手间距增大时,增大了手臂之间的夹角,两只手臂所受的力T的合力F与运发动重力平衡,由此可知合力F大小不变,由于夹角的增大,合力保持不变,只每只手臂所受力T是增大的.解答:解:运发动所受T的合力F与运发动重力大小相方向相反,故夹角增大时合力大小不变;手臂间距增大时,相当于在力图中两力T之间的夹角θ增大,假设力T大小不变,那么其合力F随夹角的增大而减小,现要保持合力F大小不变,当夹角增大时,那么T增大.应选B.点评:两个力合成时,分力大小不变,合力随分力间夹角的增大而减小,能反推出:假设保持合力不变,分力那么随夹角的增大而增大.4.〔3分〕〔2021秋•寿校级期末〕如下图,两个共点力F1、F2的大小一,夹角θ是变化的,合力为F.在θ角从0逐渐增大到180°的过程中,合力F的大小变化情况〔〕A.从最小逐渐增加B.从最大逐渐减小到零C.从最大逐渐减小D.先增大后减小考点:合力的大小与分力间夹角的关系.专题:平行四边形法那么图解法专题.分析:力的合成中,当两个共点力F1与F2合成时,同向合力最大,反向合力最小,不在一条直线上时,遵循平行四边形那么,合力范围为:|F1+F2|≥F≥|F1﹣F2|.解答:解:力是矢量,合成遵循平行四边形那么,同向合力最大,反向合力最小,根据平行四边形那么,两个分力的夹角越大,合力越小,如图,那么有C正确,ABD错误;应选:C.点评:此题关键是根据平行四边形那么作图分析,夹角越大,合力越小,合力范围为:|F1+F2|≥F≥|F1﹣F2|.5.〔3分〕〔2021秋•期末〕平面内作用于同一点的四个力假设以力的作用点为坐标原点,有F1=5N,方向沿x轴的正向;F2=6N,沿y轴正向;F3=4N,沿x轴负向;F4=8N,沿y轴负向,以上四个力的合力方向指向〔〕A.第一象限B.第二象限C.第三象限D.第四象限考点:力的合成.专题:受力分析方法专题.分析:多个力合成时,可以先合成其中的任意两个力,然后再与第三个力合成,直到合成完为止.解答:解:F1=5N,方向沿x轴的正向;F3=4N,沿x轴负向;故F1与F3的合力F13沿着x轴的正向,为1N;F2=6N,沿y轴正向;F4=8N,沿y轴负向;故F2与F4的合力F24为2N,沿着y 轴负方向;最后再将F13与F24合成,故合力F1234为N,指向第四象限;应选D.点评:此题关键先合成F1与F3,再合成F2与F4,最后得到总合力,用平行四边形那么求解合力时通常采用正交分解法,即先将各个力沿着x、y轴正交分解,求出x方向和y方向的合力,最后得到总的合力.6.〔3分〕〔2021秋•区校级期末〕一个重为20N的物体置于光滑的水平面上,当用一个F=5N的力竖直向上拉该物体时,如下图,物体受到的合力为〔〕A.15 N B.25 N C.20 N D.0 N考点:物体的弹性和弹力;力的合成.专题:受力分析方法专题.分析:当拉力为5N时,小于物体的重力,物体不能被提动,仍保持静止,根据平衡条件确物体的合力.解答:解:据题,拉力为F=5N,小于物体的重力20N,不能提动物体,物体仍保持静止,根据平衡条件可知,物体受到的合力为0.应选:D点评:此题要根据力的大小判断物体的状态,确合力的大小,不能头脑简单,得到物体的合力于重力与拉力的差15N.7.〔3分〕〔2007秋•期末〕一根轻质细绳能承受的最大拉力是G,现把一重为G的物体系在绳的中点,两手先并拢分别握住绳的两端,然后缓慢地左右对称分开,假设想绳不断,两绳间的夹角不能超过〔〕A.45°B.60° C.120° D.135°考点:力的合成.专题:受力分析方法专题.分析:把一重为G的物体系在绳的中点,将绳子左右对称分开,即两个力的合力不变且夹角在逐渐变大,故两个力逐渐变大,便到达临界条件大小为G 时进行计算.解答:解:受力分析如图:两个力的合力不变始终为G且夹角在逐渐变大,故两个力逐渐变大,两侧绳子力拉力F到达了最大为G,那么由这两侧的力在竖直方向的分量之和于重力G 得:解得:θ=120°应选:C点评:对节点进行受力分析,找到临界条件,用受力平衡列式求解即可.8.〔3分〕两个大小相的共点力F1、F2,当它们间的夹角为90°时,合力大小为20N,那么当它们之间的夹角为120°时,合力的大小为〔〕A.40 N B.10 N C.20 N D.10 N考点:力的合成.专题:受力分析方法专题.分析:两个大小相的共点力F1、F2,当它们间夹角为90°时合力大小为20N,根据平行四边形那么求出分力的大小,当夹角为120°时,再根据平行四边形那么求出合力的大小.解答:解:当两个力之间的夹角为90°时合力大小为20N,根据平行四边形那么,知F1=F2=10N.当两个力夹角为120°时,根据平行四边形那么知,F合=10N.故B正确,A、C、D错误.应选:B.点评:解决此题关键知道力的合成与分解遵循平行四边形那么,会根据平行四边形那么去求合力或分力.9.〔3分〕〔2021秋•校级月考〕设有三个力同时作用在质点P上,它们的大小和方向相当于正六边形两条边和一条对角线,如下图,这三个力中最小的力的大小为F,那么这三个力的合力于〔〕A.3F B.4F C.5F D.6F考点:力的合成.分析:多个力合成时可以先合成任意两个力,再把这两个力的合力与第三个力相合成,只到把所有的力都合成进去,即可求得最后的合力.解答:解:有图可知,F1、F2的夹角的大小为120°根据平行四边形那么可知,F1、F2的合力的大小为F,由于F3=F1+2F1cos60°=2F,所以F1、F2、F3的合力的大小为3F.应选:A.点评:对于多力的合成,不一非常逐一相合成,可以先合成任意两个,再将合力合成,效果相同.10.〔3分〕〔2021秋•区校级期中〕物体同时受到同一平面内三个力的作用,以下几组力的合力不可能为零的是〔〕A. 5 N,7 N,8 N B. 5 N,2 N,3 NC. 5 N, 1 N,10 N D.10 N,10 N,10 N考点:力的合成.分析:根据力的合成法那么可知:三个力的合力为零时,那么第三个力肯在第一二两个力的合力范围里,由此判断选项即可.解答:解:三个力合力为0时,那么任意两个力的合力与第三个力大小相,方向相反,由此可知,任意一个力在另外两个力的合力范围.A、5N和7N的合力范围为:2N﹣12N,8N在合力范围里,故三个力的合力可能为0;故A错误B、2N和3N的合力范围为:1N﹣5N,5N在合力范围里,故三个力的合力可能为0;故B错误C、1N和5N的合力范围为:4N﹣6N,10N不在合力范围里,故三个力的合力不可能为0;故C正确D、10N和10N的合力范围为:0N﹣20N,10N在合力的范围里,故三个力的合力可能为0.故D错误此题不可能的,应选:C.点评:熟悉三个力合力最小值的判方法,熟悉平衡条件的推论即其用.11.〔3分〕〔2021•〕用一根长1m的轻质细绳将一副质量为1kg的画框对称悬挂在墙壁上,绳能承受的最大张力为10N,为使绳不断裂,画框上两个挂钉的间距最大为〔g取10m/s2〕〔〕A.B.C. D.考点:力的合成与分解的运用;共点力平衡的条件及其用.分析:将重力按照力的效果进行分解,即沿两细线的方向分解,求出绳子即将断开时的临界角度〔两细线夹角〕即可得出画框上两个挂钉的最大间距.解答:解:一个大小方向确的力分解为两个大的力时,合力在分力的角平分线上,且两分力的夹角越大,分力越大,因而当绳子拉力到达F=10N的时候,绳子间的张角最大,为120°,此时两个挂钉间的距离最大;画框受到重力和绳子的拉力,三个力为共点力,受力如图.绳子与竖直方向的夹角为θ=60°,绳子长为L0=1m,那么有mg=2Fcosθ,两个挂钉的间距离,解得m,A项正确;应选:A.点评:熟练用力的合成和分解以及合成与分解中的一些规律,是解决此题的根本.二、填空题12.〔3分〕〔2021•一模〕图甲为“探究求合力的方法〞的装置.〔1〕以下说法中正确的选项是ACA.在测量同一组数据F1、F2和合力F的过程中,橡皮条结点O的位置不能变化B.弹簧测力计拉细线时,拉力方向必须竖直向下C.F1、F2和合力F的大小都不能超过弹簧测力计的量程D.为减小测量误差,F1、F2方向间夹角为90°〔2〕弹簧测力计的指针如图乙所示,由图可知拉力的大小为 4.00 N.考点:验证力的平行四边形那么.专题:题;平行四边形法那么图解法专题.分析:〔1〕该采用了“效法〞,只要明确了原理即可,判断选项中的各个说法是否正确,从而正确的解答此题;〔2〕根据弹簧秤指针的指示可读出拉力的大小.解答:解:〔1〕A、在同一组数据中,只有当橡皮条节点O的位置不发生变化时,两个力的作用效果和一个力的作用效果才相同,才可以验证平行四边形那么,故A正确;B、弹簧测力计拉细线时,方向不一向下,只有把O点拉到同一位置即可,故B错误;C、根据弹簧测力计的使用原那么可知,在测力时不能超过弹簧测力计的量程,故C正确;D、F1、F2方向间夹角为90°并不能减小误差,故D错误.应选AC.〔2〕由图乙弹簧秤的指针指示可知,拉力F的大小为:4.00N.故答案为:4.00.点评:此题考查了“效法〞的用行四边形那么根底知识,对于这些根底知识在平时练习中要不断训练,以提高解题能力;同时注意弹簧秤的读数方法.。
高一上学期16周周练语文试题Word版含答案

20XX—20XX学年上学期高一年级第十六周周测试语文试题:(共12道题)1. 下列词语中加点粗的注音全部正确的一项是()A.守拙(zhuó)三匝(zā) 呦呦(yōu) 晤面(wù) 形骸(hái)B.吹笙(shēng) 拾掇(duō) 癸丑(kuí) 峻岭(jùn) 榆柳荫后檐(yìn)C.譬如(pì) 吐哺(fǔ) 鼓瑟(sè) 修禊(xì) 曲水(qǔ)D.樊笼(fán) 暧暧(ài) 骋怀(chěnɡ) 激湍(tuān) 青青子衿(jīn)2. 下列各组词语中,书写全部正确的一组是()A.尔卜尔噬夙兴夜寐信誓旦旦雨雪霏霏B.鸷鸟不群芳泽杂揉屈心抑志欲盖弥彰C.踯躅不前情投意和窈窕无双藕断丝联D.同心离后越陌度阡譬如朝露守拙田园3. 下列各句中,加粗的成语使用恰当的一项是()A..虽然计算机应用的范围越来越广,但拥有了它并不意味着一切工作都会那么轻而易举,一挥而就。
B.歹徒在向人勒索巨额钱款时猝死于作案现场,他一生恶贯满盈,真是死得其所。
C.道德是一切制度运行的社会土壤,道德与法律在一个国家的文明框架中,唇齿相依,缺一不可。
D.虽然季羡林老先生离开我们了,但他的学生们却在各行各业的建设中,总是首当其冲。
4. 下列各句中,没有语病的一句是()A.根据本报和部分出版机构联合开展的调查显示,儿童的阅读启蒙集中在1-2岁之间,并且阅读时长是随着年龄的增长而增加的。
B.为了培养学生关心他人的美德,我们学校决定组织开展义工服务活动,三个月内要求每名学生完成20个小时的义工服务。
C.在互联网时代,各领域发展都需要速度更快、成本更低的信息网络,网络提速降费能够推动“互联网+”快速发展和企业广泛收益。
D.面对经济全球化带来的机遇和挑战,正确的选择是,充分利用一切机遇,合作应对一切挑战,引导好经济全球化走向。
高中_高一数学上学期16周周练

高一数学上学期16周周练一、选择题1、假设两个平面内分别有一条直线,这两条直线互相平行,那么这两个平面的公共点个数〔 〕A 、有限个B 、无限个C 、没有D 、没有或无限个2、以下四个命题中正确的选项是〔 〕A 、假设平面α内两条直线b a 、都平行平面β,那么βα//B 、假设直线c a c b b a ⊥⊥⊥则直线直线直线,,C 、假设直线b a b a //,,则都平行平面βD 、假设平面βαβα//,//l l 则,直线平面⊂3、以下命题中正确的选项是〔 〕A 、αα////a b b a ⇒⎭⎬⎫⊂B 、b a b a ////⇒⎭⎬⎫⊂αα C 、αα⊂⇒⎭⎬⎫b b a a //// D 、////b a a a b ααα⊂⎫⎪⇒⊄⎬⎪⎭4、如上图,平面EFGH 分别平行于CD 、AB, E 、F 、G 、H 、分别在BD,BC,AC,AD 上,AB CD ⊥, 那么EFGH 是〔 〕A 、平行四边形B 、正方形C 、矩形D 、空间四边形5、如果一条直线平行于一个平面,那么这条直线和这个平面的垂线〔 〕A 、垂直B 、相交C 、平行D 、异面6、直线αα与,则垂直,与直线a b b a ⊥的位置关系是〔 〕 A 、α⊥a B 、α//a C 、 α⊂a D 、α⊂a 或α//a7、以下命题是真命题的是〔 〕〔1〕等长的斜线段在同一平面内的射影也等长〔2〕一个平面内有无数条直线和这个平面的斜线垂直〔3〕一条直线如果和一个平面的斜线垂直,那么这条直线就垂直于这条斜线在这个平面的射影〔4〕垂直于同一条直线的两个平面平行A 、〔1〕B 、〔2〕〔4〕C 、〔2〕〔3〕D 、〔1〕〔4〕8、矩形ABCD 中,AB=1,2PA ABCD ⊥平面,PA=1,那么PC 与 平面ABC 所成的角为〔 〕A 、30︒B 、45︒C 、60︒D 、90︒9、ABC 中,AB=9,AC=15,120BAC ∠=︒,ABC 所在的平面外一点P 到三个点A 、B 、C 的距离都是14,那么点P 到平面ABC 的距离是〔 〕A 、7B 、9C 、11D 、1310、判断题A 、没有公共点的两条直线的位置关系是异面〔 〕B 、没有公共点的两条直线的位置关系是平行〔 〕C 、没有公共点的两条直线的位置关系是平行或异面〔 〕D 、假设直线l 不在平面α内,那么l 与α至多只有一个公共点〔 〕E 、分别在两个平行平面内的两条直线必定互相平行〔 〕F 、两个平面同时和第三各平面垂直,那么这两个平面必定平行〔 〕二、填空题1、空间四边形ABCD 的两对角线AC 、BD 的位置关系是2、三条直线OA 、OB 、OC 两两垂直,那么和OA 垂直的平面是3、如图,AC BC ABC ABC PA ⊥∆⊥中,面,,那么图中为直角三角形的是第3题 第4题4、如图,AB 是圆O 的直径,C 是异于A 、B 的圆周上的任意一点,PA 垂直于圆O 所在的平面,那么BC 和PC 的关系5、正方体ABCD-1111A B C D 中,E 、F 分别为1AA 、11A D 中点,那么EF 与平面11A C 所成的角为三、解答题1、如下图,PO ⊥平面ABC, AB=BC, D 为AC 的中点,BD PO=O求证:AC ⊥BP2、如图,长方体ABCD-ABCD中,P、Q、R分别为BC,CD,CC的中点,证明平面ABD与平面PQR的位置关系。
高一数学上学期16周周练试题

2017—2018 学年上学期高一年级第十六周周测试数学试题(共 13 道题)13、设会合 U{ xN | 0 x 8}, S {1,2,4,5}, T{3,5,7} ,则 S (C U T )=()A . {1,2,4}B . {1,2,3,4,5,7}C . {1,2}D . {1,2,4,5,6,8}14、函数 f ( x)1 x lg( x 2) 的定义域为()A . ( 2,1)B . [ 2,1)C .2, 1D . ( 2,1]15、 sin29()6A.3B.1 C.1D.3222216. 若角的终边上有一点 p ( 1, 1) ,则()A 、sin2 B 、 cos2 )2 ) 12C 、 sin(D 、 tan(2217、已知 sin(5) 1 , 那么 cos()2251 C .1D .2A .B .555518、半径为 2,圆心角为 的扇形的面积为( )A.432B.C.3D.3( 1 )x 2319、设 yx 3与 y 的图象的交点为 (x 0 , y 0 ) ,则 x 0 所在的区间是()2A . (0,1) B. (1,2) C .(2,3) D . (3,4)20、要获得函数 ysin(2 x) 的图象,只要将函数ysin 2x 的图象()6A .向左平移12 个单位长度 B .向右平移 个单位长度12 C .向左平移个单位长度 D .向右平移 个单位长度6621、已知 f ( x) cos(x ) 为奇函数,则的一个取值为( )A.0B. C . D .24 22、y2sin 2x单一增区间为()3A.[ k, k 55, k1] (k Z )B.[ k] (k Z )12121212C.[ k, k] (k Z )D.[k, k2] (k Z )366323、如图,ABC 为等腰直角三角形,ABC 90 .直线 l 与 AB 订交,且 l AB ,直线l 截这个三角形所得的位于直线右方的图形面积为y .点 A 到直线l 的距离为x .则y f ( x) 的图像大概为()24、已知函数f x Asin x x R,A0,0,的图象(部分)如右图所示,2则 f x 的分析式是()A.f ( x)2sin(x)( x R)6B、f ( x)2sin(2x)( x R)6C、f ( x)2sin(x)( x R)3D、f ( x)2sin(2 x)( x R)325、f ( x)x2tan()x1在 [ 3 ,) 上单一递加,则的取值范围是()62A. [k, k 2) (k Z ) B.(k2,k] ( k Z)6336C.(2,) ( k Z ) D.(, k] 36数学( 13题):13-25 ADBDC DBACB CAA。
江西省横峰中学2018届高三第16周周练数学文试题 含答

16周文科练 2017.12.11使用 命题 汪一峰 1.数列{}n a 中,已知对任意正整数n ,有123.....21nn a a a a ++++=-,则22212......n a a a +++=( )A. ()221n - B.()1413n - C. ()1213n - D. 41n - 2.已知等差数列中,有,且该数列的前项和有最大值,则使得成立的的最大值为( ) A. 11 B. 19 C. 20 D. 213.下列命题:①函数f (x )=sin 2x 一cos 2x 的最小正周期是π;②在等比数列〔n a }中,若151,4a a ==,则a 3=士2; ③设函数f (x )=()11x mm x +≠+,若21t f t -⎛⎫ ⎪⎝⎭有意义,则0t ≠ ④平面四边形ABCD 中, ()0,?0AB CD AB AD AC +=-=,则四边形ABCD 是 菱形. 其中所有的真命题是:( ) A. ①②④ B. ①④ C. ③④ D.4.已知各项均为正数的等比数列{}n a 的公比为2864,16,24q a a a a =-=,则q =__________. 5.已知等差数列{}n a , {}n b 前n 项和分别为n S 和n T ,若2113n n S n T n -=+,则1591326812a a a ab b b b ++++++=__________.6.已知数列{}n a 的前n 项和n S 满足231n n S a =-. (1)求数列{}n a 的通项公式;(2)求数列21n n a ⎧⎫-⎨⎬⎩⎭的前n 项和n T .7.已知等差数列{}n a 前n 项和n S ,等比数列{}n b 前n 项和为n T , 11a =, 11b =,224a b +=.(1)若337a b +=,求数列{}n b 的通项公式; (2)若1313T =,求5S8.已知25,a a ,是方程212270x x -+=的两根,数列{}n a 是公差为正的等差数列,数列{}n b 的前n 项和为n T ,且112n n T b =-.(n ∈N *) (Ⅰ)求数列{}n a , {}n b 的通项公式; (Ⅱ)记n c =n a n b ,求数列{}n c 的前n 项和n s .参考答案【解析】∵123.....21n n a a a a ++++=- ∴()11231.....212n n a a a a n --++++=-≥∴12n n a -=(2n ≥)当11,1n a ==也适合12n n a -=,故()1*2n n a n N -=∈ 所以{}2na 是以1为首项,4为公比的等比数列,所以()22212141 (41143)n nn a a a -+++==--,故选B.【解析】为等差数列,有最大值,则,,又,说明,, ,则 , ,,则为最小正值.选B.【解析】①函数()22sin cos cos2f x x x x =-=-,则函数的周期22T ππ==,故①正确;②在等比数列{}n a 中,若151,4a a ==,则23154a a a ==,则32a =±,又22130a a a => ,13,a a 同号, 32a =-不合题意,故②不正确;③设函数()()11x mf x m x +=≠+,则函数的定义域为{}|1x x ≠-,若21t f t -⎛⎫⎪⎝⎭有意义,则211{ 0t t t -≠-≠,即1{ 30t t ≠≠,则0t ≠且13t ≠,故③错误;④平面四边形ABCD 中, 0AB CD +=,则AB CD DC =-=,则四边形ABCD 为平行四边形,()0,0AB AD AC DB AC -⋅=∴⋅=,则四边形ABCD 的对角线垂直,则四边形ABCD 是菱形,故④正确,故选B. 4.2【解析】很明显数列的公比为正数,由题意可得: 2285516,4a a a a ==∴=,则: 564528244a a a a q q q q-=-=-=, 整理可得: 220q q --=, 结合0q >可得: 2q =.5.1516【解析】1591311377268121137744a a a a a a a a b b b b b b b b ++++===++++ 1131311313213111513316a a S b b T +⨯-====++,故答案为15166.(1)13n n a -=;(2)1133n n -+- 【解析】(1)当1n =时, 11231S a =-,得11a =,当2n ≥时, 11231n n S a --=-,将231n n S a =-与1231n n S a -=-左右相减得1233n n n a a a -=-,即13n n a a -=,又因为11a =,所以{}n a 是以1为首项,3为公比的等比数列,所以13n n a -=. (2)由(1)得121213n n n n a ---=,∴122135232113333n n n n n T ----=+++++,① 3252321333333n n n n n T ----=+++++,②,②-①得22223233nT =+++++2122133n n n ----= 1111213321313n n n ----+⨯-- 12263n n -+=-,∴1133n n n T -+=-. 7.(1) 12n n b -= (2) 当4q =-时, 7d =, 575S =;当3q =时, 0d =,试题解析:设等差数列{}n a 公差为d ,等比数列{}n b 公比为()0q q ≠有()14d q ++=,即3d q +=.(1)∵()2127d q ++=,结合3d q +=得2q =,∴12n n b -=.(2)∵23113T q q =++=,解得4q =-或3, 当4q =-时, 7d =,此时554517752S ⨯=⨯+⨯=; 当3q =时, 0d =,此时5155S a ==.8.(1)()*21n a n n N =-∈, ()*23n n b n N =∈(2)2223n n n S +=-试题解析:(1)由252512,27a a a a +=⋅=.且0d >得253,9a a ==,()5212,1,21*3n a a d a a n n N -===∴=-∈ 在112n n T b =-中,令1n =得123b = 当2n ≥时, 112n n T b =-, 11112n n T b --=-两式相减得11122n n n b b b -=-, ()1123n n b n b -=≥ ∴()1212*333n n nb n N -⎛⎫==∈ ⎪⎝⎭. (2) ()2422133n n nn c n -=-⋅= ∴231352123333n nn S -⎛⎫=++++⎪⎝⎭, 234113523212333333n n n S n n +--⎛⎫=+++++ ⎪⎝⎭, ∴234121111121223333333n n n n S +⎡⎤-⎛⎫=+++++- ⎪⎢⎥⎝⎭⎣⎦11112112193213313n n n -+⎡⎤⎛⎫⨯- ⎪⎢⎥-⎝⎭⎢⎥=+-⎢⎥-⎢⎥⎣⎦11111214442333333n n n n n ++-+⎛⎫=+--=- ⎪⎝⎭∴ 2223n nn S +=-。
2018学年高一第一学期第十六周周末练习

2018学年高一第一学期第十六周周末练习一、选择题( )1.已知A={第一象限角},B={锐角},C={小于2π的角},那么A 、B 、C 、的关系是 A. C A B ⋂= B. C B B ⋂= C. C A ⊆ D. C B A ==( )2.sin2cos3的值A.小于0B. 大于0C.等于0D.不确定( )3.设函数32log )(2-+=xx x f ,则函数)(x f 的零点所在的区间为A .)10(,B .)21(,C .2,3)(D .4),(3( )4.在直角坐标系中,若角α的终边经过点P ⎝⎛⎭⎪⎫sin 23π,cos 23π,则sin(π-α)=( )A.12B.32C.-12D.-32( )5.已知函数x x f y +=)(是偶函数,且1)2(=f ,则=-)2(fA .2B .3C .4D .5( )6.已知曲线1:cos C y x =,22π:sin 23C y x ⎛⎫=+ ⎪⎝⎭,为得到曲线2C ,则下面结论正确的是A .把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度B .把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度 C .把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度 D .把1C 上各点的横坐标缩短到原来的2倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度 ( )7.已知31)91(=a ,3log 9=b ,913=c ,则a 、b 、c 的大小关系是A .c b a >>B .b a c >>C .b c a >>D .a b c >>( )8.已知函数()sin()(0,)2f x x πωϕωϕ=+><的最小正周期为4π,且对任意实数x ,都有()()3f x f π≤成立,则()f x 的一个对称中心坐标是A.2(,0)3π-B.(,0)3π-C.2(,0)3πD.5(,0)3π( )9.定义在区间)2,0(π上的函数x y cos 2=的图象与函数x y tan 3=的图象的交点为M ,则点M到x 轴的距离为 A .23 B .3 C .1 D .21( )10.已知定义域为R 的函数)(x f 满足)1()(--=x f x f ,则函数)(x f 在区间)1,1[-上的图象可能是二、填空题 11.已知,,则______12.求值:31)8(5lg 2lg -++= . 13.已知函数)62tan()(π-=x x f ,则)4(πf _______,函数)(x f 的最小正周期是__________. 14.已知幂函数)(x f y =的图象过点)24(,,则=)3(log 3f . 15.已知函数()sin2(0)f x x ωω=->的图象关于点5,04M π⎛⎫⎪⎝⎭对称,且在区间0,2π⎡⎤⎢⎥⎣⎦上是单调函数,则ω的值为__________.16.已知函数⎪⎩⎪⎨⎧<≥-=020)1()(2x x x x f x ,若)(x f 在区间)23,(+a a 上既有最大值又有最小值,则实数a 的取值范围是 .17.设关于x 的方程220x ax --=和210x x a ---=的实根分别为12,x x 和34,x x ,若1324x x x x <<<,则实数a 的取值范围是 .三、解答题18.已知51cos sin =+θθ,),0(πθ∈.求θθcos sin -和θtan 的值;求θθθθ22cos sin cos sin 21--的值.19.已知函数f (x )=A sin(ωx +φ)(A >0,ω>0,|φ|<π2)的部分图象如图所示.(1)求函数f (x )的解析式;(2)将函数y =f (x )的图象上各点的纵坐标保持不变,横坐标缩短到原来的12倍,再把所得的函数图象向左平移π6个单位长度,得到函数y =g (x )的图象,求函数g (x )在区间⎣⎡⎦⎤0,π8上的最小值.20.已知函数a x f x x ---=+)32)(12()(1,其中a 是常数. (Ⅰ)若6=a ,且0)(≥x f ,求实数x 的取值范围;(Ⅱ)若方程0)(=x f 有两个不相等实根,求实数a 的取值范围.21.已知函数)24(log )(2-+=x a x f ,其中a 为实数. (Ⅰ)若1=a ,求函数)(x f 的定义域;(Ⅱ)若关于x 的不等式)2|2(|log )(2+->a x x f 对任意]6,3[∈x 恒成立,求实数a 的取值范围.2017-2018学年第一学期期末杭州地区(含周边)重点中学高一年级数学学科参考答案学校:缙云中学 严州中学等一、选择题BDBCD ADBCA 二、填空题11. 3- 12. 1- 13. 2 14.21 15.3π16. )0,21(-17. )1,1(- 三、解答题18.(本题满分12分) 解:(Ⅰ))62sin(22cos 2sin 3)(π+=+=x x x x f ………………4分1)632sin(2)3(=+⨯=∴πππf ……………………6分(Ⅱ)由(Ⅰ)知,)62sin(2)(π+=x x f , 当,2262πππ+=+k x 即6ππ+=k x 时2)(max =x f , ………………9分由226222πππππ+≤+≤-k x k ,得)(,63Z k k x k ∈+≤≤-ππππ所以,单调递增区间为)(],6,3[Z k k k ∈+-ππππ ……………………12分(其他解法酌情给分)19.(本题满分12分)解:(Ⅰ)令(,3)b a =λ=λλ,则4322=+λλ,得42=λ2±=∴λ, …………4分(2,23)b ∴=,或(2,23)b =-- ……………………6分 (Ⅱ)()(23)a c a c +⊥-()(23)0a c a c ∴+⋅-=, ……………………9分222324322a c a c ∴⋅=-=⨯-⨯= ………… …………12分(其他解法酌情给分)20.(本题满分14分)解:(Ⅰ)由已知,0325)2(22≥-⋅-⋅xx∴32≥x或212-≤x……………………3分 解得:3log 2≥x∴x 的取值范围是),3[log 2+∞ ……………………6分(Ⅱ)a a x f x x x x-+⋅-⋅=--⋅-=+325)2(2)32()12()(21,令xt 2=,则方程0)(=x f 有两个不相等的实根等价于方程03522=-+-a t t 有两个不相等的正实根1t ,2t ,……………………10分则有⎪⎩⎪⎨⎧>⋅>+>0002121t t t t ∆⎪⎪⎪⎩⎪⎪⎪⎨⎧>->>-⋅--⇒0230250)3(8)5(2aa 381<<-⇒a ……………………14分(其他解法酌情给分)21.(本题满分14分)解:(Ⅰ)1=a ,22log )(2-+=∴x x x f 由022>-+x x 解得:2-<x 或2>x)(x f ∴的定义域为),2()2,(+∞--∞∈ x ……………………5分 (Ⅱ)由题意)2|2(|log )24(log 22+->-+a x x a 对任意]6,3[∈x 恒成立, 即0224|2|<-+---a x a x 在]6,3[∈x 恒成立,记a x a x x g -+---=224|2|)(,则0)(max <x g又⎪⎩⎪⎨⎧<++---≥-+--=ax a x x a x a x x x g 222423224)( ……………………9分(1)当32<a ,即23<a 时a x x x g 3224)(-+--= ,此时)(x g 在]6,3[∈x 上单调递增,所以只需0)6(<g ,得37>aΦ∈∴a(2)当62>a 即3>a 时a x x a x x x g +-+--=++---=)242(224)( 又242-+-x x 在]4,3[∈x 上单调递减,]6,4[上单调递增, 0)4()(m a x<=∴g x g 得4<a 43<<∴a (3)当623≤≤a 即323≤≤a 时,由(1)和(2)可知 }37,4m ax {)}6(),4(m ax {)(maxa a g g x g --==得04<-a 且037<-a ,即437<<a , 337≤<∴a , 综上所述,437<<a . ……………………14分(其他解法酌情给分)。
高一第十六周周末测试

高一第十六周周末数学测试第I 卷(选择题)一、选择题1.若135sin -=α,且α为第四象限角,则tan α的值等于 A.512 B.512- C.125 D. 125- 2.某公司有员工500人,其中不到35岁的有125人,49~35岁的有280人,50岁以上的有95人,为了调查员工的身体健康状况,从中抽取100名员工,则应在这三个年龄段分别抽取人数为( ) A .33人,34人,33人 B .25人,56人,19人 C .30人,40人,30人 D .30人,50人,30人3.用秦九韶算法计算多项式2456()12358653f x x x x x x =+-+++在4x =-时的值时,3V 的值为( )A . -144B .-136C . -57D . 34 4.已知221sin 23cos sin θθθ+=--,则tan θ=( ) A .2 B .-1 C .-1或2 D .1或-2 5.函数()cos (0)f x x ωω=>的图象关于点3(,0)4M π对称,且在区间[0,]2π上是单调函数,则ω的值为( ) A .23 B .12 C .23或12 D .23或2 6.在区间[0,6]上随机取一个数x ,2log x 的值介于0到2之间的概率为A .21B .43C .31D .327.已知A 、B 、C 三点不共线,对平面ABC 外的任一点O ,下列条件中能确定点M 与点A 、B 、C 一定共面的是A .OM OA OB OC =++ B . 2OM OA OB OC =-- C .111333OM OA OB OC =++ D .1123OM OA OB OC =++ 8.在ABC ∆中,若22tan tan b a B A =,则ABC ∆的形状是( ) A .直角三角形 B .等腰或直角三角形 C .等腰直角三角形 D .等腰三角形 9.函数()2sin()(0,)22f x x ππωϕωϕ=+>-<<的部分图象如图所示,则,ωϕ的值分别是( )A 、2,3π-B 、2,6π-C 、4,6π-D 、4,3π10.下面程序执行后输出的结果为( ) n=5 S=0WHILE S<15 S=S + n n=n -1 WEND PRINT n ENDA .0B .1C .2D .-1 11.设α角属于第二象限,且|cos|cos22αα=-,则2α角属于( ) A .第一象限 B .第三象限 C .第一象限或第三象限 D .第四象限 12.函数()()2sin 0,2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭的部分图象如图所示,则()17012f f π⎛⎫+⎪⎝⎭的值为( )A .23-B .23+C .31-D .31+ 第II 卷(非选择题)二、填空题13.将八进制53转化为二进制的数结果是:14.为了研究某种细菌在特定环境下,随时间变化的繁殖情况,得到的实验数据如下表,并由此计算得回归直线方程为25.085.0-=∧x y ,后来因工作人员不慎将下表中的实验数据c 丢失. 天数x (天)34 5 6 7 繁殖个数y (千个) c344.56则上表中丢失的实验数据的值为______.15.从1,2,3,4,5中随机取出两个不同的数,则其和为奇数的概率为 . 16.如果向量(,1)a k =,(4,)b k =共线且方向相反,则k 等于 . 三、解答题 17.已知3sin 5θ=,θ是第二象限角,求: (1)θtan 的值; (2))32cos(πθ-的值.18.已知()()()cos ,sin ,3,1,0,m n ααα==-∈π.(1)若m n ⊥,求角α的值; (2)求||m n +的最小值.19.ABC ∆的内角C B A ,,的对边分别为c b a ,,,已知A c C a cos 2cos 3=,且3,52==c b . (1)求a 的值; (2)求)4sin(π+B 的值.20.国家射击队的队员为在2010年亚运会上取得优异成绩,正在加紧备战,经过近期训练,某队员射求该射击队员射击一次(1)射中9环或10环的概率; (2)至少命中8环的概率; (3)命中不足8环的概率.21.设函数f (x)=cos(2x +3π)+3sin2x +2a (1)求函数()f x 的单调递增区间;(2)当[0,]4x π∈时,()f x 的最小值为0,求()f x 的最大值.22.如图,在ABC ∆中,2,3==BC B π,点D 在边AB 上,DC AD =,AC DE ⊥,E 为垂足.(1)若BCD ∆的面积为33,求CD 的长; (2)若26=DE ,求角A 的大小.参考答案1.D 【解析】试题分析:α为第四象限角,512sin 5sin cos ,tan 1313cos 12ααααα=-∴===- 考点:同角三角函数基本关系式 2.B 【解析】试题分析:由已知,因为19:56:2595:280:125=,根据分层抽样方法,抽取人数分别为:25人,56人,19人 .故选B. 考点:分层抽样方法的应用. 3.B 【解析】试题分析:因为()65432356083512f x x x x x x x =+++-++可化为()(((((35)6)0)8)35)12f x x x x x x x =+++-++ ,所以061052132376340136v a v v x a v v x v v x ===+=-=+==+=-故选B.考点:秦九韶算法. 4.A 【解析】 试题分析:由221sin 23cos sin θθθ+=--可得222222sin cos 2sin cos tan 12tan cos sin 1tan θθθθθθθθθ++++=--3=-,解之得tan 2-1θ=或,又因为22cos sin θθ≠,所以2tan 1θ≠,故选A.考点:1、二倍角公式;2、“1”的代换.【方法点晴】本题是一个三角函数的二倍角公式以及“1”的代换方面的综合性问题,属于容易题.解决本题的基本思路是:“弦切”互化,为此联想到将已知式中的“1”化为22sin cos θθ+,然后再将分子分母同除以2cos θ,进而得到关于tan θ的方程,从而可解得tan θ的值.另外本题也可考虑用“万能公式”解决. 5.D 【解析】试题分析:由已知,043cos =⋅πω,则πππωk +=⋅243,即k 3432+=ω,Z k ∈,又函数在区间[0,]2π上是单调函数,可知022-≥πT ,即2221πωπ≥⋅,解得20≤<ω,所以当0=k 或1时,满足题意,即32=ω或2. 考点:三角函数图象的性质.【方法点睛】本题主要考查三角函数图象的性质.对于余弦型函数)cos(ϕω+=x A y ,函数的对称中心在x 轴上,可将对称中心的坐标代入函数关系式,当函数在区间],[b a 上为单调函数时,由三角函数图象可知区间长度2T a b ≤-,T 为函数最小正周期,可借助ωπ2=T ,即2221πωπ≥⋅,得20≤<ω,结合Z k ∈,求出ω的值. 6.A 【解析】 试题分析:24110log 214602x x p -≤≤∴≤≤∴==-,选A 考点:几何概型 7.C 【解析】试题分析:由题:因为A 、B 、C 三点不共线,对平面ABC 外的任一点O ,如果能确定点M 与点A 、B 、C 一定共面,则必然满足共起点的向量关系式中111333OM OA OB OC =++,等式右边系数和为1.考点:向量中四点共面的判定. 8.B 【解析】试题分析:由正弦定理得22tan sin tan sin A AB B=,整理得sin 2cos2A B =,又(),0,A B π∈,则有A B =或2A B π+=.故正确答案为B.考点:1、正弦定理;2、倍角公式;3、三角形形状的判定. 9.A 【解析】试题分析:由图可知,11521212T ππ=-,即T π=,所以由2T πω=可得,2ω=,所以函数()2sin(2)f x x ϕ=+,又因为函数图像过点5(,2)12π,所以522sin(2)12πϕ=⨯+,即522,122k k Z ππϕπ⨯+=+∈,又因为22ππϕ-<<,所以3πϕ=-,故应选A .考点:1、函数()sin()f x A x ωϕ=+的图像及其性质.10.A 【解析】试题分析:由题根据算法语句:while 循环语句,先判断条件是否满足,如果满足就执行循环体内的语句,执行完毕后再回来判断条件是否满足,如此重复;直到条件不满足时,循环结束。
高中物理上学期第16周训练题

金戈铁骑—————————— 教育资源共享 步入知识海洋 ————————四川省宜宾市一中2017-2018学年高中物理上学期第16周训练题一、选择题(本大题共8小题,1—5题为单项选择,6—8题为多项选择,共48分)1.如图所示,P为放在匀强电场中的天然放射源,其放出的射线在电场的作用下分成α、β、γ三束,下列判断中正确的是( ) A.a 为α射线,b 为β射线 B.a 为α射线,b 为γ射线 C.b 为γ射线,c 为α射线 D.b 为β射线,c 为γ射线2.有三个完全相同的金属小球A 、B 、C ,其中小球C 不带电,小球A 和B 带有等量的同种电荷,如图所示,A 球固定在竖直支架上,B 球用不可伸长的绝缘细线悬于A 球正上方的O 点处,静止时细线与OA 的夹角为小球C 可用绝缘手柄移动,重力加速度为g ,现在进行下列操作,其中描述与事实相符的是A. 仅将球C 与球A 接触离开后,B 球再次静止时细线中的张力比原来要小B. 仅将球C 与球B 接触离开后,B 球再次静止时细线与OA 的夹角为,仅将球C 与球A 接触离开后,B 球再次静止时细线与OA 的夹角为,则C. 剪断细线OB 瞬间,球B 的加速度等于gD. 剪断细线OB 后,球B 将沿OB 方向做匀变速直线运动直至着地 3.如图所示是一场强大小为E 、方向水平向右的匀强电场,现将一电子从A 点移动到B 点已知电子的带电量为间距离为连线与电场线成角,则可知A. 电子的电势能减小B. 电场力做功为C. 电场中A 点的电势小于B 点的电势D. AB 两点的电势差为 4.如图所示,在正点电荷Q 的电场中有M 、N 、P 、F 四点,M 、N 、P 为直角三角形的三个顶点,F 为MN 的中点,、N 、P 、F四点处的电势分别用、、、表示已知,点电荷Q 在M 、N 、P 三点所在平面内,则A. 点电荷Q 一定在MP 的中点B. 大于C. N 点的场强比P 点的场强大D. 将负试探电荷从P 点搬运到N 点,电场力做正功5.如图所示,匀强电场中,A 、B 、C 三点构成一边长为a 的等边三角形,电场强度方向平行于纸面.现有一个电子,在电场力作用下,由A 至C 动能减少W ,而质子在电场力作用下,由A 至 B 动能增加W.则该匀强电场E 的大小和方向的判定正确的是( )A.E=ae W 332,方向垂直BC 并由A 指向BC B.E=aeW63,方向垂直BC 并由A 指向BC C.E=ae W 332,方向垂直AC 并由B 指向AC D.E=aeW63,方向垂直AB 并由C 指向AB 6.图中K 、L 、M 为静电场中的三个相距很近的等势面、M 之间无电荷一带电粒子射入此静电场中后,依轨迹运动已知电势下列说法中正确的是 A. 粒子带负电B. 粒子在bc 段做减速运动C. 粒子在b 点与d 点的速度相同D. 粒子在c 点时电势能最大7.如图1-4-12所示,在y 轴上关于O 点对称的A 、B 两点有等量同种点电荷+Q ,在x 轴上C 点有点电荷-Q 且CO =OD ,∠ADO =60°.下列判断正确的是( ) A.O 点电场强度为零 B.D 点电场强度为零C.若将点电荷+q 从O 移向C ,电势能增大D.若将点电荷-q 从O 移向C ,电势能增大8.如图所示,水平面内的等边三角形ABC 的边长为L ,顶点C 恰好位于光滑绝缘直轨道CD 的最低点,光滑直导轨的上端点D 到A 、B 两点的距离均为在AB 边上的竖直投影点为一对电荷量均为的点电荷分别固定于A 、B 两点在D 处将质量为m 、电荷量为的小球套在轨道上忽略它对原电场的影响,将小球由静止开始释放,已知静电力常量为k 、重力加速度为g ,且,忽略空气阻力,则A. 轨道上D 点的场强大小为B. 小球刚到达C 点时,其加速度为零C. 小球刚到达C 点时,其动能为D. 小球沿直轨道CD 下滑过程中,其电势能先增大后减小三、实验题探究题(本大题共2小题,每空3分,共18分)9.影响平行板电容器电容的因素有______ ,在实验室中完成这个实验的方法是______ A .两极板的正对面积 B .两板间距离 C .电介质的介电常数 D .极板的材料 F .控制变量法 G .假设法 H .微小量放大法在研究影响平行板电容器电容大小因素的实验中,如图所示,把一个平行板电容器与一个静电计相连接后,给电容器带上一定电量,静电计指针的偏转指示出电容器两板间的电势差的变化,现保持B极板不动,而要使静电计指针的偏角增大,可采取的办法是______A、A板向右移一些B、A板向左移一些C、A板向上移一些D、在MN之间插入一片有机玻璃板.10.在探究两电荷间相互作用力的大小与哪些因素有关的实验中,一同学猜想可能与两电荷的间距和带电量有关他选用带正电的小球A 和球放在可移动的绝缘座上,B球用绝缘丝线悬挂于玻璃棒C点,如图所示实验时,先保持两球电荷量不变,使A球从远处逐渐向B球靠近,观察到两球距离越小,B球悬线的偏角越大;再保持两球距离不变,改变小球所带的电荷量,观察到电荷量越大,B球悬线的偏角越大实验表明:两电荷之间的相互作用力,随其距离的___________ 而增大,随其所带电荷量的___________ 而增大两空均选填“增大”、“减小”此同学在探究中应用的科学方法是___________ 选填“累积法”、“等效替代法”、“控制变量法”或“演绎法”.四、计算题(本大题共2小题,共34分)11.(14分)一质量为带电量为的小球P 自动摩擦因数倾角的粗糙斜面顶端由静止开始滑下,斜面高,斜面底端通过一段光滑小圆弧与一光滑水平面相连整个装置处在水平向右的匀强电场中,场强,忽略小球在连接处的能量损失,当小球运动到水平面时,立即撤去电场水平面上放一静止的不带电的质量也为m 的圆槽Q,圆槽光滑且可沿水平面自由滑动,圆槽的半径,如图所示在沿斜面下滑的整个过程中,P球电势能增加多少?小球P运动到水平面时的速度大小.试判断小球P能否冲出圆槽Q.12.(20分)如图所示,在距离某平面高2h处有一抛出位置P,在距P 的水平距离为处有一光滑竖直挡板端距该水平面距离为端上方整个区域内加有水平向左的匀强电场;B 端与半径为的的光滑圆轨道BC连接当传送带静止时,一带电量大小为,质量为的小滑块,以某一初速度从P点水平抛出,恰好能从AB挡板的右侧沿ABCD路径运动到D点而静止请完成下列问题求出所加匀强电场的场强大小?当滑块刚运动到C点时,求出对圆轨道的压力?若传送带转动,试讨论滑块达到D时的动能EK与传送带速率的关系?附参考答案三、实验题探究题(本大题共2小题,每空3分,共18分)9.ABC,F,AC10.减小,增大控制变量法.四、计算题(本大题共2小题,共34分)11.解:在整个过程中,电场力对P 球做功为:,根据受力分析可知,斜面对P球的支持力为:根据动能定理得:得:由代入数据可得:设当两者速度相等时,小球上升的高度为H ,根据水平方向动量守恒得:代入数据:根据机械能守恒得:,代入已知数据得:,所以小球没有冲出圆槽.答:在沿斜面下滑的整个过程中,P球电势能增加90J小球P 运动到水平面时的速度大小为.小球P不能否冲出圆槽Q.12.解:设物块从P到A运动的时间为t,水平方向的加速度大小为a,物块能够沿AB下滑,说明在A点时水平方向速度为零,则:水平方向:,其中:,竖直方向:,联立解得:;从P点到C 点根据动能定理可得:,其中,所,根据牛顿第二定律可得:,联立解得:;根据牛顿第三定律可得压力大小为9N;若传送带逆时针转动时,滑块运动的规律与传送带静止不动相同,故滑块到D点的动能为零,与传送带的速度无关;以若传送带顺时针转动,设传送带使得物体一直加速的速度大小为v,则:,当传送带静止时,根据动能定理可得:,解得:;所以传送带顺时针转动时,滑到D 点的速度与传送带速度的关系是:时,,v 带时,.答:匀强电场的场强大小为;当滑块刚运动到C点时对圆轨道的压力为9N;若传送带逆时针转动时,滑块到D点的动能为零;若传送带顺时针转动时:时,;v 带时,.金戈铁骑。
2017-2018学年高一英语下学期第十六周半月考试题

2017-2018学年高一英语下学期第十六周半月考试题第一部分:听力(共两节,满分30分)(第24套)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话,每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
What will the woman do tonight?Write a report. B.Go to a party.C.Do her housework.2.when will the speakers go on holiday?A.In June.B.In July.C.In September.3.How long is the museum open on weekdays?A.6 hours.B.7 hours.C.8 hours.4.What are the speakers mainly talking about?A.A trip.B.A coin.C.A hobby.5.Where will the man stay at 5:00?A.At home.B.At his office.C.At the train station.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答第6至7题。
What will the woman have to do tomorrow?Write a paper. B.Repair the man’s computer. C.Hand in her paper.What is the woman most likely to be?A computer programmer. B.A secretary.C.A student.听第7段材料,回答第8 至9题。
高一数学下学期 第16周周末练习 试题

心尺引州丑巴孔市中潭学校一中高一数学2021春学期第十六周双休练习班级 成绩.一、填空题〔本大题共14小题,每题5分,共计70分。
请将答案答在答卷纸指定区域,在本试卷上答题无效。
〕1、在ABC ∆中,sin :sin :sin 3:2:4A B C =,那么最大角的余弦值是 ▲ .2、假设直线l 的倾斜角为α,且1200<≤α,那么直线l 的斜率范围为 ▲ .3、假设三角形三边的长分别为,1,2(3)n n n n ++>,那么三角形的形状一定是 ▲ 三角形.4、首项为-24的等差数列,从第10项开始为正数,那么公差d 的范围 ▲ .5、ABC ∆中,1,1200==∠b A,其面积为3,那么c b a +-= ▲ .6、过P(1,4)且横截距是纵截距3倍的直线方程为 ▲ .7、在ABC ∆中,045,2,===B cm b xcm a ,假设用正弦定理解此三角形时有两个解,那么x 的取值范围是 ▲ .8、正项等比数列}{n a 中,假设,8165=⋅a a 那么=+++1032313log log log a a a __▲_____.9、等差数列}{n a 中,240,30,1849===-n n S a S ,那么n 的值为 ▲ .10、方程0)2)(2(22=+-+-n x x m x x的四个根组成一个首项为41的等差数列,那么||n m -= ▲ 11、函数()1xf x x=+,仿照等差数列求和公式的推导方法化简:1111()()()()(1)(3)(5)(7)(9)9753f f f f f f f f f ++++++++= ▲ .12、设公比为q 的等比数列{}n a 的前n 项和为n S ,假设1n S +、n S 、2n S +成等差数列,那么q =▲ .13、假设23(32)90ax aa y +-+-<表示直线23(32)90ax a a y +-+-=上方的平面区域,那么a 的取值范围是 ▲ .14、2n 个正数排成n 行n 列,如右表,其中每行数都成等比数列,每列数都成等差数列,且所有公比都相等,18,6,5565424===a a a ,那么1422a a +=_____▲_______.一中高一数学2021春学期第十六周双休练习答题卡1、__________________ 6、__________________ 11、________________2、__________________ 7、__________________ 12、________________3、__________________ 8、__________________ 13、________________4、_________________ 9、_________________ 14、________________5、_________________ 10、_________________二、解答题〔本大题共6小题,共计90分。
2018学年高一第一学期第十六周周末练习 .doc

2018学年高一第一学期第十六周周末练习一、选择题( )1.已知A={第一象限角},B={锐角},C={小于2π的角},那么A 、B 、C 、的关系是 A. C A B ⋂= B. C B B ⋂= C. C A ⊆ D. C B A ==( )2.sin2cos3的值A.小于0B. 大于0C.等于0D.不确定( )3.设函数32log )(2-+=xx x f ,则函数)(x f 的零点所在的区间为A .)10(,B .)21(,C .2,3)(D .4),(3( )4.在直角坐标系中,若角α的终边经过点P ⎝⎛⎭⎪⎫sin 23π,cos 23π,则sin(π-α)=( )A.12B.32C.-12D.-32( )5.已知函数x x f y +=)(是偶函数,且1)2(=f ,则=-)2(f A .2B .3C .4D .5( )6.已知曲线1:cos C y x =,22π:sin 23C y x ⎛⎫=+ ⎪⎝⎭,为得到曲线2C ,则下面结论正确的是A .把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度B .把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度 C .把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度 D .把1C 上各点的横坐标缩短到原来的2倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度 ( )7.已知31)91(=a ,3log 9=b ,913=c ,则a 、b 、c 的大小关系是A .c b a >>B .b a c >>C .b c a >>D .a b c >>( )8.已知函数()sin()(0,)2f x x πωϕωϕ=+><的最小正周期为4π,且对任意实数x ,都有()()3f x f π≤成立,则()f x 的一个对称中心坐标是A.2(,0)3π-B.(,0)3π-C.2(,0)3πD.5(,0)3π( )9.定义在区间)2,0(π上的函数x y cos 2=的图象与函数x y tan 3=的图象的交点为M ,则点M到x 轴的距离为 A .23 B .3 C .1 D .21( )10.已知定义域为R 的函数)(x f 满足)1()(--=x f x f ,则函数)(x f 在区间)1,1[-上的图象可能是二、填空题 11.已知,,则______12.求值:31)8(5lg 2lg -++= . 13.已知函数)62tan()(π-=x x f ,则)4(πf _______,函数)(x f 的最小正周期是__________. 14.已知幂函数)(x f y =的图象过点)24(,,则=)3(log 3f . 15.已知函数()sin2(0)f x x ωω=->的图象关于点5,04M π⎛⎫⎪⎝⎭对称,且在区间0,2π⎡⎤⎢⎥⎣⎦上是单调函数,则ω的值为__________.16.已知函数⎪⎩⎪⎨⎧<≥-=020)1()(2x x x x f x ,若)(x f 在区间)23,(+a a 上既有最大值又有最小值,则实数a 的取值范围是 .17.设关于x 的方程220x ax --=和210x x a ---=的实根分别为12,x x 和34,x x ,若1324x x x x <<<,则实数a 的取值范围是 .三、解答题18.已知51cos sin =+θθ,),0(πθ∈.求θθcos sin -和θtan 的值;求θθθθ22cos sin cos sin 21--的值.19.已知函数f (x )=A sin(ωx +φ)(A >0,ω>0,|φ|<π2)的部分图象如图所示.(1)求函数f (x )的解析式;(2)将函数y =f (x )的图象上各点的纵坐标保持不变,横坐标缩短到原来的12倍,再把所得的函数图象向左平移π6个单位长度,得到函数y =g (x )的图象,求函数g (x )在区间⎣⎡⎦⎤0,π8上的最小值.20.已知函数a x f x x ---=+)32)(12()(1,其中a 是常数.(Ⅰ)若6=a ,且0)(≥x f ,求实数x 的取值范围;(Ⅱ)若方程0)(=x f 有两个不相等实根,求实数a 的取值范围.21.已知函数)24(log )(2-+=x a x f ,其中a 为实数. (Ⅰ)若1=a ,求函数)(x f 的定义域;(Ⅱ)若关于x 的不等式)2|2(|log )(2+->a x x f 对任意]6,3[∈x 恒成立,求实数a 的取值范围.2017-2018学年第一学期期末杭州地区(含周边)重点中学高一年级数学学科参考答案学校:缙云中学 严州中学等一、选择题BDBCD ADBCA 二、填空题11. 3- 12. 1- 13. 2 14.21 15.3π16. )0,21(-17. )1,1(- 三、解答题18.(本题满分12分) 解:(Ⅰ))62sin(22cos 2sin 3)(π+=+=x x x x f ………………4分1)632sin(2)3(=+⨯=∴πππf ……………………6分(Ⅱ)由(Ⅰ)知,)62sin(2)(π+=x x f , 当,2262πππ+=+k x 即6ππ+=k x 时2)(max =x f , ………………9分由226222πππππ+≤+≤-k x k ,得)(,63Z k k x k ∈+≤≤-ππππ所以,单调递增区间为)(],6,3[Z k k k ∈+-ππππ ……………………12分(其他解法酌情给分)19.(本题满分12分)解:(Ⅰ)令(,3)b a =λ=λλ,则4322=+λλ,得42=λ2±=∴λ, …………4分(2,23)b ∴=,或(2,23)b =-- ……………………6分 (Ⅱ)()(23)a c a c +⊥-()(23)0a c a c ∴+⋅-=, ……………………9分222324322a c a c ∴⋅=-=⨯-⨯= ………… …………12分(其他解法酌情给分)20.(本题满分14分)解:(Ⅰ)由已知,0325)2(22≥-⋅-⋅xx∴32≥x或212-≤x……………………3分 解得:3log 2≥x∴x 的取值范围是),3[log 2+∞ ……………………6分(Ⅱ)a a x f x x x x-+⋅-⋅=--⋅-=+325)2(2)32()12()(21,令xt 2=,则方程0)(=x f 有两个不相等的实根等价于方程03522=-+-a t t 有两个不相等的正实根1t ,2t ,……………………10分则有⎪⎩⎪⎨⎧>⋅>+>0002121t t t t ∆⎪⎪⎪⎩⎪⎪⎪⎨⎧>->>-⋅--⇒0230250)3(8)5(2aa 381<<-⇒a ……………………14分(其他解法酌情给分)21.(本题满分14分)解:(Ⅰ)1=a ,22log )(2-+=∴x x x f 由022>-+x x 解得:2-<x 或2>x)(x f ∴的定义域为),2()2,(+∞--∞∈ x ……………………5分 (Ⅱ)由题意)2|2(|log )24(log 22+->-+a x x a 对任意]6,3[∈x 恒成立, 即0224|2|<-+---a x a x 在]6,3[∈x 恒成立,记a x a x x g -+---=224|2|)(,则0)(max <x g又⎪⎩⎪⎨⎧<++---≥-+--=ax a x x a x a x x x g 222423224)( ……………………9分(1)当32<a ,即23<a 时a x x x g 3224)(-+--= ,此时)(x g 在]6,3[∈x 上单调递增,所以只需0)6(<g ,得37>aΦ∈∴a(2)当62>a 即3>a 时a x x a x x x g +-+--=++---=)242(224)( 又242-+-x x 在]4,3[∈x 上单调递减,]6,4[上单调递增, 0)4()(m a x<=∴g x g 得4<a 43<<∴a (3)当623≤≤a 即323≤≤a 时,由(1)和(2)可知 }37,4m ax {)}6(),4(m ax {)(maxa a g g x g --==得04<-a 且037<-a ,即437<<a , 337≤<∴a , 综上所述,437<<a . ……………………14分(其他解法酌情给分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一第16周周测地理试题
姓名 班级 成绩 一、单项选择题
1.扬州、济宁从古代繁荣的商业贸易城市到后来的逐渐衰落,这表明( )
①古代河运是主要的交通运输方式
②现代城市布局中,沿江设市已毫无吸引力
③交通方式的改变,对沿线城市的分布及发展会产生很大的影响 ④沿高速公路的城市轴线已完全取代了沿江设市的布局 A .①② B .①③ C .①④ D .②④ 2.形成商业中心的主要条件是( )
A .在社会发展中有一定的政治历史地位
B .环境优美,名胜古迹多
C .地形平坦开阔,有利于商品的储存
D .交通便利,便于商品集散 4.下列关于商业街的说法,不正确的是( )
A .商业街一般建在城市的几何中心处
B .商业街一般由较多的零售商店和为消费者购物、娱乐以及享受各种服务的场所组成
C .商业街不可能建在市郊
D .商业街为商业中心的一种组织形式 读下图,完成5~6题。
5.该城市拟建的大型服装批发城应布局在图中的( )
A .①处
B .②处
C .③处
D .④处 6.影响该城市发展的主导因素是( )
A .河流
B .政策
C .铁路
D .科技 读下图,回答7—9题。
7.图中黑点表示某种地理事物,该地理事物最有可能是: A .公共汽车站 B .加油站 C .超市 D .工厂
8.从图中信息判断,①、②、③、④四地中,距
离该区域中心城市最近的是: A .① B .② C .③ D .④ 9.图中国道走向平直的主要原因是:
A .尽可能联系较多的经济据点
B .缩短线路长度,节省运营时间
C .降低筑路成本
D .少占耕地
从勘测设计到开工建设,前后经历了半个世纪,被称之为“钢铁露天路”,备受世人瞩目的青藏铁路于2005年10月15日在拉萨火车站举行贯通典礼仪式。
已于2006年7月青藏铁路全线通车。
据此回答10—11题。
10.在规划进藏铁路时,曾有川藏线、滇藏线、青藏线等多种方案,最终选择青藏线方案所考虑的主要因素是:
A .自然条件
B .国防安全
C .社会经济
D .国家政策 11. 青藏铁路约150千米的路段实施了“以桥代路”工程,主要原因是:
①铁路沿线沟壑纵横 ②避免风沙掩埋铁路 ③铁路沿线有多年冻土 ④为动物留出生态通道 A .①② B .②③ C .③④ D .①④
读某区域等高线图(图11),回答12—14题 12.影响图示公路走向的主要因素是
①城镇布局 ②地形起伏 ③河流流向 ④矿产分布 A .①② B .②③ C .③④ D .①④ 13.与丙城区位条件相类似的城市有
①大连 ②武汉 ③重庆 ④石家庄 A .①② B .②③ C .③④ D .①④
14.丁城建港的区位条件有
①纬度低、港口水域全年不冻 ②位于河流人海口,常年不淤 ③地形平坦、便于港口建设 ④水陆联运便利,腹地较广 A .①② B .②③ C .③④ D .①④
下图是某城市交通线路规划示意图,读图,完成15~16 题。
15.该市规划修建从甲到乙的铁路线,从造价、路程、环境等方面考虑,在①②③④四条待选线路中,你认为较合理的是( )
A .①
B .②
C .③
D .④ 16.该市规划建一个大型百货商场,在甲、乙、丙、丁四处中,你认为较合理的是( )
A .甲
B .乙
C .丙
D .丁
济州岛位于韩国的西南海域,是韩国的第一大岛屿,也是一座火山岛,该岛气候温和,
成为韩国人心目中的理想的度蜜月之地,岛内公路四通八达。
读图回答17~18题。
17.影响岛内公路布局的主要因素是( )
A .人口
B .地形
C .景点
D .河流
18.岛内运输方式以公路为主其主要原因是( )
A .地势起伏大
B .居住人口少
C .自然灾害较少
D .面积小,公路运输灵活方便
二、 综合题
读“山区(林区)与平原(水稻产区)商业网点示意图”,并回答下列问题:
(1)山区聚落的分布特点是________,形成原因________________。
(2)山区商业网点密度比平原地区________,原因是________________。
(3)图中山区与平原商业网点的分布表明:农村地区的集市贸易基本上是沿________自发形成的,这符合________原则。
(5)A 、B 、C 三处聚落中,最容易发展成城市的是________处,因为该处________________。
8.读某城市略图,回答下列问题。
(1)商业网点A 的布局符合________最优原则,这里发展商业的两大优势是:①____________;②____________。
(2)图中商业中心B 的布局符合________最优原则,这里发展商业的优势是
________________________________________________________________________。
(3)C 商业点分布是否合理?为什么?
解析:本题主要考查交通运输对商业网点分布位置的影响。
从图中可以看出,商业网点
A
位于城市的外环线附近,这里交通便利,此外,这里位于城市边缘,地租较低,也是商业
发展的一大优势。
商业中心B位于城区中心,这里人口密集,市场较大,符合市场最优原则。
C商业点的布局既不符合市场最优原则,也不符合交通最优原则,因为这里市场狭小,交通不便。
答案:(1)交通交通便利地租较低
(2)市场人口密集,市场广大,且市场对外的辐射能力强
(3)不合理。
这既不符合市场最优原则,也不符合交通最优原则。
高一第16周周测地理试题答案
1-5ABBAD 6-10 ADCBD 11-15 DBAAA
16、16.(1)沿公路和河流呈带状分布临近公路与河流的地方交通便利
(2)小山区路况差,交通不如平原便利,吸引的购物者比平原少。
(3)街道(或交通线)交通最优
(4)B 因为B处位于两条公路交汇处,交通最为便利。
