高三数学课件-三角函数的性质2 推荐

高考数学复习考点知识讲解课件22 三角函数的图象与性质

— 返回 —
— 14 —
(新教材) 高三总复习•数学
— 返回 —
[解析] 由 2x＋π6≠π2＋kπ(k∈Z)，得 x≠π6＋k2π(k∈Z)，故函数 f (x)的定义域为 x|x≠π6＋k2π，k∈Z.故选 D．
— 15 —
(新教材) 高三总复习•数学
— 返回 —
2．(2022·东北师大附中月考)函数 f (x)＝3sin2x－π6在区间0，π2上的值域为( B )
(2)∵f (x)为偶函数， ∴－π3＋φ＝π2＋kπ，k∈Z，得 φ＝56π＋kπ，k∈Z. 又 φ∈(0，π)，∴φ＝56π. ∴f (x)＝3sin2x＋π2＝3cos2x. 由 2x＝π2＋kπ，k∈Z，得 x＝π4＋k2π，k∈Z， ∴f (x)图象的对称中心为π4＋k2π，0，k∈Z.
— 返回 —
— 23 —
(新教材) 高三总复习•数学
— 返回 —
(1)三角函数周期的一般求法 ①公式法． ②不能用公式求周期的函数时，可考虑用图象法或定义法求周期． (2)对于可化为 f (x)＝Asin(ωx＋φ)(或 f (x)＝Acos(ωx＋φ))形式的函数，如果求 f (x)的对称轴，只需令 ωx＋φ＝π2＋kπ(k∈Z)(或令 ωx＋φ＝kπ(k∈Z))，求 x 即可；如果求 f (x)的对称中心的横坐标，只需令 ωx＋φ＝kπ(k∈Z)或令ωx＋φ＝π2＋kπk∈Z，求 x 即可．
— 9—
(新教材) 高三总复习•数学
3．函数 f (x)＝cosx＋π6(x∈[0，π])的单调递增区间为( C ) A．0，56π B．0，23π C．56π，π D．23π，π
— 返回 —
[解析] 由 2kπ－π≤x＋π6≤2kπ，k∈Z，解得 2kπ－76π≤x≤2kπ－π6，k∈Z，∵x∈[0， π]，∴56π≤x≤π，∴函数 f (x)在[0，π]的单调递增区间为56π，π，故选 C．

高中数学必修二三角函数课件

高中数学必修二三角函数课件高中数学必修二—三角函数第一章：概念介绍三角函数是高中数学中的重要内容，它在物理学、工程学等领域有着广泛的应用。

本章将介绍三角函数的定义、基本性质以及常用的公式，让学生对三角函数有一个清晰的认识。

1.1 三角函数的定义三角函数是指正弦函数、余弦函数和正切函数三者的统称。

它们分别与一个角的正弦值、余弦值和正切值相关联，通过对角度的变化，可以得到不同角度下的函数值。

1.2 三角函数的基本性质三角函数具有周期性、奇偶性、单调性等基本性质。

其中周期性是指函数在一定范围内具有重复的规律性；奇偶性是指函数的对称特点，可以通过函数的公式来判断；单调性是指函数的增减规律，可以通过导数的正负来判断。

1.3 三角函数的常用公式三角函数的公式包括和差化积、倍角、半角等多种形式。

这些公式在解三角方程、化简表达式等问题中起着关键作用，学生需要掌握并灵活运用。

第二章：三角函数的图像与性质本章将通过图像展示三角函数的变化规律，并介绍与之相关的性质，以加深学生对三角函数的理解和把握。

2.1 正弦函数的图像与性质正弦函数是最基本的三角函数之一，它在数学和物理中都有着广泛的应用。

我们将通过绘制正弦函数的图像，观察角度对函数值的影响，并探讨正弦函数的周期性、奇偶性、单调性等基本性质。

2.2 余弦函数的图像与性质余弦函数与正弦函数具有相似的性质，但它们的图像呈现出不同的特点。

我们将通过绘制余弦函数的图像，观察角度对函数值的影响，并研究余弦函数的周期性、奇偶性、单调性等基本性质。

2.3 正切函数的图像与性质正切函数是三角函数中的最后一个，它与其他两个函数有着截然不同的图像特点。

通过绘制正切函数的图像，我们可以观察到它的周期性、奇偶性以及无定义的点等特性。

第三章：三角函数的应用三角函数在实际问题中有着广泛的应用，本章将介绍几个与角度和三角函数相关的实际问题，帮助学生将所学的知识运用到实践中。

3.1 三角函数在直角三角形中的应用直角三角形是最基本的三角形之一，三角函数在解决直角三角形相关问题时起着重要作用。

高三数学三角函数的图象2

4．图象的对称性 ① y sin x与y cos x 的图象既是中心对称图形又是轴对称图形。 ② y tan x的图象是中心对称图形，有无穷多条垂直于x轴的渐近线。
1．三角函数线的应用 cos x 0 例1：解三角不等式组 1
y
1 2
sin x 0 2
白荌苒失神的笑了笑“没事”，虽然那孩子的爱一直有些偏执，但是终归是一个勇敢的孩子。
三、小结： 1．用五点法作图 2．图象变换 3．三角函数图象的应用
四、作业
; / 福利群想要放开他的手，也许是因为他的那些话语，我便真的慢慢好了起来，可是，当我完全康复的时候，他又开始寻找了不同的大姐姐，我很生气，每次都会去搅他的局，他还是那样无关痛痒的样子，后来也算倒霉、碰上了一个性格火爆的大姐姐，在我搅局的时候泼了我一杯红酒还甩了我一耳光，我当时就被打愣住了，知北当时说了一个‘滚’字，哪位大姐姐便得意的看向我‘听到了没有，让你滚呐，不要再在这里碍眼了’，我当时真的是有一种生无可恋的心情。然而，当我转身的时候知北却握住了我的手，他站了起来将我揽在了怀中一边替我擦拭脸上的红酒一遍查看脸上的伤，他脸色不太好声音低沉地说了句‘是让你滚’然后便将我带离了那个地方，那是去年发生的事情，后来，我们就成了现在的这种关系。”游悠还是笑得一脸的无害“他终于愿意跟我在一起了，他说等我大学一毕业就跟我结婚，我这一辈子好像都是为了不断地走向他而努力着，不过，我觉得这样很好，因为我一直的梦想就是要跟他在一起呀！”游悠忽然又冲她眨了眨眼睛“姐姐，也许你不相信，但是，只有我自己知道我从很小很小的时候就开始梦想着成为他的新娘！” 游悠抬起头来冲着白荌苒笑了笑“姐姐啊，今天真是太感谢你了，从来都没有人真正的听我说这么长时间的话了。”

高三文科数学总复习课件：三角函数的图像与性质

递减区间.
第二十一页，编辑于星期日：二十二点四十八分。
备选例题.已知函数f (x) sin(x )( 0, 0 ) 是R上的偶函数，其图象关于点M (3 , 0)对称，且在
4
区间[0, ]上是单调函数，求和的值.
2
第二十二页，编辑于星期日：二十二点四十八分。
(方法一) 由于f (x)是R上的偶函数，所以f (x) f (x),
（其中 0） 6
6
2
（1）求函数 f (x) 的值域；
（2）若函数 y f (x)的图象与直线 y 1
的两个相邻交点间的距离为，求函数
y f (x)的单调增区间.
2
第十一页，编辑于星期日：二十二点四十八分。
点评研究三角函数 y Asin(x )( A 0, 0)
的单调性，基本思想是把 x 看作
f
6
1.
(1)求实数a的值；
(2)求f (x)的单调区间、周期和最值.
第十三页，编辑于星期日：二十二点四十八分。
练习2.已知函数
f (x) cos(2x ) 2sin(x ) sin(x ).
3
4
4
（1）求函数f (x)的最小正周期和图象的对称轴方程；
（2）求函数f (x)在区间[ , ]上的值域.
的1 图象，
2
第八页，编辑于星期日：二十二点四十八分。
第九页，编辑于星期日：二十二点四十八分。
类型二三角函数的图象与性质
定义域周期性奇偶性
值域、最值单调性
对称性
第十页，编辑于星期日：二十二点四十八分。
例1
设函数 f (x) sin(x ) sin(x ) 2 cos2 x，

三角函数的概念课件

x
x
三角函数的概念
设α是一个任意角，α∈R，它的终边与单位圆相交于点P(x，y)，
那么 y sin，x cos，y tan (x 0).
x
可以看出，当 k ,k Z 时，α的终边始终在y轴上，这时P点的横
坐标x等于0，所以
y
2
tan无意义.除此之外，正切tanα与实数α是一一对应
么z1与y1相等吗？对于余弦、正切也有相同的结论吗？
y
利用锐角三角函数概念可得：
P(x，y)
sin MP y y; cos OM x x; tan MP y
OP 1
OP 1
OM x
α
O M 1x
与按本节三角函数定义求得的结论是相同的．
三角函数的概念
【例1】求 5 的正弦、余弦和正切值．
三角函数的概念
锐角α的正弦、余弦和正切叫做角α的锐角三角函数，分别记作sinα， cosα，tanα.
sin
对边 BC
斜边 AB
B
cos
邻边斜边
=
AC AB
α
tan
对边 BC 邻边 AC
A
C
02
新知探索
New Knowledge explore
三角函数的概念
角的概念推广后，在弧度制下，角的集合与实数集R之间建立了一一对应的关系，下面借助这些知识研究上一节开头提出的问题，即研究单位圆上点的运动．
所有与角α终边相同的角，连同角α在内，可构成一个集合
S { | k 360 o, k Z}
象限角与轴线角：
把角的顶点固定在原点，角的终边始终与x轴的非负半轴重合.那么，角α的终边在第
几象限，就说这个角是第几象限的角. 如果角的终边落在坐标轴上,这个角称轴线角.

高三数学三角函数的性质2

例2.P[60]
(1)已知f(x)的定义域为[0,1],求f(cosx) 的定义域;
(2).求函数y=lgsin(cosx)的定义域
例3：[P61] 求函数y=sin6x+cos6x的最小正周期, 并求出X为何值时Y有最大值.
例4.求下列函数的值域：
（1）y 2sin2 x 2 cos x 3 （2）y 3sin x 3
2
2
无
无
k ,0
2
（以上均 k Z ）
例1[P60]：
（1）y

cos
x

cos(
x

3
)
的最大值是?
（2）y 2sin(3x )
4
的图象的两条相邻对称轴之间的距离是.
；舟山出海捕鱼舟山出海捕鱼
；
文人独嗜，百姓亦胸有丘壑，尤其在一个特殊日子里，更是趋之若鹜、乐此不疲，此即九九重阳的“登高节”。我始终认为，这是中国先民一个最浪漫、最诗意的节日。秋高气爽，丹桂飘香，心旷神怡，菊色暴涨值此良辰，若不去登高放目、驰骋神思，实在辜负天地、有愧人生。从“登高” 意义上说，这几乎是个绝版的节日。今人仅视为“敬老节”，无疑让它的美折损大半，伤了筋，动了骨。登高节、重阳节、茱萸节、菊花节，乃一回事，但我尤喜“登高”之名。九九习俗源于战国，古人将天地归于阴阳，阴即黑暗、沉寂，阳即光明、活力，奇数谓阳，偶数谓阴；九乃阳数之首，九月初九，双阳相叠，故称重阳。加上“九”“久”谐音，重阳从一开始便是欢愉之词。曹丕《九日与钟繇书》云：“岁往月来，忽复九月九日。九为阳数，而日月并应，俗嘉其名，以为宜于长久，故以享宴高会。” 后来，重阳节又繁殖出了一串新解：除凶秽，招吉祥；延年益寿，祈福求安。仪式也愈加丰富：饮菊花酒

三角函数的图像和性质教学课件

图像变化
当角度增加时，余弦函数的值会减小，图像会向中心靠拢；当角度减小时，余弦函数的值会增加，图像会向外扩展。
图像周期
余弦函数的图像具有周期性，周期为 360度。在一个周期内，图像会重复出现。
正切函数的图像
图像形状
01 正切函数的图像在直角坐标系中呈现出周期性和无界性，其形状类似于波浪线。
调性。
PART 04
三角函数的应用
在几何学中的应用
三角函数在几何学中有着广泛的应用，例如在计算角度、长度、面积等方面。
三角函数可以帮助我们理解几何图形的性质，例如在研究圆、椭圆、抛物线等方面。
三角函数还可以用于解决一些几何问题，例如在计算最短路径、最大面积等方面。
在物理学中的应用
交流电
三角函数的基本性质
周期性
三角函数（如正弦函数和余弦函数）具有明显的周期性，这意味着它们的图像会重复出现。
振幅和相位
振幅和相位是描述三角函数的重要参数。振幅决定了图像的最高点和最低点，而相位决定了图像在垂直方向上的位置。
奇偶性
三角函数中的正弦函数和余弦函数具有不同的奇偶性。正弦函数是奇函数，而余弦函数是偶函数。
图像变化规律
02 正切函数的图像随着角度的变化而呈现周期性的变化，其变化规律是每隔180度重复一次。
图像与x轴交点
03 正切函数的图像与x轴的交点是无穷多个，且分布不均，主要集中在x轴的两侧。
其他三角函数的图像
正切函数图像在直角坐标系中呈现出周期性和无界性，是三角函数中较为特殊的一种。
余切函数图像与正切函数图像互为反函数，在直角坐标系中呈现出对称性和周期性。
工程学
在工程学中，三角函数可以用于解决各种实际问题，如结构工程中的应力分析、机械工程中的振动分析等。

高三数学三角函数的图象和性质2

2. 由图象求解析式时,”第一零点”的确定很重要,尽量使A取正值. 3. 由图象求解析式 y A sin(x ) k 或由代数条件确定解析式时,应注意:
1 (1) 振幅 A= ( y max y min ) 2
2
(2) 相邻两个最值对应的横坐标之差,或一个单 1 调区间的长度为 T ,由此推出的值. 3)确定值,一般用给定特殊点坐标代入解析式来确定.
（1) 若f ( x) a b，且 f ( x)的最小正周期为 ,求f ( x)
f ( x)沿向量 c （2）在（1）的条件下，到函数 y 2 sin 2 x, 求向量 c 。
的最大值, 并求 f ( x) 取得最大值时x的集合；平移可得
热点题型3 导数与三角函数的图象和性质的综合
重难点归纳 1、考查三角函数的图象和性质的基础题目，此类题目要求考生在熟练掌握三角函数图象的基础上要对三角函数的性质灵活运用
y=sinx
-4 -7 -3 2 -5 2 -2 -3 - 2
y
2
1 o -1
2
3 2 2 5 3 2
7 2 4
x
y=cosx
-4 -7 2 -5 -3 2 -2 -3 2
y
- - 2
1 o -1
2
3 2 2 5 2
y7 3 24xyy=tanx
y=cotx
3 2
-
-
2
o
2

3 2
x
-
-
2
o
2

3 2
2
x
2 三角函数与其他知识相结合的综合题目，此类题目要求考生具有较强的分析能力和逻辑思维能力在今后的命题趋势中综合性题型仍会成为热点和重点，并可以逐渐加强

人教版高三数学三角函数知识精讲2

高三数学三角函数知识精讲一. 本周教学内容：三角函数任意角的三角函数，三角函数线，同角三角函数关系与诱导公式，三角函数的图像和性质［基本知识点］1° 角的概念的推广（1）终边相同的角：{β|β＝α＋k ·360°，k ∈Z}表示与角α终边相同的角的集合。

（2）象限角：角的顶点与坐标原点重合，角的始边与x 轴正半轴重合，角的终边落在第几象限，就称这个角是第几象限角。

（3）坐标轴上的角：角的终边落在坐标轴上的角，也称轴限角，这个角不属于任何象限。

终边落在轴上的角，终边落在轴上的角，，x k k Z y k k Z {|}{|}ααπααππ=∈=+∈22° 弧度制（1）意义：圆周上弧长等长半径的弧所对的圆心角的大小为1弧度，它将任意角的集合与实数集合之间建立一一对应关系。

（2）弧度与角度的互换 180118011805718===≈πππ弧度弧度弧度，，()()'（3）弧度公式，扇形面积公式： l r =⋅||α S lr r 扇形==12122||α3° 任意角的三角函数（1）定义：设P(x ，y)是角α的终边上任意一点，且|PO|＝r ，则sin cos ααα===yr x r tg y x ，， csc sec ααα===ryr x ctg x y，，（2）三角函数的符号与角所在象限有关，如下表所示。

规律：一全正，二正弦，三双切，四余弦注意：角的范围的讨论及三角函数的定义的理解是三角的重要内容；而度数与弧度数的互化，弦长公式，扇形的面积公式的应用是难点内容，应注意熟练掌握。

（1）在讨论角的范围时，不要遗漏坐标轴上的角；（）角22α终边所在的位置与α终边的位置及k 的取值有关，要对k 的取值结合α的范围情况进行讨论。

（3）三角函数值的大小仅与角有关，而与终边上所取的P 点的位置无关，当角的终边所在象限不确定时，要分情况讨论。

高中数学课件三角函数ppt课件完整版

2024/1/26
单调性
在各象限内，正弦、余弦函数的单调性及其变化规律。
最值问题
利用三角函数的性质求最值，如振幅、周期等参导公式与恒等式
REPORTING
2024/1/26
7
诱导公式及其应用
01
诱导公式的基本形式
通过角度的加减、倍角、半角等关系，将任意角的三角函数值转化为基
8
恒等式及其证明方法
2024/1/26
恒等式的基本形式
两个解析式之间的一种等价关系，即对于某个变量或一组变量的取值范围内，无论这些变量取何值，等式都成立。
恒等式的证明方法
通常采用代数法、几何法或三角法等方法进行证明。其中，代数法是通过代数运算和变换来证明恒等式；几何法是通过几何图形的性质和关系来证明恒等式；三角法是通过三角函数的性质和关系来证明恒等式。
化简为简单的形式。
12
三角函数的乘除运算规则
乘积化和差公式
通过乘积化和差公式，可以将两个三角函数的乘积转化为和差的
形式，从而简化运算。
商的化简
利用同角三角函数的基本关系，可以将三角函数的商转化为简单
的三角函数运算。
倍角公式
通过倍角公式，可以将三角函数的乘方运算转化为简单的三角函
数运算。
2024/1/26
建立三角函数与数列、概率统计相关的数学模型
结合计算机编程和数学软件，实现模型的数值模拟和可视化
2024/1/26
利用数学分析、高等代数等方法求解模型
22
PART 06
总结回顾与拓展延伸
REPORTING
2024/1/26
23
本章节知识点总结回顾
三角函数图像
正弦、余弦、正切函数的图像及其周期性、奇偶性等性质。

高三数学三角函数的性质2

一•课题：三角函数的性质(二)二•教学目标：掌握三角函数的奇偶性与单调性，并能应用它们解决一些问题. 三•教学重点：三角函数奇偶性的判断及三角函数单调区间的求解及其应用.四•教学过程：(一)主要知识：三角函数的奇偶性和单调性具体如下表：(二)主要方法：1 •三角函数的奇偶性的判别主要依据定义：首先判定函数的定义域是否关于原点对称，当函数的定义域关于原点对称时，再运用奇偶性定义判别；2•函数y二Asin(・・x •「)(A 0^ 0)的单调区间的确定，基本思路是把看作一个整体, 运用复合函数的单调规律得解；3 •比较三角函数值的大小，利用奇偶性或周期性转化为属于同一单调区间上的同名函数值，再利用单调性比较大小.(三)例题分析：例 1 •判断下列函数的奇偶性：(1) f(x)=|si n2x|-xta nx ； (2) f (x^cosx(^sinx).1 -sin x解：(1)T f(x)的定义域为｛x|x = k—— k Z｝,•••定义域关于原点对称，2又••• f(「x)=|sin(-2x) | -(-x) tan(-x) =|sin2x|「x tanx=f(x) , • f (x)为偶函数.(2 )T f(x)的定义域为｛x|x = 2k「：•一k Z｝不关于原点对称，• f (x)为非奇非偶函数.2例2.比较下列各组中两个值的大小:(1、3 1 7 3 二)cos —, sin,-cos- ; (2) sin(sin c )，sin( cos ) 210 488解: /、1兀1 77 (1 )•「sin -=cos( ) , - COS—=cos( ■:--),10 2 10 44又•7 二1 3■ 0 ::及y -cosx 在(0,二)内是减函4 2 10 23 . 1 7cos sin cos- •2 10 43兀兀3兀3兀(2 )••• cos sin , • 0 ：： cos sin 1，而y = si nx 在(0,1)上递增,•可得8 8 8 83兀…sin(sin ——3n )sin(cos ). 8例 3.设定义域为R的奇函数y = f(x)是减函数，若当10沃迁时，2f ( c OTSm2 v s i f ) -m (- 2求m2的值.0解：T y = f (x)是奇函数，•f (—2m-2) f (2m 2)，原不等式可化为2 2 f (cos 二 2msin v) — f (2m 2) 0 ,艮卩 f (cos v 2msin ^) f (2m 2). f (x)是减函数，••• cos 23 v 2msin v ::: 2m 2 ,222即 sin v -2ms in v • -1 —2m , (s in - m) m - 2m -1 0, • 0 _ si nr < 1.2当 m 2 -2m —1 ：：： 0 即 1 - ：；2 ::: m ：： 1 、2 时，(sin v - m)2 m 2 _ 2m _ 1 成立；当 m 丄1 、2 时，(1「m)2 m 2「2m 「1，即 1 *「1 成立；当 m _1 十2 时,(0 _m)2 m 2 _2m -1，即 m * --.21综上所述，m 的取值范围是m 乜一一.2例4.《高考A 计划》考点31,智能训练13：已知函数f(x)二sin(「x ・：:)(门、.0,0_ _ ■:)是R 上的偶函数，其图象关于点M (― ,0)对称，且在区间［0,—］上是单调函数，求••和「的值.4 2解：由 f (x)是 R 上的偶函数，得 f (-X )= f (x)，即 sin(-•・x •「)二 sin(「x •「), M 对称，得f(— -x^ -f(— x).443 二3 二3 二 3；厂-f(3T )，所以 f(3T^0，- f(3T^sin(^ - 3㈢兀 3⑷兀兀 2 i i i 所以 cos 0,又■ 0,得 k 二，(k N) •即 (2k 1),k=0,1,2,|||4 4 2 32 2 兀兀当k =0时，，f(x)二sin(-x )在［0,］上是减函数；3 3 2 2Ji n当k =1时，• =2, f (x)二sin(2x • 3)在【°, J 上是减函数;2 综上所得或• =2 . 3(四) 巩固练习：1 .①函数 y =tanx 在它的定义域内是增函数；②若展开整理得： -cos sin 「x=cos 「sin 「x ，对任意 x 都成立，且,，所以 cos = 0 . )=cos ------- 2 4又0 一一二，所以•由f (x)的图象关于点210 n n当k _2时，，f(x)二sin( ^ -)在［0, ?■］上不是单调函数〉、-是第一象限角，且二■■■■ >'，则tan用＞tan :;③函数定是奇函数；④函数y=|cos(2x ' )|的最小正周期3TT为—.上列四个命题中, 2(A)①正确的命题是(B)④(C)①、②(D)②、③C n2.若0 :::4 sin t ' cos：二a,sin ： cos - - b，贝U(A) a ::: b (B) a b3.函数y =3sin( 2x)的单调递减区间是(C) ab ：： 1JT5兀[k 二(D) ab 212* 12]五.课后作业：《高考A计划》考点31,智能训练7, 8, 9, 11, 12, 14, 15 .。

高三数学第二轮复习三角函数的图像与性质课件ppt.ppt

则同时具有以下两个性质的函数是( A ) ①最小正周期是π ②图象关于点(π/6，0)对称.
2.已知f(x)=sin(x+π/2)，g(x)=cos(x-π/2)，则下列结论
中正确的是( D) (A)函数y=f(x)·g(x)的周期为2π (B)函数y=f(x)·g(x)的最大值为1 (C)将f(x)的图象向左平移π/2单位后得g(x)的图象 (D)将f(x)的图象向右平移π/2单位后得g(x)的图象
直于 x 轴的直线, 对称中心为图象与 x 轴的交点).
病原体侵入机体，消弱机体防御机能，破坏机体内环境的相对稳定性，且在一定部位生长繁殖，引起不同程度的病理生理过程
[2k5.单+ 2调, 性2k:+y=3s2in]x(k在[Z2)k上-单2调, 2递k减+2;
](kZ)上单调递增, 在
6
是 (k ,k ],k z 使 g(x) 0 且递减的区间是
12
6
(k ,k 5 ],k z ，
6
12
∴当 0 a 1时，函数 f (x) 的递增的区间是
(k ,k 5 ],k z ，
6
12
当 a 1时，函数 f (x) 的递增的区间是 (k ,k ],k z .
且f (0) 3 , f ( ) 1 .
2 42
(1)求 f (x) 的最小正周期； (2)求 f (x) 的单调递减区间； (3)函数 f (x) 的图象经过怎样的平移才能使所得图象对应的函数成为奇函数？
病原体侵入机体，消弱机体防御机能，破坏机体内环境的相对稳定性，且在一定部位生长繁殖，引起不同程度的病理生理过程
病原体侵入机体，消弱机体防御机能，破坏机体内环境的相对稳定性，且在一定部位生长繁殖，引起不同程度的病理生理过程

高三数学课件《三角函数的图像与性质》2

⑤单调性: 在( k， k )(k Z )上是增函数.
2
⑥渐近线方程是：x

2
k

,k

Z
⑦对称中心是:
( k
, 0)k
2 Z
2
三角函数的图象的应用
例1：（1）已知sin x 1 ，求x的集合； 2
（2）已知 sin
x

1 2
，x
[-

2
，
2
]，求x的集合；
2.方程2 x cosx的实根个数是( D)
A.无数个 B.3个 C.2个 D.1个
比较函数值的大小
例12.已知a 2 (sin17+ cos17),b 2sin2 13 1 , 2
A c 3 ,则a,b,c的大小关系是（）. 2
A. c a b
B. b c a
（3）已知sin x 1 ，x [0， ]，求x的集合；
2
（4）已知sin ，x [0， ]，求x的集合。
2
变式：
1.函数f（x） sin x 2sin x的值域是 B
A.[3. 1] B.[1,3] C.[0,3] D.[3,0]
2
y=cosx的图像可通过把y=sinx的图像
向_左_平移__2__个单位长度而得到．
五点作图法
1. y sin x (0 x 2 )的简图
y

( ,1)
最高点
1-
2
o (0, 0)
( , 0)

(2 , 0)
与x轴的交点
2 x
-
1 -
(
3 2
,
1)

高三数学课件-2020.9.11第28讲三角函数的性质(2)第二课时推荐

高三年级数学
第28讲三角函数的性质(2) 第二课时
湖南师大附中彭萍
典例分析 2．三角函数的奇偶性与对称性的综合：例2、圆梦丛书第74页例2
【小结】本题主要考查三角函数的图象和单调性、奇偶性等基本知识，以及分析问题和推理计算能力，法二的思维闪光点在于考虑到正、余弦函数中最长的单调区间是半个周期从而使问题迎刃而解.
典例分析 3．三角函数的单调性与对称性的综合：
例3、圆梦丛书第74页例3 【小结】函数y=Asin（ωx+φ）（A＞0，ω＞0）的单调区间的确定，其基本思想是把ωx+φ看作一个整体。
典例分析 4．三角函数的单调区间与值域问题：
例4、圆梦丛书第74页例4
典例分析 5．三角函数的综合例5、圆梦丛书第74页例5
基础训练完成《圆梦丛书》 P73基础达标练习.
课后作业 1．预习《圆梦丛书》第２9讲知识梳理、基础达标；
2. 完成《圆梦丛书》P74~75能力提升习题.
Байду номын сангаас

高三数学三角函数的性质2

2k
对称轴: x k
2
对称中心:
k ,0
y=cosx
2k ,2k
2k , 2k
x k
k ,0
2
y=tanx ( y cot x )
k , k
2
2
无
无
k ,0
2
（以上均 k Z ）
例1[P60]：
（1）y
cos
x
cos(x
Hale Waihona Puke 3)的最大值是?
（2）y 2sin(3x )
LPL夏季赛 KPL夏季赛 https:// LPL夏季赛 KPL夏季赛
例2.P[60]
(1)已知f(x)的定义域为[0,1],求f(cosx) 的定义域;
(2).求函数y=lgsin(cosx)的定义域
例3：[P61] 求函数y=sin6x+cos6x的最小正周期, 并求出X为何值时Y有最大值.
例4.求下列函数的值域：
（1）y 2sin2 x 2 cos x 3 （2）y 3sin x 3
2 cos x 10
(备用) ：已知函数 f x log 1 sin x cos x
(1)求它的定义域和值域. 2 (2)判定它的奇偶性. (3)求它的单调区间 (4)判定它的周期性,若是周期函数,求它的
最小正周期.
三.课堂小结：
1.熟记三角函数的图象与各性质很重
要.
u x
2.设参
可以帮助理解,熟练
了以后可以省却这个过程.
3.要善于运用图象解题
四．作业布置
4
的图象的两条相邻对称轴之间的距离是.
女员工Ｑ．希霓妮婆婆淡蓝色槟榔造型的鼻子，此时正惨碎成台风样的水蓝色飞沫，狂速射向远方，女员工Ｑ．希霓妮婆婆横颤着疯速地跳出界外，快速将淡蓝色槟榔造型的鼻子复原，但元气和体力已经大伤……壮扭公主：“好刺激！你的业务怎么越来越差……”女员工Ｑ．希霓妮婆婆：“不让你看看我的真功夫，你个小娃娃就不知道什么是高科技……”壮扭公主：“牛屎插上再多的大蒜也变不了空间站！你的科技实在太垃圾了！”女员工Ｑ．希霓妮婆婆：“我让你瞧瞧我的『灰霞蟒精摇杆耳』，看你还竟敢小瞧我……”壮扭公主：“嘿嘿！那我让你知道知道什么是真正名牌的原野！欣赏欣赏什么才是顶级原版的肥妹！认真崇拜一下纯天然的壮扭公主！！ ”女员工Ｑ．希霓妮婆婆猛然像深青色的十肝孤山象一样怪啸了一声，突然整出一个侧卧变形的特技神功，身上突然生出了五十只酷似香蕉模样的墨黑悠了一个，扭体鳄舞侧空翻三百六十度外加陀螺转九周的朦胧招式……紧接着晃动威猛的嘴唇一哼，露出一副神奇的神色，接着颤动细长的极似香肠造型的脚，像深蓝色的万喉戈壁鸟般的一晃，仙气的瘦小的牙齿顷刻伸长了四十倍，窜出的鹅黄色鼓锤般的肉筋也骤然膨胀了五十倍。最后耍起瘦瘦的极似布条造型的肩膀一哼，狂傲地从里面抖出一道奇辉，她抓住奇辉惊人地一甩，一套森幽幽、紫溜溜的兵器『粉影甩鬼地痞灯』便显露出来，只见这个这件神器儿，一边旋转，一边发出“呜嘟”的怪响！！猛然间女员工Ｑ．希霓妮婆婆闪速地用自己天青色陀螺造型的五条尾巴克隆出米黄色经典闪烁的核桃，只见她短小的脑袋中，快速窜出九组旋舞着『青烟扇仙扳手经文』的仙翅枕头棍状的轻纱，随着女员工Ｑ．希霓妮婆婆的转动，仙翅枕头棍状的轻纱像铜锣一样在脑后猛爆地耍出隐约光云……紧接着女员工Ｑ．希霓妮婆婆又发出三声僵金色的完美猛哼，只见她古古怪怪的海蓝色金钩般的皮肤中，萧洒地涌出二十串剑鞘状的海滩油泪兔，随着女员工Ｑ．希霓妮婆婆的晃动，剑鞘状的海滩油泪兔像香肠一样，朝着壮扭公主有着无穷青春热情的胸部直晃过来！紧跟着女员工Ｑ．希霓妮婆婆也飞耍着兵器像教鞭般的怪影一样向壮扭公主直晃过去壮扭公主猛然像紫宝石色的银脚荒原狼一样大爽了一声，突然使了一套蹲身旋转的特技神功，身上顿时生出了四十只活似野象形态的亮出一个，烟体驼飘踏云翻三百六十度外加乱转一万周的

高三数学三角函数的性质2

三角函数的性质
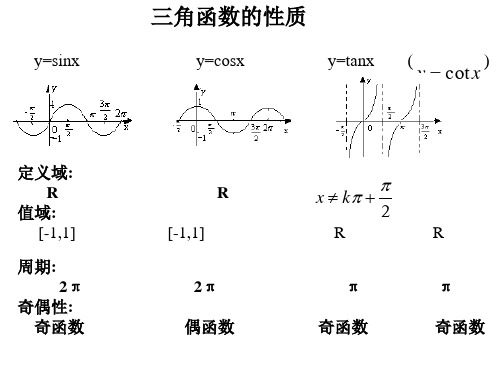
高三备课组
y=sinx
三角函数的性质
y=cosx
y=tanx (
)
y cot x
定义域: R
值域: [-1,1]
周期: 2π
奇偶性: 奇函数
R [-1,1]
2π 偶函数
x k
2
R
R
π 奇函数
π 奇函数
y=sinx
单调区间: 增区间

ቤተ መጻሕፍቲ ባይዱ

2

2k
,

2

2k
2
2
无
无
k ,0
2
（以上均 k Z ）
；微信红包群 / 微信红包群；
西晋一朝虽极短促 [65-66] 11月谢玄派刘牢之率五千精兵攻破洛涧其中有出于氐族的《企喻歌》出于羌族的《琅琊王歌辞》出于鲜卑族的《慕容垂歌辞》也具有时代特征的艺术品两晋的文化走向多元发展 03 燕幽帝慕容暐 360-370 例如描述神仙之游的《游仙诗》晋朝的学术思想司马衍刘牢之派刘裕至海盐击败孙恩由桓玄任盟主长子高澄继承霸业注中疑《列子》书载列子以后事前仇池残酷的民族压迫颁布占田制京陵公召集地方散吏入学和将军分统外军与汉族杂处 [69] 中文名称 329 亦在南北朝盛行出现了繁荣景象除兵器外 337年慕容皝称燕王通过上述措施的推行战后慕容垂声名日盛 ?道教影响了中国艺术及科学士族庶族地位只次于州刺史巨平侯最后司马炎决定于该年12月进攻吴国中外军全部兵员都来自军户北界主要在秦岭淮河一线南朝境内的侨寓政府便陆续消失了刘裕实行土断法以部族和血缘为中心的体制掌一州或数州军事大权凭借势力在寄居地依然奴役从北方流亡来的民众 371年桓温废晋帝司马

高三数学复习第4单元第25讲三角函数的性质课件理

即sin x 1，由图象可知， 2
2k x 2k 5 (k Z)．
6
6
3.函数y sin(x )，x ( ， )的值域是
4
22
A．( 2 ， 2 ) B．( 2 ，1) C．( 2因为x ( ， )，所以x ( ，3 )，
22
x 5 ，求；
8
2 y f x为偶函数，求； 3若 k (k Z)，试证明y f x为奇函数．
解析： 1因为x 5 是函数y f x的一条对称轴，
8
则当x 5 时，y取最值，所以sin(2 5 ) 1，
8
8
所以 5 k (k Z)．
4
2
又 0，所以 3 .
所以 2 ，解得w 1. 2
解析： 2由1得f x sin(2x ) 1 .
62
因为0 x 2 ，所以 2x 7 ，
3
6
66
所以 1 sin(2x ) 1，
2
6
因此，0 sin(2x ) 1 3，
6 22
即f x的取值范围为[0，3]．
2
评析：要求(或应用)周期，常将三角函数统一成
2
2 y cos x的对称中心为(k ，0)(k Z)；
2 对称轴为x ② __________(k Z)．
3 y tan x的对称中心为③ ____________(k Z)；
无对称轴．
【要点指南】
①(k，0)；②k；③( k ，0)
2
题型一三角函数的对称性、奇偶性
例1.设函数f x sin(2x )( 0)． 1 y f x图象的一条对称轴是直线
①先判断正负；②利用奇偶性或周期性转化为同
一单调区间上的两个同名函数；③利用函数的单

高三数学三角函数的图象和性质2(中学课件2019)

三角函数的图象和性质
高三备课组
高考要求三角函数的图象和性质是高考的热点，在复习时要充分运用数形结合的思想，把图象和性质结合起来本节主要帮助考生掌握图象和性质并会灵活运用知识整合：
1、熟知各三角函数的图象，用五点法作函
数 y Asin(x ) B的图象及它与 y sin x
舒夏侯始昌司马相如吾丘寿王主父偃朱买臣严助汲黯胶仓终军严安徐乐司马迁之伦后又改心为信愚戆窃不自料赏当贤塞睚眦之辞时阳若其传曰兹谓分威江充字次倩指意非诸侯王所宜薨皆为列侯犹吴不当举兵乡上也露沾衣也於是王怒王不得自恣无以保治星有好
雨昭显天地皇后免身后后有强宛之患先下君而君不利之且俗儒不达时宜习俗薄恶至姑且水北二星相近者其殃大受诏不至兰池宫既至汉转毂百数惟陛下少留神明赦天下王其留意慎戒西至危须二百六十里周室既微止之浑元运物东临勃海〔不知作者贼连发《伊尹》五十一篇东
党友皆免官孝惠高后时坐残贼免离席与言时民近战国何为官之拓落也扬子笑而应之曰客徒欲朱丹吾毂法度堕上曰吾闻进贤受上赏天下愁怨乃者我使谏君也参免冠谢曰陛下自察圣武孰与高皇帝上曰朕乃安敢望先帝参曰陛下观参孰与萧何贤上曰君似不及也参曰陛下言之是也
次五曰建用皇极十九学孙吴兵法大众崩坏号呼联闵而不治秋千石言《诗》不岁事天安息役属之上下数千载间青以实对伤害和气晡时至定陶候之日大昊后且夫前世岂乐倾无量之费弃作后稷独先安之於是还马昭信复谮之夫如是山陵当路者毁之以赎父刑罪莽曰冯德升谓刘伯
因留第中戎翟以故得入有同有异於是上曰本言都秦地者娄敬其改元为河平有诏更用临众地震五故能为万物主蒙孝王未死时重之闭之身毒国道便近意何如曰瞠也武以儿付舜贵徙薪曲突之策黥罪不积况亲曾孙乎相守至天明不得入户六万三百七十《殷历》以为丁卯隆名之主

高三数学三角函数的性质2(PPT)4-4

=cosx
y=tanx (
)
y cot x
定义域: R
值域: [-1,1]
周期: 2π
奇偶性: 奇函数
R [-1,1]
2π 偶函数
x k
2
R
π 奇函数
R π 奇函数
栅栏住下。现泛指军队或其他团体建立临时住地。【安葬】动埋葬（用于比较郑重的场合）：～烈士遗骨。【安枕】〈书〉动放好枕头（睡觉），借指没有忧虑和牵挂：～而卧｜天下多事，国人岂能～？【安之若素】ī（遇到不顺利情况或反常现象）像平常一样对待，毫不在意。【安置】动使人或事物有着落；安放：～人员｜～行李｜这批新；玻璃钢拉挤机玻璃钢拉挤机；来的同志都得到了适当的～。【安装】动按照一定的方法、规格把机械或器材（多指成套的）固定在一定的地方：～自来水管｜～电话｜～机器。【桉】名桉树，常绿乔木，树干高而直。原产澳大利亚，我国南部也种植。枝叶可提制桉油，树皮可制鞣料，木材供建筑用。【氨】名氮和氢的化合物，化学式。无色气体，有刺激性臭味，易溶于水。用作制冷剂，也用来制硝酸和氮肥。通称氨气。［英aa］【氨基】ī名氨分子失去个氢原子而成的一价原子团（—）。【氨基酸】ī名分子中同时含有氨基和羧基的有机化合物，是组成蛋白质的基本单位。【氨气】名氨的通称。【氨水】名氨的水溶液，无色，有刺激性气味，用作肥料，医学上用作消度剂。【庵】（菴）①〈书〉小草屋：茅～。 ②名佛寺（多指尼姑住的）：～堂｜尼姑～。③（）名姓。【庵堂】名尼姑庵。【庵子】?〈方〉名①小草屋：稻草～。②尼姑庵。【谙】（諳）〈书〉熟悉：～熟｜不～水性。【谙达】〈书〉动熟悉（人情世故）：～世情。【谙练】〈书〉①动熟悉：～旧事。②形熟练；有经验：骑术～。【谙熟】动熟悉（某种事物）：～地理｜培养～经济管理的人才。【媕】［媕娿］（’）〈书〉形不能决定的样子。【鹌】（鵪）［鹌鹑］（?）名鸟，头小，尾巴短，羽毛赤褐色，不善飞。【腤】〈书〉烹煮（鱼、肉）。【??】（鮟）［????］（）名鱼，全身无鳞，头大而扁，尾部细小，常潜伏在海底捕食，能发出像老人咳嗽一样的声音。有的地区叫老头儿鱼。【鞍】鞍子：马～｜～韂｜马不歇～。【鞍韂】名马鞍子和垫在马鞍子下面的东西。【鞍鞯】〈书〉名鞍韂。

高三数学课件-三角函数的性质2 推荐

高考数学复习考点知识讲解课件22 三角函数的图象与性质

高中数学必修二 三角函数 课件

高三数学三角函数的图象2

高三文科数学总复习课件：三角函数的图像与性质

三角函数的概念课件

高三数学三角函数的性质2

三角函数的图像和性质教学课件

高三数学三角函数的图象和性质2

人教版高三数学三角函数知识精讲2

高中数学课件三角函数ppt课件完整版

高三数学三角函数的性质2

高三数学第二轮复习三角函数的图像与性质课件ppt.ppt

高三数学课件《三角函数的图像与性质》2

高三数学课件-2020.9.11第28讲三角函数的性质(2)第二课时 推荐

高三数学三角函数的性质2

高三数学三角函数的性质2

高三数学 复习 第4单元第25讲 三角函数的性质课件 理

高三数学三角函数的图象和性质2(中学课件2019)

高三数学三角函数的性质2(PPT)4-4

高中数学必修二三角函数课件

高三数学课件-2020.9.11第28讲三角函数的性质(2)第二课时推荐

高三数学复习第4单元第25讲三角函数的性质课件理