《组合数学》模拟练习题
第七课二年级奥数组合数学练习题

一、空瓶子换饮料1、促销活动规定:3个空雪碧瓶子,可以换1瓶雪碧.如果买3瓶雪碧,那么,最多可以喝到__________瓶雪碧.(组合数学-空瓶子换饮料)空瓶子换饮料) A. 1 B. 3 C. 42、商店促销活动,用4个空瓶可以换1瓶水.老师和一些小朋友进店后,共买了7瓶水.如果每人喝1瓶水,那么最多有几人能喝到水?(组合数学-空瓶子换饮料)空瓶子换饮料) A. 7 B. 8 C. 9D.D. 103、师生共7人外出春游.到达后,老师要给每人买一瓶矿泉水.到商店后,他发现商店正在进行促销活动,在进行促销活动,规定每规定每3个空瓶可换1瓶矿泉水.瓶矿泉水.那么,老师最少买多少瓶矿泉水,那么,老师最少买多少瓶矿泉水,那么,老师最少买多少瓶矿泉水,就可就可以保证每人喝到一瓶?(组合数学-空瓶子换饮料)空瓶子换饮料) A. 5 B. 6 C.C. 74、促销活动规定:5个空可乐瓶子,可以换1瓶可乐.如果买5瓶可乐,那么,最多可以喝到__________瓶可乐.(组合数学-空瓶子换饮料)空瓶子换饮料) A. 1 B. 5 C. 6答案:CCAC二、过河问题1、有6个人要过河到对岸(从一个岸边到另一个岸边算渡河1次).现在只有1条小船,1个船夫,并且船上最多能容纳3个人.那么至少要渡河几次,6个人才能全部渡到对岸?(组合数学--过河问题)过河问题) A. 2 B. 3 C. 52、有8个人要过河到对岸(从一个岸边到另一个岸边算渡河1次).现在只有1条小船,并且最多能容纳3个人.那么至少要渡河几次,8个人才能全部渡到对岸?(组合数学--过河问题)河问题) A. 4 B. 5C. 73、果果、肉肉和豆豆,三人体重分别为40斤、50斤、90斤.三人要乘船到对岸(从一个岸边到另一个岸边算渡河1次)次)..现在只有1条小船,条小船,并且最多能承受并且最多能承受100斤.斤.那么至少要那么至少要渡河几次,三个人才能全部到达对岸?(组合数学--过河问题)过河问题)A. 2B. 3C. 54、有10个人要过河到对岸(从一个岸边到另一个岸边算渡河1次).现在只有1条小船,1个船夫,并且船上最多能容纳5个人.那么至少要渡河几次,10个人才能全部渡到对岸?(组合数学--过河问题)过河问题) A. 5 B. 3 C. 2答案:CBCA三、奇偶性的应用1、小马乐乐在草坪和花园之间来回奔跑.如果乐乐最初在草坪上,它第1次从草坪上跑到了花园里,第2次又从花园里跑到了草坪上……乐乐这样跑了9次之后,它跑到了草坪上,还是跑到了花园里?(组合数学--奇偶性的应用)奇偶性的应用)A. 草坪上草坪上B. 花园里花园里2、游乐园里有三个座位,牛牛开始坐在②号座位上,想了想就换到相邻的座位,想想又换到相邻的座位……那么牛牛换到第6次停下休息的时候,它坐在几号座位?(组合数学--奇偶性的应用)偶性的应用)A. ①B. ②C.C. ③3、3、元元在熊猫乐园里玩,但只能沿着黑色的线跑来跑去.但只能沿着黑色的线跑来跑去.若规定元元从一种颜色乐园跑若规定元元从一种颜色乐园跑到另一种颜色乐园叫跑一次,如果元元最初在紫色乐园,跑12次后,他最后跑到了哪种颜色乐园?(组合数学--奇偶性的应用)奇偶性的应用)A. 黄色乐园黄色乐园B. 蓝色乐园蓝色乐园C. 紫色乐园紫色乐园D. 绿色乐园绿色乐园4、4、小天鹅美美在一条小河的两岸之间来回的游.若规定美美从一岸游到另一岸叫渡河1次,如果美美最初在右岸,渡河8次后,美美游到了左岸,还是游到了右岸?(组合数学--奇偶性的应用)奇偶性的应用)A. 左岸左岸B. 右岸右岸 答案:BCCB四、奇偶性的袜子大法1、24+39的结果是奇数,还是偶数?(组合数学--奇偶性的袜子大法)奇偶性的袜子大法) A. 奇数奇数 B. 偶数偶数2、16-7的结果是奇数,还是偶数?(组合数学--奇偶性的袜子大法)奇偶性的袜子大法) A. 奇数奇数 B. 偶数偶数3、4735-2457的结果是奇数,还是偶数?(组合数学--奇偶性的袜子大法)奇偶性的袜子大法) A. 奇数奇数 B. 偶数偶数4、31+39的结果是奇数,还是偶数?(组合数学--奇偶性的袜子大法)奇偶性的袜子大法)A. 奇数奇数B. 偶数 答案:AABB五、奇偶性的捣蛋鬼大法1、8+7-6-5+4+3-2-1的结果是奇数,的结果是奇数,还是偶数?还是偶数?还是偶数?(组合数学(组合数学--奇偶性的捣蛋鬼大法) A. 奇数奇数 B. 偶数偶数2、凡凡第1天把4块糖放进盒子里,第2天从盒子里拿出2块糖,第3天又把4块糖放进盒子里,第4天又从盒子里拿出2块糖……过了几天后,盒子里会不会有21块糖?(组合数学--奇偶性的捣蛋鬼大法)奇偶性的捣蛋鬼大法) A. 会 B. 不会不会3、小山后的梨树结了50个梨.个梨.木木每天摘木木每天摘2个梨吃,个梨吃,过了若干天后,过了若干天后,过了若干天后,树上可能只剩树上可能只剩1个梨吗?(组合数学--奇偶性的捣蛋鬼大法)奇偶性的捣蛋鬼大法)A. 可能可能B. 不可能不可能4、9-8+7-6+5-4+3-2+1的结果是奇数,的结果是奇数,还是偶数?还是偶数?还是偶数?(组合数学(组合数学--奇偶性的捣蛋鬼大法)法) A. 奇数奇数 B. 偶数偶数 答案:BBBA六、画图推理1、跑步比赛的时候,小燕子、蒙蒙和大雁取得了前3名.其中小燕子在第2名,蒙蒙在第3名.根据条件,将小燕子、大雁和蒙蒙放到合适的位置.下列选项中,哪个是正确的呢?(组合数学--画图推理)画图推理)A.B.C.D.D.2、小燕子、大雁、蒙蒙、文文四个小朋友排成一队去游玩.小燕子排第二,大雁说:“我紧跟在蒙蒙的后面.”大雁排第几呢?(组合数学--画图推理)画图推理) A.B. 第二第二C. 第三第三D. 第四第四3、饭饭、旦旦、乐乐三个小朋友谈论谁的个子高.饭饭说:“旦旦比乐乐高.”旦旦说:“饭饭比乐乐高.”乐乐说:“饭饭比旦旦矮.”三个小朋友中,谁的个子最高呢?(组合数学--画图推理)画图推理) A. 饭饭饭饭 B. 旦旦旦旦 C.C. 乐乐乐乐4、跑步比赛的时候,小燕子、蒙蒙和大雁取得了前3名.其中小燕子在第2名,蒙蒙在第3名.根据条件,将小燕子、大雁和蒙蒙放到合适的位置.下列选项中,哪个是正确的呢?(组合数学--画图推理)画图推理)A.A.B.B.C.C.D.D.答案:DDBB七、有关时间的认识1、以下哪个日期是不可能出现的?(组合数学--有关时间的认识)有关时间的认识) A. 6月30日 B. 5月31日 C. 3月31日 D. 2月30日2、2013年1月1日是星期二,这个月有几个星期日呢?(组合数学--有关时间的认识)A. 3B. 4C.C. 53、2012年伦敦奥运会是闰年,那么,2014年是闰年吗?(组合数学--有关时间的认识)有关时间的认识) A. 是 B. 不是不是4、以下哪个日期是不可能出现的?(组合数学--有关时间的认识)有关时间的认识) A. 5月31日 B. 4月31日 C. 2月29日 D. 8月31日 答案:DBBB八、公元年的认识1、如下图,是公元年的时间轴,那么,公元前5年的时间点,可能在A 点,还是在B 点?(组合数学--公元年的认识)公元年的认识)A. A 点B.B. B 点2、公元123年,乐乐8岁了,乐乐出生在哪年?(组合数学--公元年的认识)公元年的认识) A. 公元前131年 B. 公元131年C. 公元前115年D. 公元115年3、公元前5年,发生了地震.2年后是哪年呢?(组合数学--公元年的认识)公元年的认识) A. 公元前7年 B. 公元7年 C. 公元3年 D. 公元前3年4、如下图,是公元年的时间轴,那么,公元15年的时间点,可能在A 点,还是在B 点?(组合数学--公元年的认识)公元年的认识)A. A 点B. B 点 答案:BDDA九、列表推理1、文文、星星和旦旦住在三层小楼里,每人单独住一层,文文住在下层,旦旦不住在中层.那么,旦旦住在哪层呢?(组合数学--列表推理)列表推理)A. 上层上层B. 中层中层C. 下层下层2、李阿姨、张阿姨、赵阿姨三人中,一位是演员,一位是工程师,一位是教师.、李阿姨、张阿姨、赵阿姨三人中,一位是演员,一位是工程师,一位是教师. 已知:(1)李阿姨比教师体重重;)李阿姨比教师体重重; (2)赵阿姨和教师体重不同;)赵阿姨和教师体重不同; (3)李阿姨和演员是朋友.)李阿姨和演员是朋友. 那么,赵阿姨的职业是什么呢?(组合数学--列表推理)列表推理)A. 工程师工程师B. 教师教师C. 演员演员3、有三户人家,每户有一个小孩.他们的名字是:旦旦(女)、文文(女)、亮亮(男),孩子的爸爸是老杨、老曹和老陈.孩子的爸爸是老杨、老曹和老陈.现在知道:(1)老杨家的孩子参加了少年女子体操队;)老杨家的孩子参加了少年女子体操队; (2)老曹的女儿不是旦旦.)老曹的女儿不是旦旦.那么,亮亮是谁家的孩子?(组合数学--列表推理)列表推理)A. 老杨老杨B. 老陈老陈C. 老曹老曹4、饭饭、小燕子和大雁在一座三层小楼里住着,每人单独住一层,饭饭住在下层,大雁不住在中层.那么,大雁住在哪层呢?(组合数学--列表推理)列表推理)A. 上层上层B. 中层中层C.C. 下层下层 答案:ACBA十、共用火柴棒1、用4根火柴棒能摆一个正方形.如果要摆出三个这么大的正方形,最少还需要增加几根火柴棒?(组合数学--共用火柴棒)共用火柴棒)A. 4B. 8C. 10D. 62、用4根火柴棒能摆一个正方形.如果要摆出四个这么大的正方形,最少还需要增加几根火柴棒?(组合数学--共用火柴棒)共用火柴棒)A. 8B. 9C. 12D. 163、最少拿掉几根火柴棒,可以使下图正好构成三个正方形?(组合数学--共用火柴棒)共用火柴棒)A. 4B. 3C. 2D. 14、用4根火柴棒能摆一个正方形.如果要摆出两个这么大的正方形,最少还需要增加几根火柴棒?(组合数学--共用火柴棒)共用火柴棒)A. 2B. 3C. 4D.D. 5 答案:DADB十一、别闲着1、豆豆看电视需要35分钟,吃花生需要30分钟,做完这两件事最少需要几分钟?(组合数学--别闲着)别闲着)A. 30B. 65C. 352、豆豆起床后做事.刷牙洗脸需要6分钟,烤面包需要10分钟,吃面包需要4分钟.那么,豆豆最少用几分钟才能做完所有事情?(组合数学--别闲着)别闲着) A. 20B. 10C.C. 143、小熊用一个平底锅煎饼,每次能同时放两块饼,煎一块饼需要4分钟(正、反面各需2分钟).小熊煎完2块饼至少需要几分钟?(组合数学--别闲着)别闲着)A. 4B. 6C. 84、乐乐洗碗需要20分钟,听音乐需要16分钟,做完这两件事最少需要几分钟?(组合数学--别闲着)别闲着)A. 16B. 20C. 36答案:CCAB十二、木板问题1、给一块小木板的两面刷漆,刷一面漆需要1分钟,但必须等到2分钟漆干后才能给另一面刷漆.那么刷完1块这样的小木板最少需要几分钟?(组合数学--木板问题)木板问题)A. 2B. 4C. 62、给一块小木板的两面刷漆,刷一面漆需要1分钟,但必须等到3分钟漆干后才能给另一面刷漆.那么刷完5块这样的小木板最少需要几分钟?(组合数学--木板问题)木板问题)A. 25B. 5C. 10 3、给一块小木板的两面刷漆,刷一面漆需要1分钟,但必须等到4分钟漆干后才能给另一面刷漆.那么刷完3块这样的小木板最少需要几分钟?(组合数学--木板问题)木板问题)A. 6B. 8C. 184、给一块小木板的两面刷漆,刷一面漆需要1分钟,但必须等到5分钟漆干后才能给另一面刷漆.那么刷完1块这样的小木板最少需要几分钟?(组合数学--木板问题)木板问题)A. 7B. 12C.C. 2答案:BCBA十三、节省等候时间1、豆豆和乐乐排队去取餐.豆豆取餐需要3分钟,分钟,乐乐取餐需要乐乐取餐需要2分钟.如果豆豆先付款,那么乐乐的等候时间是几分钟?(组合数学--节省等候时间)节省等候时间)A. 5B. 3C. 2D. 82、豆豆和乐乐排队去取餐.豆豆取餐需要1分钟,乐乐取餐需要2分钟.那谁先付款,另一个人的等候时间比较短?(组合数学--节省等候时间)节省等候时间)A. 豆豆豆豆B. 乐乐乐乐 3、豆豆和乐乐排队去取餐.豆豆取餐需要3分钟,分钟,乐乐取餐需要乐乐取餐需要10分钟.分钟.如果要使俩人所如果要使俩人所花的时间总和最短,那最短时间是几分钟?(组合数学--节省等候时间)节省等候时间)A. 13B. 16C. 234、豆豆和乐乐排队去取餐.豆豆取餐需要5分钟,分钟,乐乐取餐需要乐乐取餐需要2分钟.如果豆豆先取餐,那么乐乐的等候时间是几分钟?(组合数学--节省等候时间)节省等候时间)A. 12B. 5C. 7D. 2答案:BABB十四、扫雷游戏规则1、这是一张地雷分布图,其中A 的周围是哪几格?(组合数学--扫雷游戏规则)扫雷游戏规则)A. B 、C 、H 、G 、KB. B 、C 、D 、E 、FC. B 、C 、D 、E 、F 、G 、H 、KD. B 、H 、G2、这是一张地雷分布图,其中既在A 的周围,又在D 的周围的是哪几格?(组合数学--扫雷游戏规则)雷游戏规则)A. B 、KB. B、C、E、FC. E、F、PD. B、E、H3、这是一张地雷分布图,☆代表的数是几?(组合数学--扫雷游戏规则)扫雷游戏规则)A. 1B. 2C. 3D. 4扫雷游戏规则)4、这是一张地雷分布图,其中A的周围是哪几格?(组合数学--扫雷游戏规则)A. BB. B、FC. E、FD. B、E、F答案:ABBD十五、扫雷游戏1、这是一张地雷分布图.请把确定有地雷的格子全找出来.(组合数学--扫雷游戏)扫雷游戏)A. A、B、C、D、K、H、G、FB. A、B、C、D、FC. A、B、C、DD. A、B、C2、这是一张地雷分布图.下面哪个选项是正确的?(组合数学--扫雷游戏)扫雷游戏)A. “△”处一定有地雷.“△”处一定有地雷.B. “☆”和“□”处一定有地雷.“☆”和“□”处一定有地雷.C. “☆”和“△”处一定有地雷.“☆”和“△”处一定有地雷.D. “△”和“□”处一定有地雷.“△”和“□”处一定有地雷.3、这是一张地雷分布图.共有几个地雷?(组合数学--扫雷游戏)扫雷游戏)A. 0B. 2C. 3D. 44、这是一张地雷分布图.请把确定有地雷的格子全找出来.(组合数学--扫雷游戏)扫雷游戏)A. A 、C 、EB. A 、C 、E 、FC. A 、F 、E 、D 、CD. A 、C 、E 、F 、D 、H答案:AABC十六、认识奇偶点1、下面哪个点是奇点?(组合数学--认识奇偶点)认识奇偶点)A.A.B.B.2、下面哪个点是奇点?(组合数学--认识奇偶点)认识奇偶点)A.A.B.B.3、下图中共有__________个奇点.(组合数学--认识奇偶点)认识奇偶点)A. 0B. 1C. 24、下面哪个点是奇点?(组合数学--认识奇偶点)认识奇偶点)A.A.B.B.答案:ABCB十七、一笔画与奇偶点1、下面选项中,哪个图形不能一笔画成?(组合数学--一笔画与奇偶点)一笔画与奇偶点)A.A.B.B.C.C.D.D.2、下面选项中,哪个图形能一笔画成?(组合数学--一笔画与奇偶点)一笔画与奇偶点)A.A.B.B.C.C.3、下图从哪一点出发就可以一笔画成?(组合数学--一笔画与奇偶点)一笔画与奇偶点)A. A 或BB. A 或B 或C 或DC. D 或ED. A 或B 或C 或D 或E 或F 或G4、下面选项中,哪个图形不能一笔画成?(组合数学--一笔画与奇偶点)一笔画与奇偶点)A.A.B.B.C.C.D.D.答案:DADC 十八、多笔画转为一笔画1、下图最少需要几笔画完成?A. 1B. 2C. 32、最少去掉几条线,下图就没有奇点了?、最少去掉几条线,下图就没有奇点了?A. 1B. 2C. 0 3、最少去掉几条线,下图就可以一笔画成了?A. 0B. 1C. 24、下图最少需要几笔画完成?A. 2B. 1C. 3答案:BBBA 十九、实物图转化为点线图十九、实物图转化为点线图1、在一个公园的湖里,有4个小岛,它们之间共有4座桥.将实物图画成点线图.下列选项中正确的是哪个?(组合数学--实物转化为点线图)实物转化为点线图)A.A.B.B.2、下图是乡间的一条小河,上面建有A 、B 、C 、D 、E 、F 、G 七座桥, 你能一次不重复地走遍所有的桥吗?(每座桥最多只能走一次,可以在岛和陆地上重复地走.(组合数学--实物转化为点线图)转化为点线图)A. 能B. 不能不能 3、在一个公园的湖里,有4个小岛,它们之间共有6座桥.如果游客想一次不重复地走完所有的桥,应该从哪个岛出发?(组合数学--实物转化为点线图)实物转化为点线图)A. 岛A 或岛CB. 岛B 或岛DC. 岛A 或岛BD. 岛C 或岛D4、在一个公园的湖里,有4个小岛,它们之间共有6座桥.将实物图画成点线图.下列选项中正确的是哪个?(组合数学--实物转化为点线图)实物转化为点线图)A.A.B.B.答案:BBDB。
高二数学组合与组合的运用试题答案及解析

高二数学组合与组合的运用试题答案及解析1.某班有4个空位,安排从外校转来的3个学生坐到这4个空位上,每人一个座位,则不同的坐法有()A.24种B.43种C.34种D.4种【答案】A【解析】由题意得,每人一个座位,也就是从从4个座位选3个,然后分配到3个学生,则不同的坐法 =24种.故选:A.【考点】排列组合.2. 9件产品中,有4件一等品,3件二等品,2件三等品,现在要从中抽出4件产品来检查,至少有两件一等品的抽取方法是()A.B.C.D.【答案】D【解析】至少有两件一等品包括三种情况,第一种是恰有两件一等品,有种方法;第二种是恰有三件一等品,有种方法; 第三种是恰有四件一等品,有种方法;所以共有种方法,答案选D.【考点】排列组合3. 9件产品中,有4件一等品,3件二等品,2件三等品,现在要从中抽出4件产品来检查,至少有两件一等品的抽取方法是()A.B.C.D.【答案】D【解析】分为三类,第一类,2件一等品2件非一等品有不同取法,第二类,3件一等品1件非一等品有不同取法,第三类,4件一等品0件非一等品有不同取法,根据分类计数原理知,至少有两件一等品的不同抽取方法有++种,故选D.【考点】计数原理;组合知识4.已知,则= 。
【答案】4或9【解析】由组合数性质知:或解得:或【考点】组合数性质5.将一枚硬币连掷5次,如果出现k次正面向上的概率等于出现k+1次正面向上的概率,那么k的值为()A.0B.1C.2D.3【答案】C【解析】正面向上的次数满足二项分布,且有,由题意知,可得,那么,所以.【考点】二项分布,组合数的性质.6.某医院有内科医生5名,外科医生6名,现要派4名医生参加赈灾医疗队,如果要求内科医生和外科医生中都有人参加,则有种选法(用数字作答).【答案】310【解析】此题用间接法比较简单,从11人任选4人的方法有,其中只有内科医生的方法,只有外科医生的方法,所以按要求的方法种数为.【考点】组合及组合数的计算7.从2,3,4,5,6,7,8,9这8个数中任取2个不同的数分别作为一个对数的底数和复数,则可以组成________个不同的对数值.【答案】52【解析】C85=56,又log24=log39,又log39=log24,log23=log49,log49=log23所以可以组成52个对数值.8. 7名志愿者安排6人在周六、周日参加上海世博会宣传活动,若每天安排3人,则不同的安排方案有________种(用数字作答).【答案】140【解析】分两步:第一步,安排周六,有C种方案;第二步,安排周日,有C43种方案,故共有C73C43=140(种)不同的安排方案.9.某区有7条南北向街道,5条东西向街道(如图).则从A点走到B点最短的走法有________种.【答案】210【解析】每条东西向街道被分成6段,每条南北向街道被分成4段,从A到B最短的走法,无论怎样走,一定包括10段,其中6段方向相同,另4段方向也相同,每种走法,即是从10段中选出6段,这6段是走东西方向的(剩下4段是走南北方向的),共有C106=C104=210(种)走法.10.某地政府召集5家企业的负责人开会,已知甲企业有2人到会,其余4家企业各有1人到会,会上有3人发言,则这3人来自3家不同企业的可能情况的种数为________.【答案】16【解析】分两类:①含有甲C21C42,②不含有甲C43,共有C21C42+C43=16种.11.电脑系统中有个“扫雷”游戏,要求游戏者标出所有的雷,游戏规则是:一个方块下面有一个雷或没有雷,如果无雷,掀开方块下面就会标有数字(如果数字是0,常省略不标),此数字表明它周围的方块中雷的个数(至多八个),如图甲中的“3”表示它的周围八个方块中有且仅有3个雷.图乙是张三玩的游戏中的局部,根据图乙中信息,上方第一行左起七个方块中(方块上标有字母),能够确定下面一定没有雷的方块有,下面一定有雷的方块有 .(请填入所有选定方块上的字母)图甲图乙【答案】BDEF(3分);AC(2分)【解析】图乙中最左边的“1”和最右边的“1”,可得如下推断:由第三行最左边的“1”,可得它的上方必定是雷,最右边1的右边是雷,所以,E,F下均无雷。
排列与组合练习题

排列与组合练习题排列与组合是数学中常见的概念,它们在生活中也有着广泛的应用。
通过排列与组合的练习题,我们可以锻炼我们的逻辑思维能力,提高解决问题的能力。
下面我将给大家分享一些有趣的排列与组合练习题。
1. 假设有5个不同的水果,分别是苹果、香蕉、橙子、草莓和葡萄。
现在要从中选出3个水果,问有多少种不同的选法?解析:这是一个组合问题,可以使用组合公式进行计算。
根据组合公式,C(n, k) = n! / (k! * (n-k)!),其中n为总数,k为选取的数目。
将题目中的数据代入公式,可得C(5, 3) = 5! / (3! * (5-3)!) = 10。
所以,有10种不同的选法。
2. 在一家餐厅里,有7道菜可以选择。
现在要点一份主菜和两份配菜,问有多少种不同的点菜方式?解析:这是一个排列问题,可以使用排列公式进行计算。
根据排列公式,A(n, k) = n! / (n-k)!,其中n为总数,k为选取的数目。
将题目中的数据代入公式,可得A(7, 1) * A(6, 2) = 7! / (7-1)! * 6! / (6-2)! = 7 * 6 * 5 = 210。
所以,有210种不同的点菜方式。
3. 一家超市有8种不同的饮料,现在要选择3种饮料放入购物篮中,问有多少种不同的选择方式?解析:这是一个组合问题,可以使用组合公式进行计算。
根据组合公式,C(n, k) = n! / (k! * (n-k)!),其中n为总数,k为选取的数目。
将题目中的数据代入公式,可得C(8, 3) = 8! / (3! * (8-3)!) = 56。
所以,有56种不同的选择方式。
4. 某班有10个学生,其中3个是男生,7个是女生。
现在要从中选出3个学生组成一个小组,问有多少种不同的选择方式?解析:这是一个组合问题,可以使用组合公式进行计算。
根据组合公式,C(n, k) = n! / (k! * (n-k)!),其中n为总数,k为选取的数目。
组合数学第一章习题解答

1.34 在r,s,t,u,v,w,x,y,z的排列中,求y居x和z中间的排 列数。 解:2*7! 1.35 凸十边形的任意三条对角线不共点,试求这凸十边形 的对角线交于多少个点(交点指内部交点,顶点及外部交点除 外)。
任意4点的两条对角线有一个交点, C(10,4)
1.36 试证一整数是另一整数的平方的必要条件是除尽它的 数的数目是整(奇)数。 解:如果一个数能写成另一个整数的平方的形式。则
C(n, r) =
n C(n −1 r −1),1 ≤ r ≤ n , r
n ! n(n −1 )! = (n − r)!r! (n − r)(n − r −1 r! )! n (n −1 )! n = = C(n −1 r) , n − r (n − r −1 r! n − r )!
1.31 试证任意r个相邻数的连乘 (n+1)(n+2)...(n+r)=(n+r)!/n!被r!除尽。 从n+r个元素中取r个的组合数,C(n+r,r)=(n+r)!/n!r! 1.32 在a,b,c,d,e,f,x,x,x,y,y的排列中,要求y必须夹在 两个x之间,问这样的排列数等于多少? 7!把xyxyx看作一个元素来看待。 1.33 已知r,n,k都是正整数,r≥nk,将r个无区别的球放在 n个有标志的盒子里,每盒至少k个球,试问有多少种方案? C(n+r-nk-1,r-nk)
1.8、求1040和2030的公因数数目。 解: 等价于求(2×5)40和(2×2×5)30 的公因数数目。 C(40,1)+C(40,1)C(30,1)+C(30,1)+1=40+1200+30=1271 C(41,1)C(31,1)=1271 1.9、试证n2的整除数的数目是奇数。
组合实际问题解答练习题

组合实际问题解答练习题组合实际问题是数学中的一个重要概念,它在各个领域都有广泛的应用。
本文将介绍一些实际问题,并给出解答练习题,以帮助读者更好地理解和应用组合实际问题。
问题一:某超市有5种不同的水果,小明要买3种水果,他有多少种不同的选择?解答:根据组合实际问题的定义,我们可以使用组合数来解决这个问题。
假设超市的5种水果分别为苹果、香蕉、橙子、葡萄和樱桃。
小明要买3种水果,可以将问题转化为从5种水果中选取3种的问题,即求解C(5, 3)。
根据组合数的计算公式,C(n, r) = n! / (r! * (n-r)!),我们可以计算出C(5, 3) = 5! / (3! * 2!) = 10。
所以小明有10种不同的选择。
问题二:一个班级有10个男生和8个女生,班委会要选出3名男生和2名女生组成小组,有多少种不同的选法?解答:这个问题可以用组合数来解决。
选出3名男生可以从10个男生中选取3个,选出2名女生可以从8个女生中选取2个。
因此,问题可以转化为求解C(10, 3) * C(8, 2)。
计算C(10, 3) = 10! / (3! * 7!) = 120,C(8, 2) = 8! / (2! * 6!) = 28。
所以最终的结果为120 * 28 = 3360。
所以班委会有3360种不同的选法。
问题三:一家餐厅提供4种主菜和3种甜点,小明想点一道主菜和一道甜点,他有多少种选择?解答:这个问题类似于排列组合的问题,小明需要从4种主菜中选取一种,从3种甜点中选取一种,因此他的选择数为4 * 3 = 12。
所以小明有12种不同的选择。
问题四:某公司有8个部门,需要从这些部门中选出3个部门组成一个项目小组,其中至少有一个财务部门和一个人力资源部门,有多少种不同的选法?解答:这个问题可以用组合实际问题的思路来解决。
首先,从8个部门中选取1个财务部门有8种选择,从剩下的7个部门中选取1个人力资源部门有7种选择。
五个人住三个房间的排列组合题

五个人住三个房间的排列组合题全文共四篇示例,供读者参考第一篇示例:在生活中,我们经常会遇到排列组合的问题,比如在旅游时安排房间或者在团队活动中分配任务等等。
今天,我们就来探讨一个具体的排列组合问题:五个人住三个房间的问题。
我们将会从不同角度分析这个问题,探讨不同的排列组合方式,以及相关的数学原理和逻辑推理。
希望通过本文的阐述,能够对读者对排列组合问题有更深入的认识和理解。
让我们来看看这个问题的具体情境。
假设有五个人,分别是A、B、C、D、E,他们需要安排住宿,有三个房间可以使用。
现在就是要想办法将这五个人分配到三个房间中,使得每个房间至少有一个人,且不考虑房间的大小和舒适度。
在这种情况下,我们可以分析出不同的排列组合方式来满足这一条件。
我们来分析每个房间可能的人数组合。
由于每个房间至少有一个人,所以可能的人数组合为(1, 1, 3)、(1, 2, 2)和(1, 1, 1, 2)。
根据这个思路,我们可以将排列组合问题分解为三个子问题:将五个人分成1、1、3这样的组合、将五个人分成1、2、2这样的组合,以及将五个人分成1、1、1、2这样的组合。
接下来,我们逐一分析这三种情况。
首先考虑将五个人分成1、1、3这样的组合。
这种情况下,我们首先要选出一个人作为第一个房间的居住者,然后再从剩下的四个人中选出一个人作为第二个房间的居住者,剩下的三个人自然就是第三个房间的居住者。
根据排列组合的计算公式,这种情况下的排列数为5*4*3=60种。
接着考虑将五个人分成1、2、2这样的组合。
同样地,我们先选出一个人作为第一个房间的居住者,然后再从剩下的四个人中选出两个人作为第二个房间的居住者,剩下的两个人自然就是第三个房间的居住者。
根据排列组合的计算公式,这种情况下的排列数为5*4/2=30种。
最后考虑将五个人分成1、1、1、2这样的组合。
同样地,我们先选出一个人作为第一个房间的居住者,然后再从剩下的四个人中选出一个人作为第二个房间的居住者,再从剩下的三个人中选出一个人作为第三个房间的居住者,剩下的一个人自然就是第四个房间的居住者。
组合数学(3)

的不同的完美覆盖的个数?
解:因为是4×4棋盘,肯定能够完美覆盖。每
个骨牌覆盖2个方格,共需要8个骨牌;现在
将这8个骨牌的放置情况做下列分类: 1)8个骨牌全部水平放置, 有一种情况。
1
2) 8个骨牌中有6个水平放置,2个垂直放置,
共有四种情况。
则:
S = S1×S2
要精通加法原理和乘法原理,可以通过尝
试解决大量问题来实现。
10
设A,B为二不同类事件,若事件A有m种产生 方式,事件B有n种产生方式,则“事件A与
事件B” 有mn种产生方式
用集合论的术语,乘法原理也可描述如下:
设S,T为二集,若S为m元集,T为n元集,则
S与T的叉积之集合S×T为mn元集。
19
例7 一个由张一,王二,李三,赵四,刘五和陈六组 成的六人委员会要选出一个主席,一个秘书 和一个会计。 (a) 有多少种选择?
(b)如果张一或王二必须是主席,有多少种选法?
(c) 如果刘五必须任三职之一,有多少种选法?
(d) 如果赵四和陈六必须任职,有多少种选法?
20
解:(a)运用乘法原理,可以通过三个连续的步
有3×5×4=60种可能。
23
(d) 我们把指派赵四,陈六和其他委员中的
一个为办公室人员看作由三个连续的步骤
组成:指定赵四,指定陈六,选择剩下的那个
办公室人员。指赵四有3种方法。一旦赵四被
指定,指定陈六有2种方法。一旦赵四和陈六
被指定,有4种方法选择剩下的那个办公室人
员。根据乘法原理,有3×2×4=24种可能的选
2)求小于10000的含0的正整数的个数
解:1)小于10000的不含1的正整数可看做4位数,
组合分解练习题

组合分解练习题组合分解是一种常见的数学问题解决方法,它可以帮助我们理解和解决一系列复杂的计算问题。
通过将问题分解为更小的部分,并将这些部分重新组合,我们可以更好地理解问题的本质,并找到解决问题的方法。
在本文中,将介绍一些组合分解的练习题,以帮助读者掌握这一重要的技巧。
1. 组合分解求和给定正整数n,求1到n之间所有整数的和。
我们可以将这个问题分解为求1到(n-1)之间所有整数的和,然后再加上n本身。
这是因为1到n之间的所有整数可以分解为1到(n-1)之间的整数再加上n本身。
因此,可以使用递归的方法来求解这个问题。
例如,当n=5时,1到5之间的所有整数的和为:1 + 2 + 3 + 4 + 5 = 15。
2. 组合分解求积给定正整数n,求1到n之间所有整数的积。
我们可以将这个问题分解为求1到(n-1)之间所有整数的积,然后再乘以n本身。
这是因为1到n之间的所有整数可以分解为1到(n-1)之间的整数再乘以n本身。
同样,可以使用递归的方法来求解这个问题。
例如,当n=4时,1到4之间的所有整数的积为:1 × 2 × 3 × 4 = 24。
3. 组合分解求组合数给定非负整数n和k,求组合数C(n, k)。
组合数表示从n个元素中取出k个元素的不同组合方式的数量。
我们可以将这个问题分解为求C(n-1, k-1)和C(n-1, k)两个组合数的和。
这是因为从n个元素中取出k 个元素的组合数可以分解为从(n-1)个元素中取出(k-1)个元素的组合数再加上从(n-1)个元素中取出k个元素的组合数。
例如,当n=5,k=3时,C(5, 3)表示从5个元素中取出3个元素的不同组合方式的数量。
根据组合数的计算公式,C(5, 3) = C(4, 2) + C(4, 3) = 6 + 4 = 10。
4. 组合分解求子集数量给定一个集合S,求其所有子集的数量。
一个集合的子集是指从该集合中取出任意个元素(包括空集和全集)所组成的集合。
华师网络2014年9月课程考试《组合数学》练习题库及答案

华中师范大学职业与继续教育学院 《组合数学》练习题库及答案一、选择题1. 把101本书分给10名学生,则下列说法正确的是()A.有一名学生分得11本书B.至少有一名学生分得11本书C.至多有一名学生分得11本书D.有一名学生分得至少11本书2. 8人排队上车,其中A ,B 两人之间恰好有4人,则不同的排列方法是()A.!63⨯B.!64⨯C. !66⨯D. !68⨯3. 10名嘉宾和4名领导站成一排参加剪彩,其中领导不能相邻,则站位方法总数为()A.()4,11!10P ⨯B. ()4,9!10P ⨯C. ()4,10!10P ⨯D. !3!14-4. 把10个人分成两组,每组5人,共有多少种方法()A.⎪⎪⎭⎫ ⎝⎛510B.⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛510510 C.⎪⎪⎭⎫ ⎝⎛49 D.⎪⎪⎭⎫ ⎝⎛⨯⎪⎪⎭⎫ ⎝⎛4949 5. 设x,y 均为正整数且20≤+y x ,则这样的有序数对()y x ,共有()个A.190B.200C.210D.2206. 仅由数字1,2,3组成的七位数中,相邻数字均不相同的七位数的个数是()A.128B.252C.343D.1927. 百位数字不是1且各位数字互异的三位数的个数为()A.576B.504C.720D.3368. 设n 为正整数,则∑=⎪⎪⎭⎫ ⎝⎛nk k n 02等于()A.n 2B. 12-nC. n n 2⋅D. 12-⋅n n9. 设n 为正整数,则()k k n k k n 310⎪⎪⎭⎫ ⎝⎛-∑=的值是()A.n 2B. n 2-C. ()n 2-D.010. 设n 为正整数,则当2≥n 时,∑=⎪⎪⎭⎫ ⎝⎛-nk k k 22=()A.⎪⎪⎭⎫ ⎝⎛3nB. ⎪⎪⎭⎫ ⎝⎛+21n C. ⎪⎪⎭⎫ ⎝⎛+31n D. 22+⎪⎪⎭⎫ ⎝⎛n 11. ()632132x x x +-中23231x x x 的系数是()A.1440B.-1440C.0D.112. 在1和610之间只由数字1,2或3构成的整数个数为() A.2136- B. 2336- C. 2137- D. 2337- 13. 在1和300之间的整数中能被3或5整除的整数共有()个A.100B.120C.140D.16014. 已知(){}o n n f ≥是Fibonacci 数列且()()348,217==f f ,则()=10f ()A.89B.110C.144D.28815. 递推关系3143---=n n n a a a 的特征方程是()A.0432=+-x xB. 0432=-+x xC. 04323=+-x xD. 04323=-+x x16. 已知()⋯⋯=⨯+=,2,1,0232n a n n ,则当2≥n 时,=n a ()A.2123--+n n a aB. 2123---n n a aC.2123--+-n n a aD. 2123----n n a a 17. 递推关系()⎩⎨⎧=≥+=-312201a n a a n n n 的解为()A.32+⨯=n n n aB. ()221+⨯+=n n n aC. ()122+⨯+=n n n aD. ()n n n a 23⨯+=18. 设()⋯⋯=⨯=,2,1,025n a n n ,则数列{}0≥n n a 的常生成函数是()A.x 215-B. ()2215x - C.()x 215- D. ()2215x -19. 把15个相同的足球分给4个人,使得每人至少分得3个足球,不同的分法共有()种A.45B.36C.28D.2020. 多重集{}b a S ⋅⋅=4,2的5-排列数为()A.5B.10C.15D.2021. 部分数为3且没有等于1的部分的15-分拆的个数为()A.10B.11C.12D.1322. 设n,k 都是正整数,以()n P k 表示部分数为k 的n-分拆的个数,则()116P 的值是()A.6B.7C.8D.923. 设A ,B ,C 是实数且对任意正整数n 都有⎪⎪⎭⎫ ⎝⎛⋅+⎪⎪⎭⎫ ⎝⎛⋅+⎪⎪⎭⎫ ⎝⎛⋅=1233n C n B n A n ,则B 的值是()A.9B.8C.7D.624. 不定方程1722321=++x x x 的正整数解的个数是()A.26B.28C.30D.3225. 已知数列{}0≥n n a 的指数生成函数是()()t t e e t E 521⋅-=,则该数列的通项公式是()A.n n n n a 567++=B. n n n n a 567+-=C. n n n n a 5627+⨯+=D. n n n n a 5627+⨯-=26、6名同学排成一排,其中甲,乙两人必须排在一起的不同排法有()种。
小学四年级数的组合练习题

小学四年级数的组合练习题标题:小学四年级数学练习题说明:本份小学四年级数学练习题共有四个小节,每个小节中包含多个题目,以提升学生在数学能力方面的掌握。
请学生们认真阅读题目并仔细计算,选择正确答案,并在答题纸上作答。
题目:第一节:加减法运算题目1:请计算出以下数学表达式的结果:a) 8 + 3 - 2 = ?b) 13 - 5 + 9 = ?c) 16 - 7 + 4 - 1 = ?d) 20 + 17 - 23 = ?题目2:将下列算术表达式用数字形式表示:a) 九十五减二十一等于多少?b) 三十二加七等于多少?c) 一百减二十一加五等于多少?d) 五十加三十减十二等于多少?第二节:乘法运算题目1:请计算出以下数学表达式的结果:a) 6 × 7 = ?b) 8 × 5 × 2 = ?c) 9 × 3 - 4 = ?d) 15 - 5 × 2 = ?题目2:将下列算术表达式用数字形式表示:a) 六十乘以四等于多少?b) 七十二减去六个九等于多少?c) 三十八减去四倍六等于多少?d) 九十五减去三倍五等于多少?第三节:除法运算题目1:请计算出以下数学表达式的结果:a) 18 ÷ 3 = ?b) 42 ÷ 6 ÷ 2 = ?c) 64 ÷ (8 - 3) = ?d) 30 ÷ 5 × 2 = ?题目2:将下列算术表达式用数字形式表示:a) 六十除以五等于多少?b) 九十二减去三倍四再除以二等于多少?c) 四十八减去三等于多少?d) 八十二除以九再乘以三等于多少?第四节:综合题题目1:小明一共有48本书,他想把这些书放在6个书架上。
每个书架上要放同样多的书,并且每个书架上的书数必须是偶数。
请问他应该将书怎么分才能满足条件?题目2:一个矩形花坛的长是8米,宽是5米。
如果要在花坛周围做一圈砖,每块砖的尺寸为0.4米 × 0.2米,问需要多少块砖?题目3:甲乙两个人比体重,甲的体重是乙的4/5,乙体重比甲轻了24千克,求甲的体重是多少千克?题目4:在一个花园里,有红色的花和白色的花,共有56朵。
高中试卷-6.2.2 组合及组合数(精讲)(含答案)
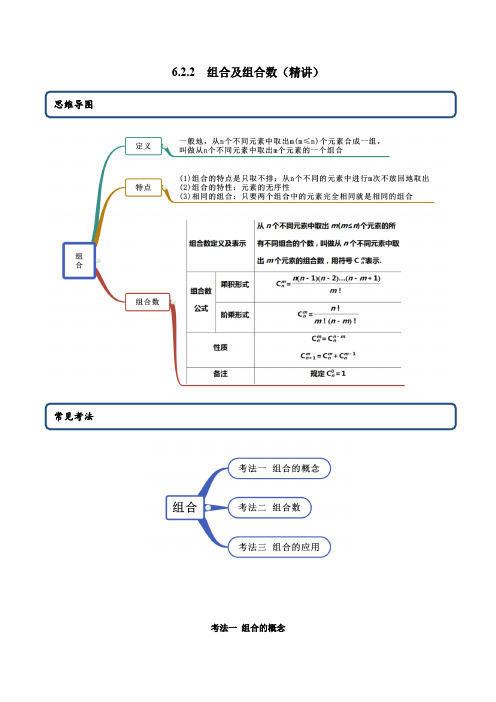
6.2.2 组合及组合数(精讲)考法一组合的概念【例1】(2020·广东湛江高二单元测试)给出下列问题:①有10个车站,共需要准备多少种车票?②有10个车站,共有多少中不同的票价?③平面内有10个点,共可作出多少条不同的有向线段?④有10个同学,假期约定每两人通电话一次,共需通话多少次?⑤从10个同学中选出2名分别参加数学和物理竞赛,有多少中选派方法?以上问题中,属于组合问题的是_________(填写问题序号).【答案】②④【解析】①有10个车站,共需要准备多少种车票?相当于从10个不同元素任取2个按一定顺序排列起来,属于排列问题;②有10个车站,共有多少中不同的票价?相当于从10个不同元素任取2个并成一组,属于组合问题;③平面内有10个点,共可作出多少条不同的有向线段?相当于从10个不同元素任取2个按一定顺序排列起来,属于排列问题;④有10个同学,假期约定每两人通电话一次,共需通话多少次?相当于从10个不同元素任取2个并成一组,属于组合问题;⑤从10个同学中选出2名分别参加数学和物理竞赛,有多少中选派方法?相当于从10个不同元素任取2个按一定顺序排列起来,属于排列问题;以上问题中,属于排列问题的是②④.【一隅三反】1.(2020·全国高二课时练习)以下四个问题中,属于组合问题的是()A.从3个不同的小球中,取出2个小球排成一列B.老师在排座次时将甲、乙两位同学安排为同桌C.在电视节目中,主持人从100名幸运观众中选出2名幸运之星D.从13位司机中任选出两位分别去往甲、乙两地【答案】C【解析】只有从100名幸运观众中选出2名幸运之星,与顺序无关,是组合问题.故选:C.2.(2020·全国高二课时练习)下列问题属于排列问题的是()①从10个人中选2人分别去种树和扫地;②从10个人中选2人去扫地;③从班上30名男生中选出5人组成一个篮球队;④从数字5,6,7,8中任取两个不同的数作为log a b中的底数与真数A.①④B.①②C.④D.①③④【答案】A【解析】排列的概念:从n 个元素中取()m m n £个元素,按照一定顺序排成一列,由题可知:①④中元素的选取有顺序,②③中元素的选取无顺序,由此可判断出:①④是排列问题,故选:A.考法二 组合数【例2】(1)(2020·广东云浮·高二期末)333345C C C ++=( )A .45C B .56C C .36C D .46C (2)(2020·湖北高二期末)满足条件23n n A C >的自然数n 有( )A .7个B .6个C .5个D .4个【答案】(1)D (2)C【解析】(2)333433434345445556C C C C C C C C C ++=++=+=.故选:D.(2)由23n n A C >得(1)(2)(1)321n n n n n --->´´,即8n <,又3n ³,且*n N Î,所以3,4,5,6,7n =.故选:C.【一隅三反】1.(2020·陕西高二期末)若()6671*n n n C C C n +-=ÎΝ,则n 等于( )A .11B .12C .13D .14【答案】B【解析】根据题意,6671n n n C C C +-=变形可得,6671n n n C C C +=+;由组合性质可得,6771n n n C C C ++=,即6711n n C C ++=,则可得到16712n n +=+Þ=.故选:B.2.(2020·林芝市第二高级中学高二期中)已知215n C =,那么2n A =( )A .20B .30C .42D .72【答案】B【解析】2156n C n =Þ=22630n A A == 答案选B3.设n 为满足不等式01222008nn n n n C C C nC ×+×<×+++的最大正整数,则n 的值为( ).A .11B .10C .9D .8【答案】D【解析】设0122nn n n n S C C C nC =+++×××+,则()()12012n n n n nn n S nC n C n C C --=+-+-+×××+,又r n rn nC C -=,01212222n n n n n n nn n S nC nC nC nC nC C n -\=++++++=×+,121n S n -\=×+,由2008S <得:122007n n -×<,72128=Q ,82256=,\78210242007´=<,89223042007´=>,n \的值为8.故选:D .4.(多选)下列等式正确的是( )A .()111mm nn n A A+++=B .()()!2!1n n n n =--C .!m m nnA C n =D .11m mn nA A n m+=-【答案】ABD【解析】A.11!(1)!(1)!(1)(1)()!()![(1)(1)]!mm n n n n n n A n A n m n m n m +++++=+×===--+-+,故正确;B.()()!(1)(2)3212!1(1)n n n n n n n n n --´´´´==---L ,故正确;C.!!m m m n nnA A C m n =¹,故错误;D.111!!(1)!()!m mn n n n A A n m n m n m n m +=×==-----,故正确.故选:ABD5.(多选)(2020·江苏省丰县中学高二期末)如下的四个命题中真命题的标号为( )A .97100162700C =B .3239910C C C +=C .12345678888888C C C C C C C 254++++++=D .10(12)x +的展开式中二项式系数最大的项是513579(4)5!x ´´´´【答案】BCD【解析】由于9731001001009998161700321C C ´´===´´,故A 错误;由组合数的性质:11mm mn nn C C C -++=,3239910C C C \+=,故B 正确;1234567808888888888C C C C C C C 22562254C C ++++++=--=-=,故C 正确;10(12)x +的展开式中二项式系数最大的项是5109876(2)5!x =´´´´513579(4)5!x ´´´´,故D 正确.故选: BCD考法三 组合应用【例3】男运动员6名,女运动员4名,其中男、女队长各1名.现选派5人外出参加比赛,在下列情形中各有多少种选派方法?(1)男运动员3名,女运动员2名;(2)至少有1名女运动员;(3)队长中至少有1人参加;(4)既要有队长,又要有女运动员.【答案】(1)120 (2)246 (3)196 (4)191【解析】(1)分两步完成:第一步,选3名男运动员,有C 36种选法;第二步,选2名女运动员,有C 24种选法.由分步计数原理可得,共有C 36· C 24=120(种)选法.(2)方法一 “至少有1名女运动员”包括以下四种情况:1女4男,2女3男,3女2男,4女1男.由分类计数原理可得总选法共有C 14C 46+C 24C 36+C 34C 26+C 44C 16=246(种).方法二 “至少有1名女运动员”的反面为“全是男运动员”,可用间接法求解.从10人中任选5人有C 510种选法,其中全是男运动员的选法有C 56种.所以“至少有1名女运动员”的选法有C 510-C 56=246(种).(3)方法一 (直接法)可分类求解:“只有男队长”的选法种数为C 48;“只有女队长”的选法种数为C 48;“男、女队长都入选”的选法种数为C 38,所以共有2C 48+C 38=196(种)选法.方法二 (间接法)从10人中任选5人有C 510种选法,其中不选队长的方法有C 58种.所以“至少有1名队长”的选法有C 510-C 58=196(种).(4)当有女队长时,其他人任意选,共有C 49种选法;当不选女队长时,必选男队长,共有C 48种选法,其中不含女运动员的选法有C 45种,所以不选女队长时的选法共有(C 48-C 45)种.所以既要有队长又要有女运动员的选法共有C 49+C 48-C 45=191(种).【一隅三反】1.(2020·江苏金湖中学)一个口袋内有3个不同的红球,4个不同的白球(1)从中任取3个球,红球的个数不比白球少的取法有多少种?(2)若取一个红球记2分,取一个白球记1分,从中任取4个球,使总分不少于6分的取法有多少种?【答案】(1) 13;(2) 22.【解析】(1 )从中任取3个球,红球的个数不比白球少的取法:红球3个,红球2个和白球1个.当取红球3个时,取法有1种;当取红球2个和白球1个时,.取法有213412C C =种.根据分类计数原理,红球的个数不少于白球的个数的取法有11213+=种.(2 )使总分不少于6分情况有两种:红球2个和白球2个,红球3个和白球1个.第一种,红球2个和白球2个,取法有223418C C =种;第二种,红球3个和白球1个,取法有31344C C =种,根据分类计数原理,使总分不少于6分的取法有18422+=种.2.(2020·云南省保山第九中学)某车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人.现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组中共抽取3名工人进行技术考核.(Ⅰ)求从甲、乙两组各抽取的人数;(Ⅱ)求从甲组抽取的工人中恰好1名女工人的概率;(Ⅲ)求抽取的3名工人中恰有2名男工人的概率.【答案】(Ⅰ)2,1;(Ⅱ)815;(Ⅲ)3175.【解析】(Ⅰ)因为车间甲组有10名工人,乙组有5名工人,所以甲、乙两组的比例是2:1,又因为从甲、乙两组中共抽取3名工人进行技术考核,所以从甲、乙两组各抽取的人数是2,1;(Ⅱ)因为车间甲组有10名工人,其中有4名女工人,所以从甲组抽取的工人中恰好1名女工人的概率1146210815p C CC==;(Ⅲ)因为车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人,所以求抽取的3名工人中恰有2名男工人的概率112166322121105105131475p C C C C C C C C C =+=.3.(2020·江苏高二)有男运动员6名,女运动员4名,其中男女队长各1名.选派5人外出比赛,在下列情形中各有多少种选派方法?(1)男运动员3名,女运动员2名;(2)至少有1名女运动员;(3)既要有队长,又要有女运动员.【答案】(1)共有3264120C C ·=(种)选法;(2)246;(3)191.【解析】⑴第一步:选3名男运动员,有36C 种选法.第二步:选2名女运动员,有24C 种选法.共有3264•120C C =(种)选法.⑵“至少1名女运动员”的反面为“全是男运动员”.从10人中任选5人,有510C 种选法,其中全是男运动员的选法有36C 种.所以“至少有1名女运动员”的选法有55106246C C -=(种).(3)当有女队长时,其他人选法任意,共有49C 种选法.不选女队长时,必选男队长,共有48C 种选法.其中不含女运动员的选法有45C 种,所以不选女队长时共有4485C C -种选法.故既要有队长,又要有女运动员的选法有444985191C C C +-=(种).。
组合数学(4)

可以把构造包含子串DEF的ABCDEF的排列看作四个
标号DEF,A,B,C的排列.由全排列定义,
6
四个对象有4!个排列。于是包含子串DEF的
ABCDEF的排列数为4!=24。
DEF A B C
例2:ABCDEF的包含字母DEF不间隔任意顺序
的排列有多少个?
7
我们可以通过两步来解决这个问题:选择字 母DEF为一个子字符串,构造DEF的一个任意 顺序的排列。由全排列定义,第一步有3!=6 种方法,根据例1,第二步可以有24种方法。根
1
种选择方法,由于必须分成两组,去掉其中的:
10 10 2 共有:1022种,又因为每个人 0 10
的年龄可以是1到60中的任意一个,年龄和可 能的分布共:60×10=600种,因此,相当于
1022个物体放在600个盒子,由鸽巢原理,至
少有两组分配在同一盒子中,在同一个盒子中
18
[解法二] 我们把不愿意彼此挨着座的两人设为: A, B 。假设A固定位置不动,B就不能排在 A的左右, A的左边只能余下的8个人,同时 A 的右边只能再余下的7个人, 其他7个位置的安排可以
. C 非B A 非B D . . . 。
19
是:7!种满足题意的 排法共: 8×7×7! =7×8!
20
生成n!个全排列的错位置排法
当n=1,排列方式只有一种,就是1。 当n=2时,先将唯一的1-排列1写出两次,并 错位置以2,即得两个2排列如下:
1
2 1
2
当n=3时,先将两个2-排列分别写出3次,共6次
21
并错位置以3, 即得3!=6个3排列如下:
1 2 132 3 1 2 3 2 1 231 2 1
数学组合综合练习题及答案

数学组合综合练习题及答案数学组合综合练习题及答案一、选择题1.某年级有6个班,分别派3名语文教师任教,每个教师教2个班,则不同的任课方法种数为( )A.C26C24C22 B.A26A24A22C.C26C24C22C33 D.A26C24C22A33[答案] A2.从单词“equation”中取5个不同的字母排成一排,含有“qu”(其中“qu”相连且顺序不变)的不同排法共有( )A.120种 B.480种C.720种 D.840种[答案] B[解析] 先选后排,从除qu外的6个字母中任选3个字母有C36种排法,再将qu看成一个整体(相当于一个元素)与选出的3个字母进行全排列有A44种排法,由分步乘法计数原理得不同排法共有C36A44=480(种).3.从编号为1、2、3、4的四种不同的种子中选出3种,在3块不同的土地上试种,每块土地上试种一种,其中1号种子必须试种,则不同的试种方法有( )A.24种 B.18种C.12种 D.96种[答案] B[解析] 先选后排C23A33=18,故选B.4.把0、1、2、3、4、5这六个数,每次取三个不同的数字,把其中最大的数放在百位上排成三位数,这样的三位数有( ) A.40个 B.120个C.360个 D.720个[答案] A[解析] 先选取3个不同的数有C36种方法,然后把其中最大的数放在百位上,另两个不同的数放在十位和个位上,有A22种排法,故共有C36A22=40个三位数.5.(2010湖南理,7)在某种信息传输过程中,用4个数字的一个排列(数字允许重复)表示一个信息,不同排列表示不同信息,若所用数字只有0和1,则与信息0110至多有两个对应位置上的数字相同的信息个数为( )A.10 B.11C.12 D.15[答案] B[解析] 与信息0110至多有两个对应位置上的数字相同的信息包括三类:第一类:与信息0110只有两个对应位置上的数字相同有C24=6(个)第二类:与信息0110只有一个对应位置上的数字相同有C14=4(个)第三类:与信息0110没有一个对应位置上的数字相同有C04=1(个)与信息0110至多有两个对应位置上的数字相同的信息有6+4+1=11(个)6.北京《财富》全球论坛开幕期间,某高校有14名志愿者参加接待工作.若每天排早,中,晚三班,每班4人,每人每天最多值一班,则开幕式当天不同的排班种数为( )A.C414C412C48 B.C1214C412C48C.C1214C412C48A33 D.C1214C412C48A33[答案] B[解析] 解法1:由题意知不同的排班种数为:C414C410C46=14×13×12×114!10×9×8×74!6×52!=C1214C412C48.故选B.解法2:也可先选出12人再排班为:C1214C412C48C44,即选B.7.(2009湖南理5)从10名大学毕业生中选3人担任村长助理,则甲、乙至少有1人入选,而丙没有入选的不同选法的种数为( ) A.85 B.56C.49 D.28[答案] C[解析] 考查有限制条件的组合问题.(1)从甲、乙两人中选1人,有2种选法,从除甲、乙、丙外的7人中选2人,有C27种选法,由分步乘法计数原理知,共有2C27=42种.(2)甲、乙两人全选,再从除丙外的其余7人中选1人共7种选法.由分类计数原理知共有不同选法42+7=49种.8.以一个正三棱柱的顶点为顶点的四面体共有( )A.6个 B.12个C.18个 D.30个[答案] B[解析] C46-3=12个,故选B.9.(2009辽宁理,5)从5名男医生、4名女医生中选3名医生组成一个医疗小分队,要求其中男、女医生都有,则不同的组队方案共有( )A.70种 B.80种C.100种 D.140种[答案] A[解析] 考查排列组合有关知识.解:可分两类,男医生2名,女医生1名或男医生1名,女医生2名,∴共有C25C14+C15C24=70,∴选A.10.设集合Ⅰ={1,2,3,4,5}.选择Ⅰ的两个非空子集A和B,要使B中最小的数大于A中最大的数,则不同的选择方法共有( ) A.50种 B.49种C.48种 D.47种[答案] B[解析] 主要考查集合、排列、组合的基础知识.考查分类讨论的思想方法.因为集合A中的最大元素小于集合B中的最小元素,A中元素从1、2、3、4中取,B中元素从2、3、4、5中取,由于A、B非空,故至少要有一个元素.1° 当A={1}时,选B的方案共有24-1=15种,当A={2}时,选B的方案共有23-1=7种,当A={3}时,选B的方案共有22-1=3种,当A={4}时,选B的方案共有21-1=1种.故A是单元素集时,B有15+7+3+1=26种.2° A为二元素集时,A中最大元素是2,有1种,选B的方案有23-1=7种.A中最大元素是3,有C12种,选B的方案有22-1=3种.故共有2×3=6种.A中最大元素是4,有C13种.选B的方案有21-1=1种,故共有3×1=3种.故A中有两个元素时共有7+6+3=16种.3° A为三元素集时,A中最大元素是3,有1种,选B的方案有22-1=3种.A中最大元素是4,有C23=3种,选B的方案有1种,∴共有3×1=3种.∴A为三元素时共有3+3=6种.4° A为四元素时,只能是A={1、2、3、4},故B只能是{5},只有一种.∴共有26+16+6+1=49种.二、填空题11.北京市某中学要把9台型号相同的电脑送给西部地区的三所希望小学,每所小学至少得到2台,共有______种不同送法.[答案] 10[解析] 每校先各得一台,再将剩余6台分成3份,用插板法解,共有C25=10种.12.一排7个座位分给3人坐,要求任何两人都不得相邻,所有不同排法的`总数有________种.[答案] 60[解析] 对于任一种坐法,可视4个空位为0,3个人为1,2,3则所有不同坐法的种数可看作4个0和1,2,3的一种编码,要求1,2,3不得相邻故从4个0形成的5个空档中选3个插入1,2,3即可.∴不同排法有A35=60种.13.(09海南宁夏理15)7名志愿者中安排6人在周六、周日两天参加社区公益活动.若每天安排3人,则不同的安排方案共有________种(用数字作答).[答案] 140[解析] 本题主要考查排列组合知识.由题意知,若每天安排3人,则不同的安排方案有C37C34=140种.14.2010年上海世博会期间,将5名志愿者分配到3个不同国家的场馆参加接待工作,每个场馆至少分配一名志愿者的方案种数是________种.[答案] 150[解析] 先分组共有C35+C25C232种,然后进行排列,有A33种,所以共有(C35+C25C232)A33=150种方案.三、解答题15.解方程Cx2+3x+216=C5x+516.[解析] 因为Cx2+3x+216=C5x+516,所以x2+3x+2=5x+5或(x2+3x+2)+(5x+5)=16,即x2-2x-3=0或x2+8x-9=0,所以x=-1或x=3或x=-9或x=1.经检验x=3和x=-9不符合题意,舍去,故原方程的解为x1=-1,x2=1.16.在∠MON的边OM上有5个异于O点的点,边ON上有4个异于O点的点,以这10个点(含O点)为顶点,可以得到多少个三角形?[解析] 解法1:(直接法)分几种情况考虑:O为顶点的三角形中,必须另外两个顶点分别在OM、ON上,所以有C15C14个,O不为顶点的三角形中,两个顶点在OM上,一个顶点在ON上有C25C14个,一个顶点在OM上,两个顶点在ON上有C15C24个.因为这是分类问题,所以用分类加法计数原理,共有C15C14+C25C14+C15C24=5×4+10×4+5×6=90(个).解法2:(间接法)先不考虑共线点的问题,从10个不同元素中任取三点的组合数是C310,但其中OM上的6个点(含O点)中任取三点不能得到三角形,ON上的5个点(含O点)中任取3点也不能得到三角形,所以共可以得到C310-C36-C35个,即C310-C36-C35=10×9×81×2×3-6×5×41×2×3-5×41×2=120-20-10=90(个).解法3:也可以这样考虑,把O点看成是OM边上的点,先从OM上的6个点(含O点)中取2点,ON上的4点(不含O点)中取一点,可得C26C14个三角形,再从OM上的5点(不含O点)中取一点,从ON上的4点(不含O点)中取两点,可得C15C24个三角形,所以共有C26C14+C15C24=15×4+5×6=90(个).17.某次足球比赛共12支球队参加,分三个阶段进行.(1)小组赛:经抽签分成甲、乙两组,每组6队进行单循环比赛,以积分及净剩球数取前两名;(2)半决赛:甲组第一名与乙组第二名,乙组第一名与甲组第二名作主客场交叉淘汰赛(每两队主客场各赛一场)决出胜者;(3)决赛:两个胜队参加决赛一场,决出胜负.问全程赛程共需比赛多少场?[解析] (1)小组赛中每组6队进行单循环比赛,就是6支球队的任两支球队都要比赛一次,所需比赛的场次即为从6个元素中任取2个元素的组合数,所以小组赛共要比赛2C26=30(场).(2)半决赛中甲组第一名与乙组第二名(或乙组第一名与甲组第二名)主客场各赛一场,所需比赛的场次即为从2个元素中任取2个元素的排列数,所以半决赛共要比赛2A22=4(场).(3)决赛只需比赛1场,即可决出胜负.所以全部赛程共需比赛30+4+1=35(场).18.有9本不同的课外书,分给甲、乙、丙三名同学,求在下列条件下,各有多少种分法?(1)甲得4本,乙得3本,丙得2本;(2)一人得4本,一人得3本,一人得2本;(3)甲、乙、丙各得3本.[分析] 由题目可获取以下主要信息:①9本不同的课外书分给甲、乙丙三名同学;②题目中的3个问题的条件不同.解答本题先判断是否与顺序有关,然后利用相关的知识去解答.[解析] (1)分三步完成:第一步:从9本不同的书中,任取4本分给甲,有C49种方法;第二步:从余下的5本书中,任取3本给乙,有C35种方法;第三步:把剩下的书给丙有C22种方法,∴共有不同的分法有C49C35C22=1260(种).(2)分两步完成:第一步:将4本、3本、2本分成三组有C49C35C22种方法;第二步:将分成的三组书分给甲、乙、丙三个人,有A33种方法,∴共有C49C35C22A33=7560(种).(3)用与(1)相同的方法求解,得C39C36C33=1680(种).。
华杯赛组合数学(杂题)练习题

第七部分:组合篇(杂题)1、【第18届华杯赛决赛A卷第2题】农谚‘逢冬数九’讲的是,从冬至之日起,每九天分为一段,依次称之为一九,二九,…,九九,冬至那天是一九的第一天.2012年12月21日是冬至,那么2013年的元旦是______九的第______天.2、【第18届华杯赛决赛A卷第9题】用四个数字4和一些加、减、乘、除号和括号,写出四个分别等于3,4,5和6的算式.3、【第18届华杯赛决赛A卷第12题】由四个相同的小正方形拼成右图.能否将连续的24个自然数分别放在图中所示的24个黑点处(每处放一个,每个数只使用一次),使得图中所有正方形边上所放的数之和都相等?若能,请给出一个例子;若不能,请说明理由.B、卷第2题】4、【第18届华杯赛决赛C农谚“逢冬数九”讲的是,从冬至之日起,每九天分为一段,依次称之为一九,二九,…,九九,冬至那天是一九的第一天.2012年12月21日是冬至,那么2013年的2月10日是______九的第______天.5、【第19届华杯赛决赛B A 、卷第6题】如右图,三个圆交出七个部分.将整数0~6分别填到七个部分中,使得每个圆内的四个数字的和都相等,那么和的最大值是______.6、【第19届华杯赛决赛A 卷第14题】在右边的算式中,字母d c b a 、、、和“□”代表十个数字0到9中的一个.其中d c b a 、、、四个字母代表不同的数字,求d c b a 、、、代表的数字之和.7、【第19届华杯赛决赛D B 、卷第13题】在右边的算式中,字母d c b a 、、、和“□”代表十个数字0到9中的一个.其中d c b a 、、、四个字母代表不同的数字,求d c b a 、、、代表的数字之和.8、【第19届华杯赛决赛C 卷第2题】在右边的算式中,每个汉字代表0至9这十个数字中的一个,相同汉字代表相同数字、不同汉字代表不同数字.则“数学竞赛”所代表的四位数是______.9、【第19届华杯赛决赛C 卷第9题】A、和C处.A处农场年产小麦50吨,B处有三个农场在一条公路边,分别在下图所示的B农场年产小麦10吨,C处农场年产小麦60吨.要在这条公路边修建一个仓库收买这些小麦.假设运费从A到C方向是每吨每千米1.5元,从C到A方向是每吨每千米1元.问仓库应该建在何处才能使运费最低?10、【第19届华杯赛决赛B卷第13题】如右图,圆周上均匀地标出十个点.将1~10这十个自然数分别放到这十个点上.用过圆心的一条直线绕圆心旋转,当线上没有标出的点时,就把1~10分成两组.对每种摆放方式,随着直线的转动有五种分组方式.对于每种分组都有一个两组数和的乘积,记五个积中最小的值为K.问所有的摆放中,K最大为多少?11、【第19届华杯赛决赛D卷第6题】如右图,三个圆交出七个部分.将整数1~7分别填到七个部分中,使得每个圆内的四个数字的和都相等,那么和的最大值是______.12、【第20届华杯赛决赛C卷第3题】将2015的十位、百位和千位的数字之和相加,得到的和写在2015个位数字之后,得到一个自然数20153,将新数的十位,百位和千位数字相加,得到的和写在20153的个位数字之后,得到201536,再操作两次,得到201536914,如此继续下去,共操作了2015次,得到一个很大的自然数,这个自然数所有数字之和等于______.13、【第20届华杯赛决赛C卷第8题】右边是一个算式,9个汉字代表数字1至9,不同的汉字代表不同的数字,则算式“盼×望+树×翠绿+天空×湛蓝”可能的最大值为______.14、【第20届华杯赛决赛C卷第14题】将530本书分给48名学生,至少有几名学生分到的书的数量相同?15、【第21届华杯赛决赛A卷第2题】中国北京在2015年7月31日获得了2022年第24届冬季奥林匹克运动会的主办权.预定该届冬奥会的开幕时间为2022年2月4日,星期______.(今天是2016年3月12日,星期六)16、【第21届华杯赛决赛A卷第6题】共有12名同学玩一种扑克游戏,每次4人参加,且任意2位同学同时参加的次数不超过1.那么他们最多可以玩______次.17、【第21届华杯赛决赛A卷第8题】两把小尺与一把大尺组成套尺,小尺可以沿着大尺滑动.大尺上每一个单位都标有自然数,第一把小尺将大尺上的11个单位等分为10,第二把小尺将大尺上9个单位等分为10,两A、两点间距离,A点在大尺的0单位把小尺的起点都为0,都分别记为1至10.现测量B处,B点介于大尺的18与19单位之间;将第一把小尺的0单位处于B点时,其单位3恰好与大尺上某一单位相合.如果将第二把小尺的0单位处置于B点,那么第二把小尺的______个单位恰好与大尺上某一单位相合.18、【第21届华杯赛决赛A卷第12题】将一个五边形沿一条直线剪成两个多边形,再将其中一个多边形沿一条直线剪成两部分,得到了三个多边形,然后将其中一个多边形沿一条直线剪成两部分,…,如此下去.在得到的多边形中要有20个五边形,则最少剪多少次?19、【第21届华杯赛决赛B卷第10题】商店春节促销,顾客每次购物支付现金时,每100元可得一张价值50元的代金券.这些代金券不能兑成现金,但可以用来购买商品,规则是:当次购物得到的代金券不能当次使用;每次购物支付的现金不少于购买商品价值的一半.李阿姨只有不超过1550元的现金,她能买到价值2300元的商品吗?如果能,给她设计一个购物方案;如果不能,说明理由.20、【第21届华杯赛决赛B卷第21题】现有下图左边所示的“四连方”纸片五种,每种的数量足够多.要在如下图右边所示的5×5方格网上,放“四连方”,“四连方”可以翻转,“四连方”的每个小方格都要与方格网的某个小方格重合,任意两个“四连方”不能有重叠部分.那么最少放几个“四连方”就不能再放了?21、【第21届华杯赛决赛C卷第2题】某月里,星期五、星期六和星期日各有5天,那么该月的第1日是星期______.22、【第21届华杯赛决赛C卷第13题】黑板上先写下一串数:1,2,3,…,100,如果每次都擦去最前面的6个,并在这串数的最后再写上擦去的6个数的和,得到新的一串数,再做同样的操作,直到黑板上剩下的数不足6个.问:(1)最后黑板上剩下的这些数的和是多少?(2)最后所写的那个数是多少?23、【第21届华杯赛决赛C卷第14题】数学竞赛,填空题8道,答对1题,得4分,未答对,得0分;问答题6道,答对1道,得7分,未答对,得0分.参赛人数400人,至少有多少人的总分相同?24、【第22届华杯赛决赛A 卷第7题,B 卷第6题】一列数,,,,,21⋅⋅⋅⋅⋅⋅n a a a 记)(i a S 为i a 的所有数字之和,如422)22(=+=S .若)()(,22,20172121--+===n n n a S a S a a a ,那么2017a 等于______.25、【第22届华杯赛决赛B A 、卷第9题】平面上有5条不同的直线,这5条直线共形成n 个交点,则n 有多少个不同的数值?26、【第22届华杯赛决赛A 卷第13题】班上共有60位同学,生日记为某月某号.问每个同学两个同样的问题:班上有几个人与你生日的月份相同?班上有几个人与你生日的号数相同(比如生日为1月12日与12月12日的号数是相同的).结果发现,在所得到的回答中包含了由0到14的所有整数,那么,该班至少有多少个同学生日相同?27、【第22届华杯赛决赛A 卷第14题】将1至9填入右图的网格中,要求每个格子填一个整数,不同格子填的数字不同,且每个格子周围的格子(即与该格子有公共边的格子)所填数字之和是该格子中所填数字的整数倍.已知左右格子已经填有数字4和5,问:标有字母X的格子所填的数字最大是多少?28、【第22届华杯赛决赛B卷第13题】一个正六边形被剖分成6个小三角形,如右图.在这些小三角形的7个顶点处填上7个不同的整数.能否找到一个填法,使得每个小三角形顶点处的3个数都按顺时针方向从小到大排列.如果可以,请给出一种填法;如果不可以,请说明理由.29、【第22届华杯赛决赛B卷第14题】7×7的方格网黑白染色,如果黑格比白格少的列的个数为m,黑格比白格多的行的个数为n,求nm 的最大值.。
组合数学练习题

组合数学练习题1. 将n 本书放在5个书架上,每个书架至少能够放n 本书. 问:(1) 将这n 本书放到这些书架上有多少种不同的方法?(2) 如果只考虑书架上书的数量,而不考虑哪本书放在什么地方,有多少种不同的方法?(基础)2.把n 个相异的球放到4个相异盒子1234,,,A A A A 中,求使得1A 含有奇数个球,2A 含有偶数个球的不同的放球方法数.(母函数)3.将充分多的苹果、香蕉、橘子和梨这4种水果装袋,要求各袋有偶数个苹果,最多2个橘子,3的倍数个香蕉,最多1个梨.如果每袋装n 个水果,求装袋的种类数.(母函数)4. 有多少个长度为n 的0与1串,在这些串中,既不包含子串010,也不包含子串101?(递推关系)5. 一个计算机系统把一个十进制数字串作为一个编码字,如果它包含偶数个0,就是有效的. 求有效的n 位编码字的个数n a .(递推关系)6.某人在距家以北n 个街区,以东n 个街区处工作,每天他走2n 个街区去上班.如果他从不穿越(但可以碰到)从家到工作地的对角线,那么他有多少条可能的道路?(基础,典型数列)7. 把 (4)n n 件彼此相异的物品分给甲、乙、丙三人,使得甲至少分得两件物品,乙和丙至少分得一件物品,有多少种不同的分法?(典型数列)8. n 个单位各派2名代表出席一个会议,2n 名代表围一圆桌坐下.试问:(1) 各单位代表入座的方案有多少种?(2) 各单位的2位代表不相邻的方案有多少种? (容斥原理)9.一部由1楼上升到10楼的电梯内共有n 位乘客,他们分别到5至10楼去,该电梯从5楼开始每层楼都停,以便让乘客决定是否离开电梯。
(1) 求n 位乘客离开电梯的不同方法的种数。
(2) 求每层楼都有人离开电梯的不同方法的种数。
(容斥原理)10.用四种颜色(红、蓝、绿、黄)涂染四台仪器A ,B ,C 和D 。
规定每台仪器只能用一种颜色并且任意两台仪器颜色都不能相同。
如果B 不允许用蓝色和红色,C 不允许用蓝色和绿色,D 不允许用绿色和黄色,问有多少种染色方案?(容斥原理,棋盘多项式)11. 某个宴会共有2n个人出席,每个人均至少认识其中的n个人. 证明:可安排这2n个人中的某4个人围圆桌而坐,使得每个人的旁边都是他所认识的人.(抽屉原理)12. 边长为1的正三角形内任选21n 个点,必有两点的距离小于等于1n.(抽屉原理)13. 用红、黄、蓝三种颜色对正六边形的顶点进行着色,共有多少种不同的方案?其中正六边形可以绕几何中心旋转或沿其对称轴翻转。
组合数学

《组合数学》 练习题一一、填空题1.从n 个不相同的元素里,每次取出m 个全不相同的元素,并且将这些元素放在圆周上进行排列,即排列好的元素列没有头尾,则其排列的个数为 。
2.计算⎥⎦⎤⎢⎣⎡-1n n = 。
3.在1和2000之间能被6整除但不能被15整除的正整数共有 个。
4.令1110()n n n n f x a x a x a x a --=++++,则()f x 的差分表中第1n +(1)n ≥+行为 .5.已知递推关系)3(1243321≥-+=---n a a a a n n n n 的一个特征根为2,则其通解为 。
6.在多项式()7521...x x x +++的展开式中的项534321x x x x 的系数是 。
7.计算⎭⎬⎫⎩⎨⎧24= 。
8.当1≥n 时,我们有 n D = (其中n D 表示集合},...,2,1{n 的更列的个数)。
9.在边长为1的正方形内任意放入5个点,则其中至少有两个点的距离小于 。
10.在1和2000之间能被6整除但不能被15整除的正整数共有 个。
二、选择题:1.百位数字不是1且各位数字互异的三位数的个数是 ( ).A 576B 504C 720D 3362.6321)32(x x x +-中23231x x x 的系数是( ) A 1440 B –1440 C . 0 D 13.递推关系⎩⎨⎧=≥+=-3)1( 2201a n a a n n n 的解为( )A 32+⋅=n n n aB 22)1(++=n n n aC 12)2(++=n n n aD n n n a 2)3(+=4.在32⨯矩形方格纸上,各个小正方形的顶点称为格点,则以格点为顶点的等腰直角三角形的个数为( ).A 24;B 38 ;C 46 ;D 50.5.设x ,y 均为正整数且y x +≤20,则这样的有序数对),(y x 共有( )个。
A 190B 200C 210D 2206. 从n 3个相邻的正整数中选出三个数,使它们的和能被3整除,共有不同选法种数为( ).A 33n C ; B 313)(C ; C 333n C ; D 3133)(3C C n +. 7. ABC ∆的三边长分别为3,5,7,则能覆盖此三角形的最小圆半径为( ).A 3.5;B 7 ;C 337 ;D 3314. 8. 由一个正方体的三个顶点所构成的正三角形的个数为( ).A 4;B 8 ;C 12 ;D 24.9. 8次射击,命中3次,其中恰有2次连续命中的情形共有( )种.A 15;B 30 ;C 48 ;D 60.10. 递推关系)3(4331≥-=--n a a a n n n 的特征方程是( )A 0432=+-x xB 0432=-+x xC 04323=+-x xD 04322=-+x x三、计算题1.求50!中2的最高次幂.2.求)(5x f 的展开式.3.从1至2000的整数中,至少能被2,3,5中的两个数整除的整数有多少个?4.一次宴会,7位来宾寄存他们的帽子,在取回他们的帽子时,问有多少种可能使得(1)没有一位来宾取回的是他自己的帽子?(2)至少有一位来宾取回的是他自己的帽子?5.解下列递推关系:⎩⎨⎧===≥+-=---.7,3,2),3( 485210321a a a n a a a a n n n n 6.设集合{0,1}S =,求在n 维向量1(,...,)n a a ,,1i a S i n ∈≤≤,中不许连续出现两个0的向量的取法数?7.求50!中2的最高次幂.8.求)(5x f 的展开式.9.设{1,2,...,2001}A =,是判断是否存在集合A 的分划1234A A A A A =⋃⋃⋃,其中集合(14)i A i ≤≤中各数字的和组成等差数列,并说明理由。
2015级组合数学复习题解答

解 设所求的数为an,则{an}的指母函数为
x2 x3 Ge ( x ) ( x )9 ( e x 1)9 2! 3! n 9 9 9 9 x ( 1)k e (9k ) x ( 1)k (9 k )n n! k 0 k k 0 k n 0
解得
13 3 65 13 3 65 n an (5 65) (5 65) n 52 52
20
12. 在一圆周上均匀地取2n个点,用n条两两 不相交的弦把这些点配成对,求所有这种配对的
方式数.
解 设所求配对的方式数为hn,则h1 = 1,则h0 = 1,
,v2k, ,v2n , 连接 设2n个点依次为 v1,v2, v1,v2k , 则将圆周一分为二,一边有2(k -1)个点,
中,要求a与b的个数之和为偶数,求这样的单词
的个数.
解 这样的单词有两类:一类包括偶数个a与 偶数个b;另一类包括奇数个a与奇数个b.设所求 的数为an,则{an}的指母函数为
2 3 x2 x4 x x Ge ( x ) (1 ) 2 (1 x ) 3 2! 4! 2! 3! 2 3 x 3 x5 x x (x ) 2 (1 x ) 3 3! 5! 2! 3!
x1 x2 x3 x4 x5 x6 x7 =14 x1 0,x7 0,xi 1, i 2, 3, , 62Fra bibliotek作变量代换
y1 x1,y7 x7,yi xi 1, i 2, 3, , 6
则原方程变成
y1 y2 y3 y4 y5 y6 y7 9 yi 0, i 1, 2, 3, , 7
高中数学练习题附带解析排列与组合的应用与计算

高中数学练习题附带解析排列与组合的应用与计算高中数学练习题附带解析——排列与组合的应用与计算在高中数学学习中,排列与组合是一个重要的概念。
排列是指从一组元素中选取若干个元素进行排列,并且排列的顺序很重要;组合是指在一组元素中选取若干个元素,组合的顺序不重要。
这两个概念在实际生活中也有广泛的应用。
本文将通过多道数学练习题来探讨排列与组合的应用与计算方法。
1. 排列的应用与计算方法题目:一家电影院有10个座位,有5个人来买票,其中3个人有特殊要求,必须坐在相邻的位置,问有多少种不同的就座方式?解析:首先,我们可以将这道题目看作是一个排列组合问题中的全排列问题。
因为这道题目中不同的“就座方式”就是从10个座位中选取5个人进行排序。
因此,全排列的结果为10 × 9 × 8 × 7 × 6。
此外,这道题目还有一个特殊的限制条件,即3个人必须坐在相邻的位置。
因此,我们需要把这3个人看成一个整体,把他们的全排列除以3!,即可得到他们的所有排列方式。
因此,最终的答案为:(10 × 9 × 8 × 7 ×6)/(3 × 2 × 1)= 5,040 种不同的就座方式。
2. 组合的应用与计算方法题目:从6个数中选出4个数,问有多少种不同的选法?解析:这道题目涉及到了组合,因为题目中不考虑数字的先后顺序,只关心选出的4个数。
因此,我们需要将这4个数看成一个组合体,从中选取出任意4个数的选法都算作一种结果。
这就是我们熟知的组合数学问题。
通过组合数学的公式,我们可以得到该问题的答案:C (6,4)= 15。
其中,C(n,m)表示从 n 个不同元素中取出 m 个不同元素的组合数。
3. 排列组合的综合应用题目:有8个人排成一列,其中有4个男生和4个女生,请问有多少种不同的排列方式,使得男女两个组内的人都不相邻?解析:这道题目中既有排列,又有组合,因此需要综合运用排列与组合的知识。
数字的拼排列与组合练习题

数字的拼排列与组合练习题1. 数字的拼排列与组合练习题2. 问题一:数字拼排列数字的拼排列是指将多个数字按照一定的规则组合起来,形成新的数字。
请按照以下拼排列规则完成练习题。
3. 一、给出数字1、2、3,请问可以组合成多少个不重复的两位数?4. 二、给出数字1、2、3、4,请问可以组合成多少个不重复的三位数?5. 三、给出数字1、2、3、4、5,请问可以组合成多少个不重复的四位数?6. 四、给出数字1、2、3、4、5、6,请问可以组合成多少个不重复的五位数?7. 答案及解析如下是每个练习题的答案与解析,以便核对和理解。
8. 问题一答案与解析:一、给出数字1、2、3,请问可以组合成多少个不重复的两位数?答案:共有6个不重复的两位数:12、13、21、23、31、32。
解析:在这个练习题中,我们需要考虑两位数的组合情况。
由于只给出了三个数字,所以每个两位数的十位数和个位数都需要从给定的数字中选择。
我们可以通过穷举法,将数字1、2、3分别放在十位和个位上,得到的所有结果即为答案。
考虑到没有重复的情况,最终得到了6个不重复的两位数。
9. 二、给出数字1、2、3、4,请问可以组合成多少个不重复的三位数?答案:共有24个不重复的三位数。
解析:在这个练习题中,我们需要考虑三位数的组合情况。
给出了四个数字,所以每个三位数的百位、十位和个位都需要从给定的数字中选择。
同样地,可以通过穷举法得到所有结果。
由于没有重复的要求,最终得到了24个不重复的三位数。
10. 三、给出数字1、2、3、4、5,请问可以组合成多少个不重复的四位数?答案:共有120个不重复的四位数。
解析:在这个练习题中,我们需要考虑四位数的组合情况。
给出了五个数字,每个四位数的千位、百位、十位和个位都需要从给定的数字中选择。
同样地,可以通过穷举法得到所有结果。
最终得到了120个不重复的四位数。
11. 四、给出数字1、2、3、4、5、6,请问可以组合成多少个不重复的五位数?答案:共有720个不重复的五位数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《组合数学》模拟练习题组合数学模拟练习题04一、 填空题1、 红、黄、蓝、白4个球在桌上排成一圈,有 种排法。
2、设P 、Q 为集合,则|P ∪Q| |P| + |Q|.3、0max i nn i≤≤⎧⎫⎛⎫=⎨⎬ ⎪⎝⎭⎩⎭。
4、设S = {1,2,3,4}中仅有2个定位的排列数N(2) = 。
5、依照字典序,排列(4576321)的下一个排列是 。
6.01.nk n k =⎛⎫= ⎪⎝⎭∑ 。
7. 72,0,1,3,1⎛⎫= ⎪⎝⎭.8. 366个人中必有 个人生日相同。
9、 (1,2,3,4)(4)D =的移位排列数。
10、解递推关系 f (r) – 4f (r-1) + 4f (r-2) = 2 r时,应设非齐次的特解为 。
11.的系数为的展开式中,34232641x x x x i i ⎪⎭⎫ ⎝⎛∑= 。
12. 在14个人中至少有 个人为同月份出生。
13. 解常系数线性齐次递推关系的常用方法称为 法 。
14. 记移位排列数为D(n),则r 定位排列数N(r) = 。
15.数值函数的推迟函数Sk(f)= 。
二、 单项选择题1、数值函数f = (1,1,1,...)的生成函数F(x) =( ) A 、(1+x)n B 、1-x C 、(1-x)-1D 、(1+x)-n2、递推关系f(n) = 4f(n -1)-4f(n -2)的特征方程有重根2,则( )是它的一般解 。
A 、C 12n -1+C 22n B 、(C 1+C 2n)2n C 、C(1+n)2n D 、C 12n +C 22n .3、由6颗不同颜色的珠子可以做成 ( )种手链。
A 、720B 、120C 、60D 、6 4、=⎪⎭⎫ ⎝⎛-∑=nk kk n 0)1(( )。
A 、2nB 、0C 、n2n -1D 、15、按照字典序,排列4517632的下一个排列是 ( ).A 、4571236B 、4517623C 、4576321D 、45213676、当r ≥k 时差分多项式P k (r) =( )A 、0B 、⎪⎭⎫ ⎝⎛k r C 、r(r -1)...(r -k+1) D 、!1k7、设F(x),G(x)分别是f 和g 的生成函数,则以下不成立的是( ) 。
A 、F(x)+G(x) 是f+g 的生成函数B 、F(x)G(x)是fg 的生成函数C 、x r F(x) 是S r (f)的生成函数D 、F(x)-xF(x) 是∇f 的生成函数.8、在无柄茶杯的四周画上四种不同的图案,共有( )种画法。
A 、24B 、12C 、6D 、39、=⎪⎭⎫ ⎝⎛∑=nk k n k 1( )。
A 、2n B 、0 C 、n2n -1 D 、110、设S={1,2,3,4,5,6,7},5-组合12367的下一个组合是 ( ).A 、12567B 、12376C 、12467D 、12456 三、 解答题1. 有4个相同的红球,5个相同的白球,那么这9个球有多少种不同的排列方式?2.公司有5台电视机,4台洗衣机,7台冰箱,现要把其中3台电视机,2台洗衣机,4台冰箱选送到展销会,试问有多少种选法?3.设S = {1, 3•2, 3•3, 2•4, 5}是一个多重集,那么由集合S的元素能组成多少个不同的四位数。
4. 09~用这十个数码,可以组成多少个恰有两个重复数码的三位数?5. 设S ={a, b, c, d, e},求S的所有3-组合(按字典序排列)。
6. 设集合S ={1, 2, 3, 4},按照字典序写出排列3124后的所有全排列。
7.试求在1到300之间那些不能被3, 5和7中任何一个整除的整数个数。
8. 数1, 2, 3, 4, 5, 6, 7, 8的全排列中,有4个数字在原来位置上,另外4个不在原来位置上的错排数目。
9. 一人在8小时内加工了40个零件,已知他在第一个小时内加工了6个零件,而最后一个小时内加工了4个零件。
证明一定存在连续的两个小时,这两个小时内至少加工了10个零件。
10. 证明在边长为2的正方形内任意5点必有两点,其距离不超过2。
11. 设数值函数 f = {1,7,72,73,...}, g ={1,6,62,63,...}, 求卷积f * g 的生成函数。
12. 用生成函数求下式之和:123123n n n n n n ⎛⎫⎛⎫⎛⎫⎛⎫⋅+⋅+⋅++⋅ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭13. 解非齐次递推关系1201693,20,1n n n a a a n a a --++=≥⎧⎨==⎩14. 解齐次递推关系120181601,0n n n a a a a a ---+=⎧⎨=-=⎩15.一教室有两排座位,每排8个,今有14名学生,5人总坐在前排,4人总在后排,问学生入座有几种方式?16. 将字母a,b,c,d,e,f,g 排成一行,使得模式beg 和cad 都不出现的排列总数是多少?17. 按照字典序写出集合S ={1,2,3,4}的前面12个全排列。
18. 求8个字母A 、B 、C 、D 、E 、F 、G 、H 的全排列中只有4个元素不在原来位置上的排列数。
19. 某次会议有10个代表参加,每一位代表至少认识其余9位中的一位,则10位代表中至少有两位代表认识的人数相等。
20. 求数值函数f = {1,-3,32,-33,...}的生成函数.21. 设初始值h(0) = 0, h(1) = 1,求解递推关系 h(n) = 5h(n -1)-6h(n -2). (n = 2,3,...)组合数学模拟练习题参考答案一、 填空题1、6;2、≤;3、2n n ⎛⎫⎪⎡⎤ ⎪ ⎪⎢⎥⎣⎦⎝⎭; 4、6 ;5、4612357.6、2 n ;7、420;8、2;9、9 ; 10、2012222rr rp p r p r ++11、60; 12、2; 13、特征方程; 14、)(r n D r n n -⎪⎭⎫ ⎝⎛- ;15、⎩⎨⎧≥--≤≤kr k r f k r )(100.二、 单项选择题1、C ;2、B ;3、C ;4、B ;5、D ;6、B ;7、B ;8、C ;9、C ; 10、D ;三、 解答题1. 解:设有限多重集S = {4•红球,5•白球}, 则9-重复排列数为:9!4!5!= 126.即9个球有126种不同的排列方式. 2. 解:547.324⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭电视机有种选法;洗衣机有种选法;冰箱有种选法由乘法法则得,5472100.324⎛⎫⎛⎫⎛⎫⨯⨯= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭共有种选法3. 解:从多重集{1, 3•2, 3•3, 2•4, 5}产生 无重复的四位数有:45P 个;有1个2-重复的四位数有:344!122!⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭个;有2个2-重复的四位数有:34!22!2!⎛⎫ ⎪⎝⎭个;有1个3-重复的四位数有:244!113!⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭个;共有120 + 216 + 18 + 32 = 386个四位数。
4. 解:991,2;11⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭第位重复有991,3;11⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭第位重复有 992,3;11⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭第位重复有99324311⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭共有个重复数码的三位数.5. 解:S ={a , b , c , d , e },按组合生成算法S 的所有3-组合:abc ->abd ->abe ->acd ->ace ->ade ->bcd ->bce ->bde ->cde6. 解:按照字典序排列算法,集合S ={1, 2, 3, 4}的3124后全排列为:3124->3142->3214->3241->3412->3421->4123->4132->4213->4231->4312->43217. 解:令A 1,A 2和A 3分别表示1到300之间能被3, 5和7整除的整数集合,则有123300300300||100,||60,||42,357A A A ⎡⎤⎡⎤⎡⎤======⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦121323300300300||20,||14,||8353757A A A A A A ⎡⎤⎡⎤⎡⎤⋂==⋂==⋂==⎢⎥⎢⎥⎢⎥⋅⋅⋅⎣⎦⎣⎦⎣⎦123300||2357A A A ⎡⎤⋂⋂==⎢⎥⋅⋅⎣⎦根据容斥原理知:123||300(1006042)(20148)2138.A A A ⋂⋂=-+++++-=8. 解:求8个数字全排列中只有4个数字不在原来位置上,其余4个数字保持不动,相当于4个数字的移位排列,其数目为:)8(.91412)2416121(24)!41!31!21!111(!4)4(分=+-=+-=+-+-=D故8个数字的全排列中只有4个数字不在原来位置上的排列数为63032456789!4!4!8)4(48=⋅⋅⋅⋅⋅=⋅=⎪⎭⎫ ⎝⎛D9. 解:去掉首尾两个小时,在其余6个小时内加工了30个零件,把这6个小时分成3个“连续的两个小时”(抽屉),根据抽屉原理:一定存在连续的两个小时,这两个小时内至少加工了10个零件。
10. 解:把边长为2的正方形,分成4个边长为1的小正方形,这4个小正方形组成4个抽屉,根据抽屉原理:正方形内任意5点必有两点落入一个小正方形内,而小正方形内两点间距离不超2(对角线长),所以正方形内必有两点,其距211. 解:数值函数f = {1,7,72,73,...}的生成函数223323()1777...1(7)(7)(7)...1.(|7|1)17F x x x x x x x x x=++++=++++=<-数值函数f = {1,6,62,63,...}的生成函数223323()1666...1(6)(6)(6)...1.(|6|1)16F x x x x x x x x x=++++=++++=<-所以卷积 f * g 的生成函数为1(16)(17)x x --. 12. 解:设数值函数{,,,,,}0123n n n n n f n ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭其生成函数23()(1)0123n n n n n n n F x x x x x x n ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+++++=+ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭两边对x 求导211()23(1)123n n n n n n F x x x n x n x n --⎛⎫⎛⎫⎛⎫⎛⎫'=+⋅+⋅++⋅=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭令 x = 1 得1232123n n n n n n n n -⎛⎫⎛⎫⎛⎫⎛⎫+⋅+⋅++⋅= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭13. 解:特征方程为:x 2 + 6x + 9 = 0 解得特征根为- 3, - 3. 因此齐次通解 (A + Br) (-3) r设非齐次的特解为 C , 代入递推关系式有 C + 6C + 9C = 3所以特解为316C =非齐次的通解3()(3)16r r a A Br =+-+为一般解,由边界条件得30163()(3)116A A B ⎧+=⎪⎪⎨⎪+-+=⎪⎩解此线性方程组得唯一解 31,1612A B =-=- 因此所求的解为313(3)(3)161216r r r a r =----+14. 解:特征方程为:x 2-8x + 16 = 0 解得特征根为4, 4.因此 a r = (A + Br)4r 为一般解,由边界条件得1()40A AB =-⎧⎨+=⎩解此线性方程组得唯一解 A = -1, B = 1因此所求的解为 (1)4rra r =-+15. 解:由5人总坐在前排,在前排选5个座位,有C 85 5!种坐法;由4人总坐在后排,在后排选4个座位,有C84 4!种坐法;在余下的7个座位中选5个座位,给余下的5人坐,有C75 5!种坐法;所以学生入座共有C85 5! C84 4! C75 5! = 28449 792 000种方式.16 . 解:仅有beg模式,或cad模式的排列数都是P(5,5)=5!(将模式捆在一起视为一个元素,再和其余4个元素构成5个元素的全排列)。
