数学实验答案-1
2021版高考数学一轮总复习第十一章计数原理和概率题组训练85n次独立重复试验与二项分布理20210

2021版高考数学一轮总复习第十一章计数原理和概率题组训练85n 次独立重复试验与二项分布理2021051541341.下列表中能成为随机变量X 的分布列的是( )答案 C2.袋中有大小相同的红球6个、白球5个,从袋中每次任意取出1个球,直到取出的球是白球时为止,所需要的取球次数为随机变量ξ,则ξ的可能值为( ) A .1,2,…,6 B .1,2,…,7 C .1,2,…,11 D .1,2,3,…答案 B解析 除白球外,其他的还有6个球,因此取到白球时取球次数最少为1次,最多为7次.故选B.3.若某一随机变量X 的概率分布如下表,且m +2n =1.2,则m -n2的值为( )X 0 1 2 3 P0.1mn0.1 A.-0.2 C .0.1 D .-0.1答案 B解析 由m +n +0.2=1,m +2n =1.2,可得m =n =0.4,m -n2=0.2.4.已知随机变量X 的分布列为P(X =k)=12k ,k =1,2,…,则P(2<X≤4)等于( )A.316B.14C.116D.516答案 A解析 P(2<X≤4)=P(X =3)+P(X =4)=123+124=316.5.若随机变量X 的分布列为则当P(X<a)=0.8A .(-∞,2] B .[1,2] C .(1,2] D .(1,2)答案 C解析 由随机变量X 的分布列知:P(X<-1)=0.1,P(X<0)=0.3,P(X<1)=0.5,P(X<2)=0.8,则当P(X<a)=0.8时,实数a 的取值范畴是(1,2].6.袋中有大小相同的5只钢球,分别标有1,2,3,4,5五个号码,任意抽取2个球,设2个球号码之和为X ,则X 的所有可能取值个数为( ) A .25 B .10 C .7 D .6答案 C解析 X 的可能取值为1+2=3,1+3=4,1+4=5=2+3,1+5=6=4+2,2+5=7=3+4,3+5=8,4+5=9.7.甲、乙两队在一次对抗赛的某一轮中有3个抢答题,竞赛规定:关于每一个题,没有抢到题的队伍得0分,抢到题并回答正确的得1分,抢到题但回答错误的扣1分(即得-1分).若X 是甲队在该轮竞赛获胜时的得分(分数高者胜),则X 的所有可能取值是________. 答案 -1,0,1,2,3解析 X =-1,甲抢到一题但答错了;X =0,甲没抢到题,或甲抢到2题,但答时一对一错;X =1时,甲抢到1题且答对或甲抢到3题,且一错两对;X =2时,甲抢到2题均答对;X =3时,甲抢到3题均答对.8.已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球,现从甲、乙两个盒内各任取2个球.设ξ为取出的4个球中红球的个数,则P(ξ=2)=________. 答案310解析 ξ可能取的值为0,1,2,3,P (ξ=0)=C 32C 42C 42C 62=15,P (ξ=1)=C 31C 42+C 32C 21C 41C 42C 62=715,又P(ξ=3)=C 31C 42C 62=130,∴P(ξ=2)=1-P(ξ=0)-P(ξ=1)-P(ξ=3)=1-15-715-130=310.9.一个盒子里装有7张卡片,其中有红色卡片4张,编号分别为1,2,3,4;白色卡片3张,编号分别为2,3,4.从盒子中任取4张卡片(假设取到任何一张卡片的可能性相同). (1)求取出的4张卡片中,含有编号为3的卡片的概率;(2)在取出的4张卡片中,红色卡片编号的最大值设为X ,求随机变量X 的分布列与数学期望.答案 (1)67 (2)175解析 (1)设“取出的4张卡片中,含有编号为3的卡片”为事件A , 则P(A)=C 21C 53+C 22C 52C 74=67. 因此取出的4张卡片中,含有编号为3的卡片的概率为67.(2)随机变量X 的所有可能取值为1,2,3,4. P(X =1)=C 33C 74=135,P(X =2)=C 43C 74=435,P(X =3)=C 53C 74=27,P(X =4)=C 63C 74=47.则随机变量X 的分布列是故随机变量X 的数学期望E(X)=1×35+2×35+3×7+4×7=5.10.在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖.某顾客从此10张奖券中任抽2张,求:(1)该顾客中奖的概率;(2)该顾客获得的奖品总价值X 元的概率分布列. 答案 (1)23(2)略解析 (1)该顾客中奖,说明是从有奖的4张奖券中抽到了1张或2张,由因此等可能地抽取,因此该顾客中奖的概率 P =C 41C 61+C 42C 102=3045=23.(或用间接法,即P =1-C 62C 102=1-1545=23).(2)依题意可知,X 的所有可能取值为0,10,20,50,60(元),且P(X =0)=C 40C 62C 102=13,P(X =10)=C 31C 61C 102=25,P(X =20)=C 32C 102=115,P(X =50)=C 11C 61C 102=215,P(X =60)=C 11C 31C 102=115.因此X 的分布列为:11.在103件,求:(1)取出的3件产品中一等品件数X 的分布列;(2)取出的3件产品中一等品件数多于二等品件数的概率. 答案 (1)略 (2)31120解析 (1)由于从10件产品中任取3件的结果数为C 103,从10件产品中任取3件,其中恰有k 件一等品的结果数为C 3kC 73-k,那么从10件产品中任取3件,其中恰有k 件一等品的概率为P(X =k)=C 3kC 73-kC 103,k =0,1,2,3.因此随机变量X 的分布列是(2)设“取出的31件一等品和2件三等品”为事件A 1,“恰好取出2件一等品”为事件A 2,“恰好取出3件一等品”为事件A 3.由于事件A 1,A 2,A 3彼此互斥,且A =A 1∪A 2∪A 3,而P(A 1)=C 31C 32C 103=340,P(A 2)=P(X =2)=740,P(A 3)=P(X =3)=1120,∴取出的3件产品中一等品件数多于二等品件数的概率为P(A)=P(A 1)+P(A 2)+P(A 3)=340+740+1120=31120. 12.(2021·大连质检)某高中共派出足球、排球、篮球三个球队参加市学校运动会,它们获得冠军的概率分别为12,13,23.(1)求该高中获得冠军个数X 的概率分布列;(2)若球队获得冠军,则给其所在学校加5分,否则加2分,求该高中得分Y 的概率分布列. 答案 (1)略 (2)略解析 (1)由题意知X 的可能取值为0,1,2,3, 则P(X =0)=(1-12)×(1-13)×(1-23)=19,P(X =1)=12×(1-13)×(1-23)+(1-12)×13×(1-23)+(1-12)×(1-13)×23=718,P(X =2)=12×13×(1-23)+(1-12)×13×23+12×(1-13)×23=718,P(X =3)=12×13×23=19.∴X 的分布列为(2)∵得分Y =5X +2(3∵X 的可能取值为0,1,2,3.∴Y 的可能取值6,9,12,15.则P(Y =6)=P(X =0)=19,P(Y =9)=P(X =1)=718,P(Y =12)=P(X =2)=718,P(Y =15)=P(X =3)=19.∴Y 的分布列为13.力打造的大型励志专业音乐评论节目,于2012年7月13日正式在浙江卫视播出.每期节目有四位导师参加.导师背对歌手,若每位参赛选手演唱完之前有导师为其转身,则该选手能够选择加入为其转身的导师的团队中同意指导训练.已知某期《中国新歌声》,6位选手演唱完后,四位导师为其转身的情形如下表所示:现从这6(1)求选出的2人导师为其转身的人数和为4的概率;(2)记选出的2人导师为其转身的人数之和为X ,求X 的分布列及数学期望E(X). 答案 (1)15(2)E(X)=5解析 (1)设6位选手中,A 有4位导师为其转身,B ,C 有3位导师为其转知,D ,E 有2位导师为其转身,F 只有1位导师为其转身.从6人中随机抽取两人有C 62=15种情形,其中选出的2人导师为其转身的人数和为4的有C 22+C 21C 11=3种,∴所求概率为P =315=15.(2)X 的所有可能取值为3,4,5,6,7.P(X =3)=C 21C 11C 62=215;P(X =4)=15;P(X =5)=1+C 21C 21C 62=515=13;P(X =6)=C 21C 11+C 22C 62=315=15;P(X =7)=C 21C 11C 62=215. ∴X 的分布列为X 3 4 5 6 7 P215151315215E(X)=3×215+4×5+5×3+6×5+7×15=5.1.由于电脑故障,使得随机变量X 的分布列中部分数据丢失(以“x,y ”代替),其分布列如下:X 1 2 3 4 5 6 P0.200.100.x50.100.1y0.20答案 2,5解析 由于0.20+0.10+(0.1x +0.05)+0.10+(0.1+0.01y)+0.20=1,得10x +y =25,又因为x ,y 为正整数,故两个数据依次为2,5.2.一实验箱中装有标号为1,2,3,3,4的5只白鼠,若从中任取1只,记取到的白鼠的标号为Y ,则随机变量Y 的分布列是________. 答案Y 1 2 3 4 P15152515解析 Y P(Y =1)=15,P(Y =2)=15,P(Y =3)=25,P(Y =4)=15.∴Y 的分布列为3.一个袋子中装有74,黄球3个,编号分别为2,4,6,从袋中任取4个球(假设取到任何一个球的可能性相同). (1)求取出小球中有相同编号的概率;(2)记取出的小球的最大编号为X ,求随机变量X 的分布列. 答案 (1)1935(2)略解析 (1)设“取出的小球中有相同编号的”为事件A ,编号相同可分成一个相同和两个相同,则P(A)=2(C 21C 31+C 32)+1C 74=1935. (2)随机变量X 的可能取值为:3,4,6. P(X =3)=1C 74=135,P(X =4)=C 21C 43+C 42C 74=25, P(X =6)=C 63C 74=47,随机变量X 的分布列为:4.一袋中装有102个球,至少得到1个白球的概率是79.(1)求白球的个数;(2)从袋中任意摸出3个球,记得到白球的个数为X ,求随机变量X 的分布列. 答案 (1)5个 (2)略解析 (1)记“从袋中任意摸出2个球,至少得1个白球”为事件A ,设袋中白球的个数为x ,则P(A)=1-C 10-x 2C 102=79,得到x =5.故白球有5个.(2)X 服从超几何分布,P(X =k)=C 5kC 53-kC 103,k =0,1,2,3.因此可得其分布列为P112 512 512 1125.(2020·福建,理)该银行卡将被锁定.小王到该银行取钱时,发觉自己不记得了银行卡的密码,但能够确认该银行卡的正确密码是他常用的6个密码之一,小王决定从中不重复地随机选择1个进行尝试.若密码正确,则终止尝试;否则连续尝试,直至该银行卡被锁定. (1)求当天小王的该银行卡被锁定的概率;(2)设当天小王用该银行卡尝试密码的次数为X ,求X 的分布列和数学期望. 答案 (1)12 (2)分布列略,E(X)=52解析 (1)设“当天小王的该银行卡被锁定”的事件为A , 则P(A)=56×45×34=12.(2)依题意得,X 所有可能的取值是1,2,3.又P(X =1)=16,P(X =2)=56×15=16,P(X =3)=56×45×1=23.因此X 的分布列为X 1 2 3 P161623因此E(X)=1×16+2×16+3×3=2.6.某中学动员学生在春节期间至少参加一次社会公益活动(下面简称为“活动”).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.(1)求合唱团学生参加活动的人均次数;(2)从合唱团中任选两名学生,求他们参加活动次数恰好相等的概率;(3)从合唱团中任选两名学生,用ξ表示这两人参加活动次数之差的绝对值,求随机变量ξ的分布列.答案 (1)2.3 (2)4199(3)略解析 依照统计图知参加活动1次、2次、3次的学生数分别为10,50,40.(1)该合唱团学生参加活动的人均次数为x -=1×10+2×50+3×40100=2.3.(2)从合唱团中任选两名学生,他们参加活动次数恰好相等的概率P =C 102+C 502+C 402C 1002=4199. (3)ξ的取值为0,1,2,ξ的分布列为7.(2020·重庆)摸奖者先从装有3个红球与4个白球的袋中任意摸出3个球,再从装有1个蓝球与2个白球的袋中任意摸出1个球.依照摸出4个球中红球与蓝球的个数,设一、二、三等奖如下:(1)求一次摸奖恰好摸到1个红球的概率; (2)求摸奖者在一次摸奖中获奖金额X 的分布列. 答案 (1)1835(2)略解析 设A i 表示摸到i 个红球,B j 表示摸到j 个蓝球,则A i (i =0,1,2,3)与B j (j =0,1)独立.(1)恰好摸到1个红球的概率为P(A 1)=C 31C 42C 73=1835.(2)X 的所有可能的值为:0,10,50,200, 则P(X =200)=P(A 3B 1)=P(A 3)P(B 1)=C 33C 73·13=1105,P(X =50)=P(A 3B 0)=P(A 3)P(B 0)=C 33C 73·23=2105,P(X =10)=P(A 2B 1)=P(A 2)P(B 1)=C 32C 41C 73·13=12105=435,P(X =0)=1-1105-2105-435=67.综上知X 的分布列为8.试销终止后(3件,当天营业终止后检查存货,若发觉存量少于2件,则当天进货补充至3件,否则不进货.将频率视为概率.(1)求当天商店不进货的概率;(2)设X 为翌日开始营业时该商品的件数,求X 的分布列和均值. 答案 (1)310 (2)114解析 (1)P(“当天商店不进货”)=P(“当天商品销售量为0件”)+P(“当天商品销售量为1件”)=120+520=310.(2)由题意知,X 的可能取值为2,3.P(X =2)=P(“当天商品销售量为1件”)=520=14;P(X =3)=P(“当天商品销售量为0件”)+P(“当天商品销售量为2件”)+P(“当天商品销售量为3件”)=120+920+520=34.故X 的分布列为X 的均值为E(X)=2×14+3×34=4.9.设ξ为随机变量,从棱长为1的正方体的12条棱中任取两条,当两条棱相交时,ξ=0;当两条棱平行时,ξ的值为两条棱之间的距离;当两条棱异面时,ξ=1. (1)求概率P(ξ=0);(2)求ξ的分布列,并求其数学期望E(ξ).解析 (1)若两条棱相交,则交点必为正方体8个顶点中的1个,过任意1个顶点恰有3条棱,因此共有8C 32对相交棱,因此P(ξ=0)=8C 32C 122=8×366=411.(2)若两条棱平行,则它们的距离为1或2,其中距离为2的共有6对,故P(ξ=2)=6C 122=111. 因此P(ξ=1)=1-P(ξ=0)-P(ξ=2)=1-411-111=611.因此随机变量ξ的分布列是因此E(ξ)=1×611+10.(2020·贵州遵义联考)2021年巴西奥运会的周边商品有80%左右为“中国制造”,所有的厂家差不多上通过层层选择才能获此殊荣.甲、乙两厂生产同一产品,为了解甲、乙两厂的产品质量,以确定这一产品最终的供货商,采纳分层抽样的方法从甲、乙两厂生产的产品共98件中分别抽取9件和5件,测量产品中的微量元素的含量(单位:毫克).下表是从乙厂抽取的5件产品的测量数据:(1)(2)当产品中的微量元素x ,y 满足x≥175,且y≥75,该产品为优等品.用上述样本数据估量乙厂生产的优等品的数量;(3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数ξ的分布列及其均值(即数学期望). 答案 (1)35 (2)14 (3)45解析 (1)乙厂生产的产品总数为5÷1498=35.(2)样品中优等品的频率为25,估量乙厂生产的优等品的数量为35×25=14.(3)ξ=0,1,2,P (ξ=i)=C 2iC 32-iC 52(i =0,1,2), ξ的分布列为3 10+1×35+2×110=45.均值E(ξ)=0×。
苏州苏州大学实验学校小学数学二年级上册第四单元阶段练习(答案解析)(1)

一、选择题1.从50里面连续减去10个5,结果是()A. 10B. 5C. 02.明明和他的2个好朋友一起到图书馆借绘本,每人借的绘本本数同样多,他们一共可能借了()本绘本。
A. 14B. 15C. 203.1根小木棍长3厘米,6根这样的小木棍连起来长()。
A. 9厘米B. 18米C. 18厘米4.两个乘数都是5,积是()。
A. 10B. 25C. 155.积是15的算式是()。
A. 10+ 5=15B. 35-20=15C. 3×5=156.1千克桃子4元钱,买5千克桃子多少元钱?用()算比较简单。
A. 加法B. 乘法C. 减法7.6+6+6+6+3可以写成()。
A. 6×4+3B. 6×4C. 5×68.一共有多少本书?列式错误的是()。
A. 5+2B. 5+5C. 5×29.6×8不能表示()。
A. 6的8倍B. 8个6相加C. 8和6相加10.与7×9-7得数相等的算式是()。
A. 6×9+9B. 7×8+7C. 7×7+711.下列算式,不能直接改写成乘法算式的是()。
A. 4+4+4+4+4B. 3+2+3+3C. 7+7+712.5个8相加的可以列式为()。
A. 8+5B. 8×5C. 5+5+5+5+513.3个4相加,写成的算式是()。
A. 4+3B. 3×4C. 4×414.小红有5盒珠子,每盒9个,分给小朋友20个后,还剩几个?正确的列式是()。
A. 5+9+20B. 5×9+20C. 5×9-2015.下面的算式中,积是16的是( )。
A. 8+8B. 4×4C. 4×3二、填空题16.,5个能换________个。
17.5个9比4个9多________,比50少________。
18.8+8+8+8+8+8=________×________=________。
数学实验作业1--答案

数学实验-作业1—及部分答案(要求:1. 每次上机课下课之前提交,文件名如:数学091朝鲁第一次作业.doc。
2. 交至邮箱:matlabzuoyetijiao@3.作业实行5分制,依次为A++,A+,A ,A-,A- -)4.作业中,需要编程实现的均要求列出你的代码,以及求解的结果)1.请上网或查阅各种资料并回答:MATLAB是什么?MATLAB能做什么?答:略2.请上网或查阅各种资料并回答:MATLAB语言突出的特点是什么?答:略3.在MATLAB软件中有几种获得帮助的途径?答:help函数,菜单栏help菜单。
4.请上网或查询MATLAB软件中inv函数的功能与特点。
答:用来求可逆矩阵的逆矩阵。
inv(A),即求已知矩阵A的逆矩阵。
5.请上网或查阅各种资料并回答:如何在MATLAB中建立向量和矩阵。
答:如在matlab中创建向量a=(2,-5,6,1);a=[2,-5,6,1];b= [2;-5;6;1];如在matlab中创建矩阵A=;A=[1,2,3;4,5,6;7,8,9];A =1 2 34 5 67 8 96.请上网或查阅各种资料并回答:在MATLAB中,向量和矩阵如何进行基本加减乘除四则运算,以及矩阵的乘法。
答:a=[2,-5,6,1];b= [1,2,3,4];求向量的和与差,直接输入a+b,a-b,即可,当然必须要求两个向量大小一致。
如:>> a=[2,-5,6,1];b= [1,2,3,4];>> a+bans =3 -3 9 5>> a-b1 -7 3 -3>> a.*bans =2 -10 18 4>> a./bans =2.0000 -2.5000 2.0000 0.2500>> a/b向量之间进行除法运算,使用不加点的矩阵除法“A/B”时,问题可以描述为:给定两个向量A、B,求一个常量x,使得A=x * B。
数学实验1-3章习题答案
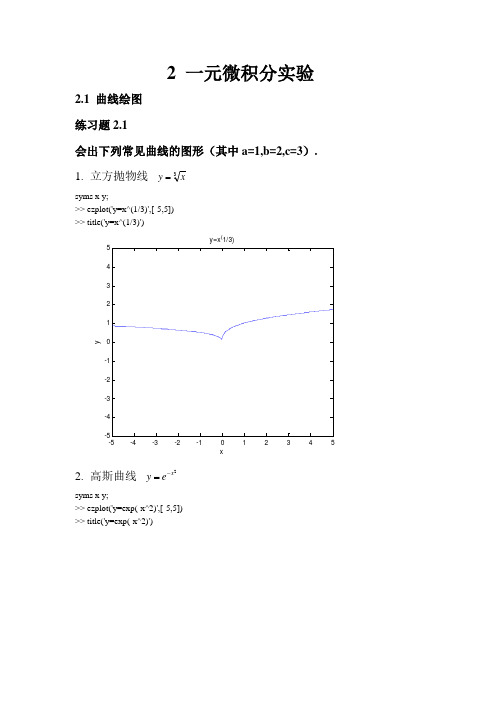
ans =
18.3287
函数的单调区间为:
(1)单调递增区间:-2<x<-1.5326 -0.7315<x<0以及1.5951<x<2;
(2)单调递减区间:-1.5326<x<-0.7315以及0<x<1.5951.
(2)
函数的图形为:
clear
>> fplot('3*x^5-20*x^3+10',[-3,3])
ans =
-3
最值2:
x=1:0.1:3;
>> y=3.*x.^5-20.*x.^3+10;
>> [m k]=max(y)
m =
199
k =
21
>> x(k)
ans =
3
驻点1及相应的二阶导数值:
clear
>> syms x y
>> y=3*x^5-20*x^3+10;
>> yxx=diff(y,x,2);
>> grid on
f=inline('100*acos(1-1/200*(r^2))+r^2*acos(1/20*r)-10*sqrt(r^2-1/400*r^4)-50*pi','r');
>> y=fzero(f,12)
y =
11.5873
3.求解下列非线性方程组在远点附近的根:
clear
>> syms x y z
>> [x y z]=solve('9*x^2+36*y^2+4*z^2-36','x^2-2*y^2-20*z','16*x-x^3-2*y^2-16*z^2',x,y,z)
(完整版)MATLAB数学实验第二版答案(胡良剑)

数学实验答案Chapter 1Page20,ex1(5) 等于[exp(1),exp(2);exp(3),exp(4)](7) 3=1*3, 8=2*4(8) a为各列最小值,b为最小值所在的行号(10) 1>=4,false, 2>=3,false, 3>=2, ture, 4>=1,ture(11) 答案表明:编址第2元素满足不等式(30>=20)和编址第4元素满足不等式(40>=10)(12) 答案表明:编址第2行第1列元素满足不等式(30>=20)和编址第2行第2列元素满足不等式(40>=10)Page20, ex2(1)a, b, c的值尽管都是1,但数据类型分别为数值,字符,逻辑,注意a与c相等,但他们不等于b(2)double(fun)输出的分别是字符a,b,s,(,x,)的ASCII码Page20,ex3>> r=2;p=0.5;n=12;>> T=log(r)/n/log(1+0.01*p)Page20,ex4>> x=-2:0.05:2;f=x.^4-2.^x;>> [fmin,min_index]=min(f)最小值最小值点编址>> x(min_index)ans =0.6500 最小值点>> [f1,x1_index]=min(abs(f)) 求近似根--绝对值最小的点f1 =0.0328x1_index =24>> x(x1_index)ans =-0.8500>> x(x1_index)=[];f=x.^4-2.^x; 删去绝对值最小的点以求函数绝对值次小的点>> [f2,x2_index]=min(abs(f)) 求另一近似根--函数绝对值次小的点f2 =0.0630x2_index =65>> x(x2_index)ans =1.2500>> z=magic(10)z =92 99 1 8 15 67 74 51 58 4098 80 7 14 16 73 55 57 64 414 81 88 20 22 54 56 63 70 4785 87 19 21 3 60 62 69 71 2886 93 25 2 9 61 68 75 52 3417 24 76 83 90 42 49 26 33 6523 5 82 89 91 48 30 32 39 6679 6 13 95 97 29 31 38 45 7210 12 94 96 78 35 37 44 46 5311 18 100 77 84 36 43 50 27 59>> sum(z)>> sum(diag(z))>> z(:,2)/sqrt(3)>> z(8,:)=z(8,:)+z(3,:)Chapter 2Page 45 ex1先在编辑器窗口写下列M函数,保存为eg2_1.m function [xbar,s]=ex2_1(x)n=length(x);xbar=sum(x)/n;s=sqrt((sum(x.^2)-n*xbar^2)/(n-1));例如>>x=[81 70 65 51 76 66 90 87 61 77];>>[xbar,s]=ex2_1(x)Page 45 ex2s=log(1);n=0;while s<=100n=n+1;s=s+log(1+n);endm=nPage 40 ex3clear;F(1)=1;F(2)=1;k=2;x=0;e=1e-8; a=(1+sqrt(5))/2;while abs(x-a)>ek=k+1;F(k)=F(k-1)+F(k-2); x=F(k)/F(k-1);enda,x,k计算至k=21可满足精度clear;tic;s=0;for i=1:1000000s=s+sqrt(3)/2^i;ends,toctic;s=0;i=1;while i<=1000000s=s+sqrt(3)/2^i;i=i+1;ends,toctic;s=0;i=1:1000000;s=sqrt(3)*sum(1./2.^i);s,tocPage 45 ex5t=0:24;c=[15 14 14 14 14 15 16 18 20 22 23 25 28 ...31 32 31 29 27 25 24 22 20 18 17 16];plot(t,c)Page 45 ex6(1)x=-2:0.1:2;y=x.^2.*sin(x.^2-x-2);plot(x,y)y=inline('x^2*sin(x^2-x-2)');fplot(y,[-2 2]) (2)参数方法t=linspace(0,2*pi,100);x=2*cos(t);y=3*sin(t); plot(x,y)(3)x=-3:0.1:3;y=x;[x,y]=meshgrid(x,y);z=x.^2+y.^2;surf(x,y,z)(4)x=-3:0.1:3;y=-3:0.1:13;[x,y]=meshgrid(x,y);z=x.^4+3*x.^2+y.^2-2*x-2*y-2*x.^2.*y+6;surf(x,y,z)(5)t=0:0.01:2*pi;x=sin(t);y=cos(t);z=cos(2*t);plot3(x,y,z)(6)theta=linspace(0,2*pi,50);fai=linspace(0,pi/2,20); [theta,fai]=meshgrid(theta,fai);x=2*sin(fai).*cos(theta);y=2*sin(fai).*sin(theta);z=2*cos(fai);surf(x,y,z)(7)x=linspace(0,pi,100);y1=sin(x);y2=sin(x).*sin(10*x);y3=-sin(x);plot(x,y1,x,y2,x,y3)page45, ex7x=-1.5:0.05:1.5;y=1.1*(x>1.1)+x.*(x<=1.1).*(x>=-1.1)-1.1*(x<-1.1);plot(x,y)page45,ex9clear;close;x=-2:0.1:2;y=x;[x,y]=meshgrid(x,y);a=0.5457;b=0.7575;p=a*exp(-0.75*y.^2-3.75*x.^2-1.5*x).*(x+y>1);p=p+b*exp(-y.^2-6*x.^2).*(x+y>-1).*(x+y<=1);p=p+a*exp(-0.75*y.^2-3.75*x.^2+1.5*x).*(x+y<=-1);mesh(x,y,p)page45, ex10lookfor lyapunovhelp lyap>> A=[1 2 3;4 5 6;7 8 0];C=[2 -5 -22;-5 -24 -56;-22 -56 -16];>> X=lyap(A,C)X =1.0000 -1.0000 -0.0000-1.0000 2.0000 1.0000-0.0000 1.0000 7.0000Chapter 3Page65 Ex1>> a=[1,2,3];b=[2,4,3];a./b,a.\b,a/b,a\bans =0.5000 0.5000 1.0000ans =2 2 1ans =0.6552 一元方程组x[2,4,3]=[1,2,3]的近似解ans =0 0 00 0 00.6667 1.3333 1.0000矩阵方程[1,2,3][x11,x12,x13;x21,x22,x23;x31,x32,x33]=[2,4,3]的特解Page65 Ex 2(1)>> A=[4 1 -1;3 2 -6;1 -5 3];b=[9;-2;1];>> rank(A), rank([A,b]) [A,b]为增广矩阵ans =3ans =3 可见方程组唯一解>> x=A\bx =2.38301.48942.0213(2)>> A=[4 -3 3;3 2 -6;1 -5 3];b=[-1;-2;1];>> rank(A), rank([A,b])ans =3ans =3 可见方程组唯一解>> x=A\bx =-0.4706-0.2941(3)>> A=[4 1;3 2;1 -5];b=[1;1;1];>> rank(A), rank([A,b])ans =2ans =3 可见方程组无解>> x=A\bx =0.3311-0.1219 最小二乘近似解(4)>> a=[2,1,-1,1;1,2,1,-1;1,1,2,1];b=[1 2 3]';%注意b的写法>> rank(a),rank([a,b])ans =3ans =3 rank(a)==rank([a,b])<4说明有无穷多解>> a\bans =110 一个特解Page65 Ex3>> a=[2,1,-1,1;1,2,1,-1;1,1,2,1];b=[1,2,3]';>> x=null(a),x0=a\bx =-0.62550.6255-0.20850.4170x0 =11通解kx+x0Page65 Ex 4>> x0=[0.2 0.8]';a=[0.99 0.05;0.01 0.95];>> x1=a*x, x2=a^2*x, x10=a^10*x>> x=x0;for i=1:1000,x=a*x;end,xx =0.83330.1667>> x0=[0.8 0.2]';>> x=x0;for i=1:1000,x=a*x;end,xx =0.83330.1667>> [v,e]=eig(a)v =0.9806 -0.70710.1961 0.7071e =1.0000 00 0.9400>> v(:,1)./xans =1.17671.1767 成比例,说明x是最大特征值对应的特征向量Page65 Ex5用到公式(3.11)(3.12)>> B=[6,2,1;2.25,1,0.2;3,0.2,1.8];x=[25 5 20]'; >> C=B/diag(x)C =0.2400 0.4000 0.05000.0900 0.2000 0.01000.1200 0.0400 0.0900>> A=eye(3,3)-CA =0.7600 -0.4000 -0.0500-0.0900 0.8000 -0.0100-0.1200 -0.0400 0.9100>> D=[17 17 17]';x=A\Dx =37.569625.786224.7690Page65 Ex 6(1)>> a=[4 1 -1;3 2 -6;1 -5 3];det(a),inv(a),[v,d]=eig(a) ans =-94ans =0.2553 -0.0213 0.04260.1596 -0.1383 -0.22340.1809 -0.2234 -0.0532v =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170d =-3.0527 0 00 3.6760 00 0 8.3766(2)>> a=[1 1 -1;0 2 -1;-1 2 0];det(a),inv(a),[v,d]=eig(a) ans =1ans =2.0000 -2.0000 1.00001.0000 -1.0000 1.00002.0000 -3.0000 2.0000v =-0.5773 0.5774 + 0.0000i 0.5774 - 0.0000i-0.5773 0.5774 0.5774-0.5774 0.5773 - 0.0000i 0.5773 + 0.0000id =1.0000 0 00 1.0000 + 0.0000i 00 0 1.0000 - 0.0000i(3)>> A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10]A =5 76 57 10 8 76 8 10 95 7 9 10>> det(A),inv(A), [v,d]=eig(A)ans =1ans =68.0000 -41.0000 -17.0000 10.0000-41.0000 25.0000 10.0000 -6.0000-17.0000 10.0000 5.0000 -3.000010.0000 -6.0000 -3.0000 2.0000v =0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209d =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887(4)(以n=5为例)方法一(三个for)n=5;for i=1:n, a(i,i)=5;endfor i=1:(n-1),a(i,i+1)=6;endfor i=1:(n-1),a(i+1,i)=1;enda方法二(一个for)n=5;a=zeros(n,n);a(1,1:2)=[5 6];for i=2:(n-1),a(i,[i-1,i,i+1])=[1 5 6];enda(n,[n-1 n])=[1 5];a方法三(不用for)n=5;a=diag(5*ones(n,1));b=diag(6*ones(n-1,1));c=diag(ones(n-1,1));a=a+[zeros(n-1,1),b;zeros(1,n)]+[zeros(1,n);c,zeros(n-1,1)] 下列计算>> det(a)ans =665>> inv(a)ans =0.3173 -0.5865 1.0286 -1.6241 1.9489-0.0977 0.4887 -0.8571 1.3534 -1.62410.0286 -0.1429 0.5429 -0.8571 1.0286-0.0075 0.0376 -0.1429 0.4887 -0.58650.0015 -0.0075 0.0286 -0.0977 0.3173>> [v,d]=eig(a)v =-0.7843 -0.7843 -0.9237 0.9860 -0.92370.5546 -0.5546 -0.3771 -0.0000 0.3771-0.2614 -0.2614 0.0000 -0.1643 0.00000.0924 -0.0924 0.0628 -0.0000 -0.0628-0.0218 -0.0218 0.0257 0.0274 0.0257d =0.7574 0 0 0 00 9.2426 0 0 00 0 7.4495 0 00 0 0 5.0000 00 0 0 0 2.5505Page65 Ex 7(1)>> a=[4 1 -1;3 2 -6;1 -5 3];[v,d]=eig(a)v =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170d =-3.0527 0 00 3.6760 00 0 8.3766>> det(v)ans =-0.9255 %v行列式正常, 特征向量线性相关,可对角化>> inv(v)*a*v 验算ans =-3.0527 0.0000 -0.00000.0000 3.6760 -0.0000-0.0000 -0.0000 8.3766>> [v2,d2]=jordan(a) 也可用jordanv2 =0.0798 0.0076 0.91270.1886 -0.3141 0.1256-0.1605 -0.2607 0.4213 特征向量不同d2 =8.3766 0 00 -3.0527 - 0.0000i 00 0 3.6760 + 0.0000i>> v2\a*v2ans =8.3766 0 0.00000.0000 -3.0527 0.00000.0000 0.0000 3.6760>> v(:,1)./v2(:,2) 对应相同特征值的特征向量成比例ans =2.44912.44912.4491(2)>> a=[1 1 -1;0 2 -1;-1 2 0];[v,d]=eig(a)v =-0.5773 0.5774 + 0.0000i 0.5774 - 0.0000i-0.5773 0.5774 0.5774-0.5774 0.5773 - 0.0000i 0.5773 + 0.0000id =1.0000 0 00 1.0000 + 0.0000i 00 0 1.0000 - 0.0000i>> det(v)ans =-5.0566e-028 -5.1918e-017i v的行列式接近0, 特征向量线性相关,不可对角化>> [v,d]=jordan(a)v =1 0 11 0 01 -1 0d =1 1 00 1 10 0 1 jordan标准形不是对角的,所以不可对角化(3)>> A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10]A =5 76 57 10 8 76 8 10 95 7 9 10>> [v,d]=eig(A)v =0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209d =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887>> inv(v)*A*vans =0.0102 0.0000 -0.0000 0.00000.0000 0.8431 -0.0000 -0.0000-0.0000 0.0000 3.8581 -0.0000-0.0000 -0.0000 0 30.2887本题用jordan不行, 原因未知(4)参考6(4)和7(1)Page65 Exercise 8只有(3)对称, 且特征值全部大于零, 所以是正定矩阵. Page65 Exercise 9(1)>> a=[4 -3 1 3;2 -1 3 5;1 -1 -1 -1;3 -2 3 4;7 -6 -7 0]>> rank(a)ans =3>> rank(a(1:3,:))ans =2>> rank(a([1 2 4],:)) 1,2,4行为最大无关组ans =3>> b=a([1 2 4],:)';c=a([3 5],:)';>> b\c 线性表示的系数ans =0.5000 5.0000-0.5000 1.00000 -5.0000Page65 Exercise 10>> a=[1 -2 2;-2 -2 4;2 4 -2]>> [v,d]=eig(a)v =0.3333 0.9339 -0.12930.6667 -0.3304 -0.6681-0.6667 0.1365 -0.7327d =-7.0000 0 00 2.0000 00 0 2.0000>> v'*vans =1.0000 0.0000 0.00000.0000 1.0000 00.0000 0 1.0000 v确实是正交矩阵Page65 Exercise 11设经过6个电阻的电流分别为i1, ..., i6. 列方程组如下20-2i1=a; 5-3i2=c; a-3i3=c; a-4i4=b; c-5i5=b; b-3i6=0;i1=i3+i4;i5=i2+i3;i6=i4+i5;计算如下>> A=[1 0 0 2 0 0 0 0 0;0 0 1 0 3 0 0 0 0;1 0 -1 0 0 -3 0 0 0; 1 -1 0 0 0 0 -4 0 0;0 -1 1 0 0 0 0 -5 0;0 1 0 0 0 0 0 0 -3; 0 0 0 1 0 -1 -1 0 0;0 0 0 0 -1 -1 0 1 0;0 0 0 0 0 0 -1 -1 1];>>b=[20 5 0 0 0 0 0 0 0]'; A\bans =13.34536.44018.54203.3274-1.18071.60111.72630.42042.1467Page65 Exercise 12>> A=[1 2 3;4 5 6;7 8 0];>> left=sum(eig(A)), right=sum(trace(A))left =6.0000right =6>> left=prod(eig(A)), right=det(A) 原题有错, (-1)^n应删去left =27.0000right =27>> fA=(A-p(1)*eye(3,3))*(A-p(2)*eye(3,3))*(A-p(3)*eye(3,3)) fA =1.0e-012 *0.0853 0.1421 0.02840.1421 0.1421 0-0.0568 -0.1137 0.1705>> norm(fA) f(A)范数接近0ans =2.9536e-013Chapter 4Page84 Exercise 1(1)roots([1 1 1])(2)roots([3 0 -4 0 2 -1])(3)p=zeros(1,24);p([1 17 18 22])=[5 -6 8 -5];roots(p)(4)p1=[2 3];p2=conv(p1, p1);p3=conv(p1, p2);p3(end)=p3(end)-4; %原p3最后一个分量-4roots(p3)Page84 Exercise 2fun=inline('x*log(sqrt(x^2-1)+x)-sqrt(x^2-1)-0.5*x');fzero(fun,2)Page84 Exercise 3fun=inline('x^4-2^x');fplot(fun,[-2 2]);grid on;fzero(fun,-1),fzero(fun,1),fminbnd(fun,0.5,1.5)Page84 Exercise 4fun=inline('x*sin(1/x)','x');fplot(fun, [-0.1 0.1]);x=zeros(1,10);for i=1:10, x(i)=fzero(fun,(i-0.5)*0.01);end;x=[x,-x]Page84 Exercise 5fun=inline('[9*x(1)^2+36*x(2)^2+4*x(3)^2-36;x(1)^2-2*x(2)^2-20*x(3);16*x(1)-x(1)^3-2*x(2)^ 2-16*x(3)^2]','x');[a,b,c]=fsolve(fun,[0 0 0])Page84 Exercise 6fun=@(x)[x(1)-0.7*sin(x(1))-0.2*cos(x(2)),x(2)-0.7*cos(x(1))+0.2*sin(x(2))];[a,b,c]=fsolve(fun,[0.5 0.5])Page84 Exercise 7clear; close; t=0:pi/100:2*pi;x1=2+sqrt(5)*cos(t); y1=3-2*x1+sqrt(5)*sin(t);x2=3+sqrt(2)*cos(t); y2=6*sin(t);plot(x1,y1,x2,y2); grid on; 作图发现4个解的大致位置,然后分别求解y1=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[1.5,2])y2=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[1.8,-2])y3=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[3.5,-5])y4=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[4,-4])Page84 Exercise 8(1)clear;fun=inline('x.^2.*sin(x.^2-x-2)');fplot(fun,[-2 2]);grid on; 作图观察x(1)=-2;x(3)=fminbnd(fun,-1,-0.5);x(5)=fminbnd(fun,1,2);fun2=inline('-x.^2.*sin(x.^2-x-2)');x(2)=fminbnd(fun2,-2,-1);x(4)=fminbnd(fun2,-0.5,0.5);x(6)=2feval(fun,x)答案: 以上x(1)(3)(5)是局部极小,x(2)(4)(6)是局部极大,从最后一句知道x(1)全局最小,x(2)最大。
上海上海外国语大学闵行实验学校小学数学二年级上册第五单元习题(答案解析)(1)
一、选择题1.图形,从左面看到的是( )。
A. B. C.2.从侧面看,看到的是().A. B. C.3.小明看到的杯子的形状是()。
A. B. C. D.4.从箭头所示的方向看过去,看到的图形是( )A. B. C.5.从上面看,看到的图形是( )。
A. B. C.6.这个小朋友看到的图形是:( )A. B. C.7.这两幅茶杯图哪一幅是从“侧面“观察得到的?( )A. B.8.下面的图形分别是从哪个方向看到的?( )A. 从正面看B. 从侧面看C. 从上面看9.请你判断:下面方案是从空中看到的“绿色金字塔”.(即此种方案按一定顺序种植,若干年后会形成“绿色金字塔”)()A. B. C. D. 10.某冷饮厅推出新款圣代,如图所示,则它的俯视图为()A. B. C. D. 11.从上面看,看到的形状是()A. B. C.12.哪幅图是在飞机上看到的这座楼房的形状? ()A. B. C.13.小辉看到的是哪张图片?()A. B.14.淘气看到的是哪副图?()A. B.15.小刚和小丽都在看同一个茶壶,请你选出小刚看到的是哪一个?()A. B. C.二、填空题16.下面右边的照片分别是谁拍的?填一填。
________________________17.观察,从________面看到的是,从________面看到的是,从________面看到的是.18.下面的图分别是谁看到的?把序号填在相应的横线上。
________________________19.夜晚,人与路灯之间的距离越近,人的影子越________,人与路灯的距离越远,人的影子越________.(填“长”或“短”)20.是________号看到的; 是________号看到的; 是________号看到的; 是________号看到的。
21.下面这些照片分别是谁拍到的?把名字填在下面。
________________________________22.下面三幅图分别是谁看到的?把他们的编号填在图片下面的横线上。
实验讲义-1-研究匀变速直线运动-答案版

实验:研究匀变速直线运动2020年3月23日1.教材第一章和第二章所有实验的汇总,包括如何测量速度,如何研究速度与时间、位移与时间的关系,测量速度的多种器材和方法的选择等等2.伽利略的科学研究方法。
把试验和逻辑推理(包括数学演算)和谐地结合起来,从而发展了人类的科学思维方式和科学研究方法。
用打点计时器做实验:1.纸带做与物体相同的运动2.纸带上记录着t,可以用刻度尺直接测量出x实验目的:研究小车的运动,尝试找到小车的运动规律实验设计:总问题:你准备如何进行这个实验,并请说明每个实验环节的目的分问题:1.如何组装?打点计时器、小车放到哪一端?先挂钩码还是先穿纸带?2.选用交流还是直流电源?220v的还是4~6v的?需要天平吗?3.先通电还是先放车?4.如何确认纸带哪段是先打出来的哪段是后打出来的?5.什么是计时点,怎么选计数点6.这个实验中需要平衡摩擦力吗?7.发现点迹间距越来越大,猜测这是一个加速运动,想要进一步确认是否为匀加速运动,可以怎么做?(测速度画v-t图看是否直线,计算∆S,计算a)8.尝试测v,理论上选取包含该点的越短的一段计算平均速度,越接近该点的瞬时速度。
实验操作中,太短的距离测量误差太大。
所以,选择适宜的一段进行测量。
9. ∆S计算10.确认是匀变速以后,如何求某点瞬时速度更合适?11.求解加速度的时候,一定要用456减123段吗?尝试使用6减1段计算,或者56减12计算,还可以用速度变化量比时间来计算。
比较所有计算式,说明为什么456减123更好。
如果只有4段怎么办?如果只有5段怎么办?如果只测得了1和5怎么办?这个结果一定不能用吗?这个实验的关键在于测量速度和加速度,除了打点计时器和纸带以外,还有哪些器材可以完成这个任务?(频闪照片、光电门、应用手机传感器的app例如phyphox)选择一条比较理想的纸带,舍掉开头的比较密集的点,确定计数始点,标明计数点,正确使用毫米刻度尺测量两点间的距离,并把测量结果填入表中,用逐差法求出加速度的值,还可求出各计数点对应的速度,做v—t图象,求得直线的斜率即为物体运动的加速度。
河南省郑州陈中实验学校2022-2023学年九年级上学期1月期末数学试题及解析

河南省郑州陈中实验学校2022-2023学年九年级上学期1月期末数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.﹣2023的绝对值等于( )A .﹣2023B .2023C .土2023D .20222.2022年北京冬奥会的奖牌“同心”表达了“天地合·人心同”的中华文化内涵,将这六个汉字分别写在某正方体的表面上,如图是它的一种展开图,则在原正方体中,与“地”字所在面相对的面上的汉字是( )A .合B .同C .心D .人3.据测算,世博会召开时,上海使用清洁能源可减少二氧化碳排放约16万吨,将16万吨用科学记数法表示为( )A .31.610⨯吨B .41.610⨯吨C .51.610⨯吨D .61.610⨯吨 4.如图,利用工具测量角,则1∠的大小为( )A .30°B .60°C .120°D .150°5.如图所示的扇形统计图描述了某校学生对课后延时服务的打分情况(满分5分),则所打分数的众数为( )A .5分B .4分C .3分D .45%6.对于反比例函数y =﹣5x,下列说法错误的是( ) A .图象经过点(1,﹣5)B .图象位于第二、第四象限C .当x <0时,y 随x 的增大而减小D .当x >0时,y 随x 的增大而增大7.小区新增了一家快递店,第一天揽件200件,第三天揽件242件,设该快递店揽件日平均增长率为x ,根据题意,下面所列方程正确的是( )A .()22001242x +=B .()22001242x -= C .()20012242x += D .()20012242x -=8.如图,点(0,3)(1,0)A B 、,将线段AB 平移得到线段DC ,若90,2ABC BC AB ∠=︒=,则点D 的坐标是( )A .(7,2)B .(7,5)C .(5,6)D .(6,5)9.如图,在Rt ABC △中,=90B ∠︒,=4BC ,=5AC ,点D 在BC 上,以AC 为对角线的所有平行四边形ADCE 中,DE 的最小值是( )A .3B .6C .8D . 1010.如图1,菱形ABCD 中,=60B ∠︒,动点P 以每秒1个单位的速度自点A 出发沿线段AB 运动到点B ,同时动点Q 以每秒2个单位的速度自点B 出发沿折线B C D --运动到点D .图2是点P 、Q 运动时,△BPQ 的面积S 随时间t 变化关系图象,则a 的值是( )A .2B .2.5C .3D .二、填空题11.已知250x y y ,则x y=______. 12.本周末一位数学老师设置了A ,B ,C ,D 四个类型的作业,要求每一个同学们从中随机抽取两个类型作业完成.那么小颖同学抽到B ,C 两类型作业的概率是________.13.科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如下表:科学家经过猜想、推测出l 与t 之间是二次函数关系.由此可以推测最适合这种植物生长的温度为____△.14.如图,D 、E 分别是ABC 的边AB 、BC 上的点,且//DE AC ,AE 、CD 相交于点O ,若125DOE COA S S =△△,则BDE CDE S S =△△______.15.如图,在矩形ABCD 中,3AB =,2BC =,将BCD △沿射线BD 平移a 个单位长度()0a >得到B C D ''',连接AB ',AD ',则当AB D ''是直角三角形时,a 的值为________.三、解答题16.(1)计算:0tan 602(0)π︒-+-(2)解方程:24830x x --=17.人口问题是“国之大者”.以习近平同志为核心的党中央高度重视人口问题,准确把握人口发展形势,有利于推动社会持续健康发展,为开启全面建设社会主义现代化国家新征程、向第二个百年奋斗目标进军创造良好的条件.某综合与实践研究小组根据我国第七次人口普查数据进行整理、描述和分析,给出部分数据信息:信息一:普查登记的全国大陆31个省、自治区、直辖市人口数的频数分布直方图如下: (数据分成6组:020x ≤<,2040x ≤<,4060x ≤<,6080x ≤<,80100x ≤<,100120x ≤≤)信息二:普查登记的全国大陆31个省、自治区、直辖市人口数(百万人)在4060x ≤<这一组的数据是:58,47,45,40,43,42,50;信息三:2010——2021年全国大陆人口数及自然增长率;请根据以上信息,解答下列问题:(1)普查登记的全国大陆31个省、自治区、直辖市人口数的中位数为______百万人.(2)下列结论正确的是______.(只填序号)△全国大陆31个省、自治区、直辖市中人口数大于等于100(百万人)的有2个地区; △相对于2020年,2021年全国大陆人口自然增长率降低,全国大陆人口增长缓慢; △2010-2021年全国大陆人口自然增长率持续降低.(3)请写出2016-2021年全国大陆人口数、全国大陆人口自然增长率的变化趋势,结合变化趋势谈谈自己的看法.18.如图,反比例函数y=k x(x >0)的图象过格点(网格线的交点)P . (1)求反比例函数的解析式;(2)在图中用直尺和2B 铅笔画出两个矩形(不写画法),要求每个矩形均需满足下列两个条件:△四个顶点均在格点上,且其中两个顶点分别是点O ,点P ;△矩形的面积等于k 的值.19.本学期小明经过一段时间的学习,想利用所学的数学知识对某小区居民楼AB 的高度进行测量.如图,先测得居民楼AB 与CD 之间的距离BD 为28m ,后站在F 点处测得居民楼CD 的顶端C 的仰角为45︒,居民楼AB 的顶端A 的仰角为55︒,已知居民楼CD 的高度为14.6m ,小颖的观测点E 距地面1.6m ,求居民楼AB 的高度(精确到1m ). (参考数据:sin550.82550.5755 1.43︒≈︒≈︒≈,cos ,tan )20.如图1,在矩形ABCD 中,AC ,BD 相交于点O ,点E 为BD 上的一个动点,连接CE 并延长到点F ,使EF CE =,连接AF .(1)若点E 与点B 重合(如图2),判断AF 与BD 的数量关系和位置关系,并说明理由;(2)若以A ,F ,B ,E 为顶点的四边形是平行四边形,3BD =,请直接写出线段BE 的长度.21.2021年7月24日,中共中央办公厅、国务院办公厅印发《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》.某学校积极响应“双减”政策,为了丰富学生校园生活,经研究决定准备购买一批体育健身器材.已知购买2个篮球和3个排球共花费440元,购买4个篮球和1个排球共花费480元.(1)求篮球和排球的单价;(2)某体育用品店有两种优惠方案,方案一:每购买一个篮球就送一个排球;方案二:购买篮球和排球的费用一律打七五折.该学校需要购买40个篮球和x 个排球(40x >).方案一的费用为1y 元,方案二的费用为2y 元.△根据题目信息,直接写出1y 与x 的的函数表达式: ;2y 与x 的函数表达式: ;△画出2y 图象,并直接写出1y ,2y 交点的坐标 ;△根据图象回答:当购买排球的数量x 满足条件 时,方案二比方案一更优惠. 22.某游乐场的圆形喷水池中心O 有一喷水管OA ,0.5OA =米,从A 点向四周喷水,喷出的水柱为抛物线且形状相同.如图,以水平方向为x 轴,点O 为原点建立平面直角坐标系,点A 在y 轴上.已知在与池中心O 点水平距离为3米时,水柱达到最高,此时高度为2米.(1)求水柱所在的抛物线(第一象限部分)的函数表达式;(2)身高为1.67m 的小颖站在距离喷水管4m 的地方,她会被水喷到吗?(3)现重新改建喷泉,升高喷水管,使落水点与喷水管距离7m ,已知喷水管升高后,喷水管喷出的水柱抛物线形状不变,且水柱仍在距离原点3m 处达到最高,则喷水管OA 要升高多少?23.【思维探究】数学兴趣小组在研究四边形的旋转时,遇到了这样的一个问题.如图1,四边形ABCD 和BEFG 都是正方形,BH AE ⊥于H ,延长HB 交CG 于点M .通过测量发现CM MG =.为了证明他们的发现,小颖想到了这样的证明方法:过点C 作CN BM ⊥于点N .她已经证明了ABH BCN ≌,但接下来的证明过程,她有些迷茫了.(1)请同学们帮小颖将剩余的证明过程补充完整;(2)【思维延伸】若将原题中的“正方形”改为“矩形”(如图2所示),且AB BG t BC BE (其中0t >),请直接写出线段CM MG 、的数量关系为 ;(3)【思维拓展】在图3中,在Rt ABC △和Rt ADE △中,9060BAC DAE ABC ADE ∠∠︒∠∠︒==,==,连接BD CE 、,F 为BD 中点,则AF 与CE 的数量关系为 .参考答案:1.B【分析】利用绝对值的代数意义,正数的绝对值是它本身,0的绝对值是0,负数的绝对值是它的相反数,据此直接计算即可.【详解】解:根据绝对值的定义可得-2023=2023;故选:B【点睛】本题考查绝对值的代数意义,掌握绝对值的意义是解题的关键.2.D【分析】根据正方体的展开图进行判断即可;【详解】解:由正方体的展开图可知“地”字所在面相对的面上的汉字是“人”;故选:D.【点睛】本题主要考查正方体的展开图相对两个面上的文字,注意正方体的空间图形,从相对面入手是解题的关键.3.C【分析】科学记数法的表示形式为10na⨯的形式,其中1≤|a|<10,n为整数,确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同,当原数绝对值大于等于10时,n是正数;当原数的绝对值<1时,n是负数.【详解】解:16万吨=160000吨=5⨯吨.1.610故选:C.【点睛】此题考查了科学记数法的表示方法.科学记数法的表示形式为10na⨯的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.4.A【分析】利用对顶角相等求解.【详解】解:量角器测量的度数为30°,∠=︒.由对顶角相等可得,130故选A.【点睛】本题考查量角器的使用和对顶角的性质,掌握对顶角相等是解题的关键.5.B【分析】根据扇形统计图中得分情况的所占比多少来判断即可;【详解】解:由扇形统计图可知:1分所占百分比:5%;2分所占百分比:10%;3分所占百分比:25%;4分所占百分比:45%;5分所占百分比:15%;可知,4分所占百分比最大,故4分出现的次数最多,△所打分数的众数为4;故选:B.【点睛】本题主要考查众数的概念,扇形统计图,理解扇形统计图中最大百分比是所打分数的众数,这是解本题的关键.6.C【分析】根据题目中的函数解析式和反比例函数的性质,可以判断各个选项中的说法是否正确,从而可以解答本题.【详解】解:反比例函数y=﹣5x,A、当x=1时,y=﹣51=﹣5,图像经过点(1,-5),故选项A不符合题意;B、△k=﹣5<0,故该函数图象位于第二、四象限,故选项B不符合题意;C、当x<0时,y随x的增大而增大,故选项C符合题意;D、当x>0时,y随x的增大而增大,故选项D不符合题意;故选C.【点睛】本题考查的是反比例函数的性质,熟练掌握反比例函数的性质是解题的关键.7.A【分析】平均增长率为x,关系式为:第三天揽件量=第一天揽件量×(1+平均增长率)2,把相关数值代入即可.【详解】解:由题意得:第一天揽件200件,第三天揽件242件,△可列方程为:()22001242x+=,故选:A.【点睛】此题考查一元二次方程的应用,得到三天的揽件量关系式是解决本题的突破点,难度一般.8.D【分析】先过点C 做出x 轴垂线段CE ,根据相似三角形找出点C 的坐标,再根据平移的性质计算出对应D 点的坐标.【详解】如图过点C 作x 轴垂线,垂足为点E ,△90ABC ∠=︒△90ABO CBE ∠+∠=︒△90CBE BCE +=︒∠△ABO BCE在ABO ∆和BCE ∆中,90ABO BCE AOB BEC =⎧⎨==︒⎩∠∠∠∠ , △ABO BCE ∆∆∽, △12AB AO OB BC BE EC === , 则26BE AO == ,22EC OB ==△点C 是由点B 向右平移6个单位,向上平移2个单位得到,△点D 同样是由点A 向右平移6个单位,向上平移2个单位得到,△点A 坐标为(0,3),△点D 坐标为(6,5),选项D 符合题意,故答案选D【点睛】本题考查了图象的平移、相似三角形的判定与性质,利用相似三角形的判定与性质找出图象左右、上下平移的距离是解题的关键.9.A【分析】根据点到直线垂线段最短及平行线间距离处处相等,结合勾股定理即可得到答案.【详解】解:△=90B ∠︒,=4BC ,=5AC ,△3AB ,△四边形ADCE 是平行四边形,△BC AE ∥,△当DE BC ⊥时,DE 最小,△=90B ∠︒,△四边形ABDE 是矩形,△3DE AB ==,故选A .【点睛】本题考查矩形判定和性质,平行四边形的性质,勾股定理及点到直线垂线段最短,解题的关键是掌握点到直线垂线段最短.10.D【分析】根据图一图二中的数据即可作出判断.【详解】如图二可知,当4t =时两点停止运动,△点P 从点A 运动到点B 用了4秒,△4AB =,△点Q 运动到点C 之前和之后,BPQ 面积算法不同,即2t =时,S 的解析式发生变化, △图2中点M 对应的横坐标为2,此时P 为AB 中点,点C 与点Q 重合,连接AC ,如图所示△菱形ABCD 中,4,60AB BC B ==∠=︒,△ABC 是等边三角形, △1,22CP AB BP AB ⊥==,△CP ==△11222a S BP CP ==⋅=⨯⨯= 故选:D .【点睛】本题考查了动点函数的图象,解决本题的关键是菱形的边长.11.52. 【分析】根据两内项之积等于两外项之积解答即可.【详解】△25x y =, △52x y =, 故答案为:52. 【点睛】本题主要考查了比例的性质,可根据比例的基本性质直接求解.12.16【分析】利用树状图列出所有情况数,找出抽到B ,C 两类的情况数,即可得到概率.【详解】解:由题意可得,由上图可得:总共有12种情况,抽到B ,C 两类的情况有2种, △21126P ==, 故答案为16. 【点睛】本题考查利用树状图求概率,解题的关键是正确画出树状图.13.-1【分析】首先利用图标得出一组对称点,然后利用二次函数对称轴与顶点(最值)得出即可.【详解】由(-2,49),(0,49)可知抛物线的对称轴为直线t=-1,故当t=-1时,植物生长的温度最快.故答案为-1.【点睛】此题主要考查了二次函数的应用以及待定系数法求二次函数解析式,得出二次函数解析式是解题关键.14.14【分析】由//DE AC ,推出DEO CAO △∽△,可得21()25DEO CAO S DE SAC ∆∆==,推出15DE BE AC BC ==,推出14BE EC =,即可求解.【详解】解://DE AC ,DEO CAO ∴∽△△, ∴21()25DEO CAO S DE S AC ==△△, 15DE BE AC BC ∴==, 14BE EC ∴=, 14BED DEC S S ∴=△△, 故答案为:14. 【点睛】本题考查相似三角形的判定和性质,解题的关键是熟练掌握相似三角形的面积比等于相似比的平方.15 【分析】分两种情况:△如图1,90D AB ''∠=︒,△如图2,90AB D ''∠=︒,分别作辅助线,构建相似三角形,证明三角形相似列比例式可得对应a 的值.【详解】解:△如图1,90D AB ''∠=︒,延长C B ''交AB 于G ,过点D 作D H AB '⊥,交BA 的延长线于H ,△90H AGB BGB ''∠=∠=∠=︒,△四边形ABCD 是矩形,△90BAD C ∠=∠=︒,2AD BC ==, △tan AD B G AB BG ABD ∠'==,即23B G BG '=, 设2B G x '=,3BG x =,△BB a '===,由平移得:DD BB ''==,△22D H x '=+,3AH BG x ==,△33AG AB BG x =-=-,△90D AB HAD BAB ''''∠=∠+∠=︒,90AD H HAD ''∠+∠=︒,△AD H GAB ''∠=∠,△90H AGB '∠=∠=︒,△D HA AGB ''∽, △D H AH AG B G '=',即223332x x x x+=-, △513x =,△513a =; △如图2,90AB D ''∠=︒,延长C B ''交AB 于M ,则C M AB '⊥,△90AMB '∠=︒,由平移得:2B C BC ''==,3C D CD ''==,同理设2B M m '=,3BM m =,则BB a '==,△33AM m =-,△90AB M D B C ''''∠+∠=︒,90MAB AB M ''∠+∠=︒,△D B C MAB ''''∠=∠,△90C AMB ''∠=∠=︒,△D C B B MA ''''∽, △C D B C MB AM ''''=',即32233m m=-, △913m =,△913a =;综上,a 【点睛】本题主要考查了矩形的性质、平移的性质、勾股定理、三角函数、三角形相似的性质和判定、直角三角形的性质等知识点;解题关键是画出两种情况的图形,依题意进行分类讨论.16.(1)1-(2)11x =+,21x =【分析】(1)根据三角函数,绝对值,0指数幂及根数运算直接计算即可得到答案;(2)移项,化二次项系数为1,配方,两边开方即可得到答案.【详解】(1)解:原式(21=+-21-1=-;(2)解:移项得,2483x x -=,两边同时除以4得,2324x x -=, 配方得,27(1)4x -=, 两边开方得,1x -=,△11x =+,21x = 【点睛】本题考查去绝对值,0指数幂,根式化简,三角函数,解一元二次方程,解题的关键是熟练掌握几种解一元二次方程的方法及选择适当的方法.17.(1)40(2)△△(3)答案见解析【分析】(1)根据已知发现中位数在第二组内,从小到大排列找出处在中间位置的一个数或两个数的平均数即可求出中位数;(2)从频数分布直方图可知,比95亿元多的省份有5个,因此处在第六名;△根据频数分布直方图进行判断即可;△根据条形图与折线图即可判断;△根据折线图即可判断;(3)根据条形图与折线图可写出2016﹣2021年全国大陆人口数、全国大陆人口自然增长率的变化趋势,根据变化趋势写出看法即可.【详解】(1)解:将这31个省、自治区、直辖市人口数从小到大排列处在中间位置的数是40百万人,因此中位数是40百万人,故答案为:40;(2)解:①全国大陆31个省、自治区、直辖市中人口数大于等于100(百万人)的有2个地区,故原结论正确,符合题意;②相对于2020年,2021年全国大陆人口自然增长率降低,全国大陆人口增长缓慢,故原结论正确,符合题意;③2010﹣2021年全国大陆人口自然增长率的情况是:2010﹣2012,2013﹣2014,2015﹣2016年增长率持续上升;2012﹣2013,2014﹣2015,2016﹣2021年增长率持续降低,故原结论错误,不符合题意.所以结论正确的是△△.故答案为:△△;(3)解:2016﹣2021年全国大陆人口数增长缓慢,全国大陆人口自然增长率持续降低.看法:放开计划生育的政策,鼓励多生优育,以免人口负增长的情况出现.【点睛】本题考查频数分布直方图、条形统计图、折线统计图,中位数,理解统计图中数量之间的关系是正确解答的前提.18.(1)4yx;(2)作图见解析.【详解】分析:(1)将P点坐标代入y=kx,利用待定系数法即可求出反比例函数的解析式;(2)根据矩形满足的两个条件画出符合要求的两个矩形即可.详解:(1)△反比例函数y=k x(x >0)的图象过格点P (2,2), △k=2×2=4,△反比例函数的解析式为y=4x; (2)如图所示:矩形OAPB 、矩形OCDP 即为所求作的图形.点睛:本题考查了作图-应用与设计作图,反比例函数图象上点的坐标特征,待定系数法求反比例函数解析式,矩形的判定与性质,正确求出反比例函数的解析式是解题的关键. 19.23m【分析】过E 作GH BD ∥,根据题意可得13CH CD DH CD EF =-=-=,根据在F 点处测得居民楼CD 的顶端C 的仰角为45︒可得13EH CH ==,281315GE =-=,最后根据居民楼AB 的顶端A 的仰角为55︒即可得到AG ,即可得到答案.【详解】解:过E 作GH BD ∥,根据题意可得,△GH BD ∥,△28GH BD ==(m), 1.6BG EF HD ===(m),△13CH CD DH CD EF =-=-=(m),△在F 点处测得居民楼CD 的顶端C 的仰角为45︒,△13EH CH ==(m),△281315GE =-=(m),△AB 的顶端A 的仰角为55︒, △tan 55 1.4315AG AG EG ︒===, △21.45AG =(m),△21.45 1.623AB AG GB =+=+≈(m),△居民楼AB 的高度为23m ,.【点睛】本题考查解直角三角形解决仰俯角问题,解题关键是作辅助线根据等腰三角形求出EH .20.(1)AF BD =且AF BD ∥;(2)1或3【分析】(1)若点E 与点B 重合根据矩形ABCD 得到AD BC =,AD BC ∥,结合EF CE =,即可得到四边形AFBD 为平行四边形;(2)先根据矩形的性质得到OC OA =,OB OD =,再根据三角形中位线的性质得到OE AF ,12OE AF =,当AB 为对角线时,如图1根据平行四边形的性质得到AF BE =,则32OB BE =,即可得到一个答案;当AB 为边时,如图,此时E 点与D 点重合,即可得到答案.【详解】(1)解:AF BD =且AF BD ∥,△四边形ABCD 是矩形,△AD BC =,AD BC ∥,△EF CE =,△AD FB =,△四边形AFBD 是平行四边形,△AF BD =,AF BD ∥;(2)解:△四边形ABCD 是矩形,△OC OA =,OB OD =,△EF CE =,△OE AF ,12OE AF =, 当AB 为对角线时,如下图△四边形AFBE为平行四边形,△AF BE=,△12OE BE=,△32OB OE BE BE=+=,△3BD=,△1BE=;当AB为边时,如下图△四边形ABEF为平行四边形,△AB EF=,△AB CD=,△此时点E与点D重合,△3BE BD==;综上所述BE的长度为1或3.【点睛】本题考查了矩形的性质:平行四边形的性质矩形都具有;矩形的四个角都是直角;也考查了平行四边形的判定和三角形中位线性质.21.(1)篮球单价为100元、排球单价为80元;(2)△y1=80x+800;y2=60x+3000;△(110,9600);见详解;△x>110.【分析】(1)设篮球单价为x元、排球单价为y元,根据等量关系购买2个篮球和3个排球共花费440元,购买4个篮球和1个排球共花费480元列二元一次方程组23440 4480x yx y+=⎧⎨+=⎩,解方程组即可;(2)△利用篮球单价×篮球个数+排球单价×优惠后的排球个数得出方案一的费用,利用篮球单价×篮球个数与排球单价×排球个数的和×0,75得出方案二的费用即可;△用描点法画y2的函数图像,列表,描点,作射线;然后让y1=y2,列方程80x+800=60x+3000,解方程即可;△根据函数图像,方案二更优惠是方案一的函数图像在方案二的函数图像上方,从而得出当x>110时,方案二比方案一更优惠.【详解】(1)解:设篮球单价为x元、排球单价为y元;根据题意,得23440 4480x yx y+=⎧⎨+=⎩,解这个方程组得10080xy=⎧⎨=⎩,篮球单价为100元、排球单价为80元;(2)解:△y1=100×40+80×(x-40)=80x+800,y2=(100×40+80x)×75%=60x+3000,故答案为:y1=80x+800;y2=60x+3000;△列表描点(0,3000),(100,9000),过这两点作射线如图,△y1=y2,△列方程80x+800=60x+3000;解得x=110,y1=80×110+800=9600,△1y,2y交点的坐标(110,9600),故答案为(110,9600);△根据函数图像,方案二更优惠,含义是y 1>y 2是指方案一的函数图像在方案二的函数图像上方,△当x >110时,方案二比方案一更优惠.故答案为x >110.【点睛】本题考查列二元一次方程组解应用题,列一次函数解析式,描点法化函数图像,解一元一次方程,利用函数图像求不等式的解集.掌握列二元一次方程组解应用题,列一次函数解析式,描点法化函数图像,解一元一次方程,利用函数图像求不等式的解集是解题关键.22.(1)21(3)26y x =-+ (2)她不会被水喷到; (3)23【分析】(1)根据图像设抛物线解析式为2()y a x h k =-+,根据题意将点(0,0.5)A 代入即可得到答案;(2)计算当4x =时y 的值,与1.67m 比较即可得到答案;(3)根据题意中形状不变得到a 不变,对称轴是3h =及过(7,0)点代入顶点式即可得到答案.【详解】(1)解:设抛物线解析式为2()y a x h k =-+,由图像可得, 3h =,2k =,图像过(0,0.5)A ,△2(03)20.5a -+= , 解得:16a =-, △21(3)26y x =--+; (2)解:当4x =时,2111(43)2 1.6766y =--+=>, △她不会被水喷到;(3)解:设解析式为2()y a x h k =-+,由题意可得,△图像形状不变,仍在距离原点3m 处达到最高,落水点与喷水管距离7m , △16a =-,3h =,过(7,0)点, △210(73)6k =--+, 解得:83k =, △218(3)63y x =--+, 当0x =时, △2187(03)636y =-⨯-+=, 72263-=, △OA 要升高23米.【点睛】本题考查二次函数实际应用及求抛物线解析式,解题的关键是根据图像及题意提取相关信息.23.(1)见解析; (2)21CM GM t =;(3)CE =.【分析】(1)如图1中,过点G 作GT NH ⊥于点T .分别证明BH CN =,TG BH =,再证明(AAS)CMN GMT ≌,可得结论;(2)如图2中,过点C 作CN MH ⊥于点N ,G 过点G 作GT NM ⊥交HM 的延长线于点T .证明AHB BNC ∽,推出1CN BC BH AB t ==,推出1CN BH t=,同法可证EHB BTG ∽,推出TG BG t BH BE==,推出TG kBH =,再证明CNM GTM ∽,可得结论;(3)结论:CE =.如图3中,延长AF 到T ,使得AF FT =,连接BT ,DT .证明CAE ABT ∽,推出EC AC AT AB==,可得结论. 【详解】(1)如图1中,过点G 作GT NH ⊥于点T .ABH BCN ≌,BH CN ∴=,同法可证EHB BTG ≌,BH TG ∴=,CN GT ∴=,CN NH ⊥,GT NH ⊥,90N GTM ∴∠=∠=︒,CMN GMT ∠=∠,(AAS)CMN GMT ∴≌,CM GM ∴=;(2)如图2中,过点C 作CN MH ⊥于点N ,G 过点G 作GT NM ⊥交HM 的延长线于点T .四边形ABCD 是矩形,90ABC AHB CNB ∴∠=∠=∠=︒,90ABH CBN ∴∠+∠=︒,90CBN BCN ∠+∠=︒,ABH BCN ∴∠=∠,AHB BNC ∴∽, ∴1CN BC BH AB t==,1CN BH t∴=, 同法可证EHB BTG ∽, ∴TG BG t BH BE==, TG tBH ∴=,90T CNM ∠=∠=︒,CMN GMT ∠=∠,CNM GTM ∴∽, ∴211BH CM CN t MG TG tBH t===. 故答案为:21CM GM t =; (3)结论:CE =.理由:如图3中,延长AF 到T ,使得AF FT =,连接BT ,DT .AF FT =,BF FD =,∴四边形ABTD 是平行四边形,AD BT ∴=,//AD BT ,180ABT BAD ∴∠+∠=︒,90CAB DAE ∠=∠=︒,180BAD CAE ∴∠+∠=︒,ABT CAE ∴∠=∠,60ABC ADE ∠∠︒==,30ACB AED ∴∠=∠=︒,AC ∴=,AE ==,∴AC AE AB BT= CAE ABT ∴∽,∴EC AC AT AB =∴2EC AF=CE ∴=.故答案为:CE =.【点睛】本题属于四边形综合题,考查了全等三角形的判定和性质,相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形或相似三角形解决问题.。
915230-MATLAB第三版实验答案

MATLAB程序设计与应用(第三版)实验参考答案实验1 MATLAB系统环境与运算基础%第1题(略)%第2题(略)%第3题%(1)z1=2*sin(85*pi/180)/(1+exp(2))%(2)x=12;y=1e-5;z2=pi/(x+y)%(3)x=[2,1+2i;-0.45,5];z2=0.5*log(x+sqrt(1+x.^2))%(3)a=-3.0:0.1:3.0;z3=(exp(0.3*a)-exp(-0.3*a))/2.*sin(a+0.3)+log((0.3+a)/2)%第4题A=[12 34 -4;34 7 87;3 65 7];B=[1 3 -1;2 0 3;3 -2 7];A*BA.*BA^3A.^3A/BB\A[A,B][A([1,3],:);B^2]%第5题A=[1 2 3 4 5;6 7 8 9 10;11 12 13 14 15;16 17 18 19 20;21 22 23 24 25] B=[3 0 16;17 -6 9;0 23 -4;9 7 0;4 13 11]C=A*B%求D方法1F=size(C)D=C(F(1)-2:F(1),F(2)-1:F(2))%求D方法2D=C(end-2:end,end-1:end)whos%第6题%(1)A=100:999;B=rem(A,21);C=length(find(B==0))%(2)A='lsdhKSDLKklsdkl';k=find(A>='A'&A<='Z');A(k)=[]实验2 MATLAB矩阵处理%第1题E=eye(3);R=rand(3,2);O=zeros(2,3);S=diag([2,3]);A=[E,R;O,S];A^2B=[E,(R+R*S);O,S^2]%第2题A=fix(10*rand(5))H=det(A)Trace=trace(A)Rank=rank(A)Norm=norm(A)%第3题H=hilb(5)P=pascal(5)Hh=det(H)Hp=det(P)Th=cond(H)Tp=cond(P)%第4题A=[-29,6,18;20,5,12;-8,8,5][V,D]=eig(A)%数学意义略%第5题方法一%(1):A=[1/2,1/3,1/4;1/3,1/4,1/5;1/4,1/5,1/6]; b=[0.95,0.67,0.52]';x=inv(A)*b%(2):B=[0.95,0.67,0.53]';x=inv(A)*B%(3):cond(A)%第5题方法二A=hilb(4)A(:,1)=[]A(4,:)=[]B=[0.95,0.67,0.52]';X=inv(A)*BB1=[0.95,0.67,0.53]';X1=inv(A)*B1N=cond(B)N1=cond(B1)Na=cond(A) %矩阵A为病态矩阵实验3 顺序结构程序设计%程序(略)实验4 选择结构程序设计%第1题程序一x=[-5.0,-3.0,1.0,2.0,2.5,3.0,5.0];y=[]; %建立存放所有y值的矩阵for x0=xif x0<0&x0~=-3y=[y,x0*x0+x0-6];elseif x0>=0&x0<5&x0~=2&x0~=3y=[y,x0*x0-5*x0+6];elsey=[y,x0*x0-x0-1];endendx %输出所有xy %输出所有y%第1题程序二x=[-5,-3,1,2,2.5,3,5];y=[];for a=1:7if x(a)<0&x(a)~=-3y=[y,(x(a))^2+x(a)-6];elseif x(a)>=0&x(a)<5&x(a)~=2&x(a)~=3y=[y,(x(a))^2-5*x(a)+6];elsey=[y,x(a)*x(a)-x(a)-1];endend%第2题程序一x=input('请输入一个百分制成绩:');if x>100|x<0disp('您输入的成绩不是百分制成绩,请重新输入。
北京市师大实验小学数学六年级下册第一单元经典习题(含答案解析)

一、选择题1.一袋饼干外包装袋上标着:净重(250±5克),表示这种饼干标准的质量是250克,实际每袋最多不超过()克。
A. 255B. 250C. 245D. 260A解析: A【解析】【解答】250+5=255(克)故答案为:A。
【分析】根据条件“ 净重(250±5克)”可知,这种饼干实际质量最少不低于250-5=245克,最多不超过250+5=255克,据此解答。
2.下列描述正确的是()。
A. 在上图上可以找到-5、20、3.5三个数对应的点B. 上图中,直线上的数不是正数就是负数C. 在0和3之间的数只有1和2A解析: A【解析】【解答】解:A:任何数都可以在数轴上找到,此选项正确;B:直线上有5个数,0不是正数,也不是负数。
此选项错误;C:在0和3之间的数有无数个。
此选项错误。
故答案为:A。
【分析】在数轴上0右边的数都是正数,左边的数都是负数,0不是正数也不是负数。
3.在-4,-9,-1.2,-0.1这些数中,最大的数是()。
A. -4B. -9C. -1.2D. -0.1D解析: D【解析】【解答】解:-9<-4<-1.2<-0.1,最大的数是-0.1。
故答案为:D。
【分析】正数都比负数大,比较负数的大小,去掉负号后比较大的数字小,去掉负号后比较小的数字大。
4.如果-个人先向东走6m记作+6m,后来这个人又走-7m,结果是()。
A. 相当于从起点向东走了13mB. 相当于从起点向东走了1mC. 相当于从起点向西走了13mD. 相当于从起点向西走了1m D解析: D【解析】【解答】解:如果一个人先向东走6m记作+6m,后来这个人又走-7m,结果是+6+(-7)=-1(米),相当于从起点向西走了1m。
故答案为:D。
【分析】向东走为正,那么向西走就为负,先向东走6m,再向西走7米,相当于从起点走向西走了1米。
5.一种饼干包装袋上标着:净重(150±5克),表示这种饼干标准的质量是150克,实际每袋最少不少于()克.A. 155B. 150C. 145C解析: C【解析】【解答】150-5=145(克)。
华东师范大学第二附属中学(实验班用)数学习题详解-1

第一章 集合与命题 1.1 集合及其表示法基础练习1.用描述法表示下列集合: (1){}14916253649,,,,,,. (2)12340251017⎧⎫⋯±±±±⎨⎬⎩⎭,,,,,.解:(1){}217y y x x x =∈*N ,,≤≤. (2)()2111n x x n n ⎧⎫-⎪⎪=±∈⎨⎬-+⎪⎪⎩⎭*N ,. 2.用列举法表示下列集合: (1){x x 是20的正约数}. (2){}2340x x x x --<∈Z ,. 解:(1){}12451020,,,,,. (2)解不等式得:{}140123x -<<⇒,,,. 3.设三元素的集合0b a a ⎧⎫⎨⎬⎩⎭,,也可表示为{}21a a b +-,,,求20102011a b +的值. 解:由已知有()()11a b =-,,,故有201020110a b +=. 4.已知全集65M aa a ⎧⎫=∈∈⎨⎬-⎩⎭N Z 且,求集合M . 解:由已知5a -=1,2,3,6,则1a =-,2,3,4,故{}1234M =-,,,. 5.给定三元集合{}21x x x -,,,求实数x 的取值范围. 解:由集合元素的互异性知0x ≠,1,2x 的取值范围是()()515151*********⎛⎛⎫⎛⎫⎛⎫-+++-∞+∞ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,,,,,6.若集合{}2210A x ax x a x =++=∈∈R R ,,中只有一个元素,求a .解:当0a =时,方程只有一个根12-,则以0a =符合题意.当0a ≠时,则关于x 的方程2210ax x ++=是一元二次方程,由于集合A 中只有一个元素,则一元二次方程2210ax x ++=有两个相等的实数根,所以440a ∆=-=,解得1a =. 综上所得,0a =,1.7.若集合{}1A x xy xy =-,,,其中x ∈Z ,y ∈Z 且0y ≠,若0A ∈.求A 中元素之和. 解:由已知及集合元素的互异性知0x y ≠,,则10xy -=. 由于 x ∈Z ,y ∈Z ,则 ()()11x y =,,(舍)或()11--,, 则 A 中元素之和为0.8.设集合{}0123S a a a a =,,,,在S 上定义运算为:i j k a a a ⊕=,其中k 为i j +被4除的余数,0i j =,,1,2,3,则求满足关系式()20x x a a ⊕⊕=的()x x S ∈的个数. 解:由于 ()20x x a a ⊕⊕=则 ()()()2mod 41mod 4x x x ⊕≡±⇒≡±.只有1a ,3a 符合所给关系式,则x 的个数为2.分析:在4元素集合上定义一个封闭运算显得抽象而陌生,在理解题目的字面含义和数学含义后,题目的结构并不复杂,可以认为就是一个条件、一个结论:(1) 题目的条件:在S 上定义了一个运算+。
2022-2023 学年度师大附中高新实验学校七年级第一次月考数学参考答案

2022-2023学年度第二学期第一次作业大检查数学答案一.选择题(共10小题)1.∠1与∠2是对顶角的为()A.B.C.D.【分析】有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角,由此即可判断.【解答】解:A、∠1与∠2,没有公共顶点,故A不符合题意;B、∠1与∠2,一个角的两边不是另一个角的两边的反向延长线,故B不符合题意;C、∠1与∠2,一个角的两边不是另一个角的两边的反向延长线,故C不符合题意;D、∠1与∠2是对顶角,故D符合题意.故选:D.2.下列实数0,,π,,其中无理数共有()A.1个B.2个C.3个D.4个【分析】无理数是指无限不循环小数,包括三方面的数:①含π的,②一些有规律的数,③开方开不尽的数,根据以上内容判断即可.【解答】解:π,,是无理数.故选:B.【点评】本题考查了无理数的定义,注意:无理数是指无限不循环小数.3.如图,直线b,c被直线a所截,则∠1与∠2是()A.对顶角B.同位角C.内错角D.同旁内角【分析】两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.【解答】解:由题意可得,∠1与∠2是直线b,c被直线a所截而成的同位角.故选:B.【点评】本题主要考查了同位角,同位角的边构成“F“形,内错角的边构成“Z“形,同旁内角的边构成“U”形.4.﹣27的立方根为()A.3B.-3C.9D.-9故选:B.【点评】本题主要考查的是立方根的定义5.下列命题是假命题的是()A.如果两条直线平行,那么内错角一定相等B.如果两条直线平行,那么同位角一定相等C.如果两个角是同旁内角,那么它们一定互补D.如果两个角是对顶角,那么它们一定相等【分析】根据平行线的判定定理与性质定理、对顶角性质判断求解即可.【解答】解:如果两条直线平行,那么内错角一定相等,故A是真命题,不符合题意;如果两条直线平行,那么同位角一定相等,故B是真命题,不符合题意;如果两个角是同旁内角,那么它们不一定一定互补,故C是假命题,符合题意;如果两个角是对顶角,那么它们一定相等,故D是真命题,不符合题意;故选:C.【点评】此题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.6.下列每组图形中,左边的图形平移后可以得到右边图形的是()A.B.C.D.【分析】根据平移的性质:大小,形状,方向不变,即可一一判定.【解答】解:选项A中的两个图形,左边的图形平移后不能得到右边的图形,故该选项不符合题意;选项B中的两个图形,左边的图形平移后不能得到右边的图形,故该选项不符合题意;选项C中的两个图形,左边的图形平移后不能得到右边的图形,故该选项不符合题意;选项D中的两个图形,左边的图形平移后能得到右边的图形,故该选项符合题意.故选:D.【点评】本题考查了平移作图,熟练掌握和运用平移作图的方法是解决本题的关键.7.下列运算正确的是()A.﹣22=4B.C.D.|﹣2|=2【分析】先化简各式,逐一判断即可解答.【解答】解:A、﹣22=﹣4,故A不符合题意;B、()3=﹣5,故B不符合题意;C、=2,故C不符合题意;D、|﹣2|=2,故D符合题意;故选:D.【点评】本题考查了实数的运算,准确熟练地进行计算是解题的关键.8.如图,平行线AB,CD被直线EF所截,FG平分∠EFD,若∠EFD=70°,则∠EGF 的度数是()A.35°B.55°C.70°D.110°【分析】先根据角平分线的定义求出∠GFD的度数,再由平行线的性质即可得出结论.【解答】解:∵FG平分∠EFD,∠EFD=70°,∴∠GFD=∠EFD=×70°=35°,∵AB∥CD,∴∠EGF=∠GFD=35°.故选:A.【点评】本题考查的是平行线的性质,用到的知识点为;两直线平行,内错角相等.9.如图,直线a、b被直线c所截,下列说法正确的是()A.当∠1=∠2时,a∥b B.当a∥b时,∠1=∠2C.当∠1+∠2=180°时,a∥b D.当∠1+∠2=90°时,a∥b【分析】根据平行线的判定定理和性质定理判断即可.【解答】解:如图:A、∵∠2与∠3互为邻补角,∴∠3=180°﹣∠2,当∠1=∠3,即∠1=180°﹣∠2时,根据同位角相等,两直线平行,一定有a∥b,故此选项不符合题意;B、∵a∥b,∴∠1=∠3,∵∠2+∠3=180°,∴∠1+∠2=180°,故此选项不符合题意;C、当∠1+∠2=180°时,∵∠2+∠3=180°,∴∠1=∠3,∴a∥b,故此选项符合题意;D、当a∥b时,∠1=∠3,∵∠3+∠2=180°,∴∠1+∠2=180°,故此选项不符合题意.故选:C.【点评】此题考查了平行线的判定与性质,熟练掌握平行线的判定定理与性质定理是解题的关键.10.如图,已知AB∥EG,BC∥DE,CD∥EF,则x、y、z三者之间的关系是()A.x﹣z=y B.x+y+z=180°C.y﹣x=z D.y﹣x=x﹣z【分析】延长AB交DE于H,依据平行线的性质,即可得到∠ABC=∠DEG,即x=z+y,进而得到x﹣z=y.【解答】解:如图所示,延长AB交DE于H,∵BC∥DE,∴∠ABC=∠AHE=x,∵CD∥EF,AB∥EG,∴∠D=∠DEF=z,∠AHE=∠DEG=z+y,∴∠ABC=∠DEG,即x=z+y,∴x﹣z=y.故选:A.【点评】此题主要考查了平行线的性质,关键是掌握平行线性质定理:两直线平行,内错角相等.二.填空题(共6小题)11.的平方根为±2.【分析】先去掉根号,再求平方根和去绝对值.【解答】解:∵=4,4的平方根为±2,∴的平方根为±2,故答案为:±2.【点评】本题考查平方根的性质,解题的关键是将计算出来.12.请写出一个小于的正整数1(答案不唯一).【分析】估算的大小,进而得出答案.【解答】解:∵<<,∴2<<3,∴比小的正整数有1.故答案为:1(答案不唯一,1或2都对).【点评】本题考查估算无理数的大小,估算出在哪两个相邻的正整数之间是解题的关键.13.把命题“邻补角互补”改写成“如果…,那么…”的形式如果两个角是邻补角.那么它们(这两个角)互补.【分析】分清题目的已知与结论,即可解答.【解答】解:把命题“邻补角互补”改写为“如果…那么…”的形式是:如果两个角是邻补角.那么它们(这两个角)互补,故答案为:如果两个角是邻补角.那么它们(这两个角)互补.【点评】本题主要考查了命题的定义,正确理解定义是关键.14.已知实数x,y满足+(y+2)2=0,则x+y=1.【分析】根据算术平方根和偶次方的非负性求出x、y的值,再代入求出即可.【解答】解:∵实数x,y满足+(y+2)2=0,∴x﹣3=0,y+2=0,∴x=3,y=﹣2,∴x+y=3+(﹣2)=1,故答案为:1.【点评】本题考查了算术平方根、偶次方的非负性和求代数式的值,能求出x、y的值是解此题的关键.15.如图,△ABC 的边BC 长为4cm .将△ABC 平移2cm 得到△A 'B 'C ',且BB '⊥BC ,则阴影部分的面积为8cm 2.【分析】根据平移的性质得出阴影部分的面积等于四边形BB 'C 'C 的面积解答即可.【解答】解:由平移可知,阴影部分的面积等于四边形BB 'C 'C 的面积=BC ×BB '=4×2=8(cm 2),故答案为:8.【点评】本题考查了四边形的面积公式和平移的性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.16.任何实数a ,可用[a ]表示不超过a 的最大整数,如[4]=4,[]=1.现对72进行如下操作:72第一次[]=8,第二次[]=2,第三次[]=1,这样对72只需进行3次操作变为1;在进行这样的3次操作后变为1的所有正整数中,最大的是255.【分析】根据用[a ]表示不超过a 的最大整数,进行计算即可解答.【解答】解:[]=15,[]=3,[]=1,而:[]=16,[]=4,[]=2,[]=1,即:只需进行3次操作后变为1的所有正整数中,最大的是:255,故答案为:255.【点评】本题考查了算术平方根,实数大小比较,理解[a ]表示不超过a 的最大整数,是解题的关键.三.解答题(共9小题)17.计算:(1)+|﹣5|﹣22(2)2-23)(+(1)解:原式=3+5-4=4(2)解:原式=32-23=+18.如图,由若干个小正方形(小正方形的边长为1)构成的网格中有一个△ABC ,△ABC 的三个顶点都在格点上,按要求进行下列作图:(只借助于网格,需写出结论)(1)画出先将△ABC 向右平移2格,再向上平移3格后的△A 'B 'C '.(2)△A 'B 'C '的面积.【分析】(1)利用平移的性质得出对应点位置,进而得出答案;(2)考察三角形的面积的算法.【解答】解:(1)如图所示:△A 'B 'C '即为所求作图形.(2)△A 'B 'C '的面积为32321=⨯⨯【点评】此题主要考查了平移变换,正确得出对应点位置是解题关键,求三角形的面积的关键是找准三角形的底边和底边上对应的高.19.数轴上的点A ,B ,C ,D 分别表示|﹣3|,﹣2.5,,﹣4.(1)在如图所示的数轴上标出点A ,B ,C ,D 的位置.(2)这四点所表示的数从小到大的关系是:﹣4<﹣2.5<<|﹣3|.【分析】(1)根据实数在数轴上的表示方法,画出数轴并标出各点的对应位置;(2)按照数轴上右边的数总比左边的大进行比较,并连接.【解答】解:(1)画数轴表示如下:(2)由(1)题数轴所示,可得﹣4<﹣2.5<<|﹣3|.故答案为:﹣4,﹣2.5,,|﹣3|.【点评】此题考查了利用数轴上的点表示有理数,及利用数轴进行有理数大小比较的能力,解题的关键是能把有理数用数轴上的点准确表示.20.在横线上填上适当的内容,完成下面的证明.已知,直线a,b,c,d的位置如图所示,∠1+∠2=180°,∠3=∠4,求证:c∥d.证明:如图,∵∠1+∠2=180°(已知),∠2+∠3=180°(平角的定义),∴∠1=∠3(同角的补角相等),又∵∠3=∠4(已知),∴∠1=∠4(等量代换),∴c∥d(内错角相等,两直线平行).【分析】由已知及邻补角的定义得到∠3=∠1,等量代换得出∠1=∠4,即可判定c∥d.【解答】证明:如图,∵∠1+∠2=180°(已知),∠2+∠3=180°(平角的定义),∴∠3=∠1(同角的补角相等),又∵∠3=∠4(已知),∴∠1=∠4(等量代换),∴c∥d(内错角相等,两直线平行).故答案为:已知;∠1;等量代换;内错角相等,两直线平行.【点评】此题考查了平行线的判定,熟记“内错角相等,两直线平行”是解题的关键.21.如图,在四边形ABCD中,AD∥BC,∠B=80°.(1)求∠BAD的度数;(2)AE平分∠BAD交BC于点E,∠BCD=50°.求证:AE∥DC.【分析】(1)根据两直线平行,同旁内角互补求出∠BAD;(2)根据角平分线的定义求出∠DAE,根据平行线的性质求出∠AEB,得到∠AEB=∠BCD,根据平行线的判定定理证明结论.【解答】(1)解:∵AD∥BC,∴∠B+∠BAD=180°,∵∠B=80°,∴∠BAD=100°;(2)证明:∵AE平分∠BAD,∴∠DAE=50°,∵AD∥BC,∴∠AEB=∠DAE=50°,∵∠BCD=50°,∴∠AEB=∠BCD,∴AE∥DC.【点评】本题考查的是平行线的判定和性质、角平分线的定义,掌握平行线的性质是解题的关键.22.已知5a+2的立方根是3,3a+b﹣1的算术平方根是4,c是的整数部分.(1)求a,b,c的值;(2)求3a﹣b+c的平方根.【分析】(1)利用立方根的意义、算术平方根的意义、无理数的估算方法,求出a、b、c 的值;(2)将a、b、c的值代入代数式求出值后,进一步求得平方根即可.【解答】解:(1)∵5a+2的立方根是3,∴5a+2=27,解得a=5,∵3a+b﹣1的算术平方根是4,∴3a+b﹣1=16,解得b=2,∵3<<4,∴的整数部分是3,∴c=3,综上所述:a=5,b=2,c=3.(2)∵a=5,b=2,c=3,∴3a﹣b+c=15﹣2+3=16,.∴3a﹣b+c的平方根是4【点评】本题考查了算术平方根、平方根、估算无理数的大小等知识点,易错点是16的平方根.23.如图,已知AB∥CD,BC平分∠ABD交AD于点E.(1)证明:∠1=∠3;(2)若AD⊥BD于点D,∠CDA=34°,求∠3的度数.【分析】(1)由角平分线的定义得到∠1=∠2,由AB∥CD可得∠2=∠3,根据等量代换可得∠1=∠3;(2)由垂直的定义得出∠ADB=90°,可得∠CDB=∠CDA+∠ADB=124°,由平行线的性质得出∠ABD=56°,根据角平分线的定义即可得解.【解答】(1)证明:∵BC平分∠ABD,∴∠1=∠2,∵AB∥CD,∴∠2=∠3,∴∠1=∠3;(2)解:∵AD⊥BD,∴∠ADB=90°,∵∠CDA=34°,∴∠CDB=∠CDA+∠ADB=34°+90°=124°,∵AB∥CD,∴∠ABD+∠CDB=180°,∴∠ABD=180°﹣124°=56°,∵BC平分∠ABD,∴∠1=∠2=∠ABD=×56°=28°,∵∠1=∠3,∴∠3=28°.【点评】此题主要考查了平行线的性质,熟记“两直线平行,内错角相等”及“两直线平行,同旁内角互补”是解题的关键.24.如果一个四位自然数的百位数字大于或等于十位数字,且千位数字等于百位数字与十位数字的和,个位数字等于百位与十位数字的差,则我们称这个四位数为“附中高新数”,例如:自然数4312,其中3>1,4=3+1,2=3﹣1,所以4312是“附中高新数”;(1)最小的“附中高新数”是1101,最大的“附中高新数”是9909;(2)若把一个“附中高新数”的千位数字与个位数字交换,得到的新数叫做这个“附中高新数”的友谊数,请证明任意一个“附中高新数”和它的友谊数的差都能被原“附中高新数”的十位数字整除;(3)若一个“附中高新数”的后三位数字所表示的数与千位数字所表示的数的7倍之差能被13整除,请求出这个“附中高新数”.【解答】解:设“附中高新数”为,且b≥c,a=b+c,d=b﹣c,a、b、c、d都是自然数,(1)当a为最小时,则a=1,∴b+c=a=1,∵b≥c,∴b=1,c=0,∴d=b﹣c=1﹣0=1,∴最小的“附中高新数”是1101,当a最大时,即a=9,∴b+c=a=9,∵b≥c,当最大时,即b最大为9,∴c=0,∴d=b﹣c=9﹣0=9,∴最大的“附中高新数”是9909,故答案为:1101,9909;(2)证明:“附中高新数”:=1000a+100b+10c+d①,友谊数:=1000d+100b+10c+a②,∵a=b+c,d=b﹣c,∴a﹣d=(b+c)﹣(b﹣c)=2c>0,∴a>d,a=2c+d,①﹣②得:999a﹣999d=999(a﹣d)=999(2c+d﹣d)=1998c,∵原“附中高新数”的十位数字为c,∴任意一个“附中高新数”和它的友谊数的差都能被原“附中高新数”的十位数字整除;(3)=100b+10c+d,∵a=b+c,d=b﹣c,∴﹣7a=100b+10c+d﹣7a=100b+10c+b﹣c﹣7(b+c)=94b+2c,由题意得:=7b+为整数,即3b+2c为13的倍数,∵0≤b≤9,0≤c≤9,b、c为整数,且1≤b+c≤9,∴2≤3b+2c≤27,∴3b+2c=13或26,①当3b+2c=13时(b≥c),得,∴“附中高新数”为5321;②若3b+2c=26(b≥c),则或(舍),∴“附中高新数”为9817,综上所述,“附中高新数”为5321或9817.【点评】本题主要考查了“附中高新数”的应用,实数的运算,理解新定义,并将其转化为实数的运算是解题的关键.25.如图1,AB∥CD,点E,F分别在直线CD,AB上,∠BEC=2∠BEF,过点A作AG ⊥BE的延长线交于点G,交CD于点N,AK平分∠BAG,交EF于点H,交BE于点M.(1)直接写出∠AHE,∠FAH,∠KEH之间的关系:∠AHE=∠FAH+∠KEH.(2)若∠BEF=∠BAK,求∠AHE.(3)如图2,在(2)的条件下,将△KHE绕着点E以每秒5°的速度逆时针旋转,旋转时间为t,当KE边与射线ED重合时停止,则在旋转过程中,当△KHE的其中一边与△ENG的某一边平行时,直接写出此时t的值.【分析】(1)根据平行线的性质和三角形的外角性质可得答案;(2)根据∠BEF=∠BAK,分别表示出∠BAK、∠BEC、∠BAK、∠KAG、∠AME和∠AHE,再由AG⊥BE,可得∠BEF的度数,则问题可解;(3)结合(2),分以下几种情况求解:①当KH∥NG时,延长KE交GN边于P,②当KH∥EG时,③当KH∥EN时,即EK与EG在同一直线上时,④当KE∥NG时,⑤当HE∥NG时.【解答】解:(1)∵AB∥CD,∴∠KEH=∠AFH,∵∠AHE是△AHF的外角,∴∠AHE=∠AFH+∠FAH,∴∠AHE=∠FAH+∠KEH.故答案为:∠AHE=∠FAH+∠KEH;(2)∵AB∥CD,∴∠BAK=∠MKE,∠ABE=∠BEC,∵,∴∠BAK=2∠BEF,∵∠BEC=2∠BEF,∴∠BAK=∠BEC,∴∠BAK=∠ABE,∴AK平分∠BAG,∴∠BAK=∠GAK=∠ABE,∵AG⊥BE,∴∠AGB=90°,∴3∠BAK=90°,∴∠BAK=∠ABE=∠GAK=30°,∴,∴∠CEF=45°,∴∠CEF=∠AFE=45°,∴∠AHE=∠AFE+∠BAK=75°.(3)①当KH∥NG时,延长KE交GN边于P,∵∠EKH=∠EPG=30°,∴∠PEG=90°﹣∠EPG=60°,∵∠GEN=90°﹣ENG=30°,∴∠PEN=∠PEG﹣∠GEN=30°,∴∠CEK=∠PEN=30°,∴当△KHE绕E点旋转30°时,EK∥GN,∴秒,②当KH∥EG时,∴∠EKH=∠KEG=30°,∴∠NEK=∠NEG+∠KEG=60°,∴∠NEK=60°,∴∠CEK=120°,∴当△KHE绕点E旋转120°时,HK∥EG,∴秒,③当KH∥EN时,即EK与EG在同一直线上时,∴∠CEK=150°,∴当△KHE绕点E旋转150°时,KH∥EN,∴秒,∴当△KEH的其中一边与△ENG的某一边平行时t的值为6秒或24秒或30秒.④当KE∥NG时,∵∠GEN=30°,∴∠CEK=90°﹣∠GEN=60°.∴当△KHE旋转60°时,KE∥NG.∴(秒).⑤当HE∥NG时,∵∠GEN=30°,∠KEH=45°,∴∠CEK=∠CEH+∠HEK=90°﹣∠GEN+∠HEK=105°.∴当△KHE旋转105°时,HE∥NG.∴(秒).当△KEH的其中一边与△ENG的某一边平行时t的值为6秒或24秒或30秒或12秒或21秒.。
2020-2021学年五年级上册数学单元检测-1.小数乘法 青岛版 (最新版)

五年级上册数学单元检测-1.(北京市第一实验小学学考复习)小数乘法一、单选题1.(北京市第一实验小学学考复习)0.02与0.002的乘积( )0.004A. >B. <C. =2.下面( )结果大于1。
A. 0.72×1B. 0.72÷1C. 0.72÷0.1D. 0.72×0.13.(上海市第二实验小学期末学业考模拟)一种铁矿石,每10克里含铁6.02克,每克铁矿石含铁______克,1000克这种铁矿石含铁______克.()A. 6.02,6020B. 0.602,602C. 0.0602,60.2D. 0.62,624.18-(1.(北京市第一实验小学学考复习)75+1.(北京市第一实验小学学考复习)25×2.4)=()A. 4B. 13.(上海市第二实验小学期末学业考模拟)25C. 12.25D. 5二、判断题5.判断对错.一个数乘0.5的结果和这个数除以2的结果一定相等.6.一个数乘小数,积一定小于这个数.7.小数加、减、乘法计算时,都要将小数点对齐。
三、填空题8.看图回答(1)买4千克香蕉需要________钱?(2)一箱苹果67.5元,每千克苹果________元?9.计算1.(北京市第一实验小学学考复习)7×0.017=________1.(北京市第一实验小学学考复习)7-0.017=________10.(1)72-37=________(2)2.5+7.9=________(3)0.25×40=________(4)1.(北京市第一实验小学学考复习)25×7×8=________11.(北京市第一实验小学学考复习)在横线上填上“>”“<”“=”5.42×0.9________5.42;0.98×1________0.98;31.(北京市第一实验小学学考复习)5×0.9________31.(北京市第一实验小学学考复习)5;4.95×1________4.95.2.5×0.8________2.5;3.(上海市第二实验小学期末学业考模拟)56×1.(北京市第一实验小学学考复习)01________3.(上海市第二实验小学期末学业考模拟)56;12.在横线上填上“>”“<”或“=”.(1)32.5×1________32.5÷0.1(2)0×400________1.(北京市第一实验小学学考复习)4÷999四、解答题13.(上海市第二实验小学期末学业考模拟)李阿姨在超市买了3kg苹果,一共花了10.8元.如果梁奶奶想买5kg这样的苹果,要花多少钱?五、综合题14.列竖式计算.(1)0.18×8.05=(2)1.(北京市第一实验小学学考复习)02÷3.(上海市第二实验小学期末学业考模拟)3≈(保留两位小数)六、应用题15.小红的爸爸从美国给小红寄回价值7.85美元的故事书,折合人民币多少元?(1美元折合人民币6.81元)参考答案一、单选题1.(北京市第一实验小学学考复习)【答案】B【解析】【解答】0.02×0.002=0.00004,所以0.02与0.002的乘积<0.004.故答案为:B【分析】根据小数乘法的计算方法计算出积,然后与0.004比较即可;小数乘小数,先按照整数乘法的计算方法计算出积,然后看两个因数中共有几位小数,就从积的右边向左数出几位点上小数点;位数不够的用0补足.2.【答案】C【解析】【解答】解:0.72×1=0.72;0.72÷1=0.72;0.72÷0.1=7.2;0.72×0.1=0.072。
数学实验(第二版)课后习题答案
贵州师范学院2012级数本一班李刚数学实验课后练习答案习题2.11. syms x y;>> x=-5:0.01:5;>> y=x.^1/2;>> plot(x,y)2. f plot('exp(-x.^2)',[-5,5])3. ezplot('x.^3+y.^3-3*x*y',[-5,5])4 . ezplot('y.^2-x.^3/(1-x)',[-5,5])5.t=0:0.1:2*pi;x=t-sin(t);y=2*(1-cos(t));plot(x,y)6. t=0:0.1:2*pi; x=cos(t).^3; >> y=sin(t).^3;>> plot(t,y)>>7: t=0:0.1:2*pi; x=cos(t); y=2*sin(t); z=3*t; plot3(x,y,z)8: x =0:0.1:2*pi; r=x; polar(x,r)9: x =0:0.1:2*pi; r=exp(x); polar(x,r)10: x=0:0.1:2*pi; r=sqrt(cos(2*x)); polar(x,r)11: x=0:0.1:2*pi; r=sqrt(sin(2*x)); polar(x,r)12: x =0:0.1:2*pi; r=1+cos(x); polar(x,r)练习2.2 1:(1)(2):syms n; limit('sqrt(n+2)-2*(sqrt(n+1))+sqrt(n)',n,inf)Ans= 0 (3):: (4):(5):(6):2:3:fplot('x.^2*sin(x.^2-x-2)',[-2,2])练习2.3 1:(2):2:练习2.4 1:(1)(2):(3)(4):2:(1):syms x;int(x^(-x),x,0,1)ans =int(x^(-x),x = 0 .. 1)vpa(ans,10)ans =1.291285997(2):syms x;int(exp(2*x)*cos(x)^3,x,0,2*pi)ans =-22/65+22/65*exp(4*pi)(3):syms x; int(exp(x^2/2)/sqrt(2*pi),x,0,1)ans =-1125899906842624/5644425081792261*i*erf(1/2*i*2^(1/2))*pi^(1/2)*2^(1/2) >> vpa(ans,10)ans =.4767191345(4):syms x;int(x*log(x^4)*asin(1/x^2),x,1,3)ans =int(x*log(x^4)*asin(1/x^2),x = 1 .. 3)>> vpa(ans,10)ans =2.459772128(5):syms x ;int(exp(x^2/2)/sqrt(2*pi),x,-inf,inf)ans =Inf(6):syms x ;int(sin(x)/x,x,0,inf)ans =1/2*pi(7):syms x ;int(tan(x)/sqrt(x),x,0,1)Warning: Explicit integral could not be found. > In sym.int at 58ans =int(tan(x)/x^(1/2),x = 0 .. 1)>> vpa(ans,10)ans =.7968288892(8):syms x ;int(exp(-x^2/2)/(1+x^4),x,-inf,inf)ans =1/4*pi^(3/2)*2^(1/2)*(AngerJ(1/2,1/2)-2/pi^(1/2)*sin(1/2)+2/pi^(1/2)*cos(1/2)-WeberE(1/2,1/2 ))>> vpa(ans,10)ans =1.696392536(9):syms x ;int(sin(x)/sqrt(1-x^2),x,0,1)ans =1/2*pi*StruveH(0,1)>> vpa(ans,10)ans =.8932437410练习2.5(1):syms n;symsum(1/n^2^n,n,1,inf)ans =sum(1/((n^2)^n),n = 1 .. Inf)(2):s yms n ;symsum(sin(1/n),n,1,inf)ans =sum(sin(1/n),n = 1 .. Inf)(3):syms n ;symsum(log(n)/n^3,n,1,inf) ans =-zeta(1,3)(4):syms n ;symsum(1/(log(n))^n,n,3,inf) ans =sum(1/(log(n)^n),n = 3 .. Inf)(5):syms n;symsum(1/(n*log(n)),n,2,inf) ans =sum(1/n/log(n),n = 2 .. Inf)(6):yms n;symsum((-1)^n*n/(n^2+1),n,1,inf)ans =-1/4*Psi(1-1/2*i)+1/4*Psi(1/2-1/2*i)-1/4*Psi(1+1/2*i)+1/4*Psi(1/2+1/2*i)第三章练习3.11:(1):a=-30:1:30;b=-30:1:30;[x,y]=meshgrid(a,b);z=10*sin(sqrt(x.^2+y.^2))./(sqrt(1+x.^2+y.^2)); meshc(x,y,z)(2):a=-30:1:30;b=-30:1:30;[x,y]=meshgrid(a,b);z=4*x.^2/9+y.^2;meshc(x,y,z)(3):(4):a=-30:1:30;b=-30:1:30;[x,y]=meshgrid(a,b); z=x.^2/3-y.^2/3; meshc(x,y,z)(5):a=-30:1:30;>> b=-30:1:30;>> [x,y]=meshgrid(a,b); >> z=x*y;>> meshc(x,y,z)(6):(7):a=-30:1:30;>> b=-30:1:30;>> [x,y]=meshgrid(a,b); >> z=sqrt(x.^2+y.^2); >> meshc(x,y,z)(8):(9):a=-30:1:30;>> b=-30:1:30;>> [x,y]=meshgrid(a,b);>> z=atan(x./y);>> meshc(x,y,z)练习3.21;a=-1:0.1:1;>> b=0:0.1:2;>> [x,y]=meshgrid(a,b);>> z=x.*exp(-x.^2-y.^2);>> [px,py]=gradient(z,0.1,0.1);>> contour(a,b,z)>> hold on>> quiver(a,b,px,py)2:a=-2:0.1:1;>> b=-7:0.1:1;>> [x,y]=meshgrid(a,b);>> z=y.^3/9+3*x.^2.*y+9*x.^2+y.^2+x.*y+9; >> plot3(x,y,z)>> grid on3:[x,y]=meshgrid(-2*pi:0.2:2*pi); z=x.^2+2*y.^2;plot3(x,y,z)hold onezplot('x^2+y^2-1',[-2*pi,2*pi]) ; grid on4:t=0:0.03:2*pi;>> s=[0:0.03:2*pi]';>> x=(0*s+1)*cos(t);y=(0*s+1)*sin(t);z=s*(0*t+1); >> mesh(x,y,z)>> hold on>> [x,y]=meshgrid(-1:0.1:1);>> z=1-x+y;>> mesh(x,y,z)5:syms x y z dx dyz=75-x^2-y^2+x*y;zx=diff(z,x),zy=diff(z,y)zx =-2*x+yzy =-2*y+x练习3.31:ezplot('x^2+y^2-2*x',[-2,2]);>> grid onsyms x y ;s=int(int(x+y+1,y,-sqrt(1-(x-1)^2),sqrt(1-(x-1)^2)),x,0,2)s =2*pi2:syms r t ;>> s=int(int(sqrt(1+r^2*sin(t)),r,0,1),t,0,2*pi)s =int(1/2*((1+sin(t))^(1/2)*sin(t)^(1/2)+log(sin(t)^(1/2)+(1+sin(t))^(1/2)))/sin(t)^(1/2),t = 0 .. 2*pi) 3:syms x y z ;>> s=int(int(int(1/(1+x+y+z)^3,z,0,1-x-y),y,0,1-x),x,0,1)s =-5/16+1/2*log(2)4:s=vpa(int(int(x*exp(-x^2-y^2),y,0,2),x,-1,10))s =0.16224980455070416645061789474030练习3.41:(1):y=dsolve('Dy=x+y','y(0)=1','x')得:y =-1-x+2*exp(x)(2):y=dsolve('Dy=2*x+y^2','y(0)=0')y =tan(t*x^(1/2)*2^(1/2))*x^(1/2)*2^(1/2)练习4.11:(1):p=[5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -6 8 0 0 0 -5 0 0]; >> x=roots(p)x =0.97680.9388 + 0.2682i0.9388 - 0.2682i0.8554 + 0.5363i0.8554 - 0.5363i0.6615 + 0.8064i0.6615 - 0.8064i0.3516 + 0.9878i0.3516 - 0.9878i-0.0345 + 1.0150i-0.0345 - 1.0150i-0.4609 + 0.9458i-0.4609 - 0.9458i-0.1150 + 0.8340i-0.1150 - 0.8340i-0.7821 + 0.7376i-0.7821 - 0.7376i-0.9859 + 0.4106i-0.9859 - 0.4106i-1.0416-0.7927(2): p=[8 36 54 23];x=roots(p)x =-1.8969 + 0.6874i-1.8969 - 0.6874i-0.70632:p1=[1 0 -3 -2 -1];p2=[1 -2 5];[q2,r2]=deconv(p1,p2)q2 =1 2 -4r2 =0 0 0 -20 19 3:syms x;f=x^4+3*x^3-x^2-4*x-3;g=3*x^3+10*x^2+2*x-3;p1=factor(f),p2=factor(g)p1 =(x+3)*(x^3-x-1)p2 =(x+3)*(3*x^2+x-1)4:syms x ;f=x^12-1;p=factor(f)p =(-1+x)*(1+x^2+x)*(1+x)*(1-x+x^2)*(1+x^2)*(x^4-x^2+1)5: (1):p=[1 0 1];q=[1 0 0 0 1];[a,b,r]=residue(p,q)a =-0.0000 - 0.3536i-0.0000 + 0.3536i0.0000 - 0.3536i0.0000 + 0.3536ib =0.7071 + 0.7071i0.7071 - 0.7071i-0.7071 + 0.7071i-0.7071 - 0.7071ir =[](2):p=[1];q=[1 0 0 0 1];[a,b,r]=residue(p,q)a =-0.1768 - 0.1768i -0.1768 + 0.1768i0.1768 - 0.1768i0.1768 + 0.1768ib =0.7071 + 0.7071i0.7071 - 0.7071i -0.7071 + 0.7071i -0.7071 - 0.7071ir =[](3):p=[1 0 1];q=[1 1 -1 -1];[a,b,r]=residue(p,q)a =0.5000-1.00000.5000b =-1.0000-1.00001.0000r =[] (4): p=[1 1 0 0 0 -8];[a,b,r]=residue(p,q)a =-4-38b =-11r =1 1 1练习 4.21:(1):D=[2 1 3 1;3 -1 2 1;1 2 3 2;5 0 6 2];det(D)ans =6(2):syms a b c dD=[a 1 0 0 ;-1 b 1 0;0 -1 c 1;0 0 -1 d];det(D)ans =a*b*c*d+a*b+a*d+c*d+12:(1):D=[1 1 1 1; a b c d;a^2 b^2 c^2 d^2;a^3 b^3 c^3 d^3];det(D)ans =b*c^2*d^3-b*d^2*c^3-b^2*c*d^3+b^2*d*c^3+b^3*c*d^2-b^3*d*c^2-a*c^2*d^3+a*d^2*c^3+a *b^2*d^3-a*b^2*c^3-a*b^3*d^2+a*b^3*c^2+a^2*c*d^3-a^2*d*c^3-a^2*b*d^3+a^2*b*c^3+a^ 2*b^3*d-a^2*b^3*c-a^3*c*d^2+a^3*d*c^2+a^3*b*d^2-a^3*b*c^2-a^3*b^2*d+a^3*b^2*c(2): s yms a b x y zD=[a*x+b*y a*y+b*z a*z+b*x; a*y+b*z a*z+b*x a*x+b*y;a*z+b*x a*x+b*y a*y+b*z];det(D)ans =3*a^3*x*z*y+3*b^3*y*x*z-a^3*x^3-a^3*y^3-b^3*z^3-a^3*z^3-b^3*x^3-b^3*y^33: (1): D=[1 1 1 1;1 2 -1 4;2 -3 -1 -5;3 1 2 11];D1=[5 1 1 1;-2 2 -1 4;-2 -3 -1 -5;0 1 2 11];D2=[1 5 1 1;1 -2 -1 4;2 -2 -1 -5;3 0 2 11];D3=[1 1 5 1;1 2 -2 4;2 -3 -2 -5;3 1 0 11];D4=[1 1 1 5;1 2 -1 -2;2 -3 -1 -2;3 1 2 0];x1=det(D1)/det(D);x2=det(D2)/det(D);x3=det(D3)/det(D);x4=det(D4)/det(D);x1,x2,x3,x4x1 =1x2 =2x3 =3x4 =-1(2):D=[5 6 0 0 0;1 5 6 0 0;0 1 5 6 0;0 0 1 5 6;0 0 0 1 5]; D1=[1 6 0 0 0;0 5 6 0 0;0 1 5 6 0;0 0 1 5 6;1 0 0 1 5]; D2=[5 1 0 0 0;1 0 6 0 0;0 0 5 6 0;0 0 1 5 6;0 1 0 1 5]; D3=[5 6 1 0 0;1 5 0 0 0;0 1 0 6 0;0 0 0 5 6;0 0 1 1 5]; D4=[5 6 0 1 0;1 5 6 0 0;0 1 5 0 0;0 0 1 0 6;0 0 0 1 5]; D5=[5 6 0 0 1;1 5 6 0 0;0 1 5 6 0;0 0 1 5 0;0 0 0 1 1]; x1=det(D1)/det(D);x2=det(D2)/det(D);x3=det(D3)/det(D);x4=det(D4)/det(D);x5=det(D5)/det(D);x1,x2,x3,x4,x5x1 =2.2662x2 =-1.7218x3 =1.0571x4 =-0.5940x5 =0.3188练习 4.3 1:A=[1 2 0;3 4 -1; 1 1 -1];B=[1 2 3;-1 0 1;-2 4 -3];A',2+A,2*A-B,A*B,A^2,A^(-1)ans =1 3 12 4 10 -1 -1ans =3 4 25 6 13 3 1ans =1 2 -37 8 -34 -2 1ans =-1 2 51 2 162 -2 7ans =7 10 -214 21 -33 5 0ans =-3.0000 2.0000 -2.00002.0000 -1.0000 1.0000-1.0000 1.0000 -2.0000 2:(1):B=[2 4 3];B'ans =243(2):A=[1 2 3];B=[2 4 3];A.*B,B.*Aans =2 8 9ans =2 8 93:(1):A=[0 1 0;1 0 0;0 0 1];B=[1 0 0;0 0 1;0 1 0];C=[1 -4 3;2 0 -1;1 -2 0];A^(-1),B^(-1),X=A^(-1)*C*B^(-1) ans =0 1 01 0 00 0 1ans =1 0 00 0 10 1 0X =2 -1 01 3 -41 0 -2(2):>> A=[1 2 3;2 2 3;3 5 1];B=[1 0 0;2 0 0;3 0 0];A^(-1),x=A^(-1)*Bans =-1.0000 1.0000 0.00000.5385 -0.6154 0.23080.3077 0.0769 -0.1538x =1 0 00 0 00 0 0练习 4.41:(1):A=[4 2 -1;3 -1 2;11 3 0];b=[2;10;8];B=[A,b];rank(A),rank(B)ans =2ans =3(2):A=[2 1 -1 1;3 -2 1 -3;1 4 -3 5];b=[1;4;-2];B=[A,b];rank(A),rank(B)ans =2ans =2(3):A=[ 1 1 1 1; 1 2 -1 4;2 -3 -1 -5;3 1 2 11];b=[5;-2;-2;0];B=[A,b];rank(A),rank(B)ans =4ans =4(4):A=[ 1 1 2 -1; 2 1 1 -1;2 2 1 2];b=[0;0;0];B=[A,b];rank(A),rank(B)ans =3ans =32:syms a;A=[-2 1 1;1 -2 1;1 1 -2];b=[-2;a;a^2];B=[A,b];rank(A),rank(B)ans =2ans =3练习4.51:(1):A=[0 1;-1 0];[a,b]=eig(A)a =0.7071 0.70710 + 0.7071i 0 - 0.7071ib =0 + 1.0000i 000 - 1.0000i(2):A=[0 0 1;0 1 0;1 0 0];[a,b]=eig(A)a =0.7071 0.7071 00 0 -1.0000-0.7071 0.7071 0b =-1 0 00 1 00 0 1(3):A=[4 1 -1;3 2 -6;1 -5 3];[a,b]=eig(A)a =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170b =-3.0527 0 00 3.6760 00 0 8.3766(4):A=[1 1 1 1;1 1 -1 -1;1 -1 1 -1;1 1 -1 1];[a,b]=eig(A)a =0.5615 0.3366 0.2673 -0.7683-0.5615 -0.3366 0.0000 -0.0000-0.5615 -0.3366 -0.5345 -0.6236-0.2326 0.8125 0.8018 -0.1447b =-1.4142 0 0 00 1.4142 0 00 0 2.0000 00 0 0 2.0000(5):A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10];[a,b]=eig(A)a =0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209b =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887(6):A=[5 6 0 0 0;1 5 6 0 0 ;0 1 5 6 0 ;0 0 1 5 6; 0 0 0 1 5 ]; [a,b]=eig(A)a =0.7843 -0.7843 -0.9860 -0.9237 -0.92370.5546 0.5546 0.0000 0.3771 -0.37710.2614 -0.2614 0.1643 -0.0000 0.00000.0924 0.0924 0.0000 -0.0628 0.06280.0218 -0.0218 -0.0274 0.0257 0.02579.2426 0 0 0 00 0.7574 0 0 00 0 5.0000 0 00 0 0 2.5505 00 0 0 0 7.4495 2:(1):A=[0 1;-1 0];[a,b]=eig(A)a =0.7071 0.70710 + 0.7071i 0 - 0.7071ib =0 + 1.0000i 00 0 - 1.0000i>> P=orth(a),B=P'*A*P,P*P'P =-0.7071 -0.70710 - 0.7071i 0 + 0.7071iB =0 + 1.0000i 0 - 0.0000i0 - 0.0000i 0 - 1.0000ians =1.0000 0 + 0.0000i0 - 0.0000i 1.0000>> inv(a)*A*a0 + 1.0000i 000 - 1.0000i3:(1):A=[2 0 0;0 3 2;0 2 3]; [a,b]=eig(A)a =0 1.0000 0-0.7071 0 0.70710.7071 0 0.7071b =1.0000 0 00 2.0000 00 0 5.0000>> P=orth(a),B=P'*A*P,P*P'P =-1.0000 0 -0.00000.0000 0.7071 0.7071-0.0000 -0.7071 0.7071B =2.0000 0.0000 0.00000.0000 1.0000 00.0000 0 5.0000ans =1.0000 -0.0000 0.0000-0.0000 1.0000 -0.00000.0000 -0.0000 1.0000(2):A=[1 1 0 -1;1 1 -1 0;0 -1 1 1;-1 0 1 1];[a,b]=eig(A)a =-0.5000 0.7071 0.0000 0.50000.5000 -0.0000 0.7071 0.50000.5000 0.7071 0.0000 -0.5000-0.5000 0 0.7071 -0.5000 b =-1.0000 0 0 00 1.0000 0 00 0 1.0000 00 0 0 3.0000 >> P=orth(a),B=P'*A*P,P*P'P =-0.5000 -0.4998 -0.4783 -0.52100.5000 -0.4822 0.5212 -0.49580.5000 0.4998 -0.4964 -0.5037-0.5000 0.5175 0.5031 -0.4786 B =-1.0000 0.0000 0.0000 0.00000.0000 2.9988 -0.0362 0.03440.0000 -0.0362 1.0007 -0.00060.0000 0.0344 -0.0006 1.0006 ans =1.0000 0.0000 0.0000 -0.00000.0000 1.0000 -0.0000 00.0000 -0.0000 1.0000 0.0000-0.0000 0 0.0000 1.0000练习5.3 1: [m,v]=unifstat(1,11)m =6v =8.33332:[m,v]=normstat(0,16)m =v =256>> s=sqrt(v)s =163:x=randn(200,6);s=std(x)s =0.9094 0.9757 0.9702 0.9393 0.9272 1.09824: x=normrnd(0,16,300,1);hist(x,10)练习 5.61:x=[352 373 411 441 462 490 529 577 641 692 743];y=[166 153 177 201 216 208 227 238 268 268 274];plot(x,y,'*')4:(1):x=[10 10 10 15 15 15 20 20 20 25 25 25 30 30 30];y=[25.2 27.3 28.7 29.8 31.1 27.8 31.2 32.6 29.7 31.7 30.1 32.3 29.4 30.8 32.8]; plot(x,y,'*')。
数学建模实验答案__数学规划模型二.

实验05 数学规划模型㈡(2学时)(第4章数学规划模型)1.(求解)汽车厂生产计划(LP,整数规划IP)p101~102(1) (LP)在模型窗口中输入以下线性规划模型max z = 2x1 + 3x2 + 4x3s.t. 1.5x1 + 3x2 + 5x3≤ 600280x1 + 250x2 + 400x3≤ 60000x1, x2, x3≥ 0并求解模型。
★(1) 给出输入模型和求解结果(见[101]):(2) (IP)在模型窗口中输入以下整数规划模型max z = 2x1 + 3x2 + 4x3s.t. 1.5x1 + 3x2 + 5x3≤ 600280x1 + 250x2 + 400x3≤ 60000x1, x2, x3均为非负整数并求解模型。
LINGO函数@gin见提示。
★(2) 给出输入模型和求解结果(见[102]模型、结果):2.(求解)原油采购与加工(非线性规划NLP ,LP 且IP )p104~107模型:已知 ⎪⎩⎪⎨⎧≤≤+≤≤+≤≤=)15001000(63000)1000500(81000)5000(10)(x x x x x xx c注:当500 ≤ x ≤ 1000时,c (x ) = 10 × 500 + 8( x – 500 ) = (10 – 8 ) × 500 + 8x112112221112212211112112122211122122max 4.8() 5.6()()500100015000.50.6,,,,0z x x x x c x x x x x x x x x x x x x x x x x x =+++-+≤++≤≤≥+≥+≥2.1解法1(NLP )p104~106将模型变换为以下的非线性规划模型:1121122212311122122111121121222123122312311122122max4.8()5.6()(1086)50010000.50.6(500)0(500)00,,500,,,,0z x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x =+++-+++≤++≤≥+≥+=++-=-=≤≤≥LINGO 软件设置:局部最优解,全局最优解,见提示。
2024届浙江省温州市南浦实验中学七年级数学第一学期期末综合测试试题含解析

2024届浙江省温州市南浦实验中学七年级数学第一学期期末综合测试试题注意事项:1.答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.如图,AB=8cm,AD=BC=5cm,则CD等于()A.1cm B.2cm C.3cm D.4cm2.下列计算正确的是()A.﹣1﹣1=0 B.2(a﹣3b)=2a﹣3b C.a3﹣a=a2D.﹣32=﹣9 3.当x=1时,的值为−2,则的值为A.− 16 B.− 8 C.8 D.164.已知y是x的一次函数,下表中列出了部分对应值,则m的值等于()x -1 0 my 1 -2 -5A.1 B.12C.0 D.-15.如图,将长方形纸片ABCD的角C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部点E处,若FH平分∠BFE,则∠GFH的度数α是()A.90°<α<180°B.0°<α<90°C.α=90°D.α随折痕GF位置的变化而变化6.下列说法正确的是( )A.将310万用科学记数法表示为3.1×107B.用四舍五入法将1.097精确到百分位为1.10C .近似数2.3与2.30精确度相同D .若用科学记数法表示的数为2.01×105,则其原数为20 1007.如图,是一个正方体的表面积展开图,相对面上所标的两个数互为倒数,那么a b c +=( )A .1516-B .1716C .1716-D .15168.一列火车正匀速行驶,它先用20秒的速度通过了一条长为160米的隧道(即从车头进入入口到车尾离开出口),又用15秒的时间通过了一条长为80米的隧道,求这列火车的长度,设这列火车的长度为x 米,根据题意可列方程为( )A .16028022015x x ++= B .160802015x x ++= C .16028022015x x --= D .1602802015x x --= 9.当1x =时,代数式31px qx ++的值为2019,则当1x =-时,代数式31px qx ++的值为( )A .-2017B .-2019C .2018D .201910.下列各组数比较大小,判断正确的是( )A .64->-B .31->+C .90->D .2537->- 11.我国计划在2020年左右发射火星探测卫星,据科学研究,火星距离地球的最近距离约为5500万千米,这个数据用科学记数法可表示为( )A .5.5×106千米B .5.5×107千米C .55×106千米D .0.55×108千米12.下列判断:①2πxy -不是单项式;②3x y -是多项式;③0不是单项式;④1x x + 是整式.其中正确的有( ) A .2个 B .1个 C .3个 D .4个二、填空题(每题4分,满分20分,将答案填在答题纸上)13.松桃县城某商店把一件商品按成本价提高50%后标价,又打8折销售,现售价为240元,设这件商品的成本价为x 元,则可列方程:______.14.有依次排列的三个数:“2,5-,8”对这三个数作如下操作:对任何相邻的两个数,都用左边的数减去右边的数,将所得之差写在这两个数之间,即可产生一个新数串:“2,7,-5,-13,8”称为第一次操作;做第二次同样的操作后又产生一个新数串:“2,-5,7,12,-5,8,-13,-21,8”……依次继续操作下去,直到第2020次操作后停止操作.则第2020次操作所得新数串中所有各数的和为_____.15.建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上,这样做的依据是:__________.16.阅读理解:a b c d ,,,是有理数,我们把符号a b c d 称为22⨯阶行列式,并且规定:a b ad bc c d =-,则满足等式112321xx +=的x 的值是____________. 17.某校报名参加甲、乙、丙、丁四个兴趣小组的学生人数如图所示,那么报名参加甲组和丙组的人数之和占所有报名人数的百分比为 .三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)已知:如图,AOB ∠是直角,AOC ∠在AOB ∠的外侧,且40AOC ∠=︒,ON 是AOC ∠的平分线,OM 是BOC ∠的平分线.(1)求MON ∠的大小;(2)当锐角AOC ∠的大小为x ︒时,试猜想(1)中MON ∠的大小是否发生改变?并通过计算说明理由.19.(5分)化简:1(93)2(1)3x x --+.20.(8分)解方程:(1)82(32)6x x -+=; (2)11223x x x -+-=-. 21.(10分)(1)()22222333a ab a ab ⎛⎫+-+- ⎪⎝⎭(2)先化简,在求值:22113122323x x y x y ⎛⎫⎛⎫--+-+ ⎪ ⎪⎝⎭⎝⎭,其中2x =-,23y =. 22.(10分)阅读下列材料:时间利用调查以自然人为调查对象,通过连续记录被调查者一天24小时的活动,获得居民在工作学习、家务劳动、休闲娱乐等活动上花费的时间,为分析居民身心健康和生活质量等提供数据支撑.2008年,我国第一次开展了时间利用调查,相距十年后的2018年,开展了第二次时间利用调查.2018年5月,北京调查总队对全市1700户居民家庭开展了入户调查,下面是根据此次调查的结果对北京市居民时间利用的特点和变化进行的分析. 北京市居民一天的时间分布情况统计图北京市居民2008年上下班的交通时间为1小时29分钟,2018年依然为1小时29分钟;2008年人均家庭劳务时间为2小时32分钟,2018年为2小时52分钟;2008年人均自由支配时间为4小时17分钟,2018年为4小时34分钟;2008年上网时间为25分钟,2018年上网时间是2008年的7.44倍.(说明:以上内容摘自北京市统计局官网),根据以上材料解答下列问题:(1)2018年采用的调查方式是;(2)图中m的值为;(3)①利用统计表,将2008年和2018年北京市居民上下班的交通时间、人均家庭劳务时间、人均自由支配时间和上网时间表示出来;②根据以上信息,说明十年间北京市居民时间利用变化最大的是,请你分析变化的原因是.23.(12分)如图,已知点C为AB上一点,AC=12cm,CB=12AC,D、E分别为AC、AB的中点,求DE的长.参考答案一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、B【解题分析】试题分析:首先根据已知条件求出线段DB的长度,再求出线段CD长度即可.解:∵AB=8cm,AD=5cm,∴BD=AB﹣AD=3cm,∵BC=5cm,∴CD=CB﹣BD=2cm,故选B.考点:直线、射线、线段.2、D【分析】根据有理数的减法、去括号、同底数幂的乘方即可解答.【题目详解】解:A.﹣1﹣1=﹣2,故本选项错误;B.2(a﹣3b)=2a﹣6b,故本选项错误;C.a3÷a=a2,故本选项错误;D.﹣32=﹣9,正确;故选:D .【题目点拨】本题考查了去括号和简单的提取公因式,掌握去括号时符号改变规律是解决此题的关键.3、A【解题分析】试题分析:∵当x=1时,的值为﹣2,∴,∴,∴=(﹣3﹣1)×(1+3)=﹣1.故选A .考点:整式的混合运算—化简求值.4、A【分析】设一次函数解析式为y=kx+b ,找出两对x 与y 的值代入计算求出k 与b 的值,即可确定出m 的值.【题目详解】解:设一次函数解析式为y=kx+b , 将x=-1,y=1;x=0,y=-2代入得:12k b b -+⎧⎨-⎩== , 解得:k=-3,b=-2,∴一次函数解析式为y=-3x-2,令y=-5,得到x=1,则m=1,故选:A .【题目点拨】此题考查待定系数法求一次函数解析式,以及一次函数图象上点的坐标特征,熟练掌握待定系数法是解题的关键. 5、C【分析】先根据折叠的性质得出CFG EFG ∠=∠,再根据角平分线的定义得出12EFH BFE ∠=∠,然后根据平角的定义、角的和差即可得.【题目详解】由折叠的性质得:CFG EFG ∠=∠ 12EFG CFE ∴∠=∠ ∵FH 平分BFE ∠12EFH BFE ∴∠=∠ ∴GFH EFG EFH ∠=∠+∠1122CFE BFE =∠+∠ 1()2CFE BFE =∠+∠1180902=⨯︒=︒即90α=︒故选:C.【题目点拨】本题考查了折叠的性质、角平分线的定义等知识点,掌握并熟记各性质与定义是解题关键.6、B【分析】A、利用科学记数法进行验证即可;B、利用四舍五入法进行验证即可;C、利用精确度的概念进行验证即可;D、利用科学记数法进行验证即可.【题目详解】解:A、将310万用科学记数法表示为3.1×106,故此选项错误;B、用四舍五入法将1.097精确到百分位为1.10,故此选项正确;C、近似数2.3精确到十分位,近似数2.30精确到百分位,所以近似数2.3与2.30精确度不同,故此选项错误;D. 若用科学记数法表示的数为2.01×105,则其原数为20 1000,故此选项错误.故选B.【题目点拨】本题考查了科学记数法与近似数,理解科学记数法的表示方法和近似数的相关概念是解决此题的关键.7、A【分析】根据正方体的展开图分别判断出a、b、c的对面,即可求出a、b、c的值,然后代入求值即可.【题目详解】解:由正方体的展开图可知:a和14是对面,b和-1是对面,c和-2是对面∴a=4,b=-1,c=1 2 -∴41151216 ab c⎛⎫+=-+-=-⎪⎝⎭故选A.【题目点拨】此题考查的是根据正方体的展开图,判断一个面的相对面和有理数的混合运算,掌握正方体相对面的判断方法和有理数的运算法则是解决此题的关键.8、B【分析】设这列火车的长度为x米,根据速度=路程÷时间结合火车的速度不变,即可得出关于x的一元一次方程,此题得解.【题目详解】设这列火车的长度为x 米,依题意,得:160802015x x ++=. 故选:B .【题目点拨】本题考查了由实际问题抽象出一元一次方程,找准等量关系,正确列出一元一次方程是解答本题的关键.9、A【分析】代入后求出p+q=2018,变形后代入,即可求出答案.【题目详解】∵当x=1时,代数式px 3+qx+1的值为2019,∴代入得:p+q+1=2019,∴p+q=2018,∴当x=-1时,代数式px 3+qx+1=-p-q+1=-(p+q )+1=-2018+1=-2017,故选:A .【题目点拨】此题考查求代数式的值,能够整体代入是解题的关键.10、D【分析】根据正数大于负数和0,0大于负数,两个负数绝对值大的反而小,即可解答.【题目详解】A. 64-<-,故错误B. 31-<+,故错误C. 90-<,故错误D. ∵25371415=-=-2121--, 又∵14152121< ∴2537->-,故正确 故选:D【题目点拨】本题考查了实数比较大小,解决本题的关键是根据正数大于负数和0,0大于负数,两个负数绝对值大的反而小. 11、B【解题分析】科学记数法的表示形式为a ×10n 的形式.其中1≤|a |<10,n 为整数,确定n 的值时,用原数的整数位数减1,即5500万=5.5×1.故选B .12、B【分析】根据单项式、多项式及整式的定义,结合所给式子即可得出答案.【题目详解】(1) 2πxy -是单项式,故(1)错误; (2) 3x y -是多项式,故(2)正确; (3)0是单项式,故(3)错误; (4)1x x +不是整式,故(4)错误; 综上可得只有(2)正确.故选B.【题目点拨】此题考查单项式,整式,多项式,解题关键在于掌握各性质定义.二、填空题(每题4分,满分20分,将答案填在答题纸上)13、00(150)0.8240x +⨯=【分析】设这件商品的成本价为x 元,则标价为00(150)x +元,打8折为00(150)0.8x +⨯,再根据打8折销售,现售价为240元即可列出方程.【题目详解】解:设这件商品的成本价为x 元,根据题意可得,00(150)0.8240x +⨯=. 故答案为:00(150)0.8240x +⨯=.【题目点拨】本题属于一元一次方程的应用,找出题目中的等量关系是解题的关键.14、-12115【分析】根据题意分别计算出第1次、第2次、第3次操作后增加的和,发现每次操作后和均增加-6,进而推出规律,求出第2020次操作所得新数串中所有各数的和.【题目详解】解:第1次操作后增加数字:7,-13,第1次操作后增加的和为:7+(-13)=-6;第2次操作后增加数字:-5,12,8,-21,第2次操作后增加的和为:-5+12+8+(-21)=-6;第3次操作后增加数字:7,-12,-5,17,-13,21,8,-29,第3次操作后增加的和为:7+(-12)+(-5)+17+(-13)+21+8+(-29)=-6;……,即每次操作后和增加-6,∴第2020次操作后和增加2020×(-6)=-12120,∴第2020次操作所得新数串中所有各数的和为2+(-5)+8+(-12120)=-12115.故答案为:-12115.【题目点拨】本题考查数字变化类规律,先分别计算出第1次、第2次、第3次操作后增加的和,从而得到:每次操作后和增加-6,是解题的关键.15、两点确定一条直线【分析】由直线公理可直接得出答案.【题目详解】建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上,沿着这条线就可以砌出直的墙,则其中的道理是:两点确定一条直线.故答案为:两点确定一条直线.【题目点拨】本题主要考查的是直线的性质,掌握直线的性质是解题的关键.16、-1【分析】根据新定义运算得到关于x的方程进行求解.【题目详解】∵11 2321x x+=∴()211 23xx+-=解得x=-1故答案为:-1.【题目点拨】此题主要考查一元一次方程的应用,解题的关键是根据题意得到方程.17、40%【解题分析】试题分析:从条形统计图可知:甲、乙、丙、丁四个兴趣小组的总人数为200人,甲、丙两个小组的人数为80人,所以报名参加甲组和丙组的人数之和占所有报名人数的百分比为80÷200×100%=40%.三、解答题(本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)45°;(2)∠MON的大小不发生改变,即∠MON=45°,理由见解析.【解题分析】(1)根据∠AOB 是直角,∠AOC=40°,可得∠AOB+∠AOC=90°+40°=130°,再利用OM 是∠BOC 的平分线,ON 是∠AOC 的平分线,即可求得答案.(2)根据∠BOC=∠AOB+∠AOC=90°+x ︒,∠MON=∠MOC-∠NOC ,可得∠MON =12∠AOB =45°. 【题目详解】(1)∵∠AOB 是直角,∠AOC=40°.∴∠BOC=∠AOB+∠AOC=90°+40°=130° ∵ON 是∠AOC 的平分线,OM 是∠BOC 的平分线∴∠COM=12∠BOC=12×130°=65°,∠CON=12∠AOC=12×40°=20°, ∴∠MON=∠COM-∠CON=65°-20°=45° (2)当锐角∠AOC 的大小为x ︒时,∠MON 的大小不发生改变,即∠MON=45°理由:当∠AOC=x ︒时,∠BOC=∠AOB+∠AOC=90°+x ︒ ∵ON 是∠AOC 的平分线,OM 是∠BOC 的平分线∴∠COM=12∠BOC=12×(90°+x ︒)=45°+12x ︒,∠CON=12∠AOC=12x ︒, ∴∠MON=∠COM-∠CON=45°+12x ︒-12x ︒=45° 【题目点拨】本题考查了角的计算和角平分线的定义等知识点的理解和掌握,难度不大,属于基础题19、3x -【分析】根据整式的加减运算法则即可求解. 【题目详解】1(93)2(1)3x x --+ 3122x x =---3x =-【题目点拨】此题主要考查整式的加减,解题的关键是熟知其运算法则.20、(1)5x =;(2)75x = 【分析】(1)去括号,移项后系数化为1即可求解;(2)方程两边同时乘6后去分母,去括号,移项合并,将x 系数化为1,即可求出解.【题目详解】解:(1)8646x x --=8664x x -=+210x =5x =故答案为:5x =.(2)()()6311221x x x --=-+6331222x x x -+=--6321223x x x -+=--57x =75x = 故答案为:75x =. 【题目点拨】此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,将未知数系数化为1,即可求解;熟练掌握一元一次方程的解法是解题的关键.21、(1)232a ab ++(2)23x y -+;589【分析】(1)根据整式的加减运算法则即可求解;(1)根据整式的加减运算法则进行化简,再代入x,y 即可求解.【题目详解】(1)()22222333a ab a ab ⎛⎫+-+-⎪⎝⎭ =2246332a ab a ab +--+=232a ab ++(2)22113122323x x y x y ⎛⎫⎛⎫--+-+ ⎪ ⎪⎝⎭⎝⎭ =22123122323x x y x y -+-+ =23x y -+把2x =-,23y =代入原式=()4329-⨯-+=458699+=. 【题目点拨】此题主要考查整式的化简求值,解题的关键是熟知整式的加减运算法则.22、(1)抽样调查;(2)1;(3)①答案见解析;②上网时间;答案不唯一.【分析】(1)根据抽样调查的定义判断即可;(2)根据扇形统计图中,所有百分比的和为1计算;(3)①利用列表法解决问题即可;②利用表格中的数据判断即可.【题目详解】解:(1)抽样调查.(2)m=100-38-4-8-3-14-11-2=1,故答案为1.(3)①十年间北京市居民时间利用的变化统计表(单位:分钟)②上网时间.答案不唯一,理由合理即可,例如:生活水平提高了.【题目点拨】本题考查扇形统计图,频数分布表等知识,解题的关键是读懂题意,熟练掌握基本知识.23、DE的长3cm【分析】根据CB、AC的关系求出AC的长度,再根据线段中点的定义可得AD=12AC,AE=12AB,然后根据DE=AE-AD计算即可得解.【题目详解】因为AC=12cm,所以CB=12AC=12×12=6 cm,所以AB=AC+ CB=12+6=18cm.因为点E为AB的中点,所以AE=12AB=9cm,因为点D为AC的中点,所以AD=12AC=6cm,所以DE=AE﹣AD=9﹣6=3cm,所以DE的长3cm.【题目点拨】本题考查了两点间的距离、中点定义,解题关键是中点定义.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.(1)[1 2 3 4;0 2 -1 1;1 -1 2 5;]+(1/2).*([2 1 4 10;0 -1 2 0;0 2 3 -2]) 2.A=[3 0 1;-1 2 1;3 4 2],B=[1 0 2;-1 1 1;2 1 1]X=(B+2*A)/23.A=[-4 -2 0 2 4;-3 -1 1 3 5]abs(A)>3%4.A=[-2 3 2 4;1 -2 3 2;3 2 3 4;0 4 -2 5]det(A),eig(A),rank(A),inv(A)求计算机高手用matlab解决。
>> A=[-2,3,2,4;1,-2,3,2;3,2,3,4;0,4,-2,5]求|A|>> abs(A)ans =(2 3 2 41 2 3 23 2 3 40 4 2 5求r(A)>> rank(A)ans =4求A-1《>> A-1ans =-3 2 1 30 -3 2 12 1 2 3-1 3 -3 4求特征值、特征向量>> [V,D]=eig(A) %返回矩阵A的特征值矩阵D 与特征向量矩阵V,V =- ++ - - +- +- + - +D ={+ 0 0 00 - 0 00 0 + 00 0 0 -将A的第2行与第3列联成一行赋给b>> b=[A(2,:),A(:,3)']b =《1 -23 2 2 3 3 -21.a=round(unifrnd(1,100))i=7;while i>=0i=i-1;b=input('请输入一个介于0到100的数字:');if b==a¥disp('You won!');break;else if b>adisp('High');else if b<adisp('Low');endendendend结果a =82请输入一个介于0到100的数字:50Low;请输入一个介于0到100的数字:75Low请输入一个介于0到100的数字:85High请输入一个介于0到100的数字:82You won!2.clear all;clc;n=input('请输入数字n=');·n1=floor(n/100); %取出百位数字n1n2=mod(floor(n/10),10); %取出十位数字n2n3=mod(n,10) ; %取出个位数字n3if n1^3+n2^3+n3^3==nfprintf('%d是“水仙花数”', n) % 注意输出格式前须有%符号elsefprintf('%d不是“水仙花”', n) % 注意输出格式前须有%符号end结果请输入数字n=234~234不是“水仙花数”>>3.price=input('请输入商品价格');switch fix(price/100)case {0,1} %价格小于200rate=0;case {2,3,4} %价格大于等于200但小于500 rate=3/100;case num2cell(5:9) %价格大于等于500但小于1000 ]rate=5/100;case num2cell(10:24) %价格大于等于1000但小于2500 rate=8/100;case num2cell(25:49) %价格大于等于2500但小于5000 rate=10/100;otherwise %价格大于等于5000rate=14/100;endprice=price*(1-rate) %输出商品实际销售价格结果!请输入商品价格250 price =4、Function f=myfun(x)x=input;)s=pi*x*xl=pi*x^24、Function y=circle(r)s=pi*x*xl=pi*x^24.syms rs=pi*r*r>l=2*pi*r5. function fibonacci(n,m)f(1)=1;f(2)=1;for i=3:max(n,m)f(i)=f(i-1)+f(i-2);endfprintf('第%d项',m)x=f(m)fprintf('前%d项',n)~s=f(1:n)COMMAND WINDOW输入:fibonacci(20,50)1.绘制])4,0[)(3sin(3π∈=x x e y x 的图像,要求用蓝色的星号画图;并且画出器官包络线3x e y ±=的图像,用红色的点划线画图。
2.用fplot 和ezplot 命令绘出函数)21sin(32t ey t +=-在区间]10,0[上的图像。
3.在同一图像窗口画三个子图要求使用指令gtext,axis,legend,title,xlabel,和ylabel : (3)'(4)]8,1[,sin 1∈=x x e y x1.x=0:pi/25:4*pi;y1=exp(x/3).*sin(3*x);y2=exp(x/3);y3=-exp(x/3);plot(x,y1,'b*',x,y2,'r-.',x,y3,'r-.')2.t=1::10;y=exp(-2*t/3).*sin(1+2*t);plot(t,y);figurefplot('exp(-2*t/3).*sin(1+2*t)',[1,10])ezplot('exp(-2*t/3).*sin(1+2*t)',[1,10])3.x=1:1/50:8;y=exp(1./x).*sin(x);subplot(1,3,3),plot(x,y,'b-');>legend('y=exp(1/x)sinx'),grid on,title('y=exp(1/x)sinx'),xlabel('x轴'),ylabel('y轴')gtext('真棒'),axis([x1 x8 y1 y10])4.x=0:pi/50:2*pi;y1=sin(x);y2=cos(x);y3=sin(2*x);plot(x,y1,'k*--',x,y2,'rs-',x,y3,'bo--'),grid ontitle('曲线y1=sin(x),y2=cos(x)与y3=sin(2*x)');xlabel('x轴'),ylabel('y轴')gtext('y1=sin(x)'),gtext('y2=cos(x)'),gtext('y3=sin(2*x)')legend('y1=sin(x)','y2=cos(x)','y3=sin(2*x)')5.绘制圆锥螺线的图像并加各种标注,圆锥螺线的参数方程为:⎪⎪⎪⎩⎪⎪⎪⎨⎧=≤≤==t z t t t t y t t t x 2)200(,6cos 6cos π 6.在同一图形窗口画半径为1的球面,柱面122=+y x 以及极坐标]2,0[,4sin 21πρ∈=t t 7.)8.用mesh 与surf 命令绘制三维曲面223y x z +=的图像,并使用不同的着色效果及光照效果。
9.绘制由函数14169222=++z y x 形成的立体图,并通过改变观测点获得该图形在各个坐标平面上的投影。
10.画三维曲面)2,2(522≤≤---=y x y x z 与平面3=z 的交线。
5.t=1:pi/50:20*pi;x=t.*cos(pi/6.*t);y=t.*sin(pi/6.*t);z=2*t;plot3(x,y,z);grid on ;>title('圆锥螺线')xlabel('x 轴');ylabel('y 轴');zlabel('z 轴');axis square6.v=[-2 2 -2 2 -2 2];subplot(1,3,1),spheretitle('以半径为1的球面'),xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴'),axis(v) subplot(1,3,2),cylindertitle('柱面'),xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴')subplot(1,3,3),t=0:pi/100:2*pi;polar(t,(1/2)*sin(4*t))title('p=(1/2)*sin(4t)')7.[X,Y]=meshgrid(-8::8);Z=X.^2+3*Y.^2;subplot(1,2,1);mesh(X,Y,Z);shading interpsubplot(1,2,2);surf(X,Y,Z);shading flat?8.[xx,yy,zz]=sphere(40);x=xx*3;y=yy*4;z=zz*2;surf(x,y,z)axis equal9.[X,Y]=meshgrid(-2::2);Z1=5-X.^2+Y.^2;subplot(1,3,1),mesh(X,Y,Z1),title('曲面');Z2=3*ones(size(X));% 创建一个和y矩阵相同大小的纯1矩阵subplot(1,3,2),mesh(X,Y,Z2),title('平面');r0=abs(Z1-Z2)<=1;ZZ=r0.*Z2;YY=r0.*Y;XX=r0.*X;subplot(1,3,3)plot3(XX(r0~=0),YY(r0~=0),ZZ(r0~=0),'*')title('交线')10.v=[-22 -22 -22];[x,y,z]=sphere(30);surf(4*x,4*y,4*z)title('半径为4的球面'),axis(v)。
