必修2第2章测验题B卷

合集下载

人教版高中化学必修2第二章《化学反应与能量》测试题(B卷)【含答案】

人教版高中化学必修2第二章《化学反应与能量》测试题（B 卷）本试卷分第一部分（选择题）和第二部分（非选择题），满分100分，考试时间40分钟。

第一部分选择题（共60分）一、单项选择题（共10小题，每小题3分，共30分。

） 1．下列反应中属吸热反应的是A ．镁与盐酸反应放出氢气B ．氢氧化钠与盐酸的反应C ．硫在氧气中燃烧D ．Ba(OH)2·8H 2O 与NH 4Cl 反应 2．对于反应2SO 2(g)＋O 2(g)2SO 3(g)，能增大正反应速率的措施是A ．增大容器容积B ．移去部分SO 3C ．通入大量O 2D ．降低体系温度 3．在2L 密闭容器中进行的反应2SO 2(g)＋O 2(g)2SO 3(g)，在10秒内反应物SO 2的物质的量由1mol 降到0.6mol ，则反应速率ν(SO 2)为A ．0.02mol/(L·s)B ．0.04mol/((L·s)C ．0.2mol/((L·s)D ．0.4mol/((L·s) 4．下列化学电池不易造成环境污染的是A ．锌锰电池B ．氢氧燃料电池C ．镍镉电池D ．铅蓄电池5．A 、B 、C 三种金属片，把A 、B 用导线连接后同时浸入稀硫酸溶液中，A 是负极；把B 、C 用导线连接后同时浸入稀硫酸溶液中，C 发生还原反应。

三种金属的活动性顺序是A ．A ＞B ＞C B ．C ＞B ＞A C ．A ＞C ＞BD ．B ＞A ＞C 6．下列装置中能构成原电池的是7．下列关于物质及其变化的说法不．正确的是 A ．各种物质都储存有化学能 B ．不少的化学反应都具有可逆性C ．物质发生化学变化时，键的断裂和生成都要释放能量G铜铜稀硫酸AG铜锌稀硫酸 CG银稀硫酸 BG铜锌乙醇 DD．物质发生化学变化时，常常伴随有物理变化8．工业上合成氨的反应为N 2(g)+3H2(g) 2NH3(g)，为了增大反应速率，提高经济效益，最理想的措施是A．增大反应物的浓度B．增大反应体系的压强C．提高反应体系的温度D．选择合适的催化剂9．下列实验中，反应速率加快是由催化剂引起的是A．双氧水中加入1~2滴1mol/L FeCl3，可迅速放出气体B．炭粉中加入KClO3，点燃时燃烧更为剧烈C．固态FeCl3和固体NaOH混合后，加入水能迅速产生沉淀D．锌与稀硫酸反应中加入少量CuSO4溶液，反应放出H2的速率加快10．氢氧燃料电池是一种高效、环境友好的发电装置，它是以铂作电极，KOH溶液作电解液，总反应为：2H2 + O2＝2H2O，正极反应为：O2 + 2H2O + 4e－＝4OH－，下列叙述不．正确的是A．H2通入负极区B．O2通入正极区C．负极反应为2H2 + 4OH－－4e－＝4H2O D．正极发生氧化反应二、多项选择题（共6小题，每小题5分，共30分。

数学必修2第二章测试题B卷

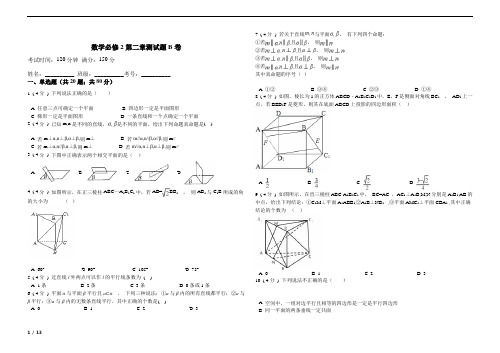
数学必修2第二章测试题B卷考试时间：120分钟满分：150分姓名：__________ 班级：__________考号：__________一、单选题（共20题；共80分）1. ( 4分) 下列说法正确的是（）A. 任意三点可确定一个平面B. 四边形一定是平面图形C. 梯形一定是平面图形D. 一条直线和一个点确定一个平面2. ( 4分) 已知m,n是不同的直线，是不同的平面，给出下列命题真命题是( )A. 若m⊥α,n⊥β,α⊥β,则m⊥B. 若m//α,n//β,α//β,则m//C. 若m⊥α,n//β,α⊥β,则m⊥D. 若m//α,n⊥β,α⊥β,则m//3. ( 4分) 下图中正确表示两个相交平面的是（）A. B. C. D.4. ( 4分) 如图所示，在正三棱柱ABC—A1B1C1中，若AB=BB1，则AB1与C1B所成的角的大小为（）A. 60°B. 90°C. 105°D. 75°5. ( 4分) 过直线l外两点可以作l的平行线条数为( )A. 1条B. 2条C. 3条D. 0条或1条6. ( 4分) 平面α与平面β平行且a⊂α，下列三种说法：①a与β内的所有直线都平行；②a与β平行；③a与β内的无数条直线平行，其中正确的个数是( )A. 0B. 1C. 2D. 3 7. ( 4分) 若关于直线与平面，有下列四个命题：①若,,且，则；②若,,且，则；③若,,且，则；④若,,且，则；其中真命题的序号（）A. ①②B. ③④C. ②③D. ①④8. ( 4分) 如图，棱长为1的正方体ABCD﹣A1B1C1D1中，E，F是侧面对角线BC1，AD1上一点，若BED1F是菱形，则其在底面ABCD上投影的四边形面积（）A. B. C. D.9. ( 4分) 如图所示，在直三棱柱ABC-A1B1C1中，BC=AC ，AC1⊥A1B,M,N分别是A1B1,AB的中点，给出下列结论：①C1M⊥平面A1ABB1,②A1B⊥NB1,③平面AMC1⊥平面CBA1 ,其中正确结论的个数为（）A. 0B. 1C. 2D. 310. ( 4分) 下列说法不正确的是（）A. 空间中，一组对边平行且相等的四边形是一定是平行四边形B. 同一平面的两条垂线一定共面1/ 13C. 过直线上一点可以作无数条直线与这条直线垂直，且这些直线都在同一个平面内D. 过一条直线有且只有一个平面与已知平面垂直11. ( 4分) 在空间四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA的中点．若AC=BD=a，且AC与BD所成的角为60°，则四边形EFGH的面积为（）A. B. C. D.12. ( 4分) 设P表示一个点，a，b表示两条直线，α，β表示两个平面，给出下列四个命题，其中正确的命题是（）①P∈a，P∈α⇒a⊂α②a∩b=P，b⊂β⇒a⊂β③a∥b，a⊂α，P∈b，P∈α⇒b⊂α④α∩β=b，P∈α，P∈β⇒P∈b．A. ①②B. ②③C. ①④D. ③④13. ( 4分) 异面直线l与m成60°，异面直线l与n成45°，则异面直线m与n成角范围是（）A. [15°，90°]B. [60°，90°]C. [15°，105°]D. [30°，105°]14. ( 4分) 如图，四棱锥P﹣ABCD中，M，N分别为AC，PC上的点，且MN∥平面PAD，则（）A. MN∥PDB. MN∥PAC. MN∥ADD. 以上均有可能15. ( 4分) 设，是不同的直线，，，是不同的平面，有以下四个命题其中正确的命题是（）A. ①④B. ①③C. ②③D. ②④16. ( 4分) 下列命题中，m，n表示两条不同的直线，a，b，γ表示三个不同的平面①若m⊥a，n∥a，则m⊥n；②若a⊥γ，b⊥γ，则a∥b；③若m∥a，n∥a，则m∥n；④若a∥b，b∥γ，m⊥a，则m⊥γ．正确的命题是（）A. ①③B. ②③C. ①④D. ②④17. ( 4分) 在四棱锥中，底面，底面为矩形，，是上一点，若，则的值为( )A. B. C. D. 418. ( 4分) 若a、b、c、d是直线，α、β是平面，且a、b⊂α，c、d⊂β，且a∥c，b∥d，则平面α与平面β ( )A. 平行B. 相交C. 异面D. 不能确定19. ( 4分) 正四棱锥（底面为正方形，顶点在底面上的射影是底面的中心）的底面边长为2，高为2，为边的中点，动点在表面上运动，并且总保持，则动点的轨迹的周长为（）A. B. C. D.20. ( 4分) 设a,b是两条直线，是两个平面，则的一个充分条件是（）A. B.C. D.二、解答题（共10题；共70分）21. ( 5分) 在正方体ABCD－A1B1C1D1中，E为AB的中点，F为AA1的中点，求证：第3页共26页◎第4页共26页（1）E、C、D1、F、四点共面；（2）CE、D1F、DA三线共点．22. ( 5分) 如图，在三棱锥P—ABC中，E、F、G、H分别是AB、AC、PC、BC的中点，且PA=PB，AC=BC、（Ⅰ）证明：AB⊥PC；（Ⅱ）证明：平面PAB//平面FGH23. ( 10分) 如图，在四棱锥中，平面，，，，.（1）求证：；（2）求多面体的体积.24. ( 10分) 如图，在四棱锥中，底面ABCD是菱形，PA＝PB，且侧面PAB⊥平面ABCD，点E是AB的中点. （1）求证：PE⊥AD；（2）若CA＝CB，求证：平面PEC⊥平面PAB．25. ( 5分) 在三棱柱ABC－A1B1C1中，M，N，P分别为A1C1，AC和AB的中点．求证：∠PNA1＝∠BCM.26. ( 5分) 如图，在正方形ABCD－A1B1C1D1中，E，F，M分别是棱B1C1，BB1，C1D1的中点，是否存在过点E，M且与平面A1FC平行的平面？若存在，请作出并证明；若不存在，请说明理由.27. ( 5分) 如图，在直三棱柱ABC﹣A1B1C1中，AC⊥BC，点D是AB的中点．求证：（1）AC⊥BC1；（2）AC1∥平面B1CD．3/ 1328. ( 10分) 如图，平行四边形ABCD中，BC=2AB=4，∠ABC=60°，PA⊥AD，E，F分别为BC，PE的中点，AF⊥平面PED．（1）求证：PA⊥平面ABCD；（2）求直线BF与平面AFD所成角的正弦值．29. ( 5分) 如图，是圆的直径，垂直圆所在的平面，是圆上的点．（1）求证：平面；（2）设为的中点，为的重心，求证：平面．30. ( 10分) 如图，在四棱柱ABCD﹣A1B1C1D1中，侧棱A1A⊥底面ABCD，AB⊥AC，AB=1，AC=AA1=2，AD=CD= ．用向量法解决下列问题：（1）若AC的中点为E，求A1C与DE所成的角；（2）求二面角B1﹣AC﹣D1（锐角）的余弦值．第7页共26页◎第8页共26页答案解析部分一、单选题1.【答案】C【考点】平面的基本性质及推论，空间图形的公理【解析】【解答】A中三点要不共线；B中空间四边形实际就是一个四面体；D中点要不在直线上这是一道立体几何概念题，选C.2.【答案】A【考点】直线与平面平行的判定，直线与平面垂直的判定【解析】【分析】B项可能是平行，相交，异面；C，D项可能垂直还可能平行【点评】此题可联系正方体中的线面关系来判定3.【答案】D【考点】平面的概念、画法及表示【解析】【解答】A中无交线；B中不可见线没有画成虚线；C中虚、实线没按画图规则画，也不正确．D的画法正确．画两平面相交时，一定要画出交线，还要注意画图规则，不可见线一般应画成虚线，有时也可以不画．故答案为:D.【分析】画两平面相交时，一定要画出交线，还要注意画图规则，不可见线一般应画成虚线，有时也可以不画.4.【答案】B【考点】异面直线及其所成的角【解析】【分析】选出向量的基底，将，用基底表示，求出两个向量的数量积，利用向量垂直的充要条件求出两个向量的夹角．【解答】设|BB1|=m，=，=，=则=+，=-?= (+)?(- )= 2-?=m2-m?mcos=0∴⊥∴CA1与C1B所成的角的大小是90°故选B5.【答案】D【考点】空间中直线与直线之间的位置关系【解析】【解答】以如图所示的正方体为例．令所在直线为直线，过外的两点可以作一条直线与平行，过外的两点不能作直线与平行，故答案为：D.【分析】结合直线与直线的位置关系，要么平行要么异面，即可得出答案。

必修2 第二章检测试卷(word版含答案)

必修2 第二章检测试卷一、选择题(本题包括18小题，每小题3分，共54分，每小题只有一个选项符合题意)1．(2020·厦门双十中学期中)达康书记又追问环保局长：那么垃圾处理中，能随便焚烧吗？焚烧垃圾会降低GDP的。

在焚烧垃圾过程中发生了( )A．吸热的非氧化还原反应B．吸热的氧化还原反应C．放热的非氧化还原反应D．放热的氧化还原反应答案 D2．化学反应中必然伴随着物质变化和能量变化，下列说法正确的是( )A．浓硫酸溶于水共价键断裂并放出大量的热，所以该过程是放热反应B．吸热反应一定要在加热或高温条件下才能进行C．上图可表示放热反应中的能量变化D．焰色反应有能量变化，所以焰色反应是化学反应答案 C3．如图是化学课外活动小组设计的用化学电源使LED灯发光的装置示意图。

下列有关该装置的说法正确的是( )A．铜片为负极，其附近的溶液变蓝，溶液中有Cu2＋产生B．如果将锌片换成铁片，电路中的电流方向将改变C．其能量转化的形式主要是“化学能→电能→光能”D．如果将稀硫酸换成柠檬汁，LED灯将不会发光答案 C4．如图所示的装置，在盛有水的烧杯中，铁圈和银圈的连接处吊着一根绝缘的细丝，使之平衡。

小心地往烧杯中央滴入CuSO4溶液。

片刻后可观察到的现象是(指悬吊的金属圈)( )A．铁圈和银圈左右摇摆不定B．保持平衡状态不变C．铁圈向下倾斜D．银圈向下倾斜答案 D5．甲：在试管中加入1 g粉末状大理石，加入4 mol·L－1盐酸20 mL(过量)；乙：在试管中加入2 g颗粒状大理石，加入4 m ol·L－1盐酸20 mL(过量)；下列CO2生成体积(折算成标准状况)V(CO2)同反应时间t的关系曲线图合理的是( )答案 D6．(2020·湖北恩施月考)一定条件下，将NO2与SO2以体积比1∶2置于密闭容器中发生NO2(g)＋SO2(g)SO3(g)＋NO(g)的可逆反应，下列能说明反应达到平衡状态的是( )A．体系压强保持不变B．混合气体颜色保持不变C．SO3和NO的体积比保持不变D．每消耗1 mol SO3的同时生成1 mol NO2答案 B7．(2020·铜陵市期中)根据如图所示示意图，下列说法不正确的是( )A．反应C(s)＋H2O(g)===CO(g)＋H2(g)，能量增加(b－a) kJ·mol－1B．该反应过程反应物断键吸收的能量大于生成物成键放出的能量C．1 mol C(s)和1 mol H2O(l)反应生成1 mol CO(g)和1 mol H2(g)吸收的热量为131.3 kJD．1 mol C(s)、2 mol H、1 mol O转变成1 mol CO(g)和1 mol H2(g)放出的热量为a kJ答案 C8．根据下面的信息，下列叙述正确的是( )⎭⎬⎫H 2g 1 mol H 2的共价键断裂吸收436 kJ 能量2H g 12O 2g 12 mol O 2的共价键断裂吸收249 kJ 能量O g 形成1 mol H 2O 的共价键释放930 kJ 能量H 2O(g) A ．2 mol H 2(g)跟1 mol O 2(g)反应生成2 mol H 2O(g)吸收能量为490 kJB ．化学反应中能量变化的大小与反应物的质量多少无关C ．1 mol H 2(g)跟0.5 mol O 2(g)反应生成1 mol H 2O(l)释放能量为245 kJD ．2 mol H 2O(g)的能量比2 mol H 2(g)与1 mol O 2(g)的能量之和低答案 D9．纽扣电池可作计算器、电子表等的电源。

高中地理第2章地表形态的塑造过关检测B卷新人教版选择性必修

第二章过关检测(B卷)(时间:60分钟满分:100分)一、单项选择题(每小题2分,共40分)盐风化是含盐溶液渗透到岩石表层的空隙或微裂隙中,因蒸发过饱和而导致盐类结晶,盐结晶膨胀而导致的岩石表面颗粒分解或脱落,地貌上形成大小不等的风化穴的物理风化作用过程。

右图为甘肃酒泉某地红色砂岩露头的盐风化穴示意图,该地平均年降水量仅为84毫米。

读图,完成第1~2题。

1.下列不属于盐风化形成条件的是( )A.干湿交替的环境B.含有孔隙的岩石C.可溶性盐类物质D.坡度较陡的地势2.下列地理事象,可能是因盐风化作用形成的是( )A.南岭地区花岗岩的球状风化B.黄土高原的千沟万壑C.敦煌莫高窟壁画的风化剥落D.云南喀斯特地貌的发育答案:1.D 2.C解析:第1题,由题目信息可知,盐风化需要盐类结晶。

可溶性盐类物质溶于水后,形成含盐溶液渗透到岩石表层的空隙或微裂隙中,随着水分的蒸发,盐类逐渐结晶、膨胀。

故盐风化需要可溶性盐类物质、含有孔隙的岩石和干湿交替的环境,而地势的陡缓对盐风化无明显影响。

第2题,敦煌莫高窟位于我国西北地区,气候干旱,降水少,昼夜温差大,风化作用明显,地表盐分多,故可能受到盐风化的影响。

黄土高原千沟万壑的地貌和云南喀斯特地貌均是由流水作用形成的;盐风化在地貌上形成大小不等的风化穴,显然花岗岩的球状风化不是因盐风化作用形成。

北京市某中学师生到中国延庆世界地质公园进行考察。

图1是学生绘制的地质素描图,图2是被誉为“小桂林”的龙庆峡景区照片,图3是延庆“硅化木”国家地质公园照片。

读图,完成第3~4题。

3.据图1和图2景观判断( )A.图1属于背斜构造B.图2属于河流堆积地貌C.图1地形主要由外力作用形成D.图2山体由花岗岩构成4.同学们向专家了解到图3“硅化木”的形成历史。

数亿年前,因火山喷发使高大林木迅速掩埋于地下,经硅化和变质形成特殊的“木化石”,后来有部分“硅化木”出露于延庆白河两岸高坡上,始被人发现。

(完整word版)高二数学必修2第二章测试题及答案(word文档良心出品)

64,那么tan^的值等于第1页（共4页）11、已知二面角〉-AB-:的平面角是锐角二,内一点C 至U :的距离为 3，点C 到棱AB 的距离为咼中数学必修咼2第二章测试题试卷满分：150分考试时间：120分钟班级 __________ 姓名 ____________ 学号 ___________ 分数 ______________一、选择题（每小题5分，共60分）1、线段AB 在平面:内，则直线 AB 与平面〉的位置关系是A 、AB 二很 B 、AB 二，C 、由线段AB 的长短而定D 、以上都不对2、下列说法正确的是A 、三点确定一个平面B 、四边形一定是平面图形3、垂直于同一条直线的两条直线一定A 、平行B 、相交C 、异面4、在正方体 ABCD - AiBGD i 中，下列几种说法正确的是PA 、AC i_ADB 、DQ i_ABC 、AC i 与 DC 成 45 角5、若直线l //平面〉，直线a 二:工，则I 与a 的位置关系是A 、I // aB 、I 与a 异面C 、I 与a 相交D 、丨与a 没有公共点6、下列命题中：（i ）、平行于同一直线的两个平面平行；（2）、平行于同一平面的两个平面平行；（3）、垂直于同一直线的两直线平行；（4）、垂直于同一平面的两直线平行 •其中正确的个数有A 、iB 、2C 、3D 、47、在空间四边形 ABCD 各边AB 、BC 、CD 、DA 上分别取E 、F 、G 、H 四点，如果与EF 、GH 能相交于点P ，那么A 、点必P 在直线AC 上B 、点P 必在直线BD 上C 、点P 必在平面ABC 内D 、点P 必在平面ABC 外8、 a , b , c 表示直线，M 表示平面，给出下列四个命题：①若a // M , b// M ，贝V a //b ;②若b M , a //b ，贝U a // M ;③若a 丄c , b 丄c ,贝V a // b ;④若a 丄M , b ±M ，贝V a // b.其中正确命题的个数有 A 、0个B 、1个C 、2个D 、3个9、点P 为厶ABC 所在平面外一点， PO 丄平面ABC 垂足为 0,若PA=PB=PC 则点 0是厶ABCW （）A 、内心B 、外心C、重心D、垂心10、在棱长为1的正方体上，分别用过共顶点的三条棱中点的平面截该正方体下的凸多面体的体积是C 、梯形一定是平面图形D 、平面〉和平面一：有不同在一条直线上的三个交点D 、以上都有可能pD 、AC i 与 B i C 成 60 角，则截去8个三棱锥后，剩317、如图，PAL 平面 ABC 平面 PABL 平面 PBC 求证：AB 丄BC （12分）CTD 、3—712、如图：直三棱柱ABC —A 1B 1C 1的体积为V ,点P 、Q 分别在侧棱AA i 和CC i 上，AP=C 1Q ，则四棱锥B —APQC 的体积为VVVVA 、 —B 、 —C 、一D 、一2 3 4 5二、填空题（每小题5分，共20分）13、已知直线 a 丄直线b, a 〃平面-,则b 与一：的位置关系为 ____________ . ________14、正方体ABC^ —A 1B 1C 1D 1中，平面AB 1D 1和平面BCQ 的位置关系为 _______________________ 15、已知PA 垂直平行四边形 ABCD 所在平面，若 PC_BD ，平行则四边形ABCD 一 -定是___________ :16. a 、3是两个不同的平面， m n 是平面a 及B 之外的两条不同直线，给出四个论断：①m_ n ②a 13③m 13④n _a以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个命题：三、解答题（共70分,要求写出主要的证明、解答过程）18、已知E 、F 、G 、H 为空间四边形 ABCD 的边AB 、BC 、CD 、DA 上的点，且 EH // FG . 求证：EH // BD. （10 分）A'P ABC'Q CA19、已知ABC 中.ACB =90；, SA_ 面ABC, AD _ SC，求证：AD _ 面SBC. （12 分）20 .如图，P从平面ABC AE1 PB, AB丄BC, AF丄PC,PA=AB=BC=2（ 1）求证：平面AEF丄平面PBC（2 ）求二面角P—BC- A的大小；（3）求三棱锥P—AEF的体积.（12分）BCC21、已知正方体ABCD -ABGD , O是底ABCD对角线的交点•。

人教B版必修2练习第二章单元测验 Word版含解析

第二章单元测验班级姓名考号分数本试卷满分分，考试时间分钟．一、选择题：本大题共小题，每小题分，共分．在下列各题的四个选项中，只有一个选项是符合题目要求的．．设直线与轴的交点是，且倾斜角为α，若将此直线绕点按逆时针方向旋转°，得到直线的倾斜角为α＋°，则( )．°≤α＜°．°≤α＜°．°＜α≤°．°＜α＜°答案：解析：由于直线与轴相交，可知α≠°.又α与α＋°都是直线的倾斜角，从而有(\\(°＜α＜°°＜α＋°＜°，))∴°＜α＜°.故选.．直线(＋－)＋(－)－＋＝与直线－－＝平行，则值为( )．－或．－或．－．答案：解析：因为两直线平行，所以有(－)＋(＋－)＝即＋－＝，∴＝－或.检验知＝时不成立，故＝－.．直线－－＝与坐标轴围成三角形的面积为( )．．．．答案：解析：直线－－＝的截距分别为、－与坐标轴围成三角形的面积为.．在空间直角坐标系中，()，()，则等于( )．．．答案：解析：＝＝.．当<<时，直线：－＝－与直线：－＝的交点在( )．第一象限．第二象限．第三象限．第四象限答案：解析：＝得交点，在第二象限．．已知三角形的三个顶点坐标分别为()，(，－)，()，则三角形的重心坐标为( )答案：解析：三角形三个顶点分别为(，，)，(，，)，(，，)，则其重心为.故所求重心坐标为.．若圆＋＋－＋＝关于直线－＋＝对称，则＋等于( )．．－．－答案：解析：∵圆心(－)，∴－－＋＝，∴＋＝.．两圆＋－－＋＝和＋－－＋＝的位置关系是( )．相离．相交．内切．外切答案：．如果点(，)在两条平行线－＋＝及－＋＝之间，则应取的整数值为( )．－．．－．答案：解析：将＝代入两直线方程得＝，＝，由<<得＝.．曲线＋＋＋－＝上到直线＋－＝距离等于的点的个数为( )．．．．答案：解析：圆心(－，－)，半径＝，＝＝－＝，∴共有个符合条件的点．．已知点(，)在直线＋＝上，则的最小值为( )．．．．答案：解析：由点(，)在直线＋＝上知，＋＝.则＋＝＋(－)＝(－＋)＝[(－＋)]＝＋当＝，＝时，有最小值.．如果圆＋(－)＝上任意一点(，)都能使＋＋≥成立，则实数的范围是( )．≥－－．≤－－．≥－．≤－答案：解析：由＋＋≥，得≥－－，要使该不等式恒成立，只需≥(－－)，令＝－－，则＋＋＝.由≤，得－－≤≤－.于是≥－.二、填空题：本大题共小题，每小题分，共分．把答案填在题中横线上．．直线－－＝与圆(－)＋(＋)＝交于，两点，则△(是原点)的面积等于．答案：解析：解方程组(\\(＝()－(),(－(＋(＋(＝))得－－＝，∵(\\(＋＝，＝－()，))∴＝－＝＝，又由点到直线距离公式，得—＝，∴△＝.．与两平行直线＋－＝和＋－＝相切，圆心在直线＋＋＝上的圆的方程是．答案：＋＝解析：设圆心为(，－－)，根据题意，有圆心到两平行直线之间的距离相等为圆的半径，所以＝⇒＝－.所以圆心坐标为，半径＝＝.所以所求圆的方程为＋＝.．若，满足(－)＋＝，则的取值范围是．答案：[]解析：解法一：由(－)＋＝，得＝－(－)≥，故(－)≤，∴≤≤.∴＝＝，由≤≤，得≤－≤，∴≤≤，则的取值范围是[]．。

人教版高中化学选择性必修二第2章分子结构与性质过关检测卷(B)含答案

第二章过关检测卷(B)(时间:75分钟满分:100分)一、选择题(本题共10小题,每小题4分,共40分。

每小题只有一个选项符合题目要求)1.共价键、离子键和范德华力是粒子之间的不同作用力,下列物质中含有两种上述作用力的是()。

①NaOH②SiO2③Na2O2④金刚石⑤NaCl⑥白磷A.①③⑥B.①②④D.③④⑤NaOH是离子化合物,Na+与OH-之间存在离子键,氧原子与氢原子之间存在共价键;②SiO2是共价化合物,只存在共价键;③Na2O2是离子化合物,Na+与O22-间存在离子键,氧原子与氧原子之间存在共价键;④金刚石中只存在共价键;⑤NaCl是离子化合物,只存在离子键;⑥白磷存在P—P共价键,白磷分子间通过范德华力结合,故选A。

2.下列有关共价键的描述,错误的是()。

A.键能:C—N<C N<C≡NB.键长:I—I>Br—Br>Cl—ClC.共价键极性:H—F<N—H:NF3<NH3答案C解析两种元素的原子形成的共价键的数目越多,键能越大,故键能大小关系为C—N<CN<C≡N,故A项正确;原子半径:I>Br>Cl,故键长大小关系为I—I>Br—Br>Cl—Cl,故B项正确;元素的电负性:F>N,故共价键极性:H—F>N—H,故C项错误;电负性:F>N>H,使成键电子对更偏向于F,成键电子对与成键电子对之间的斥力减小,键角变小,所以键角NF3<NH3,故D 项正确。

3.下列说法中错误的是()。

A.氨水中含有多种分子间氢键B.H2O的沸点比HF的沸点高,可能与氢键数目有关C.氢键X—H…Y—的三个原子总在一条直线上,HF沸点最高,是由于HF分子间存在氢键NH3分子之间存在氢键,NH3与H2O、H2O与H2O之间都存在氢键,A项正确。

氢键F—H…F的强度比O—H…O的强度大,但1个HF分子平均形成1个氢键,1个H2O分子平均形成2个氢键,所以H2O的沸点高于HF的沸点,跟分子间形成的氢键数目有关,B项正确。

高中数学(人教B版必修2)学业分层测评：第2章 2.2.1 直线方程的概念与直线的斜率 Word版含答案

学业分层测评(建议用时：45分钟)一、选择题1.下列说法正确的是( )A.一条直线和x 轴的正方向所成的正角，叫做这条直线的倾斜角B.直线的倾斜角α的取值范围是锐角或钝角C.与x 轴平行的直线的倾斜角为180°D.每一条直线都存在倾斜角，但并非每一条直线都存在斜率【解析】选项A 成立的前提条件为直线和x 轴相交，故错误；选项B 中倾斜角α的范围是0°≤α<180°，故错误；选项C 中与x 轴平行的直线，它的倾斜角为0°，故错误；选项D 中每一条直线都存在倾斜角，但是直线与y 轴平行时，该直线的倾斜角为90°，斜率不存在，故正确.【答案】 D2.若A 、B 两点的横坐标相等，则直线AB 的倾斜角和斜率分别是( )A.45°，1B.135°，－1C.90°，不存在D.180°，不存在【解析】由于A 、B 两点的横坐标相等，所以直线与x 轴垂直，倾斜角为90°，斜率不存在.故选C.【答案】 C3.若过两点A (4，y )，B (2，－3)的直线的倾斜角是135°，则y 等于( )A.1B.5C.－1D.－5【解析】由斜率公式可得：y ＋34－2＝tan 135°， ∴y ＋32＝－1，∴y ＝－5.∴选D.【答案】 D4.若直线l 的向上方向与y 轴的正方向成60°角，则l 的倾斜角为( )A.30°B.60°C.30°或150°D.60°或120°【解析】直线l 可能有两种情形，如图所示，故直线l 的倾斜角为30°或150°.故选C.【答案】 C5.直线l 过点A (1,2)，且不过第四象限，则直线l 的斜率k 的最大值是( )A.0B.1C.12D.2【解析】如图，k OA ＝2，k l ′＝0，只有当直线落在图中阴影部分才符合题意，故k ∈.故直线l 的斜率k 的最大值为2.【答案】 D二、填空题6.a ，b ，c 是两两不等的实数，则经过P (b ，b ＋c )，C (a ，c ＋a )两点直线的倾斜角为________.【解析】由题意知，b ≠a ，所以k ＝c ＋a －b ＋c a －b＝1，故倾斜角为45°.【答案】 45°7.已知三点A (－3，－1)，B (0,2)，C (m,4)在同一直线上，则实数m 的值为________.【解析】 ∵A 、B 、C 三点在同一直线上，∴k AB ＝k BC ，∴2－－0－－＝4－2m －0， ∴m ＝2.【答案】 28.在平面直角坐标系中，正△ABC 的边BC 所在直线的斜率是0，则AC ，AB 所在直线的斜率之和为________.【解析】如图，易知k AB ＝3，k AC ＝－3，则k AB ＋k AC ＝0.【答案】 0三、解答题9.已知点A (1,2)，在坐标轴上求一点P 使直线PA 的倾斜角为60°.【解】 (1)当点P 在x 轴上时，设点P (a,0)，∵A (1,2)，∴k PA ＝0－2a －1＝－2a －1. 又∵直线PA 的倾斜角为60°，∴tan 60°＝－2a －1，解得a ＝1－233. ∴点P 的坐标为⎝ ⎛⎭⎪⎫1－233，0. (2)当点P 在y 轴上时，设点P (0，b ). 同理可得b ＝2－3， ∴点P 的坐标为(0,2－3).10.已知A (2,4)，B (3,3)，点P (a ，b )是线段AB (包括端点)上的动点，求b －1a －1的取值范围.【解析】设k ＝b －1a －1，则k 可以看成点P (a ，b )与定点Q (1,1)连线的斜率.如图，当P 在线段AB 上由B 点运动到A 点时，PQ 的斜率由k BQ 增大到k AQ ，因为k BQ ＝3－13－1＝1，k AQ ＝4－12－1＝3，所以1≤k ≤3，即b －1a －1的取值范围是.1.斜率为2的直线经过点A (3,5)，B (a,7)，C (－1，b )三点，则a ，b 的值分别为( )A.4,0B.－4，－3C.4，－3D.－4,3【解析】由题意，得⎩⎪⎨⎪⎧ k AC ＝2，k AB ＝2，即⎩⎪⎨⎪⎧ b －5－1－3＝2，7－5a －3＝2，解得a ＝4，b ＝－3.【答案】 C2.已知直线l 1的斜率为1，l 2的斜率为a ，其中a 为实数，当两直线的夹角在(0°，15°)内变动时，则a 的取值范围是( )A.(0,1)B.⎝ ⎛⎭⎪⎫33，3C.⎝ ⎛⎭⎪⎫33，1∪(1，3)D.(1，3)【解析】 ∵l 1的倾斜角为45°，∴l 2的倾斜角的取值范围为(30°，45°)∪(45°，60°)，∴a 的取值范围为⎝⎛⎭⎪⎫33，1∪(1，3)，故选C. 【答案】 C3.已知直线l 1的倾斜角α1＝15°，直线l 1与l 2的交点为A ，把直线l 2绕着点A 按逆时针方向旋转到和直线l 1重合时所转的最小正角为60°，则直线l 2的斜率的值为________. 【解析】设直线l 2的倾斜角为α2，则由题意知：180°－α2＋15°＝60°，α2＝135°，k 2＝tan α2＝－tan 45°＝－1.【答案】－14.点M (x ，y )在函数y ＝－2x ＋8的图象上，当x ∈时，求y ＋1x ＋1的取值范围.【解】 y ＋1x ＋1＝y －－x －－的几何意义是过M (x ，y )，N (－1，－1)两点的直线的斜率. ∵点M 在函数y ＝－2x ＋8的图象上，且x ∈，∴设该线段为AB 且A (2,4)，B (5，－2)，设直线NA ，NB 的斜率分别为k NA ，k NB .∵k NA ＝53，k NB ＝－16，∴－16≤y ＋1x ＋1≤53. ∴y ＋1x ＋1的取值范围是⎣⎢⎡⎦⎥⎤－16，53.。

人教版高中生物必修2遗传与进化第2章综合测试试卷含答-案答案在前2

第二章综合测试答案解析一、1.【答案】B【解析】等位基因A、a位于同源染色体上，会在减数分裂过程中，随着同源染色体的分离而分离，同源染色体的分离发生在减数第一次分裂期间，所以基因A与a分开的时期也是减数第一次分裂期间，即由初级精母细胞形成次级精母细胞的过程中。

2.【答案】B【解析】甲图和乙图所示细胞中都存在同源染色体，丙图和丁图所示细胞中不存在同源染色体，A错误；精原细胞可进行有丝分裂，也可进行减数分裂，若甲图所示细胞为精原细胞，其子细胞可能会进行减数分裂（乙图所示的分裂方式），B正确；丙图所示细胞处于减数第二次分裂中期，细胞内含有2条染色体和4 个核DNA分子，而丁图所示细胞为生殖细胞，细胞内含有2条染色体和2个核DNA分子，C错误；乙图所示细胞的细胞质均等分裂，说明该细胞只能是初级精母细胞，不可能是初级卵母细胞，因此不可能存在于雌性动物体内，D错误。

3.【答案】A【解析】分析题意可知，题图表示核DNA含量的变化曲线，曲线AB段处于减数分裂前的间期，此时正在进行DNA分子的复制，A正确；曲线BC段处于减数第一次分裂时期，该过程中没有着丝粒的分裂，B错误；曲线DE段处于减数第二次分裂时期，该过程中不会出现同源染色体非姐妹染色单体间的互换，C错误；曲线FG段细胞内的染色体数目是体细胞的一半，D错误。

4.【答案】C【解析】由于F1中雄鸡均为芦花形，雌鸡均为非芦花形，设相关基因用A、a表示，可推出双亲基因型为Z A W和Z a Z a，F1基因型为Z A Z a和Z a W，控制芦花和非芦花性状的基因在Z染色体上，A正确；芦花为显性性状，且ZZ为雄性，所以雄性中芦花鸡比例大，B正确；让F1中的雌雄鸡自由交配，即Z A Z a Z a W，F2基因型为Z A Z a、Z a Z a、Z A W、Z a W，雌雄鸡都有两种表型，C错误；让F1自交产生的F2中的雌雄芦花鸡交配，即Z A Z a Z A W，F3基因型为Z A Z A、Z A Z a、Z A W、Z a W，芦花鸡占3/4，D正确。

人教B版高中数学必修二第二章同步测试试卷().docx

第二章解析几何初步（人教实验B版必修2）123A C5 6√225分.－2、B相＝0．只案中必须明确写出数值和单位）17．（本题满分12分）已知圆的方程是x2+y2－2ax+ 2（a－2）y+2=0，其中a≠1，且a∈R.（1）求证：a取不为1的实数时，上述圆恒过定点；（2）求与圆相切的直线方程；（3）求圆心的轨迹方程.18．（本题满分12分）一束光线l自A(－3,3)发出，射到x轴上，被x轴反射后与圆C：x2＋y2－4x－4y＋7＝0有公共点．(1)求反射光线通过圆心C时，光线l所在直线的方程；(2)求在x轴上，反射点M的横坐标的取值范围．19．（本题满分12分）已知圆x2＋y2－2x－4y＋m ＝0.(1)此方程表示圆，求m的取值范围；(2)若(1)中的圆与直线x＋2y－4＝0相交于M、N两点，且OM⊥ON(O为坐标原点)，求m的值；(3)在(2)的条件下，求以MN为直径的圆的方程．20.（本题满分12分）已知圆O：x2＋y2＝1和定点A(2,1)，由圆O外一点P(a，b)向圆O引切线PQ，切点为Q，|PQ|＝|PA|成立，如图．(1)求a、b间的关系；(2)求|PQ|的最小值；(3)以P为圆心作圆，使它与圆O有公共点，试在其中求出半径最小的圆的方程．21．（本题满分13分）在空间直角坐标系中，已知A（3，0，1）和B（1，0，-3），试问：（1）在y轴上是否存在点M，满足｜MA｜＝｜MB｜？（2）在y轴上是否存在点M，使△MAB为等边三角形？若存在，试求出点M的坐标. 22．（本题满分13分）如图，在平面直角坐标系xOy 中，已知圆C1：(x＋3)2＋(y－1)2＝4和圆C2：(x－4)2＋(y－5)2＝4.(1)若直线l过点A(4,0)，且被圆C1截得的弦长为23，求直线l的方程.(2)设P为平面上的点，满足：存在过点P的无穷多对互相垂直的直线l1和l2，它们分别与圆C1和C2相交，且直线l1被圆C1截得的弦长与直线l2被C2截得的弦长相等．试求所有满足条件的点P的坐标．第二章解析几何初步（人教实验B版必修2）答题纸得分：一、选择题二、填空题13． 14． 15. 16.三、计算题17.18.19.20.21.22.第二章解析几何初步（人教实验B 版必修2）答案一、选择题1.D 解析：由3a (a －23)＋(－1)×1＝0，得a ＝－13或a ＝1.2.C 解析：直线l 1：ax －y ＋b ＝0，斜率为a ，在y 轴上的截距为b ，设k 1＝a ，m 1＝b . 直线l 2：bx －y ＋a ＝0，斜率为b ，在y 轴上的截距为a ，设k 2＝b ，m 2＝a . 由A 知：因为l 1∥l 2，k 1＝k 2>0，m 1>m 2>0，即a ＝b >0，b >a >0，矛盾．由B 知：k 1<0<k 2，m 1>m 2>0，即a <0<b ，b >a >0，矛盾．由C 知：k 1>k 2>0，m 2>m 1>0，即a >b >0，可以成立．由D 知：k 1>k 2>0，m 2>0>m 1，即a >b >0，a >0>b ，矛盾．3.B 解析：点A 关于x 轴的对称点A ′(－1，－1)，A ′与圆心(5,7)的距离为10,∴ 所求的最短路程为10－2＝8.4.D 解析：圆x 2＋y 2＝1的圆心为(0,0)，半径为1，圆x 2＋y 2＝4的圆心为(0,0)，半径为2，则圆心距0<2－1＝1，所以两圆内含．5.B 解析：圆心(a,2)到直线l ：x －y ＋3＝0的距离d ＝23122a a -++=，依题意212a ⎛+⎫ ⎪⎝⎭2＋⎝ ⎛⎭⎪⎫2322＝4，解得a ＝2－1.6.D 解析：∵ 所求直线平行于直线2x ＋3y －6＝0，∴ 设所求直线方程为2x ＋3y ＋c ＝0，由|2－3＋c |22＋32＝|2－3－6|22＋32，∴ c ＝8，或c ＝－6(舍去)，∴ 所求直线方程为2x ＋3y ＋8＝0. 7.B 解析：数形结合答案容易错选D ，但要注意直线的表达式是点斜式，说明直线的斜率存在，它与直线过点(1,2)要有所区分．8.D 解析：由x =√1−y 2知，曲线表示如图所示的半圆，让直线y =x +b 在图形中平行移动，可知，当－1＜b ≤1时直线与半圆有一个公共点；当直线与半圆相切时，也与半圆只有一个公共点，此时√2=1，求得b =√2（舍去）或b =－√2.故选D.9.B 解析：∵ 圆C 的圆心为(1,1)，半径为5，∴ |PC |＝5，∴ |PA |＝|PB |＝25，∴ S ＝12×25×5×2＝10.10.C 解析：圆x 2＋y 2－4x －2y －4＝0可化为(x －2)2＋(y －1)2＝9，直线mx ＋2ny －4＝0始终平分圆周，即直线过圆心(2,1)，所以2m ＋2n －4＝0，即m ＋n ＝2，mn ＝m (2－m )＝－m 2＋2m ＝－(m －1)2＋1≤1，当m ＝1时等号成立，此时n ＝1，与“m ≠n ”矛盾，所以mn ＜1. 11.C 解析：曲线y ＝21x -表示单位圆的上半部分，画出直线l 与曲线在同一坐标系中的图象，可观察出仅当直线l 在过点(－1,0)与点(0,1)的直线与圆的上切线之间时，直线l 与曲线有两个交点．当直线l 过点(－1,0)时，m ＝1；当直线l 为圆的上切线时，m ＝2(注：m ＝－2时，直线l 为下切线)．12.A 解析：∵ 点P 在圆上，∴ 切线l 的斜率k ＝－1k OP＝－11－42＋2＝43. ∴ 直线l 的方程为y －4＝43(x ＋2)，即4x －3y ＋20＝0.又直线m 与l 平行，∴ 直线m 的方程为4x －3y ＝0. 故两平行直线的距离为d ＝4.二、填空题13.(x －1)2＋(y －1)2＝4 解析：易求得AB 的中点为(0,0)，斜率为－1，从而其垂直平分线为直线y ＝x ，根据圆的几何性质，这条直线应该过圆心，将它与直线x ＋y －2＝0联立得到圆心O (1,1)，半径r ＝|OA |＝2. 14.3 解析：过P 作圆的切线PC ，切点为C ，在Rt △POC 中，易求|PC |＝3，由切割线定理，|PA |·|PB |＝|PC |2＝3.15.±5 解析：已知直线斜率k 1＝－2，直线ax ＋2y ＋c ＝0的斜率为－2a .∵ 两直线垂直，∴ (－2)·2a ⎛⎫- ⎪⎝⎭＝－1，得a ＝－1.圆心到切线的距离为5，即|c |5＝5，∴c ＝±5，故ac ＝±5. 16.(－∞，0)∪(10，＋∞) 解析：将圆x 2＋y 2－2x ＋4y ＋4＝0化为标准方程，得(x －1)2＋(y ＋2)2＝1，圆心为(1，－2)，半径为 1.若直线与圆无公共点，即圆心到直线的距离大于半径，即d ＝55m -＞1，∴ m ＜0或m ＞10.三、计算题 17．（1）证明：将方程x 2+y 2－2ax +2（a －2）y +2=0整理得 x 2+y 2－4y +2－a （2x －2y ）=0，令{x 2+y 2−4y +2=0，x −y =0，解得{x =1，y =1，∴ 定点为（1，1）.即a 取不为1的实数时，圆恒过定点（1，1）.（2）解：易得已知圆的圆心坐标为（a ，2－a ），半径为√2|a －1|. 设所求切线方程为y =kx +b ，即kx －y +b =0，则圆心到直线的距离应等于圆的半径，即√2=√2|a -1|恒成立.整理得2（1+k 2）a 2－4（1+k 2）a +2（1+k 2）=(k +1)2a 2+2（b －2）（k +1）a +(b −2)2恒成立.比较系数可得{2(1+k 2)=(k +1)2，−4(1+k 2)=2(b −2)(k +1)，2(1+k 2)=(b −2)2，解得k =1，b =0.所以所求的切线方程是y =x .（3）解：圆心坐标为（a ，2-a ），又设圆心坐标为（x ，y ），则有{x =a ，y =2−a ，消去参数得x +y =2，即所求的圆心的轨迹方程为x +y =2.18．解：圆C 的方程可化为(x －2)2＋(y －2)2＝1.(1)圆心C 关于x 轴的对称点为C ′(2，－2)，过点A ，C ′的直线的方程x ＋y ＝0即为光线l 所在直线的方程．(2)A 关于x 轴的对称点为A ′(－3，－3)，设过点A ′的直线为y ＋3＝k (x ＋3)．当该直线与圆C 1，解得k ＝43或k ＝34，所以过点A ′的圆C 的两条切线分别为y ＋3＝43(x ＋3)，y ＋3＝34(x ＋3)．令y ＝0，得x 1＝－34，x 2＝1，所以在x 轴上反射点M 的横坐标的取值范围是[－34，1]．19.解：(1)方程x 2＋y 2－2x －4y ＋m ＝0，可化为(x －1)2＋(y －2)2＝5－m ， ∵ 此方程表示圆，∴ 5－m ＞0，即m ＜5.(2) 22240,240,x y x y m x y ⎧+--+=⎨+-=⎩消去x 得(4－2y )2＋y 2－2×(4－2y )－4y ＋m ＝0，化简得5y 2－16y ＋m ＋8＝0.设M (x 1，y 1)，N (x 2，y 2)，则121216,58,5y y m y y ⎧+=⎪⎪⎨+⎪+=⎪⎩①② 由OM ⊥ON 得y 1y 2＋x 1x 2＝0即y 1y 2＋(4－2y 1)(4－2y 2)＝0，∴16－8(y 1＋y 2)＋5y 1y 2＝0.将①②两式代入上式得16－8×165＋5×85m +＝0，解之得m ＝85.(3)由m ＝85，代入5y 2－16y ＋m ＋8＝0，化简整理得25y 2－80y ＋48＝0，解得y 1＝125，y 2＝45.∴ x 1＝4－2y 1＝－45，x 2＝4－2y 2＝125.∴ M ⎝ ⎛⎭⎪⎫－45，125，N ⎝ ⎛⎭⎪⎫125，45， ∴ MN 的中点C 的坐标为⎝ ⎛⎭⎪⎫45，85. 又|MN |＝⎝ ⎛⎭⎪⎫125＋452＋⎝ ⎛⎭⎪⎫45－1252＝855，∴ 所求圆的半径为455. ∴ 所求圆的方程为45x ⎛⎫- ⎪⎝⎭2＋85y ⎛⎫- ⎪⎝⎭2＝165.○1 20.解：(1)连接OP ，则△OQP 为直角三角形，又|PQ |＝|PA |，所以|OP |2＝|OQ |2＋|PQ |2＝1＋|PA |2，所以a 2＋b 2＝1＋(a －2)2＋(b －1)2，故2a ＋b －3＝0. (2)由(1)知，P 在直线l ：2x ＋y －3＝0上，所以|PQ |min ＝|PA |min ，为A 到直线l 的距离，所以|PQ |min ＝|2×2＋1－3|22＋12＝255. (或由|PQ |2＝|OP |2－1＝a 2＋b 2－1＝a 2＋9－12a ＋4a 2－1＝5a 2－12a ＋8＝5(a －1.2)2＋0.8，得|PQ |min ＝255.) (3)以P 为圆心的圆与圆O 有公共点，半径最小时为与圆O 相切的情形，而这些半径的最小值为圆O 到直线l 的距离减去圆O 的半径，圆心P 为过原点与l 垂直的直线l ′与l 的交点P 0，所以r ＝322＋12－1＝355－1，又l ′：x －2y ＝0，联立l ：2x ＋y －3＝0得P 0(65，35)．所以所求圆的方程为(x －65)2＋(y －35)2＝(355－1)2.21．解：（1）假设在y 轴上存在点M ，满足｜MA ｜＝｜MB ｜.因为点M 在y 轴上，可设M （0，y ，0），由｜MA ｜＝｜MB ｜，可得√32+y 2+12=√12+y 2+32，显然，此式对任意y ∈R 恒成立.这就是说y 轴上的所有点都满足｜MA ｜＝｜MB ｜. （2）假设在y 轴上存在点M ，使△MAB 为等边三角形. 由（1）可知，y 轴上的所有点都满足｜MA ｜＝｜MB ｜，所以只要｜MA ｜＝｜AB ｜就可以使得△MAB 是等边三角形.因为｜MA ｜=√10+y 2，|AB |=√(1−3)2+(0−0)2+(−3−1)2=√20，于是√10+y 2=√20，解得y =±√10，故在y轴上存在点M使△MAB为等边三角形，点M的坐标为（0，√10，0），或（0，－√10，0）. 22．解：(1)由于直线x＝4与圆C1不相交，所以直线l的斜率存在．设直线l的方程为y＝k(x－4)，圆C1的圆心到直线l的距离为d，因为圆C1被直线l截得的弦长为23，所以d＝1.由点到直线的距离公式得k(24k＋7)＝0，即k＝0或k＝－724，所以直线l的方程为y＝0或7x＋24y－28＝0.(2)设点P(a，b)满足条件，不妨设直线l1的方程为y－b＝k(x－a)，k≠0，则直线l2的方程为y－b＝－1k(x－a)．因为圆C1和C2的半径相等，且圆C1被直线l1截得的弦长与圆C2被直线l2截得的弦长相等，所以圆C1的圆心到直线l1的距离和圆C2的圆心到直线l2的距离相等，即=，整理得|1＋3k＋ak－b|＝|5k＋4－a－bk|，从而1＋3k＋ak－b＝5k＋4－a－bk或1＋3k＋ak－b＝－5k－4＋a＋bk，即(a＋b－2)k＝b－a＋3或(a－b＋8)k＝a＋b－5，因为k的取值有无穷多个，所以20,30,a bb a+-=⎧⎨-+=⎩或80,50,a ba b-+=⎧⎨+-=⎩解得5,21,2ab⎧=⎪⎪⎨⎪=-⎪⎩或3,213.2ab⎧=-⎪⎪⎨⎪=⎪⎩这样点P只可能是点P1⎝⎛⎭⎪⎫52，－12或点P2⎝⎛⎭⎪⎫－32，132.经检验点P1和P2满足题目条件．。

必修二第二章检查试卷及详细答案

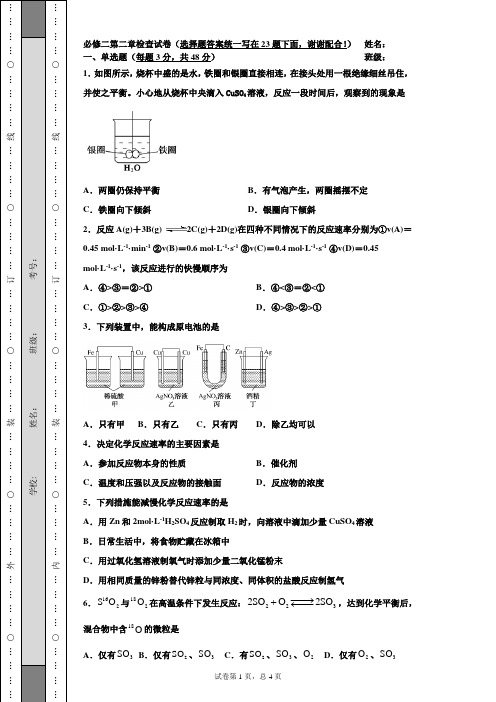
…………○…订…………………线……名：___________班级：_考号：_________…………○…订…………………线……必修二第二章检查试卷（选择题答案统一写在23题下面，谢谢配合！）姓名：一、单选题（每题3分，共48分）班级： 1．如图所示，烧杯中盛的是水，铁圈和银圈直接相连，在接头处用一根绝缘细丝吊住，并使之平衡。

小心地从烧杯中央滴入CuSO 4溶液，反应一段时间后，观察到的现象是A ．两圈仍保持平衡B ．有气泡产生，两圈摇摆不定C ．铁圈向下倾斜D ．银圈向下倾斜 2．反应A(g)＋3B(g)2C(g)＋2D(g)在四种不同情况下的反应速率分别为①v(A)＝0.45 mol·L -1·min -1 ②v(B)＝0.6 mol·L -1·s -1 ③v(C)＝0.4 mol·L -1·s -1 ④v(D)＝0.45 mol·L -1·s -1，该反应进行的快慢顺序为 A ．④>③＝②>① B ．④<③＝②<① C ．①>②>③>④D ．④>③>②>①3．下列装置中，能构成原电池的是A ．只有甲B ．只有乙C ．只有丙D ．除乙均可以4．决定化学反应速率的主要因素是 A ．参加反应物本身的性质 B ．催化剂 C ．温度和压强以及反应物的接触面 D ．反应物的浓度5．下列措施能减慢化学反应速率的是A ．用Zn 和2mol·L -1H 2SO 4反应制取H 2时，向溶液中滴加少量CuSO 4溶液B ．日常生活中，将食物贮藏在冰箱中C ．用过氧化氢溶液制氧气时添加少量二氧化锰粉末D ．用相同质量的锌粉替代锌粒与同浓度、同体积的盐酸反应制氢气6．162S O 与182O 在高温条件下发生反应：2232SO O 2SO −−→+←−−，达到化学平衡后，混合物中含18O 的微粒是○……※○……7．氯化钠是一种重要的生活、生产必需品。

第2章基因和染色体的关系B卷能力提升—高一生物学人教版(2019)必修二单元达标测试卷

第2章基因和染色体的关系B卷能力提升—2022-2023学年高一生物学人教版（2019）必修二单元达标测试卷一、单项选择题（本题包括14小题，每小题2分，共28分。

每小题只有一个选项符合题意）1.下列有关动物精子和卵细胞形成过程的叙述，错误的是( )A.次级精母细胞可能含1条X染色体，次级卵母细胞可能含2条X染色体B.精子的形成过程需要经过变形，卵细胞的形成不需要经过变形C.若细胞在减Ⅱ中期有染色体22条，则该细胞在减Ⅰ前期可产生11个四分体D.一个精原细胞和一个卵原细胞经减数分裂产生的生殖细胞数量不同2.某哺乳动物卵原细胞形成卵细胞的过程中，某时期的细胞如图所示，其中①~④表示染色体，a~h表示染色单体。

下列叙述正确的是( )A.图示细胞为次级卵母细胞，所处时期为前期ⅡB.①与②的分离发生在后期Ⅰ，③与④的分离发生在后期ⅡC.该细胞的染色体数与核DNA分子数均为卵细胞的2倍D.a和e同时进入一个卵细胞的概率为1/163.对老鼠睾丸切片进行显微观察，根据细胞中染色体的数目将正常细胞分为A、B、C 三组，每组细胞数目如表所示，下列叙述正确的是( )B.B组细胞内的性染色体组成均为一条X和一条YC.C组细胞均为精细胞D.A、B两组细胞均存在同源染色体4.下列有关观察蝗虫精母细胞减数分裂固定装片的实验的叙述，错误的是( )A.选取蝗虫作实验材料，是因为蝗虫染色体数目相对较少，染色体较大，易于观察B.实验过程中，我们可以观察到蝗虫的精母细胞进行减数分裂不同时期的动态过程C.用显微镜观察到蝗虫减数第一次分裂与减数第二次分裂中期染色体数目及排列在赤道板的方式均不同D.观察到某些细胞有染色体联会现象，这些细胞是雄性蝗虫的初级精母细胞5.研究者用不同颜色的荧光对基因型为AaBb的精原细胞的基因进行标记，显性基因A 和B分别被标记上红光和蓝光。

下列关于该细胞减数分裂过程中染色体标记情况（不考虑突变）的叙述，错误的是( )A.若次级精母细胞中有4个荧光点，则基因A、B位于同一条染色体上B.同一条染色体上可能存在3个荧光点C.蓝光和红光可能会出现在不同的细胞中D.若细胞一极出现1种颜色2个荧光点，则细胞一定处于减数第一次分裂6.下图为某动物睾丸曲细精管一个细胞中一对同源染色体示意图，图中1-8表示基因。

必修二第2章测试卷

第二章测试卷(时间：120分钟满分：150分)一、选择题(本大题共12小题，每小题5分，满分60分)1．若直线a 与b 是异面直线，b 与c 也是异面直线，则直线a 与c ( ) A ．平行 B ．异面 C ．相交 D ．都有可能【答案】D2．正方体ABCD-A 1B 1C 1D 1中，P ，Q ，R 分别是AB ，AD ，B 1C 1的中点．那么，正方体的过P ，Q ，R 的截面图形是( )A ．三角形B ．四边形C ．五边形D ．六边形【答案】D3．平行六面体ABCD-A 1B 1C 1D 1中，既与AB 共面也与CC 1共面的棱的条数为( ) A ．3 B ．4 C ．5 D ．6 【答案】C4．设m ，n 是两条不同的直线，α，β是两个不重合的平面，给定下列四个命题，其中为真命题的是( )①⎭⎪⎬⎪⎫m ⊥n n ⊂α⇒m ⊥α ②⎭⎪⎬⎪⎫m ⊥αm ⊂β⇒α⊥β ③⎭⎪⎬⎪⎫m ⊥αn ⊥α⇒m ∥n ④⎭⎪⎬⎪⎫m ⊂αn ⊂βα∥β⇒m ∥n A ．①② B ．②③ C ．③④ D ．①④【答案】B5．对两条不相交的空间直线a 与b ，必存在平面α，使得( ) A ．a ⊂α，b ⊂α B ．a ⊂α，b ∥α C ．a ⊥α，b ⊥α D ．a ⊂α，b ⊥α 【答案】B6．已知α-l-β是一个大小确定的二面角，若a ，b 是空间两条直线，则能使a ，b 所成的角为定值的一个条件是( )A ．a ∥α且b ∥βB ．a ∥α且b ⊥βC ．a ⊥α且b ∥βD ．a ⊥α且b ⊥β【答案】D7．已知直二面角α-l-β，点A ∈α，AC ⊥l ，C 为垂足，点B ∈β，BD ⊥l ，D 为垂足．若AB ＝2，AC ＝BD ＝1，则CD ＝( )A ．2B ． 3C ． 2D ．1【答案】C8．二面角α-A-B-β的平面角为锐角，C 是平面α内的一点(它不在棱AB 上)，点D 是点C 在平面β内的射影，点E 是棱AB 上满足∠CEB 为锐角的任意一点，那么( )A ．∠CEB ＝∠DEB B ．∠CEB >∠DEBC ．∠CEB <∠DEBD ．∠CEB 与∠DEB 的大小关系不定【答案】B9．如图，在棱长均为2的正四棱锥P-ABCD 中，点E 为PC 的中点，则下列命题正确的是( )A ．BE ∥平面P AD 且BE 到平面P AD 的距离为 3B ．BE ∥平面P AD 且BE 到平面P AD 的距离为263C ．BE 与平面P AD 不平行且BE 与平面P AD 所成的角大于30° D ．BE 与平面P AD 不平行且BE 与平面P AD 所成的角小于30° 【答案】D【解析】在平面PBC 中，过P 作直线l ，使l ∥BC ，则l ∥AD ，所以l 是平面PBC 与平面P AD 的交线．显然BE 与l 相交，故BE 与平面P AD 不平行．由棱长都为2，可知∠CBE ＝30°，所以BE 与平面P AD 内的直线AD 所成的角为30°.所以BE 与平面P AD 所成的角不可能大于30°.故选D.10．在矩形ABCD 中，若AB ＝3，BC ＝4，P A ⊥平面AC 且P A ＝1，则点P 到对角线BD 的距离为( )A.292B ．135C ．175D ．1195【答案】B【解析】在平面ABCD 中，过A 作AH ⊥BD 于D ，又P A ⊥BD ，所以BD ⊥平面P AH ，所以BD ⊥PH ，即PH 为点P 到对角线BD 的距离．在Rt △ABD 中，AB ＝3，AD ＝4，则BD ＝5，AH ＝AB ·AD BD ＝125.所以PH ＝P A 2＋AH 2＝135.11．(2015年福建模拟)如图，正方体ABCD-A 1B 1C 1D 1中，O 为底面ABCD 的中心，M 为棱BB 1的中点，则下列结论中错误的是( )A ．D 1O ∥平面A 1BC 1B ．MO ⊥平面A 1BC 1C ．异面直线BC 1与AC 所成的角等于60°D ．二面角MACB 等于90° 【答案】D【解析】连接B 1D 1交A 1C 1于E ，连接BO ，则四边形D 1OBE 为平行四边形，∴D 1O ∥BE ，故D 1O ∥平面A 1BC 1，A 正确．连接B 1D ，BD ，OM ，∵O 为底面ABCD 的中心，M 为棱BB 1的中点，∴MO ∥B 1D .∵B 1D ⊥平面A 1BC 1，∴MO ⊥平面A 1BC 1，B 正确．∵AC ∥A 1C 1，∴∠A 1C 1B 为异面直线BC 1与AC 所成的角．∵△A 1C 1B 为等边三角形，∴∠A 1C 1B ＝60°，C 正确．∵BO ⊥AC ，MO ⊥AC ，∴∠MOB 为二面角M －AC －B 的平面角，显然不等于90°，故D 不正确．12．(2015年山东模拟)如图在直三棱柱ABC-A 1B 1C 1中，∠ACB ＝90°，AA 1＝2，AC ＝BC ＝1，则异面直线A 1B 与AC 所成角的余弦值是( )A.63 B ．22 C.33D ．66【答案】D【解析】∵AC ∥A 1C 1，∴∠C 1A 1B 即为异面直线A 1B 与AC 所成角. 在直三棱柱ABC －A 1B 1C 1中，∴CC 1⊥AC, CC 1⊥BC .∵∠ACB ＝90°，即AC ⊥BC ，∴AC ⊥平面BCC 1B 1.∴AC ⊥BC 1.∴A 1B ＝4＋1＋1＝6，cos ∠C 1A 1B ＝A 1C 1A 1B ＝66.二、填空题(本大题共4小题，每小题5分，满分20分)13．平面α过正方体ABCD-A1B1C1D1的三个顶点B，D，A1且α与底面A1B1C1D1的交线为l，则l与B1D1的位置关系是________．【答案】平行14．如图，已知ABCD是平行四边形，P A＝PC，PD＝PB，则平面P AC与平面ABCD 的关系是________．【答案】垂直15．已知α，β，γ是三个互不重合的平面，l是一条直线，给出下列四个命题：①若α⊥β，l⊥β，则l∥α；②若l⊥α，l∥β，则α⊥β；③若l上有两个点到α的距离相等，则l∥α；④若α⊥β，α∥γ，则γ⊥β.其中正确命题的序号是________．【答案】②④16．将锐角A为60°，边长为a的菱形ABCD沿BD折成60°的二面角，则A与C之间的距离为________．【答案】3 2a【解析】设BD的中点为O，△ABD，△CBD都是边长为a的等边三角形，所以AO＝CO＝32a且AO⊥BD，CO⊥BD.所以∠AOC＝60°.所以△AOC是等边三角形，AC＝32a.三、解答题(本大题共6小题，满分70分)17．(10分)如右图，在三棱锥P ABC中，已知△ABC是等腰直角三角形，∠ABC＝90°，△P AC是直角三角形，∠P AC＝90°，∠ACP＝30°，平面P AC⊥平面ABC.(1)求证：平面P AB⊥平面PBC；(2)若PC＝2，求△PBC的面积．(1)证明：∵平面P AC⊥平面ABC，其交线为AC，P A⊥AC，P A⊂平面P AC，∴P A⊥平面ABC.∵BC⊂平面ABC，∴P A⊥BC.又AB ⊥BC ，AB ∩P A ＝A ，AB ⊂平面P AB ，P A ⊂平面P AB ， ∴BC ⊥平面P AB . 而BC ⊂平面PBC ， ∴平面P AB ⊥平面PBC .(2)【解析】由(1)得，BC ⊥平面P AB ， ∴BC ⊥PB ，即∠PBC ＝90°. 由已知PC ＝2，得AC ＝3， BC ＝22AC ＝22×3＝62. 在Rt △PBC 中，PB ＝PC 2－BC 2＝22－⎝⎛⎭⎫622＝ 102. ∴Rt △PBC 的面积S ＝12PB ×BC ＝12×62×102＝154. 18．(12分)在斜三棱柱ABC-A 1B 1C 1中，侧面ACC 1A 1⊥平面ABC ，∠ACB ＝90°.(1)求证：BC ⊥AA 1；(2)若M ，N 是棱BC 上的两个三等分点，求证：A 1N ∥平面AB 1M . 证明：(1)因为∠ACB ＝90°，所以AC ⊥CB .又侧面ACC 1A 1⊥平面ABC 且平面ACC 1A 1∩平面ABC ＝AC ，BC ⊂平面ABC ，所以BC ⊥平面ACC 1A 1.又AA 1⊂平面ACC 1A 1，所以BC ⊥AA 1. (2)连接A 1B ，交AB 1于O 点，连接MO .在△A 1BN 中，O ，M 分别为A 1B ，BN 的中点，所以OM ∥A 1N . 又OM ⊂平面AB 1M ，A 1N ⊄平面AB 1M ，所以A 1N ∥平面AB 1M .19．(12分)如图，在三棱柱BCE-ADF 中，四边形ABCD 是正方形，DF ⊥平面ABCD ，M ，N 分别是AB ，AC 的中点，G 是DF 上的一点．(1)求证：GN⊥AC；(2)若FG＝GD，求证：GA∥平面FMC.证明：(1)连接DN.∵四边形ABCD是正方形，∴DN⊥AC.∵DF⊥平面ABCD，AC⊂平面ABCD，∴DF⊥AC.又DN∩DF＝D，∴AC⊥平面DNF.∵GN⊂平面DNF，∴GN⊥AC.(2)如图，取DC的中点S，连接AS，GS.∵G是DF的中点，∴GS∥FC，AS∥CM.又GS，AS⊄平面FMC，FM，CM⊂平面FMC，∴GS∥平面FMC.∴AS∥平面FMC.而AS∩GS＝S，∴平面GSA∥平面FMC，∵GA⊂平面GSA，∴GA∥平面FMC.20．(12分)如图，棱柱ABC-A1B1C1的侧面BCC1B1是菱形，B1C⊥A1B.(1)求证：平面AB1C⊥平面A1BC1；(2)设D是A1C1上的点且A1B∥平面B1CD，求A1D∶DC1的值．(1)证明：因为侧面BCC1B1是菱形，所以B1C⊥BC1.又B1C⊥A1B，且A1B∩BC1＝B，所以B1C⊥平面A1BC1.又B1C⊂平面AB1C，所以平面AB1C⊥平面A1BC1.(2)【解析】设BC1交B1C于点E，连接DE，则DE是平面A1BC1与平面B1CD的交线．因为A1B∥平面B1CD，所以A1B∥DE.又E是BC1的中点，所以D为A1C1的中点，即A1D∶DC1＝1.21．(12分)如图，在四棱锥P-ABCD中，底面ABCD是正方形，PD⊥底面ABCD，M，N分别是P A，BC的中点且PD＝AD＝1.(1)求证：MN∥平面PCD；(2)求证：平面P AC⊥平面PBD；(3)求三棱锥P ABC的体积．(1)证明：取AD中点E，连接ME，NE，由已知M，N分别是P A，BC的中点，所以ME∥PD，NE∥CD.又ME，NE⊂平面MNE，ME∩NE＝E，所以平面MNE∥平面PCD.又MN⊂平面MNE，所以MN∥平面PCD.(2)证明：因为ABCD 为正方形，所以AC ⊥BD .又PD ⊥平面ABCD ，所以PD ⊥AC . 又PD ∩BD ＝D ，所以AC ⊥平面PBD ，AC ⊂平面P AC . 所以平面P AC ⊥平面PBD .(3)【解析】因为PD ⊥平面ABCD ，所以PD 为三棱锥P ABC 的高，三角形ABC 为等腰直角三角形，所以三棱锥P ABC 的体积V ＝13S △ABC ·PD ＝16.22．(12分)如图，在四棱锥P-ABCD 中，底面ABCD 为平行四边形，∠ADC ＝45°，AD ＝AC ＝1，O 为AC 的中点，PO ⊥平面ABCD ，PO ＝2，M 为PD 的中点．(1)求证：PB ∥平面ACM ； (2)求证：AD ⊥平面P AC ；(3)求直线AM 与平面ABCD 所成角的正切值． (1)证明：连接BD ，MO .在平行四边形ABCD 中，因为O 为AC 的中点，所以O 为BD 的中点．又M 为PD 的中点，所以PB ∥MO .因为PB ⊄平面ACM ，MO ⊂平面ACM ，所以PB ∥平面ACM .(2)证明：因为∠ADC ＝45°且AD ＝AC ＝1，所以∠DAC ＝90°，即AD ⊥AC .又PO ⊥平面ABCD ，AD ⊂平面ABCD ，所以PO ⊥AD .而AC ∩PO ＝O ，所以AD ⊥平面P AC .(3)解：取DO 中点N ，连接MN ，AN .因为M 为PD 的中点，所以MN ∥PO 且MN ＝12PO ＝1.由PO ⊥平面ABCD ，得MN ⊥平面ABCD .所以∠MAN 是直线AM 与平面ABCD 所成的角．在Rt △DAO 中，AD ＝1，AO ＝12，所以DO ＝52.从而AN ＝12DO ＝54. 在Rt △ANM 中，tan ∠MAN ＝MN AN ＝154＝455，即直线AM 与平面ABCD 所成角的正切值为455.。

高中人教数学B版必修2：第二章单元测验

(2)根据P，A，B的位置分析可知，当直线l与线段AB相交时，kPB≤k≤kPA.
因为kPA＝＝－，kPB＝＝－，
二、填空题：本大题共4小题，每小题5分，共20分．把答案填在题中横线上．
13．直线x－2y－3＝0与圆(x－2)2＋(y＋3)2＝9交于E，F两点，则△EOF(O是原点)的面积等于________．
答案：
解析：解方程组
得5x2－10x－11＝0，
∵
∴|EF|＝ |x1－x2|
＝＝4，
又由点到直线距离公式，得dO—EF＝，
4．在空间直角坐标系中，A(0,2,4)，B(1,4,6)，则|AB|等于()
A．2B．2
C. D．3
答案：D
解析：|AB|＝＝3.
5．当0<k< 时，直线l1：kx－y＝k－1与直线l2：ky－x＝2k的交点在()
A．第一象限B．第二象限
C．第三象限D．第四象限
答案：B
解析：k＝得交点，在第二象限．
解得k＝± ＝± .
三、解答题：本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤．
17．(10分)已知点A(－1，－2)和B(－3,6)，直线l经过点P(1，－5)．
(1)若直线l与直线AB平行，求直线l的方程；
(2)若直线l与线段AB相交，求直线l的斜率k的取值范围．
解：(1)kAB＝＝－4，所以直线l与直线AB平行时直线l的方程为y＋5＝－4(x－1)，化简后得：4x＋y＋1＝0.
A．1B．－1
C. D．－
答案：C
解析：∵圆心(－1,2)，∴－2a－2b＋1＝0，∴a＋b＝ .
8．两圆x2＋y2－4x－6y＋12＝0和x2＋y2－8x－6y＋16＝0的位置关系是()

新人教B2第二章试题及答案详解

x y O x y O x y O xyO河南许昌高级中学必修2（B ）第二章测试卷A 卷1．下列命题中为真命题的是（）A ．平行直线的倾斜角相等B ．平行直线的斜率相等C ．互相垂直的两直线的倾斜角互补D ．互相垂直的两直线的斜率互为相反 2. 在同一直角坐标系中，表示直线y ax =与y x a =+正确的是（）A ．B ．C ．D ．图13．已知点(1,2)A 、(3,1)B ，则线段AB 的垂直平分线l 的方程是（） A ．524=+y x B ．524=-y x C ．52=+y x D ．52=-y x4．如果直线022=++y ax 与直线023=--y x 平行，那么系数a 为（） A ．23-B ．6-C ．3-D ．32 5.空间直角坐标系中,点(3,4,0)A -和点(2,1,6)B -的距离是 ( ) A．．．9 D6．圆：012222=+--+y x y x 上的点到直线2=-y x 的距离最大值是（）A ．2B ．21+C ．221+D ．221+ 7．直线x y 2=关于x 轴对称的直线方程为.8．已知点)1,1(P 和直线l ：02043=--y x ，则过P 与直线l 平行的直线方程是，过点P 与l 垂直的直线方程是.9．直线l 经过直线0623=++y x 和0752=-+y x 的交点，且在两坐标轴上的截距相等，则直线l 的方程是______.10．方程022=++-+m y x y x 表示一个圆，则m 的取值范围是.11．求经过点)2,1(A 且到原点的距离等于1的直线方程.12．已知一曲线是与两个定点(0,0)O 、(3,0)A 距离的比为21的点的轨迹，则求此曲线的方程.B 卷1．过直线013=-+y x 与072=-+y x 的交点，且与第一条直线垂直的直线l 的方程是（）A ．073=+-y xB ．0133=+-y xC ．072=+-y xD ．053=--y x 2．已知(2,1,1),(1,1,2),(2,0,1)A B C ，则下列说法中正确的是（）Ａ.,,A B C 三点可以构成直角三角形Ｂ.,,A B C 三点可以构成锐角三角形Ｃ.,,A B C 三点可以构成钝角三角形Ｄ.,,A B C 三点不能构成任何三角形 3．已知1O ：06422=+-+y x y x 和2O ：0622=-+x y x 交于,A B 两点，则AB 的垂直平分线的方程是（）Ａ.30x y ++=Ｂ.250x y --=Ｃ.390x y --=Ｄ.4370x y -+= 4．两点)2,2(++b a A 、B ),(b a b --关于直线1134=+y x 对称，则（）Ａ.2,4=-=b a Ｂ.2,4-==b a Ｃ.2,4==b a Ｄ.2,4a b ==5．与圆02422=+-+y y x 相切，并在x 轴、y 轴上的截距相等的直线共有（） A 、6条 B 、5条 C 、4条 D 、3条6．直线2x =被圆422=+-y a x ）（所截得的弦长等于32，则a 的值为（） A 、-1或-3 B 、22-或 C 、1或3 D 、37.已知(1,2,1),(2,2,2)A B -，点P 在z 轴上，且PA PB =,则点P 的坐标为8.圆心在直线270x y --=上的圆C 与y 轴交于两点(0,4)A -，(0,2)B -，则圆C 的方程为．9．已知点(,)M a b 在直线1543=+y x 上，则22b a +的最小值为10．经过)1,2(-A 和直线1x y +=相切，且圆心在直线x y 2-=上的圆的方程为. 11．求垂直于直线0743=--y x ，且与两坐标轴构成周长为10的三角形的直线方程12．自点A(-3，3)发出的光线L 射到x 轴上，被x 轴反射，其反射光线所在直线与圆x 2+y 2-4x-4y+7=0相切，求光线L 所在直线的方程.C 卷1.如图2，圆822=+y x 内有一点(1,2)P -，AB 为过点P 且倾斜角为α的弦，（1）当α＝135０时，求AB 。

【人教B版】2017年必修2第二章学业质量标准检测试卷含解析

第二章学业质量标准检测时间120分钟，满分150分.一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中只有一个是符合题目要求的)1．已知直线经过点A (0,4)和点B (1,2)，则直线AB 的斜率为导学号 92434954( B ) A ．3 B ．－2 C ．2D ．不存在[解析] 由斜率公式得，直线AB 的斜率k ＝2－41－0＝－2.2．已知点A (1,2,2)、B (1，－3,1)，点C 在yOz 平面上，且点C 到点A 、B 的距离相等，则点C 的坐标可以为导学号 92434955( C )A ．(0,1，－1)B ．(0，－1,6)C ．(0,1，－6)D ．(0,1,6)[解析] 由题意设点C 的坐标为(0，y ，z )， ∴1＋(y －2)2＋(z －2)2＝1＋(y ＋3)2＋(z －1)2，即(y －2)2＋(z －2)2＝(y ＋3)2＋(z －1)2. 经检验知，只有选项C 满足.3．过两点(－1,1)和(3,9)的直线在x 轴上的截距是导学号 92434956( A ) A ．－32B ．－23C ．25D ．2[解析] 由题意，得过两点(－1,1)和(3,9)的直线方程为y ＝2x ＋3. 令y ＝0，则x ＝－32，∴直线在x 轴上的截距为－32，故选A ．4．(2016·沧州高一检测)方程x 2＋y 2＋ax ＋2ay ＋54a 2＋a －1＝0表示圆，则a 的取值范围是导学号 92434957( D )A ．a <－2或a >23B ．－23<a <2C ．a >1D ．a <1[解析] 由题意知，a 2＋(2a )2－4⎝⎛⎭⎫54a 2＋a －1＝－4a ＋4>0. ∴a <1. 故选D ．5．已知直线l 1：(k －3)x ＋(4－k )y ＋1＝0与l 2：2(k －3)x －2y ＋3＝0平行，则k 的值是导学号 92434958( C )A ．1或3B ．1或5C ．3或5D ．1或2[解析] 当k ＝3时，两直线显然平行；当k ≠3时，由两直线平行，斜率相等，得－k －34－k ＝2(k －3)2. 解得k ＝5，故选C ．6．直线3x －2y ＋m ＝0与直线(m 2－1)x ＋3y ＋2－3m ＝0的位置关系是导学号 92434959( C )A ．平行B ．垂直C ．相交D ．与m 的取值有关[解析] 由3×3－(－2)×(m 2－1)＝0，即2m 2＋7＝0无解. 故两直线相交.7．若点(2,2)在圆(x ＋a )2＋(y －a )2＝16的内部，则实数a 的取值范围是导学号 92434960( A )A ．－2<a <2B ．0<a <2C ．a <－2或a >2D ．a ＝±2[解析] 由题意，得(2＋a )2＋(2－a )2<16， ∴－2<a <2.8．(2016·葫芦岛高一检测)已知圆C 方程为(x －2)2＋(y －1)2＝9，直线l 的方程为3x －4y －12＝0，在圆C 上到直线l 的距离为1的点有几个导学号 92434961( B )A ．4B ．3C ．2D ．1[解析] 圆心C (2,1)，半径r ＝3，圆心C 到直线3x －4y －12＝0的距离d ＝|6－4－12|32＋(－4)2＝2，即r －d ＝1.∴在圆C 上到直线l 的距离为1的点有3个.9．(2017·安徽省巢湖四中、庐江二中第二次联考)直线2mx －(m 2＋1)y －m ＝0倾斜角的取值范围是导学号 92434962( C )A ．[0，π)B ．[0，π4]C ．[0，π4]∪[3π4，π)D ．[0，π4]∪(π2，π)[解析] ∵直线2mx －(m 2＋1)y －m ＝0的斜率k ＝2mm 2＋1，①m ≥0时m 2＋1≥2m ，∴0≤k ≤1, ②m ＜0时，－1≤k ＜0，∴直线2mx －(m 2＋1)y －m ＝0倾斜角的取值范围是[0，π4]∪[3π4，π)，故选C ．10．设m >0，则直线2(x ＋y )＋1＋m ＝0与圆x 2＋y 2＝m 的位置关系为导学号 92434963( C )A ．相切B ．相交C ．相切或相离D ．相交或相切[解析] ∵m >0，∴圆心(0,0)到直线2(x ＋y )＋1＋m ＝0的距离d ＝|1＋m |2＋2＝1＋m2，圆x 2＋y 2＝m 的半径r ＝m ，由1＋m 2－m ＝1－2m ＋m 2＝(1－m )22≥0，得d ≥r ，故选C ．11．两圆x 2＋y 2－4x ＋2y ＋1＝0与x 2＋y 2＋4x －4y －1＝0的公切线有导学号 92434964( C )A ．1条B ．2条C ．3条D ．4条[解析] x 2＋y 2－4x ＋2y ＋1＝0的圆心为(2，－1)，半径为2，圆x 2＋y 2＋4x －4y －1＝0的圆心为(－2,2)，半径为3，故两圆外切，即两圆有三条公切线.12．一辆卡车宽1. 6 m ，要经过一个半圆形隧道(半径为3. 6 m)则这辆卡车的平顶车篷篷顶距地面高度不得超过导学号 92434965( B )A ．1. 4 mB ．3. 5 mC ．3. 6 mD ．2. 0 m[解析] 圆半径OA ＝3. 6 m ，卡车宽1. 6 m ，∴AB ＝0. 8 m ，∴弦心距OB ＝3.62－0.82≈3. 5 m.二、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上) 13．若点(2，k )到直线3x －4y ＋6＝0的距离为4，则k 的值等于__－2或8__. 导学号 92434966[解析] 由题意，得|6－4k ＋6|32＋(－4)2＝4，∴k ＝－2或8.14．若直线x ＋3y －a ＝0与圆x 2＋y 2－2x ＝0相切，则a 的值为__－1或3__. 导学号 92434967[解析] 圆心为(1,0)，半径r ＝1，由题意，得|1－a |1＋3＝1，∴a ＝－1或3.15．已知直线l 垂直于直线3x ＋4y －2＝0，且与两个坐标轴构成的三角形的周长为5个单位长度，直线l 的方程为__4x －3y ＋5＝0或4x －3y －5＝0__. 导学号 92434968[解析] 由题意可设直线l 的方程为y ＝43x ＋b ，令x ＝0，得y ＝b ，令y ＝0，得x ＝－34b .∴三角形的周长为|b |＋34|b |＋54|b |＝5，解得b ＝±5，故所求直线方程为4x －3y ＋5＝0或4x －3y －5＝0.16．(2015·江苏卷)在平面直角坐标系xOy 中，以点(1,0)为圆心且与直线mx －y －2m －1＝0(m ∈R )相切的所有圆中，半径最大的圆的标准方程为__(x －1)2＋y 2＝2__. 导学号 92434969[解析] 直mx －y －2m －1＝0可化为 m (x －2)＋(－y －1)＝0，由⎩⎪⎨⎪⎧ x －2＝0－y －1＝0，得⎩⎪⎨⎪⎧x ＝2y ＝－1.∴直线过定点P (2，－1). 以点C (1,0)为圆心且与直线mx －y －2m －1＝0相切的所有圆中，最大的半径为|PC |＝(2－1)2＋(－1－0)2＝2，故圆的标准方程为(x －1)2＋y 2＝2.三、解答题(本大题共6个大题，共70分，解答应写出文字说明，证明过程或演算步骤) 17．(本题满分10分)正方形ABCD 的对角线AC 在直线x ＋2y －1＝0上，点A 、B 的坐标分别为A (－5,3)、B (m,0)(m >－5)，求B 、C 、D 点的坐标. 导学号 92434970[解析] 如图，设正方形ABCD 两顶点C 、D 坐标分别为(x 1，y 1)、(x 2，y 2).∵直线BD ⊥AC ，k AC ＝－12，∴k BD ＝2，直线BD 方程为y ＝2(x －m )，与x ＋2y －1＝0联立解得⎩⎨⎧x ＝15＋45m y ＝25－25m，点E 的坐标为⎝⎛⎭⎫15＋45m ，25－25m ， ∵|AE |＝|BE |， ∴⎝⎛⎭⎫15＋45m ＋52＋⎝⎛⎭⎫25－25m －32＝⎝⎛⎭⎫15＋45m －m 2＋⎝⎛⎭⎫25－25m 2，平方整理得m 2＋18m ＋56＝0，∴m ＝－4或m ＝－14(舍∵m >－5)，∴B (－4,0). E 点坐标为(－3,2)，∴⎩⎪⎨⎪⎧－3＝－5＋x122＝3＋y 12，∴⎩⎪⎨⎪⎧x 1＝－1y 1＝1.即点C (－1,1)，又∵⎩⎪⎨⎪⎧－3＝－4＋x222＝0＋y 22，∴⎩⎪⎨⎪⎧x 2＝－2y 2＝4，即点D (－2,4).∴点B (－4,0)、点C (－1,1)、点D (－2,4).18．(本题满分12分)已知一直线通过点(－2,2)，且与两坐标轴所围成的三角形的面积为1，求这条直线的方程. 导学号 92434971[解析] 设直线方程为y －2＝k (x ＋2)，令x ＝0得y ＝2k ＋2，令y ＝0得x ＝－2－2k ，由题设条件12⎪⎪⎪⎪－2－2k ·||2k ＋2＝1， ∴2(k ＋1)2＝|k |，∴⎩⎨⎧ k >02k 2＋3k ＋2＝0或⎩⎨⎧k <02k 2＋5k ＋2＝0， ∴k ＝－2或－12，∴所求直线方程为：2x ＋y ＋2＝0或x ＋2y －2＝0.19．(本题满分12分)已知直线y ＝－2x ＋m ，圆x 2＋y 2＋2y ＝0. 导学号 92434972 (1)m 为何值时，直线与圆相交？ (2)m 为何值时，直线与圆相切？ (3)m 为何值时，直线与圆相离？[解析] 由⎩⎪⎨⎪⎧y ＝－2x ＋mx 2＋y 2＋2y ＝0，得5x 2－4(m ＋1)x ＋m 2＋2m ＝0.Δ＝16(m ＋1)2－20(m 2＋2m )＝－4[(m ＋1)2－5]，当Δ>0时，(m＋1)2－5<0，∴－1－5<m<－1＋ 5.当Δ＝0时，m＝－1±5，当Δ<0时，m<－1－5或m>－1＋ 5.故(1)当－1－5<m<－1＋5时，直线与圆相交；(2)当m＝－1±5时，直线与圆相切；(3)当m<－1－5或m>－1＋5时，直线与圆相离.20．(本题满分12分)(2016·天水市泰安二中高一检测)直线l经过两点(2,1)、(6,3). 导学号 92434973(1)求直线l的方程；(2)圆C的圆心在直线l上，并且与x轴相切于(2,0)点，求圆C的方程.[解析](1)直线l的斜率k＝3－16－2＝12，∴直线l的方程为y－1＝12(x－2)，即x－2y＝0.(2)由题意可设圆心坐标为(2a，a)，∵圆C与x轴相切于(2,0)点，∴圆心在直线x＝2上，∴a＝1.∴圆心坐标为(2,1)，半径r＝1.∴圆C的方程为(x－2)2＋(y－1)2＝1.21．(本题满分12分)已知圆的方程为x2＋y2－2x－4y＋m＝0. 导学号 92434974(1)若圆与直线x＋2y－4＝0相交于M、N两点，且OM⊥ON(O为坐标原点)，求m的值；(2)在(1)的条件下，求以MN为直径的圆的方程.[解析](1)圆的方程可化为(x－1)2＋(y－2)2＝5－m，∴m<5.设M (x 1，y 1)、N (x 2，y 2).由⎩⎪⎨⎪⎧x ＋2y －4＝0x 2＋y 2－2x －4y ＋m ＝0，得5y 2－16y ＋m ＋8＝0， ∴y 1＋y 2＝165，y 1y 2＝m ＋85.x 1x 2＝(4－2y 1)(4－2y 2)＝16－8(y 1＋y 2)＋4y 1y 2， ∵OM ⊥ON ，∴k OM ·k ON ＝－1，即x 1x 2＋y 1y 2＝0.∴16－8(y 1＋y 2)＋5y 1y 2＝0， ∴16－8×165＋8＋m ＝0，∴m ＝85.(2)以MN 为直径的圆的方程为(x －x 1)(x －x 2)＋(y －y 1)(y －y 2)＝0，即x 2＋y 2－(x 1＋x 2)x －(y 1＋y 2)y ＝0.又x 1＋x 2＝4－2y 1＋4－2y 2＝8－2(y 1＋y 2)＝85，∴以MN 为直径的圆的方程为x 2＋y 2－85x －165y ＝0.22．(本题满分12分)(2016·吉林实验中学上学期第三次模拟)已知圆C 的圆心C 在第一象限，且在直线3x －y ＝0上，该圆与x 轴相切，且被直线x －y ＝0截得的弦长为27，直线l ：kx －y －2k ＋5＝0与圆C 相交. 导学号 92434975(1)求圆C 的标准方程.(2)求出直线l 所过的定点；当直线l 被圆所截得的弦长最短时，求直线l 的方程及最短的弦长.[解析] (1)设圆心C (a ，b )，a ＞0，b ＞0，半径为r ，则b ＝3a ，r ＝3a . 圆心C (a,3a )到直线x －y ＝0的距离d ＝|a －3a |12＋12＝2a ，(2a )2＋(7)2＝(3a )2，即a 2＝1.∵a ＞0，∴a ＝1. ∵圆心C (1,3)，半径为3，∴圆C的方程为(x－1)2＋(y－3)2＝9.(2)∵直线l：kx－y－2k＋5＝0即(x－2)k－(y－5)＝0，∴直线l过定点M(2,5). k CM＝2，弦长最短时，k l＝－12. 直线l：x＋2y－12＝0，|CM|＝5，∴最短弦长为4.。