青海省青海师范大学附属第二中学2014-2015学年高一下学期期中考试数学试题

合集下载

青海省青海师范大学附属第二中学2014_2015学年高一英语下学期期中试题(无答案)

师大二附中2014-2015学年第二学期期中考试测试卷高一年级英语第I卷（共115分）第一部分：语法和词汇知识（共20小题，每小题1.5分，满分30分）1.—Don’t forget to feed the cat while I’m away.— No, I ______.A. don’tB. won’tC. can’tD. didn’t2. With a ______ expression on her face, she is ______ about what to do next.A. puzzled; puzzlingB. puzzling; puzzledC. puzzled; puzzledD. puzzling; puzzling3. Seeing the tiger walking ______ them, the small animals ran ______ all directions.A. near; toB. to; towardsC. by; inD. towards; in4. His plan is excellent in ______, but I don’t think it will work in practice.A. theoryB. exerciseC. themeD. paper5. It was a pity ______ John wouldn’t be able to spend his vacation with me.A. thatB. whenC. whyD. whether6. The Chinese government has done what it can to prevent the A H1N1 flu ______.A. to spreadB. from spreadingC. to be spreadD. from being spread7. A civil war ______ if the three parties cannot reach an agreement.A. will take placeB. will be broken outC. took placeD. broke out8. Nothing more was heard from him ______ we began to wonder if he was dead.A. now thatB. so thatC. as ifD. as long as9. She walked around the room with her nose in the air, pretending I didn’t ______.A. liveB. existC. surviveD. breathe10. Bruce lost the game. To ______, I told him a lot of jokes.A. cheer him upB. pick him upC. cheer up himD. pick up him11. Though he is 10 years old, he doesn’t know that 2 ______ by 4 makes 8.A. multiplyingB. is multiplyingC. multipliedD. is multiplied12. Now the number of the students in our school is ______ that of five years ago.A. as twice much asB. twice as larger asC. as twice large asD. twice as large as13. They ______ to finish the projec t before Sunday, but they didn’t make it becauseof the heavy snow.A. succeededB. triedC. managedD. thought14. I comforted myself with the belief ______ my friend was right so I didn’t needto worry.A. whatB. whichC. thatD. if15. The building ______ by trees and flowers is where the girls practice dancing.A. surroundingB. is surroundingC. surroundedD. is surrounded16. ______ in Chinese tea culture, Lewis came to China to study it.A. EncouragedB. ImpressedC. PleasedD. Interested17. The teacher always waits until all the children ______ before he starts the lesson.A. get downB. set downC. put downD. settle down18. ______ I know, he isn’t coming to the party.A. As soon asB. As long asC. As well asD. As far as19. We need to make all the preparations ______ two days, because they have brought forward the date of the competition.A. beforeB. atC. amongD. within20. Billy decided to complete his journey around the world ______ give up, althoughhe was injured in an accident.A. rather thanB. other thanC. more thanD. better than第二部分：完形填空（共20小题；每小题1.5分，满分30分）阅读下面短文，从短文后所给各题的四个选项（A、B、C、D）中选出能填入空白处的最佳选项。

青海省高一下学期期中数学试卷B卷(考试)

青海省高一下学期期中数学试卷B卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分）某单位有职工200人，其中青年职工40人，现从该单位的200人中抽取40人进行健康普查，如果采用分层抽样进行抽取，则青年职工应抽的人数为（）A . 5B . 6C . 8D . 102. （2分）设奇函数f（x）的定义域为实数集R，且满足f（x+1）=f（x﹣1），当x∈[0，1）时，f（x）=2x ﹣1．则的值为（）A .B .C . 0D . 1﹣3. （2分）(2020·河南模拟) 已知底面是等腰直角三角形的三棱锥P-ABC的三视图如图所示，俯视图中的两个小三角形全等，则（）A . PA，PB，PC两两垂直B . 三棱锥P-ABC的体积为C .D . 三棱锥P-ABC的侧面积为4. （2分）若函数f（x）=xex﹣m在R上存在两个不同的零点，则m的取值范围是（）A . m＞eB . m＞﹣C . ﹣＜m＜0D . ﹣e＜m＜05. （2分） (2015高一下·济南期中) 如果点P（sinθcosθ，2cosθ）位于第三象限，那么角θ所在象限是（）A . 第一象限B . 第二象限C . 第三象限D . 第四象限6. （2分）已知正三棱柱ABC﹣A1B1C1的六个顶点在球O1上，又知球O2与此正三棱柱的5个面都相切，求球O1与球O2的表面积之比（）A . 5：1B . 2：1C . 4：1D . ：17. （2分）某中学高三文科班从甲、乙两个班各选出7名学生参加文史知识竞赛，他们取得的成绩（满分100分）的茎叶图如图，其中甲班学生成绩的平均分是85，乙班学生成绩的中位数是83，则x+y的值为（）A . 8B . 7C . 9D . 1688. （2分）已知P1（x1 ， y1）是直线l：f（x，y）=0上的一点，P2（x2 ， y2）是直线l外的一点，由方程f（x，y）+f（x1 ， y1）+f（x2 ， y2）=0表示的直线与直线l的位置关系是（）A . 互相重合B . 互相平行C . 互相垂直D . 互相斜交9. （2分） (2017高二上·玉溪期末) 为了得到函数，x∈R的图象，只需把函数y=2sinx，x∈R的图象上所有的点（）A . 向左平移个单位长度，再把所得各点的横坐标缩短到原来的倍纵坐标不变）B . 向右平移个单位长度，再把所得各点的横坐标缩短到原来的倍（纵坐标不变）C . 向左平移个单位长度，再把所得各点的横坐标伸长到原来的3倍（纵坐标不变）D . 向右平移个单位长度，再把所得各点的横坐标伸长到原来的3倍（纵坐标不变）10. （2分）已知函数f（x）=，阅读如图所示的程序框图，若输入a的值为f（1）的值，则输出的k值是（）A . 9B . 10C . 11D . 1211. （2分） (2016高一下·鞍山期中) 若样本数据x1 ， x2 ，…，x10的标准差为2，则数据2x1﹣1，2x2﹣1，…，2x10﹣1的标准差为（）A . 3B . ﹣3C . 4D . ﹣412. （2分）设，则f(x)=cos(cosx)与g(x)=sin(sinx)的大小关系是（）A . f(x)<g(x)B . f(x)>g(x)C .D . 与x的取值有关二、填空题 (共4题；共4分)13. （1分）函数y=cos（﹣x）的单调递增区间为________14. （1分）如图所示，△A′B′C′表示水平放置的△ABC在斜二测画法下的直观图，A′B′在x′轴上，B′C′与x′轴垂直，且B′C′=3，则△ABC的边AB上的高为________．15. （1分） (2016高二上·江阴期中) 直线y=kx+1与圆（x﹣3）2+（y﹣2）2=9相交于A、B两点，若AB＞4，则k的取值范围是________．16. （1分） (2019高一上·黑龙江月考) 已知函数在区间上是增函数，则下列结论正确的是________（将所有符合题意的序号填在横线上）．①函数在区间上是增函数；②满足条件的正整数的最大值为3；③ .三、解答题： (共6题；共75分)17. （10分）已知两条直线l1：3x+4y﹣2=0与l2：2x+y+2=0的交点P，求：（1）过点P且过原点的直线方程；（2）过点P且垂直于直线l3：x﹣2y﹣1=0的直线l的方程．18. （15分）(2017·衡阳模拟) 如图1为某市2017年2月28天的日空气质量指数折线图．由中国空气质量在线监测分析平台提供的空气质量指数标准如下：空气质量指数（0，50]（50，100]（100，150]（150，200]（200，300]300以上空气质量等级1级优2级良3级轻度污染4级中度污染5级重度污染6级严重污染（Ⅰ）请根据所给的折线图补全如图2所示的频率分布直方图（并用铅笔涂黑矩形区域），并估算该市2月份空气质量指数监测数据的平均数（保留小数点后一位）；（Ⅱ）在该月份中任取两天，求空气质量至少有一天为优或良的概率；（Ⅲ）如果该市对环境进行治理，治理后经统计，每天的空气质量指数近似满足X～N（75，552），则治理后的空气质量指数均值大约下降了多少？19. （10分）如图，在四棱柱ABCD﹣A1B1C1D1中，AC⊥B1D，BB1⊥底面ABCD，E、F、H分别为AD、CD、DD1的中点，EF与BD交于点G．（1）证明：平面ACD1⊥平面BB1D；（2）证明：GH∥平面ACD1 ．20. （10分） (2016高一上·密云期中) 某蔬菜基地种植西红柿，由历年市场行情得知，从二月一日起的300天内，西红柿场售价与上市时间的关系如图一的一条折线表示；西红柿的种植成本与上市时间的关系如图二的抛物线段表示．（1）写出图一表示的市场售价与时间的函数关系式p=f（t）；写出图二表示的种植成本与时间的函数关系式Q=g（t）；（2）认定市场售价减去种植成本为纯收益，问何时上市的西红柿纯收益最大？（注：市场售价各种植成本的单位：元/102㎏，时间单位：天）21. （15分） (2017高二下·濮阳期末) 濮阳市黄河滩区某村2010年至2016年人均纯收入（单位：万元）的数据如下表：年份2010201120122013201420152016年份代号x1234567人均纯收入y 2.9 3.3 3.6 4.4 4.8 5.2 5.9（Ⅰ）求y关于x的线性回归方程；（Ⅱ）利用（Ⅰ）中的回归方程，分析2010年至2016年该村人均纯收入的变化情况，并预测该村2017年人均纯收入．附：回归直线的斜率和截距的最小乘法估计公式分别为： = ， = ﹣．22. （15分）已知ω是正数，函数f（x）=2sinωx在区间上是增函数，求ω的取值范围．参考答案一、选择题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题： (共6题；共75分) 17-1、18-1、19-1、20-1、20-2、21-1、22-1、。

青海省青海师范大学附属第二中学2014-2015学年高一下学期第二次月考

师大二附中2014-2015学年第二学期月考试卷高一年级化学（满分：100分）命题：石立军审题：李辉一、选择题（每小题2分，共20分）1．已知X、Y、Z、W、R是原子序数依次增大的五种短周期主族元素，其中Y、R原子最外层电子数相等；X元素最低负价与W元素最高正价绝对值相等；工业上常用电解熔融氧化物的方法冶炼W单质；Z、W、R最高价氧化物对应的水化物两两反应均生成盐和水。

下列说法正确的是A．简单离子半径：Y＞Z＞WB．简单氢化物的热稳定性：X＞Y＞RC．W的最高价氧化物对应的水化物碱性比Z的强D．R的最高价氧化物对应的水化物化学式一定是HRO42．下列对相应有机物的描述完全正确的是①甲烷：天然气的主要成分，与氯气在光照条件下发生取代反应生成四种氯代物，其中CH3Cl 是气体。

②乙烯：一个国家石油化工发展水平的标志，可以发生加成反应和加聚反应。

③苯：平面结构，每个分子中含有3个碳碳双键，可与氢气发生加成反应生成环己烷。

④油脂：属于高分子化合物，可以发生水解反应生成甘油。

⑤蔗糖：糖尿病人尿液的成分之一，可以用新制Cu(OH)2检验。

⑥蛋白质：水解的最终产物为氨基酸，部分蛋白质遇浓硝酸显黄色。

A．①②③ B．②④⑥ C．①②⑥ D．①⑤⑥3．根据下表信息，判断以下叙述正确的是A．氢化物的还原性为H2T>H2RB．单质与稀盐酸反应的速率为L<QC．L、M、R的最高价氧化物的水化物两两之间均能反应D．离子半径：L2+<R2—4．下列叙述中，金属a的活泼性肯定比金属b的活泼性强的是A．a原子的最外层电子数比b原子的最外层电子数少B．a原子电子层数比b原子的电子层数多C．1mol a 从酸中置换H+生成的H2比1 mol b从酸中置换H＋生成的H2多D．常温时，a能从水中置换出氢，而b不能5．在密闭容器中进行X2（气）+2Y2（气）Z（气）的反应，X2、Y2、Z的起始浓度依次为0.2mol/L、0.3mol/L、0.3mol/L，当反应达到其最大限度（即化学平衡状态）时，各物质的浓度有可能的是A．c（Z）＝0.45mol/LB．c（X2）＝0.3mol/L c（Z）＝0.1 mol/LC．c（X2）＝0.5mol/LD．c（Y2）＝0.5mol/L6．金刚石与石墨是碳元素的两种结构不同的单质，彼此互称同素异形体。

2014-2015学年高一下学期期中考试数学试卷-Word版含答案

2014-2015学年高一下学期期中考试数学试卷-Word版含答案2014——2015学年下学期高一年级期中考数学学科试卷本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，考试时间120分钟第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 不等式0121≤+-x x 的解集为( )A.⎝ ⎛⎭⎪⎫－∞，－12∪[1，＋∞) B.⎣⎢⎡⎦⎥⎤－12，1C.⎝ ⎛⎦⎥⎤－∞，－12∪[1，＋∞) D. ⎝ ⎛⎦⎥⎤－12，12. 若0<<b a ，则下列不等式不能成立的是 ( ) A.ba11> B ．b a 22> C ．b a > D ．b a )21()21(> 3. 不等式16)21(1281≤<x 的整数解的个数为（）A ．10B ．11C ．12D ．134. 等差数列{}n a 中，如果39741=++a a a ，27963=++a a a ，则数列{}n a 前9项的和为( )A ．297B ．144C ．99D ．665. 已知直线1l ：01)4()3(=+-+-y k x k 与2l ：032)3(2=+--y x k 平行，则k 的值是( )A ．1或3B ．1或5C ．3或5D ．1或26. 在△ABC 中，80=a ，70=b ，45=A ，则此三角形解的情况是（） A 、一解 B 、两解 C 、一解或两解 D 、无解7. 如果0<⋅C A ，且0<⋅C B ，那么直线0=++C By Ax 不通过( ) A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限8.已知点()5,x 关于点),1(y 的对称点为()3,2--,则点()y x p ,到原点的距离为( )A ．4B ．13C ．15D ．179. 计算机是将信息转换成二进制进行处理的，二进制即“逢二进一”，如(1 101)2表示二进制数，将它转换成十进制数是1×23＋1×22＋0×21＋1×20＝13，那么将二进制数(11…114个01)2转换成十进制数是( )A ．216－1B ．216－2C ．216－3D ．216－4 10. 数列{}n a 满足21=a ，1111+-=++n n n a a a ，其前n 项积为n T ，则=2014T ( ) A.61B ．61- C ．6 D ．6- 11. 已知0,0>>y x ，且112=+yx，若m m y x 222+>+恒成立，则实数m 的取值范围是( )A ．(－∞，－2]∪[4，＋∞)B ．(－2，4)C ．(－∞，－4]∪[2，＋∞)D ．(－4，2) 12. 设数列{}n a 的前n 项和为n S ，令nS S S T nn +++=21，称n T 为数列n a a a ,,,21 的“理想数”，已知数列50021,,,a a a 的“理想数”为2004，那么数列12,50021,,,a a a 的“理想数”为( ) A ．2012 B ．2013 C ．2014 D ．2015第Ⅱ卷（非选择题共90分）19.(12分) 已知直线l 过点)2,3(P ，且与x 轴、y 轴的正半轴分别交于A ，B 两点，如图所示，求OAB ∆的面积的最小值及此时直线l 的方程．20. (12分) 某观测站C 在城A 的南偏西20˚的方向上，由A 城出发有一条公路，走向是南偏东40˚，在C 处测得距C 为31千米的公路上B 处有一人正沿公路向A 城走去，走了20千米后，到达D 处，此时C 、D 间距离为21千米，问还需走多少千米到达A 城？21. (12分) 在各项均为正数的等差数列{}n a 中，对任意的*N n ∈都有12121+=+++n n n a a a a a . (1)求数列{}n a 的通项公式n a ；(2)设数列{}n b 满足11=b ，na n nb b 21=-+，求证：对任意的*N n ∈都有212++<n n n b b b .22. (12分)设函数())0(132>+=x xx f ，数列{}n a 满足11=a ，)1(1-=n n a f a ，*N n ∈，且2≥n .(1)求数列{}n a 的通项公式； (2)对*N n ∈，设13221111++++=n n n a a a a a a S ，若ntS n 43≥恒成立，求实数t 的取值范围．答案一、选择题：（每题5分，共60分）13、 3 14、349π15、 2 16、 ①②⑤三、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．17. 解：(1)由题意，得⎩⎪⎨⎪⎧a 3a 6＝55，a 3＋a 6＝a 2＋a 7＝16.∵公差d>0，∴⎩⎪⎨⎪⎧a 3＝5，a 6＝11，∴d ＝2，a n ＝2n －1.(2)∵b n ＝a n ＋b n －1(n≥2，n ∈N *)， ∴b n －b n －1＝2n －1(n≥2，n ∈N *)．∵b n ＝(b n －b n －1)＋(b n －1－b n －2)＋…＋(b 2－b 1)＋b 1(n≥2，n ∈N *)，且b 1＝a 1＝1，∴b n ＝2n －1＋2n －3＋…＋3＋1＝n 2(n≥2，n ∈N *)． ∴b n ＝n 2(n ∈N *)．题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 D BBCCACDCDDA18. 解析 27(1)4sin cos 2180,:22B C A A B C +-=++=︒由及得 22272[1cos()]2cos 1,4(1cos )4cos 5214cos 4cos 10,cos ,20180,60B C A A A A A A A A -+-+=+-=-+=∴=︒<<︒∴=︒即 22222222(2):cos 211cos ()3.2223123,3: 2 :.221b c a A bcb c a A b c a bc bc b c b b a b c bc bc c c +-=+-=∴=∴+-=+===⎧⎧⎧=+==⎨⎨⎨===⎩⎩⎩由余弦定理得代入上式得由得或 19. 解：由题意设直线方程为x a ＋y b ＝1(a ＞0，b ＞0)，∴3a ＋2b ＝1.由基本不等式知3a ＋2b ≥26ab，即ab≥24(当且仅当3a ＝2b，即a ＝6，b ＝4时等号成立)．又S ＝12a ·b ≥12×24＝12，此时直线方程为x 6＋y4＝1，即2x ＋3y －12＝0.∴△ABO 面积的最小值为12，此时直线方程为2x ＋3y －12＝0. 20. 解据题意得图02，其中BC=31千米，BD=20千米，CD=21千米，∠CAB=60˚．设∠ACD = α ，∠CDB = β ．在△CDB 中，由余弦定理得：71202123120212cos 222222-=⨯⨯-+=⋅⋅-+=BD CD BC BD CD β，734cos 1sin 2=-=ββ．()CDA CAD ∠-∠-︒=180sin sin α ()β+︒-︒-︒=18060180sin()143523712173460sin cos 60cos sin 60sin =⨯+⨯=︒-︒=︒-=βββ在△ACD 中得1514352321143560sin 21sin sin =⨯=⋅︒=⋅=αA CD AD ．所以还得走15千米到达A 城． 21. 解：(1)设等差数列{a n }的公差为d.令n ＝1，得a 1＝12a 1a 2.由a 1>0，得a 2＝2.令n ＝2，得a 1＋a 2＝12a 2a 3，即a 1＋2＝a 1＋2d ，得d ＝1.从而a 1＝a 2－d ＝1.故a n ＝1＋(n －1)·1＝n. (2)证明：因为a n ＝n ，所以b n ＋1－b n ＝2n ，所以b n ＝(b n －b n －1)＋(b n －1－b n －2)＋…＋(b 2－b 1)＋b 1 ＝2n －1＋2n －2＋…＋2＋1 ＝2n －1.又b n b n ＋2－b 2n ＋1＝(2n －1)(2n ＋2－1)－(2n ＋1－1)2＝－2n <0，所以b n b n ＋2<b 2n ＋1.22. 解：(1)由a n ＝f ⎝⎛⎭⎪⎫1a n －1，可得a n －a n －1＝23，n ∈N *，n≥2.所以{a n }是等差数列．又因为a 1＝1，所以a n ＝1＋(n －1)×23＝2n ＋13，n ∈N *.(2)因为a n ＝2n ＋13，所以a n ＋1＝2n ＋33，所以1a n a n ＋1＝92n ＋12n ＋3＝92⎝⎛⎭⎪⎫12n ＋1－12n ＋3.所以S n ＝92⎝ ⎛⎭⎪⎫13－12n ＋3＝3n 2n ＋3，n ∈N *. S n ≥3t 4n ，即3n 2n ＋3≥3t 4n ，得t≤4n 22n ＋3(n ∈N *)恒成立．令g(n)＝4n 22n ＋3(n ∈N *)，则g(n)＝4n 22n ＋3＝4n 2－9＋92n ＋3＝2n ＋3＋92n ＋3－6(n ∈N *)．令p ＝2n ＋3，则p≥5，p ∈N *.g(n)＝p ＋9p －6(n ∈N *)，易知p ＝5时，g(n)min ＝45.所以t≤45，即实数t 的取值范围是⎝⎛⎦⎥⎤－∞，45.。

青海省青海师范大学第二附属中学2024届高一数学第二学期期末考试试题含解析

青海省青海师范大学第二附属中学2024届高一数学第二学期期末考试试题考生须知： 1．全卷分选择题和非选择题两部分，全部在答题纸上作答。

选择题必须用2B 铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。

2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。

3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。

一、选择题：本大题共10小题，每小题5分，共50分。

在每个小题给出的四个选项中，恰有一项是符合题目要求的1．己知函数()2*21,12x x n n f x n N x x x -+-⎛⎫=∈≠ ⎪++⎝⎭的最小值为n a ，最大值为n b ，若()()11n n n c a b =--，则数列{}n c 是（）A ．公差不为0的等差数列B ．公比不为1的等比数列C ．常数数列D ．以上都不对2．在等差数列{}n a 中，395724a a a a =--+，则6a =（） A ．3B ．6C ．9D ．123．已知角终边上一点，则的值为（） A ．B ．C ．D ．4．已知圆()()22:1C x a y b -+-=，设平面区域70,{30,0x y x y y +-≤Ω=-+≥≥，若圆心C ∈Ω,且圆C 与x 轴相切，则22a b +的最大值为（） A ．5B ．29C ．37D ．495．已知各项均为正数的数列{}n a 的前n 项和为n S ，且()2*212,21,n n a a S n n N+==++∈若对任意的*n N ∈，123111120n n a n a n a n a λ++++-≥++++恒成立，则实数λ的取值范围为（） A ．1,3⎛⎤-∞ ⎥⎝⎦B ．7,12⎛⎤-∞ ⎥⎝⎦C ．1,4⎛⎤-∞ ⎥⎝⎦D ．1,2⎛⎤-∞ ⎥⎝⎦6．已知等差数列{}n a 中，若412203a a d +==，，则5a =（） A ．1B ．2C ．3D ．47．已知实心铁球的半径为R ，将铁球熔成一个底面半径为R 、高为h 的圆柱，则hR=( ) A ．32B ．43C ．54D ．28．在ABC 中，已知其面积为22()S a b c =--，则cos A = （） A ．34B ．1315C ．1517D ．17199．设点P 是函数y =(),Q x y 满足260x y --=，则PQ 的最小值为（）A ．4B 2CD 410．已知0a b +<，且0b >，那么a ，b ，a -，b -的大小关系是（） A ．b a b a -<<<- B ．b a a b -<<-< C ．a b a b <-<-<D ．a b b a <-<<-二、填空题：本大题共6小题，每小题5分，共30分。

青海师大二附中高一数学期中测试试题(无答案)新人教A版

高一下学期期中测试数学试题第Ⅰ卷（选择题共36分）一、选择题(本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1、ΔABC 中, a = 1, b =3, ∠A=30°，则∠B 等于（）A ．60°B ．60°或120°C ．30°或150°D ．120°2、已知△ABC 中，AB ＝6，∠A ＝30°，∠B ＝120°，则△ABC 的面积为( )A ．9B ．18C ．93D ．183 3、在△ABC 中，已知a ＝3，b ＝4， c ＝5，则角C 为 ( )A ．90°B ．60°C ．45°D ．30°4、在等比数列中，112a =，12q =，132n a =，则项数n 为（） A. 3 B. 4 C. 5 D. 65、设11a b >>>-,则下列不等式中恒成立的是 ( )A ．11a b < B ．11a b> C ．2a b > D ．22a b > 6、不等式220ax bx ++>的解集是11(,)23-，则a b +的值是（）。

A. 10 B. 10- C. 14 D. 14- 7、设{}n a 为等差数列，则下列数列中，成等差数列的个数为（）①{}2n a ②{}n pa ③{}n pa q + ④{}n na （p 、q 为非零常数） A ．1 B ．2 C ．3 D ．48、在等差数列｛a n ｝中，前n 项和为S n ，若S 16—S 5=165，则1698a a a ++的值是（）A ．90B ．90-C ．45D ．45- 9、若不等式02)1()1(2>+-+-x m x m 的解集是R ，则m 的范围是（）A ．(1,9)B ．(,1](9,)-∞⋃+∞C ． [1,9)D ．(,1)(9,)-∞⋃+∞10. 设a ，b ，c ，d∈R ，且a >b ，c <d ，则下列结论中正确的是( )A ．a ＋c >b ＋dB ．a －c >b －dC ．ac >bdD ．a d > b c11.不等式12--x x ≥0的解集是( ) A.［2,+∞）B. (]1,∞-∪(2,+∞）C. (－∞,1)D. (－∞,1)∪［2,+∞) 12．已知x+3y-1=0，则关于y x 82+的说法正确的是（）Ａ．有最大值8 Ｂ．有最小值22 Ｃ．有最小值8 Ｄ．有最大值22二、填空题：请把答案填在题中横线上（每小题5分，共20分）.13．在△ABC 中，AB=3，13BC =，AC=4。

青海省高一下学期期中数学试卷(I)卷

青海省高一下学期期中数学试卷（I）卷姓名:________ 班级:________ 成绩:________一、填空题 (共12题；共14分)1. （1分）若函数f（x）=logt|x+1|在区间（﹣2，﹣1）上恒有 f（x）＞0，则关于t的不等式f（8t﹣1）＜f（1）的解集为________．2. （1分） (2017高一上·孝感期末) 三个数a、b、c∈（0，），且cosa=a，sin（cosb）=b，cos（sinc）=c，则a、b、c从小到大的顺序是________．3. （1分）已知函数f（x）=ln（x+），若正实数a，b满足f（2a）+f（b一1）=0，则的最小值是________4. （1分） (2015高三上·廊坊期末) 若直线ax+2by﹣2=0（a，b＞0）始终平分圆x2+y2﹣4x﹣2y﹣8=0的周长，则ab的取值范围是________ ．5. （1分）(2017·黄浦模拟) 已知sin（α+ ）= ，α∈（﹣，0），则tanα=________．6. （1分）(2017·淮北模拟) 函数的值域是________．7. （1分） (2016高一上·涞水期中) 若函数f（x）=ln（mx2﹣6mx+m+8）的定义域为实数集R，则实数m的取值范围是________8. （1分） (2017高一下·嘉兴期末) 已知sin2α﹣2cos2α=2（0＜α＜），则tanα=________．9. （1分） (2016高一上·黑龙江期中) 设方程x+2x=4的根为m，方程x+log2x=4的根为n，则m+n=________．10. （1分）已知，则当的值为________ 时取得最大值。

11. （3分）若角α的终边与单位圆交于P（﹣，），则sinα=________；cosα=________；tanα=________．12. （1分） (2017高一上·徐汇期末) 已知A={x|x≤7}，B={x|x＞2}，则A∩B=________．二、选择题 (共4题；共8分)13. （2分） (2016高二上·天心期中) 若a，b为实数，则“0＜ab＜1”是“b＜”的（）A . 充分而不必要条件B . 必要而不充分条件C . 充分必要条件D . 既不充分也不必要条件14. （2分） (2016高一上·湖州期中) 与角﹣终边相同的角是（）A .B .C .D .16. （2分）函数的图象与函数图象交点的个数是（）A . 1B . 2C . 3D . 4三、解答题 (共5题；共40分)17. （10分） (2016高一上·长春期中) 已知角α的顶点在原点，始边与x轴的非负半轴重合，终边与单位圆相交于点P（﹣，）（1）求sinα（2）求的值．18. （5分）已知扇形OAB的周长是60cm，（Ⅰ）若其面积是20cm2 ，求扇形OAB的圆心角的弧度数；（Ⅱ）求扇形OAB的最大面积．19. （10分） (2019·金华模拟) 已知函数的最小正周期为，且.（1）求和的值；（2）若，求．20. （5分）已知二次函数f（x）有两个零点0和﹣2，且f（x）最小值是﹣1，函数g（x）与f（x）的图象关于原点对称．（1）求f（x）和g（x）的解析式；（2）若h（x）=f（x）﹣λg（x）在区间[﹣1，1]上是增函数，求实数λ的取值范围．21. （10分） (2019高一上·会宁期中) 国庆期间，某旅行社组团去风景区旅游，若旅行团人数不超过20人，每人需交费用800元；若旅行团人数超过20人，则给予优惠：每多1人，人均费用减少10元，直到达到规定人数60人为止.旅行社需支付各种费用共计10000元.（1）写出每人需交费用S关于旅行团人数的函数；（2）旅行团人数x为多少时，旅行社可获得最大利润？最大利润是多少？参考答案一、填空题 (共12题；共14分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、选择题 (共4题；共8分)13-1、14-1、16-1、三、解答题 (共5题；共40分) 17-1、17-2、18-1、19-1、19-2、20-1、21-1、21-2、。

青海省青海师范大学附属第二中学2014-2015学年高一下学期第二次月考数学试题

师大二附中2014-2015学年第二学期第二次月考测试卷高一年级数学（满分：150分）命题：刘雪莲审核：樊扬扬一、选择题：(本大题共12小题，第小题5分，共60分．在每小题给出的四个选项中，只有一项符是合题目要求的．)1．在三角形ABC 中，若0cos sin ≤B A ，则三角形ABC 为( )A.锐角三角形B.钝角三角形C.直角三角形D.钝角三角形或直角三角形 2. 不可以作为数列： ,0,2,0,2，的通项公式的是（ )A. ⎪⎩⎪⎨⎧∈=∈-==++),2(0),12(2N k k n N k k n a n B. 2sin 2πn a n = C. 1)1(+-=n n a D.2)1(cos2π-=n a n 3. 下列说法：①一组数据不可能有两个众数；②一组数据的方差必须是正数；③将一组数据中的每一个数据都加上或减去同一个常数后，方差恒不变；④在频率分布直方图中，每个小长方形的面积等于相应小组的频率，其中错误的有（） A.0个 B.1个 C.2个 D.3个4. 如图所示，程序的输出结果为S ＝132，则判断框中应填( )A ．i ≥10?B ．i ≥11?C ．i ≤11?D ．i ≥12?5. 若数列{}n a 是等差数列，首项10a >，200320040a a +>，200320040a a ⋅<，则使前n 项和n S >成立的最大自然数n是( ) A ．4 005 B ．4 006 C ．4 007 D ．40086. 某大学数学系共有学生5 000人，其中一、二、三、四年级的人数比为4∶3∶2∶1，要用分层抽样的方法从数学系所有学生中抽取一个容量为200的样本，则应抽取三年级的学生人数为（）A.80B.40C.60D.207. 图1所示的茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).图1 图2已知甲组数据的中位数为15，乙组数据的平均数为16.8，则x ，y 的值分别为（） A.2，5 B.5，5 C ．5，8 D ．8，88.已知函数y =f (x )的图象如图2所示，则不等式0112>⎪⎭⎫⎝⎛-+x x f 的解集为（）A.()1,∞-B. ()1,2-C. ()2,-∞-D. ()()+∞-∞-,12,9. 已知两个变量x ，y 之间具有线性相关关系，试验测得(x ，y )的四组值分别为(1，2)，(2，4)，(3，5)，(4，7)，则y 与x 之间的回归直线方程为（）A. yˆ =0.8x +3 B. y ˆ=－1.2x +7.5 C. yˆ=1.6x +0.5 D. y ˆ=1.3x +1.2 10.设x ,y ∈R ,a ＞1,b ＞1，若a x =b y =3,32=+b a ,则yx 11+的最大值为（）A.2B.23 C.1 D.2111. 为了了解某校高三学生的视力情况，随机抽查了该校100名高三学生的视力情况，得到频率分布直方图如下图，由于不慎将部分数据丢失，但知道后5组频数和为62，设视力在4.6到4.8之间的学生数为a ，最大频率为0.32，则a 的值为( )A ．64B ．54C ．48D ．2712. 若110a b<<，则下列不等式中，正确的不等式有 ( ) ①a b ab +< ②a b > ③a b < ④2b aa b+>A .1个B .2个C .3个D .4 二、填空题：（本大题共4小题，每小题5分，共20分．把答案填在题中横线上．） 13. 为了在运行下面的程序之后得到输出y ＝25，键盘输入x 应该是________．INPUT x IF x<0 THEN y ＝(x ＋1)*(x ＋1)ELSEy ＝(x －1)*(x －1)END IF PRINT y END14. 采用系统抽样方法从960人中抽取32人做问卷调查，为此将他们随机编号为1，2，…，960，分组后在第1组中采用简单随机抽样的方法抽到的编号为9，则从编号为的30人中应抽的编号是_____.15. 已知,x y 满足约束条件10,230,x y x y --≤⎧⎨--≥⎩当目标函数z ax by =+(0,0)a b >>在该约束条件下取到最小值ab 的最大值为 .16. 等差数列{a n }中，n S 是它的前n 项之和，且76S S <，87S S >，则下列说法中： ①此数列的公差0<d ； ②9S 一定小于6S ； ③7a 是各项中最大的一项； ④7S 一定是n S 中的最大值．三、解答题：（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．）17.(10分) 已知点)1,3(),0,0(A O ，点),(y x P 满足220240330x y x y x y +-≥⎧⎪-+≥⎨⎪--≤⎩，求OP OA ⋅的最大值和最小值.18. ABC ∆中，角A ，B ，C 所对的边分别为,,a b c . 已知3,cos 2a A B A π===+. （Ｉ）求b 的值；（II ）求ABC ∆的面积.19. 画出求12－22＋32－42＋…＋992－1002的值的程序框图．20. 为了了解某地初三年级男生的身高情况，从其中的一个学校选取容量为60的（1）求出表中a ，m 的值；（2）画出频率分布直方图；(3)估计这组数据的众数、平均数和中位数.(2)用最小二乘法计算利润额y 关于销售额x 的回归直线方程；(3)当销售额为4千万元时，利用(2)的结论估计该零售店的利润额(百万元)．22. 已知函数f (x )＝14x ＋m(m >0)，当x 1、x 2∈R ，且x 1＋x 2＝1时，总有f (x 1)＋f (x 2)＝12.(1)求m 的值．(2)设S n ＝f (0n )＋f (1n )＋f (2n )＋…＋f (nn)，求S n .。

青海省高一下学期期中数学试卷(I)卷(考试)

青海省高一下学期期中数学试卷（I）卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分）设向量a＝(2，4)与向量b＝(x ， 6)共线，则实数x＝（）A . 2B . 3C . 4D . 62. （2分）向量，若与平行，则m等于（）A . -2B . 2C .D .3. （2分）已知函数的图象在处的切线斜率为（），且当时，其图象经过，则（）A .B .C .D .4. （2分）函数的定义域是（）A . [－1，＋∞)B . [－1,0)C . (－1，＋∞)D . (－1,0)5. （2分）已知等差数列{an}的前n项和为Sn ， a1=-11，a5+a6=-4，Sn取得最小值时n 的值为（）A . 6B . 7C . 8D . 96. （2分） (2019高一上·嘉兴月考) 已知函数在区间［－1,2］上的最大值为2，则的值等于（）A . 2或3B . －1或3C . 1D . 37. （2分） (2016高二上·桓台期中) 若实数x、y满足约束条件，则目标函数z=x+y的最大值为（）A . 2B . 3C . 4D . 18. （2分） (2017高二上·张掖期末) 在△ABC中，BC=7，AB=5，∠A=120°，则△ABC的面积等于（）A .B .C .D .9. （2分） (2016高二上·晋江期中) 在锐角△ABC中，已知| |=4，| |=1，S△ABC= ，则等于（）A .B . 13C .D . 1710. （2分） (2016高一下·台州期末) 在△ABC中，角A、B、C的对边分别为a，b，c，a=1，b= ，∠A=则∠B等于（）A .B .C . 或D .11. （2分）(2017·温州模拟) 设，，均为非零向量，若|（ + ）• |=|（﹣）• |，则（）A . ∥B . ⊥C . ∥ 或∥D . ⊥ 或⊥12. （2分）(2018·银川模拟) 数列的前n项的和满足则下列为等比数列的是（）A .B .C .D .二、填空题 (共4题；共4分)13. （1分） (2017高一下·济南期末) 若向量 =（1，2）， =（x，﹣1），且（ +2 ）∥ ，则x=________．14. （1分） (2015高二上·天水期末) 设Sn是数列{an}的前n项和，且a1=﹣2，Sn=2an+2，则an=________．15. （1分） (2016高一下·重庆期中) 已知船A在灯塔C北偏东85°且到C的距离为2km，船B在灯塔C西偏北25°且到C的距离为 km，则A，B两船的距离为________ km．16. （1分）求函数的最小值为________．三、解答题 (共6题；共70分)17. （10分）(2017·南通模拟) 在平面直角坐标系中，已知点A（0，0），B（4，3），若A，B，C三点按顺时针方向排列构成等边三角形ABC，且直线BC与x轴交于点D．（1）求cos∠CAD的值；（2）求点C的坐标．18. （10分）(2016·四川理) 在△ABC中，角A，B，C所对的边分别是a，b，c，且 + = ．（1）证明：sinAsinB=sinC；（2）若b2+c2﹣a2= bc，求tanB．19. （15分） (2016高三上·桓台期中) 已知向量 =（1，2）， =（﹣2，m）， = +（t2+1）， =﹣k + ，m∈R，k、t为正实数．（1）若∥ ，求m的值；（2）若⊥ ，求m的值；（3）当m=1时，若⊥ ，求k的最小值．20. （15分） (2018高一上·黑龙江期中) 定义在R上的函数y＝f（x）．对任意的a，b∈R．满足：f（a+b）＝f（a）•f（b），当x＞0时，有f（x）＞1，其中f（1）＝2．（1）求f（0），f（﹣1）的值；（2）判断该函数的单调性，并证明；（3）求不等式f（x+1）＜4的解集．21. （10分）(2017·江西模拟) 等差数列{an}的前n项和为Sn ，数列{bn}是等比数列，满足a1=3，b1=1，b2+S2=10，a5﹣2b2=a3 ．（1）求数列{an}和{bn}的通项公式；（2）令cn=an•bn，设数列{cn}的前n项和为Tn，求Tn．22. （10分） (2016高二上·桂林开学考) 已知公差d＞0的等差数列{an}中，a1=10，且a1 ， 2a2+2，5a3成等比数列．（1）求公差d及通项an；（2）设Sn= + +…+ ，求证：Sn＜．参考答案一、选择题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共70分) 17-1、17-2、18-1、18-2、19-1、19-2、19-3、20-1、20-2、20-3、21-1、21-2、22-1、22-2、。

青海省师大二附中高一数学下学期期中试卷(含解析)

2014-2015学年青海师大二附中高一（下）期中数学试卷一、选择题：（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项符是合题目要求的．）1．在一个△ABC中，若a=2，b=2，A=30°，那么B等于( )A．60°B．60°或120°C．30°D．30°或150°2．已知{a n}为等差数列，且a7﹣2a4=﹣1，a3=0，则公差d=( )A．﹣2 B．﹣C．D．23．在△ABC中，已知，则∠C=( )A．30°B．150°C．45°D．135°4．数列{a n}的前n项和为S n，若，则S5=( )A．1 B．C．D．5．设0＜b＜a＜1，则下列不等式成立的是( )A．ab＜b2＜1 B．C．2b＜2a＜2 D．a2＜ab＜16．不等式（1﹣x）（2+x）＞0的解集为( )A．（﹣2，1）B．（﹣∞，﹣2）∪（1，+∞）C．（﹣∞，1）∪（2，+∞）D．（﹣1，2）7．已知x＞2，则x+的最小值为( )A．6 B．4 C．3 D．28．对任意的实数x，不等式mx2﹣mx﹣1＜0恒成立，则实数m的取值范围是( ) A．（﹣4，0）B．（﹣4，0] C．[﹣4，0] D．[﹣4，0）9．已知非负实数x、y满足2x+3y﹣8≤0且3x+2y﹣7≤0，则x+y的最大值是( ) A．B．C．3 D．210．不等式组表示的区域为D，点P （0，﹣2），Q （0，0），则( )A．P∉D，且Q∉D B．P∉D，且Q∈D C．P∈D，且Q∉D D．P∈D，且Q∈D 11．设a＞0，b＞0．若是3a与3b的等比中项，则+的最小值为( )A．4 B．6 C．2D．212．若关于x的方程x2+ax+a2﹣1=0有一正根和一负根，则实数a的取值范围是( ) A．﹣＜a＜﹣1 B．﹣2＜a＜2 C．﹣1＜a＜1 D．1＜a＜二、填空题：（该题共4小题，每小题5分，共20分．把答案填在题中横线上．）13．a克糖水中含有b克塘（a＞b＞0），若在糖水中加入x克糖，则糖水变甜了．试根据这个事实提炼出一个不等式：__________．14．若S n为等比数列{a n}的前n项和，8a2+a5=0，则S6：S3=__________．15．已知点P（x，y）的坐标x，y满足，则x2+y2﹣4x的最大值是__________．16．设△ABC的内角A，B，C所对边的长分别为a，b，c，则下列命题正确的是__________（写出所有正确命题的编号）．①若ab＞c2，则C＜②若a+b＞2c，则C＜③若a3+b3=c3，则C＜④若（a+b）c＜2ab，则C＞⑤若（a2+b2）c2＜2a2b2，则C＞．三、解答题：（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．）17．设锐角三角形ABC的内角A，B，C的对边分别为a，b，c，a=2bsinA（Ⅰ）求B的大小；（Ⅱ）求cosA+sinC的取值范围．18．（Ⅰ）比较x2+y2+1与2（x+y﹣1）的大小；（Ⅱ）已知a，b∈R+，求证：（a+b）（a2+b2）（a3+b3）≥8a3b3．19．已知数列{a n}满足a1=1，a2=2，a n+2=，n∈N*．（1）令b n=a n+1﹣a n，证明：{b n}是等比数列；（2）求{a n}的通项公式．20．（1）已知集合A={x|x2﹣x﹣6＞0}，B={x|0＜x+a＜4}，若A∩B=∅，求实数a的取值范围；（2）已知f（x）=﹣3x2+a（6﹣a）x+b．当不等式f（x）＞0的解集为（﹣1，3）时，求实数a，b的值．21．本公司计划2008年在甲、乙两个电视台做总时间不超过300分钟的广告，广告总费用不超过9万元．甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟．假定甲、乙两个电视台为该公司所做的每分钟广告，能给公司带来的收益分别为0.3万元和0.2万元．问该公司如何分配在甲、乙两个电视台的广告时间，才能使公司的收益最大，最大收益是多少万元？22．若S n是公差不为0的等差数列{a n}的前n项和，且S1，S2，S4成等比数列．（1）求等比数列S1，S2，S4的公比；（2）若S2=4，求{a n}的通项公式；（3）设，T n是数列{b n}的前n项和，求使得对所有n∈N*都成立的最小正整数m．2014-2015学年青海师大二附中高一（下）期中数学试卷一、选择题：（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项符是合题目要求的．）1．在一个△ABC中，若a=2，b=2，A=30°，那么B等于( )A．60°B．60°或120°C．30°D．30°或150°考点：正弦定理．专题：解三角形．分析：将已知代入正弦定理即可直接求值．解答：解：由正弦定理可得：sinB===．∵0＜B＜180°，∴B=60°或120°，故选：B．点评：本题主要考查了正弦定理的简单应用，属于基本知识的考查．2．已知{a n}为等差数列，且a7﹣2a4=﹣1，a3=0，则公差d=( )A．﹣2 B．﹣C．D．2考点：等差数列．专题：计算题；方程思想．分析：利用等差数列的通项公式，结合已知条件列出关于a1，d的方程组，求解即可．解答：解：设等差数列{a n}的首项为a1，公差为d，由等差数列的通项公式以及已知条件得，即，解得d=﹣，故选B．点评：本题考查了等差数列的通项公式，熟记公式是解题的关键，同时注意方程思想的应用．3．在△ABC中，已知，则∠C=( )A．30°B．150°C．45°D．135°考点：余弦定理．专题：解三角形．分析：利用余弦定理表示出cosC，将已知等式变形后代入求出cosC的值，即可确定出C的度数．解答：解：∵a2+b2=c2+ba，即a2+b2﹣c2=ab，∴由余弦定理得：cosC==，∴∠C=45°．故选：C．点评：此题考查了余弦定理，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键．4．数列{a n}的前n项和为S n，若，则S5=( )A．1 B．C．D．考点：数列的求和．专题：计算题．分析：由=，利用裂项求和法能求出S5．解答：解：∵=，∴S5=a1+a2+a3+a4+a5==1﹣=．故选D．点评：本题考查数列前n项和的求法，是基础题．解题是要认真审题，注意裂项求法的灵活运用．5．设0＜b＜a＜1，则下列不等式成立的是( )A．ab＜b2＜1 B．C．2b＜2a＜2 D．a2＜ab＜1考点：基本不等式．专题：分析法．分析：首先对于这类选择题可以通过排除分析法作答．对于条件0＜b＜a＜1，然后根据基本不等式，各种函数的单调性的知识一个一个选项排除，即可得到答案．解答：解：对于A：ab＜b2＜1，因为0＜b＜a＜1，则乘以b不变号，即b2＜ab．故A错误．对于B：可直接根据对数函数在的单调性判断B错误．对于C：因为y=2x是单调递增函数，且0＜b＜a＜1，所以2b＜2a＜21，即2b＜2a＜2．故C正确．对于D：因为0＜b＜a＜1，则乘以a不变号，即ab＜a2．故D错误．所以答案选C．点评：此题主要考查基本不等式的应用，其中涉及到函数单调性和函数在区间值域的知识．属于综合性的问题，需要一个一个选项去分析排除．此外这类题容易出错，做题时切忌谨慎．6．不等式（1﹣x）（2+x）＞0的解集为( )A．（﹣2，1）B．（﹣∞，﹣2）∪（1，+∞）C．（﹣∞，1）∪（2，+∞）D．（﹣1，2）考点：一元二次不等式的解法．专题：不等式的解法及应用．分析：根据一元二次不等式的解集与方程根的关系，结合二次函数可得不等式的解集解答：解：不等式（1﹣x）（2+x）＞0，∴不等式（x﹣1）（x+2）＜0，∴方程（x﹣1）（x+2）=0的两根为﹣2，1，∴不等式（1﹣x）（2+x）＞0的解集为（﹣2，1），故选：A．点评：本题考查了一元二次不等式的解法，利用了因式分解法，找到与对应方程和二次函数的关系容易得到；属于基础题7．已知x＞2，则x+的最小值为( )A．6 B．4 C．3 D．2考点：基本不等式．专题：不等式的解法及应用．分析：由题意可得x﹣2＞0，可得x+=x﹣2++2，由基本不等式可得．解答：解：∵x＞2，∴x﹣2＞0，∴x+=x﹣2++2，≥2+2=6，当且仅当x﹣2=即x=4时，x+取最小值6，故选：A．点评：本题考查基本不等式求最值，凑出可用基本不等式的形式是解决问题的关键，属基础题．8．对任意的实数x，不等式mx2﹣mx﹣1＜0恒成立，则实数m的取值范围是( ) A．（﹣4，0）B．（﹣4，0] C．[﹣4，0] D．[﹣4，0）考点：函数恒成立问题．专题：计算题．分析：当m=0时，不等式显然成立；当m≠0时，根据二次函数图象的性质得到m的取值范围．两者取并集即可得到m的取值范围．解答：解：当m=0时，mx2﹣mx﹣1=﹣1＜0，不等式成立；设y=mx2﹣mx﹣1，当m≠0时函数y为二次函数，y要恒小于0，抛物线开口向下且与x轴没有交点，即要m＜0且△＜0得到：解得﹣4＜m＜0．综上得到﹣4＜m≤0．故选B．点评：本题以不等式恒成立为平台，考查学生会求一元二次不等式的解集．同时要求学生把二次函数的图象性质与一元二次不等式结合起来解决数学问题．9．已知非负实数x、y满足2x+3y﹣8≤0且3x+2y﹣7≤0，则x+y的最大值是( ) A．B．C．3 D．2考点：简单线性规划．专题：数形结合．分析：①画可行域②z为目标函数纵截距③画直线0=x+y，平移直线过（1，2）时z有最大值解答：解：画可行域如图，z为目标函数z=x+y，可看成是直线z=x+y的纵截距，画直线0=x+y，平移直线过A（1，2）点时z有最大值3．故选C．点评：本题考查线性规划问题，难度较小．目标函数有唯一最优解是我们最常见的问题，这类问题一般要分三步：画出可行域、求出关键点、定出最优解．10．不等式组表示的区域为D，点P （0，﹣2），Q （0，0），则( ) A．P∉D，且Q∉D B．P∉D，且Q∈D C．P∈D，且Q∉D D．P∈D，且Q∈D考点：二元一次不等式（组）与平面区域；元素与集合关系的判断．专题：综合题．分析：将两个点的坐标分别代入不等式组，判断点的坐标是否满足不等式组，若满足则点在区域内；若不满足说明点不在区域内．解答：解：将P的坐标代入不等式组得所以P的坐标满足不等式组，即P在区域D内同样将Q的坐标代入不等式组得，所以Q的坐标不满足不等式组，即Q不在区域D内故选C点评：本题考查判断点是否在区域内，只要判断点的坐标是否满足区域对应的不等式组即可．也可以画出区域及点，再判断点与区域的位置关系．11．设a＞0，b＞0．若是3a与3b的等比中项，则+的最小值为( ) A．4 B．6 C．2D．2考点：基本不等式；等比数列的通项公式．专题：不等式的解法及应用．分析：由题意易得正数a、b满足a+b=1，进而可得+=（+）（a+b）=2++，由基本不等式求最值可得．解答：解：a＞0，b＞0，是3a与3b的等比中项，∴3=3a•3b=3a+b，∴a+b=1，∴+=（+）（a+b）=2++≥2+2=4，当且仅当=即a=b=时取等号，故选：A．点评：本题考查基本不等式求最值，涉及等比数列的性质，属基础题．12．若关于x的方程x2+ax+a2﹣1=0有一正根和一负根，则实数a的取值范围是( ) A．﹣＜a＜﹣1 B．﹣2＜a＜2 C．﹣1＜a＜1 D．1＜a＜考点：一元二次方程的根的分布与系数的关系．专题：函数的性质及应用．分析：由题意可得△=a2﹣4（a2﹣1）＞0，且两根之积 a2﹣1＜0，由此求得a的范围．解答：解：由题意可得△=a2﹣4（a2﹣1）＞0，且两根之积a2﹣1＜0，求得﹣1＜a＜1，故选：C．点评：本题主要考查一元二次方程根的分布与系数的关系，二次函数的性质，属于基础题．二、填空题：（该题共4小题，每小题5分，共20分．把答案填在题中横线上．）13．a克糖水中含有b克塘（a＞b＞0），若在糖水中加入x克糖，则糖水变甜了．试根据这个事实提炼出一个不等式：（a＞b＞0）．考点：不等关系与不等式．专题：不等式的解法及应用．分析：利用糖水的浓度可得（a＞b＞0）即可．解答：解：由a克糖水中含有b克塘（a＞b＞0）可得糖水的浓度为；在糖水中加入x克糖，可得糖水的浓度为．∵糖水变甜了，于是可得＞；化为（a＞b＞0）．故答案为（a＞b＞0）．点评：本题考查了溶液的浓度，属于基础题．14．若S n为等比数列{a n}的前n项和，8a2+a5=0，则S6：S3=﹣7．考点：等比数列的通项公式．专题：等差数列与等比数列．分析：根据等比数列的通项公式以及前n项和公式进行求解即可．解答：解：由8a2+a5=0得a5=﹣8a2，即，∴q=﹣2，则===1+q3=1﹣8=﹣7，故答案为：﹣7．点评：本题主要考查等比数列的通项公式和前n项和公式的应用，根据条件求出公比是解决本题的关键．15．已知点P（x，y）的坐标x，y满足，则x2+y2﹣4x的最大值是12．考点：简单线性规划．专题：不等式的解法及应用．分析：先根据约束条件画出可行域，再利用几何意义求最值Z=x2+y2﹣4x的最大表示动点到定点（2，0）点的距离的平方有关，只需求出可行域内的动点到该点的距离最大值即可．解答：解：作出可行域，如图：令z=x2+y2﹣4x=（x﹣2）2+y2﹣4，∵（x﹣2）2+y2所表示的几何意义是动点到定点（2，0）的距离的平方，作出可行域：易知当为A点时取得目标函数的最大值，可知A点的坐标为（﹣2，0），代入目标函数中，可得z max=12．故答案为：12．点评：本题属于线性规划中的延伸题，对于可行域不要求线性目标函数的最值，而是求可行域内的点与原点之间的距离问题．16．设△ABC的内角A，B，C所对边的长分别为a，b，c，则下列命题正确的是①②③（写出所有正确命题的编号）．①若ab＞c2，则C＜②若a+b＞2c，则C＜③若a3+b3=c3，则C＜④若（a+b）c＜2ab，则C＞⑤若（a2+b2）c2＜2a2b2，则C＞．考点：命题的真假判断与应用；余弦定理的应用．专题：证明题；压轴题．分析：①利用余弦定理，将c2放大为ab，再结合均值定理即可证明cosC＞，从而证明C ＜；②利用余弦定理，将c2放大为（）2，再结合均值定理即可证明cosC＞，从而证明C＜；③利用反证法，假设C≥时，推出与题设矛盾，即可证明此命题正确；④⑤只需举反例即可证明其为假命题，可举符合条件的等边三角形解答：解：①ab＞c2⇒cosC=＞=⇒C＜，故①正确；②a+b＞2c⇒cosC=＞=≥=⇒C＜，故②正确；③当C≥时，c2≥a2+b2⇒c3≥ca2+cb2＞a3+b3与a3+b3=c3矛盾，故③正确；④举出反例：取a=b=c=2，满足（a+b）c≤2ab得：C=＜，故④错误；⑤举出反例：取a=b=c=，满足（a2+b2）c2≤2a2b2，此时有C=，故⑤错误故答案为①②③点评：本题主要考查了解三角形的知识，放缩法证明不等式的技巧，反证法和举反例法证明不等式，有一定的难度，属中档题三、解答题：（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．）17．设锐角三角形ABC的内角A，B，C的对边分别为a，b，c，a=2bsinA（Ⅰ）求B的大小；（Ⅱ）求cosA+sinC的取值范围．考点：正弦定理；正弦函数的定义域和值域．专题：计算题．分析：（1）先利用正弦定理求得sinB的值，进而求得B．（2）把（1）中求得B代入cosA+sinC中利用两角和公式化简整理，进而根据A的范围和正弦函数的性质求得cosA+sinC的取值范围．解答：解：（Ⅰ）由a=2bsinA，根据正弦定理得sinA=2sinBsinA，所以，由△ABC为锐角三角形得．（Ⅱ）===．由△ABC为锐角三角形知，0＜A＜，，所以．由此有≤，所以，cosA+sinC的取值范围为（，]．点评：本题主要考查了正弦定理得应用和三角函数中两角和公式的运用．涉及了正弦函数的性质，考查了学生对三角函数知识的把握．18．（Ⅰ）比较x2+y2+1与2（x+y﹣1）的大小；（Ⅱ）已知a，b∈R+，求证：（a+b）（a2+b2）（a3+b3）≥8a3b3．考点：不等式比较大小．专题：不等式．分析：（Ⅰ）作差配方即可比较出大小；（Ⅱ）利用基本不等式即可得到结论．解答：解：（Ⅰ）x2+y2+1﹣2（x+y﹣1）=（x﹣1）2+（y﹣1）2+1＞0，∴x2+y2+1＞2（x+y﹣1）；（Ⅱ）（a+b）（a2+b2）（a3+b3）≥2•2ab•2≥8a3b3，当且仅当a=b时取等号．问题得以证明．点评：本题考查了“作差法”、“配方法”“基本不等式”比较数的大小，属于基础题19．已知数列{a n}满足a1=1，a2=2，a n+2=，n∈N*．（1）令b n=a n+1﹣a n，证明：{b n}是等比数列；（2）求{a n}的通项公式．考点：等比关系的确定；数列递推式．专题：等差数列与等比数列．分析：（1）先令n=1求出b1，然后当n≥2时，求出a n+1的通项代入到b n中化简可得{b n}是以1为首项，为公比的等比数列得证；（2）由（1）找出b n的通项公式，当n≥2时，利用a n=a1+（a2﹣a1）+（a3﹣a2）++（a n﹣a n ﹣1）代入并利用等比数列的前n项和的公式求出即可得到a n的通项，然后n=1检验也符合，所以n∈N，a n都成立．解答：解：（1）证b1=a2﹣a1=1，当n≥2时，所以{b n}是以1为首项，为公比的等比数列．（2）解由（1）知，当n≥2时，a n=a1+（a2﹣a1）+（a3﹣a2）++（a n﹣a n﹣1）=1+1+（﹣）+…+==1+[1﹣（﹣）n﹣1]=，当n=1时，．所以．点评：考查学生会确定一个数列为等比数列，会利用数列的递推式的方法求数列的通项公式．以及会利用等比数列的前n项和的公式化简求值．20．（1）已知集合A={x|x2﹣x﹣6＞0}，B={x|0＜x+a＜4}，若A∩B=∅，求实数a的取值范围；（2）已知f（x）=﹣3x2+a（6﹣a）x+b．当不等式f（x）＞0的解集为（﹣1，3）时，求实数a，b的值．考点：其他不等式的解法；交集及其运算．专题：计算题；不等式的解法及应用．分析：（1）利用二次不等式的解法求出集合A，不等式组求解集合B，通过A∩B=∅，列出关系式求解即可．（2）通过二次不等式的解，推出对应方程的根，利用韦达定理求解a，b的值即可．解答：解：（1）A={x|x＜﹣2或x＞3}，B={x|﹣a＜x＜4﹣a} …∵A∩B=φ，∴∴1≤a≤2 …．（2）∵f（x）＞0的解为﹣1＜x＜3，∴x=﹣1和x=3是﹣3x2+a（6﹣a）x+b=0的两根…∴，解得…．点评：本题考查二次不等式的解法，不等式组的求法，转化思想的应用，考查计算能力．21．本公司计划2008年在甲、乙两个电视台做总时间不超过300分钟的广告，广告总费用不超过9万元．甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟．假定甲、乙两个电视台为该公司所做的每分钟广告，能给公司带来的收益分别为0.3万元和0.2万元．问该公司如何分配在甲、乙两个电视台的广告时间，才能使公司的收益最大，最大收益是多少万元？考点：简单线性规划的应用．分析：利用线性规划的思想方法解决某些实际问题属于直线方程的一个应用．本题主要考查找出约束条件与目标函数，准确地描画可行域，再利用图形直线求得满足题设的最优解．解答：解：设公司在甲电视台和乙电视台做广告的时间分别为x分钟和y分钟，总收益为z元，由题意得目标函数为z=3000x+2000y．二元一次不等式组等价于作出二元一次不等式组所表示的平面区域，即可行域．如图，作直线l：3000x+2000y=0，即3x+2y=0．平移直线l，从图中可知，当直线l过M点时，目标函数取得最大值．联立解得x=100，y=200．∴点M的坐标为（100，200）．∴z max=3000x+2000y=700000（元）答：该公司在甲电视台做100分钟广告，在乙电视台做200分钟广告，公司的收益最大，最大收益是70万元．点评：用图解法解决线性规划问题时，分析题目的已知条件，找出约束条件和目标函数是关键，可先将题目中的量分类、列出表格，理清头绪，然后列出不等式组（方程组）寻求约束条件，并就题目所述找出目标函数．然后将可行域各角点的值一一代入，最后比较，即可得到目标函数的最优解．22．若S n是公差不为0的等差数列{a n}的前n项和，且S1，S2，S4成等比数列．（1）求等比数列S1，S2，S4的公比；（2）若S2=4，求{a n}的通项公式；（3）设，T n是数列{b n}的前n项和，求使得对所有n∈N*都成立的最小正整数m．考点：等差数列与等比数列的综合；数列与不等式的综合．专题：综合题；等差数列与等比数列．分析：（1）利用数列{a n}为等差数列，S1，S2，S4成等比数列．可求出首项与公差的关系，即可求得公比；（2）由S2=4，结合（1）的结论，即可求{a n}的通项公式；（3）利用裂项法求数列{b n}的前n项和，确定T n＜，从而可得不等式，即可求得使得对所有n∈N*都成立的最小正整数m．解答：解：（1）∵数列{a n}为等差数列，∴S1=a1，S2=2a1+d，S4=4a1+6d，∵S1，S2，S4成等比数列，∴S1•S4=S22，∴，∴∵公差d不等于0，∴d=2a1∴；（2）∵S2=4，∴2a1+d=4，又d=2a1，∴a1=1，d=2，∴a n=2n﹣1．（3）∵∴…=要使对所有n∈N*恒成立，∴，∴m≥30，∵m∈N*，∴m的最小值为30．点评：本题考查等差数列与等比数列的结合，考查数列的通项与求和，考查恒成立问题，正确求和是关键．。

青海省师大附二中2014-2015学年高一(下)第一次月考数学

2014-2015学年青海省师大附二中高一（下）第一次月考数学一、选择题（共12小题，每小题5分，满分60分）1．（5分）（2015春•青海校级月考）数列1×4，2×5，3×6，…，n（n+3），…则它的前n项和S n=（）A．n（n+1）（n+2）B．n（n+1）（n+3）C．n（n+1）（n+4）D．n（n+1）（n+5）考点：数列的求和．专题：等差数列与等比数列．分析：由于a n=n（n+3）=n2+3n，12+22+32+…+n2=．利用等差数列的前n项和公式即可得出．解答：解：∵a n=n（n+3）=n2+3n，12+22+32+…+n2=．∴此数列的前n项和S n=12+22+32+…+n2+3（1+2+…+3）．=+3×=．故选：D．点评：本题考查了等差数列的通项公式及其前n项和公式、12+22+32+…+n2=，考查了推理能力与计算能力，属于中档题2．（5分）（2009秋•荣成市校级期中）下列判断正确的是（）A．a=7，b=14，A=30°，有两解 B． a=30，b=25，A=150°，有一解C．a=6，b=9，A=45°，有两解D． a=9，b=10，A=60°，无解考点：正弦定理．专题：计算题．分析：由各选项中A的度数，求出sinA的值，再由a与b的值，利用正弦定理求出sinB的值，由a 与b的大小关系，利用大边对大角判断出A与B的大小关系，即可判断出B有一解、两解或无解，得到正确的选项．解答：解：A、∵a=7，b=14，A=30°，∴由正弦定理=得：sinB==1，又B为三角形的内角，∴B=90°，C=60°，c=7，则此时三角形只有一解，此选项错误；B、∵a=30，b=25，A=150°，∴由正弦定理=得：sinB==，∵a＞b，∴150°＞A＞B，则此时B只有一解，本选项正确；C、∵a=6，b=9，A=45°，∴∴由正弦定理=得：sinB==＞，∵b＞a，∴B＞A=45°，∴此时B只有一解，本选项错误；D、∵a=9，b=10，A=60°，∴∴由正弦定理=得：sinB==＞，∵a＜b，∴60°=A＜B，此时B有两解，本选项错误，故选B点评：此题考查了正弦定理，以及三角形的边角关系，熟练掌握正弦定理是解本题的关键．3．（5分）（2014秋•济宁期末）设S n为等比数列{a n}的前n项和，8a2+a5=0，则=（）A．﹣11 B．﹣8 C．5D． 11考点：等比数列的性质．专题：转化思想．分析：由等比数列的前n项和公式，故==1+q2，由此知，应该有方程8a2+a5=0求出q的值，再代入求值，选出正确选项解答：解：∵Sn为等比数列{a n}的前n项和，8a2+a5=0∴8a1q+a1q4=0又数列是等比数列，首项不为0∴8q+q4=0，又q不为零，故有q=﹣2∴===5故选C点评：本题考查等比数列的性质，解题的关键是由8a2+a5=0求出公比q的值，再由等比数列的求和公式将用q表示出来，即可求出值，本题考查了转化的思想及计算能力，4．（5分）（2013秋•醴陵市校级期中）已知点（n，a n）（n∈N*）都在直线3x﹣y﹣24=0上，那么数列{a n}中有（）A．a7+a9＞0 B．a7+a9＜0 C．a7+a9=0 D．a7•a9=0考点：等差数列的性质．专题：等差数列与等比数列．分析：由题意可得a n=3n﹣24，进而由等差数列的性质可得a7+a9=2a8=0解答：解：∵点（n，a n）都在直线3x﹣y﹣24=0上，∴3n﹣a n﹣24=0，∴a n=3n﹣24，∴数列{a n}为等差数列，且a8=0，∴由等差数列的性质可得a7+a9=2a8=0故选：C点评：本题考查等差数列的性质，属基础题．5．（5分）（2007•海南）已知a，b，c，d成等比数列，且抛物线y=x2﹣2x+3的顶点为（b，c）则ad=（）A． 3 B． 2 C． 1 D．﹣2考点：等比数列的通项公式．专题：计算题．分析：通过配方，可得抛物线y=x2﹣2x+3的顶点为（1，2），即b=1，c=2，由等比数列的性质可得ad=bc，故问题可求．解答：解：∵y=x2﹣2x+3=（x﹣1）2+2，∴抛物线y=x2﹣2x+3的顶点为（1，2），∴b=1，c=2，又∵a，b，c，d成等比数列，∴ad=bc=2，故选B．点评：本题综合考查了二次函数的顶点和等比数列的性质，比较简单．6．（5分）（2015春•双流县校级期中）在△ABC中，若a=2bsinA，则B等于（）A．30° B．60° C．30°或150°D． 60°或120°考点：正弦定理．专题：计算题．分析：把已知的等式变形后，再利用正弦定理列出关系式，等量代换求出sinB的值，由B为三角形的内角，利用特殊角的三角函数值即可求出B的度数．解答：解：∵，∴，∵根据正弦定理，∴=，∴sinB=，又B为三角形的内角，∴B=60°或120°故选D点评：本题主要考查正弦定理的运用．正弦定理建立了三角形的边角关系，故在三角形边、角问题中常利用正弦定理来解决，熟练掌握正弦定理是解本题的关键．7．（5分）（2014秋•济宁期末）数列{a n}的通项公式a n=n2+n，则数列{}的前9项和为（）A．B．C．D．考点：数列的求和．专题：等差数列与等比数列．分析：由a n=n2+n，可得=，利用“裂项求和”即可得出．解答：解：∵a n=n2+n，∴=，则数列{}的前9项和=+…+=1﹣=．故选：A．点评：本题考查了“裂项求和”方法，考查了推理能力与计算能力，属于基础题．8．（5分）（2015春•青海校级月考）在△ABC中，A=60°，a=3，则=（）A．B．C．D．考点：正弦定理．专题：解三角形．分析：由条件利用正弦定理可得=2R 的值，再利用正弦定理花间要求的式子，从而得到结果．解答：解：由条件利用正弦定理可得=2R==2，∴==2R=2，故选：D．点评：本题主要考查正弦定理的应用，属于基础题．9．（5分）（2015•南昌校级二模）已知各项均为正数的等比数列{a n}中，3a1，成等差数列，则=（）A．27 B． 3 C．﹣1或3 D． 1或27考点：等比数列的性质．专题：等差数列与等比数列．分析：由题意可得公比q的方程，解得方程可得q，可得=q3，代值计算可得．解答：解：设等比数列{a n}的公比为q，由题意可得a3=3a1+2a2，∴a1q2=3a1+2a1q，即q2=3+2q解得q=3，或q=﹣1（舍去），∴==q3=27故选：A点评：本题考查等比数列的通项公式和性质，属基础题．10．（5分）（2014•衡阳县校级模拟）在△ABC中，若，则△ABC是（）A．等腰三角形B．等边三角形C．直角三角形D．等腰三角形或直角三角形考点：正弦定理；三角形的形状判断．专题：计算题．分析：利用正弦定理化简已知等式，变形后利用二倍角的正弦函数公式化简，得到A与B相等或互余，即可判断出三角形ABC的形状．解答：解：由正弦定理得：==，∴sinAcosA=sinBcosB，即sin2A=sin2B，∴sin2A=sin2B，∴2A=2B或2A+2B=180°，即A=B或A+B=90°，则△ABC为等腰三角形或直角三角形．故选D点评：此题考查了正弦定理，以及三角形形状的判断，熟练掌握正弦定理是解本题的关键．11．（5分）（2015春•青海校级月考）公比为2的等比数列{a n}的各项都是正数，且a3a9=16，则log2=（）A． 4 B． 5 C． 6 D． 7考点：等比数列的性质．专题：等差数列与等比数列．分析：根据等比数列的通项公式结合对数的基本运算进行求解即可．解答：解：∵公比为2的等比数列{a n}的各项都是正数，且a3a9=16，∴a6a6=16，即a6=4，则a10=a6•24=4•24=26，则log2=log226=6，故选：C．点评：本题主要考查对数的计算，以及等比数列的通项公式的应用，根据等比数列的性质是解决本题的关键．12．（5分）（2015春•青海校级月考）已知两座灯塔A和B与海洋观察站C的距离都等于a km，灯塔A在观察站C的北偏东20°，灯塔B在观察站C的南偏东40°，则灯塔A与B的距离为（）A． a km B．a km C． a km D． 2a km考点：解三角形的实际应用．专题：计算题；解三角形．分析：先根据题意求得∠ACB，进而根据余弦定理求得AB．解答：解：依题意知∠ACB=180°﹣20°﹣40°=120°，在△ABC中，由余弦定理知AB==．即灯塔A与灯塔B的距离为km．故选A点评：本题给出实际应用问题，求海洋上灯塔A与灯塔B的距离．着重考查了三角形内角和定理和运用余弦定理解三角形等知识，属于基础题．二.填空题：（该题共4小题，每小题5分，共20分．把答案填在题中横线上．）13．（5分）（2015春•青海校级月考）在△ABC的三内角A、B、C的对应边分别为a，b，c，当a2+c2≥b2+ac 时，角B的取值范围为（0°，60°，故答案为：（0°，60°﹣（n+1）2+24（n+1）﹣（﹣n2+24n）=﹣2（n+1）+25，∴当n≥2时，a n=﹣2n+25，又∵a1=S1=﹣1+24=23满足上式，∴a n=﹣2n+25；（2）∵S n=﹣n2+24n=﹣（n﹣12）2+144，∴当n=12时S n达到最大，最大值是144．点评：本题考查等差数列的前n项和，注意解题方法的积累，属于中档题．19．（12分）（2009•北京）在△ABC中，角A，B，C的对边分别为，．（Ⅰ）求sinC的值；（Ⅱ）求△ABC的面积．考点：正弦定理；同角三角函数基本关系的运用．专题：计算题．分析：（Ⅰ）由cosA=得到A为锐角且利用同角三角函数间的基本关系求出sinA的值，根据三角形的内角和定理得到C=π﹣﹣A，然后将C的值代入sinC，利用两角差的正弦函数公式化简后，将sinA和cosA代入即可求出值；（Ⅱ）要求三角形的面积，根据面积公式S=absinC和（Ⅰ）可知公式里边的a不知道，所以利用正弦定理求出a即可．解答：解：（Ⅰ）∵A、B、C为△ABC的内角，且＞0，∴A为锐角，则sinA==∴∴sinC=sin（﹣A）=cosA+sinA=；（Ⅱ）由（Ⅰ）知sinA=，sinC=，又∵，∴在△ABC中，由正弦定理，得∴a==，∴△ABC的面积S=absinC=×××=．点评：考查学生灵活运用正弦定理、三角形的面积公式及同角三角函数间的基本关系化简求值．灵活运用两角和与差的正弦函数公式化简求值．20．（12分）（2015春•青海校级月考）已知等差数列{a n}的前n项和为S n，且a2=2，S6=21（1）求数列{a n}的通项公式；（2）设b n=a n•2n，求数列{b n}的前n项和T n．考点：数列的求和；等差数列的性质．专题：等差数列与等比数列．分析：（1）设等差数列{a n}的公差为d，利用等差数列的通项公式及其前n项和公式即可得出；（2）b n=a n•2n=n•2n．利用“错位相减法”及其等比数列的前n项和公式即可得出．解答：解：（1）设等差数列{a n}的公差为d，∵a2=2，S6=21，∴，解得，∴a n=1+（n﹣1）=n．（2）b n=a n•2n=n•2n．∴数列{b n}的前n项和T n=2+2×22+3×23+…+n•2n，2T n=22+2×23+…+（n﹣1）×2n+n•2n+1，∴﹣T n=2+22+23+…+2n﹣n•2n+1=﹣n•2n+1=（1﹣n）•2n+1﹣2，∴T n=（n﹣1）×2n+1+2．点评：本题考查了“错位相减法”、等差数列与等比数列的通项公式及其前n项和公式，考查了推理能力与计算能力，属于中档题21．（12分）（2012•辽宁）在△ABC中，角A、B、C的对边分别为a，b，c．角A，B，C成等差数列．（Ⅰ）求cosB的值；（Ⅱ）边a，b，c成等比数列，求sinAsinC的值．考点：数列与三角函数的综合．专题：计算题；综合题．分析：（Ⅰ）在△ABC中，由角A，B，C成等差数列可知B=60°，从而可得cosB的值；（Ⅱ）（解法一），由b2=ac，cosB=，结合正弦定理可求得sinAsinC的值；（解法二），由b2=ac，cosB=，根据余弦定理cosB=可求得a=c，从而可得△ABC为等边三角形，从而可求得sinAsinC的值．解答：解：（Ⅰ）由2B=A+C，A+B+C=180°，解得B=60°，∴cosB=；…6分（Ⅱ）（解法一）由已知b2=ac，根据正弦定理得sin2B=sinAsinC，又cosB=，∴sinAsinC=1﹣cos2B=…12分（解法二）由已知b2=ac及cosB=，根据余弦定理cosB=解得a=c，∴B=A=C=60°，∴sinAsinC=…12分点评：本题考查数列与三角函数的综合，着重考查等比数列的性质，考查正弦定理与余弦定理的应用，考查分析转化与运算能力，属于中档题．22．（12分）（2013•浙江）在公差为d的等差数列{a n}中，已知a1=10，且a1，2a2+2，5a3成等比数列．（Ⅰ）求d，a n；（Ⅱ）若d＜0，求|a1|+|a2|+|a3|+…+|a n|．考点：数列的求和；等差数列的通项公式；等比数列的性质．专题：等差数列与等比数列．分析：（Ⅰ）直接由已知条件a1=10，且a1，2a2+2，5a3成等比数列列式求出公差，则通项公式a n可求；（Ⅱ）利用（Ⅰ）中的结论，得到等差数列{a n}的前11项大于等于0，后面的项小于0，所以分类讨论求d＜0时|a1|+|a2|+|a3|+…+|a n|的和．解答：解：（Ⅰ）由题意得，即，整理得d2﹣3d﹣4=0．解得d=﹣1或d=4．当d=﹣1时，a n=a1+（n﹣1）d=10﹣（n﹣1）=﹣n+11．当d=4时，a n=a1+（n﹣1）d=10+4（n﹣1）=4n+6．所以a n=﹣n+11或a n=4n+6；（Ⅱ）设数列{a n}的前n项和为S n，因为d＜0，由（Ⅰ）得d=﹣1，a n=﹣n+11．则当n≤11时，．当n≥12时，|a1|+|a2|+|a3|+…+|a n|=﹣S n+2S11=．综上所述，|a1|+|a2|+|a3|+…+|a n|=．点评：本题考查了等差数列、等比数列的基本概念，考查了等差数列的通项公式，求和公式，考查了分类讨论的数学思想方法和学生的运算能力，是中档题．。

青海师范大学附属第二中学2014-2015学年高一下学期第一次月考化学试卷

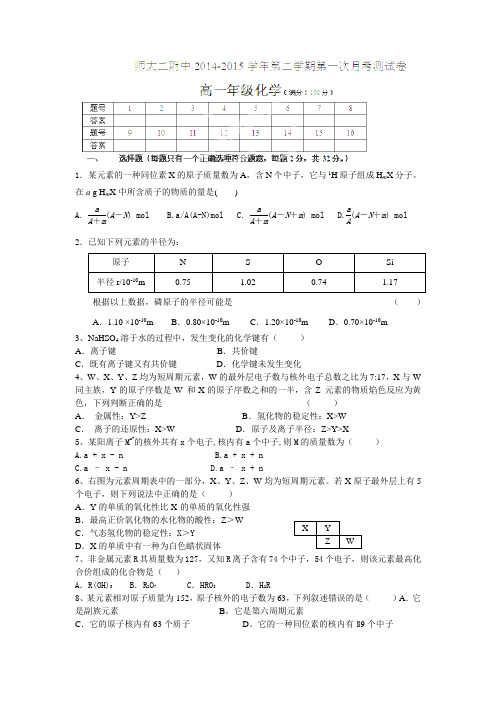
1．某元素的一种同位素X 的原子质量数为A ，含N 个中子，它与1H 原子组成H m X 分子。

在a g H m X 中所含质子的物质的量是( )A. aA ＋m (A －N ) mol B.a/A(A-N)mol C. aA ＋m (A －N ＋m ) mol D.aA(A －N ＋m ) mol 2．已知下列元素的半径为：根据以上数据，磷原子的半径可能是（） A ．1.10 ×10-10m B ．0.80×10-10m C ．1.20×10-10m D ．0.70×10-10m3、NaHSO 4溶于水的过程中，发生变化的化学键有（）A ．离子键B ．共价键C ．既有离子键又有共价键D ．化学键未发生变化4、W 、X 、Y 、Z 均为短周期元素，W 的最外层电子数与核外电子总数之比为7:17，X 与W 同主族，Y 的原子序数是W 和X 的原子序数之和的一半，含Z 元素的物质焰色反应为黄色，下列判断正确的是（）A ．金属性：Y>ZB ．氢化物的稳定性：X>WC ．离子的还原性：X>WD ．原子及离子半径：Z>Y>X5、某阳离子M n+的核外共有x 个电子,核内有a 个中子,则M 的质量数为（）A.a + x - nB.a + x + nC.a – x - nD.a – x + n6、右图为元素周期表中的一部分，X 、Y 、Z 、W 均为短周期元素。

若X 原子最外层上有5个电子，则下列说法中正确的是（）A ．Y 的单质的氧化性比X 的单质的氧化性强B C ．气态氢化物的稳定性：X ＞Y D ．X 7、非金属元素R 其质量数为127合价组成的化合物是（）A ．R(OH)3B ．R 2O 7C ．HRO 3D ．H 2R8、某元素相对原子质量为152，原子核外的电子数为63，下列叙述错误的是（）A ．它是副族元素 B 。

青海省青海师范大学附属第二中学高一化学下学期期中试题

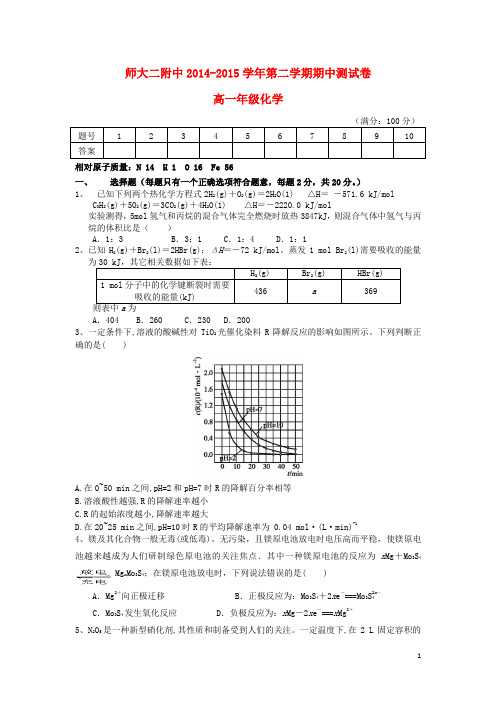
师大二附中2014-2015学年第二学期期中测试卷高一年级化学题号 1 2 3 4 5 6 7 8 9 10 答案相对原子质量：N 14 H 1 O 16 Fe 56一、选择题（每题只有一个正确选项符合题意，每题2分，共20分。

）1、已知下列两个热化学方程式2H2(g)＋O2(g)＝2H2O(1) △H＝－571.6 kJ/molC3H8(g)＋5O2(g)＝3CO2(g)＋4H2O(1) △H＝－2220.0 kJ/mol实验测得，5mol氢气和丙烷的混合气体完全燃烧时放热3847kJ，则混合气体中氢气与丙烷的体积比是（）A．1：3 B．3：1 C．1：4 D．1：12、已知H2(g)＋Br2(l)＝2HBr(g)；ΔH＝－72 kJ/mol。

蒸发1 mol Br2(l)需要吸收的能量H2(g) Br2(g) HBr(g)1 mol分子中的化学键断裂时需要436 a369吸收的能量(kJ)A．404 B．260 C．230 D．2003、一定条件下,溶液的酸碱性对TiO2光催化染料R降解反应的影响如图所示。

下列判断正确的是( )A.在0~50 min之间,pH=2和pH=7时R的降解百分率相等B.溶液酸性越强,R的降解速率越小C.R的起始浓度越小,降解速率越大D.在20~25 min之间,pH=10时R的平均降解速率为0.04 mol·(L·min)-14、镁及其化合物一般无毒(或低毒)、无污染，且镁原电池放电时电压高而平稳，使镁原电池越来越成为人们研制绿色原电池的关注焦点．其中一种镁原电池的反应为x Mg＋Mo3S4 Mg x Mo3S4；在镁原电池放电时，下列说法错误的是( )A．Mg2＋向正极迁移 B．正极反应为：Mo3S4＋2x e－===Mo3S2x－4C．Mo3S4发生氧化反应 D．负极反应为：x Mg－2x e－===x Mg2＋5、N2O5是一种新型硝化剂,其性质和制备受到人们的关注。

青海省师范大学附属第二中学高一数学下学期第一次月考试题

青海省师范大学附属第二中学2014-2015学年高一数学下学期第一次月考试题1. 数列14⨯， 25⨯，36⨯，…，(3)n n +，…则它的前n 项和n S =（）A ．1(1)(2)3n n n ++B ．1(1)(3)3n n n ++C ．1(1)(4)3n n n ++D ．1(1)(5)3n n n ++2. 不解三角形，确定下列判断中正确的是（）A. ο30,14,7===A b a ，有两解 B. ο150,25,30===A b a ,有一解 C. ο45,9,6===A b a ，有两解 D. ο60,10,9===A c b ，无解 3. 设n S 是等比数列{}n a 的前n 项和，若2580a a +=，则42S S 的值为( ) A ．-3 B ．3 C ．-5 D ．54. 已知点）,n （n a 都在直线024x 3=--y 上，那么在数列{}n a 中有（）A ．0a 97>+a B. 0a 97<+a C. 0a 97=+a D. 0a 97=•a 5. 已知d c b a ,,,成等比数列，且曲线322+-=x xy 的顶点是),(c b ，则ad 等于( )A ．3B ．2C ．1D ．-2 6. 在ABC ∆中，若A b a sin 23=，则B 等于（）A. ο30B. ο60C.ο30或ο150D. ο60或ο1207. 数列{}n a 的通项公式2n a n n =+，则数列1n a ⎧⎫⎨⎬⎩⎭的前9项和为( )A ．910B ．89C ．109D ．11108. 在ABC ∆中，ο60=A ,3=a ，则=++++CB A cb a sin sin sin （）A.338 B. 3392 C. 3326 D. 32 9. 已知各项均为正数的等比数列}{n a 中，13213,,22a a a 成等差数列，则=++1081311a a a a （） A ．27B ．3C ．1-或3D ．1或2710. 在ABC ∆中，已知abB A =cos cos ，则ABC ∆的形状是（）A.直角三角形B.等腰三角形C.等边三角形D.等腰或直角三角形 11. 公比为2的等比数列{}n a 的各项都是正数，且16a a 93=，则10a2log =（）A ．4B ．5C ．6D ．712. 已知两灯塔A 和B 与海洋观测站C 的距离都等于a km ，灯塔A 在观测站C 的北偏东20°，灯塔B 在观测站C 的南偏东40°，则灯塔A 与灯塔B 的距离为( ) A ．a km B.3a km C.2a km D ．2a km二填空题：（该题共4小题，每小题5分，共20分．把答案填在题中横线上．）13. 在△ABC 的三内角A 、B 、C 的对应边分别为a ，b ，c ，当ac b c a +≥+222时，角B 的取值范围为14.等差数列{a n }的前m 项和为30，前2m 项为100，则它的前3m 项和为________ 15. 在△ABC 中，sinA ∶sinB ∶sinC=2∶3∶4，则B 的余弦值为 16. 等差数列{}n a 和}{b n 的前n 项和分别为n n 和B A ，若32n 1-3n n n +=B A ，则1313b a 的值为_____三、解答题：（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．） 17.( 本小题满分10分)在ABC ∆中，角,,A B C 所对的边分别为,,a b c ，已知),cos ,sin (sin m A B C =→0m 且),2,(n =•=→→→n c b（1）求A(2)若求,2,32a ==c ABC ∆的面积18．(本小题满分12分) 已知数列{}n a 的前n 项和为n S =24n -n 2+=(1)求数列的通项公式；(2)当n 为何值时，n S 达到最大？最大值是多少？19. (本小题满分12分)在ABC ∆中，角,,A B C 的对边分别为,,,3a b c B π=，4cos ,5A b ==（1）求sin C 的值；（2）求ABC ∆的面积20.(本小题满分12分)已知等差数列{}n a 的前n 项和为n S ，且21,2a 62==s （1）求数列{}n a 的通项公式；（2）设n2b •=n n a ，求数列{}n b 的前n 项和n T21. (本小题满分12分) 在ABC ∆中，角,,A B C 所对的边分别为,,a b c ，角A,B,C 成等差数列（1）求B cos 的大小；（2）边,,a b c 成等比数列，求C A sin sin 的值22. (本小题满分12分) 在公差为d 的等差数列{}n a 中，已知10a 1=，且3215,22,a a a + 成等比数列（1）求n a ,d（2）若0d <，求n a a a ++++K 321a。

2014-2015学年度高一下学期期中考试数学试题_Word版含答案

2014－2015学年第二学期期中考试高一数学本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷为1-10题，共50分，第Ⅱ卷为11-20题，共100分。

全卷共计150分。

考试时间为120分钟。

第Ⅰ卷（本卷共计50 分）一．选择题：（每小题只有一个选项，每小题5分，共计50分）1．化简0015tan 115tan 1-+等于 ( ) A. 3 B.23C. 3D. 1 2. 在中，下列三角式ABC ∆ ①sin(A+B)+sinC;②cos(B+C)+cosA;③2tan 2tanCB A + ④cos 2sec 2AC B +,其中恒为定值的是 ( ) A ．①② B ②③ C ②④D ③④3. 已知函数f(x)=sin(x+2π)，g(x)=cos(x －2π)，则下列结论中正确的是( ) A ．函数y=f(x)·g(x)的最小正周期为2π B ．函数y=f(x)·g(x)的最大值为1C ．将函数y=f(x)的图象向左平移2π单位后得g(x)的图象D ．将函数y=f(x)的图象向右平移2π单位后得g(x)的图象4．圆：0y 6x 4y x 22=+-+和圆：0x 6y x 22=-+交于A 、B 两点，则AB 的垂直平分线的方程是（）．A ．03y x =++B ．05y x 2=--C ． 09y x 3=--D ．07y 3x 4=+- 5．长方体的表面积是24，所有棱长的和是24，则对角线的长是（）．Ａ．14 B ．4 C ．32 D ．23x图4-3-17．下列命题正确的是（）．A ．a//b, a⊥α⇒a⊥bB ．a⊥α, b⊥α⇒a//bC ．a⊥α, a⊥b ⇒b//αD ．a//α,a⊥b ⇒b⊥α8．圆：02y 2x 2y x 22=---+上的点到直线2y x =-的距离最小值是（）． A ．0 B ．21+ C ．222- D ．22- 9．曲线0y 4x 4y x 22=-++关于（）A ．直线4x =对称B ．直线0y x =+对称C ．直线0y x =-对称D ．直线)4,4(-对称10．已知在四面体ABCD 中，E 、F 分别是AC 、BD 的中点，若CD=2AB=4，EF ⊥AB ，则EF 与CD 所成的角为（）． A ．︒90 B ．︒45 C ．︒60D ．︒30第Ⅱ卷（本卷共计100分）二．填空题：（每小题5分，共计20分）11. 使函数f(x)=sin(2x+θ)+)2cos(3θ+x 是奇函数，且在[0，4π]上是减函数的θ的一个值____________.12．一个圆锥的母线长为4，中截面面积为π，则圆锥的全面积为____________．13．已知z ,y ,x 满足方程C ：22(3)(2)4x y ++-=，的最大值是___________．14．在三棱锥A B C P -中，已知2PC PB PA ===，︒=∠=∠=∠30CPA BPC BPA ，一绳子从A 点绕三棱锥侧面一圈回到点A 的距离中，绳子最短距离是_____________．三．解答题：(本大题共6小题，满分80分.解答须写出文字说明、证明过程和演算步骤.)15. （本小题满分12分）已知π2 <α<π,0<β<π2 ,tan α=－ 34 ,cos(β－α)= 513,求sinβ的值.ＡＢＣＰDC 1A 1B 1CBA16．（本小题满分12分）已知平行四边形ABCD 的两条邻边AB 、AD 所在的直线方程为02y 4x 3=-+；02y x 2=++，它的中心为M )3,0(，求平行四边形另外两条边CB 、CD 所在的直线方程及平行四边形的面积．17．（本小题满分14分）正三棱柱111C B A ABC -中，2BC =，6AA 1=，Ｄ、Ｅ分别是1AA 、11C B 的中点，（Ⅰ）求证：面E AA 1⊥面BCD ；（Ⅱ）求直线11B A 与平面BCD 所成的角．18．（本小题满分14分）直线L 经过点)2,1(P ，且被两直线L 1：02y x 3=+-和 L 2：01y 2x =+-截得的线段AB 中点恰好是点P ，求直线L 的方程．19.（本小题满分14分）如图,在三棱柱111-ABC A B C 中，侧棱1AA ⊥底面ABC ,,⊥AB BC D 为AC 的中点,12A A AB ==,3BC =. （1）求证：1//AB 平面1BC D ； (2) 求四棱锥11-B AAC D 的体积.20.（本小题满分14分）设关于x 函数a x a x x f 2cos 42cos )(+-= 其中02π≤≤x（1）将f(x)的最小值m 表示成a 的函数m=g(a); （2）是否存在实数a,使f(x)>0在]2,0[π∈x 上恒成立？（3）是否存在实数a ，使函数f(x) 在]2,0[π∈x 上单调递增？若存在，写出所有的a组成的集合；若不存在，说明理由。

青海省师大附二中高一数学下学期第一次月考试卷(含解析)

2014-2015学年青海省师大附二中高一（下）第一次月考数学一、选择题（共12小题，每小题5分，满分60分）1．（5分）（2015春•青海校级月考）数列1×4，2×5，3×6，…，n（n+3），…则它的前n 项和S n=（）A．n（n+1）（n+2）B．n（n+1）（n+3）C．n（n+1）（n+4）D．n（n+1）（n+5）考点：数列的求和．专题：等差数列与等比数列．分析：由于a n=n（n+3）=n2+3n，12+22+32+…+n2=．利用等差数列的前n 项和公式即可得出．解答：解：∵a n=n（n+3）=n2+3n，12+22+32+…+n2=．∴此数列的前n项和S n=12+22+32+…+n2+3（1+2+…+3）．=+3×=．故选：D．点评：本题考查了等差数列的通项公式及其前n项和公式、12+22+32+…+n2=，考查了推理能力与计算能力，属于中档题2．（5分）（2009秋•荣成市校级期中）下列判断正确的是（）A．a=7，b=14，A=30°，有两解B．a=30，b=25，A=150°，有一解C．a=6，b=9，A=45°，有两解D． a=9，b=10，A=60°，无解考点：正弦定理．专题：计算题．分析：由各选项中A的度数，求出sinA的值，再由a与b的值，利用正弦定理求出sinB 的值，由a与b的大小关系，利用大边对大角判断出A与B的大小关系，即可判断出B有一解、两解或无解，得到正确的选项．解答：解：A、∵a=7，b=14，A=30°，∴由正弦定理=得：sinB==1，又B为三角形的内角，∴B=90°，C=60°，c=7，则此时三角形只有一解，此选项错误；B、∵a=30，b=25，A=150°，∴由正弦定理=得：sinB==，∵a＞b，∴150°＞A＞B，则此时B只有一解，本选项正确；C、∵a=6，b=9，A=45°，∴∴由正弦定理=得：sinB==＞，∵b＞a，∴B＞A=45°，∴此时B只有一解，本选项错误；D、∵a=9，b=10，A=60°，∴∴由正弦定理=得：sinB==＞，∵a＜b，∴60°=A＜B，此时B有两解，本选项错误，故选B点评：此题考查了正弦定理，以及三角形的边角关系，熟练掌握正弦定理是解本题的关键．3．（5分）（2014秋•济宁期末）设S n为等比数列{a n}的前n项和，8a2+a5=0，则=（）A．﹣11 B．﹣8 C．5 D． 11考点：等比数列的性质．专题：转化思想．分析：由等比数列的前n项和公式，故==1+q2，由此知，应该有方程8a2+a5=0求出q的值，再代入求值，选出正确选项解答：解：∵Sn为等比数列{a n}的前n项和，8a2+a5=0∴8a1q+a1q4=0又数列是等比数列，首项不为0∴8q+q4=0，又q不为零，故有q=﹣2∴===5故选C点评：本题考查等比数列的性质，解题的关键是由8a2+a5=0求出公比q的值，再由等比数列的求和公式将用q表示出来，即可求出值，本题考查了转化的思想及计算能力，4．（5分）（2013秋•醴陵市校级期中）已知点（n，a n）（n∈N*）都在直线3x﹣y﹣24=0上，那么数列{a n}中有（）A．a7+a9＞0 B．a7+a9＜0 C．a7+a9=0 D．a7•a9=0考点：等差数列的性质．专题：等差数列与等比数列．分析：由题意可得a n=3n﹣24，进而由等差数列的性质可得a7+a9=2a8=0解答：解：∵点（n，a n）都在直线3x﹣y﹣24=0上，∴3n﹣a n﹣24=0，∴a n=3n﹣24，∴数列{a n}为等差数列，且a8=0，∴由等差数列的性质可得a7+a9=2a8=0故选：C点评：本题考查等差数列的性质，属基础题．5．（5分）（2007•海南）已知a，b，c，d成等比数列，且抛物线y=x2﹣2x+3的顶点为（b，c）则ad=（）A． 3 B． 2 C． 1 D．﹣2考点：等比数列的通项公式．专题：计算题．分析：通过配方，可得抛物线y=x2﹣2x+3的顶点为（1，2），即b=1，c=2，由等比数列的性质可得ad=bc，故问题可求．解答：解：∵y=x2﹣2x+3=（x﹣1）2+2，∴抛物线y=x2﹣2x+3的顶点为（1，2），∴b=1，c=2，又∵a，b，c，d成等比数列，∴ad=bc=2，故选B．点评：本题综合考查了二次函数的顶点和等比数列的性质，比较简单．6．（5分）（2015春•双流县校级期中）在△ABC中，若a=2bsinA，则B等于（）A．30°B．60°C．30°或150°D．60°或120°考点：正弦定理．专题：计算题．分析：把已知的等式变形后，再利用正弦定理列出关系式，等量代换求出sinB的值，由B 为三角形的内角，利用特殊角的三角函数值即可求出B的度数．解答：解：∵，∴，∵根据正弦定理，∴=，∴sinB=，又B为三角形的内角，∴B=60° 或120°故选D点评：本题主要考查正弦定理的运用．正弦定理建立了三角形的边角关系，故在三角形边、角问题中常利用正弦定理来解决，熟练掌握正弦定理是解本题的关键．7．（5分）（2014秋•济宁期末）数列{a n}的通项公式a n=n2+n，则数列{}的前9项和为（）A． B．C． D．考点：数列的求和．专题：等差数列与等比数列．分析：由a n=n2+n，可得=，利用“裂项求和”即可得出．解答：解：∵a n=n2+n，∴=，则数列{}的前9项和=+…+=1﹣=．故选：A．点评：本题考查了“裂项求和”方法，考查了推理能力与计算能力，属于基础题．8．（5分）（2015春•青海校级月考）在△ABC中，A=60°，a=3，则=（）A．B．C．D．考点：正弦定理．专题：解三角形．分析：由条件利用正弦定理可得=2R 的值，再利用正弦定理花间要求的式子，从而得到结果．解答：解：由条件利用正弦定理可得=2R==2，∴==2R=2，故选：D．点评：本题主要考查正弦定理的应用，属于基础题．9．（5分）（2015•南昌校级二模）已知各项均为正数的等比数列{a n}中，3a1，成等差数列，则=（）A．27 B． 3 C．﹣1或3 D． 1或27考点：等比数列的性质．专题：等差数列与等比数列．分析：由题意可得公比q的方程，解得方程可得q，可得=q3，代值计算可得．解答：解：设等比数列{a n}的公比为q，由题意可得a3=3a1+2a2，∴a1q2=3a1+2a1q，即q2=3+2q解得q=3，或q=﹣1（舍去），∴==q3=27故选：A点评：本题考查等比数列的通项公式和性质，属基础题．10．（5分）（2014•衡阳县校级模拟）在△ABC中，若，则△ABC是（）A．等腰三角形B．等边三角形C．直角三角形D．等腰三角形或直角三角形考点：正弦定理；三角形的形状判断．专题：计算题．分析：利用正弦定理化简已知等式，变形后利用二倍角的正弦函数公式化简，得到A与B 相等或互余，即可判断出三角形ABC的形状．解答：解：由正弦定理得：==，∴sinAcosA=sinBcosB，即sin2A=sin2B，∴sin2A=sin2B，∴2A=2B或2A+2B=180°，即A=B或A+B=90°，则△ABC为等腰三角形或直角三角形．故选D点评：此题考查了正弦定理，以及三角形形状的判断，熟练掌握正弦定理是解本题的关键．11．（5分）（2015春•青海校级月考）公比为2的等比数列{a n}的各项都是正数，且a3a9=16，则log2=（）A． 4 B． 5 C． 6 D．7考点：等比数列的性质．专题：等差数列与等比数列．分析：根据等比数列的通项公式结合对数的基本运算进行求解即可．解答：解：∵公比为2的等比数列{a n}的各项都是正数，且a3a9=16，∴a6a6=16，即a6=4，则a10=a6•24=4•24=26，则log2=log226=6，故选：C．点评：本题主要考查对数的计算，以及等比数列的通项公式的应用，根据等比数列的性质是解决本题的关键．12．（5分）（2015春•青海校级月考）已知两座灯塔A和B与海洋观察站C的距离都等于a km，灯塔A在观察站C的北偏东20°，灯塔B在观察站C的南偏东40°，则灯塔A与B的距离为（）A． a km B．a km C． a km D．2a km考点：解三角形的实际应用．专题：计算题；解三角形．分析：先根据题意求得∠ACB，进而根据余弦定理求得AB．解答：解：依题意知∠ACB=180°﹣20°﹣40°=120°，在△ABC中，由余弦定理知AB==．即灯塔A与灯塔B的距离为km．故选A点评：本题给出实际应用问题，求海洋上灯塔A与灯塔B的距离．着重考查了三角形内角和定理和运用余弦定理解三角形等知识，属于基础题．二.填空题：（该题共4小题，每小题5分，共20分．把答案填在题中横线上．）13．（5分）（2015春•青海校级月考）在△ABC的三内角A、B、C的对应边分别为a，b，c，当a2+c2≥b2+ac时，角B的取值范围为（0°，60°] ．考点：余弦定理．专题：解三角形．分析：根据题意和余弦定理求出cosB的范围，再根据内角的范围和余弦函数的性质求出角B的范围．解答：解：由题意得，a2+c2≥b2+ac，则a2+c2﹣b2≥ac，由余弦定理得，cosB=≥，∵0＜B＜180°，∴0°＜B≤60°，∴角B的取值范围为（0°，60°]，故答案为：（0°，60°]．点评：本题考查了余弦定理，以及余弦函数的性质，注意内角的范围，属于中档题．14．（5分）（2012•深圳校级二模）等差数列{a n}的前m项和为30，前2m项和为100，则它的前3m项和为210 ．考点：等差数列的性质．专题：计算题．分析：设前3m项和为 x，则 30，100﹣30，x﹣100 成等差数列，解出 x的值，即为所求．解答：解：等差数列{a n}的每m项的和成等差数列，设前3m项和为 x，则 30，100﹣30，x﹣100 成等差数列，故2×70=30+（x﹣100 ），x=210，故答案为：210．点评：本题考查等差数列的性质，前n项和的性质，得到 30，100﹣30，x﹣100 成等差数列，是解题的关键．15．（5分）（2013•大连一模）在△ABC中，sinA：sinB：sinC=2：3：4，则cosC的值为．考点：正弦定理；余弦定理．专题：计算题．分析：由正弦定理可得，可设其三边分别为2k，3k，4k，再由余弦定理求得cosC的值．解答：解：在△ABC中，sinA：sinB：sinC=2：3：4，由正弦定理可得，可设其三边分别为2k，3k，4k，由余弦定理可得 16k2=4k2+9k2﹣12k2cosC，解方程可得cosC=，故答案为：．点评：本题考查正弦定理、余弦定理的应用，设出其三边分别为2k，3k，4k，是解题的关键．16．（5分）（2015春•青海校级月考）已知等差数列{a n}和{b n}的前n项和分别为A n和B n，若=，则的值为．考点：等差数列的前n项和．专题：等差数列与等比数列．分析：由等差数列的性质和求和公式可得=，代值计算可得．解答：解：由等差数列的性质和求和公式可得：======故答案为：点评：本题考查等差数列的求和公式和性质，属中档题．三、解答题：（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．）17．（10分）（2015春•青海校级月考）在△ABC中，角A，B，C所对的边分别为a，b，c，已知=（sinC，sinBcosA），=（b，2c），且•=0（1）求A；（2）若a=2，c=2，求△ABC的面积．考点：平面向量数量积的运算；正弦定理；余弦定理．专题：解三角形；平面向量及应用．分析：（1）根据向量的运算得出bsinC+2csinBcosA=0，利用正弦定理边角转化得出sinBsinC+2sinCsinBcosA=0，约分即可得出cosA=﹣，求解角．（2）利用余弦定理得出cosA==﹣，求解b，利用三角形的面积公式得出即可．解答：解：（1）∵知=（sinC，sinBcosA），=（b，2c），且•=0∴bsinC+2csinBcosA=0，①根据正弦定理得出：b=2RsinB，=2RsinC，代入上式①得出：sinBsinC+2sinCsinBcosA=0，1+2cosA=0，cosA=﹣，∵0＜A＜180°∴A=120°（2）∵a=2，c=2，∴根据余弦定理得出cosA==﹣，即b2+2b﹣8=0b=2，b=﹣4（舍去），∴S=bcsinA==点评：本题利用向量考察了三角形的问题，利用正弦定理，余弦定理得出三角形的角，边，考察了学生的运算能力，属于中档题．18．（12分）（2015春•青海校级月考）已知数列{a n}的前n项和为S n=﹣n2+24n（1）求数列的通项公式；（2）当n为何值时，S n达到最大？最大值是多少？考点：数列递推式；等差数列的通项公式；等差数列的前n项和．专题：等差数列与等比数列．分析：（1）利用a n+1=S n+1﹣S n可知当n≥2时有a n=﹣2n+25，验证当n=1时是否成立即可；（2）通过配方，结合二次函数的知识即得结论．解答：解：（1）∵S n=﹣n2+24n，∴S n+1=﹣（n+1）2+24（n+1），∴a n+1=S n+1﹣S n=[﹣（n+1）2+24（n+1）]﹣（﹣n2+24n）=﹣2（n+1）+25，∴当n≥2时，a n=﹣2n+25，又∵a1=S1=﹣1+24=23满足上式，∴a n=﹣2n+25；（2）∵S n=﹣n2+24n=﹣（n﹣12）2+144，∴当n=12时S n达到最大，最大值是144．点评：本题考查等差数列的前n项和，注意解题方法的积累，属于中档题．19．（12分）（2009•北京）在△ABC中，角A，B，C的对边分别为，．（Ⅰ）求sinC的值；（Ⅱ）求△ABC的面积．考点：正弦定理；同角三角函数基本关系的运用．专题：计算题．分析：（Ⅰ）由cosA=得到A为锐角且利用同角三角函数间的基本关系求出sinA的值，根据三角形的内角和定理得到C=π﹣﹣A，然后将C的值代入sinC，利用两角差的正弦函数公式化简后，将sinA和cosA代入即可求出值；（Ⅱ）要求三角形的面积，根据面积公式S=absinC和（Ⅰ）可知公式里边的a不知道，所以利用正弦定理求出a即可．解答：解：（Ⅰ）∵A、B、C为△ABC的内角，且＞0，∴A为锐角，则sinA==∴∴sinC=sin（﹣A）=cosA+sinA=；（Ⅱ）由（Ⅰ）知sinA=，sinC=，又∵，∴在△ABC中，由正弦定理，得∴a==，∴△ABC的面积S=absinC=×××=．点评：考查学生灵活运用正弦定理、三角形的面积公式及同角三角函数间的基本关系化简求值．灵活运用两角和与差的正弦函数公式化简求值．20．（12分）（2015春•青海校级月考）已知等差数列{a n}的前n项和为S n，且a2=2，S6=21 （1）求数列{a n}的通项公式；（2）设b n=a n•2n，求数列{b n}的前n项和T n．考点：数列的求和；等差数列的性质．专题：等差数列与等比数列．分析：（1）设等差数列{a n}的公差为d，利用等差数列的通项公式及其前n项和公式即可得出；（2）b n=a n•2n=n•2n．利用“错位相减法”及其等比数列的前n项和公式即可得出．解答：解：（1）设等差数列{a n}的公差为d，∵a2=2，S6=21，∴，解得，∴a n=1+（n﹣1）=n．（2）b n=a n•2n=n•2n．∴数列{b n}的前n项和T n=2+2×22+3×23+…+n•2n，2T n=22+2×23+…+（n﹣1）×2n+n•2n+1，∴﹣T n=2+22+23+…+2n﹣n•2n+1=﹣n•2n+1=（1﹣n）•2n+1﹣2，∴T n=（n﹣1）×2n+1+2．点评：本题考查了“错位相减法”、等差数列与等比数列的通项公式及其前n项和公式，考查了推理能力与计算能力，属于中档题21．（12分）（2012•辽宁）在△ABC中，角A、B、C的对边分别为a，b，c．角A，B，C成等差数列．（Ⅰ）求cosB的值；（Ⅱ）边a，b，c成等比数列，求sinAsinC的值．考点：数列与三角函数的综合．专题：计算题；综合题．分析：（Ⅰ）在△ABC中，由角A，B，C成等差数列可知B=60°，从而可得cosB的值；（Ⅱ）（解法一），由b2=ac，cosB=，结合正弦定理可求得sinAsinC的值；（解法二），由b2=ac，cosB=，根据余弦定理cosB=可求得a=c，从而可得△ABC为等边三角形，从而可求得sinAsinC的值．解答：解：（Ⅰ）由2B=A+C，A+B+C=180°，解得B=60°，∴cosB=；…6分（Ⅱ）（解法一）由已知b2=ac，根据正弦定理得sin2B=sinAsinC，又cosB=，∴sinAsinC=1﹣cos2B=…12分（解法二）由已知b2=ac及cosB=，根据余弦定理cosB=解得a=c，∴B=A=C=60°，∴si nAsinC=…12分点评：本题考查数列与三角函数的综合，着重考查等比数列的性质，考查正弦定理与余弦定理的应用，考查分析转化与运算能力，属于中档题．22．（12分）（2013•浙江）在公差为d的等差数列{a n}中，已知a1=10，且a1，2a2+2，5a3成等比数列．（Ⅰ）求d，a n；（Ⅱ）若d＜0，求|a1|+|a2|+|a3|+…+|a n|．考点：数列的求和；等差数列的通项公式；等比数列的性质．专题：等差数列与等比数列．分析：（Ⅰ）直接由已知条件a1=10，且a1，2a2+2，5a3成等比数列列式求出公差，则通项公式a n可求；（Ⅱ）利用（Ⅰ）中的结论，得到等差数列{a n}的前11项大于等于0，后面的项小于0，所以分类讨论求d＜0时|a1|+|a2|+|a3|+…+|a n|的和．解答：解：（Ⅰ）由题意得，即，整理得d2﹣3d﹣4=0．解得d=﹣1或d=4．当d=﹣1时，a n=a1+（n﹣1）d=10﹣（n﹣1）=﹣n+11．当d=4时，a n=a1+（n﹣1）d=10+4（n﹣1）=4n+6．所以a n=﹣n+11或a n=4n+6；（Ⅱ）设数列{a n}的前n项和为S n，因为d＜0，由（Ⅰ）得d=﹣1，a n=﹣n+11．则当n≤11时，．当n≥12时，|a1|+|a2|+|a3|+…+|a n|=﹣S n+2S11=．综上所述，|a1|+|a2|+|a3|+…+|a n|=．点评：本题考查了等差数列、等比数列的基本概念，考查了等差数列的通项公式，求和公式，考查了分类讨论的数学思想方法和学生的运算能力，是中档题．。