有理数全章复习

合集下载

第1章有理数(单元复习课件)(知识导图+考点梳理+数学活动+课本复习题)七年级数学上册人教版2024

时间
第一季度
第二季度
第三季度
第四季度
盈利/万元
-6.8
-10.7
31.5
27.8
31.5> 27.8 > -6.8 > -10.7
6. 某年我国人均水资源比上年的增幅是 -5.6%. 后续
三年各年比上年的增幅分别是 -4.0%，13.0%，-9.6%.
这些增幅中哪个最小？增幅是负数说明什么？
-9.6%最小
（1）一般地，数轴上表示数 a 的点与原点的距离叫作数 a 的绝对值，记作| a |，
读作“a的绝对值”.
（2）绝对值的性质（非负性）.
一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0 的绝对值是
0.
即： ①如果a>0，那么￨a￨= a；
②如果a=0，那么￨a￨= 0；
③如果a<0，那么￨a￨= -a.
7. 在数轴上表示下列各数、并将这些数按从小到大的顺序排列，
再用“<”连接起来.
3，-4，0，2，-2，-1
-4
-4
-3
-2
-1
0
-2
-1
0
-4 < -2 < -1 <
1
2
3
2
3
0 < 2 < 3
4
知识梳理
4. 相反数
（1）相反数：只有符号不同的两个数,互为相反数；
（2）相反数的几何意义：
在数轴上位于原点两侧并且到原点距离相等的两个点所表示
–(–2) > –|+2|
（3）+|–3| 和 |–(+5)|；（4）–(+ ) 和 –|–
（3）+|–3| = 3， |–(+5)| = 5；

有理数总复习

a 10b第一章有理数总复习知识点梳理：1.正数与负数：负数产生的必要性；具有相反意义的量。

2.有理数的分类：3.数轴、相反数、倒数、绝对值：（1）数轴的三要素是：________________________________（2）只有符号不同的两个数叫做互为____________，a 的相反数为___ ；（3）互为倒数的两个数乘积是，没有倒数；（4）一个正数的绝对值是____________；一个负数的绝对值是____________；零的绝对值是_______.（5）有理数的大小比较：方法一：0 一切正数，0 一切负数；两个负数作比较，绝对值大的 .方法二：在数轴上，________表示的数总比________表示的数大。

4.科学记数法：把一个大于10的数表示成a ×10n 的形式，（其中a 是____________ ，n 是____________ ）5.近似数【自主学习、巩固训练】要求：自主完成下列各题，并把自己疑惑的、不懂的做好批注，时间10分钟.1. 在 -1，+7， 0， 23-， 516中，正数有（） A 、1个 B 、2个 C 、3个 D 、4个2.在–2，+3.5，0，32-，–0.7，11中．负分数有…………（） A 、l 个 B 、2个 C 、3个 D 、4个3. 下列数据是近似数的是（）A.小白数学得了90分B. 小明身高约173cmC.数学课本有86页D.（1）班有45名同学4.如图，，那么下列结论正确的是( ) A ．a 比b 大 B ．b 比a 大C ．a 、b 一样大D ．a 、b 的大小无法确定5.我国最长的河流长江全长约为6300千米，用科学记数法表示为（）A. 63×102千米B. 6.3×102千米或者有理数有理数C. 6.3×104千米D. 6.3×103千米6.用数轴上的点表示下列有理数，并求其相反数、倒数和绝对值。

第一章有理数复习

有理数分数整数正整数 0 负整数正分数负分数
自然数
有理数的分类
有理数的另一种分类
有理数 0 有理数有理数数分数数分数
分类的的数数. 数数
分类
（1）零既不是正数也不是负数，零）零既不是正数也不是负数，大于负数，正数大于零。大于负数，正数大于零。（2）零的相反数是它本身，零的绝）零的相反数是它本身，对值是它本身，对值是它本身，零的任何非零次幂是零。（3）零是绝对值最小的有理数。）零是绝对值最小的有理数。（4）零乘以任何数为零，零除以任）零乘以任何数为零，何不为零的数为零。何不为零的数为零。（5）零没有倒数，零不能做除数。）零没有倒数，零不能做除数。
有理数
正数、正数、负数在实际生活中的应用
外国语学校对七年级女生进行了仰卧起坐的测试，以能做36个为标准个为标准，测试，以能做个为标准，超过的次数用正数表不足的次数用负数表示，其中8名女生的成绩示，不足的次数用负数表示，其中名女生的成绩如下 2 -1 0 3 -2 -4 1 0 名女生的成绩分别是多少？（1）这8名女生的成绩分别是多少？）名女生的成绩分别是多少名女生有百分之几达到标准？（2）这8名女生有百分之几达到标准？）名女生有百分之几达到标准（3）她们共做了多少个仰卧起坐？）她们共做了多少个仰卧起坐？
1.零是整数吗自然数一定是整数吗自然数零是整数吗?自然数一定是整数吗零是整数吗自然数一定是整数吗?自然数一定是正整数吗?整数一定是自然数吗整数一定是自然数吗? 一定是正整数吗整数一定是自然数吗
零是整数；自然数一定是整数；零是整数；自然数一定是整数；自然数不一定是正整数，因为零也是自然数；一定是正整数，因为零也是自然数；整数不一定是自然数，不一定是自然数，因为负整数不是自然数。

有理数全章复习

有理数全章复习理解有理数的概念和性质：有理数是指可以表示为两个整数的比值的数，这里的整数可以是正整数、负整数或零。

有理数的性质主要包括有理数的加减乘除运算性质、有理数大小的比较，以及有理数的乘方、开方运算等。

一、有理数的加减乘除运算性质：1.有理数的加法性质：-交换律：a+b=b+a-结合律：(a+b)+c=a+(b+c)-存在零元素：a+0=a-存在相反元素：a+(-a)=02.有理数的减法性质：-减法的定义：a-b=a+(-b)-减法与加法的关系：a-b=a+(-b)3.有理数的乘法性质：-交换律：a*b=b*a-结合律：(a*b)*c=a*(b*c)-分配律：a*(b+c)=a*b+a*c4.有理数的除法性质：-除法的定义：a÷b=a*(1/b)二、有理数的大小比较：1.同号比大小：正数大于负数，负数小于正数；正数之间、负数之间，绝对值大的数大。

2.异号比大小：两个数绝对值相比，绝对值大的数小。

三、有理数的乘方和开方运算：1.有理数的乘方：-正数的指数性质：a^m*a^n=a^(m+n)-负数的指数性质：a^(-m)=1/a^m-零的指数性质：a^0=1（a≠0）- 乘方的分配律：(ab)^n = a^n * b^n2.有理数的开方：-非负数的开方：√a*√a=a（a≥0）- 开方的分配律：√(ab) = √a * √b有理数的应用：1.在数轴上表示有理数：-正数表示：从0向右的数轴上的点表示，数值与点的位置对应。

-负数表示：从0向左的数轴上的点表示，数值与点的位置对应。

-零的表示：数轴上的0点表示。

2.数与有理数的运算：-数的加减法：将数转换为有理数进行运算。

-有理数与有理数的加减法：按照有理数的加减法规则进行运算。

3.比例与比例运算：-比例的定义：两个比例相等叫做比例，表示为a:b=c:d。

- 比例的性质：比例的两个比值相等，乘法性质：a:b = ac:bd。

-比例方程的解法：根据比例的性质，设置比例方程求解。

《有理数》全章复习与巩固(提高)知识讲解

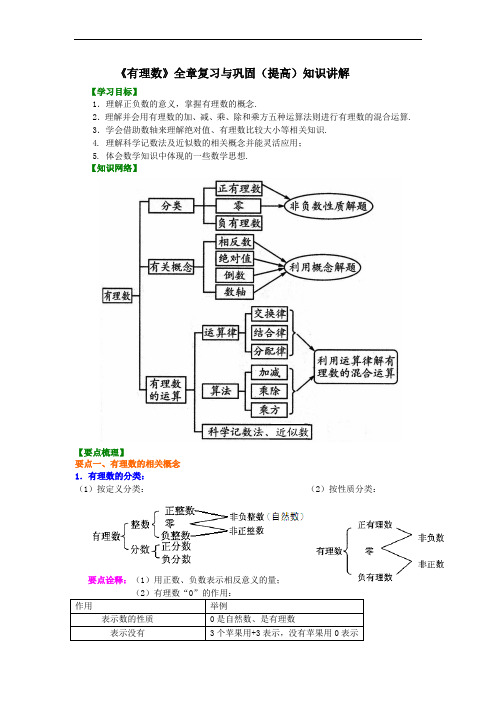
《有理数》全章复习与巩固（提高）知识讲解【学习目标】1．理解正负数的意义，掌握有理数的概念.2．理解并会用有理数的加、减、乘、除和乘方五种运算法则进行有理数的混合运算.3．学会借助数轴来理解绝对值、有理数比较大小等相关知识.4. 理解科学记数法及近似数的相关概念并能灵活应用；5. 体会数学知识中体现的一些数学思想.【知识网络】【要点梳理】要点一、有理数的相关概念1．有理数的分类：（1）按定义分类：（2）按性质分类：要点诠释：（1）用正数、负数表示相反意义的量；作用举例表示数的性质0是自然数、是有理数表示没有3个苹果用+3表示，没有苹果用0表示2．数轴：规定了原点、正方向和单位长度的直线．要点诠释：（1）一切有理数都可以用数轴上的点表示出来，数轴上的点不都表示的是有理数，如π．（2）在数轴上，右边的点所对应的数总比左边的点所对应的数大．3．相反数：只有符号不同的两个数互称为相反数，0的相反数是0．要点诠释：（1）一对相反数在数轴上对应的点位于原点两侧，并且到原点的距离相等，这两点是关于原点对称的．（2）求任意一个数的相反数，只要在这个数的前面添上“-”号即可．（3）多重符号的化简：数字前面“-”号的个数若有偶数个时，化简结果为正，若有奇数个时，化简结果为负． 4．绝对值：（1)代数意义：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．数a 的绝对值记作a ．（2)几何意义：一个数a 的绝对值就是数轴上表示数a 的点与原点的距离．要点二、有理数的运算 1 ．法则：（1）加法法则：①同号两数相加，取相同的符号，并把绝对值相加．②绝对值不相等的异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值．③一个数同0相加，仍得这个数．（2）减法法则：减去一个数，等于加这个数的相反数．即a-b=a+(-b) ．（3）乘法法则：①两数相乘，同号得正，异号得负，并把绝对值相乘．②任何数同0相乘，都得0．（4）除法法则：除以一个不等于0的数，等于乘这个数的倒数．即a÷b=a·1b(b≠0) ．（5）乘方运算的符号法则：①负数的奇次幂是负数，负数的偶次幂是正数；②正数的任何次幂都是正数，0的任何非零次幂都是0． (6)有理数的混合运算顺序：①先乘方，再乘除，最后加减；②同级运算，从左到右进行； ③如有括号，先做括号内的运算，按小括号、中括号、大括号依次进行．要点诠释：“奇负偶正”口诀的应用：（1）多重负号的化简，这里奇偶指的是“－”号的个数，例如：－[－（－3）]=－3，－[+（－3）]=3．（2）有理数乘法，当多个非零因数相乘时，这里奇偶指的是负因数的个数，正负指结果中积的符号，例如：（－3）×（－2）×（－6）=－36，而（－3）×（－2）×6=36．（3）有理数乘方，这里奇偶指的是指数，当底数为负数时，指数为奇数，则幂为负；指数为偶数，则幂为正，例如： 2(3)9-=， 3(3)27-=-．2．运算律：（1）交换律: ① 加法交换律:a+b=b+a ； ②乘法交换律:ab=ba ；（2）结合律: ①加法结合律： (a+b)+c=a+(b+c)； ②乘法结合律：（ab ）c=a(bc)（3）分配律：a(b+c)=ab+ac 要点三、有理数的大小比较比较大小常用的方法有：（1）数轴比较法；（2）法则比较法：正数大于0，0大于负数，正数大于负数；两个负数，绝对值大的反而小；(3) 作差比较法．（4）作商比较法；（5)倒数比较法．要点四、科学记数法、近似数及精确度1.科学记数法：把一个大于10的数表示成10na ⨯的形式（其中110a ≤<，n 是正整数），此种记法叫做科学记数法．例如：200 000=5210⨯．2.近似数：接近准确数而不等于准确数的数，叫做这个精确数的近似数或近似值.如长江的长约为6300㎞，这里的6300㎞就是近似数.要点诠释：一般采用四舍五入法取近似数，只要看要保留位数的下一位是舍还是入.3.精确度：一个近似数四舍五入到哪一位，就称这个数精确到哪一位，精确到的这一位也叫做这个近似数的精确度. 要点诠释：（1）精确度是指近似数与准确数的接近程度.（2）精确度有两种形式：①精确到哪一位．②保留几个有效数字．这两种的形式的意义不一样，一般来说精确到哪一位可以表示误差绝对值的大小，例如精确到0.1米，说明结果与实际数相差不超过0.05米，而有效数字往往用来比较几个近似数哪个更精确些. 【典型例题】类型一、有理数相关概念1．已知x 与y 互为相反数，m 与n 互为倒数，|x+y |+（a-1）2＝0，求a 2-(x+y+mn)a+(x+y)2009+(-mn)2010的值．【思路点拨】(1)若有理数x 与y 互为相反数，则x+y ＝0，反过来也成立． (2)若有理数m 与n 互为倒数，则mn ＝1，反过来也成立．【答案与解析】解：因为x 与y 互为相反数，m 与n 互为倒数，（a-1）2≥0，所以x+y ＝0，mn ＝1，a ＝1，所以a 2-(x+y+mn)a+(x+y)2009+(-mn)2010＝a 2-(0+1)a+02009+(-1)2010＝a 2-a+1．∵a＝1，∴原式＝12-1+1＝1【总结升华】要全面正确地理解倒数，绝对值，相反数等概念. 举一反三：【变式1】选择题（1）已知四种说法：①|a|=a 时，a>0；|a|=-a 时， a<0. ②|a|就是a 与-a 中较大的数. ③|a|就是数轴上a 到原点的距离. ④对于任意有理数，-|a|≤a≤|a|. 其中说法正确的个数是（） A ．1 B ．2 C ．3 D ．4（2）有四个说法：①有最小的有理数 ②有绝对值最小的有理数 ③有最小的正有理数 ④没有最大的负有理数上述说法正确的是（）A ．①② B．③④ C．②④ D．①② （3）已知(-ab)3>0，则（）A ．ab<0B ．ab>0C ．a>0且b<0D ．a<0且b<0 （4）若|x-1|+|y+3|+|z-5|=0，则(x+1)(y-3)(z+5)的值是（） A ．120 B ．-15 C ．0 D ．-120 （5）下列各对算式中，结果相等的是（）A ．-a 6与(-a)6B ．-a 3与|-a|3C ．[(-a)2]3与(-a 3)2D ．(ab)3与ab 3【答案】（1）C ；（2）C ；（3）A ；（4）D ；(5)C【变式2】（呼伦贝尔）中国的陆地面积约为9 600 000km 2，把9 600 000用科学记数法表示为．【答案】9.6×106．2.（江西校级模拟）如果m ，n 互为相反数，那么|m+n ﹣2016|=________．【思路点拨】先用相反数的意义确定出m+n=0，从而求出|m+n ﹣2016|. 【答案】2016.【解析】解：∵m ，n 互为相反数， ∴m+n=0，∴|m+n ﹣2016|=|﹣2016|=2016；故答案为2016．【总结升华】此题是绝对值题，主要考查了绝对值的意义，相反数的性质，熟知相反数的意义是解本题的关键．类型二、有理数的运算3．(1)211143623324⎛⎫⎛⎫⎛⎫⎛⎫-----+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭(2)5153()( 1.5)()1244-÷⨯-÷- ()()23541(3)24121522⎛⎫-÷-⨯-⨯-+ ⎪⎝⎭(4)137775111 2.534812863⎡⎤⎛⎫⎛⎫⎛⎫+--÷--÷⨯- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦(5)()1003221511221132⎛⎫----÷- ⎪⎝⎭+--⨯【答案与解析】解：（1）原式21111143622332412=-++-= （2）原式543421215239=-⨯⨯⨯=-（3）原式3132(4)12(1516)104=-÷-⨯-⨯-+=-（4）原式12561[1(2)1]()233253=+-++-⨯⨯-=（5）1125112()41192---÷-=+--⨯原式 3.9=-【总结升华】有理数的混合运算有很多技巧，如：正、负数分别相加；分数中，同分母或分母有倍数关系的分数结合相加；除法转化为乘法、正向应用乘法分配律：a(b+c)＝ab+ac ；逆向应用分配律：ab+ac ＝a(b+c)等. 举一反三：【变式】（1）225117832[()10.25]199[()2]7148923-÷⨯-⨯-⨯--（2）23155115(1)()()(2)()299229-⨯---⨯-+-⨯【答案】解：（1）225117832[()10.25]199[()2]7148923-÷⨯-⨯-⨯--251471834()199(2)492584929=⨯⨯-⨯-⨯- 118343()199(2)449292=-⨯-⨯-⨯20(3)3=--2033=-+123=（2）23155115(1)()()(2)()299229-⨯---⨯-+-⨯955515()()()()499289=⨯---⨯-+-⨯5951()()942817224=-⨯++=-4. 先观察下列各式：11111434⎛⎫=- ⎪⨯⎝⎭；111147347⎛⎫=- ⎪⨯⎝⎭； 11117103710⎛⎫=- ⎪⨯⎝⎭；…；1111(3)33n n n n ⎛⎫=- ⎪++⎝⎭，根据以上观察，计算： 1111447710+++⨯⨯⨯ (1)20052008+⨯的值．【答案与解析】解：原式111111111111343473710320052008⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭… 111111111344771020052008⎛⎫=-+-+-+⋅⋅⋅+- ⎪⎝⎭1113200812007320086692008⎛⎫=- ⎪⎝⎭=⨯=【总结升华】根据题中提供的拆项方法把每一项拆成11133n n ⎛⎫- ⎪+⎝⎭的形式，然后再进行计算．举一反三：【变式】用简单方法计算：120180148124181++++ 【答案】解：原式=1111111111115(...)244668810101222446101224++++=-+-++-=⨯⨯⨯⨯⨯ 类型三、数学思想在本章中的应用5．（香洲区校级二模）（1）阅读下面材料：点A ，B 在数轴上分别表示实数a ，b ，A ，B 两点之间的距离表示为|AB|．当A，B两点中有一点在原点时，不妨设点A在原点，如图（1），|AB|=|OB|=|b|=|a﹣b|；当A，B两点都不在原点时，①如图（2），点A，B都在原点的右边，|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|；②如图（3），点A，B都在原点的左边，|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣（﹣a）=|a﹣b|；③如图（4），点A，B在原点的两边，|AB|=|OA|+|OB|=|a|+|b|=a+（﹣b）=|a﹣b|；综上，数轴上A，B两点之间的距离|AB|=|a﹣b|．（2）回答下列问题：①数轴上表示2和5的两点之间的距离是，数轴上表示﹣2和﹣5的两点之间的距离是，数轴上表示1和﹣3的两点之间的距离是；②数轴上表示x和﹣1的两点A和B之间的距离是，如果|AB|=2，那么x为；③当代数式|x+1|+|x﹣2|取最小值时，相应的x的取值范围是．④解方程|x+1|+|x﹣2|=5．【答案与解析】解：①数轴上表示2和5的两点之间的距离是|2﹣5|=3；数轴上表示﹣2和﹣5的两点之间的距离是|﹣2﹣（﹣5）|=3；数轴上表示1和﹣3的两点之间的距离是|1﹣（﹣3）|=4．②数轴上表示x和﹣1的两点A和B之间的距离是|x﹣（﹣1）|=|x+1|，如果|AB|=2，那么x为1或﹣3．③当代数式|x+1|十|x﹣2|取最小值时，∴x+1≥0，x﹣2≤0，∴﹣1≤x≤2．④当x≤﹣1时，﹣x﹣1﹣x+2=5，解得x=﹣2；当﹣1＜x≤2时，3≠5，不成立；当x＞2时，x+1+x﹣2=5，解得x=3．故答案为：3，3，4，|x+1|，1或﹣3，﹣1≤x≤2．【总结升华】此题综合考查了数轴、绝对值的有关内容，用几何方法借助数轴来求解，体现了数形结合的优点．类型四、规律探索6.下面两个多位数1248624…，6248624…都是按照如下方法得到的：将第1位数字乘以2，若积为一位数，将其写在第2位；若积为两位数，则将其个位数字写在第2位．对第2位数字再进行如上操作得到第3位数字……，后面的每一位数字都是由前一位数字进行如上操作得到的．当第1位数字是3时，仍按如上操作得到一个多位数，则这个多位数前100位的所有数字之和是( )．A．495 B．497 C．501 D．503【思路点拨】多位数1248624…是怎么来的？当第1个数字是1时，将第1位数字乘以2得2，将2写在第2位上，再将第2位数字2乘以2得4，将其写在第3位上，将第3位数字4乘以2的8，将8写在第4位上，将第4位数字8乘以2得16，将16的个位数字6写在第5位上，将第5位数字6乘以2得12，将12的个位数字2写在第6位上，再将第6位数字2乘以2得4，将其写在第7位上，以此类推．根据此方法可得到第一位是3的多位数后再求和．【答案】A【解析】按照法则可以看出此数为362 486 248…，后面6248循环，所以前100位的所有数字之和是3+(6+2+4+8)×24+6+2+4＝495，所以选A ．【总结升华】特例助思，探究规律，这类题主要是通过观察分析，从特殊到一般来总结发现规律，并表示出来．举一反三：【变式】世界上著名的莱布尼茨三角形如图所示，则排在第10行从左边数第3个位置上的数是（）．A ．1132 B ．1360 C ．1495 D ．1660【答案】B 提示：观察发现：分子总是1，第n 行的第一个数的分母就是n ，第二个数的分母是第一个数的（n-1）倍，第三个数的分母是第二个数的分母的(1)2n-倍．根据图表的规律，则第10行从左边数第3个位置上的数是111094360=⨯⨯．。

有理数全章复习(按知识点分类复习)

第一章有理数全章复习考点一：用正负数表示相反意义的量1、七年级一班某次数学测验的平均成绩为80分，数学老师以平均成绩为基准，记作0，把小龙、小聪、小梅、小莉、小刚这五位同学的成绩简记为+10，–15，0，+20，–2．问这五位同学的实际成绩分别是多少分2、如果规定收入为正，支出为负．收入500 元记作500元，那么支出237元应记作( ) A ．－500元B ．－237元C ．237元D ．500元3.有4包真空小包装火腿，每包以标准克数〔450克〕为基准，超过的克数记作正数，不足的克数记作负数，以下数据是记录结果，其中表示实际克数最接近标准克数的( )A ．+2B ．－3C ．+3D ．+44.某商店出售三种不同品牌的大米，米袋上分别标有质量如下表：现从中任意拿出两袋不同品牌的大米，这两袋大米的质量最多相差 ( )A ．B ．C ．D ．考点二：有理数的分类1、_______、_______和_________成为整数，__________和__________统称为分数。

___________和_________统称为有理数。

练习稳固：1、在–2，+3.5，0，32-，–0.7，11中．负分数有……………………〔〕 A 、l 个 B 、2个 C 、3个 D 、4个2、不超过3)23(-的最大整数是………………………………………〔〕 A 、–4 B –3 C 、3 D 、43．在数8.3、－4、0、－〔－5〕、+6、－|－10|、1中,正数有____ 个； 4、以下说法中正确的个数有 ( )①一个有理数不是整数就是分数 ②一个有理数不是正数就是负数 ③一个整数不是正的，就是负的 ④一个分数不是正的，就是负的A 1B 2C 3D 45、在数＋8.3，－4，－0.8，0，90，－｜－24｜中，__________是正数，____________不是整数。

6、比132-大而比123小的所有整数的和为 __________ 。

第一章《有理数》复习总结

第一章《有理数》复习总结有理数是整数和分数的统称，包括正数、负数和零。

有理数可以表示为p/q的形式，其中p和q都是整数，且q不等于0。

p称为分子，q称为分母。

1.有理数的大小比较：(1)对于同号的有理数，绝对值越大，数值越大；(2)对于异号的有理数，正数大于负数，绝对值越小，数值越大。

2.有理数的加减乘除：(1)加法：拆分有理数，按照整数部分和小数部分相加；(2)减法：将减数变为相反数，再进行加法运算；(3)乘法：分别计算分子和分母的乘积，然后化简；(4)除法：将除数变为倒数，再进行乘法运算。

3.有理数的约分和化简：(1)约分：将分子和分母同时除以最大公因数，使得分数不可再约分；(2)化简：将带有分数线的有理数化为最简形式。

4.有理数的绝对值：(1)正数的绝对值是其本身；(2)负数的绝对值是其相反数；(3)零的绝对值是零。

5.有理数的相反数：(1)正数的相反数是负数；(2)负数的相反数是正数；(3)零的相反数是零。

6.计算混合数的值：(1)将整数部分和小数部分分开，分别计算；(2)将结果相加或相减，得到最终的结果。

7.有理数的乘方：(1)有理数的整数次方，将底数连乘或连除相应次数；(2)底数是分数，将底数化为整数的形式进行计算。

8.有理数的乘法逆元：(1)有理数的乘法逆元是其倒数；(2)除零外，任意非零有理数的乘法逆元存在。

9.有理数的混合运算：(1)先进行括号内的运算，再进行乘除法运算，最后进行加减法运算；(2)若有多个加法或减法运算，按照从左到右的顺序进行。

10.有理数在坐标轴上的表示：(1)正数表示点在原点的右侧；(2)负数表示点在原点的左侧；(3)零表示点在原点。

有理数在数学中有着广泛的应用，比如在数轴上定位、计算中的加减乘除、分数和小数的运算等。

学好有理数不仅需要掌握各种运算规则和性质，还需要大量的练习和实践。

通过不断的练习和思考，可以提高解决实际问题的能力，培养思维和逻辑思维能力。

总之，有理数作为数学的一个重要概念，是我们平日生活中接触最多的数的形式。

有理数知识点总结---超级实用

- 1 --bb a-a0第一章有理数全章系统复习资料例1、若0,b 0,a <>且b a >，你能比较b a b a --,,,的大小吗？用“>”号把它们连结起来。

分析：直接比较有一定的难度，此时如果借助数轴来求解就比较方便了，首先可以确定a 在原点的右侧，b 在原点左侧，并可以知道离开原点的距离是a 大。

解：将b a b a --,,,，在数轴上表示如右图：所以a -b b a <<<-1.0既，也。

2.正整数、零和负整数统称为；正分数和负分数统称为；和统称为有理数。

2.把一些数放在一起，就组成一个数的，简称数集。

3.零和正数统称为，零和负数统称为。

4.正整数和零统称为，又统称为；零和负整数统称为。

（一）把下列各数填在相应的集合中：8、-1、-0.4、35、0、13-、6、9、317-、114、-19正数集合：﹛ …﹜ 负数集合：﹛ …﹜ 整数集合：﹛ …} 分数集合：﹛ …﹜非正数集合：﹛ …﹜ 非负数集合：﹛ …﹜ 非正整数集合：﹛ …﹜非负整数集合：﹛ …﹜（二）判断题：1. 一个有理数不是正数就是分数。

（）2. 一个有理数不是整数就是分数。

（）3. 有限小数和无限小数都是有理数。

（）4. 0C ︒表示没有温度。

（）（三）选择题：6. 下列说法正确的是（） A.一个有理数不是正数就是负数 B.一个有理数不是整数就是分数C.有理数指整数、分数、正有理数、零、负有理数这五类D. 以上结论都不对7. 在下列说法中不正确的是（） A. 如果a 是有理数，那么2a 是偶数 B. 一个整数不是奇数就是偶数C. 一个数不能同时既为正数也为负数D. 0是最小的自然数（四）填空题：10.非负整数与正整数的区别是非负整数包括，而正整数不包括。

11.自然数包括和。

12.从负有理数集合中去掉负分数，得到集合。

人教版七年级上有理数全章总复习及试题

人教版七年级上有理数全章总复习及试题1.1 正数与负数一、必记概念:0既 ,也。

在实际生活中，常常用正数和负数表示具有意义的量。

如果上升10米记作+10米,那么下降5米记作。

二、练习：1. 下列结论中错误的是（）A. 零是整数B. 零不是正数 C。

零是偶数 D. 零不是自然数2. 如果顺时针旋转30°记作-30°，那么逆时针旋转45°记作。

3. 某人向东走5米，又回头向西走5米，此人实际距原地米.4. 如果中午以后的2小时记作+2小时，那么+2小时前3小时应记作。

5。

观察下面依次排列的一列数，你能发现它们排列的规律是什么吗？后面空格内的三个数是什么,试把它写出来.(1) 2、-3、4、-5、6、、、、…（2） 1、2、3、5、8、、、、…6. “一个数前面加‘-’，它一定是负数”对吗?1。

2 有理数1.2。

1 有理数一、必记概念：1. 正整数、零和负整数统称为 ;正分数和负分数统称为 ;和统称为有理数。

2。

把一些数放在一起,就组成一个数的，简称数集。

3。

零和正数统称为 ,零和负数统称为。

4. 正整数和零统称为，又统称为；零和负整数统称为。

二、练习:(一）把下列各数填在相应的集合中：-1、-0。

4、35、0、13-、6、9、317-、114、-19正数集合：﹛…﹜负数集合：﹛…﹜整数集合：﹛…﹜分数集合:﹛…﹜非正数集合:﹛…﹜非负数集合：﹛…﹜非正整数集合:﹛…﹜非负整数集合:﹛…﹜（二）判断题：1. 一个有理数不是正数就是分数。

( ）2。

一个有理数不是整数就是分数。

( ）3。

有限小数和无限小数都是有理数。

（ )4. 0C︒表示没有温度。

（ )（三）选择题:5。

下列说法:（1）零是正数；（2）零是整数；（3）零是有理数；（4）零是非负数；(5)零是偶数。

其中正确的说法的个数为( )A. 2个B. 3个C. 4个 D。

5个6. 下列说法正确的是（）A。

一个有理数不是正数就是负数B. 一个有理数不是整数就是分数C. 有理数是指整数、分数、正有理数、零、负有理数这五类D。

章复习第1章有理数

章复习第1章有理数一、有理数的意义1、正数：________________的数叫做正数，如:__________.2、负数：________________的数叫做负数，如:__________.3、______既不是正数，也不是负数，而是正数与负数的分界.在我们所认识的数中，______是唯一的“中性”数. 一切______数 < 0 <一切______数.4、有理数：______________________叫做有理数。

（或者：数位有限的数以及数位无限但循环的数叫做有理数。

）有理数的两种分类：或者与有理数相关的重要概念1、数轴：规定了______、______和______的______叫数轴.用途:任何有理数都可以在数轴上表示（但数轴上的点不都表示有理数，有些点表示的数不是有理数.）.数轴上表示的数，右边（正半轴上）的数(____数)>____>左边（负半轴上）的数(____数).2、相反数：如果两个数只有符号不同，那么我们称其中一个数是另一个数的相反数．特别地，0的相反数是0.注：①任何一个有理数，都有两方面的特性，分别是正负性和绝对值，“只有符号不同的两个数”中的“只有”指的是除了符号外，两个数的绝对值完全相同；②这是相反数的代数意义。

相反数的几何定义：在数轴上位于原点的两侧，并且与原点的距离相等的两点所表示的两个数，称为互为相反数．注：相反数是成对出现的，不是单独存在的。

相反数的性质：①任何数都有相反数，并且只有一个相反数；②正数的相反数是负数，负数的相反数是正数．特别地，0的相反数是0；③互为相反数的两个数之和为O；反之，和为O的两个数一定互为相反数。

相反数的表示法(求法)：一般地，对任意一个数a，它的相反数为-a.这里a表示任意的数，可以是正数、负数，也可以是0．3、绝对值：在数轴上表示数a的点与原点的距离叫做数a的绝对值，记作|a|．（这是绝对值的几何意义）绝对值的代数意义：正数的绝对值是它本身；负数的绝对值是它的相反数；零的绝对值是零．用式子表示为：注：①无论是绝对值的几何定义，还是绝对值的代数定义，都揭示了绝对值的一个重要性质——非负性．也就是说，任何一个有理数的绝对值都是非负数，即对任意有理数a，都有|a|≥0.②当a<O时，-a>O.即当a<O时，|a|=-a是一个正数。

七年级第一章有理数全章复习

七年级第一章有理数全章复习
第一章有理数
一、有理数分类
复习练习：
1、下面关于有理数的说法正确的是（ A ）
A. 整数集合和分数集合合在一起就是有理数集合
B. 正数集合与负数集合合在一起就构成整数集合
C. 正数和负数统称为有理数
D. 正数、负数和零统称为有理数
2、若两个有理数的和是正数，那幺一定有结论（ D ）
A. 两个加数都是正数
B. 两个加数有一个是正数
C. 一个加数正数，另外一个加数为零
D. 两个加数不能同为负数
4. 下面说法正确的有（ B ）
①一个有理数不是整数就是分数②一个有理数不是正数就是负数③一个整数不是正数就是负数④一个分数不是正数就是负数
A.1 个
B.2 个
C.3 个
D.4 个
二、数轴
1、像这样规定了原点、正方向和单位长度的直线叫做数轴.
2、数轴的三要素：原点、正方向、单位长度,缺一不可.
3、在数轴上比较两个有理数大小的法则：
①在数轴上表示的两个数，右边的数总比左边的大。

第一章有理数章节复习

解：（1）4.8×105=480 000；（2）9.7×106=9 700 000；（3）1.0×107=10 000 000；（4）2.75×104=27 500；（5）6.414×103=6 414．
1. 在有理数中，最大的负整数是_-__1_，最小的正整数是__1___，最小的非负整数是__0___，最大的非正整数是___0___． 2. 下列说法错误的是（ D ）
A.没有最大的有理数
B.没有最小的有理数
C.最大的负整数是-1
3. 下列说法正确的是( B )
D.最小的自然数是1
A.一个有理数，不是正数，就是负数
（2）乘方的符号法则：正数的任何次幂都是正数；负数的奇次幂是负数，负数的偶次幂是正数；
零的正整数次幂都是零. 6.有理数的混合运算 (1)先乘方，再乘除，最后加减； (2)同级运算，从左到右进行； (3)如有括号，先做括号内的运算，按小括号、中括号、大括号依次进行.
四、科学记数法 1.定义：把大于10的数记成a×10n的形式，其中a是整数数位只有一位的
考点一正数和负数
【例3】 1.在下列各组中，哪个选项表示互为相反意义的量（ A ）
A.足球比赛胜5场与负5场
B.向东走3千米，再向南走3千米
C.增产10吨粮食与减产-10吨粮食 D.下降的反义词是上升
【点睛】解题关键是理解“正”和“负”的相对性，确定一对具有相反意义的量．此题的难点在“增产10吨粮食与减产-10吨粮食”在这一点上要理解“-”就是减产的意思
【例5】将下列各数分别填入下列相应的圈内：
3.5
，-3.5，0 ，|-2|，-2，-135
，-
1 3
，0.5
正数
3.5，|-2|，0.5

有理数整章复习题

有理数复习一．选择题（共10小题）1．如果收入10元记作+10元，那么支出10元记作（）A．+20 元B．+10元C．﹣10元D．﹣20元2．下列各数：﹣2，+2，+3.5，0，﹣，﹣0.7，11，+π，其中负分数有（）A．1个B．2个C．3个D．4个3．a的相反数为﹣3，则a等于（）A．﹣3B．3C．±3D．4．4.5+（﹣3.2）﹣（﹣1.1）+_______＝1，横线上应填入（）A．2.4B．﹣2.4C．1.4D．﹣1.45．下列各组数中，相等的是（）A．﹣9和﹣B．﹣|﹣9|和﹣（﹣9）C．9和|﹣9|D．﹣9和|﹣9|6．如图，数轴上点A对应的数是，将点A沿数轴向左移动2个单位至点B，则点B对应的数是（）A．﹣B．﹣2C．D．7．下面的说法正确的是（）A．有理数的绝对值一定比0大B．有理数的相反数一定比0小C．如果两个数的绝对值相等，那么这两个数相等D．互为相反数的两个数的绝对值相等8．已知﹣m＜2＜m，若有理数m在数轴上对应的点为M，则点M在数轴上可能的位置是（）A．B．C．D．9．若a＞b，则下列各式正确的为（）A．|a|＞|b|B．|a|＜|b|C．|a|＞b D．a＞|b|10．设a为最小的正整数，b为最大的负整数，c是绝对值最小的有理数，则a+b﹣c的值为（）A．0B．2C．﹣2D．2或﹣2二．填空题（共4小题）11．已知在数轴上A点表示的数为﹣3，则与A点相隔18个单位长度的点表示的数为．12．某班5名学生在一次数学测试中的成绩以120为标准，超过的分数记为正数，不足的分数记为负数，记录如下：﹣4，+9，﹣1，0，+6，则他们的平均成绩是分．13．若|a|＝3，|b|＝2，则a﹣b的绝对值为．14．一天早晨的气温是﹣5℃，中午上升了10℃，半夜又下降了7℃，则半夜的气温是℃．三．解答题（共8小题）15．今年夏天某市发生特大山洪泥石流灾害，该市消防总队迅即出动兵力驰援灾区，在抗险救灾中，消防官兵的冲锋舟沿东西方向的河流抢救灾民，早晨从A地出发，晚上到达B 地，约定向东为正方向，当天的航行路程记录如下（单位：千米）：+14，﹣9，+8，﹣7，+13，﹣6，+10（1）B地在A地何处？（2）冲锋舟距离A地最远在东或西方向多少千米？（3）若冲锋舟每千米耗油0.5升，出发时油箱还剩20升汽油，求途中至少还需补充多少升汽油？16．把下列各数填在相应的大括号内15，﹣，0.81，﹣3，，﹣3.1，﹣4，171，0，3.14正整数集合{ …}负整数集合{ …}整数集合{ …}分数集合{ …}．17．数a在数轴上的位置如图所示，且|a+1|＝2，则|3a+7|＝．18．阅读材料：在数轴上5与﹣2所对的两点之间的距离：|5﹣（﹣2）|＝7．在数轴上点A、B分别表示数a、b，则A、B两点之间的距离AB＝ǀa﹣bǀ＝ǀb﹣aǀ．请回答下列问题：（1）数轴上表示﹣2和﹣5的两点之间的距离是；数轴上表示数x和3的两点之间的距离表示为．数轴上表示数和的两点之间的距离表示为ǀx+2ǀ．（2）当表示数x的点在﹣2与3之间移动时，| x﹣3|+|x+2|＝．（3）要使|x﹣3|+|x+2|＝9，则x为．（4）当|x﹣3|+|x+2|＝5时，x的取值范围为．19．在数轴上把下列各数表示出来，并用“＜”连接各数．﹣|﹣3.5|，1，0，﹣（﹣2），﹣（+1），420．计算：（1）（﹣13）+（﹣7）﹣（+20）﹣（﹣40）+（+16）；（2）（+）+（﹣）+（+1）+（﹣）；（3）（+1.9）+3.6﹣（﹣10.1）+1.4；（4）1+2﹣3+﹣4.25．21．如图，数轴上点A、B表示的有理数分别为a、b，并求出2a﹣b的值．（1）根据题意：a＝，b＝；（2）求2a﹣b的值．22．已知：|a﹣2|+|b+|＝0，求a+b a的值．一．选择题（共10小题，每题3分）1．在（﹣1）5、（﹣1）4、﹣23，（﹣3）2这四个数中，负数有几个（）A．0个B．1个C．2个D．3个2．在0，2，﹣3，﹣这四个数中，最小的数是（）A．0B．2C．﹣3D．﹣3．﹣2的绝对值是（）A．2B．﹣2C．2或﹣2D．或﹣4．如图，数轴上的点A、B关于原点对称，则点B表示的数是（）A．2B．﹣2C．±2D．05．2019年3月21日，春分，雪至．哈尔滨市的最低气温是﹣8℃，最高气温是1℃，则这一天哈尔滨市的最高气温与最低气温的差是（）A．﹣9℃B．9℃C．7℃D．﹣7℃6．﹣（﹣6）等于（）A．﹣6B．6C．D．±67．若m﹣n＞0，则下列各式中一定正确的是（）A．m＞n B．mn＞0C．D．﹣m＞﹣n8．数轴上，到原点距离是8的点表示的数是（）A．8和﹣8B．0和﹣8C．0和8D．﹣4和49．若ab＞0，a+b＜0，则（）A．a、b都为负数B．a、b都为正数C ．a 、b 中一正一负D ．以上都不对10．下列四个算式：①﹣2﹣3＝﹣1；②2﹣|﹣3|＝﹣1；③（﹣2）3＝﹣6；④﹣2÷＝﹣6．其中，正确的算式有（）A ．0个B ．1个C ．2个D ．3个二．填空题（共5小题，每题4分）11．如果向东走10米记作+10米，那么向西走15米可记作米．12．已知a 、b 互为相反数，c 、d 互为倒数，那么2a +2b ﹣5cd ＝．13．对于任意有理数a 、b ，定义运算如下：a *b ＝（a ﹣b ）×（a +b ），则（﹣3）*5的值为14．在数轴上，若点A 表示﹣2，则到点A 距离等于2的点所表示的数为．15．若有理数a <0，b<0，则b a b a b a b a --+--+，，，中最大的是．三．解答题（共17小题）16．计算（共8分，每题2分）（1）﹣10﹣（﹣3）+（﹣5）（2）﹣2.5÷×（﹣）（3）（﹣2）2×5﹣（﹣2）3÷4 （4）÷（﹣2）﹣×﹣÷417．（6分）下列有理数：﹣1，2，5，﹣1（1）将上列各数在如上图的数轴上表示出来；（2）将上列各数从小到大排列，并用“＜”符号连接．18．（6分）已知有理数a、b互为相反数且a≠0，c、d互为倒数，有理数m和﹣2在数轴上表示的点相距3个单位长度，求|m|﹣+﹣cd的值．19．（8分）在学习完《有理数》后，小奇对运算产生了浓厚的兴趣．借助有理数的运算，定义了一种新运算“⊕”，规则如下：a⊕b＝a×b+2×a．（1）求2⊕（﹣1）的值；（2）求﹣3⊕（﹣4⊕）的值；（3）试用学习有理数的经验和方法来探究这种新运算“⊕”是否具有交换律？请写出你的探究过程．20．（10分）规定两数a，b之间的一种运算，记作（a，b）：如果a c＝b，那么（a，b）＝c．例如：因为23＝8，所以（2，8）＝3．（1）根据上述规定，填空：（3，9）＝，（5，125）＝，（﹣，）＝，（﹣2，﹣32）＝．（2）令（4，5）＝a，（4，6）＝b，（4，30）＝c，试说明下列等式成立的理由：（4，5）+（4，6）＝（4，30）．21．（12分）元旦放假时，小明一家三口一起乘小轿车去探望爷爷、奶奶和姥爷、姥姥．早上从家里出发，向东走了5千米到超市买东西，然后又向东走了2.5千米到爷爷家，下午从爷爷家出发向西走了10千米到姥爷家，晚上返回家里．（1）若以小明家为原点，向东为正方向，用1个单位长度表示1千米，请将超市、爷爷家和姥爷家的位置在下面数轴上分别用点A、B、C表示出来；（2）超市和姥爷家相距多少千米？（3）若小轿车每千米耗油0.08升，求小明一家从出发到返回家，小轿车的耗油量．。

有理数全章复习

第1章有理数(单元复习课件)(知识导图+考点梳理+数学活动+课本复习题)七年级数学上册人教版2024

有理数总复习

第一章 有理数复习

有理数全章复习

《有理数》全章复习与巩固(提高)知识讲解

有理数全章复习(按知识点分类复习)

第一章《有理数》复习总结

有理数知识点总结---超级实用

人教版七年级上有理数全章总复习及试题

章复习 第1章 有理数

七年级第一章有理数全章复习

第一章 有理数章节复习

有理数整章复习题

第一章有理数复习

章复习第1章有理数

第一章有理数章节复习