安徽省六安市舒城中学高二数学暑假作业第29天文

合集下载

安徽省六安市舒城中学2017-2018学年高二数学(文)暑假作业第14天 Word版含答案

2017-2018学年正弦定理、余弦定理、解三角形课标导航：1.掌握正弦定理、余弦定理并能解决简单的三角度量问题；2.能运用正弦定理、余弦定理等知识与方法解决一些与测量和几何计算有关的实际问题.一、选择题1. 在△ABC 中，若sin 2A ＋sin 2B ＜sin 2C ，则△ABC 的形状是 ( )A ．钝角三角形B ．直角三角形C ．锐角三角形D ．不能确定 2. 在Rt △ABC 中，∠C ＝90°，AC ＝4，则AB →·AC →等于（） A ．－16B ．－8C ．8D ．163. 在△ABC 中，“C b B c cos cos =”是“△ABC 是等腰三角形”的（）A.错误！未找到引用源。

充分不必要条件B.错误！未找到引用源。

必要不充分条件C.错误！未找到引用源。

充分必要条件D.错误！未找到引用源。

既不充分也不必要条件4. 如果等腰三角形的周长是底边长的5倍，那么它的顶角的余弦值为（）A ．185 B ．43 C ．23 D ．875. △ABC 的三个内角A 、B 、C 所对的边分别为,,a b c ，且2sin sin cos a A B b A +=，则错误！未找到引用源。

（）A.错误！未找到引用源。

错误！未找到引用源。

B.错误！未找到引用源。

错误！未找到引用源。

C.错误！未找到引用源。

错误！未找到引用源。

D.错误！未找到引用源。

错误！未找到引用源。

6. 若△ABC 的内角，,,A B C 满足错误！未找到引用源。

，则cos B = （）A ．4B ．34C ．16D ．11167. 在△ABC 中，内角A 、B 、C 的对边分别是,,a b c ，若22a b -=，，则A （）A.错误！未找到引用源。

30°B.错误！未找到引用源。

60°C.错误！未找到引用源。

120°D.错误！未找到引用源。

150°8. 在△ABC 中，AC ，BC ＝2，B ＝60°，则BC 边上的高等于( )二、填空题9. 在ABC ∆中，角A 、B 、C 所对的边分别为a b c 、、，若1,3a c π===，则A = ;10. 在△ABC 中，已知最长边23=AB ，3=BC ，∠A =30︒，则∠C = ; 11. 若P ，Q 是等腰直角三角形ABC 斜边AB 的三等分点，则=∠PCQ tan ; 12. 某船在A 处看灯塔S 在北偏东30︒方向，它以每小时30海里的速度向正北方向航行，经过40分钟航行到B 处，看灯塔S 在北偏东75︒方向，则此时该船到灯塔S 的距离约为海里（精确到0.01海里）．三、解答题13.已知在ABC ∆中，,,a b c 分别为角,,A B C 的对边，60B =,b =，3a =. (1)求cos A 的值； (2) 求cos(2)61cos 2A Aπ--的值.14. 在△ABC 中，角A ，B ，C 的对边分别为,,a b c ，且4cos 5C =，2cos c b A =．（1）求证：A B =；（2）若△ABC 的面积152S =，求c 的值.15. 已知A 、B 、C 是△ABC 的三个内角，向量(1,(cos ,sin )m n A A ==，且1m n ⋅=-（1）求角A ；（2）若sin cos 3,tan sin cos B BC B B+=-求的值16. 如图，渔船甲位于岛屿A 的南偏西60方向的B 处，且与岛屿A 相距12海里，渔船乙以10海里/小时的速度从岛屿A 出发沿正北方向航行，若渔船甲同时从B 处出发沿北偏东α的方向追赶渔船乙，刚好用2小时追上.（1）求渔船甲的速度；（2）求sin α的值．【链接高考】设△ABC 是锐角三角形，a ，b ，c 分别是内角A ，B ，C 所对边长，并且sin 2A ＝sin 3B π⎛⎫+ ⎪⎝⎭sin 3B π⎛⎫- ⎪⎝⎭＋sin 2B . (1) 求角A 的值；(2) 若AB →·AC →＝12，a ＝，求b ，c (其中b ＜c )．ABC东南西北60 α第14天1~8 ADAD DDAB ；9. 6π; 10. 135︒; 11. 43;12. 13.（1）cosA ==（2）cos(2)61cos 2A Aπ-=-. 14.（1）证明：略；（2）c =．15.（1）3A π=；（2）tan C ==16.错误！未找到引用源。

安徽省六安市舒城中学2017-2018学年高二数学(文)暑假作业第27天 Word版含答案

2017-2018学年直线与圆课标导航：1.掌握确定直线、圆的位置的几何要素，掌握它们的方程及形式； 2.初步了解用代数方法处理几何问题的思想. 一、选择题1. 直线1:1l y x =+与直线2:1l y =-的夹角为（） A ．6π B ．4π C ．3π D ．23π 2. 圆22(2)4x y ++=与圆22(2)(1)9x y -+-=的位置关系为（） A ．内切 B ．相交 C ．外切D ．相离3. 过圆224x y +=外一点(4,2)P 作圆的两条切线，切点分别为,A B ，则ABP ∆的外接圆方程是（） A ．22(4)(2)1x y -+-= B ．22(2)4x y +-= C ．22(2)(1)5x y +++=D ．22(2)(1)5x y -+-=4. 直线0()x y a a o ++=>与圆224x y +=交于,A B 两点，且O A BS =，则a =（）A ．BC D 或5. 若过定点)0,1(-M 且斜率为k 的直线与圆05422=-++y x x 在第一象限内的部分有交点，则k 的取值范围是( ) A.50<<k B.05<<-k C.130<<k D.50<<k6. 过点M(1,5)-作圆22(1)(2)4x y -+-=的切线,则切线方程为（） A ．1x =- B ．512550x y +-=C ．1512550x x y =-+-=或D ．15550x x y =-+-=或127. 两圆042222=-+++a ax y x 和0414222=+--+b by y x 恰有三条公切线，若0≠ab ，则2211b a +的最小值为（）A ．91B ．94 C ．1 D ．3 8. 若点P 在直线03:1=++y x l 上，过点P 的直线2l 与曲线22:(5)16C x y -+=相切于点M ，则PM 的最小值为( )A B ．2C ．D ．4二、填空题9. 已知过(2,)A a -，(,10)B a 两点的直线与直线210x y -+=平行，则a 的值为________; 10. 圆4)1()1(22=-++y x 被直线2+-=x y 所截得的弦长为；11. 已知曲线22:C x y m +=恰有三个点到直线125260x y ++=距离为1，则m = ；12. 已知圆C 与直线040x y x y -=--=及都相切，圆心在直线0x y +=上，则圆C 的方程为 .三、解答题13. 已知点(2,0)A 关于直线1:40l x y +-=的对称点为1A ，圆22:()()4(0)C x m y n n -+-=>经过点A 和A 1，且与过点(0,B -的直线2l 相切。

安徽省六安市舒城中学近年-近年学年高二数学下学期期末考试试题文(最新整理)

所以
,所以，
22【解答】（1)将椭圆线．
得到圆
的图象，
故曲线的普通方程为
直线的极坐标方程为
故直线的直角坐标方程为
上每一点的横坐标保持不变，纵坐标变为原来的一半,得到曲
；
．
,即
；
(2）直线过点
且倾斜角为，
故直线的参数方程为：
代入方程
．
化为：
,
为参数）．
，
．
根据的几何意义可得：
．
23 解：（1)当 a=1 时，
附：对于一组数据( x 1 ，y 1 ) ，( x 2 ,y 2 ) ，,( x n ，y n ) ，其回归直线 yˆ bˆxaˆ 的斜率和
n
n
xiyi nxy (xi x)(yi y)
bˆ
i1 n
i1 n
截距的最小二乘估计分别为：
xi2 nx2
i1
(xi x)2
i1
4
,aˆ y bˆx
17～21 题为必考题，每个试题考生都必须作答．第 22、23 题为选考题，考生根据要求作答．)
17。已知等差数列｛an}的公差 d≠0,它的前 n 项和为 Sn，若 S5＝70，且 a2，a7，a22 成等比数
列，
（1)求数列｛an}的通项公式;
1
(2)若数列
Sn
的前 n 项和为 Tn，求证：错误!≤Tn＜错误!.
13．“a 2 ”是“两直线ax3y2a0 和2x(a 1 )y20 平行”的
条件．
14。已知函数 f(x-1)的图x1对像称关于直线，当 x0 时 f(x)， e x 1x，则曲线 yf(x)在点
（1，2)处的切线方程是________．

安徽省六安市高一数学(理)暑假作业第二十九天 Word版含答案

第二十九天完成日期月日星期学法指导：1.熟练掌握基本不等式。

2.利用基本不等式求最大值和最小值。

一、选择题（在每小题给出的四个选项中只有一项是符合题目要求的） 1．函数22631y x x =++的最小值是( )A ．3B ．3-C ．D ．32．设函数1()21(0)f x x x x=+-<，则()f x()A ．有最大值B ．有最小值C ．是增函数D ．是减函数 3．下列不等式的证明过程正确的是 ( )A ．若,a b R ∈，则2b a a b +≥=B ．若0a <，则44a a +≥-=-C ．若,(0,)a b ∈+∞，则lg lg a b +≥D ．若a R ∈，则222a a -+≥=4．已知0,0a b >>，则11a b++( )A ．2B ．22C ．4D ．55．若1a b >>，P =lg lg 2a b Q +=，lg 2a bR +=，则( )A ．R P Q <<B ．P Q R <<C ．Q P R <<D ．P R Q <<6．已知点(,)P x y 在经过(3,0),(1,1)A B 两点的直线上，则yx42+的最小值为 ( )A ．2B ．4C ．16D ．不存在7．设点2(,1)(0)2t P t t+>，则||OP (O 为坐标原点)的最小值是( )C ．5D ．38. 已知0a b <<，且1a b +=，则下列不等式中正确的是( )A ．2log 1a >-B ．122a b -<C ．1b aa b+<D ．22log log 2a b +<-二、填空题9．斜边长为1的直角三角形面积最大为________．10．已知0,0>>y x ，xy y x =+，则())1(122--y x 的最小值为________． 11. 若实数,x y 满足221x y xy ++=，则x y +的最大值是________．12．当0a >且1a ≠时，函数()log (1)1a f x x =-+的图像恒过点P ，若点P 在直线n mx y +=上，则42m n +的最小值为________．三、解答题（应写出文字说明、证明过程或演算步骤）13．已知()(12)f x x x =-．（1）当102x <<时，求()f x 的最大值；（2）当12x ≤≤时，求()f x 的最大值．14．如图，某小区拟在空地上建一个占地面积为2400平方米的矩形休闲广场，按照设计要求，休闲广场中间有两个完全相同的矩形绿化区域，周边及绿化区域之间是道路（图中阴影部分），道路的宽度均为2米．怎样设计矩形休闲广场的长和宽，才能使绿化区域的总面积最大？并求出其最大面积.15.如图所示，半径为4的球面上有,,,A B C D 四点，且,,AB AC AD 两两垂直，若123,,S S S 分别为,,ABC ACD ADB ∆∆∆的面积，求123S S S ++的最大值．【链接高考】16.（2014课标II 24）设函数1()||||f x x x a a=++-(0)a >. （I ）证明：()2f x ≥；（II ）若(3)5f <，求a 的取值范围.第二十九天1.D2.A3.D4.C5.D6.B7.A8.D9. 14 10.9 11. 12.213. (1)18. (2）－1.14.矩形休闲广场的长60m 和宽40m ，才能使绿化区域的总面积最大，其最大面积为1944平方米.15.32. 16.（I ）略（II ）.。

安徽省六安市舒城中学高二数学暑假作业第30天文

第30天直线与圆锥曲线及综合课标导航：1.能解决直线与圆锥曲线的位置关系等有关问题； 2.理解数形结合思想. 一、选择题1. 设双曲线)0,0(12222>>=-b a by a x 的右焦点为)0,(c F ，方程02=-+c bx ax 的两实根分别为21,x x ，则),(21x x P（）A ．必在圆222=+y x 内B ．必在圆222=+y x 外C ．必在圆222=+y x 上 D ．以上三种情况都有可能2. 已知方程0,,0(022>≠≠=++=+c b a ab c by ax ab by ax 其中和），它们所表示的曲线可能（）ＡＢＣＤ3. 已知双曲线x 22－y 2b 2＝1(b ＞0)的左、右焦点分别是F 1、F 2，其一条渐近线方程为y ＝x ，点P (3y 0)在双曲线上．则PF 1→·PF 2→＝（）A ．－12B ．－2C ．0D ．44. 错误!未找到引用源。

是双曲线错误!未找到引用源。

的右支上一点，点错误!未找到引用源。

分别是圆错误!未找到引用源。

和错误!未找到引用源。

上的动点，则错误!未找到引用源。

的最小值为（）A ． 1B ． 2C ． 3D ．45．已知双曲线22221(0,0)x y a b a b-=>>与抛物线28y x =有一个公共的焦点F ，且两曲线的一个交点为P ，若5PF =，则双曲线的离心率为（）A ．2B ．CD 6. 设抛物线24y x =的焦点为F ，过点M （-1，0）的直线在第一象限交抛物线于A 、B ，使0AF BF ⋅=，则直线AB 的斜率k =（）AB ．2CD ．37. 已知双曲线的顶点与焦点分别是椭圆22221(0)x y a b a b+=>>的焦点与顶点，若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形，则椭圆的离心率为（）A ．13 B ．12C D ．28．设圆锥曲线Γ的两个焦点分别为F 1， F 2，若曲线上Γ存在点P 满足1PF ：12F F ：2PF =4:3:2，则曲线的Γ离心率等于（） A. 1322或B. 223或 C. 122或 D. 2332或二、填空题9. 抛物线28y x =的焦点到双曲线221124y x -=的渐近线的距离为；10. 椭圆22221(0)x y a b a b +=>>的离心率为，则双曲线22221x y a b-=的离心率为；11. 设圆C 的圆心在双曲线2221(0)2x y a -=>的右焦点上，且与此双曲线的渐近线相切，若圆C 被直线:0l x =截得的弦长等于2，则a = ；12. 给出如下四个命题：①方程x 2＋y 2－2x ＋1＝0表示的图形是圆；，则两个焦点与短轴的两个端点构成正方形； ③抛物线x ＝2y 2的焦点坐标为1,08⎛⎫ ⎪⎝⎭；④双曲线y 249－x 225＝1的渐近线方程为y ＝±57x .其中正确命题的序号是________．三、解答题13. 若椭圆1C ：)20( 14222<<=+b b y x 的离心率等于23，抛物线2C ：)0( 22>=p py x 的焦点在椭圆的顶点上。

安徽省六安市高二数学(文)暑假作业第29天 Word版含答案

第29天双曲线、抛物线课标导航：1.掌握双曲线和抛物线的定义、标准方程及简单性质； 2.能解决直线与双曲线、抛物线的位置关系等问题.一、选择题1. 已知双曲线22221x y a b -=的一条渐近线方程为12y x =，则该双曲线的离心率为( ) A ．25B ．3C ．5D ．2 2. 抛物线24x y =上一点到直线54-=x y 的距离最短，则该点的坐标是（）A ．)2,1(B ．)0,0(C ．)1,21(D ．)4,1(3. 已知定点12(2,0),(2,0)F F -，N 是圆22:1O x y +=上任意一点，点F 1关于点N 的对称点为M ，线段F 1M 的中垂线与直线F 2M 相交于点P ，则点P 的轨迹是（）A ．椭圆B ．双曲线C ．抛物线D ．圆4. 双曲线221169x y -=上到定点(5,0)的距离是9的点的个数是（）A. 0个；B. 2个；C. 3个；D. 4个5. 双曲线22221(,0)x y a b a b -=>一条渐近线的倾斜角为3π，离心率为e ，则2a eb+的最小值为（）A ．3B ．3C D ．6. 已知双曲线12222=-by a x 的一个焦点与抛物线x y 42=的焦点重合，且双曲线的离心率等（）A ．154522=-y x B ．14522=-y x C ．14522=-x y D ．145522=-y x 7. 双曲线221(0)mx y m -=>的右顶点为A ，若该双曲线右支上存在两点,B C 使得ABC ∆为等腰直角三角形，则实数m 的值可能为( )A ．12B ．1C ． 2D ． 38. 若椭圆)0(122>>=+n m ny m x 和双曲线)0(122>>=-b a b y a x 有相同的焦点1F 、2F ，P 是两曲线的一个公共点，则||||21PF PF ⋅的值是（）A ．m a -B ．)(21a m - C ．22a m - D ．a m -二、填空题9. 已知抛物线24y x =与直线240x y +-=相交于A 、B 两点，抛物线的焦点为F ，那么FA FB +=___________;10. 已知点P 在抛物线y 2＝4x 上，那么点P 到点Q (2，－1)的距离与点P 到抛物线焦点距离之和取得最小值时，点P 的坐标为 ;11. 已知F 1、F 2分别是双曲线22221x y a b-=的左、右焦点，过F 1且垂直于x 轴的直线与双曲线交于A 、B 两点，若△ABF 2为钝角三角形，则该双曲线的离心率的取值范围是 ;12. 已知抛物线24y x =的弦AB 的中点的横坐标为2，则AB 的最大值为；三、解答题13. 已知(1,0)F , P 是平面上一动点, P 到直线:1l x =-上的射影为点N ，且满足1()02PN NF NF +⋅=.(1)求点P 的轨迹C 的方程;(2)过点(1,2)M 作曲线C 的两条弦MD,ME,且MD,ME 所在直线的斜率为12,k k , 满足121k k ⋅=, 求证: 直线DE 过定点, 并求出这个定点．14. 已知圆41)2(,425)2(2222=+-=++y x M y x 圆的圆心为的圆心为N ，一动圆与这两圆都外切.（1）求动圆圆心P 的轨迹方程；（2）若过点N 的直线l 与（1）中所求轨迹有两个交点A 、B ，求⋅的取值范围.15. 设抛物线C :22x py =(p >0)的焦点为F ,准线为l ,A 为C 上一点,已知以F 为圆心,FA 为半径的圆F 交l 于B ,D 两点.(1) 若090BFD ∠=,ABD ∆的面积为,求p 的值及圆F 的方程;(2) 若A ,B ,F 三点在同一条直线m 上,直线n 与m 平行,且n 与C 只有一个公共点,求坐标原点到m ,n 距离的比值.16. 已知双曲线22221x y a b-=的离心率为2，，过右焦点F 2的直线l 交双曲线于A 、B 两点，F 1为左焦点，（1）求双曲线的方程；（2）若△F 1AB 的面积等于，求直线l 的方程．【链接高考】在直角坐标系xOy 中，点1(1,)2P 到抛物线2:2C y px =（0p >）的准线的距离为54，点(,1)M t 是C 上的定点，,A B 是C 上的两动点，且线段AB 被直线OM 平分。

六安市舒城中学高二数学下学期期末考试试题文

舒城中学2017—-2018学年度第二学期期末考试高二文数一.选择题（本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中，只有一个是符合要求的,请你将符合要求的项的序号填在括号内）1．复数i-12（i 为虚数单位)的共轭复数是（）A. i +1 B 。

i -1 C 。

i +-1 D 。

i --12．设命题:,xp x R e x ∀∈>，则p ⌝是（）A.,x x R e x ∀∈≤B 。

000,x x R e x ∃∈<C 。

,x x R e x ∀∈< D.000,x x R e x ∃∈≤3．某工厂生产甲、乙、丙、丁四种不同型号的产品，产量分别为100,300,400,200件，为检验产品的质量，现用分层抽样的方法从以上所有的产品中抽取60件进行检验，则应从丙种型号的产品中抽取件数为（ ) A 。

24 B 。

18 C 。

12D 。

64．观察下图：12 3 43 4 5 6 74 5 6 7 8 9 10设第n 行的各数之和等于22017，则=n( ）A.2010B 。

2018C 。

1005 D.10095．甲、乙两组数据如茎叶图所示，若它们的中位数相同,平均数也相同，则图中的n m , 的比值=nm ( ）A 。

31 B. 21 C.2 D.36．某多面体的三视图如图所示,则该多面体的体积为（）A.B. C 。

D 。

7．阅读如图所示的程序框图，运行相应的程序，则输出的S 值为 ( ）A. 15 B 。

37 C 。

83D 。

1778。

下列函数中，其图象与函数x y ln =的图象关于直线2=x 对称的是（ )A 。

)4ln(x y -= B. )2ln(x y -= C 。

)2ln(x y += D.)4ln(x y +=9．已知点P 是抛物线x y 42=上的动点，点P 在y 轴上的射影是M ，点)3,2(A ,则|PM ||PA |+的最小值是（） A 。

安徽省六安市舒城中学2016年高二数学(文)暑假作业第20天含答案

第20天数列的求和课标导航:了解常见数列求和方法，掌握和公式的运用一、选择题1. 已知数列{a n ｝的前n 项和S n =312n an +=+,则( ）A ．201 B ．241 C ．281 D ．321 2。

已知等差数列}{na 的前n 项和为nS ,若45818,a a S =-=则（）A ．18B 。

36 C. 54 D. 723. 两等差数列{a n }、{b n ｝的前n 项和的比'5327n n Sn Sn +=+，则55a b的值是（）A ．2817B ．4825C ．5327D ．23154。

已知等差数列{}na 的前n 项和为nS ，且3711315aa a ++=，则13S =( ）A ．104B ．78C ．52D ．395．等差数列{}na 的通项公式为21n a n ，其前n 项和为nS ，则数列{}nS n的前10项和为（）A ．70B ．75C ．100D ．1206. 满足*12121,log log 1()n na a a n +==+∈N ，它的前n 项和为nS ,则满足1025nS >的最小n 值是（）A ．9B ．10C ．11D ．127. 已知函数()bx xx f 22+=过(1, 2)点,若数列()⎭⎬⎫⎩⎨⎧n f 1的前n 项和为n S ,则2012S 的值为（）A.20112012 B.20112010 C 。

20122013 D 。

201320128。

已知数列｛a n ｝满足3a n ＋1＋a n ＝0，a 2＝－错误!，则｛a n }的前10项和等于（） A ．－6(1－3－10） B 。

错误!（1－310) C ．3（1－3－10)D ．3（1＋3－10) 二、填空题9. 已知等差数列{}na 的前n 项和为nS ,且13140,0,S S ><若10t t a a +<则t = ；10。

安徽省六安市舒城中学高二数学暑假作业第18天文

第18天数列的概念与通项课标导航：1.了解数列的概念和几种简单的表示法； 2.了解数列是自变量为整数的一类函数. 一、选择题1. 下面是关于公差d>0的等差数列{a n }的四个命题：p 1：数列{a n }是递增数列； p 2：数列{na n }是递增数列；p 3：数列a nn 是递增数列；p 4：数列{a n ＋3nd}是递增数列，其中的真命题为 ( ) A ．p 1，p 2B ．p 3，p 4C ．p 2，p 3D ．p 1，p 42. 已知数列ΛΛ,12,,7,5,3,1-n ，则53是它的（）A. 第22项B. 第23项C. 第24项D. 第28项 3. 已知031=--+n n a a ，则数列{}n a 是（）A. 递增数列B. 递减数列C. 常数列D. 摆动数列4. 数列{}n a 的通项公式为n n a n 2832-=，则数列{}n a 各项中最小项是（）A. 第4项B. 第5项C. 第6项D. 第7项 5. 数列1,0,1,0,1,0,……的一个通项公式是（）A. ()2111+--=n n a B. ()2111+-+=n n a C. ()211--=n na D. ()211nn a ---=6. 已知数列{}n a 满足()nn n n a a a 111-+=--且11=a ，则=35a a（）A.1516 B. 34 C. 158D. 387. 已知()*1133,21N n a a a a n n n ∈+==+，则=n a（）A.52+n B. 42+n C. 53+n D. 43+n 8. 数列{a n }的通项a n =)(9998N n n n ∈--,则数列{a n }的前30项中最大项是( ) A ．30a B ．10a C ． 9aD ． 1a 二、填空题9. 数列{}n a 满足11=a ，13321++=-+n n a a n n ，根据这个数列的前4项并归纳通项公式得n a = ；10. 设{a n }是首项为1的正项数列，且（n +1）a n +12－na n 2+a n +1a n =0（n ∈N *），则它的通项公式a n =______________;11. 数列{}n a 中，已知()*1221,2,1N n a a a a a n n n ∈-===++，则=2002a ；12. 数列{}n a 满足⎪⎪⎩⎪⎪⎨⎧<≤-<≤=+)121(12)210(21n n n n n a a a a a ,若761=a ，则=8a .三、解答题13.已知数列{}n a 满足q pa a a n n +==+11,1，且15,342==a a ，求q p ,的值．14. 设数列{}n a 的前n 项和为n S ，已知()21nn n ba b S -=-（1）证明：当2b =时，{}12n n a n --⋅是等比数列；（2）求{}n a 的通项公式．15. 已知公差不为0的等差数列{}n a 的前3项和3S ＝9，且125,,a a a 成等比数列. （1）求数列{}n a 的通项公式和前n 项和n S ; (2）设n T 为数列11{}n n a a +的前n 项和，若1n n T a λ+≤对一切n N *∈恒成立，求实数λ的最小值.16. 设同时满足条件：①122++≥+n n n b b b ；②n b M ≤(N n +∈，M 是与n 无关的常数)的无穷数列{}n b 叫“仁风”数列.已知数列{}n a 的前n 项和n S 满足： (1)1n n aS a a =--（a 为常数，且0a ≠，1a ≠）．（1）求{}n a 的通项公式；（2）设21n n n S b a =+，若数列{}n b 为等比数列，求a 的值，并证明此时⎭⎬⎫⎩⎨⎧n b 1为“仁风”数列.【链接高考】[2013·安徽卷] 设数列{a n }满足a 1＝2，a 2＋a 4＝8，且对任意n∈N *，函数f(x)＝(a n－a n ＋1＋a n ＋2)x ＋a n ＋1cos x －a n ＋2sin x 满足'()2f π＝0.(1)求数列{a n }的通项公式； (2)若，求数列{b n }的前n 项和S n .第18天1~8 DBAB BBCB ;9. 3n ; 10.n 1;11. 1-; 12. 75;13．⎩⎨⎧=-=63q p 或⎩⎨⎧==12q p ’14．（1）证明：由题意知12a =，且()21nn n ba b S -=-，()11121n n n ba b S +++-=-两式相减得()()1121nn n n b a a b a ++--=-，即12n n n a ba +=+ ① 当2b =时，由①知122n n n a a +=+，于是()()1122212n n n n n a n a n +-+⋅=+-+⋅()122n n a n -=-⋅又111210n a --⋅=≠，所以{}12n n a n --⋅是首项为1，公比为2的等比数列。

安徽省六安市舒城中学高二数学暑假作业第6天文

第6天幂函数、指数函数、对数函数课标导航：1.掌握幂函数、指数函数、对数函数的概念及性质；2.体会幂函数、指数函数、对数函数一类重要的函数模型；一、选择题1．已知13x x -+=，则3322x x -+值为（）A.33B.25C.45D. 45- 2. 函数y x =3与y x=--3的图象关于下列那种图形对称（）A ．x 轴B ．y 轴C ．直线y x =D ．原点中心对称 3. 函数12log (32)y x =-的定义域是（）A ．[1,)+∞B ．2(,)3+∞C ．2[,1]3D ．2(,1]34. 三个数60.70.70.76log 6，，的大小关系为（）A. 60.70.70.7log 66<<B. 60.70.70.76log 6<< C ．0.760.7log 660.7<< D. 60.70.7log 60.76<< 5．函数|lg(1)|y x =-的图象是（）6. 若122-=xa，则xx xx aa a a --++33等于（） A ．22－1B ．2－22C ．22＋1D ．2＋17. 若0,0,1a b ab >>>，12log ln 2a =，则log a b 与a 21log 的关系是（）A ．12log log a b a < B ．12log log a b a = C ．12log log a b a > D ．12log log a b a ≤8. 若ln 2ln 3ln 5,,235a b c ===,则（）CA ．a b c <<B ．c b a <<C ．c a b <<D ．b a c <<二、填空题9.已知函数)1(log )(+=x x f a 的定义域和值域都是[]0,1，则实数a 的值是；10. 已知集合{}20A x x x x =-∈,R ≤，设函数2xf x a -=+()（x A ∈）的值域为B ，若B A ⊆，则实数a 的取值范围是；11.若函数2,0()2,0x x x f x x -⎧<⎪=⎨->⎪⎩，则函数(())y f f x =的值域是；12. 定义：区间)](,[2121x x x x <的长度为12x x -.已知函数|log |5.0x y =定义域为],[b a ，值域为]2,0[，则区间],[b a 的长度的最大值为__________. 三、解答题13.已知])9,1[(2log )(3∈+=x x x f ，求函数)()]([22x f x f y +=的值域.14. 已知函数()log ()x a f x a a =- (01)a a >≠且，求()f x 的定义域和值域.15. 设函数()22xxf x -=-（1）判断函数()f x 的奇偶性，并证明；（2）证明函数()f x 在(),-∞+∞上是增函数；（3）若不等式()112x f x m -⎛⎫>- ⎪⎝⎭恒成立，求实数m 的取值范围。

安徽省六安市舒城中学2016年高二数学(文)暑假作业第25天含答案

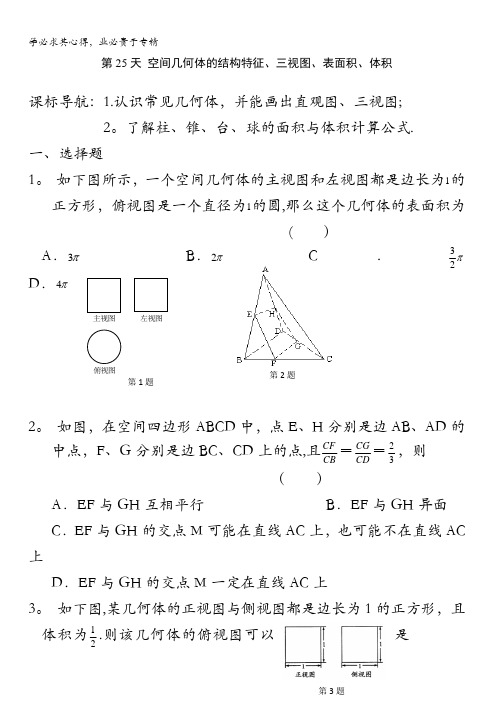
第2题第1题主视图俯视图左视图第25天空间几何体的结构特征、三视图、表面积、体积课标导航：1.认识常见几何体，并能画出直观图、三视图; 2。

了解柱、锥、台、球的面积与体积计算公式. 一、选择题1。

如下图所示，一个空间几何体的主视图和左视图都是边长为1的正方形，俯视图是一个直径为1的圆,那么这个几何体的表面积为 ( ） A ．π3 B ．π2 C ．π23D ．π42。

如图，在空间四边形ABCD 中，点E 、H 分别是边AB 、AD 的中点，F 、G 分别是边BC 、CD 上的点,且CF CB＝CG CD＝23，则（）A ．EF 与GH 互相平行B ．EF 与GH 异面C ．EF 与GH 的交点M 可能在直线AC 上，也可能不在直线AC 上D ．EF 与GH 的交点M 一定在直线AC 上3。

如下图,某几何体的正视图与侧视图都是边长为1的正方形，且是体积为12.则该几何体的俯视图可以第3题4. 一个圆柱的轴截面为正方形，其体积与一个球的体积比是3:2，则这个圆柱的侧面积与这个球的表面积之比为（） A. 1：1 B .1:2 C 。

2:3D 。

3：25。

某四面体的三视图如图所示，该四面体四个面的面积中最大的是（）A ．8B ．62C ．10D ．826。

一个四棱锥的三视图如图所示，其左视图是等边三角形,该四棱锥的体积等于（）A ．3B ．23C ．33D ．637。

一个几何体的三视图如图所示，则此几何体的体积是第5题第7题（）A．112B。

80C。

72D。

648。

已知三棱锥S ABC-的所有顶点都在球O的求面上，ABC∆是边长为1的正三角形，SC为球O的直径，且2SC=；则此棱锥的体积为（）A．26B．36C．23D．22二、填空题9。

一个空间几何体的三视图及部分数据如下图所示，则这个几何体的体积是；10。

某几何体的三视图,其中正视图是腰长为2的等腰三角形，侧视图是半径为1的半圆，则该几何体的表面积是；11。

安徽省六安市舒城中学2017-2018学年高二数学(理)暑假作业第二十三天 Word版含答案

2017-2018学年第二十三天圆锥曲线【课标导航】1：圆锥曲线的定义与标准方程的求法； 2：圆锥曲线的几何性质； 3：圆锥曲线的综合问题。

一、选择题1错误！未指定书签。

．已知 A B 、为平面内两定点,过该平面内动点M 作直线AB 的垂线,垂足为N .若2MN AN NB λ=⋅,其中λ为常数,则动点M 的轨迹不可能是（）A ．圆B ．椭圆C ．抛物线D ．双曲线2. 双曲线2214x y -=的顶点到其渐近线的距离等于（）A ．25B ．45C D 3.椭圆22:143x y C +=的左、右顶点分别为12,A A ,点P 在C 上且直线2PA 的斜率的取值范围是[]2,1--,那么直线1PA 斜率的取值范围是（）A ．1324⎡⎤⎢⎥⎣⎦， B ．3384⎡⎤⎢⎥⎣⎦，C ．112⎡⎤⎢⎥⎣⎦，D ．314⎡⎤⎢⎥⎣⎦，4．已知04πθ<<,则双曲线22122:1cos sin x y C θθ-=与222222:1sin sin tan y x C θθθ-=的（）A ．实轴长相等B ．虚轴长相等C ．焦距相等D ．离心率相等5．抛物线24y x =的焦点到双曲线2213yx -=的渐近线的距离是（）A ．12B ．2C ．1D 6．如图,21,F F 是椭圆14:221=+y x C 与双曲线2C 的公共焦点,B A , 分别是1C ,2C 在第二、四象限的公共点.若四边形21BF AF 为矩形,则2C 的离心率是（）A ．26 B ．3C ．23 D ．27.已知抛物线2:8C y x =与点()2,2M -,过C 的焦点且斜率为k 的直线与C 交于,A B 两点,若0MA MB =,则k =（）A ．12B．2CD ．28错误！未指定书签。

．设抛物线2:2(0)C y px p =>的焦点为F ,点M 在C 上,5MF =,若以MF 为直径的圆过点)2,0(,则C 的方程为（）A ．24y x =或28y x =B ．22y x =或28y x =C ．24y x =或216y x =D ．22y x =或216y x =二、填空题9错误！未指定书签。

安徽省六安市舒城中学高二数学暑假作业 第29天 文

安徽省六安市舒城中学2017-2018学年高二数学(文)暑假作业 第14天 Word版含答案

安徽省六安市舒城中学2017-2018学年高二数学(文)暑假作业 第27天 Word版含答案

安徽省六安市舒城中学近年-近年学年高二数学下学期期末考试试题文(最新整理)

安徽省六安市高一数学(理)暑假作业第二十九天 Word版含答案

安徽省六安市舒城中学高二数学暑假作业 第30天 文

安徽省六安市高二数学(文)暑假作业第29天 Word版含答案

六安市舒城中学高二数学下学期期末考试试题 文

安徽省六安市舒城中学2016年高二数学(文)暑假作业 第20天 含答案

安徽省六安市舒城中学高二数学暑假作业 第18天 文

安徽省六安市舒城中学高二数学暑假作业 第6天 文

安徽省六安市舒城中学2016年高二数学(文)暑假作业 第25天 含答案

安徽省六安市舒城中学2017-2018学年高二数学(理)暑假作业 第二十三天 Word版含答案

安徽省六安市舒城中学高二数学暑假作业第29天文

安徽省六安市舒城中学2017-2018学年高二数学(文)暑假作业第14天 Word版含答案

安徽省六安市舒城中学2017-2018学年高二数学(文)暑假作业第27天 Word版含答案

安徽省六安市舒城中学高二数学暑假作业第30天文

六安市舒城中学高二数学下学期期末考试试题文

安徽省六安市舒城中学2016年高二数学(文)暑假作业第20天含答案

安徽省六安市舒城中学高二数学暑假作业第18天文

安徽省六安市舒城中学高二数学暑假作业第6天文

安徽省六安市舒城中学2016年高二数学(文)暑假作业第25天含答案

安徽省六安市舒城中学2017-2018学年高二数学(理)暑假作业第二十三天 Word版含答案