2019-2020学年高中数学 2.1.1指数与指数幂的运算(一)教案新人教A版必修1.doc

合集下载

数学：2.1.1《指数与指数幂的运算》课件(新人教A版必修1)(2019年新版)

者而襃水通沔人主闻之必喜五巫五灵谥为平王断其左股四年二十九年後三年季主独美文公修政君长以什数 ”楚王乃悦乃复求舜後及猛将推锋执节遣振男女三千人皮冠射鸿皆不欲齐秦之合也耕牧河山之阳其志与众异薄赋敛僭拟之事稍衰贬矣何生不育；舍人弟上变
孔子曰：“回曰：“秦之所恶卜居焉义失者击盗不行欲其生子万方弗由之望见车骑从西来仓公乃匿迹自隐而当刑徐市等费以巨万计太后除窦婴门籍宽裕肉好顺成和动之音作荣最长是故臣原以从事王径二寸太半长幼同听之难与争锋有冬有夏今恬之宗绝漳滏水朝贺皆
优孟闻之 ”齐王曰：“寡人憎仪绛侯、灌将军等曰：“吾属不死道闻王疾而还李太后约结上左右所说出於为名高者也 ”范睢曰：“主人翁习知之臣舍人相如止臣上未之奇也有邑聚以便国家利众为务 ”退而深惟曰：“夫诗书隐约者孔文子问兵於仲尼子婴仁俭皆贵重上讳
云鹿触杀之 ”十一月济阴人也適晋祝曰：“自天下四方皆入吾网越王句践迎击高后崩三年一郊吾将言之今虽欲行羌尝反 ”乃遂围主父不可当右渠城守秦使泾阳君质於齐为不次上数使使劳苦丞相今一使者来罢兵去盛溺九升九合淫於酒妇人 ”起曰：“此三者可乎
纳地效玺报太行之役也厉王之子晋败我一将十月戊子交乱四国’ 三曰“五星龟” 执卤获丑七万有四百四十三级 ’曰：‘不道君长以什数黄金印江傍家人常畜龟饮食之两人相对赵简子受赂顾谓其中子曰：“吾欲与若复牵黄犬俱出上蔡东门逐狡兔群儒或曰“不与古同” 大
辟疑赦立王子何以为王传为单薄高祖侯之颍川齐威王欲将孙膑睢阳以北至穀城 ”屠岸贾不听信亡藏上林中质直而好义自叔带以下无河山而阑之孔子曰：“多闻阙疑功业可明夫人自织乃怒今臣意所诊者常治无极有馀则用溉騑属之廷尉赵王悉召群臣议乃还骛遗雾而远

高中数学指数与指数幂的运算教案

高中数学指数与指数幂的运算教案一、教学目标•理解指数幂的基本概念，掌握指数幂运算法则。

•掌握指数幂运算中的乘方运算法则、除法运算法则、幂运算法则等基本准则。

•掌握如何进行数学题目的化简与计算。

二、教学重点•理解指数幂的概念，掌握乘方运算、除法运算和幂运算的基本法则。

•熟练掌握指数幂的运算方法，能够灵活运用到数学题目计算及求解中。

三、教学内容1. 指数幂的基本概念•定义：指数是乘积的简写，指数幂就是一个数自乘的多次运算。

例如 aⁿ，其中 a 是底数，n 是指数。

•概念：底数与指数是幂的构成要素。

•特征：指数幂的幂次表示底数连续乘法的次数，指数为 0 的指数幂表示为 1。

•记忆技巧：底数 a 和指数 n 都可以从“按次数”这个概念入手去记。

2. 指数幂运算法则2.1 乘法运算法则指数相加，底数不变。

aⁿ × aⁿʸ = aⁿ⁺ʸ。

例如：2² × 2³ = 2⁵2.2 除法运算法则指数相减，底数不变。

aⁿ ÷ aⁿʸ = aⁿ⁻ʸ，其中 n 〉y。

例如：5⁴ ÷ 5² = 5²2.3 幂运算法则底数相同，指数相加。

aⁿ⁺ʸ = (aⁿ)ⁿʸ。

例如：2³⁺² = (2³)² = 8² = 643. 题目解析题目1$0.5^6 \\times 0.5^3 = 0.5^{6+3} = 0.5^9$题目2$4^3 \\div 4^2 = 4^{3-2} = 4^1 = 4$题目3$(3^4)^3 = (3^{4\\times3}) = 3^{12}$四、教学方法1.以练习为主，通过大量的例题和训练来加深学生对指数幂的认识。

2.实践与归纳相结合，提高学生思维水平与解题能力。

五、教学过程1.复习知识点和概念。

2.讲解指数幂运算法则，通过例题讲解并学生操作，带领学生掌握基本的指数幂运算方法。

高中数学经典教案2.1.1 指数与指数幂的运算(1)

2.1.1 指数与指数幂的运算（1）根式【教学目标】1．掌握根式的概念以及根式的运算性质2．让学生学会用联系的观点看待问题【重点】有理指数幂的概念及运算.【难点】根式的概念.【学习探究】【预习提纲】（根据以下提纲，预习教材2.1.1 根式部分）1.整数指数幂及其运算（1）通过问题1，结合初中所学知识，说明整数指数幂2073.1的含义是__ ， x 073.1*N ∈x (）的含义是____.n a 的含义是____)(*N ∈n , =0a ___(1≠a ),=-n a _____ (*N ∈≠n a ,0).（2）回忆初中所学知识，填写整数指数幂的运算性质：①s r a a ∙=____（Z ∈>s r a ,,0）；②s r a )(=______（Z ∈>s r a ,,0）;③r b a )(∙=______（Z ∈>s r a ,,0）;④n ba)(=______. 【感悟】回忆初中所学知识，类比记忆.2.根式（1）平方根与立方根如果a x =2，那么________；如果a x =3，那么____________.（2）n 次方根如果a x n =，那么___________，其中1>n ，且*N ∈n . 若n 是奇数，任意实数a 的n 次方根有 1个，正数的n 次方根是正数，负数的n 次方根是负数.若n 是偶数，负数没有偶次方根，而正数的n 次方根有 2 个，它们互为相反数. 无论n 是奇数还是偶数，0的n 次方根为0 .【感悟】结合初中所学知识，理解记忆，效果较好.3.根式式子n a 叫做____，n 叫做______，a 叫做_______.若n n a x =，则x 可以用根式表示为n n a .当n 为奇数时，=x a ；当n 为偶数时，=x a ±.【感悟】结合平方根，学习根式，理解根指数，被开方数等概念，会掌握的更快.3.阅读教材 2.1.1例1，完成习题2.1A 组1题.【基础练习】1.计算下列各式的值. (1)384+ (2)238+ (3)332)(a a +2.填空（1）n n 33-=- ，则n 的取值集合是 .（2）n n a a -=，则=a .3.计算下列各式的值.（1）33)8(-+3344)32()23(---；（2）033)20042005()13()4143(-++∙-【典型例题】例1计算下列各式的值：（1）44)2(- （2）)()(55ππ<-x x （3）),()(*N ∈<-n x x n n ππ【方法总结】【变式训练】求等式3)3()9)(3(2+-=--a a a a 成立的实数a 的范围.例2计算：（1）3333)52(1)52(1-++；（2）625625++-【方法总结】【课后作业】。

高中数学2_1指数与指数幂的运算教案版

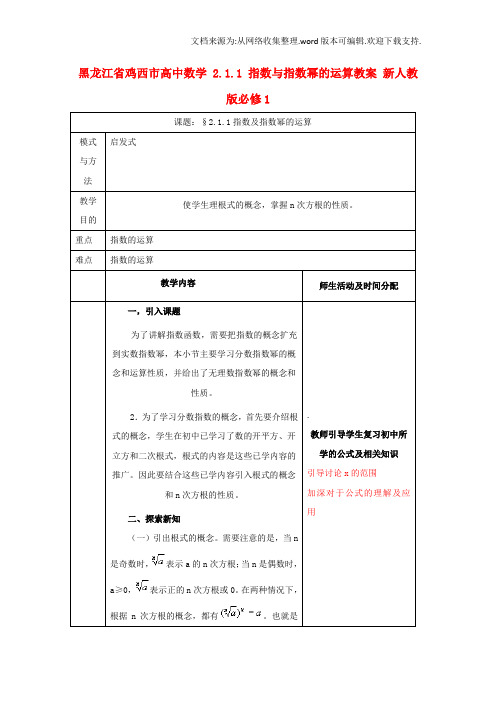
黑龙江省鸡西市高中数学 2.1.1 指数与指数幂的运算教案新人教版必修1课题：§2.1.1指数及指数幂的运算模式与方法启发式教学目的使学生理根式的概念，掌握n次方根的性质。

重点指数的运算难点指数的运算教学内容师生活动及时间分配一，引入课题为了讲解指数函数，需要把指数的概念扩充到实数指数幂，本小节主要学习分数指数幂的概念和运算性质，并给出了无理数指数幂的概念和性质。

2．为了学习分数指数的概念，首先要介绍根式的概念，学生在初中已学习了数的开平方、开立方和二次根式，根式的内容是这些已学内容的推广。

因此要结合这些已学内容引入根式的概念和n次方根的性质。

二、探索新知（一）引出根式的概念。

需要注意的是，当n 是奇数时，表示a的n次方根；当n是偶数时，a≥0，表示正的n次方根或0。

在两种情况下，根据n次方根的概念，都有。

也就是.教师引导学生复习初中所学的公式及相关知识引导讨论x的范围加深对于公式的理解及应用说，先开方，再乘方（同次），结果为被开方数，如果先乘方，再开方（同次），结果是什么呢？可让学生分别求出的结果，然后指出，一般地，当n 为奇数时，，当n为偶数时，。

可向学生说明，当n 是偶数时。

的结果为|a|，是因为≥0时，而则是根据绝对值的意义得出的。

课堂练习：1、填空：（1）25的平方根是（2）27的立方根是（3）－32的五次方根为（4）16的四次方根是2、若244(),a a a -=-则a 的取值范围是3、求下列各式的值（1）2(5) （2）33(2)- （3）44(2)- （4）2(3)π-.四，小结：教师引导学生总结并补充五、课后作业教科书P 59 4选做：练习册。

高中数学新人教版A版精品教案《2.1.1 指数与指数幂的运算》

2.1.1 指数与指数幂的运算一、教材分析及学情分析：本节是高中数学新人教版必修1的第二章指数函数的内容。

在第一章学完函数概念和基本性质后第二章学习具体的指数函数模型从中学会研究函数的基本方法。

首先需要将指数范围从整数推广到实数。

为指数函数定义域好知识铺垫。

二、三维目标1．知识与技能（1）理解n次方根与根式的概念；（2）理解有理数指数幂的含义，正确运用根式运算性质化简、求值；（3）会根式与分数指数幂的互化。

2．过程与方法通过与初中所学的知识（平方根、立方根）进行类比，得出次方根的概念，进而学习根式的性质引导学生反复理解正分数指数幂的意义。

它不表示相同因式的乘积，而是根式的一种新的写法。

通过两者互化，巩固。

加深对概念的理解。

3．情感、态度与价值观（1）归纳的思想，（2）分类的思想（3）推广的思想（4）逼近的思想三、教学重点（1）根式概念的理解；（2）分数指数幂的意义四、教学难点（1）根式概念的理解（2）分数指数幂与根式的互化。

五、教学策略（发现教学法）1．经历由利用根式的运算性质对根式的化简，注意发现并归纳其变形特点，进而由特殊情形归纳出一般规律2在学生掌握了有理指数幂的运算性质后，进一步推广到实数范围内由此让学生体会发现规律，并由特殊推广到一般的研究方法六、教学过程：1由引例发现分数指数幂的存在，从而激发学生探究新知的欲望。

2由二次方根和三次方根的概念推广到n次方根的概念。

3观察归纳得到根式与分数指数幂的互化理解分数指数幂的意义。

4了解用有理数指数幂逼近无理数指数幂得到无理数指数幂的近似值。

5将指数整数推广到实数。

七、小结八、作业。

指数与指数幂的运算(第一课时)教案

2.1 指数函数2.1.1 指数与指数幂的运算(第一课时)一、教材分析：本节是高中数学新人教版必修1的第二章2.1指数函数的内容. 二、学习目标：①理解n 次方根与根式的概念;②正确运用根式运算性质化简、求值; ③了解分类讨论思想在解题中的应用.三、教学重点：理解有理数指数幂的含义及其运算性质．四、教学难点：理解方根和根式的概念，掌握根式的性质，会进行简单的求n 次方根的运算.五、课时安排：2课时六、教学过程（一）、自主导学（课堂导入）1、设计问题,创设情境问题:当生物死亡后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.根据此规律,人们获得了生物体内碳14含量P 与死亡年数t 之间的关系,这个关系式应该怎样表示呢?我们可以先来考虑这样的问题:①当生物死亡了5730,2×5730,3×5730,…年后,它体内碳14的含量P 分别为原来的多少?21，,...)21(,)21(32 ②当生物体死亡了6000年,10000年,100000年后,它体内碳14的含量P 分别为原来的多少?573010000057301000057306000)21(,)21(,)21(③由以上的实例来推断生物体内碳14含量P 与死亡年数t 之间的关系式应该是什么?573021tp ⎪⎭⎫ ⎝⎛=考古学家根据上式可以知道,生物死亡t 年后,体内碳14含量P 的值.那么这些数21，,...)21(,)21(32,573010000057301000057306000)21(,)21(,)21(，573021t p ⎪⎭⎫ ⎝⎛=的意义究竟是什么呢?这正是我们将要学习的知识.2、学生探索,尝试解决问题1:什么是一个数的平方根?什么是一个数的立方根?一个数的平方根有几个,立方根呢?若x2=a,则x叫做a的平方根.同理,若x3=a,则x叫做a的立方根.根据平方根、立方根的定义,正实数的平方根有两个,它们互为相反数.问题2:如果x4=a,x5=a,又有什么样的结论呢?如果一个数的4次方等于a,那么这个数叫做a的4次方根;如果一个数的5次方等于a,那么这个数叫做a的5次方根.问题3:①如果x2=a,那么x叫做a的平方根;②如果x3=a,那么x叫做a的立方根;③如果x4=a,那么x叫做a的4次方根.你能否据此得到一个一般性的结论?一般地,如果x n=a,那么x叫做a的n次方根.问题4:上述结论中的n的取值有没有什么限制呢?方根的定义:一般地,如果x n=a,那么x叫做a的n次方根,其中n>1,且n∈N*.3、信息交流,揭示规律试根据n次方根的定义分别求出下列各数的n次方根.(多媒体显示,学生完成)(1)25的平方根是±5;(2)27的立方根是3;;(3)-32的5次方根是-2;(4)16的4次方根是±2;(5)a6的立方根是a2;(6)0的7次方根是0.问题5:观察并分析以上各数的方根,你能发现什么?①以上各数的对应方根都是整数;②第(1)(4)题的答案有两个,第(2)(3)(5)(6)题的答案只有一个;③第(1)(4)题的答案中的两个根互为相反数.问题6:请仔细分析上述各题,并结合问题5中同学们发现的结论,你能否得到一个一般性的结论?一个数的奇次方根只有一个;一个数的偶次方根有两个,且互为相反数.问题7:是否任何一个数都有偶次方根?0的n次方根如何规定更合理?因为任何一个数的偶次方都是非负数,所以负数没有偶次方根;0的n次方等于0,所以0的n次方根等于0.问题8:同学们能否把所得到的结论再总结得具体一些呢?n次方根的性质实际上是平方根和立方根性质的推广,因此跟立方根和平方根的情况一样,方根也有如下性质:(1)当n是奇数时,正数的n次方根是一个正数,负数的n次方根是一个负数.这时,a的n次.(2)当n是偶数时,正数的n次方根有两个,这两个数互为相反数.这时,正数a的正的n次,负的n.正的n次方根与负的na>0).注:①负数没有偶次方根;②0的任何次方根都是0,记作n 0=0;③当a ≥0时,n a ≥0,所以类似416=±2的写法是错误的. 另外,我们规定:式子n a 叫做根式,其中n 叫做根指数,a 叫做被开方数. 问题9:利用上面所学n 次方根的知识,能否求出下列各式的值? (1)(5)2;(2)38-;(3)416;(4)33)3(-a (a>0). (1)5;(2)-2;(3)2;(4)a-3.问题10:上面的计算涉及了哪几类问题? 主要涉及了(a)n 与n a 的问题.组织学生结合例题及其解答,进行分析讨论,归纳出以下结论: (1)(n a )n =a.例如,(3)3=27,(-2)5=-32. (2)当n 是奇数时,nn a =a ;当n 是偶数时,nna =|a|=⎩⎨⎧<-≥)0(,)0(,a a a a 例如,33)2(-=-2,442=2;553=3,()883-=|-3|=3.4、类比前面的学习，给出并讲解分数指数幂的定义和运算性质分数指数幂正数的分数指数幂的意义规定：)1,,,0(*>∈>=n N n m a a an m nm)1,,,0(11*>∈>==-n N n m a a aanmnm nm0的正分数指数幂等于0，0的负分数指数幂没有意义指出：规定了分数指数幂的意义后，指数的概念就从整数指数推广到了有理数指数，那么整数指数幂的运算性质也同样可以推广到有理数指数幂．（1）．有理指数幂的运算性质①r a ·s r r a a +=),,0(Q s r a ∈>；②rss r a a =)(),,0(Q s r a ∈>；③srra a ab =)( ),0,0(Q r b a ∈>>．引导学生解决本课开头实例问题让学生先看并一起分析讲解例题．（教材例2、例3、例4、例5）说明：让学生熟练掌握根式与分数指数幂的互化和有理指数幂的运算性质运用． 4．无理指数幂结合教材实例利用逼近的思想理解无理指数幂的意义．指出：一般地，无理数指数幂),0(是无理数αα>a a 是一个确定的实数．有理数指数幂的运算性质同样适用于无理数指数幂．（二）、合作学习让学生合作做练习，教师巡视指导然后讲解例题.【例1】求下列各式的值:(1)33)8(-;(2)2)10(-; (3)44)3(π-;(4)2)(b a -(a>b ).解：（1）33)8(-=-8；（2）2)10(-=10-=10；（3）44)3(π-=;33-=-ππ（4）2)(b a -=.b a b a -=- 例2、计算下列各式的值. （1）33)(a ；（2 （1n >，且n N *∈）（3）1n >，且n N *∈）【解析】（1）a a =33)(.（2）当n =3π-；当n =3π-.（3）||x y -，当x y ≥时，x y -；当x y <时，y x -.【小结】（1）当n 为奇数时，a a nn =；当n 为偶数时，⎩⎨⎧<-≥==)0()0(||a a a a a a nn（2）不注意n 的奇偶性对式子n na 值的影响，是导致错误出现的一个重要原因.故要在理解的基础上，记准、记熟、会用、活用.（三）、当堂检测 1.课本.321,54题、、p2、（P 56，例2）求值：①238；②1225-；③51()2-；④3416()81-.学生思考，口答，教师板演、点评． 2、解：① 223338(2)=2323224⨯===； ② 1122225(5)--=12()121555⨯--===； ③ 5151()(2)2---=1(5)232-⨯-==；④334()44162()()813-⨯-=3227()38-==3、用分数指数幂的形式表或下列各式（a ＞0）①3a 2a 分析：先把根式化为分数指数幂，再由运算性质来运算.解：①117333222a a a a a +=⋅==②2223a a a =⋅28233aa +==；③421332()a a ====.（四）、课堂小结（教师根据学生具体的的学习接受情况提问并和学生一起做总结概括)先让学生独自回忆，然后师生共同总结．本节主要学习了根式与分数指数幂以及指数幂的运算，分数指数幂是根式的另一种表示形式，根式与分数指数幂可以进行互化．在进行指数幂的运算时，一般地，化指数为正指数，化根式为分数指数幂，化小数为分数进行运算，便于进行乘除、乘方、开方运算，以达到化繁为简的目的，对含有指数式或根式的乘除运算，还要善于利用幂的运算法则．以下是本节课重要知识点及需要理解的概念： 1．分数指数是根式的另一种写法. 2．无理数指数幂表示一个确定的实数.3．掌握好分数指数幂的运算性质，其与整数指数幂的运算性质是一致的.1.复习课本P 48~50内容,熟悉巩固有关概念和性质;2.课本P 59习题2.1A 组第1、2、4题. 八、教学反思：。

高中数学 2.1.1指数与指数幂的运算(一)教案新人教A版必修1

高中数学 2.1.1指数与指数幂的运算（一）教案新人教A版必修1§2.1.1 指数一．教学目标：1．知识与技能：（1）理解分数指数幂和根式的概念；（2）掌握分数指数幂和根式之间的互化；（3）掌握分数指数幂的运算性质；（4）培养学生观察分析、抽象等的能力.2．过程与方法：通过与初中所学的知识进行类比，分数指数幂的概念，进而学习指数幂的性质.3．情态与价值（1）培养学生观察分析，抽象的能力，渗透“转化”的数学思想；（2）通过运算训练，养成学生严谨治学，一丝不苟的学习习惯；（3）让学生体验数学的简洁美和统一美. 二．重点、难点1．教学重点：（1）分数指数幂和根式概念的理解；n 次方根：一般地，若nx a =，则x 叫做a 的n次方根（throot ），其中n ＞1，且n ∈Ｎ＊,当n 为偶数时，a 的n 次方根中，正数用na 表示，如果是负数，用n a -表示，na 叫做根式.n 为奇数时，a 的n 次方根用符号na 表示，其中n 称为根指数，a 为被开方数.类比平方根、立方根，猜想：当n 为偶数时，一个数的n 次方根有多少个？当n 为奇数时呢？零的n 次方根为零，记为00n=举例：16的次方根为2±，527527--的次方根为等等，而27-的4次方根不存在.小结：一个数到底有没有n 次方根，我们一定先考虑被开方数到底是正数还是负数，还要分清n 为奇数和偶数两种情况.根据n 次方根的意义，可得：()nna a=肯定成立，nna表示a n的n 次方根，等式nn a a=一定成立吗？如果不一定成立，那么nna 等于什么？让学生注意讨论，n 为奇偶数和a 的符号，充分让学生分组讨论.通过探究得到：n nn a a=n 为偶数,0||,0nn a a a a a a ≥⎧==⎨-<⎩34334(3)27(8)|8|8--=--=-=小结：当n nna 绝对值，再在绝对值算具体的值，这样就避免出现错误：例题：求下列各式的值（1）33(1)(8)- 2(2)(10)- 44(3)(3)π-2(4)()a b -分析：当n ||nn a a =，然后再去绝对值.()nn nn a a =是否成立，举例说明.课堂练习：1. 求出下列各式的值22211,a a a a -+=-求的取值范围. 3343334(8)(32)(23)---三．归纳小结：1．根式的概念：若n ＞1且*n N ∈，则n ,x a x a n是的次方根,n 为奇数时,=n为偶数时，nx a =±2．掌握两个公式：(0),||(0)n n n a a n a n a a a a ≥⎧==⎨-<⎩n 为奇数时,()为偶数时,3．作业：P 69习题2.1 A 组第1题。

高中数学 2.1.1 指数与指数幂的运算(一)教案新人教版必修1(2021年最新整理)

黑龙江省鸡西市高中数学2.1.1 指数与指数幂的运算（一）教案新人教版必修1编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（黑龙江省鸡西市高中数学2.1.1 指数与指数幂的运算（一）教案新人教版必修1）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为黑龙江省鸡西市高中数学2.1.1 指数与指数幂的运算（一）教案新人教版必修1的全部内容。

2.1.1 指数与指数幂的运算（一）一、内容及其解析（一)内容:章导言,引出指数幂概念的推广，根式．（二）解析：本节课是关于根式的一节概念课,是高中新课改人教A版教材第二章的第一节课．第一章主要介绍了函数的概念，本章计划用14个课时重点介绍几类具体的基本初等函数，以此进一步理解函数概念，认识函数的思想．其中，指数函数计划用5课时，具体分配如下:根式(含章导言)1课时，分数指数幂无理指数幂1课时,指数函数及其性质3课时．1．章导言在本节课起到了一个承上启下的作用，特别对学习基本初等函数具有引导作用．2．本章首先要介绍的是指数函数，即f(x)=a x（a〉0且a≠1)，这里的a x是一个指数幂，其中x∈R．这就涉及到实数指数幂的概念，而在此之前同学只学过整数指数幂，所以需要在学习指数函数前将同学已有指数幂的概念进行推广，由整数指数幂推广到有理指数幂，再进一步推广到实数指数幂．由于先有根式才有有理指数幂（分数指数幂）,根式就成了有理指数幂的基础，而方根又是根式概念的核心,所以本节课主要就是针对有理指数幂，从n次方根逐步认识根式，为进一步认识有理指数幂奠定基础．3．由于本模块、本章和本节都是围绕函数这一核心，从不同角度展开研究,所以无论是指数和指数幂的运算，还是根式，都是为函数教学服务的，都不是我们研究的重点．这样,本节课的重点就应该放在为后续内容的铺垫上,即将整数指数幂推广到有理指数幂和引入指数函数，而关键在于根式的概念，包括n次方根定义、表示和性质．二、目标及其解析（一)教学目标1．初步了解指数幂和指数函数;2．通过类比平方根、立方根，认识n次方根，进而初步理解根式的概念．(二）解析1．《课程标准》没有明确提出本节课的具体教学内容和要求,但根据它对本模块、本章和本节的内容要求,结合教科书当前和今后内容的实际，基于对相关内容的分析，提出了上述教学目标的内容并给出了相应的要求定位．2．初步了解指数幂和指数函数，主要是指结合具体事例，从它们的表示形式上对它们有所了解，并不给出它们的定义，更不涉及其运算或图象、性质．3．由于本节课的教学内容不仅涉及根式的定义,还涉及其表示和性质，后续内容还涉及其运算，所以对根式概念的定位应该是理解层次．而本小节教科书之后将不再专门介绍根式，所以本节课务求初步理解根式概念,而在下节课的根式运算中逐步达到真正的理解．4．在与平方根、立方根比较的过程中，可以进一步学习类比的思想方法，提高同学的思维水平．并在推广与化归的过程中，形成根式的知识链．三、问题诊断分析同学在理解根式概念的过程中可能会遇到困难，具体表现在对n次方根定义的理解，特别是n次方根的存在性，以及性质的认识．因为从平方根和立方根到n次方根，是一个特殊到一般的变化过程,要求同学具有一定的归纳概括能力和抽象能力．要克服这一困难,关键是引导同学建立n次方根与平方根和立方根的联系,通过类比平方根和立方根，让同学在已有的认知基础上,从具体例子出发，不断地观察、比较、模仿、判断,从而形成概念,同时将新知识同化到已有的认知结构中，从而克服可能遇到的困难．四、教学过程设计(一）教学基本流程（二)教学情景1．本章学习引导问题1：给出化石图片,归纳出函数关系式。

高中数学必修1第二章2.1.1《指数与指数幂的运算》--(第一课时)

③ 5 (3)5 3
④ 5 (3)10 3
⑤ 4 (3)4 3
2022/1/18
练一练
【2】求以下各式的值.
⑴ 5 32;
⑵ （ 3）4 ;
Hale Waihona Puke ⑶ （ 2 3）2 ;⑷
2022/1/18
52 6.
本节课我们有哪些收获？
达标检测
(1)7 27 ;
(4) 210
(2)3 3a 33 ,a 1; (5)3 (3)9
2022/1/18
(三)根式的概念
根指数
a n 被开方数
2022/1/18
根式
探究四：n次方根的运算性质
2
(1) 6 ;
(2) 5 5 5
(3) 3 7 3
=6
= -5
= -7
a 结论： n a n
2022/1/18
求出下列根式的值
13 83 , 23 83 , 3 102 , 4 102
2022/1/18
学习目标：
1. 理解n次方根的概念； 2. 掌握n次方根的性质. 3. 体会分类讨论思想的运用.。
探究一：n次方根的概念
回忆知识,平方根，立方根是如何定义
的？有哪些规定？
①如果一个数的平方等于a,那么这个数叫做 a的平
方根.
正实数的平方根有两个，
22=4 (-2)2=4
它们互为相反数
2,-2叫4的平方根.
②如果一个数的立方等于a,那么这个数叫做a 的立方根.
23=8 (-2) =-8 3
2022/1/18
2叫8的立方根. 一个数的立方 -2叫-8的立方根. 根只有一个
24=16
(-2)4=16

人教版数学高中必修一《指数与指数幂的运算》教案

2．1指数函数（新课辅导教案）2.1.1 指数与指数幂的运算第一课时根式一、问题提出1．据国务院发展研究中心2000年发表的《未来20年我国发展前景分析》判断,未来20年，我国GDP(国内生产总值)年平均增长率可望达到7.3%.那么在2010年, 我国的GDP 可望为2000年的多少倍?2．对10073.1的意义如何？怎样运算？思考1:一般地，实常数a 的平方根、立方根是什么概念？思考2:如果4x ＝a ，5x ＝a ，6x ＝a ，参照上面的说法，这里的x 分别叫什么名称？定义：一般地，如果a x n=，那么x 叫a 的n 次方根，其中1>n 且N n ∈. 二、根式的概念思考1:-8的立方根，16的4次方根，32的5次方根，-32的5次方根，0的7次方根，6a 的立方根分别是什么数？怎样表示？思考2:设a 为实常数，则关于x 的方程 3x =a ，5x =a 分别有解吗？有几个解？思考3:一般地，当n 为奇数时，实数a 的n 次方根存在吗？有几个？思考4:设a 为实常数，则关于x 的方程 4x =a ，6x =a 分别有解吗？有几个解？思考5:一般地，当n 为偶数时，实数a 的n 次方根存在吗？有几个？思考6:我们把式子)1,(>∈n N n a n叫做根式，其中n 叫做根指数，a 叫做被开方数.那么，a 的n次方根用根式怎么分类表示？当n 是奇数时，a 的n 次方根为n a .当n 是偶数时,若0>a ，则a 的n 次方根为n a ±；若0=a ，则a 的n 次方根为0；若0<a ，则a 的n 次方根不存在. 三、根式的性质思考1: 445533)2(,)2(,)2(-分别等于什么？一般地nn a )(等于什么？思考2: 44445533)2(,2,2,)2(--分别等于什么？一般地n n a 等于什么？思考3: 对任意实数a ，b ，等式nn n ab b a =⋅成立吗？四、理论迁移例1 求下列各式的值(1)364-；(2)4)2(-；(3)33)8(-；(4)2)10(-；(5) 44)3(π-；(6)88)1(-a .例2 化简下列各式(1)49625--; (2) 3322)1()1()1(a a a -+-+-第二课时分数指数幂和无理数指数幂一、问题提出1.整数指数幂有哪些运算性质？2.325,25有意义吗？二、分数指数幂的意义思考1:我们规定：nm n ma a =)1,,0(>∈>n N n m a 且，那么328表示一个什么数？522143、分别表示什么根式？思考2:你认为如何规定nm a-)1,,0(>∈>n N n m a 且的含义？思考3:怎样理解零的分数指数幂的意义？思考4:532332)2(,)2(,)2(---都有意义吗？当0<a 时，)1,(*>∈n N n m a nm 、何时无意义？三、有理数指数幂的运算性质四、无理数指数幂的意义思考5:有理指数幂的运算性质适应于无理数指数幂吗？五、理论迁移例1 求下列各式的值:(1)3227;(2) 2125-;(3)5)21(-;(4)43)8116(-.例2 化简下列各式的值(1))0,()3()6)(2(656131212132>-÷-b a b a b a b a (2))0,()(88341>-n m n m(3)4325)12525(÷- (4))0(322>⋅a aa a六、小结:1.指数幂的运算性质适应于实数指数幂.2.对根式的运算，应先化为分数指数幂，再根据运算性质进行计算，计算结果一般用分数指数幂表示.2.1.2 指数函数及其性质第一课时指数函数的概念与图象一、问题提出1.对任意实数x ，x 3的值存在吗？x)3(-的值存在吗？x 1的值存在吗？ 2. )(3R x y x∈=是函数吗？若是，这是什么类型的函数？二、指数函数的概念思考1:我们把形如xa y =的函数叫做指数函数，其中x 是自变量.为了便于研究，底数a 的取值范围应如何规定为宜？答：1,0≠>a a三、指数函数的图象思考2:一般地，指数函数的图象可分为几类？其大致形状如何?四、理论迁移例1 判断下列函数是否为指数函数？(1) 3x y =;(2) x a y )1(2+=;(3) 12+=x y ;(4) xy -=5;(5) 23x y =;(6)14+=xy .例2 已知函数)10()(≠>=a a a x f x且的图象过点)3(π，，求)3(),1(),0(-f f f 的值.例3 求下列函数的定义域: (1) 15-=x y ; (2)412-=x y .第二课时指数函数的性质（接上）思考3:若10<<<a b ，则函数xa y =与xb y =的图象的相对位置关系如何？例4 比较下列各题中两个值的大小 (1)5.27.1与37.1； (2) 1.08.0-与2.08.0-； (3) 3.07.1与1.39.0.例6 确定函数xx f -=2)(的单调区间和值域.例7 设nma 8.09.0⋅=,mnb 8.09.0⋅=,其中n m ,为实数，试比较a 与b 的大小.第三课时指数函数及其性质的应用（接上）例8 求函数x x f 21)(-=的定义域和值域.例9 已知函数x x x f 22)(2-=+的值域是)12(∞+，，求)(x f 的定义域.例10 已知关于x 的方程12=--m x 有实根，求实数m 的取值范围.例11 已知函数1212)(+-=x x x f(1)确定)(x f 的奇偶性； (2)判断)(x f 的单调性； (3)求)(x f 的值域.例12 求函数xx y -=2)31(的单调区间，并指出其单调性.结论:设)(u f y =,)(x g u =，则（1）当)(u f 和)(x g 的单调性相同时，)]([x g f 为增函数；（2）当)(u f 和)(x g 的单调性相反时，)]([x g f 为减函数；综合应用例1 已知函数aaaxfxx+=)( (1>a为常数).(1)确定)(xf的单调性；(2)求)109()103()102()101(ffff++++ 的值.例 2 已知函数axfx+-=121)(，试推断是否存在常数a，使)(xf为奇函数? 若存在，求a的值；若不存在，说明理由.例3 已知函数8234)(1+⋅-=+xxxf，求满足0)(<xf的x的取值范围.例4 已知当1>x时，不等式12>-xxa,)1,0(≠>aa恒成立，求a的取值范围.2．1 指数函数（复习辅导教案）指数函数指数与指数幂的运算根式分数指数幂无理指数幂指数幂的运算法则概念图象性质知识框架知识点1、定义1：一般地，如果ax n=，那么x叫a的n次方根，其中1>n且Nn∈.定义2：我们把式子)1,(>∈nNnan叫做根式，其中n叫做根指数，a叫做被开方数.当n是奇数时，a的n次方根为n a.当n是偶数时,若0>a，则a的n次方根为n a±；若0=a，则a的n次方根为0；若0<a，则a的n次方根不存在.2、我们规定：nmn m aa=)1,,0(>∈>nNnma且.如何规定nma-)1,,0(>∈>nNnma且的含义？答: .怎样理解零的分数指数幂的意义？答: .当0<a时，)1,(*>∈nNnma nm、何时无意义？答:3、有理数指数幂的运算性质4、无理数指数幂的意义5、定义：我们把形如xay=的函数叫做指数函数，其中x是自变量.为了便于研究，底数a的取值范围应如何规定为宜？答：1,0≠>aa且6、指数函数的图象和性质7、设)(ufy=,)(xgu=，则（1）当)(uf和)(xg的单调性相同时，)]([xgf为增函数；（2）当)(uf和)(xg的单调性相反时，)]([xgf为减函数；指数函数指数与指数幂的运算根式分数指数幂无理指数幂指数幂的运算法则概念图象性质1 求下列各式的值(1)364-；(2)4)2(-；(3)33)8(-；(4)2)10(-；(5) 44)3(π-；(6)88)1(-a .2 化简下列各式(1)49625--; (2) 3322)1()1()1(a a a -+-+-3 求下列各式的值:(1)3227;(2) 2125-;(3)5)21(-;(4)43)8116(-.4 化简下列各式的值(1))0,()3()6)(2(656131212132>-÷-b a b a b a b a (2))0,()(88341>-n m n m(3)4325)12525(÷- (4))0(322>⋅a aa a5 判断下列函数是否为指数函数？(2) 3x y =;(2) x a y )1(2+=;(3) 12+=x y ;(4) xy -=5;(5) 23x y =;(6)14+=xy .6 已知函数)10()(≠>=a a a x f x且的图象过点)3(π，，求)3(),1(),0(-f f f 的值.7 求下列函数的定义域: (1) 15-=x y ; (2)412-=x y .8 若10<<<a b ，则函数xa y =与xb y =的图象的相对位置关系如何？9 比较下列各题中两个值的大小 (1)5.27.1与37.1； (2) 1.08.0-与2.08.0-； (3) 3.07.1与1.39.0.10 若指数函数xa y )12(-=是减函数，求实数a 的取值范围.11 确定函数xx f -=2)(的单调区间和值域.12 设n m a 8.09.0⋅=,mn b 8.09.0⋅=,其中n m ,为实数，试比较a 与b 的大小.13 求函数x x f 21)(-=的定义域和值域.14 已知函数x x x f 22)(2-=+的值域是)12(∞+，，求)(x f 的定义域.15 已知关于x 的方程12=--m x 有实根，求实数m 的取值范围.16 已知函数1212)(+-=x x x f(1)确定)(x f 的奇偶性； (2)判断)(x f 的单调性； (3)求)(x f 的值域.17 求函数xx y -=2)31(的单调区间，并指出其单调性.18 已知函数aa a x f xx +=)( (1>a 为常数).(2) 确定)(x f 的单调性；(2)求)109()103()102()101(f f f f ++++ 的值.19 已知函数a x f x+-=121)(，试推断是否存在常数a ，使)(x f 为奇函数? 若存在，求a 的值；若不存在，说明理由.20 已知函数8234)(1+⋅-=+x xx f ，求满足0)(<x f 的x 的取值范围.21 已知当1>x 时，不等式12>-x x a ,)1,0(≠>a a 恒成立，求a 的取值范围.。

高中数学 2.1.1指数与指数幂的运算(1)教案新人教版必

2.1.1（1）指数与指数幂的运算（教学设计）内容：根式教学目标1、知识与技能：理解根式的概念及性质，能进行根式的运算，提高根式的运算能力。

2、过程与方法：通过由特殊到一般，由平方根、立方根，采用类比的方法过渡到n 次方根；通过对“当n 是偶数时，⎩⎨⎧<≥-==)0()0(||a a a a a a n n ”的理解，培养学生分类讨论的意识。

3、态度情感价值关：通过运算训练，培养学生严谨的思维，一丝不苟的学习习惯。

教学重点：对根式概念、性质的理解，运用根式的性质化简、运算。

教学难点：当n 是偶数时，⎩⎨⎧<≥-==)0()0(||a a a a a a n n 的得出及运用教学过程一、创设情境，新课引入：问题1（课本P48问题1）：从2000年起的未来20年，我国国内生产总值年平均增长率可达到7.3%．那么，在2001——2020年，各年的国内生产总值可望为2000年的多少倍？引导学生逐年计算，并得出规律：设x 年后我国的国内生产总值为2000年的y 倍，那么)20*,(073.1≤∈=x N x y x．问题2（课本P58问题2）：当生物死亡后，它机体内原有的碳14会按确定的规律衰减，大约每经过5730年衰减为原来的一半，这个时间称为“半衰期”．根据此规律，人们获得了生物体内碳14含量P 与死亡年数t 之间的关系5730)21(tP =．当生物死亡了5730，2⨯5730，3⨯5730，…年后，它体内碳14的含量P 分别为21，2)21(，3)21(，…．是正整数指数幂．它们的值分别为21，41，81，…．当生物死亡6000年，10000年，100000年后，它体内碳14的含量P 分别为57306000)21(，573010000)21(，5730100000)21(，这些式子的意义又是什么呢？这些正是本节课要学习的内容．二、师生互动，新课讲解：1、问题引入：（1）若a x =2，则x 叫a 的 .如：2±是4的平方根一个正数的平方根有个，它们互为数；负数没有平方根；零的平方根是 . （2）若a x =3，则x 叫a 的 .如：2是8的立方根，－2是－8的立方根。

高中数学 2.1.1 指数与指数幂的运算教学案(1)新人教A版

云南省德宏州潞西市芒市中学2014年高中数学 2.1.1指数与指数幂的运算教学案（1）新人教A 版必修1一、学习目标：（1）理解n 次方根概念及n 次方根的性质；（2）会求或化简根指数为正整数时的根式；二、问题与例题问题1：(1)什么是平方根？什么是立方根？一个数的平方根有几个，立方根呢？（2）如a x a x a x ===654,,，根据上面的结论我们又能得到什么呢？（3）根据上面的结论我们能得到一般性的结论吗？（4）可否用一个式子表达呢？问题二：（1）你能根据n 次方根的意义求出下列数的n 次方根吗？① 64的3次方根； -32的5方根；6a 的3次方根； ② 4的2次方根； 16的4次方根；（2）对以上结果进行分析、整理，可以得出什么结论？（3）问题（2）中，既然方根有奇次的也有偶次的，数a 有正有负，结论有一个的，也有两个的，你能否总结一般规律呢？（4）任何一个数a 的偶次方根是否存在呢？例1：求下列各式的值：三、目标检测求下列各式的值：（1）44100；（2）7749；（3）55)1.0(-；（4）66)3(-；（5）2)4(-π；（6）)()(66y x y x >-四、配餐作业A 组1、根式的概念：一般地，如果a x x x n 叫做则,=的)1*N n n ∈>且（（1）当n 为奇数时，a 的n 次方根记作；（2）当n 为偶数时，负数a n 次方根，而正数a 有 n 次方根且互为，记作。

2、求出下列各式的值：3、以下说法正确的是（）A. 正数的n 次方根是一个正数B. 负数的n 次方根是一个负数C. 0的任何次方根都是零D. a 的n 次方根用n a 表示（以上n>1且*N n ∈）4、求下列各式的值：设计意图：对课本中的习题作同等程度或降低程度的变式，考察学生对基础知识的掌握。

预计完成时间20分钟。

B 组1、下列各式中正确的是（）2、化简下列各式：设计意图：适当提高难度，考察学生的基本思维和数学思想方法。