三角形五心及其性质
三角形的五心及性质

重心三角形三条中线的交点叫做三角形重心。
定理:设三角形重心为O,BC边中点为D,则有AO = 2 OD。
重心坐标为三顶点坐标平均值。
外心三角形三边的垂直平分线的交点,称为三角形外心。
外心到三顶点距离相等。
过三角形各顶点的圆叫做三角形的外接圆,外接圆的圆心即三角形外心,这个三角形叫做这个圆的内接三角形。
内心三角形的内切圆的圆心简称为三角形的内心,即三角形三个角平分线的交点。内心有下列优美的性质:
性质1设I为△ABC的内心,则I为其内心的充要条件是:到△ABC三边的距离相等。
性质2设I为△ABC的内心,则∠BIC=90°+1/2∠A,类似地还有两式;反之亦然。
性质3设I为△ABC内一点,AI所在直线交△ABC的外接圆于D。I为△ABC内心的充要条件是ID=DB=DC。
性质5三角形一内角平分线与其外接圆的交点到另两顶点的距离与到内心的距离相等;反之,若I为△ABC的∠A平分线AD(D在△ABC的外接圆上)上的点,且DI=DB,则I为△ABC的内心。
性质6设I为△ABC的内心,BC=a,AC=b,AB=c,∠A的平分线交BC于K,交△ABC的外接圆于D,则AI/KI =AD/DI =DI/DK = (b+c)/a。
外心三角形的外接圆的圆心简称三角形的外心.即三角形三边中垂线的交点。外心有如下一系列优美性质:
性质1三角形的外心到三顶点的距离相等,反之亦然。
性质2设O为△ABC的外心,则∠BOC=2∠A,或∠BOC=360°-2∠A(还有两式)。
性质3设三角形的三条边长,外接圆的半径、面积分别为a、b、c,R、S△,则R=abc/4S△。
三角形只有一个垂心。
旁心与三角形的一边及其他两边的延长线都相切的圆叫做三角形的旁切圆,旁切圆的圆心叫做三角形旁心。
三角形五心性质总汇

三角形的五心1.内心:三角形三条内角平分线的交点,也是三角形内切圆的圆心。
角平分线性质:到角两边距离相等. 内心性质:到三角形三边距离相等。
2.重心:三角形三条中线交点中线性质:将三角形面积等分成两部分.重心性质:分三角形的中线两段长比例为2:1(长:短)3.外心:三角形三边垂直平分线的交点,三角形外接圆圆心。
垂直平分线性质:到线段两端点距离相等。
外心性质:到三角形三个顶点距离相等。
4.旁心:三角形一个内角平分线与另外两个外角的平分线的交点。
旁心性质:三角形的四心(内心、重心、垂心、外心)只有一个, 但旁心有三个,旁心到三角形三边所在直线距离相等。
三角形中有许多重要的特殊点,特别是三角形的“五心”,在解题时有很多应用,在本节中将分别给予介绍.三角形的“五心”指的是三角形的外心,内心,重心,垂心和旁心.1、三角形的外心三角形的三条边的垂直平分线交于一点,这点称为三角形的外心(外接圆圆心). 三角形的外心到三角形的三个顶点距离相等. 都等于三角形的外接圆半径.锐角三角形的外心在三角形内; 直角三角形的外心在斜边中点; 钝角三角形的外心在三角形外. 2、三角形的内心三角形的三条内角平分线交于一点,这点称为三角形的内心(内切圆圆心). 三角形的内心到三边的距离相等,都等于三角形内切圆半径. 内切圆半径r 的计算:设三角形面积为S ,并记p =12(a +b +c ),则r =Sp .特别的,在直角三角形中,有 r =12(a +b -c ). 3、三角形的重心 三角形的三条中线交于一点,这点称为三角形的重心. 上面的证明中,我们也得到了以下结论:三角形的重心到边的中点与到相应顶点的距离之比为 1∶ 2.4、三角形的垂心 三角形的三条高交于一点,这点称为三角形的垂心.斜三角形的三个顶点与垂心这四个点中,任何三个为顶点的三角形的垂心就是第四个点.所以把这样的四个点称为一个“垂心组”. A B COABCDE F GAB CD E F I aIKHE F D A BCM5、三角形的旁心三角形的一条内角平分线与另两个外角平分线交于一点,称为三角形的旁心(旁切圆圆心).每个三角形都有三个旁切圆.重心的性质:1、重心到顶点的距离与重心到对边中点的距离之比为2∶1。
中考数学之三角形五心定律

三角形五心定律三角形的重心,外心,垂心,内心和旁心称之为三角形的五心。
三角形五心定理是指三角形重心定理,外心定理,垂心定理,内心定理,旁心定理的总称.重心定理:三角形的三条边的中线交于一点。
该点叫做三角形的重心。
三中线交于一点可用燕尾定理证明,十分简单。
(重心原是一个物理概念,对于等厚度的质量均匀的三角形薄片,其重心恰为此三角形三条中线的交点,重心因而得名)重心的性质:1、重心到顶点的距离与重心到对边中点的距离之比为2︰1。
2、重心和三角形任意两个顶点组成的3个三角形面积相等。
即重心到三条边的距离与三条边的长成反比。
3、重心到三角形3个顶点距离的平方和最小。
4、在平面直角坐标系中,重心的坐标是顶点坐标的算术平均数,即其重心坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3)。
5. 以重心为起点,以三角形三顶点为终点的三条向量之和等于零向量。
外心定理:三角形外接圆的圆心,叫做三角形的外心。
外心的性质:1、三角形的三条边的垂直平分线交于一点,该点即为该三角形的外心。
2、若O是△ABC的外心,则∠BOC=2∠A(∠A为锐角或直角)或∠BOC=360°-2∠A(∠A为钝角)。
3、当三角形为锐角三角形时,外心在三角形内部;当三角形为钝角三角形时,外心在三角形外部;当三角形为直角三角形时,外心在斜边上,与斜边的中点重合。
4、外心到三顶点的距离相等垂心定理:三角形的三条高(所在直线)交于一点,该点叫做三角形的垂心。
垂心的性质:1、三角形三个顶点,三个垂足,垂心这7个点可以得到6个四点圆。
2、三角形外心O、重心G和垂心H三点共线,且OG︰GH=1︰2。
(此直线称为三角形的欧拉线(Euler line))(除正三角形)3、垂心到三角形一顶点距离为此三角形外心到此顶点对边距离的2倍。
4、垂心分每条高线的两部分乘积相等。
定理证明已知:ΔABC中,AD、BE是两条高,AD、BE相交于点O,连接CO并延长交AB于点F ,求证:CF⊥AB证明:连接DE∵∠ADB=∠AEB=90度∴A、B、D、E四点共圆∴∠ADE=∠ABE又∵∠ODC=∠OEC=90度∴O、D、C、E四点共圆∴∠ACF=∠ADE=∠ABE又∵∠ABE+∠BAC=90度∴∠ACF+∠BAC=90度∴CF⊥AB因此,垂心定理成立!内心定理:三角形内切圆的圆心,叫做三角形的内心。
三角形五心及其性质延伸

三角形五心及其性质延伸1.内心:三角形三条内角平分线的交点,也是三角形内切圆的圆心。
角平分线性质:到角两边距离相等. 内心性质:到三角形三边距离相等。
延伸:①内角平分线定理如图,AD 为△ABC证明过程如下:作BE//AC 交其延长线于E,又∵BE//AC,易证△ADC ∽ △EDB, 得证。
②外角平分线定理如图,AD 为△ABC 的外角平分线,交BC延长线于D证明过程如下:作CE//AB 交AD 于E,ABDCEcbcABCDEF又∵CE//AB,易证△ADB ∽ △EDC,得证。
③三角形内角平分线长公式如图,AD 为△ABC证明过程如下:作BE//AC 交其延长线于交其于F 。
由前文的内角平分线定理可知,△ADC∽ △EDB,而△ABE 为等腰三角形,④内心到三边距离r(三角形内切圆半径)设三角形面积为S ,则有cb cAFBDCEBC证明过程如下:连接OA,OB,OC.S△AOBS△AOC =S△BOC =又∵S=S△AOB + S△AOC+ S△BOC ,即2.重心:三角形三条中线交点中线性质:将三角形面积等分成两部分.重心性质:分三角形的中线两段长比例为2:1(长:短)如图:AD,BE,CF为△ABC三条中线,G为其重心,则有证明过程如下:作BH//FC交AD延长线于H,易证△GDC ≌△HDB又∵BH//FG,F为AB中点,∴G也为AH.延伸:三角形中线长公式AGFECB DHAFBDC如图,AD 为△ABC 的中线,则有证明过程如下:作BE//AC 交AD 延长线于E,易证△ADC ≌ △EDB ,∵BE//AC交其 延长线于F 。
又AB=c ,∴故3.外心:三角形三边垂直平分线的交点,三角形外接圆圆心。
垂直平分线性质:到线段两端点距离相等。
外心性质:到三角形三个顶点距离相等。
内心到三顶点距离R(三角形外接圆半径)某边除以它对角正弦的2倍) 证明过程于下:连接AO 并延长交圆O 于D,则AD 为圆直径,AD=2R.AD同弧AB 所对的圆周角相等),∴即延伸①:正弦定理由于变形得到正弦定理每边除以它所对角的正弦为2R) 延伸②:余弦定理证明过程如下:作交其于D4.旁心:三角形一个内角平分线与另外两个外角的平分线的交点。
三角形五心定律

三角形五心定律
形外部;当三角形为直角三角形时,外心在斜边上,与斜边的中点重合。
4、外心到三顶点的距离相等。
三、三角形垂心定理
三角形的三条高(所在直线)交于一点,该点叫做三角形的垂心。
垂心的性质:
1、三角形外心O、重心G和垂心H三点共线,且OG︰GH=1︰2。
2、垂心到三角形一顶点距离为此三角形外心到此顶点对边距离的2倍。
3、垂心分每条高线的两部分乘积相等。
四、三角形内心定理
三角形内切圆的圆心,叫做三角形的内心。
内心的性质:
1、三角形的三条内角平分线交于一点。
该点即为三角形的内心。
2、直角三角形的内心到边的距离等于两直角边的和减去斜边的差的二分之一。
3、O为三角形的内心,A、B、C分别为三角形的三个顶点,延长AO交BC边于N,则有AO:ON=AB:BN=AC:CN=(AB+AC):BC
4、△ABC中,R和r分别为外接圆为和内切圆的半径,O和I分别为其外心和内心,则OI^2=R^2-2Rr.
5、(内角平分线分三边长度关系)△ABC中,0为内心,∠A 、∠B、∠C的内角平分线分别交BC、AC、AB于Q、P、R,则BQ/QC=c/b, CP/PA=a/c, BR/RA=a/b.
6、内心到三角形三边距离相等。
三角形的五心

三角形的五心重心定义:三角形三条中线的交点叫做三角形重心。
性质:(1)设三角形重心为O,BC边中点为D,则有AO = 2 OD。
(2)三角形的重心与三顶点的连线所构成的三个三角形面积相等;(3)重心坐标为三顶点坐标平均值。
(4)以三角形的重心将三角形支起,三角形会保持平衡。
外心定义:三角形三边的垂直平分线的交点,称为三角形外心。
性质:(1)外心到三顶点距离相等。
(2)过三角形各顶点的圆叫做三角形的外接圆,外接圆的圆心即三角形外心,这个三角形叫做这个圆的内接三角形。
(3)三角形有且只有一个外接圆。
内心定义:三角形内心为三角形三条内角平分线的交点。
性质:(1)与三角形各边都相切的圆叫做三角形的内切圆。
(2)内切圆的圆心即是三角形内心。
(3)内心到三角形三边距离相等,这个三角形叫做圆的外切三角形。
(4)三角形有且只有一个内切圆。
垂心定义:三角形三边上的三条高线所在直线的交点,称为三角形垂心。
性质:(1)锐角三角形的垂心在三角形内;直角三角形的垂心在直角的顶点;钝角三角形的垂心在三角形外.。
(2)三角形只有一个垂心。
旁心定义:(1)与三角形的一边及其他两边的延长线都相切的圆叫做三角形的旁切圆,旁切圆的圆心叫做三角形旁心。
(2)三角形的一条内角平分线与其他两个角的外角平分线交于一点,即三角形的旁心。
性质:(1)旁心到三角形一边及其他两边延长线的距离相等。
(2)三角形有三个旁切圆,三个旁心。
这三个旁心到三角形三条边的延长线的距离相等。
五心的性质:三角形的五心有许多重要性质,它们之间也有很密切的联系,如:(1)三角形的重心与三顶点的连线所构成的三个三角形面积相等;(2)三角形的外心到三顶点的距离相等;(3)三角形的垂心与三顶点这四点中,任一点是其余三点所构成的三角形的垂心;(4)三角形的内心、旁心到三边距离相等;(5)三角形的垂心是它垂足三角形的内心;或者说,三角形的内心是它旁心三角形的垂心;(6)三角形的外心是它的中点三角形的垂心;(7)三角形的重心也是它的中点三角形的重心;(8)三角形的中点三角形的外心也是其垂足三角形的外心.(9)三角形的任一顶点到垂心的距离,等于外心到对边的距离的二倍.详细性质垂心三角形三边上的高的交点称为三角形的垂心。
三角形的五“心”及其性质

三角形的五“心”及其性质
三角形的五心是指三角形内部的五个特殊点,包括重心、外心、内心、垂心和旁心。
1. 重心:三角形三个顶点与其对边的中点连接所交于一点,这个点被
称为重心。
重心到三角形三边的距离相等,重心将三角形划分为三个
面积相等的小三角形。
2. 外心:三角形三个顶点的垂直平分线相交于一点,这个点被称为外心。
外心是三角形外接圆圆心,即三角形三个顶点与外心的连线的长
度相等。
3. 内心:三角形三个顶点的角平分线相交于一点,这个点被称为内心。
内心是三角形内切圆圆心,即三角形三条边与内心的连线的垂直距离
相等。
4. 垂心:三角形三个顶点的高的延长线相交于一点,这个点被称为垂心。
垂心是三角形三条高的交点,即垂心到三角形三个顶点所在的直
线距离相等。
5. 旁心:三角形的旁心有三个,分别对应三条边。
旁心是指三角形的
外切圆圆心,即三角形的一条边外边的一条角的角平分线与另外两条
边延长线的交点。
这些五心有一些重要的性质:
- 重心是三角形的重要重心之一,它将三角形分成三个面积相等的小三
角形。
- 外心是三角形外接圆圆心,外接圆的直径是三角形的边长,外心到三
个顶点的距离相等。
- 内心是三角形内切圆圆心,内接圆与三个边相切,内心到三个边的距
离相等。
- 垂心是三角形三条高的交点,垂心到三个顶点所在的直线距离相等。
- 旁心是三角形外切圆圆心,外切圆与三条边相切,旁心到相对应的边
的距离相等。
三角形五心的性质【超全总结】

word格式-可编辑-感谢下载支持重心的性质:(三条中线的交点)1、重心到顶点的距离与重心到对边中点的距离之比为2︰1。
2、重心和三角形任意两个顶点组成的3个三角形面积相等。
即重心到三条边的距离与三条边的长成反比。
3、重心到三角形3个顶点距离的平方和最小。
4、在平面直角坐标系中,重心的坐标是顶点坐标的算术平均数,即其重心坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3。
5. 以重心为起点,以三角形三定点为终点的三条向量之和等于零向量。
外心的性质:(三条边的垂直平分线的交点)1、若O是△ABC的外心,则∠BOC=2∠A(∠A为锐角或直角)或∠BOC=360°-2∠A(∠A为钝角)。
2、当三角形为锐角三角形时,外心在三角形内部;当三角形为钝角三角形时,外心在三角形外部;当三角形为直角三角形时,外心在斜边上,与斜边的中点重合。
3、计算外心的坐标应先计算下列临时变量:d1,d2,d3分别是三角形三个顶点连向另外两个顶点向量的点乘。
C1=d2d3,c2=d1d3,c3=d1d2;c=c1+c2+c3。
外心坐标:( (c2+c3)/2c,(c1+c3)/2c,(c1+c2)/2c )。
4、外心到三顶点的距离相等垂心的性质:(三条高的交点)1、三角形三个顶点,三个垂足,垂心这7个点可以得到6个四点圆。
2、三角形外心O、重心G和垂心H三点共线,且OG︰GH=1︰2。
(此直线称为三角形的欧拉线)3、垂心到三角形一顶点距离为此三角形外心到此顶点对边距离的2倍。
4、垂心分每条高线的两部分乘积相等。
内心的性质:(三个内角的角平分线的交点)1、直角三角形的内心到边的距离等于两直角边的和减去斜边的差的二分之一。
2、P为ΔABC所在空间中任意一点,点O是ΔABC内心的充要条件是:Po=(a×PA+b×PB+c×PC)/(a+b+c).3、O为三角形的内心,A、B、C分别为三角形的三个顶点,延长AO交BC边于N,则有AO:ON=AB:BN=AC:CN=(AB+AC):BC4、(欧拉定理) ΔABC中,R和r分别为外接圆为和内切圆的半径,O和I分别为其外心和内心,则OI2=R2-2Rr.5、(内角平分线分三边长度关系)△ABC中,O为内心,∠A、∠B、∠C的内角平分线分别交BC、AC、AB于Q、P、R,则BQ/QC=c/b, CP/PA=a/c, BR/RA=a/b.6、内心到三角形三边距离相等。
三角形五心及其性质

三角形的三条高的交点叫做三角形的垂心。
三角形垂心的性质设△ABC的三条高为AD、BE、CF,其中D、E、F为垂足,垂心为H,角A、B、C的对边分别为a、b、c,p=(a+b+c)/2.1、锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外. 2、三角形的垂心是它垂足三角形的内心;或者说,三角形的内心是它旁心三角形的垂心;3、垂心H关于三边的对称点,均在△A BC的外接圆上。
4、△ABC中,有六组四点共圆,有三组(每组四个)相似的直角三角形,且A H•HD=BH•HE=CH•HF。
5、 H、A、B、C四点中任一点是其余三点为顶点的三角形的垂心(并称这样的四点为一—垂心组)。
6、△AB C,△ABH,△BC H,△ACH的外接圆是等圆。
7、在非直角三角形中,过H的直线交AB、AC所在直线分别于P、Q,则 AB/AP•tanB+AC/A Q•tanC=tan A+tanB+tan C。
8、三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍。
9、设O,H分别为△ABC的外心和垂心,则∠BAO=∠HAC,∠ABH=∠OBC,∠BCO=∠HCA。
10、锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍。
11、锐角三角形的垂心是垂足三角形的内心;锐角三角形的内接三角形(顶点在原三角形的边上)中,以垂足三角形的周长最短。
12、西姆松定理(西姆松线):从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。
13、设锐角△ABC内有一点T,那么T是垂心的充分必要条件是PB*PC*BC+PB*P A*AB+PA*PC*AC=AB*BC*CA。
垂心的向径定义设点H为锐角三角形ABC的垂心,向量OH=h,向量OA=a,向量OB=b,向量OC=c,则h=(ta nA a +tanB b +tanC c)/(tanA+ta nB+tanC).垂心坐标的解析解:设三个顶点的坐标分别为(a1,b1)(a2,b2)(a3,b3),那么垂心坐标x=Δx/2/Δ,y=-Δy/2/Δ。
中考数学之三角形五心定律

三角形五心定律三角形的重心,外心,垂心,内心和旁心称之为三角形的五心。
三角形五心定理是指三角形重心定理,外心定理,垂心定理,内心定理,旁心定理的总称.重心定理:三角形的三条边的中线交于一点。
该点叫做三角形的重心。
三中线交于一点可用燕尾定理证明,十分简单。
(重心原是一个物理概念,对于等厚度的质量均匀的三角形薄片,其重心恰为此三角形三条中线的交点,重心因而得名)重心的性质:1、重心到顶点的距离与重心到对边中点的距离之比为2︰1。
2、重心和三角形任意两个顶点组成的3个三角形面积相等。
即重心到三条边的距离与三条边的长成反比。
3、重心到三角形3个顶点距离的平方和最小。
4、在平面直角坐标系中,重心的坐标是顶点坐标的算术平均数,即其重心坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3)。
5. 以重心为起点,以三角形三顶点为终点的三条向量之和等于零向量。
外心定理:三角形外接圆的圆心,叫做三角形的外心。
外心的性质:1、三角形的三条边的垂直平分线交于一点,该点即为该三角形的外心。
2、若O是△ABC的外心,则∠BOC=2∠A(∠A为锐角或直角)或∠BOC=360°-2∠A(∠A为钝角)。
3、当三角形为锐角三角形时,外心在三角形内部;当三角形为钝角三角形时,外心在三角形外部;当三角形为直角三角形时,外心在斜边上,与斜边的中点重合。
4、外心到三顶点的距离相等垂心定理:三角形的三条高(所在直线)交于一点,该点叫做三角形的垂心。
垂心的性质:1、三角形三个顶点,三个垂足,垂心这7个点可以得到6个四点圆。
2、三角形外心O、重心G和垂心H三点共线,且OG︰GH=1︰2。
(此直线称为三角形的欧拉线(Euler line))(除正三角形)3、垂心到三角形一顶点距离为此三角形外心到此顶点对边距离的2倍。
4、垂心分每条高线的两部分乘积相等。
定理证明已知:ΔABC中,AD、BE是两条高,AD、BE相交于点O,连接CO并延长交AB于点F ,求证:CF⊥AB证明:连接DE∵∠ADB=∠AEB=90度∴A、B、D、E四点共圆∴∠ADE=∠ABE又∵∠ODC=∠OEC=90度∴O、D、C、E四点共圆∴∠ACF=∠ADE=∠ABE又∵∠ABE+∠BAC=90度∴∠ACF+∠BAC=90度∴CF⊥AB因此,垂心定理成立!内心定理:三角形内切圆的圆心,叫做三角形的内心。
三角形五心及其性质

三角形的三条高的交点叫做三角形的垂心。
三角形垂心的性质设△ABC的三条高为AD、BE、CF,其中D、E、F为垂足,垂心为H,角A、B、C的对边分别为a、b、c,p=(a+b+c)/2.1、锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外.2、三角形的垂心是它垂足三角形的内心;或者说,三角形的内心是它旁心三角形的垂心;3、垂心H关于三边的对称点,均在△ABC的外接圆上。
4、△ABC中,有六组四点共圆,有三组(每组四个)相似的直角三角形,且AH•HD=BH•HE=CH•HF。
5、H、A、B、C四点中任一点是其余三点为顶点的三角形的垂心(并称这样的四点为一—垂心组)。
6、△ABC,△ABH,△BCH,△ACH的外接圆是等圆。
7、在非直角三角形中,过H的直线交AB、AC所在直线分别于P、Q,则AB/AP•tanB+AC/AQ•tanC=tanA+tanB+tanC。
8、三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍。
三角形重心已知:△ABC中,D为BC中点,E为AC中点,AD与BE交于O,CO延长线交AB于F。
求证:F为AB中点。
证明:根据燕尾定理,S△AOB=S△AOC,又S△AOB=S△BOC,∴S△AOC=S△BOC,再应用燕尾定理即得AF=BF,命题得证。
重心的几条性质:1.重心到顶点的距离与重心到对边中点的距离之比为2:1。
2.重心和三角形3个顶点组成的3个三角形面积相等。
3.重心到三角形3个顶点距离的平方和最小。
4.在平面直角坐标系中,重心的坐标是顶点坐标的算术平均,即其坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3);空间直角坐标系——横坐标:(X1+X2+X3)/3 纵坐标:(Y1+Y2+Y3)/3 竖坐标:(Z1+Z2+Z3)/35.重心和三角形3个顶点的连线的任意一条连线将三角形面积平分。
证明:刚才证明三线交一时已证。
6.重心是三角形内到三边距离之积最大的点。
三角形五心定律

数学定理
01 重心定理
03 垂心定理 05 旁心定理
目录
02 外心定理 04 内心定理 06 特殊
基本信息
三角形五心定理,是指三角形重心定理、外心定理、垂心定理、内心定理,以及旁心定理的总称。三角形的 重心,外心,垂心,内心和旁心称之为三角形的五心。
重心定理
重心定理
三角形的三条边的中线交于一点,该点叫做三角形的重心。 重心的性质: 1、重心到顶点的距离与重心到对边中点的距离之比为2︰1。 2、重心和三角形任意两个顶点组成的3个三角形面积相等。即重心到三条边的距离与三条边的长成反比。 3、重心到三角形3个顶点距离的平方和最小。 4、在平面直角坐标系中,重心的坐标是顶点坐标的算术平均数,即其重心坐标为 5.以重心为起点,以三角形三顶点为终点的三条向量之和等于零向量。
内心定理
内心定理
三角形内切圆的圆心,叫做三角形的内心。 内心的性质: 1、三角形的三条内角平分线交于一点。该点即为三角形的内心。 2、直角三角形的内心到边的距离等于两直角边的和与斜边的差的二分之一。 3、P为ΔABC所在空间中任意一点,点0是ΔABC内心的充要条件是:向量P0=(a×向量PA+b×向量PB+c×向 量PC)/(a+b+c). 4、O为三角形的内心,A、B、C分别为三角形的三个顶点,延长AO交BC边于N,则有 AO:ON=AB:BN=AC:CN=(AB+AC):BC 5、(欧拉定理)⊿ABC中,R和r分别为外接圆为和内切圆的半径,O和I分别为其外心和内心,则OI^2=R^22Rr. 6、(内角平分线分三边长度关系) △ABC中,0为内心,∠A、∠B、 ∠C的内角平分线分别交BC、AC、AB于Q、P、R, 则BQ/QC=c/b, CP/PA=a/c, BR/RA=a/b.
三角形的五心性质

三角形的五心性质内心是三条角平分线的交点,它到三边的距离相等。
外心是三条边垂直平分线的交点,它到三个顶点的距离相等。
重心是三条中线的交点,它到顶点的距离是它到对边中点距离的2倍。
垂心是三条高的交点,它能构成很多直角三角形相似。
旁心是一个内角平分线与其不相邻的两个外角平分线的交点,它到三边的距离相等。
(1)重心和三顶点的连线所构成的三个三角形面积相等;(2)外心到三顶点的距离相等;(3)垂心与三顶点这四点中,任一点是其余三点构成的三角形的垂心;(4)内心、旁心到三边距离相等;(5)垂心是三垂足构成的三角形的内心;(6)外心是中点三角形的垂心;(7)中心也是中点三角形的重心;(8)三角形的中点三角形的外心也是其垂足三角形的外心。
三角形的五心定理重心定理:三角形的三条中线交于一点,这点到顶点的距离是它到对边中点距离的2倍,该点叫做三角形的重心。
外心定理:三角形的三边的垂直平分线交于一点,该点叫做三角形的外心。
垂心定理:三角形的三条高交于一点,该点叫做三角形的垂心。
内心定理:三角形的三内角平分线交于一点,该点叫做三角形的内心。
旁心定理:三角形一内角平分线和另外两顶点处的外角平分线交于一点,该点叫做三角形的旁心。
三角形有三个旁心。
重心的几条性质:1、重心到顶点的距离与重心到对边中点的距离之比为2:1。
2、重心和三角形3个顶点组成的3个三角形面积相等。
3、重心到三角形3个顶点距离的平方和最小。
4、在平面直角坐标系中,重心的坐标是顶点坐标的算术平均,即其坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3);空间直角坐标系——横坐标:(X1+X2+X3)/3 纵坐标:(Y1+Y2+Y3)/3 竖坐标:(z1+z2+z3)/35、三角形内到三边距离之积最大的点。
线段的重心线段的重心就是线段的中点平行四边形的重心平行四边形的重心就是它两条对角线的交点三角形的重心、外心、垂心、内心、旁心称为三角形的五心,它们都是三角形的重要相关点。
中考数学点睛三角形五心及其性质延伸
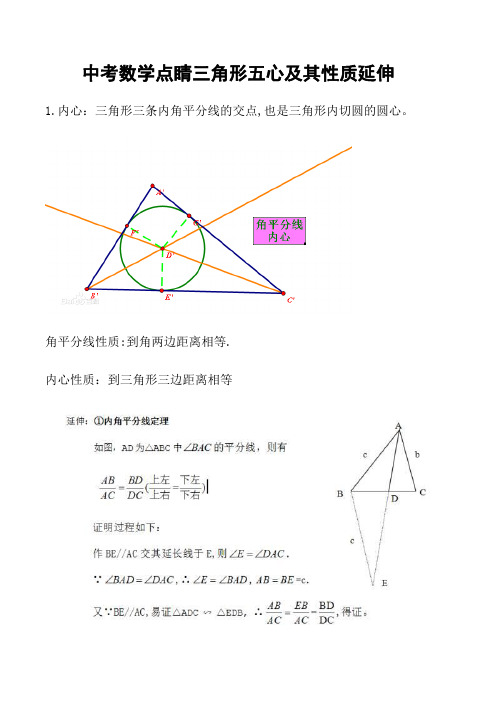
中考数学点睛三角形五心及其性质延伸1.内心:三角形三条内角平分线的交点,也是三角形内切圆的圆心。
角平分线性质:到角两边距离相等.
内心性质:到三角形三边距离相等
4.旁心:三角形一个内角平分线与另外两个外角的平分线的交点。
旁心性质:三角形的四心(内心、重心、垂心、外心)只有一个,但旁心有三个,旁心到三角形三边所在直线距离相等。
4、三角形的垂心
三角形的三条高交于一点,这点称为三角形的垂心.
斜三角形的三个顶点与垂心这四个点中,任何三个为顶点的三角形的垂心就是第四个点.所以把这样的四个点称为一个“垂心组”.。
三角形的五心

三角形的中心,重心,垂心,内心,外心。
五心的定义和性质是什么如果你知道了三角形的重心,垂心,内心,外心,那么对以等边三角形,这四心是合一的,也叫中心,中心具有所有四心的性质。
需要补充的是三角形还有一个旁心,通常把三角形的重心,外心,垂心,内心和旁心称之为三角形的五心。
一、三角形重心定理三角形的三条边的中线交于一点。
该点叫做三角形的重心。
重心位置:于三角形内部三中线交于一点可用燕尾定理证明,十分简单。
(重心原是一个物理概念,对于等厚度的质量均匀的三角形薄片,其重心恰为此三角形三条中线的交点,重心因而得名)重心的性质:1、重心到顶点的距离与重心到对边中点的距离之比为2︰1。
2、重心和三角形任意两个顶点组成的3个三角形面积相等。
即重心到三条边的距离与三条边的长成反比。
3、重心到三角形3个顶点距离的平方和最小。
4、在平面直角坐标系中,重心的坐标是顶点坐标的算术平均数,即其重心坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3。
二、三角形垂心定理三角形的三条高(所在直线)交于一点,该点叫做三角形的垂心。
垂心的位置:于锐角三角形内部,直角三角形的两只角边交点,钝角三角形的外部。
垂心的性质:1、三角形三个顶点,三个垂足,垂心这7个点可以得到6个四点圆。
2、三角形外心O、重心G和垂心H三点共线,且OG︰GH=1︰2。
(此直线称为三角形的欧拉线(Euler line))3、垂心到三角形一顶点距离为此三角形外心到此顶点对边距离的2倍。
4、垂心分每条高线的两部分乘积相等。
定理证明已知:ΔABC中,AD、BE是两条高,AD、BE交于点O,连接CO并延长交AB于点F ,求证:CF ⊥AB证明:连接DE ∵∠ADB=∠AEB=90度∴A、B、D、E四点共圆∴∠ADE=∠ABE∵∠EAO=∠DAC ∠AEO=∠ADC∴ΔAEO∽ΔADC∴AE/AO=AD/AC ∴ΔEAD∽ΔOAC ∴∠ACF=∠ADE=∠ABE又∵∠ABE+∠BAC=90度∴∠ACF+∠BAC=90度∴CF⊥AB因此,垂心定理成立!三、三角形内心定理三角形内切圆的圆心,叫做三角形的内心。
三角形的五心及性质

三角形的五心及性质重心三角形三条中线的交点叫做三角形重心。
定理:设三角形重心为O,BC边中点为D,则有AO = 2 ODAO = 2 OD。
重心坐标为三顶点坐标平均值。
外心三角形三边的垂直平分线的交点,称为三角形外心。
外心到三顶点距离相等。
过三角形各顶点的圆叫做三角形的外接圆,外接圆的圆心即三角形外心,这个三角形叫做这个圆的内接三角形。
三角形有且只有一个外接圆。
内心三角形内心为三角形三条内角平分线的交点。
与三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心即是三角形内心,内心到三角形三边距离相等。
这个三角形叫做圆的外切三角形。
三角形有且只有一个内切圆。
垂心三角形三边上的三条高线的交点,称为三角形垂心。
锐角三角形的垂心在三角形内;直角三角形的垂心在直角的顶点;钝角三角形的垂心在三角形外.。
三角形只有一个垂心。
旁心与三角形的一边及其他两边的延长线都相切的圆叫做三角形的旁切圆,旁切圆的圆心叫做三角形旁心。
三角形的一条内角平分线与其他两个角的外角平分线交于一点,即三角形的旁心。
旁心到三角形一边及其他两边延长线的距离相等。
三角形有三个旁切圆,三个旁心。
这三个旁心到三角形三条边的延长线的距离相等。
五心的性质三角形的五心有许多重要性质,它们之间也有很密切的联系,如:1)三角形的重心与三顶点的连线所构成的三个三角形面积相等;2)三角形的外心到三顶点的距离相等;3)三角形的垂心与三顶点这四点中,任一点是其余三点所构成的三角形的垂心;4)三角形的内心、旁心到三边距离相等;5)三角形的垂心是它垂足三角形的内心;或者说,三角形的内心是它旁心三角形的垂心;6)三角形的外心是它的中点三角形的垂心;7)三角形的重心也是它的中点三角形的重心;8)三角形的中点三角形的外心也是其垂足三角形的外心.9)三角形的任一顶点到垂心的距离,等于外心到对边的距离的二倍.垂心 三角形三边上的高的交点称为三角形的垂心。
三角形垂心有下列有趣的性质:设△ABC 的三条高为AD AD、、BE BE、、CF CF,其中,其中D 、E 、F 为垂足,垂心为H 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形的三条高的交点叫做三角形的垂心。
三角形垂心的性质设△ABC的三条高为AD、BE、CF,其中D、E、F为垂足,垂心为H,角A、B、C的对边分别为a、b、c,p=(a+b+c)/2.1、锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外.2、三角形的垂心是它垂足三角形的内心;或者说,三角形的内心是它旁心三角形的垂心;3、垂心H关于三边的对称点,均在△ABC的外接圆上。
4、△ABC中,有六组四点共圆,有三组(每组四个)相似的直角三角形,且AH•HD=BH•HE=CH•HF。
5、H、A、B、C四点中任一点是其余三点为顶点的三角形的垂心(并称这样的四点为一—垂心组)。
6、△ABC,△ABH,△BCH,△ACH的外接圆是等圆。
7、在非直角三角形中,过H的直线交AB、AC所在直线分别于P、Q,则AB/AP•tanB+AC/AQ•tanC=tanA+tanB+tanC。
8、三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍。
9、设O,H分别为△ABC的外心和垂心,则∠BAO=∠HAC,∠ABH=∠OBC,∠BCO=∠HCA。
10、锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍。
11、锐角三角形的垂心是垂足三角形的内心;锐角三角形的内接三角形(顶点在原三角形的边上)中,以垂足三角形的周长最短。
12、西姆松定理(西姆松线):从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。
13、设锐角△ABC内有一点T,那么T是垂心的充分必要条件是PB*PC*BC+PB*PA*AB+PA*PC*AC=AB*BC*CA。
垂心的向径定义设点H为锐角三角形ABC的垂心,向量OH=h,向量OA=a,向量OB=b,向量OC=c,则h=(tanA a +tanB b +tanC c)/(tanA+tanB+tanC).垂心坐标的解析解:设三个顶点的坐标分别为(a1,b1)(a2,b2)(a3,b3),那么垂心坐标x=Δx/2/Δ,y=-Δy/2/Δ。
其中,Δ=det([x2-x1,x3-x2,y2-y1,y3-y2]);Δx=det([(x1+x2)*(x2-x1)+(y1+y2)*(y2-y1),y2-y1;(x2+x3)*(x3-x2)+(y2+y3)*(y3-y2),y3-y2]);Δy=det([x3-x2,(y2+y3)*(y3-y2);x3-x1,(y3+y1)*(y3-y1)+(x2-x1)*(x1-x3)]);垂心的向量特征:三角形ABC内一点O,向量OA•OB=OB•OC=OC•OA,则点O是三角形的垂心证明由OA•OB=OB•OC,得OA•OB-OC•OB=0(OA-OC)•OB=0CA•OB=0,即OB垂直于AC边同理由OB•OC=OC•OA,可得OC垂直于AB边由OA•OB=OC•OA,得OA垂直于BC边显然点O是三角形的垂心三角形的重心重心是三角形三边中线的交点,三线交一点可用燕尾定理证明,十分简单。
证明过程又是塞瓦定理的特例。
三角形重心已知:△ABC中,D为BC中点,E为AC中点,AD与BE交于O,CO延长线交AB于F。
求证:F为AB中点。
证明:根据燕尾定理,S△AOB=S△AOC,又S△AOB=S△BOC,∴S△AOC=S△BOC,再应用燕尾定理即得AF=BF,命题得证。
重心的几条性质:1.重心到顶点的距离与重心到对边中点的距离之比为2:1。
2.重心和三角形3个顶点组成的3个三角形面积相等。
3.重心到三角形3个顶点距离的平方和最小。
4.在平面直角坐标系中,重心的坐标是顶点坐标的算术平均,即其坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3);空间直角坐标系——横坐标:(X1+X2+X3)/3 纵坐标:(Y1+Y2+Y3)/3 竖坐标:(Z1+Z2+Z3)/35.重心和三角形3个顶点的连线的任意一条连线将三角形面积平分。
证明:刚才证明三线交一时已证。
6.重心是三角形内到三边距离之积最大的点。
其它规则图形的重心注:下面的几何体都是均匀的,线段指细棒,平面图形指薄板。
三角形的重心就是三边中线的交点。
线段的重心就是线段的中点。
平行四边形的重心就是其两条对角线的交点,也是两对对边中点连线的交点。
平行六面体的重心就是其四条对角线的交点,也是六对对棱中点连线的交点,也是四对对面重心连线的交点。
圆的重心就是圆心,球的重心就是球心。
锥体的重心是顶点与底面重心连线的四等分点上最接近底面的一个。
四面体的重心同时也是每个定点与对面重心连线的交点,也是每条棱与对棱中点确定平面的交点。
三角形的旁切圆(与三角形的一边和其他两边的延长线相切的圆)的圆心叫做旁心。
旁心是一个三角形内角平分线与其不相邻的两个外角平分线的交点,它到三角形三边的距离相等。
如图,点M就是△ABC的一个旁心。
三角形任意两角的外角平分线和第三个角的内角平分线的交点。
一个三角形有三个旁心,而且一定在三角形外。
若设O为△ABC的旁心,用向量表示则有aOA=bOB+cOC1、三角形一内角平分线和另外两顶点处的外角平分线交于一点,该点即为三角形的旁心。
2、每个三角形都有三个旁心。
内心是三角形三条内角平分线的交点,即内切圆的圆心。
内心是三角形角平分线交点的原理:经圆外一点作圆的两条切线,这一点与圆心的连线平分两条切线的夹角(原理:角平分线上点到角两边距离相等)。
内心定理:三角形的三个内角的角平分线交于一点。
该点叫做三角形的内心。
注意到内心到三边距离相等(为内切圆半径),内心定理其实极易证。
若三边分别为l1,l2,l3,周长为p,则内心的重心坐标为(l1/p,l2/p,l3/p)。
直角三角形的内心到边的距离等于两直角边的和减去斜边的差的二分之一。
双曲线上任一支上一点与两焦点组成的三角形的内心在实轴的射影为对应支的顶点。
三角形内心的性质设⊿ABC的内切圆为☉O(半径r),角A、B、C的对边分别为a、b、c,p=(a+b+c)/2。
1、三角形的三条角平分线交于一点,该点即为三角形的内心。
2、三角形的内心到三边的距离相等,都等于内切圆半径r。
3、r=S/p。
证明:S△ABC=S△OAB+S△OAC+S△OBC=(cr+br+ar)/2=rp, 即得结论。
△ABC中,∠C=90°,r=(a+b-c)/2。
5、∠BOC=90°+A/2。
6、点O是平面ABC上任意一点,点O是⊿ABC内心的充要条件是:a(向量OA)+b(向量OB)+c(向量OC)=向量0。
7、点O是平面ABC上任意一点,点I是⊿ABC内心的充要条件是:向量OI=[a(向量OA)+b(向量OB)+c(向量OC)]/(a+b+c)。
8、⊿ABC中,A(x1,y1),B(x2,y2),C(x3,y3),那么⊿ABC内心I的坐标是:(ax1/(a+b+c)+bx2/(a+b+c)+cx3/(a+b+c),ay1/(a+b+c)+by2/(a+b+c)+cy3/(a+b+c)。
9、(欧拉定理)⊿ABC中,R和r分别为外接圆为和内切圆的半径,O和I分别为其外心和内心,则OI^2=R^2-2Rr。
10、(内角平分线分三边长度关系)角平分线分对边与该角的两边成比例。
证明:△ABC中,AD是∠A的角平分线,D在BC上,abc 是角的对边ABC,d=AD。
由于正弦定理b/sinB=c/sinC d=R1sinB=R2sinC,R1是△ABD的外接圆半径,R2是△ACD 的外接圆半径,所以R1/R2=sinC/sinB=c/b.又BD=R1sinBAD,CD=R2sinCAD,∠CAD=∠BAD,所以BD/CD=R1/R2=c/b=AB/AC三角形外接圆的圆心叫做三角形的外心.三角形外接圆的圆心也就是三角形三边中垂线的交点,三角形的三个顶点就在这个外接圆上.三角形外心的性质设⊿ABC的外接圆为☉G(R),角A、B、C的对边分别为a、b、c,p=(a+b+c)/2.1:(1)锐角三角形的外心在三角形内;(2)直角三角形的外心在斜边上,与斜边中点重合;(3)钝角三角形的外心在三角形外.2:∠BGC=2∠A,(或∠BGC=2(180°-∠A).3:点G是平面ABC上一点,那么点G是⊿ABC外心的充要条件是:(向量GA+向量GB)·向量AB= (向量GB+向量GC)·向量BC=(向量GC+向量GA)·向量CA=向量0.4:点G是平面ABC上一点,点P是平面ABC上任意一点,那么点G是⊿ABC外心的充要条件是:(1)向量PG=((tanB+tanC)向量PA+(tanC+tanA)向量PB+(tanA+tanB)向量PC)/2(tanA+tanB+tanC).或(2)向量PG=(cosA/2sinBsinC)向量PA+(cosB/2sinCsinA)向量PB+(cosC/2sinAsinB)向量PC.5:三角形三条边的垂直平分线的交于一点,该点即为三角形外接圆的圆心.外心到三顶点的距离相等。
6:R=abc/4S⊿ABC.正弦定理:2R=a/sinA=b/sinB=c/sinC。
