带p-laplacian算子四阶四点边值问题的迭代解
含有p-Laplacian算子n阶多点边值问题在共振条件下非负解的存在性

曲 阜 师 范 大 学
Junl o Q f N r l ora f uu oma
V0 _ 8 No. l3 1
Jn 0 2 a .2 1
含有 PL pai -a l a c n算子 n阶 多点 边值 问题在共振 条件下非 负解的存在性
1 引
言
对 于二 阶线 性 常微分 方程 多点边 值 问题可解 性 的研 究是 由 It l n和 Mo ev首先 开 始 的 ,见 文献 [.] ie s 1 . 2
此后 , 便有了诸多关于非线性有限多点边值 问题的研究 . 。 但是在共振条件下 , 含有 pLp c n -al i 算子 n aa 阶奇异多点边值 问题却很 少有人研究 , 本文主要运用推广到算子 . Ⅳ在锥上的零点指数 , 讨论 了含 有 P .
_÷ Ke rL.
定义 2 3 设 力为 中的有界开集 , . 若有 Q ) l中的有界集 , Ⅳ( 为 , 且 ( 一 ) ) , Q ( 为 中的紧集 , 则 称 Ⅳ在 上为 一 紧的. H= j i 则 H. n L y 令 L+ - P, , C d o 为线性双射 , 且有有界逆算子满足
m一 2
(. ) 1 1
() ” ) 0 = ( =… = 0
’ )= ,()=∑ o ( , ( 0 “1 0 / ) i “
(2 1) .
其 ( = Iu > = ,+ = f0 ]R R 续R= ,) ∈(,, 中 M l- Pl 古 寺 1:, ד 连 , [∞; c0) ) 2 ; u ; P ,[ 1 一 + 0 。 (1
孟 令 君 , 刘 立 山
( 曲阜师范大学数学科学学院 , 7 15 山东省 曲阜市 ) 2 36 ,
laplacian算子matlab程序

laplacian算子matlab程序Laplacian算子是常用的图像处理算法之一,它可以用于边缘检测、图像增强等应用。
在Matlab中,我们可以使用Laplacian算子对图像进行处理并得到边缘信息。
本文将介绍如何使用Matlab编写Laplacian算子的程序,并展示算法在图像处理中的实际应用。
Laplacian算子的定义如下:L(x, y) = ∂²I(x, y)/∂x² + ∂²I(x, y)/∂y²其中,L(x, y)是Laplacian算子的输出,I(x, y)是输入图像,∂²I(x, y)/∂x²和∂²I(x, y)/∂y²分别是图像在水平和竖直方向上的二阶导数。
在Matlab中,我们可以使用内置的函数`fspecial`和`imfilter`实现Laplacian算子。
具体步骤如下:步骤1:读取图像首先,我们需要读取一幅图像作为输入。
可以使用`imread`函数读取图像,并使用`imshow`函数显示图像。
```matlabimage = imread('input.jpg');imshow(image);```步骤2:构造Laplacian算子的卷积核在Matlab中,我们可以使用`fspecial`函数构造一个Laplacian算子的卷积核。
Laplacian算子的卷积核通常取如下形式:```0 -1 0-1 4 -10 -1 0```可以使用`fspecial('laplacian')`函数生成Laplacian算子的卷积核。
为了增强边缘效果,我们可以对卷积核进行归一化处理,使其元素之和为1。
```matlablaplacian = fspecial('laplacian');laplacian = laplacian / sum(abs(laplacian(:)));```步骤3:应用Laplacian算子使用`imfilter`函数将Laplacian算子应用到图像上。
laplacian算子

laplacian算子
Laplacian算子的概念可以追溯到17,18世纪时期的拉普拉斯,他是贝尔定理的发现者。
它是一种线性微分运算符,可以在几何物理学和数学中被广泛的应用。
在数学领域,它的作用是函数本身的二阶微分的求取,也就是函数的梯度及曲率的求取。
在图像处理中,Laplacian算子可以用来检测边缘和角点,所以在应用上非常广泛。
对拉普拉斯算子来说,它的应用主要有三个方面:边缘检测、受激响应和角点检测。
首先,它可用来检测图像边缘,即在连续的图像域中,其像素值发生了重大变化,这种变化称为边缘。
通过拉普拉斯算子,可以得到图像中存在的边界,这种算法在现实世界中也被广泛使用,比如在自动驾驶领域中就经常使用拉普拉斯算子来检测路径的边缘,以便更好的控制行驶方向。
此外,拉普拉斯算子也可以用来检测受激响应,它可以通过响应的极大值检测来检测图像的受激响应,使用Laplacian算子可以找到极大值位置,从而判断出图像中存在的灰度特征点,这样就可以将不同图像生成一张总图,便于研究不同图像之间的关系。
最后,Laplacian算子可以用来检测角点,这种技术相当普遍,利用Laplace拉普拉斯算子可以检测出图像中的角点。
当选择的模板大小和阈值较小时,仅有非常强烈的角点会被检测到,而其他稍弱的角点会被忽略;当选择的模板大小和阈值较大时,会检测到更多的角点,但也增加了误报率。
Laplacian算子是一个非常重要的工具,在计算机视觉中得到了
广泛的应用。
它可以用来检测图像中的边缘,受激响应和角点。
它的本质是一个二阶梯度,具有十分重要的特性,如果能够准确的检测到这些边缘甚至角点,将会大大的提升我们的图像识别能力。
带p-Laplacian算子的分数阶微分方程边值问题在无穷区间中解的存在性

o n a n u n b o u n d e d d o ma i n a r e o b t a i n e d . Ke y wo r d s f r a c t i o n l a d i f e r e n t i a l e q u a t i o n;b o u n d a r y v lu a e p ob r l e m ;i n i f n i t e i n t e r v l ;f a i x e d p o i n t t h e o r e m
近年来 , 分数阶微分方程在国内外引起 了极大 的研究兴趣 , 特别是边值 问题解 的存在性 4 。 . 据作者所
知, 目 前很少有学者研究带 p - L a p l a c i a n 算子的分数阶微分方程边值问题解 的存在性 剖, 尤其是无穷区间中
解 的存在性研究甚少 . 无穷区间上的边值问题在物理学 、 自然科学等领域中有很多实际应用 , 如不稳定的气体通过半无穷带气 孔媒介问题 , 孤立中子的电势问题等 - l 0 ] . 因此 , 对它的研究具有重要的意义. 受以上文献的启发 , 本文主要利用 S c h a u d e r 不动点定理研究如下一类带 P — L a p l a c i a n 算子的分数阶微分 方程边值问题在无穷 区间中解 的存在性 : 『 +咖 ( + ( t ) ); t , u ( t ) , : ( t ) ) , t E( 0 ,+O 0) ,
2 . C o l l e g e o f ci S e n c e s . C h i n a U n i v e si r t y o f Mi n i n g a n d T e c h n o l o g y , X u z h o u 2 2 1 1 1 6, C h i n a )
一类p—laplace方程边值问题解的存在性

一类p—laplace方程边值问题解的存在性理解一类p-Laplace方程边值问题解的存在性:1. p—Laplace方程简介p—Laplace方程是一种常见的椭圆型偏微分方程,它在空间变换、热传导中也有广泛的应用。
它的解由p—Laplace方程决定:∂u/∂x+∂v/∂y=u^(p-2)f,其中p是大于等于1的任意常数,u,v是满足边界条件的函数,x,y是定义域内的坐标,f是常函数。
2. 一类p—Laplace方程边值问题的存在性一类p—Laplace方程的边值问题的存在性取决于其常数p的大小。
如果p大于1,那么该方程有唯一解;如果p小于1,那么该方程可能有无穷多解;如果p=1,则该方程常有唯一解,又有可能出现无穷多解。
3. p—Laplace方程边值问题解的存在性判定判定一类p—Laplace方程边值问题解的存在性,要仔细检查边界条件是否符合两个条件:(1)任意的边界函数都必须满足给定边界条件;(2)边界条件必须对所有满足方程组调和函数,如成反馈函数、空间变换函数等来施加有效制约。
缺一不可,边值问题解才能有存在性。
4. p>1时一类p—Laplace方程边值问题解的存在性当p大于1时,p—Laplace方程边值问题解有唯一解。
这是因为二阶偏微分方程组只能有一个解, p大于1时,椭圆型经ene变换可以转化为二阶偏微分方程组,根据拓扑的余定理,二阶偏微分方程组必有唯一解,故这时候方程解有存在性。
5. p<1时一类p-Laplace方程边值问题解的存在性当p小于1时,p—Laplace方程边值问题解可能有无穷多解。
这是因为当p<1时,椭圆型经ene变换不能转化为二阶偏微分方程组,根据拓扑的余定理,任一条件的任何解,如满足给定的边界条件,都是经en变换回解法所得,因此这种情况下该方程解有无穷多解的存在性。
6. p=1时一类p—Laplace方程边值问题解的存在性当p等于1时,p—Laplace方程边值问题解存在性有两种情形:(1)如果边界条件符合两个条件(前面讲到),有唯一解;(2)另一种情形是,如果边界条件不完全符合两个条件,则可能出现无穷多解。
具p-Laplacian算子时滞微分方程边值问题解的存在唯一性

>o 使得 任意 的 ∈U,>T, 有 I f一l , t j 都 () i s I 。 E 为定 义在 ( 一ro )R) m ()<£令 [ ,o , 上的 所有 函数 z的集
合 , 且 z在 [ ,。 上连 续 可微 且 导数 连 续 有界 。E 是 一个 B n c 并 0。 ) a a h空 间 , 定义 其 范 数 l・l 为 I 一 I l £ I z
ma m x I () , pI f 1, x{ a z £ Is () )z∈E。 u z
一 r O : 手
引理 1 设 z ∈c( 一, c ) R) O o ) 的连续可 微 函数 , z是边值 问题 ( ) ( ) E ,o 上 的 [ . o , 为[ ,o 上 , 则 1~ 3在 0o )
一
个解 , 当且仅 当
f f, ()
一
一r f O, ≤ ≤
1翰。 ) f 。 ( ff t。 , ) ≥ d o
() 5
定理 1 假设
I t zI f(, ) ≤F(, l I ,f 2 ∈E ,o xc( 一r 0 , xR, , t I ,2I (, ) o o ) ) , [ , ] R)
J n 2 1 u . 02
具 一 a lc n算 子 时滞 微分 方 程 边 值 问题 L pai a 解 的存在 唯一 性
韦 煜明 , 王 勇 , 艳秋 , 唐 范江 华
( 广西 师 范 大 学 数学 科学 学 院 , 西 桂 林 5 1 0 ) 广 4 0 4
摘
要 : 文 主 要研 究 无 穷 区 间上 具有 户 L pai 本 一al a c n算 子 的 时滞 微分 方 程 边 值 问题 解 的 存 在 性 和 唯 一 性 , 利用
laplace积分的几种计算方法

laplace 积分的几种计算方法Laplace 积分是一种数学技巧,用于解决带有指数或高阶微分项的微分方程。
它通常用于求解线性高阶常微分方程的解析解。
Laplace 积分的几种计算方法包括:初值问题法:这种方法的基本思想是将Laplace 积分表示为初值问题的形式,然后使用常规的数值求解方法求解。
公式如下:{y (n )+a 1y (n−1)+a 2y (n−2)+⋯+a n−1y ′+a n y =g (t )y (t 0)=y 0y (1)(t 0)=y 1⋯y (n−1)(t 0)=y n−1 反演积分法:这种方法的基本思想是通过反演积分将Laplace 积分转化为函数值的形式,然后再使用常规的数值求解方法求解。
公式如下:L −1[F (s )]=12πi ∫e st F (s )ds c+i ∞c−i ∞其中,L −1[F (s )] 表示 Laplace 反演,c 是极点的实部,i 是虚数单位。
分段线性插值法:这种方法的基本思想是将 Laplace 积分分成若干个子区间,然后在每个子区间内使用线性插值法求解。
公式如下:L −1[F (s )]≈∑t i −t i−12ni=1[f (t i−1)+f (t i )]+O (ℎ2)其中,t i 是分段点,ℎ 是分段间隔。
牛顿迭代法:这种方法的基本思想是使用牛顿迭代法对 Laplace 积分进行近似求解。
公式如下:x k+1=x k −F (x k )F ′(x k )其中,x k 是迭代变量,F (x ) 是待求解的 Laplace 积分函数。
分数阶差分格式:这种方法的基本思想是使用分数阶差分格式对 Laplace 积分进行近似求解。
公式如下:1ℎα∑(−1)i−1i!ni=1(αi)(x−t i)α−i f(t i)+O(ℎα+1)其中,ℎ是分段间隔,α是差分阶数,t i是分段点,f(t i)是待求解的Laplace 积分函数。
这些方法均可用于求解Laplace 积分,但其适用范围和精度有所不同,应根据具体问题选择适当的方法。
【国家自然科学基金】_p-laplacian边值问题_基金支持热词逐年推荐_【万方软件创新助手】_20140803
推荐指数 10 6 4 4 3 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
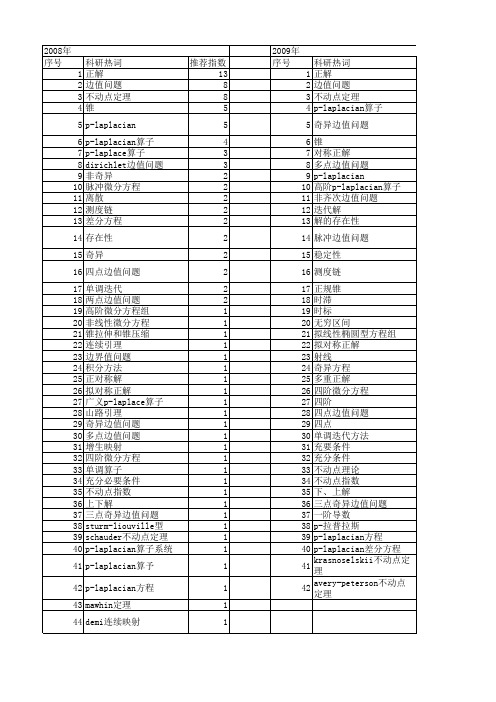
科研热词 正解 边值问题 不动点定理 p-laplacian算子 奇异边值问题 锥 对称正解 多点边值问题 p-laplacian 高阶p-laplacian算子 非齐次边值问题 迭代解 解的存在性 脉冲边值问题 稳定性 测度链 正规锥 时滞 时标 无穷区间 拟线性椭圆型方程组 拟对称正解 射线 奇异方程 多重正解 四阶微分方程 四阶 四点边值问题 四点 单调迭代方法 充要条件 充分条件 不动点理论 不动点指数 下、上解 三点奇异边值问题 一阶导数 p-拉普拉斯 p-laplacian方程 p-laplacian差分方程 krasnoselskii不动点定理 avery-peterson不动点定理
推荐指数 13 8 8 5 5 4 3 3 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42
科研热词 推荐指数 正解 6 边值问题 5 不动点定理 5 p-laplacian方程 3 迭代解 2 奇异脉冲方程 2 p-laplacian算子 2 p-laplacian 2 高阶导数 1 锥 1 连续引理 1 脉冲 1 测度链 1 正解的存在性 1 时滞 1 时标 1 拟线性化 1 拟对称正解 1 拟对称 1 广义p-laplace算子 1 山路引理 1 山路定理 1 存在 1 奇异混合单调算子 1 多点边值问题 1 多个正解 1 增生映射 1 四点边值问题 1 单调迭代 1 单调算子 1 半直线 1 全连续 1 不动点 1 上下解 1 三点边值问题 1 一阶导数 1 一维p-laplacian算子 1 p-拉普拉斯算子 1 p-laplacian边值问题 1 p-laplace算子 1 p-laplace 1 p-lapace差分方程边值问题 1 leray-schauder度 1 leray-schauder不动点定理 1 dirichlet边值问题 1 demi连续映射 1 banach空间 1 avery-peterson不动点定理 1 (ps)条件 1 (c)条件 1
Laplace讲解全

cm (s p)m
cm1 (s p)m1
c1
s p
cm
F
(s)
(s
p)m
s
p
cm1
1 1!
d ds
F(s)(s
p) m
s p
ck 1 (m k)
d (mk) ! d smk
F(s)(s p)m
s p
c1
1 (m 1)!
d (m1) ds m1
F(s)(s p)m
s p
f (t)
利用微分性质求 L[cos 2 t] , 设f (t) cos2 t
则f ' (t) 2 cost( sin t) sin 2t
对上式两边取L变换:sF (s) f (0) 2 s2 22
f (t) cot2 t, f (0) 1. F(s) 1 [ 2 1] s s2 22 s2 2
0
f () Lim s
1
s0 (s 4)(s 3)
Lim
s
s0 s 2 7s 12
0
例:求
L1
(s
4 p)5
解:
L1
4 s5
?
L tn
m(m 1) m!
s n1
s n1
两边取
L1
即
L1
s
n!
n1
t
n
L1
1 s n1
tn n!
L1
1 s5
3. Laplace变换性质
一.线性性质
若 , 是常数,L[ f1(t) ]= f1 (s) , L[ f2 (t) ]=F2 (s)
,则 L[f1 (t) f2 (t)]=F1 (s) F2 (s)
laplacian算子原理

laplacian算子原理Laplacian算子,也称为拉普拉斯算子或者是Laplacian运算符,是数学分析和微分方程领域中的一种重要算子。
该算子的定义依赖于场的某些物理性质,例如温度、压力、声波、电势等等。
它能够描述场在某个点的局部变化情况,通常被广泛应用于各种物理现象的研究中,例如热传导、电磁场、流体动力学等领域。
本文将对Laplacian算子的原理进行详细介绍,阐述其在物理学与数学领域的应用。
1. Laplacian算子的定义Laplacian算子是指对向量场中的标量场进行二阶求导,通常用符号Δ表示。
在三维欧几里得空间中,Laplacian算子的定义如下:Δf = ∂²f / ∂x² + ∂²f / ∂y² + ∂²f / ∂z²其中f为标量场,x、y、z分别为欧几里得空间中的三个坐标轴。
2. Laplacian算子的性质Laplacian算子具有以下性质:(1) 它是一个线性算子,即若f、g为标量场,则Δ(f+g) = Δf + Δg。
(2) 对于一些基本的分析函数,它们的Laplacian算子有确定的表达式。
例如:- 对于常数函数f(x)=c,Δf = 0;- 对于一元二次函数f(x) = ax² + bx + c,Δf = 2a;- 对于正弦函数f(x) = sin(x),Δf = - sin(x);- 对于余弦函数f(x) = cos(x),Δf = - cos(x)。
(3) Laplacian算子是旋转不变的,即对于任何旋转变换,其结果的Laplacian算子与变换前的结果相同。
(4) Laplacian算子有很好的泊松方程性质,即在某些特定条件下,对于一些给定的边界条件,可以通过求解其泊松方程来得到相应的函数解。
3. Laplacian算子的物理意义Laplacian算子在物理学中有着广泛的应用。
具体来说,它可以描述不同物理量在空间中的变化:(1) 热传导:在热传导中,热量的传导速率与温度场的梯度有关。
拉普拉斯(Laplace)方程

(1.13)
实例三:膜平衡方程 在第三章中我们研究了膜的振动方程
ρ
∂2u ∂t2
=
T
∂2u ∂x2
+
∂2u ∂y2
+ F (t, x, y).
(1.14)
特别地,当研究在不随时间而变换的外力F (x, y)作用下的膜的平衡问题时,膜的位移 函数u和时间t无关,此时方程(1.14) 可化为膜平衡方程
∂2u ∂x2
位质量的质点的引力−→F (x,
y,
z)其大小为
m r2
,而作用的方向为−P−P→0,即作用方向沿着这
两点的连线指向P0点,其中r = (x − x0)2 + (y − y0)2 + (z − z0)2表示点P0与点P 的距
离。−→F (x, y, z)可以写成下述向量的形式
−→F (x,
y,
z)
=
第五章 Laplace方程
Laplace方程(又称调和方程)和Poisson方程是最典型的椭圆型方程,它们具有广泛 的应用背景,譬如静电学中的电势以及牛顿万有引力理论中的引力势均满足这类椭圆 型方程(它们在静电学和引力理论中分别被称为静电场方程和静态引力场方程)。本章我 们介绍关于Laplace方程和Poisson方程的一些基本知识、方法和结果。在第一节中我们 介绍了Laplace方程和Poisson方程的导出以及定解条件的提法。在第二节中我们介绍变 分法,着重介绍在物理、力学等领域中具有重要应用的变分问题及变分原理(实际上, 许多常微分方程问题和数学物理方程的定解问题常常可归结为变分问题)。在第三节中 我们应用Green公式,建立了Laplace方程解的平均值定理,并证明了关于调和函数的 极值原理,进而应用该极值原理证明了第一边值问题解的唯一性和稳定性。在第四节 中,我们首先引入著名的Green函数,讨论了它的一些基本性质,并着重介绍了求解特 殊区域(球、半空间和圆)上的Laplace方程的第一边值问题解的表达式的静电源法。在 第五节中,我们利用在第四节中建立的Poisson公式进一步讨论了调和函数的另外一些 重要性质,譬如Harnack定理等等。在第六节中我们证明了Laplace方程的强极值原理, 并利用它讨论了Laplace方程的第二边值问题解的唯一性。
一类具有p-Laplacian算子的Plate方程全局吸引子的性质

应用数学MATHEMATICA APPLICATA2022,35(3):634-641一类具有p-Laplacian算子的Plate方程全局吸引子的性质孟凤娟,刘存才,张昶(江苏理工学院数理学院,江苏常州213001)摘要:本文旨在研究一类具有p-Laplacian算子的Plate方程全局吸引子的性质.关于这类方程吸引子存在性已有很多结果,然而关于吸引子性质的研究不多,并且关于吸引子维数的估计已知结果都是有限维.本文证明了吸引子里多重平衡点的存在性,特别地,在一定条件下得到了吸引子维数随着参数的变化可以任意大.关键词:全局吸引子;平衡点;李亚普诺夫泛函;Plate方程中图分类号:O175AMS(2010)主题分类:35L05;35B41文献标识码:A文章编号:1001-9847(2022)03-0634-081.引言Plate方程作为一类重要的物理模型,其最早来源于工程力学.在连续介质力学中,板被定义为厚度非常小的平面结构,通过梁理论可以得出板方程对于平板力学的数学描述.在物理学上,关于板的理论有很多,例如:Mindlin-Reissner板、Kirchhoff薄板动力学、Reissner-Stein理论、Von Karman方程.研究板方程的目的主要是计算载荷板材承受的变形和压力,因此,研究板方程具有很强的物理意义和实际用途.Plate方程的数学研究起源于Woinowsky-Krieger在文[1]中所建立的弹性振动方程:∂2u ∂t2+EIϱ∂4u∂x4−(Hϱ+EA2ϱl∫l[∂u(ξ,t)∂ξ]2dξ)∂2u∂x2=0,其中E是Young模量,ϱ是杆的密度,A是横截面积,l是杆长,E是初始的轴向张力.这类问题的严格数学分析及解的整体存在性与渐近性的研究始于Ball在文[2]中关于弹性梁方程稳定性的讨论.关于Plate方程解的渐近行为的研究近年来受到广泛关注.如:在非线性项满足临界增长与f(u).u≥0时,Khanmamedov在文[3-4]中分别研究了带有弱阻尼αu t与内部阻尼a(x)u t的Plate方程在无界区域上全局吸引子的存在性,吸引子的正则性及分形维数的有限性.2009年,Kolbasin在文[5]中研究了带有位移依赖阻尼σ(u)u t的Plate方程在有界区域上吸引子的存在性.2013年,马巧珍等在文[6]中得到了带有强阻尼项∆u t的Plate方程指数吸引子的存在性.2014年,KANG在文[7]中研究了带有µ∆u t−∆u tt的非自治Plate方程分别在区间H2(Ω)×H1(Ω)与H4(Ω)×H3(Ω)中拉回吸引子存在性.最近,Khanmanedov在文[8]中研究了带有非局部非线性项f(∥∇u∥L2(R n))|u|p−2∆u的Plate方程在无界域上的渐近性.∗收稿日期:2021-08-12基金项目:国家自然科学基金(12026431,11701230,11801227,11801228);江苏高校“青蓝工程”资助作者简介:孟凤娟,女,汉族,山东人,教授,研究方向:非线性泛函分析.第3期孟凤娟等:一类具有p -Laplacian 算子的Plate 方程全局吸引子的性质635本文考虑具有p -Laplacian 算子的Plate 方程 u tt −∆u t +∆2u −div(|∇u |p −2∇u )+φ(u )=0,(x,t )∈Ω×R +,u =∆u =0,(x,t )∈∂Ω×R +,u (x,0)=u 0(x ),u t (x,0)=u 1(x ),x ∈Ω,(1.1)全局吸引子的性质,其中Ω⊂R N 是具有光滑边界∂Ω的有界区域.首先假设(H 1)当N ≥3时,2≤p ≤2N −2N −2,当N =1,2时,p ≥2;(H 2)φ(s )=|s |m −1s −β|s |γs ,其中,当N >4,m =N +2N −4,当N ≤4时,m >0,0<γ<m −1,a 0是正常数,β>β0充分大,β0将在引理3.3给出.具有p -Laplacian 算子的Plate 方程(1.1)作为弹塑性微观结构模型在物理和力学中具有广泛的应用.例如在空间维数N =1和N =2情况下,分别描述了弹塑性杆的纵向运动和反平面剪切变形[9].系统(1.1)解的存在性,解的渐近行为等性质得到广泛研究,如:当空间维数N =1时,方程(1.1)变为u tt −u xxt +u xxxx −(|u x |p −2u x )x +φ(u )=0.不考虑耗散作用的影响,结合低阶非线性项与小的高阶弥散微观结构项之间的相互作用,AN 和Peirce [9]在一维情形下研究了如下方程u tt +u xxxx =a (u 2x )x 的系列问题.陈国旺和杨志坚[10]研究了比上式更一般的方程初边值问题u tt −σ(u x )x +u xxxx =f,整体解的存在性以及有限时刻解爆破的充分条件.高维情形下,杨志坚等在文[11-12]中研究了如下方程u tt −div {σ(|∇u |2∇u )−λ∆u t +∆2u +h (u t )+g (u )=f (x )在h ≡0以及h =0情形下,非线性项g 次临界和临界情形下初值问题解的长时间行为,证明了对应无穷维动力系统全局吸引子的存在性,Hausdoff维数和分形维数的有限性.综上,关于系统(1.1)全局吸引子的存在性已有很多文献讨论,但全局吸引子的几何结构的研究诸如吸引子维数的估计和指数吸引子尚鲜见.本文的主要目的是揭示当参数β足够大时系统(1.1)全局吸引子里平衡点的多重性.所运用的工具是临界点理论中的Z 2指标.系统(1.1)具有整体的Lyapunov 泛函并且由于φ(u )关于u 是奇的,所以该Lyapunov 泛函是偶的(见引理2.4).一般来讲,如果一个系统具有Lyapunov 泛函并且有全局吸引子,那么全局吸引子一定是平衡点集的不稳定流形的并.特别地,如果平衡点集是离散的,则全局吸引子可看成是所有平衡点不稳定流形的并,另一方面,系统的吸引子总是所有有界完全轨道的并,每个有界完全轨道是连接两个不同平衡点,而且每一个平衡点均由完全有界轨道连接它.所以,平衡点越多,吸引子的结构越复杂.因此,研究平衡点的多重性对揭示全局吸引子的结构有重要的意义.关于具有Lyapunov 泛函的偏微分方程全局吸引子结构的描述最早是Henry 在文[13]中给出,在该文中,作者以Chaffee-Infante 抛物方程为模型,用分歧理论的方法从平衡点之间轨道连接的角度给出了吸引子结构的详细描述.在文[14-15]中作者考虑了Chaffee-Infante 方程{u t −u xx =λ(u −u 3),u (0)=u (π)=0的分歧问题,其中λ≥0.并且证明了当n 2<λ<(n +1)2时该系统全局吸引子里有2n +1个不动点.通过文[14-15]的分析我们知道当0≤λ<1时原点是稳定的平衡点,但是,每当λ2穿过一个特征值,全局吸引子里将多出一对不稳定的平衡点.因而当λ充分大时,从原点出发将出现一系列的鞍结分叉从而可得到平衡点的对数也将无穷大.636应用数学2022另一方面,在文[16]中,作者利用Z2指标证明了方程−∆u=λf(u)在f是次临界增长并且是奇函数的假设下,当λ→∞时解的个数趋于无穷大.在文[17]中作者考虑了扰动问题−∆u=f(x,u)+ϵg(x,u)多重解的存在性并且利用Z2指标证明了对任意的自然数j,都存在ϵj>0使得对任意的0<ϵ≤ϵj都至少存在j个不同的解.受文[13-17]的启发,最近,钟承奎等在文[18]中结合临界点理论中的下降流思想和Z2指标理论来估算具有Lyapunov泛函的对称动力系统全局吸引子的两个不相交子集的Z2指标,其中Lyapunov泛函在其中一个子集上是正的,在另一个子集上是负的,进而得到全局吸引子里多重平衡点的存在性.作为该理论的应用,作者考虑了一类反应扩散方程全局吸引子里多重平衡点的存在性.Plate方程与反应扩散方程有着本质的区别,关于Plate方程全局吸引子中平衡点个数的估计的问题,至今还没有人进行研究,本文我们就运用[18]中的理论给出Plate方程在一定条件下平衡点的多重性以及一族吸引子分形维数随着参数的变化是任意大的.2.预备知识本节我们给出本文所需要的一些基本概念和结论,首先给出无穷维动力系统的相关定义和理论.定义2.1[19−20]假设算子族{S(t)}:X→X,t≥0,满足1)S(0)=Id(恒等变换);2)S(t)S(s)=S(t+s),∀t,s≥0;3)当t n→t并且在X中x n→x时,S(t n)x n→S(t)x,则称{S(t)}:X→X,t≥0是X上的C0半群.定义2.2[19−20]设X是完备的度量空间,{S(t)}t≥0是X上的连续半群,称{S(t)}t≥0是渐近紧的,如果对相空间X中的任何有界点列{x n}∞n=1以及t n→∞,{S(t n)x n}∞n=1有收敛子列.定义2.3[19−20]设X是完备的度量空间,{S(t)}t≥0是X上的连续半群,称X中的子集A是{S(t)}t≥0的全局吸引子,如果A满足1)(紧性)A是X中的一个紧集;2)(不变性)S(t)A=A,∀t≥0;3)(吸引性)对于X中的任何有界子集B,都有dist(S(t)B,A)→0(t→∞),其中dist(A,B)表inf y∈B dist(x,y).示Hausdorff半距离,定义为dist(A,B)=supx∈A引理2.1[19]设{S(t)}t≥0是完备度量空间X上的连续半群,则{S(t)}t≥0在X中存在全局吸引子当且仅当1){S(t)}t≥0在X中有有界吸收集;2){S(t)}t≥0在X上是渐近紧的.定义2.4[15,20]设H为Banach空间,{S(t)}t≥0是定义在H上的半群,X⊂H是它的一个正不变集,称Φ:X→R是{S(t)}t≥0定义在X上的Lyapunov泛函如果1)对任意给定的u0∈X,函数t→Φ(S(t)u0)关于时间t是非增的;2)存在τ>0,使得Φ(S(τ)u0)=Φ(u0),那么u0是半群S(t)的一个平衡点(不动点).称动力系统(X,S t)为梯度系统,若系统在整个相空间X上存在一个Lyapunov泛函.下面,我们给出系统(1.1)解的存在唯一性以及相应半群全局吸引子的存在性结果,详见文[11-12])等.引理2.2设(H1),(H2)成立,则对任何T>0及初值(u0,u1)∈(H2(Ω)∩H1(Ω))×L2(Ω),(Ω))×L2(Ω)).系统(1.1)的解存在并且唯一,(u,u t)∈C([0,T];(H2(Ω)∩H1第3期孟凤娟等:一类具有p -Laplacian 算子的Plate 方程全局吸引子的性质637对任给t ∈R 定义映射S (t ):(u 0,u 1)→(u (t ),u t (t )).(2.1)由引理2.2,易得{S (t )}t ≥0在能量相空间(H 2(Ω)∩H 10(Ω))×L 2(Ω)中是C 0-半群.引理2.3设(H 1),(H 2)成立,则对任何β,系统(1.1)所生成的半群{S (t )}t ≥0在空间(H 2(Ω)∩H 10(Ω))×L 2(Ω)中存在全局吸引子A β.对一个具有Lyapunov 泛函的奇连续半群,在全局吸引子具有对称结构的前提下,钟承奎等在[18]中借助于“原点是对应的Lyapunov 泛函的局部极小点”这一假设,估计了原点的吸引域边界的Z 2指标,进而对半群{S (t )}t ≥0在全局吸引子内平衡点的个数做了估算,具体结论如下:引理2.4[18]设X 是一个Banach 空间,{S (t )}t ≥0是X 上的一个C 0半群.假设{S (t )}t ≥0满足下列条件:(A 1)对任意的t ≥0,S (t )是奇的;(A 2)在X 上,{S (t )}t ≥0有一个全局吸引子A ;(A 3)在X 上,{S (t )}t ≥0有一个C 0Lyapunov 偶泛函F ;(A 4)存在B (0,ρ)(以0为中心,ρ为半径的球),对任意的u ∈B (0,ρ),t →∞都有S (t )u →0,并且F |∂B (0,ρ)≥α>F (0)=0,其中α是一个给定的正常数;(A 5)存在一个X 的n 维子空间X n 和一个正常数R (>ρ),使得F |X n ∩∂B (0,R )≤0.则有下列结论(i)半群{S (t )}t ≥0在A ∩F −1([α,∞))中至少有n 对不动点;(ii)半群{S (t )}t ≥0在A ∩F −1((−∞,0))中至少有n 对不动点.3.主要结果引理3.1设(H 1),(H 2)成立,对任何给定的β,由系统(1.1)诱导出的解半群是奇的,定理2.3中得到的全局吸引子A β是对称的.证对任何初值(u 0,u 1)∈(H 2(Ω)∩H 10(Ω))×L 2(Ω),显然(−u 0,−u 1)∈(H 2(Ω)∩H 10(Ω))×L 2(Ω).设(u (t ),u t (t ))是系统(1.1)对应初值(u 0,u 1)的唯一的解.由于φ是奇函数,从而(−u (t ),−u t (t ))是系统(1.1)对应初值(−u 0,−u 1)的唯一解.因此,S (t )(−u 0,−u 1)=(−u (t ),−u t (t ))=−S (t )(u 0,u 1),从而S (t )是奇的.下面我们将验证A β的对称性.设B 0=B (0,R )={(u,u t )∈(H 2(Ω)∩H 10(Ω))×L 2(Ω),∥(u,u t )∥(H 2(Ω)∩H 10(Ω))×L 2(Ω)≤R }是半群S (t )的对称吸收集.假设(y,y t )∈A β,则存在一个序列{x n ,x nt }∞n =1⊂B 0及t n →∞(当n →∞时),使得在(H 2(Ω)∩H 10(Ω))×L 2(Ω)内S (t n )(x n ,x nt )→(y,y t ).因为半群S (t )是奇的,从而在(H 2(Ω)∩H 10(Ω))×L 2(Ω)中有S (t n )(−x n ,−x nt )=−S (t n )(x n ,x nt )→(−y,−y t ).因此,A β是对称的.定义能量泛函F (u,u t )=∫Ω{12(|∆u |2+|u t |2)+1p |∇u |p +Φ(u )}d x,(3.1)其中Φ(u )=∫u 0φ(s )d s 是φ(u )的原函数.引理3.2由(3.1)所给出的泛函F (u,u t )是半群{S (t )}t ≥0在空间(H 2(Ω)∩H 10(Ω))×L 2(Ω)上的Lyapunov 偶泛函.证设(u,u t )=S (t )(u 0,u 1)是系统(1.1)对应初值(u 0,u 1)的解.用u t 乘以(1.1)并在Ω上积分可得∥u t ∥2L 2(Ω)+d d t ∫Ω{12(|∆u |2+|u t |2)+1p |∇u |p +Φ(u )}d x =0,即d d t F (S (t )(u 0,u 1))=−∥u t ∥2L 2(Ω).(3.2)638应用数学2022因而对每个给定的初值(u 0,u 1)∈(H 2(Ω)∩H 10(Ω))×L 2(Ω),函数t →F (S (t )(u 0,u 1))是非增的.如果存在某个τ>0使得F (S (τ)(u,u t ))=F (u,u t ).从(3.2)可知,当0≤t ≤τ时S (t )(u,u t )=(u,u t ).因此F (S (nτ)(u,u t ))=F (S ((n −1)τ)S (τ)(u,u t ))=F (S ((n −1)τ)(u,u t )=···=F (u,u t ).重复上面的过程可得对任意的n ∈Z +,当0≤t ≤nτ时S (t )(u,u t )=(u,u t ).所以对任意的t ≥0,S (t )(u,u t )=(u,u t ).因此由(3.1)定义的F (u,u t )是算子半群的{S (t )}t ≥0的Lyapunov 泛函.结合(3.1)和(H 2)易知,F (u,u t )=F (−(u,u t )),即F 是偶的.引理3.3对任何自然数n ,存在X 的一n 维子空间X n 和一正常数R ,使得F |X n ∩∂B (0,R )≤0.证由假设(H 2),可得Φ(u )=∫u 0φ(s )d s =∫u 0(|s |m −1s −β|s |γs )d s =1m +1|u |m +1−βγ+2|u |γ+2,对任何自然数n,设X n 是(H 2(Ω)∩H 10(Ω))×L 2(Ω)的一个n 维子空间,A n ={(u,u t )∈X n :∥∆u ∥L 2(Ω)+∥u t ∥L 2(Ω)=1},则A n 是空间(H 2(Ω)∩H 10(Ω))×L 2(Ω))的紧集,并且存在正常数δ使得inf (u,v )∈A n ∥u ∥γ+2L γ+2(Ω)=δ.设RA n ={R (u,u t ):(u,u t )∈A n },则对R (u,u t )∈RA n ,利用H¨o lder 不等式和Sobolev 嵌入H 2(Ω)∩H 10(Ω) →L m +1(Ω)及H 2(Ω)∩H 10(Ω) →L γ+2(Ω)可得F (R (u,u t ))=∫Ω{12R 2(|∆u |2+|u t |2)+1p R p |∇u |p +1m +1R m +1|u |m +1−βγ+2R γ+2|u |γ+2}d x ≤12R 2+CR m +1−βγ+2R γ+2δ,对固定的R,取β0=1δ(R −r +CR m −r −1)(γ+2),则当β≥β0时,F (R (u,u t ))≤0.(3.3)引理3.4设(H 1),(H 2)成立,对每个给定的β,A β为系统(1.1)的全局吸引子,由(3.1)所定义的F 是半群{S (t )}t ≥0在(H 2(Ω)∩H 10(Ω))×L 2(Ω)中的Lyapunov 泛函.则存在原点的一个邻域B (0,ρ),(ρ<R )使得(i)对任意的(u,u t )∈B (0,ρ),当t →∞时,S (t )(u,u t )→0,(ii)F |∂B (0,ρ)≥α>F (0,0)=0,其中α是一个固定的正常数.证由Sobolev 嵌入H 2(Ω)∩H 10(Ω) →L 2n N −4(Ω) →L m +1N −4(Ω)及H 2(Ω)∩H 10(Ω) →L γ+2(Ω),可得F (u,u t )=∫Ω{12(|∆u |2+|u t |2)+1p |∇u |p +Φ(u )}d x,≥12∥∆u ∥2L 2(Ω)+12∥u t ∥2L 2(Ω)+C ∥u ∥m +1L m +1(Ω)−βγ+2∥u ∥γ+2L γ+2(Ω)≥12∥∆u ∥2L 2(Ω)+12∥u t ∥2L 2(Ω)+C ∥u ∥m +1L m +1(Ω)−βγ+2C ∥∆u ∥γ+2L 2(Ω).(3.4)由于γ>0,γ+2>2,当∥∆u ∥L 2(Ω)充分小时,∥∆u ∥γ+2L 2(Ω)可由∥∆u ∥2L 2(Ω)控制.上式意味着存在0<ρ1<R 使得当(u,u t )∈B (0,ρ1)={(u,u t )∈(H 2(Ω)∩H 10(Ω))×L 2(Ω),∥(u,u t )∥(H 2(Ω)∩H 10(Ω))×L 2(Ω)≤ρ1}时,F |∂B (0,ρ1)≥α1>F (0,0)=0,(3.5)其中,α1是一个给定的正常数.下面我们将验证当ρ<ρ1及α2<α1成立时,F |B (0,ρ)<α2.F (u,u t )=∫Ω{12(|∆u |2+|u t |2)+1p |∇u |p +Φ(u )}d x,第3期孟凤娟等:一类具有p -Laplacian 算子的Plate 方程全局吸引子的性质639≤12∥∆u ∥2L 2(Ω)+12∥u t ∥2L 2(Ω)+1p ∥∇u ∥p L p (Ω)+C ∥∆u ∥m +1L 2(Ω)−βγ+2∥u ∥γ+2L γ+2(Ω)≤12∥∆u ∥2L 2(Ω)+12∥u t ∥2L 2(Ω)+1p∥∇u ∥p L p (Ω)+C ∥∆u ∥m +1L 2(Ω),由上述不等式可知当(u,u t )∈B (0,ρ),ρ→0时F (u,u t )→0,从而存在某个ρ<ρ1使得F |B (0,ρ)<α2.(3.6)由(3.4),我们还可知存在某个α>0使得F |∂B (0,ρ)≥α>F (0,0)=0.(3.7)由引理3.2知F 是一个Lyapunov 泛函,则F (S (t )(u 0,u 1))关于时间t 是递减的,结合(3.5),(3.6)可得,对任给t ≥0,F |S (t )B (0,ρ)<α2.(3.8)因此对任给t ≥0,S (t )B (0,ρ)⊂B (0,ρ1).(3.9)否则,存在某个t 0及(u 0,u 1)∈B (0,ρ)使得S (t 0)(u 0,u 1)∈X \B (0,ρ1).根据S (t )的连续性,存在t 1满足0<t 1≤t 0并且S (t 1)(u 0,u 1)∈∂B (0,ρ1).因为F |∂B (0,ρ1)≥α1,可得F (S (t 1)ϕ0)≥α1,与(3.8)矛盾.因此,对任何(u 0,u 1)∈B (0,ρ)及t ≥0,S (t )(u 0,u 1)∈B (0,ρ1).下面我们将验证对任何初值(u 0,u 1)∈B (0,ρ1),算子半群只有原点是平衡点.即∀(u 0,u 1)∈B (0,ρ),S (t )(u 0,u 1)=(u 0,u 1)⇒(u 0,u 1)=0.(3.10)由于算子半群的平衡点对应于系统稳态方程的解,即{u 1=0,∆2u 0−div(|∇u 0|p −2∇u 0)+φ(u 0)=0.因而要验证(3.10)成立,只需证明∫Ω(|∆u |2−div(|∇u |p −2∇u )u +φ(u )u )dx =0⇒u =0.由(H 1),(H 2)可得∫Ω(|∆u |2−div(|∇u |p −2∇u )u +φ(u )u )d x ≥∫Ω(|∆u |2d x +∥∇u ∥pL p (Ω)−Cβ∫Ω|u |(γ+2)d x +C ∫Ω|u |m +1d x ≥C (∫Ω|u |2n N −4d x )N −4N −Cβ∫Ω|u |(γ+2)d x +C ∫Ω|u |m +1d x≥C ∫Ω|u |(γ+2)d x )2γ+2d x −Cβ∫Ω|u |(γ+2)d x +C ∫Ω|u |m +1d x.(3.11)注意2γ+2<1并且γ+2<m +1,Cβ∫Ω|u |(γ+2)d x 可以被C ∫Ω|u |(γ+2)d x )2γ+2d x 和C ∫Ω|u |m +1d x 控制,结合(3.9),我们可选择适当的ρ,使得对任何S (t )(u 0,u 1)=(u,u t )=(0,0),∫Ω(|∆u |2−div(|∇u |p −2∇u )u +φ(u )u )d x >0成立.因此我们已证明对任给(u,u t )∈B (0,ρ1)\(0,0),S (t )(u,u t )=(u,u t ).根据(3.5),(3.6)和(3.10),我们可以得到对任给(u 0,u 1)∈B (0,ρ),当t →∞时,S (t )(u 0,u 1)→0.(3.12)由引理2.3可知系统(1.1)存在全局吸引子,再根据引理2.1可知{S (t )}t ≥0是渐近紧的.因此,对任给初值(u 0,u 1)∈B (0,ρ)及t n →∞,{S (t n )ϕ0}有一个收敛子列,即当t n k →∞时S (t n k )(u 0,u 1)→(u ′0,u ′1).(3.13)640应用数学2022要证(3.12),只需证明(u′0,u′1)=0.由Lyapunov泛函的定义(定义2.4)可得F(S(t)(u′,u′1))≤F((u′,u′1)),∀t>0.(3.14)我们断言对某个τ>0F(S(τ)(u′0,u′1))=F((u′,u′1)).(3.15)下面将用反证法来验证(3.15).若(3.15)不成立,则对任给t>0,F(S(t)(u′0,u′1))<F((u′,u′1)).(3.16)从而当ε>0充分小时,存在t′>0满足F(S(t′0)(u′,u′1))<F((u′,u′1))−ε.(3.17)根据(3.13),可得当t nk→∞时S(t nk+t′)(u0,u1)→S(t′)(u′,u′1).(3.18)根据F的连续性和(3.18),可得当t nk→∞时F(S(t nk +t′)(u0,u1))→F(S(t′)(u′,u′1)),(3.19)并且由(3.13)可得当t nk→∞时F(S(t nk+t′)(u0,u1))→F((u′,u′1)).(3.20)结合(3.19)和(3.20),我们有F(S(t′0)(u′,u′1))=F((u′,u′1)),这与(3.17)矛盾.因此(3.15)成立.由Lyapunov泛函的定义,(u′0,u′1)是S(t)的不动点,即对任给∀t>0,S(t)(u′,u′1)=(u′,u′1).结合(3.5)(3.6)和(3.10),我们有(u′0,u′1)=0,即(3.12)成立.结合(3.7)和(3.12),引理3.4得以证明.由引理3.1-3.4可知,由引理2.2生成的算子半群(2.1)满足引理2.4的所有条件,根据引理2.4可得:定理3.1假设(H1),(H2)成立,对每个给定的β,Aβ是(1.1)的全局吸引子,由(3.1)定义的F是算子半群{S(t)}t≥0在空间(H2(Ω)∩H1(Ω))×L2(Ω)中的Lyapunov泛函.则对任意自然数n,存在β充分大使得{S(t)}t≥0在Aβ∩F−1([α,∞))内至少有n对不同的不动点,并且在Aβ∩F−1((−∞,0))内至少有n对不同的不动点.在文[9]中,我们知道任何一个分形维数为n的紧集与R2n+1之间都存在一个一一的线性奇的H¨o lder连续映射.类似于文[30]中推论1.1,由引理3.1-3.4及引理2.4可得如下推论:推论3.1假设(H1),(H2)成立,对任何给定的β,Aβ是系统(1.1)全局吸引子.则我们有下列结论:limβ→∞dim Aβ=∞.参考文献:[1]WOINOWSKY K.The efect of an axial force on the vibration of hinged bars[J].J.Appl.Mech.,1950,17:35-36.[2]BALL J.Stability theory for an extensible beam[J].J.Differential Equations,1973,14:399-41.[3]KHANMAMEDOV A.Existence of a global attractor for the plate equation with a critical exponentin an unbounded domain[J].Appl.Math.Lett.,2005,18(7):827-832.[4]KHANMAMEDOV A.Global attractors for the plate equation with a localized damping and a criticalexponent in an unbounded domain[J].J.Differential Equations,2006,225:528-548.[5]KOLBASIN S.Attractors for Kirchhoff’s equation with a nonlinear damping coefficient[J].NonlinearAnal.,2009,71:2361-2371.[6]MA Qiaozhen,YANH Yun,ZYAHG Xiaoliang.Existence of exponential attractors for the plateequations with strong damping[J].Electron.J.Differential Equations,2013,114:1-10.第3期孟凤娟等:一类具有p-Laplacian算子的Plate方程全局吸引子的性质641[7]KANG J.Pullback attractors for a non-autonomous plate equations[J].Appl.Anal.,2014,93:875-888.[8]KHANMAMEDOV A,SIMSEK S.Existence of the global attractor for the plate equation withnonlocal nonlinearity in R n[J].Discrete Contin.Dyn.Syst.Ser.B,2016,21:151-172.[9]AN Lianjun,PIERCE A.A weakly nonlinear analysis of elasto-plastic-microstructure models[J].SIAM Journal on Applied Mathematics,1995,55:136-155.[10]CHEN Guowang,YANG Zhijian.Existence and non-existence of global solutions for a class of non-linear wave equations[J].Math.Methods Appl.Sci.,2000,23:615-631.[11]YANG Zhijian.Longtime behavior for a nonlinear wave equation arising in elasto-plasticow[J].Math.Methods Appl.Sci.,2009,32:1082-1104.[12]YANG Zhijian,JIN Baoxia.Gloal attractor for a class of Kirchhoffmodels[J].Journal of MathematicalPhysics,2009,50:032701.[13]HENRY D.Geometric Theory of Semilinear Parabolic Equations[M].Lecture Notes in Math.Berlin:Springer,1981.[14]CHEN Shaowei,LI Shujiei.On a nonlinear elliptic eigenvalue problem[J].J.Math.Anal.Appl.,2005,307:691-698.[15]HALE J K.Asymptotic Behavior of Dissipative Systems[M].Providence,RI:AMS,1988.[16]ROBINSON J.Infinite-Dimensional Dynamical Systems,An Introduction to Dissipative ParabolicPDEs and the Theory of Global Attractors[M].Cambridge:Cambridge University Press,2001. [17]LI Shujie,LIU Zhaoli.Perturbations from symmetric elliptic boundary value problems[J].J.Differ-ential Equations,2002,185:271-280.[18]ZHONG Chengkui,YOU Bo,YANG Rong.The existence of multiple equilibrium points in a globalattractor for some symmetric dynamical systems[J].Nonlinear Analysis Real World Application,2014, 19:31-44.[19]LADYZHENSKAYA O.Attractors for Semigroups and Evolution Equations[M].Cambridge:Cam-bridge University Press,1991.[20]TEMAM R.Infinite-dimensional Systems in Mechanics and Physics[M].New York:Springer-Verlag,1997.Property of Global Attractor for a Class of Plate Equationwith p-LaplacianMENG Fengjuan,LIU Cuncai,ZHANG Chang(School of Mathematics and Physics,Jiangsu University of Technology,Changzhou213001,China)Abstract:This paper is concerned with a class of Plate equation with p-Laplacian.Many re-searchers have studied the existence of attractors for these equations.However,there are not many studies on the property of the attractor,especially,the estimates on the dimension of the attractor are finite.In this paper,we investigate the property of the attractor for the equation by getting the existence of multiple equilibrium points in attractor,in particular,we obtain the dimension of of attractor can be arbitrarily large with the change of parameters under certain conditions.Key words:Global attractor;Equilibrium point;Lyapunov functional;Plate equation。
laplacian算子锐化例题

标题:laplacian算子在图像处理中的应用与例题分析一、laplacian算子简介laplacian算子是一种在图像处理中常用的算子,它可以用于图像的边缘检测和图像的锐化处理。
laplacian算子的原理是通过计算像素点的二阶导数来寻找图像中的边缘或者进行图像的锐化处理。
在图像处理中,边缘检测和图像锐化是非常重要的步骤,因此 laplacian算子得到了广泛的应用。
二、laplacian算子的应用1. 边缘检测laplacian算子可以通过计算图像像素的二阶导数来检测图像中的边缘。
当像素的二阶导数值达到局部极值时,就可以判断该像素点是图像的边缘点。
在边缘检测中,laplacian算子可以帮助我们找到图像中存在的边缘,从而进行后续的图像处理工作。
边缘检测是图像处理中的一个基本问题,laplacian算子的应用使得边缘检测更加准确和高效。
2. 图像锐化除了边缘检测,laplacian算子还可以用于图像的锐化处理。
图像的锐化是指增强图像中的细节和纹理,使得图像更加清晰和真实。
通过对图像进行laplacian算子的运算,可以突出图像中的细节和边缘,从而实现图像的锐化处理。
图像锐化是图像处理中的一个重要步骤,它可以改善图像的质量和增强图像的视觉效果。
三、laplacian算子的例题分析下面我们通过一个具体的例题来分析laplacian算子在图像处理中的应用。
例题:使用laplacian算子对下面的图像进行边缘检测和图像锐化处理。
(插入一张图像)通过计算图像的laplacian算子,我们可以得到图像的二阶导数,从而找到图像中的边缘和强化图像的细节。
接下来我们将逐步分析具体的操作步骤。
1. laplacian算子的计算我们需要定义laplacian算子的模板。
常见的laplacian算子模板包括3x3和5x5两种。
我们以3x3的laplacian算子模板为例进行计算。
(插入laplacian算子的3x3模板图)对于给定的图像,我们可以通过对每个像素点进行laplacian算子的计算来得到图像的二阶导数。
带有非局部源和吸收项的P-Laplacian方程解的熄灭

2 主 要结 论 及 证 明
定理 l 当r < 1 时, 假设p一 1 = g , 如果 2 N < p < 2 R x< I I 一 A 或者 1 < p ≤
引理 1 m 设 A 是问题 一 d i v ( 1
u∈
l
)= A 1 1 一 , ∈ , 1 1 。 n = O的第一特征值 , 则对任意
( ) , 有A I 『 “J d ≤ l “J d ・
设y ( £ ) 是 定义 在 [ 0 , +∞ ) 上 的非负 绝对 连 续 函 数 , 且满 足 : d y +a y ≤0
关键 词 : P - L a p l a c i a n方程 ; 熄灭 ; 非局 部 源 中图分类 号 : 0 1 7 5 . 2 9 文 献标 志码 : A
1 预 备 知识
考虑 带有 非局 部源 和 吸收项 的 P — L a p l a c i a n方程 :
一
d i V ( 『 Vu J p - 2 Vu )=A ( x , t ) d x— r E力, f >0
[ 1 2 ]研究了 1 / , 一 d W (1 u 【 u )=A u 锯的熄灭 , 得到了P—l:q 是熄灭临界指数 ; 文献[ 1 3 ] 研究了 “ 一 d i v (I Vu I Vu )=A u 一 』 B u 解 的熄灭 , 得到了当q=1 时, P一1=r 是熄灭临界指数 以及 当q<1 时
{ ( ) : 0 , ∈ a , £ > 0 【 ( i o ) : u 。 x ) , ∈
laplacian算子matlab程序

laplacian算子matlab程序
(实用版)
目录
1.引言
2.拉普拉斯算子概述
3.MATLAB 编程实现拉普拉斯算子
4.结论
正文
1.引言
拉普拉斯算子在图像处理、信号处理等领域具有广泛的应用。
在MATLAB 中,我们可以通过编程实现拉普拉斯算子,从而方便地进行相关研究和应用。
本文将介绍拉普拉斯算子的概念,并给出在 MATLAB 中实现拉普拉斯算子的方法。
2.拉普拉斯算子概述
拉普拉斯算子是一种线性算子,用于求解离散信号的频域表示。
拉普拉斯算子的定义为:
L = [1 - 2*cos(π/N)] / (π/N)
其中,N 表示信号长度。
拉普拉斯算子在信号处理中的应用包括滤波、去噪等。
3.MATLAB 编程实现拉普拉斯算子
在 MATLAB 中,我们可以通过以下步骤实现拉普拉斯算子:
(1) 创建一个信号,例如长度为 N 的均匀分布信号 x = (0:N-1)";
(2) 计算拉普拉斯算子的逆 Z 变换:Y = fft(x, N) / N;
(3) 对信号进行拉普拉斯变换:X = ifft(Y, N) / N;
(4) 计算拉普拉斯算子的频域表示:H = fft(X, N) / N;
(5) 通过逆 Z 变换得到原始信号的频域表示:H_inv = ifft(H, N) / N;
(6) 对比原始信号和拉普拉斯变换后的信号,可以观察到拉普拉斯算子的作用。
4.结论
通过 MATLAB 编程实现拉普拉斯算子,我们可以更好地理解其在信号处理和图像处理等领域的应用。
