第四届2012全国大学生数学竞赛试题(非数学类_)
历届全国大学生数学竞赛(非数学专业类)初赛试题统计分析

第24卷第3期2021年5月高等数学研究STUDIESIN COLLEGE MATHEMATICSVol24,No.3May2021doi:10.3969/j.issn.1008-1399.2021.03.022历届全国大学生数学竞赛(非数学专业类)初赛试题统计分析刘烁—,马丽娜2,吴克坚—,徐清华—,王瑞星—,赵清波1$•空军军医大学基础医学院数学物理教研室,陕西西安,710032*2.陕西师范大学数学与信息科学学院,陕西西安,710062)摘要本文对历届全+大学生数学竞赛(非数学专业类)初赛试题及答案进行了统计分析,剖析了竞赛试题的命题理念与结构特点,并提出竞赛准备的几点建议•关键词大学生数学竞赛;统计分析中图分类号O13文献标识码A文章编号1008-1399(2021)03-0077-03Statistical Analyses of the Chinese Mathematics Competitionsfor Non-Mathematical ProfessionalsLIU Shuo1,MA Lina2,WU Kejian1,XU Qinghua1,WANG Ruixing,and ZHAO Qingbo1 (18TeachingandResearchLaboratoryofMathematicsandPhysics!SchoolofBasic Medical!AirForce MedicalUniversity!Xian710032,PRC;28Co l ege of Mathematics and Information Science!Shaanxi Normal University!Xi'an710062!PRC)Abstract With al the past test questions of the Chinese Mathematics Competitions for Non-Mathematical Professionals,this paper presents the statistics of the questions'proposition idea and structural character-iDticD!andputDforwardDomeDuggeDtionD.Keywords TheChineDe MathematicDCompetitionD!DtatiDticalanalyDiD为激励大学生学习数学的兴趣,进一步推动高等学校数学课程的改革和建设,提高大学数学课程的教学水平,发现和选拔数学创新人才,自2009年起,中国数学会每年举办一次全国大学生数学竞赛(The Chinese Mathematics Competitions(简称CMC)).竞赛的参赛对象为大学本科二年级及二年级以上的在校大学生,分为数学专业类和非数学专业类两组,数学专业类竞赛内容为大学本科数学专业基础课的教学内容,非数学专业类竞赛内容为大收稿日期:2020-05-28修改日期:2020-09-01作者简介:刘烁(1979—),男,湖南安乡人,硕士,副教授,主要从事生物数学传染病动力学模型研究,Email:liushuo912@.通讯作者:赵清波(1966—),女,河南洛阳人,硕士,教授,主要从事卫生统计学研究,Email:zhaoqbo@.学本科理科高等数学课程的教学内8竞赛分为初赛和决赛进行,试题均由全国大学生数学竞赛委员会统一组织专家命制.分区初赛由各省(市、区、军队院校)数学会负责组织选拔,使用全国统一试题,在同一时间内进行考试;决赛由全国大学生数学竞赛工作小组和承办单位负责组织实施.作为一项面向本科生的全国性高水平学科竞赛,全国大学生数学竞赛为青年学子提供了一个展示数学基本功和数学思维的舞台,为高校发现和选拔优秀数学人才并进一步促进数学课程建设的改革和发展积累了调研素材.竞赛试题在所考查的知识内容、题量分布与命题理念方面有何特点,在解题方法上应该怎样准备,是许多大学数学老师和学生十78高等数学研究2021年5月分关心的问题,有鉴于此,笔者对历届全国大学生数学竞赛(非数学专业类)初赛的试题进行了全面的统计分析,希望能有助于大家进一步明确全国大学生数学竞赛的试题特点与复习教学目标,从而更好地加强教学及备考的针对性.一、历届全国大学生数学竞赛(非数学专业类)初赛试题统计分析1.试题来源及整体情况试题来源于全国大学生数学竞赛资源网,网址:.选取2009年至2019年共11届全国大学生数学竞赛(非数学专业类)初赛试题,共101题,总分值1100分.2.题将11届试题的每一道题按题型、分值、所考查的知识点、用到的解题方法进行整理,利用python 统计题型分布,知识点及解题方法出现的频次.(1)题量除2011年9道,2009年和2012年11道外,其余均为10道题.(2)型题型主要有填空、计算、证明、综合(既有证明又有计算)四类。
2009-16大学生数学竞赛真题(非数学类)--整理20171002

n=1
n=1
9
2013 年 第五届全国大学生数学竞赛预赛试卷
一、 解答下列各题(每小题 6 分共 24 分,要求写出重要步骤)
( )n
1.求极限 lim 1+ sin π 1+ 4n2 . n→∞
∫ 2.证明广义积分 +∞ sin x dx 不是绝对收敛的 0x
3.设函数 y = y ( x) 由 x3 + 3x2 y − 2 y3 = 2 确定,求 y ( x) 的极值。
二、(5
分)求极限 lim( ex
+
e2x
+"+
e nx
e
)x
,其中 n 是给定的正整数.
x→0
n
∫ 三、(15 分)设函数 f (x) 连续,g(x) = 1 f (xt)dt ,且 lim f (x) = A ,A 为常数,求 g′(x)
0
x→0 x
并讨论 g′(x) 在 x = 0 处的连续性.
(1)
∫∫
S
ρ
(
z x, y,
z
)
dS
;(2)
∫∫
S
z
(
λ
x
+
3μ
y
+ν
z
)
dS
( ) ( ) ( ) 六.(本题 12 分)设 f(x)是在 −∞, +∞ 内的可微函数,且 f 、 x < mf x ,其 ( ) 中 0 < m < 1 , 任 取 实 数 a0 , 定 义 an = ln f an−1 , n = 1, 2,..., 证 明 :
平面与路径3 x x+1 sin t dt
第四届全国大学生数学竞赛决赛试题与解答

1 1 x2 [(` 1 + x 2 ) ln(1 + x 2 ) − x 2 ]arctan x − ∫ [ln(1 + x 2 ) − ]dx 1 + x2 2 2 1 x 3 (1 + x 2 )ln(1 + x 2 ) − x 2 − 3⎤ = arctan x ⎡ − ln(1 + x 2 ) + x + C (3 分) ⎣ ⎦ 2 2 2 =
(2 分)
f ′( x) = − f 2 ( x) ,并且 f (0) = e0 = 1
由此可求得 f ( x ) =
1 . (3 分) x +1
1 ≤1 x
即 f ( x ) ≤ f (1) + 1 , f ( x ) 有上界. (4 分) 由于 f ( x ) 在 [1, +∞ ) 上单调增加且有上界,所以 lim f ( x ) 存在. (1 分)
−u ( x )
求 y ( x) = e ,
x
−2 x
f ( x, x) 所满
,其中 u =
∫
0
f (t ) d t .
⎡ ⎛ ⎞⎤ ln x − ln a ln x + ln(ln a ) 2ln a ⎢ ⎜ ln ax ⎟ ⎥ ln x − ln a 2 ln a ⎞ 2ln a ⎛ 1. 解 lim ⎢ ln( x ln a ) ⋅ ln ⎜ (4 分) = lim ln ⎜1 + ⎥ ⎟ ⎟ x →0 + x ⎥ x →0+ ⎝ ln x − ln a ⎠ ⎢ ⎜ ln ⎟ ⎢ ⎥ ⎝ a ⎠⎦ ⎣
2 z 2 = 2 z , 就有
Fz = ∫ G ρ
全国大学生数学竞赛初赛2012年第四届《非数学专业》竞赛题目及答案解析高清无水印版

2012年第四届全国大学生数学竞赛初赛(非数学类)试卷及参考答案一、简答下列各题(本题共5个小题,每题6分,共30分) 1.求极限()12lim!.n n n →∞【参考答案】:因为2211ln !!,n n n n e而211ln1ln 2ln ln !,12n n n n n且ln lim 0.n n n 所以1ln1ln 2ln lim 0.12n n n n即 21lim ln !0n n n 21lim ! 1.n n n 2.求通过直线2320,:55430x y z L x y z ⎧⎪+-+=⎪⎪⎨⎪+-+=⎪⎪⎩的两个相互垂直的平面12,ππ,使其中一个平面过点()4,3,1.-【参考答案】:过直线L 的平面束方程为 23255430x y z x y z ,即 (25)534230.x y z 若平面1 过点 4,3,1 ,代入得0 ,即 ,从而1 的方程为3410.x y z 若平面束中的平面2 与1 垂直,则 3(25)451340. 解得3, 从而平面2 的方程为2530.x y z 3.已知函数(,),ax byz u x y e+=且20ux y∂=∂∂,确定常数,a b ,使函数(,)z z x y =满足方程20.z z zz x y x y∂∂∂--+=∂∂∂∂ 【参考答案】:(,),ax by z u e au x y x x (,),ax by zu e bu x y y y2(,),ax by z u ue b a abu x y x y x y21(1)(1)(,),ax by z z z u uz e b a ab a b u x y x y x y x y若是上式等于0,只有 1(1)(1)(,)0u ub a ab a b u x y x y,由此可得 1.a b 4.设()u u x =连续可微,(2)1u =,且()()32d d Lx y u x x uu y +++⎰在右半平面上与路径无关,求().u x 【参考答案】:由32u x u x y u yx,得34x u u u ,即214dx x u du u, 这是一个一阶线性微分方程,于是由公式有通解为ln 2ln 2442uux e u edu C uudu C u uC 由(2)1u 得0C ,所以1/3.2x u5.求极限lim d .x x x t +【参考答案】:因为当1x 时,x x xxdt0x所以lim0.x xx第二题:(10分)计算20|sin |d .xe x x +∞-⎰【参考答案】:由于220(1)1|sin ||sin |nn k xxk k ex dx ex dx12(1)11sin nk k x k k e xdx应用分部积分法,有1222(1)11sin 15k k x k k e xdx e e所以有 222011|sin |15n n x k k e x dx e e212221151n e e e e 当(1)n x n 时,(1)2220|sin ||sin ||sin |n x n x x x e x dx e x dx e x dx当n ,由两边夹法则,得2222011|sin |lim |sin |.51xxxx e ex dx ex dx e【注】如果最后不用夹逼准则,而用2222011|sin |lim |sin |.51n xxn e ex dx ex dx e需要先说明20|sin |x e x dx收敛。
2012第四届试题及答案

(4, −3,1) ;
(3) 已 知 函 数 z = u ( x, y )e
ax + by
∂ 2u = 0, 确 定 常 数 a 和 b , 使 函 数 z = z ( x, y ) 满 足 方 程 ,且 ∂x∂y
∂ 2 z ∂z ∂z − − + z =0; ∂x∂y ∂x ∂y
(4) 设函数 u = u ( x) 连续可微, u (2) = 1 , 且 ( x + 2 y )udx + ( x + u 3 )udy 在右半平面上与路径无关,
F (t + Δt ) − F (t ) , 这是一个在厚度为 Δt 的球壳上的积分. 原点到球壳边缘上的点的射线和
z 轴夹角在 θ t + Δt 和 θ t 之间. 我们使用球坐标变换来做这个积分, 由积分的连续性可知, 存在
α = α (Δt ) , θ t + Δt ≤ α ≤ θ t , 使得
1 f ′′(0) + ο (1) 1 f ′′(0) 1 = 1 − lim = 1− = …………………(3 分) 2 x →0 f '( x) − f '(0) 2 f ′′(0) 2 x
⎛ x3 ⎜ x f (u ) ∴ lim = lim ⎝ x →0 f ( x ) sin 3 u x →0 ⎛ u3 ⎜ ⎝
….(2 分)
⎧ x2 + y2 = z S : 在曲线 上任取一点 ( x, y, z ) , 则原点到的点的射线和 z 轴的夹角 ⎨ 2 2 2 2 x y z t + + = ⎩
为
θt = arccos = arccos
z t
g . 取 Δt > 0 , 则 θ t > θ t + Δt . 对于固定的 t > 0 , 考虑积分差 t
历届全国大学生数学竞赛预赛试卷

历届全国⼤学⽣数学竞赛预赛试卷全国⼤学⽣数学竞赛预赛试卷(⾮数学类)2009年第⼀届全国⼤学⽣数学竞赛预赛试卷(⾮数学类)⼀、填空题(每⼩题5分,共20分)1.计算()ln(1)d yx y x y ++=??____________,其中区域D 由直线1=+y x 与两坐标轴所围成三⾓形区域.2.设)(x f 是连续函数,且满⾜220()3()d 2f x x f x x =--?,则()f x =____________.3.曲⾯2222x z y =+-平⾏平⾯022=-+z y x 的切平⾯⽅程是__________.4.设函数)(x y y =由⽅程29ln )(y y f e xe=确定,其中f 具有⼆阶导数,且1≠'f ,则=22d d xy________________. ⼆、(5分)求极限xenx x x x ne e e )(lim 20+++→Λ,其中n 是给定的正整数. 三、(15分)设函数)(x f 连续,10()()g x f xt dt =?,且A x x f x =→)(lim 0,A 为常数,求()g x '并讨论)(x g '在0=x 处的连续性.四、(15分)已知平⾯区域}0,0|),{(ππ≤≤≤≤=y x y x D ,L 为D 的正向边界,试证:(1)-=---Lx y Lx yx ye y xe x ye y xed d d d sin sin sin sin ;(2)2sin sin 25d d π?≥--Ly yx ye y xe.五、(10分)已知xxexe y 21+=,xx exe y -+=2,x xx e exe y --+=23是某⼆阶常系数线性⾮齐次微分⽅程的三个解,试求此微分⽅程.六、(10分)设抛物线c bx ax y ln 22++=过原点.当10≤≤x 时,0≥y ,⼜已知该抛物线与x 轴及直线1=x 所围图形的⾯积为31.试确定c b a ,,,使此图形绕x 轴旋转⼀周⽽成的旋转体的体积V 最⼩.七、(15分)已知)(x u n 满⾜1()()1,2,n xnn u x u x x e n -'=+=L ,且n eu n =)1(,求函数项级数∑∞=1)(n n x u 之和.⼋、(10分)求-→1x 时,与∑∞=02n n x 等价的⽆穷⼤量.2010年第⼆届全国⼤学⽣数学竞赛预赛试卷(⾮数学类)⼀、(25分,每⼩题5分)(1)设22(1)(1)(1)nnx a a a =+++L ,其中||1,a <求lim .n n x →∞(2)求21lim 1x xx ex -→∞+ ?.(3)设0s >,求0(1,2,)sx nn I e x dx n ∞-==?L .(4)设函数()f t有⼆阶连续导数,1(,)r g x y f r ??==,求2222g g x y ??+??. (5)求直线10:0x y l z -=??=?与直线2213:421x y z l ---==--的距离. ⼆、(15分)设函数()f x 在(,)-∞+∞上具有⼆阶导数,并且()0f x ''>,lim ()0x f x α→+∞'=>,lim ()0x f x β→-∞'=<,且存在⼀点0x ,使得0()0f x <.证明:⽅程()0f x =在(,)-∞+∞恰有两个实根.三、(15分)设函数()y f x =由参数⽅程22(1)()x t t t y t ψ?=+>-?=?所确定,且22d 3d 4(1)y x t =+,其中()t ψ具有⼆阶导数,曲线()y t ψ=与22132t u y e du e-=+在1t =出相切,求函数()t ψ. 四、(15分)设10,nn n k=>=∑,证明:(1)当1α>时,级数1nn na S α+∞=∑收敛;(2)当1α≤且()n s n →∞→∞时,级数1nn na S α+∞=∑发散. 五、(15分)设l 是过原点、⽅向为(,,)αβγ,(其中2221)αβγ++=的直线,均匀椭球2222221x y z a b c++≤(其中0c b a <<<,密度为1)绕l 旋转. (1)求其转动惯量;(2)求其转动惯量关于⽅向(,,)αβγ的最⼤值和最⼩值.六、(15分)设函数()x ?具有连续的导数,在围绕原点的任意光滑的简单闭曲线C 上,曲线积分422d ()d 0L xy x x y x y ?+=+??的值为常数.(1)设L 为正向闭曲线22(2)1x y -+=,证明422d ()d 0L xy x x yx y ?+=+??;(2)求函数()x ?;(3)设C 是围绕原点的光滑简单正向闭曲线,求422d ()d C xy x x y x y ?++??.2011年第三届全国⼤学⽣数学竞赛预赛试卷(⾮数学类)⼀、计算下列各题(本题共3⼩题,每⼩题各5分,共15分)(1)求11cos 0x x x -→??;(2).求111lim ...12n n n n n →∞??++++++;(3)已知()2ln 1arctan tt x e y t e=+=-,求22d d y x .⼆、(本题10分)求⽅程()()24d 1d 0x y x x y y +-++-=的通解.三、(本题15分)设函数()f x 在0x =的某邻域内具有⼆阶连续导数,且()()()0,0,0f f f '''均不为0,证明:存在唯⼀⼀组实数123,,k k k ,使得()()()()12320230lim0h k f h k f h k f h f h→++-=. 四、(本题17分)设2221222:1x y z a b c∑++=,其中0a b c >>>,2222:z x y ∑=+,Γ为1∑与2∑的交线,求椭球⾯1∑在Γ上各点的切平⾯到原点距离的最⼤值和最⼩值.五、(本题16分)已知S 是空间曲线22310x y z ?+=?=?绕y 轴旋转形成的椭球⾯的上半部分(0z ≥)(取上侧),∏是S 在(,,)P x y z 点处的切平⾯,(,,)x y z ρ是原点到切平⾯∏的距离,,,λµν表⽰S 的正法向的⽅向余弦.计算:(1)()d ,,SzS x y z ρ??;(2)()3d Sz x y z S λµν++??六、(本题12分)设()f x 是在(,)-∞+∞内的可微函数,且()()f x mf x '<,其中01m <<,任取实数0a ,定义1ln (),1,2,...n n a f a n -==,证明:11()n n n a a ∞-=-∑绝对收敛.七、(本题15分)是否存在区间[]0,2上的连续可微函数()f x ,满⾜(0)(2)1f f ==,()1f x '≤,2()d 1f x x ≤?请说明理由.2012年第四届全国⼤学⽣数学竞赛预赛试卷(⾮数学类)⼀、(本⼤题共5⼩题,每⼩题6分,共30分)解答下列各题(要求写出重要步骤).(1)求极限21lim(!)n n n →∞.(2)求通过直线2320:55430x y z l x y z +-+=??+-+=?的两个互相垂直的平⾯1π和2π,使其中⼀个平⾯过点(4,3,1)-.(3)已知函数(,)ax byz u x y e+=,且20ux y=.确定常数a 和b ,使函数(,)z z x y =满⾜⽅程20z z zz x y x y--+=?. (4)设函数()u u x =连续可微,(2)1u =,且3(2)d ()d Lx y u x x u u y +++?在右半平⾯与路径⽆关,求(,)u x y .(5)求极限1limx xx t +.⼆、(本题10分)计算20sin d x e x x +∞-?.三、(本题10分)求⽅程21sin2501x x x=-的近似解,精确到0.001. 四、(本题12分)设函数()y f x =⼆阶可导,且()0f x ''>,(0)0f =,(0)0f '=,求330() lim ()sin x x f u f x u→,其中u 是曲线()y f x =上点(,())P x f x 处的切线在x 轴上的截距. 五、(本题12分)求最⼩实数C ,使得满⾜10 ()d 1f x x =?的连续函数()f x都有1f dx C ≤?.六、(本题12分)设()f x 为连续函数,0t >.区域Ω是由抛物⾯22z x y =+和球⾯2222x y z t ++=(0)z >所围起来的部分.定义三重积分222()()d F t f x y z v Ω=++,求()F t 的导数()F t ''.七、(本题14分)设1n n a ∞=∑与1n n b ∞=∑为正项级数,证明:(1)若()111lim 0n n n n n a a b b →∞++->,则级数1n n a ∞=∑收敛;(2)若()111lim 0n n n n n a a b b →∞++-<,且级数1n n b ∞=∑发散,则级数1n n a ∞=∑发散. 2013年第五届全国⼤学⽣数学竞赛预赛试卷(⾮数学类)⼀、解答下列各题(每⼩题6分,共24分,要求写出重要步骤) 1.求极限(lim 1sin nn →∞+.2.证明⼴义积分0sin d xx x+∞不是绝对收敛的.3.设函数()y y x =由323322x x y y +-=确定,求()y x 的极值.4.过曲线0)y x =≥上的点A 作切线,使该切线与曲线及x 轴所围成的平⾯图形的⾯积为34,求点A 的坐标.⼆、(满分12分)计算定积分2sin arctan d 1cos xx x e I x xππ-?=+?.三、(满分12分)设()f x 在0x =处存在⼆阶导数(0)f '',且()0lim 0x f x x →=.证明:级数11n f n ∞=??∑收敛.四、(满分12分)设(),()0()f x f x m a x b π'≤≥>≤≤,证明2sin ()d baf x x m≤. 五、(满分14分)设∑是⼀个光滑封闭曲⾯,⽅向朝外.给定第⼆型的曲⾯积分()()()333d d 2d d 3d d I x x y z y y z x z z x y ∑=-+-+-??.试确定曲⾯∑,使积分I 的值最⼩,并求该最⼩值.六、(满分14分)设22d d ()()a aC y x x y I r x y -=+?,其中a 为常数,曲线C为椭圆222x xy y r ++=,取正向.求极限lim ()a r I r →+∞.七、(满分14分)判断级数()()1111212n n n n ∞=+++++∑L 的敛散性,若收敛,求其和. 2014年第六届全国⼤学⽣数学竞赛预赛试卷(⾮数学类)⼀、填空题(共有5⼩题,每题6分,共30分)1.已知1x y e =和1x y xe =是齐次⼆阶常系数线性微分⽅程的解,则该⽅程是.2.设有曲⾯22:2S z x y =+和平⾯022:=++z y x L .则与L 平⾏的S 的切平⾯⽅程是.3.设函数()y y x =由⽅程21sin d 4y xt x t π-??=所确定.求d d x y x ==.4.设1(1)!nn k kx k ==+∑,则=∞→n n x lim .5.已知130()lim 1x x f x x e x →??++= ??,则=→20)(lim x x f x . ⼆、(本题12分)设n 为正整数,计算21d 1cos ln d d ne I x x x π-??=. 三、(本题14分)设函数()f x 在]1,0[上有⼆阶导数,且有正常数,A B 使得()f x A ≤,|"()|f x B ≤.证明:对任意]1,0[∈x ,有2 2|)('|B A x f +≤.四、(本题14分)(1)设⼀球缺⾼为h ,所在球半径为R .证明该球缺体积为2)3(3h h R -π,球冠⾯积为Rh π2;(2)设球体12)1()1()1(222≤-+-+-z y x 被平⾯6:=++z y x P 所截的⼩球缺为Ω,记球缺上的球冠为∑,⽅向指向球外,求第⼆型曲⾯积分d d d d d d I x y z y z x z x y ∑=++??.五、(本题15分)设f 在],[b a 上⾮负连续,严格单增,且存在],[b a x n ∈,使得-=b ann n dx x f a b x f )]([1)]([.求n n x ∞→lim .六、(本题15分)设2222212n n n nA n n n n =++++++L ,求??-∞→n n A n 4lim π. 2015年第七届全国⼤学⽣数学竞赛预赛试卷(⾮数学类)⼀、填空题(每⼩题6分,共5⼩题,满分30分)(1)极限2222sin sin sin lim 12n n n n n n n n πππ→∞??+++= ?+++ ?L . (2)设函数(),z zx y =由⽅程,0z z F x y y x ?++= ??所决定,其中(),F u v 具有连续偏导数,且0u v xF yF +≠则z zxy x y+=. (3)曲⾯221z x y =++在点()1,1,3M-的切平⾯与曲⾯所围区域的体积是.(4)函数()[)[)3,5,00,0,5x f x x ?∈-?=?∈??在(]5,5-的傅⽴叶级数在0x =收敛的是.(5)设区间()0,+∞上的函数()u x 定义域为()2xt u x e dt +∞-=?,则()u x 的初等函数表达式是.⼆、(12分)设M 是以三个正半轴为母线的半圆锥⾯,求其⽅程. 三、(12分)设()f x 在(),a b 内⼆次可导,且存在常数,αβ,使得对于(),x a b ?∈,有()()()f x f x f x αβ'=+,则()f x 在(),a b 内⽆穷次可导.四、(14分)求幂级数()()30211!nn n x n ∞=+-+∑的收敛域及其和函数.五、(16分)设函数()f x 在[]0,1上连续,且()()110,1f x dx xf x dx ==??.试证:(1)[]00,1x ?∈使()04f x >;(2)[]10,1x ?∈使()14f x =.五、(16分)设(),f x y 在221x y +≤上有连续的⼆阶偏导数,且2222xx xy yy f f f M ++≤.若()()()0,00,0,00,00x y f f f ===,证明:()221,4x y f x y dxdy +≤≤.2016年第⼋届全国⼤学⽣数学竞赛预赛试卷(⾮数学类)⼀、填空题(每⼩题5分,满分30分)1、若()f x 在点x a =可导,且()0f a ≠,则()1lim nn f a n f a →∞?+=__________. 2、若()10f =,()1f '存在,求极限()()220sin cos tan3lim1sin x x f x x xI ex→+=-.3、设()f x 有连续导数,且()12f =,记()2x z f e y =,若zz x=,求()f x 在0x >的表达式. 4、设()sin 2x f x e x =,求02n a π<<,()()40f .5、求曲⾯22 2x z y =+平⾏于平⾯220x y z +-=的切平⾯⽅程.⼆、(14分)设()f x 在[]0,1上可导,()00f =,且当()0,1x ∈,()01f x '<<,试证当()0,1a ∈,()()()230d d aaf x xf x x >?.三、(14分)某物体所在的空间区域为222:22x y z x y z Ω++≤++,密度函数为222x y z ++,求质量()222d d d M x y z x y z Ω=++.四、(14分)设函数()f x 在闭区间[]0,1上具有连续导数,()00f =,()11f =,证明:()10111lim 2nn k k n f x dx fn n →∞=-=- ? ?∑?. 五、(14分)设函数()f x 在闭区间[]0,1上连续,且()1d 0I f x x =≠?,证明:在()0,1内存在不同的两点12,x x ,使得()()12112f x f x I+=. 六、(14分)设()f x 在(),-∞+∞可导,且()()(2f x f x f x =+=.⽤Fourier 级数理论证明()f x 为常数.2017年第九届全国⼤学⽣数学竞赛预赛试卷(⾮数学类)⼀、1.已知可导函数f (x )满⾜?+=+xx tdt t f x xf 01sin )(2)(cos ,则()f x =_________.2.求??+∞→n n n 22sin lim π.3.设(,)w f u v =具有⼆阶连续偏导数,且==+u x cy v x cy -,,其中c 为⾮零常数.则21xx yy w w c -=_________. 4.设()f x 有⼆阶导数连续,且(0)'(0)0,"(0)6f f f ===,则240(sin )lim x f x x →=____.5.不定积分sin 2sin 2(1sin )x e xI dx x -=-?=________. 6.记曲⾯222z x y =+和z =围成空间区域为V ,则三重积分Vzdxdydz =___________.⼆、(本题满分14分)设⼆元函数(,)f x y 在平⾯上有连续的⼆阶偏导数.对任何⾓度α,定义⼀元函数()(cos ,sin )g t f t t =ααα.若对任何α都有(0)0dg dtα=且22(0)0d g dt α>.证明)0,0(f 是(,)f x y 的极⼩值. 三、(本题满分14分)设曲线Γ为在2221x y z ++=,1x z +=,0,0,0x y z ≥≥≥上从(1,0,0)A 到(0,0,1)B 的⼀段.求曲线积分?Γ++=xdz zdy ydx I.四、(本题满分15分)设函数()0f x >且在实轴上连续,若对任意实数t ,有||()1t x ef x dx +∞---∞≤?,则,()a b a b ?<,2()2bab a f x dx -+≤. 五、(本题满分15分)设{}n a 为⼀个数列,p 为固定的正整数。
第四届全国大学生数学竞赛决赛试题及答案(非数学组)

于是 I = I1 + I 2 = 1 + π
3 8
六、 (本题 15 分) 若对任意收敛于 0 的数列 { xn } 级数 ∑ an xn 都收敛,证明级数 ∑ an 收敛.
n =1 n =1
∞ ∞
令 Sn = ∑ ak ,xn = 证明: 用反证法. 若级数 ∑ an 发散,
n =1 k =1
∞
而 g (0) = f 2 (0) + [ f '(0)] = 4 且 0 ∈ [ξ1 , ξ 2 ] , 知 g (ξ ) = max g ( x) ≥ 4 , 由此可得 ξ ∈ (ξ1 , ξ 2 ) , 根据 Fermat
2
x∈[ξ1 ,ξ 2 ]
定理, g '(ξ ) = 0 ,即
g '(ξ ) = 2 f (ξ ) f '(ξ ) + 2 f '(ξ ) f ''(ξ ) = 0 .
3 2
3 2 2
⋅ 2dxdy =
=
G ρ 2π 2 1 ⋅ rdr = G ρπ ln 2. 2 ∫0 ∫1 r 2
三、 (本题 15 分)
f ( x) 在 [1, +∞] 连续可导, f ' ( x) =
x
⎡ 1 1 1 ⎤ − ln(1 + ) ⎥ , 证明 ⎢ 2 x ⎦ 1 + f ( x) ⎣ ⎢ x ⎥
证明:在 [−2,0] 和 [0, 2] 上分别使用 Lagrange 中值定理,分别 ∃ξ1 ∈ (−2,0), ξ 2 ∈ (0, 2) 使得 f (0) − f (−2) = 2 f '(ξ1 ), f (2) − f (0) = 2 f '(ξ 2 ) . 令 g ( x) = f 2 ( x) + [ f '( x)] ,考虑 g ( x) 在闭区间 [ξ1 , ξ 2 ] 上的最大值,记 g (ξ ) = M = max g ( x) . 由于
最近五届全国大学生高等数学竞赛真题及答案(非数学类)

目录第一届全国大学生数学竞赛预赛试卷 ........................................................................................... 1 第二届全国大学生数学竞赛预赛试卷 ........................................................................................... 7 第三届全国大学生数学竞赛预赛试卷 ......................................................................................... 11 第四届全国大学生数学竞赛预赛试卷 ......................................................................................... 18 第五届全国大学生数学竞赛预赛试卷 .. (23)(参加高等数学竞赛的同学最重要的是好好复习高等数学知识,适当看一些辅导书及相关题目,主要是一些各大高校的试题。
)2009年 第一届全国大学生数学竞赛预赛试卷一、填空题(每小题5分,共20分)1.计算=--++⎰⎰y x yx x yy x Dd d 1)1ln()(____________,其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.解: 令v x u y x ==+,,则v u y v x -==,,v u v u y x d d d d 1110det d d =⎪⎪⎭⎫ ⎝⎛-=, v u uvu u u y x yx x yy x DDd d 1ln ln d d 1)1ln()(⎰⎰⎰⎰--=--++⎰⎰⎰⎰----=---=1021000d 1)ln (1ln d )d ln 1d 1ln (u uu u u u u u u u v v uuv u u u u u ⎰-=12d 1u uu (*) 令u t -=1,则21t u -=dt 2d t u -=,42221t t u +-=,)1)(1()1(2t t t u u +-=-,⎰+--=0142d )21(2(*)tt t⎰+-=1042d )21(2t t t 1516513221053=⎥⎦⎤⎢⎣⎡+-=t t t 2.设)(x f 是连续函数,且满足⎰--=2022d )(3)(x x f x x f , 则=)(x f ____________.解: 令⎰=20d )(x x f A ,则23)(2--=A x x f ,A A x A x A 24)2(28d )23(202-=+-=--=⎰,解得34=A 。
历届全国大学生高等数学竞赛真题及答案非数学类

前三届高数竞赛预赛试题(非数学类)(参加高等数学竞赛的同学最重要的是好好复习高等数学知识,适当看一些辅导书及相关题目,主要是一些各大高校的试题。
)2009年 第一届全国大学生数学竞赛预赛试卷一、填空题(每小题5分,共20分)1.计算=--++⎰⎰y x yx x yy x Dd d 1)1ln()(____________,其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.解: 令v x u y x ==+,,则v u y v x -==,,v u v u y x d d d d 1110det d d =⎪⎪⎭⎫ ⎝⎛-=, v u u v u u u y x y x x yy x D D d d 1ln ln d d 1)1ln()(⎰⎰⎰⎰--=--++⎰⎰⎰⎰----=---=1021000d 1)ln (1ln d )d ln 1d 1ln (u uu u u u u u u u v v uuv u u u u u ⎰-=12d 1u uu (*) 令u t -=1,则21t u -=dt 2d t u -=,42221t t u +-=,)1)(1()1(2t t t u u +-=-,⎰+--=0142d )21(2(*)tt t⎰+-=1042d )21(2t t t 1516513221053=⎥⎦⎤⎢⎣⎡+-=t t t2.设)(x f 是连续函数,且满足⎰--=2022d )(3)(x x f x x f , 则=)(x f ____________.解: 令⎰=20d )(x x f A ,则23)(2--=A x x f ,A A x A x A 24)2(28d )23(202-=+-=--=⎰,解得34=A 。
因此3103)(2-=x x f 。
3.曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是__________. 解: 因平面022=-+z y x 的法向量为)1,2,2(-,而曲面2222-+=y x z 在),(00y x 处的法向量为)1),,(),,((0000-y x z y x z y x ,故)1),,(),,((0000-y x z y x z y x 与)1,2,2(-平行,因此,由x z x =,y z y 2=知0000002),(2,),(2y y x z x y x z y x ====,即1,200==y x ,又5)1,2(),(00==z y x z ,于是曲面022=-+z y x 在)),(,,(0000y x z y x 处的切平面方程是0)5()1(2)2(2=---+-z y x ,即曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是0122=--+z y x 。
历届全国大学生数学竞赛真题及答案非数学类

高数竞赛预赛试题〔非数学类〕〔参加高等数学竞赛的同学最重要的是好好复习高等数学知识,适当看一些辅导书及相关题目,主要是一些各大高校的试题。
〕2021年 第一届全国大学生数学竞赛预赛试卷 一、填空题〔每题5分,共20分〕1.计算=--++⎰⎰y x yx x yy x D d d 1)1ln()(,其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.解:令vx u y x ==+,,那么vu y v x -==,,v u v u y x d d d d 1110det d d =⎪⎪⎭⎫⎝⎛-=,v u u v u u u y x y x x yy x D D d d 1ln ln d d 1)1ln()(⎰⎰⎰⎰--=--++⎰⎰⎰⎰----=---=1021000d 1)ln (1ln d )d ln 1d 1ln (u uu u u u u u u u v v u uv u u u u u〔*〕令u t -=1,那么21t u -=dt 2d t u -=,42221t t u +-=,)1)(1()1(2t t t u u +-=-,⎰+--=0142d )21(2(*)t t t⎰+-=1042d )21(2t t t 151651322153=⎥⎦⎤⎢⎣⎡+-=t t t 2.设)(x f 是连续函数,且满足⎰--=2022d )(3)(x x f x x f , 那么=)(x f .解:令⎰=20d )(x x f A ,那么23)(2--=A x x f ,A A x A x A 24)2(28d )23(202-=+-=--=⎰,解得。
因此。
3.曲面平行平面022=-+z y x 的切平面方程是.解:因平面022=-+z y x 的法向量为)1,2,2(-,而曲面在),(00y x 处的法向量为)1),,(),,((0000-y x z y x z y x ,故)1),,(),,((0000-y x z y x z y x 与)1,2,2(-平行,因此,由x z x =,y z y 2=知0000002),(2,),(2y y x z x y x z y x ====,即1,200==y x ,又5)1,2(),(00==z y x z ,于是曲面22=-+z y x 在)),(,,(0000y x z y x 处的切平面方程是0)5()1(2)2(2=---+-z y x ,即曲面 平行平面022=-+z y x 的切平面方程是0122=--+z y x 。
2012第四届全国大学生数学竞赛四川赛区获奖名单

2012第四届全国大学生数学竞赛四川赛区获奖名单更新时间:2012-11-6 16:55:252012第四届全国大学生数学竞赛四川赛区评奖工作已经结束,经过全国大学生数学竞赛四川赛区组委会专家评审,现将四川赛区本次获奖名单公布如下:第四届全国大学生数学竞赛四川赛区数学类奖名单赛区一等奖编号姓名性别学校名称学院名称参赛类型准考证1周超男四川大学应用数学数学专业201202王宇男四川大学应用数学数学专业201203陈攀男电子科技大学数学数学专业201204周世奇男电子科技大学数学数学专业201205戴烜中男四川大学吴玉章学院数学专业201206邓田娟女四川大学数学基地班数学专业201207杨爽女乐山师范学院数学与应用数学数学专业201208任偲骐男四川大学应用数学数学专业201209李昊天男四川大学数学大类数学专业2012010李波男乐山师范学院数学与应用数学数学专业2012011傅费思男四川大学应用数学数学专业20120赛区二等奖编号姓名性别学校名称学院名称参赛类型准考证1李姗蔓女宜宾学院数学与应用数学数学专业201202李佑铭男四川大学数学与应用数学(基础) 数学专业201203孔祥飞男电子科技大学数学数学专业201204石云鹏男四川大学数学大类数学专业201205佘睿男四川大学基地班数学专业201206郭汝驰男四川大学应用数学数学专业201207常建龙男电子科技大学数学数学专业2012010402 16 8鲁东男西南交通大学数学数学专业2012010803 16 9雷文超男四川大学信息与计算科学数学专业2012010807 20 10岳阳男西南交通大学计算数学专业2012010703 21 11罗开宝男内江师范学院数学与应用数学专业数学专业2012010905 22 12胡方涛男电子科技大学数学数学专业2012010730 23 13余东洲男四川大学数学大类数学专业2012010401 24 14涂代源男四川大学应用数学数学专业2012010422 24 15何俊材男四川大学应用数学数学专业2012010427 24 16孙硕男电子科技大学数学数学专业2012010829 24 17钟友林男四川大学应用数学数学专业2012011027 24 赛区三等奖编号姓名性别学校名称学院名称参赛类型准考证号名次1唐浩耘男四川大学应用数学数学专业2012010127 29 2谭大超男乐山师范学院数学与应用数学数学专业2012010214 29 3纪圣塨男西南交通大学数学数学专业2012010710 29 4赵威男四川大学数学大类数学专业2012011003 29 5胡留春男西南交通大学统计数学专业2012011119 29 6张瑞梅女内江师范学院数学与应用数学专业数学专业2012011224 29 7周义满男电子科技大学数学数学专业2012010129 35 8李艳晶女四川师范大学数学与应用数学数学专业2012010228 35 9夏王洋男四川大学应用数学数学专业2012010706 35 10王玖玮男四川大学应用数学数学专业2012010801 35 11杨红明男电子科技大学数学数学专业2012010808 35 12王琦男四川大学数学基地班数学专业2012010310 40 13周玲女四川大学数学大类数学专业2012010330 40 14李福团男西南交通大学计算数学专业2012010906 40 15唐志骥男四川大学数学与应用数学(金融)数学专业2012011129 40 16刘春燕女西华师范大学数学与应用数学数学专业2012010221 44 17王世莉女乐山师范学院数学与应用数学数学专业2012010413 4418胡又壬女四川大学基地班数学专业2012010816 4419阳密女四川师范大学数学与应用数学数学专业2012011107 4420刘连林男西南交通大学数学数学专业2012010105 4821侯振铎男四川大学数学基地班数学专业2012010202 4822张鹏成男四川大学吴玉章学院数学专业2012010227 4823王凯男四川大学数学大类数学专业2012011202 4824李洋洋男中国民航飞行学院信息0902 数学专业2012011221 4825郭凯迪女四川大学数学与经济创新班数学专业2012010120 4826王豪男四川民族学院数学与应用数学专业数学专业2012010404 48第四届全国大学生数学竞赛四川赛区非数学类获名单赛区一等奖编号姓名性别学校名称学院名称参赛类型准考证号名1 姚青松男西南交通大学经济学非数学专业2012023420 12 刘同科男电子科技大学计算机非数学专业2012023715 23 郑飞洋男电子科技大学物电非数学专业2012023214 34 孙健男电子科技大学通信非数学专业2012022301 45 胡欢男电子科技大学微固非数学专业2012023004 56 李娇女电子科技大学生命非数学专业2012024823 57 马骥男电子科技大学自动化非数学专业2012022613 78 汪威男电子科技大学数理基科班非数学专业2012022428 89 赵旭男西南交通大学材料成型非数学专业2012023218 810 陈宣奇男电子科技大学微固非数学专业2012024110 811 李辉男电子科技大学物电非数学专业2012023128 1112 孟帆男电子科技大学电工非数学专业2012021612 1213 王冰川男西华大学自动化非数学专业2012022720 1314 何加智男电子科技大学物电非数学专业2012022724 1415 许亿志男电子科技大学通信非数学专业2012021528 1516 吴昊男西南交通大学茅以升学院非数学专业2012022919 1517 温勇兵男四川大学制造学院非数学专业2012024524 1518 张亦弛男电子科技大学微固非数学专业2012024822 1519 余锦斌男电子科技大学通信非数学专业2012022014 1920 王洋男中国民航飞行学院计科0901 非数学专业2012022427 1921 朱启勋男电子科技大学通信非数学专业2012023601 1922 解为良男西南交通大学测绘工程非数学专业2012023606 2223 颜在满男西南交通大学生命学院非数学专业2012023814 2224 邹艳波男成都理工大学电气工程及其自动化非数学专业2012024014 2225 李斯文男四川大学高分子科学与工程学院非数学专业2012023714 2526 娄舜男电子科技大学光电非数学专业2012023903 2527 胡勇男电子科技大学光电非数学专业2012024028 2528 屈伸男电子科技大学数理基科班非数学专业2012024322 2529 何涛男电子科技大学机电非数学专业2012024806 2530 李珂男西南交通大学热能与动力工程非数学专业2012021630 3031 卢享男电子科技大学计算机非数学专业2012023827 3032 陈勇男西南石油大学电气工程非数学专业2012024122 30赛区二等奖编号姓名性别学校名称学院名称参赛类型准考证号名1 舒海男电子科技大学物电非数学专业2012021713 332 赵海林男电子科技大学通信非数学专业2012024001 333 张永伟男电子科技大学数理基科班非数学专业2012024225 334 米从威男电子科技大学物电非数学专业2012021807 365 余坤益男四川大学化学学院非数学专业2012022905 366 张齐艳男四川大学高分子科学与工程学院非数学专业2012024226 367 郭甜甜女电子科技大学自动化非数学专业2012024628 368 沙永祥男四川大学建筑与环境学院非数学专业2012023226 409 陈军伟男四川大学水利水电学院非数学专业2012023405 4010 徐霈强男成都信息工程学院大气科学非数学专业2012024019 4011 时北极男西南交通大学力学非数学专业2012024723 4012 徐晓燕女成都理工大学旅游管理非数学专业2012024724 4013 李裕宇男西南交通大学软件工程非数学专业2012022629 4514 王刚男四川大学物理学院非数学专业2012023915 4515 黄睿捷男四川大学化学学院非数学专业2012024114 4516 钱华明男电子科技大学机电非数学专业2012024427 4517 肖电坤男西南交通大学土木非数学专业2012021523 4918 邵俊波男四川大学建筑与环境学院非数学专业2012022403 4919 刘岩男西南交通大学力学非数学专业2012022801 4920 陈廷君男西南交通大学土木非数学专业2012022906 4921 王林男成都理工大学土木工程非数学专业2012023006 4922 张志业女成都理工大学资源勘查工程非数学专业2012023125 4923 何永成男西南交通大学土木非数学专业2012024516 4924 张峰男四川大学电气信息学院非数学专业2012024616 4925 王迪松男电子科技大学数理基科班非数学专业2012024824 4926 李孟林男电子科技大学数理基科班非数学专业2012024826 4927 郭文博男电子科技大学自动化非数学专业2012022729 5928 薄文斐男电子科技大学物电非数学专业2012022808 5929 叶雷男四川大学制造学院非数学专业2012023205 5930 王玉东男四川大学物理学院非数学专业2012023222 5931 游军杰男四川大学电气信息学院非数学专业2012023527 5932 谭启贵男西南石油大学油气储运非数学专业2012024617 5933 郭焱林男四川大学电气信息学院非数学专业2012021801 6534 陶源男电子科技大学通信非数学专业2012022030 6535 孟楠男电子科技大学英才非数学专业2012022120 6536 张志伟男成都理工大学公共事业管理非数学专业2012022518 6537 张一幸男电子科技大学数理基科班非数学专业2012022704 6538 张三锋男电子科技大学微固非数学专业2012022810 6539 李坤男电子科技大学通信非数学专业2012023020 6540 赵晓凤女四川大学水利水电学院非数学专业2012023914 6541 李行健男电子科技大学数理基科班非数学专业2012024128 6542 凡航男四川大学电气信息学院非数学专业2012024415 6543 黎燕文男西南交通大学土木学院非数学专业2012021404 7544 宋昌意男电子科技大学通信非数学专业2012021510 7545 康文武男四川大学电子信息学院非数学专业2012022203 7546 王欣男西南科技大学土木非数学专业2012023101 7547 周大鸥男成都理工大学核工程与核技术非数学专业2012023207 7548 张路男西南石油大学石油工程非数学专业2012023502 7549 刘鹏男西华大学热动非数学专业2012023809 75赛区三等奖编号姓名性别学校名称学院名称参赛类型准考证号名1 付雪冬女电子科技大学自动化非数学专业2012021816 822 郭达鸿男西南交通大学力学与工程非数学专业2012022016 823 李飞跃男四川大学工商管理学院非数学专业2012022214 824 徐文男西南交通大学测绘非数学专业2012022621 825 应宏辉男电子科技大学物电非数学专业2012023906 826 颜峰男电子科技大学自动化非数学专业2012024113 827 邵春雨女电子科技大学光电非数学专业2012024417 828 刘忠智男成都理工大学物探非数学专业2012024604 829 刘丰男四川大学物理学院非数学专业2012022401 9010 张磊男西南交通大学电气非数学专业2012022425 9011 郭尚岐男电子科技大学数理基科班非数学专业2012022524 9012 万文杰男成都理工大学核工程与核技术非数学专业2012022830 9013 齐佳宏男四川大学建筑与环境学院非数学专业2012022913 9014 罗文刚男西南科技大学机械非数学专业2012022915 9015 尤成宇男西南财经大学保险非数学专业2012023306 9016 许加宝男中国民航飞行学院飞构1102 非数学专业2012023705 9017 赵亚丽女四川大学电子信息学院非数学专业2012023802 9018 韩小宁男西南交通大学茅机非数学专业2012024606 9019 林碧玉女西南交通大学地学学院非数学专业2012021508 1020 汪冬兵男西南交通大学土木非数学专业2012021602 1021 王雪微女电子科技大学物电非数学专业2012021608 1022 莫一奉男四川大学电气信息学院非数学专业2012022103 1023 许度男西南交通大学土木工程非数学专业2012022213 1024 池启康男四川大学电子信息学院非数学专业2012022811 1025 王智坚男成都学院自动化非数学专业2012022816 1026 张恩来男四川大学建筑与环境学院非数学专业2012023301 1027 孙继发男电子科技大学自动化非数学专业2012023625 1028 潘誉男电子科技大学能源非数学专业2012023822 1029 何彪男电子科技大学微固非数学专业2012023916 1030 马世琪男电子科技大学通信非数学专业2012024021 1031 何伟男四川大学锦江学院土木工程非数学专业2012021611 1132 张熙男电子科技大学数理基科班非数学专业2012021814 1133 丁祎晓男电子科技大学微固非数学专业2012022318 1134 郑炯卫男电子科技大学微固非数学专业2012022429 1135 汤华男四川大学电气信息学院非数学专业2012022505 1136 吕彦璆女电子科技大学电工非数学专业2012022512 1137 孙建东男宜宾学院电子信息非数学专业2012022520 1138 宋泽良男成都学院机械设计非数学专业2012022714 1139 冯俊羲男四川大学电子信息学院非数学专业2012023126 1140 牛玉宁女成都理工大学核工程与核技术非数学专业2012023401 1141 黎渺军男四川大学电气信息学院非数学专业2012023414 1142 张邦健男内江师范学院物理学非数学专业2012023707 1143 尹鑫鑫男电子科技大学生命非数学专业2012024018 1144 郝勇男电子科技大学物电非数学专业2012024302 1145 杨云帆男西南交通大学茅以升学院非数学专业2012024608 1146 郭征明男四川大学建筑与环境学院非数学专业2012024623 1147 蒋勇男西南交通大学机械非数学专业2012021422 1248 阮艳女成都理工大学测控技术与仪器非数学专业2012021505 1249 刘海男四川大学锦江学院土木工程非数学专业2012021725 1250 李凯男电子科技大学英才非数学专业2012021823 1251 陈程男四川大学物理学院非数学专业2012021928 1252 肖龙男电子科技大学机电非数学专业2012022101 1253 陈晋荣男成都理工大学勘查技术与工程非数学专业2012022606 1254 夏建雄男四川大学物理学院非数学专业2012022712 1255 孙立志男四川大学电气信息学院非数学专业2012022902 1256 陈宇皓男西华大学热动非数学专业2012023127 1257 冯琳女西南交通大学交控非数学专业2012023217 1258 汪迁男四川大学建筑与环境学院非数学专业2012023323 1259 张庆伟男电子科技大学成都学院通信工程非数学专业2012024313 1260 熊林云男四川大学吴玉章学院非数学专业2012024811 1261 罗明有男宜宾学院生物工程非数学专业2012021719 1462 徐明男西南科技大学土木非数学专业2012021829 1463 魏于量男西南交通大学土木非数学专业2012022114 1464 王握男西南交通大学交通运输非数学专业2012022123 1465 张海波男电子科技大学光电非数学专业2012022210 1466 郑力铭男西南石油大学化学工程非数学专业2012023201 1467 徐斌男电子科技大学物电非数学专业2012023209 1468 李广西男电子科技大学计算机非数学专业2012023329 1469 黄凯文男西南交通大学土木非数学专业2012023522 1470 陈国钱男西南科技大学核工非数学专业2012023719 1471 安盼盼女西南交通大学信息学院非数学专业2012024009 1472 舒秉亮男电子科技大学通信非数学专业2012024330 1473 涂洋男成都理工大学电气工程及其自动化非数学专业2012024404 1474 唐静女四川大学工商管理学院非数学专业2012024505 1475 谭孝元男成都理工大学电气工程及其自动化非数学专业2012024511 1476 鲁宇航男成都理工大学空间信息与数字技术非数学专业2012021730 1577 朱贵平男西南石油大学石油工程非数学专业2012022007 1578 石茂林男四川大学物理学院非数学专业2012022514 1579 丁占岭男四川大学吴玉章学院非数学专业2012023619 1580 李宜筱女西南科技大学核工非数学专业2012023702 1581 郑康立男成都学院通信工程非数学专业2012024813 15。
第四届全国大学生数学竞赛试题(非数学类)2012

第四届全国大学生数学竞赛预赛试卷(非数学类,2012)一、(本题共5小题,每小题各6分,共30分)解答下列各题 (1)求极限21lim(!);n n n →∞ (2)求通过直线2320:55430x y z L x y z +−+=⎧⎨+−+=⎩的两个相互垂直的平面1π和2π,使其中一个平面过点(4,-3,1); (3)已知函数(,)ax byz u x y e +=,且20u x y ∂=∂∂,确定常数a 和b ,使函数(,)z z x y =满足方程20z z z z x y x y∂∂∂−−+=∂∂∂∂; (4)设函数()u u x =连续可微,(2)1u =,且3(2)()L x y udx x u udy +++∫在右半平面上与路径无关,求();u x(5)求极限1lim ;x x x + 二、(本题10分) 计算20sin x e x dx +∞−∫三、(本题10分) 求方程21sin 2501x x x=−的近似解,精确到0.001. 四、(本题12)设函数()y f x =二阶可导,且()0,(0)0,(0)0,f x f f ′′′>== 求330()lim ()sin x x f u f x u→,其中u 是曲线()y f x =上点(,())P x f x 处的切线在x 轴上的截距。
五、(本题12)求最小实数C ,使得对满足10()1f x dx =∫的连续的函数()f x ,都有10f dx C ≤∫。
六、(本题12)设()f x 为连续函数,0t >,区域Ω是由抛物面22z x y =+和球面2222x y z t ++=所围起来的上半部分,定义三重积分222()()F t f x y z dv Ω=++∫∫∫。
求()F t 的导数()F t ′。
七、(本题14) 设1n n a∞=∑与1n n b ∞=∑为正项级数,那么(1) 若111lim(0,n n n nn a a b b →∞++−>则1n n a ∞=∑收敛; (2) 若111lim(0,n n n n n a a b b →∞++−<且1n n b ∞=∑发散,则1n n a ∞=∑发散。
第四届全国大学生数学竞赛非数学类预赛试卷
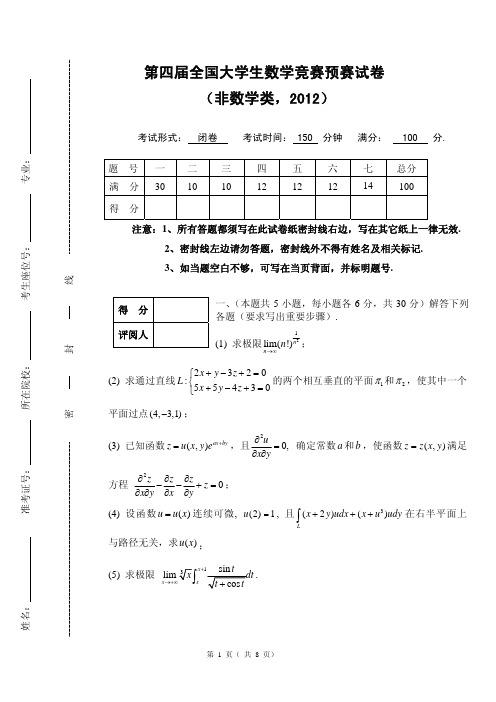
部分.定义三重积分
F(t) = ∫∫∫ f (x2 + y2 + z2 )dv . Ω
求 F(t) 的导数 F′(t) .
考生编号: 线
封
所在院校:
密
准考证号:
姓名:
第 7 页( 共 8 页)
得分 评阅人
七、(本题 14 分)
∞
∞
设 ∑ an 与 ∑ bn 为正项级数,那么
n=1
n=1
∑ (1)若
专业:
考生编号: 线
封
所在院校:
密
准考证号:
姓名:
第 3 页( 共 8 页)
得分 评阅人
三、(本题 10 分) 求方程 x2 sin 1 = 2x − 501的近似解,精确到 0.001.
x
第 4 页( 共 8 页)
得分 评阅人
四、(本题 12 分) 设函数 y = f (x) 二阶可导,且 f ′′(x) > 0 , f (0) = 0 ,
与路径无关,求 u(x) ;
∫ (5) 求极限 lim 3 x x+1 sin t dt .
x→+∞ x t + cos t
封
所在院校:
密
准考证号:
姓名:
第 1 页( 共 8 页)
第 2 页( 共 8 页)
得分 评阅人
二、(本题 10 分)
∫ 计算 +∞ e−2x | sin x | dx . 0
f
′(0)
=
0 ,求 lim x→0
f
x3 f (u) (x) sin3 u
,其中
u
是曲线
y
=
f
(x)
最近五届全国大学生高等数学竞赛真题及答案(非数学类)

目录第一届全国大学生数学竞赛预赛试卷 ........................................................................................... 1 第二届全国大学生数学竞赛预赛试卷 ........................................................................................... 7 第三届全国大学生数学竞赛预赛试卷 ......................................................................................... 11 第四届全国大学生数学竞赛预赛试卷 ......................................................................................... 18 第五届全国大学生数学竞赛预赛试卷 .. (23)(参加高等数学竞赛的同学最重要的是好好复习高等数学知识,适当看一些辅导书及相关题目,主要是一些各大高校的试题。
)2009年 第一届全国大学生数学竞赛预赛试卷一、填空题(每小题5分,共20分)1.计算=--++⎰⎰y x yx x yy x Dd d 1)1ln()(____________,其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.解: 令v x u y x ==+,,则v u y v x -==,,v u v u y x d d d d 1110det d d =⎪⎪⎭⎫ ⎝⎛-=, v u uvu u u y x yx x yy x DDd d 1ln ln d d 1)1ln()(⎰⎰⎰⎰--=--++⎰⎰⎰⎰----=---=1021000d 1)ln (1ln d )d ln 1d 1ln (u uu u u u u u u u v v uuv u u u u u ⎰-=12d 1u uu (*) 令u t -=1,则21t u -=dt 2d t u -=,42221t t u +-=,)1)(1()1(2t t t u u +-=-,⎰+--=0142d )21(2(*)tt t⎰+-=1042d )21(2t t t 1516513221053=⎥⎦⎤⎢⎣⎡+-=t t t 2.设)(x f 是连续函数,且满足⎰--=2022d )(3)(x x f x x f , 则=)(x f ____________.解: 令⎰=20d )(x x f A ,则23)(2--=A x x f ,A A x A x A 24)2(28d )23(202-=+-=--=⎰,解得34=A 。
全国大学生数学竞赛试题解答及评分标准(非数学类)

全国大学生竞赛历年试题名师精讲(非数学类)(2009-—2013)第五届全国大学生数学竞赛预赛试卷(非数学类)一、 解答下列各题(每小题6分共24分,要求写出重要步骤)1。
求极限(lim 1sin nn →∞+。
解因为()sin sin 2sinn ππ==……(2分);原式lim 1exp lim ln 1sin nn n n →∞→∞⎡⎤⎛⎫⎛⎫=+=+⎢⎥ ⎢⎥⎝⎝⎣⎦…exp lim n n →∞⎛= ⎝2.证明广义积分0sin xdx x ⎰不是绝对收敛的解 记()1sin n n nx a dx xππ+=⎰,只要证明0n n a ∞=∑发散即可。
……………………(2分)因为()()()()10112sin sin 111n n n a x dx xdx n n n ππππππ+≥==+++⎰⎰.…………(2分) 而()021n n π∞=+∑发散,故由比较判别法nn a∞=∑发散。
……………………………………(2分)3。
设函数()y y x =由323322x x y y +-=确定,求()y x 的极值。
解 方程两边对x 求导,得22236360x xy x y y y ''++-= ………………(1分)故()2222x x y y y x+'=-,令0y '=,得()200x x y x +=⇒=或2x y =-………(2分) 将2x y =-代入所给方程得2,1x y =-=,将0x =代入所给方程得0,1x y ==-,…………………………………(2分)又()()()()()2222222222422x xy y y x x x y yy x y y x ''++--+-''=-()()()0,1,02,1,0200220010,1020x y y x y y y y ''====-==+---''''==-<=>-, 故()01y =-为极大值,()21y -=为极小值.…………………………(3分)4.过曲线)0y x ≥上的点A 作切线,使该切线与曲线及x 轴所围成的平面图形的面积为34,求点A 的坐标. 解 设切点A的坐标为(t ,曲线过A点的切线方程为y -=令0y =,由切线方程得切线与x 轴交点的横坐标为02x t =-。
全国大学生数学竞赛大纲(非数学专业组)

中国大学生数学竞赛竞赛大纲(初稿)为了进一步推动高等学校数学课程的改革和建设,提高大学数学课程的教学水平,激励大学生学习数学的兴趣,发现和选拔数学创新人才,更好地实现“中国大学生数学竞赛”的目标,特制订本大纲。
一、竞赛的性质和参赛对象“中国大学生数学竞赛”的目的是:激励大学生学习数学的兴趣,进一步推动高等学校数学课程的改革和建设,提高大学数学课程的教学水平,发现和选拔数学创新人才。
“中国大学生数学竞赛”的参赛对象为大学本科二年级及二年级以上的在校大学生。
二、竞赛的内容“中国大学生数学竞赛”分为数学专业类竞赛题和非数学专业类竞赛题。
(二)中国大学生数学竞赛(非数学专业类)竞赛内容为大学本科理工科专业高等数学课程的教学内容,具体内容如下:一、函数、极限、连续1.函数的概念及表示法、简单应用问题的函数关系的建立.2.函数的性质:有界性、单调性、周期性和奇偶性.3.复合函数、反函数、分段函数和隐函数、基本初等函数的性质及其图形、初等函数.4.数列极限与函数极限的定义及其性质、函数的左极限与右极限.5.无穷小和无穷大的概念及其关系、无穷小的性质及无穷小的比较.6.极限的四则运算、极限存在的单调有界准则和夹逼准则、两个重要极限.7.函数的连续性(含左连续与右连续)、函数间断点的类型.8.连续函数的性质和初等函数的连续性.9.闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理).二、一元函数微分学1. 导数和微分的概念、导数的几何意义和物理意义、函数的可导性与连续性之间的关系、平面曲线的切线和法线.2. 基本初等函数的导数、导数和微分的四则运算、一阶微分形式的不变性.3. 复合函数、反函数、隐函数以及参数方程所确定的函数的微分法.4. 高阶导数的概念、分段函数的二阶导数、某些简单函数的n阶导数.5. 微分中值定理,包括罗尔定理、拉格朗日中值定理、柯西中值定理和泰勒定理.6. 洛必达(L’Hospital)法则与求未定式极限.7. 函数的极值、函数单调性、函数图形的凹凸性、拐点及渐近线(水平、铅直和斜渐近线)、函数图形的描绘.8. 函数最大值和最小值及其简单应用.9. 弧微分、曲率、曲率半径.三、一元函数积分学1.原函数和不定积分的概念.2. 不定积分的基本性质、基本积分公式.3. 定积分的概念和基本性质、定积分中值定理、变上限定积分确定的函数及其导数、牛顿-莱布尼茨(Newton-Leibniz )公式.4. 不定积分和定积分的换元积分法与分部积分法.5. 有理函数、三角函数的有理式和简单无理函数的积分.6. 广义积分.7. 定积分的应用:平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力及函数的平均值.四.常微分方程1. 常微分方程的基本概念:微分方程及其解、阶、通解、初始条件和特解等.2. 变量可分离的微分方程、齐次微分方程、一阶线性微分方程、伯努利(Bernoulli )方程、全微分方程.3. 可用简单的变量代换求解的某些微分方程、可降阶的高阶微分方程:),()n (x f y =),,(y x f y '='' ),(y y f y '=''.4. 线性微分方程解的性质及解的结构定理.5. 二阶常系数齐次线性微分方程、高于二阶的某些常系数齐次线性微分方程.6. 简单的二阶常系数非齐次线性微分方程:自由项为多项式、指数函数、正弦函数、余弦函数,以及它们的和与积7. 欧拉(Euler )方程.8. 微分方程的简单应用五、向量代数和空间解析几何1. 向量的概念、向量的线性运算、向量的数量积和向量积、向量的混合积.2. 两向量垂直、平行的条件、两向量的夹角.3. 向量的坐标表达式及其运算、单位向量、方向数与方向余弦.4. 曲面方程和空间曲线方程的概念、平面方程、直线方程.5. 平面与平面、平面与直线、直线与直线的夹角以及平行、垂直的条件、点到平面和点到直线的距离.6. 球面、母线平行于坐标轴的柱面、旋转轴为坐标轴的旋转曲面的方程、常用的二次曲面方程及其图形.7. 空间曲线的参数方程和一般方程、空间曲线在坐标面上的投影曲线方程.六、多元函数微分学1. 多元函数的概念、二元函数的几何意义.2. 二元函数的极限和连续的概念、有界闭区域上多元连续函数的性质.3. 多元函数偏导数和全微分、全微分存在的必要条件和充分条件.4. 多元复合函数、隐函数的求导法.5. 二阶偏导数、方向导数和梯度.6. 空间曲线的切线和法平面、曲面的切平面和法线.7. 二元函数的二阶泰勒公式.8. 多元函数极值和条件极值、拉格朗日乘数法、多元函数的最大值、最小值及其简单应用.七、多元函数积分学1.二重积分和三重积分的概念及性质、二重积分的计算(直角坐标、极坐标)、三重积分的计算(直角坐标、柱面坐标、球面坐标).2.两类曲线积分的概念、性质及计算、两类曲线积分的关系.3.格林(Green)公式、平面曲线积分与路径无关的条件、已知二元函数全微分求原函数.4.两类曲面积分的概念、性质及计算、两类曲面积分的关系.5.高斯(Gauss)公式、斯托克斯(Stokes)公式、散度和旋度的概念及计算.6.重积分、曲线积分和曲面积分的应用(平面图形的面积、立体图形的体积、曲面面积、弧长、质量、质心、转动惯量、引力、功及流量等)八、无穷级数1.常数项级数的收敛与发散、收敛级数的和、级数的基本性质与收敛的必要条件.2.几何级数与p级数及其收敛性、正项级数收敛性的判别法、交错级数与莱布尼茨(Leibniz)判别法.3.任意项级数的绝对收敛与条件收敛.4.函数项级数的收敛域与和函数的概念.5.幂级数及其收敛半径、收敛区间(指开区间)、收敛域与和函数.6.幂级数在其收敛区间内的基本性质(和函数的连续性、逐项求导和逐项积分)、简单幂级数的和函数的求法.7.初等函数的幂级数展开式.8.函数的傅里叶(Fourier)系数与傅里叶级数、狄利克雷(Dirichlei)定理、函数在[-l,l]上的傅里叶级数、函数在[0,l]上的正弦级数和余弦级数。
