logistic模型和最小二乘资料讲解
logistic模型

Logistic模型简介Logistic回归模型是一种常用的分类模型,用于对二分类问题进行建模和预测。
该模型基于Logistic函数,将连续的输出映射到了概率值,可以方便地用于分类任务。
基本原理Logistic函数Logistic函数,也被称为Sigmoid函数,是一种常见的激活函数,公式如下:$$ f(x) = \\frac{1}{1 + e^{-x}} $$Logistic函数具有如下特点: - 输出范围在0到1之间,可以看作是一个概率值;- 在x趋近于正无穷时,输出趋近于1,在x趋近于负无穷时,输出趋近于0; - 当x=0时,输出值为0.5,此时分类为不确定。
Logistic回归模型Logistic回归模型通过将Logistic函数作用于线性回归模型的输出,将连续的输出转换为0和1的概率值。
模型的数学表达式如下:$$ P(y=1|x; w) = \\frac{1}{1 + e^{-(w_0 + w_1x)}} $$其中,P(P=1|P;P)表示在给定输入x的情况下,预测y=1的概率;P0和P1是模型的参数,通过训练数据进行估计。
对于二分类问题,可以将上式进一步扩展为:$$ P(y=c|x; w) = \\frac{e^{w_c \\cdot x}}{\\sum_{k=1}^{C} e^{w_k \\cdot x}} $$其中,C为类别数量,P P为类别c的参数,P为输入。
模型训练Logistic回归模型的训练目标是最大化似然函数。
似然函数描述了模型参数在给定训练样本的情况下的概率,即给定参数值时样本出现的可能性。
似然函数的数学表达式如下:$$ L(w) = \\prod_{i=1}^{N} P(y_i|x_i; w) $$其中,P P为第i个样本的真实标签,P P为其对应的特征,P为总样本数量。
为了计算方便,常常使用对数似然函数,即:$$ l(w) = \\log(L(w)) = \\sum_{i=1}^{N} \\log(P(y_i|x_i; w)) $$训练时使用梯度下降法最小化对数似然函数,通过迭代更新参数P,直至收敛为止。
logistic回归模型

Logistic回归模型
• 列联表中的数据是以概率的形式把属性变量联系 起来的,而概率p的取值在0与1之间,因此,要把
概率 p (x)与 x 之间直接建立起函数关系是不合
适的。即 (x) x
Logistic回归模型
• 因此,人们通常把p的某个函数f(p)假设为变量的 函数形式,取 f ( p) ln (x) ln p
1 (x) 1 p
• 称之为logit函数,也叫逻辑斯蒂变换。 • 因此,逻辑斯蒂变换是取列联表中优势的对数。
当概率在0-1取值时,Logit可以取任意实数,避免 了线性概率模型的结构缺陷。
Logistic回归模型
假设响应变量Y是二分变量,令 p P(Y 1) ,影响Y
的因素有k个 x1, xk,则称:
多项logit模型
• 前面讨论的logit模型为二分数据的情况,有时候 响应变量有可能取三个或更多值,即多类别的属 性变量。
• 根据响应变量类型的不同,分两种情况:
–响应变量为定性名义变量; –响应变量为定性有序变量;
• 当名义响应变量有多个类别时,多项logit模型应 采取把每个类别与一个基线类别配成对,通常取 最后一类为参照,称为基线-类别logit.
• 为二分数据的逻辑斯ln 1蒂pp回归g(模x1,型,,xk简) 称逻辑斯蒂 回归模型。其中的k个因素称为逻辑斯蒂回归模型 的协变量。
• 最重要的逻辑斯蒂回归模型是logistic线性回归模 型,多元logit模型的形式为:
ln
p 1 p
0
1x1
k xk
Logistic回归模型
• 其中,0, 1, , k 是待估参数。根据上式可以得到
多项logit模型
Logistic回归模型

Logistic 回归模型1 Logistic 回归模型的基本知识 1.1 Logistic 模型简介主要应用在研究某些现象发生的概率p ,比如股票涨还是跌,公司成功或失败的概率,以及讨论概率p 与那些因素有关。
显然作为概率值,一定有10≤≤p ,因此很难用线性模型描述概率p 与自变量的关系,另外如果p 接近两个极端值,此时一般方法难以较好地反映p 的微小变化。
为此在构建p 与自变量关系的模型时,变换一下思路,不直接研究p ,而是研究p 的一个严格单调函数)(p G ,并要求)(p G 在p 接近两端值时对其微小变化很敏感。
于是Logit 变换被提出来:ppp Logit -=1ln)( (1)其中当p 从10→时,)(p Logit 从+∞→∞-,这个变化范围在模型数据处理上带来很大的方便,解决了上述面临的难题。
另外从函数的变形可得如下等价的公式:XT X T T eep X ppp Logit βββ+=⇒=-=11ln)( (2)模型(2)的基本要求是,因变量(y )是个二元变量,仅取0或1两个值,而因变量取1的概率)|1(X y P =就是模型要研究的对象。
而T k x x x X ),,,,1(21 =,其中i x 表示影响y 的第i 个因素,它可以是定性变量也可以是定量变量,Tk ),,,(10ββββ =。
为此模型(2)可以表述成:kx k x kxk x k k ee p x x p p βββββββββ+++++++=⇒+++=- 11011011011ln (3)显然p y E =)(,故上述模型表明)(1)(ln y E y E -是k x x x ,,,21 的线性函数。
此时我们称满足上面条件的回归方程为Logistic 线性回归。
Logistic 线性回归的主要问题是不能用普通的回归方式来分析模型,一方面离散变量的误差形式服从伯努利分布而非正态分布,即没有正态性假设前提;二是二值变量方差不是常数,有异方差性。
最小二乘法分类

最小二乘法分类最小二乘法(Least Squares Method)是一种常用的参数估计方法,用于寻找一个函数模型的最佳拟合参数,使得模型的预测值与观测值的残差平方和最小化。
这种方法最早由高斯提出,并被广泛应用于统计学和计算机科学等领域。
本文将介绍最小二乘法的基本原理、应用场景以及相关的算法和评估指标。
一、基本原理:最小二乘法用于求解形如y = f(x;θ) 的函数模型的参数θ,其中y是观测值,x是自变量,f是函数模型。
最小二乘法的目标是找到最佳的参数θ,使得模型的预测值与实际观测值之间的残差平方和最小化。
具体步骤如下:1. 定义函数模型:根据具体问题,选择适当的函数模型,如线性模型、多项式模型、指数模型等。
2. 表达目标函数:根据函数模型和参数θ,将目标函数表达为关于θ的函数形式。
3. 定义损失函数:通常采用残差的平方和作为损失函数,即Loss = Σ(y_i - f(x_i;θ))^2 。
4. 求解参数θ:通过最小化损失函数,即求解使得∂Loss/∂θ = 0 的参数θ。
5. 参数估计:根据求解得到的参数θ,即可获得最佳的函数模型。
二、应用场景:最小二乘法在各个领域都有广泛的应用,以下是一些常见的应用场景:1. 线性回归:最小二乘法用于拟合线性回归模型,求解自变量与因变量之间的关系。
2. 特征选择:最小二乘法可用于特征选择,筛选对目标变量影响最大的特征。
3. 数据压缩:通过最小二乘法可以估计出一个低维子空间,将高维数据进行压缩。
4. 图像处理:最小二乘法可用于图像去噪、图像恢复等问题,如使用低秩矩阵模型对图像进行恢复。
5. 信号处理:最小二乘法可用于信号滤波、信号恢复等问题,如基于 DCT 的音频和图像压缩。
三、算法与评估指标:1. 最小二乘法的数值解:在实际应用中,最小二乘法的数值解可以通过各种数值优化算法来求解,包括梯度下降法、牛顿法、共轭梯度法等。
2. 算法评估指标:常用的评估指标包括残差平方和(Residual Sum of Squares, RSS)、均方误差(Mean Square Error, MSE)以及决定系数(Coefficient of Determination, R^2)等。
logistic数学模型

logistic数学模型Logistic数学模型是一种常用的回归模型,用于预测二元变量的概率。
它在很多领域中都有广泛的应用,例如医学、金融、市场营销等。
这个模型的基本形式是一个S形曲线,也称为sigmoid函数,它的输出值范围在0到1之间。
在Logistic模型中,我们通过输入变量的线性组合来估计输出变量的概率。
具体而言,我们将输入变量的线性组合作为指数函数的参数,然后将指数函数的结果转化为概率值。
Logistic数学模型有很多优点。
首先,它可以处理二元变量的概率预测,这在很多实际问题中非常有用。
其次,它具有很好的解释性,我们可以通过模型的系数来解释不同变量对输出变量的影响程度。
此外,由于sigmoid函数的特性,Logistic模型对异常值具有一定的鲁棒性。
在应用Logistic数学模型时,我们通常需要进行模型拟合和参数估计。
模型拟合是指通过给定的数据集,找到最适合的模型参数,使得模型的预测结果与实际观测值尽可能接近。
参数估计可以使用最大似然估计等方法来进行。
在实际应用中,我们还需要评估Logistic模型的性能。
常用的评估指标包括准确率、精确率、召回率、F1值等。
这些指标可以帮助我们评估模型的预测能力,并根据需要进行模型调整和改进。
除了基本的Logistic数学模型,还有一些扩展模型可以用于处理更复杂的问题。
例如,多项Logistic回归模型可以用于处理多类别变量的概率预测。
此外,Logistic模型还可以与其他模型结合,形成混合模型,以提高预测性能。
尽管Logistic数学模型在很多领域中都有广泛的应用,但它也有一些局限性。
首先,Logistic模型假设自变量和因变量之间存在线性关系,这在一些实际问题中可能不成立。
其次,Logistic模型对于异常值较敏感,需要进行异常值处理。
此外,当自变量之间存在多重共线性时,Logistic模型的解释性会受到影响。
Logistic数学模型是一种常用的回归模型,用于预测二元变量的概率。
Logistic回归模型基本知识

Logistic 回归模型1 Logistic 回归模型的基本知识 1.1 Logistic 模型简介主要应用在研究某些现象发生的概率p ,比如股票涨还是跌,公司成功或失败的概率,以及讨论概率p 与那些因素有关。
显然作为概率值,一定有10≤≤p ,因此很难用线性模型描述概率p 与自变量的关系,另外如果p 接近两个极端值,此时一般方法难以较好地反映p 的微小变化。
为此在构建p 与自变量关系的模型时,变换一下思路,不直接研究p ,而是研究p 的一个严格单调函数)(p G ,并要求)(p G 在p 接近两端值时对其微小变化很敏感。
于是Logit 变换被提出来:ppp Logit -=1ln)( (1)其中当p 从10→时,)(p Logit 从+∞→∞-,这个变化范围在模型数据处理上带来很大的方便,解决了上述面临的难题。
另外从函数的变形可得如下等价的公式:XT XT T ee p Xppp Logit βββ+=⇒=-=11ln )( (2)模型(2)的基本要求是,因变量(y )是个二元变量,仅取0或1两个值,而因变量取1的概率)|1(X y P =就是模型要研究的对象。
而Tk x x x X ),,,,1(21 =,其中i x 表示影响y 的第i 个因素,它可以是定性变量也可以是定量变量,Tk ),,,(10ββββ =。
为此模型(2)可以表述成:kx k x k x k x kk eep x x pp βββββββββ+++++++=⇒+++=- 11011011011ln (3)显然p y E =)(,故上述模型表明)(1)(lny E y E -是k x x x ,,,21 的线性函数。
此时我们称满足上面条件的回归方程为Logistic 线性回归。
Logistic 线性回归的主要问题是不能用普通的回归方式来分析模型,一方面离散变量的误差形式服从伯努利分布而非正态分布,即没有正态性假设前提;二是二值变量方差不是常数,有异方差性。
最小二乘算法原理

最小二乘算法原理最小二乘算法是一种用来求解最优拟合直线或曲线的方法。
其原理是通过最小化实际观测值与拟合值之间的差异平方和,来找到最合适的模型参数。
假设我们有n个数据点,其中每个数据点由自变量x和因变量y组成。
最小二乘算法的目标是找到一条拟合直线(或曲线),使得所有数据点到该直线(或曲线)的距离之和最小。
首先,我们需要定义一个模型函数,表示拟合直线(或曲线)的形式。
例如,对于线性函数来说,模型函数可以表示为:y= a + bx,其中a和b是需要求解的模型参数。
然后,我们计算每个数据点与模型函数的差异,记为残差或误差。
对于线性函数来说,残差可以表示为:ε = y - (a + bx)。
接下来,我们计算残差的平方和(Sum of Squared Residuals,SSR),即将每个残差平方后求和。
SSR表示了实际观测值与拟合值之间的整体偏差。
最小二乘算法的关键步骤是,通过求解模型参数的偏导数并令其等于零,来找到使得SSR最小的模型参数。
对于线性函数来说,我们可以通过求解下面的正规方程组来得到最优参数的估计值:∂SSR/∂a = -2Σ(y - (a + bx)) = 0∂SSR/∂b = -2Σx(y - (a + bx)) = 0将上述方程化简后,我们就可以得到最优参数的估计值:a = (Σy - bΣx) / nb = (nΣxy - ΣxΣy) / (nΣx^2 - (Σx)^2)其中,Σ表示对所有数据点求和,n表示数据点的个数。
通过最小二乘算法,我们可以得到拟合直线(或曲线)的最优参数估计值,从而使得实际观测值与拟合值之间的差异最小化。
最小二乘算法被广泛应用于数据分析、回归分析、信号处理等领域。
Logistic回归模型 (2)

欢迎共阅Logistic 回归模型1 Logistic 回归模型的基本知识 1.1 Logistic 模型简介主要应用在研究某些现象发生的概率p ,比如股票涨还是跌,公司成功或失败的概率,以及讨论概率p 与那些因素有关。
显然作为概率值,一定有10≤≤p ,因此很难用线性模型描述概率p 与自变量的关系,另外如果p 接近两个极端值,此时一般方法难以较好地反映p究p Logit (1) (2)1的概率i 个(3)差形式服从伯努利分布而非正态分布,即没有正态性假设前提;二是二值变量方差不是常数,有异方差性。
不同于多元线性回归的最小二乘估计法则(残差平方和最小),Logistic 变换的非线性特征采用极大似然估计的方法寻求最佳的回归系数。
因此评价模型的拟合度的标准变为似然值而非离差平方和。
定义1 称事件发生与不发生的概率比为 优势比(比数比 odds ratio 简称OR),形式上表示为OR=kx k x e pp βββ+++=- 1101 (4)定义2 Logistic 回归模型是通过极大似然估计法得到的,故模型好坏的评价准则有似然值来表征,称-2ˆln ()L β为估计值βˆ的拟合似然度,该值越小越好,如果模型完全拟合,则似然值ˆ()L β为1,而拟合似然度达到最小,值为0。
其中ˆ()lnL β表示βˆ的对数似然函数值。
定义3 记)ˆ(βVar 为估计值βˆ的方差-协方差矩阵,21)]ˆ([)ˆ(ββVar S =为βˆ的标准差矩阵,则称k i S w iii i ,,2,1,ˆ[2 ==β (5)为iβˆ (6) 1.22 2.1因变量(反应变量)分为两类,取值有两种,设事件发生记为y=1,不发生记为 y=0,设自变量T k x x x X ),,,(21 =是分组数据,取有限的几个值;研究事件发生的概率)|1(X y P =与自变量X 的关系,其Logistic 回归方程为:k k x x X y P X y P βββ+++=== 110)|0()|1(ln 或 kx k x kxk x ee X y P ββββββ+++++++== 1101101)|1( 例2.1.1 分组数据[1] 在一次住房展销会上,与房地产商签订初步购房意向书的有n=325人,在随后的3个月时间内,只有一部分顾客购买了房屋。
数学建模模型常用的四大模型及对应算法原理总结

数学建模模型常用的四大模型及对应算法原理总结四大模型对应算法原理及案例使用教程:一、优化模型线性规划线性回归是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,在线性回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。
如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。
案例实操非线性规划如果目标函数或者约束条件中至少有一个是非线性函数时的最优化问题叫非线性规划问题,是求解目标函数或约束条件中有一个或几个非线性函数的最优化问题的方法。
建立非线性规划模型首先要选定适当的目标变量和决策变量,并建立起目标变量与决策变量之间的函数关系,即目标函数。
然后将各种限制条件加以抽象,得出决策变量应满足的一些等式或不等式,即约束条件。
整数规划整数规划分为两类:一类为纯整数规划,记为PIP,它要求问题中的全部变量都取整数;另一类是混合整数规划,记之为MIP,它的某些变量只能取整数,而其他变量则为连续变量。
整数规划的特殊情况是0-1规划,其变量只取0或者1。
多目标规划求解多目标规划的方法大体上有以下几种:一种是化多为少的方法,即把多目标化为比较容易求解的单目标,如主要目标法、线性加权法、理想点法等;另一种叫分层序列法,即把目标按其重要性给出一个序列,每次都在前一目标最优解集内求下一个目标最优解,直到求出共同的最优解。
目标规划目标规划是一种用来进行含有单目标和多目标的决策分析的数学规划方法,是线性规划的特殊类型。
目标规划的一般模型如下:设xj是目标规划的决策变量,共有m个约束条件是刚性约束,可能是等式约束,也可能是不等式约束。
设有l个柔性目标约束条件,其目标规划约束的偏差为d+, d-。
设有q个优先级别,分别为P1, P2, …, Pq。
在同一个优先级Pk中,有不同的权重,分别记为[插图], [插图](j=1,2, …, l)。
logistic模型最小二乘法matlab代码

logistic模型最小二乘法matlab代码逻辑回归模型是一种用于解决分类问题的方法,它可以通过对样本特征进行适当的处理以预测离散类型数据(如0和1)的概率。
在这篇文章中,我们将展示如何使用最小二乘法来训练逻辑回归模型。
具体实现采用MATLAB进行编程。
1. 数据准备首先,我们需要准备有标签的数据集。
在这里,我们将使用一个简单的二元分类数据集来展示。
数据集是一个csv文件格式,包含两个列:x和y,以及一个类别列ones和zeros。
2. 数据预处理在创建逻辑回归模型之前,我们应该对数据进行一些预处理,这些处理包括:特征缩放、特征映射和特征提取。
我们在这里展示如何通过MATLAB实现特征缩放。
假设我们已经加载了数据集,并将其保存在一个名为data的矩阵中。
我们可以通过以下代码对数据进行处理:% scale features to 0-1 rangedata(:,1) = (data(:,1) - min(data(:,1))) / (max(data(:,1)) - min(data(:,1)));data(:,2) = (data(:,2) - min(data(:,2))) / (max(data(:,2)) - min(data(:,2)));3. 实现逻辑回归模型在这一步中,我们将展示如何通过最小二乘法来训练逻辑回归模型,并使用MATLAB实现。
我们首先定义模型参数矩阵theta和目标变量y,其中目标变量y可以是任意二进制值(如0或1)。
然后,我们使用最小二乘法估计theta的值。
% initialize model parameterstheta = zeros(size(data,2),1);y = data(:,3);% estimate model parameters using least squarestheta = inv(data'*data) * data' * y;4. 预测新的样本完成模型训练之后,我们可以使用它来预测新的样本。
logistic模型原理

logistic模型原理什么是logistic模型?Logistic模型是一种用于分类问题的数学模型,也被称为逻辑回归模型。
它是一种广义线性模型,适用于二分类问题,即输出结果只有两个类别。
通过将特征进行适当的映射和转换,logistic模型可以将输入特征和输出结果之间的关系建模,并根据特征的变化预测输出结果所属的类别。
Logistic模型的原理如下:1. 建立假设函数:Logistic模型的假设函数基于sigmoid函数,形式为:hθ(x) = g(θ^T * x)其中hθ(x)表示预测的输出结果,g表示sigmoid函数,θ是特征的权重参数,x是输入特征向量。
2. 定义sigmoid函数:Sigmoid函数的表达式为:g(z) = 1 / (1 + e^(-z))sigmoid函数的值域在[0, 1]之间,可以将实数映射到概率值上。
3. 构建逻辑回归的损失函数:逻辑回归使用最大似然估计来估计模型参数。
假设训练样本的输出结果是二分类的,标记为0或1。
对于给定的输入特征x,其输出结果为y∈{0,1}。
令p(y=1 x)表示给定特征x的情况下,输出结果为1的概率。
根据最大似然估计,似然函数为:L(θ) = Π(p(yi=1 xi)^yi * (1-p(yi=1 xi))^(1-yi))对上式取对数,可以得到对数似然函数:l(θ) = Σ(yi * log(p(yi=1 xi)) + (1-yi) * log(1-p(yi=1 xi)))其中yi表示真实输出结果,p(yi=1 xi)表示根据假设函数预测输出结果为1的概率。
为了得到模型参数θ,我们需要最小化损失函数J(θ):J(θ) = -1/m * l(θ)4. 求解最优参数:通过梯度下降等优化算法,可以求解最优的模型参数θ,使得损失函数最小化。
5. 利用模型进行预测:得到最优参数θ后,通过假设函数hθ(x)可以预测输入特征x对应的输出结果。
这就是Logistic模型的基本原理和步骤。
logistic模型

logistic模型概述logistic模型是一种常用的统计模型,用于分析二分类问题。
它通过将线性模型的输出映射到[0,1]区间内的概率值,从而得到分类结果。
logistic模型在各个领域都有广泛的应用,如金融风险评估、医学诊断等。
原理logistic模型基于logistic函数,也称为sigmoid函数。
该函数的形式为:f(x) = 1 / (1 + e^(-x))其中,x为线性模型的输出。
logistic函数的特点是将任意实数映射到[0,1]区间内,且在x等于0时取值为0.5。
这使得logistic模型的输出可以理解为事件发生的概率。
参数估计logistic模型的参数估计一般采用最大似然估计法。
最大似然估计法的基本思想是找到使得已观察到的数据出现的可能性最大的参数值。
对于logistic模型而言,参数估计可以通过优化算法来实现,如梯度下降、牛顿法等。
模型评估针对logistic模型的评估可以采用多种指标,常见的包括准确率、精确率、召回率和F1值等。
准确率是指模型预测正确的样本占总样本数的比例;精确率是指模型预测为正类的样本中实际为正类的比例;召回率是指实际为正类的样本中被模型预测为正类的比例;F1值是精确率和召回率的调和平均数。
示例我们以一个虚拟的购买预测模型为例来演示logistic模型的应用。
假设我们有一个电商网站的用户行为数据,包括用户的浏览历史、收藏商品等信息。
我们希望利用这些数据来预测用户是否会购买某一商品。
首先,我们需要将用户的行为数据转化为特征。
比如,我们可以将用户的浏览次数、购物车商品数量等作为特征变量。
然后,我们将用户的购买行为作为目标变量。
接下来,我们使用logistic模型进行训练,并得到模型的参数。
在模型训练完成后,我们可以使用模型来预测新样本的购买概率。
根据阈值的设定,我们可以将概率大于等于阈值的样本划分为正类,将概率小于阈值的样本划分为负类。
这样,我们就可以得到对新样本的购买预测结果。
最小二乘法的原理及证明

最小二乘法的原理及证明最小二乘法是一种常用的数据拟合方法,它的本质是通过寻找最小化残差平方和的参数组合进行数据拟合。
在现实生活中,很多实际问题都可以通过最小二乘法来求解,如线性回归、曲线拟合、方程求解等。
本文将介绍最小二乘法的原理及证明。
一、最小二乘法的原理最小二乘法是一种基于误差最小化的思想进行模型参数求解的方法。
对于含有n个数据点的模型,其最小二乘法的表示形式为:$min[\sum_{i=1}^n(y_i-f(x_i))^2]$其中,$y_i$为第i个数据点的观测值,$f(x_i)$为模型在$x_i$处的预测值。
最小二乘法的目的是寻找一个最优的模型参数集合,使得预测值与观测值之间的误差平方和最小。
以线性回归为例,线性回归模型的基本形式为:$y=\beta_0+\beta_1x+\epsilon$其中,$\beta_0$和$\beta_1$为线性回归的系数,$\epsilon$为误差项。
通过最小二乘法,我们需要求解$\beta_0$和$\beta_1$,使得预测值与真实值之间的残差平方和最小。
在实际应用中,最小二乘法可以通过求解模型参数的偏导数,进而得到参数的估计值。
同时,最小二乘法还可以通过矩阵运算的形式进行求解,这种方法称为矩阵最小二乘法。
二、最小二乘法的证明最小二乘法的原理可以通过数学证明来得到。
在数学推导中,我们需要利用概率论和统计学的相关知识。
1、最小二乘法的基本假设首先,我们需要对最小二乘法做出一些假设。
最小二乘法的假设包括:(1)数据点满足线性关系;(2)误差项满足高斯分布;(3)误差项具有同方差性;(4)误差项之间相互独立。
在这些假设的基础上,我们可以得出以$X$为自变量,$Y$为因变量的线性模型:$Y=\beta_0+\beta_1X+\epsilon$其中,$\beta_0$和$\beta_1$为线性模型的系数,$\epsilon$为误差项。
我们需要利用概率论和统计学的方法,通过参数的似然函数来求解模型的系数。
logistic回归模型

logistic回归模型一、模型简介在实际分析中,有时候因变量为分类变量,例如阴性阳性、性别、血型等,此时使用线性回归模型进行拟合会出现问题。
因此,我们需要找出其他解决思路,那就是logit变换(逻辑变换)。
逻辑变换将某种结果出现的概率和不出现的概率之比称为优势比P/(1-P),并取其对数,使之与自变量之间呈线性关系,从而解决了线性回归模型无法保证因变量只有两个取值的问题。
经过逻辑变换的线性模型称为logistic回归模型(逻辑回归模型),属于广义线性回归模型的范畴。
逻辑回归可以预测某个结果出现的概率,对因变量进行变换的方法很多,并不只有逻辑变换一种。
二、模型估计方法逻辑回归不能使用普通最小二乘估计,而使用极大似然估计或迭代重加权最小二乘法IRLS(XXX)。
使用极大似然估计的好处是,这是一种概率论在参数估计中的应用,正好和我们对因变量的概率预测相符合。
极大似然估计基于这样的思想:如果某些参数能使这个样本出现的概率最大,那就把这个参数作为估计的真实值。
三、优势比odds根据因变量的取值不同,逻辑回归可以分为四种:二分类逻辑回归、有序多分类逻辑回归、无序多分类逻辑回归、配对逻辑回归。
优势比odds是逻辑回归中的一个重要概念,指某种结果出现的概率和不出现的概率之比,通过逻辑变换,优势比可以被用作因变量进行拟合。
对于一些特殊情况,还需具体问题具体分析,不能一味地使用逻辑变换。
在二分类逻辑回归中,自变量可以是连续变量、二分类变量和多分类变量。
对于多分类变量,需要引入哑变量进行处理。
哑变量也称为虚拟变量,取值通常为0或1,代表参照分类和比较分类。
需要注意避免共线性,定义k-1个哑变量(包含截距)或k个哑变量(不包含截距)。
有序多分类变量指各因变量之间存在等级或程度差异。
对于因变量为有序分类变量的数据,可以通过拟合因变量个数-1个的逻辑回归模型,称为累积逻辑模型来进行。
这种方式依次将因变量按不同的取值水平分割成若干个二分类变量,然后再依次拟合二分类逻辑回归模型。
普通最小二乘法和logit模型

普通最小二乘法(Ordinary Least Squares, OLS)和Logit模型是统计学中常用的两种回归分析方法。
它们分别适用于不同的数据类型和分析目的,在实际研究中应用广泛。
一、普通最小二乘法(OLS)普通最小二乘法是回归分析中最基本的方法之一,它的主要思想是通过最小化观测数据与回归模型预测值之间的残差平方和来确定模型的参数估计值。
简而言之,OLS试图找到一条最能拟合数据的线,使得观测值与模型预测值的误差平方和最小。
在使用OLS进行回归分析时,需要满足一些假设前提。
数据应该呈现线性关系。
误差项应该是独立同分布的。
自变量之间不应该存在多重共线性。
只有在这些假设成立的情况下,OLS才能够给出有效的参数估计和显著性检验结果。
二、Logit模型Logit模型是一种广义线性模型,它常用于处理二分类问题,例如判断一个人是否患有某种疾病、是否购物某种产品等。
Logit模型的特点是能够将输出值限定在0和1之间,因此非常适合处理概率问题。
在Logit模型中,因变量通常用二项分布,自变量经过线性组合后通过逻辑函数(Logistic Function)转化为概率。
Logistic Function的形式为:\[p(x)=\frac{1}{1+e^{-z}}\]其中,\(p(x)\)表示概率,\(z\)为线性组合函数。
通过Logit模型可以得到各个自变量对于因变量的影响程度,这对于解释变量间的相互作用关系非常有用。
在实际应用中,Logit模型通常通过最大似然估计来确定模型参数。
使用Logit模型时,需要注意数据的合理性和模型的拟合度,以免出现过拟合或欠拟合的情况。
三、两种方法的比较1. 数据类型适用性:OLS适用于连续型数据的回归分析,而Logit模型适用于二分类问题的概率预测。
2. 假设前提:OLS对数据的要求相对较为严格,需要确保数据线性相关、误差项独立同分布等假设成立;而Logit模型对数据类型的要求相对较小,更适用于实际应用场景。
最小二乘法

最小二乘法最小二乘法(Least Squares Method)是一种统计学上常用的参数估计方法,通过最小化观测数据与理论模型之间的误差的平方和,来估计模型的参数。
在统计学和数学中,最小二乘法被广泛应用于曲线拟合、回归分析、数据处理以及信号处理等领域。
最小二乘法的基本思想是,通过找到可以使得各观测数据与理论模型预测的数据之间的差异最小的参数估计值,从而得到最佳的拟合结果。
它是一种数学上比较成熟且有效的方法,可以用来解决具有一定误差的线性和非线性函数拟合问题。
在应用最小二乘法时,首先需要建立数学模型来描述观测数据与自变量之间的关系。
这个数学模型可以是线性的,也可以是非线性的,根据实际问题的特点来确定。
然后,根据观测数据和数学模型,利用最小二乘法的原理来求解模型的参数估计值。
最小二乘法的基本步骤如下:1. 建立数学模型:通过分析问题的背景和要求,确定观测数据与自变量之间的关系,并建立数学模型。
2. 确定误差函数:定义误差函数,它是观测数据与数学模型之间的差异度量。
3. 最小化误差函数:通过最小化误差函数,即求解误差函数的导数为0的参数估计值,来得到最佳的模型拟合结果。
4. 评估拟合结果:通过各种统计指标和图示分析来评估最小二乘拟合的效果,并对结果进行解释和验证。
最小二乘法的优点在于它是一种数学上比较简单和直观的方法,并且在实际应用中得到了广泛的应用。
它能够充分考虑观测数据的误差,通过最小化误差的平方和来估计模型的参数,从而得到较为可靠的拟合结果。
最小二乘法的应用非常广泛,涵盖了许多学科领域,如物理学、经济学、工程学、生物学和地球科学等。
在曲线拟合中,最小二乘法可以用来拟合直线、曲线和曲面等;在回归分析中,最小二乘法可以用来建立回归模型,并进行参数估计和显著性检验;在数据处理中,最小二乘法可以用来进行信号滤波和数据平滑等。
总之,最小二乘法是一种重要的数学和统计方法,在许多实际问题中起着重要的作用。
它不仅可以用来拟合曲线和回归分析,还可以应用于信号处理、数据处理和参数估计等领域。
Logistic回归模型的参数估计为什么不能采用最小二乘法?

Logistic回归模型的参数估计为什么不能采⽤最⼩⼆乘法? logistic回归模型的参数估计问题,是可以⽤最⼩⼆乘⽅法的思想进⾏求解的,但和经典的(或者说⽤在经典线性回归的参数估计问题)最⼩⼆乘法不同,是⽤的是“迭代重加权最⼩⼆乘法”(IRLS, Iteratively Reweighted Least Squares)。
本质上不能使⽤经典的最⼩⼆乘法的原因在于,logistic回归模型的参数估计问题不能“⽅便地”定义“误差”或者“残差”。
下⾯是对经典线性回归问题和logistic回归问题的⼀些讨论。
(1)最⼩⼆乘/最⼩⼆乘法、最⼩⼆乘估计和极⼤似然估计的区别 最⼩⼆乘/最⼩⼆乘法可以看成是⼀种朴素的思想,即如果某种差异可以量化为实数,那么我们就可以(⾃然地)把这些差异的平⽅相加,将这个和作为⼀种⽬标函数。
我记得我们⾼代有节课专门讲过“⼆乘”的矩阵形式,以及相关的“最⼩”这⼀优化⽬标的矩阵运算等等。
最⼆乘估计是指⽤最⼩⼆乘法对统计模型中的参数进⾏估计的估计⽅法。
除了最⼩⼆乘估计,还有常⽤的极⼤似然估计、矩估计等参数估计的⽅法。
对经典线性回归模型的参数估计来说,最⼩⼆乘估计和极⼤似然估计的结果是等价的,换句话说,对于其他模型,这种等价性就可能不成⽴。
对于logistic回归模型来说,极⼤似然估计是没有解析解(closed form solution)的。
最⼩⼆乘估计和极⼤似然估计的不同在于优化的⽬标函数不同。
最⼩⼆乘估计因为是⽤的最⼩⼆乘法,⽬标函数就是前⾯提到的那种“⾃然地”对“误差”或者“残差”的处理⽅式(这⾥“误差”和“残差”之所以加引号,是因为我们为了理解⽅便赋予了操作对象“某种差异”实际的意义); 极⼤似然估计的⽬标函数是似然函数。
可见,前者的⽬标函数依赖于我们对“误差”的选取,⽽后者依赖于数据的具体概率分布。
最⼩⼆乘估计有很多良好的性质,这些性质是不依赖于具体概率分布的,仅需要满⾜Gauss-Markov假设即可。
logistic模型和最小二乘
记误差
ri yi f ( x, ti ),
r (r1, r2 ,, rn )T
确定x的方法: 求x使得误差平方和
rT r ( yi f ( x, ti ))2
最小
MATLAB最小二乘拟合
• 命令 lsqcurvefit • 基本用法 [x,resnorm,res]=lsqcurvefit(@f,x0,t,y,lb,ub) 输入:@f =f(x,t) x0=参数初值 t=自变量向量 y=函数值向量 lb ub =参数的上下界 输出 x=参数估计值 resnom=<r, r>(误差平方和) res= r(误差向量)
r=0.2557, xm=392.1 专家估计
阻滞增长模型(Logistic模型)
模型检验
用模型计算2000年美国人口,与实际数据比较
x(2000 x(1990 x x(1990 rx(1990 1 x(1990 / xm ] ) ) ) )[ )Βιβλιοθήκη x(2000 274.5 )
f=x(1)/(1+(x(1)/3.9-1)*exp(-x(2)*t)); 2. 和前面相同,只要将 myexp 换为mylogistic
LOGSTIC模型结果
两个模型结果比较
线性化后再参数估计
对指数模型
y x0 e
rt
取对数后, ln y ln x0 rt 对 ln x0 , r的估计可以采用线性回 归
x(t ) x0 e
rt
x(t ) x0 (e ) x0 (1 r )
r t
t
随着时间增加,人口按指数规律无限增长
指数增长模型的应用及局限性
• 与19世纪以前欧洲一些地区人口统计数据吻合 • 适用于19世纪后迁往加拿大的欧洲移民后代
logistic模型原理

logistic模型原理Logistic模型是一种用于建立二分类问题的概率模型,它是在广义线性模型(Generalized Linear Models, GLMs)的基础上发展而来的。
Logistic模型的目标是对给定的输入变量进行分类,并输出该输入变量属于某一类别的概率。
在Logistic模型中,通过sigmoid函数(也称为Logistic函数)将线性回归模型的输出限定在0和1之间。
这是因为sigmoid函数具有S形曲线,保证了输出值处于概率的范围内。
Logistic模型的数学表达式如下:P(Y=1|X) = 1 / (1 + exp(-h(X)))P(Y=0|X) = exp(-h(X)) / (1 + exp(-h(X)))其中,P(Y=1|X)表示当输入变量为X时,输出变量为1的概率;P(Y=0|X)表示当输入变量为X时,输出变量为0的概率;h(X)表示线性回归模型的输出。
Logistic模型的参数估计通常使用极大似然估计法来进行求解。
在训练过程中,通过最大化对数似然函数来寻找最优参数值,使得模型对训练数据的拟合度最大化。
Logistic模型具有以下特点:1. 输出值是一个概率,可以用于对样本进行分类。
2. 模型的输出范围在0和1之间,可以表示为属于某一类别的概率。
3. 模型可以通过参数估计进行求解,通常使用梯度下降等优化算法。
Logistic模型常被应用于很多领域,如医学诊断、金融风险评估、信用评分等。
其优点包括建模简单、计算速度快、模型解释性强等。
总结起来,Logistic模型是一种用于分类问题的概率模型,通过sigmoid函数将线性回归模型的输出映射到0和1之间,可以表示为属于某一类别的概率。
它的参数估计通常使用极大似然估计方法进行求解,适用于很多实际应用场景。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
阻滞增长模型(Logistic模型)
人口增长到一定数量后,增长率下降的原因:
资源、环境等因素对人口增长的阻滞作用
且阻滞作用随人口数量增加而变大
r是x的减函数
假设 r(x) r sx (r, s 0) r~固有增长率(x很小时)
xm~人口容量(资源、环境能容纳的最大数量)
function f=myexp(x,t) f=x(1)*exp(x(2)*t);
• 2.建立M文件myexpexec.m t=0:21 y=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6, 50.2,62.9,76.0,92.0,106.5,123.2,131.7,150.7, 179.3,204.0,226.5,251.4,281.4] x0=[4,0.3]; [x,norm,res]=lsqcurvefit(@myexp,x0,t,y)
f=x(1)/(1+(x(1)/3.9-1)*exp(-x(2)*t)); 2. 和前面相同,只要将 myexp 换为mylogistic
LOGSTIC模型结果
两个模型结果比较
线性化后再参数估计
对指数模型
y x0ert 取对数后, ln y ln x0 rt 对ln x0, r的估计可以采用线性回 归
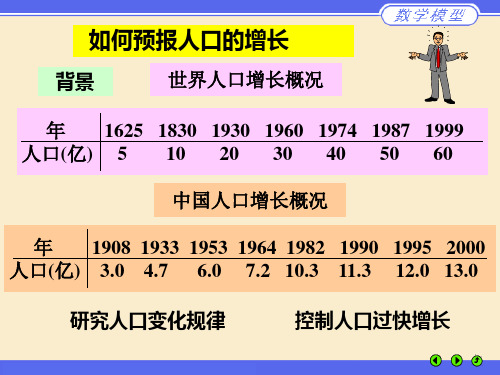
研究人口变化规律
控制人口过快增长
常用的计算公式 今年人口 x0, 年增长率 r
k年后人口
x x (1 r)k
k
0
指数增长模型——马尔萨斯提出 (1798)
基本假设 : 人口(相对)增长率 rdx dt rx, x(0) x0
x(t t) x(t) rt x(t)
为待定的参数向量
记误差 ri yi f (x, ti ),
r (r1, r2 , , rn )T
确定x的方法: 求x使得误差平方和
rT r ( yi f (x,ti ))2
最小
MATLAB最小二乘拟合
• 命令 lsqcurvefit • 基本用法 [x,resnorm,res]=lsqcurvefit(@f,x0,t,y,lb,ub) 输入:@f =f(x,t) x0=参数初值 t=自变量向量 y=函数值向量 lb ub =参数的上下界 输出 x=参数估计值
模型应用——预报美国2010年的人口
加入2000年人口数据后重新估计模型参数
r=0.2490, xm=434.0
x(2010)=306.0(实际308.7)
Logistic 模型在经济领域中的应用(如耐用消费品的售量)
最小二乘拟合
问题:给定 ti , yi , i 1,2,...n 拟合一个函数 y=f(x,t),其中x
MATLAB线性回归命令
• b = regress(y,X) 返回回归系数向量b, • 线性模型 y = Xb, • X 是 n×p 矩阵, y 是观察值向量
使用线性回归的M文件
• t=0:21 • y=[3.9,5.3,7.2,9.6, …,251.4,281.4]; • logy=log(y); logy=logy'; • X=[ones(22,1) t']; • b=regress(logy,X); • x(1)=exp(b(1));x(2)=b(2); • y1=myexp(x,t); • plot(t,y,'+',t,y1,'*');
阻滞增长模型(Logistic模型)
参数估计 用指数增长模型或阻滞增长模型作人口 预报,必须先估计模型参数 r 或 r, xm
• 利用统计数据用最小二乘法作拟合
例:美国人口数据(单位~百万)
1860 1870 1880 …… 1960 1970 1980 1990 31.4 38.6 50.2 …… 179.3 204.0 226.5 251.4
如何预报人口的增长
背景
世界人口增长概况
年 1625 1830 1930 1960 1974 1987 1999 人口(亿) 5 10 20 30 40 50 60
中国人口增长概况
年 1908 1933 1953 1964 1982 1990 1995 2000 人口(亿) 3.0 4.7 6.0 7.2 10.3 11.3 12.0 13.0
r(xm ) 0
s r r(x) r(1 x )
xm
xm
阻滞增长模型(Logistic模型)
dx rx dt
dx/dt
dx r(x)x rx(1 x )
dt
xm
x
xm
xm/2
0 xm/2
xm x
x0 0
t
x(t)
xm
1 ( xm 1)e rt
x0
x(t)~S形曲线, x增加先快后慢
resnom=<r, r>(误差平方和) res= r(误差向量)
例子
已知美国人口数据如下(单位~百万) 1860 1870 1880 …… 1960 1970 1980 1990 31.4 38.6 50.2 …… 179.3 204.0 226.5 251.4 用指数增长模型作人口预报
估计模型参数 r的MATLAB方法 1.建立M文件 myexp.m
专家估计
r=0.2557, xm=392.1
阻滞增长模型(Logistic模型) 模型检验
用模型计算2000年美国人口,与实际数据比较
x(2000 ) x(1990 ) x x(1990 ) rx(1990 )[1 x(1990 ) / xm ]
x(2000) 274.5 实际为281.4 (百万)
x(t) x e rt 0
x(t) x0 (er )t x0 (1 r)t
随着时间增加,人口按指数规律无限增长
指数增长模型的应用及局限性
• 与19世纪以前欧洲一些地区人口统计数据吻合 • 适用于19世纪后迁往加拿大的欧洲移民后代 • 可用于短期人口增长预测 • 不符合19世纪后多数地区人口增长规律 • 不能预测较长期的人口增长过程
• 3. 利用MATLAB作图,比较结果 • plot(t,y,'+'); • hold on; • y1=myexp(x,t); % 理论数据 • plot(t,y1,'*');
指数模型结果
• 如果用LOGISTIC 模型作拟合,步骤相同 • 1.建立m文件 mylogistic.m function f=mylogistic(x,t)
