3.3 勾股定理的简单应用-2020秋苏科版八年级数学上册课件(共15张PPT)
合集下载
苏教版八年级数学上册《勾股定理的简单应用》赛课课件

勾股定理的简单应用
苏科版数学八年级上册
3.3勾股定理的简单应用
做一做:
李叔叔想要检测雕塑 底座正面的AD边和BC边 是否分别垂直于底边AB, 但他随身只带了卷尺.
(1)你能替他想办法完成任务吗?
做一做:
(2)李叔叔量得AD长 是30厘米,AB长是40厘 米,BD长是50厘米, AD边垂直于AB边吗? 为什么?
做一做:
(3)小明随身只有一个 长度为20厘米的刻度尺, 他能有办法检验AD边是 否垂直于AB边吗?BC 边与AB边呢?
问题的延伸Leabharlann 下图是学校的旗杆,旗杆上的绳子垂 到了地面,并多出了一段,现在老师想知 道旗杆的高度,你能帮老师想个办法吗? 请你与同伴交流设计方A 案?
图(1)
C 图(2) B
小明发现旗杆上的绳子垂到地面还多1米,如图(1), 当他们把绳子的下端拉开5米后,发现下端刚好接触地 面,如图(2),你能帮他们把旗杆的高度和绳子的长 度计算出来吗?请你与同伴交流并回答用的是什么方法.
谢谢观赏
You made my day!
我们,还在路上……
解:设水池的水深AC为x尺,则这根芦苇长 AD=AB=(x+1)尺,
在直角三角形ABC中,BC=5尺, 由勾股定理,得BC2+AC2=AB2,
即 52+ x2= (x+1)2
25+ x2= x2+2 x+1, 2 x=24,
∴ x=12, x+1=13
答:水池的水深12尺,这根芦苇长13尺.
通过今天的学习, 用你自己的话说说你的收获和体会?
A
图(1)
C 图(2) B
试一试:
在我国古代数学著作《九
苏科版数学八年级上册
3.3勾股定理的简单应用
做一做:
李叔叔想要检测雕塑 底座正面的AD边和BC边 是否分别垂直于底边AB, 但他随身只带了卷尺.
(1)你能替他想办法完成任务吗?
做一做:
(2)李叔叔量得AD长 是30厘米,AB长是40厘 米,BD长是50厘米, AD边垂直于AB边吗? 为什么?
做一做:
(3)小明随身只有一个 长度为20厘米的刻度尺, 他能有办法检验AD边是 否垂直于AB边吗?BC 边与AB边呢?
问题的延伸Leabharlann 下图是学校的旗杆,旗杆上的绳子垂 到了地面,并多出了一段,现在老师想知 道旗杆的高度,你能帮老师想个办法吗? 请你与同伴交流设计方A 案?
图(1)
C 图(2) B
小明发现旗杆上的绳子垂到地面还多1米,如图(1), 当他们把绳子的下端拉开5米后,发现下端刚好接触地 面,如图(2),你能帮他们把旗杆的高度和绳子的长 度计算出来吗?请你与同伴交流并回答用的是什么方法.
谢谢观赏
You made my day!
我们,还在路上……
解:设水池的水深AC为x尺,则这根芦苇长 AD=AB=(x+1)尺,
在直角三角形ABC中,BC=5尺, 由勾股定理,得BC2+AC2=AB2,
即 52+ x2= (x+1)2
25+ x2= x2+2 x+1, 2 x=24,
∴ x=12, x+1=13
答:水池的水深12尺,这根芦苇长13尺.
通过今天的学习, 用你自己的话说说你的收获和体会?
A
图(1)
C 图(2) B
试一试:
在我国古代数学著作《九
【苏科版】数学八年级上册 勾股定理的简单应用 P标准课件

.
A
x
10-x
C
B
3
练一练
“引葭赴岸”是《九章算术》中另一道题“今 有池方一丈,葭生其中央,出水一尺,引葭 赴岸,适与岸齐.问水深、葭长各几何?”
∴
A
D2例2 在△ABC中,AB=26,BC=20,BC边上的中
+B线解A:D∵=A2D4是,BC求边A上C.的中线,
D
1
2
2
= A
∴∵ABDD2=+CBDD=2=576+BC1=001=0.676 AB2=262=676
3.3 勾股定理的简单应用
例1:九章算术中的“折竹”问题:今有竹高 一丈,末折抵地,去根三尺,问折者高几何?
意思是:有一根竹子原高1丈(1丈=10尺), 中部有一处折断,竹梢触地面处离竹根3尺,试 问折断处离地面多高?
解:如图,设AC是x尺,则AB是 (10-x)尺.
∵∠C=90° ∴x∴2+C3A22+=CB(2=10A-B2x)2
苏科版数学八年级上册 勾股定理的简单应用 P标准课件-精品课件ppt(实用版)
练一练
已知某校有一块四边形空地ABCD,如图,经测 量∠B=90°,AB=30m,BC=40m,CD=130m ,DA=120m, 求这块地的面积。
BA
C
苏科版数学八年级上册 勾股定理的简单应用 P标准课件-精品课件ppt(实用版)
苏科版数学八年级上册 勾股定理的简单应用 P标准课件-精品课件ppt(实用版)
1955年希腊曾经发行了一枚纪念邮票.
苏科版数学八年级上册 勾股定理的简单应用 P标准课件-精品课件ppt(实用版)
苏科版数学八年级上册 勾股定理的简单应用 P标准课件-精品课件ppt(实用版)
练一练
A
x
10-x
C
B
3
练一练
“引葭赴岸”是《九章算术》中另一道题“今 有池方一丈,葭生其中央,出水一尺,引葭 赴岸,适与岸齐.问水深、葭长各几何?”
∴
A
D2例2 在△ABC中,AB=26,BC=20,BC边上的中
+B线解A:D∵=A2D4是,BC求边A上C.的中线,
D
1
2
2
= A
∴∵ABDD2=+CBDD=2=576+BC1=001=0.676 AB2=262=676
3.3 勾股定理的简单应用
例1:九章算术中的“折竹”问题:今有竹高 一丈,末折抵地,去根三尺,问折者高几何?
意思是:有一根竹子原高1丈(1丈=10尺), 中部有一处折断,竹梢触地面处离竹根3尺,试 问折断处离地面多高?
解:如图,设AC是x尺,则AB是 (10-x)尺.
∵∠C=90° ∴x∴2+C3A22+=CB(2=10A-B2x)2
苏科版数学八年级上册 勾股定理的简单应用 P标准课件-精品课件ppt(实用版)
练一练
已知某校有一块四边形空地ABCD,如图,经测 量∠B=90°,AB=30m,BC=40m,CD=130m ,DA=120m, 求这块地的面积。
BA
C
苏科版数学八年级上册 勾股定理的简单应用 P标准课件-精品课件ppt(实用版)
苏科版数学八年级上册 勾股定理的简单应用 P标准课件-精品课件ppt(实用版)
1955年希腊曾经发行了一枚纪念邮票.
苏科版数学八年级上册 勾股定理的简单应用 P标准课件-精品课件ppt(实用版)
苏科版数学八年级上册 勾股定理的简单应用 P标准课件-精品课件ppt(实用版)
练一练
苏科版数学八年级上册勾股定理的简单应用精品课件PPT

其中线段AB表示竹子折断部分,用线段CB来表
示竹梢触地处离竹根的距离.设AC=x,则AB=
(10-x)尺.
A
由勾股定理得:
∴x2+32=(10-x)2
解得:x=4.55
(10-X) X
∴折断处离地面4.55尺。
C3
B
苏科版数学八年级上册3.3 勾股定理的简单应用 课件
苏科版数学八年级上册3.3 勾股定理的简单应用 课件
•
3、在生命的每一个阶段,阿甘的心中 只有一 个目标 在指引 着他, 他也只 为此而 踏实地 、不懈 地、坚 定地奋 斗,直 到这一 目标的 完成, 又或是 新的目 标的出 现。
•
4、让学生有个整体感知的过程。虽然 这节课 只教学 做好事 的部分 ,但是 在研读 之前我 让学生 找出风 娃娃做 的事情 ,进行 板书, 区分好 事和坏 事,这 样让学 生能了 解课文 大概的 资料。
2、(2015 •毕节改编)下列各组数据中的三个数作为 三角2、形(的2边01长3黔,江其南中州能)构一成直直角角三三角角形形三的边是长( 为3、) 4、x,
则x2A=.3_,2_45_,或_6_7 B.9,12,15 C.6,7,8 D.2,3,4 3、3、在写△出AB几C中组,常∠见C=勾90股°数,。若a:b=3:4,c=15,则 a=_3_、_,4b、=_5_;___.6、8、10; 9、12、 15
感谢观看,欢迎指导!
苏科版数学八年级上册3.3 勾股定理的简单应用 课件
回忆归纳
勾股定理: 直角三角形的两条直角边a、
b的平方和等于斜边c的平方
A
变形:
a2+b2=c2 c2 -b2=a2
c
b
B
a
苏科版数学八年级上册. 勾股定理的简单应用 课件ppt演讲教学

速度沿北偏东30°方向向C移动,且台风中心
风力不变,若城市受到的风力达到或 A
超过四级,则称受台风影响.
D
(1)该城市是否会受到这次台风
的影响?为什么?
苏科版数学八年级上册. 勾股定理的简单应用 课件ppt演讲教学
B
苏科版数学八年级上册. 勾股定理的简单应用 课件ppt演讲教学
可怕的台风
(2)若受到台风影响,那么台风影响该城 市的持续时间有多长?
⑵求证:AB2 - AC2=2BC·DE. A
苏科版数学八年级上册. 勾股定理的简单应用 课件ppt演讲教学
B
DEC
苏科版数学八年级上册. 勾股定理的简单应用 课件ppt演讲教学
休闲一时种光圆柱形饮料容器,测得底面半 径为2.5㎝,高为12㎝,吸管放进杯里, 杯口外面至少要露出4㎝,问吸管要做多 长?
ac
△ABC中
a2 b2 c2
Cb
C 900
A
苏科版数学八年级上册. 勾股定理的简单应用 课件ppt演讲教学
苏科版数学八年级上册. 勾股定理的简单应用 课件ppt演讲教学
带着勾股定理去旅行
苏科版数学八年级上册. 勾股定理的简单应用 课件ppt演讲教学
我们出发了 苏科版数学八年级上册. 勾股定理的简单应用 课件ppt演讲教学
在圆柱下底面上的A
么走 会最
点有一只蚂蚁,它想 近呢?
绕圆柱侧面爬行一圈,
从点A爬到正上方的
点B处, 蚂蚁爬行的
A
最短路程是多少?
(π的值取3)
苏科版数学八年级上册. 勾股定理的简单应用 课件ppt演讲教学
苏科版数学八年级上册. 勾股定理的简单应用 课件ppt演讲教学
B
苏科版数学八年级上册勾股定理的简单应用精品课件PPT

勾股定理的应用(1)
苏科版数学八年级上册3.3 勾股定理的简单应用(1) 课件
学习目标
能运用勾股定理解决实际问题.
苏科版数学八年级上册3.3 勾股定理的简单应用(1) 课件
苏科版数学八年级上册3.3 勾股定理的简单应用(1) 课件
自学指导
请看P.65-66练习前面的内容: 1.回忆所学勾股定理内容; 2.注意例题是如何运用勾股定理 求出一些线段长度的. 6分钟后比谁能仿照例题解决一 些实际问题.
苏科版数学八年级上册3.3 勾股定理的简单应用(1) 课件
苏科版数学八年级上册3.3 勾股定理的简单应用(1) 课件
问题3
在台风“麦莎” 的袭击中,一棵大 树在离地面9米处 断裂,树的顶部落 在离树根底部12米 处。这棵树折断之 前有多高?
苏科版数学八年级上册3.3 勾股定理的简单应用(1) 课件
苏科版数学八年级上册3.3 勾股定理的简单应用(1) 课件
苏科版数学八年级上册3.3 勾股定理的简单应用(1) 课件
知识回味
勾股定理: 直角三角形的两条直角边的 平方和等于斜边的平方
cb a
苏科版数学八年级上册3.3 勾股定理的简单应用(1) 课件
a2+b2=c2
苏科版数学八年级上册3.3 勾股定理的简单应用(1) 课件
____4_8_c_m_2____.
苏科版数学八年级上册3.3 勾股定理的简单应用(1) 课件
苏科版数学八年级上册3.3 勾股定理的简单应用(1) 课件
自学检测二
1 P.66 练习 1 2 P.66 练习 2
3 一种盛饮料的圆柱形杯(如图),测得内部 底面半径为2.5㎝,高为12㎝,吸管放进杯里, 杯口外面至少要露出4.6㎝,问吸管要做多长?
苏科版数学八年级上册3.3 勾股定理的简单应用(1) 课件
学习目标
能运用勾股定理解决实际问题.
苏科版数学八年级上册3.3 勾股定理的简单应用(1) 课件
苏科版数学八年级上册3.3 勾股定理的简单应用(1) 课件
自学指导
请看P.65-66练习前面的内容: 1.回忆所学勾股定理内容; 2.注意例题是如何运用勾股定理 求出一些线段长度的. 6分钟后比谁能仿照例题解决一 些实际问题.
苏科版数学八年级上册3.3 勾股定理的简单应用(1) 课件
苏科版数学八年级上册3.3 勾股定理的简单应用(1) 课件
问题3
在台风“麦莎” 的袭击中,一棵大 树在离地面9米处 断裂,树的顶部落 在离树根底部12米 处。这棵树折断之 前有多高?
苏科版数学八年级上册3.3 勾股定理的简单应用(1) 课件
苏科版数学八年级上册3.3 勾股定理的简单应用(1) 课件
苏科版数学八年级上册3.3 勾股定理的简单应用(1) 课件
知识回味
勾股定理: 直角三角形的两条直角边的 平方和等于斜边的平方
cb a
苏科版数学八年级上册3.3 勾股定理的简单应用(1) 课件
a2+b2=c2
苏科版数学八年级上册3.3 勾股定理的简单应用(1) 课件
____4_8_c_m_2____.
苏科版数学八年级上册3.3 勾股定理的简单应用(1) 课件
苏科版数学八年级上册3.3 勾股定理的简单应用(1) 课件
自学检测二
1 P.66 练习 1 2 P.66 练习 2
3 一种盛饮料的圆柱形杯(如图),测得内部 底面半径为2.5㎝,高为12㎝,吸管放进杯里, 杯口外面至少要露出4.6㎝,问吸管要做多长?
八年级数学上册第三章勾股定理:勾股定理的简单应用同步ppt课件新版苏科版

太阳能真空管AC有多长?
C B
【解析】在Rt△ABC中,由勾股定理,得
AC=
=
=150(cm).
答:太阳能真空管AC长150 cm.
勾股定理的应用
已知:如图,在Rt△ABC和Rt△A′B′C′中, ∠C=∠C′=90°,AB=A′B′,AC=A′C′.
求证: ABC≌△A′B′C′.
证明:在Rt△ABC和Rt△A′B′C′中, ∠C=∠C′=90° 根据勾股定理,得
发现
13 是直角边分别为2,3的直角三角形的斜边长。
B
13
2 3 AC O 1 2 3 13
提问 你能用语言叙述一下作图过程吗?
1 在数轴上找到点A,使OA=3; 2 作直线l⊥OA,在l上取一点B,使AB=2; 3 以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,
则点C即为表示 13的点。
1.如图,池塘边有两点A,B,点C是与BA方向成直角的AC 方的距 离(结果取整数).
解: AB BC 2 AC 2 602 202 40 2 57m.
2.如图,太阳能热水器的支架AB长
A
为90 cm,与AB垂直的BC长为120 cm.
4.如图,在平面直角坐标系中有两 点A(5,0)和B(0,4),求这两点间 的距离.
解: OA2 OB2 52 42 41
5.在数轴上作出表示 20 的点. 解:点A即为表示 20 的点.
6.飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶 上方3 km处,过了20 s,飞机距离这个男孩头顶5 km.这 一过程中飞机飞过的距离是多少千米?
【解析】在Rt△ABC中,
C
?
B
3 5
答:飞机飞过的距离是4 km.
最新苏科版八年级数学上册精品课件-3.3勾股定理的简单应用

上方3 km处,过了20 s,飞机距离这个男孩头顶5 km.这
• 单击此处编辑母版文本样式
一过• 程第中二飞级机飞过的距离是多少千米?
• 第三级
【解析】在• R第t四△级 ABC中,
• 第五级
C
?
B
3 5
答:飞机飞过的距离是4 km.
A
单击此处编母版标题样式
• 单击此处编辑母版课文堂本样小式结
• 第•二第级三级化非直角三角形为直角三角形
知识讲解
利• 单用击勾此股处定编理辑解母决版文实本际样问式题
• 第二级
• 第三级
例1 一个门• 第框四的级 尺寸如图所示,一块长3 m, 宽2.2 m的长方• 形第五薄级木板能否从门框内通过? 为什么?
已知条件有哪些?
单击此处编母版标题样式
• 观单击察此处编辑母版文本样式
1.木板• 第能二横级着或竖着从门框通过吗?
单击此处编母版标题样式
2.如图,等边三角形的边长是6.求: •(单1)击高此A处D编的辑长母;版文本样式 (2•)第这•二第个级三三级 角形的面积. 解:(1)• 第A四D级⊥BC于D,则BD=CD=3.
• 第五级
在Rt△ABD中,由勾股定理
AD2=AB2-BD2=62-32=27,故AD=3 3 ≈5.2
• 单击此处编辑解母:版在R文t△本A样OB式中,根据勾股定理,
• 第二级 OB2=AB2-OA2=2.62-2.42=1.
A • 第三级 OB=1.
C
• 第四级
• 第在五R级 t△COD中,根据勾股定理,
OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15.
O BD
OD 3.15 1.77, BD OD OB 1.77 1 0.77.
苏教科版初中数学八年级上册-3.3勾股定理的应用PPT课件

A
20
23
B
(3)在一个内腔长30cm、宽40 cm、 zxxk
高50 cm的木箱中放一根笔直的细玻璃 管,这根玻璃管的长度至多为多少cm?
B
C
A
D
(4)在图中,如果在箱内的A处有一
只昆虫,它要在箱壁上爬行到B处,至
少要爬多远?
.B
.A
C
D
. B
.
C
B
A
D
50
A 30 D 40 C 图①
. B
zxxk
2.7勾股定理的应用(三)
例1. 蚂议最短路程问题. (1) 如图所示。有一个圆柱,它的高等
于12厘米,底面半径等于3厘米。在圆柱下 底面的A点有一只蚂蚁,它想吃到上底面的 A点相对的B点处的事物,沿着圆柱侧面需 要爬行的最短路程是多少? (п的值取3)
(2)如图是一个三级台阶,它的每一级的长宽和 高分别为20dm、3dm、2dm,A和B是这个台阶两个 相对的端点,A点有一只蚂蚁,想到B点去吃可口 的食物,则蚂蚁沿着台阶面爬到B点最短 路程是_____________.
.
C
C
B
A
D
40
A 30 D 50 图②
. B B
50
.C
C
C
A
D
40
A 30 D 图③
例2.如图,A,B是直线l外同侧的两点,且点 A和点B到l的距离分别是3㎝和5㎝,AB=12㎝, 若点P在l上移动,求PA+PB的最小值。
·B ·A
l
例3.有一个如图所示的长方体的透明玻璃鱼缸, 假设其长AD=80cm,高AB=60cm,水深为AE =40cm,在水面上紧贴内壁G处有一鱼饵,G在水 面线EF上,且EG=60cm,一小虫想从鱼缸外的 A点沿壁爬进鱼缸内G处吃鱼饵. (1)动物应该走怎样的路线才使爬的路线最短呢? 请在图中画出它爬行的路线,并用箭头标注. (2)求小动物爬行的最短路线长.
苏科版数学八年级上册勾股定理的简单应用优质PPT4

苏科版数学八年级上册勾股定理的简 单应用 优质PPT 4
B
C
B
苏科版数学八年级上册勾股定理的简 单应用 优质PPT 4 苏科版数学八年级上册勾股定理的简 单应用 优质PPT 4
苏科版数学八年级上册勾股定理的简 单应用 优质PPT 4
变式:
如果把盒子换成长为3cm,宽为2cm, 高为1cm的长方体,蚂蚁沿着表面需要 爬行的最短路程又是多少呢?
感悟方程思想
已知长方形ABCD如图折叠,使点D落在 BC边上的点F处,已知AB=8,BC=10,求 EC的长。
你能说出图中哪些线段的长?
A
10
D
?
8-x
8 10
8-x
6
F4 C
10
求折痕AE的长。
苏科版数学八年级上册勾股定理的简 单应用 优质PPT 4
苏科版数学八年级上册勾股定理的简 单应用 优质PPT 4
初中数学 八年级(上册)
3.3 勾股定理的简单应用
勾股定理你知多少?
说出来与大家分享吧!
赵爽弦图
勾股世界
两千两千多多年年前前,,古古希腊希有腊个有哥拉个毕达哥拉斯 学斯学派派,,他他们们首首先发先现发了勾现股了定勾理,股因定此 理,因此在 在国国外外人人们们通通常常称勾称股勾定理股为定毕理达哥为拉毕斯 达哥拉斯定 定理理。。为为了了纪纪念念毕达毕哥达拉斯哥学拉派斯,1学95派5 ,1955年希 年腊希曾腊经曾经发发行行了了一一枚枚纪念纪票念。邮票。
B
苏科版数学八年级上册勾股定理的简 单应用 优质PPT 4
A
苏科版数学八年级上册勾股定理的简 单应用 优质PPT 4
分析:有3种情况,六条路线。
(1)经过前面和上底面;
苏教版八年级数学上册《勾股定理的简单应用》赛课课件

6、“教学的艺术不在于传授本领,而在于激励、唤醒、鼓舞”。2021年11月2021/11/82021/11/82021/11/811/8/2021
▪7、“教师必须懂得什么该讲,什么该留着不讲,不该讲的东西就好比是学生思维的器,马上使学生在思维中出现问题。”“观察是 思考和识记之母。”2021/11/82021/11/8November 8, 2021
做一做:
(3)小明随身只有一个 长度为20厘米的刻度尺, 他能有办法检验AD边是 否垂直于AB边吗?BC 边与AB边呢?
问题的延伸
下图是学校的旗杆,旗杆上的绳子垂 到了地面,并多出了一段,现在老师想知 道旗杆的高度,你能帮老师想个办法吗? 请你与同伴交流设计方A 案?
图(1)
C 图(2) B
▪1、“手和脑在一块干是创造教育的开始,手脑双全是创造教育的目的。” ▪2、一切真理要由学生自己获得,或由他们重新发现,至少由他们重建。 ▪3、反思自我时展示了勇气,自我反思是一切思想的源泉。 ▪4、好的教师是让学生发现真理,而不只是传授知识。 ▪5、数学教学要“淡化形式,注重实质.
勾股定理的简单应用
苏科版数学八年级上册
3.3勾股定理的简单应用
做一做:
李叔叔想要检测雕塑 底座正面的AD边和BC边 是否分别垂直于底边AB, 但他随身只带了卷尺.
(1)你能替他想办法完成任务吗?
做一做:
(2)李叔叔量得AD长 是30厘米,AB长是40厘 米,BD长是50厘米, AD边垂直于AB边吗? 为什么?
解:设水池的水深AC为x尺,则这根芦苇长 AD=AB=(x+1)尺,
在直角三角形ABC中,BC=5尺, 由勾股定理,得BC2+AC2=AB2,
即 52+ x2= (x+1)2
▪7、“教师必须懂得什么该讲,什么该留着不讲,不该讲的东西就好比是学生思维的器,马上使学生在思维中出现问题。”“观察是 思考和识记之母。”2021/11/82021/11/8November 8, 2021
做一做:
(3)小明随身只有一个 长度为20厘米的刻度尺, 他能有办法检验AD边是 否垂直于AB边吗?BC 边与AB边呢?
问题的延伸
下图是学校的旗杆,旗杆上的绳子垂 到了地面,并多出了一段,现在老师想知 道旗杆的高度,你能帮老师想个办法吗? 请你与同伴交流设计方A 案?
图(1)
C 图(2) B
▪1、“手和脑在一块干是创造教育的开始,手脑双全是创造教育的目的。” ▪2、一切真理要由学生自己获得,或由他们重新发现,至少由他们重建。 ▪3、反思自我时展示了勇气,自我反思是一切思想的源泉。 ▪4、好的教师是让学生发现真理,而不只是传授知识。 ▪5、数学教学要“淡化形式,注重实质.
勾股定理的简单应用
苏科版数学八年级上册
3.3勾股定理的简单应用
做一做:
李叔叔想要检测雕塑 底座正面的AD边和BC边 是否分别垂直于底边AB, 但他随身只带了卷尺.
(1)你能替他想办法完成任务吗?
做一做:
(2)李叔叔量得AD长 是30厘米,AB长是40厘 米,BD长是50厘米, AD边垂直于AB边吗? 为什么?
解:设水池的水深AC为x尺,则这根芦苇长 AD=AB=(x+1)尺,
在直角三角形ABC中,BC=5尺, 由勾股定理,得BC2+AC2=AB2,
即 52+ x2= (x+1)2
苏科版数学八年级上册3.3 勾股定理的简单应用 课件
展开
2、立体图形
平面图形
勾股定理
直角三角形模型。
课课练:p62.8
二 正方体中的最值问题
1.如图,在棱长为10 cm 的正方体的一个顶 点A处有一只蚂蚁,现要向顶点B处爬行,已 知蚂蚁爬行的速度是1cm/s,且速度保持不 变,问蚂蚁能否在20 s内从A爬到B?
食物
B
A
如图,在棱长为10 cm 的正方体的一个顶 点A处有一只蚂蚁,现要向顶点B处爬行, 已知蚂蚁爬行的速度是1cm/s,且速度保持 不变,问蚂蚁能否在20 s内从A爬到B?
B B
A
三.长方体中的最值问题
3、在长30cm、宽50 cm、高40 cm
. 的木箱中,如果在箱内的A处有一只昆
虫爬, 多远它?要在箱壁上爬行到B处B,至少要
40
.A
C
50
30 D
.B
40
C
B
.
50
A 30 D
40
A 30 D 50
C
图①
.
C 50 B
B
40
50
.C
C
A 30 D
40
A 30 D 图②
. C 30 B
B
40
.D 5C0
30
C
A
40
D
50
A
图③
◆在上面的木箱中,如果在箱外的A处
有一只昆虫.
⑴它要在箱壁上爬行到箱内的D处,至
少要爬多远?
B
⑵它要在箱壁上
爬行到箱内的C
处,至少要爬多 远?
C
A
D
.
40
c A 30 D 50
图①
四、台阶中的最值问题
苏教八年级数学上册《勾股定理的简单应用》赛课课件

做一做:
(3)小明随身只有一个 长度为20厘米的刻度尺, 他能有办法检验AD边是 否垂直于AB边吗?BC 边与AB边呢?
问题的延伸
下图是学校的旗杆,旗杆上的绳子垂 到了地面,并多出了一段,现在老师想知 道旗杆的高度,你能帮老师想个办法吗? 请你与同伴交流设计方A 案?
图(1)
C 图(2) B
小明发现旗杆上的绳子垂到地面还多1米,如图(1), 当他们把绳子的下端拉开5米后,发现下端刚好接触地 面,如图(2),你能帮他们把旗杆的高度和绳子的长 度计算出来吗?请你与同伴交流并回答用的是什么方法.
A
图(1)
C 图(2) B
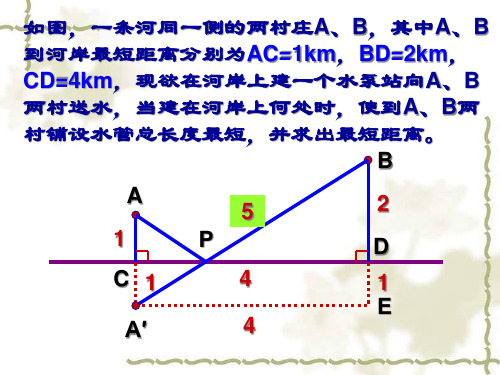
试一试:
在我国古代数学著作《九
章算术》中记载了一道有趣的 问题,这个问题的意思是:有
D
C
B
一个水池,水面是一个边长为
10尺的正方形,在水池的中央
有一根新生的芦苇,它高出水 面1尺,如果把这根芦苇垂直拉 A
向岸边,它的顶端恰好到达岸
边的水面,请问这个水池的深
度和这根芦苇的长度各是多少?
解:设水池的水深AC为x尺,则这根芦苇长 AD=AB=(x+1)尺,
在直角三角形ABC中,BC=5尺, 由勾股定理,得BC2+AC2=AB2,
即 52+ x2= (x+1)2
25+ x2= x2+2 x+1, 2 x=24,
∴ x=12, x+1=13
答:水池的水深12尺,这根芦苇长13尺.
通过今天的学习, 用你自己的话说说你的收获和体会?
本节课主要是应用勾股定理和它的逆定理来解 决实际问题,在应用定理时,应注意: 1.没有图的要按题意画好图并标上字母. 2.不要用错定理. 你学会了吗?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
随堂练习
2.如图,校园内有两棵树,一棵树高13 m,另一棵树高8 m, 两树相距12 m,一只小鸟从一棵树的顶端飞到另一棵树的 顶端,小鸟至少要飞( D ) A.10 m B.11 m C.12 m D.13 m
随堂练习
3.木工师傅想利用木条制作一个直角三角形的工具,那么 下列各组数据不符合直角三角形的三边长的是( D ) A.3 cm,4 cm,5 cm B.6 cm,8 cm,10 cm C.5 cm,12 cm,13 cm D.13 cm,16 cm,18 cm
解:∵AD是BC边上的中线,且BC=20,
BD 1 BC=10 2
∵AD2+BD2=576+100=676,
AB 2=262=676,
B
A DC
∴AD2+BD2=AB2,
∴ ∠ADB=90°,AD垂直平分BC.
∴AC=AB=26.
课程讲授
1 勾股定理的简单应用
例3 如图,已知CD=6cm,AD=8cm, ∠ADC=90°, BC=24cm,AB=26cm,求阴影部分面积.
= (DE+CE)·( DE- BE)
=BD·CD.
课堂小结
勾股定理的简 单应用
勾股定理 的应用
勾股定理的实 际应用
第3章 勾股定理
3.3 勾股定理的简单应用
新知导入 课程讲授
随堂练习 课堂小结
知识要点
勾股定理的简单应用
新知导入
看一看: 从远处看,斜拉桥的索塔、桥面与拉索组
成许多直角三角形。
新知导入
想一想: 已知桥面以上索塔AB的高,怎样计算
AC,AD,AE,AF,AG的长.
A
G B C DE F
课程讲授
1 勾股定理的简单应用
归纳: 1.勾股定理主要应用于求线段的长度、 图形的周长、面积. 2.利用题中所给条件构造直角三角形,解决实 际问题.
随堂练习
1.如图,一轮船以16海里/时的速度从港口A出发向东北方向 航行,另一轮船以12海里/时的速度同时从港口A出发向东南 方向航行,离开港口2小时后,则两船相距( C ) A.25海里 B.30海里 C.40海里 D.50海里
随堂练习
4.如图,在△ABC中,AB=AC,D点在CB 延长线上,
求证:AD2-AB2=BD·CD.
A
证明:过点A作AE⊥BC于点E.
∵AB=AC,∴BE=CE.
在Rt △ADE中,AD2=AE2+DE2. D 在Rt △ABE中,AB2=AE2+BE2.
B EC
= DE2- BE2
= (DE+BE)·( DE- BE)
(10-x)
示竹子折断部分,用线段OB来表 x
示竹梢触地处离竹根的距离.设 OA=x,则AB=10-x.
O 3
B
由勾股定理得
∴x2+32=(10-x)2.
解得x=4.55,
∴折断处离地面4.55尺.
课程讲授
1 勾股定理的简单应用
例2 如图,在△ABC中,AB=26,BC=20,BC边上的
中线AD=24,求AC.
1 勾股定理的简单应用
例1 九章算术中的“折竹”问题:今有竹高一丈, 末折抵地,去根三尺,问折者高几何?意思是:有一根竹 子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面 处离竹根3尺,试问折断处离地面多高?
课程讲段 A
AB来表示竹子,其中线段AB表
C
A
D
B
课程讲授
1 勾股定理的简单应用
解:在Rt△ADC中,
C
∵AC2=AD2+CD2(勾股定理)
=82+62=100,
∴AC=10.
A
D
∵AC2+BC2=102+242=676=262,
B
∴△ACB为直角三角形(勾股定理的逆定理).
∴S阴影部分=S△ACB-S△ACD =120-24 =96.
课程讲授
