2021版高考数学(文)大一轮人教A广西专用滚动测试卷二(第一_五章)
2021版高考数学(文)大一轮人教A广西专用单元质检八 立体几何(A)

单元质检八立体几何(A)(时间:45分钟满分:100分)单元质检卷第17页一、选择题(本大题共5小题,每小题7分,共35分)1.若平面α⊥平面β,且平面α内的一条直线a垂直于平面β内的一条直线b,则()A.直线a必垂直于平面βB.直线b必垂直于平面αC.直线a不一定垂直于平面βD.过a的平面与过b的平面垂直答案:C解析:α⊥β,a⊂α,b⊂β,a⊥b,当α∩β=a时,b⊥α;当α∩β=b时,a⊥β,其他情形则未必有b⊥α或a⊥β,所以选项A,B,D都错误,故选C.2.(2019云南曲靖沾益四中高三三模)如图,一个透明的球形装饰品内放置了两个共底面的圆锥,且这两个圆锥的顶点和底面圆周都在这个球面上,已知圆锥底面面积是这个球面,则较大圆锥与较小圆锥的体积之比为()面积的316A.2∶1B.3∶1C.4∶1D.5∶1答案:B解析:不妨设球的半径为4,则球的表面积为64π,圆锥的底面积为12π,所以圆锥的底面半径为2√3.由几何体的特征知球心到圆锥底面的距离、球的半径以及圆锥底面的半径三者可以构成一个直角三角形,由此可以求得球心到圆锥底面的距离是√42-(2√3)2=2,所以圆锥体积较小者的高为4-2=2,同理可得圆锥体积较大者的高为4+2=6.又这两个圆锥的底面相同,所以较大圆锥与较小圆锥的体积之比等于它们的高之比,即3∶1,故选B. 3.(2019广东潮州高三二模)一个几何体的三视图如图所示,该几何体外接球的表面积为()A.28πB.32πC.36πD.112π3答案:D解析:该几何体是一个底面为正方形的四棱锥,其中一个侧面为正三角形且与底面垂直,分别过正方形底面和正三角形侧面的中心作面的垂线,交点为外接球球心,由勾股定理求得球的半径为√283,表面积为112π3.4.我国古代数学名著《孙子算经》中有如下问题:“今有筑城,上广二丈,下广五丈四尺,高三丈八尺,长五千五百五十尺,秋程人功三百尺.问:须工几何?”意思是:“现要筑造底面为等腰梯形的直棱柱的城墙,其中底面等腰梯形的上底为2丈,下底为5.4丈,高为3.8丈,直棱柱的侧棱长为5 550 尺.如果一个秋天工期的单个人可以筑出300立方尺,问:一个秋天工期需要多少个人才能筑起这个城墙?”(注:一丈等于十尺)( ) A.24 642 B.26 011 C.52 022 D.78 033 答案:B解析:根据棱柱的体积公式,可得城墙所需土方为20+542×38×5550=7803300(立方尺),一个秋天工期所需人数为7803300300=26011,故选B .5.在空间四面体ABCD 中,平面ABD ⊥平面BCD ,且DA ⊥平面ABC ,则△ABC 的形状是( )A.锐角三角形B.直角三角形C.钝角三角形D.不能确定 答案:B解析:作AE ⊥BD ,交BD 于E ,∵平面ABD ⊥平面BCD ,∴AE ⊥平面BCD ,BC ⊂平面BCD , ∴AE ⊥BC.而DA ⊥平面ABC ,BC ⊂平面ABC , ∴DA ⊥BC.又∵AE ∩AD=A ,∴BC ⊥平面ABD.而AB ⊂平面ABD ,∴BC ⊥AB , 即△ABC 为直角三角形.故选B .二、填空题(本大题共3小题,每小题7分,共21分)6.已知四棱锥P-ABCD 的三视图如图所示,则此四棱锥外接球的半径为 .答案:√5解析:因为三视图对应的几何体是四棱锥,顶点在底面的射影是底面矩形的长边的中点,底面边长分别为4,2,满足侧面PAD⊥底面ABCD,△PAD为等腰直角三角形,且高为2,如×√42+22=√5.图所示,可知外接球球心为底面对角线的交点,可求得球半径为127.已知PA垂直于平行四边形ABCD所在的平面,若PC⊥BD,则平行四边形ABCD的形状一定是.答案:菱形解析:因为PA⊥平面ABCD,BD⊂平面ABCD,所以PA⊥BD.又PC⊥BD,且PC⊂平面PAC,PA⊂平面PAC,PC∩PA=P,所以BD⊥平面PAC.又AC⊂平面PAC,所以BD⊥AC.又四边形ABCD是平行四边形,所以四边形ABCD是菱形.8.已知A,B,C,D是球面上不共面的四点,AB=AC=√3,BD=CD=√2,BC=√6,平面ABC⊥平面BCD,则此球的体积为.π答案:8√23解析:如图所示,设球心坐标为O,连接OD,交BC于点E,连接AE,由题意可知OE2+AE2=OA2.设球的半径R=OD=OA=x,由题意,得(√22-x)2+(√62)2=x 2,解得x=√2,则此球的体积为V=43πR 3=8√23π. 三、解答题(本大题共3小题,共44分)9.(14分)如下的三个图中,左面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在右面画出(单位:cm).(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图; (2)按照给出的尺寸,求该多面体的体积;(3)在所给直观图中连接BC',证明BC'∥平面EFG. 答案:(1)解如图:(2)解所求多面体体积V=V 长方体-V 正三棱锥=4×4×6-13×(12×2×2)×2=2843(cm 3).(3)证明在长方体ABCD-A'B'C'D'中,连接AD',则AD'∥BC'.因为E ,G 分别为AA',A'D'的中点, 所以AD'∥EG.从而EG ∥BC'.又BC'⊄平面EFG ,所以BC'∥平面EFG.10.(15分)(2019全国Ⅱ,文17)如图,长方体ABCD-A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1.(1)证明:BE⊥平面EB1C1;(2)若AE=A1E,AB=3,求四棱锥E-BB1C1C的体积.答案:(1)证明由已知得B1C1⊥平面ABB1A1,BE⊂平面ABB1A1,故B1C1⊥BE.又BE⊥EC1,所以BE⊥平面EB1C1.(2)解由(1)知∠BEB1=90°.由题设知Rt△ABE≌Rt△A1B1E,所以∠AEB=∠A1EB1=45°,故AE=AB=3,AA1=2AE=6.作EF⊥BB1,垂足为F,则EF⊥平面BB1C1C,且EF=AB=3.所以,四棱锥E-BB1C1C的体积V=1×3×6×3=18.311.(15分)如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1⊥底面ABC,AC⊥AB,AC=AB=AA1=2,∠AA1B1=60°,E,F分别为棱A1B1,BC的中点.(1)求三棱柱ABC-A1B1C1的体积;(2)在直线AA1上是否存在一点P,使得CP∥平面AEF?若存在,求出AP的长;若不存在,说明理由.解:(1)在三棱柱ABC-A1B1C1中,A1B1=AB.因为AB=AA 1=2,所以A 1B 1=AA 1=2.又因为∠AA 1B 1=60°,连接AB 1,所以△AA 1B 1是边长为2的正三角形. 因为E 是棱A 1B 1的中点,所以AE ⊥A 1B 1,且AE=√3. 又AB ∥A 1B 1,所以AE ⊥AB. 又侧面ABB 1A 1⊥底面ABC , 且侧面ABB 1A 1∩底面ABC=AB ,又AE ⊂侧面ABB 1A 1,所以AE ⊥底面ABC ,所以三棱柱ABC-A 1B 1C 1的体积为V=S △ABC ·AE=12AB ·AC ·AE=12×2×2×√3=2√3. (2)在直线AA 1上存在点P ,使得CP ∥平面AEF.理由如下:连接BE 并延长,与AA 1的延长线相交,交点为P.连接CP. 因为A 1B 1∥AB ,故PEPB =PA 1PA=A 1E AB.因为E 为棱A 1B 1的中点,AB=A 1B 1,所以A 1E AB =12,所以PE=EB.又F 为棱BC 的中点,所以EF 为△BCP 的中位线, 所以EF ∥CP.又EF ⊂平面AEF ,CP ⊄平面AEF , 所以CP ∥平面AEF.故在直线AA 1上存在点P ,使得CP ∥平面AEF. 此时,PA 1=AA 1=2,所以AP=2AA 1=4.快乐分享,知识无界!感谢您的下载!由Ruize收集整理!。
2021版高考数学(文)大一轮人教A广西专用单元质检十一 概率

单元质检十一概率(时间:45分钟满分:100分)单元质检卷第25页一、选择题(本大题共6小题,每小题7分,共42分)1.若某群体中的成员只用现金支付的概率为0.45,既用现金支付也用非现金支付的概率为0.15,则不用现金支付的概率为()A.0.3B.0.4C.0.6D.0.7答案:B解析:设不用现金支付的概率为P,则P=1-0.45-0.15=0.4.2.从装有3个红球、2个白球的袋中任取3个球,若事件A=“所取的3个球中至少有1个白球”,则事件A的对立事件是()A.1个白球、2个红球B.2个白球、1个红球C.3个都是红球D.至少有1个红球答案:C解析:事件A=“所取的3个球中至少有1个白球”说明有白球,白球的个数可能是1或2或3,和事件“1个白球、2个红球”“2个白球、1个红球”“至少有1个红球”都能同时发生,既不互斥,也不对立.故选C.3.(2019宁夏平罗中学高三四模)现有4本不同的书平均分给两名同学,则语文书、数学书恰好分给一位同学的概率为()A.12B.13C.16D.112答案:B解析:4本不同的书平均分给两名同学的基本情况有6种,语文书、数学书恰好分给一位同学的基本情况有2种,故所求概率为13.4.已知函数f(x)=2x(x<0),其值域为D,在区间(-1,2)上随机取一个数x,则x∈D的概率是()A.12B.13C.14D.23答案:B解析:函数f(x)=2x(x<0)的值域为(0,1),即D=(0,1),则在区间(-1,2)上随机取一个数x,x∈D的概率P=1-02-(-1)=13.故选B.5.七巧板是我国古代劳动人民的发明之一,它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的.一个用七巧板拼成的正方形如图所示,若在此正方形中任取一点,则此点取自阴影部分的概率是()A.14B.18C.38D.316答案:B解析:不妨设小正方形的边长为1,则两个最小的等腰直角三角形的边长为1,1,√2,左上角的等腰直角三角形的边长为√2,√2,2,两个最大的等腰直角三角形的边长为2,2,2√2,即大正方形的边长为2√2, 所以所求概率P=1-12×2+1+1+2×28=18.6.已知P 是△ABC 所在平面内一点,4PB ⃗⃗⃗⃗⃗ +5PC ⃗⃗⃗⃗⃗ +3PA⃗⃗⃗⃗⃗ =0.现将一粒红豆随机撒在△ABC 内,则红豆落在△PBC 内的概率是( ) A .14 B .13C .512D .12答案:A解析:依题意,易知点P 位于△ABC 内,作PB 1⃗⃗⃗⃗⃗⃗⃗ =4PB ⃗⃗⃗⃗⃗ ,PC 1⃗⃗⃗⃗⃗⃗⃗ =5PC ⃗⃗⃗⃗⃗ ,PA 1⃗⃗⃗⃗⃗⃗⃗ =3PA ⃗⃗⃗⃗⃗ ,则PB 1⃗⃗⃗⃗⃗⃗⃗ +PC 1⃗⃗⃗⃗⃗⃗⃗ +PA 1⃗⃗⃗⃗⃗⃗⃗ =0,点P 是△A 1B 1C 1的重心. S △PB 1C 1=S △PC 1A 1=S △PA 1B 1, 而S △PBC =(14×15)S △PB 1C 1, S △PCA =(13×15)·S △PC 1A 1,S△PAB=(13×14)S △PA 1B 1,因此S △PBC ∶S △PCA ∶S △PAB =3∶4∶5, 即S △PBCS△PBC+S △PCA +S △PAB =33+4+5=14,即红豆落在△PBC 内的概率等于14,故选A .二、填空题(本大题共2小题,每小题7分,共14分)7.已知实数x ∈[2,30],执行如图所示的程序框图,则输出的x 不小于103的概率是 .答案:914解析:已知实数x∈[2,30],经过第一次循环得到x=2x+1,n=2;经过第二次循环得到x=2(2x+1)+1,n=3;经过第三次循环得到x=2[2(2x+1)+1]+1,n=4;此时退出循环,输出的值为8x+7.令8x+7≥103得x≥12.由几何概型可知输出的x不小于103的概率为30-1230-2=914.8.两名教师对一篇初评为“优秀”的作文复评,若批改成绩都是两位正整数,且十位数字都是5,则两名教师批改成绩之差的绝对值不超过2的概率为.答案:0.44解析:用(x,y)表示两名教师的批改成绩,则(x,y)的所有可能情况为10×10=100(种).当x=50时,y可取50,51,52,共3种可能;当x=51时,y可取50,51,52,53,共4种可能;当x=52,53,54,55,56,57时,y的取法均有5种,共30种可能;当x=58时,y可取56,57,58,59,共4种可能;当x=59时,y可取57,58,59,共3种可能.综上可得,两名教师批改成绩之差的绝对值不超过2的情况有44种.由古典概型的概率公式可得,所求概率为P=44100=0.44.三、解答题(本大题共3小题,共44分)9.(14分)已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.(1)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?(2)设抽出的7名同学分别用A,B,C,D,E,F,G表示,现从中随机抽取2名同学承担敬老院的卫生工作.①试用所给字母列举出所有可能的抽取结果;②设M 为事件“抽取的2名同学来自同一年级”,求事件M 发生的概率.解:(1)由已知,甲、乙、丙三个年级的学生志愿者人数之比为3∶2∶2,由于采用分层抽样的方法从中抽取7名同学,因此应从甲、乙、丙三个年级的学生志愿者中分别抽取3人、2人、2人.(2)①从抽出的7名同学中随机抽取2名同学的所有可能结果为{A,B},{A,C},{A,D},{A,E},{A,F},{A,G},{B,C},{B,D},{B,E},{B,F},{B,G},{C,D},{C,E},{C,F},{C,G},{D,E},{D,F},{D,G},{E,F},{E,G},{F,G},共21种.②由①,不妨设抽出的7名同学中,来自甲年级的是A,B,C,来自乙年级的是D,E,来自丙年级的是F,G,则从抽出的7名同学中随机抽取的2名同学来自同一年级的所有可能结果为{A,B},{A,C},{B,C},{D,E},{F,G},共5种. 所以,事件M 发生的概率P (M )=521.10.(15分)某保险公司利用简单随机抽样的方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:(1)若每辆车的投保金额均为2 800元,估计赔付金额大于投保金额的概率;(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4 000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4 000元的概率.解:(1)设A 表示事件“赔付金额为3000元”,B 表示事件“赔付金额为4000元”,以频率估计概率得P (A )=1501000=0.15,P (B )=1201000=0.12.因为投保金额为2800元,赔付金额大于投保金额对应的情形是3000元和4000元, 所以其概率为P (A )+P (B )=0.15+0.12=0.27.(2)设C 表示事件“投保车辆中新司机获赔4000元”,由已知,样本车辆中车主为新司机的有0.1×1000=100辆,而赔付金额为4000元的车辆中,车主为新司机的有0.2×120=24辆.所以样本车辆中新司机车主获赔金额为4000元的频率为24100=0.24,由频率估计概率得P (C )=0.24.11.(15分)甲、乙两人玩一种游戏,每次由甲、乙各出1到5根手指头,若和为偶数,算甲赢,否则算乙赢.(1)若以A 表示和为6的事件,求P (A ).(2)现连玩三次,若以B 表示甲至少赢一次的事件,C 表示乙至少赢两次的事件,试问B 与C 是否为互斥事件?为什么?(3)这种游戏规则公平吗?说明理由.解:(1)甲、乙各出1到5根手指头,共有5×5=25(种)可能结果,和为6的有(1,5),(5,1),(2,4),(4,2),(3,3),共有5种可能结果,故P (A )=525=15.(2)B与C不是互斥事件,理由如下:B与C都包含“甲赢一次,乙赢两次”,事件B与事件C 可能同时发生,故不是互斥事件.(3)和为偶数的有13种可能结果,甲赢的概率为P=1325>12,故这种游戏规则不公平.快乐分享,知识无界!感谢您的下载!由Ruize收集整理!。
2021版高考数学(文)大一轮人教A广西专用考点33 基本不等式及其应用

考点规范练33 基本不等式及其应用考点规范练A 册第24页基础巩固1.下列不等式一定成立的是( ) A.lg (x 2+14)>lg x (x>0) B.sin x+1sinx ≥2(x ≠k π,k ∈Z ) C.x 2+1≥2|x|(x ∈R ) D.1x +1>1(x ∈R ) 答案:C解析:因为x>0,所以x 2+14≥2·x ·12=x ,所以lg (x 2+14)≥lg x (x>0),故选项A 不正确; 当x ≠k π,k ∈Z 时,sin x 的正负不定,故选项B 不正确; 由基本不等式可知选项C 正确; 当x=0时,1x +1=1,故选项D 不正确.2.已知a>0,b>0,a ,b 的等比中项是1,且m=b+1a ,n=a+1b ,则m+n 的最小值是( ) A.3 B.4C.5D.6答案:B解析:由题意知ab=1,则m=b+1a =2b ,n=a+1b =2a ,故m+n=2(a+b )≥4√ab =4(当且仅当a=b=1时,等号成立).3.小王从甲地到乙地往返的时速分别为a 和b (a<b ),其全程的平均时速为v ,则( ) A.a<v<√ab B.v=√ab C.√ab <v<a+b 2D.v=a+b 2答案:A解析:设甲、乙两地相距s ,则小王往返两地用时为s a +sb , 从而v=2ssa +s b=2aba+b .∵0<a<b ,∴√ab <a+b 2,2ab a+b >2ab 2b=a ,∴2a+b <√ab,即2aba+b<√ab,∴a<v<√ab.4.已知圆x2+y2+4x-2y-1=0上存在两点关于直线ax-2by+2=0(a>0,b>0)对称,则1a +4b的最小值为()A.8B.9C.16D.18答案:B解析:由圆的对称性可得,直线ax-2by+2=0必过圆心(-2,1),所以a+b=1.所以1a +4b=(1a+4b)(a+b)=5+ba+4ab≥5+4=9,当且仅当ba=4ab,即2a=b=23时等号成立,故选B.5.若正数x,y满足4x2+9y2+3xy=30,则xy的最大值是()A.43B.53C.2D.54答案:C解析:由x>0,y>0,得4x2+9y2+3xy≥2×(2x)×(3y)+3xy(当且仅当2x=3y时等号成立), 则12xy+3xy≤30,即xy≤2,故xy的最大值为2.6.设x,y∈R,a>1,b>1,若a x=b y=3,a+b=2√3,则1x +1y的最大值为()A.2B.32C.1 D.12答案:C解析:由a x=b y=3,1x +1y=1log a3+1log b3=lga+lgblg3=lg(ab)lg3,又a>1,b>1,所以ab≤(a+b2)2=3,所以lg(ab)≤lg3,从而1x +1y≤lg3lg3=1,当且仅当a=b=√3时等号成立.7.已知x>1,则log x9+log27x的最小值是.答案:2√63解析:∵x>1,∴log x9+log27x=2lg3lgx +lgx3lg3≥2√23=2√63,当且仅当x=3√6时等号成立.∴log x9+log27x的最小值为2√63.8.(2019河北涞水波峰中学高三模拟一)已知x>0,y>0,且4x +1y=1,若x+y≥m2+m+3恒成立,则实数m的取值范围是.答案:[-3,2]解析:x+y=(x+y)(4x +1y)=5+xy+4yx≥5+2√xy×4yx=9,当且仅当x=6,y=3时等号成立,所以x+y的最小值为9,所以m2+m+3≤9,m2+m-6≤0,解得-3≤m≤2,即实数m的取值范围是[-3,2].9.某公司购买一批机器投入生产,据市场分析,每台机器生产的产品可获得的总利润y(单位:万元)与机器运转时间x(单位:年)的关系为y=-x2+18x-25(x∈N*).则当每台机器运转年时,年平均利润最大,最大值是万元.答案:58解析:每台机器运转x年的年平均利润为yx =18-(x+25x),而x>0,所以yx≤18-2√25=8,当且仅当x=5时,年平均利润最大,最大值为8万元.10.已知a,b∈R,且a-3b+6=0,则2a+18的最小值为.答案:14解析:∵a-3b+6=0,∴a-3b=-6.∵a,b∈R,∴2a>0,18>0.∴2a+18≥2a-3b2√2-6=14,当且仅当2a=18,即a=-3,b=1时取等号.11.某种饮料分两次提价,提价方案有两种,方案甲:第一次提价p%,第二次提价q%;方案乙:每次都提价p+q2%,若p>q>0,则提价多的方案是.答案:乙解析:设原价为a,则方案甲提价后为a(1+p%)(1+q%),方案乙提价后为a(1+p+q2%)2.由于(1+p%)(1+q%)<[(1+p%)+(1+q%)2]2=(1+p+q2%)2,因此提价多的是方案乙.12.设a,b均为正实数,求证:1a2+1b2+ab≥2√2.答案:证明因为a ,b 均为正实数,所以1a 2+1b 2≥2√1a 2·1b 2=2ab , 当且仅当1a =1b ,即a=b 时,等号成立, 又因为2ab +ab ≥2√2ab ·ab =2√2, 当且仅当2ab =ab 时,等号成立, 所以1a +1b +ab ≥2ab +ab ≥2√2,当且仅当{1a 2=1b 2,2ab=ab ,即a=b=√24时,等号成立.能力提升13.已知不等式2x 2-axy+y 2≥0对任意x ∈[1,2]及y ∈[1,3]恒成立,则实数a 的取值范围是( ) A.a ≤2√2B.a ≥2√2C.a ≤113D.a ≤92答案:A解析:因为2x 2-axy+y 2≥0,且y ≠0, 所以2(x y )2-a xy +1≥0.令t=xy ,则不等式变为2t 2-at+1≥0. 由x ∈[1,2],y ∈[1,3],可知t ∈[13,2], 即2t 2-at+1≥0在t ∈[13,2]时恒成立. 由2t 2-at+1≥0可得a ≤2t 2+1t,即a ≤2t+1t .又2t+1t ≥2√2t ·1t =2√2,当且仅当2t=1t ,即t=√22时等号成立,所以2t+1t 取得最小值2√2,所以有a ≤2√2,故选A . 14.已知不等式|y+4|-|y|≤2x +a2x 对任意实数x ,y 都成立,则实数a 的最小值为( ) A.1 B.2C.3D.4答案:D解析:令f (y )=|y+4|-|y|, 则f (y )≤|y+4-y|=4,即f (y )max =4.∵不等式|y+4|-|y|≤2x +a2x 对任意实数x ,y 都成立, ∴2x +a2x ≥f (y )max =4,∴a ≥-(2x )2+4×2x =-(2x -2)2+4恒成立; 令g (x )=-(2x )2+4×2x ,则a ≥g (x )max =4,∴实数a 的最小值为4. 15.已知x>0,a 为大于2x 的常数. (1)求函数y=x (a-2x )的最大值; (2)求y=1a -2x -x 的最小值.解:(1)∵x>0,a>2x ,∴y=x (a-2x )=12×2x (a-2x )≤12×[2x+(a -2x )2]2=a 28,当且仅当x=a4时取等号, 故函数y=x (a-2x )的最大值为a 28. (2)y=1a -2x -x=1a -2x +a -2x 2−a 2≥2√12−a 2=√2−a 2,当且仅当x=a -√22时取等号.故y=1a -2x -x 的最小值为√2−a2.16.某工厂某种产品的年固定成本为250万元,每生产x 千件,需另投入成本为C (x )(单元:万元),当年产量不足80千件时,C (x )=13x 2+10x (单位:万元).当年产量不少于80千件时,C (x )=51x+10000x-1 450(单位:万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.(1)写出年利润L (x )(单位:万元)关于年产量x (单位:千件)的函数解析式; (2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?解:(1)因为每件商品售价为0.05万元,则x 千件商品销售额为0.05×1000x 万元,依题意得,当0<x<80时,L (x )=(0.05×1000x )-13x 2-10x-250=-13x 2+40x-250; 当x ≥80时,L (x )=(0.05×1000x )-51x-10000x +1450-250=1200-(x +10000x),则L (x )={-13x 2+40x -250,0<x <80,1200-(x +10000x ),x ≥80.(2)当0<x<80时,L (x )=-13(x-60)2+950,此时,当x=60时,L (x )取得最大值L (60)=950.当x ≥80时,L (x )=1200-(x +10000x)≤1200-2√x ·10000x=1200-200=1000,当且仅当x=10000x时,即x=100时,L (x )取得最大值1000.因为950<1000,所以当年产量为100千件时,该厂在这一商品的生产中所获利润最大.最大利润为1000万元.高考预测17.若a ,b 满足ab=a+b+3,求ab 的取值范围. 解:∵ab=a+b+3,∴a+b=ab-3, ∴(a+b )2=(ab-3)2. ∵(a+b )2≥4ab , ∴(ab-3)2≥4ab ,即(ab )2-10ab+9≥0,故ab ≤1或ab ≥9. 因此ab 的取值范围是(-∞,1]∪[9,+∞).快乐分享,知识无界!感谢您的下载!由Ruize收集整理!。
广西省南宁市2021届新高考第二次大联考数学试卷含解析

广西省南宁市2021届新高考第二次大联考数学试卷一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.中国古代数学著作《算法统宗》中有这样一个问题;“三百七十八里关,初行健步不为难,次后脚痛递减半,六朝才得到其关,要见每朝行里数,请公仔细算相还.”其意思为:“有一个人走了378里路,第一天健步走行,从第二天起脚痛每天走的路程是前一天的一半,走了6天后到达目的地,求该人每天走的路程.”由这个描述请算出这人第四天走的路程为( ) A .6里 B .12里C .24里D .48里【答案】C 【解析】 【分析】设第一天走1a 里,则{}n a 是以1a 为首项,以12为公比的等比数列,由题意得1661(1)2378112a S -==-,求出1192a =(里),由此能求出该人第四天走的路程. 【详解】设第一天走1a 里,则{}n a 是以1a 为首项,以12为公比的等比数列, 由题意得:1661(1)2378112a S -==-, 解得1192a =(里),∴34111()1922428a a =⨯=⨯=(里).故选:C . 【点睛】本题考查等比数列的某一项的求法,考查等比数列等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题. 2.已知α是第二象限的角,3tan()4πα+=-,则sin 2α=( ) A .1225B .1225-C .2425D .2425-【答案】D 【解析】利用诱导公式和同角三角函数的基本关系求出2cos α,再利用二倍角的正弦公式代入求解即可. 【详解】因为3tan()4πα+=-, 由诱导公式可得,sin 3tan cos 4ααα==-, 即3sin cos 4αα=-, 因为22sin cos 1αα+=, 所以216cos 25α=, 由二倍角的正弦公式可得,23sin 22sin cos cos 2αααα==-,所以31624sin 222525α=-⨯=-. 故选:D 【点睛】本题考查诱导公式、同角三角函数的基本关系和二倍角的正弦公式;考查运算求解能力和知识的综合运用能力;属于中档题.3.已知集合{2,3,4}A =,集合{},2B m m =+,若{2}A B =I ,则m =( ) A .0 B .1C .2D .4【答案】A 【解析】 【分析】根据2m =或22m +=,验证交集后求得m 的值. 【详解】因为{2}A B =I ,所以2m =或22m +=.当2m =时,{2,4}A B =I ,不符合题意,当22m +=时,0m =.故选A.【点睛】本小题主要考查集合的交集概念及运算,属于基础题.4.空间点到平面的距离定义如下:过空间一点作平面的垂线,这个点和垂足之间的距离叫做这个点到这个平面的距离.已知平面α,β,λ两两互相垂直,点A α∈,点A 到β,γ的距离都是3,点P 是αA .33-B .3C .332- D .32【答案】D 【解析】 【分析】建立平面直角坐标系,将问题转化为点P 的轨迹上的点到x 轴的距离的最小值,利用P 到x 轴的距离等于P 到点A 的距离得到P 点轨迹方程,得到()26399y x =-+≥,进而得到所求最小值.【详解】如图,原题等价于在直角坐标系xOy 中,点()3,3A ,P 是第一象限内的动点,满足P 到x 轴的距离等于点P 到点A 的距离,求点P 的轨迹上的点到x 轴的距离的最小值. 设(),P x y ,则()()2233y x y =-+-,化简得:()23690x y --+=,则()26399y x =-+≥,解得:32y ≥, 即点P 的轨迹上的点到β的距离的最小值是32. 故选:D . 【点睛】本题考查立体几何中点面距离最值的求解,关键是能够准确求得动点轨迹方程,进而根据轨迹方程构造不等关系求得最值.5.已知底面为正方形的四棱锥,其一条侧棱垂直于底面,那么该四棱锥的三视图可能是下列各图中的( )A .B .C .D .【答案】C 【解析】试题分析:通过对以下四个四棱锥的三视图对照可知,只有选项C 是符合要求的.考点:三视图6.已知函数()()4,2x f x x g x a x =+=+,若[]121,3,2,32x x ⎡⎤∀∈∃∈⎢⎥⎣⎦,使得()()12f x g x ≥,则实数a 的取值范围是( ) A .1a ≤ B .1a ≥ C .0a ≤ D .0a ≥【答案】C 【解析】试题分析:由题意知,当11,32x ⎡⎤∈⎢⎥⎣⎦时,由()4424f x x x x x=+≥⋅=,当且仅当4x x =时,即2x =等号是成立,所以函数()f x 的最小值为4,当[]22,3x ∈时,()2xg x a =+为单调递增函数,所以()()min 24g x g a ==+,又因为[]121,3,2,32x x ⎡⎤∀∈∃∈⎢⎥⎣⎦,使得()()12f x g x ≥,即()f x 在1,32x ⎡⎤∈⎢⎥⎣⎦的最小值不小于()g x 在[]2,3x ∈上的最小值,即44a +≤,解得0a ≤,故选C . 考点:函数的综合问题.【方法点晴】本题主要考查了函数的综合问题,其中解答中涉及到基本不等式求最值、函数的单调性及其应用、全称命题与存在命题的应用等知识点的综合考查,试题思维量大,属于中档试题,着重考查了学生分析问题和解答问题的能力,以及转化与化归思想的应用,其中解答中转化为()f x 在1,32x ⎡⎤∈⎢⎥⎣⎦的最小7.已知集合{}1,2,3,,M n =L (*n N ∈),若集合{}12,A a a M =⊆,且对任意的b M ∈,存在{},1,0,1λμ∈-使得i j b a a λμ=+,其中,i j a a A ∈,12i j ≤≤≤,则称集合A 为集合M 的基底.下列集合中能作为集合{}1,2,3,4,5,6M =的基底的是( ) A .{}1,5 B .{}3,5C .{}2,3D .{}2,4【答案】C 【解析】 【分析】根据题目中的基底定义求解. 【详解】因为11213=-⨯+⨯,21203=⨯+⨯, 30213=⨯+⨯, 41212=⨯+⨯,51213=⨯+⨯, 61313=⨯+⨯,所以{}2,3能作为集合{}1,2,3,4,5,6M =的基底, 故选:C 【点睛】本题主要考查集合的新定义,还考查了理解辨析的能力,属于基础题.8.ABC V 是边长为E 、F 分别为AB 、AC 的中点,沿EF 把AEF V 折起,使点A 翻折到点P 的位置,连接PB 、PC ,当四棱锥P BCFE -的外接球的表面积最小时,四棱锥P BCFE -的体积为( )A B C D 【答案】D 【解析】 【分析】首先由题意得,当梯形BCFE 的外接圆圆心为四棱锥P BCFE -的外接球球心时,外接球的半径最小,通过图形发现,BC 的中点即为梯形BCFE 的外接圆圆心,也即四棱锥P BCFE -的外接球球心,则可如图,四边形BCFE 为等腰梯形,则其必有外接圆,设O 为梯形BCFE 的外接圆圆心,当O 也为四棱锥P BCFE -的外接球球心时,外接球的半径最小,也就使得外接球的表面积最小,过A 作BC 的垂线交BC 于点M ,交EF 于点N ,连接,PM PN ,点O 必在AM 上,E 、F 分别为AB 、AC 的中点,则必有AN PN MN ==,90APM ∴∠=o ,即APM △为直角三角形.对于等腰梯形BCFE ,如图:因为ABC V 是等边三角形,E 、F 、M 分别为AB 、AC 、BC 的中点, 必有MB MC MF ME ===,所以点M 为等腰梯形BCFE 的外接圆圆心,即点O 与点M 重合,如图132PO OC BC ∴===222336PA AO PO =-=-= 所以四棱锥P BCFE -底面BCFE 的高为362PO PA AM ⋅⨯== 113131362332334342P BCFE BCFE ABC V S h S h -==⨯=⨯⨯⨯=V 故选:D. 【点睛】9.框图与程序是解决数学问题的重要手段,实际生活中的一些问题在抽象为数学模型之后,可以制作框图,编写程序,得到解决,例如,为了计算一组数据的方差,设计了如图所示的程序框图,其中输入115x =,216x =,318x =,420x =,522x =,624x =,725x =,则图中空白框中应填入( )A .6i >,7SS = B .6i …7SS = C .6i >,7S S = D .6i …,7S S = 【答案】A 【解析】 【分析】依题意问题是()()()22212712020207S x x x ⎡⎤=-+-+⋯+-⎣⎦,然后按直到型验证即可. 【详解】根据题意为了计算7个数的方差,即输出的()()()22212712020207S x x x ⎡⎤=-+-+⋯+-⎣⎦, 观察程序框图可知,应填入6i >,7SS =, 故选:A. 【点睛】本题考查算法与程序框图,考查推理论证能力以及转化与化归思想,属于基础题. 10.3481(3)(2)x x x+-展开式中x 2的系数为( ) A .-1280 B .4864C .-4864D .1280【答案】A根据二项式展开式的公式得到具体为:()23174268811322x C x C x x ⎡⎤⎡⎤⎛⎫⎛⎫-+⋅-⎢⎥ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦⎢⎥⎣⎦化简求值即可.【详解】根据二项式的展开式得到可以第一个括号里出33x 项,第二个括号里出1x项,或者第一个括号里出4x ,第二个括号里出21x ,具体为:()23174268811322x C x C x x ⎡⎤⎡⎤⎛⎫⎛⎫-+⋅-⎢⎥ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦⎢⎥⎣⎦化简得到-1280 x 2 故得到答案为:A. 【点睛】求二项展开式有关问题的常见类型及解题策略:(1)求展开式中的特定项.可依据条件写出第1r +项,再由特定项的特点求出r 值即可.(2)已知展开式的某项,求特定项的系数.可由某项得出参数项,再由通项写出第1r +项,由特定项得出r 值,最后求出其参数.11.双曲线22221(0,0)x y a b a b-=>>的右焦点为F ,过点F 且与x 轴垂直的直线交两渐近线于,M N 两点,与双曲线的其中一个交点为P ,若(,)OP OM ON R λμλμ=+∈u u u r u u u u r u u u r ,且625λμ=,则该双曲线的离心率为( )A B .12C .12D 【答案】D 【解析】 【分析】根据已知得本题首先求出直线与双曲线渐近线的交点,再利用OP OM ON λμ=+u u u r u u u u r u u u r,求出点()()bc P c a λμλμ⎛⎫+- ⎪⎝⎭,,因为点P 在双曲线上,及c e a =,代入整理及得241e λμ=,又已知625λμ=,即可求出离心率. 【详解】由题意可知bc bc M c N c a a ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭,,,,代入OP OM ON λμ=+u u u r u u u u r u u u r 得:()()bc P c a λμλμ⎛⎫+- ⎪⎝⎭,,代入双曲线方程22221x y a b -=整理得:241e λμ=,又因为625λμ=,即可得到e =,本题主要考查的是双曲线的简单几何性质和向量的坐标运算,离心率问题关键寻求关于a ,b ,c 的方程或不等式,由此计算双曲线的离心率或范围,属于中档题. 12.已知过点(1,1)P 且与曲线3y x =相切的直线的条数有( ). A .0 B .1 C .2 D .3【答案】C 【解析】 【分析】设切点为()00x ,y ,则300y x =,由于直线l 经过点()1,1,可得切线的斜率,再根据导数的几何意义求出曲线在点0x 处的切线斜率,建立关于0x 的方程,从而可求方程. 【详解】若直线与曲线切于点()()000x ,y x 0≠,则32000000y 1x 1k x x 1x 1x 1--===++--, 又∵2y'3x =,∴200y'x x 3x ==,∴2002x x 10--=,解得0x 1=,01x 2=-, ∴过点()P 1,1与曲线3C :y x =相切的直线方程为3x y 20--=或3x 4y 10-+=, 故选C . 【点睛】本题主要考查了利用导数求曲线上过某点切线方程的斜率,求解曲线的切线的方程,其中解答中熟记利用导数的几何意义求解切线的方程是解答的关键,着重考查了运算与求解能力,属于基础题. 二、填空题:本题共4小题,每小题5分,共20分。
广西南宁市、玉林市、贵港市等2025届高三大练习(二)数学试题

广西南宁市、玉林市、贵港市等2025届高三大练习(二)数学试题注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知角α的顶点与坐标原点O 重合,始边与x 轴的非负半轴重合,它的终边过点(3,4)P --,则tan 24πα⎛⎫+ ⎪⎝⎭的值为( ) A .247-B .1731-C .247D .17312. “1sin 2x =”是“2()6x k k Z ππ=+∈”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件3.在边长为23的菱形ABCD 中,60BAD ∠=︒,沿对角线BD 折成二面角A BD C --为120︒的四面体ABCD (如图),则此四面体的外接球表面积为( )A .28πB .7πC .14πD .21π4.如图,在ABC 中,,(,),2AD AB BD xAB yAC x y R AD ⊥=+∈=,且12AC AD ⋅=,则2x y +=( )A .1B .23-C .13-D .34-5.执行如图所示的程序框图,则输出的结果为( )A .40322017B .20152016C .20162017D .201510086.已知函数2()ln(1)f x x x-=+-,则函数(1)=-y f x 的图象大致为( )A .B .C .D .7.在ABC ∆中,角,,A B C 的对边分别为,,a b c ,3C π=,若()6,m c a b =-,(,6n a b c =-,且//m n ,则ABC ∆的面积为( ) A .3B .932C .332D .338.已知(1)nx λ+展开式中第三项的二项式系数与第四项的二项式系数相等,2012(1)n n n x a a x a x a x λ+=++++,若12242n a a a ++⋅⋅⋅=,则012(1)nn a a a a -+-⋅⋅⋅+-的值为( )A .1B .-1C .8lD .-819.已知20,()1(0),{|()},{|(())()}a f x ax x x A x f x x B x f f x f x x >=-+>=≤=≤≤,若A B φ=≠则实数a 的取值范围是( ) A .(0,1]B .3(0,]4C .3[,1]4D .[1,)+∞10.已知抛物线C :24x y =的焦点为F ,过点F 的直线l 交抛物线C 于A ,B 两点,其中点A 在第一象限,若弦AB的长为254,则AF BF =( ) A .2或12B .3或13C .4或14D .5或1511.函数()y f x =()x R ∈在(]1∞-,上单调递减,且(1)f x +是偶函数,若(22)(2)f x f -> ,则x 的取值范围是( ) A .(2,+∞) B .(﹣∞,1)∪(2,+∞) C .(1,2)D .(﹣∞,1)12.设函数()()ln 1f x x =-的定义域为D ,命题p :x D ∀∈,()f x x ≤的否定是( ) A .x D ∀∈,()f x x > B .0x D ∃∈,()00f x x ≤ C .x D ∀∉,()f x x >D .0x D ∃∈,()00f x x >二、填空题:本题共4小题,每小题5分,共20分。
广西桂林、崇左市2021届高三联合调研考试(二模)数学(文)答案

2
,则
f
6
=
.
16. 已知函数 f x x2ln x a 1有两个不同的零点,则实数 a 的取值范围是
ቤተ መጻሕፍቲ ባይዱ
.
【文科数学试卷 第 2 页(共 4 页)】
三、解答题:解答应写出文字说明,证明过程或演算步骤. 第 17-21 题为必考题,
每个试题考生都必须作答。第 22、23 题为选考题,考生根据要求做答。
C. 1,1
D. 0,1
A. 1
B. 2
C. 2
D. 3
3.
已知
f
x
2x1 3,
log2 1 x
x
,
x
1,
1,
则
f
f
3
A. 1
B. 1
C. 2
D. 2
4.若 sin cos 2 ,则 sin 2
A. 1
B. 1
C. 1
D. 1
2
2
5. 已知中心在坐标原点的椭圆 C 的右焦点为 F 2,0 ,且其离心率为 1 ,则 C 的方程为
2021 年高考桂林市第二次调研考试
数学(文科)
考生注意: 1. 本卷满分 150 分,考试时间 120 分钟。 2. 考生作答时,请将答案答在答题卡上,选择题每小题选出答案后,用 2B 铅笔把答题卡
上对应题目的答案标号涂黑,非选择题请用直径 0.5 毫米黑色墨水签字笔在答题卡上各题的答 题区域内作答,超出答题卡区域书写的答案无效,在试题卷草稿上作答无效。
A. 1
B. 1
C. 1
D. 1
2
4
【文科数学试卷 第 1 页(共 4 页)】
8. 《聊斋志异》中有这样一首诗:“挑水砍柴不堪苦,请归但求穿墙术. 得诀自诩无所阻, 额上坟起终不悟.”在这里我们称形如以下等式具有“穿墙术”:
2021版高考数学(文)大一轮人教A广西专用滚动测试卷四(第一_九章)

滚动测试卷四(第一~九章)(时间:120分钟 满分:150分)滚动测试卷第13页一、选择题(本大题共12小题,每小题5分,共60分)1.若集合M={x |(12)x≥1},N={x|y=lg(x+2)},则M ∩N 等于( ) A.[0,+∞) B.(-2,0] C.(-2,+∞) D.(-∞,-2)∪[0,+∞)答案:B解析:因为集合M={x |(12)x≥1}={x |(12)x≥(12)0}, 所以M={x|x ≤0},N={x|y=lg(x+2)}={x|x>-2},所以M ∩N={x|x ≤0}∩{x|x>-2}={x|-2<x ≤0}.2.设复数√3-i 2 021在复平面内对应的点为A ,则过原点和点A 的直线的倾斜角为( ) A.π6 B.-π6 C.2π3 D.5π6答案:D解析:设直线的倾斜角为α,α∈[0,π),∵复数√3-i 2021=√3-i 在复平面内对应的点是A (√3, -1),原点(0,0),直线过原点和点A ,∴直线的斜率k=√3-0=-√33,即tan α=-√33,∴α=5π6.故选D . 3.(2019广西桂林、崇左联合模拟)将函数f (x )=sin (2x +π3)的图象向右平移π6个单位,得到函数g (x )的图象,则下列说法不正确的是( ) A.g (x )的周期为πB.x=π6是g (x )图象的一条对称轴 C.g (π6)=√32D.g (x )为奇函数 答案:B解析:g (x )=sin2x ,周期为π,A 正确;g (π6)=sin π3=√32,B 不正确,C 正确;g (x )=sin2x 为奇函数,D 正确.4.已知函数y=f (x )的定义域为{x|x ≠0},满足f (x )+f (-x )=0,当x>0时,f (x )=ln x-x+1,则函数y=f (x )的大致图象是( )答案:A解析:因为函数y=f (x )的定义域为{x|x ≠0},满足f (x )+f (-x )=0,所以函数f (x )是奇函数,排除C 项,D 项.当x=e 时,f (e)=1-e +1=2-e <0,排除B 项,A 项正确.5.已知向量a ,b 满足|a |=1,(a+b )⊥a ,(2a+b )⊥b ,则向量a ,b 的夹角为( ) A.π6B.π4C.π3D.3π4答案:D解析:设向量a ,b 的夹角为θ, 因为|a |=1,(a+b )⊥a ,(2a +b )⊥b , 所以(a+b )·a =1+|b |cos θ=0,① (2a+b )·b =2|b |cos θ+|b |2=0.② 由①②可得cos θ=-√22,θ=3π4,故选D .6.已知双曲线x 2a 2−y 2b 2=1(a>0,b>0)的一条渐近线平行于直线l :x+2y+5=0,双曲线的一个焦点在直线l 上,则双曲线的方程为( ) A.x 220−y 25=1B.x 25−y 220=1C.3x 225−3y 2100=1 D.3x 2100−3y 225=1答案:A解析:∵双曲线x 2a 2−y 2b 2=1(a>0,b>0)的一条渐近线平行于直线l :x+2y+5=0,双曲线的一个焦点在直线l 上, ∴{-ba =-12,c =-5,a 2+b 2=c 2,解得{a =2√5,b =√5.∴双曲线方程为x 220−y 25=1.7.如图,在△ABC 中,点D 在AC 上,AB ⊥BD ,BC=3√3,BD=5,sin ∠ABC=2√35,则CD 的长为( )A.√14B.4C.2√5D.5答案:B解析:由题意可得, sin ∠ABC=2√35=sin (π2+∠CBD)=cos ∠CBD ,再根据余弦定理可得,CD 2=BC 2+BD 2-2BC ·BD ·cos ∠CBD=27+25-2×3√3×5×2√35=16, 可得CD=4.8.某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在侧(左)视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为( )A.2√17B.2√C.3D.2答案:B解析:如图所示,易知N 为CD⏜的中点,将圆柱的侧面沿母线MC 剪开,展平为矩形MCC'M',易知CN=14CC'=4,MC=2,从M 到N 的路程中最短路径为MN.在Rt △MCN 中,MN=√MC 2+NC 2=2√5.9.已知P 为抛物线y 2=4x 上一个动点,Q 为圆x 2+(y-4)2=1上一个动点,则点P 到点Q 的距离与点P 到直线x=-1的距离之和的最小值是( )A.5B.8C.√17-1D.√15-1 答案:C解析:抛物线y 2=4x 的焦点为F (1,0),圆x 2+(y-4)2=1的圆心为E (0,4),半径为1.根据抛物线的定义可知,点P 到准线的距离等于点P 到焦点的距离,所以当P ,Q ,E ,F 四点共线时,点P 到点Q 的距离与点P 到直线x=-1的距离之和最小,为|QF|=|EF|-r=√42+1-1=√17-1.10.设等差数列{a n}的前n项和为S n,若a2=-11,a5+a9=-2,则当S n取最小值时,n等于()A.9B.8C.7D.6答案:C解析:设等差数列的首项为a1,公差为d,由a2=-11,a5+a9=-2,得{a1+d=-11,a1+6d=-1,解得{a1=-13,d=2.∴a n=-15+2n.由a n=-15+2n≤0,解得n≤152.∴当S n取最小值时,n=7.11.已知f(x)是定义域为(-∞,+∞)的奇函数,满足f(1-x)=f(1+x),若f(1)=2,则f(1)+f(2)+f(3)+…+f(50)=()A.-50B.0C.2D.50答案:C解析:∵f(-x)=f(2+x)=-f(x),∴f(x+4)=f[(x+2)+2]=-f(x+2)=f(x).∴f(x)的周期为4.∵f(x)为奇函数,∴f(0)=0.∵f(2)=f(1+1)=f(1-1)=f(0)=0,f(3)=f(-1)=-f(1)=-2,f(4)=f(0),∴f(1)+f(2)+f(3)+f(4)=0.∴f(1)+f(2)+…+f(50)=f(49)+f(50)=f(1)+f(2)=2.12.已知F1,F2是椭圆C:x 2a2+y2b2=1(a>b>0)的左、右焦点,A是C的左顶点,点P在过A且斜率为√36的直线上,△PF1F2为等腰三角形,∠F1F2P=120°,则C的离心率为()A.23B.12C.13D.14答案:D解析:∵A(-a,0),△PF1F2为等腰三角形, ∴|PF2|=|F1F2|=2c.过点P 作PE ⊥x 轴,∵∠F 1F 2P=120°,∴∠PF 2E=60°.∴|F 2E|=c ,|PE|=√3c ,∴P (2c ,√3c ).∵k PA =√36,∴PA 所在直线方程为y=√36(x+a ). ∴√3c=√36(2c+a ).∴e=ca =14.二、填空题(本大题共4小题,每小题5分,共20分)13.用[x ]表示不大于实数x 的最大整数,方程lg 2x-[lg x ]-2=0的实根个数是 . 答案:3解析:令lg x=t ,则得t 2-2=[t ].作y=t 2-2与y=[t ]的图象,知t 2-2=[t ]有3个解, 分别是t=-1,t=2,还有一解在1<t<2内. 当1<t<2时,[t ]=1,所以t=√3.故得x=110,x=100,x=10√3,即共有3个实根.14.(2019河北衡水中学高三大联考)设实数x ,y 满足约束条件{x +y ≤0,x -y -2≤0,x ≥0,则z=3x+2y 的最大值为 . 答案:1解析:不等式组表示的平面区域(阴影部分)如图所示,平移直线y=-32x ,可知当直线y=-32x+z2经过点P (1,-1)时,z=3x+2y 取最大值1.15.已知圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为78,SA 与圆锥底面所成角为45°.若△SAB 的面积为5√15,则该圆锥的侧面积为 . 答案:40√2π解析:设O 为底面圆圆心,∵cos ∠ASB=78,∴sin ∠ASB=√1-(78)2=√158.∴S △ASB =12×|AS|·|BS|·√158=5√15.∴SA 2=80.∴SA=4√5.∵SA 与圆锥底面所成的角为45°,∠SOA=90°, ∴SO=OA=√22SA=2√10.∴S 圆锥侧=πrl=4√5×2√10×π=40√2π.16.(2019广东深圳高三二调)如图①,在等腰直角三角形ABC 中,斜边AB=4,D 为AB 的中点,将△ACD 沿CD 折叠得到如图②所示的三棱锥C-A'BD.若三棱锥C-A'BD 的外接球的半径为√5,则∠A'DB= .图①图②答案:2π3解析:设△A'BD的外接圆半径为r,∠A'DB=2θ,其中θ∈(0,π2),并设A'B的中点为M,DM=b,A'M=a,则有a2+(b-r)2=r2,由于a2+b2=4,由此可得br=2.又因为1+r2=5,所以r=2,b=1,而cosθ=b2=12,所以∠A'DB=2θ=2π3.三、解答题(本大题共6小题,共70分)17.(10分)已知△ABC的内角A,B,C的对边分别为a,b,c,且b cos A+√33a=c.(1)求cos B;(2)如图,D为△ABC外一点,在平面四边形ABCD中,∠D=2∠B,且AD=1,CD=3,BC=√6,求AB的长.解:(1)在△ABC中,由正弦定理,得sin B cos A+√33sin A=sin C.又C=π-(A+B),所以sin B cos A+√33sin A=sin(A+B),即sin B cos A+√33sin A=sin A cos B+cos A sin B,所以sin A cos B=√33sin A.又A∈(0,π),所以sin A≠0,所以cos B=√33.(2)因为∠D=2∠B,所以cos D=2cos2B-1=-13.在△ACD中,AD=1,CD=3,由余弦定理,得AC2=AD2+CD2-2AD·CD·cos D=1+9-2×1×3×(-13)=12,则AC=2√3.在△ABC中,BC=√6,AC=2√3,cos B=√33,由余弦定理,得AC2=AB2+BC2-2AB·BC·cos B,即12=AB2+6-2·AB×√6×√33,化简得AB2-2√2AB-6=0,解得AB=3√2(负值舍去).故AB的长为3√2.18.(12分)(2019广东汕头二模)如图,等边三角形PAC所在平面与梯形ABCD所在平面垂直,且有AD∥BC,AB=AD=DC=2,BC=4.(1)证明:AB⊥平面PAC;(2)求点D到平面PAB的距离.答案:(1)证明取BC中点M,连接AM,则四边形AMCD为菱形,即有AM=MC=12BC,所以AB⊥AC.∵AB⊂平面ABCD,平面ABCD⊥平面PAC,平面ABCD∩平面PAC=AC,∴AB⊥平面PAC.(2)解由(1)可得PA=AC=2√3,∠ABC=60°,∠BAD=120°.取AC的中点O,连接PO,则PO⊥AC,PO=3.∵PO⊂平面PAC,平面PAC⊥平面ABCD,平面PAC∩平面ABCD=AC,∴PO⊥平面ABCD.V D-PAB=V P-ABD=13S△ABD·PO=1 3×12×2×2×sin120°×3=√3.由(1)有AB⊥平面PAC,得AB⊥PA, ∴S△PAB=12×2×2√3=2√3.设点D 到平面PAB 的距离为d , ∵V D-PAB =13S △PAB ·d ,∴d=32.19.(12分)已知动圆C 与圆E :x 2+(y-1)2=14外切,并与直线y=-12相切.(1)求动圆圆心C 的轨迹Γ;(2)若从点P (m ,-4)作曲线Γ的两条切线,切点分别为A ,B ,求证:直线AB 恒过定点. 答案:(1)解由题意知,圆E 的圆心E (0,1),半径为12. 设动圆圆心C (x ,y ),半径为r. 因为圆C 与直线y=-12相切, 所以d=r ,即y+12=r.①因为圆C 与圆E 外切,所以|CE|=12+r , 即√x 2+(y -1)2=12+r.②联立①②,消去r ,可得x 2=4y.所以动圆圆心C 的轨迹Γ是以E (0,1)为焦点,y=-1为准线的抛物线.(2)证明由已知得直线AB 的斜率一定存在.不妨设直线AB 的方程为y=kx+b. 联立{x 2=4y ,y =kx +b ,整理,得x 2-4kx-4b=0,其中Δ=16(k 2+b )>0. 设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=4k ,x 1x 2=-4b.③由抛物线的方程可得,y=14x 2,∴y'=12x.∴过点A (x 1,y 1)的抛物线的切线方程为y-y 1=12x 1(x-x 1),又y 1=14x 12,代入切线方程整理得,y=12x 1x-14x 12.∵切线过P (m ,-4),代入整理得,x 12-2mx 1-16=0,同理可得x 22-2mx 2-16=0.∴x 1,x 2为关于x 的方程x 2-2mx-16=0的两个根, ∴x 1+x 2=2m ,x 1x 2=-16.④由③④可得,x 1x 2=-4b=-16,x 1+x 2=4k=2m.∴b=4,k=m 2,直线AB 的方程为y=m2x+4.∴直线AB 恒过定点(0,4).20.(12分)已知各项为正数的等比数列{a n }的前n 项和为S n ,数列{b n }的通项公式b n ={n ,n 为偶数,n +1,n 为奇数(n ∈N *),若S 3=b 5+1,b 4是a 2和a 4的等比中项.(1)求数列{a n }的通项公式; (2)求数列{a n ·b n }的前n 项和T n .解:(1)∵数列{b n }的通项公式b n ={n ,n 为偶数,n +1,n 为奇数(n ∈N *),∴b 5=6,b 4=4.设各项为正数的等比数列{a n }的公比为q ,q>0, ∵S 3=b 5+1=7,∴a 1+a 1q+a 1q 2=7.① ∵b 4是a 2和a 4的等比中项,∴b 42=a 2·a 4=a 32=16,解得a 3=a 1q 2=4,② 由①②得3q 2-4q-4=0, 解得q=2或q=-23(舍去),∴a 1=1,∴a n =2n-1. (2)当n 为偶数时, T n =(1+1)·20+2·2+(3+1)·22+4·23+(5+1)·24+…+[(n-1)+1]·2n-2+n ·2n-1 =(20+2·2+3·22+4·23+…+n ·2n-1)+(20+22+…+2n-2), 设H n =20+2·2+3·22+4·23+…+n ·2n-1,① 2H n =2+2·22+3·23+4·24+…+n ·2n ,② ①-②,得-H n =20+2+22+23+…+2n-1-n ·2n =1-2n1-2-n ·2n =(1-n )·2n -1, ∴H n =(n-1)·2n +1,∴T n =(n-1)·2n +1+1-4n21-4=(n -23)·2n +23. 当n 为奇数,且n ≥3时,T n =T n -1+(n+1)·2n-1=(n -53)·2n-1+23+(n+1)·2n-1=(2n -23)·2n-1+23,经检验,T 1=2符合上式,∴T n ={(2n -23)·2n -1+23,n 为奇数,(n -23)·2n+23,n 为偶数.21.(12分)(2019广东潮州高三二模)如图,已知椭圆x 2a 2+y 2b 2=1(a>b>0),点A (2,0)是它的右端点,弦BC 过椭圆的中心O ,且AC ⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ =0,|BC ⃗⃗⃗⃗⃗ |=2|AC⃗⃗⃗⃗⃗ |.(1)求椭圆的标准方程;(2)设P ,Q 为椭圆上不重合的两点,∠PCQ 的平分线总是垂直于x 轴,且存在实数λ,使得PQ ⃗⃗⃗⃗⃗ =λAB ⃗⃗⃗⃗⃗ ,求λ的最大值.解:(1)依题意可知a=2.∵AC⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ =0,∴∠ACB=90°. 又|BC ⃗⃗⃗⃗⃗ |=2|AC ⃗⃗⃗⃗⃗ |,∴|OC ⃗⃗⃗⃗⃗ |=|AC⃗⃗⃗⃗⃗ |, ∴△AOC 是等腰直角三角形.∵A (2,0),∴C (1,1).∵点C 在椭圆上,∴14+1b =1,∴b 2=43,∴所求椭圆的标准方程为x 24+y 243=1. (2)对于椭圆上两点P ,Q ,∵∠PCQ 的平分线总是垂直于x 轴,∴PC 与CQ 所在直线关于直线x=1对称.设k PC =k (k ≠0),则k CQ =-k ,则直线PC 的方程为y-1=k (x-1)⇒y=k (x-1)+1,①直线CQ 的方程为y-1=-k (x-1)⇒y=-k (x-1)+1,②将①代入x 24+3y 24=1,得(1+3k 2)x 2-6k (k-1)x+3k 2-6k-1=0.③∵C (1,1)在椭圆上,∴x=1是方程③的一个根,∴x P =3k 2-6k -11+3k 2.以-k 替换k ,得到x Q =3k 2+6k -13k 2+1,x P -x Q =-12k 1+3k 2,y P -y Q =-4k1+3k 2. 又|PQ ⃗⃗⃗⃗⃗ |=√(x P -x Q )2+(y P -y Q )2=√(-12k 1+3k )2+(-4k 1+3k )2=√1609k 2+1k 2+6≤2√303,当且仅当9k 2=1k 2,即k 2=13,k=±√33时取等号.∵|AB ⃗⃗⃗⃗⃗ |=√10,PQ ⃗⃗⃗⃗⃗ =λAB ⃗⃗⃗⃗⃗ ,∴λmax =2√303√10=2√33. 22.(12分)已知函数f (x )=x-1x -a ln x ,(1)若f (x )无极值点,求a 的取值范围;(2)设g (x )=x+1x -(ln x )2,当a 取(1)中的最大值时,求g (x )的最小值;(3)证明:∑i=1n √2i (2i +1)>ln 2n+12+1(n ∈N *).答案:(1)解求导函数,可得f'(x )=x 2-ax+1x 2.∵函数f (x )无极值点,∴方程x 2-ax+1=0在区间(0,+∞)内无根或有唯一根, ∴方程a=x+1x 在区间(0,+∞)内无根或有唯一根,又x+1x ≥2(当且仅当x=1时取等号),∴(x +1x )min =2,∴a ≤2.故a 的取值范围是(-∞,2].(2)解当a=2时,f (x )=x-1x -2ln x ,g (x )=x+1x -(ln x )2,由(1)知,f (x )在区间(0,+∞)内是增函数,当x ∈(0,1)时,f (x )=x-1x -2ln x<f (1)=0,即x-1x <2ln x<0;当x ∈(1,+∞)时,f (x )=x-1x -2ln x>f (1)=0,即x-1x >2ln x>0; ∴当x>0时,|x -1x |≥|2ln x|=|ln x 2|,令x 2=t>0,∴|√t -t |≥|ln t|, 两边平方,得t+1t -2≥(ln t )2,∴当t>0时,t+1t -2≥(ln t )2成立,当且仅当t=1时取等号,∴当x=1时,函数g (x )取最小值2.(3)证明由上知,当x>1时,x+1x -(ln x )2>2, ∴当x>1时,√x −√x >ln x 成立, 令x=2n +12n ,得√2n +12n −√2n 2n +1>ln 2n +12n , 即n n >ln2n +12, ∴不等式:∑i=1n √2i (2i +1)>ln 21+12+…+ln 2n +12 >ln 21+221+1+…+ln 2n +22n +1=ln (2n ·20+121+1·…·2n -1+12n +1)=ln 2n+12n +1. 即∑i=1n √2i (2i +1)>ln 2n+12+1(n ∈N *).快乐分享,知识无界!感谢您的下载!由Ruize收集整理!。
21高考数学理导学大一轮人教A广西专用滚动测试卷二第一~五章 含解析

滚动测试卷二(第一~五章)(时间:120分钟满分:150分)滚动测试卷第5页一、选择题(本大题共12小题,每小题5分,共60分)1.集合A={x∈N||x-1|≤1},B={x|y=√1-x2},则A∩B的子集个数为()A.1B.2C.4D.8答案:C解析:∵集合A={x∈N||x-1|≤1}={0,1,2},B={x|y=√1-x2}={x|-1≤x≤1},∴A∩B={0,1}.∴集合A∩B的子集个数为22=4,故选C.2.1+2i1-2i=()A.-45−35i B.-45+35iC.-35−45i D.-35+45i答案:D解析:1+2i1-2i =(1+2i)(1+2i)(1-2i)(1+2i)=1-4+4i5=-35+45i.3.下列结论正确的是()A.若命题p:∀x>0,都有x2>0,则p:∃x0≤0,使得x02≤0B.若命题p和p∨q都是真命题,则命题q也是真命题C.在△ABC中,a,b,c是内角A,B,C所对的边,则a<b的充要条件是cos A>cos BD.命题“若x2+x-2=0,则x=-2或x=1”的逆否命题是“x≠-2或x≠1,则x2+x-2≠0”答案:C解析:若命题p:∀x>0,都有x2>0,则p:∃x0>0,使得x02≤0.故A项错误;若命题p和p∨q都是真命题,则命题q可能是真命题,也可能是假命题.故B项错误;在△ABC中,由a<b可知0<A<B<π,而y=cos x在区间(0,π)内单调递减,故cos A>cos B,C 项正确;命题“若x2+x-2=0,则x=-2或x=1”的逆否命题是“x≠-2且x≠1,则x2+x-2≠0”.故D项错误.故选C.4.如图,阴影区域是由函数y=cos x的一段图象与x轴围成的封闭图形,则这个阴影区域的面积是()A.1B.2C.π2 D.π答案:B解析:由题意可知阴影区域的面积是S=-∫ π23π2cos x d x=-sin x |π23π2=2.故选B .5.(2019广东汕头高三二模)已知f (x )是定义在R 上的奇函数,满足f (1+x )=f (1-x ),且f (1)=a ,则f (2)+f (3)+f (4)=( ) A.0 B.-a C.a D.3a 答案:B解析:由f (1+x )=f (1-x ),且f (x )是R 上的奇函数,可知f (x )是周期为4的周期函数,f (0)=0,所以f (4)=f (0)=0,f (3)=f (-1)=-f (1)=-a ,f (2)=f (1+1)=f (1-1)=f (0)=0,所以f (2)+f (3)+f (4)=0-a+0=-a.6.(2019广东汕头二模)函数f (x )=√3cos (x -π2)+cos(π-x )的单调递增区间为( ) A.[-5π6+2kπ,π6+2kπ],k ∈Z B.[-2π3+2kπ,π3+2kπ],k ∈ZC.[-π3+2kπ,2π3+2kπ],k ∈Z D.[-π6+2kπ,5π6+2kπ],k ∈Z答案:C解析:f (x )=√3cos (x -π2)+cos(π-x )=√3sin x-cos x=2sin (x -π6),由-π2+2k π≤x-π6≤π2+2k π,k ∈Z ,得-π3+2k π≤x ≤2π3+2k π,k ∈Z ,所以f (x )的单调递增区间为-π3+2k π,2π3+2k π,k ∈Z . 7.函数y=ln (1-x1+x )+sin x 的图象大致为( )答案:A解析:易知f (x )=ln (1-x1+x )+sin x 的定义域为(-1,1),且f (-x )=ln (1+x1-x )+sin(-x )=-ln (1-x1+x )-sin x=-f (x ),即函数f (x )是奇函数,图象关于原点对称,排除选项C,D;又f (12)=ln 13+sin 12=sin 12-ln 3<0,故排除选项B,所以选A .8.在四边形ABCD 中,AC ⊥BD ,且AC=2,BD=3,则AB ⃗⃗⃗⃗⃗ ·CD ⃗⃗⃗⃗⃗ 的最小值为( ) A.134B.-134 C.154 D.-154答案:B解析:设AC 与BD 相交于点O ,以O 为原点,AC ,BD 为坐标轴建立平面直角坐标系,设C (a ,0),D (0,b ),则A (a-2,0),B (0,b-3), 故AB ⃗⃗⃗⃗⃗ =(2-a ,b-3),CD ⃗⃗⃗⃗⃗ =(-a ,b ). ∴AB ⃗⃗⃗⃗⃗ ·CD ⃗⃗⃗⃗⃗ =a (a-2)+b (b-3) =(a-1)2+(b -32)2−134.∴当a=1,b=32时,AB ⃗⃗⃗⃗⃗ ·CD ⃗⃗⃗⃗⃗ 取得最小值-134.9.设偶函数f (x )对任意x ∈R ,都有f (x+3)=-1f (x ),且当x ∈[-3,-2]时,f (x )=4x ,则f (107.5)=( ) A.10 B.110C.-10D.-110答案:B解析:∵f (x+3)=-1f (x ), ∴f (x+6)=-1f (x+3)=-1-1f (x )=f (x ).∴函数f (x )是以6为周期的函数.∴f (107.5)=f (6×17+5.5)=f (5.5)=-1f (2.5)=-1f (-2.5)=-14×(-2.5)=110.故选B .10.已知函数y=sin(πx+φ)-2cos(πx+φ)(0<φ<π)的图象关于直线x=1对称,则sin 2φ=( ) A.-45B.-35C.35D.45答案:A解析:y=sin(πx+φ)-2cos(πx+φ) =√5sin(πx+φ-α), 其中sin α=√5,cos α=√5.∵函数y 的图象关于直线x=1对称, ∴π+φ-α=π2+k π,k ∈Z , 即φ=α-π2+k π,k ∈Z . ∴sin 2φ=sin 2(α-π2+kπ) =sin(2α-π+2k π)=sin(2α-π) =-sin 2α=-2sin αcos α =-2×√5×√5=-45,故选A . 11.在△ABC 中,内角A ,B ,C 的对边分别是a ,b ,c.若cos B=14,sinCsinA =2,且S △ABC =√154,则b=( ) A.4 B.3 C.2D.1答案:C解析:由cos B=14,0<B<π,得sin B=√154. 又sinCsinA =2,得ca =2,即c=2a. 由S △ABC =√154=12ac sin B=a 2·√154,得a=1.所以c=2.由b 2=a 2+c 2-2ac cos B=1+4-2×1×2×14=4,得b=2.12.已知函数y=f (x )是定义在R 上的偶函数,且当x>0时,不等式f (x )+x ·f'(x )<0成立,若a=30.2f (30.2),b=(log π2)f (log π2),c=(log 214)f (log 214),则a ,b ,c 之间的大小关系为( ) A.a>c>b B.c>a>b C.c>b>a D.b>a>c 答案:C解析:构造函数g (x )=xf (x ),则g'(x )=f (x )+xf'(x ),当x>0时,不等式f (x )+x ·f'(x )<0成立, ∴当x>0时,g'(x )<0,函数g (x )单调递减.∵函数y=f (x )是定义在R 上的偶函数, ∴g (-x )=-xf (-x )=-xf (x )=-g (x ), ∴g (x )在R 上是奇函数, ∴g (x )在R 上是减函数.∵a=30.2f (30.2),b=(log π2)f (log π2),c=(log 214)f (log 214),log 214=-2,而-2<log π2<30.2, ∴c>b>a.故选C .二、填空题(本大题共4小题,每小题5分,共20分) 13.已知tan (x +π4)=-2,则sin 2x+2cos 2x= . 答案:45解析:∵tan (x +π4)=tanx+11-tanx=-2,∴tan x=3,则sin 2x+2cos 2x=2tanx+2tan x+1=45.14.已知函数f (x )={-2e x ,x ≤0,lnx ,x >0(其中e 为自然对数的底数),则函数y=f (f (x ))的零点是 . 答案:e解析:令f (x )=t ,则y=f (t ).由f (t )=0,可得t=1; 由f (x )=1,可得x=e .故函数y=f (f (x ))的零点是e .15.我国南宋著名数学家秦九韶在他的著作《数书九章》卷五“田域类”里有一个题目:“问有沙田一段,有三斜,其小斜一十三里,中斜一十四里,大斜一十五里.里法三百步.欲知为田几何.”这道题讲的是有一个三角形沙田,三边分别为13里,14里,15里,假设1里按500米计算,则该三角形沙田外接圆的半径为 米. 答案:4 062.5解析:由题意画出图象,如图所示,且AB=13里=6 500米,BC=14里=7 000米,AC=15里=7 500米, 在△ABC 中,由余弦定理有cos B=AB 2+BC 2-AC 22AB ·BC=132+142-1522×13×14=513,B 为锐角,sinB=√1-cos 2B =1213,设△ABC 外接圆半径为R , 则由正弦定理有bsinB =2R ,R=b2sinB =7 5002×1213=4 062.5米.16.在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,若AB ⃗⃗⃗⃗⃗ ·AC ⃗⃗⃗⃗⃗ =BA ⃗⃗⃗⃗⃗ ·BC⃗⃗⃗⃗⃗ =1,则c= .答案:√2解析:由内角A ,B ,C 所对的边分别为a ,b ,c ,可知AB=c ,AC=b ,BC=a.由AB ⃗⃗⃗⃗⃗ ·AC ⃗⃗⃗⃗⃗ =BA ⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ , 得cb cos A=ca cos B.故由正弦定理,得sin B cos A=cos B sin A , 即sin(B-A )=0.因为-π<B-A<π,所以B=A ,从而b=a.由已知BA ⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ =1,得ac cos B=1. 故由余弦定理知ac ·a 2+c 2-b 22ac=1,即a 2+c 2-b 2=2,故c=√2.三、解答题(本大题共6小题,共70分)17.(10分)设向量a =(4cos α,sin α),b =(sin β,4cos β),c =(cos β,-4sin β). (1)若a 与b -2c 垂直,求tan(α+β)的值; (2)求|b +c |的最大值;(3)若tan αtan β=16,求证:a ∥b . (1)解因为a 与b -2c 垂直,所以a ·(b -2c )=4cos αsin β-8cos αcos β+4sin αcos β+8sin αsin β=4sin(α+β)-8cos(α+β)=0,因此tan(α+β)=2. (2)解由b +c =(sin β+cos β,4cos β-4sin β), 得|b +c |=√(sinβ+cosβ)2+(4cosβ-4sinβ)2 =√≤4√2.又当β=k π-π4(k ∈Z )时,等号成立,所以|b +c |的最大值为4√2.(3)证明由tan αtan β=16, 得16cos αcos β=sin αsin β, 故a ∥b .18.(12分)某公司为了获得更大的收益,每年要投入一定的资金用于广告促销,经调查,每年投入广告费t 百万元,可增加销售额约为-t 2+7t 百万元.(1)若该公司将一年的广告费控制在4百万元之内,则应投入多少广告费,才能使该公司由此增加的收益最大?(2)现该公司准备共投入5百万元,分别用于广告促销和技术改造,经预测,每投入技术改造费x (1≤x ≤5)百万元,可增加的销售额约为12x 2+4ln x 百万元,请设计一个资金分配方案,使该公司由此增加的收益最大.(注:收益=销售额-投入,这里除了广告费和技术改造费,不考虑其他的投入) 解:(1)设每年投入t 百万元的广告费后增加的收益为f (t )百万元, 则由f (t )=(-t 2+7t )-t=-t 2+6t=-(t-3)2+9(0≤t ≤4).∴当t=3时,f (t )取得最大值9,即投入3百万元的广告费时,该公司由此增加的收益最大. (2)用于技术改造的资金为x 百万元,则用于广告促销的资金为(5-x )百万元, 设由此增加的收益是g (x )百万元.则g (x )=12x 2+4ln x+[-(5-x )2+7(5-x )]-5=-12x 2+3x+4ln x+5. g'(x )=-x+3+4x =-x 2-3x -4x=-(x -4)(x+1)x,1≤x ≤5.则当1≤x<4时,g'(x )>0;当4<x ≤5时,g'(x )<0. ∴当x=4时,g (x )取得最大值.即4百万元用于技术改造,1百万元用于广告促销,该公司由此增加的收益最大. 19.(12分)函数f (x )=A sin(ωx+φ)(A >0,ω>0,0<φ<π2)的部分图象如图所示.(1)求f (x )的解析式;(2)设g (x )=[f (x -π12)]2,求函数g (x )在区间[-π6,π3]上的最大值,并确定此时x 的值. 解:(1)由题图,知A=2,T4=π3, 则2πω=4×π3,即ω=32.又f (-π6)=2sin [32×(-π6)+φ] =2sin (-π4+φ)=0, ∴sin (φ-π4)=0. ∵0<φ<π2,-π4<φ-π4<π4,∴φ-π4=0,即φ=π4,∴f (x )的解析式为f (x )=2sin (32x +π4).(2)由(1)可得f (x -π12)=2sin [32(x -π12)+π4]=2sin (32x +π8), g (x )=[f (x -π12)]2=4×1-cos(3x+π4)2=2-2cos (3x +π4),∵x ∈[-π6,π3],∴-π4≤3x+π4≤5π4,∴当3x+π4=π,即x=π4时,g (x )max =4.20.(12分)(2019广东深圳高三二模)已知在△ABC 中,AB=√2BC ,AC=2√5,点D 在边AC 上,且AD=2CD ,∠ABD=2∠CBD. (1)求∠ABC 的大小; (2)求△ABC 的面积.解:(1)依题意,设∠ABD=2∠CBD=2θ,则∠ABC=3θ. ∵0<∠ABC<π,∴0<θ<π3.在△BAD 中,由正弦定理,得ABsin∠ADB =ADsin∠ABD , ∴sin ∠ADB=ABsin∠ABDAD.在△BCD 中,由正弦定理,得BCsin∠BDC =CDsin∠CBD , ∴sin ∠BDC=BCsin∠CBDCD.∵∠ADB+∠BDC=π,∴sin ∠ADB=sin ∠BDC. 又AB=√2BC ,AD=2CD ,∴√2BCsin2θ2CD=BCsinθCD,∴√2sin θcos θ=sin θ.∵0<θ<π3,∴cos θ=√22,∴θ=π4.∴∠ABC=3θ=3π4.(2)在△ABC 中,由余弦定理,得AC 2=AB 2+BC 2-2AB ·BC cos ∠ABC , ∴(2√5)2=(√2BC )2+BC 2-2√2BC ·BC cos 3π4, 解得BC=2.∴S △ABC =12AB ·BC ·sin ∠ABC=12×√2BC 2sin 3π4=2.21.(12分)已知函数f (x )=x 3+ax 2-x+c ,且a=f'(23).(1)求a 的值;(2)求函数f (x )的单调区间; (3)设函数g (x )=(f (x )-x 3)·e x ,若当x ∈[-3,2]时,函数g (x )单调递增,求实数c 的取值范围. 解:(1)由f (x )=x 3+ax 2-x+c ,得f'(x )=3x 2+2ax-1. 当x=23时,得a=f'(23)=3×(23)2+2a×23-1,解得a=-1. (2)由(1)可知,f (x )=x 3-x 2-x+c , 则f'(x )=3x 2-2x-1=3(x +13)(x-1), 由f'(x )>0,得x<-13或x>1; 由f'(x )<0,得-13<x<1.所以f (x )的单调递增区间是(-∞,-13)和(1,+∞),f (x )的单调递减区间是(-13,1).(3)函数g (x )=(f (x )-x 3)·e x =(-x 2-x+c )·e x ,有g'(x )=(-2x-1)e x +(-x 2-x+c )e x =(-x 2-3x+c-1)e x ,因为函数g (x )在x ∈[-3,2]上单调递增,所以h (x )=-x 2-3x+c-1≥0在x ∈[-3,2]上恒成立. 故只要h (x )在区间[-3,2]上的最小值h (2)≥0即可,解得c ≥11,所以c 的取值范围是[11,+∞).22.(12分)已知函数f (x )=x 2+2cos x ,g (x )=e x (cos x-sin x+2x-2),其中e ≈2.718 28…是自然对数的底数.(1)求曲线y=f (x )在点(π,f (π))处的切线方程.(2)令h (x )=g (x )-af (x )(a ∈R ),讨论h (x )的单调性并判断有无极值,有极值时求出极值. 解:(1)由题意f (π)=π2-2, 又f'(x )=2x-2sin x , 所以f'(π)=2π,因此曲线y=f (x )在点(π,f (π))处的切线方程为y-(π2-2)=2π(x-π),即y=2πx-π2-2. (2)由题意得h (x )=e x (cos x-sin x+2x-2)-a (x 2+2cos x ),因为h'(x )=e x (cos x-sin x+2x-2)+e x (-sin x-cos x+2)-a (2x-2sin x ) =2e x (x-sin x )-2a (x-sin x ) =2(e x -a )(x-sin x ), 令m (x )=x-sin x , 则m'(x )=1-cos x ≥0,所以m (x )在R 上单调递增.因为m (0)=0,所以当x>0时,m (x )>0;当x<0时,m(x)<0.①当a≤0时,e x-a>0,当x<0时,h'(x)<0,h(x)单调递减,当x>0时,h'(x)>0,h(x)单调递增,所以当x=0时h(x)取到极小值,极小值是h(0)=-2a-1;②当a>0时,h'(x)=2(e x-e ln a)(x-sin x),由h'(x)=0得x1=ln a,x2=0.(ⅰ)当0<a<1时,ln a<0,当x∈(-∞,ln a)时,e x-e ln a<0,h'(x)>0,h(x)单调递增;当x∈(ln a,0)时,e x-e ln a>0,h'(x)<0,h(x)单调递减;当x∈(0,+∞)时,e x-e ln a>0,h'(x)>0,h(x)单调递增.所以当x=ln a时h(x)取到极大值.极大值为h(ln a)=-a[ln2a-2ln a+sin(ln a)+cos(ln a)+2],当x=0时h(x)取到极小值,极小值是h(0)=-2a-1;(ⅱ)当a=1时,ln a=0,所以当x∈(-∞,+∞)时,h'(x)≥0,函数h(x)在区间(-∞,+∞)内单调递增,无极值;(ⅲ)当a>1时,ln a>0,所以当x∈(-∞,0)时,e x-e ln a<0,h'(x)>0,h(x)单调递增;当x∈(0,ln a)时,e x-e ln a<0,h'(x)<0,h(x)单调递减;当x∈(ln a,+∞)时,e x-e ln a>0,h'(x)>0,h(x)单调递增.所以当x=0时h(x)取到极大值,极大值是h(0)=-2a-1;当x=ln a时h(x)取到极小值,极小值是h(ln a)=-a[ln2a-2ln a+sin(ln a)+cos(ln a)+2].综上所述:当a≤0时,h(x)在区间(-∞,0)内单调递减,在区间(0,+∞)内单调递增,函数h(x)有极小值,极小值是h(0)=-2a-1;当0<a<1时,函数h(x)在区间(-∞,ln a)和(0,+∞)内单调递增,在区间(ln a,0)内单调递减,函数h(x)有极大值,也有极小值,极大值是h(ln a)=-a[ln2a-2ln a+sin(ln a)+cos(ln a)+2],极小值是h(0)=-2a-1;当a=1时,函数h(x)在区间(-∞,+∞)上单调递增,无极值;当a>1时,函数h(x)在区间(-∞,0)和(ln a,+∞)内单调递增,在(0,ln a)内单调递减,函数h(x)有极大值,也有极小值,极大值是h(0)=-2a-1,极小值是h(ln a)=-a[ln2a-2ln a+sin(lna)+cos(ln a)+2].。
2021版高考数学(文)大一轮人教A广西专用滚动测试卷一(第一_三章)

2021版⾼考数学(⽂)⼤⼀轮⼈教A⼴西专⽤滚动测试卷⼀(第⼀_三章)滚动测试卷⼀(第⼀~三章)(时间:120分钟满分:150分)滚动测试卷第1页⼀、选择题(本⼤题共12⼩题,每⼩题5分,共60分)1.(2019⼴西崇左天等⾼级中学考前适应)设全集U=R ,集合A={x|x>0},B={x|-3-3} C.{x|x ≤0或x ≥1} D.{x|x ≤-3} 答案:D解析:∵A ∪B={x|x>-3},∴?U (A ∪B )={x|x ≤-3}. 2.函数y=√log 12(2x -1)的定义域为( )A.(12,+∞) B.[1,+∞)C.(12,1]D.(-∞,1)答案:C解析:要使函数有意义,需{log 12(2x -1)≥0,2x -1>0,解得12所以函数的定义域是(12,1].3.已知幂函数f (x )的图象经过点(4,2),则幂函数f (x )具有的性质是( ) A.在其定义域上为增函数 B.在其定义域上为减函数 C.奇函数 D.定义域为R 答案:A解析:设幂函数f (x )=x a ,∵幂函数的图象过点(4,2), ∴4a=2,∴a=12,∴f (x )=x 12(x ≥0),由f (x )的性质知,f (x )是⾮奇⾮偶函数,定义域为[0,+∞),在定义域内⽆最⼤值,在定义域内单调递增.故选A .4.下列判断错误的是( )A.命题“若am 2≤bm 2,则a ≤b ”是假命题B.命题“?x ∈R ,x 3-x 2-1≤0”的否定是“?x 0∈R ,x 03?x 02-1>0”C .“若a=1,则直线x+y=0和直线x-ay=0互相垂直”的逆否命题为真命题 D.命题“p ∨q 为真命题”是命题“p ∧q 为真命题”的充分不必要条件答案:D解析:A 项中,当m=0时,满⾜am 2≤bm 2,但a 可以⼤于b ,故命题是假命题,故正确; B 项显然正确;C 项中,原命题是真命题,故其逆否命题也为真命题,故正确;D 项中,p ∨q 为真命题,可知p ,q ⾄少有⼀个为真,但推不出p ∧q 为真命题,故错误.故选D .5.下列函数中,既是奇函数,⼜在区间(0,+∞)内单调递增的是( ) A .y=sin xB .y=-x 2+1xC .y=x 3+3xD .y=e |x|答案:C解析:选项A,C 中函数为奇函数,但函数y=sin x 在区间(0,+∞)内不是单调函数,故选C . 6.若函数y=x 2-3x-4的定义域为[0,m ],值域为[-254,-4],则m 的取值范围是( ) A .(0,4] B .[32,4]C .[32,3]D .[32,+∞)答案:C解析:y=x 2-3x-4=(x -32)2254.当x=0或x=3时,y=-4,故32≤m ≤3. 7.设函数f (x )={5x -m ,x <1,2x,x ≥1,若f (f (45))=8,则m=( ) A.2 B.1C.2或1D.12答案:B解析:∵f (f (45))=8,∴f (4-m )=8.若4-m<1,即3sinx x 2的部分图象⼤致为( )答案:D解析:(⽅法⼀)易知g (x )=x+sinx x 2为奇函数,其图象关于原点对称.所以y=1+x+sinx x 2的图象只需把g (x )的图象向上平移⼀个单位长度,选项D 满⾜.(⽅法⼆)当x=1时,f (1)=1+1+sin1=2+sin1>2,排除A,C . ⼜当x →+∞时,y →+∞,B 项不满⾜,D 满⾜.9.若函数f (x )=|log a x|-2-x (a>0,a ≠1)的两个零点是m ,n ,则( ) A .mn=1 B .mn>1 C .mn<1 D .以上都不对答案:C解析:由f (x )=0,得|log a x|=2-x,函数y=|log a x|,y=2-x=(12)x的图象如图所⽰,由图象可知,n>1,01,则有-log a m=(12)m,log a n=(12)n,两式两边分别相减得log a (mn )=(12)n(12)m<0,∴010.某公司为激励创新,计划逐年加⼤研发资⾦投⼊.若该公司2015年全年投⼊研发资⾦130万元,在此基础上,每年投⼊的研发资⾦⽐上⼀年增长12%,则该公司全年投⼊的研发资⾦开始超过200万元的年份是( )(参考数据:lg 1.12≈0.05,lg 1.3≈0.11,lg2≈0.30) A.2018年 B.2019年 C.2020年 D.2021年答案:B解析:设从2015年后第n 年该公司全年投⼊的研发资⾦开始超过200万元, 由已知得130×(1+12%)n >200,∴1.12n >200130,两边取常⽤对数得n lg1.12>lg 200130, ∴n>lg2-lg1.3lg1.12≈0.30-0.110.05=3.8.∴n ≥4,故选B .11.已知函数y=f (x )是定义在R 上的偶函数,且当x>0时,不等式f (x )+x ·f'(x )<0成⽴,若a=30.2·f (30.2),b=(log π2)·f (log π2),c=(log 214)·f (log 214),则a ,b ,c 的⼤⼩关系为( ) A .c>b>a B .c>a>b C .b>a>c D .a>c>b 答案:A解析:设F (x )=xf (x ),当x>0时,F'(x )=[xf (x )]'=f (x )+xf'(x )<0,即函数F (x )在区间(0,+∞)内单调递减,⼜y=f (x )在R 上是偶函数,则F(x )在R 上是奇函数,从⽽F (x )在R 上单调递减,⼜30.2>1,04<0,即30.2>log π2>log 214,所以F (30.2)4),即ax -1+sin πx 在[0,1)内的最⼤值为m ,在(1,2]上的最⼩值为n ,则m+n=( ) A.-2 B.-1C.1D.2答案:D解析:可知f (x )=xx -1+sin πx=1+1x -1+sin πx.记g (x )=1x -1+sin πx ,则当x ∈[0,1)时,g (2-x )=12-x -1+sin π(2-x )=11-x -sin πx=-(1x -1+sinπx) =-g (x ),即在区间[0,1)∪(1,2]上,函数f (x )关于点(1,1)中⼼对称,故m+n=2. ⼆、填空题(本⼤题共4⼩题,每⼩题5分,共20分)13.能够说明“设a ,b ,c 是任意实数,若a>b>c ,则a+b>c ”是假命题的⼀组整数a ,b ,c 的值依次为 .答案:-1,-2,-3(答案不唯⼀)解析:答案不唯⼀,如令a=-1,b=-2,c=-3,则a>b>c ,⽽a+b=-3=c ,能够说明“设a ,b ,c 是任意实数,若a>b>c ,则a+b>c ”是假命题.14.已知函数f (x )是奇函数,当x>0时,f (x )=a x (a>0,且a ≠1),且f (lo g 124)=-3,则a 的值为 . 答案:√3解析:∵奇函数f (x )满⾜f (lo g 124)=-3,⽽lo g 124=-2<0,∴f (-2)=-3,即f (2)=3,⼜∵当x>0时,f (x )=a x (a>0,且a ≠1),∴f (2)=a 2=3,解之,得a=√3.15.已知a ∈R ,设函数f (x )=ax-ln x 的图象在点(1,f (1))处的切线为l ,则l 在y 轴上的截距为 . 答案:1解析:∵f (x )=ax-ln x ,∴f'(x )=a-1x ,f'(1)=a-1,f (1)=a ,则切线l ⽅程为y-a=(a-1)(x-1),即y=(a-1)x+1,则l 在y 轴上的截距为1.16.已知函数f (x )=x 2+2x ,g (x )=(12)x-m.若?x 1∈[1,2],?x 2∈[-1,1],使f (x 1)≥g (x 2),则实数m 的取值范围是 . 答案:[-52,+∞)解析:?x 1∈[1,2],?x 2∈[-1,1],使f (x 1)≥g (x 2),只需f (x )=x 2+2x 在区间[1,2]上的最⼩值⼤于等于g (x )=(12)x-m 在区间[-1,1]上的最⼩值.因为f'(x )=2x-2x 2=2(x 3-1)x 2≥0在区间[1,2]上恒成⽴,且f'(1)=0,所以f (x )=x 2+2x 在区间[1,2]上单调递增,所以f (x )min =f (1)=12+21=3.因为g (x )=(12)x-m 在区间[-1,1]上单调递减, 所以g (x )min =g (1)=12-m , 所以12-m ≤3,即m ≥-52.三、解答题(本⼤题共6⼩题,共70分) 17.(10分)已知函数f (x )=a-22+1.(1)求f (0);(2)探究f (x )的单调性,并证明你的结论;(3)若f (x )为奇函数,求满⾜f (ax )2+1=a-1.(2)f (x )在R 上单调递增.证明如下:∵f (x )的定义域为R ,∴任取x 1,x 2∈R 且x 12x 1+1-a+22x 2+1=2·(2x 1-2x 2)(1+2x 1)(1+2x 2), ∵y=2x 在R 上单调递增,且x 10,2x 2+1>0. ∴f (x 1)-f (x 2)<0,即f (x 1)∴f (-x )=-f (x ),即a-22-x +1=-a+22+1,解得a=1(或⽤f (0)=0去解). ∴f (ax )⼜∵f (x )在R 上单调递增,∴x<2. ∴x 的取值范围为(-∞,2).18.(12分)已知f (x )是定义在R 上的奇函数,且对任意实数x ,恒有f (x+2)=-f (x ).当x ∈[0,2]时,f (x )=2x-x 2.(1)求证:f (x )是周期函数;(2)当x ∈[2,4]时,求f (x )的解析式;(3)求f(0)+f(1)+f(2)+…+f(2 015)的值.答案:(1)证明因为f(x+2)=-f(x),所以f(x+4)=-f(x+2)=f(x).所以f(x)是周期为4的周期函数.(2)解当x∈[-2,0]时,-x∈[0,2].由已知得f(-x)=2(-x)-(-x)2=-2x-x2,⼜f(x)是奇函数,所以f(-x)=-f(x)=-2x-x2,所以f(x)=x2+2x.⼜当x∈[2,4]时,x-4∈[-2,0],所以f(x-4)=(x-4)2+2(x-4).⼜f(x)是周期为4的周期函数,所以f(x)=f(x-4)=(x-4)2+2(x-4)=x2-6x+8.从⽽求得当x∈[2,4]时,f(x)=x2-6x+8.(3)解f(0)=0,f(2)=0,f(1)=1,f(3)=-1.⼜f(x)是周期为4的周期函数,所以f(0)+f(1)+f(2)+f(3)=f(4)+f(5)+f(6)+f(7)=…=f(2008)+f(2009)+f(2010)+f(2011)=f(2012)+f(2013)+f(2014)+f(2015)=0.所以f(0)+f(1)+f(2)+…+f(2015)=0.19.(12分)随着⼈们⽣活⽔平的不断提⾼,⼈们对餐饮服务⾏业的要求也越来越⾼,由于⼯作繁忙⽆法抽出时间来享受美味,这样⽹上外卖订餐应运⽽⽣.若某商家的⼀款外卖便+4(x-16)2,其中当每⽉的销售量y(单位:千盒)与销售价格x(单位:元/盒)满⾜关系式y=ax-1212(1)求a的值;(2)假设该款便当的⾷物材料、员⼯⼯资、外卖配送费等所有成本折合为每盒12元(只考虑销售出的便当盒数),试确定销售价格x 的值,使该店每⽉销售便当所获得的利润最⼤.(结果保留⼀位⼩数)解:(1)当x=14时,y=21,代⼊关系式y=a+4(x-16)2,x-12+16=21,解得a=10.得a2+4(x-16)2,(2)由(1)可知,便当每⽉的销售量y=10x-12所以每⽉销售便当所获得的利润+4(x-16)2]f(x)=(x-12)[10x-12=10+4(x-12)(x-16)2,从⽽f'(x )=4(x-16)(3x-40). 令f'(x )=0,得x=403, 当x ∈(12,403)时,f'(x )>0,函数f (x )单调递增;当x ∈(403,16)时,f'(x )<0,函数f (x )单调递减, 所以当x=403≈13.3时,函数f (x )取得最⼤值.故当销售价格为13.3元/盒时,该店每⽉销售便当所获得的利润最⼤. 20.(12分)已知函数f (x )=ln x-ax+b x (a ,b ∈R ),且对任意x>0,都有f (x )+f (1x )=0. (1)求a ,b 的关系式;(2)若f (x )存在两个极值点x 1,x 2,且x 11)=0, 故f (1)=-a+b=0,即a=b.(2)由(1)可知f (x )=ln x-ax+a x ,且x>0, 则f'(x )=1x -a-ax 2=-ax 2+x -ax 2.令g (x )=-ax 2+x-a ,要使f (x )存在两个极值点x 1,x 2,则y=g (x )有两个不相等的正数根,因此,{a >0,12a>0,Δ=1-4a 2>0,g (0)=-a <0或{a <0,12a>0,Δ=1-4a 2>0,g (0)=-a >0,解得02. 21.(12分)已知函数f (x )=e xax +x+1,其中a ∈R .(1)若a=0,求函数f (x )的定义域和极值.(2)当a=1时,试确定函数g (x )=f (x )-1的零点个数,并证明.解:(1)当a=0时,函数f (x )=e xx+1的定义域为{x|x ∈R ,且x ≠-1},f'(x )=xe x(x+1)2. 令f'(x )=0,得x=0.当x 变化时,f'(x )和f (x )的变化情况如下: x(-∞,-1)(-1,0)(0,+∞)所以f (x )的单调递减区间为(-∞,-1),(-1,0);单调递增区间为(0,+∞). 故当x=0时,函数f (x )有极⼩值f (0)=1. 函数f (x )⽆极⼤值.(2)函数g (x )存在两个零点.证明过程如下: 由题意,函数g (x )=e xx 2+x+1-1. 因为x 2+x+1=(x +12)2+34>0, 所以函数g (x )的定义域为R . 求导,得g'(x )=e x (x 2+x+1)-e x (2x+1)(x 2+x+1)2=e x x (x -1)(x 2+x+1)2,令g'(x )=0,得x故函数g (x )的单调递减区间为(0,1);单调递增区间为(-∞,0),(1,+∞). 当x=0时,函数g (x )有极⼤值g (0)=0; 当x=1时,函数g (x )有极⼩值g (1)=e3-1.因为函数g (x )在区间(-∞,0)内单调递增,且g (0)=0,所以对于任意x ∈(-∞,0),g (x )≠0. 因为函数g (x )在区间(0,1)内单调递减,且g (0)=0,所以对于任意x ∈(0,1),g (x )≠0. 因为函数g (x )在区间(1,+∞)内单调递增,且g (1)=e3-1<0,g (2)=e 27-1>0,所以函数g (x )在区间(1,+∞)内有且仅有⼀个x 0,使得g (x 0)=0,故函数g (x )存在两个零点(即0和x 0).22.(12分)(2019河北衡⽔中学⾼三下学期四调)已知函数f (x )=ax ln x-bx 2-ax. (1)若曲线y=f (x )在点(1,f (1))处的切线⽅程为x+y+12=0,求a ,b 的值; (2)当a ≤0,b=12时,?x 1,x 2∈(1,e),都有|f (x 1)-f (x 2)||x 1-x 2|<3,求a 的取值范围.解:(1)因为f'(x )=a ln x+a-2bx-a=a ln x-2bx , 所以f'(1)=-2b=-1,f (1)=-b-a=-32, 所以b=12,a=1.(2)当a ≤0,b=12时,f'(x )=a ln x-x ,当x ∈(1,e)时,f'(x )<0恒成⽴,所以f(x)在区间(1,e)内单调递减.不妨设1f(x2),则|f(x1)-f(x2)||x1-x2|<3等价于f(x1)-f(x2)<3x2-3x1,即f(x1)+3x1即函数h(x)=f(x)+3x在区间(1,e)内单调递增.所以h'(x)=a ln x-x+3≥0,即a≥x-3lnx 在区间(1,e)内恒成⽴.令g(x)=x-3lnx,则g'(x)=lnx-1+3x(lnx)2.令y=ln x-1+3x ,则y'=1x3x=x-3x<0在区间(1,e)内恒成⽴,所以y=ln x-1+3x 在区间(1,e)内单调递减,且当x=e时,y=3e>0,所以y>0在区间(1,e)内恒成⽴,即g'(x)>0在区间(1,e)内恒成⽴,所以g(x)在区间(1,e)内单调递增, 所以g(x)所以a≥e-3.所以实数a的取值范围是[e-3,0].快乐分享,知识⽆界!感谢您的下载!由Ruize收集整理!。
人教A版高中数学选修广西专用阶段滚动检测二课时提能训练文新,

【全程复习方略】(广西专用)2013版高中数学 阶段滚动检测(二)课时提能训练 文 新人教版第一~五章 (120分钟 150分) 第I 卷(选择题 共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(滚动单独考查)“m<14”是“一元二次方程x 2+x +m =0有实数解”的( )(A)充分不必要条件 (B)充分必要条件 (C)必要不充分条件 (D)既不充分又不必要条件2.(滚动交汇考查)若定义:a ⊕b =a -b ,a ⊗b =|a +b|,则“-2≤x≤2”是“f(x)=24x x (2)2⊕⊗--有意义”的( )(A)充分而不必要条件 (B)必要而不充分条件 (C)充要条件 (D)既不充分也不必要条件3.若AB u u u r =(1,1),AC u u u r =(3,8),AD u u u r=(0,1),BC u u u r +CD u u u r =(a ,b),则a +b =( )(A)-1 (B)0 (C)1 (D)24.(2012·玉林模拟)曲线y =2sin(x +π4)cos(x -π4)与直线y =12在y 轴右侧的交点按横坐标从小到大依次记为P 1、P 2、P 3、…,则|P 2P 4|等于( ) (A)π (B)2π (C)3π (D)4π5.(2012·北海模拟)已知tanα=-12,则sinα+2cosα4cosα-4sinα的值是( )(A)52 (B)-52 (C)14 (D)-146.(滚动单独考查)已知f(1-x 1+x )=1-x 21+x 2,则f(x)的解析式为( )(A)f(x)=x 1+x 2 (B)f(x)=-2x1+x 2(C)f(x)=2x 1+x 2 (D)f(x)=-x1+x27.(2012·柳州模拟)已知两点M(-1,-6),N(3,0),点P(-73,y)分有向线段MN u u u u r 的比为λ,则λ,y 的值为( ) (A)-14,8 (B)14,-8(C)-14,-8 (D)4,188.给定两个向量a =(3,4),b =(2,1),若(a +x b )⊥(a -b ),则x 的值等于( ) (A)-3 (B)32 (C)3 (D)-329.函数y =sin(2x +π3)图象的对称轴方程可能是( )(A)x =-π6 (B)x =-π12(C)x =π6 (D)x =π1210.(滚动单独考查)y =e x+e-xe x -e-x 的图象大致为( )11.(2012·梧州模拟)若点H 是△ABC 的垂心,且OH u u u r =OA u u u r +OB u u u r +OC u u u r,则点O 是△ABC 的( )(A)垂心 (B)内心 (C)外心 (D)重心12.如图所示,在平面四边形ABCD 中,若AC =3,BD =2,则(AB u u u r+DC u u u r )·(AC u u u r +BD u u u r)=( )(A)7 (B)6 (C)5 (D)4第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上) 13.将函数y =f(x)的图象按向量a =(1,-1)平移后所得图象的解析式为y =x 2-2x +2,则函数y =f(x)的解析式为 . 14.(2012·贺州模拟)已知sinx =55,x∈(π2,3π2),则tan(x -π4)= . 15.(2012·杭州模拟)甲船在A 处观察乙船,乙船在它的北偏东60°的方向,两船相距a 海里,乙船正向北行驶,若甲船是乙船速度的3倍,则甲船应取 方向才能追上乙船;追上时甲船行驶了 海里. 16.给出下列4个命题:①非零向量a ,b 满足|a |=|b |=|a -b |,则a 与a +b 的夹角为30°; ②“a ·b >0”是“a ,b 的夹角为锐角”的充要条件;③将函数y =|x +1|的图象按向量a =(-1,0)平移, 得到的图象对应的函数表达式为y =|x +2|;④在△ABC 中,若(AB u u u r +AC u u u r )·(AB u u u r -AC u u ur )=0,则△ABC 为等腰三角形.其中正确的命题是 .(注:把你认为正确的命题的序号都填上)三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤) 17.(10分)(2012·南宁模拟)已知函数f(x)=sin x 2cos x 2+cos 2x 2-2(1)求函数的最小正周期. (2)求函数f(x)在区间[π,17π12]上的最大值和最小值. 18.(12分)已知向量m =(2cos 2x ,sinx),n =(1,2cosx). (1)若m ⊥n 且0<x <π,试求x 的值;(2)设f(x)=m ·n ,试求f(x)的对称轴方程、对称中心.19.(12分)(2012·郑州模拟)在锐角三角形ABC 中,已知内角A 、B 、C 所对的边分别为a 、b 、c ,且满足2sinB(2cos 2B2-1)=-3cos2B.(1)求B 的大小;(2)如果b =2,求△ABC 的面积S △ABC 的最大值.20.(12分)如图所示,P 是△ABC 内一点,且满足AP u u u r +2BP u u u r+3CP u u u r =0,设Q 为CP 延长线与AB 的交点,求证:CQ u u u r=2CP u u u r .21.(12分)如图所示,设抛物线y 2=2px(p >0)的焦点为F ,经过点F 的直线交抛物线于A 、B 两点,点C 在抛物线的准线上,且BC∥x 轴,证明:直线AC 经过原点O.(用向量方法证明)22.(12分)(滚动交汇考查)已知函数f(x)=log 4(4x+1)+kx(k∈R)是偶函数. (1)求k 的值;(2)设g(x)=log 4(a·2x-43a),若函数f(x)与g(x)的图象有且只有一个公共点,求实数a 的取值范围.答案解析1.【解题指南】本题考查充分、必要条件,一元二次方程根的判定.先求出一元二次方程x 2+x +m =0有实数解的条件,再分析与m<14的关系.【解析】选A.由“一元二次方程x 2+x +m =0有实数解”得:12-4m ≥0⇒m ≤14,则m<14是m ≤14的充分不必要条件.2.【解析】选B.由题意,f(x)=4-x2|x -2|-2,由⎩⎪⎨⎪⎧4-x 2≥0|x -2|≠2得函数f(x)的定义域为[-2,0)∪(0,2].∴-2≤x ≤2时,f(x)不一定有意义.故选B.3.【解析】选A.∵BC u u u r +CD u u u r =BD u u u r =AD u u u r -AB u u u r=(-1,0),∴a =-1,b =0,∴a +b =-1.4.【解析】选A.2sin(x +π4)cos(x -π4)=2sin 2(x +π4)=1-cos[2(x +π4)]=1+sin2x ,其最小正周期为π,又|P 2P 4|显然是一个最小正周期,故选A. 5.【解析】选C.∵tan α=-12,∴sin α+2cos α4cos α-4sin α=tan α+24-4tan α=-12+24-4×(-12)=32×16=14. 6.【解析】选C.(特殊值法):对于f(1-x 1+x )=1-x21+x 2,令x =0,代入其中有f(1)=1. 经检验只有选项C 满足f(1)=1. 【一题多解】(换元法):选C.令t =1-x 1+x ,由此得x =1-t1+t ,所以f(t)=1-(1-t 1+t )21+(1-t 1+t )2=2t1+t 2,从而f(x)的解析式为f(x)=2x 1+x2. 7.【解析】选C.由题意,得⎩⎪⎨⎪⎧-73=-1+3λ1+λy =-6+01+λ,解得⎩⎪⎨⎪⎧y =-8λ=-14,故选C.8.【解析】选A.依题意(a +x b )·(a -b )=0,即a 2+(x -1)a ·b -x b 2=0, 又a =(3,4),b =(2,1), 则25+10(x -1)-5x =0, 解得x =-3.9.【解析】选D.令2x +π3=k π+π2(k ∈Z),得x =k π2+π12(k ∈Z),令k =0得该函数的一条对称轴为x =π12.本题也可用代入验证法来解.10.【解析】选A.函数有意义,需使e x-e -x≠0,其定义域为{x|x ≠0}. 又因为y =e x+e -xe x -e -x =e 2x+1e 2x-1=1+2e 2x -1,所以当x >0时函数为减函数,故选A. 11.【解析】选C.OH u u u r =OA u u u r +OB u u u r +OC u u u r ⇒AH u u u r =OB u u ur +OC u u u r , 取BC 的中点D ,则OB u u u r +OC u u u r =2OD u u u r ,∴AH u u u r=2OD u u u r .又∵AH ⊥BC ,∴OD ⊥BC , ∴点O 在BC 的中垂线上. 同理点O 在CA 、AB 的中垂线上, 所以点O 是△ABC 的外心.12.【解题指南】用已知模的向量AC u u u r 、BD u u u r 表示目标向量AB u u u r 、DC u u ur . 【解析】选C.由于AB u u u r =AC u u u r +CB u u u r ,DC u u u r =DB u u u r +BC u u ur , 所以AB u u u r +DC u u u r =AC u u u r +CB u u u r +DB u u u r +BC u u u r =AC u u u r -BD u u u r.(AB u u u r +DC u u u r )·(AC u u u r +BD u u u r )=(AC u u u r -BD u u u r )·(AC u u u r +BD u u u r )=AC u u u r 2-BD u u u r 2=9-4=5.13.【解析】设(x ,y)为函数y =f(x)图象上任一点,点(x ′,y ′)为平移后的对应点,则⎩⎪⎨⎪⎧x ′=x +1y ′=y -1,代入y ′=x ′2-2x ′+2,整理得y =x 2+2.故所求函数的解析式为y =x 2+2.答案:y =x 2+2 14.【解析】∵sinx =55,x ∈(π2,3π2), ∴tanx =-12,∴tan(x -π4)=tanx -11+tanx =-3.答案:-315.【解析】如图所示,设到C 点甲船追上乙船,乙船到C 点用的时间为t ,乙船速度为v ,则BC =tv ,AC =3tv ,B =120°, 由正弦定理知BC sinCAB =ACsinB ,∴1sinCAB =3sin120°, ∴sinCAB =12,∴∠CAB =30°,∴∠ACB =30°,∴BC =AB =a ,∴AC 2=AB 2+BC 2-2AB ·BCcos120° =a 2+a 2-2a 2·(-12)=3a 2, ∴AC =3a. 答案:北偏东30°3a16.【解析】①考虑向量和、差的平行四边形法则,不难判断结论正确;②当a ,b 的夹角为0°时,a ·b >0也成立,结论错误;③由两个函数图象容易判断结论正确;④可得AB u u u r 2=AC u u u r 2,即AB =AC ,正确.所以①③④正确. 答案:①③④17.【解题指南】(1)利用降幂公式将f(x)化为y =Asin(ωx +φ)+B 的形式求最小正周期.(2)利用整体代换的思想求最值.【解析】(1)f(x)=sin x 2cos x 2+cos 2x 2-2=12sinx +1+cosx2-2 =12(sinx +cosx)-32 =22sin(x +π4)-32, ∴最小正周期T =2πω=2π.(2)由(1)知f(x)=22sin(x +π4)-32, ∵x ∈[π,1712π],∴x +π4∈[54π,53π],当x +π4=32π,即x =54π时,f(x)有最小值,f(54π)=-22-32, 当x +π4=54π,即x =π时,f(x)有最大值,f(π)=-2.【方法技巧】解三角函数问题的变形技巧重视三角函数的“三变”:“三变”是指“变角、变名、变式”.变角:对角的拆分要尽可能化成同名、同角、特殊角;变名:尽可能减少函数名称;变式:对式子变形一般要尽可能有理化、整式化、降低次数等.在解决求值、化简、证明问题时,一般是观察角度、函数名、所求(或所证明)问题的整体形式中的差异,再选择适当的三角公式恒等变形.18.【解析】(1)m ⊥n ⇒2cos 2x +2sinxcosx =0⇒cos2x +sin2x +1=0⇒2sin(2x +π4)=-1 ⇒sin(2x +π4)=-22.∵0<x <π,∴2x +π4∈(π4,9π4),∴2x +π4=5π4或7π4,∴x =π2或3π4.(2)由(1)得f(x)=2sin(2x +π4)+1, 令2x +π4=k π+π2,k ∈Z ,可得x =k π2+π8,k ∈Z ,即对称轴方程为x =k π2+π8,k ∈Z ,令2x +π4=k π,k ∈Z ,可得x =k π2-π8,k ∈Z.即对称中心坐标为(k π2-π8,0),k ∈Z.19.【解析】(1)2sinB(2cos 2B2-1)=-3cos2B⇒2sinBcosB =-3cos2B ⇒tan2B =-3, ∵0<B <π2,∴0<2B <π,∴2B =2π3,∴B =π3.(2)由(1)知B =π3,∵b =2,由余弦定理,得:4=a 2+c 2-ac ≥2ac -ac =ac(当且仅当a =c =2时等号成立), ∵△ABC 的面积S △ABC =12acsinB =34ac ≤3,∴△ABC 面积的最大值为 3.20.【证明】∵AP u u u r =AQ u u u r +QP u u u r, BP u u u r =BQ u u u r +QP u u u r ,∴(AQ u u u r +QP u u u r )+2(BQ u u u r +QP u u u r)+3CP u u u r =0, ∴AQ u u u r +3QP u u u r +2BQ u u u r+3CP u u u r =0,又∵A ,B ,Q 三点共线,C ,P ,Q 三点共线,故可设AQ u u u r =λBQ u u u r ,CP u u u r =μ QP u u u r,∴λ BQ u u u r +3QP u u u r +2BQ u u u r +3μ QP u u u r=0, ∴(λ+2)BQ u u u r +(3+3μ)QP u u u r=0. 而BQ u u u r ,QP u u u r 为不共线向量,∴⎩⎪⎨⎪⎧λ+2=03+3μ=0.∴λ=-2,μ=-1.∴CP u u u r =-QP u u u r =PQ u u u r. 故CQ u u u r =CP u u u r +PQ u u u r=2CP u u u r .21.【解题指南】先由FA FB u u u r u u u r ∥建立点A ,B 坐标之间的关系, 再证OAOC u u u r u u u r∥即可. 【证明】设A(x 1,y 1),B(x 2,y 2),又F(p2,0),则C(-p2,y 2),则FA u u u r =(x 1-p 2,y 1),FB u u u r =(x 2-p2,y 2),∵FA u u u r 与FB u u u r共线,∴(x 1-p 2)y 2-(x 2-p2)y 1=0,即x 1-p 2y 1=x 2-p 2y 2,代入x 1=y 212p ,x 2=y 222p 整理得,y 1·y 2=-p 2.∵OA u u u r =(x 1,y 1),OC u u u r =(-p2,y 2),x 1y 2+p 2y 1=y 212p ·(-p 2y 1)+p 2y 1=0,∴OA u u u r 与OC u u u r共线,即A 、O 、C 三点共线,也就是说直线AC 经过原点O.【方法技巧】利用向量法解决解析几何问题(1)利用向量法来解决解析几何问题,首先要将线段看成向量,求得向量坐标从而进行运算. (2)平面向量在解析几何中的应用,是以解析几何中的坐标为背景的一种向量描述.它主要强调向量的坐标运算,将向量问题转化为坐标问题,进而利用直线和圆锥曲线的位置关系的相关知识来解答.22.【解析】(1)由函数f(x)是偶函数可知:f(x)=f(-x), ∴log 4(4x+1)+kx =log 4(4-x+1)-kx ,∴log 44x +14-x +1=-2kx ,即x =-2kx 对一切x ∈R 恒成立,∴k =-12.(2)函数f(x)与g(x)的图象有且只有一个公共点,即方程log 4(4x +1)-12x =log 4(a ·2x-43a)有且只有一个实根,化简得方程2x +12x =a ·2x-43a 有且只有一个实根,令t =2x >0,则方程(a -1)t 2-43at -1=0有且只有一个正根,①a =1⇒t =-34,不合题意;②a -1≠0且Δ=0⇒a =34或-3,若a =34⇒t =-2,不合题意;若a =-3⇒t =12,③一个正根与一个负根,即-1a -1<0⇒a>1, 综上:实数a 的取值范围是{-3}∪(1,+∞).。
21高考英语导学大一轮人教广西专用滚动测试2 含解析

滚动测试二第一部分听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5 段对话。
每段对话后有一个小题,从题中所给的 A、B、C 三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话前,你都有5秒钟的时间阅读题目;听完后,各小题给出5秒钟的作答时间。
每段对话仅读一遍。
1.What does the woman like best?A.Water.B.Coffee.C.Tea.2.What are the speakers talking about?A.Market research.B.A job interview.C.An exam paper.3.What was the woman doing?A.Looking for something.B.Admiring a building.C.Selling flowers.4.What will the man probably do?A.Prepare for a test.B.Go to meet friends.C.Rest at home.5.What did the man buy yesterday?A.Shirts.B.Trousers.C.Shoes.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答第6、7题。
6.How is the man probably feeling now?A.Sorry.B.Angry.C.Worried.7.What does the woman want to do?A.Try on some new dresses.B.Wait outside with friends.C.Buy the man something.听第7段材料,回答第8、9题。
广西桂林市、崇左市2021届高考数学联考试卷(文科)(二模)(含答案解析)

广西桂林市、崇左市2021届高考数学联考试卷(文科)(二模)一、单选题(本大题共12小题,共60.0分)1.已知集合A={(x,y)︳x2+y2=1},B={(x,y)︳x+y=1},则集合A∩B的元素个数为()A. 4B. 3C. 2D. 12.若复数z=a+bi(a、b∈R),则下列正确的是()A. |z2|>|z|2B. |z2|=|z|2C. |z2|<|z|2D. |z|2=z23.函数f(x)=2x2−mx+3,当x∈(−∞,−2]时是减函数,x∈[−2,+∞)时是增函数,则f(1)等于()A. −3B. 13C. 7D. 由m而定的常数4.设α∈(0,π2),β∈(π2,π),若1−cosαsinα=1+cosβsinβ,则下列结论一定正确的是()A. sinα=sinβB. sinα=−cosβC. sinα=cosβD. sin2α=sin2β5.设椭圆x22+y2=1的两个焦点为F1,F2,且P点的坐标为(√22 , √32),则|PF1|+|PF2|=()A. 1B. √2C. 2D. 2√26.等差数列{a n}中,a1>0,S n是前n项和且S9=S18,则当n=()时,S n最大.A. 12B. 13C. 12或13D. 13或147.曲线上的点到直线的最短距离是()A. B. C. D. 08.如果:在10进制中2004=4×100+0×101+0×102+2×103,那么类比:在5进制中数码2004折合成十进制为()A. 29B. 254C. 602D. 20049.已知P是圆x2+y2=1上的一动点,则P点到直线l:x+y−2√2=0的距离的最大值为()A. 1B. 3C. 2D. 2√210.在2h内将某种药物注射进患者的血液中.在注射期间,血液中的药物含量呈线性增加;停止注射后,血液中的药物含量呈指数衰减.能反映血液中药物含量Q随时间t变化的图象是()A. B.C.D.11. 数列{a n }满足a n +a n+1=1 (n ∈N ∗),a 2=2,S n 是数列{a n }的前n 项和,则S 31为( )A. 14B. 15C. 16D. 1712. 已知双曲线的右准线与渐近线在第四象限的交点为,双曲线的右焦点为,则所在直线的斜率是( )A.B.C.D.二、单空题(本大题共4小题,共20.0分)13. 已知等边△ABC 的边长为1,D 为边AC 的中点,则AB ⃗⃗⃗⃗⃗ ⋅BD⃗⃗⃗⃗⃗⃗ = ______ . 14. 设变量x ,y 满足约束条件{x −y ≥−1x +y ≤4y ≥a ,目标函数z =3x −2y 的最小值为−4,则a 的值是______.15. 已知函数f(x)=sin(2x +φ),若f(π12)−f(−5π12)=2,则函数f(x)的单调增区间为______. 16. 设函数f(x)={1−sinπx,−2≤x <0(19)x ,x ≥0,若关于x 的方程f(x)−a =0有三个不等实根x 1,x 2,x 3,且x 1+x 2+x 3=−52,则a = ______ . 三、解答题(本大题共7小题,共82.0分)17. 在△ABC 中,内角A 、B 、C 的对应边分别为a 、b 、c ,且cosBcosC =−b2a+c . (Ⅰ)求角B 的大小;(Ⅱ)b =√13,a +c =4,且a >c ,求△ABC 的面积.18. 如图,在三棱锥S −ABC 中,侧面SAB 与侧面SAC 均为等边三角形,∠BAC =90°,O 为BC 中点. (1)证明:SO ⊥平面ABC ;(2)(理科)求二面角A −SC −B 的余弦值. (文科)若AB =2,求三棱锥A −SBC 的体积.19. 某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上40间产品作为样本称出它们的重量(单位:克),重量的分组区间为(490,495],(495,500],…(510,515],由此得到样本的频率分布直方图,如图所示.(Ⅰ)根据频率分布直方图,求重量超过505克的产品数量;(Ⅱ)在上述抽取的40件产品中任取2件,设Y 为重量超过505克的产品数量,求Y 的数学期望.20. 已知函数f(x)=12x 2−(a +1)x +alnx . (1)当a =log 32时,求f(x)的单调区间; (2)若a <−12,函数g(x)=f(x)x在x =x 0处取得最小值,证明:0<f(x 0)<(e −1)(e −a).21. 已知抛物线C :y 2=4x 的焦点为F ,准线为l ,过l 上一点P 作抛物线C 的两条切线,切点为A ,B . (1)求证:直线AB 过焦点F ;(2)若|PA|=8,|PB|=6,求|PF|的值.22. 在直角坐标系xOy 中,将单位圆x 2+y 2=1上各点的横坐标扩大为原来的2倍,纵坐标不变得到曲线C ,以O 为极点,x 轴正半轴为极轴,建立极坐标系. (1)求曲线C 的参数方程;(2)设M 为C 上一点,N 点的板坐标为(2,π2),求|MN|的最大值及此时点M 的坐标.23. 设不等式组{|x −1|+2>|x +2||x −1|<|x +2|的解集为M ,且a ,b ∈M .(1)证明:|a +3b|<2(2)试比较|1−4ab|与2|a −b|的大小,并说明理由【答案与解析】1.答案:C解析:本题主要考查集合的基本元素,根据点集关系转化为直线和圆的位置公式是解决本题的关键,属于基础题.根据集合关系转化为直线和圆的位置关系即可得到结论.解:集合A的元素为半径为1的圆上的点构成的集合,集合B的元素为直线x+y=1上的点构成的集合,圆心到直线的距离d=√2=√22<1,即直线x+y=1和圆相交,则直线和圆有2个公共点,故集合A∩B的元素个数为2个,故选:C.2.答案:B解析:解:∵z2=(a+bi)2=a2+2abi+(bi)2=a2−b2+2abi;∴|z2|=√(a2−b2)2+(2ab)2=√a4+2a2b2+b4=a2+b2;又∵|z|=2+b2;∴|z|2=a2+b2.即|z2|=|z|2.故选:B.3.答案:A解析:本题考查了二次函数的图象与性质的应用问题,是基础题.解:二次函数f(x)=2x2−mx+3的图象是抛物线,当x∈[−2,+∞]时增函数,当x∈(−∞,−2]时是减函数,∴抛物线的对称轴是x=m4=−2,解得m=−8,∴f(x)=2x2−8x+3,∴f(1)=2−8+3=−3.故选A.4.答案:A解析:解:由已知可得:1−cosαsinα=1−1−tan2α21+tan2α22tanα21+tan2α2=1+1−tan2β21+tan2β22tanβ21+tan2β2=1+cosβsinβ,从而有:tanα2tanβ2=1,得sinα2sinβ2=cosα2cosβ2故有:cos(α+β2)=0∵α∈(0,π2),β∈(π2,π),∴π4<α+β2<3π4∴α+β=π∴sinα=sin(π−β)=sinβ故选:A.由万能公式化简可得cos(α+β2)=0,由已知可求得π4<α+β2<3π4,从而α+β=π,故可得sinα=sin(π−β)=sinβ.本题主要考查了三角函数中的恒等变换应用,属于基本知识的考查.5.答案:D解析:解:经验证P的椭圆上的一点,椭圆x22+y2=1的两个焦点为F1,F2,且P点的坐标为(√22 , √32),则|PF1|+|PF2|=2a=2√2.故选:D.判断P的位置,利用椭圆的定义,转化求解即可.本题考查椭圆的简单性质的应用,椭圆定义的应用,是基本知识的考查.6.答案:D解析:解:设等差数列{a n}的公差是d,由S9=S18得,9a1+9×82×d=18a1+18×172×d,解得d=−113a1,∴S n=na1+n(n−1)2×d=−126a1⋅n2+2726a1n,∵a1>0,∴当n=27时,即n=13或14时,S n最大,2故选:D.由等差数列的前n项和公式化简S9=S18,求出a1与d的关系式,利用二次函数的性质求出S n最大时n的值.本题考查等差数列的前n项和公式,以及利用二次函数的性质求出S n最大,属于中档题.7.答案:A解析:本题考查导数的几何意义及点到直线的距离公式,在曲线y=ln(2x−1)上设出一点,然后求出该点处的导数值,由该导数值等于直线2x−y+3=0的斜率求出点的坐标,然后由点到直线的距离公式求解.解:设曲线y=ln(2x−1)上的一点是P(m,n)则过P的切线必与直线2x−y+3=0平行.由,所以切线的斜率,解得m=1,n=ln(2−1)=0.即P(1,0)到直线的最短距离是.故选A.8.答案:B解析:解:(2004)5=2×53+4=254.故选B.本题考查的知识点是类比推理,由10进制的转换方法类比推理出5进制的转换方法,5进制与十进制数之间的转换,只要我们根据10进制转换方法逐位进行转换,即可得到答案.类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).9.答案:B解析:先利用点到直线的距离公式求得圆心到直线l的距离,则将此距离加上半径,即为所求.本题主要考查直线和圆的位置关系,点到直线的距离公式的应用,属于基础题.=2,解:圆心(0,0)到直线l:x+y−2√2=0的距离d=√2|2故P点到直线l:x+y−2√2=0的距离的最大值为d+r=2+1=3,故选:B.10.答案:B解析:解:在注射期间,血液中的药物含量呈线性增加,则第一段图象为直线,且为增函数,排除A,D,停止注射后,血液中的药物含量呈指数衰减.排除C.能反映血液中药物含量Q随时间t变化的图象是B.故选:B.根据在注射期间,血液中的药物含量呈线性增加;停止注射后,血液中的药物含量呈指数衰减即可得出.本题考查了直线与指数函数的图象与性质,考查了推理能力与计算能力,属于基础题.11.答案:A解析:解:数列{a n}满足a n+a n+1=1(n∈N∗),a2=2,∴a1+2=1,解得a1=−1.则S31=a1+(a2+a3)+(a4+a5)+⋯+(a30+a31)=−1+1×15=14.故选:A.数列{a n}满足a n+a n+1=1(n∈N∗),a2=2,可得a1+2=1,解得a1.利用S31=a1+(a2+a3)+ (a4+a5)+⋯+(a30+a31)即可得出.本题考查了数列分组求和、数列递推关系,考查了推理能力与计算能力,属于中档题.12.答案:A解析:解:由双曲线得a=4,b=3,c=5,右焦点F(5,0),因此双曲线的右准线方程为,双曲线的渐近线方程为y=,联立,解得(舍去)或,即,因此PF 所在直线的斜率为,故选A .13.答案:−34解析:解:因为△ABC 为等边三角形,所以AB ⃗⃗⃗⃗⃗ ⋅BD⃗⃗⃗⃗⃗⃗ =1×√32cos150°=−34; 故答案为:−34.所求利用数量积公式解答,其中向量的夹角为150°.本题考查了向量的数量积的定义和等边三角形的性质,属于基础题.14.答案:−1解析:解:作出约束条件所对应的可行域(如图),目标函数z =3x −2y 可化为y =32x −12z , 平移直线y =32x −12z 可知, 由{x −y =−1y =a , 解得x =a −1,y =a , ∴A(a −1,a),当直线经过点A 截距取最大值,z 最小, ∴3(a −1)−2a =−4, 解得a =−1故答案为:−1.作出可行域,变形目标函数并平移直线y =32x −12z 可得结论.本题考查简单线性规划,准确作图、利用目标函数的几何意义求最值是解决问题的关键,属于中档题.15.答案:[kπ−5π12,kπ+π12],k ∈Z解析:解:∵函数f(x)=sin(2x +φ),若f(π12)−f(−5π12)=2, 函数f(x)的周期为π,则f(π12)=sin(π6+φ)=1,f(−5π12)=sin(−5π6+φ)=−1,故π6+φ=2kπ+π2,且−5π6+φ=2kπ−π2,k ∈Z ,即φ=2kπ+π3,k ∈Z .故f(x)=sin(2x +π3 ).令2kπ−π2≤2x +π3≤2kπ+π2,解得kπ−5π12≤x ≤kπ+π12,k ∈Z . 故答案为:[kπ−5π12,kπ+π12],k ∈Z .本题主要考查正弦函数的图象特征,正弦函数的值域、单调性,属于中档题. 由条件可得π6+φ=2kπ+π2,且−5π6+φ=2kπ−π2,k ∈Z ,求得φ的值,可得f(x)的解析式,再利用正弦函数的单调性得出结论.16.答案:13解析:解:如图所示,画出函数f(x)的图象, 不妨设x 1<x 2<x 3,则x 1+x 2=2×(−32)=−3, 又x 1+x 2+x 3=−52, ∴x 3=12. ∴a =(19)12=13. 故答案为:13.如图所示,画出函数f(x)的图象,不妨设x 1<x 2<x 3,则x 1+x 2=2×(−32),又x 1+x 2+x 3=−52,可得x 3,代入aa =(19)x 3即可得出a .本题考查了函数的图象与性质、数形结合思想方法,考查了推理能力与计算能力,属于中档题.17.答案:解:(Ⅰ)利用正弦定理化简已知等式得:cosBcosC =−sinB2sinA+sinC,整理得:2sinAcosB+sinCcosB+cosCsinB=0,即2sinAcosB=−sin(B+C)=−sinA,∵sinA≠0,∴cosB=−12,∵B为三角形内角,∴B=120°;(Ⅱ)∵b=√13,cosB=−12,a+c=4,∴由余弦定理得:b2=a2+c2−2accosB,即13=a2+c2+ac=(a+c)2−ac=16−ac,∴ac=3,则S△ABC=12acsinB=12×3×√32=3√34.解析:(Ⅰ)已知等式利用正弦定理化简,整理后利用两角和与差的正弦函数公式及诱导公式化简,根据sin A不为0,求出cos B的值,由B为三角形内角,利用特殊角的三角函数值即可求出B的度数;(Ⅱ)利用余弦定理列出关系式,再利用完全平方公式化简,将b,a+c及cos B的值代入求出ac的值,再由sin B的值,利用三角形面积公式即可求出三角形ABC的面积.此题考查了正弦、余弦定理,两角和与差的正弦函数公式,以及三角形面积公式,熟练掌握定理及公式是解本题的关键.18.答案:证明:(1)由题设知AB=AC=SB=SC=SA,连结OA,△ABC为等腰直角三角形,∴OA=OB=OC=√22SA,且AO⊥BC,又△SBC为等腰三角形,故SO⊥BC,且SO=√22SA,从而OA2+SO2=SA2.∴△SOA为直角三角形,SO⊥AO.又AO∩BO=O.∴SO⊥平面ABC.解:(2)(理科)(法一:几何法):取SC的中点M,连结AM,OM,由(1)知SO=OC,SA=AC.得OM⊥SC,AM⊥SC.∴∠OMA为二面角A−SC−B的平面角.由AO⊥BC,AO⊥SO,SO∩BC=O得AO⊥平面SBC.∴AO⊥OM.又AM =√32SA , 故sin∠AMO =AO AM =√2√3=√63,cos∠AMO =√33, ∴二面角A −SC −B 的余弦值为√33. (法二:向量法):以O 为原点,OB 为x 轴,OA 为y 轴,OS 为z 轴,建立空间直角坐标系, 设AB =2,则A(0,√2,0),B(√2,0,0),C(−√2,0,0),S(0,0,√2),SA ⃗⃗⃗⃗⃗ =(0,√2,−√2),SB ⃗⃗⃗⃗⃗ =(√2,0,−√2),SC⃗⃗⃗⃗⃗ =(−√2,0,−√2), 设平面SAB 的法向量n⃗ =(x,y ,z), 则{n ⃗ ⋅SA ⃗⃗⃗⃗⃗ =√2y −√2z =0n⃗ ⋅SB ⃗⃗⃗⃗⃗ =√2x −√2z =0,取x =1,得n ⃗ =(1,1,1), 设平面SBC 的法向量m⃗⃗⃗ =(0,1,0), 设二面角A −SC −B 的平面角为θ,则cosθ=|m ⃗⃗⃗ ⋅n ⃗⃗ ||m ⃗⃗⃗ |⋅|n ⃗⃗ |=3=√33. ∴二面角A −SC −B 的余弦值为√33. (2)(文科)∵AB =2,∴S △BAC =12×AB ×AC =12×2×2=2, SO =√22SA =√2,∴三棱锥A −SBC 的体积:V A−SBC =V S−ABC =13×√2×2=2√23. 解析:(1)由题设知AB =AC =SB =SC =SA ,连结OA ,推导出SO ⊥BC ,SO ⊥AO ,由此能证明SO ⊥平面ABC .(2)(理科)几何法:取SC 的中点M ,连结AM ,OM ,则OM ⊥SC ,AM ⊥SC ,∠OMA 为二面角A −SC −B 的平面角,由此能求出二面角A −SC −B 的余弦值.向量法:以O 为原点,OB 为x 轴,OA 为y 轴,OS 为z 轴,建立空间直角坐标系,利用向量法能求出二面角A −SC −B 的余弦值.(2)(文科)三棱锥A −SBC 的体积V A−SBC =V S−ABC .本题考查线面垂直的证明,考查二面角的余弦值的求法,考查三棱锥的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、函数与方思想、数形结合思想,是中档题.19.答案:解:(Ⅰ)重量超过505克的产品数量是40×(0.05×5+0.01×5)=12件;(Ⅱ)Y的所有可能取值为0,1,2;P(Y=0)=C282C402=63130,P(Y=1)=C121C281C402=56130,P(Y=2)=C122C402=11130,Y的分布列为:∴E(Y)=0×63130+1×56130+2×11130=3965=35.解析:(Ⅰ)重量超过505克的产品结合频率分布直方图可知有两个部分,求出两矩形的面积,根据重量超过505克的产品数量等于该频率乘以样本容量即可;(Ⅱ)Y的所有可能取值为0,1,2,然后利用组合数分别求出它们的概率,列出分布列即可求Y的数学期望.本题主要考查了频率分布直方图,以及组合及组合数公式的应用,考查数学期望.属于中档题.20.答案:(1)解:由f(x)=12x2−(a+1)x+alnx,得f′(x)=x−(a+1)+ax =(x−1)(x−a)x(x>0),0<a=log32<1,由f′(x)>0,得0<x<log32或x>1,则f(x)的单调递增区间为(0,log32),(1,+∞).由f′(x)<0,得log32<x<1,则f(x)的单调递减区间为(log32,1);(2)证明:g(x)=12x−a−1+alnxx,g′(x)=x2+2a(1−lnx)2x2,设ℎ(x)=x2+2a(1−lnx),∵a<−12,∴ℎ(x)在(0,+∞)上为增函数,又ℎ(1)=1+2a<0,ℎ(e)=e2>0,∴∃t∈(1,e),ℎ(t)=0,当0<x<t时,g′(x)<0;当x>t时,g′(x)>0.故x0=t且x02+2a=2alnx0,f(x0)=12x02−(a+1)x0+alnx0=12x02−(a+1)x0+12x02+a=(x0−1)(x0−a),∵a<−12,x0∈(1,e),∴0<f(x 0)<(e −1)(e −a).解析:(1)求出原函数的导函数,得到导函数的零点,由导函数在不同区间段内的符号可得原函数的单调性;(2)对g(x)求导,得到函数的单调性,由单调性得到函数取得最小值时的x 值,代入f(x)解析式,结合a 与x 0的范围即可证明结论.本题考查对数的应用,考查利用导数研究函数的单调性,函数的最值与零点问题,综合性较强,难度较大.21.答案:解:(1)设点A(x 1,y 1),B(x 2,y 2),P(−1,a)、设直线PA :y −y 1=k 1(x −x 1),联立{y −y 1=k 1(x −x 1)y 2=4x整理可得:y 2−4k 1y +4y 1k 1−4x 1=0, 由△=0 得1−k 1y 1+k 12x 1=0 又y 12=4x 1,故1−k 1y 1+14k 12y 12=0, 故(12k 1y 1−1)2=0,故k PA =k 1=2y 1,故直线PA 的方程为:y −y 1=2y 1(x −x 1),即yy 1=2x +2x 1, 同理k PB =2y 2,直线PB 的方程为:yy 2=2x +2x 2. 又P 在直线PA ,PB 上∴{ay 1=−2+2x 1ay 2=−2+2x 2, 故A (x 1,y 1),B(x 2,y 2),在直线ay =−2+2x 上,故直线AB 的方程为ay =−2+2x.令y =0,得x =1,∴直线AB 过焦点F .(2)由(1)知联立{ay =−2+2x y 2=4x消x 得:y 2−2ay −4=0 , 故y 1+y 2=2a ,y 1y =−4,故k PA ⋅k PB =2y 1⋅2y 2=−1, 故直线PA 与直线PB 垂直,从而|AB|=√PA 2+PB 2=10,又{y 12=4x 1y 22=4x 2∴y 12−y 22=4(x 1−x 2),k AB =y 1−y 2x 1−x 2=4y 1+y 2=2a , 又k PF =a−0−1−1=−a 2,k PF ⋅k AB =−1,故PF ⊥AB ,∴|PF|=6×810=245.解析:(1)设A ,B ,P 的坐标,设直线PA ,PB 的方程与抛物线联立,求出两根之和及两根之积,由判别式为0及点A ,B 在抛物线上可得直线PA ,PB 的斜率与A ,B 的纵坐标的关系,由于P 在两条直线上,可得直线AB 的方程ay =−2+2x 上,可得直线AB 恒过定点(1,0),即直线过抛物线的焦点;(2)由(1)可得直线AB 的方程,与抛物线联立求出两根之和及两根之积,进而求出直线PA ,PB 的斜率之积为−1,所以直线PA ,PB 互相垂直,可得弦长|AB|的值,A ,B 代入抛物线的方程作差可得直线AB 的斜率,求出PF 的斜率与AB 的斜率之积为−1,进而求出PF 的值.本题考查抛物线的性质及直线恒过定点的应用,直线互相垂直的性质,属于中档题.22.答案:解:(1)由题意,可得曲线C 的直角坐标方程为x 24+y 2=1,则其参数方程为{x =2cosθy =sinθ(θ为参数);(2)由N 得极坐标为(2,π2),得N 得直角坐标为(0,2),∴|MN|=√4cos 2θ+(sinθ−2)2=√−3(sinθ+23)2+283.当sinθ=−23时,|MN|取得最大值为2√213, 此时M(±2√53,−23). 解析:(1)由坐标变换可得曲线C 的方程,由平方关系转化为参数方程;(2)求出N 的直角坐标,由两点间的距离公式可得|MN|,平方后利用三角函数求最值.本题考查简单曲线的极坐标方程,考查参数方程与普通方程的互化,训练了利用三角函数求最值,是中档题.23.答案:解:(1)令f(x)=|x −1|−|x +2|={3, x ≤−2−2x −1, −2<x <1−3, x ≥1,由题意可得−2<|x −1|−|x +2|<0,即−2<−2x −1<0,解得−12<x <12;则M ={x|−12<x <12};∴|a +3b|≤|a|+3|b|<12+3×12=2; ∴原题得证.(2)由(1)可得a 2<14,b 2<14;∵|1−4ab|2−4|a −b|2=(1−8ab +16a 2b 2)−4(a 2−2ab +b 2)=(4a 2−1)(4b 2−1)>0,∴|1−4ab|2>4|a −b|2,故|1−4ab|>2|a−b|.解析:(1)构造出新函数f(x)=|x−1|−|x−2|,将f(x)转换为分段函数,求出解集,之后利用|a+ 3b|≤|a|+3|b|证明不等式;(2)根据利用作差法比较大小,得出关系.本题主要考查绝对值不等式的解法,属于中档题.。
2021年广西高考文科数学真题及参考答案
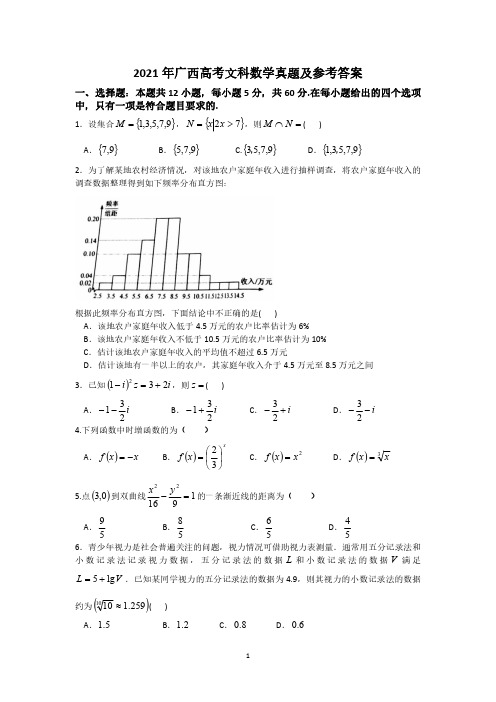
2021年广西高考文科数学真题及参考答案一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{}9,7,5,3,1=M ,{}72>=x x N ,则=⋂N M ()A .{}9,7B .{}9,7,5 C.{}9,7,53,D .{}9,7,53,1,2.为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:根据此频率分布直方图,下面结论中不正确的是()A .该地农户家庭年收入低于4.5万元的农户比率估计为6%B .该地农户家庭年收入不低于10.5万元的农户比率估计为10%C .估计该地农户家庭年收入的平均值不超过6.5万元D .估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间3.己知()i z i 2312+=-,则=z ()A .i 231--B .i 231+-C .i +-23D .i --234.下列函数中时增函数的为()A .()xx f -=B .()xx f ⎪⎭⎫⎝⎛=32C .()2xx f =D .()3xx f =5.点()0,3到双曲线191622=-y x 的一条渐近线的距离为()A .59B .58C .56D .546.青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L 和小数记录法的数据V 满足V L lg 5+=.已知某同学视力的五分记录法的数据为4.9,则其视力的小数记录法的数据约为()259.11010≈()A .5.1B .2.1C .8.0D .6.07.在一个正方体中,过顶点A 的三条棱的中点分别为G F E ,,.该正方体截去三棱锥EFG A -后,所得多面体的三视图中,正视图如右图所示,则相应的侧视图是()A .B .C .D .8.在ABC ∆中,已知︒=120B ,19=AC ,2=AB ,则=BC ()A .1B .2C .5D .39.记n S 为等比数列{}n a 的前n 项和,若42=S ,64=S ,则=6S ()A .7B .8C .9D .1010.将3个1和2个0随机排成一行,则2个0不相邻的概率为()A .3.0B .5.0C .6.0D .8.011.若⎪⎭⎫ ⎝⎛∈20πα,,αααsin 2cos 2tan -=,则=αtan ()A .1515B .55C .35D .31512.设()x f 是定义域为R 的奇函数,且()()x f x f -=+1.若3131=⎪⎭⎫ ⎝⎛-f ,则=⎪⎭⎫⎝⎛35f ()A .35-B .31-C .31D .35二、填空题:本题共4小题,每小题5分,共20分。
2021年广西南宁三中高考数学二模试卷(文科)(附答案详解)

2021年广西南宁三中高考数学二模试卷(文科)一、单选题(本大题共12小题,共60.0分)1. (2021·甘肃省·模拟题)已知集合A ={x|−2<x ≤1},B ={−2,−1,0,1},则A ∩B =( )A. {−2,−1,0,1}B. {−1,0,1}C. {−1,0}D. {−2,−1,0}2. (2021·广西壮族自治区南宁市·模拟题)设复数z =i−31+i ,则z 的共轭复数z −=( )A. −1+2iB. 1+2iC. −1−2iD. 1−2i3. (2021·广东省佛山市·单元测试)设命题p :∀x >1,x >lnx ;则¬p 为( )A. ∃x 0>1,x 0>lnx 0B. ∃x 0≤1,x 0≤lnx 0C. ∃x 0>1,x 0≤lnx 0D. ∀x >1,x ≤lnx4. (2021·广西壮族自治区南宁市·模拟题)已知a ⃗ =(1,−1),b ⃗ =(−1,3),则a⃗ ⋅(2a ⃗ +b ⃗ )=( )A. 0B. 1C. −1D. 25. (2021·江西省·模拟题)某几何体的三视图如图所示,已知图中圆的半径都为1,则此几何体的体积为( )A. π4 B. π2 C. 3π4 D. π6. (2021·浙江省·模拟题)设变量x 、y 满足约束条件{y ≤42x −3y ≤−22x +y ≥6,则目标函数z =x +y 的最小值是( )A. 1B. 3C. 4D. 57. (2021·陕西省西安市·模拟题)函数f(x)=cosx−x 2e x的图象大致为( )A. B.C. D.8.(2021·宁夏回族自治区银川市·模拟题)在等比数列{a n}中,a1+a3=10,a5+a7=160,则a1=()A. 0B. 1C. 2D. 49.(2020·黑龙江省哈尔滨市·单元测试)已知圆(x−1)2+y2=4内一点P(2,1),则过P点最短弦所在的直线方程是()A. x−y+1=0B. x+y−3=0C. x+y+3=0D. x=210.(2021·广西壮族自治区南宁市·模拟题)执行如图所示的程序框图,若输出的S是30,则判断框内的条件可以是()A. n≥6B. n≥8C. n>10D. n≥1011.(2021·陕西省西安市·模拟题)已知椭圆x2a2+y2b2=1(a>b>0)的右焦点为F,离心率为√32,过点F的直线l交椭圆于A,B两点,若AB的中点为(1,1),则直线l的斜率为()A. −14B. −34C. −12D. 112.(2021·陕西省西安市·模拟题)已知直线l是曲线f(x)=x4−2x3在点(1,f(1))处的切线,点P(m,n)是直线l上位于第一象限的一点,则m+2nm⋅n的最小值为()A. 4B. 9C. 25D. 16二、单空题(本大题共4小题,共20.0分)13.(2021·体验省·单元测试)已知一组数据4,2a,3−a,5,6的平均数为4,则a的值是.14.(2021·福建省厦门市·模拟题)已知f(x)=sin(2x+φ)(0<φ<π)是偶函数,则)=______ .f(π615.(2021·甘肃省金昌市·模拟题)在边长为6的正方形中有一封闭曲线围成的阴影区域,,则阴影区域的面从该正方形区域内任取一点,若该点落在阴影区域内的概率为49积为______ .16.(2021·广西壮族自治区南宁市·模拟题)在长方体ABCD−A1B1C1D1中,AB=AD=6,AA1=2,M为棱BC的中点,动点P满足∠APD=∠CPM,则点P的轨迹与长方体的侧面DCC1D1的交线长等于______ .三、解答题(本大题共7小题,共82.0分)17.(2021·安徽省·单元测试)已知△ABC的角A,B,C的对边分别为a,b,c,满足(b−a)(sinB+sinA)=(b−c)sinC.(1)求A;(2)从下列条件中:①a=√3;②S△ABC=√3中任选一个作为已知条件,求△ABC周长的取值范围.18.(2021·广西壮族自治区南宁市·模拟题)某校数学课外兴趣小组为研究数学成绩是否与性别有关,统计了本校高三年级每名学生一学期数学成绩的平均分(采用百分制),剔除平均分在40分以下的学生后,共有男生300名,女生200名现采用分层随机抽样的方法,从中抽取了100名学生,按性别分为两组,并将两组学生的成绩分为6组,得到如表.附表及公式:其中n=a+b+c+d,K2=n(ad−bc)2.(a+b)(c+d)(a+c)(b+d)P(K2≥k)0.1000.0500.0100.001 k 2.706 3.841 6.63510.828(1)估计男、女生各自的平均分(同一组数据用该组区间中点值作代表),从计算结果判断数学成绩与性别是否有关;(2)规定成绩在80分以上为优秀,请你根据已知条件补全所列的2×2列联表,并判断是否有90%以上的把握认为“数学成绩与性别是否有关”.优秀非优秀合计男生女生合计19.(2021·江西省萍乡市·模拟题)在如图所示的空间几何体中,两等边三角形△ACD与△ABC互相垂直,AC=BE=4,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.(1)求证:DE//平面ABC;(2)求点B到平面ADE的距离.20.(2021·河南省平顶山市·单元测试)已知椭圆C:x2a2+y2b2=1(a>b>0)的左、右焦点分别是F1,F2,上、下顶点分别是B1,B2,离心率e=12,短轴长为2√3.(1)求椭圆C的标准方程;(2)过F2的直线l与椭圆C交于不同的两点M,N,若MN⊥B1F2,试求△F1MN内切圆的面积.21.(2021·安徽省·模拟题)已知函数f(x)=kx2+2x−lnx.(1)当k=1时,求在x=1处的切线方程;(2)若f(x)在定义域上存在极大值,求实数k的取值范围.22.(2014·山西省临汾市·模拟题)在直角坐标系xOy中,曲线C1的参数方程是{x=√3cosαy=sinα(α是参数).以原点O为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程是ρsin(θ+π4)=4√2(1)求曲线C1的普通方程与曲线C2的直角坐标方程;(2)设P为曲线C1上的动点,求点P到C2上点的距离的最小值,并求此时点P的直角坐标.23.(2021·广西壮族自治区南宁市·模拟题)已知f(x)=|x−a|+|x+b|(a>0,b>0).(1)当a=2,b=1时,解不等式f(x)≥9;(2)若f(x)的最小值为2,求1a+1+12b的最小值.答案和解析1.【答案】B【知识点】交集及其运算【解析】解:∵A={x|−2<x≤1},B={−2,−1,0,1},∴A∩B={−1,0,1}.故选:B.进行交集的运算即可.本题考查了交集及其运算,考查了计算能力,属于基础题.2.【答案】C【知识点】复数的四则运算【解析】解:∵z=(i−3)(1−i)2=−2+4i2=−1+2i,∴z−=−1−2i.故选:C.利用复数的运算法则、共轭复数的定义即可得出.本题考查了复数的运算法则、共轭复数的定义,考查了推理能力与计算能力,属于基础题.3.【答案】C【知识点】全称量词命题、存在量词命题的否定及真假判定【解析】解;∵命题是全称命题的否定,是特称命题,只否定结论.∴¬p:∃x0>1,x0≤lnx0故选:C.根据全称命题的否定是特称命题进行判断.本题主要考查含有量词的命题的否定,比较基础.4.【答案】A【知识点】向量的数量积【解析】解:由已知条件可得a⃗2=1+1=2,a⃗⋅b⃗ =1×(−1)−1×3=−4,因此,a⃗⋅(2a⃗+b⃗ )=2a⃗2+a⃗⋅b⃗ =2×2−4=0.利用向量的数量积的运算法则,求解即可. 本题考查向量的数量积的求法,是基础题.5.【答案】D【知识点】空间几何体的三视图【解析】解:根据几何体三视图转换为几何体的直观图,该几何体为34个球体; 故V =34×43⋅π⋅13=π. 故选:D .首先把三视图转换为几何体的直观图,进一步利用球的体积公式的应用求出结果. 本题考查的知识要点:三视图和几何体的直观图之间的转换,几何体的体积公式的应用,主要考查学生的运算能力和数学思维能力,属于基础题.6.【答案】C【知识点】简单的线性规划【解析】解:由约束条件作出可行域如图,联立{2x −3y =−22x +y =6,解得A(2,2),化z =x +y 为y =−x +z ,由图可知,当直线y =−x +z 过A 时, 直线在y 轴上的截距最小,z 有最小值为2+2=4, 故选:C .由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,把最优解的坐标代入目标函数得答案.本题考查简单的线性规划,考查数形结合思想,是中档题.【知识点】函数图象的作法 【解析】解:f(−x)=cos(−x)−(−x)2e −x=cosx−x 2e −x≠f(x),即f(x)不为偶函数,其图象不关于y 轴对称,故排除A ,C ;当x =0时,f(x)=1e >0,故排除D , 故选项B 符合函数f(x), 故选:B .先判断函数的奇偶性,再根据函数的零点和函数值的特点即可判断.本题考查了函数图象的识别,掌握函数的奇偶性和函数值的特点是解题的关键,属于基础题.8.【答案】C【知识点】等比数列的通项公式 【解析】解:在等比数列{a n }中, ∵a 1+a 3=10,a 5+a 7=160, ∴{a 1+a 1q 2=10a 1q 4+a 1q 6=160, 解得q 2=4,a 1=2. 故选:C .利用等比数列的通项公式列出方程组,能求出首项.本题考查等比数列的首项的求法,考查等比数列的性质等基础知识,考查运算求解能力,是基础题.9.【答案】B【知识点】直线与圆的位置关系及判定 【解析】解:如图:圆心坐标D(1,0),要使过P点的弦最短,则圆心到直线的距离最大,即DP⊥BC时,满足条件,=1,此时DP的斜率k=1−02−1则弦BC的斜率k=−1,则此时对应的方程为y−1=−1(x−2),即x+y−3=0,故选B.根据圆的性质,确定最短弦对应的条件,即可得到结论.本题主要考查直线方程的求解,根据直线和圆的位置关系确定最短弦满足的条件是解决本题的关键.10.【答案】D【知识点】程序框图【解析】解:由程序框图,其执行结果如下:1、S=0,n=0:n=2,S=2,执行循环体;2、S=2,n=2:n=4,S=6,执行循环体;3、S=6,n=4:n=6,S=12,执行循环体;4、S=12,n=6:n=8,S=20,执行循环体;5、S=20,n=8:n=10,S=30,跳出循环体,输出S=30;∴框内条件应为n≥10.故选:D.模拟执行程序框图,依次写出每次循环得到的n,S的值,根据已知即可得解判断框内本题主要考查了循环结构的程序框图,正确判断退出循环的条件是解题的关键,属于基础题.11.【答案】A【知识点】椭圆的性质及几何意义【解析】解:设A(x1,y1),B(x2,y2),则AB的中点坐标为(x1+x22,y1+y22),由题意可得x1+x2=2,y1+y2=2,将A,B的坐标的代入椭圆的方程:{x12a2+y12b2=1x22 a2+y22b2=1,作差可得x12−x22a2+y12−y22b2=0,所以y1−y2x1−x2=−b2a2⋅x1+x2y1+y2=−b2a2,又因为离心率e=ca =√32,所以1−b2a2=34,所以−b2a2=−14,即直线AB的斜率为−14,故选:A.设A,B的坐标,代入椭圆的方程,作差可得直线AB的斜率的表达式,再由椭圆的离心率可得a,b的关系,进而求出直线AB的斜率.本题考查椭圆的性质及点差法求直线的斜率,属于基础题.12.【答案】B【知识点】导数的几何意义【解析】解:f(x)=x4−2x3的导数为f′(x)=4x3−6x2,可得在点(1,f(1))处的切线的斜率为4−6=−2,切点为(1,−1),切线的方程为y+1=−2(x−1),即为2x+y=1,则2m+n=1(m,n>0),所以m+2nm⋅n =(2m+n)(1n+2m)=5+2mn+2nm≥5+2×2=9,当且仅当m=n=13时,取得等号.则m+2nm⋅n的最小值为9.求得f(x)的导数,可得切线的斜率和切点,进而得到切线的方程,由乘“1”法和基本不等式,可得所求最小值.本题考查导数的运用:求切线的方程,以及基本不等式的运用:求最值,考查方程思想和转化思想、运算能力,属于中档题.13.【答案】2【知识点】平均数、中位数、众数【解析】【分析】本题考查平均数的定义的运用,属于基础题.运用平均数的定义,解方程可得a的值.【解答】解:一组数据4,2a,3−a,5,6的平均数为4,则4+2a+(3−a)+5+6=4×5,解得a=2.故答案为:2.14.【答案】12【知识点】正弦、余弦函数的图象与性质【解析】解:∵f(x)=sin(2x+φ)(0<φ<π)是偶函数,∴φ=π2,f(x)=cos2x,则f(π6)=cosπ3=12,故答案为:12.由题意利用函数的奇偶性,求出函数的解析式,可得f(π6)的值.本题主要考查三角函数的奇偶性,属于基础题.15.【答案】16【知识点】几何概型【解析】解:设阴影部分的面积为S ,结合几何概型公式可得:S 6×6=49,解得:S =16. 故答案为:16.由题意结合几何概型计算公式得到关于面积的方程,解方程即可求得最终结果. 本题考查几何概型及其应用,重点考查学生对基础概念的理解和计算能力,属于中档题.16.【答案】2π3【知识点】简单多面体(棱柱、棱锥、棱台)及其结构特征 【解析】解:如下图所示:当P 在面DCC 1D 1内时,AD ⊥面DCC 1D 1,CM ⊥面DCC 1D 1;又∠APD =∠MPC ,在Rt △PDA 与Rt △PCM 中,∵AD =6,则MC =3,∴tan∠APD =ADPD=tan∠MPC =MCPC,则6PD =3PC ,即PD =2PC.在平面DCC 1D 1中,以DC 所在直线为x 轴,以DC 的垂直平分线为y 轴建立平面直角坐标系,则D(−3,0),C(3,0),设P(x,y),由PD =2PC ,得√(x +3)2+y 2=2√(x −3)2+y 2, 整理得:x 2−10x +y 2+9=0,即(x −5)2+y 2=16. ∴点P 的轨迹是以F(5,0)为圆心,半径为4的圆. 设圆F 与面DCC 1D 1的交点为E 、M , 作EK 垂直x 轴于点K ,则sin∠EFK =EK EF=24=12;∴∠EFK =π6;故点P 的轨迹与长方体的面DCC 1D 1的交线为劣弧ME ⏜,所以劣弧ME ⏜的长为π6×4=2π3.由题意画出图形,由角的关系得到边的关系,然后再在平面DCC1D1内建系,求出P的轨迹方程,确定点P的轨迹与长方体的面DCC1D1的交线,进而求得交线长.本题考查棱柱的结构特征、圆的方程、弧长问题,考查数学运算能力及直观想象能力,属于难题.17.【答案】解:(1)因为(b−a)(sinB+sinA)=(b−c)sinC,由正弦定理得(b−a)(b+a)=(b−c)c,即b2+c2−a2=bc,由余弦定理得cosA=b2+c2−a22bc =12,A∈(0,π),所以A=π3.(2)选择①a=√3.由正弦定理bsinB =csinC=asinA=2,即△ABC周长l=2sinB+2sinC+√3=2sinB+2sin(2π3−B)+√3=3sinB+√3cosB+√3=2√3sin(B+π6)+√3,∵B∈(0,2π3)∴π6<B+π6<5π6,12<sin(B+π6)≤1,即△ABC周长的取值范围(2√3,3√3],选择②S△ABC=√3.,得S△ABC=12bcsinA=√34bc=√3,得bc=4.由余弦定理得a2=b2+c2−bc=(b+c)2−3bc=(b+c)2−12,即△ABC周长l=a+b+c=√(b+c)2−12+b+c,∵b+c≥2√bc=4,当且仅当b=c=2时等号成立.∴l=a+b+c≥√42−12+4=6,即△ABC周长的取值范围[6,+∞).【知识点】正弦定理及变形、辅助角公式(三角函数的叠加及应用(北师))、三角形面积公式、利用余弦定理解决范围与最值问题、由基本不等式求最值或取值范围、利用正弦定理解决范围与最值问题、利用余弦定理解三角形【解析】本题主要考查了正弦定理,余弦定理,三角函数恒等变换的应用,正弦函数的性质,三角形的面积公式,基本不等式在解三角形中的综合应用,考查了计算能力和转化思想,属于中档题.(1)由正弦定理化简已知等式可得b 2+c 2−a 2=bc ,由余弦定理得cos A 的值,结合A 的范围可求A 的值.(2)选择①a =√3.由正弦定理,三角函数恒等变换的应用可求△ABC 周长l =2√3sin(B +π6)+√3,可求B +π6的范围,根据正弦函数的性质可求△ABC 周长的取值范围;选择②利用三角形的面积公式可得bc =4,由余弦定理得a 2=(b +c)2−12,根据基本不等式可求b +c ≥2√bc =4,即可得解△ABC 周长的取值范围.18.【答案】(1)男生的平均分x −1=45×3+55×9+65×18+75×15+85×6+95×960=71.5,女生的平均分x −2=45×6+55×4+65×5+75×10+85×13+95×240=71.5,从男、女生各自的平均分来看,数学成绩与性别无关;(2)由题表可知,在抽取的100名学生中,男生组中成绩优秀的有15人,女生组中成绩优秀的有15人,据此可得2×2列联表如下:计算可得K 2=100×(15×25−15×45)230×70×60×40≈1.786<2.706,所以没有90%以上的把握认为“数学成绩与性别是否有关”.【知识点】独立性检验【解析】(1)利用平均数的计算公式求解即可;(2)由题中的信息,补全2×2列联表,由公式计算K 2的值,对照临界值表中的数据,即可得到答案.本题考查了特征数的求解以及独立性检验的应用,解题的关键是掌握平均数的计算公式以及独立性检验的方法,属于基础题.19.【答案】(1)证明:取AC 中点O ,连接BO ,DO ,由题知,BO 为∠ABC 的平分线,BO⊥AC,DO⊥AC,设点F是点E在平面ABC上的射影,由题知,点F在BO上,连接EF,则EF⊥平面ABC.∵平面ACD⊥平面ABC,平面ACD∩平面ABC=AC,DO⊂平面ACD,DO⊥AC,∴DO⊥平面ABC,∴DO//EF,……………………………………………………………(2分)∵BE和平面ABC所成的角为60°,即∠EBF=60°,∴EF=2√3,又DO=2√3,∴四边形EFOD为平行四边形,∴DE//BO,…………………………………(5分)BO⊆平面ABC,DE⊄平面ABC,∴DE//平面ABC.……………………………………(6分) (2)解:设点B到平面ADE的距离为d,由V B−ADE=V A−BDE得:13S△ADE⋅d=13S△BDE⋅2……………………………(8分)1 3⋅12⋅AD⋅DE⋅d=13⋅12⋅ED⋅DO⋅2……………………………(10分)解得d=√3.………………………………(12分)【知识点】线面平行的判定、利用空间向量求点、线、面之间的距离【解析】(1)取AC中点O,连接BO,DO,证明BO⊥AC,DO⊥AC,连接EF,说明EF⊥平面ABC.推出DO⊥AC,利用BE和平面ABC所成的角为60°,证明DE//BO,推出DE//平面ABC.(2)设点B到平面ADE的距离为d,由V B−ADE=V A−BDE得:13S△ADE⋅d=13S△BDE⋅2,求解距离即可.本题考查直线与平面垂直以及直线与平面平行的判定定理的应用,等体积法的应用,点、线、面距离的求法,是中档题.20.【答案】解:(1)由题意可得{ca =122b=2√3,又a2=b2+c2,解得a2=4,b2=3,所以椭圆C的方程为x24+y23=1.(2)由B1(0,√3),F2(1,0),知B1F2的斜率为−√3,因为MN ⊥B 1F 2,故MN 的斜率为√33,则直线l 的方程为y =√33(x −1),即x =√3y +1,联立{x 24+y 23=1x =√3y +1,得13y 2+6√3y −9=0, 设M(x 1,y 1),N(x 2,y 2),则y 1+y 2=−6√313,y 1y 2=−913,则△F 1MN 的面积为S =c ⋅|y 1−y 2|=√(y 1+y 2)2−4y 1y 2=2413, 则△F 1MN 的周长L =4a =8, 即S =12LR ,得内切圆R =2S L=613,所以△F 1MN 的内切圆面积为πR 2=36169π.【知识点】直线与椭圆的位置关系、椭圆的概念及标准方程【解析】(1)由离心率e =12,短轴长为2√3,列方程组,解得a ,b ,进而可得椭圆的方程.(2)由题可知B 1F 2的斜率为−√3,又MN ⊥B 1F 2,得MN 的斜率为√33,写出直线l 的方程,联立椭圆的额方程,设M(x 1,y 1),N(x 2,y 2),结合韦达定理可得y 1+y 2,y 1y 2,进而可得△F 1MN 的周长L =4a =8,则内切圆R =2S L,进而可得△F 1MN 的内切圆面积.本题考查椭圆的方程,直线与椭圆的相交问题,解题中需要一定的计算能力,属于中档题.21.【答案】解:(1)k =1时,f(x)=x 2+2x −lnx ,f′(x)=2x +2−1x ,因为f(1)=3,f′(1)=3,故f(x)在x =1处的切线方程为y −3=3(x −1),即y =3x ; (2)f′(x)=2kx +2−1x =2kx 2+2x−1x,x >0,设g(x)=2kx 2+2x −1,①当k =0时,g(x)=0可得x =12,易得,当0<x <12时,g(x)<0,即f′(x)<0,f(x)单调递减, 当x >12时,g(x)>0,即f′(x)>0,f(x)单调递增, 故f(x)有极小值,没有极大值;②当k >0时,△=4+8k >0,由g(x)=0得,x =√1+2k−12k,当0<x <√1+2k−12k时,g(x)<0,即f′(x)<0,f(x)单调递减,当x >√1+2k−12k,g(x)>0,即f′(x)>0,f(x)单调递增,故f(x)有极小值,没有极大值; ③当k <0时,△=4+8k ,当k ≤−12时,△=4+8k ≤0,f′(x)≤0,f(x)单调递减,没有极大值, 当−12<k <0时,△=4+8k >0, 由g(x)=0得,x =√1+2k−12k,或x =−√1+2k−12k,当0<x <√1+2k−12k时,g(x)<0,即f′(x)<0,f(x)单调递减,当√1+2k−12k<x <−√1+2k−12k,g(x)>0,即f′(x)>0,f(x)单调递增,当x >−√1+2k−12k,g(x)<0,即f′(x)<0,f(x)单调递减,故f(x)在x =−√1+2k−12k取得极大值,综上−12<k <0.【知识点】导数的几何意义、利用导数研究函数的极值【解析】(1)把k =1代入,对函数求导,然后结合导数的几何意义即可求解; (2)先对函数求导,结合导数与单调性的关系讨论k 的范围,确定函数单调性,进而确定极值的存在情况,可求.本题主要考查了导数的几何意义及利用导数研究函数的单调性,体现了分类讨论思想的应用.22.【答案】解:(1)由曲线C 1:{x =√3cosαy =sinα,可得{√3=cosαy =sinα,两式两边平方相加得:(√3)2+y 2=1,即曲线C 1的普通方程为:x 23+y 2=1.由曲线C 2:ρsin(θ+π4)=4√2得:√22ρ(sinθ+cosθ)=4√2,即ρsinθ+ρcosθ=8,所以x +y −8=0, 即曲线C 2的直角坐标方程为:x +y −8=0.(2)由(1)知椭圆C 1与直线C 2无公共点,椭圆上的点P(√3cosα,sinα)到直线x +y −8=0的距离为d =√3cosα+sinα−8|√2=|2sin(α+π3)−8|√2,∴当sin(α+π3)=1时,d 的最小值为3√2,此时点P 的坐标为(32,12).【知识点】简单曲线的极坐标方程【解析】(1)由条件利用同角三角函数的基本关系把参数方程化为直角坐标方程,利用直角坐标和极坐标的互化公式x =ρcosθ、y =ρsinθ,把极坐标方程化为直角坐标方程. (2)求得椭圆上的点P(√3cosα,sinα)到直线x +y −8=0的距离为d =√3cosα+sinα−8|√2=|2sin(α+π3)−8|√2,可得d 的最小值,以及此时的α的值,从而求得点P 的坐标.本题主要考查把参数方程、极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,正弦函数的值域,属于基础题.23.【答案】解:(1)当a =2,b =1时,f(x)=|x −2|+|x +1|≥9,所以{x ≤−1−2x +1≥9或{−1<x ≤23≥9或{x >22x −1≥9,(3分)解得:x ≤−4或x ≥5,故解集为(−∞,−4]∪[5,+∞);(5分)(2)由a >0,b >0,所以f(x)=|x −a|+|x +b|≥|x +b −x +a|=|a +b|=a +b , 当且仅当(x −a)(x +b)≤0,即−b ≤x ≤a 时,等号成立. 若f(x)的最小值为2,则a +b =2,所以(a +1)+b =3,(7分)1a +1+12b =13(1a +1+12b )((a +1)+b)=13(32+b a +1+a +12b )≥13(32+2√12)=13(32+√2)=12+√23当且仅当ba+1=a+12b,即a =5−3√2,b =3√2−3时,等号成立.(9分)所以1a+1+12b 的最小值为12+√23.(10分)【知识点】函数的最值、不等式和绝对值不等式 【解析】(1)去掉绝对值,转化求解不等式的解集即可. (2)由推出a +b =2,利用基本不等式转化求解最值即可.本题考查绝对值不等式的解法,基本不等式的应用,考查转化思想以及计算能力,是中档题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
滚动测试卷二(第一~五章)(时间:120分钟 满分:150分)滚动测试卷第5页一、选择题(本大题共12小题,每小题5分,共60分)1.(2019广东中山一中高三下学期冲刺)已知集合A={x|y=log 2(x-2)},B={x|x 2≥9},则A ∩(∁R B )=( ) A.[2,3) B.(2,3) C.(3,+∞) D.(2,+∞) 答案:B解析:由题意可知,A={x|x>2},B={x|x ≤-3或x ≥3}, 所以∁R B={x|-3<x<3}, 所以A ∩(∁R B )={x|2<x<3}.2.(2019广东深圳高三二模)已知复数z 1=3+4i,z 2=34+i,则z 1·z 2等于( ) A.254 B.43iC.254−43iD.-254i答案:A解析:由已知得,z 2=34-i,所以z 1·z 2=(3+4i)(34-i)=254.3.下列结论正确的是( ) A.若命题p :∀x>0,都有x 2>0,则p :∃x 0≤0,使得x 02≤0B.若命题p 和p ∨q 都是真命题,则命题q 也是真命题C.在△ABC 中,a ,b ,c 是内角A ,B ,C 所对的边,则a<b 的充要条件是cos A>cos BD.命题“若x 2+x-2=0,则x=-2或x=1”的逆否命题是“x ≠-2或x ≠1,则x 2+x-2≠0” 答案:C解析:若命题p :∀x>0,都有x 2>0,则p :∃x 0>0,使得x 02≤0.故A 项错误;若命题p 和p ∨q 都是真命题,则命题q 可能是真命题,也可能是假命题.故B 项错误;在△ABC 中,由a<b 可知0<A<B<π,而y=cos x 在(0,π)内单调递减,故cos A>cos B ,C 项正确; 命题“若x 2+x-2=0,则x=-2或x=1”的逆否命题是“x ≠-2且x ≠1,则x 2+x-2≠0”.故D 项错误.故选C .4.命题“存在x ∈[0,2],x 2-x-a ≤0为真命题”的一个充分不必要条件是( ) A.a ≤0B.a ≥-1C.a ≥-14D.a ≥3答案:D解析:∵存在x ∈[0,2],x 2-x-a ≤0为真命题,∴a ≥(x 2-x )min =[(x -12)2-14]min=-14.因此上述命题的一个充分不必要条件是a ≥3.故选D .5.(2019广东汕头高三二模)已知f (x )是定义在R 上的奇函数,满足f (1+x )=f (1-x ),且f (1)=a ,则f (2)+f (3)+f (4)=( ) A.0 B.-a C.a D.3a 答案:B解析:由f (1+x )=f (1-x ),且f (x )是R 上的奇函数,可知f (x )是周期为4的周期函数,f (0)=0,所以f (4)=f (0)=0,f (3)=f (-1)=-f (1)=-a ,f (2)=f (1+1)=f (1-1)=f (0)=0,所以f (2)+f (3)+f (4)=0-a+0=-a.6.函数f (x )=A sin(ωx+φ)(其中A >0,|φ|<π2)的部分图象如图所示,将函数f (x )的图象( )可得g (x )=sin (2x +π4)的图象.A.向右平移π12个单位长度 B.向左平移π24个单位长度 C.向左平移π12个单位长度 D.向右平移π24个单位长度答案:D解析:由函数f (x )=A sin(ωx+φ)的部分图象知,A=1,T4=7π12−π3=π4, ∴T=2πω=π,解得ω=2,由五点法画图知,2×π3+φ=π,解得φ=π3,∴f (x )=sin (2x +π3), 又y=sin [2(x -π24)+π3]=sin (2x +π4),∴将函数f (x )的图象向右平移π24个单位长度,可得g (x )=sin (2x +π4)的图象,故选D . 7.函数y=ln (1-x1+x )+sin x 的图象大致为( )答案:A解析:易知f (x )=ln (1-x1+x )+sin x 的定义域为(-1,1),且f (-x )=ln (1+x1-x )+sin(-x )=-ln (1-x1+x )-sin x=-f (x ),即函数f (x )是奇函数,图象关于原点对称,排除选项C,D;又f (12)=ln 13+sin 12=sin 12-ln3<0,故排除选项B,所以选A .8.(2019河北邯郸大名一中高三模拟)已知菱形ABCD 的边长为2,∠DAB=60°,点E ,F 分别为BC ,CD 的中点,则AE ⃗⃗⃗⃗⃗ ·BF ⃗⃗⃗⃗⃗ =( ) A.3 B.1 C.3√32D.32答案:D解析:因为点E 为BC 的中点,所以AE ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +BE ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +12BC ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +12AD ⃗⃗⃗⃗⃗ .因为点F 为CD 的中点,所以BF ⃗⃗⃗⃗⃗ =BC ⃗⃗⃗⃗⃗ +CF ⃗⃗⃗⃗⃗ =AD ⃗⃗⃗⃗⃗ +12CD ⃗⃗⃗⃗⃗ =AD ⃗⃗⃗⃗⃗ +12BA ⃗⃗⃗⃗⃗ =AD ⃗⃗⃗⃗⃗ −12AB ⃗⃗⃗⃗⃗ . 所以AE ⃗⃗⃗⃗⃗ ·BF ⃗⃗⃗⃗⃗ =(AB ⃗⃗⃗⃗⃗ +12AD ⃗⃗⃗⃗⃗ )·(AD ⃗⃗⃗⃗⃗ -12AB ⃗⃗⃗⃗⃗ )=AB ⃗⃗⃗⃗⃗ ·AD ⃗⃗⃗⃗⃗ −12AB ⃗⃗⃗⃗⃗ 2+12AD ⃗⃗⃗⃗⃗ 2−14AD ⃗⃗⃗⃗⃗ ·AB ⃗⃗⃗⃗⃗ =34AB ⃗⃗⃗⃗⃗ ·AD ⃗⃗⃗⃗⃗ −12|AB ⃗⃗⃗⃗⃗ |2+12|AD ⃗⃗⃗⃗⃗ |2. 因为菱形ABCD 的边长为2,所以|AB ⃗⃗⃗⃗⃗ |=|AD ⃗⃗⃗⃗⃗ |=2. 又因为∠DAB=60°,所以AE ⃗⃗⃗⃗⃗ ·BF ⃗⃗⃗⃗⃗ =34AB ⃗⃗⃗⃗⃗ ·AD ⃗⃗⃗⃗⃗ −12|AB ⃗⃗⃗⃗⃗ |2+12|AD ⃗⃗⃗⃗⃗ |2=34AB ⃗⃗⃗⃗⃗ ·AD ⃗⃗⃗⃗⃗ =34|AB ⃗⃗⃗⃗⃗ |·|AD ⃗⃗⃗⃗⃗ |cos ∠DAB=34×2×2×12=32.故选D .9.若不等式tt +9≤a ≤t+2t 在t ∈(0,2]上恒成立,则a 的取值范围是( ) A.[16,1] B.[213,1]C.[16,413]D.[16,2√2]答案:B解析:∵函数y=t+2t 2=1t +2t 2在t ∈(0,2]上为减函数, ∴当t=2时,y=t+2t 2的最小值为1. 令f (t )=tt 2+9,则f'(t )=9-t 2(t 2+9)2.当t ∈(0,2]时,f'(t )>0,故f (t )在区间(0,2]上为增函数,故当t=2时,f (t )=tt +9的最大值为213. 故由题意知(tt +9)max≤a ≤(t+2t )min,即213≤a ≤1.10.已知函数y=sin(πx+φ)-2cos(πx+φ)(0<φ<π)的图象关于直线x=1对称,则sin 2φ=( ) A.-45 B.-35C.35D.45答案:A解析:y=sin(πx+φ)-2cos(πx+φ)=√5sin(πx+φ-α), 其中sin α=√5,cos α=√5.∵函数y 的图象关于直线x=1对称, ∴π+φ-α=π2+k π,k ∈Z , 即φ=α-π2+k π,k ∈Z .∴sin2φ=sin2(α-π2+kπ)=sin(2α-π+2k π) =sin(2α-π)=-sin2α=-2sin αcos α =-2×√5×√5=-45,故选A . 11.在△ABC 中,内角A ,B ,C 的对边分别是a ,b ,c.若cos B=14,sinCsinA =2,且S △ABC =√154,则b=( ) A.4 B.3 C.2D.1答案:C解析:由cos B=14,0<B<π,得sin B=√154. 又sinCsinA =2,得ca =2,即c=2a. 由S △ABC =√154=12ac sin B=a 2·√154,得a=1.所以c=2.由b 2=a 2+c 2-2ac cos B=1+4-2×1×2×14=4,得b=2.12.已知函数y=f (x )是定义在R 上的偶函数,且当x>0时,不等式f (x )+x ·f'(x )<0成立,若a=30.2f (30.2),b=(log π2)f (log π2),c=(log 214)f (log 214),则a ,b ,c 之间的大小关系为( )A.a>c>bB.c>a>bC.c>b>aD.b>a>c答案:C解析:构造函数g (x )=xf (x ),则g'(x )=f (x )+xf'(x ), 当x>0时,不等式f (x )+x ·f'(x )<0成立, ∴当x>0时,g'(x )<0,函数g (x )单调递减. ∵函数y=f (x )是定义在R 上的偶函数, ∴g (-x )=-xf (-x )=-xf (x )=-g (x ),∴g (x )在R 上是奇函数,∴g (x )在R 上是减函数.∵a=30.2f (30.2),b=(log π2)f (log π2),c=(log 214)f (log 214),log 214=-2,而-2<log π2<30.2, ∴c>b>a.故选C .二、填空题(本大题共4小题,每小题5分,共20分) 13.已知tan (x +π4)=-2,则sin 2x+2cos 2x= . 答案:45解析:∵tan (x +π4)=tanx+11-tanx=-2,∴tan x=3,则sin2x+2cos 2x=2tanx+2tan x+1=45. 14.设函数f (x )={x +1,x ≤0,2x ,x >0,则满足f (x )+f (x -12)>1的x 的取值范围是 .答案:(-14,+∞)解析:由题意得当x>12时,2x+2x -12>1恒成立,即x>12;当0<x ≤12时,2x +x-12+1>1恒成立,即0<x ≤12;当x ≤0时,x+1+x-12+1>1,解得x>-14,即-14<x ≤0. 综上,x 的取值范围是(-14,+∞).15.我国南宋著名数学家秦九韶在他的著作《数书九章》卷五“田域类”里有一个题目:“问有沙田一段,有三斜,其小斜一十三里,中斜一十四里,大斜一十五里.里法三百步.欲知为田几何.”这道题讲的是有一个三角形沙田,三边分别为13里,14里,15里,假设1里按500米计算,则该三角形沙田外接圆的半径为 米. 答案:4 062.5解析:由题意画出图形,如图所示,且AB=13里=6500米,BC=14里=7000米,AC=15里=7500米, 在△ABC 中,由余弦定理得cos B=AB 2+BC 2-AC 22AB ·BC=132+142-1522×13×14=513,B 为锐角,sin B=√1-cos 2B =1213, 设△ABC 外接圆半径为R , 则由正弦定理有bsinB =2R ,R=b2sinB =75002×1213=4062.5米.16.在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,若AB ⃗⃗⃗⃗⃗ ·AC ⃗⃗⃗⃗⃗ =BA ⃗⃗⃗⃗⃗ ·BC⃗⃗⃗⃗⃗ =1,则c= .答案:√2解析:由内角A ,B ,C 所对的边分别为a ,b ,c , 可知AB=c ,AC=b ,BC=a.由AB ⃗⃗⃗⃗⃗ ·AC ⃗⃗⃗⃗⃗ =BA ⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ ,得cb cos A=ca cos B. 故由正弦定理,得sin B cos A=cos B sin A ,即sin(B-A )=0.因为-π<B-A<π, 所以B=A ,从而b=a.由已知BA ⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ =1,得ac cos B=1. 故由余弦定理知ac ·a 2+c 2-b 22ac=1,即a 2+c 2-b 2=2,故c=√2.三、解答题(本大题共6小题,共70分)17.(10分)设向量a =(4cos α,sin α),b =(sin β,4cos β),c =(cos β,-4sin β). (1)若a 与b -2c 垂直,求tan(α+β)的值; (2)求|b +c |的最大值;(3)若tan αtan β=16,求证:a ∥b .答案:(1)解因为a 与b -2c 垂直,所以a ·(b -2c )=4cos αsin β-8cos αcos β+4sin αcos β+8sin αsin β=4sin(α+β)-8cos(α+β)=0,因此tan(α+β)=2. (2)解由b +c =(sin β+cos β,4cos β-4sin β), 得|b +c |=√(sinβ+cosβ)2+(4cosβ-4sinβ)2 =√≤4√2.又当β=k π-π4(k ∈Z )时,等号成立,所以|b +c |的最大值为4√2.(3)证明由tan αtan β=16,得16cos αcos β=sin αsin β,故a ∥b .18.(12分)某公司为了获得更大的收益,每年要投入一定的资金用于广告促销,经调查,每年投入广告费t 百万元,可增加销售额约为-t 2+7t 百万元.(1)若该公司将一年的广告费控制在4百万元之内,则应投入多少广告费,才能使该公司由此增加的收益最大?(2)现该公司准备共投入5百万元,分别用于广告促销和技术改造,经预测,每投入技术改造费x (1≤x ≤5)百万元,可增加的销售额约为12x 2+4ln x 百万元,请设计一个资金分配方案,使该公司由此增加的收益最大.(注:收益=销售额-投入,这里除了广告费和技术改造费,不考虑其他的投入)解:(1)设投入t 百万元的广告费后增加的收益为f (t )百万元, 则由f (t )=(-t 2+7t )-t=-t 2+6t=-(t-3)2+9(0≤t ≤4),∴当t=3时,f (t )取得最大值9,即投入3百万元的广告费时,该公司由此增加的收益最大. (2)用于技术改造的资金为x 百万元,则用于广告促销的资金为(5-x )百万元, 设由此增加的收益是g (x )百万元.则g (x )=12x 2+4ln x+[-(5-x )2+7(5-x )]-5=-12x 2+3x+4ln x+5. g'(x )=-x+3+4x =-x 2-3x -4x=-(x -4)(x+1)x,1≤x ≤5.则当1≤x<4时,g'(x )>0;当4<x ≤5时,g'(x )<0.∴当x=4时,g (x )取得最大值.即4百万元用于技术改造,1百万元用于广告促销,该公司由此增加的收益最大. 19.(12分)(2019广东蕉岭中学高三下学期第一次适应性考试)设函数f (x )=√3sin(ωx+φ)(ω>0,-π2<φ<π2)的图象的一个对称中心为(π12,0),且图象的一个最高点与相邻最低点的距离为√π24+12. (1)求ω,φ的值; (2)若f (α2+π12)=√34(0<α<π2),求cos (α+π4)的值.解:(1)由函数图象的一个最高点与相邻最低点的距离为√π24+12得,(πω)2+12=π24+12, 解得ω=2.故f (x )=√3sin(2x+φ).因为函数f (x )=√3sin(2x+φ)的图象的一个对称中心为(π12,0),所以2×π12+φ=k π,k ∈Z . 又因为-π2<φ<π2,所以φ=-π6.(2)由(1)知,f (x )=√3sin (2x -π6),所以f (α2+π12)=√3sin [2(α2+π12)-π6]=√3sin α=√34, 所以sin α=14.因为0<α<π2,所以cos α=√154. 所以cos (α+π4)=√22(cos α-sin α)=√22×√15-14=√30-√28. 20.(12分)已知函数f (x )=sin 2x-cos 2x+2√3sin x cos x (x ∈R ). (1)求f (x )的最小正周期;(2)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若f (A )=2,c=5,cos B=17,求△ABC 的中线AD 的长.解:(1)f (x )=-cos2x+√3sin2x=2sin (2x -π6), ∴T=2π2=π,∴函数f (x )的最小正周期为π. (2)由(1)知f (x )=2sin (2x -π6),∵在△ABC 中f (A )=2,∴sin (2A -π6)=1, ∴2A-π6=π2,∴A=π3, 又cos B=17,∴sin B=4√37, ∴sin C=sin(A+B )=√32×17+12×4√37=5√314, 在△ABC 中,由正弦定理csinC =asinA ,得5√314=√32,∴a=7,∴BD=72.在△ABD 中,由余弦定理得AD 2=AB 2+BD 2-2AB ·BD ·cos B=52+(72)2-2×5×72×17=1294,∴AD=√1292. 21.(12分)已知函数f (x )=x 3+ax 2-x+c ,且a=f'(23).(1)求a 的值;(2)求函数f (x )的单调区间; (3)设函数g (x )=(f (x )-x 3)·e x ,若当x ∈[-3,2]时,函数g (x )单调递增,求实数c 的取值范围. 解:(1)由f (x )=x 3+ax 2-x+c ,得f'(x )=3x 2+2ax-1. 当x=23时,得a=f'(23)=3×(23)2+2a×23-1, 解得a=-1.(2)由(1)可知,f (x )=x 3-x 2-x+c , 则f'(x )=3x 2-2x-1=3(x +13)(x-1), 由f'(x )>0,得x<-13或x>1; 由f'(x )<0,得-13<x<1.所以f (x )的单调递增区间是(-∞,-13)和(1,+∞),f (x )的单调递减区间是(-13,1). (3)函数g (x )=(f (x )-x 3)·e x =(-x 2-x+c )·e x ,有g'(x )=(-2x-1)e x +(-x 2-x+c )e x =(-x 2-3x+c-1)e x , 因为函数g (x )在x ∈[-3,2]上单调递增,所以h (x )=-x 2-3x+c-1≥0在x ∈[-3,2]上恒成立.故只要h (x )在区间[-3,2]上的最小值h (2)≥0即可,解得c ≥11,所以c 的取值范围是[11,+∞).22.(12分)已知函数f (x )=12x 2-a ln x (a ∈R ).(1)若函数f (x )在x=2处的切线方程为y=x+b ,求a ,b 的值; (2)若函数f (x )在区间(1,+∞)内为增函数,求a 的取值范围; (3)讨论方程f (x )=0的解的个数,并说明理由. 解:(1)因为f'(x )=x-ax (x>0),又f (x )在x=2处的切线方程为y=x+b , 所以{2-a2=1,2-aln2=2+b ,解得a=2,b=-2ln2.(2)若函数f (x )在区间(1,+∞)内为增函数, 则f'(x )=x-ax ≥0在区间(1,+∞)内恒成立,即a ≤x 2在区间(1,+∞)内恒成立,所以a ≤1.(3)当a=0时,f (x )在定义域(0,+∞)内恒大于0,此时方程无解. 当a<0时,f'(x )=x-ax >0在区间(0,+∞)内恒成立,所以f (x )在区间(0,+∞)内为增函数. 因为f (1)=12>0,f (e 1a)=12e 2a -1<0, 所以方程有唯一解. 当a>0时,f'(x )=x-ax =x 2-a x=(x+√a )(x -√a )x.因为当x ∈(0,√a )时,f'(x )<0, 则f (x )在区间(0,√a )内为减函数; 当x ∈(√a ,+∞)时,f'(x )>0,则f (x )在区间(√a ,+∞)内为增函数.所以当x=√a 时,f (x )有极小值,即最小值为f (√a )=12a-a ln √a =12a (1-ln a ). 当a ∈(0,e)时,f (√a )=12a (1-ln a )>0,方程无解; 当a=e 时,f (√a )=12a (1-ln a )=0,此方程有唯一解x=√e . 当a ∈(e,+∞)时,f (√a )=12a (1-ln a )<0, 因为f (12)>0,且√a >1,所以方程f (x )=0在区间(0,√a )内有唯一解. 因为当x>1时,(x-ln x )'>0,所以x-ln x>1, 所以x>ln x.所以f (x )=12x 2-a ln x>12x 2-ax.因为2a>√a >1,所以f (2a )>12(2a )2-2a 2=0,所以方程f (x )=0在区间(√a ,+∞)内有唯一解. 所以方程f (x )=0在区间(e,+∞)内有两解. 综上,当a ∈[0,e)时,方程无解; 当a<0或a=e 时,方程有唯一解; 当a>e 时,方程有两解.快乐分享,知识无界!感谢您的下载!由Ruize收集整理!。
