MATLAB7 答案
MATLAB语言与控制系统仿真-参考答案-第7章
7.3控制系统根轨迹分析MATLAB 仿真实训7.3.1实训目的1. 掌握运用MATLAB 绘制180度、0度根轨迹图的编程方法;2. 学会通过根轨迹图获取相关信息的方法;3. 利用仿真结果对系统根轨迹进行分析;4.学会通过根轨迹图分析和解决一些实际问题。
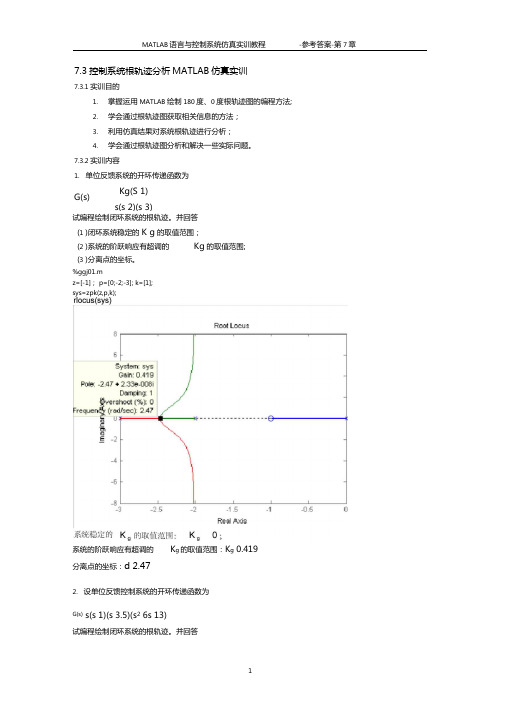
7.3.2实训内容1. 单位反馈系统的开环传递函数为试编程绘制闭环系统的根轨迹。
并回答 (1 )闭环系统稳定的 K g 的取值范围; (2 )系统的阶跃响应有超调的 Kg 的取值范围;(3 )分离点的坐标。
%ggj01.mz=[-1]; p=[0;-2;-3]; k=[1]; sys=zpk(z,p,k);系统的阶跃响应有超调的 K g 的取值范围:K g 0.419分离点的坐标:d 2.472. 设单位反馈控制系统的开环传递函数为G(s) s(s 1)(s 3.5)(s 2 6s 13)试编程绘制闭环系统的根轨迹。
并回答G(s)Kg(S 1) s(s 2)(s 3)(1 )闭环系统稳定的K的取值范围;(2) 根轨迹与虚轴的交点坐标; (3) 分离点的坐标。
ggj02.m%根轨迹仿真实训第 2题 n=1;d=co nv([1,0],co nv([1,1],co nv([1,3.5],[1,6,13]))); rlocus( n,d)10 -s由图上数据可知:闭环系统稳定的 K 的取值范围:0 K 70.9 ; 根轨迹与虚轴的交点坐标:j1.02 ;分离点的坐标:d 0.403。
3. 设单位反馈控制系统的开环传递函数为KG(s)- s(s 4)( s 4s 20)试编程绘制闭环系统的根轨迹。
并回答 (1 )闭环系统稳定的K 的取值范围;(2) 根轨迹与虚轴的交点坐标; (3) 各个分离点的坐标。
%根轨迹仿真实训第 3题Root Locus640 ■2-10-40 2斗6Real AxisDaimninn- -Fl IT10125System 割g j : i go^ainc £4祁怎比〕:3.15Pole : -2 + 7.51e-D06i Damping: 1 Overshoot (%): 0 Frequency (racVsec): 2由图上数据可知:闭环系统稳定的 K 的取值范围:0 K 262 ; 根轨迹与虚轴的交点坐标:j3.18 ;分离点的坐标:d,2,d 2,32 j2.45。
MATLAB 实验七答案

实验七模型参数建立一、实验目的1、熟悉Matlab软件中数据拟合命令2、进一步熟悉用初等数学建模的一些方法3、掌握数学模型中参数的确定方法二、实验基本知识若数据(x1,y1),…(xn,yn)要拟合是m次多项式函数,y = a1xm + a2xm -1 + ... + amx + am +1则可用命令格式:a=polyfit(x,y,m)其中X,Y是数据向量,m是多项式的次数。
返回的a是系数构成的向量:a = [a1 a2 ...am am+1 ]二、实验内容1 有一只对温度敏感的电阻,已经测得了一组温度t 和电阻R的数据,试建立R 和t关系。
解先看一下温度与电阻大概存在什么关系:输入如下命令t=[20.5 32.7 51 73 95.7];R=[765 826 873 942 1032];plot(t,R,'r*')xlabel('t'),ylabel('R')aa=polyfit(t,R,1);说明R和t的关系是线性关系,则可用polyfit命令来拟合它的系数aa=polyfit(t,R,1);a=aa(1)b=aa(2)运行得:a=3.3987b=702.0968这样得到R与t的关系为:R=3.3987t+ 702.09682 一册书的成本费y 与印刷的册数x 有关,统计数据如下,试用 y=a+b/x 去拟合以上数据。
Matlab 程序: x=1:10; x1=1./x;y=[10.15 5.52 4.08 2.85 2.11 1.62 1.41 1.30 1.21 1.15]; A=polyfit(x1,y,1); x=1:10;y = 0.1382 + 10.2487./ x plot(x,y,'-r*')y = 0.1382 + 10.2487/x已知应力--应变关系可以用一条指数曲线来描述,即假设解 选取指数函数作拟合时,在拟合前需作变量代换,化为k 1,k 2的线性函数ε-ε=σ2k 1e kε-ε⨯=σ=⨯===-=-=+ε==-=εσ=ε-=εσ5209.4943231112010112021e 100275.45209.494k 100275.43009.8k ln a 5209.494k a a a z k ln a k a ln z k k ln ,,,,,k lna=[1.55 2.47 2.93 3.03 2.89]b=[500 1000 1500 2000 2375]*10^(-6) d=[3.103 2.465 1.953 1.517 1.219]*10^(3) c=log(d)aa=polyfit(b,c,1)。
matlab第七章课后题答案

matlab第七章课后题答案第一题分解因式syms x y z>> A=x^9-1;>> factor(A)ans =(x-1)*(x^2+x+1)*(x^6+x^3+1) 解(1)>> B=x^4+x^3+2*x^2+x+1;>> factor(B)ans =(x^2+1)*(x^2+x+1) 解(2)> C=125*x^6+75*x^4+15*x^2+1;>> factor(C)ans =(5*x^2+1)^3 解(3)> D=x^2+y^2+z^2+z*(x*y+y*z+z*x);>> factor(D)ans =x^2+y^2+z^2+z*x*y+y*z^2+z^2*x 解(4)第二题化简表达式syms x y a b>> s=y/x+x/y;>> simplify(s)ans =(x^2+y^2)/x/y 解(1)s=sqrt(a+sqrt(a^2-b))/2+sqrt(a-sqrt(a^2-b))/2;ans =1/2*(a+(a^2-b)^(1/2))^(1/2)+1/2*(a-(a^2-b)^(1/2))^(1/2) 解(2)s=2*cos(x)^2*x-sin(x)^2*x;>> simplify(s)ans =x*(3*cos(x)^2-1) 解(3)s=sqrt(3+2*(sqrt2)) 第三题求函数的极限> syms x>> f=(x^2-6*x+8)/(x^2-5*x+4);> limit(f,x,4)ans =2/3 解(1)>> f=abs(x)/x;>> limit(f,x,0)ans =NaN 解(2)f=(sqrt(1+x^2)-1)/x;>> limit(f,x,0)ans =0 解(3)f=(x+1/x)^x;>> limit(f,x,inf,'left')ans =Inf 解(4)第四题求函数的符号导数f=3*(x^2)-5*x+1;>> diff(f)ans =6*x-5 解(1)y’>> diff(f,x,2)ans =6 解(1)> y=sqrt(x+sqrt(x+sqrt(x)));>> diff(y)ans =1/2/(x+(x+x^(1/2))^(1/2))^(1/2)*(1+1/2/(x+x^(1/2))^(1/2)* (1+1/2/x^(1/2))) 解(2)diff(y,x,2)ans =-1/4/(x+(x+x^(1/2))^(1/2))^(3/2)*(1+1/2/(x+x^(1/2))^(1/2)*(1+1 /2/x^(1/2)))^2+1/2/(x+(x+x^(1/2) )^(1/2))^(1/2)*(-1/4/(x+x^(1/2))^(3/2)*(1+1/2/x^(1/2))^2-1/8/(x+x^(1/2))^(1/2)/x^(3/2)) 解(2)y=sin(x)-x^2/2;> diff(y)ans =cos(x)-x 解(3)>> diff(y,x,2)ans =-sin(x)-1 解(3)syms x y z>> z=x+y-sqrt(x^2+y^2);>> diff(z,x,y)ans =1-1/(x^2+y^2)^(1/2)*y 解(4)>> diff(y,x)ans =0 解(4)第五题求不定积分x=sym('x');>> f=1/(x+a);>> int(f)ans =log(x+a) 解(1)>> f=(1-3*x)^3;>> int(f)ans =-1/12*(1-3*x)^4 解(2)>> f=(1/(sin(x)^2*cos(x)^2));>> int(f)ans =1/sin(x)/cos(x)-2/sin(x)*cos(x) 解(3)>> f=x^2/(sqrt(a^2+x^2));>> int(f)ans =1/2*x*(a^2+x^2)^(1/2)-1/2*a^2*log(x+(a^2+x^2)^(1/2)) 解(4)第六题求定积分> x=sym('x');> int((x*(2-sin(x)^2))^12,0,1)ans =-13072167041243000966100527033032931/1439431206610157 332070400000000000*sin(1)^19 *cos(1)-6398861758307370972493847449067915934618360845299932 3027852007/820274272 498737105178830959457441284892917760000000000*cos(1)*s in(1)+417844027386435896683 78350956709518241555640967463723429593/1230411408748 105657768246439186161927339376640000000000*sin(1)^3*cos(1)-6287598784304532394386769772554886862775718358540 017487607/179434997109098741757869272381315281070325 7600000000000*sin(1)^7*cos(1)-117903417317/3522410053632*sin(1)^23*cos(1)+93129118771 020938708526771772323524014639/1529945519744217245425650892800000000000*sin(1)^1 7*cos(1)-2677966496932891906 2789407028617562008014032541099/65676988573810175970 43504106365255680000000000* sin(1)^10-9093666156737053001410403050886921533204877134531540 1/53375584364747317 6140678428961747763200000000*cos(1)^2+2541573211/1467 67085568*sin(1)^24+940325057 70279736611460220749/16522396770089041920000000000*si n(1)^20+2704734082846637530 0822998906838403821858600396601/46703636319153902912 30936253415292928000000000*sin(1)^8+5542192477209543230894137867604219553503/255 75581466676109936796106752000000000*sin(1)^16+6290548805350754451916704658025155 325352197570086424587493/20 1864371747736084477602931428979691204116480000000000 0*sin(1)^9*cos(1)-74888453896 484988301898479573506809/175613581237857810540134400 0000000*sin(1)^18-66275838868 9551809679364987359346538465101954279/84285468669723 0591620583026983541145600000000*sin(1)^14+47417160064207694184289443781709965432 75038000761225969993/153801 4260935132072210308048982702409174220800000000000*sin(1)^5*cos(1)-273698005143037 11474211657412466731397670944577/1002665095819570213 96215456910540800000000000*sin(1)^15*cos(1)+18044178399358284974551495/22109663333 532016**********sin(1)^21*cos(1)+159018588498544047612814017616772807534595903672 788230889/18504234076875807 7437802687143231383603773440000000000*sin(1)^13*cos(1)-42990929319556261053136947 04999192498272936575705473777243/2220508089225096929 253632245718776603245281280000000000*sin(1)^11*cos(1)+7264479585721640057236136324 9893595045872001672201/160 1267530942419528422035286885243289600000000*sin(1)^4-179168559345113148705406926 00563709435304263998599/3002376620517036615791316162 909831168000000000*sin(1)^6-3 228431702614231399553/6979060395685611307008*sin(1)^22 +1809464903223467961506769 2014871302547716716561173/86693624917429432280974254 20402137497600000000*sin(1)^12+90821203400667453448262867129549773153665801090519 0650989336891/1066356554248 3582367324802472946736703607930880000000000 解(1)int(x/(x^2+x+1),-1,1)ans =1/2*log(3)-1/6*3^(1/2)*pi 解(2)> int((x*sin(x))^2,0,pi)ans =1/6*pi^3-1/4*pi 解(3)第七题求级数之和n=sym('n');>> s1=symsum((-1)*(2*n+1)/2^n,n,0,inf)s1 =-6 解(1)>> s2=symsum(x^(2*n-1)/2^n-1,n,1,inf)s2 =sum(x^(2*n-1)/(2^n)-1,n = 1 .. Inf) 解(2)s3=symsum(1/(2*n+1)^2,n,0,inf)s3 =1/8*pi^2 解(3)s4=symsum(1/n*(n+1)*(n+1),n,1,inf)s4 =Inf 解(4)第八题求泰勒展开式>> x=sym('x');f1=x^4-5*x^3+x^2-3*x+4;f2=(exp(x)+exp(-x))/2;f3=tan(x);f4=sin(x)^2;f5=sqrt(x^3+x^2+5*x+3);taylor(f1,4,4)ans =-140+21*x+37*(x-4)^2+11*(x-4)^3 解(1)taylor(f2,5,0)ans =1+1/2*x^2+1/24*x^4 解(2)taylor(f3,3,2)ans =tan(2)+(1+tan(2)^2)*(x-2)+tan(2)*(1+tan(2)^2)*(x-2)^2 解(3)taylor(f4,8,0)x^2-1/3*x^4+2/45*x^6 解(4)taylor(f5,5,0)ans =3^(1/2)+5/6*3^(1/2)*x-13/72*3^(1/2)*x^2+137/432*3^(1/2)*x^3-2909/10368*3^(1/2)* x^4 解(5)第九题求非线性方程的解x=solve(‘a*x^2+b*x+c=0’,’x’)x =1/2/a*(-b+(b^2-4*a*c)^(1/2))1/2/a*(-b-(b^2-4*a*c)^(1/2)) 解(1)x=solve(‘2*sin(3*x-pi/4)=1’,’x’)x =5/36*pi 解(2)x=solve(‘sin(x)-sqrt(3)*cos(x)=sqrt(2)’,’x’)x =-atan(2*(1/4*2^(1/2)+1/4*3^(1/2)*2^(1/2))*2^(1/2)/(3^(1/2)-1))+pi-atan(2*(1/4*2^(1/2)-1/4*3^(1/2)*2^(1/2))*2^(1/2)/(1+3^(1/2)))-pi 解(3)x=solve(‘x^2+10*(x-1)*sqrt(x)+14*x+1=0’,’x’)x =(2^(1/2)-1)^2(-4+17^(1/2))^2 解(4)第十题求方程组的解[x,y]=solve(‘ln(x/y)=9’,’exp(x+y)=3’,’x,y’)x =exp(9)*log(3)/(exp(9)+1)log(3)/(exp(9)+1) 解(1)[x,y,z]=solve(‘(4*x^2)/(4*x^2+1)=y’,’(4*y^2)/(4*y^2+1) =z’,’(4*z^2)/(4*z^2+ 1)=x’,’x,y,z’)x =y =0 解(2)z =第十一题求初值y=dsolve('x*(D2y)+(1-n)*(Dy)+y=0','y(0)=Dy(0)=0','x')第十二题,求特解[x,y]=dsolve(‘Dx=3*x+4*y’,’Dy=5*x-7*y’,’x(0)=0’,’y(0)=0’,’t’)x =y =解(1)。
中南大学matlab课后习题(7)

第一章思考练习1.与一般的Windows程序一样,启动MATLAB系统有3种常见方法:(1)使用Windows“开始”菜单。
(2)运行MATLAB系统启动程序matlab.exe。
(3) 利用快捷方式。
要退出MATLAB系统,也有3种常见方法:(2) 在MATLAB命令窗口输入Exit或Quit命令。
(3) 单击MATLAB主窗口的“关闭”按钮。
2.matlab用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,主要包括MATLAB和Simulink两大部分。
它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案3.可以在第一个物理行之后加上三个小黑点并按回车键,然后再下一个物理行输入其他部分。
4.help命令会显示当前帮助系统中的所有项目,即搜索路径中所有的目录名称,只显示那些与关键字中完全匹配的结果。
Lookfor命令对搜索范围内的M文件经行搜索,条件比较宽泛。
第二章(1) w=sqrt(2)*(1+0.34245*10^(-6)(2)a=3.5b=5c=9.8x=(2*pi*a+(b+c)/(pi+a*b*c)-exp(2))/(tan(b+c)+a)(3)a=3.32b=7.9y=2*pi*a^2*((1-pi/4)*b-(0.8333-pi/4)*a)(4) t=[2,1-3i;5,-0.65]Z=0.5*exp(2*t)*log(t+sqrt(1+t.*t))2. A=[-1,5,-4;0,7,8;3,61,7];B=[8,3,-1;2,5,3;-3,2,0];(1)A+6*B A^2-B+eye(2)A*B A.*B B.*A(3)A/B B\A(4)[A,B] [A([1,3],:);B^2]3.(1)A=[23,10,-0.778,0;41,-45,65,5;32,5,0,32;6,-9.54,54,3.14]; K=find(A>10&A<25);A(K)(2)A=[23,10,-0.778,0;41,-45,65,5;32,5,0,32;6,-9.54,54,3.14]; B=A(1:3,:) C=A(:,1:2) D=A(2:4,3:4) E=B*C(3)E<D E&D E|D ~E|~D5. A=[-29,6,18;20,5,12;-8,8,5];[V,D]=eig(A)A*V=V*D第三章1.f=input('输入一个数:','s');f(end :-1:1)2.(1)if语句score=input('请输入成绩:');if score>=90&&score<=100disp('A');elseif score>=80&&score<=89disp('B');elseif score>=70&&score<=79disp('C');elseif score>=60&&score<=69;disp('D');elseif score<60&&score>=0;disp('E');elsedisp('出错');End(2)用switch语句score=input('请输入成绩:');switch fix(score/10)case {9,10}disp('A');case {8}disp('B');case {7}disp('C');case {6}disp('D');case {0,1,2,3,4,5}disp('E');otherwisedisp('出错');End3.b=max(a)c=min(a)b=0c=0for i=1:20if a(i)>bb=a(i);endif a(i)<cc=a(i);End4.a=[-3:0.1:3];b=((exp(0.3.*a)-exp(-0.3.*a))./2)c=sin(a+0.3)for i=1:61y=(exp(0.3*a(i))-exp(-0.3*a(i)))/2*sin(a(i)+0.3)+log((0.3+a(i))/2) End5.(1)A=0;n=100for i=1:nA=1/n/n+A;End(2)A=1;n=10000;for i=1:nA=(2*n*n*2)/((2*n-1)*(2*n+1))*A;end6. A=rand(5,6)n=input('ÇëÊäÈëÒ»¸ön');if n>5n=5A(n,n)elseA(n)7.f1.m 代码:function m=f1(n)m=n+10*log(n^2+5);f2.m 代码:function m=f2(n)m=0;for i=1:nm=m+i*(i+1);end在命令文件p3_11.m 中调用f1.m 和f2.mp3_11.m 代码如下:y1=f1(40)/(f1(30)+f1(20));y2=f2(40)/(f2(30)+f2(20));y1y28.∑=1001k k 函数文件factor1.m 代码如下:function f=factor1(k)if k==1f=1;elsef=factor1(k-1)+k;end∑=5012^k k 函数文件factor2.m 代码:function f=factor2(k)if k==1f=1;elsef=factor2(k-1)+^2;end∑=101/1k k 函数文件factor3.m 代码:function f=factor3(k)if k==1f=1;elsef=factor3(k-1)+1/k;end思考练习2.N=[1,2,3,4,5]A=N.*2B=N./4C=1./ND=1./(N./2)./(N./2)/43.B=0for i=1:20A(i)=fix((99-10+1)*rand(1)+10);B=A(i)+B;endB=B/20for i=1:20if A(i)<B&rem(A(i),2)==0A(i)end第四章.1.(1).x=-12:0.001:12;y=x-x.^3/6;plot(x,y);xlabel('x 轴');ylabel('y 轴');title('Y=X-X^3/3!');(2)t=0:0.01:2*pi;x=8.*cos(t);y=4*sqrt(2).*sin(t);plot(x,y)2.t=-pi:pi/10:pi;y=1./(1+exp(-t));subplot(2,2,1);bar(t,y,'b');title('bar(t,y,''b'')');axis([-5,5,-3,3]); subplot(2,2,2);stairs(t,y,'k');title('stairs (t,y,''k'')');axis([-5,5,-3,3]); subplot(2,2,3);stem(t,y,'m');title('stem (t,y,''m'')');axis([-5,5,-3,3]); subplot(2,2,4);loglog(t,y,'g');title('loglog(t,y,''g'')');axis([-5,5,-3,3]);3.(1) t=0:pi/100:2*pi;y=5*cos(t)+4;polar(t,y,'-*')(2)t=-pi/3:pi/100:pi/3;r=5*sin(t).^2./cos(t);polar(t,r,'-*')4.(1)t=0:pi/100:2*pi;x=exp(-t/20).*cos(t);y=exp(-t/20).*sin(t);z=t;plot3(x,y,z)(2) [x,y]=meshgrid(-5:5);z=ones(11);surf(x,y,z);shading interp;5.[x,y,z]=sphere(50);m=moviein(100);for i=1:100surf(i*x,i*y,i*z);shading interpcolormap(hot);axis equalaxis([-100,100,-100,100,-100,100]) axis offm(:,i)=getframe;End思考练习2.(1)x=1:0.1:10a=exp((x.^2)/2)y=a.*1/2/piplot(x,y)(2)t=-pi:0.1:2*piX=t.*sin(t)Y=t.*cos(t)plot(X,Y)3.t=0:0.00005:pi;x=sin(3*t).*cos(t);y1=2*x-0.5;y2=sin(3*t).*sin(t);plot(x,y2,x,y1);hold onk=find(abs(y2-y1)<1e-4);x1=x(k);y3=2*x1-0.5;plot(x1,y3,'rp')4.x=-pi*6:0.1:pi*6y=sin(1./x)plot(x,y)fplot('sin(1./x)',[-pi*6,pi*6],1e-4)5.(1)x=1:0.1:10y=12./xpolar(x,y)(2)x=-pi/6:0.1:pi/6y=3*sin(x).*cos(x)./(sin(x).^3+cos(x).^3) polar(x,y)6.(1)[u,v]=meshgrid(-pi:pi/100:pi);x=3*u.*sin(v);y=2*u.*cos(v);z=4*u.*u;mesh(x,y,z);(2)[x,y]=meshgrid(-3:6/100:3);z=-5./(1+x.*x+y.*y);mesh(x,y,z)第五章1.A=randn(10,5)(1) X=mean(A)Y=std(A,0,1)(2) max(max(A))min(min(A))(3) B=sum(A,2)sum(B)(4) sort(A);sort(A,2,'descend')2.(1)t=0:15:90;x1=[0,0.2588,0.5000,0.7071,0.8660,0.9659,1.0000];a1=0:1:90;y1=interp1(t,x1,a1,'spline')x2=[0,0.2679,0.5774,1.0000,1.7320,3.7320,NaN]; a2=0:1:75;y2= interp1(t,x2,a2,'spline')p1=polyfit(t,x1,5);Z1=polyval(p1,a1)p2=polyfit(t,x2,5);z2=polyval(p2,a2)(2)X=[1 4 9 16 25 36 49 64 81 100];Y=1:10;X1=1:100;Y1=interp1(X,Y,X1,'cubic')3.4.P=[2,-3,5,13];Q=[1,5,8];p=polyder(P)p1=polyder(P,Q)[p,q]= polyder(P,Q)5.P1=[1,2,4,0,5];P2=[1,0];P3=[1,2,3];1) P4=conv(P2,P3)P4=[0,1,2,3,0];P=P1+P42) x=roots(P)3) A=[-1,1.2,-1.4;0.75,2,3.5;0,5,2.5];Y=polyval(P,A)4)Z=polyvalm(P,A)第六章1.(1)>> A=[1/2,1/3,1/4;1/3,1/4,1/5;1/4,1/5,1/6];B=[0.95,0.67,0.52]';x=A\B (2)>> A=[1/2,1/3,1/4;1/3,1/4,1/5;1/4,1/5,1/6];B=[0.95,0.67,0.53]';x=A\B (3)>> cond(A)2.(1)建立函数文件funx.m,命令如下;Function fx=funx(x)fx=x^41+x^3+1;调用fzero函数求根,命令如下;>> z=fzero(@funx,-1)(2) 建立函数文件sin.m,命令如下;Function fx=sin(x)fx=x-(sin(x))/x;调用fzero函数求根,命令如下;>> z=fzero(@sin,0.5)(3) 建立函数文件myfun.m,命令如下;function q=myfun(p)x=p(1);y=p(2);z=p(3);q(1)=sin(x)+y^2+log(z)-7;q(2)=3*x+2^y-z^3+1;q(3)=x+y+z-5;调用fsolve函数求根,命令如下;>> options=optimset('Display','off');x=fsolve(@myfun,[1,1,1]',options)3.(1) 建立函数文件funt.m,命令如下;function yp=funt(t,y)yp=-y*(1.2+sin(10*t));求微分方程,程序如下:>> t0=0;tf=5;y0=1;[t,y]=ode23(@funt,[t0,tf],y0)(2) 建立函数文件funr.m,命令如下;function yp=funr(t,y)yp=cos(t)-(y)/(1+t^2);求微分方程,程序如下:>> t0=0;tf=5;y0=1;[t,y]=ode23(@funr,[t0,tf],y0)4.建立函数文件mymax.m命令如下:function fx=mymax(x)fx=-1*(1+x^2)/(1+x^4);求最大值,程序如下:>> [x,y]=fminbnd(@mymax,0,2)5.编写目标函数M文件fop.m,命令如下:function f=fop(x)f=-1*(x(1)^(1/2)+x(2)^(1/2)+x(3)^(1/2)+x(4)^(1/2)); 设定约束条件,并调用fmincon函数求解此约束最优化问题,程序如下:>>x0=[200,200,200,200];A=[1,0,0,0;1.21,1,0,0;1.331,1.21,1,0;1.4641,1.331,1.21,1];b=[400,440,484,532.4];Ib=[0,0,0,0];options=optimset('Display','off');[x,y]=fmincon(@fop,x0,A,b,[],[],Ib,[],[],options)思考练习1,(1)矩阵求逆:>> A=[2,3,5;3,7,4;1,-7,1];b=[10,3,5]';x=inv(A)*b矩阵除法:>> A=[2,3,5;3,7,4;1,-7,1];b=[10,3,5]';x=A\b矩阵分解:>> A=[2,3,5;3,7,4;1,-7,1];b=[10,3,5]';[L,U]=lu(A);x=U\(L\b)(2)矩阵求逆:>> A=[6,5,-2,5;9,-1,4,-1;3,4,2,-2;3,-9,0,2];b=[-4,13,1,11]';x=inv(A)*b矩阵除法:>> A=[6,5,-2,5;9,-1,4,-1;3,4,2,-2;3,-9,0,2];b=[-4,13,1,11]';x=A\b矩阵分解:>> A=[6,5,-2,5;9,-1,4,-1;3,4,2,-2;3,-9,0,2];b=[-4,13,1,11]'; [L,U]=lu(A);x=U\(L\b)2.(1)建立函数文件fun1.m,命令如下:function fx=fun1(x)fx=3*x+sin(x)-exp(x);调用fzero函数求根,命令如下;>> y=fzero(@fun1,1.5)(2) 建立函数文件fun2.m,命令如下:function fx=fun2(x)fx=1-(1/x)+5;调用fzero函数求根,命令如下;>> y=fzero(@fun2,1)(3) 建立函数文件myfun3.m,命令如下;function q=fun3(p)x=p(1);y=p(2);q(1)=x^2+y^2-9;q(2)=x+y-1;调用fsolve函数求根,命令如下;>> options=optimset('Display','off');x=fsolve(@fun3,[1,1]',options)3.(1)建立函数文件fun5.m,命令如下:function ydot=fun5(t,y)ydot(1)=(2-3*y(2)-2*t*y(1))/(1+t^2);ydot(2)=y(1);ydot=ydot';求解微分方程,命令如下:>> t0=0;tf=5;x0=[0,1];[t,y]=ode45(@fun5,[t0,tf],x0);[t,y](2) (1)建立函数文件fun5.m,命令如下:function ydot=fun6(t,y)ydot(1)=cos(t)+(5*y(1)*cos(2*t))/(t+1)^2-y(2)-y(3)/(3+sin(t)); ydot(2)=y(1);ydot(3)=y(2);ydot=ydot';求解微分方程,命令如下:>> t0=0;tf=5;x0=[0,1];[t,y]=ode45(@fun5,[t0,tf],x0);[t,y]4.建立函数文件max.m命令如下:function fx=max(x)fx=-1*(sin(x)+cos(x^2));求最大值,程序如下:>> [x,y]=fminbnd(@mymax,0,pi)5.编写目标函数M文件fop.m,命令如下:function f=topm(x)f=-1*x*(3-2*x)^2;设定约束条件,并调用fmincon函数求解此约束最优化问题,程序如下:>>x0=[0];A=[1];b=[1.5];Ib=[0];options=optimset('Display','off');[x,y]=fmincon(@top,x0,A,b, [],[],Ib,[],[],options)第七章1.function f=f1(x)f=sin(x)./x;function f=f2(x)f=[1./((x-0.3).^2+0.01)-1./((x-0.9).^2+0.04)-6];[I,n]=quad(@f1,0,2)[S,n]=quad(@f2,0,1)2.f=inline('exp(-x.^2-y.^2)','x','y');I1=dblquad(f,0,1,0,1)f=inline('abs(cos(x+y))','x','y');I2=dblquad(f,0,pi,0,pi)3. X=0.3:0.2:1.5;Y=[0.3895,0.6598,0.9147,1.1611,1.3971,1.6212,1.8325];trapz(X,Y)4. x=0:pi/5:2*pi;for n=1:3nDX=diff(sin(x),n)end5. f=inline('sin(x)./(x+cos(2.*x))');g=inline('[cos(x).*(x+cos(2.*x))-sin(x).*(1-2.*sin(2.*x))]./(x+cos(2.*x)).^2');x=0:0.01:2*pi;p=polyfit(x,f(x),5);dp=polyder(p);dpx=polyval(dp,x);dx=diff(f([x,2*pi+0.01]))/0.01;gx=g(x);plot(x,dpx,x,dx,'-',x,gx,':')思考练习1.求解定积分的数值方法有梯形法、辛普森法、高斯法等,基本思想是将整个积分区间分成n个子区间,而每个小的子区间上的定积分的值可近似求得。
MATLAB 课后部分答案

P77 第2章1、>> x=2;>> y=power(x,3)+(x-0.98).^2./(x+1.35).^3-5*(x+1./x)>> x=4;>> y=power(x,3)+(x-0.98).^2./(x+1.35).^3-5*(x+1./x)7、>> mat=rand(4,5);>> m=1;>> for i=1:2for j=1:5if mat(i,j)>0.3b(m)=mat(i,j);m=m+1;endendend>> b8、>> V=inv(A)>> A=rand(5,5);10、>> A=[1 4 8 13;-3 6 -5 -9;2 -7 -12 -8];B=[5 4 3 -2;6 -2 3 -8;-1 3 -9 7]; >> C=A*B??? Error using ==> mtimesInner matrix dimensions must agree.>> C=A.*BC =5 16 24 -26-18 -12 -15 72-2 -21 108 -5611、>> x=linspace(0,2*pi,125);>> y=cos((x).*(0.5+3*sin(x)./(1+x.^2)));>> plot(x,y)13、>> x=-2:0.1:2;y=-2:0.1:2;>> [X,Y]=meshgrid(x,y);>> Z=X.^2.*exp(-X.^2-Y.^2);>> mesh(Z)建立一个M函数文件mycos.m,程序如下:function y=mycos(x)clear allx=input('请输入x的值')y=1./((x-2).^2+0.1)+1./((x-3).^3+0.01)在命令窗口输入:mycosP123 第3章1、>> x=[446 714 950 1422 1634];y=[7.04 4.28 3.40 2.54 2.13];>> xi=500:500:1500;>> yi=interp1(x,y,xi,'linear')4、>> p=[3 4 7 2 9 12];>> roots(p)8、>> a=[2 4 9;4 2 4;9 4 18];>> [V,D]=eig(a) %V的列向量是相应的特征向量,对角阵D的对角元素为a的特征值10、>> p1=[-1 4 0];p2=[-1 -4 0];>> A=polyder(p1);B=polyder(p2);>> A1=roots(A);B1=roots(B);>> y=4*A1-4*B1-A1.^2-B1.^213、>> syms x y>> Ex=int(int(x.*12.*y.^2,y,0,x),x,0,1)>> Ey=int(int(y.*12.*y.^2,x,y,1),y,0,1)>> Exy=Ex.*Ey14、>> A=rand(4,4);>> [L,U]=lu(A)>> [Q,R]=qr(A)P183 第4章1、>> n=-2*pi:0.01:2*pi;>> N=12;x=cos(n*pi./6);>> X=fft(x,N)>> nx=((n>=0)&(n<=11)); hx=((n>=0)&(n<=5)); >> xn=0.8*nx;hn=hx;>> y=conv(xn,hn)4、>> n=0:11;h=0:5;>> nx=((n>=0)&(n<=11)); hx=((n>=0)&(n<=5)); >> xn=0.8*nx;hn=hx;>> M=length(xn);N=length(hn);>> L=pow2(nextpow2(M+N-1));>> Xk=fft(xn,L);Hk=fft(hn,L);>> Yk=Xk.*Hk;>> yn=ifft(Yk,L)5、>> num=[2 3 0];den=[1 0.4 1];>> [z,p,k]=tf2zp(num,den)6、>> num=[4 15.6 6 2.4 -6.4];den=[3 2.4 6.3 -11.4 6]; >> [z,p,k]=tf2zp(num,den)>> zplane(z,p)7、>> num=[18 0 0 0];den=[18 3 -4 -1];>> [r,p,k]=residuez(num,den)9、建立一个M函数文件,程序如下:clear allN=10;[z,p,k]=buttap(N);[A,B,C,D]=zp2ss(z,p,k);wc1=100;wc2=200;[At,Bt,Ct,Dt]=lp2bp(A,B,C,D,wc1,wc2);[num1,den1]=ss2tf(At,Bt,Ct,Dt);[num2,den2]=impinvar(num1,den1);dimpulse(num2,den2)10、建立一个M函数文件,程序如下:clear allwp=100*2*pi;ws=200*2*pi;Rp=2;Rs=15;Fs=500;[N,Wc]=buttord(wp,ws,Rp,Rs,'s'); %选择滤波器的最小阶数[z,p,k]=buttap(N);[B,A]=zp2tf(z,p,k);[num,den]=bilinear(B,A,Fs); %模拟滤波器的传递函数转换为数字滤波器的传递函数freqz(num,den)11、建立一个M函数文件,程序如下:clear allN=48;w=[0.35,0.65];B=fir1(N,w,'bandpass'); %返回一个N阶的带通滤波器freqz(B) %绘制滤波器的频率响应曲线12、建立一个M函数文件,程序如下:clear allN=37;wc=0.3*pi;B=fir1(N,wc);freqz(B) %绘制滤波器的频率响应曲线13、建立一个M函数文件,程序如下:clear allN=55;F=[0:1/55:1];A=[ones(1,28),zeros(1,N-27)];B=fir2(N,F,A);freqz(B) %绘制滤波器的频率响应曲线15、建立一个M函数文件,程序如下:clear allwc=0.4*pi/(2*pi);N=12;[B,A]=butter(N,wc);%设计N阶截止频率为wc的Butterworth低通数字滤波器的传递函数模型m=dimpulse(B,A,101);stem(m,'.')P277 第6章2、建立一个M函数文件,程序如下:function [h,l]=huffmancode(P)if length(find(P<0))~=0,error('Not a prod.vector')endif abs(sum(P)-1)>10e-10error('Not a prod.vector')endn=length(P);for i=1:n-1for j=i:nif P(i)<=P(j)p=P(i);P(i)=P(j);P(j)=p;endendenddisp('概率分布'),PQ=P;m=zeros(n-1,n);for i=1:n-1[Q,l]=sort(Q);m(i,:)=[l(1:n-i+1),zeros(1,i-1)];Q=[Q(1)+Q(2),Q(3:n),1];endfor i=1:nc(i,:)=blanks(n*n);endc(n-1,n)='0';c(n-1,2*n)='1';for i=2:n-1c(n-i,1:n-1)=c(n-i+1,n*(find(m(n-i+1,:)==1))-(n-2):n*(find(m(n-i+1,:)==1)));c(n-1,n)='0';c(n-i,n+1:2*n-1)=c(n-i,1:n-1);c(n-i,2*n)='1';for j=1:i-1c(n-i,(j+1)*n+1:(j+2)*n)=c(n-i+1,n*(find(m(n-i+1,:)==j+1)-1)+1:n*find(m(n-i+1,:)==j+1));endendfor i=1:nh(i,1:n)=c(1,n*(find(m(1,:)==i)-1)+1:find(m(1,:)==i)*n);ll(i)=length(find(abs(h(i,:))~=32));endl=sum(P.*ll); %计算平均码长在命令窗口中输入:>> P=[0.20 0.15 0.13 0.12 0.1 0.09 0.08 0.07 0.06];>> [h,l]=huffmancode(P)3、建立一个M函数文件,程序如下:function[sqnr,a_quan,code]=u_pcm(a,n)% U_PCM 一个序列均匀的PCM编码.% n=量化级数的数目(偶数).% sqnr=输入信号量化噪声比(偶数)。
matlab课后习题答案1到6章

欢迎共阅习题二1.如何理解“矩阵是MATLAB 最基本的数据对象”? 答:因为向量可以看成是仅有一行或一列的矩阵,单个数据(标量)可以看成是仅含一个元素的矩阵,故向量和单个数据都可以作为矩阵的特例来处理。
(2) 删除矩阵A 的第7号元素。
答:A(7)=[](3) 将矩阵A 的每个元素值加30。
答:A=A+30;(4) 求矩阵A 的大小和维数。
答:size(A);ndims(A);(5) 将向量 t 的0元素用机器零来代替。
答:t(find(t==0))=eps; (6) 将含有12个元素的向量 x 转换成34⨯矩阵。
答:reshape(x,3,4); (7) 求一个字符串的ASCII码。
答:abs(‘123’); 或E 。
答:B=A(1:3,:); C=A(:,1:2); D=A(2:4,3:4);E=B*C;(2) 分别求E<D 、E&D 、E|D 、~E|~D 和find(A>=10&A<25)。
答:E<D=010001⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦,E&D=110111⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦,11⎡⎤⎢⎥答:student(1).id='0001';student(1).name='Tom'; student(1).major='computer';student(1).grade=[89,78,67,90,86,85]; 8.建立单元矩阵B 并回答有关问题。
B{1,1}=1;B{1,2}='Brenden';B{2,1}=reshape(1:9,3,3); B{2,2}={12,34,2;54,21,3;4 ,23,67};(1)size(B)和ndims(B)的值分别是多少?答:size(B) 的值为2, 2。
ndims(B) 的值为2。
(2)B(2)和B(4)的值分别是(2)建立5×6随机矩阵A,其元素为[100,200]范围内的随机整数。
MATLAB习题参考答案(胡良剑,孙晓君)

% 如图(4.31) % 如图(4.32)
图(4.31)error
4 2 2 2
图(4.32)
(4)曲面 z = x + 3 x + y − 2 x − 2 y − 2 x y + 6, x < 3,−3 < y < 13 解: >> xa=linspace(-3,3,100);ya=linspace(-3,13,100); >> [x,y]=meshgrid(xa,ya); >> z=x.^4+3*x.^2+y.^2-2*x-2*y-2*x.^2.*y+6; >> mesh(x,y,z) >> surf(x,y,z)
解:建立 M 文件 pxy 如下: xa=-2:0.05:2;ya=xa; nx=length(xa);ny=length(ya); [x,y]=meshgrid(xa,ya); z=zeros(nx,ny); [a1,b1]=find(x+y>1); %第 a1 列 b1 行对应的 x+y>1 (x 对应列;y 对应行) %第 a1 列对应的 x 值是 xa(a1);第 b1 行对应的 y 值是 ya(b1) z((a1-1)*ny+b1)=0.5457*exp(-0.75*ya(b1).^2-3.75*xa(a1).^2-1.5*xa(a1)); [a2,b2]=find(x+y<=1&x+y>-1); z((a2-1)*ny+b2)=0.7575*exp(-ya(b2).^2-6*xa(a2).^2); [a3,b3]=find(x+y<=-1); z((a3-1)*ny+b3)=0.5457*exp(-0.75*ya(b3).^2-3.75*xa(a3).^2+1.5*xa(a3)); surf(x,y,z); 命令窗口: >> pxy 运行结果如右图: 或者 M 文件如下: clear;close; xa=-2:0.1:2;ya=-2:0.1:2;[x,y]=meshgrid(xa,ya); z=zeros(size(x)); k1=find(x+y>1); z(k1)=0.5457*exp(-0.75*y(k1).^2-3.75*x(k1).^2-1.5*x(k1)); k2=find(x+y<=1&x+y>-1); z(k2)=0.7575*exp(-y(k2).^2-6*x(k2).^2); k3=find(x+y<-1); z(k3)=0.5457*exp(-0.75*y(k3).^2-3.75*x(k3).^2+1.5*x(k3)); mesh(x,y,z); 6、运行 demo 解:>>demo 7、查询 trapz 的功能、用法、目录、程序结构、相同目录下其它文件 解: >> help trapz ――功能用法 >> type trapz――程序结构,源码 >> which trapz――所在目录 >> help C:\MATLAB6p5\toolbox\matlab\datafun――该目录下其它文件
MATLAB习题参考答案

第1章 MATLAB简介1、MA TLAB的主要特点有:①语言简洁,编程效率高。
②人机界面友善,交互性好。
③绘图功能强大,便于数据可视化。
④学科众多、领域广泛的MATLAB工具箱。
⑤源程序的开放性。
MATLAB的典型应用领域有:①自动控制②汽车③电子④仪器仪表⑤生物医学⑥信号处理⑦通信等。
2、填空题⑴命令窗口、命令历史窗口、当前目录窗口⑵查阅、保存、编辑⑶清除图形窗、清除命令窗口中显示内容、清除MATLAB工作空间中保存的变量。
3、如果想查看某一变量具体内容或者对其修改操作,可以在工作空间中双击该变量名称,可以打开数组编辑器,在数组编辑器中可以查看变量的具体内容,也可以对其修改。
如果想删除MATLAB内存中的变量,可以在工作空间中选中该变量,然后利用工作空间窗口的菜单命令或工具条中的快捷图标进行删除。
4、1+2+3+4+5+... (+ 后面可以直接跟...,也可以在+和...中加一个空格。
)6+7+8+91+2+3+4+5 ... (5后面必须跟一个空格,不能直接跟...,否则报错,这在预置一个+6+7+8+9 大数组时很重要。
)第2章矩阵与数值数组1、填空题:⑴非数、无穷大、机器零阈值,浮点数相对精度,eps= 2.2204e-016。
⑵全下标、单下标。
2、阅读程序题:(本题主要考察数组的寻访、赋值和简单运算,提示:带;的语句不显示结果)⑴ans =2 3 7Sa =102030A =1 20 5 30 910 4 6 8 10⑵ A =1 3 5 7 9 11 13 152 4 6 8 10 12 14 16ans =1 5 9 132 6 10 143 7 11 154 8 12 16A =0 0 5 7 0 0 13 152 4 0 0 10 12 0 0⑶ ans =-1 -46 4ans =3 05 -2ans =3 69 12ans =3 69 123、A=magic(4);L=A<10L =0 1 1 01 0 0 11 1 1 01 0 0 14、省略。
matlab课后习题及答案

第一章5题已知a=4.96,b=8.11,计算)ln(b a e b a +-的值。
解:clearclca=4.96;b=8.11;exp(a-b)/log(a+b)ans =0.01676题已知三角形的三边a=9.6,b=13.7,c=19.4,求三角形的面积。
提示:利用海伦公式area =))()((c s b s a s s ---计算,其中S=(A+B+C)/2.解:clearclca=9.6;b=13.7;c=19.4;s=(a+b+c)/2area=sqrt(s*(s-a)*(s-b)*(s-c))s =21.3500第二章8题已知S=1+2+2^2+2^3+……+2^63,求S 的值解:clearclcS=0;for i=0:1:63S=S+2^i;endSS =1.8447e+0199题分别用for 和while 循环结构编写程序,计算∑=-1001n 1n 2)(的值。
解:clearclcs=0;for n=1:100s=s+(2*n-1);endss =10000clearclcn=1;s=0;while n<=100s=s+(2*n-1);n=n+1;endss =10000第三章2题在同一坐标下绘制函数x ,,2x -,2x xsin(x)在()∏∈,0x 的曲线。
解:clearclcx=0:0.2:pi;y1=x;y2=x.^2;y3=-(x.^2);y4=x.*sin(x);plot(x,y1,'-',x,y2,'-',x,y3,'-',x,y4,'-')00.51 1.52 2.53-10-8-6-4-22468109题用不同的线型和颜色在同一坐标内绘制曲线y1=2e x 5.0 、y2=sin(2∏x )的图形。
解:clearclcx=0:0.01:pi;y1=2*exp(-0.5*x);y2=sin(2*pi*x);plot(x,y1,'b:',x,y2,'r--')00.51 1.52 2.53 3.5-1-0.50.511.52第四章1题对表达式f=3238641+++x x x 进行化简。
matlab课后练习习题及答案详解

matlab课后习题及答案详解第1章MATLAB概论与其余计算机语言对比较,MATLAB语言突出的特色是什么?MATLAB拥有功能强盛、使用方便、输入简捷、库函数丰富、开放性强等特色。
MATLAB系统由那些部分构成?MATLAB系统主要由开发环境、MATLAB数学函数库、MATLAB语言、图形功能和应用程序接口五个部分组成。
安装MATLAB时,在选择组件窗口中哪些部分一定勾选,没有勾选的部分此后怎样补安装?在安装MATLAB时,安装内容由选择组件窗口中个复选框能否被勾选来决定,能够依据自己的需要选择安装内容,但基本平台(即MATLAB选项)一定安装。
第一次安装没有选择的内容在补安装时只要依据安装的过程进行,不过在选择组件时只勾选要补装的组件或工具箱即可。
MATLAB操作桌面有几个窗口?怎样使某个窗口离开桌面成为独立窗口?又怎样将离开出去的窗口从头搁置到桌面上?在MATLAB操作桌面上有五个窗口,在每个窗口的右上角有两个小按钮,一个是封闭窗口的Close按钮,一个是能够使窗口成为独立窗口的Undock 按钮,点击Undock按钮就能够使该窗口离开桌面成为独立窗口,在独立窗口的view菜单中选择Dock,,菜单项就能够将独立的窗口从头防备的桌面上。
怎样启动M文件编写/调试器?在操作桌面上选择“成立新文件”或“翻开文件”操作时,M文件编写/调试器将被启动。
在命令窗口中键入edit命令时也能够启动M文件编写/调试器。
储存在工作空间中的数组能编写吗?怎样操作?储存在工作空间的数组能够经过数组编写器进行编写:在工作空间阅读器中双击要编写的数组名翻开数组编写器,再选中要改正的数据单元,输入改正内容即可。
命令历史窗口除了能够察看前方键入的命令外,还有什么用途?命令历史窗口除了用于查问从前键入的命令外,还能够直接履行命令历史窗口中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到M文件中。
怎样设置目前目录和搜寻路径,在目前目录上的文件和在搜寻路径上的文件有什么差别?目前目录能够在目前目录阅读器窗口左上方的输入栏中设置,搜寻路径能够经过选择操作桌面的file菜单中的SetPath菜单项来达成。
第7章 MATLAB数值微分与积分_习题答案

1第7章 MATLAB 数值微分与积分习题7一、选择题1.diff([10,15])的值是( )。
AA .5B .10C .15D .252.数值积分方法是基于( )的事实。
DA .求原函数很困难B .原函数无法用初等函数表示C .无法知道被积函数的精确表达式D .A ,B ,C 三个选项3.求数值积分时,被积函数的定义可以采取( )。
DA .函数文件B .内联函数C .匿名函数D .A ,B ,C 三个选项4.以下选项不能用来求数值积分的函数是( )。
BA .quadgkB .quad2C .integralD .integral25.以下选项不是离散傅里叶变换的函数是( )。
CA .fftB .fft2C .fft1D .fftn二、填空题1.在MATLAB 中,没有直接提供求 的函数,只有计算 的函数diff 。
数值导数,向前差分2.基于变步长辛普森法,MATLAB 给出了 函数和 函数来求定积分。
quad ,quadl3.MA TLAB 提供了基于全局自适应积分算法的 函数来求定积分,该函数的积分限 (可以或不可以)为无穷大。
integral ,可以4.MATLAB 提供的 、 、 函数用于求二重积分的数值解, 、 函数用于求三重积分的数值解。
integral2,quad2d ,dblquad ,integral3,triplequad5.MA TLAB 提供了离散傅里叶变换函数fft ,对应的逆变换函数是 。
ifft三、应用题1.求函数在指定点的数值导数。
(1)2346x x x x f 22ππππ,,,,cos sin)(=+= (2)321x 1x x f 2,,,)(=+=2(1):(2):直接用导数函数求:f=inline('x./sqrt(x.^2+1)');f(1)用拟合函数求:f=inline('sqrt(x.^2+1)');x=0:0.001:5;p=polyfit(x,f(x),5);dp=polyder(p);dpx=polyval(dp,1)2.求定积分。
MATLAB全部实验及答案
3)A^3和A.^3
4)[A,B]和[A([1,3],:);B^2]
2、设有矩阵A和B,A=[1 2 3 4 5;6 7 8 9 10;11 12 13 14 15;16 17 18 19 20;21 22 23 24 25],B=[3 0 16;17 -6 9;0 23 -4;9 7 0;4 13 11]
使用Windows的“开始”菜单。
运行MATLAB系统的启动程序matlab.exe。
利用桌面上的快捷方式。
MATLAB主窗口
命令窗口(Command Window)
当前目录窗口(Current Directory)
工作空间窗口(Workspace)
命令历史窗口(Command History)
2、下列符号中哪些是MATLAB的合法变量名?用给变量赋值的方法在机器上验证你的答案(3vars、global、help、My_exp、sin、X+Y、_input、E-4、AbCd、AB_C_。)
6、利用MATLAB提供的rand函数和圆整函数随机生成4X3整数矩阵A,进行如下操作
1)A各列元素的平均值和中值
平均值
>> A_mean=mean(A)
A_mean =
0.5000 0.7500 0.7500
中值
>> A_median=median(A)
A_median =
0.5000 1.0000 1.0000
整数类型的运算函数
创建逻辑类型数据的函数
MATLAB的逻辑运算
MATLAB的关系运算
格式化字符
三、主要仪器及耗材
计算机
四、实验内容和步骤
1、已知A=[12 34 -4;34 7 87;3 65 7],B=[1 3 -1;2 0 3;3 -2 7],求下列表达式的值:
《MATLAB7.x》程序设计语言(第二版)课后题答案

《MATLAB7.x》程序设计语言(第二版)部分课后习题答案(楼顺天,姚若玉,沈俊霞编著)说明:所有答案均是本人在备考过程中亲自整理的,收录了一部分题目的答案。
答案可能存在不足甚至谬误,很多算法也可能不是最优的,仅供参考。
本人尽力整理的一点点心血,希望对大家有所帮助。
第二章8、 a=rand(5,5);[i,j]=find(a>0.5);for u=1:length(i);b(u)=a(i(u),j(u));endb'10、aa=any(a');i=find(aa==0)a(i,:)=[];第四章1、function flag=isprime(m)%m为素数,flag=1%m不为素数,flag=0k=sqrt(m);flag=1;for i=2:k;if rem(m,i)==0;flag=0;breakendendm=input('input an integer\n');flag=isprime(m);if flag==1disp([num2str(m),'是素数'])elsedisp([num2str(m),'不是素数'])end4、function [x1,x2]=jfc(a,b,c)d=b^2-4*a*c;if d>0;x1=(-b-sqrt(d))/(2*a);x2=(-b+sqrt(d))/(2*a);elseif d==0;x1=-b/(2*a);a=input('a=');b=input('b=');c=input('c=');[x1,x2]=jfc(a,b,c);if x1~=x2;disp('原方程存在两个不同的根')disp(['x1=',num2str(x1)])disp(['x2=',num2str(x2)]);elseif x1==x2;disp('原方程存在两个相同的根')disp(['x1=x2=',num2str(x1)])elsedisp('原方程的根不存在')end%MATLAB上机作业,184页习题4,求二次方程的实根function [s1,s2]=solve(a,b,c)d=b^2-4*a*c;if d>0s1=(-b-sqrt(d))/(2*a)s1=(-b-sqrt(d))/(2*a)%disp(['原方程有两个不同的根'num2str(s1)'和'nums2tr(s2)]) elseif d==0s1=(-b-sqrt(d))/(2*a);s1=(-b-sqrt(d))/(2*a);%disp(['原方程有两个相同的根'num2str(s1))elsedisp('原方程无实根')endend5、x=-3:0.01:3;if x>=-3 & x<-1;y=(-x.^2-4*x-3)/2;elseif x>=-1 & x<1;y=-x.^2+1;elsey=(-x.^2+4*x-3)/2;endplot(x,y)6、%MATLAB上机作业,184页习题6,点不同按钮产生不同分布的数s=menu('请选择随机数类型','U[-10,10]','U[-5,5]','U[-1,1]','N(0,1)');switch scase 1,n=(rand(1)-0.5)*20;case 2,n=(rand(1)-0.5)*10;case 3,n=(rand(1)-0.5)*2;endn7、load a.txt[m,n]=size(a);w=zeros(m,1);for i=1:m;w(i)=(2*a(i,1)+3*a(i,2)+2*a(i,3)+4*a(i,4)+2.5*a(i,5)+a(i,6))/14.5;endw8、function k=jj(i)if i<=10k=0.1*i;elseif i<=20k=1+(i-10)*0.05;elseif i<=40k=1.5+(i-20)*0.02;elsek=1.9+(i-40)*0.01;ends=0;a=2;b=1;for i=1:15;s=s+a/b;c=b;b=a;a=a+c;ends9、a=ones(15,1);b=ones(15,1);c=ones(15,1);a(1)=2;c(1)=2;for i=2:15;a(i)=b(i-1)+a(i-1);b(i)=a(i-1);c(i)=a(i)./b(i)endsum(c)第五章3、t=1:1:10;t=t';y=[4.842,4.362,3.754,3.368,3.169,3.083,3.304,3.016,3.012,3.005]';x1=[ones(size(t)),exp(-t)];x2=[ones(size(t)),t.*exp(-t)];p1=x1\y;p2=x2\y;grid on,legend('给定数据','y1拟合','y2拟合')5、(1)function dy=cwf(t,y)dy=[5*y(1)-5*y(2)-6*y(3);3*y(1)-2*y(2)+5*y(3);2*y(1)-y(2)-4*y(3)];x0=[1,-4,5];tspan=[13,16];[t,y]=ode45('cwf',tspan,x0);plot(t,y)(2)function dy=cwf(t,y)dy=[y(1)+2*y(2)-3*y(3)+y(4);3*y(1)+y(3)-2*y(4);y(1)-2*y(2)+5*y(4);2*y(1)+3*y(2)+y(4)];x0=[1,-1,2,1];tspan=[15,16];[t,y]=ode45('cwf',tspan,x0);plot(t,y)7、t=1:10;tt=1:0.01:10;y=[15,39.5,66,85.5,89,67.5,12,-86.4,-236.9,-448.4];p1=polyfit(t,y,2);y1=polyval(p1,tt);p2=polyfit(t,y,3);y2=polyval(p2,tt);plot(t,y,'b*',tt,y1,'r-',tt,y2,'c-');legend('样本点','二次拟合','三次拟合'),grid on10&11、pa=[2 3 -4];pb=[4 -2 5];pc=[3 -2 5 6];d1=conv(pa,pb)[q2,r2]=deconv(pc,pa)[q3,r3]=deconv(pc,pb)dy1=polyder(pa,pb)[q2,r2]=polyder(pc,pa)[q3,r3]=polyder(pc,pb)12、x=-5:1:5;xx=-5:0.01:5;y=10.*exp(-abs(x));y1=interp1(x,y,xx,'nearest');y2=interp1(x,y,xx,'linear');y3=interp1(x,y,xx,'spline');y4=interp1(x,y,xx,'cubic');plot(x,y,'*',xx,y1,'r-',xx,y2,'c-',xx,y3,'k-',xx,y4,'g-')grid on,legend('样本点','最临近内插','线性内插','三次样条内插','三次曲线内插')13、a=rand(1,50);amax=max(a)vara=(std(a))^2b=randn(1,50);bmax=max(a)bmin=min(a)ub=mean(a)varb=(std(a))^214、t=[0,0.2,0.4,0.6,0.8,1,2,5]';tt=0:0.01:5;y=[1,1.51,1.88,2.13,2.29,2.4,2.6,-4]';p1=polyfit(t,y,3);y1=polyval(p1,tt);x=[ones(size(t)),exp(t)];p2=x\y;y2=p2(1)+p2(2)*exp(tt);plot(t,y,'k*',tt,y1,'r-',tt,y2,'b-')legend('样本点','三次多项式拟合','指数拟合'),grid on 17、function y=jifen1(x)y=exp(-2*x);function y=jifen2(x)y=exp(2*x);function y=jifen3(x)y=x.^2-3*x+0.5;z1=quadl('jifen1',0,2)z2=quadl('jifen2',0,2)z3=quadl('jifen3',-1,1)19、function z=jifen(x,y)z=exp(-x*y)-2*x*y;q=dblquad('jifen',0,1,-1,1)20、function dy=cwf(t,y)dy=[0.5-y(1);y(1)-4*y(2)];x0=[1,-0.5];tspan=[0,25];[t,y]=ode45('cwf',tspan,x0);plot(y(1,:),y(2,:));grid on亲爱的朋友,上文已完,为感谢你的阅读,特加送另一篇范文,如果下文你不需要,可以下载后编辑删除,谢谢!道路施工方案1、工程概况2、编制说明及编制依据3、主要施工方法及技术措施3.1施工程序3.2施工准备3.3定位放线3. 4土方开挖3.5卵石路基施工3.6天然砾基层施工3. 7高强聚酯土工格楞3.8水泥稳定砂砾基层施工3.9路缘石施工3. 10玻璃纤维土工格栅施工3.11沥青面层施工3. 12降水施工4、质量控制措施5、雨季施工安排6、安全技术措施1.工程概况本项目建设的厂址位于新疆石河子市。
楼顺天第二版matlab7.x程序设计语言答案之欧阳家百创编

P83欧阳家百(2021.03.07)No.3>> A=5-round(100*rand(50,2))/10A =0.8000 -4.20004.10005.0000-1.0000 0.40000.3000 0.8000-2.0000 0.4000-2.0000 -2.7000-1.4000 1.80004.7000 -2.80004.3000 0.30001.8000 4.6000-0.3000 3.2000-1.5000 -2.20000.9000 0.3000-3.2000 3.5000-2.2000 1.6000-4.7000 -1.1000-0.3000 3.10001.7000 -2.40003.9000 2.6000-1.1000 -4.2000-2.8000 2.30000.8000 -2.70004.1000 3.10002.3000 2.10003.50004.10002.2000 -0.80000.6000 -1.8000-0.3000 -0.50000.4000 0.7000-3.8000 -1.4000-0.2000 -1.5000-4.4000 -1.8000-1.4000 -1.4000-4.6000 -4.50002.6000 2.9000-1.8000 -2.10002.1000 2.6000-1.7000 3.8000-2.0000 -1.10004.3000 0.50002.5000 0.40002.8000 -1.6000-1.7000 -2.7000-3.4000 1.50001.6000 -1.6000-2.8000 0.8000-1.8000 -3.40004.9000 -3.3000-1.0000 2.40001.1000 -1.1000No.6>> A=randn(10,10)A =-0.4326 -0.1867 0.2944 -0.3999 -1.6041 -1.0106 0.0000 0.5689 0.6232 0.3899-1.6656 0.7258 -1.3362 0.6900 0.2573 0.6145 -0.3179 -0.2556 0.7990 0.08800.1253 -0.5883 0.7143 0.8156 -1.0565 0.5077 1.0950 -0.3775 0.9409 -0.63550.2877 2.1832 1.6236 0.7119 1.4151 1.6924 -1.8740 -0.2959 -0.9921 -0.5596-1.1465 -0.1364 -0.6918 1.2902 -0.8051 0.5913 0.4282 -1.4751 0.2120 0.44371.1909 0.1139 0.8580 0.6686 0.5287 -0.6436 0.8956 -0.2340 0.2379 -0.94991.1892 1.0668 1.2540 1.1908 0.2193 0.3803 0.7310 0.1184 -1.0078 0.7812-0.0376 0.0593 -1.5937 -1.2025 -0.9219 -1.0091 0.5779 0.3148 -0.7420 0.56900.3273 -0.0956 -1.4410 -0.0198 -2.1707 -0.0195 0.04031.4435 1.0823 -0.82170.1746 -0.8323 0.5711 -0.1567 -0.0592 -0.0482 0.6771 -0.3510 -0.1315 -0.2656>> [i,j]=find(-0.5<A<0.5)i =2538 9 8 1 3 5 8 9 1 6 8 4 5 4 7 8 3 4 6 9 j = 1 1 2 2 3 3 3 3 4 5 5 5 5 5 6 6 6 7 810101010>> length(j)ans =26P146No.5clear;x=-3:0.1:3;figure(1)y1=2*x+5;y2=x.^2-3*x+1;subplot(1,2,1),plot(x,y1),title('函数1')axis([-3 3 -5 5])subplot(1,2,2),plot(x,y2),title('函数2')axis([-3 3 -5 5])No.7clear;x=[190 33 45 42 45];h=pie(x,{'生活费','资料费','电话费','购买衣服','其他费用'})explode=[0 1 0 0 0];figure(1)pie(x,{'生活费','资料费','电话费','购买衣服','其他费用'})title('每月消费比例')h =175.0033 176.0023 177.0022 178.0022 179.0022 180.0022 181.0022 182.0022 183.0022 184.0022No.9[x,y]=meshgrid([-2:0.25:2]);>> z=x.^2+y.^2+sin(x*y);>> contour3(x,y,z,30)surface(x,y,z,'EdgeColor',[.8 .8 .8],'FaceColor','none')>> grid off>> view(-15,25)P184No.1clear;function [t]=sushu(n)n=input(‘输入的数是’)A=sqrt(n);k=floor(A);for i=2:kif mod(n,i)==0t=0;break;elset=1;endendNo.3zeros_num_all = 0;for i=1:2006zeros_num = zeroscnt1(i);%zeros_num = zeroscnt2(i);zeros_num_all = zeros_num + zeros_num_all;enddisp(['1~2006中“0”的个数为:',num2str(zeros_num_all)]) zeroscnt1函数:function num = zeroscnt1(data)data_str = num2str(data);num_vec = find(data_str == '0');num = length(num_vec);zeroscnt2函数function num = zeroscnt2(data)num = 0;while(data>=1)if mod(data,10) == 0num = num + 1;data = fix(data/10);elsedata = fix(data/10);endendNo.5i=0;for x=-3:0.01:3i=i+1;X(i)=x;if and(x>=-3,x<-1)Y(i)=(-x*x-4*x-3)/2;elseif and(x>=-1,x<1)Y(i)=-x*x+1;elseY(i)=(-x*x+4*x-3)/2; endendplot(X,Y)No.8clear;I=input(‘个人完成的利润为’) if I<=10y=I*0.1elseif I>10&I<=20y=10*10+(I-10)*0.05 elseif I>20&I<=40y=10*0.15+(I-20)*0.02 elseif I>40y=10*0.17+(I-40)*0.01 end>> m02个人完成的利润为25I =25y =1.6000No.9clear;i=1;s=0;a1=1;a2=1;while i<16k=a1;a1=a1+a2;a2=k;s=s+a1/a2;i=i+1;end>> ss =24.5701P263No.1a =1 9 87 2 53 -2 7>> det(a)ans =-442>> inv(a)ans =-0.0543 0.1787 -0.06560.0769 0.0385 -0.11540.0452 -0.0656 0.1380(2)>> b=[1 0 -7 5;0 -26 7 2;7 4 3 5;8 -3 2 15]b =1 0 -7 50 -26 7 27 4 3 58 -3 2 15>> det(b)ans =-9334>> inv(b)ans =0.1501 0.0654 0.3046 -0.1603-0.0509 -0.0471 -0.0312 0.0336-0.1697 -0.0204 -0.0703 0.0827-0.0676 -0.0416 -0.1593 0.1478No.22,(1)>> a1=[1 2 3;2 2 5;3 5 1];>> b1=[11;12;31];x1=inv(a1)*b1x1 =1.80005.2000-0.4000(2)a2=[3 1 0 5;0 6 7 3;0 4 3 0;2 -1 2 6];b2=[2;4;7;8];>> x2=inv(a2)*b2x2 =28.1892-9.4595-14.6216No.3clear;t=1:1:10;t=t';y=[4.842,4.362,3.754,3.368,3.169,3.083,3.304,3.016,3.012,3.005]'; x1=[ones(size(t)),exp(-t)];x2=[ones(size(t)),t.*exp(-t)];p1=x1\y;p2=x2\y;tt=linspace(1,10,1000);plot(t,y,'*',tt,p1(1)+p1(2)*exp(-tt),'r-',tt,p2(1)+p2(2)*tt.*exp(-tt),'c-') grid on,legend('给定数据','y1拟合','y2拟合')No.7clear;t=1:10;tt=1:0.01:10;y=[15,39.5,66,85.5,89,67.5,12,-86.4,-236.9,-448.4];p1=polyfit(t,y,2);y1=polyval(p1,tt);p2=polyfit(t,y,3);y2=polyval(p2,tt);plot(t,y,'b*',tt,y1,'r-',tt,y2,'c-');legend('样本点','二次拟合','三次拟合'),grid onNo.8p1,p2,p3,p4p1 =1 -2 -34 2p2 =1 -7 5 31 -30p3 =1 -1 -25 25p4 =-2 3 1 5 8 0>> roots(p1),roots(p2),roots(p3),roots(p4)ans =2.41421.4142-1.4142-0.4142ans =5.0000-2.00001.0000ans =-5.00005.00001.0000ans =2.41760.0148 + 1.3215i0.0148 - 1.3215i-0.9473No.9y11=polyval(p1,-1.5),y12=polyval(p1,2.1),y13=polyval(p1,3.5)y11 =1.0625y12 =-1.9039y13 =43.5625>> y21=polyval(p2,-1.5),y22=polyval(p2,2.1),y23=polyval(p2,3.5) y21 =-36.5625y22 =11.7711y23 =-10.3125>> y31=polyval(p3,-1.5),y32=polyval(p3,2.1),y33=polyval(p3,3.5) y31 =56.8750y32 =-22.6490y33 =-31.8750>> y41=polyval(p4,-1.5),y42=polyval(p4,2.1),y43=polyval(p4,3.5) y41 =26.2500y42 =24.7733y43 =-468.125013,15,20No.13>> a=rand(1,50);amax=max(a)amin=min(a)ua=mean(a)vara=(std(a))^2b=randn(1,50);bmax=max(a)bmin=min(a)ub=mean(a)varb=(std(a))^2amax =0.9706amin =0.0318ua =0.5661vara =0.0977bmax =0.9706bmin =0.0318ub =0.5661varb =0.0977No.15>> t=0:1/199:1;>> x=3*sin(2*pi*20*t)+10*sin(2*pi*200*t+0.25*pi)+10*randn(size(t)); >> y=fft(x);>> m=abs(y);>> f=(0:length(y)-1)'*199/length(y);>> figure(1)>> subplot(2,1,1),plot(t,x),grid on>> title('信号检测')>> ylabel('Input\itx'),xlabel('Time')>> subplot(2,1,2),plot(f,m)>> ylabel('Abs.Magnitude'),grid on>> xlabel('Frequency(Hertz)')No.16t=0:pi/50:2*pi;x1=sin(w*t)+randn(size(t));x2=cos(w*t)+randn(size(t));x3=sin(w*t)+randn(size(t));R1=corrcoef(x1,x2)R2=corrcoef(x1,x3)y1=randn(size(t));y2=randn(size(t));y3=randn(size(t));Q1=corrcoef(y1,y2)Q2=corrcoef(y1,y3)R1 =1.0000 0.04200.0420 1.0000R2 =1.0000 0.26410.2641 1.0000Q1 =1.0000 -0.0791-0.0791 1.0000Q2 =1.0000 0.02540.0254 1.0000No.20M函数:function dy=diffequat1(t,y)dy=[0.5-y(1);y(1)-4*y(2)];Matble:>> X0=[1;-0.5];>> tspan=[0,50];>> clear all>> X0=[1;-0.5];>> tspan=[0,25];>> [T,X]=ode45('diffequat1',tspan,X0);>> figure(1)>> subplot(2,1,1),plot(T,X(:,1),'r'),title('x_{1}'),grid on >> subplot(2,1,2),plot(T,X(:,2),'k'),title('x_{2}'),grid on >> figure(2)>> plot(X(:,1),X(:,2)),title('系统轨迹'),grid on>> xlabel('x_{1}'),ylabel('x_{2}')P313No.2A=[65 76 78 87 76;64 78 67 87 95;64 65 78 88 76;78 90 81 83 85;67 89 87 78 86;69 74 78 81 82];A(:,:,2)=[67 87 67 78 65;65 76 87 67 59;78 90 67 87 86;74 67 87 67 87;89 67 87 87 86;80 80 81 82 84];A(:,:,3)=[67 80 82 85 87;87 87 87 87 87;85 75 65 75 75;80 89 89 89 89;79 79 79 79 79;90 90 67 78 90];A(:,:,4)=[78 78 78 78 78;67 89 76 87 82;78 56 76 87 67;90 92 89 87 86;78 89 78 67 89;91 90 85 85 86];A(:,:,5)=[68 87 86 86 86;78 90 76 76 78;78 98 78 76 87;78 97 87 67 75;78 90 65 76 89;67 87 78 87 78];A(:,:,6)=[87 87 87 87 78;78 87 90 78 76;75 78 76 75 74;76 87 85 86 88;88 77 90 87 89;85 87 88 90 83];A(:,:,7)=[68 87 85 84 80;88 80 89 85 90;78 79 70 79 88;88 78 91 88 80;69 87 86 85 83;80 88 78 78 87];A(:,:,8)=[67 80 82 85 87;87 87 87 88 87;85 79 65 75 75;80 89 89 89 89;79 79 79 79 79;90 90 67 78 90];A(:,:,9)=[67 87 67 78 65;65 76 88 67 59;78 90 67 87 86;74 67 87 67 87;80 67 87 87 86;80 80 81 82 84];A(:,:,10)=[87 78 78 78 78;67 89 76 87 82;78 56 76 87 67;90 90 89 87 86;78 89 78 67 89;91 90 85 85 86];gra=Afor i=1:length(gra)mean_gra=mean(mean(gra(6,5,i)));a(i,1)=mean_gra;disp([num2str(i) '宿舍平均分是' num2str(mean_gra)]);endsit=sort(a);disp('排名如下')for i=1:10disp(['第' num2str(11-i) '名分数是' num2str(sit(i,1))]);end结果:gra(:,:,1) =65 76 78 87 7664 78 67 87 9564 65 78 88 7678 90 81 83 8567 89 87 78 8669 74 78 81 82gra(:,:,2) =67 87 67 78 6565 76 87 67 5978 90 67 87 8674 67 87 67 87 89 67 87 87 86 80 80 81 82 84。
MATLAB作业7参考答案

MATLAB作业7参考答案1、试生成满足正态分布2N的30000 个伪随机数,对其均值和方差进行验(0.5,1.4)证,并用直方图的方式观察其分布与理论值是否吻合,若改变直方图区间的宽度会得出什么结论?解:用下面的语句可以生成随机数,并计算均值和方差,可见,其结果接近给定的数值。
>> x=normrnd(0.5,1.4,30000,1);>>m=mean(x), s=std(x)m =0.49974242123102s =1.40033494141044>> xx=-5:0.3:5; yy=hist(x,xx); bar(xx,yy/length(x)/0.3); hold onx0=-5:0.1:5; y0=normpdf(x0,0.5,1.5); plot(x0,y0)>> xx=-5:0.8:5; yy=hist(x,xx); bar(xx,yy/length(x)/0.8);hold on; plot(x0,y0)2、某研究者对随机抽取的一组保险丝进行了实验,测出使保险丝烧断的电流值为10.4, 10.2,12.0, 11.3, 10.7, 10.6, 10.9, 10.8, 10.2, 12.1,假设这些值α≤的条件下求出这些保险丝的溶断电流及其满足正态分布,试在置信水平0.05置信区间。
解:方法①由normfit() 函数可以直接求出置信区间,亦即溶断电流的均值为10.92,其置信区间为(10:43; 11:41)。
>> x=[10.4,10.2,12,11.3,10.7,10.6,10.9,10.8,10.2,12.1];>> [m1,s1,ma,sa]=normfit(x,0.05); m1, mam1 =10.92000000000000ma =10.43271643434768 11.40728356565233方法②采用T 检验函数即可判定是否接受均值为mean(x) 的检验,也能求出同样的均值与置信区间>> x=[10.4,10.2,12,11.3,10.7,10.6,10.9,10.8,10.2,12.1];mean(x)ans =10.92000000000000>> [H,p,ci]=ttest(x,mean(x),0.05)H =p =1ci =10.43271643434768 11.407283565652333、假设测出某随机变量的12 个样本为9.78, 9.17, 10.06, 10.14, 9.43, 10.60, 10.59, 9.98, 10.16,10.09, 9.91, 10.36,试求其方差及方差的置信区间。
MATLAB课后习题集附标准答案

第2章 MATLAB概论1、与其他计算机语言相比较,MATLAB语言突出的特点是什么?答:起点高、人机界面适合科技人员、强大而简易的作图功能、智能化程度高、功能丰富,可扩展性强.2、MATLAB系统由那些部分组成?答:开发环境、MATLAB数学函数库、MATLAB语言、图形功能、应用程序接口3、安装MATLAB时,在选择组件窗口中哪些部分必须勾选,没有勾选的部分以后如何补安装?答:在安装MATLAB时,安装内容由选择组件窗口中各复选框是否被勾选来决定,可以根据自己的需要选择安装内容,但基本平台(即MATLAB选项)必须安装.第一次安装没有选择的内容在补安装时只需按照安装的过程进行,只是在选择组件时只勾选要补装的组件或工具箱即可.矚慫润厲钐瘗睞枥庑赖。
4、MATLAB操作桌面有几个窗口?如何使某个窗口脱离桌面成为独立窗口?又如何将脱离出去的窗口重新放置到桌面上?聞創沟燴鐺險爱氇谴净。
答:在MATLAB操作桌面上有五个窗口,在每个窗口的右下角有两个小按钮,一个是关闭窗口的Close 按钮,一个是可以使窗口称为独立的Undock按钮,点击Undock按钮就可以使该窗口脱离桌面称为独立窗口,在独立窗口的view菜单中选择Dock,菜单项就可以将独立的窗口重新防止的桌面上.残骛楼諍锩瀨濟溆塹籟。
5、如何启动M文件编辑/调试器?答:在操作桌面上选择“建立新文件”或“打开文件”操作时,M文件编辑/调试器将被启动.在命令窗口中键入edit命令时也可以启动M文件编辑/调试器.酽锕极額閉镇桧猪訣锥。
6、存储在工作空间中的数组能编辑吗?如何操作?答:存储在工作空间的数组可以通过数组编辑器进行编辑:在工作空间浏览器中双击要编辑的数组名打开数组编辑器,再选中要修改的数据单元,输入修改内容即可.彈贸摄尔霁毙攬砖卤庑。
7、命令历史窗口除了可以观察前面键入的命令外,还有什么用途?答:命令历史窗口除了用于查询以前键入的命令外,还可以直接执行命令历史窗口中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到M文件中.謀荞抟箧飆鐸怼类蒋薔。
实验七 matlab求解级数有关计算

实验七 matlab 求解级数有关计算1.级数的基本概念常数项级数:称用加号将数列n a 的项连成的式子+++++n a a a a 321为(常数项)无穷级数,简记为∑∞=1n na。
称级数∑∞=1n na前n 项构成的和∑==++++=nk kn n a a a a a S 1321为级数的部分和。
若SS n n =∞→lim ,则称级数∑∞=1n na收敛,其和为S 。
Taylor 级数:设函数)(x f 在包含a x =的区域内具有各阶导数,则称幂级数+-++-+-+=-∑∞=n n n n n a x n a f a x a f a x a f a f a x n a f )(!)()(!2)())((')()(!)()(2)2(0)(为函数)(x f 在a x =的Taylor 级数,当0=a 时称为Maclaurin(麦克劳林)级数。
2.级数的MATLAB 命令MATLAB 中主要用symsum,taylor 求级数的和及进行Taylor 展开。
例1 先用taylor 命令观测函数x y sin =的Maclaurin 展开式的前几项,例如观测前6项, 相应的MA TLAB 代码为:>>clear; syms x;>>taylor(sin(x),0,1) >>taylor(sin(x),0,2) >>taylor(sin(x),0,3) >>taylor(sin(x),0,4) >>taylor(sin(x),0,5) >>taylor(sin(x),0,6)结果为:ans =0 ans =x ans =xans =x-1/6*x^3 ans =x-1/6*x^3ans =x-1/6*x^3+1/120*x^5然后在同一坐标系里作出函数x y sin =和它的Taylor 展开式的前几项构成的多项式函数,,!5!3,!3,533 x x x y x x y x y +-=-==的图形,观测这些多项式函数的图形向x y sin =的图形的逼近的情况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题答案第1章1-2(1)使用Windows“开始”菜单。
(2)运行MATLAB系统启动程序matlab.exe。
(3)利用快捷方式。
1-3 MATLAB系统主要由开发环境、MATLAB函数库、MATLAB语言、图形功能和应用程序接口五个部分组成。
1-4窗口:M文件编辑/调试器、历史指令窗、当前目录浏览器、工作空间浏览器、内存数组编辑器、交互界面分类目录窗、及帮助导航/浏览器和图形窗。
1-5在操作桌面上选择建立新文件或打开文件操作时,M文件编辑/调试器将被启动。
在命令窗口中键入edit命令时也可以启动M文件编辑/调试器。
MATLAB的开发环境中包括了专门的M文件编辑器,该编辑器不但提供了M文件的编辑功能,同时还与MATLAB的开发环境一起实现了MATLAB命令和函数文件的运行与调试。
1-6Copy 将所选历史命令拷贝到剪贴板EvaluateSelection 运行所选历史命令CreateM-File 打开编辑器,将所选历史命令复制到编辑器DeleteSelection 删除所选历史命令(不确认是否删除) DeletetoSelection 从头删除到所选历史命令(不确认是否删除) DeleteEntireHistory 清除全部历史命令(将弹出对话框确认是否清除)1-7当用户在MATLAB命令窗口输入一条命令后,MATLAB按照一定次序寻找相关的文件。
基本的搜索过程是:(1)检查该命令是不是一个变量。
(2)检查该命令是不是一个内部函数。
(3)检查该命令是否当前目录下的M文件。
(4)检查该命令是否MATLAB搜索路径中其他目录下的M文件。
用户可以将自己的工作目录列入MATLAB搜索路径,从而将用户目录纳入MATLAB系统统一管理。
设置搜索路径的方法有:(1)用path命令设置搜索路径。
例如,将用户目录c:\mydir加到搜索路径下,可在命令窗口输入命令:2MTALB 7.X 程序设计path(path,’d:\my’)(2) 用对话框设置搜索路径1-8在MATLAB中有多种获得帮助的途径:(1)帮助浏览器:选择view菜单中的Help菜单项或选择Help菜单中的MATLAB Help 菜单项可以打开帮助浏览器;(2)help命令:在命令窗口键入help 命令可以列出帮助主题,键入help 函数名可以得到指定函数的在线帮助信息;(3)lookfor命令:在命令窗口键入lookfor 关键词可以搜索出一系列与给定关键词相关的命令和函数;注意:lookfor和模糊查询查到的不是详细信息,通常还需要在确定了具体函数名称后用help命令显示详细信息。
第2章2-1FORMAT SHORT 默认设置,以两位整数和4位小数形式输出FORMAT LONG 以16 位十进制数形式输出FORMAT SHORT E以5位十进制数加指数形式输出FORMAT LONG E 以16位十进制数加指数形式输出FORMAT SHORT G 从format short和format short e中自动选择最佳输出形式FORMAT LONG G 从format long和format long e中自动选择最佳输出形式FORMAT HEX 以16位十六进制数形式输出FORMAT + 以正号、负号和零形式输出FORMAT BANK 以两位小数形式输出FORMAT RAT 以近似分数形式输出2-2x=[4+8i 3+5i 2-7i 1+4i 7-5i;3+2i 7-6i 9+4i 3-9i 4+4i];Rx=real(x)Ix=imag(x)Ax=abs(x)Cx=conj(x)CCx=x'2-3x=-5:2:5 %建立行向量length(x) %向量x的长度x(1) %x的第一个元素习题答案 3x(end) % x的最后一个元素x' % 向量转置为列向量y=linspace(-5,5,8) %建立行向量y' % 向量转置为列向量2-4执行结果为:ans =3 3ans =2ans =9a12 =1ah1 =8 1 6al1 =834ah1_3 =8 1 64 9 2al1_3 =8 63 74 2a =8 1 6 03 5 7 04 9 2 00 0 0 9a =8 1 6 03 5 7 04MTALB 7.X 程序设计4 9 2 0a =8 1 63 5 74 9 22-5执行结果为:ans =6ans =151ans =-3 1 5ans =7 3-2 6-3 5ans =612-15ans =-6 6 6-12 12 12-10 10 10ans =14 7 126 -12 1410 -19 4ans =7 2 34 10 12-9 -3 5习题答案 5ans =38 15 42-42 29 54-38 7 22ans =49 1 94 25 369 1 25ans =0.0976 0.4634 -0.4146-0.1707 0.4390 -0.02440.5732 -0.9024 0.9390ans =0.1429 2.0000 0.33331.0000 0.4000 0.3333-1.0000 -3.0000 0.20002-6执行结果为:ans =1-23ans =1 2 3ans =1 3-2 -43 5ans =1 2 33 4 5ans =5 6 7 8ans =86MTALB 7.X 程序设计ans =6 7 810 11 122-7已知角度[]60=x,求x的正弦、余弦、正切和余切。
4530在三角函数运算中,自变量可以是角度也可以是弧度。
x=[30 45 60]; x1=x/180*pi;sin(x1),cos(x1),tan(x1),cot(x1)% 自变量是弧度sind(x),cosd(x),tand(x),cotd(x) %自变量是角度2-8x=10:99;length(x((rem(10:99,5)==0)))2-9x=10:20;log10(x)/log10(3)2-10a=[1.55 -1.45 1.45 -1.55];floor(a),ceil(a),round(a),fix(a) 执行结果为:ans =1 -2 1 -2ans =2 -1 2 -1ans =2 -1 1 -2ans =1 -1 1 -12-11s1=upper('China');s2='china';s3=lower('Chinese');c1=strcmp(s1,s2)c2=strcmpi(s1,s2)c3=strncmp(s1,s3,4)c4=strncmpi(s1,s3,2)执行结果为:c1 =c2 =1习题答案7c3 =c4 =12-12执行结果为:ans =5 5 5 5ans =-3 -1 1 3ans =20ans =4 6 6 4ans =1 8 9 4ans =1 4 9 16ans =16 8 4 2ans =2 4 8 16 16 8 4 22-13执行结果为:ans =2h =2l =3ans =6ans =[2x2 double]ans =8MTALB 7.X 程序设计[1x27 char] [2x2 double] [2x2 double] ans =[2x2 double][]ans =[2x2 double] [2x2 double][3x3 double] []ans =0 -31 0ans =ans =-3ans =0 1c =[1x27 char ] [2x2 double] [2x2 double] [2x2 double] [3x3 double] [] [] [] [ 5] c =[1x27 char ] [2x2 double] [2x2 double] [2x2 double] [3x3 double] [] 2-14t.college='computer'='Wang Ming';t.number='19990101';t.sex='man';='MATLAB';t.corse.class='2004';t.corse(2).name='maple';t.corse(2).class='2005';t2.college='computer'='zhang Ming';t2.number='19990101';习题答案9t2.sex='man';='math';t2.corse.class='2006';t2.corse(2).name='MATLAB';t2.corse(2).class='2005';t2.corse(3).name='math';t2.corse(3).class='2006';t第3章3-1a=[1 5 8;3 0 -4];b=[6 -7 3;5 0 2];a>ba>=ba<ba<=ba==ba~=b执行结果为:ans =0 1 10 0 0ans =0 1 10 1 0ans =1 0 01 0 1ans =1 0 01 1 1ans =0 0 00 1 0ans =10MTALB 7.X 程序设计1 1 11 0 13-2执行结果为:x =0 0 0 0 1 1 1 1 1y =0 0 0 0 0 1 0 0 03-3a=reshape(-6:2:12,2,5)L=a>6; %产生与A同型的0—1逻辑值数组x=find(a>6);a(L) % 把L中逻辑值1对应的A元素取出x %大于6的元素在原数组中的序号3-4执行结果为:x =0 0 0 0 0 0 0 1 1y =1 1 1 1 0 0 0 0 0L =1 1 1 1 0 0 0 1 1aL =1.00002.10003.20004.3000 8.7000 9.8000 xh =1 2 3 4 8 93-5a=reshape(-6:2:12,2,5);b=reshape(-8:3:19,2,5);la=a&b;lb=a|b;islogical_la=islogical(la)islogical_lb=islogical(lb)any_lab=any([la,lb])all_lab=all([la,lb])执行结果为:islogical_la =1islogical_lb =1any_lab =1 1 1 1 1 1 1 1 1 1 all_lab =1 0 1 1 1 1 1 1 1 1 3-6a=magic(3);b=magic(4);P1=rem(a,3)==0;P2=rem(b,3)==0;a(P1)b(P2)3-7执行结果为:all_a =1 0 1 1 1any_a =1 1 1 1 1isnan_a =0 0 0 0 00 0 0 0 0isinf_a =0 0 0 0 00 0 0 0 0isfinite_a =1 1 1 1 11 1 1 1 13-8a=input('Please input a matrix? ');if isreal(a)==1sign(a)elsedisp('The matrix isnot real matrix') end3-9x=input('请输入x的值:');if isreal(x)==0disp('No defination')elseif x>=-1 & x<=1y=x.^2+1elsey=x+1end程序2:x=input('请输入x的值:');isreal_x=isreal(x);switch isreal_xcase 1if x>1|x<-1y=1+xelsey=x.^2+1endcase 0disp('No defination')end3-10x=input('please enter x value:');if x<0 & x~=-3y=x.^2+x-6elseif x>=0&x~=2&x~=3&x<10y=x.^2-5*x+6elsey=x.^2-x-1end3-11执行结果:a =2 -1 0 0 0 0 -1 2 -1 0 0 0 0 -1 2 -1 0 0 0 0 -1 2 -1 0 0 0 0 -1 2 -1 3-12s= 1083-13程序1:y=0;for n=1:100f=1/n/n/n;y=y+f;n=n+1;endy程序2:y=0;n=1;while n<=100f=1/n/n/n;y=y+f;n=n+1;endy3-14n=input('please enter n value:');s=0;for i=1:2:ns=s+i;ends3-15程序:a=0;b=3;n=1000;h=(b-a)/n;x=a:h:b;f=x./(x.^2-1);for i=1:ns(i)=(f(i)+f(i+1))*h/2;ends=sum(s)3-16程序1:n=input('Please enter n:');y1=0;for i=1:n;y1=y1+1/i/i;y=sqrt(6*(y1));endy程序2:n=input('Please enter the number n:');i=1:n;f=1./i.^2;y1=sum(f);y=sqrt(6*(y1))3-17m=input('矩阵行数:m=');n= input('矩阵列数:n=');for i=1:mfor j=1:ndisp(['输入第',num2str(i),'行,第', num2str(j),'列元素']) A(i, j) = input (… ‟)endend3-18程序1:function y=f2(x)y=x.^3+2*x.^2+1;y=f2([-5 -3 -1 1 3 5])程序2:f=inline('x.^3+2*x.^2+1');f([-5 -3 -1 1 3 5])3-19for month=1:12;switch monthcase{3,4,5}season='spring'case{6,7,8}season='summer'case{9,10,11}season='autumn'otherwiseseason='winter'endend3-203-21定义函数文件:function z=ff(x,y)z=x^2+exp(x+y)-y*log(x)-3;调用:z=ff(2,4)第4章4-1结果为:In cotd at 16y =0 0.5000 0.8660 1.0000 0.8660 0.5000 01.0000 0.8660 0.5000 0 -0.5000 -0.8660 -1.00000 0.5774 1.7321 Inf -1.7321 -0.5774 0Inf 1.7321 0.5774 0 -0.5774 -1.7321 Inf y_2_max =11InfInfy_max =Infy_2_min =-1.0000-1.7321-1.7321y_min =-1.73214-2cx=cov(x) ,cy=cov(y)cxy=cov(x,y) 4-3执行结果为:ans =9 -36 30-36 192 -18030 -180 180ans =9192180ans =30 -180 180-36 192 -1809 -36 30ans =30 -36 9-180 192 -36180 -180 30ans =30 -180 180-36 192 -1809 -36 30ans =9 -36 30 -36 192 -180 30 -180 180ans =9 0 0-36 192 030 -180 180ans =9 -36 300 192 -1800 0 1804-4定义函数文件:function x4_4(a)%a matrix[m n]=size(a);if m==ndet_a=det(a)if det_a~=0inv_a=inv(a)endelsedisp('no inverse')pinv_a=pinv(a)disp('no det')endrank_a=rank(a)>> x4_4([1 -6 3 2;3 -5 4 0;-1 -11 2 4])no inversepinv_a =-0.1000 0.1860 -0.03000.5000 -0.2500 -0.25000.7000 -0.2020 -0.29001.0000 -0.5400 -0.3000no detrank_a =3>> x4_4([1 2 1 0;6 2 4 1;0 2 1 0;3 1 4 1])det_a =1inv_a =1.0000 0 -1.0000 0-3.0000 1.0000 3.0000 -1.00006.0000 -2.0000 -5.0000 2.0000-24.0000 7.0000 20.0000 -6.0000rank_a =44-5a=[1 1 3 2;-1 1 -1 3;5 -2 8 9;-1 3 1 7];rank(a)ans =3线性相关4-6a=[2 2 -1;1 -2 4;5 8 2]; [X,D]=eig(a)X =0.0000 -0.7160 0.2760-0.4472 0.4200 -0.7472-0.8944 0.5576 0.6045D =6.0000 0 00 1.6056 00 0 -5.60564-7A=[6 5 -2 5;9 -1 4 -1;3 4 2 -2;3 -9 2 0];b=[-4 13 1 11]'; inv(A)*b A=[6 5 -2 5;9 -1 4 -1;3 4 2 -2;3 -9 2 0];b=[-4 13 1 11]'; A\bans =-8.33332.000027.000018.0000A=[6 5 -2 5;9 -1 4 -1;3 4 2 -2;3 -9 2 0];b=[-4 13 1 11]';Ab=[A,b]; rref(Ab)ans =1.0000 0 0 0 -8.33330 1.0000 0 0 2.00000 0 1.0000 0 27.00000 0 0 1.0000 18.00004-9x=[1 1 3;4 3 2;1 2 5]*inv([1 1 -1;2 1 0;1 1 1])x =-1 0 20 1 2-1 -1 44-10p=[1 0 -2 -5];r=roots(p);for ii=1:length(r)if r(ii)>=0&r(ii)<=3r(ii)endendans =2.09464-11(1))(x f 、)(x g 的根;p1=[3 -1 2 1 0 3];p2=[1/3 1 -3 -1];roots(p1),roots(p2)ans =0.7330 + 0.7416i0.7330 - 0.7416i-0.8952-0.1188 + 1.0066i-0.1188 - 1.0066ians =-4.75882.0642-0.3054(2))()(x g x f +,)()(x g x f ⋅和)()(x g x f ;p1+[0 0 p2]ans =3.0000 -1.0000 2.3333 2.0000 -3.0000 2.0000p1p1 =3 -1 2 1 0 3conv(p1,p2)ans =1.00002.6667 -9.3333 2.3333 -4.0000 -4.0000 2.0000 -9.0000-3.0000 [r p k]=residue(p1,p2)r =-792.245022.1035-0.8584p =-4.75882.0642-0.3054k =9 -30 177(3))(x f 、)(x g 、)()(x g x f 的导数。
