二章圆波导
波导中微波的模式

波导中微波的模式波导是一种用来传输微波信号的导波结构,由金属壁面构成,中间空腔内充满介质。
在波导中,微波信号通过内部的反射而传播,产生各种模式。
不同模式具有不同的传播特性和分布特点,对于波导设计和应用都非常重要。
本文将介绍波导中常见的几种微波模式。
1.矩形波导模式:矩形波导是最常见的一种波导类型,由金属矩形管道组成。
在矩形波导中,有许多不同的模式,包括正交模式(TE模式)和纵向模式(TM模式)。
(1)TE模式:TE模式是横向电场模式,在矩形波导中,电场垂直于波导的横截面方向。
TE模式的特点是不含有磁场分量,只有电场分量。
TE模式分为TE10,TE20,TE01等不同的阶次。
(2)TM模式:TM模式是纵向磁场模式,在矩形波导中,磁场沿波导的横截面方向。
TM模式的特点是不含有电场分量,只有磁场分量。
TM模式也分为TM10,TM20,TM01等不同的阶次。
矩形波导模式的分布特点是波束在波导内壁上反射,形成驻波模式。
TE和TM模式可以共存,交替出现。
2.圆形波导模式:圆形波导是由金属圆管构成的波导结构。
圆形波导模式与矩形波导模式类似,也有TE模式和TM模式,但其阶次的确定方式略有不同。
(1)TE模式:TE模式是横向电场模式,电场沿着圆柱壁面方向。
TE 模式中的波动电场与壁面垂直,并且没有磁场分量。
(2)TM模式:TM模式是纵向磁场模式,磁场沿着圆柱壁面方向。
TM 模式中的波动磁场与壁面垂直,并且没有电场分量。
与矩形波导不同的是,圆形波导模式的阶次由径向模式数目(m)和角向模式数目(n)两个参数共同确定。
例如,TE11模式表示径向和角向模式都为13.表面波模式:除了矩形和圆形波导模式外,波导中还存在一种特殊的模式,称为表面波模式。
表面波模式是指波在波导壁面上沿着壁面传播的模式,不进一步传播到波导的深处。
表面波模式包括射线波、栅波和电磁波导模式。
射线波模式是指波束沿着表面传播,而不发散或收敛;栅波模式是指波束被壁面上的栅格结构所限制;电磁波导模式是指在电磁波导中,电磁波束是由电和磁场的耦合形成的。
圆波导

cTE
mn
2a
mn
cTM
mn
2a
mn
在所有的模式中,TE11模截止波长最长,其次为 TM01模,三种典型模式的截止波长分别为
cTE 3.4126a
11
cTM 2.6127 a
01
cTE 1.6398a
01
微波工程基础
5
第二章 规则金属波导之圆波导
圆波导中各模式截止波长的分布图
11
第二章 规则金属波导之圆波导
磁场有径向 和轴向分量
(3)低损耗的TE01模
波导内壁电流:
TE01模的场分布
圆波导三种模式的导体衰减曲线
J s n H a a z H z a H z
TE01 模是圆波导的高次模式,比它低的模式有 TE11 、TM01 、 TE21 ,它与TM11是简并模。它也是圆对称模故无极化简并。
方圆波导变换器
TE11模的截止波长最长,是圆波导中的最低次模,也是主模。圆 波导中模的场分布与矩形波导的模的场分布很相似,因此工程上容 易通过矩形波导的横截面逐渐过渡变为圆波导,从而构成方圆波导 变换器。 但由于圆波导中极化简并模的存在,所以很难实现单模传输,因 此圆波导不太适合于远距离传输场合。 微波工程基础
微波工程基础
7
第二章 规则金属波导之圆波导
极化简并
旋转
利用极化兼并现象制成极化衰减器、极化变换器等
微波工程基础
8
第二章 规则金属波导之圆波导
(c)传输功率 TEmn和TMmn模的传输功率分别为:
PTE mn
2 πa m 2 2 Z H ( 1 ) J TE mn m (kc a) 2 2 2 m kc k a 2
第2-6章 圆形波导
(3)低损耗TE01模
①电磁场沿 方向不变化,场具有轴对称性; ②只有 E分量,在r = 0 及r = a 处,
u mn E mn J m a
Hz 0
场沿半径按贝塞尔函数或按其导数的规律变化,波型指数n 表示场沿半径分布的最大值个数;场沿圆周方向按正弦或余 弦函数形式变化,波型指数m表示场沿圆周分布的整波数。
2. 圆波导的传输参数
• TEmn导模的各参数:
波阻抗:
Z TE
E k Er H Hr
k cmn
式中
u mn为 J m (k c a)的根。
u mn E z (r , , z ) E mn J m a
基本解为:
cos m jz r e sin m
则得一般解:
u mn cos m jz E z (r , , z ) E mn J m r e a sin m m 0 n 1
u mn ja E r E mn J m m 0 n 1 u mn a
E
m 0 n 1
cos m j (t z ) r sin m e u mn sin m j (t z ) jma 2 E mn J m 2 a r cos m e u mn r
场沿圆周方向按正弦或余弦函数形式变化,波型 指数m表示场沿圆周分布的整波数。
2)TM模 则
Hz = 0,
圆形波导的理论分析和特性
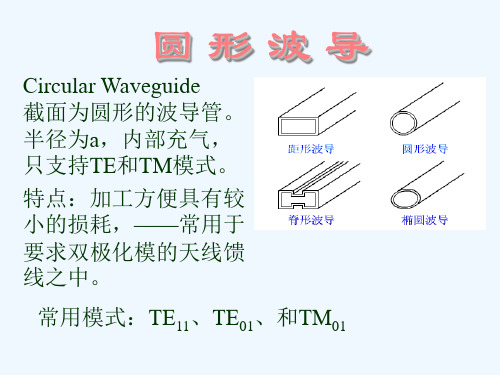
传播常数: mn k k 截至波长: cmn 截至频率 2 a u 'mn v
u 'mn k a
2
2
3.2 18
3.2 19 3.2 20
f cmn
cmn
u 'mn 2 a
其中贝塞尔函数最小根u11'=1.841对应TE11模。 c=3.41a;次低模为根u01=3.832, c=1.64a
圆形波导分析 – TM modes.(续四)
波导阻抗: Z TM Ef Er Hf H r w k
2 2 cmn 2
3.2 25
2
传播常数: mn k k 截至波长: cmn 截至频率 2 a u mn v
u mn k a
m 0 n 1
u m n co s m f j ( w t z ) jw m a 2 E mn J m ( r) e 2 si n m f u mn r a co s m f j ( w t z ) jw a ' u mn E mn J m ( r) e sin m f u mn a
3.2 26
3.2 27 3.2 28
f cmn
cmn
u mn 2 a
其中贝塞尔函数最小根 u01=2.405对应TM01模。 c=2.62a
圆形波导的特性
圆形波导模的传输条件是c> 或fc<f;传输特性 与矩形波导类似,为高通器件。 圆形波导存在两种模式简并现象: TE0n与TMm0的模兼并; 另一种是m非零的TEmn与TMmn模的极化简并。 圆形波导的基模—— 主模为TE11,其截止波长最长(TE11=3.41a) 次模为TM01,其截止波长最长(TM01=2.62a)
圆形波导
场沿圆周方向按正弦或余弦函数形式变化,波 型指数m表示场沿圆周分布的整波数。
TEmn导模的各参数:
波阻抗:
Z TE
Er H
E Hr
k
传播常数: mn
k2
k2 cmn
k
2
um n
2
a
截止波长: 截止频率:
cmn
2a
u m n
f cmn
k cmn
2
um n
2a
▪TE11模
u11 1.841对应本征值为最小值
bh k
传播常数: mn
k2
k2 cmn
k2
umn
2
a
截止波长:
cmn
2a
u mn
截止频率:
f cmn
k cmn
2
umn
2a
TM01模
u01 2.405 最小值 c 2.62a
圆波导中的 传输特性:
圆波导中传输条件 l c > l , f > fc
圆波导的主模是TE11模,cTE11 3.41a ; TM01模为次主模 cTE11 2.62a
必须为整数m
cos m () B1 cos m B2 sin m B sin m ,
m 0,1,2,...
由于圆波导结构具有轴对称性,场的极化方向具有不
确定性,使导波场在φ方向存在 cos m和sin m两
种可能的分布。它们独立存在,相互正交(两个线性 无关的独立成份),截止波长相同,构成同一波导的 极化简并模。
R(贝塞尔方程)的解为
R(r) A1J m (kc r) A2Ym (kc r) 式中 J m (k为crm) 阶贝塞尔函数,
微波技术基础第二章课后答案---杨雪霞

2-1 波导为什么不能传输TEM 波?答:一个波导系统若能传输TEM 波型,则在该系统中必须能够存在静电荷静电核或恒定电流,而在单导体所构成的空心金属波导馆内,不可能存在静电荷或恒定电流,因此也不可能传输TEM 波型。
2-2 什么叫波型?有哪几种波型?答:波型是指每一种能够单独地在规则波导中存在的电磁场的一种分布状态。
根据场的横向分量与纵向分量之间的关系式划分波型,主要有三种:TEM 波(0z E =,0z H =),TE 波(0z E =,0z H ≠),TM 波(0z E ≠,0z H =) 2-3 何谓TEM 波,TE 波和TM 波?其波阻抗和自由空间波阻抗有什么关系?答:0z E =,0z H =的为TEM 波;0z E =,0z H ≠为TE 波;0z E ≠,0z H =为TM 波。
TE 波阻抗:x TE y E wuZ H ηβ===>TM 波阻抗:x TM y E Z H w βηε=== 其中η为TEM 波在无限答煤质中的波阻抗。
2-4 试将关系式y z x H H jw E y z ε∂∂-=∂∂,推导为1()zx y H E j H jw yβε∂=+∂。
解:由y H 的场分量关系式0j zy H H eβ-=(0H 与z 无关)得:y y H j H zβ∂=-∂利用关系式y z x H H jw E y zε∂∂-=∂∂可推出: 11()()y z zx y H H H E j H jw y z jw yβεε∂∂∂=+=+∂∂∂ 2-5 波导的传输特性是指哪些参量?答:传输特性是指传输条件、传播常数、传播速度、波导波长、波形阻抗、传输功率以与损耗和衰减等。
2-6何为波导的截止波长c λ?当工作波长λ大于或小于c λ时,波导内的电磁波的特性有何不同?答: 当波沿Z 轴不能传播时呈截止状态,处于此状态时的波长叫截止波长,定义为2c ck πλ=; 当工作波长大于截止波长时,波数c k k <,此时电磁波不能在波导中传播; 当工作波长小于截止波长时,波数c k k >,此时电磁波能在波导内传播;2-7 矩形波导中的截止波长c λ和波导波长g λ,相速度p υ和群速度g υ有什么区别和联系?它们与哪些因素有关? 答:波导波长为2g πλλβ==>,c λ为截止波长群速为g c υ=<,相速为p υ=,且2p g c υυ⋅=,与c ,工作波长λ,截止波长c λ有关。
圆波导、同轴线、带状线、微带线简介

1、3 带状线简介
带状线的结构 带状线的结构如下图所示,由一个宽度为W, 厚度为t的中心导带和相距为d的上、下两块接地 板构成,接地板之间填充 r 的均匀介质。 带状线支持TEM波传输,这也是带状线的主 模式。同时带状线可认为是由同轴线演变而来, 故存在高次波形TE或TM模。一般可通过选择带 状线的横向尺寸来抑制高次模的出现,当取 min min b W 时可保证TEM波主模单模工 2 r 2 r 作。
2.7 10 Rs r Z 0 A 30 (b t ) c 0.16 Rs B Z 0b
r Z0 120
r Z0 120
带状线简介
Rs f / 为导体表面电阻,且 式中,
2W 1 b t 2b t A 1 ln bt bt t
同轴线简介
同轴线结构图
同轴线简介
同轴线的场方程 求解同轴线中的TEM波各场量,就是在柱坐标系 下求解横向分布函数φ所满足的拉普拉斯方程。 求得的同轴线中TEM波的横向场分量为:
E0 j z Et ar e r E0 j z HБайду номын сангаасt a e r
其中,E0是振幅常数,η =120π/ 是TEM波的 波阻抗。
圆波导
圆波导TM01场结构分布图
圆波导 线(ρ=0)附近最强。根据上述特点,它可以有 效地和轴向流动的电子流交换能量, 由此将其应 用于微波电子管中的谐振腔及直线电子加速器中 的工作模式。
1、2 同轴线简介 同轴线的概念 同轴线是一种典型的双导体传输系统, 它由内、 外同轴的两导体柱构成, 中间为支撑介质。其中, 内、 外半径分别为a和b, 填充介质的磁导率和介电常数 分别为μ 和ε。 同轴线是微波技术中最常见的TEM模传输线,它 既能支持TEM波传输,也能支持TE、TM波传播。 同时,同轴线是一种宽频带微波传输线,因此它得 到广泛的应用。其结构如下图所示。
FEKO应用2-圆波导圆极化天线上课讲义

F E K O应用2-圆波导圆极化天线FEKO应用2:天线系列内容:圆波导圆极化天线一、模型描述1.1模型描述:图1:波导圆极化天线-全模型示意图1.2计算方法描述:采用矩量法-MLFMM1.3计算参数:圆波导主模圆极化-TE11模式12.5GHz高次模圆极化-TE21模式 15GHz计算该类天线的圆极化辐射方向图。
二、主要流程:启动CadFEKO,新建一个工程:Circular_waveguide_TE11_LHC.cfx,在以下的各个操作过程中,可以即时保存做过的任何修正。
2.1:定义变量:在CadFEKO中左侧的树型浏览器中双击“Variables”节点,依次定义如下变量:工作频率:freq=12.5e9工作波长:lam = c0/freq波导波长:lam_w=0.0293圆波导半径:wg_r=0.51*lam圆波导高度:wg_L=2*lam_w开口圆喇叭开口半径:horn_r=lam开口圆喇叭底部半径:horn_r0=0.65*lam开口圆喇叭高度:horn_L=3.05*lam图2:变量定义2.2:模型建立:圆波导天线模型建立:点击菜单“Construct”,选择“Cylinder”,弹出“Create Cylinder”对话框:在“Geometry”标签:Base centre (B): (U: 0.0; V: 0.0; N: -wg_L-horn_L)Radius (R):wg_rHeight(H):wg_LLabel:waveguide点击“Create”;点击“F5”快捷键,在3D视图中适中显示模型。
图3:定义圆波导天线波导部分点击菜单“Construct”,选择“Cone”,弹出“Create Cone”对话框:在“Geometry”标签:Base centre (B): (U: 0.0; V: 0.0; N: - horn_L)Base Radius (Rb):horn_r0Height(H):horn_LTop radius (Rt): horn_rLabel:flare点击“Create”;图4:定义圆波导天线波导部分在左侧树型浏览器中,展开“Model->Geometry”节点,同时选中新建的模型“waveguide”和“flare”,点击鼠标右键“Apply->Union”(或直接点击键盘的U 键),把新生成的模型更名为“horn”;在左侧树型浏览器中,选中模型“horn”,点击鼠标右键,选择“Apply->Simplify”,弹出“Simplify geometry”对话框,采用默认设置,进行模型冗余处理,(会删除模型waveguide和flare中间的公共面-因为该面的前向和后向区域材料相同,且该面的属性也与前后向区域材料相同);在3D视图中,选中新建模型horn的顶部面元(z=0的面),点击鼠标右键,选择“Del”,删除该面元;图5:删除顶部面元在3D视图区域,进入面选模式(光标定在模型的某一面上,依次点击鼠标左键,可以在体选、面选上自动切换),选中新建喇叭天线“horn”的最底部面元(z=-(wg_h+horn_L)的面元),点击鼠标右键,选择“Properties”,弹出“Face properties”对话框:进入“Meshing”标签:勾选:Local mesh sizeMesh size: lam/15点击“OK”按钮。
2章10圆波导

E (r , , z, t ) -
Hr E r (r , , z, t ) H
但此模式不是圆波导中的最低模式故在使用时必须设法避免圆波导中的电磁波圆波导中的电磁波圆波导中常用的三种模式圆波导中常用的三种模式tete0101除低次模以外te01模也是圆波导中常用的一种模式其截止波长为c164a013832代入场解表达式得场结构如右图所示从场分量表示式可看出该模式的各分量均与变量无关因此场分布是轴对称的电场只有分量电力线为横截面内的一个个同心圆故将这个模式也称为圆电模式磁场有r和分量在ra附近只有磁场的纵向分量所以壁表面电流是只有分量的环状电流与环状电流对应的衰减常数随着频率的升高是单调下降的此波型在毫米波段得到广泛应用
H 1 E E 2 2 ( z j z ) r (k ) r
1 j E z H z H r 2 2 ( ) r (k ) r
E H z 1 H 2 2 (j z ) r r (k )
求得Hz以后,就可求出其余电磁场分量:
1 a ' ni cos n j (t z ) Hr E Er= j B( ) J n ( r ) e Z TM ni a sin n 1 j n a 2 ni sin n j (t z ) H Er E= B( ) J n ( r ) e Z TM r ni a cos n
E H z 1 H 2 (j z ) r r (k 2)
kca =μni
kc =μni / a
圆波导场分布推导

⎞ ⎟⎟⎠
B
⎛ ⎜ ⎝
cos mϕ sin mϕ
⎞ ⎟ ⎠
由
Nm(x)的性质,
lim
x→0
Nm
(
x
)
→
−∞
,可得
A2=0,因此有
Hz
(ρ,ϕ,
z)
=
A1 BJ m
( Kc ρ
)
⎛ ⎜ ⎝
cos mϕ sin mϕ
⎞ ⎟
e−
⎠
jβ z
Step 2: 横向分量用纵向分量表示 在圆柱坐标系中有
alρ ρ alϕ alz
Φ
(ϕ
)
=
B1
cos
mϕ
+
B2
sin
mϕ
=
B
⎛ ⎜ ⎝
cos mϕ sin mϕ
⎞ ⎟ ⎠
对于方程(1),如何求解?
其实方程(1)是应用广泛的 Bessel 方程。关于 Bessel 方程和 Bessel 函数,请自学。
因此可以得到 R(ρ)的特殊解:
R(
ρ
)
=
A1 J m
( Kc ρ
)
+
A2 Nm
alρ ρ alϕ alz
JG ∇× A=
1
∂
∂
∂ =1 ∂
∂ − jβ
ρ ∂ρ ∂ϕ ∂z ρ ∂ρ ∂ϕ
Aρ ρ Aϕ Az
Aρ ρ Aϕ Az
JJG
JG
由 ∇ × H = jωε E 可得
JG
JJG
由 ∇ × E = jωμ H 可得
⎧1 ⎪⎪ ρ
∂H z ∂ϕ
+
jβ Hϕ
=
2-光纤结构、导波原理及制造

15:22
20
光纤:结构、导波原理和制造
(b)标量解的特征方程
特征方程由边界条件给出 r=a时 Ey与 E y 在边界上连续,由E(r,, z)可得
r
AJ m (U ) CK m (W ) AUJ m '(U ) CWK m '(W ) 其中,U ua,W wa.
由贝塞尔函数的递推公式
其中u k n a, w k n a
2 2 0 1 2 2 2 2 0 2
15:22
30
光纤:结构、导波原理和制造
传播常数β的本征方程为:
J u K w J u n2 K w m 2 1 1 m m m 2 m 2 2 2 uJ m u wK m w uJ m u n1 wK m w k0 n1 u w
第二章 光纤:结构、导波原 理及制造
光纤:结构、导波原理和制造
主要内容
2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 光纤模式和结构 圆波导的模式理论 单模光纤 梯度折射率光纤 光纤材料 光纤制造 光缆 光缆铺设方法
《现代光纤通信技术》
2
光纤:结构、导波原理和制造
2.1 光纤模式和结构
E =CK m r e
Ⅱ y
jm
e-j t- z 来自2 2 2 式中w2= 2-k2 = 2-k0 n2
采用同样的方法可以求得磁场的解为:
纤芯
包层
H =BJ m ur e
Ⅰ y Ⅱ y
jm
e
-j t- z
H =DK m wr e
jm
圆形波导的理论分析和特性

2
对任意r,f均成立,左右两端均必须为常数: (设为kf2),则有:
圆形波导分析 6 – TE modes(续一)
d F(f ) 2 kf F(f ) 0 2 df
2 2 2
3.2 7 / 8
d R(r ) dR(r ) 2 2 r r (kc kf ) R(r ) 0 2 dr dr
w
kc2 k 2 2 ; k w 2 /
H z 0 f Ez 0 r H w z r r E z r f
Ef
umn cos mf j (w t z ) j ma 2 Emn J m ( r) e 2 sin mf umn a
umn cos mf j (w t z ) Ez Emn J m ( r) e sin mf a m 0 n 1 Hr
圆形波导分析 2 -- 纵横关系
j Ez w H z Er 2 kc r r f j Ez H z Ef 2 w kc r f r j H z w Ez Hr 2 kc r r f j H z Ez Hf 2 w kc r f r
umn ' cos mf j (w t z ) H z H mn J m ( r) e sin mf a m 0 n 1
圆形波导分析6 – TE modes(续四).
此解说明,圆形波导可以支持无穷多种导模TEmn
场沿径向按贝塞尔函数或其导数的规律变化。
波型指数n表示沿半径分布的最大值个数;
圆形波导的特性
2.3 圆形波导解析

Z TM
j
1 H t 2 j z ˆ t E z Kc
1 ˆ ˆ t r r r
式中
§2.3 圆形波导
于是,得到横向场分量的解: cos m jz ' Er j E0 J m ( K c r ) e sin m Kc
立体图:Page73 图2-24
§2.3 圆形波导
2.3.5 TM01 波型
——Er
---------Hφ
TM01波型的场量表达式为
2.405 jz Er j E0 J1( r )e 2.405 R
R
z
Ez E0 J 0 (
2.405 jz r )e R
×× ××
2.405 H j E0 J 1 ( r ) e j z 2.405 R
t2 1 1 2 2 2 2 r r r r 2
横向算子为
§2.3 圆形波导
纵向场满足
2 2 t Ez ( r , ) Kc Ez ( r , ) 0
2 2 t H z ( r , ) Kc H z (r , ) 0
柱坐标下为
2 Ez r 2
截止波长
Er j
(c )TE o 3.41R
11
(2-140)
H 0 R 2
1.841 sin jz J r e 1 2 (1.841) r R cos
' 1.841 cos jz J1 r e
将m=1、 n=1 代 入TE 波型的 场方程
§2.3 圆形波导
圆形波导管:横截面为圆形的空心金属波导管
作用:可作为传输系统用于多路通信中,也常用来 构成圆柱形谐振腔、旋转关节,等元件。
圆形波导的截止频率

圆形波导的截止频率圆形波导是一种常见的波导结构,其截止频率是指在该波导中传播的电磁波的最低频率。
在圆形波导中,电磁波以圆形的横截面模式传播,具有较低的传输损耗和较高的传输效率。
本文将从圆形波导的结构特点、工作原理以及截止频率的影响因素等方面进行探讨。
我们来了解一下圆形波导的结构特点。
圆形波导由一个中心导体和一个外圆形导体组成,中心导体位于外圆形导体的中心轴线上。
中心导体和外圆形导体之间的空间被称为波导空间,电磁波在这个空间中传播。
由于圆形波导的结构对电磁波的传播路径有一定的限制,因此只有当电磁波的频率高于一定的数值时,才能在圆形波导中传播,这个频率就是圆形波导的截止频率。
我们来探讨一下圆形波导的工作原理。
当电磁波的频率高于圆形波导的截止频率时,电磁波可以在圆形波导中传播。
在传输过程中,电磁波沿着圆形波导的轴线方向传播,并在导体表面发生反射。
由于圆形波导的结构对电磁波的传播路径有限制,电磁波在圆形波导中的传播速度比在自由空间中的传播速度要慢。
这导致了电磁波在圆形波导中的波长变短,频率增加。
当电磁波的频率低于圆形波导的截止频率时,电磁波无法在圆形波导中传播,会被波导壁反射回去。
截止频率是圆形波导的一个重要参数,它受到多种因素的影响。
首先,截止频率与波导的几何尺寸密切相关。
波导的直径越大,截止频率就越低,允许传播的频率范围也就越宽。
相反,波导的直径越小,截止频率就越高,允许传播的频率范围也就越窄。
其次,截止频率还与波导中的材料特性有关。
不同材料的介电常数和磁导率会影响电磁波的传播速度和波长,进而影响截止频率。
此外,波导的长度也会对截止频率产生影响,长度越长,截止频率越低。
在实际应用中,圆形波导的截止频率决定了它的使用范围。
当需要传输高频率的电磁波时,可以选择直径较大的圆形波导,以保证传输的稳定性和效率。
而当需要传输低频率的电磁波时,可以选择直径较小的圆形波导,以减小系统的尺寸和成本。
同时,根据截止频率的不同,还可以设计出多种不同的圆形波导结构,以满足不同频率范围的应用需求。
射频技术基础:第2.3圆形波导
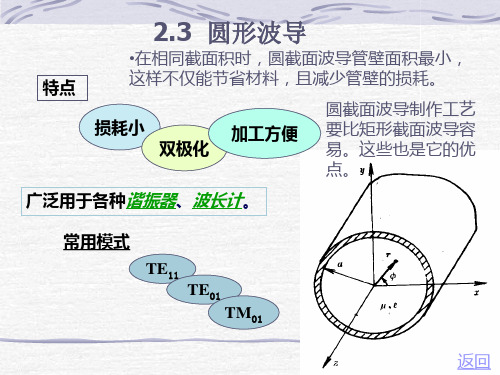
贝塞尔函数
Jn u
1k
u n 2k
k 0 k! n k ! 2
J0 u J1 u
J2 u
k0
1
k
u2k 22k (k !)2
u
1k
u2k
2k 0
22k k !(k 1)!
u2 22 k 0
1k
u2k
22k k !(k 2)!
诺伊曼函数 Yn u
Jn u cos n J n u sin n
∵ Ym (kc ) 0 而场在ρ =0处应为有限 ∴A2=0
2.3 圆形波导
特点
•在相同截面积时,圆截面波导管壁面积最小, 这样不仅能节省材料,且减少管壁的损耗。
损耗小
加工方便
双极化
圆截面波导制作工艺 要比矩形截面波导容 易。这些也是它的优 点。
广泛用于各种谐振器、波长计。
常用模式
TE11 TE01 TM01
返回
一. 与矩形波导一样, 圆波导也只能传输TE和TM波型。设圆 形波导外导体内径为a, 并建立如图 2-6 所示的圆柱坐标。
2)TM模
Hz = 0,
则 Ez (r, , z) E0z (r, )e jz
利用分离变量法求得解后代入边界条件可得本征值
kcmn
umn a
,m
0,1,2,...n
1,2,...
式中 umn 为 J m (kca) 的根。
基本解为:
Ez
(r,,
z)
Emn J m
umn a
r cos m sin m
Ez
m0 n1
E
mn
J
m
umn a
r
cos m sin m
圆波导截止波长计算公式

圆波导截止波长计算公式
圆波导截止波长计算公式是用来计算圆波导中最低能传播的电磁波波长的公式。
圆波导是一种常用的传输线,它可以传输高频电磁波,广泛应用于微波通信、雷达、卫星通信等领域。
圆波导的截止波长是指在圆波导中最低能传播的电磁波波长。
当电磁波的波长小于截止波长时,电磁波无法在圆波导中传播。
因此,圆波导的截止波长是圆波导能够传输的最低频率的电磁波波长。
圆波导截止波长计算公式为:
λc = 2πa/√(εr- (b/a)^2)
其中,λc为圆波导的截止波长,a为圆波导的半径,b为圆波导中心导体的半径,εr为圆波导的相对介电常数。
圆波导截止波长计算公式的推导基于圆波导中的电磁波方程和边界条件。
通过求解电磁波方程和边界条件,可以得到圆波导中最低能传播的电磁波波长。
圆波导截止波长计算公式的应用非常广泛。
在微波通信、雷达、卫星通信等领域中,圆波导是一种常用的传输线。
通过计算圆波导的截止波长,可以确定圆波导能够传输的最低频率的电磁波波长,从而确定圆波导的传输性能。
圆波导截止波长计算公式是圆波导传输性能的重要参数之一。
通过
计算圆波导的截止波长,可以确定圆波导能够传输的最低频率的电磁波波长,从而确定圆波导的传输性能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
H
r
H0
j
kc
cos m Jm (kcr) sin m
e z
H0
kc
J
m
(kc
r
)
cos sin
m m
e
z
H
H0
m
kc2 r
J
m
(kc
r
)
sin cos
m m
e
z
(13)
其中, J'm是(k第cr)一类m阶Bessel函数的导数。
二、圆波导一般解
3. 边界条件 圆波导包含三种边界条件
• 有限条件 f(r=0)≠∞ • 周期条件f( 0 )=f( 2 ) • 理想导体条件地ft(r=R)=0
1 r2
2 2
2 z2
2
2 x2
2 y 2
2 z 2
圆波导包含三种边界条件
•有限条件 f(r=0)≠∞ • 周期条件f( 0 )=f( 2 ) • 理想导体条件ft(r=R)=0
其中t表示切向分量
二、圆波导一般解
各种波导之间的差异主要是横向边界条件不同,由 此可以得到各种不同的波型和模式,很自然,为了 适合圆波导,应该采用圆柱坐标系。 分析方法: 1、利用波动方程求解纵向场分量Ez,Hz的通解 2、根据边界条件求特解 3、利用横纵关系式求解所有场分量的表达式 4、根据表达式讨论其截至特性、传输性和场结构。
r2 R
2 Rz r2
r R
R r
kc2r
2
1
2 2
z
0
显然,可以令一常数-m2
1
d 2
d 2
m2
(7)
r 2
d2R dr 2
r
dR dr
(kc2r 2
m2 )R
0
二、圆波导一般解
其解分别是
( )
c1
cos
m
c2
sin
m
cos m
sin
m
R(r
)
c3
J
m
(kc
r
)
c4
Nm
(kc
其中t表示切向分量
有限条件导致圆波导体不出现Neumann函数。 周期边界条件要求m为整数阶。
二、圆波导一般解
理想导体边界条件要求r=R处, E=0,也即
J m (kc R) 0
设 m是n m阶Bessel函数导数的第n个根,则
(14)
kc R m n (n 1, 2, 3, ) (15)
kc
z
H
j
kc2r
H
0
J
m
mn
R
r
sin cos
m m
e
j
z
Hz
H0Jm
mn
R
r
sin cos
m m
e j z
J
v
(
x)
cos(v ) sin(v
)
J
v
(
x)
二、圆波导一般解
利用纵向分量表示横向分量
H j E
E jH
1
r
H
z
H z
j Er
1
r
Ez
E z
j Hr
(11)
Hzr
Hz r
j E
(10)
1
r
r
(rH ) Hr 来自 j Ez注意到
Ezr
Ez r
j H
1
r
r
(rE )
Er
j Hz
z
二、圆波导一般解
可以把上面两个Maxwell旋度方程分解成两组
j Er
H
1 r
Hz
Er
j H
Ez r
Hr
j E
Hz r
j Hr
E
1 r
Ez
(12)
H
1 kc2
j
Ez r
r
Hz
Er
1 kc2
j
r
Hz
Ez r
2.2 圆波导
我们已经研究了矩形波导,对于 圆波导的提出应该有它的理由。
一、圆波导的一些特点 在矩形波导应用之后, 还有必要提出圆波导吗?当然,既然
要用圆波导,有其优点存在。
主要有: 1.实践的需要 结构几何对称性——独特用途如,雷达的旋转搜索。如果没有 旋转关节,那只好发射机跟着转。象这类应用中, 圆波导成了 必须要的器件。
m n
R
2 c
c
2 R m n
(16)
二、圆波导一般解
圆波导TE波场表达形式 γ =jβ,H0=k2c Hm,n
Er
j
m
kc2r
H0Jm
mn
R
r
sin cos
m m
e
j
z
E
j kc
H0 Jm
mn
R
r
sin cos
m m
e
j
z
Ez 0
Hr
j
kc
H0 Jm
mn
R
r
sin cos
m m
e
j
r
)
Jm (kcr) Nm (kcr)
(8)
其中c1,c2,c3,c4为常数。m=0,1,2,…为整数。
Jm (kcr)为第一类m阶Bessel函数 Nm (kcr)为第二类m阶Bessel函数(Neumann函数)
二、圆波导一般解
对于Neumann函数最大特点是x→0,Nm(x)→-∞。
而空心波导,中间没有导体的条件下不可能出现 Neumann函数。
Hz
cos m H0 Jm (kcr) sin m
e z
(9)
2. 纵向分量法
贝塞尔函数曲线
U’11=1.841
U01=2.40 5
J 0 '(x) J1 (x)
J
v
(
x)
x 2
v
k 0
k!(v
x2 4
2
k
1)
Nv
(x)
很容易引出一个品质因数F
F Pmax S aL
很明显,数字研究早就指出:在相同周长的条件下, 圆面积最大
思考:圆波导与矩形波导区别?
思考:圆波导与矩形波导区别?
截面形状不同 采用不同坐标系 波动方程的表现
形式不同
形状不同导致边界条 件的表现形式不同
解的形式不同
拉普拉斯算子
2
1 r
r
r
r
Hr
1 kc2
j
r
Ez
Hz r
E
1 kc2
r
Ez
j
Hz r
二、圆波导一般解
j, H0 kc2Hm,n
TE模式
Ez
0; H z
H0
Jm
(kc r )
cos m sin m
e
z
有
Er
H0
j m
kc2 r
Jm
(kcr)
sin m cos m
e
z
E
相同的周长圆的面积最大
可见,要探索小衰减,大功率传输线,想到圆波 导是自然的。
特点小结:损耗小;用于天线馈线;也可用于较远距离的 传输线;广泛用作微波谐振腔。
2.功率容量和衰减是波导传输线十分重要的两个指 标。这个问题从广义上看
功率容量 衰减 a
Pmax S(其中S是截面) L(其中L是周长)
二、圆波导一般解
1. 它们也可以划分为TE和TM波。
我们以TE波作为例子,这时 Ez=0
z分量分别满足
2
H
z
k2Hz
0
H r
z
|rR
0
对于圆柱坐标
2
1 r
r
r
r
1 r2
2 2
2 z2
假设
H z R(r)( )Z (z)
(1)
(2) (3)
二、圆波导一般解
同样可解出 Z ( z) ce z
(4)
于是
H z R(r)( )e z
(5)
且满足
2
1 r
r
r
r
...
2Hz r2
1 Hz r r
1 r2
2Hz 2
kc2 H z
(6)
其中
2 kc2 k 2
二、圆波导一般解
2Rz r2
1R r r
R r2
2z 2
kc2 H z
等式两边除以ΦR,乘上r2
