水力学第2-7章答案(吕宏兴__裴国霞等)
水力学答案完整版

第一章 绪论答案1-1.20℃的水2.5m 3,当温度升至80℃时,其体积增加多少? [解] 温度变化前后质量守恒,即2211V V ρρ= 又20℃时,水的密度31/23.998m kg =ρ 80℃时,水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆ 1-2.当空气温度从0℃增加至20℃时,运动粘度ν增加15%,重度γ减少10%,问此时动力粘度μ增加多少(百分数)? [解] 原原ρννρμ)1.01()15.01(-+==原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμ此时动力粘度μ增加了3.5%。
1-3.有一矩形断面的宽渠道,其水流速度分布为μρ/)5.0(002.02y hy g u -=,式中ρ、μ分别为水的密度和动力粘度,h 为水深。
试求m h 5.0=时渠底(y =0)处的切应力。
[解] μρ/)(002.0y h g dy du -=)(002.0y h g dydu -==∴ρμτ 当h =0.5m ,y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4.一底面积为45×50cm 2,高为1cm 的木块,质量为5kg ,沿涂有润滑油的斜面向下作等速运动,木块运动速度u=1m/s ,油层厚1cm ,斜坡角22.620 (见图示),求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时,等速下滑y u AT mg d d sin μθ== 001.0145.05.062.22sin 8.95sin ⨯⨯⨯⨯==δθμu A mg =s Pa 08376.0⋅ 1-5.已知液体中流速沿y 方向分布如图示三种情况,试根据牛顿内摩擦定律y ud d μτ=,定性绘出切应力沿y[解]1-6.为导线表面红绝缘,将导线从充满绝缘涂料的模具中拉过。
《水力学》第二章答案

第二章:水静力学 一:思考题2-1.静水压强有两种表示方法,即:相对压强和绝对压强2-2.特性(1)静水压强的方向与受压面垂直并指向手压面;(2)任意点的静水压强的大小和受压面的方位无关,或者说作用于同一点上各方向的静水压强都相等. 规律:由单位质量力所决定,作为连续介质的平衡液体内,任意点的静水压强仅是空间坐标的连续函数,而与受压面的方向无关,所以p=(x,y,z)2-3答:水头是压强的几何意义表示方法,它表示h 高的水头具有大小为ρgh 的压强。
绝对压强预想的压强是按不同的起点计算的压强,绝对压强是以0为起点,而相对压强是以当地大气压为基准测定的,所以两者相差当地大气压Pa.绝对压强小于当地大气压时就有负压,即真空。
某点负压大小等于该点的相对压强。
Pv=p'-pa2-4.在静水压强的基本方程式中C g p z =+ρ中,z 表示某点在基准面以上的高度,称为位置水头,g p ρ表示在该点接一根测压管,液体沿测压管上升的高度,称为测压管高度或压强水头,g p z ρ+称为测压管水头,即为某点的压强水头高出基准面的高度。
关系是:(测压管水头)=(位置水头)+(压强水头)。
2-5.等压面是压强相等的点连成的面。
等压面是水平面的充要条件是液体处于惯性坐标系,即相对静止或匀速直线运动的状态。
2-6。
图中A-A 是等压面,C-C,B-B 都不是等压面,因为虽然位置高都相同,但是液体密度不同,所以压强水头就不相等,则压强不相等。
2-7.两容器内各点压强增值相等,因为水有传递压强的作用,不会因位置的不同压强的传递有所改变。
当施加外力时,液面压强增大了Ap∆,水面以下同一高度的各点压强都增加Ap∆。
2-8.(1)各测压管中水面高度都相等。
(2)标注如下,位置水头z,压强水头h,测压管水头p.图2-82-9.选择A2-10.(1)图a 和图b 静水压力不相等。
因为水作用面的面积不相等,而且作用面的形心点压强大小不同。
《水力学》第二章答案

第二章:水静力学一:思考题2-1.静水压强有两种表示方法,即:相对压强和绝对压强2-2.特性(1)静水压强的方向与受压面垂直并指向手压面;(2)任意点的静水压强的大小和受压面的方位无关,或者说作用于同一点上各方向的静水压强都相等. 规律:由单位质量力所决定,作为连续介质的平衡液体内,任意点的静水压强仅是空间坐标的连续函数,而与受压面的方向无关,所以p=(x,y,z)2-3答:水头是压强的几何意义表示方法,它表示h高的水头具有大小为p gh的压强。
绝对压强预想的压强是按不同的起点计算的压强,绝对压强是以0为起点,而相对压强是以当地大气压为基准测定的,所以两者相差当地大气压Pa.绝对压强小于当地大气压时就有负压,即真空。
某点负压大小等于该点的相对压强。
Pv=p'-pa2-4•在静水压强的基本方程式中z+〃=C中,z表示某点在基准面以上的高度,/pg称为位置水头,*表示在该点接一根测压管,液体沿测压管上升的高度,称为测p g压管高度或压强水头,z+亠称为测压管水头,即为某点的压强水头高出基准面p g的高度。
关系是:(测压管水头)=(位置水头)+(压强水头)。
2-5.等压面是压强相等的点连成的面。
等压面是水平面的充要条件是液体处于惯性坐标系,即相对静止或匀速直线运动的状态。
2-6。
图中A-A是等压面,C-C,B-B都不是等压面,因为虽然位置高都相同,但是液体密度不同,所以压强水头就不相等,则压强不相等。
2-7.两容器内各点压强增值相等,因为水有传递压强的作用,不会因位置的不同压强的传递有所改变。
当施加外力时,液面压强增大了坐,水面以下同一高度A的各点压强都增加坐。
A2-8.(1)各测压管中水面高度都相等。
(2)标注如下,位置水头z,压强水头h,测压管水头p・2-10・(1)图a和图b静水压力不相等。
因为水作用面的面积不相等,而且作用面的形心点压强大小不同。
所以静水压力Pa>Pb・(2)图c和图d静水压力大小相等。
水力学第27章答案吕宏兴裴国霞等

2-1 解:(1)p A+γ水·ΔH=γH·Δh;所以p A=γH·Δh-γ水·ΔH=38.02kP a(γH=13.6γ水)(2)测压管长度:p A=γ水·h 所以h= p A/γ水=38.02×103/9.8×103=3.88m2-3 解:P A-γh=p B-γ(h1+h2+h)+γH h1所以,p A-p B=γH h1-γ(h1+h2)=13.6×9.8×0.53-9.8×(0.53+1.2) =53.68kPa2-6解:p A=γH(h1+h2)-γ(h1+h2)=13.6××9.8××0.53-9.8×(0.53+1.2)=53.68kp a 2-7 解:(1)左支:绝对:p c'=p0'+γh0=86.5+9.8×2=106.1kPa(2)右支:p c'=p a+γ水h;h=(p c'-p a)/γ水=(106.1-9.8)/9.8=0.827m 2-8 解:p A=0.6p a=0.6×98=58.8kp a(1)左支:p A=γh1 h1=p A/γ=58.8/9.8=6m(2)右支:p A+γh=γH h2 h2=(p A+γh)/γH=0.456m2-10解:设管嘴内的绝对压强为p',则p'+γh= p aP v=p a- p'=γh=9.8×0.6=5.886kp a2-12解:(1)设容器底部面积为S,相对压强为P,对容器底部进行受力分析:由牛顿第二定律:ΣF=m·a;-(P+G)=-m·a 所以得出p·s+γ·s·h=ρ·s·h·ap=ρ·h·a -γh=γh/g·a-γh=γh(a/g-1)p=9.8×2(4.9/9.8-1)=-9.8kN/㎡(2)相对压强为0 p=γh(1-a/g)=0 由式可知a/g-1=0a=g=9.8m/s2时,p=02-142-16解:下游无水时,h1=1.2m,h2=1.85m,b=3m(1)求静水总压力P方法10:P=Ωb=1/2[γh1+γ(h1+h2)]×AB×b=1/2×9.8×(2×1.2+1.85)×2.14×3=133.7kN方法20:P=γh c A=γ(h1+h2/2)×AB×b=133.7kN(2)计算P的作用点D的位置:e=l/3·(2h1+h2ˊ)/(h1+h2ˊ)=0.915m(其中hˊ=h1+h2)(3)计算T:因为ΣM a=0 则:P·AC+G·AO·cos600 其中:AC=AB-e=2.14-0.915=AO=AB/2133.7×(2.14-0.915)+9.8×2.14/2×1/2=T×2.14×1/2所以T=158kN下游有水时,AB=2.14,b=3m,p A=γh1=9.8×1.2=11.76kPa,p A=p B (1)静水总压力P左=γ·h c1A1=9.8×(h1+h2/2)×AB×b=P1=133.7kN (其中h c1=h1+h2/2 A1=AB×b)e1=0.915mP右=γ·h c2A2=9.8×h2/2×AB×b=P2=58.2kN(其中h c2=h2/2)e2=l/3=2.14/3=0.71m(2)因为ΣM a=0P1×(AB-e1)+G×AO×cos600=T×AB×cos600+P2×(AB-e2)T=80.2kN2.18已知:H=3m,b=5m,R=4.3m,θ=450 求P 及作用点 H=Rsin450=4.3×22=3m (1)水平分力:P x =γh e A x =9.8×1.5×3×5=220.5(KN) (2)铅垂分力:P z =γv=γΩ×b=9.8×1.143×5=56.01(KN) 其中:Ω=S 梯OABC —S 扇OAC =8.4-7.257=1.143㎡ S 梯OABC =0.5×[4.3+(4.3-3)]×3=8.4㎡ S 扇OAC =360450πR 2=360450×3.14×4.32=7.257㎡ (3)P=PPzx22+=01.565.22022+=227.5(KN )(4)P 与水平面的夹角α: α=arctanPPxz =arctan5.22001.56=14.250=14015` 2-192-20 解:已知b=10m ,k=8m(1)夹角计算:Sin β1=(173-170)/8=3/8=0.375(cos β1=550.5/8)β1=22.020Sin β2=(170-165)/8=5/8=0.625(cos β2=0.781) β2=38.680(2)水平方向水压力P x :(闸门宽b=10m)公式:P x =γh c A x =9.8×4×8×10=3136kN(另法:P x =1/2×9.8×8×8×10=kN )(3)垂直方向水压力P z =γV关键计算压力体体积V=[三角形ofc (11.12㎡)+扇形ocd (33.88㎡)-梯形ofed (34.36)]×b所以 V=(11.12+33.86-34.36)×10=10.636×10=106.36m ³P z =γV=9.8×106.36=1042.33kN(4)总压力P:P=(P x 2+P z 2)=3304.7kN作用方向α=arctan1042.3/3304.7=17.51P 与水平面夹角17.510,且过o 点。
(完整)水力学第二章思考题答案

(完整)水力学第二章思考题答案2.1。
恒定流:如果在流场中任何空间点上所有的运动要素都不随时间而改变.非恒定流:如果在流场中任何空间点上有任何一个运动要素是随时间而变化。
均匀流:水流的流线为相互平行的直线.非均匀流:水流的流线不是相互平行的直线。
渐变流:水流的流线虽然不是相互平行的直线,但几乎近于平行的直线.急变流:水流的流线之间夹角很大或者流线的曲率半径很小.按运动要素是否彼此平行的直线分为均匀流和非均匀流,而非均匀流按流线的不平行和弯曲程度又分为渐变流和急变流。
渐变流重要性质为:过水断面上近似服从静压分布:Z+P/y=C2.2。
此时的A₁υ₁=A₂υ₂符合连续方程.两个断面无支流,且上游水位恒定,则下游通过的流量一定,则流量保持平衡,满足该公式。
2。
3能量方程:Ζ₁+Ρ₁/ρg+α₁(μ₁)²/2g=Ζ₂+Ρ₂/ρg+α₂(μ₂)²/2g+hw’。
Ζ₁:位置水头;Ρ₁/ρg:压强水头;(μ₁)²/2g:流速水头;Ζ₂:单位位能;Ρ₂/ρg:单位压能;(μ₂)²/2g:单位动能;hw’:水头损失。
能量意义:在总流中任意选取两个过水断面,该两断面上液流所具有的总水头若为H₁和H₂,则:H₁=H₂+hw。
2.4这些说法都不对.对于理想液体来说,在无支流进去的情况下,其各断面的流量总和是相等的,根据能量方程:Ζ₁+Ρ₁/ρg+α₁(μ₁)²/2g=Ζ₂+Ρ₂/ρg+α₂(μ₂)²/2g+hw’,及连续方程:A ₁υ₁=A₂υ₂。
可以看出:只要其流量不改变,能量的总和就不会变。
则水是由流速大地方向流速小的地方流这种说法就是错误的。
总流的动量方程:ΣF=ρQ(Β₂υ₂-Β₁υ₁),也说明了这一点。
2.5总水头线:把各断面H=Ζ+Ρ/ρg+α(μ)²/2g描出的点子连接起来得到的线就是总水头线;测压管水头线:把各断面的(Ζ+Ρ/ρg)值的点子连接起来得到的线就是测压管水头线。
水力学第2-7章参考答案(吕宏兴__裴国霞等)

2-1 解:(1)p A+γ水·ΔH=γH·Δh;所以p A=γH·Δh-γ水·ΔH=38.02kP a(γH=13.6γ水)(2)测压管长度:p A=γ水·h 所以h= p A/γ水=38.02×103/9.8×103=3.88m2-3 解:P A-γh=p B-γ(h1+h2+h)+γH h1所以,p A-p B=γH h1-γ(h1+h2)=13.6×9.8×0.53-9.8×(0.53+1.2) =53.68kPa2-6解:p A=γH(h1+h2)-γ(h1+h2)=13.6××9.8××0.53-9.8×(0.53+1.2)=53.68kp a 2-7 解:(1)左支:绝对:p c'=p0'+γh0=86.5+9.8×2=106.1kPa(2)右支:p c'=p a+γ水h;h=(p c'-p a)/γ水=(106.1-9.8)/9.8=0.827m 2-8 解:p A=0.6p a=0.6×98=58.8kp a(1)左支:p A=γh1 h1=p A/γ=58.8/9.8=6m(2)右支:p A+γh=γH h2 h2=(p A+γh)/γH=0.456m2-10解:设管嘴内的绝对压强为p',则p'+γh= p aP v=p a- p'=γh=9.8×0.6=5.886kp a2-12解:(1)设容器底部面积为S,相对压强为P,对容器底部进行受力分析:由牛顿第二定律:ΣF=m·a;-(P+G)=-m·a 所以得出p·s+γ·s·h=ρ·s·h·ap=ρ·h·a -γh=γh/g·a-γh=γh(a/g-1)p=9.8×2(4.9/9.8-1)=-9.8kN/㎡(2)相对压强为0 p=γh(1-a/g)=0 由式可知a/g-1=0a=g=9.8m/s2时,p=02-142-16解:下游无水时,h1=1.2m,h2=1.85m,b=3m(1)求静水总压力P方法10:P=Ωb=1/2[γh1+γ(h1+h2)]×AB×b=1/2×9.8×(2×1.2+1.85)×2.14×3=133.7kN方法20:P=γh c A=γ(h1+h2/2)×AB×b=133.7kN(2)计算P的作用点D的位置:e=l/3·(2h1+h2ˊ)/(h1+h2ˊ)=0.915m(其中hˊ=h1+h2)(3)计算T:因为ΣM a=0 则:P·AC+G·AO·cos600 其中:AC=AB-e=2.14-0.915=AO=AB/2133.7×(2.14-0.915)+9.8×2.14/2×1/2=T×2.14×1/2所以T=158kN下游有水时,AB=2.14,b=3m,p A=γh1=9.8×1.2=11.76kPa,p A=p B (1)静水总压力P左=γ·h c1A1=9.8×(h1+h2/2)×AB×b=P1=133.7kN (其中h c1=h1+h2/2 A1=AB×b)e1=0.915mP右=γ·h c2A2=9.8×h2/2×AB×b=P2=58.2kN(其中h c2=h2/2)e2=l/3=2.14/3=0.71m(2)因为ΣM a=0P1×(AB-e1)+G×AO×cos600=T×AB×cos600+P2×(AB-e2)T=80.2kN2.18已知:H=3m,b=5m,R=4.3m,θ=450 求P 及作用点 H=Rsin450=4.3×22=3m (1)水平分力:P x =γh e A x =9.8×1.5×3×5=220.5(KN) (2)铅垂分力:P z =γv=γΩ×b=9.8×1.143×5=56.01(KN) 其中:Ω=S 梯OABC —S 扇OAC =8.4-7.257=1.143㎡ S 梯OABC =0.5×[4.3+(4.3-3)]×3=8.4㎡ S 扇OAC =360450πR 2=360450×3.14×4.32=7.257㎡ (3)P=PPzx22+=01.565.22022+=227.5(KN )(4)P 与水平面的夹角α: α=arctanPPxz =arctan5.22001.56=14.250=14015` 2-192-20 解:已知b=10m ,k=8m(1)夹角计算:Sin β1=(173-170)/8=3/8=0.375(cos β1=550.5/8)β1=22.020Sin β2=(170-165)/8=5/8=0.625(cos β2=0.781) β2=38.680(2)水平方向水压力P x :(闸门宽b=10m)公式:P x =γh c A x =9.8×4×8×10=3136kN(另法:P x =1/2×9.8×8×8×10=31363136kN )(3)垂直方向水压力P z =γV关键计算压力体体积V=[三角形ofc (11.12㎡)+扇形ocd (33.88㎡)-梯形ofed (34.36)]×b所以 V=(11.12+33.86-34.36)×10=10.636×10=106.36m ³P z =γV=9.8×106.36=1042.33kN(4)总压力P:P=(P x 2+P z 2)=3304.7kN作用方向α=arctan1042.3/3304.7=17.51P 与水平面夹角17.510,且过o 点。
【最新试题库含答案】水力学第二章课后答案_0

水力学第二章课后答案:篇一:水力学第二章课后答案1 2 6 11答案在作业本2.12 (注:书中求绝对压强)用多管水银测压计测压,图中标高的单位为m,试求水面的压强p0。
解: p0?p4??3.0?1.4??g?p5??2.5?1.4??Hgg??3.0?1.4??g?pa??2.3?1.2??Hgg??2.5?1.2??g??2.5?1.4??Hgg??3.0?1.4??g ?pa ??2.3?2.5?1.2?1.4??Hgg??2.5?3.0?1.2?1.4??g?pa????2.3?2.5?1.2?1.4??13.6??2.5?3.0?1.2?1.4??g???g?pa?265.00(kPa)答:水面的压强p0?265.00kPa。
2-12形平板闸门AB,一侧挡水,已知长l=2m,宽b=1m,形心点水深hc=2m,倾角?=45?,闸门上缘A处设有转轴,忽略闸门自重及门轴摩擦力,试求开启闸门所需拉力T。
解:(1)解析法。
P?pC?A?hC?g?bl?1000?9.807?2?1?2?39.228(kN)bl3IChC222yD?yC???????2.946CyCAsin?sin4512?blsin45sin?2-13矩形闸门高h=3m,宽b=2m,上游水深h1=6m,下游水深h2=4.5m,试求:(1)作用在闸门上的静水总压力;(2)压力中心的位置。
解:(1)图解法。
压强分布如图所示:∵ p????h1?h???h2?h????g??h1?h2??g??6?4.5??1000?9.807?14.71(kPa)P?p?h?b?14.71?3?2?88.263(kN)b合力作用位置:在闸门的几何中心,即距地面(1.5m,)处。
2(2)解析法。
P1?p1A??g?h1?1.5??hb??6?1.5??9807?3?2?264.789(kN) bh3IC1?2h2?yD1?yC2??4.5???4.5?? yC2A4.5?bh4.5?12??1??20.25?0.75??4.667(m) 4.5P2?p2A??g?h2?1.5??hb?3?9.807?3?2?176.526(kN) yD2?yC1?IC1?2IC?12??yC1????3?0.75??3.25(m) yC1AyC1?A?3合力:P?P1?P2?88.263(kN)合力作用位置(对闸门与渠底接触点取矩):yDP?P1?h1?yD1??P2?h2?yD2?。
水力学第二章课后习题答案
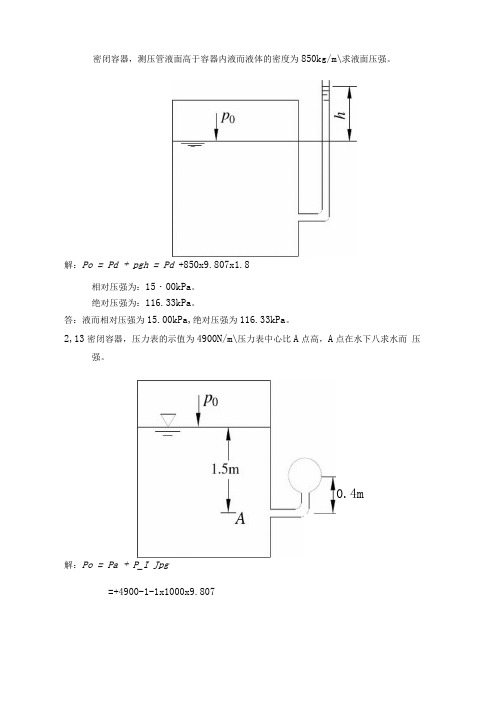
密闭容器,测压管液面高于容器内液而液体的密度为850kg/m\求液面压强。
解:Po = Pd + pgh = Pd +850x9.807x1.8相对压强为:15・00kPa。
绝对压强为:116.33kPa。
答:液而相对压强为15.00kPa,绝对压强为116.33kPa。
2,13密闭容器,压力表的示值为4900N/m\压力表中心比A点高,A点在水下八求水而压强。
0.4m解:Po = Pa + P_I Jpg=+4900-1-1x1000x9.807=Pa —5.888 (kPa)相对压强为:-5.888kPa 。
绝对压强为:95.437 06 答:水而相对压强为-5.888kPa. 绝对压强为95.437 kPa 。
解:(1)总压力:(2)支反力: 不同之原因: & = A ・p = 4pg X3X3 = 353,052 (kN) R = %=林+%=%+Qg(lxlxl + 3x3x3)=1绻 +9807 x28 = 274.596 kN +%总压力位底面水压力与面积的乘枳,为圧力体XQg 。
而支座反力与水体 重量及箱体重力相平衡,而水体重量为水的实际体积XQg 。
答:水箱底面上总压力是353.052kN. 4个支座的支座反力是274.596kNO2.14盛满水的容器,顶口装有活塞A.宜径dr 容器底的直径D G 高hr 如活塞上加 力2520N(包括活塞自重),求容器底的压强和总压力。
3m Im解:(1)容器底的压强:Pn = P A +pgh = 25^ + 9807xl.8 = 37.706 (kPa)(相对压强)(2)容器底的总压力:pQ = App =^D~ -Po = -^XI"X37.706x 10^ = 29.614 (kN) 答:容器底的压强为37.706kPa,总圧力为29・614kN。
用多皆水银测压计测圧,图中标髙的单位为m,试求水而的压强po。
Po v3.0_yL4隶解^ 〃0=久-(3・0-1・4)必=p5+(2・5-14)%g-(3・0-l ・4)Qg =Pa +(2・3-l ・2)%g-(2・5-l ・2)Qg+(2・5-l ・4)%g-(3・0-14)Qg=化+(2・3+2・5-1・2-14)乐 g-(2・5+3・0 - L2-14)Qg = N+[(2・3 + 2・5-l ・2-l ・4)xl3・6-(2・5 + 3・0-l ・2-l ・4)Qg]Qg=几+265.00 (kPa)答:水而的压强Po=265・OOkPa 。
《水力学》第二章答案

第二章:水静力学 一:思考题2-1.静水压强有两种表示方法,即:相对压强和绝对压强2-2.特性(1)静水压强的方向与受压面垂直并指向手压面;(2)任意点的静水压强的大小和受压面的方位无关,或者说作用于同一点上各方向的静水压强都相等. 规律:由单位质量力所决定,作为连续介质的平衡液体内,任意点的静水压强仅是空间坐标的连续函数,而与受压面的方向无关,所以p=(x,y,z)2-3答:水头是压强的几何意义表示方法,它表示h 高的水头具有大小为ρgh 的压强。
绝对压强预想的压强是按不同的起点计算的压强,绝对压强是以0为起点,而相对压强是以当地大气压为基准测定的,所以两者相差当地大气压Pa.绝对压强小于当地大气压时就有负压,即真空。
某点负压大小等于该点的相对压强。
Pv=p'-pa2-4.在静水压强的基本方程式中C g p z =+ρ中,z 表示某点在基准面以上的高度,称为位置水头,g p ρ表示在该点接一根测压管,液体沿测压管上升的高度,称为测压管高度或压强水头,g p z ρ+称为测压管水头,即为某点的压强水头高出基准面的高度。
关系是:(测压管水头)=(位置水头)+(压强水头)。
2-5.等压面是压强相等的点连成的面。
等压面是水平面的充要条件是液体处于惯性坐标系,即相对静止或匀速直线运动的状态。
2-6。
图中A-A 是等压面,C-C,B-B 都不是等压面,因为虽然位置高都相同,但是液体密度不同,所以压强水头就不相等,则压强不相等。
2-7.两容器内各点压强增值相等,因为水有传递压强的作用,不会因位置的不同压强的传递有所改变。
当施加外力时,液面压强增大了Ap∆,水面以下同一高度的各点压强都增加Ap∆。
2-8.(1)各测压管中水面高度都相等。
(2)标注如下,位置水头z,压强水头h,测压管水头p.图2-8 2-9.选择A2-10.(1)图a 和图b 静水压力不相等。
因为水作用面的面积不相等,而且作用面的形心点压强大小不同。
《水力学》第二章答案

第二章:水静力学 一:思考题2-1.静水压强有两种表示方法,即:相对压强和绝对压强2-2.特性(1)静水压强的方向与受压面垂直并指向手压面;(2)任意点的静水压强的大小和受压面的方位无关,或者说作用于同一点上各方向的静水压强都相等. 规律:由单位质量力所决定,作为连续介质的平衡液体内,任意点的静水压强仅是空间坐标的连续函数,而与受压面的方向无关,所以p=(x,y,z)2-3答:水头是压强的几何意义表示方法,它表示h 高的水头具有大小为ρgh 的压强。
绝对压强预想的压强是按不同的起点计算的压强,绝对压强是以0为起点,而相对压强是以当地大气压为基准测定的,所以两者相差当地大气压Pa.绝对压强小于当地大气压时就有负压,即真空。
某点负压大小等于该点的相对压强。
Pv=p'-pa2-4.在静水压强的基本方程式中C g p z =+ρ中,z 表示某点在基准面以上的高度,称为位置水头,g p ρ表示在该点接一根测压管,液体沿测压管上升的高度,称为测压管高度或压强水头,g p z ρ+称为测压管水头,即为某点的压强水头高出基准面的高度。
关系是:(测压管水头)=(位置水头)+(压强水头)。
2-5.等压面是压强相等的点连成的面。
等压面是水平面的充要条件是液体处于惯性坐标系,即相对静止或匀速直线运动的状态。
2-6。
图中A-A 是等压面,C-C,B-B 都不是等压面,因为虽然位置高都相同,但是液体密度不同,所以压强水头就不相等,则压强不相等。
2-7.两容器内各点压强增值相等,因为水有传递压强的作用,不会因位置的不同压强的传递有所改变。
当施加外力时,液面压强增大了Ap∆,水面以下同一高度的各点压强都增加Ap∆。
2-8.(1)各测压管中水面高度都相等。
(2)标注如下,位置水头z,压强水头h,测压管水头p.图2-82-9.选择A2-10.(1)图a 和图b 静水压力不相等。
因为水作用面的面积不相等,而且作用面的形心点压强大小不同。
水力学第二章的课后答案详解

1 2 6 11答案在作业本2.12(注:书中求绝对压强)用多管水银测压计测压,图中标高的单位为m ,试求水面的压强0p 。
水Δ3.0p 0水Δ1.4Δ2.5Δ1.2Δ2.3汞解:4 3.0 1.4p p g5 2.5 1.4 3.0 1.4Hgp g g 2.3 1.22.5 1.22.5 1.43.0 1.4a HgHgp ggg g2.3 2.5 1.2 1.42.53.0 1.2 1.4aHgp g g2.32.5 1.2 1.413.6 2.53.0 1.2 1.4ap g g265.00ap (kPa )答:水面的压强0p 265.00kPa 。
2-12形平板闸门AB ,一侧挡水,已知长l =2m ,宽b =1m ,形心点水深c h =2m ,倾角=45,闸门上缘A 处设有转轴,忽略闸门自重及门轴摩擦力,试求开启闸门所需拉力T 。
lbαB AThc解:(1)解析法。
10009.80721239.228C C Pp Ah g bl(kN )3222212222.946122sinsin 4512sin 45sinC CD CC C blI h y y h y Abl2-13矩形闸门高h=3m,宽b=2m,上游水深1h=6m,下游水深2h=4.5m,试求:(1)作用在闸门上的静水总压力;(2)压力中心的位置。
h h2h1解:(1)图解法。
压强分布如图所示:h1h2p∵12p h h h h g12h h g6 4.510009.80714.71(kPa)14.713288.263P p h b(kN)合力作用位置:在闸门的几何中心,即距地面(1.5m,)2b处。
(2)解析法。
111 1.56 1.5980732264.789P p Ag h hb(kN )3221221124.54.54.5 4.512C D C C bh I h y y y Abh120.250.754.6674.5(m )222 1.539.80732176.526P p A g h hb (kN )22211111130.753.253C CD C C C C I I y y yy A y A(m)合力:1288.263PP P (kN )合力作用位置(对闸门与渠底接触点取矩):111222D D D y PP h y P h y 111222D D DP h y P h y y P264.7896 4.667176.526 4.5 3.2588.2631.499(m )答:(1)作用在闸门上的静水总压力88.263kN ;(2)压力中心的位置在闸门的几何中心,即距地面(1.5m,)2b处。
水力学 第二章课后题答案

r • H • D 2[ ]
rHD 2
9.8 14000 200 2 14000000
0.98cm
2.1 盛有同种介质(密度A =B
=1200kg/m 3 )的两容器,其中心
点A、B位于同一高程,今用U形
差压计测定A、B点之压差(差
压计内盛油,密度 0=
800kg/m 3),A点还装有一水银
测压计。其它有关数据如图题1-
2所示(s=5cm,
h 1
=20cm,h=4cm)
问:
1. A、B两点之压差为多少?
解:当下游无水时: 水平分力
Px rhC 1Ax1 9.8 13 26 1 3312.4KN(水平向右)
垂直分力
Pz rV1 9.8 梯形abcd 1 9.8 0.5 (26 18) 4 1 862.04KN(竖直向下)
当下游有水时 水平分力
Px rhC 1Ax1 rhc2Ax 2 3312.4 9.8 3 6 1 3316KN(水平向右)
(1)相同,不相等 (2)减小,上升
2.5 压力体的概念是什么?如何确定压力体的范围及作用力 方向?
压力体是计算总压力垂直分力 FPZ 的概念,只是作为计算
曲面上垂直压力的一个数值当量,不是由实际水体构成。
由受压曲面本身、通过曲面的四个边缘向自由液面作的
铅垂面、自由液面或其延伸面围成的体积就是压力体。压力 体位于受压面同一侧的叫做实压力体,液体压力向下;压力 体位于受压面异侧的叫做虚压力体,液体压力向上。
2
98
1 ctg 60
2
2
P
1 2
2 sin 60
则拉力 T 139.5KN
2.8 有—直立的矩形自动 翻板闸门,门高H为5m, 如果要求水面超过门顶h 为lm时,翻板闸门即可
《水力学》第二章答案

第二章:水静力学 一:思考题2-1.静水压强有两种表示方法,即:相对压强和绝对压强2-2.特性(1)静水压强的方向与受压面垂直并指向手压面;(2)任意点的静水压强的大小和受压面的方位无关,或者说作用于同一点上各方向的静水压强都相等. 规律:由单位质量力所决定,作为连续介质的平衡液体内,任意点的静水压强仅是空间坐标的连续函数,而与受压面的方向无关,所以p=(x,y,z)2-3答:水头是压强的几何意义表示方法,它表示h 高的水头具有大小为ρgh 的压强。
绝对压强预想的压强是按不同的起点计算的压强,绝对压强是以0为起点,而相对压强是以当地大气压为基准测定的,所以两者相差当地大气压Pa.绝对压强小于当地大气压时就有负压,即真空。
某点负压大小等于该点的相对压强。
Pv=p'-pa2-4.在静水压强的基本方程式中C g p z =+ρ中,z 表示某点在基准面以上的高度,称为位置水头,g p ρ表示在该点接一根测压管,液体沿测压管上升的高度,称为测压管高度或压强水头,g p z ρ+称为测压管水头,即为某点的压强水头高出基准面的高度。
关系是:(测压管水头)=(位置水头)+(压强水头)。
2-5.等压面是压强相等的点连成的面。
等压面是水平面的充要条件是液体处于惯性坐标系,即相对静止或匀速直线运动的状态。
2-6。
图中A-A 是等压面,C-C,B-B 都不是等压面,因为虽然位置高都相同,但是液体密度不同,所以压强水头就不相等,则压强不相等。
2-7.两容器内各点压强增值相等,因为水有传递压强的作用,不会因位置的不同压强的传递有所改变。
当施加外力时,液面压强增大了Ap∆,水面以下同一高度的各点压强都增加Ap∆。
2-8.(1)各测压管中水面高度都相等。
(2)标注如下,位置水头z,压强水头h,测压管水头p.图2-82-9.选择A2-10.(1)图a 和图b 静水压力不相等。
因为水作用面的面积不相等,而且作用面的形心点压强大小不同。
【最新试题库含答案】水力学第二章课后答案

水力学第二章课后答案篇一:水力学第二章答案(吕宏兴__裴国霞等)2-1 解:(1)pA+γ水·ΔH=γH·Δh;所以pA=γH·Δh-γ水·ΔH=38.02kPa(γH=13.6γ水)(2)测压管长度:pA=γ水·h 所以h= pA/γ水=38.02×103/9.8×103=3.88m2-3 解:PA-γh=pB-γ(h1+h2+h)+γHh1所以,pA-pB=γHh1-γ(h1+h2)=13.6×9.8×0.53-9.8×(0.53+1.2) =53.68kPa2-6解:pA=γH(h1+h2)-γ(h1+h2)=13.6××9.8××0.53-9.8×(0.53+1.2)=53.68kpa2-7 解:(1)左支:绝对:pc =p0 +γh0=86.5+9.8×2=106.1kPa(2)右支:pc =pa+γ水h;h=(pc -pa)/γ水=(106.1-9.8)/9.8=0.827m2-8 解:pA=0.6pa=0.6×98=58.8kpa(1)左支:pA=γh1 h1=pA/γ=58.8/9.8=6m(2)右支:pA+γh=γHh2 h2=(pA+γh)/γH=0.456m2-10解:设管嘴内的绝对压强为p ,则p +γh= paPv=pa- p =γh=9.8×0.6=5.886kpa2-12解:(1)设容器底部面积为S,相对压强为P,对容器底部进行受力分析:由牛顿第二定律:ΣF=m·a;-(P+G)=-m·a 所以得出p·s+γ·s·h=ρ·s·h·ap=ρ·h·a -γh=γh/g·a-γh=γh(a/g-1)篇二:《水力学》第二章答案第二章:水静力学一:思考题2-1.静水压强有两种表示方法,即:相对压强和绝对压强2-2.特性(1)静水压强的方向与受压面垂直并指向手压面;(2)任意点的静水压强的大小和受压面的方位无关,或者说作用于同一点上各方向的静水压强都相等. 规律:由单位质量力所决定,作为连续介质的平衡液体内,任意点的静水压强仅是空间坐标的连续函数,而与受压面的方向无关,所以p=(x,y,z)2-3答:水头是压强的几何意义表示方法,它表示h高的水头具有大小为?gh的压强。
水力学第二章课后答案

1 2 6 11 答案在作业本2.12(注:书中求绝对压强)用多管水银测压计测压,图中标高的单位为m,试求水面的压强 p0。
p0 3.0水2.52.3水1.4 1.2汞解: p0 p4 3.0 1.4gp5 2.5 1.4Hg g3.0 1.4gp a 2.3 1.2Hg g2.5 1.2g 2.5 1.4Hgg3.0 1.4 gp a 2.3 2.51.2 1.4Hg g 2.5 3.0 1.2 1.4gp a 2.3 2.51.2 1.413.6 2.5 3.0 1.2 1.4g gp a265.00 (kPa)答:水面的压强p0265.00kPa。
2-12 形平板闸门AB,一侧挡水,已知长 l =2m,宽 b =1m,形心点水深h c =2m,倾角 = 45 ,闸门上缘A处设有转轴,忽略闸门自重及门轴摩擦力,试求开启闸门所需拉力 T 。
Th c AbBlα解:( 1)解析法。
P p C A h C g bl1000 9.8072 1 239.228 (kN)I C h C bl 32222y D122 2y Csin h C sin 45o122 2.946 y C Abl12sin sin 45o2-13 矩形闸门高 h =3m,宽 b =2m,上游水深 h1 =6m,下游水深 h2 =4.5m,试求:( 1)作用在闸门上的静水总压力;(2)压力中心的位置。
h1h2h解:( 1)图解法。
压强分布如图所示:h1h2p∵p h1h h2h gh1h2g6 4.5 1000 9.80714.71( kPa)P p h b 14.71 3 288.263 (kN)合力作用位置:在闸门的几何中心,即距地面(1.5m, b) 处。
2(2)解析法。
11g 11.5 hb6 1.59807 3 2 264.789 (kN )Pp A hI Cbh 3 1h 2 yD1yC 24.5 122y C2 A 4.5 bh4.5 4.5121 20.250.754.667 (m )4.5P 2 p 2 A g h 2 1.5 hb 3 9.807 32(kN )176.526yD 2yC1I C1y C 21 I C132 0.753.25 (m )y C1 A yC1 A 3合力: PP 1 P 2 88.263 (kN )合力作用位置(对闸门与渠底接触点取矩) :y D P P 1 h 1yD1P 2 h 2yD 2P 1 h 1yD1 P 2 h 2yD 2y DP264.7896 4.667 176.5264.5 3.2588.2631.499 (m )答:( 1)作用在闸门上的静水总压力 88.263kN ;(2)压力中心的位置在闸门的几何中心,即距地面 (1.5m, b) 处。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2-1 解:(1)p A+γ水·ΔH=γH·Δh;所以p A=γH·Δh-γ水·ΔH=(γH=γ水)(2)测压管长度:p A=γ水·h 所以h= p A/γ水=×103/×103=3.88m2-3 解:P A-γh=p B-γ(h1+h2+h)+γH h1所以,p A-p B=γH h1-γ(h1+h2)=×× = 2-6解:p A=γH(h1+h2)-γ(h1+h2)=××××解:(1)左支:绝对:p c'=p0'+γh0=+×2=(2)右支:p c'=p a+γ水h; h=(p c'-p a)/γ水=()/=0.827m 2-8 解:p A==×98=(1)左支:p A=γh1 h1=p A/γ==6m(2)右支:p A+γh=γH h2 h2=(p A+γh)/γH=0.456m 2-10解:设管嘴内的绝对压强为p',则p'+γh= p aP v=p a- p'=γh=×=2-12解:(1)设容器底部面积为S,相对压强为P,对容器底部进行受力分析:由牛顿第二定律:ΣF=m·a;-(P+G)=-m·a 所以得出p·s+γ·s·h=ρ·s·h·ap=ρ·h·a -γh=γh/g·a-γh=γh(a/g-1)p=×2=㎡(2)相对压强为0 p=γh(1-a/g)=0 由式可知 a/g-1=0a=g=9.8m/s2时,p=02-142-16解:下游无水时,h1=,h2=,b=3m(1)求静水总压力P方法10:P=Ωb=1/2[γh1+γ(h1+h2)]×AB×b=1/2××(2×+××3=方法20:P=γh c A=γ(h1+h2/2)×AB×b=(2)计算P的作用点D的位置:e=l/3·(2h1+h2ˊ)/(h1+h2ˊ)=0.915m(其中hˊ=h1+h2)(3)计算T:因为ΣM a=0 则:P·AC+G·AO·cos600 其中:AC=AB-e= AO=AB/2×所以 T=158kN下游有水时,AB=,b=3m,p A=γh1=×=,p A=p B(1)静水总压力P 左=γ·h c1A 1=×(h 1+h 2/2)×AB ×b=P 1= (其中h c1=h 1+h 2/2 A 1=AB ×b ) e 1=P 右=γ·h c2A 2=×h 2/2×AB ×b=P 2=(其中h c2=h 2/2) e 2=l/3=3=0.71m(2) 因为ΣM a =0P 1×(AB-e 1)+G ×AO ×cos600=T ×AB ×cos600+P 2×(AB-e 2) T=已知:H=3m,b=5m,R=,θ=450 求P 及作用点H=Rsin450=×22=3m(1)水平分力:P x =γh e A x =××3×5=(KN) (2)铅垂分力:P z =γv=γΩ×b=××5=(KN) 其中:Ω=S 梯OABC —S 扇OAC =-=㎡ S 梯OABC =×[+()]×3=㎡ S 扇OAC =360450πR 2=360450××=㎡ (3)P=PPzx22+=01.565.22022+=(KN )(4)P 与水平面的夹角α: α=arctanPPxz =arctan5.22001.56==14015`2-192-20 解:已知b=10m,k=8m(1)夹角计算:Sinβ1=(173-170)/8=3/8=(cosβ1=8)β1= Sinβ2=(170-165)/8=5/8=(cosβ2=)β2=(2)水平方向水压力P x:(闸门宽b=10m)公式:P x=γh c A x=×4×8×10=3136kN(另法:P x=1/2××8×8×10=kN)(3)垂直方向水压力P z=γV关键计算压力体体积V=[三角形ofc(㎡)+扇形ocd(㎡)-梯形ofed()]×b 所以 V=(+)×10=×10=106.36m³P z=γV=×=(4)总压力P:P=(P x2+P z2)=作用方向α==P与水平面夹角,且过o点。
解:已知ABCD宽度b=5m(1)作用于BC弧上的水平分力:(两种方法)压力图法:P x=Ωb=γΔH×2R×b=×1×2×1×5=98(KN)分析法:P x左=γh c左A x=×(ΔH+R)×(2R×b)=×2×2×5=196(KN)P x右=γh c右A x=×R×2R×b=×1×2×5=98(KN)P=P x左—P x右=98(KN)方向水平向右(2)作用于AB弧上的铅垂分力P z:P z=γv可见P z左,P z右大小相等,方向相反,故P z=0故作用在BC段上的静水总压力P=P z=98KN,方向过O点水平向右。
水力学第四章已知:l=10m,d=50mm,h= Q=90247.0=(m 3/s)求λ V=A Q =5.002.4027.00π=1.4m/s圆管(计算均匀流沿程水头损失的一个基本公式);达西—威廉巴赫公式h f =λd l gv 22h f =h=(ABO 无局部水头损失)故λ=vh ldg f22=已知:棱柱体渠道,均匀流,紊流粗糙区。
A=24m 2,X=12m,v=s, J=.求n一般渠道中的流动为均匀流V=C RJ =JR n2131,故n=vJR 213=(3) 谢才公式:v=C RJ J=RCA Q 222=kQ 22其中A=4πd 2 R=4d C=R n611n 取 k=AC R =R n321×4πd 2=(m 3/s) 故h f=kQ 22l=(m)(n=,k=,h f =3.33m 偏小)水力学第五章(2)有压管道中的恒定流已知:预制混凝土引水管 查表(P118)n=~D=1m,l=40m, = D 上 =70m,D 下 =60.5m ,D 管底=62.0m 求Q 解:自由出流流量公式Q=μc A Hog2 n 取作用水头H o == (管道形心点与上有水面的距离) A=π4D 2= π4㎡ μc =ξλ∑++dl 11假设在阻力平方区 λ=cg28C=n R61=013.01×)41(61=(m 21/s) 故 λ=cg28= μc =ξλ∑++dl 11 =Q=×π4×5.7.2g =(m 3/s) V=A Q =436.6π=8.10m/s>1.2m/s 原假设成立 已知Z s =4.5m,l=20m,d=150mm,l 1=12m,d 1=150mm,λ= ξ自网=,ξ水泵阀= ,ξ90=,若h v ≤6m,求:(1)Q 泵(2)Z(5)解:水泵安装高度为: Z s ≤h v -(α+γdl 11+ξ∑)gv22故v2max=(h v -Z s )2g/(α+dl11 +ξ∑)=×(1+× 15.012++ =故v max =(m/s) Q max ==×421d π=(m 3/s)(4) 对于自流管:Q=μc A gz 2 作用水头Z=Q 2/μ2cA 22g其中A=42d π=μc =ξλ∑+dl1=1215.02003.01+++=故Z=6.19018.0378.00269.0222⨯⨯=(m)已知:d=0.4m,H=4m,Z=1.8m,l 1=8m,l2=4m,l3=12m求(1)Q (2)p min 的断面位置及h vmax解:(1)淹没出流:Q=μc A gz 2 μc =ξλ∑+dl1(n 的取值及ξ的取值都要明确)取n 为,c=n1R61=013.01×)44.0(61=(m 21/s) λ=cg28=故μc =.13.025.24.01248029.01+⨯++++⨯=A=42d π=4π×4.02=(㎡)故Q=××42⨯g =(m 3/s)(3)最小压强发生在第二转折处(距出口最远且管道最高) n= 对上游1-1,2-2,列能量方程,0-0为上游水面0+γpa+0=(Z -2d )+γP 2+g v 222∂+(λd l +ζ∑)g v 222V 2=A Q =1256.0473.0=(m/s) h v =γP Pa2-=Z -2d +(ζλ∑++dl1)+gv 222=dl l21+ζ网ζ弯6.19766.32=(m)解:如P145例5 法1:取C h =130采用哈森-威廉森S=d871.491013.1⨯×Ch852.11=d871.472.137421S 1=×1010-(d 1=1200mm) S 2=×1010-(d 2=1000mm) S 3=×1010-(d 3=800mm)假设J 节点压力水头为h=25(m)(5m<h<30m) 设A,B,C 的水位分别为D A =30m,D B =15m,D C =0 利用h f =QSl852.1 h f1=30-25=5m=S 1Q852.11l1=×1010-×750Q852.11Q 1=(m 3/s)并联:h f 1=hf 2=hf 3即k l Q 21121=k l Q 22222=k l Q 23323l 1=l 2=l3所以Q 2=Q k 12/k 1Q3=Q k 13/k 1k=R AC 故k1=421d π×λg8×)4(121dk 2=422d π×λg8×)4(221dk3=423d π×λg8×)4(321dλ相同故kk 12=)(1225d d =32k k 13=)(1325d d =243所以Q2=32Q 1=(m 3/s) Q3=243Q 1=(m 3/s)另法:利用达西公式h f =gd lv 22λV=42d π且h f1=h f2=h f3 得到d Q 5121=d Q 5222=d Q 5323 即1521Q =2522Q =3523Q所以Q2=32Q 1=(m 3/s) Q 3=243Q 1=(m 3/s)水力学第六章(5) 明渠恒定均匀流已知h=1.2m,b=2.4m,m=,n=,i=求v 和Q 解:A=(b+mh)h=+××= χ=b+2h m21+=+2××5.121+=6.73mR=χA=0.75m V=C Ri =Rni32=025.0016.0×75.032=(m 3/s)Q=vA=×=(m 3/s) 已知:n=,b=8m,i=80021,求Q (断面为矩形m=0) βm=2(m21+-m)=2=hb mmhm=4mA m =b m h m =8×4=32m2χm=bm+2hm=16m R m=χmm A=2mC=n1261=028.01×261= Q=R A n i 32=2323280001028.01⨯⨯=(m 3/s) 已知:矩形渡槽,b=1.5m,l =116.5m,Q=7.65m 3/s,D 进口=52.06m h=1.7m,求i 及D 出口 Q=AC Ri i=RCA Q222A=bh=×=2.55m 2χ=b+2h=+2×=4.9mR=χA =9.455.2=0.52m C=R n 611=52.061013.01=69 所以i=52.06955.265.7222⨯⨯=D 出口=D 进口-i l =51.64m解:χ1=b+h m21+=3.677mχ2=1.5mnr=χχχχ212211++n n =5.1677.35.1025.0677.30275.0+⨯+⨯=A=(b+b+mh)×2h =3.56m 2χ=b+h m 21++h=5.177m R=χA =0.688m C=R n611=)688.0(610268.01⨯=(s m /21) Q=AC Ri =××002.0688.0⨯=(m 3/s)已知:b=3.4m,梯形m=,i=65001,渠底至堤顶的高差为3.2m (3)安全超高a=,Q=67m 3/s 解:(2)h= A=(b+mh)h=+××=㎡χ=b+2h m 21+=+2××5.121+=13.1mR=χA=1.54m C=nR61 查表取n=0.03 C=03.054.161=(s m/21)Q=AC Ri =××6500154.1⨯=11.09m 3/s v=AQ=0.55m/s v 不冲=v R ×R 41=0.95m/s>v 不冲 (3)当h=时 A=(b+mh)h=+××=㎡χ=b+2h m 21+=+2×5.121+=8.81mR=χA =81.848.8=0.96m 当n=,C=n R 61=03.096.061=(s m/21)Q=AC Ri =××650096.0=3.41m 3/s v=A Q =48.841.3=0.4m/s v ''=0.5m/s>v 所以在此条件下会发生淤积水力学第七章7-6 梯形 水跃 Q=25m ³/s ,b=5m ,m=,h 2=,求h 1解:q=Q/b=5㎡/s 查图法h 2/q 2/3=52/3=1/=N=mq 2/3/b=×52/3/5= 由此查附图IV 可知: h 1/q 2/3= h 1=7-7 矩形水平渠:b=5.0m, Q=50m ³/s, h 1=0.5m ,判别水跃形式,求h 2解:q=Q/b=10㎡/sFr 12=v 2/gh 1=(Q/bh 1)2/gh 1=, Fr 1=>,可见水跃为强水跃. h 2=h 1/2[(1+8Fr 12)]=6.14m。
