空间问题的四面体单元

合集下载

几何-空间几何-正四面体专题

几何-空间几何-正四面体专题一．选择题（共6小题）1．已知棱长为a的正四面体ABCD内切球O，经过该棱锥A﹣BCD的中截面为M，则O到平面M的距离为（）A．B．C．D．2．已知正四面体ABCD的棱长为1，球O与正四面体的各棱都相切，且球心在正四面体的内部，则球O的表面积为（）A．4πB．2πC．D．3．已知球O在一个棱长为的正四面体内，如果球O是该正四面体的最大球，那么球O的表面积等于（）A．B．C．2πD．4．半径为1的球面上的四点A，B，C，D是一个正四面体的顶点，则这个正四面体的棱长是（）A．B．C．D．5．正四棱锥P﹣ABCD的侧棱长和底面边长都等于a，有两个正四面体的棱长也都等于a．当这两个正四面体各有一个面与正四棱锥的侧面PAD，侧面PBC完全重合时，得到一个新的多面体，该多面体是（）A．五面体B．七面体C．九面体D．十一面体6．（2006•江西）如图，在四面体ABCD中，截面AEF经过四面体的内切球（与四个面都相切的球）球心O，且与BC，DC分别截于E、F，如果截面将四面体分成体积相等的两部分，设四棱锥A﹣BEFD与三棱锥A﹣EFC的表面积分别是S1，S2，则必有（）A．S1＜S2B．S1＞S2C．S1=S2D．S1，S2的大小关系不能确定二．填空题（共14小题）7．已知棱长为a的正四面体ABCD有内切球O，经过该棱锥A﹣BCD三侧棱中点的截面为α，则O到平面α的距离为_________．8．在正四面体ABCD中，其棱长为a，若正四面体ABCD有一个内切球，则这个球的表面积为_________．9．已知正四面体棱长为a，则它的外接球表面积为_________．10．正四面体ABCD的棱长为1，则其外接球球面上A、B两点间的球面距离为_________．11．正四面体ABCD的棱长为1，棱AB∥平面α，则正四面体上所有点在平面α内的射影所构成的图形面积的取值范围为_________．12．（2006•浙江）正四面体ABCD的棱长为1，棱AB∥平面α，则正四面体上的所有点在平面α内的射影构成的图形面积的取值范围是_________．13．已知正四面体ABCD的棱长为1，若以的方向为左视方向，则该正四面体的左视图与俯视图面积和的取值范围为_________．14．四面体ABCD中，AB=CD=6，其余的棱长均为5，则与该四面体各个表面都相切的内切球的半径长等于_________．15．正四面体的棱长为a，它的体积为_________．16．棱长为1的正四面体ABCD中，对棱AB、CD之间的距离为_________．17．已知球O是棱长为12的正四面体S﹣ABC的外接球，D，E，F分别是棱SA，SB，SC的中点，则平面DEF 截球O所得截面的面积是_________．18．与四面体的一个面及另外三个面的延长面都相切的球称为该四面体的旁切球，则棱长为1的正四面体的旁切球的半径r=_________．19．已知结论：“在正三角形ABC中，若D是BC的中点，G是三角形ABC重心，则=2”．若把该结论推广到空间，则有结论：“在正四面体ABCD中，若△BCD的中心为M，四面体内部一点O到四面体各面的距离都相等，则=_________．20．设等边△ABC的边长为a，P是△ABC内的任意一点，且P到三边AB，BC，CA的距离分别为d1，d2，d3，则有d1+d2+d3为定值；由以上平面图形的特性类比空间图形：设正四面体ABCD的棱长为a，P是正四面体ABCD内的任意一点，且P到四个面ABC、ABD、ACD、BCD的距离分别为d1，d2，d3，d4，则有d1+d2+d3+d4为定值_________．几何-空间几何-正四面体专题参考答案与试题解析一．选择题（共6小题）1．已知棱长为a的正四面体ABCD内切球O，经过该棱锥A﹣BCD的中截面为M，则O到平面M的距离为（）A．B．C．D．考点：点、线、面间的距离计算；棱锥的结构特征。

汽车结构有限元分析03单元类型及单元分析

1.一维单元分析； 2.二维单元分析； 3.三维单元分析； 4.板壳单元； 5.其它各种单元介绍； 6.单元选用；
1.一维单元分析
主要有：杆单元、梁单元、管单元等。
1.1杆单元---最简单的两节点一维单元，用于杆件承受轴向力分析。
设杆单元横截面积为Ａ，长度为l，轴向分布载荷q为(x) 。单元2个节点的位移向量为： e ui u j T
由空间弹性力学几何方程，得应变表达式：
{} [B]{ }e [[B1 ][B2 ][B20 ]]{ }e
由空间弹性力学物理方程，单元内的应力可以表示成：
[ ] [D][ ] [D][B]{ }e [S]{ }e
单元刚度矩阵为：
[k]e
[B]T [D][B]dV
[k1e1
[k
e 21
这其中设定单元位移模式，利用虚功原理建立单元节点力与节点位移关系并组建单元刚度矩阵的过程，我们将其称为单元分析。
为了使有限元法的解在单元尺寸逐步趋小时能够收敛于精确解，所构造的单元位移函数必须满足以下三方面的条件：
1）位移模式中必须包括反映刚体位移的项；
2）位移模式中必须包括反映常应变的线性位移项；
这样空间梁单元就由3个节点组成i,，j,k 点必
须在一个平面内，但不能共线。i节点到j节
点为单元坐标系的x轴，y轴(或z轴)在节点i、
j和k构成的平面上且与x轴垂直，应用右手定
则可以确定另一坐标iz, 轴j, k(或y轴)。
三点
确定后，单元坐标系即确定，梁单元的截面
方位也就完全确定下来。所增加的一个用于
] ]
[k1e2 ]
[k
e 22
]
[k1e20
[k

机械结构有限元分析---空间问题有限元

U Nd e
d e1 d e2 d e3 d e 4 de d e5 d e 6 d e 7 d e8 displacement components at node 1 displacement components at node 2 (1, -1, 1)6 displacement components at node 3 displacement components at node 4 displacement components at node 5 displacement components at node 6 displacement components at node 7 displacement components at node 8
06
制作：南昌航空大学————贺红林，2014
6.2 四结点四面体单元
一、位移模式
单元结点位移向量
T T T { }e [ iT T j m n ]
z
n m i j y
x
T
[u i vi wi u j v j w j u m v m wm u n v n wn ]
位移函数
u a1 a2 x a3 y a4 z
(-1, -1, -1)1 (1, -1, -1)2 3(1, 1, -1) (-1, -1, 1)5

8(-1, 1, 1)
7 (1, 1, 1)

4(-1, 1, -1)

u1 d ei v1 w 1
N N1
(i 1, 2, ,8)
N2
N3
bi Ab 1 i A3 A1bi [ Si ] [ D][ Bi ] 6V A2 ci 0 A2 di

空间几何中的平行四面体的性质

空间几何中的平行四面体的性质平行四面体是一种常见的几何体，具有一些特殊的性质。

本文将介绍平行四面体的定义、特征、性质和应用。

一、定义平行四面体是一个具有四个面，并且每两个面都平行的多面体。

它是空间中的一个四面体，其中相邻的面是平行的。

二、特征1. 面的性质：平行四面体的四个面都是平行的，其中相邻的面是平行的，而且任意两个非相邻的面之间也是平行的。

2. 边的性质：平行四面体有六条边，每条边和另外三条边都平行。

3. 顶点的性质：平行四面体有四个顶点，并且每个顶点都连接着三条边。

4. 高度的性质：平行四面体有四条高，每条高是从一个顶点垂直地下垂到另一个面上。

5. 体积的性质：平行四面体的体积可以通过计算底面积与高度的乘积来得到。

三、性质1. 平行四面体的对角线相交于一个点，该点被称为中心。

2. 平行四面体的每个角都是锐角或钝角，不存在直角和平角。

3. 平行四面体的底面积相等的两个平行四面体，它们的体积相等。

4. 平行四面体的两条对边相等的两个平行四面体，它们的体积相等。

5. 平行四面体的每个侧面都是一个平行四边形。

6. 平行四面体的平面对角面积比等于它们的底面积比。

四、应用1. 建筑工程：平行四面体可以用于建筑物的结构设计，例如某些立柱或桥梁的设计中。

2. 几何分析：平行四面体的性质在几何分析中具有重要意义，可以用于计算面积、体积等参数。

3. 空间定位：平行四面体可以用于空间定位和坐标系统的建立，有助于测量和定位目标位置。

总结：平行四面体是一个具有四个平行的面的几何体，具有特殊的性质。

它在建筑工程、几何分析和空间定位等领域都有着广泛的应用。

通过了解平行四面体的定义、特征、性质和应用，我们可以更好地理解和应用这一几何形体。

正四面体的性质及应用

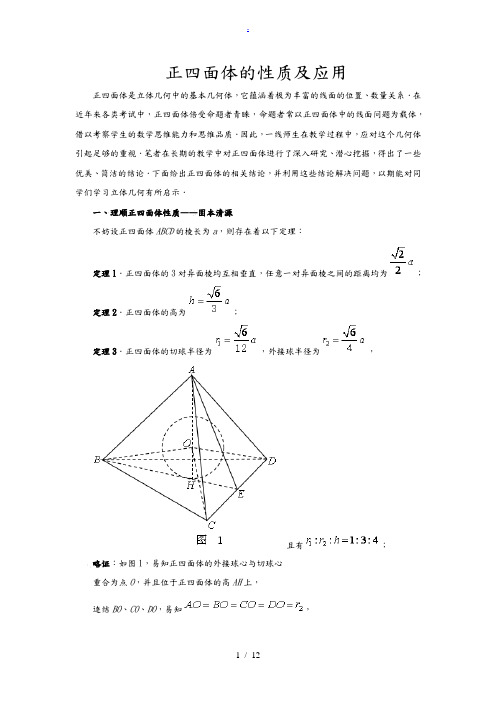
正四面体的性质及应用正四面体是立体几何中的基本几何体，它蕴涵着极为丰富的线面的位置、数量关系．在近年来各类考试中，正四面体倍受命题者青睐，命题者常以正四面体中的线面问题为载体，借以考察学生的数学思维能力和思维品质．因此，一线师生在教学过程中，应对这个几何体引起足够的重视．笔者在长期的教学中对正四面体进行了深入研究、潜心挖掘，得出了一些优美、简洁的结论．下面给出正四面体的相关结论，并利用这些结论解决问题，以期能对同学们学习立体几何有所启示．一、理顺正四面体性质——固本清源不妨设正四面体ABCD的棱长为a，则存在着以下定理：定理1．正四面体的3对异面棱均互相垂直，任意一对异面棱之间的距离均为；定理2．正四面体的高为；定理3．正四面体的切球半径为，外接球半径为，且有；略证：如图1，易知正四面体的外接球心与切球心重合为点O，并且位于正四面体的高AH上，连结BO、CO、DO，易知，且，从而AO、BO、CO、DO两两所确定的平面将正四面体分割成四个形状相同的正三棱锥：，，且每一个小正三棱锥的高都是切球的半径，于是有，即，亦即有，所以，．故定理4．正四面体的全面积为，体积为；定理5．正四面体底面任一点O到三个侧面的距离的之和；正四面体任意一点到四个侧面的距离之和(仿定理3利用体积分割法易证)．定理6．正四面体的侧棱与其底面所成的线面角大小为；定理7．正四面体相邻侧面所成的二面角的大小为；略证：设相邻两个侧面所成的角为，由于四个侧面的面积均相等，所以由射影面积公式知．定理8．设正四面体的侧棱与底面所成的角为，相邻两个侧面所成的二面角记为，则有略证：如图1所示，易知，，由H为的中心，易知，从而．定理9．正四面体的外接球的球心与切球的球心O重合且为正四面体的中心；中心与各个顶点的四条连线中两两夹角相等，其大小为，此角即为化学中甲烷分子结构式中的键位角．略证：如图1，在三角形AOB中，，，由余弦定理可求得，于是．同理可得．定理10．正四面体接于一正方体，且它们共同接于同一个球，球的直径等于正方体的对角线．二、运用正四面体性质——化繁为易1．巧算空间距离例1．一个球与正四面体的6条棱都相切，若正四面体的棱长为a，则求此球的体积．分析一：由定理10知，将正四面体嵌于正方体的部，然后再利用正四面体的棱与球相切，则该半径与正方体的切半径相等进行求解．解法一．如图2所示，将正四面体补成正方体，易知与正四面体的各棱相切的球即为正方体的切球．∵正四面体的棱长为a，∴正方体的棱长为．∴正方体的切球半径．∴．分析二：根据正四面体的对称性，结合定理1可知，该球的球心应位于正四面体的中心，其直径即为正四面体相对棱之间的距离．解法二．∵正四面体的棱长为a，∴由定理1可知，相对棱间的距离为．即该球的半径为．∴．例2．在棱长为2的正四面体木块ABCD的棱AB上有一点P（），过P点要锯出与棱AB垂直的截面，当锯到某个位置时因故停止，这时量得在面ABD上锯痕，在面ABC上的锯缝，求锯缝MN的值．解：如图3，取AB的中点E，连结CE，DE，则为正四面体相邻两面的二面角的平面角，由条件知∠MPN也是正四体相邻两面的二面角的平面角，即∠NPM＝∠CED，由定理7可知，于是，在中，由余弦定理得，∴2．妙求空间角例3．设P为空间一点，PA、PB、PC、PD是四条射线，若PA、PB、PC、PD两两所成的角相等，则这些角的余弦值为．解：如图4，构造正四面体ABCD，设P为四面体的中心，则PA、PB、PC、PD两两所成的角相等，设，由正四面体的性质，可知余弦值为例4．如图5，在正四面体ABCD中，E、F分别为棱AD、BC的中点，连结AF、CE．⑴求异面直线直线AF和CE所成的角；⑵求CE与面BCD所成的角．解：⑴连结FD，在平面AFD，过点E作EG∥AF交DF于点G．则是异面直线AF与CE所成的角（或其补角）．设正四面体ABCD的棱长为a，可得，，．由余弦定理可求得．故异面直线AF与CE所成的角为．⑵由已知易知平面AFD⊥平面BCD，在平面AFD，过点E作EH⊥FD于点H，连结CH，则∠ECH为CE与平面BCD所成的角．∵EH为正四面体高的一半，由正四面体性质的定理2知．∴．∴CE与底面BCD所成的角为．例5．如图6，正四面体ABCD的四个顶点在同一个球面上，CC1和DD1是该球的直径，求面ABC与面AC1D1所成角的正弦值．解：由正四面体性质定理10知正四面体接于一球，该正方体也接于此球，且正方体的对角线为此球的直径，如图所示，即CC1、DD1为该球的直径．连结C1D1，交AB于点M，连结MC．∵MC⊥AB，MD1⊥AB，∴∠CMD1为平面ABC与平面AC1D1所成的角．设正方体棱长为a，在中，．∴平面ABC与平面ACD所成的角的正弦值为．归纳反思：正四面体是立体几何中一个重要的数学问题载体，在平时的学习过程中若能有意识地研究它、利用它，就能较好地培养我们数学思维的“方向感”和思路的“归属感”，有助于促进自己数学思维空间的拓展、数学品质的提升．1.在正四面体P ABC-中，D、E、F分别是AB、BC、CA的中点，下面四个结论中不成立的是②．①//BC面PDF；②面PDF⊥面ABC；③DF⊥面PAE；④面PAE⊥面ABC．2.正四面体ABCD中，AB与平面ACD所成角的余弦值为3．3.如图，正四面体ABCD的棱长为2，点E，F分别为棱AD，BC的中点，则EF BA的值为()A．4B．4-C．2-D．24.以下说法 ①三个数20.3a =，2log 0.3b =，0.32c =之间的大小关系是b a c <<；②已知：指数函数()(0,1)x f x a a a =>≠过点(2,4)，则log 41a y =；③已知正四面体的边长为2cm ，则其外接球的体积为33cm π； ④已知函数()y f x =的值域是[1，3]，则()(1)F x f x =-的值域是[0，2]；⑤已知直线//m 平面α，直线n 在α，则m 与n 平行．其中正确的序号是①③．5.在正四面体A BCD -中，M 为AB 的中点，则直线CM 与AD 所成角的余弦值为()A ．12B ．2C ．3D ．23选：C ．6.在正四面体ABCD 中，E 、F 分别为棱AD 、BC 的中点，连接AF 、CE ，则异面直线AF 和CE 所成角的正弦值为()A ．13B ．23C ．24D ．5 选：D ．【点评】本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力．在立体几何中找平行线是解决问题的一个重要技巧，这个技巧就是通过三角形的中位线找平行线，如果试题的已知中涉及到多个中点，则找中点是出现平行线的关键技巧．本题易错点在于要看清是求异面直线AF 和CE 所成角的正弦值，而不是余弦值，不要错选答7.如图所示，在正四面体A BCD -中，E 是棱AD 的中点，P 是棱AC 上一动点，BP PE +的最小值为7，则该正四面体的外接球的体积是()A 6πB ．6πC 36D ．32π 选：A ．8.棱长为1的正四面体ABCD 中，E 为棱AB 上一点（不含A ，B 两点），点E 到平面ACD 和平面BCD 的距离分别为a ，b ，则11a b +的最小值为6 【考点】7F ：基本不等式及其应用【专题】31：数形结合；35：转化思想；5F ：空间位置关系与距离；5T ：不等式【分析】设点O 是正三角形ACD 的中心，连接OB ，作EF AO ⊥，垂足为点F ．AO 交CD 于点M ，则点M 为CD 的中点．设(01)AE AB λλ=<<．23AO AM =，3AM ，22BO AB AO =-．由//EF BO ，可得6EF BO a λ===．同理可得：6)b EN λ=-．代入利用基本不等式的性质即可得出．【解答】解：如图所示，设点O 是正三角形ACD 的中心，连接OB ，作EF AO ⊥，垂足为点F ．AO 交CD 于点M ，则点M 为CD 的中点．设(01)AE AB λλ=<<．223333AO AM ===， 226BO AB AO ∴=- //EF BO ，6EF BO a λ∴===．同理可得：6)b EN λ==-．∴21111161()11(1)()2a b λλλλλλ+=+=⨯=+---当且仅当12λ=时取等号．故答案为：9.已知M 是正四面体ABCD 棱AB 的中点，N 是棱CD 上异于端点C ，D 的任一点，则下列结论中，正确的个数有()（1）MN AB ⊥；（2）若N 为中点，则MN 与AD 所成角为45︒；（3）平面CDM ⊥平面ABN ；（4）存在点N ，使得过MN 的平面与AC 垂直．A ．1个B ．2个C ．3个D ．4个【考点】LM ：异面直线及其所成的角；LO ：空间中直线与直线之间的位置关系；LW ：直线与平面垂直；LY ：平面与平面垂直【专题】14：证明题【分析】连接CM 、DM ，可证明出AB ⊥平面CDM ，从而MN AB ⊥，得（1）正确；取AC 中点E ，连接EM 、EN ，利用三角形中位线定理证明出EN 、NM 所成的直角或锐角，就是异面直线MN 、AD 所成的角，再通过余弦定理，可以求出MN 与AD 所成角为45︒，故（2）正确；根据（1）的正确结论：MN AB ⊥，结合平面与平面垂直的判定定理，得到（3）正确；对于（4），若存在点N ，使得过MN 的平面与AC 垂直，说明存在N 的一个位置，使MN AC ⊥．因此证明出“不论N 在线段CD 上的何处，都不可能有MN AC ⊥”，从而说明不存在点N ，使得过MN 的平面与AC 垂直．【解答】解：（1）连接CM 、DM正ABC ∆中，M 为AB 的中点CM AB ∴⊥同理DM AB ⊥，结合MC M D M =AB ∴⊥平面CDM ，而MN ⊆平面CDMMN AB ∴⊥，故（1）是正确的；（2）取AC 中点E ，连接EM 、ENADC ∆中，E 、N 分别是AC 、CD 的中点//EN AD ∴，12EN AD =． EN ∴、NM 所成的直角或锐角，就是异面直线MN 、AD 所成的角设正四面体棱长为2a ，在MCD ∆中，2CM DM a === 则Rt MNC ∆中122CN a a =⨯=∴MN = 在MNE ∆中，122ME EN a a ==⨯=∴222cos 2EN MN EM ENM EN MN +-∠==⨯⨯ 45ENM ∴∠=︒，即异面直线MN 、AD 所成的角是45︒，故（2）正确；（3）由（1）的证明知：AB ⊥平面CDMAB ⊂平面ABN∴平面ABN ⊥平面CDM ，故（3）正确；（4）若有MN AC ⊥，根据（1）的结论MN AB ⊥，因为AB 、AC 相交于A 点，所以MN ⊥平面ABCMCD ∆中，CM MD ==，2CD a =2221cos 023CM MD CD CMD CM MD +-∴∠==> 可得CMD ∠是锐角，说明点N 在线段CD 上从C 到D 运动过程中， CMN ∠的最大值是锐角，不可能是直角，因为CM ⊂平面ABC ，CM 与NM 不能垂直，以上结论与MN ⊥平面ABC 矛盾，故不论N 在线段CD 上的何处，都不可能有MN AC ⊥．因此不存在点N ，使得过MN 的平面与AC 垂直．综上所述，正确的命题为（1）（2）（3）故选：C ．10.棱长为a 的正四面体中，给出下列命题：①正四面体的体积为324a V =；②正四面体的表面积为2S ；③切球与外接球的表面积的比为1:9；④正四面体的任意一点到四个面的距离之和均为定值．上述命题中真命题的序号为②③④．【考点】LE ：棱柱、棱锥、棱台的侧面积和表面积；LF ：棱柱、棱锥、棱台的体积【专题】31：数形结合；35：转化思想；49：综合法；5F ：空间位置关系与距离【分析】①正四面体的高h ==，体积为213V =，计算即可判断出正误；②正四面体的表面积为24S a =，即可判断出正误；③分别设切球与外接球的半径为r ，R ，则23143r ⨯，解得r ；R +=，解得R ，即可判断出正误； ④正四面体的任意一点到四个面的距离之和为H，则221133H ⨯=【解答】解：①正四面体的高h =，体积为3231324a V ==≠，因此不正确；②正四面体的表面积为224S a =，正确；③分别设切球与外接球的半径为r ，R ，则2314312r ⨯=，解得r =；R +=，解得R ． :1:3r R ∴=，因此表面积的比为1:9，正确；④正四面体的任意一点到四个面的距离之和为H ，则221133H ⨯=化简可得：H =，即为正四面体的高，均为定值，正确．上述命题中真命题的序号为②③④．。

四面体中若干问题的探论

四面体中若干问题的探论【摘要】四面体的相关问题经常作为高考和竞赛的考题背景，自然也就成为中学数学研究的重点之一.本文首先用代数和几何两种不同的方法讨论了:六正数构成四面体六条棱长的充要条件，然后又从平面几何和立体几何两个角度对充要条件的应用展开了较深入的思考,然后再根据这个充要条件推导出了四面体的六棱求积公式等一系列重要的结论，最后本文把三角形的两个优美的结论，在四面体中作了类比推广，同时也是对《中学数学研究》提出的:数学疑难系列之六，做了完整的回答。

【关键词】四面体；充要条件；余弦定理About some questions in the tetrahedronZeng zhong-jun【Abstract】The related questions of tetrahedron frequently as the college entrance examination and the competition examination question background, also becomes one of the middle school mathematics research. This article first used the algebra and the geometry methods discussed the necessary and sufficient conditions of six positive number constitution tetrahedron six leng long, then have launched the thorough ponder from the plane geometry and the solid geometry twoangles to the necessary and sufficient condition application, then acted according to this necessary and sufficient condition to infer the tetrahedron six leng quadrature formula again and so on a series of important conclusions, finally this article the triangle two exquisite conclusions, has made in the tetrahedron the analogy promotion, simultaneously was also proposes to "Middle school Mathematics Research": Sixth mathematics difficult series, have given the complete reply.【Key words】Tetrahedron；Sufficient and necessary condition；Cosine theorem1.引言我们知道三角形和四面体分别是平面几何和立体几何中最简单的封闭图形,在过去的学习过程中,我们对三角形的相关性质研究得比较多,也得出了很多优美的结论.但是对于四面体的相关问题的研究就显得较少,可以说四面体是一片很有开发空间的“土地”,可以成为中学数学探究性学习的很好的课题,同时也可以作为中学数学教师加强数学基本功练习的不错的素材.本文就不同角度对四面体的一些基本性质做了比较深入的思考,也得出了很多重要的结论.2. 六正数构成四面体六棱长的充要条件定理1设, , , , , 为六正数,则这六正数构成四面体六条棱长的充要条件是:=++- ＞0(其中:和，和，和各为四面体的一组对棱).2.1 定理1的代数证明证明:如图1所示四面体,因为; 分别为, 的三边.易知＞＞.所以,对于及有:＞+ + (1)＞+ + (2)当二面角的平面角或时，易知四点共面.(1) 当二面角的平面角时,建立如图2所示的直角坐标系,则有: , 假设两点坐标分别为:, 那么我们有:，，，解方程组可得两点的坐标分别为,(其中: =-- - + + + ,且由(1),(2)式可知,, ).(2) 当二面角的平面角时,建立如图3所示的直角坐标系, 则有: ,由(1)的推导过程,同理可得两点的坐标分别为:, .由两点间的距离公式可知:(其中:=- + + + + - + + - ).因为四面体的四个顶点,则二面角的平面角应满足:,从而有:＜＜LLLLLLLLLLLLLLLLLLLLL(3)将不等式(3)平方得:,即有＜＜整理得: ＜两边同时平方:＜(4)把, , 代入(4)式中,整理化简得:++- ＞0由于以上求解过程步步可逆,所以:六正数和, 和, 和构成四面体的六条棱长的充要条件是: (其中:和, 和, 和各为四面体的一组对棱).2.2 定理1的几何证明证明:如图4所示四面体,设, , 则有:由(5),(6)可知:由,且,可知.又在上为减函数,所以,即: ＞(9)对于而言:①当时,由在上为减函数可知: .②当时,由可知:,又因在上为增函数,所以所以: 对于,且都有由(9),(10)可知:＜＜(11)即: - ＜＜+所以,即＜,所以＜• ,不等式两边同时平方可知- + ＜化简整理可得:1+ - - - ＞(12)又在，，中,由余弦定理可知:=(13)=(14)=(15)把(13),(14),(15)分别代入(12)式中有:1+ • •- -- ＞0去分母化简整理可知:++- ＞0由于以上求解过程步步可逆,所以:六正数和, 和, 和构成四面体的六条棱长的充要条件是: (其中:和, 和, 和各为四面体的一组对棱).2.3 关于定理1的说明及推论对于定理1的充要条件,很容易认为:只要对于的三边: , 的三边:, 的三边: , 的三边:分别满足构成三角形的条件,就可以保证六正数和, 和, 和可以构成四面体的六条棱长(其中: 和, 和, 和各为四面体的一组对棱).其实不然,例如:=10, =9, =7, =8, =14, =11时,, , , 都存在,但是=-552321＜0.由上述定理可知,这样的六正数不能构成四面体的三组对棱长,从而不能构成四面体.由定理1的代数证明过程,容易知道:当二面角的平面角或时,四点共面,此时有:或,即:= ,所以:= ,从而:其实由定理1的几何证明过程，同样可以得出：当(5),(6),(7)式中的七个不等式中任何一个取时，四点共面，此时显然可以推出：因此,我们有如下推论:推论1 六正数构成四面体三组对棱的充要条件是:推论2 空间四点共面的充要条件是: .2.4 定理1及其推论的应用下面根据定理1,给出已知四面体六棱长求该四面体的体积公式:定理2已知四面体的三组对棱分别为和, 和, 和,且,则四面体的体积为：证明:如图5,过四面体顶点作底面的垂线交于点,连结,且设,则有:, , .因四点共面,由推论2可知把, , 代如中整理有:-= (16)在中,由海伦公式有:(其中).平方整理有,代入(16)式中得: ,又,所以此公式非常简洁,很好记忆,特别适合求已知四面体六条棱长的非特殊四面体的体积,但是此公式的弱点是计算量较大.特别地:令,可得等腰四面体(三组对棱分别相等的四面体)的体积公式:令:可得正三棱锥的体积公式:令可得正四面体的体积公式: 令, , 可得垂直四面体(存在一个顶点出发的三条棱两两垂直的四面体)的体积公式:例1 (2003年全国高中数学联赛)如图6所示,在中,, , 是的中点.将沿折起,使两点间的距离为,求此三棱锥的体积.解: 由题意可知,分别记, , .所以由定理2即得:例2如图7,已知四面体的棱长, , , , , ,求四面体的体积.解:设= , = , = , = , = , = 所以由定理2即得:为了简化定理2的计算量,下面我们给出已知四面体由一个顶点出发的三条棱长及其中每两条棱的夹角，求其体积的公式：定理3已知四面体由顶点出发的三条棱长分别为.其中, , 则这个四面体的体积为：证明:如图8所示,过A作于H,过H作于M,于N,连结, 则,且易知, .从而:因为四点在以为直径的圆上,即为外接圆直径.=== =从而四面体的体积:= =定理3相对于定理2的优点在于大大降低了求体积的计算量.对于上述例1，例2这类已知四面体的六棱长求该四面体体积的问题,当然也可以用定理3来完成，只需要用余弦定理求出对应的,再代入定理3的公式即可.对于推论2即: 空间四点共面的充要条件,在三角形的有关计算和一些数学奥赛定理的证明中,有着广泛的应用,下面举例说明:例3已知三角形三边长,求中线长.如图9所示,在四边形中,令: ,则即为的中线.把代入中,化简即得中线长.例4证明斯得瓦尔特(Stewart)定理: 已知及边两点间一点，求证:+ -=如图9,在四边形中,令: ,则点D位于B,C两点之间.把代入中,整理即得:,即:+ -=例5证明西姆松(Simson)定理,即:已知三角形的三边长,求其内角平分线长.如图9,在四边形中,令: ,,即:, ,则AD即为的的角平分线,把, 代入中,整理可得:角平分线长(其中:).3.三角形的两个性质在四面体中的类比推广类比是根据两类不同对象之间在某些方面有相同或相似之处，猜测它们在其他方面也可能相同或相似，并做出某些判断的方法.在中学数学教学过程中，类比思想是一种重要的具有创造性的思想，有助于发现、解决问题，是数学知识拓展的原动力之一.由于三角形和四面体分别是平面几何和立体几何中最简单的封闭图形，下面就三角形的两个性质在四面体中做类比推广.3.1 五心俱全且有两心重合的四面体为正四面体大家都知道一个三角形有外心，内心，重心，垂心，界心(4)并且有两心重合的三角形为正三角形.文[3]提出了数学疑难之6:四心俱全且有两心重合的四面体是否正四面体?.是一个十分有趣的问题,经过笔者的研究发现，对于四面体而言我们有如下定理：定理4五心(即四面体的外心,内心,重心,垂心, )俱全且有两心重合的四面体为正四面体.为了得到定理4,我们先给出以下三个引理:引理1(5)若点P是四面体内一点, 则点P是四面体重心的充要条件是:= = = .引理2(6)若四面体的四条高相等且相交于一点,则该四面体为正四面体.引理3(7)垂心存在的四面体(非正三棱锥)的垂心,内心,外心,及界心构成以重心为中心的平行四边形的四个顶点.为了证明定理4,我们先证明如下命题:命题1 垂心存在且重心和内心重合的四面体为正四面体.证明:如图10,设ABCD是垂心存在的四面体,点P同时为四面体ABCD的重心和内心,且设底面ABC,BCD ,CDA ,DAB上的高分别为,设点P到ABC,BCD ,CDA ,DAB上的距离分别为.因点P为四面体ABCD的重心,由引理1知,= = = ,又P为内心,则,∴,∴.又Q四面体ABCD的垂心存在,即四条高线交于一点,由引理2可知,四面体ABCD为正四面体.命题2 垂心和外心重合的四面体为正四面体.证明:如图11,点P为四面体ABCD的垂心和外心,连结PA,PB,PC,PD,延长DP交面ABC于点0,连结AO,BO,CO.因P为四面体的垂心,所以DP⊥面ABC,AP⊥面BCD,∴BC⊥面ADP,∴AO⊥BC同理可得:BO⊥AC,CO⊥AB,∴为O的垂心ΔABC.又因P为四面体的外心,则PA=PB=PC ,又PO⊥面ABC ,所以ΔAOP≌ΔBOP≌ΔCOP, ∴AO=BO=CO,即0为ΔABC的外心, ∴ΔABC有两心重合,所以ΔABC为等边三角形.同理: ΔBCD,ΔCDA,ΔDAB也为等边三角形.∴四面体ABCD为正四面体.命题3 垂心和内心重合的四面体为正四面体.证明:如图12, 点P为四面体ABCD的垂心和内心,连结PA,PB,PC,PD,并延长DP,AP分别交面ABC,BCD于点O,Q,连结AO,DQ,Q,P为四面体垂心,∴PO=PQ又∠APO=DPQ,∴ΔAPO ≌ΔDPQ,所以:AP=DP.同理可得AP=BP=CP=D=,∴点P为四面体ABCD的外心,所以:四面体ABCD的垂心和外心重合.由结论2可知,四面体ABCD为正四面体.命题4 垂心存在且内心和外心重合的四面体为正四面体.证明:如图13, 点P为四面体ABCD的外心和内心,过点P 作PO1,PO2,PO3,PO4分别垂直于面BCD,ACD,ABD,ABC,垂足分别为O1,O2,O3,O4,并连结PA,PB,PC.因P为四面体ABCD的外心,所以:AP=BP=CP,又Q,PO4⊥面ABC ,所以：ΔPO4A≌ΔPO4B ≌ΔPO4C , ∴AO4=BO4=CO4即O4为ΔABC的外心,同理:O1O2O3分别为ΔBCD, ΔACD, ΔABD的外心.又P为四面体ABCD的内心,则:PO3=PO4 ∴ΔPO4B≌ΔPO3B,∴BO3=BO4,即ΔBCD,ΔACD,ΔABD,ΔADC的外接圆半径全相等.ΔAO4B≌ΔAO3B,∴∠AO4B=AO3B ,同理可得: ∠BO4C=∠BO1C, ∠BO1D=∠BO3D, ∠AO3D=∠AO2D, ∠AO4C=∠AO2C, ∠CO1D=∠CO3D,不妨设：∠AO4B=∠AO3B= ,∠BO4C=∠BO1C= ,∠BO1D=∠BO3D= ,∠AO3D=AO2D= ,∠AO4C=AO2C= ,∠CO1D=∠CO2D=(17)+(19)得: =1200LLL(21)(18)+(20)得:,比较(21)(22)得,即, ≌, 同理: , .即:四面体为等腰四面体(三组对棱分别相等的四面体). ≌≌≌, ∴SABC=SBCD=SCDA=SDAB,∴( 的意义同命题1).又Q四面体ABCD的垂心存在,即四条高线交于一点,由引理2可知,四面体ABCD为正四面体.当四面体ABCD垂心存在,且界心和重心重合或界心和内心重合时,由引理3可知,内心和重心重合,再由命题1可得如下结论:命题5 垂心存在且重心和界心重合的四面体为正四面体.命题6 垂心存在且内心和界心重合的四面体为正四面体.当四面体ABCD的垂心和重心重合或外心和重心重合时,由引理3可知,垂心和重心重合,再由命题2可得如下结论: 命题7 垂心和重心重合的四面体为正四面体.命题8 垂心存在且重心和外心重合的四面体为正四面体.当四面体ABCD的垂心存在, 且外心和界心重合时,由引理3可知,垂心和内心重合,再由命题3可得如下结论: 命题9 垂心存在且外心和界心重合的四面体为正四面体.当四面体ABCD的垂心和界心重合时,由引理3可知,内心和外心重合,再由命题4可得如下结论:命题10 垂心和界心重合的四面体为正四面体.综上命题1到命题10可知:五心俱全且有两心重合的四面体为正四面体，从而定理4得证.但如果四面体的垂心不存在,则命题1, 命题4, 命题5, 命题6的结论应为等腰四面体(三组对棱分别相等的四面体),证明略.3.2 四面体余弦定理普通高级中学课本在高一(下)向量部分给出了解斜三角形的一个有力工具――余弦定理，下面我们就把余弦定理类比推广到四面体中，不妨称之为“四面体余弦定理”.定理5如图14，在四面体ABCD中，设顶点A,B,C,D所对面的面积分别为S1,S2,S3,S4.其中每两面所夹的二面角分别为( ),则：= + + -- - ；= + +- - -= + + -- -= + + -- -证明:过顶点A作于O,由射影面积公式有：= + + =+ +(23)同理：= + +(24)= + +(25)= + +(26)由(24)得= - + ，两边同时乘以得：= - +(27)同上可得：= - +(28)= -+(29)(27)+(28)+(29)得：=+ + - --再将(23)式带入上式左边有：= + + -- -用同样的方法可以证明：= + + -- -= + + -- -= + + -- -以上即为“四面体余弦定理”的内容，证明及表达式.如果在四面体ABCD中从一点出发的三条棱，两两垂直即共点的三个面两两垂直，不妨设D为此顶点，此时有：，.由四面体余弦定理可得，这就是勾股定理在四面体中的推广，可以称为“四面体勾股定理”.参考文献[1]付增德.数学疑难之9:6正数如何构成四面体的6棱长?[J].中学数学研究(广州),2007(3) .[2]曾中君. 6正数构成四面体3组对棱长的充要条件[J].中学数学研究(广州).本文已收到用稿通知,文章登记编号:07-1611.[3]许鲔潮.数学疑难之6:四心俱全且有两心重合的四面体是否正四面体?[J].中学数学研究,2006(12).[4]邓胜.四面体界点,界心及其坐标公式[J].中学数学,2002(11).[5]段惠民.也谈重心向量形式的应用[J].数学通讯,2004(13).[6]虞关寿.四面体与平行六面体的关系探析[J].数学通讯,2005(9).[7]黄华松.垂心存在的四面体若干心的一个性质[J].数学通讯,2006(3).[8]朱德祥.初等数学复习及研究(立体几何)[M].北京:人民教育出版社,1960.[9]曾中君.直线y=kx(k=a/b)上的点到椭圆最短距离的讨论[J].数学教学通讯,2007(1)收稿日期：2011-04-22“本文中所涉及到的图表、公式、注解等请以PDF格式阅读”。

空间几何中的平行四面体

空间几何中的平行四面体在空间几何学中，平行四面体是一个非常重要的概念。

它是由四个平行的且不在同一平面的三角形构成的多面体。

本文将介绍平行四面体的定义及性质，并给出一些相关的例子和应用。

一、平行四面体的定义平行四面体是由四个平行的且不在同一平面的三角形所组成的多面体。

它具有以下特点：1. 四个面都是三角形。

2. 相邻两个面之间的边都是平行的。

3. 任意两个不相邻的面之间的距离是相等的。

二、平行四面体的性质1. 平行四面体的对棱平行且相等。

对任意的棱AB和CD，若AB ∥ CD，则有AB=CD。

2. 平行四面体的对顶角平等。

对任意的顶点O和底面P，若∠AOC=∠BOD，则有∠DOP=∠COP。

3. 平行四面体的任意两个面之间的距离相等。

对于任意的两个面ACDF和BCEF，有AC=BD。

4. 平行四面体的四条棱构成的四面体是平行四面体，且与原平行四面体全等。

5. 平行四面体的底面积乘以高等于体积。

设底面为底的面积为S，其高为H，则平行四面体的体积V=SH/3。

三、平行四面体的例子1. 双峰山：双峰山位于中国的广东省韶关市。

它的山势独特，由四个平行的山脊组成，形成了一个平行四面体的形状。

2. 锡尔河四面体：位于俄罗斯的锡尔河口以北，是一个由四条平行的山脉组成的地貌景观。

3. 钻石：钻石的晶体结构可以看作是一个平行四面体的形状，钻石的每个面都是一个等边三角形。

四、平行四面体的应用1. 三维建模：在计算机图形学和三维建模领域，平行四面体常被用于表示物体的三维空间结构。

2. 计算几何：平行四面体是计算几何中的重要概念，可以用来求解空间中的各种几何问题。

3. 数学教学：在数学教学中，通过平行四面体的例子可以引导学生理解三维空间的概念，并进行相关的几何推理。

总结：平行四面体是空间几何学中的一个重要概念，它由四个平行的且不在同一平面的三角形组成。

它具有一系列独特的性质，如对棱平行且相等、对顶角平等等。

平行四面体在实际生活中也有很多应用，如三维建模、计算几何等。

5.1.15.1等参数单元及空间问题分析

注：等参单元的刚度积分一般很难有解析式，必须进行数值积分，目前普遍采用高斯数值积分法（略）。
5.1.2等参单元小结
1、等参单元存在的充要条件是|J|≠0
为了保证能进行等参变换(即总体坐标与局部坐标一一对应)，通常要求总体坐标系下的单元为凸，即不能有内角大于或等于或接近180度情况。
2、等参单元的优点是当单元边界呈二次以上的曲线时，容易用很少的单元去逼近曲线边界。
4
Ni
,
1 4
1
i
1i
i = 1,2,3,4
同矩形单元位移形函数
2）单元应变
将位移表达式代入几何方程得等参单元的应变
u
0
0
x ε 0 u
x
v y
0
v
N1 ,
y
0
0 N1
N2 0
0 N2
N3 0
0 N4 N3 0
0
u1
N4能很好地适应曲线边界和准确地模拟结构形状，又能具有较高次的位移模式，
等参单元（iso-parametric element）的概念：等参数单元就是对单元几何形状和单元内的参变量函数采用相同数目的节点参数和相同的形函数进行变换而设计出的一种新型单元。
思路：任意直四边形可看成是正四边形(常称为母元)的变形，由于正四边形（母元）的位移函数、单刚矩阵均已得到，则可利用正四边形单元的结果研究任意四边形。
。
5.1.1 平面4节点等参单元 1）等参变换（坐标映射）
目的：建立矩形母单元与任意四边形单元的坐标映射关系
已知：
xi yi
f
ii
（i=
1,2,3,4）求，：
x y
f
解法：插值 x 1 2 3 4

空间四面体的外接球和内切球问题

空间四面体的外接球和内切球问题
概述
空间四面体的外接球和内切球问题是几何学中的一个重要问题。

外接球是指与四面体的四个顶点都接触的球，内切球则是指与四面
体的每个面都相切的球。

这两个球体在几何学和物理学中都有广泛
的应用。

外接球的存在性和唯一性
对于任意给定的四面体，是否存在一个与之外切的球？答案是
肯定的。

根据几何学原理，四面体的外接球的球心一定位于四个顶
点的垂直平分面的交点上。

而外接球的半径等于球心与任意一个顶
点的距离。

内切球的存在性和唯一性
同样，对于任意给定的四面体，是否存在一个与之内切的球？
答案也是肯定的。

内切球的球心一定位于四个面的角平分线的交点上，而内切球的半径等于球心到四个面的距离的最小值。

解决方法
虽然存在多种方法来计算空间四面体的外接球和内切球，但最
常用的方法是使用线性代数和解析几何的技巧。

通过分析四面体的
顶点坐标和面的方程，可以求解外接球和内切球的半径和球心坐标。

应用领域
空间四面体的外接球和内切球在许多领域都有应用，比如计算
机图形学、物理学和工程学。

在计算机图形学中，外接球和内切球
可以用来优化渲染技术和三维模型的建模。

在物理学中，外接球和
内切球可以用来分析四面体的形状和体积。

在工程学中，外接球和
内切球可以用来优化结构设计和空间布局。

结论
空间四面体的外接球和内切球问题是一个重要且有趣的几何学
问题。

通过使用适当的解决方法和分析工具，我们可以计算出外接
球和内切球的半径和球心坐标，并在实际应用中发挥重要的作用。

空间几何中的相似四面体性质

空间几何中的相似四面体性质相似四面体是空间几何中一种重要的几何体，它具有一些独特的性质和特点。

本文将从四面体的定义入手，介绍相似四面体的基本概念、性质和应用。

一、四面体的定义四面体是由四个不在同一平面上的点所确定的多面体，它有四个面、六条棱和四个顶点。

四面体的六条棱两两相交于一点，这个点被称为四面体的顶点。

二、相似四面体的定义相似四面体是指具有相似形状但不一定相等的四个三角面的四面体。

当四面体的对应边成比例时，我们可以称它们为相似四面体。

三、相似四面体的性质1. 相似比例相似四面体的相似比例是指两个相似四面体的对应边的比值相等。

假设有两个相似四面体ABCD和A'B'C'D'，则它们的相似比例可以表示为AB/A'B' = AC/A'C' = AD/A'D' = BC/B'C' = BD/B'D' = CD/C'D'。

2. 体积比相似四面体的体积比是指两个相似四面体体积的比值等于它们的边长比的三次方。

假设有两个相似四面体ABCD和A'B'C'D'，它们的体积比可以表示为(Volume ABCD)/(Volume A'B'C'D') = (AB/A'B')^3 = (AC/A'C')^3 = (AD/A'D')^3 = (BC/B'C')^3 = (BD/B'D')^3 = (CD/C'D')^3。

3. 高度比相似四面体的高度比是指两个相似四面体相应高度的比值等于它们的边长比，也等于它们的体积比的三次方根。

四、相似四面体的应用1. 尺规作图相似四面体的性质可以应用于尺规作图中。

例如，给定一个已知的四面体，利用相似四面体的性质，我们可以通过尺规作图构造出与给定四面体相似的另一个四面体。

空间问题的四面体单元

第三章轴对称、三维和高次单元§3-2 空间问题的四面体单元空间问题的有限单元法，和平面问题及轴对称问题的有限单元法的原理和分析过程完全相同。

由于空间问题应采用三维坐标系，因此单元的自由度、刚度矩阵的元素个数，方程组内方程个数等要较平面问题和轴对称问题多，所以空间问题的规模一般比轴对称问题和平面问题大得多。

它要求计算机的内存大，且计算时间长，费用高。

这些问题都给三维有限单元法的具体运用带来许多困难。

和平面问题一样，空间有限单元法采用单元也是多种多样的，其中最简单的是四节点四面体单元。

采用四面体单元和线性位移模式来处理空间问题，可以看作平面问题中三角形单元的推广。

在采用四面体单元离散化后的空间结构物中，一系列不相互重叠的四面体之间仅在节点处以空间铰相互连接。

四节点四面体单元仅在四个顶点处取为节点，其编号为i,j,m,p 。

每个单元的计算简图如图3-7所示。

在位移法中，取节点位移为基本未知量，四节点四面体单元共有十二个自由度(位移分量)，其节点位移列阵为{}[]Tpp p m m m j jj i i ip m j i ew v u w v u w v u w v u =⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=δδδδδ其子矩阵 {}[]i ii i w v u =δ (i,j,m)相应的节点力列阵为{}[]Tp m j ie F F F F F -图3-7 空间四面体单元其子矩阵 {}[]Ti i i i W V U F =一、单元法位移函数结构中各点的位移是坐标x 、y 、z 的函数。

当单元足够小时，单元内各点的位移可用简单的线性多项式来近似描述，即⎪⎭⎪⎬⎫+++=+++=+++=z y x w z y x v z y x u 121110087654321αααααααααααα (3-49) 式中1α，2α，…，12α是十二个待定系数，它们可由单元的节点位移和坐标确定。

假定节点i,j,m,p 的坐标分别为(i x i y i z )、(j x j y j z )、(m x m y m z )、 (p x p y p z )，将它们代入(3-49)式的第一式可得各个节点在x 方向的位移⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧+++=+++=+++=+++=p p p p m m m m j j j j i i i i z y x u z y x u z y x u z y x u 4321432143214321αααααααααααααααα (3-50)解上述线性方程组，可得到1α，2α，3α，4α，再代入(3-50)式，得])()()()[(61p p p p p m m m m m jj j j j i i i i i u z d y c x b a u z d y c x b a u z d y c x b a u z d y c x b a Vu +++-+++++++-+++=(3-51) 其中V 为四面体ijmp 的体积，a i ,b i ，…，c p ,d p 为系数。

判断---四面体-公共边法

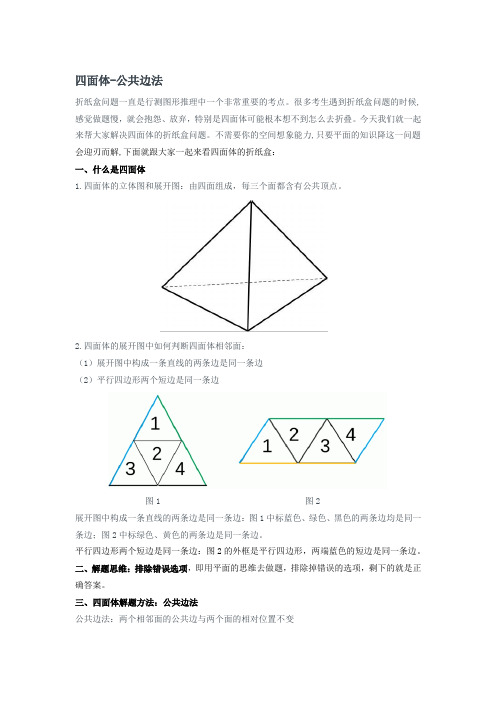
四面体-公共边法
折纸盒问题一直是行测图形推理中一个非常重要的考点。

很多考生遇到折纸盒问题的时候,感觉做题慢，就会抱怨、放弃，特别是四面体可能根本想不到怎么去折叠。

今天我们就一起来帮大家解决四面体的折纸盒问题。

不需要你的空间想象能力,只要平面的知识降这一问题会迎刃而解,下面就跟大家一起来看四面体的折纸盒：
一、什么是四面体
1.四面体的立体图和展开图：由四面组成，每三个面都含有公共顶点。

2.四面体的展开图中如何判断四面体相邻面：
（1）展开图中构成一条直线的两条边是同一条边
（2）平行四边形两个短边是同一条边
图1 图2
展开图中构成一条直线的两条边是同一条边：图1中标蓝色、绿色、黑色的两条边均是同一条边；图2中标绿色、黄色的两条边是同一条边。

平行四边形两个短边是同一条边：图2的外框是平行四边形，两端蓝色的短边是同一条边。

二、解题思维：排除错误选项，即用平面的思维去做题，排除掉错误的选项，剩下的就是正确答案。

三、四面体解题方法：公共边法
公共边法：两个相邻面的公共边与两个面的相对位置不变
图1 图2
图2中的两个面分别是图1中的面2和面3，面2和面3的公共边在展开图中与面3的箭头并不垂直，但是在立体图中，面3的箭头垂直于面2和面3的公共边，所以展开图与平面图不一致，可以排除。

题型示例：
左边给定的是纸盒外表面的展开图，右边哪一项能够由它折叠而成：
四个选项中都是面2和面4，所以可以画出面2和面4的公共边，面2的虚线与公共边相交却不垂直，可以排除C、D两个选项，面4的两个短线与公共边都相交，排除B项，所以选择A项。

判断---四面体-画边法

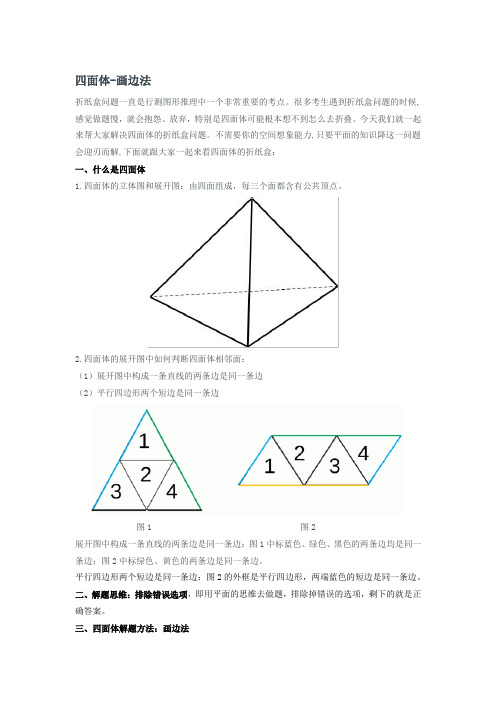
四面体-画边法折纸盒问题一直是行测图形推理中一个非常重要的考点。

很多考生遇到折纸盒问题的时候,感觉做题慢，就会抱怨、放弃，特别是四面体可能根本想不到怎么去折叠。

今天我们就一起来帮大家解决四面体的折纸盒问题。

不需要你的空间想象能力,只要平面的知识降这一问题会迎刃而解,下面就跟大家一起来看四面体的折纸盒：一、什么是四面体1.四面体的立体图和展开图：由四面组成，每三个面都含有公共顶点。

2.四面体的展开图中如何判断四面体相邻面：（1）展开图中构成一条直线的两条边是同一条边（2）平行四边形两个短边是同一条边图1 图2展开图中构成一条直线的两条边是同一条边：图1中标蓝色、绿色、黑色的两条边均是同一条边；图2中标绿色、黄色的两条边是同一条边。

平行四边形两个短边是同一条边：图2的外框是平行四边形，两端蓝色的短边是同一条边。

二、解题思维：排除错误选项，即用平面的思维去做题，排除掉错误的选项，剩下的就是正确答案。

三、四面体解题方法：画边法画边法：1.找到同一个面的唯一点（起点）2.按同一个方向（顺/逆时针）给唯一点所在的面的三个边标号3.结合选项排除图1 图2 图3找唯一点：如图1的左右有2个红点，但这2个红点在图3中不容易区分，找不到对应的红点；如果将上面的顶点标红（图2），则能很容易在图3中找到对应的点（与直线相交的点），即唯一点（能马上识别出来的点）。

图4 图5按同一个方向（顺/逆时针）给唯一点所在的面的三个边标号，展开图和立体图形的方向要保持一致。

直线面上与直线相交的顶点是唯一点，以该点作为起点，在直线面上沿着顺时针方向转一圈，标记1、2、3（如图4），图5的立体图按照相同的方式标号。

结合选项排除：图4的边1对应的是箭头面，图5的边1对应两条直线的面，与图4不一致，可以排除。

题型示例：左边给定的是纸盒外表面的展开图，右边哪一项能够由它折叠而成：本题通过相对位置不容易观察，展开图中有直线面，与顶点的交点比较容易确认，可以作为唯一点，且选项均有该面，找到唯一点后，顺时针画一圈标记1、2、3。

几何-空间几何-正四面体专题教程

点评：本题考查球的内接体的表面积问题，找出表面积的共有特征是解题简化的关键，是中档题．
二．填空题（共 14 小题） 7．已知棱长为 a 的正四面体 ABCD 有内切球 O，经过该棱锥 A﹣BCD 三侧棱中点的截面为α，则 O 到平面α的距离为
．
考点：点、线、面间的距离计算。 1455213
专题：计算题。分析：
，
BO2﹣OE2=BE2，
所以 OE= 球的表面积为：4π•OE2= 故答案为：
点评：本题考查正四面体的内切球的表面积，是一道典型题目，考试常考题，考查空间想象能力，计算能力，是
©2010-2012 菁优网
为（）
A．4π
B．2π
C．
D．
3．已知球 O 在一个棱长为的正四面体内，如果球 O 是该正四面体的最大球，那么球 O 的表面积等于（）
A．
B．
C．2π
D．
4．半径为 1 的球面上的四点 A，B，C，D 是一个正四面体的顶点，则这个正四面体的棱长是（）
A．
B．
C．
D．
5．正四棱锥 P﹣ABCD 的侧棱长和底面边长都等于 a，有两个正四面体的棱长也都等于 a．当这两个正四面体各有
又∵球的半径 R=1 ∴正四面体棱长 l 与外接球半径 R 的关系
l=
得 l=
故选 D 点评：
注意牢记：边长为 1 的正三角形，高为，内切圆的半径为，外接圆半径为；棱长为 1 的正四面体，
侧高为，侧面内切圆的半径为，侧面外接圆半径为；高为，内切球半径为，外接球半径为
5．正四棱锥 P﹣ABCD 的侧棱长和底面边长都等于 a，有两个正四面体的棱长也都等于 a．当这两个正四面体各有

有限元四面体及六面体单元

(4-113)
(4-114)
空间问题有限元分析
基本概念 4节点四面体 7.单元刚度矩阵
基本概
空间问题有限元分析
基本概念 4节点四面体 7.单元刚度矩阵
基本概念
空间问题有限元分析
单元刚度矩阵
空间问题有限元分析
4节点四面体
22%
单元刚度矩阵
40%
(4-104)
(4-105)
空间问题有限元分析
基本概念
4节点四面体
2.单元位移场的表达
将式(9-3)代入节点条件(9-4)中，可求取待定系数(ai，bi，ci)，i＝0，1，2，3。在求得待定系数后，可重写式(9-3)为
(4-106)
(4-107)
空间问题有限元分析
基本概念 4节点四面体单元应变场的表达
(4-116)
空间问题有限元分析
基本概念
8节点正六面体
2.单元位移场的表达
该单元有8个节点，因此每个方向的位移场可以设定8个待定系数，根据确定位移模式的基本原则（从低阶到高阶、唯一确定性），选取该单元的位移模式为
(4-117)
(4-118)
空间问题有限元分析
基本概念
8节点正六面体
3.其它物理参量的表达
空间问题有限元分析
(4-102)
(4-103)
基本概念 4节点四面体 4节点四面体单元几何和节点描述
空间问题有限元分析
基本概念
4节点四面体
2.单元位移场的表达
该单元有4个节点，单元的节点位移有12个自由度(DOF)。因此每个方向的位移场可以设定4个待定系数，根据节点个数以及确定位移模式的基本原则（从低阶到高阶的完备性、唯一确定性），选取该单元的位移模式为

小学教育ppt课件教案认识正四面体的形状和特征

科学技术领域中的价值
数学研究
正四面体是数学研究中的重要对象之一，涉及到几何学、拓扑学等多个分支，对于推动数学理论的发展具有重要意义。
物理实验
在物理实验中，正四面体可以作为实验器材的一部分，用于研究光学、力学等物理现象。
计算机图形学
正四面体在计算机图形学中常被用作三维模型的基本单元，用于构建复杂的三维场景和动画效果。
02
5. 教师总结学生的探究结果，并给出相关拓展知识。
07 总结评价与反思
CHAPTER
关键知识点总结回顾
正四面体的定义
正四面体是一个由四个全等的等边三角形组成的立体图形。
正四面体的性质
正四面体的每个面都是等边三角形，每个角都是相等的，且任意两个相邻面之间的二面角都是相等的。
正四面体的应用
正四面体在几何学中有着广泛的应用，如在建筑设计、工程绘图和科学研究等领域中常常出现。
正四面体的性质
正四面体有4个面、4个顶点、6条棱，每个面都是等边三角形，每个顶点引出3条棱，任意两个顶点间的距离相等。
正四面体与其他多面体关系
与正三棱锥的关系
正四面体可以看作是正三棱锥的特殊情况，当正三棱锥的底面是正三角形且侧棱与底面垂直时，即为正四面体。
与其他正多面体的关系
正四面体是五种正多面体之一，其他四种分别是正六面体、正八面体、正十二面体和正二十面体。
1. 教师布置小组探究任务，要求学生寻找生活中类似正四面体结构的物体。
3. 小组内讨论并整理探究结果，准备向全班汇报。
2. 学生分组进行探究，记录找到的物体并拍摄照片。
小组探究：寻找生活中类似结构物体
01
4. 各小组依次向全班汇报探究结果，展示找到的类似正四面体结构的物体及其应用场景。

八面体空隙和四面体空隙

八面体空隙和四面体空隙1 八面体空隙八面体空隙是一种山体内景观特征，它是一种在一定高度上自然发育的孔洞形状。

它的呈现形式大致是穿透式的，以类似八边形的形态在上层石头内贯穿，下部呈广义圆弧型。

它形态有多样，大小不一。

八面体空隙在地质学上主要是由水文成因和空间形态学成因确定的。

1.1 水文成因在水文成因形成的八面体空隙，首先是由均质岩体中的压裂作用、液化作用和流溶作用等地质物理地貌现象驱动，作用于深层节理，形成节理口，并沿坡位区是持续穿透，破坏下位岩体构造运动，改变岩体的形态和力学状态，从而形成八面体空隙。

1.2 空间形态学成因空间形态学成因形成的八面体空隙是由周围空间条件直接控制，一般在夹块裂解、山地龟裂、崴脊繁枝等空间条件下容易发育。

在一定的深度上穿透并与其他构造元素分离出一定大小及形态的空间，从而形成八面体空隙。

2 四面体空隙四面体空隙属于特殊的孔洞形态，是一种由若干棱面、四面体和六棱柱组成的孔洞，是矿、岩体或石质物构成的透明孔眼，形状多样，大小不一。

主要有水文和空间形态学两种发育模式。

2.1 水文成因四面体空隙的水文成因是由均质岩体的地质构造运动和空间形态学变化驱动的，是一种部分填充土壤的山体内景观特征。

它的形成除了水流在内部、外部岩体结构裂缝纹面上的摩擦作用外，还与气温、气压、地温和应力密切相关。

2.2 空间形态学成因四面体空隙的空间形态学成因是指在固体岩体在运动中形成的“体形-张力-裂隙”模型和空间-条件-作用关系的几何构造，在受均质岩体沿断裂剪切的应变作用，面部的棱边破坏、沿着断裂中裂缝运动和发展。

此时此刻，它可以发育为三维的四边形、圆柱形、类似八的形态，也可以以更复杂的形状出现，尺寸与根部也是不一样的。

体心立方堆积的四面体空隙和八面体空隙个数

体心立方堆积的四面体空隙和八面体空隙个数在物理和化学的世界里，体心立方堆积可谓是一颗璀璨的明珠。

想象一下，一个有点儿像我们常见的骰子的形状，里面却藏着一片神秘的天地。

体心立方堆积，听起来高深莫测，但其实它在我们生活中随处可见。

像一些金属的晶体结构，里面其实有不少空隙，就像我们生活中总有一些不太完美的小角落。

咱们今天就来聊聊这个堆积方式里的两种重要空隙——四面体空隙和八面体空隙，真的是个大有学问的话题。

四面体空隙，这个名字听起来是不是像某种高科技产品？它就是在体心立方结构中形成的一个小空间，形状就像一个小四面体。

想象一下，一个小小的金字塔，有四个面、四个角。

这个空隙的数量可不少，真是让人感到惊讶。

在体心立方的每个晶胞中，能够形成八个这样的四面体空隙。

听到这里，可能有小伙伴在想，八个？是不是觉得这就像买一送一的促销活动？没错，每个晶胞里的四面体空隙就像是一个个隐藏的小宝藏，等待着我们去发现。

接着再说说八面体空隙。

这个名字也不简单，是个正八面体的形状，感觉像是一个迷你版的游戏骰子。

嘿，想象一下，如果你把一个正方体想象成一块饼，那么八面体空隙就像是这个饼里挖出来的小洞。

每个体心立方晶胞中，竟然能形成四个八面体空隙，简直就像在一块蛋糕上切出四个小圆圈，别看小，滋味可不小。

这四个八面体空隙也是一个个能被小原子填充的空间，仿佛在为整体的稳定性做着贡献。

这两种空隙之间的关系就像是老朋友一样亲密。

四面体空隙和八面体空隙虽然形状不同，但都在同一个晶胞里“共处”，为体心立方结构增添了不少层次感。

就像一家人里，父母和孩子各有各的角色，互相支撑，互相依赖。

四面体空隙多一些，八面体空隙少一些，但彼此的存在让整个结构变得更加稳固。

你想啊，光是空隙的数量就有点儿像是一场家里的聚会，四面体空隙像是热情的主办方，八面体空隙则是默默付出的助手，缺一不可。

说到这里，很多人可能会觉得这些数学和物理的东西有点枯燥，其实不然！这些空隙就像是生活中那些看似不起眼的小细节，偶尔却能起到决定性的作用。

(试卷)奥赛经典-奥林匹克数学中的几何问题---第二十二章一般四面体的性质及应用

第二十二章一般四面体的性质及应用【基础知识】四面体是三角形在空间的直接推广，三角形的很多性质及其证法可以推广到四面体上去．四面体的许多性质可以借助于平行六面体来证．性质1任意四面体六个内二面角的平分面交于一点，这点到四面体四个面的距离相等，该点称为四面体的内切球球心（简称四面体的内心）．内切球与四面体四个面内切．若四面体ABCD 的体积为V ，顶点A 所对的侧面面积为A S ，类似地有B S ，C S ，D S （后面所设均同此），其内切球半径记为r ，则3A B C DVr S S S S =+++．性质2任意四面体六条棱的垂直平分面交于一点，这点到四面体四顶点的距离相等，该点称为四面体的外接球球心（简称四面体的外心）．外接球通过四面体四顶点．若四面体ABCD 的体积为V ，其三对对棱的长分别为1a ，a ；1b ，b ；1c ，c ，其外接球半径为R ，则1624Q R V V===注其中Q 即为以三对对棱乘积为边的三角形面积．性质3任意四面体的四条中线（每一顶点与其对面重心的连线）交于一点，而且每条中线从各该顶点算起都被这点分为31∶之比，这点称为四面体的重心．性质4任意四面体的共顶点的（二面角的棱共顶点）三个内二面角的平分面与另三个内二面角的补（或外）二面角的平分面交于一点，这点到四面体四个面的距离相等，该点称为四面体的旁切球球心（简称四面体的旁心），且一个四面体有四个旁心，旁切球与四面体的一个侧面外切，与其他三个侧面的延展面相切．若与四面体ABCD 的顶点A 所对的面外切，与其余三个侧面的延展面相切的旁切球半径记为A r ，类似地有B r ，C r ，D r ，其他记号同前，则 3A B C D A V r S S S S =++-，3B A C D B Vr S S S S =++-，3C A B D C V r S S S S =+++，3D A B C DVr S S S S =+++．性质5（射影定理）四面体任意一个侧面的面积等于其他三个侧面在这个侧面上的射影面积之和．即在四面体ABCD 中，若记AB θ为棱AB 所在的内二面角的大小，其余类同，则有 cos cos cos A B CD C BD D BC S S S S θθθ=⋅+⋅+⋅， cos cos cos B C AD D AC A CD S S S S θθθ=⋅+⋅+⋅， cos cos cos C D AB A BD B AD S S S S θθθ=⋅+⋅+⋅， cos cos cos D A BC B AC C AB S S S S θθθ=⋅+⋅+⋅．性质6（余弦定理）四面体任意一个侧面的面积的平方，等于其他三个侧面的面积的平方和减去这三个侧面中每两个面面积及其所夹二面角余弦之积的两倍之和．即在四面体ABCD 中，有22222cos 2cos 2cos A B C D B C AD C D AB B D AC S S S S S S S S S S θθθ=++-⋅⋅-⋅⋅-⋅，22222cos 2cos 2cos B C D A C D AB C A BD D A BC S S S S S S S S S S θθθ=++-⋅⋅-⋅⋅-⋅，22222cos 2cos 2cos C A B D A B CD A D BC B D AC S S S S S S S S S S θθθ=++-⋅⋅-⋅⋅-⋅，22222cos 2cos 2cos D A B C A B AB A C BD B C AD S S S S S S S S S S θθθ=++-⋅⋅-⋅⋅-⋅．注顺次用A S ，B S ，C S ，D S 去乘射影定理中各式并相加整理即得以上第一式，其余各式类同．性质7（体积公式一）四面体体积13=倍底面面积与底面上的高的乘积．即11113333A AB BC CD D v S h S h S h S h =⋅=⋅=⋅=⋅．性质8（体积公式二）四面体的体积等于它的任意两个面的面积及其所夹二面角正弦之积的三分之二，除以这两个面的公共棱长．即对四面体ABCD ，有2sin 2sin 2sin 2sin 3333C D AB A D BC A B CD B C DAS S S S S S S S V AB BC CD DAθθθθ⋅⋅⋅⋅⋅⋅⋅⋅====2sin 2sin 33B DAC A C BDS S S S AC BDθθ⋅⋅⋅⋅=．注由2111sin sin 3332C C C AB C AB h AB V S h S h S AB θθ⋅⋅=⋅=⋅⋅=⋅⋅=⋅斜高斜高2sin 3C DABS S ABθ⋅⋅等即证得．性质9（体积公式三）四面体的体积等于共顶点的三条棱长乘积与该顶点三面角的特征值乘积的六分之一，即对于四面体ABCD ，若共顶点A 的三条棱长分别为a ，b ，c ，顶点A 处的三个面角分别为α，β，γ则有()1166v abc S A =⋅=16abc =，()12ωαβγ=++．其中()S A =A的三面角的特征值．注由111sin sin 332V S h ab C γβ=⋅=⋅⋅⋅⋅性质10（体积公式四）若记1P ，2P ，3P分别为四面体相对两棱（互为异面的两条棱）的积的平方，再乘以另外四条棱的平方和与这对棱的平方和的差所得的积；P 为四面体每个面上三条棱的积的平方和，则四面体的体积V 性质11（正弦定理一）在四面体ABCD 中，有（1）sin sin sin sin C D AB A D BC B C DA B D ACAB BC DA ACS S S S S S S S θθθθ===⋅⋅⋅⋅⋅⋅⋅⋅2sin sin 3A B CD A C BD CD BD S S S S Vθθ===⋅⋅⋅⋅；（2）22sin sin sin sin sin sin 9A B C D AB CD AD BC AC BD S S S S AB CD AD BC AC BDVθθθθθθ⋅⋅⋅⋅⋅⋅===⋅⋅⋅；（3）若()sin A 表示顶点A 处的三棱中，任意两棱上的二面角的正弦与这两条棱夹角的正弦三者的积，余类同，则()()()()22sin sin sin sin 9C A B C D A B DS S S S S S S S A B C D V====．注此性质由性质8即证．性质12（正弦定理二）四面体中各个面上三条棱长的积与其所对三面角的特征值之比都相等，该比值等于六条棱长的积与体积的六倍之比，即对四面体ABCD ，有 ()()()()BC CD BD AC CD AD AB BD AD AB BC ACS A S B S C S D ⋅⋅⋅⋅⋅⋅⋅⋅===6AB BC CD BD AC ADV⋅⋅⋅⋅⋅=．注此性质由性质9即证，性质13（对棱所成角公式）四面体一对对棱所成角的余弦等于其他两对对棱平方和之差的绝对值与这对对棱乘积的二倍之比．即对四面体ABCD ，有 ¼()cos ,AB CD =()()22222BC AD AC BD AB CD+-+⋅；¼()cos ,BC AD =()()22222AB CD AC BD BC CD+-+⋅；¼()cos ,AC BD =()()22222BCAD AB DC AC BD+-+⋅；注其证明可参见第18章中例1或补成平行六面体，运用三角形余弦定理及平行四边形的对角线平方和等于四边平方和即证．性质14（对棱距离公式）若a 和1a ，b 和1b ，c 和1c 是四面体的三对对棱长，三对对棱之间的距离分别记为()1,d a a ，()1,d b b ，()1,d c c ，则 ()112,Vd a a =；()1,d b b =()1212,Vd c c =．注补成平行六面体证．性质15若四面体的一对对棱长分别为a ，1a ，这对对棱间的距离为d ，对棱所成的角为θ，则四面体的体积V 为11sin 6V aa d θ=⋅．性质16（二面角平分面定理）四面体二面角的内（或外）平分面分所对的棱得两条线段和这个二面角的两个面的面积对应成比例．性质17（空间张角公式）设过四面体ABCD 的棱BC 的截面EBC 交所对的棱AD 于E ，二面角A BC E --，E BC D --的大小分别为1θ，2θ，则 ()1212sin sin sin EBCDBC ABCS S S θθθθ+=+△△△．性质18（空间莱布尼兹公式）设四面体ABCD 的六条棱长分别为a ，b ，c ，d ，e ，f ，G 为其重心，P 为空间中任一点，则()()2222222222211416PG PA PB PC PD a b c d e f =+++-+++++性质19（空间塞瓦定理）设E ，F ，G ，H ，M ，N 分别为四面体ABCD 的棱CD ，DB ，BC ，AD ，AB ，AC 上的点，若六个平面ABE ，ACF ，ADG ，BCH ，CDM ，DBN 共点，则 1CE DH AM BGED HA MB GC⋅⋅⋅= 性质20（空间梅涅劳斯定理）平面KLMN 交四面体ABCD 的棱AB ，BD ，CD ，AC 于K ，L ，M ，N ，则1AK BL DM CNKB LD MC NA⋅⋅⋅=．证明设四边形KLMN 是四面体ABCD 被平面α所截的截面，1AA ，1BB ，1CC ，1DD 是平面α的垂线（1A ，1B ，1C ，1D 分别为垂足）．考察棱AB 与平面α相交的部分，显然11AA K BB K △△≌，则11AA AK KB BB =．同理，11BB BL LD DD =,11DD BM MC CC =,11CC CN NA AA =．以上四式两边相乘即证．性质21（空间斯特瓦尔特定理）在四面体ABCD 中．AD BC ⊥，过棱BC 作截面BCE 交棱AD 于E ，则222214BCE ABC BCD DE AE S S S BC AE DE AD AD =⋅+⋅-⋅⋅△△△．证明如图221-，作AF BC ⊥于F ，连BF ，DF ．注意到AD BC ⊥，知BC ⊥面ADF ，所以BC EF ⊥，BC EF ⊥．记AEF α∠=．在AEF △中，由余弦定理，有 2222cos AF EF AE AE EF α=+-⋅⋅．上式两边同乘以2BC 后，整理得EFBDC图22-1A222244cos 4BCE ABCBCES BC AE S AE BC S α+⋅-=⋅⋅△△△．同理在DEF △中，有222244cos 4BCE BCDBCES BE DE S DE BC S α+⋅--=⋅⋅△△△．由上述两式消去α，整理便证得结论．推论1当ABC BCD S S =△△时，有22214BCE ABCS S BC AE DE =-⋅⋅△△．推论2当E 为AD 中点时，有222221112216BCE ABC BCD S S S BC AD =+-⋅△△△ 推论3当面BCE 平分二面角A BC D --时，有2214BCE ABC BCD S S S BC AE DE =⋅-⋅⋅△△△．事实上，由ABC EABC BCD EBCD S V AE S V DE ==△△，有BCD ABC BCD S DE AD S S =+△△△，ABC ABC BCDS AECD S S =+△△△．由此即证．推论4当AEk ED=时，有 ()222222111141BCE ABC BCD k k S S S AD BC k k k =+-⋅⋅⋅+++△△△．性质22四面体ABCD 中，E ，F ，G ，H 分别在棱AB ，BC ，CD ，DA 上，且1AE EB λ=，2BFFCλ=， 3CG GD λ=，4DHHA λ=，则内接四面体EFGH 的体积与四面体ABCD 的体积之间有关系式 ()()()()1234123411111EFGH ABCDV V λλλλλλλλ⋅⋅⋅-=⋅++++．证明连ED ，BG ，得四棱锥E FBDG -，G EBDH -．在CBD △，ABD △中，有 ()()33232311111CFG CBD S CF CG S CB CD λλλλλλ⋅==⋅=⋅++++△△， ()()11141411111AEH ABD S AF AH S AB AD λλλλλλ⋅==⋅=⋅++++△△， ()()23223111FBDG CBD CFG CBD CBD S S S S S λλλλλ-++==++△△△△， ()()14414111ABD AFH EBDH ABD ABD S S S S S λλλλλ-++==++△△△△．又()()()2321231111G FBDG FBDG ACBD CBD V S BE V S AB λλλλλλ-++=⋅=+++△ ()()()1441341111G EBDH EBDH CABD ABD V S GD V S CD λλλλλλ-++=⋅=+++△， ()()13111EBDG BDG ABDC BDC V S BE DG BE V S AB DC AB λλ=⋅=⋅=++△△．设六面体EGFBDH 的体积为V '，则()()()()124224142324241231411111E FBDG G EBDH EBDG V V V V λλλλλλλλλλλλλλλλλλ--+++++++'=+-=++++ 设六面体FHEACG 的体积为V ''，则()()()()123134121334131231411111F GCAH H FCAE HACF V V V V λλλλλλλλλλλλλλλλλλ--+++++++'=+-=++++当B ，F 在平面EHG 的同侧时，有()EFGH ABCD V V V V '''=+-．当C ，F 在平面EHG 的同侧时，有()EFGH ABCD V V V V '''==+．综合，得()EFGH ABCD V V V V '''=-+．即证．注由此性质可得E ，F ，G ，H 共面的充要条件是1AE BF CG DH EB FC GD HA⋅⋅⋅=．【典型例题与基本方法】例1已知三棱锥S ABC -的底面是正三角形，A 点在侧面SBC 上的射影H 是SBC △的垂心，二面角H AB C --的平面角等于30︒，SA =S ABC -的体积．（1999年全国高中联赛题）解如图222-，由题设，知AH ⊥面SBC ，作BH SC ⊥于E ，则由三垂线定理知SC ⊥面ABE ．设S 在面ABC 的射影为O ，则SO ⊥面ABC ．由三垂线定理的逆定理，可知CO AB ⊥于F ．同理，BO AC ⊥．故O 为ABC △的中心，从而SA SB SC ===又CF AB ⊥，CF 是EF 在面ABC 上的射影，由三垂线定理知EF AB ⊥，所以EFC ∠是二面角H AB C --的平面角，故30EFC ∠=︒，cos6030OC SC =⋅︒=︒，tan603SO OC =⋅︒=．又OC AB =，则3AB ==，所以，21333S ABC V -=⋅例2证明：任意一个四面体总有一个顶点，由这个顶点出发的三条棱可以构成一个三角形的三边．（IMO 10-试题）证明利用反证法来证，设四面体ABCD 中AB 是最长的棱，如果任意一个顶点出发的三条都不能构成一个三角形，则对由A 出发的三条棱，有AB AC AD +≥．又对由B 出发的三条棱，有BA BC BD +≥．两式相加，得2AB AC AD BC BD +++≥．()*但在ABC △与ABD △中，有AB AC BC <+，AB AD BD <+．此两式相加，有 2AB AC AD BC BD <+++．上式与()*式矛盾，故原结论获证．注和这道试题类似的命题还有（1）任意四面体的三组对棱之和可以构成一个三角形的三边；（2）任意四面体的三组对棱之积可以构成一个三角形的三边；FOCBE HS图22-2A（波兰1975～1976年竞赛题）（3）任意四面体的三组对棱的平方和可以构成一个三角形的三边．例3若一个四面体恰有一棱之长大于1，求证这四面体的体积18V≤．证明如图223-，设AB是这个四面体的最长的棱，则ACD△，BCD△的边长不大于1．作BCD△的高BE和ACD△的高AF，则BE，AF1a≤表示CD的长度），四面体的高AO h AF=-≤111332BCDV h S a=⋅△≤()21424a a=-，而()()()()22431213a a a a a-=---+-≤，故当1a=时，()24a a-取最大值3，故31248V=≤．例4证明：在四面体中至多有一个顶点具有如下性质：该顶点处的任何两个平面角之和都大于180︒．（第22届莫斯科竞赛题）证明假定顶点A和B都具备所述的性质，则有180CAB DAB∠+∠>︒及180CBA DBA∠+∠>︒，但是作为CAB△和DAB△的全部6个内角之和也只有180180︒+︒，此为矛盾，从而原结论获证．例5设d是任意四面体的相对棱间距离的最小值，h是四面体的最小高的长．证明2d h>．（第24届全俄竞赛题）证明如图224-，为确定起见，假定h是四面体ABCD中由顶点A所引出的高，而d是棱AB和CD之间的距离．经过顶点B引直线l CD∥，过点A作平面垂直于棱CD交CD于F，交l于E，于是AEF△的高AH和FG就分别等于h和d．由于AEF△的第三条高等于四面体ABCD的某一条高，所以其值不小于h，因此AF EF≤，且图22-3B C图22-4HGlFE BDAC2h AH AE AF FE d FG FE FE+==<≤，此即为所证．例6试证：过四面体相对棱的中点的任一截面平分四面体的体积．（IMO 29-预选题）证法1如图225-，设M 和P 分别是四面体ABCD 的棱AC 和BD 的中点，MNPQ 是四面体ABCD 的一个包含线段MP 的截面，因为P 为BD 的中点，则BCP CDP S S =△△，即有ABCP ACDP V V =．因此，要证截面MNPQ 将四面体ABCD 分成体积相等的两部分，只要证明AMNP V 与OMPQ V 相等就可以了．由N 和Q 分别作平面APC 的垂线，垂足分别为E ，F ，如图225-．因为M 为AC 的中点，则有APM CPM S S =△△，故要证AMNP CMPQ V V =，只要证NE FQ =即可．设MP 与NQ 交于点O ，易证E ，O ，F 三点共线．要证NE FQ =，只要证明NO OQ =就可以了（通过Rt Rt NEO QFO △△≌得到）．为此，考察两个平行平面，异面直线AB 和CD 分别在这两个平面上（如图226-）．因为MP 是连接AC ，BD 中点的线段，所以它在与上述两平面平行的平面上，这个平面到两已知平面的距离相等．由于线段NQ 与MP 相交于O ，所以O 等分线段NQ ，即有NO OQ =．故结论获证．注上述证明中，没有对截面MNPQ 的形状进行讨论．若对其形状进行讨论，则有下述两种证法．证法2如图227-，设M ，P 分别是四面体ABCD 的对棱AC ，BD 的中点．OF E P QNMA BD图22-5N OP M QBDCA图22-6当截面是平行四边形或特殊三角形时，证明比较简单（略）．当截面是一般四边形MNPQ 时．由AM CM =，有A MNPQ C MNPQ V V --=又在ABC △中，对截线MNG 应用梅涅劳斯定理，有1AM CG BNMC GB NA⋅⋅=．从而，有1CG BNGB NA⋅=．同理，在BCD △中，有1BP DQ CG PD QC GB ⋅⋅=，即1DQ CGQC GB⋅=．于是BN DQ NA QC =,得BN DQBA DC=．又1C BPN Q APD V BN CDV BA QD--⋅==⋅,即C BPN Q APD V V --=．故C MNPQ C BPN A MNPQ Q APD V V V V ---+=+一．证毕．证法3前面同证法2，下证截面为一般四边形MNPQ 时的情形．记A d 表示顶点A 到截面MNPQ 的距离（其余类同），设N 分AB 的比为m n ∶．则由M ，P 分别是AC ，BD 的中点，可知Q 点分CD 的比C A D B d d CQ AN mQD d d NB n====．由A C d d =，有A MNPQ C MNPQ V V --=．又13113APD Q APDQ APD C BPNBPN C APD S d V AB QD m n n V NB CD n m n S d ----⋅+==⋅=⋅=+⋅△．即Q APD C BPN V V --=．故C MNPQ C BPN A MNPQ Q APD V V V V ----+=+．例7如图228-，设四面体1234A A A A 的外接球与内切球的半径分别为R 与r ，则3R r ≥．图22-7DG证明设O 为四面体的外心，i A 所对的面的面积为(14)i S i ≤≤，球心O 到i A 所对的面的距离为(14)i d i ≤≤，四面体体积为V ，过顶点1A 的高11A H h =，则易知1111d OA d R h +=+≥，从而()111113S d R S h V +⋅=≥，即1111133S d S R V ⋅+⋅≥．同理2221133S d S R V ⋅+⋅≥，3331133S d S R V ⋅+≥， 4441133S d S R V +⋅≥．以上四式相加，并注意()1122334413S d S d S d S d V ⋅+⋅++⋅=，有4113i i V R S V =+⋅∑≥4，即419i i R S V =⋅∑≥．因4113i i V r S ==⋅∑，从而44113i i i i R S r S ==⋅⋅∑∑≥，即3R r ≥．例8在四面体1234A A A A 中，顶点i A 所对的面的面积为(14)i S i ≤≤，侧面面积为k S ，j S 的两侧面所夹的内二面角的大小记为,k j()14k j <≤≤，棱k j A A 的中点记为kj M ，含点kj M 与另两顶点（不含顶点k A ，j A ）的三角形称为四面体的一个中线面（或一棱与对棱中点的面），这个中线面的面积记为kj S ()14k j <≤≤，则()22212cos ,4kj k j k j S S S S S k j =++⋅⋅，其中k ，j 满足14k j <≤≤．证明对四面体1234A A A A ，由性质6，有223434131423242cos cos 1,3cos 1,42,32,4S S S S S S S S S S S S +=⋅⋅++⋅+⋅⋅+⋅⋅+⋅⋅及221212131423242cos 1,2cos 1,3cos 1,4cos 2,3cos 2,4S S S S S S S S S S S S +=⋅⋅+⋅⋅+⋅⋅+⋅⋅+⋅⋅．亦即13142324cos 1,3cos 1,4cos 2,3cos 2,4S S S S S S S S ⋅⋅++⋅+⋅⋅+⋅⋅2212122cos 1,2S S S S =+-⋅⋅．图22-843A 2A对四面体13412A A A M 和四面体23412A A A M 分别运用性质6，有2222123423411112cos 3,44422S S S S S S =++-⋅⋅⋅-3242112cos 2,32cos 2,422S S S S ⋅⋅-⋅⋅⋅，2222123413411112cos 3,44422S S S S S S =++-⋅⋅⋅-3141112cos 1,32cos 1,422S S S S ⋅⋅⋅-⋅⋅⋅上述两式相加，并将前面结果代入，有()22222123412131412cos 1,3cos 1,42S S S S S S S S S =+++-⋅⋅-⋅-232434cos 2,3cos 2,4cos 3,4S S S S S S ⋅⋅-⋅⋅-⋅⋅2212131411cos 1,3cos 1,422S S S S S S =+-⋅⋅-⋅-232411cos 2,3cos 2,422S S S S ⋅⋅-⋅⋅()222212121212cos 1,22S S S S S S =+-+-⋅ ()2212121cos 1,22S S S S =++⋅．故()22212121212cos 1,24S S S S S =++⋅⋅．同理，得()22212cos ,4kj k j k j S S S S s k j =++⋅⋅．注由性质5，有421412cos ,k j t k j i S S k j S =⋅⋅=∑∑≤≤≤，则推知()22214141412cos ,4kj k j k j k j k j k j S S S S S k j <<⎡⎤=++⋅⋅⎢⎥⎣⎦∑∑∑≤≤≤≤≤≤≤ 444222111134i i i i i i S S S ===⎛⎫=+= ⎪⎝⎭∑∑∑ 例9设G 为四面体1234A A A A 的重心，则222222221232434213143444GA A A A A A A GA A A A A A A +++=+++ 222222223121424412132344GA A A A A A A GA A A A A A A =+++=+++21434k j k j A A =∑≤≤≤．43图22-9证明如图229-，连A ，G 并延长交面234A A A 于点1G ，则1G 是234A A A △的重心，连21A G 并延长交34A A 于M ，则M 是34A A 的中点．连1A M ，对12A A M △及点1G 应用斯特瓦尔特定理，有2221121211212211AG A M A A MG A M A G A M A G MG ⋅=⋅+⋅-⋅⋅．而21121A G G M =∶∶，则2222111212122339AG A A A M A M =+-．()* 由三角形中线公式，有 ()224211212341124A M A A A A A A =+-,()222222324341124A M A A A A A A =+-, 并将其代入()*，有()()2222222111213142324341139AG A A A A A A A A A A A A =++-++．从而()()222222232221111213142324342324343314164GA A G A A A A A A A A A A A A A A A A A A ⎛⎫==+++++-++ ⎪⎝⎭．故22222123243414344k j k j GA A A A A A A A A <+++=∑≤≤．同理可证其他三式均等于例10设R ，r 分别为四面体1234A A A A 的外接球半径与内切球半径，i h 为顶点i A 到所对面的距离，内切球切各顶点i A 所对的面于i A '(1234)i =，，，．求证：（Ⅰ）21416k j k j A A R <∑≤≤≤；（Ⅱ）4214194k j i k j i A A h <=∑∑≤≤≤（Ⅲ）422164i i h r =∑≥；（Ⅳ）141419nk j k j i k j k j i A A A A X <<=''∑∑∑≤≤≤≤≤．证明（Ⅰ）设O ，G 分别为四面体1234A A A A 的外心和重心，延长1A G ，交面234A A A 于1G ，则1G 为234A A A △的重心，连21A G 交34A A 于M 点，则M 点为34A A 中点，如图229-．由例9中证明，知2222222111213142324341[3()()]9AG A A A A A A A A A A A A =++-++．同理，在四面体234OA A A 中，有222222212342324341[3()()]9OG OA OA OA A A A A A A =++-++．()222223243419R A A A A A A =-++ 由于G 为四面体重心，由性质3，知1131AG GG =．于是，在11AOG △中，对点G 应用斯特瓦尔特定理，有 ()222211111[433]16OG OG OA AG =+- 2222222121314232434116()()16R A A A A A A A A A A A A ⎡⎤=-++-++⎣⎦．由于20OG ≥，故21416k j k j A A R <∑≤≤≤．（Ⅱ）显然11AG h ≥，则()()22222221121314232434139h A A A A A A A A A A A A ⎡⎤++-++⎣⎦≤．同理，对2h ，3h ，3h 也有类似于上述的不等式．此四式相加，得4214194k j i k j i A A h <=∑∑≤≤≤．（Ⅲ）由13i i V S h =()1,2,3,4i =，则有4411113ii i iSh V ===∑∑又由4113i i V S r ==⋅∑，则4111i ih r ==∑．由14411234114i i h h h h h =⎛⎫ ⎪⎝⎭∑≥，有()412344h h h h r ≥．故()()()114222222212341234448h h h h h h h h r r ⎡⎤+++=⎣⎦≥≥4．（Ⅳ）四面体1234A A A A ''''的外接球半径记为R '，则214116k j k j R A A <'''∑≤≤≥．又四面体1234A A A A ''''的外接球半径恰是四面体1234A A A A 的内切球半径，故R r '=．于是4222214119999166416k j i k j i R A A h r R <='=∑∑≤≤≥≥≥≥14k j k j A A <''∑≤≤．故214149k j kj k j k j A A R A A <<'''∑∑≤≤≤≤≥8≥．例11四面体1234A A A A 中，外接球半径为R ，体积为V ，过顶点k A ，j A 的中线面为()14kj S k j <≤≤．试证：141k j kjS <∑≤≤ 证明设1d ，2d ，3d 与1θ，2θ，3θ分别为三对对棱12A A ，34A A ；13A A ，24A A ；14A A ，23A A 的距离与夹角，则由性质15，有1234111sin 6V A A A A d θ=⋅⋅⋅，亦即113346V d A A A A ⋅≤．同理，有213246V d A A A A ⋅≤，314236Vd A A A A ⋅≥．取34A A 的中点M ，则121212112MA A S S A A d =⋅△≥，同理，可得关于kj S 的不等式，从而412113214323324234111111112k j kj S A A d A A d A A d A A d A A d A A d <⎛⎫+++++ ⎪⋅⋅⋅⋅⋅⋅⎝⎭∑1≤≤≤122141413k j k j k j k j A A A A V <<⎫⎪⎭∑∑≤≤≤≤≤)12216R =例12设四面体1234A A A A 的内心为I ，记k j A IA △的面积为kj S '，顶点i A 所对的面的面积为i S ．试证：4141kji k j i S S <='∑≤≤ 证明过I 作1IA '⊥面234A A A 于1A '，作34IN A A ⊥于N ，若记面积为k S ，j S 的两侧面夹角为()14kj k j θ<≤≤，则易见11212A NI θ'∠=．设r 为四面体1234A A A A 的内切球半径，则在1Rt IA N '△中，有121sin 2rIN θ=,则34121212sin 2A A r S θ⋅'=．由性质8，有1212342sin 3S S V A A θ⋅⋅=，于是消去34A A ，得12121221cos 32S V S S θ'⋅=⋅，注意到4113i i V S r ==⋅∑，则1212124121cos 2ii S S S S θ='''=⋅∑．对上述两边取∑，并用canchy 不等式，有1241414121cos 2kj k j k j ii S S θ<<=⎫'=⋅⎪⎭∑∑∑≤≤≤≤ 12241414121cos 2k j k j kj k j k j i i S S S S S θ<<=⎡⎤⎛⎫⎛⎫⋅⋅⋅⋅⎢⎥ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦∑∑∑≤≤≤≤≤．()* 注意到性质5，有1212313414cos cos cos S S S S θθθ=⋅+⋅+⋅，即42213121423411cos cos cos 2222i i S S S S θθθ==⋅+⋅+⋅∑，对上式两边同乘以1S 后，再两边取∑，有241141cos 42kj i k j i k j S S S θ=<⎛⎫=⋅⋅ ⎪⎝⎭∑∑≤≤．又由对称平均不等式，有1421141146i k j i k j S S S =<⎛⎫=⋅ ⎪⎝⎭∑∑≤≤ 于是，由()*式（将上述结果代入()*式）即有414114kj i k j i S S <='∑≤≤．例13四面体1234A A A A 的三组对棱乘积的平方和不小于各侧面面积平方和的4倍，即若令12A A a =，34A A a '=，13A A b =，24A A b '=，14A A c =，23A A c '=，顶点i A 所对面的面积为()1234i S i =，，，，则 222222222212344()a a b b C C S S S S '''+++++≥，其中等号当且仅当各对棱的平方和相等．证明对234A A A △应用海伦一秦九韶公式，有 ()24442222221122216S a b c a b a c b c '''''''''=---+++ 同理，()24442222222122216S a b c a b a c b c '''=---+++， ()2444222223122216S a b c a b a c b c '''=---+++， ()24442222224122216S a b c a b a c b c '''=---+++．以上四式相加并整理，得22221234S S S S +++=()()()()()()(){}2222222222222222222221416a a b b a a c c b b c c a a b b c c ⎡⎤⎡⎤⎡⎤'''''''''-+-+-+-+-+-++++⎣⎦⎣⎦⎣⎦()22222214a ab bc c '''++≤．例14四面体1234A A A A 内一点P 到顶点i A 及i A 所对的面的距离分别为i l ，i d ，顶点i A 到所对的面的距离为()1234i h i =，，，，34k ≥ ．求证：41423ki k i i i l h d =⎛⎫ ⎪+⎝⎭∑≥．证明先证一个结论：设()01,2,3,4i x i >=，41i i x a ==∑，则4143ki k i i x a x =⎛⎫ ⎪-⎝⎭∑≥．其中等号当且仅当1234x x x x ===时取得．事实上，由()443333()44i i i i x a x a x a x ⎡⎤+-⎛⎫-=⎢⎥ ⎪⎝⎭⎣⎦≤，有443343k kk i i k i x x a x a ⎛⎫⎛⎫⎪ ⎪-⎝⎭⎝⎭≥，从而 4434444433314114443343k k k kk ii i i k ki i i x x x a x a a ===⎛⎫ ⎪⎛⎫⎛⎫ ⎪⋅=⎪ ⎪- ⎪⎝⎭⎝⎭⎪⎝⎭∑∑∑≥≥ 下证原题：设四面体1234A A A A 的体积为V ，如图2210-，作11A H ⊥面234A A A 于1H ，作11PE A H ⊥于E ，作1PD ⊥面234A A A 于1D ，则11A P l =，11PD d =，111A H h =．设i A 所对面的面积为(1234)i S i =，，，，则()1111111113S l S d S A E d S h V ⋅+⋅+==≥，从而2341133PA A A S l V V ⋅-≥．同理，1342233PA A A S l V V ⋅-≥，1243333PA A A S l V V ⋅-≥， 1234433PA A A S l V V ⋅-≥．从而()13412412322334493PA A A PA A A PA A A V S l S l S l V V V +++-+≥()234111632PA A A V V S h d =+=+，即111112233442l S l h d S l S l S l '+++≥．同理，222221133442l S l h d S l S l S l +++≥，333331122442l S l h d S l S l S l +++≥，444441122332l S l h d S l S l S l +++≥．令()1,2,3,4i i i x l R i =⋅=，由前述结论，得4411423kki i ki i i i i l x h d a x ==⎛⎫⎛⎫ ⎪ ⎪+-⎝⎭⎝⎭∑∑≥≥．【解题思维策略分析】1．解四面体的有关问题时，要善于与三角形类比A 3A 4图22-10例15一个球内切于四面体，将每个切点与该点所在面的三顶点连结起来，这样形成的每面的三个角（以切点为顶点）组成一个集合．试证这四个集合是相等的．（第16届普特南竞赛题）证明设四面体的顶点为()1234i P i =，，，，又设i Q 是正对着i P 的面与球相切的切点．用i ，j ，k ，l 表示{}1234，，，的不同元素，由于i j PQ 与i k PQ 是从同一顶点向球所作的切线，故ij i k PQ PQ =．同理，i j i k PQ PQ =，从而i j l i k l PQ p PQ P △△≌（边，边，边）．于是i j l i k l PQ P PQ P ∠=∠，并用il θ表示这种角，即有il li θθ=.由于以i Q 为顶点的三个角相加是2π，故有2334422πθθθ++=，3441132πθθθ++=，4112242πθθθ++=，1223312πθθθ++=．将这些等式的前两个相加减去后两个，且利用ij ji θθ=．得3412220θθ-=，即1234θθ=．又由对称性，得ij kj θθ=．()*以1Q 为顶点的角是23θ，34θ，42θ，由()*式，它们分别等于以2Q 为顶点的三个角，即41θ，34θ，13θ．由对称性，在所有四个面上的中心角都有同样的情形．证毕，注第26届IMO 由前苏联提供的预选题：“四面体ABCD 的内切球与面ABD 和DBC 分别相切于K 和M 点，证明：AKB DMC ∠=∠．”显然，这道试题是例15的特殊情形．例16已知ABC △的面积力S △，外接圆半径为R ，过A ，B ，C 作平面ABC 的垂线，并在平面ABC 的同一侧的垂线分别取1A ，1B ，1C ，使1a AA h =，1b BB h =，1c CC h =，这里a h ，b h ，c h 分别表示边BC ，CA ，AB 边上的高．求四个平面11A B C ，11B C A ，11C A B ，ABC 所围成的四面体的体积．解求解此问题的关键是确定这个四面体的四个顶点的位置．设平面11A B C 与直线AB 相交于K 点，则点K 在11A B 上．由11AA BB ∥知11a b h AA KA b ACKB BB h a BC====．因此，K 是BCA ∠的外角平分线与BA 的交点，从而平面11A B C 与ABC 的交线是BCA ∠的外角平分线．同理，类似可得：平面11B C A 与ABC 的交线是CAB ∠的外角平分线．上述两条外角平分线的交点是ABC △的旁心B I ，因此B I 就是平面11A B C ，11B C A 与ABC 的公共点，即为所求四面体的一个顶点．这样，旁心A I ，B I ，C I 是所求四面体的三个顶点．设第四个顶点为P ，则P 是平面11A B C 和11B C A 的公共点，因而在直线1B B I 上，P 在平面ABC 上的射影在B BI 上，也在A AI 上，因而P 的射影就是ABC △的内心I ．由相似三角形，1PI AA ∥，且1A P 与AI 相交于A I ，可得1a A a A ar rII PI PI AA h AI r -===，其中r 为ABC △的内切圆半径，a r 为劳切圆半径．设ABC △的周长为2l ，则11221a a a a r r S S l a l PE h r a l l a ---=⋅=⋅=-△．由平面几何知识，易证A B C I I I △的面积为 ()1222a b c S a b c S S ar br cr l a l b l c ⎛⎫'=+++=+++ ⎪---⎝⎭△△△()()()2abc S l a l b l c ⋅=---△．故所求体积()()()211332A B C PI I I S abc S V S PI l l a l b l c ⋅'=⋅=⋅⋅---△△△1433abc S R ==⋅△．例17在四面体1234A A A A 中，顶点i A 所对的面的面积记为()1234i S i =，，，，以i j A A 为棱的二面角为il θ，则（Ⅰ）2142cos 3ij k j θ<∑≤≤≥；（Ⅱ）6141cos 3ij k j θ<≤≤≤C ．证明联想到在ABC △中，运用三角形射影定理并结合柯西不等式，有2223cos cos cos 4A B C ++≥，31cos cos cos 2A B C ⋅⋅≤，于是有下述证法：（Ⅰ）由性质5，1234324423cos cos cos S S S S θθθ=⋅+⋅+⋅，由Cauchy 不等式，有221234324423(cos cos cos )S S S S θθθ=⋅+⋅+⋅()()222222234342423cos cos cos S S S θθθ++++≤，从而22221342423222234cos cos cos S S S S θθθ++++≥．同理，还有类似于上式的三个式子，四式相加，得2444222141112cos 4111i ii ij k j i i i i i i S x x S S x x θ<===⎛⎫==-++ ⎪---⎝⎭∑∑∑∑≤≤≥ ()1234141ix x x x x =-++++-∑()4411111641143133i i i ix x ==⎛⎫⎡⎤=-+-⋅-+= ⎪⎢⎥-⎣⎦⎝⎭∑∑≥．故2142cos 3ijk j θ<∑≤≤≥．（Ⅱ）由1234324423cos cos cos S S S S θθθ=⋅+⋅+⋅≥．同理，还有类似于上式的三个不等式，此四式相乘，化简即得6141cos 3ij k j θ<∏≤≤≤．注将三角形与四面体的上述两个不等式各统一为（Ⅰ）2111cos ,2k j n n i j n<++∑≤≤≥；（Ⅱ）()11211cos ,n n i j n i j n -+<+∏≤≤≤，其中2n =为三角形的，3n =为四面体的．2．善于将有关问题进行转化例18四面体ABCD 三个侧面ABD ，ACD ，BCD 上，由顶点D 引出的中线与底面ABC △对应边所成的角相等，证明：每个侧面的面积小于另外两个侧面面积之和．（1997年波兰竞赛题）证明设E ，F ，G 分别是边AB ，BC ，CA 的中点，连结DE ，DF ，DG 如图2211- （a ）．设DE 与AB 所成角为θ，则 1sin sin 2DAB S DE AB DE FG θθ=⋅⋅=⋅⋅△， 1sin sin 2DBC S DF BC DF GE θθ=⋅⋅=⋅⋅△， 1sin sin 2DCA S DG CA DG EF θθ=⋅⋅=⋅⋅△．由于sin 0θ>，所要证明的命题转化为证明：在四面体DEFG 中，任意一组对棱的乘积小于另两组对棱乘积之和．为此，我们来证明： DE FG DF GE DG EF ⋅<⋅+⋅．将四面体DEFG 的面DFG △绕FG 翻转到底面所在的平面上，得D FG '△如图2211- （b ）．在四边形D FFG '中，显然，有D G DG '=，D F DF '=．由Ptolemy （托勒密）不等式，有D E GF D F GE D G EF DF GE DG EF '''⋅++⋅=⋅+⋅≤．设D E '与GF 交于点O ，由DFG D FG '△△≌，得DO D O '=．在DOE △中， DE DO OE D O OE D E ''<+=+=．故DE GF D E GF DF GE DG EF '⋅<⋅⋅+⋅≤．从而原题得证．例19给出三个四面体()123i i i i A B C D i =，，，过点i B ，i C ，i D 作平面i α，i β，i γ() 123i =，，分别与棱i i A B ，i i A C ，i i A D 垂直()123i =，，．如果九个平面i α，i β，i γ()123i =，，相交于一点E ，而三点1A ，2A ，3A 在同一直线l 上，求三个四面体的外接球面的交集（形状怎样？位置怎样？）．（CMO 3-试题）解由于几何元素太多，画出准确的全图几乎不可能．为此，画出一个局部图．COCDEFGABDEFG(b)(a)图22-11连1A E 与1B E 如图2212- （a ），可知111A B B E ⊥，此表明以1A E 为直径的球过1A ，1B ，E 三点．同样可知，这球过1A ，1B ，1C ，1D ，E 五点，此表明中心在1A E 的中点1O ，直径为1A E 的球也正好是四面体1111A B C D 的外接球．类似地可定出四面体i i i i A B C D 的外接球直径和中心()123i =，，．于是问题转化为到直线123A A A 及其线外一点E 所决定的平面上来了．这个平面与三个球的交线是三个圆，它们有一个公共点E ，从E 向直线123A A A 作垂线，垂足为E '，显然E '是E 关于直线123O O O 的对称点，所以E 与E '是这三圆的公共点．由此知以EE '为直径且垂直于直线123A A A 的圆就是三个四面体的外接球的交集．当E 在直线123A A A 上时，此圆就退化为一个点E ．此时三个球面相切于E 点．例20如图22-13，过四面体PABC 的重心G 的任一直线l 与四个面分别相交于M ，N ，S ，T 四点．求证：11110GM GN GS GT+++=u u u u r u u u r u u u r u u u r ．（《数学通报》问题1362题）证明设1G 为ABC △的重心，连1PG ，并设直线L 与直线1PG 确定的平面α与侧面ABC 的交线分别与ABC △的三边交于1A ，1B ，1C ．连1PA ，1PB ，1PC ，在平面α内，直线l 与1PA ，1PB ，1PC ，11A B 的交点分别为M ，N ，S ，T ．因G 是四面体重心，1G 是ABC △的重心，由重心性质，知G 分1PG u u u u r所成的比为31∶，且1112111110G A G B G C ++=u u u u r u u u u u r u u u u r ．231B 1图22-12(a)(b)B 1lG 1C 1A 1G TPNMSAC B图22-13以1G 为原点，以直线11G A 为x 轴，建立平面直角坐标系如图2214-．设()1,0A a ，()1,0B b ，()1,0C c ，(),P m n ，别由1112121110G A G B G C ++=u u u u r u u u u u r u u u u u r ，知1110a b c ++=，,44m n G ⎛⎫ ⎪⎝⎭．由两点式得直线1PA ，1PB ，1PC ，11A B 的方程分别为()n y x a m a =--，()ny x b m b=--， ()ny x c m c=--，0y = 设直线l 的参数方程为 1cos 41sin 4x m t y n t αα⎧=+⋅⎪⎪⎨⎪=+⋅⎪⎩（α为倾斜角，t 为参数）并设M ，N ，S ，T 对应的参数分别为1t ，2t ，3t ，4t ．将直线l 的方程分别代入直线1PA ，1PB ，1PC ，11A B 方程，得 114sin 4cos 4sin 33m n t na nααα-⋅-⋅=+， 214sin 4cos 4sin 33m n t nb nααα-⋅-⋅=+， 314sin 4cos 4sin 43m n t nc nααα-⋅-⋅=+，414sin t n α-= 由1110a b c++=，得123411110t t t t +++=，故11110GM GN GS GT +++=u u u ur u u u r u u u r u u u r ． 3．适当构作辅助体例21求证：若四面体相对棱间的距离分别为1d ，2d ，3d ，则四面体的体积V 不小于13123d d d ．图22-14证明如2215-，过四面体ABCD 的三组对棱AB 与CD ，AD 与BC ，AC 与BD ，分别引三对相互平行的平面，得平行六面体（或以四面体ABCD 的棱为侧面对角线构作平行六面体），各相对面的距离分别等于四面体三组对棱的距离，又易知该平行六面体的体积正好是四面体ABCD 体积的3倍．在底面11A DB C 中，作1EF CA ⊥于E ，则1EF B D ⊥．设垂足为F ，则EF 不小于平面11A AC C 与平面11DD BB 间的距离，即3EF d ≥．又12AC d ≥，所以1123A DB CS d d ⋅≥Y ．又平面11A DB C 与平面11AD BC 的距离为1d ，因此， 1111111123AD BC A DB C A DB C V S d d d d -=⋅⋅⋅≥Y ．Suoyi 12313ABCD V d d d ≥．例22设a ，b 为四面体ABCD 的一对对棱AB 与CD 的长，r 为四面体内切球半径，求证：()2abr a b <+．（第22届全苏竞赛题）证明如图2416-，过AB 与CD 分别作ABEF Y 与CDGH Y ，使得AF CD ∥，CH AB ∥，连AC ，BH ，EG ，FD ，得一个平行六面体AFEB CDGH -（或以四面体ABCD 的三棱CA ，CB ，CD 为共顶点的棱构成平行六面体）．设AB 与CD 之间的距离为d ，它们所成的角为θ，则由性质15，知1sin 6V ab d θ=⋅⋅四面体．设a h 为ABD △中AB 边上的高，显然D 到AB 的距离大于D 到面AFEB 的距离，即a h d >，而1122ABD a S a h ad =⋅>△．同理，12ABC S ad >△，12ACD S bd >△，12BCD S bd >△．于是，四面体ABCD 的表面积D B CA EFC 1D 1A 1B 1图22-15GABCDHFE图22-16()ABD ABC ACD BCD S S S S S a b d =+++>+△△△△表．注意到性质1，即13V S r =⋅表，得到()3sin 222V abd abd ab r S S S a b θ⋅==<+表表表≤ 4．注意运用向量知识求解例23设平面α，β，γ，δ与四面体ABCD 的外接球面分别切于点A ，B ，C ，D ．证明：如果平面α与β的交线与直线CD 共面，则γ与δ的交线与直线AB 共面．（1981年保加利亚竞赛题）证明设四面体ABCD 的外心为O ，半径为R ．令OA a =u u u r ，OB =b u u u r ，OC c =u u u r ，CD d =u u u r．对空间中任意一点X ，令OX x =u u u r，则222222R =====a b c b d ．因为OA α⊥，所以平面α上的点X 满足()0⋅-=a x a ，即2⋅a x =R ．同理，平面β，γ，δ上的点X 分别满足2R ⋅=b x ，2⋅c x =R ，2R ⋅=d x ．注意到，对任意不同时为零的数λ，μ，有方程()()2R λλλμ⋅⋅+a b x =．给出了一个过平面α与β的交线l 的平面（因0λλ≠a +b ，且对任意X l ∈，有2R ⋅=⋅a x b x =．另外，对空间中任意一点X 也存在一对不同时为零的数λ，μ，使得()()220R R λμ⋅-+⋅-=a x b x ．即适当选取λ与μ，可使相应的平面过点X ．因此直线CD 与直线l 共面的充要条件是：关于未知数λ与μ的方程组()()()()22220,0,R R R R λμλμ⎧⋅-+⋅-=⎪⎨⋅-+⋅-=⎪⎩a c b c a c b c 有非零解，即有()()()()2222R R R R ⋅-⋅-=⋅-⋅-a c b c a b b c ．同理可证，平面γ与δ的交线和直线AB 共面的充要条件为()()()()2222R R R R ⋅-⋅-=⋅-⋅-c a d b c b d a ．因为上面得到的两个条件是等价的，所以题中结论得证．例24设四面体ABCD 对应于各顶点的高分别为a h ，b h ，c h ，d h ，在各高线上分别取1A ，1B ，1C ，1D ，使1a k AA h =，1a k BB h =，1c k CC h =，1dkDD h =为任一实数．求证：四面体1111A B C D 的重心合于四面体ABCD 的重心．证明令AB b =u u u r ，AC c =u u u r ，AD d =u u u r ，根据向量矢量积的意义，知同BD BC ⨯u u u r u u u r 的方向是对应A 点高线的方向，而它的长度是BCD △面积的2倍．设A 点对应高线的单位向量为i ，则2BCDBD BCi S ⨯=△u u u r u u u r，而()()BD BC ⨯=-⨯-=⨯⨯⨯d b c d b d +d c +c b u u u r u u u r ．故2i S⨯⨯⨯=b d +dc +c d．同理，设B ，C ，D 点对应的高线的单位向量分别为j ，k ，l ，则22ACD ACD AC AD S S ⨯⨯=△△c d j =u u u r u u u r ，2ADB S ⨯△d b k =，2ABCS ⨯△b c l =．若设四面体ABCD 的体积为V ，因而()16a k k AA h V ==⨯⨯⨯i =b d +d c +c d u u u r ．同理，()16k BB V =⨯c d u u u r ，()16k CC V =⨯d b u u u u r ，()16kDD V =⨯b c u u u u r ．因而，有11110AA BB CC DD +++=u u u r u u u r u u u u r u u u u u r．又设1O 为四面体1111A B C D 的重心，则()1111111114AO A B AC A D =++u u u u r u u u u r u u u u r u u u u r()11111114A A AB BB A A AC CC A A AD DD =++++++++u u u r u u ur u u u r u u u r u u u r u u u u r u u u r u u u r u u u u r ()11111144A A AA BB CC DD =++++b +c +d +u u u r u u u r u u u r u u u u r u u u u r ()114A A =-b +c +d u u u r ．而111AO AA A O =+u u u u r u u u r u u u u r ，故()114AO AO ==b +c +d u u u u r u u u r，这表示1O 与O 重合．【模拟实战】习题A1．在三棱锥S ABC -的棱SA ，SB ，SC 上分别取点1A ，1B ，1C ，使得11SA SA SB SB ⋅=⋅1SC SC =⋅．证明：点A ，B ，C ，1A ，1B ，1C ．在同一球面上．（第15届全俄竞赛题）2．在四面体ABCD 内求作一点P ，使四个四面体的体积比满足P BCD P CDA P DAB P ABC V V V V αβγδ----=∶∶∶∶∶∶，其中α，β，γ，δ为给定的正数．3．设P ，Q ，R 分别是四面体ABCD 的棱AC ，AD ，AB 或延长线上的点，E ，F 在BC 上，且BE EF FC ==，AE ，AF 分别与RP 交于点G ，H ．记四面体APQR 与AGHQ 的体积分别为V ，1V ．求证：13V V ≥，当且仅当RP BC ∥或RP 与BC 重合时等号取得．4．四面体ABCD 内接于半径为R 的球，且球心O 在四面体内部．求证：四面体ABCD 至少有一条棱长． 5．在四面体ABCD 中，P 为各棱长之和，V 为其体积，用()CD S 表示过四面体棱CD 及相对棱AB 中点。