三角形的分类方法
三角形的分类与计算

三角形的分类与计算三角形是几何学中的基本图形之一,由三条边和三个内角组成。
在三角形中,根据边的长度和角的大小,可以对其进行分类。
同时,通过已知的边长或角度,可以进行相关计算。
下面将对三角形的分类和计算进行详细介绍。
一、三角形的分类根据边长的不同,可以将三角形分为以下三类:1.等边三角形:等边三角形是指三条边的长度相等的三角形。
在等边三角形中,三个角的度数也相等,均为60度。
等边三角形是一种特殊的等腰三角形。
2.等腰三角形:等腰三角形是指有两边的长度相等的三角形。
在等腰三角形中,两个底角的度数相等。
如果等腰三角形的底边也相等,则称为等边等腰三角形。
3.普通三角形:普通三角形是指三边的长度都不相等的三角形。
在普通三角形中,三个角的度数也不相等。
根据角的大小,可以将三角形分为以下三类:1.锐角三角形:锐角三角形是指三个内角都小于90度的三角形。
在锐角三角形中,三边的长度可能相等,也可能不相等。
2.直角三角形:直角三角形是指一个内角等于90度的三角形。
直角三角形的两条边相互垂直,其中一个内角为直角。
3.钝角三角形:钝角三角形是指三个内角中至少有一个大于90度的三角形。
在钝角三角形中,两长边的长度可能相等,也可能不相等。
二、三角形的计算1.边长计算:a.如果已知三角形的三个内角度数,则可以利用三角形内角和定理计算出未知边的长度。
三角形内角和定理是指三角形的三个内角度数之和等于180度。
b.如果已知三角形的两个边的长度和夹角,则可以利用余弦定理或正弦定理计算出第三边的长度。
c.如果已知三角形的一个边的长度和两个夹角,则可以利用正弦定理计算出其余两边的长度。
2.面积计算:三角形的面积可以通过以下公式计算:面积=底边长度×高/2其中,高是指从顶点到底边的垂直距离。
3.三角函数计算:三角函数是三角形中的重要概念,包括正弦、余弦和正切。
这些函数可以用来计算三角形中的边长和角度,例如:a. 正弦定理:a/sinA = b/sinB = c/sinC,其中a、b、c是三角形的边长,A、B、C是对应的内角度数。
三角形的分类及性质

三角形的分类及性质三角形是几何学中最基本的形状之一,它由连结三条线段的端点组成。
在几何学中,根据三角形的边长和角度,可以对其进行分类。
本文将对三角形的分类及其性质进行探讨。
I. 等边三角形等边三角形是一种特殊的三角形,其三条边的长度相等。
由于每个内角都是60度,所以它也是等角三角形。
等边三角形具有以下性质:1. 三条边相等。
2. 三个内角均为60度。
3. 等边三角形的高、中线、垂心和重心重合。
II. 等腰三角形等腰三角形是指两条边相等的三角形。
等腰三角形也具有一些特殊性质:1. 两条边相等。
2. 两个底角相等。
3. 等腰三角形的高、中线、垂心和重心可以不重合。
III. 直角三角形直角三角形有一个内角为90度(直角)。
直角三角形的特点有:1. 有一个90度的内角。
2. 两个锐角相加必为90度。
3. 直角三角形的斜边最长,其他两边为短边。
IV. 钝角三角形钝角三角形至少有一个内角大于90度。
钝角三角形具有以下性质:1. 有一个大于90度的内角。
2. 其余两个内角和小于90度。
3. 钝角三角形的两边之和大于第三边。
V. 锐角三角形锐角三角形的三个内角都小于90度。
锐角三角形的特性包括:1. 三个内角都小于90度。
2. 三条边的长度可能不等。
3. 锐角三角形的高、中线、垂心和重心一般不会重合。
总结:通过以上分类和性质的介绍,我们可以看出三角形的多样性。
不同类型的三角形具有不同的边长和角度特性,这些特性在几何学中起到重要的作用。
了解不同类型三角形的性质可以帮助我们更好地理解几何学的基础知识,并在解决实际问题时能够灵活运用。
注意:以上只是对三角形分类及性质的简要介绍,随着对几何学的深入学习,我们将进一步了解三角形的相关性质及其在几何学中的应用。
三角形的分类

三角形的分类三角形,这可是咱们数学世界里的“常客”。
从小学开始,咱们就和三角形打交道啦。
先来说说三角形的分类方法吧。
三角形按照角的大小来分,可以分成锐角三角形、直角三角形和钝角三角形。
锐角三角形呢,就是它的三个角都小于 90 度,一个个角都像小锐角一样活泼俏皮。
比如说,咱们拿三角板来比划,那个最小的三角板,它的每个角都小小的、尖尖的,这就是锐角三角形的样子。
直角三角形就比较有特点啦,它有一个角正好是 90 度,像个站岗的士兵,笔直笔直的。
还记得小时候搭积木不?有时候咱们搭出一个形状,其中有一个角怎么都推不倒,直直的,那八成就是个直角三角形啦。
钝角三角形呢,它有一个角大于 90 度小于 180 度,这个角就像个懒洋洋的家伙,张得大大的。
再按照边的长短来分,三角形又能分成等边三角形、等腰三角形和一般三角形。
等边三角形可有趣啦,它的三条边都一样长,就像三个好兄弟,谁也不偏袒谁,长度都相等。
我记得有一次在公园里,看到花坛的形状,三边都长得一模一样,当时我就想,这可不就是咱们数学里的等边三角形嘛。
等腰三角形呢,它有两条边长度相等,就像一对双胞胎姐妹,总有那么两条边长得特别像。
有一回我在家整理书架,发现一本旧书里夹着一张纸,上面画着一个等腰三角形,一下子就让我想起了课堂上讲的知识。
一般三角形就是三条边都不一样长的,它们各有各的脾气,长短不一。
在生活中,三角形的身影也是无处不在。
比如,咱们家里的晾衣架,那一个个的支架组合起来,不就是好多三角形嘛,这样能让晾衣架更稳固。
还有自行车的车架,也是利用了三角形的稳定性,咱们骑着车在路上飞驰,可多亏了这些三角形在默默支撑着呢。
再看看那些漂亮的建筑,有的屋顶就是三角形的,既能排水又美观。
学习三角形的分类,可不仅仅是为了考试得分哦,更是为了让咱们能更好地理解这个丰富多彩的世界。
当我们看到这些三角形的时候,能够一下子就认出它们的类型,是不是感觉特别有成就感呢?总之,三角形的分类虽然看似简单,但是用处可大着呢!希望大家都能和三角形成为好朋友,在数学的海洋里畅游得更欢快!。
三角形的分类

三角形的分类三角形是几何学中研究的基本图形之一,根据边长和角度的关系,可以将三角形分为不同的类型。
在本文中,我们将探讨常见的三角形分类及其特点。
一、根据边长分类1. 等边三角形:等边三角形的三条边长度都相等。
由于其特殊的性质,它的三个内角也相等,每个角均为60度。
等边三角形是一种特殊的等腰三角形。
2. 等腰三角形:等腰三角形的两边长度相等,而底边长度不相等。
等腰三角形的两个底角也相等。
3. 等腰直角三角形:等腰直角三角形是一种融合了等腰三角形和直角三角形的特性的三角形。
它的两条直角边长度相等,而斜边的长度与两条直角边长度之比为√2。
4. 普通三角形:普通三角形的三条边长度都各不相等。
它没有特殊的性质,是最一般的三角形形状。
二、根据角度分类1. 直角三角形:直角三角形的一个角为直角(90度),另外两个角为锐角和钝角。
直角三角形是最常见和易于理解的三角形类型,也是勾股定理的基础。
2. 锐角三角形:锐角三角形的三个内角均为锐角,即小于90度。
3. 钝角三角形:钝角三角形的三个内角中,至少有一个是钝角,即大于90度。
三、根据边长和角度综合分类1. 等腰锐角三角形:等腰锐角三角形是一种既有等腰特性又有锐角特性的三角形。
它的两边长度相等,而三个内角均为锐角。
2. 等腰钝角三角形:等腰钝角三角形具有等腰特性和钝角特性。
它的两边长度相等,至少有一个内角是钝角。
3. 等腰直角三角形:已在前面的内容中介绍过,等腰直角三角形是一种融合了等腰三角形和直角三角形的特性的三角形。
三角形的分类不仅仅是对三角形形状的描述,也涉及到其性质和特点。
通过对不同类型三角形的学习,我们可以更深入地了解几何形状及其相关概念。
总结:三角形根据边长和角度的特点可以分为等边三角形、等腰三角形、等腰直角三角形和普通三角形。
根据角度的不同,三角形可以分为直角三角形、锐角三角形和钝角三角形。
此外,还有一些特殊类型的三角形,如等腰锐角三角形、等腰钝角三角形和等腰直角三角形。
三角形的分类和性质

三角形的分类和性质
三角形的分类和性质
三角形的分类:常见的三角形按边分有普通三角形,等腰三角;按角分有直角三角形、锐角三角形、钝角三角形等,其中锐角三角形和钝角三角形统称斜三角形。
按角分
1、锐角三角形:三个角都小于90度。
2、直角三角形:其中一个角等于90度。
3、钝角三角形:其中一个角一定大于90度,钝角大于九十度且小于一百八
十度。
按边分
不等边三角形:3条边都不相等。
等腰三角形:有2条边相等。
等边三角形:3条边都相等。
三角形是由同一平面内不在同一直线上的三条线段“首尾”顺次连接所组成的封
闭图形,在数学、建筑学有应用。
三角形的性质
1、三角形三个内角的和等于180度。
2、三角形任何两边的和大于第三边。
3、三角形任意两边之差小于第三边。
4、三角形的外角等于与它不相邻的两个内角的和。
三角形怎么分类(一)

三角形怎么分类(一)引言概述:三角形是几何学中最基本的图形之一,根据三角形的边长和角度关系,可以将其分类为不同类型。
本文将详细讨论三角形的分类方法,并分析每一类别的特征和性质。
通过了解三角形的分类,我们可以更好地理解和应用几何学中的相关概念和定理。
正文:1. 根据边长分类1.1 等边三角形1.2 等腰三角形1.3 不等边三角形1.4 直角三角形1.5 钝角三角形1.6 锐角三角形1.7 等腰锐角三角形1.8 等腰钝角三角形1.9 ...(根据需要进行补充)2. 根据角度分类2.1 锐角三角形2.2 直角三角形2.3 钝角三角形2.5 余弦三角形2.6 绝对余弦三角形2.7 ...(根据需要进行补充)3. 根据边长和角度关系分类3.1 等腰直角三角形3.2 等腰钝角三角形3.3 锐角等边三角形3.4 直角等腰三角形3.5 ...(根据需要进行补充)4. 根据内角和外角之和分类4.1 内角和为180°的三角形4.2 外角和为360°的三角形4.3 内角和小于180°的三角形4.4 内角和大于180°的三角形4.5 ...(根据需要进行补充)5. 根据特殊性质分类5.1 等角三角形5.2 相似三角形5.3 相等三角形5.5 ...(根据需要进行补充)总结:通过对三角形的分类方法进行细致的探讨,我们可以深入理解不同类型三角形的特征和性质。
从边长、角度、边长和角度关系、内外角之和以及特殊性质的角度考虑,我们能够更好地应用几何学中的定理和概念,并解决与三角形相关的问题。
熟练掌握三角形的分类方法不仅扩展了我们对几何学的认识,也为我们在实际应用中提供了更多便利和创新的思路。
因此,通过学习本文所介绍的三个大点分类方法,并结合具体例子进行练习和应用,有助于进一步巩固和拓展我们对三角形分类的认识。
三角形的认识认识三角形的基本概念和分类

三角形的认识认识三角形的基本概念和分类三角形的认识:认识三角形的基本概念和分类三角形是几何学中最基本的图形之一,它由三条线段组成,连接起来形成一个封闭的三边形。
在本文中,我们将深入探讨三角形的基本概念及其分类。
一、三角形的基本概念三角形由三条线段组成,分别称为三角形的三边。
三边的交点称为三角形的顶点。
除此之外,三角形还包括三个内角和三个外角。
三个内角相加的和总是等于180度。
二、三角形的分类根据三角形内角的大小和三边的长短,三角形可以被分为以下几类:等边三角形、等腰三角形、直角三角形、锐角三角形和钝角三角形。
1. 等边三角形等边三角形的三边长度完全相等,且三个内角都为60度。
等边三角形具有对称性和稳定性,常见于图案设计和建筑结构中。
2. 等腰三角形等腰三角形的两边长度相等,且两个对应的内角也相等。
第三边可以不等于两边长度,但不会超过两边之和。
等腰三角形在几何学中非常常见,如金字塔的侧面、高楼大厦的屋顶等。
3. 直角三角形直角三角形的一个内角为90度,通常被称为直角。
直角三角形最著名的例子是勾股定理。
根据勾股定理,直角三角形的两直角边的平方之和等于斜边的平方。
4. 锐角三角形锐角三角形的所有内角都小于90度,即三个内角都是锐角。
锐角三角形的三边长度也会有所不同。
5. 钝角三角形钝角三角形至少有一个内角大于90度,称为钝角。
其他两个内角则是锐角或直角。
钝角三角形的形状更为扁平,内角较小的两边会相对较长。
结论:三角形作为几何学中最基本的图形之一,具有丰富的性质和分类。
通过了解三角形的基本概念和分类,我们可以更好地理解和应用几何学的原理。
对于根据三边长度和内角大小对三角形进行分类的方法,我们应该加以熟记,并在实际问题中加以应用,以便更好地理解和解决相关问题。
总之,三角形的认识是我们学习几何学的基础,通过深入了解三角形的基本概念和分类,我们可以更好地应用几何学知识,解决实际问题,实现几何学在日常生活中的应用和价值。
三角形按边分类可以分为哪三种

三角形按边分类可以分为哪三种三角形按边分类可以分为不等边三角形、等腰三角形、等边三角形三种。
等边三角形三边相等,等腰三角形有两边相等,不等边三角形三边都不等。
三角形按边分类可以分为不等边三角形、等腰三角形、等边三角形三种。
等边三角形三边相等,等腰三角形有两边相等,不等边三角形三边都不等。
三角形分类1、不等边三角形;不等边三角形,数学定义,指的是三条边都不相等的三角形叫不等边三角形。
2、等腰三角形;等腰三角形,指两边相等的三角形,相等的两个边称为这个三角形的腰。
等腰三角形中,相等的两条边称为这个三角形的腰,另一边叫做底边。
两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
3、等边三角形。
等边三角形〔又称正三角形〕,为三边相等的三角形,其三个内角相等,均为60°,它是锐角三角形的一种。
等边三角形也是最稳定的构造。
等边三角形是特殊的等腰三角形,所以等边三角形拥有等腰三角形的一切性质。
三角形的性质1、在平面上三角形的内角和等于180°〔内角和定理〕。
2、在平面上三角形的外角和等于360°〔外角和定理〕。
3、在平面上三角形的外角等于与其不相邻的两个内角之和。
推论:三角形的一个外角大于任何一个和它不相邻的内角。
4、一个三角形的三个内角中最少有两个锐角。
5、在三角形中至少有一个角大于等于60度,也至少有一个角小于等于60度。
6、三角形任意两边之和大于第三边,任意两边之差小于第三边。
7、在一个直角三角形中,假设一个角等于30度,那么30度角所对的直角边是斜边的一半。
8、直角三角形的两条直角边的平方和等于斜边的平方〔勾股定理〕。
9、直角三角形斜边的中线等于斜边的一半。
10、三角形的三条角平分线交于一点,三条高线的所在直线交于一点,三条中线交于一点。
三角形的分类

小红是这样分的
三角形的分类
锐角三角形
按角分 直角三角形 钝角三角形
三个角都是锐角的三角形
有一个角是直角的三角形 有一个角是钝角的三角形
锐角三角形
图形
图形
图形
直角三角形
钝角三角形
按角分:锐角三角形; 直角三角形; 钝角三角形.
锐角三角形返回直角三Fra bibliotek形返回
钝角三角形
返回
三角形的分类
等腰三角形 按边分
两条边相等的三角形
等边三角形
不等边三角形
三条边都相等的三角形
三条边都不相等的三角形
一般三角形
等腰三角形 等边三角形
等腰三角形
腰
腰
底角
底角
底
等腰三角形的两条腰相等,两个底角也相等。
等边三角形
等边三角形的三条边相等, 三个内角也相等,都是60度。
不等边三角形
不等边三角形的三条边都不相等,三个角也不相等
小明是这样分的
三角形分类的三种方法

三角形分类的三种方法三角形是一个简单而有趣的几何形状,它由三个连接在一起的线段组成。
根据其边长和角度的特征,可以将三角形分为不同的类型。
下面将介绍三种常用的分类方法。
一、根据边长分类1.等边三角形:每条边的长度相等。
等边三角形的三个内角也相等,每个角为60度。
2.等腰三角形:两条边的长度相等。
等腰三角形的两个底角也相等,而顶角则可以不相等。
3.普通三角形:三条边的长度都不相等。
根据边长的分类方法主要侧重于三角形的边长特征,可以很直观地判断三角形的类型。
二、根据角度分类1.直角三角形:其中一个内角为90度,被称为直角。
直角三角形的两个较短边长度可以相等,也可以不等。
2.钝角三角形:其中一个内角大于90度,被称为钝角。
钝角三角形的三个内角之和大于180度。
3.锐角三角形:三个内角都小于90度,被称为锐角。
锐角三角形的三个内角之和等于180度。
根据角度的分类方法主要关注于三角形内部角度的特征,能更直观地了解三角形的角度情况。
三、根据边长和角度分类1.等边等角三角形:边长相等并且角度也相等的三角形。
即等边三角形的每个角都是60度。
2.等腰等角三角形:边长两两相等并且角度也相等的三角形。
即等腰三角形的两个底角相等。
3.普通三角形:边长都不相等,并且角度也不相等的三角形。
根据边长和角度的分类方法是较为全面的,同时考虑了三角形的边长和角度特征。
总结起来,三角形的分类方法主要有根据边长、角度以及边长和角度相结合三种,每种方法针对不同的特征,能够更全面地了解三角形的类型。
此外,还有一些其他的分类方法,如根据三边的关系分类(如等腰直角三角形、等腰钝角三角形等),但以上所介绍的三种方法是最常用和最基本的分类方法。
三角形的分类

三角形的分类三角形是几何学中最基本的形状之一,它由三条边和三个角组成。
根据其边长和角度关系的不同,三角形可以分为不同的类型。
本文将介绍三角形的分类及其特点。
一、按照边长分类1. 等边三角形:三条边的长度完全相等。
等边三角形的三个角也相等,每个角都等于60度。
等边三角形是一种特殊的等腰三角形。
2. 等腰三角形:至少有两条边的长度相等。
等腰三角形的两个底角(底边对应的两个角)相等。
3. 普通三角形:三条边的长度各不相等的三角形称为普通三角形。
二、按照角度分类1. 直角三角形:其中一个角为直角(90度)。
直角三角形的边长关系满足勾股定理,即a²+b²=c²,其中a和b为两条直角边的长度,c为斜边的长度。
2. 钝角三角形:其中一个角大于90度。
钝角三角形的其他两个角都是锐角。
3. 锐角三角形:所有角都小于90度的三角形称为锐角三角形。
三、按照边长和角度关系分类1. 等边等角三角形:即既是等边三角形,又是等角三角形的三角形。
2. 等腰等角三角形:既是等腰三角形,又是等角三角形的三角形。
3. 普通三角形:所有边长和角度都不相等的三角形。
四、其他特殊三角形1. 等腰直角三角形:既是等腰三角形,又是直角三角形的三角形。
等腰直角三角形的两个等腰角均为45度。
2. 等腰钝角三角形:既是等腰三角形,又是钝角三角形的三角形。
3. 等腰锐角三角形:既是等腰三角形,又是锐角三角形的三角形。
在实际应用中,我们可以通过观察三角形的边长和角度关系,来判断三角形的类型。
例如,在建筑设计中,我们需要确保三角形的各个边长和角度满足设计要求,以保证建筑结构的稳定性和美观性。
总结:三角形是几何学中最基本的形状,根据边长和角度关系的不同,可以分为等边三角形、等腰三角形、普通三角形、直角三角形、钝角三角形和锐角三角形等不同类型。
了解三角形的分类及其特点,有助于我们在实际应用中更好地理解和运用相关知识。
三角形的分类

一、三角形的分类
1.按角分类:2.按边分类:
等腰三角形与等边三角形之间的关系: 三角形的分类
在三角形中,
三个角都是锐角的三角形叫做锐角三角形;有一个角是直角的三角形叫做直角三角形;有一个角是钝角的三角形叫做钝角三角形.锐角三角形和钝角三角形统称为斜三角形.
等腰三角形是指至少有两条边相等的三角形;等边三角形是指三条边都相等的三角形;等边三角形是特殊的等腰三角形.
爱智康
2018/06/12
已知,,,是三角形的三边,且满足,是判断这个三角形的形状.a b c ++=0(a −b )2(b −c )2(c −a )2。
三角形按边分类可以分为哪三种

三角形按边分类可以分为哪三种三角形按边分类可以分为不等边三角形、等腰三角形、等边三角形三种。
等边三角形三边相等,等腰三角形有两边相等,不等边三角形三边都不等。
扩展资料三角形分类1、不等边三角形;不等边三角形,数学定义,指的是三条边都不相等的三角形叫不等边三角形。
2、等腰三角形;等腰三角形,指两边相等的三角形,相等的两个边称为这个三角形的腰。
等腰三角形中,相等的两条边称为这个三角形的腰,另一边叫做底边。
两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
3、等边三角形。
等边三角形(又称正三角形),为三边相等的.三角形,其三个内角相等,均为60°,它是锐角三角形的一种。
等边三角形也是最稳定的结构。
等边三角形是特殊的等腰三角形,所以等边三角形拥有等腰三角形的一切性质。
三角形的性质1、在平面上三角形的内角和等于180°(内角和定理)。
2、在平面上三角形的外角和等于360°(外角和定理)。
3、在平面上三角形的外角等于与其不相邻的两个内角之和。
推论:三角形的一个外角大于任何一个和它不相邻的内角。
4、一个三角形的三个内角中最少有两个锐角。
5、在三角形中至少有一个角大于等于60度,也至少有一个角小于等于60度。
6、三角形任意两边之和大于第三边,任意两边之差小于第三边。
7、在一个直角三角形中,若一个角等于30度,则30度角所对的直角边是斜边的一半。
8、直角三角形的两条直角边的平方和等于斜边的平方(勾股定理)。
9、直角三角形斜边的中线等于斜边的一半。
10、三角形的三条角平分线交于一点,三条高线的所在直线交于一点,三条中线交于一点。
三角形的分类

三角形的分类三角形是我们在数学中常见的几何图形之一,它具有丰富的特性和多样的分类方式。
接下来,让我们一起深入了解三角形的分类。
首先,按照角的大小来分类,三角形可以分为锐角三角形、直角三角形和钝角三角形。
锐角三角形,顾名思义,就是三角形的三个角都小于 90 度。
这种三角形的特点是三个内角都是锐角,它的三条边长度之间的关系比较灵活。
想象一下,一个锐角三角形就像是一个充满活力、充满朝气的三角形,三个角都“精神饱满”,角度都不大。
直角三角形就比较特别了,它有一个角恰好是 90 度。
这个 90 度的角被称为直角,而与直角相对的那条边叫做斜边,另外两条边叫做直角边。
直角三角形在我们的生活中应用非常广泛。
比如,建筑工人在建造房屋时,经常会用到直角三角形的原理来确保墙角是垂直的。
钝角三角形则是有一个角大于 90 度小于 180 度。
这个大于 90 度的角就是钝角。
钝角三角形看起来就有点“不协调”,有一个角“懒洋洋”地张得很大。
接着,按照边的长度关系,三角形可以分为等边三角形、等腰三角形和一般三角形。
等边三角形,它的三条边长度都相等。
由于三条边长度相等,所以三个角也相等,每个角都是 60 度。
等边三角形就像是一个完美平衡的图形,三边相等,角度也相等,给人一种整齐、和谐的美感。
等腰三角形则是有两条边长度相等。
这两条相等的边叫做腰,另一条边叫做底边。
相对应的,相等的两个角叫做底角,另一个角叫做顶角。
等腰三角形在几何图形的组合和构建中经常出现。
而一般三角形就是三条边长度都不相等的三角形。
这种三角形的特点是边和角的关系比较复杂,需要通过具体的测量和计算来确定其特性。
不同类型的三角形在数学和实际生活中都有着独特的应用和意义。
比如,在建筑设计中,需要考虑不同三角形的稳定性和结构强度;在物理学中,三角形的知识可以用于计算力的合成和分解;在计算机图形学中,三角形是构建复杂图形的基本单元。
锐角三角形由于其内角都比较小,所以在受力分析时,它的稳定性相对较弱,但在一些需要灵活变化的结构中可能会被用到。
三角形的分类

三角形的分类三角形是几何学中最常见和最基本的图形之一。
根据其特性,三角形可以分为不同的类型。
以下是三角形的一些主要分类:1等边三角形:三条边都相等的三角形称为等边三角形。
这种三角形的所有角都是相等的,每个角都是60度。
等边三角形是一种特殊的等腰三角形。
2等腰三角形:有两条边长度相等的三角形称为等腰三角形。
这种三角形的两个底角是相等的,顶角与两个底角的和加起来等于180度。
直角三角形:有一个角是90度的三角形称为直角三角形。
这种三角形的斜边长等于其两条直角边的平方和的平方根。
直角三角形的一个锐角是45度。
钝角三角形:有一个角大于90度的三角形称为钝角三角形。
这种三角形的钝角对应的边比其他两边长。
锐角三角形:所有角都小于90度的三角形称为锐角三角形。
这种三角形的所有边都相等。
斜三角形:三条边长度不相等的三角形称为斜三角形。
斜三角形可以进一步分为钝角斜三角形和锐角斜三角形,取决于其最大的角是钝角还是锐角。
这些分类可以根据三角形的不同特性进行进一步的细分。
例如,等腰三角形可以进一步分为等边等腰三角形和底角与顶角不相等的等腰三角形等。
还有等腰直角三角形等腰钝角三角形等特殊形式。
三角形的分类对于理解几何学中的基本概念和性质非常重要。
通过掌握不同类型的三角形的特性和关系,我们可以更好地理解几何学中的基本原理和应用。
三角形是数学几何中一个非常基础且重要的概念,而三角形的分类也是学生需要掌握的一项重要技能。
根据边长和角的特征,三角形可以分为以下几类:等边三角形等腰三角形、直角三角形和普通三角形。
等边三角形是一种三边长度相等的三角形,其中三个角的大小也相等。
等边三角形的判定方法是:如果一个三角形的三边长度相等,那么这个三角形就是等边三角形。
等边三角形是一个特殊的等腰三角形。
等腰三角形是一种两边长度相等的三角形,其中两个角的大小也相等。
等腰三角形的判定方法是:如果一个三角形有两条边的长度相等,那么这个三角形就是等腰三角形。
三角形的分类
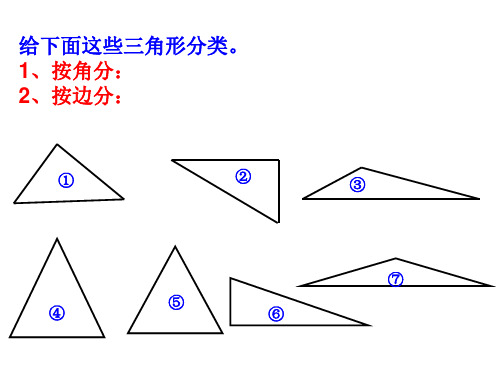
①
②
③
⑦ ④ ⑤ ⑥
1、按角分: 、按角分:
三个角都是锐角的三角形叫做
①
④
⑤
锐角三角形
② ⑥ ③
有一个角是直角的三角形叫做
直角三角形
有一个角是钝角的三角形叫做
钝角三角形
⑦
每个三角形都至少有两个锐角,另外一个角是锐角,直角,钝角中的一个。 每个三角形都至少有两个锐角,另外一个角是锐角,直角,钝角中的一个。
给下面这些三角形分类。 给下面这些三角形分类。 1、按角分: 、按角分: 2、按边分: 、按边分:
①
②
③
⑦ ④ ⑤ ⑥
不等边三角形和等腰三角形。 不等边三角形和等腰三角形。
2、按边分: 、按边分:
④
⑦
⑤
等腰三角形
等腰三角形
等边三角形
三角形的分类与内角和

三角形的分类与内角和三角形的分类三角形是由三条线段组成的几何图形,它的分类主要基于其边长和角度大小。
根据边长的不同,三角形可以分为以下三种分类:1.等边三角形:所有边长相等的三角形被称为等边三角形。
它的三个内角也相等,每个角都为60度。
等边三角形是一种特殊的等腰三角形。
2.等腰三角形:只有两条边长相等的三角形被称为等腰三角形。
它的两个内角也相等。
3.普通三角形:除了等腰三角形和等边三角形之外的所有三角形都被称为普通三角形。
它的三个边长和三个内角都可以不相等。
三角形的内角和三角形的内角和是指三个内角的度数之和。
根据三角形的性质,我们知道一个三角形的内角和总是等于180度。
设三角形的三个内角分别为A、B和C,它们的度数分别为α、β和γ。
则有以下等式成立:α + β + γ = 180°根据这个等式,我们可以得到一些有趣的结论:•当三角形是等边三角形时,它的每个内角的度数都为60度,所以三个内角的和为180度。
•当三角形是等腰三角形时,它的两个内角的度数相等,假设为x度。
则有:x + x + γ = 180°,化简得到:2x + γ = 180°,进而可以计算出γ的度数。
•当三角形是普通三角形时,它的三个内角的度数都可以不相等。
我们可以通过已知两个内角的度数,来计算出第三个内角的度数。
例如,已知α和β的度数,可以通过以下等式计算出γ的度数:α + β + γ = 180°。
总结三角形是一种常见的几何图形,根据其边长和角度大小的不同,可以分为等边三角形、等腰三角形和普通三角形。
三角形的内角和总是等于180度,无论其是等边三角形、等腰三角形还是普通三角形。
通过已知两个内角的度数,我们可以计算出第三个内角的度数。
对于等腰三角形和普通三角形,我们可以利用已知的条件计算出内角的度数。
以上是对三角形的分类与内角和的介绍。
三角形是几何学中重要的概念,对于解决与角度和边长相关的问题十分有用。
分类三角形的题目

分类三角形的题目
以下就是小编给大家盘点的分类三角形的题目,仅供大家参考。
三角形的分类有很多种方法,以下是常见的两种分类方式及相关题目:
一、按角分类
1、锐角三角形:三个角都是锐角的三角形。
2、直角三角形:有一个角是直角的三角形。
3、钝角三角形:有一个角是钝角的三角形。
相关题目:
判断下列三角形属于哪一类:
1、三角形的三个角分别为30°、60°、90°。
(直角三角形)
2、三角形的三个角分别为80°、50°、50°。
(锐角三角形)
二.按边分
1、等边三角形:三条边都相等的三角形。
2、等腰三角形:至少有两条边相等的三角形。
3、不等边三角形:三条边都不相等的三角形。
相关题目:
下列三角形中,一定是等边三角形的是()。
A.有两个角是60°的三角形
B.三个角都相等的三角形
C.有一个角是60°的等腰三角形
答案选B。
根据等边三角形的判定定理:三个角都相等的三角形是等边三角形,可得选项B正确;而选项A和选项C只是满足等边三角形的其中一个条件,不能确定该三角形一定是等边三角形。
以上是关于三角形分类的两种常见方式及相关题目示例,希望对你有所帮助!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形的分类方法
作者:梦恰
来源:《小学生学习指导_趣味课堂·中年级》2019年第04期
“观察下面这些三角形,你们可以发现哪些知識呢?”林老师在黑板上画好了九个三角形。
(如下图)
“这个简单。
”拉拉抢着说,“这九个三角形都是由三条线段围成的,都有三个顶点、三个内角、三条边。
”
“还有吗?”林老师继续发问。
咪咪用手比了比说:“有了,①、④、⑥、⑨这四个三角形都有三个锐角,所以这些三角形都是锐角三角形。
”
“③、⑤、⑦这三个三角形都有一个直角,所以都是直角三角形。
”木木指着图形,说出了自己的发现。
“②、⑧这两个三角形是钝角三角形,因为它们都有一个钝角。
”兰兰眼尖,找出了与众不同的三角形。
“哇,你们真厉害,按‘角’的不同,给三角形分类,还有哪种分类方法呢?”林老师又抛出问题。
“可以按‘边’的不同给这些三角形分类。
”兰兰反应快,又说出了自己的看法,“①、③、⑤、⑨这四个三角形都是一般三角形,因为这些三角形的三条边都不相等。
”
木木受到启发,说:“②、④、⑦、⑧这四个三角形,只有两条腰相等,所以这些三角形都是等腰三角形。
”
“⑥这个三角形是等边三角形,它的三条边都相等,也叫正三角形。
”咪咪指着图⑥,比画着三条边的长度。
“还可以发现哪些知识?”林老师又问道。
“⑥既是锐角三角形,又是等边三角形,因为这个三角形的三个角相等,三条边也相等。
”咪咪又说出了自己的发现。
“⑦是等腰直角三角形,因为这个三角形既有一个角是直角,又有两条边相等。
”拉拉补充说。
兰兰看了看,想了想,补充说:“②、⑧这两个三角形既有一个角是钝角,又有两条边相等,所以它们是等腰钝角三角形。
”
林老师这下满意了,伸出双手,为同学们的精彩发言竖起大拇指。
