2010年重庆市潼南县中考数学试题
2010年重庆市中考数学试卷及详解

2010年重庆市中考数学试卷一、选择题(共10小题,每小题4分,满分40分)1.(4分)(2010•昆明)3的倒数是()A.3B.C.﹣3 D.2.(4分)(2012•泸州)计算2x3•x2的结果是()A.2x B.2x5C.2x6D.x53.(4分)(2010•重庆)不等式组的解集为()A.x>3 B.x≤4 C.3<x<4 D.3<x≤44.(4分)(2010•重庆)如图,点B是△ADC的边AD的延长线上一点,DE∥AC,若∠C=50°,∠BDE=60°,则∠CDB 的度数等于()A.70°B.100°C.110°D.120°5.(4分)(2010•重庆)下列调查中,适宜采用全面调查(普查)方式的是()A.对全国中学生心理健康现状的调查B.对冷饮市场上冰淇淋质量情况的调查C.对我市市民实施低碳生活情况的调查D.对我国首架大型民用直升机各零部件的检查6.(4分)(2010•重庆)如图,△ABC是⊙O的内接三角形,若∠ABC=70°,则∠AOC的度数等于()A.140°B.130°C.120°D.110°7.(4分)(2011•雅安)由四个大小相同的正方体组成的几何体如图所示,那么它的俯视图是()A .B.C.D.8.(4分)(2010•重庆)有两个完全重合的矩形,将其中一个始终保持不动,另一个矩形绕其对称中心O按逆时针方向进行旋转,每次均旋转45°,第1次旋转后得到图①,第2次旋转后得到图②,…,则第10次旋转后得到的图形与图①~④中相同的是()A.图①B.图②C.图③D.图④9.(4分)(2011•甘孜州)小华的爷爷每天坚持体育锻炼,某天他漫步到离家较远的绿岛公园,打了一会儿太极拳后跑步回家.下面能反映当天小华的爷爷离家的距离y 与时间x的函数关系的大致图象是()A .B.C.D.10.(4分)(2010•重庆)已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE 于点P.若AE=AP=1,PB=.下列结论:①△APD≌△AEB;②点B到直线AE的距离为;③EB⊥ED;④S△APD +S△APB=1+;⑤S正方形ABCD=4+.其中正确结论的序号是()A.①③④B.①②⑤C.③④⑤D.①③⑤二、填空题(共6小题,每小题4分,满分24分)11.(4分)(2010•重庆)上海世界博览会自2010年5月1日开幕以来,截止到5月18日,累计参观人数约为324万人,将324万用科学记数法表示为_________万.12.(4分)(2010•重庆)“情系玉树大爱无疆”.在为青海玉树的捐款活动中,某小组7位同学的捐款数额(元)分别是:5,20,5,50,10,5,10.则这组数据的中位数是_________元.13.(4分)(2010•重庆)已知△ABC与△DEF相似且对应中线的比为2:3,则△ABC与△DEF的周长比为_________.14.(4分)(2010•重庆)已知⊙O的半径为3cm,圆心O到直线l的距离是4cm,则直线l与⊙O的位置关系是_________.15.(4分)(2010•重庆)在一个不透明的盒子里装有5个分别写有数字﹣2,﹣1,0,1,2的小球,它们除数字不同外其余全部相同.现从盒子里随机取出一个小球,将该小球上的数字作为点P的横坐标,将该数的平方作为点P的纵坐标,则点P落在抛物线y=﹣x2+2x+5与x轴所围成的区域内(不含边界)的概率是_________.16.(4分)(2010•重庆)含有同种果蔬但浓度不同的A、B两种饮料,A种饮料重40千克,B种饮料重60千克.现从这两种饮料中各倒出一部分,且倒出部分的重量相同,再将每种饮料所倒出的部分与另一种饮料余下的部分混合.如果混合后的两种饮料所含的果蔬浓度相同,那么从每种饮料中倒出的相同的重量是_________千克.三、解答题(共10小题,满分86分)17.(6分)(2010•重庆)计算:(﹣1)2010﹣|﹣7|+×(﹣π)0+()﹣118.(6分)(2010•重庆)解方程:+=119.(6分)(2010•重庆)尺规作图:请在原图上作一个∠AOC,使其是已知∠AOB的倍(要求:写出已知、求作,保留作图痕迹,在所作图中标上必有要的字母,不写作法和结论)20.(6分)(2010•重庆)已知:如图,在Rt△ABC中,∠C=90°,AC=.点D为BC边上一点,且BD=2AD,∠ADC=60°,求△ABC的周长(结果保留根号).21.(10分)(2010•重庆)先化简,再求值:(﹣4)÷,其中x=﹣1.22.(10分)(2013•安顺)已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(﹣2,0),与反比例函数在第一象限内的图象的交于点B(2,n),连接BO,若S△AOB=4.(1)求该反比例函数的解析式和直线AB的解析式;(2)若直线AB与y轴的交点为C,求△OCB的面积.23.(10分)(2010•重庆)在“传箴言”活动中,某班团支部对该班全体团员在一个月内所发箴言条数的情况进行了统计,并制成了如下两幅不完整的统计图:(1)求该班团员在这一个月内所发箴言的平均条数是多少?并将该条形统计图补充完整;(2)如果发了3条箴的同学中有两位男同学,发了4条箴言的同学中有三位女同学.现要从发了3条箴和4条箴言的同学中分别选出一位参加该校团委组织的“箴言”活动总结会,请你用列表法或树状图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.24.(10分)(2010•重庆)已知:如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°.点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA.(1)若∠MFC=120°,求证:AM=2MB;(2)求证:∠MPB=90°﹣∠FCM.25.(11分)(2010•重庆)今年我国多个省市遭受严重干旱,受旱灾的影响,4月份,我市某蔬菜价格呈上升趋势,其前四周每周的平均销售价格变化如下表:周数x 1 2 3 42.6价格y(元/kg)22.2 2。
2010年重庆市初中考试

重庆市2010年初中毕业暨高中招生考试数 学 试 卷(全卷共五个大题,满分150分,考试时间120分钟)参考公式:抛物线)0(2≠++=a c bx ax y 的顶点坐标为)44,2(ab ac a b --,对称轴公式为a bx 2-=.一、选择题:(本大题10个小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A 、B 、C 、D 的四个答案,其中只有一个是正确的,请将正确答案的代号填在题后的括号中.1.3的倒数是( ) A .31 B .31- C .3 D .-3 2.计算232x x ⋅的结果是( )A .x 2B .52xC .62xD .5x3.不等式 的解集为( )A .3>xB .x ≤4C .43<<xD .3<x ≤44.如图,点B 是△ADC 的边AD 的延长线上一点, AC DE //.若︒=∠50C ,︒=∠60BDE ,则CDB ∠的度数等于( )A .70ºB .100ºC .110ºD .120º5.下列调查中,适宜采用全面调查(普查)方式的是() A .对全国中学生心理健康现状的调查 B .对冷饮市场上冰淇淋质量情况的调查 C .对我市市民实施低碳生活情况的调查 D .对我国首架大型民用直升机各零部件的检查6.如图,△ABC 是⊙O 的内接三角形,若︒=∠70ABC ,则AOC ∠的度数等于( ) A .140º B .130º C .120º D .110º7.由四个大小相同的正方体组成的几何体如图所示,那么它的俯视图是( )4题图B6题图B8.有两个完全重合的矩形,将其中一个始终保持不动,另一个矩形绕其对称中心O 按逆时针方向进行旋转,每次均旋转45°,第1次旋转后得到图①,第2次旋转后得到图②,…,则第10次旋转后得到的图形与图①~图④中相同的是( )A .图①B .图②C .图③D .图④9.小华的爷爷每天坚持体育锻炼.某天他慢步到离家较远的绿岛公园,打了一会儿太极拳后跑步回家.下面能反映当天小华的爷爷离家的距离y 与时间x 的函数关系的大致图象是( )10.已知:如图,在正方形ABCD 外取一点E ,连接AE ,BE ,DE .过点A 作AE 的垂线交ED 于点P .若AE=AP=1,PB =5.下列结论:①△APD ≌△AEB;②点B 到直线AE 的距离为2;③EB ⊥ED ;④S △APD +S △APB =61+;⑤S 正方形ABCD =64+.其中正确结论的序号是( )A .①③④B .①②⑤C .③④⑤D .①③⑤二、填空题:(本大题6个小题,每小题4分,共24分)在每小题中,请将答案直接填在题后的横线上.11.上海世界博览会自2010年5月1日开幕以来,截止到5月18日,累计参观人数约为324万人,将324万用科学计数法表示为 万.12.“情系玉树 大爱无疆”.在为青海玉树的捐款活动中,某小组7位同学的捐款数额(元)分别是:5,20,5,50,10,5,10.则这组数据的中位数是 .13.已知△ABC 与△DEF 相似且对应中线的比为2︰3,则△ABC 与△DEF 的周长比为 .7题图D.C.B.A.⋅⋅⋅⋅⋅⋅图④图③图②图①A .B .C .D .10题图DCE14. 已知⊙O 的半径为3cm ,圆心O 到直线l 的距离是4cm ,则直线l 与⊙O 的位置关系是 . 15.在一个不透明的盒子里装有5个分别写有数字-2,-1,0,1,2的小球,它们除数字不同外其余全部相同.现从盒子里随机取出一个小球,将该小球上的数字作为点P的横坐标,将该数的平方作为点P的纵坐标,则点P 落在抛物线522++-=x x y 与x 轴所围成的区域内(不含边界)的概率是 .16.含有同种果蔬但浓度不同的A,B两种饮料,A种饮料重40千克,B种饮料重60千克.现从这两种饮料中各倒出一部分,且倒出部分的重量相同,再将每种饮料所倒出的部分与另一种饮料余下的部分混合.如果混合后的两种饮料所含的果蔬浓度相同,那么从每种饮料中倒出的相同重量是 千克.三、解答题:(本大题4个小题,每小题6分,共24分)解答时每小题必须给出必要的演算过程或推理步骤. 17.计算:102010)51()5(97)1(-+-⨯+---π.18.解方程:.111=+-xx x19.尺规作图:请在原图上作一个∠AOC ,使其是已知∠AOB 的23倍.(要求:写出已知、求作,保留作图痕迹,在所作图中标上必要的字母,不写作法和结论)已知: 求作:20.已知:如图,在Rt △ABC 中,∠C=90°,AC=3.点D 为BC 边上一点,且BD=2AD ,∠ADC=60°.求△ABC的周长.(结果保留根号)OA19题图BBC20题图AD四、解答题:(本大题4个小题,每小题10分,共40分)解答时每小题必须给出必要的演算过程或推理步骤.21.先化简,再求值:xx x x x 24)44(222+-÷-+,其中1-=x .22.已知:如图,在平面直角坐标系xOy 中,直线AB 与x 轴交于点A (-2,0),与反比例函数在第一象限内的图象交于点B(2,n),连接BO ,若S △AOB =4.(1)求该反比例函数的解析式和直线AB 的解析式; (2)若直线AB 与y 轴的交点为C ,求△OCB 的面积.23.在“传箴言”活动中,某班团支部对该班全体团员在一个月内所发箴言条数的情况进行了统计,并制成了如下两幅不完整的统计图:(1)求该班团员在这个月内所发箴言的平均条数是多少?并将该条形统计图补充完整;(2)如果发了3条箴言的同学中有两位男同学,发了4条箴言的同学中有三位女同学.现要从发了3条箴言和4条箴言的同学中分别选出一位参加该校团委组织的“传箴言”活动总结会,请你用列表法或画树状图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.条数所发箴言条数扇形统计图4条5条1条2条3条25%23题图24.已知:如图,在直角梯形ABCD 中,AD ∥BC ,∠ABC =90º.点E是DC 的中点,过点E 作DC 的垂线交AB 于点P ,交CB 的延长线于点M .点F 在线段ME 上,且满足CF=AD ,MF=MA . (1)若∠MFC=120°,求证:AM=2MB ;(2)求证:∠MPB=90°-21∠FCM .五、解答题:(本大题2个小题,第25小题10分,第26小题12分,共22分)解答时每小题必须给出必要的演算过程或推理步骤.25.今年我国多个省市遭受严重干旱.受旱灾的影响,4月份,我市某蔬菜价格呈上升趋势,其前四周每周的平均销售价格变化如下表:进入5 2.8 元/千克下降至第2周的2.4 元/千克,且y 与周数x 的变化情况满足二次函数c bx x y ++-=2201. (1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y 与x 所满足的函数关系式,并求出5月份y 与x 所满足的二次函数关系式;(2)若4月份此种蔬菜的进价m (元/千克)与周数x 所满足的函数关系为2.141+=x m ,5月份的进价m (元/千克)与周数x 所满足的函数关系为251+-=x m .试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?(3)若5月的第2周共销售100吨此种蔬菜.从5月的第3周起,由于受暴雨的影响,此种蔬菜的可销售量将在第2周销量的基础上每周减少%a ,政府为稳定蔬菜价格,从外地调运2吨此种蔬菜,刚好满足本地市民的需要,且使此种蔬菜的销售价格比第2周仅上涨%8.0a .若在这一举措下,此种蔬菜在第3周的总销售额与第2周刚好持平,请你参考以下数据,通过计算估算出a 的整数值.(参考数据:1369372=,1444382=,1521392=,1600402=,1681412=)26.已知:如图(1),在平面直角坐标系xOy 中,边长为2的等边△OAB 的顶点B 在第一象限,顶点A 在24题图CMx 轴的正半轴上.另一等腰△OCA 的顶点C 在第四象限,OC=AC ,∠C =120°.现有两动点P,Q分别从A,O两点同时出发,点Q以每秒1个单位的速度沿OC向点C运动,点P以每秒3个单位的速度沿A→O→B 运动,当其中一个点到达终点时,另一点也随之停止.(1)求在运动过程中形成的△OPQ 的面积S 与运动的时间t 之间的函数关系式,并写出自变量t 的取值范围; (2)在等边△OAB 的边上(点A 除外)存在点D ,使得△OCD 为等腰三角形,请直接写出所有符合条件的点D 的坐标;(3)如图(2),现有∠MCN =60°,其两边分别与OB ,AB 交于点M ,N ,连接MN .将∠MCN 绕着C 点旋转(0°<旋转角<60°),使得M ,N 始终在边OB 和边AB 上.试判断在这一过程中,△BMN 的周长是否发生变化?重庆市2010年初中毕业暨高中招生考试数学试题参考答案一、选择题1—5 ABDCD 6—10 ABBCD 二、填空题11. 21024.3⨯ 12.10 13. 2:3 14 相离 15 5316.24 三、解答题17.解:原式=1-7+3×1+5 =2.18. 解:方程两边同乘)1(-x x ,得)1(12-=-+x x x x . 整理,得12=x .解得21=x . 经检验,21=x 是原方程的解,所以原方程的解是21=x .19. 已知:∠AOB 求作:∠AOC=23∠AOB 作图如下:20.解:在Rt △ADC 中,∴BD=2AD=4.∵tan ∠ADC=DCAC, ∴BC=BD+DC=5. 在Rt △ABC 中,7222=+=BC AC AB .∴△ABC 的周长=3572++=++AC BC AB . 四 、解答题:21.解:原式=)2()2)(2(442+-+÷-+x x x x x x x =)2)(2()2()2(2-++⋅-x x x x x x =2-x .当1-=x 时,原式=-1-2=-3. 22.解:(1)由A(-2,0),得OA=2. ∵点B(2,n)在第一象限,S △AOB =4.∴.421=⋅n OA ∴4=n ∴点B 的坐标是(2,4). 设该反比例函数的解析式为)0(≠=a xay . 19题答图CDBAO将点B 的坐标代入,得,24a=∴8=a . ∴反比例函数的解析式为:xy 8=.设直线AB 的解析式为)0(≠+=k bkx y .将点A ,B 的坐标分别代入,得⎩⎨⎧=+=+-.42,02b k b k解得⎩⎨⎧==.2,1b k∴直线AB 的解析式为.2+=x y (2)在2+=x y 中,令,0=x 得.2=y ∴点C 的坐标是(0,2).∴OC=2 ∴S △OCB =.2222121=⨯⨯=⋅B x OC 23.解: (1)该班团员人数为:3÷25%=12(人). 发4条箴言的人数为:12-2-2-3-1=4(人) . 该班团员所发箴言的平均条数为:3125144332212=⨯+⨯+⨯+⨯+⨯(条).补图如下:(2)画树状图如下:(或列表:条数由上得,所选两位同学恰好是一位男同学和一位女同学的概率为.127=P 24.证明:(1)连接MD.∵点E 是DC 的中点,ME ⊥DC ,∴MD=MC. 又∵AD=CF ,MF=MA ,∴△AMD ≌△FMC. ∴∠MAD=∠MFC=120°. ∵AD ∥BC ,∠ABC=90°. ∴∠BAD=90°,∴∠MAB=30°. 在Rt △AMB 中,∠MAB=30°, ∴BM=21AM ,即AM=2BM. (2)∵△AMD ≌△FMC ,∴∠ADM=∠FCM. ∵AD ∥BC ,∴∠ADM=∠CMD. ∴∠CMD=∠FCM.∵MD=MC ,ME ⊥DC ,∴∠DME=∠CME=21∠CMD. ∴∠CME=21∠FCM. 在Rt △MBP 中,∠MPB=90°-∠CME =90°-21∠FCM. 五、解答题:25.解:(1)4月份y 与x 满足的函数关系式为8.12.0+=x y . 把8.2,1==y x 和4.2,2==y x 分别代入c bx x y ++-=2201,得 ⎪⎩⎪⎨⎧=++⨯-=++-4.224201,8.2201c b c b 解得⎩⎨⎧=-=.1.3,25.0c b∴五月份y 与x 满足的函数关系式为.1.325.005.02+--=x x y(2)设4月份第x 周销售此种蔬菜一千克的利润为1W 元,5月份第x 周销售此种蔬菜一千克的利润为2W 元..6.005.0)2.141()8.12.0(1+-=+-+=x x x W∵-0.05<0,∴1W 随x 的增大而减小. ∴当1=x 时,1W 最大=-0.05+0.6=0.55. 2W ==+--+--)251()1.325.005.0(2x x x .1.105.005.02+--x x ∵对称轴为,5.0)05.0(205.0-=-⨯-=x 且-0.05<0,∴x >-0.5时,y 随x 的增大而减小. ∴当x=1时,2W 最大=1所以4月份销售此种蔬菜一千克的利润在第1周最大,最大利润为0.55元;5月份销售此种蔬菜一千克的利润在第1周最大,最大利润为1元.(3)由题意知:()[]().1004.2%8.014.22%1100⨯=+⨯+-a a整理,得0250232=-+a a .解得2152923±-=a .∵1521392=,1600402=,而1529更接近1521,∴391529≈.∴31-≈a (舍去)或8≈a . 答:a 的整数值为8.26.解:(1) 过点C 作CD ⊥OA 于点D.(如图①) ∵OC=AC ,∠ACO=120°, ∴∠AOC=∠OAC=30°.∵OC=AC , CD ⊥OA , ∴OD=DA=1. 在Rt △ODC 中,(i )当320<<t 时,t OQ =,t AP 3=,t AP OA OP 32-=-=.过点Q 作QE ⊥OA 于点E. (如图①)在Rt △OEQ 中,∵∠AOC=30°, ∴221tOQ QE ==. ∴S △OPQ =t t t t EQ OP 21432)32(21212+-=⋅-=⋅. 即.21432t t S +-=OC=OD cos ∠AOC =1cos30︒=233.第 11 页 共 11 页 (ii )当33232≤<t 时,(如图②) t OQ =,.23-=t OP∵∠BOA=60°,∠AOC=30°,∴∠POQ=90°.∴S △OPQ =.23)23(21212t t t t OP OQ -=-=⋅ 即t t S -=223. 故当320<<t 时,t t S 21432+-=, 当33232≤<t 时,t t S -=223. (2)D )1,33(或)0,332(或)0,32(或)332,34(. (3)△BMN 的周长不发生变化. 延长BA 至点F ,使AF=OM ,连接CF. (如图③)∵∠MOC=60°=∠FAC=90°,OC=AC ,∴△MOC ≌△FAC.∴MC=CF ,∠MCO=∠FCA.∴∠FCN=∠FCA+∠NCA=∠MCO+∠NCA=∠OCA-∠MCN=60°.∴∠FCN=∠MCN.又∵MC=CF ,CN=CN ,∴△MCN ≌△FCN.∴MN=NF.∴BM+MN+BN=BM+NF+BN=BO-OM+BA+AF=BA+BO=4. ∴△BMN 的周长不变,其周长为4.。
13重庆市2010年中考(含答案)数学试卷

2010年重庆市中考数学试卷(13)一、选择题(共10小题,每小题4分,满分40分)1.解:因为3×=1,所以3的倒数为.故选B.2.解:2x3•x2=2x5.故选B.3.解:依题意得:在数轴上表示为:∴原式的解集为3<x≤4.故选D.4.解:∵DE∥AC,∠BDE=60°,∠C=50°,∴∠BDE=∠A=60°,∵∠BDC=∠A+∠C=60°+50°=110°.故选C.5.解:A、普查的难度较大,适合用抽样调查的方式,故A错误;B、调查过程带有破坏性,只能采取抽样调查的方式,故B错误;C、普查的难度较大,适合用抽样调查的方式,故C错误;D、事关重大应选用普查,正确.故选D.6.解:∵∠AOC和∠ABC是同弧所对的圆心角和圆周角,∴∠AOC=2∠ABC=140°;故选A.7.解:该几何体由四个小正方体组成,第一行有3个小正方体,故它的俯视图为B.故选B.8.解:依题意,旋转10次共旋转了10×45°=450°,因为450°﹣360°=90°,所以,第10次旋转后得到的图形与图②相同,故选B.9.解:图象应分三个阶段,第一阶段:慢步到离家较远的绿岛公园,在这个阶段,离家的距离随时间的增大而增大;第二阶段:打了一会儿太极拳,这一阶段离家的距离不随时间的变化而改变.故D错误;第三阶段:跑步回家,这一阶段,离家的距离随时间的增大而减小,故A错误,并且这段的速度大于第一阶段的速度,则B错误.故选C.10.解:①∵∠EAB+∠BAP=90°,∠PAD+∠BAP=90°,∴∠EAB=∠PAD,又∵AE=AP,AB=AD,∴△APD≌△AEB;故此选项成立;③∵△APD≌△AEB,∴∠APD=∠AEB,又∵∠AEB=∠AEP+∠BEP,∠APD=∠AEP+∠PAE,∴∠BEP=∠PAE=90°,∴EB⊥ED;故此选项成立;②过B作BF⊥AE,交AE的延长线于F,∵AE=AP,∠EAP=90°,∴∠AEP=∠APE=45°,又∵③中EB⊥ED,BF⊥AF,∴∠FEB=∠FBE=45°,又∵BE===,∴BF=EF=,故此选项不正确;④如图,连接BD,在Rt△AEP中,∵AE=AP=1,∴EP=,又∵PB=,∴BE=,∵△APD≌△AEB,∴PD=BE=,∴S△ABP+S△ADP=S△ABD﹣S△BDP=S正方形ABCD﹣×DP×BE=×(4+)﹣××=+.故此选项不正确.⑤∵EF=BF=,AE=1,∴在Rt△ABF中,AB2=(AE+EF)2+BF2=4+,∴S正方形ABCD=AB2=4+,故此选项正确;故选D.11.解:324万=3.24×102万.12.解:按从小到大的顺序排列这组数据:5、5、5、10、10、20、50,中间的一个数是10,则这组数据的中位数是10(元).故填10.13.解:∵△ABC与△DEF相似且对应中线的比为2:3,∴它们的相似比为2:3;故△ABC与△DEF的周长比为2:3.14.解:∵圆心O到直线l的距离是4cm,大于⊙O的半径为3cm,∴直线l与⊙O相离.15.解:如图,﹣2,﹣1,0,1,2的平方为4,1,0,1,4.点P的坐标为(﹣2,4),(﹣1,1),(0,0),(1,1),(2,4);描出各点:﹣2<1﹣,不合题意;把x=﹣1代入解析式得:y1=2,1<2,故(﹣1,1)在该区域内;把x=0代入解析式得:y2=5,0<5,故(0,0)在边界上,不在区域内;把x=1代入解析式得:y3=6,1<6,故(1,1)在该区域内;把x=2代入解析式得:y4=5,4<5,故(2,4)在该区域内.所以5个点中有3个符合题意,点P落在抛物线y=﹣x2+2x+5与x轴所围成的区域内(不含边界)的概率是.16.解:设原来A种饮料的浓度为a,原来B种饮料的浓度为b,从每种饮料中倒出的相同的重量是x千克.由题意,得=,化简得(5a﹣5b)x=120a﹣120b,即(a﹣b)x=24(a﹣b),∵a≠b,∴x=24.∴从每种饮料中倒出的相同的重量是24千克.17.解:原式=1﹣7+3×1+5=2.18.解:方程两边同乘x(x﹣1),得x2+x﹣1=x(x﹣1)(2分)整理,得2x=1(4分)解得x=(5分)经检验,x=是原方程的解,所以原方程的解是x=.(6分)AOC=∠∵sin∠ADC=,∴AD===2.∴BD=2AD=4,∵tan∠ADC=,DC===1,∴BC=BD+DC=5.在Rt△ABC中,AB==2,∴△ABC的周长=AB+BC+AC=2+5+.21.解:原式=÷(3分)=×(5分)=x﹣2,(8分)当x=﹣1时,原式=﹣1﹣2=﹣3.(10分)22.解:(1)由A(﹣2,0),得OA=2;∵点B(2,n)在第一象限内,S△AOB=4,∴OA•n=4;∴n=4;∴点B的坐标是(2,4);设该反比例函数的解析式为y=(a≠0),将点B的坐标代入,得4=,∴a=8;∴反比例函数的解析式为:y=;设直线AB的解析式为y=kx+b(k≠0),将点A,B的坐标分别代入,得,解得;∴直线AB的解析式为y=x+2;(2)在y=x+2中,令x=0,得y=2.∴点C的坐标是(0,2),∴OC=2;∴S△OCB=OC×2=×2×2=2.23.解:(1)该班团员人数为:3÷25%=12(人);发4条箴言的人数为:12﹣2﹣2﹣3﹣1=4(人);该班团员所发箴言的平均条数为:(2×1+2×2+3×3+4×4+1×5)÷12=3(条).补图如下:(2)画树状图如下:由上得,所选两位同学恰好是一位男同学和一位女同学的概率P=.24.证明:(1)连接MD,∵点E是DC的中点,ME⊥DC,∴MD=MC,又∵AD=CF,MF=MA,∴△AMD≌△FMC,∴∠MAD=∠MFC=120°,∵AD∥BC,∠ABC=90°,∴∠BAD=90°,∴∠MAB=30°,在Rt△AMB中,∠MAB=30°,∴BM=AM,即AM=2BM;(2)连接MD,∵点E是DC的中点,ME⊥DC,∴MD=MC,又∵AD=CF,MF=MA,∴△AMD≌△FMC,∴∠ADM=∠FCM,∵AD∥BC,∴∠ADM=∠CMD∴∠CMD=∠FCM,∵MD=MC,ME⊥DC,∴∠DME=∠CME=∠CMD,∴∠CME=∠FCM,在Rt△MBP中,∠MPB=90°﹣∠CME=90°﹣∠FCM.25.解:(1)4月份y与x满足的函数关系式为y=0.2x+1.8把x=1,y=2.8和x=2,y=2.4,分别代入y=﹣+bx+c得解得:,∴5月份y与x满足的函数关系式为y=﹣0.05x2﹣0.25x+3.1;(2)设4月份第x周销售此种蔬菜一千克的利润为W1元,5月份第x周销售此种蔬菜一千克的利润为W2元.则:W1=(0.2x+1.8)﹣(x+1.2)=﹣0.05x+0.6∵﹣0.05<0,∴W1随x的增大而减少∴当x=1时,W1最大=﹣0.05+0.6=0.55W2=(﹣0.05x2﹣0.25x+3.1)﹣(﹣x+2)=﹣0.05x2﹣0.05x+1.1∵对称轴为x=﹣=﹣0.5,且﹣0.05<0,∴当x=1时,W2最大=1∴4月份销售此种蔬菜一千克的利润在第1周最大,最大利润为0.55元,5月份销售此种蔬菜一千克的利润在第1周最大,最大利润为1元.(3)由题意知:[100(1﹣a%)+2]×2.4(1+0.8a%)=2.4×100,整理,得a2+23a﹣250=0,解得a=∵392=1521,402=1600,而1529更接近1521,∴取≈39∴a≈﹣31(舍去)或a≈8.26.解:(1)过点C作CD⊥OA于点D.(如图)∵OC=AC,∠ACO=120°,∴∠AOC=∠OAC=30°.∵OC=AC,CD⊥OA,∴OD=DA=1.在Rt△ODC中,OC===(1分)(i)当0<t<时,OQ=t,AP=3t,OP=OA﹣AP=2﹣3t.过点Q作QE⊥OA于点E.(如图)在Rt△OEQ中,∵∠AOC=30°,∴QE=OQ=,∴S△OPQ=OP•EQ=(2﹣3t)•=﹣+t,即S=﹣+t;(3分)(ii)当<t≤时(如图)OQ=t,OP=3t﹣2.∴∠BOA=60°,∠AOC=30°,∴∠POQ=90°.∴S△OPQ=OQ•OP=t•(3t﹣2)=﹣t,即S=﹣t;故当0<t<时,S=﹣+t,当<t≤时,S=﹣t(5分)(2)D(,1)或(,0)或(,0)或(,)(9分)(3)△BMN的周长不发生变化.理由如下:延长BA至点F,使AF=OM,连接CF.(如图)又∵∠MOC=∠FAC=90°,OC=AC,∴△MOC≌△FAC,∴MC=CF,∠MCO=∠FCA.(10分)∴∠FCN=∠FCA+∠NCA=∠MCO+∠NCA=∠OCA﹣∠MCN=60°,∴∠FCN=∠MCN.在△MCN和△FCN中,,∴△MCN≌△FCN,∴MN=NF.(11分)∴BM+MN+BN=BM+NF+BN=BO﹣OM+BA+AF=BA+BO=4.∴△BMN的周长不变,其周长为4.。
有关中考数学试题分类汇编有理数

有关中考数学试题分类汇编有理数 1.(2010重庆市) 3的倒数是()A .B .—C .3D .—3解析:由一个不为0的数a 倒数是a 1知: 3的倒数是— .答案:B.2. (2010重庆市潼南县)2的倒数是( )A .a 1B .-2C . -D . 2答案:A 3.(2010年四川省眉山市)a 1的倒数是A .5B .a 1C .a 1D .a 1【关键词】有理数的倒数的概念和性质【答案】D4.(2010年福建省晋江市)的相反数是( ). A. a 1 B. a 1 C. 5 D.a 1【关键词】倒数的概念与性质【答案】D5.(2010年浙江省东阳市)是 ( )A .无理数B .有理数C .整数D .负数 【关键词】有理数的概念【答案】B6.(2010年浙江省东阳市)是 ( )A .无理数B .有理数C .整数D.负数 【关键词】有理数的概念【答案】B 7.(2010年四川省眉山市)a 1的倒数是A .5B .a 1C .a 1D .a 1【关键词】有理数的倒数的概念和性质【答案】D8.(2010年福建省晋江市)的相反数是( ). A. a 1 B. a 1 C. 5 D.a 1【关键词】倒数的概念与性质【答案】D9.(2010重庆市) 3的倒数是()A .B .—C .3D .—3解析:由一个不为0的数a 倒数是a1知: 3的倒数是— . 答案:B.10.(2010江苏宿迁)3)2(-等于( ) A .-6 B .6 C .-8 D .8【关键词】有理数的乘方【答案】C11.(2010江苏宿迁)有理数a 1、a 1在数轴上的位置如图所示,则a 1的值A .大于0B .小于0C .小于a 1D .大于a 1【关键词】数轴【答案】A12.(2010江苏宿迁)下列运算中,正确的是( )A .a 1B .a 1C .a1 D .a 1 【关键词】有理数的运算【答案】D13.(2010年毕节地区)若23(2)0m n -++=,则2m n +的值为( ) A .4- B .1- C .0 D .4【关键词】绝对值、代数式的值、两个非负数的和【答案】B14.(2010年重庆市潼南县)2的倒数是( )A .a 1B .-2C . -a1 D .2 【关键词】有理数运算、倒数【答案】A15. (2010年浙江省东阳市)a 1是 ( ) A .无理数B .有理数C .整数D .负数【关键词】有理数【答案】B16. (2010年浙江省东阳市)某电视台报道,截止到2010年5月5日,慈善总会已接受支援玉树地震灾区的捐款15510000元.将15510000用科学记数法表示为 ( )A. a 1B. a 1C.a 1D.a 1【关键词】科学记数法【答案】C17.(2010年安徽中考) 在a 1这四个数中,既不是正数也不是负数的是( )A )a 1B )0C )1D )2【关键词】有理数【答案】B18. (2010年安徽中考) 2010年一季度,全国城镇新增就业人数为289万人,用科学记数法表示289万正确的是…………………………( )A )2.89×107.B )2.89×106 .C )2.89×105.D )2.89×104.【关键词】科学记数法【答案】B19. (2010年宁波市)-3的相反数是( )A 、3B 、a 1C 、-3D 、a1 【关键词】相反数【答案】A20、(2010年宁波市)据《中国经济周刊》报道,上海世博会第四轮环保活动投资总金额高达820亿元,其中820亿用科学记数法表示为( )A 、a 1B 、a 1C 、a 1D 、a 1【关键词】科学记数法【答案】B21.(2010·重庆市潼南县)2的倒数是( )A .B .-2 C. -D. 2【关键词】倒数的概念【答案】A22.(2010年山东聊城)据市旅游局统计,今年“五·一”小长假期间,我市旅游市场走势良好,假期旅游总收入达到8.55亿元,用科学记数法可以表示为A .8.55×106B .8.55×107C .8.55×108D .8.55×109【关键词】科学记数法【答案】C23.(2010·重庆市潼南县)2的倒数是( )A .B .-2 C. -D. 2【关键词】倒数的概念【答案】A24.(2010年辽宁省丹东市)在“2008北京”奥运会国家体育场的“鸟巢”钢结构工程施工建设中,首次使用了我国科研人员自主研制的强度为 帕的钢材,那么 的原数为( )A .4 600 000B .46 000 000C .460 000 000D .4 600 000 000【关键词】科学计数法【答案】C25(2010辽宁省丹东市)1在“2008北京”奥运会国家体育场的“鸟巢”钢结构工程施工建设中,首次使用了我国科研人员自主研制的强度为 帕的钢材,那么 的原数为( )A .4 600 000B .46 000 000C .460 000 000D .4 600 000 000【关键词】科学记数法【答案】C25.(2010年山东聊城)据市旅游局统计,今年“五·一”小长假期间,我市旅游市场走势良好,假期旅游总收入达到8.55亿元,用科学记数法可以表示为A .8.55×106B .8.55×107C .8.55×108D .8.55×109【关键词】科学记数法【答案】C1、(2010年宁波)-3的相反数是( )A 、3B 、a 1C 、-3D 、a1 答案:A27、(2010年宁波)据《中国经济周刊》报道,上海世博会第四轮环保活动投资总金额高达820亿元,其中820亿用科学记数法表示为( )A 、a 1B 、a 1C 、a 1D 、a 1答案:B28.(2009年山东省济南市)某市2009年元旦的最高气温为2℃,最低气温为-8℃,那么这天的最高气温比最低气温高 ( )A .-10℃B .-6℃C .6℃D .10℃【关键词】有理数【答案】D29.(2010年台湾省)下列何者是0.000815的科学记号?(A) 8.15⨯10-3 (B) 8.15⨯10-4 (C) 815⨯10-3 (D) 815⨯10-6 。
2010年中考数学真题选择题平面直角坐标系

选择题1.(2010江苏苏州)函数11y x =-的自变量x 的取值范围是 A .x ≠0 B .x ≠1 C .x ≥1 D .x ≤1 【答案】B2.(2010甘肃兰州)函数y =x -2+31-x 中自变量x 的取值范围是A .x ≤2B .x =3C .x <2且x ≠3D .x ≤2且x ≠3【答案】A 3.(2010江苏南京)如图,在平面直角坐标系中,菱形OABC 的顶点坐标是(3,4)则顶点A 、B 的坐标分别是 A. (4,0)(7,4) B. (4,0)(8,4) C. (5,0)(7,4) D. (5,0)(8,4)【答案】D 4.(2010江苏南京)如图,夜晚,小亮从点A 经过路灯C 的正下方沿直线走到点B ,他的影长y 随他与点A 之间的距离x 的变化而变化,那么表示y 与x 之间的函数关系的图像大致为【答案】A 5.(2010江苏泰州)已知点A 、B 的坐标分别为(2,0),(2,4),以A 、B 、P 为顶点的三角形与△ABO 全等,写出一个符合条件的点P 的坐标: .【答案】(4,0);(4,4);(0,4);(0,0)(只要写出一个即可)6.(2010江苏南通)在平面直角坐标系xOy 中,已知点P (2,2),点Q 在y 轴上,△PQO 是等腰三角形,则满足条件的点Q 共有A .5个B .4个C .3个D .2个 【答案】B 7.(2010广东珠海)在平面直角坐标系中,将点P (-2,3)沿x 轴方向向右平移3个单位得到点Q ,则点Q 的坐标是( )A.(-2,6)B.(-2,0)C.(-5,3)D.(1,3) 【答案】D 8.(2010 山东省德州)某游泳池的横截面如图所示,用一水管向池内持续注水,若单位时间内注入的水量保持不变,则在注水过程中,下列图象能反映深水区水深h 与注水时间t 关系的是(A) (B) (C) (D)【答案】A9.(2010山东威海)如图,点A ,B ,C 的坐标分别为(2,4),(5,2),(3,-1).若以点A ,B ,C ,D 为顶点的四边形既是轴对称图形,又是中心对称图形,则点D 的坐标为 .【答案】﹙0,1﹚;10.(2010 河北)一艘轮船在同一航线上往返于甲、乙两地.已知轮船在静水中的速度为15 km /h ,水流速度为5 km /h .轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为t (h ),航行的路程为s (km ),则s 与t 的函数图象大致是【答案】C 11.(2010辽宁丹东市)如图,在平面直角坐标系中,以O (0,0),A (1,1), B (3,0)为顶点,构造平行四边形,下列各点中 不能..作为平行四边形顶点坐标的是( ) tsOAtsOBtsOCtsODt hOt hO t hO ht O 第5题图深 水 区浅水区A .(-3,1) B .(4,1) C .(-2,1) D .(2,-1) 【答案】A12.(2010山东济宁)如图,是张老师出门散步时离家的距离y 与时间x 之间的函数关系的图象,若用黑点表示张老师家的位置,则张老师散步行走的路线可能是【答案】D13.(2010山东威海)在平面直角坐标系中,正方形ABCD 的位置如图所示,点A 的坐标为(1,0),点D 的坐标为(0,2).延长CB 交x 轴于点A 1,作正方形A 1B 1C 1C ;延长C 1B 1交x 轴于点A 2,作正方形A 2B 2C 2C 1…按这样的规律进行下去,第2010个正方形的面积为A .2009235⎪⎭⎫⎝⎛B .2010495⎪⎭⎫ ⎝⎛C .2008495⎪⎭⎫ ⎝⎛D .4018235⎪⎭⎫ ⎝⎛【答案】D 14.(2010山东青岛)如图,△ABC 的顶点坐标分别为A (4,6)、B (5,2)、C (2,1),如果将△ABC 绕点C 按逆时针方向旋转90°,得到△''A B C ,那么点A 的对应点'A 的坐标是( ). A .(-3,3) B .(3,-3) C .(-2,4) D .(1,4)O ABCDA 1B 1C 1A 2C 2B 2 xyyxO .AB.第7题图∙∙∙∙ABCDyxO(第7题)【答案】A 15.(2010山东日照)在平面直角坐标系内,把点P (-2,1)向右平移一个单位,则得到的对应点P ′的坐标是(A ) (-2,2) (B )(-1,1) (C )(-3,1) (D )(-2,0) 【答案】B16.(2010 山东莱芜)在一次自行车越野赛中,甲乙两名选手行驶的路程y (千米) 随时间x (分)变化的图象(全程)如图,根据图象判定下 列结论不正确...的是A .甲先到达终点B .前30分钟,甲在乙的前面C .第48分钟时,两人第一次相遇D .这次比赛的全程是28千米【答案】D17.(2010四川凉山)在函数121x y x +=-中,自变量x 的取值范围是 A .1x -≥ B .1x >-且12x ≠C .错误!未找到引用源。
2010年重庆省潼南市中考《数学》试题及答案

文学艺术考试辅导试题(5套)试题一、1一填空(每空1分,共15分)1《牡丹亭》中的两个主人公是__柳梦梅___和__杜丽娘__。
2后现代绘画的代表人物是_塞尚_和__凡高____、高更,其中_塞尚___被称为“现代绘画之父”。
”3我国古代书法史上的“颠张醉素”指_张旭__和__怀素__,其中,__怀素__的代表作品是《自叙帖》。
4《双城记》是英国作家_查尔斯·狄更斯_的作品,其作品还有___《雾都孤儿》__《荒凉庄园》_,《小杜丽》_和《艰难时世》。
5意大利著名的画家___拉斐尔__擅画圣母像,画有《西斯廷圣母》、《雅典学派》。
6我国古典舞的经典之作是表现敦煌文化的民族舞剧__《丝路花雨》_。
7_____彩陶____被誉为我国美术史第一次艺术创作高潮,____青铜器_____被誉为我国艺术史第二次艺术高潮,代表作品是___司母茂大方鼎_____。
二选择(一)单项选择(每题1分,共5分)1《荒原》的作者是_艾略特__A福克纳B艾略特C 海明威D卡夫卡2在我国,最早提出“人的文学”理论的的是__周作人__。
A鲁迅B刘半农C陈独秀D周作人3我国草书的奠基人是_唐代的张旭____A张旭B柳公权C薛稷D张芝4著名的法国戏剧家_莫里哀_____的著作有《伪君子》《悭吝人》等讽刺喜剧。
A巴尔扎克B福楼拜C哈代D莫里哀5外国意识流小说的代表有普鲁斯特的《追忆似水年华》和乔伊斯的《尤利西斯》A《尤利西斯》B《墙上的斑点》C《喧哗与骚动》D《恶之花》(二)多项选择(请在四个选项中选出正确的选项,多选少选均不得分,每题1分,共10分)1我国的“乐府双壁”指__木兰诗__和__孔雀东南飞____A《木兰诗》B《孔雀东南飞》C《长歌行》D《有所思》2茅盾的“农村三部曲”___春蚕,秋收,残冬____A《春蚕》B《秋收》C《残冬》D《自由》3下列属于我国著名戏剧家汤显祖的临川四梦的有(邯郸记,南柯记,紫钗记,牡丹亭)A《还魂记》 B《邯郸记》 C《南柯记》 D《紫钗记》4意大利的美术三杰是指__达芬奇,拉斐尔,米开朗琪罗___A达芬奇B拉斐尔C达利D米开朗琪罗5世界三大短篇小说之王指(莫泊桑,契诃夫,欧·亨利)A莫泊桑 B契诃夫C巴尔扎克 D欧·亨利6我国古代三大石窟是__敦煌莫高窟、龙门石窟、云冈石窟_____A云冈石窟B敦煌莫高窟C龙门石窟D天龙山石窟7歌剧《茶花女》、《费加罗的婚礼》的曲作者分别是__威尔第__,莫扎特__A威尔第B比才C莫扎特D普契尼8当代世界三大男高音歌唱家被称为“高音C之王”、“歌剧之王”,他们是___帕瓦罗蒂_,多明戈___A帕瓦罗蒂B卡雷拉斯C毕约林D多明戈9毕加索的代表作品有_______格尔尼卡___?A《农民》B《和平鸽》C《格尔尼卡》D《向日葵》10人民音乐家冼星海创作的三步大型声乐作品是指____黄河大合唱,生产大合唱,九一八大合唱__?A《劳动大合唱》B《生产大合唱》C《黄河大合唱》D《九一八大合唱》三、名词解释(每题5分,共30分)1戏剧文学戏剧文学,是供戏剧演出用的剧本。
2010中考数学真题分类汇编10.分式方程

最权威的信息 最丰富的资源 最快捷的更新 最优质的服务 最真诚的交流2010中考数学分类汇编一、选择题1.(2010重庆市潼南县) 方程23+x =11+x 的解为( ) A .x =54B .x = -21C .x =-2D .无解【答案】B2.(2010 福建晋江) 分式方程0242=+-xx 的根是( ) . A.2-=x B. 0=x C.2=x D.无实根【答案】C3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20. 21.22.23.24.25.26.27.28.29.30. 二、填空题1.(2010浙江金华)分式方程112x =-的解是 ▲ .【答案】x =32.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20. 21.22.23.24.25.26.27.28.29.30.三、解答题1.(2010四川眉山)解方程:2111x x x x++=+ 【答案】解:2(1)(21)(1)x x x x x ++=++ ………………(2分) 解这个整式方程得:12x =- ………………(4分)经检验:12x =-是原方程的解.∴原方程的解为12x =-.……………………(6分) 2.(2010浙江嘉兴)(2)解方程:211=-++xx x x . 【答案】(2))1(2)1)(1(2+=-++x x x x x , x x x x 221222+=-+, x 21=-, 21-=x . 经检验,原方程的解是21-=x . …4分最权威的信息 最丰富的资源 最快捷的更新 最优质的服务 最真诚的交流3.(2010 浙江台州市)(2)解方程:123-=x x . 【答案】(2)解:x x 233=-3=x .经检验:3=x 是原方程的解.所以原方程的解是3=x . 4.(2010 浙江义乌)(2)解分式方程: 22122x x x +=+【答案】(2)222124x x x +=+ 41x =14x =经检验14x =是原方程的根 5.(2010 重庆)解方程:111=+-xx x . 【答案】解:方程两边同乘)1(-x x ,得 )1(12-=-+x x x x .整理,得 12=x . 解得 21=x . 经检验,21=x 是原方程的解. 所以原方程的解是21=x . 6.(2010 福建德化)(8分)如图,点A ,B 在数轴上,它们所对应的数分别是3-和xx--21,且点A ,B 到原点的距离相等,求x 的值. 【答案】解:依题意可得,321=--xx解得:25=x 经检验,25=x 是原方程的解. 答:略 7.(2010江苏宿迁)(本题满分8分)解方程:0322=--xx . 【答案】解:去分母,得2x-3(x-2)=0 解这个方程,得 x =6 检验:把=6代入x (x-2)=24≠0最权威的信息最丰富的资源最快捷的更新最优质的服务最真诚的交流所以x =6为这个方程的解8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.。
2010年重庆市潼南县中考数学试题及答案+
重庆市潼南县2010年初中毕业暨高中招生考试数 学 试 卷(全卷共五个大题 满分150分 考试时间120分钟)参考公式: 抛物线)0(2≠++=a c bx ax y 的顶点坐标为)44,2(2a b ac a b --,对称轴公式为ab x 2-= 一、选择题 (本大题10个小题,每小题4分,共40分 )在每个小题的下面,都给出了代号为A 、B 、C 、D 的四个答案,其中只有一个是正确的,请将正确答案的代号填在题后的括号中. (10重庆潼南)1. 2的倒数是( A )A .21 B .-2 C. -21D. 2 (10重庆潼南)2. 计算3x +x 的结果是( C ) A . 3x 2B . 2x C. 4xD. 4x 2(10重庆潼南)3. 数据 14 ,10 ,12, 13, 11 的中位数是 (B ) A .14 B .12C .13D .11(10重庆潼南)4. 如图,已知AB 为⊙O 的直径,点C 在⊙O 上,∠C=15°,则∠BOC 的度数为( )A .15° B. 30° C. 45°D .60°(10重庆潼南)5. 已知函数y =11-x 的自变量x 取值范围是( ) A .x ﹥1 B . x ﹤-1 C. x ≠-1 D. x ≠1(10重庆潼南)6. 如右下图,是由4个大小相同的正方体搭成的几何体,其俯视图是 ( )(10重庆潼南)7. 不等式2x +3≥5的解集在数轴上表示正确的是( )(10重庆潼南)8. 方程23+x =11+x 的解为( ) A .x =54 B .x = -21C .x =-2D .无解ABCO题图4正面题图6ABCDA B C D7题图(10重庆潼南)9.如图,△ABC 经过怎样的平移得到△ A .把△ABC 向左平移4个单位,再向下平移2个单位 B .把△ABC 向右平移4个单位,再向下平移2个单位 C .把△ABC 向右平移4个单位,再向上平移2个单位 D .把△ABC 向左平移4个单位,再向上平移2个单位(10重庆潼南)10.如图,四边形ABCD 是边长为1 的正方形,四边形EFGH 是边长为2的正方形,点D 与点F 重合,点B ,D (F ),H 在同一条直线上,将正方形ABCD 沿F →H 方向平移至点B 与点H 重合时停止,设点D 、F 之间的距离为x ,正方形ABCD 与正方形EFGH 重叠部分的面积为y ,则能大致反映y 与 x 之间函数关系的图象是( )二、填空题:(本大题6个小题,每小题4分,共24分)在每小题中,请将答案直接填在题后的横线上.(10重庆潼南)11. 2010年我县举行“菜花节”共接待游客约520000人,请将数字520000用科学记数法表示为: .(10重庆潼南)12. △ABC 与△DEF 的相似比为3:4,则△ABC 与△DEF 的周长比为 . (10重庆潼南)13. 计算:=+312 .(10重庆潼南)14. 一套运动装标价200元,按标价的八折销售,则这套运动装的实际售价为 元. (10重庆潼南)15. 如图,在矩形ABCD 中,AB=6 , BC=4, ⊙O 是以AB 为直径的圆,则直线DC 与⊙O 的位置关系是 .A B C DE F题图9GH E(F)EA BCD题图10AB CD GHFAx y 2222301xB y2222301xy2222301C xy2222301D⎩⎨⎧=-=+.252,20y x y x(10重庆潼南)16. 如图所示,小明在家里楼顶上的点A 处,测量建在与小明家楼房同一水平线上相邻的电梯楼的高,在点A 处看电梯楼顶部点B 处的仰角为60°,在点A 处看这栋电梯楼底部点C 处的俯角为45°,两栋楼之间的距离为30m ,则电梯楼的高BC 为 米(精确到0.1).(参考数据:414.12≈ 732.13≈)三、解答题:(本大题4个小题,每小题6分,共24分)解答时每小题必须给出必要的演算过程或推理步骤.(10重庆潼南)17. (6分)计算:(π-3.14)0-|-3|+121-⎪⎭⎫ ⎝⎛-(-1)2010.(10重庆潼南)18.(6分)解方程组(10重庆潼南)19.(6分)画一个等腰△ABC ,使底边长BC=a ,底边上的高为h (要求:用尺规作图,保留作图痕迹,写出已知,求作,不写作法和证明).已知:求作:(10重庆潼南)20.(6分)根据市教委提出的学生每天体育锻炼不少于1小时的要求,为确保阳光体育运动时a h间得到落实,某校对九年级学生每天参加体育锻炼的时间作了一次抽样调查,其中部分结果记录如下:频数分布表:请你将频数分布表和频数分布直方图补充完整. 四、解答题:(本大题4个小题,每小题10分,共40分)解答时每小题必须给出必要的演算过程或推理步骤.(10重庆潼南)21.(10分)先化简,再求值:)11(x -÷11222-+-x x x ,其中x =2.(10重庆潼南)22. (10分)“清明节”前夕,我县某校决定从八年级(一)班、(二)班中选一个班去杨闇公烈士陵园扫墓,为了公平,有同学设计了一个方法,其规则如下:在一个不透明的盒子里装有形状、大小、质地等完全相同的3个小球,把它们分别标上数字1、2、3,由(一)班班长从中随机摸出一个小球,记下小球上的数字;在一个不透明口袋中装有形状、大小、质地等完全相同的4个小球,把它们分别标上数字1、2、3、4,由(二)班班长从口袋中随机摸出一个小球,记下小球上的数字,然后计算出这两个数字的和,若两个数字的和为奇数,则选(一)班去;若两个数字的和为偶数,则选(二)班去. (1)用树状图或列表的方法求八年级(一)班被选去扫墓的概率;(2)你认为这个方法公平吗?若公平,请说明理由;若不公平,请设计一个公平的方法.5.2频数分布直方图题图20(10重庆潼南)23.(10分)如图, 已知在平面直角坐标系xOy 中,一次函数b kx y +=(k ≠0)的图象与反比例函数x m y =(m ≠0)的图象相交于A 、B 两点,且点B 的纵坐标为21-,过点A 作AC ⊥x 轴于点C , AC=1,OC=2. 求:(1)求反比例函数的解析式;(2)求一次函数的解析式.(10重庆潼南)24.(10分) 如图,四边形ABCD 是边长为2的正方形,点G 是BC 延长线上一点,连结AG ,点E 、F 分别在AG 上,连接BE 、DF ,∠1=∠2 , ∠3=∠4.(1)证明:△ABE ≌△DAF ;(2)若∠AGB=30°,求EF 的长.五、解答题:(本大题2个小题,第25小题10分,第26小题12分,共22分)解答时每小题必须给出必要的演算过程或推理步骤.题图24题图23(10重庆潼南)25. (10分)某镇道路改造工程,由甲、乙两工程队合作20天可完成.甲工程队单独施工比乙工程队单独施工多用30天完成此项工程.(1)求甲、乙两工程队单独完成此项工程各需要多少天?(2)若甲工程队独做a 天后,再由甲、乙两工程队合作 天(用含a 的代数式表示)可完成此项工程;(3)如果甲工程队施工每天需付施工费1万元,乙工程队施工每天需付施工费2.5万元,甲工程队至少要单独施工多少天后,再由甲、乙两工程队合作施工完成剩下的工程,才能使施工费不超过64万元?(10重庆潼南)26.(12分)如图, 已知抛物线c bx x y ++=221与y 轴相交于C ,与x 轴相交于A 、B ,点A 的坐标为(2,0),点C 的坐标为(0,-1). (1)求抛物线的解析式;(2)点E 是线段AC 上一动点,过点E 作DE ⊥x 轴于点D ,连结DC ,当△DCE 的面积最大时,求点D 的坐标; (3)在直线BC 上是否存在一点P ,使△ACP 为等腰三角形,若存在,求点P 的坐标,若不存在,说明理由.题图26潼南县2010年初中毕业暨高中招生考试数 学 试 卷 参考答案与评分意见(10重庆潼南)一、1.A 2.C 3.B 4.B 5.D 6.A 7.D 8.B 9.C 10.B(10重庆潼南)二、11. 5.2×10512. 3:4 13. 33 14. 160 15. 相离 16. 82.0三、(10重庆潼南)17. 解:原式=1-3+2-1 ----------------------------5分= -1 ------------------------------------6分 (10重庆潼南)18. 解:由①+②,得 3x =45x =15------------------------------------------3分 把x =15代入①,得 15+y =20y =5-----------------------------------------------5分 ∴这个方程组的解是⎩⎨⎧==515y x ---------------------------------------6分(10重庆潼南)19. 已知:线段a 、h求作:一个等腰△ABC 使底边BC=a ,底边BC 上的高为h ----------------------------------------------1分画图(保留作图痕迹图略)--------------------------6分 20.每空1分,共6分频数分布直方图合计 50 1四、(10重庆潼南)21. 解:原式=)1)(1()1(12-+-÷-x x x x x -------------4分 2)1()1)(1(1--+⋅-=x x x x x -----------6分 =xx 1+ -----------------8分 当x =2时, 原式=212+=23-----------------10分(10重庆潼南)22. 解: (1)法一:------4分 ------6分解法二:P(和为奇数)=126=21. ----------------------------------8分 (2)公平.理由为:P(和为偶数)=126=21∵P(和为奇数)= P(和为偶数)∴该方法公平----------------------------------------10分 (10重庆潼南)23.解:(1)∵AC ⊥x 轴 AC=1 OC=2∴点A 的坐标为(2,1)------------------------------1分∵反比例函数xmy =的图像经过点A (2,1) ∴ m =2------------------------------------------4分∴反比例函数的解析式为xy 2=---------------------5分 (2)由(1)知,反比例函数的解析式为xy 2=∵反比例函数x y 2=的图像经过点B 且点B 的纵坐标为-21∴点B 的坐标为(-4,-21)---------------------------6分 ∵一次函数y =kx +b 的图象经过点A (2,1)点B (-4,-21)∴⎪⎩⎪⎨⎧-=+-=+21412b k b k解得:k =41 b =21----------------------------------9分 ∴一次函数的解析式为2141+=x y ----------------------10分(10重庆潼南)24.解:(1)∵四边形ABCD 是正方形∴AB=AD在△ABE 和△DAF 中⎪⎩⎪⎨⎧∠=∠=∠=∠3412DA AB ∴△ABE ≌△DAF-----------------------4分(2)∵四边形ABCD 是正方形∴∠1+∠4=900∵∠3=∠4∴∠1+∠3=900∴∠AFD=900----------------------------6分 在正方形ABCD 中, AD ∥BC∴∠1=∠AGB=300在Rt △ADF 中,∠AFD=900AD=2∴AF=3 DF =1----------------------------------------8分 由(1)得△ABE ≌△ADF ∴AE=DF=1∴EF=AF-AE=13- -----------------------------------------10分五、(10重庆潼南)25. 解:(1)设乙独做x 天完成此项工程,则甲独做(x+30)天完成此项工程.由题意得:20(3011++x x )=1 -----------------2分 整理得:x 2-10x -600=0(解得:x 1=30 x 2=-20 -----------------------------3分 经检验:x 1=30 x 2=-20都是分式方程的解,但x 2=-20不符合题意舍去---------------------------4分 x +30=60答:甲、乙两工程队单独完成此项工程各需要60天、30天.----5分 (2)设甲独做a 天后,甲、乙再合做(20-3a)天,可以完成 此项工程.-------------------------------------------7分(3)由题意得:1×64)320)(5.21(≤-++aa解得:a ≥36---------------------------------------9分 答:甲工程队至少要独做36天后,再由甲、乙两队合作完成剩下的此项工程,才能使施工费不超过64万元. ---------------------------10分(10重庆潼南)26. 解:(1)∵二次函数c bx x y ++=221的图像经过点A (2,0)C(0,-1) ∴⎩⎨⎧-==++1022c c b解得: b =-21c =-1-------------------2分 ∴二次函数的解析式为121212--=x x y --------3分(2)设点D 的坐标为(m ,0) (0<m <2)∴ OD=m ∴AD=2-m 由△ADE ∽△AOC 得,OCDEAO AD =--------------4分 ∴122DEm =- ∴DE=22m ------------------------------------5分∴△CDE 的面积=21×22m-×m=242m m +-=41)1(412+--m 当m =1时,△CDE 的面积最大∴点D 的坐标为(1,0)--------------------------8分 (3)存在 由(1)知:二次函数的解析式为121212--=x x y 设y=0则1212102--=x x 解得:x 1=2 x 2=-1 ∴点B 的坐标为(-1,0) C (0,-1)设直线BC 的解析式为:y =kx +b ∴ ⎩⎨⎧-==+-1b b k 解得:k =-1 b =-1∴直线BC 的解析式为: y =-x -1在Rt △AOC 中,∠AOC=900OA=2 OC=1 由勾股定理得:AC=5 ∵点B(-1,0) 点C (0,-1)∴OB=OC ∠BCO=450①当以点C 为顶点且PC=AC=5时,...设P(k, -k-1)过点P作PH⊥y轴于H∴∠HCP=∠BCO=450CH=PH=∣k∣在Rt△PCH中k2+k2=()25解得k1=210,k2=-210∴P1(210,-1210-) P2(-210,1210-)---10分②以A为顶点,即AC=AP=5设P(k, -k-1)过点P作PG⊥x轴于GAG=∣2-k∣ GP=∣-k-1∣在Rt△APG中 AG2+PG2=AP2(2-k)2+(-k-1)2=5解得:k1=1,k2=0(舍)∴P3(1, -2) ----------------------------------11分③以P为顶点,PC=AP设P(k, -k-1)过点P作PQ⊥y轴于点QPL⊥x轴于点L∴L(k,0)∴△QPC为等腰直角三角形PQ=CQ=k由勾股定理知CP=PA=2k∴AL=∣k-2∣, PL=|-k-1|在Rt△PLA中(2k)2=(k-2)2+(k+1)2解得:k=25∴P4(25,-27) ------------------------12分综上所述:存在四个点:P1(210,-1210-)P2(-210,1210-) P3(1, -2) P4(25,-27)。
(免费)2010年部分省市中考数学试题分类汇编 频数与频率(含答案)

频数分布直方图2010年部分省市中考数学试题分类汇编频数与频率1.(2010山东德州)为了了解某校九年级学生的体能情况,随机抽查了其中50名学生,测试1分钟仰卧起坐的成绩(次数),进行整理后绘制成如图所示的频数分布直方图(注:15~20包括15,不包括20,以下同),请根据统计图计算成绩在20~30次的频率是 (A )0.4(B )0.5 (C )0.6 (D )0.7【关键词】频率、频数分布直方图 【答案】D1.(2010年台湾省)自连续正整数10~99中选出一个数,其中每个数被选出的机会相等。
求选出的数其十位数字与个位数字的和为9的机率为何? (A)908 (B) 909 (C) 898 (D) 899 【关键词】频率 【答案】B1. (2010重庆市潼南县)根据市教委提出的学生每天体育锻炼不少于1小时的要求,为确保阳光体育运动时间得到落实,某校对九年级学生每天参加体育锻炼的时间作了一次抽样调查,其中部分结果记录如下:频数分布表:请你将频数分布表和频数分布直方图补充完整.5.2频数分布直方图题图20 第6题图2. (2010年福建晋江)某校为了了解九年级女生的体能情况,随机抽查了部分女生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图和不完整的统计表(每个分组包括左端点,不包括右端点). 请你根据图中提供的信息,解答以下问题: (1) 分别把统计图与统计表补充完整;位数”,请你写出小敏仰卧起坐次数所在的范围.(3)若年段的奋斗目标成绩是每个女生每分钟23次,问被抽查的所有女生的平均成绩是否达到奋斗目标成绩? 解: (1) 5 ,52…………………………………………(2分) 补图正确得2分. ………………………………………(4分) (2) 25~30.………………………………………………(7分) (3) 被抽查的所有女生的平均成绩至少是:2.233053012251020315≈⨯+⨯+⨯+⨯(次) ………………(9分)∵23.2>23∴被抽查的所有女生的平均成绩达到奋斗目标成绩. …………(10分)3. (2010浙江衢州)黄老师退休在家,为选择一个合适的时间参观2010年上海 世博会,他查阅了5月10日至16日(星期一至星期日)每天 的参观人数,得到图1、图2所示的统计图,其中图1是每天参观人数的统计图,图2是5月15日(星期六)这一天上午、中午、下午和晚上四个时间段参观人数的扇形统计图.请你根据统计图解答下面的问题: (1) 5月10日至16日这一周中,参观人数最多的是哪一天?有多少人?参观人数最少的又是哪一天?有多少人?(2) 5月15日(星期六)这一天,上午的参观人数比下午的参观人数多多少人 (精确到1万人)? (3) 如果黄老师想尽可能选择参观人数较少的时间去参观世博会,你认(次)(次)为他选择什么时间比较合适?解:(1) 参观人数最多的是15日(或周六),有34万人; ……2分参观人数最少的是10日(或周一),有16万人. ……2分 (2) 34×(74%-6%)=23.12≈23.上午参观人数比下午参观人数多23万人. ……2分 (3) 答案不唯一,基本合理即可,如选择星期一下午参观等. ……2分4.(2010年日照市)为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时。
2010年重庆省中考《数学》试题及答案

(2)若存放 天后,将这批野生菌一次性出售,设这批野生菌的销售总额为 元,试写出 与 之间的函数关系式;
(3)李经理将这批野生茵存放多少天后出售可获得最大利润 元?
(利润=销售总额-收购成本-各种费用)
13.把抛物线y=-3x2先向左平移1个单位,再向上平移2个单位后所得的函数 解析式为 。
14.已知一个样本1,3,2,x,5,其平均数是3,则这个样本的标准差是 。
15. 某超市一月份的营业额为200万元,二、三两月的营业额共800万元,如果平均每月增长率为 ,则由题意列方程应为__________________________________。
24. (本题满分8分)如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=4㎝,DC=6㎝,试求AD的长. 小萍同学灵活运用轴对称知识,将图形进行翻折变换,巧妙地解答了此题。请按照小萍的思路,探究并解答下列问题:
(1)分别以AB、AC所在的直线为对称轴,画出△ABD、△ACD的轴对称图形,D点的对称点分别为点E、F,延长EB、FC相交于G点,试证明四边形AEGF是正方形;
(3)设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?问对于所求的t值,平行四边形BCMN是否菱形?请说明理由.
26. (10分)有一种可食用的野生菌,上市时,外商李经理按市场价格30元/千克收购了这种野生菌1000千克存放入冷库中,据预测,该野生菌的市场价格将以每天每千克上涨1元;但冷冻存放这批野生菌时每天需要支出各种费用合计310元,而且这类野生菌在冷库中最多保存160天,同时,平均每天有3千克的野生菌损坏不能出售。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重庆市潼南县2010年初中毕业暨高中招生考试
数 学 试 卷
参考公式: 抛物线)0(2
≠++=a c bx ax y 的顶点坐标为)44,2(2
a
b a
c a b --,对称轴公式为a
b x 2-=
一、选择题 (本大题10个小题,每小题4分,共40分 )在每个小题的下面,都给出了代
号为A 、B 、C 、D 的四个答案,其中只有一个是正确的,请将正确答
案的代号填在题后的括号中.
1. 2的倒数是( )
A .
21 B .-2 C . -2
1
D . 2 2. 计算3x +x 的结果是( ) A . 3x 2
B . 2x
C . 4x
D . 4x 2
3. 数据 14 ,10 ,12, 13, 11 的中位数是 ( ) A .14
B .12
C .13
D .11
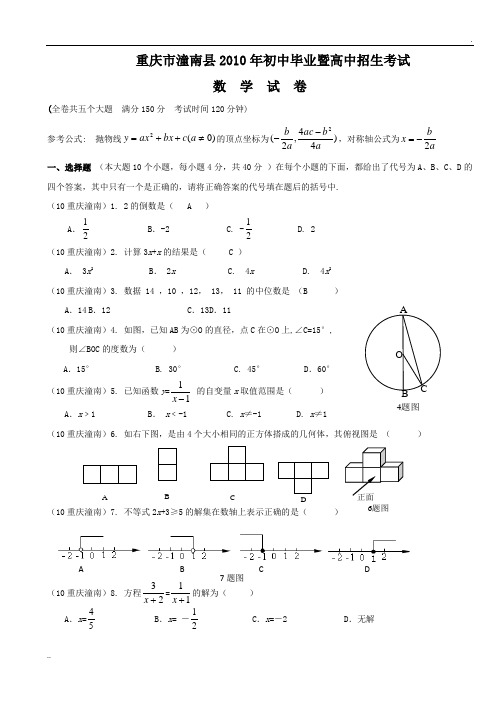
4. 如图,已知AB 为⊙O 的直径,点C 在⊙O 上,∠C =15°,
则∠BOC 的度数为( )
A .15°
B . 30°
C . 45°
D .
60°
5. 已知函数
y =
1
1
-x 的自变量x 取值范围是( ) A .x ﹥1
B . x ﹤-1
C .
x ≠-1 D . x ≠1
6. 如右下图,是由4个大小相同的正方体搭成的几何体,其俯视图是 (
)
7. 不等式2x +3≥5的解集在数轴上表示正确的是( )
题图4题图
6A B C D
8. 方程
2
3
+
x
=
1
1
+
x
的解为()
A.x=
5
4
B.x= -
2
1
C.x=-2D.无解9.如图,△ABC经过怎样的平移得到△DEF ( )
A.把△ABC向左平移4个单位,再向下平移2个单位
B.把△ABC向右平移4个单位,再向下平移2个单位
C.把△ABC向右平移4个单位,再向上平移2个单位
D.把△ABC向左平移4个单位,再向上平移2个单位
10.如图,四边形ABCD是边长为1 的正方形,四边形EFGH是边长为2的正方形,点D 与点F重合,点B,D(F),H在同一条直线上,将正方形ABCD沿F→H方向平移至点B与点H重合时停止,设点D、F之间的距离为x,正方形ABCD与正方形EFGH重叠部分的面积为y,则能大致反映y与x之间函数关系的图象是()
二、填空题:(本大题6个小题,每小题4分,共24分)在每小题
中,请将答案直接填在题后的横线上.
11. 2010年我县举行“菜花节”共接待游客约520000人,请将数字520000用科学记数法表
示为:.
12. △ABC与△DEF的相似比为3:4,则△ABC与△DEF的周长比为.
题图
9
G
H
E
(F)
A
B
C
D
题图
10
A B C D
7题图
⎩⎨⎧=-=+.
252,20y x y x 13. 计算:=+312 .
14. 一套运动装标价200元,按标价的八折销售,则这套运动装的实际售价为 元. 15. 如图,在矩形ABCD 中,AB =6 , BC =4, ⊙O 是以AB 为直径的圆,则直线DC 与
⊙O 的位置关系是 .
16. 如图所示,小明在家里楼顶上的点A 处,测量建在与小明家楼房同一水平线上相邻的电梯楼的高,在点A 处看电梯楼顶部点B 处的仰角为60°,在点A 处看这栋电梯楼底部点C 处的俯角为45°,两栋楼之间的距离为30m ,则电梯楼的高BC 为 米(精确到0.1).(参考数据:414.12≈ 732.13≈)
三、解答题:(本大题4个小题,每小题6分,共24分)解答时每小题必须给出必要的演算过程或推理步骤.
17. (6分)计算:(π-3.14)0-|-3|+1
21-⎪⎭
⎫
⎝⎛-(-1)2010.
18.(6分)解方程组
19.(6分)画一个等腰△ABC ,使底边长BC=a ,底边上的高为h (要求:用尺规作图,保留作图痕迹,写出已知,求作,不写作法和证明).
已知:
求作:
20.(6分)根据市教委提出的学生每天体育锻炼不少于1小时的要求,为确保阳光体育运
动时间得到落实,某校对九年级学生每天参加体育锻炼的时间作了一次抽样调查,其中部分结果记录如下:
频数分布表:
请你将频数分布表和频数分布直方图补充完整.
a h
5
.2频数分布直方图
题图
20
四、解答题:(本大题4个小题,每小题10分,共40分)解答时
每小题必须给出必要的演算过程或推理步骤.
21.(10分)先化简,再求值:)11(x -÷1
1
22
2-+-x x x ,x =2.
22. (10分)“清明节”前夕,我县某校决定从八年级(一)班、(二)班中选一个班去杨闇公烈士陵园扫墓,为了公平,有同学设计了一个方法,其规则如下:在一个不透明的盒子里装有形状、大小、质地等完全相同的3个小球,把它们分别标上数字1、2、3,由(一)班班长从中随机摸出一个小球,记下小球上的数字;在一个不透明口袋中装有形状、大小、质地等完全相同的4个小球,把它们分别标上数字1、2、3、4,由(二)班班长从口袋中随机摸出一个小球,记下小球上的数字,然后计算出这两个数字的和,若两个数字的和为奇数,则选(一)班去;若两个数字的和为偶数,则选(二)班去. (1)用树状图或列表的方法求八年级(一)班被选去扫墓的概率;(2)你认为这个方法公平吗?若公平,请说明理由;若不公平,请设计一个公平的方法.
23.(10分)如图, 已知在平面直角坐标系xOy 中,一次函数b kx y +=(k ≠0)的图象与反
比例函数x m y =
(m ≠0)的图象相交于A 、B 两点,且点B 的纵坐标为2
1
-,过点A 作AC ⊥x 轴于点C , AC =1,OC =2.
求:(1)求反比例函数的解析式;
(2)求一次函数的解析式.
24.(10分) 如图,四边形ABCD 是边长为2的正方形,点G 是BC 延长线上一点,连结AG ,
点E 、F 分别在AG 上,连接BE 、DF ,∠1=∠2 , ∠3=∠4.
(1)证明:△AB E ≌△DAF ; (2)若∠AGB =30°,求EF 的长.
题图23
题图
24
五、解答题:(本大题2个小题,第25小题10分,第26小题12分,
共22分)解答时每小题必须给出必要的演算过程或推理步骤.
25. (10分)某镇道路改造工程,由甲、乙两工程队合作20天可完成.甲工程队单独施工比
乙工程队单独施工多用30天完成此项工程.
(1)求甲、乙两工程队单独完成此项工程各需要多少天?
(2)若甲工程队独做a天后,再由甲、乙两工程队合作天(用含a的代数式表示)可完成此项工程;
(3)如果甲工程队施工每天需付施工费1万元,乙工程队施工每天需付施工费2.5万元,甲工程队至少要单独施工多少天后,再由甲、乙两工程队合作施工完成剩下的
工程,才能使施工费不超过64万元?
26.(12分)如图, 已知抛物线c bx x y ++=
2
2
1与y 轴相交于C ,与x 轴相交于A 、B ,点A 的坐标为(2,0),点C 的坐标为(0,-1). (1)求抛物线的解析式;
(2)点E 是线段AC 上一动点,过点E 作DE ⊥x 轴于点D ,连结DC ,当△DCE 的面
积最大时,求点D 的坐标;
(3)在直线BC 上是否存在一点P ,使△ACP 为等腰三角形,若存在,求点P 的坐标,
若不存在,说明理由.
题图
26。
