高一上数学周测(8)

合集下载

第三章函数的概念与性质单元检测卷(含解析)—2024-2025学年高一上学期数学必修第一册

第三章　函数的概念与性质（单元检测卷）一、单选题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.函数y ＝－x 2＋2x ＋3的定义域为( )A.[－3，1] B.[－1，3]C.(－∞，－3]∪[1，＋∞)D.(－∞，－1]∪[3，＋∞)2.已知函数y ＝f(x ＋1)定义域是[－2，3]，则函数y ＝f(x －1)的定义域是( )A.[0，5] B.[－1，4]C.[－3，2]D.[－2，3]3.已知函数f(x)＝Error!若f(－a)＋f(a)≤0，则实数a 的取值范围是( )A.[－1，1] B.[－2，0]C.[0，2]D.[－2，2]4.设f(x)是定义域为R 的奇函数，且f(1＋x)＝f(－x)．若f ＝13，则f ＝( )A.－53B.－13C.13D.535.二次函数的图象的顶点为(0，－1)，对称轴为y 轴，则二次函数的解析式可以为( )A .y ＝－14x 2＋1B.y ＝14x 2－1C .y ＝4x 2－16 D.y ＝－4x 2＋166.拟定从甲地到乙地通话m min的话费(单位：元)符合f(m)＝{3.71，0＜m ≤4，1.06×(0.5×[m]＋2)，m ＞4，其中[m]表示不超过m 的最大整数，从甲地到乙地通话5.2min 的话费是A.3.71元 B.4.24元C.4.77元D.7.95元7.若函数f(x)在R 上是减函数，则下列关系式一定成立的是( )A.f(a)＞f(2a) B.f(a 2)＜f(a)C.f(a 2＋a)＜f(a)D.f(a 2＋1)＜f(a 2)8.若函数f (x)是奇函数，且当x>0时，f (x)＝x 3＋x ＋1，则当x<0时，f (x)的解析式为( )A .f (x)＝x 3＋x －1B .f (x)＝－x 3－x －11()3 5()3C .f (x)＝x 3－x ＋1D .f (x)＝－x 3－x ＋1二、多选题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，有选错的得0分，部分选对的得部分分．9.已知f (2x －1)＝4x 2，则下列结论正确的是( )A .f (3)＝9 B.f (－3)＝4C .f (x)＝x 2D.f (x)＝(x ＋1)210.函数f(x)的图象是折线段ABC ，如图所示，其中点A ，B ，C 的坐标分别为(－1，2)，(1，0)，(3，2)，以下说法正确的是( )A.f(x)＝Error!B.f(x －1)的定义域为[－1，3]C.f(x ＋1)为偶函数D.若f(x)在[m ，3]上单调递增，则m 的最小值为111.下列说法正确的是( )A.若幂函数的图象经过点，则该幂函数的解析式为y ＝x -3B.若函数f(x)＝，则f(x)在区间(－∞，0)上单调递减C.幂函数y ＝x α(α＞0)始终经过点(0，0)和(1，1)D.若函数f(x)＝x ，则对于任意的x 1，x 2∈[0，＋∞)有f(x 1)＋f(x 2)2≤f 三、填空题：本题共3小题，每小题5分，共15分．把答案填在题中横线上．12.设f(x)＝11－x，则f(f(x))＝__________13.已知二次函数f(x)＝ax 2＋2ax ＋1在区间[－3，2]上的最大值为4，则a 的值为________14.若函数f(x)＝ax 2＋bx ＋3a ＋b 是偶函数，定义域为[a －1，2a]，则a ＝________，b ＝________四、解答题：本题共5小题，共77分．解答时应写出文字说明、证明过程或演算步骤．1(,2)845x-12x x ()2+15.（13分）已知幂函数f(x)＝(m2－5m＋7)x－m-1(m∈R)为偶函数．(1)求f的值；(2)若f(2a＋1)＝f(a)，求实数a的值．16.（14分）已知函数f(x)＝Error!(1)求f(f(f(5)))的值；(2)画出函数的图象．17.（16分）某公司生产一种电子仪器的固定成本为20 000元，每生产一台仪器需增加投入100元，已知总收益满足函数：R(x)＝{400x－12x2，0≤x≤400，80 000，x＞400，其中x是仪器的月产量．(1)将利润表示为月产量的函数f(x)；(2)当月产量为何值时，公司所获利润最大？最大利润为多少元？(总收益＝总成本＋利润)18.（16分）已知函数f(x)＝x21＋x2＋1，x∈R．1 () 2(1)判断并证明函数的奇偶性；(2)求f(x)＋f 的值；(3)计算f(1)＋f(2)＋f(3)＋f(4)＋f ＋f ＋f ．19.（18分）已知二次函数f(x)＝x 2－2(a －1)x ＋4．(1)若a ＝2，求f(x)在[－2，3]上的最值；(2)若f(x)在区间(－∞，2]上单调单减，求实数a 的取值范围；(3)若x ∈[1，2]，求函数f(x)的最小值．参考答案及解析：一、单选题1()x 1()21()31()41.B 解析：由题意，令－x 2＋2x ＋3≥0，即x 2－2x －3≤0，解得－1≤x ≤3，所以函数的定义域为[－1，3]．故选B ．2.A 解析：由题意知－2≤x ≤3，所以－1≤x ＋1≤4，所以－1≤x －1≤4，得0≤x ≤5，即y ＝f(x －1)的定义域为[0，5]．3.D 解析：依题意，可得Error!或Error!或Error!解得－2≤a ≤2．4.C 解析：由题意，f ＝f ＝f ＝－f ＝－f ＝－f ＝f ＝13．5.B 解析：把点(0，－1)代入四个选项可知，只有B 正确．故选B ．6.C 解析：f(5.2)＝1.06×(0.5×[5.2]＋2)＝1.06×(0.5×5＋2)＝4.77．7.D 解析:因为f(x)是R 上的减函数，且a 2＋1＞a 2，所以f(a 2＋1)＜f(a 2)．故选D ．8.A 解析：∵函数f (x)是奇函数，∴f (－x)＝－f (x)，当x<0时，－x>0，∵x>0时，f (x)＝x 3＋x ＋1，∴f (－x)＝(－x)3－x ＋1＝－x 3－x ＋1，∴－f (x)＝－x 3－x ＋1，∴f (x)＝x 3＋x －1．即x<0时，f (x)＝x 3＋x －1．故选A ．二、多选题9.BD 解析：令t ＝2x －1，则x ＝t ＋12，∴f (t)＝4＝(t ＋1)2．∴f (3)＝16，f (－3)＝4，f (x)＝(x ＋1)2．故选BD ．10.ACD 解析：由图可得当－1≤x ＜1时，图象过(1，0)，(－1，2)两点，设f(x)＝kx ＋b ，∴Error!解得Error!＝－x ＋1，当1≤x ≤3时，根据图象过点(1，0)，(3，2)，同理可得f(x)＝x －1，∴f(x)＝Error!A 正确；由图可得f(x)的定义域为[－1，3]，关于x ＝1对称，∴f(x －1)的定义域为[0，4]，f(x ＋1)为偶函数，即B 错误，C 正确；当f(x)在[m ，3]上单调递增，则1≤m ＜3，故m 的最小值为1，D 正确．故选ACD ．11.CD 解析：若幂函数的图象经过点，则该幂函数的解析式为y ＝，故A 错误；函数f(x)＝是偶函数且在(0，＋∞)上单调递减，故在(－∞，0)上单调递增，故B 错误；幂函数y ＝x α(α＞0)始终经过点(0，0)和(1，1)，故C 正确；对任意的x 1，x 2∈[0，＋∞)，要证f(x 1)＋f(x 2)2≤f ，即x 1＋x 22≤x 1＋x 22，即x 1＋x 2＋2x 1x 24≤x 1＋x 22，即(x 1－x 2)2≥0，易知成立，故D 正确．三、填空题5()32(1)3+2()3-2(31[1(3+-1()31()3-2t 1()2+1(,2)813x -45x -12x x ()2+12.答案：x －1x (x ≠0且x ≠1)解析：f(f(x))＝11－11－x ＝11－x －11－x＝x －1x ．13.答案：－3或38解析：f(x)的对称轴为直线x ＝－1．当a ＞0时，f(x)max ＝f(2)＝4，解得a ＝38；当a ＜0时，f(x)max ＝f(－1)＝4，解得a ＝－3．综上所述，a ＝38或a ＝－3．14.答案：13，0解析：因为偶函数的定义域关于原点对称，所以a －1＝－2a ，解得a ＝13．又函数f(x)＝13x 2＋bx＋b ＋1为二次函数，结合偶函数图象的特点，则－b2×73＝0，易得b ＝0．四、解答题15.解：(1)由m 2－5m ＋7＝1，得m ＝2或m ＝3．当m ＝2时，f(x)＝x -3是奇函数，所以不满足题意，所以m ＝2舍去；当m ＝3时，f(x)＝x -4，满足题意，所以f(x)＝x -4．所以f ＝＝16．(2)由f(x)＝x -4为偶函数且f(2a ＋1)＝f(a)，得|2a ＋1|＝|a|，即2a ＋1＝a 或2a ＋1＝－a ，解得a ＝－1或a ＝－13．16.解：(1)因为5＞4，所以f(5)＝－5＋2＝－3．因为－3＜0，所以f(f(5))＝f(－3)＝－3＋4＝1．因为0＜1＜4，所以f(f(f(5)))＝f(1)＝12－2×1＝－1，即f(f(f(5)))＝－1．(2)图象如图所示．1()241()217.解：(1)设月产量为x 台，则总成本为(20 000＋100x)元，从而f(x)＝{－12x 2＋300x －20 000，0≤x ≤400，60 000－100x ，x ＞400．(2)当0≤x ≤400时，f(x)＝－12(x －300)2＋25 000，所以当x ＝300时，f(x)max ＝25 000．当x ＞400时，f(x)＝60 000－100x 单调递减，f(x)＜60 000－100×400＝20 000＜25 000．所以当x ＝300时，f(x)max ＝25 000，即每月生产300台仪器时利润最大，最大利润为25 000元．18.解：(1)f(x)是偶函数，理由如下．f(x)的定义域为R ，关于y 轴对称．因为f(－x)＝(－x)21＋(－x)2＋1＝x 21＋x 2＋1＝f(x)，所以f(x)＝x 21＋x 2＋1是偶函数．(2)因为f(x)＝x 21＋x 2＋1，所以f ＝＋1＝1x 2＋1＋1，所以f(x)＋f ＝3．(3)由(2)可知f(x)＋f ＝3，又因为f(1)＝32，所以f(1)＋f(2)＋f(3)＋f(4)＋ff ＋f ＋f ＝f(1)＋＝32＋3×3＝21219.解：(1)当a ＝2时，f(x)＝x 2－2x ＋4，x ∈[－2，3]，因为f(x)的对称轴为x ＝1，所以f(x)在[－2，1]上单调递减，在[1，3]上单调递增，所以当x ＝1时，f(x)取得最小值为f(1)＝1－2＋4＝3，当x ＝－2时，f(x)取得最大值为f(－2)＝22＋4＋4＝12．1()x 221()x 11()x +1(x 1()x 1()21()31()4111[f (2)f ()][f (3)f ()][f (4)f ()]234+++++(2)二次函数f(x)＝x 2－2(a －1)x ＋4的对称轴为x ＝a －1，f(x)在区间(－∞，2]单调递减，则a －1≥2，解得a≥3．所以实数a 的取值范围为[3，＋∞)．(3)二次函数f(x)＝x 2－2(a －1)x ＋4的对称轴为x ＝a －1，当a －1≤1，则a≤2，此时f(x)在[1，2]上单调递增，所以f(x)min ＝f(1)＝1－2(a －1)＋4＝7－2a ．当1＜a －1＜2，则2＜a ＜3，此时f(x)在[1，a －1]上单调递减，在[a －1，2]上单调递增，所以f(x)min ＝f(a －1)＝(a －1)2－2(a －1)2＋4＝－a 2＋2a ＋3．当a －1≥2，则a ≥3，此时f(x)在[1，2]上单调递减，所以f(x)min ＝f(2)＝22－4(a －1)＋4＝12－4a ．综上，f(x)min ＝{7－2a ，a ≤2，－a 2＋2a ＋3，2＜a ＜3，12－4a ，a ≥3．。

江苏无锡市湖滨中学2024-2025学年高一(上)数学第8周阶段性训练模拟练习【含答案】

江苏无锡市湖滨中学2024-2025学年高一（上）数学第8周阶段性训练模拟练习一．选择题（共7小题）1．幂函数在（0，+∞）上单调递增，则m的值为（）A．2B．3C．4D．2或42．已知正数x，y满足＝2，则x+2y的最小值为（）A．7B．14C．18D．93．若不等式ax2+bx+c＞0的解集为{x|﹣1＜x＜2}，那么不等式a（x2+1）+b（x﹣1）+c＞2ax的解集为（）A．{x|﹣2＜x＜1}B．{x|x＜﹣2或x＞1}C．{x|x＜0或x＞3}D．{x|0＜x＜3}4．已知函数，若存在x1，x2∈R，且x1≠x2，使得f（x1）＝f（x2），则实数a的取值范围为（）A．（﹣∞，4）B．C．（﹣∞，3）D．（﹣∞，8）5．已知函数f（x）＝a x﹣2+1（a＞0，且a≠1）恒过定点M（m，n），则函数g（x）＝n﹣m x不经过（）A．第一象限B．第二象限C．第三象限D．第四象限6．已知集合A＝，B＝{x|（x﹣2a）（x﹣a2﹣1）＜0}，若A∩B＝∅，则实数a的取值范围为（）A．{a|a＞2}B．{a|a≥2}C．{a|a＝1或a≥2}D．{a|a≥1}7．已知函数y＝f（x）的定义域为（﹣∞，﹣1）∪（﹣1，+∞），且f（x﹣1）为奇函数，当x＜﹣1时，f （x）＝﹣2x2﹣8x﹣7，则方程的所有根之和等于（）A．﹣4B．﹣2C．0D．2二．多选题（共6小题）（多选）8．下列命题为真命题的是（）A．若a＞b＞0，则ac2＞bc2B．若a＜b＜0，则a2＞ab＞b2C．若a＞b＞0且c＜0，则D．若﹣1≤x＜y≤5，则﹣6≤x﹣y＜0（多选）9．下列选项正确的是（）A．若x≠0，则x的最小值为2B．若正实数x，y满足x+2y＝1，则的最小值为8C．的最小值为2D．函数（x＜0）的最大值是0（多选）10．已知函数f（x）＝若互不相等的实数x1，x2，x3满足f（x1）＝f（x2）＝f（x3），则x1+x2+x3的值可以是（）A．﹣8B．﹣7C．﹣6D．﹣5（多选）11．设正实数m，n满足m+n＝2，则下列说法正确的是（）A．的最小值为1B．的最小值为C．的最大值为2D．m2+n2的最大值为2（多选）12．若函数y＝a x+b﹣1（a＞0，且a≠1）的图象不经过第二象限，则需同时满足（）A．a＞1B．0＜a＜1C．b＞0D．b≤0（多选）13．下列说法不正确的是（）A．命题“∀x＜1，都有x2＜1”的否定是“∃x≥1，使得x2≥1”B．集合A＝{﹣2，1}，B＝{x|ax＝2}，若A∩B＝B，则实数a的取值集合为{﹣1，2}C．方程3x2+a（a﹣6）x﹣3＝0有一个根大于1，另一个根小于1的充要条件是0＜a＜6 D．若存在使不等式x2﹣2x﹣m＜0上能成立，则实数m的取值范围是（0，+∞）三．填空题（共5小题）14．已知函数f（x）＝，且f（a）＝14，则f（﹣a）的值为．15．已知x＞y＞0，不等式恒成立，则实数m的取值范围是．16．已知幂函数f（x）＝（m2+m﹣5）x m在（0，+∞）上单调递减，则m＝．17．若，则函数f（x）的值域为．18．已知a，b∈R，若函数f（x）＝（1﹣x2）（x2+ax+b）的图象关于直线x＝﹣2对称，且对于任意正数x 都有x2﹣ax+t≥bx成立，则a+b＝，实数t的最小值是．四．解答题（共3小题）19．已知函数．（Ⅰ）求函数f（x）的零点；（Ⅱ）证明：函数f（x）在区间（0，+∞）上单调递增；（Ⅲ）若x＞0时，f（ax2+2a）＞0恒成立，求正数a的取值范围．20．已知二次函数f（x）＝ax2+bx+c（a＞0，a，b，c∈R），f（1）＝1，对任意x∈R，f（x﹣2）＝f（﹣x），且f（x）≥x恒成立．（1）求二次函数f（x）的解析式；（2）若函数g（x）＝4f（x）﹣2x+|x﹣λ|的最小值为2，求实数λ的值．21．已知定义在R上的函数是奇函数．（1）求实数a的值；（2）求f（x）的值域；（3）证明f（x）在R上为减函数并解不等式．参考答案与试题解析一．选择题（共7小题）1．【解答】解：幂函数中，m2﹣6m+9＝1，解得m＝2或m＝4，当m＝2时，f（x）＝x﹣1，在（0，+∞）上是单调减函数，不满足题意；当m＝4时，f（x）＝x5，在（0，+∞）上是单调增函数，满足题意；所以m的值是4．故选：C．2．【解答】解：由已知可得（）＝1，则x+2y＝＝（8+2+））＝（10+8）＝9，当且仅当，即x＝6，y＝时取得最小值为9，故选：D．3．【解答】解：因为不等式ax2+bx+c＞0的解集为{x|﹣1＜x＜2}，所以﹣1和2是方程ax2+bx+c＝0的两个根，且a＜0，所以，解得b＝﹣a，c＝﹣2a，所以不等式a（x2+1）+b（x﹣1）+c＞2ax化为a（x2+1）﹣a（x﹣1）﹣2a＞2ax，由a＜0，可整理得x2﹣3x＜0，解得0＜x＜3，所以不等式的解集为{x|0＜x＜3}．故选：D．4．【解答】解：由题意知，y＝﹣x2+ax的对称轴为，当，即a＜4时，根据二次函数的性质可知，一定存在x1，x2∈R，使得f（x1）＝f（x2）；当，即a≥4时，由题意知，﹣22+2a＞4a﹣5，解得，不合题意；综上，实数a的取值范围为（﹣∞，4）．故选：A．5．【解答】解：∵f（x）＝a x﹣2+1（a＞0，且a≠1）恒过定点（2，2），∴m＝n＝2，∴g（x）＝2﹣2x，∴g（x）为减函数，且过点（0，1），∴g（x）的函数图象不经过第三象限．故选：C．6．【解答】解：解分式不等式可得，A＝{x|﹣1＜x≤4}，∵a2+1≥2a，∴a＝1时，B＝∅，满足A∩B＝∅，a≠1时，B＝{x|2a＜x＜a2+1}，∵A∩B＝∅，得，解得a≥2；综上，实数a的取值范围为{a|a＝1或a≥2}故选：C．7．【解答】解：因为f（x﹣1）为奇函数，所以f（x﹣1）关于（0，0）对称，所以f（x）关于（﹣1，0）对称，即f（x）＝﹣f（﹣2﹣x）．当x＜﹣1时，f（x）＝﹣2x2﹣8x﹣7，当x＞﹣1时，﹣2﹣x＜﹣1，f（x）＝﹣f（﹣2﹣x）＝2（x+2）2+8（﹣2﹣x）+7＝2x2﹣1，所以f（x）＝．因为，所以或，解得，，，，所以x1+x2+x3+x4＝﹣4．故选：A．二．多选题（共6小题）8．【解答】解：对于A，若a＞b＞0，c＝0，则ac2＝bc2，故A错误，对于B，若a＜b＜0，则a2＞ab，ab＞b2，∴a2＞ab＞b2，故B正确，对于C，若a＞b＞0，则a2＞b2＞0，∴，又∵c＜0，∴，故C正确，对于D，若﹣1≤x＜y≤5，则x﹣y＜0，且﹣5≤﹣y＜1，∴﹣6≤x﹣y＜0，故D正确，故选：BCD．9．【解答】解：对于A，当x＜0时，，故A错误，对于B，∵x＞0，y＞0，x+2y＝1，则＝＝2++＝，当且仅当，即x＝，y＝时，等号成立，故的最小值为8，故B正确，对于C，令，t，y＝在[，+∞）上单调递增，则y的最小值为y＝，故C错误，对于D，当x＜0时，，当且仅当，即x＝﹣1时，等号成立，故y＝2+x+≤0，即函数y的最大值为0，故D正确．故选：BD．10．【解答】接：根据f（x）解析式作出f（x）的图像，再作y＝k交f（x）于三点，横坐标分别为x1，x2，x3，由图像易知x2+x3＝0，所以x1+x2+x3＝x1，令f（x）＝﹣5，解得x1＝﹣3；令f（x）＝3，解得x1＝﹣7；故x1+x2+x3∈（﹣7，﹣3]，故选：CD．11．【解答】解：对于A，因为m＞0，n＞0，所以，当且仅当m＝n＝1时等号成立，故有最大值1，故A错；对于B，因为m+n＝2，所以＝，当且仅当时，即m＝2﹣2，n＝4﹣2时等号成立，故B正确；对于C，，当且仅当m＝n＝1时等号成立，所以，故C正确；对于D，m2+n2＝（m+n）2﹣2mn＝4﹣2mn，由A有mn≤1，则﹣2mn≥﹣2，所以m2+n2≥2，当且仅当m＝n＝1时等号成立，故D错．故选：BC．12．【解答】解：函数y＝a x+b﹣1（a＞0，a≠1）的图象，由函数y＝a x（a＞0，a≠1）的图象向上平移（b﹣1）单位得到；若0＜a＜1，则函数图象经过第二象限；若a＞1，b﹣1+1≤0，则函数图象不经过第二象限；所以a＞1，b≤0，满足题意．故选：AD．13．【解答】解：对于A：命题的否定是：“∃x＜1，使得x2≥1”，故A不正确；对于B：A∩B＝B⇒B⊆A，A＝{﹣2，1}的子集有ϕ，{﹣2}，{1}，{﹣2，1}，当B＝∅时，显然有a＝0；当B＝{﹣2}时，﹣2a＝2⇒a＝﹣1；当B＝{1}时，a•1＝2⇒a＝2；当B＝{﹣2，1}，不存在a，符合题意，∴实数a值集合为{﹣1，0，2}，故B不正确；对于C：令f（x）＝3x2+a（a﹣6）x﹣3，由f（1）＜0得a2﹣6a＜0，即0＜a＜6，故C正确；对于D：若存在使不等式x2﹣2x﹣m＜0上能成立，则存在，使得m＞x2﹣2x，等价于m＞（x2﹣2x）min，，因为当x＝1时（x2﹣2x）min＝﹣1，∴m＞﹣1，故D不正确．故选：ABD．三．填空题（共5小题）14．【解答】解：根据题意，函数f（x）＝＝+＝+2，则有f（﹣x）＝﹣+2，则f（x）+f（﹣x）＝4，若f（a）＝14，则f（﹣a）＝﹣10，故答案为：﹣10．15．【解答】解：由题意，不等式恒成立，即，∵x＞y＞0，∴，当且仅当（x﹣y）2＝4y2时取等号，∴m2﹣2m+2≤5，解得﹣1≤m≤3．故答案为：[﹣1，3]．16．【解答】解：∵幂函数f（x）＝（m2+m﹣5）x m在（0，+∞）上单调递减，∴，解得m＝﹣3．故答案为：﹣3．17．【解答】解：令t＝，t≥0，则x＝1﹣t2，所以原函数可转化为g（t）＝1﹣t2+t＝﹣（t﹣）2+，t≥0，由二次函数的性质可得g（t）≤g（）＝，所以函数f（x）的值域为（﹣∞，]．故答案为：（﹣∞，]．18．【解答】解：由f（x）＝（1﹣x2）（x2+ax+b）＝0，可得x＝1，或x＝﹣1，或x2+ax+b＝0，因为f（x）的图象关于直线x＝﹣2对称，所以f（﹣1）＝f（﹣3）＝0，f（1）＝f（﹣5）＝0，所以﹣3和﹣5是方程x2+ax+b＝0的两个根，所以，得，所以a+b＝8+15＝23，所以不等式x2﹣ax+t≥bx可化为x2﹣8x+t≥15x，所以t≥﹣x2+23x，令y＝﹣x2+23x，则其对称轴为，所以当时，y＝﹣x2+23x取得最大值，其最大值为，所以，所以实数t的最小值是．故答案为：23；．四．解答题（共3小题）19．【解答】解：（Ⅰ）因为，所以x≠﹣1，令，则有2x2＝x+1，即2x2﹣x﹣1＝0，解得x＝1或，所以f（x）的零点为x＝1或；（Ⅱ）证明：任取x1，x2∈（0，+∞），x1＜x2，则，因为0＜x1＜x2，所以，即f（x1）﹣f（x2）＜0，f（x1）＜f（x2），所以函数f（x）在区间（0，+∞）上单调递增；（Ⅲ）若x＞0时，f（ax2+2a）＞0恒成立，即f（ax2+2a）＞f（1）恒成立，因为a＞0，所以ax2+2a＞0，又函数f（x）在区间（0，+∞）上单调递增，所以“f（ax2+2a）＞f（1）恒成立”等价于“ax2+2a＞1恒成立”，即在x∈（0，+∞）上恒成立，又因为，故a的取值范围为．20．【解答】解：（1）因为对任意x∈R，f（x﹣2）＝f（﹣x），所以a（x﹣2）2+b（x﹣2）+c＝a（﹣x）2+b（﹣x）+c，即（2b﹣4a）x+4a﹣2b＝0对任意x∈R成立，所以b＝2a，因为f（1）＝1，所以a+b+c＝1，所以c＝1﹣3a，又对任意x∈R，f（x）≥x恒成立，所以ax2+2ax+（1﹣3a）≥x，即ax2+（2a﹣1）x+（1﹣3a）≥0在R上恒成立，所以Δ＝（2a﹣1）2﹣4a（1﹣3a）＝16a2﹣8a+1＝（4a﹣1）2≤0，所以，，所以函数．（2）由题意，①当时，，，②当时，，λ＝±1，不符合题意，舍去，③当时，，，综上所述，实数．21．【解答】解：（1）因为定义在R上的函数是奇函数，所以f（0）＝0，即＝0，解得a＝1，所以f（x）＝，f（﹣x）＝＝＝﹣f（x），符合题意，故a的值为1．（2）f（x）＝＝＝﹣+，因为2x＞0，所以2x+1＞1，0＜＜1，﹣＜﹣+＜，所以f（x）的值域为（﹣，）．（3）证明：在R上任取x1＜x2，则f（x1）﹣f（x2）＝﹣+﹣（﹣+）＝﹣＝，因为x1＜x2，所以﹣＞0，+1＞0，+1＞0，所以f（x1）﹣f（x2）＞0，即f（x1）＞f（x2），所以f（x）在R上为减函数，因为f（x）为奇函数，所以等价于f（t﹣1）＞﹣f（）＝f（﹣），所以t﹣1＜﹣，解得t＜0，即不等式的解集为（﹣∞，0）．。

高一上数学测试题及答案

高一上数学测试题及答案一、选择题（每题3分，共30分）1. 下列哪个选项是不等式2x - 5 < 0的解集？A. x < 2.5B. x > 2.5C. x < -2.5D. x > -2.5答案：A2. 函数f(x) = 3x^2 - 2x + 5在x = 1处的导数是：A. 4B. 5C. 6D. 7答案：B3. 集合A = {1, 2, 3}，集合B = {2, 3, 4}，A∩B是：A. {1}B. {2, 3}C. {3, 4}D. {1, 2, 3, 4}答案：B4. 直线y = 2x + 1与x轴的交点坐标是：A. (-0.5, 0)B. (0.5, 0)C. (0, 1)D. (1, 0)答案：A5. 圆x^2 + y^2 = 9的半径是：A. 3B. 6C. 9D. 18答案：A6. 函数y = sin(x)的周期是：A. 2πB. πC. 1D. 4π答案：A7. 抛物线y^2 = 4x的焦点坐标是：A. (1, 0)B. (0, 1)C. (2, 0)D. (0, 2)答案：C8. 等差数列{an}的首项a1 = 2，公差d = 3，其第5项a5是：A. 17B. 14C. 13D. 11答案：A9. 已知三角形ABC的三边长分别为a、b、c，且满足a^2 + b^2 = c^2，那么三角形ABC是：A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能确定答案：B10. 函数f(x) = x^3 - 3x^2 + 4在区间(1, 2)上是：A. 单调递增B. 单调递减C. 先增后减D. 先减后增答案：D二、填空题（每题4分，共20分）11. 已知等比数列{bn}的首项b1 = 4，公比q = 2，那么b3 =__________。

答案：1612. 函数f(x) = x^2 - 4x + 3的最小值是 __________。

答案：-113. 圆心在原点，半径为5的圆的标准方程是 __________。

襄阳市普通高中 2022-2023 学年度上学期期末教学质量检测统一测试高一数学(含答案解析)

襄阳市普通高中 2022-2023 学年度上学期期末教学质量检测统一测试高一数学1. 已知全集U =R ，集合A ={x|1≤x ≤2}，B ={−1,1,2,3}，那么阴影部分表示的集合为A. {−1,3}B. {1,2,3}C. {1,3}D. {−1,2,3}2. 命题“∀x >0，x 2−x ≤1”的否定是( ) A. ∀x ≤0，x 2−x ≤1 B. ∀x >0，x 2−x >1 C. ∃x ≤0，x 2−x ≤1D. ∃x >0，x 2−x >13. 下列函数中，值域为(0,+∞)的是 A. f(x)=√x B. f(x)=x +1x (x >0) C. f(x)=√x+1 D. f(x)=1−1x (x >1)4. 已知一个扇形的周长为8，则当该扇形的面积取得最大值时，圆心角大小为A. π6 B. π4 C. 32 D. 25. 下列选项中，是“不等式2x 2−x −m >0在x ∈R 上恒成立”的一个必要不充分条件的是A. m ≤−18B. m <−18C. m <−14D. −18<m <−146. 已知f(x)是定义在R 上的奇函数，且f(x)=−f(x −2)，当x ∈(0,1]时，f(x)=3x −1，则f(log 336)=A. −12 B. −54C. 54 D. 127. 设函数f(x)=2tan(ωx −π3)(ω>0)的图象的一个对称中心为(π6,0)，则f(x)的一个最小正周期是( )A. π3B. π4C. π5D. 2π58. 我们知道二氧化碳是温室性气体，是全球变暖的主要元凶.在室内二氧化碳含量的多少也会对人体健康带来影响.下表是室内二氧化碳浓度与人体生理反应的关系室内二氧化碳浓度不大于0.1%(0.1%即为1000ppm)，所以室内要换气，保持二氧化碳浓度水平不高于标准值.经测定，某中学刚下课时，一个教室内二氧化碳浓度为2000ppm，若开窗通风后二氧化碳浓度y%与经过时间t(单位：分钟)的关系式为y=0.05+λe−t9(λ∈R)，则该教室内的二氧化碳浓度达到国家标准需要开窗通风时间至少约为(参考数据：ln3≈1.099，ln5≈1.609)A. 8分钟B. 9分钟C. 10分钟D. 11分钟9. 已知θ∈(0,π)，sinθ+cosθ=15，则下列结论正确的是A. θ∈(π2,π) B. cosθ=35C. tanθ=−34D. sinθ⋅cosθ=−122510. 已知函数f(x)=log a|x−2|+2(a>0且a≠1)的图象经过定点A，且点A在角θ的终边上，则1tanθ+1sinθ的值可能是( )A. √13+34B. √13+32C. √5+14D. √5+1211. 已知关于x的不等式ax2+bx+c≤0的解集是{x|x≤−2或x≥6}，则下列说法正确的是A. a<0B. 不等式bx+c>0的解集是{x|x<−3}C. 不等式cx2−bx+a<0的解集是{x|−16<x<12}D. a+b+c>012. 已知定义在R上的函数f(x)的图象连续不断，若存在常数λ(λ∈R)，使得f(x+λ)+λf(x)=0对于任意的实数x恒成立，则称f(x)是回旋函数.给出下列四个命题，正确的命题是( )A. 函数f(x)=a(其中a为常数，a≠0)为回旋函数的充要条件是λ=−1B. 函数f(x)=2x+1是回旋函数C. 若函数f(x)=a x(0<a<1)为回旋函数，则λ<0D. 函数f(x)是λ=2的回旋函数，则f(x)在[0,2022]上至少有1011个零点13. 已知tan(π+α)=−2，则sinα−4cosαsinα+cosα=___________.14. 已知幂函数f(x)=x a，指数函数g(x)=a x(a>0，且a≠1)，若f(x)在[12,2]上的最大值为4，则g(f(a+1))=__________.15. 若函数f(x)=x2−6x+2+a在区间(1,4)内有零点，则实数a的取值范围是__________16. 甲、乙两人解关于x的方程2x+b⋅2−x+c=0，甲写错了常数b，得到的根为x=−2或x=log2174，乙写错了常数c，得到的根为x=0或x=1，则原方程所有根的和是__________.17. 已知集合A={x|a−1≤x≤2a+1}，B={x|−2≤x≤4}.在①A∪B=B;②"x∈A”是“x∈B”的充分不必要条件;③A∩B=⌀这三个条件中任选一个，补充到本题第(2)问的横线处，求解下列问题.(1)当a=3时，求∁R(A∩B);(2)若__________，求实数a的取值范围.18. 求下列各式的值：(1)已知a，b是方程x2+6x+3=0的两个实根，求ba +ab的值;(2)化简√823−(log2510)−1+4log23+√4lg22−4lg2+1，并求值.19. 随着我国经济发展，医疗消费需求增长，人们健康观念转变以及人口老龄化进程加快等因素的影响，医疗器械市场近年来一直保持了持续增长的趋势，某医疗公司为了进一步增加市场竞争力，计划改进技术生产某产品.已知生产该产品的年固定成本为300万元，最大产能为80台.每生产x台，需另投入成本G(x)万元，且G(x)={2x2+80x,0<x≤40201x+3600x−2020,40<x≤80，由市场调研知，该产品每台的售价为200万元，且全年内生产的该产品当年能全部销售完.(1)写出年利润W(x)万元关于年产量x台的函数解析式(利润=销售收入一成本);(2)当该产品的年产量为多少台时?公司所获利润最大，最大利润是多少?20. 已知二次函数f(x)=ax2+bx+c(a,b,c∈R)，f(0)=14，f(1)=1，且对任意的x∈R，都有f(x−2)=f(−x)成立.(1)求二次函数f(x)的解析式;(2)若函数g(x)=4f(x)−x+|x−λ|的最小值为2，求实数λ的值.21. 设函数f(x)=ka x−a−x(a>0且a≠1，k∈R)，若f(x)是定义在R上的奇函数且f(1)= 32.(1)求k和a的值;(2)判断其单调性(无需证明)，并求关于t的不等式f(2t+3)<f(t2−5)成立时，实数t的取值范围;(3)函数g(x)=a2x+a−2x−6f(x)，x∈[1,2]，求g(x)的值域.22. 函数f(x)=Asin(ωx+φ)(其中A>0，ω>0，|φ|<π2)的部分图象如图所示，把函数f(−x)的图象向右平移π4个单位，得到函数g(x)的图象.(1)当x∈R时，求函数g(x)的单调递减区间;(2)对于∀x1∈[−π12,π3]，是否总存在唯一的实数x2∈[π6,34π]，使得f(x1)+g(x2)=m成立?若存在，求出实数m的值或取值范围;若不存在，说明理由.答案和解析1.【答案】A【解析】【分析】本题考查Venn图，属于基础题.【解答】解：由图知，阴影部分表示(∁U A)∩B={−1,3).2.【答案】D【解析】【分析】本题考查命题的否定，属于基础题.【解答】解：命题“∀x>0，x2−x≤1”的否定是∃x>0，x2−x>1.3.【答案】C【解析】【分析】本题主要考查函数的值域的求法，属于基础题。

中职数学三角函数单元测试题

中职数学三角函数单元测试题高一年级数学注意事项：1.本试卷共4页，满分共100分，考试时间为90分钟； 2.请将答案填写到答题卡上. 一、选择题（4×10=40分）1. 若角α的终边过点)34(-，P ，则αcos 的值为（）4.A 3.B - 54.C 53.D -2. 已知角α的终边上一点)43(，-P ，那么=+ααcos sin （）51.A - 51.B 257.C - 257.D3. 若角α的终边过点)30cos 30(sin ︒-︒，，则αsin 等于（）21.A 21.B - 23.C - 33.D - 4. 若角α的终边上一点)43(--，P ，则=-)2cos(a π（）2524.A -257.B - 257.C 2524.D 5. 若0cos sin >⋅αα，则角α所在的象限为（）第一或第三象限角.A . 第一或第四象限角.B 第二或第三象限角.C 第二或第四象限角.D6. 求。

15sin -15cos 22的值（）21.A 21.B23.C 33.D - 7. 已知0tan cos >⋅θθ，那么角θ是（）0cos 0sin .A <>θθ且0cos sin .B <⋅θθ0tan 0cos .C >>θθ且0tan cos .D >⋅θθ8. )619sin(π-的值等于（） 21.A 21.B - 23.C 23.D - 9. ︒+︒240tan 600sin 的值等于（）23.A -23.B 321.C +- 321.D + 10. 设)20(33tan παα<<=，，则α等于（） 6.A π676.B ππ或3.C π 343.D ππ或二、填空题（4×5=20分）11.已知α是第二象限角，则|sin |sin cos |cos |αααα+的值是__________.11. 若54sin -=θ，0tan >θ，则=θcos _________.13. 若=∈-=θππαα2tan )23(53cos ，则，，且__________.14. ____20s 80sin 20cos 80cos 。

高一数学周测试卷

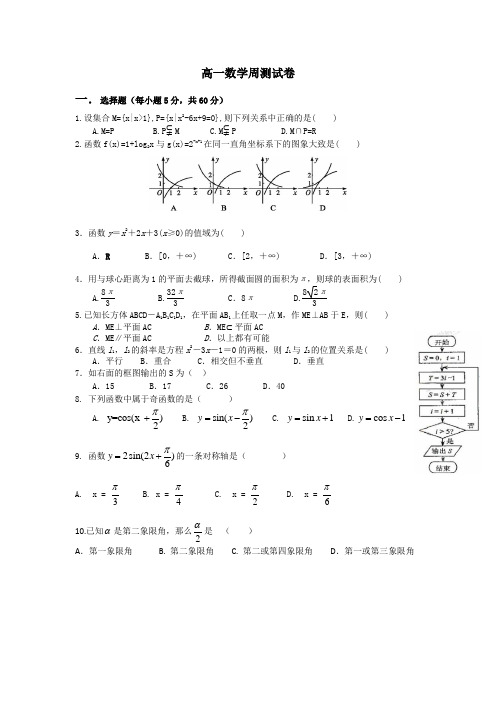
高一数学周测试卷一．选择题（每小题5分，共60分）1.设集合M={x|x>1},P={x|x 2-6x+9=0},则下列关系中正确的是( )A.M=PB.P ⫋MC.M ⫋PD.M ∩P=R2.函数f(x)=1+log 2x 与g(x)=2-x+1在同一直角坐标系下的图象大致是( )3．函数y ＝x 2＋2x ＋3(x ≥0)的值域为( )A ．RB ．[0，＋∞)C ．[2，＋∞)D ．[3，＋∞) 4．用与球心距离为1的平面去截球，所得截面圆的面积为π，则球的表面积为( ) A.8π3 B.32π3 C ．8π D.82π35.已知长方体ABCD －A 1B 1C 1D 1，在平面AB 1上任取一点M ，作ME ⊥AB 于E ，则( ) A ．ME ⊥平面AC B ．ME ⊂平面ACC ．ME ∥平面ACD ．以上都有可能6．直线l 1，l 2的斜率是方程x 2－3x －1＝0的两根，则l 1与l 2的位置关系是( )A ．平行B ．重合C ．相交但不垂直D ．垂直7．如右面的框图输出的S 为（）A ．15B ．17C ．26D ．408. 下列函数中属于奇函数的是（）A. y=cos(x )2π+B. sin()2y x π=- C. sin 1y x =+ D.cos 1y x =- 9. 函数2sin(2)6y x π=+的一条对称轴是（）A. x = 3πB. x = 4πC. x = 2πD. x = 6π 10.已知α是第二象限角，那么2α是（） A ．第一象限角 B. 第二象限角 C. 第二或第四象限角 D ．第一或第三象限角11.设()f x 是定义域为R ，最小正周期为32π的函数，若cos ,(0)(),2sin ,(0)x x f x x x ππ⎧-≤<⎪=⎨⎪≤<⎩则15()4f π-等于（）A.2 B. 1 C. 0 D.2- 12.右图是函数2|)(|x sin(2y π<φφ+ω=的图象，那么（）（A ）6,1110π=φ=ω （B ）6,1110π-=φ=ω （C ）6,2π=φ=ω （D ）6,2π-=φ=ω二、填空题（每题5分，共20分） 13．已知定点A(－1，3)，B(4，2)，以A 、B 为直径作圆，与x 轴有交点C ，则交点C 的坐标是________．14．在长为12cm 的线段AB 上任取一点C ，现作一矩形，使邻边长分别等于线段AC 、CB 的长，则该矩形面积大于20cm 2的概率为__________．15. 函数1y tan 34x π⎛⎫=- ⎪⎝⎭的定义域为 16.已知0tan ,0sin ><θθ，那么θ是第象限角。

2024-2025学年上海华二普陀高一上学期数学周测试卷及答案(2024.09)

1华二普陀2024学年第一学期高一年级数学月周测2024.09一、填空题（本大题共有12题,满分36分） 1.不等式13x x+≤的解集为______. 2.已知D 为一个非空数集，语句“任意的3,10x D x ∈+>”的否定形式是______. 3.设全集{}22,4,5U m m =+−，集合{}2,1A m =−，若{}1A =，则实数m =______. 4.已知:2 x α≠或3y ≠，:5 x y β+≠，则α是β的______条件. 5.不等式()()()343120x x x x ++++≥的解集为______.6.已知关于x 的不等式2243x x a a −+≥−在[]1,4x ∈上有解，则实数a 的取值范围是______.7.已知关于x 的不等式260mx x m−≥−的解集为A ，若2A ∉，则实数m 的取值范围是______.8.2024届欧洲杯以西班牙夺冠圆满结束，小明统计了其所在班级50名同学中支持德国，西班牙，英格兰的人数，每人都至少支持其中一个队伍，有15人这三支队伍都支持，18人不支持德国，20人不支持西班牙，16人不支持英格兰，则仅支持两支队伍的同学的人数为______.9.若关于x 的不等式22820046x x mx mx m −+≤++−的解集为R ，则实数m 的取值范围是______. 10.已知集合{}2280A x x x =+−≥，{}2240B x x ax =−+≤，若0a >，且A B 中恰有2个整数元素，则实数a 的取值范围为______.11.用A 表示非空集合A 中元素的个数，定义,,A B A B A B B A B A ⎧−≥⎪*=⎨−>⎪⎩，若{}0,1A =，()(){}2230B x x axxax =+++=，1A B *=，则实数a 的所有可能取值构成集合S ，则S =______.（请用列举法表示）212.若集合{}1,2,3,,10A =⋯，集合B A ⊆，且B ≠∅，记()W B 为B 中元素的最大值与最小值之和，则对所有的B ，()W B 的平均值是______. 二、选择题(本大题共有4题,满分12分,每题3分)13.设a 、b 是非零实数，若a b <，则下列不等式成立的是（） A.22a b <B.22ab a b <C.2211ab a b<D.b a a b< 14.已知二次函数()()20f x x x a a =++>，若()0f m <，则()1f m +的值是（） A.正数B.负数C.零D.符号与m 有关15.对于集合A 、B ，定义集合运算{}A B x x A x B −=∈∉且，给出下列三个结论：（1）()()A B B A −−=∅；（2）()()()()A B B A A B A B −−=−；（3）若A B =，则A B −=∅；则其中所有正确结论的序号是（） A.（1）（2）B.（1）（3）C.（2）（3）D.（1）（2）（3）16.设全集{}1,2,3,4,5,6,7,8,9,10U =，给出条件：①A U ⊆；②若x A ∈，则2x A ∉；③若x A ∈，则2x A ∉.那么同时满足三个条件的集合A 的个数为（） A.0个B.16个C.32个D.64个三、解答题（本大题满分52分）． 17.（本题满分6分）解关于x 的不等式：221ax x +≥+.318．（本题满分8分，第1小题满分4分，第2小题满分4分）已知{}240A x x x =+=，(){}222110B x x a x a =+++−=. （1）若A 是B 的子集，求实数a 的值；（2）若B 是A 的子集，求实数a 的取值范围.19．（本题满分8分，第1小题满分4分，第2小题满分4分）（1）对任意的x R ∈，使得()()221230x k x k k −++−−>成立，求实数k 的取值范围；（2）对任意的[]1,2x ∈−，使得()()221230x t x t t −++−−<成立，求实数t 的取值范围；20．（本题满分12分，第1小题满分6分，第2小题满分6分）已知一元二次方程()()22330k x mx k n −++−=，其中k 、m 、n 均为实数. （1）若方程有两个整数根，且k 为整数，2k m =+，1n =，求方程的整数根；（2）若方程有两个实数根1x 、2x ，满足()()()()112212x x k x x k x k x k −+−=−−，且k 为最大的负整数，试判断2m ≤是否成立？请说明理由.421．（本题满分18分，第1小题满分5分，第2小题满分6分，第3小题满分7分）对于四个正数x ，y ，z ，w ，如果xw yz <，那么称(),x y 是(),z w 的“下位序列”. （1）对于2，7，3，11，试问()2,7是否为()3,11的“下位序列”；（2）设a ，b ，c ，d 均为正数，且(),a b 是(),c d 的“下位序列”，试判断,,c a a c d b b d++之间的大小关系；（3）设正整数n 满足条件：对集合()0,2022内的每个正整数m ，总存在正整数k ，使得(),2022m 是(),k n 的“下位序列”，且(),k n 是()12023m ,+的“下位序列”，求正整数n 的最小值.5参考答案一、填空题1.1|02x x x ⎧⎫≥<⎨⎬⎩⎭或; 2.存在3,10x D x ∈+≤; 3.3−; 4.必要不充分;5.{}|432x x x x −≤≤−≥=−或-1或;6.[]1,4−;7.(][),34,−∞⋃+∞;8.16人;9.()2,0−; 10.135,62⎡⎫⎪⎢⎣⎭；11.{− 12.1111.用A 表示非空集合A 中元素的个数，定义,,A B A BA B B A B A ⎧−≥⎪*=⎨−>⎪⎩，若{}0,1A =，()(){}2230B x x axxax =+++=，1A B *=，则实数a 的所有可能取值构成集合S ，则S =______.（请用列举法表示）【答案】{−【解析】根据题意,{}01A ,=,则有2A =,又因为()(){}22|30B x x ax x ax =+++=, 即得B 表示方程()()2230x axxax +++=实数根的个数，解这个方程得(1)20x ax +=，或(2)230x ax ++=解方程(1)得120,x x a ==−，解方程(2)得,若2120a −>,即a >或a <−时,方程有两个不等实根分别为34x x ==若2120a −=,即a =−a =,方程有且只有一个实根；若2120a −<,即a −<时,方程没有实数根.综上可得,当a >或a <−,4B =当a =−a =,3B =；当0a =时,1B =所以(1)当A B …时,*1A B A B =−=，即得1B =，此时可得0a =； (2)当A B <时,即得3B =,此时可得a =−a =;故答案为:{0,−.6二、选择题13.C 14.A 15.D 16.C15.对于集合A 、B ，定义集合运算{}A B x x A x B −=∈∉且，给出下列三个结论：（1）()()A B B A −−=∅；（2）()()()()A B B A A B A B −−=−；（3）若A B =，则A B −=∅；则其中所有正确结论的序号是（） A.（1）（2） B.（1）（3）C.（2）（3）D.（1）（2）（3）【答案】D【解析】对于结论(1),{}|,A B x x A x B −=∈∉且是Venn 图中的第1部分{}|,B A x x A x B −=∉∈且是Venn 图中的第3部分,()()A B B A ∴−⋂−=∅,故正确; 对于结论(2)()(),A B B A −⋃−是Venn 图中的第1、3部分,()()A B A B ⋃−⋂也是Venn 图中的第1、3部分，()()()()A B B A A B A B ∴−⋃−=⋃−⋂,故正确；对于结论(3),若A B =,则{|A B x x A −=∈且}x A ∉=∅,故正确;故选:D .16.设全集{}1,2,3,4,5,6,7,8,9,10U =，给出条件：①A U ⊆；②若x A ∈，则2x A ∉；③若x A ∈，则2x A ∉.那么同时满足三个条件的集合A 的个数为（） A.0个 B.16个C.32个D.64个【答案】C【解析】由题意可知,若1A ∈,则2,4,8A A A ∈∈∈;若1A ∈,则2,4,8A A A ∈∈∈. 此时,1,2,4,8的放置有2种;若3A ∈,则6A ∈;若3A ∈,则6A ∈,此时3,6的放置有2种;7若5A ∈,则10A ∈;若5A ∈,则10A ∈,此时,5,10的放置有2种. 7、9的放置没有限制,各有2种.综上所述,满足条件的集合A 的个数为5232=.故选:C. 三．解答题17.当2a =时,原不等式的解集为{|x x R ∈且1}x ≠−；当2a >时,原不等式的解集为{|0x x …或1}x <−; 当2a <时,原不等式的解集为{|10}x x −<…. 18.（1）1a =（2）1a a ≤−或=119.（1）1313k k <−>或（2）122⎛+− ⎝⎭20．（本题满分12分，第1小题满分6分，第2小题满分6分）已知一元二次方程()()22330k x mx k n −++−=，其中k 、m 、n 均为实数. （1）若方程有两个整数根，且k 为整数，2k m =+，1n =，求方程的整数根；（2）若方程有两个实数根1x 、2x ，满足()()()()112212x x k x x k x k x k −+−=−−，且k 为最大的负整数，试判断2m ≤是否成立？请说明理由. 【答案】（1）方程的整数根为0,1,2,3。

2023-2024学年深圳市实验学校光明部高一第一次周测数学试题及答案

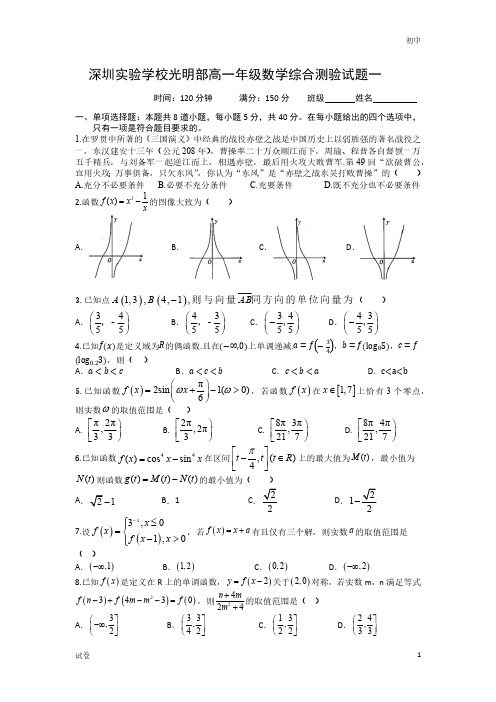
深圳实验学校光明部高一年级数学综合测验试题一时间：120分钟满分：150分班级姓名一、单项选择题：本题共8道小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.在罗贯中所著的《三国演义》中经典的战役赤壁之战是中国历史上以弱胜强的著名战役之一，东汉建安十三年（公元208年），曹操率二十万众顺江而下，周瑜、程普各自督领一万五千精兵，与刘备军一起逆江而上，相遇赤壁，最后用火攻大败曹军.第49回“欲破曹公，宜用火攻；万事俱备，只欠东风”，你认为“东风”是“赤壁之战东吴打败曹操”的（）A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件2.函数31()f x x x=-的图像大致为（）A ．B ．C ．D ．3.已知点()()1,3,4,1,A B AB -则与向量同方向的单位向量为（）A ．3455⎛⎫ ⎪⎝⎭，-B ．4355⎛⎫ ⎪⎝⎭-C ．3455⎛⎫- ⎪⎝⎭，D ．4355⎛⎫- ⎪⎝⎭，4.已知f (x )是定义域为R 的偶函数.且在(−∞,0)上单调递减.a =f −b =f (log 85)，c =f(log 0.23)，则（）A ．a <b <cB ．a <c <bC ．c <b <aD ．c<a<b5.已知函数()π2sin 1(0)6f x x ωω⎛⎫=+-> ⎪⎝⎭，若函数()f x 在[]1,7x ∈上恰有3个零点，则实数ω的取值范围是（）A. π2π,33⎡⎫⎪⎢⎣⎭B. 2π,2π3⎡⎫⎪⎢⎣⎭C. 8π3π,217⎡⎫⎪⎢⎣⎭D. 8π4π,217⎡⎫⎪⎢⎣⎭6.已知函数44()cos sin f x x x =-在区间,()4t t t R π⎡⎤-∈⎢⎥⎣⎦上的最大值为()M t ，最小值为()N t 则函数()()()g t M t N t =-的最小值为（）A 1-B ．1C D ．1-7.设()()3,01,0x x f x f x x -⎧≤⎪=⎨->⎪⎩，若()f x x a =+有且仅有三个解，则实数a 的取值范围是（）A ．(),1-∞B ．()1,2C ．()0,2D ．(),2-∞8.已知()f x 是定义在R 上的单调函数，()2y f x =-关于()2,0对称，若实数m ，n 满足等式()()()23430f n f m m f -+--=，则2424n mm ++的取值范围是（）A ．3,2⎛⎤-∞ ⎥⎝⎦ B ．33,42⎛⎤ ⎥⎝⎦ C ．13,22⎛⎤ ⎥⎝⎦ D ．24,33⎛⎤⎥⎝⎦二、多项选择题：本题共3小题，每小题6分，共18分。

湖北鄂东南省级示范高中教育教学改革联盟学校2024-2025学年高一上学期起点考试数学试题(含解析)

2024年秋季鄂东南省级示范高中教育教学改革联盟学校起点考试高一数学试题考试时间：2024年10月14日上午8：00—10：00 试卷满分：150分一､选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合，则（）A.B.C.D.2.命题“”的否定为（）A. B.C. D.3.已知集合，则集合A 的所有非空子集的个数为（）A.5个B.6个C.7个D.8个4.下列各组函数表示相同函数的是（）A. B.C. D.5.设，则“”是“”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.已知，则正确的结论是（）A. B.C.D.与的大小不确定7.已知关于的不等式的解集为，则关于的不等式的解集为（）A. B.，或C. D.{1,0,1,2,3},{12}A B xx =-=-<≤∣A B ⋂={1,0}-{1,0,1}-{0,1}{0,1,2}2[1,3],320x x x ∀∈--+≤2000[1,3],320x x x ∃∈--+≥2[1,3],320x x x ∃∈--+>2[1,3],320x x x ∀∈--+≥2000[1,3],320x x x ∃∉--+≥86A x x ⎧⎫⎨⎬⎩⎭=∈∈-N N ()1,()|1|f x x g x x =+=+0()1,()f x g x x ==2()()f m g n ==32(),()1x xf xg x xx +==+x ∈R |32|3x -≤(2)0x x -≤1,c a b >==a b <a b>a b =a b x 20ax bx c ++>{23}xx <<∣x 20bx ax c ++<615x x ⎧⎫-<<⎨⎬⎩⎭{1x x <-∣6}5x >213x x ⎧⎫-<<⎨⎬⎩⎭213x x x ⎧⎫<->⎨⎬⎩⎭，或8.若正实数满足，不等式有解，则的取值范围是（）A. B.C. D.二､多选题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.9.图中阴影部分用集合符号可以表示为（）A. B.C. D.10.若，且，则下列说法正确的是（）A.有最大值有最大值2C.有最小值5 D.11.下列命题正确的有（）A.若方程有两个根，一个大于1另一个小于1，则实数的取值范围为B.设，若且，则C.设，命题是命题的充分不必要条件D.若集合和至少有一个集合不是空集，则实数的取值范围是或三､填空题：本题共3小题，每小题5分，共15分.12.已知函数的定义域为，则函数的定义域为______.,x y 24x y +=212131m m x y +>++m 4,13⎛⎫-⎪⎝⎭4,(1,)3⎛⎫-∞-⋃+∞ ⎪⎝⎭41,3⎛⎫- ⎪⎝⎭4(,1),3⎛⎫-∞-⋃+∞ ⎪⎝⎭()U ()B A C ⋂⋃ðU (()())A B B C ⋂⋃⋂ð()()U A C B⋃⋂ð()()()()U UA BC B ⋂⋃⋂ðð0,0a b >>41a b +=ab 1161a a b +2216a b +2210ax x -+=a (0,1),a b ∈R 12a b -……24a b +……54210a b -……,a b ∈R :p a b >:||||q a a b b >{}{}2220,220,A xx x a B x x ax A =+-==++=∣∣B a a (1)a -…()y f x =[3,2]-(21)1f x y x +=+13.已知为二次函数，满足，则函数______.14.设集合，函数，已知，且，则的取值范围为______.四､解答题：本题共5小题，共77分.解答应写出文字说明､证明过程或演算步骤.15.（13分）已知集合.（1）若，求；（2）若，求实数的取值范围.16.（15分）设命题：对任意，不等式恒成立，命题：存在使得不等式成立.（1）若为真命题，求实数的取值范围；（2）若命题与命题一真一假，求实数的取值范围.17.（15分）已知关于的不等式.（1）若不等式的解集为或，求的值；（2）求关于的不等式的解集.18.（17分）某公司销售甲､乙两种产品，根据市场调查和预测，甲产品的利润（万元）与投资额（万元）成正比，其关系如图（1）所示；乙产品的利润（万元）与投资额（万元）的算术平方根成正比，其关系式如图（2）所示，（1）分别将甲､乙两种产品的利润表示为投资额的函数；（2）若该公司投资万元资金，并全部用于甲､乙两种产品的营销，问：怎样分配这万元投资，才能使公司获得最大利润？其最大利润为多少？19.（17分）设，其中，记.（1）若，求的值域；()f x 2()(1)2f x f x x ++=()f x =[0,1),[1,3]M N ==21,()63,x x Mf x x x N+∈⎧=⎨-∈⎩a M ∈(())f f a M ∈a {68},{123}A xx B x m x m =-<=++∣∣………1m =()A B ⋂R ðA B A ⋃=m p [0,1]x ∈2234x m m --…q [1,1]x ∈-2210x x m -+-…p m p q m x 31,1ax x a x +->∈-R {1xx <∣2}x >a x y x y x (0)a a >a 22()21,()41f x x tx g x x tx =-+=-++0t >()min{(),()}F x f x g x =1t =()F x（2）若，记函数对任意，总存在，使得成立，求实数的取值范围；（3）若，求实数的取值范围.2024年秋季鄂东南省级示范高中教育教学改革联盟学校起点考试高一数学参考答案0t >2()()1h x f x tx t =+-+1,x t t ⎡⎤∈⎢⎥⎣⎦1,22m t t⎡⎤∈⎢⎥⎣⎦()h x m =t 13[0,3],()22x F x ∀∈-≤t一､选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.【答案】D【详解】因为，所以.故选：D.2.【答案】B【详解】由全称命题的否定为特称命题知：原命题的否定为：故选：B 3.【答案】C 【详解】由题设，，即8可被整除且，故集合A 的所有非空子集的个数为4.【答案】D【解答】解：与的对应关系不同，不是同一函数：定义域不同，不是同一函数：，而的定义域为，不是同一函数：与的定义域都为，对应关系相同，是同一函数.故途：D.5.【答案】D【解答】根据题意，不等式，则，即，解集为不等式，即，解集为，因为且，所以“”是“”的既不充分也不必要条件，故选：D.6.【解新】方法一：特值法取特殊值，令，则易知，排除B ，C ，还不能排除D ，猜测选A.方法二：作差法，分析法{1,0,1,2,3),{12}A Bxx =-=-<≤∣{}0,1,2A B ⋂=2000[1,3],320x x x ∃∈--+>86x∈-N 6x -60,x x ->∈N {2,4,5},A ∴=3217-=()1f x x =+()1g x x =+0()1,()f x g x x ==()f m =R 2()g n =[0,)∞+32()1x xf x x +=+()g x x =R 323x -...3323x -- (15)33x -≤≤15,33⎤-⎥⎦()20x x -…02x ……[]0,2[]15,0,233-⊂[]150,2,33⎤⊄-⎥⎦324x -…()20x x -…2c =1a b ==-a b <要比较比较与的大小（遇到二次根式可考虑平方去掉恨号）比较的大小与的大小..，故.故选：A.方法三：有理化法，故选A.7.【答案】A【解答】因为不等式的解集为，所以2和3是方程的两个实数解，且；由根和系数的关系知，所以；所以不等式可化为，叫，解得，所求不等式的解集为故选：A.8.【答栥】B 【详解】由a b -=-=-,a b +⇔24c ⇔2c +4c ⇔c c <<a b <====1100.c c ∴+>->⇒>⇒>>1.c ∀><a b <20ax bx c ++>{23}xx <<∣20ax bx c ++=0a <2323b ac a ⎧+=-⎪⎪⎨⎪⨯=⎪⎩5,6b a c a =-=20bx ax c ++<2560ax ax a -++<2560x x --<615x -<<615x x ⎧⎫-<<⎨⎬⎩⎭，仅当，即时等号成立.要使不等式有解，只需.所以.故选：B二､多选题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.9.【答案】AD【解答】解：图中阴影部分用集合符号可以表示为或.故选：AD.10.【答案】AC【解答】解：对于A ，，当且仅当且，当时取等号，不以有最大值故A 正确，对于B.因为.，当且仅当时取等号，，故B 错误对于C ，，当且仅当且叫且，即时取等号，所以有最小值5，故C 正确()()412112111421441616163y x x y x y x y x y ⎡⎡⎤+⎛⎫⎡⎤⎢+=+++=⨯++≥⨯+=⎢⎥ ⎪⎣⎦+++⎢⎝⎭⎣⎦⎣()411y x xy +=+13,2x y ==212131m m x y +>++()()221434341033m m m m m m +>⇒+-=+->()4,1,3m ∞∞⎛⎫∈--⋃+ ⎪⎝⎭()()U B A C ⋂⋃ð()()()()U UA B C B ⋂⋃⋂ðð211(4)1444416a b ab ab +=⨯≤⨯=4a b =41a b +=11,82b a ==ab 1,1624442a b a b a b +=++≤+++=+≤142a b ==+144115a a b a b a a b a b a b ++=+=++≥+=4b a a b =41,a b +=2a b =41a b +=11,36a b ==1aa b+对于D.因为.所以，所以，当且仅当且，即时取等号，所以有最小值，故错误.故选：AC 11.【答案】ABD 【解答】选项A ：函数有两个两点，，而且一个大于1另一个小于1.则或，解得.实数的取值范围为，故A 正确；选项B ：令，则.由解得所以.因为，所以，则.故B 正确；选项C ：若既有；若显然有；若，则，而，所以，故可以推出若，当时，如果，不等式显然成立，此时有如果，则有，因而当时，，此时有.因而，敬可以推出，综合知是的充要条件221624a b ab +⨯…()222222161624(4)a b a b ab a b +++⨯=+ (22)2(4)11622a b a b ++≥=4a b =41a b +=11,82b a ==2216a b +12D ()()221f x x x x α=-+∈R 0a ∴≠()01210a f a >⎧⎨=-+<⎩()01210a f a <⎧⎨=-+>⎩01a <<∴a ()0,1,a b u a b v +=-=24,12u v …………a b u a b v +=⎧⎨-=⎩22u v a u v b +⎧=⎪⎪⎨-⎪=⎪⎩424222322u v u v a b u v u v u v +--=⋅-⋅=+-+=+24,336u v ............5310u v +......54210a b - (22)0,a b a b >≥>a a b b >0,a b ≥>0a a b b >>0a b >>22a b <22,a a a b b b =-=-a a b b >a b >||||a ab b >a a b b >0b <0a ≥1a b >0a <22a b ->-1a b >0b ≥0a >22a b >a b >a a b b >a b >p q故C 不正确；选项D ：假设两个方程无实根（即均是空集），则有.所以当或时，两个方程至少有一个方程有实根，即两个集合至少有一个不是空集.故填或，故D 正确三､填空题：本题共3小题，每小题5分，共15分.12.【答案】【详解】由题意得：，解得：，由，解得：，故函数的定义域是.13.【答案】【解答】解：设，满足，所以，解得则函数.14.【答案】【解答】解：因为.所以，则，由，可得，解得.,A B 1221Δ440Δ480a a a a ⎧<-⎧=+<⎪⎪⇒⎨⎨=-<<<⎪⎪⎩⎩1a <<-a ≤1a -…a ≤1a ≥-[)12,11,2⎛⎤--⋃- ⎥⎝⎦3212x -≤+≤122x -≤≤10+≠x 1≠-x [)12,11,2⎛⎤--⋃- ⎥⎝⎦()2f x x x=-()2f x ax bx c =++()()212f x f x x ++=()()()2221(1)12f x f x ax bx c a x b x c x ++=+++++++=2212201200a a ab b a bc c ⎧==⎧⎪⎪+=⇒=-⎨⎨⎪⎪++==⎩⎩()2f x x x =-11,32⎛⎤ ⎥⎝⎦a M ∈()[)211,3f a a =+∈()()()632136f f a a a =-+=-()()ff a M ∈0361a -< (1132)a <≤故答案为：.四､解答题：本题共5小题，共77分.解答应写出文字说明､证明过程或演算步骤.15.（13分）【解答】解：（1）时，，则或，则或（2），等价于，当，则，船得，符合题意当.则，解得.综上，实数的取值范围为16.（15分）【解析】（1）因为为真命题，所以对任意不等式恒成立，所以其中，所以，解得，有以的取值范围，（2）若为真命题，即存在.使得不等式成立，则，其中，1]，而，所以，故：因为一真一假.所以为真命题，为假命题或为假命题，为真命题，若为真命题，为假命题，则，所以；若为假命题，为真命题.则或，所以.综上，或，所以的取值范围为.17.（15分）【解答】解：（1）不等式可化为，原不等式的解集为或.故；11,32⎛⎤ ⎥⎝⎦1m ={25}B xx =<∣…{2R B x x =<∣ð5}x >(){62A A B xx ⋂=-<<∣ð58}x <…A B A ⋃=B A ⊆B =∅123m m +>+2m <-B ≠∅12316238m m m m +≤+⎧⎪+>-⎨⎪+≤⎩522m -≤≤m 5,2∞⎛⎤- ⎥⎝⎦p [0,1],x ∈2234x m m -- (2)min (23)4x m m -≥-[]0,1x ∈234m m --…13m ……m []1,3q []1,1x ∈-2210x x m -+-…()2min210x x m -+-…[1x ∈-()2min212x x m m -+-=-+20m -+…2m ….p q p q p q p q 132m m ≤≤⎧⎨>⎩23m <≤p q 12m m <⎧⎨≤⎩32m m >⎧⎨≤⎩1m <1m <23m <…m ()(],12,3∞-⋃ 311ax x x +->-()()210ax x -->{1xx <∣2}x >1a =（2）①当时，不等式为，解得：②当时，方程的两根分别为，（i ）当时，，故不等式的解为：（ii ）当时，若，即时，不等式的解为或.若，即时，不等式的解为；考，即时，不等式得解为或.综上可知，当时，不等式的解集为；当时，不等式的解集为当时，不等式的解集为或；当时，不等式的解集为，当时，不等式的解集为或.18.（17分）【解答】解：（1）由题知，甲产品的利润函数为乙产品的利润函数为.由题知，函数经过d 点，有，所以.函数经过点，有由，所以.（2）设乙产品的投资金额为万元，则甲产的投资金额为万元.所获得总利润为万元，则，0a =220x -+>1x <0a ≠()2220ax a x -++=21,a0a <21a <21x a<<0a >21a >02a <<1x <2x a >21a=2a =1x ≠21a <2a >2x a <1x >0a <21x x a ⎧⎫<<⎨⎬⎩⎭0a ={}|1x x <02a <<{1xx <∣2}x a >2a ={}1x x ≠∣2a >{1xx >∣2}x a <()(0)f x kx x =…())0g x x =>()f x ()1.8,0.4510.45 1.8,4k k ==()()104f x x x =…()g x ()9,3.75 3.75=54k =())0g x x =…(0)x x a <…()a x -y ()1,(0)4y a x x a =+-<…令，则，函数图象开口问上，对称轴为，所以当时，函数在上单调递增，当，即时，.时，函数在上递增，在上递减，当，即时，有最大值.综上得：时，乙产品投资万元，甲产品投资万元，该公司可获得最大利润，最大利润为万元.时，乙产品投资万元：时，乙产品投资万元，印产品投资万元，该公司可获得最大利润，最大利润为万元19.【解答】（1），即作图可知，函数的最大值为值域为.（2）由题意，只需在上的值域为的子集即可，因为，所以，对称轴为，由得，t =2x t =()2251151.44444y t a t t t a =+-=-++5541224t =-=-⨯502<⎡⎣t =x a =y 52>50,2⎡⎤⎢⎥⎣⎦52⎛ ⎝52t =254x =y 42516a +52>254254a ⎛⎫- ⎪⎝⎭42516a +52a 52>254254a ⎛⎫- ⎪⎝⎭42516a +()()2221,41f x x x g x x x =-+=-++ ()()()22623,f xg x x x x x ∴-=-=-()()(),03,,3,f x x F x g x x ⎧≤≤⎪∴=⎨>⎪⎩()[]()()2221,0,3,41,,03,.x x x F x x x x ∞∞⎧-+∈⎪=⎨-++∈-⋃+⎪⎩()F x ()()3 4.F F x =(],4∞-()h x 1,x t t ⎡⎤∈⎢⎥⎣⎦1,22t t⎡⎤⎢⎥⎣⎦0t >()2222324t h x x tx t x t ⎛⎫=-+=-+ ⎪⎝⎭2t x =1,x t t ⎡⎤∈⎢⎥⎣⎦1t >①当，即在的图象可知，，由题意得由（时取等号.放第一个式子成立，由第二个式子得故此时②当，即时，在递减，在上递增.此时最小值为，最大值为，所以，综上，所求的范围为.（3）.①当时，无解，②当时，解得.12t t ≤1t <≤()h x 1,t t ⎡⎤⎢⎥⎣⎦2221()1,h x r t t ⎡⎤∈+-⎢⎥⎣⎦22211122t t t t t⎧≤+-⎪⎨⎪≥⎩221111t t +-≥=1t =02t <…1t <≤12t t >1>()h x 1,2t t ⎡⎫⎪⎢⎣⎭,2t t ⎡⎤⎢⎥⎣⎦2324t t h ⎛⎫= ⎪⎝⎭2()h t t =2231422t t t t ⎧≥⎪⎨⎪≤⎩2t ≤≤2t <≤t (1,2]()()131222F x F x -≤⇔-≤≤()()()22623,f xg x x tx x x t -=-=- ∴01t <≤()()[]()(]()()()1,,0,3,32,,3,3.31,f t f x x t F x f t g x x t g ⎧⎧≥-∈⎪⎪=∴≤⎨⎨∈⎪⎪≥-⎩⎩13t <<()()[]()()1,,0,3,32,f t F x f x x f ⎧≥-⎪=∈∴⎨≤⎪⎩43t ≤≤③当时，，解得，舍去.综上，3t ≥()()[](),0,3,31F x f x x f =∈∴≥-116t ≤413≤≤。

2024-2025学年湖北省孝感市孝感高级中学高一(上)开学数学试卷(含答案)

2024-2025学年湖北省孝感高级中学高一（上）开学数学试卷一、单选题：本题共8小题，每小题5分，共40分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.命题“∃x∈R，使得x2−3=2”的否定为( )A. ∀x∉R，x2−3≠2B. ∃x∈R，x2−3≠2C. ∃x∉R，x2−3=2D. ∀x∈R，x2−3≠22.已知集合A={x|x−3x+4<0}，B={x|x∈Z,86−x∈N}，则A∩B=( )A. {−2}B. {−2,2}C. {−2,2,4}D. {−2,2,4,5}3.下列命题为真命题的是( )A. 若a2>b2，则a>bB. 若a>b，c>d，则a−c>b−dC. 若a>b>0，c>d，则da <cbD. 若0<a<b<c，则ac−a<bc−b4.中国宋代的数学家秦九韶曾提出“三斜求积术”，即假设在平面内有一个三角形，边长分别为a，b，c，三角形的面积s可由公式s=p(p−a)(p−b)(p−c)求得，其中p为三角形周长的一半，这个公式也被称为海伦一秦九韶公式.现有一个三角形的边长满足a+c=10，b=6，则此三角形面积的最大值为( )A. 10B. 82C. 12D. 935.命题“∃x∈[−1,1]，x2−2x−a>0”为假命题的一个充分不必要条件是( )A. a>2B. a>3C. a≥3D. a≤26.为了丰富学生的课余生活，某校开设了篮球社团、话剧社团、志愿者协会，高一某班学生共有28人参加了学校社团，其中有15人参加篮球社团，有8人参加话剧社团，有14人参加志愿者协会，同时参加篮球社团和话剧社团的有3人，同时参加篮球社团和志愿者协会的有3人，同时参加话剧社团和志愿者协会的有4人，只参加志愿者协会的有( )人．A. 8B. 9C. 10D. 117.关于x的不等式ax2+bx+c<0的解集为{x|x<2或x>3}，则下列选项正确的是( )A. a>0B. 不等式bx2−ax+c>0的解集为{x|−65<x<1}C. a−b+c>0D. 不等式cx+b<0的解集为{x|x>56}8.设a>b>0，且a2−b2=2，则2a2+3b2−4ab的最小值是( )A. 4B. 2C. 1D. 34二、多选题：本题共3小题，共18分。

湖南省长沙市周南中学2024-2025学年高一上学期第一阶段性测试(10月)数学试题

湖南省长沙市周南中学2024-2025学年高一上学期第一阶段性测试（10月）数学试题一、单选题1．下列各图中，不能表示y 是x 的函数的是（）A ．B ．C ．D ．2．已知：11(a b a b>∈R ,，且0)ab ≠，下列不等关系一定成立的是（） A ．a b > B ．a b < C ．a b ab +>D ．22ab a b >3．已知集合{}3,N A x x x =≤∈，{}221,,B m m m =-，{}3,,32C m m =-，若B C =，则A B⋂的子集个数为（） A ．2B ．4C ．7D ．84．已知函数()y f x =的定义域为[]1,4-，则21f x y += ）A ．[]5,5-B ．31,2⎛⎤ ⎥⎝⎦C ．(]1,5D ．35,2⎡⎤-⎢⎥⎣⎦5．已知(31)4,1(),1a x a x f x ax x -+<⎧=⎨-≥⎩是定义在R 上的减函数，则实数a 的取值范围是（）A ．11,83⎡⎫⎪⎢⎣⎭B ．11,83⎡⎤⎢⎥⎣⎦C ．10,3⎡⎤⎢⎥⎣⎦D ．10,3⎛⎤ ⎥⎝⎦6．为了加强家校联系，王老师组建了一个由学生､家长和教师组成的QQ 群.已知该群中男学生人数多于女学生人数，女学生人数多于家长人数，家长人数多于教师人数，教师人数的两倍多于男学生人数.则该QQ 群人数的最小值为（）A ．20B ．22C ．26D ．287．若a b >，且2ab =，则22(1)(1)a b a b-++-的最小值为（）A．2 B．4 C．4 D．28．关于函数()()1xf x x x=∈+R 的性质，①等式()()0f x f x -+=对x ∈R 恒成立；②函数()f x 的值域为()1,1-；③若12x x ≠，则一定有()()12f x f x ≠；④存在无数个0x ，满足()0011f x f x ⎛⎫+=- ⎪⎝⎭其中正确结论个数为（）A ．1B ．2C ．3D ．4二、多选题9．命题:p x ∃∈R ，210x x -+=．命题q ：任意两个等边三角形都相似．关于这两个命题，下列判断正确的是（） A ．p 是真命题 B ．:p x ⌝∀∈R ，210x x -+≠C ．q 是真命题D ．q ⌝：存在两个等边三角形，它们不相似10．已知集合{}222|80A x x a x a =++-=,{}2|(2)0B x x =+=,且A B A B =I U ．集合D 为a的取值组成的集合，则下列关系中正确的是（）A ．2D -∈B ．2D ∉C ．D ∅⊆D ．0D ∉11．德国著名数学家狄利克雷在数学领域成就显著，以其命名的函数R 1,Q()0,Q x f x x ∈⎧=⎨∈⎩ð，被称为狄利克雷函数，其中R 为实数集，Q 为有理数集，则以下关于狄利克雷函数()f x 的结论中，正确的是（）A ．函数()f x 满足：()()f x f x -=B ．函数()f x 的值域是[]0,1C ．对于任意的x ∈R ，都有()()1f f x =D ．在()f x 图象上不存在不同的三个点、、A B C ，使得ABC V 为等边三角形三、填空题12．已知14,263x y x y -≤-≤-≤+≤，则8z x y =-的取值范围是. 13．在22{|1}1x A x x -=<+，22{|0}B x x x a a =++-<，设全集U =R ，若“x A ∈”是“x B ∈”的充分不必要条件，则实数a 的取值范围是 14．设函数()f x 的定义域为R ，满足1(1)()2f x f x +=，且当(0,1]x ∈时，()(1)f x x x =--.若对任意[,)x m ∈+∞，都有8()9f x ≤，则m 的取值范围是.四、解答题15．已知集合{}|()(2)0A x x m x =-+<，{}|0B x x m =+<. (1)当1m =时，求A B ⋂；(2)若A B B =U ，求实数m 的取值范围． 16．已知函数()()2,0af x x x x x=+∈≠R ． (1)若1a =，求()f x 在{10x x ∈-≤<R 或01}x <≤上的值域； (2)证明：当0a >时，函数()f x在区间,∞⎛- ⎝⎦上单调递增． 17．已知()y f x =在()0,∞+上有意义，单调递增且满足()()()()21,f f xy f x f y ==+．(1)求证：()()22f x f x =；(2)求不等式的()()32f x f x ++≤的解集．18．我们知道，当0a b ≥>时，如果把2,,112a b a b a b ++排成一列的话，一个美丽、大方、优雅的均值不等式链2__________11a ba b ≥≥≥≥+便款款的、含情脉脉的降临在我们面前.这个均值不等式链神通巨大，可以解决很多很多的由定值求最值问题. （1）填空写出补充完整的该均值不等式链；2__________11a b a b≥≥≥≥+（2）如果定义：当0a b ≥>时，a b -为,a b 间的“缝隙”.2a b +间的“缝隙”为M ，2a b+N ，请问M 、N 谁大？给出你的结论并证明. 19．对于函数()f x ，若存在0x ∈R ，使()00f x x =成立，则称0x 为()f x 的不动点．(1)已知函数()23f x x x =--，求函数()f x 的不动点；(2)若对于任意的b ∈R ，二次函数()()218f x ax b x b =+-+-（0a ≠）恒有两个相异的不动点，求实数a 的取值范围；(3)若函数()()211f x mx m x m =-+++在区间()0,2上有唯一的不动点，求实数m 的取值范围．。

2022-2023学年北师大版高一上数学月考试卷(含解析)

2022-2023学年高中高一上数学月考试卷学校：____________ 班级：____________ 姓名：____________ 考号：____________考试总分：95 分考试时间： 120 分钟注意事项：1．答题前填写好自己的姓名、班级、考号等信息; 2．请将答案正确填写在答题卡上;卷I （选择题）一、选择题（本题共计 8 小题，每题 5 分，共计40分）1. ，，若，则的值为（）A.B.或C.D.2. 某中学的学生积极参加体育锻炼，其中有名学生喜欢篮球或足球，名学生喜欢篮球，名学生喜欢足球，则该中学既喜欢篮球又喜欢足球的学生数是( )A.B.C.D.3. 已知，，若，则 A.B.C.D.4. 已知集合，，则（）A.A ={a,a +b,a +2b}B ={a,ac,a }c 2A =B c −1−1−12−12185766346485254A ={1,x,y}B ={1,,2y}x 2A =B x −y =()1211432A ={x|−8>0}2x B ={x|x −1>6}A ∪B =(3,+∞)(7,+∞)B.C.D.5. 已知“”是“”的充分不必要条件，则的取值范围为( )A.B.C.D.6. 已知集合，，若，则实数的取值范围为（）A.B.C.D.7. 已知命题：实数满足，命题：实数满足．若是的充分不必要条件，则实数的取值范围为( )A.B.C.D.8. 正数，满足＝，且恒成立，则实数的取值范围是（）A.B.C.D.(7,+∞)(3,7)(−∞,7)x >k <13x +1k (−∞,−1][1,+∞)[2,+∞)(2,+∞)A ={x|−2≤x ≤−1}B ={y|y =−2x +a,x ∈A}A ⊆B a [−5,−4][4.5][−3,−6][3,6]p x −+6x −8>0x 2q x −(m +1)x +m <0(m >1)x 2p q m 1<m <41<m ≤4m >4m ≥4a b 2a +b 12−4−≤t −ab −−√a 2b 212t (−∞,]2–√2[,+∞)2–√2[−,]2–√22–√2[,+∞)12二、多选题（本题共计 4 小题，每题 5 分，共计20分）9. 下列关于空集的说法中，正确的有（）A.B.C.D.10. 若集合＝恰有两个子集，则的值可能是（）A.B.C.D.或11. 下列结论中正确的是（）A.“”是“”的充要条件B.函数的最小值为C.命题“”的否定是“”D.若函数有负值，则实数的取值范围是或12. 下列命题中正确的是( )A.的最小值是B.的最大值是C.的最大值是D.有最大值卷II （非选择题）三、填空题（本题共计 1 小题，共计5分）∅∈∅∅⊆∅∅∈{∅}∅⊆{∅}A {x |a −2x −1＝0}x 2a 0−1101ab >0>0ab y =++2x 2−−−−−√1+2x 2−−−−−√2∀x >1,−x >0x 2∃≤1,−≤0x 0x 20x 0y =−ax +1x 2a a >2a <−2y =+3x 2+2x 2−−−−−√2y =x +(x <0)1x −2y =2−3x −(x >0)4x 2−43–√y =+3x 2+2x 2−−−−−√13. （5分）若命题“ ，”为假命题，则的取值范围是________.四、解答题（本题共计 6 小题，每题 5 分，共计30分）14. 已知集合，，若，求实数的值．15. 已知椭圆，，分别为椭圆的左顶点和右焦点，过的直线交椭圆于点，．若，且当直线轴时，．求椭圆的方程；设直线，的斜率分别为，，问是否为定值？并证明你的结论；记的面积为，求的最大值．16. 已知函数的最小值等于．（1）求的值；（2）若正数，，满足，求的最大值． 17. 解不等式． 18. 设命题：对任意，不等式恒成立，命题：存在，使得不等式成立．若为真命题，求实数的取值范围；若为假命题，为真命题，求实数的取值范围． 19. 已知函数.求关于的不等式的解集；若不等式对任意恒成立，求实数的取值范围．∃x ∈R +2mx +m +2<0x 2m A ={x|−3x +2=0}x 2B ={x|−ax +a −1=0}x 2A ∪B =A a C :+=1(a >b >0)x 2a 2y 2b 2A F C F l C P Q AF =3l ⊥x PQ =3(1)C (2)AP AQ k 1k 2k 1k 2(3)△APQ S S f(x)=|x +m|−|2x −4|(m >0)3m a b c a +b +c =3m ++a −√b √c √<0x −3x +7p x ∈[0,1]2x −2≥−3m m 2q x ∈[−1,1]−x +m −1≤0x 2(1)p m (2)p ∧qp ∨q m f (x)=−4x +5(x ∈R)x 2(1)x f (x)<2(2)f (x)>m −3x ∈R m参考答案与试题解析2022-2023学年高中高一上数学月考试卷一、选择题（本题共计 8 小题，每题 5 分，共计40分）1.【答案】C【考点】集合的相等【解析】根据集合相等确定元素关系即可得到结论．【解答】解：∵，，∴若，则①或②，由①消去得，当时，集合，不成立，由②消去得，当或时，当时，此时，满足条件.故选：.2.【答案】D【考点】Venn 图表达集合的关系及运算【解析】记“该中学学生喜欢篮球”为事件，“该中学学生喜欢足球”为事件，则“该中学学生喜欢篮球或足球”为事件，“该中学学生既喜欢篮球又喜欢足球”为事件·，然后根据积事件的概率公式可得结果．【解答】解：记“该中学喜欢篮球的学生”为集合，“该中学喜欢足球的学生”为集合，A ={a,a +b,a +2b}B ={a,ac,a }c 2A =B {a +b =ac a +2b =ac 2{a +b =ac 2a +2b =acb c =1c =1B =B ={a,a,a}b c =1c =1c =−12c =−12b =−a 34C A B A +B A B P (A ⋅B)=P (A)+P (B)−P (A +B)A B A ∪B则“该中学喜欢篮球或足球的学生”为集合，如图，所以该中学既喜欢篮球又喜欢足球的学生数为人.故选.3.【答案】C【考点】集合的无序性集合的相等【解析】化简，，利用，即可得出结论．【解答】解：，假设，解得或(舍去)，(舍去)，该假设不合题意；假设，解得，，该假设满足题意；.故选.4.【答案】A【考点】并集及其运算【解析】A ∪B =85A ∩B =63+76−85=54D A B A =B ∵A =B {x =，x 2y =2y ，∴x =0x =1y =0∴{=y ，x 2x =2y ，∴(2y =y )2y =14x =12∴∴x −y =−=121414C无【解答】解：因为，，所以．故选．5.【答案】C【考点】必要条件、充分条件与充要条件的判断【解析】求出的等价条件，然后利用充分条件和必要条件的定义进行判断求解．【解答】解：由得，解得或．要使“”是“”的充分不必要条件，则．故选.6.【答案】A【考点】集合的包含关系判断及应用集合关系中的参数取值问题【解析】由已知先求出集合，然后结合集合的包含关系即可直接求解．【解答】解：因为，，若，则解得：.故选.7.A ={x|x >3}B ={x|x >7}A ∪B =(3,+∞)A <13x +1<13x +1−1=<03x +1−x +2x +1x <−1x >2x >k <13x +1k ≥2C B A ={x|−2≤x ≤−1}B ={y|y =−2x +a,x ∈A}={y|2+a ≤y ≤4+a}A ⊆B {4+a ≥−1,2+a ≤−2,−5≤a ≤−4A【答案】D【考点】根据充分必要条件求参数取值问题【解析】先求出，为真时的值，再利用充分必要条件求解即可.【解答】解：由，可得，由，可得.∵是的充分不必要条件，∴，∴.故选.8.【答案】B【考点】不等式恒成立问题基本不等式在最值问题中的应用【解析】由，，＝得，＝，于是问题转化为：恒成立，令＝，求得的最大值，只需即可．【解答】∵，，＝，∴＝，∴恒成立，转化为恒成立，令＝＝，又由，，＝得：＝，∴（当且仅当，时取“＝”）；∴＝．p q x −+6x −8>0x 22<x <4−(m +1)x +m <0x 21<x <m p q {x|2<x <4} {x|1<x <m}m ≥4D a >0b >02a +b 14+a 2b 21−4ab t ≥2+4ab −ab −−√12f(a,b)2+4ab −ab −−√12f(a,b)t ≥f(a,b)max a >0b >02a +b 14+a 2b 21−4ab 2−4−≤t −ab −−√a 2b 212t ≥2+4ab −ab −−√12f(a,b)2+4ab −=4(ab +−)ab −−√1212ab −−√184−(+)ab −−√14234a >0b >02a +b 112a +b ≥22ab −−−√ab ≤18a =14b =12f(a,b)max 4−=(+)18−−√142342–√2≥–√．二、多选题（本题共计 4 小题，每题 5 分，共计20分）9.【答案】B,C,D【考点】集合的包含关系判断及应用【解析】此题暂无解析【解答】略10.【答案】A,B【考点】子集与真子集【解析】恰有两个子集的集合只有一个元素，进而求解．【解答】集合恰有两个子集，则集合中只有一个元素，当＝时，，满足题意；当时，＝＝，即＝，此时＝，满足题意；故的值为，．11.【答案】A,D【考点】命题的真假判断与应用t ≥2–√2A A a 0a ≠0△4+4a 0a −1A {−1}a 0−1必要条件、充分条件与充要条件的判断命题的否定【解析】此题暂无解析【解答】解：对于，由，能得到，反之也成立，故正确.对于，由基本不等式可知当且仅当，解得，无解，所以等号不成立，所以取不到最小值，错误；对于，命题""的否定是“”，故错误.对于，函数有负值，则，解得或，故正确.故选.12.【答案】B,C【考点】命题的真假判断与应用基本不等式基本不等式在最值问题中的应用【解析】结合基本不等式以及基本不等式取得最值的条件对每个选项进行分析即可求解.【解答】解：对于，，当且仅当时取等号，解得无解，即式子最小值取不到，故错误；对于，时，，当且仅当时取等号成立，故正确；A ab >0>0a b AB +≥2,+2x 2−−−−−√1+2x 2−−−−−√=+2x 2−−−−−√1+2x 2−−−−−√=−1x 2B C ∀x >1,−x >0x 2∃>1,−≤0x 0x 20x 0C D y =−ax +1x 2Δ=−4>0(−a)2a >2a <−2D AD A y ==++3x 2+2x 2−−−−−√+2x 2−−−−−√1+2x 2−−−−−√≥2=2⋅+2x 2−−−−−√1+2x 2−−−−−√−−−−−−−−−−−−−−−−√=+2x 2−−−−−√1+2x 2−−−−−√x 2A B x <0y =x +=−[(−x)+(−)]1x 1x ≤−2=−2(−x)⋅(−)1x−−−−−−−−−−√x =−1B =2−3x −≤2−2=2−4−−−−−对于，时，，当且仅当时取等号，即式子的最大值是，故正确；对于，由中结论可知，无最大值，故错误.故选.三、填空题（本题共计 1 小题，共计5分）13.【答案】【考点】全称命题与特称命题命题的否定【解析】由于命题：“，使得”为假命题，可得命题的否定是：“，”为真命题，因此，解出即可．【解答】解：∵命题：“，使得”为假命题，∴命题的否定是：“，”为真命题，∴，即，解得，∴实数的取值范围是．故答案为：．四、解答题（本题共计 6 小题，每题 5 分，共计30分）14.【答案】解：由题得，∵，∴，∴或或或．当时，，无解；当时，得；当时，C x >0y =2−3x −≤2−2=2−44x 3x ⋅4x −−−−−√3–√3x =4x 2−43–√CD A y =+3x 2+2x 2−−−−−√D BC [−1,2]∃x ∈R +2mx +m +2<0x 2∀x ∈R +2mx +m +2≥0x 2Δ≤0∃x ∈R +2mx +m +2<0x 2∀x ∈R +2mx +m +2≥0x 2Δ≤04−4(m +2)≤0m 2−1≤m ≤2m [−1,2][−1,2]A ={1,2}A ∪B =A B ⊆A B =∅{1}{2}{1,2}B =∅Δ=−4(a −1)<0a 2B ={1}{1+1=a,1×1=a −1,a =2B ={2}{2+2=a,2×2=a −1,无解；当时，得．综上可知，或．【考点】集合关系中的参数取值问题根与系数的关系【解析】【解答】解：由题得，∵，∴，∴或或或．当时，，无解；当时，得；当时，无解；当时，得．综上可知，或．15.【答案】解：设椭圆的右焦点为，，则，①由，得，②又当直线轴时，，的横坐标为，将代入中，得，则，③联立①②③，解得，，，所以椭圆的方程为．为定值．证明如下：显然，直线不与轴垂直，可设的方程为，B ={1,2}{1+2=a,1×2=a −1,a =3a =2a =3A ={1,2}A ∪B =A B ⊆A B =∅{1}{2}{1,2}B =∅Δ=−4(a −1)<0a 2B ={1}{1+1=a,1×1=a −1,a =2B ={2}{2+2=a,2×2=a −1,B ={1,2}{1+2=a,1×2=a −1,a =3a =2a =3(1)F(c,0)c >0=+a 2b 2c 2AF =3a +c =3l ⊥x P Q c x =c +=1x 2a 2y 2b 2y =±b 2a PQ ==32b 2a =4a 2=3b 2=1c 2C +=1x 24y 23(2)k 1k 2−14PQ y PQ x =my +1=122联立椭圆方程，消去并整理得，又设，，由韦达定理得从而，，所以，即，故得证．由知，所以．令，，则，设函数，由知，在上为增函数，得，即时，，此时取得最大值为．【考点】圆锥曲线中的定点与定值问题利用导数研究函数的最值根与系数的关系直线与椭圆结合的最值问题+=1x 24y 23x (3+4)+6my −9=0m 2y 2P(,)x 1y 1Q(,)x 2y 2 +=−y 1y 26m 3+4m 2=y 1y 2−93+4m 2+=(m +1)+(m +1)=x 1x 2y 1y 283+4m 2=(m +1)(m +1)=x 1x 2y 1y 2−12+4m 23+4m 2==k 1k 2y 1y 2(+2)(+2)x 1x 2y 1y 2+2(+)+4x 1x 2x 1x 2===−−93+4m 2++4−12+4m 23+4m 2163+4m 2−93614=−k 1k 214(3)(2) +=−，y 1y 26m 3+4m 2=，y 1y 2−93+4m 2S =AF ⋅|−|=|−|=12y 1y 232y 1y 232(+−4y 1y 2)2y 1y 2−−−−−−−−−−−−−−√==1832(−+6m 3+4m 2)2363+4m 2−−−−−−−−−−−−−−−−−−−−√+1m 2(3+4m 2)2−−−−−−−−−−√=18+1m 29(+1+6(+1)+1m 2)2m 2−−−−−−−−−−−−−−−−−−−−−−√=1819(+1)++6m 21+1m 2−−−−−−−−−−−−−−−−−−−− t =+1m 2t ≥1S =(t ≥1)189t ++61t −−−−−−−−−√g(t)=9t +(t ≥1)1t (9t +)'=9−=>01t 1t 29−1t 2t 2g(t)[1,+∞)t =1m =0[g(t)=9×1+=10]min 11S =1810+6−−−−−√92椭圆的标准方程【解析】对第（1）问，由，，及可求得，；对第（2）问，可先设直线的方程与，的坐标，联立直线与椭圆的方程，由韦达定理建立交点坐标的关系，将用坐标表示，再探求定值的存在性；对第（3）问，根据，将用参数表示，从而得到面积关于函数，根据此函数的形式特点，可求得面积的最大值．【解答】解：设椭圆的右焦点为，，则，①由，得，②又当直线轴时，，的横坐标为，将代入中，得，则，③联立①②③，解得，，，所以椭圆的方程为．为定值．证明如下：显然，直线不与轴垂直，可设的方程为，联立椭圆方程，消去并整理得，又设，，由韦达定理得从而，，所以，即，故得证．由知，所以AF =3PQ =3=+a 2b 2c 2a 2b 2PQ P Q k 1k 2=AF ⋅|−|S △APQ 12y 1y 2|−|y 1y 2m m (1)F(c,0)c >0=+a 2b 2c 2AF =3a +c =3l ⊥x P Q c x =c +=1x 2a 2y 2b 2y =±b 2a PQ ==32b 2a =4a 2=3b 2=1c 2C +=1x 24y 23(2)k 1k 2−14PQ y PQ x =my +1+=1x 24y 23x (3+4)+6my −9=0m 2y 2P(,)x 1y 1Q(,)x 2y 2 +=−y 1y 26m 3+4m 2=y 1y 2−93+4m 2+=(m +1)+(m +1)=x 1x 2y 1y 283+4m 2=(m +1)(m +1)=x 1x 2y 1y 2−12+4m 23+4m 2==k 1k 2y 1y 2(+2)(+2)x 1x 2y 1y 2+2(+)+4x 1x 2x 1x 2===−−93+4m 2++4−12+4m 23+4m 2163+4m 2−93614=−k 1k 214(3)(2) +=−，y 1y 26m 3+4m 2=，y 1y 2−93+4m 2S =AF ⋅|−|=|−|=12y 1y 232y 1y 232(+−4y 1y 2)2y 1y 2−−−−−−−−−−−−−−√=18−−−−−−−−−−．令，，则，设函数，由知，在上为增函数，得，即时，，此时取得最大值为．16.【答案】【考点】基本不等式基本不等式在最值问题中的应用【解析】此题暂无解析【解答】此题暂无解答17.【答案】解：∵．∴可得：∴解得：．∴不等式的解集为．【考点】分式不等式的解法一元二次不等式的解法==1832(−+6m 3+4m 2)2363+4m 2−−−−−−−−−−−−−−−−−−−−√+1m 2(3+4m 2)2−−−−−−−−−−√=18+1m 29(+1+6(+1)+1m 2)2m 2−−−−−−−−−−−−−−−−−−−−−−√=1819(+1)++6m 21+1m 2−−−−−−−−−−−−−−−−−−−− t =+1m 2t ≥1S =(t ≥1)189t ++61t −−−−−−−−−√g(t)=9t +(t ≥1)1t (9t +)'=9−=>01t 1t 29−1t 2t 2g(t)[1,+∞)t =1m =0[g(t)=9×1+=10]min 11S =1810+6−−−−−√92<0x −3x +7{(x −3)(x +7)<0，x +7≠0，−7<x <3{x |−7<x <3}【解析】（1）由题意可得：，或，进而即可得解．【解答】解：∵．∴可得：∴解得：．∴不等式的解集为．18.【答案】解：∵命题：对任意，不等式恒成立，而，有，，解得，∴为真命题时，实数的取值范围是.命题：存在，使得不等式成立，只需，∵，，，解得，即命题为真时，实数的取值范围是.由题意，命题，一真一假，若为假命题，为真命题，则解得；若为假命题，为真命题，则解得.综上所述，实数的取值范围为或.【考点】一元二次不等式的解法复合命题及其真假判断逻辑联结词“或”“且”“非”【解析】{x −3>0x +7<0{x −3<0x +7>0<0x −3x +7{(x −3)(x +7)<0，x +7≠0，−7<x <3{x |−7<x <3}(1)p x ∈[0,1]2x −2≥−3m m 2x ∈[0,1]=−2(2x −2)min ∴−2≥−3m m 21≤m ≤2p m 1≤m ≤2(2)q x ∈[−1,1]−x +m −1≤0x 2≤0(−x +m −1)x 2min −x +m −1=+m −x 2(x −)12254∴=−+m (−x +m −1)x 2min 54∴−+m ≤054m ≤54q m m ≤54p q p q m <1或m >2,m ≤,54m <1q p 1≤m ≤2,m >,54<m ≤254m m <1<m ≤254x ∈[0,1],≥−3m(2x −2)2命题为真，只需，根据一次函数的单调性，转化为求关于的一元二次不等式；（2）命题为真，只需，根据二次函数的性质，求出的范围，依题意求出真假，和假真时，实数的取值范围．【解答】解：∵命题：对任意，不等式恒成立，而，有，，解得，∴为真命题时，实数的取值范围是.命题：存在，使得不等式成立，只需，∵，，，解得，即命题为真时，实数的取值范围是.由题意，命题，一真一假，若为假命题，为真命题，则解得；若为假命题，为真命题，则解得.综上所述，实数的取值范围为或.19.【答案】解：∵，∴，，∴，故不等式的解集为.∵不等式对任意恒成立，∴恒成立.∵，∴，∴即，故的取值范围为.【考点】不等式恒成立问题二次函数的性质P x ∈[0,1],≥−3m (2x −2)min m 2m 4x ∈[−1,1],≤0(−x +m −1)x 2min m P 4P 4m (1)p x ∈[0,1]2x −2≥−3m m 2x ∈[0,1]=−2(2x −2)min ∴−2≥−3m m 21≤m ≤2p m 1≤m ≤2(2)q x ∈[−1,1]−x +m −1≤0x 2≤0(−x +m −1)x 2min −x +m −1=+m −x 2(x −)12254∴=−+m (−x +m −1)x 2min 54∴−+m ≤054m ≤54q m m ≤54p q p q m <1或m >2,m ≤,54m <1q p 1≤m ≤2,m >,54<m ≤254m m <1<m ≤254(1)−4x +5<2x 2−4x +3<0x 2(x −3)(x −1)<01<x <3(1,3)(2)f (x)>m −3x ∈R f(x >m −3)min f(x)=(x −2+1)2f(x =1)min m −3<1m <4m (−∞，4)一元二次不等式的解法【解析】此题暂无解析【解答】解：∵，∴，，∴，故不等式的解集为.∵不等式对任意恒成立，∴恒成立.∵，∴，∴即，故的取值范围为.(1)−4x +5<2x 2−4x +3<0x 2(x −3)(x −1)<01<x <3(1,3)(2)f (x)>m −3x ∈R f(x >m −3)min f(x)=(x −2+1)2f(x =1)min m −3<1m <4m (−∞，4)。

高一数学上学期第八次周考试题及答案

开化中学高一年级数学周考卷（8）班级姓名学号一．选择题（每小题5分，共50分） 1.已知函数的定义域为 …………………………………………………………………（）．．．．2．已知集合，，则……………………………( ) ．．．． 3．在区间上为增函数的是 ………………………………………………………………………( )．．．． 4．设函数则的值为 ……………………………………………( )．．．．5．若函数= 的定义域为,则实数的取值范围是…………………………( )．．．．6.设函数则方程一定存在根的区间是 …………………………………（）．(-1,1) ．(0,1)．(1,2) ． (2,3)7．已知函数在定义域上单调，则实数的取值范围为 ………………( )．．．．8．已知集合，若集合有且仅有一个元素，则实数的取值范围是 …………………………………………………………………………………………………………( )．．．()f x =A (,1)-∞B (,1]-∞C (1,)+∞D [1,)+∞{|2}S x x =<2{|340}T x x x =--≤()R S T =A (2,4)B [2,4]C (,4)-∞D (,4]-∞(,0)-∞A 1=y B 21x y +=C 122---=x x y D 21xy x-=-221,1()2,1,x x f x x x x ⎧-≤⎪=⎨+->⎪⎩1(2)f f ⎛⎫⎪⎝⎭A 18B 89C 1516D 2716-()f x 3442++-mx mx x R m A (,)-∞+∞B 3[0,)4C 3(,)4+∞D 3(0,)4()24,xf x x =+-()0f x =A B C D 25,1,()11, 1.x ax x f x x x ⎧-+<⎪=⎨+≥⎪⎩R a A (,2]-∞B [2,)+∞C [4,)+∞D [2,4]23{|0,(1,1)}2A x x x k x =--=∈-A k A 159[,){}2216--B 15(,)22C 95[,)162-． 9．已知若函数则函数……………………( ) ．有最小值为，有最大值为．无最小值，有最大值为．有最小值为，无最大值．无最值10.若函数是偶函数，函数是奇函数，则a +b 是……………（）．1 ．-．-1二、填空题（每小题5分，共25分） 11. 计算 .12．函数和互为反函数，则的值为 .13.已知三个函数的零点依次为r , s , t , 则r , s , t 的大小关系为__ .14．关于x 的方程有实根，且一个大于2，一个小于2，则m 取值范围为_ __ __.15．已知函数，若函数在区间内存在零点，则实数的取值范围为 .三、解答题（本大题共5小题，共75分） 16．（本题满分15分）计算：（1）；（2）D 9[,)16-+∞{},,,,,a ab Max a b b a b ≥⎧=⎨<⎩{}2()|4|,f x Max x x x =-()f x A 04B 4C 0D ()lg(101)xf x ax =++4()2x xb g x -=A 12B C 12D 31log 53+=()2xf x =()log a g x x =1()2g 2()2,()2,()log xf x xg x xh x x x =+=-=+22(1)40x m x m +++-=2()34f x x x a =+-()f x (1,1)-a 21023213(2)(9.6)(3)(1.5)48-----+52551log 352log log log 14;50+-17. 已知集合A =，集合B =.（1）若，求实数m 的值；（2）若，求实数m 的取值范围。

河南省南阳市第二完全学校高级中学2022-2023学年高一上学期第三次(线上)周考数学试卷

2022年11月高一数学第三次周考试卷考试时间：120分钟；考试分数：150分第I 卷（选择题）一、单项选择题（本大题共6小题，每小题5分，共30分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

）1．为了解某中学高一年级600名学生的身高情况，抽查了其中100名学生的身高进行统计分析．下列叙述正确的是（）A ．以上调查属于全面调查B ．每名学生是总体的一个个体C ．100名学生的身高是总体的一个样本D ．600名学生是总体2．当a>1时，在同一坐标系中，函数x a y =与x y a log =的图像为（）A ．B ．C ．D ．3．盒子中有5只螺丝钉，其中有2只是坏的，现从盒中随机地抽取2只，那么至少1只坏的概率是（）A ．710B ．310C ．35D ．7204．某工厂生产甲、乙、丙三种型号的产品，产品数量之比为3：5：7，现用分层抽样的方法抽出容量为n 的样本，其中甲种产品有18件，则样本容量n=（）A ．45B ．54C ．90D ．1265．演讲比赛共有9位评委分别给出某选手的原始评分，评定该选手的成绩时，从9个原始评分中去掉1个最高分、1个最低分，得到7个有效评分.7个有效评分与9个原始评分相比，不变的数字特征是A ．中位数B ．平均数C ．方差D ．极差6．某鱼业养殖场新进1000尾鱼苗，测量其体长(单位：毫米)，将所得数据分成6组，其分组及频数情况如下表：分组(单位：毫米)[)70,75[)75,80[)80,85[)85,90[)90,95[)95,100频数100100m 350150n已知在按以上6个分组做出的频率分布直方图中，[)95,100分组对应小矩形的高为0.01，则下列说法正确的是（）A ．260m =B ．鱼苗体长在[)90,100上的频率为0.16C ．鱼苗体长的中位数一定落在区间[)80,85内D ．这批鱼苗体长平均数为85毫米7．已知对数函数log a y x =，且在区间[)3,+∞上恒有1y <-，则实数a 的取值范围是（）A ．()1,3；B ．10,3⎛⎫ ⎪⎝⎭；C ．1,13⎛⎫ ⎪⎝⎭；D ．()3,+∞．8．2020年春节前后，一场突如其来的新冠肺炎疫情在全国蔓延，疫情就是命令，防控就是责任.在党中央的坚强领导和统一指挥下，全国人民众志成城、团结一心，掀起了一场坚决打赢疫情防控阻击战的人民战争.下面的图表展示了2月14日至29日全国新冠肺炎疫情变化情况，根据该折线图，下列结论错误的是（）A ．16天中每日新增确诊病例数量在下降且19日的降幅最大B ．16天中每日新增确诊病例的中位数小于新增疑似病例的中位数C ．16天中新增确诊、新增疑似、新增治愈病例的极差均大于2000D ．21日至29日每日新增治愈病例数量均大于新增确诊与新增疑似病例之和二、多项选择题（本大题共2小题，每小题5分，共10分。

高一数学周考卷

高一数学周考卷（考试时间：90分钟，满分：100分）一、选择题（每题2分，共30分）1. （2分）若a=3，b=2，则a+b的值为（）A. 5B. 5C. 1D. 12. （2分）下列函数中，奇函数是（）A. y=x^2B. y=|x|C. y=x^3D. y=x^2+x3. （2分）已知等差数列{an}，a1=1，a3=3，则公差d为（）A. 1B. 2C. 3D. 44. （2分）下列命题中，真命题是（）A. 任意两个平行线之间的距离相等B. 任意两个平行四边形的面积相等C. 任意两个等腰三角形的底角相等D. 任意两个等边三角形的面积相等5. （2分）若函数f(x)=2x+1，则f(1)的值为（）A. 1B. 0C. 1D. 26. （2分）直线y=2x+1与x轴的交点坐标为（）A. (0,1)B. (1,0)C. (1,0)D. (0,1)7. （2分）若三角形的三边长分别为3、4、5，则该三角形是（）A. 等边三角形B. 等腰三角形C. 直角三角形D. 钝角三角形二、判断题（每题1分，共20分）8. （1分）若a>b，则ab一定大于0。

（）9. （1分）等差数列的任意两项之差等于公差。

（）10. （1分）平行线的斜率相等。

（）11. （1分）函数y=2x+1的图像是一条直线。

（）12. （1分）若两个角的和为180度，则这两个角互为补角。

（）13. （1分）圆的面积与半径成正比。

（）14. （1分）三角形的三条高线交于一点。

（）三、填空题（每空1分，共10分）15. （1分）若a=5，b=3，则ab=______。

16. （1分）函数f(x)=x^2的图像是一个______。

17. （1分）等差数列的通项公式为an=a1+(n1)d，其中d表示______。

18. （1分）若一个等腰三角形的底角为45度，则顶角为______度。

19. （1分）直线y=kx+b中，k表示______。

2024-2025学年贵州省部分学校高一上学期联考数学试题(含答案)

2024-2025学年贵州省部分学校高一上学期联考数学试题一、单选题：本题共8小题，每小题5分，共40分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.下列各组对象能构成集合的是( )A. 中国著名的数学家B. 高一(2)班个子比较高的学生C. 不大于5的自然数D. 约等于3的实数2.已知ab>bc，则下列不等式一定成立的是( )A. a>cB. a<cC. ab <cbD. ab>cb3.已知a>0，b>0，且a+3b=6，则ab的最大值是( )A. 9B. 6C. 43D. 34.金钱豹是猫科豹属中的一种猫科动物.根据以上信息，可知“甲是猫科动物”是“甲是金钱豹”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件5.若x>−1，P=1x+2+1，Q=1−x，则( )A. P≥QB. P≤QC. P>QD. P<Q6.已知−5≤2a+b≤1，−1≤a+2b≤3，则a−b的最大值是( )A. 1B. 2C. 4D. 87.已知p是q的充分不必要条件，q是s的充要条件，s是r的充分不必要条件，r是q的必要不充分条件，则p 是s的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件8.学校统计某班45名学生参加音乐、科学、体育3个兴趣小组的情况，其中有20名学生参加了音乐小组，有21名学生参加了科学小组，有22名学生参加了体育小组，有24名学生只参加了1个兴趣小组，有12名学生只参加了2个兴趣小组，则3个兴趣小组都没参加的学生有( )A. 5名B. 4名C. 3名D. 2名二、多选题：本题共3小题，共18分。

在每小题给出的选项中，有多项符合题目要求。

9.已知命题p:有些三角形是轴对称图形，命题q:梯形的对角线相等，则( )A. p是存在量词命题B. q是全称量词命题C. p是假命题D. ¬q是真命题10.已知函数y=ax2+bx+c的部分图象如图所示，则( )A. abc<0B. b+c>0C. 2a+b+c<0D. 关于x的不等式cx2+bx+a>0的解集为{x|−13<x<1}11.若S是含有n个元素的数集，则称S为n数集S.n数集S中含有m(m≤n)个元素的子集，称为S的m子集.若在n数集S的任何一个t(4≤t≤n)子集中，存在4个不同的数a，b，c，d，使得a+b=c+d，则称该S的t子集为S的等和子集.下列结论正确的是( )A. 3数集A有6个非空真子集B. 4数集B有6个2子集C. 若集合C={1,2,3,4,6}，则C的等和子集有2个D. 若集合D={1,2,3,4,6,13,20,40}，则D的等和子集有24个三、填空题：本题共3小题，每小题5分，共15分。

高一(上)数学第二章函数单元测试题7-8 人教版

高一(上)数学第二章函数单元测试题7-8(时间：45分钟满分100分)一、选择题1．若3a=2,则log 38-2log 36用a 的代数式可表示为（）（A ）a-2 （B ）3a-(1+a)2 （C ）5a-2 （D ）3a-a 22.2log a (M-2N)=log a M+log a N,则NM的值为（）（A ）41（B ）4 （C ）1 （D ）4或1 3．已知x 2+y 2=1,x>0,y>0,且log a (1+x)=m,logaya n xlog ,11则=-等于（）（A ）m+n （B ）m-n （C ）21(m+n) （D ）21(m-n)4.如果方程lg2x+(lg5+lg7)lgx+lg5·lg7=0的两根是α、β，则α·β的值是（）（A ）lg5·lg7（B ）lg35（C ）35 （D ）351 5.已知log 7[log 3(log 2x)]=0，那么x 21-等于（）（A ）31（B ）321 （C ）221 （D ）331 6．函数y=lg （112-+x）的图像关于（）（A ）x 轴对称（B ）y 轴对称（C ）原点对称（D ）直线y=x 对称 7．函数y=log 2x-123-x 的定义域是（）（A ）（32，1）⋃（1，+∞）（B ）（21，1）⋃（1，+∞）（C ）（32，+∞）（D ）（21，+∞）8．函数y=log 21(x 2-6x+17)的值域是（）（A ）R （B ）[8，+∞]（C ）（-∞，-3）（D ）[3，+∞] 9．函数y=log 21(2x 2-3x+1)的递减区间为（）（A ）（1，+∞）（B ）（-∞，43］（C ）（21，+∞）（D ）（-∞，21］10．函数y=(21)2x +1+2,(x<0)的反函数为（）（A ）y=-)2(1log )2(21>--x x （B ）)2(1log )2(21>--x x（C ）y=-)252(1log )2(21<<--x x （D ）y=-)252(1log )2(21<<--x x11.若log m 9<log n 9<0,那么m,n 满足的条件是（）（A ）m>n>1 （B ）n>m>1 （C ）0<n<m<1 （D ）0<m<n<112.log a132<，则a 的取值X 围是（）（A ）（0，32）⋃（1，+∞）（B ）（32，+∞）（C ）（1,32）（D ）（0，32）⋃（32，+∞）13．若1<x<b,a=log ２b x,c=log a x,则a,b,c 的关系是（）（A ）a<b<c （B ）a<c<b （C ）c<b<a （D ）c<a<b 14.下列函数中，在（0，2）上为增函数的是（）（A ）y=log 21(x+1) （B ）y=log 212-x（C ）y=log 2x 1（D ）y=log 21(x 2-4x+5) 15.下列函数中，同时满足：有反函数，是奇函数，定义域和值域相同的函数是（）（A ）y=2x x e e -+（B ）y=lg xx+-11（C ）y=-x3（D ）y=x16.已知函数y=log a (2-ax)在[0，1]上是x 的减函数，则a 的取值X 围是（）（A ）（0，1）（B ）（1，2）（C ）（0，2）（D ）[2，+∞) 17．已知g(x)=log a 1+x (a>0且a ≠1)在（-1，0）上有g(x)>0，则f(x)=a1+x 是（）（A ）在（-∞，0）上的增函数（B ）在（-∞，0）上的减函数（C ）在（-∞，-1）上的增函数（D ）在（-∞，-1）上的减函数18．若0<a<1,b>1,则M=a b ，N=log b a,p=b a的大小是（）（A ）M<N<P （B ）N<M<P （C ）P<M<N （D ）P<N<M19．“等式log 3x 2=2成立”是“等式log 3x=1成立”的（）（A ）充分不必要条件（B ）必要不充分条件（C ）充要条件（D ）既不充分也不必要条件 20．已知函数f(x)=x lg ,0<a<b,且f(a)>f(b)，则（）（A ）ab>1 （B ）ab<1 （C ）ab=1 （D ）(a-1)(b-1)>0 二、填空题1．若log a 2=m,log a 3=n,a 2m+n=。

浙江宁波市效实中学2024-2025学年新高一上学期分班考试数学试卷(解析版)

效实中学新高一数学能力测试试题卷一、填空题1. 已知 0x 是关于 x 的方程 210x ax −−=的根. 当 32a =− 时， 0x = ___; 当2a =时，3001x x −=_______ 【答案】 ①. 12或2− ②. 8+或8− 【解析】【分析】直接解方程可得第一空，利用整体的思想及方程的思想可先化简代数式，并代入方程的根计算即可得第二空.【详解】显然32a =−时，方程可化为()()22320212x x x x +−==−+，解之得012x =或02x =−； 2a =时，有202101x x x −−=⇒=+01x =，且20021x x =+，对于()()()()2200030000011222141xx x x x x x x x −++−===+，当01x =+时，0448x +=+当01x =时，0448x +=−. 故答案为：12或2−；8+8−. 2. 已知实数a ，b ，c 满足2221a b c ++=，则ab bc ca ++的最小值为___，此时 22a b ab ++=______ 【答案】 ①. 12−##0.5− ②. 12##0.5 【解析】【分析】由()20a b c ++≥求出ab bc ca ++的最小值，此时()c a b =−+，再将两边平方，代入2221a b c ++=求出22a b ab ++. 【详解】因为()()222220a b c ab bc ca a b c +++++=++≥，所以()2221122ab bc ca a b c ++≥−++=−，当且仅当0a b c ++=时取等号，所以ab bc ca ++的最小值为12−，此时()c a b =−+，则()()2222212c a b a ab b =−×+=++，则222222212a ab b b a b c a +++++=+=，所以2212a b ab ++=.故答案为：12−；123. 对实数m ，n .定义运算 “⊗”为: m n mn n ⊗=+. 已知关于x 的方程()14x a x ⊗⊗=−.若该方程有两个相等的实数根，则实数a 的值是___，若该方程有两个不等负根，则实数a 的取值范围是___. 【答案】 ①. 0 ②. 0a > 【解析】【分析】首先化简()x a x ⊗⊗，即可得到方程()()2414110a x a x ++++=，再根据()410Δ0a +≠= 计算第一空，由根判别式及韦达定理得到不等式组，即可得到第二空. 【详解】因为a x ax x ⊗=+，所以()()()()()()211x a x x ax x x ax x ax x a x a x ⊗⊗=⊗+=+++=+++，又()14x a x ⊗⊗=−，所以()()211104a x a x ++++=，即()()2414110a x a x ++++=，若该方程有两个相等的实数根，则()()()2410Δ1611610a a a +≠ =+−+= ，解得0a =；若该方程有两个不等负根，则()()()()2410Δ16116101041a a a a+≠=+−+> >+ ，解得0a >，所以实数a 的取值范围是0a >. 故答案为：0；0a >4. 如图，AB 是半圆O 的直径，弦AD ，BC 相交于点P ， 60DPB ∠= ，D 是弧BC 的中点. 则ACAB的值为_______的【答案】12##0.5 【解析】【分析】依题意可得90ACB ∠= ，即可求出30CAD ∠= ，再由D 是弧BC 的中点，得到CAD BAD ∠=∠，即可求出CAB ∠【详解】∵AB 是半圆O 的直径， ∴90ACB ∠= ，∵60APC DPB ∠=∠= ， ∴30CAD ∠= ，∵D 是 BC的中点， ∴30∠=∠= CAD BAD ， ∴60CAB ∠= ， ∴1cos cos 602AC CAB AB ∠===．故答案为：12． 5. 记()()2211xyx y A xy−−=. 若a b c abc ++=，则abbc ca A A A A =++的值为_________【答案】4 【解析】【分析】依题意a 、b 、c 均不为0，根据所给定义表示出ab A ，bc A ，ca A ，再通分计算可得. 【详解】依题意a 、b 、c 均不0，又()()222222111aba b a b a b A abab−−−−+==，为()()222222111bcb c c b c cb A bcb −−−−=+=，()()222222111cac a c a c ca A caa −−−−=+=，且a b c abc ++=，所以222222222222111ab bc ca bc ac a b a b c b c b c a c a A A A A ab −−−+++−−−=++=++222222222222a a a b b babc abc c a c b c a b c a c b c b b c a c a abc −−+−−−+−+++= 222222222222a a cc a c b c a b c a c b c b b c a c a a b b ab b−−++−−−−=+++ ()()()222222a a cabc a c b c ab a b c c b cb a b c c a ca b b a b c a b −−+++−−+++−−+++=222222222222abc a c b c a b ab abc c b abc b c c b c a ca abc c aabca ab b −−+++−−=++++−−++ 44abcabc=. 故答案为：46. 若一条直线过ABC 的内心，且平分ABC 的周长. 则该直线分ABC 所成的两个图形的面积之比为_______ 【答案】1:1 【解析】【分析】设ABC 的内心为O ，内切圆的半径为r ，作出图形，再由面积公式计算可得. 【详解】设ABC 的内心为O ，内切圆的半径为r ，内切圆与三边的切点分别为D 、E 、F ，则OE OF OD r ===，且OE BC ⊥，OF AC ⊥，OD AB ⊥，过ABC 的内心，且平分ABC 的周长的直线m ，与BC 交于点M ，AC 交于点N ，则AB AN BM CN CM ++=+，又()12ABMN ANO ABO BMO S S S S AN AB BM r =++=++ ， ()12CMN CNO CMO S S S CN CM r =+=+ ，所以ABMN CMN S S = ，即该直线分ABC 所成的两个图形的面积之比为1:1. 故答案为：1:17. 如果甲的身高数或体重数至少有一项比乙大. 则称甲不亚于乙. 在 100 个小伙子中，如果某人不亚于其他 99 人，就称他为棒小伙子，那么 100 个小伙子中的棒小伙子最多可能有 _________人. 【答案】100 【解析】【分析】先讨论有两个、三个小伙子时棒小伙子的最多个数，再设想100个人时的极端情况，分类讨论即可. 【详解】先考虑两个小伙子的情形，如果甲的身高＞乙的身高，且乙的体重＞甲的体重，可知“棒小伙子”最多有2人．再考虑三个小伙子的情形，如果甲的身高＞乙的身高＞丙的身高，且丙的体重＞乙的体重＞甲的体重，可知“棒小伙子”最多有3人．由此可以设想，当有100个小伙子时，设每个小伙子为()1,2,,100i A i = ，其身高为i x ，体重为i y ，当121100i i x x x x x +>>>>>> 且1009911 i i y y y y y +>>…>>…>> 时，由身高看，i A 不亚于12100,,i i A A A ++ ，由体重看，i A 不亚于1121,,,i i A A A − ，所以，i A 不亚于其他99人，i A 为“棒小伙子”，因此，100个小伙子中的“棒小伙子”最多可能有100个．故答案为：100．8. 如果直角三角形的三边都是 200 以内的正整数，且较长的两边长相差 1 . 那么这样的直角三角形有____________个. 【答案】9 【解析】【分析】利用勾股定理及数的性质计算即可.【详解】不妨设该直角三角形的是三边长依次为,,1x y y +，其中200,N x y x y ∗≤<∈、，由勾股定理知()2222121x y y x y +=+⇒=+，显然21y +为大于1且小于401的奇数，所以x 为大于1且小于20的奇数，则3,5,7,9,11,13,15,17,19x =，即满足题意的直角三角形有9个. 故答案为：99. 用()S n 表示自然数n 的数字和. 例如: ()10101S =+=，()90990918S =++=.若对任意自然数n ，都有()n S n x +≠. 则满足这个条件的最大的两位整数x 的值是_________. 【答案】97 【解析】【分析】列出90,,80n = 时()n S n +的值，再判断80n <且n 为自然数时()n S n +的取值情况，即可得解.【详解】因()909099S +=，()8989106S +=，()8888104S +=， ()8787102S +=，()8686100S +=，()858598S +=，()848496S +=， ()838394S +=，()828292S +=，()818190S +=，()808088S +=，当80n <且n 为自然数时，()797995n S n +≤++=，当90n >且n 为自然数时，nn +SS (nn )>99，所以若对任意自然数n ，都有()n S n x +≠， x 的值为97. 故答案为：9710. 把一副扑克牌从上到下按照大王、小王、黑桃 A 、红桃 A 、方块 A 、梅花 A 、黑桃 2 、红桃 2、方块 2、梅花 2、...、黑桃 K 、红桃 K 、方块 K 、梅花 K 的顺序依次叠成一叠，然后执行步骤①: 把整叠牌最上面一张丢掉，再执行步骤②: 把整叠牌最上面一张移到整叠牌的最下面，再执行步骤①，再执行步骤②， ...... 步骤①和步骤②依次执行直至整叠牌只剩下一张，请问：最后剩下的这张牌是_________. 【答案】红桃J 【解析】【分析】根据规律分析每轮丢掉的牌与剩下的牌，即可分析出最后剩下的牌. 【详解】不妨将54张牌按照上述顺序依次标号为1，2，，54，第一轮将丢掉1，3，5，，53；第二轮将丢掉2，6，10，，54，此时需将4号移到整叠牌的最下面，剩下的牌从上到下按顺序依次为8，12，16，20，24，28，32，36，40，44，48，52，4；第三轮将丢掉：8，16，24，32，40，48，4，此时需将12号移到整叠牌的最下面，为剩下的牌从上到下按顺序依次为20，28，36， 44，52，12；第四轮将丢掉：20，36， 52，剩下的牌从上到下按顺序依次为28，44，12；第五轮将丢掉：28，12，故最后剩下的为44；又241042+×=，所以第44张为红桃J ，故最后剩下的这张牌是红桃J . 故答案为：红桃J11. 若实数 a b ，满足a b +=，则 a 的取值范围为_________. 【答案】0a ≥ 【解析】【分析】利用根式的意义先确定0a ≥，再利用换元法及反比例函数、二次函数的性质计算即可.【详解】由题意易知00a b a b +≥ −≥ ，所以0a ≥，①显然0a =时，0b =，②当0a >时，不妨设b ta =，此时()()101110a b t a t a b t a +=+≥⇒−≤≤−=−≥，则()()()21141t a t a t +=⇒+=−若1t =，则00a b a b −=⇒== 若1t =−，则00a b a b +=⇒==，也不符合题意，所以11t −<<，即()()()()()2222418418411181142111t t a t t t t t −−+ ===−=−− ++ +++，易知11t −<<时1101221t t<+<⇒<+，令11m t =+，则211842a m =−− ，由二次函数的性质可知211180242a >−−= ，综上，0a ≥. 故答案为：0a ≥.12. 已知()()21R f x ax x =−∈，若关于 x 的方程 ()f x x = 与 ()()f f x x = 都有解，且两个方程的解完全相同，则实数 a 的取值范围是_________. 【答案】1344a −≤≤ 【解析】【分析】分0a =与0a ≠进行讨论，当0a ≠时结合一元二次方程的根的判别式与条件两个方程可知2210a x ax a +−+=要么没有实根，要么实根是方程210ax x −−=的根，计算即可得. 【详解】由已知()210f x x ax x =⇒−−=，()()()22110f f x x a ax x =⇒−−−= ()()342222221110a x a x x a axx a x ax a ⇒−−+−=−−+−+=，由题意可知210ax x −−=有实根， ①当0a =时，有()1f x =−，即1x =−，令()()f f x x =，即()11f x −=−=，符合要求；②当0a ≠时，()f x x =有解，则140a ∆=+≥，解得14a ≥−，要满足题意，此时2210a x ax a +−+=要么没有实根，要么实根是方程210ax x −−=的根，若2210a x ax a +−+=没有实根，则()22410a a a ∆=−−<，解得34a <；若2210a x ax a +−+=有实根且实根是方程210ax x −−=的根，则由方程210ax x −−=，得22a x ax a +，代入2210a x ax a +−+=，有210ax +=．由此解得12x a =−，再代入得111042a a +−=，由此34a =，综上所述， a 的取值范围是1344a −≤≤．故答案为：1344a −≤≤.二、解答题13. 已知函数()22f x x bx c =−++在1x =时有最大值1. （1）求实数⋅b c 的值；（2）设0m n <<，若当m x n ≤≤时，()f x 最小值为1n ，最大值为1m，求m ，n 的值. 【答案】（1）4− （2）1m =，n =【解析】的【分析】（1）依题意可得()1411b f = =，即可求出b 、c 的值；（2）由（1）可得()()2211f x x =−−+，即可得到1m ≥，从而得到()1f m m =且()1f n n=，从而得到m ，n 是关于x 的方程()21211x x−−+=的两个解，即可求出m 、n 的值.【小问1详解】因()22f x x bx c =−++在1x =时有最大值1，则()14121bf b c = =−++=，解得41b c = =− ，所以4b c ⋅=−；【小问2详解】由（1）可得()()22241211f x x x x =−+−=−−+，则()1f x ≤，又0m n <<，所以11m≤，则1m ≥，所以当m x n ≤≤时()f x 单调递减，所以()()21211f m m m=−−+=，且()()21211f n n n=−−+=，所以m ，n 是关于x 的方程()21211x x−−+=的两个解，即()()212210x x x −−−=，解方程得11x =，2x =3x =，又1m n ≤<，所以1m =，n =.为。

高一数学周练(含答案)

高一数学周练一、单选题(共40分)1．若集合{4},{31}M x N x x =<=≥∣，则M N ⋂=（） A ．{}02x x ≤< B ．123x x ⎧⎫≤<⎨⎬⎩⎭C ．{}316x x ≤<D ．1163x x ⎧⎫≤<⎨⎬⎩⎭2．函数 y = ） A ．3,2⎛⎫-∞- ⎪⎝⎭B ．3,2⎡⎫-+∞⎪⎢⎣⎭C ．[)0,+∞D ．(],3∞--][)0,+∞.3．“角α，β的终边关于y x =轴对称”是“22sin sin 1αβ+=”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件【答案】A【分析】根据三角函数的性质的即可判断求解.【详解】若角α，β的终边关于y x =轴对称，则sin α＝cos β，则2222sin sin cos sin =1αβββ+=+；若22sin sin 1αβ+=，则22sin =cos αβ，则sin α＝±cos β，则角α，β的终边关于y x =或y ＝－x 轴对称；综上，“角α，β的终边关于y x =轴对称”是“22sin sin 1αβ+=”的充分不必要条件. 故选：A.4．已知方程ln 112x x =-的实数解为0x ，且()0,1x k k ∈+，*k ∈N ，则k =（） A ．1 B ．2 C ．3 D ．4【答案】D【解析】先转化为两个简单函数判断交点所在区间的大致范围，再由零点判定定理确定即可．【详解】解：112lnx x =-，令()g x lnx =，()112h x x =-在同一坐标系画出图象可得由图可知01x >，令()211f x lnx x =+-，()()129(27)0f f ln =-->，()()23(27)(35)0f f ln ln =-->， ()()34(35)(43)0f f ln ln =-->， ()()45(43)(51)0f f ln ln =--<，()04,5x ∴∈4k ∴=，故选：D ．【点睛】本题主要考查函数零点所在区间的求法，图象法和零点判定定理．将函数的零点问题转化为两个函数交点的问题是常用的手段，属于基础题．5．如图是下列四个函数中的某个函数在区间[3,3]-的大致图像，则该函数是（）A ．3231x xy x -+=+B ．321x xy x -=+C ．22cos 1x xy x =+ D ．22sin 1xy x =+6．将函数()sin (0)3f x x ωω⎛⎫=+> ⎪⎝⎭的图像向左平移π2个单位长度后得到曲线C ，若C关于y 轴对称，则ω的最小值是（） A ．16B ．14C ．13D ．127．记函数()sin (0)4f x x b ωω⎛⎫=++> ⎪⎝⎭的最小正周期为T ．若23T ππ<<，且()y f x =的图象关于点3,22π⎛⎫ ⎪⎝⎭中心对称，则2f π⎛⎫= ⎪⎝⎭（）A ．1B ．32C ．52 D ．38．已知函数()131,0ln ,0x x f x x x +⎧-⎪=⎨>⎪⎩若函数()()g x f x a =-有3个零点，则a 的取值范围是（） A ．()0,1 B ．(]0,2C ．()2,+∞D ．()1,+∞【答案】A【分析】要使函数()()g x f x a =-有三个零点，则()f x a =有三个不相等的实根，即()f x 与y a =的图象有三个交点，结合函数的性质及图象即可得出.【详解】要使函数()()g x f x a =-有三个零点，则()f x a =有三个不相等的实根，即()f x 与y a =的图象有三个交点，当1x ≤-时，113x f x在(],1-∞-上单调递减，()0,1f x ；当10-<≤x 时，()131x f x +=-在(]1,0-上单调递增，()0,2f x ；当0x >时，()ln f x x =在()0,∞+上单调递增，()f x ∈R ；由()f x 与y a =的图象有三个交点，结合函数图象可得()0,1a ∈，故选：A.二、多选题(共20分)9．已知函数f （x ）＝2sin （2x ﹣6π），则如下结论：其中正确的是（） A ．函数f （x ）的最小正周期为π； B ．函数f （x ）在[6π，512π]上的值域为[1； C ．函数f （x ）在7(,)312ππ上是减函数；D ．函数y ＝f （x ）的图象向左平移6π个单位得到函数y ＝2sin2x 的图象，10．下列结论正确的是（）A ．若α，β的终边相同，则αβ-的终边在x 的非负半轴上B ．函数()log 1a f x x =+（0a >且1a ≠）恒过定点(),2aC ．函数()22x f x x =-只有两个零点D ．己知一扇形的圆心角60α=︒，且其所在圆的半径3R =，则扇形的弧长为π11．如图，摩天轮的半径为40m ，其中心O 点距离地面的高度为50m ，摩天轮按逆时针方向匀速转动，且20min 转一圈，若摩天轮上点P 的起始位置在最高点处，则摩天轮转动过程中（）A ．转动10min 后点P 距离地面10mB ．若摩天轮转速减半，则转动一圈所需的时间变为原来的12C ．第17min 和第43min 点P 距离地面的高度相同D ．摩天轮转动一圈，点P 距离地面的高度不低于70m 的时间为5min 【详解】解：摩天轮2010t t ππ=，(02)ϕπ是以轴正半轴为始边，轴正半轴为始边，为终边的角为P 的纵坐标为又由题知，P 点起始位置在最高点处，2π5070，1102t，020t ， 0210t ππ，103t ππ或52310tπππ，解得1003t 或50203t ， 20min 3，故D 错误．故选：AC ．12．给出下面四个结论，其中正确的是（） A ．函数()()ln sin f x x =的定义域是()0,π. B ．()sin sin 122x xf x =+的值域为52,2⎡⎤⎢⎥⎣⎦.C ．函数()sin 2f x x x =-+在区间()2,4上有唯一一个零点.D ．角πα6=是1cos 22α=-的必要不充分条件.三、填空题(共20分)13．已知sin π3a ⎛⎫- ⎪⎝⎭＝13，则cos 5π()6a -＝________．【详解】sin 14．定义在R 上的偶函数()f x ，当],(0x ∈-∞时，()f x 单调递减，则()()231f x f x +<-的解集为______．15．已知α为第二象限角，cos 2sin()24απα⎛⎫--+= ⎪⎝⎭，则cos α=___________.16．函数sin(2)4y x π=+的图像与直线y ＝a 在(0，98π)上有三个交点，其横坐标分别为1x ，2x ，3x ，则123x x x ++的取值范围为_______.8442⎝⎭πππ利用对称性求出答案四、解答题(共70分)17．已知全集U =R ，集合{}2|2150A x x x =--<，集合()(){}2|210B x x a x a =-+-<. （1）若1a =，求UA 和B ；（2）若A B A ⋃=，求实数a 的取值范围. ）UA ={x ∴x {|3U A x x ∴=-或5}x ，若1a =，则集合{|(2B x x =-（2）因为A B A ⋃=，所以当B =∅时，221a a =-，解当B ≠∅时，即1a ≠时，）可知集合{|A x =-22135a a --，解得15a，且综上所求，实数a 的取值范围为：15a-．【点睛】本题主要考查了集合的基本运算，考查了一元二次不等式的解法，是基础题．18．已知函数()()()sin 20f x x ϕϕ=+<<π的图象关于点,012⎛⎫- ⎪⎝⎭对称.(1)求ϕ的值；(2)将函数()y f x =的图象向右平移6π个单位，然后将所得的图象上各点的横坐标缩小到原来的12倍（纵坐标不变），得到函数()y g x =的图象.当0,4x π⎡⎤∈⎢⎥⎣⎦时，求函数()g x 的值域.19．已知函数2()2sin 1f x x x θ=+-，1[]2x ∈．（1）当6πθ=时，求()f x 的最大值和最小值；（2）若()f x 在1[]2x ∈上是单调函数，且[0,2)θπ∈，求θ的取值范围．443366【详解】试题分析：（1）当时，在上单调递减，在上单调递增当时，函数有最小值当时，函数有最小值（2）要使在31[,]22x ∈-上是单调函数，则或即或，又解得：20．已知函数()sin()0,||2f x x ωϕωϕ⎛⎫=+>< ⎪⎝⎭的部分图象如图所示.（1）写出函数f （x ）的最小正周期T 及ω、φ的值；（2）求函数f （x ）在区间,44ππ⎡⎤-⎢⎥⎣⎦上的最大值与最小值.,44ππ⎡⎤-⎢⎥⎣⎦当23x π+=21．已知二次函数2()21(0)g x mx mx n m =-++>在区间[0，3]上有最大值4，最小值0．（1）求函数()g x 的解析式；（2）设()2()g x x f x x-=．若()220x xf k -⋅在[3,3]x ∈-时恒成立，求k 的取值范围．22．已知函数()21log 1x f x x -=+． (1)若()1f a =，求a 的值；(2)判断函数()f x 的奇偶性，并证明你的结论；(3)若()f x m ≥对于[)3,x ∈+∞恒成立，求实数m 的范围．【答案】(1)3- (2)奇函数，证明见解析f a=，）()1-3为奇函数，证明如下：，解得：x。

高一上数学周测(8)

第三章 函数的概念与性质 单元检测卷(含解析)—2024-2025学年高一上学期数学必修第一册

江苏无锡市湖滨中学2024-2025学年高一(上)数学第8周阶段性训练模拟练习【含答案】

高一上数学测试题及答案

襄阳市普通高中 2022-2023 学年度上学期期末教学质量检测统一测试高一数学(含答案解析)

中职数学三角函数单元测试题

高一数学周测试卷

2024-2025学年上海华二普陀高一上学期数学周测试卷及答案(2024.09)

2023-2024学年深圳市实验学校光明部高一第一次周测数学试题及答案

湖北鄂东南省级示范高中教育教学改革联盟学校2024-2025学年高一上学期起点考试数学试题(含解析)

2024-2025学年湖北省孝感市孝感高级中学高一(上)开学数学试卷(含答案)

湖南省长沙市周南中学2024-2025学年高一上学期第一阶段性测试(10月)数学试题

2022-2023学年北师大版高一上数学月考试卷(含解析)

高一数学上学期第八次周考试题及答案

河南省南阳市第二完全学校高级中学2022-2023学年高一上学期第三次(线上)周考数学试卷

高一数学周考卷

2024-2025学年贵州省部分学校高一上学期联考数学试题(含答案)

高一(上)数学第二章函数单元测试题7-8 人教版

浙江宁波市效实中学2024-2025学年新高一上学期分班考试数学试卷(解析版)

高一数学周练(含答案)

第三章函数的概念与性质单元检测卷(含解析)—2024-2025学年高一上学期数学必修第一册