海南中学九年级下学期期中试卷

合集下载

海南九年级期中试卷语文【含答案】

海南九年级期中试卷语文【含答案】专业课原理概述部分一、选择题1. 下列哪个字在古代汉语中通常表示“水”？A. 氵B. 水字底C. 水部首D. 水字旁2. 《离骚》的作者是谁？A. 屈原B. 宋玉C. 墨子D. 庄子3. 以下哪个成语出自《论语》？A. 温故知新B. 画龙点睛C. 对牛弹琴D. 井底之蛙4. 下列哪个朝代不属于中国古代文学史上的“唐宋八大家”？A. 唐朝B. 宋朝C. 元朝D. 明朝5. 下列哪个词牌名出自《诗经》？A. 关雎B. 江南C. 蒹葭D. 桃夭二、判断题1. 《红楼梦》是中国古代四大名著之一。

（√）2. “赋、比、兴”是《诗经》的主要表现手法。

（√）3. “唐诗、宋词、元曲、明清小说”概括了中国古代文学的发展脉络。

（√）4. “床前明月光，疑是地上霜”出自李白的《静夜思》。

（√）5. “但愿人长久，千里共婵娟”出自苏轼的《水调歌头》。

（√）三、填空题1. “三人行，必有我师焉”出自《论语》中的哪一篇？2. “山不在高，有仙则名”出自哪篇古文？3. “洛阳亲友如相问，一片冰心在玉壶”出自哪位诗人的作品？4. “先天下之忧而忧，后天下之乐而乐”出自哪篇古文？5. “春眠不觉晓，处处闻啼鸟”出自哪位诗人的作品？四、简答题1. 请简要介绍《三国演义》的主要人物及故事梗概。

2. 请简要介绍《水浒传》的主要人物及故事梗概。

3. 请简要介绍《西游记》的主要人物及故事梗概。

4. 请简要介绍《红楼梦》的主要人物及故事梗概。

5. 请简要介绍《诗经》的主要内容和艺术特点。

五、应用题1. 请以“我的家乡”为题，写一篇短文，不少于200字。

2. 请以“我最喜欢的一位诗人”为题，写一篇短文，不少于200字。

3. 请以“读书的好处”为题，写一篇短文，不少于200字。

4. 请以“我的梦想”为题，写一篇短文，不少于200字。

5. 请以“环保意识”为题，写一篇短文，不少于200字。

六、分析题1. 请分析《庐山谣》中的“飞流直下三千尺，疑是银河落九天”所运用的修辞手法及其效果。

2024-2025学年海南省海口市美兰区重点名校第二学期初三年级期中考试英语试题试卷含答案

2024-2025学年海南省海口市美兰区重点名校第二学期初三年级期中考试英语试题试卷注意事项：1．答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

Ⅰ. 单项选择1、The UN colorful activities on April 20 to celebrate Chinese Language Day.A．held B．missed C．kept2、Mr. Green is very strict with his children, and he ______ allows them to watch TV on school days.A．always B．usually C．sometimes D．never3、The summer holiday is coming , We`re going to have______ holiday.A．a two-month B．a two-months C．two months D．two-months4、You’d better _______ too much meat. You are much too fat.A．not eat B．eat otherC．not to eat D．don’t eat5、—Excuse me, where is the nearest bookstore around here?—Just go along Center Street and turn left. Xinhua bookstore is ______ your right.A．in B．on C．at D．to6、She usually has ________ egg and some porridge for ________ breakfast.A．an; the B．an; \ C．a; the D．a; \7、The mobile phone has infl uenced people’s life a lot since it _________.A．invents B．inventedC．is invented D．was invented8、— Why do you like living in the countryside?一Because there's noise and fewer cars there.A．less B．little C．fewer D．few9、The terrible earthquake happened ________ 13: 46 ________ the afternoon of March 11th.A．on; in B．at: on C．at; in D．on; on10、I like watching table tennis matches and favourite player is Fan Zhendong.A．my B．your C．his D．herⅡ. 完形填空11、完形填空（10小题，每小题1分，共10分）先通读短文，掌握其大意，然后从A、B、C、D四个选项中选出一个可以填入相应空白处的最佳答案，并将其标号填入答题卡相应位置。

海南省海南中学九年级物理下学期期中试题(无答案)

海南省海南中学2012届九年级物理下学期期中试题（无答案）一、请你来选择（每题2分共22分）1．在以下实验事实中，能说明分子间存在着引力的是（）A．红墨水滴在水中后水被染成了红色B．两个光滑的铅块压紧后会黏在一起C．水与酒精充分混合后总体积会变小 D．要将固体和液体压缩感觉非常困难2．神舟七号载人飞船于2008年9月25日发射升空，并成功实施了中国航天员首次空间出舱活动，如图宇航员出舱后在舱外停留的那一刻（）A．以地球为参照物，飞船是静止的B．以地球为参照物，宇航员是静止的C．以飞船为参照物，宇航员是静止的D．以月球为参照物，宇航员和飞船都是静止的3.小英和妈妈住在河师大沁园宾馆时，在卫生间发现了一种旅行用的“两面针”牙膏，如图所示，根据你的观察和生活经验，你认为下列说法错误的是（）A.挤压牙膏时可反映出力能使物体发生形变B.新的整支牙膏受到的重力是5牛C.牙膏盖上的条纹是为了增大摩擦D.牙膏盖子中间的尖锐物是为了增大压强4. 某同学在实验课上做模拟大自然中“雨”的形成实验时，锥形瓶中注入少量的温水，稍后取一干燥的表面皿盖在瓶口在表面皿中放置一些冰块（如右图所示）；稍后发现在瓶口出现朦胧的“白雾”，表面皿底部看到有小水滴，小水滴逐变大，最终下落到瓶内，由此实验可知雨滴形成的过程和物态变化，下列说法正确的是（）A．水蒸气下降时遇热凝结成水滴，物态变化为液化B．水蒸气上升时遇冷凝结成水滴，物态变化为液化C．水蒸气上升时遇冷凝结成水滴，物态变化为汽化D．水蒸气下降时遇热凝结成水滴，物态变化为汽化5．假设一架战斗机正在空中某一高度做匀速飞行，另一架空中加油机给其加油，加油后战斗机仍以原来的高度和速度做匀速飞行，则战斗机的( )A．动能增加，势能减少，机械能不变 B．动能不变，势能不变，机械能不变C．动能减少，势能不变，机械能减少 D．动能增加，势能增加，机械能增加6．一支铅笔放在水平桌面上处于静止，下列哪对力是平衡力（）A．铅笔受到的重力与桌面对铅笔的支持力B．铅笔受到的重力与铅笔对桌面的压力C．铅笔对桌面的压力与桌面对铅笔的支持力D．铅笔受到的重力与桌子受到的重力7．如图所示，电源电压不变，闭合开关S，滑动变阻器的滑片由a向b移动过程中，下列说法中正确的是（）A．电流表示数减大B．电压表示数减小C．电压表、电流表示数的比值增小D．定值电阻R l消耗的电功率减小8．水在日常生活中有着不可替代的作用，如果水的密度、沸点、凝固点、比热容等性质发生变化。

海南九年级期中试卷【含答案】

海南九年级期中试卷【含答案】专业课原理概述部分一、选择题（每题1分，共5分）1. 下列哪个城市是海南省的省会？A. 三亚B. 海口C. 儋州D. 文昌2. 海南省位于中国的哪个方位？A. 东部B. 南部C. 西部D. 北部3. 海南省的气候类型属于？A. 热带雨林气候B. 热带草原气候C. 亚热带季风气候D. 热带沙漠气候4. 海南省的官方语言是什么？A. 英语B. 汉语C. 海南话D. 傣语5. 海南省的简称是？A. 琼B. 桂C. 粤D. 渝二、判断题（每题1分，共5分）1. 海南省是中国面积最大的省份。

（）2. 海南省的旅游资源丰富，有“东方夏威夷”之称。

（）3. 海南省的省会是三亚。

（）4. 海南省位于北回归线以南。

（）5. 海南省的经济支柱是农业。

（）三、填空题（每题1分，共5分）1. 海南省的省会是______。

2. 海南省位于中国的______方位。

3. 海南省的气候类型属于______。

4. 海南省的官方语言是______。

5. 海南省的简称是______。

四、简答题（每题2分，共10分）1. 请简述海南省的地理位置。

2. 请简述海南省的气候特点。

3. 请简述海南省的旅游资源。

4. 请简述海南省的经济支柱。

5. 请简述海南省的文化特色。

五、应用题（每题2分，共10分）1. 请举例说明海南省的一种旅游资源，并说明其吸引力。

2. 请举例说明海南省的一种特色美食，并说明其特点。

3. 请举例说明海南省的一种传统节日，并说明其庆祝方式。

4. 请举例说明海南省的一种民间艺术，并说明其特色。

5. 请举例说明海南省的一种经济作物，并说明其经济价值。

六、分析题（每题5分，共10分）1. 请分析海南省的旅游业对当地经济发展的影响。

2. 请分析海南省的气候条件对农业生产的影响。

七、实践操作题（每题5分，共10分）1. 请设计一条海南省的旅游路线，包括主要景点和活动安排。

2. 请设计一份海南省的特色美食菜单，包括菜品名称和特点。

海南省九年级下学期期中数学试卷A卷

海南省九年级下学期期中数学试卷A卷一、选择题 (共12题；共24分)1. （2分）﹣8的相反数是（）A . 8B . ﹣C .D . ﹣82. （2分）据统计，2015年广州地铁日均客运量均为6 590 000人次，将6 590 000用科学记数法表示为（）A . 6.59×104B . 659×104C . 65.9×105D . 6.59×1063. （2分）由5个大小相同的正方体组成的几何体如图所示，其主视图是（）A .B .C .D .4. （2分）若x+y=1，则代数式3（4x﹣1）﹣2（3﹣6y）的值为（）A . -8B . 8C . -3D . 35. （2分）剪纸是扬州的非物质文化遗产之一，下列剪纸作品中是中心对称图形的是（）A .B .C .D .6. （2分）对于一组统计数据：3，4，2，2，4，下列说法错误的是（）A . 中位数是3B . 平均数是3C . 方差是0.8D . 众数是47. （2分）如图，在Rt△ABC中，∠ABC=90°．AB=BC．点D是线段AB上的一点，连结CD．过点B作BG⊥CD，分别交CD、CA于点E、F，与过点A且垂直于AB的直线相交于点G，连结DF，给出以下四个结论：① = ；②若点D是AB的中点，则AF= AB；③当B、C、F、D四点在同一个圆上时，DF=DB；④若 = ，则S△ABC=9S△BDF ，其中正确的结论序号是（）A . ①②B . ③④C . ①②③D . ①②③④8. （2分）如图，菱形ABCD的周长为20cm，DE⊥AB，垂足为E，cosA=，则下列结论中正确的个数为（）①DE=3cm；②EB=1cm；③S菱形ABCD=15cm2A . 3个B . 2个C . 1个D . 0个9. （2分）若将抛物线y=2x2先向左平移2个单位，再向下平移1个单位得到一个新的抛物线，则新抛物线的顶点坐标是A . (-2,1)B . (-2,-1)C . (2,1)D . (2,-1)10. （2分））我校七年级某班的师生到距离8千米的农场学农，出发小时后，小亮同学骑自行车从学校按原路追赶队伍，结果他们同时到达农场．已知小亮骑车的速度比队伍步行的速度每小时快6千米．若设队伍步行的速度为每小时x千米，则可列方程（）A .B .C .D .11. （2分）已知A（-1，y1），B（2，y2）两点在双曲线y=上，且 y1＞y2 ，则m的取值范围是（）A . m>0B . m＜0C . m>-D . m＜-12. （2分）小王利用计算机设计了一个程序，输入和输出的数据如下表：输入…12345…输出……那么，当输入数据8时，输出的数据是（）A .B .C .D .二、填空题 (共4题；共4分)13. （1分）当a=2016时，分式的值是________．14. （1分）有6张卡片，每张卡片上分别写有不同的从1到6的一个自然数，从中任意抽出一张卡片，不放回，再抽出一张卡片，以第一次抽取的数字为十位数，第二次抽取的数字为个位数，则组成的两位数是6的倍数的概率是________.15. （1分）如图，OA的方向是北偏东15°，OC的方向是北偏西40°，若∠AOC=∠AOB，则OB的方向是________．16. （1分）若一次函数y=（3a﹣2）x+6随着x的增大而增大，则a的取值范围是________．三、解答题 (共7题；共97分)17. （10分）（1）计算：（2）化简：18. （10分）综合题。

上海海南中学初中数学九年级下期中经典练习卷(答案解析)

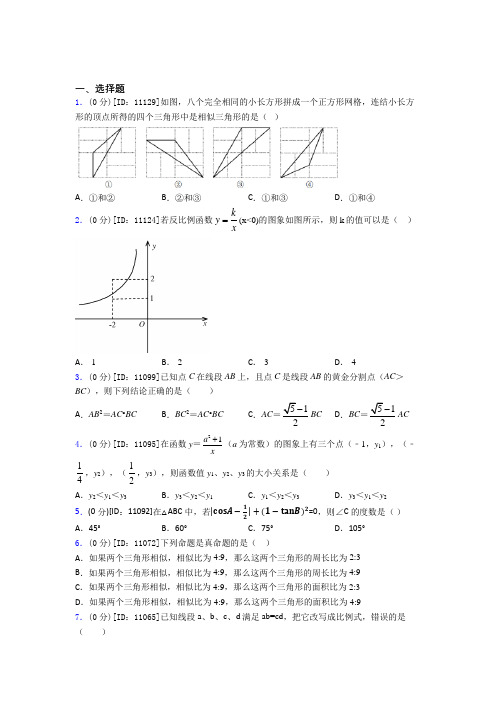
一、选择题1．(0分)[ID：11129]如图，八个完全相同的小长方形拼成一个正方形网格，连结小长方形的顶点所得的四个三角形中是相似三角形的是（）A．①和②B．②和③C．①和③D．①和④2．(0分)[ID：11124]若反比例函数kyx=(x<0)的图象如图所示，则k的值可以是（）A．-1B．-2C．-3D．-43．(0分)[ID：11099]已知点C在线段AB上，且点C是线段AB的黄金分割点（AC＞BC），则下列结论正确的是（）A．AB2＝AC•BC B．BC2＝AC•BC C．AC 51-BC D．BC51-AC4．(0分)[ID：11095]在函数y＝21ax+（a为常数）的图象上有三个点（﹣1，y1），（﹣1 4，y2），（12，y3），则函数值y1、y2、y3的大小关系是（）A．y2＜y1＜y3B．y3＜y2＜y1C．y1＜y2＜y3D．y3＜y1＜y2 5．(0分)[ID：11092]在△ABC中，若|cosA−12|+(1−tanB)2=0，则∠C的度数是（）A．45°B．60°C．75°D．105°6．(0分)[ID：11072]下列命题是真命题的是（）A．如果两个三角形相似，相似比为4:9，那么这两个三角形的周长比为2:3B．如果两个三角形相似，相似比为4:9，那么这两个三角形的周长比为4:9C．如果两个三角形相似，相似比为4:9，那么这两个三角形的面积比为2:3D．如果两个三角形相似，相似比为4:9，那么这两个三角形的面积比为4:97．(0分)[ID：11065]已知线段a、b、c、d满足ab=cd，把它改写成比例式，错误的是（）A．a：d＝c：b B．a：b＝c：d C．c：a＝d：b D．b：c＝a：d 8．(0分)[ID：11056]如图，在以O为原点的直角坐标系中，矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上，反比例函数kyx= (x＞0)与AB相交于点D，与BC相交于点E，若BD=3AD，且△ODE的面积是9,则k的值是( )A．92B．74C．245D．129．(0分)[ID：11046]在△ABC中，若|sinA-32|+(1-tanB)2=0，则∠C的度数是( )A．45°B．60°C．75°D．105°10．(0分)[ID：11044]如图，某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度，他们通过调整测量位置，使斜边DF与地面保持平行，并使边DE 与旗杆顶点A在同一直线上，已知DE=0.5m，EF=0.25m，目测点D到地面的距离DG=1.5m，到旗杆的水平距离DC=20m，则旗杆的高度为( )A．105 m B．(105 1.5)+ mC．11.5m D．10m11．(0分)[ID：11042]如图所示，在△ABC 中，AB＝6，AC＝4，P 是AC 的中点，过 P 点的直线交AB 于点Q，若以 A、P、Q 为顶点的三角形和以A、B、C为顶点的三角形相似，则AQ 的长为 ( )A．3B．3或43C．3或34D．4312．(0分)[ID：11039]在反比例函数4yx=的图象中，阴影部分的面积不等于4的是（）A．B． C．D．13．(0分)[ID：11034]下列四个几何体中，主视图与左视图相同的几何体有（）A．1个B．2个C．3个D．4个14．(0分)[ID：11033]给出下列函数：①y=﹣3x+2；②y=3x；③y=2x2；④y=3x，上述函数中符合条作“当x＞1时，函数值y随自变量x增大而增大“的是（）A．①③B．③④C．②④D．②③15．(0分)[ID：11063]已知点P是线段AB的黄金分割点（AP＞PB），AB=4，那么AP 的长是（）A．252-B．25-C．251-D．52-二、填空题16．(0分)[ID：11230]如图，在△ABC中，CD、BE分别是△ABC的边AB、AC上的中线，则DF EFBF CF++=________。

海南初三初中数学期中考试带答案解析

海南初三初中数学期中考试班级:___________ 姓名：___________ 分数：___________一、选择题1. 2的相反数是（）A．2B．﹣2C．D．2.下列各式不是二次根式的是（）A．B．C．D．3.数据1，0，4，3的平均数是（）A．3B．2.5C．2D．1.5 4.已知图中的两个三角形全等，则∠α的度数是（）A．72°B．60°C．58°D．50°5.如图，DE是△ABC的中位线，若BC的长为3cm，则DE的长是（）A．2cm B．1.5cm C．1.2cm D．1cm 6.当x=﹣2时，代数式x+1的值是（）A．﹣1B．﹣3C．1D．37.要使式子在实数范围内有意义，则x的取值范围是（）A．x≥1B．x＜1C．x≤1D．x≠18.在下列各式中，与（a﹣b）2一定相等的是（）A．a2+2ab+b2B．a2﹣b2C．a2+b2D．a2﹣2ab+b29.方程x（x+1）=0的解是（）A．x="0"B．x=﹣1C．x1=0，x2=﹣1D．x1=0，x2=110.矩形ABCD 的面积是16，它的长与宽的比为4：1，则该矩形的宽为（） A ．1 B ．2 C ．3D ．411.一次函数y=﹣x+2的图象是（）A ．B ．C ．D ．12.若x 1，x 2是一元二次方程x 2﹣5x+6=0的两个根，则x 1+x 2的值是（） A ．1 B ．5 C ．﹣5D ．613.点M （﹣5，2）关于x 轴对称的坐标是（） A ．（﹣5，﹣2） B ．（5，﹣2）C ．（5，2）D ．（﹣5，2）14.将二次函数y=x 2﹣2x+3化为y=（x ﹣h ）2+k 的形式，结果为（）A ．y=（x+1）2+4B ．y=（x ﹣1）2+4C ．y=（x+1）2+2D ．y=（x ﹣1）2+2二、填空题1.“a 的2倍与1的和”用代数式表示是．2.已知点A （3，﹣6）是二次函数y=ax 2上的一点，则这二次函数的解析式是．3.二次函数y=x 2+2x ﹣3的图象的顶点坐标，对称轴是直线，最小值是．4.将抛物线y=x 2+1向下平移2个单位，向右平移3个单位，则此时抛物线的解析式是．三、解答题1.（1）计算：﹣3×（﹣2）2；（2）用公式法解：x 2﹣3x ﹣1=0．2.目前我省小学和初中在校生共136万人，其中小学在校生人数比初中在校生人数的2倍少2万人．问目前我省小学和初中在校生各有多少万人？3.在正方形网格中，△ABC 各顶点都在格点上，点A 、C 的坐标分别为（﹣5，1）、（﹣1，4），结合所给的平面直角坐标系解答下列问题：（1）画出△ABC 关于y 轴对称的△A 1B 1C 1；（2）画出△ABC 关于x 轴对称的△A 2B 2C 2；（3）点C 1的坐标是；点C 2的坐标是．4.如图，在△ABC中，∠ACB=90°，∠CAB=30°，△ABD是等边三角形，E是AB的中点，连接CE并延长交AD 于F．求证：（1）△AEF≌△BEC；（2）四边形BCFD是平行四边形．5.如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为x=1，且抛物线经过A（﹣1，0）、C（0，﹣3）两点，与x 轴交于另一点B．（1）求这条抛物线所对应的函数关系式；（2）在抛物线的对称轴x=1上求一点M，使点M到点A的距离与到点C的距离之和最小，并求出此时点M的坐标．四、计算题根据图1，图2所提供的信息，解答下列问题：（1）2007年海南省城镇居民人均可支配收入为元，比2006年增长 %；（2）求2008年海南省城镇居民人均可支配收入（精确到1元），并补全条形统计图；（3）根据图1指出：2005﹣2008年海南省城镇居民人均可支配收入逐年（填“增加”或“减少”）．海南初三初中数学期中考试答案及解析一、选择题1. 2的相反数是（）A．2B．﹣2C．D．【解析】根据相反数的定义，求解得2的相反数为：﹣2．故选：B．【考点】相反数2.下列各式不是二次根式的是（）A．B．C．D．【答案】D【解析】根据二次根式的定义，可得，，都是二次根式，无意义，故选：D．【考点】二次根式的定义3.数据1，0，4，3的平均数是（）A．3B．2.5C．2D．1.5【答案】C【解析】只要运用求平均数公式：，即可求平均数为：（1+0+4+3）=2．故选C．【考点】算术平均数4.已知图中的两个三角形全等，则∠α的度数是（）A．72°B．60°C．58°D．50°【答案】D【解析】要根据已知的对应边去找对应角，并运用“全等三角形对应角相等”即可由图中的两个三角形全等，a与a，c与c分别是对应边，那么它们的夹角就是对应角，所以∠α=50°.故选：D．【考点】全等三角形5.如图，DE是△ABC的中位线，若BC的长为3cm，则DE的长是（）A．2cm B．1.5cm C．1.2cm D．1cm【答案】B【解析】三角形中位线的性质：三角形的中位线平行于第三边，且等于第三边的一半；本题利用定理计算即可由BC的长为3cm，得DE=1.5．故选B．【考点】三角形中位线定理6.当x=﹣2时，代数式x+1的值是（）A．﹣1B．﹣3C．1D．3【解析】把x=﹣2直接代入x+1 =﹣2+1=﹣1．故选A ．【考点】代数式求值7.要使式子在实数范围内有意义，则x 的取值范围是（） A ．x≥1 B ．x ＜1 C ．x≤1D ．x≠1【答案】A【解析】根据被开方数大于等于0，列式得，x ﹣1≥0，解得x≥1．故选：A ．【考点】二次根式有意义的条件8.在下列各式中，与（a ﹣b ）2一定相等的是（）A ．a 2+2ab+b 2B ．a 2﹣b 2C ．a 2+b 2D ．a 2﹣2ab+b 2【答案】D【解析】根据完全平方公式：（a ﹣b ）2=a 2﹣2ab+b 2．判定即可. 故选D ．【考点】完全平方公式9.方程x （x+1）=0的解是（） A ．x="0" B ．x=﹣1 C ．x 1=0，x 2=﹣1 D ．x 1=0，x 2=1【答案】C【解析】此题考查了学生用降次的方法解一元二次方程的思想，即可由x （x+1）=0，得到x=0，x+1=0，解得x 1=0，x 2=﹣1．故选C ．【考点】解一元二次方程-因式分解法10.矩形ABCD 的面积是16，它的长与宽的比为4：1，则该矩形的宽为（） A ．1 B ．2 C ．3 D ．4【答案】B【解析】设矩形的宽为x ，则长为4x ．根据题意得：4x 2=16，所以x 2=4．根据算术平方根的意义可得x=2．故选：B ．【考点】算术平方根11.一次函数y=﹣x+2的图象是（）A ．B ．C ．D ．【答案】D【解析】因为﹣1＜0，2＞0，根据一函数的性质，可以判断，直线过二、四、一象限．也可求出与x 轴、y 轴的交点，直接连线．如：根据k=﹣1，b=2可知，直线过二、四、一象限，且截距是2．故选D ．【考点】一次函数的图象12.若x 1，x 2是一元二次方程x 2﹣5x+6=0的两个根，则x 1+x 2的值是（） A ．1 B ．5 C ．﹣5D ．6【答案】B【解析】依据一元二次方程根与系数的关系可知，x 1+x 2=﹣，这里a=1，b=﹣5，依据一元二次方程根与系数得：x 1+x 2=5．故选B ．【考点】根与系数的关系13.点M （﹣5，2）关于x 轴对称的坐标是（） A ．（﹣5，﹣2） B ．（5，﹣2）C ．（5，2）D ．（﹣5，2）【答案】A【解析】由关于原x 轴对称的点的纵坐标互为相反数，横坐标相等，得M （﹣5，2）关于x 轴对称的坐标是（﹣5，﹣2），故选：A ．【考点】关于x 轴、y 轴对称的点的坐标14.将二次函数y=x 2﹣2x+3化为y=（x ﹣h ）2+k 的形式，结果为（）A ．y=（x+1）2+4B ．y=（x ﹣1）2+4C ．y=（x+1）2+2D ．y=（x ﹣1）2+2【答案】D【解析】本题是将一般式化为顶点式，由于二次项系数是1，只需加上一次项系数的一半的平方来凑成完全平方式即可得y=x 2﹣2x+3=x 2﹣2x+1﹣1+3=（x ﹣1）2+2．故选：D ．【考点】二次函数的三种形式二、填空题1.“a 的2倍与1的和”用代数式表示是．【答案】2a+1【解析】根据题意可知a 的2倍即为2a ，2a 与1的和，所以代数式为2a+1．【考点】列代数式2.已知点A （3，﹣6）是二次函数y=ax 2上的一点，则这二次函数的解析式是．【答案】y=﹣x 2【解析】将点A （3，﹣6）代入y=ax 2，利用待定系数法法求该二次函数的解析式即可得﹣6=9a ，解得a=﹣；因此该二次函数的解析式为：y=﹣x 2．【考点】待定系数法求二次函数解析式3.二次函数y=x 2+2x ﹣3的图象的顶点坐标，对称轴是直线，最小值是．【答案】（﹣1，﹣4）；x=﹣1，﹣4【解析】把二次函数解析式整理成顶点式形式， y=x 2+2x ﹣3=x 2+2x+1﹣4=（x+1）2﹣4，可求顶点坐标为（﹣1，﹣4）；对称轴是直线x=﹣1，最小值时﹣4．【考点】1、二次函数的性质；2、二次函数的最值4.将抛物线y=x 2+1向下平移2个单位，向右平移3个单位，则此时抛物线的解析式是．【答案】y=x 2﹣6x+8【解析】根据“上加下减，左加右减”的原则，由抛物线y=x 2+1向下平移2个单位后的解析式为：y=x 2+1﹣2=x 2﹣1．再向右平移3个单位所得抛物线的解析式为：y=（x ﹣3）2﹣1，即y=x 2﹣6x+8．【考点】二次函数图象与几何变换三、解答题1.（1）计算：﹣3×（﹣2）2；（2）用公式法解：x 2﹣3x ﹣1=0．【答案】（1）-10（2）x 1=，x 2=【解析】（1）先计算乘方和根号，再计算乘法，最后计算加减即可；（2）公式法求解可得．试题解析：（1）原式=2﹣3×4=2﹣12=﹣10；（2）∵a=1，b=﹣3，c=﹣1， ∴b 2﹣4ac=9+4=13＞0， ∴x=，即x 1=，x 2=．【考点】1、解一元二次方程-公式法；2、二次根式的性质与化简2.目前我省小学和初中在校生共136万人，其中小学在校生人数比初中在校生人数的2倍少2万人．问目前我省小学和初中在校生各有多少万人？【答案】90,46【解析】设初中在校生为x 万人．根据小学在校生人数比初中在校生人数的2倍少2万人，表示出小学在校生人数，从而根据总人数是136万，列方程求解．试题解析：设初中在校生为x 万人，依题意得：x+（2x ﹣2）=136 解得：x=46∴2x ﹣2=2×46﹣2=90（万人）答：目前我省小学在校生为90万人，初中在校生为46万人．【考点】一元一次方程的应用3.在正方形网格中，△ABC 各顶点都在格点上，点A 、C 的坐标分别为（﹣5，1）、（﹣1，4），结合所给的平面直角坐标系解答下列问题：（1）画出△ABC 关于y 轴对称的△A 1B 1C 1；（2）画出△ABC 关于x 轴对称的△A 2B 2C 2；（3）点C 1的坐标是；点C 2的坐标是．【答案】图形见解析【解析】（1）找出对称点A 1、B 1、C 1，连点成线即可得出结论；（2）找出对称点A 2、B 2、C 2，连点成线即可得出结论；（3）根据点C 的坐标，结合对称点的特点即可找出点C 1、C 2的坐标，此题得解．试题解析：（1）画出△ABC 关于y 轴对称的△A 1B 1C 1，如图1所示．（2）画出△ABC 关于x 轴对称的△A 2B 2C 2，如图2所示．（3）∵点C的坐标为（﹣1，4），∴点C1的坐标是（1，4）；点C2的坐标是（﹣1，﹣4）．故答案为：（1，4）；（﹣1，﹣4）．【考点】作图-轴对称变换4.如图，在△ABC中，∠ACB=90°，∠CAB=30°，△ABD是等边三角形，E是AB的中点，连接CE并延长交AD 于F．求证：（1）△AEF≌△BEC；（2）四边形BCFD是平行四边形．【答案】证明见解析【解析】（1）利用等边三角形的性质得出∠DAB=60°，即可得出∠ABC=60°，进而求出△AEF≌△BEC（ASA）；（2）利用平行线的判定方法以及直角三角形的性质得出CF∥BD，进而求出答案．试题解析：（1）∵E是AB中点，∴AE=BE，∵△ABD是等边三角形，∴∠DAB=60°，∵∠CAB=30°，∠ACB=90°，∴∠ABC=60°，在△AEF和△BEC中，∴△AEF≌△BEC（ASA）；（2）∵∠DAC=∠DAB+∠BAC，∠DAB=60°，∠CAB=30°，∴∠DAC=90°，∴AD∥BC，∵E是AB的中点，∠ACB=90°，∴EC=AE=BE，∴∠ECA=30°，∠FEA=60°，∴∠EFA=∠BDA=60°，∴CF∥BD，∴四边形BCFD是平行四边形．【考点】1、平行四边形的判定；2、全等三角形的判定与性质5.如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为x=1，且抛物线经过A（﹣1，0）、C（0，﹣3）两点，与x轴交于另一点B．（1）求这条抛物线所对应的函数关系式；（2）在抛物线的对称轴x=1上求一点M ，使点M 到点A 的距离与到点C 的距离之和最小，并求出此时点M 的坐标．【答案】（1）y=x 2﹣2x ﹣3；（2）（1，﹣2）【解析】（1）利用待定系数设抛物线的解析式为y=ax 2+bx+c ，代入求出即可；（2）根据令x 2﹣2x ﹣3=0，解得x 1=﹣1，x 2=3，所以B 点坐标为（3，0），进而求出直线BC 的解析式，即可得出M 点的坐标．试题解析：（1）设抛物线的解析式为y=ax 2+bx+c ，则有：，解得：所以抛物线的解析式为y=x 2﹣2x ﹣3；（2）令x 2﹣2x ﹣3=0，解得x 1=﹣1，x 2=3，所以B 点坐标为（3，0）．设直线BC 的解析式为y=kx+b ，则，解得，所以直线解析式是y=x ﹣3．当x=1时，y=﹣2．所以M 点的坐标为（1，﹣2）．【考点】1、待定系数法求二次函数解析式，2、待定系数法求一次函数解析式四、计算题根据图1，图2所提供的信息，解答下列问题：（1）2007年海南省城镇居民人均可支配收入为元，比2006年增长 %；（2）求2008年海南省城镇居民人均可支配收入（精确到1元），并补全条形统计图；（3）根据图1指出：2005﹣2008年海南省城镇居民人均可支配收入逐年（填“增加”或“减少”）．【答案】（1）10997，17.1；（2）图形见解析（3）增加【解析】（1）2007年海南省城镇居民人均可支配收入从条形统计图中即可读出；比2006年增长从折线统计图中即可读出．（2）2008年海南省城镇居民人均可支配收入结合2008年的增长率在2007年的基础上即可计算．然后画图即可．（3）因为增长率都是正数，所以总在增长．试题解析：（1）10997，17.1；（2）10997×（1+14.6%）≈12603（元）所补全的条形图如图所示；（3）增加．【考点】1、条形统计图；2、折线统计图。

海南九年级期中试卷【含答案】

海南九年级期中试卷【含答案】专业课原理概述部分一、选择题（每题1分，共5分）1. 下列哪个城市是海南省的省会？A. 三亚B. 海口C. 儋州D. 文昌2. 海南省位于中国的哪个方位？A. 东部B. 南部C. 西部D. 北部3. 海南省的气候类型属于？A. 热带雨林气候B. 热带季风气候C. 亚热带季风气候D. 温带季风气候4. 海南省的主要经济作物有哪些？A. 橡胶、椰子、胡椒B. 棉花、茶叶、甘蔗C. 水稻、小麦、玉米D. 苹果、梨、桃子5. 海南省的旅游资源丰富，其中哪个景点被称为“天涯海角”？A. 亚龙湾B. 天涯海角C. 大东海D. 西岛二、判断题（每题1分，共5分）1. 海南省的简称是“琼”。

（）2. 海南省的行政中心是三亚市。

（）3. 海南省的气候特点是全年高温多雨。

（）4. 海南省的主要粮食作物是水稻和小麦。

（）5. 海南省的旅游景点有亚龙湾、天涯海角、大东海等。

（）三、填空题（每题1分，共5分）1. 海南省的简称是______。

2. 海南省的行政中心是______。

3. 海南省的气候特点是______。

4. 海南省的主要粮食作物是______。

5. 海南省的旅游景点有______、______、______等。

四、简答题（每题2分，共10分）1. 请简述海南省的地理位置和气候特点。

2. 请列举海南省的主要经济作物和旅游资源。

3. 请简述海南省的行政区划和人口分布。

4. 请简述海南省的历史和文化特点。

5. 请简述海南省的经济发展现状和未来规划。

五、应用题（每题2分，共10分）1. 请计算海南省的总面积和人口密度。

2. 请分析海南省的气候特点对农业发展的影响。

3. 请列举海南省的三大旅游城市及其主要景点。

4. 请分析海南省的经济发展优势和劣势。

5. 请设计一条海南省的旅游路线，包括主要景点和行程安排。

六、分析题（每题5分，共10分）1. 请分析海南省的地理位置和气候特点对经济发展的影响。

海南九年级期中试卷【含答案】

海南九年级期中试卷【含答案】专业课原理概述部分海南九年级期中试卷一、选择题（每题1分，共5分）1. 下列哪种动物是海南省特有的珍稀物种？A. 海南孔雀雉B. 海南兔C. 海南坡鹿D. 海南金钱龟2. 海南省的气候类型主要是？A. 热带雨林气候B. 热带季风气候C. 亚热带季风气候D. 温带季风气候3. 海南省的省会是？A. 三亚B. 海口C. 琼海D. 儋州4. 海南岛与大陆之间的海峡是？A. 琼州海峡B. 台湾海峡C. 巴士海峡D. 马六甲海峡5. 海南省的主要经济作物是？A. 橡胶B. 水稻C. 棉花D. 小麦二、判断题（每题1分，共5分）1. 海南省是中国最南端的省份。

（）2. 海南省的方言主要是闽南语。

（）3. 海南省的旅游业是其重要的经济支柱。

（）4. 海南省的矿产资源丰富，有“南海石油城”之称。

（）5. 海南省的环岛高速公路是中国最长的环岛高速公路。

（）三、填空题（每题1分，共5分）1. 海南省的简称是______。

2. 海南省的行政区域划分为______个地级市和______个自治州。

3. 海南省的最高峰是______。

4. 海南省的国家级风景名胜区有______个。

5. 海南省的四大名菜是______、______、______、______。

四、简答题（每题2分，共10分）1. 简述海南省的地理位置和地形特点。

2. 简述海南省的气候特点。

3. 简述海南省的旅游资源。

4. 简述海南省的历史文化。

5. 简述海南省的经济特点。

五、应用题（每题2分，共10分）1. 请列举海南省的三个旅游景点，并简要介绍其特色。

2. 请简述海南省的农业发展情况。

3. 请简述海南省的工业发展情况。

4. 请简述海南省的交通发展情况。

5. 请简述海南省的环境保护情况。

六、分析题（每题5分，共10分）1. 分析海南省发展旅游业的优势和劣势。

2. 分析海南省发展农业的优势和劣势。

七、实践操作题（每题5分，共10分）1. 设计一份海南省旅游攻略，包括景点选择、交通方式、住宿推荐等。

海南省海口市国兴中学2023-2024学年九年级下学期期中考试物理试题A卷(含答案)

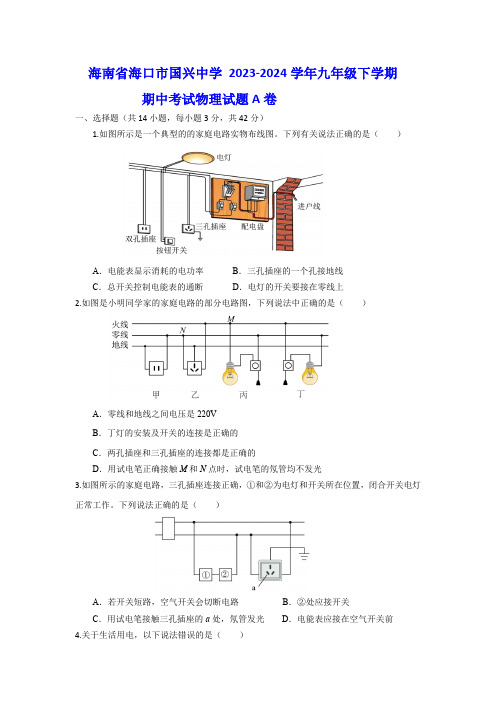
海南省海口市国兴中学2023-2024学年九年级下学期期中考试物理试题A卷一、选择题（共14小题，每小题3分，共42分）1.如图所示是一个典型的的家庭电路实物布线图。

下列有关说法正确的是（）A．电能表显示消耗的电功率B．三孔插座的一个孔接地线C．总开关控制电能表的通断D．电灯的开关要接在零线上2.如图是小明同学家的家庭电路的部分电路图，下列说法中正确的是（）A．零线和地线之间电压是220VB．丁灯的安装及开关的连接是正确的C．两孔插座和三孔插座的连接都是正确的D．用试电笔正确接触M和N点时，试电笔的氖管均不发光3.如图所示的家庭电路，三孔插座连接正确，①和②为电灯和开关所在位置，闭合开关电灯正常工作。

下列说法正确的是（）A．若开关短路，空气开关会切断电路B．②处应接开关C．用试电笔接触三孔插座的a处，氖管发光D．电能表应接在空气开关前4.关于生活用电，以下说法错误的是（）A BC DA．发生如图所示的触电时，漏电保护器会切断电流B．绝缘皮破损容易造成短路，也容易造成触电事故C．图中电能表与空气开关允许通过的最大电流相同D．保险丝是用铅锑合金制作的，电阻比较大、熔点比较低5.图所示的是关于生活用电的四个情境，下列说法中正确的是（）A．图甲：使用螺丝刀试电笔时不能用指尖抵住上端的金属帽B．图乙：与三孔插座中标有①的插孔相连的是火线C．图丙：人站在干燥的木凳上同时接触火线和零线，不会触电D．图丁：用电器的总功率过大，容易发生火灾6.对下列四幅图的表述正确的是（）A. 甲图反映的是电动机的工作原理B. 乙图能实现电能转化为机械能C. 丙图闭合开关后，小磁针N极逆时针偏转D. 丁图中小磁针N极顺时针偏转7.如图所示是某同学设计的探究电流通过导体时产生热的多少与哪些因素有关的实验装置。

两个透明容器中密封着等量的空气，U形管中液面高度的变化反映密闭空气温度的变化。

下列说法正确的是（）A. 通电一段时间，两个透明容器中空气内能增大是通过做功的方式改变B. 该实验装置不能探究电流通过导体产生的热量与通电时间的关系C. 若要探究电流通过导体产生的热量与电流的关系，右侧透明容器中应接入阻值是5Ω的电阻D. 若要探究电流通过导体产生的热量与电阻的关系，右侧透明容器中应接入阻值是10Ω的电阻8.如图所示是生活中常见的刷卡机，当人们将带有磁条的信用卡在刷卡机指定位置刷一下，刷卡机的检测头就会产生感应电流便可读出磁条上的信息。

海南初三初中数学期中考试带答案解析

海南初三初中数学期中考试班级:___________ 姓名：___________ 分数：___________一、选择题1.下列方程是一元二次方程的是（）A．2x+3="0"B．y2+x﹣2="0"C．+x2="1"D．x2+1=02.下列函数解析式中，一定为二次函数的是（）A．y=3x﹣1B．y=ax2+bx+c C．s=2t2﹣2t+1D．y=x2+3.二次函数y=x2+2x﹣1的最小值是（）A．﹣1B．﹣2C．1D．24.下列这些复杂的图案都是在一个图案的基础上，在“几何画板”软件中拖动一点后形成的，它们中每一个图案都可以由一个“基本图案”通过连续旋转得来，旋转的角度正确的是（）A．30°B．45°C．60°D．90°5.一元二次方程x（x﹣1）=0的解是（）A．x="0"B．x="1"C．x=0或x=﹣1D．x=0或x=16.抛物线y=x2+4的顶点坐标是（）A．（4，0）B．（﹣4，0）C．（0，﹣4）D．（0，4）7.如图，将等腰三角板向右翻滚，依次得到b、c、d，下列说法中，不正确的是（）A．a到b时旋转B．a到c是平移C．a到d是平移D．b到c是旋转8.二次函数y=x2+4x﹣5的图象的对称轴为（）A．x="4"B．x=﹣4C．x="2"D．x=﹣29.某厂一月份的总产量为500吨，三月份的总产量达到为700吨．若平均每月增长率是x，则可以列方程（）A．500（1+2x）="700"B．500（1+x2）="700"C．500（1+x）2="700"D．700（1+x2）=50010.将抛物线y=x 2向左平移2个单位长度，再向下平移3个单位长度，得到的抛物线的函数表达式为（）A ．y=（x+2）2﹣3B ．y=（x+2）2+3C ．y=（x ﹣2）2+3D ．y=（x ﹣2）2﹣311.已知x 1、x 2是一元二次方程x 2﹣4x+1=0的两个根，则x 1+x 2等于（）A ．﹣4B ．﹣1C ．1D ．412.风车应做成中心对称图形，并且不是轴对称图形，才能在风口处平稳旋转．现有一长条矩形硬纸板（其中心有一个小孔）和两张全等的矩形薄纸片，将纸片粘到硬纸板上，做成一个能绕着小孔平稳旋转的风车．正确的粘合方法是（）A ．B ．C ．D ．13.如图，在正方形ABCD 中，E 为DC 边上的点，连接BE ，将△BCE 绕点C 顺时针方向旋转90°得到△DCF ，连结EF ，若∠BEC=70°，那么∠CEF 的度数为（）A ．20°B ．25°C ．40°D ．45°14.一次函数y=ax+b 与二次函数y=ax 2+bx+c 在同一坐标系中的图象可能是（）A ．B ．C ．D ．15.关于函数y=x 2+2x ，下列说法正确的是①图形是轴对称图形 ②图形经过点（﹣1，1） ③图形有一个最低点 ④当x ＞1时，y 随x 的增大而增大．二、填空题1.方程3x 2﹣2x ﹣1=0的一次项系数是，常数项是．2.点A （﹣1，2）关于原点对称点B 的坐标是．三、解答题1.关于x 的一元二次方程2x 2﹣4x+m ﹣1=0有两个相等的实数根，则m 的值为．2.解下列方程：（1）x 2﹣2x=﹣1；（2）（x+3）2=2x （x+3）．3.如图是抛物线形拱桥，当拱顶高离水面2m 时，水面宽4m ．若水面下降了2.5m ，水面的宽度增加多少？4.如图，正方形ABCD 与正方形A 1B 1C 1D 1关于某点中心对称，已知A ，D 1，D 三点的坐标分别是（0，4），（0，3），（0，2）．（1）求对称中心的坐标．（2）写出顶点B ，C ，B 1，C 1的坐标．5.如图，将一块正方形空地划出部分区域进行绿化，原空地一边减少了2m ，另一边减少了3m ，剩余一块面积为20m 2的矩形空地，则原正方形空地的边长是多少？6.已知二次函数y=x 2﹣4x+3．（1）该函数的顶点坐标是，与x 轴的交点坐标是；（2）在平面直角坐标系中，用描点法画出该二次函数的图象；（3）根据图象回答：当0≤x ＜3时，y 的取值范围是．7.已知：如图，二次函数y=ax2+bx+c的图象与x轴交于A、B两点，其中A点坐标为（﹣1，0），点C（0，5），另抛物线经过点（1，8），M为它的顶点．（1）求抛物线的解析式；（2）求△MCB的面积．（3）在坐标轴上，是否存在点N，满足△BCN为直角三角形？如存在，请直接写出所有满足条件的点N．海南初三初中数学期中考试答案及解析一、选择题1.下列方程是一元二次方程的是（）A．2x+3="0"B．y2+x﹣2="0"C．+x2="1"D．x2+1=0【答案】D【解析】根据一元二次方程的定义：只含有一个未知数，并且未知数的最高次数是2的整式方程叫一元二次方程进行分析即可知：A、不是一元二次方程，故此选项错误；B、不是一元二次方程，故此选项错误；C、不是一元二次方程，故此选项错误；D、是一元二次方程，故此选项正确；故选：D．【考点】一元二次方程的定义2.下列函数解析式中，一定为二次函数的是（）A．y=3x﹣1B．y=ax2+bx+c C．s=2t2﹣2t+1D．y=x2+【答案】C【解析】根据二次函数的定义，可得：A、y=3x﹣1是一次函数，故A错误；B、y=ax2+bx+c （a≠0）是二次函数，故B错误；C、s=2t2﹣2t+1是二次函数，故C正确；D、y=x2+不是二次函数，故D错误；故选：C．【考点】二次函数的定义3.二次函数y=x2+2x﹣1的最小值是（）A．﹣1B．﹣2C．1D．2【答案】B【解析】用配方法可得y=x2+2x﹣1=（x+1）2﹣2，可见二次函数y=x2+2x﹣1的最小值是﹣2．故选B．【考点】二次函数的最值4.下列这些复杂的图案都是在一个图案的基础上，在“几何画板”软件中拖动一点后形成的，它们中每一个图案都可以由一个“基本图案”通过连续旋转得来，旋转的角度正确的是（）A．30°B．45°C．60°D．90°【答案】C【解析】观察每一个图案都可以由一个“基本图案”通过连续旋转得到，就是看这个图形可以被通过中心的射线平分成几个全等的部分，即可由每一个图案都可以被通过中心的射线平分成6个全等的部分，则旋转的角度是60度．故选C．【考点】利用旋转设计图案5.一元二次方程x（x﹣1）=0的解是（）A．x="0"B．x="1"C．x=0或x=﹣1D．x=0或x=1【答案】D【解析】方程利用两数相乘积为0，两因式中至少有一个为0，因此可由方程x（x﹣1）=0，可得x=0或x﹣1=0，解得：x=0或x=1．故选：D．【考点】解一元二次方程-因式分解法6.抛物线y=x2+4的顶点坐标是（）A．（4，0）B．（﹣4，0）C．（0，﹣4）D．（0，4）【答案】D【解析】二次函数y=ax2+k的顶点坐标是（0，k），直接由抛物线y=x2+4的顶点坐标是（0，4）．故选D．【考点】二次函数的性质7.如图，将等腰三角板向右翻滚，依次得到b、c、d，下列说法中，不正确的是（）A．a到b时旋转B．a到c是平移C．a到d是平移D．b到c是旋转【答案】B【解析】根据旋转、平移的判断方法，可知：A．a到b是以直角顶点为旋转中心的旋转，本项正确；B．a到c不是沿直线移动一定距离得到新图形，所以不是平移，本项错误；C．a到d是沿直线移动一定距离得到新图形是平移，本项正确；D．b到c是以点A为旋转中心的旋转，本项正确．故选：B．【考点】几何变换的类型8.二次函数y=x2+4x﹣5的图象的对称轴为（）A．x="4"B．x=﹣4C．x="2"D．x=﹣2【答案】D【解析】直接利用抛物线的对称轴公式由二次函数y=x 2+4x ﹣5的图象的对称轴为：x==﹣2．故选：D ．【考点】二次函数的性质9.某厂一月份的总产量为500吨，三月份的总产量达到为700吨．若平均每月增长率是x ，则可以列方程（）A ．500（1+2x ）="700"B ．500（1+x 2）="700"C ．500（1+x ）2="700"D ．700（1+x 2）=500【答案】C【解析】主要考查增长率问题，一般用增长后的量=增长前的量×（1+增长率），如果设平均每月增率是x ，那么根据三月份的产量可以设平均每月增率是x ，二月份的产量为：500×（1+x ）；三月份的产量为：500（1+x ）2=700；故选C ．【考点】由实际问题抽象出一元二次方程10.将抛物线y=x 2向左平移2个单位长度，再向下平移3个单位长度，得到的抛物线的函数表达式为（）A ．y=（x+2）2﹣3B ．y=（x+2）2+3C ．y=（x ﹣2）2+3D ．y=（x ﹣2）2﹣3【答案】A【解析】先确定抛物线y=x 2的顶点坐标为（0，0），再根据点平移的规律得到点（0，0）平移后所得对应点的坐标为（﹣2，﹣3），然后根据顶点式写出平移后的抛物线解析式为y=（x+2）2﹣3．故选：A ．【考点】二次函数图象与几何变换11.已知x 1、x 2是一元二次方程x 2﹣4x+1=0的两个根，则x 1+x 2等于（）A ．﹣4B ．﹣1C ．1D ．4【答案】D【解析】据一元二次方程的根与系数的关系得到两根之和,即韦达定理，两根之和是﹣，两根之积是．由方程x 2﹣4x+1=0的两个根是x 1，x 2，可得x 1+x 2=﹣（﹣4）=4．故选D ．【考点】根与系数的关系12.风车应做成中心对称图形，并且不是轴对称图形，才能在风口处平稳旋转．现有一长条矩形硬纸板（其中心有一个小孔）和两张全等的矩形薄纸片，将纸片粘到硬纸板上，做成一个能绕着小孔平稳旋转的风车．正确的粘合方法是（）A ．B ．C ．D ．【解析】抓住一点：风车应做成中心对称图形，并且不是轴对称图形，结合选项进行判断：A、是中心对称图形，并且不是轴对称图形，符合题意；B、不是中心对称图形，是轴对称图形，不符合题意；C、是中心对称图形，也是轴对称图形，不符合题意；D、不是中心对称图形，是轴对称图形，不符合题意；故选A．【考点】利用旋转设计图案13.如图，在正方形ABCD中，E为DC边上的点，连接BE，将△BCE绕点C顺时针方向旋转90°得到△DCF，连结EF，若∠BEC=70°，那么∠CEF的度数为（）A．20°B．25°C．40°D．45°【答案】D【解析】由旋转的性质可得∠BCE=∠DCF=90°，且CE=CF，可得∠CEF=45°，故选D．【考点】1、旋转的性质；2、正方形的性质14.一次函数y=ax+b与二次函数y=ax2+bx+c在同一坐标系中的图象可能是（）A．B．C．D．【答案】B【解析】先由一次函数y=ax+b图象得到字母系数的正负，再与二次函数y=ax2+bx+c的图象相比较看是否一致，即：A、由抛物线可知，a＜0，x=﹣＜0，得b＞0，由直线可知，a＞0，b＞0，故本选项错误；B、由抛物线可知，a＜0，x=﹣＜0，得b＜0，由直线可知，a＜0，b＜0，故本选项正确；C、由抛物线可知，a＞0，x=﹣＞0，得b＜0，由直线可知，a＞0，b＞0，故本选项错误；D、由抛物线可知，a＜0，x=﹣＜0，得b＜0，由直线可知，a＞0，b＞0，故本选项错误．【考点】1、二次函数的图象；2、一次函数的图象15.关于函数y=x 2+2x ，下列说法正确的是①图形是轴对称图形 ②图形经过点（﹣1，1） ③图形有一个最低点 ④当x ＞1时，y 随x 的增大而增大．【答案】①③④【解析】 ∵y=x 2+2x=（x+1）2﹣1，∴函数图象为抛物线，对称轴为x=﹣1，开口向上 ∴图形是轴对称图形，故①正确；函数有最小值，故③正确；当x ＞﹣1时，y 随x 的增大而增大，∴当x ＞1时，y 随x 的增大而增大，故④正确；当x=﹣1时，代入可得y=﹣1≠1，故图象不过（﹣1，1）点，故②不正确；综上可知正确的是①③④．【考点】1、二次函数的性质；2、二次函数的最值二、填空题1.方程3x 2﹣2x ﹣1=0的一次项系数是，常数项是．【答案】﹣2；﹣1【解析】根据任何一个关于x 的一元二次方程经过整理，都能化成如下形式ax 2+bx+c=0（a≠0）．这种形式叫一元二次方程的一般形式．其中ax 2叫做二次项，a 叫做二次项系数；bx 叫做一次项；b 叫做一次项系数，c 叫做常数项，可由方程3x 2﹣2x ﹣1=0的一次项系数是﹣2，常数项是﹣1.【考点】一元二次方程的一般形式2.点A （﹣1，2）关于原点对称点B 的坐标是．【答案】（1，﹣2）【解析】根据关于原点对称的点的坐标特点：它们的坐标符号相反,可直接得到点A （﹣1，2）关于原点对称点B 的坐标是（1，﹣2）．【考点】关于原点对称的点的坐标三、解答题1.关于x 的一元二次方程2x 2﹣4x+m ﹣1=0有两个相等的实数根，则m 的值为．【答案】3【解析】根据题意可知△=b 2-4ac=0，即42﹣4×2×（m ﹣1）=0，解得m=3.【考点】根的判别式2.解下列方程：（1）x 2﹣2x=﹣1；（2）（x+3）2=2x （x+3）．【答案】（1）x 1=x 2=1（2）x 1=﹣3，x 2=3【解析】（1）方程的左右两边同时加上一次项系数一半的平方，左边就是完全平方式，右边就是常数，然后利用平方根的定义即可求解．（2）先移项，然后通过提取公因式对等式的左边进行因式分解．试题解析：（1）∵x 2﹣2x=﹣1，∴（x ﹣1）2=0，∴x 1=x 2=1．（2）（x+3）2=2x （x+3），（x+3）（x+3﹣2x ）=0，（x+3）（3﹣x ）=0，x+3=0或3﹣x=0，解得 x 1=﹣3，x 2=3．【考点】1、解一元二次方程-因式分解法；2、解一元二次方程-配方法3.如图是抛物线形拱桥，当拱顶高离水面2m 时，水面宽4m ．若水面下降了2.5m ，水面的宽度增加多少？【答案】2【解析】根据已知得出直角坐标系，进而求出二次函数解析式，再通过把y=﹣2.5代入抛物线解析式得出水面宽度，即可得出答案．试题解析：建立平面直角坐标系，设横轴x 通过AB ，纵轴y 通过AB 中点O 且通过C 点，则通过画图可得知O 为原点，抛物线以y 轴为对称轴，且经过A ，B 两点，OA 和OB 可求出为AB 的一半2米，抛物线顶点C 坐标为（0，2），设顶点式y=ax 2+2，把A 点坐标（﹣2，0）代入得a=﹣0.5，∴抛物线解析式为y=﹣0.5x 2+2，当水面下降2.5米，通过抛物线在图上的观察可转化为：当y=﹣2.5时，对应的抛物线上两点之间的距离，也就是直线y=﹣1与抛物线相交的两点之间的距离，可以通过把y=﹣2.5代入抛物线解析式得出：﹣2.5=﹣0.5x 2+2，解得：x=±3，所以水面宽度增加到6米，比原先的宽度当然是增加了2米．【考点】二次函数的应用4.如图，正方形ABCD 与正方形A 1B 1C 1D 1关于某点中心对称，已知A ，D 1，D 三点的坐标分别是（0，4），（0，3），（0，2）．（1）求对称中心的坐标．（2）写出顶点B ，C ，B 1，C 1的坐标．【答案】（1）（0，2.5）（2）（﹣2，4），（﹣2，2），（2，1），（2，3）【解析】（1）根据对称中心的性质，可得对称中心的坐标是D 1D 的中点，据此解答即可．（2）首先根据A ，D 的坐标分别是（0，4），（0，2），求出正方形ABCD 与正方形A 1B 1C 1D 1的边长是多少，然后根据A ，D 1，D 三点的坐标分别是（0，4），（0，3），（0，2），判断出顶点B ，C ，B 1，C 1的坐标各是多少即可．试题解析：（1）根据对称中心的性质，可得对称中心的坐标是D 1D 的中点，∵D 1，D 的坐标分别是（0，3），（0，2），∴对称中心的坐标是（0，2.5）．（2）∵A ，D 的坐标分别是（0，4），（0，2），∴正方形ABCD 与正方形A 1B 1C 1D 1的边长都是：4﹣2=2，∴B ，C 的坐标分别是（﹣2，4），（﹣2，2）， ∵A 1D 1=2，D 1的坐标是（0，3），∴A 1的坐标是（0，1），∴B 1，C 1的坐标分别是（2，1），（2，3），综上，可得顶点B ，C ，B 1，C 1的坐标分别是（﹣2，4），（﹣2，2），（2，1），（2，3）．【考点】1、中心对称；2、坐标与图形性质5.如图，将一块正方形空地划出部分区域进行绿化，原空地一边减少了2m ，另一边减少了3m ，剩余一块面积为20m 2的矩形空地，则原正方形空地的边长是多少？【答案】7m【解析】可设原正方形的边长为xm ，则剩余的空地长为（x ﹣2）m ，宽为（x ﹣3）m ．根据长方形的面积公式方程可列出，进而可求出原正方形的边长．试题解析：设原正方形的边长为xm ，依题意有（x ﹣3）（x ﹣2）=20，解得：x 1=7，x 2=﹣2（不合题意，舍去）即：原正方形空地的边长是7m ．【考点】一元二次方程的应用6.已知二次函数y=x 2﹣4x+3．（1）该函数的顶点坐标是，与x 轴的交点坐标是；（2）在平面直角坐标系中，用描点法画出该二次函数的图象；（3）根据图象回答：当0≤x ＜3时，y 的取值范围是．【答案】（1）（2，﹣1），（1，0），（3，0）；（3）﹣1≤y≤3【解析】（1）把函数解析式整理成顶点式形式，然后写出顶点坐标即可，再令y=0，解关于x 的一元二次方程即可得到与x 轴的交点坐标；（2）根据二次函数与坐标轴的交点和顶点坐标作出图象即可；（3）根据函数图象写出y 的取值范围即可．试题解析：（1）∵y=x 2﹣4x+3=（x ﹣2）2﹣1，∴顶点坐标为（2，﹣1）令y=0，则x 2﹣4x+3=0，解得x 1=1，x 2=3，所以，与x 轴的交点坐标是（1，0），（3，0）；（2）如图所示；（3）0≤x ＜3时，y 的取值范围是﹣1≤y≤3．【考点】1、二次函数与不等式的关系，2、抛物线与x 轴的交点问题，3、二次函数的性质7.已知：如图，二次函数y=ax 2+bx+c 的图象与x 轴交于A 、B 两点，其中A 点坐标为（﹣1，0），点C （0，5），另抛物线经过点（1，8），M 为它的顶点．（1）求抛物线的解析式；（2）求△MCB 的面积．（3）在坐标轴上，是否存在点N ，满足△BCN 为直角三角形？如存在，请直接写出所有满足条件的点N ．【答案】（1）y=﹣x 2+4x+5（2）15（3）存在，（0，0）或（0，﹣5）或（﹣5，0）【解析】（1）把A （﹣1，0），C （0，5），（1，8）三点代入二次函数解析式，解方程组即可．（2）先求出M 、B 、C 的坐标，根据即可解决问题．（3）分三种情①C 为直角顶点；②B 为直角顶点；③N 为直角顶点；分别求解即可．试题解析：（1）∵二次函数y=ax 2+bx+c 的图象经过A （﹣1，0），C （0，5），（1，8），则有：，解得．∴抛物线的解析式为y=﹣x 2+4x+5．（2）令y=0，得（x ﹣5）（x+1）=0，x 1=5，x 2=﹣1，∴B （5，0）．由y=﹣x 2+4x+5=﹣（x ﹣2）2+9，得顶点M （2，9）如图1中，作ME ⊥y 轴于点E ，可得 =（2+5）×9﹣×4×2﹣×5×5=15．（3）存在．如图2中，∵OC=OB=5， ∴△BOC 是等腰直角三角形， ①当C 为直角顶点时，N 1（﹣5，0）．②当B 为直角顶点时，N 2（0，﹣5）．③当N 为直角顶点时，N 3（0，0）．综上所述，满足条件的点N 坐标为（0，0）或（0，﹣5）或（﹣5，0）．【考点】1、二次函数，2、三角形的面积，3、直角三角形的判定和性质。

海口市第一中学2024届九年级下学期期中考试数学(A卷)试卷(含解析)

海南省海口市第一中学2023-2024学年九年级下学期期中考试数学试题A卷一、选择题（共14小题，每小题3分，共42分）1. 下列运算正确的是（）A. B.C. D.答案：D解析：解：A、和不是同类项，不能合并，该选项不符合题意；B、，该选项不符合题意；C、，该选项不符合题意；D、，该选项符合题意；故选：D．2. 不等式组的解集在数轴上表示正确的是（）A. B.C. D.答案：A解析：解：，解得，解得，利用数轴表示为：．故选：A．3. 如图，直线l1∥l2，将一直角三角尺按如图所示放置，使得直角顶点在直线l1上，两直角边分别与直线l1、l2相交形成锐角∠1、∠2且∠1＝25°，则∠2的度数为（）A. 25°B. 75°C. 65°D. 55°答案：C解析：如图，∵∠1＝25°，∠BAC＝90°，∴∠3＝180°-90°-25°=65°，∵l1∥l2，∴∠2＝∠3＝65°，故选C．4. 如图，在等腰△ABC中，AB＝AC＝4cm，∠B＝30°，点P从点B出发，以cm/s的速度沿BC方向运动到点C停止，同时点Q从点B出发，以1cm/s的速度沿BA—AC方向运动到点C停止．若△BPQ的面积为y（），运动时间为x（s），则下列最能反映y与x之间函数关系的图象是( )A. B. C. D.答案：D解析：如图1，作AH⊥BC于H，∵AB＝AC＝4cm，∴BH＝CH．∵∠B＝30°，∴AH＝AB＝2，∴BH＝AH＝2，∴BC＝2BH＝4．∵点P运动的速度为cm/s，Q点运动的速度为1cm/s，∴点P从B点运动到C需8s，Q点运动到C需8s．分类讨论：①当0≤x≤4时，作QD⊥BC于D，如图1，由题意可知BQ＝x，BP＝x，在Rt△BDQ中，DQ＝BQ＝x，∴y＝＝；②当4<x≤8时，作QD⊥BC于D，如图2，由题意可知CQ＝8-x，BP＝x，在Rt△CDQ中，DQ＝CQ＝(8-x)，∴y＝＝+x．综上所述，y＝．故选：D．5. 如图，下列选项中不是正六棱柱的三视图的是（　）A. B. C. D.答案：A解析：正六棱柱三视图分别为：三个左右相邻的矩形，两个左右相邻的矩形，正六边形．故选A．6. 下列计算正确的是（）A. B. C. D.答案：B解析：解：A. ，故此选项错误；B. ，正确；C. ，故此选项错误；D. ，故此选项错误．故选：B．7. 如图是一个隧道的横截面，它的形状是以O为圆心的圆的一部分，，直线交圆于E，，则圆的半径为（）A. 4B. 3C.D.答案：C解析：解：连接，∵，根据垂径定理：，设圆的半径是，在中，有，即：，解得：，∴圆的半径长是，故选：C．8. 如图所示，抛物线的顶点为，与x轴的交点A在点和之间，以下结论：①;②;③;④，其中正确的有（）A. 1个B. 2个C. 3个D. 4个答案：B解析：解：由图象可得：抛物线与x轴有两个交点，∴有两个不同的根，∴，故①错误；∵抛物线的顶点为，与x轴的交点A在点和之间，∴与x轴的另一交点在点和之间，∴时，，故②错误；∵抛物线的顶点为，∴，即，故③正确；当时，，故④正确；故选：B．9. 如图，正比例函数的图象与反比例函数的图象相交于A、B两点，其中点A的横坐标为2，当时，x的取值范围是（）A. 或B. 或C. 或D. 或答案：A解析：解：正比例函数与反比例函数的图象均关于原点对称，点的横坐标为2，点的横坐标为．由函数图象可知，当或时，正比例函数的图象在反比例函数图象的上方，当时，的取值范围是或．10. 二次函数的图象如图所示，有下列结论：①；②；③若m 为任意实数，则；④；⑤若，且，则．其中，正确结论的个数为（）A. 1B. 2C. 3D. 4答案：B解析：解：①抛物线开口方向向下，则．抛物线对称轴位于y轴右侧，则a、b异号，即．抛物线与y轴交于正半轴，则，所以．故①错误．②∵抛物线对称轴为直线，∴，即，故②正确；③∵抛物线对称轴为直线，抛物线开口方向向下，∴函数的最大值为，∴当时，，即，故③错误；④∵抛物线与x轴的一个交点在的左侧，而对称轴为直线，∴关于直线的对称点为，抛物线与x轴的另一个交点在的右侧，∴当时，，∴，⑤∵，∴，∴，∴，而，∴，即，∵，∴，故⑤正确．综上所述，正确的有②⑤．故选：B．11. 如图，P是⊙O外一点，PA，PB分别和⊙O切于A，B，C是弧AB上任意一点，过C作⊙O的切线分别交PA，PB于D，E，若△PDE的周长为12，则PA等于( )A. 12B. 6C. 8D. 10答案：B解析：解：∵PA、PB、DE分别切⊙O于A、B、C，∴PA=PB，DA=DC，EC=EB；∵△PDE的周长为12，∴PD+DE+PE=PD+DA+EB+PE=PA+PB=12，∴PA=PB=6．故选B．12. 数学知识在生产和生活中被广泛应用，下列实例所应用的最主要的几何知识，说法正确的是（）A. 射击时，瞄准具的缺口、准星和射击目标在同一直线上，应用了“两点确定一条直线”；B. 车轮做成圆形，应用了“圆是中心对称图形”；C. 学校门口的伸缩门由菱形而不是其他四边形组成，应用了“菱形的对角线互相垂直平分”；D. 地板砖可以做成矩形，应用了“矩形对边相等”．答案：A解析：解：A、在正常情况下，射击时要保证瞄准的一只眼在准星和缺口确定的直线上，才能射中目标，应用了“两点确定一条直线”，故符合题意；B、因为圆上各点到圆心的距离相等，所以车轮中心与地面的距离保持不变，坐车的人感到非常平稳，故不符合题意；C、学校门口的伸缩门由菱形而不是其他四边形组成，应用了“菱形四边相等和平行四边形的不稳定性”，故不符合题意；D、地板砖可以做成矩形，应用了“矩形四个内角都是直角”的性质，故不符合题意．故选：A．13. 如图，∠1＝∠2＝58°，根据尺规作图痕迹，可得∠ADB 的度数是（）A. 58°B. 60°C. 61°D. 122°答案：C解析：解：根据尺规作图痕迹可得，AD平分，则，∵，∴，，∴，故选：C14. 学校为创建“书香校园”购买了一批图书．已知购买科普类图书花费10000元，购买文学类图书花费9000元，其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元，且购买科普书的数量比购买文学书的数量少100本．求科普类图书平均每本的价格是多少元？若设科普类图书平均每本的价格是x元，则可列方程为（）A. ﹣=100B. ﹣=100C. ﹣=100D. ﹣=100答案：B解析：解：科普类图书平均每本的价格是x元，则可列方程为：﹣=100，故选B．二、非选择题（共58分）15. 如图，⊙的半径为2，点A，B，C都在⊙上，若．则的长为_____（结果用含有的式子表示）答案：##解析：，，，⊙的半径为2，，故答案为：．16. 计算：．答案：解析：解：17. 如图，在矩形ABCD中，AC是对角线．（1）实践与操作：利用尺规作线段AC的垂直平分线，垂足为点O，交边AD于点E，交边BC于点F（要求：尺规作图并保留作图痕迹，不写作法，标明字母），（2）猜想与证明：试猜想线段AE与CF的数量关系，并加以证明．答案：（1）作图见解析（2），证明见解析小问1解析：解：如图，小问2解析：解：．证明如下：∵四边形ABCD是矩形，∴．∴．∵EF为AC的垂直平分线，∴．∴．∴．18. （1）计算：．（2）解不等式组：．答案：（1）；（2）-7<x≤1．解析：解：（1）原式；（2）解不等式：x-3（x-2）≥4，得：x≤1，解不等式：，得：x>-7，则不等式组的解集为：-7<x≤1．19. 如图1所示，已知AB，CD是⊙O的直径，T是CD延长线的一点，⊙O的弦AF交CD于点E，且AE ＝EF，OA2＝OE•OT．（1）如图1，求证：BT是⊙O的切线；（2）在图1中连接CB，DB，若，求tan T的值；（3）如图2，连接DF交AB于点G，过G作GP⊥CD于点P，若BT，DT＝6．求：DG的长．答案：（1）详见解析；（2）CD是圆的直径；（3）解析：解：（1）证明：CD是⊙O的直径，⊙O的弦AF交CD于点E，且AE＝EF，∴CD⊥AF，∠AEO＝90°，∴AO2＝OE•OT，AB是圆的直径，，又∠AOE＝∠BOT，∴△AOE∽△TOB，∴∠OBT＝∠AEO＝90°，∴BT是⊙O切线；（2）CD是圆的直径，∴∠CBD＝90°，又∠OBT＝90°，∴∠CBO＝∠DBT，∵OB＝OC，∴∠C＝∠OBC，∴∠C＝∠DBT，又∠T＝∠T，∴△DBT∽△BCT，∴，设DT＝m（m＞0），则BT＝2m，CT＝4m，则CD＝3m，OB＝OD＝1.5m，在Rt△OBT中，，（3）∵∠OBT＝90°，∴OB2+BT2＝OT2，设半径为r，又BT＝6，DT＝6，r2+（6）2+（r+6）2，解得：r＝3，∴△AOE∽△TOB，，即：，∴OE＝1，AE＝2，∵GP⊥CD于点P，∠AEO＝90°，∴∠AEO＝∠GPO，又∠AOE＝∠GOP，∴△AOE∽△GOP，∴，设：OP＝a，则PG＝2a，PD＝OD﹣OP＝3﹣a，而△PDG∽△EDF，则，即：，解得：，∴，在Rt△PDG中，．20. 如图1，抛物线与轴交于A,B两点，与轴交于点C，AB=4，矩形OBDC的边CD=1，延长DC交抛物线于点E.（1）求抛物线的表达式；（2）如图2，点P是直线EO上方抛物线上的一个动点，过点P作y轴的平行线交直线EO于点G，作PH EO，垂足为H.设PH的长为l，点P的横坐标为m，求l与m的函数关系是（不必写出m的取值范围），并求出l的最大值；（3）如果点N是抛物线对称轴上的一点，抛物线上是否存在点M，使得以M,A,C,N为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的M的坐标；若不存在，请说明理由.答案：（1）抛物线解析式为y=﹣x2﹣x+2；（2）l=﹣（m+）2+，最大值为；（3）（2，﹣）或（﹣4，﹣）或（﹣2，2）．解析：解：（1）∵矩形OBDC的边CD=1，∴OB=1，∵AB=4，∴OA=3，∴A（﹣3，0），B（1，0），把A、B两点坐标代入抛物线解析式可得，解得，∴抛物线解析式为y=﹣x2﹣x+2；（2）在y=﹣x2﹣x+2中，令y=2可得2=﹣x2﹣x+2，解得x=0或x=﹣2，∴E（﹣2，2），∴直线OE解析式y=﹣x，由题意可得P（m，﹣m2﹣m+2），∵PG∥y轴，∴G（m，﹣m），∵P在直线OE的上方，∴PG=﹣m2﹣m+2﹣（﹣m）=﹣m2﹣m+2=﹣（m+）2+，∵直线OE解析式为y=﹣x，∴∠PGH=∠COE=45°，∴l=PG=[﹣（m+）2+]=﹣（m+）2+，∴当m=﹣时，l有最大值，最大值为；（3）①当AC为平行四边形的边时，则有MN∥AC，且MN=AC，如图，过M作对称轴的垂线，垂足为F，设AC交对称轴于点L，则∠ALF=∠ACO=∠FNM，在△MFN和△AOC中∴△MFN≌△AOC（AAS），∴MF=AO=3，∴点M到对称轴的距离为3，又y=﹣x2﹣x+2，∴抛物线对称轴为x=﹣1，设M点坐标为（x，y），则|x+1|=3，解得x=2或x=﹣4，当x=2时，y=﹣，当x=﹣4时，y=，∴M点坐标为（2，﹣）或（﹣4，﹣）；②当AC为对角线时，设AC的中点为K，∵A（﹣3，0），C（0，2），∴K（﹣，1），∵点N在对称轴上，∴点N的横坐标为﹣1，设M点横坐标为x，∴x+（﹣1）=2×（﹣）=﹣3，解得x=﹣2，此时y=2，∴M（﹣2，2）；综上可知点M的坐标为（2，﹣）或（﹣4，﹣）或（﹣2，2）．。

海南九年级期中试卷数学

海南九年级期中试卷数学专业课原理概述部分一、选择题（每题1分，共5分）1. 若一个三角形的两边分别为8cm和10cm，且这两边的夹角为90°，则这个三角形的周长为多少cm？A. 16cmB. 18cmC. 26cmD. 34cm2. 已知一组数据的平均数为10，中位数为12，众数为15，则这组数据中可能存在的数值是？A. 5B. 10C. 12D. 153. 若函数f(x) = 2x + 3，则f(3)的值为多少？A. 3B. 6C. 9D. 124. 在直角坐标系中，点(3, 4)关于y轴的对称点的坐标是？A. (-3, 4)B. (3, -4)C. (-3, -4)D. (4, 3)5. 若一个等差数列的首项为2，公差为3，则第10项的值为多少？A. 29B. 30C. 31D. 32二、判断题（每题1分，共5分）1. 平行四边形的对角线互相平分。

（）2. 一组数据的中位数和平均数相等。

（）3. 两个负数相乘的结果是正数。

（）4. 在同一平面内，两条直线如果不平行，则一定相交。

（）5. 任何一个正整数都可以表示为2的幂的整数倍。

（）三、填空题（每题1分，共5分）1. 若一个等腰三角形的底边长为8cm，腰长为10cm，则这个三角形的周长为______cm。

2. 若一组数据的平均数为15，且数据个数为5，则这组数据的总和为______。

3. 若函数f(x) = x^2 4x + 4，则f(2)的值为______。

4. 在直角坐标系中，点(1, 2)到原点的距离为______。

5. 若一个等差数列的公差为2，第5项的值为15，则首项的值为______。

四、简答题（每题2分，共10分）1. 简述勾股定理的内容。

2. 什么是函数？给出一个具体的函数例子。

3. 什么是等差数列？给出一个具体的等差数列例子。

4. 什么是平行四边形？给出一个具体的平行四边形例子。

5. 什么是概率？给出一个具体的概率例子。

海口九年级期中数学试卷【含答案】

海口九年级期中数学试卷【含答案】专业课原理概述部分一、选择题（每题1分，共5分）1. 若一个正方形的边长为a，则它的对角线长是（）。

A. a/2B. a√2C. 2aD. a²2. 下列哪个数是无理数？（）A. √9B. √16C. √3D. √13. 若x² 5x + 6 = 0，则x的值为（）。

A. 2 或 3B. 1 或 6C. -2 或 -3D. -1 或 -64. 下列哪个图形不是正多边形？（）A. 等边三角形B. 等腰梯形C. 正方形D. 正五边形5. 若一组数据为2, 4, 6, 8, 10，则这组数据的平均数是（）。

A. 4B. 6C. 8D. 10二、判断题（每题1分，共5分）1. 任何两个奇数相加的结果一定是偶数。

（）2. 0是有理数。

（）3. 两条平行线的斜率一定相等。

（）4. 若a > b，则a² > b²。

（）5. 任何数乘以0都等于0。

（）三、填空题（每题1分，共5分）1. 若一个圆的半径为r，则它的面积是______。

2. 若一个等差数列的首项为a，公差为d，则第n项的通项公式是______。

3. 若一个直角三角形的两个直角边分别为3和4，则它的斜边长是______。

4. 若一个函数f(x) = x² 2x + 1，则f(1)的值是______。

5. 若一组数据为1, 3, 5, 7, 9，则这组数据的中位数是______。

四、简答题（每题2分，共10分）1. 请简述勾股定理。

2. 请简述等差数列和等比数列的区别。

3. 请简述一次函数的性质。

4. 请简述二次函数的图像特点。

5. 请简述概率的基本概念。

五、应用题（每题2分，共10分）1. 一个长方形的长是10cm，宽是5cm，求它的面积。

2. 若一组数据为2, 4, 6, 8, 10，求这组数据的平均数。

3. 若一个等差数列的首项为2，公差为3，求第5项的值。