最新备战中考数学专题练习(全国通用)-相似三角形判定定理(含解析)
中考数学相似三角形分类专练 证明相似三角形中的对应线段成比例重难点专练(解析版)

同上,AB可以与DE对应,也可以与DF对应,∴相似比可能是 ,也可能是 ,C不一定成立;
∵∠A=∠D,即∠A与∠D是对应角,∴它们的对边一定是对应比,即BC与EF是对应比,
∴相似比为 ,∴D一定成立,
故选D.
【考点知悉】
本题考查相似三角形的性质,注意相似三角形的性质是针对对应角和对应边而言的.
17.如图,点D、E分别在 的边AB、AC上,且 ,若DE=3,BC=6,AC=8,则 _______.
18.如图,点D、E、F分别位于△ABC的三边上,满足DE∥BC,EF∥AB,如果AD:DB=3:2,那么BF:FC=_____.
19.如图,在△ABC中,AB=9,AC=6,D为AB边上一点,且△ABC∽△ACD,则AD=__.
∴这个三角形的边长扩大到原来的4倍,
故选B.
【考点知悉】
本题考查了相似三角形的相似比和周长比之间的关系,属于简单题,熟练掌握相似三角形的性质是解题关键.
10.D
【思路点拨】
根据①直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项.②每一条直角边是这条直角边在斜边上的射影和斜边的比例中项,进行判断即可.
30.如图, , , , ,则 ________.
31.如图,△ABC中,DE∥BC, ,△ADE的面积为8,则△ABC的面积为______
三、解答题
32.已知:如图,AB是半圆O的直径,弦CD∥AB,动点P、Q分别在线段OC、CD上,且DQ=OP,AP的延长线与射线OQ相交于点E、与弦CD相交于点F(点F与点C、D不重合),AB=20,cos∠AOC= .设OP=x,△CPF的面积为y.
∴ ,
2022年中考数学真题-专题15 相似三角形(1)(全国通用解析版)

专题15 相似三角形一.选择题1. 在设计人体雕像时,使雕像上部(腰部以上)与下部(腰部以下)的高度比,等于下部与全部的高度比,可以增加视觉美感.如图,按此比例设计一座高度为2m 的雷锋雕像,那么该雕像的下部设计高度约是( )(结果精确到0.01m .参1.414≈ 1.732≈2.236≈)A. 0.73mB. 1.24mC. 1.37mD. 1.42m【答案】B【解析】 【分析】设雕像的下部高为x m ,由黄金分割的定义得51,22x求解即可. 【详解】解:设雕像的下部高为x m ,则上部长为(2-x )m ,∵雕像上部(腰部以上)与下部(腰部以下)的高度比,等于下部与全部的高度比, 雷锋雕像为2m , ∴51,22x ∴51 1.24x, 即该雕像的下部设计高度约是1.24m ,故选:B .【点睛】本题考查了黄金分割的定义,熟练掌握黄金分割的定义及黄金比值是解题的关键.2. 神奇的自然界处处蕴含着数学知识.动物学家在鹦鹉螺外壳上发现,其每圈螺纹的直径与相邻螺纹直径的比约为0.618.这体现了数学中的( )A. 平移B. 旋转C. 轴对称D. 黄金分割【答案】D【解析】 【分析】根据黄金分割的定义即可求解.【详解】解:动物学家在鹦鹉螺外壳上发现,其每圈螺纹的直径与相邻螺纹直径的比约为0.618.这体现了数学中的黄金分割.故选:D【点睛】本题考查了黄金分割的定义,黄金分割是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,其比值为12,约等于0.618,这个比例被公认为是最能引起美感的比例,因此被称为黄金分割.熟知黄金分割的定义是解题关键.3. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A ,B ,C 都在横线上.若线段3AB =,则线段BC 的长是( )A. 23B. 1C. 32D. 2【答案】C【解析】【分析】过点A 作五条平行横线的垂线,交第三、四条直线,分别于D 、E ,根据题意得2AD DE =,然后利用平行线分线段成比例定理即可求解.【详解】解:过点A 作五条平行横线的垂线,交第三、四条直线,分别于D 、E , 根据题意得2AD DE =,∵BD CE ∥, ∴2AB AD BC DE==, 又∵3AB =, ∴1322BC AB ==故选:C【点睛】本题考查了平行线分线段成比例的应用,作出适当的辅助线是解题的关键.4. 在ABC 中(如图),点D 、E 分别为AB 、AC 的中点,则:ADE ABC SS =( )A. 1:1B. 1:2C. 1:3D. 1:4【答案】D【解析】【分析】证出DE 是ABC ∆的中位线,由三角形中位线定理得出//DE BC ,12DE BC =,证出ADE ABC ∆∆,由相似三角形的面积比等于相似比的平方即可得出结论. 【详解】解:点D 、E 分别为AB 、AC 的中点,DE ∴是ABC ∆的中位线,//DE BC ∴,12DE BC =, ADE ABC ∴, 211:24ADE ABC S S ⎛⎫∴== ⎪⎝⎭. 故选:D .【点睛】本题考查了相似三角形的判定与性质、三角形中位线定理;熟练掌握三角形中位线定理,证明三角形相似是解决问题的关键.5. 将一张以AB 为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片ABCD ,其中90A ∠=︒,9AB =,7BC =,6CD =,2AD =,则剪掉的两个直角三角形的斜边长不可能...是( )A. 252B. 454C. 10D. 354【答案】A【解析】【分析】根据题意,画出相应的图形,然后利用相似三角形的性质和分类讨论的方法,求出剪掉的两个直角三角形的斜边长,然后即可判断哪个选项符合题意.【详解】解:当△DFE ∽△ECB 时,如图,∴DF FE DE EC CB EB==, 设DF =x ,CE =y , ∴9672x y y x +==+,解得:274214x y ⎧=⎪⎪⎨⎪=⎪⎩, ∴2145644DE CD CE =+=+=,故B 选项不符合题意; ∴2735244EB DF AD =+=+=,故选项D 不符合题意;如图,当△DCF ∽△FEB 时,∴DC CF DF FE EB FB==, 设FC =m ,FD =n , ∴6927m n n m ==++,解得:810m n =⎧⎨=⎩, ∴FD =10,故选项C 不符合题意;8614BF FC BC =+=+=,故选项A 符合题意;故选:A【点睛】本题考查相似三角形的性质、矩形的性质,解答本题的关键是明确题意,利用分类讨论的方法解答.6. 若ABC DEF △△,6BC =,4EF =,则AC DF =( ) A. 49 B. 94 C. 23 D. 32【答案】D【解析】【分析】根据,ABC ,,DEF ,可以得到,BC AC EF DF =然后根据BC =6,EF =4,即可求解.【详解】解:∵ABC DEF △△ ∴,BC AC EF DF=6BC =,4EF =, ∴AC DF =63=42故选D【点睛】本题考查了相似三角形的性质,掌握相似三角形的性质是解题的关键. 7. 如图,在ABC 中,D 、E 分别为线段BC 、BA 的中点,设ABC 的面积为S 1,EBD 的面积为S 2.则21S S =( )A. 12B. 14C. 34D. 78 【答案】B【解析】【分析】先判定EBD ABC ,得到相似比为12,再根据两个相似三角形的面积比等于相似比的平方,据此解题即可.【详解】解:,D 、E 分别为线段BC 、BA 的中点, ,12BE BD AB BC ==, 又,B B ∠=∠,,EBD ABC ,相似比为12, ,22114S BE S AB ⎛⎫== ⎪⎝⎭, 故选:B .【点睛】此题考查相似三角形的判定与性质等知识,是重要考点,难度较易,掌握相关知识是解题关键.8. 如图,在Rt ABC 和Rt BDE 中,90ABC BDE ∠=∠=︒,点A 在边DE 的中点上,若AB BC =,2DB DE ==,连结CE ,则CE 的长为( )A.C. 4【答案】D【解析】【分析】过点E 作EF ⊥BC ,交CB 延长线于点F ,过点A 作AG ⊥BE 于点G ,根据等腰直角三角形的性质可得BE =BED =45°,进而得到AB BC ==22EG AG AE ===,BG =,再证得△BEF ∽△ABG ,可得BF EF ==,然后根据勾股定理,即可求解.【详解】解:如图,过点E 作EF ⊥BC ,交CB 延长线于点F ,过点A 作AG ⊥BE 于点G ,在Rt BDE 中,∠BDE =90°,2DB DE ==,∴BE ==BED =45°,∵点A 在边DE 的中点上,∴AD =AE =1,∴AB ==∴AB BC ==∵∠BED =45°,∴△AEG 是等腰直角三角形,∴22EG AG AE ===,∴BG =, ∵∠ABC =∠F =90°,∴EF ∥AB ,∴∠BEF =∠ABG ,∴△BEF ∽△ABG , ∴BE BF EF AB AG BG ====,解得:BF EF==,∴5CF=,∴CE故选:D【点睛】本题主要考查了相似三角形的判定和性质,等腰直角三角形的判定和性质,勾股定理,熟练掌握相似三角形的判定和性质,等腰直角三角形的判定和性质,勾股定理是解题的关键.9. ABC的三边长分别为2,3,4,另有一个与它相似的三角形DEF,其最长边为12,则DEF的周长是()A. 54B. 36C. 27D. 21【答案】C【解析】【分析】根据相似三角形的性质求解即可.【详解】解:∵,ABC与,DEF相似,△ABC的最长边为4,,DEF的最长边为12,∴两个相似三角形的相似比为1:3,,,DEF的周长与,ABC的周长比为3:1,,,DEF的周长为3×(2+3+4)=27,故选:C.【点睛】本题主要考查了相似三角形的性质,熟知相似三角形的周长之比等于相似之比是解题的关键.10. 如图,在△ABC中,点D、E分别在边AB、AC上,若DE∥BC,23 ADDB=,DE=6cm,则BC的长为()A. 9cmB. 12cmC. 15cmD. 18cm 【答案】C【解析】【分析】根据平行得到ADE ABC ∆∆,根据相似的性质得出AD DE AB BC =,再结合23AD DB =,DE =6cm ,利用相似比即可得出结论. 【详解】解:在△ABC 中,点D 、E 分别在边AB 、AC 上,若DE ∥BC , ADE B ∴∠=∠,A A ∠=∠,ADE ABC ∴, AD DE ABBC ∴=, 23AD DB=, 25DE AD AD BC AB AD DB ∴===+, 6cm DE =,55615cm 22DE BC ⨯∴===, 故选:C .【点睛】本题考查利用相似求线段长,涉及到平行线的性质、两个三角形相似的判定与性质等知识点,熟练掌握相似三角形的判定与性质是解决问题的关键. 11. 如图,ABC 与DEF 位似,点O 是它们的位似中心,且位似比为1∶2,则ABC 与DEF 的周长之比是( )A. 1∶2B. 1∶4C. 1∶3D. 1∶9【答案】A【解析】 【分析】根据位似图形是相似图形,位似比等于相似比,相似三角形的周长比等于相似比即可求解.【详解】解:∵ABC 与DEF 位似∴ABC DEF ∽△△∵ABC 与DEF 的位似比是1:2∴ABC 与DEF 的相似比是1:2∴ABC 与DEF 的周长比是1:2故选:A .【点睛】本题考查了位似变换,解题的关键是掌握位似变换的性质和相似三角形的性质.12. 如图,ABC 与DEF 位似,点O 为位似中心,相似比为2:3.若ABC 的周长为4,则DEF 的周长是( )A. 4B. 6C. 9D. 16【答案】B【解析】【分析】根据周长之比等于位似比计算即可.【详解】设DEF 的周长是x ,∵ ABC 与DEF 位似,相似比为2:3,ABC 的周长为4,∴4:x =2:3,解得:x =6,故选:B .【点睛】本题考查了位似的性质,熟练掌握位似图形的周长之比等于位似比是解题的关键.13. 如图是一张矩形纸片ABCD ,点E 为AD 中点,点F 在BC 上,把该纸片沿EF 折叠,点A ,B 的对应点分别为A B A E ''',,与BC 相交于点G ,B A ''的延长线过点C .若23BF GC =,则AD AB的值为( )A. C. 207 D. 83 【答案】A【解析】【分析】令BF =2x ,CG =3x ,FG =y ,易证CGA CFB ''△∽△,得出CG A G CF B F '=',进而得出y =3x ,则AE =4x ,AD =8x ,过点E 作EH ⊥BC 于点H ,根据勾股定理得出EH =,最后求出AD AB的值. 【详解】解:过点E 作EH ⊥BC 于点H ,又四边形ABCD 为矩形,∴∠A =∠B =∠D =∠BCD =90°,AD =BC ,∴四边形ABHE 和四边形CDEH 为矩形,∴AB =EH ,ED =CH , ∵23BF GC =, ∴令BF =2x ,CG =3x ,FG =y ,则CF =3x +y ,2B F x '=,52x y A G -'=, 由题意,得==90CA G CB F ''︒∠∠,又GCA '∠为公共角,∴CGA CFB ''△∽△, ∴CG A G CF B F'=', 则53232x yx x y x-=+,整理,得()()30x y x y +-=,解得x =-y (舍去),y =3x ,∴AD =BC =5x +y =8x ,EG =3x ,HG =x ,在Rt △EGH 中EH 2+HG 2=EG 2,则EH 2+x 2=(3x )2,解得EH=, EH=-x (舍),∴AB=,∴AD AB ==. 故选:A .【点睛】本题考查了矩形的判定和性质,相似三角形的判定和性质,勾股定理求边长等知识,借助于相似三角形找到y =3x 的关系式是解决问题的关键.14. 如图,已知BD 是矩形ABCD 的对角线,AB =6,BC =8,点E ,F 分别在边AD ,BC 上,连结BE ,DF .将△ABE 沿BE 翻折,将△DCF 沿DF 翻折,若翻折后,点A ,C 分别落在对角线BD 上的点G ,H 处,连结GF .则下列结论不正确...的是( )A. BD =10B. HG =2C. EG FH ∥D. GF ⊥BC【答案】D【解析】 【分析】根据矩形的性质以及勾股定理即可判断A ,根据折叠的性质即可求得,HD BG ,进而判断B ,根据折叠的性质可得90EGB FHD ∠=∠=︒,进而判断C 选项,根据勾股定理求得CF 的长,根据平行线线段成比例,可判断D 选项 【详解】BD 是矩形ABCD 的对角线,AB =6,BC =8,8,6BC AD AB CD ∴====10BD ∴==故A 选项正确,将△ABE 沿BE 翻折,将△DCF 沿DF 翻折,6BG AB ∴==,6DH CD ==4DG ∴=,4BH BD HD =-=1010442HG BH DG ∴=--=--=故B 选项正确,,EG BD HF DB ⊥⊥,,EG ,HF ,故C 正确设AE a =,则EG a =,8ED AD AE a ∴=-=-,EDG ADB ∠=∠tan tan EDG ADB ∴∠=∠ 即6384EG AB DG AD === 344a ∴= 3AE ∴=,同理可得3CF =若FG CD ∥ 则CF BF =GD BG 342,563CF GD BF BG ===, ∴CF BF ≠GD BG , FG ∴不平行CD ,即GF 不垂直BC ,故D 不正确.故选D【点睛】本题考查了折叠的性质,矩形的性质,勾股定理,平行线分线段成比例,掌握以上知识是解题的关键.15. 如图,四边形ABCD 为正方形,将EDC △绕点C 逆时针旋转90︒至HBC ,点D ,B ,H 在同一直线上,HE 与AB 交于点G ,延长HE 与CD 的延长线交于点F ,2HB =,3HG =.以下结论:,135EDC ∠=︒;,2EC CD CF =⋅;,HG EF =;,sin 3CED ∠=.其中正确结论的个数为( )A. 1个B. 2个C. 3个D. 4个【答案】D【解析】 【分析】利用旋转的性质,正方形的性质,可判断①正确;利用三角形相似的判定及性质可知②正确;证明∽GBH EDC △△,得到DC EC HB HG=,即32⋅==CD HG a EC HB ,利用HEC △是等腰直角三角形,求出2=HE ,再证明∽HGB HDF △△即可求出3EF =可知③正确;过点E 作EM FD ⊥交FD 于点M ,求出sin 3∠==ME EFC EF ,再证明=∠∠DEC EFC ,即可知④正确. 【详解】解:∵EDC △旋转得到HBC ,∴=∠∠EDC HBC ,∵ABCD 为正方形,D ,B ,H 在同一直线上,∴=18045=135∠︒-︒︒HBC ,∴=135∠︒EDC ,故①正确;∵EDC △旋转得到HBC ,∴EC HC =,90ECH ∠=︒,∴=45∠︒HEC ,∴=18045=135∠︒-︒︒FEC ,∵=∠∠ECD ECF ,∴EFC DEC ∽△△,∴EC FC DC EC=, ∴2EC CD CF =⋅,故②正确;设正方形边长为a ,∵=45∠+∠︒GHB BHC ,=45∠+∠︒GHB HGB ,∴=∠∠=∠BHC HGB DEC ,∵=135∠=∠︒GBH EDC ,∴∽GBH EDC △△, ∴DC EC HB HG =,即32⋅==CD HGaEC HB ,∵HEC △是等腰直角三角形,∴2=HE ,∵∠=∠GHB FHD ,=135∠=∠︒GBH HDF ,∴HBG HDF ∽, ∴HBHGHD HF =2=,解得:3EF =,∵3HG =,∴HG EF =,故③正确;过点E 作EM FD ⊥交FD 于点M ,∴=45∠︒EDM ,∵2ED HB ==,∴==MD ME∵3EF =,∴sin ∠==ME EFC EF ∵=45∠+∠︒DEC DCE ,=45∠+∠︒EFC DCE ,∴=∠∠DEC EFC ,∴sin sin 3∠=∠==ME DEC EFC EF ,故④正确 综上所述:正确结论有4个,故选:D【点睛】本题考查正方形性质,旋转的性质,三角形相似的判定及性质,解直角三角形,解题的关键是熟练掌握以上知识点,结合图形求解.16. 如图所示,在菱形ABCD 中,对角线AC 与BD 相交于点O ,过点C 作CE BD ∥交AB 的延长线于点E ,下列结论不一定正确的是( )A. 12OB CE =B. ACE 是直角三角形C. 12BC AE =D. BE CE =【答案】D【解析】 【分析】由菱形的性质可知AC DB ⊥,AO OC =,由两直线平行,同位角相等可以推出90ACE AOB ∠=∠=︒,再证明Rt ACE Rt AOB △,得出12OB CE =,12AB AE =,由直角三角形斜边中线等于斜边一半可以得出12BC AE =.现有条件不足以证明BE CE =.【详解】解:∵在菱形ABCD 中,对角线AC 与BD 相交于点O ,∴AC DB ⊥,AO OC =,∴90AOB ∠=︒,∵CE BD ∥,∴90ACE AOB ∠=∠=︒,∴ACE 是直角三角形,故B 选项正确;∵90ACE AOB ∠=∠=︒,CAE OAB ∠=∠,∴Rt ACERt AOB △, ∴12OB AB OA CE AE AC ===, ∴12OB CE =,12AB AE =,故A 选项正确; ∴BC 为Rt ACE 斜边上的中线, ∴12BC AE =,故C 选项正确; 现有条件不足以证明BE CE =,故D 选项错误;故选D .【点睛】本题考查菱形的性质,平行线的性质,相似三角形的判定与性质以及直角三角形斜边中线的性质,难度一般,由菱形的性质得出AC DB ⊥,AO OC =是解题的关键.17. 如图,在Rt ABC 中,90ACB ∠=︒,以其三边为边向外作正方形,连结CF ,作GM CF ⊥于点M ,BJ GM ⊥于点J ,⊥AK BJ 于点K ,交CF 于点L .若正方形ABGF 与正方形JKLM 的面积之比为5,CE =,则CH 的长为( )A. B. 32+ C.【答案】C【解析】 【分析】设CF 交AB 于P ,过C 作CN ⊥AB 于N ,设正方形JKLM 边长为m ,根据正方形ABGF 与正方形JKLM 的面积之比为5,得AF =AB ,证明△AFL ≌△FGM (AAS ),可得AL =FM ,设AL =FM =x ,在Rt △AFL 中,x 2+(x +m )2=)2,可解得x =m ,有AL =FM =m ,FL =2m ,从而可得AP =,FP =52m ,BP ,即知P 为AB 中点,CP =AP =BP ,由△CPN ∽△FP A ,得CN =m ,PN =12m ,即得AN m ,而tan ∠BAC =BC CN AC AN ==,又△AEC ∽△BCH ,根据相似三角形的性质列出方程,解方程即可求解.【详解】解:设CF 交AB 于P ,过C 作CN ⊥AB 于N ,如图:设正方形JKLM 边长为m ,∴正方形JKLM 面积为m 2,∵正方形ABGF 与正方形JKLM 的面积之比为5,∴正方形ABGF 的面积为5m 2,∴AF =AB ,由已知可得:∠AFL =90°-∠MFG =∠MGF ,∠ALF =90°=∠FMG ,AF =GF , ∴△AFL ≌△FGM (AAS ),∴AL =FM ,设AL =FM =x ,则FL =FM +ML =x +m ,在Rt △AFL 中,AL 2+FL 2=AF 2,∴x 2+(x +m )2=)2,解得x =m 或x =-2m (舍去),∴AL =FM =m ,FL =2m ,1tan ,22AP AL m AFL AF FL m ∠==== 1,2=∴AP ,5,2m BP AB A FP P ====-==∴ ∴AP =BP ,即P 为AB 中点,∵∠ACB =90°,∴CP =AP =BP∵∠CPN =∠APF ,∠CNP =90°=∠F AP ,∴△CPN ∽△FP A ,,CP CN PN FP AF AP ∴==即2522m == ∴CN =m ,PN =12m ,∴AN =AP +PN=12m ∴tan ∠BAC=BC CN AC AN ==, ∵△AEC 和△BCH 是等腰直角三角形,∴△AEC ∽△BCH ,,BC CH AC CE∴=10CE ==CH ∴=故选:C .【点睛】本题考查正方形性质及应用,涉及全等三角形判定与性质,相似三角形判定与性质,勾股定理等知识,解题的关键是用含m 的代数式表示相关线段的长度.18. 如图,某零件的外径为10cm ,用一个交叉卡钳(两条尺长AC 和BD 相等)可测量零件的内孔直径AB .如果OA :OC =OB :OD =3,且量得CD =3cm ,则零件的厚度x 为( )A. 0.3cmB. 0.5cmC. 0.7cmD. 1cm【答案】B【解析】【分析】求出△AOB和△COD相似,利用相似三角形对应边成比例列式计算求出AB,再根据外径的长度解答.【详解】解:∵OA:OC=OB:OD=3,∠AOB=∠COD,∴△AOB∽△COD,∴AB:CD=3,∴AB:3=3,∴AB=9(cm),∵外径为10cm,∴19+2x=10,∴x=0.5(cm).故选:B.【点睛】本题考查相似三角形的应用,解题的关键是利用相似三角形的性质求出AB的长.二、填空题19. 在20世纪70年代,我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”,在全国大规模推广,取得了很大成果.如图,利用黄金分割法,所做EF将矩形窗框ABCD分为上下两部分,其中E为边AB的黄金分割点,即2=⋅.已知AB为2米,则线段BE的长为______米.BE AE AB【答案】1)##15【解析】【分析】根据点E 是AB 的黄金分割点,可得AE BE BE AB ==,代入数值得出答案.【详解】∵点E 是AB 的黄金分割点,∴12AE BE BE AB -==. ∵AB=2,,∴1BE =)米.故答案为:1).【点睛】本题主要考查了黄金分割的应用,掌握黄金比是解题的关键. 20. 如图,已知在△ABC 中,D ,E 分别是AB ,AC 上的点,DE BC ∥,13AD AB =.若DE =2,则BC 的长是______.【答案】6【解析】 【分析】根据相似三角形的性质可得13DE AD BC AB ==,再根据DE =2,进而得到BC 长.【详解】解:根据题意,∵DE BC∥,∴△ADE∽△ABC,∴13 DE ADBC AB==,∵DE=2,∴213 BC=,∴6BC=;故答案为:6.【点睛】本题考查了相似三角形的判定和性质,解题的关键是掌握相似三角形的性质进行计算.21. 如图,在△ABC中,点D、E分别是AB、AC的中点,若△ADE的面积为2,则△ABC的面积为_____.【答案】8.【解析】【分析】证△ADE∽△ABC,得2 ADEABCS DES BC⎛⎫= ⎪⎝⎭△△.【详解】解:∵D、E分别是AB、AC的中点,∴DE∥BC,DE=12BC,∴∠ADE=∠B,∠AED=∠C,∴△ADE∽△ABC,∴2ADEABCS DES BC⎛⎫= ⎪⎝⎭△△,∵S△ADE=2,∴S△ABC=4S△ADE=4×2=8.故答案为8.【点睛】考核知识点:相似三角形性质.利用三角形中位线性质是关键.22. 如图,ABC 和DEF 是以点O 为位似中心的位似图形.若:2:3OA AD =,则ABC 与DEF 的周长比是_________.【答案】2:5【解析】【分析】根据位似图形的性质,得到OCA OFD ∆∆,根据:2:3OA AD =得到相似比为25CA OA OA FD OD OA AD ===+,再结合三角形的周长比等于相似比即可得到结论. 【详解】解:ABC 和DEF 是以点O 为位似中心的位似图形, ∴OCAOFD ∆∆, ∴CA OA FD OD=,:2:3OA AD =, ∴25CA OA OA FD OD OA AD ===+, ∴根据ABC 与DEF 的周长比等于相似比可得25ABC DEF C CA C FD ∆∆==, 故答案为:2:5.【点睛】本题考查相似图形的性质,掌握位似图形与相似图形的关系,熟记相似图形的性质是解决问题的关键.23. 如图,已知等腰ABC 的顶角BAC ∠的大小为θ,点D 为边BC 上的动点(与B 、C 不重合),将AD 绕点A 沿顺时针方向旋转θ角度时点D 落在D 处,连接BD '.给出下列结论:①ACD ABD '≅△△;②ACB ADD '△△;③当BD CD =时,ADD '的面积取得最小值.其中正确的结论有________(填结论对应的序号).【答案】①②③【解析】【分析】依题意知,ABC 和ADD '是顶角相等的等腰三角形,可判断②;利用SAS 证明ADC AD B '≌△△, 可判断①;利用面积比等于相似比的平方,相似比为AD AC,故最小时ADD '面积最小,即AD BC ⊥,等腰三角形三线合一,D 为中点时 .【详解】∵AD 绕点A 沿顺时针方向旋转θ角度得到AD '∴DAD θ'∠=,AD AD ='∴CAB DAD '∠=∠即CAD DAB DAB BAD '∠+∠=∠+∠∴CAD BAD '∠=∠,CAD BAD AC AB AD AD ∠=∠⎧⎪=⎨⎪='⎩' 得:ADC AD B '≌△△(SAS )故①对∵ABC 和ADD '是顶角相等的等腰三角形∴ACB ADD '△△故②对 ∴2()AD D ABC S AD S AC'=△△ 即AD 最小时AD D S '△最小当AD BC ⊥时,AD 最小由等腰三角形三线合一,此时D 点是BC 中点故③对故答案为:①②③【点睛】本题考查全等三角形的判定和性质,相似三角形的判定和性质,手拉手模型,选项③中将面积与相似比结合是解题的关键 .24. 如图,已知F 是ABC 内的一点,FD BC ∥,FE AB ∥,若BDFE 的面积为2,13BD BA =,14BE BC =,则ABC 的面积是________.【答案】12【解析】【分析】延长EF 、DF 分布交AC 于点M 、N ,可以得到相似三角形并利用相似三角形分别求出AM 、MN 、CN 之间的关系,从而得到三角形的面积关系即可求解.【详解】解:如图所示:延长EF 、DF 分布交AC 于点M 、N ,FD BC∥,FE AB∥,13BD BA=,14BE BC=,∴32CE BE AD BD==,,32CM CE AN ADAM BE CN BD∴====,,∴令AM x=,则3CM x=,4AC x∴=,28143333AN AC x CN AC x∴====,,53MN x∴=,∴5589NM NMAN MC==,,25:6425:81NMF NAD NMF MECS S S S==△△△△:,:,∴设256481NMF NAD MECS a S a S a===△△△,,,56FECNS a∴=四边形,2120ABCS a∴=+△,264421209ADNABCS a ADS a AB⎛⎫∴===⎪+⎝⎭△,求出112a=,212012ABCS a∴=+=△,故答案为:12.【点睛】本题考查了相似三角形中的A型,也可以利用平行线分线段成比例知识,具有一定的难度,不断的利用相似三角形的性质:对应线段成比例进行求解线段的长度;利用相似三角形的面积之比等于相似比的平方是解题的关键.25. 如图,已知菱形ABCD 的边长为2,60DAB ∠=︒,E 为AB 的中点,F 为CE 的中点,AF 与DE 相交于点G ,则GF 的长等于___________.【解析】【分析】连接FB ,作CG AB ⊥交AB 的延长线于点G .由菱形的性质得出60CBG DAB ∠=∠=︒,2AD AB BC CD ====,解直角BGC ∆求出CG =,1BG =,推出FB 为ECG ∆的中位线,进而求出FB ,利用勾股定理求出AF ,再证明AEG ABF ∆∆,得出12AG GF AF ==. 【详解】解:如图,连接FB ,作CG AB ⊥交AB 的延长线于点G .∵四边形ABCD 是边长为2的菱形,∴//AD BC ,2AD AB BC CD ====,∵60DAB ∠=︒,∴60CBG DAB ∠=∠=︒,∴sin 2CG BC CBG =⋅∠==1cos 212BG BC CBG =⋅∠=⨯=, ∵E 为AB 的中点,∴1AE EB ==,∴BE BG =,即点B 为线段EG 的中点,又∵F 为CE 的中点,∴FB 为ECG ∆的中位线,∴//FB CG,122FB CG ==, ∴FB AB ⊥,即ABF ∆是直角三角形,∴AF === 在AED ∆和BGC ∆中, AD BC DAE CBG AE BG =⎧⎪∠=∠⎨⎪=⎩,‘∴AED BGC ∆≅∆,∴90AED BGC ∠=∠=︒,∴90AEG ABF ∠=∠=︒,又∵GAE FAB ∠=∠,∴AEGABF ∆∆, ∴12AG AE AF AB ==,∴124AG AF ==,∴4GF AF AG =-=.. 【点睛】本题考查菱形的性质,平行线的性质,三角函数解直角三角形,三角形中位线的性质,相似三角形的判定与性质等,综合性较强,添加辅助线构造直角BGC∆是解题的关键.26. 如图,在矩形ABCD中,AB=6,BC=8,点M、N分别是边AD、BC的中点,某一时刻,动点E从点M出发,沿MA方向以每秒2个单位长度的速度向点A 匀速运动;同时,动点F从点N出发,沿NC方向以每秒1个单位长度的速度向点C匀速运动,其中一点运动到矩形顶点时,两点同时停止运动,连接EF,过点B作EF的垂线,垂足为H.在这一运动过程中,点H所经过的路径长是_____.【解析】∆∆,【分析】根据题意知EF在运动中始终与MN交于点Q,且AQM FQNNQ MQ=点H在以BQ为直径的PN上运动,运动路径长为PN的长,求出:1:2,BQ及PN的圆角,运用弧长公式进行计算即可得到结果.【详解】解:∵点M、N分别是边AD、BC的中点,连接MN,则四边形ABNM是矩形,AD==4,∴MN=AB=6,AM=BN=12根据题意知EF在运动中始终与MN交于点Q,如图,∵四边形ABCD 是矩形,∴AD //BC ,∴AQMFQN ∆∆, ∴12NF NQ EM MQ == ∴123NQ MN == 当点E 与点A 重合时,则NF =122AM =, ∴BF =BN +NF =4+2=6,∴AB =BF =6∴ABF ∆是等腰直角三角形,∴45,AFB ∠=︒∵BP ⊥AF ,∴45PBF ∠=︒由题意得,点H 在以BQ 为直径的PN 上运动,运动路径长为PN 长,取BQ 中点O ,连接PO ,NO ,∴∠PON =90°,又90,BNQ ∠=︒∴BQ ===∴12ON OP OQ BQ ====,∴PN故答案为:2【点睛】本题主要考查了相似三角形的判定与性质,勾股定理,圆周角定理,以及弧长等知识,判断出点H 运动的路径长为PN 长是解答本题的关键.27. 如图,ABC 中,点E 、F 分别在边AB 、AC 上,12∠=∠.若4BC =,2AF =,3CF =,则EF =______.【答案】85【解析】【分析】易证△AEF ∽△ABC ,得EF AF BC AC =即EF AF BC AF CF=+即可求解. 【详解】解:∵∠1=∠2,∠A =∠A ,∴△AEF ∽△ABC , ∴EF AF BC AC =,即EF AF BC AF CF=+ ∵4BC =,2AF =,3CF =, ∴2423EF =+,∴EF=85,故答案为:85.【点睛】本题考查相似三角形的判定与性质,熟练掌握相似三角形的判定与性质定理是解题的关键.28. 如图是钉板示意图,每相邻4个钉点是边长为1个单位长的小正方形顶点,钉点A,B的连线与钉点C,D的连线交于点E,则AB与CD是否垂直?______(填“是”或“否”);AE=______.【答案】,. 是,.5【解析】【分析】(1)证明△ACG≌△CFD,推出∠CAG=∠FCD,证明∠CEA=90°,即可得到结论;(2)利用勾股定理求得AB的长,证明△AEC∽△BED,利用相似三角形的性质列式计算即可求解.【详解】(1)如图:AC=CF=2,CG=DF=1,∠ACG=∠CFD=90°,∴△ACG≌△CFD,∴∠CAG=∠FCD,∵∠ACE+∠FCD=90°,∴∠ACE+∠CAG=90°,∴∠CEA=90°,∴AB与CD是垂直的,故答案为:是;(2)AB=∵AC ∥BD ,∴△AEC ∽△BED , ∴AC AE BD BE =,即23AE BE =, ∴25AE BE =,∴AE =25BE .【点睛】本题考查了相似三角形的判定和性质,全等三角形的判定和性质,解答本题的关键是明确题意,找出所求问题需要的条件.29. 如图,在ABC 中,点D 在AB 边上,点E 在AC 边上,请添加一个条件_________,使ADE ABC △△∽.【答案】∠ADE =∠B (答案不唯一).【解析】【分析】已知有一个公共角,则可以再添加一个角从而利用有两组角对应相等的两个三角形相似来判定或添加夹此角的两边对应成比例也可以判定.【详解】解∶∵∠A =∠A ,∴根据两角相等的两个三角形相似,可添加条件∠ADE =∠B 或∠AED =∠C 证ADE ABC△△∽相似;根据两边对应成比例且夹角相等,可添加条件AD AEAB AC=证ADE ABC△△∽相似.故答案为∶∠ADE=∠B(答案不唯一).【点睛】此题考查了本题考查了相似三角形的判定,解题的关键是掌握相似三角形的判定方法.30. 如图,四边形ABCD是正方形,点E在边BC的延长线上,点F在边AB上,以点D为中心将DCE绕点D顺时针旋转90︒与DAF△恰好完全重合,连接EF交DC于点P,连接AC交EF于点Q,连接BQ,若·AQ DP=BQ=______.【解析】【分析】通过,DFQ=,DAQ=45°证明A、F、Q、D四点共圆,得到∠FDQ=∠F AQ=45°,∠AQF=∠ADF,利用等角对等边证明BQ=DQ=FQ=EQ,并求出DE=,通过有两个角分别相等的三角形相似证明AFQ PED∽,得到AQ DP DE FQ⋅=⋅=BQ代入DE、FQ中即可求出.【详解】连接PQ,∵DCE绕点D顺时针旋转90︒与DAF△完全重合,,DF=DE,∠EDF=90°,DAF DCE≌,,,DFQ=,DEQ=45°,,ADF=,CDE,,四边形ABCD是正方形,AC是对角线,∴∠DAQ=∠BAQ=45°,,,DFQ=,DAQ=45°,,,DFQ、,DAQ是同一个圆内弦DQ所对的圆周角,即点A、F、Q、D在同一个圆上(四点共圆),∴∠FDQ=∠F AQ=45°,∠AQF=∠ADF,,,EDQ=90°-45°=45°,,DQE=180°-,EDQ-,DEQ=90°,,FQ=DQ=EQ,,A、B、C、D是正方形顶点,∴AC、BD互相垂直平分,∵点Q在对角线AC上,∴BQ=DQ,,BQ=DQ=FQ=EQ,,∠AQF=∠ADF,,ADF=,CDE,,∠AQF=,CDE,,,F AQ=,PED=45°,∽,,AFQ EPD,AQ FQ=,DE DP,AQ DP DE FQ⋅=⋅=,BQ=DQ=FQ=EQ,∠DQE=90°,,DE =,,DE FQ BQ ⋅=⋅=∴BQ ==,【点睛】本题综合考查了相似三角形、全等三角形、圆、正方形等知识,通过灵活运用四点共圆得到等弦对等角来证明相关角相等是解题的巧妙方法.三、解答题31. 如图,在ABC 中,点D ,E ,F 分别在边AB ,AC ,BC 上,连接DE ,EF ,已知四边形BFED 是平行四边形,DE 1BC 4=.(1)若8AB =,求线段AD 的长.(2)若ADE 的面积为1,求平行四边形BFED 的面积.【答案】(1)2 (2)6【解析】【分析】(1)利用平行四边形对边平行证明ADE ABC △△∽,得到DE AD BC AB=即可求出; (2)利用平行条件证明ADE EFC ∽,分别求出ADE EFC 与、ADE ABC 与的相似比,通过相似三角形的面积比等于相似比的平方分别求出EFC S、ABC S ,最后通过BFED ABC EFC ADE S S S S =--求出.【小问1详解】∵四边形BFED 是平行四边形,,∥DE BC ,,ADE ABC △△∽,,DE AD BC AB =, ,DE 1BC 4=, ∴AD 1AB 4=, ,118244AD AB ==⨯=;【小问2详解】∵四边形BFED 是平行四边形,,∥DE BC ,EF AB ∥,DE =BF ,,,AED ECF EAD CEF ∠=∠∠=∠,,ADE EFC ∽ ,2ADE EFC S DE S FC ⎛⎫= ⎪⎝⎭, ∵DE 1BC 4=,DE =BF , ∴43FC BC DE DE DE DE =-=-=, ,133DE DE FC DE ==, ,221139ADE EFC S DE S FC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭, ,ADE ABC △△∽,DE 1BC 4=, ∴2211416ADE ABC S DE S BC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭, ,1ADE S =△,,9,16EFC ABC SS ==, ,16916BFED ABC EFC ADES S S S =--=--=. 【点睛】本题考查了相似三角形,熟练掌握相似三角形的面积比等于相似比的平方、灵活运用平行条件证明三角形相似并求出相似比是解题关键.32. 华师版八年级下册数学教材第121页习题19.3第2小题及参考答案.证明:设CE 与DF 交于点O ,∵四边形ABCD 是正方形,∴90B DCF ∠=∠=︒,BC CD =.∴90BCE DCE ∠+∠=︒.∵CE DF ⊥,∴90COD ∠=︒.∴90CDF DCE ∠+∠=︒.∴CDF BCE ∠=∠.∴CBE DFC ≌△△. ∴CE DF =.某数学兴趣小组在完成了以上解答后,决定对该问题进一步探究(1)【问题探究】如图,在正方形ABCD 中,点E 、F 、G 、H 分别在线段AB 、BC 、CD 、DA 上,且EG FH ⊥.试猜想EG FH的值,并证明你的猜想.(2)【知识迁移】如图,在矩形ABCD 中,AB m =,BC n =,点E 、F 、G 、H 分别在线段AB 、BC 、CD 、DA 上,且EG FH ⊥.则EG FH=______.(3)【拓展应用】如图,在四边形ABCD 中,90DAB ∠=︒,60ABC ∠=︒,AB BC =,点E 、F 分别在线段AB 、AD 上,且CE BF ⊥.求CE BF的值.【答案】(1)1,理由见解析(2)n m(3【解析】【分析】(1)过点A 作AM ∥HF 交BC 于点M ,作AN ∥EG 交CD 的延长线于点N ,利用正方形ABCD ,AB =AD ,∠ABM =∠BAD =∠ADN =90°求证△ABM ≌△ADN 即可;(2)过点A 作AM ∥HF 交BC 于点M ,作AN ∥EC 交CD 的延长线于点N ,利用在长方形ABCD 中,BC =AD ,∠ABM =∠BAD =∠ADN =90°求证△ABM ∽△ADN .再根据其对应边成比例,将已知数值代入即可;(3)如图3中,过点C 作CM ⊥AB 于点M .设CE 交BF 于点O .证明△CME ∽△BAF ,推出BCE BF CM A =,可得结论. 【小问1详解】解:1EG FH=,理由为: 过点A 作AM ∥HF 交BC 于点M ,作AN ∥EG 交CD 的延长线于点N ,∵四边形ABCD 是正方形,∴AB ∥CD ,AD ∥BC ,∴四边形AMFH 是平行四边形,四边形AEGN 是平行四边形,∴AM =HF ,AN =EG ,在正方形ABCD 中,AB =AD ,∠ABM =∠BAD =∠ADN =90°∵EG ⊥FH ,∴∠NAM =90°,∴∠BAM =∠DAN ,在△ABM 和△ADN 中,∠BAM =∠DAN ,AB =AD ,∠ABM =∠ADN∴△ABM ≌△AND ,∴AM =AN ,即EG =FH , ∴1EG FH=; 【小问2详解】解:过点A 作AM ∥HF 交BC 于点M ,作AN ∥EC 交CD 的延长线于点N ,∵四边形ABCD 是矩形,∴AB ∥CD ,AD ∥BC ,∴四边形AMFH 是平行四边形,四边形AEGN 是平行四边形,∴AM =HF ,AN =EG ,在矩形ABCD 中,BC =AD ,∠ABM =∠BAD =∠ADN =90°,∵EG ⊥FH ,∴∠NAM =90°,∴∠BAM =∠DAN .∴△ABM ∽△ADN , ∴AM AB AN AD=, ∵AB m =,BC AD n ==,AM =HF ,AN =EG , ∴HF m EG n=, ∴EG n FH m=; 故答案为:n m ; 【小问3详解】解:∵60ABC ∠=︒,AB BC =,∴ABC ∆是等边三角形,∴设AB BC AC a ===,过点CN AB ⊥,垂足为N ,交BF 于点M ,则12AN BN a ==,在Rt BCN ∆中,CN ===, ∵CN AB ⊥,CE BF ⊥,∴90ABF BMN ∠+∠=︒,90ECN CMF ∠+∠=︒,又∵CMF BMN ∠=∠,∴ABF ECN ∠=∠,∵CN AB ⊥,90DAB ∠=︒,∴90DAB CNE ∠=∠=︒,∴NCE ABF ∆∆∽, ∴CE CN BF AB=,即22CE BF a ==. 【点睛】本题属于四边形综合题,考查了正方形的性质,矩形的性质,全等三角形的判定和性质,相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形或相似三角形解决问题.33. 小东在做九上课本123页习题:“1也是一个很有趣的比.已知线段AB (如图1),用直尺和圆规作AB 上的一点P ,使AP :AB =1.”小东的作法是:如图2,以AB 为斜边作等腰直角三角形ABC ,再以点A 为圆心,AC 长为半径作弧,交线段AB 于点P ,点P 即为所求作的点.小东称点P 为线段AB 的“趣点”.。
相似三角形-2022年中考数学专练(解析版)

热点07 相似三角形相似三角形在中考数学中的地址永远都是无法撼动的第一,不管是对相似三角形性质、判定、亦或是应用的考察,都有出题类型多变,出题形式随意的特点,并且,因为其高度的融合性,不管是在选择题、填空题、解答题的压轴题中,都可以作为压轴题的问题背景出现,也是解决压轴题问题不可或缺的方法途径。
基于以上特征,相似三角的考察难度可以从中等跨越到较难,属于中考数学中较为重要的压轴考点。
1.相似三角形的性质:分类记忆——边、角、线、面积+周长;相似三角形的性质有:对应边成比例、对应角相等、对应边上的“三线”之比=相似比、对应面积之比=相似比的平方、对应周长之比=相似比。
另外,相似三角形之前还有有关平行线分线段成比例的基本性质的考察。
2.相似三角形的判定:重点记“AA”与“SAS”类型,小题勿忘“SSS”类型;相似三角形的判定方法中,最常用的是有两个角对应相等的两个三角形相似,其次是对应角相等,对应边成比例的两个三角形相似。
三边对应成比例的两个三角形相似不长出现,但是个别小题,特别是和网格结合的问题小题中,也是有出现几率的。
3.相似三角形的应用:理解题意、提炼模型、注意特殊要求;相似三角形的应用多与实际生活结合,考察树或者楼的高度、物体的某些边的长度等。
此时通常需要自己提炼出应用的相似模型,并根据需要添加辅助线等,个别时候还会要求结果符合一定的要求,需要特点别注意。
当相似三角形与函数结合考察时,通常为压轴题,需要同时注意相似三角形与函数各自的性质的融合。
相似三角形的考察热点有:平行线分线段成比例的基本性质、相似三角形的性质、判定以及其综合应用。
近几年也常考察相似里的几何模型,如:手拉手模型、K型图模型、A字图与8字图模型、母子三角形模型等。
A卷(建议用时:60分钟)1.(2021•攀枝花·中考真题)若(x、y、z均不为0),则=.【分析】设比值为k,然后用k表示出x、y、z,再代入比例式进行计算即可得解.【解答】解:设===k(k≠0),则x=6k,y=4k,z=3k,所以,==3.故答案为:3.2.(2021•百色·中考真题)如图,△ABC中,AB=AC,∠B=72°,∠ACB的平分线CD交AB于点D,则点D是线段AB的黄金分割点.若AC=2,则BD=.【分析】证AD=CD=BC,再证△BCD∽△BAC,得BC:AB=BD:BC,则AD:AB=BD:AD,得点D是AB边上的黄金分割点,AD>BD,求出AD=AB=﹣1,即可求解.【解答】解:∵AB=AC=2,∴∠B=∠ACB=72°,∠A=36°,∵CD平分∠ACB,∴∠ACD=∠BCD=36°,∴∠A=∠ACD,∴AD=CD,∵∠CDB=180°﹣∠B﹣∠BCD=72°,∴∠CDB=∠B,∴BC=CD,∴BC=AD,∵∠B=∠B,∠BCD=∠A=36°,∴△BCD∽△BAC,∴BC:AB=BD:BC,∴AD:AB=BD:AD,∴点D是AB边上的黄金分割点,AD>BD,∴AD=AB=﹣1,∴BD=AB﹣AD=2﹣(﹣1)=3﹣,故答案为:3﹣.3.(2021•哈尔滨·中考真题)如图,在△ABC中,DE∥BC,AD=2,BD=3,AC=10,则AE的长为()A.3B.4C.5D.6【分析】根据平行线分线段成比例由DE∥BC得到,然后根据比例的性质可求出AE.【解答】解:∵DE∥BC,∴,∵AD=2,BD=3,AC=10,∴,∴AE=4.故选:B.4.(2021•上海·中考真题)如图所示,已知在梯形ABCD中,AD∥BC,=,则=.【分析】过D作DM⊥BC于M,过B作BN⊥AD于N,由四边形BMDN是矩形,可得DM=BN,=,根据AD∥BC,可得==,=,即可得到=.【解答】解:过D作DM⊥BC于M,过B作BN⊥AD于N,如图:∵AD∥BC,DM⊥BC,BN⊥AD,∴四边形BMDN是矩形,DM=BN,∵=,∴=,∴=,∵AD∥BC,∴==,∴=,∴=,故答案为:.5.(2021•镇江·中考真题)如图,点D,E分别在△ABC的边AC,AB上,△ADE∽△ABC,M,N分别是DE,BC的中点,若=,则=.【分析】根据相似三角形对应中线的比等于相似比求出,根据相似三角形面积的比等于相似比的平方解答即可.【解答】解:∵M,N分别是DE,BC的中点,∴AM、AN分别为△ADE、△ABC的中线,∵△ADE∽△ABC,∴==,∴=()2=,故答案为:.6.(2021•湘潭·中考真题)如图,在△ABC中,点D,E分别为边AB,AC上的点,试添加一个条件:,使得△ADE与△ABC相似.(任意写出一个满足条件的即可)【分析】根据相似三角形判定定理:两个角相等的三角形相似;夹角相等,对应边成比例的两个三角形相似,即可解题.【解答】解:添加∠ADE=∠C,又∵∠A=∠A,∴△ADE∽△ACB,故答案为:∠ADE=∠C(答案不唯一).7.(2021•巴中·中考真题)如图,△ABC中,点D、E分别在AB、AC上,且==,下列结论正确的是()A.DE:BC=1:2B.△ADE与△ABC的面积比为1:3C.△ADE与△ABC的周长比为1:2D.DE∥BC【分析】根据相似三角形的判定与性质进行逐一判断即可.【解答】解:∵==,∴AD:AB=AE:AC=1:3,∵∠A=∠A,∴△ADE∽△ABC,∴DE:BC=1:3,故A错误;∵△ADE∽△ABC,∴△ADE与△ABC的面积比为1:9,周长的比为1:3,故B和C错误;∵△ADE∽△ABC,∴∠ADE=∠B,∴DE∥BC.故D正确.故选:D.8.(2021•恩施州·中考真题)如图,在4×4的正方形网格中,每个小正方形的边长都为1,E为BD与正方形网格线的交点,下列结论正确的是()A.CE≠BD B.△ABC≌△CBD C.AC=CD D.∠ABC=∠CBD【分析】根据勾股定理可以得到BC、CD、BD的长,再根据勾股定理的逆定理可以得到△BCD的形状,利用相似三角形的判定与性质,可以得到EF的长,然后即可得到CE的长,从而可以得到CE和BD的关系;根据图形,很容易判断△ABC≌△CBD和AC=CD不成立;再根据锐角三角函数可以得到∠ABC 和∠CBD的关系.【解答】解:由图可得,BC==2,CD==,BD==5,∴BC2+CD2=(2)2+()2=25=BD2,∴△BCD是直角三角形,∵EF∥GD,∴△BFE∽△BGD,∴,即,解得EF=1.5,∴CE=CF﹣EF=4﹣1.5=2.5,∴=,故选项A错误;由图可知,显然△ABC和△CBD不全等,故选项B错误;∵AC=2,CD=,∴AC≠CD,故选项C错误;∵tan∠ABC==,tan∠==,∴∠ABC=∠CBD,故选项D正确;故选:D.9.(2021•内江·中考真题)在同一时刻,物体的高度与它在阳光下的影长成正比.在某一时刻,有人测得一高为1.8m的竹竿的影长为3m,某一高楼的影长为60m,那么这幢高楼的高度是()A.18m B.20m C.30m D.36m【分析】设此高楼的高度为x米,再根据同一时刻物高与影长成正比例出关于x的比例式,求出x的值即可.【解答】解:设这幢高楼的高度为x米,依题意得:=,解得:x=36.故这幢高楼的高度为36米.故选:D.10.(2021•兰州·中考真题)如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为5m时,标准视力表中最大的“”字高度为72.7mm,当测试距离为3m时,最大的“”字高度为()A.121.17mm B.43.62mm C.29.08mm D.4.36mm【分析】直接利用平行线分线段成比例定理列比例式,代入可得结论.【解答】解:由题意得:CB∥DF,,∵AD=3m,AB=5m,BC=72.7mm,,∴DF=43.62(mm),故选:B.11.(2021•锦州·中考真题)如图,△ABC内接于⊙O,AB为⊙O的直径,D为⊙O上一点(位于AB下方),CD交AB于点E,若∠BDC=45°,BC=6,CE=2DE,则CE的长为()A.2B.4C.3D.4【分析】连接CO,过点D作DG⊥AB于点G,连接AD,因为CE=2DE,构造△DGE∽△COE,求出DG=3,设GE=x,则OE=2x,DG=3,则AG=6﹣3x,BG=6+3x,再利用△AGD∽△ADB,列出方程即可解决.【解答】解:方法一、连接CO,过点D作DG⊥AB于点G,连接AD,∵∠BDC=45°,∴∠CAO=∠CDB=45°,∵AB为⊙O的直径,∴∠ACB=∠ADB=90°,∴∠CAB=∠CBA=45°,∵BC=6,∴AB=BC=12,∵OA=OB,∴CO⊥AB,∴∠COA=∠DGE=90°,∵∠DEG=∠CEO,∴△DGE∽△COE,∴=,∵CE=2DE,设GE=x,则OE=2x,DG=3,∴AG=6﹣3x,BG=6+3x,∵∠ADB=∠AGB=90°,∠DAG=∠BAD,∴△AGD∽△ADB,∴DG2=AG•BG,∴9=(6﹣3x)(6+3x),∵x>0,∴x=,∴OE=2,在Rt△OCE中,由勾股定理得:CE=,方法二、∵∠CDB=∠A=45°,∴∠ABC=∠A=45°,∵∠BCE=∠DCB,∴△BCE∽△DCB,∴BC2=CE×CD,设DE=x,则CE=2x,∴(6)2=2x×3x,∵x>0,∴x=2,∴CE=4,故选:D.12.(2021•连云港·中考真题)如图,△ABC中,BD⊥AB,BD、AC相交于点D,AD=AC,AB=2,∠ABC=150°,则△DBC的面积是()A.B.C.D.【分析】过点C作BD的垂线,交BD的延长线于点E,可得△ABD∽△CED,可得==,由AD=AC,AB=2,可求出CE的长,又∠ABC=150°,∠ABD=90°,则∠CBD=60°,解直角△BCE,可分别求出BE和BD的长,进而可求出△BCD的面积.【解答】解:如图,过点C作BD的垂线,交BD的延长线于点E,则∠E=90°,∵BD⊥AB,CE⊥BD,∴AB∥CE,∠ABD=90°,∴△ABD∽△CED,∴==,∵AD=AC,∴=,∴===,则CE=,∵∠ABC=150°,∠ABD=90°,∴∠CBE=60°,∴BE=CE=,∴BD=BE=,∴S△BCD=•BD•CE=×=.故选:A.13.(2021•济南·中考真题)如图,一个由8个正方形组成的“C”模板恰好完全放入一个矩形框内,模板四周的直角顶点M,N,O,P,Q都在矩形ABCD的边上,若8个小正方形的面积均为1,则边AB的长为.【分析】如解答图所示,连接EG,则∠OEP=90°,由题意得,小正方形的边长为1,根据勾股定理得出OP=,根据矩形的性质可判定△OEP∽△QBM,得到===,进而得出BM=,QB=,利用AAS证明△QBM≌△MAN,根据全等三角形的性质及线段的和差即可得解.【解答】解:如下图所示,连接EG,则∠OEP=90°,由题意得,小正方形的边长为1,∴OP===,∵四边形ABCD是矩形,∴∠B=∠C=∠A=90°,∠MQP=90°,∴∠BMQ=∠CQP=90°﹣∠MQP,同理∠EPO=∠CQP=90°﹣∠QPC,∴∠BMQ=∠EPO,又∠OEP=∠B=90°,∴△OEP∽△QBM,∴===,∴BM===,QB===,∵∠B=∠A=90°,∠NMQ=90°,∴∠BMQ=∠ANM=90°﹣∠AMN,在△QBM和△MAN中,,∴△QBM≌△MAN(AAS),∴AM=QB=,∴AB=BM+AM=+=.故答案为:.14.(2021•鄂州·中考真题)如图,在▱ABCD中,点E、F分别在边AD、BC上,且∠ABE=∠CDF.(1)探究四边形BEDF的形状,并说明理由;(2)连接AC,分别交BE、DF于点G、H,连接BD交AC于点O.若=,AE=4,求BC的长.【分析】(1)利用∠ABE=∠CDF以及平行四边形的性质,求证BE∥DF,AD∥BC即可判断四边形BEDF 的形状;(2)设AG=2a,通过已知条件即可推出的值,再通过求证△AGE∽△CGB,利用相似比即可求出BC的长.【解答】解:(1)四边形BEDF为平行四边形,理由如下:∵四边形ABCD为平行四边形,∴∠ABC=∠ADC,∵∠ABE=∠CDF,∴∠EBF=∠EDF,∵四边形ABCD为平行四边形,∴AD∥BC,∴∠EDF=∠DFC=∠EBF,∴BE∥DF,∵AD∥BC,∴四边形BEDF为平行四边形;(2)设AG=2a,∵,∴OG=3a,AO=5a,∵四边形ABCD为平行四边形,∴AO=CO=5a,AC=10a,CG=8a,∵AD∥BC,∴△AGE∽△CGB,∴,∵AE=4,∴BC=16.15.(2021•聊城·中考真题)如图,在△ABC中,AB=AC,⊙O是△ABC的外接圆,AE是直径,交BC 于点H,点D在上,连接AD,CD过点E作EF∥BC交AD的延长线于点F,延长BC交AF于点G.(1)求证:EF是⊙O的切线;(2)若BC=2,AH=CG=3,求EF和CD的长.【分析】(1)由题意可证∠BAE=∠CAE,由等腰三角形的性质可得AE⊥BC,由平行线的性质可证EF ⊥AE,可得结论;(2)在Rt△OHC中,利用勾股定理可求半径,可得AE的长,通过证明△AEF∽△AHG,可得,可求EF的长,通过证明△DCG∽△BAG,可得,可求CD的长.【解答】证明:(1)∵AB=AC,∴=,∵AE是直径,∴=,∴∠BAE=∠CAE,又∵AB=AC,∴AE⊥BC,又∵EF∥BC,∴EF⊥AE,∴EF是⊙O的切线;(2)连接OC,设⊙O的半径为r,∵AE⊥BC,∴CH=BH=BC=1,∴HG=HC+CG=4,∴AG===5,在Rt△OHC中,OH2+CH2=OC2,∴(3﹣r)2+1=r2,解得:r=,∴AE=,∵EF∥BC,∴△AEF∽△AHG,∴,∴=,∴EF=,∵AH=3,BH=1,∴AB===,∵四边形ABCD内接于⊙O,∴∠B+∠ADC=180°,∵∠ADC+∠CDG=180°,∴∠B=∠CDG,又∵∠DGC=∠AGB,∴△DCG∽△BAG,∴,∴=,∴CD=.B卷(建议用时:80分钟)1.(2021•大庆·中考真题)已知==,则=.【分析】设===k,分别求出x、y、z的值,代入所求式子化简即可.【解答】解:设===k,∴x=2k,y=3k,z=4k,∴===,故答案为.2.(2021•德阳·中考真题)我们把宽与长的比是的矩形叫做黄金矩形.黄金矩形给我们以协调、匀称的美感,世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计.已知四边形ABCD是黄金矩形,边AB的长度为﹣1,则该矩形的周长为.【分析】分两种情况:①边AB为矩形的长时,则矩形的宽为3﹣,求出矩形的周长即可;②边AB为矩形的宽时,则矩形的长为=2,求出矩形的周长即可.【解答】解:分两种情况:①边AB为矩形的长时,则矩形的宽为×(﹣1)=3﹣,∴矩形的周长为:2(﹣1+3﹣)=4;②边AB为矩形的宽时,则矩形的长为:(﹣1)÷=2,∴矩形的周长为2(﹣1+2)=2+2;综上所述,该矩形的周长为2+2或4.3.(2021•阿坝州·中考真题)如图,直线l1∥l2∥l3,直线a,b与l1,l2,l3分别交于点A,B,C和点D,E,F.若AB:BC=2:3,EF=9,则DE的长是()A.4B.6C.7D.12【分析】根据平行线分线段成比例定理得出AB:BC=DE:EF,再求出答案即可.【解答】解:∵l1∥l2∥l3,∴AB:BC=DE:EF.∵AB:BC=2:3,EF=9,∴DE=6.故选:B.4.(2021•宿迁·中考真题)如图,在△ABC中,AB=4,BC=5,点D、E分别在BC、AC上,CD=2BD,CE=2AE,BE交AD于点F,则△AFE面积的最大值是.【分析】连接DE.首先证明DE∥AB,推出S△ABE=S△ABD,推出S△AEF=S△BDF,可得S△AEF=S△ABD,求出△ABD面积的最大值即可解决问题.【解答】解:连接DE.∵CD=2BD,CE=2AE,∴==2,∴DE∥AB,∴△CDE∽△CBA,∴==,∴==,∵DE∥AB,∴S△ABE=S△ABD,∴S△AEF=S△BDF,∴S△AEF=S△ABD,∵BD=BC=,∴当AB⊥BD时,△ABD的面积最大,最大值=××4=,∴△AEF的面积的最大值=×=,故答案为:5.(2021•盘锦·中考真题)“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学著作《九章算术》中的“井深几何”问题,它的题意可以由示意图获得,设井深为x尺,所列方程正确的是()A.=B.=C.=D.=【分析】如图,设AD交BE于K.利用相似三角形的性质求解即可.【解答】解:如图,设AD交BE于K.∵DK∥BC,∴△EKD∽△EBC,∴=,∴=,故选:A.6.(2021•临沂·中考真题)如图,点A,B都在格点上,若BC=,则AC的长为()A.B.C.2D.3【分析】根据相似三角形的判定和性质可以得到AB的长,然后由图可知AC=AB﹣BC,然后代入数据计算即可.【解答】解:作CD⊥BD于点D,作AE⊥BD于点E,如右图所示,则CD∥AE,∴△BDC∽△BEA,∴,∴=,解得BA=2,∴AC=BA﹣BC=2﹣=,故选:B.7.(2021•湘西州·中考真题)如图,在△ECD中,∠C=90°,AB⊥EC于点B,AB=1.2,EB=1.6,BC =12.4,则CD的长是()A.14B.12.4C.10.5D.9.3【分析】由∠ABE=∠C,∠E=∠E,证明△ABE∽△DCE,得=,即可求解.【解答】解:∵EB=1.6,BC=12.4,∴EC=EB+BC=14,∵AB⊥EC,∴∠ABE=90°,∵∠C=90°,∴∠ABE=∠C,又∵∠E=∠E,∴△ABE∽△DCE,∴=,即=,解得:CD=10.5,故选:C.8.(2021•益阳·中考真题)如图,Rt△ABC中,∠BAC=90°,tan∠ABC=,将△ABC绕A点顺时针方向旋转角α(0°<α<90°)得到△AB′C′,连接BB′,CC′,则△CAC′与△BAB′的面积之比等于.【分析】证明△ACC′∽△ABB′,可得=()2,解决问题.【解答】解:由旋转的性质可知,∠BAC=∠B′AC′,∴∠BAB′=∠CAC′,∵AB=AB′,AC=AC′,∴=,∴△ACC′∽△ABB′,∴=()2,∵∠CAB=90°,∴tan∠ABC==,∴=()2=.故答案为:9:4.9.(2021•常州·中考真题)如图,在△ABC中,AC=3,BC=4,D、E分别在CA、CB上,点F在△ABC 内.若四边形CDFE是边长为1的正方形,则sin∠FBA=.【分析】连接AF,过点F作FG⊥AB于G,由四边形CDFE是边长为1的正方形可得AD=2,BE=3,根据勾股定理求出AB=5,AF=,BF=,设BG=x,利用勾股定理求出x=3,可得FG=1,即可得sin∠FBA的值.【解答】解:连接AF,过点F作FG⊥AB于G,∵四边形CDFE是边长为1的正方形,∴CD=CE=DF=EF=1,∠C=∠ADF=90°,∵AC=3,BC=4,∴AD=2,BE=3,∴AB==5,AF==,BF==,设BG=x,∵FG2=AF2﹣AG2=BF2﹣BG2,∴5﹣(5﹣x)2=10﹣x2,解得:x=3,∴FG==1,∴sin∠FBA==.故答案为:.10.(2021•绵阳·中考真题)如图,在△ACD中,AD=6,BC=5,AC2=AB(AB+BC),且△DAB∽△DCA,若AD=3AP,点Q是线段AB上的动点,则PQ的最小值是()A.B.C.D.【分析】根据相似三角形的性质得到=,得到BD=4(负值舍去),AB=BD=4,过B作BH⊥AD 于H,根据等腰三角形的性质得到AH=AD=3,根据勾股定理得到BH===,当PQ⊥AB时,PQ的值最小,根据相似三角形的性质即可得到结论.【解答】解:∵△DAB∽△DCA,∴=,∴=,解得:BD=4(负值舍去),∵△DAB∽△DCA,∴,∴AC=,∵AC2=AB(AB+BC),∴(AB)2=AB(AB+BC),∴AB=4,∴AB=BD=4,过B作BH⊥AD于H,∴AH=AD=3,∴BH===,∵AD=3AP,AD=6,∴AP=2,当PQ⊥AB时,PQ的值最小,∵∠AQP=∠AHB=90°,∠P AQ=∠BAH,∴△APQ∽△ABH,∴,∴=,∴PQ=,故选:A.11.(2021•温州·中考真题)由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.过点D作DF的垂线交小正方形对角线EF的延长线于点G,连结CG,延长BE交CG于点H.若AE=2BE,则的值为()A.B.C.D.【分析】如图,过点G作GT⊥CF交CF的延长线于T,设BH交CF于M,AE交DF于N.设BE=AN =CM=DF=a,则AE=BM=CF=DN=2a,想办法求出BH,CG,可得结论.【解答】解:如图,过点G作GT⊥CF交CF的延长线于T,设BH交CF于M,AE交DF于N.设BE =AN=CM=DF=a,则AE=BM=CF=DN=2a,∴EN=EM=MF=FN=a,∵四边形ENFM是正方形,∴∠EFH=∠TFG=45°,∠NFE=∠DFG=45°,∵GT⊥TF,DF⊥DG,∴∠TGF=∠TFG=∠DFG=∠DGF=45°,∴TG=FT=DF=DG=a,∴CT=3a,CG==a,∵MH∥TG,∴△CMH∽△CTG,∴CM:CT=MH:TG=1:3,∴MH=a,∴BH=2a+a=a,∴==,故选:C.12.(2021•山西·中考真题)如图,在△ABC中,点D是AB边上的一点,且AD=3BD,连接CD并取CD 的中点E,连接BE,若∠ACD=∠BED=45°,且CD=6,则AB的长为.【分析】取AD中点F,连接EF,过点D作DG⊥EF于G,DH⊥BE于H,设BD=a,由三角形中位线定理可得DF=a,EF∥AC,DE=3,通过证明四边形DGEH是正方形,可得DE=DG=3,DH∥EF,通过证明△BDH∽△DFG,可得,可求BH的长,在Rt△DHB中,利用勾股定理可求BD的长,即可求解.【解答】解:如图,取AD中点F,连接EF,过点D作DG⊥EF于G,DH⊥BE于H,设BD=a,∴AD=3BD=3a,AB=4a,∵点E为CD中点,点F为AD中点,CD=6,∴DF=a,EF∥AC,DE=3,∴∠FED=∠ACD=45°,∵∠BED=45°,∴∠FED=∠BED,∠FEB=90°,∵DG⊥EF,DH⊥BE,∴四边形EHDG是矩形,DG=DH,∴四边形DGEH是正方形,∴DE=DG=3,DH∥EF,∴DG=DH=3,∵DH∥EF,∴∠BDH=∠DFG,∴△BDH∽△DFG,∴,∴=,∴BH=2,∴BD===,∴AB=4,故答案为:4.13.(2021•鞍山·中考真题)如图,△ABC的顶点B在反比例函数y=(x>0)的图象上,顶点C在x 轴负半轴上,AB∥x轴,AB,BC分别交y轴于点D,E.若==,S△ABC=13,则k=.【分析】过点B作BF⊥x轴于点F,通过设参数表示出三角形ABC的面积,从而求出参数的值,再利用三角形ABC与矩形ODBF的关系求出矩形面积,即可求得k的值.【解答】解:如图,过点B作BF⊥x轴于点F.∵AB∥x轴,∴△DBE∽△OCE,∴=,∵==,∴====,设CO=3a,DE=3b,则AD=2a,OE=2b,∴,OD=5b,∴BD=,∴AB=AD+DB=,∵S△ABC===13,∴ab=,∵S矩形ODBF=BD•OD===18,又∵反比例函数图象在第一象限,∴k=18,故答案为18.14.(2021•营口·中考真题)如图,AB是⊙O直径,点C,D为⊙O上的两点,且=,连接AC,BD 交于点E,⊙O的切线AF与BD延长线相交于点F,A为切点.(1)求证:AF=AE;(2)若AB=8,BC=2,求AF的长.【分析】(1)利用AB是⊙O直径,AF是⊙O的切线,得到∠DAF=∠ABF,利用=得到∠ABF=∠CAD,进而证得∠F=∠AEF,根据等角对等边即可证得AF=AE;(2)利用勾股定理求得AC,利用△BCE∽△BAF得到=,求得CE=AF=AE,根据AE+CE =AC即可求得AF.【解答】(1)证明:连接AD,∵AB是⊙O直径,∴∠ADB=∠ADF=90°,∴∠F+∠DAF=90°,∵AF是⊙O的切线,∴∠F AB=90°,∴∠F+∠ABF=90°,∴∠DAF=∠ABF,∵=,∴∠ABF=∠CAD,∴∠DAF=∠CAD,∴∠F=∠AEF,∴AF=AE;(2)解:∵AB是⊙O直径,∴∠C=90°,∵AB=8,BC=2,∴AC===2,∵∠C=∠F AB=90°,∠CEB=∠AEF=∠F,∴△BCE∽△BAF,∴=,即=,∴CE=AF,∵AF=AE,∴CE=AE,∵AE+CE=AC=2,∴AE=,∴AF=AE=.15.(2021•杭州·中考真题)如图,锐角三角形ABC内接于⊙O,∠BAC的平分线AG交⊙O于点G,交BC边于点F,连接BG.(1)求证:△ABG∽△AFC.(2)已知AB=a,AC=AF=b,求线段FG的长(用含a,b的代数式表示).(3)已知点E在线段AF上(不与点A,点F重合),点D在线段AE上(不与点A,点E重合),∠ABD =∠CBE,求证:BG2=GE•GD.【分析】(1)根据∠BAC的平分线AG交⊙O于点G,知∠BAG=∠F AC,由圆周角定理知∠G=∠C,即可证△ABG∽△AFC;(2)由(1)知=,由AC=AF得AG=AB,即可计算FG的长度;(3)先证△DGB∽△BGE,得出线段比例关系,即可得证BG2=GE•GD.【解答】(1)证明:∵AG平分∠BAC,∴∠BAG=∠F AC,又∵∠G=∠C,∴△ABG∽△AFC;(2)解:由(1)知,△ABG∽△AFC,∴=,∵AC=AF=b,∴AB=AG=a,∴FG=AG﹣AF=a﹣b;(3)证明:∵∠CAG=∠CBG,∠BAG=∠CAG,∴∠BAG=∠CBG,∵∠ABD=∠CBE,∴∠BDG=∠BAG+∠ABD=∠CBG+∠CBE=∠EBG,又∵∠DGB=∠BGE,∴△DGB∽△BGE,∴=,∴BG2=GE•GD.16.(2021•罗湖区·中考真题)如图,在四边形ABCD中,AB=AD,AC与BD交于点E,∠ADB=∠ACB.(1)求证:=;(2)若AB⊥AC,AE:EC=1:2,F是BC中点,求证:四边形ABFD是菱形.【分析】(1)利用相似三角形的判定得出△ABE∽△ACB,进而求出答案;(2)首先证明AD=BF,进而得出AD∥BF,即可得出四边形ABFD是平行四边形,再利用AD=AB,得出四边形ABFD是菱形.【解答】证明:(1)∵AB=AD,∴∠ADB=∠ABE,又∵∠ADB=∠ACB,∴∠ABE=∠ACB,又∵∠BAE=∠CAB,∴△ABE∽△ACB,∴=,又∵AB=AD,∴=;(2)设AE=x,∵AE:EC=1:2,∴EC=2x,由(1)得:AB2=AE•AC,即AB2=x•3x∴AB=x,又∵BA⊥AC,∴BC=2x,∴∠ACB=30°,∵F是BC中点,∴BF=x,∴BF=AB=AD,连接AF,则AF=BF=CF,∠ACB=30°,∠ABC=60°,又∵∠ABD=∠ADB=30°,∴∠CBD=30°,∴∠ADB=∠CBD=∠ACB=30°,∴AD∥BF,∴四边形ABFD是平行四边形,又∵AD=AB,∴四边形ABFD是菱形.。
专题28 相似三角形篇(解析版)

专题28 相似三角形考点一:比例1. 比例的性质:①基本性质:两内项之积等于量外项之积。
即若d c b a ::=,则ad bc =。
②合比性质:若d c b a =,则d d c b b a +=+。
③分比性质:若d c b a =,则d d c b b a -=-。
④合分比性质:若d c b a =,则d c d c b a b a -+=-+。
⑤等比性质:若n m d c b a ===...,则n m d c b a n d b m c a ====++++++.........。
2. 比例线段:若四条线段d c b a ,,,,如果其中两条线段的比(即它们的长度比)与另两条线段的比相等,如d c b a ::=(即ad bc =),我们就说这四条线段是成比例线段,简称比例线段。
3. 平行线分线段成比例:三条平行线被两条直线所截,所得的对应线段成比例。
即如图:有EFDE BC AB =;DFDE AC AB =;DFEF AC BC =。
推论:①平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
②如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边。
③平行于三角形的一边,并且和其他两边(或两边的延长线)相交的直线,所截得的三角形的三边与原三角形的三边对应成比例。
1.(2022•镇江)《九章算术》中记载,战国时期的铜衡杆,其形式既不同于天平衡杆,也异于称杆.衡杆正中有拱肩提纽和穿线孔,一面刻有贯通上、下的十等分线.用该衡杆称物,可以把被称物与砝码放在提纽两边不同位置的刻线上,这样,用同一个砝码就可以称出大于它一倍或几倍重量的物体.图为铜衡杆的使用示意图,此时被称物重量是砝码重量的 倍.【分析】根据比例的性质解决此题.【解答】解:由题意得,5m被称物=6m砝码.∴m被称物:m砝码=6:5=1.2.故答案为:1.2.2.(2022•巴中)如图,在平面直角坐标系中,C为△AOB的OA边上一点,AC:OC=1:2,过C作CD ∥OB交AB于点D,C、D两点纵坐标分别为1、3,则B点的纵坐标为( )A.4B.5C.6D.7【分析】根据CD∥OB得出,根据AC:OC=1:2,得出,根据C、D两点纵坐标分别为1、3,得出OB=6,即可得出答案.【解答】解:∵CD∥OB,∴,∵AC:OC=1:2,∴,∵C 、D 两点纵坐标分别为1、3,∴CD =3﹣1=2,∴,解得:OB =6,∴B 点的纵坐标为6,故选:C .3.(2022•临沂)如图,在△ABC 中,DE ∥BC ,32 DB AD ,若AC =6,则EC =( )A .56B .512C .518D .524【分析】利用平行线分线段成比例定理解答即可.【解答】解:∵DE ∥BC ,∴=,∴,∴,∴EC =.故选:C .4.(2022•丽水)如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A ,B ,C 都在横线上.若线段AB =3,则线段BC 的长是( )A .32B .1C .23D .2【分析】过点A 作平行横线的垂线,交点B 所在的平行横线于D ,交点C 所在的平行横线于E ,根据平行线分线段成比例定理列出比例式,计算即可.【解答】解:过点A作平行横线的垂线,交点B所在的平行横线于D,交点C所在的平行横线于E,则=,即=2,解得:BC=,故选:C.5.(2022•襄阳)如图,在△ABC中,D是AC的中点,△ABC的角平分线AE交BD于点F,若BF:FD=3:1,AB+BE=33,则△ABC的周长为 .【分析】如图,过点F作FM于点M,FN⊥AC于点N,过点D作DT∥AE交BC于点T.证明AB =3AD,设AD=CD=a,证明ET=CT,设ET=CT=b,则BE=3b,求出a+b,可得结论.【解答】解:如图,过点F作FM⊥AB于点M,FN⊥AC于点N,过点D作DT∥AE交BC于点T.∵AE平分∠BAC,FM⊥AB,FN⊥AC,∴FM=FN,∴===3,∴AB=3AD,设AD =DC =a ,则AB =3a ,∵AD =DC ,DT ∥AE ,∴ET =CT ,∴==3,设ET =CT =b ,则BE =3b ,∵AB +BE =3,∴3a +3b =3,∴a +b =,∴△ABC 的周长=AB +AC +BC =5a +5b =5,故答案为:5.6.(2022•哈尔滨)如图,AB ∥CD ,AC ,BD 相交于点E ,AE =1,EC =2,DE =3,则BD 的长为( )A .23B .4C .29D .6【解答】解:∵AB ∥CD ,∴△ABE ∽△CDE ,∴=,即=,∴BE =1.5,∴BD =BE +DE =4.5.故选:C .7.(2022•雅安)如图,在△ABC 中,D ,E 分别是AB 和AC 上的点,DE ∥BC ,若12 BD AD ,那么BCDE =( )A .94B .21C .31D .32【分析】根据相似三角形的判定定理和性质定理解答即可.【解答】解:∵DE ∥BC ,∴△ADE ∽△ABC ,∴=,∵=,∴=,∴==.故选:D .8.(2022•凉山州)如图,在△ABC 中,点D 、E 分别在边AB 、AC 上,若DE ∥BC ,32 BD AD ,DE =6cm ,则BC 的长为( )A .9cmB .12cmC .15cmD .18cm【分析】根据=,得到=,根据DE ∥BC ,得到∠ADE =∠B ,∠AED =∠C ,得到△ADE ∽△ABC ,根据相似三角形对应边成比例即可得出答案.【解答】解:∵=,∴=,∵DE ∥BC ,∴∠ADE =∠B ,∠AED =∠C ,∴△ADE ∽△ABC ,∴=,∴=,∴BC =15(cm ),故选:C .9.(2022•鞍山)如图,AB ∥CD ,AD ,BC 相交于点E ,若AE :DE =1:2,AB =2.5,则CD 的长为 .【分析】由平行线的性质求出∠B =∠C ,∠A =∠D ,其对应角相等得△EAB ∽△EDC ,再由相似三角形的性质求出线段CD 即可.【解答】解:∵AB ∥CD ,∴∠B =∠C ,∠A =∠D ,∴△EAB ∽△EDC ,∴AB :CD =AE :DE =1:2,又∵AB =2.5,∴CD =5.故答案为:5.10.(2022•上海)如图,在△ABC 中,∠A =30°,∠B =90°,D 为AB 中点,E 在线段AC 上,BC DE AB AD ,则AC AE = .【分析】利用平行线截线段成比例解答.【解答】解:∵D 为AB 中点,∴=.当DE ∥BC 时,△ADE ∽△ABC ,则===.当DE 与BC 不平行时,DE =DE ′,=.故答案是:或.11.(2022•宜宾)如图,△ABC 中,点E 、F 分别在边AB 、AC 上,∠1=∠2.若BC =4,AF =2,CF =3,则EF = .【分析】由∠1=∠2,∠A =∠A ,得出△AEF ∽△ABC ,再由相似三角形的性质即可得出EF 的长度.【解答】解:∵∠1=∠2,∠A =∠A ,∴△AEF ∽△ABC ,∴,∵BC =4,AF =2,CF =3,∴,∴EF =,故答案为:.考点二:相似三角形的性质1.相似图形的概念:把形状相同的图形称为相似图形。
2020年中考数学必考考点压轴题 专题24 相似三角形判定与性质(含答案)

专题24相似三角形判定与性质1.相似三角形:对应角相等,对应边成比例的两个三角形叫做相似三角形。
相似多边形对应边的比叫做相似比。
2.三角形相似的判定方法:(1)定义法:对应角相等,对应边成比例的两个三角形相似。
(2)平行法:平行于三角形一边的直线和其他两边(或两边延长线)相交,构成的三角形与原三角形相似。
(3)判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似,可简述为两角对应相等,两三角形相似。
(4)判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应相等,并且夹角相等,那么这两个三角形相似,可简述为两边对应成比例且夹角相等,两三角形相似。
(5)判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似,可简述为三边对应成比例,两三角形相似。
3.直角三角形相似判定定理:①以上各种判定方法均适用②定理:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
③垂直法:直角三角形被斜边上的高分成的两个直角三角形与原三角形相似。
4.相似三角形的性质:(1)相似三角形的对应角相等,对应边成比例(2)相似三角形对应高的比、对应中线的比与对应角平分线的比都等于相似比(3)相似三角形周长的比等于相似比(4)相似三角形面积的比等于相似比的平方。
【例题1】(2019•海南省)如图,在Rt△ABC中,∠C=90°,AB=5,BC=4.点P是边AC上一动点,过点P作PQ∥AB交BC于点Q,D为线段PQ的中点,当BD平分∠ABC时,AP的长度为()B.C.D.A.【答案】B.【解析】本题考查的是相似三角形的判定和性质,掌握相似三角形的判定定理和性质定理是解题的关键.根据勾股定理求出AC,根据角平分线的定义、平行线的性质得到∠QBD=∠BDQ,得到QB=QD,根据相似三角形的性质列出比例式,计算即可.∵∠C=90°,AB=5,BC=4,∴AC==3,∵PQ∥AB,∴∠ABD=∠BDQ,又∠ABD=∠QBD,∴∠QBD=∠BDQ,∴QB=QD,∴QP=2QB,∵PQ∥AB,∴△CPQ∽△CAB,∴==,即==,解得,CP=,∴AP=CA﹣CP=【例题2】(2019•四川省凉山州)在▱ABCD中,E是AD上一点,且点E将AD分为2:3的两部分,连接BE、AC相交于F,则S△AEF:S△CBF是.【答案】4:25或9:25.【解析】本题考查的是相似三角形的判定和性质、平行四边形的性质,掌握相似三角形的面积比等于相似比的平方是解题的关键.分AE:ED=2:3、AE:ED=3:2两种情况,根据相似三角形的性质计算即可.①当AE:ED=2:3时,∵四边形ABCD是平行四边形,∴AD∥BC,AE:BC=2:5,∴△AEF∽△CBF,:S△CBF=()2=4:25;∴S△AEF②当AE:ED=3:2时,:S△CBF=()2=9:25。
中考数学复习----《相似三角形的性质》知识点总结与专项练习题(含答案)

中考数学复习----《相似三角形的性质》知识点总结与专项练习题(含答案) 知识点总结1. 相似图形的概念:把形状相同的图形称为相似图形。
2. 相似三角形的概念:如果两个三角形的对应边的比相等,对应角相等,那么这两个三角形相似。
3. 相似三角形的性质:①相似三角形的对应角相等,对应边的比相等。
对应边的比叫做相似比。
②相似三角形的周长比等于相似比,面积比等于相似比的平方。
相似三角形的对应线段(对应中线、对应角平分线、对应边上的高)的比也等于相似比。
练习题1、(2022•兰州)已知△ABC ∽△DEF ,21=DE AB ,若BC =2,则EF =( ) A .4 B .6 C .8 D .16【分析】利用相似三角形的性质可得,代入即可得出EF 的长.【解答】解:∵△ABC ∽△DEF ,∴, ∵=,BC =2, ∴, ∴EF =4,故选:A .2、(2022•贺州)如图,在△ABC 中,DE ∥BC ,DE =2,BC =5,则S △ADE :S △ABC 的值是( )A .253B .254C .52D .53 【分析】根据相似三角形的面积比等于相似比的平方计算即可.【解答】解:∵DE ∥BC ,∴S △ADE ∽S △ABC ,∵DE =2,BC =5,∴S △ADE :S △ABC 的值为, 故选:B .3、(2022•甘肃)若△ABC ∽△DEF ,BC =6,EF =4,则DF AC =( ) A .94 B .49 C .32 D .23 【分析】根据△ABC ∽△DEF ,可以得到,然后根据BC =6,EF =4,即可得到的值.【解答】解:∵△ABC ∽△DEF ,∴, ∵BC =6,EF =4,∴=,故选:D .4、(2022•绍兴)将一张以AB 为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片ABCD ,其中∠A =90°,AB =9,BC =7,CD =6,AD =2,则剪掉的两个直角三角形的斜边长不可能是( )A .225B .445C .10D .435 【分析】根据题意,画出相应的图形,然后利用相似三角形的性质和分类讨论的方法,求出剪掉的两个直角三角形的斜边长,然后即可判断哪个选项符合题意.【解答】解:如右图1所示,由已知可得,△DFE ∽△ECB ,则,设DF=x,CE=y,则,解得,∴DE=CD+CE=6+=,故选项B不符合题意;EB=DF+AD=+2=,故选项D不符合题意;如图2所示,由已知可得,△DCF∽△FEB,则,设FC=m,FD=n,则,解得,∴FD=10,故选项C不符合题意;BF=FC+BC=8+7=15;如图3所示:此时两个直角三角形的斜边长为6和7;故选:A.5、(2022•连云港)△ABC的三边长分别为2,3,4,另有一个与它相似的三角形DEF,其最长边为12,则△DEF的周长是()A.54B.36C.27D.21【分析】(1)方法一:设2对应的边是x,3对应的边是y,根据相似三角形的对应边的比相等列等式,解出即可;方式二:根据相似三角形的周长的比等于相似比,列出等式计算.【解答】解:方法一:设2对应的边是x,3对应的边是y,∵△ABC∽△DEF,∴==,∴x=6,y=9,∴△DEF的周长是27;方式二:∵△ABC∽△DEF,∴=,∴=,∴C△DEF=27;故选:C.。
(完整word版)九年级数学相似三角形知识点及习题

相似三角形要点一、本章的两套定理第一套(比例的有关性质): b a n d b m c a n d b n m d c b a =++++++⇒≠+++=== :)0(等比性质 涉及概念:①第四比例项②比例中项③比的前项、后项,比的内项、外项④黄金分割等。
二、有关知识点:1.相似三角形定义: 对应角相等,对应边成比例的三角形,叫做相似三角形。
2.相似三角形的表示方法:用符号“∽”表示,读作“相似于”。
3.相似三角形的相似比: 相似三角形的对应边的比叫做相似比。
4.相似三角形的预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所截成的三角形与原三角形相似。
5.相似三角形的判定定理:(1)三角形相似的判定方法与全等的判定方法的联系列表如下:类型斜三角形 直角三角形 全等三角形的判定 SASSSS AAS (ASA ) HL 相似三角形的判定 两边对应成比例夹角相等 三边对应成比例 两角对应相等一条直角边与斜边对应成比例 从表中可以看出只要将全等三角形判定定理中的“对应边相等”的条件改为“对应边成比例”就可得到相似三角形的判定定理,这就是我们数学中的用类比的方法,在旧知识的基础上找出新知识并从中探究新知识掌握的方法。
6.直角三角形相似:(1)直角三角形被斜边上的高分成两个直角三角形和原三角形相似。
(2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
7.相似三角形的性质定理:(1)相似三角形的对应角相等。
(2)相似三角形的对应边成比例。
(3)相似三角形的对应高线的比,对应中线的比和对应角平分线的比都等于相似比。
(4)相似三角形的周长比等于相似比。
(5)相似三角形的面积比等于相似比的平方。
8.相似三角形的传递性 如果△ABC ∽△A 1B 1C 1,△A 1B 1C 1∽△A 2B 2C 2,那么△ABC ∽A 2B 2C 2三、注意1、相似三角形的基本定理,它是相似三角形的一个判定定理,也是后面学习的相似三角形的判定定理的基础,这个定理确定了相似三角形的两个基本图形“A ”型和“ X ”型。
相似三角形的判定及习题精讲(含答案)

14.75或27, 提示:当小多边形的周长为45时,大多边形的周长为 ×45=75;当大多边形的周长为45时,小多边形的周长为 ×45=27。 15.100cm和40cm
(二)选择题: 1. D 2.A 。 提示:过E作EG//AD交BD于G,则 = = ,设BG=2k, GD=3k, 则BD=5k, CD=15k,
A、 B、 C、 D、
6.正方形ABCD中,E是AD中点,BM⊥CE于M,AB=6cm, 则BM的长为 ( )。
A、12 cm B、
cm C、3 cm D、 cm 7.要把一个三角形的面积扩大到原来面积的8倍,而它的形状不变, 那么它的边长要增大到原来的( )倍。
A、2 B、4 C、2 D、64 8.梯形ABCD中,AD//BC,AC、BD交于E点,SΔADE∶SΔADC=1∶3, 则SΔADE∶SΔDBC=( )。 A、1∶3 B、1∶4 C、1∶5 D、1∶6 (三)已知:如图,在ΔABC中,AD为中线,E在AB上,AE=AC,CE交 AD于F,EF∶FC=3∶5,
(五)略 (六)提示:过点D作DM//AC交BC于M,证ΔBDM∽ΔBAC及 ΔQDM∽ΔQBD,通过等比代换可得。
(七)本题由正方形在三角形中的位置不同引起分类讨论。提示如 下: 解:直角三角形内接正方形有两种不同的位置。 如下图:
(1)如图(1),作CP⊥AB于P,交GF于H,则CH⊥GF, ∵ GF//AB, ∴ ΔCGF∽ΔCAB, ∴ = , ∵ ∠ACB=90°,AC=8,BC=6由勾股定理得AB=10, ∵ AC·BC=AB·CP, ∴ CP= = = , 设GF=x, 则CH=
∵ EG//PD,∴ = = =
3.C 4. A 5.D
6.B。 提示:如图,易证ΔBMC∽ΔCDE, ∵ ED=
初三数学13 相似三角形-2024年中考数学真题分项汇编(全国通用)(解析版)

专题13 相似三角形一.选择题1.(2022·黑龙江哈尔滨)如图,,,AB CD AC BD ∥相交于点E ,1,2,3AE EC DE ===,则BD 的长为( )A .32B .4C .92D .6【答案】C【分析】根据相似三角形对应边长成比例可求得BE 的长,即可求得BD 的长.【详解】∵//AB CD ∴ABE CDE ∽ ∴AE BE EC DE= ∵1,2,3AE EC DE ===,∴32BE =∵BD BE ED =+ ∴92BD = 故选:C .【点睛】本题考查了相似三角形的对应边长成比例,解题的关键在于找到对应边长.2.(2022·广西贺州)如图,在ABC 中,25DE BC DE BC ==∥,,,则:ADE ABC S S 的值是( )A .325B .425C .25D .35【答案】B【分析】根据相似三角形的判定定理得到ADE ABC ,根据相似三角形的面积比等于相似比的平方计算,得到答案.【详解】解:25DE BC DE BC ==∥,,∴ADE ABC ,∴2224525ADE ABC S DE S BC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭ ,故选:B .【点睛】此题考查相似三角形的判定和性质,掌握相似三角形的面积比等于相似比的平方是解题的关键.3.(2022·广西梧州)如图,以点O 为位似中心,作四边形ABCD 的位似图形''''A B C D ﹐已知'13OA OA =,若四边形ABCD 的面积是2,则四边形''''A B C D 的面积是( )A .4B .6C .16D .18【答案】D 【分析】两图形位似必相似,再由相似的图形面积比等于相似比的平方即可求解.【详解】解:由题意可知,四边形ABCD 与四边形''''A B C D 相似,由两图形相似面积比等于相似比的平方可知:''''22'1139ABCD A B C D S OA S OA ⎛⎫⎛⎫= ⎪= ⎪= ⎪ ⎪⎝⎭⎝⎭,又四边形ABCD 的面积是2,∴四边形''''A B C D 的面积为18,故选:D .【点睛】本题考察相似多边形的性质,属于基础题,熟练掌握相似图形的性质是解决本题的关键.4.(2022·四川雅安)如图,在△ABC 中,D ,E 分别是AB 和AC 上的点,DE ∥BC ,若AD BD =21,那么DE BC =( )A .49B .12C .13D .23【答案】D【分析】先求解2,3AD AB =再证明,ADE ABC ∽可得2.3DE AD BC AB ==【详解】解: AD BD =21,2,3AD AB ∴= DE ∥BC ,,ADE ABC ∴ ∽ 2,3DE AD BC AB ∴== 故选D 【点睛】本题考查的是相似三角形的判定与性质,证明ADE ABC △△∽是解本题的关键.5.(2022·内蒙古包头)如图,在边长为1的小正方形组成的网格中,A ,B ,C ,D 四个点均在格点上,AC 与BD 相交于点E ,连接,AB CD ,则ABE △与CDE △的周长比为( )A .1:4B .4:1C .1:2D .2:1【答案】D 【分析】运用网格图中隐藏的条件证明四边形DCBM 为平行四边形,接着证明ABE CDE ∽,最后利相似三角形周长的比等于相似比即可求出.【详解】如图:由题意可知,3DM =,3BC =, ∴DM BC =,而DM BC ∥,∴四边形DCBM 为平行四边形,∴AB DC ∥,∴BAE DCE ∠=∠,ABE CDE ∠=∠,∴ABE CDE ∽,∴21ABE CDE C AB C CD ===△△.故选:D .【点睛】本题考查了平行四边形的判定与性质、相似三角形的判定与性质及勾股定理,熟练掌握相关知识并正确计算是解题关键.6.(2022·黑龙江绥化)如图,在矩形ABCD 中,P 是边AD 上的一个动点,连接BP ,CP ,过点B 作射线,交线段CP 的延长线于点E ,交边AD 于点M ,且使得ABE CBP =∠∠,如果2AB =,5BC =,AP x =,PM y =,其中25x < .则下列结论中,正确的个数为( )(1)y 与x 的关系式为4y x x =-;(2)当4AP =时,ABP DPC ∽;(3)当4AP =时,3tan 5EBP ∠=.A .0个B .1个C .2个D .3个【答案】C 【分析】(1)证明ABM APB ∽,得AB AM AP AB=,将2AB =,AP x =,PM y =代入,即可得y 与x 的关系式;(2)利用两组对应边成比例且夹角相等,判定ABP DPC ∽;(3)过点M 作MF BP ⊥垂足为F ,在Rt APB △中,由勾股定理得BP 的长,证明FPM APB ∽,求出MF ,PF ,BF 的长,在Rt BMF △中,求出tan EBP ∠的值即可.【详解】解:(1)∵在矩形ABCD 中,∴AD BC ∥,90A D ∠=∠=︒,5BC AD ==,2AB DC ==,∴APB CBP ∠=∠,∵ABE CBP =∠∠,∴ABE APB ∠=∠,∴ABM APB ∽,∴AB AM AP AB=,∵2AB =,AP x =,PM y =,∴22x y x -=,解得:4y x x=-,故(1)正确;(2)当4AP =时,541DP AD AP =-=-=,∴12DC DP AP AB ==,又∵90A D ∠=∠=︒,∴ABP DPC ∽,故(2)正确;(3)过点M 作MF BP ⊥垂足为F ,∴90A MFP MFB ∠=∠=∠=︒,∵当4AP =时,此时4x =,4413y x x =-=-=,∴3PM =,在Rt APB 中,由勾股定理得:222BP AP AB =+,∴BP ===,∵FPM APB ∠=∠,∴FPM APB ∽,∴MF PF PM AB AP PB ==,∴24MF PF ==∴MF =PF =∴BF BP PF =-=∴3tan 4MF EBP BF ∠===故(3)不正确;故选:C .【点睛】本题主要考查相似三角形的判定和性质,勾股定理的应用,矩形的性质,正确找出相似三角形是解答本题的关键.7.(2022·湖北鄂州)如图,定直线MN ∥PQ ,点B 、C 分别为MN 、PQ 上的动点,且BC =12,BC 在两直线间运动过程中始终有∠BCQ =60°.点A 是MN 上方一定点,点D 是PQ 下方一定点,且AE ∥BC ∥DF ,AE =4,DF =8,ADBC 在平移过程中,AB +CD 的最小值为()A .B .C .D .【答案】C 【分析】如图所示,过点F 作FH CD ∥交BC 于H ,连接EH ,可证明四边形CDFH 是平行四边形,得到CH =DF =8,CD =FH ,则BH =4,从而可证四边形ABHE 是平行四边形,得到AB =HE ,即可推出当E 、F 、H 三点共线时,EH +HF 有最小值EF 即AB +CD 有最小值EF ,延长AE 交PQ 于G ,过点E 作ET ⊥PQ 于T ,过点A 作AL ⊥PQ 于L ,过点D 作DK ⊥PQ 于K ,证明四边形BEGC 是平行四边形,∠EGT =∠BCQ =60°,得到EG =BC =12,然后通过勾股定理和解直角三角形求出ET 和TF 的长即可得到答案.【详解】解:如图所示,过点F 作FH CD ∥交BC 于H ,连接EH ,∵BC DF FH CD ∥∥,,∴四边形CDFH 是平行四边形,∴CH =DF =8,CD =FH ,∴BH =4,∴BH =AE =4,又∵AE BC ∥,∴四边形ABHE 是平行四边形,∴AB =HE ,∵EH FH EF +≥,∴当E 、F 、H 三点共线时,EH +HF 有最小值EF 即AB +CD 有最小值EF ,延长AE 交PQ 于G ,过点E 作ET ⊥PQ 于T ,过点A 作AL ⊥PQ 于L ,过点D 作DK ⊥PQ 于K ,∵MN PQ BC AE ∥∥,,∴四边形BEGC 是平行四边形,∠EGT =∠BCQ =60°,∴EG =BC =12,∴=cos =6=sin GT GE EGT ET GE EGT ⋅⋅∠,∠,同理可求得8GL AL ==,,4KF DK ==,,∴2TL =,∵AL ⊥PQ ,DK ⊥PQ ,∴AL DK ∥,∴△ALO ∽△DKO ,∴2AL AO DK DO==,∴2133AO AD DO AD ====∴24OL OK ===,,∴42TF TL OL OK KF =+++=,∴EF ==故选C .【点睛】本题主要考查了平行四边形的性质与判定,相似三角形的性质与判定,勾股定理,解直角三角形,正确作出辅助线推出当E 、F 、H 三点共线时,EH +HF 有最小值EF 即AB +CD 有最小值EF 是解题的关键.8.(2022·广西贵港)如图,在边长为1的菱形ABCD 中,60ABC ∠=︒,动点E 在AB 边上(与点A 、B 均不重合),点F 在对角线AC 上,CE 与BF 相交于点G ,连接,AG DF ,若AF BE =,则下列结论错误的是( )A .DF CE =B .120BGC ∠=︒C .2AF EG EC =⋅D .AG【答案】D【分析】先证明△BAF ≌△DAF ≌CBE ,△ABC 是等边三角形,得DF =CE ,判断A 项答案正确,由∠GCB +∠GBC =60゜,得∠BGC =120゜,判断B 项答案正确,证△BEG ∽△CEB 得BE CE GE BE= ,即可判断C 项答案正确,由120BGC ∠=︒,BC =1,得点G 在以线段BC 为弦的弧BC 上,易得当点G 在等边△ABC 的内心处时,AG 取最小值,由勾股定理求得AG D 项错误.【详解】解:∵四边形ABCD 是菱形,60ABC ∠=︒,∴AB =AD =BC =CD ,∠BAC =∠DAC =12∠BAD =12(180)ABC ⨯︒-∠=60ABC ︒=∠,∴△BAF ≌△DAF ≌CBE ,△ABC 是等边三角形,∴DF =CE ,故A 项答案正确,∠ABF =∠BCE ,∵∠ABC =∠ABF +∠CBF =60゜,∴∠GCB +∠GBC =60゜,∴∠BGC =180゜-60゜=180゜-(∠GCB +∠GBC )=120゜,故B 项答案正确,∵∠ABF =∠BCE ,∠BEG =∠CEB ,∴△BEG ∽△CEB ,∴BE CE GE BE = ,∴2BE GE CE = ,∵AF BE =,∴2AF GE CE = ,故C 项答案正确,∵120BGC ∠=︒,BC =1,点G 在以线段BC 为弦的弧BC 上,∴当点G 在等边△ABC 的内心处时,AG 取最小值,如下图,∵△ABC 是等边三角形,BC =1,∴BF AC ⊥,AF =12AC =12,∠GAF =30゜,∴AG =2GF ,AG 2=GF 2+AF 2,∴2221122AG AG ⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭, 解得AG D 项错误,故应选:D【点睛】本题主要考查了菱形的基本性质、等边三角形的判定及性质、圆周角定理,熟练掌握菱形的性质是解题的关键.9.(2022·贵州贵阳)如图,在ABC 中,D 是AB 边上的点,B ACD ∠=∠,:1:2AC AB =,则ADC 与ACB △的周长比是( )A .B .1:2C .1:3D .1:4【答案】B 【分析】先证明△ACD ∽△ABC ,即有12AC AD CD AB AC BC ===,则可得12AC AD CD AB AC BC ++=++,问题得解.【详解】∵∠B =∠ACD ,∠A =∠A ,∴△ACD ∽△ABC ,∴AC AD CD AB AC BC ==,∵12AC AB =,∴12AC AD CD AB AC BC ===,∴12AC AD CD AC AD CD AB AC BC AB AC BC ++====++,∴△ADC 与△ACB 的周长比1:2,故选:B .【点睛】本题主要考查了相似三角形的判定与性质,证明△ACD ∽△ABC 是解答本题的关键.10.(2022·广西)已知△ABC 与△A 1B 1C 1是位似图形,位似比是1:3,则△ABC 与△A 1B 1C 1的面积比( )A .1 :3B .1:6C .1:9D .3:1【答案】C【分析】根据位似图形的面积比等于位似比的平方,即可得到答案.【详解】∵△ABC 与△A 1B 1C 1是位似图形,位似比是1:3,∴△ABC 与△A 1B 1C 1的面积比为1:9,故选:C .【点睛】本题考查位似图形的性质,熟练掌握位似图形的面积比等于位似比的平方是解题的关键.11.(2022·山东临沂)如图,在ABC 中,∥DE BC ,23AD DB =,若6AC =,则EC =( )A .65B .125C .185D .245【答案】C【分析】由∥DE BC ,23AD DB =,可得2,3AD AE DB EC ==再建立方程即可.【详解】解: ∥DE BC ,23AD DB =,2,3AD AE DB EC ∴== 6AC =,62,3CE CE -∴= 解得:18.5CE =经检验符合题意故选C 【点睛】本题考查的是平行线分线段成比例,证明“23AD AE DB EC ==”是解本题的关键.12.(2022·山东威海)由12个有公共顶点O 的直角三角形拼成如图所示的图形,∠AOB =∠BOC =∠COD =…=∠LOM =30°.若S △AOB =1,则图中与△AOB 位似的三角形的面积为( )A .(43)3B .(43)7C .(43)6D .(34)6【答案】C【分析】根据题意得出A 、O 、G 在同一直线上,B 、O 、H 在同一直线上,确定与△AOB 位似的三角形为△GOH ,利用锐角三角函数找出相应规律得出OG=6x ,再由相似三角形的性质求解即可.【详解】解:∵∠AOB =∠BOC =∠COD =…=∠LOM =30°∴∠AOG =180°,∠BOH =180°,∴A 、O 、G 在同一直线上,B 、O 、H 在同一直线上,∴与△AOB 位似的三角形为△GOH ,设OA =x ,则OB=1cos30OA x ==︒,∴OC=24cos303OB x x ==︒,∴OD=3cos30OC x ==︒,…∴OG=6x ,∴6OG OA =,∴12643GOH AOB S S ⎛⎫== ⎪⎝⎭ ,∵1AOB S = ,∴643GOH S ⎛⎫= ⎪⎝⎭ ,故选:C .【点睛】题目主要考查利用锐角三角函数解三角形,找规律问题,相似三角形的性质等,理解题意,找出相应边的比值规律是解题关键.二.填空题13.(2022·贵州黔东南)如图,折叠边长为4cm 的正方形纸片ABCD ,折痕是DM ,点C 落在点E 处,分别延长ME 、DE 交AB 于点F 、G ,若点M 是BC 边的中点,则FG =______cm.【答案】53【分析】根据折叠的性质可得DE =DC =4,EM =CM =2,连接DF ,设FE =x ,由勾股定理得BF ,DF ,从而求出x 的值,得出FB ,再证明FEG FBM ∆∆ ,利用相似三角形对应边成比例可求出FG .【详解】解:连接,DF 如图,∵四边形ABCD 是正方形,∴4,90.AB BC CD DA A B C CDA ︒====∠=∠=∠=∠=∵点M 为BC 的中点,∴114222BM CM BC ===⨯=由折叠得,2,4,ME CM DE DC ====∠90,DEM C ︒=∠=∴∠90DEF ︒=,90,FEG ∠=︒设,FE x =则有222DF DE EF =+∴2224DF x =+又在Rt FMB ∆中,2,2FM x BM =+=,∵222FM FB BM =+∴FB ==∴4AF AB FB =-=在Rt DAF ∆中,222,DA AF DF +=∴2224(44,x +=+解得,124,83x x ==-(舍去)∴4,3FE =∴410233FM FE ME =+=+=∴83FB ==∵∠90DEM ︒=∴∠90FEG ︒=∴∠,FEG B =∠又∠.GFE MFB =∠∴△FEG FBM∆ ∴,FG FE FM FB=即4310833FG =∴5,3FG =故答案为:53【点睛】本题主要考查了正方形的性质,折叠的性质,勾股定理,相似三角形的判定与性质,正确作出辅助线是解答本题的关键.14.(2022·上海)如图,在△ABC 中,∠A =30°,∠B =90°,D 为AB 中点,E 在线段AC 上,AD DE AB BC=,则AE AC =_____.【答案】12或14【分析】由题意可求出12DE BC =,取AC 中点E 1,连接DE 1,则DE 1是△ABC 的中位线,满足112DE BC =,进而可求此时112AE AC =,然后在AC 上取一点E 2,使得DE 1=DE 2,则212DE BC =,证明△DE1E2是等边三角形,求出E1E2=14AC ,即可得到214AE AC =,问题得解.【详解】解:∵D 为AB中点,∴12AD DE AB BC ==,即12DE BC =,取AC 中点E 1,连接DE 1,则DE 1是△ABC 的中位线,此时DE 1∥BC ,112DE BC =,∴112AE AD AC AB ==,在AC 上取一点E 2,使得DE 1=DE 2,则212DE BC =,∵∠A =30°,∠B =90°,∴∠C =60°,BC =12AC ,∵DE 1∥BC ,∴∠DE1E2=60°,∴△DE1E2是等边三角形,∴DE 1=DE 2=E1E2=12BC ,∴E1E2=14AC ,∵112AE AC =,∴214AE AC =,即214AE AC =,综上,AE AC 的值为:12或14,故答案为:12或14.【点睛】本题考查了三角形中位线的性质,平行线分线段成比例,等边三角形的判定和性质以及含30°角的直角三角形的性质等,根据12DE BC =进行分情况求解是解题的关键.15.(2022·北京)如图,在矩形ABCD 中,若13,5,4AF AB AC FC ===,则AE 的长为_______.【答案】1【分析】根据勾股定理求出BC ,以及平行线分线段成比例进行解答即可.【详解】解:在矩形ABCD 中:AD BC ∥,90ABC ∠=︒,∴14AE AF BC FC ==,4BC =,∴144AE =,∴1AE =,故答案为:1.【点睛】此题考查了勾股定理以及平行线分线段成比例,掌握平行线分线段成比例是解题的关键.16.(2022·江苏常州)如图,在Rt ABC △中,90C ∠=︒,9AC =,12BC =.在Rt DEF 中,90F ∠=︒,3DF =,4EF =.用一条始终绷直的弹性染色线连接CF ,Rt DEF 从起始位置(点D 与点B 重合)平移至终止位置(点E 与点A 重合),且斜边DE 始终在线段AB 上,则Rt ABC △的外部被染色的区域面积是______.【答案】28【分析】过点F 作AB 的垂线交于G ,同时在图上标出,,M N F '如图,需要知道的是Rt ABC 的被染色的区域面积是MNF F S '梯形,所以需要利用勾股定理,相似三角形、平行四边形的判定及性质,求出相应边长,即可求解.【详解】解:过点F 作AB 的垂线交于G ,同时在图上标出,,M N F '如下图:90C ∠=︒ ,9AC =,12BC =,15AB ∴==,在Rt DEF 中,90F ∠=︒,3DF =,4EF =.5DE ∴==,15510AE AB DE =-=-= ,//,EF AF EF AF ''= ,∴四边形AEFF '为平行四边形,10AE FF '∴==,11622DEF S DF EF DE GF =⋅=⋅= ,解得:125GF =, //DF AC ,,DFM ACM FDM CAM ∴∠=∠∠=∠,DFM ACM ∴ ∽,13DM DF AM AC ∴==,1115344DM AM AB ∴===,//BC AF ' ,同理可证:ANF DNC ' ∽,13AF AN BC DN '∴==,345344DN AN AB ∴===,451530444MN DN DM ∴=-=-=,Rt ABC 的外部被染色的区域面积为130121028245MNF F S '⎛⎫=⨯+⨯= ⎪⎝⎭梯形,故答案为:28.【点睛】本题考查了直角三角形,相似三角形的判定及性质、勾股定理、平行四边形的判定及性质,解题的关键是把问题转化为求梯形的面积.17.(2022·广西)数学兴趣小组通过测量旗杆的影长来求旗杆的高度,他们在某一时刻测得高为2米的标杆影长为1.2米,此时旗杆影长为7.2米,则旗杆的高度为______米.【答案】12【分析】根据同时、同地物高和影长的比不变,构造相似三角形,然后根据相似三角形的性质解答.【详解】解:设旗杆为AB ,如图所示:根据题意得:ABC DEF ∆∆ ,∴DE EF AB BC= ∵2DE =米, 1.2EF =米,7.2BC =米,∴2 1.2=7.2AB 解得:AB =12米.故答案为:12.【点睛】本题考查了中心投影、相似三角形性质的应用,解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.18.(2022·广东深圳)已知ABC 是直角三角形,90,3,5,B AB BC AE ∠=︒===连接CE 以CE 为底作直角三角形CDE 且,CD DE =F 是AE 边上的一点,连接BD 和,BF BD 且45,FBD ∠=︒则AF 长为______.【分析】将线段BD 绕点D 顺时针旋转90︒,得到线段HD ,连接BH ,HE ,利用SAS 证明EDH CDB ∆≅∆,得5EH CB ==,90HED BCD ∠=∠=︒,从而得出////HE DC AB ,则ABF EHF ∆∆∽,即可解决问题.【详解】解:将线段BD 绕点D 顺时针旋转90︒,得到线段HD ,连接BH ,HE ,BDH ∴∆是等腰直角三角形,又EDC ∆ 是等腰直角三角形,HD BD ∴=,EDH CDB ∠=∠,ED CD =,()EDH CDB SAS ∴∆≅∆,5EH CB ∴==,90HED BCD ∠=∠=︒,90EDC ∠=︒ ,90ABC ∠=︒,////HE DC AB ∴,,ABF EHF BAF HEF ∴∠=∠∠=∠,ABF EHF ∴∆∆∽,∴==-AB AF AF EH EF AE AF ,AE =∴35=AF ∴=,【点睛】本题主要考查了等腰直角三角形的性质,全等三角形的判定与性质,相似三角形的判定与性质等知识,解题的关键是作辅助线构造全等三角形.19.(2022·广西河池)如图,把边长为1:2的矩形ABCD 沿长边BC ,AD 的中点E ,F 对折,得到四边形ABEF ,点G ,H 分别在BE ,EF 上,且BG =EH =25BE =2,AG 与BH 交于点O ,N 为AF 的中点,连接ON ,作OM ⊥ON 交AB 于点M ,连接MN ,则tan ∠AMN =_____.【答案】58##0.625【分析】先判断出四边形ABEF 是正方形,进而判断出△ABG ≌△BEH ,得出∠BAG =∠EBH ,进而求出∠AOB =90°,再判断出△AOB ~△ABG ,求出OA OB ==△OBM ~△OAN ,求出BM =1,即可求出答案.【详解】解:∵点E ,F 分别是BC ,AD 的中点,∴11,22AF AD BE BC ==,∵四边形ABCD 是矩形,∴∠A =90°,AD ∥BC ,AD =BC ,∴12AF BE AD ==,∴四边形ABEF 是矩形,由题意知,AD =2AB ,∴AF =AB ,∴矩形ABEF 是正方形,∴AB =BE ,∠ABE =∠BEF =90°,∵BG =EH ,∴△ABG≌△BEH(SAS),∴∠BAG=∠EBH,∴∠BAG+∠ABO=∠EBH+∠ABO=∠ABG=90°,∴∠AOB=90°,∵BG=EH=25BE=2,∴BE=5,∴AF=5,∴AG==∵∠OAB=∠BAG,∠AOB=∠ABG,∴△AOB∽△ABG,∴OA OB ABAB BG AG==,即52OA OB==∴OA OB==∵OM⊥ON,∴∠MON=90°=∠AOB,∴∠BOM=∠AON,∵∠BAG+∠FAG=90°,∠ABO+∠EBH=90°,∠BAG=∠EBH,∴∠OBM=∠OAN,∴△OBM~△OAN,∴OB BM OA AN=,∵点N是AF的中点,∴1522AN AF==,52BM=,解得:BM=1,∴AM=AB-BM=4,∴552tan48ANAMNAM∠===.故答案为:5 8【点睛】此题主要考查了矩形性质,正方形性质和判定,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理,求出BM 是解本题的关键.20.(2022·内蒙古赤峰)如图,为了测量校园内旗杆AB 的高度,九年级数学应用实践小组,根据光的反射定律,利用镜子、皮尺和测角仪等工具,按以下方式进行测量:把镜子放在点O 处,然后观测者沿着水平直线BO 后退到点D ,这时恰好能在镜子里看到旗杆顶点A ,此时测得观测者观看镜子的俯角α=60°,观测者眼睛与地面距离CD =1.7m ,BD =11m ,则旗杆AB 的高度约为_________m . 1.7≈)【答案】17【分析】如图容易知道CD ⊥BD ,AB ⊥BD ,即∠CDO =∠ABO =90°.由光的反射原理可知∠COD =∠AOB =60°,这样可以得到△COD ∽△AOB ,然后利用对应边成比例就可以求出AB .【详解】解:由题意知∠COD =∠AOB =60°,∠CDE =∠ABE =90°,∵CD =1.7m ,∴OD =60CD tan =︒≈1(m),∴OB =11-1=10(m),∴△COD ∽△AOB .∴CD OD AB OB =,即1.7110AB =,∴AB =17(m),答:旗杆AB 的高度约为17m .故答案为:17.【点睛】本题考查了解直角三角形的应用,相似三角形的应用,本题只要是把实际问题抽象到相似三角形中,利用相似三角形的性质就可以求出结果.21.(2022·湖北鄂州)如图,在边长为6的等边△ABC 中,D 、E 分别为边BC 、AC 上的点,AD 与BE 相交于点P ,若BD =CE =2,则△ABP 的周长为 _____.【答案】6+【分析】如图所示,过点E 作EF ⊥AB 于F ,先解直角三角形求出AF ,EF ,从而求出BF ,利用勾股定理求出BE 的长,证明△ABD ≌△BCE 得到∠BAD =∠CBE ,AD =BE ,再证明△BDP ∽△ADB ,得到62BP PD==,即可求出BP ,PD ,从而求出AP ,由此即可得到答案.【详解】解:如图所示,过点E 作EF ⊥AB 于F ,∵△ABC 是等边三角形,∴AB =BC ,∠ABD =∠BAC =∠BCE =60°,∵CE =BD =2,AB =AC =6,∴AE =4,∴cos 2sin AF AE EAF EF AE EAF =⋅∠==⋅∠=,,∴BF =4,∴BE =又∵BD =CE ,∴△ABD ≌△BCE (SAS ),∴∠BAD =∠CBE ,AD =BE ,又∵∠BDP =∠ADB ,∴△BDP ∽△ADB ,∴BD BP DP AD AB BD==,62BP PD==,∴BP PD =∴AP AD AP =-=,∴△ABP 的周长=6AB BP AP ++=故答案为:6+【点睛】本题主要考查了等边三角形的性质,解直角三角形,勾股定理,相似三角形的性质与判定,全等三角形的性质与判定,正确作出辅助线是解题的关键.22.(2022·山东潍坊)《墨子·天文志》记载:“执规矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,正方形ABCD 的面积为4,以它的对角线的交点为位似中心,作它的位似图形A B C D '''',若:2:1A B AB ='',则四边形A B C D ''''的外接圆的周长为___________.【答案】【分析】根据正方形ABCD 的面积为4,求出2AB =,根据位似比求出4A B ''=,周长即可得出;【详解】解: 正方形ABCD 的面积为4,∴2AB =,:2:1A B AB ''=,∴4A B ''=,∴A C ''==所求周长=;故答案为:.【点睛】本题考查位似图形,涉及知识点:正方形的面积,正方形的对角线,圆的周长,解题关键求出正方形ABCD 的边长.23.(2022·内蒙古包头)如图,在Rt ABC 中,90ACB ∠=︒,3AC BC ==,D 为AB 边上一点,且BD BC =,连接CD ,以点D 为圆心,DC 的长为半径作弧,交BC 于点E (异于点C ),连接DE ,则BE的长为___________.【答案】3##3-+【分析】过点D 作DF ⊥BC 于点F ,根据题意得出DC DE =,根据等腰三角形性质得出CF EF =,根据90ACB ∠=︒,3AC BC ==,得出AB =CF x =,则3BF x =-,证明DF AC ,得出BF BDCF AD=,列出关于x 的方程,解方程得出x 的值,即可得出3BE =.【详解】解:过点D 作DF ⊥BC 于点F ,如图所示:根据作图可知,DC DE =,∵DF ⊥BC ,∴CF EF =,∵90ACB ∠=︒,3AC BC ==,∴AB ===∵3BD BC ==,∴3AD =,设CF x =,则3BF x =-,∵90ACB ∠=︒,∴AC BC ⊥,∵DF BC ⊥,∴DF AC ,∴BF BDCF AD =,即3x x -=,解得:x =,∴226CE x ===-,∴3363BE CE =-=-+=.故答案为:3.【点睛】本题主要考查了等腰三角形的性质和判定,勾股定理,平行线分线段成比例定理,平行线的判定,作出辅助线,根据题意求出CF 的长,是解题的关键.24.(2022·江苏泰州)如图上,Δ,90,8,6,ABC C AC BC ∠=== 中O 为内心,过点O 的直线分别与AC 、AB 相交于D 、E ,若DE=CD+BE ,则线段CD 的长为__________.【答案】2或12##12或2【分析】分析判断出符合题意的DE 的情况,并求解即可;【详解】解:①如图,作//DE BC ,OF BC OG AB ⊥⊥,,连接OB ,则OD ⊥AC ,∵//DE BC ,∴OBF BOE ∠=∠∵O 为ABC ∆的内心,∴OBF OBE ∠=∠,∴BOE OBE ∠=∠∴BE OE =,同理,CD OD =,∴DE=CD+BE ,10AB ===∵O 为ABC ∆的内心,∴OF OD OG CD ===,∴BF BG AD AG==,∴6810AB BG AG BC CD AC CD CD CD =+=-+-=-+-=∴2CD =②如图,作DE AB ⊥,由①知,4BE =,6AE =,∵ACB AED CAB EAD ∠=∠∠=∠,∴ABC ADE ∆∆ ∴AB ADAC AE=∴1061582AB AE AD AC ⋅⨯===∴151822CD AC AD =-=-=∵92DE ===∴19422DE BE CD =+=+=∴12CD =故答案为:2或12.【点睛】本题主要考查三角形内心的性质、勾股定理、三角形的相似,根据题意正确分析出符合题意的情况并应用性质定理进行求解是解题的关键.25.(2022·黑龙江绥化)如图,60AOB ∠=︒,点1P 在射线OA 上,且11OP =,过点1P 作11PK OA ⊥交射线OB 于1K ,在射线OA 上截取12PP ,使1211PPPK =;过点2P 作22P K OA ⊥交射线OB 于2K ,在射线OA 上截取23P P ,使2322P P P K =.按照此规律,线段20232023P K 的长为________.20221【分析】解直角三角形分别求得11PK ,22P K ,33P K ,……,探究出规律,利用规律即可解决问题.【详解】解:11PK OA ⊥ ,11OPK ∴△是直角三角形,在11Rt OPK 中,60AOB ∠=︒,11OP =,12111tan 60PP PK OP ∴==⋅︒=11PK OA ⊥ ,22P K OA ⊥,1122PK P K ∴∥,2211OP K OPK ∴△∽△,222111P K OP PK OP ∴=,=221P K ∴,同理可得:2331P K =+,3441P K =,……,11n n n P K -∴=,2022202320231P K ∴=,20221.【点睛】本题考查了图形的规律,解直角三角形,平行线的判定,相似三角形的判定与性质,解题的关键是学会探究规律的方法.26.(2022·黑龙江)如图,在平面直角坐标系中,点1A ,2A ,3A ,4A ……在x 轴上且11OA =,212OA OA =,322OA OA =,432OA OA =……按此规律,过点1A ,2A ,3A ,4A ……作x轴的垂线分别与直线y =交于点1B ,2B ,3B ,4B ……记11OA B ,22OA B △,33 OA B ,44 OA B ……的面积分别为1S ,2S ,3S ,4S ……,则2022S =______.【答案】2【分析】先求出11A B =,可得11OA B S =112233n n A B A B A B A B ⋯⋯∥∥∥∥,从而得到11OA B ∽22OA B △∽33 OA B ∽44 OA B ∽……∽n n OA B △,再利用相似三角形的性质,可得11OA B S ∶22OA B S ∶33OA B S ∶44OA B S ∶……∶n n OA B S =()()()2222231:2:2:2::2n ,即可求解.【详解】解:当x =1时,y =,∴点(1B ,∴11A B =∴11112OA B S =⨯= ,∵根据题意得:112233n n A B A B A B A B ⋯⋯∥∥∥∥,∴11OA B ∽22OA B △∽33 OA B ∽44 OA B ∽……∽n n OA B △,∴11OA B S ∶22OA B S ∶33OA B S ∶44OA B S :……∶n n OA B S = OA 12∶OA 22∶OA 32∶……∶OAn 2,∵11OA =,212OA OA =,322OA OA =,432OA OA =,……,∴22OA =,2342OA ==,3482OA ==,……,12n n OA -=,∴11OA B S ∶22OA B S ∶33OA B S ∶44OA B S ∶……∶n n OA B S =()()()2222231246221:2:2:2::21:2:2:2::2n n --= ,∴11222n n n OA B OA B S S -= ,∴220222202222S ⨯-==故答案为:2【点睛】本题主要考查了图形与坐标的规律题,相似三角形的判定和性质,明确题意,准确得到规律,是解题的关键.27.(2022·广西)如图,在正方形ABCD 中,AB =,对角线,AC BD 相交于点O .点E 是对角线AC 上一点,连接BE ,过点E 作EF BE ⊥,分别交,CD BD 于点F 、G ,连接BF ,交AC 于点H ,将EFH △沿EF 翻折,点H 的对应点H '恰好落在BD 上,得到EFH '△若点F 为CD 的中点,则EGH '△的周长是_________.【答案】5+【分析】过点E 作PQ //AD 交AB 于点P ,交DC 于点Q ,得到BP =CQ ,从而证得BPE ≌EQF △,得到BE =EF ,再利用BC =F 为中点,求得BF ==BE EF ===,再求出2EO ==,再利用AB //FC ,求出ABH CFH △∽△21AH CH ==,求得216833AH =⨯=,18833CH =⨯=,从而得到EH =AH -AE =1610233-=,再求得EOB GOE △∽△得到21242OG ===,求得EG OG =1, 过点F 作FM ⊥AC 于点M ,作FN ⊥OD 于点N ,求得FM =2,MH =23,FN =2,证得Rt FH N '△≌Rt FMH 得到23H N MH '==,从而得到ON =2,NG =1,25133GH '=+=,从而得到答案.【详解】解:过点E 作PQ //AD 交AB 于点P ,交DC 于点Q ,∵AD //PQ ,∴AP =DQ ,BPQ CQE ∠=∠,∴BP =CQ ,∵45ACD ∠=︒,∴BP =CQ =EQ ,∵EF ⊥BE ,∴90PEB FEQ ∠+∠=︒∵90PBE PEB ∠+∠=︒∴PBE FEQ ∠=∠,在BPE 与EQF △中BPQ FQE PB EQPBE FEQ ∠=∠⎧⎪=⎨⎪∠=∠⎩∴BPE ≌EQF △,∴BE =EF ,又∵BC AB ==F 为中点,∴CF =∴BF ==∴BE EF ===,又∵4BO ==,∴2EO ==,∴AE =AO -EO =4-2=2,∵AB //FC ,∴ABH CFH △∽△,∴AB AH CF CH=,21AH CH ==,∵8AC ==, ∴216833AH =⨯=,18833CH =⨯=,∴EH =AH -AE =1610233-=,∵90BEO FEO ∠+∠=︒,+90BEO EBO ∠∠=︒,∴FEO EBO ∠=∠,又∵90EOB EOG ∠=∠=︒,∴EOB GOE△∽△∴EG OG OE BE OE OB==,21242OG ===,∴EG OG =1,过点F 作FM ⊥AC 于点M ,∴FM=MC 2=,∴MH =CH -MC =82233-=, 作FN ⊥OD 于点N ,2,FN ==,在Rt FH N '△与Rt FMH 中FH FH FN FM'=⎧⎨=⎩∴Rt FH N '△≌Rt FHM∴23H N MH '==,∴ON =2,NG =1,∴25133GH '=+=,∴10533EGH C EH EG GH EH EG GH '''=++=++=△,故答案为:【点睛】本题考查了正方形的性质应用,重点是与三角形相似和三角形全等的结合,熟练掌握做辅助线是解题的关键.28.(2022·辽宁)如图,在正方形ABCD 中,E 为AD 的中点,连接BE 交AC 于点F .若6AB =,则AEF 的面积为___________.【答案】3【分析】由正方形的性质可知1113222AE AD AB BC ====,//AD BC ,则有AEF CBF ∽△△,然后可得12EF AE BF BC ==,进而问题可求解.【详解】解:∵四边形ABCD 是正方形,6AB =,∴6AD BC AB ===,//AD BC ,∴AEF CBF ∽△△,∴EF AE BF BC=,∵E 为AD 的中点,∴1113222AE AD AB BC ====,∴12EF AE BF BC ==,192ABE S AE AB =⋅= ,∴13EF BE =,∴133AEF ABE S S == ;故答案为3.【点睛】本题主要考查正方形的性质及相似三角形的性质与判定,熟练掌握正方形的性质及相似三角形的性质与判定是解题的关键.29.(2022·贵州贵阳)如图,在四边形ABCD 中,对角线AC ,BD 相交于点E ,6cm AC BC ==,90ACB ADB ∠=∠=︒.若2BE AD =,则ABE △的面积是_______2cm ,AEB ∠=_______度.【答案】 36-36- 112.5【分析】通过证明ADE BCE ,利用相似三角形的性质求出23m AE =,263m CE =-,再利用勾股定理求出其长度,即可求三角形ABE 的面积,过点E 作EF ⊥AB ,垂足为F ,证明AEF 是等腰直角三角形,再求出AE CE =,继而证明()Rt BCE Rt BFE HL ≅ ,可知122.52EBF EBC ABC ∠=∠=∠=︒,利用外角的性质即可求解.【详解】90,ACB ADB AED BEC ∠=∠=︒∠=∠ ,ADE BCE ∴ ,AD AE BC BE∴=,6,2BC AC BE AD === ,设,2AD m BE m ==,62m AE m∴=,23m AE ∴=,263m CE ∴=-,在Rt BCE 中,由勾股定理得222BC CE BE +=,22226(6)(2)2m m ∴+-=,解得236m =-或236m =+ 对角线AC ,BD 相交于点E ,236m ∴=-,12AE ∴=-,6CE ∴=,∴(2111263622ABE S AE BC =⋅⋅=⨯-⨯=- ,过点E 作EF ⊥AB ,垂足为F ,90,ACB AC BC ∠=︒= ,45BAC ABC AEF ∴∠=∠=︒=∠,6AE AF AE CE ∴====,BE BE = ,()Rt BCE Rt BFE HL ∴≅ ,122.52EBF EBC ABC ∴∠=∠=∠=︒,112.5AEB ACB EBC ∴∠=∠+∠=︒,故答案为:36-,112.5.【点睛】本题考查了相似三角形的判定和性质,勾股定理,等腰直角三角形的判定和性质,全等三角形的判定和性质及三角形外角的性质,熟练掌握知识点是解题的关键.三.解答题30.(2022·河北)如图,某水渠的横断面是以AB 为直径的半圆O ,其中水面截线MN AB ∥.嘉琪在A 处测得垂直站立于B 处的爸爸头顶C 的仰角为14°,点M 的俯角为7°.已知爸爸的身高为1.7m .(1)求∠C 的大小及AB 的长;(2)请在图中画出线段DH ,用其长度表示最大水深(不说理由),并求最大水深约为多少米(结果保留小数点后一位).(参考数据:tan 76︒取4 4.1)【答案】(1)=76C ∠︒, 6.8(m)AB =(2)见详解,约6.0米【分析】(1)由水面截线MN AB ∥可得BC AB ⊥,从而可求得76C ∠=︒,利用锐角三角形的正切值即可求解.(2)过点O 作O H M N ⊥,交MN 于D 点,交半圆于H 点,连接OM ,过点M 作MG ⊥OB 于G ,水面截线MN AB ∥,即可得DH 即为所求,由圆周角定理可得14BOM ∠=︒,进而可得ABC OGM ,利用相似三角形的性质可得4OG GM =,利用勾股定理即可求得GM 的值,从而可求解.(1)解:∵水面截线MN AB∥BC AB ∴⊥,90ABC ∴∠=︒,90=76C CAB ∴∠=︒-∠︒,在t R ABC 中,90ABC ∠=︒, 1.7BC =,tan 76 1.7AB AB BC ∴︒==,解得 6.8(m)AB ≈.(2)过点O 作O H M N ⊥,交MN 于D 点,交半圆于H 点,连接OM ,过点M 作MG ⊥OB 于G ,如图所示:水面截线MN AB ∥,OH AB ⊥,DH MN ∴⊥,GM OD =,DH ∴为最大水深,7BAM ∠=︒ ,214BOM BAM ∴∠=∠=︒,90ABC OGM ∠=∠=︒ ,且14BAC ∠=︒,ABC OGM ∴ ,OG MG AB CB ∴=,即6.8 1.7OG MG =,即4OG GM =,在Rt OGM △中,90OGM ∠=︒, 3.42AB OM =≈,222OG GM OM ∴+=,即2224(3.4)GM GM +=(),解得0.8GM ≈,= 6.80.86DH OH OD ∴-=-≈,∴最大水深约为6.0米.【点睛】本题考查了解直角三角形,主要考查了锐角三角函数的正切值、圆周角定理、相似三角形的判定及性质、平行线的性质和勾股定理,熟练掌握解直角三角形的相关知识是解题的关键.31.(2022·吉林)下面是王倩同学的作业及自主探究笔记,请认真阅读并补充完整.【作业】如图①,直线12l l ∥,ABC 与DBC △的面积相等吗?为什么?解:相等.理由如下:设1l 与2l 之间的距离为h ,则12ABC S BC h =⋅ ,12DBC S BC h =⋅△.∴ABC DBC S S = .【探究】(1)如图②,当点D 在1l ,2l 之间时,设点A ,D 到直线2l 的距离分别为h ,h ',则ABC DBC S h S h ='△△.证明:∵ABC S(2)如图③,当点D 在1l ,2l 之间时,连接AD 并延长交2l 于点M ,则ABC DBC S AM S DM =△△.证明:过点A 作AE BM ⊥,垂足为E ,过点D 作DF BM ⊥,垂足为F ,则90AEM DFM ∠=∠=︒,∴AE ∥ .∴AEM △∽ .∴AE AM DF DM =.由【探究】(1)可知ABC DBC S S =△△ ,∴ABC DBC S AM S DM =△△.(3)如图④,当点D 在2l 下方时,连接AD 交2l 于点E .若点A ,E ,D 所对应的刻度值分别为5,1.5,0,ABC DBC S S △△的值为 .【答案】(1)证明见解析(2)证明见解析(3)73【分析】(1)根据三角形的面积公式可得11,22ABC DBC S S BC h BC h '=⋅=⋅ ,由此即可得证;(2)过点A 作AE BM ⊥,垂足为E ,过点D 作DF BM ⊥,垂足为F ,先根据平行线的判定可得AE DF ,再根据相似三角形的判定可证AEM DFM ~ ,根据相似三角形的性质可得AE AM DF DM=,然后结合【探究】(1)的结论即可得证;(3)过点A 作AM BC ⊥于点M ,过点D 作DN BC ⊥于点N ,先根据相似三角形的判定证出AME DNE ~ ,再根据相似三角形的性质可得73AM AE DN DE ==,然后根据三角形的面积公式可得12ABC S BC AM =⋅ ,12DBC S BC DN =⋅ ,由此即可得出答案.(1)证明:12ABC S BC h =⋅ ,12DBC BC h S '=⋅ ,ABC DBC S h S h ∴='.(2)证明:过点A 作AE BM ⊥,垂足为E ,过点D 作DF BM ⊥,垂足为F ,则90AEM DFM ∠=∠=︒,AE DF ∴∥.AEM DFM ~∴ .AE AM DF DM∴=.由【探究】(1)可知ABC DBC S AE S DF= ,ABC DBC S AM S DM ∴= .(3)解:过点A 作AM BC ⊥于点M ,过点D 作DN BC ⊥于点N ,则90AME DNE ∠=∠=︒,AM DN ∴ ,AME DNE ∴~ ,AM AE DN DE∴=, 点,,A E D 所对应的刻度值分别为5,1.5,0,5 1.5 3.5AE ∴=-=, 1.5DE =,3.571.53AM DN ∴==,又12ABC S BC AM =⋅ ,12DBC S BC DN =⋅ ,73ABCDBC S AM S DN =∴= ,故答案为:73.【点睛】本题考查了相似三角形的判定与性质、平行线的判定、三角形的面积等知识点,熟练掌握相似三角形的判定与性质是解题关键.32.(2022·山东青岛)如图,在Rt ABC △中,90,5cm,3cm ACB AB BC ∠=︒==,将ABC 绕点A 按逆时针方向旋转90︒得到ADE ,连接CD .点P 从点B 出发,沿BA 方向匀速运动,速度为1cm/s ;同时,点Q 从点A 出发,沿AD 方向匀速运动,速度为1cm/s .PQ 交AC 于点F ,连接,CP EQ .设运动时间为(s)(05)t t <<.解答下列问题:(1)当EQ AD ⊥时,求t 的值;(2)设四边形PCDQ 的面积为()2cm S ,求S 与t 之间的函数关系式;(3)是否存在某一时刻t ,使PQ CD ∥?若存在,求出t 的值;若不存在,请说明理由.【答案】(1)16s 5(2)213714210S t t =-+(3)存在,65s 29t =【分析】(1)利用AQE AED △∽△得AQ AE AE AD =,即445t =,进而求解;(2)分别过点C ,P 作,CM AD PN BC ⊥⊥,垂足分别为M ,N ,证ABC CAM △∽△得,AB BC AC CA AM CM ==,求得121655AM CM ==,再证BPN BAC △∽△得BP PN BA AC=,得出45PN t =,根据ABC ACD APQ BPC PCDQ S S S S S S ==+-- 四边形即可求出表达式;(3)当PQ CD ∥时AQP ADC ∠=∠,易证APQ MCD △∽△,得出AP AQ MC MD =,则5161355t t -=,进而求出t 值.(1)解:在Rt ABC △中,由勾股定理得,4AC ===∵ABC 绕点A 按逆时针方向旋转90︒得到ADE。
相似三角形性质与判定专项练习30题(有答案)
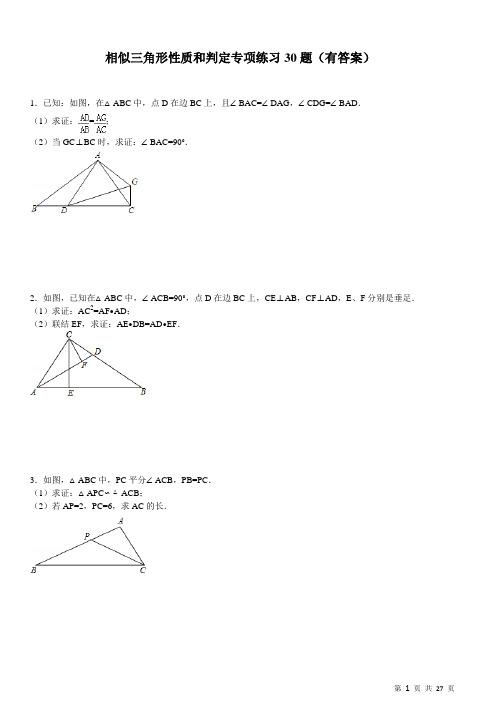
相似三角形性质和判定专项练习30题(有答案)1.已知:如图,在△ABC中,点D在边BC上,且∠BAC=∠DAG,∠CDG=∠BAD.(1)求证:=;(2)当GC⊥BC时,求证:∠BAC=90°.2.如图,已知在△ABC中,∠ACB=90°,点D在边BC上,CE⊥AB,CF⊥AD,E、F分别是垂足.(1)求证:AC2=AF•AD;(2)联结EF,求证:AE•DB=AD•EF.3.如图,△ABC中,PC平分∠ACB,PB=PC.(1)求证:△APC∽△ACB;(2)若AP=2,PC=6,求AC的长.4.如图,在平行四边形ABCD中,过B作BE⊥CD,垂足为点E,连接AE,F为AE上一点,且∠BFE=∠C.(1)求证:△ABF∽△EAD;(2)若AB=4,∠BAE=30°,求AE的长.5.已知:如图,△ABC中,∠ABC=2∠C,BD平分∠ABC.求证:AB•BC=AC•CD.6.已知△ABC,∠ACB=90°,AC=BC,点E、F在AB上,∠ECF=45°,设△ABC的面积为S,说明AF•BE=2S 的理由.7.等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.(1)若AE=CF;①求证:AF=BE,并求∠APB的度数;②若AE=2,试求AP•AF的值;(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.8.如图所示,AD,BE是钝角△ABC的边BC,AC上的高,求证:=.9.已知:如图,在△ABC中,AB=AC,DE∥BC,点F在边AC上,DF与BE相交于点G,且∠EDF=∠ABE.求证:(1)△DEF∽△BDE;(2)DG•DF=DB•EF.10.如图,△ABC、△DEF都是等边三角形,点D为AB的中点,E在BC上运动,DF和EF分别交AC于G、H 两点,BC=2,问E在何处时CH的长度最大?11.如图,AB和CD交于点O,当∠A=∠C时,求证:OA•OB=OC•OD.12.如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外).连接EB,过E作EF⊥AB,交AB的延长线为F.(1)猜测直线BE和直线AC的位置关系,并证明你的猜想.(2)证明:△BEF∽△ABC,并求出相似比.13.已知:如图,△ABC中,点D、E是边AB上的点,CD平分∠ECB,且BC2=BD•BA.(1)求证:△CED∽△ACD;(2)求证:.14.如图,△ABC中,点D、E分别在BC和AC边上,点G是BE边上一点,且∠BAD=∠BGD=∠C,联结AG.(1)求证:BD•BC=BG•BE;(2)求证:∠BGA=∠BAC.15.已知:如图,在△ABC中,点D是BC中点,点E是AC中点,且AD⊥BC,BE⊥AC,BE,AD相交于点G,过点B作BF∥AC交AD的延长线于点F,DF=6.(1)求AE的长;(2)求的值.16.如图,△ABC中,∠ACB=90°,D是AB上一点,M是CD中点,且∠AMD=∠BMD,AP∥CD交BC延长线于P点,延长BM交PA于N点,且PN=AN.(1)求证:MN=MA;(2)求证:∠CDA=2∠ACD.17.已知:如图,在△ABC中,已知点D在BC上,联结AD,使得∠CAD=∠B,DC=3且S△ACD:S△ADB﹦1﹕2.(1)求AC的值;(2)若将△ADC沿着直线AD翻折,使点C落点E处,AE交边BC于点F,且AB∥DE,求的值.18.在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F.(1)求证:△ABC∽△FCD;(2)若DE=3,BC=8,求△FCD的面积.19.如图,△ABC为等边三角形,D为BC边上一点,以AD为边作∠ADE=60°,DE与△ABC的外角平分线CE 交于点E.(1)求证:∠BAD=∠FDE;(2)设DE与AC相交于点G,连接AE,若AB=6,AE=5时,求线段AG的长.20.如图所示,△ABC中,∠B=90°,点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC 边向点C以2cm/s的速度移动.(1)如果P,Q分别从A,B同时出发,经几秒,使△PBQ的面积等于8cm2?(2)如果P,Q分别从A,B同时出发,并且P到B后又继续在BC边上前进,Q到C后又继续在CA边上前进,经过几秒,使△PCQ的面积等于12.6cm2?21.已知:如图,△ABC是等边三角形,D是AB边上的点,将DB绕点D顺时针旋转60°得到线段DE,延长ED 交AC于点F,连接DC、AE.(1)求证:△ADE≌△DFC;(2)过点E作EH∥DC交DB于点G,交BC于点H,连接AH.求∠AHE的度数;(3)若BG=,CH=2,求BC的长.22.如图,在△ABC中,CD平分∠ACB,BE∥BC交AC于点E.(1)求证:AE•BC=AC•CE;(2)若S△ADE:S△CDE=4:3.5,BC=15,求CE的长.23.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,(1)求证:AC2=AB•AD;(2)求证:CE∥AD;(3)若AD=4,AB=6,求的值.24.在△ABC中,∠CAB=90°,AD⊥BC于点D,点E为AB的中点,EC与AD交于点G,点F在BC上.(1)如图1,AC:AB=1:2,EF⊥CB,求证:EF=CD.(2)如图2,AC:AB=1:,EF⊥CE,求EF:EG的值.25.如图,M、N、P分别为△ABC三边AB、BC、CA的中点,BP与MN、AN分别交于E、F.(1)求证:BF=2FP;(2)设△ABC的面积为S,求△NEF的面积.26.在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,E、F分别是AC,BC边上一点,且CE=AC,BF=BC,(1)求证:;(2)求∠EDF的度数.27.如图,△ABC是等边三角形,且AB∥CE.(1)求证:△ABD∽△CED;(2)若AB=6,AD=2CD,①求E到BC的距离EH的长.②求BE的长.28.如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连接CC′交斜边于点E,CC′的延长线交BB′于点F.(1)若AC=3,AB=4,求;(2)证明:△ACE∽△FBE;(3)设∠ABC=α,∠CAC′=β,试探索α、β满足什么关系时,△ACE与△FBE是全等三角形,并说明理由.29.如图,△ABC是等边三角形,∠DAE=120°,求证:(1)△ABD∽△ECA;(2)BC2=DB•CE.30.如图,在Rt△ABC中,∠C=90°,且AC=CD=,又E,D为CB的三等分点.(1)证明:△ADE∽△BDA;(2)证明:∠ADC=∠AEC+∠B;(3)若点P为线段AB上一动点,连接PE,则使得线段PE的长度为整数的点P的个数有几个?请说明理由.相似三角形性质和判定专项练习30题参考答案:1.解:(1)∵∠ADC=∠B+∠BAD,且∠CDG=∠BAD,∴∠ADG=∠B;∵∠BAC=∠DAG,∴△ABC∽△ADG,∴=.(2)∵∠BAC=∠DAG,∴∠BAD=∠CAG;又∵∠CDG=∠BAD,∴∠CDG=∠CAG,∴A、D、C、G四点共圆,∴∠DAG+∠DCG=180°;∵GC⊥BC,∴∠DCG=90°,∴∠DAG=90°,∠BAC=∠DAG=90°.2.解:(1)如图,∵∠ACB=90°,CF⊥AD,∴∠ACD=∠AFC,而∠CAD=∠FAC,∴△ACD∽△AFC,∴,∴AC2=AF•AD.(2)如图,∵CE⊥AB,CF⊥AD,∴∠AEC=∠AFC=90°,∴A、E、F、C四点共圆,∴∠AFE=∠ACE;而∠ACE+∠CAE=∠CAE+∠B,∴∠ACE=∠B,∠AFE=∠B;∵∠FAE=∠BAD,∴△AEF∽△ADB,∴AE:AD=BD:EF,∴AE•DB=AD•EF.3.解:(1)∵PB=PC,∴∠B=∠PCB;∵PC平分∠ACB,∴∠ACP=∠PCB,∠B=∠ACP,∵∠A=∠A,∴△APC∽△ACB.(2)∵△APC∽△ACB,∴,∵AP=2,PC=6,AB=8,∴AC=4.∵AP+AC=PC=6,这与三角形的任意两边之和大于第三边相矛盾,∴该题无解.4.(1)证明:∵AD∥BC,∴∠C+∠ADE=180°,∵∠BFE=∠C,∴∠AFB=∠EDA,∵AB∥DC,∴∠BAE=∠AED,∴△ABF∽△EAD;(2)解:∵AB∥CD,BE⊥CD,∴∠ABE=90°,∵AB=4,∠BAE=30°,∴AE=2BE,由勾股定理可求得AE=5.证明:∵∠ABC=2∠C,BD平分∠ABC,∴∠ABD=∠DBC=∠C,∴BD=CD,在△ABD和△ACB中,,∴△ABD∽△ACB,∴=,即AB•BC=AC•BD,∴AB•BC=AC•CD.6.证明:∵AC=BC,∴∠A=∠B,∵∠ACB=90°,∴∠A=∠B=45°,∵∠ECF=45°,∴∠ECF=∠B=45°,∴∠ECF+∠1=∠B+∠1,∵∠BCE=∠ECF+∠1,∠2=∠B+∠1;∴∠BCE=∠2,∵∠A=∠B,∴△ACF∽△BEC.∴,∴AC•BC=BE•AF,∴S△ABC=AC•BC=BE•AF,∴AF•BE=2S.7.(1)①证明:∵△ABC为等边三角形,∴AB=AC,∠C=∠CAB=60°,又∵AE=CF,在△ABE和△CAF中,,∴△ABE≌△CAF(SAS),∴AF=BE,∠ABE=∠CAF.又∵∠APE=∠BPF=∠ABP+∠BAP,∴∠APE=∠BAP+∠CAF=60°.∴∠APB=180°﹣∠APE=120°.②∵∠C=∠APE=60°,∠PAE=∠CAF,∴△APE∽△ACF,∴,即,所以AP•AF=12(2)若AF=BE,有AE=BF或AE=CF两种情况.①当AE=CF时,点P的路径是一段弧,由题目不难看出当E为AC的中点的时候,点P经过弧AB的中点,此时△ABP为等腰三角形,且∠ABP=∠BAP=30°,∴∠AOB=120°,又∵AB=6,∴OA=,点P的路径是.②当AE=BF时,点P的路径就是过点C向AB作的垂线段的长度;因为等边三角形ABC的边长为6,所以点P 的路径为:.所以,点P经过的路径长为或3.8.证明:∵AD,BE是钝角△ABC的边BC,AC上的高,∴∠D=∠E=90°,∵∠ACD=∠BCE,∴△ACD∽△BCE,∴=.9.证明:(1)∵AB=AC,∴∠ABC=∠ACB,∵DE∥BC,∴∠ABC+∠BDE=180°,∠ACB+∠CED=180°.∴∠BDE=∠CED,∵∠EDF=∠ABE,∴△DEF∽△BDE;(2)由△DEF∽△BDE,得.∴DE2=DB•EF,由△DEF∽△BDE,得∠BED=∠DFE.∵∠GDE=∠EDF,∴△GDE∽△EDF.∴,∴DE2=DG•DF,∴DG•DF=DB•EF.10.解:设EC=x,CH=y,则BE=2﹣x,∵△ABC、△DEF都是等边三角形,∴∠B=∠DEF=60°,∵∠B+∠BDE=∠DEF+∠HEC,∴∠BDE=∠HEC,∴△BED∽△CHE,∴,∵AB=BC=2,点D为AB的中点,∴BD=1,∴,即:y=﹣x2+2x=﹣(x﹣1)2+1.∴当x=1时,y最大.此时,E在BC中点11.解:∵∠A=∠C,∠AOD=∠BOC,∴△OAD∽△OCB,∴=,∴OA•OB=OC•OD.12.解:(1)猜测BE和直线AC垂直.证明:∵△AEC是等边三角形,∴AE=CE,∵四边形ABCD是正方形,∴AB=CB,∵BE=BE,∴△AEB≌△CEB(SSS).∴∠AEB=∠CEB,∵AE=CE,∴BE⊥AC;(2)∵△AEC是等边三角形,∴∠EAC=∠AEC=60°,∵BE⊥AC,∴∠BEA=∠AEC=30°,∵四边形ABCD是正方形,∴∠BAC=45°,∴∠BAE=15°,∴∠EBF=45°,∵EF⊥BF,∴∠F=90°,∴∠EBF=∠BAC,∠F=∠ABC,∴△BEF∽△ACB,延长EB交AC于G,设AC为2a,则BG=a,EB=a﹣a,∴相似比是:===13.证明:(1)∵BC2=BD•BA,∴BD:BC=BC:BA,∵∠B是公共角,∴△BCD∽△BAC,∴∠BCD=∠A,∵CD平分∠ECB,∴∠ECD=∠BCD,∴∠ECD=∠A,∵∠EDC=∠CDA,∴△CED∽△ACD;(2)∵△BCD∽△BAC,△CED∽△ACD,∴=,=,∴.14.证明:(1)∵∠DBG=∠EBC,∠BGD=∠C,∴△BDG∽△BEC,∴=,则BD•BC=BG•BE;(2)∵∠DBA=∠ABC,∠BAD=∠C,∴△DBA∽△ABC,∴=,即AB2=BD•BC,∵BD•BC=BG•BE,∴AB2=BG•BE,即=,∵∠GBA=∠ABE,∴△GBA∽△ABE,∴∠BGA=∠BAC.15.解:(1)∵在△ABC中,点D是BC中点,点E是AC中点,且AD⊥BC,BE⊥AC,∴AC=AB=BC,∴△ABC是等边三角形,∴∠C=60°,∵BF∥AC,∴∠CBF=∠C=60°,∵AD⊥BC,∴∠FDB=90°,∴∠F=30°,∵DF=6,∴BD=2,∵AE=EC=BD=DC,∴AE=2;(2)∵∠BDF=90°,∠F=30°,BD=2,∴BF=2DB=4,∵AC∥BF,∴△AEG∽△FBG,∴=()2=.16.证明:(1)∵AP∥CD,∴∠AMD=∠MAN,∠BMD=∠MNA,∵∠AMD=∠BMD,∴∠MAN=∠MNA,∴MN=MA.(2)如图,连接NC,∵AP∥CD,且PN=AN.∴==,∴MC=MD,∴CN为直角△ACP斜边AP的中线,∴CN=NA,∠NCA=∠NAC,∵AP∥CD,∴∠NAC=∠ACD,∴∠NCM=2∠ACD,∵∠CMN=∠DMB,∠DMA=∠BMD,∴∠CMD=∠DMA,在△CMN和△DMA中,,∴△CMN≌△DMA(SAS),∠ADM=∠NCM=2∠ACD.即:∠CDA=2∠ACD.17.解:(1)∵S△ACD:S△ADB﹦1:2,∴BD=2CD,∵DC=3,∴BD=2×3=6,∴BC=BD+DC=6+3=9,∵∠CAD=∠B,∠C=∠C,∴△ABC∽△DAC,∴=,即=,解得AC=3;(2)由翻折的性质得,∠E=∠C,DE=CD=3,∵AB∥DE,∴∠B=∠EDF,∵∠CAD=∠B,∴∠EDF=∠CAD,∴△EFD∽△ADC,∴=()2=()2=18.(1)证明:∵D是BC的中点,DE⊥BC,∴BE=CE,∴∠B=∠DCF,∵AD=AC,∴∠FDC=∠ACB,∴△ABC∽△FCD;(2)解:过A作AG⊥CD,垂足为G.∵AD=AC,∴DG=CG,∴BD:BG=2:3,∵ED⊥BC,∴ED∥AG,∴△BDE∽△BGA,∴ED:AG=BD:BG=2:3,∵DE=3,∴AG=,∵△ABC∽△FCD,BC=2CD,∴=()2=.∵S△ABC=×BC×AG=×8×=18,∴S△FCD=S△ABC=.19.(1)证明:∵△ABC为等边三角形,∴∠B=60°,由三角形的外角性质得,∠ADE+∠FDE=∠BAD+∠B,∵∠ADE=60°,∴∠BAD=∠FDE;(2)解:如图,过点D作DH∥AC交AB于H,∵△ABC为等边三角形,∴△BDH是等边三角形,∴∠BHD=60°,BD=BH,∴∠AHD=180°﹣60°=120°,∵CE是△ABC的外角平分线,∴∠ACE=(180°﹣60°)=60°,∴∠DCE=60°+60°=120°,∴∠AHD=∠DCE=120°,又∵AH=AB﹣BH,CD=BC﹣BD,∴AH=CD,在△AHD和△DCE中,,∴△AHD≌△DCE(ASA),∴AD=DE,∵∠ADE=60°,∴△ADE是等边三角形,∴∠DAE=∠DEA=60°,AE=AD=5,∵∠BAD=∠BAC﹣∠CAD=60°﹣∠CAD,∠EAG=∠DAE﹣∠CAD=60°﹣∠CAD,∴∠BAD=∠EAG,∴△ABD∽△AEG,∴=,即=,解得AG=.20.解:(1)设x秒时,点P在AB上,点Q在BC上,且使△PBQ面积为8cm2,由题意得(6﹣x)•2x=8,解之,得x1=2,x2=4,经过2秒时,点P到距离B点4cm处,点Q到距离B点4cm处;或经4秒,点P到距离B点2cm处,点Q到距离B点8cm处,△PBQ的面积为8cm2,综上所述,经过2秒或4秒,△PBQ的面积为8cm2;(2)当P在AB上时,经x秒,△PCQ的面积为:×PB×CQ=×(6﹣x)(8﹣2x)=12.6,解得:x1=(不合题意舍去),x2=,经x秒,点P移动到BC上,且有CP=(14﹣x)cm,点Q移动到CA上,且使CQ=(2x﹣8)cm,过Q作QD⊥CB,垂足为D,由△CQD∽△CAB得,即QD=,由题意得(14﹣x)•=12.6,解之得x1=7,x2=11.经7秒,点P在BC上距离C点7cm处,点Q在CA上距离C点6cm处,使△PCQ的面积等于12.6cm2.经11秒,点P在BC上距离C点3cm处,点Q在CA上距离C点14cm处,14>10,点Q已超出CA的范围,此解不存在.综上所述,经过7秒和秒时△PCQ的面积等于12.6cm221.(1)证明:如图,∵线段DB顺时针旋转60°得线段DE,∴∠EDB=60°,DE=DB.∵△ABC是等边三角形,∴∠B=∠ACB=60°.∴∠EDB=∠B.∴EF∥BC.∴DB=FC,∠ADF=∠AFD=60°.∴DE=DB=FC,∠ADE=∠DFC=120°,△ADF是等边三角形.∴AD=DF.∴△ADE≌△DFC.(2)解:由△ADE≌△DFC,得AE=DC,∠1=∠2.∵ED∥BC,EH∥DC,∴四边形EHCD是平行四边形.∴EH=DC,∠3=∠4.∴AE=EH.∴∠AEH=∠1+∠3=∠2+∠4=∠ACB=60°.∴△AEH是等边三角形.∴∠AHE=60°.(3)解:设BH=x,则AC=BC=BH+HC=x+2,由(2)四边形EHCD是平行四边形,∴ED=HC.∴DE=DB=HC=FC=2.∵EH∥DC,∴△BGH∽△BDC.∴.即.解得x=1.∴BC=3.22.(1)证明:∵DE∥BC,∴∠ADE=∠B,∠AEC=∠ACB,∴△ADE∽△ABC,∴=,∵DE∥BC,∴∠EDC=∠BCD,∵CD平分∠ACB,∴∠BCD=∠DCE,∴∠DCE=∠EDC,∴DE=CE,∴=,即AE•BC=AC•CE;(2)∵S△ADE:S△CDE=4:3.5,∴AE:CE=4:3.5,∴=,∵由(1)知=,∴=,解得DE=6,∵DE=CE,∴CE=8.23.(1)证明:∵AC平分∠DAB,∴∠DAC=∠CAB,∵∠ADC=∠ACB=90°,∴△ADC∽△ACB,∴AC2=AB•AD;(2)证明:∵E为AB的中点,∴CE=AB=AE,∴∠EAC=∠ECA,∵∠DAC=∠CAB,∴∠DAC=∠ECA,∴CE∥AD;(3)解:∵CE∥AD,∴△AFD∽△CFE,∴AD:CE=AF:CF,∵CE=AB,∴CE=×6=3,∵AD=4,∴,∴.24.(1)证明:如图1,在△ABC中,∵∠CAB=90°,AD⊥BC于点D,∴∠CAD=∠B=90°﹣∠ACB.∵AC:AB=1:2,∴AB=2AC,∵点E为AB的中点,∴AB=2BE,∴AC=BE.在△ACD与△BEF中,,∴△ACD≌△BEF,∴CD=EF,即EF=CD;(2)解:如图2,作EH⊥AD于H,EQ⊥BC于Q,∵EH⊥AD,EQ⊥BC,AD⊥BC,∴四边形EQDH是矩形,∴∠QEH=90°,∴∠FEQ=∠GEH=90°﹣∠QEG,又∵∠EQF=∠EHG=90°,∴△EFQ∽△EGH,∵AC:AB=1:,∠CAB=90°,∴∠B=30°.在△BEQ中,∵∠BQE=90°,∴sinB==,∴EQ=BE.在△AEH中,∵∠AHE=90°,∠AEH=∠B=30°,∴cos∠AEH==,∴EH=AE.∵点E为AB的中点,∴BE=AE,∴EF:EG=EQ:EH=BE:AE=1:=:3.25.(1)证明:如图1,连接PN,∵N、P分别为△ABC边BC、CA的中点,∴PN∥AB,且.∴△ABF∽△NPF,∴.∴BF=2FP.(2)解:如图2,取AF的中点G,连接MG,∴MG∥EF,AG=GF=FN.∴△NEF∽△NMG,∴S△NEF=S△MNG=×S△AMN=××S△ABC=S.26.(1)证明:∵CD⊥AB,∴∠CDB=∠ADC=90°,∴∠ACD+∠BCD=90°,∵∠ACB=90°,∴∠A+∠ACD=90°,∴∠A=∠BCD,∴△ADC∽△CDB,∴=;(2)解:∵CE=AC,BF=BC,∴===,又∵∠A=∠BCD,∴∠ACD=∠B,∴△CED∽△BFD,∴∠CDE=∠BDF,∴∠EDF=∠EDC+∠CDF=∠BDF+∠CDF=∠CDB=90°.27.解;(1)∵AB∥CE,∴∠A=∠DCE,又∵∠ADB=∠EDC,∴△ABD∽△CED;(2)①过点E作EH⊥BF于点H,∵△ABC是等边三角形,△ABD∽△CED,AB=6,AD=2CD,∴==,∠A=∠ACB=60°,∴CE=3,∵AB∥CE,∴∠A=∠DCE=60°,∴∠ECH=180°﹣∠ACB﹣∠DCE=180°﹣60°﹣60°=60°,∴EH=CE•sin60°=3×=;②在Rt△ECH中,∵∠ECH=60°,CE=3,∴CH=CE•cos60°=3×=,∴BH=BC+CH=6+=,∴BE===3.28.(1)解:∵AC=AC′,AB=AB′,∴由旋转可知:∠CAB=∠C′AB′,∴∠CAB+∠EAC′=∠C′AB′+∠EAC′,即∠CAC′=∠BAB′,又∵∠ACB=∠AC′B′=90°,∴△ACC′∽△ABB′,∵AC=3,AB=4,∴==;(2)证明:∵Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,∴AC=AC′,AB=AB′,∠CAB=∠C′AB′,(1分)∴∠CAC′=∠BAB′,∴∠ABB′=∠AB′B=∠ACC′=∠AC′C,∴∠ACC′=∠ABB′,(3分)又∵∠AEC=∠FEB,∴△ACE∽△FBE.(4分)(3)解:当β=2α时,△ACE≌△FBE.理由:在△ACC′中,∵AC=AC′,∴∠ACC′=∠AC′C====90°﹣α,(6分)在Rt△ABC中,∠ACC′+∠BCE=90°,即90°﹣α+∠BCE=90°,∴∠BCE=90°﹣90°+α=α,∵∠ABC=α,∴∠ABC=∠BCE,(8分)∴CE=BE,由(2)知:△ACE∽△FBE,∴△ACE≌△FBE.(9分)29.证明:(1)∵△ABC是等边三角形,∠DAE=120°,∴∠DAB+∠CAE=60°,∵∠ABC是△ABD的外角,∴∠DAB+∠D=∠ABC=60°,∴∠CAE=∠D,∵∠ABC=∠ACB=60°,∴∠ABD=∠ACE=120°,∴△ABD∽△ECA;(2)∵△ABD∽△ECA,∴=,即AB•AC=BD•CE,∵AB=AC=BC,∴BC2=BD•CE30.(1)证明:∵AC=CD=DE=EB=,又∠C=90°,∴AD=2,∴=,==,∴=,又∵∠ADE=∠BDA,∴△ADE∽△BDA;(2)证明:∵△ADE∽△BDA,∴∠DAE=∠B,又∵∠ADC=∠AEC+∠DAE,∴∠ADC=∠AEC+∠B;(3)解:∵点P为线段AB上一动点,根据勾股定理得:AE==,BE=,∴PE的最大值为.作EF⊥AB,则EF=,则PE的最小值为∴≤EP≤,∵EP为整数,即EP=1,2,3,结合图形可知PE=1时有两个点,所以PE长为整数的点P个数为4个.。
中考数学复习---相似三角形综合压轴题练习(含答案解析)

中考数学复习---相似三角形综合压轴题练习(含答案解析)一.平行线分线段成比例(共1小题)1.(2022•襄阳)如图,在△ABC中,D是AC的中点,△ABC的角平分线AE 交BD于点F,若BF:FD=3:1,AB+BE=3,则△ABC的周长为.【答案】5【解答】解:如图,过点F作FM⊥AB于点M,FN⊥AC于点N,过点D作DT∥AE交BC于点T.∵AE平分∠BAC,FM⊥AB,FN⊥AC,∴FM=FN,∴===3,∴AB=3AD,设AD=DC=a,则AB=3a,∵AD=DC,DT∥AE,∴ET=CT,∴==3,设ET=CT=b,则BE=3b,∵AB+BE=3,∴3a+3b=3,∴a+b=,∴△ABC的周长=AB+AC+BC=5a+5b=5,故答案为:5.二.相似三角形的性质和判定2.(2022•鞍山)如图,在正方形ABCD中,点E为AB的中点,CE,BD交于点H,DF⊥CE于点F,FM平分∠DFE,分别交AD,BD于点M,G,延长MF交BC于点N,连接BF.下列结论:①tan∠CDF=;②S△EBH:S△DHF =3:4;③MG:GF:FN=5:3:2;④△BEF∽△HCD.其中正确的是.(填序号即可).【答案】①③④【解答】解:如图,过点G作GQ⊥DF于点Q,GP⊥EF于点P.设正方形ABCD的边长为2a.∵四边形ABCD是正方形,∴∠ABC=∠BCD=90°,∵AE=EB=a,BC=2a,∵DF⊥CE,∴∠CFD=90°,∴∠ECB+∠DCF=90°,∵∠DCF+∠CDF=90°,∴∠CDF=∠ECB,∴tan∠CDF=,故①正确,∵BE∥CD,∴===,∵EC===a,BD=CB=2a,∴EH=EC=a,BH=BD=a,DH=BD=a,在Rt△CDF中,tan∠CDF==,CD=2a,∴CF=a,DF=a,∴HF=CE﹣EH﹣CF=a﹣a﹣a=a,∴S△DFH=•FH•DF=×a×a=a2,∵S△BEH=S△ECB=××a×2a=a2,∴S△EBH:S△DHF=a2:a2=5:8,故②错误.∵FM平分∠DFE,GQ⊥EF,GP⊥FE,∴GQ=GP,∵==,∴=,∴BG=DG,∵DM∥BN,∴==1,∴GM=GN,∵S△DFH=S△FGH+S△FGD,∴×a×a=××GP+×a×GQ,∴GP=GQ=a,∴FG=a,过点N作NJ⊥CE于点J,设FJ=NJ=m,则CJ=2m,∴3m=a,∴m=a,∴FN=m=a,∴MG=GN=GF+FN=a+a=a,∴MG:GF:FN=a:a:a=5:3:2,故③正确,∵AB∥CD,∴∠BEF=∠HCD,∵==,==,∴=,∴△BEF∽△HCD,故④正确.故答案为:①③④.3.(2022•眉山)如图,四边形ABCD为正方形,将△EDC绕点C逆时针旋转90°至△HBC,点D,B,H在同一直线上,HE与AB交于点G,延长HE与CD的延长线交于点F,HB=2,HG=3.以下结论:①∠EDC=135°;②EC2=CD•CF;③HG=EF;④sin∠CED=.其中正确结论的个数为()A.1个B.2个C.3个D.4个【答案】D【解答】解:∵△EDC旋转得到△HBC,∴∠EDC=∠HBC,∵ABCD为正方形,D,B,H在同一直线上,∴∠HBC=180°﹣45°=135°,∴∠EDC=135°,故①正确;∵△EDC旋转得到△HBC,∴EC=HC,∠ECH=90°,∴∠HEC=45°,∴∠FEC=180°﹣45°=135°,∵∠ECD=∠ECF,∴△EFC∽△DEC,∴,∴EC2=CD•CF,故②正确;设正方形边长为a,∵∠GHB+∠BHC=45°,∠GHB+∠HGB=45°,∴∠BHC=∠HGB=∠DEC,∵∠GBH=∠EDC=135°,∴△GBH∽△EDC,∴,即,∵△HEC是等腰直角三角形,∴,∵∠GHB=∠FHD,∠GBH=∠HDF=135°,∴△HBG∽△HDF,∴,即,解得:EF=3,∵HG=3,∴HG=EF,故③正确;过点E作EM⊥FD交FD于点M,∴∠EDM=45°,∵ED=HB=2,∴,∵EF=3,∴,∵∠DEC+∠DCE=45°,∠EFC+∠DCE=45°,∴∠DEC=∠EFC,∴,故④正确综上所述:正确结论有4个,故选:D.4.(2022•东营)如图,已知菱形ABCD的边长为2,对角线AC、BD相交于点O,点M,N分别是边BC、CD上的动点,∠BAC=∠MAN=60°,连接MN、OM.以下四个结论正确的是()①△AMN是等边三角形;②MN的最小值是;③当MN最小时S△CMN=S菱形ABCD;④当OM⊥BC时,OA2=DN•AB.A.①②③B.①②④C.①③④D.①②③④【答案】D【解答】解:∵四边形ABCD是菱形,∴AB=CB=AD=CD,AB∥CD,AC⊥BD,OA=OC,∴∠BAC=∠ACD=60°,∴△ABC和△ADC都是等边三角形,∴∠ABM=∠ACN=60°,AB=AC,∵∠MAN=60°,∴∠BAM=∠CAN=60°﹣∠,∴△BAM≌△CAN(ASA),∴AM=AN,∴△AMN是等边三角形,故①正确;当AM⊥BC时,AM的值最小,此时MN的值也最小,∵∠AMB=90°,∠ABM=60°,AB=2,∴MN=AM=AB•sin60°=2×=,∴MN的最小值是,故②正确;∵AM⊥BC时,MN的值最小,此时BM=CM,∴CN=BM=CB=CD,∴DN=CN,∴MN∥BD,∴△CMN∽△CBD,∴===,∴S△CMN=S△CBD,∵S△CBD=S菱形ABCD,∴S△CMN=×S菱形ABCD=S菱形ABCD,故③正确;∵CB=CD,BM=CN,∴CB﹣BM=CD﹣CN,∴CM=DN,∵OM⊥BC,∴∠CMO=∠COB=90°,∵∠OCM=∠BCO,∴△OCM∽△BCO,∴=,∴OC2=CM•CB,∴OA2=DN•AB,故④正确,故选:D.5.(2022•绍兴)将一张以AB为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片ABCD,其中∠A=90°,AB =9,BC=7,CD=6,AD=2,则剪掉的两个直角三角形的斜边长不可能是()A.B.C.10D.【答案】A【解答】解:如右图1所示,由已知可得,△DFE∽△ECB,则,设DF=x,CE=y,则,解得,∴DE=CD+CE=6+=,故选项B不符合题意;EB=DF+AD=+2=,故选项D不符合题意;如图2所示,由已知可得,△DCF∽△FEB,则,设FC=m,FD=n,则,解得,∴FD=10,故选项C不符合题意;BF=FC+BC=8+7=15;如图3所示:此时两个直角三角形的斜边长为6和7;故选:A.6.(2022•连云港)如图,将矩形ABCD沿着GE、EC、GF翻折,使得点A、B、D恰好都落在点O处,且点G、O、C在同一条直线上,同时点E、O、F在另一条直线上.小炜同学得出以下结论:①GF∥EC;②AB=AD;③GE =DF;④OC=2OF;⑤△COF∽△CEG.其中正确的是()A.①②③B.①③④C.①④⑤D.②③④【答案】B【解答】解:由折叠性质可得:DG=OG=AG,AE=OE=BE,OC=BC,∠DGF=∠FGO,∠AGE=∠OGE,∠AEG=∠OEG,∠OEC=∠BEC,∴∠FGE=∠FGO+∠OGE=90°,∠GEC=∠OEG+∠OEC=90°,∴∠FGE+∠GEC=180°,∴GF∥CE,故①正确;设AD=2a,AB=2b,则=OG=AG=a,AE=OE=BE=b,∴CG=OG+OC=3a,在Rt△CGE中,CG2=GE2+CE2,(3a)2=a2+b2+b2+(2a)2,解得:b=a,∴AB=AD,故②错误;在Rt△COF中,设OF=DF=x,则CF=2b﹣x=2a﹣x,∴x2+(2a)2=(2a﹣x)2,解得:x=a,∴DF=×a=a,2OF=2×a=2a,在Rt△AGE中,GE==a,∴GE=DF,OC=2OF,故③④正确;无法证明∠FCO=∠GCE,∴无法判断△COF∽△CEG,故⑤错误;综上,正确的是①③④,故选:B.7.(2022•遂宁)如图,正方形ABCD与正方形BEFG有公共顶点B,连接EC、GA,交于点O,GA与BC交于点P,连接OD、OB,则下列结论一定正确的是()①EC⊥AG;②△OBP∽△CAP;③OB平分∠CBG;④∠AOD=45°;A.①③B.①②③C.②③D.①②④【答案】D【解答】解:∵四边形ABCD、四边形BEFG是正方形,∴AB=BC,BG=BE,∠ABC=90°=∠GBE,∴∠ABC+∠CBG=∠GBE+∠CBG,即∠ABG=∠EBC,∴△ABG≌△CBE(SAS),∴∠BAG=∠BCE,∵∠BAG+∠APB=90°,∴∠BCE+∠APB=90°,∴∠BCE+∠OPC=90°,∴∠POC=90°,∴EC⊥AG,故①正确;取AC的中点K,如图:在Rt△AOC中,K为斜边AC上的中点,∴AK=CK=OK,在Rt△ABC中,K为斜边AC上的中点,∴AK=CK=BK,∴AK=CK=OK=BK,∴A、B、O、C四点共圆,∴∠BOA=∠BCA,∵∠BPO=∠CPA,∴△OBP∽△CAP,故②正确,∵∠AOC=∠ADC=90°,∴∠AOC+∠ADC=180°,∴A、O、C、D四点共圆,∵AD=CD,∴∠AOD=∠DOC=45°,故④正确,由已知不能证明OB平分∠CBG,故③错误,故正确的有:①②④,故选:D.8.(2022•金华)如图是一张矩形纸片ABCD,点E为AD中点,点F在BC上,把该纸片沿EF折叠,点A,B的对应点分别为A′,B′,A′E与BC相交于点G,B′A′的延长线过点C.若=,则的值为()A.2B.C.D.【答案】A【解答】解:连接FG,CA′,过点G作GT⊥AD于点T.设AB=x,AD=y.∵=,∴可以假设BF=2k,CG=3k.∵AE=DE=y,由翻折的性质可知EA=EA′=y,BF=FB′=2k,∠AEF=∠GEF,∵AD∥CB,∴∠AEF=∠EFG,∴∠GEF=∠GFE,∴EG=FG=y﹣5k,∴GA′=y﹣(y﹣5k)=5k﹣y,∵C,A′,B′共线,GA′∥FB′,∴=,∴=,∴y2﹣12ky+32k2=0,∴y=8k或y=4k(舍去),∴AE=DE=4k,∵四边形CDTG是矩形,∴CG=DT=3k,∴ET=k,∵EG=8k﹣5k=3k,∴AB=CD=GT==2k,∴==2.解法二:不妨设BF=2,CG=3,连接CE,则Rt△CA'E≌Rt△CDE,推出A'C =CD=AB=A'B',==1,推出GF=CG=3,BC=8,在Rt△CB'F,勾股得CB'=4则A'B'=2,故选:A.9.(2022•乐山)如图,等腰△ABC的面积为2,AB=AC,BC=2.作AE∥BC且AE=BC.点P是线段AB上一动点,连结PE,过点E作PE的垂线交BC的延长线于点F,M是线段EF的中点.那么,当点P从A点运动到B 点时,点M的运动路径长为()A.B.3C.2D.4【答案】B【解答】解:如图,过点A作AH⊥BC于点H.当点P与A重合时,点F与C重合,当点P与B重合时,点F的对应点为F″,点M的运动轨迹是△ECF″的中位线,M′M″=CF″,∵AB=AC,AH⊥BC,∴BH=CH,∵AE∥BC,AE=BC,∴AE=CH,∴四边形AHCE是平行四边形,∵∠AHC=90°,∴四边形AHCE是矩形,∴EC⊥BF″,AH=EC,∵BC=2,S△ABC=2,∴×2×AH=2,∴AH=EC=2,∵∠BEF″=∠ECB=∠ECF″,∴∠BEC+∠CEF″=90°,∠CEF″+∠F″=90°,∴∠BEC=∠F″,∴△ECB∽△F″CE,∴EC2=CB•CF″,∴CF″==6,∴M′M″=3故选:B.10.(2022•海南)如图,菱形ABCD中,点E是边CD的中点,EF垂直AB交AB的延长线于点F,若BF:CE=1:2,EF=,则菱形ABCD的边长是()A.3B.4C.5D.【答案】B【解答】解:过点D作DH⊥AB于点H,如图,∵四边形ABCD是菱形,∴AD=AB=CD,AB∥CD.∵EF⊥AB,DH⊥AB,∴DH∥EF,∴四边形DHFE为平行四边形,∴HF=DE,DH=EF=.∵点E是边CD的中点,∴DE=CD,∴HF=CD=AB.∵BF:CE=1:2,∴设BF=x,则CE=2x,∴CD=4x,DE=HF=2x,AD=AB=4x,∴AF=AB+BF=5x.∴AH=AF﹣HF=3x.在Rt△ADH中,∵DH2+AH2=AD2,∴.解得:x=±1(负数不合题意,舍去),∴x=1.∴AB=4x=4.即菱形ABCD的边长是4,故选:B.11.(2022•黑龙江)如图,正方形ABCD的对角线AC,BD相交于点O,点F 是CD上一点,OE⊥OF交BC于点E,连接AE,BF交于点P,连接OP.则下列结论:①AE⊥BF;②∠OPA=45°;③AP﹣BP=OP;④若BE:CE =2:3,则tan∠CAE=;⑤四边形OECF的面积是正方形ABCD面积的.其中正确的结论是()A.①②④⑤B.①②③⑤C.①②③④D.①③④⑤【答案】B【解答】解:①∵四边形ABCD是正方形,∴AB=BC=CD,AC⊥BD,∠ABD=∠DBC=∠ACD=45°.∴∠BOE+∠EOC=90°,∵OE⊥OF,∴∠FOC+∠EOC=90°.∴∠BOE=∠COF.在△BOE和△COF中,,∴△BOE≌△COF(ASA),∴BE=CF.在△BAE和△CBF中,,∴△BAE≌△CBF(SAS),∴∠BAE=∠CBF.∵∠ABP+∠CBF=90°,∴∠ABP+∠BAE=90°,∴∠APB=90°.∴AE⊥BF.∴①的结论正确;②∵∠APB=90°,∠AOB=90°,∴点A,B,P,O四点共圆,∴∠APO=∠ABO=45°,∴②的结论正确;③过点O作OH⊥OP,交AP于点H,如图,∵∠APO=45°,OH⊥OP,∴OH=OP=HP,∴HP=OP.∵OH⊥OP,∴∠POB+∠HOB=90°,∵OA⊥OB,∴∠AOH+∠HOB=90°.∴∠AOH=∠BOP.∵∠OAH+BAE=45°,∠OBP+∠CBF=45°,∠BAE=∠CBF,∴∠OAH=∠OBP.在△AOH和△BOP中,,∴△AOH≌△BOP(ASA),∴AH=BP.∴AP﹣BP=AP﹣AH=HP=OP.∴③的结论正确;④∵BE:CE=2:3,∴设BE=2x,则CE=3x,∴AB=BC=5x,∴AE==x.过点E作EG⊥AC于点G,如图,∵∠ACB=45°,∴EG=GC=EC=x,∴AG==x,在Rt△AEG中,∵tan∠CAE=,∴tan∠CAE===.∴④的结论不正确;⑤∵四边形ABCD是正方形,∴OA=OB=OC=OD,∠AOB=∠BOC=∠COD=∠DOA=90°,∴△OAB≌△OBC≌△OCD≌△DOA(SAS).∴.∴.由①知:△BOE≌△COF,∴S△OBE=S△OFC,∴.即四边形OECF的面积是正方形ABCD面积的.∴⑤的结论正确.综上,①②③⑤的结论正确.故选:B.12.(2022•辽宁)如图,在正方形ABCD中,对角线AC,BD相交于点O,点E是OD的中点,连接CE并延长交AD于点G,将线段CE绕点C逆时针旋转90°得到CF,连接EF,点H为EF的中点.连接OH,则的值为.【答案】【解答】解:以O为原点,平行于AB的直线为x轴,建立直角坐标系,过E 作EM⊥CD于M,过F作FN⊥DC,交DC延长线于N,如图:设正方形ABCD的边长为2,则C(1,1),D(﹣1,1),∵E为OD中点,∴E(﹣,),设直线CE解析式为y=kx+b,把C(1,1),E(﹣,)代入得:,解得,∴直线CE解析式为y=x+,在y=x+中,令x=﹣1得y=,∴G(﹣1,),∴GE==,∵将线段CE绕点C逆时针旋转90°得到CF,∴CE=CF,∠ECF=90°,∴∠MCE=90°﹣∠NCF=∠NFC,∵∠EMC=∠CNF=90°,∴△EMC≌△CNF(AAS),∴ME=CN,CM=NF,∵E(﹣,),C(1,1),∴ME=CN=,CM=NF=,∴F(,﹣),∵H是EF中点,∴H(,0),∴OH=,∴==.故答案为:.13.(2022•辽宁)如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,点P为斜边AB上的一个动点(点P不与点A、B重合),过点P作PD⊥AC,PE⊥BC,垂足分别为点D和点E,连接DE,PC交于点Q,连接AQ,当△APQ为直角三角形时,AP的长是.【答案】3或2【解答】解:在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,∴∠BAC=30°,∴AB=2BC=2×2=4,∴AC===2,当∠APQ=90°时,如图1,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,∴∠BAC=30°,∴AB=2BC=2×2=4,∴AC===2,∵∠APQ=∠ACB=90°,∠CAP=∠BAC,∴△CAP∽△BAC,∴,即,∴AP=3,当∠AQP=90°时,如图2,∵PD⊥AC,PE⊥BC,∠ACB=90°,∴四边形DPEC是矩形,∴CQ=QP,∵∠AQP=90°,∴AQ垂直平分CP,∴AP=AC=2,综上所述,当△APQ为直角三角形时,AP的长是3或2,故答案为:3或2.14.(2022•绍兴)如图,AB=10,点C是射线BQ上的动点,连结AC,作CD ⊥AC,CD=AC,动点E在AB延长线上,tan∠QBE=3,连结CE,DE,当CE=DE,CE⊥DE时,BE的长是.【答案】或5【解答】解:如图,过点C作CT⊥AE于点T,过点D作DJ⊥CT交CT的延长线于点J,连接EJ.∵tan∠CBT=3=,∴可以假设BT=k,CT=3k,∵∠CAT+∠ACT=90°,∠ACT+∠JCD=90°,∴∠CAT=∠JCD,在△ATC和△CJD中,,∴△ATC≌△CJD(AAS),∴DJ=CT=3k,AT=CJ=10+k,∵∠CJD=∠CED=90°,∴C,E,D,J四点共圆,∵EC=DE,∴∠CJE=∠DJE=45°,∴ET=TJ=10﹣2k,∵CE2=CT2+TE2=(CD)2,∴(3k)2+(10﹣2k)2=[•]2,整理得4k2﹣25k+25=0,∴(k﹣5)(4k﹣5)=0,∴k=5和,∴BE=BT+ET=k+10﹣2k=10﹣k=5或,故答案为:5或.15.(2022•甘肃)如图,在矩形ABCD中,AB=6cm,BC=9cm,点E,F分别在边AB,BC上,AE=2cm,BD,EF交于点G,若G是EF的中点,则BG的长为cm.【答案】【解答】解:∵四边形ABCD是矩形,∴AB=CD=6cm,∠ABC=∠C=90°,AB∥CD,∴∠ABD=∠BDC,∵AE=2cm,∴BE=AB﹣AE=6﹣2=4(cm),∵G是EF的中点,∴EG=BG=EF,∴∠BEG=∠ABD,∴∠BEG=∠BDC,∴△EBF∽△DCB,∴=,∴=,∴BF=6,∴EF===2(cm),∴BG=EF=(cm),故答案为:.16.(2022•新疆)如图,四边形ABCD是正方形,点E在边BC的延长线上,点F在边AB上,以点D为中心,将△DCE绕点D顺时针旋转90°与△DAF 恰好完全重合,连接EF交DC于点P,连接AC交EF于点Q,连接BQ,若AQ•DP=3,则BQ=.【答案】【解答】解:如图,连接DQ,∵将△DCE绕点D顺时针旋转90°与△DAF恰好完全重合,∴DE=DF,∠FDE=90°,∴∠DFE=∠DEF=45°,∵四边形ABCD是正方形,∴∠DAC=45°=∠BAC,∴∠DAC=∠DFQ=45°,∴点A,点F,点Q,点D四点共圆,∴∠BAQ=∠FDQ=45°,∠DAF=∠DQF=90°,∠AFD=∠AQD,∴DF=DQ,∵AD=AB,∠BAC=∠=45°,AQ=AQ,∴△ABQ≌△ADQ(SAS),∴BQ=QD,∠AQB=∠AQD,∵AB∥CD,∴∠AFD=∠FDC,∴∠FDC=∠AQB,又∵∠BAC=∠DFP=45°,∴△BAQ∽△PFD,∴,∴AQ•DP=3=BQ•DF,∴3=BQ•BQ,∴BQ=,故答案为:.17.(2022•苏州)如图,在矩形ABCD中,=.动点M从点A出发,沿边AD向点D匀速运动,动点N从点B出发,沿边BC向点C匀速运动,连接MN.动点M,N同时出发,点M运动的速度为v1,点N运动的速度为v2,且v1<v2.当点N到达点C时,M,N两点同时停止运动.在运动过程中,将四边形MABN沿MN翻折,得到四边形MA′B′N.若在某一时刻,点B的对应点B′恰好与CD的中点重合,则的值为.【答案】【解答】解:如图,设AD交A′B′于点Q.设BN=NB′=x.∵=,∴可以假设AB=2k,CB=3k,∵四边形ABCD是矩形,∴AD=BC=3k,CD=AB=2k,∠C=∠D=90°,在Rt△CNB′中,CN2+CB′2=NB′2,∴(3k﹣x)2+k2=x2,∴x=k,∴NB′=k,CN=3k﹣k=k,由翻折的性质可知∠A′B′N=∠B=90°,∴∠DB′Q+∠CB′N=90°,∠CB′N+∠CNB′=90°,∴∠DB′Q=∠CNB′,∵∠D=∠C=90°,∴△DB′Q∽△CNB′,∴DQ:DB′:QB′=CB′::NB′=3:4:5,∵DB′=k,∴DQ=k,∵∠DQB′=∠MQA′,∠D=∠A′,∴△DQB′∽△A′QM,∴A′Q:A′M:QM=DQ:DB′:QB′=3:4:5,设AM=MA′=y,则MQ=y,∵DQ+QM+AM=3k,∴k+y+y=3k,∴y=k,∴===,解法二:连接BB′,过点M作MH⊥BC于点H.设AB=CD=6m,CB=9m,设BN=NB′=n,则n2=(3m)2+(9m﹣n)2,∴n=5m,CN=4m,由△BB′C∽△MNH,可得=2m,∴AM=BH=3m,∴===,故答案为:.18.(2022•湖北)如图1,在△ABC中,∠B=36°,动点P从点A出发,沿折线A→B→C匀速运动至点C停止.若点P的运动速度为1cm/s,设点P的运动时间为t(s),AP的长度为y(cm),y与t的函数图象如图2所示.当AP恰好平分∠BAC时t的值为.【答案】2+2【解答】解:如图,连接AP,由图2可得AB=BC=4cm,∵∠B=36°,AB=BC,∴∠BAC=∠C=72°,∵AP平分∠BAC,∴∠BAP=∠PAC=∠B=36°,∴AP=BP,∠APC=72°=∠C,∴AP=AC=BP,∵∠PAC=∠B,∠C=∠C,∴△APC∽△BAC,∴,∴AP2=AB•PC=4(4﹣AP),∴AP=2﹣2=BP,(负值舍去),∴t==2+2,故答案为:2+2.19.(2022•随州)如图1,在矩形ABCD中,AB=8,AD=6,E,F分别为AB,AD的中点,连接EF.如图2,将△AEF绕点A逆时针旋转角θ(0°<θ<90°),使EF⊥AD,连接BE并延长交DF于点H.则∠BHD的度数为,DH的长为.【答案】90°,.【解答】解:如图,设EF交AD于点J,AD交BH于点O,过点E作EK⊥AB于点K.∵∠EAF=∠BAD=90°,∴∠DAF=∠BAE,∴=,∴△DAF∽△BAE,∴∠ADF=∠ABE,∵∠DOH=∠AOB,∴∠DHO=∠BAO=90°,∴∠BHD=90°,∵AF=3,AE=4,∠EAF=90°,∴EF==5,∵EF⊥AD,∴•AE•AF=•EF•AJ,∴AJ=,∴EJ===,∵EJ∥AB,∴=,∴=,∴OJ=,∴OA=AJ+OJ=+=4,∴OB===4,OD=AD﹣AO=6﹣4=2,∵cos∠ODH=cos∠ABO,∴=,∴DH=.故答案为:90°,.20.(2022•娄底)如图,已知等腰△ABC的顶角∠BAC的大小为θ,点D为边BC上的动点(与B、C不重合),将AD绕点A沿顺时针方向旋转θ角度时点D落在D′处,连接BD′.给出下列结论:①△ACD≌△ABD′;②△ACB∽△ADD′;③当BD=CD时,△ADD′的面积取得最小值.其中正确的结论有(填结论对应的应号).【答案】①②③【解答】解:由题意可知AC=AB,AD=AD′,∠CAD=∠BAD′,∴△ACD≌△ABD′,故①正确;∵AC=AB,AD=AD′,∠BAC=∠D′AD=θ,∴=,∴△ACB∽△ADD′,故②正确;∵△ACB∽△ADD′,∴=()2,∵当AD⊥BC时,AD最小,△ADD′的面积取得最小值.而AB=AC,∴BD=CD,∴当BD=CD时,△ADD′的面积取得最小值,故③正确;故答案为:①②③.21.(2022•牡丹江)如图,在等腰直角三角形ABC和等腰直角三角形ADE中,∠BAC=∠DAE=90°,点D在BC边上,DE与AC相交于点F,AH⊥DE,垂足是G,交BC于点H.下列结论中:①AC=CD;②AD2=BC•AF;③若AD=3,DH=5,则BD=3;④AH2=DH•AC,正确的是.【答案】②③【解答】解:①∵△ABC是等腰直角三角形,∴∠B=∠ACB=45°,∵∠ADC=∠B+∠BAD,而∠BAD的度数不确定,∴∠ADC与∠CAD不一定相等,∴AC与CD不一定相等,故①错误;②∵∠BAC=∠DAE=90°,∴∠BAD=∠CAE,∵∠B=∠AED=45°,∴△AEF∽△ABD,∴=,∵AE=AD,AB=BC,∴AD2=AF•AB=AF•BC,∴AD2=AF•BC,故②正确;④∵∠DAH=∠B=45°,∠AHD=∠AHD,∴△ADH∽△BAH,∴=,∴AH2=DH•BH,而BH与AC不一定相等,故④不一定正确;③∵△ADE是等腰直角三角形,∴∠ADG=45°,∵AH⊥DE,∴∠AGD=90°,∵AD=3,∴AG=DG=,∵DH=5,∴GH===,∴AH=AG+GH=2,由④知:AH2=DH•BH,∴(2)2=5BH,∴BH=8,∴BD=BH﹣DH=8﹣5=3,故③正确;本题正确的结论有:②③故答案为:②③.22.(2022•丹东)如图,四边形ABCD是边长为6的菱形,∠ABC=60°,对角线AC与BD交于点O,点E,F分别是线段AB,AC上的动点(不与端点重合),且BE=AF,BF与CE交于点P,延长BF交边AD(或边CD)于点G,连接OP,OG,则下列结论:①△ABF≌△BCE;②当BE=2时,△BOG的面积与四边形OCDG面积之比为1:3;③当BE=4时,BE:CG=2:1;④线段OP的最小值为2﹣2.其中正确的是.(请填写序号)【答案】①②【解答】解:①∵四边形ABCD是菱形,∴AB=BC=AD=CD,∴∠ABC=60°,∴△ABC是等边三角形,∴∠BAC=∠ABC=60°,在△ABF和△BCE中,,∴△ABF≌△BCE(SAS),故①正确;②由①知:△ABC是等边三角形,∴AC=AB=6,∵AF=BE=2,∴CF=AC﹣AF=4,∵四边形ABCD是菱形,∴AD∥BC,OB=OD,OA=OC,∴△AGF∽△CBF,S△BOG=S△DOG,S△AOD=S△COD,∴,∴,∴AG=3,∴AG=,∴S△AOD=2S△DOG,∴S△COD=2S△DOG,∴S四边形OCDG=S△DOG+S△COD=3S△DOG=3S△BOG,故②正确;③如图1,∵四边形ABCD是菱形,∴AB∥CD,∴△CGF∽△ABF,∴,∴,∴CG=3,∴BE:CG=4:3,故③不正确;④如图2,由①得:△ABF≌△BCE,∴∠BCE=∠ABF,∴BCE+∠CBF=∠ABF+∠CBF=∠ABC=60°,∴∠BPC=120°,作等边三角形△BCH,作△BCH的外接圆I,则点P在⊙I上运动,点O、P、I共线时,OP最小,作HM⊥BC于M,∴HM==3,∴PI=IH=,∵∠ACB+∠ICB=60°+30°=90°,∴OI===,∴OP最小=OI﹣PI=﹣2,故④不正确,故答案为:①②.三.相似三角形的应用23.(2022•衢州)希腊数学家海伦给出了挖掘直线隧道的方法:如图,A,B是两侧山脚的入口,从B出发任作线段BC,过C作CD⊥BC,然后依次作垂线段DE,EF,FG,GH,直到接近A点,作AJ⊥GH于点J.每条线段可测量,长度如图所示.分别在BC,AJ上任选点M,N,作MQ⊥BC,NP⊥AJ,使得==k,此时点P,A,B,Q共线.挖隧道时始终能看见P,Q处的标志即可.(1)CD﹣EF﹣GJ=km.(2)k=.【答案】1.8;.【解答】解:(1)CD﹣EF﹣GJ=5.5﹣1﹣2.7=1.8(km);(2)连接AB,过点A作AZ⊥CB,交CB的延长线于点Z.由矩形性质得:AZ=CD﹣EF﹣GJ=1.8,BZ=DE+FG﹣CB﹣AJ=4.9+3.1﹣3﹣2.4=2.6,∵点P,A,B,Q共线,∴∠MBQ=∠ZBA,又∵∠BMQ=∠BZA=90°,∴△BMQ∽△BZA,∴=k===.故答案为:1.8;.24.(2022•温州)如图是某风车示意图,其相同的四个叶片均匀分布,水平地面上的点M在旋转中心O的正下方.某一时刻,太阳光线恰好垂直照射叶片OA,OB,此时各叶片影子在点M右侧成线段CD,测得MC=8.5m,CD =13m,垂直于地面的木棒EF与影子FG的比为2:3,则点O,M之间的距离等于米.转动时,叶片外端离地面的最大高度等于米.【答案】10,(10+)【解答】解:解法一:如图,过点O作OP∥BD,交MG于P,过P作PN ⊥BD于N,则OB=PN,∵AC∥BD,∴AC∥OP∥BD,∴=,∠EGF=∠OPM,∵OA=OB,∴CP=PD=CD=6.5,∴MP=CM+CP=8.5+6.5=15,tan∠EGF=tan∠OPM,∴OM=×15=10;∵DB∥EG,∴∠EGF=∠NDP,∴sin∠EGF=sin∠NDP,即=,∴OB=PN=,以点O为圆心,OA的长为半径作圆,当OB与OM共线时,叶片外端离地面的高度最大,其最大高度等于(10+)米.解法二:如图,设AC与OM交于点H,过点C作CN⊥BD于N,∵HC∥EG,∴∠HCM=∠EGF,∵∠CMH=∠EFG=90°,∴△HMC∽△EFG,∴==,即=,∴HM=,∵BD∥EG,∴∠BDC=∠EGF,∴tan∠BDC=tan∠EGF,设CN=2x,DN=3x,则CD=x,∴x=13,∴x=,∴AB=CN=2,∴OA=OB=AB=,在Rt△AHO中,∵∠AHO=∠CHM,∴sin∠AHO==,∴=,∴OH=,∴OM=OH+HM=+=10(米),以点O为圆心,OA的长为半径作圆,当OB与OM共线时,叶片外端离地面的高度最大,其最大高度等于(10+)米.故答案为:10,(10+).49。
初中数学《相似三角形》压轴30题含解析

相似三角形(压轴必刷30题专项训练)一.填空题(共9小题)1(2020秋•虹口区校级月考)一张等腰三角形纸片,底边长为15cm ,底边上的高长22.5cm .现沿底边依次从下往上裁剪宽度均为3cm 的矩形纸条,如图所示.已知剪得的纸条中有一张是正方形,则这张正方形纸条是第6张.【分析】设第x 张为正方形,如图,△ADE ∽△ABC ,则DE BC =AM AN,从而计算出x 的值即可.【解答】解:如图,设第x 张为正方形,则DE =3(cm ),AM =(22.5-3x )(cm ),∵△ADE ∽△ABC ,∴DE BC =AM AN ,即315=22.5-3x 22.5,解得x =6.故答案为:6.【点评】本题考查了相似三角形的判定和性质,等腰三角形的性质以及正方形的性质,注:相似三角形的对应边之比等于对应边上的高之比.2(2019秋•浦东新区校级月考)如图,在平行四边形ABCD 中,E 是边BC 上的点,AE 交BD 于点F ,如果BE BC=23,那么BF FD =23.【分析】由平行四边形的性质可证△BEF ∽△DAF ,再根据相似三角形的性质得BE :DA =BF :DF 即可解.【解答】解:ABCD 是平行四边形,∴BC ∥AD ,BC =AD∴△BEF ∽△DAF∴BE :DA =BF :DF∵BC =AD∴BF :DF =BE :BC =2:3.【点评】本题考查了平行四边形的性质及相似三角形的判定定理和性质.3(2017秋•虹口区校级月考)如图,直角三角形ABC 中,∠ACB =90°,AB =10,BC =6,在线段AB上取一点D ,作DF ⊥AB 交AC 于点F ,现将△ADF 沿DF 折叠,使点A 落在线段DB 上,对应点记为A 1;AD 的中点E 的对应点记为E 1,若△E 1FA 1∽△E 1BF ,则AD =165.【分析】利用勾股定理列式求出AC ,设AD =2x ,得到AE =DE =DE 1=A 1E 1=x ,然后求出BE 1,再利用相似三角形对应边成比例列式求出DF ,然后利用勾股定理列式求出E 1F ,然后根据相似三角形对应边成比例列式求解得到x 的值,从而可得AD 的值.【解答】解:∵∠ACB =90°,AB =10,BC =6,∴AC =AB 2-BC 2=102-62=8,设AD =2x ,∵点E 为AD 的中点,将△ADF 沿DF 折叠,点A 对应点记为A 1,点E 的对应点为E 1,∴AE =DE =DE 1=A 1E 1=x ,∵DF ⊥AB ,∠ACB =90°,∠A =∠A ,∴△ABC ∽△AFD ,∴AD AC =DF BC ,即2x 8=DF 6,解得DF =32x ,在Rt △DE 1F 中,E 1F =DF 2+DE 12=3x 22+x 2=13x 2,又∵BE 1=AB -AE 1=10-3x ,△E 1FA 1∽△E 1BF ,∴E 1F A 1E 1=BE 1E 1F ,∴E 1F 2=A 1E 1•BE 1,即(13x 2)2=x (10-3x ),解得x =85,∴AD 的长为2×85=165.故答案为:165.【点评】本题考查了相似三角形的性质,主要利用了翻折变换的性质,勾股定理,相似三角形对应边成比例,综合题,熟记性质并准确识图是解题的关键.4(2021秋•普陀区校级月考)如图,在△ABC 中,4AB =5AC ,AD 为△ABC 的角平分线,点E 在BC 的延长线上,EF ⊥AD 于点F ,点G 在AF 上,FG =FD ,连接EG 交AC 于点H .若点H 是AC 的中点,则AG FD的值为43.【分析】解题关键是作出辅助线,如解答图所示:第1步:利用角平分线的性质,得到BD =54CD ;第2步:延长AC ,构造一对全等三角形△ABD ≌△AMD ;第3步:过点M 作MN ∥AD ,构造平行四边形DMNG .由MD =BD =KD =54CD ,得到等腰△DMK ;然后利用角之间关系证明DM ∥GN ,从而推出四边形DMNG 为平行四边形;第4步:由MN ∥AD ,列出比例式,求出AG FD的值.【解答】解:已知AD 为角平分线,则点D 到AB 、AC 的距离相等,设为h .∵BD CD =S △ABD S △ACD =12AB ⋅h 12AC ⋅h =AB AC =54,∴BD =54CD .如图,延长AC ,在AC 的延长线上截取AM =AB ,则有AC =4CM .连接DM .在△ABD 与△AMD 中,AB =AM ∠BAD =∠MAD AD =AD ∴△ABD ≌△AMD (SAS ),∴MD =BD =54CD .过点M 作MN ∥AD ,交EG 于点N ,交DE 于点K .∵MN ∥AD ,∴CK CD =CM AC =14,∴CK =14CD ,∴KD =54CD .∴MD =KD ,即△DMK 为等腰三角形,∴∠DMK =∠DKM .由题意,易知△EDG 为等腰三角形,且∠1=∠2;∵MN ∥AD ,∴∠3=∠4=∠1=∠2,又∵∠DKM =∠3(对顶角)∴∠DMK =∠1,∴DM ∥GN ,∴四边形DMNG 为平行四边形,∴MN =DG =2FD .∵点H 为AC 中点,AC =4CM ,∴AH MH=23.∵MN ∥AD ,∴AG MN =AH MH ,即AG 2FD =23,∴AG FD =43.故答案为:43.方法二:如图,有已知易证△DFE ≌△GFE ,故∠5=∠B +∠1=∠4=∠2+∠3,又∠1=∠2,所以∠3=∠B ,则可证△AGH ∽△ADB设AB =5a ,则AC =4a ,AH =2a ,所以AG /AD =AH /AB =2/5,而AD =AG +GD ,故GD /AD =3/5,所以AG :GD =2:3,F 是GD 的中点,所以AG :FD =4:3.【点评】本题是几何综合题,难度较大,正确作出辅助线是解题关键.在解题过程中,需要综合利用各种几何知识,例如相似、全等、平行四边形、等腰三角形、角平分线性质等,对考生能力要求较高.5(2022秋•普陀区校级月考)如图,点A 1,A 2,A 3,A 4在射线OA 上,点B 1,B 2,B 3在射线OB 上,且A 1B 1∥A 2B 2∥A 3B 3,A 2B 1∥A 3B 2∥A 4B 3.若△A 2B 1B 2,△A 3B 2B 3的面积分别为1,4,则图中三个阴影三角形面积之和为10.5.【分析】已知△A 2B 1B 2,△A 3B 2B 3的面积分别为1,4,且两三角形相似,因此可得出A 2B 2:A 3B 3=1:2,由于△A 2B 2A 3与△B 2A 3B 3是等高不等底的三角形,所以面积之比即为底边之比,因此这两个三角形的面积比为1:2,根据△A 3B 2B 3的面积为4,可求出△A 2B 2A 3的面积,同理可求出△A 3B 3A 4和△A 1B 1A 2的面积.即可求出阴影部分的面积.【解答】解:△A 2B 1B 2,△A 3B 2B 3的面积分别为1,4,又∵A 2B 2∥A 3B 3,A 2B 1∥A 3B 2,∴∠OB 2A 2=∠OB 3A 3,∠A 2B 1B 2=∠A 3B 2B 3,∴△B 1B 2A 2∽△B 2B 3A 3,∴B 1B 2B 2B 3=12=A 2B 2A 3B 3,∴A 2A 3A 3A 4=12.∵S △A 2B 2A 3S △B 2A 3B3=12,△A 3B 2B 3的面积是4,∴△A 2B 2A 3的面积为=12×S △A 2B 2B 3=12×4=2(等高的三角形的面积的比等于底边的比).同理可得:△A 3B 3A 4的面积=2×S △A 3B 2B 3=2×4=8;△A 1B 1A 2的面积=12S △A 2B 1B 2=12×1=0.5.∴三个阴影面积之和=0.5+2+8=10.5.故答案为:10.5.【点评】本题的关键是利用平行线证明三角形相似,再根据已给的面积,求出相似比,从而求阴影部分的面积.6(2017秋•徐汇区校级月考)设△ABC 的面积为1,如图①,将边BC 、AC 分别2等分,BE 1、AD 1相交于点O ,△AOB 的面积记为S 1;如图②将边BC 、AC 分别3等分,BE 1、AD 1相交于点O ,△AOB 的面积记为S 2;⋯,依此类推,则S n 可表示为 12n +1 .(用含n 的代数式表示,其中n 为正整数)【分析】连接D 1E 1,设AD 1、BE 1交于点M ,先求出S △ABE 1=1n +1,再根据AB D 1E 1=BM ME 1=n +1n 得出S △ABM :S △ABE 1=(n +1):(2n +1),最后根据S △ABM :1n +1=(n +1):(2n +1),即可求出S n .【解答】解:如图,连接D 1E 1,设AD 1、BE 1交于点M ,∵AE1:AC =1:(n +1),∴S △ABE 1:S △ABC =1:(n +1),∴S △ABE 1=1n +1,∵AB D 1E 1=BM ME 1=n +1n ,∴BM BE 1=n +12n +1,∴S △ABM :S △ABE 1=(n +1):(2n +1),∴S △ABM :1n +1=(n +1):(2n +1),∴S n =12n +1.故答案为:12n +1.【点评】此题考查了相似三角形的判定与性质,用到的知识点是相似三角形的判定与性质、平行线分线段成比例定理、三角形的面积,关键是根据题意作出辅助线,得出相似三角形.7(2018秋•南岗区校级月考)已知菱形ABCD 的边长是6,点E 在直线AD 上,DE =3,连接BE 与对角线AC 相交于点M ,则MC AM的值是 2或23 .【分析】由菱形的性质易证两三角形相似,但是由于点E 的位置未定,需分类讨论.【解答】解:分两种情况:(1)点E 在线段AD 上时,△AEM ∽△CBM ,∴MC AM =BC AE=2;(2)点E在线段AD的延长线上时,△AME∽△CMB,∴MCAM =BCAE=23.【点评】本题考查了相似三角形的性质以及分类讨论的数学思想;其中由相似三角形的性质得出比例式是解题关键.注意:求相似比不仅要认准对应边,还需注意两个三角形的先后次序.8(2020秋•虹口区校级月考)如图,在△ABC中,∠ACB的内、外角平分线分别交BA及其延长线于点D、E,BC=2.5AC,则ABAD+ABAE=5.【分析】根据CD平分∠ACB,可得ABDA=BCAC,根据CE平分∠ACB的外角,可得DEAE=BCAC,进而可得结果.【解答】解:∵CD平分∠ACB,∴AB DA =BC AC,∴BD+DADA =BC+ACAC,∴AB DA =BC+ACAC,①∵CE平分∠ACB的外角,∴DE AE =BC AC,∴BE-AEAE =BC-ACAC,∴AB AE =BC-ACAC,②①+②得,AB AD +ABAE=BC+ACAC+BC-ACAC=2BCAC=2×2.5=5.故答案为:5.【点评】主要考查了相似三角形的判定及其性质的应用问题;解题的关键是灵活运用相似三角形的性质来分析、判断、推理或解答.9(2022秋•黄浦区校级月考)如图,在等腰△ABC中,AB=AC,点P在BA的延长线上,PA=1 4AB,点D在BC边上,PD=PC,则CDBC的值是 34 .【分析】过点P 作PE ∥AC 交DC 延长线于点E ,根据等腰三角形判定与性质,平行线的性质可证PB =PE ,再证△PCE ≌△PDB ,可得BD =CE ,再利用平行线分线段成比例的PA AB=CE BC ,结合线段的等量关系以及比例的性质即可得出结论.【解答】解:如图,过点P 作PE ∥AC 交DC 延长线于点E ,∵AB =AC ,∴∠B =∠ACB ,∵AC ∥PE ,∴∠ACB =∠E ,∴∠B =∠E ,∴PB =PE ,∵PC =PD ,∴∠PDC =∠PCD ,∴∠BPD =∠EPC ,∴在△PCE 和△PDB 中,PC =PD ∠BPD =∠EPC PB =PE,∴△PCE ≌△PDB (SAS ),∴BD =CE ,∵AC ∥PE ,∴PA AB =CE BC ,∵PA =14AB ,∴CE BC =14,∴BD BC =14,∴CD BC =34.故答案为:34.【点评】本题考查了等腰三角形的判定与性质,平行线分线段成比例,以及全等三角形的判定,解决问题的关键是正确作出辅助线,列出比例式.二.解答题(共21小题)10(2017秋•虹口区校级月考)在△ABC 中,∠CAB =90°,AD ⊥BC 于点D ,点E 为AB 的中点,EC 与AD交于点G ,点F 在BC 上.(1)如图1,AC :AB =1:2,EF ⊥CB ,求证:EF =CD .(2)如图2,AC :AB =1:,EF ⊥CE ,求EF :EG 的值.【分析】(1)根据同角的余角相等得出∠CAD =∠B ,根据AC :AB =1:2及点E 为AB 的中点,得出AC =BE ,再利用AAS 证明△ACD ≌△BEF ,即可得出EF =CD ;(2)作EH ⊥AD 于H ,EQ ⊥BC 于Q ,先证明四边形EQDH 是矩形,得出∠QEH =90°,则∠FEQ =∠GEH ,再由两角对应相等的两三角形相似证明△EFQ ∽△EGH ,得出EF :EG =EQ :EH ,然后在△BEQ 中,根据正弦函数的定义得出EQ =12BE ,在△AEH 中,根据余弦函数的定义得出EH =32AE ,又BE =AE ,进而求出EF :EG 的值.【解答】(1)证明:如图1,在△ABC 中,∵∠CAB =90°,AD ⊥BC 于点D ,∴∠CAD =∠B =90°-∠ACB .∵AC :AB =1:2,∴AB =2AC ,∵点E 为AB 的中点,∴AB =2BE ,∴AC =BE .在△ACD 与△BEF 中,∠CAD =∠B ∠ADC =∠BFE =90°AC =BE,∴△ACD ≌△BEF ,∴CD =EF ,即EF =CD ;(2)解:如图2,作EH ⊥AD 于H ,EQ ⊥BC 于Q ,∵EH ⊥AD ,EQ ⊥BC ,AD ⊥BC ,∴四边形EQDH 是矩形,∴∠QEH =90°,∴∠FEQ =∠GEH =90°-∠QEG ,又∵∠EQF =∠EHG =90°,∴△EFQ ∽△EGH ,∴EF :EG =EQ :EH .∵AC :AB =1:3,∠CAB =90°,∴∠B =30°.在△BEQ 中,∵∠BQE =90°,∴sin B =EQ BE =12,∴EQ =12BE .在△AEH中,∵∠AHE=90°,∠AEH=∠B=30°,∴cos∠AEH=EHAE =32,∴EH=32AE.∵点E为AB的中点,∴BE=AE,∴EF:EG=EQ:EH=12BE:32AE=1:3=3:3=33.【点评】本题考查了相似三角形的判定和性质、全等三角形的判定和性质、矩形的判定和性质,解直角三角形,综合性较强,有一定难度.解题的关键是作辅助线,构造相似三角形,并且证明四边形EQDH是矩形.11(2021秋•杨浦区校级月考)如图,已知在菱形ABCD,点E是AB的中点,AF⊥BC于点F,连接EF、ED、DF,DE交AF于点G,且DE⊥EF.(1)求证:AE2=EG•ED;(2)求证:BC2=2DF•BF.【分析】(1)根据直角三角形的性质得到AE=FE,根据菱形的性质得到AD∥BC,求得∠DAG=∠AFB =90°,然后证明△AEG∽△DEA,即可得到结论;(2)由AE=EF,AE2=EG•ED,得到FE2=EG•ED,推出△FEG∽△DEF,根据相似三角形的性质得到∠EFG=∠EDF,根据相似三角形的判定和性质即可得到结论.【解答】证明:(1)∵AF⊥BC于点F,∴∠AFB=90°,∵点E是AB的中点,∴AE=FE,∴∠EAF=∠AFE,∵四边形ABCD是菱形,∴AD∥BC,∴∠DAG=∠AFB=90°,∵DE⊥EF,∴∠FEG=90°,∴∠DAG=∠FEG,∵∠AGD=∠FGE,∴∠EFG=∠ADG,∴∠EAG=∠ADG,∵∠AEG=∠DEA,∴△AEG∽△DEA,∴AE DE =EG AE,∴AE2=EG•ED;(2)∵AE=EF,AE2=EG•ED,∴FE2=EG•ED,∴EF DE =EGEF,∵∠FEG=∠DEF,∴△FEG∽△DEF,∴∠EFG=∠EDF,∴∠BAF=∠EDF,∵∠DEF=∠AFB=90°,∴△ABF∽△DFE,∴AB DF =BF EF,∵四边形ACBD是菱形,∴AB=BC,∵∠AFB=90°,∵点E是AB的中点,∴FE=12AB=12BC,∴BC DF =BF12BC,∴BC2=2DF•BF.【点评】本题考查了相似三角形的判定和性质,菱形的性质,直角三角形的性质,正确的识别图形是解题的关键.12(2021秋•杨浦区校级月考)如图,已知在平行四边形ABCD中,AE:ED=1:2,点F为DC的中点,连接BE、AF,BE与AF交于点H.(1)求EH:BH的值;(2)若△AEH的面积为1,求平行四边形ABCD的面积.【分析】(1)延长AF,BC交于点G,证明△ADF≌△GCF(AAS),可得AD=CG=BC,所以BG=2BC,根据AE:ED=1:2,可得AE:AD=1:3,AE:BG=1:6,,证明△AEH∽△GBH,即可解决问题;(2)在△AEH中,设AE=x,AE边上的高为h,△BGH中,BG边上的高为h′,可得平行四边形ABCD的高为h+h′,BC=3x,根据△AEH的面积为1,可得x•h=2,所以h′=6h,进而可以求平行四边形ABCD 的面积.【解答】解:(1)如图,延长AF,BC交于点G,∵四边形ABCD是平行四边形,∴AD ∥BC ,AD =BC ,∴∠D =∠DCG ,∠DAF =∠G ,∵点F 为DC 的中点,∴DF =CF ,在△ADF 和△GCF 中,∠D =∠FCG ∠DAF =∠G DF =CF,∴△ADF ≌△GCF (AAS ),∴AD =CG ,∴AD =CG =BC ,∴BG =2BC ,∵AE :ED =1:2,∴AE :AD =1:3,∴AE :BG =1:6,∵AD ∥BC ,∴△AEH ∽△GBH ,∴EH :BH =AE :BG =1:6;(2)在△AEH 中,设AE =x ,AE 边上的高为h ,△BGH 中,BG 边上的高为h ′,∴平行四边形ABCD 的高为h +h ′,BC =3x ,∵△AEH 的面积为1,∴12x •h =1,∴x •h =2∵△AEH ∽△GBH ,∴h :h ′=1:6,∴h ′=6h ,∴h +h ′=7h ,∴平行四边形ABCD 的面积=BC •(h +h ′)=3x •7h =21xh =42.【点评】本题考查了相似三角形的判定和性质,平行四边形的性质,平行线分线段成比例等知识,添加恰当辅助线构造相似三角形是解题的关键.13(2021春•徐汇区校级月考)如图,在菱形ABCD 中,点E 在对角线AC 上,点F 在BC 的延长线上,EF =EB ,EF 与CD 相交于点G ;(1)求证:EG •GF=CG •GD ;(2)联结DF ,如果EF ⊥CD ,那么∠FDC 与∠ADC 之间有怎样的数量关系?证明你的结论.【分析】(1)先证明△BCE ≌△DCE ,得∠EDC =∠EBC ;利用此条件再证明∠DGE ∽△FGC ,即可得到EG •GF =CG •GD.(2)利用第(1)题的结论,可证明△DGE ∽△FGC ,再利用三角形内角外角关系,即可得到∠ADC 与∠FDC 的关系.【解答】解:(1)证明:∵点E 在菱形ABCD 的对角线AC 上,∴∠ECB =∠ECD ,∵BC =CD ,CE =CE ,∴△BCE ≌△DCE ,∴∠EDC =∠EBC ,∵EB =EF ,∴∠EBC =∠EFC ;∴∠EDC =∠EFC ;∵∠DGE =∠FGC ,∴△DGE ∽△FGC ;∴EGCG =GD FG∴EG •GF =CG •GD ;(2)∠ADC =2∠FDC .证明:∵EG CG =GD FG ,∴EG DG =CG FG,又∵∠DGF =∠EGC ,∴△CGE ∽△FGD ,∵EF ⊥CD ,DA =DC ,∴∠DAC =∠DCA =∠DFG =90°-∠FDC ,∴∠ADC =180°-2∠DAC =180°-2(90°-∠FDC )=2∠FDC .【点评】本题主要考查了全等三角形的判定及性质、相似三角形的判定及性质、菱形的性质等知识点的综合应用,解题时注意:相似三角形的对应角相等,对应边成比例.在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用.14(2021秋•宝山区校级月考)如图,四边形DEFG 是△ABC 的内接正方形,AB =BC =6cm ,∠B =45°,则正方形DEFG 的面积为多少?【分析】过A 作AH ⊥BC 于H ,交GF 于M ,于是得到△ABH 是等腰直角三角形,求得AH =BH =2222AB =32cm ,由△AGF ∽△ABC ,得到GF BC =AM AH,求得GF =(62-6)cm ,即可得到结论.【解答】解:过A 作AH ⊥BC 于H ,交GF 于M ,∵∠B =45°,∴AH =BH =22AB =32cm ,∵GF ∥BC ,∴△AGF ∽△ABC ,∴GF BC =AM AH,即GF 6=32-GF 32,∴GF =(62-6)cm ,∴正方形DEFG 的面积=GF 2=(62-6)2=(108-722)cm .【点评】本题考查了相似三角形的判定与性质,正方形的四条边都相等的性质,利用相似的性质:对应边的比值相等求出正方形的边长是解答本题的关键.15(2021秋•松江区月考)如图,在平行四边形ABCD 中,点E 为边BC 上一点,联结AE 并延长AE 交DC 的延长线于点M ,交BD 于点G ,过点G 作GF ∥BC 交DC 于点F .求证:DF FC =DM CD.【分析】由GF ∥BC ,根据平行线分线段成比例定理,可得DF FC,又由四边形ABCD 是平行四边形,可得AB =CD ,AB ∥CD ,继而可证得DM AB =DG BG ,则可证得结论.【解答】证明:∵GF ∥BC ,∴DF FC =DG BG,∵四边形ABCD 是平行四边形,∴AB =CD ,AB ∥CD ,∴DM AB =DG BG ,∴DF FC =DM CD.【点评】此题考查了平行分线段成比例定理以及平行四边形的性质,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.16(2021秋•松江区月考)如图,在Rt △ABC 中,∠ACB =90°,CD ⊥AB 于D ,E 是AC 的中点,DE 的延长线与BC 的延长线交于点F .(1)求证:FD FC =BD DC ;(2)若BC FC =54,求BD DC的值.【分析】(1)根据直角三角形斜边上中线性质求出DE =EC ,推出∠EDC =∠ECD ,求出∠FDC =∠B ,根据∠F =∠F 证△FBD ∽△FDC ,即可;(2)根据已知和三角形面积公式得出S △BDC S △FDC =54,S △BDF S △FDC =94,根据相似三角形面积比等于相似比的平方得出S △BDFS △FDC =BD DC 2=94,即可求出BD DC.【解答】(1)证明:∵CD ⊥AB ,∴∠ADC =90°,∵E 是AC 的中点,∴DE =EC ,∴∠EDC =∠ECD ,∵∠ACB =90°,∠BDC =90°∴∠ECD +∠DCB =90°,∠DCB +∠B =90°,∴∠ECD =∠B ,∴∠FDC =∠B ,∵∠F =∠F ,∴△FBD ∽△FDC ,∴FD FC =BD DC(2)解:∵BC FC =54,∴S △BDCS △FDC =54,∴S △BDFS △FDC =94,∵△FBD ∽△FDC ,∴S △BDF S △FDC =BD DC2=94,∴BD DC=32.【点评】本题考查了相似三角形的性质和判定,三角形的面积,注意:相似数据线的面积比等于相似比的平方,题目比较好,有一定的难度.17(2021春•黄浦区校级月考)如图,四边形ABCD 是矩形,E 是对角线AC 上的一点,EB =ED 且∠ABE =∠ADE .(1)求证:四边形ABCD 是正方形;(2)延长DE 交BC 于点F ,交AB 的延长线于点G ,求证:EF •AG =BC •BE .【分析】(1)根据邻边相等的矩形是正方形即可证明;(2)由AD ∥BC ,推出EF DE =EC EA ,同理DC AG =EC EA,由DE =BE ,四边形ABCD 是正方形,推出BC =DC,可得EFBE =BCAG解决问题;【解答】(1)证明:连接BD.∵EB=ED,∴∠EBD=∠EDB,∵∠ABE=∠ADE,∴∠ABD=∠ADB,∴AB=AD,∵四边形ABCD是矩形,∴四边形ABCD是正方形.(2)证明:∵四边形ABCD是矩形∴AD∥BC,∴EF DE =EC EA,同理DCAG=ECEA,∵DE=BE,四边形ABCD是正方形,∴BC=DC,∴EF BE =BC AG,∴EF•AG=BC•BE.【点评】本题考查相似三角形的判定和性质、矩形的性质、正方形的性质和判定等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.18(2021秋•浦东新区校级月考)如图,在△ABC中,DE∥BC,EF∥CD,求证:AD2=AF•AB.【分析】由DE∥BC,EF∥CD,可得△ADE∽△ABC,△AFE∽△ADC,然后由相似三角形的对应边成比例,证得结论.【解答】证明:∵DE∥BC,EF∥CD,∴△ADE∽△ABC,△AFE∽△ADC,∴AD:AB=AE:AC,AF:AD=AE:AC,∴AD:AB=AF:AD,∴AD2=AF•AB.【点评】此题考查了相似三角形的判定与性质.注意掌握相似三角形的对应边成比例.19(2020秋•浦东新区月考)在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F.(1)求证:△ABC∽△FCD;(2)若DE=3,BC=8,求△FCD的面积.【分析】(1)由DE⊥BC,D是BC的中点,根据线段垂直平分线的性质,可得BE=CE,又由AD=AC,易得∠B=∠DCF,∠FDC=∠ACB,即可证得△ABC∽△FCD;(2)首先过A作AG⊥CD,垂足为G,易得△BDE∽△BGA,可求得AG的长,继而求得△ABC的面积,然后由相似三角形面积比等于相似比的平方,求得△FCD的面积.【解答】(1)证明:∵D是BC的中点,DE⊥BC,∴BE=CE,∴∠B=∠DCF,∵AD=AC,∴∠FDC=∠ACB,∴△ABC∽△FCD;(2)解:过A作AG⊥CD,垂足为G.∵AD=AC,∴DG=CG,∴BD:BG=2:3,∵ED⊥BC,∴ED∥AG,∴△BDE∽△BGA,∴ED:AG=BD:BG=2:3,∵DE=3,∴AG=92,∵△ABC∽△FCD,BC=2CD,∴S△FCDS△ABC=(CDBC)2=14.∵S△ABC=12×BC×AG=12×8×92=18,∴S△FCD=14S△ABC=92.【点评】此题考查了相似三角形的判定与性质以及等腰三角形的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.20(2021春•静安区校级月考)已知:如图,在菱形ABCD中,点E在边BC上,点F在BA的延长线上,BE=AF,CF∥AE,CF与边AD相交于点G.求证:(1)FD=CG;(2)CG2=FG•FC.【分析】(1)根据菱形的性质得到∠FAD =∠B ,根据全等三角形的性质得到FD =EA ,于是得到结论;(2)根据菱形的性质得到∠DCF =∠BFC ,根据平行线的性质得到∠BAE =∠BFC ,根据全等三角形的性质得到∠BAE =∠FDA ,等量代换得到∠DCF =∠FDA ,根据相似三角形的判定和性质即可得到结论.【解答】证明:(1)∵在菱形ABCD 中,AD ∥BC ,∴∠FAD =∠B ,在△ADF 与△BAE 中,AF =BE ∠FAD =∠B AD =BA,∴△ADF ≌△BAE ,∴FD =EA ,∵CF ∥AE ,AG ∥CE ,∴EA =CG ,∴FD =CG ;(2)∵在菱形ABCD 中,CD ∥AB ,∴∠DCF =∠BFC ,∵CF ∥AE ,∴∠BAE =∠BFC ,∴∠DCF =∠BAE ,∵△ADF ≌△BAE ,∴∠BAE =∠FDA ,∴∠DCF =∠FDA ,又∵∠DFG =∠CFD ,∴△FDG ∽△FCD ,∴FD FC=FG FD ,FD 2=FG •FC ,∵FD =CG ,∴CG 2=FG •FC .【点评】本题考查了相似三角形的判定和性质,全等三角形的判定和性质,菱形的性质,熟练掌握相似三角形的性质是解题的关键.21(2021秋•浦东新区校级月考)如图,梯形ABCD 中,AD ∥BC ,BC =2AD ,点E 为边DC 的中点,BE 交AC 于点F .求:(1)AF :FC 的值;(2)EF :BF 的值.【分析】(1)延长BE 交直线AD 于H ,如图,先由AD ∥BC 得到△DEH ∽△CEB ,则有DH BC =DE CE,易得DH =BC ,加上BC =2AD ,所以AH =3AD ,然后证明△AHF ∽△CFB ,再利用相似比可计算出AF :FC 的值;(2)由△DEH ∽△CEB 得到EH :BE =DE :CE =1:1,则BE =EH =12BH ,由△AHF ∽△CFB 得到FH :BF =AF :FC =3:2;于是可设BF =2a ,则FH =3a ,BH =BF +FH =5a ,EH =52a ,接着可计算出EF =FH -EH =12a ,然后计算EF :BF 的值.【解答】解:(1)延长BE 交直线AD 于H ,如图,∵AD ∥BC ,∴△DEH ∽△CEB ,∴DH BC =DE CE,∵点E 为边DC 的中点,∴DE =CE ,∴DH =BC ,而BC =2AD ,∴AH =3AD ,∵AH ∥BC ,∴△AHF ∽△CFB ,∴AF :FC =AH :BC =3:2;(2)∵△DEH ∽△CEB ,∴EH :BE =DE :CE =1:1,∴BE =EH =12BH ,∵△AHF ∽△CFB ,∴FH :BF =AF :FC =3:2;设BF =2a ,则FH =3a ,BH =BF +FH =5a ,∴EH =52a ,∴EF =FH -EH =3a -52a =12a ,∴EF :BF =12a :2a =1:4.【点评】本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;在运用相似三角形的性质时,主要通过相似比得到线段之间的关系.22(2021秋•浦东新区校级月考)已知:如图,在△ABC 中,BD 是∠ABC 的平分线,过点D 作DE ∥CB ,交AB 于点E ,AD DC =13,DE =6.(1)求AB 的长;(2)求S △ADE S △BCD.【分析】(1)由∠ABD =∠CBD ,DE ∥BC 可推得∠EDB =∠CBD ,进而推出∠ABD =∠EDB ,由此可得BE =DE =6,由DE ∥BC 可得AE EB =AD DC=13,进而证得AE =2,于是可得结论;(2)△ADE 看成以DE 为底,高为h 1,△BCD 看成以BC 为底,高为h 2,由平行线分线段成比例定理和相似三角形的性质可得h 1h 2=AD DE =13,DE BC =14,进而证得结论.【解答】解:(1)BD 平∠ABC ,∴∠ABD =∠CBD ,∵DE ∥BC ,∴∠EDB =∠CBD ,∴∠ABD =∠EDB ,∴BE =DE =6,∵DE ∥BC ,∴AE EB =AD DC =13,∴AE 6=13,∴AE =2,∴AB =AE +BE =8;(2)△ADE 看成以DE 为底,高为h 1,△BCD 看成以BC 为底,高为h 2,∵DE ∥CB ,∴△AED ∽△ABC ,∴h 1h 2=AD DE =13,DE BC =14,∴S △ADE S △BCD =12DE ⋅h 112BC ⋅h 2=112.【点评】本题主要考查了等腰三角形的性质,平行线分线段成比例定理和相似三角形的性质,三角形的面积等知识,熟练应用平行线分线段成比例定理和相似三角形的性质是解决问题的关键.23(2022春•长宁区校级月考)已知:如图,在平行四边形ABCD 中,AC 、DB 交于点E ,点F 在BC 的延长线上,联结EF 、DF ,且∠DEF =∠ADC .(1)求证:EFBF =AB DB;(2)如果BD 2=2AD •DF ,求证:平行四边形ABCD 是矩形.【分析】(1)由已知条件和平行四边形的性质易证△ADB ∽△EBF ,再由相似三角形的性质:对应边的比值相等即可证明:EF BF =AB DB;(2)由(1)可得BD 2=2AD •BF ,又因为BD 2=2AD •DF ,所以可证明BF =DF ,再由等腰三角形的性质可得∠DEF =90°,所以∠ADC =∠DEF =90°,进而可证明平行四边形ABCD 是矩形.【解答】解:(1)证明:∵平行四边形ABCD ,∴AD ∥BC ,AB ∥DC∴∠BAD +∠ADC =180°,又∵∠BEF +∠DEF =180°,∴∠BAD +∠ADC =∠BEF +∠DEF ,∵∠DEF =∠ADC ,∴∠BAD =∠BEF ,∵AD ∥BC ,∴∠EBF =∠ADB ,∴△ADB ∽△EBF ,∴EF BF =AB DB;(2)∵△ADB ∽△EBF ,∴AD BD =BE BF,在平行四边形ABCD 中,BE =ED =12BD ,∴AD •BF =BD •BE =12BD 2,∴BD 2=2AD •BF ,又∵BD 2=2AD •DF ,∴BF =DF ,∴△DBF 是等腰三角形,∵BE =DE ,∴FE ⊥BD ,即∠DEF =90°,∴∠ADC =∠DEF =90°,∴平行四边形ABCD 是矩形.【点评】本题考查了平行四边形的性质、相似三角形的判断和性质以及矩形的判断,其中(2)小题证明△DBF 是等腰三角形是解题的关键.24(2021秋•宝山区校级月考)已知,如图,在梯形ABCD中,AD∥BC,BC=6,点P是射线AD上的点,BP交AC于点E,∠CBP的角平分线交AC于点F,且CF=13AC时.求AP+BP的值.【分析】延长BF交射线AP于M,根据AD∥BC,根据两直线平行,内错角相等可得∠M=∠CBM,再根据角平分线的定义可得∠PBM=∠CBM,从而得到∠M=∠PBM,根据等角对等边可得BP=PM,求出AP+BP=AM,再根据AC=13CF求出AE=2CF,然后根据△MAF和△BCF相似,利用相似三角形对应边成比例列式求解即可.【解答】解:如图,延长BF交射线AP于M,∵AD∥BC,∴∠M=∠CBM,∵BF是∠CBP的平分线,∴∠PBM=∠CBM,∴∠M=∠PBM,∴BP=PM,∴AP+BP=AP+PM=AM,∵CF=13AC,则AF=2CF,由AD∥BC得,△MAF∽△BCF,∴AMBC =AFCF=2,∴AM=2BC=2×6=12,即AP+BP=12.【点评】本题考查了相似三角形的判定与性质,角平分线的定义,平行线的性质,延长BF构造出相似三角形,求出AP+BP=AM并得到相似三角形是解题的关键,也是本题的难点.25(2020秋•虹口区校级月考)已知:如图,已知△ABC与△ADE均为等腰三角形,BA=BC,DA= DE.如果点D在BC边上,且∠EDC=∠BAD.点O为AC与DE的交点.(1)求证:△ABC∽△ADE;(2)求证:DA•OC=OD•CE.【分析】(1)根据三角形的外角的性质和角的和差得到∠B=∠ADE,由于BABC=DADE=1,根据得到结论;(2)根据相似三角形的性质得到∠BAC=∠DAE,于是得到∠BAD=∠CAE=∠CDE,证得△COD∽△EOA,根据相似三角形的性质得到OCOE =ODOA,由∠AOD=∠COE,推出△AOD∽△COE,根据相似三角形的性质即可得到结论.【解答】证明:(1)∵∠ADC =∠ABC +∠BAD =∠ADE +∠EDC ,∴∠B =∠ADE ,∵BA BC=DA DE =1,∴△ABC ∽△ADE ;(2)∵△ABC ∽△ADE ,∴∠BAC =∠DAE ,∴∠BAD =∠CAE =∠CDE ,∵∠COD =∠EOA ,∴△COD ∽△EOA ,∴OC OE =OD OA,∵∠AOD =∠COE ,∴△AOD ∽△EOC ,∴DA :CE =OD :OC ,即DA •OC =OD •CE .【点评】本题考查了相似三角形的判定和性质,三角形的外角的性质,熟练掌握相似三角形的判定定理是解题的关键.26(2021秋•金山区校级月考)已知:如图,在梯形ABCD 中,AD ∥BC ,点E 在边AD 上,CE 与BD 相交于点F ,AD =4,AB =5,BC =BD =6,DE =3.(1)求证:△DFE ∽△DAB ;(2)求线段CF 的长.【分析】(1)AD ∥BC ,DE =3,BC =6,DF FB =DE BC=36=12,DF DA =DE DB .又∠EDF =∠BDA ,即可证明△DFE ∽△DAB .(2)由△DFE ∽△DAB ,利用对应边成比例,将已知数值代入即可求得答案.【解答】证明:(1)∵AD ∥BC ,DE =3,BC =6,∴DF FB =DE BC =36=12,∴DF BD =12,∵BD =6,∴DF =2.∵DA =4,∴DF DA =24=12,DE DB =36=12.∴DF DA=DE DB .又∵∠EDF =∠BDA ,∴△DFE ∽△DAB .(2)∵△DFE ∽△DAB ,∴EF AB =DE DB .∵AB =5,∴EF 5=36,∴EF =52=2.5.∵DE ∥BC ,∴CFEF =BC DE .∴CF 2.5=63,∴CF =5.(或利用△CFB ≌△BAD ).【点评】此题考查学生对梯形和相似三角形的判定与性质的理解和掌握,第(2)问也可利用△CFB ≌△BAD 求得线段CF 的长,不管学生用了哪种方法,只要是正确的,就要积极地给予表扬,以此激发学生的学习兴趣.27(2020秋•宝山区月考)如图,正方形DEFG 的边EF 在△ABC 的边BC 上,顶点D 、G 分别在边AB 、AC 上,已知△ABC 的边BC =15,高AH =10,求正方形DEFG 的边长和面积.【分析】高AH 交DG 于M ,如图,设正方形DEFG 的边长为x ,则DE =MH =x ,所以AM =10-x ,再证明△ADG ∽△ABC ,则利用相似比得到x 15=10-x 10,然后根据比例的性质求出x ,再计算x 2的值即可.【解答】解:高AH 交DG 于M ,如图,设正方形DEFG 的边长为x ,则DE =MH =x ,∴AM =AH -MH =10-x ,∵DG ∥BC ,∴△ADG ∽△ABC ,∴DG BC =AM AH,即x 15=10-x 10,∴x =6,∴x 2=36.答:正方形DEFG 的边长和面积分别为6,36.【点评】本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;也考查了正方形的性质.28(2021秋•闵行区校级月考)如图,在Rt △ABC 中,∠ACB =90°,CD ⊥AB ,M 是CD 上的点,DH ⊥BM 于H ,DH 的延长线交AC 的延长线于E .求证:(1)△AED ∽△CBM ;(2)AE •CM =AC •CD .【分析】(1)由于△ABC 是直角三角形,易得∠A +∠ABC =90°,而CD ⊥AB ,易得∠MCB +∠ABC =90°,利用同角的余角相等可得∠A =∠MCB ,同理可证∠1=∠2,而∠ADE =90°+∠1,∠CMB =90°+∠2,易证∠ADE =∠CMB ,从而易证△AED ∽△CBM ;(2)由(1)知△AED ∽△CBM ,那么AE :AD =CB :CM ,于是AE •CM =AD •CB ,再根据△ABC 是直角三角形,CD 是AB 上的高,易知△ACD ∽△CBD ,易得AC •CD =AD •CB ,等量代换可证AE •CM =AC •CD .【解答】证明:(1)∵△ABC 是直角三角形,∴∠A +∠ABC =90°,∵CD ⊥AB ,∴∠CDB =90°,即∠MCB +∠ABC =90°,∴∠A =∠MCB ,∵CD ⊥AB ,∴∠2+∠DMB =90°,∵DH ⊥BM ,∴∠1+∠DMB =90°,∴∠1=∠2,又∵∠ADE =90°+∠1,∠CMB =90°+∠2,∴∠ADE =∠CMB ,∴△AED ∽△CBM ;(2)∵△AED ∽△CBM ,∴AE BC =AD CM,∴AE •CM =AD •CB ,∵△ABC 是直角三角形,CD 是AB 上的高,∴△ACD ∽△CBD ,∴AC :AD =CB :CD ,∴AC •CD =AD •CB ,∴AE •CM =AC •CD .【点评】本题考查了相似三角形的判定和性质、直角三角形斜边上的高所分成的两个三角形与这个直角三角形相似.解题的关键是证明∠A =∠MCB 以及∠ADE =∠CMB .29(2022秋•徐汇区校级月考)如图,在直角坐标平面内有点A (6,0),B (0,8),C (-4,0),点M 、N 分别为线段AC 和射线AB 上的动点,点M 以2个单位长度/秒的速度自C 向A 方向做匀速运动,点N 以5个单位长度/秒的速度自A 向B 方向做匀速运动,MN 交OB 于点P .(1)求证:MN :NP 为定值;(2)若△BNP 与△MNA 相似,求CM 的长;(3)若△BNP 是等腰三角形,求CM 的长.【分析】(1)过点N 作NH ⊥x 轴于点H ,然后分两种情况进行讨论,综合两种情况,求得MN :NP 为定值53.(2)当△BNP 与△MNA 相似时,当点M 在CO 上时,只可能是∠MNB =∠MNA =90°,所以△BNP ∽△MNA ∽△BOA ,所以AM AN =AB AO ,所以10-2k 5k =106,k =3031,即CM =6031;当点M 在OA 上时,只可能是∠NBP =∠NMA ,所以∠PBA =∠PMO ,根据题意可以判定不成立,所以CM =6031.(3)由于等腰三角形的特殊性质,应分三种情况进行讨论,即BP =BN ,PB =PN ,NB =NP 三种情况进行讨论.【解答】证明:(1)过点N 作NH ⊥x 轴于点H ,设AN =5k ,得:AH =3k ,CM =2k ,①当点M 在CO 上时,点N 在线段AB 上时:∴OH =6-3k ,OM =4-2k ,∴MH =10-5k ,∵PO ∥NH ,∴MN NP =MH OH=10-5k 6-3k =53,②当点M 在OA 上时,点N 在线段AB 的延长线上时:∴OH =3k -6,OM =2k -4,∴MH =5k -10,∵PO ∥NH ,∴MN NP =MH OH=5k -103k -6=53;解:(2)当△BNP 与△MNA 相似时:①当点M 在CO 上时,只可能是∠MNB =∠MNA =90°,∴△BNP ∽△MNA ∽△BOA ,∴AMAN =AB AO,。
【中考数学】2022-2023学年易错常考专题训练—相似三角形(含解析)

【中考数学】2022-2023学年易错常考专题训练—相似三角形1.如图,抛物线与x 轴交于A 、B 两点(点A 在点B 的左边),与y 轴213222y x x =-++交于点C ,连接.BC(1)求点A 、B 、C 的坐标;(2)设x 轴上的一个动点P 的横坐标为t ,过点P 作直线轴,交抛物线于点N ,交直PN x ⊥线于点M .BC ①当点P 在线段上时,设的长度为s ,求s 与t 的函数关系式;AB MN ②当点P 在线段上时,是否存在点P ,使得以O 、P 、N 三点为顶点的三角形与OB 相似?若存在,请求出点P 的坐标;若不存在,请说明理由.COB △2.如图,抛物线经过,,三点.()4,0A ()10B ,()0,2C -(1)求出抛物线的解析式;(2)P 是抛物线在第一象限上的一动点,过P 作PM ⊥x 轴,垂足为M ,是否存在P 点,使得以A ,P ,M 为顶点的三角形与△OAC 相似?若存在,请求出符合条件的点P 的坐标;若不存在,请说明理由;(3)若抛物线上有一点D (点D 位于直线AC 的上方且不与点B 重合)使得,DCA ABCS S=△△直接写出点D 坐标.3.如图,已知,,抛物线经过、两点,交轴于点()2,0A -()4,0B 2y ax bx c =++A B y .点是第一象限内抛物线上的一点,连接,.为上的动点,过点()0,4C P AC BC M OB 作轴,交抛物线于点,交于点.M PM x ⊥P BC Q(1)求抛物线的函数表达式;(2)过点作,垂足为点,设点的坐标为请用含的代数式表示线段P PN BC ⊥N M ()0m ,m 的长,并求出当为何值时有最大值,最大值是多少?PN m PN (3)试探究在运动过程中,是否存在这样的点,使得以,,为顶点的三角形M Q O M Q 与相似.若存在,请求出此时点的坐标;若不存在,请说明理由.AOC Q 4.如图,在平面直角坐标系中,抛物线与两坐标轴分别相交于xOy 213442y x x =-++三点.A B C ,,(1)求证:;90ACB ∠=︒(2)点是第一象限内抛物线上的动点,过点作轴的垂线交于点,交轴于点D D x BCE x .F①②点是的中点,若以点为顶点的三角形与相似,求点的坐标.G AC C D E ,,AOG D 5.如图,在平面直角坐标系中,矩形ABCD 的边BC 与x 轴、y 轴的交点分别为C (8,0),B (0,6),CD =5,抛物线y =ax 2﹣x +c (a ≠0)过B ,C 两点,动点M 从点D 开始以154每秒5个单位长度的速度沿D→A→B→C 的方向运动到达C 点后停止运动.动点N 从点O 以每秒4个单位长度的速度沿方向运动,到达C 点后,立即返回,向CO 方向运动,到达O 点后,又立即返回,依此在线段OC 上反复运动,当点M 停止运动时,点N 也停止运动,设运动时间为t .(1)求抛物线的解析式;(2)求点D 的坐标;(3)当点M ,N 同时开始运动时,若以点M ,D ,C 为顶点的三角形与以点B ,O ,N 为顶点的三角形相似,直接写出t 的值.6.如图.在平面直角坐标系中.抛物线与x 轴交于A 、B 两点,与y 轴交212y x bx c =++于点C .点A 的坐标为,点C 的坐标为.已知点是线段上的动()1,0-()0,2-(),0E m AB 点(点E 不与点A ,B 重合).过点E 作轴交抛物线于点P ,交于点F .PE x ⊥BC(1)求该抛物线的表达式;(2)若,请求出m 的值;:1:2EF PF =(3)是否存在这样的m ,使得与相似?若存在,求出此时m 的值;若不存在,BEP △ABC 请说明理由;(4)当点E 运动到抛物线对称轴上时,点M 是x 轴上一动点,点N 是抛物线上的动点,在运动过程中,是否存在以C 、B 、M 、N 为顶点的四边形是平行四边形?若不存在,请说明理由;若存在,请直接写出点M 的坐标.7.如图,抛物线与y 轴交于点A ,与轴交于点,,P 是26y ax bx =+-x ()3,0B -()1,0C 线段下方抛物线上的一个动点,过点Р作轴的垂线,交轴于点H ,交于点AB x x AB D .设点P 的横坐标为.()30t t -<<(1)求抛物线的解析式.(2)用含t 的式子表示线段的长,并求线段长度的最大值.PD PD (3)连接,当与相似时,求点P 的坐标.AP DPA DHB △8.如图,抛物线与轴交于点,与轴交于点,点234y x bx c =-++x ()4,0A y ()0,3B 为线段上一动点,过点且垂直于轴的直线与直线及抛物线分别交于(),0M m OA M x AB 点,.P N(1)求抛物线的解析式,并写出此抛物线的对称轴和顶点坐标;(2)如果以点P ,N ,B ,O 为顶点的四边形为平行四边形,求的值;m (3)如果以B ,P ,N 为顶点的三角形与相似,求点的坐标.APM △M 9.如图,抛物线经过,两点,与y 轴交于点B ,P 为抛物2y x bx c =-++()4,0A ()1,0C -线上的动点,连接AB ,BC ,PA ,PC ,PC 与AB 相交于点Q .(1)求抛物线的解析式;(2)若P 为第一象限抛物线上的动点,设的面积为,的面积为,当APQ △1S BCQ △2S 时,求点P 的坐标;215S S -=(3)是否存在点P ,使,若存在,直接写出点P 的坐标:若不存在,说45PAB CBO ∠+∠=︒明理由.10.如图,在平面直角坐标系中,抛物线与x 轴的正、负半轴分别交xOy 23y ax bx =++于点B 、A ,与y 轴交于点C ,已知,,.5AB =tan 3CAB ∠=:3:4OC OB =(1)求该抛物线的表达式;(2)设该抛物线的对称轴分别与x 轴、交于点E 、F ,求的长;BC EF (3)在(2)的条件下,联结,如果点P 在该抛物线的对称轴上,当和相似CE CEP △CEB 时,求点P 的坐标11.如图,直线分别交轴、轴于点,过点的抛物线31255y x =-+x y A B ,A 与轴的另一交点为,与轴交于点,抛物线的对称轴交2y x bx c =-++x C y ()04D ,l 于点,连接交于点.AD E OE AB F(1)求抛物线的解析式;(2)求证:;OE AB ⊥(3)为抛物线上的一动点,直线交于点,是否存在这样的点,使以P PO AD M P 为顶点的三角形与相似?若存在,求点的横坐标;若不存在,请说明A O M ,,ACD P 理由.12.如图,以D 为顶点的抛物线交x 轴于A 、B 两点,交y 轴于点C ,直212y x bx c=-++线的表达式为.BC 6y x =-+(1)求抛物线的表达式;(2)在直线上存在一点P ,使的值最小,求此最小值;BC PO PA +(3)在x 轴上是否存在一点Q ,使得以A 、C 、Q 为顶点的三角形与相似?若存在,BCD △请求出点Q 的坐标;若不存在,请说明理由.13.如图,在平面直角坐标系中,抛物线与x 轴交于点A 和点2()0y ax bx c ac =++≠B (点A 在点B 的左侧),与y 轴交于点C .若线段的长满足,OA OB OC 、、2OC OA OB =⋅则这样的抛物线称为“黄金”抛物线.如图,抛物线为“黄金”抛物线,22(0)y ax bx a =++≠其与x 轴交点为A ,B (其中B 在A 的右侧),与y 轴交于点C .且4OA OB=(1)求抛物线的解析式;(2)若P 为上方抛物线上的动点,过点P 作,垂足为D .AC PD AC ⊥①求的最大值;PD ②连接,当与相似时,求点P 的坐标.PC PCD ACO △14.在平面直角坐标系中,O 为坐标原点,直线与x 轴交于点B ,与y 轴交于点3y x =-+C .二次函数的图像过B ,C 两点,且与x 轴交于另一点A ,点M 为线段2y ax 2x c =++OB 上的一个动点(不与端点O ,B 重合).(1)求二次函数的表达式;(2)如图①,过点M 作y 轴的平行线l 交于点F ,交二次函数的图像于BC 2y ax 2x c =++点E ,记的面积为,的面积为,当时,求点E 的坐标;CEF 1S BMF 2S 1212S S =(3)如图②,连接,过点M 作的垂线,过点B 作的垂线,与交于点CM CM 1l BC 2l 1l2l G ,试探究的值是否为定值?若是,请求出的值;若不是,请说明理由.CG CM CGCM 15.如图1,已知抛物线与轴交于两点,与轴交于2y xbx c =-++x ()()2,0,4,0A B -y 点.C (1)求的面积;ABC (2)如图2,点是抛物线上第一象限的一点,且,求点的坐标;P PAB ACO ∠=∠P (3)若点是直线上一点,请在图3中探究:抛物线在轴上方的部分上是否存在点N 2y =x ,使得是以点为直角顶点的等腰直角三角形?若存在,请直接写出所有满足M CMN M 条件的点的坐标;若不存在,请说明理由.M 16.如图,在平面直角坐标系中,已知抛物线经过,xOy 2y ax x c =++()2,0A -两点,直线与轴交于点.()0,4B 3x =x C(1)求,的值;a c (2)经过点的直线分别与线段,直线交于点,,且与的面O AB 3x =D E BDO △OCE △积相等,求直线的解析式;DE (3)是抛物线上位于第一象限的一个动点,在线段和直线上是否分别存在点,P OC 3x =F ,使,,,为顶点的四边形是以为一边的矩形?若存在,求出点的坐G B F G P BF F 标;若不存在,请说明理由.答案:1.(1),,;()10A -,()40B ,()02C ,(2)①;②点P()()221210212042t t t s t t t ⎧--≤<⎪⎪=⎨⎪-+≤≤⎪⎩2.(1)215222y x x =-+-(2)存在,(2,1)(3)点的坐标为(3,1)D 3.(1)2142y x x =-++,当时,有最大值2m =PN (3)存在,或48,33Q ⎛⎫ ⎪⎝⎭84,33Q ⎛⎫ ⎪⎝⎭4.(1)1(2)①;②或.9(4,6)D 25(3,)4D 5.(1)2315684y x x =-+(2)(11,4)或2356.(1);213222y x x =--(2);2m =(3)存在,m 的值为0或3;(4)存在,M 点的坐标为或或()7,0()1,0M 7.(1);2246y x x =+-(2);线段长度的最大值为.226PD t t =--PD 92(3)或()2,6P --755,48P ⎛⎫-- ⎪⎝⎭8.(1),对称轴:,顶点坐标239344y x x =-++32x =375,216⎛⎫ ⎪⎝⎭(2)2(3)或11,09M ⎛⎫ ⎪⎝⎭()3,0M 9.(1)234y x x =-++(2)或16P(,)26P (,)(3)()3,4P 10.(1)239344y x x =-++(2)158EF =(3)P 的坐标为:或.3,52⎛⎫ ⎪⎝⎭39,24⎛⎫ ⎪⎝⎭11.(1)抛物线解析式为234y x x =-++(2)2(3)存在,点的横坐标为P 12.(1)21262y x x =-++(2)10(3)当Q 的坐标为或时,以A 、C 、Q 为顶点的三角形与相似()00,()180,BCD △13.(1)213222y x x =--+(2)①PD ②P 坐标为或(3,2)-325()28,-14.(1);223y x x =-++(2);(1,4)E(3)15.(1)24(2)1523(,)416P (3)存在,或()3,5M 16.(1),12a =-4c =(2)23y x =-(3)存在这样的点,点的坐标为或F F (2,0)。
专题14相似三角形判定定理的证明(2个知识点6种题型1种中考考法)解析版-初中数学北师大版9年级上册

【答案】△AMF∽△BGM,△DMG∽△DBM,△EMF∽△EAM,证明见解析. 【分析】根据相似三角形的判定定理可以直接写出图中有 3 对相似三角形;可以利用相似三角形的判定定 理两组角对应相等的两个三角形相似来证明△AMF∽△BGM. 【详解】图中的相似三角形有:△AMF∽△BGM,△DMG∽△DBM,△EMF∽△EAM. 以下证明△AMF∽△BGM. ∵∠AFM=∠DME+∠E(外角定理),∠DME=∠A=∠B(已知),∴∠AFM=∠DME+∠E=∠A+∠E=∠ BMG,∠A=∠B,∴△AMF∽△BGM. 【点睛】本题考查了相似三角形的判定.解答此题,要找出对应角相等来证明三角形相似. 【变式】(2022 秋·九年级课时练习)如图,在 △ABC 和 △ADE 中,∠BAD=∠CAE, ∠ABC=∠ADE. (1)写出图中两对相似三角形(不得添加字母和线); (2)请证明你写出的两对相似三角形.
∴△ABC∽△A′B′C′.
【点睛】本题主要考查了相似三角形的证明,作出辅助线,证明△ADE≌△A′B′C′,是解题的关键.
【例 3】(2022 秋·九年级课时练习)已知:在△ABC 和△A′B′C′中,
AB AB
BC BC
AC AC
2023年中考数学一轮复习之必考点题型全归纳与分层精练-相似三角形(解析版)

专题22相似三角形【专题目录】技巧1:巧用“基本图形”探索相似条件技巧2:巧作平行线构造相似三角形技巧3:证比例式或等积式的技巧【题型】一、相似图形的概念和性质【题型】二、平行线分线段成比例定理【题型】三、相似三角形的判定【题型】四、相似三角形的性质【题型】五、利用相似三角形解决实际问题【题型】六、位似图形的概念与性质【题型】七、平面直角坐标系与位似图形【考纲要求】1、了解比例线段的有关概念及其性质,并会用比例的性质解决简单的问题.2、了解相似多边形,相似三角形的概念,掌握其性质和判定并会运用.3、了解位似变换和位似图形的概念,掌握并运用其性质.【考点总结】一、相似图形及比例线段解直相似图形在数学上,我们把形状相同的图形称为相似图形.相似多边形若两个边数相同的多边形,它们的对应角相等、对应边成比例,则这两个多边形叫做相似多边形。
特征:对应角相等,对应边成比例。
比例线段的定义在四条线段a,b,c,d中,如果其中两条线段的比等于另外两条线段的比,即a cb d(或a∶b=c∶d),那么这四条线段a,b,c,d叫做成比例线段,简称比例线段.【考点总结】二、相似三角形【技巧归纳】技巧1:巧用“基本图形”探索相似条件相似三角形的四类结构图:1.平行线型.2.相交线型.角三角形的应用比例线段的性质(1)基本性质:a b =c d ad =bc ;(2)合比性质:a b =c d a +b b =c +d d ;(3)等比性质:若a b =c d =…=m n (b +d +…+n ≠0),那么a +c +…+m b +d +…+n =a b.黄金分割点C 把线段AB 分成两条线段AC 和BC ,如果AC AB =BC AC ,则线段AB 被点C 黄金分割,点C 叫线段AB 的黄金分割点,AC 与AB 的比叫做黄金比.3.子母型.4.旋转型.【类型】一、平行线型1.如图,在△ABC 中,BE 平分∠ABC 交AC 于点E ,过点E 作ED ∥BC 交AB 于点D.(1)求证:AE·BC =BD·AC ;(2)如果S △ADE =3,S △BDE =2,DE =6,求BC 的长.【类型】二、相交线型2.如图,点D ,E 分别为△ABC 的边AC ,AB 上的点,BD ,CE 交于点O ,且EO BO =DO CO,试问△ADE 与△ABC 相似吗?请说明理由.【类型】三、子母型3.如图,在△ABC 中,∠BAC =90°,AD ⊥BC 于点D ,E 为AC 的中点,ED 的延长线交AB 的延长线于点F.求证:AB AC =DF AF .【类型】四、旋转型4.如图,已知∠DAB =∠EAC ,∠ADE =∠ABC.求证:(1)△ADE ∽△ABC ;(2)AD AE =BD CE .参考答案1.(1)证明:∵ED ∥BC ,∴∠ADE =∠ABC.又∵∠A =∠A ,∴△ADE ∽△ABC.∴AE AC =DE BC.∵BE 平分∠ABC ,∴∠DBE =∠EBC.∵ED ∥BC ,∴∠DE B =∠EBC.∴∠DBE =∠DEB.∴DE =BD.∴AE AC =BD BC.即AE·BC =BD·AC.(2)解:设h △ADE 表示△ADE 中DE 边上的高,h △BDE 表示△BDE 中DE 边上的高,h △ABC 表示△ABC 中BC 边上的高.∵S △ADE =3,S △BDE =2,∴S △ADE S △BDE =12·DE·h △ADE 12·DE·h △BDE =h △ADE h △BDE =32.∴h △ADE h △ABC =35.∵△ADE ∽△ABC ,∴DE BC =h △ADE h △ABC =35.∵DE =6,∴BC =10.2.解:相似.理由如下:因为EO BO =DO CO,∠BO E =∠COD ,∠DOE =∠COB ,所以△BOE ∽△COD ,△DOE ∽△COB.所以∠EBO =∠DCO ,∠DEO =∠CBO.因为∠ADE =∠DCO +∠DEO ,∠ABC =∠EBO +∠CBO ,所以∠ADE =∠ABC.又因为∠A =∠A ,所以△ADE ∽△ABC.3.证明:∵∠BAC =90°,AD ⊥BC 于点D ,∴∠BAC =∠A DB =90°.又∵∠CBA =∠ABD(公共角),∴△ABC ∽△DBA.∴AB AC =DB DA,∠BAD =∠C.∵AD ⊥BC 于点D ,E 为AC 的中点,∴DE =EC.∴∠BDF =∠CDE =∠C.∴∠BDF =∠BAD.又∵∠F =∠F ,∴△DBF ∽△ADF.∴DB AD =DF AF .∴AB AC =DF AF.(第3题)点拨:当所证等积式或比例式运用“三点定型法”不能定型或能定型而不相似,条件又不具备成比例线段时,可考虑用中间比“搭桥”,称为“等比替换法”,有时还可用“等积替换法”,例如:如图,在△ABC 中,AD ⊥BC 于点D ,D E ⊥AB 于点E ,DF ⊥AC 于点F ,求证:AE·AB =AF·AC.可由两组“射影图”得AE·AB=AD 2,AF·AC =AD 2,∴AE·AB =AF·AC.4.证明:(1)∵∠DAB =∠EAC ,∴∠DAE =∠BAC.又∵∠ADE =∠ABC ,∴△ADE ∽△ABC.(2)∵△ADE ∽△ABC ,∴AD AE =AB AC.∵∠DAB =∠EAC ,∴△ADB ∽△AEC.∴AD AE =BD CE.技巧2:巧作平行线构造相似三角形【类型】一、巧连线段的中点构造相似三角形1.如图,在△ABC 中,E ,F 是边BC 上的两个三等分点,D 是AC 的中点,BD 分别交AE ,AF 于点P ,Q ,求BP PQ QD.【类型】二、过顶点作平行线构造相似三角形2.如图,在△ABC 中,AC =BC ,F 为底边AB 上一点,BFAF =32,取CF 的中点D ,连接AD 并延长交BC 于点E ,求BE EC 的值.【类型】三、过一边上的点作平行线构造相似三角形3.如图,在△ABC 中,AB >AC ,在边AB 上取一点D ,在AC 上取一点E ,使AD =AE ,直线DE 和BC的延长线交于点P.求证:BP CP =BD EC .【类型】四、过一点作平行线构造相似三角形4.如图,在△ABC 中,点M 为AC 边的中点,点E 为AB 上一点,且AE =14AB ,连接EM 并延长交BC 的延长线于点D.求证:BC =2CD.参考答案1.解:如图,连接DF ,∵E ,F 是边BC 上的两个三等分点,∴BE =EF =FC.∵D 是AC 的中点,∴AD =CD.∴DF 是△ACE 的中位线.∴DF ∥AE ,且DF =12AE.∴DF ∥PE.∴∠BEP =∠BFD.又∵∠EBP 为公共角,∴△BEP ∽△BFD.∴BE BF =BP BD.∵BF =2BE ,∴BD =2BP.∴BP =PD.∴DF =2PE.∵DF ∥AE ,∴∠APQ =∠FDQ ,∠PAQ =∠DFQ.∴△APQ ∽△FDQ.∴PQ QD =AP DF.设PE =a ,则DF =2a ,AP =3a.∴PQQD =AP DF =3 2.∴BP PQ QD =53 2.2.解:如图,过点C 作CG ∥AB 交AE 的延长线于点G.∵CG ∥AB ,∴∠DAF =∠G.又∵D 为C F 的中点,∴CD =DF.在△ADF 和△GDC DAF =∠G ,ADF =∠CDG ,=CD ,∴△ADF ≌△GDC(AAS ).∴AF =CG.∵BF AF =32,∴AB AF =5 2.∵AB ∥CG ,∴∠CGE =∠BAE ,∠BCE =∠ABE.∴△ABE ∽△GCE.∴BE EC =AB CG =AB AF =52.3.证明:如图,过点C 作CF ∥AB 交DP 于点F ,∴∠PFC =∠PDB ,∠PCF =∠PBD.∴△PCF ∽△PBD.∴BP CP =BD CF.∵AD ∥CF ,∴∠ADE =∠EFC.∵AD =AE ,∴∠ADE =∠AED.∵∠AED =∠CEP ,∴∠EFC =∠CEP.∴EC =CF.∴BP CP =BD EC.4.证明:(方法一)如图①,过点C 作CF ∥A B ,交DE 于点F ,(第4题①)∴∠FCD =∠B.又∵∠D 为公共角,∴△CDF ∽△BDE.∴CF BE =CD BD.∵点M 为AC 边的中点,∴AM =CM.∵CF ∥AB ,∴∠A =∠MCF.又∵∠AME =∠CM F ,∴△AME ≌△CMF.∴AE =CF.∵AE =14AB ,BE =AB -AE ,∴BE =3AE.∴AE BE =13.∵CF BE =CD BD,∴AE BE =CD BD =13,即BD =又∵BD =BC +CD ,∴BC =2CD.(第4题②)(方法二)如图②,过点C 作CF ∥DE ,交AB 于点F ,∴AE AF =AM AC.又∵点M 为AC 边的中点,∴AC =2AM.∴2AE =AF.∴AE =EF.又∵AE AB =14,∴BF EF=2.又∵CF ∥DE ,∴BF FE =BC CD =2.∴BC =2CD.(第4题③)(方法三)如图③,过点E 作EF ∥BC ,交AC 于点F ,∴∠AEF =∠B.又∵∠A 为公共角,∴△AEF ∽△ABC.∴EF BC =AE AB =AF AC.由AE =14AB ,知EF BC =AE AB =AF AC =14,∴EF =14BC ,AF =14AC.由EF ∥CD ,易证得△EFM ∽△DCM ,∴EF CD =MF MC.又∵AM =MC ,∴MF =12MC ,∴EF =12CD.∴BC =2CD.(第4题④)(方法四)如图④,过点A 作AF ∥BD ,交DE 的延长线于点F ,∴∠F =∠D ,∠FAE =∠B.∴△AEF ∽△BED.∴AE BE =AF BD.∵AE =14AB ,∴AE =13BE.∴AF =13BD.由AF ∥CD ,易证得△AFM ∽△CDM.又∵AM =MC ,∴AF =CD.∴CD =13BD.∴BC =2CD.点拨:由已知线段的比,求证另外两线段的比,通常添加平行线,构造相似三角形来求解.技巧3:证比例式或等积式的技巧【类型】一、构造平行线法1.如图,在△ABC 中,D 为AB 的中点,DF 交AC 于点E ,交BC 的延长线于点F ,求证:AE·CF =BF·EC.2.如图,已知△ABC 的边AB 上有一点D ,边BC 的延长线上有一点E ,且AD =CE ,DE 交AC 于点F ,求证:AB·DF =BC·EF.【类型】二、三点定型法3.如图,在▱ABCD 中,E 是AB 延长线上的一点,DE 交BC 于F.求证:DC AE =CF AD .4.如图,在△ABC 中,∠BAC =90°,M 为BC 的中点,DM ⊥BC 交CA 的延长线于D ,交AB 于E.求证:AM 2=MD·ME.【类型】三、构造相似三角形法5.如图,在等边三角形ABC中,点P是BC边上任意一点,AP的垂直平分线分别交AB,AC于点M,N.求证:BP·CP=BM·CN.【类型】四、等比过渡法6.如图,在△ABC中,AB=AC,DE∥BC,点F在边AC上,DF与BE相交于点G,且∠EDF=∠ABE.求证:(1)△DEF∽△BDE;(2)DG·DF=DB·EF.7.如图,CE是Rt△ABC斜边上的高,在EC的延长线上任取一点P,连接AP,作BG⊥AP于点G,交CE于点D.求证:CE2=DE·PE.【类型】五、两次相似法8.如图,在Rt△ABC中,AD是斜边BC上的高,∠ABC的平分线BE交AC于E,交AD于F.求证:BF BE =AB BC .9.如图,在▱ABCD 中,AM ⊥BC ,AN ⊥CD ,垂足分别为M ,N.求证:(1)△AMB ∽△AND ;(2)AM AB =MN AC .【类型】六、等积代换法10.如图,在△ABC 中,AD ⊥BC 于D ,DE ⊥AB 于E ,DF ⊥AC 于F.求证:AE AF =AC AB .【类型】七、等线段代换法11.如图,在等腰三角形ABC 中,AB =AC ,AD ⊥BC 于点D ,点P 是AD 上一点,CF ∥AB ,延长BP 交AC 于点E ,交CF 于点F ,求证:BP 2=PE·PF.12.如图,已知AD 平分∠BAC ,AD 的垂直平分线EP 交BC 的延长线于点P.求证:PD 2=PB·PC.参考答案1.证明:如图,过点C 作CM ∥AB 交DF 于点M.∵CM ∥AB ,∴∠FCM =∠B ,∠FMC =∠FDB.∴△CMF ∽△BDF.∴BF CF =BD CM.又∵CM ∥AD ,∴∠A =∠ECM ,∠ADE =∠CME.∴△ADE ∽△CME.∴AE EC =AD CM.∵D 为AB 的中点,∴BD =AD.∴BD CM =AD CM .∴BF CF =AE EC.即AE·CF =BF·EC.2.证明:过点D 作DG ∥BC ,交AC 于点G ,易知△DGF ∽△ECF ,△ADG ∽△ABC.∴EF DF =CE DG ,AB BC =AD DG.∵AD =CE ,∴CE DG =AD DG .∴AB BC =EF DF.即AB·DF =BC·EF.点拨:过某一点作平行线,构造出“A ”型或“X ”型的基本图形,通过相似三角形转化线段的比,从而解决问题.3.证明:∵四边形ABCD 是平行四边形,∴A E ∥D C ,∠A =∠C.∴∠CDF =∠E.∴△FCD ∽△DAE.∴DC AE =CF AD.4.证明:∵DM ⊥BC ,∠BAC =90°,∴∠B +∠BEM =90°,∠D +∠DEA =90°.∵∠BEM =∠DEA ,∴∠B =∠D.又∵M 为BC 的中点,∠BAC =90°,∴BM =AM.∴∠B =∠BAM.∴∠BAM =∠D.即∠EAM =∠D.又∵∠AME =∠DMA.∴△AME ∽△DMA.∴AM MD =ME AM.即AM 2=MD·ME.5.证明:如图,连接PM ,PN.∵MN 是AP 的垂直平分线,∴MA =MP ,NA =NP.∴∠1=∠2,∠3=∠4.又∵△ABC 是等边三角形,∴∠B =∠C =∠1+∠3=60°.∴∠2+∠4=60°.∴∠5+∠6=120°.又∵∠6+∠7=180°-∠C =120°,∴∠5=∠7.∴△BPM ∽△CNP.∴BP CN =BM CP.即BP·CP =BM·CN.6.证明:(1)∵AB =AC ,∴∠ABC =∠ACB.∵DE ∥BC ,∴∠ABC +∠EDB =180°,∠ACB +∠FED =180°.∴∠FED =∠EDB.又∵∠EDF =∠DBE ,∴△DEF ∽△BDE.(2)由△DEF ∽△BDE 得DE BD =EF DE.即DE 2=DB·EF.又由△DEF ∽△BDE ,得∠GED =∠EFD.∵∠GDE =∠EDF ,∴△GDE ∽△EDF.∴DG DE =DE DF.即DE 2=DG·DF.∴DG·DF =DB·EF.7.证明:∵BG ⊥AP ,PE ⊥AB ,∴∠AEP =∠DEB =∠AGB =90°.∴∠P +∠PAB =90°,∠PAB +∠AB G =90°.∴∠P =∠ABG.∴△AEP ∽△DEB.∴AE DE =PE BE.即AE·BE =PE·DE.又∵∠CEA =∠BEC =90°,∴∠CAB +∠ACE =90°.又∵∠ACB =90°,∴∠CAB +∠CBE =90°.∴∠ACE =∠CBE.∴△AEC CEB.∴AE CE =CE BE.即CE 2=AE·BE.∴CE 2=DE·PE.8.证明:由题意得∠BDF =∠BAE =90°.∵BE 平分∠ABC ,∴∠DBF =∠ABE.∴△BDF ∽△BAE.∴BD AB =BF BE.∵∠BAC =∠BDA =90°,∠ABC =∠DBA.∴△ABC ∽△DBA.∴AB BC =BD AB.∴BF BE =AB BC.9.证明:(1)∵四边形ABCD 为平行四边形,∴∠B =∠D.∵AM ⊥BC ,AN ⊥CD ,∴∠AMB =∠AND =90°.∴△AMB ∽△AND.(2)由△AMB ∽△AND 得AM AN =AB AD,∠BAM =∠DAN.又AD =BC ,∴AM AN =AB BC.∵AM ⊥BC ,AD ∥BC ,∴∠MAD =∠AMB =90°.∴∠B +∠BAM =∠MAN +∠NAD =90°.∴∠B =∠MAN.∴△AMN ∽△BAC.∴AM AB =MN AC.10.证明:∵AD ⊥BC ,DE ⊥AB ,∴∠ADB =∠AED =90°.又∵∠BAD =∠DAE ,∴△ABD ∽△ADE.∴AD AB =AE AD.即AD 2=AE·AB.同理可得AD 2=AF·AC.∴AE·AB =AF·AC.∴AE AF =AC .11.证明:连接PC ,如图所示.∵AB =AC ,AD ⊥BC ,∴AD 垂直平分BC ,∠ABC =∠ACB.∴BP =CP.∴∠1=∠2∴∠ABC -∠1=∠ACB -∠2,即∠3=∠4.∵CF ∥AB ,∴∠3=∠F.∴∠4=∠F.又∵∠CPF =∠CPE ,∴△CPF ∽△EPC.∴CP PE =PF CP,即CP 2=PF·PE.∵BP =CP ,∴BP 2=PE·PF.12.证明:如图,连接PA ,∵EP 是AD 的垂直平分线,∴PA =PD.∴∠PD A =∠PAD.∴∠B +∠BAD =∠DAC +∠CAP.又∵AD 平分∠BAC ,∴∠BAD =∠DAC.∴∠B =∠CAP.又∵∠APC =∠BPA ,∴△PAC ∽△PBA.∴PA PB =PC PA.即PA 2=PB·PC.∵PA =PD ,∴PD 2=PB·PC.【题型讲解】【题型】一、相似图形的概念和性质例1、如图,在△ABC 中,DE ∥AB ,且CD BD =32,则CE CA 的值为()A .35B .23C .45D .32【答案】A【提示】根据平行线分线段成比例定理得到比例式即可解答.【详解】解:∵DE //AB ,∴32CE CD AE BD ==∴CE CA 的值为35.故答案为A .【题型】二、平行线分线段成比例定理例2、如图,在ABC ∆中,//DE BC ,9AD =,3DB =,2CE =,则AC 的长为()A .6B .7C .8D .9【答案】C 【提示】根据平行线分线段成比例定理,由DE ∥BC 得AD AE DB EC =,然后利用比例性质求EC 和AE 的值即可【详解】∵//DE BC ,∴AD AE DB EC =,即932AE =,∴6AE =,∴628AC AE EC =+=+=.故选C .【题型】三、相似三角形的判定例3、如图,已知DAB CAE ∠=∠,那么添加下列一个条件后,仍然无法判定A ABC DE ∽△△的是()A .AB AC AD AE =B .AB BC AD DE =C .B D ∠=∠D .C AED∠=∠【答案】B【提示】利用相似三角形的判定依次判断可求解.【详解】解:∵∠DAB=∠CAE ,∴∠DAE=∠BAC ,A 、若AB AC AD AE =,且∠DAE=∠BAC ,可判定△ABC ∽△ADE ,故选项A 不符合题意;B 、若AB BC AD DE =,且∠DAE=∠BAC ,无法判定△ABC ∽△ADE ,故选项B 符合题意;C 、若∠B=∠D ,且∠DAE=∠BAC ,可判定△ABC ∽△ADE ,故选项C 不符合题意;D 、若∠C=∠AED ,且∠DAE=∠BAC ,可判定△ABC ∽△ADE ,故选项D 不符合题意;故选:B .【题型】四、相似三角形的性质例4、如图,在ABC ∆中,D 、E 分别是AB 和AC 的中点,15BCED S =四边形,则ABC S ∆=()A .30B .25C .22.5D .20【答案】D【提示】首先判断出△ADE ∽△ABC ,然后根据相似三角形的面积比等于相似比的平方即可求出△ABC 的面积.【详解】解:根据题意,点D 和点E 分别是AB 和AC 的中点,则DE ∥BC 且DE=12BC ,故可以判断出△ADE ∽△ABC,根据相似三角形的面积比等于相似比的平方,可知ADE S ∆:ABC S ∆=1:4,则BCED S 四边形:ABC S ∆=3:4,题中已知15BCED S =四边形,故可得ADE S ∆=5,ABC S ∆=20故本题选择D【题型】五、利用相似三角形解决实际问题例5、为测量某河的宽度,小军在河对岸选定一个目标点A ,再在他所在的这一侧选点B ,C ,D ,使得AB ⊥BC ,CD ⊥BC ,然后找出AD 与BC 的交点E ,如图所示.若测得BE =90m ,EC =45m ,CD =60m ,则这条河的宽AB 等于()A .120mB .67.5mC .40mD .30m【答案】A 【解析】∵∠ABE=∠DCE,∠AEB=∠CED,∴△ABE ∽△DCE,∴AB BE CD CE=.∵BE =90m ,EC =45m ,CD =60m ,∴()906012045AB m ⨯==故选A.【物高问题】【题型】六、位似图形的概念与性质例6、如图,△ABC 与△DEF 位似,点O 为位似中心.已知OA ∶OD =1∶2,则△ABC 与△DEF 的面积比为()A .1∶2B .1∶3C .1∶4D .1∶5【答案】C【提示】根据位似图形的性质即可得出答案.【详解】由位似变换的性质可知,//,//AB DE AC DF∴12OA OB OD OE ==12AC OA DF OD ∴==∴△ABC 与△DEF 的相似比为:1∶2∴△ABC 与△DEF 的面积比为:1∶4故选C .【题型】七、平面直角坐标系与位似图形例7、如图,三角板在灯光照射下形成投影,三角板与其投影的相似比为2:5,且三角板的一边长为8cm .则投影三角板的对应边长为()A .20cmB .10cmC .8cmD .3.2cm【答案】A【提示】根据对应边的比等于相似比列式进行计算即可得解.【详解】解:设投影三角尺的对应边长为xcm ,∵三角尺与投影三角尺相似,∴8:x =2:5,解得x =20.故选:A .相似三角形(达标训练)一、单选题1.如图,已知∥DE BC ,12AD BD =,则ADE V 与ABC 的周长之比为()A .1:2B .1:4C .1:9D .1:3【答案】D 【分析】根据平行线的性质及相似三角形的判定定理可得:ABC ADE ∽,相似三角形的对应边成比例,且周长比等于相似比,据此即可解答.【详解】解:∵∥DE BC ,∴ADE B ∠=∠,∵A A ∠=∠,∴ABC ADE ∽,∵AD :DB =1:2,∴AD :AB =1:3,∴13ADE ABC C C ∆∆=::,即ADE 与ABC 的周长比为1:3.故选:D .【点睛】题目主要考查相似三角形的判定与性质,平行线的性质,熟练掌握相似三角形的判定定理及其性质是解题关键.2.如图,在ABC 中,高BD 、CE 相交于点.F 图中与AEC △一定相似的三角形有()A .1个B .2个C .3个D .4个【答案】C 【分析】利用相似三角形的判定方法可得AEC △∽ADB ,AEC △∽FEB ,AEC △∽FDC △,可求解.【详解】解:A A ∠=∠ ,90AEC ADB ∠=∠=︒,AEC ∴ ∽ADB ,ACE ABD ∴∠=∠,又90AEC BEC ∠=∠=︒ ,AEC ∴ ∽FEB ,ACE ACE ∠=∠ ,90AEC ADB ∠=∠=︒,AEC ∴ ∽FDC △,故选C【点睛】本题考查了相似三角形的判定,掌握相似三角形的判定方法是解题的关键.3.在△ABC 中,D 、E 分别是AB 、AC 的中点,则△ADE 与△ABC 的面积之比为()A .16B .14C .13D .12【答案】B【分析】容易证明两个三角形相似,求出相似比,相似三角形的周长之比等于相似比,面积比等于相似比的平方.【详解】解:由题意得DE 为△ABC 的中位线,那么DE ∥BC ,DE :BC =1:2.∴△ADE ∽△ABC ,∴△ADE 与△ABC 的周长之比为1:2,∴△ADE 与△ABC 的面积之比为:4,即14.故选:B .【点睛】此题考查的是相似三角形的性质,三角形中位线定理,掌握相似三角形的周长之比等于相似比,面积比等于相似比的平方是解决此题关键.4.如图,D 是ABC 的边BC 上的一点,那么下列四个条件中,不能够判定△ABC 与△DBA 相似的是()A .C BAD∠=∠B .BAC BDA ∠=∠C .AC AD BC AB =D .2AB BD BC=⋅【答案】C【分析】由相似三角形的判定定理即可得到答案.【详解】解:C BAD ∠=∠,B B ∠=∠,ABC ∽DBA ,故选项A 不符合题意;BAC BDA ∠=∠,B B ∠=∠,ABC ∽DBA ,故选项B 不符合题意;AC AD BC AB=,但无法确定ACB ∠与BAD ∠是否相等,所以无法判定两三角形相似,故选项C 符合题意;2AB BD BC =⨯即AB BC BD AB=,B B ∠=∠,ABC ∽DBA ,故选项D 不符合题意.故选:C .【点睛】本题考查相似三角形的判定定理,熟练掌握相关定理是解题的关键.5.已知ABC ∽A B C ''' ,AD 和A D ''是它们的对应角平分线,若8AD =,12A D ''=,则ABC 与A B C ''' 的面积比是()A .2:3B .4:9C .3:2D .9;4【答案】B【分析】根据相似三角形的性质:对应角平分线的比等于相似比,面积的比等于相似比的平方求解即可.【详解】ABC ∽A B C ''' ,AD 和A D ''是它们的对应角平分线,8AD =,12A D ''=,∴两三角形的相似比为::8:122:3AD A D '==',则ABC 与'''A B C 的面积比是:4:9.故选:B【点睛】本题考查的是相似三角形的性质,熟知相似三角形面积的比等于相似比的平方是解答此题的关键.二、填空题6.如图所示,某校数学兴趣小组利用标杆BE 测量建筑物的高度,已知标杆BE 高为1.5m ,测得AB =3m ,AC =10m ,则建筑物CD 的高是_____m .【答案】5【分析】根据题意和图形,利用三角形相似的性质,可以计算出CD 的长,从而可以解答本题.【详解】∵EB ⊥AC ,DC ⊥AC ,∴EB ∥DC ,∴AEB ADC ∠=∠,ABE ACD ∠=∠,又∵A A ∠=∠,∴△ABE ∽△ACD ,∴AB AC =BE CD,∵BE =1.5m ,AB =3m ,AC =10m ,∴3 1.510CD=,解得,5CD =,即建筑物CD 的高是5m ,故答案为:5.【点睛】本题考查了相似三角形的应用、相似比等知识,正确得出相似三角形是解题的关键.7.如图所示,要使ABC ADE ~,需要添加一个条件__________(填写一个正确的即可)【答案】ADE B∠=∠【分析】根据已有条件,加上一对角相等就可以证明ABC 与ADE V 相似,依据是:两角对应相等的两个三角形相似.【详解】解:添加ADE B ∠=∠,A A∠=∠ ABC ADE∴ ~故答案为:ADE B ∠=∠.【点睛】本题主要考查了三角形相似的判定方法,牢记三角形相似的判定方法是做出本题的关键.三、解答题8.如图,在△ABC 中,D ,E 分别是AB ,AC 边上的点,且AD :AB =AE :AC =2:3.(1)求证:△ADE∽△ABC;(2)若DE=4,求BC的长.【答案】(1)见解析(2)BC=6.【分析】(1)直接根据相似三角形的判定方法判定即可;(2)利用相似三角形的性质即可求解.(1)证明:∵∠A=∠A,AD:AB=AE:EC=2:3,即23 AD AEAB EC==,∴△ADE∽△ABC;(2)解:∵△ADE∽△ABC,∴AD DEAB BC=,243BC=,∴BC=6.【点睛】本题考查了三角形的判定和性质,熟记各图形的性质并准确识图是解题的关键.相似三角形(提升测评)一、单选题1.如图,在菱形ABCD中,点E在AD边上,EF∥CD,交对角线BD于点F,则下列结论中错误的是()A .DE DF AE BF =B .EF DF AD DB =C .EF DF CD BF =D .EF DF CD DB=【答案】C【分析】根据已知及平行线分线段成比例定理进行分析,可得CD ∥BF ,依据平行线成比例的性质和相似三角形的性质即可得到答案.【详解】解:∵四边形ABCD 是平行四边形,∴AB ∥CD ,AB =CD ,∵EF ∥CD ,∴EF ∥AB ,∴DE DF AE BF =,△DEF ∽△DAB ,∴EF DF AB DB=,∵AB =AD =CD ,∴EF DF AD DB =,EF DF CD DB=,∴选项A 、B 、D 正确;选项C 错误;故选:C .【点睛】此题考查平行四边形的性质、相似三角形的判定与性质以及平行线分线段成比例定理;熟练掌握平行四边形的性质,证明三角形相似是解决问题的关键.2.如图1为一张正三角形纸片ABC ,其中D 点在AB 上,E 点在BC 上.今以DE 为折线将B 点往右折后,BD 、BE 分别与AC 相交于F 点、G 点,如图2所示.若10AD =,16AF =,14DF =,8BF =,则CG 的长度为多少?()A .7B .8C .9D .10【答案】C 【分析】根据三角形ABC 是正三角形,可得∠A =∠B =60°,△AFD ∽△BFG ,即可求出FG =7,而AD =10,DF =14,BF =8,可得AB =32=AC ,故CG =AC -AF -FG =9.【详解】解: 三角形ABC 是正三角形,60A B ∴∠=∠=︒,AFD BFG ∠=∠ ,AFD BFG ∴∆∆∽,∴DF AF FG BF =,即14168FG =,7FG ∴=,10AD = ,14DF =,8BF =,32AB ∴=,32AC ∴=,321679CG AC AF FG ∴=--=--=;故选:C .【点睛】本题考查等边三角形中的翻折问题,解题的关键是掌握翻折的性质,证明AFD BFG ∆∆∽,从而求出FG 的长度.3.如图,在平面直角坐标系中有A ,B 两点,其中点A 的坐标是(-2,1),点B 的横坐标是2,连接AO ,BO .已知90AOB ∠=︒,则点B 的纵坐标是()A .B .4CD .2【答案】B 【分析】先过点A 作AC x ⊥轴于点C ,过点B 作BD x ⊥轴于点D ,构造相似三角形,再利用相似三角形的性质列出比例式,计算求解即可.【详解】解:过点A 作AC x ⊥轴于点C ,过点B 作BD x ⊥轴于点D ,则90ACO ODB ∠=∠=︒,90B BOD ∠+∠=︒,90AOB ∠=︒Q ,90AOC BOD ∴∠+∠=︒,B AOC ∴∠=∠,ACO ∴ ∽ODB △,AC CO OD DB∴=,又A 的坐标是()2,1-,点B 的横坐标是2,∴AC =1,CO =2,OD =2,122DB∴=,即4DB =,∴:B 的纵坐标是4.故选:B .【点睛】本题主要考查了相似三角形的判定与性质,通过作垂线构造相似三角形是解决问题的关键.4.如图,D 是ABC △的边上的一点,过点D 作BC 的平行线交AC 于点E ,连接BE ,过点D 作BE 的平行线交AC 于点F ,则下列结论错误的是()A .AD AF BD EF =B .AF DF AE EB =C .=AD AE AB AC D .CAF FE DE B =【答案】D【分析】根据DF BE ∥,DE BC ∥找到对应线段成比例或相似三角形对应线段的比相等,判断即可.【详解】解:DF BE ∥,AD AF BD EF∴=,故A 选项比例式正确,不符合题意;DF BE ∥,ADF ABE ∴△∽△,DF AF EB AE∴=,故B 选项比例式正确,不符合题意;DE BC ∥,AD AE AB AC∴=,故C 选项比例式正确,不符合题意;DE BC ∥,DE AF BC FEAF AC =≠∴故D 选项比例式不正确,符合题意.故选D .【点睛】本题主要考查了平行线分线段成比例,相似三角形的判定和性质,解题的关键是找准对应线段.二、填空题5.如图,小明想测量一棵树的高度,他发现树的影子落在了地上和墙上,此时测得地面上的影长BD 为4m ,墙上的影子CD 长为1m ,同一时刻一根长为1m 的垂直于地面上的标杆的影长为0.5m ,则树的高度为______m .【答案】9【分析】设地面影长对应的树高为m x ,根据同时同地物高与影长成正比列出比例式求出x ,然后加上墙上的影长CD 即为树的高度.【详解】解:设地面影长对应的树高为m x ,由题意得,140.5x =,解得8x =,墙上的影子CD 长为1m ,∴树的高度为()819m +=.故答案为:9.【点睛】本题考查利用投影求物高.熟练掌握同时同地物高与影长成正比是解题的关键.6.如图,梯形ABCD 中,AD BC ∥,2BC AD =,点F 在BC 的延长线上,AF 与BD 相交于点E ,与CD 边相交于点G .如果2AD CF =,那么DEG ∆与CFG ∆的面积之比等于______.【答案】16:7##167【分析】根据ADG FCG ∆∆∽和ADE FBE ∆∆∽,根据相似三角形对应边成比例和相似三角形的面积比等于相似比的平方,即可求解.【详解】解:AD BC ,ADG FCG ∴∆∆∽,2AD AG CF GF∴==,∴ADG ∆与CFG ∆的面积之比4:1,AD BC ,ADE FBE ∴∆∆∽,25AD AE BF EF ∴==,令GF a =,则2AG a =,设,2AE x EG a x ==-,:(2)2:5x a a x ∴+-=,67x a ∴=,68,77AE a EG a ∴==,:3:4AE EG =,∴DEG ∆与ADE ∆的面积之比是4:3,∴DEG ∆与CFG ∆的面积之比是16:7.故答案为:16:7.【点睛】此题考查了相似三角形的判定与性质,熟练掌握并运用:相似三角形对应边成比例、相似三角形三、解答题7.如图,正方形ABCD 和正方形CEFG 中,点D 在CG 上,BC =1,CE =3,连接AF 交CG 于点K ,H 是AF 的中点,连接CH .(1)求tan ∠GFK 的值;(2)求CH 的长.【答案】(1)12(2)CH =【分析】(1)由正方形的性质得出AD =CD =BC =1,CG =FG =CE =3,,AD BC GF BE ∥∥,∠G =90°,证出ADK FGK V :V ,得出比例式求出3342GK DG ==,即可得出结果;(2)由正方形的性质求出AB =BC =1,CE =EF =3,∠E =90°,延长AD 交EF 于M ,连接AC 、CF ,求出AM =4,FM =2,∠AMF =90°,根据正方形性质求出∠ACF =90°,根据直角三角形斜边上的中线性质求出12CH AF =,根据勾股定理求出AF ,即可得出结果.(1)解:∵四边形ABCD 和四边形CEFG 是正方形,∴AD =CD =BC =1,CG =FG =CE =3,,AD BC GF BE ∥∥,∠G =90°,∴DG =CG -CD =2,AD GF ∥,∴ADK FGK V :V ,∴DK :GK =AD :GF =1:3,∴3342GK DG ==,∴312tan 32GK GFK FG ∠===;(2)解:∵正方形ABCD 和正方形CEFG 中,点D 在CG 上,BC =1,CE =3,∴AB =BC =1,CE =EF =3,∠E =90°,延长AD 交EF 于M ,连接AC 、CF ,如图所示:则AM =BC +CE =1+3=4,FM =EF-AB =3-1=2,∠AMF =90°,∵四边形ABCD 和四边形GCEF 是正方形,∴∠ACD =∠GCF =45°,∴∠ACF =90°,∵H 为AF 的中点,∴12CH AF =,在Rt △AMF 中,由勾股定理得:22224225AF AM FM =+=+=,∴152CH AF ==.【点睛】本题考查了相似三角形的判定与性质、三角函数、勾股定理,正方形的性质,直角三角形斜边上的中线性质;本题有一定难度,特别是(2)中,需要通过作出辅助线运用直角三角形斜边上的中线性质才能得出结果.8.如图所示,BEF 的顶点E 在矩形ABCD 对角线AC 的延长线上,13BC AB AE ==,,与FB 交于点G ,连接AF ,满足ABF ∽CEB ,其中A 对应C B ,对应E F ,对应B(1)求证:30FAD ∠=︒.(2)若13CE =,求tan FEA ∠的值.【答案】(1)见解析937【分析】(1)由相似可得FAB BCE ∠∠=,再由矩形的性质得AD BC ∥90DAB ABC ∠∠==︒,,从而可求得180FAD DAB DAC ∠∠∠++=︒,则有FAD BAC ∠∠=,即可求得FAD ∠的度数;(2)结合(1)可求得73AE =,再由相似的性质求得33AF =tan FEA ∠的值.(1)ABF ∽CEB ,FAB BCE ∠∠∴=,四边形ABCD 是矩形,∴90AD BC DAB ABC ∠=∠=︒∥,,DAC ACB ∴∠=∠,180BCE ACB ∠∠+=︒ ,180FAB DAC ∠∠∴+=︒,即180FAD DAB DAC ∠∠∠++=︒,90180FAD DAC ∠∠∴+︒+=︒,90FAD DAC ∠∠∴+=︒,90DAB ∠=︒ ,90BAC DAC ∠∠∴+=︒,FAD BAC ∠∠∴=,在Rt ABC中,tan 3BC BAC AB ∠== ,30BAC ∴∠=︒,30FAD ∠∴=︒;(2)由(1)得9030ABC BAC ∠∠=︒=︒,,2212AC BC ∴==⨯=,17233AE AC CE ∴=+=+=,ABF ∽CEB ,AF AB BC CE∴=,即113AF =,∴=AF 由(1)得:90FAD DAC ∠∠+=︒,则90FAE ∠=︒,在Rt FAE中,tan 3AF FEA AE ∠==【点睛】本题主要考查相似三角形的性质,矩形的性质,解直角三角形,解答的关键是结合图形及相应的性质求得FAD BAC ∠∠=.。
初中数学经典相似三角形练习题(附参考答案)

初中数学经典相似三角形练习题(附参考答案)初中数学经典相似三角形练习题(附参考答案)一、题目描述在初中数学中,相似三角形是一个非常重要的概念。
本文为您提供一些经典的相似三角形练习题,通过解答这些练习题可以提高学生的解题能力和对相似三角形的理解。
本文附有详细的参考答案,供学生进行自我检测和复习。
二、练习题1. 已知△ABC和△DEF相似,AB = 6cm,BC = 8cm,AC = 10cm,DE = 9cm,计算EF的长度。
2. △ABC与△DEF相似,AB = 2cm,BC =3.5cm,AC = 4cm,EF= 7cm,求DE的长度。
3. 在△ABC中,角A的度数为50°,角B的度数为70°,BC = 8cm。
若与△ABC相似的三角形的边长分别为10cm和12cm,求与△ABC相似的三角形的第三边的长度。
4. 在△ABC中,∠B = 90°,AC = 10cm,BC = 12cm。
若与△ABC相似的三角形的第二边为16cm,求与△ABC相似的三角形的第三边的长度。
5. 已知△ABC与△DEF相似,AB = 6cm,AC = 8cm,DE = 12cm,若EF = 18cm,求BC的长度。
6. 高度为5cm的小树和高度为12cm的大树的影子长度之比为2:3。
如果小树的影子长度为10cm,求大树的影子长度。
7. 一个航拍无人机垂直飞行,发现自己离地面的垂直距离与航拍无人机的长度(包括机身和旋翼)的比例为3:2。
如果航拍无人机的长度为120cm,求离地面的垂直距离。
8. 在一个旅游小组中,由5名成年人和7名儿童组成,其平均年龄为30岁。
如果另一个旅游小组由2名成年人和3名儿童组成,其平均年龄为24岁。
求这两个旅游小组的总年龄之比。
三、参考答案1. 根据相似三角形的性质可知,EF与AC的比例应与DE与BC的比例相等。
即 EF/AC = DE/BC。
代入已知值,得 EF/10 = 9/8。
最新九年级中考数学专题: 二次函数综合题(相似三角形问题)含答案
2023年九年级中考数学专题: 二次函数综合题(相似三角形问题)1.如图1,抛物线()221y x m m =--+(m 为常数)与x 轴交于A B 、两点(点B 在点A 右侧),与y 轴交于点C .(1)下列说法:①抛物线开口向上,①点C 在y 轴正半轴上;①12m >;①抛物线顶点在直线21y x =-+上,其中正确的是_______;(2)如图2,若直线21y x =-+与该抛物线交于M N 、两点(点M 在点N 下方),试说明:线段MN 的长是一个定值,并求出这个值;(3)在(2)的条件下,设直线21y x =-+与y 轴交于点D ,连接BM BN BD 、、,当:1:2DN MN =时,求此时m 的值,判断MBN △与MDB △是否相似,并说明理由.2.在平面直角坐标系xOy 中,抛物线()260y ax ax c a =-+>与x 轴交于A 、B 两点(点A 在点B 的左侧),顶点为C ,直线AC 交y 轴于点D ,连接BD ,且ABD △与ABC 的面积之比为1:2.(1)顶点C 的横坐标为__________; (2)求点B 的坐标;(3)连接CO ,将BCO 绕点C 按逆时针方向旋转一定的角度后,点B 与点A 重合,此时点O 恰好也在y 轴上,求抛物线的表达式.3.如图,抛物线2y x bx c =-++与x 轴交于点()1,0A -,()3,0B ,与y 轴交于点C ,点D 是直线BC 上方抛物线上一动点.(1)求抛物线的解析式;(2)如图1,过点D 作DE x ⊥轴于点E ,交直线BC 于点M .当2DM ME =时,求点D 的坐标; (3)如图2,设AB 的中点为点N ,过点D 作DF BC ⊥于点F ,连接CD 、CN ,使得以C 、D 、F 三点为顶点的三角形与CNO 相似,请直接写出点D 的坐标.4.如图,在平面直角坐标系xOy 中,抛物线()2y a x h k =-+与x 轴相交于O ,A 两点,顶点P 的坐标为()2,1-.点B 为抛物线上一动点,连接,AP AB ,过点B 的直线与抛物线交于另一点C .(1)求抛物线的函数表达式;(2)若点B 的横坐标与纵坐标相等,ABC OAP ∠=∠,且点C 位于x 轴上方,求点C 的坐标; (3)若点B 的横坐标为t ,90ABC ∠=︒,请用含t 的代数式表示点C 的横坐标,并求出当0t <时,点C 的横坐标的取值范围.5.如图,在平面直角坐标系xOy 中,抛物线213442y x x =-++与两坐标轴分别相交于A ,B ,C 三点(1)求证:①ACB =90°(2)点D 是第一象限内该抛物线上的动点,过点D 作x 轴的垂线交BC 于点E ,交x 轴于点F . ①求DE +BF 的最大值;①点G 是AC 的中点,若以点C ,D ,E 为顶点的三角形与AOG 相似,求点D 的坐标.6.在平面直角坐标系xOy 中,已知抛物线L 与x 轴交于,A B 两点,且经过点(0,2)C -,抛物线的顶点D 的坐标为325,28⎛⎫- ⎪⎝⎭.(1)求抛物线L 的函数表达式;(2)如图1,点E 为第四象限抛物线L 上一动点,过点E 作EG BC ⊥于点G ,求EG 的最大值,及此时点E 的坐标;(3)如图2,连接,AC BC ,过点O 作直线//l BC ,点,P Q 分别为直线l 和抛物线L 上的点.试探究:在第一象限是否存在这样的点,P Q ,使PQB CAB ∽.若存在,请求出所有符合条件的点P 的坐标;若不存在,请说明理由.7.如图所示,已知抛物线21y x =-与x 轴交于A 、B 两点,与y 轴交于点C .(1)求A 、B 、C 三点的坐标;(2)过点A 作AP ①CB 交抛物线于点P ,求四边形ACBP 的面积;(3)在x 轴上方的抛物线上是否存在一点M ,过M 作MG ①x 轴于点G ,使以A 、M 、G 三点为顶点的三角形与①PCA 相似?若存在,请求出M 点的坐标;否则,请说明理由.8.如图,在同一直角坐标系中,抛物线1L :28y ax bx =++与x 轴交于()8,0A -和点C ,且经过点()2,12B -,若抛物线1L 与抛物线2L 关于y 轴对称,点A 的对应点为'A ,点B 的对应点为'B .(1)求抛物线2L 的表达式;(2)现将抛物线2L 向下平移后得到抛物线3L ,抛物线3L 的顶点为M ,抛物线3L 的对称轴与x 轴交于点N ,试问:在x 轴的下方是否存在一点M ,使MNA '与ACB '△相似?若存在,请求出抛物线的3L 表达式;若不存在,说明理由.9.如图,在平面直角坐标系中,抛物线26y ax bx =++与x 轴交于点(1,0),(3,0)A B -,与y 轴交于点C ,点P 是第一象限内抛物线上的动点. (1)求抛物线的解析式;(2)连接BC 与OP ,交于点D ,当:PD OD 的值最大时,求点P 的坐标;(3)点M 在抛物线上运动,点N 在y 轴上运动,是否存在点M 、点N 使90CMN ∠=︒,且CMN △与BOC 相似,若存在,请直接写出点M 的坐标.10.如图,已知抛物线23y ax bx =+-与x 轴交于()2,0A -、()6,0B 两点,与y 轴交于C 点,设抛物线的顶点为D .过点D 作DE x ⊥轴,垂足为E .P 为线段DE 上一动点,(),0F m 为x 轴上一点,且PC PF ⊥.(1)求抛物线的解析式:(2)①当点P 与点D 重合时,求m 的值;①在①的条件下,将COF 绕原点按逆时针方向旋转90︒并平移,得到111C O F △,点C ,O ,F 的对应点分别是点1C ,1O ,1F ,若COF 的两个顶点恰好落在抛物线上,直接写出点1F 的坐标; (3)当点P 在线段DE 上运动时,求m 的变化范围.11.综合与实践如图1,抛物线y =﹣83x 2﹣94x +6与x 轴交于点A 和点B (点A 在点B 的左侧),与y 轴交于点C .(1)求直线AC 的表达式;(2)点E 在抛物线的对称轴上,在平面内是否存在点F ,使得以点A ,C ,E ,F 为顶点的四边形是矩形?若存在,请直接写出点E 的坐标;若不存在,请说明理由;(3)如图2,设点P 从点O 出发以1个单位长度/秒的速度向终点A 运动,同时点Q 从点A 出发以54个单位长度/秒的速度向终点C 运动,运动时间为t 秒,当①OPQ 的平分线恰好经过OC 的中点时,求t 的值.12.抛物线23y x bx =-++与x 轴交于(3,0),(1,0)A B -两点,与y 轴交于点C ,点D 为抛物线的顶点.(1)求抛物线的表达式及顶点D 的坐标; (2)在直线AC 上方的抛物线上找一点P ,使12ACPACDSS =,求点P 的坐标;(3)在坐标轴上找一点M ,使以点B ,C ,M 为顶点的三角形与ACD △相似,直接写出点M 的坐标.13.如图,将抛物线2443y x =-+平移后,新抛物线经过原抛物线的顶点C ,新抛物线与x 轴正半轴交于点B ,联结BC ,tanB 4=,设新抛物线与x 轴的另一交点是A ,新抛物线的顶点是D .(1)求点D 的坐标;(2)设点E 在新抛物线上,联结,AC DC ,如果CE 平分DCA ∠,求点E 的坐标;(3)在(2)的条件下,将抛物线2443y x =-+沿x 轴左右平移,点C 的对应点为F ,当DEF 和ABC 相似时,请直接写出平移后得到抛物线的表达式.14.在平面直角坐标系xOy 中,已知二次函数2(0)y ax bx c a =++≠的图象与x 轴交于A B ,两点(点A 在点B 的左边),与y 轴交于点C ,其顶点的横坐标为1,且过点(2)3,和(312)--,. (1)求此二次函数的表达式;(2)若直线:(0)l y kx k =≠与线段BC 交于点D (不与点B C ,重合),则是否存在这样的直线l ,使得以B O D ,,为顶点的三角形与BAC 相似?若存在,求出该直线的函数表达式及点D 的坐标;若不存在,请说明理由;(3)若点P 是位于该二次函数对称轴右边图象上不与顶点重合的任意一点,试比较锐角PCO ∠与ACO ∠的大小(不必证明),并写出此时点P 的横坐标p x 的取值范围.15.如图1,在平面直角坐标系中,抛物线2y x bx c =-++经过点A 和点()10B ,,交y 轴于点()0,3C .(1)求抛物线的解析式及顶点D 的坐标;(2)点P 是抛物线上A 、D 之间的一点,过点P 作PE x ⊥轴于点E ,PG y ⊥轴,交抛物线于点G ,过点G 作GF x ⊥轴于点F ,当矩形PEFG 的周长最大时,求点P 的坐标;(3)如图2,连接AD 、BD ,点M 在线段AB 上(不与A 、B 重合),作直线MN x ⊥轴交抛物线于点N ,是否存在点M ,使得AMN 与OBC 相似?若存在,求出点M 的坐标;若不存在,请说明理由.16.在平面直角坐标系xOy 中,已知抛物线2y ax bx c =++与x 轴交于()1,0A -,()4,0B 两点,与y 轴交于点()0,2C -.(1)求抛物线的函数表达式;(2)如图1,点D 为第四象限抛物线上一点,连接AD ,BC 交于点E ,求DEAE的最大值; (3)如图2,连接AC ,BC ,过点O 作直线//l BC ,点P ,Q 分别为直线l 和抛物线上的点,试探究:在第一象限是否存在这样的点P ,Q ,使PQB CAB ∽.若存在,请求出所有符合条件的点P 的坐标;若不存在,请说明理由.17.如图1,在平面直角坐标xoy 系中,已知抛物线y =-12x 2+bx +c 与x 轴交于点A (﹣4,0)、B(2,0),与y 轴交于点C . (1)求抛物线的解析式;(2)如图2,沿直线AC 平移抛物线y =-12x 2+bx +c ,使得A 、C 两点的对应点E 、F 始终在直线AC上.①设在平移过程中抛物线与y 轴交于点M ,求点M 纵坐标的最大值;①试探究抛物线在平移过程中,是否存在这样的点E ,使得以A 、E 、B 为顶点的三角形与①ABF 相似.若存在,请求出此时点E 的坐标;若不存在,请说明理由.18.如图,已知二次函数y =ax 2+bx +c 的图象经过点A (﹣1,0),B (4,0),E (1,3),与y 轴交于点C .(1)求该二次函数表达式;(2)判断△ABC 的形状,并说明理由;(3)P 为第一象限内该二次函数图象上一动点,过P 作PQ ∥AC ,交直线BC 于点Q ,作PM ∥y 轴交BC 于M .①求证:△PQM ∽△COA ; ②求线段PQ 的长度的最大值.19.如图,直线y x n =-+与x 轴交于点(4,0)A ,与y 轴交于点B ,抛物线2y x bx c =-++经过点A ,B .(1)求抛物线的解析式;(2)(m,0)E 为x 轴上一动点,过点E 作ED x ⊥轴,交直线AB 于点D ,交抛物线于点P ,连接BP . ①点E 在线段OA 上运动,若BPD ∆直角三角形,求点E 的坐标;①点E 在x 轴的正半轴上运动,若45PBD CBO ∠+∠=︒.请直接写出m 的值.20.如图,点A ,B 都在x 轴上,过点A 作x 轴的垂线交抛物线24y x x =-+于点C ,过点B 作x 轴的垂线交该抛物线于点D ,点C ,D 都在第一象限,点D 在点C 的右侧,DE AC ⊥于点E ,连结CD ,BE ,//CD EB .(1)若2OA =,求AB 的长.(2)若点A 是线段OB 的中点,求点E 的坐标.(3)根据(2)的条件,连结OD ,动点P 在线段OB 上,作PQ OD ⊥交OD 于点Q ,当PDQ 与CDE △相似时,求OQOD的值.答案1.(1)①①①;(3)m =3,相似;m =1,不相似2.(1)3;(2)(5,0);(3)2y 3.(1)2y x 2x 3=-++;(2)()2,3D ;(3)57,24D ⎛⎫ ⎪⎝⎭或315,24⎛⎫ ⎪⎝⎭4.(1)214y x x =-或21(2)14y x =--;(2)点C 的坐标为(6,3)或51,4⎛⎫- ⎪⎝⎭;(3)164t t --+;12C x ≥ 5.(1)(2)①9;①(4,6)D 或25(3,)4D .6.(1)213222y x x =--;(2)max ()=EG E 的坐标为(2,3)-;(3)存在,点P 的坐标为6834,99⎛⎫ ⎪⎝⎭或⎝⎭. 7.(1)A (-1,0),B (1,0),C (0,-1);(2)四边形ACBP 的面积为4;(3)M 点的坐标为(-2,3)或(43,79)或(4,15). 8.(1)抛物线2L 的解析式为21382y x x =-++.(2)函数3L 的解析式为:2121322y x x =-+-或2126323y x x =-+-. 9.(1)2 246y x x =-++;(2)点P 的坐标为315,22⎛⎫ ⎪⎝⎭;(3)存在,点M 的坐标为939,48⎛⎫ ⎪⎝⎭. 10.(1)2134y x x =--;(2)①4;①1(2,9)16或13(6-,49)144;(3)748m ≤≤ 11.(1)直线AC 的表达式为364y x =+;(2)点E 1的坐标为20(3,)3--;点E 2的坐标为(3,10)-;点E 3的坐标为(3,3-+;点E 4的坐标为(3,3--;(3)t 的值为5.12.(1)223y x x =--+;(1,4)D -;(2)⎝⎭P 或⎝⎭;(3)点M 的坐标为(0,0)或(9,0)-,或10,3⎛⎫- ⎪⎝⎭. 13.(1)16(1,)3-;(2)(2,4)-;(3)242()433y x =-++或241()4312y x =--+ 14.(1)2y x 2x 3=-++;(2)存在,点D 的坐标分别为3944⎛⎫ ⎪⎝⎭,或(12),; (3)当5p x >时,锐角PCO ACO ∠<∠;当5p x =时,锐角PCO ACO ∠=∠;当25p x <<时,锐角PCO ACO ∠>∠.15.(1)223y x x =--+,()1,4-;(2)()2,3P -;(3)存在,()2,0-或2,03⎛⎫ ⎪⎝⎭16.(1)213222y x x =--;(2)45;(3)存在,点P 的坐标为6834,99⎛⎫ ⎪⎝⎭或⎝⎭17.(1)2142y x x =--+;(2)①6;①存在,E (62--或(62--18.(1)二次函数表达式为:213222y x x =-++ ;(2)△ABC 为直角三角形;(3); 19.(1)234y x x =-++;(2)①(2,0)或(3,0);①7m =或134.20.(1;(2)1296,749E ⎛⎫ ⎪⎝⎭;(3)2或4932。
中考数学专题训练:相似三角形(附参考答案)

中考数学专题训练:相似三角形(附参考答案)1.若a3=b2,则a+bb的值为( )A.32B.53C.52D.232.如图,在△ABC中,DE∥BC,AD=2,BD=3,AC=10,则AE的长为( )A.3 B.4C.5 D.63.如图,AD∥BE∥FC,直线l1,l2分别与三条平行线交于点A,B,C和点D,E,F.若AB=3,BC=5,DF=12,则EF的长为( )A.4.5 B.6C.7.5 D.84.如图,小雅同学在利用标杆BE测量建筑物的高度时,测得标杆BE高1.2 m,又知AB∶BC=1∶8,则建筑物CD的高是( )A.9.6 m B.10.8 mC.12 m D.14 m5.如图,在平面直角坐标系中,△ABC的三个顶点分别为A(1,2),B(2,1),C(3,2).现以原点O为位似中心,在第一象限内作与△ABC的相似比为2的位似图形△A′B′C′,则顶点C′的坐标是( )A.(2,4) B.(4,2)C.(6,4) D.(5,4)6.如图(单位:mm),小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为5 m时,标准视力表中最大的“E”字高度为72.7 mm,当测试距离为3 m时,最大的“E”字高度为( )A.121.17 mm B.43.62 mmC.29.08 mm D.4.36 mm7.如图,AC是□ABCD的对角线,点E在CD的延长线上,连接BE分别交AC,AD 于点F,G,则下列式子一定正确的是( )A.AFCF =AGDGB.ABCE=CFAFC.BFFG =EFBFD.ADDG=ABDE8.如图,在△ABC中,D,E分别为边AB,AC上的点,试添加一个条件:________________________,使得△ADE与△ABC相似.(任意写出一个满足的条件即可)9.如图,已知在梯形ABCD中,AD∥BC,S△ABDS△BCD =12,则S△BOCS△BCD=______.10.如图,在矩形ABCD中,若AB=3,AC=5,AFFC =14,则AE的长为_____.11.如图,为了测量山坡的护坡石坝高,把一根长为4.5 m 的竹竿AC斜靠在石坝旁,量出竿上AD长为1 m时,它离地面的高度DE为0.6 m,则坝高CF为________m.12.已知在平面直12角坐标系中,△AOB的顶点分别为A(2,1),B(2,0),O(0,0).若以原点O为位似中心,相似比为2,将△AOB放大,则点A的对应点的坐标为__________________________.13.如图,在△ABC中,点D,E分别是AB,AC的中点.若S△ADE=2,则S△ABC=_____.14.如图,在平面直角坐标系中,△ABC与△ODE是位似图形,则它们位似中心的坐标是____________.15.如图,在△ABC和△DEC中,∠A=∠D,∠BCE=∠ACD.(1)求证:△ABC∽△DEC;(2)若S△ABC∶S△DEC=4∶9,BC=6,求EC的长.16.如图,在△ABC中,AB=4,BC=5,点D,E分别在BC,AC上,CD=2BD,CE =2AE,BE交AD于点F,则△AFE面积的最大值是______.17.小孔成像的示意图如图所示,光线经过小孔O,物体AB在幕布前形成倒立的实像CD(点A,B的对应点分别是C,D).若物体AB的高为6 cm,小孔O到物体和实像的水平距离BE,CE分别为8 cm,6 cm,则实像CD的高度为________cm.18.如图,在正方形ABCD中,点E是边CD上一点,连接BE,以BE为对角线作正方形BGEF,边EF与正方形ABCD的对角线BD相交于点H,连接AF,有以下五个结论:①∠ABF=∠DBE;②△ABF∽△DBE;③AF⊥BD;④2BG2=BH·BD;⑤若CE∶DE=1∶3,则BH∶DH=17∶16.你认为其中正确的是____________.(填写序号)19.已知,如图1,若AD是△ABC中∠BAC的内角平分线,通过证明可得ABAC =BDCD,同理,若AE是△ABC中∠BAC的外角平分线,通过探究也有类似的性质.请你根据上述信息,求解如下问题:如图2,在△ABC中,BD=2,CD=3,AD是△ABC的内角平分线,则△ABC的BC边上的中线长l的取值范围是_____________.20.如图,在等腰三角形ABC中,AB=AC,点E,F在线段BC上,点Q在线段AB 上,且CF=BE,AE2=AQ·AB.求证:(1)∠CAE=∠BAF;(2)CF·FQ=AF·BQ.21.在等腰三角形ABC中,AB=AC,点D是边BC上一点(不与点B,C重合),连接AD.(1)如图1,若∠C=60°,点D关于直线AB的对称点为点E,连接AE,DE,则∠BDE=________.(2)若∠C=60°,将线段AD绕点A顺时针旋转60°得到线段AE,连接BE.①在图2中补全图形;②探究CD与BE的数量关系,并证明.(3)如图3,若ABBC =ADDE=k,且∠ADE=∠C,试探究BE,BD,AC之间满足的数量关系,并证明.参考答案1.C 2.B 3.C 4.B 5.C 6.B 7.C8.ADAB =AEAC(答案不唯一) 9.2310.1 11.2.712.(4,2)或(-4,-2)13.8 14.(4,2) 15.(1)证明略(2)EC=916.43 17.4.5 18.①②③④ 19.12<l<25220.(1)证明略(2)证明略21.(1)30°(2)①图略②CD与BE的数量关系为CD=BE,证明略(3)AC=k(BD+BE),证明略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
备战中考数学专题练习(全国通用)-相似三角形判定定理(含解析)一、单选题1.如图,△ABC中,∠BCD=∠A,DE∥BC,与△ABC相似的三角形(△ABC自身除外)的个数是()A. 1个B. 2个C. 3个D. 4个2.如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①、②、③、④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是()A. ①与②相似B. ①与③相似C. ①与④相似D. ②与④相似3.如图,P为线段AB上一点,AD与BC交于E,∠CPD=∠A=∠B,BC交PD于F,AD交PC 于G,则图中相似三角形有()A. 1对B. 2对C. 3对D. 4对4.如图,若D、E分别为△ABC中AB、AC边上的点,且∠AED=∠B ,AD=3,AC=6,DB=5,则AE的长度为()A. B. C. D. 45.如图,小明把一个边长为10的正方形DEFG剪纸贴在△ABC纸片上,其中AB=AC=26,BC=20,正方形的顶点D,G分别在边AB、AC上,且AD=AG,点E、F在△ABC内部,则点E到BC 的距离为()A. 1B. 2C.D.6.如图,能使△ACD∽△BCA全等的条件是()A. B. AC2=CD CB C. D. CD2=AD BD7.如图,已知点P在△ABC的边AC上,下列条件中,不能判断△ABP∽△ACB的是()A. ∠ABP=∠CB. ∠APB=∠ABCC. AB2=AP•ACD.8.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是()A. ∠ABP=∠CB. ∠APB=∠ABCC. =D.9.如图,在△ABC中,点D在AB上,下列条件能使△BCD和△ABC相似的是()A. ∠ACD=∠BB. ∠ADC=∠ACBC. AC2=AD•ABD. BC2=BD•BA10.如图,已知△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列一个条件后,仍无法判定△ABC∽△DAE的是()A. =B. ∠B=∠DC. AD∥BCD. ∠BAC=∠D二、填空题11.如图,△ABC中,点D、E分别是AB、AC边上的点,欲使△ADE∽△ACB,则需添加的一个条件是________.(只写一种情况即可)12.如图,在□ABCD中,AB=6,AD=8,∠B=60°,∠BAD 与∠CDA的角平分线AE、BF相交于点G,且交BC于点E、F,则图中阴影部分的面积是________.13.在Rt△ABC中,C为直角顶点,过点C作AB的垂线,若D为垂足,若AC、BC为方程x2﹣6x+2=0的两根,则AD•BD的值等于________14.如图,若CD是Rt△ABC斜边CD上的高,AD=3cm,CD=4cm,则BC的长等于________ cm.15.如图,路灯距离地面8米,身高1.6米的小亮站在距离灯的底部(点O)20米的A处,则小亮的影子AM长为________ 米.16.如图,在梯形ABCD中,AB∥DC,AD=2,BC=6,若△AOB的面积等于6,则△AOD的面积等于________.17.如图,△ABC中,AB=5,BC=3,CA=4,D为AB的中点,过点D的直线与BC交于点E,若直线DE截△ABC所得的三角形与△ABC相似,则DE=________ .18.已知菱形ABCD的边长是8,点E在直线AD上,若DE=3,连接BE与对角线AC相交于点M,则的值是________.19.如图,AB、CD相交于点O,试添加一个条件使得△AOD∽△COB,你添加的条件是________ .(只需写一个)三、解答题20.如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在BD上由点B向点D方向移动,当点P移到离点B多远时,△APB和△CPD相似?21.如图,中,为上一点,,,,求的长.四、综合题22.在菱形ABCD中,AB=2 ,AC是对角线,∠B=60°,点E在BC边上,点F在DC边上,且∠EAF=60°,AE与DC的延长线交于点M,AF与BC的延长线交于点N.(1)如图1,若点E为BC边上的中点.①求证:△ACM≌△ACN;(2)如图2,若点E为BC边上的任意点(不与点B,C重合),请说明CM•NC是一个定值.23.如图,在△ABC中,∠C=90°,AB=10,BC=8,P、Q分别是AB、BC边上的点,且AP=BQ=a (其中0<a<8).(1)若PQ⊥BC,求a的值;(2)若PQ=BQ,把线段CQ绕着点Q旋转180°,试判别点C的对应点C’是否落在线段QB 上?请说明理由.24.如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB于D.(1)求证:△ACB∽△ADE;(2)求AD的长度.25.如图,已知AD为△ABC的角平分线,∠ADE=∠B。
(1)求证:△ABD∽△ADE。
(2)若AB =9,AE=4求AD的长。
答案解析部分一、单选题1.【答案】B【考点】相似三角形的判定【解析】【解答】∵DE∥BC∴∴△BCD∽△ABC∴有两个与△ABC相似的三角形故答案为:B.【分析】根据平行于三角形一边的直线,截其它两边,所截得的三角形与原三角形相似得出△ADE ∽△ABC, 由有两个角对应相等的三角形三角形相似得出△BCD∽△ABC,从而得出有两个与△ABC相似的三角形。
2.【答案】B【考点】相似三角形的判定【解析】【解答】解:∵OA:OC=OB:OD,∠AOB=∠COD,∴△AOB∽△COD,故答案为:B.【分析】根据相似三角形的判定方法两边对应成比例且夹角相等两三角形相似;得到△AOB∽△COD.3.【答案】C【考点】相似三角形的判定【解析】【分析】先根据条件证明△PCF∽△BCP,利用相似三角形的性质:对应角相等,再证明△APD∽△PGD,进而证明△APG∽△BFP再证明时注意图形中隐含的相等的角。
【解答】∵∠CPD=∠B,∠C=∠C,∴△PCF∽△BCP.∵∠CPD=∠A,∠D=∠D,∴△APD∽△PGD.∵∠CPD=∠A=∠B,∴∠APG=∠BFP,∴△APG∽△BFP.故选C.【点评】本题考查相似三角形的判定.识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角。
4.【答案】D【考点】相似三角形的判定与性质【解析】【解答】∵∠A=∠A ,∠AED=∠B ,∴△ADE∽△ACB ,∴AE:AB=AD:AC ,又∵AD=3,AC=6,DB=5,∴AB=AD+DB=8,∴AE=8×3÷6=4.故选D .【分析】根据相似三角形的判定首先证出△ADE∽△ACB ,然后根据相似三角形的性质得出AE:AB=AD:AC ,从而求出AE的长度.5.【答案】B【考点】相似三角形的判定与性质【解析】【解答】解:过点A作AM⊥BC,交DG于点H,BC于点M,∵AB=AC,BC=20,∴BM=MC=BC=10,∴AH==24,∵正方形的顶点D,G分别在边AB、AC上,且AD=AG,∴DG⊥AH,DH=HG=DG,∵DG=10,∴DH=5,∵∠BAM=∠MAB,∠ABC=∠ADH,∴△ADH∽△ABM,∴,∴∴AD=13,∴AH=HM=12,∴点E到BC的距离为:12﹣10=2;故选B.【分析】过点A作AM⊥BC,交DG于点H,BC于点M,根据等腰三角形的性质和勾股定理求出AH,再根据正方形的顶点D,G分别在边AB、AC上,且AD=AG,得出DG⊥AH,DH=HG= DG,求出DH,再根据AA证出△ADH∽△ABM,求出AD,从而得出AH,最后根据HM的长减去正方形的长就是点E到BC的距离,代值计算即可得出答案.6.【答案】B【考点】相似三角形的判定【解析】∵∠C=∠C当∠ADC=∠BAC或∠CAD=∠B或CD:AC=AC:BC或AC 2 =CD CB∴当AC 2 =CD CB时,△ACD ∽△BCA故选B.7.【答案】D【考点】相似三角形的判定【解析】【解答】解:A、∵∠A=∠A,∠ABP=∠C,∴△ABP∽△ACB,故本选项错误;B、∵∠A=∠A,∠APB=∠ABC,∴△ABP∽△ACB,故本选项错误;C、∵∠A=∠A,AB2=AP•AC,即,∴△ABP∽△ACB,故本选项错误;D、根据和∠A=∠A不能判断△ABP∽△ACB,故本选项正确;故选:D.【分析】根据相似三角形的判定定理(①有两角分别相等的两三角形相似,②有两边的比相等,并且它们的夹角也相等的两三角形相似)逐个进行判断即可.8.【答案】D【考点】相似三角形的判定【解析】【解答】A、当∠ABP=∠C时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项不符合题意;B、当∠APB=∠ABC时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项不符合题意;C、当时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项不符合题意;D、无法得到△ABP∽△ACB,故此选项符合题意.故答案为:D.【分析】(1)当∠ABP=∠C时,而∠A是公共角,所以根据有两个角相等的两个三角形相似可得△ABP∽△ACB;(2)当∠APB=∠ABC时,方法同(1)可得△ABP∽△ACB;(3)当,而∠A是公共角,根据两边的比相等,且这两边的夹角也相等,那么这两个三角形相似可得△ABP∽△ACB;(4)当,虽然∠A是公共角,但不符合相似三角形的判定定理,所以不能判断两个三角形相似。
9.【答案】D【考点】相似三角形的判定【解析】【解答】解:若BC2=BD•BA,则有=,且∠B=∠B,∴△BCD∽△BAC,故选D【分析】由两边对应成比例且夹角相等得到三角形相似即可得证.10.【答案】B【考点】相似三角形的判定【解析】【解答】解:∵∠C=∠AED=90°,=,∴△ABC∽△DAE,故选项A可以证明相似;∵∠C=∠AED=90°,∠B=∠D,∴△ABC∽△ADE,故B选项错误;∵AD∥BC,∴∠B=∠DAE,∵∠C=∠AED=90°,∴△ABC∽△DAE,故选项C可以证明相似;∵∠BAC=∠D,∠C=∠AED=90°,∴△ABC∽△DAE,故选项D可以证明相似;故选B.【分析】根据已知及相似三角形的判定方法对各个选项进行分析,从而得到最后答案.二、填空题11.【答案】∠ADE=∠C或∠AED=∠B或【考点】相似三角形的判定【解析】【解答】解:∵∠A=∠A∴当∠ADE=∠C或∠AED=∠B或时,△ADE∽△ABC,故答案为:∠ADE=∠C或∠AED=∠B或【分析】已知∠A等于∠A,再添加一个对应角相等或对应边成比例即可证△ADE∽△ACB。
