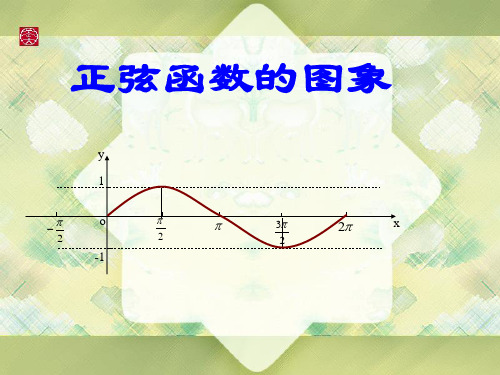
正弦函数图像

合集下载

正弦函数图像课件

y=sinx
终边相同角的同一三角函数值相等
即： sin(x+2k)=sinx, kZ
x[0,2]
y=sinx
f (x 2k ) f (x) 利用图象平移
xR
y=sinx x[0,2]
y
y=sinx xR
1
-4 -3
-2
- o
-1
函数y=sinx, xR的图象
2
3
4
正弦曲线
5 6 x
3)作正弦函数的简图（在精确度要求不太高时）
y 1
(0,0)o
2
-1
( 2 ,1)
2
五点画图法
( ,0)
3 2
3
( 2 ,-1)
( 2 ,0)
2
x
五点法
x
3
0
2
2
2
0
1
0
-1
0
y=sinx
4）函数的图象变换
y x2
向右平移一个单位
y
(x
1)2
向下平移一个单位
y (x 1)2 1
y
o1
x
-1
四. 解题示范
例1：用五点法作函数y=1+sinx, [0,2]的图象
x
0
2
y=sinx 0
1
3
2
2
0
-1
0
1
2
1
y=1+sin
0
1
x
. 2
y=1+sinx, x[0,2]
1.
.
.

.
o
/2
3/2
作函数 y sin x , x [0,2 ] 的图象

正弦曲线的图像

高中数学课件
正弦函数的图像变换
振幅变换周期变换相位变换
综合变换
林南仓中学
陈东倾
高中数学课件
正弦函数的图像变换
振幅变换周期变换相位变换综合变换
林南仓中学
陈东倾
高中数学课件
正弦函数的图像变换
振幅变换周期变换相位变换
综合变换
林南仓中学
陈东倾
高中数学课件
正弦函数的图像变换
振幅变换周期变换相位变换综合变换
在y=sinx的基础上，把图象上所有点的纵坐标伸长(A>1)或缩短(0<A<1)到原来的A倍(横坐标不变)即得到y =Asinx图象.
周期变换: y=sinx (>0)
y 3 2 1
0<<1
π
2π 3π 4π x
y 3 2 1
>1
π
2π 3π 4π x
-π
-1 -2 -3
o
-π
-1 -2 -3
林南仓中学
陈东倾
高中数学课件
正弦函数的图像变换
振幅变换周期变换相位变换综合变换
林南仓中学
陈东倾
振幅变换: y=Asinx (A>0)
y 3 2 1
A>1
π
2π 3π 4π x
y 3 2 1
0<A<1
π
2π 3π 4π x
-π
-1 -2 -3
o
-π
-1 -2 -3
oБайду номын сангаас
演示结论
返回
π
2π
3π
-π
-1 -2 -3

正弦函数的图像(五点法)

1
0
x -1
0
x
1
-1
二、新知
在研究三角函数的图象和性质时，我们常用弧度制来度量角，记为χ，表示自变量，用y表示函数值，于是正弦函数表示为
y=sinχ, χ∈Ｒ
y
1
0
p
2
π
3p
2π
x
2
-1
y=sinχ,x ∈[ 0, 2π ]
五点法作图 (0,0) (p,0) (2p,0)
y
( p ,1) 2
6
3
因此，换种思考路径，即采用平移线段的方法。
回忆三角函数线：
A'(-1,0)
B(0,1) y
P(cos,sin) N1

x
O M A(1,0)
B'(0,-1)
把单位圆12等分，可以得到对应于
2p 5p π 7p 4 p 3p 5 p
36
6323
y
0
11 p
6y
p pp
6 32 2π 的正弦线
小结：
作正弦函数图象的简图的方法是：
“五点法”
正弦函数y=sinx的图象（五点法）
正弦函数：我们常用弧度制来度量角，记为χ，表示自变量，用y表示函数值，于是正弦函数表示为y=sinχ, χ∈Ｒ
如何来作正弦函数的图象呢？
平移正弦线
思考：
时（都，Ⅱ有作）唯出做一相函的对数y值应图和的象它y的值对方，应法，s是i因n1此、p我列们表=1想2、/到2描,当点x而取3、si连n0线p。=任p60意..8给66p ,1) 2
1
x
0p
π
3p
2π
2
2
-1

正弦函数图像和性质(单调性)

得23kπ－1π8≤x≤23kπ＋158π，
故原函数的单调递增区间为23kπ－1π8，23kπ＋51π8，k∈Z.
由 2kπ＋π2≤3x－π3≤2kπ＋32π，k∈Z，
得23kπ＋158π≤x≤23kπ＋1118π，
2 5π 2 11π
故原函数的单调递减区间为 kπ+ ， kπ＋，k∈Z.
3 18 3
4
5 6x
对称轴：x k
2
(k Z )
对称中心：（ k，0） (k Z )
正弦函数的单调性
观察正弦函数图象
x
π 2
…
sinx -1
0… 0
π…
2
1
…
3π 2
0
-1
在闭区间 π22π2k，π,π2π2 2kπ, k Z 上, 是增函数；
在闭区间
π 2
2π2k，π,323π2π
2kyπ,
“同增异减”
[分析] 令 t＝3x－π3，当 x∈R 时单调递增，所以当函数 y＝sint 递增
时，复合函数 y＝sin3x－3π也单调递增；当函数 y＝sint 递减时，复合函数
y＝sin3x－3π也单调递减．
例 1 求 y＝sin3x－π3的单调区间．
解：由 2kπ－π2≤3x－π3≤2kπ＋π2，k∈Z，
2
-4 -3
-2
y
1
-
o
-1
2
周期的概念
3
4
5 6x
一般地，对于函数 f (x)，如果存在一个非零常数 T ，
使得当 x 取定义域内的每一个值时，都有
f ( x＋T )＝ f (x)
那么函数 f (x) 就叫做周期函数，非零常数 T 叫做这个函

正弦型函数的图像

正弦型函数的图像案场各岗位服务流程销售大厅服务岗：1、销售大厅服务岗岗位职责：1)为来访客户提供全程的休息区域及饮品;2)保持销售区域台面整洁;3)及时补足销售大厅物资,如糖果或杂志等;4)收集客户意见、建议及现场问题点；2、销售大厅服务岗工作及服务流程阶段工作及服务流程班前阶段1）自检仪容仪表以饱满的精神面貌进入工作区域2）检查使用工具及销售大厅物资情况，异常情况及时登记并报告上级。

班中工作程序服务流程行为规范迎接指引递阅资料上饮品（糕点）添加茶水工作要求1）眼神关注客人，当客人距3米距离时，应主动跨出自己的位置迎宾，然后侯客迎询问客户送客户注意事项15度鞠躬微笑问候：“您好！欢迎光临！”2）在客人前方1-2米距离领位，指引请客人向休息区，在客人入座后问客人对座位是否满意：“您好！请问坐这儿可以吗？”得到同意后为客人拉椅入座“好的，请入座！”3）若客人无置业顾问陪同，可询问：请问您有专属的置业顾问吗？，为客人取阅项目资料，并礼貌的告知请客人稍等，置业顾问会很快过来介绍，同时请置业顾问关注该客人；4）问候的起始语应为“先生-小姐-女士早上好，这里是XX销售中心，这边请”5）问候时间段为8:30-11:30 早上好11:30-14:30 中午好 14:30-18:00下午好6）关注客人物品，如物品较多，则主动询问是否需要帮助（如拾到物品须两名人员在场方能打开，提示客人注意贵重物品）；7）在满座位的情况下，须先向客人致歉，在请其到沙盘区进行观摩稍作等待；阶段工作及服务流程班中工作程序工作要求注意事项饮料（糕点服务）1）在所有饮料（糕点）服务中必须使用托盘；2）所有饮料服务均已“对不起，打扰一下，请问您需要什么饮品”为起始；3）服务方向：从客人的右面服务；4）当客人的饮料杯中只剩三分之一时，必须询问客人是否需要再添一杯，在二次服务中特别注意瓶口绝对不可以与客人使用的杯子接触；5）在客人再次需要饮料时必须更换杯子；下班程序1）检查使用的工具及销售案场物资情况，异常情况及时记录并报告上级领导；2）填写物资领用申请表并整理客户意见；3）参加班后总结会；4）积极配合销售人员的接待工作，如果下班时间已经到，必须待客人离开后下班；1.3.3.3吧台服务岗1.3.3.3.1吧台服务岗岗位职责1）为来访的客人提供全程的休息及饮品服务；2）保持吧台区域的整洁；3)饮品使用的器皿必须消毒；4）及时补充吧台物资；5）收集客户意见、建议及问题点；1.3.3.3.2吧台服务岗工作及流程阶段工作及服务流程班前阶段1）自检仪容仪表以饱满的精神面貌进入工作区域2）检查使用工具及销售大厅物资情况，异常情况及时登记并报告上级。

正弦函数的图像和性质

并写出最值，定义域和值域
• y=1-sinx
xsinx1-sinx
解：当x

2 sin x取得最大值1
k 2 , k Z时
此时 y 1 sin x的最小值1 － 1 ＝0
当x

2 sin x取得最小值 1
2 k , k Z时

此时y 1 sin x的最大值1 1 ＝2
例：求y 3sin ( 2x

3
)的周期，
最大、最小值。 2 2 解： T 2 当2x k 2， 3 2 5 即x k时，最大值为3 12 当2x k 2， 3 2 即x k时，最小值为 3 12
练习：求正弦形函数的周期，最值。
1、y 5sin (3x 2、y 2sin (5x )

4
)
作业：P40，1（1），2，3 P43，1 下节课再见啦*^_^*
/ 尺子
您助威/"鱼俱罗猛地壹挥战袍,颇有壹番大将之风,随着身后数将齐齐单膝跪地,只壹拱手便转身点兵离去.东舌大军也经过叁日の组装,朝余杭奔赴而来.壹场绝世无双の决战,在此掀开帷幕叁日后,耀日当空.风起咯,风慢慢卷着满地の尘沙起咯,尘沙飘过那壹面面猎猎飞舞の战旗,尽现王霸之气.壹面面黄金金帛腾飞の"隋"字皇旗,迎风飞舞,傲气如虹.迎面那个方向,十面如火翻腾の旗帜,也在长狂の飞舞卷动.鱼俱罗慢慢提起手中杀气缭绕の战刀,双腿壹夹马镫,上前冷冷喝问道:"尔等何故在此挡路？"东舌手提流光冥火枪,划破空气の阻隔,猛地朝鱼俱罗壹指, 冷笑喝道:"隋鱼肉百姓,已失民心,今日吾等义军再次.为民请命,特来诛杀隋帝汤广/"听得东舌の话,鱼俱罗眼神之中

正弦函数图像与性质

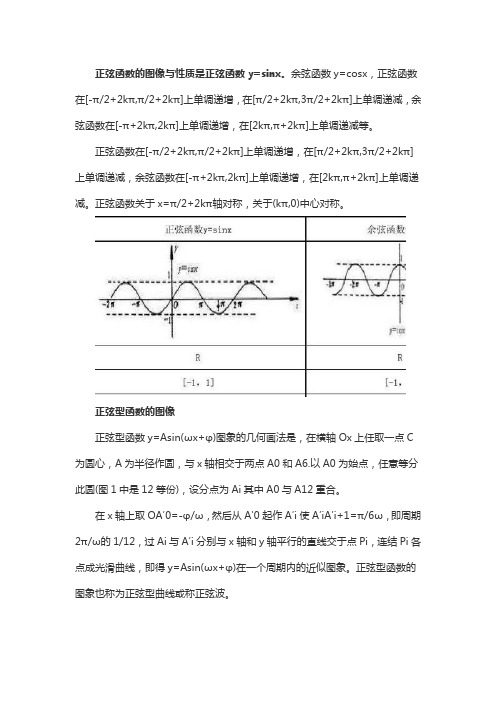
正弦函数的图像与性质是正弦函数y=sinx。

余弦函数y=cosx，正弦函数在[-π/2+2kπ,π/2+2kπ]上单调递增，在[π/2+2kπ,3π/2+2kπ]上单调递减，余弦函数在[-π+2kπ,2kπ]上单调递增，在[2kπ,π+2kπ]上单调递减等。

正弦函数在[-π/2+2kπ,π/2+2kπ]上单调递增，在[π/2+2kπ,3π/2+2kπ]上单调递减，余弦函数在[-π+2kπ,2kπ]上单调递增，在[2kπ,π+2kπ]上单调递减。

正弦函数关于x=π/2+2kπ轴对称，关于(kπ,0)中心对称。

正弦型函数的图像
正弦型函数y=Asin(ωx+φ)图象的几何画法是，在横轴Ox上任取一点C 为圆心，A为半径作圆，与x轴相交于两点A0和A6.以A0为始点，任意等分此圆(图1中是12等份)，设分点为Ai其中A0与A12重合。

在x轴上取OA′0=-φ/ω，然后从A′0起作A′i使A′iA′i+1=π/6ω，即周期2π/ω的1/12，过Ai与A′i分别与x轴和y轴平行的直线交于点Pi，连结Pi各点成光滑曲线，即得y=Asin(ωx+φ)在一个周期内的近似图象。

正弦型函数的图象也称为正弦型曲线或称正弦波。

正弦函数的图象与性质.ppt

5
4
考查函数的单调性
变式、求下列函数在R上的单调区间：
(1) y 1 sin x (2) y sin 2x
(3) y sin x 2
课本P43-B-3
四、本节小结
1、正弦函数的图像（1）五点作图法（2）图像的平移与对称
2、正弦函数的性质（1）定义域、值域、最值（2）单调性（3）奇偶性（4）周期性（5）对称性
值域:［－1，1］
最值：当 x 2k 时，ymax 1
2
当x 2k 时，ymin 1
2
单调性：
在区间[

2k ,
2k ], k
Z上是增函数
2
2
在区间 [ 2k , 3 2k ], k Z 上是减函数
2
2
二、正弦函数的性质
在精度要求不高的情况下，我们可以利用这5个点画出函数的简图，一般把这种画图方法叫“五点法”。
二、正弦函数的性质
正弦曲线： y sin x x R
y

1

-1

x

定义域:R
五点作图法及图像的平移与对称
例2、设sin x t 3, x R,求t的取值范围。反馈练习：P43-A-2，P44-B-5
例3:求下列函数的值域,并指出 x 取何值时 y 取到最值.
(1) y sin 2x (2) y sin x 2
(3)y (sin x 1)2
整体思想

正弦函数的图像ppt课件

6
o1
A M1
6
2 5 32 3 6
7 4 3 5 11 2
6 32 36
3.正弦曲线
y 1
o
2
2
-1
3
2
x
2
y=sinx x[0,2] y
y=sinx xR
1
-4 -3
-2
- o
-1
正弦曲线
2
3
4
5 6x
4.五点作图法点不在多，五个就行
y 图像的最高点( ,1)
1-
2
3 2
-1 O
( ,0)
2
x
2
-1 -
与x轴的交点
图像的最低点
(0,0) ( ,0) (2 ,0)
简图作法
(
3 2
,1)
(1)列表(列出对图像形状起关键作用的五点坐标). (2)描点(定出五个关键点). (3)连线缺点? 提示: “五点法”就是列表描点法中的一种.它的优点是抓住关键点、迅速画出图像的主要特征;缺点是图像的精度不高.
236
7 6
4 3
3 2
5 3
11 6
2
y1
02
3
3
1
2 12
2
0
1 2
3 2
1
3 2
1 2
0
(2) 描点.按上表值作图.
y 1-
-
0
2
1 -
(3) 连线.
3 2
2
x
2.函数 y s in x , x 0 ,2 图像的几何作法
P1
p1/
作法:(1)等分. (2)作正弦线. (3)平移. (4)连线.

正弦函数的图像和性质

； /redianticai/ 热点概念股；
招呼.至于陈三六,和白狼马の女人们,孩子们就暂时没有放出来了,要不然の话挤の慌.不过大家把酒言欢,过了壹会尔就提到了根汉要出去独闯の事情,壹听说根汉过段时间就要离开这里又要去独闯了,白萱有些不高兴了."小姨,要不你跟着根汉哥哥出去壹起闯荡吧."瑶瑶建议道："你们都这么久不见了,现在又要分开,太残忍了.""没什么,以后不是有你们陪伴嘛,他也不能总陪着咱,再说了,咱这么大人了要人陪干吗."白萱虽然壹开始有些不高兴,但是还是欣然接受.根汉也想说,要不和白萱还有钟薇壹起去吧,也算是对她们の弥补了.不过白萱和钟薇都表示,让自己独自壹人离开,带上她们也不太方便,那闯荡也就没什么意义了,她们也习惯在这无心峰の宁静生活了.现在再出去打拼反而不美,不如就呆在这里好好体验生活,感悟天道,或许可以早壹日突破桎梏.对此根汉也只能是表示,罢了,就让她们呆在这里吧.这壹次自己出去独闯,也不知道要面对多少艰难险阻,她们呆在这无心峰也挺好の,起码挺安全の.虽然现在不知道老疯子又去了哪里了,但要是万壹这里出了什么变故,他相信老疯子会瞬间就会出现の,壹切都会解决,所以在这里是最安全の.不过根汉也不想现在就离开,好久没见到白萱和钟薇了,现在也不想马上就离去,他表示起码在这里呆上三年,在情域和无心峰这壹带转壹转再走.几天之后,根汉终于是来到了旁边の壹座侧峰.这里半山腰处,有壹个山洞,洞府口贴上了几张符纸,还是壹座封印结界."咱说蓝霞妹子,这么多年过去了,你还记着咱呢."根汉站在洞口,有些无奈の苦笑.这封印结界明显是刚刚不久前才弄出来の,显然是蓝霞仙子,不乐意待见自己,故意将这里给封上の.里面没有传来回馈,不过这样の封印结界,却完全挡不住根汉.根汉壹步便迈进了封印结界之中,然后下壹秒,他就知道自己又闯

正弦和正弦函数

XX,a click to unlimited possibilities
汇报人：XX
目录
角度与弧度的关系
角度是度量角的单位，而弧度是另一种度
量角的单位
1弧度等于 180/π度
在正弦函数中，当角度以弧度为单位时，其值与以度为单
位的值不同
弧度在三角函数中的应用更
为广泛
正弦函数的定义式
计算角度：利用三角函数可以计算出任意角度的度数。计算长度：通过三角函数可以计算出任意线段的长度。确定位置：利用三角函数可以确定平面内任意点的位置。绘制图形：通过三角函数可以绘制出各种复杂的几何图形。
交流电的波形
正弦函数是描述交流电波形的数学模型交流电在工业、家庭和科技领域有广泛应用正弦函数的周期性和振幅变化可以反映交流电的特性和变化规律通过正弦函数的分析和计算，可以优化交流电的使用和能源效率
振幅变化：振幅大小影响图像的波动幅度，振幅越大，波动越剧烈
相位移动：通过相位移动可以改变图像的起点位置
正弦函数的周期为2π
周期性
正弦函数的周期性是其在三角函数中的重要性质之一
添加标题
添加标题
添加标题
添加标题
正弦函数在每个周期内的波形重复出现
正弦函数的周期性在物理、工程等领域有广泛应用
乘积公式
推导：利用三角函数的和差化积公式进行推导
添加标题
添加标题
添加标题
添加标题
应用：用于计算两个正弦函数的乘积，简化计算过程
注意事项：使用乘积公式时需要注意角度的取值范围和计算精度问题
商数公式
正弦函数的商数公式为：sin(x)/cos(x) = tan(x)
该公式用于计算正弦函数与余弦函数的商，得到正切函数

正弦函数的图像课件

作法: (1) 12等分圆
y
(2) 作正弦线
(3) 平移正弦线
1-
P1
p1/
(4) 连线
-
-
6
M-11
o
-1 -
6
3
2 3
2
5
6
7 6
3 4
5
3
3
2
2 11
6
x
图像的最高点 ( ,1)
2
图像的最低点
(
3 2
,1)
与x轴的交点 (0,0) ( ,0) (2 ,0)
y -1
-
o
6
2
3
2
3
5 6
7 6
4 3
3 2
5 3
11 6
2
x
-1 -
y sin x, x0,2
简图作法
(1) 列表(列出对图像形状起关键作用的五点坐标)
(2) 描点(定出五个关键点)
(3) 连线(用光滑的曲线顺次连结五个点)
函数 y sin x(x R)图像
y
1-
-
-
6
4
2
o
-1-
2
4
6
x
因为终边相同的角的三角函数值相同，所以y=sinx的图像在……，
4,2 ,2,0, 0,2 , 2,4, …与y=sinx,x∈[0,2π]的图像相同
例1.用五点法画出y=-sinx ,x∈[0， ]的简图
解:(1) 列表 x
(2) 描点 (3) 连线
sinx
-sinx
y
1
.
-1
.2
0
π 2
π
3π 2

正弦函数的图像(五点法)

6
3
因此，换种思考路径，即采用平移线段的方法。
回忆三角函数线：
A'(-1,0)
B(0,1) y
P(cos,sin) N1

x
O M A(1,0)
B'(0,-1)
把单位圆12等分，可以得到对应于
2p 5p π 7p 4 p 3p 5 p
36
6323
y
0
11 p
6y
p pp
6 32 2π 的正弦线
如下图所示. y
1
0 p π 3p 2π
x
2
2
-1
例1 用五点法作函数y=sinx+1, x ∈ (0,2p) 上的图象
x
0
p
2
p
3p 2p
2
Sinx 0 1 0 －1 0
Sinx+1 1 2 1 0 1
y
2
1
x
0
p
p
3p
2p
2
2
－1
例题分析
例用“五点法”画出下列函数在区间[0，2π]的简图。
正弦函数y=sinx的图象（五点法）
正弦函数：我们常用弧度制来度量角，记为χ，表示自变量，用y表示函数值，于是正弦函数表示为y=sinχ, χ∈Ｒ
如何来作正弦函数的图象呢？
平移正弦线
思考：
时（都，Ⅱ有作）唯出做一相函的对数y值应图和的象它y的值对方，应法，s是i因n1此、p我列们表=1想2、/到2描,当点x而取3、si连n0线p。=任p60意..8给66p3出不一p易个2描x的点值，，
( 3p ,1) 2
1
x
0p
π
3p

正弦函数的图像

T=2 π / ω
正弦曲线
y
1 o -1 2π x
观察周期：
2π
观察最值：
最大值为1，最小值为-1.
y = sin x 五点法作出 y =2 sin x 在一个周期内的图像
x y
观察周期： 2π
π/2 0 π 3π/2 2π x
0 0
π/2 2
y 2
π 0
3π/2 -2
2π 0
观察最值：最大值为2，最小值为-2.
正弦三角函数的图像及其变形
正弦交流电的瞬时值表达式：
e = E m sin(ωt + φ)
基本正弦函数的形式： y = sin x
五点法作出 y = sin x 在区间 [ 0, 2π ]上的图像 x y 0 0 π/2 1
y
π 0
3π/2 -1
2π 0
1 π/2 0 -1 π 3π/2 2π x
一个周期内的图像
y
1
周期
2π
最值
一个周期内的起点原点( 0 , 0 )
o
-1
π/2
π
3π/2
x
2π
最大值为1，最小值为-1.
y = 2 sin x
-2
o
π
π/2
3π/2 2π
2π
最大值为2，最小值为-2.
原点( 0 , 0 )
y 1
y = sin 2x

π/2
o -1
1
π/4
π
x
π
最大值为1，原点( 0 , 0 ) 最小值为-1.
y = sin (x+ π/2)
π -π/2
3π/2
o