数学建模:运算符号
关于数学建模方面的知识

关于数学建模⽅⾯的知识关于数学建模⽅⾯的知识⼀、数学模型的定义现在数学模型还没有⼀个统⼀的准确的定义,因为站在不同的⾓度可以有不同的定义.不过我们可以给出如下定义:“数学模型是关于部分现实世界和为⼀种特殊⽬的⽽作的⼀个抽象的、简化的结构.”具体来说,数学模型就是为了某种⽬的,⽤字母、数学及其它数学符号建⽴起来的等式或不等式以及图表、图象、框图等描述客观事物的特征及其内在联系的数学结构表达式.⼀般来说数学建模过程可⽤如下框图来表明:数学是在实际应⽤的需求中产⽣的,要解决实际问题就必需建⽴数学模型,从此意义上讲数学建模和数学⼀样有古⽼历史.例如,欧⼏⾥德⼏何就是⼀个古⽼的数学模型,⽜顿万有引⼒定律也是数学建模的⼀个光辉典范.今天,数学以空前的⼴度和深度向其它科学技术领域渗透,过去很少应⽤数学的领域现在迅速⾛向定量化,数量化,需建⽴⼤量的数学模型.特别是新技术、新⼯艺蓬勃兴起,计算机的普及和⼴泛应⽤,数学在许多⾼新技术上起着⼗分关键的作⽤.因此数学建模被时代赋予更为重要的意义.⼆、建⽴数学模型的⽅法和步骤1. 模型准备要了解问题的实际背景,明确建模⽬的,搜集必需的各种信息,尽量弄清对象的特征.2. 模型假设根据对象的特征和建模⽬的,对问题进⾏必要的、合理的简化,⽤精确的语⾔作出假设,是建模⾄关重要的⼀步.如果对问题的所有因素⼀概考虑,⽆疑是⼀种有勇⽓但⽅法⽋佳的⾏为,所以⾼超的建模者能充分发挥想象⼒、洞察⼒和判断⼒,善于辨别主次,⽽且为了使处理⽅法简单,应尽量使问题线性化、均匀化.3. 模型构成根据所作的假设分析对象的因果关系,利⽤对象的内在规律和适当的数学⼯具,构造各个量间的等式关系或其它数学结构.这时,我们便会进⼊⼀个⼴阔的应⽤数学天地,这⾥在⾼数、概率⽼⼈的膝下,有许多可爱的孩⼦们,他们是图论、排队论、线性规划、对策论等许多许多,真是泱泱⼤国,别有洞天.不过我们应当牢记,建⽴数学模型是为了让更多的⼈明了并能加以应⽤,因此⼯具愈简单愈有价值.4. 模型求解可以采⽤解⽅程、画图形、证明定理、逻辑运算、数值运算等各种传统的和近代的数学⽅法,特别是计算机技术.⼀道实际问题的解决往往需要纷繁的计算,许多时候还得将系统运⾏情况⽤计算机模拟出来,因此编程和熟悉数学软件包能⼒便举⾜轻重.5. 模型分析对模型解答进⾏数学上的分析. “横看成岭侧成峰,远近⾼低各不同”,能否对模型结果作出细致精当的分析,决定了你的模型能否达到更⾼的档次.还要记住,不论那种情况都需进⾏误差分析,数据稳定性分析.三、数模竞赛出题的指导思想传统的数学竞赛⼀般偏重理论知识,它要考查的内容单⼀,数据简单明确,不允许⽤计算器完成.对此⽽⾔,数模竞赛题是⼀个“课题”,⼤部分都源于⽣产实际或者科学研究的过程中,它是⼀个综合性的问题,数据庞⼤,需要⽤计算机来完成.其答案往往不是唯⼀的(数学模型是实际的模拟,是实际问题的近似表达,它的完成是在某种合理的假设下,因此其只能是较优的,不唯⼀的),呈报的成果是⼀编“论⽂” .由此可见“数模竞赛”偏重于应⽤,它是以数学知识为引导计算机运⽤能⼒及⽂章的写作能⼒为辅的综合能⼒的竞赛.四、竞赛中的常见题型赛题题型结构形式有三个基本组成部分:1. 实际问题背景涉及⾯宽——有社会,经济,管理,⽣活,环境,⾃然现象,⼯程技术,现代科学中出现的新问题等.⼀般都有⼀个⽐较确切的现实问题. 若⼲假设条件有如下⼏种情况:1)只有过程、规则等定性假设,⽆具体定量数据;2)给出若⼲实测或统计数据;3)给出若⼲参数或图形;4)蕴涵着某些机动、可发挥的补充假设条件,或参赛者可以根据⾃⼰收集或模拟产⽣数据.要求回答的问题往往有⼏个问题,⽽且⼀般不是唯⼀答案。
matlab数值运算和符号运算

《深度探讨:从数值运算到符号运算的MATLAB应用》在科学计算领域中,MATLAB无疑是一个不可或缺的工具。
它被广泛应用于数学建模、数据分析、图形可视化和算法开发等领域。
在MATLAB中,数值运算和符号运算是两个核心概念,它们分别在不同的领域中发挥着重要作用。
本文将从数值运算和符号运算两个方面展开讨论,带您深入探索MATLAB的应用价值。
一、数值运算1. MATLAB中的数值数据类型在MATLAB中,常见的数值数据类型包括整数、浮点数和复数等。
它们在科学计算中有着广泛的应用,例如在矩阵运算、微分方程求解和优化算法中。
2. 数值计算函数的应用MATLAB提供了丰富的数值计算函数,包括线性代数运算、插值和拟合、统计分布和随机数生成等。
这些函数为科学计算提供了强大的支持,使得复杂的数值计算变得更加简单高效。
3. 数值方法在实际问题中的应用通过具体的案例,我们可以深入了解MATLAB在实际问题中的数值计算方法。
通过有限元分析解决结构力学问题、通过数值积分求解物理方程、通过数值微分求解工程问题等。
二、符号运算1. MATLAB中的符号计算工具MATLAB提供了符号计算工具包,可以进行符号变量的定义、代数运算、微分积分和方程求解等。
这为数学建模、符号推导和精确计算提供了强大的支持。
2. 符号计算函数的应用通过具体的例子,我们可以深入了解MATLAB中符号计算函数的应用。
利用符号计算求解微分方程、利用符号变量定义复杂的代数表达式等。
3. 符号计算在科学研究中的应用通过详细的案例,我们可以了解符号计算在科学研究中的应用。
利用符号计算推导物理模型、利用符号运算求解工程问题等。
总结与展望:通过本文的深度探讨,我们对MATLAB中的数值运算和符号运算有了全面的了解。
数值运算为我们提供了高效的数值计算工具,而符号运算则为我们提供了精确的符号计算工具。
这两者相辅相成,在不同的领域中发挥着重要的作用。
希望通过本文的阐述,读者可以更加深入地理解MATLAB中数值运算和符号运算的应用,提升科学计算的能力和水平。
数学建模——MATLAB命令大全

正割
Sech
双曲正割
Asech
反双曲正割
Csc
余割
Csch
双曲余割
Acsc
反余割
Acsch
反双曲余割
Cot
余切
Coth
双曲余切
Acot
反余切
Acoth
反双曲余切
指数函数
Exp
指数
Log
自然对数
Log10
常用对数
Sqrt
平方根
复数函数
Abs
绝对值
Argle
相角
Conj
复共轭
Image
复数虚部
Real
Dbode
离散Bode图
Dnichols
离散Nichols图
Dnyquist
离散Nyquist图
Dsigma
离散奇异值频域图
Fbode
连续系统的快速Bode图
Freqs
拉普拉斯变换频率响应
Freqz
Z变换频率响应
Ltifr
低级频率响应函数
Margin
增益和相位裕度
Nichols
Nichols图
Ngrid
变数值为字符串
Isstr
当变量为字符串时其值为真
Blanks
空串
Deblank
删除尾部的空串
Str2mat
从各个字符串中形成文本矩阵
Eval
执行由MATLAB表达式组成的串
字符串比较
Strcmp
比较字符串
Findstr
在一字符串中查找另一个子串
Upper
变字符串为大写
Lower
变字符串为小写
Isletter
第2讲 数学建模MATLAB入门

3、数学函数 、
函 数 名 称 函 数 名 称
sin(x) cos(x) tan(x) abs(x) min(x) sqrt(x) log(x) sign(x)
正弦函数 余弦函数 正切函数 绝对值 最小值 开平方 自然对数 符号函数
asin(x) acos(x) atan(x) max(x) sum(x) exp(x) log10 ( x) fix(x)
MATLAB (matrix1)
2、矩阵中元素的操作 、
的第r行 (1)矩阵 的第 行:A(r,:) )矩阵A的第 ( ,:) 的第r列 (:,r) (2)矩阵 的第 列:A(:, ) )矩阵A的第 (:, 的每一列, 拉伸为一个列向量: (:) (3)依次提取矩阵 的每一列,将A拉伸为一个列向量:A(:) )依次提取矩阵A的每一列 拉伸为一个列向量 的第i 列构成新矩阵:A(i1:i2, j1:j2) (4)取矩阵 的第 1~i2行、第j1~j2列构成新矩阵 )取矩阵A的第 的第i 构成新矩阵:A(i2:-1:i1,:) (5)以逆序提取矩阵 的第 1~i2行,构成新矩阵 )以逆序提取矩阵A的第 : 的第j 构成新矩阵:A(:, j2:-1:j1 ) (6)以逆序提取矩阵 的第 1~j2列,构成新矩阵 )以逆序提取矩阵A的第 : 的第i 构成新矩阵:A(i1:i2,: ] ,:)=[ (7)删除 的第 1~i2行,构成新矩阵 )删除A的第 的第j 构成新矩阵:A(:, (8)删除 的第 1~j2列,构成新矩阵 :, j1:j2)=[ ] )删除A的第 拼接成新矩阵: (9)将矩阵 和B拼接成新矩阵:[A B];[A;B] )将矩阵A和 拼接成新矩阵 ; ; MATLAB (matrix2)
(2)数组 数组运算 )数组-数组运算 当两个数组有相同维数时, 当两个数组有相同维数时,加、减、乘、除、 幂运算可按元素对元素方式进行的, 元素对元素方式进行的 幂运算可按元素对元素方式进行的,不同大小或维 数的数组是不能进行运算的. 数的数组是不能进行运算的
数学运算中参量右下角两条竖杠和垂直

数学运算中参量右下角两条竖杠和垂直在数学运算中,我们经常会遇到一些特殊的符号和标记,它们可能并不是常见的加减乘除等运算符号,但却在特定的情境下扮演着重要的角色。
其中,一个常见且具有特殊意义的符号就是右下角两条竖杠和垂直符号。
这个符号在数学运算和数学表达中具有一定的特殊性,接下来我们将从深度和广度的角度对这个符号进行全面评估,以便更深入地理解它的意义和用途。
1. 符号说明右下角两条竖杠和垂直符号是用来表示取绝对值的数学符号。
在数学中,绝对值表示一个数距离原点的距离,无论这个数是正数还是负数,其绝对值都为正数。
这一点可以用符号来简洁表示,即“|x|”,其中“x”表示需要求绝对值的数。
右下角的两条竖杠和垂直符号也可以表示向量的模,即向量的大小。
2. 使用示例在实际的数学运算中,右下角两条竖杠和垂直符号常常出现在绝对值、向量模等情境中。
当我们需要求解一个数的绝对值时,就会使用这个符号来表示。
另外,在物理学和工程学中,表示向量大小时也会使用这个符号。
在这些情况下,右下角的两条竖杠和垂直符号起到了简洁明了地表示数学概念的作用。
3. 我的个人观点和理解在我看来,右下角两条竖杠和垂直符号是数学运算中非常重要的一个表示符号。
它能够简洁清晰地表示数的绝对值和向量的模,帮助我们在数学运算和理论推导中更加简便地表达和理解这些概念。
它也提醒着我们,在进行数学运算和物理推导时要注重数的正负和向量的方向,以便得到正确的结果和结论。
总结回顾通过本文的分析,我们对右下角两条竖杠和垂直符号在数学运算中的作用有了更深入的理解。
我们了解到它是用来表示数的绝对值和向量的模的重要符号,能够在各种数学运算和理论推导中起到简洁明了的作用。
我们也明白了在实际应用中,正确理解和使用这个符号对于得到准确的数学结果和物理结论非常重要。
在今后的学习和工作中,我们应该注重对这个符号的理解和应用,以提高数学运算和理论推导的准确性和效率。
结论右下角两条竖杠和垂直符号在数学运算中扮演着重要的角色,它是表示绝对值和向量模的重要符号,能够简洁明了地表达这些数学概念。
matlab 求解符号方程

一、背景介绍Matlab是一种强大的数学软件,常用于数学建模、仿真、数据分析等领域。
在工程和科学研究中,求解符号方程是一个常见的问题,Matlab提供了丰富的符号计算工具,可以帮助用户高效地求解符号方程。
二、Matlab符号计算工具1. 符号变量定义在Matlab中,我们可以通过syms命令定义符号变量,使用符号变量进行符号运算。
例如:```matlabsyms x y```2. 求解符号方程Matlab提供了solve函数,可以用来求解符号方程。
solve函数的基本语法如下:```matlabsol = solve(equations, variables)```其中,equations表示要求解的方程组,variables表示待求解的变量。
solve函数会返回符号方程的解。
三、示例接下来,我们通过一个示例来演示如何使用Matlab求解符号方程。
假设我们要求解如下的符号方程:```matlabsyms xeqn = x^2 - 4*x + 3 == 0;sol = solve(eqn, x);disp(sol);```运行以上代码,可以得到方程x^2 - 4*x + 3 = 0的解为x = 1或x = 3。
四、注意事项在使用Matlab求解符号方程时,有一些需要注意的事项:1. 可能存在多解或无解的情况,在求解后需要对解进行检查;2. 符号计算是一种复杂的运算,可能存在数值精度问题,需要注意数值的精确性;3. 在求解复杂的方程组时,可能需要对方程组进行化简或变形,以提高求解效率。
五、总结通过Matlab的符号计算工具,我们可以较为方便地求解符号方程,实现高效的符号计算。
在工程和科学研究中,这些工具能够帮助我们快速解决复杂的数学问题,提高工作效率。
希望本文的介绍和示例能够帮助读者更好地理解和应用Matlab的符号计算工具。
Matlab在求解符号方程方面具有广泛的应用。
通过利用Matlab的符号计算工具,用户可以轻松地进行符号方程的求解和符号计算,并获得高精度的结果。
建模中的布尔运算

建模中的布尔运算建模中的布尔运算在计算机编程和建模领域中,布尔运算是最基本和重要的运算之一。
布尔运算是基于布尔代数的数学理论而来,它用于处理逻辑和比较问题,它只有两种结果:真和假。
在建模中包含了许多布尔运算的应用,例如逻辑运算、真值表、条件语句等等。
布尔代数是基于逻辑、代数和符号表示法的数学分支,在20世纪初被引入到电子工程中。
它提供了一种用于处理逻辑语句的数学理论,尤其是用于处理真和假值的语句。
在布尔代数中,只有两种值:真和假,分别用1和0表示。
逻辑技术和布尔代数已广泛应用于电路设计、自动化控制、计算机科学和通信等领域。
布尔运算的逻辑运算符号包括以下几种:与(&)、或(|)、非(~)和异或(^)。
这些运算符的使用方法如下:1. 与运算(&):对两个输入的布尔值进行比较。
只有当两个输入都是真值时,输出才是真值,否则是假值。
2. 或运算(|):对两个输入的布尔值进行比较。
只有当任意一个输入为真值时,输出才是真值,否则是假值。
3. 非运算(~):是单个输入的比较。
当输入为真值时,输出为假值,反之亦然。
4. 异或运算(^):与或运算不同,异或运算只有在两个输入值不同时才会输出真值,如果两个输入值相等,则输出假值。
在建模过程中,布尔运算可用于创建逻辑函数,它们可以根据输入的值来计算输出,并用于控制建模系统的行为、状态和功能。
逻辑函数可以通过真值表来表示,这是一个表格形式,其中列表示所有可能的输入组合和对应的输出值。
可以使用布尔运算来构建这些真值表以确定逻辑函数的输出值。
条件语句也是建模中广泛使用布尔运算的一个示例。
条件语句可根据输入值中条件的真假情况执行不同的操作。
它可以使用“假-否则”语法结构来实现,这意味着它将先验证一个条件语句是否为真值,如果是,它将执行操作并继续代码;如果条件语句为假值,那么就会执行其他操作。
布尔运算的另一个重要应用场景是在电路设计和逻辑门,其中布尔运算表示不同的逻辑门之间的相互关系。
数学建模符号说明

三、符号说明H(θ):太阳高度角;t:当地时刻δ:太阳赤纬角;∅:当地纬度;H′(θ):享受日照所需仰角;H:高层住宅楼房总高度;h:该楼层的高度;L:楼间距;Sum:一天内享受日照累计时间;T:超过6h的天数;Month-day:超过6h的日期;t i-t i+1(i=1,2,3……):享受日照时间段;θ:太阳直射点纬度(正值表示北半球,负值表示南半球);ω:地球公转角速度;∆t i(i=1,2……):某天距春分的时间差;H ijk(I,j,k=1,2……)(i为楼号,j为单元号,k为楼层):未售出楼层的高度;Sum_time:全年某楼层享受到日照的总小时数;P1,P2,P3,P4:价格、交通、环境、噪音的权重;d+,d−:正负偏差变量;EX1,EX2,EX3,EX4:消费者在价格、交通、环境、噪音的期望值;a:该楼房基价;b%:逐层递增率;W ij(i=1,2……7)(j=1,2……14)(i表示楼层,j表示楼号):某楼层的售价;X ij(i=1,2……14)(j=1,2……):各楼的交通状况值;Y ij(i=1,2……)(j=1,2……):各楼环境值;Z ij(i=1,2……)(j=1,2……):楼层所受噪音干扰指数;五、模型推广本论文模型可推广适用于城市住宅购房参考。
六、参考文献[1]M·得瓦洛夫斯基、金大勤等,《阳光与建筑》,北京:中国建筑工业出版社,1981。
[2]李旭光,城市居住区日照的认识误区及对策[J],住宅科技,2005,(1)。
[3]赵文凯,日照标准与日照间距的关系,城市规划,2003,27(1)。
[4]关于居住区设计规范中日照问题的研究[c]。
数学建模MATLAB特殊符号
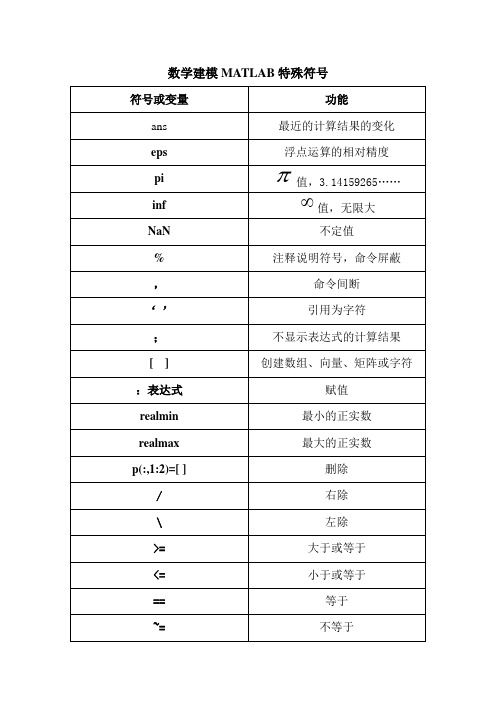
数学建模MATLAB特殊符号| 或~ 非“&”和“|”操作符可比较两个标量或两个同阶矩阵.对于矩阵来说必须符合规则,如果A和B都是0-1矩阵,则A&B或A|B也都是0-1矩阵,这个0-1矩阵的元素是A和B 对应元素之间逻辑运算的结果,逻辑操作符认定任何非零元素都为真,给出“1”,任何零元素都为假,给出“0”.非(或逻辑非)是一元操作符,即~A:当A是非零时结果为“0”;当A为“0”时,结果为“1”.因此下列两种表示:p | (~p) 结果为1.p &(~p) 结果为0.any和all函数在连接操作时很有用,设x是0-1向量,如果x中任意有一元素非零时,any(x)返回“1”,否则返回“0”;all(x)函数当x的所有元素非零时,返回“1”,否则也返回“0”.这些函数在if语句中经常被用到.如:if all(A<5)do somethingend还有"&&"和"||"运算符,Matlab中的逻辑运算"&&"与"&","||"与"|"的区别如下:&&和||被称为&和|的short circuit形式,A&B(1)首先判断A的逻辑值,然后判断B的值,然后进行逻辑与的计算。
(2)A和B可以为矩阵(e.g. A=[1 0],B=[0 0])。
A&&B(1)首先判断A的逻辑值,如果A的值为假,就可以判断整个表达式的值为假,就不需要再判断B的值。
(2)A和B不能是矩阵,只能是标量。
"|"与“||”同理。
A&&B 首先判断A的逻辑值,如果A的值为假,就可以判断整个表达式的值为假,就不需要再判断B的值。
这种用法非常有用,如果A是一个计算量较小的函数,B是一个计算量较大的函数,那么首先判断A对减少计算量是有好处的。
scilab代数符号运算

scilab代数符号运算
Scilab是一种开源的数学建模和仿真软件,它提供了丰富的数
学函数和工具,包括代数符号运算。
在Scilab中进行代数符号运算,可以使用符号变量和符号表达式来表示和操作代数表达式。
首先,你可以使用`syms`命令创建符号变量,比如:
syms x y.
这样就创建了符号变量x和y。
然后,你可以使用这些符号变
量来构建符号表达式,比如:
expr = x^2 + 2xy + y^2。
这样就创建了一个符号表达式expr,表示x^2 + 2xy + y^2。
接下来,你可以对这些符号表达式进行各种代数运算,比如展开、因式分解、求导、求积分等。
例如,你可以使用`expand`函数
来展开表达式:
expanded_expr = expand(expr)。
这样就得到了表达式expr的展开形式。
此外,你还可以使用`factor`函数对表达式进行因式分解:
factored_expr = factor(expr)。
这样就得到了表达式expr的因式分解形式。
如果你想对表达式进行求导,可以使用`diff`函数:
derivative = diff(expr, x)。
这样就得到了表达式expr对x的导数。
同样地,如果你想对表达式进行积分,可以使用`integrate`函数:
integral = integrate(expr, x)。
这样就得到了表达式expr对x的积分。
总之,Scilab提供了丰富的符号运算功能,可以帮助你进行各种代数运算,并且可以方便地进行符号数学建模和分析。
希望这些信息能够帮助到你。
数学符号累加

数学符号累加【原创实用版】目录1.引言:介绍数学符号累加的概念2.正文1.引言数学符号累加是数学中一种重要的运算方式,它能够帮助我们简化复杂的计算过程,使数学问题变得易于理解和解决。
在数学领域,累加符号有着广泛的应用,从基础的加法运算到高级的数学建模等。
本文将从累加符号的表示方法、运算规则和应用实例三个方面,详细介绍数学符号累加的相关知识。
2.正文a.累加符号的表示方法数学中,累加符号通常用∑(求和)表示。
在具体的问题中,求和符号∑会与一个表示范围的标注一起使用,表示从范围标注的第一个数加到范围标注的第 n 个数。
例如:∑(i=1 到 n)ai,表示将序列中的前 n 个数相加。
b.累加符号的运算规则累加符号遵循交换律、结合律等基本的运算规则,具体如下:交换律:对于任意的实数 a 和 b,有∑ai=∑bi。
结合律:对于任意的实数 a、b 和 c,有∑(ai+bj)=∑ai+∑bj。
分配律:对于任意的实数 a、b 和 c,有∑(a(bi+cj))=∑a(bi)+∑a(cj)。
此外,还需要注意以下几点:1.当求和范围为负数时,表示从范围标注的第 n 个数加到范围标注的第一个数。
例如:∑(i=n 到 1)ai。
2.求和符号∑可以与函数符号 f 一起使用,表示对函数 f 的值进行求和。
例如:∑(x=a 到 b)f(x)。
c.累加符号的应用实例累加符号在数学中有着广泛的应用,下面举两个实例:例 1:计算等差数列的前 n 项和已知等差数列{an}的首项 a1=1,公差 d=2,求前 n 项和 Sn。
解:根据等差数列的求和公式,Sn=∑(i=1 到 n)ai=∑(i=1 到 n)(a1+(i-1)d)=n(a1+an)/2=n(1+(n-1)2)/2=n(2n-1)。
例 2:计算从 1 到 100 的所有偶数的和解:假设所求和为 S,则 S=∑(i=1 到 50)2i。
由于 2i=2*i,因此 S=2∑(i=1 到 50)i=2*(1+2+3+...+50)=2*50*51/2=1275。
[整理版]数学建模复习内容带习题答案
![[整理版]数学建模复习内容带习题答案](https://img.taocdn.com/s3/m/1d0fd2d059f5f61fb7360b4c2e3f5727a5e924ad.png)
考试内容分布:1、线性规划2题,有1题需编程;2、非线性规划2题,有1题需编程;3、微分方程1题,需编程;4、差分方程2题,纯计算,不需编程;5、插值2题,拟合1题,纯计算,不需编程;;6、综合1题(4分),纯计算,不需编程。
一、列出下面线性规划问题的求解模型,并给出matlab计算环境下的程序1.某车间有甲、已两台机床,可用于加工三种工件,假定这两台车床的可用台时数分别为800和900,三种工件的数量分别为400,600和500,且已知用两种不同车床加工单位数量不同工件所需的台时数和加工费用如下表。
问怎样分配车床的加工任务,才能即满足加工工件的要求,又使加工费用最低。
(答案见课本P35, 例1)2.有两个煤厂A,B,每月进煤分别不少于60t、100t,它们负责供应三个居民区的用煤任务,这三个居民区每月需用煤分别为45t, 75t, 40t。
A厂离这三个居民区分别为10km, 5km, 6km,B厂离这三个居民区分别为4km, 8km, 15km,问这两煤厂如何分配供煤,才能使总运输量最小?(1)问题分析设A煤场向这三个居民区供煤分别为x1,x2,x3;B煤场向这三个居民区供煤分别为x4,x5,x6,则min f=10*x1+5*x2+6*x3+4*x4+8*x5+15*x6,再根据题目约束条件来进行解题。
(2) 模型的求解>> f=[10 5 6 4 8 15];>> A=[-1 -1 -1 0 0 00 0 0 -1 -1 -1-1 0 0 -1 0 00 -1 0 0 -1 00 0 -1 0 0 -1];>> b=[-60;-100;-45;-75;-40];>> Aeq=[];>> beq=[];>> vlb=zeros(6,1);>> vub=[];>> [x,fval]=linprog(f,A,b,Aeq,beq,vlb,vub)Optimization terminated.(3) 结果分析x =0.0000 20.000040.0000 45.0000 55.0000 0.0000 fval =960.0000即A 煤场分别向三个居民区供煤0t,20t,40t ;B 煤场分别向三个居民区供煤45t,55t,0t 可在满足条件下使得总运输量最小。
数学建模的基本步骤

数学建模的基本步骤数学建模的基本步骤一、数学建模题目1) 以社会,经济,管理,环境,自然现象等现代科学中出现的新问题为背景,一般都有一个比较确切的现实问题。
2) 给出若干假设条件:1. 只有过程、规则等定性假设;2. 给出若干实测或统计数据;3. 给出若干参数或图形等。
根据问题要求给出问题的优化解决方案或预测结果等。
根据问题要求题目一般可分为优化问题、统计问题或者二者结合的统计优化问题,优化问题一般需要对问题进行优化求解找出最优或近似最优方案,统计问题一般具有大量的数据需要处理,寻找一个好的处理方法非常重要。
二、建模思路方法1、机理分析根据问题的要求、限制条件、规则假设建立规划模型,寻找合适的寻优算法进行求解或利用比例分析、代数方法、微分方程等分析方法从基本物理规律以及给出的资料数据来推导出变量之间函数关系。
、数据分析法对大量的观测数据进行统计分析,寻求规律建立数学模型,2 采用的分析方法一般有:1). 回归分析法( 数理统计方法)- 用于对函数f(x) 的一组观测值)i=1,2,…,n,确定函数的表达式。
(xi,fi2) . 时序分析法-- 处理的是动态的时间序列相关数据,又称为过程统计方法。
3) 、多元统计分析( 聚类分析、判别分析、因子分析、主成分分析、生存数据分析)3、计算机仿真(又称统计估计方法): 根据实际问题的要求由计算机产生随机变量对动态行为进行比较逼真的模仿,观察在某种规则限制下的仿真结果(如蒙特卡罗模拟)。
三、模型求解: 模型建好了,模型的求解也是一个重要的方面,一个好的求解算法与一个合适的求解软件的选择至关重要,常用求解软件有matlab ,mathematica ,lingo ,lindo ,spss,sas 等数学软件以及c/c++ 等编程工具。
Lingo 、lindo 一般用于优化问题的求解,spss ,sas 一般用于统计问题的求解,matlab ,mathematica 功能较为综合,分别擅长数值运算与符号运算。
数学建模符号说明

符号说明1.(0)x ——n 个元素的数列;2.()(1)(0)1()ki x k x i ==∑; 3.()d k ——x )1(的灰导数;4.(1)z ——()1x 的紧邻均值数列;5.(1)(1)(1)()0.5()0.5(1)z k x k x k =+-;6.a ——称为发展系数;7.1()z k ()——称为白化背景值; 8.b 称为灰作用量;9.Y 为数据向量;10.B 为数据矩阵;11.u 为参数向量;12.X ——总人口随时间变化的拟合函数; 13A ——人口结构变化率;14.Q ——病床总需求;15.C ——肺癌患病人数;16.D ——胃癌患病人数;17.1E ——肺癌在市级医院的病床需求;18.2E ——肺癌在区级医院的病床需求; 19.1F ——胃癌在市级医院的病床需求;20.2F ——胃癌在区级医院的病床需求;fhj(i): 指公园i 年非户籍人人口数hj(i) :指公园i 年户籍人人口数N : 床位数ϕ :每日入院患者数目不稳定而引入的调整系数 T :患者平均每年入院天数xjgs:指疾病心肌梗塞tnb:指疾病糖尿病D :一年总天数h :患者数目符号说明()i a t --------------------第t 时间区间内第i 个年龄段人口总数 ()i c t --------------------第t 时间区间内第i 个年龄段人口总数占总人口的比例 ()k i c t --------------------第t 时间区间内第i 个年龄段中第k 年龄值人口总数占总人口的比例()A t --------------------第t 时间区间内各年龄段人口总数的向量 ()P t --------------------第t 时间区间各年龄段人口总数向量转移矩阵 ()i b t -------------------第t 时间区间内第i 个年龄段人的生育率 ()i d t -------------------第t 时间区间内第i 个年龄段人的死亡率 ()k i d t -----------------第t 时间区间内第i 个年龄段中第k 年龄值的死亡率 ()i s t -------------------第t 时间区间内第i 个年龄段人的存活率 ()h t --------------------- 第t 时间区间男性人数与女性人数的比值 ()i e t ---------------------第t 时间区间内第i 个年龄段育龄妇女的生育率 m---------------------------每个年龄段上年龄值的数目1.x 预测变量:表示年份2.f (x )表示人口数,具体见模型的建立与求解3.i F : 各级别医院个数 4.i y : 每年的患病人数 5.iw : 不同类型的医疗机构床位数i P : 深圳市总人口数N : 各年龄层所占的比例 i Q : 各区域床位需求: 全市床位需求Q总A: 2000年-2010年的年份矩阵B: 2000年-2010年的年末常住人口数矩阵b: 每年年末常住人口数it: 年份()x t: 年末常住人口数E: 相对误差K: 环境可容纳的人口最大数量x: 初始时刻人数r: 人口增长率t: 初始时刻a: 全市的儿童比例1a: 青中年人口比例2a: 老年人口比例3Y: 全市医疗床位总需求总Q: 各区医疗床位需求nD: 各区年龄结构比例W: 全区总人数R: 全市总床位数Z: 住院率F: 各级别医院个数iy: 每年的患病人数iw: 不同类型的医疗机构床位数iB——出生率;tD——死亡率;tM——迁入人口;itM——迁出人口;otP t——本年的实际人口;()(1)P t ——下一年的人口预测值;4、定义符号说明Q——非常住人口总和;非Q——进入城镇务工、经商、和从事劳动服务的暂住人口总和;1Q——为探亲访友、旅游、求学、治病等而外出的人员;2Q——无职业、无收入、无暂住证的三无人员即盲流人口;3p——比例因素;X——深圳市t当年G DP总量;tGDPX——常住人口GDP值;b——进入城镇务工、经商、和从事劳动服务的暂住人口总和的初始值1p——探亲访友人数的概率;2Q——旅行人数;旅Q——外来学习人数;学Q——外来求医人数;医b——其他人数。
数学建模定义符号说明1

2.定义符号说明:x i表示按照第i种模式切割I型号玻璃的块数(i=1,2,3...,20);表示按照第j种模式切割II型号玻璃的块数yj(j=1,2,3,...,20);3.模型建立:此问题为建筑公司下料问题,其与钢管易拉罐下料问题,自来水分派问题,奶制品的生产销售问题非常相似,都属于数学优化模型。
所以我们可以用一些数学规划的相关知识来解决。
按照假设把这其中规格的窗户分为两组,如表1:1200x800 1200x650 1100x750 700x600A1500x850 1200x750 800x600BI,II型号玻璃分别以这两组的窗户的尺寸进行切割,例如I 型号玻璃按照A组切割,可以切3块1200x800,1块1200x650和1块700x600;II 玻璃按照A组切割,可以切3块1200x800,4块1200x650和2块700x600等等多种方案,这多种方案由表2,3表示:表2模式尺寸1200x801200x651100x75700x600 余量1 4 6 0 0 0 0 0 0 141 1202 3 5 1 1 1 1 1 1 117 963 2 5 3 0 0 0 0 0 99 133.54 2 4 2 4 0 0 0 0 94.5 05 2 4 2 1 2 1 2 1 93 109.56 2 4 1 1 2 3 2 3 171 1087 2 4 0 0 2 4 2 4 358.5 61.58 1 3 5 5 0 0 0 0 39 189 1 3 4 4 0 2 0 2 34.5 1210 1 3 2 3 6 4 6 4 21 611 1 3 1 2 7 5 7 5 57 4212 1 3 0 0 8 0 8 0 93 193.513 0 2 5 0 1 0 1 0 93 256.514 0 2 3 0 4 12 4 12 40.5 015 0 1 3 7 6 0 6 0 39 5416 0 0 2 8 2 0 2 0 120 7217 0 0 2 4 4 0 4 0 118.5 136.518 0 0 1 2 3 1 3 1 73.5 319 0 0 1 0 6 0 6 0 112.5 020 0 0 0 0 12 0 12 0 21 0表31500x850 1200x750 800x600 余量模式尺寸1 3 4 0 1 0 0 142.5 962 2 4 1 0 1 2 132 903 2 3 0 2 3 0 126 133.54 1 3 3 1 1 2 79.5 127.55 1 3 2 0 3 4 73.5 121.56 1 2 1 4 5 0 67.5 817 1 2 0 3 7 2 61.5 758 0 2 4 2 0 4 165 699 0 2 3 1 4 6 63 6310 0 2 0 0 9 8 93 5711 1 4 0 208.512 1 3 2 202.513 1 2 4 196.514 1 1 6 190.515 1 0 10 88.5对A 组建立的模型为:决策变量 x i y j 它们为非负整数;决策目标 分别以切割后剩余的余料量和切割原料玻璃的总块数为最小目标,由表2,3可以得到目标函数 MinM1=141x1+117x+99x3+94.5x4+93x5+171x6+358.5x7+39x8+34.5x9+21x10+57x11+93x12+93x13+40.5x14+39x15+120x16+118.5x17+73.5x18+112.5x19+21x20+120y1+96y2+133.5y3+109.5y5+108.y6+61.5y7+18y8+12y9+6y10+42y11+193.5y12+256.5y13+54y15+72y16+136.5y17+3y18 ;(1) Min M2=∑=201i i x +∑=201j j y ;(2)约束条件:4x1+3x2+2x3+2x4+2x5+2x6+2x7+x8+x9+x10+x11+x12+6y1+5y2+5y3+4y4+4y5+4y6+4y7+3y8+3y9+3y10+3y11+3y12+2y13+2y14+y15 >=540 (3)x2+3x3+2x4+2x5+x6+5x8+4x9+2x10+x11+5x13+3x14+3x15+2x16+2x 17+x18+x19+y2+4y4+y5+y6+5y8+4y9+3y10+2y11+7y15+8y16+4y17+2y18 >=480 (4)x2+2x5+2x6+2x7+6x10+7x11+8x12+x13+4x14+6x15+2x16+4x17+3x1 8+6x19+12x20+y2+y5+3y6+4y7+2y9+4y10+5y11+12y14+y18 >=480 (5)x2+2x5+2x6+2x7+6x10+7x11+8x12+x13+4x14+6x15+2x16+4x17+3x1 8+6x19+12x20+y2+y5+3y6+4y7+2y9+4y10+5y11+12y14+y18 >=600 (6)模型求解:将(1)(3)(4)(5)(6)构成的整数线性规划模型输入LINDO如下:min141x1+117x2+99x3+94.5x4+93x5+171x6+358.5x7+39x8+34.5x9+21x10+57x11+93x12+93x13+40.5x14+39x15+120x16+118.5x17+73.5x18+112.5x19+21x20+120y1+96y2+133.5y3+109.5y5+108y6+61.5y7+18y8+12y9+6y10+42y11+19 3.5y12+256.5y13+54y15+72y16+136.5y17+3y18st4x1+3x2+2x3+2x4+2x5+2x6+2x7+x8+x9+x10+x11+x12+6y1+5y2+5y3+4y4+4y5 +4y6+4y7+3y8+3y9+3y10+3y11+3y12+2y13+2y14+y15 >=540x2+3x3+2x4+2x5+x6+5x8+4x9+2x10+x11+5x13+3x14+3x15+2x16+2x17+x18+x 19+y2+4y4+y5+y6+5y8+4y9+3y10+2y11+7y15+8y16+4y17+2y18 >=480x2+2x5+2x6+2x7+6x10+7x11+8x12+x13+4x14+6x15+2x16+4x17+3x18+6x19+12x20+y2+y5+3y6+4y7+2y9+4y10+5y11+12y14+y18 >=480x2+2x5+2x6+2x7+6x10+7x11+8x12+x13+4x14+6x15+2x16+4x17+3x18+6x19+1 2x20+y2+y5+3y6+4y7+2y9+4y10+5y11+12y14+y18 >=600end求解可得到解如下:Global optimal solution found.Objective value: 0.000000Total solver iterations: 6V ariable V alue Reduced CostX1 0.000000 141.0000X2 0.000000 117.0000X3 0.000000 99.00000X4 0.000000 94.50000 X5 0.000000 93.00000 X6 0.000000 171.0000 X7 0.000000 358.5000 X8 0.000000 39.00000 X9 0.000000 34.50000 X10 0.000000 21.00000 X11 0.000000 57.00000 X12 0.000000 93.00000 X13 0.000000 93.00000 X14 0.000000 40.50000 X15 0.000000 39.00000 X16 0.000000 120.0000 X17 0.000000 118.5000 X18 0.000000 73.50000 X19 0.000000 112.5000 X20 0.000000 21.00000 Y1 0.000000 120.0000 Y2 0.000000 96.00000 Y3 0.000000 133.5000 Y5 0.000000 109.5000 Y6 0.000000 108.0000 Y7 0.000000 61.50000 Y8 0.000000 18.00000 Y9 0.000000 12.00000 Y10 0.000000 6.000000 Y11 0.000000 42.00000 Y12 0.000000 193.5000 Y13 0.000000 256.5000 Y15 0.000000 54.00000 Y16 0.000000 72.00000 Y17 0.000000 136.5000 Y18 0.000000 3.000000 Y4 120.0000 0.000000 Y14 50.00000 0.000000Row Slack or Surplus Dual Price1 0.000000 -1.0000002 40.00000 0.0000003 0.000000 0.0000004 120.0000 0.0000005 0.000000 0.000000即按照模式4切割II号玻璃120块和模式14切割II号玻璃50块使得余量最小;为0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[n,d]=numden(s) – 该函数提取符号表达式s的分子和分母,分别将它们存放在n与d中。
例 对表达式 f=x/y+y/x 进行通分。
– syms x y
– f=x/y+y/x;
– [n,d]=numden(f)
– n=
–
x^2+y^2
– d=
– y*x
12
基本的符号运算(续)
因式分解与展开
6
符号计算基础(续)
考察符号变量和数值变量的差别
例
a=sym('a');b=sym('b');c=sym('c');d=sym('d'); %定义4个符号变量
w=10;x=5;y=-8;z=11;
%定义4个数值变量
A=[a,b;c,d]
%建立符号矩阵A
B=[w,x;y,z]
%建立数值矩阵B
det(A) det(B)
主要内容 符号计算基础 符号函数及其应用 符号积分 级数 符号方程求解 其他常用命令
4
符号计算基础
MATLAB定义了一种符号数据类型
– 运算对象为符号对象
» 符号常量:无变量的符号表达式称作符号常量 » 符号变量 » 符号表达式
建立符号对象
– x=sym(‘x’) 创建单个符号常量/变量x
» 符号常量: x不为变量 » 符号变量: x为字符、字符串、表达式或字符表达式
MATLAB 符号运算
1
x a xa
lim
xa
x2 a2
s2
1
1 2
1 3
1 4
d2x
dt 2 d2y
dt 2
y x
0 0
sin x 4xdt
2t
(1)n1 1 n
x2 y2 5 2x2 3xy 2y2 0
2
符号运算
什么是符号运算?
– 直接对抽象的符号对象进行计算,结果以标准的符号形式来表示。 – 可以获得比数值计算更一般的结果。
%计算符号矩阵A的行列式 %计算数值矩阵B的行列式
7
符号计算基础(续)
比较符号常数与数值在代数运算时的差别
例
pi1=sym('pi');k1=sym('8');k2=sym('2');k3=sym('3'); % 定义符号变量
pi2=pi;r1=8;r2=2;r3=3;
% 定义数值变量
sin(pi1/3)
% 计算符号表达式值
sin(pi2/3)
% 计算数值表达式值
sqrt(k1)
% 计算符号表达式值
sqrt(r1)
% 计算数值表达式值
sqrt(k3+sqrt(k2))
% 计算符号表达式值
sqrt(r3+sqrt(r2))
% 计算数值表达式值
8
基本的符号运算(续)
基本的符号运算
– 符号表达式的四则运算 »+ , - , * , / 。
的MATLAB命令。
符号表达式例子以及MATLAB等效表达式
符号表达式
1 2xn
y 2x cos(x 2 ) sin(2x)
a b
M c
d
MATLAB表达式
' 1/(2*x^n) ' y= ' 1/sqrt(2*x) ' ' cos(x^2)-sin(2*x) ' M=sym( ' [a,b;c,d] ' )
10
基本的符号运算(续)
例
u f=sym('2*x^2+3*x-5') u g=sym('x^2-x+7') u f+g u f-g u f*g u f/g u f^3
11
基本的符号运算(续)
符号表达式的提取分子和分母运算(分式通分)
– 如果符号表达式是一个有理分式或可以展开为有理分式,可利用 numden函数来提取符号表达式中的分子或分母。其一般调用格式为:
13
基本的符号运算(续)
表达式展开:expand(S)
– 例 展开表达式f=(x+1)5和f=sin(x+y) – syms x y – f=(x+1)^5; – expand(f) – f=sin(x+y); – expand(f)
14
基本的符号运算(续)
符号表达式的同类项合并:collect(S,n)
– 它最初是由加拿大的滑铁卢(Waterloo)大学开发的。当要求MATLAB进行符号 运算时,它就请求Maple去计算并将结果返回到MAT箱(函数)集合,有符 号具表。达式的运算,复合、简化、微分、积分以及求解代数方程和微分方程的3 工
符号运算的特点:
– 运算以推理解析的方式进行,因此不受计算误差积累问题困扰; – 计算结果或给出完全正确的封闭解,或给出任意精度的数值解(当封闭解不存在
时);
– 符号计算指令的调用比较简单,经典教科书公式相近; – 计算所需时间较长,有时难以忍受。
MATLAB符号运算是通过集成在MATLAB中的符号运算工具箱(symbolic math toolbox)来实现的。符号数学工具箱中的工具是建立在功能强大的称作 Maple软件的基础上。
– syms用于方便地一次创建多个符号变量,调用格式为: syms a b c d .
» 这种格式定义符号变量时不需要在变量名上加字符分界符('),变量间用空格 而不要用逗号分隔。
» 书写简洁意义清楚,建议使用。
5
符号计算基础(续)
符号表达式
– 含有符号对象的表达式称为符号表达式
MATLAB在内部把符号表达式表示成字符串,以与数字变 量或运算相区别;否则,这些符号表达式几乎完全象基本
– 符号表达式的提取分子和分母运算
» numden
– 因式分解与展开
» factor,expand
– 表达式化简
» simplify,simple
– 符号表达式与数值表达式之间的转换
» sym,numeric,eval
9
基本的符号运算(续)
符号表达式的四则运算
– 符号表达式的四则运算和其他表达式的运算并无不同,但要注意 ,其运算结果依然是一个符号表达式。
– factor(S) 对S分解因式,S是符号表达式或符号矩阵。 – expand(S) 对S进行展开,S是符号表达式或符号矩阵。 – collect(S) 对S合并同类项,S是符号表达式或符号矩阵。 – collect(S,v) 对S按变量v合并同类项,S是符号表达式或符号矩阵 例1: 对表达式f=x9-1进行因式分解。 – syms x – f=factor(x^9-1) 例2:对大整数12345678901234567890进行因式分解 – factor(sym('12345678901234567890'))
