柳浩 3
冶金工程专业卓越工程师教育培养学生工程能力的实践教学改革

当前我国高等工程教育主要存在的问题是脱离工程实践。
教育部为促进高等教育面向社会需求培养人才于2011年启动“卓越工程师教育培养计划”,目的是全面提高工程教育人才的培养质量,提升工程人才的工程素质,适应我国科技发展和产业升级的需要。
冶金工艺性专业主要是针对传统的钢铁产业,涉及冶金工程专业、材料成型及控制工程专业,本科人才目标定位是培养具备较高的工程素质和解决工程实际问题能力的现场工程师。
工程素质集中体现在综合性、系统性、实践性和创新性。
然而,在现行的实验教学体系中,学生工程素质的培养是薄弱环节。
以冶金工程专业为例,冶金工程专业原有“冶金物化”“冶金自动化”“传输原理”“专业综合实验”四门依序开设的专业实验课程体系。
其中前三者课带随堂实验,实验教学依附于理论课,实验项目多为理论的验证,综合多个知识点或具备工程环境的实验项目较少;实验内容与工程实践结合不够,没有突出工艺性专业应用性和实践性的特点,不利于培养学生的综合实践能力和工程素质。
因此,必须通过冶金工程专业实验教学体系与课程内容的改革,搭建新的工程实践教学平台,建立产学研实验教学新模式,培养学生的工程素质和知识集成能力,使人才适应国际标准的要求。
一、贯穿工程素质培养的实验教学体系改革创新思路冶金工程实验教学改革表明,只有让学生在实验过程中充分动脑、动手,才能有效提升学生的综合素质和工程能力。
实验课程设置必须融合各学科知识,并以梯级能力培养为主线,专业实践能力培养为重点,不断优化实践教学体系,提高学生的工程实践能力。
梯级能力培养包括学生基本动手能力的培养、基本实践能力的训练、专业实践能力的强化和综合应用能力的提高,分别对应专业基础实验教学平台、专业综合实验教学平台和科研创新性实验教学平台。
1.实验教学打破按课程开设课内实验和集中实验的格局,全部开设独立实验课程。
4门独立设置的实验课程包括“冶金传输原理实验”32学时(2学分)、“冶金自动化技术实验”16学时(1学分)、“冶金原理实验”集中安排2周(2学分)、“专业综合实验”集中安排2周(2学分)。
评审编号
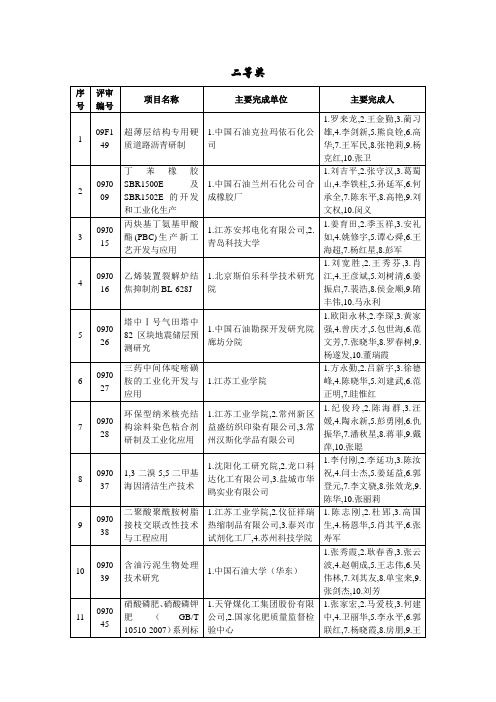
09J009
丁苯橡胶SBR1500E及SBR1502E的开发和工业化生产
1.中国石油兰州石化公司合成橡胶厂
1.刘吉平,2.张守汉,3.葛蜀山,4.李铁柱,5.孙延军,6.何承全,7.陈东平,8.高艳,9.刘文权,10.闵义
3
09J015
丙炔基丁氨基甲酸酯(PBC)生产新工艺开发与应用
1.江苏安邦电化有限公司,2.青岛科技大学
13
09J049
稠油油藏热采监测资料解释及调堵参数研究
1.中国石油大学(北京),2.中国石油化工股份有限公司胜利油田分公司,3.中国石油化工股份有限公司河南油田分公司,4.中国石油天然气股份有限公司辽河油田分公司
1.刘慧卿,2.宁正福,3.张红玲,4.庞占喜,5.刘仁静,6.王庆,7.王增林,8.王晗,9.刘欣,10.张瑛
34
09J175
20kt/a异丙醇胺装置
1.赛鼎工程有限公司,2.化学工业第二设计院宁波工程有限公司
1.陈发挥,2.隋保有,3.刘佩绅,4.颜焕敏,5.郭仁君,6.周剑,7.吴泽安,8.沈洪飞,9.温雪莲,10.徐斌
35
09J178
疏松砂岩稠油油藏注蒸汽开采工艺配套技术
1.中国石油大学(华东),2.中石化胜利油田分公司孤东采油厂
1.江南大学,2.中国化工经济技术发展中心,3.湖南出入境检验检疫局检验检疫技术中心,4.天津市检验检疫科学技术研究院
1.王利兵,2.胥传来,3.王晓兵,4.冯智劼,5.李宁涛,6.吕刚,7.张园,8.于艳军,9.赵黎华,10.周磊
39
09J198
三环唑原药国家标准GB12685-2006、三环唑可湿性粉剂国家标准GB20701-2006的制定
25
09J117
工业锅炉节能减排问题探析

后缓解能源危机的主要途径 。那么 , 如何做好 工业 锅炉的节能 减排工作是我们要探讨 的问题 。
1 工 业 锅炉 应 用 现 状
在操作中 , 多数锅炉存在无 运行状 态检测 仪的特点 , 而且 有的工业锅炉仅 只有机械运行件的控制装 置 , 运行过程极 为不
严格。
工业锅炉是工业 和社会使用 的必需消耗 品, 它主要是为工
业锅炉制造许可证 , 其 主要生产类 型就是层然锅炉 , 占到燃煤锅
炉总数的 9 6 % 以上。根据权威数据显示 , 仅2 0 1 1 年全国锅炉总
规, 不断加强对管理人员 的培训 , 使 管理人 员在不 断更新 观念 的基础上 , 提高锅炉 的有效运行效 率。
3 . 1 完善 各项 节 能减 排 法 规
.
0 引言
术力量 薄弱 , 在节 能 技 术 的新 产 品推 广 上 还 有 待进 一 步 的 提高。
2 . 3 燃 烧技 术及 设 备 水 平 较 低
随着全球化进程 的 日益加快 , 环境污染越来越受到人们 的 广泛关注…。我国是发展 迅速 的新兴 国家 , 污染物排 放 、 能源 消耗所 占比重越来越 受到关注 。在 我 国主要的能 源结构是 以
采用 图纸 间的互相借鉴 , 依葫芦画瓢 , 很少采用新 的科学 工艺 。
在有些锅炉制造过程中 , 不仅装配工艺极 其简单 、 质量粗 糙 , 而 且风量的调节性能也很差 , 排风 机设计 不密封 , 产 品质 量严重 不合格。有 的制造商在制造中 , 锅炉的横向风压呈现不均衡分
布, 侧墙与炉子排风 口间漏风相当严重 , 导致在实 际使用 中, 很
锅炉都在 低负荷下运行 。据不完全统计 , 我 国的工业锅 炉平均
中山市三叶斑潜蝇寄主种类及危害情况

中山市三叶斑潜蝇寄主种类及危害情况柳浩;刘春燕;李宁东;曾玲【摘要】对中山市5个无公害蔬菜生产基地的调查结果表明,在大田蔬菜种植期间,三叶斑潜蝇主要嗜食危害6科14种寄主植物,包括菊科的茼蒿、非洲菊和莴苣,伞形科的西芹和香芹,豆科的豆角、四季豆,茄科的番茄和枸杞,葫芦科的冬瓜、西葫芦、黄瓜,以及十字花科的芥菜和白菜等蔬菜品种,对其他蔬菜种类没有发现危害.【期刊名称】《广东农业科学》【年(卷),期】2012(039)007【总页数】5页(P92-96)【关键词】三叶斑潜蝇;美洲斑潜蝇;寄主;危害【作者】柳浩;刘春燕;李宁东;曾玲【作者单位】中山市农业局农业技术推广中心,广东中山5284033;华南农业大学资源环境学院昆虫生态室,广东广州510642;广东省森林病虫害防治与检疫总站,广东广州510173;中山市农业局农业技术推广中心,广东中山5284033;华南农业大学资源环境学院昆虫生态室,广东广州510642【正文语种】中文【中图分类】S476三叶斑潜蝇(Liriomyza trifolii)是世界上重要的检疫性蔬菜害虫[1-2],已知其可危害25科300多种植物[3-5],而且随着扩散面积的增大,寄主范围也在逐渐扩大。
三叶斑潜蝇入侵我国大陆后,尤其是在广东地区,常与美洲斑潜蝇在同一生境中生存危害,国内对于美洲斑潜蝇的研究已较为透彻[6-10],国外对于三叶斑潜蝇的研究报道较多[11-14],而对该虫的寄主危害情况、田间种群发生动态,目前国内尚没有报道。
我们已对广东省73个菜场中,三叶斑潜蝇对寄主蔬菜危害的选择性和危害程度进行了初步普查[15]。
在此基础上,我们对中山市三叶斑潜蝇寄主种类及危害进行了调查,现将研究结果报道如下。
1 材料与方法试验于2007年1~12月每月上旬进行调查;调查地点为中山市港口镇西街菜场、南区福涌村菜场、坦洲镇定发菜场、大涌镇青岗菜场和沙朗隆平村菜场,菜场均为无公害蔬菜生产基地。
含非谐振节点滤波器的耦合矩阵综合方法

含非谐振节点滤波器的耦合矩阵综合方法柳浩;李胜先【摘要】基于非谐振节点理论,提出了一种改进的直接耦合矩阵综合方法.通过将非谐振节点看作谐振点,采用经典耦合矩阵综合方法得到耦合矩阵,再对矩阵作相似变换,使非谐振节点位置相对应的元素不含传输零点信息,并对其所在行列作比例变换,使其还原为非谐振节点,直接综合得到可用于设计含非谐振节点滤波器的耦合矩阵.这种综合方法简化了含非谐振节点滤波器的综合、拓扑重构和性能仿真,Matlab和HFSS仿真结果验证了这种综合方法的合理性和可行性.【期刊名称】《中国空间科学技术》【年(卷),期】2016(036)002【总页数】4页(P46-49)【关键词】滤波器;耦合矩阵;非谐振节点;谐振点;相似变换;传输零点【作者】柳浩;李胜先【作者单位】中国空间技术研究院西安分院,西安 710000;中国空间技术研究院西安分院,西安 710000【正文语种】中文【中图分类】TN713Key words:filter;coupling matrix;nonresonating node;resonatingnode;similarity transformation;transmission zero广义切比雪夫滤波器广泛应用在各种微波系统中,如卫星通信系统、雷达系统等,在通过实现有限传输零点来提高选择性[1]方面,交叉耦合方法要实现N阶N个传输零点,需要源与负载的直接耦合,这样就限制了带通滤波器输入与输出间的隔离。
另外,提取极点技术需要主通路上增加额外的相位,增加了滤波器的体积和质量。
为了消除以上两种方法固有的缺陷,2004年, Amari和Rosenberg首先提出了非谐振节点[2](Non-Resonating Node,NRN)的概念,可实现N阶N个传输零点而不需要源与负载的直接耦合。
谐振器与非谐振节点的模块化设计特性也非常优越,通过级联产生传输零点的单元结构,使级联单元独立控制其相对应的零点。
4年级成绩计算系统

2014-11-11
静宁县城关小学四年级
班 学号 级 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 五 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 语文 姓名 樊燕妮 陈蕾蕾 汪勃宇 王林源 陈新 邹嘉月 张文博 高邈 胡岩峰 闫博雅 孙昱 陈淮 张雨彤 张元浩 沙家宝 景雨轩 靳佳妮 王家乐 吕宛怡 郜育辰 夏宏民 李佩月 张佳 景诗云 席权 杨涛涛 李珊珊 郭芮瑄 吕浩科 王瑞琪 张博 王桓 翟敏 白锭峰 杨希玺 席楠 杨莹煊 马磊 于源 孙艺凡 牟晶晶 总分 班级名 全级 次 名次 总分 数学 班级名 全级名 次 次 总分 英语
班成绩表
科学 思品 语数外三科 总分 五科 班级名 全级名 次 次
班级 全级名 班级 全级 班级 全级 班级 全级 总分 总分 总分 名次 次 名次 名次 名次 名次 名次 名次
二 二
1 2
徐菲 张韵涵
城关小学成绩计算系统
2014-11-11
静宁县城关小学四年级
班 学号 级 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 二 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 语文 姓名 靳鑫 戴英杰 李旻燕 何沛儒 王小烨 张迎博 尤钰翔 李颜冰 田子果 王璇 王新宇 李腾 王锦 张妍 陈静茹 刘越宏 柳成晨 王灵慧 方保霖 雷尊岩 胡东鹏 刘康 杜江虎 魏誉 柴皓淇 马瑛 王辰 黎雨彤 吕佳昕 韩启立 张剑飞 徐硕键 王铖 何娜 苟淑贤 郭思琳 任高卓 张芮菡 胡子昱 张帆 王亚辉 总分 班级名 全级 次 名次 总分 数学 班级名 全级名 次 次 总分 英语
不同生殖生长阶段高温胁迫对水稻产量和品质的影响

核农学报2023,37(9):1872~1883Journal of Nuclear Agricultural Sciences不同生殖生长阶段高温胁迫对水稻产量和品质的影响季平1, **柳浩1, **叶世河1刘金龙1匡佳丽1龙莎1杨洪涛1, 2刘晓龙1, 2, *(1宜春学院生命科学与资源环境学院,江西宜春336000;2江西省高等学校硒农业工程技术研究中心,江西宜春336000)摘要:为探究不同生殖生长阶段高温胁迫对水稻产量损失及稻米品质的影响,以水稻品种黄华占(HHZ)和Y两优1577(YLY1577)为材料,以白天32 ℃/晚上26 ℃为对照(CK),分别在孕穗期(始穗前7 d,HS1)及始穗后1~7(HS2)、8~14(HS3)、15~21(HS4)和22~28 d(HS5)进行高温胁迫(白天38 ℃/晚上32 ℃),测定水稻植株生长发育、产量结构和稻米品质的变化。
结果表明,孕穗期高温对水稻幼穗发育影响最大,始穗后1~7 d高温对结实率影响最大,8~14 d高温对千粒重影响最大。
HHZ、YLY1577分别在始穗后1~7、8~14 d高温胁迫下的产量损失最大。
孕穗期高温对稻米品质影响较小。
与对照相比,始穂后1~28 d高温使稻米加工品质降低,垩白粒率和垩白度增加;总淀粉、直链淀粉、蔗糖含量和胶稠度降低,蛋白质、葡萄糖和果糖含量增加;淀粉最终黏度、消减值和糊化温度增加,崩解值降低。
始穗后8~14 d高温对稻米的外观和食味品质影响最大,其次为始穗后15~21和1~7 d。
综上,孕穗期高温主要通过抑制幼穗生长发育影响产量形成。
始穗后1~14 d是高温胁迫影响水稻产量的关键时期,主要通过降低结实率和千粒重抑制产量形成。
始穗后8~21 d是稻米品质对高温胁迫的敏感时期,始穗后8~14 d遭遇高温胁迫可能会导致水稻产量和稻米品质的双重损失。
本研究结果为不同生育期高温胁迫下水稻的产量和品质评估提供了科学依据。
四、项目名称废轮胎修筑高性能沥青路面关键技术及工程应用(一)申报

四、项目名称:废轮胎修筑高性能沥青路面关键技术及工程应用(一)申报奖种:科学技术进步奖一等奖(二)所在专业评审组名称:交通运输(三)项目简介:本项目属于公路路基、路面工程科学技术领域。
废轮胎是一种可利用的再生资源,它其中富含的优质橡胶和抗老化剂等材料可以替代当前普遍应用但价格昂贵的SBS改性材料,广泛应用于高性能沥青路面的修筑。
据统计,每修筑1km橡胶沥青路面可消耗近万条废轮胎,从而代替了传统高污染、高耗能的废轮胎处理方式,实现了废轮胎资源化升级利用。
但长期以来,由于缺乏橡胶沥青应用技术标准、工业化生产装备、橡胶沥青混凝土设计方法和施工工法等关键技术,严重制约了废轮胎筑路技术及规模产业化的发展。
自2001年起,本项目依托国家及行业科研开发、节能减排和技术推广任务开始立项研究。
主要技术创新如下:(1)攻克了橡胶沥青互逆反应的控制机理等核心技术难题。
(2)研发了高性能、大功率橡胶沥青生产装备并实现产业化。
(3) 创建了橡胶沥青混凝土设计理论和方法。
(4) 开发了低噪声、抗开裂、钢桥面铺装及预防性养护等功能型高性能橡胶沥青混凝土。
2007年本项目成果即被列入首批交通运输部“材料节约和循环利用专项行动计划”重点推广项目,修筑了科技示范工程,并成功应用于北京奥运会、长安街大修等重大道路工程。
编制国家标准1部,行业和地方标准 6 部,指南 2部,形成国家及行业工法6 项,地方性规范10余项。
本项目获得国家授权发明专利8项,实用新型专利2项;获省部级科技一等奖 4项,二等奖 2 项;出版原创性专著1部;培养博士9名,硕士26名,培训工程技术人员3000余人。
在引领绿色交通技术发展的同时,促进产业全面升级,并取得了显著的社会经济效益,总体技术达到国际领先水平。
(五)推广应用情况:依据本项目成果先后编制标准7部、指南2部,形成各级工法6项。
“橡胶沥青及混凝土”已被许多地区纳入地方推广应用的典型材料和结构。
2007年,本项目成果即被交通运输部列为首批“材料节约和循环利用专项行动计划”重点推广应用技术之一。
四、项目名称废轮胎修筑高性能沥青路面关键技术及工程应用(一)申报

四、项目名称:废轮胎修筑高性能沥青路面关键技术及工程应用(一)申报奖种:科学技术进步奖一等奖(二)所在专业评审组名称:交通运输(三)项目简介:本项目属于公路路基、路面工程科学技术领域。
废轮胎是一种可利用的再生资源,它其中富含的优质橡胶和抗老化剂等材料可以替代当前普遍应用但价格昂贵的SBS改性材料,广泛应用于高性能沥青路面的修筑.据统计,每修筑1km橡胶沥青路面可消耗近万条废轮胎,从而代替了传统高污染、高耗能的废轮胎处理方式,实现了废轮胎资源化升级利用。
但长期以来,由于缺乏橡胶沥青应用技术标准、工业化生产装备、橡胶沥青混凝土设计方法和施工工法等关键技术,严重制约了废轮胎筑路技术及规模产业化的发展.自2001年起,本项目依托国家及行业科研开发、节能减排和技术推广任务开始立项研究。
主要技术创新如下:(1)攻克了橡胶沥青互逆反应的控制机理等核心技术难题.(2)研发了高性能、大功率橡胶沥青生产装备并实现产业化。
(3)创建了橡胶沥青混凝土设计理论和方法。
(4)开发了低噪声、抗开裂、钢桥面铺装及预防性养护等功能型高性能橡胶沥青混凝土。
2007年本项目成果即被列入首批交通运输部“材料节约和循环利用专项行动计划”重点推广项目,修筑了科技示范工程,并成功应用于北京奥运会、长安街大修等重大道路工程。
编制国家标准1部,行业和地方标准 6 部,指南 2部,形成国家及行业工法6 项,地方性规范10余项。
本项目获得国家授权发明专利 8项,实用新型专利2项;获省部级科技一等奖 4项,二等奖 2 项;出版原创性专著1部;培养博士9名,硕士26名,培训工程技术人员3000余人。
在引领绿色交通技术发展的同时,促进产业全面升级,并取得了显著的社会经济效益,总体技术达到国际领先水平。
依据本项目成果先后编制标准7部、指南2部,形成各级工法6项。
“橡胶沥青及混凝土”已被许多地区纳入地方推广应用的典型材料和结构。
2007年,本项目成果即被交通运输部列为首批“材料节约和循环利用专项行动计划”重点推广应用技术之一。
基于DSP的太阳能跟踪控制系统研究

Ke r s ta k n o to t o DS s l re e g y wo d : r c i g c n r l me h d; P; o a n r y
器 的精 度要 靠高精 度 的传感 器 , 精密 的 实验 电路 来
1 引 言
理论 分 析 表 明 : 用 相 同 功 率 的太 阳 能 电 池 采
Ab ta t I o sd ro h n c u a y a d p o n ii t re e c b l y o u r n o a n r y t a k n y t m. Th s s r c : n c n i e ft e ia c r c n o ra t n e f r n e a i t fc r e ts l r e e g r c i g s se — i i p p r p e e t i h p e i in s l re e g r c i g s s e wh c s h o t o t o h to i t a k n v m e tc m— a e r s n s a h g - r c s o a n r y ta k n y t m ih u et e c n r l o me h d t a b t r c i g mo e n o b n d wih p o o lc rc d t c in ta k n , a d u e DS s c n r l r c r h p Th u s r u h y t a k d b h bt i e t h t ee t i e e t r c i g o n s P a o tol o ec i. e e s n i o g l r c e y t e o i
2017年赤峰市汉授初一(11)班学生基线测试
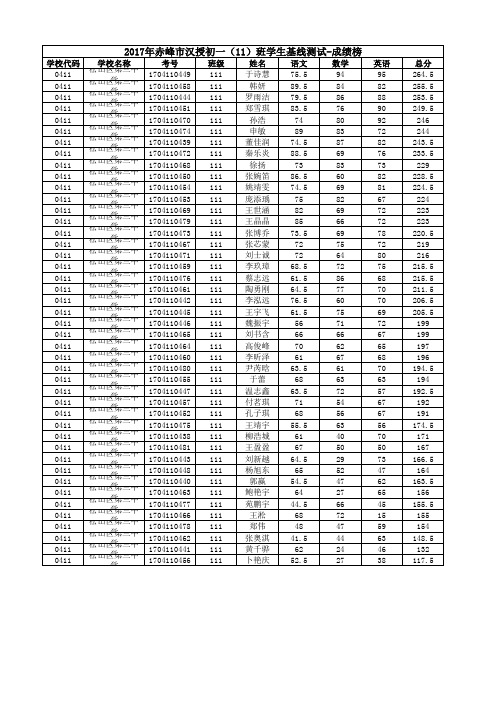
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42
学校代码 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 0411 学校名称 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 松山区第三中学 考号 1704110449 1704110458 1704110444 1704110451 1704110470 1704110474 1704110439 1704110472 1704110468 1704110450 1704110454 1704110453 1704110469 1704110479 1704110473 1704110467 1704110471 1704110459 1704110476 1704110461 1704110442 1704110445 1704110446 1704110465 1704110464 1704110460 1704110480 1704110455 1704110447 1704110457 1704110452 1704110475 1704110438 1704110481 1704110443 1704110448 1704110440 1704110463 1704110477 1704110466 1704110478 1704110462 1704110441 1704110456 班级 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 111 姓名 于诗慧 韩妍 罗雨洁 郑雪琪 孙浩 申敏 董佳润 秦乐炎 徐扬 张婉笛 姚靖雯 庞添瑀 王世涵 王晶晶 张博乔 张芯蒙 刘士诚 李玖璋 蔡志远 陶勇刚 李泓远 王宇飞 魏振宇 刘书含 高俊峰 李昕泽 尹芮晗 于蕾 温志鑫 付茗琪 孔子琪 王靖宇 柳浩城 王盈盈 刘新越 杨旭东 郭赢 鲍艳宇 苑鹏宇 王淞 郑伟 张奥淇 黄千骅 卜艳庆 语文 75.5 89.5 79.5 83.5 74 89 74.5 88.5 73 86.5 74.5 75 82 85 73.5 72 72 68.5 61.5 64.5 76.5 61.5 56 66 70 61 63.5 68 63.5 71 68 55.5 61 67 64.5 65 54.5 64 44.5 68 48 41.5 62 52.5 数学 94 84 86 76 80 83 87 69 83 60 69 82 69 66 69 75 64 72 86 77 60 75 71 66 62 67 61 63 72 54 56 63 40 50 29 52 47 27 66 72 47 44 24 27 英语 95 82 88 90 92 72 82 76 73 82 81 67 72 72 78 72 80 75 68 70 70 69 72 67 65 68 70 63 57 67 67 56 70 50 73 47 62 65 45 15 59 63 46 38 总分 264.5 255.5 253.5 249.5 246 244 243.5 233.5 229 228.5 224.5 224 223 223 220.5 219 216 215.5 215.5 211.5 206.5 205.5 199 199 197 196 194.5 194 192.5 192 191 174.5 171 167 166.5 164 163.5 156 155.5 155 154 148.5 132 117.5
经鼻内镜翼管神经切断术治疗过敏性鼻炎患者的效果

经鼻内镜翼管神经切断术治疗过敏性鼻炎患者的效果曹俊强【摘要】目的观察经鼻内镜翼管神经切断术治疗过敏性鼻炎患者的效果.方法选取2014年10月至2016年1月临颍县人民医院收治的86例过敏性鼻炎患者,依照手术方案分为对照组和观察组,各43例.对照组接受经鼻内镜下鼻甲黏膜下剥离术,观察组接受经鼻内镜翼管神经切断术,术后随访1a.观察两组临床疗效、手术时间、住院时间、术中出血量和并发症发生率.结果观察组患者总有效率高于对照组,术中出血量低于对照组,手术时间和住院时间均短于对照组,并发症发生率低于对照组,差异有统计学意义(P<0.05).结论经鼻内镜翼管神经切断术治疗过敏性鼻炎效果显著,能减少术中出血量,降低并发症发生率,改善其预后,促进康复进程.【期刊名称】《河南医学研究》【年(卷),期】2018(027)011【总页数】2页(P2001-2002)【关键词】经鼻内镜翼管神经切断术;过敏性鼻炎;疗效【作者】曹俊强【作者单位】临颍县人民医院耳鼻喉科河南漯河 462600【正文语种】中文【中图分类】R765.2过敏性鼻炎为鼻腔黏膜变应性疾病,主要由接触变应原引起,临床表现为连续喷嚏、阵发性鼻痒、鼻涕量多清稀、鼻塞,部分患者伴有失嗅、咽喉痒、眼痒,虽不能危及患者生命,但严重影响其生活质量[1]。
过敏性鼻炎易反复发作,难以根治,治疗关键在于避免与变应原接触。
传统治疗多采用抗组胺药、糖皮质激素、抗白三烯药等暂缓鼻部症状,但易引发内分泌失调、血压升高等不良反应,不宜长期服用。
随着医学技术的发展,手术成为治疗过敏性鼻炎的常见方式。
目前临床常采用下鼻甲黏膜下剥离术,疗效尚可,但术中出血多,并发症发生率高[2]。
本研究旨在观察经鼻内镜翼管神经切断术治疗过敏性鼻炎患者的效果。
1 资料与方法1.1 一般资料选取2014年10月至2016年1月临颍县人民医院收治的86例过敏性鼻炎患者,依照手术方案分为对照组和观察组,各43例。
小儿腺样体肥大的临床治疗

20 8 6 . 06,( )
[ ] 王红 洛, 5 范崇盛, 薛柯凡. 样体 肥大 16倒疗 效观 察. 腺 5 中国误诊 学杂 志 , 0 ,( ) 2 333 . 0
用智慧和勤劳谱写人生华彩篇章——记全国劳动模范北京市政路桥控股建材集团总工程师柳浩

大 部分 时 问都泡 在 工地 上 。
当 时 , 已有 身 孕 , 她 尚未 度 过前 3 月危 险期 。 个 就这样 , 她 瞒 着 大 家 跑 工 地 、 试 做 验, 终于在做 了母亲 的同时 ,
也 获得 事 业 上 的 丰 收—— 上 述 研 究 成 果 被 认 定 为 具
行 业 采 风 器
Spe al si es por ci Bu n s Re t
用智慧和勤劳谱 写人生华彩篇章
记全 国劳动模 范 北京市政路桥控股建材集 团总工程 师柳浩
爱 岗敬 业 甘 做 默 默 无 闻 的“ 路 石 " 铺
-
4 9 9 4年 8月 , 浩 从 西 安公 路 学 院研 究 生 毕 业 分 2 0 柳 0 2年 , 当北 京获 得 2 0 0 8年奥 运 会举 办权 后 , 政府 市
个 性 化 方 案 , 续 为 杏 石 1 I 六 环 路 西 沙 屯 收 费 实 施 的北京 长 安街 大 修工 程 , 陆 3路 3、 全程 l O多 k 道路 全 部 m
Z 1 ̄ 5 9竹 第 8 席荭 川 00 期( ) 2 巷 投 盯
1
器 行业采风
Sp i ecal Busne s Rep t i s or
采 用 了抗 车辙 路 面结 构 , 共计 使 用 抗 车辙 沥青 混 合 料 修工 程 就抽取 了 4 0多个 。由于这些 工作 不能 影 响交 0 4万余 吨 。“ 车 辙技 术 ” 抗 作为 北京 市建 国六 十周 年科 通 , 在夜 间进 行 , 夜 间加班 工作是 家常便 饭 。加 上 要 她
I配到北京 , 一直从 事道路材料研究工作 , 至今 已 决 定对 二 环路进 行 改造 。她承 担 了为二 环路 改造 工程
三维激光扫描技术在道路工程测量中的应用

三维激光扫描技术在道路工程测量中的应用摘要:道路工程勘察测量工作是工程建设的基础与保障,因而测量质量广受人们的关注。
现阶段,随着我国社会经济的快速发展,道路工程的作用愈加重要,对道路工程测量的要求也越来越高。
因此,传统的测量技术已经较难满足当下道路工程测量的需要,因此应当引入当先的新兴技术。
基于此,本文首先对三维激光扫描技术进行阐述,进而深入探究了其在道路工程测量中部分场景的应用。
关键词:三维激光扫描,道路工程,测量,应用引言:道路施工测量作为道路施工质量的基础和保证,有助于道路工程建设的开展[1]。
当下,随着建设项目的快速增加,通过调研可以发现,新技术方法正在不断开发并应用于实际测量过程。
在道路测量工作中通常使用现代技术手段和设备,但通常只能应用在较为平坦的路段,并且无法将测量工作和测量数据三维化,因此测量数据在实际应用过程中通过无法将结果进行准确的展示。
随着技术的进步,三维激光扫描技术已经引起人们的注意,并越来越多地用于道路工程测量中。
使用三维激光扫描技术进行道路工程测量不仅可以使测量数据三维化,而且可以在空间上描述测量区域,从而使测量数据更准确,参考值更高,有助于道路工程测量的长期发展。
1.三维激光扫描技术相关概述三维激光扫描技术主要采用激光测距原理,其通过记录要测量表面上大量密集点的3D坐标,根据相应的反射率和纹理信息,可以快速构建测量对象的三维模型,进而将点、线、面以及文字等展示在地图数据信息上[2]。
三维激光扫描技术具体包括数据采集的硬件部分和数据处理的软件部分。
根据不同的载体,又可以分为航空、车载、地面便携三种类型[3]。
它采用扫描技术来测量待加工工件的尺寸和形状,主要用于逆向工程、表面读取、工件的三维测量场景中。
对于现有的三维对象(样本或模型),无需技术文档即可快速测量对象的轮廓收集数据,并且可以对其进行配置、编辑、修改进而产生通用输出格式。
三维激光扫描技术的核心是云、建模、空间网格扫描等模块。
基于表面活性技术的温拌沥青混合料应用研究

步研 究 。根 据确定 的级配 ,采用 常 规拌 和与 温
设计 验证 思路 为对 HM A与 多种 WMA进行
拌对 照 的方式 ,进行 马歇 尔试 验 ,表 3为通 过不
3 0
石
油
沥
青
2 1 年第 2 01 5卷
同拌和 方式 以及温 拌技 术不 同拌 和温度下 试验 得
到 的主要 体积 指标 。
用 较多 的是 直 投 式 D T温 拌 添 加 剂 ,是 一 种 表 A 面活性 剂 的水 溶 液 ,呈 碱性 。D T温 拌 工艺 中 , A 表面活 性剂分 子 由亲油端 和亲水 端组 成 ,在 水溶
在 3 左右 ,相当于生产 1 混合料将节省 1 0c l C t —
15k 燃油,由于集料加热温度大大降低 ,缩短 . g
科 学的参考建议 ,并促进节能减排低碳环保的温拌 沥青混合料更好地发展 。
关 键 词 :温 拌 添加剂 路 面 维修
温 拌 沥青混 合 料 WMA ( r xA pa ) Wam Mi shl t
亲油端 结合 沥青 ,胶 团发生 反转 。 由于水 的蒸 发 散失 与界 面条件 密切 相关 ,因此 毛细 空间 中存 在
沥青混 合料 生产 中拌 和的工 作性 以及更 有效 的可
压实性 能 。
目前温拌 技术 主要 有三种 :
a 沥青发泡 技术 ,即 通过 少 量 的水 或 者 发 )
泡 剂喷洒 进热 沥青 中 ,在 水蒸气 作用 下形 成膨胀 腔 里 ,在短时 间 内降低沥 青 的粘 度 ; b 有机 添加剂 技术 ,有 机添 加 剂能 够在 9 ) O
不可逆 的 ,其最 终残余 量不 足沥青 用量 的 1 。 %
八年级学生名次

数学 127 130 129 122 121 125 124 125 129 119 106 119 123 100 115 117 110 115 130 124 92 115 124 105 105 106 114 118 95 54 85 78 87 41 35 35 57 40 28 12 14 24 14 15 9 0
王增科 王丽 彭彩霞 刘崇鑫 曲高阳 尹盈盈 孙逸文 温连馨 张知龙 泮慧忠 杜永霖 赵孟佳 李国浩 欧亚洲 郭新龙 孙雪 王慧 李群 刘欣宇 李亚萍 车文超 周巧燕 尚秀梅 潘志坚 孙伟龙 张高睿 刘迪 李诺 闫子龙 孙瑞超 刘晶 曲阳凯 耿鹏程 曲晓龙 李杨 赵月宝 刘萌琪 卫晓腾 刘炳宇 王文萍 郭泰 曲苗苗 刘航 王建宁 杜震 王康
语文 115 114 113 108 112 111 108 114 112 110 90 105 93 105 98 92 96 93 94 104 86 80 95 96 80 76 57 79 91 75 80 86 69 69 55 66 69 47 44 0 27 20 31 61
数学 118 124 124 119 129 116 124 118 124 118 127 129 125 110 109 113 83 94 91 71 86 79 87 42 90 59 96 69 53 30 21 25 47 44 72 46 34 17 17 45 9 3 12 0
八年级第二学期期中考试学生成绩表
考号 3081 3002 3004 3126 3007 3242 3048 3043 3213 3046 3090 3132 3053 3012 3129 3059 3135 3057 3257 3101 3050 3224 3061 3222 3259 3218 3109 3229 3147 3227 3103 3069 3264 3266 3071 3195 3111 3035 3192 3075 3037 3039 3197 3079 3120 3084
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
编号2014010355 研究类型理论研究分类号O15College of Arts﹠Science of Hubei Normal University学士学位论文Bachelor’s Thesis论文题目分块矩阵的性质与应用作者姓名柳浩学号2010311010355所在院系数学系学科专业名称数学与应用数学导师及职称谢涛讲师论文答辩时间2014年5月15日本科毕业论文诚信承诺书目录1.引言 (1)2.分块矩阵的概念 (1)3.分块矩阵的运算性质 (1)3.1分块矩阵的加法 (2)3.2分块矩阵的乘法 (3)3.3分块矩阵的转置 (5)3.4对角分块矩阵的一些性质 (6)4 分块矩阵的相关定理及其证明 (6)5 利用分块矩阵计算行列式 (10)5.1 利用定理1计算行列式 (10)5.2 利用定理2计算行列式 (12)5.3 利用定理3计算行列式 (13)5.4 利用定理4计算行列式 (18)5.5 利用定理5计算行列式 (20)5.6 利用定理6计算行列式 (22)6.总结: (24)参考文献 (25)分块矩阵的性质与应用柳浩(指导老师,谢涛老师)(湖北师范学院文理学院中国黄石 435002)摘要:分块矩阵是矩阵理论中的一个重要内容,在高等代数中有着很重要的应用.矩阵分块的思想来源于对矩阵运算复杂度和储存思想的考虑,矩阵分块能降低矩阵的阶数,使矩阵条理更清晰并简化运算.本文从研究行列式以及分块矩阵的基本性质入手,在查阅了大量文献的基础上,给出了与行列式计算有关的分块矩阵相关定理.将分块矩阵降阶的思想应用在行列式计算过程中,推导出了借助分块矩阵进行行列式计算的多种方法,最后通过具体的例子对比说明,很多时候借助分块矩阵计算行列式比用行列式的常规方法计算更简单、直观、清晰.关键词:分块矩阵;行列式中图分类号:O15Properties and Application of Block MatrixLiu Hao (Tutor:Xie Tao)Abstract: Block Matrix is an important content of Matrix theory, which has a significant usage in Advanced Algebra. The idea of Block Matrix comes from the considerationof the memory storage and the complexity of Matrix Manipulation. Block Matrixcan reduce the exponent number of Matrix to make the consecution of Matrixclearer and the operation of Matrix easier. This article starts with basic properties ofMatrix, and gives some main conclusions of Block Matrix on the basis of accessinga lot of literature. And then, we use the reduction thoughts of Block Matrix inprocess of determinant calculation to derive multiple methods of determinantcalculation with the block matrix. At last, we use object lessons to compare, showsthat computing the determinant by means of block matrix is often more simple,intuitive and clear than conventional methods of determinant calculation.Key words: block matrix; determinant分块矩阵的性质与应用柳浩(指导老师,谢涛老师)(湖北师范学院文理学院 中国 黄石 435002)1.引言在高等代数中,矩阵是一项非常重要的内容,也是高等数学的很多分支研究问题的工具.当我们处理阶数较高或者具有特殊结构的矩阵时,用一般处理低阶矩阵的方法,往往会比较困难,为了研究问题的方便,也为了显示出矩阵中某些部分的特性,我们常常把一个大型矩阵分成若干子块.把每个子块矩阵看成是一个元素,从而构成分块矩阵.分块矩阵形象地揭示了一个复杂或是特殊矩阵的内部本质结构.利用矩阵分块可以把高阶矩阵划分为阶数较低的“块”,然后对这些以“块”为单位的矩阵施行矩阵的运算.本文就分块矩阵的加法与数量乘法、乘法等运算性质以及行列式展开等方面的应用作了较为深入的研究.2.分块矩阵的概念将一个矩阵用若干条横线和竖线分成许多个小矩阵,将每个小矩阵称为这个矩阵的子块,以子块为元素的形式上的矩阵称为分块矩阵.为了说明这个方法,我们来看以下的一个例子,在矩阵A=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-1011012100100001=⎥⎦⎤⎢⎣⎡E A E O 212中, E 2表示2级单位矩阵,而 A 1=⎥⎦⎤⎢⎣⎡-1121, O=⎥⎦⎤⎢⎣⎡0000 这就是我们所说的矩阵的分块.3.分块矩阵的运算性质分块矩阵的运算在形式上和数字矩阵的运算完全一样,只要进行运算的矩阵的分块适当,分块矩阵有类似于普通矩阵的运算法则:3.1分块矩阵的加法设A ,B 都是n m ⨯矩阵,并且对A ,B 用同样的方法进行分块:111212122212k k l l lk A A A A A A A A A A ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦ 111212122212k k l l lk B B B B B B B B B B ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦其中,ij ij A B 都是i j m n ⨯矩阵,即,ij ij A B 使同型矩阵,那么111112121121212222221122k k k k l l l l lk lk A B A B A B A BA B A B A B A B A B A B +++⎡⎤⎢⎥+++⎢⎥+=⎢⎥⎢⎥+++⎣⎦应注意的是,利用分块法对两个同型矩阵进行加法运算时,两个矩阵必须采用相同的分块法.下面我们通过一个例题来详细了解加法的运算法则.例1:100000,001001a a Ab b ⎛⎫ ⎪⎪= ⎪⎪⎝⎭设000100000001a a B b b ⎛⎫⎪⎪= ⎪ ⎪⎝⎭, .A B +求 解:将,A B 分块100000001001a a A b b ⎛⎫⎪⎪= ⎪ ⎪⎝⎭12A O ,OA ⎛⎫=⎪⎝⎭其中121,01;1a A a bA b ⎛⎫=⎪⎝⎭⎛⎫=⎪⎝⎭12000100000001a B O a B ,OB b b ⎛⎫⎪⎛⎫ ⎪==⎪ ⎪⎝⎭ ⎪⎝⎭其中120,10;1a B a bB b ⎛⎫=⎪⎝⎭⎛⎫=⎪⎝⎭111021,0112a a a A B a a a ⎛⎫⎛⎫⎛⎫+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭221021,1122b b b A B b b b ⎛⎫⎛⎫⎛⎫+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭1122AO B O A B O A OB ⎛⎫⎛⎫+=+ ⎪ ⎪⎝⎭⎝⎭2100120000210022a a b b ⎛⎫⎪ ⎪=⎪ ⎪⎝⎭.同理,设A 都是n m ⨯矩阵,把A 进行分块:111212122212k k l l lk A A A A A A A A A A ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦,a 为任意数,则111212122212k k l l lk aA aA aA aA aA aA aA aA aA aA ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦.3.2分块矩阵的乘法数乘运算: 设分块矩阵t s ij n m A A ⨯⨯=)(,k 为任意数,则分块矩阵与k 的数乘为t s ij kA kA ⨯=)(.乘法运算: 一般地说,设sn ik a A )(=,nm kj b B )(=,将矩阵A 、B 分块,⎪⎪⎪⎪⎪⎭⎫⎝⎛=st s s t t A A A A A A A A A A212222111211,⎪⎪⎪⎪⎪⎭⎫⎝⎛=tr t t r r B B B B B B B B B B 212222111211, 其中每个ij A 是j i n s ⨯小矩阵,每个ij B 是j i m n ⨯小矩阵,于是有⎪⎪⎪⎪⎪⎭⎫⎝⎛==sr s s r r C C C C C C C C C AB C 212222111211, 其中ij C 是j i k m ⨯矩阵,=ij C ∑=ni ijij BA 1.应该注意,在进行乘法运算求乘积AB 时,对矩阵A 、B 分块要求,矩阵A 的列的分法必须与矩阵B 的行的分法一致.矩阵的乘法不适合交换律,即一般来说,没有BA AB =.分块矩阵是一类特殊的矩阵,它的乘法同样不适合交换律.根据上文所述分块矩阵也是一个矩阵,因此有与一般矩阵的加法、数乘、乘法的运算性质相同.不过,分块矩阵运算时应注意以下几点:(1) 进行加法运算时,对应子块的结构需相同;(2) 进行数乘运算时,必须对每一子块都乘以相同的数; (3) 进行乘法运算时,不能随意交换两个相乘子块的顺序.在具体运算过程中,我们要灵活地分块,目的是使运算更简便.而对于乘法,在矩阵A 与矩阵B 相乘时,对B 的一个分块方式,A 可以有几种分块方式都可与B 相乘,同样对A 的一个分块方式,B 也是如此.但不论怎样分块,始终坚持相乘的两个矩阵前一个矩阵列的分法与后一个矩阵行的分法一致,因为只有这样乘积才有意义.例如,已知⎪⎪⎪⎭⎫ ⎝⎛=200010001A ,⎪⎪⎪⎭⎫ ⎝⎛=011010100101B ,我们把B 分块为⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛222122011010100101B B E E , 其中2E 为二阶单位阵,这时若只考虑乘法的相容性,A 可以分块为⎪⎪⎪⎭⎫ ⎝⎛200010001、⎪⎪⎪⎭⎫ ⎝⎛200010001或⎪⎪⎪⎭⎫⎝⎛200010001,我们可以看到第一种分法中有单位块,而⎪⎪⎭⎫ ⎝⎛=222A OO E A , 对于乘法运算显然更加简便,即=AB ⎪⎪⎪⎭⎫ ⎝⎛200010001⎪⎪⎪⎭⎫⎝⎛011010100101⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=222122222B B E E A OO E ⎪⎪⎭⎫⎝⎛=2222212222B A B A E E ⎪⎪⎪⎭⎫⎝⎛=022*********.例2]1[:用分块法计算AB ,其中51241421,53100120020-⎛⎫⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭A B解:,A B 如上分块,⎪⎪⎭⎫ ⎝⎛=22211211A AA A A ⎪⎪⎭⎫⎝⎛=232221131211B B B B B B B其中11122122421(0,0),(5),,,12⎛⎫⎛⎫====⎪ ⎪-⎝⎭⎝⎭A A A A()()()0,20,0,01,1342,51232221131211===⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=B B B B B B ; 令==C AB ⎪⎪⎭⎫⎝⎛232221131211C C CC C C ,其中 =+=2112111111B A B A C )0()0)(5(51)00(=+⎪⎪⎭⎫⎝⎛,=+=2212121112B A B A C )00(()()()1002051342=+⎪⎪⎭⎫⎝⎛,=+=2312131113B A B A C )0()0)(5(01)00(=+⎪⎪⎭⎫⎝⎛-,=+=2122112121B A B A C ⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-514)0(21511024,=+=2222122122B A B A C ⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-332014)20(2113421024,=+=2322132123B A B A C ⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-04)0(21011024.故==C AB ⎪⎪⎪⎭⎫⎝⎛---=⎪⎪⎭⎫ ⎝⎛0335420141401000232221131211C C CC C C . 值得注意的是,利用分块法对两个矩阵进行乘法运算时,左矩阵列的分法和右矩阵行的分法必须完全相同. 3.3分块矩阵的转置对于一有rs 块的分块矩阵1111s r rs A A A A A ⎛⎫⎪=⎪ ⎪⎝⎭,有11111111T T s r TT T r rs s sr A A A A A A A A A A ⎛⎫⎛⎫⎪ ⎪=⇒= ⎪⎪⎪ ⎪⎝⎭⎝⎭值得注意的是,转置时,每一个小块也要转置,并且它的位置也要行列对调. 3.4对角分块矩阵的一些性质对于方阵A ,经过分块后,非0对角块都只在主对角线上,而且每个小块都是方阵;即120000000000s A A A A ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭,其中(1,2,)i A i s =都是方阵,那么称A 为分块对角矩阵.有如下性质: (1)行列式12s A A A A =.(2)若0(1,2,,)i A i s ≠=则0A ≠,并且有11112100000000000s A A A A ----⎛⎫ ⎪⎪= ⎪ ⎪ ⎪⎝⎭. (3)分块对角阵的乘法,111122220000000000000000s s s s A B A B A B A B A B A B ⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪ ⎪⎪ ⎪= ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭. (4)分块对角阵的转置,120000000000s A A A A ⎛⎫ ⎪⎪= ⎪⎪⎝⎭,那么1200000000000TT TT s A A A A ⎛⎫ ⎪⎪= ⎪ ⎪ ⎪⎝⎭. 4 分块矩阵的相关定理及其证明定义1]2[ 在一个n 级行列式D 中任意选定k 行k 列)(n k ≤.位于这些行和列的交点上的2k 个元素按照原来的次序组成一个k 级行列式M ,称为行列式D 的一个k 级子式.当n k <时,在D 中划去这k 行k 列后余下的元素按照原来的次序组成的k n -级行列式M '称为k 级子式M 的余子式.引理(拉普拉斯定理)设在行列式D 中任意取定了k )11(-≤≤n k 个行.由这k 行元素所组成的一切k 级子式与它们的代数余子式的乘积的和等于行列式D .定理1 设A 是m 阶方阵,B 是n m ⨯阶矩阵,C 是n 阶矩阵,则C A CO BA =. 证明: 利用拉普拉斯定理,只要将行列式CO B A按后n 行展开,在其所有的n 阶子式中,除C 外至少包含一列零向量,因此它们的值为零.而C 的余子式为A ,且C 位于整个矩阵的第n m m m +++,,2,1 行,第n m m m +++,,2,1 列,即可得C A CO BA =. 类似地行列式的形式为CB O A时,由行列式的转置值不变,因此仍有C A C A C B OA =''='''.通过上面的定理,我们自然想到,若是将行列式CO B A换成OC B A又会有怎样的结论,它的值等于B C 吗? 定理2 设A 、B 、C 均为n 阶方阵,则B C OC B A n 2)1(-=. 证明: 将拉普拉斯定理应用于上式的后n 行,在其所有n 阶子式中,除C 外至少包含一列零向量,因此它们的值为零.而C 的余子式为B ,且C 位于整个矩阵的第n n n n +++,,2,1 行, 第n ,,2,1 列,因此C B OC BA s )1(-=, 其中偶数+=+⋅⋅⋅+++++⋅⋅⋅+++=2)21()()2)(1(n n n n n n s ,即B C OC B A n 2)1(-=. 定理 3 ⎥⎦⎤⎢⎣⎡=D C B A P 是分块n 阶矩阵,其中A 为r 阶方阵,B 为s r ⨯阶阵,C 为r s ⨯阶阵,D 为s 阶方阵.(1) 若A 可逆,则B CA D A P 1--=; (2) 若D 可逆,则B CD A D P 1--=. 证明: (1) 当0≠A 时,有⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---B CA D O B A D C B A I CA O I 11 两边取行列式可得=P A B CA D 1--.(2) 当0≠D 时,有⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---D C O C BD A D C B A I O BD I 11 两边取行列式可得P =D B CD A 1--.将定理3中条件特殊化,可得到如下推论.推论1 设A 、B 、C 、D 分别是r ,s r ⨯,r s ⨯,s 矩阵,则有(1)CB D DCB E r -=;(2)BC A E C BA s-=.证明:(1) 只需在定理3中令r E A =,即有CB D CBD O BE D C B E rr -=-=.(2) 只需在定理3中令s E B =,即有BC A E CO BC A E CB A ss-=-=.推论2 设B 、C 分别是s r ⨯,r s ⨯,则有BC E CB E E CB E r s sr -=-=.证明: 只需在定理3中令r E A =,s E B =,则有BC E CB E E CB E r s sr -=-=.定理4[]5,4 设A 、B 、C 、D 都是n 阶方阵,则(1) 当0≠A 且CA AC =时,=DC BA CB AD - (2) 当A 0≠且BA AB =时,=DC BA CB DA -;(3) 当0≠D 且CD DC =时,=DC BA BC AD -; (4) 当0≠D 且BD DB =时,=DC BA BC DA -.证明:由A 、B 、C 、D 均为n 阶方阵,当0≠A 且CA AC =时,利用定理3得=DC BA AB CA D 1--B ACA AD 1--=B CAA AD 1--= CB AD -=,即=DC BA CB AD -, (2)、(3)、(4)类似可得.定理5[]7,6 设A 、B 都是n 阶方阵,则有B A B A AB BA -+=. 证明: 根据分块矩阵性质有BA O BBA A AB B B A A B B A -+=++= B A B A -+=.定理6[]8 设A 为n 阶可逆方阵,α与β均为n 维列向量,则)1(1βαβα-+=+A A A T T .证明: 因⎪⎪⎭⎫⎝⎛-+=⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-10110T TT A AE βαββαα, (1) ⎪⎪⎭⎫⎝⎛+=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛--αβαβαβ1110110A AA A ET T T , (2) (1)式、(2)式两边各取行列式,又1110=-=-TEE βα, 从而有)1(11αβαββα-+=+=-A A A A T T T.5 利用分块矩阵计算行列式在行列式计算的过程中,若是该行列式的结构符合上述定理条件的要求,就可按照该定理进行矩阵分块,利用定理的结论计算行列式.其中的关键是如何对行列式进行分块,什么样的行列式能进行分块.我们在运用分块矩阵计算行列式时,要仔细观察行列式的结构,先确定运用哪个公式来进行计算,再对行列式进行相应的分块.在计算的过程中,也可能遇到可以运用分块矩阵计算的行列式,因此不仅要牢记公式,也要学会灵活运用.5.1 利用定理1计算行列式能够利用定理1求解的行列式的类型为CO B A 或CB O A ,下面给出具体例子. 例3 计算行列式530012000215311210241210--=H . 解: 方法1(利用定理1)对行列式H 分块,CO BA H =, 其中⎪⎪⎪⎭⎫ ⎝⎛-=531102210A ,⎪⎪⎪⎭⎫ ⎝⎛-=211241B ,⎪⎪⎭⎫⎝⎛=5312C .根据定理1,有75312531102210=-==C A H .方法2(化三角形法) 将行列式H 化为上三角形.530012000215311210241210--=H 53012000215311210222321----=5312000412103674022321----=270000120004132141003674022321-----= 7=.方法3(降阶法)530012000215311210241210--=H 5300120012104121153001200215341212-⋅--⋅-= 53001200121041211530012001041041212-⋅----⋅-= 5301201215312010412---⋅-= 531253122-⋅=7=.显然方法1更简单,利用定理1计算例1极大简化了计算. 5.2 利用定理2计算行列式对于可以利用定理2计算的行列式,其结构特点是OC B A型.下面是利用定理2计算行列式的具体例子. 例4 计算行列式=H 0000000000000626151333231262322211615131211ba ab a b a a a a a a a a a a a a a a a . 解: 方法1(利用定理2)利用定理2结论,对行列式H 分块,OC BA H =, 其中⎪⎪⎪⎭⎫ ⎝⎛=333231232221131211a a a a a a a a a A ,⎪⎪⎪⎭⎫⎝⎛=a a aa a a B 000261615,⎪⎪⎪⎭⎫ ⎝⎛=b a a b a bC 626151000, 因此=H =-B C 9)1(33b a -. 方法2(降阶法)=H 000000000000626151333231262322211615131211ba ab a baa a a a a a a a a a a a a a 00000000062615133323126232221ba ab a b a a a a a a a a a a -= 0000623332262322ba baa a a a a a ab -=0003326232ba a a a a ab -= aa a ab 0263-=33b a -=.方法3(定义法)这是一个六阶行列式,在展开式中应有!6项,但是由于其有很多零元素,所以不等于零的项就大大减少了,展开式中一般形式是654321654321j j j j j j a a a a a a ,显然,如果41≠j ,那么11j a 这一项就为零,因此只考虑41=j 的那些项;同理,只考虑14=j 的那些项,而由于第五行只有非零元素51a 和b ,所以只考虑25=j ,同理有52=j ,63=j ,36=j .根据定义即可计算P ,即=H 33)456123()1(b a τ-33339)1(b a b a -=-=.从上面的例子我们看到,将方法2、3与方法1比较,方法2解题步骤更多更复杂,而方法3比较抽象,要有很好的观察力,显然利用分块矩阵来解题时,行列式的结构很清楚明了,解题过程也更简单. 5.3 利用定理3计算行列式下面是利用定理3计算行列式的例子.例5 计算n 2阶行列式b cb c d a da H=,其中0≠a .解: 方法1(利用定理3)对行列式分块,令DC BA H =, 其中⎪⎪⎪⎭⎫ ⎝⎛=a a A ,⎪⎪⎪⎭⎫ ⎝⎛=b b B ,⎪⎪⎪⎭⎫ ⎝⎛=c c C ,⎪⎪⎪⎭⎫ ⎝⎛=d d D .A 、B 、C 、D 均为n 阶方阵,0≠=n a A 得A 可逆. 因为⎪⎪⎪⎭⎫⎝⎛--=----d ca b d ca b D CA B 111,所以n n cd ab d ca b a D CA B A H )()(11-=-=-=--.方法2(降阶法)b cb c d a da H=121200000000---=n n b c b c d a d a d cb bc b c da d a a2222---=n n b cb c d a da cdb cbc d a d a ab== n cd ab )(-.方法3(化三角形法)利用行列式的性质,将H 化为上三角形,即bc b cd a da H=1--=cda b b c d a da110----=cda b cda d dadan n cda b a )(1--=n cd ab )(-=.从上面例子可以看到,行列式H 是一个高阶抽象行列式,比较上面三种方法,显然方法1更为简单,而且在利用定理3将行列式进行分块之后,该行列式的结构便十分清晰,计算过程也很简单明. 例6[]9 计算行列式nn a a a a D ++++=11111111111111111111321,其中n i a ,,2,1,01 =≠. 解:方法1(利用定理3)对该行列式先加边,再将加边后的行列式的第1行乘1-加到其余各行, 得nn a a a a D ++++=111110111110111110111110111111321na a a 0010000100010011111121----=, 令)1(=A ,)1,,1,1( =B ,⎪⎪⎪⎪⎪⎭⎫⎝⎛---=111C ,⎪⎪⎪⎪⎪⎭⎫⎝⎛=n a a a D21, 由于01≠a ,且B 可逆,从而==D C B A D n n n i a a a a a B CA D A 211111)(∑=--+=-)11(11∑∏==+=ni in i i a a . 方法2(化三角形法)先对行列式加边处理,再利用行列式的性质,将n D 化为三角形.100000111111111111111111111111321n n a a a a D ++++=11111111100001000010000321------=n a a a a11111111000010010010001010000113211n n n i i a a a a a a -----=-=∏∑∏=-=+-----=ni in n ni i a a a a a a a 11321111111110100000100000010000001)11(11∑∏==+=ni ini i a a . 从上面的例子我们可以看到,在利用公式计算行列式时,并不一定在最开始时就进行分块.有时候,我们可以先对行列式进行变换,再使用公式计算行列式.同时,我们也认识到行列式的计算是十分灵活的,如上面的方法1就将加边法和定理3结合起来使用,所以在计算行列式时要学会灵活运用知识.方法2中运用矩阵的初等变换将行列式化成三角形,计算过程比较繁琐且容易出错.但是在什么样的情况下利用定理3求行列式值比较简便,还有待进一步讨论,下面将给出一类特殊的行列式的例子. 例7[]10 求形如11110111011110 -----=M的n 阶(n 为偶数)反对称行列式的值. 解: 将M 按如下分块,B CA D A DC B A M 1--==,其中⎪⎪⎭⎫ ⎝⎛-=0110A ,⎪⎪⎭⎫ ⎝⎛=111111 B ,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------=111111 C ,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---=011101110 D 因为01≠=A ,所以A 可逆.又有⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎪⎪⎭⎫⎝⎛------=-11111101101111111 B CA , 所以1242=======--A M M M D M n n .从此例可以推广,形如⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛------=00a a a a a a a a a a a a M (0≠a )的n 阶(n 为偶数)的反对称矩阵,其行列式的值为n a .上面总结了定理3在一类特殊行列式上的应用,当遇到这类问题时可直接使用上述结论.当然,在其他某些数字行列式的计算上也可直接运用定理3,也可先经过行列式的某些变换使其数字更简单结构更明了,再使用定理3来计算. 5.4 利用定理4计算行列式定理3虽给出了计算行列式的一种方法,但计算过程相对繁琐,计算中涉及到多次求逆和矩阵相乘,同时也不易记忆.而定理4可以说是定理3的推论,在实际应用中定理4更常用.下面将给出相关例子. 例8 计算例3所给的n 2阶行列式. 解: A 、C 如例3所给,DC BA H =,而且CA AC =,则有 =H =-CD AB cdab cdab cdab ---n cd ab )(-=.注意:(1)这里并不需要0≠a 这个条件;(2)在用定理4计算高阶行列式时,A 和C 有一个是n 阶单位矩阵或是n 阶数量矩阵时,那么计算方法会更简便. 例9 计算行列式=H 1210520132211111-. 解: 方法1[]11(利用定理4)对H 进行分块⎪⎪⎭⎫ ⎝⎛=D C B A H ,其中⎪⎪⎭⎫ ⎝⎛=2111A ,⎪⎪⎭⎫ ⎝⎛-=3211B ,⎪⎪⎭⎫ ⎝⎛=1001C ,⎪⎪⎭⎫⎝⎛=1252D .显然A 可逆且CA AC =,故=H CB AD -, 所以1010453==H .方法2(化三角形法)利用行列式的性质,将行列式H 化为三角形.=H =-12105201322111111210411041101111--5100020041101111-=10500020041101111=-=.方法3(降阶法)=H 12141141112104110411011111210520132211111--=--=-=-=5100204115102=10.我们可以看到利用定理4计算例2的过程比利用定理3和其他方法计算时更简单. 5.5 利用定理5计算行列式对于能用定理5求解的行列式,我们往往很容易看出来,而且分块也很简单.下面给出具体例子. 例10 计算行列式=P 0000a b ca cb bc a c b a 的值.解:方法1(利用定理5)将对行列式P 进行分块,=P AB BA , 其中⎪⎪⎭⎫ ⎝⎛=00a a A ,⎪⎪⎭⎫⎝⎛=b c c b B ,则由定理5可得=P =A B B A B A +B A -⋅bc a ca b b c a c a b ----++= ))()()((c b a c b a b c a c b a ---+-+++=.方法2(降解法)将行列式P 按第一行展开,可得P ab c c b ca cbc a c b ba b a c a b bc a a 000000⋅-⋅+⋅= )()()(322223322c c b c a c ba bc b b a ac ab a -+---+-+-=222222444222c b c a b a c b a ---++=))()()((c b a c b a b c a c b a ---+-+++=.方法3(列归一法)将行列式的第2、3、4列都加到第1列.P 000a b c b a a c c b a b c c b a c b a c b a ++++++++=101011)(a b a c bc c b a c b a ++=cb a a b ca b a c cb bc a cb ac b a ---------++=0001)( cb a a bc a b a c cb bc a c b a ---------++=)( bca cb ac a bcb bc c b a c b a --++-----++-++=0)(bc a c a bc b b c c b a c b a -------+-++=001))((])()[)((22c a b c b a c b a ---+-++=))()()((c b a c b a b c a c b a ---+-+++=.此题看似简单,但若是计算方法不佳,计算起来也不会轻松.比较上面三种方法,可以看到,利用定理5计算此题极大的简化了计算过程.5.6 利用定理6计算行列式在利用定理6计算n 阶行列式时,要根据具体情况,把原来行列式的元素组成的矩阵分成两部分,其中一部分是n 阶可逆矩阵A ,该矩阵一般为对角矩阵,那么其行列式和逆矩阵比较容易求出;另一部分是n 维列向量α和β组成的乘积T αβ.这种分法是利用定理6计算n 阶行列式的难点,需要有较强的观察力.下面列举两个具体例子加以说明. 例11 计算行列式=D ba a a a ab a a a a a b a a a a a ba n n n n ++++321321321321.解:方法1(利用定理6)令⎪⎪⎪⎪⎪⎭⎫⎝⎛=b b b A,Tn a a a ),,,(21⋅⋅⋅=α,T )1,,1,1(⋅⋅⋅=β, 则=T βα⎪⎪⎪⎪⎪⎭⎫⎝⎛111 ()n a a a ,,21⎪⎪⎪⎪⎪⎭⎫⎝⎛=n n n a a a a a a a a a 212121, 而且TA D βα+=,又由于n b A =,并且=-βα1A T∑=-ni iab11,从而由定理4知,)()1()1(11111∑∑=-=--+=+=+=+=ni i n ni i n T T a b ba b b A A A D βαβα.方法2(利用方阵特征值与行列式的关系) 令矩阵⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛++++=b a a a a a ba a a a ab a a a a a ba A n n n n321321321321,则+=n bE A =⎪⎪⎪⎪⎪⎭⎫⎝⎛n n n a a a a a aa a a 212121+n bE n A .显然,n bE 的n 个特征值为b b b ,,, ,n A 的n 特征值为0,,0,0,1∑=n i i a ,故A 的特征值为b b b a b ni i ,,,,1 ∑=+,由方阵特征值与对应行列式的关系知=D )(11b a bni i n +∑=-.方法3(化三角形法)=D ba a a a ab a a a a a b a a a a a ba n n nn ++++3213213213211001010100111321b a b a b a b a b n n +=101000010321b a b a b a b a b n n i i n∑==nb =)1(1+∑=ni i b a )(11b a b ni i n +=∑=-.例12 计算行列式nn n n n n b a x b a b a b a b a x b a b a b a b a x D +++=212221212111(1>n ).解:当0=x 时,0=D ;当0≠x 时,设⎪⎪⎪⎪⎪⎭⎫⎝⎛=x x x A ,Tn T n b b b a a a ),,,(,),,,(2121 ==βα, 由此可得TA D αβ+=,⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=n n n n n n n n Tb a b a b a b a b a b a b a b a b a b b b a a a2122212121112121),,,(αβ, 再因nx A =,且=-αβ1A T∑=-ni i i b a x11,由定理6可得)()1(111∑=--+=+=+=ni i i n T Tb a x xA A A D αβαβ.容易看出,运用定理6计算行列式也有一定的规律可循,计算这类行列式时一定要弄清它的结构,对行列式进行合理分块,这样计算过程会得到很大简化.6.总结:分块矩阵是矩阵计算问题中一种重要的技巧,尤其是在遇到高阶矩阵,复杂矩阵还有抽象矩阵的问题时,使用起来更为方便.参考文献[1] 李师正.高等代数解题方法现技巧[M].北京:高等教育出版社,2004[2] 北京大学数学系几何与代数教研室前代数小组.高等代数(第三版)[M].北京:高等教育出版社,2003[3] 高白俊.分块矩阵的初等变换及其应用[J].伊犁师范学院学报,2007(12):15-17[4] 刘国良.分块矩阵行列式的一些结果[J]. 石家庄职业技术学院学报,2003(08):52-53[5] 胡景明.分块矩阵在求高阶行列式中的应用[J].河北工程技术高等专科学校学报,2004(12):51-53[6] 高振兴.矩阵分块与应用[J].辽宁师范大学学报,2011(06):157-160[7] 王莲花,李念伟.分块矩阵在行列式计算中的应用[J].河南教育学院学报,2005(03):12-15[8] 张燕.分块矩阵行列式的性质及其应用[J].高等函授学报,2010(12):31-33[9] 廖军.分块矩阵求n阶行列式的值[J].文山师范高等专科学校学报,2004(06):164-168[10] 吕智颖,李晓红,石国庆.分块行列式的第一降阶定理在行列式计算与证明中的应用[J].高师理科学刊,2005(2):11-13[11] 彭丽清.矩阵分块在行列式计算中的应用[J].忻州师范学院学报,2006(04):31-32。
