12.3相对论的速度变换
相对论的速度变换

P =mv
E = mc
2
2
c v= P E
m0c
2 2
2
E = mc =
v 1− 2 c
=
m0c
2 4
1 c 2 1− 2 2 P c E
2 c 2 2 2 4 E 1 − 2 P = m0 c E
28
解得:
2 4 E 2= P 2 c 2 + m 0 c
或:
E = ( Pc) + E0
●按相对论,粒子间相互作用时,满足能量守 恒关系:
∑ E = ∑ (m c ) = const
2 i i i i
∑ m = const
i i
说明物质间相互作用时质量守恒。 如原子核反应中质量守恒:
∑m + ∑m = ∑m '+ ∑m
0 k 0
k
'
反应前后静质量和动质量可以相互转化。
23
例:氢弹核聚变反应引起的质能变化
1
2
1 v2 ≈ 1+ 2 2c
m0 2 2 ∴ EK = m0c + v − m0c 2
2
1 2 = m0v 2
●根据 EK = mc − m0 c
2 2
牛顿力学动能公式
=
m0 v 1− 2 c
2
c − m0c
2
2
17
得到粒子速率由动能表示的关系:
−2 E 2 2 v = c 1 − 1 + K 2 m0c
v v dt − dx 1 − u x dx − vdt u x − v c = c dt dx′ = dt dt ′ = = 2 2 1− β 2 1− β 2 1− β 1− β
《相对论的速度变换定律 质量和能量的关系》课件1

自主学习
名师解疑
分类例析
二、质量和速度的关系
m=
m0 1-vc22
(1)式中m0是物体静止时的质量(也称为静质量),m是物体以
速度v运动时的质量.这个关系式称为相对论质速关系.
(2)v≪c时,近似地m=m0.
自主学习
名师解疑
分类例析
(3) 微 观 粒 子 的 运 动 速 度 很 高 , 它 的 质 量 明 显 地 大 于 静 止 时 质 量.例如回旋加速器中被加速的粒子质量会变大,导致做圆周运 动的周期变大后,它的运动与加在D形盒上的交变电压不再同步, 回旋加速器的加速能量因此受到了限制. 特别提醒 (1)物体的质量会随速度的增大而增大. (2)物体运动的质量要大于静止质量.
自主学习
名师解疑
分类例析
【变式1】 若一宇宙飞船对地以速度v运动,宇航员在飞船内沿同方向 测得光速为c,问在地上的观察者看来,光速应为v+c吗? 解析 由相对论速度变换公式u=1u+′u+′c2vv,式中u′、v分别 为v和c.代入公式求得光对地速度u=1v++vcc2c=cvv+ +cc=c. 答案 在地面的观察者看来,光速是c不是v+c.
自主学习
名师解疑
分类例析
【变式3】 已知电子的静止能量为0.511
MeV,若电子的动能为0.25
MeV,则它所增加的质量Δm与静止质量m0的比值近似为 ( ).
A.0.1 B.0.2 C.0.5 D.0.9
自主学习
名师解疑
分类例析
解析 由题意E=m0c2 即m0c2=0.511×106×1.6×10-19 J① ΔE=Δmc2 即Δmc2=0.25×106×1.6×10-19 J② 由②①得Δmm0 =00..52151≈0.5,故只有C项正确. 答案 C
4、相对论的速度变换公式

结论 :
沿两个惯性系相对运动方向发生的两个事 件,在其中一个惯性系中表现为同时的, 在 另一惯性系中观察则不同时。
1
——同时的相对性
精选完整ppt课件
6
二、运动时钟的变慢
二、运动时钟的变慢
v
M
h
v
v
M
M
M
cΔt 2h
A
A vΔt
B
2
对于车厢内的人: t
2h c
对于车厢外的人:t
4h2 c2 v2
t t 1 v 2 c
时间延缓效应并
不是说由于相对运动 而使钟发生了结构性 变化,是由于不同观 测者进行量度时引起 的一种观测效应。这
t t
1 v 2 c
种效应是相对的。对
于同一参考系,v=0,
就不存在这种效应了。
当v接近光速时,
这种偏差是非常大的。
①相对性原理: 对于不同的惯性系,物理规律
(包括力学和电磁学)都是一样的。
②光速不变原理: 光速与惯性系的选择无关。
注意:速度要接近光速时,相对论效应才会明显。
一、“同时”的相对性
在一个参考系中是同时发生的两件事,在 相对于此参考系运动的另一个参考系中观测不 是同时发生,这就是“同时”的相对性。
v u v 1 .4 c
V大于光速可能吗?
P105页
一、相对论的速度变换
根据时空相对性,狭义相对论给出:在
以速率u相对于参考系S运动的参考系S'中,
一物体沿与u相同的方向以速率v' 运动时, 在参考系S中,它的速率为:
u v
v
1
uv c2
s y s' y'
教科版选修3-4 第6章 第4节 相对论的速度变换公式 质能关系
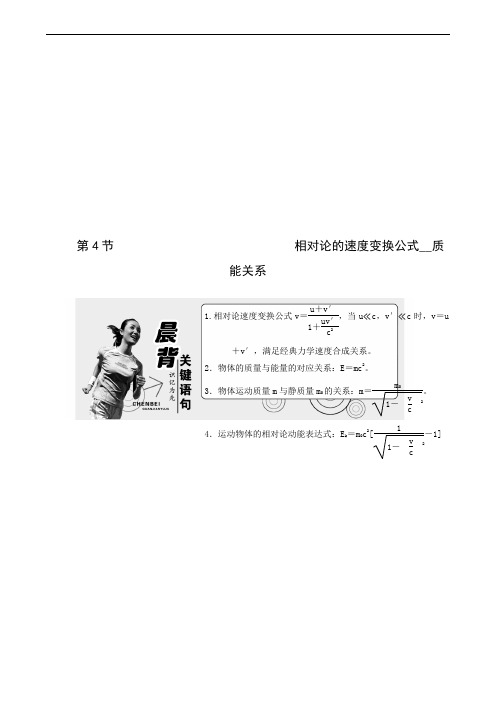
第4节相对论的速度变换公式__质能关系1.相对论速度变换公式v =u +v′1+uv′c2,当u ≪c ,v′≪c 时,v =u+v′,满足经典力学速度合成关系。
2.物体的质量与能量的对应关系:E =mc 2。
3.物体运动质量m 与静质量m 0的关系:m =m 01-v c 2。
4.运动物体的相对论动能表达式:E k =m 0c 2[11-v c2-1]v′沿着火车前进的方向相对火车运动,那么这个人相对地面的速度v 为v =u +v′1+uv′c2。
理解这个公式时请注意:(1)如果车上的人的运动方向与火车的运动方向相反,则v′取负值。
(2)如果u ≪c ,v′≪c ,这时v′uc 2可忽略不计,这时相对论的速度合成公式可近似变为v =v′+u 。
(3)如果v′与u 的方向垂直或成其他角度时,情况比较复杂,上式不适用。
[学后自检]┄┄┄┄┄┄┄┄┄┄┄┄┄┄(小试身手)在高速运动的火车上,设车对地面的速度为v ,车上的人以速度u′沿着火车前进的方向相对火车运动,那么他相对地面的速度u 与u′+v 的关系是( )A .u =u′+vB .u <u′+vC .u >u′+vD .以上均不正确解析:选B 按照经典的时空观,u =u′+v ,而实际上人对地面的速度按照相对论速度公式计算,u =u′+v1+u′v c2,因此u 比u′与v 之和要小,但只有在u′和v 的大小接近光速时才能观察此差别。
相对论质量和能量[自读教材·抓基础]1.质能关系式E =mc 2。
式中m 是物体的质量,E 是它具有的能量。
由此可见,物体质量越大,其蕴含的能量越大。
能量与质量成正比。
2.相对论质量 m =m 01-v 2c2(m 0指静质量); 与静质量对应的静能量为E 0=m 0c 2。
[跟随名师·解疑难]1.对质速关系m =m 01-v c2的理解(1)式中m 0是物体静止时的质量(也称为静质量),m 是物体以速度v 运动时的质量。
第18课狭义相对论II——动量和能量

0
2
1− 2
• =
≈ 0 +
0 2
2
1− 2
1
2
2 0 2
2
≈ 0 +
1
0 2
2
物体静止时的质能
动能
• Einstein由此假设,物体的能量 =
2
=
0 2
2
1− 2
相对论中的能量
• 这个假设能满足能量守恒吗?
•
•
=
2
• =
0
2
1− 2
•=
0
•=
2
大家能感受到这
些公式的美吗?
2
1− 2
=
02
2
1− 2
= ( −
)/
2
1−
2
2
y
A
参
考
系
A’
参
考
系
在A参考系中
以速度v向x
方向运动
速度u
ut
x
(
• =
′
′
′
=
(
−
2
1− 2
)
2
−/
2
1− 2
)
=
(−)
(−/2)
=
−
1−/2
• 一起来验证光速不变,无法通过速度叠加超光速。
A’
参
考
系
= ( − )/ 1 −
2
2
′ =
′ =
1−
2
2
′
= ( −
相对论中速度转换

相对论中速度转换Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!相对论是现代物理学的一门基础理论,其研究对象是在高速运动状态下的物体和光。
相对论的提出,彻底改变了人们对空间和时间的认识,揭示了高速运动下的物体具有与经典力学完全不同的性质。
在相对论中,速度是一个非常重要的物理量。
在低速情况下,经典力学和相对论的速度转换公式是一致的。
但在高速情况下,由于爱因斯坦相对论的出现,速度转换并不遵循简单的加法规则。
相对论中的速度转换公式是一种非常独特且重要的规律,它为我们理解高速运动下物体的行为提供了重要的参考。
相对论速度变换的数学推导

相对论速度变换的数学推导相对论是爱因斯坦于1905年提出的革命性物理理论,改变了我们对时间、空间和物质与能量的观念。
其中一个重要的概念就是速度变换。
在经典力学中,速度是一个矢量,由物体在单位时间内移动的距离和方向决定。
然而,在相对论中,速度不再是简单的向量,而是涉及时间和空间的复杂概念。
为了推导相对论速度变换的数学表达式,我们首先需要定义一些变量。
假设有两个参考系,一个是S系,另一个是S'系。
S系是一个静止的参考系,而S'系是相对于S系以速度v沿x轴方向运动的参考系。
我们将物体在S系中的速度表示为u,而在S'系中的速度表示为u'。
根据相对论的基本假设,光的速度在任何参考系中都是恒定的,即光速不变原理。
因此,我们可以将光速作为一个常量c来表示。
现在,我们来考虑一个物体在S系中以速度u运动,那么在S'系中的速度应该如何表示呢?根据相对论的基本原理,两个参考系之间的转换关系可以通过洛伦兹变换来描述。
洛伦兹变换的数学形式如下:x' = γ(x - vt)y' = yz' = zt' = γ(t - vx/c^2)其中,x,y,z和t是S系中的空间和时间坐标,x',y',z'和t'是S'系中的空间和时间坐标,v是S'相对于S系的相对速度,c是光速,γ是洛伦兹因子,定义为γ = 1/√(1 - (v^2/c^2))。
根据洛伦兹变换的定义,我们可以推导出物体在S'系中的速度u'与在S系中的速度u之间的关系。
我们可以通过对上述变换关系中x'和t'的导数来找到答案。
首先,对x'求导数,有:dx'/dt = d(γ(x - vt))/dt= γ(dx/dt - v(dx/dt))= γ(u - v)同样的,对t'求导数,有:dt'/dt = d(γ(t - vx/c^2))/dt= γ(dt/dt - (v/c^2)(dx/dt))= γ(1 - (v/c^2)u)我们知道,速度的定义是速度等于位移对时间的导数,即v = dx/dt。
相对论的速度变换公式 质能关系

= 1.125×108 m/s
二、对相对论质量和质能方程的理解
1、相对论质量:物体的质量会随物体的速度的增大而增大,物体
以速度v运动时的质量m与静止时的质量m0之间的关系
m m0
(1)v≪c时,(
v c
1
v c
2
m为运动质量>m0为静止质量
)2=0此时有m=m0,也就是说:低速运动的物体
,可认为其质量与物体的运动状态无关.
☆如果车上人运动方向与火车运动方向相反,则u取负值。
一、对相对论的速度变换公式的理解
1.当物体运动方向与参考系相对地面的运动方向相反 时,公式中的u′取负值.
2.若物体运动方向与参考系运动方向不共线,此式不 可用.
3.由公式可知:u一定比u′+v小,但当u′和v都比c小 得多时,可认为u=u′+v,这就是低速下的近似,即经 典力学中的速度叠加.
(3)物体的能量变化ΔE与质量变化Δm的对应关系为:ΔE=Δmc2.
二、对相对论质量和质能方程的理解
例3、太阳由于向四面空间辐射能量,每秒损失了质量 4×109kg 。求太阳的辐射功率。
解:设太阳的辐射功率为P:
Pmc2 mc2 t 1
代入数据:P=4109(3108)2 =3.61026J/s =3.61026W
B
K系
中 国 航 天
中 国 航 天
A ux
。可知K′系相对K系是速度为
v = 2.0×108 m/s
飞船A 在K系中的速度为
ux = 2.5×108 m/s
飞船A 在K’系中的速度为
ux´=
u 1
x
v c
v ux
2
= 1
2.5×108 2.0×108
相对论速度变换矩阵

相对论速度变换矩阵相对论速度变换矩阵(Lorentz变换矩阵)是狭义相对论中重要的数学工具,用于描述物体在不同参考系中的速度变换关系。
该矩阵由荷兰物理学家洛伦兹于1904年提出,是狭义相对论的基础之一。
为了理解相对论速度变换矩阵,首先需要了解相对论中的两个重要概念:光速不变和事件。
根据狭义相对论的基本假设,光速在任何参考系中都是不变的,即光的速度在不同参考系中保持不变。
而事件是指在时空中发生的一系列物理现象,如两个物体相对运动、光信号的传播等。
在相对论中,我们常常需要描述在一个参考系中观察到的物体速度如何在另一个参考系中观察。
这就涉及到相对论速度变换矩阵的应用。
假设有两个参考系S和S',其中S'相对于S以速度v沿着x轴运动。
设在S系中有一个物体以速度u沿着x轴运动,则在S'系中观察到的速度记为u'。
根据相对论速度变换矩阵的定义,我们可以得到如下的变换关系:u' = (u - v) / (1 - uv/c^2)其中c为光速。
这个矩阵表达式告诉我们,在相对论中,物体的速度不仅仅取决于其自身的速度,还受到参考系的选择和相对速度的影响。
当相对速度v趋近于光速时,u'的值将趋近于光速,这是相对论的一个重要结论,即无论物体自身的速度如何,其速度在任何参考系中都不会超过光速。
相对论速度变换矩阵的推导过程较为复杂,需要运用洛伦兹变换公式和矢量运算等数学工具。
具体推导细节在此不再详述,感兴趣的读者可以参考相关的狭义相对论教材或论文进行深入了解。
相对论速度变换矩阵的应用广泛,不仅仅局限于物体速度的变换。
它在许多领域都有重要的应用,如粒子物理学、天体物理学、电动力学等。
特别是在粒子物理学中,研究高速运动的粒子和反粒子,相对论速度变换矩阵是不可或缺的工具之一。
除了速度变换,相对论速度变换矩阵还可以用于描述时间和空间的变换。
根据洛伦兹变换公式,时间和空间在不同参考系中也会发生变换。
高中物理 第六章 相对论 4 相对论的速度变换公式 质能关系 5 广义相对论点滴

4 相对论的速度变换公式 质能关系5 广义相对论点滴(选学)[学习目标] 1.知道相对论速度变换公式、相对论质量和质能方程.2.了解广义相对论的基本原理.3.初步了解广义相对论的几个主要观点以及主要观测证据.一、相对论的速度变换设高速行驶的火车对地面的速度为u ,车上的人相对火车以速度v ′运动,那么人相对地面的速度v 为:v =v ′+u1+uv ′c2.二、相对论质量和能量1.物体以速度v 运动时的质量m 与静止时的质量m 0之间的关系是:m =m 01-v 2c2.2.爱因斯坦质能关系式:E =mc 2,m 是物体的质量,E 是它具有的能量. 三、广义相对论点滴 1.广义相对论的基本原理(1)广义相对性原理:在任何参考系中物理规律都是一样的.(2)等效原理:一个不受引力作用的加速系统跟一个受引力作用的惯性系统是等效的. 2.广义相对论的几个结论(1)光在引力场中传播时,将会发生偏折. (2)引力作用使光波发生频移. (3)在引力场中时间会延缓.(4)当两个天体相互绕转时,会向外界辐射引力波. [即学即用] 判断下列说法的正误.(1)根据相对论速度变换公式,两个物体的速度无论多大,它们的相对速度也不会大于光速c.( √)(2)在相对论力学中,物体静止时的质量最小.( √)(3)根据质能方程,质量可以转化为能量,能量可以转化为质量.( ×)(4)一个均匀的引力场与一个做匀速运动的参考系等价,这就是著名的等效原理.( ×)一、相对论速度变换公式[导学探究] 一列车正以u =50m/s 的速度高速行驶,列车内一乘客以相对列车v =5 m/s 的速度向前跑,站台上的观察者测得该乘客的速度是多大?若列车的速度是0.9c ,乘客的速度是0.5c ,那么站台上的观察者测得该乘客的速度是0.9c +0.5c =1.4c 吗?为什么? 答案 站台上的观察者测得该乘客的速度是55m/s.不是.因为根据狭义相对论原理,光速c 是极限速度,任何物体的速度不可能超过光速. [知识深化] 对相对论速度变换公式的理解(1)公式v =v ′+u1+v ′u c2是矢量式.若人运动方向与火车运动方向相同,则v ′取正值.若人运动方向与火车运动方向相反,则v ′取负值.(2)如果u ≪c ,v ′≪c 时,uv ′c 2可忽略不计,这时相对论的速度变换公式可近似为v =v ′+u .(3)若v ′=c ,u =c ,则v =c ,表明一切物体的速度都不能超过光速.(4)该变换公式只适用于同一直线上匀速运动速度的变换,对于更复杂的情况不适用. 例1 一粒子以0.05c 的速率相对实验室参考系运动.此粒子衰变时发射出一个电子,电子相对于粒子的速度为0.8c ,电子的衰变方向与粒子运动方向相同,求电子相对于实验室参考系的速度. 答案 0.817c解析 已知v ′=0.05c ,u =0.8c . 由相对论速度变换公式得v =u +v ′1+uv ′c2=(u +v ′)c 2c 2+uv ′=(0.8c +0.05c )c 2c 2+0.8c ×0.05c ≈0.817c .二、相对论质量和质能方程[导学探究] 回旋加速器中磁场一次次把粒子拉到狭缝处,狭缝处的电场一次次加速带电粒子.假如回旋加速器的半径可以增大到很大,磁感应强度足够大,经回旋加速器加速的粒子的速度可以达到任意速度甚至超过光速吗?为什么? 答案 速度不可以超过光速.因为回旋加速器的理论基础是粒子在磁场中做圆周运动的周期(T =2πm qB)等于交变电场的周期;速度较小时粒子的质量m 可以认为不变,周期T 不变,电场变化与粒子圆周运动同步,但速度较大时,粒子质量增大明显,粒子做圆周运动的周期T 变大,无法做到圆周运动的周期与交变电场的周期同步. [知识深化] 对相对论质量的理解 (1)相对论质量m =m 01-(v c)2.(2)因为总有v <c ,所以运动物体的质量m 总要大于它静止时的质量m 0,但当v ≪c 时,m ≈m 0,所以低速运动的物体,可认为其质量与运动速度无关.(3)微观粒子的速度很大,因此粒子质量明显大于静止质量.例2 为使电子的质量增加到静止质量的两倍,需有多大的速度( ) A.6.0×108m/s B.3.0×108m/s C.2.6×108m/s D.1.5×108m/s答案 C解析 由相对论质速关系式m =m 01-⎝ ⎛⎭⎪⎫v c 2可得到v =c1-⎝ ⎛⎭⎪⎫m 0m2=c1-⎝ ⎛⎭⎪⎫122=32c ≈2.6×108m/s ,故选C.例3 1905年,爱因斯坦创立了“相对论”,提出了著名的质能方程,下面涉及对质能方程理解的几种说法中正确的是( ) A.若物体能量增大,则它的质量增大 B.若物体能量增大,则它的质量减小 C.E =mc 2中能量E 其实就是物体的内能 D.由ΔE =Δmc 2知质量和能量可以互相转化 答案 A解析 由爱因斯坦质能方程可知,物体具有的与质量相对应的能量称为质能.E =mc 2表明质量与能量之间存在一一对应的关系,物体吸收或放出能量,则对应其质量会增加或减少,质量与能量并没有相互转化,B 、D 项错误,A 项正确;E =mc 2中能量E 包括静止能量E 0和动能E k ,而非物体的内能,C 项错误.三、广义相对论的几个结论例4 (多选)下列说法中正确的是( ) A.物质的引力使光线弯曲B.光线弯曲的原因是介质不均匀而非引力作用C.在强引力的星球附近,时间进程会变慢D.广义相对论可以解释引力红移现象答案 ACD解析 从广义相对论的两个基本假设可以得出:物质的引力使光线弯曲;引力场的存在使得空间不同位置的时间进程出现差别,如在矮星表面的引力很强,那里的时间进程变慢,从而导致引力红移,所以正确的选项为A 、C 、D.1.光线在引力场中弯曲,以及引力红移现象都是在引力场很强的情况下产生的.2.光在同一种均匀介质中沿直线传播的现象,在我们的日常生活中仍然成立.1.(相对论速度变换公式)一高能加速器沿相反方向射出两个粒子,速度均为0.6c ,则它们的相对速度大小是多少? 答案 0.88c解析 以其中任意一个粒子为运动参考系,要求的就是另一个粒子在该运动参考系下的运动速度v ′.由题意知,运动参考系相对静止参考系的速度u =0.6c ,另一粒子相对于静止参考系的速度v =-0.6c .根据相对论速度变换公式v =v ′+u 1+v ′u c2,可知-0.6c =v ′+0.6c1+v ′·0.6c c2.可解得v ′≈-0.88c故两粒子的相对速度大小为0.88c .2.(相对论质量)星际火箭以0.8c 的速率飞行,其静止质量为运动质量的百分之几? 答案 60%解析 设星际火箭的静止质量为m 0′,运动质量为m ′, 则m 0′m ′=m 0′m 0′1-(0.8c c)2×100%=60%.3.(质能方程)一电子(m 0=9.1×10-31kg)以0.99c 的速率运动.问:(1)电子的总能量是多大?(2)电子的经典力学的动能与相对论的动能的比值是多大? 答案 (1)5.8×10-13J (2)0.08解析 (1)电子的总能量为:E =mc 2=m 01-(v c)2·c 2=9.1×10-311-(0.99c c)2×(3×108)2J ≈5.8×10-13J.(2)电子的经典力学动能为:E k =12m 0v 2=12m 0(0.99c )2.相对论的动能为:E k ′=E -E 0=mc 2-m 0c 2E k E k ′=12m 0(0.99c )2mc 2-m 0c 2=12×0.99211-(0.99c c)2-1≈0.08.4.(广义相对论)(多选)下列说法中正确的是( )A.在任何参考系中,物理规律都是相同的,这就是广义相对性原理B.在不同的参考系中,物理规律都是不同的,例如牛顿运动定律仅适用于惯性参考系C.一个均匀的引力场与一个做匀速运动的参考系等价,这就是著名的等效原理D.一个均匀的引力场与一个做匀加速运动的参考系等价,这就是著名的等效原理 答案 AD解析 根据广义相对论基本原理可知,选项A 、D 正确.一、选择题考点一 相对论速度变换公式1.(多选)在一列相对于地面速度为v 的高速行驶的火车上,车上的人以速度u ′沿着火车前进方向相对于火车运动,根据相对论速度变换公式,下列说法正确的是( ) A.人相对于地面的速度小于人的速度和火车速度之和 B.人相对于地面的速度大于人的速度和火车速度之和C.只要人和火车的速度足够大,人相对于地面的速度可以超过光速D.不管人和火车的速度多大,人相对于地面的速度都小于光速 答案 AD2.设想有一艘飞船以v =0.8c 的速度在地球上空飞行,如果这时从飞船上沿其运动方向抛出一物体,该物体相对于飞船的速度为0.9c ,从地面上的人看来,物体的速度为( )A.1.7cB.0.1cC.0.99cD.无法确定答案 C解析 根据相对论速度变换公式:v =v ′+u1+v ′u c2,得v =0.9c +0.8c1+0.9c ×0.8c c2≈0.99c .3.火箭以35c 的速度飞离地球,在火箭上向地球发射一束高能粒子,粒子相对地球的速度为45c ,其运动方向与火箭的运动方向相反.则粒子相对火箭的速度大小为( )A.75cB.c 5C.3537cD.5c13 答案 C解析 由相对论速度变换公式v =v ′+u 1+v ′u c 2,可得-45c =35c +v ′1+35cv ′c2,解得v ′=-3537c ,负号说明与v 方向相反. 考点二 相对论质量4.(多选)关于物体的质量,下列说法正确的是( ) A.在牛顿力学中,物体的质量是保持不变的B.在牛顿力学中,物体的质量随物体的速度变化而变化C.在相对论力学中,物体静止时的质量最小D.在相对论力学中,物体的质量随物体速度的增大而增大 答案 ACD解析 在牛顿力学中,物体的质量是保持不变的,故选项A 正确,B 错误;在相对论力学中,由于物体的速度v 不可能达到光速c ,所以v <c,1-(v c)2<1,根据m =m 01-(v c)2,可知选项C 、D 均正确.5.(多选)电子的电荷量为1.6×10-19C ,质量为9.1×10-31kg ,一个电子被电压为106V 的电场加速后,关于该电子的质量和速度,以下说法正确的是( ) A.电子的质量不变 B.电子的质量增大C.电子的速度可以达到1.9cD.电子的速度不可能达到c 答案 BD解析 电子被电场加速后,根据m =m 01-(v c)2可知,随电子速度的增大,其质量也增大,故A 错误,B 正确;此时不能根据eU =12m 0v 2求速度,任何物体的速度都不可能超过光速c ,故C 错误,D 正确. 考点三 质能方程6.如图1所示,鸡蛋和乒乓球都静止在地面上,关于二者所具有的能量关系,下列说法中正确的是( )图1A.鸡蛋大B.乒乓球大C.一样大D.无法进行比较答案 A解析 物体所具有的能量和其质量有关,根据质能方程,质量越大,所具有的能量越大,所以鸡蛋具有的能量大于乒乓球具有的能量.7.已知电子的静止能量为0.511MeV ,若电子的动能为0.25MeV ,则它所增加的质量Δm 与静止质量m 0的比值近似为( ) A.0.1B.0.2C.0.5D.0.9 答案 C解析 由题意E =m 0c 2即m 0c 2=0.511×106×1.6×10-19J ①ΔE =Δmc 2即Δmc 2=0.25×106×1.6×10-19J ②由②①得Δm m 0=0.250.511≈0.5,故C 项正确. 考点四 广义相对论8.(多选)下列说法中,正确的是( )A.由于太阳引力场的影响,我们有可能看到太阳后面的恒星B.强引力作用可使光谱线向红端偏移C.引力场越强的位置,时间进程越快D.由于物质的存在,实际的空间是弯曲的 答案 ABD解析 由广义相对论可知:物质的引力使光线弯曲,因此选项A 、D 正确;在引力场中时间进程变慢,而且引力越强,时间进程越慢,因此我们能观察到引力红移现象,所以选项B 正确,C 错误.9.在日全食的时候,通过仪器可以观察到太阳后面的恒星,这说明星体发出的光( ) A.经太阳时发生了衍射 B.可以穿透太阳及其他障碍物 C.在太阳引力场作用下发生了弯曲 D.经过太阳外的大气层时发生了折射 答案 C解析 根据爱因斯坦的广义相对论可知,光线在太阳引力场作用下发生了弯曲,所以可以在适当的时候(如日全食时)通过仪器观察到太阳后面的恒星,故C 正确,A 、B 、D 错误. 二、非选择题10.(相对论质量)设宇宙射线粒子的能量是其静止能量的k 倍,则粒子运动时的质量等于其静止质量的________倍,粒子运动速度是光速的________倍. 答案 kk 2-1k解析 依据爱因斯坦的质能方程E =mc 2,宇宙射线粒子的能量是其静止能量的k 倍,则其质量等于其静止质量的k 倍;再由相对论质量公式m =m 01-⎝ ⎛⎭⎪⎫v c 2得v c =k 2-1k . 11.(质能方程)一被加速器加速的电子,其能量为 3.00×109eV ,(m 0=9.1×10-31kg ,c =3×108m/s)试问:(1)这个电子的动质量是其静质量的多少倍? (2)这个电子的速率是多少?答案 (1)5.86×103(2)2.999999955×108m/s 解析 (1)由相对论质能关系E =mc 2和E 0=m 0c 2可得电子的动质量m 与静质量m 0之比为m m 0=E E 0=3.00×109×1.6×10-199.1×10-31×(3×108)2≈5.86×103. (2)由m =m 01-v 2c2可得v =1-m 20m2·c =0.999999985c =2.999999955×108m/s.。
相对论速度变换

相对论速度变换
相对论速度变换是由爱因斯坦在他制定相对论时所提出的一个重要概念,它是指一个物体可以在不同的情况下由一个固定的相对速度变化到另一个特定的相对速度,而不会实际产生时间上的偏移,只会有相对论的研究才能使这种游戏可以藉由领域中的某种力学力学,广泛的用于虚拟现实的游戏平台中。
相对论速度变换的核心理念建立在爱因斯坦的一般相对论里,它引入“转换原理”来容易理解物理场中存在的绝对“速度”只是物理学力在特定条件下构成的另一种范畴。
当它被提出时,相对论速度变换提出了很多疑问,尤其是在物理学上的,因为它本身就有一定的矛盾,因为它表现出的“绝对”的概念,就这个框架内不能存在任何绝对的变量,所以引发了很多疑问。
但是爱因斯坦的几乎每一个重大的物理发现都跟时间有关,越来越多的物理学家也会运用上证明它的各种数学模型或者考虑它,特别是在时间校准,钟振及其它关于时间有关的知识领域里,据此推导出时间校准机制,并用来确定某种特定和时间有关的事件,从最初的两极光布朗(Polarization of light Brown)实验,到最新的 GPS(Global Positioning System)定位系统,相对论速度变换已成为一种跨时空的概念,它可以为我们提供更加准确的定位功能和其它的科技应用,也可以简化许多比较复杂的相对论原理领域里的推导,从而有效地为特定的理论和实际技术应用领域提供便利。
今天相对论速度变换已被广泛用于工程学,尤其是在特定的应用场景下,可以极大加强系统性能,在更加高层次上,它也正朝着通过简化、重复利用相对论基础知识,更高效地应用于更大领域的目标努力。
随着科学技术的发展,相对论速度变换也在不断发展和完善,更准确地让物理学和技术可以更容易的推导和应用。
相对论速度变换

相对论速度变换相对论速度变换是相对论的基本概念之一,它是描述物体相对运动的关键。
相对论速度变换的概念最初是由爱因斯坦提出的,他指出,在相对论中,物体的速度不再遵循经典物理学中常见的加法规则,而是遵循一种新的数学公式。
本文将重点介绍相对论速度变换的基本概念和公式,以及其在实际物理学中的应用。
基本概念在经典物理学中,两个物体相对运动时,它们的速度可以用简单的加减法来计算。
例如,如果两个物体a和b相对运动的速度分别为va和vb,则它们相对速度为vb-va。
这种速度计算方法在日常生活和大多数工程中都非常有用。
然而,在相对论中,事情就变得有些复杂。
在相对论中,物体的速度不能简单地用加减法相加,因为当物体的相对速度接近光速时,加减法的结果会是错误的。
相对论速度变换是一种新的速度计算方法,其目的是在描述物体的相对速度时,避免出现类似的问题。
相对论速度变换的基本思想可以用洛伦兹变换来描述,这是一种广义相对论中用来描述物体运动轨迹变化的数学公式。
洛伦兹变换中的关键概念包括“运动暂态”、“长度收缩”和“时间膨胀”等,这些概念都是相对论速度变化的基础。
公式推导假设有空间中的两个参考系S和S',它们之间的相对运动速度为v。
假设一个事件发生在S系中,且该事件具有时刻t和位置x。
根据洛伦兹变换的定义,该事件在S'系中的时刻t'和位置x'可以用如下公式计算:x' = (x - vt)/sqrt(1 - v^2/c^2)t' = (t - vx/c^2)/sqrt(1 - v^2/c^2)其中,c是光速。
在相对论速度变换中,我们关心的是两个物体之间的相对速度。
因此,我们可以通过以下公式计算参考系S'中物体B的速度u',假设物体B相对于参考系S中的速度为u:u' = (u - v)/(1 - vu/c^2)这个公式描述了相对论速度变换的基本规则,它告诉我们,在参考系S中测量物体B 的速度是u,而在参考系S'中测量物体B的速度是u'。
狭义相对论洛仑兹速度变换资料

由此可得洛仑兹速 度x分量的变换公式
dx
dx udt 1 u2 / c2
(ux u)dt , 1u2 / c2
dt
dt udx / c2 1u2 / c2
(1 uvx / c2 )dt , 1u2 / c2
vx
vx u . 1 vxu / c2
{范例13.3} 洛仑兹速度变换
[讨论]
{范例13.3} 洛仑兹速度变换
(1)根据洛仑兹坐标变换,推导x方向上速度变换公式。A飞船 在地面上以0.5c的速度运动,B飞船在地面上以0.8c的速度同 向运动,那么B飞船相对于A飞船的速度是多少?如果B飞船 在地面上以0.8c的速度相向运动,结果又如何? (2)根据洛仑 兹坐标变换,推导y方向或z方向上速度变换公式以及合速度
vx
0.8c 0.5c 1 0.8 0.5
0.5c
可见:在同向运动时,B飞船相对A飞船的速度大于0.3c。
如果B飞船与A飞船相向运动,则vx = -0.8c,可得B飞船在S'系中的速度
vx
0.8c 0.5c 1 (0.8) 0.5
0.9286c
在相向运动时,B飞船相对A飞船的速度仍然小于光速。
当u = -c时,有 vx' = c,也说明 相同的问题。
{范例13.3} 洛仑兹速度变换
(2)根据洛仑兹坐标变换,推导y方向或z方向上速度变换公式
以及总速度的变换公式。在太阳参考系中观察,一束星光垂
直射向地面,速率为c,而地球以速率u垂直于光线运动。求 在地面上测量,这束星光速度的大小与方向如何?
vx
1
vx vxu
u /c
2
,
vy
vy 1 u2 1 vxu /
第六章 第4节 相对论的速度变换公式 质能关系

u′沿着火车前进的方向相对火车运动,那么他相对地面的速度
u 与 u′+v 的关系是
()
A.u=u′+v
B.u<u′+v
C.u>u′+v
D.以上均不正确
解析:按照经典的时空观,u=u′+v,而实际上人对地面的速度 按照相对论速度公式计算,u=1u+′u+′c2vv,因此 u 比 u′与 v 之和要 小,但只有在 u′和 v 的大小接近光速时才能观察此差别。
(2)如果 u ≪c,v′≪c,这时v′c2 u可忽略不计,这时相 对论的速度合成公式可近似变为 v=v′+u。
(3)如果 v′与 u 的方向垂直或成其他角度时,情况比较 复杂,上式不适用。
[学后自检]┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄(小试身手)
在高速运动的火车上,设车对地面的速度为 v,车上的人以速度
D.在相对论力学中,物体的质量随物体速度的增大而增大
解析:在牛顿力学中,物体的质量是保持不变的,故选项 A
正确,B 错误;在相对论力学中,由于物体的速度 v 不可能
达到光速 c,所以 v<c,1-(vc)2<1,根据 m=
m0 ,可判 1-vc2
断选项 C、D 均正确。
答案:ACD
3.设想有一艘飞船以 v=0.8c 的速度在地球上空飞行,如果这时
(2)对于一个以速率 v 运动的物体,其动能
Ek=m(3)物体的总能量 E 为动能与静质能之和,即 E=Ek+E0= mc2(m 为动质量)。
(4)由质能关系式可知 ΔE=Δmc2。
[学后自检]┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄(小试身手) 星际火箭以 0.8c 的速率飞行,其静止质量为运动质量的多少倍?
m/s=5.9×106
上述计算表明,加速后的电子还属于低速的,可以使用经典的
相对论速度变换公式

相对论速度变换公式是由爱因斯坦提出的相对论原理与牛顿运动定律结合而产生的,关于时间和空间的变化定律。它解释了在不同的参照系中,时间和空间发生的变化。该公式是由以下三个参数组成的:
1.α是速度的量(α=V/c),其中V表示物体相对于参照系速度,c表示光速;
2.2.γ是Lorentz系数γ的一个重要参数;
3.3.Δx,Δt是时间和长度的变化量,这也是相对论速度变换公式的主要参数。
4.
根据相对论速度变换公式,当物体以夹角λ相对于光速运动时,物体的距离和时间的变化将满足如下关系:Δx'=γ[Δx-VΔt],Δt'=γ[Δt-VΔx/c2]。在这里,γ=1/(1-α2),α=V/c,V表示物体相对于参照系(即光速c)的速度,c表示光速,Δx'是物体在参照系中测出的距离。
7.相对论速度变换公式已经广泛应用于物理、力学和天文学等方面,发挥着重要作用。
5.
换句话说,当物体以相对于光速V的速度运动时,物体的时间和空间的变化将受到物理上的干扰,从而产生影响的变换关系称为“相对论速度变换公式”。这一变换公式提出了距离、时间及其变化的物理关系,用于客观评价物体不同参照系的距离、时间的变化。
6.
总的来说,相对论速度变换公式对于理解物以相对于光速运动时,距离时间和变化之间的变化关系,具有重要意义。
高中物理第六章相对论第4讲相对论的速度变换公式质能

二、广义相对论点滴(选学) 1.广义相对性原理和等效原理
(1)广义相对性原理 在__任__何__参__考__系__中物理规律都是_一__样___的. (2)等效原理 一个不受引力作用的加速度系统跟一个受引力作用的 _惯__性__系__统___是等效的. 2.支持广义相对论的几个观测结果 (1)光在引力场中传播时,将会发生__偏__折__,而不再是直线 传播. (2)引力作用使光波发生__频__移__.
第4讲 相对论的速度变换公式 质能关系
第5讲 广义相对论点滴(选学)
[目标定位] 1.知道相对论速度变换公式、相对论质量和质能 方程.2.了解广义相对论的基本原理.3.初步了解广义相对论的几 个主要观点以及主要观测证据.
一、相对论的速度变换公式 质能关系
1.相对论的速度变换
在以速率u相对于参考系S运动的参考系S′中,一物体沿与
(3)在引力场中时间也会__延__缓__,引力越强,时钟就走得越 __慢____. (4)水星绕太阳运动的轨道与根据牛顿万有引力定律计算所 得的不一致. (5)当两个天体相互绕转时,会向外界辐射出__引__力__波____. 3.宇宙的演化 (1)20世纪40年代末,物理学家伽莫夫把宇宙膨胀与粒子反 应理论结合起来,提出宇宙大爆炸假说. (2)宇宙大爆炸理论最大说服力的证据是宇宙背景辐射的发 现.
解析 已知 v=0.05c,ux′=0.8c. 由相对论速度叠加公式得 ux=1u+x′ux+c′2vv=cu2x+′u+x′vvc2, ux=c20+.8c0+.8c0×.050c.05c2c≈0.817c. 答案 0.817c
二、对相对论质量和质能方程的理解
1.相对论质量 物体的质量会随物体的速度增大而增大,物体以速度 v 运 动 时 的 质 量 m 与 静 止 时 的 质 量 m0 之 间 的 关 系 m = 1m-0 vc2.
相对论的速度变换公式质能方程

1、速度变换公式: v u v '
1
uv ' c2
2、质量变化公式:
m
3、质能方程:
m0
1
v2 c2
E mc2
狭义相对论简介
1、两个基本假设; 2、两个重要结论; 3、三个重要公式。
E E E 物体运动时的质量要比静止时质量大。
这就是我们过去熟悉k的动能表达式,这也能让我0们看出,牛顿力学是相对论力学在低速情况下的特例。
物体运动时的能量与物体静能量之差
当v《c时,m≈m0,
2
E mc 2 当v’=c时,v=c,
m c 当v’=c时,v=c,
0 选修3-4第六章 相对论
2
E m c Ek 当u和v’都远小于光0速c时,v=u+v0’
对 论 的 质 量 变
时的质量m0之间有下面的关系:
静质量
动质量
m m0
1
v2 c2
物体运动 的速率
换
相 对 论 的
m 上式表明:
m0
1
v2 c2
m0
质
量 物体运动时的质量要比静止时质量大。
变
换
当v《c时,m≈m0,
即在经典力学中,质量保持不变。
物体的质量m与它所包含的
质
能量E存在确定的关系:
度 他相对于地面的速度v是多大?
变 换
v u v'
当v’=c时,v=c,
1
uv ' c2
满足光速不变原理。
相 对 论
v u v'
1
uv ' c2
的
速 当u和v’都远小于光速c时,v=u+v’
度 变 换
相对论速度变换公式推导

相对论速度变换公式推导相对论是物理学中的一门重要分支,它研究的是运动物体之间的相对关系。
其中最基础且核心的概念就是:光速不变原理。
在相对论中,光速不变原理被认为是一个普适的规律。
具体来说,任何一个固定光源所发出的光线,传播速度都是恒定的,不受光源和接收器的相对运动状态影响。
相对论中的速度变换,指的是两个物体之间的相对速度,即在两个物体分别以不同的速度(相对于某个参考系)移动时,它们在对方眼中的速度。
这个速度变换是相对论中的一个重要问题,也是相对论中的一个核心概念。
在相对论中,一个物体的速度不仅取决于该物体本身不动时的速度,还取决于观察其运动的参考系的状态。
相对论速度变换公式可以用来计算两个物体之间的相对速度,具体推导过程如下:假设有两个物体A和B,它们分别以速度v1和v2相对于参考系S0运动。
另设观察者S以速度v0在参考系S0中运动,同时观测物体A和物体B。
则A物体相对于S的速度为v1-v0,B物体相对于S的速度为v2-v0。
然而上述公式不是最终答案。
根据相对论理论,速度不是像牛顿力学一样简单相加的,而是需要对速度进行洛伦兹变换,才能算出物体的实际物理速度。
相对论速度变换公式即为所求。
通过洛伦兹变换,我们可以得到物体A和物体B之间的相对速度公式:v = (v1-v2)/(1 - v1v2/c^2)其中,v1为物体A的速度,v2为物体B的速度,c为光速,v为相对速度。
当两个物体的速度都非常小,即远远小于光速时,相对论速度变换公式退化为牛顿力学公式:v = v1 - v2。
综上所述,相对论速度变换公式是用于计算两个相对运动的物体之间的相对速度的公式。
相对论理论指出,速度之间并不是简单相加的关系,不能直接进行运算,而需要进行洛伦兹变换。
相对论速度变换公式的推导过程比较复杂,但是通过渐进分析以及高数知识可以计算得出。
作为物理学教材中的一部分,相对论速度变换公式对于我们理解相对论的使用和基本事实有着很大的指导意义。
漆安慎《普通物理学教程:力学》第二版《相对论简介》单元思维方法分析一览表
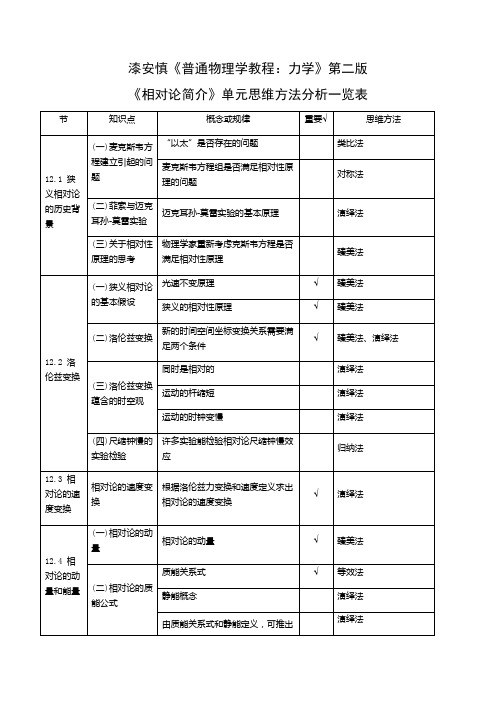
物理学家重新考虑克斯韦方程是否满足相对性原理
臻美法
12.2洛伦兹变换
(一)狭义相对论的基本假设
光速不变原理
√
臻美法
狭义的相对性原理
√
臻美法
(二)洛伦兹变换
新的时间空间坐标变换关系需要满足两个条件
√
臻美法、演绎法
(三)洛伦兹变换蕴含的时空观
同时是相对的
演绎法
运动的杆缩短
演绎法
漆安慎《普通物理学教程:力学》第二版
《相对论简介》单元思维方法分析一览表
节思维方法
12.1狭义相对论的历史背景
(一)麦克斯韦方程建立引起的问题
“以太”是否存在的问题
类比法
麦克斯韦方程组是否满足相对性原理的问题
对称法
(二)菲索与迈克耳孙-莫雷实验
迈克耳孙-莫雷实验的基本原理
演绎法
运动的时钟变慢
演绎法
(四)尺缩钟慢的实验检验
许多实验能检验相对论尺缩钟慢效应
归纳法
12.3相对论的速度变换
相对论的速度变换
根据洛伦兹力变换和速度定义求出相对论的速度变换
√
演绎法
12.4相对论的动量和能量
(一)相对论的动量
相对论的动量
√
臻美法
(二)相对论的质能公式
质能关系式
√
等效法
静能概念
演绎法
由质能关系式和静能定义,可推出总能等于动能加静能
归纳法
臻美法
(二)等效原理和广义相对性原理
弱等效原理
等效法
强等效原理
等效法
广义相对性原理
等效法
局域惯性系
微元法、建模法
*12.6引力场与弯曲时空
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§12.3 相对论的速度变换
上页
下页
返回
结束
第十二章 相对论简介
§12.3 相对论的速度变换
设坐标系S 相对于坐标系S 以速度 u 沿 x 轴正向 运动, 则对于S系而言:
dx vx , dt 则对于S 系而言: dx v ,y v y , dt
光向后的速度
这正是光速不变原理所要求的.
上页 下页
cu v c uc 1 2 c c u v c uc 1 2 c
返回
结束
第十二章 相对论简介
作业:P448
12.3.3
上页
下页
返回
结束
上页 下页 返回 结束
第十二章 相对论简介
这就是B相对A的速度.同样可得A相对B的速度
0.995c
/ x
注意:从地面测量,二者相互接近的速度仍为1.8c 。 洛仑兹速度变换表明:两个小于光速的速度合 成小于光速;两个速度中有一个等于光速,或两个 速度都等于光速,合成速度等于光速.这样,普遍结 论是:通过速度变换,在任何惯性系中物体的运动 速度都不可能超过光速,也就是说,光速是物体运 动的极限速度.
dz vz dt dz v z dt
dx 1 dt dt v (v x u ) (12.3.1) x dt dt dt 1 2
上页 下页 返回 结束
第十二章 相对论简介
u t (t 2 x ) c dt d u (1 u v ) ( t 2 x ) 2 x c dt dt c
解 设地球为S系,火箭A为S´系. A的运动 u vA 0.9c 已知B在S系中的速度 速度
(S´系) A B
地球 ( S系 x
vx vB 0.9c
则B相对A的运动速度,就是B相对S′参考系测得的
x u ux
/ x
1
c
2
0.9c 0.9c 1.8c 0.995c 1.81c 0.9c 0.9c 1 c2
1 dt dt 1 u v 2 x c
2
代入(12.3.1)式中得
vx u v' x u 1 2 vx c
上页 下页 返回 结束
第十二章 相对论简介
vx u v' x u 1 2 vx c
1 v' y vy u 1 2 vx c
2
v x u vx u 1 2 v x c
上页 下页 返回 结束
第十二章 相对论简介
菲涅尔研究介质对其中光速的影响实验结果
c c kv n
k 11/ n
2
上页
下页
返回
结束
第十二章 相对论简介
例:有一辆火车以速度u相对地面作匀速直线运动. 在火车上向前和向后射出两道光,求光相对地面的速 度. 解 以地面为S系,火车为S′系,则光相对车向前 的速度为 v c,向后的速度 v c ,则得 x x 光向前的速度
1 vy v y u 1 2 v x c
2
1 v' z vz u 1 2 vx c
2
1 vz v z u 1 2 v x c
2
正变换
上页 下页
逆变换
返回 结束
第十二章 相对论简介
例:设有两个火箭A、B相向运动,在地面测得A、B的 速度沿x轴正方向各为 vA 0.9c , B 0.9c .试求它们 v 0.9c -0.9c 相对运动的速度.
