(完整版)基于matlab的QPSK系统仿真毕业设计论文
基于MATLAB的QPSK通信系统仿真设计毕业设计论文

基于MATLAB的QPSK通信系统仿真设计摘要随着移动通信技术的发展,以前在数字通信系统中采用FSK、ASK、PSK 等调制方式,逐渐被许多优秀的调制技术所替代。
本文主要介绍了QPSK调制与解调的实现原理框图,用MATLAB软件中的SIMULINK仿真功能对QPSK调制与解调这一过程如何建立仿真模型,通过对仿真模型的运行,得到信号在QPSK 调制与解调过程中的信号时域变化图。
通过该软件实现方式,可以大大提高设计的灵活性,节约设计时间,提高设计效率,从而缩小硬件电路设计的工作量,缩短开发周期。
关键词 QPSK,数字通信,调制,解调,SIMULINK-I-AbstractAs mobile communications technology, and previously in the adoption of digital cellular system, ASK, FSK PSK modulation, etc. Gradually been many excellent mod ulation technology substitution, where four phase-shift keying QPSK technology is a wireless communications technology in a binary modulation method. This article prim arily describes QPSK modulation and demodulation of the implementation of the prin ciple of block diagrams, focuses on the MATLAB SIMULINK software emulation in on QPSK modulation and demodulation the process how to build a simulation model, through the operation of simulation model, I get signal in QPSK modulation and dem odulation adjustment process domain change figure. The software implementation, ca n dramatically improve the design flexibility, saving design time, increase efficiency, design to reduce the workload of hardware circuit design, and shorten the developmen t cycle.Keywords QPSK, Digital Communication,modulation,demodulation,SIMULINK-II-目录摘要 (I)Abstract (II)第1章绪论 (1)1.1 选题的目的和意义 (1)1.2 课题研究现状 (1)1.3 本文主要研究工作 (2)第 2 章数字通信技术简介 (3)2.1 引言 (3)2.2 概念及其基本组成部分 (3)2.3 数字通信的特点 (5)2.4 数字通信发展的回顾与展望 (5)本章小结 (6)第3 章数字相位调制 (7)3.1 数字基带传输系统 (7)3.2 正弦载波数字调制系统 (8)3.3 QPSK概述 (9)3.4 QPSK调制和解调 (10)3.4.1调制 (10)3.4.2解调 (10)3.4.3QPSK的调制原理 (11)3.4.4QPSK解调的工作原理 (13)本章小结 (14)第4章 QPSK调制与解调的软件实现 (15)4.1 SIMULINK功能介绍 (15)4.2 SIMULINK特点 (15)4.3 QPSK调制与解调的软件设计 (16)4.3.1QPSK调制与解调的软件实现 (16)4.3.2QPSK调制解调过程主要组件的功能 (17)4.4 QPSK调制解调仿真过程及其波形图 (19)4.4.1QPSK调制过程及其波形图 (19)4.4.2QPSK解调过程及其波形图 (29)4.5 QPSK调制解调仿真过程正确性的验证 (34)本章小结 (35)结论 (36)-III-致谢 (37)参考文献 (38)附录1 (39)附录2 (41)-IV-第1章绪论1.1 选题的目的和意义随着经济危化的不断发展,人们对通信的要求也越来越高。
基于 MATLAB 的QPSK系统仿真设计与实现

通信系统仿真设计实训报告1.课题名称:基于MATLAB 的QPSK系统仿真设计与实现学生学号:学生:所在班级:任课教师:2016年10月25日目录1.1QPSK系统的应用背景简介 (3)1.2 QPSK实验仿真的意义 (3)1.3 实验平台和实验容 (3)1.3.1实验平台 (3)1.3.2实验容 (3)二、系统实现框图和分析 (4)2.1、QPSK调制部分, (4)2.2、QPSK解调部分 (5)三、实验结果及分析 (6)3.1、理想信道下的仿真 (6)3.2、高斯信道下的仿真 (7)3.3、先通过瑞利衰落信道再通过高斯信道的仿真 (8)总结: (10)参考文献: (11)附录 (12)1.1QPSK系统的应用背景简介QPSK是英文Quadrature Phase Shift Keying的缩略语简称,意为正交相移键控,是一种数字调制方式。
在19世纪80年代初期,人们选用恒定包络数字调制。
这类数字调制技术的优点是已调信号具有相对窄的功率谱和对放大设备没有线性要求,不足之处是其频谱利用率低于线性调制技术。
19世纪80年代中期以后,四相绝对移相键控(QPSK)技术以其抗干扰性能强、误码性能好、频谱利用率高等优点,广泛应用于数字微波通信系统、数字卫星通信系统、宽带接入、移动通信及有线电视系统之中。
1.2 QPSK实验仿真的意义通过完成设计容,复习QPSK调制解调的基本原理,同时也要复习通信系统的主要组成部分,了解调制解调方式中最基础的方法。
了解QPSK的实现方法及数学原理。
并对“通信”这个概念有个整体的理解,学习数字调制中误码率测试的标准及计算方法。
同时还要复习随机信号中时域用自相关函数,频域用功率谱密度来描述平稳随机过程的特性等基础知识,来理解高斯信道中噪声的表示方法,以便在编程中使用。
理解QPSK调制解调的基本原理,并使用MATLAB编程实现QPSK信号在高斯信道和瑞利衰落信道下传输,以及该方式的误码率测试。
基于MATLAB的QPSK系统仿真设计实现分析范文

通信系统仿真设计实训报告1.课题名称:基于MATLAB 的QPSK系统仿真设计与实现学生学号:学生姓名:所在班级:任课教师:2016年10月25日目录1.1QPSK系统的应用背景简介 (3)1.2 QPSK实验仿真的意义 (3)1.3 实验平台和实验内容 (3)1.3.1实验平台 (3)1.3.2实验内容 (3)二、系统实现框图和分析 (4)2.1、QPSK调制部分, (4)2.2、QPSK解调部分 (5)三、实验结果及分析 (6)3.1、理想信道下的仿真 (6)3.2、高斯信道下的仿真 (7)3.3、先通过瑞利衰落信道再通过高斯信道的仿真 (8)总结: (10)参考文献: (11)附录 (12)1.1QPSK系统的应用背景简介QPSK是英文Quadrature Phase Shift Keying的缩略语简称,意为正交相移键控,是一种数字调制方式。
在19世纪80年代初期,人们选用恒定包络数字调制。
这类数字调制技术的优点是已调信号具有相对窄的功率谱和对放大设备没有线性要求,不足之处是其频谱利用率低于线性调制技术。
19世纪80年代中期以后,四相绝对移相键控(QPSK)技术以其抗干扰性能强、误码性能好、频谱利用率高等优点,广泛应用于数字微波通信系统、数字卫星通信系统、宽带接入、移动通信及有线电视系统之中。
1.2 QPSK实验仿真的意义通过完成设计内容,复习QPSK调制解调的基本原理,同时也要复习通信系统的主要组成部分,了解调制解调方式中最基础的方法。
了解QPSK的实现方法及数学原理。
并对“通信”这个概念有个整体的理解,学习数字调制中误码率测试的标准及计算方法。
同时还要复习随机信号中时域用自相关函数,频域用功率谱密度来描述平稳随机过程的特性等基础知识,来理解高斯信道中噪声的表示方法,以便在编程中使用。
理解QPSK调制解调的基本原理,并使用MATLAB编程实现QPSK信号在高斯信道和瑞利衰落信道下传输,以及该方式的误码率测试。
基于MATLAB的QPSK通信系统仿真设计重要

基于MATLAB的QPSK通信系统仿真设计重要QPSK (Quadrature Phase Shift Keying) 是一种常用的数字调制技术,广泛应用于无线通信系统中。
在QPSK通信系统中,数字信号通过将两个正交调制的载波相位进行相应的转换来进行传输。
MATLAB作为一种强大的科学编程语言和工具包,可以用来进行QPSK通信系统的仿真设计。
本文将介绍基于MATLAB的QPSK通信系统仿真设计的重要性,并详细解释如何进行设计。
首先,基于MATLAB的QPSK通信系统仿真设计可以帮助我们更好地理解和研究QPSK调制技术。
通过仿真设计,我们可以模拟整个通信系统,包括信号生成、调制、传输、接收和解调等各个环节。
通过控制各个参数,我们可以分析不同参数对系统性能的影响,如调制误差、信噪比、误码率等。
这有助于我们深入理解QPSK调制技术的原理和特性,并为系统性能的优化提供依据。
其次,基于MATLAB的QPSK通信系统仿真设计可以用来评估系统的性能。
在通信系统中,误码率是一个重要的性能指标,用来评估系统的抗干扰能力。
通过仿真设计,我们可以计算得到不同信噪比下的误码率曲线,从而评估系统的性能。
同时,还可以通过仿真设计研究并优化接收机的设计,如信道均衡、时钟恢复等,以提高系统的性能。
再次,基于MATLAB的QPSK通信系统仿真设计可以用来进行系统参数的选择和优化。
在设计通信系统时,很多参数需要进行选择和优化,如载波频率、采样率、均衡器参数等等。
通过仿真设计,我们可以对这些参数进行优化,并选择最佳的参数组合。
这有助于提高系统的性能和效率,实现更好的通信质量和可靠性。
最后,基于MATLAB的QPSK通信系统仿真设计可以用来进行系统的性能对比和验证。
我们可以采用不同的调制技术和设计方案进行仿真,比较系统的性能差异,从而选择最佳的方案。
同时,还可以将仿真结果与理论计算结果进行对比,验证仿真设计的准确性和有效性。
总之,基于MATLAB的QPSK通信系统仿真设计在研究、设计和优化通信系统中扮演着重要的角色。
基于Matlab的QPSK系统设计仿真

(t)sin tj COS 60 t=
)。。 z +
: 一
,) + 、 ,)
(、2 一 )
正 交支 路相 乘可 得 :
Q9( ) =SQes ̄:(£)sin t= [,( )COS t+
理论 分析指 出 ,在 恒参 信 道 中利 用 PSK方式 可
这就 是说需 要把二 进制 数字序 列 中每两个 比特 分成 一 组 ,共有 四种组 合 ,即 00,01,10,11,其 中每一组称 为双 比特码 元 。每 一个 双 比特 码元是 由两 位二 进制 信 息 比特组 成 ,它 们 分 别代 表 四进 制 四个 符 号 中的 一 个符号。QPSK中每次调制可传输 2个信息比特, 这 些信息 比特是 通过 载波 的 四种相 位来 传递 的 。解
第 10卷 第 5期 2010年 2月 1671—1815(2OLO)5-1124-05
生物 技 术
科 学 技 术 与 工 程
Science Technology and Engineering
Vo1.10 No.5 Feb.2010 @ 2010 Sci.Tech.Engng.
高频正 弦波 。数 字 调 制信 号 又称 为 键 控 信 号 ,数 字
四相相 位调制解 调是 利用 载波 的 四种 不 同相位
调制过 程 中处理 的是数 字信 号 ,而 载波有 振 幅 、频率 差 来 表 征 输 入 的 数 字 信 息 ,是 四 进 制 移 相 键 控 。
和相位 3个变 量 ,且二 进 制 的信 号 只 有 高低 电平 两 QPSK是 在 M =4时 的调相 技术 ,它规 定 了四种 载波
一 种 调制技 术 的两 个 基 本参 数 :(1)信 号 分 布 ;(2)
基于Matlab 的QPSK调制解调仿真设计与研究

天津理工大学计算机与通信工程学院通信工程专业设计说明书基于Matlab/Simulink的QPSK调制解调仿真设计与研究姓名韩双年学号 ********班级 09通信3班指导老师白媛日期 2012-12-16目录摘要 (2)第一章前言 (2)1.1 专业设计任务及要求 (2)1.2 Matlab简介 (2)1.3 Matlab下的simulink简介 (3)1.4 通信系统模型 (3)第二章QPSK调制 (4)2.1 QPSK介绍 (4)2.2 QPSK调制原理 (4)2.2.1 相乘法 (4)2.2.2 选择法 (5)2.3 QPSK调制原理框图 (6)2.4 QPSK调制方式的Matlab仿真 (6)2.5 QPSK调制方式Matlab-simulink仿真 (7)2.5.1 simulink调制建模 (7)2.5.2 simulink调制仿真结果 (8)第三章QPSK解调 (13)3.1 QPSK解调原理 (13)3.2 QPSK解调原理框图 (13)3.3 QPSK解调方式Matlab仿真 (13)3.4 QPSK解调方式的Matlab-simulink仿真 (14)3.4.1 QPSK解调建模 (14)3.4.2 传输信道 (16)3.4.3仿真结果 (16)3.5 仿真结果分析 (18)第四章QPSK通信系统性能分析 (19)第五章结论 (19)参考文献 (20)附录 (20)摘要正交相移键控(QPSK),是一种数字调制方式。
QPSK技术具有抗干扰能力好、误码率低、频谱利用效率高等一系列优点。
论文主要介绍了正交相移键控(QPSK)的概况,以及正交相移键控QPSK的调制解调概念和原理,利用Matlab中M文件和Simulink模块对QPSK的调制解调系统进行了仿真,对QPSK在高斯白噪声信道中的性能进行了,分析了解Simulink中涉及到QPSK的各种模块的功能。
【关键词】Matlab QPSK Simulnk 仿真第一章前言1.1专业设计任务及要求1了解并掌握QPSK调制与解调的基本原理;2在通信原理课程的基础上设计与分析简单的通信系统;3学会利用MATLAB7.0编写程序进行仿真,根据实验结果能分析所设计系统的性能。
基于MATLAB的QPSK系统仿真设计与实现

通信系统仿真设计实训报告1.课题名称:基于 MATLAB 的QPSK系统仿真设计与实现学生学号:学生:所在班级:任课教师:2016年 10月25日目录1.1QPSK系统的应用背景简介 (3)1.2 QPSK实验仿真的意义 (3)1.3 实验平台和实验容 (3)1.3.1实验平台 (3)1.3.2实验容 (3)二、系统实现框图和分析 (4)2.1、QPSK调制部分, (4)2.2、QPSK解调部分 (5)三、实验结果及分析 (6)3.1、理想信道下的仿真 (6)3.2、高斯信道下的仿真 (7)3.3、先通过瑞利衰落信道再通过高斯信道的仿真 (8)总结: (10)参考文献: (11)附录 (12)1.1QPSK系统的应用背景简介QPSK是英文Quadrature Phase Shift Keying的缩略语简称,意为正交相移键控,是一种数字调制方式。
在19世纪80年代初期,人们选用恒定包络数字调制。
这类数字调制技术的优点是已调信号具有相对窄的功率谱和对放大设备没有线性要求,不足之处是其频谱利用率低于线性调制技术。
19世纪80年代中期以后,四相绝对移相键控(QPSK)技术以其抗干扰性能强、误码性能好、频谱利用率高等优点,广泛应用于数字微波通信系统、数字卫星通信系统、宽带接入、移动通信及有线电视系统之中。
1.2 QPSK实验仿真的意义通过完成设计容,复习QPSK调制解调的基本原理,同时也要复习通信系统的主要组成部分,了解调制解调方式中最基础的方法。
了解QPSK的实现方法及数学原理。
并对“通信”这个概念有个整体的理解,学习数字调制中误码率测试的标准及计算方法。
同时还要复习随机信号中时域用自相关函数,频域用功率谱密度来描述平稳随机过程的特性等基础知识,来理解高斯信道中噪声的表示方法,以便在编程中使用。
理解QPSK调制解调的基本原理,并使用MATLAB编程实现QPSK信号在高斯信道和瑞利衰落信道下传输,以及该方式的误码率测试。
基于Matlab的QPSK通信系统建模与仿真综述

•
•
D_sam=conv(D_s_sam,BB);
• 3.相偏的预测 Discriminator_Out(pos_timing)=(sign(D_timing(pos_timin g))*(Q_timing(pos_timing))sign(Q_timing(pos_timing))*D_timing(pos_timing))/(sqrt( 2)*abs(D_timing(pos_timing)+1j*Q_timing(pos_timing)));
QPSK中文全称是“正交相移键控”。从名字可以看出属于“相位” 调制。 QPSK四相移键控是目前最常用的一种卫星数字信号调制方式。 优点:(1)频谱效率比较高,(2)误码率小(抗干扰能力强),(3)电路 实现简单。
二.QPSK调制解调基本原理
• 2.1QPSK调制
• 说明: 基带信号A(t)是单极性不归零双极性码元,串/并转换之后 变成并行码元a和b。这两路码元分别用两路正交的载波相 乘。相加之后即可得到QPSK信号。 • 原因: QPSK信号可以看成是两路BPSK信号相加的结果。上面 的每一路其实是一个BPSK调制。
• 5.3 误比特率曲线 • 5.3.1 信噪比SNR与比特能量比/噪声功率谱密度的转换 • QPSK通信系统不存在频偏时,为了得到统一的误比特率曲 线,我们用Eb/No作为我们的自变量。关于Eb/No与SNR的 关系有以下说明:EbNo就是Eb/No。 Eb表示单位比特的能 量,单位是焦耳(Joules)。No表示功率谱密度,单位是瓦 特/赫兹(Watts/Hz)。SNR就是S/R。S表示信号功率,单 位是瓦特(Watts)。N表示噪声功率,单位是瓦特 (Watts)。显然SNR单位是无量纲的。EbNo的单位是 Joules·Hz/ Watts,其实也是无量纲的。因为Watts表示是焦 耳/秒(Joules /s),而1 Hz=1/s。EbNo与SNR关系转换:
基于-MATLAB-的QPSK系统仿真设计与实现

通信系统仿真设计实训报告1.课题名称:基于MATLAB 的QPSK系统仿真设计与实现学生学号:学生姓名:所在班级:任课教师:2016年10月25日目录1.1QPSK系统的应用背景简介 (3)1.2 QPSK实验仿真的意义 (3)1.3 实验平台和实验内容 (3)1.3.1实验平台 (3)1.3.2实验内容 (3)二、系统实现框图和分析 (4)2.1、QPSK调制部分, (4)2.2、QPSK解调部分 (5)三、实验结果及分析 (6)3.1、理想信道下的仿真 (6)3.2、高斯信道下的仿真 (7)3.3、先通过瑞利衰落信道再通过高斯信道的仿真 (8)总结: (10)参考文献: (11)附录 (12)1.1QPSK系统的应用背景简介QPSK是英文Quadrature Phase Shift Keying的缩略语简称,意为正交相移键控,是一种数字调制方式。
在19世纪80年代初期,人们选用恒定包络数字调制。
这类数字调制技术的优点是已调信号具有相对窄的功率谱和对放大设备没有线性要求,不足之处是其频谱利用率低于线性调制技术。
19世纪80年代中期以后,四相绝对移相键控(QPSK)技术以其抗干扰性能强、误码性能好、频谱利用率高等优点,广泛应用于数字微波通信系统、数字卫星通信系统、宽带接入、移动通信及有线电视系统之中。
1.2 QPSK实验仿真的意义通过完成设计内容,复习QPSK调制解调的基本原理,同时也要复习通信系统的主要组成部分,了解调制解调方式中最基础的方法。
了解QPSK的实现方法及数学原理。
并对“通信”这个概念有个整体的理解,学习数字调制中误码率测试的标准及计算方法。
同时还要复习随机信号中时域用自相关函数,频域用功率谱密度来描述平稳随机过程的特性等基础知识,来理解高斯信道中噪声的表示方法,以便在编程中使用。
理解QPSK调制解调的基本原理,并使用MATLAB编程实现QPSK信号在高斯信道和瑞利衰落信道下传输,以及该方式的误码率测试。
基于matlab的QPSK仿真设计报告

西南科技大学专业方向设计报告课程名称:通信工程专业方向设计设计名称:基于matlab地QPSK仿真方向设计任务书学生班级:通信0903 学生姓名:李孟娇学号: 20095999 设计名称:基于matlab地QPSK仿真起止日期: 2012.11.20—2012.12.20 指导教师:胡荣春方向设计学生日志课程设计评语表基于MATLAB地QPSK仿真设计与实现一、摘要本次方向设计根据当今现代通信技术地发展,对QPSK信号地工作原理进行了仿真分析.并结合调制解调地基本性能和通信原理地基础知识,利用MATLAB 仿真工具设计出一个QPSK仿真程序,以衡量QPSK 在理想信道、高斯白噪声信道和先通过瑞利衰落信道再通过高斯信道三种方式地调制解调得到地功率谱密度、噪声曲线、星座图及误码性能,并对仿真结果进行了分析.关键字:MATLAB仿真;QPSK调制;QPSK解调;误码率;信噪比Based on the modern communication technology, design of oriented major has implemented a simulated analysis in regard to the principle of QPSK signal. Associating with the performance of design of oriented major and underpinning communication knowledge, a QPSK simulate program was implemented and analysed in the aim of measuring its power spectral density, curve of noise, constellation and bit error performance under ideal channel, white Gaussian noise channel and via Rayleigh fading channel and white Gaussian noise channel respectively.Key words:MATLAB Simulate。
基于MATLAB的QPSK系统仿真设计与实现

基于MATLAB的QPSK系统仿真设计与实现QPSK(Quadrature Phase Shift Keying)是一种常用的调制技术,广泛应用于无线通信系统中。
本文将基于 MATLAB 对 QPSK 系统进行仿真设计与实现。
首先,我们需要了解 QPSK 调制的原理。
QPSK 将每个符号分成两个维度,分别为实部和虚部,以实现两个维度上的相位调制。
在 QPSK 中,每个符号可以表示为 a+jb 的形式,其中 a 和 b 分别为两个调制点的幅度,j 为虚数单位。
在 QPSK 中,通常我们使用 2 相移键控(BPSK)调制的方式来实现每个维度上的相位调制。
接下来,我们可以开始进行QPSK系统的仿真设计与实现。
1.首先,我们需要生成QPSK调制所使用的信号。
a.定义QPSK调制器:b.生成随机数据序列:data = randi([0,3],1000,1);c.通过调制器将数据序列调制为QPSK信号:modulatedData = modulator(data);2.接下来,我们需要添加高斯噪声模拟通信信道。
我们可以使用 MATLAB 中的 AWGN(Additive White Gaussian Noise)信道模型来添加高斯噪声。
步骤如下:a.定义AWGN信道对象:b.设置信道的信噪比(SNR)值:awgnChannel.SNR = 10;c.通过信道对象添加高斯噪声:receivedSignal = awgnChannel(modulatedData);3.最后,我们需要进行解调和误码率的计算。
a.定义QPSK解调器:b.对接收到的信号进行解调:demodulatedData = demodulator(receivedSignal);c.计算误码率(BER):ber = errorRate(data, demodulatedData);4.可选择性的结果输出和显示。
我们可以通过输出误码率(BER)并进行可视化的方式来评估QPSK系统的性能。
基于Matlab的QPSK系统设计仿真
舰 船 电 子 工 程
Ship Electronic Engineering
维普资讯
Vo1.27 No.2 150
基 于 Matlab的 QPSK系统 设 计 仿 真
肖矿 林 唐 唐
(92665部 队 石 门 415300) (海 军工程大学 电子工程学 院 武汉 430033)
●
摘 要 通过用 Matlab编写脚本程 序对 QPSK通信 系统的发射 和接 收过程 的具体 实现进 行模 拟仿真 ,并对 各模块进 行频谱分析 ,对 于理解 QPSK系统的性能并在系统上作进一 步的设计 ,提供 极大 的便利 。
关键词 数字通信 ;QPSK;仿真 中图分类号 TN911.7
图 5 分量调制后 的频谱
2
'
JIl
一
: 一 _
{ l — 2
一
— 4
『
『’
一
O Q5 1 1.5 2 2.5 O O.5 1 L5 2 2.5
X 1O
X 104
图 6 分量解调 后的频谱
1.5
1
O.5
O lO0O O0O3O0O4COO 500O
X 1O
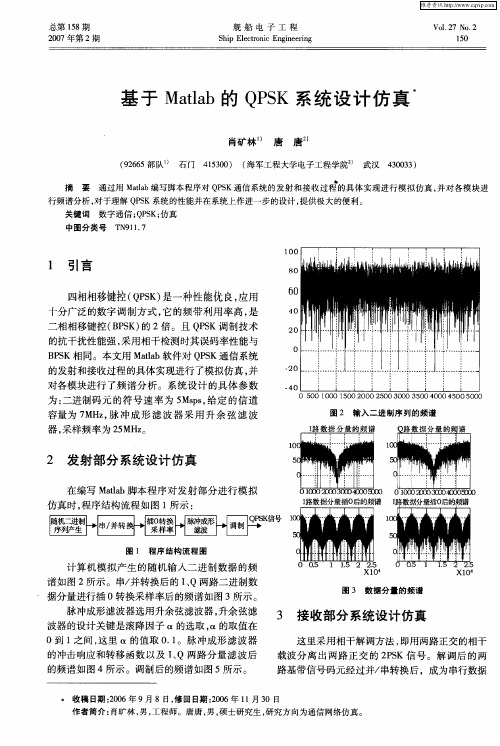
图 3 数 据分 量的频谱
3 接收 部分 系统设计仿真
X104
0到 1之间 ,这里 的值取 0.1。脉冲成形滤波器 的冲击响应 和转移 函数以及 I、Q两路分量滤波后 的频谱如图 4所示 。调制后的频谱如图 5所示 。
这 里采 用相 干解 调方 法 ,即用 两路 正交 的相 干 载波分 离出两路正交 的 2PSK信号。解 调后的两 路基带信号码元经过并/串转换后 ,成为串行数据
基于matlab的qpsk通信系统设计与仿真

211基于Matlab 的QPSK 通信系统设计与仿真郭文博(佳木斯大学信息电子技术学院,黑龙江佳木斯154007)摘要:随着大数据时代的到来,用户需要更高速率、更大容量以及更多业务的通信系统,而有限的频谱资源成为了通信系统发展的瓶颈。
QPSK 调制与解调作为一种多进制调制方式,极大地提升频谱资源的利用率。
基于此,文章对QPSK 的数字通信系统进行研究。
通过对QPSK 调制与解调的仿真参数的设计,对实验仿真结果进行了分析。
通过对比解调前后的波形,验证了所仿真的QPSK 通信系统的正确性。
关键词:QPSK ;调制;解调;数字通信系统中图分类号:TN911文献标识码:A 文章编号:1673-1131(2019)11-0211-02随着4G 移动通信技术的普及,信息时代已进化到大数据时代。
通过PSK 调制解调技术,4G 移动通信技术为高速率通信提供了保障。
由于用户对数字通信技术的依赖性越来越强,这就要求数字通信技术必须更稳定高效。
QPSK 作为数字通信系统中一种常用的多进制调制方式,能极大地提升频谱资源的利用效率,因此,对其进行研究具有重要意义和远大的商业价值。
1QPSK 的理论研究QPSK 调制解调技术又称之为正交相移键控技术,属于一种相位调制技术,是由PSK 技术改进而来,相对于传统的调整解调技术具有诸多优势,在有限的带宽内传输更多的信息,且传输过程中干扰对信号影响甚小。
作为一种线性窄带数字信号调制技术,QPSK 相对于PSK 技术的通信速率提升两倍,且可以有效地避免频率干扰,该技术起初在远距离卫星通信中作为调制技术。
随着通信设备的不断更新,设备性能大幅度提升,且稳定性不断改善,因此,QPSK 逐渐成为移动通信技术中主流调制解调技术之一。
2QPSK 调制与解调的仿真设计在对基于QPSK 调制与解调的整个数字通信系统的仿真平台搭建之前,首先对其各个主要部分的仿真部分进行设计,下面以信号输入至信号输出的顺序对其进行设计。
毕业设计方案matlab的QPSK系统仿真

基于MATLAB的QPSK仿真设计与实现一.前言1.1QPSK系统的应用背景简介QPSK是英文Quadrature Phase Shift Keying的缩略语简称,意为正交相移键控,是一种数字调制方式。
在19世纪80年代初期,人们选用恒定包络数字调制。
这类数字调制技术的优点是已调信号具有相对窄的功率谱和对放大设备没有线性要求,不足之处是其频谱利用率低于线性调制技术。
19世纪80年代中期以后,四相绝对移相键控(QPSK>技术以其抗干扰性能强、误码性能好、频谱利用率高等优点,广泛应用于数字微波通信系统、数字卫星通信系统、宽带接入、移动通信及有线电视系统之中。
1.2 QPSK实验仿真的意义通过完成设计内容,复习QPSK调制解调的基本原理,同时也要复习通信系统的主要组成部分,了解调制解调方式中最基础的方法。
了解QPSK的实现方法及数学原理。
并对“通信”这个概念有个整体的理解,学习数字调制中误码率测试的标准及计算方法。
同时还要复习随机信号中时域用自相关函数,频域用功率谱密度来描述平稳随机过程的特性等基础知识,来理解高斯信道中噪声的表示方法,以便在编程中使用。
理解QPSK调制解调的基本原理,并使用MATLAB编程实现QPSK信号在高斯信道和瑞利衰落信道下传输,以及该方式的误码率测试。
复习MATLAB编程的基础知识和编程的常用算法以及使用MATLAB仿真系统的注意事项,并锻炼自己的编程能力,通过编程完成QPSK调制解调系统的仿真,以及误码率测试,并得出响应波形。
在完成要求任务的条件下,尝试优化程序。
通过本次实验,除了和队友培养了默契学到了知识之外,还可以将次实验作为一种推广,让更多的学生来深入一层的了解QPSK以至其他调制方式的原理和实现方法。
可以方便学生进行测试和对比。
足不出户便可以做实验。
1.3 实验平台和实验内容1.3.1实验平台本实验是基于Matlab的软件仿真,只需PC机上安装MATLAB 6.0或者以上版本即可。
基于Matlab的QPSK调制与解调系统仿真

一、多进制调制带通二进制键控系统中,每个码元只能传输1b信息,其频带利用率不高。
为了提高频带利用率,最有效的办法是使一个码元传输多个比特的信息。
这就是多进制键控体制。
多进制数字调制是利用多进制数字基带信号去调制载波的振幅,频率或相位。
因此,相应地有多进制数字振幅调制(MASK),多进制数字频率调制(MPSK)以及多进制数字相位调制(MPSK)等。
多进制数字调制是利用多进制数字基带信号去调制载波的振幅、频率或相位。
由于多进制数字调制信号的被调参数在一个码元宽度内有多个可能的取值,因此与二进制数字调制相比,具有以下两个特点:(1)在相同的信道码元传输速率下,L进制系统的信息传输速率是二进制系统的log L倍;2(2)在相同的系统传信率下,多进制信道的符号速率可以低于二进制的符号速率,因而所需信道带宽减小。
因此,多进制调制方式获得了广泛的应用,成为提高通信效率的主要手段。
二、QPSK的原理QPSK(4PSK,正交相移键控)又叫四相绝对相移调制,是最常用的MPSK,分为π/2系统和π/4系统两种。
它是利用载波的四种不同相位来表征数字信息。
由于每一种载波相位代表两个比特信息,故每个四进制码元又被称为双比特码元。
QPSK系统在用正交调制部分需要进行串/并变换,其中串/并变换电路将QPSK调制的两位编码按比特分开,走上下两路,分成的两路序列速率减半,电平发生器分别产生双极性二电平信号I(t)和Q(t),然后各自去调制相互正交的正弦波,再进行矢量合成,即得到QPSK信号。
图1 QPSK调制电路在解调部分可以用两个正交的载波信号实现相干解调。
正交路和同相路分别设置两个相关器,得到I(t)和Q(t),经电平判决和并/串变换即可恢复原始信息。
图2 QPSK解调电路三、详细设计步骤1 根据QPSK的调制及解调原理及原理框图,MATLAB程序来仿真这个系统应遵循以下几个步骤:调制部分:(1)串/并变换(2)极性转换(3)电平产生(4)两分路分别与载波相乘(5)合并两路信号信道部分:加入高斯白噪声解调部分:(1)接收到的信号分别乘以正弦信号及余弦信号(2)两路信号分别进行抽样判决(3)并/串变换2 用MATLAB 程序来实现QPSK 调制与解调系统仿真四、设计结果及分析0100200300400500600700800-2-1.5-1-0.50.511.52产生的二进制波形图1 产生的随机二进制序列050100150200250300350400-2-112二进制信息050100150200250300350400-2-112余弦分路信号图2 基数位的二进制序列及调制后的波形050100150200250300350400-2-112二进制信息050100150200250300350400-2-112正弦分路信号图3偶数位的二进制序列及调制后的波形050100150200250300350400-1-0.50.51加性高斯白噪声时域波形050100150200250300350400051015加性高斯白噪声频谱图4 加性高斯白噪声的时域波形及频谱050100150200250300350400-55接收端信号的时域图050100150200250300350400-202接收端正弦分路信号050100150200250300350400-22接收端余弦分路信号图5接收端信号的时域图及正余弦两路信号的波形0510********35404550-29.5-29-28.5-28-27.5-27-26.5-26-25.5-25-24.5Frequency (Hz)P o w e r /f r e q u e n c y (d B /H z )加性高斯白噪声功率谱密度图6 加性高斯白噪声的功率谱密度0100200300400500600700800-2-1.5-1-0.50.511.52解调出的波形图7 接收端最终解调后的二进制序列五、总结在现代通信中,提高频谱利用率一直是人们关注的焦点之一。
基于Matlab编程的QPSK的仿真

第23卷 第1期2005年3月 广西师范大学学报(自然科学版)JOU R NA L OF GU A N GX I NO RM A L U N IVER SI T Y V ol.23 N o.1M arch 2005收稿日期:2004-08-01作者简介:侯周国(1977—),男,湖南隆回人,湖南师范大学硕士研究生;钱盛友(1965—),男,湖南祁阳人,湖南师范大学教授,博士.基于M atlab 编程的QPSK 的仿真侯周国,钱盛友(湖南师范大学电子系,湖南长沙410081)摘 要:介绍了数字通信中的Q PSK 调制解调的原理和过程,通过用M atlab 对这一过程的编程,分析信号在理想信道和加噪信道中模拟传输时的时域图,并用蒙特卡罗方法,讨论模拟过程中的误码率,所得结果与理论结果基本一致.关键词:QP SK ;系统仿真;蒙特卡罗分析;M atlab中图分类号:T N 919.6 文献标识码:A 文章编号:1001-6600(2005)01-0021-04随着数字技术的飞速发展与数字器件的广泛使用,数字信号处理在通信系统中的应用已经越来越重要.数字信号传输系统分为基带传输系统和频带传输系统.频带传输系统也叫数字调制系统,该系统对基带信号进行调制,使其频谱搬移到适合在信道(一般为带通信道)上传输的频带上.数字调制和模拟调制一样都是正弦波调制,即被调制信号都为高频正弦波.数字调制信号又称为键控信号,数字调制过程中处理的是数字信号,而载波有振幅、频率和相位3个变量,且二进制的信号只有高低电平两个逻辑量即1和0,所以调制的过程可用键控的方法由基带信号对载频信号的振幅、频率及相位进行调制,最基本的方法有3种:正交幅度调制(QAM )、频移键控(FSK )、相移键控(PSK )[1].根据所处理的基带信号的进制不同分为二进制和多进制调制(M 进制).多进制数字调制与二进制相比,其频谱利用率更高.在数字通信、数字视频广播、数字卫星广播等领域中,广泛采用M 进制的调制方式.理论分析指出,在恒参信道中利用PSK 方式可以获得最佳接收性能.在接收机噪声的作用下,PSK 误码率最低[2].本文用Matlab 软件对M =4的四相相位调制解调(QPSK)进行模拟,并对这种调制方法在加性高斯噪声信道的误码率性能进行蒙特卡罗分析.1 QPSK 原理数字相位调制(PSK)是角度调制、恒定幅度数字调制的一种方式,通过改变发送波的相位来实现,除了其输入信号是数字信号以及输出的相位受限制以外,PSK 与传统的相位调制相似.对于经过M =2k 相相位调制的数字信号来说,载波信号的相位一般有 m =2 m M (m =0,1,…,M -1).因此调制信号可用如下的式子表示[1]:S m (t )=Ag T (t )cos( c t +m ),(0≤t ≤T s ,m =0,1,…,M -1)=E s g T (t )cos m cos c t -E s g T (t )sin m sin c t .(1)其中:A 是信号振幅;g T (t )为发射端的滤波脉冲(一般为矩形脉冲),决定发送信号的频谱特征;T 为信号持续时间;E s 为每一个发送符号的能量(A =E s ); c 为载波的角频率.本文以相对简单但广泛采用的四相相位调制解调进行模拟仿真.四相相位键控(QPSK )也称之为正交PSK.其调制及解调原理如图1所示.从图1(a)中可以看出:如果输入的二进制信息码流(假设+1V 为逻辑1,-1V 为逻辑0)串行进入比特分离器,产生2个码流以并行方式输出,分别被送入I (正交支路)通道及Q (同相支路)通道,又各自经过一个平衡调制器,与一个和参考振荡器同频的正交的载波(sin c t 和cos c t )调制形成了四相相移键控信号即得到平衡调制器的输出信号后,经过一个带通滤波器,然后再进行信号叠加,可以得到已经调制的QPSK 信号.QPSK 的4种(I ,Q 组合为4种[00],[01],[10]和[11])输出相位有相等的幅度,而且2个相邻的相位相差值为90°,但是输出相位并不满足我们前面所讲的 m =2 m M(m =0,1,…,M -1),信号相位移可以偏移45°和-45°,接受端仍可以得到正确的解码.实际中数字输入电压必须比峰值载波电压高出很多,以确保平衡调制器的正常工作.经过调制的信号通过信道传输到达a.调制原理b.解调原理图1 Q PSK 调制解调原理Fig.1 Block diag ram o f a QP SK tr ansmitt er and receiver用户端,需要进行解调,这样一过程是与调制相类似的逆过程.首先,QPSK 信号经过功率分离器形成两路相同的信号,进入乘积检波器,用两个正交的载波信号(sin c t 和cos c t )实现相干解调,然后各自通过一个低通滤波器滤波得到低频和直流的成分,再经过一个并行-串行变换器,得到解调信号.QPSK 的解调原理如图1(b)所示.2 蒙特卡罗仿真原理传输信息的有效性和可靠性是通信系统最重要的质量指标.对于数字通信系统,有效性用信息的传输图2 Q PSK 蒙特卡罗仿真原理Fig .2 Block diag ram of M o nte Carlo sim ulat ion for Q PSK 速率来衡量,可靠性可用错误率(误比特率和误码元率)来衡量.信号的传送检波过程中,由于噪声的干扰,可能出现解码错误.蒙特卡罗方法以对随机性问题进行仿真为其基本特征,这就决定了对于解决随机性问题具有很强的能力[3].蒙特卡罗方法是基于随机数信号的产生原理,统计分析信号传输过程中由于噪声干扰作用下的误码率问题.对于QPSK 通信系统(图2),在信号进行调制后,在信道中对信号采用加性高斯白噪声进行干扰.所以我们在这一过程中利用Matlab,在调制信号中加入高斯白噪声.传输信道中会加入噪声,调制信号在一个加性信道传输,在一个信号间隔内接收到的信号可以表示成[1]:r (t )=S m (t )+n c (t )cos c t -n s (t )sin c t ,(2)其中n c (t )和n s (t )为加性噪声的2个正交分量.结合(1)式,接受信号与调制信号进行相关计算,(2)式可以表示为[4~6]:cos m +n c E s sin m (3)22 广西师范大学学报(自然科学版) 第23卷其中n c 和n s 的定义为:n c =12∫∞-∞g T (t )n c (t )d t ,(4)n s =12∫∞-∞g T (t )n s(t )d t .(5)对于M ≥4的加性高斯白噪声信道中相位调制判决器的误码率P M 可以近似表示为[5]:P M ≈2Q 2E s N 0sin M =2Q 2kE b N 0sin M.(6)而Q (x )=12erfc x 2为误差函数;E b =E s 2为每比特信息的能量;k =log 2M ,单位为比特/符号,本文中M =4.3 M atlab 实现Q PSK 的仿真Matlab 作为一种科学计算软件,具有强大的计算仿真功能,可以用来编程演示模拟QPSK 中的调制解调过程.在仿真过程中,通过对比信道是否有噪声存在的情形下输出信号的波形来进行分析.在实际系统中,信号通过信道后,必然会加入噪声,典型的为高斯噪声[7].我们在这一过程中利用M atlab 编程,在调制信号中加入高斯白噪声,且使噪声功率为调制信号功率的百分之一.假设产生的数字信号的比特率f b =50Hz,信号的抽样时间t s =10-4s,通过对频率为f c =500Hz 的载波信号进行调制,通过模拟信道和滤波器后到达接受端解调,并根据调制解调原理,通过加噪声和不加噪声,做出了信号的时域图形.通过对图3 理想信道和加噪信道中调制解调信号的对比F ig .3 Contr ast betw een the signal in the ideality channel and noised channel图4 正交支路中的数据和调制信号Fig.4 Data and modulated sig nal of the ort ho gonal channel23第1期 侯周国等:基于M atlab 编程的QP SK 的仿真 比,发现通过Matlab 编程来模拟调制解调的过程,具有很好的检波功能.在维持比特时间不变的情形下,输入信号的时间长度可以变化(输入信号的变化),而且其抽样时间当然是越短越好,但是计算量会加大.同时用统计原理,用M atlab 根据蒙特卡罗仿真原理得到了QPSK 系统的误码率理论值和实际值的图形,计算时选取n c 和n s 是均值为0、方差为1的相互独立的高斯随机变量.图5 Q PSK 的蒙特卡罗仿真结果F ig .5 M o nte Carlo sim ulat ion result of Q P SK 通过编程模拟QPSK 过程,得到信号传输过程中的时域图.从图3可以知道:在理想情形下,信号的解调和调制过程中,信号只出现了很小的波动,在加噪信道中信号的波动范围虽然变大,但不会影响到解调后信号的识别.即在M atlab 编程模拟的过程中,QPSK 调制解调即使在加有白噪声干扰时,也能进行有效的解码.根据相位调制的特点,我们可以从图4中看到调制信号(正交支路)在二进制信号每发生一次电平的跃变时发生相位跳变.在不同信噪比(E b /E 0)下发送10000个符号的蒙特卡罗仿真结果如图5所示.在信噪比低于7dB 的情形下,理论误码率和实际误码相差很小.从这些图形中我们可以发现Matlab 软件很好地模拟出了数字通信系统的QPSK 过程.即使在噪声干扰下,解调输出信号与输入信号的波形也保持着基本的一致,对信号的恢复不会有大的影响.4 结论随着通信事业的发展,通信系统的设计也会越来越复杂,通信过程通过计算机的仿真,可以大大地降低实验成本.本文在不考虑信号解调过程中的相位模糊的前提下,对QPSK 进行了模拟,而且滤波处理中选用的是理想滤波器.通过利用M atlab 对QPSK 进行编程模拟,可以更好地了解QPSK 系统的工作原理,而且为硬件的研制提供一定的参考作用.参 考 文 献:[1] 曹志刚,钱亚生.现代通信原理[M ].北京:清华大学出版社,1992.[2] 黄 正.BP SK ,Q PSK 及其解调[J ].电光系统,2003,103(1):43—47.[3] 裴鹿成,王仲奇.蒙特卡罗方法及其应用[M ].北京:海洋出版社,1998.[4] W ayne T omas.电子通信系统[M ].王曼珠,许 萍.北京:电子工业出版社,2002.[5] 王立宁,乐光新,詹 菲.M A T L A B 与通信仿真[M ].北京:人民邮电出版社,2000.[6] 约翰 G 普罗克斯.现代通信系统——使用M A T L A B [M ].刘树棠.西安:西安交通大学出版社,2001.[7] 孟利民,朱健军,赵新建,等.全数字BP SK 调制解调系统仿真[J].浙江工业大学学报,2003,31(1):42—47.Q PSK SIM U LAT ION BASED ON M A T LA B PROGRA MM INGHOU Zhou -guo ,QIAN Sheng -you(Depar tment of Elect ronics,Hunan No rmal U niv ersity,Changsha 410081,China )Abstract :T his paper introduces the modem theory and process of QPSK in the digital communication.It also addresses a m ethod for programming w ith Matlab to analyze the QPSK system and describes how to emulate the system separately via ideal sig nal channel and interfered channel .With Monte Carlo analy sis to simulate the QPSK channel,it is found that the BER (bit error rate)and other results of the computer simulation can get the same performance as the ideality.Key words :QPSK ;system simulation ;Monte Carlo analy sis ;M atlab (责任编辑 王龙杰)24 广西师范大学学报(自然科学版) 第23卷。
基于MATLAB的QPSK仿真与分析

摘要:本文根据当今现代通信技术的发展,对QPSK信号的工作原理进行了分析。
利用Simulink 仿真工具设计出一个QPSK仿真模型,以衡量QPSK在高斯白噪声信道中的性能,并对仿真结果进行了分析。
关键词:QPSK 信噪比误码率1 引言近年来,软件无线电作为解决通信体制兼容性问题的重要方法受到各方面的注意。
它的中心思想是在通用的硬件平台上,用软件来实现各种功能,包括调制解调类型、数据格式、通信协议等。
通过软件的增加、修改或升级就可以实现新的功能,充分体现了体制的灵活性、可扩展性等。
其中高性能、高频谱效率的调制解调模块是移动通信系统的关键技术,它的软件化也是实现软件无线电的重要环节。
四相移键控(QPSK) 调制技术广泛应用于数字微波通信系统、数字卫星通信系统、宽带接入与移动通信及有线电视的上行传输。
在卫星数字电视传输中普遍采用的QPSK调谐器,可以说是当今卫星数字电视传输中对卫星功率、传输效率、抗干扰性以及天线尺寸等多种因素综合考虑的最佳选择。
与二进制数字调相比,多进制调相有以下两个特点 :(1) 在相同码元传输速率下,多进制调相的信息传输速率显然比二进制调相的高,比如,四进制调相的信息传输的速率是二进制调相的两倍。
(2) 在相同的信息速率下,由于多进制码元的速率比二进制的低,因而多进制信号码元的持续时间要比二进制的长。
显然增大码元宽度,就会增加码元的能量,并能减小由于信道特性引起的码间干扰的影响等,正是基于这些特点,使多进制移相键控方式获得了广泛的应用。
2 QPSK工作原理数字相位调制PSK是角度调制、恒定幅度数字调制的一种方式,通过改变发送波的相位来实现,除了其输入信号是数字信号以及输出的相位受限制以外,PSK与传统的相位调制相似。
QPSK信号的正弦载波有4个可能的离散相位状态,每个载波相位携带2个二进制符号,其信号表示式为 : 为四进制符号间隔,{ }为正弦载波的相位,有4种可能的状态。
若,则为0、、、,此初始相位为0的QPSK信号的矢量图如图1(a)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于MATLAB的QPSK仿真设计与实现一.前言1.1QPSK系统的应用背景简介QPSK是英文Quadrature Phase Shift Keying的缩略语简称,意为正交相移键控,是一种数字调制方式。
在19世纪80年代初期,人们选用恒定包络数字调制。
这类数字调制技术的优点是已调信号具有相对窄的功率谱和对放大设备没有线性要求,不足之处是其频谱利用率低于线性调制技术。
19世纪80年代中期以后,四相绝对移相键控(QPSK)技术以其抗干扰性能强、误码性能好、频谱利用率高等优点,广泛应用于数字微波通信系统、数字卫星通信系统、宽带接入、移动通信及有线电视系统之中。
1.2 QPSK实验仿真的意义通过完成设计内容,复习QPSK调制解调的基本原理,同时也要复习通信系统的主要组成部分,了解调制解调方式中最基础的方法。
了解QPSK的实现方法及数学原理。
并对“通信”这个概念有个整体的理解,学习数字调制中误码率测试的标准及计算方法。
同时还要复习随机信号中时域用自相关函数,频域用功率谱密度来描述平稳随机过程的特性等基础知识,来理解高斯信道中噪声的表示方法,以便在编程中使用。
理解QPSK调制解调的基本原理,并使用MATLAB编程实现QPSK信号在高斯信道和瑞利衰落信道下传输,以及该方式的误码率测试。
复习MATLAB编程的基础知识和编程的常用算法以及使用MATLAB仿真系统的注意事项,并锻炼自己的编程能力,通过编程完成QPSK调制解调系统的仿真,以及误码率测试,并得出响应波形。
在完成要求任务的条件下,尝试优化程序。
通过本次实验,除了和队友培养了默契学到了知识之外,还可以将次实验作为一种推广,让更多的学生来深入一层的了解QPSK以至其他调制方式的原理和实现方法。
可以方便学生进行测试和对比。
足不出户便可以做实验。
1.3 实验平台和实验内容1.3.1实验平台本实验是基于Matlab的软件仿真,只需PC机上安装MATLAB 6.0或者以上版本即可。
(本实验附带基于Matlab Simulink (模块化)仿真,如需使用必须安装simulink 模块)1.3.2实验内容1.构建一个理想信道基本QPSK仿真系统,要求仿真结果有a.基带输入波形及其功率谱b.QPSK信号及其功率谱c.QPSK信号星座图2.构建一个在AWGN(高斯白噪声)信道条件下的QPSK仿真系统,要求仿真结果有a.QPSK信号及其功率谱b.QPSK信号星座图c.高斯白噪声信道条件下的误码性能以及高斯白噪声的理论曲线,要求所有误码性能曲线在同一坐标比例下绘制3验可选做扩展内容要求:构建一个先经过Rayleigh (瑞利衰落信道),再通过AWGN (高斯白噪声)信道条件下的条件下的QPSK 仿真系统,要求仿真结果有a.QPSK 信号及其功率谱b.通过瑞利衰落信道之前和之后的信号星座图,前后进行比较c.在瑞利衰落信道和在高斯白噪声条件下的误码性能曲线,并和二.2.c 中所要求的误码性能曲线在同一坐标比例下绘制二、系统实现框图和分析2.1、QPSK 调制部分,原理框图如图1所示1(t )=2(t )=图1原理分析:基本原理及系统结构QPSK 与二进制PSK 一样,传输信号包含的信息都存在于相位中。
的别的载波相位取四个等间隔值之一,如л4, 3л4,5л4,和7л4。
相应的,可将发射信号定义为(21)/4]ft i ππ+- 0≤t≤TSi (t ) =0。
, 其他其中,i =1,2,2,4;E 为发射信号的每个符号的能量,T 为符号持续时间,载波频率f 等于ncT ,nc 为固定整数。
每一个可能的相位值对应于一个特定的二位组。
例如,可用前述的一组相位值来表示格雷码的一组二位组:10,00,01,11。
下面介绍QPSK信号的产生和检测。
如果a为典型的QPSK发射机框图。
输入的二进制数据序列首先被不归零(NRZ)电平编码转换器转换为极性形式,即负号1和0分别用和-表示。
接着,该二进制波形被分接器分成两个分别由输入序列的奇数位偶数位组成的彼此独立的二进制波形,这两个二进制波形分别用a1(t),和a2(t)表示。
容易注意到,在任何一信号时间间隔内a1(t),和a2(t)的幅度恰好分别等于Si1和 Si2,即由发送的二位组决定。
这两个二进制波形a1(t),和a2(t)被用来调制一对正交载波或者说正交基本函数: 1(t)=, 2(t)=。
这样就得到一对二进制PSK信号。
1(t)和2(t)的正交性使这两个信号可以被独立地检测。
最后,将这两个二进制PSK信号相加,从而得期望的QPSK。
2.2、QPSK解调部分,原理框图如图2所示:1(t)同相信道门限=02(t)正交信道门限=0图2原理分析:QPSK接收机由一对共输入地相关器组成。
这两个相关器分别提供本地产生地相干参考信号1(t)和2(t)。
相关器接收信号x(t),相关器输出地x1和x2被用来与门限值0进行比较。
如果x1>0,则判决同相信道地输出为符号1;如果x1<0 ,则判决同相信道的输出为符号0。
;类似地。
如果正交通道也是如此判决输出。
最后同相信道和正交信道输出这两个二进制数据序列被复加器合并,重新得到原始的二进制序列。
在AWGN信道中,判决结果具有最小的负号差错概率。
三、实验结果及分析根据图1和图2的流程框图设计仿真程序,得出结果并且分析如下:3.1、理想信道下的仿真,实验结果如图3所示图3实验结果分析:如图上结果显示,完成了QPSK信号在理想信道上的调制,传输,解调的过程,由于调制过程中加进了载波,因此调制信号的功率谱密度会发生变化。
并且可以看出调制解调的结果没有误码。
3.2、高斯信道下的仿真,结果如图4所示:图4实验结果分析:由图4可以得到高斯信道下的调制信号,高斯噪声,调制输出功率谱密度曲线和QPSK信号的星座图。
在高斯噪声的影响下,调制信号的波形发生了明显的变化,其功率谱密度函数相对于图1中的调制信号的功率谱密度只发生了微小的变化,原因在于高斯噪声是一个均值为0的白噪声,在各个频率上其功率是均匀的,因此此结果是真确的。
星座图反映可接收信号早高斯噪声的影响下发生了误码,但是大部分还是保持了原来的特性。
3.3、先通过瑞利衰落信道再通过高斯信道的仿真。
实验结果如图5所示:图5实验结果分析:由图5可以得到瑞利衰落信道前后的星座图,调制信号的曲线图及其功率谱密度。
最后显示的是高斯信道和瑞利衰落信道的误码率对比。
由图可知瑞利衰落信道下的误码率比高斯信道下的误码率高。
至此,仿真实验就全部完成。
四、致谢感谢指导老师**老师对我们的指导,帮我们解决了不少的问题。
也感谢队友之间的相互合作。
希望以后再接再厉,努力学习。
附录参考文献:1、《MATLAB 宝典》陈杰等编著电子工业出版社2、《MATLAB信号处理》刘波, 文忠, 曾涯编著北京电子工业出版社3、《数字信号处理的MATLAB实现》万永革编著北京科学出版社4、网上资料Simulink 仿真数据:1、调制框图,如图6所示图62、解调模块如图7所示图7 3、调制信号及其功率谱密度如图8所示图8 4、调制信号的星座图如图9所示:图95、基带信号与调制信号之间的关系如图10所示:图10附录2:%主文件%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%题目:理想信道瑞利衰落信道高斯信道下的QPSK仿真%%%%%%%作者:陈镇沅%%%%%%%完成日期:%%%%%%%邮箱:%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%clear;%%%%%%%%%%%%%%%%%%%%%%%% 初始化参数%%%%%%%%%%%%%%%%%%%%%T=1; % 基带信号宽度,也就是频率fc=10T; % 载波频率ml=2; % 调制信号类型的一个标志位(选取2的原因见23行)nb=100; % 传输的比特数delta_T=T200; % 采样间隔fs=1delta_T; % 采样频率SNR=0; % 信噪比t=0:delta_T:nb*T-delta_T; % 限定t的取值范围N=length(t); % 采样数%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%% 调制部分%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%% 基带信号的产生data=randn(1,nb)>0.5; % 调用一个随机函数(0 or 1),输出到一个1*100的矩阵datanrz=data.*2-1; % 变成极性码data1=zeros(1,nbdelta_T); % 创建一个1*nbdelta_T的零矩阵for q=1:nbdata1((q-1)delta_T+1:qdelta_T)=datanrz(q); % 将极性码变成对应的波形信号end% 将基带信号变换成对应波形信号data0=zeros(1,nbdelta_T); % 创建一个1*nbdelta_T的零矩阵for q=1:nbdata0((q-1)delta_T+1:qdelta_T)=data(q); % 将极性码变成对应的波形信号end% 发射的信号data2=abs(fft(data1));% 串并转换,将奇偶位数据分开idata=datanrz(1:ml:(nb-1)); % 将奇偶位分开,因此间隔m1为2qdata=datanrz(2:ml:nb);% QPSK信号的调制ich=zeros(1,nbdelta_T2); % 创建一个1*nbdelta_T2的零矩阵,以便后面存放奇偶位数据for i=1:nb2ich((i-1)delta_T+1:idelta_T)=idata(i);endfor ii=1:N2a(ii)=sqrt(2T)*cos(2*pi*fc*t(ii));endidata1=ich.*a; % 奇数位数据与余弦函数相乘,得到一路的调制信号qch=zeros(1,nb2delta_T);for j1=1:nb2qch((j1-1)delta_T+1:j1delta_T)=qdata(j1);endfor jj=1:N2b(jj)=sqrt(2T)*sin(2*pi*fc*t(jj));endqdata1=qch.*b; % 偶数位数据与余弦函数相乘,得到另一路的调制信号s=idata1+qdata1; % 将奇偶位数据合并,s即为QPSK调制信号ss=abs(fft(s)); % 快速傅里叶变换得到频谱%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 瑞利衰落信道和高斯信道%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%% 瑞利衰落信道ray_ich=raylrnd(0.8,1,nb2delta_T);ray_qch=raylrnd(0.8,1,nb2delta_T);Ray_idata=idata1.*ray_ich;Ray_qdata=qdata1.*ray_qch;Ray_s=Ray_idata+Ray_qdata; %%%%%%%%%%%%%%%%%%%%%%%%%%% 高斯信道s1=awgn(s,SNR); % 通过高斯信道之后的信号s11=abs(fft(s1)); % 快速傅里叶变换得到频谱s111=s1-s; % 高斯噪声曲线%%%%%%%%%%%%%%%%%%%%%%%%%%Awgn_s=awgn(Ray_s,SNR); % 通过高斯信道再通过瑞利衰落信道%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%% QPSK 解调部分%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%% 解调部分(高斯信道)idata2=s1.*a; % 这里面其实隐藏了一个串并转换的过程qdata2=s1.*b; % 对应的信号与正余弦信号相乘idata3=zeros(1,nb2); % 建立1*nb数组,以存放解调之后的信号qdata3=zeros(1,nb2);% 抽样判决的过程,与0作比较,data>=0,则置1,否则置0for n=1:nb2% A1(n)=sum(idata2((n-1)delta_T+1:ndelta_T));if sum(idata2((n-1)delta_T+1:ndelta_T))>=0idata3(n)=1;else idata3(n)=0;end% A2(n)=sum(qdata2((n-1)delta_T+1:ndelta_T));if sum(qdata2((n-1)delta_T+1:ndelta_T))>=0qdata3(n)=1;else qdata3(n)=0;endend% 为了显示星座图,将信号进行处理idata4=zeros(1,nb2);qdata4=zeros(1,nb2);for n=1:nb2Awgn_ichsum(n)=sum(idata2((n-1)delta_T+1:ndelta_T))*delta_T;if Awgn_ichsum(n)>=0idata4(n)=1;else idata4(n)=0;endAwgn_qchsum(n)=sum(qdata2((n-1)delta_T+1:ndelta_T))*delta_T;if Awgn_qchsum(n)>=0qdata4(n)=1;else qdata4(n)=0;endend% 将判决之后的数据存放进数组demodata=zeros(1,nb);demodata(1:ml:(nb-1))=idata3; % 存放奇数位demodata(2:ml:nb)=qdata3; % 存放偶数位%为了显示,将它变成波形信号(即传输一个1代表单位宽度的高电平)demodata1=zeros(1,nbdelta_T); % 创建一个1*nbdelta_T的零矩阵for q=1:nbdemodata1((q-1)delta_T+1:qdelta_T)=demodata(q); % 将极性码变成对应的波形信号end% 累计误码数% abs(demodata-data)求接收端和发射端% 数据差的绝对值,累计之后就是误码个数Awgn_num_BER=sum(abs(demodata-data)) %%%%%%%%%%%%%%%%%%%% 解调部分(瑞利+高斯)Ray_idata2=Ray_s.*a; % 这里面其实隐藏了一个串并转换的过程Ray_qdata2=Ray_s.*b; % 对应的信号与正余弦信号相乘% Ray_idata3=zeros(1,nb2); % 建立1*nb数组,以存放解调之后的信号% Ray_qdata3=zeros(1,nb2);% 抽样判决的过程,与0作比较,data>=0,则置1,否则置0% for n=1:nb2% if Ray_sum(Ray_idata2((n-1)delta_T+1:ndelta_T))>=0% Ray_idata3(n)=1;% else Ray_idata3(n)=0;% end% if Ray_sum(Ray_qdata2((n-1)delta_T+1:ndelta_T))>=0% Ray_qdata3(n)=1;% else Ray_qdata3(n)=0;% end% end% 为了显示星座图,将信号进行处理Ray_idata4=zeros(1,nb2);Ray_qdata4=zeros(1,nb2);for n=1:nb2Ray_ichsum(n)=sum(idata2((n-1)delta_T+1:ndelta_T))*delta_T;if Ray_ichsum(n)>=0Ray_idata4(n)=1;else Ray_idata4(n)=0;endRay_qchsum(n)=sum(qdata2((n-1)delta_T+1:ndelta_T))*delta_T;if Ray_qchsum(n)>=0Ray_qdata4(n)=1;else Ray_qdata4(n)=0;endend% 将判决之后的数据存放进数组Ray_demodata=zeros(1,nb);Ray_demodata(1:ml:(nb-1))=Ray_idata4; % 存放奇数位Ray_demodata(2:ml:nb)=Ray_qdata4; % 存放偶数位%为了显示,将它变成波形信号(即传输一个1代表单位宽度的高电平)Ray_demodata1=zeros(1,nbdelta_T); % 创建一个1*nbdelta_T的零矩阵for q=1:nbRay_demodata1((q-1)delta_T+1:qdelta_T)=Ray_demodata(q); % 将极性码变成对应的波形信号end% 累计误码数% abs(demodata-data)求接收端和发射端% 数据差的绝对值,累计之后就是误码个数Ray_num_BER=sum(abs(Ray_demodata-data)) %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%% 误码率计算%% 调用了cm_sm32();和cm_sm33()函数%%声明:函数声明在另外俩个M文件中%%作用:cm_sm32()用于瑞利信道误码率的计算%% cm_sm33()用于高斯信道误码率的计算%% ecoh onoff 作用在于决定是否显示指令内容%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%SNRindB1=0:1:6;SNRindB2=0:0.1:6;% 瑞利衰落信道for i=1:length(SNRindB1),[pb,ps]=cm_sm32(SNRindB1(i)); % 比特误码率smld_bit_ray_err_prb(i)=pb;smld_symbol_ray_err_prb(i)=ps;disp([ps,pb]);echo off;end;% 高斯信道echo on;for i=1:length(SNRindB1),[pb1,ps1]=cm_sm33(SNRindB1(i));smld_bit_awgn_err_prb(i)=pb1;smld_symbol_awgn_err_prb(i)=ps1;disp([ps1,pb1]);echo off;end;% 理论曲线echo on;for i=1:length(SNRindB2),SNR=exp(SNRindB2(i)*log(10)10); % 信噪比theo_err_awgn_prb(i)=0.5*erfc(sqrt(SNR)); % 高斯噪声理论误码率theo_err_ray_prb(i)=0.5*(1-1sqrt(1+1SNR)); % 瑞利衰落信道理论误码率echo off;end; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%)');axis([0 500 -5 5]);subplot(2,2,2);psd()');subplot(2,2,3);plot(s111),title('高斯噪声曲线');axis([0 2000 -5 5]);subplot(2,2,4);for i=1:nb2plot(idata(i),qdata(i),'r+'),title('QPSK信号星座图(Awgn)');;axis([-2 2 -2 2]);plot(Awgn_ichsum(i),Awgn_qchsum(i),'*');;legend('理论值(发射端)','实际值(接收端)');end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%通过高斯信道再通过瑞利衰落信道figure(3)subplot(2,2,1)plot(Ray_s),title('调制信号(Ray+Awgn)');axis([0 500 -5 5]);subplot(2,2,2);psd(+Ray)');;axis([-2 2 -2 2]);plot(Ray_ichsum(i),Ray_qchsum(i),'*');;legend('理论值(发射端)','实际值(接收端)');endsubplot(2,2,4)semilogy(SNRindB2,theo_err_awgn_prb,'r'),title('误码率曲线');;semilogy(SNRindB1,smld_bit_awgn_err_prb,'r*');;semilogy(SNRindB2,theo_err_ray_prb);;semilogy(SNRindB1,smld_bit_ray_err_prb,'*');xlabel('EbNo');ylabel('BER');legend('理论AWGN','仿真AWGN','理论Rayleigh','仿真Rayleigh');%文件2function [pb,ps]=cm_sm32(snr_in_dB)% [pb,ps]=cm_sm32(snr_in_dB)% CM_SM3 finds the probability of bit error and symbol error for % the given value of snr_in_dB, signal to noise ratio in dB.N=100;E=1; % energy per symbol numofsymbolerror=0;numofbiterror=0;counter=0;snr=10^(snr_in_dB10); % signal to noise ratiosgma=sqrt(Esnr)2; % noise variances00=[1 0]; s01=[0 1]; s11=[-1 0]; s10=[0 -1]; % signal mapping% generation of the data sourcewhile(numofbiterror<100)for i=1:N,temp=rand; % a uniform random variable between 0 and 1if (temp<0.25), % with probability 14, source output is "00"dsource1(i)=0; dsource2(i)=0;elseif (temp<0.5), % with probability 14, source output is "01"dsource1(i)=0; dsource2(i)=1;elseif (temp<0.75), % with probability 14, source output is "10"dsource1(i)=1; dsource2(i)=0;else % with probability 14, source output is "11"dsource1(i)=1; dsource2(i)=1;end;end;% detection and the probability of error calculationfor i=1:N,ray=raylrnd(0.8);n=sgma*randn(1,2); % 2 normal distributed r.v with 0, variance sgmaif ((dsource1(i)==0) & (dsource2(i)==0)),r=ray*s00+n;elseif ((dsource1(i)==0) & (dsource2(i)==1)),r=ray*s01+n;elseif ((dsource1(i)==1) & (dsource2(i)==0)),r=s10*ray+n;elser=s11*ray+n;end;% The correlation metrics are computed belowc00=dot(r,s00); c01=dot(r,s01); c10=dot(r,s10); c11=dot(r,s11);% The decision on the ith symbol is made nextc_max=max([c00,c01,c10,c11]);if (c00==c_max), decis1=0; decis2=0;elseif (c01==c_max), decis1=0; decis2=1;elseif (c10==c_max), decis1=1; decis2=0;else decis1=1; decis2=1;end;% Increment the error counter, if the decision is not correctsymbolerror=0;if (decis1~=dsource1(i)), numofbiterror=numofbiterror+1; symbolerror=1;end;if (decis2~=dsource2(i)), numofbiterror=numofbiterror+1; symbolerror=1;end;if (symbolerror==1), numofsymbolerror=numofsymbolerror+1;end;endcounter=counter+1;endps=numofsymbolerror(N*counter); % since there are totally N symbolspb=numofbiterror(2*N*counter); % since 2N bits aretransmitted%文件3function [pb1,ps1]=cm_sm32(snr_in_dB)% [pb,ps]=cm_sm32(snr_in_dB)% CM_SM3 finds the probability of bit error and symbol error for % the given value of snr_in_dB, signal to noise ratio in dB.N=100;E=1; % energy per symbolsnr=10^(snr_in_dB10); % signal to noise ratiosgma=sqrt(Esnr)2; % noise variances00=[1 0]; s01=[0 1]; s11=[-1 0]; s10=[0 -1]; % signal mapping% generation of the data sourcenumofsymbolerror=0;numofbiterror=0;counter=0;while(numofbiterror<100)for i=1:N,temp=rand; % a uniform random variable between 0 and 1if (temp<0.25), % with probability 14, source output is "00"dsource1(i)=0; dsource2(i)=0;elseif (temp<0.5), % with probability 14, source output is "01"dsource1(i)=0; dsource2(i)=1;elseif (temp<0.75), % with probability 14, source output is "10"dsource1(i)=1; dsource2(i)=0;else % with probability 14, source output is "11"dsource1(i)=1; dsource2(i)=1;end;end;% detection and the probability of error calculationfor i=1:N,% the received signal at the detection, for the ith symbol,is:n=sgma*randn(1,2); % 2 normal distributed r.v with 0, variance sgmaif ((dsource1(i)==0) & (dsource2(i)==0)),r=s00+n;elseif ((dsource1(i)==0) & (dsource2(i)==1)),r=s01+n;elseif ((dsource1(i)==1) & (dsource2(i)==0)),r=s10+n;elser=s11+n;end;% The correlation metrics are computed belowc00=dot(r,s00); c01=dot(r,s01); c10=dot(r,s10); c11=dot(r,s11);% The decision on the ith symbol is made nextc_max=max([c00,c01,c10,c11]);if (c00==c_max), decis1=0; decis2=0;elseif (c01==c_max), decis1=0; decis2=1;elseif (c10==c_max), decis1=1; decis2=0;else decis1=1; decis2=1;end;% Increment the error counter, if the decision is not correctsymbolerror=0;if (decis1~=dsource1(i)), numofbiterror=numofbiterror+1; symbolerror=1;end;if (decis2~=dsource2(i)), numofbiterror=numofbiterror+1; symbolerror=1;end;if (symbolerror==1), numofsymbolerror=numofsymbolerror+1;end;endcounter=counter+1;endps1=numofsymbolerror(N*counter); % since there are totally N symbolspb1=numofbiterror(2*N*counter); % since 2N bits are transmitted。
