2011圆

合集下载

2011年中考数学试题汇编---圆与圆的位置关系

选择题（每小题x 分，共y 分）（2011•吉林省）15.如图，两个等圆⊙A ⊙B 分别与直线l 相切于点C 、D,连接AB,与直线l 相交于点O ,∠AOC=300,连接AC.BC,若AB=4，则圆的半径为（ B ）A21B 1C 3D 2 （2011•张家界）7、已知两圆相外切，连心线长度是10厘米，其中一圆的半径为6厘米，则另一圆的半径是（D ）A 、16厘米B 、10厘米C 、6厘米D 、4厘米7、（2008•宁德）如图，国际奥委会会旗上的图案是由五个圆环组成，在这个图案中反映出的两圆位置关系有（ B ）A 、内切、相交B 、外离、相交C 、外切、外离D 、外离、内切（2011•襄阳市）9．在△ABC 中，∠C=90°．AC=3cm ．BC=4cm ，若⊙A ．⊙B 的半径分别为1cm ，4cm ．则⊙A 与⊙B 的位置关系是AA ．外切B ．内切C ．相交D ．外离（2011•扬州市）4．已知相交两圆的半径分别为4和7，则它们的圆心距可能是（ C ） A ．2 B ．3 C ．6 D ．11（2011•铜仁）6．已知⊙O 1与⊙O 2的半径分别为6cm 、11cm ，当两圆相切时，其圆心距d 的值为（ D ）A 、0cmB 、5cmC 、17cmD 、5cm 或17cm（2011•达州）7、如图4，国际奥委会会旗上的图案是由五个圆环组成，在这个图案中反映出的两圆位置关系有BA.、内切、相交 B 、外离、相交 C 、外切、外离D 、外离、内切（2011•陕西省）7．同一平面内的两个圆，他们的半径分别为2和3 ，圆心距为d,当51 d 时，两圆的位置关系是【 B 】A 、外离B 、相交C 、内切或外切D 、内含（2011•天津）(6) 已知⊙1O 与⊙2O 的半径分别为3 cm 和4 cm ，若12O O =7 cm ，则⊙1O 与⊙2O 的位置关系是D(A) 相交 (B) 相离 (C) 内切 (D) 外切〔2011•浙江省台州市〕8．如图是一个组合烟花的横截面，其中16个圆的半径相同，点A 、B 、C 、D 分别是四个角上的圆的圆心，且四边形ABCD 为正方形．若圆的半径为r ，组合烟花的高为h ，则组合烟花侧面包装纸的面积至少需要(接缝面积不计)【 D 】 A ．rh π26 B ．rh rh π+24 C ．rh rh π212+ D ．rh rh π224+3. （2011台湾台北，25）如图(九)，圆A 、圆B 的半径分别为4、2，且AB ＝12。

魔法少女小圆

重要设定
• 丘比能够实现少女一个愿望的魔法使者。一般人类无法看见，能够在一定范围内和与被它选中的
人进行心灵感应对话，但是交流的内容主要还是通过丘比来进行中转。真实名称是Incubator（孵化机）。在动画中只在吃东西的时候才会开口，背后的红色圆圈可以打开盛放悲伤之种，自称有无数个替身。曾千方百计引诱小圆成为魔法少女，因为没有感情故不认为自己的行为有任何不妥。目的是为了满足自己所属种族的能量消耗、避免整个宇宙的热寂而选择牺牲人类。新生成的世界规则中改为直接收集魔法少女灵核中的绝望凝结作为能量来源。
1411070114
魔法少女小圆
魔法少女小圆
简介
成就
剧集重要设定
简介
• 《魔法少女小圆》（日语：魔法少女まどか☆ マギカ；拉丁语：Puella Magi Madoka Magica‎ ）是一部由日本动画公司SHAFT制作，于2011年 1月起开始在MBS电视台播放的日本深夜动画。 • 《魔法少女小圆》总共12集，编剧虚渊玄，导演新房昭之。在2011年12月的《Newtype》杂志上公布了小圆剧场版的启动，2部总集篇《起始的物语》《永远的物语》，以及1部全新的故事《叛逆的物语》于2013年10月26日在日本上映。
成就
• 该作电视动画开播之后，即以压倒性实力横扫海内外的排行、评选，日本各大动画奖、巴黎动画展皆一致给予最高评价。翌年荣膺第15回日本文化厅媒体艺术祭的 “动画大赏”，亦表示其艺术价值已具有日本政府认可的历史地位。
剧集
•第1话似乎在梦中见过的样子...... 挚爱的家人与好友陪伴在身旁，有时开心，就读国二的鹿目圆，过着如此和平的生活。某天晚上，圆做了一个神奇的梦。 •第2话那真是太令人高兴了丘比受到转学生晓美焰的攻击。圆与沙耶香在保护丘比时遭遇危机，被魔法少女巴麻美所救。她说——两人有一个能实现任何愿望的机会，但是得背负残酷的使命 •第3话已经什麼都不怕了圆与沙耶香陪同麻美讨伐魔女。麻美成为魔法少女的理由揭晓了。两人在某天傍晚，发现恭介所住的医院，有一颗即将孵化的悲叹之种。 •第4话奇迹与魔法，都是存在的目睹麻美与魔女的壮烈决战，圆放弃成为魔法少女。来到失去主人的麻美房间，圆对于自己的怯懦落下眼泪。 •第5话不可能有所後悔沙耶香成为魔法少女，从魔女手中救出好友。看到恭介的手迅速康复，她感受着无比的幸福。另一方面，瞭望台上的杏子，正暗中观察着这样的沙 •第6话这样绝对有问题沙耶香与圆，回头寻找昨天由於杏子闯入而追丢的使魔。沙耶香不惜与杏子交战的意志，使得个性温和的圆哑口无言。在这个时候，焰基于某个目的，试着与杏子进行接触。

2011山东中考数学总复习圆

2011山东中考数学总复习圆（22）圆3 〖考试内容〗弧长，扇形的面积.圆锥的侧面积、全面积〖考试要求〗会计算弧长及扇形的面积，会计算圆锥的侧面积和全面积. 〖考点复习〗 1．弧长[例1]半径为1的⊙O 中，120º的圆心角所对的弧长是（） A ．3πB ．23π C ．π D ．32π2．扇形的面积[例2]．一个扇形的圆心角是120°，它的面积为3πcm 2，那么这个扇形的半径是（） A 、3cm Ｂ、3cm Ｃ、6cm Ｄ、9cm 3．圆锥的侧面积[例3一个底面半径为5cm ，母线长为16cm 的圆锥，它的侧面展开图的面积是……（） A 、80πcm 2 B 、40πcm 2C 、80cm 2D 、40cm 2[例4]如图，圆锥的母线长为5cm ，高线长是4cm ，则圆锥的底面积是( )cm 2 A 、3π B 、9π C 、16π D 、25π 〖考题训练〗1．如图，是排洪水管的横截面，若此管道的半径为54cm ，水面以上部分的弓形弧的弧长为30πcm ，则这段弓形弧所对的圆心角的度数为_________º2．如图，当半径为30cm 的转动轮转过120︒角时，传送带上的物体A 平移的距离为 cm 。

3．在一个地球仪的赤道上用铁丝打一个箍，现将铁丝箍半径增大1米，需增加ｍ米长的铁丝，假设地球的赤道上也有一个铁箍，同样半径增大1米，需增加ｎ米长的铁丝，则ｍ与ｎ的大小关系是（）A 、ｍ＞ｎB 、ｍ＜ｎC 、ｍ＝ｎD 、不能确定4．如图，水平位置的圆柱形油桶的截面半径是R ，油面高为23R ，截面上有油的弓形（阴影部分）的面积为＿＿＿＿。

（结果不取近似值）5．如图，AB 是⊙O 的直径，点D 、E 是半圆的三等分点，AE 、BD 的延长线交于点C 。

若CE ＝2，则图中阴影部分的面积是（）A 、43π－ 3B 、23πC 、23π－ 3D 、13π6．如图是小明制作的一个圆锥形纸帽的示意图.围成这个纸帽的纸的面积为cm 2(π取3.14).7．已知圆锥的底面周长为20πcm ，母线长为10cm ，那么这个圆锥的侧面积是_________㎝2(结果保留π).8．小红要过生日了，为了筹备生日聚会，准备自己动手用纸板制作圆锥形的生日礼帽。

湖北省2011年中考数学试题分类解析11 圆

2011年中考数学试题分类解析汇编专题11：圆一、选择题1. （佛山3分）若O 的一条弧所对的圆周角为60︒，则这条弧所对的圆心角是A 、30︒B 、60︒C 、120︒D 、以上答案都不对【答案】C 。

【考点】同弧所对圆周角与圆心角的关系。

【分析】根据同弧所对圆周角是圆心角的一半的定理，直接得出结果。

故选C 。

2. （广州3分）如图，AB 切⊙O 于点B ，OA ＝2AB ＝3，弦BC ∥OA ，则劣弧BC的弧长为A 3错误！未找到引用源。

B 、错误！2C 、πD 、错误！未找到引用源。

32π【答案】A 。

【考点】弧长的计算，切线的性质，特殊角的三角函数值，平行线的性质。

【分析】要求劣弧 BC的长首先要连接OB ，OC ，由AB 切⊙O 于点B ，根据切线的性质得到OB ⊥AB ，在Rt △OBA 中，OA ＝2错误！未找到引用源。

，AB ＝3，利用三角函数求出∠BOA ＝60°，同时得到OB ＝12OA ＝得到∠BOA ＝∠CBO ＝60°，于是有∠BOC ＝60°，最后根据弧长公式计算出劣弧 BC 的长=1803。

故选A 。

3.（茂名3分）如图，⊙O 1、⊙O 2相内切于点A ，其半径分别是8和4，将⊙O 2沿直线O 1O 2平移至两圆相外切时，则点O 2移动的长度是A 、4B 、8C 、16D 、8或16【答案】D 。

【考点】圆与圆的位置关系，平移的性质。

【分析】由题意可知点O 2可能向右移，此时移动的距离为⊙O 2的直径长；如果向左移，则此时移动的距离为⊙O 1的直径长。

∵⊙O 1、⊙O 2相内切于点A ，其半径分别是8和4，如果向右移：则点O 2移动的长度是4×2=8，如果向左移：则点O 2移动的长度是8×2=16．∴点O 2移动的长度8或16。

故选D 。

4.（清远3分）如图，点A 、B 、C 在⊙O 上，若∠BAC ＝20º，则∠BOC 的度数为A ．20ºB ．30ºC ．40ºD ．70º【答案】C 。

2011年高考数学试题分类解析(九)--直线和圆的方程

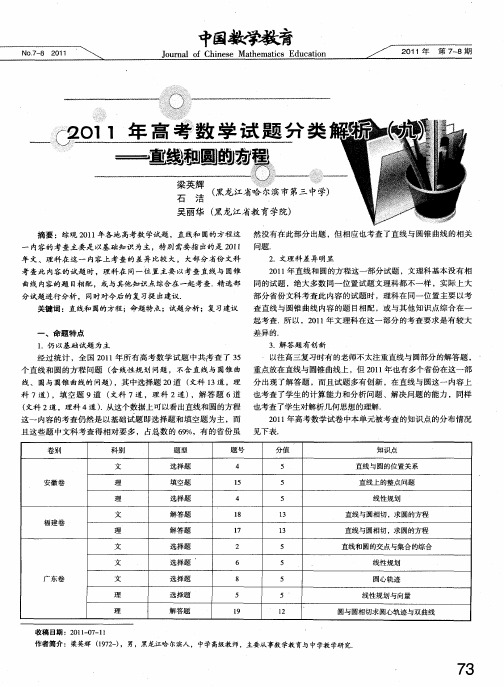
２１年高考数学试卷中本单元被考查的知识点的分布情况０１
且这些题中文科考查得相对要多，占总数的６％，有的省份虽见下表９
卷别科别
文安徽卷理理文福建卷
题型
选择题填空题选择题解答题
题号
４１５４１８
起考查．以，２１所０１年文理科在这一部分的考查要求是有较大
差异的．３答题有创新．解
关键词：直线和圆的方程；命题特点；试题分析；复习建议
命题特点
一
、
１．仍以基础试题为主
经过统计，全国２１０１年所有高考数学试题中共考查了３５
二、亮点扫描
当ｍ≤０，时集合Ａ对应以（，Ｏ为圆心、以ｌ为半径２）ｍｌ
在２１年直线和圆的方程这部分试题中，有亮点的试题很的圆及圆内区域，集合曰对应两条平行线之间的区域，要使０１
多，有些试题也非常有新意，对学生要求的能力也比较强，学ＡｎＢ≠ ，只需圆心到较近的直线的距离小于等于半径，即
理理
选择题选择题填空题选择题选择题选择题填空题
９１０１３４１１７１２
５５５５５。５５
直线与圆的位置轨迹圆的方程线性规划圆与圆，圆心距线性规划线性规划
辽宁卷
２１年直线和圆的方程这一部分试题，文理科基本没有相０１
曲线内容的题目相配，或与其他知识点综合在一起考查．选部同的试题，绝大多数同一位置试题文理科都不一样，实际上大精

2011二模四边形、圆答案

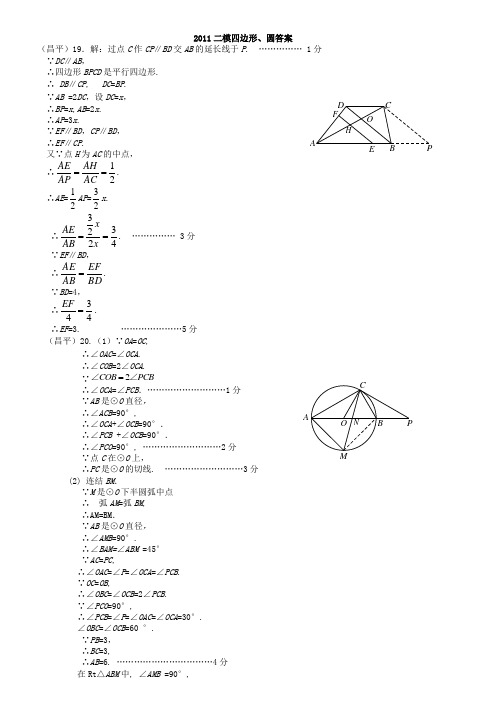
2011二模四边形、圆答案（昌平）19．解：过点C 作CP ∥BD 交AB 的延长线于P . …………… 1分 ∵DC ∥AB ，∴四边形BPCD 是平行四边形. ∴ DB ∥CP , DC =BP . ∵AB =2DC ，设DC =x ，∴BP =x ,AB =2x .∴AP =3x .∵EF ∥BD ，CP ∥BD ，∴EF ∥CP .又∵点H 为AC 的中点， ∴12A E A H A PA C ==.∴AE =21AP =32x .∴33224xAEAB x ==. …………… 3分 ∵EF ∥BD ， ∴BD EFAB AE =. ∵BD =4， ∴344EF =.∴EF =3. …………………5分（昌20.（1）∵OA =OC ,∴∠OAC =∠OCA .∴∠COB =2∠OCA .∵2C O B P C B =∠∠∴∠OCA =∠PCB ．………………………1分∵AB 是⊙O 直径，∴∠ACB =90°,∴∠OCA +∠OCB =90°．∴∠PCB +∠OCB =90°．∴∠PCO =90°, ………………………2分∵点C 在⊙O 上，∴PC 是⊙O 的切线. ………………………3分 (2) 连结BM ．∵M 是⊙O 下半圆弧中点 ∴ 弧AM =弧BM , ∴AM=BM ．∵AB 是⊙O 直径， ∴∠AMB =90°.∴∠BAM=∠ABM =45° ∵AC =PC ,∴∠OAC =∠P =∠OCA =∠PCB . ∵OC =OB ,∴∠OBC =∠OCB =2∠PCB . ∵∠PCO =90°,∴∠PCB =∠P =∠OAC =∠OCA =30°. ∠OBC =∠OCB =60 °. ∵PB =3， ∴BC =3,∴AB =6. ……………………………4分在Rt △ABM 中, ∠AMB =90°,PH O FED C BA N MO PCB A根据勾股定理，得AM =23 . ……………………………5分（朝阳）19．解：（1）连接OA ，∵AD 为⊙O 切线， ∴ ∠OAD=90°．…… 1分 ∵sinD=12， ∴∠D=30°．……………… 2分 ∴∠AOC=60°．∴∠ABC=12∠AOC=30°． ……………… 3分（2）在Rt △OAD 中，∠D=30°，OD=20.∴OA=12OD=10． ∵OE ⊥AC ，OA=OC ， ∴∠AOE=30°，AE=12OA=5．∴AC=2AE=10.∵BC 是⊙O 的直径， ∴∠BAC=90°．在Rt △BAC 中，AB=103tan A C A B C=∠， ………………………… 4分在Rt △ABE 中，BE=22513AB AE +=． ………………………… 5分(东城)19.（本小题满分5分）解：（1）证明：∵BD 是∠ABC 的平分线，∴ ∠1=∠2.∵ AD //BC ，∴∠2=∠3. ∴ ∠1=∠3.∴AB=AD . ---------------------2分（2）作AE ⊥BC 于E ，DF ⊥BC 于F .∴ EF=AD=AB .∵ ∠ABC ＝60°，BC =3AB ， ∴ ∠BAE =30°. ∴ BE =21AB . ∴ BF =23AB=21BC .∴ BD=DC .∴ ∠C =∠2.∵ BD 是∠ABD 的平分线， ∴ ∠1=∠2=30°.∴ ∠C =30°. -------------------------5分（东城）20.（本小题满分5分）解：（1）CD 与圆O 相切． …………………1分证明：连接OD ，则∠AOD =2∠AED =2⨯45︒=90︒． …………………2分 ∵四边形ABCD 是平行四边形，∴AB //DC ．∴∠CDO =∠AOD =90︒．∴OD ⊥CD ． …………………3分 ∴CD 与圆O 相切．（2）连接BE ，则∠ADE =∠ABE ．∴sin ∠ADE =sin ∠ABE =65． …………………4分EB CAO DEB CAO DAB CDEOABCD 123E F∵AB 是圆O 的直径，∴∠AEB =90︒，AB =2⨯3=6．在Rt △ABE 中，sin ∠ABE =ABAE =65．∴AE =5 ．（房山）19．解：过点B 作BE ⊥AC 交CD 于E ，过点A 作AF ⊥CB 于F ∵CD ∥AB ，AB=AC ， ∴四边形ABEC 是菱形---------------------------------------1分 ∴BE=CE=AB ∵∠BAC=120°∴∠ABC=30°，∠ABE=60°，∠BED=60° ∵CD=2AB ，BD=2∴△ABC 是等边三角形，AB=2--------------------------------------------------------------------2分在△ABF 中，∠AFB=90°, ∠ABC=30°，AB =2∴BF=3，AF=1---------------------------------------------------------------------------3分 ∴BC=23-------------------------------------------------------------------------------4分 ∴△ABC 的面积为3-------------------------------------------------------------------------------5分（房山）20．解：（1）直线BD 与O 相切．------------------------------------------------------------------1分证明：如图1，连结O D ．O A O D = ， ∴A A D O ∠=∠． 90C ∠= ， ∴90CBD CDB ∠+∠=．又C B D A ∠=∠ ， ∴90ADO CDB ∠+∠=．∴90ODB ∠= ．∴直线BD 与O 相切-------------------------------------2分（2）解法一：如图1，连结D E ．90C ∠=， 2B C =，B D =52∴4cos 5B C C B D B D∠==----------------------------------------------------3分AE 是O 的直径， ∴90ADE ∠=．∴cos A DA A E=．∵C B D A ∠=∠，∴A DA E =BCBD =45．-------------------4分∵AE=2AO ∴A D A O =85------------------------------------------------------5分解法二：如图2，过点O 作O H A D ⊥于点H ． ∴12A H D H A D ==．∴cos A H A A O= F E ABC D（图1）CB AO DE（图2）HCBAO DE3310sin .1010∠==A E A B C =A B231DCBAOE90C ∠=， 2B C =，B D =52∴4cos 5B C C B D B D∠==．------------------------- 3分∵C B D A ∠=∠， ∴A H A O =BC BD =45．---------------------------------4分 ∴A D A O =85----------------------------------------5分（丰台）19. 解：如图，分别过点、A D 作AE BC ⊥于点E ，D F B C ⊥于点F ．………………………………1分∴AE D F ∥．又AD BC ∥，∴四边形A E F D 是矩形．2EF AD ∴==．…………………………………2分 ,⊥= BD DC BD DC ，6B C =，∴△BDC 是等腰直角三角形，……………………3分 132∴====D F B F A E B C ．3D F B F ∴==，1BE BF EF =-=．………………………………4分在R t △A B E 中，90ABE ∠= ， 2210AB AE BE∴=+=,∴ ．5分 …………5分（丰台）20. （1）证明：联结OD ， ∴OD =OA ， ∴∠1=∠2，∵BC 为⊙O 的切线，∴∠ODB =90°，…………1分 ∵∠C =90°，∴∠ODB =∠C ， ∴OD ∥AC ，∴∠3=∠2，………………………2分 ∴∠1=∠3 ，∴AD 是∠BAC 的平分线. ……3分（2）解：在Rt △ABC 中，∠C =90°, tan B =34， AC = 3， ∴BC =4，AB =5，………………………………………………………4分在Rt △ODB 中, tan B =34O D BD =，设一份为x ，则OD=OA=3x ,则BD=4x ,OB=5x ， ∴AB =8x ，∴8x=5,解得x=58，∴半径OA =158. …………………………………………………………5分（海淀）19．解：作DE //AC ,交BC 的延长线于点E ,作DF ⊥BE,垂足为F. …………..1分∵AD //BC ,∴四边形ACED 为平行四边形.∴AD=CE=3，BE=BC+CE=8. .……………………..2分F EOD CB A∵AC ⊥BD ， ∴DE ⊥BD.∴△BDE 为直角三角形，90.BD E ∠=︒ ∵∠DBC =30°，BE =8,∴4,4 3.DE BD == …….……………………..4分在直角三角形BDF 中∠DBC =30°,∴23DF =. …….……………………..5分（海淀）20．（1）证明：连结OC .∵CD 是O ⊙的切线，∴OC ⊥CD.∴90O C M ∠=︒. …….……………………..1分 ∵//C D AB ,∴180O C M C O A ∠+∠=︒. ∵AM ⊥CD,∴90AM C ∠=︒.∴在四边形OAMC 中90O AM ∠=︒ .∵OA 为O ⊙的半径,∴AM 是O ⊙的切线 .…….……………………..2分（2）连结OC ,BC .∵CD 是O ⊙的切线， ∴OC ⊥CD . ∴90O C M ∠=︒. ∵AM ⊥CD , ∴90AM C ∠=︒. ∴//O C AM .∴12∠=∠.∵OA= OC ,∴32∠=∠. 即BAC C AM ∠=∠. …….……………………..3分易知90AC B ∠=︒，∴BAC C AM △∽△. …….……………………..4分 ∴AB AC ACAM=.即224AC AB AM =⋅=.∴26AC =. …….……………………..5分(怀柔)19. （1）证法一：如图，连接O D ．22.52DAB DOC DAB ∠=∠=∠， 45DOC ∴∠= 1分又45ACD ∠=，18090ODC ACD DOC ∴∠=-∠-∠=，2分即O D C D ⊥．C D ∴是O 的切线． 3分（2）解：由（1）可得：O D C △是等腰直角三角形．4分22AB = ，A B 是直径， 2OD OB ∴==．5分22OC OD ∴==．22BC OC OB ∴=-=-．6分（怀柔）20.解：（1）∵四边形 ABCD 是正方形∴∠BCF+∠FCD=900BC=CD 1分∵△ECF 是等腰直角三角形，DBMAOC1图2图OABDMC123B A DC EF21E A CBD ∴∠ECD+∠FCD=900. CF=CE 2分 ∴∠BCF=∠ECD.∴△BCF ≌△DCE 3分(2)在△BFC 中，BC=5，CF=3，∠BFC=900.∴BF=2222534BC CF -=-=. 4分∵△BCF ≌△DCE ，∴DE=BF=4，∠BFC=∠DEC=∠FCE=900.∴DE ∥FC ∴△DGE ∽△CGF 5分 ∴DG ：GC=DE ：CF=4：3. 6分（门头沟）19. 解：如图，分别过点A 、D 作AE ⊥BC 于点E ，DF ⊥BC 于点F ． ……………………1分∴ AE // DF ．又∵ AD // BC ，∴ 四边形AEFD 是矩形．∴ EF =AD =3． ……………………………………… 2分 ∵ BD ⊥CD ，∠C =60°，BC =43， ∴ DC =BC ·cos60°=143232⨯=．∴ CF =DC ·cos60°=12332⨯=．∴ AE =DF = DC ·sin60°=32332⨯=． …………………………………………… 3分∴23BE BC EF CF =--=． ………………………………………………………… 4分在Rt △ABE 中，∠AEB =90°，∴ AB =22223(23)21AE BE +=+=． ………………………………………… 5分（门头沟）20．解：（1）由直径A B 平分 CD ，可证A B C D ⊥． ······················ 1分 BF 与O ⊙相切，A B 是O ⊙的直径，AB BF ∴⊥．···························2分 C D B F ∴∥． ·························· 3分（2）连结B D . A B 是O ⊙的直径， 90A D B ∴∠=°.在R t AD B △中，3cos cos 4A C == ，428AB =⨯=，3cos 864A D A B A ∴=⋅=⨯=． ··················· 4分在R t AED △中，39cos 642A E A D A =⋅=⨯=，∴ DE =2222937622AD AE⎛⎫-=-=⎪⎝⎭．由直径A B 平分 CD ，可求237C D DE ==． ····················· 5分（平谷）19．解：(1)∵ AC =BC , AD = BE , ∠CAD =∠CBE , ∴ △ADC ≌△BEC ……………………………………..1分∴ DC =EC ,∠1=∠2. ……………………………………2分 ∵ ∠1+∠BCD =90°， ∴ ∠2+∠BCD =90°. 所以 △DCE 是等腰直角三角形…………………………..3分 (2) ∵ △DCE 是等腰直角三角形. ∴ ∠CDE =45°. ∵ ∠BDC =135°，∴ ∠BDE =90°……………………………………….4分 ∵ BD :CD =1:2,设BD =x ，则CD =2x ，DE =x 22，BE =3x.FE DC B A AD F BCO EOE B D A CH O F EDCBA∴.31sin ==∠BEBD BED (5)（平谷）20.（1）证明：连接OD ．………………………….1分 ∵ OD = OB ， ∴ ∠B =∠ODB . ∵ A B A C =，∴ B C ∠=∠． ∴ ∠ODB =∠C .∴ OD ∥AC ．………………………………………2分∵ DE ⊥ AC ， ∴ OD ⊥DE .∴DE 是O ⊙的切线．………………………………………………………………………3分 (2) 解：连接AD , ∵ AB 为直径， ∴ ∠ADB =90°．∵120AB AC BAC =∠=，°， ∴ 30B C ∠=∠=°. ∴ AD =121=AB ．∵ 在Rt △AED 中，DE ⊥ AC ,∠DAE =60°， ∴ AE =2121=AD ，DE =23．…………………………………………………………….4分∴ EC =.23212=-∴ .833232321S =⨯⨯=∆DEC ……………………………………………………………..5分（石景山）19．解：（1）作出线段C D ' ………………………………… 1分过点D 作BC DF ⊥于F ,过点A 作BC AH ⊥于H ∵四边形ABCD 是等腰梯形，AD ∥BC 易证()22-621===BH FC︒=∠=∠90ADF EDF过点'C 作E C '垂直于AD 的延长线于点E ∴︒=∠='∠90DFC C DE∵线段DC 绕点D 逆时针旋转90°，得到线段C D ' ∴︒='∠90C CD ,C D DC '=∴︒=∠+∠9031，︒=∠+∠9032 ∴21∠=∠∴CFD ∆≌ED C '∆ ………………………… 2分 ∴2=='FC C E ∴=∆'ADC S 2222121'=⨯⨯=⋅E C AD …………………… 3分（2）在'AEC Rt ∆中，52tan ='∠C DA ,2='C E∴5=EA ∵2=AD∴3=ED …………………………… 4分由CFD ∆≌ED C '∆得： 3==ED DF在DFC Rt ∆中，由勾股定理得：13=CD∴13==CD AB ……………………………5分（石景山）20．解：（1）证明：联结BE ………………………………1分321H EFC 'ABCD∵ BC 为直径 ∴E ∠=90°∴︒=∠+∠90EHB EBH∵ AC AH =, ABC AF 为△的角平分线 ∴ACH AHC ∠=∠ ∵EHB AHC ∠=∠ ∴ACH EHB ∠=∠ ∵E 点为弧BD 的中点 ∴DBE ECB ∠=∠∴︒=∠+∠90ACH ECB ……………2分 ∴ AC 是⊙O 的切线（2) ∵ AC 是⊙O 的切线 ∴︒=∠90ACB∵10,6==AB AC ∴8=BC∵AC AH = ∴4=BH …………………………………………3分又∵DBE ECB ∠=∠，E ∠为公共角 ∴BEH △∽CEB △∴2184===CBBH ECBE …………………………………………4分∴在EBC Rt △中，可得222)21(BC EC EC =+,5516=EC ………………………………5分（顺义）19. 解：（1）∵四边形A B C D 是矩形，∴90A D ∠=∠=︒，7,4AD BC DC AB ====.∴ 90APE AEP ∠+∠=︒ ∵P E P C ⊥ ∴90E P C ∠=︒∴90APE D PC ∠+∠=︒∴A E P D P C ∠=∠--------------------------------------1分 ∴A E P D P C ∆∆∴P EA PC PD C= -------------------------------------------2分∵P E C ∆是等腰三角形，90E P C ∠=︒∴ P E C P = ∴ 4AP D C ==∴ 3P D A D A P =-= ------------------------------3分（2）设P D x =, 则7A P x =-∵P E A PC PD C = ∴74P E xC P -= -------------------------------------------4分在C P E ∆中, 90E P C ∠=︒, 30P E C ∠=︒∴3tan 303C PPE =︒=∴3P EC P = ∴734x -=∴743x =-∴43AP = ---------------------------------------------5分（顺义）20. (1）证明：连结O C由D C 是切线得O C D C ⊥-------------------------------1分又AD D C ⊥ AD O C ∥DCBOAE∴D A C A C O ∠=∠又由O A O C =得BAC AC O ∠=∠ D AC BAC ∴∠=∠∴ ECBC = ∴B C E C = --------------------------------------------2分（2）解：A B 为直径∴90A C B ∠=° 又B A C B E C ∠=∠∴ cos cos 8AC AB BAC AB BEC =⋅∠=⋅∠= 226BC AB AC∴=-=--------------------------3分∴ 3sin 5B AC ∠= ----------------------------------4分又D AC BAC BEC ∠=∠=∠ 且AD D C ⊥24sin sin 5C D A C D A C A C B A C ∴=∠=∠=·· --------5分（西城）20．解：（1）作DM ⊥AB 于点M ，CN ⊥AB 于点N ．（如图3）∵ AB ∥D C ，DM ⊥AB ，CN ⊥AB ，∴ ∠DMN =∠CNM =∠MDC =90︒． ∴ 四边形MNCD 是矩形. ∵4C D =，∴ MN =CD = 4．∵ 在梯形ABC D 中，AB ∥D C ，5AD BC ==， ∴ ∠DAB =∠CBA ，DM=CN ． ∴ △ADM ≌△BCN ．又∵10AB =， ∴ AM =BN =()11(104)322AB M N -=⨯-=．∴ MB =BN +MN =7．……………………………………………………………2分∵ 在Rt △AMD 中，∠AMD =90︒，AD =5，AM =3， ∴ 224D M AD AM=-=．∴ 4tan 7D M ABD BM∠==．……………………………………………………3分（2）∵ EF AB ⊥，∴ ∠F =90︒．∵∠DMN =90︒， ∴ ∠F =∠DMN .∴ DM ∥EF ．∴ △BDM ∽△BEF ． ∵ D E BD =，∴12BM BD BFBE==．∴ BF =2BM =14． ……………………………………………………………4分 ∴ AF =BF -AB =14-10=4． …………………………………………………5分（西城）21．（1）证明：如图4．∵ 点A 是劣弧BC 的中点，∴ ∠ABC ＝∠ADB ．………………………1分又∵ ∠BAD ＝∠EAB ，图 4E COFADB 图3M N QP(图2)DCBAHGPBA∴ △ABE ∽△ADB ．………………………2分∴ABADAE AB=．∴ 2A B A E A D =⋅．………………………………………………………3分（2）解：∵ AE =2，ED =4，∴()22612AB AE AD AE AE ED =⋅=+=⨯=．∴23AB =（舍负）．………………………………………………………4分∵ BD 为⊙O 的直径，∴ ∠A =90︒．又∵ DF 是⊙O 的切线，∴ DF ⊥BD.∴ ∠BDF =90︒．在Rt △ABD 中，233tan 63A B A D B A D∠===，∴ ∠ADB =30︒．∴ ∠ABC =∠ADB =30︒. ∴∠DEF=∠AEB=60︒，903060ED F BD F AD B ∠=∠-∠=︒-︒=︒．∴ ∠F =18060D EF ED F ︒-∠-∠=︒． ∴ △DEF 是等边三角形．∴ EF = DE =4．………………………………………………………………5分（延庆）19.解：（1）如图过B 点作BE ⊥CD ，垂足为E 在Rt ∆BEC 中，∠BEC=90度， tanC=34，AD=BE=4∴ tanC=34CEBE=，CE=3由勾股定理可得BC=5AB=DE=2∴CD=5 ∴ S 梯形ABCD=144)52(21=⨯+ （2）解法一：如图过点P 作PN ⊥CD ，交CD 于点N ，交AB 的延长线于M 已知条件可知点P 是点D 沿AQ 翻折而得到的，推得AP=4 梯形ABCD ∴AB ∥CD ∴∠MBP=∠C在Rt ∆BMP 中，∠BMP=90度，BP=x ,tan ∠BMP=tan ∠C=34可推得MP=x 54，BM=x 53在Rt ∆AMP 中，利用勾股定理可推得222AP MPAM=+ 即16)54()532(22=++x x整理方程得0601252=--x x 解之满足条件的52146+-==x BP 。

2011中考复习之圆补充训练

2011年中考复习之《圆》补充训练1.如图，在Rt ABC △中，90C ∠= ，BE 平分ABC ∠交AC 于点E ，点D 在AB 边上且DE BE ⊥．⑴判断直线AC 与DBE △外接圆的位置关系，并说明理由；⑵若6AD AE ==，BC ．2. 已知：如图，在Rt ABC △中，90C ∠=，点O 在AB 上，以O 为圆心，OA 长为半径的圆与AC AB ，分别交于点D E ，，且CBD A ∠=∠．⑴判断直线BD 与O 的位置关系，并证明你的结论；⑵若:8:5AD AO =，2BC =，求BD 的长3. 如图所示，ABC △是直角三角形，90ABC ∠=，以AB 为直径的O 交AC 于点E ，点D 是BC 边的中点，连结DE ．⑴求证：DE 与O 相切；⑵若O3DE =，求AE ．4. 如图，AB 为半圆O 的直径，点C 在半圆O 上，过点O 作BC 的平行线交AC 于点E ，交过点A的直线于点D ，且BAC D ∠=∠.⑴求证：AD 是半圆O 的切线；⑵若2=BC ，2=CE ，求AD .5. 如图，点D 是⊙O 的直径CA 延长线上一点，点B 在⊙O 上，且AB ＝AD ＝AO ．⑴求证：BD 是⊙O 的切线．⑵若点E 是劣弧BC 上一点，AE 与BC 相交于点F ，△BEF 的面积为8，cos ∠BFA ＝23，求△ACF 的面积．6.已知：如图，ABC △中，AB AC =，以AB 为直径的O 交BC 于点P ，PD AC ⊥于点D ． ⑴求证：PD 是O 的切线；⑵若1202CAB AB ∠== ，，求BC 的值．A BCD OP7.如图，AB 、BC 、CD 分别与⊙O 切于E 、F 、G ，且AB ∥CD ．连接OB 、OC ，延长CO 交⊙O 于点M ，过点M 作MN ∥OB 交CD 于N ．⑴求证：MN 是⊙O 的切线；⑵当0B =6cm ，OC =8cm 时，求⊙O 的半径及MN 的长．8.如图，AB 是⊙O 的直径，∠BAC =30°，M 是OA 上一点，过M 作AB 的垂线交AC 于点N ，交BC 的延长线于点E ，直线CF 交EN 于点F ，且∠ECF =∠E . ⑴证明CF 是⊙O 的切线；⑵设⊙O 的半径为1，且AC =CE ，求MO 的长.9. 在Rt △ABC 中，BC =9， CA =12，∠ABC 的平分线BD 交AC 与点D ， DE ⊥DB 交AB 于点E ．⑴设⊙O 是△BDE 的外接圆，求证:AC 是⊙O 的切线;⑵设⊙O 交BC 于点F ，连结EF ，求EFAC的值．10.如图，已知O 的直径AB 垂直于弦CD 于点E ，过C 点作CG AD ∥交AB 的延长线于点G ，连接CO 并延长交AD 于点F ，且CF AD ⊥． ⑴试问：CG 是O 的切线吗？说明理由；⑵请证明：E 是OB 的中点；⑶若8AB =，求CD 的长．E F GODCBA11. 如图，在⊙O 中，∠ACB =∠BDC =60°，AC =cm 32，⑴求∠BAC 的度数；⑵求⊙O 的周长；⑶连接AD ，求证：DB =DA +DC .CB DA E12. 如图，ABC △内接于O ，过点A 的直线交O 于点P ，交BC 的延长线于点D ，2AB AP AD = ．⑴求证：AB AC =；⑵如果60ABC ∠=，O 的半径为1，且P 为 AC 的中点，求AD 的长．13.如图，⊙O 是Rt △ABC 的外接圆，AB 为直径， ∠ABC =30°，CD 是⊙O 的切线，ED ⊥AB 于F ，⑴判断△DCE 的形状；⑵设⊙O 的半径为1，且OF =213-，求证△DCE ≌△OCB ．14.如图，AC 是圆O 的直径，10AC =厘米，PA PB ，是圆O 的切线，A B ，为切点．过A 作AD BP ⊥，交BP 于D 点，连结AB BC ，． ⑴；⑵若切线AP 的长为12厘米，求弦AB 的长．P15.如图，⊙O 是△ABC 的外接圆，FH 是⊙O 的切线，切点为F ，FH ∥BC ，连结AF 交BC 于E ，∠ABC 的平分线BD 交AF 于D ，连结BF ． ⑴证明：AF 平分∠BAC ；⑵证明：BF ＝FD ；⑶若EF ＝4，DE ＝3，求AD 的长．16.如图，已知AB 是⊙O 的直径，过⊙O 上的点C 的切线交AB 的延长线于E ，AD⊥EC 于D 且交⊙O 于F 。

2011年中考数学圆与圆复习题

圆与圆知识考点：1、掌握两圆的内外公切线长的性质和求切线长的方法（转化为解直角三角形）。

2、掌握有关两圆的内、外公切线的基本图形，以及这类问题添加辅助线的方法，会结合圆的切线的性质解决有关两圆公切线的问题。

精典例题：【例1】如图，⊙O1与⊙O2外切于P ，AB 是两圆的外公切线，切点为A 、B ，我们称△PAB 为切点三角形，切点三角形具有许多性质，现总结如下：（1）△PAB 是直角三角形，并且∠APB ＝900；（2）△PAB 的外接圆与连心线O1O2相切；（3）以O1O2为直径的圆与Rt △PAB 的斜边AB 相切；（4）斜边AB 是两圆直径的比例中项；（5）若⊙O1、⊙O2的半径为1R 、2R ，则PA ∶PB ∶AB ＝1R ∶2R ∶21R R +；（6）内公切线PC 平分斜边AB ；（7）△CO1O2为直角三角形。

这些结论虽然在证题时仍需证明，但有了这些基本结论作基础，可帮助你迅速找到解题思路，可以提高解题速度，下面用一个具体的例子来说明。

例1图1例1图2F如图2，⊙A 和⊙B 外切于P ，CD 为两圆的外公切线，C 、D 分别为切点，PT 为内公切线，PT 与CD 相交于点T ，延长CP 、DP 分别与两圆相交于点E 、F ，又⊙A 的半径为9，⊙B 的半径为4。

（1）求PT 的长；（2）求证：PF PE PD PC ⋅=⋅；（3）试在图中找出是线段PA 和PB 比例中项的线段，并加以证明。

分析：图中的基本图形是切点三角形，易证T 为CD 的中点，∠CPD ＝900，PT 即为外公切线长的一半，CF 、DE 分别为两圆直径，且互相平行，问题就解决了。

略解；（1）作BG ⊥AC 于G ，则CD ＝BG ＝12)49()49(22=--+∴PT ＝CT ＝TD ＝21CD ＝6证明（2）PT ＝21CD ，∴∠CPD ＝900∴CF 、DE 分别是⊙A 和⊙B 的直径又∵CD 切两圆于C 、D ，∴FC ⊥CD ，ED ⊥CD∴CF ∥DE ，∴PD PFPE CP =，∴PF PE PD PC ⋅=⋅ （3）图中是PA 和PB 比例中项的线段有PT 、CT 、DT （证明略）【例2】如图，⊙O 和⊙O '内切于点B ，⊙O '经过O ，⊙O 的弦AE 切⊙O '于点C ，AB 交⊙O '于D 。

2011中考复习圆章节补充训练

山东省17市2011年中考数学试题分类解析汇编专题11 圆

山东17市2011年中考数学试题分类解析汇编专题11：圆一. 选择题1.（日照4分）已知AC⊥BC 于C ，BC ＝a ，CA ＝b ，AB ＝c ，下列选项中⊙O 的半径为aba b+的是【答案】D 。

【考点】三角形的内切圆与内心，切线的性质，正方形的判定和性质，解一元一次方程，相似三角形的判定和性质。

【分析】设圆的半径是r 。

A 、设圆切BC 于D ，切AC 于E ，切AB 于F ，连接OD ，OE ，OF ，如图，根据切线的性质可得到正方形OECD ，AE ＝AF ，BD ＝BF ，则a －r ＋b －r ＝c ，∴r＝2a b c+-，故本选项错误；B 、设圆切AB 于F ，连接OF ，如图，则OF ＝r ，AO ＝b －r ，△BCA∽△OFA，∴OF AOCB AB =，即r rb a c-=，∴r＝aba c+，故本选项错误；C 、连接OE 、OD ，根据AC 、BC 分别切圆O 于E 、D ，如图，根据切线的性质可得到正方形OECD ，则OE ＝r ，AE ＝b －r ，△BCA∽△OEA，∴OE AEBC AC=，即r rb a b-=，∴r＝ab a b +，故本选项正确；D 、设圆切BC 于D ，连接OD ，OA ，则BD ＝a ＋r ，由BA ＝BD 得c ＝a ＋r ，即r ＝c －a ，故本选项错误。

故选C 。

2.（滨州3分）如图，在平面直角坐标系中，正方形ABCO 的顶点A 、C 分别在y 轴、x 轴上，以AB 为弦的⊙M 与x 轴相切．若点A 的坐标为（0，8），则圆心M 的坐标为A 、（﹣4，5）B 、（﹣5，4）C 、（5，﹣4）D 、（4，﹣5）【答案】D 。

【考点】垂径定理，勾股定理，正方形的性质。

【分析】过点M 作MD⊥AB 于D ，交OC 于点E ，连接AM 。

设⊙M 的半径为r ．∵以边AB 为弦的⊙M 与x 轴相切，AB∥OC，∴DE⊥CO。

∴DE 是⊙M 直径的一部分。

2011年山东省圆中考专题(答案)

2011山东中考数学分类------圆一、选择题1.（淄博 11,4分）如图，矩形ABCD 中，AB=4，以点B 为圆心，BA 为半径画弧交BC 于点E ，以点O 为圆心的⊙O 与弧AE ，边AD ，DC 都相切．把扇形BAE 作一个圆锥的侧面，该圆锥的底面圆恰好是⊙O ，则AD 的长为（）A ．4B ．92C ．112D ．5 【答案】D 。

2.（临沂 6,3分）如图，⊙O 的直径CD=5cm ，AB 是⊙O 的弦，AB⊥CD，垂足为M ，OM ：OD=3：5 ．则AB 的长是（）A 、2cm B 、3cm C 、4cm D 、2cm 故选C ．3，（•滨州3,3分）如图，在平面直角坐标系中，正方形ABCO 的顶点A 、C 分别在 y 轴、x 轴上，以AB 为弦的⊙M 与x 轴相切．若点A 的坐标为（0，8），则圆心M 的坐标为（） A 、（﹣4，5） B 、（﹣5，4）C 、（5，﹣4） D 、（4，﹣5）故选D ．4（济宁 5,3分）．已知⊙O 1与⊙O 2相切，⊙O 1的半径为9 cm ，⊙O 2的半径为2 cm ，则O 1O 2的长是 A ．1 cm B ．5 cmC ．1 cm 或5 cmD ．0.5cm 或2.5cm5（济宁 9.3分）如图，如果从半径为9cm 的圆形纸片剪去13圆周的一个扇形，将留下的扇形围成一个圆锥（接缝处不重叠），那么这个圆锥的高为（） A ．6cm B ．35cm C ．8cm D ．53cm6，（泰安 10,3分）.如图，⊙O 的弦AB 垂直平分半径OC ，若AB=,6⊙O 的半径为（A ）2 （B ）22 （C ）22 （D ）267（泰安 14,3分）一圆锥的侧面展开图是半径为2的半圆，则该圆锥的全面积是（A ）5π （B ）4π （C ）3π （D ）2π 8 (日照 11．4分)已知AC ⊥BC 于C ，BC =a ，CA =b ，AB =c ，下列选项中⊙O 的半径为ba ab的是（第9题）剪去9（莱芜 11,3分）将一个圆心角是90º的扇形围成一个圆锥的侧面，则该圆锥的侧面积S 侧和底面积S 底的关系是【 D 】A ．S 侧＝S 底B ．S 侧＝2S 底C ．S 侧＝3S 底D ．S 侧＝4S 底 10（青岛 3,3分）已知⊙O 1与⊙O 2的直径分别是4cm 和6cm ，O 1O 2＝5cm ，则两圆的位置关系是【】 A ．外离 B ．外切 C ．相交 D ．内切11（青岛 7,3分）7．如图1，在正方形铁皮上剪下一个扇形和一个半径为1cm 的圆形，使之恰好围成图2所示的一个圆锥，则圆锥的高为【】 A ．17cm B ．4cm C ．15cm D ．3cm12、（2011•潍坊9,3分）如图，半径为1的小圆在半径为9的大圆内滚动，且始终与大圆相切，则小圆扫过的阴影部分的面积为（） A 、17π B 、32π C 、49π D 、80π 故选B ．13（枣庄 7,3分）7．如图，PA 是O ⊙的切线，切点为A ，P A =23,∠APO =30°，则O ⊙的半径为（） A .1B .3C .2D .4二、填空 1、（济宁 13,3分）如图，在Rt △ABC 中，∠C=90°，BC=4cm ，以点C 为圆心，以3cm 长为半径作圆，则⊙C 与AB 的位置关系是。

2.4史密斯圆图(2011完成)

由此可见线上移动长度在圆图上反射系数转动一周改变度刻度尺标度范围为且零点位置通的周期为即设在传输线上有ab两点且ab两点相位差为a离信源近b离负载近则从b到a相角减小圆图中应顺时针旋转即从负载端向信号源方向移动时顺时针旋转a离负载近b离信源近则从b到a相角增大圆图中应逆时针旋转即从信号源向负载方向移动时逆时针旋转
2 z
B z (A)
l
A
(B)
若 z A zB （A离信源近,B离负载近),则从B到A相角减小,圆图中应顺时针旋转，即从负载端向信号源方向移动时，Γ顺时针旋转 ; 若 z A （A离负载近，B离信源近),则从B到A相角增大,圆图中 zB 应逆时针旋转,即从信号源向负载方向移动时，Γ逆时针旋转。
' 2
z
1 1 ( 1) ''2 x x
2
2
圆心坐标
x 0
1 1
'
1 x
''
1 半径 x
x0
'
1 0.5
x 1 x 1 2 x 1

2 1
0
0.5
1
1 1 1
2

1
0.5
0
"
-0.5 -1
x0
2
-2
0.5

圆
的关系，固有时称等

圆也为等

关系，即一一对应
圆，它们形状相同，但
标度值不同，标度值后面讲。
4、等电阻圆和等电抗圆
现将反射系数 Γ 分为实部和虚部两部分，Γ=Γ′+jΓ″，其中Γ′ 为实部，jΓ″为虚部，那么式（2.4.1）可改写为
r jx 1 ' j'' 1 j

2011年江苏省初中青年数学教师优秀课教案：圆(南京·濮磊)

圆上各点到圆心的距离都等于半径；（纯粹）
到圆心距离等于半径的点都在圆上.（完备）
学生交流，相互讨论后，教师请学生回答，得出圆的集合定义：
圆是平面内到定点距离等于定长的点的集合.
类比得到：
点P在⊙O内 d＜r
点P在⊙O外 d＞r
圆的内部可以看成是平面内到圆心的距离小于半径的点的集合；
圆的外部可以看成是平面内到圆心的距离大于半径的点的集合.
（二）过程与方法目标
1．通过观察、操作、交流的过程，培养学生动手能力、探究问题的能力以及合作交流的能力．
2．经历探究、归纳的过程，丰富数学活动经验，体会从特殊到一般的研究方法，以及数形结合和转化的数学思想．
（三）情感态度目标
经历圆的有关概念的形成过程，引导学生用数学的眼光和运动、集合的观点去认识世界、解决问题.激发学生爱生活的情感．通过小组交流活动，培养学生合作学习的意识和探索研究的精神．
（1）平面上的圆把平面上的点分成几个部分？
学生思考后回答：圆上的点、圆外的点、圆内的点.
教师追问：圆上的点具有怎样的特征？
学生思考后回答，其他学生补充后，可得：圆上各点到圆心的距离都等于半径.
设⊙O的半径为r，点P到圆心的距离OP＝d，则有：
点P在⊙O上 d＝r.
（2）几何画板演示
（i）如图：已知点A在半径为5的圆O上，过点A作AH⊥x轴，垂足为H.若OH=3，求AH.
（ii）学生探索：请找出与定点O距离为5的格点，这样的点你能找出几个？
（iii）学生探索：请找出与定点O距离为5的点，这样的点你能找出几个？
（3）几何画板动画呈现，让学生直观感受.结合（2）的探索和（1）的操作过程，学生得出：到圆心距离等于半径的点都在圆上.点P在⊙O上 d＝r.

2011圆习题课学案

ABCOP AB O F AC BDE 圆习题课学案出题人：班级姓名学号一、基础训练1、已知⊙O 的半径为6cm ，OP=5cm ，则点P 在圆2、已知⊙O 的半径为3cm ，圆心Ｏ到直线ａ的距离是４cm ，则直线ａ与⊙O 的位置关系是3、如图，PA 、PB 是⊙O 的切线，切点分别是A 、B ，如果∠P=60°，那么∠AOB 等于（）Ａ、60° Ｂ、90° Ｃ、120° Ｄ、150° 4、已知1o 的半径是8cm ，2o 的半径是3cm ，若12O O =4cm ，则这两圆的位置关系是 5、用反证法证明“两直线平行，同位角相等”的第一步是假设： 6、如图，在Ｒｔ△ＡＢＣ中，∠Ｃ＝９０°，若ＡＣ＝３cm ，ＢＣ＝４cm ，则△ＡＢＣ的外接圆的半径是7、如图，⊙O 内切于△ＡＢＣ，切点分别是D 、E 、F ，已知∠B=50°，∠C=60°，那么∠EDF 等于（）A 、40° Ｂ、55° Ｃ、65° Ｄ、70°第１题第５题第７题二、例题选讲例题1：如图，PA 、PB 是⊙O 的切线，⊙O 的半径是2cm ，∠APB=60°，求：（1）PA 、PB 、PC 的长；（2）四边形AOBP 的面积例题2：如图，AB 是⊙O 的直径，DC 切⊙O 于点C ，AD ⊥DC ，垂足为D.（1）求证：AC 平分∠BAD （2）若AB=10，∠BAD=60°，求AC 的长PDOBCAE 12I B C A例题3；如图，已知⊙O 是△ＡＢＣ的外接圆，ＡＢ为直径，若PA ⊥AB ，PO 过AC 的中点M ，求证：ＰＣ是⊙O 的切线三、课堂检测1、已知方程2540x x -+=的两根分别是1o 和2o 的半径，且12O O ＝3，那么两圆的位置关是（）Ａ、相交Ｂ、外切Ｃ、内切Ｄ、相离2、如图，AB 、AC 是⊙O 的两条弦，∠A=30°，过点C 的切线与OB 的延长线交于点D ，则∠D 的度数是3、如图，在△ＡＢＣ中，I 是内心，∠B ＩC=115°，则∠A=第2题第3题第4题4、尺规作图：画△ＡＢＣ的外接圆5、如图，AB 是⊙O 的直径，DE ⊥AC ，D 是线段BC 的中点，求证：DE 是⊙O 的切线 B O CDABACOABDBE AOCCDOAPBOAPBC6、如图，PA与⊙O相切于点A，弦AB⊥OP，垂足为C，ＯＰ与⊙O相交于点Ｄ，已知OA=2，OP=4。

九年级《圆》复习

（第6题） A B OD7题DCAO 第11题2010-2011年度九年级《圆》有关复习选择题是一种常见的命题形式,它一般由题干和选择支两部分组成.题干指命题的条件,选择支是几个供选择的结论.选择题属于客观性试题,概论性强,小巧灵活,覆盖面广,既可以考查基础知识掌握的情况,又能检查分析、判断问题的能力。

所以，想解好选择题，就要扎扎实实地掌握基础知识，加强基本功训练，同时注意培养自己的数学能力，锻炼思维的灵敏性。

选择题历年都是中考的必考题型，主要考查对基本知识和基本技能的掌握情况，但方法越来越灵活，常见的方法一般有七种： 1．直接求解法：直接根据选择题的题设，通过计算、推理、判断得出正确选项．2．排除法：有些选择题根据题设条件和有关知识，从4个答案中，排除3个答案，根据答案的唯一性，确定正确的答案，这种方法也称为剔除法或淘汰法或筛选法．3．特殊值法：根据命题条件．’选择题中所研究的量可以在某个范围内任意取值，这时可以取满足条件的一个或若干特殊值代人进行检验，从而得出正确答案． 4．验证法：直接将各选择支中的结论代人题设条件进行检验，从而选出符合题意的答案． 5．作图法：有的选择题可通过命题条件的，作出函数的图象或几何图形，借助于图象或图形的直观性从中找出正确答案．这种应用“数形结合”来解数学选择题的方法，我们称之为“作图法” 6．定义法：运用相关的定义、概念、定理、公理等内容，作出正确选择的一种方法．7．综合法：为了对选择题迅速、正确地作出判断，有时需要综合运用前面介绍的几种方法．解选择题的原则是既要注意题目特点，充分应用供选择的答案所提供的信息，又要有效地排除错误答案可能造成的干扰，须注意以下几点：（1）要认真审题；（2）要大胆猜想；（3）要小心验证；（4）先易后难，先简后繁． 1．（2010安徽省中中考）如图，⊙O 过点B 、C 。

圆心O 在等腰直角△ABC 的内部，∠BAC ＝900，OA ＝1，BC ＝6，则⊙O 的半径为（）A ）10B ）32C ）23D ）132．（2010安徽芜湖）如图所示，在圆⊙O 内有折线OABC ，其中OA ＝8，AB ＝12，∠A ＝∠B ＝60°，则BC 的长为（）A ．19B ．16C ．18D ．20 3．（2010甘肃兰州）有下列四个命题：①直径是弦；②经过三个点一定可以作圆；③三角形的外心到三角形各顶点的距离都相等；④半径相等的两个半圆是等弧．其中正确的有（）A ．4个B ．3个C ． 2个D ． 1个4．（2010甘肃兰州）将量角器按如图所示的方式放置在三角形纸板上，使点C 在半圆上．点A 、B 的读数分别为86、30，则∠ACB 的大小为（）A ．15︒ B ．28︒ C ．29︒ D ．34︒ 5．（2010山东烟台）△ ABC 内接于⊙O ，D 为线段AB 的中点，延长OD 交⊙O 于点E ，连接AE ，BE ，则下列五个结论①AB ⊥DE,②AE=BE,③OD=DE,④∠AEO=∠C,⑤,正确结论的个数是（） A 、2 B 、3 C 、4 D 、5 6．（2010 浙江台州市）如图，⊙O 的直径CD ⊥AB ，∠AOC =50°，则∠CDB 大小为 ( )A ．25° B ．30° C ．40° D ．50°7．（2010 河北）如图3，在5×5正方形网格中，一条圆弧经过A ，B ，C 三点，那么这条圆弧所在圆的圆心是（）A ．点P B ．点Q C ．点R D ．点M8．（2010 山东省德州）已知三角形的三边长分别为3,4,5，则它的边与半径为1的圆的公共点个数所有可能的情况是（）(A)0，1，2，3 (B)0，1，2，4 (C)0，1，2，3，4 (D)0，1，2，4，5 9．（2010年贵州毕节）如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为则该半圆的半径为（）A. (4 cmB. 9 cmC.D. 10．（2010湖北荆门）如图，MN 是半径为1的⊙O 的直径，点A O 上，∠AMN =30°，B 为AN 弧的中点，点P 是直径MN 则P A+PB 的最小值为（）A ．22B ．2C ．1D ．2 11．（2010湖南郴州）如图，AB 是O 的直径，CD 为弦，CD AB ⊥于E ，则下列结论中不成立．．．的是（）Ａ．A D ∠=∠ Ｂ．CE DE = Ｃ．90ACB ∠=Ｄ．CE BD =B A 第14题图 A B D 图(15)2N（第16题）第16题图(第20题) 第10题图A B 单位：mm l 1 l 212．（2010湖北荆州）△ABC 中，∠A=30°，∠C=90°，作△ABC 的外接圆．如图，若弧A B 的长为12cm ，那么弧AC 的长是（）A ．10cmB ．9cmC ．8cmD ．6cm 13．(2010江苏苏州)如图，已知A 、B 两点的坐标分别为 (2，0)、(0，2)，⊙C 的圆心坐标为(－1，0)，半径为1．若D 是⊙C 上的一个动点，线段DA 与y 轴交于点E ，则△ABE 面积的最小值是（）A ．2 B ．1C ．2D ．214．（2010山东青岛）如图，在Rt △ABC 中，∠C = 90°，∠B = 30°， BC = 4 cm ，以点C 为圆心，以2 cm 的长为半径作圆，则⊙C 与 AB 的位置关系是（）． A ．相离 B ．相切 C ．相交 D ．相切或相交 15．（2010台湾）图(15)为△ABC 和一圆的重叠情形，此圆与直线 BC 相切于C 点，且与AC 交于另一点D 。

2011中考数学真题解析95 圆的基本性质(含答案)

考点：圆周角定理；坐标与图形性质；勾股定理；锐角三角函数的定义。
专题：计算题。
分析：连接AB，利用圆周角定理得∠C=∠ABO，将问题转化到Rt△ABO中，利用锐角三角函数定义求解．
解答：解：如图，连接AB，
由圆周角定理，得∠C=∠ABO，
在Rt△ABO中，OA=3，OB=4，由勾股定理，得AB=5，
16.（2011，四川乐山，6，3分）如图，CD是⊙O的弦，直径AB过CD的中点M，若∠BOC=40°，则∠ABD=（）
A.40°B.60° C.70°D.80°
考点：垂径定理；圆周角定理。
专题：计算题。
分析：∠BOC与∠BDC为所对的圆心角与圆周角，根据圆周角定理可求∠BDC，由垂径定理可知AB⊥CD，在Rt△BDM中，由互余关系可求∠ABD．
9.（2011，台湾省，27,5分）如图，圆O为△ABC的外接圆，其中D点在上，且OD⊥AC．已知∠A=36°，∠C=60°，则∠BOD的度数为何？（）
A、132B、144
C、156D、168
考点：圆周角定理。
专题：计算题。
分析：连接CO，由圆周角定理可求∠BOC，由等腰三角形的性质求∠BCO，可得∠OCA，利用互余关系求∠COD，则∠OBD=∠BOC+∠COD．
∴AB=2AM，
∵CD=5cm，
∴OD=OA= CD= ×5= cm，
∵OM：OD=3：5，
∴OM= OD= × = ，
∴在Rt△AOM中，AM= = =2，
∴AB=2AM=2×2=4cm．
故选C．
点评：本题考查的是垂径定理及勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
12.（2011泰安，10，3分）如图，⊙O的弦AB垂直平分半径OC，若AB＝，则⊙O的半径为（）

《圆》课标解读

《圆》课标解读一、课标要求《义务教育数学课程标准（2011年版）》在“学段目标”的“第二学段”中提出“探索一些图形的形状、大小和位置关系，了解一些几何体和平面图形的基本特征；体验简单图形的运动过程，能在方格纸上画出简单图形运动后的图形，了解确定物体位置的一些基本方法；掌握测量、识图和画图的基本方法”“在观察、实验、猜想、验证等活动中，发展合情推理水平，能实行有条理的思考，能比较清楚地表达自己的思考过程与结果”“在使用数学知识和方法解决问题的过程中，理解数学的价值”。

《义务教育数学课程标准（2011年版）》在“课程内容”的“第一学段”中提出“能辨认长方形、正方形、三角形、平行四边形、圆等简单图形”“会用长方形、正方形、三角形、平行四边形或圆拼图”；又在“第二学段”中指出“通过观察、操作，理解平行四边形、梯形和圆，知道扇形，会用圆规画圆”“通过操作，了解圆的周长与直径的比为定值，掌握圆的周长公式；探索并掌握圆的面积公式，并能解决简单的实际问题”“通过观察、操作等活动，进一步理解轴对称图形及其对称轴，能在方格纸上画出轴对称图形的对称轴；能在方格纸上补全一个简单的轴对称图形”“能从平移、旋转和轴对称的角度欣赏生活中的图案，并使用它们在方格纸上设计简单的图案”。

《义务教育数学课程标准（2011年版）》在“实施建议”中提出：“数学活动经验的积累是提升学生数学素养的重要标志。

协助学生积累数学活动经验是数学教学的重要目标，是学生持续经历、体验各种数学活动过程的结果。

数学活动经验需要在‘做’的过程和‘思考’的过程中积淀，是在数学学习活动过程中逐步积累的”。

二、课标解读（一）以实践活动引领学生学习，增强学生动手操作、自主探索的水平本单元教材在各知识板块的编排中，都体现了上述的理念与内容，即以实践性的活动让学生“做”起来，在“做”的过程中，引发学生的“思考”，进而主动探索，最终理解概念（或得出结论）。

在实际教学中，教师应注意多让学生动手操作，通过画一画、剪一剪、围一围、拼一拼等多种形式，协助学生理解圆的基本特征，探索圆的周长、面积计算公式。

圆在生活中的应用

圆在生活中的应用作者：邓革周来源：《初中生·考试》2011年第11期中考中，利用圆的相关知识解决生活中的实际问题的题型经常出现?郾请看下面的例子?郾一、应用垂径定理解决实际问题例1 （2010年南宁卷）如图1，用一块直径为a的圆形桌布平铺在对角线长为a的正方形桌面上，若四周下垂的最大长度相等，则桌布下垂的最大长度x为 ?郾分析：先画出其对应的几何图形，再解答?郾解：如图2，⊙O为桌布，正方形ABCD为桌面，连接AO，过点O作OE⊥AB分别交AB、■于F、E两点?郾在Rt△AFO中，OA=■，由垂径定理及勾股定理可知OF=■a. ∴ x=EF=OE-OF=■a?郾温馨小提示：用垂径定理解题时，需作出圆心到弦的垂线段（即弦心距），垂足为弦的中点，利用半径、弦心距和弦的一半组成的直角三角形来达到求解的目的?郾在弦长a、弦心距d、半径r及弓形高h中，已知任意两个的值就可以求出其他两个的值?郾针对性训练1 在圆柱形油槽内装有一些油，截面如图3，油面宽AB为6分米，如果再注入一些油后，油面AB上升1分米，油面宽变为8分米，圆柱形油槽直径MN为（）?郾A?郾 6分米 B?郾 8分米C?郾 10分米 D?郾 12分米二、应用两圆相切的性质解决实际问题例2 （2011年天水卷）如图4，一个长方体的香烟盒，装满大小均匀的20支香烟，打开香烟盒的顶盖后，20支香烟排成三行?郾经测量，一支香烟的直径为0?郾75cm，长约8?郾4cm?郾（1）试计算烟盒顶盖ABCD的面积；（计算结果不取近似值）（2）制作这样一个烟盒至少需要多少cm2的纸张？（不计重叠粘合部分，计算结果精确到0?郾1cm2，■≈1?郾73）分析：从实体中抽象出几何图形，利用正多边形和两圆外切的性质求出AB，两圆的连心线经过切点?郾解：（1）如图5，作O1E⊥O2O3 ?郾∵ O1O2=O2O3=O1O3=0?郾75=■（cm），∴ O1E=■×■=■（cm）.∴ AB=2O1E+2R=■（cm），AD=7×■=■（cm）?郾∴ S矩形ABCD=AB·AD=■×■=■（cm2）?郾（2）制作这样一个烟盒至少需要纸张的面积为：S=2（■+■×8?郾4+■×8?郾4）≈144?郾1（cm2）?郾温馨小提示：活用两圆相切的性质是解这类题的关键?郾针对性训练2 图7是一个组合烟花（图6）的横截面，其中16个圆的半径相同，点O1、O2、O3、O4是四个角上圆的圆心，且四边形O1O2O3O4是正方形?郾若圆的半径为r，组合烟花的高度为h，则组合烟花侧面包装纸的面积至少需要（接缝面积不计）（）?郾A?郾26πrh B?郾 24rh＋πrh C?郾 12rh－2πrh D?郾 24rh＋2πrh三、应用弧长公式和扇形面积公式解决实际问题例3 （2011年朝阳卷）如图8是一纸杯，母线AC与EF延长后形成的立体图形是圆锥，该圆锥的侧面展开图是扇形OAB，经测量，纸杯上开口的直径为6cm，下底面直径为4cm，EF=8cm，求扇形OAB的圆心角及这个纸杯的表面积?郾（面积的结果用π表示）?郾分析：纸杯表面积=纸杯侧面积+纸杯下底面的面积?郾解：由题意可知■=6π，■=4π?郾设∠AOB=n°，AO=R，则CO=R-8?郾由弧长公式得■=6π，■=4π?郾解方程组6×180=nR,4×180=nR-8n. ∴n=45,R=24?郾即扇形OAB的圆心角是45°?郾又∵ R=24，R-8=16，∴ S扇形OCD=■×4π×16=32π，S扇形OAB=■×6π×24=72π?郾∴ S纸杯侧面积=S扇形OAB-S扇形OCD=72π-32π=40π.∴ S纸杯底面积=π·22=4π，S纸杯表面积=40π+4π=44π?郾温馨小提示：圆柱的侧面展开图是矩形，矩形的长等于底面圆的周长c，宽等于母线长l，如果圆柱的底面半径为r，则S圆柱侧=c·l=2πrl?郾圆锥的侧面展开图是扇形，扇形的弧长等于圆锥底面圆的周长c，半径等于圆锥母线长l，若圆锥的底面半径为r，扇形的圆心角为α，则α=■·360°，S圆锥侧=■c·l=πrl?郾针对性训练3 如图9，圆柱底面半径为2cm，高为9πcm，点A、B分别是圆柱两底面圆周上的点，且A、B在同一母线上，用一棉线从A顺着圆柱侧面绕3圈到B，求棉线最短为 cm?郾四、应用圆的知识进行方案设计例4 （2008年南通卷）在一次数学探究性学习活动中，某学习小组要制作一个圆锥体模型，操作规则是：在一块边长为16cm的正方形纸片上剪出一个扇形和一个圆，使得扇形围成圆锥的侧面时，圆恰好是该圆锥的底面?郾他们首先设计了如图10所示的方案一，发现这种方案不可行，于是调整了扇形和圆的半径，设计了如图10所示的方案二?郾（两个方案中，圆与正方形相邻两边及扇形的弧均相切?郾方案一中扇形的弧与正方形的两边相切）（1）说明方案一不可行的理由；（2）判断方案二是否可行？若可行，请确定圆锥的母线长及其底面圆的半径；若不可行，请说明理由?郾分析：方案是否可行，关键是看底面圆的周长与扇形的弧长是否相等?郾利用两圆相切的性质求出圆的半径?郾解：（1）理由如下：∵扇形的弧长＝16×■＝8π，圆锥底面周长＝2πr，∴ 2πr=8π，即圆的半径为4cm?郾所给正方形纸片的对角线长为16■cm，而制作这样的圆锥实际需要正方形纸片的对角线长为16+4+4■=（20+4■）cm，20+4■>16■，故方案一不可行?郾（2）方案二可行?郾求解过程如下：设圆锥底面圆的半径为rcm，圆锥的母线长为Rcm，则（1+■）r+R=16■，2πr=■.解得R=■，r=■?郾温馨小提示：两圆外切，圆心距等于两半径之和，圆锥底面圆的周长等于侧面展开图扇形的弧长?郾针对性训练4 （经典题）现需测量一井盖（圆形），但只有一把角尺（尺的两边互相垂直，一边有刻度，且两边长度都大于井盖的直径），请结合图形，用文字说明测量方法，写出测量步骤?郾井盖和角尺如图11所示?郾针对性训练参考答案：1?郾 C 2?郾 D 3?郾15π4?郾如图12所示，把角尺顶点A放在井盖边缘，这样就产生了90°的圆周角，设角尺的一边与井盖边缘交于B点，另一边与井盖的边缘交于C点，度量BC的长，即可求出井盖的直径?郾■。