2014年全国高中数学联合竞赛加试不等式另解

合集下载

2014年全国各地高考数学试题及解答分类大全(不等式)

2014年全国各地高考数学试题及解答分类大全（不等式）一、选择题：1（2014安徽理）y x ,满足约束条件⎪⎩⎪⎨⎧≥+-≤--≤-+02202202y x y x y x ，若ax y z -=取得最大值的最优解不唯一，则实数a 的值为（）A,121-或 B.212或 C.2或1 D.12-或解析：数形结合求解。

考点：1.线性规划求参数的值.2.(2014福建文)要制作一个容积为34m ，高为1m 的无盖长方体容器，已知该溶器的底面造价是每平方米20元，侧面造价是是每平方米10元，则该容器的最低总造价是（）.80.120.160.240A B C D 元元元元3.(2014福建文)已知圆()()22:1C x a y b -+-=，设平面区域70,70,0x y x y y +-≤⎧⎪Ω=-+≥⎨⎪≥⎩，若圆心C =Ω,且圆C 与x 轴相切，则22a b +的最大值为（）.5.29.37.49A B C D 4.(2014北京理)若x 、y 满足20200x y kx y y +-≥⎧⎪-+≥⎨⎪≥⎩，且z y x =-的最小值为4-，则k 的值为（）A．2B．2-C．12D．12-【答案】D 【解析】可行域如图所示，当0>k 时，知x y z -=无最小值，当0<k 时，目标函数线过可行域内A点时z 有最小值，联立⎩⎨⎧=+-=020y kx y ，解之得⎪⎭⎫ ⎝⎛-0,2k A ，420min -=+=k z ，即21-=k .5、(2014广东文)若变量,x y 满足约束条件280403x y x y +≤⎧⎪≤≤⎨⎪≤≤⎩，则2z x y =+的最大值等于A.7B.8C .10 D.11答案:C提示:作出可行域(为一个五边形及其内部区域),易知在点(4,2)处目标函数取到最大值10.选C.6.(2014广东理)若变量x 、y 满足约束条件11y x x y y ≤⎧⎪+≤⎨⎪≤-⎩，且2z x y =+的最大值和最小值分别为M和m ，则M m -=（）A.8B.7C.6D.5截距最大，此时z 取最大值M ，即()2213M =⨯+-=；()336M m -=--=，故选C.7．(2014湖北文)若变量x ，y＋y ≤4，－y ≤2，≥0，y ≥0，则2x ＋y 的最大值是()A ．2B ．4C ．7D ．84．C[解析]＋y ≤4，－y ≤2，≥0，y ≥0表示的可行域如下图阴影部分所示．设z ＝2x ＋y ，平移直线2x ＋y ＝0，易知在直线x ＋y ＝4与直线x －y ＝2的交点A (3，1)处，z ＝2x2=-+y x 02=+-y kx A=-x y＋y 取得最大值7.故选C.8．(2014湖北理)由不等式组x ≤0，y ≥0，y －x －2≤0确定的平面区域记为Ω1，不等式组x ＋y ≤1，x ＋y ≥－2确定的平面区域记为Ω2，在Ω1中随机取一点，则该点恰好在Ω2内的概率为()A.18B.14C.34D.787．D [解析]作出Ω1，Ω2表示的平面区域如图所示，S Ω1＝S △AOB ＝12×2×2＝2，S △BCE ＝12×1×12＝14，则S 四边形AOEC ＝S Ω1－S △BCE ＝2－14＝74.故由几何概型得，所求的概率P ＝S 四边形AOEC S Ω1＝742＝78.故选D.9.(2014江西理)（不等式选做题）对任意,x y R ∈,111x x y y -++-++的最小值为（）A.1 B.2 C.3 D.4【答案】B【解析】()|1||||1||1|1||11|123x x y y x x y y -++-++≥--+--+=+=10.(2014全国大纲文)不等式组(2)0||1x x x +>⎧⎨<⎩的解集为（）A ．{|21}x x -<<-B ．{|10}x x -<<C ．{|01}x x <<D ．{|1}x x >11.(2014全国新课标Ⅰ文)设x ，y 满足约束条件,1,x y a x y +≥⎧⎨-≤-⎩且z x ay =+的最小值为7，则a =（A ）-5（B ）3（C ）-5或3（D ）5或-3【答案】：B 【解析】：画出不等式组对应的平面区域，如图所示.在平面区域内，平移直线0x ay +=，可知在点A 11,22a a -+⎛⎫⎪⎝⎭处，z 取得最值，故117,22a a a -++=解之得a = -5或a = 3.但a = -5时，z取得最大值，故舍去，答案为a = 3.选B.12.(2014全国新课标Ⅰ理)不等式组124x y x y +≥⎧⎨-≤⎩的解集记为D .有下面四个命题：1p ：(,),22x y D x y ∀∈+≥-，2p ：(,),22x y D x y ∃∈+≥,3P ：(,),23x y D x y ∀∈+≤，4p ：(,),21x y D x y ∃∈+≤-.其中真命题是A .2p ，3P B .1p ，4p C.1p ，2p D .1p ，3P 【答案】：C【解析】：作出可行域如图：设2x y z +=，即122zy x =-+，当直线过()2,1A -时，min 220z =-+=，∴0z ≥，∴命题1p 、2p 真命题，选C.13.(2014全国新课标Ⅱ文)设x ，y 满足约束条件0103310x y x y x y ≥⎧⎪--≤⎨⎪-+≥-⎩+，则z =2x +y 的最大值为()A．8B．7C．2D．1【答案解析】A．解析：作图即可.考点：考查二元一次不等式组的应用，中等题.14.(2014全国新课标Ⅱ理)设x ，y 满足约束条件03103507x y x x y y ≤⎧⎪-+≤⎨⎪--≥-⎩+，则z =2x -y 的最大值为()A.10B.8C.3D.2【答案解析】B.解析：作图即可.考点：考查二元一次不等式组的应用，中等题.15.(2014山东理)已知实数,x y 满足xya a <（01a <<），则下列关系式恒成立的是（A ）221111x y >++（B ）22ln(1)ln(1)x y +>+（C ）sin sin x y >（D ）22x y>15.【答案】D【解析】y x a a a yx>∴<<<10, 但不能判断22y x >（如1,0-==y x ）∴排除A,B;x y sin = 是周期函数，∴排除C;3x y = 是单调递增函数，∴D 正确.16.(2014山东文)已知实数,x y 满足(01)x ya a a <<<，则下列关系式恒成立的是(A)33x y>(B)sin sin x y >(C)22ln(1)ln(1)x y +>+(D)221111x y >++16.【答案】A【解析】由)10(<<<a a a yx得，y x >，但是不可以确定2x 与2y 的大小关系，故C 、D 排除，而x y sin =本身是一个周期函数，故B 也不对，33y x >正确。

答案与评分细则(14年高中数学联赛四川试题)

2014年全国高中数学联赛（四川）参考答案及评分标准说明：1、评阅试卷时，请依据评分标准.选择题和填空题只设5分和0分两档；其它各题的评阅，请严格按照评分标准规定的评分档次给分，不要再增加其它中间档次.2、如果考生的解答题方法和本解答不同，只要思路合理，步骤正确，在评阅时可参考本评分标准适当划分档次评分，5分一个档次，不要再增加其它中间档次. 一、选择题（本大题共6个小题，每小题5分，共30分）1、D2、B3、A4、B5、C6、C 二、填空题（本大题共6个小题，每小题5分，共30分）7、326 8、14 9、80 10、0 11、5 12、28 三、解答题（本大题共4个小题，每小题20分，共80分）13、已知a 为常数，函数1()ln(1xf x ax x−=−+．（1）求函数()f x 的单调递减区间；（2）若83a =−，求()f x 的极值．解：（1）函数()f x 的定义域为(1,1)−．()ln(1)ln(1)f x x x ax =−−+−，2112()111f x a a x x x −−′=−−=−−+− (5分) 因为11x −<<，故2221x−≤−−； ① 当2a >−时，()0f x ′<恒成立，故单调递减区间为(1,1)−； ② 当2a =−时，(1,0)x ∈−时()0f x ′<；0x =时()0f x ′=； (0,1)x ∈时()0f x ′<；故单调递减区间为(1,1)−；③ 当2a <−时，由()0f x ′<知221a x−<−，即22a x a +>1x <<或者1x −<<；故单调递减区间为，(1,−．综上所述，当2a ≥−时，单调递减区间为(1,1)−；当2a <−时，单调递减区间为，(1,−−年全国高中数学联赛（四川）试题（2）823a =−<−，由()0f x ′=知驻点为12x =−，或12x =；于是: 112x −<<−时'()0f x <；1122x −<<时'()0f x >；112x <<时'()0f x <．（15分）所以，()f x 有极小值14()ln 323f −=−+，有极大值14()ln 323f =−．（20分）14、已知不等式31cos 4cos sin 3222≤++−a x a x x 对一切R x ∈恒成立，求实数a 的取值范围．解：设31cos 4cos sin 3)(222−++−=a x a x x x f ，则28cos 4cos 4)(22−++−=a x a x x f 令x t cos =，则]1,1[−∈t故当]1,1[−∈t 时，22()44280g t t at a =−++−≤恒成立二次函数()g t 的对称轴2a t =， ①当12a≤−，即2a ≤−时，()g t 在]1,1[−∈t 上单减，故有()g t 的最大值2(1)4320g a a −=−−≤，解得42a −≤≤−；（5分）②当112a −<<，即22a −<<时，有()g t 的最大值2(22802ag a =−≤，解得22a −<<；（10分） ③当12a≥，即2a ≥时，()g t 在]1,1[−∈t 上单增，故有()g t 的最大值2(1)4320g a a =+−≤，解得24a ≤≤；（15分）综上可知，所求a 的取值范围是[4,4]−．（20分）15、已知k 为给定正整数，数列{}n a 满足13a =，2*211(31)3()k n n a S n −+=−+∈N ，其中n S 是{}n a 的前n 项和．令3121log ()()n n b a a a n n =∈"*N ,记213||2kk i i T b ==−∑．若k T ∈*N ,求k 的所有可能值．解：由条件知22121212(31)333k k k a +−−=−×+=，又 2211(31)3k n n a S −+=−+，2211(31)3k n n a S −−=−+（2n ≥）故2211(31)k n n n a a a −+−=−，即22113k n n a a −+=．于是2223221212)3(2)n k n k k n a a n +−−−−==≥，显然1n =也符合．所以，数列{}n a 的通项公式22321()n k k n a n +−−=∈*N ．（5分）从而3121log ()n n b a a a n ="111(223)21ni i k n k ==⋅+−−∑1121n k −=+−．（10分）于是1()32221n n k b k −+−=−，从而n k ≤时302n b −<；1n k ≥+时302nb −>．所以222111333||()()22221kk kk i i i i i i k k T b b b k ===+=−=−+−=−∑∑∑．（15分）因为k T ∈*N ，即2(21)|k k −，故2(21)|(411)k k −−+，于是(21)|1k − 故211k −=，解得1k =．所以所求k 的所有可能值为1k =．（20分）16、过椭圆22132x y +=的右焦点F 作两条垂直的弦AB 、CD ，设AB 、CD 的中点分别为M 、N ．（1）求证：直线MN 必过定点，并求出这个定点；（2）若弦AB 、CD 的斜率均存在，求△FMN 的面积的最大值．解：（1）由题意知，(1,0)F ．① 当弦AB 、CD 的斜率均存在，设AB 的斜率为k ，则CD 的斜率为1k−．设:(1)AB y k x =−，代入椭圆方程22132x y +=，得2222(32)6(36)0k x k x k +−+−=，所以223232A B M x x k x k +==+，22(1)32M M k y k x k −=−=+，故点22232(,3232k kM k k −++．因为CD ⊥AB ，所以将点M 的坐标中的k 换为1k −，即得点2232(,)2323kN k k ++．（5分）（i ）当1k ≠±时，22222222332332332MNk kk k k k k k +++=−++24210(1)56633k k k k k +−==−−，此时直线MN 的方程为222253()233323k ky xk k k −−=−+−+，则直线MN 过定点3(,0)5．（ii ）当1k =±时，易得直线MN 的方程为35x =，也过点3(,0)5． ② 当弦AB 或弦CD 的斜率不存在时，易知直线MN 为x 轴，也过点3(,0)5．综上可知，直线MN 必过定点E 3(,0)5．（10分）（2）由（1）知S △FMN =1||||2M N EF y y ⋅⋅− 2212253223k kk k −=−++2222(1)(32)(23)k k k k +=++ （15分）不妨设0k >，则6424222222222212101012(12212)(1)(32)(23)(32)(23)k k k k k k S k k k k −−++−+−−′==++++ 由0S ′=知1k =．又(0,1)k ∈时，0S ′>; (1,)k ∈+∞时，0S ′<; 故当1k =时，S 有最大值为425．所以，△FMN 的面积的最大值是425．（20分）。

2014年全国高中数学联赛A卷真题word版

一试一、填空题1. 若正数b a ,满足()b a b a +=+=+632log log 3log 2，则b a 11+的值为________.2. 设集合⎭⎬⎫⎩⎨⎧≤≤≤+213b a b a 中的最大元素与最小元素分别为m M ,，则m M -的值为__________.3. 若函数()12-+=x a x x f 在[)+∞,0上单调递增，则实数a 的取值范围是__________.4. 数列{}n a 满足21=a ，()()*+∈++=N n a n n a n n 1221，则=+++2013212014a a a a Λ . 5. 正四棱锥ABCD P -中，侧面是边长为1的正三角形，N M ,分别是边BC AB ,的中点，则异面直线MN 与PC 之间的距离是__________.6. 设椭圆Γ的两个焦点是21,F F ，过点1F 的直线与Γ交于点Q P ,.若212F F PF =，且1143QF PF =,则椭圆Γ的短轴与长轴的比值为__________.7. 设等边三角形ABC 的内切圆半径为2，圆心为I .若点P 满足1=PI ，则APB ∆与APC ∆的面积之比的最大值为__________.8. 设D C B A ,,,是空间四个不共面的点，以21的概率在每对边之间连一条边，任意两对点之间是否连边是相互独立的，则B A ,可用（一条边或者若干条边组成的）空间折线连接的概率为__________.二、解答题9. 平面直角坐标系xOy 中，P 是不在x 轴上的一个动点，满足条件：过P 可作抛物线x y 42=的两条切线，两切点连线P l 与PO 垂直.设直线P l 与直线PO ，x 轴的交点分别为R Q ,.（1）证明R 是一个定点；（2）求QR PQ 的最小值. 10. 数列{}n a 满足61π=a ，()n n a a sec arctan 1=+()*∈N n .求正整数m ，使得1001sin sin sin 21=⋅⋅⋅m a a a Λ. 11. 确定所有的复数α，使得对任意复数21,z z ()2121,1,z z z z ≠<，均有 ()()222121z z z z αααα++≠++.二试一、设实数c b a ,,满足1=++c b a ，0>abc .求证：412+<++abc ca bc ab .二、如图，在锐角ABC ∆中，︒≠∠60BAC ，过点B 、C 分别作ABC ∆的外接圆⊙O 的切线BD 、EC ，且满足BC CE BD ==.直线DE 与AB 、AC 的延长线分别交于点F 、G .设CF 与BD 交于点M ，CE 与BG 交于点N .求证：AN AM =.三、设{}100,,3,2,1Λ=S .求最大的整数k ，使得S 有k 个互不相同的非空子集，具有性质：对这k 个子集中任意两个不同子集，若它们的交非空，则它们交集中的最小元素与这两个子集中的最大元素均不相同.四、设整数201421,,,x x x Λ模2014互不同余，整数201421,,,y y y Λ模2014也互不同余. 证明：可将201421,,,y y y Λ重新排列为201421,,,z z z Λ，使得201420142211,,,z x z x z x +++Λ模4028互不同余.。

2014年全国高中数学联赛江苏赛区复赛参考答案与评分标准(加试)

取正整数 k1 满足 1－ 1k1＞cos nt，由（1）可知存在正整数 n，使得 cos n＞1－ 1k1＞22001145．这与使 cosn＞22001145成立的正整数 n 的个数是 t 矛盾．
所以存在无穷多个正整数 n，使得 cosn＞22001145．
………………………50 分
2014 年全国高中数学联赛江苏赛区复赛试4 卷（加试）参考答案第 4 页共 4 页
从而 n＜36，又因为 n 为偶数，所以 n≤34．
……………… 40 分
（3）证明 n=34 能取到．
不妨设凸 34 边形内角中只有两个值 x 和 x－20°，它们相间出现，各为一半，
有 17(2x－20°)＝32×180°，x＝301570°＜180°．x－20°＞0，
知存在满足条件的凸 34 边形．
({x}＝x－［x］，［x］表示不大于 x 的最大整数)．将区间［0，1)分成 M 个小区间：［0，M1 )，［M1 ，M2 )，…，［MM－1，1)，由抽屉原理可知，一定存在 1≤i＜j≤M+1，使得{iα}，{jα}在同一个小区间，
因此，|{jα}－{iα}|＜M1 ，从而|nα－(［jα］－［iα］)|＜M1 ，
而当 n 为偶数时，且 x1，x2，…，xn 中一半取 2，一半取 8 时，等号成立．故当且仅当 n 为偶数，且 x1，x2，…，xn 中一半取 2，一半取 8 时等号成立．
…………………………… 40 分
2014 年全国高中数学联赛江苏赛区复赛试2 卷（加试）参考答案第 2 页共 4 页
Printed with FinePrint trial version - purchase at
⎩⎨⎧ 由①②知，必须有

2014年全国高中数学联赛试题及答案详解(A卷)

2013
解：由题设
an

2(n 1) n
an1

2(n 1) n

2n n 1 an2

2(n 1) n

2n n 1

23 2
a1

2n1 (n
1)
．
记数列{an} 的前 n 项和为 Sn ，则
Sn =
2 + 2 × 3 + 22 × 4 + + 2n−1(n +1)
2015 2013

2015
．
2013
5. 正四棱锥 P ABCD 中，侧面是边长为 1 的正三角形，M , N 分别是边 AB, BC 的中
点，则异面直线 MN 与 PC 之间的距离是
．
答案： 2 ． 4
解：设底面对角线 AC, BD 交于点 O ，过点 C 作直
线 MN 的垂线，交 MN 于点 H ．由于 PO 是底面的垂线，故 PO CH ，又
解：记 f (z) (z )2 z ．则
f (z1) f (z2 ) (z1 )2 z1 (z2 )2 z2
(z1 z2 2)(z1 z2 ) z1 z2 ．
①
假如存在复数 z1, z2 ( z1 , z2 1, z1 ≠ z2 ) ，使得 f (z1) f (z2 ) ，则由①知，
连接的情况数．
(1) 有 AB 边：共 25 32 种情况．
(2) 无 AB 边，但有 CD 边：此时 A ， B 可用折线连接当且仅当 A 与 C ， D 中至少一
点相连，且 B 与 C ， D 中至少一点相连，这样的情况数为 (22 1)(22 1) 9 ．

2014年全国高中数学联合竞赛试题及解答.(B卷)

（也可以猜出通项，用数学归纳法证明）
2014B 10、（本题满分 20 分）设 x1, x2 , x3 是多项式方程 x3 10x 11 0 的三个根.
⑴已知 x1, x2 , x3 都落在区间 5,5 之中，求这三个根的整数部分；（5 分）
2014 年全国高中数学联合竞赛试题（B 卷）第 4 页共 10 页
以得到 an3 an 12 ，说明 a3k1,a3k ,a3k1分别是公差为12 的等差数列，首先分别为 a2 5 ， a3 9 ， a4 13 。又 a1, a2 , a3 , a4 成公差为 4 的等差数列，所有 an 也是公差为 4 的等差数列，
an 4n 3。
由过
AD
，
BE
交点的直线系方程为
x0 (x 2) 2(2 x0 2 y0
)

y

x 2

2y0 ( 2 x0
y 1) 2y0

0
，
把 C(2,1)
代入可得

1，此时直线系就变为
x0 (x 2(2 x0
2) 2y0
)

y

x

2

件 A 共包含 45 C153 。由于在 52 张牌随机抽取 5 张的基本事件个数为 C552 ，于是事件 A 发生的概率
为 45 C153
C
5 52
0.5071，从而 P( A) 1 0.5071 0.4929 。
2014B 8、设 g(x) x(1 x) ，是定义在区间[0,1]上的函数，则函数 y xg (x) 的图像与 x

2014年全国高中数学联赛湖北省预赛试题及参考答案(高二)

2014年全国高中数学联合竞赛湖北省预赛试题参考答案（高二年级）一、填空题（本题满分90分，每小题9分。

直接将答案写在横线上。

）1. 已知正整数数列}{n a 满足n n n a a a +=++12，∈n *N ．若15711=a ，则1a = 3 .2. 函数x x x x y 22cos 2cos sin sin -+=的值域为11[22---+.3. 在△ABC 中，︒=30A ，232=⋅，则△ABC 的最大角的余弦值为12-．4．在直角坐标平面内，曲线3|||1||1|=+++-y x x 围成的图形的面积是 5 .5．若2113>+--a a 恒成立，则a的取值范围是[1,1-.6. 去掉集合{|10000,A n n n =≤∈*N }中所有的完全平方数和完全立方数后，将剩下的元素按从小到大的顺序排成一个数列，这个数列的第2014项为 2068 .7．在四面体ABCD 中，3AB AC ==，4BD BC ==，⊥BD 面ABC ，则四面体ABCD 的外接球的半径为10.8. 三对夫妻排成一排照相，仅有一对夫妻相邻的概率为25.9. 若A a ∈且A a A a ∉+∉-1,1，则称a 为集合A 的孤立元素.那么，集合{M =1，2，3，4，5，6，7，8，9}的无孤立元素的4元子集有 21 个.10. 共焦点的椭圆与双曲线的离心率分别为21,e e ，若椭圆的短轴长为双曲线的虚轴长的2倍，则2111e e +的最大值为52.二、解答题（本题满分60分，每小题20分。

）11. 当1||≤x 时，不等式2210px qx p +-+≥恒成立，试求q p +的最大值．解法1 令]1,1[,12)(2-∈+-+=x p qx px x f . （1）先考虑0p >时的情况，①若114q p -≤-≤，即44p q p -≤≤，则由题意知()04qf p-≥，即 22()()1044q q p q p p p ⋅-+⋅--+≥，整理得2218()22q p +-≤.设cos q r θ=，12p -=，其中0r ≤≤，[0,2]θπ∈，则1sin cos )2p q r θθ+=++.设(0,)2πϕ∈，且tan ϕ= 1(sin cos cos sin )2p q r θϕθϕ+=++1sin()2r θϕ=++1122≤+=，等号成立的条件是：r =1sin 3θ=，cos 3θ=，即23p =，43q =. …………………10分②若14qp-<-，即4q p >，则由(1)10f p q -=-+≥得1q p ≤+，所以41p q p <≤+，从而可得13p <，此时52123p q p +≤+<<； ③若14qp->，即p q 4-<，则302p q p +≤-<<； …………………15分（2）当0p ≤时，由(1)2110f p q p p q -=--+=-+≥得1q p ≤+，故212p q p +≤+<. 综合可知：q p +的最大值为2． …………………20分解法二特殊值法.在不等式2210px qx p +-+≥中取特殊值21-=x ，得2≤+q p ． …………………10分当且仅当34,32==q p 时，0)21(3431343412222≥+=++=+-+x x x p qx px ．所以，q p +的最大值为2． …………………20分12. 设B A ,是双曲线λ=-222y x 上的两点，点)2,1(N 是线段AB 的中点，线段AB 的垂直平分线交双曲线于D C ,两点．（1）确定λ的取值范围；（2）试判断D C B A ,,,四点是否共圆？并说明理由．解（1）依题意，可设直线AB 的方程为2)1(+-=x k y ，代入双曲线方程并整理得222(2)2(2)[(2)2]0k x k k x k λ-+---+= ①设),(),,(2211y x B y x A ，则21,x x 是方程①的两个不同实根，于是可知22224(2)4(2)[(2)2]0k k k k λ∆=-+--+> ②且2212)2(2kk k x x --=+．又)2,1(N 是线段AB 的中点，故12)2(2=--k k k ，解得1=k ，故直线AB 的方程为1(1)2y x =⋅-+，即1y x =+．将1=k 代入②，得0)21(44>++λ，解得1->λ．又CD 是线段AB 的垂直平分线，故CD 所在直线的方程是)1(2--=-x y ，即3+-=x y ，将其代入双曲线方程，整理得09262=--+λx x ③由题意，方程③也有两个不同实根，所以2164(29)0λ∆=--->，解得9λ>-．又0λ≠，于是可得：λ的取值范围为(1,0)(0,)-+∞． …………………10分（2）设),(),,(4433y x D y x C ，线段CD 的中点为),(00y x M ，则43,x x 是方程③的两根，所以643-=+x x ，9243--=λx x ，于是32430-=+=x x x ，6300=+-=x y ．于是，由弦长公式可得34|||CD x x =-===.又方程①即01222=---λx x ，同理可得||AB ==.显然||||CD AB <，又CD 是线段AB 的垂直平分线，假设存在(1,0)(0,)λ∈-+∞使得D C B A ,,,四点共圆，则CD 必为该圆的直径，点M 为圆心．又点M 到直线AB 的距离为d ===222222||||||()3642AB MA MB d λ==+=+=+．又 22||()3642CD λ==+，所以2222||||||||MD MC MB MA ===．故当(1,0)(0,)λ∈-+∞时，D C B A ,,,四点均在以(3,6)M -为圆心、为半径的圆上．…………………20分13. 在单调递增数列}{n a 中，12a =，24a =，且12212,,+-n n n a a a 成等差数列，22122,,++n n n a a a 成等比数列， ,3,2,1=n ．（1）求数列}{n a 的通项公式；（2）设数列}1{n a 的前n 项和为n S ，证明：43(3)n n S n >+，*n ∈N ．解（1）因为数列{}n a 为单调递增数列，120a =>，所以0n a >（*n ∈N ）. 由题意得221212n n n a a a -+=+，221222n n n a a a ++=，于是+=-n n n a a a 22222222+n n a a ，化简得+=-2222n n a a 22+n a，所以数列为等差数列.又32126a a a =-=，23429a a a ==，所以数列2=，公差为1d =1n =+，从而22(1)n a n =+.结合221222n n n a a a --=可得21(1)n a n n -=+.因此，当n 为偶数时n a =21(2)4n +，当n 为奇数时n a =(1)(3)4n n ++. 所以数列}{n a 的通项公式为211(1)(3)1(2)[1(1)][1(1)]2424n nn n n n a ++++=+-⋅++-⋅217(1)48n n n +-=++.…………………10分（2）因为n a 22217(1)1(2)11(2)(3)48444n n n n n n n n +-+=++≤++=<++，所以 14114()(2)(3)23n a n n n n >=-++++， 11a S n =21a +31a + +n a 1+111111114[()()()()]34451223n n n n >-+-++-+-++++ 1144()333(3)nn n =-=++，所以43(3)n n S n >+，*n ∈N ． …………………20分。

2014年高中数学联赛试题及其解答

加试
一、（本题满分 40 分）设实数a、b、c满足a + b + c = 1，abc＞0，求证：ab + bc + ca＜ √ + 。
证明方法一：因为abc＞0，故a、b、c全为正数，或一正两负。（Ⅰ）若a、b、c中一正两负，不妨设a＞0，b、c＜0，则ab + bc + ca = a(b + c) + bc = a(b + c) + bc = [1 − (b + c)](b + c) + bc = (b + c) − b − − ＜0＜ √ + 。
解答：我们考虑存在复数z 、z ，|z |、|z |＜1，z ≠ z ，使得(z + α) + αz =
(z + α) + αz 的充要条件。此时
(z + α) + αz = (z + α) + αz
⇔ α(z − z ) = (z − z )(z + z + 2α)
⇔ α[(z − z ) + 2(z − z )] = (z − z )(z + z )
3、若函数f(x) = x + a|x − 1|在[0， + ∞)上单调递增，则实数a的取值范围是
。
x − ax + a，x ∈ 0，1
解答：根据条件知f(x) =
。f(x)在 0，1 单调递增的充要
x + ax − a，x ∈ 1， + ∞
条件为 ≤ 0 ⇔ a ≤ 0；f(x)在 1， + ∞ 单调递增的充要条件为− ≤ 1 ⇔ a ≥ −2。故实数

2014年全国高中数学联合竞赛试题及解答.(A卷)

1 。 100
，a n 1 arctan(sec a n ) ，（n N ）求正整数 m ， 6 , ) ，且 tan a n 1 sec a n 2 2
★解析：由已知条件可知，对任意正整数 n ， a n 1 ( 由于 sec a n 0 ，故 a n 1 (0,
2014 年全国高中数学联合竞赛试题（A 卷）
第 2 页共 11 页
2a | QF1 | | QF2 || PF1 | | PF2 | 2c 4
于是 | QF2 || PF1 | | PF2 | | QF1 | 2c 1 设 H 为线段 PF1 的中点，则 | F1 H | 2, | QH | 5 ，且有 F2 H PF1 。由勾股定理知，
① ②
2014 年全国高中数学联合竞赛试题（A 卷）
第 4 页共 11 页
而点 P 的坐标 ( a, b) 同时满足①，②。故 A ， B 的坐标均满足方程
by 2( x a )
③ ( x1 , y1 ) ， ( x 2 , y 2 )
故③就是直线 AB 的方程。直线 PO 与 AB 的斜率分别为从而③即为 y
tan a m tan a1 tan a 2 … sec a1 sec a 2 sec a m

tan a m tan a1 tan a 2 … （利用①） tan a 2 tan a3 tan a m 1
2014 年全国高中数学联合竞赛试题（A 卷）
第 5 页共 11 页

2 2 2 2 2 2 5
48 3 。 64 4
二、解答题：本大题共 3 小题，共 56 分。解答应写出文字说明、证明过程或演算步骤。 2014A 9、（本题满分 16 分）平面直角坐标系 xOy 中， P 是不在 x 轴上的一个动点，满足条件：过 P 可作抛物线 y 4 x 的两条切线，两切点连线 l P 与 PO 垂直.设直线 l P 与直线 PO ， x 轴的交点分别为 Q, R 。 ⑴证明： R 是一个定点； ⑵求

2014年全国高中数学联赛试题及解答

全国高中数学联合竞赛试题（A 卷）一试一、填空题（本大题共8小题，每小题8分，共64分）1. 若正数,a b 满足()2362log 3log log a b a b +=+=+，则11a b+的值为________．答案：设连等式值为k ，则232,3,6k k ka b a b --==+=，可得答案108分析：对数式恒等变形问题，集训队讲义专门训练并重点强调过2. 设集合3|12b a b a ⎧⎫+≤≤≤⎨⎬⎩⎭中的最大元素与最小你别为,M m ，则M m -的值为______．答案：33251b a +≤+=，33b a a a+≥+≥，均能取到，故答案为5-分析：简单最值问题，与均值、对勾函数、放缩有关，集训队讲义上有类似题 3. 若函数()21f x x a x =+-在[0,)+∞上单调递增，则实数a 的取值范围是______．答案：零点分类讨论去绝对值，答案[]2,0-分析：含绝对值的函数单调性问题，集训队讲义专门训练并重点强调过4. 数列{}n a 满足12a =，()()*1221n n n a a n N n ++=∈+，则2014122013a a a a =+++______．答案：()1221n n n aa n ++=+，迭乘得()121n n a n -=+，()212232421n n S n -=+⨯+⨯+++，乘以公比错位相减，得2n n S n =，故答案为20152013．分析：迭乘法求通项，等差等比乘积求前n 项和，集训队讲义专门训练并重点强调过5. 正四棱锥P ABCD -中，侧面是边长为1的正三角形，,M N 分别是边,AB BC 的中点，则异面直线MN与PC 之间的距离是________．答案：OB 为公垂线方向向量，故距离为12OB =分析：异面直线距离，也可以用向量法做，集训队讲义专门练并重点强调过6. 设椭圆Γ的两个焦点是12,F F ，过点1F 的直线与Γ交于点,P Q ．若212PF F F =，且1134PF QF =，则椭圆Γ的短轴与长轴的比值为________．答案：不妨设焦点在x 轴（画图方便），设114,3PF QF ==，焦距为2c ，224a c =+，可得△2PQF 三边长为7,21,2c c +，过2F 作高，利用勾股可得5c =．分析：椭圆中常规计算，与勾股定理、解三角形、斯特瓦尔特等有关，集训队讲义训练过相关7. 设等边三角形ABC 的内切圆半径为2，圆心为I ．若点P 满足1PI =，则△APB 与△APC 的面积之比的最大值为________．答案：sin sin APB APC S PABS PAC ∠=∠，又两角和为60最大，即AP 与(),1I 切于对称轴右侧8. 设,,,A B C D 是空间中四个不共面的点，以12的概率在每对点之间连一条边，任意两点之间是否连边是相互独立的，则,A B 之间可以用空间折线（一条边或者若干条边组成）连结的概率为_______．答案：总连法64种，按由A 到B 最短路线的长度分类．长度为1，即AB 连其余随意，32种；长度为2，即AB 不连，ACB 或ADB 连，其余随意，ACB 连8种，故共88214+-=种（一定注意,ACB ADB 同时连被算了2次，根据CD 是否连有2种情形）；长度为3，两种情形考虑ACDB ，ACDB 连、,,AB CB AD 均不连只有1种，故连法为2种；综上，答案483644=分析：组合计数，分类枚举，难度不大但容易算错，集训队讲义训练过类似题目二、解答题（本大题共3小题，共56分）9. （本题满分16分）平面直角坐标系xOy 中，P 是不在x 轴上的一个动点，满足条件：过P 可作抛物线24y x =的两条切线，两切点连线P l 与PO 垂直．设直线P l 与直线PO ，x 轴的交点分别为,Q R ．（1）证明：R 是一个定点；（2）求PQQR的最小值．答案：（1）设(),P a b ，()()1122,,,A x y B x y ，0,0a b ≠≠，()11:2PA yy x x =+，()22:2PB yy x x =+ 故,A B 两点均适合方程()2by a x =+，利用垂直，可得2a =-，故交点为定点()2,0（2）∵2a =-，故,2PO PR b bk k =-=-，设OPR α∠=，则α为锐角，1tan PQ QR α=，利用两角差的正切公式，可得282PQ b QR b+=≥．分析：涉及圆锥曲线切点弦方程、两直线夹角公式、不等式求最值，集训队讲义专门训练并重点过10. （本题满分20分）数列{}n a 满足16a π=，()()*1arctan sec n n a a n N +=∈．求正整数m ，使得121sin sin sin 100m a a a ⋅⋅⋅=．答案：由反函数值域，知,22n a ππ⎛⎫∈- ⎪⎝⎭，2222132tan sec tan 1tan 3n n n n a a a +-==+==，1212112122311tan tan tan tan tan tan tan sin sin sin sec sec sec tan tan tan tan m m m m m m a a a a a a a a a a a a a a a a a ++⋅⋅⋅=⋅=⋅==故3333m =分析：涉及简单反三角函数、数列通项公式求法，集训队讲义对类似题目进行过训练11. （本题满分20分）确定所有的复数α，使得对任意复数()121212,,1,z z z z z z <≠，均有()()221122z z z z αααα++≠++．答案：转换命题为计算存在12,z z 使得相等时的充要条件存在12,z z 使得相等，记()()2f z z z αα=++，()()()()()1212121220f z f z z z z z z z αα-=++-+-=，则()()()1212122z z z z z z αα-=-++-，故12122222z z z z a ααα=++≥-->-，故2α<；若2α<，令12,22z i z i ααββ=-+=--，其中012αβ<<-，则12z z ≠，122i ααββ-±≤-+<，计算121212,2,2z z z z i z z i αββ+=--=-=-并代入，知()()12f z f z =．综上，满足条件的α为,2Z αα∈≥二试一、（本题满分40分）设实数,,a b c满足1a b c++=，0abc>．求证：14ab bc ca++<．a b c≥≥>，则1a≥1c≤．)ab bc ca c++-+⎭12c-，故有()()111122c c cc cc c⎛---≤-+-⎭⎝⎭由于1110,3333c-≥+≥>310c->，故原不等式成立．方法2：不妨设0a b c≥≥>，则13a≥c，设()()1f b ab bc ca ab c c=++=+-，()f b递增f⇔，()())()1f b ab a b a b⎛'=--=-⎝，()010f b'≥⇔≥⇔≤≥故()f b a；题目转化为21ac+=，a c≥，记()()222212g a a ac a a a=+-=+--()()262621g a a a⎫'=-+=-⎪⎭，由于13a≥1=，得1532a=，115,332a⎛⎫∈ ⎪⎝⎭时g'151,322⎫⎪⎝⎭时()g a在13或12max1124g g⎛⎫==⎪⎝⎭分析：一道偏函数化的不等式题，可以将其放缩为一元函数，也可以拿导数与调整法很快做出来，集训队讲义上两种方法都训练过．二、（本题满分40分）在锐角三角形ABC中，60BAC∠≠，过点,B C分别作三角形ABC的外接圆的切线,BD CE，且满足BD CE BC==．直线DE与,AB AC的延长线分别交于点,F G．设CF与BD交于点M，CE与BG交于点N．证明：AM AN=．答案：设△ABC三边为,,a b c，则BD CE a==，先计算AM，∵,BFD ABC BDF DBC BAC∠=∠∠=∠=∠，∴△BFD∽△CBA．由比例可知acDFb=，故BM BC bBDDF c==，故abBMb c=+，故由余弦定理知()2222cosab abAM c c A Bb c b c⎛⎫=+-⋅+⎪++⎝⎭222cosab abcc Cb c b c⎛⎫=++⎪++⎝⎭，整理可得此式关于,b c对称故可知22AM AN=分析：由于一旦,,a b c三边确定则图形固定，所以通过相似、比例、余弦定理计算的思路比较显然GF ED三、（本题满分50分）设{}1,2,3,,100S =．求最大的整数k ，使得S 有k 个互不相同的非空子集，具有性质：对这k 个子集中任意两个不同子集，若它们的交非空，则它们交集中的最小元素与这两个子集中的最大元素均不相同．答案：一方面，取包含1的、至少含2个元素的所有子集，共9921-个，显然满足题意；另外归纳证对于{}1,2,3,,S n =，任取()123n n -≥个子集，均存在两个的交集中最小的等于某个中最大的当3n =时，将7个非空子集分为三类：{}{}{}31,32,3，{}{}21,2，{}{}11,2,3．任取四个必有两个同类．假设n k =时命题成立，当1n k =+时，如果取出的2k 个子集中至少有12k -个不含1k +，利用归纳假设知成立；如果不含1k +的不足12k -，则至少有121k -+个含有1k +，而S 含有1k +的子集共2k 个，可以配成12k - 对，使得每对中除了公共元素1k +外，其余恰为1到n 的互补子集，这样，如果选出121k -+个，则必有两个除1k +外不交，故命题成立．综上，k 的最大值为9921-．分析：集合中的组合最值问题，比较常规的一道题，类似感觉的题集训队讲义在组合中的归纳法中有过四、（本题满分50分）设整数122014,,,x x x 模2014互不同余，整数122014,,,y y y 模2014也互不同余．证明：可将122014,,,y y y 重新排列为122014,,,z z z ，使得112220142014,,,x z x z x z +++模4028互不同余．答案：不妨设()mod 2014i i x y i ≡≡，1,2,,2014i =．下面对i y 序列进行1007次调整从而构成i z 序列：若i i x y +与10071007i i x y +++模4028不同余，则1007,i i y y +不调整；否则，交换1007,i i y y +位置，1,2,,2014i =．下证，进行1007次调整后，得到的i z 序列一定满足条件．任意挑选一列()1,2,,1007i i x z i +=，只需证其与10071007i i x z +++、()1,2,,1007,j j x z j j i +=≠、10071007j j x z +++模4028不同余即可由i z 构造方法，i i x z +与10071007i i x z +++不同余是显然的，因为不可能调整前后均同余，故只需看另两个；首先，对于不同的,i j ，2i 与2j 模4028不同余，否则会导致()mod 2014i j ≡．若,i j y y 均未调整，则()2mod 2014i i x z i +≡，()100710072mod 2014j j j j x z x z j +++≡+≡，故成立；若,i j y y 均已调整，则()21007mod 2014i i x z i +≡+，()1007100721007mod 2014j j j j x z x z j +++≡+≡+，故成立；若只有一个被调整过，不妨设i y 未调整、j y 已调整，则()2mod 2014i i x z i +≡， ()1007100721007mod 2014j j j j x z x z j +++≡+≡+，若()4028|21007i j --，则()1007|i j -，矛盾，故同样成立．综上，构造的i z 序列满足条件．全国高中数学联赛试题及解答高中联赛试题分析从试题类型来看，今年代数、几何、数论、组合4部分所占的比例为：代数37.3%，几何26.7%，数论16.7%，组合19.3%．这方面和历年情况差不多，但具体的知识点差别极大．一试第7题填空题可谓出人意表，虽然解答是用三角函数的方法处理的，对比历年试题，这题毫无疑问也是顶替了三角函数的位置．但本题却是一道彻头彻尾的平面几何题．从图中不难看出，最值情况在相切时取到，剩下的只是利用三角函数处理了一下计算上的问题．其余填空题中，第1~6题和往年出题风格类似，第8题概率计算略显突兀，本题几乎不需要用到计数的技巧，而是用单纯枚举的方法即可解决．放在填空题最后一题的位置不免显得难度不够．一试三道解答题中，第9题和第10题均不太难，所考知识点也和往年类似，无需多说．第11题又再次爆了冷门，考了一道复数问题．联赛已经多年没有考复数的大题了，许多学生都没有准备．可以说，这次一下戳中了学生的罩门．相信本题最终的得分率不容乐观．而本次试题中最特殊的要数加试中的平面几何题了．一反从1997年开始保持到如今的惯例，没有将平面几何题放在加试的第一题．而且本题实则为《中等数学》2012年第12期中的数学奥利匹克高中训练题中的原题，这无疑又让此题失色不少．今年的加试第一题放了一道不等式问题，虽然近几年不等式考察得较少，但是不等式一直是数学竞赛中的热门，在历年联赛中多有出现．考虑到本题难度并不大，放在联赛加试第一题还是非常合适的．全国高中数学联赛试题及解答加试第三题组合最值问题的出题风格一如既往，可以从很极端的情况下猜出答案，再进行证明．值得一提的是本题题干描述有歧义，最后一句“则它们交集中的最小元素与这两个子集中的最大元素均不相同”中，记最小元素为a ，两个最大元素为b 和c ．本句话中到底是指a 、b 、c 这3个数互不相同还是指a b ≠且a c ≠，无疑是容易让人误解的．希望今后联赛试题中能避免出现这种情况．加试第四题虽说考察的是数论中的同余知识，但更多考察的是构造法技巧，这也符合联赛加试中试题综合各方面知识的出题思想．从难度上来说本题难度不算太大，只要能从较小的数开始构造并寻找规律，找出2014的构造并不显得困难．但本题的出题背景无疑和以下题目相关：“n 为给定正整数，()122,,,n x x x 和()122,,,n y y y 均为1~2n 的一个排列，则112222,,,n n x y x y x y +++这2n 个数不可能模2n 互不同余．” 总的说来，本次联赛考察的知识点和往年比差别较大，但从试卷难度来说，和前两年是相当的．预计今年联赛的分数线可能比去年略低．。

不等式高中数学竞赛教案

不等式高中数学竞赛教案
一、教学目标：
1. 掌握不等式的基本性质和解不等式的方法；
2. 提高解决实际问题中的不等式的能力；
3. 增强学生对数学竞赛题型的理解和应对能力。

二、教学重点：
1. 不等式的基本性质；
2. 解不等式的方法；
3. 实际问题中的不等式应用。

三、教学内容：
1. 不等式的定义和基本性质；
2. 不等式的解法及解不等式的常用技巧；
3. 实际问题中的不等式应用。

四、教学步骤：
1. 引入不等式的概念，引导学生理解不等式与等式的区别和联系；
2. 教授不等式的基本性质和常见不等式的性质；
3. 演示解不等式的方法，包括一元一次不等式、一元二次不等式等；
4. 给学生布置练习题，巩固所学内容；
5. 引导学生尝试解决实际问题中的不等式，并与同学分享解题思路。

五、教学工具：
1. 教材《高中数学竞赛教程》；
2. 黑板、彩色粉笔；
3. 习题册、试卷。

六、教学评价：
1. 根据学生的课堂表现和作业完成情况评定成绩；
2. 鼓励学生多参加数学竞赛，提高解决问题的能力。

七、教学反思：
1. 随着教学内容的不断深入，要及时调整教学方法，关注学生的学习情况；
2. 在课堂上鼓励学生提问和讨论，促进学生之间的互动和合作。

以上是一份高中数学竞赛不等式教案范本，希望对您有所帮助。

祝您教学顺利！。

高中数学竞赛解题方法篇(不等式)

高中数学竞赛中不等式的解法摘要：本文给出了竞赛数学中常用的排序不等式，平均值不等式，柯西不等式和切比雪夫不等式的证明过程，并挑选了一些与这几类不等式相关的一些竞赛题进行了分析和讲解。

希望对广大喜爱竞赛数学的师生有所帮助。

不等式在数学中占有重要的地位，由于其证明的困难性和方法的多样性，而成为竞赛数学中的热门题型.在解决竞赛数学中的不等式问题的过程中，常常要用到几个著名的代数不等式：排序不等式、平均值不等式、柯西不等式、切比雪夫不等式.本文就将探讨这几个不等式的证明和它们的一些应用.1．排序不等式定理1设1212...,...n n a a a b b b ≤≤≤≤≤≤，则有1211...n n n a b a b a b -+++ (倒序积和)1212...n r r n r a b a b a b ≤+++（乱序积和） 1122 ...n n a b a b a b ≤+++（顺序积和）其中1,2,...,n r r r 是实数组1,2,...,n b b b 一个排列，等式当且仅当12...n a a a ===或12...n b b b ===时成立.（说明：本不等式称排序不等式，俗称倒序积和乱序积和顺序积和.）证明：考察右边不等式，并记1212...n r r n r S a b a b a b =+++。

不等式1212...nr r n r S a b a b a b ≤+++的意义：当121,2,...,n r r r n===时，S 达到最大值1122 ...n n a b a b a b +++.因此，首先证明n a 必须和n b 搭配，才能使S 达到最大值.也即，设n r n <且n b 和某个()k a k n <搭配时有.n n k n n r k r n n a b a b a b a b +≤+ （1-1）事实上， ()()()0n n n n nk r k n n r n r n k a b a b a b a b b b a a +-+=--≥不等式（1-1）告诉我们当nr n <时，调换n b 和n r b 的位置（其余n-2项不变），会使和S 增加.同理，调整好n a 和n b 后，再调整1n a -和1n b -会使和增加.经过n 次调整后，和S 达到最大值1122 ...n n a b a b a b +++，这就证明了1212...n r r n r a b a b a b +++1122 ...n n a b a b a b ≤+++.再证不等式左端,由1211...,...n n n a a a b b b -≤≤≤-≤-≤≤-及已证明的不等式右端，得1211(...)nn n a b a b a b --+++1212(...)n r r n r a b a b a b ≥-+++即 1211...n n n a b a b a b -+++1212...n r r n r a b a b a b ≤+++ .例1 （美国第3届中学生数学竞赛题）设a,b,c 是正数，求证：3()a b c a b ca b c abc ++≥.思路分析：考虑两边取常用对数，再利用排序不等式证明. 证明：不妨设ab c ≥≥，则有lg lg lg a b c ≥≥根据排序不等式有：lg lg lg lg lg lg a a b b c c a b b c c a ++≥++lg lg lg lg lg lg a a b b c c a c b a c b ++≥++ 以上两式相加，两边再分别加上 lg lg lg a a b b c c ++有 3(lg lg lg )()(lg lg lg )a a b b c c a b c c a b ++≥++++ 即 lg lg 3a b ca b cab c abc ++≥故 3()a b c a b cab c abc ++≥ .例2 设a,b,c R +∈，求证：222222333222a b b c c a a b c a b c c a b bc ca ab+++++≤++≤++. 思路分析：中间式子每项都是两个式子之和，将它们拆开，再用排序不等式证明. 证明：不妨设ab c ≥≥，则 222a b c ≥≥且111c b a≥≥根据排序不等式，有222222111a b c a b c c a b a b c++≥++222222111a b c a b c b c a a b c++≥++ 两式相加除以2，得222222222a b b c c a a b c c a b+++++≤++再考虑333ab c ≥≥，并且111bc ca ab≥≥ 利用排序不等式，333333111 a b c a b c bc ca ab ca ab bc++≥++333333111 a b c a b c bc ca ab ab bc ac++≥++ 两式相加并除以2，即得222222333222a b b c c a a b c c a b bc ca ab+++++≤++ 综上所述，原不等式得证.例3 设12120...,0...n n a a a b b b ≤≤≤≤≤≤≤≤，而1,2,...,n i i i 与1,2,...,n j j j 是1,2,...,n 的两个排列. 求证：1111r snnnni j r sr s r s a b a b r sr s ====≥++∑∑∑∑. （1-2）思路分析：已知条件中有两组有序实数，而式（1-2）具有“积和”形式，考虑使用排序不等式.证明：令 1s nj rs b d r s==+∑（r=1,2,...,n ）显然 12...n d d d ≥≥≥ 因为 12...n b b b ≤≤≤ ，且111...(1)1r n r n r ≤≤≤++-+ 由排序不等式1nsr s b d r s =≤+∑ 又因为 12...n a a a ≤≤≤所以 11rnnr r i r r r a d a d ==≤∑∑且111nnnsr r r r s r b a a d r s ===≤+∑∑∑（注意到r a ≥0）故11111r ssrn nn nni j j iri rr s r s r a b b a a dr s r s =======++∑∑∑∑∑11111nn nn ns r s r r r r r s r s b a ba d a r s r s=====≥≥=++∑∑∑∑∑ 故原式得证.2.均值不等式定理2 设12,,...,n a a a 是n 个正数，则()()()()H n G n A n Q n ≤≤≤称为均值不等式.其中，121()111...nH n a a a =+++，()G n =12...()na a a A n n+++=，()Q n =分别称为12,,...,n a a a 的调和平均数，几何平均数，算术平均数，均方根平均数. 证明：先证 ()()G n A n ≤.记c= i ia b c=，则原不等式12...n b b b n ⇔+++≥其中 12121...( (1)n n b b b a a a c == 取 12,,...,n x x x 使 11212123,,...,,n n n x x xb b b x x x --=== 则 1.n n x b x = 由排序不等式，易证111221......n n n n x x x b b b n x x x -+++=+++≥下证()()A n Q n ≤因为 222212121...[(...)n n a a a a a a n+++=+++22212131()()...()n a a a a a a +-+-++-2222232421()()...()...()n n n a a a a a a a a -+-+-++-++-]2121(...)n a a a n≥+++ 所以12...n a a a n +++≤从上述证明知道，当且仅当12...n a a a ===时，不等式取等号.下面证明 ()()H n G n ≤对n 个正数12111,,...,na a a ，应用 ()()G n H n ≤，得12111...n a a a n +++≥即 ()()H n G n ≤（等号成立的条件是显然的）.例4已知2201,0a x y <<+=，求证：1log ()log 28x y a a a a +≤+. 证明：由于 01a <<，0,0x y a a >>，有xy aa +≥=从而log ()log log 22xy a a a x ya a ++≤=+下证128x y +≤ ，即 14x y +≤。

2014年高中数学联赛安徽省赛区试题及解答

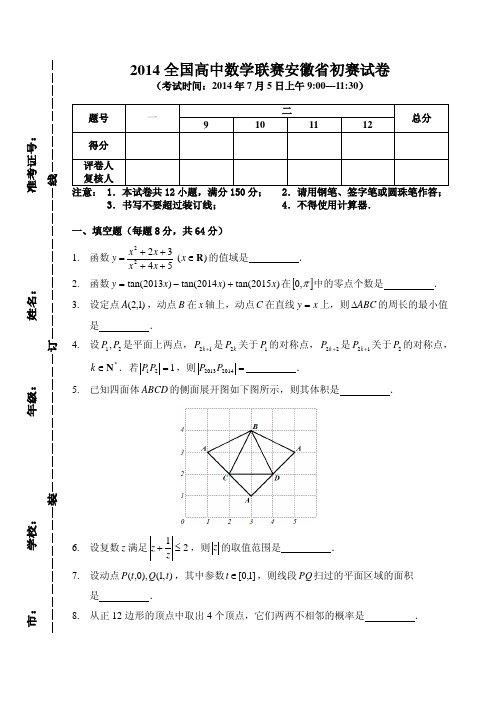
c
c3 c
c
这与ω 是无理数矛盾．
-----22 分
设被取出的 4 个顶点的编号从小到大为 a,b, c, d ．若它们两两不相邻，则有
x = b − a − 2 ≥ 0，y = c − b − 2 ≥ 0，z = d − c − 2 ≥ 0
当a
= 1 时，满足
d
≤ 11即
x
+
y
+
z
≤
4
的 (x,
y,
z)
共有
C
3 7
=
15 个；
当a
≥
2
时，满足
d
≤ 12 即
是整数，这与ω ∈ (1,2)矛盾．因此，ω 是无理数．
-----13 分
（2）假设ω 还满足 aω 2 + bω + c = 0 (a,b, c ∈ Z, a ≠ 0) ，则有
aω 2 + bω + c = 0 ω 3 − ω −1 = 0
(1) . 将第（1）式乘ω 减去第（2）式乘 a 得
(2)
1 3
单调增，在
x=−源自1 3处取得极大值
2 33
−1<
0 ，在 −
1, 3
1 3
单调减，在
x
=
1 处取得极小值 3
−
2 33
−1
<
0
，在 −
∞,−
1 3
单调增．再由
f
(1)
=
−1 <
0，f
(2)
=
5
>
0 知，
方程 f (x) = 0 有唯一的实根ω ∈ (1,2)．

2014年全国高中数学联赛江苏赛区复赛参考答案与评分细则（一试）[1]

2014年全国高中数学联赛江苏赛区复赛参考答案与评分细则（一试）[1]2014年全国高中数学联赛江苏赛区复赛参考答案与评分细则一试一、填空题（本题满分64分，每小题8分）1．在△ABC中，若c cos B＝12，b sin C＝5，则c＝．答案：13．解：根据正弦定理，得c sin B＝b sin C＝5，所以c2＝(c cos B)2＋(c sin B)2＝132，从而c＝13．2．函数f(x)＝x＋1(x+1)3＋1(x＞0)，则函数取得最小值时，所对应的x值是．答案：43－1．解：由f(x)＝x＋1(x+1)3＋1＝13(x＋1)＋13(x＋1)＋13(x＋1)＋1(x+1)3≥44(13)3，等号当且仅当13(x＋1)＝1(x+1)3，即x＝43－1．（本题也可求导）3．对于任意的实数a∈(－2，4]，都有x2－ax＋9＞0成立，则实数x的取值范围为．答案：R．解：当a∈(－2，4]时，△＝a2－36＜0，故x2－ax＋9＞0恒成立，从而x的取值范围是R．4．已知等比数列{a n}的公比为q，前n项和S n＞0（n＝1，2，3，…），则q的取值范围是．答案：(－1，0)∪(0，＋∞)．解：因为S n＞0（n＝1，2，3，…），所以a1＞0．当q＝1，S n＝na1＞0成立．当q≠1，S n＝a1(1－q n)1－q＞0（n＝1，2，3，…）恒成立，所以q∈(－1，0)∪(0，1)∪(1，＋∞)．综上q的取值范围是(－1，0)∪(0，＋∞)．5．已知5件产品中有3件合格品，2件次品．每次任取一个检验，检验后不再放回，恰好经过3次检验找出2件次品的概率为．答案：3 10．解：恰好3次找出2件次品，有三种情况：（1）第1次，第3次找出次品；（2）第2次，第3次找出次品，（3）前三次均为正品．若第1次，第3次找出次品的25×34×13＝110；若第2次，第3次找出次品的概率35×24×13＝110．若前3次均找出的是正品的概率35×24×13＝110，故恰好经过3次检验找出2件次品的概率为110＋110＋110＝310．6．点A 是椭圆x 2a 2＋y 2＝1(a ＞1)的上顶点，B 、C 是该椭圆上的另外两点，且△ABC 是以点A为直角顶点的等腰直角三角形．若满足条件的△ABC 只有一解，则椭圆的离心率的范围为．答案：(0，63]．解：设等腰直角三角形的一边所在直线方程为：y ＝kx ＋1(k ＞0)，它与椭圆的另一个交点B 的横坐标为－2ka 21＋a 2k 2，从而点C 的横坐标为2ka 2a 2＋k 2．由AB ＝AC ，得(1＋k 2)×4k 2a 4(1＋a 2k 2)2＝(1＋1k 2)×4k 2a 4(a 2＋k 2)2，化简得：k 3－a 2k 2＋ka 2－1＝0，由题意知，此方程的解只有k ＝1．而k 3－a 2k 2＋ka 2－1＝(k －1)［k 2－(a 2－1)k ＋1］＝0，要使上述方程有惟一的正数解k ＝1，则(a 2－1)2－4≤0，即1＜a ≤3（a ＝3时，方程的解惟一）．所以其离心率的取值范围是(0，63]．7．方程x ＋2y ＋3z ＝2014的非负整数解(x ，y ，z )的个数为．答案：339024．解：方程x ＋2y ＝k 的非负整数解(x ，y )个数为［k2］＋1，所以，方程x ＋2y ＝2014－3z 的非负整数解的个数为671∑z =0{［2014－3z 2］＋1}＝671∑z =0(1007－2z )＋671∑z =0［z2］＋672 ＝672×1007－670×672＋335×336＝339024．8．计算：2014∑k =1[－3＋8k ＋14]＝．答案：40115．解：令t ＝－3＋8k ＋14，则k ＝2t 2＋3t ＋1．因此[－3＋8k ＋14]＝n 当且仅当2n 2＋3n ＋1≤k ＜2(n ＋1)2＋3(n ＋1)＋1，n ∈N ．由于2×302＋3×30＋1＝1891，2×312＋3×31＋1＝2016，所以 2014∑k =1[－3＋8k ＋14]＝30∑n =1n [2(n ＋1)2＋3(n ＋1)＋1－(2n 2＋3n ＋1)]－30 ＝30∑n =1(4n 2＋5n )－30＝4(12＋22＋…＋302)＋5(1＋2＋…＋30)－30＝40115．二、解答题（本题满分16分）设数列{a n }的前n 项和为S n ，a 1≠0，2S n +1－3S n ＝2a 1，n ∈N *．（1）证明数列{a n }为等比数列；（2）若a 1，a p (p ≥3)两项均为正整数，且存在正整数m ，使a 1≥m p －1，a p ≤(m ＋1) p －求a n ．解：（1）由题意2S 2－3S 1 =2a 1，得2a 2－3a 1=0．由a 1≠0，得 a 2a 1＝32．………………………… 2分又 2S n +1－3S n ＝2a 1，2S n +2－3S n +1＝2a 1，得 2a n +2－3a n +1＝0，n ∈N *．由a 1≠0，得a n +1≠0，故a n +2a n +1＝32．所以数列{a n }为等比数列．………………………… 6分（2）由（1）知a p =a 1×(32p －1．因为a 1，a p ∈N *，所以a 1=k ×2p －1，k ∈N *，从而a p = k ×3 p －1．………………………… 10分由a 1≥m p －1，a p ≤(m ＋1) p －1，得k ×2p －1≥m p －1，k ×3p －1≤(m +1) p －1，即m ≤2×p －1k ，m ＋1≥3×k ，作差得1≥p －1k ，即k ≤1，所以k ＝1．所以 a n ＝2p －1×(32)n －1．………………………… 16分已知动点A ，B 在椭圆x 28＋y 24＝1上，且线段AB 的垂直平分线始终过点P (－1，0)．（1）求线段AB 中点M 的轨迹方程；（2）求线段AB 长度的最大值．解：（1）设点A ，B 的坐标为A (x 1，y 1)，B (x 2，y 2)，线段AB 的中点M 的坐标为(x 0，y 0)．当AB 与x 轴垂直时，线段AB 的中点M 的坐标为(－2，0)．当AB 与x 轴不垂直时，因为点A ，B 在椭圆x 28＋y 24＝1上，所以x 128＋y 124＝1，x 228＋y 224＝1．从而(x 1－x 2)(x 1＋x 2)8＋(y 1－y 2)(y 1＋y 2)4＝0，即y 1－y 2x 1－x 2＝－x 02y 0．因为线段AB 的垂直平分线始终过点P (－1，0)，所以y 1－y 2x 1－x 2×y 0x 0＋1＝－1，从而x 0＝－2．即线段AB 中点M 的轨迹方程为x ＝－2，－2＜y ＜2．…………………… 8分（2）当AB 与x 轴垂直时，AB ＝22．当AB 与x 轴不垂直时，由（1）知，直线AB 的方程为y －y 0＝1y 0(x ＋2)．…………………… 12分由y －y 0＝1y 0(x ＋2)，x 28＋y 24＝1，得(y 02＋2)x 2＋4(y 02＋2)x ＋2y 04＋8＝0．所以x 1＋x 2＝－4，x 1x 2＝2y 04＋8y 02＋2．从而AB ＝(1＋1y 02)×[16－4×2y 04＋8y 02＋2])＝8(y 02＋1)(2－y 02)y 02＋2＝22×－[(y 02＋2)＋4y 02＋2]＋5，其中－2＜y 0＜2，且y 0≠0，所以AB ＜22．所以线段AB 长度的最大值为22．…………………… 20分设a ，b ，c ，d 都是整数，p ＝a 2＋b 2是素数．如果p |c 2＋d 2，证明：c 2＋d 2p 可以表示为两个整数的平方和．证明：因为p | c 2＋d 2，所以c 2＋d 2＝pm ，其中m 为整数．于是m ＝c 2＋d 2p ＝(c 2＋d 2)(a 2＋b 2)p 2＝(c ＋d i)(c －d i)(a ＋b i)(a －b i)p 2，一方面，m ＝(c ＋d i)(c －d i)(a ＋b i)(a －b i)p 2＝(ca －db )2＋(da ＋cb )2p 2，（1）另一方面，m ＝(c ＋d i)(c －d i)(a ＋b i)(a ＋b i)p 2＝(ca ＋db )2＋(da －cb )2p 2，（2）…………………………………… 10分注意到(ca ＋db )(ca －db )＝c 2a 2－d 2b 2＝(pm －d 2)a 2－d 2b 2 ＝pma 2－d 2(a 2＋b 2) ＝p (ma 2－d 2)．因为p 是素数，所以ca ＋db 和ca －db 中至少有一个数能被p 整除．……………………………… 15分当ca －db 能被p 整除时，令ca －db ＝pt ，t 是整数，根据（1），因为m 是整数，所以da ＋cb 也被p 整除．令da ＋cb ＝ps ，s 是整数，则c 2＋d 2p ＝m ＝t 2＋s 2．当ca ＋db 能被p 整除时，同理可证：c 2＋d 2p 也可以表示为两个整数的平方和．……………………………… 20分。

2014年全国高中数学联赛加试_A卷_试题及参考答案

在三角形Ａ由余弦ＢＭ中，ＢＭ＝Ｂ＋Ａ， ∠Ａ定理得
２２ａｂａｂｃ（２２ＡＭ２＝ｃ＋（ｃｏｓＡ＋Ｂ）２－）ｂ＋ｃｂ＋ｃ２２２２２ａｂａｂｃ·ａ＋ｂ－ｃ２２＝ｃ＋（２＋）ｂ＋ｃ２ａｂｂ＋ｃ
数学竞赛之窗
ＭＣＢＣＢＤＡＣＬＣ，＝＝＝＝ＭＦＦＤＦＤＡＢＬＢ
因此ＬＭ ∥ＢＦ．同理，由此推出ＬＮ ∥ＣＧ．
１［２（２２２２２）＝（＋ｃ＋ａｂ＋ｃ（ａ＋ｂ２ｃｂ）ｂ＋ｃ
２）（）］－ｃｂ＋ｃ
ｚｘｓｓ．ｃｂｔ．ｃｎｋｉ．ｎｅｔｚｘｓｓｈｉｎａｏｕｒｎａｌ．ｎｅｔ．ｃｎ网址：电子邮箱：＠ｃｐｊ
·２８·
中学生数学 ·２高中）０１５年１月上 · 第５０５期（
ｎ－１
若不然，我们有ｘｍｏｄｉ＋ｙｉ＝ｘｉ＋ｋ＋ｙｉ＋ｋ（，，两式相加可得４ｋ）ｘｘｍｏｄ４ｋ）ｙｙｉ＋ｉ＋ｋ ≡ ｉ＋ｋ＋ｉ（，于是ｘ，但２ｘ２ｘｍｏｄ４ｋ）ｘｍｏｄ２ｋ）ｉ≡ ｉ＋ｋ（ｉ≡ ｉ＋ｋ（ …，互不同余，特别地，ｘｘｘ０１４（＝２ｋ）１，２，２０１４模２，矛盾．ｘｘｍｏｄ２ｋ）ｉｉ＋ｋ（由上述构造方法知ｚ …，ｚｚｙ１，２，２ｋ是ｙ１，２， …，记ｗ …，下面ｘｚｉ＝１，２，２ｋ．ｙ２ｋ的排列．ｉ＝ｉ＋ｉ， …，这只需证明，验证ｗ１，ｗ２，ｗ２ｋ互不同余．ｋ模４对任意整数ｉ、、ｉ＋ｋ、模１≤ ｉｗｗｗ＜ｊ，ｊ≤ｋ，ｉ、ｊｗｊ＋ｋ（４ｋ两两不同余＊）注意，前面的构造方式已保证，（ｏｗｍｏｄ４ｋ）ｗｄ４ｋ）ｉｗｉ＋ｋ（ｊｗｊ＋ｋｍ（＊＊）情形一：且ｚ则由前面的构造方ｚｙｙｉ＝ｉ，ｊ＝ｊ．式可知，ｗｗｉ（ｍｏｄ２ｋ）ｊｉ≡ ｗｉ＋ｋ ≡ ２ｊ ≡ｗｊ＋ｋ ≡ ２（）ｍｏｄ２ｋ．由于２，故易知ｗｉｍｏｄ２ｋ）２ｊ（ｉ与ｗｉ＋ｋ模及ｗｊ＋ｋ模２从而２ｋ不同余，ｗｋ不同余，ｉ＋ｋ与ｗｊ再结合（可见（得证．模４ｋ更不同余，＊＊）＊）情形二：且ｚ则由前面的构ｚｙｙｉ＝ｉ＋ｋ，ｊ＝ｊ＋ｋ．造方式可知，ｗｗ２ｉ＋ｋ（ｍｏｄ２ｋ）ｊｉ≡ｗｉ＋ｋ ≡ ｊ ≡ｗｊ＋ｋ ≡２）＋ｋ（ｍｏｄ２ｋ．同样有ｗ及ｗｉ＋ｋ模２ｋ不同余，ｗｉ与ｗｉ＋ｋ与ｊ与情形一相同地可知ｗｊ及ｗｊ＋ｋ模２ｋ不同余．（得证．＊）情形三：且ｚ（ｉ＝ｙ且ｚｚｙｙｉ＝ｉ，ｉ＋ｋ，ｊ＝ｊ＋ｋｚｊ＝的情形与此相同）则由前面的构造方式可知．ｙｊ，ｗｗ２ｉ（ｍｏｄ２ｋ）ｊ＋ｋｉ≡ｗｉ＋ｋ ≡ ｊ ≡ｗｊ＋ｋ ≡２（ｍｏｄ２ｋ）．由于ｋ是奇数，故２），更有２ｉｋ（ｍｏｄ２ｉ２ｊ＋，因此仍然有ｗ及ｗｊ＋ｋ模ｋ（ｍｏｄ２ｋ）２ｊ＋ｉ与ｗｊ及ｗｊ＋ｋ模２从而２ｋ不同余，ｗｋ不同余．ｉ＋ｋ与ｗｊ（得证．＊）因此本题得证．

2014年全国高中数学联合竞赛一试试题(B卷)解析

如图，l3
:
x0x 4
+
y0y
=
1，
令 x = −2 得 E −2, 2 + x0 . 2y0
令 y = −1 得 D 4(1 + y0), −1 . x0
则 |EA| = 2 + x0 ，
|AC |
2y0
|CB| = |BD|
x0 ，|DP | = 2(1 + y0) |P E|
y0 + 1
2 + x0 2y0
所以函数 xg(x) 的图像与 x 轴所围成图形的面积是 1 · 1
1
2
π=
π.
222
16
二、解答题：本大题共 3 小题，满分 56 分. 解答应写出文字说明、证明过程或演
算步骤.
第3页共5页
9. 设数列 {an} 的前 n 项和 Sn 组成的数列满足 Sn + Sn+1 + Sn+2 = 6n2 + 9n + 7
1，tan ∠P F1F2
=
1 2
,
tan
∠P
F2F1
=
−2.
则
a
=
.
解答
作 P M ⊥ x 轴，设 |F2M | = x，则
tan ∠P F2M = 2 ⇒ |P M | = 2|F2M | = 2x，
tan
∠P F1F2
=
1 2
⇒
|F1M |
=
2|P M |
=
4x，
于是 |F√1F2| = 3x ⇒ S△P F1F2 = 3x2 = 1
⇒x=
3 3
⇒
|F1F2|

2014年全国高中数学联赛一试二试试题整理详解汇编(一试二试为A卷)(教师版)

一、填空题（本大题共8小题，每小题8分，共64分） 1.若正数b a ,)log(log 3log 232b a b a +=+=+,则ba 11+的值为__________. 【答案】1082.设集合}21|3{≤≤≤+b a b a中的最大值与最小值分别为m M ,，则m M -=_________. 【答案】523-【解析】33125,1,2 5.1a b b a b M a ≤≤≤+≤+====由知，当时，得最大元素 33322332 3.b a a a b m a a a+≥+≥⋅====又，当时，得最小元素 3.若函数|1|)(2-+=x a x x f 在),0[+∞上单调递增，则a 的取值范围为_______. 【答案】[-2,0].【解析】2[1,)()1, 2.2af x x ax a a +∞=+-≤≥-在上，单调递增，等价于-即在 2[0,1](),00.2af x x ax a a =+-≤≤上，单调递增等价于-，即[2,0].a -因此实数的取值范围是 4.数列}{n a 满足)(1)2(2,211⋅+∈++==N n a n n a a n n ，则2013212014...a a a a +++=_________. 【答案】20152013. 【解析】122(1)2(1)21n n n n n n a a a n n n --++==⋅=⋅⋅⋅-112(1)2232(1).12n n n a n n n -+⋅=⋅⋅⋅⋅⋅=+- {},n n a n S 记数列的前项和为则2n-1=2+23+24++21)n S n ⨯⨯⋅⋅⋅+（23n=22+23+24++21)n S n ⨯⨯⨯⋅⋅⋅+所以2（122(1)(2222)n n n n S n --=+-++⋅⋅⋅++将上面两式相减，得2(1)22.n n n n n =+-=201320142013122013220152015.220132013aa a a⨯==++⋅⋅⋅+⨯故5.已知正四棱锥ABCDP-中，侧面是边长为1的正三角形，NM,分别是边BCAB,的中点，则异面直线MN与PC之间的距离是_____________.【答案】24【解析】设底面对角线AC,BD交于点O，过点C作直线MN的垂线，交MN于点H.由于PO是底面的垂线，故PO⊥CH，又AC⊥CH，所以CH与平面POC垂直，故CH⊥PC.因此CH是直线MN与PC的公垂线段，又CH=22,24CN=MN PC故异面直线与之间的2.4距离是6.设椭圆Γ的两个焦点是21,FF，过点1F的直线与Γ交于点QP,，若||||212FFPF=，且||4||311QFPF=，则椭圆Γ的短轴与长轴的比值为__________.【答案】26726,b T=因此椭圆的短轴与长轴的比值为26ba=7.设等边三角形ABC 的内切圆半径为2，圆心为I 。