点的存在性的证明方法的分析
零点的存在性定理

06 参考文献
参考文献
01
[1] 张三. (2018). 零点存在性定理研究. 科学出版社.
02
[2] 李四, 王五. (2020). 数学分析中的零点存在性定理及其 应用. 高等教育出版社.
03
[3] 刘海涛. (2015). 实数完备性与零点存在性定理. 清华大 学出版社.
THANKS FOR WATCHING
扩展二
总结词
探索零点存在性定理在多维空间的应用
详细描述
零点存在性定理主要应用于一维实数线上。然而,这 个定理也可以推广到多维空间中。通过研究高维空间 中函数的零点存在性,可以揭示出更多有趣的数学现 象和性质。
扩展三
总结词
将零点存在性定理与其他数学定理结合
详细描述
零点存在性定理可以与其他重要的数学定理结合使用, 以解决更复杂的问题。例如,它可以与极限理论、积分 理论等结合,用于证明更广泛的数学命题。这种结合可 以促进数学不同分支之间的交叉融合,推动数学的发展 。
证明方法二
总结词
利用极限的存在性和函数值的符号变化证明。
详细描述
首先,我们需要证明函数在某一点的极限存在,并且函数值从正变为负或从负变为正。这样,我们可 以确定函数在这一点附近有零点。通过分析函数在区间两端的取值和变化趋势,我们可以找到这样的 点,从而证明零点的存在性。
证明方法三
总结词
利用导数和函数的单调性证明。
感谢您的观看
推论一
推论一
如果函数在区间两端取值异号,则函数在此区间内至少存在 一个零点。
证明
假设函数在区间$[a, b]$两端取值异号,即$f(a) cdot f(b) < 0$。 根据连续函数的性质,函数在区间$[a, b]$上必存在至少一个零 点,使得$f(c) = 0$,其中$c in (a, b)$。
Banach空间上的不动点理论及其应用

Banach空间上的不动点理论及其应用Banach空间是数学中的一个重要概念,它在函数分析领域具有广泛的应用。
不动点理论是研究映射在自身上是否存在不动点的数学理论。
本文将介绍Banach空间上的不动点理论,探讨其应用领域和意义。
一、Banach空间的定义和性质Banach空间是一个完备的向量空间,具有一个范数,使得该空间中的任意Cauchy序列收敛于该空间中的某一元素。
Banach空间的一个重要性质是完备性,即任意柯西序列在该空间内收敛。
Banach空间的完备性对于不动点理论的推导和证明至关重要。
二、不动点理论的基本概念在Banach空间上,给定一个映射F,若存在一个元素x使得F(x) = x,则称x为F的不动点。
不动点理论研究的是映射在自身上是否存在不动点,并通过各种方法寻找和证明不动点的存在性和唯一性。
三、不动点理论的证明方法1. 压缩映射原理:若存在一个常数k (0<k<1),使得对于任意x和y,有d(F(x),F(y)) ≤ kd(x,y),其中d为Banach空间中的距离函数。
则F为压缩映射,且存在唯一的不动点。
2. 构造性证明:通过构造合适的映射函数,找到不动点的存在性和唯一性。
3. Brouwer不动点定理:对于n维球面上的连续映射,存在至少一个不动点。
4. Kakutani不动点定理:对于凸紧合集上的凸映射,存在至少一个不动点。
等等。
四、应用领域不动点理论在许多领域具有广泛的应用,包括:1. 微分方程:通过不动点理论,可以证明微分方程存在解,且解的存在是稳定的。
2. 经济学:不动点理论在经济学中的应用较为常见,特别是涉及到均衡分析和最优化问题。
3. 优化问题:通过将优化问题转化为不动点问题,可以使用不动点理论来解决各种优化问题。
4. 图像处理:不动点理论在图像处理中的应用,如图像恢复、压缩感知等方面具有重要意义。
5. 动力学系统:不动点理论在动力学系统中的应用广泛,通过不动点理论可以研究动力学系统的稳定性和渐进行为。
论文正文-浅谈函数的零点问题

学士学位论文题目浅谈函数的零点问题浅谈函数的零点问题摘要:浅谈函数零点问题实质上就是说,函数零点的存在性,零点唯一性,零点的个数问题及其应用的问题。
本文运用零点定理、罗尔定理及其推广和微分中值定理、介值定理等多个重要定理对函数零点存在性、唯一性、个数问题进行多方面的解答,结合典型例题分析、讨论并证明相关问题,得出解决此类问题的解决方法,使得今后在学习函数零点的过程中得到了简便、全面的答题策略。
关键词:函数零点定理 罗尔定理 唯一性 存在性 零点个数 一、预备知识1. 概念及定理函数零点定义:对于函数()y f x =,我们把使()0f x =的实数x 叫做函数()y f x =的零点。
二、零点的存在性问题2.1 在数学学习中,函数零点的存在性问题始终都是人们研究的热点可课题。
可以用零点定理解决,也能用罗尔定理、函数最值、函数的幂级数展开式及微分中值定理解决此问题。
(1)零点定理 :若函数在区间[,]a b 上的图像时连续不断的一条曲线,且满足()()0f a f b <,那么,函数()y f x =在区间(,)a b 内有零点,即存在(,)c a b ∈,使得()0f c =。
这个c 也就是方程()0f x =的实根。
零点定理的证明:不妨设()0,()0.f a f b <> 令{|()0,[,]}.E x f x x a b =<∈由()0f a <知,E ≠∅ 且b 为E 的一个上界, 于是 根据确界存在原理, 存在sup [,]E a b ξ=∈ ,下证()0f ξ=(注意到()0,()0,f a f b ≠≠ 故此时必有(),a b ξ∈)事实上,()1若()0,f ξ<则[,)a b ξ∈。
由函数连续的局部保号性知存在0,σ>对()1,,()0x f x ξξσ∈+<存在11,sup x E x E ∈>,这与sup E 为E 的上界矛盾;()2若()0,f ξ>则(,].a b ξ∈仍由函数连续的局部保号性知存在0,σ>对()1,,()0x f x ξσξ∈->存在1x 为E 的一个上界,且1,x ξ< 这又与sup E 为E 的最小上界矛盾。
数论的方法和技巧 04数论中的存在性问题

数论中的存在性问题知识要点与基本方法在数论问题中回答满足一些条件的某对象存在或不存在的问题我们称之为数论存在性问题.它与其它数学存在性问题在理论上是一样的,区别是,其内容是数论知识方面的. 基本方法:解决数论存在性问题没有什么死的方法,也没有什么固定的程式,所用知识是普遍的,采取的方法也是灵活多样的.但由于数论存在性问题是数学竞赛中难度较大的,并且又是常见的题型,因此,对其解决的方法我们给出大致的归纳如下:1.反证法. 2.数学归纳法. 3.按模分类. 4.高斯函数. 5.试验,猜想,证明. 6.构造法. (1)按归纳方式构造 (2)用阶乘构造 (3)用非十进制记数构造 7.数论知识的综合运用.赛题精讲1.关于反证法例1 已知n 是已确定的正整数,)(k f r =是使满足n r ≤≤1的整数r 与满足n k ≤≤1的整数k 对应的函数,且当21k k <时,恒有)()(21k f k f ≤.证明:存在整数)1(n m m ≤≤,使m m f =)(恒成立.【分析】 因n 的大小不知道,函数f 的对应关系情况复杂,故很难确定符合条件的m ,不妨用反证法.证明:若对任何n m ≤≤1的m ,均有m m f ≠)(,则由1)1(≥f 和1)1(≠f ,可知2)1(≥f .于是,2)1()2(≥≥f f ,即2)2(≥f ,又2)2(≠f .故3)2(≥f ,同理可得4)3(≥f ,…,n n f ≥-)1(,1)(+≥n n f .这与n n f ≤≤)(1矛盾.故,存在整数)1(n m m ≤≤,使m m f =)(.2.关于数学归纳法例2 在黑板上依次写出数a 1=1,a 2,a 3,…,法则如下:如果2-n a 为自然数且未写出过,则写21-=+n n a a ,否则就写31+=+n n a a ,证明:所有出现在该序列中的完全平方数都是由写在它前面的那个数加3得到的.【分析】 关键是根据在黑板上写数的法则,归纳证明:m k 5≤时,55+=+k k a a ,继而,考虑平方数被5除的余数特征.证明:首先用归纳法证明如下断言:“当m n 5=时,由1到n 的所有自然数全都被写出,且255-=m a m ,而对于任何m k 5≤,都必有55+=+k k a a .” 当n =5时,依据法则有 431121=+=→=a a a2223=-=→a a 5334=+=→a a 3245=-=→a a 6356=+=→a a .假定当m n 5=时,由1到5m 的所有整数均已被写出,且255-=m a m .于是,按下来的5个数就只能是1515+=+m a m ,4531525+=+=++m a a m m 2522535+=-=++m a a m m 5533545+=+=++m a a m m 3524555+=-=++m a a m m如此即完成了归纳过程.进而考虑到平方数被5除的余数只能是4、1和0,又显然出现在序列中的被5除余4,1和0的数,都是通过写在它前面的那个数加3得到的,因此命题得证.例3 证明:存在无穷多个合数n ,使得1123---n n 是n 的倍数. 证明:∵只要x 与y 为不相等的整数,k 为自然数,则k k y x y x --|∴要证1123---n n 可被n 整除,注意到n 为合数,可知,只要1|2-n t ① ∴t k n 21⋅=-则当视t x 23=,ty 22=时,就有k k k k k k n n y x tttt-=-=-=-⋅⋅--)2()3(2323222211可被n y x tt =-=-2223整除 于是123122--=-tt n ∴要①成立,只要13|22-tt下面用归纳法证明:对一切自然数t ,数132-t都可被22+t 整数. 当1=t 时,结论显然 假设对m t =时结论成立, 则当1+=m t 时,有 )13)(13(132221-+=-+mm m前一因子132+m 可被2整数,后一因子132-m由归纳假设可知可被22+m 整除.∴当1+=m t 时,132-t可被22+t 整除. 从而对一切自然数t ,数132-t可被22+t 整除. ∴存在无穷多个合数n ,使得1123---n n 是n 的倍数. 【评注】 注意到tt n 2223-=,2≥t ,则显然n 为合数. 因此:)23)(23()2()3(23231111111122222222222222---------+=-=-=-⋅⋅t t t t t t t t tt3.关于按模分类按模分类可以实现“大”向“小”,“多”向“少”,“无限”向“有限”,“无序”向“有序”,“不定”向“确定”的转化.例4 非常数的正整数无穷数列{a n }满足递推关系121+=+n n a a 或12-n a ,n =1,2,…,求证:数列{a n }中至少有一项为合数.【分析】本题关键是考察a n 的取值情况,a n 的取值由a 1确定,但a 2可有2个取值,a 3可有4个取值,……,a n 可有12-n 个取值,因此,无法确定a n .用什么办法可把不定的递推关系转化成确定的递推关系呢?我们相到了“模”.因a n 均为奇数)2(≥n ,故按mod 2分类不行,可考虑mod 3.证明:由于{a n }是递增数列,不妨设31>a (否则去掉前面若干项即可). (i)若01≡a (mod 3),则1|3a ,得证.(ii)若11≡a (mod 3),a 1为质数(若a 1为合数已得证) 对1212+≡a a ,有02≡a (mod 3),得证, 对1212-≡a a ,有12≡a (mod 3),从而, 对1223+≡a a ,有03≡a (mod 3),得证, 对1223-≡a a ,有13≡a (mod 3),从而, …或者得证,或者1≡n a (mod 3). 若都有121≡≡≡≡≡ n a a a (mod 3) 则121-=+n n a a于是)1(211-=-+n n a a ,从而1)1(211+-=+a a n n应用费马小定理,得01)1(1)1(211111≡+-≡+-≡-a a a a a (mod a 1) ∴1|1a a a于是1a a 为合数,得证.(iii)若21≡a (mod 3),可类似于(ii)进行讨论.4.关于高斯函数的应用][x y =叫高斯函数,记号[x ]表示不超过x 的最大整数.如0]215[=-,1]128.0[-=-,19]98.19[=等等.含有记号[x ]的数学问题,一方面因为它是整数,所以经常与数论问题联系在一起,再则[x ]满足不等式1][][1+<≤<-x x x x ,因而借助于不等式又容易使问题得到解决.数论问题中有一类是与高斯函数有关的存在性问题,解决是应抓住高斯函数的特殊性解题.下面的例子还得注意归纳法的应用.例 5 设非负整数列a 1, a 2, …, a 1999,对于任意的整数i , j ,且1999≤+j i ,有1++≤≤++j i j i j i a a a a a ,证明:存在实数x ,使得对于n =1,2,…,1999,有][nx a n =.分析与证明:本题是证明存在x ,使][nx a n =,根据高斯函数定义,应有11+<≤<-n n a nx a nx 即n a x n a nn 1+<≤ 这个不等式应对n =1,2,…,1999都成立.于是,x 应该同时属于1999个区间n a n [, ]1na n +,可以想象出来,如果x 存在,则x 应为na n的最大者. 我们取 }m a x {na x n=这样,只要证明对一切∈m {1,2,…,1999},都有nax m a n m ≥>+1 即可,也就是na m a nm >+1 n m ma n na >+(2)我们采用数学归纳法证明这个不等式. 当1==n m 时,式(2)成立. 设m , n 均小于k 时,式(2)成立. 当m , n 中较大的一个为k 时,有两种情况: (I )n =k ,此时设r qm n +=,m r <≤0,由已知有 q a qa a a a a a a r m r m m q r qm n ++≤≤+++≤++≤- 21)1(由归纳假设r m ma r ra >+,则n na r mq na mq r ra mqa mq ma mqa ma m m m m r m n +=++=+++<++≤故式(2)成立.(II )m =k ,设r qn m +=,n r <≤0 由题设,有r n r n m a qa a aq a +≥≥+≥ r n m na naq na +≥n r n n r n m ma n na ra ma n na nqa n na >++-=++≥+这最后一步是由归纳假设n r ra n na >+ 于是,式(2)成立.以上我们证明了式(2)成立,从而,对一连串区n a n [, ]1n a n +中,只要x 取na n 的最大者,就能满足题目要求.例 6 证明:对任一个自然数)2(≥k k ,存在一个无理数,使得对每一个自然数m ,1][-≡m r (mod k )【分析】 如何考虑结论1][-≡m r (mod k )呢?这相当于01][≡+m r (mod k ),但是带有取整记号不便于思考.应注意到一个事实,如果10<<s ,则1][+=+m m m r s r .于是,问题转化为是否存在这样的无理数r 和10<<s ,使得m m s r +能被k 整除.同时又知道这样一个事实,若s r +与B 都是整数,且s r +与rs 都能被k 整除时,对正整数m ,m m s r +也能被k 整除.这样,问题又转化为是否存在这样的无理数r 和10</<s ,使得s r +与rs 都是整数且能被k 整除.这使我们想到韦达定理.证明:首先证明,当s r +与rs 为整数,且能够被k 整除时,对所有正整数m ,m m s r +也是整数,且能被k 整除.设kp s r =+,kq rs =,其中k 是正整数,p , q 是整数,则 )2(22)(222222q kq k kq p k rs s r s r -=-=-+=+即22s r +是整数,且能被k 整除.假设s r +,22s r +,33s r +,…,11--+m m s r 都是整数且能被k 整除,由于 )())((2211----+-++=+m m m m m m s r rs s r s r s r则m m s r +是整数,且能被k 整除. 于是,用数学归纳法完成了证明.下面只需证明,存在这样的r 和s ,其中r 是无理数,s 满足10<<s ,s r +和rs 是整数,且能被k 整除,为此,考虑方程02=+-kq kpx x如果r , s 存在,且10<<s ,则必须满足不等式组 1240,042222<--<>-=∆kq p k kp kq p k 即 042>>>q p k qp 显然,对任一自然数)2(≥k k ,这样的整数q , p 是存在的. 为使r 是无理数,只要kq p k 422-不是完全平方数即可. 为此选择k q =,则)4(42222-=-p k kq p k当2=p 时,0422=-kq p k 与0422>-=∆kq p k 矛盾,∴2=p 不符合题目要求. 当3≥p 时,若42-p 是完全平方数,设224t p =-,则422=-t p ,有 4))((=-+t p t p由于t p +与t p -具有相同的奇偶性,所以不存在两个不同的偶数之积为4. 即42-p 不是完全平方数.从而2224k p k -不是完全平方数,这时r 就是无理数. 此时,10<<s ,则01][≡+=+m m m r s r (mod k )5.关于试验,猜想,证明的存在性问题例7 记kk I 1111=.求证:存在无穷多个正整数n ,使I 1,I 2,…,I n 除以n 给出互不相 同的余数.试验:I n :1,11,111,1111,…,k1111,….2不符合;3除以I 1,I 2,I 3的余数分别是1, 2,0;4,5,6,7,8均不符合;9除以I 1~I 9的余数分别是1~8及0;10,11也非所求.但12以后的试算就变得复杂,甚至不可能,停止.回顾我们试算的结果,可以作出猜想:r n 3=,∈r N *证明:(i)对r 的归纳法可证明r I r 3|3,但r I r 31|3/+(留给读者) (ii)用反证法证明I 1,I 2,…,I n 是mod n 的完全剩余类)3(r n =.若有r j i 3≤<,使j i I I ≡(mod )3r ,则由i j I 10=,i i j I I +-及(10, 1)3=r 知i j r I -|3 即存在正整数r k 3<,使k r I |3.令k 为最小的这种数,设s k p r +⋅=3,k s <≤0 ∵s k k p k I I I r ++++=-)11010()1(3 ,(规定I 0=0),又k r I |3,r I r 3|3 ∴s r I |3于是0=s ,有r k 3|,t k 3=,r t <≤1由(i)知t I t 3|3.但t I t 31|3/+,故k r I I t =/3|3.此与k r I |3矛盾. 例8 证明:存在无穷多个自然数n ,使得22|+n n ,12|1+-n n . 试验,显然,2≥n ,∴从2开始试算. 22|22+,12|122+-22|33+/,22|44+/,22|55+/ 22|66+且12|56+再往下试验,22|77+/,12|88+/,22|99+/如果再继续试验就麻烦了,不妨思考以上成立的两个数2和6. 6可以写成222+经检验22|22626++,12|12626++ 这是因为66226=+,65126=+,而)1222)(12(2)12(2225556056566+++++=+=+于是22|6666+因)1222)(12(1)2(1255460611666+-+-+=+=+ 又有12|6566+,由以上试验可以猜想出,当22|+n n 且12|1+-n n 时, 22|222++nn ,且12|122++nn下面我们证明这个结论,这就把讨论存在性问题转化为一个结论确定的论证性问题. 证明:显然,22|22+,12|122+- 假设存在∈n N ,使得22|+n n 且12|1+-n n 由22|+n n 可知,n |2,n |4/由12|1+-n n 可知,存在∈k N ,使得k n n )1(12-=+ 其中1|2-/n ,k |2/M n k n n)12(12121)1(2+=+=+--,∈M N于是12|1221++-nn对此式两边同乘以2,有22|2222+++nn由于22|+n n ,n |4/,则nt n =+22,t 为奇数.T n nt n)12(121222+=+=++,∈T N即有12|1222+++nn于是,当22|+n n ,12|1+-n n ,n |2,n |4/时,必有22|2222+++nn 且12|1222+++nn因此,由2=n 可生成6222=+,66226=+,2266+,…等等.如此下去,可以得到无穷多个符合题目要求的自然数n .6.构造法首先指出的是,构造的思索过程,实如同摸着石头过河,走一步看一步,通过不断的修正“凑”出符合要求的对象.(1)按归纳方式构造例9 证明,对任意∈n N ,2≥n ,存在一个由n 个整数构成的集合ξ,使得对ξ中的任意两个不同的数a ,b ,均有ab b a |)(2-.证明:我们对n 采用归纳的构造 当2=n 时,取=2ξ{1,2}即可设k n =时,存在含k 个元素的集合=k ξ{a 1,a 2,…,a k } 满足条件,即对任意k j i ≤<≤1,均有j i j i a a a a |)(2-令A =a 1…a k ,考虑如下的1+k 个数 A ,A +a 1,A +a 2,…,A +a k构成集合1+k ξ,则容易验证1+k ξ满足题中的条件.【评注】上述归纳的关键是令A =a 1…a k ,选集合=+1k ξ{A ,A +a 1,A +a 2,…,A +a k } 例10 对任意2≥n ,证明,存在n 个不同的正整数a 1,a 2,a 3,…,a n 使得 )(|)(j i j i a a a a +- j i ≠(,i ,j =1,2,…,n )证明:用归纳方式构造当2=n 时,取a 1=1,a 2=2,即可假设已有n 个正整数a 1<a 2<…<a n !符合要求,则1+n 个数 a n !,a n !+a 1,a n !+a 2,…,a n !+a n 符合要求事实上 +∈+⋅=-+++N )!(2!)!(!)!(i in n i n n i n a a a a a a a a a (i =1,2,…,n )又不妨设j i >,(i , j =1,2,…,n ),则 ji ji n j n i n j n i n a a a a a a a a a a a a a A -++=+-++++=)!(2)!()!()!()!(∵)(|)(j i j i a a a a +-(归纳假设),且)!(2|)(n j i a a a -,所以∈A N + (2)用阶乘构造例11 证明:可把正整数集N +分拆成两个子集A ,B ,使得A 中任3个数都不成等差数列,而且不存在由B 中无穷多个数构成的等差数列.证明:令∈+=n n n A |!{N +},A N B -=若B 中含有首项为a 1,公差为d 的无限长等差数列,则此数列中的一项 A d a d a d d d a a ∈+++=+++)()!(]1)!([1111与所设矛盾,故B 中不会无穷多项组成的等差数列. 又对任意正整数1≥>>k n m ,有)!(2)!()!(2)!(3)!(!)!()!(n n m n n m n m n m m m m m k k +>++=+≥+≥+>+++所以,A 中任3数不成等差数列. (3)采用非十进制记数构造例12 证明:可以用4种颜色对正整数1,2,…,2000染色,使它不会有由7个同色数组成的等差数列.证明:问题等价于把集合=ξ{1,2,…,2000}分折成4个非空子集M 1,M 2,M 3,M 4,使得)(j i M M j i ≠=φ ,ξ=4321M M M M因为2000763>⨯,所以,ξ中的每个数都可以表示成至多4位的7进制数(abcd )7.这里a ,b ,c ,d ∈(0, 1, 2, …, 6)设ξ∈=77)(|){(abcd abcd A i ,i b ≠,i c ≠,}i d ≠,i =1,2,3,4对任意ξ∈x ,由于每个7进制正整数末3位数上至少有1,2,3,4中的一个数字未出现,例如x 的末3位数中未出现4,则4A x ∈,所以,ξ=4321A A A A下证:集合A i (i =1, 2, 3, 4)中不含由7项构成的等差数列.反设某个A i 中含有由7项构成的等差数列:a , a +d , …, a +6d (a 为首项,d 为公差). 若d |7/,d |72/,仿上可得到这个等差数列中必有一项,它的7进制表示中从右数的第三位数字为i ,矛盾.若d |73,则20007663>⨯≥d ,矛盾.综上证得集合A i (i =1, 2, 3, 4)中任意7个数不成等差数列,最后,令11A M =,122A A M =,2133A A A M =,32144A A A A M =,得到符合要求的分拆. 7.关于数论知识的综合运用例13 确定是否存在满足下列条件的正整数n ,n 恰好能够被2000个互不相同的质数整除,且12+n 能够被n 整除.【分析】 本题是数学归纳法,整除知识,代数变形的综合运用.由于题目中所要确定的n ,是恰好可被2000个互不相互的质数整除,故可考虑用数学归纳法证明一个更一般的命题.证明:先证明一个引理.引理 对于每一个整数2>a ,存在一个质数p 满足1|3+a p ,但p 不能整除1+a .证:假设对某个2>a ,引理不成立,则12+-a a 的每一个质因子都要整除1+a ,而恒等式3)2)(1(12+-+=+-a a a a 说明能够整除12+-a a 的唯一质数是3,换言之,12+-a a 是3的方幂,又∵从假设有3整除1+a ,即1+a 是3的倍数,∴2-a 也是3的倍数,于是12+-a a 能够被3整除,但不能被9整除,故得12+-a a 恰等于3.另一方面,由2>a 知312>+-a a ,∴矛盾,从而引理得证. 按下来证明一个更一般的命题:“对于每一个自然数k ,一定存在一个自然数n 满足).12(|+n n n |3,且n 恰好能够被k 个互不相同的质数整除.”当1=k 时,3=n 即可使命题成立. 假设当m k =,1≥m 时,命题成立.当1+=m k 时,因为)12(|+n n ,n 可以写成1(3≥⋅l t l ,t |3/)的形式,则n 必为奇数, 且)122(|32+-n n利用恒等式 )122)(12(1223+-+=+n n n n 可知 )12(|33+n n根据上面引理,存在一个奇质数p 满足)12(|3+n p .但p 不能整除12+n ,于是,自然数)(3)1(k n p k n ⋅=+,即满足命题对于1+k 的要求,归纳法完成.例14 (1)正整数p ,q ,r ,a 满足2ra pq =,且r 是素数,p ,q 互素.证明:p ,q 中有一个是完全平方数;(2)是否存在素数p ,使得)12(1-+p p 是完全平方数.解:(1)设m k m k k p p p p 2121=,n s n s s q q q q 2121=,l t l t t a a a a 2121=,其中p i , q j , a h 均为素数,且(p i , q j )=1,则有l n m t l t t s n s s k m k k a a ra q q q p p p 222212121212121 ⋅=⋅⋅⋅由于r 是素数,则p ,q 中不被r 整除的那个数一定是完全平方数. (2)设21)12(b p p =-+当2=p 时,则142=b ,不可能,当2>p 时,设12+=q p ,由于2|b p ,所以b p |,设pa b =,则有221)12(a p p p =-+,即211)12)(12(pa p p =+-++由于p 是素数,12(1-+p ,1)121=++p ,由(1)可知2112c p =-+或2112c p =++ 若2112c p =-+,则1221+=+c p .由于1≥p ,则12|4+p ,而)1(|42+/c ,矛盾.若2112c p =++,则)1)(1(1221+-=-=+c c c p ,于是121q c =-,221q c =+,且21q q <,121+=+q q q ,所以,有22212=-q q ,2)12(2121=--q q q若121=q ,则01=q ,21212=--q q 矛盾.若221=q ,则11=q ,11212=--q q ,112=-q q ,22=q ,于是2=q ,5=p ,635)12(1⨯=-+p p 不是完全平方数.因此,不存在正整数p ,使得)12(1-+p p 是完全平方数.。
4 第二部分 专题五 第4讲 圆锥曲线中的定点、定值、存在性问题

上一页
返回导航
下一页
第二部分 专题五 解析几何
15
解:(1)由题意知,直线 AB 的方程为 y=x+p2.
由y=x+p2,得 x2=2py
y2-3py+p42=0.
设 A(x3,y3),B(x4,y4),则 y3+y4=3p. 所以|AB|=y3+y4+p=4p=16,所以 p=4. 所以抛物线 C 的方程为 x2=8y.
上一页
返回导航
下一页
第二部分 专题五 解析几何
12
因为|D→A+D→B|=|D→A-D→B|,所以D→A⊥D→B,即D→A·D→B=0, 即(x1+2,y1)·(x2+2,y2)=x1x2+2(x1+x2)+4+y1y2=0, 所以43m+2-4k122+2×3-+84mkk2+4+3m32+-41k22k2=0, 所以 7m2-16mk+4k2=0, 解得 m1=2k,m2=27k,且均满足 3+4k2-m2>0, 当 m1=2k 时,l 的方程为 y=kx+2k=k(x+2),直线恒过点(-2,0),与已知矛盾; 当 m2=27k 时,l 的方程为 y=kx+27k=kx+27,直线恒过点-27,0. 综上,直线 l 过定点,定点坐标为-27,0.
上一页
返回导航
下一页
第二部分 专题五 解析几何
8
思维方法 解得 k=-m+2 1.【关键 2:设出直线 l 的方程,并与椭圆方程联立消去 y 得到关于 x 的一元二次方程,利用根与系数的关系及条件找到直线 l 中两个参数的关系】 当且仅当 m>-1 时,Δ >0,于是 l:y=-m+2 1x+m,即 y+1=-m+2 1(x-2),所以 l 过定点(2,-1). 【关键 3:将 k=-m+2 1代入直线 l 的方程,变形得到直线所过定点(2,-1)】
高中数学中常见的证明方法

高中数学中常见的证明方法一、直接证明法直接证明法是最基本也是最常见的证明方法之一。
它通过对所要证明的命题进行逻辑推理和分析,直接给出证明的过程和结论。
要使用直接证明法,一般需要明确以下几个步骤:1. 提出所要证明的命题:首先,明确所要证明的命题,即要证明的结论。
2. 建立前提条件:在进行证明前,需要明确前提条件,即已知条件或已知命题。
3. 逻辑推理:通过逻辑推理和分析,根据已知条件和逻辑关系,逐步推导出结论。
4. 结论:最后,根据已有的证明过程,给出结论。
二、间接证明法间接证明法又称反证法,它是通过假设所要证明的命题不成立,然后推导出与已知事实矛盾的结论,从而证明所要证明的命题是正确的。
间接证明法的一般步骤如下:1. 假设反命题:首先,假设所要证明的命题的反命题是正确的。
2. 推导过程:根据假设和已知条件,通过逻辑推理进行推导,尽可能多地得到信息。
3. 矛盾结论:最终推导出一个与已知事实矛盾的结论。
4. 否定假设:由于假设的反命题与已知事实矛盾,所以可以否定假设,即所要证明的命题是正确的。
间接证明法常用于证明一些数学定理、存在性证明和最大最小值的存在性等问题。
三、数学归纳法数学归纳法是一种常用的证明方法,特别适用于证明一类命题或定理,如整数性质、等差数列的性质等。
它基于两个基本步骤:基本情况的验证和归纳假设的使用。
数学归纳法的一般步骤如下:1. 基本情况的验证:首先,验证当命题成立的最小情况,通常是n=1或n=0的情况。
2. 归纳假设的使用:假设当n=k时命题成立,即假设命题对于某个特定的正整数k是成立的。
3. 归纳步骤的推理:在归纳假设的基础上进行推理和分析,证明当n=k+1时命题也成立。
4. 归纳法的结论:根据归纳步骤的推理和基本情况的验证,可以得出结论,即所要证明的命题对于所有正整数都成立。
数学归纳法在数学推理和定理证明中有着广泛的应用,尤其适用于证明具有递推性质的命题。
四、逆否命题证明法逆否命题证明法是通过对命题的逆否命题进行证明,从而间接地证明所要证明的命题。
高中数学讲义:零点存在的判定与证明

零点存在的判定与证明一、基础知识:1、函数的零点:一般的,对于函数()y f x =,我们把方程()0f x =的实数根0x 叫作函数()y f x =的零点。
2、零点存在性定理:如果函数()y f x =在区间[],a b 上的图像是连续不断的一条曲线,并且有()()0f a f b ×<,那么函数()y f x =在区间(),a b 内必有零点,即()0,x a b $Î,使得()00f x =注:零点存在性定理使用的前提是()f x 在区间[],a b 连续,如果()f x 是分段的,那么零点不一定存在3、函数单调性对零点个数的影响:如果一个连续函数是单调函数,那么它的零点至多有一个。
因此分析一个函数零点的个数前,可尝试判断函数是否单调4、几个“不一定”与“一定”(假设()f x 在区间(),a b 连续)(1)若()()0f a f b ×<,则()f x “一定”存在零点,但“不一定”只有一个零点。
要分析()f x 的性质与图像,如果()f x 单调,则“一定”只有一个零点(2)若()()0f a f b ×>,则()f x “不一定”存在零点,也“不一定”没有零点。
如果()f x 单调,那么“一定”没有零点(3)如果()f x 在区间(),a b 中存在零点,则()()f a f b ×的符号是“不确定”的,受函数性质与图像影响。
如果()f x 单调,则()()f a f b ×一定小于05、零点与单调性配合可确定函数的符号:()f x 是一个在(),a b 单增连续函数,0x x =是()f x 的零点,且()0,x a b Î,则()0,x a x Î时,()0f x <;()0,x x b Î时,()0f x >6、判断函数单调性的方法:(1)可直接判断的几个结论:① 若()(),f x g x 为增(减)函数,则()()f x g x +也为增(减)函数② 若()f x 为增函数,则()f x -为减函数;同样,若()f x 为减函数,则()f x -为增函数③ 若()(),f x g x 为增函数,且()(),0f x g x >,则()()f x g x ×为增函数(2)复合函数单调性:判断()()y f g x =的单调性可分别判断()t g x =与()y f t =的单调性(注意要利用x 的范围求出t 的范围),若()t g x =,()y f t =均为增函数或均为减函数,则()()y f g x =单调递增;若()t g x =,()y f t =一增一减,则()()y f g x =单调递减(此规律可简记为“同增异减”)(3)利用导数进行判断——求出单调区间从而也可作出图像7、证明零点存在的步骤:(1)将所证等式中的所有项移至等号一侧,以便于构造函数(2)判断是否要对表达式进行合理变形,然后将表达式设为函数()f x (3)分析函数()f x 的性质,并考虑在已知范围内寻找端点函数值异号的区间(4)利用零点存在性定理证明零点存在例1:函数()23x f x e x =+-的零点所在的一个区间是( )A.1,02æö-ç÷èø B.10,2æöç÷èø C.1,12æöç÷èø D.31,2æöç÷èø思路:函数()f x 为增函数,所以只需代入每个选项区间的端点,判断函数值是否异号即可解:1211234022f e -æöæö-=+×--=-<ç÷ç÷èøèø,()020f =-<11232022f æö=+×-=-<ç÷èø()12310f e e =+-=->()1102f f æö\×<ç÷èø01,12x æö\Îç÷èø,使得()00f x =答案:C例2:函数()()ln 1f x x x =-+的零点所在的大致区间是( )A.31,2æöç÷èø B.3,22æöç÷èøC.()2,eD.(),e +¥思路:先能判断出()f x 为增函数,然后利用零点存在性判定定理,只需验证选项中区间端点函数值的符号即可。
放缩取点证明零点存在性问题

f (x)=ex-
a x
<ex-
a ex 1
=g(x) .
令g(x)=0,
ex 1 1 4a 2
x ln 1 1 4a 2
取 x2 ln 1
1 4a 2
,则有:f (x2)<g(x2) =0 .
结合f (x)的单调性可知, f (x)在(x2 , x1)必存在 唯一的变号零点.
此法难点在于如何对ex进行放缩 f (x)=ex-ax2 f ′(x)=ex-2ax f ′′(x)=ex-2a
1°a≤0时, f (x)无零点;
2°0<a≤ e 时, f ′(x)≥0 ,f (x)递增,无零点; 2
3°a> e 时,令f ′′(x)=0, x=ln2a 2
f ′(x)在(0,ln2a)单调递减,在(ln2a,+)单调递增.
由例2可知f ′(x)必有两个变号零点x1,x2,(x1<x2)
y
f ′(x)
f (x)在(0,x1 )单调递增, 在(x1 , x2)单调递减, 在(x2,+)单调递增.
ln2a x
O x1
x2
y f (x)
1
O x1
x2 x
f (x)在(0,x1 )无零点,
在x2处由极小值f (x2) ,
f ′(x2)=0 e x2 2ax2
(2016·全国新课标Ⅰ卷·理·21)已知函数 f (x)=(x-2)ex+a(x-1)2 有两个零点.
(Ⅰ) 求 a 的取值范围; 可放缩成-3 (Ⅱ) 设 x1, x2 是 f (x) 的两个零点 ,
取 x1 1
1 4a 2
,则有:f (x1)>g(x1) =0 .
若取 x1= a 和x1=a,则效果更佳,几何解释如下图:
浅论数学分析中极限问题的存在性和若干求解方法

浅论数学分析中极限问题的存在性和若干求解方法微积分的思想在公元前7世纪就已经产生,但并不是十分明显。
在公元前3世纪,伟大的阿基米德就利用穷竭法求出了抛物线、螺线、圆的面积以及椭球体、抛物面体等各种复杂几何体的表面积、体积公式。
在中国,三国时期的刘徽发明了世界闻名的割圆术。
南朝时的祖氏父子更是将圆周率计算到了小数点后七位。
此外祖暅之提出的祖暅原理也比西方早了一个多世纪。
而这些成就大多也包含了微积分的思想在其中。
直到15世纪初,人们的科学技术开始要求更加强劲的数学工具。
具体来说有不同领域的四个问题促使了微积分最终的发明。
这四个问题是:运动中速度、加速度、距离之间的虎丘问题,尤其是非匀速运动,使瞬时变化率的研究成为必要;曲线求切线问题,例如要确定透镜曲面上任意一点的法线等;从求炮弹的最大射程,到求行星轨道的近日点与远日点等问题提出的求函数的极大值或极小值问题;当然还有千百年来人们一直在研究如何计算长度、面积、体积与重心等问题。
其中,第一、第二、第三促进微分的发展,第四问题促进积分的发展。
微分与积分起初是互相独立发展的,开普勒、伽利略、费马、笛卡尔、卡瓦列里、巴罗等人做出了不可忽略的贡献,直到牛顿和莱布尼兹对微分和积分进行了统一。
牛顿从1664年开始研究微积分。
1665年5月,牛顿发明了“流数术(微分法)”,1666年5月,发明“反流数术(积分法)”,并于1666年10月将其整理成文,命名为《流数简论》(未发表)。
这是历史上第一本系统描述微积分的学术书籍。
在1673年,莱布尼兹提出特征三角形(ds,dx,dy),并认识到特征三角形在微分中的重要意义,又因为牛顿使用的运算符号过于复杂,所以当代的数学分析采用的是莱布尼兹的符号体系。
数学是十分严谨的学科,追求精确的证明。
但是整个微积分体系都是建立在无穷的层面的,是十分模糊的概念。
于是还有一批数学家便投身与微积分的严格化的论述。
这项工作最终是由柯西完成的,1821年,柯西发表《工科大学分析教程》;1823年,柯西发表《无穷小计算教程概论》;1929年,柯西发表《微积分学讲义》,这三本著作建立了一个沿用至今的微积分模型,并严格定义了如极限、实数、无穷小等概念。
一阶非线性常微分方程解的存在性定理—Picard-Lindelof定理

⼀阶⾮线性常微分⽅程解的存在性定理—Picard-Lindelof定理上⼀节简单介绍了可求解的⼀阶常微分⽅程的解法,因为⼤部分⾮线性⽅程是不可解的,所以需要给出解的存在性的证明。
本节主要介绍⼀阶⾮线性常微分⽅程Cauchy问题(E)dydx=f(x,y),y(x0)=y0.解的存在性定理Picard-Lindelof定理(有的书上称它为Cauchy-Lipschitz定理). 对⼀阶常微分⽅程解的存在性理论作出重要贡献的数学家有Cauchy、Lipschitz、Picard、Lindelof、Peano等,其中Picard提出的Picard迭代法尤其值得关注。
据传Picard证明Picard—Lindelof定理的原始论⽂⾜⾜有三四百页,后来数学家Banach把Picard的⽅法抽象出来证明了著名的Banach不动点定理。
Banach不动点定理是分析学中最重要的定理之⼀,也是⽤的最多的定理之⼀,它在线性⽅程组求解迭代⽅法的收敛性、常微分⽅程的两点边值问题、隐函数定理、Lax-Milgram定理甚⾄代数⽅程解的存在性等问题中均有重要应⽤。
许多微分⽅程(组)通过转化为等价的积分⽅程再利⽤不动点理论来证明解的存在性。
本节也采⽤这⼀框架来探索⽅程(E)解的存在性。
为此,⾸先利⽤Picard迭代给出Banach不动点定理的证明。
定理1 (Banach) 设X为Banach空间(即完备的赋范空间,完备的意思指所有的Cauchy列均收敛),f:X→X为压缩映射,即存在常数k,0<k<1,对任意x,y∈X有‖f(x)−f(y)‖≤k‖x−y‖,则映射f:X→X有且只有⼀个不动点x∈X.证明:任取x0∈X,构造Picard迭代x n+1=f(x n),n≥0.则‖x n+1−x n‖=‖f(x n)−f xn−1‖≤k‖x n−x n−1‖≤⋯≤k n‖x1−x0‖.设m>n≥0,由三⾓不等式和上式得‖x m−x n‖≤m−1∑p=n‖x p+1−x p‖≤k n1−k‖x1−x0‖,当m,n→∞时,‖x m−x n‖→0, 故序列{x n}为Cauchy列,由X的完备性知存在x∞∈X使得lim f:X\to X满⾜Lipschitz条件,显然连续.故x_{\infty}=\lim_{n\to\infty}x_{n+1}=\lim_{n\to\infty}f(x_{n})=f(\lim_{n\to\infty}x_{n})=f(x_{\infty}).存在性得证。
高一数学函数的零点存在定理及其应用分析总结

零点存在定理:如果函数f(x)在区间[a, b]上连续,且f(a)·f(b)<0,则f(x)在区间(a, b)内有零点。
单调性判断:根据零点存在定理,如果函数f(x)在区间[a, b]上有零点,则f(x)在区间(a, b)上至少有一个单调区间。
应用实例:例如,判断函数f(x)=x^3-x在区间[-1, 1]上的单调性,可以通过零点存在定理来判断。
结合实际应用:结合实际例子,理解定理的应用方法和技巧
注意定理的局限性:了解定理的局限性和适用条件
掌握定理的应用范围:了解定理的应用条件和适用范围
感谢您的观看
注意事项:在使用零点存在定理判断函数单调性时,需要注意函数的连续性和零点的存在性。
在研究函数图像中的应用
求解函数方程:通过零点存在定理,可以求解函数方程,得到函数的解析式
确定函数图像的零点:通过零点存在定理,可以确定函数图像的零点位置
判断函数图像的性质:通过零点存在定理,可以判断函数图像的连续性、单调性等性质
研究函数图像的极限:通过零点存在定理,可以研究函数图像的极限,得到函数的极限值
在解决实际问题中的应用
零点存在定理在解决实际问题中的应用广泛,如求解方程、优化问题等
零点存在定理在解决实际问题时,需要注意定理的适用条件和范围,避免错误应用
零点存在定理在解决实际问题时,需要结合实际问题的具体情况,灵活运用
零点存在定理的数学表达
零点存在定理:如果函数f(x)在区间[a, b]上连续,且f(a)·f(b)<0,则函数f(x)在区间(a, b)内至少有一个零点。
零点:函数f(x)的零点是指使得f(x)=0的x值。
பைடு நூலகம்
连续函数:如果函数f(x)在区间[a, b]上每一点x都有定义,且对于任意的ε>0,存在δ>0,使得当|x-x0|<δ时,|f(x)-f(x0)|<ε,则称f(x)在区间[a, b]上是连续的。
18第一部分 板块二 专题五 解析几何 第4讲 圆锥曲线中的定点、定值、存在性问题(大题)

解 假设存在常数 λ 使得|AB|+|CD|=λ|AB|·|CD|成立,则 λ=|A1B|+|C1D|. 由题意知,l1,l2的斜率存在且均不为零, 设l1的方程为y=kx+1, 则由yx=2=k4xy+,1, 消去 y 得 x2-4kx-4=0. 设A(x1,y1),B(x2,y2),则x1+x2=4k,x1x2=-4.
(2)若过F的直线交抛物线C于不同的两点A,B(均与P不重合),直线PA,PB分别 交抛物线的准线l于点M,N.试判断以MN为直径的圆是否过点F,并说明理由.
解 以MN为直径的圆一定过点F,理由如下: 设A(x1,y1),B(x2,y2), 设直线AB的方程为x=my+1(m∈R),代入抛物线C:y2=4x, 化简整理得y2-4my-4=0, 则yy11+y2=y2=-44m,,
例 1 (2019·济南模拟)已知抛物线 C1:y2=2px(p>0)与椭圆 C2:x42+y32=1 有一个相同的
焦点,过点A(2,0)且与x轴不垂直的直线l与抛物线C1交于P,Q两点,P关于x轴的对 称点为M. (1)求抛物线C1的方程;
解 由题意可知抛物线的焦点为椭圆的右焦点,坐标为(1,0), 所以p=2,所以抛物线的方程为y2=4x.
例3 (2019·济南模拟)设M是抛物线E:x2=2py(p>0)上的一点,抛物线E在点M处 的切线方程为y=x-1. (1)求E的方程;
解 方法一 由xy2==x2-py1,, 消 y 得 x2-2px+2p=0.
由题意得Δ=4p2-8p=0,
因为p>0,所以p=2.
故抛物线E:x2=4y.
方法二 设 Mx0,2xp20 ,
由(1)知P(4,4), 所以直线 PA 的方程为 y-4=xy11--44(x-4)=myy1-1-43(x-4), 令 x=-1 得 y=4mm-y15-y31+8,即 M-1,4mm-y15-y31+8,
解析函数零点的孤立性及唯一性定理

对于超越函数,如三角函数、指数函数等,其零点往往难 以直接求解,需要采用数值方法逼近。例如,求解 $sin(x)=0$的零点,可以采用二分法或迭代法。由于 $sin(x)$是周期函数,其零点有无穷多个,因此需要结合 问题的实际背景选择合适的求解方法。
06
总结与展望
研究成果总结
解析函数零点的孤立 性
解析函数的性质
解析函数在其定义域内具有连续性和可微性,因此在其零点周围的小邻域内,函数值可以由泰勒级数展开式近似 表示。若零点非孤立,则在这个小邻域内存在其他零点,使得泰勒级数展开式在该点处也为零,这与解析函数的 性质相矛盾。
零点孤立性的应用
确定函数零点的个数
通过判断函数在某点处的零点是否为孤立零点,可以确定函数在该点处的零点个数。若为零点,则在该点处函数值为 零;若非零点,则在该点处函数值不为零。
零点性质
分析函数零点的性质,如是否是重根、是否可导 等。
解析函数及其性质
解析函数定义
01
解析函数是指在定义域内处处可导的函数,具有良好的分析性
质。
解析函数的性质
02
包括可微性、连续性、可积性等,这些性质使得解析函数在数
学分析中占有重要地位。
解析函数与实函数的区别
03
解析函数的研究范围扩展到复数域,而实函数仅限于实数域。
04
解析函数零点与多项式根 的关系
多项式根的性质
多项式根的存在性
对于任意非零多项式,其在复数域内至少有 一个根。
多项式根的个数
n次多项式的根最多有n个,重根按重数计算。
多项式根的分布
多项式的根在复数平面上分布,且对于实系 数多项式,虚根成对出现。
解析函数零点与多项式根的联系
点的存在性的证明方法的分析

点的存在性的证明方法的分析点在数学中是一个抽象概念,它象征着数学中最基本的地位。
虽然它抽象的性质使其难以完全证明存在性,但却有一些有效的方法可以引入点的存在性。
本文就点的存在性的证明方法进行分析。
首先要了解的是定义点的存在性的证明的术语。
一般来说,“存在性证明”是指提出一个特定的结论,证明其存在的方法。
具体来说,“证明点的存在性”就是指提出特定的结论:一个或多个点存在于一个特定的空间中,并进行有效地证明。
常用的证明点存在性的方法有两种,分别是几何学方法和抽象数学方法。
几何学方法,即物体在空间中的位置和形状的分析,可以用来证明点的存在。
抽象数学方法,即以数学形式表达物体的位置和形状,可以用来证明点的存在。
几何学方法可以用许多种不同的方法来证明点的存在性。
一种常用的方法是采用几何定理,结合集合理论分析关系,证明点的存在性。
例如,可以证明三角形ABC中点A存在,并通过相关定理证明,比如半平面交定理。
此外,可以用下列定义来说明点的存在性:一点存在于某物中,当且仅当取出该物中的任意一份,都可以在其中找到该点。
结合上述定义和表达式,可以用数学方法证明点的存在性。
抽象数学方法用来证明点的存在性,可以用数学运算和逻辑推理来解决问题。
首先,要用数学形式描述物体的位置和形状。
然后,要建立逻辑推理,用数学运算证明物体中某点的存在性。
例如,假设存在一条直线L,可以使用数学运算证明该直线上一定存在一点P,且P到L两点距离最短。
总之,以上就是点的存在性的证明方法的分析。
几何学方法和抽象数学方法可以有效地证明点的存在性,而且可以使用数学定理和逻辑推理来证明点的存在性,使得点的存在性的证明变得更加容易。
在实践中,只要使用这些方法,就可以相应地证明点的存在性,从而解决实际问题。
罗尔定理在函数零点问题中的应用(可编辑)

罗尔定理在函数零点问题中的应用(可编辑)罗尔定理在函数零点问题中的应用本科毕业论文题目罗尔定理在函数零点问题中的应用系别数学与信息科学学院专业数学与应用数学指导教师评阅教师班级级2班姓名学号年 5 月 10 日目录摘要…………………………………………………………………………………………………? Abstract……………………………………………………………………………………?引言……………………………………………………………………………………… (1)1概念及定理 (1)2罗尔定理在函数零点问题中的应用 (3)2.1 罗尔定理在函数零点存在性问题中的应用 (3)2.2 罗尔定理在函数零点个数问题中的应用 (4)2.3 罗尔定理在函数零点唯一性证明中的应用 (5)2.4 罗尔定理与几个特殊多项式函数的零点分布问题..........................................52.4.1 Laguerre多项式 (5)2.4.2 Hermite多项式....................................................................................6 2.4.3勒让德多项式 (8)2.5 多变元情形下的罗尔定理及其在几何学上的应用 (9)结束语……………………………………………………………………………………… (10)参考文献……………………………………………………………………………………… (11)致谢……………………………………………………………………………………… (12)摘要:在介绍了罗尔定理的基础上,通过综合应用类比法、分析法、演绎推理法将罗尔定理在一元实函数中进行了推广,得到了在“任意区间”上罗尔定理的结论成立,同时得到了在“函数在区间内除有限个点处存在正(或负)无穷的导数外,其他点均有有限导数”的情形下罗尔定理的结论仍然成立.将罗尔定理在复变函数(解析函数)中进行了推广,得到了向量值函数中的一个重要结论.结合典型例题,分析、讨论并证明了罗尔定理及推广后的罗尔定理在函数零点问题中的实际应用,同时证明了在几何学上的具体应用,用广义罗尔定理证明了三个特殊多项式,说明了罗尔定理不仅具有重要的理论意义,而且还有很好的应用价值.关键词:函数;函数零点;罗尔定理;应用Abstract: On the basis of the Rolle theorem, through analogy,combined application, analysis and deductive reasoning method, the promotion of Rolle theorem in the real function of one dollar. Thentheconclusion of Rolle Theorem set up in the “free range”. At thesame time,on the condition of “function in the range of a finite number of points in addition to positive or negative derivative of the infinite,the other points are limited derivative”, Rolle theorem remain valid. Rolle theorem promote in the complex function analytic functions.Vector-valued functions has been an important conclusion. Combined witha typical example, and analysis, discussion and proof of Rolle theoremand the promoted Rolle are application practically in the function against. At the same time, the specific application in the geometry isproved. Using the generalized Rolle theorem prove three special polynomial. Rolle theorem shows not only an important theoretical significance, but also very good practical value Key words: function; function against; rolle theorem; application引言对函数零点问题的研究一直是微积分理论研究中的一个重要课题,解决这一问题常用的工具是微积分中的零点定理、费马定理、罗尔定理、拉格朗日中值定理、柯西中值定理等,对于不同的理论和方法有不同的使用范围和各自的优缺点.罗尔定理是基于费马定理且能导出拉格朗日中值定理和柯西中值定理的一个著名定理,因此对罗尔定理的研究一直以来都是微积分理论研究中一个比较活跃的方向.根据罗尔定理,若函数在闭区间上连续、开区间内可导,则在端点和的取值就决定了内某点的微分性质,尽管的取值一般情况下不易求出,但它并不影响罗尔定理的应用.由于它的这个优越性质,将它应用于函数零点问题中就具有明显的优越性.因此,长期以来人们都想削弱罗尔定理的三个限制条件,以便将它用于更加广泛的领域.至今,人们在文献[1]-[5]中将其在一元实函数中进行了推广,将“有限区间”推广到了“任意区间、任意端值”上,并且将“处处可导”推广到了“在区间内除有限个点处存在正(或负)无穷的导数外,均有有限导数”,削弱了严格的限制,同时讨论了一些函数的零点问题.在罗尔定理的应用中,构造辅助函数十分重要.2003年,文献[6]利用找原函数的思想,通过不定积分的过程来寻求辅助函数,得到了应用罗尔定理构造辅助函数的一种方法.但罗尔定理只能用于一元实函数,能否将它推广到多元函数中呢?1995年Furi与Martelli经过研究将其推广到了向量值函数中,并将其应用到了几何学上.这样罗尔定理不仅可以用于实函数,也可以用于复变函数的零点问题中.本文根据大量的文献整理与综合,首先给出了罗尔定理及其推广形式,进而应用这些结论分析讨论了其在实函数和复变函数零点问题中的具体应用.1 概念及定理1.1 函数零点的定义如果存在实数,使得,则称为函数的零点. 函数的零点又称为方程的实根.讨论函数零点的存在性,确定函数零点的个数,证明函数零点的唯一性的问题,统称为函数的零点问题.1.2 罗尔定理[7]若函数满足如下条件:1 在闭区间上连续;2在开区间内可导;3,则在内至少存在一点,使得.罗尔定理的几何意义是说:在每一点都可导的一段连续曲线上,如果曲线的两端点高度相等,则至少存在一条水平切线.1.3 推广的罗尔定理推广1:若函数在有限区间或无限区间内满足:1可导;2 .则在内至少存在一点,使得.推广2:若函数满足:1在上连续;2在内除有限个点处存在正无穷或负无穷的导数外,均有有限导数;3.则在中至少存在一点,使得.推广3(广义罗尔定理):设函数在有限或无穷的区间中的任意一点处有有限的导数,且,则在中至少存在一点,使得.推广4向量值函数中的推广:设, (1)上连续; (2)内可微; (3)存在非零向量,使得对任意的成立; (4)存在非零向量,使得对任意的,恒为常数; (5)存在非零向量,使得对任意的,不变号.若除满足(1)(2)两个条件外,还满足(3)(4)(5)中的任意一个,则至少存在一点,使得(注意到为矩阵),即与向量组正交.罗尔定理仅仅适用于连续的一元实函数,推广1、2和3是对它在实函数中的进一步推广,这样可以让罗尔定理摆脱太严格的限制,同时推广的罗尔定理就可以在任意区间、任意端值上使用了,从而使其在实函数中的应用更加广阔.但是罗尔定理的最大缺陷就是只能用于一元连续实函数,因此推广4将其从本质上推广到了向量值函数中,从而能将罗尔定理从代数学中推广到几何学中,与日常的生产生活联系更加紧密.2 罗尔定理在函数零点问题中的应用零点问题就是指零点的存在性、唯一性以及个数的问题,这一问题的解决可以采用高等数学中的零点定理、费马定理、拉格朗日中值定理等微积分方法,不同的方法在不同的环境中有各自的优越性.罗尔定理在函数零点问题中的应用十分广泛,无论是零点的存在性、唯一性还是个数问题,应用罗尔定理都能得到很好的解决.2.1 罗尔定理在函数零点存在性问题中的应用在数学学科中,函数零点的存在性问题始终都是人们研究的热点课题.虽然这一问题的解决可以用零点定理,但在难以认定正负值点的时候,就需要换一种方法,其中罗尔定理就是一种很好的方法.用罗尔定理讨论函数零点问题时可以采用以下方法.对函数的原函数使用罗尔定理:若在闭区间上,并且,则在上至少存在一点,使得. 例1 设函数是定义在闭区间上的连续函数,且,证明存在,使得. 分析:如果用零点定理,则令,但的值是正还是负,难以确定,因此考虑改用罗尔定理.证明:令,则.那么 (因为),所以.又因为,所以由罗尔定理可知,存在,使得. 针对难以确定正负值点的函数零点存在性问题,采用罗尔定理能方便而又快速的给我们提供解决方法,因为它并不要求求出区间内的端点值或者说判断端点值的正负,而只需要知道它是否连续、可微就可以了.针对这一类问题,通常采用的方法就是对函数的原函数使用罗尔定理.但由于罗尔定理的限制太严格了,它要求三个限制条件必须同时满足,只要有一个条件不满足,罗尔定理就不一定成立,这就大大的限制了罗尔定理的使用范围,因此在难以确定函数是否连续、可微时直接使用罗尔定理反而会增加解题的难度,加大计算量.2.2 罗尔定理在函数零点个数问题中的应用在数学学习和生产生活中,零点的个数问题始终是一个重要的问题.讨论一个函数到底有几个零点,通常可以采用先确定至多有几个零点,再确定至少有几个零点,从而得出零点的个数,在这过程中罗尔定理就显示出了它的优越性.例2 讨论方程的零点个数. 解:设函数,显然在定义域内是连续函数.分别令得所以在区间各至少有一个零点,即方程至少有三个实根.令,这个函数在区间上连续且单调递增,,所以在有唯一的零点,所以由罗尔定理可知在至多有两个零点.同理可知在至多有三个零点.综上所述,方程在恰好有三个零点.将方程转化为函数,再利用微积分的方法解决问题,这是一种重要的思想,即化归的思想,是一种常用的解题策略.2.3 罗尔定理在函数零点唯一性证明中的应用在函数零点问题中,讨论某个函数的零点是否唯一,是一种常见的题型,并且在实际生活中也具有重要的意义.罗尔定理为这类题型提供了一个有力的工具.例3 已知在上二阶可微,,,,则在内只有一个实根.证明:首先证明存在性.过定点做曲线的切线:,则切线与轴的交点,由(向上凸的),显然有.下面采用反证法证明唯一性.若存在使得,则由罗尔定理可知,存在使得.这与是矛盾的.所以只有一点,使得.唯一性的证明通常都比较困难,一般从正面入手很难解决问题,然而从反面思考,往往有“柳暗花明又一村”的感觉.在零点唯一性的证明中,罗尔定理能较好地发挥它独特的性质.2.4 罗尔定理与几个特殊多项式函数的零点分布问题在研究有关多项式的问题时,多项式的零点分布是经常遇到并且非常重要的问题之一.在解决的方法中,罗尔定理是一个很好的工具,但是罗尔定理的要求非常严格,三个条件必须同时满足,定理才成立.因此我们利用推广的罗尔定理解决这个问题.以下就是用罗尔定理解决三种特殊多项式的例子.2.4.1 Laguerre多项式在区间上带权函数的正交多项式序列中的多项式称为Laguerre多项式,其表达式为.例4 证明多项式所有的根都是正根. 证明:因为, ,依此类推可知是次多项式.可见,至多只有个实根.设函数,则.由广义罗尔定理知,存在,使得.现设至少有个零点,且.分析的结构易知,是一个与一个次多项式的乘积,即 ,其中是一个多项式.则,由广义罗尔定理知,存在,使得.根据数学归纳法,至少有个正根.又由于恒不为零,所以至少有个正根.由前面可知最多只能有个实根,所以只有个实根,且都是正实根.2.4.2 Hermite多项式在实际生活中,函数在某区间上存在,但函数往往很复杂,甚至没有明显的解析表达式,因此常用插值法去构造一个既能反映函数特征又便于计算的较为简单的函数以替代函数.不同的实际问题,选用的插值函数也会不同.Hermite多项式就经常被选为插值函数.在区间上带权函数的正交多项式序列中的多项式称为Hermite多项式,其表达式为.例5 证明多项式所有的根都是实数. 证明:显然是一个次多项式. 设函数,则, ,可见有一个实数根,有两个相异的实数根. 现假设有个相异的实根,并记作.分析的结构可知.因为有个相异的实根,因此可令,即,其中为一个非零常数.又由于,根据罗尔定理得,存在使得,即在之间至少存在个相异实根.又由于,根据广义罗尔定理可知,必存在,使得.同理,,由广义罗尔定理知必存在,使得.综上所述,至少有个实根.所以由数学归纳法知至少有个相异的实根.从而至少有个相异的实根.但是是的一个次多项式,故恰有个根(实根或复根),即的所有根都是实根.2.4.3 勒让德多项式伴随勒让德多项式(Associated Legendre polynomials)有时被简称为勒让德多项式.数学上,勒让德函数指以下勒让德微分方程的解:为求解方便一般也写成如下斯图姆-刘维尔形式(Sturm-Liouville form): 上述方程及其解函数因法国数学家阿德里安-马里?勒让德而得名.勒让德方程是物理学和其他技术领域常常遇到的一类常微分方程.当试图在球坐标系中求解三维拉普拉斯方程(或相关的其他偏微分方程)时,问题便会归结为勒让德方程的求解. 例6 证明勒让德多项式的一切零点都是实数且含于区间中.证明:设,因为是次多项式,且恒不为0,所以是次多项式,由代数定理可知它至多只有个实零点.由于,由广义罗尔定理知,至少存在一点,使得.假设至少有个实零点.分析的结构可将写为以下结构 ,其中为次多项式. 因为,由罗尔定理可知存在,使得,即至少有个零点,并且全部在区间之间. 由数学归纳法可知至少有个实零点,且全部介于区间之间.由于恒不为0,所以至少有个实零点.而由前面知道是次多项式,它至多有个实零点.所以恰有个实零点,且全部介于区间之间.勒让德多项式的应用十分广泛,但如何证明它的零点是一个难点,以上例子就提供了一种很好的方法.2.5 多变元情形下的罗尔定理及其在几何学上的应用在微积分学中,关于多变元映像(从多元函数到向量值函数)的极限(包括连续性)、微分、积分及其性质,一般都是考虑一元函数的性质能否平移或推广过来.但罗尔定理的不足之处就是对向量值函数不成立,因此1995年Marden[8],1992年Evard 与Jafari[9]在复变(解析函数)情形下揭示了罗尔定理的本质,1995年Furi 与Martelli[10]对向量值函数进行了推广:在闭域上连续,开域内可微的向量值函数,罗尔定理情形下的边界函数值确定了开域内某点的微分性质.这样该结果就可以应用于几何学.例7 设定义为,并满足下列条件:在上连续;在内可微;存在中的平面,对任意的..则存在.使得在曲面上处的切平面平行于平面.这里表示的值域,或者表示的曲面.证明:设,则表示平面的法向量.由条件3)可知,对任意的,都有与正交.由罗尔定理的推广4知,存在,使得与向量组正交.又因为,在上处的切平面向量式参数方程为.这里,为参数.所以,切平面的法线与平行,从而切平面平行于平面. 罗尔定理仅仅适用于一元函数,这样就在很大程度上限制了罗尔定理的应用范围.但它的良好本质却能启发我们将其推广到向量值函数中,从而就能解决一类几何问题,为数学问题的解决提供了更多的工具.结束语利用罗尔定理的理论和方法,可以较细致的研究函数零点问题.根据罗尔定理的意义,可以将其从限制条件上和本质上进行多方位的推广,从而扩大应用领域. 通过对罗尔定理的简单分析探究,掌握了该定理的结构形式,学习了运用类比的思维方法推广该定理的过程,分析讨论了罗尔定理的实际应用.首先将罗尔定理在一元函数中进行推广,削弱了罗尔定理的限制条件.紧接着利用罗尔定理的实质将其在向量值函数中进行了推广,得到“在闭域上连续、开域内可微的向量值函数,罗尔定理情形下的边界函数值确定了开域内某点的微分性质”,从而将结果应用于几何学.最后,应用罗尔定理及其推广形式举例说明了它们在证明函数零点存在性、函数零点个数、函数零点唯一性、三类特殊多项式函数的零点分布问题,并举例说明了多变元情形下的罗尔定理在几何学上的应用.至于如何应用罗尔定理构造辅助函数,以及解决函数零点问题的各种微积分方法(如费马定理、拉格中值定理等)的优缺点比较这两个问题未做讨论.参考文献[1] 孙兰敏.洛尔定理的2个推广形式[J].衡水学院学报,2005,71:1-2.[2] 汪军.广义罗尔定理及其应用实例[J].辽宁工程技术大学学报,2000,191:93.[3] 张志军.多变元情形下的洛尔定理及其应用[J].西北师范大学学报,1998,34(1):84?87.[4] 潘黎霞.对广义罗尔定理证明并在求函数的零点上的应用[J].甘肃科技,2005,217:115-116.[5] 周敦.微分中值定理的推广及其应用[J].钦州师专钦州教院学报.1994,81:54-56.[6] 王艳萍,余学军.应用罗尔定理时一种辅助函数构造法[J].南阳师范学院,2003,29:18-21.[7] 华东师范大学数学系.数学分析:上册[M].北京:高等教育出版,2005.[8] Marden M.The search for a Rolle's theorem in the complexdomains[J].Amer,Math.Monthly,1985,92:643-650.[9] Evard J C,Jafari F.A complex Rolle'stheorem[J].Amer,Math.Monthly,1992,99:856-861.[10] Furi M,Martelli M.A multidimensional version of Rolle'stheorem[J].Amer.Math.Monthly,1995,102:243-249.致谢时光荏苒,岁月如梭,转眼毕业将至.值此论文完成之际,我谨向所有关心、爱护、帮助过我的人表示最诚挚的感谢与最美好的祝愿. 通过毕业论文的写作,我真正体会到了科学的严谨性.任何一门科学,我们都必须以认真严谨的态度去对待它,不能以自己的主观臆断去评判真理,而应以真理去认识客观世界.在论文写作过程中,我熟悉了电脑的一些基本操作,学会了论文的排版格式.经过一、二、三稿的整理和修改,我明白了一个道理??踏踏实实做人,明明白白做事.在这四年里,无论成功还是失败,许多长辈和朋友都给了我一如既往的支持与鼓励.在这里我要首先感谢我的父母、我的亲人朋友们,他们给了我无微不至的关怀,陪我一起度过二十多年的酸甜苦辣,对他们的感激之情,不知该如何表达,千言万语,只能化成实际行动,让我用一生报答他们!其次我要感谢内江师范学院可敬的老师们,尤其是我的导师――吕晓亚,她用为人师表的高尚品格和渊博深厚的学术造诣,为我们树立了的崇高的榜样,开启了人类智慧的大门.最后,衷心感谢程冲、邓平等寝室朋友们在学习时给予我的关心和帮助!。
立体几何中的存在性问题教案
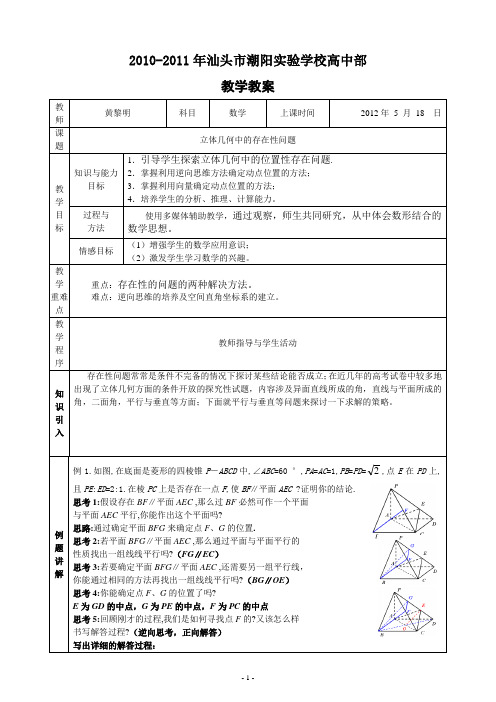
(2010·浙江·理·T20)如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形.E,F,O分别是PA,PB,AC的中点,AC=16 ,PA=PC=10.
证明:在△ABO内存在一点M使得FM⊥平面BOE,并求点M到OA,OB的距离.
提示:建系后设点M坐标为(x,y, 0 )
思考8:如何用向量来确定PC上的动点F的位置?
(令 ,通过λ的值来确定点F的位置)
思考9:如何用向量来表示BF∥平面AEC?
( ,其中 为平面ACE的法向量)
思考1Байду номын сангаас:如何求λ的值?(利用 建立方程求出λ)
写出详细的解答过程:
【方法归纳】点F是线PC上的点,一般可设 ,求出λ即可确定点F的位置
课堂练习.(2010·湖南·理·T18)
答案:AM=3
向量方法:建立适当的坐标系
令 ,利用 求出λ的值,但要注意,
根据线面垂直的条件还欠一组线面垂直,故还需证明PA⊥BC
或PA⊥MC
小结
作业
[课堂小结]
对存在性问题常采用以下两种方法:
1、(几何方法)先通过命题成立的必要条件探索出命题成立的充分条件,再从正面入手证明;
2、(向量方法)把几何问题转化为代数问题,探索出命题成立的条件
2010-2011年汕头市潮阳实验学校高中部
教学教案
教师
黄黎明
科目
数学
上课时间
2012年5月18日
课题
立体几何中的存在性问题
教学目标
知识与能力目标
1.引导学生探索立体几何中的位置性存在问题.
2.掌握利用逆向思维方法确定动点位置的方法;
3.掌握利用向量确定动点位置的方法;
关于函数零点的存在性证明的讨论

㊀㊀㊀149㊀㊀关于函数零点的存在性证明的讨论关于函数零点的存在性证明的讨论Һ刘顺琴㊀(厦门大学嘉庚学院,福建㊀漳州㊀363105)㊀㊀ʌ摘要ɔ在很多专业的专升本或研究生入学考试中,高等数学都是必考学科.在考试题型当中,有一类关于函数形态的经典题型,这就是讨论函数零点的存在性或者证明函数的零点在给定区间上的个数的问题.本文我们将对一些常用的方法进行总结与讨论.ʌ关键词ɔ高等数学;零点存在定理;罗尔定理;单调性高等数学是高等学府里理工科学生的必修科目之一,在理工类学生的专升本考试或者研究生入学考试当中,也是必考科目之一.由此可见,高等数学十分重要.高等数学以函数为核心,系统地介绍了函数的极限㊁导数㊁导数的应用㊁不定积分㊁定积分㊁微分方程㊁空间解析几何及多元函数的微积分等内容.高等数学作为一门研究函数的学科,有很多经典的问题.本文主要从应用零点定理展开的证明㊁应用微分中值定理展开的证明㊁利用单调性证明根的个数三方面进行总结和讨论.一㊁应用零点定理展开的证明闭区间上的连续函数具有很多的特殊性质,比如最值定理㊁介值定理㊁有界性定理,还有零点定理(根的存在性定理),其中零点定理就可以用来证明函数在给定区间上有零点.零点定理:设函数f(x)在闭区间[a,b]上连续,且f(a)f(b)<0,则在开区间(a,b)内,至少存在一个ξɪ(a,b),使得f(ξ)=0.该定理的条件和结论都比较简单,在几何上也是非常直观的,所以利用该定理来证明,思路简单㊁直接.利用零点定理证明零点的存在性的步骤:第一步:构造闭区间上的连续函数;第二步:验证闭区间上的连续性和端点函数值的异号性;第三步:得出结论.例1㊀证明方程x=asinx+b(a>0,b>0)至少有一个正根,并且它不超过a+b.证明:该题相当于证明函数f(x)=x-asinx-b在开区间(0,a+b]内至少有一个零点.所以证明如下:令f(x)=x-asinx-b,则根据初等函数在有定义的区间内都连续,可以得出f(x)=x-asinx-b在闭区间[0,a+b]上连续,且f(0)=0-asin0-b=-b<0,f(a+b)=(a+b)-asin(a+b)-b=a[1-sin(a+b)].由于sin(a+b)ɤ1,所以下面分两种情况讨论:情况一:sin(a+b)=1.若sin(a+b)=1,则f(a+b)=(a+b)-asin(a+b)-b=a[1-sin(a+b)]=0,则x=a+b为方程所要求的不超过a+b的正根;情况二:sin(a+b)<1.若sin(a+b)<1,则f(a+b)=(a+b)-asin(a+b)-b=a[1-sin(a+b)]>0,此时f(0)f(a+b)<0,根据零点定理,在开区间(0,a+b)内,存在一个f(x)=x-asinx-b的零点,即x=asinx+b在开区间(0,a+b)内有一根.综上,该题得证.证明该题的时候,要注意分类讨论,零点定理只是其中的一种情况.二㊁应用微分中值定理展开的证明在函数的导数部分,有三个非常重要的微分中值定理:罗尔定理㊁拉格朗日中值定理㊁柯西定理.这三个定理都可以用来证明函数的导函数在给定区间内有根,其中以罗尔定理的应用最为典型.罗尔定理:设函数f(x)满足:(1)f(x)在闭区间[a,b]上连续,(2)f(x)在开区间(a,b)内可导,(3)f(a)=f(b),则在开区间(a,b)内至少存在一个ξ,使得fᶄ(ξ)=0.该定理区别于零点定理,首先条件要求更高,结论也发生了比较大的变化,是由原函数的性质推导出来的导函数的零点的存在性.该定理在直观上可以描述为连续可导㊀㊀㊀㊀㊀150㊀的函数的两个等高点之间至少有一个导函数的零点.例2㊀设f(x)=x(x-1)(x-2) (x-100),不求导数,判断f(x)的导函数有几个零点.解:根据初等函数的连续性和可导性可知,函数f(x)=x(x-1)(x-2) (x-100)在(-ɕ,+ɕ)上任意点连续且可导,且易知f(0)=f(1)=f(2)= =f(100)=0,则在(0,1)内,至少存在ξ1,使得fᶄ(ξ1)=0;同理在(1,2)内㊁在(2,3)内㊁ ㊁在(99,100)内,均各有一个使fᶄ(x)=0的x,注意到这些区间互不交叉,所以fᶄ(x)至少有100个零点;又由于f(x)是101次多项式,所以fᶄ(x)是100次多项式,根据多项式的零点理论可知,fᶄ(x)至多有100个零点.综合上面两种情况可知,fᶄ(x)恰好有100个零点.事实上,根据上面的讨论过程,我们还可以知道fᵡ(x)恰好有99个零点,f‴(x)恰好有98个零点,f(n)(x)(1ɤnɤ100)恰好有(101-n)个零点.该题的题意清晰,证明难度较低,我们接着来看例3.例3㊀设f(x)在[0,a]上连续,在(a,b)内可导,f(a)=0,0<a,证明存在ξɪ(0,a),使得2f(ξ)+ξfᶄ(ξ)=0.思路:该题相当于证明2f(x)+xfᶄ(x)在(a,b)内有零点,显然直接使用零点定理条件不足,考虑使用罗尔定理,此时2f(x)+xfᶄ(x)的原函数在直观上求不出来.这种情况一般可以描述为:考虑用罗尔定理证明f(x)的零点的存在性,但是f(x)的原函数求不出来,此时应该考虑适当选择恒正函数μ(x),对μ(x)f(x)的原函数使用罗尔定理.例如证明fᶄ(x)+P(x)f(x)-Q(x)在(a,b)内有零点,相当于证明任意恒正函数μ(x)[fᶄ(x)+P(x)f(x)-Q(x)]在(a,b)内有零点,一般取μ(x)=eʏP(x)dx,此时有eʏP(x)dx[fᶄ(x)+P(x)f(x)-Q(x)]=[eʏP(x)dxf(x)-ʏeʏP(x)dxQ(x)dx]ᶄ.这就转化成了证明函数F(x)=eʏP(x)dxf(x)-ʏeʏP(x)dxQ(x)dx的导函数在(a,b)内有零点.下面用该思路来证明例3.证明:2f(x)+xfᶄ(x)=0等价于2xf(x)+fᶄ(x)=0,此处P(x)=2x,Q(x)=0,则构造函数F(x)=eʏ2xdxf(x)-ʏeʏ2xdx㊃0dx=x2f(x),则根据函数的连续性和可导性可知,F(x)=x2f(x)在闭区间[0,a]上连续,在开区间(a,b)内可导,且依据条件F(0)=02f(0)=0,F(a)=a2f(a)=0,则F(x)=x2f(x)在闭区间[0,a]上满足罗尔定理的条件,结论自然也是成立的,所以存在ξɪ(0,a),使得Fᶄ(ξ)=2ξf(ξ)+ξ2fᶄ(ξ)=0,又由于ξʂ0,所以有2f(ξ)+ξfᶄ(ξ)=0.例3证明结束.有时候,证明函数在区间[a,b]内有零点,可以转化为证明函数在包含在[a,b]的小区间内有根.比如下方的例4.例4㊀已知函数f(x)在区间[0,1]内二阶可导,且f(0)=f(1).证明:存在ξɪ[0,1],使得(1-ξ)fᵡ(ξ)=3fᶄ(ξ).证明:由题设f(0)=f(1)和f(x)在区间[0,1]内二阶可导易知,f(x)在区间[0,1]上满足罗尔定理,所以存在aɪ(0,1),使得fᶄ(a)=0.另外由结论(1-ξ)fᵡ(ξ)=3fᶄ(ξ),我们希望构造函数(1-x)fᵡ(x)-3fᶄ(x)的原函数,这在直观上是不好求的,令u(x)=(1-x)2,则u(x)[(1-x)fᵡ(x)-3fᶄ(x)]=(1-x)3fᵡ(x)-3(1-x)2fᶄ(x)的原函数是好构造的,令F(x)=(1-x)3fᶄ(x),则F(a)=F(1)=0,且易知F(x)在区间[a,1]上满足罗尔定理的条件,则存在ξɪ[a,1],使得Fᶄ(ξ)=(1-ξ)3fᵡ(ξ)-3(1-ξ)2fᶄ(ξ)=0,即(1-ξ)3fᵡ(ξ)=3(1-ξ)2fᶄ(ξ),又因为(1-ξ)2>0,所以(1-ξ)fᵡ(ξ)=3fᶄ(ξ),该例题得证.关于函数的构造,经常考虑利用两个函数的零点.例如f(a)=g(b)=0,则构造F(x)=f(x)g(x),F(x)满足F(a)=F(b)=0.例4已经充分说明了这一点:fᶄ(x)满足fᶄ(a)=0,g(x)=(1-x)3满足g(1)=0,所以构造了F(x)=f(x)g(x)=(1-x)3fᶄ(x).在学习了定积分之后,会出现证明含有定积分和导数的方程的根的存在性的问题.例5㊀已知f(x)在闭区间[0,1]上连续,且f(0)=ʏ10f(x)dx=0,求证:ʏx0f(t)dt=xf(x)在(0,1)内有根.证明:令F(x)=ʏx0f(t)dtx,0<xɤ1,0,x=0.ìîíïïïï容易验证F(x)在[0,1]上满足罗尔中值定理,所以根㊀㊀㊀151㊀㊀据结论,存在ξɪ(0,1),使得Fᶄ(ξ)=ξf(ξ)-ʏξ0f(t)dtξ2=0,从而得到ξf(ξ)-ʏξ0f(t)dt=0,也就证明了ʏx0f(t)dt=xf(x)在(0,1)内有根.从以上几个例子可以看出,利用中值定理证明函数在给定区间内有根的关键是构造出合适的函数,而函数也恰好是高等数学最基本的研究对象.三㊁利用单调性证明根的个数上面两种情况均只涉及函数在给定区间内零点的存在性.存在性告诉我们函数在给定区间内至少有一个零点,但是关于零点个数却没有办法解出.事实上,结合单调性和函数的极值,或者说结合函数的图像,关于函数的零点的存在性和个数可轻易解决.首先给出关于单调性的定理:定理:区间(a,b)内,fᶄ(x)>0,则f(x)在(a,b)内单调递增;区间(a,b)内,fᶄ(x)<0,则f(x)在(a,b)内单调递减.例6㊀设函数f(x)=2lnx-x2+2.(1)求f(x)的单调性;(2)证明方程f(x)=0有两个不同的实根.(1)解:f(x)的定义域为(0,+ɕ),fᶄ(x)=2x-2x=2(1-x)(1+x)x.令fᶄ(x)=0,得x1=-1(舍去),x2=1.列表如下:x(0,1)1(1,+ɕ)fᶄ(x)+0-f(x)ʏ极大值ˌ如表所示,f(x)在(0,1]上单调递增,在[1,+ɕ)上单调递减.(2)证明:f(x)在1e,1[]上连续,在[1,e]上也连续.f1e()=2ln1e-1e2+2=-1e2<0,f(1)=2ln1-1+2=1>0,f(e)=2lne-e2+2=4-e2<0.根据零点定理,存在ξ1ɪ1e,1(),ξ2ɪ(1,e),使得f(ξ1)=0且f(ξ2)=0.综上可得方程f(x)=0至少有两个不同的实根,结合单调性可知,f(x)=0恰好有两个不同的实根.四㊁结㊀语对于同类问题的研究思考及区分,能够在一定程度上提高学生的发散思维能力,增强学生的学习兴趣,提高学生的学习能力.学生在学期总结或知识点总结时进行必要的题型总结,能够强化自身综合思维能力,掌握解题技巧,并且轻松地举一反三.ʌ参考文献ɔ[1]刘顺琴.空间解析几何中关于平面对称的若干问题[J].数学学习与研究,2019(14):112-113.[2]刘顺琴.空间直角坐标系下点到直线的距离的几种计算方法[J].数学学习与研究,2020(26):28-29.[3]赵姣珍,卢昌义,文利.浅析思维导图在独立院校高等数学教学中的应用[J].数学学习与研究,2020(26):26-27.[4]徐荣聪.高等数学[M].厦门:厦门大学出版社,2016.[5]江蓉,周敏.素质教育背景下提高大学数学课堂教学质量的若干方法[J].西南师范大学学报(自然科学版),2015(4):176-180.[6]吴慧卓.高等数学教学中渗透课程思政的探索与思考[J].大学数学,2019(5):40-43.[7]葛仁福.基于研究性学习的数学分析教学实践[J].数学教育学报,2013,22(1):80-82.[8]薛丽娟.基于 互联网+ 的高等数学教学改革实践与效果研究[J].黑龙江生态工程职业学院学报,2020(2):139-142.[9]丁慧,崔国范,王亚南.应用技术型大学高等数学有效教学模式研究[J].黑龙江高教研究,2016(9):173-176.[10]王伟,刘伟,马晓峰,等.大班授课㊁小班研讨教学模式在高等数学课程中的实施[J].高师理科学刊,2015,35(5):67-69.[11]孟津,王科.高职高专数学教学改革的必由之路:将数学建模的思想和方法融入高等数学课程教学中[J].成都电子机械高等专科学校学报,2007(1):41-45.[12]吕琳琳.OBE教育理念下的高等数学教学改革探索与研究[J].黑龙江科学,2019,10(11):60-61.。
高考数学解析几何专题讲义第16讲--定点问题

3 3
x2
ty2
1
②
由①②知 AB 的方程为 3 x ty 1 ,即 x 3(1 ty)
③
3
易知右焦点 F ( 3, 0) 满足③ 故直线 AB 恒过定点 F ( 3, 0)
(2)略
【例 2-2】(2019 全国Ⅲ文 21)已知曲线 C : y x2 ,D 为直线 y = - 1 上的动点,过 D 作 C 的两条切线, 切
【解法一】 F (1, 0), k (a2 , 0) ,先探索,当 m 0 时,直线 l ox 轴,则 ABED 为矩形,由对称性知,AE 与
BD 交于定点 N ( a2 1, 0) , 2
证明:设 A(x1, y1)B(x2 , y2 )E(a2 , y1) ,当 m 变化时首先 AE 过定点 N
2 2
+ +
(y + y2 =
1)2 3 1
=
(4)2 3Þ
ìïx = 0 ïî y = 1
即两圆的公共点为(0,1)
因此所求点 T 如果存在,只能是(0,1),事实上.点(0,1)就是所求点,证明如下 当 l 与 x 轴垂直时,以 AB 为直径的圆过 T(0,1)
当 l 与 x 轴不垂直时,设直线 l : y = kx - 1 3
且以 AB 为直径的圆过椭圆 C 的右顶点。求证:直线 l 过定点,并求出该定点坐标.
y kx m
【解析】设
A(x1,
y1), B(x2 ,
y2 ) ,由 3x2
4y2
得 12
(3 4k 2 )x2 8mkx 4(m2 3) 0
64m2k 2 16(3 4k 2 )(m2 3) 0
2
2
点分别为 A,B.
连续时间Dynkin博弈的纳什均衡点存在性的一个新证明

中的凸集$
定理% 的 证 明 主 要 分 为 # 步#第 % 步 证 明 对 于
Copyright©博看网. All Rights Reserved.
第#期
张宜劼#连续时间 H:/I2/博弈的纳什均衡点存在性的一个新证明
%&&
每个固定* 8 $9"3!9$:"是拟;凹泛函%第$步 设9?%'9@%$此时
!"""/$0/ * - $ !#""/ 关于时间. 右连续$左极限存在$0/ 关
于 时 间.是 连 续 的 $
!$""/ 是上鞅$0/ 是下鞅$
!%",.( ,$"./ #0/.$0.% # ".$ $当参与人同 时停止时取等号$
!&",.% (.$ $'!".%% "6'!".%$ "# '!".$% "6 '!".$$ "$ 那么存在 !%%+ $%$+ "* $" 2$" 为与1%$1$ 相关博弈
$ 由 条 件 !" "可 知 8-?
"# >! '"*
##% "# #$
必要性*由一致可积的定义知对任意"% "$存
$ 在充分大的$ $使8-?
"# >! '"成立*由
##% "# #$
此可得
则
O2/!8-?3!5$4""( 8-?3!5$5"(
4*" 5*"
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
meh d frt e p o i g o e e itn e o h o n n d f r n t o r vn ft x se c ft e p i t i e e t o h h i
, lt、
占 的存 在 性 的证 明方 法 的分 析
郑 昌红
( 北经 济学 院统计 与应 用数 学 系 湖北 ・ 湖 武汉 400 ) 3 2 5
中 图分 类号 : 6 2 G 4
文献 标 识码 : A
文 章编 号 :6 2 7 9 ( 0 】7 0 8 0 17 — 842 1 2— 9 —2 1
设 ) 0 1 连续, 在f1 = ,3 且 o- )证明对任何自然数 )  ̄1,
n ,
terms fh ni osu co 'i cn ut it cn io, hoe ec t uu n tn ) od c bly odt n ot o n f i ,n 2 i i i uiz em t hoe ;wtot o t uu n tn r od ti F r a T erm3 i u cni os u cos n - le ) h n f i oc
看 0 。 1 )0 而 0 ) 一 <。 )
) 0 , 1m ) 1- ) 一 _ ) - f l f
我 们 经 常 会 碰 到 这 样 一类 问 题 , 定 一 定 的 已知 条 件 , 给 要证明至少存在一点 , 使得这 点满 足某个条 件。这类 问题 , 首先我们通 常能想到 的方法就是用根的存在定理 、介值定 理、 中值定理等 。构造相应的辅助 函数 、 设定相应 的区间 , 然 后验证条件 , 即可 得 出 结 论 。 然 而 , 些 问题 并 不 满 足 这 些 有 定理的条件 , 这时候我们 就无法用 常规 的方法进行证 明了。 下面我们通过几个具体 的问题来对证 明点 的存在性 的方法
∞, 存 在 一 个 数 l , 则 > 当 ( l , )_ < ; l ) 0 一 时 ( 10 又 i m
关键词
数 理 论
连 续 根 的 存 在 定 理 介 值 定 理 中值 定 理 卖
= 。所以则存在—个数 > , > 时 , )1 0 +。, O当x M2 > > 。从而得到: 凡 ) 。1M2l 在卜 一 , + 1 上连续 , 且 一 M广1 -< , + )10 ) 1 0 < 1> > , 由根 的存在定理知 : 一 一 2 ) 在(M 1 - 中至少存在一点 , 得 1 使 )0 即方 程 )X =, - n )0 少 有 一 个根 。 =至 用根 的存在定理的时候 ,构造的函数必须是某个 闭区
e fc , ma sHub i i e Unv r i o o o c , 0 5, u n, ie st f Ec n mi s43 20 W ha Hub i y e, Chia n
_( 厂 卅 )厂( = - )0在 [ 1 ] 至少 有 一 个 解 , 般 想 法 是 0一 上 , ~
c ran c n i o sT e e a eg n rl r ec n i o s1i O et i o d t n . h r r e ea l t e o dt n :) C — i yh i n
n iuo s c n to , o e i y tlzng t e c a a trsi s n tn u o di nprv t u i i h h r ce itc a d i b i
+ , 以l ∞ 所 i F m
( 一 。,i ) 。 l m
一
)+ 。给定 一 个 数 G I根 据 以 l = =, i a r
) :
分 , 用 费马 定 理 和 中值 定理 证 明 : ) 连 续 或 者 可 导 条 件 利 3无 时 . 常 需 要用 实数 理论 进行 分 析 通
间 上 的连 续 函 数 。当直 接 证 明 无法 证 的 时候 , 考 虑 用 反 不妨 证 法 , 下例 : 如
A ay i f t e Pr v n e h d f r h it n e o An l ss o h o i g M t o o t e Ex se c f t e P i t/ h n h n h n h o n /Z e g C a g o g
摘 要 本 文 主要 讨 论 了在 给 定 不 同 的条 件 下 .证 明点 的
存 在 性 的一 般 分析 方 法。 大 体 上 分 成 三 种情 况 : )连 续 条 1
件, 利用 连 续 函数 的性 质 及 其定 理 进 行 证 明 : 可 导或 者 积 2)
: 。 由于 一 时 ,L+ ∞ , + 时 , 。。 ∞ _ ,一 ∞
均可以求得相应 的点 , 使得 只 = )只
。
分 析 : 难 看 出 , 以 设 数 )厂 ) ) 不 可 = (+ 一 ,
,Байду номын сангаас
1 ] 一 , 则 ) 为连续函数 。 这个问题等价于证 明方程 )
r o; d u n mb rt e r; a n mb rt e r ot me im u e oy r l u e o y h e h Au h r d r s e a me to t t t sa d Ap l d Mah t o a d e s D p r n f ai i n p i t — S t S sc e
u t i t ,、so e r v d b t ii gr a u e e r . ci l yi i f n p o e yu i zn e ln mb rt o y bi t t l h
Ke y w o d c n i o st te r m o h e se e f he r s o tnu u ; he h o e f t e xitnc o t
