《解析几何》 各类竞赛试题选讲
解析几何竞赛题选

25.[决赛试题](13 分)已知两直线的方程: L : x = y = z , L ' : x = y = z − b 。(1)问: 1a 1
参数 a, b 满足什么条件时, L 与 L ' 是异面直线?(2)当 L 与 L ' 不重合时,求 L ' 绕 L 旋转 所生成的旋转面 π 的方程,并指出曲面 π 的类型。
=
(1 a
, 0, −
1)× c
(0,1, 0)
=
(1 c
, 0,
1 ). a
若π
平行于l2 ,则λ
=
−
1 a
.在直线l2上取点M
(a,
0, 0),则M 到平面π的距离
即为l1与l2的距离2d,即
(2d )2 =
22
,⇒ 1 = 1 + 1 + 1 .
1 a2
+
1 b2
+
1 c2
d 2 a2 b2 c2
t 可以是任意的,所以,这时, π 的方程为:
⎧ x+y+z=b
⎪
⎨ ⎪⎩
x
2
+
y2
+
z2
≥
5 6
b2
,
π 的类型: a = 1 且 b ≠ 0 时, L 与 L ' 平行,π 是一柱面; a ≠ 1且 b = 0 时, L 与 L ' 相交, π 是一锥面( a = −2 时 π 是平面);当 a ≠ 1且 b ≠ 0 时,π 是单叶双曲面( a = −2 时,π 是
+ +
(z (z
+ 1) 2 −1)2
,
即
大学解析几何考试题及答案详解

大学解析几何考试题及答案详解一、选择题1. 下列哪个选项不是平面直角坐标系中的点的坐标表示?A. (x, y)B. (y, x)C. (-3, 4)D. (2, -5)答案:B详解:在平面直角坐标系中,点的坐标表示为有序数对 (x, y),其中 x 表示横坐标,y 表示纵坐标。
选项 B 中的表示 (y, x) 与常规的坐标表示不符,因此不是正确的坐标表示。
2. 已知点 A(2, 3) 和点 B(5, 1),线段 AB 的中点 M 的坐标是多少?A. (3, 2)B. (4, 2)C. (3.5, 2)D. (2, 1)答案:B详解:线段的中点坐标可以通过求两个端点坐标的平均值得到。
对于点 A(2, 3) 和点 B(5, 1),中点 M 的坐标为:M(x, y) = ((x1 + x2) / 2, (y1 + y2) / 2) = ((2 + 5) / 2,(3 + 1) / 2) = (3.5, 2)因此,正确答案是 C,但选项 B 也正确,这里可能是题目选项设置的错误。
二、填空题1. 如果一条直线的斜率 k = 2,且通过点 (1, 3),那么这条直线的方程是 ____________。
答案:y - 3 = 2(x - 1)详解:已知直线的斜率 k 和一个点 (x1, y1),可以使用点斜式方程 y - y1 = k(x - x1) 来表示直线。
将已知的斜率 k = 2 和点 (1, 3) 代入,得到直线方程 y - 3 = 2(x - 1)。
2. 椭圆的标准方程是 ________,其中 a 和 b 是椭圆的长半轴和短半轴。
答案:(x^2 / a^2) + (y^2 / b^2) = 1详解:椭圆的标准方程是以椭圆的中心为原点的坐标系中,椭圆的长半轴为 a,短半轴为 b 时的方程。
这个方程描述了所有到椭圆两个焦点距离之和等于常数 2a 的点的集合。
三、解答题1. 已知直线 l1: y = x + 1 与直线 l2: y = -2x + 6 相交于点 P。
解析几何综合题选讲 - 答案

平面几何与圆锥曲线综合题选讲1、在平面直角坐标系xOy中,已知圆心在第二象限,半径为的圆C 与直线y x =相切于坐标原点O ,椭圆22219x y a +=与圆C 的一个交点到椭圆两焦点的距离之和为10. (1)求圆C 的方程;(2)试探究圆C 上是否存在异于原点的点Q ,使Q 到椭圆右焦点F 的距离等于线段OF 的长.若存在,请求出点Q 的坐标;若不存在,请说明理由. 19解:(1) 设圆C 的圆心为 (m , n )(m <0,n >0)依题意可得1n m ⎧=-⎪= 解得22m n =-⎧⎨=⎩∴所求的圆的方程为 22(2)(2)8x y ++-=(2) 由已知可得 210a = ∴ 5a = ∴ 椭圆的方程为221259x y += , 右焦点为 F( 4, 0);设00(,)Q x y ,依题意22002200(2)(2)8(4)16x y x y ⎧++-=⎪⎨-+=⎪⎩解得00412,55x y ==或000,0x y ==(舍去) ∴存在点412(,)55Q 2、设b >0,椭圆方程为222212x y b b+=,抛物线方程为28()x y b =-。
如图所示,过点F (0,b +2)作x 轴的平行线,与抛物线在第一象限的交点为G 。
已知抛物线在点G 的切线经过椭圆的右焦点F 1。
(1)求满足条件的椭圆方程和抛物线方程; (2)设A 、B 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点P ,使得△ABP 为直角三角形? 若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标)。
【解析】(1)由28()x y b =-得218y x b =+,当2y b =+得4x =±,∴G 点的坐标为(4,2)b +,1'4y x =,4'|1x y ==, 过点G 的切线方程为(2)4y b x -+=-即2y x b =+-,令0y =得2x b =-,1F ∴点的坐标为(2,0)b -,由椭圆方程得1F 点的坐标为(,0)b ,2b b ∴-=即1b =,即椭圆和抛物线的方程分别为2212x y +=和28(1)x y =-;(2)过A 作x 轴的垂线与抛物线只有一个交点P ,∴以PAB ∠为直角的Rt ABP ∆只有一个, 同理∴ 以PBA ∠为直角的Rt ABP ∆只有一个。
第二轮专题-解析几何.

解析几何题选讲ABCD 的面积的最大值为2.过抛物线y 2 2px (p 0)的焦点F 且倾斜角为60°的直线I 与抛物 A 、B 两点,贝y LA 匸1的值等于 (C )|BF |离心率是纽55C 的右焦点F 做直线I 交椭圆C 于A,B 两点 交y 轴于M.若MA =解:(I )x 2+5y 2=5;(n )A(x i , y i ), B(X 2, y 2), F(2,0), M(O,y 。
)解法1:由2(x 1 x 2) 2x 1x 21 24 2(x 1 x 2) x 1x 22 1.已知AC 、BD 为圆0:x 2y 4的两条相互垂直的弦,垂足为 Mi,J 2 ,则四边形3.已知中心在坐标原点的椭圆C 的焦点在x 轴上,它的一个顶点是抛物线y=-x 2的焦点,4入 1 AF ; MB =X 2BF 求证: 入1+入2为定值, 线在第一、四象限分别交于 (I )求椭圆方程;(n )过椭圆 ••• MAX 11(2 X 1)①②,1AF ,.・.¥1 y 。
1 y1•••有 F— )2=5,整理得2+10 21 +5-5 y o =0,同理有2+1022 +5 - 5yo =0,解法2:由①有1—x —,同理2 X 1X 2 2 X 25y i 25话6个方程,7个未知数:x i ,y i ,X 2,y 2,y o ,入i ,入2. 消去X i ,y i ,x 2,y 2,y o ,得入1与入2的关系.(2)证明:易求出椭圆C 的右焦点F (24}・ 设 A (j',』> (七,必).M (O,y :),显然直线f 的斜率存在,设直找f 的方程为y =走(丈一2) 1 代入方程普+ y = l 并整理,得(1 +5护)止'一20护工+ 20护一5 = 0*・ ] 2Qk- 20/一 5又 M A —( .11 *的—” J *M S =(芒:•加—,“)* 兀P= (2 —一$1) tEF — (2 — JT.1 — y J q 而 M A=A I 兀A M B=A J IJP,即(jTj M )=人1 <2 — 茁[.—yi ) 1,为―yj =e (2——yj*t iT 1£ J ■:町 丄_ 2(咼 十)—Z TI A 二4, L 2知tffj 岡的屮・1>为坐标K 点a 焦点在丄轴上.斜率为J ii 过椭鬪右焦点F 的E I 纱空椭闘于/1小M 点JPt + cW 勺ei =〔緘=1)扶线.(1)求椭圈的离心率;⑵设M 为椭岡L 任意一点・fl.曲二入(71十川必(心怎 1<山正明;入:+^为定ffl.5y2 5,再用韦达定理… X ii(2 X i )① y i y o i yi② X 22(2 X 2)③ y 2 y o2丫2④解法3:于是y 2X ・・ J LI 十" 2—jTi ~^2—x^ 1—+事〉+工】站由?P1+FIR=(J] +芒“+ $2)*农=(3 ・一】)・F5久+ ?JS 与a共线*得3(yi+;』+ (文|十jr/ = 0・又5-1 =口1 —广・,2=』僅一C3+ .rj —2f)+ (巧 +号)=0, A .r, + .巧= 即活务=瓠所以宀3从肌=/7二歹=普鼻故离心率¥= — =餐.a J(2)证明;由(1)知/ = 3/化所以獅圆土r+恂=1(口>方>0)可化为J'+3y = 36\ a' b'设(菇=(4*几由已打得(小$)=A<Xi』)+"(皮¥)*二TM(2$)在椭圆上+'$ =人$1 +/<丫齐/•CA J I 十“工2 )£十3(入M十“为= 36<即F (卅 + ^y])+//(」";+ ^yl)+ 2A// (Xi j )=:"丄①由{1)知 ■=弓-匸‘ =寺WIjfiH, + 3$| y, = j + j'l — r) C.t j — r) = lTB.r2 — 3(.T J 十丁工十3广7nF 十= 0-又# +工诟二引几土 + 3$;=貂'*代入①得L故F +/为定值•定值为1・ _________________________5.已知P(4,0)是圆x 2+y 2=36内的一点A, B 是圆上两个动点,且/ APB=90。
历年全国高中数学联赛《解析几何》专题真题汇编

历年全国高中数学联赛《解析几何》专题真题汇编1、已知点A 为双曲线x 2-y 2=1的左顶点,点B 和点C 在双曲线的右分支上,△ABC 是等边三角形,则△ABC 的面积是 ( C )(A) 33 (B) 233 (C) 33 (D) 633、若实数x, y 满足(x+5)2+(y12)2=142,则x 2+y 2的最小值为( )(A) 2 (B) 1 (C) 3 (D)2 【答案】B【解析】利用圆的知识结合数形结合分析解答,22x y +表示圆上的点(x,y )到原点的距离。
4、直线134=+yx 椭圆191622=+y x 相交于A ,B 两点,该圆上点P ,使得⊿PAB 面积等于3,这样的点P 共有( )(A) 1个 (B) 2个 (C) 3个 (D) 4个【答案】B5、设a ,b ∈R ,ab ≠0,那么直线ax -y +b=0和曲线bx 2+ay 2=ab 的图形是( )【答案】B6、过抛物线y 2=8(x +2)的焦点F 作倾斜角为60°的直线,若此直线与抛物线交于A 、B 两点,弦AB 的中垂线与x 轴交于点P ,则线段PF 的长等于( ) (A)163 (B) 83 (C) 1633 (D) 8 3 【答案】A【解析】抛物线的焦点为原点(0,0),弦AB 所在直线方程为y=3x ,弦的中点yxO Ox yO xyyx O A. B. C.D.在y=pk =43上,即AB中点为(43,43),中垂线方程为y=-33(x-43)+43,令y=0,得点P的坐标为163.∴PF=163.选A.7、已知M={(x,y)|x2+2y2=3},N={(x,y)|y=mx+b}.若对于所有的m∈R,均有M∩N≠∅,则b的取值范围是( )A.[-62,62] B.(-62,62) C.(-233,233] D.[-233,233] 【答案】A【解析】点(0,b)在椭圆内或椭圆上,⇒2b2≤3,⇒b∈[-62,62].选A.8、方程13cos2cos3sin2sin22=-+-yx表示的曲线是()A.焦点在x轴上的椭圆B.焦点在x轴上的双曲线C.焦点在y轴上的椭圆D.焦点在y轴上的双曲线【答案】C9、设圆O1和圆O2是两个定圆,动圆P与这两个定圆都相切,则圆P的圆心轨迹不可能是()【答案】A【解析】设圆O1和圆O2的半径分别是r1、r2,|O1O2|=2c,则一般地,圆P的圆心轨迹是焦点为O1、O2,且离心率分别是212rrc+和||221rrc-的圆锥曲线(当r1=r2时,O1O2的中垂线是轨迹的一部份,当c=0时,轨迹是两个同心圆)。
高中数学联赛解析几何专题练习(详解版)

高中数学联赛解析几何专题练习(详解版)一、单选题1.已知12F F 、分别为双曲线()222210,?0x y a b a b-=>>的左、右焦点,P 为双曲线右支上任一点。
若212PF PF 的最小值为8a ,则该双曲线的离心率e 的取值范围是( )。
A .(1, 3] B .(1,2] C .[2,3] D .[3,十∞) 2.对0b a >>,取第1象限的点(),k k k A x y ()1,2,,k n =L ,使a ,1x ,2x ,L n x ,b 成等差数列,而a ,1y ,2y ,L ,n y ,b 成等比数列.则各点1A 、2A 、L 、n A 与射线():0l y x x =>的关系为( ).A .各点均在射线l 的上方B .各点均在射线l 上C .各点均在射线l 的下方D .不能确定 3.若直线4x π=被曲线C :()()()()arcsin arccos arcsin arccos 0x a x a y a y a --+--=所截得的弦长为d ,当a 变化时d 的最小值是( ).A .4πB .3πC .2πD .π4.直线l 在平面上α,直线m 平行于平面α,并与直线l 异面.动点P 在平面上α,且到直线l 、m 的距离相等.则点P 的轨迹为( ).A .直线B .椭圆C .抛物线D .双曲线5.已知1F 、2F 为椭圆与双曲线的公共焦点,P 为它们的一个公共点,且1260F PF ∠=o .则该椭圆与双曲线的离心率之积的最小值为().A.3 B.2 C .l D6.过椭圆2212x y +=的右焦点2F 作倾斜角为45︒的弦AB .则AB 为( ). A.3 B.3 C.3 D.37.点P (0,2)关于直线210x y +-=的对称点坐标是A .(-2,0)B .(-1,0)C .(0.-1)D .62,55⎛⎫-- ⎪⎝⎭. 8.以双曲线2214x y m-=的离心率为半径、右焦点为圆心的圆与双曲线的渐近线相切.则m =( )A .32B .43C .54D .65 9.记()()()223,03x F x y x y y y ⎛⎫=-++≠ ⎪⎝⎭.则(),F x y 的最小值是( ). A .125 B .165 C .185 D .410.设1A 、2A 为椭圆()222210x y a b a b+=>>的左、右顶点.若在椭圆上存在异于点1A 、2A 的点P ,使得20PO PA ⋅=u u u v u u u u v ,其中,O 为坐标原点,则椭圆的离心率e 的取值范围是( ).A .10,2⎛⎫ ⎪⎝⎭B .⎛ ⎝⎭C .1,12⎛⎫ ⎪⎝⎭D .⎫⎪⎪⎝⎭二、填空题11.若实数x 、y 满足x -=,则x 的取值范围是______.12.在平面直角坐标系中,如果x 与y 都是整数,就称点(,)x y 为整点,下列命题中正确的是_____________(写出所有正确命题的编号)①存在这样的直线,既不与坐标轴平行又不经过任何整点②如果k 与b 都是无理数,则直线y kx b =+不经过任何整点③直线l 经过无穷多个整点,当且仅当l 经过两个不同的整点④直线y kx b =+经过无穷多个整点的充分必要条件是:k 与b 都是有理数⑤存在恰经过一个整点的直线13.抛物线22y x =的一条弦被()4,2A 平分,那么这条弦所在的直线方程是__________. 14.已知双曲线()222210,0x y a b a b-=>>的左、右焦点分别为1F 、2F ,过点1F 作圆222x y a +=的切线,与双曲线的右支交于点P ,且1245F PF o ∠=。
(黄倩霞)大学生数学竞《解析几何》培训讲义
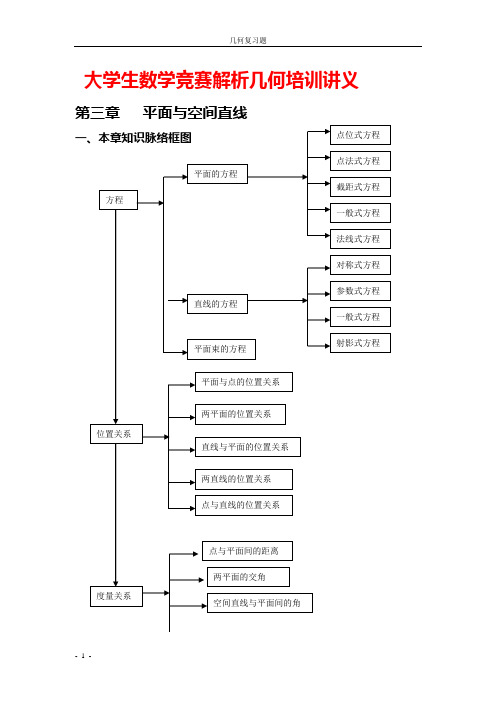
大学生数学竞赛解析几何培训讲义第三章平面与空间直线二、本章重点及难点解析几何最显著的特点就是用代数方法来研究几何.因此学习解析几何不仅要有良好空间图形的认知能力,而且更要有一些必要的代数知识,特别是向量代数知识.作为最简单的曲面与曲线——平面与空间直线来说,图形的认知应该是比较容易的,关键是要学会灵活运用有关它们的一些数量、向量以及向量形式的方程,比如平面上或直线上的点的坐标、平面的法向量、直线的方向向量、平面的向量式方程以及直线的向量式参数方程等来解决有关几何问题.本章的重点是:● 平面的各种形式的方程及其相互转换; ● 直线的各种形式的方程及其相互转换; ● 点、平面及直线的关系. 本章的难点是:● 点与平面的离差,平面划分空间问题; ● 向量式方程的运用;● 灵活运用某些点、平面的法向量、直线的方向向量,平面束等来解决一些几何问题.三、本章的基本知识要点1.平面的方程在中学的立体几何中,读者知道了一个公理:空间中不在一条直线上的三个点可以确定唯一的平面,还知道两个定理:①空间的两条相交直线可以确定准一的平面,②垂直于平面的直线同时垂直平面内的一切直线.通过上述的知识和利用矢量运算,可以得到以下平面的方程.(1)向量式方程:b v a u r r o++= (3.1)其中u,v 为参数.在仿射坐标系下,{}o o o o z y x r ,,= ,{}z y x r ,,= ,{}{}222111,,,,,Z Y X b Z Y X a ==将它们代人式(3.1),可得到下述参数式方程.(2)参数式方程⎪⎩⎪⎨⎧++=++=++=vZ u Z z z v Y u Y y y v X u X x x O O o 212121 (3.2)由于向量b a r r o,,-共面,可以得到下述混合积方程.(3)混合积方程:0),,(=-b a r r o(3.3)将对应的向量的坐标代入式(3. 3)中,可得到下述点位式方程.(4)点位式(或行列式)方程0222111=---Z Y X Z Y X z z y y x x o o o (3.4)将式(3.4)中的行列式按第一行展开,可得到下述一般方程.(5)一般方程(或称为普遍式方程)0=+++D Cz By Ax (3.5)这是一个三元一次方程.当D 不等于零时,可以得到下述截距式方程.(6)裁距式方程1=++czb y a x (3.6) 为了便于讨论点到平面的距离和点与平面的位量关系,将平面方程的讨论限制在直角坐标系下.在空间直角坐标系下.设平面上点Mo 的径矢{}00000,,z y x r OM ==,平面上任意一点M 的径矢{}z y x r ,,== 以及平面的法向量{}C B A ,,=,由于n M⊥0,所以通过0)(0=-∙r r n(3.7) 可以得到平面的点法式方程. (7)点法式方程0)()()(000=-+-+-z z C y y B x x A (3. 8)格式(3. 8)展开整理后,仍可以得到与式(3.5)类似的三元一次方程.为了计算点到平面距离和讨论点与平面的相对位置,需要指定平面的法矢.将取自原点O 出发,垂直于平面π的矢量指定为平面π的法矢,有了指定法矢的平面常被称为有向平面.此时平面π上任意点M 的径矢{}z y x r OM ,,==与平面π的单位法矢{}γβαcos ,cos ,cos 0=n 有下面的关系:p r n =⋅(3.9)其中p 是非负的.是原点O 到平面π的距离.将式(3 9)中各矢量的坐标代入,可得到下述的法式方程.(8)法式方程0cos cos cos =-++p z y x γβα (3.10)将一般方程0=+++D Cz By Ax 转化为法式方程时,需要在方程两边同时乘上法化因子22211C B A n ++±=±=λ 其中λ的正负号选取应满足0 p D =-λ,即0≠D 时,取λ与D 异号,当D=0时,取λ与第一个变量的系数同号.例如,0≠A 取0 A λ(9)三点式方程0131313121212111=---------z z y y x x z z y y x x z z y y x x (3.11) 这个方程可以看做与式(3.4)为同一类.2.平面与点的相关位置(1)点0M 与平面间π的离差p r n -⋅=δ (3.12)其中0n 为原点指平面π的单位法矢矢, ,00r OM=p 为原点O 到平面π的距离.式(3.12)也可以写成代数表达式p z y x -++=γβαδc o s c o s c o s 000 (3.13) 原点)0,0,0(O 与平面π间的离差为p -=δ,反映出原点O 、平面π、及其单位法矢0n之间的关系.点与平面间的离差是一个代数值,它的正负号反映出点在平面的侧向.在平面π同侧的点,δ的符号相同;对于在平面π异仍的点,δ的符号相反;平面π上的点,δ等于零.点与平面向的离差公式(3.13)可以将空间不在平面上的点分成两部分.同理,两个相交的平面将空间的点分成四部分.(2)点),,(0000z y x M 与平面0=+++D Cz By Ax 间的距离为 222000CB A DCz By Ax d +++++==(3.14)3.两平面的相关位置 空间两平面0:11111=+++D z C y B x A π0:22222=+++D z C y B x A π 有以下的关系:(1)1π与2π相交222111::::C B A C B A ≠⇔ (2) 1π与2π平行21212112D D C C B B A A ≠==⇔(3) 1π与2π重合21212112D D C C B B A A ===⇔在空间直角坐标系下,两平面1π与2π间的交角是用两平面二面角的平面角1(π∠,2π)来表示,并且常取其中的锐角来表示.根据平面与其法矢垂直的关系,记θ=∠),(21n n,可以得到222222212121212121212121cos ),(cos CB A CB AC C B B A A n n n n ++++++=⋅==∠ θππ (3.15)同时,两平面1π与2π垂直的充要条件是0212121=++C C B B A A4.空间直线的方程在中学的立体几何课程中有一个公理:空间不重合的两点可以确定唯一的直线.读者容易知道直线上任意两个不重合的点可以确定一个直线的方向向量.因此,在空间取定坐标系,并设直线l 上一定点Mo 的径矢{}00000,,z y x r OM ==,直线 l 上任意点M 的径矢为{}z y x r ,,= ,直线l 的方向向量v,可以得到直线l 的向量式方程“(1)向量式方程v t r r o+= (3.16)其中t 为参数.(2)参数方程⎪⎩⎪⎨⎧+=+=+=Ztz z Yt y y Xt x x O O o (3.17)由式(3.17)梢去参数t ,可以得到直线l 的对称式方程.(3)对称式方程(或称直线l 的标准方程)Zz z Y y y X x x 000-=-=- (3.18) 在式(3.18)中,方向效Z Y X ,,是一组不全为零的数.如果其中有一个为零, 例 如0=X .此时,可以设⎪⎩⎪⎨⎧-=-=Z z z Yy y x x 000如果其中有两个数为零,例如0,0==Y X ,此时.可以设⎩⎨⎧==00y y x x这样可以得到相对应的直线方程.通过空间两点),,(1111z y x M 和),,(2222z y x M ,可以得到直线的两点式方程.(4)两点式方程121121121z z z z y y y y x x x x --=--=-- (3.19)空间直线可以看做是两个相交平面的交线,所以可以得到直线一般方程. (5)直线的一般方程⎩⎨⎧=+++=+++0022221111D z C y B x A D z C y B x A (3.20)其中系数222111::::C B A C B A ≠。
高中数学竞赛与强基计划试题专题:解析几何

高中数学竞赛与强基计划试题专题:解析几何一、单选题1.(2020·北京·高三强基计划)从圆224x y +=上的点向椭圆22:12x C y +=引切线,两个切点间的线段称为切点弦,则椭圆C 内不与任何切点弦相交的区域面积为()A .2πB .3πC .4πD .前三个答案都不对2.(2022·北京·高三校考强基计划)内接于椭圆22149x y +=的菱形周长的最大值和最小值之和是()A .B .CD .上述三个选项都不对3.(2020·湖北武汉·高三统考强基计划)已知直线1211::22l y x l y x =-=,,动点P 在椭圆22221(0)x y a b a b +=>>上,作1//PM l 交2l 于点M ,作2//PN l 交1l 于点N .若22PM PN +为定值,则()A .2ab =B .3ab =C .2a b =D .3a b=4.(2020·北京·高三强基计划)设直线3y x m =+与椭圆2212516x y +=交于A ,B 两点,O 为坐标原点,则OAB面积的最大值为()A .8B .10C .12D .前三个答案都不对5.(2022·贵州·高二统考竞赛)如图,1C ,2C 是离心率都为e 的椭圆,点A ,B 是分别是2C 的右顶点和上顶点,过A ,B 两点分别作1C 的切线1l ,2l .若直线1l ,2l 的斜率分别为1k ,2k ,则12k k 的值为()A .2eB .21e -C .21e -D .21e 6.(2020·湖北武汉·高三统考强基计划)过椭圆22149x y +=的中心作两条互相垂直的弦AC 和BD ,顺次连接,,,A B C D 得一四边形,则该四边形的面积可能为()A .10B .12C .14D .167.(2019·贵州·高三校联考竞赛)设椭圆C :()222210x y a b a b +=>>的左、右焦点分别为12,F F ,其焦距为2c .点322c N ⎛⎫⎪ ⎪⎝⎭在椭圆的内部,点M 是椭圆C 上的动点,且112||MF MN F +<恒成立,则椭圆C 的离心率的取值范围是()A .⎛ ⎝⎭B .⎫⎪⎪⎝⎭C .⎫⎪⎪⎝⎭D .⎝⎭二、多选题8.(2022·贵州·高二统考竞赛)如图,M ,N 分别是Rt ABC △两直角边上的动点,P 是线段MN 的中点,则以下结论正确的是()A .当△AMN 的面积为定值时,点P 的轨迹为双曲线一支B .当|MN |为定值时,点P 的轨迹为一圆弧C .当||||AM AN +为定值时,点P 的轨迹为不含端点线段D .当△AMN 的周长为定值时,点P 的轨迹为抛物线9.(2020·北京·高三校考强基计划)已知A ,B 分别为双曲线2214x y -=的左、右顶点,P 为该曲线上不同于A ,B 的任意一点设,,∠=∠= PAB PBA PAB αβ的面积为S ,则()A .tan tan αβ⋅为定值B .tantan22αβ⋅为定值C .tan()S αβ⋅+为定值D .cot()S αβ⋅+为定值10.(2020·北京·高三校考强基计划)已知点(1,1),(1,0)A Q ,P 为椭圆22143x y +=上的动点,则||||PA PQ +的()A .最大值为4B .最大值为4C .最小值为4-D .最小值为4三、填空题11.(2022·江苏南京·高三强基计划)设F ,l 分别为双曲线()22411212x y --=的右焦点与右准线,椭圆Γ以F和l 为其对应的焦点及准线,过F 作一条平行于y =的直线,交椭圆Γ于A 、B 两点,若Γ的中心位于以AB 为直径的圆外,则椭圆离心率e 的范围为___________.12.(2018·山东·高三竞赛)若直线65280x y --=交椭圆22221x ya b+=(0a b >>,且2a 、b 为整数)于点A 、C .设()0,B b 为椭圆的上顶点,而ABC 的重心为椭圆的右焦点2F ,则椭圆的方程为______.13.(2022·新疆·高二竞赛)设z 为复数,若方程2297--=z z 表示一条圆锥曲线,则此曲线的离心率=e ___________.14.(2021·全国·高三竞赛)已知集合{}22(,)|||||,0,(,)|1,044x y A x y x y t t B x y m m ⎧⎫=+>=+≤<<⎨⎩≤⎬⎭满足B A ⊆,若P 为集合B 的边界线C 上任意一点,12F F 、为曲线C 的焦点,I 为12PF F △的内心,直线1IF 和2IF 的斜率分别为12k k 、,且1213k k ⋅=-则t 的最小值为________.15.(2021·全国·高三竞赛)已知ABCD Y 的四个顶点均在双曲线2214y x -=上,点(0,1)P 在边AB 上,且12AP PB =,则ABCD Y 的面积等于_______.四、解答题16.(2022·湖北武汉·高三统考强基计划)设F 为椭圆C :22194x y +=的左焦点,P 为椭圆C 上的一点(1)作正方形FPAB (F ,P ,A ,B 按逆时针排列)当P 沿着椭圆运动一周,求动点B 的轨迹方程.(2)设()3,2Q 为椭圆外一点,求PQ PF +的取值范围.17.(2018·全国·高三竞赛)一束直线12,,l l 的每条均过xOy 平面内的抛物线2:C y x =的焦点,()1i l i ≥与抛物线C 交于点i A 、i B .若1l 的斜率为1,()2i l i ≥的斜率为1+2014l 的解析式.18.(2018·福建·高三竞赛)已知1F 、2F 分别为椭圆()2222:10x y C a b a b +=>>的左、右焦点,点3P ⎛⎫ ⎪⎝⎭在椭圆C 上,且12F PF △的垂心为5,33H ⎛⎫- ⎪ ⎪⎝⎭.(1)求椭圆C 的方程;(2)设A 为椭圆C 的左顶点,过点2F 的直线l 交椭圆C 于D 、D 两点.记直线AD 、AE 的斜率分别为1k 、2k ,若1212k k +=-,求直线l 的方程.19.(2018·江西·高三竞赛)若椭圆221259x y +=上不同的三点()11,A x y ,94,5B ⎛⎫ ⎪⎝⎭,()22,C x y 到椭圆右焦点的距离顺次成等差数列,线段AC 的中垂线l 交x 轴于点T ,求直线BT 的方程.20.(2018·湖北·高三竞赛)已知O 为坐标原点,()1,0N ,点M 为直线=1x -上的动点,MON ∠的平分线与直线MN 交于点P ,记点P 的轨迹为曲线E .(1)求曲线E 的方程;(2)过点11,22Q ⎛⎫-- ⎪⎝⎭作斜率为k 的直线l ,若直线l 与曲线E 恰好有一个公共点,求k 的取值范围.21.(2021·全国·高三竞赛)过抛物线22y px =(p 为不等于2的质数)的焦点F ,作与x 轴不垂直的直线l 交抛物线于M 、N 两点,线段MN 的垂直平分线交MN 于P 点,交x 轴于Q 点.(1)求PQ 中点R 的轨迹L 的方程;(2)证明:L 上有无穷多个整点(横、纵坐标均为整数的点),但L 上任意整点到原点的距离均不是整数.22.(2021·全国·高三竞赛)已知椭圆22:12+=x E y 的右焦点为(c,0)F ,上顶点为M ,圆222:()(0)F x c y r r -+=>,问:椭圆E 上是否存在两点P 、Q 使得圆F 内切于三角形MPQ 若存在,求出直线PQ 的方程;若不存在,请说明理由.23.(2021·全国·高三竞赛)如图所示,()(),0P a b a b <<为抛物线2:4F y x =外一点,过P 引抛物线Γ的两条切线PA PB 、,切点分别为A 、B .在线段PA 上取两点D 、E ,使得PD AE =.若过D 、E 两点的直线12l l 、分别切抛物线Γ于M 、N 两点(异于A ).求四边形MNAB 面积的最大值.24.(2021·全国·高三竞赛)已知椭圆22122:1(0)x y C a b a b+=>>,其右焦点为F ,过F 作直线l 交椭圆1C 于A 、B 两点(l 与x 轴不重合),设线段AB 中点为D ,连结OD (O 为坐标原点),直线OD 交椭圆1C 于M 、N 两点,若A 、M 、B 、N 四点共圆,且||8||3MN OD =,求椭圆1C 的离心率.25.(2018·甘肃·高三竞赛)已知椭圆2222:1x y C a b+=过点()0,2M ,且右焦点为()2,0F .(1)求椭圆C 的方程;(2)过点F 的直线l 与椭圆C 交于,A B 两点,交y 轴于点P .若,PA mAF PB nBF ==,求证:m n +为定值;(3)在(2)的条件下,若点P 不在椭圆C 的内部,点Q 是点P 关于原点O 的对称点,试求三角形QAB 面积的最小值.26.(2018·山东·高三竞赛)已知圆22:4O x y +=与曲线:3C y x t =-,(),A m n ,(),B s p ,(),,,m n s p *∈N 为曲线C 上的两点,使得圆O 上任意一点到点A 的距离与到点B 的距离之比为定值()1k k >,求t 的值.27.(2022·福建·高二统考竞赛)已知椭圆C :()222210x y a b a b+=>>的离心率为12,1A 、2A 分别为椭圆C 的左、右顶点,1F 、2F 分别为椭圆C 的左、右焦点,B 为椭圆C 的上顶点,且11BA F ∆的外接圆半径为3.(1)求椭圆C 的方程;(2)设与x 不垂直的直线l 交椭圆C 于P 、Q 两点(P 、Q 在x 轴的两侧),记直线1A P 、2PA 、2A Q 、1QA 的斜率分别为1k 、2k 、3k 、4k .已知()142353k k k k +=+,求2F PQ ∆面积的取值范围.28.(2022·新疆·高二竞赛)如图,已知ABC 内接于抛物线2:=E x y ,且边,AB AC 所在直线分别与抛物线2:4=M y x 相切,F 为抛物线M 的焦点.求证:(1)边BC 所在直线与抛物线M 相切;(2)A ,C ,B ,F 四点共圆.(2021·全国·高三竞赛)已知(2,1)S 为椭圆22Γ:182x y+=上的点,对椭圆Γ上的任意两点P 、Q ,用如下办法定义它们的“和”P Q +:过点S 作一条平行于PQ (若点P 与Q 重合,则直线PQ 表示椭圆Γ在P 处的切线)的直线l 与椭圆Γ交于不同于S 的另一点,记作P Q +(若l 与椭圆Γ相切,则规定S 为P Q +).并规定n nP P P P=+++个.29.若点(0,P Q ,求P Q +、2P 以及100P 的坐标.30.在椭圆Γ上是否存在不同于S 的点P ,满足3P S =?若存在,求出所有满足条件的点P 的坐标;若不存在,请说明理由.高中数学竞赛与强基计划试题专题:解析几何答案一、单选题1.(2020·北京·高三强基计划)从圆224x y +=上的点向椭圆22:12x C y +=引切线,两个切点间的线段称为切点弦,则椭圆C 内不与任何切点弦相交的区域面积为()A .2πB .3πC .4πD .前三个答案都不对【答案】A【分析】算出椭圆内与切点弦不相交的点的边界的方程,从而可求区域的面积.【详解】设圆224x y +=上一点为(2cos ,2sin )P θθ,则对应切点弦所在直线l 的方程为2cos 2sin 12xy θθ⋅+⋅=即cos 2sin 1x y θθ+=,1≥,故椭圆C 内不与任何切点弦相交的区域面积即为椭圆2241x y +=围成的面积,其面积为1ππ122⨯⨯=.2.(2022·北京·高三校考强基计划)内接于椭圆22149x y +=的菱形周长的最大值和最小值之和是()A.B.CD .上述三个选项都不对【答案】D【分析】求出椭圆的极坐标方程,设内接于椭圆22149x y +=的菱形为ABCD ,()12,,,2A B πρθρθ⎛⎫+ ⎪⎝⎭,分别求出22,OA OB ,再根据222AB OA OB =+,结合三角恒等变换化简,再根据三角函数的性质求出AB 的最大值和最小值,即可得解.【详解】解:由22149x y +=,得229436x y +=,化为极坐标方程为223645cos ρθ=+,设内接于椭圆22149x y +=的菱形为ABCD ,则OA OB ⊥,设()12,,,2A B πρθρθ⎛⎫+ ⎪⎝⎭,则22123645cos OA ρθ==+,22222363645sin 45cos 2OB ρπθθ==+⎛⎫++ ⎪⎝⎭,所以2221222363645cos 45sin AB ρρθθ=+=+++2223613361325162025sin cos 36sin 24θθθ⨯⨯==+++,当2sin 20θ=时,2AB 取得最大值,即AB所以菱形的周长的最大值为当2sin 21θ=时,2AB 取得最小值,即AB 的最小值为13,所以菱形的周长的最小值为13,所以内接于椭圆22149x y +=的菱形周长的最大值和最小值之和是1313=.3.(2020·湖北武汉·高三统考强基计划)已知直线1211::22l y x l y x =-=,,动点P 在椭圆22221(0)x y a b a b +=>>上,作1//PM l 交2l 于点M ,作2//PN l 交1l 于点N .若22PM PN +为定值,则()A .2ab =B .3ab =C .2a b =D .3a b=【答案】C【分析】根据四边形OMPN 是平行四边形,得到2222PM PN OM ON +=+为定值,然后将取特殊位置(),0P a ,()0,P b 求解.,易知由四边形OMPN 是平行四边形,所以2222PM PN OM ON +=+为定值,取点(),0P a 时,由()1212y x a y x ⎧=-⎪⎪⎨⎪=-⎪⎩,解得24a x a y ⎧=⎪⎪⎨⎪=-⎪⎩,所以,24a a M ⎛⎫- ⎪⎝⎭,由对称性得:,24a a N ⎛⎫ ⎪⎝⎭,所以22258OM ON a +=,取点()0,P b 时,由1212y x b y x ⎧=+⎪⎪⎨⎪=-⎪⎩,解得2x bb y =-⎧⎪⎨=⎪⎩,所以,2b M b ⎛⎫- ⎪⎝⎭,由对称性得:,2b N b ⎛⎫ ⎪⎝⎭,所以22252OM ON b +=,所以225582a b =,即2a b =,4.(2020·北京·高三强基计划)设直线3y x m =+与椭圆2212516x y +=交于A ,B 两点,O 为坐标原点,则OAB面积的最大值为()A .8B .10C .12D .前三个答案都不对【答案】B【分析】联立直线方程和椭圆方程后消元,利用公式可求面积的表达式,再利用基本不等式可求面积的最大值.【详解】由22312516y x m x y =+⎧⎪⎨+=⎪⎩可得22241150254000x mx m ++-=,()22222500424125400160024116000m m m ∆=-⨯-=⨯->,故m而241241AB ==,故1122ABOS AB ==△2224120210241m m+-⨯==,当且仅当m=等号成立,故OAB面积的最大值为10,5.(2022·贵州·高二统考竞赛)如图,1C,2C是离心率都为e的椭圆,点A,B是分别是2C的右顶点和上顶点,过A,B两点分别作1C的切线1l,2l.若直线1l,2l的斜率分别为1k,2k,则12k k的值为()A.2e B.21e-C.21e-D.21e【答案】C【详解】不妨设22122:1x yCa b+=,222222:x yCa bλ+=(0,1)a bλ>>>,∴,(,0)(0,)A aB bλλ,11:()l y k x aλ=-代入1C的方程得:()2222322422211120b a k x a k x a k a bλλ+-+-=,()()()23222224222111Δ240a kb a k a k a bλλ=--+-=,化简得()221221bkaλ=-.22:l y k x bλ=+代入22221x ya b+=得()22222222222220b a k x a bk x a b a bλλ+-+-=.()()()222222222222Δ240a bkb a k a b a bλλ=-+-=.化简得()222221bkaλ-=.∴422124bk ka=,∴222212221b a ck k ea a-===-,6.(2020·湖北武汉·高三统考强基计划)过椭圆22149x y+=的中心作两条互相垂直的弦AC和BD,顺次连接,,,A B C D得一四边形,则该四边形的面积可能为()A.10B.12C.14D.16【答案】B【分析】设()11,A x y,()22,B x y,设x轴正方向旋转到与向量OA 同向所转过的角为α,利用三角函数的定义表示,A B的坐标,代入椭圆方程,求得223636,OA OB关于α的函数表达式,进而得到223636OA OB关于α的函数表达式,利用三角函数恒定变形化简,然后利用三角函数的性质求得其取值范围,进而得到四边形面积的取值范围,从而做出选择.【详解】设()11,A x y ,()22,B x y ,设x 轴正方向旋转到与向量OA同向所转过的角为α,并根据题意不妨设OA 到OB 为逆时针旋转π2,则11cos ,sin .x OA y OA αα⎧=⎪⎨=⎪⎩,22cos sin ,2sin cos .2x OB OB y OB OB πααπαα⎧⎛⎫=+=- ⎪⎪⎪⎝⎭⎨⎛⎫⎪=+= ⎪⎪⎝⎭⎩22149x y +=,229436x y +=,2222369cos 4sin 5cos 4OA ααα=+=+, 22223694cos 5sin 4sin OBααα=+=+,2222236362516925cos sin 36sin 23636,44OA OBααα⎡⎤=+=+∈⎢⎥⎣⎦,∴36136,2OA OB ⎡⎤∈⎢⎥⎣⎦,1442,1213ABCD S OA OB ⎡⎤=∈⎢⎥⎣⎦,当4πα=时取到最小值14413,当0α=时取得最大值12.只有选项B 中的12在此范围内7.(2019·贵州·高三校联考竞赛)设椭圆C :()222210x y a b a b +=>>的左、右焦点分别为12,F F ,其焦距为2c .点322c N ⎛⎫⎪ ⎪⎝⎭在椭圆的内部,点M 是椭圆C上的动点,且112||MF MN F +<恒成立,则椭圆C 的离心率的取值范围是()A.⎛ ⎝⎭B.⎫⎪⎪⎝⎭C.,121⎛⎫⎪ ⎪⎝⎭D.⎝⎭【答案】D【详解】由322c N ⎛⎫ ⎪ ⎪⎝⎭在椭圆的内部,得22229142c c a b +<,即222222924b c a c a b +<,从而422441590a a c c -+>,得到4291540e e -+>,因此()()2231340e e -->.因为0<e <1,所以3e 2-4<0,故3e 2<1,得到0e <<.又由112||MF MN F +<恒成立,即22||a MN MF +-<恒成立,等价于()2max2||a MN MF +-<,亦即22a NF +<,等价于2a ,即2a e >.e <<二、多选题8.(2022·贵州·高二统考竞赛)如图,M ,N 分别是Rt ABC △两直角边上的动点,P 是线段MN 的中点,则以下结论正确的是()A .当△AMN 的面积为定值时,点P 的轨迹为双曲线一支B .当|MN |为定值时,点P 的轨迹为一圆弧C .当||||AM AN +为定值时,点P 的轨迹为不含端点线段D .当△AMN 的周长为定值时,点P 的轨迹为抛物线【答案】ABC【详解】建立如图的直角坐标设(),P x y ,则(2,0)M x ,(0,2)N y ,0x >,0y >,对于A ,当Rt △AMN 面积为定值()20k k >时,12222x y k ⋅⋅=,∴(0)x y k k ⋅=>轨迹为双曲线一支,所以A 正确.对于B ,若2(0)MN d d =>,则222222444x y d x y d +=⋅+=,(0,0)x y >>是一圆弧,所以B 正确.对于C ,当2(0)AM AN t t +=>时,222(0,0)x y t x y +=>>,即(0,0)x y t x y +=>>为空端点线段,所以C 正确.对于D ,当Rt △AMN 的周长为定值2C 时,则222x y C ++,即(0,0)x y C x y +=>>,()C x y =-+,∴22222222x y C Cx Cy xy x y +=--+++,所以2(22)2x C y Cx C -=-,2222Cx C y x C-=-轨迹为双曲线一支,所以D 错误.9.(2020·北京·高三校考强基计划)已知A ,B 分别为双曲线2214x y -=的左、右顶点,P 为该曲线上不同于A ,B 的任意一点设,,∠=∠= PAB PBA PAB αβ的面积为S ,则()A .tan tan αβ⋅为定值B .tantan22αβ⋅为定值C .tan()S αβ⋅+为定值D .cot()S αβ⋅+为定值【答案】AC【分析】利用三角换元得到P 的坐标为2,tan ,0,cos 2P πθθθ⎛⎫⎛⎫∈⎪ ⎪⎝⎭⎝⎭,利用斜率公式可求,αβ与θ的关系,化简后可得,αβ的关系,故可判断AB 的正误,根据面积公式可求S (用θ表示),故可判断CD 的正误.【详解】不妨设2,tan ,0,cos 2P πθθθ⎛⎫⎛⎫∈⎪ ⎪⎝⎭⎝⎭,则tan sin tan 22(1cos )(2)cos θθαθθ==+--,tan sin tan 22(1cos )2cos θθβθθ=-=---,1||tan 2tan 2S AB θθ=⋅⋅=,因此2114tan ,tan ,221t t S t t αβ==-=-,其中tan 2t θ=.对于选项A ,1tan tan 4αβ=-为定值.对于选项B ,由于22224tantan22tan tan 1tan tan tantan 2222αβαβαβαβ=⎛⎫-++ ⎪⎝⎭,因此若tantan22αβ为定值,则tantan 22αβ+为定值,从而tan 2α和tan 2β是确定的值,矛盾,对于选项C ,D ,有()2112122tan()115122t t t t t tαβ--+==-+⋅,因此tan()S αβ⋅+是定值,cot()S αβ⋅+不是定值.10.(2020·北京·高三校考强基计划)已知点(1,1),(1,0)A Q ,P 为椭圆22143x y +=上的动点,则||||PA PQ +的()A.最大值为4B.最大值为4C.最小值为4-D.最小值为4【答案】BD【分析】利用椭圆的定义可求||||PA PQ +的最值.【详解】注意到Q 为椭圆的右焦点,设其椭圆的左焦点为(1,0)Q '-,则()()||||||44||PA PQ PA PQ PA PQ +=+-=-''+,而||PA PQ -'的取值范围是,AQ AQ ''-⎡⎤⎣⎦,即[,因此所求最大值为4,最小值为4三、填空题11.(2022·江苏南京·高三强基计划)设F ,l 分别为双曲线()22411212x y --=的右焦点与右准线,椭圆Γ以F 和l 为其对应的焦点及准线,过F作一条平行于y =的直线,交椭圆Γ于A 、B 两点,若Γ的中心位于以AB 为直径的圆外,则椭圆离心率e 的范围为___________.【答案】⎫⎪⎪⎭【详解】由双曲线方程可知其焦准距为3,则椭圆Γ的焦准距23b c=(同侧焦点和准线),如图,设椭圆中心为O,建立平面直角坐标系,设F :()222210x y a b a b+=>>,()11,A x y ,()22,B x y ,直线AB方程:)y x c =+,联立直线AB 和椭圆Γ可得:()222222223630b a x a cx a c a b +++-=,由韦达可得:212222212226+=-+33=+3a x x b a a c x x b a ⋅⎧⎪⎪⎨⎪⎪⎩,由椭圆中心O 位于以AB 为直径的圆外,则有12120OA OB x x y y ⋅=+>,结合韦达定理可得:222242222422222233330333a c a b b a c a b b b a b a b a----+=>+++,所以422441030a a c c -+<,即423e 10e 40-+<,e 1<<,12.(2018·山东·高三竞赛)若直线65280x y --=交椭圆22221x ya b+=(0a b >>,且2a 、b 为整数)于点A 、C .设()0,B b 为椭圆的上顶点,而ABC 的重心为椭圆的右焦点2F ,则椭圆的方程为______.【答案】2212016x y +=【详解】设()11,A x y ,()22,C x y ,由题意ABC 的重心为椭圆的右焦点2F ,整理得213x x c +=,21y y b +=-.由()11,A x y ,()22,C x y 在直线65280x y --=上,得到212165y y x x -=-.由()11,A x y ,()22,C x y 在椭圆()222210x y a b a b +=>>上,得到2211221x y a b +=,2222221x y a b+=.两式相减并整理得()()()()2212122121635y y y y b b a x x x x c +---==⋅+-,整理得225a bc =.①本号资料全部来源于微信公#众号:数学第六感因为()11,A x y ,()22,C x y 在直线65280x y --=上,所以有1165280x y --=,2265280x y --=.将123x x c +=,12y y b +=-代入得()635560c b ⨯---=,整理得18556c b +=.②联立①②,且注意到a 、b 为整数,解得2c =,4b =,220a =.故所求的椭圆方程为2212016x y +=.13.(2022·新疆·高二竞赛)设z 为复数,若方程2297--=z z 表示一条圆锥曲线,则此曲线的离心率=e ___________.【答案】4【详解】令||,|3|,|3|=-=+=z a z b z c ,则27-=a bc .由复数的几何意义知222218+=+b c a .所以由前两式知2()32-=b c,即||-=b c ,故||3||3||6--+=<z z .因此z6的双曲线,14.(2021·全国·高三竞赛)已知集合{}22(,)|||||,0,(,)|1,044x y A x y x y t t B x y m m ⎧⎫=+>=+≤<<⎨⎩≤⎬⎭满足B A ⊆,若P 为集合B 的边界线C 上任意一点,12F F 、为曲线C 的焦点,I 为12PF F △的内心,直线1IF 和2IF 的斜率分别为12k k 、,且1213k k ⋅=-则t 的最小值为________.【详解】因为12F F 、为曲线C 的焦点,I 为12PF F △的内心,若曲线C 的方程为22221x y a b +=,则I 的轨迹方程为22221x y c bc c a +=⎛⎫ ⎪+⎝⎭,故有22121.3bc c a c k k ⎛⎫ ⎪+⎝⎭=-=-⋅可知::2:a b c =,所以3m =.设(2cos )P θθ为曲线C上一点,则有|2cos ||t θθ≥+恒成立,即t ≥15.(2021·全国·高三竞赛)已知ABCD Y 的四个顶点均在双曲线2214y x -=上,点(0,1)P 在边AB 上,且12AP PB =,则ABCD Y 的面积等于_______.【答案】4【分析】由对称性,知O 为平行四边形的中心,设()00,A x y ,得()002,32B x y --,将点A 、B 的坐标代入双曲线方程,求得A 、B 的坐标,利用等面积法知4ABCD AOB S S = △,代入即可求解.【详解】由平行四边形的对称性与双曲线的对称性,知O 为平行四边形的中心,由A 、B 、C 、D 四点在两支双曲线上各有两点,不妨设A 、D 在左支上,B 、C 在右支上,如图:考虑A 、B 关于双曲线中心的对称点,A B '',因为单支双曲线上不存在四点构成平行四边形,知,A C B D =''=,所以ABCD Y 的对称中心为O .设()00,A x y ,由12AP PB =,得()002,32B x y --.将点A 、B 的坐标代入双曲线方程得()22002020*******y x y x ⎧-=⎪⎪⎨-⎪-=⎪⎩,解得:00814x y ⎧=⎪⎪⎨⎪=-⎪⎩或00814x y ⎧=-⎪⎪⎨⎪=-⎪⎩所以A B x x ⎧=⎪⎪⎨⎪=⎪⎩或A B x x ⎧=⎪⎪⎨⎪=⎪⎩.故242||21ABCDADB AOB A B S S S OP x x ===⋅-=⨯⨯YV V.四、解答题16.(2022·湖北武汉·高三统考强基计划)设F 为椭圆C :22194x y +=的左焦点,P 为椭圆C上的一点(1)作正方形FPAB (F ,P ,A ,B 按逆时针排列)当P 沿着椭圆运动一周,求动点B 的轨迹方程.(2)设()3,2Q 为椭圆外一点,求PQ PF +的取值范围.【答案】(1)((22=149x x -+.(2)【详解】(1)如图所示,将椭圆C绕其左焦点()F 逆时针旋转90 ,得到椭圆'C,注意到在正方形FPAB 中,点B 可以看成也是由点P 绕点F 逆时针旋转90 而形成的,由于点P 在椭圆C 上运动,则点B 在椭圆'C 上运动.求B 的轨迹方程,也就是求椭圆'C 的方程.注意到椭圆'C的中心坐标为(,从而'C的方程为((22=149x x +.(2)如图所示,|||||PQ PFQF +≥当且仅当,,P F Q 三点共线,即P 运动到1P 位置时,等号成立.记椭圆C 的右焦点为)E,注意到()||||=||2||=||||6PQ PF PQ a PE PQ PE ++--+,显然有||||||=PQ PE QE -≤从而||||6PQ PF +≤+,当且仅当,,P E Q 三点共线,即P 运动到2P 位置时,等号成立.||||6PQ PF ≤+≤即PQ PF+的取值范围17.(2018·全国·高三竞赛)一束直线12,,l l 的每条均过xOy 平面内的抛物线2:C y x =的焦点,()1i l i ≥与抛物线C 交于点i A 、i B .若1l 的斜率为1,()2i l i ≥的斜率为1+2014l 的解析式.【答案】((()()201520152014201411112411y x -⎛⎫=⋅- ⎪⎝⎭-【详解】易知抛物线焦点1,04P ⎛⎫⎪⎝⎭.设()1:1,2,4i i l y k x i ⎛⎫=-= ⎪⎝⎭ ,并与2y x =联立知点i A 、i B 的横坐标i A x 、i B x 满足关于x 的方程()2222120216i i i k k x k x -++=且i i A B x x ≠.则i ii i A B A B x =-=221i i k k +=.从而,当2i≥时,有1111i i k k -==+.记{}n F 满足121F F ==及递推关系21n n n F F F ++=+则{}n F 为斐波那契数列其通项公式为n nn F ⎡⎤⎛⎥=- ⎥⎝⎭⎝⎭⎦.下面证明:1i i iF k F +=对一切正整数i 成立.由2111F k F ==,知i=1时结论成立.设i=t 时结论成立.则121111111t t t t t t t t t F F F F k k F F F +++++++=+=+==即i=t+1时结论也成立.由数学归纳法知1i i iF k F +=对一切正整数i 成立.特别地,201520142014F k F =.从而,2014l的解析式为((()()201520152014201411112411y x +-⎛⎫=⋅- ⎪⎝⎭-.【注】本题亦可用不动点方法求数列{}i k 的通项.18.(2018·福建·高三竞赛)已知1F 、2F 分别为椭圆()2222:10x y C a b a b +=>>的左、右焦点,点3P ⎛⎫ ⎪⎝⎭在椭圆C 上,且12F PF △的垂心为5,33H ⎛⎫- ⎪ ⎪⎝⎭.(1)求椭圆C 的方程;(2)设A 为椭圆C 的左顶点,过点2F 的直线l 交椭圆C 于D 、D 两点.记直线AD 、AE 的斜率分别为1k 、2k ,若1212k k +=-,求直线l 的方程.【答案】(1)22143x y +=(2)()21y x =-【详解】设()1,0F c -,()2,0F c .由12F PF的垂心为53H ⎫-⎪⎪⎝⎭,得12F H PF ⊥.所以12531F H PF k k -⋅==-,224593c -=,解得21c =.由点P ⎫⎪⎪⎝⎭在椭圆C 上,得2224119a b +=.结合2221a b c -==,解得24a =,23b =.所以椭圆C 的方程为22143x y +=.(2)由(1)知()2,0A -,()21,0F .若l 的斜率不存在,则由对称性,知120k k +=,不符合要求.若l 的存在,设为k ,则l 的方程为()1y k x =-.由()221143y k x x y ⎧=-⎪⎨+=⎪⎩,得()22224384120k x k x k +-+-=.①设()11,D x y ,()22,E x y ,则2122843k x x k +=+,212241243k x x k -=+.所以()()1212121212112222k x k x y y k k x x x x --+=+=+++++()()()12121234331122222x x k k x x x x ⎡⎤++⎛⎫=-+-=⋅-⎢⎥⎪++++⎢⎥⎝⎭⎣⎦()()221222121222834344322412824244343k x x k k k k k x x x x k k ⎡⎤⎛⎫+⎢⎥ ⎪⎡⎤+++⎝⎭⎢⎥=⋅-=⋅-⎢⎥⎢⎥-+++⎢⎥⎣⎦+⨯+⎢⎥++⎣⎦()222222238161221122412161612k k k k k k k k k k ⎡⎤++⎛⎫+⎢⎥=⋅-=⋅-=- ⎪-+++⎢⎥⎝⎭⎣⎦.又1212k k +=-,因此2k =,直线l 的方程为()21y x =-.19.(2018·江西·高三竞赛)若椭圆221259x y +=上不同的三点()11,A x y ,94,5B ⎛⎫ ⎪⎝⎭,()22,C x y 到椭圆右焦点的距离顺次成等差数列,线段AC 的中垂线l 交x 轴于点T ,求直线BT 的方程.【答案】252064x y -=【详解】用a 、b 、c 分别表示椭圆的半长轴、半短轴及半焦距之长度,则5a =,3b =,4c =,右焦点为()4,0F ,且准线方程为2a x c=,由21AFca a x c=-,22CF c a a x c=-,得1455AF x =-,2455CF x =-,根据等差性质,2AF CF BF +=,而95BF =,即12441855555x x ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭,所以128x x +=.①设线段AC 的中点为D ,则其坐标为124,2y y D +⎛⎫ ⎪⎝⎭,又设点T 的坐标为()0,0T x ,则AC 的中垂线DT 的方程为()12121242y y x xy x y y +--=---.因()0,0T x 在此直线上,故有()1212012042y y x xx y y +--=---,即()221201242y y x x x --=-.②又根据A 、B 在椭圆上,得()221192525y x =-,()222292525y x =-,所以()()22121212925y y x x x x -=-+-,据①,即有()22121236225y y x x -=--.③再据②③得06425x =,即点T 的坐标为64,025T ⎛⎫⎪⎝⎭,于是直线BT 的方程为252064x y -=.20.(2018·湖北·高三竞赛)已知O 为坐标原点,()1,0N ,点M 为直线=1x -上的动点,MON ∠的平分线与直线MN 交于点P ,记点P 的轨迹为曲线E .(1)求曲线E 的方程;(2)过点11,22Q ⎛⎫-- ⎪⎝⎭作斜率为k 的直线l ,若直线l 与曲线E 恰好有一个公共点,求k 的取值范围.【答案】(1)()201y x x =≤<(2)11,132⎧⎫+⎪⎪⎛⎤-⎨⎬⎥⎝⎦⎪⎪⎩⎭ 【详解】(1).设()(),,1,P x y M t -,易知01x ≤<.因为OP 平分MON ∠,所以OM MP PN ON==,所以)11,x x +-①)0y t y -=-.②由①②可得21y t x =-,代入①得到11x x +=-E 的方程为()201y x x =≤<.(2).记()()1,1,1,1A B -,则11,3QA QB k k ==-.直线l 的方程为1122y k x ⎛⎫+=+ ⎪⎝⎭,与抛物线方程2y x =联立,消去x 得()21102ky y k -+-=当直线l 与抛物线2y x =相切于点T 时,()1210k k ∆=--=,解得1,2k =当1k k ==T y =T 在曲线E 上;当212k k ==时,T y =,切点T 不在曲线E 上.若直线l 与曲线E 恰好有一个公共点,则有QB QA k k k <≤或k =,故所求k的取值范围为1,13⎛⎤-⋃ ⎥⎝⎦⎪⎪⎩⎭.21.(2021·全国·高三竞赛)过抛物线22y px =(p 为不等于2的质数)的焦点F ,作与x 轴不垂直的直线l 交抛物线于M 、N 两点,线段MN 的垂直平分线交MN 于P 点,交x 轴于Q 点.(1)求PQ 中点R 的轨迹L 的方程;(2)证明:L 上有无穷多个整点(横、纵坐标均为整数的点),但L 上任意整点到原点的距离均不是整数.【答案】(1)24()(0)y p x p y =-≠;(2)证明见解析.【详解】(1)抛物线22y px =的焦点为(,0)2p ,设l 的直线方程为()(0)2p y k x k =-≠.由得222y pxp y k x ⎧=⎪⎨⎛⎫=- ⎪⎪⎝⎭⎩得222221(2)04k x pk p x p k -++=.设M 、N 的横坐标分别为12x x 、,由21222pk p x x k ++=,得22122222,()2222P Px x pk p pk p p px y k k k k+++===-=,而PQ l ⊥,故PQ 的斜率为1k -,PQ 的方程为2212()2p pk py x k k k +-=--.代入0Q y =得222223222Q pk p pk px p k k ++=+=.设动点R 的坐标为(),x y ,则:21()21()22p Q P Qp x x x p k p y y y k ⎧=+=+⎪⎪⎨⎪=+=⎪⎩,因此222()4(0)p p x p y y k-==≠,故PQ 中点R 的轨迹L 的方程为24()(0)y p x p y =-≠.(2)显然对任意非零整数t ,点2((41),)p t pt +都是L 上的整点,故L 上有无穷多个整点.反设L 上有一个整点(),x y 到原点的距离为整数()0m m ≥,不妨设0,0x y >>,则:22224()x y m y p x p ⎧+=⎨=-⎩①②,因为p 是奇质数,于是|p y ,从②可推出|p x ,再由①可推出|p m .令111,,x px y py m pm ===,则有22211121141x y m y x ⎧+=⎨=-⎩③④,由③,④得2211114x x m -+=,于是2211(81)(8)17x m +-=,即()()111181881817x m x m +++-=,于是111181817,8181x m x m ++=+-=,得111x m ==,故10y =,有10y py ==,但L 上的点满足0y ≠,矛盾!因此,L 上任意点到原点的距离不为整数.22.(2021·全国·高三竞赛)已知椭圆22:12+=x E y 的右焦点为(c,0)F ,上顶点为M ,圆222:()(0)F x c y r r -+=>,问:椭圆E 上是否存在两点P 、Q 使得圆F 内切于三角形MPQ 若存在,求出直线PQ的方程;若不存在,请说明理由.【答案】存在,PQ的方程为(260x y +-+-=.【详解】假设这样的P 、Q 存在,且设()()1122,,,P x y Q x y ,由题意知(0,1),(1,0)M F ,所以直线()111:10MP y x x y x --+=.因为该直线与圆F 相切,则d r =r =,两边平方化简得()()2222111111x y r x y ⎡⎤+-=+-⎣⎦,整理得()()()()22221111111210r x ryx y -+--+-=.因为()221121x y =-,消去1x 得()()()()()2222111112111210r y r yx y -⋅-+--+-=.因为11y ≠,两边同时除以11y -,得()()()()221111211120r y r y x -⋅++---=,整理得()()221121310x ryr -+-+-=,即点P 在直线()()2221310x r y r -+-+-=上.同理,点Q 也在直线()()2221310x r y r -+-+-=上,因此直线PQ 的方程为()()2221310x r y r -+-+-=.又因为直线PQ 圆Fr=,解得r =因此直线PQ 存在且直线PQ的方程为(260x y +-+-=.23.(2021·全国·高三竞赛)如图所示,()(),0P a b a b <<为抛物线2:4F y x =外一点,过P 引抛物线Γ的两条切线PA PB 、,切点分别为A 、B .在线段PA 上取两点D 、E ,使得PD AE =.若过D 、E 两点的直线12l l 、分别切抛物线Γ于M 、N 两点(异于A ).求四边形MNAB 面积的最大值.【详解】设()()()()11220000,,,,,,,A x y B x y M x y N x y '',则直线AP 的方程为()112y y x x =+,直线BP 的方程为()222y y x x =+,故有121242y y a y y b ⎧=⎪⎪⎨+⎪=⎪⎩,同理可得1010,22E D y y y yy y '++==,又因为PD AE =,所以1E D y y b y +=+,即002y y b +'=,故12121200424AB MN y y k k x x y y b y y '-=====-++,因此//AB MN .直线AB 的方程为22by x a =+,直线MN 的方程为0000004y y y x y y y y '''=+++,即0022y y by x '=+,故两平行线间的距离d ',||AB ===||MN =所以00|4|1(||||))24MNABy y a S d AB MN '-=⋅+=⋅,其中0204a y y b ≤'≤,可令22004,b a A b y y X '-=-=,则:1(4MNAB S A X =-218=+3183⎛≤ ⎝⎭当22001(4)9b y y b a '-=-时取到最大值.24.(2021·全国·高三竞赛)已知椭圆22122:1(0)x y C a b a b+=>>,其右焦点为F ,过F 作直线l 交椭圆1C 于A 、B 两点(l 与x 轴不重合),设线段AB 中点为D ,连结OD (O 为坐标原点),直线OD 交椭圆1C 于M 、N 两点,若A 、M 、B 、N 四点共圆,且||8||3MN OD =,求椭圆1C 的离心率.【分析】先将椭圆与直线联立,结合韦达定理表示出D 坐标,再结合直线OD 交椭圆1C 于M 、N 两点,若A 、M 、B 、N 四点共圆,且||8||3MN OD =,求出2,3M ⎛ ⎝⎭再代入椭圆求出a ,进而求出离心率.【详解】不妨设椭圆1C 的半焦距1c =,则221b a =-,椭圆右焦点为(1,0)F .设:1l x ky =+,将1x ky =+,代入22221x ya b+=消去x 化简整理得()()()222222222110a k k a y a ky a -++---=.显然,方程判别式Δ0>,设()(),,,A A B B A x y B x y .由韦达定理知()2222221A B a k y y a k k a-+=--+,从而()()22222222222211122222A B D A B a k x x ax ky ky a k k a a k k a ⎛⎫-+==++=-+= ⎪ ⎪-+-+⎝⎭,()2222211D D a k x y k a k k a--==--+,于是()22222222221,a k a D a k k a a k k a ⎛⎫-- ⎪ ⎪-+-+⎝⎭.所以直线OD 的方程为()221a x y a k =--.设圆AMBN 的方程为222:0C x y Dx Ey F ++++=,直线l 直线MN 的方程为()232:(1)01a C x ky x y a k ⎛⎫--+= ⎪ ⎪-⎝⎭,由于3C 经过12C C 、的交点,且123C C C 、、均为二次曲线,则存在常数12λλ、,使得()()2222212222(1)11a x y x ky x y x y Dx Ey Fa b a k λλ⎛⎫⎛⎫--+=+-+++++ ⎪ ⎪ ⎪-⎝⎭⎝⎭,比较方程两边xy 系数知()2201a k a k -+=-,即2221a k a =-,由对称性不妨设k =.代入点D 的坐标得1,22D a ⎛- ⎪ ⎪⎝⎭,又||8||3MN OD =,得点2,3M ⎛ ⎝⎭,而M 在1C上,故22222311a a ⎛⎛⎫ ⎪ ⎝⎭⎝⎭+=-,解得a =于是1C的离心率为3c e a ==.25.(2018·甘肃·高三竞赛)已知椭圆2222:1x y C a b+=过点()0,2M ,且右焦点为()2,0F .(1)求椭圆C 的方程;(2)过点F 的直线l 与椭圆C 交于,A B 两点,交y 轴于点P .若,PA mAF PB nBF ==,求证:m n +为定值;(3)在(2)的条件下,若点P 不在椭圆C 的内部,点Q 是点P 关于原点O 的对称点,试求三角形QAB 面积的最小值.【详解】(1)由题意b=2,c=2,所以28a =,椭圆C 的方程为22184x y +=.(2)设A 、B 、P 的坐标分别为()()()1122,,,,0,x y x y t .由PA mAF = 知121m x m =+,11ty m=+.又点A 在椭圆C 上,则22211184m t m m ⎛⎫⎛⎫ ⎪ ⎪++⎝⎭⎝⎭+=,整理得222840m m t +-+=.由PB nBF =,同理得到222840n n t +-+=.由于A 、B 不重合,即m n ≠,故m 、n 是二次方程222840x x t +-+=的两根,所以m+n=-4,为定值.(3)依题意,直线l 的方程为12x yt+=,即()22t y x =--,与椭圆C 的方程联立,消去y 并整理,得()2222244160t xt x t +-+-=,()()42221642416321280t t tt ∆=-+-=+>,所以221212224416,22t t x x x x t t -+=⋅=++,而1212122QAB S t x x t x x ∆=⋅⋅-=⋅-()()22222121212=4QAB S t x x t x x x x ∆⎡⎤=-+-⎣⎦()42222216166422t t tt t ⎡⎤-⎢⎥=-⎢⎥++⎣⎦()2222321282t t t +=⋅+.()2243212t ⎡⎤⎢⎥=-⎢⎥+⎣⎦由已知,点P 不在椭圆C 的内部,得2t ,即24t ,所以2QAB S ∆的最小值为82563299⨯=,故三角形QAB 面积的最小值为163.26.(2018·山东·高三竞赛)已知圆22:4O x y +=与曲线:3C y x t =-,(),A m n ,(),B s p ,(),,,m n s p *∈N 为曲线C 上的两点,使得圆O 上任意一点到点A 的距离与到点B 的距离之比为定值()1k k >,求t 的值.【答案】43t =【详解】设(),P x y 为圆O 上任意一点,则由题意知PA k PB=.即222PA k PB =,于是()()()()22222x m y n k x s y p ⎡⎤-+-=-+-⎣⎦,整理得()()()()22222222222222111k s m kp nmn k s p x y x y k k k --+-++--=---.因此点P 的轨迹是一个圆.因为(),P x y 为圆上任意一点,所以此圆与圆22:4O x y +=必为同一个圆,于是有()22201k s m k --=-,()22201k p nk --=-,()()22222241mn k s p k +-+=-,整理得20k s m -=,20k p n -=,所以()()()()()22222424222222222411m n k s p k sk p k s p ks p k k +-++-+==+=--.因为s ,*p N ∈,所以21s ≥,21p ≥,从而22242k s p =≤+.又因为1k >,所以1s p ==,22k =,2m n ==.因此将()2,2A ,()1,1B ,代入3y x t =-,得43t =.27.(2022·福建·高二统考竞赛)已知椭圆C :()222210x y a b a b+=>>的离心率为12,1A 、2A 分别为椭圆C 的左、右顶点,1F 、2F 分别为椭圆C 的左、右焦点,B 为椭圆C 的上顶点,且11BA F ∆的外接圆半径为3.(1)求椭圆C 的方程;(2)设与x 不垂直的直线l 交椭圆C 于P 、Q 两点(P 、Q 在x 轴的两侧),记直线1A P 、2PA 、2A Q 、1QA 的斜率分别为1k 、2k 、3k 、4k .已知()142353k k k k +=+,求2F PQ ∆面积的取值范围.【答案】(1)2211612x y +=(2)0,2⎛ ⎝⎭【详解】(1)由椭圆C 的离心率为12,知12c a =,于是112BF a c OF ===,所以1=30F BO ∠︒,1=60BFO ∠︒,11=120BF A ∠︒,又AB ===,且11BA F ∆所以11==2sin sin1203AB BF A ∠⨯︒,解得=2c ,因此,=4a,b =所以,椭圆C 的方程为2211612x y +=.(2)如图,易知直线l 斜率不为0,设l 方程为x ty m =+,由22=++=11612x ty m x y ⎧⎪⎨⎪⎩,得()2223463480t y mty m +++-=,设()11,P x y ,()22,Q x y ,则122634mt y y t -+=+,212234834m y y t -=+,由(1)知,()14,0A -,()24,0A ,所以122211111222111134441643PA PA y y y y k k k k x x x y ⋅=⋅=⋅===-+---,同理,123434OA QA k k k k ⋅=⋅=-,因为()142353k k k k +=+,所以()2323335443k k k k --=+,()2323233543k k k k k k +-⋅=+,由l 与x 不垂直可得230k k +≠,所以23920k k =-,即22920PA QA k k ⋅=-,所以121294420y y x x ⋅=---,()()1212209440y y ty m ty m ++-+-=,于是()()()()22121292094940t y y t m y y m ++-++-=,()()()222223486920949403434m mt t t m m t t --+⋅+-⋅+-=++,整理得2340m m --=,解得1m =-或=4m ,因为P 、Q 在x 轴的两侧,所以2122348034m y y t -=<+,44m -<<,又1m =-时,直线l 与椭圆C 有两个不同的交点,因此1m =-,直线l 恒过点()1,0D -,。
高中数学竞赛专题讲座(解析几何)

高中数学竞赛专题讲座(解析几何)一、基础知识1.椭圆的定义,第一定义:平面上到两个定点的距离之和等于定长(大于两个定点之间的距离)的点的轨迹,即|PF 1|+|PF 2|=2a (2a>|F 1F 2|=2c). 第二定义:平面上到一个定点的距离与到一条定直线的距离之比为同一个常数e(0<e<1)的点的轨迹(其中定点不在定直线上),即e dPF =||(0<e<1). 第三定义:在直角坐标平面内给定两圆c 1: x 2+y 2=a 2, c 2: x 2+y 2=b 2, a, b ∈R +且a ≠b 。
从原点出发的射线交圆c 1于P ,交圆c 2于Q ,过P 引y 轴的平行线,过Q 引x 轴的平行线,两条线的交点的轨迹即为椭圆。
2.椭圆的方程,如果以椭圆的中心为原点,焦点所在的直线为坐标轴建立坐标系,由定义可求得它的标准方程,若焦点在x 轴上,列标准方程为12222=+b y a x (a>b>0), 参数方程为⎩⎨⎧==θθsin cos b y a x (θ为参数)。
若焦点在y 轴上,列标准方程为12222=+b y a y (a>b>0)。
3.椭圆中的相关概念,对于中心在原点,焦点在x 轴上的椭圆12222=+by a x , a 称半长轴长,b 称半短轴长,c 称为半焦距,长轴端点、短轴端点、两个焦点的坐标分别为(±a, 0), (0, ±b ), (±c, 0);与左焦点对应的准线(即第二定义中的定直线)为c a x 2-=,与右焦点对应的准线为c a x 2=;定义中的比e 称为离心率,且ace =,由c 2+b 2=a 2知0<e<1.椭圆有两条对称轴,分别是长轴、短轴。
4.椭圆的焦半径公式:对于椭圆=+2222by a x 1(a>b>0), F 1(-c, 0), F 2(c, 0)是它的两焦点。
解析几何竞赛题选

a2 + 2 (a + 2)2
(x
+
y
+
z
− b)2
−
2b a+2
(x
+
y
+
z
− b)
− b2
=
0
,
当 a = −2 时,由⑤得, x + y + z = b ,这表明,π 在这个平面上。
同时,将④代入③,有 x2 + y2 + z2 = 6t2 + 2bt + b2 = 6(t + 1 b)2 + 5 b2 。由于 66
=
sin(π
−
α
+
β
)
=
α sin(
+
β
)
2R 2
2
22
m
L
β Cα γ
n
= sin α cos β + cos α sin β = l
22
2 2 2R
1
−
m2 4R2
+
m 2R
1
−
l2 4R
2
.
n=l
1−
m2 4R2
+m
1
−
l2 4R2
,
两边平方得解之即得证。
c B
l M
十六、ΔABC的面积为1,点E, F,G分别在边 BC,CA, AB上,AE于点R处平分BF, BF于点 S处平分CG,CG于点T 处平分AE, 求ΔRST的面积。
+ +
(z (z
+ 1) 2 −1)2
,
即
⎧x
高一数学竞赛培训《解析几何部分》

高一上期数学竞赛培训资料(15)——解析几何部分(3)——直线和圆的位置关系知识归纳一、知识要点:1、直线和圆的位置关系判断:(1)直线方程和圆的方程联立:220y kx b x y Dx Ey F =+⎧⎨++++=⎩⇔20Ax Bx C ++=⇔000∆>⇔⎧⎪∆=⇔⎨⎪∆<⇔⎩相交相切相离 (2)设圆的半径为r ,圆心到直线的距离为d ,则:⇔d r d r d r <⇔⎧⎪=⇔⎨⎪>⇔⎩相交相切相离2、过定点00(,)P x y 作圆:C 222()()x a y b r -+-=的切线l ,切线l 的方程的求法:(1)点P 在圆C 上:则切线l 的方程为:200()()()()x a x a y b y b r --+--=(2)点P 在圆C 外:(有两条)设切线l 的方程为:00()y y k x x -=- (切线的斜率k 存在时)由圆心到直线的距离等于半径得:d r == 可解得斜率k 的值:1k 和2k (若只有一解,则必定有一条切线的斜率不存在!) (3)过圆外一定点00(,)P x y 作圆:C 222()()x a y b r -+-=引两条切线,切点为,A B ,则切点弦AB 所在直线的方程为:200()()()()x a x a y b y b r --+--= 3、圆和圆的位置关系:将两圆的方程联立:221112222200x y D x E y F x y D x E y F ⎧++++=⎨++++=⎩⇔0Ax By C ++= 该二元一次方程为两圆的根轴..的方程(该直线上一点向两圆引切线,则切线长相等)。
(1)两圆相交时,该直线为两圆的公共弦;(2)两圆相切时,该直线为过切点的公切线。
二、题型示例:类型一:1、已知x y 、是实数,且满足2246120x y x y +--+=,试求: (1)xy 的最值; (2) 22x y +的最值; (3) x y +的最值; (4) 2x y -的最值. 归纳解法:类型二:22kx =+有唯一解,则实数k 的取值范围是 ;3、设{(,)|1A x y y ==+,{(,)|(2)4}B x y y k x ==-+,若A B 中含有2个元素,则实数k的取值范围是解法:类型三:作图4、如图,某公园有A 、B和,且A 、B 景点间相距2km ,今欲在该小路上设一观景点,使两景点在同时进入视线时有最佳的观赏和拍摄效果,则观景点应设于何处?原问题————尺规作图:过A 、B 两点作圆,使之与定直线l 相切。
第08讲 解析几何-2009-2017全国高中数学联赛分类汇编 含解析

2009-2017全国高中数学联赛分类汇编第08讲:解析几何1、(2009一试2)已知直线:90L x y +-=和圆22:228810M x y x y +---=,点A 在直线L 上,B ,C 为圆M 上两点,在ABC ∆中,45BAC ∠=︒,AB 过圆心M ,则点A横坐标范围为.【答案】[]36,【解析】设()9A a a -,,则圆心M 到直线AC 的距离sin 45d AM =︒,由直线AC 与圆M 相交,得d 36a ≤≤.2、(2009一试5)椭圆22221x y a b+=()0a b >>上任意两点P ,Q ,若OP OQ ⊥,则乘积OP OQ ⋅的最小值为. 【答案】22222a b a b + 【解析】设()cos sin P OP OP θθ,,ππcos sin 22Q OQ OQ θθ⎛⎫⎛⎫⎛⎫±± ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,.由P ,Q 在椭圆上,有222221cos sin a b OP θθ=+ ①222221sin cos a b OQ θθ=+ ②①+②得22221111a b OP OQ+=+.于是当OP OQ ==时,OP OQ 达到最小值22222a b a b +.3、(2010一试3)双曲线122=-y x 的右半支与直线100=x 围成的区域内部(不含边界)整点(纵横坐标均为整数的点)的个数是.【答案】98004、(2011一试7)直线012=--y x 与抛物线xy 42=交于B A ,两点,C 为抛物线上的一点,︒=∠90ACB ,则点C 的坐标为. 【答案】)2,1(-或)6,9(-即0)(24)(21212212214=⋅++-+⋅++-y y t y y t x x t x x t , 即03161424=---t t t,即0)14)(34(22=--++t t t t.显然0142≠--t t,否则01222=-⋅-t t,则点C 在直线012=--y x 上,从而点C 与点A或点B 重合.所以0342=++t t,解得3,121-=-=t t.故所求点C 的坐标为)2,1(-或)6,9(-.5、(2012一试4)抛物线22(0)ypx p =>的焦点为F,准线为l,,A B 是抛物线上的两个动点,且满足3AFB π∠=.设线段AB的中点M 在l上的投影为N ,则||||MN AB 的最大值是.【答案】1【解析】由抛物线的定义及梯形的中位线定理得.2AF BFMN +=在AFB ∆中,由余弦定理得2222cos3ABAF BF AF BF π=+-⋅2()3AF BF AF BF =+-⋅22()3()2AF BF AF BF +≥+-22().2AF BF MN +==当且仅当AF BF =时等号成立。
解析几何基础100题知识讲解

解析几何基础100题一、选择题:2 2 c1.若双曲线与与1的离心率为5,则两条渐近线的方程为a, b, 4八XY XYc^XY XYcA ——0B — - 0C - - 0D - - 09 16 16 9 3 4 4 3解答:C易错原因:审题不认真,混淆双曲线标准方程中的a和题目中方程的a的意义。
2.椭圆的短轴长为2,长轴是短轴的2倍,则椭圆的中心到其准线的距离是A 8 .5B 4 ,5C 8,3D 久35 5 3 3解答:D易错原因:短轴长误认为是b3.过定点(1,2)作两直线与圆x2 y2 kx 2y k2 15 0相切,则k的取值范围是A k>2B -3<k<2C k<-3 或k>2D 以上皆不对解答:D易错原因:忽略题中方程必须是圆的方程,有些学生不考虑D2 E2 4F 02 24 .设双曲线4 匕1(a b 0)的半焦距为C,直线L过(a,0),(0,b)两点, a b已知原点到直线L的距离为 % ,则双曲线的离心率为A 2B 2 或毡C 屐D 273 3 3解答:D易错原因:忽略条件a b。
对离心率范围的限制。
5.已知二面角l 的平面角为,PA , PB , A, B为垂足,且PA=4,PB=5设A、B到二面角的棱l的距离为别为x,y,当变化时,点(x,y)的轨迹是下列图形中的A B C D解答:D易错原因:只注意寻找x,y的关系式,而未考虑实际问题中x,y的范围。
6.若曲线y 值~4与直线y k(x 2)+3有两个不同的公共点,则实数k的取值范围是3 一 3 _A 0 k 1B 0 k -C 1 k -D lkO 4 4解答:C易错原因:将曲线y 犷7转化为x2y24时不考虑纵坐标的范围;另外没有看清过点(2,-3)且与渐近线y x平行的直线与双曲线的位置关系。
7. P(-2,-2)、Q(0,-1)取一点R(2,m)使PR| 十 | RQ| 最小,则m=A 1B 0C - 1D - -2 3正确答案:D 错因:学生不能应用数形结合的思想方法,借助对称来解题。
专题讲座:解析几何难题汇总题目与答案

专题讲座:解析几何难题汇总题目与答案
在浙江高考数学卷中,解析几何常常以极高的难度出现在第21题这样的压轴大题中。
尤其是18,19两年的解析几何大题,极大的计算量让不少同学“止步于此”。
但是反观平常的模拟卷中,第21题的解析几何却往往考了一些二级结论或是简单计算即可完成的题目,非常不符合高考的“趋势”,同学们也往往因此没有意识到自己的解析几何能力还是不足够的。
今天,数海漫游为了让你们体会到高考考场上做解析几何的“煎熬”,特地选择了5道非常有难度的解析几何题让你们感受一下。
希望同学们可以每题限时20分钟完成,分多天完成,深刻体会出如何在“设点”与“设线”间游刃有余地彳亍。
需要pdf版(有留做题空间)的学生和老师都可以加入公众号群:553633223探讨数学问题,共享学习资料。
题目与解答·严禁盗用:
第一题:
难度:★★★★☆第二题:
难度:★★★★☆
第三题:
难度:★★★★☆
第四题:
难度:★★★☆☆
第五题:
难度:★★★★☆
题目来源包括:嘉兴,温中,学军等地的模拟题。
题目复杂,但其中主要思想就是把复杂的题目剖分,慢慢简化题目,最后问题也迎刃而解。
不过没做对的同学也不要灰心!!
把题目记在纠错本上,自己多多回顾!
题目不是最重要的,该学习的其实是思想。
竞赛试题选讲之解析几何

高中数学竞赛专题讲座之四:解析几何一、选择题部分1.(集训试题)过椭圆C :12322=+y x 上任一点P ,作椭圆C 的右准线的垂线PH (H 为垂足),延长PH 到点Q ,使|HQ|=λ|PH|(λ≥1)。
当点P 在椭圆C 上运动时,点Q 的轨迹的离心率的取值范围为 ( )A .]33,0( B .]23,33(C .)1,33[D .)1,23(解:设P(x 1, y 1),Q(x, y),因为右准线方程为x=3,所以H 点的坐标为(3, y)。
又∵HQ=λPH ,所以λ+-=11PQ HP ,所以由定比分点公式,可得:⎪⎩⎪⎨⎧=-+=yy x x 11)1(3λλ,代入椭圆方程,得Q 点轨迹为123)]1(3[222=++-y x λλ,所以离心率e=)1,33[321322322∈-=-λλλ. 故选C.2.(2006年南昌市)抛物线顶点在原点,对称轴为x 轴,焦点在直线3x-4y =12上,则抛物线方程为(D)A .212y x =-B .212y x =C .216y x =-D .216y x =3.(2006年江苏)已知抛物线22y px =,O 是坐标原点,F 是焦点,P 是抛物线上的点,使得△POF 是直角三角形,则这样的点P 共有(B )A .0个B .2个C .4个D .6个4.(200 6天津)已知一条直线l 与双曲线12222=-by a x (0>>a b )的两支分别相交于P 、Q 两点,O 为原点,当OQ OP ⊥时,双曲线的中心到直线l 的距离d 等于(A ) A .22ab ab- B .22a b ab- C .aba b 22- D .ab a b 22-5.(2005全国)方程13cos 2cos 3sin 2sin 22=-+-y x 表示的曲线是( ) A .焦点在x 轴上的椭圆 B .焦点在x 轴上的双曲线C .焦点在y 轴上的椭圆D .焦点在y 轴上的双曲线 解:),23cos()22cos(,223220,32ππππππ->-∴<-<-<∴>+ 即 .3sin 2sin >又,03cos 2cos ,03cos ,02cos ,32,220>-∴<>∴<<<<πππ方程表示的曲线是椭圆.)()4232sin(232sin22)3cos 2(cos )3sin 2(sin *++-=--- π,0)4232sin(.423243,432322,0232sin ,02322>++∴<++<∴<+<<-∴<-<-πππππππ.0)(<*∴式即∴-<-.3cos 2cos 3sin 2sin 曲线表示焦点在y 轴上的椭圆,选C 。
竞赛中的解析几何解答题(一)

竞赛中解析几何问题(二)解答题部分
1. (2000)已知C 0:x 2+y 2=1和C 1:122
22=+b y a x (a >b >0)。
试问:当且仅当a ,b 满足什么条件时,对C 1上任意一点P ,均存在以P 为项点,与C 0外切,与C 1内接的平行四边形?并证明你的结论。
2. (2001)设曲线C 1:1222
=+y a
x (a 为正常数)与C 2:y 2=2(x+m)在x 轴上方公有一个公共点P 。
(1)求实数m 的取值范围(用a 表示);
(2)O 为原点,若C 1与x 轴的负半轴交于点A ,当0<a<21时,试求⊿OAP 的面积的最大值(用a 表示)。
3. (2008)如图,P 是抛物线22y x =上的动点,点B C 、在y 轴上,圆22(1)1x y -+=内切于PBC ∆,求PBC ∆面积的最小值.
4. (2010)已知抛物线26y x =上的两个动点A (1x ,1y )和B (2x ,2y ),其中12x x ≠且124x x +=.线段AB 的垂直平分线与x 轴交于点C ,求ABC ∆面积的最大值.。
辅导讲座数学五讲:《解析几何》各类竞赛试题选讲

高中数学竞赛专题讲座之五:《解析几何》各类竞赛试题选讲一、选择题1.(04某某)已知曲线C :x x y 22--=与直线0:=-+m y x l 有两个交点,则m 的取值X 围是(C)A .)2,12(--B .)12,2(--C .)12,0[-D .)12,0(-2.(05全国)方程13cos 2cos 3sin 2sin 22=-+-y x 表示的曲线是 ( )A .焦点在x 轴上的椭圆B .焦点在x 轴上的双曲线C .焦点在y 轴上的椭圆D .焦点在y 轴上的双曲线3.(06某某)已知两点A (1,2), B (3,1) 到直线L 的距离分别是25,2-,则满足条件的直线L 共有( C )条.A .1B .2C .3D .4解: 由,5=AB 分别以A ,B 为圆心,2,5为半径作两个圆,则两圆外切,有三条共切线。
正确答案为C.4.(06某某)过原点O 引抛物线224y x ax a =++的切线,当a 变化时,两个切点分别在抛物线( )上 A .2213,22y x y x == B .2235,22y x y x ==C .22,3y x y x ==D .223,5y x y x ==5.若在抛物线)0(2>=a ax y 的上方可作一个半径为r 的圆与抛物线相切于原点O ,且该圆与抛物线没有别的公共点,则r 的最大值是(A ) A .a 21 B .a1C .aD .a 26.(06某某)已知抛物线y 2=2px ,o 是坐标原点,F 是焦点,P 是抛物线上的点,使得△POF是直角三角形,则这样的点P 共有(B) A .0个 B .2个 C .4个 D .6个7.(06全国)如图3,从双曲线22221(0,0)x y a b a b-=>>的左焦点F 引圆222x y a +=的切线,切点为T .延长FT交双曲线右支于P 点.若M 为线段FP 的中点,O 为坐 标原点,则||||MO MT -与b a -的大小关系为( ) A .||||MO MT b a ->-B .||||MO MT b a -=-C .||||MO MT b a -<-D .不确定8.(05某某)双曲线12222=-by a x 的左焦点为1F ,顶点为21,A A ,P 是该双曲线右支上任意一点,则分别以线段211,A A PF 为直径的两圆一定 ( )A .相交B .内切C .外切D .相离解:设双曲线的另一个焦点为2F ,线段1PF 的中点为C ,在△P F F 21中,C 为1PF 的中点,O 为21F F 的中点,从而|)||(|21||212112A A PF PF OC -==,从而以线段211,A A PF 为直径的两圆一定内切.9.点A 是直线x y l 3:=上一点,且在第一象限,点B 的坐标为(3,2),直线AB 交x 轴正半轴于点C ,那么三角形AOC 面积的最小值是(A )10.(02某某)已知A (-7,0),B (7,0),C (2,-12)三点,若椭圆的一个焦点为C ,且过A 、B 两点,此椭圆的另一个焦点的轨迹为( )(奥析263) A .双曲线 B .椭圆 C .椭圆的一部分D .双曲线的一部分 11.(03全国)过抛物线)2(82+=x y 的焦点F 作倾斜角为60O 的直线。
解析几何竞赛辅导

若不允许共线。 如图,在正三角形 ABC 的内切圆上任取一点 P ,使得
向量 PA , PB , PC , PO 不共线便满足要求。
A
O P B C
( PA + PB ) ⋅ ( PC + PO )
= OA + OB + 2 PO ⋅ OC + 2 PO
( (
)(
)
2 2
= 2 PO − OC ⋅ 2 PO + OC = 4 PO − OC = 0
XF1 ( x, y ) + YF2 ( x, y ) = 0
共轭方向: a11 XX ′ + a12 ( XY ′ + X ′ ) + a22YY ′ = 0 Y 主方向:即共轭又垂直的方向
⎛ a11 ⎜ ⎝ a12
a12 ⎞ ⎛ X ⎞ ⎛X ⎞ ⎟⎜ ⎟ = λ ⎜ ⎟ a22 ⎠ ⎝ Y ⎠ ⎝Y ⎠
r (u, v) = ( x(u , v), y (u , v), z (u , v))
求点运动所成的曲线方程, ( x(t ), y (t ), z (t )) 求点运动所成的曲面方程, ( x(u , v), y (u , v), z (u , v)) 求空间直线运动所成的曲面方程, 直线: ( At + x0 , Bt + y0 , Ct + z0 ) ,参数 s 直线族:( A( s )t + x0 ( s ), B ( s )t + y0 ( s ), C ( s )t + z0 ( s ) )
三、空间的直线和平面 平面方程,直线方程,相互位置关系,平面束。 直线
x − x0 y − y0 z − z0 和 = = X Y Z
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《解析几何》 各类竞赛试题选讲一、选择题1、(04湖南)已知曲线C :x x y 22--=与直线0:=-+m y x l 有两个交点,则m 的取值范围是(C) A .)2,12(-- B .)12,2(-- C .)12,0[-D .)12,0(-2. (05全国)方程13cos 2cos 3sin 2sin 22=-+-yx表示的曲线是( )A. 焦点在x 轴上的椭圆B. 焦点在x 轴上的双曲线C. 焦点在y 轴上的椭圆D. 焦点在y 轴上的双曲线3、(06浙江)已知两点A (1,2), B (3,1) 到直线L 的距离分别是25,2-,则满足条件的直线L共有( C )条。
(A )1 (B )2 (C )3 (D )4 解: 由,5=AB 分别以A ,B 为圆心,2,5为半径作两个圆,则两圆外切,有三条共切线。
正确答案为C 。
4.(06安徽)过原点O 引抛物线224y x ax a=++的切线,当a 变化时,两个切点分别在抛物线( )上A 、2213,22yx y x==B 、2235,22yx y x==C 、22,3y x y x== D 、223,5yx y x==5.若在抛物线)0(2>=a ax y 的上方可作一个半径为r 的圆与抛物线相切于原点O ,且该圆与抛物线没有别的公共点,则r 的最大值是 ( A ).(A)a21 (B)a1 (C)a (D)a 26. (06江苏)已知抛物线y 2=2px ,o 是坐标原点,F 是焦点,P 是抛物线上的点,使得△POF 是直角三角形,则这样的点P 共有( B ) (A)0个 (B)2个 (C)4个 (D)6个 7、(06全国)如图3,从双曲线22221(0,0)x y a b ab-=>>的左焦点F 引圆222x y a +=的切线,切点为T .延长FT 交双曲线右支于P 点。
若M 为线段FP 的中点,O 为坐标原点,则||||MO MT -与b a -的大小关系为 ( ) A.||||MO MT b a ->- B.||||MO MT b a -=- C. ||||MO MT b a -<- D.不确定8.(05四川)双曲线12222=-by ax 的左焦点为1F ,顶点为21,A A ,P 是该双曲线右支上任意一点,则分别以线段211,A A PF 为直径的两圆一定( )(A )相交 (B )内切 (C )外切 (D )相离解:设双曲线的另一个焦点为2F ,线段1PF 的中点为C ,在△P F F 21中,C 为1PF 的中点,O 为21F F 的中点,从而|)||(|21||212112A A PF PF OC -==,从而以线段211,A A PF 为直径的两圆一定内切。
9、点A 是直线x y l 3:=上一点,且在第一象限,点B 的坐标为(3,2),直线AB 交x 轴正半轴于点C ,那么三角形AOC 面积的最小值是 ( A ) 10.(02湖南)已知A (-7,0),B (7,0),C (2,-12)三点,若椭圆的一个焦点为C ,且过A 、B 两点,此椭圆的另一个焦点的轨迹为( )(奥析263) (A )双曲线 (B )椭圆 (C )椭圆的一部分 (D )双曲线的一部分11、(03全国)过抛物线)2(82+=x y 的焦点F 作倾斜角为60O的直线。
若此直线与抛物线交于A 、B 两点,弦AB 的中垂线与轴交于点P ,则线段PF 的长等于( )(奥析263) (A )316 (B )38 (C )3316 (D )38二、填空题1、若a ,b ,c 成等差数列,则直线ax +by +c = 0被椭圆22128xy+=截得线段的中点的轨迹方程为2. (04湖南)设P 是椭圆191622=+yx上异于长轴端点的任意一点,1F 、2F 分别是其左、右焦点,O为中心,则=+⋅221||||||OP PF PF ___25________.3.(05湖南)一张坐标纸对折一次后,点)4,0(A 与点)0,8(B 重叠,若点)8,6(C 与点),(n m D 重叠,则=+n m _______________;解:可解得对称轴方程为62-=x y ,由2168,6)6(28-=---+=+m n m n 得2,7,6.7==n m ,所以8.14=+n m4. 在正△ABC ∆中,D 、E 分别是AB 、AC 的中点,则以B 、C 为焦点且过点D 、E 的双曲线的1+ .5、(03全国)设F 1、F 2是椭圆14922=+yx的两个焦点,P 是椭圆上的一点,且|PF 1|:|PF 2|=2:1.则三角形PF 1F 2的面积为 . (奥析264)6、(04全国)给定两点M (-1,2),N (1,4),点P 在x 轴上移动. 当MPN ∠取最大时,点P 的坐标为 . (奥析265)7、(03山东)设曲线64222+=+x y x 上与原点距离最大和最小的点分别为M 、N ,则|MN|= . (奥析266)8、(04全国)已知}.|),{(},32|),{(22b mx y y x N y x y x M +===+=若对于所有的R m ∈,均有φ≠⋂N M ,则b 的取值范围是 (奥析267)9、(00全国)平面上的整点到直线25x -15y+12=0的距离中的最小值是8534.10、(99全国)满足不等式(|x |-1)2+(|y |-1)2 <2的整点的个数有 16 .11、(00河北)在圆x 2+y 2-5x=0内,过点)23,25(有三条弦的长度成等比数列. 则其公比的取值范围为]25,552[.12、设P 是抛物线y 2=2x 上的点,Q 是圆(x -5)2+y 2=1上的点,则|PQ|的最小值为 2 .三、解答题1、已知抛物线y 2=4ax (0<a<1)的焦点为F ,以A (a+4,0)为圆心,|AF|为半径在x 轴上方作半圆交抛物线与不同的两点M 、N ,设P 为线段MN 的中点.(1)求|MF|+|NF 的值.(2)是否存在这样的a 的值,使||MF|、|PF|、|NF|成等差数列?如存在,求出a 的值;如不存在,说明理由。
答案(1)8;(2)不存在。
(利用定义法)2、圆x 2+y 2=8,点A (2,0),动点M 在圆上,0为原点,求OMA ∠的最大值。
(方法大全1)3、已知曲线m y x M =-22:,0>x ,m 为正常数.直线l 与曲线M 的实轴不垂直,且依次交直线x y =、曲线M 、直线x y -=于A 、B 、C 、D 4个点,O 为坐标原点.(1) 若||||||CD BC AB ==,求证:AOD ∆的面积为定值; (2)若BOC ∆的面积等于AOD ∆面积的31,求证:||||||CD BC AB ==.解:(1)设直线l :b kx y +=代入m y x =-22得:02)1(222=----m b bkx x k ,0>∆得:0)1(22>-+k m b ,设),(11y x B ,),(22y x C ,则有22112kbk x x -=+,22211)(km b x x -+-=,设),(33y x A ,),(44y x D ,易得:kb x -=13,kb x +-=14,由||||||CD BC AB ==得||31||AD BC =,A CQ故||31||4321x x x x -=-,代入得|12|311)(4)12(22222kbkm b k bk -=-++-,整理得:)1(8922-=km b ,又|1|2||kbOA -=,|1|2||kbOD +=,︒=∠90AOD ,∴AOD S ∆=m k b89|1|22=-为定值。
(2)设BC 中点为P ,AD 中点为Q 则22112kbk x x x p -=+=,24312kbk x x x Q -=+=,所以Q P x x =,P 、Q 重合,从而||||DP AP =,从而||||CD AB =,又BOC ∆的面积等于AOD ∆面积的31,所以||31||AD BC =,从而||||||CD BC AB ==。
4、已知点A()0,5和曲线()0,5221422≥≤≤=-y x y x上的点、、P P 21…、n P 。
若A P 1、A P 2、…、A P n 成等差数列且公差d >0,(1). 试将d 表示为n 的函数关系式.(2). 若⎪⎭⎫⎝⎛∈51,51d ,是否存在满足条件的)(*N n n ∈.若存在,求出n 可取的所有值,若不存在,说明理由.解(1). ∵d>0,故为递增数列 ∴A P 1最小,A P n 最大。
由方程()0,5221422≥≤≤=-y x y x知)0,5(A 是它的右焦点,L: 54=x 是它的右准线, ∴251⋅=A P 3=A P n于是d n )1()25(3---= ∴ )1(155>--=n n d - - - - - - - - - - -5分(2) ∵)51,51(∈d ∴5115551<--<n 设)5526,455(--∈n 又∵*N n ∈ ∴n 取最大值14, n 取最小值8.∴n 可取8、9、10、11、12、、13、14这七个值。
- - - - - - - - -- - - - -9分 5、(03山东)椭圆C :122=+ByAx 与直线 :x+2y=7相交于P 、Q 两点,点R 的坐标为(2,5).若PQR ∆是等腰三角形,OPRQ 90=∠,求A 、B 的值。
(奥析265)6、(04全国)在平面直角坐标系xoy 中,给定三点4(0,),(1,0),(1,0)3A B C -,点P 到直线BC 的距离是该点到直线AB ,AC 距离的等比中项。
(Ⅰ)求点P 的轨迹方程;(Ⅱ)若直线L 经过A B C ∆的内心(设为D ),且与P 点的轨迹恰好有3个公共点,求L 的斜率k 的取值范围。
解:(Ⅰ)直线AB 、AC 、BC 的方程依次为44(1),(1),033y x y x y =+=--=。
点(,)P x y 到AB 、AC 、BC 的距离依次为12311|434|,|434|,||55d x y d x y d y =-+=+-=。
依设,2222123,|16(34)|25d d d x y y =--=得,即22222216(34)250,16(34)250x y y x y y --+=---=或,化简得点P 的轨迹方程为圆S :22222320171280x y y y y ++-=-+-=2与双曲线T:8x ......5分(Ⅱ)由前知,点P 的轨迹包含两部分圆S :2222320x y y ++-= ① 与双曲线T :2171280y y -+-=28x ②因为B (-1,0)和C (1,0)是适合题设条件的点,所以点B 和点C 在点P 的轨迹上,且点P 的轨迹曲线S 与T 的公共点只有B 、C 两点。
