6位2进制
二进制转换

数据在计算机中的表示与存储自然界的信息是丰富多彩的,有数值、文字、声音、图形、图像、视频等,但是计算机本质上只能处理二进制的“0”和“1”,因此必须将各种信息转换成为计算机能够接受和处理的二进制数据,这种转换往往由外部设备和计算机自动进行。
1数值数据的表示二进制数据的表示二进制数据只有“0”和“1”两个符号,其进位基数为2。
加法运算的基本规则是“逢二进一”,减法运算的基本规则是“借一当二”,其他规则都可以由此推出。
2 字符数据的表示英文字符的表示英文字符包括数字、字母、符号、控制符号等,目前广泛采用ASCII码(美国标准信息交换编码),它用1个字节的低7位(最高位为0)表示128个不同的字符,包括大写和小写的26个英文字母,0~9的10个数字,33个通用运算符和标点符号,以及33个控制码。
中文字符的表示GB2312-80在计算机中,不同的硬件和软件对二进制代码的存储单位是不一致的,但是基本存储单位是以8位二进制为一个字节。
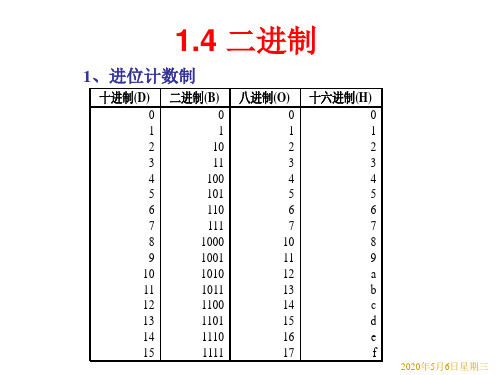
进制的转换1进位计数制1.二进制(B)二进制数只有两个代码“0”和“1”,所有的数据都由它们的组合来实现。
二进制数据在进行运算时,遵守“逢二进一,借一当二”的原则2.十六进制(H)十六进制数采用0~9和A、B、C、D、E、F六个英文字母一起构成十六个代码。
2 二进制与十进制的相互转换将每一位数字乘以它的权,再以十进制的方法相加就可以得到它的十进制的值(注意,小数点左侧相邻位的权为20,从右向左,每移一位,幂次加1)。
【例1】(10110.011)B=1×24+0×23+1×22+1×21+0×20+0×2-1 +1×2-2+1×2-3=(22.375)D(2)十进制数据转换成二进制采用的是“除2取余”的方法。
★3由于16=24,所以在将二进制数转换成十六进制数时,从最右侧开始,每四位二进制数划为一组,用一位十六进制数代替,也称为“以四换一”;十六进制数转换成二进制数时正好相反,一位十六进制数用四位二进制数来替换,也称“以一换四”。
二进制—搜狗百科

二进制—搜狗百科展开全文二进制十进制数转换为二进制数、八进制数、十六进制数的方法:二进制数、八进制数、十六进制数转换为十进制数的方法:按权展开求和法二进制与十进制(1)二进制转十进制方法:“按权展开求和”例:(1011.01) 2 =(1×2^3+0×2^2+1×2^1+1×2^0+0×2^(-1)+1×2^(-2) )10 =(8+0+2+1+0+0.25)10=(11.25)10规律:个位上的数字的次数是0,十位上的数字的次数是1,......,依次递增,而十分位的数字的次数是-1,百分位上数字的次数是-2,......,依次递减。
注意:不是任何一个十进制小数都能转换成有限位的二进制数。
(2)十进制转二进制· 十进制整数转二进制数:“除以2取余,逆序排列”(除二取余法)例:(89)10 =(1011001)289÷2 (1)44÷2 022÷2 011÷2 (1)5÷2 (1)2÷2 01· 十进制小数转二进制数:“乘以2取整,顺序排列”(乘2取整法)例: (0.625)10= (0.101)20.625X2=1.25 (1)0.25 X2=0.50 00.50 X2=1.00 (1)十进制1至100的二进制表示:0=01=12=103=114=1005=1016=1107=1118=10009=1001 10=1010 11=1011 12=1100 13=1101 14=1110 15=1111 16=10000 17=10001 18=10010 19=10011 20=10100 21=10101 22=10110 23=10111 24=11000 25=11001 26=11010 27=11011 28=11100 29=11101 30=11110 31=11111 32=100000 33=100001 34=100010 35=10001137=100101 38=100110 39=100111 40=101000 41=101001 42=101010 43=101011 44=101100 45=101101 46=101110 47=101111 48=110000 49=110001 50=110010 51=110011 52=110100 53=110101 54=110110 55=110111 56=111000 57=111001 58=111010 59=111011 60=111100 61=111101 62=111110 63=111111 64=1000000 65=100000167=1000011 68=1000100 69=1000101 70=1000110 71=1000111 72=1001000 73=1001001 74=1001010 75=1001011 76=1001100 77=1001101 78=1001110 79=1001111 80=1010000 81=1010001 82=1010010 83=1010011 84=1010100 85=1010101 86=1010110 87=1010111 88=1011000 89=1011001 90=1011010 91=1011011 92=1011100 93=1011101 94=1011110 95=101111197=1100001 98=1100010 99=1100011 100=1100100 101=1100101 102=1100110 103=1100111 104=1101000 105=1101001 106=1101010 107=1101011 108=1101100 109=1101101 110=1101110 111=1101111 112=1110000 113=1110001 114=1110010 115=1110011 116=1110100 117=1110101 118=1110110 119=1110111 120=1111000 121=1111001 122=1111010 123=1111011 124=1111100 125=1111101127=1111111128=10000000八进制与二进制二进制数转换成八进制数:从小数点开始,整数部分向左、小数部分向右,每3位为一组用一位八进制数的数字表示,不足3位的要用“0”补足3位,就得到一个八进制数。
二进制,八进制,十进制,十六进制之间的转换

二进制,八进制,十进制,十六进制之间的转换1.什么是二进制二进制是计算技术中广泛采用的一种数制。
二进制数据是用0和1两个数码来表示的数。
它的基数为2,进位规则是“逢二进一”,借位规则是“借一当二”,由18世纪德国数理哲学大师莱布尼兹发现。
当前的计算机系统使用的基本上是二进制系统,数据在计算机中主要是以补码的形式存储的。
计算机中的二进制则是一个非常微小的开关,用“开”来表示1,“关”来表示0。
信息的存储单位位(Bit) :度量数据的最小单位字节(Byte):最常用的基本单位,一个字节有8位b7 b6 b5 b4 b3 b2 b1 b01 0 0 1 0 1 0 1 =27+24+22+20=149K字节1k=1024 byteM(兆)字节 1M=1024KG(吉)字节 1G=1024MT(太)字节 1T=1024G曾经听人说,一个c,c++大神,就靠输入,0和1就可以装好操作系统,不知道是不是真的,嘿嘿2.十进制转换1234[10进制] 0 1 2 3 4 5 6 7 8 9 0 当数位上的值超过9就要进11000+200+30+4=1*103+2*102+3*101+4*100=12341011[2进制] 0 1 当数位上的值超过1就要进11*23+0*22+1*21+1*20=8+0+2+1=111011[8进制]0 1 2 3 4 5 6 7 当数位上的值超过7就要进11*83+1*81+1*80=512+8+1=5211011[16进制]0 1 2 3 4 5 6 7 8 9 A B C D E F 当数位上的值超过15就要进1 1*163+1*161+1*160=4096+16+1=4113当然其他进制转换成10进制是最简单的了,我想聪明的你肯定会了。
3.二进制转换首先来看十进制到二进制:除2取余数最后把余数倒过来 100101比如:十进制数37所以转换成的二进制数字为:100101再来八进制到二进制:一个八进制的位拆分成一个三位的二进制数比如:[八进制]6166拆分成 1101拆分成0016拆分成110所以转换成的二进制数字为:110001110再来十六进制到二进制:一个八进制的位拆分成一个四位的二进制数比如:[十六进制]6166拆分成01101拆分成00016拆分成0110所以转换成的二进制数字为:110000101104.八进制转换十进制到八进制:除8取余数最后把余数倒过来同时我们也可以先将十进制转换成二进制,然后将二进制又转换成八进制比如:2456 转化成八进制数字:46302456/8=307,余0;307/8=38,余3;38/8=4,余6;4/8=0,余4。
计算机二进制转换
1.4 二进制
1、进位计数制
十进制(D) 二进制(B)
0
0
1
1
2
10
3
11
4
100
5
101
6
110
7
111
8
1000
9
1001
10
1010
11
1011
12
1100
13
1101
14
1110
15
1111
八进制(O)
0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17
十六进制(H)
0 1 2 3 4 5 6 7 8 9 a b c d e f
2020年5月6日星期三
2. 十进制转化成 r 进制 整数部分:除以 r取余数,直到商为0,余数从下到上排列。 小数部分:乘以 r取整数,整数从上到下排列。
例 100.345(D)~=1100100.01011(B)
100(D)=144(O)=64(H)
11 0110 1110.1101 01(B)=36E.D4(H)
36 E D4
后边补两个零0100
1 101 101 110.110 101(B)= 1556.65(O)
15 5 6 6 5
2020年5月6日星期三
• 111010101.10111(B)= 725.56 (O) • 111010101.10111(B)= 1D5.B8 (H) • 7421.046(O)=111100010001.000100110(B) • 1ABC.EF1(H)=1101010111100.111011110001(B) • 8 4 2 1 001011010
二进制八进制十进制十六进制之间的转换方法

二进制八进制十进制十六进制之间的转换方法二进制、八进制、十进制和十六进制是计算机中常用的数制表示方法。
在进行转换时,可以利用其数制规则和特点来进行相互转换。
以下将详细介绍二进制、八进制、十进制和十六进制之间的转换方法。
1.二进制转八进制:二进制数是由0和1组成的数,八进制数是由0-7组成的数。
每3位二进制数可以转换为1位的八进制数,所以将二进制数从右到左以3位一组进行分组,并用八进制数表示每组即可。
2.二进制转十进制:二进制数转换为十进制数的方法是将二进制数分别乘以2的n次方,并将结果相加,其中n从0开始递增,对应于从右到左的二进制位数。
3.二进制转十六进制:二进制数转换为十六进制数的方法是将二进制数分组为4位一组,然后将每组转换为十六进制数。
4.八进制转二进制:八进制数转换为二进制数的方法是将八进制数的每位转换为对应的3位二进制数。
例如:将八进制数326转换为二进制数,可以将其每位转换为对应的3位二进制数,得到结果:011010110。
5.八进制转十进制:八进制数转换为十进制数的方法是将八进制数分别乘以8的n次方,并将结果相加,其中n从0开始递增,对应于从右到左的八进制位数。
例如:将八进制数326转换为十进制数,可以分别计算3*8^2+2*8^1+6*8^0,得到结果:2066.八进制转十六进制:将八进制数转换为十六进制数,首先将八进制数转换为二进制数,然后将二进制数转换为十六进制数。
例如:将八进制数326转换为十六进制数,可以先将其转换为二进制数011010110,然后将二进制数转换为十六进制数,得到结果:D67.十进制转二进制:将十进制数转换为二进制数的方法是将十进制数不断除以2,然后将余数逆序排列,最后将得到的余数连接在一起。
8.十进制转八进制:将十进制数转换为八进制数的方法是将十进制数不断除以8,然后将余数逆序排列,最后将得到的余数连接在一起。
例如:将十进制数214转换为八进制数,可以依次计算214/8=26余6,26/8=3余2,3/8=0余3、最后将得到的余数逆序排列,得到结果:3269.十进制转十六进制:将十进制数转换为十六进制数的方法是将十进制数不断除以16,然后将余数逆序排列,对于10~15的余数,分别用A~F表示,最后将得到的余数连接在一起。
二进制转换算法

一、概念1.十进制十进制使用十个数字0、1、2、3、4、5、6、7、8、9记数,基数为10,逢十进一; 历史上第一台电子数字计算机ENIAC是一台十进制机器,其数字以十进制表示,并以十进制形式运算;设计十进制机器比设计二进制机器复杂得多;而自然界具有两种稳定状态的组件普遍存在,如开关的开和关,电路的通和断,电压的高和低等,非常适合表示计算机中的数;设计过程简单,可靠性高;因此,现在改为二进制计算机;2. 二进制二进制以2为基数,只用0和1两个数字表示数,逢2进一;二进制与遵循十进制数遵循一样的运算规则,但显得比十进制更简单;例如:1加法:0+0=0 0+1=1 1+0=1 1+1=02减法:0-0=0 1-1=0 1-0=1 0-1=13乘法:00=0 01=0 10=0 11=14除法:0/1=0 1/1=1,除数不能为0二、进制转换1.二进制与十进制数间的转换1二进制转换为十进制将每个二进制数按权展开后求和即可;请看例题:把二进制数2=122+021+120+12-1+02-2+12-3=10二进制数转换为十进制数:二进制数第0位的权值是2的0次方,第1位的权值是2的1次方……所以,设有一个二进制数:0110 0100,转换为10进制为:下面是竖式:0110 0100 换算成十进制第0位 0 20= 0第1位 0 21= 0第2位 1 22= 4第3位 0 23= 0第4位 0 24= 0第5位 1 25= 32第6位 1 26= 64第7位 0 27= 0+---------------------------100用横式计算为:0 20 + 0 21 + 1 22 + 1 23 + 0 24 + 1 25 + 1 26 + 0 27 = 100 0乘以多少都是0,所以我们也可以直接跳过值为0的位:1 22 + 1 23 + 1 25 + 1 26 = 1002十进制转换为二进制一般需要将十进制数的整数部分与小数部分分开处理;整数部分计算方法:除2取余法请看例题:用2辗转相除至结果为1将余数和最后的1从下向上倒序写就是结果例如302302/2 = 151 余0151/2 = 75 余175/2 = 37 余137/2 = 18 余118/2 = 9 余09/2 = 4 余14/2 = 2 余02/2 = 1 余0故二进制为0十进制整数转二进制数:"除以2取余,逆序输出"例: 8910=101100122 892 44 (1)2 22 02 11 02 5 (1)2 2 (1)2 1 00 (1)小数部分计算方法:乘2取整法,即每一步将十进制小数部分乘以2,所得积的小数点左边的数字0或1作为二进制表示法中的数字,第一次乘法所得的整数部分为最高位;请看例题:例:0.62510= 20.625X 21.25X 20.5X 21.0将10转换成二进制;10=21.1250.250. 51. 02.二进制与十六进制数间的转换二进制十六进制0 01 110 211 3100 4101 5110 6111 71000 81001 91010 A1011 B1100 C1101 D1110 E1111 F(1)二进制数转换成十六进制数二进制数转换成十六进制数方法如下,以二进制数1101110为例:将二进制数从右面开始以四位为一组分组,最左面不够四位的补0,按上表查得对应的十六进制数,组合起来以后就成了;4个2进制位为一个16进制数如01011100,可看成是两组2进制数0101和1100,则这个数就是16进制的5C;0110 1110的十六进制数是6E2 十六进制转换成二进制方法十六进制转换成二进制方法如下,以十六进制数3E为例:将十六进制的每一位转换成四位二进制数,不足四位的在左面补0,组合起来即可得到二进制数;3E的二进制数是00111110,既是111110进制转16进制:10转16用传统的计算方式可以了,就是大于15小于256的10进制数除以16为的值为十位的16进制数,其余数为个位的16进制数,没余数则个位为0;如61的16进制是3D,61除以16得3余13,3作十位数,13转成D为个位数;16转10:用相反的道理,将十位数乘以16加上个位数;如5A,将5乘以16得80,加上A 的10进制10,结果是90;十六进制数转换成十进制数:2进制,用两个阿拉伯数字:0、1;8进制,用八个阿拉伯数字:0、1、2、3、4、5、6、7;10进制,用十个阿拉伯数字:0到9;16进制16进制就是逢16进1,但我们只有0~9这十个数字,所以我们用A,B,C,D,E,F这五个字母来分别表示10,11,12,13,14,15;字母不区分大小写;十六进制数的第0位的权值为16的0次方,第1位的权值为16的1次方,第2位的权值为16的2次方……所以,在第NN从0开始位上,如果是是数 X X 大于等于0,并且X小于等于 15,即:F表示的大小为 X 16的N次方;假设有一个十六进数 2AF5, 那么如何换算成10进制呢用竖式计算:2AF5换算成10进制:5 160+ F 161 + A 162 + 2 163 = 10997别忘了,在上面的计算中,A表示10,而F表示15现在可以看出,所有进制换算成10进制,关键在于各自的权值不同;4.二进制转为 8 进制二进制转为 8 进制,可以 3 位二进制位编为一组不够左侧补 0,然后从右边开始每三位按如下方式替换:000 --- 0,001 --- 1,010 --- 2,011 --- 3,100 --- 4,101 --- 5,110 --- 6,111 --- 7.比如转换二进制数那么分组为001 110 101 010 100 按照转换方法对应转换1 6 52 4所以 2 = 165248又如转换为 16 进制0000 --- 0, 0001 --- 1, 0010 --- 2, 0011 --- 30100 --- 4, 0101 --- 5, 0110 --- 6, 0111 --- 71000 --- 8, 1001 --- 9, 1010 --- A, 1011 --- B1100 --- C, 1101 --- D, 1110 --- E, 1111 --- F此时分组为 4 位二进制数为一组比如转换二进制 011010,分组:0010 1010 1001 0101 10102 A 9 5 A。
各进制之间的转换方法及表格

各进制之间的转换方法及表格进制之间的转换方法及表格:在计算机科学和数学领域中,进制是使用不同的基数来表示数字的一种方法。
常见的进制包括二进制、八进制、十进制和十六进制。
在这些进制之间进行转换非常重要,因为不同的进制在不同的场景中具有不同的优势和适用性。
下面我将详细介绍各种进制之间的转换方法,并提供一个表格以方便参考。
1.二进制转换为十进制:-方法:将二进制数每一位与2的幂相乘,然后求和。
2.十进制转换为二进制:-方法:使用短除法将十进制数连续除以2,直到商为0为止,然后依次取所得余数,从最后一个除数开始。
3.十进制转换为八进制:-方法:使用短除法将十进制数连续除以8,直到商为0为止,然后依次取所得余数,从最后一个除数开始。
-示例:将十进制数219转换为八进制数:219÷8=27余3,27÷8=3余3,3÷8=0余3、所以219的八进制表示为3334.八进制转换为十进制:-方法:将八进制数每一位与8的幂相乘,然后求和。
-示例:将八进制数333转换为十进制数:(3*8^2)+(3*8^1)+(3*8^0)=2195.十进制转换为十六进制:-方法:使用短除法将十进制数连续除以16,直到商为0为止,然后依次取所得余数,从最后一个除数开始。
十六进制中的10到15分别用字母A到F表示。
-示例:将十进制数255转换为十六进制数:255÷16=15余15,15÷16=0余15、所以255的十六进制表示为FF。
6.十六进制转换为十进制:-方法:将十六进制数每一位与16的幂相乘,然后求和。
十六进制中的A到F分别用数字10到15表示。
-示例:将十六进制数3FF转换为十进制数:(3*16^2)+(15*16^1)+(15*16^0)=1023下面是一个表格,展示了各种进制之间的转换方法和示例:进制转换,二进制,十进制,八进制,十六进制---------,----------,-------,-------,---------十进制转二进制,/,47,/,/十进制转八进制,/,219,333,/八进制转十进制,/,333,/,/十进制转十六进制,/,255,/,FF十六进制转十进制,/,3FF,/,/通过上述的转换方法和表格,我们可以在不同的进制之间进行转换,进而满足不同场景下对数据的需求。
二进制代码转换

二进制代码转换二进制代码转换在计算机科学和电子时代,二进制代码转换是一个基本的概念,在程序设计和计算机编程中非常重要。
二进制代码是计算机可以识别的唯一的代码形式,也是计算机最基本的语言。
因此,掌握二进制代码转换的方法和技巧非常重要,不仅可以提高程序设计、编程等技能,还可以更深入地了解计算机在各种应用领域的基本原理和机制。
二进制代码的基本概念二进制代码是一种用于表示数字、字母和符号的计算机语言。
二进制代码由0和1组成,是一种二进制系统,其本质是利用电子或光学信号在计算机内部传输和处理信息。
二进制代码包含两种数学运算:加法和乘法。
在二进制代码中,加法通常表示整数加法,而乘法则表示乘法或除法。
二进制代码由8位(即一个字节)或16位(即2个字节)等不同长度的片段组成。
这些片段称为二进制数或二进制位。
二进制代码的转换方法二进制代码转换是将一个数值或数据从一种数据组织形式转换为另一种数据组织形式的过程。
通常情况下,二进制代码转换涉及到以下几种转换形式:二进制转十进制,十进制转二进制,二进制转八进制,八进制转二进制,二进制转十六进制,十六进制转二进制等。
1、二进制转十进制二进制转换为十进制的方法是:将二进制数中的每一位乘以2的幂(从0开始),并将结果相加。
例如,将二进制数1101转换为十进制时:(1)1 × 2^3 +(1 × 2^2) +(0 × 2^1) +(1 × 2^0) =8 + 4 + 0 + 1 =13因此,二进制数1101转换为十进制为13。
2、十进制转二进制十进制转换为二进制的方法是:用2除以十进制数,求商和余数,将余数记录下来,然后将商再除以2,继续求商和余数。
重复此步骤,直到商为0。
倒序排列记录的余数即为转换后的二进制数。
例如,将十进制数14转换为二进制时:14 ÷ 2 =商=7,余数07 ÷ 2 =商=3,余数13 ÷ 2 =商=1,余数11 ÷2 =商=0,余数1因此,十进制数14转换为二进制为1110。
各进制间换算关系

各进制之间换算关系1、二进制数、八进制数、十六进制数转十进制数有一个公式:二进制数、八进制数、十六进制数的各位数字分别乖以各自的基数的(N-1)次方,其和相加之和便是相应的十进制数。
个位,N=1;十位,N=2...举例:110B=1*2的2次方+1*2的1次方+0*2的0次方=0+4+2+0=6D110Q=1*8的2次方+1*8的1次方+0*8的0次方=64+8+0=72D110H=1*16的2次方+1*16的1次方+0*16的0次方=256+16+0=272D 2、十进制数转二进制数、八进制数、十六进制数方法是相同的,即整数部分用除基取余的算法,小数部分用乘基取整的方法,然后将整数与小数部分拼接成一个数作为转换的最后结果。
例:见四级指导16页。
3、二进制数转换成其它数据类型3-1二进制转八进制:从小数点位置开始,整数部分向左,小数部分向右,每三位二进制为一组用一位八进制的数字来表示,不足三位的用0补足,就是一个相应八进制数的表示。
010110.001100B=26.14Q八进制转二进制反之则可。
3-2二进制转十进制:见13-3二进制转十六进制:从小数点位置开始,整数部分向左,小数部分向右,每四位二进制为一组用一位十六进制的数字来表示,不足四位的用0补足,就是一个相应十六进制数的表示。
00100110.00010100B=26.14H十进制转各进制要将十进制转为各进制的方式,只需除以各进制的权值,取得其余数,第一次的余数当个位数,第二次余数当十位数,其余依此类推,直到被除数小于权值,最后的被除数当最高位数。
一、十进制转二进制如:55转为二进制2|5527――1 个位13――1 第二位6――1 第三位3――0 第四位1――1 第五位最后被除数1为第七位,即得110111二、十进制转八进制如:5621转为八进制8|5621702 ―― 5 第一位(个位)87 ―― 6 第二位10 ―― 7 第三位1 ――2 第四位最后得八进制数:127658三、十进制数十六进制如:76521转为十六进制16|765214726 ――5 第一位(个位)295 ――6 第二位18 ――6 第三位1 ――2 第四位最后得1276516二进制与十六进制的关系2进制0000 0001 0010 0011 0100 0101 0110 011116进制0 1 2 3 4 5 6 72进制1000 1001 1010 1011 1100 1101 1110 111116进制8 9 a(10) b(11) c(12) d(13) e(14) f(15)可以用四位数的二进制数来代表一个16进制,如3A16 转为二进制为:3为0011,A 为1010,合并起来为00111010。
二进制计数法的规律。

二进制计数法的规律。
二进制计数法是一种计数系统,其中只有两个数字0和1用来表示所有的数值。
它是一种适用于计算机和电子设备的最基本、最常用的计数方式。
在二进制计数法中,每一位的值表示2的幂次方。
下面是关于二进制计数法规律的详细解释:1. 二进制数字的表示:在二进制计数法中,每一位数字称为一个二进制位(bit),它的值只能是0或1。
二进制数在右侧的位是低位,而最左侧的位是高位。
例如,二进制数1101表示为:(1 x 2^3) + (1 x2^2) + (0 x 2^1) + (1 x 2^0),即十进制数13。
2. 二进制位的权重:在二进制计数法中,每一位的权重是2的幂次方。
最右侧的位(低位)的权重为2^0,接下来的位的权重依次加倍,即2^1、2^2、2^3,依此类推。
例如,二进制数1101中,最右侧的位(低位)权重为2^0=1,接下来的位权重为2^1=2, 2^2=4,2^3=8。
3. 二进制数的递增规律:二进制数的递增规律是从低位到高位递增。
最低位为0,当该位达到最大值1时,进位到下一位,当前位重置为0。
如此反复,直到最高位也达到最大值,就完成了所有的二进制数的表示。
4. 二进制数的进位规律:当二进制位达到1时,进位到下一位。
当一个位进位时,相当于将当前位值加上当前位的权重值,然后该位重置为0。
例如,二进制数1101加1时,最右侧的位进位,所以变为1,接下来的位重置为0,得到二进制数1110。
5. 二进制数的补码表示:在计算机中,为了表示负数,通常使用二进制数的补码形式。
补码是指将正数的二进制表示反转后再加1得到的值。
这种表示方法简化了负数运算,同时还可以表示正数和负数的范围相同。
6. 二进制与其他进制的转换:二进制与其他进制之间可以相互转换。
例如,将十进制数转换为二进制时,可以使用除2取余的方法,不断将商除以2,直到商为0,然后逆序排列余数得到二进制数。
将二进制转换为十进制时,可以将每一位的值乘以相应位的权重,然后求和得到十进制数。
二进制与字符编码

⼆进制与字符编码进制进制也就是进位制,是⼈们规定的⼀种进位⽅法。
对于任何⼀种进制---X进制,就表⽰某⼀位置上的数运算时是逢X进⼀位。
⼗进制是逢⼗进⼀,⼗六进制是逢⼗六进⼀,⼆进制就是逢⼆进⼀,以此类推,x进制就是逢x进位。
⼆进制是计算技术中⼴泛采⽤的⼀种数制。
⼆进制数据是⽤0和1两个数码来表⽰的数。
它的基数为2,进位规则是“逢⼆进⼀”,借位规则是“借⼀当⼆”,由18世纪德国数理哲学⼤师莱布尼兹发现。
当前的计算机系统使⽤的基本上是⼆进制系统,数据在计算机中主要是以补码的形式存储的。
计算机中的⼆进制则是⼀个⾮常微⼩的开关,⽤“开”来表⽰1,“关”来表⽰0。
20世纪被称作第三次科技⾰命的重要标志之⼀的计算机的发明与应⽤,因为数字计算机只能识别和处理由‘0’.‘1’符号串组成的代码。
其运算模式正是⼆进制。
19世纪爱尔兰逻辑学家乔治布尔对逻辑命题的思考过程转化为对符号"0''.''1''的某种代数演算,⼆进制是逢2进位的进位制。
0、1是基本算符。
因为它只使⽤0、1两个数字符号,⾮常简单⽅便,易于⽤电⼦⽅式实现。
⼗进制:逢⼗进⼀表⽰数字: 0123456789⼆进制:逢⼆进⼀表⽰数字: 0 1⼋进制:逢⼋进⼀表⽰数字: 01234567作⽤:在某些编程语⾔⾥提供了使⽤⼋进制符号来表⽰数字的能⼒,⽽且还是有⼀些⽐较古⽼的Unix应⽤在使⽤⼋进制。
和⼆进制之间的转换: 2-->8 : 取三合⼀ 8-->2 :取⼀分三⼗六进制:逢⼗六进⼀表⽰数字: 01234567ABCDEF字符编码字符编码(英语:Character encoding)也称字集码,是把字符集中的字符编码为指定集合中某⼀对象(例如:⽐特模式、⾃然数序列、8位组或者电脉冲),以便⽂本在计算机中存储和通过通信⽹络的传递。
常见的例⼦包括将拉丁字母表编码成摩斯电码和ASCII。
其中,ASCII将字母、数字和其它符号编号,并⽤7⽐特的⼆进制来表⽰这个整数。
十进制、二进制、八进制、十六进制之间的换算规律

◆十进制转二进制:二进制是计算技术中广泛采用的一种数制。
二进制数据是用0和1两个数码来表示的数。
它的基数为2,进位规则是“逢二进一”,借位规则是“借一当二”,由18世纪德国数理哲学大师莱布尼兹发现。
当前计算机系统使用的基本上是二进制系统。
用2辗转相除至结果为1将余数和最后的1从下向上倒序写就是结果例如302302/2 = 151 余0151/2 = 75 余175/2 = 37 余137/2 = 18 余118/2 = 9 余09/2 = 4 余14/2 = 2 余02/2 = 1 余0故二进制为100101110◆二进制转十进制从最后一位开始算,依次列为第0、1、2...位第n位的数(0或1)乘以2的n次方得到的结果相加就是答案例如:01101011.转十进制:第0位:1乘2的0次方=11乘2的1次方=20乘2的2次方=01乘2的3次方=80乘2的4次方=01乘2的5次方=321乘2的6次方=640乘2的7次方=0然后:1+2+0+8+0+32+64+0=107.二进制01101011=十进制107.好了,现在对二进制和十进制之间的换算有了初步的了解了吧,下面,我们就进一步深入了解二者之间的其他换算规律:二进制转十进制,十进制转二进制的算法一、二进制数转换成十进制数由二进制数转换成十进制数的基本做法是,把二进制数首先写成加权系数展开式,然后按十进制加法规则求和。
这种做法称为"按权相加"法。
二、十进制数转换为二进制数十进制数转换为二进制数时,由于整数和小数的转换方法不同,所以先将十进制数的整数部分和小数部分分别转换后,再加以合并。
1. 十进制整数转换为二进制整数十进制整数转换为二进制整数采用"除2取余,逆序排列"法。
具体做法是:用2去除十进制整数,可以得到一个商和余数;再用2去除商,又会得到一个商和余数,如此进行,直到商为零时为止,然后把先得到的余数作为二进制数的低位有效位,后得到的余数作为二进制数的高位有效位,依次排列起来。
六位二进制数

六位二进制数
六位二进制数是一个由六个二进制位组成的数。
二进制是一种数值表示法,它使用0和1来表示数值。
在二进制中,每一位的值只能是0或1。
因此,一个六位的二进制数可以表示的最大值为2的6次方,即64。
在计算机科学中,二进制数被广泛用于各种计算和数据存储中。
六位二进制数可以表示的范围从000000(十进制的0)到111111(十进制的63)。
这种数值范围在计算机中被广泛使用,例如在8位二进制数中,范围从0到255。
当涉及到六位二进制数的具体例子时,可以考虑以下几种情况:十进制转换为二进制:
例如,将十进制的12转换为六位二进制数。
首先,可以将12分解为2的幂次方之和,即12 = 8 + 4 + 0。
然后,将每个幂次方转换为二进制数,即8 = 1000(二进制),4 = 0100(二进制),0 = 0000(二进制)。
因此,12的六位二进制表示为100001。
二进制转换为十进制:
例如,将六位二进制数110101转换为十进制。
可以使用以下公式:十进制= 二进制数x 2的幂次方之和。
在这个例子中,110101可以分解为1 x 2的5次方+ 1 x 2的4次方+ 0 x 2的3次方+ 1 x 2的2次方+ 0 x 2的1次方+ 1 x 2的0次方= 45。
计算机内存中的表示:
在计算机内存中,数据通常以二进制形式存储。
一个六位二进制
数可以存储在六个字节(Byte)的内存中。
例如,六位二进制数110001可以存储在内存中的六个字节中,每个字节存储两位二进制数。
这些例子可以帮助理解六位二进制数在计算机科学中的应用和转换。
二进制与十进制的计算公式

二进制与十进制的计算公式-CAL-FENGHAI.-(YICAI)-Company One110进制数转换为2进制数给你一个十进制,比如:6,如果将它转换成二进制数呢10进制数转换成二进制数,这是一个连续除2的过程:把要转换的数,除以2,得到商和余数,将商继续除以2,直到商为0。
最后将所有余数倒序排列,得到数就是转换结果。
听起来有些糊涂我们结合例子来说明。
比如要转换6为二进制数。
“把要转换的数,除以2,得到商和余数”。
那么:要转换的数是6, 6 ÷ 2,得到商是3,余数是0。
(不要告诉我你不会计算6÷3!)“将商继续除以2,直到商为0……”现在商是3,还不是0,所以继续除以2。
那就: 3 ÷ 2, 得到商是1,余数是1。
“将商继续除以2,直到商为0……”现在商是1,还不是0,所以继续除以2。
那就: 1 ÷ 2, 得到商是0,余数是1(拿笔纸算一下,1÷2是不是商0余1!)“将商继续除以2,直到商为0……最后将所有余数倒序排列”好极!现在商已经是0。
我们三次计算依次得到余数分别是:0、1、1,将所有余数倒序排列,那就是:110了!6转换成二进制,结果是110。
把上面的一段改成用表格来表示,则为:(在计算机中,÷用 / 来表示)2如果是在考试时,我们要画这样表还是有点费时间,所更常见的换算过程是使用下图的连除:(图:1)请大家对照图,表,及文字说明,并且自已拿笔计算一遍如何将6转换为二进制数。
说了半天,我们的转换结果对吗二进制数110是6吗你已经学会如何将二进制数转换成10进制数了请现在就计算一下110换成10进制是否就是6。
二进制数转换为十进制数二进制数第0位的权值是2的0次方,第1位的权值是2的1次方……所以,设有一个二进制数:0110 0100,转换为10进制为:下面是竖式:0110 0100 换算成十进制第0位 0 * 20 = 0第1位 0 * 21 = 0第2位 1 * 22 = 4第3位 0 * 23 = 0第4位 0 * 24 = 0第5位 1 * 25 = 32第6位 1 * 26 = 64第7位 0 * 27 = 0 +3---------------------------100用横式计算为:0 * 20 + 0 * 21 + 1 * 22 + 1 * 23 + 0 * 24 + 1 * 25 + 1 * 26 + 0 * 27 = 1000乘以多少都是0,所以我们也可以直接跳过值为0的位:1 * 22 + 1 * 23 + 1 * 25 + 1 * 26 = 1004。
二进制与十进制的计算公式

10进制数转换为2进制数给你一个十进制,比如:6,如果将它转换成二进制数呢?10进制数转换成二进制数,这是一个连续除2的过程:把要转换的数,除以2,得到商和余数,将商继续除以2,直到商为0。
最后将所有余数倒序排列,得到数就是转换结果.听起来有些糊涂?我们结合例子来说明。
比如要转换6为二进制数。
“把要转换的数,除以2,得到商和余数"。
那么:要转换的数是6, 6 ÷ 2,得到商是3,余数是0。
(不要告诉我你不会计算6÷3!)“将商继续除以2,直到商为0……”现在商是3,还不是0,所以继续除以2。
那就: 3 ÷ 2, 得到商是1,余数是1.“将商继续除以2,直到商为0……”现在商是1,还不是0,所以继续除以2。
那就: 1 ÷ 2, 得到商是0,余数是1 (拿笔纸算一下,1÷2是不是商0余1!)“将商继续除以2,直到商为0……最后将所有余数倒序排列"好极!现在商已经是0。
我们三次计算依次得到余数分别是:0、1、1,将所有余数倒序排列,那就是:110了!6转换成二进制,结果是110。
把上面的一段改成用表格来表示,则为:(在计算机中,÷用 / 来表示)如果是在考试时,我们要画这样表还是有点费时间,所更常见的换算过程是使用下图的连除:(图:1)请大家对照图,表,及文字说明,并且自已拿笔计算一遍如何将6转换为二进制数.说了半天,我们的转换结果对吗?二进制数110是6吗?你已经学会如何将二进制数转换成10进制数了,所以请现一下110换成10进制是否就是6.二进制数转换为十进制数二进制数第0位的权值是2的0次方,第1位的权值是2的1次方……所以,设有一个二进制数:0110 0100,转换为10进制为:下面是竖式:0110 0100 换算成十进制第0位 0 * 20 = 0第1位 0 * 21 = 0第2位 1 * 22 = 4第3位 0 * 23 = 0第4位 0 * 24 = 0第5位 1 * 25 = 32第6位 1 * 26 = 64第7位 0 * 27 = 0 +----—-—-—-----—--—---—-—---100用横式计算为:0 * 20 + 0 * 21 + 1 * 22 + 1 * 23 + 0 * 24 + 1 * 25 + 1 * 26 + 0 * 27 = 100 0乘以多少都是0,所以我们也可以直接跳过值为0的位:1 * 22 + 1 * 23 + 1 * 25 + 1 * 26 = 100。
二进制

二进制、八进制、十进制、十六进制数的转换方法一)、数制计算机中采用的是二进制,因为二进制具有运算简单,易实现且可靠,为逻辑设计提供了有利的途径、节省设备等优点,为了便于描述,又常用八、十六进制作为二进制的缩写。
一般计数都采用进位计数,其特点是:(1)逢N进一,N是每种进位计数制表示一位数所需要的符号数目为基数。
(2)采用位置表示法,处在不同位置的数字所代表的值不同,而在固定位置上单位数字表示的值是确定的,这个固定位上的值称为权。
在计算机中:D7 D6 D5 D4 D3 D2 D1 D0 只有两种0和18 4 2 1二)、数制转换不同进位计数制之间的转换原则:不同进位计数制之间的转换是根据两个有理数如相等,则两数的整数和分数部分一定分别相等的原则进行的。
也就是说,若转换前两数相等,转换后仍必须相等。
有四进制十进制:有10个基数:0 ~~ 9 ,逢十进一二进制:有2 个基数:0 ~~ 1 ,逢二进一八进制:有8个基数:0 ~~ 7 ,逢八进一十六进制:有16个基数:0 ~~ 9,A,B,C,D,E,F (A=10,B=11,C=12,D =13,E=14,F=15) ,逢十六进一1、数的进位记数法N=a n-1*p n-1+a n-2*p n-2+…+a2*p2+a1*p1+a0*p02、十进制数与P进制数之间的转换①十进制转换成二进制:十进制整数转换成二进制整数通常采用除2取余法,小数部分乘2取整法。
例如,将(30)10转换成二进制数。
将(30)10转换成二进制数2| 30 ….0 ----最右位2 15 (1)2 7 (1)2 3 (1)1 ….1 ----最左位∴(30)10=(11110)2将(30)10转换成八、十六进制数8| 30 ……6 ------最右位3 ------最左位∴(30)10 =(36)816| 30 …14(E)----最右位1 ----最左位∴(30)10 =(1E)163、将P进制数转换为十进制数把一个二进制转换成十进制采用方法:把这个二进制的最后一位乘上20,倒数第二位乘上21,……,一直到最高位乘上2n,然后将各项乘积相加的结果就它的十进制表达式。
