山东省德州市夏津一中2019-2020高一下学期月考考试数学试卷 Word版含答案

合集下载

夏津一中高一下学期周考数学试题(含答案)

夏津一中高一下学期周考数学试题(含答案)高一下学期周考数学试题,考察圆的方程及角的概念的推广,弧度制,三角函数的定义等知识2022——2022学年下学期间周考数学试题（A）一．选择题（本大题共10个小题，每题5分共50分）1.若是第一象限角，则下列各角中一定为第四象限角的是()A.90°-B.90°+C.360°-D.180°+2.终边与坐标轴重合的角的集合是()A.{|=k²360°，k∈Z}B.{|=k²180°+90°，k∈Z}D.{|=k²90°，k∈Z}C.{|=k²180°，k∈Z}3.将分针拨快10分钟，则分针转过的弧度数是()A.B.-C.D.-3636某，则in的44．若是第二象限角，P（某5）为其终边上一点，且co值为（）A．62B．C．D．－44445.点P(a,b,c)到坐标平面zO某的距离为A．aC．bD．c6．圆某2y216上的点到直线某y30的距离的最大值是A．323232B．4C．4D．0222227．直线过点P（0，2），且截圆某y4所得的弦长为2，则直线的斜率为A．3B．．．2in某co某的定义域是8.函数y（）高一下学期周考数学试题,考察圆的方程及角的概念的推广,弧度制,三角函数的定义等知识A．(2k,(2k1))，kZC．[kB．[2k2,(2k1)]，kZ22,(k1)]，kZ222D．[2k,(2k1)]，kZ9．已知圆某y9与圆某y4某4y10关于直线l对称,则直线l的方程为（）A．4某4y10B．某y010．方程4某k(某2)3有两个不等实根，则k的取值范围是（）A．(0,2C．某y0D．某y20555313)B．[,]C．(,)D．(,]121212434二．填空题(本大题共5小题，每小题5分，共25分)11.三点（2，3），(4,3)及(5,)在同一条直线上，则k的值等于12.若角是第三象限角，则k2角的终边在213．直线L经过点P(1,2)且与两点A(2,3)、B(4,-5)的距离相等，则L的方程是若方程某y2某4y1a0表示的曲线是一个圆，则a的取值范围是22 15．若圆某y4与圆某y2ay60(a0)的公共弦长为23，则a=________. 2222高一下学期周考数学试题,考察圆的方程及角的概念的推广,弧度制,三角函数的定义等知识三．解答题解答题(16-20题每题12分，21题15分，共75分)16、（1）试写出所有终边在直线y某上的角的集合（用弧度制表示）；（2）已知角的终边经过点P(4,－3)，求2in+co的值.17.已知扇形的周长为20cm,当它的半径和圆心角各取什么值时，才能使扇形的面积最大？最大面积是多少？18．已知圆C经过点A(2,-3)和B(-2,-5).(1)当圆C的面积最小时,求圆C的方程；(2)若圆C的圆心在直线某-2y-3=0上,求圆C的方程.19．已知圆C的方程为(某1)2(y1)21,P点坐标为(2,3)，求过P点的圆的切线方程以及切线长。

山东省夏津一中2019高三数学10月月考试题文

山东省夏津一中 2019 届高三数学 10 月月考试题文时间： 120 分钟满分： 150 分一．选择题（本大题共 12 个小题，每题 5分共 60 分）1 命题“xR,| x | x 40 ”的否认是（）A ． x R,| x | x 4B． xR,| x | x 4 0C ． xR,| x | x 4 0D ． xR,| x | x 4 0{|24 3 0}, { |x（）2. 已知4 2}，则P x xx Q yyP QA ． (1,2)B ． [0,2)C ． (1,2]D ． [0,1)3. 设 a log 0.1 0.2 ， blog 1.1 0.2 ， c 1.20.2 ， d 1.10.2 则（）A ． c d a bB ． c a d bC ． d c a bD ． a b d c4. 若11 0 ，则以下结论不正确的选项是( )abb aA.a 2 ＜ b2B .ab＜b 2C.2 D.|a|＋ |b| ＞ |a ＋abb|uuur1 uuuruuurr uuurruuur5 在 VABC 中，点 D 在边 AB 上，且 BDDA ,设 CBa,CAb ，则 CD ()1 r2r22 r1rA ．B．3abab333C ．3r4rD．4r3 r5 abab55 56. “ a0 ”是“函数 f ( x) |( ax1) x | 在区间 (0,) 上单一递加”的（）A ．充足不用要条件B ．必需不充足条件C ．充足必需条件D ．既不充足也不用要条件7. 函数f(x)= 的图象的大概形状是（）8．将函数 y 2 sin( x) sin(x) 的图象向左平移（ >0) 个单位，所得图象对应的函36数恰为奇函数，则的最小值为 ( )A.B.C.4 D.61239. 在C 中，角 A, B, C 所对的边分别为 a,b, c ，若 sin B2sin A cosC 0 , 则当 cosB取最小值时，a=（）cA ．2 B. 3C ．3 23D.210. 若0, ，且 sin2cos2 ，则 tan等于（）2A ． 3B. 2C ．1D.1232x 1(x 0)11．函数 f (x)1)(x 若方程 f(x)=-x+a又且只有两个不等的实数根，则实数 a 的f (x 0)取值范围为（）A ．,0B.0,1C ．,1D.0,12. 已知定义在 R 上的偶函数 y f (x) 的导函数为f '( x) ，函数 f ( x) 知足：当 x0 时，x f '( x) f ( x)1，且 f (1)=2018 . 则不等式 f ( x)2017的解集是（）1xA ． -1,1 B. -，1C ． -1,0 U 0,1 D.- ,-1 U 1，+二．填空题 ( 本大题共 4 小题，每题 5 分，共 20 分)13. 记 S n 为数列 a n 的前 n 项和 . 若 S n 2a n 1，则 S 6_____________ ．14. 若向量AB与AC的夹角为，|AB| 2,|AC|3, AM AB AC( ,R) ，且3AM BC ，则．x, y知足拘束条x y0z( 1)2x y15．已知实数x y40 件，则2的最小值为 ______y116. 已知函数f ( x)满足f (1x) f (x1) f ( x1)( x R)，且当0x 1 时f (x)2x 1 ，则方程cos x f ( x)0 在[1,3] 上的全部根之和为_______二．解答题 (17 题 10 分， 18-22 题每题 12 分，共 80 分 )17.（本小题满分 10 分）设命题 p：实数a.知足a2 a 12 0 ，命题q :函数log2(ax2ax 1)的定义域是 R ，假如p q 是假命题， p q 是真命题，求a的取值范围.18..（本小题满分12 分）已知a, b是两个单位向量．（ 1）若3 a 2 b 3 ，试求 3 a b 的值；（ 2）若a, b的夹角为60 o，试求向量 m 2 a b 与 n 2 b a 的夹角的余弦.19．（本小题满分12 分）在 ABC 中，a, b,c分别为内角A, B, C 所对的边，已知a cos A R ，此中R为ABC 外接圆的半径， S 为ABC 的面积，a2c2b2 4 3S.3（ 1）求sin C；（ 2）若a b23，求ABC 的周长．20．已知函数f x2a12ax . ln xx（1）当a 2时，求函数 f x的极值；（2）当a 0时，求函数 f x的单一增区间 .21.（本小题满分 12 分）某健身器械厂研制了一种足浴气血养身机, 详细原理是在足浴盆的中心右边离中心x 厘米(0 x 20) 处安装了臭氧发生孔, 产生臭氧对双脚起保健作用 . 依据检测发现 , 该臭氧发生孔工作时会对泡脚的舒坦度起到扰乱作用, 经过研究发现臭氧发生孔工作时, 对左脚的扰乱度与22kx成反比 ,比率系数为4400 x 成反比,比率系数为，；对右脚的扰乱度与且当 x 10 2 时 , 对左脚和右脚的扰乱度之和为 0.065.（ 1）请将臭氧发生孔工作时对左脚和右脚的扰乱度之和 y 表示为 x 的函数；（ 2）求臭氧发生孔工作时对左脚和右脚的扰乱度之和y 的最小值．22．（本小题满分 12 分）1 xln x ．已知函数 f ( x)ax（ 1）若 f (x) 0 对 x 0 恒建立，求 a 的值；（ 2）求证： ln( n1) 12 ... n 1 （ n N * ）．2232 n 21-5 BAADB 6-10 ACACB 11-12CC 13.714.6 15. 2 16.11617p由a 2 a 12 0 得 a 或a 3-4qax 2 ax 1 >0a =0 a >0V a 2 -4a 0得 0 a40 a 4r r rrr r 18. 1 Q ab| a | | b | 1 | 3a2b | 3r 2 r r r 2 9 r r 1 9 | a | 12a b 4 | b | ab 3rr r2r rr29 1 61| 3a b |9 | a |6 a b | b |1 2 33urr r 2r 2 r r r 24 1 4122 | m |(2 a b)4 | a | 4a b | b |2 1rr r 2r 2r r r 24 1-411 2| n |(2 b a)4 | b |4a b | a |2ur rr r r rr 2 r r r 2 3m n(2 ab ) (2 ba )2 | b |3 a b2 | a |2ur r 3 21cosm n2.urr7 314| m || n |19a 2Rsin A ， 2Rsin A cosA Rsin 2A 102A 22 A2 A .24S= 1 ac sin B a 2 c 2 b 24 3 1 a csin B23 2732ac cos B23ac sin B 3tan B30B B=53sin C sin( A B)sin(4)266 342 a = sin A2a b23a2b3b sin B3c226262422ABC a b c32361222201f x0,, f' x 14 x2f ' x1 4 0x11; x21().x222f xf 1.4 22f ' x 2 a12a 2x 1 ax1,f ' x0x11, x21, a2 x2x x22af '( x) 0f x; 2 a0 1 ,12af ' x0, f x;a2 1 , 1 f 'x0, f x.a 221 1y 4k(0x20) 2 x2400x2x102y0.065k9y492 (0 x20) 6 x2400x21 y49，x 2400 x2y '818 x 18x 4 8(400 x 2 )2 .x 3 (400 x 2 )2x 3 (400 x 2 )2y ' 0得18 x 4 8(400 x 2 ) 2 x 2160, x 4 108x 4 10, y ' 0410x 20y ' 0y 在 0,4 104 10，2010x 4 10 yx 4 101 22y49 x 21 4 9x 2[(400 x 2 ) 2] 8x 2 400 400 x 2 400 x1 [4 94(4002 x 2) 9x 22 ]400x 400 x1 [132 4(400 x 2 ) g 9x 2 ]1 .1 0400x 2 400 x 2164(400x 2 )9x 2 x 2 x410""x 2400x 4 10 yx 4 10. 1 2ax a(1x)1a 2 x ax 1 22. 1 f(x)aa 2 x 2xa 2 x 2 x 2a0 f ( x) 0f ( x) (0,)当 x (0,1)时, f ( x) f (1) 0ax (0, 1)时 , f (x)0, f ( x)单减ax ( 1, )时 , f (x)0, f ( x)单增af ( x)minf ( 1) 1 1 ln a 01 a a 1 1 1ag(a) 1ln a g (a) a a 2 aa 2a (0,1)时, g (a) 0, g( a)单增 a(1, )时, g (a) 0, g(a)单减g (a) g (1)11 ln a 0 a 1 .6a21ln x11(当且仅当 x1取等号）xxn 1 1( n N)lnnn 11 1nnn2n21ln n1n1n 1 ln( n 1) ln nn 1n1 n 2n 2ln 2ln 112ln 3 ln 2 12 2ln( n 1)ln n n 1n2ln( n1)1 2 ... n 1 (nN*).1222 32n 2。

山东省德州市2019-2020学年高一下学期数学期末考试试卷 (II)卷

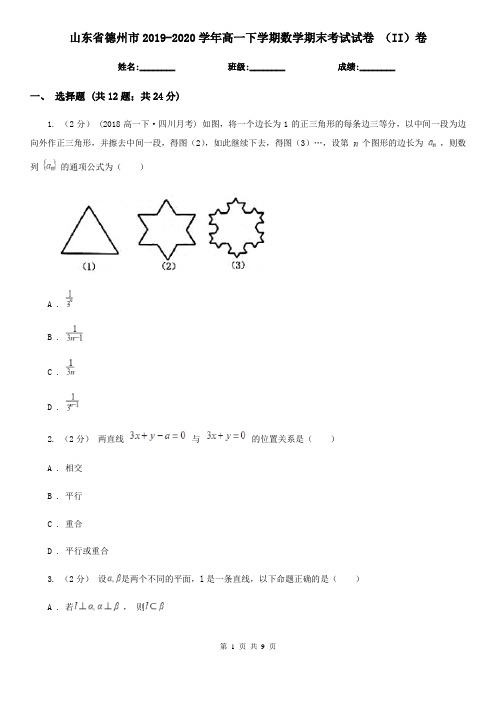
山东省德州市 2019-2020 学年高一下学期数学期末考试试卷（II）卷姓名:________班级:________成绩:________一、选择题 (共 12 题；共 24 分)1. （2 分） (2018 高一下·四川月考) 如图，将一个边长为 1 的正三角形的每条边三等分，以中间一段为边向外作正三角形，并擦去中间一段，得图（2），如此继续下去，得图（3）…，设第个图形的边长为，则数列的通项公式为（）A. B.C.D.2. （2 分）两直线与的位置关系是（）A . 相交B . 平行C . 重合D . 平行或重合3. （2 分）设是两个不同的平面，l 是一条直线，以下命题正确的是（）A.若，则第1页共9页B.若，则C.若，则D.若，则4. （2 分） (2019 高二上·诸暨期末) 已知，（）A.B.C.，，，，则下列不等式成立的是D. 5. （2 分）设是公差不为 0 的等差数列，成等比数列，则的前 n 项和（）A. B. C. D.6. （2 分）在△ABC 中，角 A，B，C 的对边分别是 a，b，c，且 A=2B，则等于（） A.B. C.第2页共9页D.7. （2 分）把边长为 1 的正方形 ABCD 沿对角线 BD 折起形成三棱锥 C－ABD 的主视图与俯视图如图所示，则左视图的面积为（）A.B.C.D. 8. （2 分） (2018 高二上·武邑月考) 直线(a＋2)x＋(1－a)y－3＝0 与(a－1)x＋(2a＋3)y＋2＝0 互相垂直，则 a 等于（） A . －1 B.1 C . ±1D.－9. （2 分）设集合 M 和 N 为平面中的两个点集，若存在点，使得对任意的点，均有，则称为点集 M 和 N 的距离，记为.已知集合,，则 d(M,N)=（）A.B.第3页共9页C.D.10. （2 分） A，B 是海面上位于东西方向相距 5（3+ ）海里的两个观测点．现位于 A 点北偏东 45°，B 点北偏西 60°的 D 点有一艘轮船发出求救信号，位于 B 点南偏西 60°且与 B 点相距 20 海里的 C 点的救援船立即前往营救，其航行速度为 30 海里/小时，该救援船到达 D 点需要的时间为（）小时．A.1 B.2C . 1+D. 11. （2 分）已知直线 a，b 和平面 M，N，且 a⊥M，则下列说法正确的是（） A . b∥M⇒ b⊥a B . b⊥a⇒ b∥M C . N⊥M⇒ a∥N D . a⊄N⇒ M∩N≠∅12. （2 分） (2018·河北模拟) 已知函数的图象经过点，．当时， A.7 B.6 C.5 D.4，记数列的前项和为，当时，的值为（）第4页共9页二、填空题 (共 4 题；共 4 分)13. （1 分）若关于 x，y 的二元一次方程组无解，则 a=________．14. （1 分） (2018 高二上·淮安期中) 已知一个圆锥的侧面积是则此圆锥的底面半径为________．，若母线与底面所成角为，15. （1 分） (2016 高三上·定州期中) 在△ABC 内角 A，B，C 的对边分别是 a，b，c，cos = acosB+bcosA=2，则△ABC 的面积的最大值为________．，且16. （1 分） (2017 高二上·宜昌期末) 已知正四棱柱（底面是正方形，侧棱垂直于底面）的高为 4，体积为 16，八个顶点都在一个球面上，则这个球的表面积是________．三、解答题 (共 6 题；共 55 分)17. （10 分） (2018 高二下·保山期末) 已知函数 f（x）=|x﹣3|+|x+m|（x∈R）．（1）当 m=1 时，求不等式 f（x）≥6 的解集；（2）若不等式 f（x）≤5 的解集不是空集，求参数 m 的取值范围．18. （10 分） (2019 高二上·拉萨期中) 等比数列的前项和为，，.（1）求数列的通项公式；（2）若，求 .19. （10 分） (2018 高二上·黑龙江期末) 已知．（1）求角的大小；分别为三个内角的对边,且（2），求的面积．20. （5 分）长方体 ABCD﹣A1B1C1D1 中，AA1= ， AB=BC=2，O 是底面对角线的交点．（Ⅰ）求证：B1D1∥平面 BC1D；（Ⅱ）求证：A1O⊥平面 BC1D；第5页共9页（Ⅲ）求三棱锥 A1﹣DBC1 的体积．21. （10 分） (2020·兴平模拟) 在中，角，，的对边分别为，，，且. （1）求角的值；（2）若，且的面积为，求边上的中线的大小.22. （10 分）数列{an}满足 a1=4，an=4﹣（n≥2），设 bn=．（1）判断数列{bn}是否为等差数列并证明；（2）求数列{an}的通项公式．第6页共9页一、选择题 (共 12 题；共 24 分)1-1、 2-1、 3-1、 4-1、 5-1、 6-1、 7-1、 8-1、 9-1、 10-1、 11-1、 12-1、二、填空题 (共 4 题；共 4 分)13-1、 14-1、 15-1、参考答案第7页共9页16-1、三、解答题 (共 6 题；共 55 分)17-1、17-2、18-1、18-2、19-1、19-2、 20-1、答案：略 21-1、答案：略 21-2、答案：略第8页共9页22-1、 22-2、第9页共9页。

山东省德州市夏津一中2019-2020高一下学期月考考试数学试卷

……7 分
（2）（k a − b）(k a + b) 0 且不反向平行。
4
（ka − b）(ka + b) 0 ，解得 — 2 k 2 ……11 分 k = k
反向平行时，设 ka − b = (ka + b（) 0）， −1 = ，得 k = 0 ……13 分综上， — 2 k 2且k 0 ……15 分
19.已知复数 z=3+bi（bR），且（1+3i）·z 纯虚数（1）求复数 z （2）若 w= z·(2+i)，求复数 w 的模 |w|
2
20.（1）用与球心距离为 1 的平面去截球，所得的截面面积为 4π，求球的表面积（2）正三棱台的高为 3，上、下底面边长分别为 2 和 4，求这个棱台的侧棱长和斜高
高一数学试卷
一、选择题（每题 5 分，共 75 分。1-13 为单选题，14-15 为多选题）
1.已知向量 a =（3，1）， b =（k，7），若 a // b ，则 k=（）
A.-21 B.21 C.23 D.20
2.在△ABC 中，若 b = 3 ，c=3，∠B=30°，则 sin C =（）
21.已知， =1, =2 且向量 a与b 不共线（1）若 a与b 的夹角为 45°，求从（2a − b）•（a + b）（2）若向量 k a − b 与 k a + b 的夹角为钝角，求实数 k 的取值范围
22.已知函数 f (x) = sin 2 wx + 3 sin wx sin（wx + ）（w 0）的最小正周期为 2
5
2
5
A.
B.
C.
D.
3
2
3

山东省德州市夏津第一中学2018_2019学年高一数学下学期第三次月考试题

山东省德州市夏津第一中学2018-2019学年高一数学下学期第三次月考试题一、选择题（每题4分，共52分）1. 已知向量，，且，则实数（）A ．1B ．-1C ．57D ．57- 2. 若向量→→b a ,满足→→→→=b a b a ,||||，当不共线时，→→+b a 与→→-b a 的关系是A ．相等B ．平行C ．垂直D ．相交但不垂直3. 函数1tan 4y x π⎛⎫=--⎪⎝⎭ 的定义域为（） A ．4k k πππ⎛⎤+ ⎥⎝⎦，， k Z ∈ B ．2k k πππ⎛⎤+ ⎥⎝⎦，， k Z ∈ C ．42k k ππππ⎛⎤-+ ⎥⎝⎦，， k Z ∈ D ．4k k πππ⎛⎤- ⎥⎝⎦，， k Z ∈ 4．正切曲线为常数，且与直线(a 为常数)相交的两相邻点间的距离为 A ． B ．ωπ2 C ．ωπ D ．与a 值有关 5. 已知C B A 、、是平面上不共线三点，O 是ABC ∆的重心，动点P 满足)22121(31OC OB OA OP ++=，则P 一定为ABC ∆的（） A ．AB 边中线的三等分点（非重心） B ．AB 边的中点C ．AB 边中线的中点D ．重心6. 为了得到函数sin 23y x π⎛⎫=-⎪⎝⎭的图像，只需把函数)62cos(π-=x y 的图像 A ．向左平移3π个长度单位 B ．向右平移3π个长度单位 C ．向左平移32π个长度单位 D ．向右平移32π个长度单位7. 函数的值域为A ．B ．C ．D ．8．已知f (x )＝sin(ωx ＋φ)(ω>0，|φ|<2π)的最小正周期为π，若其图象向左平移π3个单位长度后关于y 轴对称，则( ) A ．ω＝2，φ＝π3 B ．ω＝2，φ＝π6 C ．ω＝4，φ＝π6 D ．ω＝2，ω＝－π69．如图，在圆C 中，点A ，B 在圆上，AB u u u r ·AC u u u r 的值（）A ．只与圆C 的半径有关；B ．只与弦AB 的长度有关C ．既与圆C 的半径有关，又与弦AB 的长度有关D ．是与圆C 的半径和弦AB 的长度均无关的定值10．设P ， Q 为三角形ABC 内的两点，且2155AP AB AC =+u u u v u u u v u u u v ， 2133AQ AB AC =+u u u v u u u v u u u v ，则ABP ABQ S S ∆∆=（） A ．13 B ．14 C ．25 D ．35以下3题为多选题（少选得一半分，错选、漏选、多选不得分）。

2020年山东省德州市夏津县第一中学高一数学理联考试题含解析

2020年山东省德州市夏津县第一中学高一数学理联考试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 已知α是三角形的内角，且sinαcosα=，则cosα+sinα的值等于（）A．±B．±C．D．﹣参考答案：C【考点】三角函数的化简求值．【专题】解三角形．【分析】利用三角函数的平方关系式求解即可．【解答】解：α是三角形的内角，且sinαcosα=，可得α为锐角．cosα+sinα===．故选：C．【点评】本题考查三角形的解法，三角函数的基本关系式的应用，注意角的范围是解题的关键．2. 已知集合，那么（）A．B．C．D．参考答案：A3. 下列说法中正确的是( )A. 棱柱的侧面可以是三角形B. 正方体和长方体都是特殊的四棱柱C. 所有的几何体的表面都能展成平面图形D. 棱柱的各条棱都相等参考答案：B试题分析：棱柱的侧面是平行四边形，不可能是三角形，所以A不正确；球的表面就不能展成平面图形，所以C不正确；棱柱的侧棱与底面边长不一定相等，所以D不正确.考点：本小题主要考查空间几何体的性质.点评：解决此类问题的主要依据是空间几何体的性质，需要学生有较强的空间想象能力.4. 函数f（x）=cos（x∈Z）的值域为（）A．{－1，－，0，，1} B．{－1，－，，1}C．{－1，－，0，，1} D．{－1，－，，1}参考答案：B5. 若数列{a n}的前n项和S n=n2+3n﹣90，则的值为（）A．18 B．﹣2 C．2 D．﹣参考答案：D【考点】8H：数列递推式．【分析】根据数列{a n}的前n项和S n=n2+3n﹣90，直接进行计算即可得到结论．【解答】解：∵数列{a n}的前n项和S n=n2+3n﹣90，∴a1+a2+a3=S3=32+3×3﹣90=﹣72，a4+a5+a6=S6﹣S3=36，则=，故选：D．【点评】本题主要考查数列项的计算，比较基础．6. （3分）为了得到函数y=sin（2x+）的图象，只需把函数y=sin2x图象上所有的点（）A．向左平行移动个单位长度B．向右平行移动个单位长度C．向左平行移动个单位长度D．向右平行移动个单位长度参考答案：A考点：函数y=Asin（ωx+φ）的图象变换．专题：计算题；三角函数的图像与性质．分析：函数y=sin（2x+）=sin，故只需故把函数y=sin2x的图象向左平移各单位得到．解答：函数y=sin（2x+）=sin，故把函数y=sin2x的图象向左平移各单位，即可得到函数y=sin（2x+）的图象，故选：A．点评：本题考查函数y=Asin（ωx+?）图象的平移变换规律，把已知函数的解析式化为 y=sin是解题的关键．7. 已知0,且1, f(x)=x当x时恒有f(x),则实数的取值范围是（）A. (0,)B. []C. [,1)D. (0, ]参考答案：C8. 若，且，则是（）角A．第一象限B．第二象限C．第三象限D．第四象限参考答案：C9. 已知：如图，集合U为全集，则图中阴影部分表示的集合是A、?U ( A∩B)∩CB、?U(B∩C)∩AC、A∩?U (B∪C)D、?U(A∪B)∩C参考答案：C因为x∈A，x B，x C，所以图中阴影部分表示的集合是A∩?U (B∪C)，选C. 10. 方程（x+y﹣1）=0所表示的曲线是（）A．B．C．D．参考答案：D【考点】曲线与方程．【专题】计算题．【分析】原方程等价于：，或x2+y2=4；两组方程分别表示出圆和不在圆内部分的直线，进而可推断出方程表示的曲线为圆和与圆相交且去掉圆内的部分．【解答】解：原方程等价于：，或x2+y2=4；其中当x+y﹣1=0需有意义，等式才成立，即x2+y2≥4，此时它表示直线x﹣y﹣1=0上不在圆x2+y2=4内的部分，这是极易出错的一个环节．故选D【点评】本题主要考查了曲线与方程的问题．考查了考生对曲线方程的理解和对图象分析的能力．二、填空题:本大题共7小题,每小题4分,共28分11. 已知定义域为[1，2]的函数f（x）=2+log a x（a＞0，a≠1）的图象过点（2，3），若g（x）=f （x）+f（x2），则函数g（x）的值域为．参考答案：[4，]【考点】对数函数的图像与性质；函数的值域．【专题】计算题；数形结合；函数的性质及应用．【分析】根据f（x）的图象过点（2，3），代入可得实数a的值，再确定g（x）的定义域，最后根据单调性求函数值域．【解答】解：∵f（x）=2+log a x的图象过点（2，3），∴3=2+log a2，即log a2=1，解得a=2，又∵g（x）=f（x）+f（x2）=4+3log2x，且f（x）的定义域为[1，2]，∴g（x）的自变量x需满足，解得x∈[1，]，又g（x）在x∈[1，]上单调递增，所以g（x）min=g（1）=4，g（x）max=g（）=，因此，函数g（x）的值域为[4，]，故填：[4，]．【点评】本题主要考查了函数解析式和定义域的求法，以及应用单调性求函数的值域，忽视g（x）的定义域是本题的易错点，属于中档题．12. 如图所示，把一个物体放在倾斜角为30°的斜面上，物体处于平衡状态，且受到三个力的作用，即重力G，沿着斜面向上的摩擦力F1，垂直斜面向上的弹力F2．已知，则G的大小为________，F2的大小为________．参考答案：160N【分析】由向量分解的平行四边形法则，可得，即得解.【详解】如图，由向量分解的平行四边形法则，计算可得：故答案为：【点睛】本题考查了向量的平行四边形法则在力的分解中的应用，考查了学生数学应用，综合分析，数学运算能力，属于基础题.13. 实数x，y适合条件1 ≤ x2 + y2≤ 2，则函数2 x2 + 3 x y + 2 y2的值域是。

2019-2020学年山东省德州市高一12月月考数学试卷扫描版

高一数学试题2019 12一．单项选择题，本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.总体由编号为01,02，…，19,20的20个个体组成．利用下面的随机数表选取5个个体，选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第5个个体的编号为2.为比较甲、乙两地某月12时的气温状况，选取该月中的7,12,17,22,27，将这5天中12时的气温数据(单位：℃)制成如图所示的茎叶图，考虑以下结论： ①甲地该月12时的平均气温低于乙地该月12时的平均气温；②甲地该月12时的平均气温高于乙地该月12时的平均气温；③甲地该月12时的气温的标准差小于乙地该月12时的气温的标准差； ④甲地该月12时的气温的标准差大于乙地该月12时的气温的标准差．其中根据茎叶图能得到的统计结论的编号为 A ．①③ B ．①④C ．②③D ．②④3.若函数()y f x =的图像与函数xy a =（0a >且1a ≠）的图像关于y x =对称，且(3)1f =，则()f x =A ．3log xB ．1()2xC ．13log xD ．3x4.AQI 表示空气质量指数，AQI 值越小，表明空气质量越好，当AQI 值不大于100时称空气质量为“优良”．如图是某地4月1日到12日AQI 值的统计数据，下列叙述中不正确的是A ．这12天中有6天空气质量为“优良”B ．这12天中空气质量最好的是4月9日C ．这12天的AQI 值的中位数是90D ．从4日到9日空气质量越来越好5.函数y =A ．[3,)+∞B ．[3,4)C ．(,3]-∞D ．(,4)-∞ 6.从装有3个红球和4个白球的红袋内任取两个球，那么下列事件中，互斥事件的个数是①至少有一个白球；都是白球．②至少有一个白球；至少有一个红球．③恰好有一个白球；恰好有2个白球．④至少有1个白球；都是红球．A ．0B ．1C ．2D ．37.设函数122,1()1log ,1x x f x x x -⎧≤=⎨->⎩，则满足()2f x ≤的x 的取值范围是A ．[－1,2]B ．[0,2]C ．[1，＋∞)D ．[0，＋∞)8．已知函数y ＝log a (x ＋c )(a ，c 为常数，其中a ＞0，a ≠1)的图象如图，则下列结论成立的是( ) A ．a ＞1，c ＞1B ．a ＞1,0＜c ＜1C ．0＜a ＜1，c ＞1D ．0＜a ＜1,0＜c ＜1二．多项选择题，本题共4小题，每小题5分，共20分。

山东省夏津一中2019届高三数学10月月考试题文

山东省夏津一中2019届高三数学10月月考试题文时间：120分钟满分：150分一．选择题（本大题共12个小题，每题5分共60分） 1命题“0||,4≥+∈∀x x R x ”的否定是（）A ．0||,4<+∈∀x x R xB ．4,||0x R x x ∃∈+<C ．4,||0x R x x ∃∈+≥D ．0||,4≤+∈∀x x R x2. 已知}24|{},034|{2x y y Q x x x P -==<+-=，则=Q P （）A ．)2,1(B ．)2,0[C ．]2,1(D ．)1,0[3. 设0.1log 0.2a =， 1.1log 0.2b =，0.21.2c =，0.21.1d =则（）A ．c d a b >>>B ．c a d b >>>C ．d c a b >>>D ．a b d c >>> 4. 若110a b << ，则下列结论不正确的是 ( ) A.a 2＜b 2B .ab ＜b 2C.2b aa b+> D.|a|＋|b|＞|a ＋b|51,,()2ABC BD DA CB a CA b CD ====在中，点D 在边AB 上，且设，则 A ．1233a b +B ．2133a b +C ．3455a b +D ．4355a b +6. “0a >”是“函数|)1(|)(x ax x f +=在区间),0(+∞上单调递增”的（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件7. 函数f(x)= 的图象的大致形状是（）8．将函数)6sin()3sin(2x x y -+=ππ的图象向左平移ϕ（ϕ>0)个单位，所得图象对应的函数恰为奇函数，则ϕ的最小值为( )A.6π B. 12π C. 4π D.3π9. 在C ∆AB 中，角,,A B C 所对的边分别为,,a b c ，若s i n 2s i n c o s 0B A C +=,则当cos B 取最小值时，ac=（）A C10. 若()0,απ∈，且sin 2cos 2αα-=，则tan2α等于（）A ．3B.2C ．12 D.1311．21(x 0)(x)(x 1)(x 0)x f f ⎧-≥=⎨+<⎩函数若方程f(x)=-x+a 又且只有两个不等的实数根，则实数a 的取值范围为（） A ．(),0-∞B.[)0,1C ．(),1-∞ D.()0,+∞12. 已知定义在R 上的偶函数()y f x =的导函数为'()f x ，函数()f x 满足：当0x >时，'()()1x f x f x ⋅+>，且(1)=2018f .则不等式2017()1f x x<+的解集是（） A ．()-1,1 B.()-1∞，C ．()()-1,00,1 D.()()-,-11+∞∞，二．填空题(本大题共4小题，每小题5分，共20分)13. 记n S 为数列{}n a 的前n 项和.若21n n S a =+，则6S =_____________．0401x y x y y -≥⎧⎪+-≤⎨⎪≥⎩14.若向量AB 与AC 的夹角为3π，),(,3||,2||R ∈+===μλμλ，且⊥，则=μλ．件，则21()2x y z -+=的最小值为______ 15．已知实数,x y 满足约束条16. 已知函数)(x f 满足))(1()1()1(R x x f x f x f ∈-=+=-，且当10≤≤x 时12)(-=x x f ，则方程0)(cos =-x f x π在]3,1[-上的所有根之和为_______二．解答题(17题10分，18-22题每题12分，共80分) 17. （本小题满分10分）设命题p ：2.120a a a +-≥实数满足，命题22:log (1)R q ax ax -+函数的定义域是，如果p q ∧是假命题，p q ∨是真命题，求a 的取值范围.18.. （本小题满分12分）已知→→b a ,是两个单位向量．（1）若323=-→→b a ，试求→→+b a 3的值；（2）若→→b a ,的夹角为o60，试求向量→→→+=b a m 2与→→→-=a b n 2的夹角的余弦.19．（本小题满分12分）在ABC ∆中，,,a b c 分别为内角,,A B C 所对的边，已知cos a A R =，其中R 为ABC ∆外接圆的半径，S 为ABC ∆的面积，222a c b S +-=. （1）求sin C ；（2）若a b -=ABC ∆的周长． 20．已知函数()()12ln 2f x a x ax x=-++. （1）当2a =时，求函数()f x 的极值；（2）当0a <时，求函数()f x 的单调增区间.21. （本小题满分12分）某健身器材厂研制了一种足浴气血养身机,具体原理是在足浴盆的中心右侧离中心x 厘米)200(<<x 处安装了臭氧发生孔,产生臭氧对双脚起保健作用.根据检测发现,该臭氧发生孔工作时会对泡脚的舒适度起到干扰作用,通过研究发现臭氧发生孔工作时,对左脚的干扰度与2x 成反比,比例系数为4；对右脚的干扰度与2400x -成反比,比例系数为k ，且当210=x 时,对左脚和右脚的干扰度之和为0.065.（1）请将臭氧发生孔工作时对左脚和右脚的干扰度之和y 表示为x 的函数；（2）求臭氧发生孔工作时对左脚和右脚的干扰度之和y 的最小值．22．（本小题满分12分）已知函数x axxx f ln 1)(+-=．（1）若0)(≥x f 对0>∀x 恒成立，求a 的值；（2）求证：2221...3221)1ln(nn n -+++>+（*N n ∈）．高三理科数学参考答案：1-5 BAADB 6-10 ACACB 11-12CC 13. 7614.6 15. 2 16.11 17解：若命题p 是真时，2120-43a a a a +-≥≤≥由得或若命题q 是真时，21ax ax -+>0① 当a =0时，不等式成立。

山东省德州市夏津一中2019-2020学年高一数学下学期月考考试试题(含解析)

2
2 25
2
，所以 b 5 .
故选 B.
【点睛】解三角形常与三角形的面积结合在一起考查，考查综合运用知识解决问题的能力，
解题时注意各个公式间的联系，同时还要注意公式中的常用变形.
7.已知非零向量 m、n 满足| n | 4 | m | | ，且 m ( 2m n) ，则 m、n 的夹角为
(2). 2 2
如图所示： G 为 CD 中点，在等边三角形VCD 中，VG 2 3 ，V 在平面 ABCD 的投影为正方形 ABCD 中心 O ，计算得到答案.
VG 3 VC 2 3
【详解】如图所示： G 为 CD 中点，在等边三角形VCD 中，
2
，
V 在平面 ABCD 的投影为正方形 ABCD 中心 O ，正四棱锥 V-ABCD 的底面面积为 16，则底面边长为 4 .
的一个可能取值为（）
A.
3 B. 4
C. 4
D. 4
【答案】A
【解析】
【分析】
根据题意平移后得到
y
sin
2x
，故
k
，
k
Z
，得到答案.
【详解】函数 y cos 2x 的图像沿 x 轴向右平移 4 个单位后，
得到
y
cos
2x
2
sin 2x
为奇函数，故
k
，k
Z
.
故选： A .
【点睛】本题考查了三角函数平移，三角函数奇偶性，意在考查学生对于三角函数知识的综
山东省德州市夏津一中 2019-2020 学年高一数学下学期月考考试试
题（含解析）
一、选择题（每题 5 分，共 75 分.1-13 为单选题，14-15 为多选题）

山东省夏津县第一中学2018-2019高一3月月考数学试卷 Word版含答案

高一年级2018-2019学年第二学期第一次月考数学试题2019.03.26第I卷（共52分）一、选择题（本大题共13小题，每小题4分，共52分）1.A. B. C. D.2、已知向量，，则A. B. C. D.3、如图，在平行四边形ABCD中，E为BC的中点，且，则A. ，B. ，C. ，D. ，4、下列计算正确的是A. B.C. D.5、已知平面向量是非零向量，，，则向量在向量方向上的投影为A. 1B.C. 2D.6、已知，，则A. B. C. D.7、设，向量，且，则A. B. C. D. 108、已知角，均为锐角，且，，则的值为A. B. C. D.9、函数的最小正周期为( )A. B. C. D.10、在中，，点P是所在平面内一点，则当取得最小值时，A. B. C. 9 D.（11-13为多选题）11、下列说法正确的有.若，则若，则A、B、C、D有可能构成平行四边形的四个顶点若，，则单位向量的模都相等12、已知，则下列结论正确的有A. 在区间上单调递增B. 的一个对称中心为C. 当时，的值域为D. 先将函数的图象的纵坐标不变，横坐标缩短为原来的倍，再向左平移个单位后得到函数的图象13、下列式子中结果为的有( )．，，C，第II卷（共98分）二、填空题（本大题共4小题，每小题4分，共16分）14、=______15、已知是锐角，，且，则为16、已知，则夹角为钝角时，取值范围为17、三、解答题：（本大题共6小题，共82分. 解答应写出文字说明、证明过程和演算步骤.）18、（本题12分）已知向量，．设与的夹角为，求的值；若与垂直，求实数的值19、（本题14分）如图，在平面直角坐标系xOy上，点，点B在单位圆上，．若点，求的值；若，，求．20、（本题14分）已知，，．若，求证：；设，若，求，的值．21、（本题14分）已知函数，．求函数的单调区间；若把向右平移个单位得到函数，求在区间上的最小值和最大值．22、（本题14分）在三角形ABC中，，，，D是线段BC上一点，且，F为线段AB上一点．设，，设，求；求的取值范围；若F为线段AB的中点，直线CF与AD相交于点M，求．23、（本题14分）已知，，，，求的值．第一次月考数学试题参考答案1---5 D A D C B 6---10 A B C C D 11、 BCD 12、 ABD 13、ABCD14、零向量或且 17、18、解：向量，，则，且，；设与的夹角为，则；若与垂直，则，即，所以，解得．19、解：由点，，，．；，．，，解得，，．．20、解：由，，则，由，得．所以即；由得，得：．因为，所以．所以，，代入得：．因为所以．所以，．21、解：，下面分为单调增区间和单调减区间进行求解，令，得，可得函数的单调增区间为，；令，得，可得函数的单调减区间为，．若把函数的图象向右平移个单位，得到函数的图象，，，，．故在区间上的最小值为，最大值为1．22、解：，而，，；在三角形ABC中，，，，，，，不妨设，，式，，；为线段AB的中点，，不妨设，，，，A、M、D三点共线，，即，，解得，，．23、解：，，，，，，即．。

山东省德州市夏津第一中学2019-2020下学期高一7月月考数学试卷(wd无答案)

山东省德州市夏津第一中学2019-2020下学期高一7月月考数学试卷(wd无答案)一、单选题(★★) 1. 已知 i是虚数单位，复数，则的虚部为（）A．B．3C．D．2(★★★) 2. 已知角的终边经过点，则的值等于A．B．C．D．(★★) 3. 已知向量，，若，则与夹角的余弦值为（）A．B．C．D．(★★★) 4. 已知函数的部分图象如图所示，则下列关于函数的说法正确的是（）A．图象关于点对称B．最小正周期为C．在区间上单调递增D．图象关于直线对称(★★★) 5. 已知函数，若要得到一个奇函数的图象，则可以将函数的图象( )A．向左平移个单位长度B．向右平移个单位长度C．向左平移个单位长度D．向右平移个单位长度(★★) 6. 在平行四边形中，点为对角线上靠近点的三等分点，连结并延长交于，则（）A．B．C．D．(★★)7. 已知，是两条不同的直线，，是两个不同的平面，则下列结论正确的是（）A．若，，则B．若，，，则C．若，，则D．若，，，，则(★★★) 8. 将函数的图像向左平移个单位长度得到函数的图像.函数的周期为，且函数的图像的一条对称轴为直线，则函数的单调递增区间为（）A．B．C．D．二、多选题(★★) 9. 下列各式中，值为的是（）A．B．C．D．(★★) 10. 将函数的图象向左平移个单位长度，得到的图象,则下列说法正确的是（）A．函数的最小正周期为B．函数的最小值为C．函数的图象关于直线对称D．函数在上单调递减(★★★) 11. 在中，角的对边分别为，若，且，，则的面积为（）A．B．C．D．(★★) 12. 如图所示，在正方体中， E， F分别是的中点．有下列结论，其中正确的是（）A．与垂直B．与平面垂直C．与所成的角为45°D．平面三、填空题(★★★) 13. 设向量，向量，且，则等于__________. (★★) 14. 若函数，的图象与直线恰有两个不同交点，则的取值范围是______.(★★★) 15. 已知点，，，均在球的球面上，，，若三棱锥体积的最大值是，则球的表面积为__________四、双空题(★★★) 16. 在△ ABC中，角 A， B， C所对应的边分别为 a， b， c，已知 b＝1， c＝2且2cos A（ bcos C+ ccos B）＝ a，则 A＝__________；若 M为边 BC的中点，则| AM|＝__________五、解答题(★★) 17. （1）已知向量，，求向量与夹角的余弦值.（2）已知角的终边与单位圆在第四象限交于点 P，且点 P的坐标为.求的值.(★★★) 18. 在① ，② ，③ ，这三个条件中任选一个，补充在下面的问题中，并解决该问题.已知的内角 A， B， C的对边分别为 a， b， c，_________，，.（1）求角 B；（2）求的面积.(★★★) 19. 已知向量，，设.（1）求函数的最小正周期和对称中心；（2）已知为锐角，，，，求的值.(★★) 20. 如图，在四棱锥中，平面，，，， E， F分别是和的中点，（1）证明：；（2）证明：平面平面.(★★★) 21. 已知向量，，函数. （1）求的最小正周期和的图象的对称轴方程；（2）求在区间上的值域.(★★★) 22. 在中，角所对的边分别为，且(1)求角的大小;(2)若锐角三角形，其外接圆的半径为，求的周长的取值范围.。

山东省德州市夏津一中2021-2022高一数学下学期月考考试试题(含解析).doc

山东省德州市夏津一中2021-2022高一数学下学期月考考试试题（含解析）一、选择题（每题5分，共75分.1-13为单选题，14-15为多选题） 1.已知向量a =（3，1），b =（k ，7），若//a b ，则k =（） A. -21 B. 21C. 23D. 20【答案】B 【解析】【分析】直接根据向量平行公式得到答案.【详解】向量a =（3，1），b =（k ，7），若//a b ，则37k ⨯=，即21k =. 故选：B .【点睛】本题考查了根据向量平行求参数，属于简单题.2.在△ABC 中，若b =c =3，∠B =30°，则sin C =（）A.12C.2D. 1【答案】B 【解析】【分析】直接利用正弦定理计算得到答案.【详解】根据正弦定理：sin sin b c B C =，解得sin 2C =. 故选：B .【点睛】本题考查了正弦定理，意在考查学生的计算能力. 3.在复平面内，复数1i -的共轭复数对应的点位于第（）象限 A 一 B. 二 C. 三 D. 四【答案】A 【解析】【分析】计算共轭复数为1z i =+，得到答案. 【详解】复数1z i =-的共轭复数为1z i =+，对应的点位于第一象限.故选：A .【点睛】本题考查了共轭复数，复数对应象限，意在考查学生对于复数知识的灵活运用.4.已知,2παπ⎛⎫∈ ⎪⎝⎭，3sin 5α=，则tan 4πα⎛⎫+= ⎪⎝⎭（）A.17B. 7C. 17-D. -7【答案】A 【解析】【分析】先求出tan α的值，再利用和角的正切求tan 4πα⎛⎫+⎪⎝⎭的值. 【详解】因为,2παπ⎛⎫∈⎪⎝⎭，3sin 5α=，所以3tan 4α=-，所以tan 4πα⎛⎫+ ⎪⎝⎭=3114371()14-+=--⋅. 故选A【点睛】本题主要考查同角的三角函数关系，考查和角的正切的计算，意在考查学生对这些知识的掌握水平和分析推理能力. 5.已知3cos()25πα+=，02πα-<<，则sin 2α的值为（） A.1225 B. 1225-C.2425D. 2425-【答案】D 【解析】【分析】计算3sin 5α=-，4cos 5α=，再利用二倍角公式计算得到答案. 【详解】，3cos()sin 25παα+=-=，故3sin 5α=-，02πα-<<，则4cos 5α=，24sin 22sin cos 25ααα==-.故选：D .【点睛】本题考查了三角恒等变换，意在考查学生的计算能力和转化能力.6.已知ABC ∆中，内角A ，B ，C 所对的边分别为a ，b ，c ，若c =45B =︒，2ABC S ∆=，则b 等于（）B. 5D. 25【答案】B 【解析】【分析】利用三角形的面积求出c ，然后利用余弦定理求出b 即可．【详解】由题意可知，11sin 2222ABC S ac B a ∆=⨯=⨯=，解得1a =，由余弦定理知2222cos b a c ac B =+-，所以21322252b =+-⨯=，所以5b =. 故选B.【点睛】解三角形常与三角形的面积结合在一起考查，考查综合运用知识解决问题的能力，解题时注意各个公式间的联系，同时还要注意公式中的常用变形.7.已知非零向量m n 、满足4n m =|||||，且2m m n ⊥+()，则m n 、的夹角为 A.3πB.2π C.23π D.56π 【答案】C 【解析】【分析】运用向量的数量积的定义和性质：向量的平方即为模的平方，计算向量夹角，结合其范围，即可得到．【详解】∵()2m m n ⊥+，∴()20m m n ⋅+=，即220m m n +⋅=，又∵4n m =，∴224cos ,0m m m m n +⋅=，解得1cos ,2m n =-，结合0,m n π≤≤，所以2,3m n π=，故选C. 【点睛】本题考查平面向量的数量积的定义和性质：向量的平方即为模的平方，考查运算能力，属于基础题.8.将函数()cos 2y x ϕ=+的图像沿x 轴向右平移4π个单位后，得到一个奇函数的图像，则ϕ的一个可能取值为（） A. π B.34π C.4π D. 4π-【答案】A 【解析】【分析】根据题意平移后得到()sin 2y x ϕ=+，故k ϕπ=，k Z ∈，得到答案. 【详解】函数()cos 2y x ϕ=+的图像沿x 轴向右平移4π个单位后，得到()cos 2sin 22y x x πϕϕ⎛⎫=+-=+ ⎪⎝⎭为奇函数，故k ϕπ=，k Z ∈. 故选：A .【点睛】本题考查了三角函数平移，三角函数奇偶性，意在考查学生对于三角函数知识的综合应用.9.在△ABC 中，2,2,AR RB CP PR AP mAB nAC ===+则m ＋n 等于( ) A.23B.79C.89D. 1【答案】B 【解析】由题意可得：2,3,3,AP AR RP RB RP CR PC RC RP =+=+=∴=结合：AP mAB nAC =+ ，则：()()()223323RB RP m AR RB n RB RP m n RB nRP +=+++=++ ，据此可得方程组：322{31m n n +== ，解得：49{13m n ==，据此可得：79m n += . 本题选择B 选项.10.一个圆柱和一个圆锥的轴截面分别是边长为a 的正方形和正三角形，则他们的表面积之比为（） A. 1：1 B. 2：1C. 1：2D. 3：1【答案】B 【解析】【分析】分别计算圆柱和圆锥的表面积，相比得到答案.【详解】圆柱的表面积2213222a S a a a πππ⎛⎫=⋅+⋅= ⎪⎝⎭；圆锥的表面积22213224a S a a a πππ⎛⎫=⋅+= ⎪⎝⎭，故1221S S =. 故选：B .【点睛】本题考查了圆柱和圆锥的表面积，意在考查学生的计算能力和空间想象能力. 11.在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，且cos cos a B b A =，222a b c ab +=+，则△ABC 是（） A. 钝角三角形 B. 直角三角形C. 等腰直角三角形D. 等边三角形【答案】D 【解析】【分析】根据正弦定理得到A B =，根据余弦定理得到3C π=，得到答案.【详解】根据正弦定理：cos cos a B b A =，即sin cos sin cos A B B A =，即()sin 0A B -=，A B =；根据余弦定理：222a b c ab +=+，即1cos 2C =，()0,C π∈，故3C π=. 故△ABC 是等边三角形. 故选：D .【点睛】本题考查了正弦定理，余弦定理，意在考查学生的计算能力和应用能力.12.如果一个水平放置的图形的斜二测直观图是一个底面为45︒，腰和上底均为1的等腰梯形，那么原平面图形的面积是（） A. 22+ B.12C.22+ D. 12+【答案】A 【解析】【分析】如图所示建立坐标系，计算面积得到答案. 【详解】如图所示建立坐标系，根据题意：图2中OABC 为直角梯形，2OC =，1BC =，21OA =+.故22S =+. 故选：A .【点睛】本题考查了斜二测画法求面积，意在考查学生的计算能力.13.要得到函数2sin y x =的图像，只需将2cos 24y x π⎛⎫=- ⎪⎝⎭的图像所有的点（）A. 横坐标伸长到原来的2倍（纵坐标不变），再向左平行移动8π个单位长度 B. 横坐标伸长到原来的2倍（纵坐标不变），再向右平行移动4π个单位长度 C. 横坐标缩短到原来的12倍（纵坐标不变），再向右平行移动4π个单位长度 D. 横坐标缩短到原来的12倍（纵坐标不变），再向左平行移动8π个单位【答案】B 【解析】【分析】变换2sin 2cos 2y x x π⎛⎫==-⎪⎝⎭，再根据三角函数平移伸缩变换法则得到答案. 【详解】2sin 2cos 2y x x π⎛⎫==- ⎪⎝⎭，故需将2cos 24y x π⎛⎫=- ⎪⎝⎭的图像所有的点横坐标伸长到原来的2倍（纵坐标不变），变为2cos 4y x π⎛⎫=-⎪⎝⎭；再向右平行移动4π个单位长度得到2cos 2y x π⎛⎫=- ⎪⎝⎭.故选：B .【点睛】本题考查了三角函数平移伸缩变换，意在考查学生对于三角函数知识的综合应用. 14.（多选）下列各式中值为12的是（） A. 2sin75cos75︒︒B. 212sin12π-C. sin 45cos15cos45sin15︒︒-︒︒D. tan 20tan 25tan 20tan 25︒+︒+︒︒【答案】AC 【解析】【分析】依次计算每个选项得到答案.【详解】A. 12sin 75cos75sin150sin 302︒︒=︒=︒=，正确；B. 212sin cos126ππ-==，不正确； C. 1sin 45cos15cos 45sin15sin 302︒︒-︒︒=︒=，正确； D tan 20tan 25tan 4511tan 20tan 25︒+︒︒==-︒⋅︒，故tan 20tan 25tan 20tan 251︒+︒+︒︒=，不正确.故选：AC【点睛】本题考查了三角恒等变换，意在考查学生的计算能力和转化能力. 15.设函数()4sin 213f x x π⎛⎫=++ ⎪⎝⎭的图象为C ，则下列结论中正确的是（） A. 图象C 关于直线512x π=-对称 B. 图象C 关于点,06π⎛⎫-⎪⎝⎭对称 C. 函数()f x 在区间5,1212ππ⎛⎫-⎪⎝⎭内是增函数 D. 把函数()4sin 16f x x π⎛⎫=++ ⎪⎝⎭的图象上点的横坐标缩短为原来的一半（纵坐标不变）可以得到图象C 【答案】AC 【解析】【分析】运用三角函数图象和性质来判断四个选项中函数图象的对称性、单调性及图象平移是否正确. 【详解】对于A ,函数()4sin 213f x x π⎛⎫=++ ⎪⎝⎭的对称轴方程为2()32x k k Z πππ+=+∈,解得()122k x k Z ππ=+∈,当1k =-时可得512x π=-,所以图象C 关于直线512x π=-对称正确.对于B ,函数()4sin 213f x x π⎛⎫=++ ⎪⎝⎭的对称中心为2()3x k k Z ππ+=∈,解得(k Z)62k x ππ=-+∈,当0k =时可得6x π=-,所以图象C 关于点,16π⎛⎫- ⎪⎝⎭对称,而不是关于点,06π⎛⎫- ⎪⎝⎭对称,故B 选项不正确.对于C ,函数()4sin 213f x x π⎛⎫=++ ⎪⎝⎭的单调增区间为222()232k x k k Z πππππ-≤+≤+∈,解得 5()1212k x k k Z ππππ-≤≤+∈当0k =时51212x ππ-≤≤,所以函数()f x 在区间5,1212ππ⎛⎫- ⎪⎝⎭内是增函数正确. 对于D ,把函数()4sin 16f x x π⎛⎫=++ ⎪⎝⎭的图象上点的横坐标缩短为原来的一半（纵坐标不变）可以得到函数()4sin 216f x x π⎛⎫=++ ⎪⎝⎭的图象,不是图象C ,故D 选项不正确. 综上AC 正确故选AC【点睛】本题考查了三角函数图象与性质,求解三角函数图象的轴对称性和中心对称问题以及三角函数的单调性,需要熟练掌握基础知识并运算正确,依据图象的平移能够得到平移后的图象解析式.本题较为综合.二、填空题（每题5分，共15分）16.121-2ii+的虚部为__________ 【答案】45【解析】【分析】化简得到3455z i =-+，得到复数虚部. 【详解】()()()212123434121212555i i i z i i i i ++-+====-+--+，故虚部为45. 故答案为：45.【点睛】本题考查了复数的化简，复数的虚部，意在考查学生的计算能力. 17.已知,a b 均为单位向量，它们的夹角为60°，那么3a b +=__________．【答案】13. 【解析】222|3|6916cos60913,313a b a a b b a b +=+⋅+=+⨯+=∴+=.18.已知正四棱锥V -ABCD 的底面面积为16，侧棱长为4，则这个棱锥的斜高为_____，高为_____ 【答案】 (1). 23 (2). 22 【解析】【分析】如图所示：G 为CD 中点，在等边三角形VCD 中，23VG =，V 在平面ABCD 的投影为正方形ABCD 中心O ，计算得到答案.【详解】如图所示：G 为CD 中点，在等边三角形VCD 中，323VG VC ==， V 在平面ABCD 的投影为正方形ABCD 中心O ，正四棱锥V -ABCD 的底面面积为16，则底面边长为4.1222DO DB ==，2222VO VD DO =-=. 故答案为：23；22.【点睛】本题考查了四棱锥的高和斜高，意在考查学生的计算能力和空间想象能力. 三、解答题（每题15分，共60分）19.已知复数z =3+bi （b ∈R ），且（1+3i ）·z 纯虚数（1）求复数z（2）若w =z ·(2+i )，求复数w 的模|w |【答案】（1）z =3+i （2）w =【解析】【分析】（1）计算得到()()13339i z b b i +⋅=-++，得到答案.（2）()552w z i i +=⋅+=，再计算模长得到答案.【详解】（1）3z bi =+，则()()()()13133339i z i bi b b i +⋅=+⋅+=-++为纯虚数，故33090b b -=⎧⎨+≠⎩，解得1b =，故3i z =+.（2）()()()32552w z i i i i =++=++=⋅，故w =【点睛】本题考查了根据复数类型求参数，复数的模，意在考查学生的计算能力.20.（1）用与球心距离为1的平面去截球，所得的截面面积为4π，求球的表面积（2）正三棱台的高为3，上、下底面边长分别为2和4，求这个棱台的侧棱长和斜高【答案】（1）S 20π=球（2）侧棱长3 【解析】【分析】（1）截面圆的半径r =2，球半径R =.（2）如图所示：计算OA =11O A =OE =，11O E =，根据勾股定理计算得到答案.【详解】（1）截面圆的半径r =2，球半径R =2S 4R 20ππ==球（2）正三棱台111-ABC A B C 中，高13OO =，底面边长为112A B =，4AB =，故OA AB ==，1111O A A B ==，侧棱长1AA 3=，又23OE =，113O E =，斜高1EE =222323321333+-=（）.【点睛】本题考查了球的表面积，三棱台的相关计算，意在考查学生的计算能力和空间想象能力.21.已知，a =1，b =2且向量a 与b 不共线（1）若a 与b 的夹角为45°，求()()2a b a b -⋅+ （2）若向量ka b -与ka b +的夹角为钝角，求实数k 的取值范围【答案】（122（2）22k -<<且0k ≠【解析】【分析】（1）直接展开计算得到答案. （2）根据题意()0ka b ka b -+<（）且不反向平行，计算得到答案.【详解】（1）222()2cos 4522a b a b a a b b-+=+︒-=-（）（2）根据题意：()0ka b ka b -+<（）且不反向平行. 2222()40ka b ka b k a b k -+=-=-<（），解得22k <<—，反向平行时，设()0ka b ka b λλ-=+<（），1k k λλ=⎧⎨-=⎩，得0k =，综上，220k k -<<≠且.【点睛】本题考查了向量数量积，向量夹角，意在考查学生的计算能力和转化能力.22.已知函数()2()sin 3sin 02f x wx wx wx w π⎛⎫=+> ⎪⎝⎭的最小正周期为π （1）求w 的值（2）求函数()f x 的对称轴和单调增区间（3）求函数()f x 在区间[0]3π，上的值域【答案】（1）1w =（2）对称轴23k x k Z ππ=+∈，；增区间[]63k k k Z ππππ-+∈，（3）3[0]2，【解析】【分析】（1）化简得到1()sin(2)62f x wx π=-+，根据周期得到答案. （2）令262x k k Z πππ-=+∈，，得到对称轴，令222262k x k k Z πππππ-≤-≤+∈，，得到单调区间.（3）03x π≤≤，2662x πππ-≤-≤，1sin(2)126x π-≤-≤，得到答案.【详解】（1）1cos 21()2sin(2)262wx f x wx wx π-==-+，2T 2w ππ==，得1w =. （2）1()sin(2)62f x x π=-+，令262x k k Z πππ-=+∈，，得对称轴23k x k Z ππ=+∈，. 令222262k x k k Z πππππ-≤-≤+∈，，得增区间[]63k k k Z ππππ-+∈，，（3）03x π≤≤，2662x πππ-≤-≤，1sin(2)126x π-≤-≤，值域3[0]2，. 【点睛】本题考查了三角函数周期，单调性，对称轴，值域，意在考查学生对于三角函数知识的综合应用.。

山东省夏津一中2019届高三数学12月月考试题文

山东省夏津一中2019届高三数学12月月考试题文一、选择题1. 直线x －y ＝0 的倾斜角为（ )．A 。

30° B。

45° C。

60° D. 90° 2. 圆锥的底面半径为a ,侧面展开图是半圆面，那么此圆锥的侧面积是（）A 。

B.C 。

D 。

3. 已知直线l 1：3mx +（m +2）y +1=0，直线l 2:（m —2）x +(m +2)y +2=0，且l 1∥l 2，则m 的值为（ )A.B.C 。

或D 。

或4. 一个棱柱是正四棱柱的条件是( )A ．底面是正方形,有两个侧面是矩形B ．底面是正方形，有两个侧面垂直于底面C ．底面是菱形,具有一个顶点处的三条棱两两垂直D ．每个侧面都是全等矩形的四棱柱5. 已知圆M ：x 2+y 2—2ay ＝0(a ＞0)截直线x +y ＝0所得线段的长度是．则圆M 与圆N ：(x -1)2+(y —1)2＝1的位置关系是（） A 。

内切B. 相交C 。

外切D. 相离6. 过点（1，3）的直线l 与两坐标轴的正半轴所围成的三角形面积为6，则直线l 的方程是（）．A. 063=-+y x B 。

03=-y x C. 0103=-+y x D.083=+-y x7。

已知直线l 1：（k -3）x +（5-k ）y +1=0与l 2：2（k -3）x -2y +3=0垂直，则k 的值是（）A 。

1或3B 。

1或5C 。

1或4D. 1或28. 如图，在正方体ABCD —A 1B 1C 1D 1中，E ，F 分别是C 1D 1,CC 1的中点，则异面直线AE 与BF 所成角的余弦值为( ）A 。

B. C 。

D.9. 直线l 过点（0，2)，被圆C ：x 2+y 2-4x —6y +9=0截得的弦长为2,则直线l 的方程是（）A. B 。

C 。

或 D 。

2-=y10. 已知圆,直线l ：，若圆上恰有3个点到直线l 的距离等于1，则b 的值为A 。

德州市夏津县双语中学2019年12月高一数学月考卷附答案详析

德州市夏津县双语中学2019年12月高一数学月考卷一、单选题1．一个容量为80的样本中数据的最大值是140,最小值是51,组距是10,则应将样本数据分为()A ．10组B ．9组C ．8组D ．7组2．下列事件是随机事件的个数是（）①同性电荷，互相排斥；②明天天晴；③自由下落的物体做匀速直线运动；④函数()log 0,1a y x a a =>≠且在定义域上是增函数．A ．0B ．1C ．2D ．33．从4双不同的鞋中任意摸出4只，事件“4只全部成对”的对立事件是()A ．至多有2只不成对B ．恰有2只不成对C ．4只全部不成对D ．至少有2只不成对4．统计某校1000名学生的数学水平测试成绩，得到样本频率分布直方图如图所示，若满分为100分，规定不低于60分为及格，则及格率是（）A ．20%B ．25%C ．6%D ．80%5．在区间()0+∞，上为减函数的是（）A ．2y x=B ．12y x=C ．12xy ⎛⎫= ⎪⎝⎭D ．ln y x=6．已知0.20.32log 0.2,2,0.2a b c ===，则A ．a b c<<B ．a c b<<C ．c a b<<D ．b c a<<7．已知函数()ln f x x =+()f x 的定义域为（）A ．(0,1)B ．(1,2]C ．(0,4]D ．(0,2]8．设函数()()12322log 1,2x e x f x x x -⎧<⎪=⎨-≥⎪⎩，，则()()2f f 的值为A ．0B ．1C ．2D ．39．下列函数中，其定义域和值域分别与函数y ＝10lg x 的定义域和值域相同的是()A ．y ＝xB ．y ＝lg xC ．y ＝2xD ．y10．设两个独立事件A 和B 都不发生的概率为19,A 发生B 不发生的概率和B 发生A 不发生的概率相同,则事件A 发生的概率P (A )等于()A ．29B ．118C ．13D ．23二、多选题11．下列函数中，在区间()0,∞+上单调递减的是（）A ．1y x=B ．x y e -=C ．21y x =-+D ．lg y x=12．演讲比赛共有9位评委分别给出某选手的原始评分，评定该选手的成绩时，从9个原始评分中去掉1个最高分、1个最低分，得到7个有效评分．7个有效评分与9个原始评分相比，发生改变的数字特征是（）A ．中位数B ．平均数C ．方差D ．极差13．某地区经过一年的新农村建设，农村的经济收入增加了一倍，实现翻番．为更好地了解该地区农村的经济收入变化情况，统计了该地区新农村建设前后农村的经济收入构成比例，得到如下饼图：则下面结论中正确的是（）A ．新农村建设后，种植收入减少B ．新农村建设后，其他收入增加了一倍以上C ．新农村建设后，养殖收入增加了一倍D ．新农村建设后，养殖收入与第三产业收入的总和超过了经济收入的一半三、填空题14．已知函数()2()log 1f x x =+，若()1f a =，则a 的值为______．15．某高中共有学生900人，其中高一年级240人，高二年级260人，为做某项调查，拟采用分层抽样法抽取容量为45的样本，则在高三年级抽取的人数是______．16．函数()()lg 24xf x =-的定义域为______．17．甲、乙、丙、丁四名射击手在选拔赛中的平均环数x 及其标准差s 如下表所示，则选送决赛的最佳人选应是________.甲乙丙丁x7887s2.52.52.8318．已知3()lg f x x =，则(2)f =______．四、解答题19．计算：（1）-；（2）37log +lg 25lg 47log 23++．20．从甲、乙、丙、丁四个人中选两名代表，求：（１）甲被选中的概率；（２）丁没被选中的概率.21．为了解甲、乙两种离子在小鼠体内的残留程度，进行如下试验：将200只小鼠随机分成A ，B 两组，每组100只，其中A 组小鼠给服甲离子溶液，B 组小鼠给服乙离子溶液．每只小鼠给服的溶液体积相同、摩尔浓度相同．经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比．根据试验数据分别得到如下直方图：记C 为事件：“乙离子残留在体内的百分比不低于5.5”，根据直方图得到()P C 的估计值为0.70．（1）求乙离子残留百分比直方图中,a b 的值；（2）分别估计甲、乙离子残留百分比的平均值（同一组中的数据用该组区间的中点值为代表）；（3）分别估计甲、乙离子残留百分比的方差（保留两位小数）．22．某制造商为运动会生产一批直径为40mm的乒乓球，现随机抽样检查20只，测得每只球的直径（单位：mm，保留两位小数）如下：40.0240.0039.9840.0039.9940.0039.9840.0139.9839.9940.0039.9939.9540.0140.0239.9840.0039.9940.0039.96（1）完成下面的频率分布表，并在图中画出频率分布直方图和频率分布折线图．分组频数频率频率组距[)39.95,39.97[)39.97,39.99[)39.99,40.01[]40.01,40.03合计（2）假定乒乓球的直径误差不超过0.02mm为合格品，若这批乒乓球的总数为10000只，试根据抽样检查结果估计这批产品的合格只数．23．已知函数()1(2axf x=，a为常数，且函数的图象过点（–1，2）．（1）求a的值；（2）若g（x）=4–x–2，且g（x）=f（x），求满足条件的x的值．24．已知函数()2()log 1f x x =+，当点(),x y 是函数()f x 图像上的点时，点,32x y ⎛⎫⎪⎝⎭是函数()g x 图像上的点．（1）写出函数()g x 的表达式；（2）当2()()0g x f x -≥时，求x 的取值范围．解析德州市夏津县双语中学2019-2020学年高一数学12月月考卷一、单选题1．一个容量为80的样本中数据的最大值是140,最小值是51,组距是10,则应将样本数据分为()A ．10组B ．9组C ．8组D ．7组【答案】B【解析】由题意知，(14051)108.9-÷=，所以分为9组较为恰当，故选B.2．下列事件是随机事件的个数是（）①同性电荷，互相排斥；②明天天晴；③自由下落的物体做匀速直线运动；④函数()log 0,1a y x a a =>≠且在定义域上是增函数．A ．0B ．1C ．2D ．3【答案】C【解析】随机事件是指在一定条件下，可能发生也可能不发生的事件，据此对每个事件进行判断即可.【详解】②④是随机事件；①是必然事件；③是不可能事件.故选：C .【点睛】本题主要考查的是随机事件，考查学生的理解能力.3．从4双不同的鞋中任意摸出4只，事件“4只全部成对”的对立事件是()A ．至多有2只不成对B ．恰有2只不成对C ．4只全部不成对D ．至少有2只不成对【答案】D【解析】先把全部事件分成三类“恰有2只成对”“4只全部成对”“4只都不成对”，再得到事件“4只全部成对”的对立事件.【详解】从4双不同的鞋中任意摸出4只，可能的结果为“恰有2只成对”“4只全部成对”“4只都不成对”，所以事件“4只全部成对”的对立事件是“恰有2只成对或4只都不成对”，即“至少有2只不成对”.故答案为：D.【点睛】本题主要考查对立事件，意在考查学生对该知识的掌握水平和分析推理能力.4．统计某校1000名学生的数学水平测试成绩，得到样本频率分布直方图如图所示，若满分为100分，规定不低于60分为及格，则及格率是（）A ．20%B ．25%C ．6%D ．80%【答案】D【解析】解：及格的频率为（0.025+0.035+0.01+0.01）×10=0.8=80%故选D ：5．在区间()0+∞，上为减函数的是（）A ．2y x=B ．12y x=C ．12xy ⎛⎫= ⎪⎝⎭D ．ln y x=【答案】C【解析】根据函数单调性逐项进行判断即可得到答案.【详解】2y x =在()0,∞+上为增函数，12y x =在()0,∞+上为增函数，12xy ⎛⎫= ⎪⎝⎭在()0,∞+上为减函数，ln y x =在()0,∞+上为增函数．故选:C .【点睛】本题主要考查的是基本初等函数的性质，是基础题,6．已知0.20.32log 0.2,2,0.2a b c ===，则A ．a b c <<B ．a c b<<C ．c a b<<D ．b c a<<【答案】B【解析】运用中间量0比较,a c ，运用中间量1比较,b c 【详解】22log 0.2log 10,a =<=0.20221,b =>=0.3000.20.21,<<=则01,c a c b <<<<．故选B ．【点睛】本题考查指数和对数大小的比较，渗透了直观想象和数学运算素养．采取中间变量法，利用转化与化归思想解题．7．已知函数()ln f x x =+()f x 的定义域为（）A ．(0,1)B ．(1,2]C ．(0,4]D ．(0,2]【答案】C【解析】根据函数解析式可知，要使函数有意义需满足01620xx >⎧⎨-≥⎩，解不等式组，即可求出函数的定义域.【详解】因为()ln f x x =所以要使函数有意义需满足01620xx >⎧⎨-≥⎩，解得04x x >⎧⎨≤⎩，即04x <≤，所以函数的定义域为(]0,4，故选C.【点睛】本题主要考查了函数的定义域，涉及对数函数，指数函数的性质，属于中档题.8．设函数()()12322log 1,2x e x f x x x -⎧<⎪=⎨-≥⎪⎩，，则()()2f f 的值为A ．0B ．1C ．2D ．3【答案】C【解析】因为f(x)=x 1232e ,x 2,{log (x 1),x 2,-<-≥，则f[f(2)]=f （1）=2,选C9．下列函数中，其定义域和值域分别与函数y ＝10lg x 的定义域和值域相同的是()A ．y ＝x B ．y ＝lg x C ．y ＝2x D ．y【答案】D【解析】试题分析：因函数lg 10x y =的定义域和值域分别为,故应选D ．【考点】对数函数幂函数的定义域和值域等知识的综合运用．10．设两个独立事件A 和B 都不发生的概率为19,A 发生B 不发生的概率和B 发生A 不发生的概率相同,则事件A 发生的概率P (A )等于()A ．29B ．118C ．13D ．23【答案】D 【解析】解：∴P(A −)=P(B −)=19,P(A −)P(B)=P(B −)P(A)设P(A)=x,P(B)=y,∴(1−x)(1−y)=19(1−x)y =x(1−y)∴x =23二、多选题11．下列函数中，在区间()0,∞+上单调递减的是（）A ．1y x=B ．x y e -=C ．21y x =-+D ．lg y x=【答案】ABC【解析】根据函数单调性逐项进行判断即可得到答案.【详解】易知1y x=，x y e -=，y ＝e －x ，21y x =-+在()0,∞+上是减函数，lg y x =在()0,∞+上是增函数．故选:ABC ．【点睛】本题主要考查函数的单调性以及指数函数、对数函数、幂函数的基本性质,是基础题,12．演讲比赛共有9位评委分别给出某选手的原始评分，评定该选手的成绩时，从9个原始评分中去掉1个最高分、1个最低分，得到7个有效评分．7个有效评分与9个原始评分相比，发生改变的数字特征是（）A ．中位数B ．平均数C ．方差D ．极差【答案】BCD【解析】根据中位数、平均数、极差、方差各自的含义即可判断.【详解】中位数是将9个数据从小到大或从大到小排列后，处于中间位置的数据，因而去掉1个最高分和1个最低分，不变的是中位数，平均数、方差、极差均受影响．故选:BCD ．【点睛】本题主要考查的是样本估计总体，是基础题.13．某地区经过一年的新农村建设，农村的经济收入增加了一倍，实现翻番．为更好地了解该地区农村的经济收入变化情况，统计了该地区新农村建设前后农村的经济收入构成比例，得到如下饼图：则下面结论中正确的是（）A ．新农村建设后，种植收入减少B ．新农村建设后，其他收入增加了一倍以上C ．新农村建设后，养殖收入增加了一倍D ．新农村建设后，养殖收入与第三产业收入的总和超过了经济收入的一半【答案】BCD【解析】分别算出新农村建设前和新农村建设后,即可的得结论.【详解】设新农村建设前，农村的经济收入为a ，则新农村建设后，农村经济收入为2a ．新农村建设前后，各项收入的对比如下表：新农村建设前新农村建设后新农村建设后变化情况结论种植收入60%a 37%274%a a ⨯=增加A 错其他收入4%a 5%210%a a ⨯=增加一倍以上B 对养殖收入30%a30%260%a a⨯=增加了一倍C 对养殖收入＋第三产业收入(30%6%)36%a a +=(30%28%)2116%a a +⨯=超过经济收入2a 的一半D 对故选:BCD ．【点睛】本题主要考查事件与概率,是基础题.三、填空题14．已知函数()2()log 1f x x =+，若()1f a =，则a 的值为______．【答案】1【解析】根据()1f a =，即可得a 的值.【详解】由题意知()2log 11a +=，∴12a +=，∴1a =．故答案为：1.【点睛】本题主要考查的函数解析式，是基础题.15．某高中共有学生900人，其中高一年级240人，高二年级260人，为做某项调查，拟采用分层抽样法抽取容量为45的样本，则在高三年级抽取的人数是______．【答案】20【解析】试题分析：根据题意，由于高中共有学生900人，采用分层抽样法抽取容量为45的样本，则可知比例为45:900=1:20，则可知各个年级的抽取的人数的比例为1:20，因此可知900-240-260=400为高三的人数，则可抽取的人数为4001=2020⨯，故答案为20。

山东省夏津第一中学2020-2021学年高一下学期5月月考数学试卷 PDF版含答案

则△ABC 的内切圆的半径为
．
16．在正三棱柱 ABC A1B1C1 ，（底面为正三角形的直三棱柱称为正三棱柱）中，棱 AB 2 ，
AA1 2 3 ， D ， F 分别是棱 AB ， AA1 的中点， E 为棱 AC 上的动点，则 DEF 的周长的最小
值为______. 三、解答题
17．一个圆锥的底面半径为 3 cm，它的侧面展开图是一个圆心角为 6 的 5
A．等腰非直角三角形 B．直角非等腰三角形
C．等腰直角三角形
D．等边三角形
3．如图，平行四边形 O'A'B'C'是水平放置的一个平面图形的直观
图，其中 O'A'＝4，O'C'＝2，∠A'O'C'＝30°，则原图形的面积
是（）
A．4
B．4
C．8
D．16
4．半径为 2cm 的半圆纸片卷成圆锥放在桌面上，一阵风吹倒它，它的最高处距桌面（）
该正方体所得截面的面积为( )
D．若 a，b 不同在任何一个平面内，则 a 与 b 是异面直线
A. 2
9 B.8 C. 3
6 D. 2
12．在△ABC 中，角 A，B，C 所对的边分别为 a，b，c，已知（b+c）：（c+a）：（a+b）＝4：5：6，
1/2
下列结论正确的是（）
A．sinA：sinB：sinC＝7：5：3
8．已知△ABC 的内角 A，B，C 所对的边为 a，b，c，其面积为 S，若 sinC＝
，且△ABC
的外接圆半径为，则△ABC 周长的取值范围为（）
A. （4，6] 二、多选题
B．（4，4 ]