小升初几何必考知识点
小升初几何问题总复习

小升初几何问题总复习一、小升初考试热点及命题方向圆和立体几何近两年虽然不是考试热点,但在小升初考试中也会时常露面。
因为立体图形考察学生的空间想象能力,可以反映学生的本身潜能;而另一方面,初中很多知识点都是建立在空间问题上,所以可以说学校考察立体也是为初中选拔知识链接性好的学生。
二、2015年考点预测2015年的小升初考试如果考察圆与立体几何,不会难度太大,只需掌握我们本讲中所介绍的几类基本题型,就可成功在握。
考试热点将会出现在诸如水位问题和三维视图问题等题型。
三、典型例题解析1 与圆和扇形有关的题型【例1】(★★)如下图,等腰直角三角形ABC的腰为10厘米;以A为圆心,EF为圆弧,组成扇形AEF;阴影部分甲与乙的面积相等。
求扇形所在的圆面积。
【解】:等腰三角形的角为45度,则扇形所在圆的面积为扇形面积的8倍。
而扇形面积为等腰三角形面积:S=1/2×10×10=50。
则:圆的面积为400。
【例2】(★★★)草场上有一个长20米、宽10米的关闭着的羊圈,在羊圈的一角用长30米的绳子拴着一只羊(见左下图)。
问:这只羊能够活动的范围有多大?【解】:(此题十分经典)如右上图所示,羊活动的范围可以分为A,B,C三部分,所以羊活动的范围是【例3】(★★)在右图中,两个四分之一圆弧的半径分别是2和4,求两个阴影部分的面积差。
【解】:我们只要看清楚阴影部分如何构成则不难求解。
左边的阴影是大扇形减去小扇形,再扣除一个长方形中的不规则白色部分,而右边的阴影是长方形扣除这块不规则白色部分,那么它们的差应为大扇形减去小扇形,再减去长方形。
则为:π/4×4×4-π/4×2×2-4×2=3×3.14-8=1.42。
【例4】(★★★)如图,ABCD 是正方形,且FA=AD=DE=1,求阴影部分的面积。
(取π=3)【解】:先看总的面积为1/4的圆,加上一个正方形,加上一个等腰直角三角形,然后扣除一个等腰直角三角形,一个1/4圆,一个45度的扇形。
小学生必背几何知识点总结

小学生必背几何知识点总结一、基本概念1. 点、线、面:点是没有长度、宽度和高度的;线是由无限多个点连在一起形成的;面是由无限多条线连在一起形成的。
2. 直线、射线、线段:直线是没有端点的;射线是一个端点发散而出的,另一个方向无限延伸的部分;线段是由两个端点确定的部分。
3. 角:由两条射线的公共端点所围成的图形称为角,公共端点称为角的顶点,两条射线称为角的两边。
4. 三角形:由三条线段所围成的图形称为三角形。
5. 四边形:由四条线段所围成的图形称为四边形。
二、基本图形的性质1. 三角形的内角和:所有内角和为180°。
2. 三角形的外角和:所有外角和为360°。
3. 直角三角形:一个角为90°的三角形称为直角三角形。
4. 等边三角形:三条边相等的三角形称为等边三角形。
5. 等腰三角形:两条边相等的三角形称为等腰三角形。
6. 直线上的角:直线上的两个相邻角互为补角,补角的和为180°。
三、平行线和垂直线1. 平行线:在同一平面内,不相交且方向相同的两条直线称为平行线。
2. 垂直线:在同一平面内,相交且相交角为90°的两条直线称为垂直线。
3. 平行线交叉:平行线交叉时,所得的对应角相等、内错角相加为180°、外错角相加为180°。
4. 垂直线交叉:垂直线交叉时,所得的相邻角相加为180°。
四、长方形、正方形、菱形和梯形1. 长方形:对角线相等、相对边相等且两两平行的四边形称为长方形。
2. 正方形:对角线相等、四个边相等且四个角为90°的四边形称为正方形。
3. 菱形:对角线相等、四个边相等的四边形称为菱形。
4. 梯形:有两边平行的四边形称为梯形。
五、圆的基本性质1. 圆心和半径:圆心是圆的中心点,半径是圆心到圆上任意一点的距离。
2. 圆的周长:圆的周长等于直径乘以π,即C=πd。
3. 圆的面积:圆的面积等于半径平方乘以π,即A=πr²。
小升初几何基础知识点总结

小升初几何基础知识点总结一、点、线、面的基本概念1. 点:点是最基本的几何图形,没有长度、宽度和高度,只有位置,用字母标记。
2. 直线:由无数个相邻的点组成,无限延伸,两点确定一条直线。
3. 线段:是直线的一部分,有固定的长度。
4. 射线:是一个端点和它在同一侧直线上的所有点组成的全体。
二、角的概念和性质1. 角的概念:两条线段共同端点为顶点,分别位于这两条线段的两侧的两条射线组成的图形。
2. 角的度量:用度来表示角的大小,一个圆共360度。
3. 角的种类:锐角、直角、钝角。
4. 角的性质:相邻角、对顶角、、补角、同位角等。
三、平行线和平行四边形1. 平行线:在一个平面内,不相交且在同一方向的直线称为平行线。
2. 平行线的性质:平行线上的平行线,平行线上的平行线等于90度,直线被平行线截断时,对应角相等。
3. 平行四边形:对边平行的四边形,对角相等。
四、三角形1. 三角形:是由三条线段相互连接而成的简单的封闭图形。
2. 三角形的角:内角和为180度,外角等于其对边内角的和。
3. 三角形的性质:等边三角形的三边相等,等腰三角形的两边相等,直角三角形的一个角为90度。
4. 三角形的分类:按边长分为等边三角形、等腰三角形、普通三角形;按角度分为直角三角形、锐角三角形、钝角三角形。
五、四边形1. 四边形:是由四条线段相互连接而成的封闭图形。
2. 四边形的性质:内角和为360度。
3. 四边形的分类:矩形、正方形、平行四边形、菱形、梯形。
六、圆的概念1. 圆:一个平面内到一个固定点的距离恒定为r的所有点的集合。
2. 圆的性质:圆上任意一点到圆心的距离相等。
3. 圆的周长和面积计算公式:周长C = 2πr,面积S = πr²。
总结:以上是小升初几何基础知识点的总结,掌握这些知识点对于学生来说是非常重要的,这也是他们在学习几何课程中的基础。
希望学生能够通过学习,牢固掌握这些知识点,为之后的学习打下坚实基础。
小升初几何高频考点汇总与方法总结(上)

小升初几何高频考点汇总与方法总结(上)几何是小升初数学中的重要内容之一。
掌握几何的高频考点是提高学生成绩的关键。
本文将汇总小升初几何的高频考点,并总结一些解题方法。
1. 直线、线段与射线- 直线:没有端点的线段。
- 线段:由两个端点确定的部分。
- 射线:由一条直线和一个端点组成的部分。
2. 角的基本概念- 锐角:小于90度的角。
- 直角:等于90度的角。
- 钝角:大于90度但小于180度的角。
- 平角:等于180度的角。
3. 三角形- 等边三角形:三条边都相等的三角形。
- 等腰三角形:两条边相等的三角形。
- 直角三角形:有一个90度角的三角形。
4. 平行线和垂直线- 平行线:在同一个平面上,永远不相交的直线。
- 垂直线:相交成直角的两条线。
5. 长方形和正方形- 长方形:四个角都是直角的四边形。
- 正方形:四条边和四个角都相等的四边形。
解题方法总结1. 画图:根据题目条件,画出几何图形,有助于理清思路和找出解题方法。
2. 角的性质:利用角的性质分析题目,包括角的大小关系、角的补角和余角等。
3. 图形分割:将复杂的几何图形分割成简单的几何图形,利用简单图形的性质解题。
4. 度量关系:利用已知条件和角的度量关系求解未知量。
5. 图形相似:利用图形相似的性质,推导出未知量的关系式,求解题目。
以上是小升初几何的高频考点和解题方法的总结,希望能对学生在几何方面的研究和备考有所帮助。
参考资料:- 教材《小学数学》- 教辅资料《小升初数学模拟试卷》注意:以上内容仅为个人总结,不能确认是否完全准确。
如有不妥之处,请以正式教材为准。
小升初奥数几何的五大模型知识点

小升初奥数几何的五大模型知识点让学生体会到数学源于生活、用于生活的同时,更应该让学生体会到数学高于生活,体会到数学可以带动社会的发展,带动生活质量的提高,这样更能激发学生学好数学。
以下是无忧考网整理的相关资料,希望对您有所帮助。
【篇一】等积模型①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比;③夹在一组平行线之间的等积变形,如右图;反之,如果,则可知直线AB平行于CD.④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形);⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.【篇二】鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形.共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.在中,D、E分别是AB、AC上的点如图⑴(或D在BA的延长线上,E在AC上)蝴蝶定理任意四边形中的比例关系(“蝴蝶定理”):①或者②蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.梯形中比例关系(“梯形蝴蝶定理”)【篇三】相似模型(一)金字塔模型(二)沙漏模型所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;⑵相似三角形的面积比等于它们相似比的平方;⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半.相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具.在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.燕尾定理在三角形ABC中,AD,BE,CF相交于同一点O,那么上述定理给出了一个新的转化面积比与线段比的手段,因为和的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三角形中的三角形面积对应底边之间提供互相联系的途径。
小升初平面几何常考五大模型

一、等积变换模型1、等底等高的两个三角形面积相等。
2、两个三角形高相等,面积比等于它们的底之比。
3、两个三角形底相等,面积比等于它的的高之比。
二、共角定理模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等到于对应角(相等角或互补角)两夹边的乘积之比。
三、蝴蝶定理模型(说明:任意四边形与四边形、长方形、梯形,连接对角线所成四部的比例关系是一样的。
)四、相似三角形模型相似三角形:是形状相同,但大小不同的三角形叫相似三角形。
相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比。
相似三角形的面积比等于它们相似比的平方。
五、燕尾定理模型正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,正方形BEFG的边长为4,则△DEK的面积为由题知DC/GP=GC/PK,即DC/(DC-4)=(4+PK)/PK,令DC=a,PK=c,则a=4+c,则S△DEK=a^2+16+c*(4-c)/2+c^2-ac-a(4+a)/2=a^2/2+c^2/2-ac-2a+2c+16=(c+4)^2/2+c^2/2-c( c+4)-2(c+4)+2c+16=16。
1、图17是一个正方形地板砖示意图,在大正方形ABCD中AA1=AA2=BB1=BB2=CC1=CC2=DD1=D D2,中间小正方形 EFGH的面积是16平方厘米,四块蓝色的三角形的面积总和是72平方厘米,那么大正方形ABCD的面积是多少平方厘米?分析与解连AC和BD两条大正方形的对角线,它们相交于O,然后将三角形AOB放在D PC处(如图18和图19)。
已知小正方形EFGH的面积是16平方厘米,所以小正方形EFGH的边长是4厘米。
又知道四个蓝色的三角形的面积总和是72平方厘米,所以两个蓝色三角形的面积是72÷2=36平方厘米,即图19的正方形OCPD中的小正方形的面积是36平方厘米,那么这个正方形的边长就是6厘米。
总集篇-七种典型几何模型【七大考点】-2024年小升初数学(解析版)

总集篇·七种典型几何模型【七大考点】【第一篇】专题解读篇本专题是难点03:总集篇·七种典型几何模型。
本部分内容以七种典型几何模型为主,其中包括一半模型、等高模型、等积变形模型、鸟头模型、蝴蝶模型、相似模型、燕尾模型等,绝大部分考点属于思维拓展内容,考点考题综合性极强,难度极大,建议作为小升初复习难点内容,再根据学生实际水平和总体掌握情况,选择部分考点进行讲解,一共划分为七个考点,欢迎使用。
【第二篇】目录导航篇【考点一】几何模型其一:一半模型 (2)【考点二】几何模型其二:等高模型 (3)【考点三】几何模型其三:等积变形 (7)【考点四】几何模型其四:鸟头模型 (13)【考点五】几何模型其五:蝴蝶模型(风筝模型或任意四边形模型) (16)【考点六】几何模型其六:相似模型 (20)【考点七】几何模型其七:燕尾模型 (24)【第三篇】知识总览篇【第四篇】典型例题篇【考点一】几何模型其一:一半模型。
【方法点拨】对于长方形来说,最简单的一半就是连接对角线,当然通过等积变形还可以得到很多很多一半,最为常见的就是长方形中的一座山的样子的三角形。
【典型例题】如图,在长方形中有3块面积已经给出,求阴影部分的面积是( )。
A.10B.11C.12D.13解析:通过观察图形发现,已知三角形的面积和阴影部分图形的面积没有直接的联系,那不妨换个角度,在这个长方形中有两个长方形一半的三角形,那么这两个三角形的面积相加应该等于长方形面积,但是由于有重叠部分,两个三角形没有占满整个长方形,那么空出来的部分其实就和重叠部分面积相同,即重叠等于未覆盖。
阴影面积=5+3+4=12,选C。
【对应练习】如图所示,长方形ABCD中,三角形APD的面积是25,三角形BQC的面积为35,则阴影部分面积为多少?【考点二】几何模型其二:等高模型。
【方法点拨】三角形面积的计算公式是三角形面积=底×高÷2。
从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积。
小升初六年级奥数——几何(平面图形)

一、分数百分数问题,比和比例这是六年级的重点内容,在历年各个学校测试中所占比例超级高,重点应该把握好以下内容:对单位1的正确明白得,明白甲比乙多百分之几和乙比甲少百分之几的区别;求单位1的正确方式,用具体的量去除以对应的分率,找到对应关系是重点;分数比和整数比的转化,了解正比和反比关系;通过对“份数”的明白得结合比例解决和倍(按比例分派)和差倍问题;二、行程问题应用题里最重要的内容,因为综合考察了学生比例,方程的运用和分析复杂问题的能力,因此常常作为压轴题显现,重点应该把握以下内容:路程速度时刻三个量之间的比例关系,即当路程一按时,速度与时刻成反比;速度一按时,路程与时刻成正比;时刻一按时,速度与路程成正比。
专门需要强调的是在很多题目中必然要先去找到那个“必然”的量;当三个量均不相等时,学会通过其中两个量的比例关系求第三个量的比;学会用比例的方式分析解决一样的行程问题;有了以上基础,进一步增强多次相遇追及问题及火车过桥流水行船等特殊行程问题的明白得,重点是学会如何去分析一个复杂的题目,而不是一味的做题;三、几何问题几何问题是各个学校考察的重点内容,分为平面几何和立体几何两大块,具体的平面几何里分为直线形问题和圆与扇形;立体几何里分为表面积和体积两大部份内容。
学生应重点把握以下内容:等积变换及面积中比例的应用;与圆和扇形的周长面积相关的几何问题,处置不规那么图形问题的相关方式;立体图形面积:染色问题、切面问题、投影法、切挖问题;立体图形体积:简单体积求解、体积变换、浸泡问题;四、数论问题常考内容,而且能够应用于策略问题,数字谜问题,计算问题等其他专题中,相当重要,应重点把握以下内容:把握被特殊整数整除的性质,如数字和能被9整除的整数必然是9的倍数等;最好了解其中的道理,因为那个方式能够用在许多题目中,包括一些数字谜问题;把握约数倍数的性质,会用分解质因数法,短除法,辗转相除法求两个数的最大公因数和最小公倍数;学会求约数个数的方式,为了提高灵活运用的能力,需了解那个方式的原理;了解同余的概念,学会把余数问题转化成整除问题,下面的那个性质是超级有效的:两个数被第三个数去除,若是所得的余数相同,那么这两个数的差就能够被那个数整除;能够解决求一个多位数除以一个较小的自然数所得的余数问题,例如求1011121314…9899除以11的余数,和求20202020除以13的余数这种问题;五、计算问题计算问题通常在前几个题目中显现概率较高,要紧考察两个方面,一个是大体的四那么运算能力,同时,一些速算巧算及裂项换元等技术也常常成为考察的重点。
小升初平面几何常考五大模型知识分享

一、等积变换模型1、等底等高的两个三角形面积相等。
2、两个三角形高相等,面积比等于它们的底之比。
3、两个三角形底相等,面积比等于它的的高之比。
二、共角定理模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等到于对应角(相等角或互补角)两夹边的乘积之比。
三、蝴蝶定理模型(说明:任意四边形与四边形、长方形、梯形,连接对角线所成四部的比例关系是一样的。
)四、相似三角形模型相似三角形:是形状相同,但大小不同的三角形叫相似三角形。
相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比。
相似三角形的面积比等于它们相似比的平方。
五、燕尾定理模型正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,正方形BEFG的边长为4,则△DEK的面积为由题知DC/GP=GC/PK,即DC/(DC-4)=(4+PK)/PK,令DC=a,PK=c,则a=4+c,则S△DEK=a^2+16+c*(4-c)/2+c^2-ac-a(4+a)/2=a^2/2+c^2/2-ac-2a+2c+16=(c+4)^2/2+c^2/2 -c(c+4)-2(c+4)+2c+16=16。
1、图17是一个正方形地板砖示意图,在大正方形ABCD中AA1=AA2=BB1=BB2=CC1=CC2=DD1=D D2,中间小正方形 EFGH的面积是16平方厘米,四块蓝色的三角形的面积总和是72平方厘米,那么大正方形ABCD的面积是多少平方厘米?分析与解连AC和BD两条大正方形的对角线,它们相交于O,然后将三角形AOB放在D PC处(如图18和图19)。
已知小正方形EFGH的面积是16平方厘米,所以小正方形EFGH的边长是4厘米。
又知道四个蓝色的三角形的面积总和是72平方厘米,所以两个蓝色三角形的面积是72÷2=36平方厘米,即图19的正方形OCPD中的小正方形的面积是36平方厘米,那么这个正方形的边长就是6厘米。
小升初数学几何归纳知识点

小升初数学几何概括知识点
为大家供给了小升初数学几何概括知识点,供大家复习
备考使用。
(1)平面图形知识 ;(2) 平面图形的周长和面积 ;(3) 立体图形的认识 ;(4) 立体图形的表面积和体积。
(1)平面图形知识
①直线、射线、线段的特色、联系与差别。
②角的特色、角的分类、角的胸怀方法。
③垂直与平行。
④三角形的特色,分类 ( 按边分、按角分 ) 。
⑤四边形。
每
类图形的特色,特别与一般的关系。
⑥圆与扇形。
圆的特
色、直径、半径的特色,扇形与圆的关系。
⑦轴对称图形。
( 能画出学过的轴对称图形的对称轴)
要求:①掌握特色、成立联系,让学生感觉到点到线,线到面、面到体的联系。
②能依据图形特色进行合理的判断、选择。
(2)平面图形的周长和面积①理解周长与面积观点。
②掌握每种图形的周长与面积计算公式及推导过程。
③能应用公式灵巧解决问题。
①长方体、正方体、圆
柱、圆锥的特色。
②长、正方体的关系。
(3)立体图形的表面积和体积
②会求长方体、正方体、圆柱的表面积和体积 ; 圆锥的体积。
③成立这四种立体图形体积计算的联系。
④增强体积与表面积的差别、体积与容积的区其他对照训
练。
以上就是为大家供给的小升初数学几何概括知识点,希望能
够对大家实用,更多有关内容,请大家实时锁定!。
小升初数学总复习精讲精练7:立体几何的认识及表面积、体积和容积 精讲精练(含答案解析)

小升初数学总复习专题汇编精讲精练专题19 立体几何的认识及表面积和体积(一)(一)长方体1、特征六个面都是长方形(有时有两个相对的面是正方形)。
相对的面面积相等,12条棱相对的4条棱长度相等。
有8个顶点。
相交于一个顶点的三条棱的长度分别叫做长、宽、高。
两个面相交的边叫做棱。
三条棱相交的点叫做顶点。
把长方体放在桌面上,最多只能看到三个面。
长方体或者正方体6个面的总面积,叫做它的表面积。
2、计算公式:s=2(ab+ah+bh) V=sh V=abh(二)正方体1、特征六个面都是正方形六个面的面积相等12条棱,棱长都相等有8个顶点正方体可以看作特殊的长方体2、计算公式:S表=6a² v=a³(三)圆柱1、圆柱的认识圆柱的上下两个面叫做底面。
圆柱有一个曲面叫做侧面。
圆柱两个底面之间的距离叫做高。
进一法:实际中,使用的材料都要比计算的结果多一些,因此,要保留数的时候,省略的位上的是4或者比4小,都要向前一位进1。
这种取近似值的方法叫做进一法。
2、计算公式:s侧=ch s表=s侧+s底×2 v=sh/3(四)圆锥1、圆锥的认识圆锥的底面是个圆,圆锥的侧面是个曲面。
从圆锥的顶点到底面圆心的距离是圆锥的高。
测量圆锥的高:先把圆锥的底面放平,用一块平板水平地放在圆锥的顶点上面,竖直地量出平板和底面之间的距离。
把圆锥的侧面展开得到一个扇形。
2、计算公式:v= sh/3(五)球1、认识球的表面是一个曲面,这个曲面叫做球面。
球和圆类似,也有一个球心,用O表示。
从球心到球面上任意一点的线段叫做球的半径,用r表示,每条半径都相等。
通过球心并且两端都在球面上的线段,叫做球的直径,用d表示,每条直径都相等,直径的长度等于半径的2倍,即d=2r。
2、计算公式:d=2r四、周长和面积1、平面图形一周的长度叫做周长。
2、平面图形或物体表面的大小叫做面积。
3、常见图形的周长和面积计算公式一.长方体和正方体的表面积【例3】(龙州县期末)求长方体的占地面积就是长方体的()A.表面积B.体积C.底面积D.侧面积【解答】解:要求一个长方体的是求这个长方体的底面积.故选:C.【变式3-1】(南山区期末)正方体的棱长扩大到原来的2倍,表面积扩大到原来的4倍,体积扩大到原来的()倍.A.2B.4C.6D.8【解答】解:一个正方体棱长扩大2倍,则体积扩大2228⨯⨯=倍.答:体积扩大到原来的8倍.故选:D.【变式3-2】(合肥期末)一个长方体木块长6厘米,宽4厘米,高2厘米.如果把它切成两个相同的小长方体,表面积比原来最少增加16平方厘米,最多增加平方厘米.⨯⨯=(平方厘米)【解答】解:42216⨯⨯=(平方厘米)64248答:表面积比原来最少增加16平方厘米,最多增加48平方厘米.故答案为:16、48.【变式3-3】(黄冈期末)一个长方体的纸抽盒,在它的上面有一个长方形口(如图),这个纸抽盒的表面积是多少平方厘米?⨯+⨯+⨯⨯-⨯【解答】解:(2413247137)2142=++⨯-(31216891)228=⨯-571228=-114228=(平方厘米)1114答:这个纸抽盒的表面积是1114平方厘米.【变式3-4】(武汉月考)在一个长、宽、高分别是10厘米、8厘米、5厘米的长方体的8个顶点处,分别截下一个棱长1厘米的正方体后,剩下物体的表面积是多少平方厘米?体积是多少立方厘米?⨯+⨯+⨯⨯【解答】解:(10810585)2=++⨯(805040)2=⨯1702=(平方厘米);340⨯⨯-⨯⨯⨯10851118=-4008=(立方厘米),392答:剩下物体的表面积是340平方厘米,体积是392立方厘米.二.长方体和正方体的体积【例2】(肥城市期末)把一个棱长是2分米的正方体木块放入一个长12分米、宽9分米、高8分米的长方体盒子里面,最多能放()个正方体木块.A.90B.96C.108【解答】解:1226÷=(个)⋯(分米)924÷=(排)1÷=(层)824⨯⨯=(个)64496答:最多能放96个正方体木块.故选:B.【变式2-1】(鹿邑县期末)用混凝土铺一段长为80米、宽为15米的路面,混凝土厚为25厘米.一辆运料车每次最多运6立方米的混凝土,这辆运料车至少运()次才能完成任务.A.5000B.200C.50=米【解答】解:25厘米0.25⨯⨯÷80150.256=⨯÷12000.256=÷3006=(次)50答:这辆运料车至少运50次才能完成任务.故选:C.【变式2-2】(龙州县期末)一个商品盒是正方体形状,棱长为6厘米,这个商品盒的体积是216立方厘米,在这个盒的四周贴上商标,贴商标的面积是平方厘米.⨯⨯=(立方厘米)【解答】解:666216⨯⨯=(平方厘米)664144答:这个商品盒的体积是216立方厘米,贴商标的面积是144平方厘米.故答案为:216;144.【变式2-3】(环江县期中)一个长方体如果高缩短3cm就变成一个正方体,这时体积比原来缩小375cm,原长方体的体积是多少立方厘米?÷=(平方厘米)【解答】解:75325因为5的平方是25,所以原来长方体的底面边长是5厘米,25(53)⨯+258=⨯200=(立方厘米)答:原来长方体的体积是200立方厘米.【变式2-4】(蒙城县期末)一根2.5米长的长方体木料,把它截成3段后,表面积增加了264dm ,这根木料的体积是多少立方米?【解答】解:64平方分米964=平方米,0.644 2.5÷⨯0.16 2.5=⨯0.4=(立方米),答:这根木料的体积是0.4立方米. 二. 圆柱的侧面积、表面积和体积【例3】(环江县期中)用一张长6.28cm ,宽1dm 的长方形铁皮,围成一个圆柱体,这个圆柱的侧面积是( )A .231.4cmB .3.14 2mC .212.56cmD .262.8cm【解答】解:110dm cm =6.281062.8⨯=(平方厘米)答:这个圆柱的侧面积是62.8平方厘米.故选:D .【变式3-1】(黄冈期末)一个底面内半径是3cm 的瓶子装了一些水,把瓶盖拧紧并倒放时水的高度见图①,正放时水的高度见图②,则瓶内水的体积是( 3)cm .A .54πB .90πC .60πD .36π【解答】解:236π⨯⨯ 96π=⨯⨯354()cm π=答:瓶内水的体积是354cm π.故选:A . 【变式3-2】.(黄冈期中)如图,把一个体积是3360cm 的圆柱形木料削成一个陀螺,陀螺的体积为 240 3cm .【解答】解:33602180()cm ÷=1801803+÷18060=+3240()cm =答:陀螺的体积为3240cm .故答案为:240. 【变式3-3】把一个底面积为125.6平方厘米,高18厘米的圆锥体铝锭熔铸成一个长10厘米,宽8厘米的长方体,这个长方体的高是多少厘米?【解答】解:1125.618(108)3⨯⨯÷⨯753.680=÷9.42=(厘米),答:这个长方体的高是9.42厘米.【变式3-4】(•防城港模拟)已知一个内直径是8cm 的饮料瓶内还剩饮料的高度是6cm ,要解决“这个瓶子的容积是多少”这个问题,可以怎么解决?把你想到的办法表达清楚,不必解答.【解答】解:把瓶盖拧紧倒置放平,无饮料部分为圆柱体,根据瓶子的容积=无饮料部分圆柱的体积+饮料部分圆柱体体积计算,其中需要测量的是无饮料部分圆柱的高度,底面直径已知,由圆柱体积=底面积⨯高,即可求出瓶子的容积.真题强化演练一.选择题94.2cm.这个圆柱体积减少( 1.(杭州)一个圆柱体,如果把它的高截短3cm,它的表面积减少23)cm.A.30B.31.4C.235.5D.94.2【解答】解:半径:94.2(2 3.14)3÷⨯÷=÷÷94.2 6.283153=÷=(厘米)5体积:94.252⨯÷=÷4712=(立方厘米)235.5答:这个圆柱体积减少235.5立方厘米.故选:C.2.(桂林)下面三个结论,不正确的是()A.棱长相等的两个正方体,体积一定相等B.周长相等的两个长方形,面积一定相等C.周长相等的两个正方形,面积一定相等D.表面积相等的两个长方体,体积不一定相等【解答】解:A.如果两个正方体的棱长总和相等,那么两个正方体的棱长一定相等,则体积一定相等.B.可以举例证明,当长方形的周长是24厘米时:一种长是10厘米,宽是2厘米,面积是20平方厘米;另一种长是8厘米,宽是4厘米,面积是32平方厘米;很显然20平方厘米不等于32平方厘米.所以说周长相等的两个长方形,面积也一定相等,这种说法是错误的.C.正方形的周长=边长4⨯;因为周长相等,所以边长也相等.边长⨯边长=面积,所以它们的面积也一定相等.D.如长宽高分别为2,4,6的长方体表面积为88,体积为48;长宽高分别为2,2,10的长方体表面积为88,体积为40.故表面积相等的两个长方体,它们的体积不一定相等,题干的说法是正确的.故选:B.3.(邹平县)做一个铁皮烟囱需要多少铁皮,就是求烟囱的()A.表面积B.体积C.侧面积【解答】解:因为,烟囱是通风的,是没有上下两个底的,所以,做一个铁皮烟囱需要多少铁皮,就是求烟囱的侧面积,故选:C.4.(•萧山区模拟)把一个圆柱形木头截成相等的三段,表面积()A.不变B.增加2个底面C.增加3个底面D.增加4个底面【解答】解:把一个圆柱形木头截成相等的三段,需要截2次,共增加底面:224⨯=(个).故选:D.5.(•萧山区模拟)把一个体积为9.42立方分米的圆锥放入底面半径为4分米的圆柱形装水容器中(水浸没且无溢出),水面上升了多少分米,列式正确的是()A.9.423(3.1444)÷÷⨯⨯B.9.42(3.1444)÷⨯⨯C.9.423(3.1444)⨯÷⨯⨯D.9.429(3.1444)⨯÷⨯⨯【解答】解:2) 9.42(3.144÷⨯9.4250.24=÷0.1875=(分米)答:水面上升了0.1875分米.故选:B .6.(宁波模拟)甲、乙两个正方体棱长之比是1:3,则甲、乙两个正方体的( )A .棱长总和的比是1:3B .底面积之比是1:3C .表面积之比是1:6D .体积之比是1:9 【解答】解:因为甲、乙两个正方体棱长之比是1:3,所以A 、棱长总和的比是(112):(312)1:3⨯⨯=,故选项正确; B 、底面积之比是(11):(33)1:9⨯⨯=,故选项错误; C 、表面积之比是(116):(336)1:9⨯⨯⨯⨯=,故选项错误; D 、体积之比是(111):(333)1:27⨯⨯⨯⨯=,故选项错误. 故选:A .二.填空题7.(•鄞州区)把一个圆柱体木料横切成两个圆柱(图1),表面积增加了25.122cm ,纵切成两个半圆柱(图2),则表面积增加了248cm ,原来这个圆柱的体积是 75.36 3cm .【解答】解:圆柱的底面积:25.12212.56÷=(平方厘米), 底面半径的平方:12.56 3.144÷=,因为2的平方是4,所以圆柱的底面半径是2厘米, 圆柱的高:482(22)÷÷⨯244=÷6=(厘米)体积:23.1426⨯⨯3.1446=⨯⨯75.36=(立方厘米)答:这个圆柱的体积是75.36立方厘米.故答案为:75.36.8.(•宁波)一段圆柱形木料,如果截成两段,表面积增加6平方分米;如果沿直径切开,表面积增加8平方分米,这个圆柱的表面积是 15 平方分米.(3)π≈【解答】解:圆柱的底面积是:623÷=(平方分米)331÷=(分米)即半径的平方是1,111⨯=,所以半径1r =分米圆柱的高是:82(12)÷÷⨯42=÷2=(分米)圆柱的表面积:31223⨯⨯⨯+123=+15=(平方分米)答:这段木料的表面积是15平方分米.故答案为:15.9.(•衢州)如图所示,把一个高是5厘米的圆柱切成若干等份,拼成一个近似的长方体.拼成后的长方体的表面积比原来圆柱体的表面积增加了230cm .原来圆柱的侧面积是 30π 平方厘米,拼成后的近似长方体的体积是 立方厘米.(结果保留)π【解答】解:底面半径为:30253÷÷=(厘米)侧面积为:325π⨯⨯⨯30π=⨯30π=(平方厘米)体积为:235π⨯⨯45π=⨯45π=(立方厘米)答:原来圆柱的侧面积是30π平方厘米,拼成后的近似长方体的体积是45π立方厘米.故答案为:30π;45π;10.(•杭州模拟)一个正方体的体积是327m ,它的棱长是 3 m ,表面积是 2m .【解答】解:因为:3327a m =所以:3a m =;336⨯⨯96=⨯254()m =答:它的棱长是3m ,表面积是254m .故答案为:3,54.11.(•萧山区模拟)一个长方体的长宽高分别为8cm ,4cm ,4cm ,把它分成两个棱长为4cm 的正方体,总表面积比原来 增加 (填“增加”或“减少” )了 2cm .【解答】解:442⨯⨯162=⨯ 32=(平方厘米),答:总面积比原来增加了32平方厘米.故答案为:增加,32.12.(•萧山区模拟)一个长方体,若将它的长增加4cm ,则体积增加380cm ;若将它的宽增加4cm ,则体积增加3128cm ;若将它的高增加3cm ,则体积增加3120cm .原长方体的体积是 160 3cm ,表面积是 2cm .【解答】解:80420÷=(平方厘米)128432÷=(平方厘米)120340÷=(平方厘米)表面积:(203240)2++⨯922=⨯184=(平方厘米)体积:2()203240abh =⨯⨯ 2()25600abh =所以:160abh =(立方厘米)答:原来长方体的体积是160立方厘米,表面积是184平方厘米.故答案为:160、184.三.判断题13.(•临汾)棱长是6厘米的正方体,表面积和体积相等. ⨯ .(判断对错)【解答】解:因为正方体的表面积和体积单位不相同,没法比较它们的大小,所以原题说法是错误的.故答案为:⨯.14.(•海曙区)把一个棱长是a 厘米的正方体任意截成两个长方体,这两个长方体表面积之和是26a 平方厘米. ⨯ (判断对错)【解答】解:262a a a ⨯+⨯⨯2262a a =+28a =故答案为:⨯.15.(•萧山区模拟)当圆柱的底面直径和高都是5厘米时,圆柱的侧面展开图是一个正方形. ⨯ (判断对错)【解答】解:因为把圆柱体的侧面沿高剪开,得到一个长方形,这个长方形的长是圆柱的底面周长,长方形的宽是圆柱的高,如果得到的是正方形,这就说明圆柱的底面周长与高相等;所以题干说法错误.故答案为:⨯.16.(•山丹县模拟)圆柱体的高扩大2倍,侧面积就扩大2倍. ⨯ .(判断对错)【解答】解:圆柱的侧面积是由它的底面周长和高两个条件决定的,它的高扩大2倍,底面周长是否不变没有确定,如果底面周长不变,侧面积就扩大2倍,如果高扩大2倍底面周长缩小2倍,那么侧面积就不变,由此得此:圆柱体的高扩大2倍,侧面积就扩大2倍,这种说法是错误的. 故答案为:⨯.17.(鹤岗期末)表面积相等的两个圆柱,它们的体积也一定相等. 错误 .(判断对错)【解答】解:比如,第一个圆柱体的底半径是12r =,高是110h =,表面积212 3.14210 3.1422S =⨯⨯⨯+⨯⨯,12.561012.562=⨯+⨯,125.625.12=+,150.7=;第二个圆柱的底半径是24r =,高22h =,表面积222 3.1442 3.1442S =⨯⨯⨯+⨯⨯, 25.122 3.14162=⨯+⨯⨯,50.24100.48=+,150.72=;显然12S S =;21 3.14210V =⨯⨯,3.14410=⨯⨯,125.6=;22 3.1442V =⨯⨯,3.14162=⨯⨯,100.48=;但是12V V ≠;所以表面积相等的两个圆柱,它们的体积也一定相等.此说法错误.故答案为:错误.四.应用题18.(•益阳模拟)如下图所示,把底面直径为8厘米的圆柱切成若干等份,拼成一个近似的长方体.这个长方体的表面积比原来增加80平方厘米,那么圆柱的体积是多少立方厘米?【解答】解:底面半径:824÷=(厘米)圆柱的高:802410÷÷=(厘米)圆柱体积(长方体体积):23.14410⨯⨯3.141610=⨯⨯502.4=(立方厘米)答:圆柱的体积是502.4立方厘米.19.(•益阳模拟)一个高是15厘米的圆柱,如果它的高增加2厘米,那么它的表面积就增加125.6平方厘米,原来这个圆柱的体积是多少立方厘米?【解答】解:125.6262.8÷=(厘米)23.14(62.8 3.142)15⨯÷÷⨯23.141015=⨯⨯3.1410015=⨯⨯31415=⨯4710=(立方厘米)答:原来这个圆柱的体积是4710立方厘米.20.(•萧山区模拟)一个圆柱形容器中装有水,先把一个棱长为6cm的正方体铁块浸没在水中,水面上升了5cm.再把一个圆锥形铅锤浸没在水中,水面又上升了3cm.这个铅锤的体积是多少?(浸没过程中水均没有溢出)【解答】解:设圆锥的体积为x立方厘米,则(666):5:3x⨯⨯=5648x=129.6x=答:圆锥的体积为129.6立方厘米.21.(•萧山区模拟)如右图,在一个装有部分水的圆柱形玻璃缸中,放入一个铁块,结果溢出了26毫升的水.这个铁块的体积是多少?【解答】解:23.14(102)826⨯÷⨯+3.1425826=⨯⨯+62826=+654=(立方厘米)答:这个铁块的体积是654立方厘米.五.解答题22.(•杭州)有半径分别是6cm 和8cm ,深度相等的圆柱形容器甲和乙,把容器甲装满水倒入容器乙中,水深比容器的34低1cm ,求容器的深.【解答】解:设容器的高为h ,22368(1)4h h ππ⨯=⨯⨯-,两边同时除以π,33664(1)4h h =⨯-,364864h h =-,1264h =,12126412h ÷=÷,163h =. 答:容器的高是163厘米.23.(•桂林)一个长方体水箱,从里面量它的长是1.2dm ,宽是4dm ,高是8dm ,这个水箱最多能装水多少升?【解答】解:1.248⨯⨯,4.88=⨯,38.4=(立方分米),38.4立方分米38.4=升;答:这个水箱最多能装水38.4升.24.(•文成县)一个瓶子内直径8厘米,装入10厘米高的水后,盖好瓶子倒过来(如图),量得空余部分的高是2.5厘米,求这个瓶子的容积是多少毫升?【解答】解:根据题意可知,第二个图上部空白部分的高为2.5cm ,水的高度是10cm ,瓶子的容积实际是内直径8厘米、高是(10 2.5)+厘米的圆柱的体积,所以瓶子的容积:23.14(82)(2.510)⨯÷⨯+,3.141612.5=⨯⨯,3628()cm =,628=(毫升);答:瓶子的容积为628毫升.25.(•湘潭模拟)把一个底面半径是4厘米,高是6分米的铁制圆锥体放入盛满水的桶里,将有多少立方厘米的水溢出?【解答】解:660dm cm =213.144603⨯⨯⨯13.1416603=⨯⨯⨯150.24603=⨯⨯50.2420=⨯ 31004.8()cm =答:将有1004.8立方厘米的水溢出.26.(•杭州模拟)一个圆柱形水池,底面半径3米,池高1.5米,这个水池最多可盛水多少吨?(1立方米的水重1吨)【解答】解:水池的容积(水的体积)2:3.143 1.542.39⨯⨯=(立方米),水的吨数:42.39142.39⨯=(吨).答:这个水池最多可盛水42.39吨.27.(•杭州模拟)小明把一块橡皮泥揉成圆柱形,切成三块(如图),表面积增加了50.24平方厘米,切成四块(如图),表面积增加了96平方厘米,这块橡皮泥的体积是多少立方厘米?【解答】解:根据题意得250.24412.56()cm ÷=50.244 3.14÷÷12.56 3.14=÷2=4()cm=⨯422所以半径是2厘米.÷÷9682=÷122=(厘米)6⨯=(立方厘米)12.56675.36答:这块橡皮泥的体积是75.36立方厘米.小升初数学总复习专题汇编精讲精练专题20 立体几何的体积和容积(二)(一)长方体1、特征六个面都是长方形(有时有两个相对的面是正方形)。
小升初数学专项突破(五)几何初步知识

小升初数学专项突破(五)几何初步知识一、基本概念1、基本概念几何学:是数学的一门分科,研究物体的形状、大小和相互位置。
几何图形:由若干个点、线、面、体组合在一起,叫做几何图形。
包括平面图形和立体图形。
平面图形:图形上的所有的点在一个平面内。
如:平行四边形、长方形、正方形、梯形、三角形、圆形。
立体图形:图形上的所有的点不全在一个平面内。
如:长方体、正方体、圆柱、圆锥、球。
2、线(1)、直线:性质:①经过一点,可以画无数条直线;②经过两点,只能画一条直线;③两条直线相交,只有一个交点;④直线没有端点,可以向两个方向无限延伸,不能度量。
表示方法:①直线上任意两点的大写字母表示,如直线AB;②用一个小写字母表示,如直线a。
(2)、射线:只有一个端点,以端点为界,只能向一方无限延伸,也不能度量。
表示方法:用表示端点和射线上另外一点的两个大写字母表示,并且把表示端点的字母写在前面,如射线AB,A是端点。
(3)、线段:直线上两点之间的一段叫做线段。
这两点叫做线段的端点。
性质:线段是直线的一部分,有长短,可度量。
在连结两点的所有线中,线段最短。
表示方法:①用表示它的两个端点的大写字母来表示,如线段AB;②用一个小写字母表示,如线段a。
(4)、两点间的距离:连结两点之间的线段的长度,叫做两点间的距离,简称距离。
例如,A、B两点间的距离,就是线段AB的长度。
(5)、垂直和垂线:如果两条直线相交成直角,那么这两条直线互相垂直。
其中一条直线是另一条直线的垂线,它们的交点叫做垂足。
垂直符号用“⊥”表示。
如图。
两条直线相交不成直角时,其中的一条叫做另一条的斜线。
点到直线的距离:从直线外一点到这条直线所画垂线段的长度。
垂线的性质:①过直线上或直线外一点,有且只有一条直线和已知直线垂直。
②从直线外一点到这条直线上各点所连的线段中,垂线段最短。
(6)、平行线:在同一平面内不相交的两条直线叫做平行线。
两条直线互相平行,从一条直线上的任意一点向另一条直线引垂线,所得的平行线间的垂直线段的长度,叫做这两条平行线的距离。
小升初几何知识点梳理总结

小升初几何知识点梳理总结1线、角1直线没有端点,没有长度,可以无限延伸。
2射线只有一个端点,没有长度,射线可以无限延伸,并且射线有方向。
3在一条直线上的一个点可以引出两条射线。
4线段有两个端点,可以测量长度。
圆的半径、直径都是线段。
5角的两边是射线,角的大小与射线的长度没有关系,而是跟角的两边叉开的大小有关,叉得越大角就越大。
6几个易错的角边关系:(1)平角的两边是射线,平角不是直线。
(2)三角形、四边形中的角的两边是线段。
(3)圆心角的两边是线段。
7两条直线相交成直角时,这两条直线叫做互相垂直。
其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足。
8从直线外一点到这条直线所画的垂直线段的长度叫做点到直线的距离。
9在同一个平面上不相交的两条直线叫做平行线。
2三角形1任何三角形内角和都是180度。
2三角形具有稳定的特性,三角形两边之和大于第三边,三角形两边之差小于第三边。
3任何三角形都有三条高。
4直角三角形两个锐角的和是90度。
5两个三角形等底等高,则它们面积相等。
6面积相等的两个三角形,形状不一定相同。
3正方形面积1.正方形面积:边长×边长2.正方形面积:两条对角线长度的积÷24三角形、四边形的关系1两个完全一样的三角形能组成一个平行四边形。
2两个完全一样的直角三角形能组成一个长方形。
3两个完全一样的等腰直角三角形能组成一个正方形。
4两个完全一样的梯形能组成一个平行四边形。
5圆把一个圆割成一个近似的长方形,割拼成的长方形的长相当于圆周长的一半,宽相当于圆的半径。
则长方形的面积等于圆的面积,长方形的周长比圆的周长增加r×2。
半圆的周长等于圆的周长的一半加直径。
半圆的周长公式:C=pd¸2+d或C=pr+2r在同一个圆里,半径扩大或缩小多少倍,直径和周长也扩大或缩小相同的倍数。
而面积扩大或缩小以上倍数的平方倍。
6圆柱、圆锥把圆柱的侧面展开,得到一个长方形,这个长方形的长等于圆柱的底面的周长,宽等于圆柱的高。
小升初几何专业知识点总结

小升初几何专业知识点总结一、直线1、直线的定义:不含端点的完全由无数个点构成的一条路径。
2、直线上的点:直线可以由无数个点构成,其中任意两个点可以确定一条直线。
3、直线的性质:(1) 一条直线上的任意两点都可以确定一条唯一的直线。
(2) 两条直线要么相交于一点,要么平行,要么重合。
4、直线的表示方法:直线可以用两点确定,也可以用方程的形式表示。
5、直线的倾斜角:直线与水平线之间的夹角称为直线的倾斜角。
6、直线的斜率:直线的斜率可以表示为△y/△x 或者(y₂ - y₁)/(x₂ - x₁),表示直线的倾斜程度。
7、直线的方程:直线的方程可以表示为y = kx + b的形式,其中k为斜率,b为截距。
二、角1、角的定义:两条线段α和β共有一个端点A,并且α和β没有任何公共内点,则称α和β构成一个角,记为∠AOB。
2、角的度量:(1) 角的度量可以用角度来表示,1度= π/180弧度。
(2) 角的度量也可以用弧度来表示,一个弧长等于半径长的弧所对应的角称为1弧度。
3、角的种类:(1) 锐角:角的度数小于90°。
(2) 直角:角的度数等于90°。
(3) 钝角:角的度数大于90°。
4、角的性质:(1) 对顶角:两条交叉的直线AB和CD上的对顶角互为相等。
(2) 同位角:两条平行直线上的同位角互为相等。
(3) 内角和:平行线的两气相交内角和为180°。
5、角的平分线:将一个角平分为两个角,使得这两个角的度数分别为原来角的一半,称这条线为角的平分线。
6、垂直角:两条相交直线的两个相邻角,称为垂直角,垂直角相等。
三、多边形1、多边形的定义:是一个由三条或者三条以上的线段组成的简单闭合图形。
2、多边形的种类:(1) 三角形:三条边和三个角。
(2) 四边形:四条边和四个角。
(3) 五边形:五条边和五个角。
(4) 六边形:六条边和六个角。
3、多边形的性质:(1) 内角和:多边形的内角和为180°。
苏教版六年级数学小升初专题复习五几何初步知识
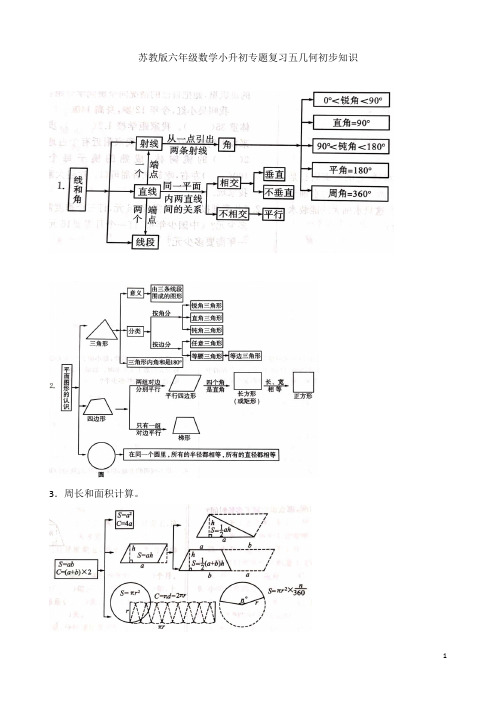
苏教版六年级数学小升初专题复习五几何初步知识3.周长和面积计算。
4.立体图形一、定义1.线段:用直尺把两点连接起来,就得到一条线段,线段长就是这两点间的距离。
两点间所有连线中线段最短。
2.射线:把线段的一端无限延长,可以得到条射线。
手电筒发出的光、太阳射出的光线都可看成是射线。
3.直线:把线段的两端无限延长,可以得到一条直线。
二、直线、线段、射线的比较名称三、同一平面上线与线的关系同一平面上的两条直线或平行或相交。
1.垂线:两条直线相交成直角时,这两条直线叫作互相垂直,其中一条直线叫作另一条直线的垂线,这两条直线的交点叫作垂足。
2.平行线:在同一平面内不相交的两条直线叫作平行线。
(1)平行线之间的距离处处相等;(2)平行线间垂线段最短,并且有无数条;(3)垂直于同一条直线的两条直线互相平行。
3.点到直线的连线中,垂线段最短4.线段AB的垂直平分线上的任意一点到线段两端的连线相等。
一、角的分类角:从一点起画两条射线,所组成的图形叫作角。
角两边叉开得越大,角越大;角的大小与角两边的长短无关。
二、角的测量利用量角器可以画角或量出角的度数。
首先将量角器的中心与角的顶点重合,然后再将量角器的零刻度线与角的一边重合,另一条边所对准的刻度就是这个角的度数。
注意要分清是内刻度线还是外刻度线。
三、画角画角的方法有很多,我们应该学会用量角器画指定大小的角。
画角时,首先要确定角的顶点,并画出角的一条边,然后将量角器的中心和零刻度线与角的顶点和画好的一条边都分别重合,数出量角器上所画角的度数,做好标记,然后连接顶点和标记,这样就画好了一个指定度数的角。
要注意美观。
形一、平行四边形和梯形(四边形)圆定义:两组对边分别平行的四边形叫作平行四边形。
只有一组对边平行的四边形叫作梯形。
二、三角形(由三条线段围成的图形)1.按角分2.按边分3.等腰三角形的特征和性质两腰相等,两底角相等,底边上的高是底边的垂直平分线。
4.等边三角形的特征和性质,5.三角形的一些特征和性质 (1)三角形具有稳定性; (2)三角形内角和是180º(3)三角形中任意两边之和大于第三边(4)在三角形中大角所对的边也大;在直角三角形中,斜边最长 (5)在等腰直角三角形中,斜边上的高等于斜边的一半三、圆(封闭的曲线图形) 1.圆的各部分名称在同一个圆内,有无数条直径和半径,所有的直径都相等,所有的半径都相等。
小升初复习重难点一几何五大模型

小升初复习重难点一几何五大模型几何五大模型一、五大模型简介(1)等积变换模型1、等底等高的两个三角形面积相等;2、两个三角形高相等,面积之比等于底之比,如图①所示,S[sub]1[/sub]:S[sub]2[/sub]=a:b;3、两个三角形底相等,面积在之比等于高之比,如图②所示,S[sub]1[/sub]:S[sub]2[/sub]=a:b;4、在一组平行线之间的等积变形,如图③所示,S[sub]△ACD[/sub]=S[sub]△BCD[/sub];反之,如果S[sub]△ACD[/sub]=S[sub]△BCD[/sub],则可知直线AB平行于CD。
例、如图,三角形ABC的面积是24,D、E、F分别是BC、AC、AD的中点,求三角形DEF的面积。
(2)鸟头(共角)定理模型1、两个三角形中有一个角相等或互补,这两个三角形叫共角三角形;2、共角三角形的面积之比等于对应角(相等角或互补角)两夹边的乘积之比。
如图下图三角形ABC中,D、E分别是AB、AC上或AB、AC延长线上的点则有:S[sub]△ABC[/sub]:S[sub]△ADE[/sub]=(AB×AC):(AD×AE)我们现在以互补为例来简单证明一下共角定理!如图连接BE,根据等积变化模型知,S[sub]△ADE[/sub]:S[sub]△ABE[/sub]=AD:AB、S[sub]△ABE[/sub]:S[sub]△CBE[/sub]=AE:CE,所以S[sub]△ABE[/sub]:S[sub]△ABC[/sub]=S[sub]△ABE[/sub]:(S[sub]△ABE[/sub]+S[sub]△CBE[/sub])=AE:AC,因此S[sub]△ADE[/sub]:S[sub]△ABC[/sub]=(S[sub]△ADE[/sub]:S[sub]△ABE[/sub])×(S[sub]△ABE[/sub]:S[sub]△ABC[/sub])=(AD:AB)×(AE:AC)。
小升初复习重难点一几何五大模型

一、五大模型简介(1)等积变换模型1、等底等高的两个三角形面积相等;2、两个三角形高相等,面积之比等于底之比,如图①所示,S[sub]1[/sub]:S[sub]2[/sub]=a:b;3、两个三角形底相等,面积在之比等于高之比,如图②所示,S[sub]1[/sub]:S[sub]2[/sub]=a:b;4、在一组平行线之间的等积变形,如图③所示,S[sub]△ACD[/sub]=S[sub]△BCD[/sub];反之,如果S[sub]△ACD[/sub]=S[sub]△BCD[/sub],则可知直线AB平行于CD。
例、如图,三角形ABC的面积是24,D、E、F分别是BC、AC、AD的中点,求三角形DEF的面积。
(2)鸟头(共角)定理模型1、两个三角形中有一个角相等或互补,这两个三角形叫共角三角形;2、共角三角形的面积之比等于对应角(相等角或互补角)两夹边的乘积之比。
如图下图三角形ABC中,D、E分别是AB、AC上或AB、AC延长线上的点则有:S[sub]△ABC[/sub]:S[sub]△ADE[/sub]=(AB×AC):(AD×AE)我们现在以互补为例来简单证明一下共角定理!如图连接BE,根据等积变化模型知,S[sub]△ADE[/sub]:S[sub]△ABE[/sub]=AD:AB、S[su b]△ABE[/sub]:S[sub]△CBE[/sub]=AE:CE,所以S[sub]△ABE[/sub]:S[sub]△ABC[/sub]=S[sub]△ABE[/sub]:(S[sub]△ABE[/sub]+S[sub]△CBE[/sub])=AE:AC,因此S[sub]△ADE[/sub]:S[sub]△ABC[/sub]=(S[sub]△ADE[/sub]:S[sub]△ABE[/sub])×(S[sub]△ABE[/sub]:S[sub]△ABC[/sub])=(AD:AB)×(AE:AC)。
