专题15 双曲线—三年高考(2015-2017)数学(文)真题分项版解析(原卷版)
2017年高考数学(文)黄金易错点:专题15-椭圆、双曲线、抛物线(含答案)

1.已知方程x 2m 2+n -y 23m 2-n =1表示双曲线,且该双曲线两焦点间的距离为4,则n 的取值范围是( ) A .(-1,3) B .(-1,3) C .(0,3) D .(0,3)答案 A2.已知双曲线x 24-y 2b 2=1(b >0),以原点为圆心,双曲线的半实轴长为半径长的圆与双曲线的两条渐近线相交于A ,B ,C ,D 四点,四边形ABCD 的面积为2b ,则双曲线的方程为( ) A.x 24-3y 24=1 B.x 24-4y 23=1 C.x 24-y 24=1 D.x 24-y 212=1 答案 D解析 由题意知双曲线的渐近线方程为y =±b2x ,圆的方程为x 2+y 2=4,联立⎩⎪⎨⎪⎧x 2+y 2=4,y =b 2x ,解得⎩⎪⎨⎪⎧x =44+b2,y =2b4+b 2,或⎩⎪⎨⎪⎧x =-44+b2,y =-2b4+b 2,即第一象限的交点为⎝⎛⎭⎪⎫44+b 2,2b 4+b 2.由双曲线和圆的对称性得四边形ABCD 为矩形,其相邻两边长为84+b 2,4b4+b 2,故8×4b 4+b 2=2b ,得b 2=12.故双曲线的方程为x 24-y 212=1.故选D.3.已知F 1,F 2是双曲线E :x 2a 2-y 2b 2=1的左,右焦点,点M 在E 上,MF 1与x 轴垂直,sin ∠MF 2F 1=13,则E 的离心率为( ) A.2B.32C.3D .2答案 A4.已知F 1、F 2为椭圆x 225+y 216=1的左、右焦点,若M 为椭圆上一点,且△MF 1F 2的内切圆的周长等于3π,则满足条件的点M 有( ) A .0个 B .1个 C .2个 D .4个答案 C解析 由椭圆方程x 225+y 216=1可得a 2=25,b 2=16,∴a =5,b =4,c =3.由椭圆的定义可得|MF 1|+|MF 2|=2a =10,且|F 1F 2|=2c =6,∴△MF 1F 2的周长|MF 1|+|MF 2|+|F 1F 2|=10+6=16. 设△MF 1F 2的内切圆的半径为r , 由题意可得2πr =3π,解得r =32.设M (x 0,y 0), 则12MF F S=12(|MF 1|+|MF 2|+|F 1F 2|)·r =12|F 1F 2|·|y 0|,即12×16×32=12×6·|y 0|, 解得|y 0|=4.∴y 0=±4. ∴M (0,4)或(0,-4).即满足条件的点M 有2个.故选C.5.已知圆x 2+y 2=a 216上点E 处的一条切线l 过双曲线x 2a 2-y 2b2=1(a >0,b >0)的左焦点F ,且与双曲线的右支交于点P ,若OE →=12(OF →+OP →),则双曲线的离心率是______________.答案264解析 如图所示,设双曲线的右焦点为H ,连接PH ,因为直线l 与圆相切,所以PF ⊥OE . 又OE ∥PH ,所以PF ⊥PH .在Rt △PFH 中,|FH |2=|PH |2+|PF |2, 即(2c )2=(a 2)2+(5a2)2,整理得c a =264,即e =264.6.经过椭圆x 24+y 23=1的右焦点的直线l 交抛物线y 2=4x 于A 、B 两点,点A 关于y 轴的对称点为C ,则OB →·OC →=________. 答案 -5由题意知C (-x 1,y 1),∴OB →·OC →=(x 2,y 2)·(-x 1,y 1)=-x 1x 2+y 1y 2=-1-4=-5. 7.若抛物线y 2=4x 上的点M 到焦点的距离为10,则M 到y 轴的距离是________. 答案 9解析 抛物线y 2=4x 的焦点F (1,0).准线为x =-1,由M 到焦点的距离为10,可知M 到准线x =-1的距离也为10,故M 的横坐标满足x M +1=10,解得x M =9,所以点M 到y 轴的距离为9.8.已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为12,且点(1,32)在该椭圆上.(1)求椭圆C 的方程;(2)过椭圆C 的左焦点F 1的直线l 与椭圆C 相交于A ,B 两点,若△AOB 的面积为627,求圆心在原点O 且与直线l 相切的圆的方程. 解 (1)由题意可得e =c a =12,又a 2=b 2+c 2, 所以b 2=34a 2.因为椭圆C 经过点(1,32),所以1a 2+9434a 2=1,解得a =2,所以b 2=3, 故椭圆C 的方程为x 24+y 23=1.(2)由(1)知F 1(-1,0),设直线l 的方程为x =ty -1, 由⎩⎪⎨⎪⎧x =ty -1,x 24+y 23=1消去x ,得(4+3t 2)y 2-6ty -9=0, 显然Δ>0恒成立,设A (x 1,y 1),B (x 2,y 2), 则y 1+y 2=6t 4+3t 2,y 1y 2=-94+3t 2,9.已知椭圆C 的长轴左,右顶点分别为A ,B ,离心率e =22,右焦点为F ,且AF →·BF →=-1.(1)求椭圆C 的标准方程;(2)若P 是椭圆C 上的一动点,点P 关于坐标原点的对称点为Q ,点P 在x 轴上的射影点为M ,连接QM 并延长交椭圆于点N ,求证:∠QPN =90°. (1)解 依题意,设椭圆C 的方程为x 2a 2+y 2b 2=1(a >b >0),则A (-a,0),B (a,0),F (c,0),由e =c a =22,得a =2c .①由AF →·BF →=-1,得(c +a,0)·(c -a,0)=c 2-a 2=-1.② 联立①②,解得a =2,c =1, 所以b 2=1,故椭圆C 的标准方程为x 22+y 2=1.(2)证明 设P (x 1,y 1),N (x 2,y 2), 由题意知x i ≠0,y i ≠0(i =1,2), 且x 1≠x 2,易错起源1、圆锥曲线的定义与标准方程例1、(1)△ABC 的两个顶点为A (-4,0),B (4,0),△ABC 周长为18,则C 点轨迹方程为( ) A.x 216+y 29=1(y ≠0) B.y 225+x 29=1(y ≠0) C.y 216+x 29=1(y ≠0) D.x 225+y 29=1(y ≠0) (2)在平面直角坐标系中,已知△ABC 的顶点A (-4,0)和C (4,0),顶点B 在椭圆x 225+y 29=1上,则sin A +sin Csin B=________.答案 (1)D (2)54解析 (1)∵△ABC 的两顶点A (-4,0),B (4,0),周长为18,∴|AB |=8,|BC |+|AC |=10.∵10>8,∴点C 到两个定点的距离之和等于定值,满足椭圆的定义,∴点C 的轨迹是以A ,B 为焦点的椭圆,∴2a =10,2c =8,∴b =3.∴椭圆的标准方程是x 225+y 29=1(y ≠0).故选D.(2)由椭圆方程知其焦点坐标为(-4,0)和(4,0),恰分别为△ABC 的顶点A 和C 的坐标,由椭圆定义知|BA |+|BC |=2a =10,在△ABC 中,由正弦定理可知,sin A +sin C sin B =|BC |+|BA ||AC |=108=54. 【变式探究】(1)已知双曲线的一个焦点与抛物线x 2=24y 的焦点重合,其一条渐近线的倾斜角为30°,则该双曲线的标准方程为( ) A.x 29-y 227=1 B.y 29-x 227=1 C.y 212-x 224=1 D.y 224-x 212=1 (2)抛物线y 2=4x 上的两点A ,B 到焦点的距离之和为8,则线段AB 的中点到y 轴的距离为________. 答案 (1)B (2)3【名师点睛】(1)准确把握圆锥曲线的定义和标准方程及其简单几何性质,注意焦点在不同坐标轴上时,椭圆、双曲线、抛物线方程的不同表示形式.(2)求圆锥曲线方程的基本方法就是待定系数法,可结合草图确定. 【锦囊妙计,战胜自我】 1.圆锥曲线的定义(1)椭圆:|PF 1|+|PF 2|=2a (2a >|F 1F 2|); (2)双曲线:||PF 1|-|PF 2||=2a (2a <|F 1F 2|);(3)抛物线:|PF |=|PM |,点F 不在直线l 上,PM ⊥l 于M . 2.求解圆锥曲线标准方程“先定型,后计算”所谓“定型”,就是曲线焦点所在的坐标轴的位置;所谓“计算”,就是指利用待定系数法求出方程中的a 2,b 2,p 的值. 易错起源2、圆锥曲线的几何性质例2 (1)椭圆Γ:x 2a 2+y 2b 2=1(a >b >0)的左,右焦点分别为F 1,F 2,焦距为2c .若直线y =3(x+c )与椭圆Γ的一个交点M 满足∠MF 1F 2=2∠MF 2F 1,则该椭圆的离心率等于________. (2)已知双曲线x 2a 2-y 2b 2=1的左、右焦点分别为F 1、F 2,过F 1作圆x 2+y 2=a 2的切线分别交双曲线的左、右两支于点B 、C ,且|BC |=|CF 2|,则双曲线的渐近线方程为( ) A .y =±3x B .y =±22x C .y =±(3+1)xD .y =±(3-1)x答案 (1)3-1 (2)C易得直线BC 的斜率为a b ,cos ∠CF 1F 2=bc ,又由双曲线的定义及|BC |=|CF 2|可得 |CF 1|-|CF 2|=|BF 1|=2a , |BF 2|-|BF 1|=2a ⇒|BF 2|=4a ,故cos ∠CF 1F 2=b c =4a 2+4c 2-16a 22×2a ×2c⇒b 2-2ab -2a 2=0⇒(b a )2-2(b a )-2=0⇒ba =1+3,故双曲线的渐近线方程为y =±(3+1)x .【变式探究】(1)设椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左,右焦点分别为F 1,F 2,P 是C 上的点,PF 2⊥F 1F 2,∠PF 1F 2=30°,则椭圆C 的离心率为( )A.36 B.13 C.12 D.33(2)设双曲线x 2a 2-y 2b 2=1(a >0,b >0)的右焦点为F ,右顶点为A ,过F 作AF 的垂线与双曲线交于B ,C 两点,过B ,C 分别作AC ,AB 的垂线,两垂线交于点D ,若D 到直线BC 的距离小于a +a 2+b 2,则该双曲线的渐近线斜率的取值范围是( ) A .(-1,0)∪(0,1) B .(-∞,-1)∪(1,+∞)C .(-2,0)∪(0,2)D .(-∞,-2)∪(2,+∞) 答案(1)D(2)A由x 2a 2-y2b 2=1可知A (a,0),F (c,0). 易得B ⎝⎛⎭⎫c ,b 2a ,C ⎝⎛⎭⎫c ,-b 2a . ∵k AB =b 2ac -a =b 2a c -a ,∴k CD =aa -cb 2. ∵k AC =b 2a a -c =b 2a a -c ,∴k BD =-aa -cb 2. ∴l BD :y -b 2a=-a a -cb 2(x -c ),【名师点睛】(1)明确圆锥曲线中a ,b ,c ,e 各量之间的关系是求解问题的关键.(2)在求解有关离心率的问题时,一般并不是直接求出c 和a 的值,而是根据题目给出的椭圆或双曲线的几何特点,建立关于参数c ,a ,b 的方程或不等式,通过解方程或不等式求得离心率的值或范围. 【锦囊妙计,战胜自我】1.椭圆、双曲线中,a ,b ,c 之间的关系 (1)在椭圆中:a 2=b 2+c 2,离心率为e =ca =1-b a 2;(2)在双曲线中:c 2=a 2+b 2,离心率为e =ca=1+b a2.2.双曲线x 2a 2-y 2b 2=1(a >0,b >0)的渐近线方程为y =±ba x .注意离心率e 与渐近线的斜率的关系.易错起源3、直线与圆锥曲线例3、如图,在平面直角坐标系xOy 中,已知椭圆x 2a 2+y 2b 2=1(a >b >0)的离心率为22,且右焦点F 到直线l :x =-a 2c的距离为3.(1)求椭圆的标准方程;(2)过F 的直线与椭圆交于A ,B 两点,线段AB 的垂直平分线分别交直线l 和AB 于点P ,C ,若|PC |=2|AB |,求直线AB 的方程. 解 (1)由题意,得c a =22且c +a 2c =3,解得a =2,c =1,则b =1, 所以椭圆的标准方程为x 22+y 2=1.(2)当AB ⊥x 轴时,|AB |=2,又|CP |=3,不合题意.当AB 与x 轴不垂直时,设直线AB 的方程为y =k (x -1),A (x 1,y 1),B (x 2,y 2), 将直线AB 的方程代入椭圆方程, 得(1+2k 2)x 2-4k 2x +2(k 2-1)=0, 则x 1,2=2k 2±21+k 21+2k 2,C 的坐标为⎝ ⎛⎭⎪⎫2k 21+2k 2,-k 1+2k 2,且|AB |=x 2-x 12+y 2-y 12=1+k2x 2-x 12=221+k 21+2k 2.若k =0,则线段AB 的垂直平分线为y 轴,与直线l 平行,不合题意.【变式探究】(1)设抛物线y 2=8x 的准线与x 轴交于点Q ,若过点Q 的直线l 与抛物线有公共点,则直线l 的斜率的取值范围为( ) A .-12,12]B .-2,2]C .-1,1]D .-4,4](2)设椭圆C :x 24+y 23=1与函数y =tan x4的图象相交于A 1,A 2两点,若点P 在椭圆C 上,且直线P A 2的斜率的取值范围是-2,-1],那么直线P A 1斜率的取值范围是________. 答案 (1)C (2)38,34]解析 (1)由题意知抛物线的准线为x =-2,∴Q (-2,0),显然,直线l 的斜率存在,故设直线l 的方程为y =k (x +2),由⎩⎪⎨⎪⎧y =k x +2,y 2=8x ,得k 2x 2+4(k 2-2)x +4k 2=0,当k =0时,x =0,此时交点为(0,0),当k ≠0时,Δ≥0, 即4(k 2-2)]2-16k 4≥0,解得-1≤k <0或0<k ≤1, 综上,k 的取值范围为-1,1],故选C.【名师点睛】解决直线与圆锥曲线问题的通法是联立方程,利用根与系数的关系,设而不求思想,弦长公式等简化计算;涉及中点弦问题时,也可用“点差法”求解. 【锦囊妙计,战胜自我】判断直线与圆锥曲线公共点的个数或求交点问题有两种常用方法(1)代数法:即联立直线与圆锥曲线方程可得到一个关于x ,y 的方程组,消去y (或x )得一元方程,此方程根的个数即为交点个数,方程组的解即为交点坐标. (2)几何法:即画出直线与圆锥曲线的图象,根据图象判断公共点个数.1.点F 为椭圆x 2a 2+y 2b 2=1(a >b >0)的一个焦点,若椭圆上存在点A 使△AOF 为正三角形,那么椭圆的离心率为( ) A.22 B.32C.2-12D.3-1答案 D解析 如图所示,设F 为椭圆的右焦点,点A 在第一象限,由已知得直线OA 的斜率为k =tan60°=3,2.已知椭圆C 1:x 2m 2+y 2=1(m >0)与双曲线C 2:x2n 2-y 2=1(n >0)的焦点重合,e 1,e 2分别为C 1,C 2的离心率,则( )A .m >n 且e 1e 2>1B .m >n 且e 1e 2<1C .m <n 且e 1e 2>1D .m <n 且e 1e 2<1 答案 A解析 由题意可得:m 2-1=n 2+1,即m 2=n 2+2,又∵m >0,n >0,故m >n . 又∵e 21·e 22=m 2-1m 2·n 2+1n 2=n 2+1n 2+2·n 2+1n2 =n 4+2n 2+1n 4+2n 2=1+1n 4+2n 2>1,∴e 1·e 2>1. 3.已知双曲线C :x 23-y 2=1的左,右焦点分别为F 1,F 2,过点F 2的直线与双曲线C 的右支相交于P ,Q 两点,且点P 的横坐标为2,则△PF 1Q 的周长为( ) A.1633B .5 3 C.1433D .4 3答案 A4.设抛物线E :y 2=2px (p >0)的焦点为F ,点M 为抛物线E 上一点,|MF |的最小值为3,若点P 为抛物线E 上任意一点,A (4,1),则|P A |+|PF |的最小值为( ) A .4+32B .7C .4+2 3D .10答案 B解析 由题意,|MF |的最小值为3,∴p2=3,∴p =6,∴抛物线E :y 2=12x ,抛物线y 2=12x 的焦点F 的坐标是(3,0); 设点P 在准线上的射影为D , 则根据抛物线的定义可知|PF |=|PD |,∴要求|P A |+|PF |取得最小值,即求|P A |+|PD |取得最小值,当D ,P ,A 三点共线时|P A |+|PD |最小,为4-(-3)=7,故选B.5.已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)与抛物线y 2=8x 有一个共同的焦点F ,两曲线的一个交点为P ,若|PF |=5,则点F 到双曲线的渐近线的距离为( ) A. 3 B .2 C. 6 D .3答案 A解析 ∵抛物线y 2=8x 的焦点为F (2,0),∴双曲线x 2a 2-y 2b 2=1(a >0,b >0)的一个焦点F 的坐标为(2,0),∴c 2=a 2+b 2=4.①∵P 是两曲线的一个交点,且|PF |=5, ∴x p +2=5,∴x p =3,∴y 2p =24. ∵P (x p ,y p )在双曲线x 2a 2-y 2b2=1上,6.已知点A (2,4)在抛物线y 2=2px (p >0)上,且抛物线的准线过双曲线x 2a 2-y2b 2=1(a >0,b >0)的一个焦点,若双曲线的离心率为2,则该双曲线的方程为____________. 答案 x 2-y 23=1解析 ∵点A (2,4)在抛物线y 2=2px (p >0)上, ∴16=4p ,解得p =4. ∴抛物线的准线方程为x =-2.又抛物线的准线过双曲线x 2a 2-y 2b 2=1(a >0,b >0)的一个焦点,∴c =2,又e =ca =2,∴a =1,则b 2=c 2-a 2=4-1=3, ∴双曲线的方程为x 2-y 23=1.7.一动圆与已知圆O 1:(x +3)2+y 2=1外切,与圆O 2:(x -3)2+y 2=81内切,则动圆圆心的轨迹方程为__________. 答案 x 225+y 216=1解析 两定圆的圆心和半径分别是O 1(-3,0),r 1=1; O 2(3,0),r 2=9.设动圆圆心为M (x ,y ),半径为R ,则由题设条件, 可得|MO 1|=R +1,|O 2M |=9-R . ∴|MO 1|+|MO 2|=10>|O 1O 2|=6.由椭圆的定义知点M 在以O 1,O 2为焦点的椭圆上,且2a =10,2c =6,∴b 2=16. ∴动圆圆心的轨迹方程为x 225+y 216=1.8.过椭圆x 25+y 24=1的右焦点作一条斜率为2的直线与椭圆交于A ,B 两点,O 为坐标原点,则△AOB 的面积为________. 答案 539.已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为12,椭圆的短轴端点与双曲线y22-x 2=1的焦点重合,过点P (4,0)且不垂直于x 轴的直线l 与椭圆C 相交于A ,B 两点. (1)求椭圆C 的方程; (2)求OA →·OB →的取值范围.解 (1)由双曲线y 22-x 2=1得其焦点为(0,±3),∴b = 3.又由e =c a =12,a 2=b 2+c 2,得a 2=4,c =1.故椭圆C 的方程为x 24+y 23=1.(2)由题意可知直线l 的斜率存在,设直线l 的方程为y =k (x -4),由⎩⎪⎨⎪⎧y =k x -4,x 24+y 23=1,消去y ,得(4k 2+3)x 2-32k 2x +64k 2-12=0, 由Δ=(-32k 2)2-4(4k 2+3)(64k 2-12)>0, 得k 2<14.10.如图所示,抛物线y 2=4x 的焦点为F ,动点T (-1,m ),过F 作TF 的垂线交抛物线于P ,Q 两点,弦PQ 的中点为N .(1)证明:线段NT 平行于x 轴(或在x 轴上); (2)若m >0且|NF |=|TF |,求m 的值及点N 的坐标.(1)证明 易知抛物线的焦点F (1,0),准线x =-1,动点T (-1,m )在准线上,则kTF =-m2.当m =0时,T 为抛物线准线与x 轴的交点,这时PQ 为抛物线的通径,点N 与焦点F 重合,显然线段NT 在x 轴上.当m ≠0时,由条件知kPQ =2m ,所以直线PQ 的方程为y =2m (x -1),联立⎩⎪⎨⎪⎧y 2=4x ,y =2m x -1,得x 2-(2。
三年高考2015_2017高考数学试题分项版解析专题16抛物线文20171101135

专题16 抛物线1.2017课标II ,文12】过抛物线2:4C y x =的焦点F ,C 于点M (M 在轴上方),为C 的准线,点N 在上且MN l ⊥,则M 到直线NF 的距离为【答案】C【考点】直线与抛物线位置关系【名师点睛】直线和圆锥曲线的位置关系,一般转化为直线方程与圆锥曲线方程组成的方程组,利用韦达定理或求根公式进行转化,涉及弦长的问题中,应熟练地利用根与系数关系,设而不求法计算弦长;涉及垂直关系时也往往利用根与系数关系、设而不求法简化运算;涉及过焦点的弦的问题,可考虑用圆锥曲线的定义求解.涉及中点弦问题往往利用点差法. 2.【2014,安徽文3】抛物线241x y =的准线方程是( )A . 1-=yB . 2-=yC . 1-=xD . 2-=x 【答案】A . 【解析】试题分析:题中抛物线的标准形式为24x y =,则其准线方程为1y =-,故先A .考点:抛物线的准线方程.【名师点睛】在求解抛物线标准方程过程中,先要将给定方程转化成标准形式如2(0)y Ax A =≠,则其焦点坐标为(,0)4A ,准线方程为4Ax =-;若2(0)x Ay A =≠,则其焦点坐标为(0,)4A ,准线方程为4Ay =-.3. 【2014全国1,文10】已知抛物线C : x y =2的焦点为F ,()00,A x y 是C 上一点,x F A 045=,则0x =( ) A. 1 B. 2 C. 4 D. 8 【答案】A 【解析】试题分析:根据抛物线的定义:到焦点的距离等于到准线的距离,又抛物线的准线方程为:14x =-,则有:01||4AF x =+,即有001544x x +=,可解得01x =. 考点:抛物线的方程和定义【名师点睛】本题主要考查了抛物线的定义和性质,同时考查了考生分析问题、转换问题的能力.4. 【2014辽宁文8】已知点(2,3)A -在抛物线C :22y px =的准线上,记C 的焦点为F ,则直线AF 的斜率为( ) A .43-B .1-C .34-D .12- 【答案】C【考点定位】1、抛物线的标准方程和简单几何性质;2、直线的斜率.【名师点睛】本题考查抛物线的标准方程、抛物线的几何性质、直线的斜率公式..注意从已知出发,确定焦点F 的坐标,进一步确定直线的斜率.本题是一道基础题,在较全面考查抛物线等基础知识的同时,考查考生的计算能力及分析问题解决问题的能力.5.【2014四川,文10】已知F 是抛物线2y x =的焦点,点A ,B 在该抛物线上且位于轴的两侧,2OA OB ⋅=(其中O 为坐标原点),则ABO ∆与AFO ∆面积之和的最小值是( )A .B .C .8D 【答案】B 【解析】试题分析:据题意得1(,0)4F ,设1122(,),(,)A x y B x y ,则221122,x y x y ==,221212122,2y y y y y y +==-或121y y =,因为,A B 位于轴两侧所以.所以122y y =-两面积之和为121122S x =-221221121111112248y y y y y y y y =-+⨯⨯=-+⨯111218y y y =++⨯11298y y =+112938y y =+≥. 【考点定位】1、抛物线;2、三角形的面积;3、重要不等式.【名师点睛】在圆锥曲线的问题中,我们通常使用设而不求的办法,此题中,我们设出1122(,),(,)A x y B x y 两点坐标,由2OA OB ⋅=,得122y y =-,接下来表示出ABO ∆与AFO ∆面积之和,利用基本不等式即可求得最小值,利用基本不等式时,要注意“一正,二定,三相等”.6.【2015高考陕西,文3】已知抛物线22(0)y px p =>的准线经过点(1,1)-,则抛物线焦点坐标为( )A .(1,0)-B .(1,0)C .(0,1)-D .(0,1)【答案】B【解析】由抛物线22(0)y px p =>得准线2px =-,因为准线经过点(1,1)-,所以2p =, 所以抛物线焦点坐标为(1,0),故答案选B 【考点定位】抛物线方程和性质.【名师点睛】1.本题考查抛物线方程和性质,采用待定系数法求出p 的值.本题属于基础题,注意运算的准确性.2.给出抛物线方程要求我们能够找出焦点坐标和直线方程,往往这个是解题的关键.7. 【2016高考四川文科】抛物线24y x =的焦点坐标是( ) (A)(0,2) (B) (0,1) (C) (2,0) (D) (1,0) 【答案】D考点:抛物线的定义.【名师点睛】本题考查抛物线的定义.解析几何是中学数学的一个重要分支,圆锥曲线是解析几何的重要内容,它们的定义、标准方程、简单的性质是我们重点要掌握的内容,一定要熟记掌握.8.【2014全国2,文10】设F 为抛物线2:=3C y x 的焦点,过F 且倾斜角为30︒的直线交C 于A ,B 两点,则 AB =( )(A (B ) (C )12 (D )【答案】C【解析】由题意,得3(,0)4F .又因为0k tan 303==,故直线AB 的方程为3y (x )34=-,与抛物线2=3y x 联立,得21616890x x -+=,设1122(x ,y ),(x ,y )A B ,由抛物线定义得,12x x AB p =++=168312162+=,选C . 【考点定位】直线与圆锥曲线的位置关系【名师点睛】本题考查了抛物线的标准方程,焦半径公式,属于中档题,深入理解抛物线的定义是解题的关键,注意韦达定理的使用.9.【2016高考新课标2文数】设F 为抛物线C :y 2=4x 的焦点,曲线y =kx(k >0)与C 交于点P ,PF ⊥x 轴,则k =( )(A )12 (B )1 (C )32(D )2【答案】D考点: 抛物线的性质,反比例函数的性质.【名师点睛】抛物线方程有四种形式,注意焦点的位置. 对函数y =kx(0)k ≠,当0k >时,在(,0)-∞,(0,)+∞上是减函数,当0k <时,在(,0)-∞,(0,)+∞上是增函数.10.【2017天津,文12】设抛物线24y x =的焦点为F ,准线为l .已知点C 在l 上,以C 为圆心的圆与y 轴的正半轴相切于点A.若120FAC ∠=︒,则圆的方程为 .【答案】22(1)(1x y ++= 【解析】试题分析:设圆心坐标为(1,)C m -,则(0,)A m ,焦点(1,0)F ,(1,0),(1,)AC AF m =-=-,1cos 21AC AF CAF AC AF⋅∠===-⋅,m =,由于圆C 与y 轴得正半轴相切,则取m =,所求圆得圆心为(1-,半径为1,所求圆的方程为22(1)(1x y ++=.【考点】1.抛物线的方程;2.圆的方程.【名师点睛】本题设计比较巧妙,考查了圆,抛物线的方程,同时还考查了向量数量积的坐标表示,本题只有一个难点,就是0120CAF ∠=,会不会用向量的坐标表示cos CAF ∠,根据图象,可设圆心为()1,C m -,那么方程就是()()2211x y m ++-=,若能用向量的坐标表示角,即可求得m ,问题也就迎刃而解了.11.【2014上海,文4】若抛物线y 2=2px 的焦点与椭圆15922=+y x 的右焦点重合,则该抛物线的准线方程为___________. 【答案】2x =-.【考点】椭圆与抛物线的几何性质【名师点睛】1.涉及抛物线几何性质的问题常结合图形思考,通过图形可以直观地看出抛物线的顶点、对称轴、开口方向等几何特征,体现了数形结合思想解题的直观性. 2.求抛物线方程应注意的问题(1)当坐标系已建立时,应根据条件确定抛物线方程属于四种类型中的哪一种;(2)要注意把握抛物线的顶点、对称轴、开口方向与方程之间的对应关系; (3)要注意参数p 的几何意义是焦点到准线的距离,利用它的几何意义来解决问题. 12.【2014高考陕西版文第11题】抛物线24y x =的准线方程为________. 【答案】1x =- 【解析】试题分析:由抛物线的几何性质知:抛物线24y x =的准线方程为1x =-,故答案为1x =-. 考点:抛物线的几何性质.【名师点晴】本题主要考查的是抛物线的几何性质,属于容易题,解题时直接利用抛物线的几何性质即可求得其准线方程13.【2017课标1,文20】设A ,B 为曲线C :y =24x 上两点,A 与B 的横坐标之和为4.(1)求直线AB 的斜率;(2)设M 为曲线C 上一点,C 在M 处的切线与直线AB 平行,且AM ⊥BM ,求直线AB 的方程.【答案】(1)1; (2)7y x =+.于是直线AB 的斜率12121214y y x x k x x -+===-. (2)由24x y =,得2xy'=.设M (x 3,y 3),由题设知312x=,解得32x =,于是M (2,1).设直线AB 的方程为y x m =+,故线段AB 的中点为N (2,2+m ),|MN |=|m +1|.将y x m =+代入24x y =得2440x x m --=.当16(1)0m ∆=+>,即1m >-时,1,22x =±从而12||AB x x -=.由题设知||2||AB MN =,即2(1)m =+,解得7m =. 所以直线AB 的方程为7y x =+. 【考点】直线与圆锥曲线的位置关系【名师点睛】本题主要考查直线与圆锥曲线位置关系,所使用方法为韦达定理法:因直线的方程是一次的,圆锥曲线的方程是二次的,故直线与圆锥曲线的问题常转化为方程组关系问题,最终转化为一元二次方程问题,故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一,尤其是弦中点问题,弦长问题,可用韦达定理直接解决,但应注意不要忽视判别式的作用. 14.【2017浙江,21】(本题满分15分)如图,已知抛物线2x y =,点A11()24-,,39()24B ,,抛物线上的点)2321)(,(<<-x y x P .过点B 作直线AP 的垂线,垂足为Q .(Ⅰ)求直线AP 斜率的取值范围; (Ⅱ)求||||PQ PA ⋅的最大值. 【答案】(Ⅰ))1,1(-;(Ⅱ)2716试题解析:(Ⅰ)设直线AP 的斜率为k ,则2121412-=+-=x x x k ,∵1322x -<<,∴直线AP 斜率的取值范围是)1,1(-.(Ⅱ)联立直线AP 与BQ 的方程110,24930,42kx y k x ky k ⎧-++=⎪⎪⎨⎪+--=⎪⎩ 解得点Q 的横坐标是)1(23422+++-=k k k x Q ,因为|PA1)2x +=)1(12++k k |PQ |= 1)1)(1()(1222++--=-+k k k x x k Q ,所以|PA ||PQ |=3)1)(1(+--k k令3)1)(1()(+--=k k k f ,因为2)1)(24()('+--=k k k f ,所以 f (k )在区间)21,1(-上单调递增,)1,21(上单调递减,因此当k =12时,||||PQ PA ⋅取得最大值2716. 【考点】直线与圆锥曲线的位置关系【名师点睛】本题主要考查直线方程、直线与抛物线的位置关系等基础知识,同时考查解析几何的基本思想方法和运算求解能力,通过表达||PA 与||PQ 的长度,通过函数3)1)(1()(+--=k k k f 求解||||PQ PA ⋅的最大值.15.【2016高考新课标1文数】(本小题满分12分)在直角坐标系xOy 中,直线l :y =t (t ≠0)交y 轴于点M ,交抛物线C :22(0)y px p =>于点P ,M 关于点P 的对称点为N ,连结ON 并延长交C 于点H . (I )求OH ON;(II )除H 以外,直线MH 与C 是否有其它公共点?说明理由. 【答案】(I )2(II )没有把直线MH 的方程x tpt y 2=-,与px y 22=联立得04422=+-t ty y ,解得t y y 221==,即直线MH 与C 只有一个公共点,所以除H 以外直线MH 与C 没有其它公共点.试题解析:(Ⅰ)由已知得),0(t M ,),2(2t pt P .又N 为M 关于点P 的对称点,故),(2t pt N ,ON 的方程为x t p y =,代入px y 22=整理得0222=-x t px ,解得01=x ,p t x 222=,因此)2,2(2t pt H . 所以N 为OH 的中点,即2||||=ON OH . (Ⅱ)直线MH 与C 除H 以外没有其它公共点.理由如下: 直线MH 的方程为x t p t y 2=-,即)(2t y ptx -=.代入px y 22=得04422=+-t ty y ,解得t y y 221==,即直线MH 与C 只有一个公共点,所以除H 以外直线MH 与C 没有其它公共点.考点:直线与抛物线【名师点睛】高考解析几何解答题大多考查直线与圆锥曲线的位置关系,直线与圆锥曲线的位置关系是一个很宽泛的考试内容,主要由求值、求方程、求定值、最值、求参数取值范围等几部分组成;解析几何中的证明问题通常有以下几类:证明点共线或直线过定点;证明垂直;证明定值问题.其中考查较多的圆锥曲线是椭圆与抛物线,解决这类问题要重视方程思想、函数思想及化归思想的应用.16.2016高考新课标Ⅲ文数]已知抛物线C :22y x =的焦点为F ,平行于轴的两条直线12,l l 分别交C 于,A B 两点,交C 的准线于P Q ,两点.(I )若F 在线段AB 上,R 是PQ 的中点,证明AR FQ ;(II )若PQF ∆的面积是ABF ∆的面积的两倍,求AB 中点的轨迹方程. 【答案】(Ⅰ)见解析;(Ⅱ)21y x =-.试题解析:由题设)0,21(F .设b y l a y l ==:,:21,则0≠ab ,且)2,21(),,21(),,21(),,2(),0,2(22b a R b Q a P b b B a A +---. 记过B A ,两点的直线为,则的方程为0)(2=++-ab y b a x . .....3分 (Ⅰ)由于F 在线段AB 上,故01=+ab . 记AR 的斜率为1k ,FQ 的斜率为2k ,则222111k b aaba ab a b a a b a k =-=-==--=+-=, 所以ARFQ . ......5分(Ⅱ)设与轴的交点为)0,(1x D , 则2,2121211b a S x a b FD a b S PQF ABF-=--=-=∆∆. 由题设可得221211ba x ab -=--,所以01=x (舍去),11=x . 设满足条件的AB 的中点为),(y x E . 当AB 与轴不垂直时,由DE AB k k =可得)1(12≠-=+x x yb a . 而y ba =+2,所以)1(12≠-=x x y . 当AB 与轴垂直时,E 与D 重合,所以,所求轨迹方程为12-=x y . ....12分 考点:1、抛物线定义与几何性质;2、直线与抛物线位置关系;3、轨迹求法.【方法归纳】(1)解析几何中平行问题的证明主要是通过证明两条直线的斜率相等或转化为利用向量证明;(2)求轨迹的方法在高考中最常考的是直接法与代入法(相关点法),利用代入法求解时必须找准主动点与从动点.17. 【2015高考湖南,文20】(本小题满分13分)已知抛物线21:4C x y =的焦点F 也是椭圆22222:1y x C a b+=(0)a b >>的一个焦点,1C 与2C 的公共弦长为F 的直线与1C 相交于,A B 两点,与2C 相交于,C D 两点,且AC 与BD 同向. (I )求2C 的方程;(II )若AC BD =,求直线的斜率.【答案】(I )22198y x += ;(II)2234341212()4()4x x x x x x x x +-=+-,设直线的斜率为,则的方程为1y kx =+,联立直线与抛物线方程、直线与椭圆方程、利用韦达定理进行计算即可得到结果.试题解析:(I )由21:4C x y =知其焦点F 的坐标为(0,1),因为F 也是椭圆2C 的一个焦点,所以221a b -= ①; 又1C 与2C 的公共弦长为1C 与2C 都关于y 轴对称,且1C 的方程为21:4C x y =,由此易知1C 与2C 的公共点的坐标为3()2,229614a b ∴+= ②, 联立①②得229,8a b ==,故2C 的方程为22198y x +=。
专题16 抛物线—三年高考(2015-2017)数学(文)真题分项版解析(原卷+解析版)

专题16 抛物线原卷1-5页+解析5-24页1.2017课标II ,文12】过抛物线2:4C y x =的焦点F ,C 于点M (M 在x 轴上方),l 为C 的准线,点N 在l 上且MN l ⊥,则M 到直线NF 的距离为B. C. D. 2.【2014,安徽文3】抛物线241x y =的准线方程是( )A . 1-=yB . 2-=yC . 1-=xD . 2-=x3. 【2014全国1,文10】已知抛物线C : x y =2的焦点为F ,()00,A x y 是C 上一点,x F A 045=,则0x =( ) A. 1 B. 2 C. 4 D. 84. 【2014辽宁文8】已知点(2,3)A -在抛物线C :22y px =的准线上,记C 的焦点为F ,则直线AF 的斜率为( ) A .43-B .1-C .34-D .12- 5.【2014四川,文10】已知是抛物线的焦点,点,在该抛物线上且位于轴的两侧, (其中为坐标原点),则与面积之和的最小值是( ) A .B .C .D .6.【2015高考陕西,文3】已知抛物线22(0)y px p =>的准线经过点(1,1)-,则抛物线焦点坐标为( )A .(1,0)-B .(1,0)C .(0,1)-D .(0,1)7. 【2016高考四川文科】抛物线24y x =的焦点坐标是( ) (A)(0,2) (B) (0,1) (C) (2,0) (D) (1,0)8.【2014全国2,文10】设F 为抛物线2:=3C y x 的焦点,过F 且倾斜角为30︒的直线交C 于A ,B 两点,则 AB =( )(A (B )6 (C )12 (D )9.【2016高考新课标2文数】设F 为抛物线C :y 2=4x 的焦点,曲线y =kx(k >0)与C 交于点P ,PF ⊥x 轴,则k =( )(A )12 (B )1 (C )32(D )210.【2017天津,文12】设抛物线24y x =的焦点为F ,准线为l .已知点C 在l 上,以C 为圆心的圆与y 轴的正半轴相切于点A.若120FAC ∠=︒,则圆的方程为 .11.【2014上海,文4】若抛物线y 2=2px 的焦点与椭圆15922=+y x 的右焦点重合,则该抛物线的准线方程为___________.12.【2014高考陕西版文第11题】抛物线24y x =的准线方程为________.13.【2017课标1,文20】设A ,B 为曲线C :y =24x 上两点,A 与B 的横坐标之和为4.(1)求直线AB 的斜率;(2)设M 为曲线C 上一点,C 在M 处的切线与直线AB 平行,且AM ⊥BM ,求直线AB 的方程.14.【2017浙江,21】(本题满分15分)如图,已知抛物线2x y =,点A11()24-,,39()24B ,,抛物线上的点)2321)(,(<<-x y x P .过点B 作直线AP 的垂线,垂足为Q .(Ⅰ)求直线AP 斜率的取值范围;(Ⅱ)求||||PQ PA ⋅的最大值.15.【2016高考新课标1文数】(本小题满分12分)在直角坐标系xOy 中,直线l :y =t (t ≠0)交y 轴于点M ,交抛物线C :22(0)y px p =>于点P ,M 关于点P 的对称点为N ,连结ON 并延长交C 于点H . (I )求OH ON;(II )除H 以外,直线MH 与C 是否有其它公共点?说明理由.16.[2016高考新课标Ⅲ文数]已知抛物线C :22y x =的焦点为F ,平行于x 轴的两条直线12,l l 分别交C 于,A B 两点,交C 的准线于P Q ,两点.(I )若F 在线段AB 上,R 是PQ 的中点,证明AR FQ ;(II )若PQF ∆的面积是ABF ∆的面积的两倍,求AB 中点的轨迹方程.17. 【2015高考湖南,文20】(本小题满分13分)已知抛物线21:4C x y =的焦点F 也是椭圆22222:1y x C a b+=(0)a b >>的一个焦点,1C 与2C 的公共弦长为,过点F 的直线l 与1C 相交于,A B 两点,与2C 相交于,C D 两点,且AC 与BD同向.(I )求2C 的方程;(II )若AC BD =,求直线l 的斜率.18.【2016高考浙江文数】(本题满分15分)如图,设抛物线22(0)y px p =>的焦点为F ,抛物线上的点A 到y 轴的距离等于|AF |-1. (I )求p 的值;(II )若直线AF 交抛物线于另一点B ,过B 与x 轴平行的直线和过F 与AB 垂直的直线交于点N ,AN 与x轴交于点M .求M 的横坐标的取值范围.19.【2015高考浙江,文19】(本题满分15分)如图,已知抛物线211C 4y x =:,圆222C (1)1x y +-=:,过点P(t,0)(t>0)作不过原点O 的直线PA ,PB 分别与抛物线1C 和圆2C 相切,A ,B 为切点. (1)求点A ,B 的坐标; (2)求PAB ∆的面积.注:直线与抛物线有且只有一个公共点,且与抛物线的对称轴不平行,则该直线与抛物线相切,称该公 共点为切点.20.【2014福建,文21】((本小题满分12分) 已知曲线Γ上的点到点(0,1)F 的距离比它到直线3y =-的距离小2.(1)求曲线Γ的方程;(2)曲线Γ在点P 处的切线l 与x 轴交于点A .直线3y =分别与直线l 及y 轴交于点,M N ,以MN 为直径作圆C ,过点A 作圆C 的切线,切点为B ,试探究:当点P 在曲线Γ上运动(点P 与原点不重合)时,线段AB 的长度是否发生变化?证明你的结论. 21.【2015高考福建,文19】已知点F 为抛物线2:2(0)E y px p =>的焦点,点(2,)A m 在抛物线E 上,且3AF =. (Ⅰ)求抛物线E 的方程;(Ⅱ)已知点(1,0)G -,延长AF 交抛物线E 于点B ,证明:以点F 为圆心且与直线GA 相切的圆,必与直线GB 相切.解析1.2017课标II ,文12】过抛物线2:4C y x =的焦点F ,C 于点M (M 在x 轴上方),l 为C 的准线,点N 在l 上且MN l ⊥,则M 到直线NF 的距离为B. C. D. 【答案】C【考点】直线与抛物线位置关系【名师点睛】直线和圆锥曲线的位置关系,一般转化为直线方程与圆锥曲线方程组成的方程组,利用韦达定理或求根公式进行转化,涉及弦长的问题中,应熟练地利用根与系数关系,设而不求法计算弦长;涉及垂直关系时也往往利用根与系数关系、设而不求法简化运算;涉及过焦点的弦的问题,可考虑用圆锥曲线的定义求解.涉及中点弦问题往往利用点差法. 2.【2014,安徽文3】抛物线241x y =的准线方程是( )A . 1-=yB . 2-=yC . 1-=xD . 2-=x 【答案】A . 【解析】试题分析:题中抛物线的标准形式为24x y =,则其准线方程为1y =-,故先A .考点:抛物线的准线方程.【名师点睛】在求解抛物线标准方程过程中,先要将给定方程转化成标准形式如2(0)y Ax A =≠,则其焦点坐标为(,0)4A ,准线方程为4Ax =-;若2(0)x Ay A =≠,则其焦点坐标为(0,)4A ,准线方程为4Ay =-.3. 【2014全国1,文10】已知抛物线C : x y =2的焦点为F ,()00,A x y 是C 上一点,x F A 045=,则0x =( ) A. 1 B. 2 C. 4 D. 8 【答案】A 【解析】试题分析:根据抛物线的定义:到焦点的距离等于到准线的距离,又抛物线的准线方程为:14x =-,则有:01||4AF x =+,即有001544x x +=,可解得01x =.考点:抛物线的方程和定义【名师点睛】本题主要考查了抛物线的定义和性质,同时考查了考生分析问题、转换问题的能力.4. 【2014辽宁文8】已知点(2,3)A -在抛物线C :22y px =的准线上,记C 的焦点为F ,则直线AF 的斜率为( ) A .43-B .1-C .34-D .12- 【答案】C【考点定位】1、抛物线的标准方程和简单几何性质;2、直线的斜率.【名师点睛】本题考查抛物线的标准方程、抛物线的几何性质、直线的斜率公式..注意从已知出发,确定焦点F 的坐标,进一步确定直线的斜率.本题是一道基础题,在较全面考查抛物线等基础知识的同时,考查考生的计算能力及分析问题解决问题的能力.5.【2014四川,文10】已知F 是抛物线2y x =的焦点,点A ,B 在该抛物线上且位于x 轴的两侧,2OA OB ⋅=(其中O 为坐标原点),则ABO ∆与AFO ∆面积之和的最小值是( ) A .2 B .3 CD【答案】B 【解析】试题分析:据题意得1(,0)4F ,设1122(,),(,)A x y B x y ,则221122,x y x y ==,221212122,2y y y y y y +==-或121y y =,因为,A B 位于x 轴两侧所以.所以122y y =-两面积之和为12211111224S x y x y y =-+⨯⨯221221121111112248y y y y y y y y =-+⨯⨯=-+⨯111218y y y =++⨯11298y y =+112938y y =+≥. 【考点定位】1、抛物线;2、三角形的面积;3、重要不等式.【名师点睛】在圆锥曲线的问题中,我们通常使用设而不求的办法,此题中,我们设出1122(,),(,)A x y B x y 两点坐标,由2OA OB ⋅=,得122y y =-,接下来表示出ABO ∆与AFO ∆面积之和,利用基本不等式即可求得最小值,利用基本不等式时,要注意“一正,二定,三相等”.6.【2015高考陕西,文3】已知抛物线22(0)y px p =>的准线经过点(1,1)-,则抛物线焦点坐标为( )A .(1,0)-B .(1,0)C .(0,1)-D .(0,1) 【答案】B【解析】由抛物线22(0)y px p =>得准线2px =-,因为准线经过点(1,1)-,所以2p =, 所以抛物线焦点坐标为(1,0),故答案选B 【考点定位】抛物线方程和性质.【名师点睛】1.本题考查抛物线方程和性质,采用待定系数法求出p 的值.本题属于基础题,注意运算的准确性.2.给出抛物线方程要求我们能够找出焦点坐标和直线方程,往往这个是解题的关键.7. 【2016高考四川文科】抛物线24y x =的焦点坐标是( ) (A)(0,2) (B) (0,1) (C) (2,0) (D) (1,0) 【答案】D考点:抛物线的定义.【名师点睛】本题考查抛物线的定义.解析几何是中学数学的一个重要分支,圆锥曲线是解析几何的重要内容,它们的定义、标准方程、简单的性质是我们重点要掌握的内容,一定要熟记掌握.8.【2014全国2,文10】设F 为抛物线2:=3C y x 的焦点,过F 且倾斜角为30︒的直线交C 于A ,B 两点,则 AB =( )(A (B )6 (C )12 (D )【答案】C【解析】由题意,得3(,0)4F .又因为0k tan 30==,故直线AB 的方程为3y )4=-,与抛物线2=3y x 联立,得21616890x x -+=,设1122(x ,y ),(x ,y )A B ,由抛物线定义得,12x x AB p =++=168312162+=,选C . 【考点定位】直线与圆锥曲线的位置关系【名师点睛】本题考查了抛物线的标准方程,焦半径公式,属于中档题,深入理解抛物线的定义是解题的关键,注意韦达定理的使用.9.【2016高考新课标2文数】设F 为抛物线C :y 2=4x 的焦点,曲线y =kx(k >0)与C 交于点P ,PF ⊥x 轴,则k =( )(A )12 (B )1 (C )32(D )2【答案】D考点: 抛物线的性质,反比例函数的性质.【名师点睛】抛物线方程有四种形式,注意焦点的位置. 对函数y =kx(0)k ≠,当0k >时,在(,0)-∞,(0,)+∞上是减函数,当0k <时,在(,0)-∞,(0,)+∞上是增函数.10.【2017天津,文12】设抛物线24y x =的焦点为F ,准线为l .已知点C 在l 上,以C 为圆心的圆与y 轴的正半轴相切于点A.若120FAC ∠=︒,则圆的方程为 .【答案】22(1)(1x y ++-= 【解析】试题分析:设圆心坐标为(1,)C m -,则(0,)A m ,焦点(1,0)F ,(1,0),(1,)AC AF m =-=-,1cos 2AC AF CAF AC AF ⋅∠===-⋅,m =,由于圆C 与y轴得正半轴相切,则取m =,所求圆得圆心为(-,半径为1,所求圆的方程为22(1)(1x y ++-=. 【考点】1.抛物线的方程;2.圆的方程.【名师点睛】本题设计比较巧妙,考查了圆,抛物线的方程,同时还考查了向量数量积的坐标表示,本题只有一个难点,就是0120CAF ∠=,会不会用向量的坐标表示cos CAF ∠,根据图象,可设圆心为()1,C m -,那么方程就是()()2211x y m ++-=,若能用向量的坐标表示角,即可求得m ,问题也就迎刃而解了.11.【2014上海,文4】若抛物线y 2=2px 的焦点与椭圆15922=+y x 的右焦点重合,则该抛物线的准线方程为___________. 【答案】2x =-.【考点】椭圆与抛物线的几何性质【名师点睛】1.涉及抛物线几何性质的问题常结合图形思考,通过图形可以直观地看出抛物线的顶点、对称轴、开口方向等几何特征,体现了数形结合思想解题的直观性. 2.求抛物线方程应注意的问题(1)当坐标系已建立时,应根据条件确定抛物线方程属于四种类型中的哪一种; (2)要注意把握抛物线的顶点、对称轴、开口方向与方程之间的对应关系; (3)要注意参数p 的几何意义是焦点到准线的距离,利用它的几何意义来解决问题. 12.【2014高考陕西版文第11题】抛物线24y x =的准线方程为________. 【答案】1x =- 【解析】试题分析:由抛物线的几何性质知:抛物线24y x =的准线方程为1x =-,故答案为1x =-. 考点:抛物线的几何性质.【名师点晴】本题主要考查的是抛物线的几何性质,属于容易题,解题时直接利用抛物线的几何性质即可求得其准线方程13.【2017课标1,文20】设A ,B 为曲线C :y =24x 上两点,A 与B 的横坐标之和为4.(1)求直线AB 的斜率;(2)设M 为曲线C 上一点,C 在M 处的切线与直线AB 平行,且AM ⊥BM ,求直线AB 的方程.【答案】(1)1; (2)7y x =+.于是直线AB 的斜率12121214y y x x k x x -+===-. (2)由24x y =,得2xy'=.设M (x 3,y 3),由题设知312x=,解得32x =,于是M (2,1).设直线AB 的方程为y x m =+,故线段AB 的中点为N (2,2+m ),|MN |=|m +1|.将y x m =+代入24x y =得2440x x m --=.当16(1)0m ∆=+>,即1m >-时,1,22x =±从而12|||AB x x -=.由题设知||2||AB MN =,即2(1)m =+,解得7m =. 所以直线AB 的方程为7y x =+. 【考点】直线与圆锥曲线的位置关系【名师点睛】本题主要考查直线与圆锥曲线位置关系,所使用方法为韦达定理法:因直线的方程是一次的,圆锥曲线的方程是二次的,故直线与圆锥曲线的问题常转化为方程组关系问题,最终转化为一元二次方程问题,故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一,尤其是弦中点问题,弦长问题,可用韦达定理直接解决,但应注意不要忽视判别式的作用.14.【2017浙江,21】(本题满分15分)如图,已知抛物线2x y =,点A11()24-,,39()24B ,,抛物线上的点)2321)(,(<<-x y x P .过点B 作直线AP 的垂线,垂足为Q .(Ⅰ)求直线AP 斜率的取值范围; (Ⅱ)求||||PQ PA ⋅的最大值. 【答案】(Ⅰ))1,1(-;(Ⅱ)2716试题解析:(Ⅰ)设直线AP 的斜率为k ,则2121412-=+-=x x x k ,∵1322x -<<,∴直线AP 斜率的取值范围是)1,1(-.(Ⅱ)联立直线AP 与BQ 的方程110,24930,42kx y k x ky k ⎧-++=⎪⎪⎨⎪+--=⎪⎩ 解得点Q 的横坐标是)1(23422+++-=k k k x Q ,因为|P A|=1)2x +=)1(12++k k |PQ |=1)1)(1()(1222++--=-+k k k x x k Q ,所以|P A ||PQ |=3)1)(1(+--k k令3)1)(1()(+--=k k k f ,因为2)1)(24()('+--=k k k f ,所以 f (k )在区间)21,1(-上单调递增,)1,21(上单调递减,因此当k =12时,||||PQ PA ⋅取得最大值2716. 【考点】直线与圆锥曲线的位置关系【名师点睛】本题主要考查直线方程、直线与抛物线的位置关系等基础知识,同时考查解析几何的基本思想方法和运算求解能力,通过表达||PA 与||PQ 的长度,通过函数3)1)(1()(+--=k k k f 求解||||PQ PA ⋅的最大值.15.【2016高考新课标1文数】(本小题满分12分)在直角坐标系xOy 中,直线l :y =t (t ≠0)交y 轴于点M ,交抛物线C :22(0)y px p =>于点P ,M 关于点P 的对称点为N ,连结ON并延长交C 于点H . (I )求OH ON;(II )除H 以外,直线MH 与C 是否有其它公共点?说明理由. 【答案】(I )2(II )没有把直线MH 的方程x tpt y 2=-,与px y 22=联立得04422=+-t ty y ,解得t y y 221==,即直线MH 与C 只有一个公共点,所以除H 以外直线MH 与C 没有其它公共点.试题解析:(Ⅰ)由已知得),0(t M ,),2(2t pt P . 又N 为M 关于点P 的对称点,故),(2t p t N ,ON 的方程为x t p y =,代入px y 22=整理得0222=-x t px ,解得01=x ,p t x 222=,因此)2,2(2t pt H . 所以N 为OH 的中点,即2||||=ON OH . (Ⅱ)直线MH 与C 除H 以外没有其它公共点.理由如下: 直线MH 的方程为x t p t y 2=-,即)(2t y ptx -=.代入px y 22=得04422=+-t ty y ,解得t y y 221==,即直线MH 与C 只有一个公共点,所以除H 以外直线MH 与C 没有其它公共点.考点:直线与抛物线【名师点睛】高考解析几何解答题大多考查直线与圆锥曲线的位置关系,直线与圆锥曲线的位置关系是一个很宽泛的考试内容,主要由求值、求方程、求定值、最值、求参数取值范围等几部分组成;解析几何中的证明问题通常有以下几类:证明点共线或直线过定点;证明垂直;证明定值问题.其中考查较多的圆锥曲线是椭圆与抛物线,解决这类问题要重视方程思想、函数思想及化归思想的应用.16.[2016高考新课标Ⅲ文数]已知抛物线C :22y x =的焦点为F ,平行于x 轴的两条直线12,l l 分别交C 于,A B 两点,交C 的准线于P Q ,两点.(I )若F 在线段AB 上,R 是PQ 的中点,证明AR FQ ;(II )若PQF ∆的面积是ABF ∆的面积的两倍,求AB 中点的轨迹方程. 【答案】(Ⅰ)见解析;(Ⅱ)21y x =-.试题解析:由题设)0,21(F .设b y l a y l ==:,:21,则0≠ab ,且)2,21(),,21(),,21(),,2(),0,2(22b a R b Q a P b b B a A +---. 记过B A ,两点的直线为l ,则l 的方程为0)(2=++-ab y b a x . .....3分 (Ⅰ)由于F 在线段AB 上,故01=+ab . 记AR 的斜率为1k ,FQ 的斜率为2k ,则222111k b aaba ab a b a a b a k =-=-==--=+-=, 所以AR FQ . ......5分 (Ⅱ)设l 与x 轴的交点为)0,(1x D , 则2,2121211b a S x a b FD a b S PQF ABF -=--=-=∆∆. 由题设可得221211b a x a b -=--,所以01=x (舍去),11=x . 设满足条件的AB 的中点为),(y x E . 当AB 与x 轴不垂直时,由DE AB k k =可得)1(12≠-=+x x yb a . 而y ba =+2,所以)1(12≠-=x x y . 当AB 与x 轴垂直时,E 与D 重合,所以,所求轨迹方程为12-=x y . ....12分考点:1、抛物线定义与几何性质;2、直线与抛物线位置关系;3、轨迹求法.【方法归纳】(1)解析几何中平行问题的证明主要是通过证明两条直线的斜率相等或转化为利用向量证明;(2)求轨迹的方法在高考中最常考的是直接法与代入法(相关点法),利用代入法求解时必须找准主动点与从动点.17. 【2015高考湖南,文20】(本小题满分13分)已知抛物线21:4C x y =的焦点F 也是椭圆22222:1y x C a b+=(0)a b >>的一个焦点,1C 与2C 的公共弦长为,过点F 的直线l 与1C 相交于,A B 两点,与2C 相交于,C D 两点,且AC 与BD同向.(I )求2C 的方程;(II )若AC BD =,求直线l 的斜率.【答案】(I )22198y x += ;(II) .2234341212()4()4x x x x x x x x +-=+-,设直线l 的斜率为k ,则l 的方程为1y kx =+,联立直线与抛物线方程、直线与椭圆方程、利用韦达定理进行计算即可得到结果.试题解析:(I )由21:4C x y =知其焦点F 的坐标为(0,1),因为F 也是椭圆2C 的一个焦点,所以221a b -= ①; 又1C 与2C 的公共弦长为,1C 与2C 都关于y 轴对称,且1C的方程为21:4C x y =,由此易知1C 与2C 的公共点的坐标为3()2,229614a b∴+= ②,联立①②得229,8a b ==,故2C 的方程为22198y x +=。
专题25 选修部分—三年高考(2015-2017数学(文)真题分项版解析(原卷版)(批量下载)

精品“正版”资料系列,由本公司独创。
旨在将“人教版”、”苏教版“、”北师 大版“、”华师大版“等涵盖几乎所有版本的教材教案、课件、导学案及同步练习和 检测题分享给需要的朋友。
本资源创作于2020年8月,是当前最新版本的教材资源。
包含本课对应 内容,是您备课、上课、课后练习以及寒暑假预习的最佳选择。
专题25 选修部分1.【2017课标1,文22】在直角坐标系xOy 中,曲线C 的参数方程为3cos ,sin ,x y θθ=⎧⎨=⎩(θ为参数),直线l 的参数方程为4,1,x a t t y t =+⎧⎨=-⎩(为参数). (1)若1-=a ,求C 与l 的交点坐标;(2)若C 上的点到l ,求a .2【2017课标1,文23】已知函数4)(2++-=ax x x f ,|1||1|)(-++=x x x g . (1)当1=a 时,求不等式)()(x g x f ≥的解集;(2)若不等式)()(x g x f ≥的解集包含[–1,1],求a 的取值范围.3.【2017课标II ,文22】 在直角坐标系xOy 中,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线1C 的极坐标方程为cos 4ρθ=。
(1)M 为曲线1C 上的动点,点P 在线段OM 上,且满足||||16OM OP ⋅=,求点P 的轨迹2C 的直角坐标方程; (2)设点A 的极坐标为(2,)3π,点B 在曲线2C 上,求OAB △面积的最大值。
4.【2017课标II ,文23】已知330,0,2a b a b >>+=。
证明: (1)55()()4a b a b ++≥;(2)2a b +≤。
5.【2017课标3,文22】在直角坐标系xOy 中,直线1l 的参数方程为2+,,x t y kt =⎧⎨=⎩(t 为参数),直线2l 的参数方程为2,,x m m my k =-+⎧⎪⎨=⎪⎩(为参数).设l 1与l 2的交点为P ,当k 变化时,P 的轨迹为曲线C .(1)写出C 的普通方程;(2)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,设l 3:ρ(cos θ+sin θ)=0,M 为l 3与C 的交点,求M 的极径.6.【2017课标3,文23】已知函数()f x =│x +1│–│x –2│.(1)求不等式()f x ≥1的解集;(2)若不等式()f x ≥x 2–x +m 的解集非空,求实数m 的取值范围.7【2017江苏,21】A. [选修4—1:几何证明选讲](本小题满分10分)如图,AB 为半圆O 的直径,直线PC 切半圆O 于点C ,AP ⊥PC ,P 为垂足. 求证:(1);PAC CAB ∠=∠ (2)2AC AP AB =⋅.B. [选修4—2:矩阵与变换](本小题满分10分)已知矩阵0110,.1002B ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦A A=[0110] ,B=[1002].(1)求AB ;(2)若曲线221:182x y C +=在矩阵AB 对应的变换作用下得到另一曲线2C ,求2C 的方程.C. [选修4-4:坐标系与参数方程](本小题满分10分)在平面坐标系中xOy 中,已知直线l 的参考方程为x 82tty =-+⎧⎪⎨=⎪⎩(t 为参数),曲线C 的参数方程为22,x s y ⎧=⎪⎨=⎪⎩(s 为参数).设P 为曲线C 上的动点,求点P 到直线l 的距离的最小值.D.[选修4-5:不等式选讲](本小题满分10分)已知,,,a b c d 为实数,且22224,16,a b c d +=+=证明8.ac bd +≤【2016,2015,2014高考】1. 【 2014湖南文12】在平面直角坐标系中,曲线2:1x C y ⎧=+⎪⎪⎨⎪=+⎪⎩(t 为参数)的普通方程为___________.2. 【2016高考天津文数】如图,AB 是圆的直径,弦CD 与AB 相交于点E ,BE =2AE =2,BD =ED ,则线段CE 的长为__________.3.【2015高考湖南,文12】在直角坐标系xOy 中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系.若曲线C 的极坐标方程为2sin ρθ=,则曲线C 的直角坐标方程为_____.4.【2014高考陕西版文第15题】(不等式选做题)设R n m b a ∈,,,,且5,522=+=+nb ma b a ,则22n m +的最小值为______.5. 【2014高考陕西版文第15题】(几何证明选做题)如图,ABC ∆中,6=BC ,以BC 为直径的半圆分别交AC AB ,于点F E ,,若AE AC 2=,则EF =_______.6. 【2014高考陕西版文第15题】(坐标系与参数方程选做题)在极坐标系中,点)6,2(π到直线1)6sin(=-πθρ的距离是_______.7. 【2014高考广东卷.文.14】(坐标系与参数方程选做题)在极坐标系中,曲线1C 和2C 的方程分 别为22cossin ρθθ=和cos 1ρθ=,以极点为平面直角坐标系的原点,极轴为x 轴正半轴,建立平面直角坐标系,则曲线1C 和2C 交点的直角坐标为_________.8. 【2014高考广东卷.文.15】(几何证明选讲选做题)如图1,在平行四边形ABCD 中,点E 在AB 上且AE EB 2=,AC 与DE 交于点F ,则CDF AEF ∆=∆的周长的周长.9.【2015高考广东,文14】(坐标系与参数方程选做题)在平面直角坐标系x y O 中,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系.曲线1C 的极坐标方程为()cos sin 2ρθθ+=-,曲线2C的参数方程为2x ty ⎧=⎪⎨=⎪⎩(t 为参数),则1C 与2C 交点的直角坐标为 .10. 【2015高考广东,文15】(几何证明选讲选做题)如图1,AB 为圆O 的直径,E 为AB 的延长线上一点,过E 作圆O 的切线,切点为C ,过A 作直线C E 的垂线,垂足为D .若4AB =,C E =,则D A = .三、解答题1. 【2015高考陕西,文22】选修4-1:几何证明选讲如图,AB 切O 于点B ,直线AO 交O 于,D E 两点,,BC DE ⊥垂足为C .(I)证明:CBD DBA ∠=∠ (II)若3,AD DC BC ==,求O 的直径.2. 【2015高考陕西,文23】选修4-4:坐标系与参数方程在直角坐标版权法xOy 吕,直线l的参数方程为132(x t t y ⎧=+⎪⎪⎨⎪=⎪⎩为参数),以原点为极点,x轴的正半轴为极轴建立极坐标系,C的极坐标方程为ρθ=.(I)写出C 的直角坐标方程;(II)P 为直线l 上一动点,当P 到圆心C 的距离最小时,求点P 的坐标.3. 【2015高考陕西,文24】选修4-5:不等式选讲已知关于x 的不等式x a b +<的解集为{|24}x x << (I)求实数,a b 的值;(II)+的最大值.4. 【2016高考新课标1文数】(本小题满分10分)选修4-1:几何证明选讲 如图,△OAB 是等腰三角形,∠AOB =120°.以O 为圆心,OA 为半径作圆.(I)证明:直线AB 与O 相切;(II)点C ,D 在⊙O 上,且A ,B ,C ,D 四点共圆,证明:AB ∥CD .5. 【2016高考新课标1文数】(本小题满分10分)选修4—4:坐标系与参数方程 在直角坐标系xy 中,曲线C 1的参数方程为(t 为参数,a >0).在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,曲线C 2:ρ=.(I )说明C 1是哪一种曲线,并将C 1的方程化为极坐标方程; (II )直线C 3的极坐标方程为,其中满足tan=2,若曲线C 1与C 2的公共点都在C 3上,求a .6.【2014全国2,文22】(本小题满分10分)选修4-1:几何证明选讲 如图,P 是O 外一点,PA 是切线,A 为切点,割线PBC 与O 相交于,B C ,2PC PA =,D 为PC 的中点,AD 的延长线交O 于点E .证明:(Ⅰ)BEEC =;(Ⅱ)22AD DEPB ⋅=7. 【2014全国2,文23】(本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xOy 中,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,半圆C 的极坐标方程为2cos ,[0,]2πρθθ=∈.(Ⅰ)求C 得参数方程;(Ⅱ)设点D 在C 上,C 在D 处的切线与直线:2l y =+垂直,根据(1)中你得到的参数方程,确定D 的坐标.8. 【2014全国2,文24】(本小题满分10分)选修4-5:不等式选讲 设函数1()||||(0)f x x x a a a=++-> (Ⅰ)证明:()2f x ≥;(Ⅱ)若(3)5f <,求a 的取值范围.9. 【2016高考新课标1文数】(本小题满分10分),选修4—5:不等式选讲 已知函数.(I )在答题卡第(24)题图中画出的图像;(II )求不等式的解集.10.【2014全国1,文22】如图,四边形ABCD 是O 的内接四边形,AB 的延长线与DC的延长线交于点E ,且CB CE =.(I )证明:D E ∠=∠; (II )设AD 不是O 的直径,AD 的中点为M ,且MB MC =,证明:ADE ∆为等边三角形.11. 【2014全国1,文23】已知曲线194:22=+y x C ,直线⎩⎨⎧-=+=t y t x l 222:(t 为参数) (1)写出曲线C 的参数方程,直线l 的普通方程;(2)过曲线C 上任意一点P 作与l 夹角为30°的直线,交l 于点A ,求PA 的最大值与最小值.12. 【2014全国1,文24】若,0,0>>b a 且ab ba =+11 (I )求33b a +的最小值;(II )是否存在b a ,,使得632=+b a ?并说明理由.13. 【2015高考新课标1,文22】选修4-1:几何证明选讲 如图AB 是O 直径,AC 是O 切线,BC 交O 与点E .(I )若D 为AC 中点,求证:DE 是O 切线;(II )若OA = ,求ACB ∠的大小.14. 【2016高考新课标2文数】如图,在正方形中,分别在边上(不与端点重合),且,过点作,垂足为.(Ⅰ) 证明:四点共圆; (Ⅱ)若,为的中点,求四边形的面积.15. 【2016高考新课标2文数】在直角坐标系xOy 中,圆C 的方程为22(6)25x y ++=.(Ⅰ)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,求C 的极坐标方程; (Ⅱ)直线l 的参数方程是cos sin x t y t αα=⎧⎨=⎩(t 为参数), l 与C 交于,A B 两点,||AB =,求l 的斜率.16. 【2016高考新课标2文数】已知函数11()||||22f x x x =-++,M 为不等式()2f x <的解集.(Ⅰ)求M ;(Ⅱ)证明:当,a b M ∈时,|||1|a b ab +<+.17. 【2015高考新课标1,文23】选修4-4:坐标系与参数方程在直角坐标系xOy 中,直线1:2C x =-,圆()()222:121C x y -+-=,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系. (I )求12,C C 的极坐标方程. (II )若直线3C 的极坐标方程为()πR 4θρ=∈,设23,C C 的交点为,M N ,求2C MN ∆ 的面积.18. 【2015高考新课标1,文24】(本小题满分10分)选修4-5:不等式选讲 已知函数()12,0f x x x a a =+--> . (I )当1a = 时求不等式()1f x > 的解集;(II )若()f x 图像与x 轴围成的三角形面积大于6,求a 的取值范围.19.【2014年.浙江。
专题25 选修部分—三年高考(2015-2017)数学(文)真题分项版解析(解析版)

1.【2017课标1,文22】在直角坐标系xOy 中,曲线C 的参数方程为3cos ,sin ,x y θθ=⎧⎨=⎩(θ为参数),直线l 的参数方程为4,1,x a t t y t =+⎧⎨=-⎩(为参数). (1)若1-=a ,求C 与l 的交点坐标;(2)若C 上的点到l a . 【答案】(1)(3,0),2124(,)2525-;(2)8a =或16a =-.试题解析:(1)曲线C 的普通方程为2219x y +=. 当1a =-时,直线l 的普通方程为430x y +-=.由2243019x y x y +-=⎧⎪⎨+=⎪⎩解得30x y =⎧⎨=⎩或21252425x y ⎧=-⎪⎪⎨⎪=⎪⎩. 从而C 与l 的交点坐标为(3,0),2124(,)2525-. (2)直线l 的普通方程为440x y a +--=,故C 上的点(3cos ,sin )θθ到l 的距离为d =.当4a ≥-时,d=8a =; 当4a <-时,d=,所以16a =-. 综上,8a=或16a =-.【考点】参数方程【名师点睛】本题为选修内容,先把直线与椭圆的参数方程化为直角坐标方程,联立方程,可得交点坐标,利用椭圆的参数方程,求椭圆上一点到一条直线的距离的最大值,直接利用点到直线的距离公式,表达椭圆上的点到直线的距离,利用三角有界性确认最值,进而求得参数a 的值.2【2017课标1,文23】已知函数4)(2++-=ax x x f ,|1||1|)(-++=x x x g . (1)当1=a 时,求不等式)()(x g x f ≥的解集;(2)若不等式)()(x g x f ≥的解集包含[–1,1],求a 的取值范围.【答案】(1){|1x x -<≤;(2)[1,1]-.试题解析:(1)当1a =时,不等式()()f x g x ≥等价于2|1||1|40x x x x -+++--≤.① 当1x <-时,①式化为2340x x --≤,无解;当11x -≤≤时,①式化为220x x --≤,从而11x -≤≤;当1x >时,①式化为240x x +-≤,从而1x <≤所以()()f x g x ≥的解集为{|1x x -<≤. (2)当[1,1]x ∈-时,()2g x =.所以()()f x g x ≥的解集包含[1,1]-,等价于当[1,1]x ∈-时()2f x ≥.又()f x 在[1,1]-的最小值必为(1)f -与(1)f 之一,所以(1)2f -≥且(1)2f ≥,得11a -≤≤.所以a 的取值范围为[1,1]-. 【考点】不等式选讲【名师点睛】形如||||x a x b c -+-≥(或c ≤)型的不等式主要有两种解法:(1)分段讨论法:利用绝对值号内式子对应方程的根,将数轴分为(,]a -∞,(,]a b ,(,)b +∞ (此处设a b <)三个部分,在每部分去掉绝对值号并分别列出对应的不等式求解,然后取各个不等式解集的并集.(2)图像法:作出函数1||||y x a x b =-+-和2y c =的图像,结合图像求解.3.【2017课标II ,文22】 在直角坐标系xOy 中,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线1C 的极坐标方程为cos 4ρθ=。
2015-2017解析几何全国卷高考真题版

2015-2017解析几何全国卷高考真题1、(2015年1卷5题)已知M (00,x y )是双曲线C :2212x y -=上的一点,12,F F 是C 上的两个焦点,若120MF MF •<,则0y 的取值围是( )(A )(-3,3) (B )(-6,6)(C )(3-,3) (D )() 【答案】A【解析】由题知12(F F ,220012x y -=,所以12MF MF •=0000(,),)x y x y -•- =2220003310x y y +-=-<,解得033y -<<,故选 A.考点:双曲线的标准方程;向量数量积坐标表示;一元二次不等式解法.2、(2015年1卷14题)一个圆经过椭圆221164x y +=的三个顶点,且圆心在x 轴的正半轴上,则该圆的标准方程为 . 【答案】22325()24x y -+=【解析】设圆心为(a ,0),则半径为4a -,则222(4)2a a -=+,解得32a =,故圆的方程为22325()24x y -+=. 考点:椭圆的几何性质;圆的标准方程3、(2015年1卷20题)在直角坐标系xoy 中,曲线C :y=24x 与直线y kx a =+(a >0)交与M,N 两点,(Ⅰ)当k=0时,分别求C 在点M 和N 处的切线方程;(Ⅱ)y 轴上是否存在点P ,使得当k 变动时,总有∠OPM=∠OPN ?说明理由.【答案】0y a --=0y a ++=(Ⅱ)存在【解析】 试题分析:(Ⅰ)先求出M,N 的坐标,再利用导数求出M,N.(Ⅱ)先作出判定,再利用设而不求思想即将y kx a =+代入曲线C 的方程整理成关于x 的一元二次方程,设出M,N 的坐标和P 点坐标,利用设而不求思想,将直线PM ,PN 的斜率之和用a 表示出来,利用直线PM ,PN 的斜率为0,即可求出,a b 关系,从而找出适合条件的P 点坐标.试题解析:(Ⅰ)由题设可得)M a,()N a -,或()M a -,)N a .∵12y x '=,故24x y =在x=C在,)a 处的切线方程为y a x -=-0y a --=.故24x y =在x=-处的到数值为C在(,)a -处的切线方程为y a x -=+0y a ++=.0y a --=0y a ++=. (Ⅱ)存在符合题意的点,证明如下:设P (0,b )为复合题意得点,11(,)M x y ,22(,)N x y ,直线PM ,PN 的斜率分别为12,k k . 将y kx a =+代入C 得方程整理得2440x kx a --=. ∴12124,4x x k x x a +==-. ∴121212y b y b k k x x --+=+=1212122()()kx x a b x x x x +-+=()k a b a+. 当b a =-时,有12k k +=0,则直线PM 的倾斜角与直线PN 的倾斜角互补, 故∠OPM=∠OPN ,所以(0,)P a -符合题意.考点:抛物线的切线;直线与抛物线位置关系;探索新问题;运算求解能力4、(2015年2卷7题)过三点(1,3)A ,(4,2)B ,(1,7)C -的圆交y 轴于M ,N 两点,则||MN =( )A .26B .8C .46D .10 【解析】由已知得321143AB k -==--,27341CB k +==--,所以1AB CB k k =-,所以AB CB ⊥,即ABC ∆为直角三角形,其外接圆圆心为(1,2)-,半径为5,所以外接圆方程为22(1)(2)25x y -++=,令0x =,得2y =±,所以MN =C .考点:圆的方程.5、(2015年2卷11题).已知A,B为双曲线E的左,右顶点,点M在E上,∆ABM为等腰三角形,且顶角为120°,则E的离心率为()A.5 B.2 C.3 D.2【解析】设双曲线方程为22221(0,0)x ya ba b-=>>,如图所示,AB BM=,0120ABM∠=,过点M作MN x⊥轴,垂足为N,在Rt BMN∆中,BN a=,3MN a=,故点M的坐标为(2,3)M a a,代入双曲线方程得2222a b a c==-,即222c a=,所以2e=,故选D.考点:双曲线的标准方程和简单几何性质.6、(2015年2卷20题)(本题满分12分)已知椭圆222:9(0)C x y m m+=>,直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M.(Ⅰ)证明:直线OM的斜率与l的斜率的乘积为定值;(Ⅱ)若l过点(,)3mm,延长线段OM与C交于点P,四边形OAPB能否为平行四边形?若能,求此时l的斜率,若不能,说明理由.【解析】(Ⅰ)设直线:l y kx b=+(0,0)k b≠≠,11(,)A x y,22(,)B x y,(,)M MM x y.将y kx b=+代入2229x y m+=得2222(9)20k x kbx b m+++-=,故12229Mx x kbxk+==-+,299M Mby kx bk=+=+.于是直线OM的斜率9MOMMykx k==-,即9OMk k⋅=-.所以直线OM 的斜率与l 的斜率的乘积为定值. (Ⅱ)四边形OAPB 能为平行四边形. 因为直线l 过点(,)3mm ,所以l 不过原点且与C 有两个交点的充要条件是0k >,3k ≠. 由(Ⅰ)得OM 的方程为9y x k =-.设点P 的横坐标为P x .由2229,9,y x kx y m ⎧=-⎪⎨⎪+=⎩得2222981Pk m x k =+,即P x =.将点(,)3m m 的坐标代入直线l 的方程得(3)3m k b -=,因此2(3)3(9)M mk k x k -=+.四边形OAPB 为平行四边形当且仅当线段AB 与线段OP 互相平分,即2P M x x ==2(3)23(9)mk k k -⨯+.解得14k =24k =.因为0,3i i k k >≠,1i =,2,所以当l的斜率为4或4+OAPB 为平行四边形.考点:1、弦的中点问题;2、直线和椭圆的位置关系.7、(2016年1卷5题)(5)已知方程222213x y m n m n-=+-表示双曲线,且该双曲线两焦点间的距离为4,则n 的取值围是(A )()1,3- (B)(- (C )()0,3 (D)( 【答案】A考点:双曲线的性质【名师点睛】双曲线知识一般作为客观题学生出现,主要考查双曲线几何性质,属于基础题.注意双曲线的焦距是2c 不是c,这一点易出错.8、(2016年1卷10题)以抛物线C 的顶点为圆心的圆交C 于A 、B 两点,交C 的准线于D 、E两点.已知|AB |=,|DE|=则C 的焦点到准线的距离为 (A)2 (B)4 (C)6 (D)8 【答案】B考点:抛物线的性质.【名师点睛】本题主要考查抛物线的性质及运算,注意解析几何问题中最容易出现运算错误,所以解题时一定要注意运算的准确性与技巧性,基础题失分过多是相当一部分学生数学考不好的主要原因.9、(2016年1卷20题)(本小题满分12分)设圆222150x y x ++-=的圆心为A ,直线l 过点B (1,0)且与x 轴不重合,l 交圆A 于C ,D 两点,过B 作AC 的平行线交AD 于点E . (I )证明EA EB +为定值,并写出点E 的轨迹方程;(II )设点E 的轨迹为曲线C 1,直线l 交C 1于M ,N 两点,过B 且与l 垂直的直线与圆A 交于P ,Q 两点,求四边形MPNQ 面积的取值围.【答案】(Ⅰ)13422=+y x (0≠y )(II ))38,12[ 试题解析:(Ⅰ)因为||||AC AD =,AC EB //,故ADC ACD EBD ∠=∠=∠, 所以||||ED EB =,故||||||||||AD ED EA EB EA =+=+.又圆A 的标准方程为16)1(22=++y x ,从而4||=AD ,所以4||||=+EB EA . 由题设得)0,1(-A ,)0,1(B ,2||=AB ,由椭圆定义可得点E 的轨迹方程为:13422=+y x (0≠y ). (Ⅱ)当l 与x 轴不垂直时,设l 的方程为)0)(1(≠-=k x k y ,),(11y x M ,),(22y x N .由⎪⎩⎪⎨⎧=+-=134)1(22y x x k y 得01248)34(2222=-+-+k x k x k . 则3482221+=+k k x x ,341242221+-=k k x x .所以34)1(12||1||22212++=-+=k k x x k MN . 过点)0,1(B 且与l 垂直的直线m :)1(1--=x k y ,A 到m 的距离为122+k ,所以 1344)12(42||22222++=+-=k k k PQ .故四边形MPNQ 的面积 341112||||212++==k PQ MN S . 可得当l 与x 轴不垂直时,四边形MPNQ 面积的取值围为)38,12[.当l 与x 轴垂直时,其方程为1=x ,3||=MN ,8||=PQ ,四边形MPNQ 的面积为12. 综上,四边形MPNQ 面积的取值围为)38,12[. 考点:圆锥曲线综合问题【名师点睛】高考解析几何解答题大多考查直线与圆锥曲线的位置关系,直线与圆锥曲线的位置关系是一个很宽泛的考试容,主要由求值、求方程、求定值、最值、求参数取值围等几部分组成, .其中考查较多的圆锥曲线是椭圆与抛物线,解决这类问题要重视方程思想、函数思想及化归思想的应用.10、(2016年2卷4题)圆2228130x y x y +--+=的圆心到直线10ax y +-= 的距离为1,则a=(A )43- (B )34- (C(D )2【解析】A圆化为标准方程为:,故圆心为,,解得,故选A .11、(2016年2卷11题)已知1F ,2F 是双曲线E :22221x y a b-=的左,右焦点,点M 在E 上,1MF 与x 轴垂直,sin 2113MF F ∠= ,则E 的离心率为(B )32(C(D )2 【解析】A离心率,由正弦定理得. 12、(2016年2卷20题)(本小题满分12分)已知椭圆E :2213x y t +=的焦点在x 轴上,A 是E 的左顶点,斜率为(0)k k >的直线交E 于A ,M 两点,点N 在E 上,MA ⊥NA.(I )当4t =,AM AN =时,求△AMN 的面积; (II )当2AM AN =时,求k 的取值围.2228130x y x y +--+=()()22144x y -+-=()14,1d ==43a =-1221F F e MF MF =-122112sin 31sin sin 13F F Me MF MF F F ====---【解析】 ⑴当时,椭圆E 的方程为,A 点坐标为, 则直线AM 的方程为.联立并整理得, 解得或,则因为,所以 因为,,,整理得, 无实根,所以. 所以的面积为. ⑵直线AM 的方程为,联立并整理得,解得或所以 所以因为所以,整理得,. 4t =22143x y +=()20-,()2y kx =+()221432x y y k x ⎧+=⎪⎨⎪=+⎩()2222341616120k x k x k +++-=2x =-228634k x k -=-+222861223434k AMk k -=+=++AM AN ⊥21212413341AN k kk =⎛⎫++⋅- ⎪⎝⎭AM AN =0k >212124343k k k=++()()21440k k k --+=2440k k -+=1k =AMN △221112144223449AM⎫==⎪+⎭(y k x =(2213x y t y k x ⎧+=⎪⎨⎪=+⎩()222223230tk x x t k t +++-=x =x =AM =+=3AN k k+2AM AN =23k k+23632k k t k -=-因为椭圆E 的焦点在x 轴,所以,即,整理得.13、(2016年3卷11题)已知O 为坐标原点,F 是椭圆C :22221(0)x y a b a b +=>>的左焦点,,A B 分别为C 的左,右顶点.P 为C 上一点,且PF x ⊥轴.过点A 的直线l 与线段PF 交于点M ,与y 轴交于点E .若直线BM 经过OE 的中点,则C 的离心率为( ) (A )13(B )12 (C )23 (D )34【答案】A考点:椭圆方程与几何性质.【思路点拨】求解椭圆的离心率问题主要有三种方法:(1)直接求得,a c 的值,进而求得e的值;(2)建立,,a b c 的齐次等式,求得b a 或转化为关于e 的等式求解;(3)通过特殊值或特殊位置,求出e .14、(2016年3卷16题)已知直线l :30mx y m ++=与圆2212x y +=交于,A B 两点,过,A B 分别做l 的垂线与x 轴交于,C D 两点,若AB =,则||CD =__________________.【答案】43t >236332k k k ->-()()231202k k k +-<-2k <考点:直线与圆的位置关系. 【技巧点拨】解决直线与圆的综合问题时,一方面,要注意运用解析几何的基本思想方法(即几何问题代数化),把它转化为代数问题;另一方面,由于直线与圆和平面几何联系得非常紧密,因此,准确地作出图形,并充分挖掘几何图形中所隐含的条件,利用几何知识使问题较为简捷地得到解决.15、(2016年3卷20题)已知抛物线C :22y x =的焦点为F ,平行于x 轴的两条直线12,l l 分别交C 于,A B 两点,交C 的准线于P Q ,两点. (I )若F 在线段AB 上,R 是PQ 的中点,证明ARFQ ;(II )若PQF ∆的面积是ABF ∆的面积的两倍,求AB 中点的轨迹方程.【答案】(Ⅰ)见解析;(Ⅱ)21y x =-.试题解析:由题设)0,21(F .设b y l a y l ==:,:21,则0≠ab ,且 )2,21(),,21(),,21(),,2(),0,2(22ba Rb Q a P b b B a A +---.记过B A ,两点的直线为l ,则l 的方程为0)(2=++-ab y b a x . .....3分 (Ⅰ)由于F 在线段AB 上,故01=+ab .记AR 的斜率为1k ,FQ 的斜率为2k ,则222111k b a aba ab a b a a b a k =-=-==--=+-=,所以AR FQ . ......5分(Ⅱ)设l 与x 轴的交点为)0,(1x D ,则2,2121211b a S x a b FD a b S PQF ABF -=--=-=∆∆.由题设可得221211b a x a b -=--,所以01=x (舍去),11=x .设满足条件的AB 的中点为),(y x E .当AB 与x 轴不垂直时,由DE ABk k =可得)1(12≠-=+x x yb a .而y ba =+2,所以)1(12≠-=x x y . 当AB 与x 轴垂直时,E 与D 重合,所以,所求轨迹方程为12-=x y . ....12分 考点:1、抛物线定义与几何性质;2、直线与抛物线位置关系;3、轨迹求法.【方法归纳】(1)解析几何中平行问题的证明主要是通过证明两条直线的斜率相等或转化为利用向量证明;(2)求轨迹的方法在高考中最常考的是直接法与代入法(相关点法),利用代入法求解时必须找准主动点与从动点.16、(2017年1卷15题)已知双曲线2222:x y C a b-,(0a >,0b >)的右顶点为A ,以A 为圆心,b 为半径作圆A ,圆A 与双曲线C 的一条渐近线交于M ,N 两点,若60MAN ∠=︒,则C 的离心率为_______.【解析】如图,OA a =,AN AM b ==∵60MAN ∠=︒,∴AP =,OP =∴tan AP OP θ==又∵tan b aθ=b a =,解得223a b =∴e ==17、(2017年1卷20题)已知椭圆C :22221x y a b+=()0a b >>,四点()111P ,,()201P ,,31P ⎛- ⎝⎭,41P ⎛ ⎝⎭中恰有三点在椭圆C 上. (1)求C 的方程;(2)设直线l 不经过2P 点且与C 相交于A 、B 两点,若直线2P A 与直线2P B 的斜率的和为1-,证明:l 过定点.【解析】(1)根据椭圆对称性,必过3P 、4P又4P 横坐标为1,椭圆必不过1P ,所以过234P P P ,,三点 将()23011P P ⎛- ⎝⎭,,代入椭圆方程得 222113141b ab ⎧=⎪⎪⎨⎪+=⎪⎩,解得24a =,21b = ∴椭圆C 的方程为:2214x y +=.(2)①当斜率不存在时,设()():A A l x m A m y B m y =-,,,, 221121A A P A P B y y k k m m m----+=+==- 得2m =,此时l 过椭圆右顶点,不存在两个交点,故不满足. ②当斜率存在时,设()1l y kx b b =+≠∶()()1122A x y B x y ,,,联立22440y kx b x y =+⎧⎨+-=⎩,整理得()222148440k x kbx b +++-= 122814kb x x k -+=+,21224414b x x k -⋅=+则22121211P A P B y y k k x x --+=+()()21212112x kx b x x kx b x x x +-++-=222228888144414kb k kb kbk b k --++=-+()()()811411k b b b -==-+-,又1b ≠ 21b k ⇒=--,此时64k ∆=-,存在k 使得0∆>成立. ∴直线l 的方程为21y kx k =-- 当2x =时,1y =-所以l 过定点()21-,.18、(2017年2卷9题)若双曲线C:22221x y a b-=(0a >,0b >)的一条渐近线被圆()2224x y -+=所截得的弦长为2,则C 的离心率为( )A .2B .3C .2D .233【命题意图】主要考查双曲线的性质及直线与圆的位置关系,意在考查考生的转化与化归思想. 【解析】解法一:常规解法根据双曲线的标准方程可求得渐近线方程为by x a=±,根据直线与圆的位置关系可求得圆心到渐进线的距离为3,∴ 圆心到渐近线的距离为221b ab a ⋅⎛⎫+ ⎪⎝⎭,即2231b ab a ⋅=⎛⎫+ ⎪⎝⎭,解得2e =.解法二:待定系数法设渐进线的方程为y kx =,根据直线与圆的位置关系可求得圆心到渐进线的距离为3,∴ 圆心到渐近线的距离为221k k +,即2231k k =+,解得23k =;由于渐近线的斜率与离心率关系为221k e =-,解得2e =.19、(2017年2卷16题)已知F 是抛物线C:28y x =的焦点,M 是C 上一点,F M 的延长线交y 轴于点N .若M 为F N 的中点,则F N = .【命题意图】本题主要考查抛物线的定义及直线与抛物线的位置关系,意在考查考生的转化与 化归思想运算求解的能力 【解析】解法一:几何法习. 20、(2017年2卷20题)设O 为坐标原点,动点M 在椭圆C :2212x y +=上,过M 做x 轴的垂线,垂足为N ,点P 满足2NP NM =.(1) 求点P 的轨迹方程;(2) 设点Q 在直线x =-3上,且1OP PQ ⋅=.证明:过点P 且垂直于OQ 的直线l 过C 的左焦点F .【命题意图】椭圆,定值问题的探索;运算求解能力【基本解法】(Ⅰ)解法一:相关点法求轨迹:设()00,M x y ,()0,0N x ,(),P x y ,则:()0,NP x x y =-,()00,NM y =. 又2NP NM =,所以:())00,0,x x y y -=,则:00,x x y ==.又()00,M x y 在椭圆C 上,所以:220012x y +=。
高考化学化学反应中的能量变化—三年高考(2015-2017)化学真题分项版解析(解析版)

1.【2017江苏卷】通过以下反应可获得新型能源二甲醚(CH3OCH3 )。
下列说法不正确...的是①C(s) + H2O(g)CO(g) + H2 (g) ΔH1 = a kJ·mol−1②CO(g) + H2O(g)CO2 (g) + H2 (g) ΔH 2 = b kJ·mol−1③CO2 (g) + 3H2 (g)CH3OH(g) + H2O(g) ΔH 3 = c kJ·mol−1④2CH3OH(g)CH3OCH3 (g) + H2O(g) ΔH 4 = d kJ·mol−1A.反应①、②为反应③提供原料气B.反应③也是CO2资源化利用的方法之一C.反应CH3OH(g)CH3OCH3 (g) +H2O(l)的ΔH =kJ·mol−1D.反应2CO(g) + 4H2 (g) CH3OCH3 (g) + H2O(g)的ΔH = ( 2b + 2c + d ) kJ·mol−1【答案】C【名师点睛】本题以合成新能源二甲醚为背景,考查学生对简单化工流程的反应原理、能量的转化关系、化学反应焓变的概念、盖斯定律的运用等知识的掌握和理解程度,同时关注了节能减排、工业三废资源化处理、开发利用新能源等社会热点问题。
2.【2016海南卷】油酸甘油酯(相对分子质量884)在体内代谢时可发生如下反应:C57H104O6(s)+80O2(g)=57CO2(g)+52H2O(l)已知燃烧1kg该化合物释放出热量3.8×104kJ。
油酸甘油酯的燃烧热△H为A.3.8×104kJ·mol-1B.-3.8×104kJ·mol-1C.3.4×104kJ·mol-1D.-3.4×104kJ·mol-1【答案】D【解析】试题分析:燃烧热指的是燃烧1mol可燃物生成稳定的氧化物所放出的热量。
2015-2017全国卷(文)真题汇编-解析几何-S

高考全国卷文科真题汇编_解析几何(2017 全国1 文科)5.已知F 是双曲线C :x 2-23y =1的右焦点,P 是C 上一点,且PF 与x轴垂直,点A 的坐标是(1,3).则△APF 的面积为A .13B .1 2C .2 3D .3 2(2017 全国1 文科)12.设A 、B 是椭圆C :2213x y m+=长轴的两个端点,若C 上存在点M满足∠AMB =120°,则m 的取值范围是A .(0,1][9,)+∞B .[9,)+∞C .(0,1][4,)+∞D .[4,)+∞(2017 全国1 文科)20.设A ,B 为曲线C :y =24x 上两点,A 与B 的横坐标之和为4. (1)求直线AB 的斜率;(2)设M 为曲线C 上一点,C 在M 处的切线与直线AB 平行,且AM ⊥BM ,求直线AB 的方程.(2017 全国2 文科)5. 若1a >,则双曲线2221x y a-=的离心率的取值范围是A. ∞)B. 2)C. (1D. 12(,)(2017 全国2 文科)12. 过抛物线2:4C y x =的焦点F C 于点M(M 在x 轴上方),l 为C 的准线,点N 在l 上且MN l ⊥,则M 到直线NF 的距离为A. B.C.D.(2017 全国2 文科)20.设O 为坐标原点,动点M 在椭圆C :2212x y +=上,过M 做x 轴的垂线,垂足为N ,点P 满足NP =.(1)求点P 的轨迹方程; (2)设点Q 在直线3x =-上,且1OP PQ ⋅=.证明:过点P 且垂直于OQ 的直线l 过C 的左焦点F .(2016 全国1 文科)5.直线l 经过椭圆的一个顶点和一个焦点,若椭圆中心到l 的距离为其短轴长的41,则该椭圆的离心率为() A.31 B.21 C.32 D.43(2016全国1 文科)13.设直线a x y 2+=与圆C :02222=--+ay y x 相交于A ,B 两点,若32=AB ,则圆C 的面积为_________(2016 全国1 文科)20.在直角坐标系xOy 中,直线l :y =t (t ≠0)交y 轴于点M ,交抛物线C :22(0)y px p =>于点P ,M 关于点P 的对称点为N ,连结ON 并延长交C 于点H .(I )求OH ON;(II )除H 以外,直线MH 与C 是否有其它公共点?说明理由.(2016 全国2 文科)5.设F为抛物线C:y2=4x的焦点,曲线y=(k>0)与C交于点P,PF⊥x轴,则k=()A.B.1 C.D.2(2016 全国2 文科)6.圆x2+y2﹣2x﹣8y+13=0的圆心到直线ax+y﹣1=0的距离为1,则a=()A.﹣B.﹣C.D.2(2016 全国2 文科)21.已知A是椭圆E:+=1的左顶点,斜率为k(k>0)的直线交E与A,M两点,点N在E上,MA⊥NA.(I)当|AM|=|AN|时,求△AMN的面积(II)当2|AM|=|AN|时,证明:<k<2.(2015 全国1 文科)5.已知椭圆E 的中心在坐标原点,离心率为12,E 的右焦点与抛物线C :y ²=8x 的焦点重合,A ,B 是C 的准线与E 的两个焦点,则|AB|= (A )3 (B )6 (C )9 (D )12(2015 全国1 文科)16.已知F 是双曲线C :x 2-82y =1的右焦点,P 是C 的左支上一点,A (0,66).当△APF 周长最小是,该三角形的面积为(2015 全国1 文科)20.已知过点A(0,1)且斜率为k 的直线l 与圆C(x-2)2+(y-3)2=1交于M,N 两点.(1) 求K 的取值范围;(2) 若OM ·ON=12,其中0为坐标原点,求︱MN ︱.。
专题16 抛物线—三年高考(2015-2017)数学(文)真题分项版解析(原卷版)(打包下载)

专题16 抛物线1.2017课标II ,文12】过抛物线2:4C y x =的焦点F ,C 于点M (M 在x 轴上方),l 为C 的准线,点N 在l 上且MN l ⊥,则M 到直线NF 的距离为B. C. D. 2.【2014,安徽文3】抛物线241x y =的准线方程是( )A . 1-=yB . 2-=yC . 1-=xD . 2-=x3. 【2014全国1,文10】已知抛物线C : x y =2的焦点为F ,()00,A x y 是C 上一点,x F A 045=,则0x =( ) A. 1 B. 2 C. 4 D. 84. 【2014辽宁文8】已知点(2,3)A -在抛物线C :22y px =的准线上,记C 的焦点为F ,则直线AF 的斜率为( )A .43-B .1-C .34-D .12- 5.【2014四川,文10】已知F 是抛物线2y x =的焦点,点A ,B 在该抛物线上且位于x 轴的两侧, 2OA OB ⋅=(其中O 为坐标原点),则ABO ∆与AFO ∆面积之和的最小值是( )A .2B .3CD 6.【2015高考陕西,文3】已知抛物线22(0)y px p =>的准线经过点(1,1)-,则抛物线焦点坐标为( )A .(1,0)-B .(1,0)C .(0,1)-D .(0,1)7. 【2016高考四川文科】抛物线24y x =的焦点坐标是( ) (A)(0,2) (B) (0,1) (C) (2,0) (D) (1,0)8.【2014全国2,文10】设F 为抛物线2:=3C y x 的焦点,过F 且倾斜角为30︒的直线交C 于A ,B 两点,则 AB =( )(A (B )6 (C )12 (D )9.【2016高考新课标2文数】设F 为抛物线C :y 2=4x 的焦点,曲线y =kx(k >0)与C 交于点P ,PF ⊥x 轴,则k =( )(A )12 (B )1 (C )32(D )210.【2017天津,文12】设抛物线24y x =的焦点为F ,准线为l .已知点C 在l 上,以C 为圆心的圆与y 轴的正半轴相切于点A.若120FAC ∠=︒,则圆的方程为 .11.【2014上海,文4】若抛物线y 2=2px 的焦点与椭圆15922=+y x 的右焦点重合,则该抛物线的准线方程为___________.12.【2014高考陕西版文第11题】抛物线24y x =的准线方程为________.13.【2017课标1,文20】设A ,B 为曲线C :y =24x 上两点,A 与B 的横坐标之和为4.(1)求直线AB 的斜率;(2)设M 为曲线C 上一点,C 在M 处的切线与直线AB 平行,且AM ⊥BM ,求直线AB 的方程.14.【2017浙江,21】(本题满分15分)如图,已知抛物线2x y =,点A11()24-,,39()24B ,,抛物线上的点)2321)(,(<<-x y x P .过点B 作直线AP 的垂线,垂足为Q .(Ⅰ)求直线AP 斜率的取值范围;(Ⅱ)求||||PQ PA ⋅的最大值.15.【2016高考新课标1文数】(本小题满分12分)在直角坐标系xOy 中,直线l :y =t (t ≠0)交y 轴于点M ,交抛物线C :22(0)y px p =>于点P ,M 关于点P 的对称点为N ,连结ON 并延长交C 于点H . (I )求OHON; (II )除H 以外,直线MH 与C 是否有其它公共点?说明理由.16.[2016高考新课标Ⅲ文数]已知抛物线C :22y x =的焦点为F ,平行于x 轴的两条直线12,l l 分别交C 于,A B 两点,交C 的准线于P Q ,两点.(I )若F 在线段AB 上,R 是PQ 的中点,证明ARFQ ;(II )若PQF ∆的面积是ABF ∆的面积的两倍,求AB 中点的轨迹方程.17. 【2015高考湖南,文20】(本小题满分13分)已知抛物线21:4C x y =的焦点F 也是椭圆22222:1y x C a b+=(0)a b >>的一个焦点,1C 与2C 的公共弦长为,过点F 的直线l 与1C 相交于,A B 两点,与2C 相交于,C D 两点,且AC 与BD 同向. (I )求2C 的方程;(II )若AC BD =,求直线l 的斜率.18.【2016高考浙江文数】(本题满分15分)如图,设抛物线22(0)y px p =>的焦点为F ,抛物线上的点A 到y 轴的距离等于|AF |-1. (I )求p 的值;(II )若直线AF 交抛物线于另一点B ,过B 与x 轴平行的直线和过F 与AB 垂直的直线交于点N ,AN 与x轴交于点M .求M 的横坐标的取值范围.19.【2015高考浙江,文19】(本题满分15分)如图,已知抛物线211C 4y x =:,圆222C (1)1x y +-=:,过点P(t,0)(t>0)作不过原点O 的直线PA ,PB 分别与抛物线1C 和圆2C 相切,A ,B 为切点. (1)求点A ,B 的坐标; (2)求PAB ∆的面积.注:直线与抛物线有且只有一个公共点,且与抛物线的对称轴不平行,则该直线与抛物线相切,称该公 共点为切点.20.【2014福建,文21】((本小题满分12分) 已知曲线Γ上的点到点(0,1)F 的距离比它到直线3y =-的距离小2.(1)求曲线Γ的方程;(2)曲线Γ在点P 处的切线l 与x 轴交于点A .直线3y =分别与直线l 及y 轴交于点,M N ,以MN 为直径作圆C ,过点A 作圆C 的切线,切点为B ,试探究:当点P 在曲线Γ上运动(点P 与原点不重合)时,线段AB 的长度是否发生变化?证明你的结论. 21.【2015高考福建,文19】已知点F 为抛物线2:2(0)E y px p =>的焦点,点(2,)A m 在抛物线E 上,且3AF =. (Ⅰ)求抛物线E 的方程;(Ⅱ)已知点(1,0)G -,延长AF 交抛物线E 于点B ,证明:以点F 为圆心且与直线GA 相切的圆,必与直线GB 相切.专题17 立体几何中线面位置关系1.【2017课标1,文6】如图,在下列四个正方体中,A ,B 为正方体的两个顶点,M ,N ,Q 为所在棱的中点,则在这四个正方体中,直接AB 与平面MNQ 不平行的是A .B .C .D .2.【2017课标3,文10】在正方体1111ABCD A B C D 中,E 为棱CD 的中点,则( )A .11A E DC ⊥B .1A E BD ⊥C .11A E BC ⊥D .1AE AC ⊥3.【2014高考广东卷.文.9】若空间中四条直线两两不同的直线..,满足,,,则下列结论一定正确的是( ) A . B .C ..既不平行也不垂直D ..的位置关系不确定4.【2016高考山东文数】已知直线a ,b 分别在两个不同的平面α,b 内,则“直线a 和直线b 相交”是“平面α和平面b 相交”的( )(A )充分不必要条件(B )必要不充分条件 (C )充要条件 (D )既不充分也不必要条件5.【2015高考广东,文6】若直线1l 和2l 是异面直线,1l 在平面α内,2l 在平面β内,l 是平面α与平面β的交线,则下列命题正确的是( )A .l 至少与1l ,2l 中的一条相交B .l 与1l ,2l 都相交C .l 至多与1l ,2l 中的一条相交D .l 与1l ,2l 都不相交 6. 【2016高考上海文科】如图,在正方体ABCD −A 1B 1C 1D 1中,E 、F 分别为BC 、BB 1的中点,则下列直线中与直线EF 相交的是( )(A)直线AA 1(B)直线A 1B 1(C)直线A 1D 1 (D)直线B 1C 17.【2014辽宁文4】已知m ,n 表示两条不同直线,α表示平面,下列说法正确的是( ) A .若//,//,m n αα则//m n B .若m α⊥,n α⊂,则m n ⊥ C .若m α⊥,m n ⊥,则//n α D .若//m α,m n ⊥,则n α⊥8.【2015高考湖北,文5】12,l l 表示空间中的两条直线,若p :12,l l 是异面直线;q :12,l l 不相交,则( )A .p 是q 的充分条件,但不是q 的必要条件B .p 是q 的必要条件,但不是q 的充分条件C .p 是q 的充分必要条件D .p 既不是q 的充分条件,也不是q 的必要条件9.【2015高考浙江,文4】设α,β是两个不同的平面,l ,m 是两条不同的直线,且l α⊂,m β⊂( )A .若l β⊥,则αβ⊥B .若αβ⊥,则l m ⊥C .若//l β,则//αβD .若//αβ,则//l m10.【2014年.浙江卷.文6】设m 、n 是两条不同的直线,α、β是两个不同的平面,则( )A.若n m ⊥,α//n ,则α⊥mB.若β//m ,αβ⊥,则α⊥mC.若β⊥m ,β⊥n ,α⊥n ,则α⊥mD.若n m ⊥,β⊥n ,αβ⊥,则α⊥m 11.【2017课标1,文18】如图,在四棱锥P-ABCD 中,AB//CD ,且90BAP CDP ∠=∠=.(1)证明:平面PAB ⊥平面PAD ;(2)若PA =PD =AB =DC ,90APD ∠=,且四棱锥P-ABCD 的体积为83,求该四棱锥的侧面积.12.【2017山东,文18】(本小题满分12分)由四棱柱ABCD -A 1B 1C 1D 1截去三棱锥C 1- B 1CD 1后得到的几何体如图所示,四边形ABCD 为正方形,O 为AC 与BD 的交点,E 为AD 的中点,A 1E⊥平面ABCD ,(Ⅰ)证明:1AO ∥平面B 1CD 1;(Ⅱ)设M 是OD 的中点,证明:平面A 1EM ⊥平面B 1CD 1.13.【2017江苏,15】 如图,在三棱锥A-BCD 中,AB ⊥AD , BC ⊥BD , 平面ABD ⊥平面BCD , 点E ,F (E 与A ,D 不重合)分别在棱AD ,BD 上,且EF ⊥AD . 求证:(1)EF ∥平面ABC ; (2)AD ⊥AC .14.【2016高考北京文数】(本小题14分)如图,在四棱锥ABCD P -中,⊥PC 平面ABCD ,,AB DC DC AC ⊥∥ (I )求证:DC PAC ⊥平面; (II )求证:PAB PAC ⊥平面平面;(III )设点E 为AB 的中点,在棱PB 上是否存在点F ,使得//PA 平面C F E ?说明理由.15.【2014四川,文18】(本小题满分12分)(第15题)ADBC EF在如图所示的多面体中,四边形和都为矩形。
专题02 函数—三年高考(2015-2017)数学(文)真题分项版解析(原卷版)
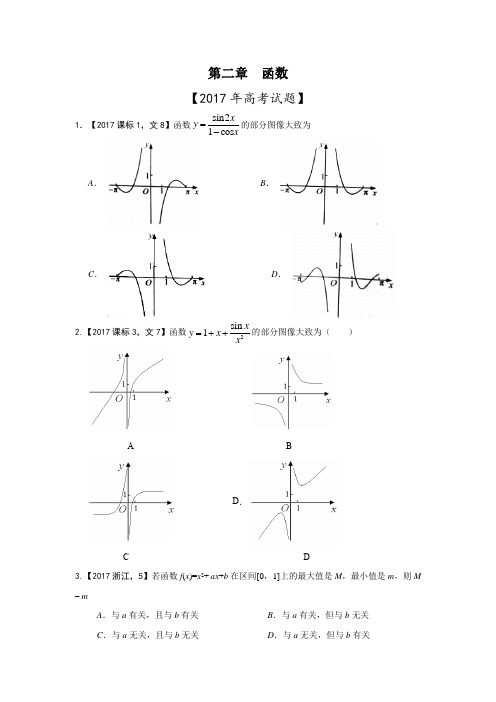
第二章 函数【2017年高考试题】1.【2017课标1,文8】函数sin21cos x y x=-的部分图像大致为 A . B .C .D .2.【2017课标3,文7】函数2sin 1x y x x =++的部分图像大致为( )A BD .C D3.【2017浙江,5】若函数f (x )=x 2+ ax +b 在区间[0,1]上的最大值是M ,最小值是m ,则M – mA .与a 有关,且与b 有关B .与a 有关,但与b 无关C .与a 无关,且与b 无关D .与a 无关,但与b 有关4.【2017北京,文5】已知函数1()3()3x x f x =-,则()f x (A )是偶函数,且在R 上是增函数(B )是奇函数,且在R 上是增函数(C )是偶函数,且在R 上是减函数(D )是奇函数,且在R 上是增函数5.【2017北京,文8】根据有关资料,围棋状态空间复杂度的上限M 约为3361,而可观测宇宙中普通物质的原子总数N 约为1080.则下列各数中与M N最接近的是 (参考数据:lg3≈0.48)(A )1033 (B )1053(C )1073 (D )10936.【2017山东,文9】设()()121,1x f x x x <<=-≥⎪⎩,若()()1f a f a =+,则1f a ⎛⎫= ⎪⎝⎭ A. 2 B. 4 C. 6 D. 87.【2017天津,文6】已知奇函数()f x 在R 上是增函数.若0.8221(log ),(log 4.1),(2)5a fb fc f =-==,则,,a b c 的大小关系为 (A )a b c <<(B )b a c <<(C )c b a <<(D )c a b <<8.【2017课标II ,文8】函数2()ln(28)f x x x =-- 的单调递增区间是A.(,2)-∞-B. (,1)-∞-C. (1,)+∞D. (4,)+∞9.【2017课标1,文9】已知函数()ln ln(2)f x x x =+-,则A .()f x 在(0,2)单调递增B .()f x 在(0,2)单调递减C .y =()f x 的图像关于直线x =1对称D .y =()f x 的图像关于点(1,0)对称 10.【2017山东,文10】若函数()e x f x (e=2.71828,是自然对数的底数)在()f x 的定义域上单调递增,则称函数()f x 具有M 性质,下列函数中具有M 性质的是A . ()2x f x -= B. ()2f x x = C. ()3xf x -= D. ()cos f x x =11.【2017天津,文8】已知函数||2,1,()2, 1.x x f x x x x +<⎧⎪=⎨+≥⎪⎩设a ∈R ,若关于x 的不等式()||2x f x a ≥+在R 上恒成立,则a 的取值范围是 (A )[2,2]-(B)[-(C)[-(D)[-12.【2017课标II ,文14】已知函数()f x 是定义在R 上的奇函数,当(,0)x ∈-∞时,32()2f x x x =+,则(2)f = ________.13.【2017北京,文11】已知0x ≥,0y ≥,且x +y =1,则22x y +的取值范围是__________.14.【2017课标3,文16】设函数10()20x x x f x x +≤⎧=⎨>⎩,,,,则满足1()()12f x f x +->的x 的取值范围是__________.15【2017山东,文14】已知f (x )是定义在R 上的偶函数,且f (x +4)=f (x -2).若当[3,0]x ∈- 时,()6x f x -=,则f (919)= .16.【2017江苏,11】已知函数31()2e e x xf x x x =-+-, 其中e 是自然对数的底数. 若2(1)(2)0f a f a -+≤,则实数a 的取值范围是 .17.【2017江苏,14】设()f x 是定义在R 且周期为1的函数,在区间[0,1)上,2,,(),,x x D f x x x D ⎧∈⎪=⎨∉⎪⎩其中集合1,*n D x x n n -⎧⎫==∈⎨⎬⎩⎭N ,则方程()lg 0f x x -=的解的个数是 . 【2016,2015,2014高考题】1. 【2016高考新课标1文数】若0a b >>,01c <<,则( )(A )log a c <log b c (B )log c a <log c b (C )a c <b c (D )c a >c b2. 【2014高考北京文第2题】下列函数中,定义域是R 且为增函数的是( )A.x y e -=B.3y x = C.ln y x = D.y x =3. 【2014高考北京文第8题】加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下,可食用率p 与加工时间t (单位:分钟)满足的函数关系2p at bt c =++(a 、b 、c 是常数),下图记录了三次实验的数据.根据上述函数模型和实验数据,可以得到最佳加工时间为( )A.3.50分钟B.3.75分钟C.4.00分钟D.4.25分钟4. 【2014高考北京文第6题】已知函数()26log f x x x =-,在下列区间中,包含()f x 零点的区间是( )A.()0,1B.()1,2C.()2,4D.()4,+∞5. 【2015高考北京,文3】下列函数中为偶函数的是( )A .2sin y x x =B .2cos y x x =C .ln y x =D .2x y -=6. 【2014高考广东卷.文.5】下列函数为奇函数的是( )A .122x x - B .3sin x x C .2cos 1x + D .22xx +7. 【2016高考新课标1文数】函数22x y x e =-在[]2,2-的图像大致为( ) (A )(B )(C )(D )8. 【2015高考广东,文3】下列函数中,既不是奇函数,也不是偶函数的是( )A .2sin y x x =+B .2cos y x x =-C .122x xy =+ D .sin 2y x x =+9. 【 2014湖南文4】下列函数中,既是偶函数又在区间(,0)-∞上单调递增的是( )21.()A f x x= 2.()1B f x x =+ 3.()C f x x = .()2x D f x -= 10. 【2016高考新课标2文数】下列函数中,其定义域和值域分别与函数y=10lg x 的定义域和值域相同的是( )(A )y =x (B )y =lg x (C )y =2x (D )y= 11. 【2016高考新课标2文数】已知函数f (x )(x ∈R )满足f (x )=f (2-x ),若函数y =|x 2-2x -3| 与y =f (x ) 图像的交点为(x 1,y 1),(x 2,y 2),…,(x m ,y m ),则1=mii x =∑( ) (A)0 (B)m (C) 2m (D) 4m12. 【2014山东.文3】 函数1log 1)(2-=x x f 的定义域为( )A. (0,2)B. (0,2]C. ),2(+∞D. [2,)+∞13. 【2014山东.文6】已知函数log ()(,a y x c a c =+为常数,其中0,1)a a >≠的图象如右图,则下列结论成立的是( )A.1,1a c >>B.1,01a c ><<C.01,1a c <<>D.01,01a c <<<<14. [2016高考新课标Ⅲ文数]已知4213332,3,25a b c ===,则( )(A) b a c << (B)a b c << (C) b c a << (D) c a b << 15. 【2016高考浙江文数】函数y =sin x 2的图象是( )16. 【2015高考山东,文2】设0.6 1.50.60.60.6 1.5a b c ===,,,则a b c ,,的大小关系是( ) (A )a b c << (B ) a c b << (C )b a c << (D )b c a <<17. 【2014山东.文5】 已知实数,x y 满足(01)x y aa a <<<,则下列关系式恒成立的是( )A.33x y >B.sin sin x y >C.22ln(1)ln(1)x y +>+D.221111x y >++ 18. 【2016高考浙江文数】已知a ,b >0,且a ≠1,b ≠1,若log >1a b ,则( )A.(1)(1)0a b --<B. (1)()0a a b -->C. (1)()0b b a --<D. (1)()0b b a -->19. 【2015高考山东,文8】若函数21()2x x f x a+=-是奇函数,则使3f x >()成立的x 的取值范围为( )(A )( ) (B)() (C )0,1() (D )1,+∞()20. 【2015高考山东,文10】设函数3,1()2,1x x b x f x x -<⎧=⎨≥⎩,若5(())46f f =,则b = ( ) (A )1 (B )78 (C )34 (D)1221. 【2016高考浙江文数】已知函数f (x )=x 2+bx ,则“b <0”是“f (f (x ))的最小值与f (x )的最小值相等”的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件22. 【2015高考陕西,文4】设10()2,0x x f x x ⎧≥⎪=⎨<⎪⎩,则((2))f f -=( ) A .1- B .14 C .12 D .3223. 【2016高考浙江文数】已知函数()f x 满足:()f x x ≥且()2,x f x x ≥∈R .( )A.若()f a b ≤,则a b ≤B.若()2bf a ≤,则a b ≤C.若()f a b ≥,则a b ≥D.若()2b f a ≥,则a b ≥24. 【2014高考陕西版文第7题】下了函数中,满足“()()()f x y f x f y +=”的单调递增函数是( ) (A )()3f x x = (B )()3x f x = (C )()23f x x = (D )()12x f x ⎛⎫= ⎪⎝⎭25. 【2015高考陕西,文9】 设()sin f x x x =-,则()f x =( )A .既是奇函数又是减函数B .既是奇函数又是增函数C .是有零点的减函数D .是没有零点的奇函数26. 【2015高考陕西,文10】设()ln ,0f x x a b =<<,若p f =,()2a b q f +=,1(()())2r f a f b =+,则下列关系式中正确的是( ) A .q r p =< B .q r p => C .p r q =< D .p r q =>27. 【2016高考北京文数】已知(2,5)A ,(4,1)B ,若点(,)P x y 在线段AB 上,则2x y -的最大值为( )A.−1B.3C.7D.828. 【2016高考北京文数】下列函数中,在区间(1,1)- 上为减函数的是( ) A.11y x=- B.cos y x = C.ln(1)y x =+ D.2x y -= 29. 【2014四川,文7】已知,,,,则下列等式一定成0b >5log b a =lg b c =510d =立的是( )A 、B 、C 、D 、30. 【2015高考四川,文5】下列函数中,最小正周期为π的奇函数是( )(A )y =sin (2x +2π) (B )y =cos (2x +2π) (C )y =sin 2x +cos 2x (D )y =sinx +cosx31.【2016高考上海文科】设()f x 、()g x 、()h x 是定义域为R 的三个函数,对于命题:①若()()f x g x +、()()f x h x +、()()g x h x +均为增函数,则()f x 、()g x 、()h x 中至少有一个增函数;②若()()f x g x +、()()f x h x +、()()g x h x +均是以T 为周期的函数,则()f x 、()g x 、()h x 均是以T 为周期的函数,下列判断正确的是( )A 、①和②均为真命题B 、①和②均为假命题C 、①为真命题,②为假命题D 、①为假命题,②为真命题32. 【2015高考四川,文8】某食品的保鲜时间y (单位:小时)与储藏温度x (单位:℃)满足函数关系kx b y e +=( 2.718...e =为自然对数的底数,,k b 为常数).若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,则该食品在33℃的保鲜时间是( )(A )16小时 (B )20小时 (C )24小时 (D )21小时33. 【2014全国1,文5】设函数)(),(x g x f 的定义域为R ,且)(x f 是奇函数,)(x g 是偶函数,则下列结论中正确的是( )A.)()(x g x f 是偶函数B. )(|)(|x g x f 是奇函数C. |)(|)(x g x f 是奇函数D. |)()(|x g x f 是奇函数34.【2015高考新课标1,文10】已知函数1222,1()log (1),1x x f x x x -⎧-≤=⎨-+>⎩ ,且()3f a =-,则(6)f a -=( )(A )74- (B )54- (C )34- (D )14- 35. 【2016高考山东文数】若函数()y f x =的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称()y f x =具有T 性质.下列函数中具有T 性质的是( ) d ac =a cd =c ad =d a c =+(A )sin y x = (B )ln y x = (C )e x y = (D )3y x =36. 【2015高考新课标1,文12】设函数()y f x =的图像与2x a y +=的图像关于直线y x=-对称,且(2)(4)1f f -+-=,则a =( )(A ) 1- (B )1 (C )2 (D )4 37. 【2014年.浙江卷.文7】已知函数c bx ax x x f +++=23)(,且3)3()2()1(0≤-=-=-<f f f ,则( )A.3≤cB.63≤<cC. 96≤<cD.9>c38. 【2016高考山东文数】已知函数f(x )的定义域为R.当x <0时,f(x )=x 3-1;当-1≤x ≤1时,f(-x )= —f(x );当x >12时,f(x +12)=f(x —12).则f(6)= ( ) (A )-2 (B )-1(C )0 (D )239. 【2015高考浙江,文5】函数()1cos f x x x x ⎛⎫=-⎪⎝⎭(x ππ-≤≤且0x ≠)的图象可能为( )A .B .C .D .40. 【2014年.浙江卷.文8】在同一坐标系中,函数)0()(>=x x x f a,x x g a log )(=的图象可能是( )41. 【2016高考四川文科】某公司为激励创新,计划逐年加大研发奖金投入.若该公司2015年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是( )(参考数据:lg1.12=0.05,lg1.3=0.11,lg2=0.30)(A)2018年 (B) 2019年 (C)2020年 (D)2021年42. 【2014高考重庆文第4题】下列函数为偶函数的是( ).()1A f x x =-2.()B f x x x =+ .()22x x C f x -=-.()22x x D f x -=+ 43. 【2014高考重庆文第10题】已知函数13,(1,0](),()()1,1]1,(0,1]x f x g x f x mx m x x x ⎧-∈-⎪==---+⎨⎪∈⎩且在(内有且仅有两个不同的零点,则实数m 的取值范围是( ) A.91(,2](0,]42-- B.111(,2](0,]42-- C.92(,2](0,]43-- D.112(,2](0,]43-- 44. 【2015高考重庆,文3】函数22(x)log (x 2x 3)f =+-的定义域是( )(A) [3,1]- (B) (3,1)-(C) (,3][1,)-∞-+∞ (D) (,3)(1,)-∞-+∞ 45. 【2014,安徽文5】设 1.1 3.13log 7,2,0.8a b c ===则( )A .c a b <<B .b a c <<C .a b c <<D .b c a <<46. 【2015高考安徽,文4】下列函数中,既是偶函数又存在零点的是( ) (A )y =lnx (B )21y x =+ (C )y =sinx (D )y =cosx47. 【2015高考安徽,文10】函数()32f x ax bx cx d =+++的图像如图所示,则下列结论成立的是( )(A )a >0,b <0,c >0,d >0 (B )a >0,b <0,c <0,d >0 (C )a <0,b <0,c <0,d >0 (D )a >0,b >0,c >0,d <048. 【2014,安徽文9】若函数()12f x x x a =+++的最小值3,则实数a 的值为 ( )A .5或8B .1-或5C . 1-或4-D .4-或849.【2014天津,文4】设,,log ,log 2212-===πππc b a 则( )A.c b a >>B.c a b >>C.b c a >>D.a b c >>50. 【2015高考天津,文8】已知函数22||,2()(2),2x x f x x x ì-?ï=í->ïî,函数()3(2)g x f x =--,则函数y ()()f x g x =-的零点的个数为( ) (A) 2 (B) 3 (C)4 (D)551. 【2015高考天津,文7】 已知定义在R 上的函数||()21()x m f x m -=-为实数为偶函数,记0.5(log 3),a f =2b (log 5),c (2)f f m ==,则,,a b c ,的大小关系为( )(A) b c a << (B) b c a << (C) b a c << (D) b c a << 52.【2014年普通高等学校招生全国统一考试湖北卷9】已知)(x f 是定义在R 上的奇函数,当0≥x 时,x x x f 3)(2-=,则函数3)()(+-=x x f x g 的零点的集合为( ) A.{1,3} B.{3,1,1,3}--C.{2D.{2-53. 【2015高考湖北,文6】函数256()lg 3x x f x x -+=-的定义域为( )A .(2,3)B .(2,4]C .(2,3)(3,4]D .(1,3)(3,6]-54. 【2015高考湖北,文7】设x ∈R ,定义符号函数1,0,sgn 0,0,1,0.x x x x >⎧⎪==⎨⎪-<⎩则( ) A .|||sgn |x x x = B .||sgn ||x x x = C .||||sgn x x x =D .||sgn x x x =55. 【2014福建,文8】若函数()log 0,1a y x a a =>≠且的图象如右图所示,则下列函数正确的是 (56. 【2014福建,文9】要制作一个容积为34m ,高为1m 的无盖长方体容器,已知该溶器的底面造价是每平方米20元,侧面造价是是每平方米10元,则该容器的最低总造价是 ( ).80.120.160.240A B C D 元元元元57. 【2015高考福建,文3】下列函数为奇函数的是()A.y =B .x y e =C .cos y x =D .x x y e e -=-58. 【2014辽宁文3】已知132a -=,21211log ,log 33b c ==,则( ) A .a b c >> B .a c b >> C .c a b >> D .c b a >>59. (2014课标全国Ⅰ,文5)设函数f (x ),g (x )的定义域都为R ,且f (x )是奇函数,g (x )是偶函数,则下列结论中正确的是( ).A .f (x )g (x )是偶函数B .|f (x )|g (x )是奇函数C .f (x )|g (x )|是奇函数D .|f (x )g (x )|是奇函数60. 【2015新课标2文11】如图,长方形的边AB =2,BC =1,O 是AB 的中点,点P 沿着边BC ,CD 与DA 运动,记BOP x ∠= ,将动点P 到A ,B 两点距离之和表示为x 的函数()f x ,则的图像大致为( )A .B .C .D .61. 【2015新课标2文12】设函数21()ln(1||)1f x x x=+-+,则使得()(21)f x f x >-成立的x 的取值范围是( ) A .1,13⎛⎫ ⎪⎝⎭ B .()1,1,3⎛⎫-∞+∞ ⎪⎝⎭C .11,33⎛⎫-⎪⎝⎭ D .11,,33⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭62. 【2014辽宁文10】已知()f x 为偶函数,当0x ≥时,1cos ,[0,]2()121,(,)2x x f x x x π⎧∈⎪⎪=⎨⎪-∈+∞⎪⎩,则不等式1(1)2f x -≤的解集为( ) A .1247[,][,]4334 B .3112[,][,]4343-- C .1347[,][,]3434 D .3113[,][,]4334-- 63. 【2014辽宁文11】 将函数3sin(2)3y x π=+的图象向右平移2π个单位长度,所得图象对应的函数( ) A .在区间7[,]1212ππ上单调递减B .在区间7[,]1212ππ上单调递增 C .在区间[,]63ππ-上单调递减 D .在区间[,]63ππ-上单调递增 二、填空题1. 【2016高考四川文科】已知函数()f x 是定义在R 上的周期为2的奇函数,当0<x <1时,()4xf x =,则5()(1)2f f -+= .2. 【2015高考北京,文10】32-,123,2log 5三个数中最大数的是 . 3. 【2015高考湖南,文14】若函数()|22|xf x b =--有两个零点,则实数b 的取值范围是_____.4. 【 2014湖南文15】若()()ax ex f x++=1ln 3是偶函数,则=a ____________.5. 【2014高考陕西版文第12题】已知42a=,lg x a =,则x =________. 6. 【2014高考陕西版文第14题】已知0,1)(≥+=x xxx f ,若++∈==N n x f f x f x f x f n n )),(()(),()(11,则)(2014x f 的表达式为________.7. 【2014全国2,文15】偶函数)(x f y =的图像关于直线2=x 对称,3)3(=f ,则)1(-f =________.8. 【2016高考上海文科】已知点(3,9)在函数xa x f +=1)(的图像上,则________)()(1=-x f x f 的反函数. 9. 【2014四川,文13】设是定义在R 上的周期为2的函数,当时,()f x [1,1)x ∈-,则 . 10. 【2015高考四川,文12】lg 0.01+log 216=_____________.11. 【2015高考四川,文15】已知函数f (x )=2x ,g (x )=x 2+ax (其中a ∈R ).对于不相等的实数x 1,x 2,设m =1212()()f x f x x x --,n =1212()()g x g x x x --,现有如下命题:①对于任意不相等的实数x 1,x 2,都有m >0;②对于任意的a 及任意不相等的实数x 1,x 2,都有n >0; ③对于任意的a ,存在不相等的实数x 1,x 2,使得m =n ; ④对于任意的a ,存在不相等的实数x 1,x 2,使得m =-n . 其中真命题有___________________(写出所有真命题的序号).12. 【2014年.浙江卷.文15】设函数⎪⎩⎪⎨⎧>-≤++=0,0,22)(22x x x x x x f ,若2))((=a f f ,则=a .13. 【2016高考浙江文数】设函数f (x )=x 3+3x 2+1.已知a ≠0,且f (x )–f (a )=(x –b )(x –a )2,x ∈R ,则实数a =_____,b =______.14. 【2015高考浙江,文9】计算:2log = ,24log 3log 32+= . 15. 【2015高考浙江,文12】已知函数()2,166,1x x f x x x x ⎧≤⎪=⎨+->⎪⎩,则()2f f -=⎡⎤⎣⎦ ,()f x 的最小值是 .16. 【2014,安徽文11】34331654+log log 8145-⎛⎫+=⎪⎝⎭________. 17. 【2016高考山东文数】已知函数2||,()24,x x m f x x mx m x m ≤⎧=⎨-+>⎩其中0m >,若存在实数b ,使得关于x 的方程f (x )=b 有三个不同的根,则m 的取值范围是________________. 18. 【2014,安徽文14】若函数()()R x x f ∈是周期为4的奇函数,且在[]2,0上的解析式为()⎩⎨⎧≤<≤≤-=21,sin 10),1(x x x x x x f π,则_______641429=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛f f . 242,10,(),01,x x f x x x ⎧-+-≤<=⎨≤<⎩3()2f =19. 【2016高考北京文数】函数()(2)1xf x x x =≥-的最大值为_________. 20. 【2015高考安徽,文14】在平面直角坐标系xOy 中,若直线a y 2=与函数1||--=a x y 的图像只有一个交点,则a 的值为 . 21. 【2015高考安徽,文11】=-+-1)21(2lg 225lg. 22. 【2014天津,文12】函数2()lg f x x =的单调递减区间是________.23. 【2014天津,文14】已知函数()⎪⎩⎪⎨⎧>-≤++=0,220,452x x x x x x f 若函数x a x f y -=)(恰有4个零点,则实数a 的取值范围为_______24. 【2014年普通高等学校招生全国统一考试湖北卷15】如图所示,函数)(x f y =的图象由两条射线和三条线段组成.若R ∈∀x ,)1()(->x f x f ,则正实数a 的取值范围是 .25. 【2015高考湖北,文13】函数2π()2sin sin()2f x x x x =+-的零点个数为_________.26. 【2014上海,文3】设常数a R ∈,函数2()1f x x x a =-+-,若(2)1f =,则(1)f = .27. 【2014上海,文9】设,0,()1,0,x a x f x x x x -+≤⎧⎪=⎨+>⎪⎩若(0)f 是()f x 的最小值,则a 的取值范围是 .28. 【2014上海,文11】若2132)(x x x f -=,则满足0)(<x f 的x 取值范围是 .29. 【2016高考天津文数】已知函数2(43)3,0()(01)log (1)1,0a x a x a x f x a a x x ⎧+-+<⎪=>≠⎨++≥⎪⎩且在R上单调递减,且关于x 的方程|()|23xf x =-恰有两个不相等的实数解,则a 的取值范围是_________.30. 【2014福建,文15】(函数()⎩⎨⎧>+-≤-=0,ln 620,22x x x x x x f 的零点个数是__________.31. 【2015高考福建,文15】若函数()2()x af x a R -=∈满足(1)(1)f x f x +=-,且()f x 在[,)m +∞单调递增,则实数m 的最小值等于_______.32. 【2015新课标2文13】已知函数()32f x ax x =-的图像过点(-1,4),则a = .33. (2014课标全国Ⅰ,文15)设函数()113e ,1,,1,x x f x x x -⎧<⎪=⎨⎪≥⎩则使得f (x )≤2成立的x 的取值范围是__________.34. 【2014辽宁文16】对于0c >,当非零实数a ,b 满足22420a ab b c -+-=,且使|2|a b +最大时,124a b c++的最小值为 .三、解答题1.【2015高考湖北,文17】a 为实数,函数2()||f x x ax =-在区间[0,1]上的最大值记为()g a . 当a =_________时,()g a 的值最小.2. 【2014上海,文20】(本题满分14分)本题有2个小题,第一小题满分6分,第二小题满分1分.设常数0≥a ,函数aax f x x -+=22)((1)若a =4,求函数)(x f y =的反函数)(1x fy -=;(2)根据a 的不同取值,讨论函数)(x f y =的奇偶性,并说明理由.3. 【2016高考上海文科】(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.已知a ∈R ,函数()f x =21log ()a x+.(1)当 1a =时,解不等式()f x >1;(2)若关于x 的方程()f x +22log ()x =0的解集中恰有一个元素,求a 的值;(3)设a >0,若对任意t ∈1[,1]2,函数()f x 在区间[,1]t t +上的最大值与最小值的差不超过1,求a 的取值范围.。
专题07三角函数—三年高考(2015-2017)数学(文)真题分项版解析(原卷版)

专题07三角函数—三年高考(2015-2017)数学(文)真题分项版解析(原卷版)专题7 三角函数1.【2017课标3,文6】函数1ππ()sin()cos()536f x x x =++-的最大值为() A .65 B .1 C .35 D .152.【2017课标II ,文3】函数π()sin(2)3f x x =+的最小正周期为A.4πB.2πC. πD.π23.【2017课标3,文4】已知4sin cos 3αα-=,则sin 2α=()A .79-B .29-C .29D .794.【2017山东,文4】已知3cos 4x =,则cos2x =A.14-B.14C.18-D.185.【2017天津,文7】设函数()2sin(),f x x x ω?=+∈R ,其中0,||πω?><.若5π11π()2,()0,88f f ==且()f x 的最小正周期大于2π,则(A )2π,312ω?==(B )211π,312ω?==-(C )111π,324ω?==-(D )17π,324ω?==6.【2017山东,文7】函数2cos 2y x x =+最小正周期为A.π2 B. 2π3C.πD. 2π 7.【2014福建,文7】将函数sin y x =的图象向左平移2π个单位,得到函数()y f x =的函数图象,则下列说法正确的是()()()()() (32).-02A y f x B y f x C y f x x D y f x πππ=====是奇函数的周期是的图象关于直线对称的图象关于点,对称8.【2015高考福建,文6】若5s i n 13α=-,且α为第四象限角,则tan α的值等于() A .125 B .125- C .512 D .512-9.(2014课标全国Ⅰ,文7)在函数①y =cos|2x |,②y =|cos x |,③πcos 26y x ?=+ ,④πtan 24y x ?=- ??中,最小正周期为π的所有函数为( ).A .①②③B .①③④C .②④D .①③10.【2014天津,文8】已知函数()cos (0),.f x x x x R ωωω=+>∈在曲线()y f x =与直线1y =的交点中,若相邻交点距离的最小值为3π,则()f x 的最小正周期为()A.2π B.23π C.π D.2π11.【2015高考新课标1,文8】函数()cos()f x x ω?=+的部分图像如图所示,则()f x 的单调递减区间为()(A )13(,),44k k k Z ππ-+∈ (B )13(2,2),44k k k Z ππ-+∈(C )13(,),44k k k Z -+∈(D )13(2,2),44k k k Z -+∈12.【2016高考新课标2文数】函数=sin()y A x ω?+的部分图像如图所示,则()(A )2sin(2)6y x π=-(B )2sin(2)3y x π=-(C )2sin(2+)6y x π=(D )2sin(2+)3y x π=13.【2014年.浙江卷.文4】为了得到函数x x y 3c os 3s in +=的图象,可以将函数x y 3cos 2=的图象()A.向右平移12π个单位长 B.向右平移4π个单位长C.向左平移12π个单位长 D.向左平移4π个单位长 14.【2016高考新课标2文数】函数π()cos 26cos()2f x x x =+-的最大值为()(A )4(B )5(C )6 (D )7[2016高考新课标Ⅲ文数]若tan 13θ=,则cos2θ=()(A )45-(B )15-(C )15(D )4515. 【2014四川,文3】为了得到函数sin(1)y x =+的图象,只需把函数sin y x =的图象上所有的点()A .向左平行移动1个单位长度B .向右平行移动1个单位长度C .向左平行移动π个单位长度D .向右平行移动π个单位长度16.【2015高考山东,文4】要得到函数4y sin x =-(3π)的图象,只需要将函数4y sin x =的图象()(A )向左平移12π个单位(B )向右平移12π个单位(C )向左平移3π个单位(D )向右平移3π个单位 17.【2016高考天津文数】已知函数)0(21sin 212sin )(2>-+=ωωωx xx f ,R x ∈.若)(x f 在区间)2,(ππ内没有零点,则ω的取值范围是()(A )]81,0((B ))1,85[]41,0( (C )]85,0((D )]85,41[]81,0(18.【2014高考陕西版文第2题】函数()cos(2)4f x x π=+的最小正周期是().2A π.B π.2C π.4D π 19. 【2015高考陕西,文6】“sin cos αα=”是“cos20α=”的() A 充分不必要条件B 必要不充分条件C 充分必要条件D 既不充分也不必要20.【2016高考新课标1文数】若将函数y =2sin (2x +π6)的图像向右平移14个周期后,所得图像对应的函数为()(A )y =2sin(2x +π4) (B )y =2sin(2x +π3) (C )y =2sin(2x –π4) (D )y =2sin(2x –π3)21.【2017课标II ,文13】函数()2cos sin f x x x =+的最大值为 .22.【2017江苏,5】若π1tan(),46α-=则tan α=.23.【2017课标1,文15】已知π(0)2a ∈,,tan α=2,则πcos ()4α-=__________.24. 【2016高考四川文科】=. 25.【2016高考浙江文数】已知22cossin 2sin()(0)x x A x b A ω?+=++>,则A =______,b =______.26.[2016高考新课标Ⅲ文数]函数sin y x x =的图像可由函数2sin y x =的图像至少向右平移_____________个单位长度得到.27.【2015高考浙江,文11】函数()2sin sin cos 1f x x x x =++的最小正周期是,最小值是.28.【2016高考新课标1文数】已知θ是第四象限角,且sin(θ+π4)=35,则tan(θ–π4)=. 29.【2015湖南文15】已知ω>0,在函数y=2sin ωx 与y=2cos ωx 的图像的交点中,距离最短的两个交点的距离为2,则ω =_____.30.【2015高考天津,文14】已知函数()()sin cos 0f x x x ωωω=+>,x ∈R ,若函数()f x 在区间(),ωω-内单调递增,且函数()f x 的图像关于直线x ω=对称,则ω的值为.31. 【2014高考重庆文第13题】将函数()()??<≤->+=220sin π?πω?ω,x x f 图像上每一点的横坐标缩短为原来的一半,纵坐标不变,再向右平移6π个单位长度得到x y sin =的图像,则=??6πf ______. 32.【2015高考四川,文13】已知sin α+2cos α=0,则2sin αcos α-cos 2α的值是______________. 33.【2017北京,文16】已知函数())2sin cos 3f x x -x x π=-.(I )f (x )的最小正周期;(II )求证:当[,]44x ππ∈-时,()12f x ≥-. 0750sin34.【2017浙江,18】(本题满分14分)已知函数f (x )=sin2x –cos 2x –sin x cos x (x ∈R ).(Ⅰ)求)32(πf 的值.(Ⅱ)求)(x f 的最小正周期及单调递增区间.35.【2015高考重庆,文18】已知函数f(x)=122cos x .(Ⅰ)求f (x )的最小周期和最小值,(Ⅱ)将函数f (x )的图像上每一点的横坐标伸长到原来的两倍,纵坐标不变,得到函数g (x )的图像.当x ∈,2ππ??时,求g(x)的值域. 36.【2015高考安徽,文16】已知函数2()(sin cos )cos2f x x x x =++(Ⅰ)求()f x 最小正周期;(Ⅱ)求()f x 在区间[0,]2π上的最大值和最小值.37.【2015高考福建,文21】已知函数()2cos 10cos 222x x x f x =+.(Ⅰ)求函数()f x 的最小正周期;(Ⅱ)将函数()f x 的图象向右平移6π个单位长度,再向下平移a (0a >)个单位长度后得到函数()gx 的图象,且函数()g x 的最大值为2.(ⅰ)求函数()gx 的解析式;(ⅱ)证明:存在无穷多个互不相同的正整数0x ,使得()00g x >.38.【2015高考湖北,文18】某同学用“五点法”画函数π()sin()(0,||)2f x A x ω?ω?=+><在某一个周期内的图象时,列表并填入了部分数据,如下表:(Ⅰ)请将上表数据补充完整,填写在答题卡上相应位置...........,并直接写出函数()f x 的解析式;(Ⅱ)将()y f x =图象上所有点向左平行移动π6个单位长度,得到()y g x =图象,求 ()y g x =的图象离原点O 最近的对称中心.39.【2016高考北京文数】(本小题13分)已知函数)0(2cos cos sin 2)(>+=ωωωωx x x x f 的最小正周期为π. (1)求ω的值;(2)求)(x f 的单调递增区间.40.【2014高考北京文第16题】(本小题满分13分)函数()3sin 26f x x π?=+的部分图象如图所示. (1)写出()f x 的最小正周期及图中0x 、0y 的值;(2)求()f x 在区间,212ππ??--上的最大值和最小值.41.【2016高考山东文数】(本小题满分12分)设2()π)sin (sin cos )f x x x x x =--- .(I )求()f x 得单调递增区间;(II )把()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移π3个单位,得到函数()y g x =的图象,求π()6g 的值. 42.【2015高考北京,文15】(本小题满分13分)已知函数()2sin 2xf x x =-.(I )求()f x 的最小正周期;(II )求()f x 在区间20,3π??上的最小值.43.【2015高考广东,文16】(本小题满分12分)已知tan 2α=.(1)求tan 4πα?+ ??的值;(2)求2sin 2sin sin cos cos 21ααααα+--的值.44. 【2014高考广东卷.文.16】(本小题满分12分)已知函数()sin 3f x A x π?=+,x R ∈,且5122f π??=. (1)求A 的值;(2)若()()ff θθ--=0,2πθ??∈ ,求6f πθ??-.。
三年高考2015_2017高考数学试题分项版解析专题5双曲线文

专题15 双曲线1.【2017课表1,文5】已知F 是双曲线C :1322=-y x 的右焦点,P 是C 上一点,且PF 与x轴垂直,点A 的坐标是(1,3),则△APF 的面积为A .B .1 2C .2 3D .3 2【答案】D【考点】双曲线【名师点睛】本题考查圆锥曲线中双曲线的简单运算,属容易题.由双曲线方程得)0,2(F ,结合PF 与x 轴垂直,可得3||=PF ,最后由点A 的坐标是(1,3),计算△APF 的面积.2.【2017课标II ,文5】若1a >,则双曲线2221x y a-=的离心率的取值范围是A. )+∞B.C. (1D. (1,2) 【答案】C【解析】由题意222222111c a e a a a+===+,因为1a >,所以21112a <+<,则1e <<故选C.【考点】双曲线离心率【名师点睛】解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于,,a b c 的方程或不等式,再根据,,a b c 的关系消掉得到,a c 的关系式,而建立关于,,a b c 的方程或不等式,要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.3.【2017天津,文5】已知双曲线22221(0,0)x y a b a b-=>>的左焦点为F ,点A 在双曲线的渐近线上,OAF △是边长为2的等边三角形(O 为原点),则双曲线的方程为(A )221412x y -=(B )221124x y -=(C )2213x y -=(D )2213y x -=【答案】D 【解析】试题分析:由题意结合双曲线的渐近线方程可得:22202tan 60c c a b ba ⎧⎪=⎪=+⎨⎪⎪==⎩,解得:221,3ab ==,双曲线方程为:2213y x -=,本题选择D 选项. 【考点】双曲线方程【名师点睛】本题主要考查的是双曲线的标准方程和双曲线的简单几何性质,属于基础题.解题时要注意、、的关系222c a b =+,否则很容易出现错误.解本题首先画图,掌握题中所给的几何关系,再结合双曲线的一些几何性质,得到,,a b c 的关系,联立方程,求得,,a b c 的值。
三年高考(2015-2017)高考数学试题分项版解析 专题15 双曲线 文

专题15 双曲线1.【2017课表1,文5】已知F 是双曲线C :1322=-y x 的右焦点,P 是C 上一点,且PF 与x轴垂直,点A 的坐标是(1,3),则△APF 的面积为A .B .1 2C .2 3D .3 2【答案】D【考点】双曲线【名师点睛】本题考查圆锥曲线中双曲线的简单运算,属容易题.由双曲线方程得)0,2(F ,结合PF 与x 轴垂直,可得3||=PF ,最后由点A 的坐标是(1,3),计算△APF 的面积.2.【2017课标II ,文5】若1a >,则双曲线2221x y a-=的离心率的取值范围是A. 2,)+∞B. 2,2)C. 2)D. (1,2) 【答案】C【解析】由题意222222111c a e a a a+===+,因为1a >,所以21112a <+<,则12e <<故选C.【考点】双曲线离心率【名师点睛】解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于,,a b c 的方程或不等式,再根据,,a b c 的关系消掉得到,a c 的关系式,而建立关于,,a b c 的方程或不等式,要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.3.【2017天津,文5】已知双曲线22221(0,0)x y a b a b-=>>的左焦点为F ,点A 在双曲线的渐近线上,OAF △是边长为2的等边三角形(O 为原点),则双曲线的方程为(A )221412x y -=(B )221124x y -=(C )2213x y -=(D )2213y x -=【答案】D 【解析】试题分析:由题意结合双曲线的渐近线方程可得:22202tan 603c c a b ba⎧⎪=⎪=+⎨⎪⎪==⎩,解得:221,3a b ==,双曲线方程为:2213y x -=,本题选择D 选项. 【考点】双曲线方程【名师点睛】本题主要考查的是双曲线的标准方程和双曲线的简单几何性质,属于基础题.解题时要注意、、的关系222c a b =+,否则很容易出现错误.解本题首先画图,掌握题中所给的几何关系,再结合双曲线的一些几何性质,得到,,a b c 的关系,联立方程,求得,,a b c 的值。
专题05 函数图象与方程—三年高考(2015-2017)数学(理)真题分项版解析(解析版)

【答案】C
【解析】如图所示,把函数 y log2 x 的图象向左平移一个单位得到
y log2(x 1)的图象 x 1时两图象相交,不等式的解为 1 x 1,用集合表示
解集选 C 【考点定位】本题考查作基本函数图象和函数图象变换及利用函数图象解不等式等有关知识, 体现了数形结合思想. 【名师点睛】本题考查作基本函数图象和函数图象变换及利用函数图象解不等式等有关知识,
4.【2016
高考天津理数】已知函数
f(x)=
x2
(4a
3) x
3a,
x
0,
(a>0,且
a≠1)在
R
loga (x 1) 1, x 0
上单调递减,且关于 x 的方程| f (x) | 2 x 恰好有两个不相等的实数解,则 a 的取值
范围是( )
(A)(0, 2 ] (B)[ 2 , 3 ]
3
34
a
3
3
4
y x2 (4a 3)x 3a 与 直 线 y 2 x 相 切 , 也 符 合 题 意 , ∴ 实 数 a 的 去 范 围 是
[1 , 2] {3},故选 C. 33 4
考点:函数性质综合应用
2018 年暑假系统班,全国钜惠,99 元 16 课时
5.【2015 高考新课标 2,理 10】如图,长方形 ABCD 的边 AB 2 , BC 1,O 是 AB 的 中点,点 P 沿着边 BC , CD 与 DA 运动,记 BOP x .将动 P 到 A 、 B 两点距离之和 表示为 x 的函数 f (x) ,则 y f (x) 的图像大致为( )
三次方程仅有一个实根的是
.(写出所有正确条件的编号)
2018 年暑假系统班,全国钜惠,99 元 16 课时
三年高考2015_2017高考数学试题分项版解析专题18双曲线理20171102337

专题 18 双曲线1.【2017课标 II ,理 9】若双曲线 C :xy22( a 0 , b 0)的一条渐近线被圆221a b22x 2y 4所截得的弦长为 2,则 C 的离心率为()A . 2B .3C .2D .2 3 3【答案】A 【解析】即:422 c ac2,整理可得: c 24a 2 ,3e双曲线的离心率c2。
故选A 。
24 2a【考点】双曲线的离心率;直线与圆的位置关系,点到直线的距离公式【名师点睛】双曲线的离心率是双曲线最重要的几何性质,求双曲线的离心率(或离心率的取 值范围),常见有两种方法: ①求出 a ,c ,代入公式e c ; a②只需要根据一个条件得到关于 a ,b ,c 的齐次式,结合 b 2=c 2-a 2转化为 a ,c 的齐次式, 然后等式(不等式)两边分别除以 a 或 a 2转化为关于 e 的方程(不等式),解方程(不等式)即可 得 e (e 的取值范围)。
2.【2017课标3,理5】已知双曲线C:x y22221(a>0,b>0)的一条渐近线方程为a b15xy有公共焦点,则 C 的方程为 22yx ,且与椭圆12123A .xyB .2218 10xyC .2214 5 xyD .2215 4x y22143【答案】B 【解析】试题分析:双曲线 C : xy22(a >0,b >0)的渐近线方程为 y b x 221,ab a椭圆中: a 212,b 2 3,c 2a 2b 29,c 3,椭圆,即双曲线的焦点为3, 0,b5a2据此可得双曲线中的方程组: c 2 a 2 b 2 c 3,解得: a 24,b 25 , 则双曲线C 的方程为xy21 . 45故选 B .3.【2017天津,理 5】已知双曲线xy2 2 221( 0, 0)a b 的左焦点为 F ,离心率为2 .若 a b经过 F 和 P (0, 4)两点的直线平行于双曲线的一条渐近线,则双曲线的方程为 (A )x y (B )22144 xy(C ) 2218 8 xy(D )2214 8x y22184【答案】 B4xy22【解析】由题意得,选 B.a b ,1 c 4,ab 2 21c8 82【考点】双曲线的标准方程【名师点睛】利用待定系数法求圆锥曲线方程是高考常见题型,求双曲线方程最基础的方法就是依据题目的条件列出关于a,b,c的方程,解方程组求出a,b,另外求双曲线方程要注意巧设双曲线(1)双曲线过两点可设为mx2ny21(mn 0),(2)与x y22221共渐近线的双a b曲线可设为x y2222(0),(3)等轴双曲线可设为x2y2(0)等,均为待定系a b数法求标准方程.4.【2016高考新课标1卷】已知方程x y22221表示双曲线,且该双曲线两焦点间m n3m n的距离为4,则n的取值范围是( )(A )1,3(B )1,3(C )0,3(D )0,3【答案】A 【解析】试题分析:x y22表示双曲线,则221m2n3m2nm n3m nc2m2n 3m2n 4m2,其中是半焦距∴m2n 3m2,由双曲线性质知:∴焦距2c 22m 4,解得m 1,∴1n 3,故选A.考点:双曲线的性质5.【2016高考新课标2理数】已知F1,F2是双曲线Ex y22:1的左,右焦点,点M在Ea b22上,MF与轴垂直,sin11,则E的离心率为()MF F213(A)2(B)32(C)3(D)2【答案】A【解析】3试题分析:因为MF 垂直于 x 轴,所以 1bb22MF 1, MF 2 2a,因为sinaa1MF F ,2 13即b2MFa 1MFb222aa1 3,化简得b a ,故双曲线离心率 e 1 b2.选A.a考点:双曲线的性质.离心率.【名师点睛】区分双曲线中 a ,b ,c 的关系与椭圆中 a ,b ,c 的关系,在椭圆中 a 2=b 2+c 2, 而在双曲线中 c 2=a 2+b 2.双曲线的离心率 e ∈(1,+∞),而椭圆的离心率 e ∈(0,1).6.【2015高考新课标 2,理 11】已知 A ,B 为双曲线 E 的左,右顶点,点 M 在 E 上,∆ABM 为等 腰三角形,且顶角为 120°,则 E 的离心率为() A . 5B .C . 3D . 2【答案】D【考点定位】双曲线的标准方程和简单几何性质.【名师点睛】本题考查双曲线的标准方程和简单几何性质、解直角三角形知识,正确表示点 M 的坐标,利用“点在双曲线上”列方程是解题关键,属于中档题. 7.【2015高考四川,理 5】过双曲线y2x 21的右焦点且与 x 轴垂直的直线,交该双曲线3的两条渐近线于A,B两点,则AB()4(A)4 3 3(B)2 3(C)6(D ) 4 3【答案】D 【解析】双曲线的右焦点为 F (2,0),过 F 与 x 轴垂直的直线为 x 2 ,渐近线方程为y2x 20,将3x 2 代入y2x 20得: y 2 12, y 2 3, | AB | 4 3 .选dreamsummit.38.【2016高考天津理数】已知双曲线xy22=1(b >0),以原点为圆心,双曲线的实半轴长4b2为半径长的圆与双曲线的两条渐近线相交于 A 、B 、C 、D 四点,四边形的 ABCD 的面积为 2b ,则双曲线的方程为()(A )x (B )223y =144x4(C )22y=14 3xy22=1(D )4b2xy 224 12=1【答案】D 【解析】试 题 分 析 : 根 据 对 称 性 , 不 妨 设 A 在 第 一 象 限 , A (x , y ) , ∴4xx y422b42b by x y4,242b216b b∴xy b2 12b4222,故双曲线的方程为x y ,故选D.221412考点:双曲线渐近线【名师点睛】求双曲线的标准方程关注点:(1)确定双曲线的标准方程也需要一个“定位”条件,两个“定量”条件,“定位”是指确定焦点在哪条坐标轴上,“定量”是指确定a,b的值,常用待定系数法.5(2)利用待定系数法求双曲线的标准方程时应注意选择恰当的方程形式,以避免讨论. ①若双曲线的焦点不能确定时,可设其方程为 Ax 2+By 2=1(AB <0). ②若已知渐近线方程为 mx +ny =0,则双曲线方程可设为 m 2x 2-n 2y 2=λ(λ≠0). 9.【2015高考新课标 1,理 5】已知 M (x 0 , y 0 )是双曲线 C :x 22y 2 1上的一点, FF1,2是 C 上的两个焦点,若MF 1 MF 2 0 ,则y 的取值范围是( )(A )(-3 3 ,33 ) (B )(- 3 6, 36)(C )( 22 , 2 22 2 , 2 2 33)(D )(2 3 , 2 3 3 3 )【答案】A【 解 析 】 由 题 知FF ,1(3, 0), 2 ( 3, 0)x 20 2 y, 所 以0 1 2MFMF=12( 3 x ,y )( 3 x ,y ) =x 2y 2y 2,解得3 3 0 1 03 3 y,故选33A.10.【2015高考重庆,理 10】设双曲线 xy22 221(a >0,b >0)的右焦点为 1,过 F 作AF 的a b垂线与双曲线交于 B ,C 两点,过 B ,C 分别作 AC ,AB 的垂线交于点 D .若 D 到直线 BC 的距离小 于 a a 2 b 2 ,则该双曲线的渐近线斜率的取值范围是 ( ) A 、 (1,0)(0,1)B 、(,1) (1,)C、(2,0)(0,2)D、(,2)(2,)【答案】A【解析】由题意b b22A(a,0),B(c,),C(c,),由双曲线的对称性知D在轴上,设D(x,0),a a6由BD AC得b b22a a1,解得c x a cc xb4a2(ca),所以b4c x a a ba c22a2(c a),所以b4a2222c a bb 0b1221,因a a此渐近线的斜率取值范围是(1,0)(0,1),选A.【考点定位】双曲线的性质.【名师点晴】求双曲线的渐近线的斜率取舍范围的基本思想是建立关于a,b,c的不等式,根据已知条件和双曲线中a,b,c的关系,要据题中提供的条件列出所求双曲线中关于a,b的不等关系,解不等式可得所求范围.解题中要注意椭圆与双曲线中a,b,c关系的不同.11.【2015高考安徽,理4】下列双曲线中,焦点在y轴上且渐近线方程为y2x的是()(A)y2x21(B)4x24y21(C)y24x21(D)x2y214【答案】C12.【2015高考湖北,理8】将离心率为的双曲线C的实半轴长和虚半轴长b(a b)同时增加1m(m 0)个单位长度,得到离心率为e的双曲线C,则()22A.对任意的a,b,e e B.当a b时,e e;当a b时,e e121212C.对任意的a,b,e e D.当a b时,e e;当a b时,e e121212【答案】D7ea b b 22abb【解析】依题意,211 ( )aa(a m )(b m )b m22e21() ,2,a ma m因为b abm ab bm ab am m (b a ),由于 m0, a 0 ,b0,a ma (a m )a (a m )bb m b b m b b m 所以当 ab 时, 0 1, 01, ( )2()2 ,所以,ee ;aa m a a maa m12bb b mb mbb m 当 ab 时, 1, 1,所以 ( )2()2 ,所以,而ee .a a ma a m aa m12所以当 a b 时, ee ;当 a b 时, ee .1212【考点定位】双曲线的性质,离心率.【名师点睛】分类讨论思想是一种重要的数学思想方法.分类讨论的时应做到:分类不重不漏; 标准要统一,层次要分明;能不分类的要尽量避免或尽量推迟,决不无原则地讨论. 13.【2015高考福建,理 3】若双曲线xy22E :1 的左、右焦点分别为9 16F F ,点 P 在双 1, 2曲线 E 上,且 PF,则13P F 等于( )2A .11B .9C .5D .3【答案】B14.【2017课标1,理】已知双曲线C:x2y2221(a>0,b>0)的右顶点为A,以A为圆心,a bb为半径作圆A,圆A与双曲线C的一条渐近线交于M、N两点.若∠MAN=60°,则C的离心率为________.【答案】23 3【解析】试题分析:8如图所示,作 AP MN ,因为圆 A 与双曲线 C 的一条渐近线交于 M 、N 两点,则 MN 为双曲线的渐近线byx上的点,且 A (a ,0) , AM ANb a而 APMN ,所以 PAN 30 , 点 A (a ,0) 到直线b y x 的距离aAP| b |1b a22在 Rt PAN 中, cos PAN PANA代入计算得 a 2 3b 2 ,即 a 3b由 c 2 a 2 b 2 得 c 2b 所以e c 2b2 3.a3b3【考点】双曲线的简单性质.xy2215.【2017山东,理 14】在平面直角坐标系 xOy 中,双曲线221 a 0,b0 的右支与 ab焦点为 F 的抛物线 x 22pxp0交于 A ,B 两点,若 AFBF4 OF ,则该双曲线的渐近线方程为.【答案】2yx2p p p【解析】试题分析:|AF||BF|=y y4y y p,A B A B222922x y1因为a b2220a y pb y a b22222x2py2,所以2pb2y y p a2bA B2a渐近线方程为2yx.2【考点】1.双曲线的几何性质.2.抛物线的定义及其几何性质.【名师点睛】1.在双曲线的几何性质中,渐近线是其独特的一种性质,也是考查的重点内容.对渐近线:(1)掌握方程;(2)掌握其倾斜角、斜率的求法;(3)会利用渐近线方程求双曲线方程的待定系数.求双曲线方程的方法以及双曲线定义和双曲线标准方程的应用都和与椭圆有关的问题相类似.因此,双曲线与椭圆的标准方程可统一为Ax2By21的形式,当A 0,B 0,A B 时为椭圆,当AB0时为双曲线.2.凡涉及抛物线上的点到焦点距离时,一般运用定义转化为到准线距离处理.16.【2017北京,理9】若双曲线y2x21的离心率为3,则实数m=_________.m【答案】2x217.【2015高考北京,理10】已知双曲线2210的一条渐近线为3x y 0,则ay aa.【答案】331 x2【解析】双曲线的渐近线方程为y a2yx,210a a101 3 3x y0 y3x , a0,则3, aa3【考点定位】本题考点为双曲线的几何性质,正确利用双曲线的标准方程,求出渐近线方程, 利用已给渐近线方程求参数.【名师点睛】本题考查双曲线的几何性质,重点考查双曲线的渐近线方程,本题属于基础题, 正确利用双曲线的标准方程,求出渐近线方程,求渐近线方程的简单方法就是把标准方程中的 “1”改“0”,利用已知渐近线方程,求出参数a 的值. 18.【2016高考山东理数】已知双曲线 E : xy22221(a >0,b >0),若矩形 ABCD 的四个顶a b点在 E 上,AB ,CD 的中点为 E 的两个焦点,且 2|AB |=3|BC |,则 E 的离心率是_______. 【答案】2 【解析】b 2试题分析:假设点 A 在第一象限,点 B 在第二象限,则 A(c, )ab2,B(c,) ,所以a| AB|(舍去),2b ,| BC | 2c ,由 2 AB3 BC , c 2a 2b 2 得离心率 e 2 或 e12a2所以 E 的离心率为 2. 考点:双曲线的几何性质【名师点睛】本题主要考查双曲线的几何性质.本题解答,利用特殊化思想,通过对特殊情况 的讨论,转化得到一般结论,降低了解题的难度.本题能较好的考查考生转化与化归思想、一 般与特殊思想及基本运算能力等.19.【2015江苏高考,12】在平面直角坐标系 xOy 中, P 为双曲线 x 2 y 2 1右支上的一个动点。
专题15双曲线-三年高考数学(文)真题分类汇编(2015-2017)

专题 15 双曲线1.【 2017 课标 1,文 5】已知 F 是双曲线 C:x 2 y 21 的右焦点, P 是 C 上一点,且 PF 与 x 轴垂直,点3A 的坐标是 (1, 3),则△APF 的面积为1 1C.2D .3A. B .3 23 22.【 2017 课标 II,文 5】若a 1 ,则双曲线x2y 2的离心率的取值范围是[根源学* 科*网 Z*X*X*K] a2 1A. ( 2, )B. ( 2,2)C. (1, 2)D. (1,2)3.【 201 7 天津,文5】已知双曲线x2 y21(a 0, b 0) 的左焦点为 F ,点A在双曲线的渐近线上,a2 b2△ OAF 是边长为 2 的等边三角形(O 为原点),则双曲线的方程为(A) x2 y 2 1 (B)x2y2 1(C)x2y2 1(D) x2 y2 14 12 12 4 3 34.【 2015 高考湖南,文 6】若双曲线x2 y21的一条渐近线经过点(3,-4),则此双曲线的离心率为() a2 b2A 、7B、5C、4 53 4 3D 、35.【 2015 高考安徽,文 6】以下双曲线中,渐近线方程为y 2x 的是() [根源学* 科* 网] ( A)x2 y 2 1 (B) x2 y 2 14 4( C)x2 y2 1 (D) x2 y2 12 26.【2014 天津,文6】已知双曲线x2 y21(a 0, b 0) 的一条渐近线平行于直线 l : y 2x 10, 双曲线a 2b2的一个焦点在直线l 上,则双曲线的方程为()x2 y 2 x2 y21 3x2 3y21 D.3x 2 3y21A. 1B.5 C.100 100 255 20 20 257.【 2015 高考天津, 文 5 】已知双曲线2- 2 = 1(a > 0, b > 0)的一个焦点为F (2,0),x2y2且双曲线的渐近线与a b圆 (x - 2) 2+ y2= 3 相切 ,则双曲线的方程为()x 2 y 2= 1x 2y 2=1(C)x 2 - y2= 1(D) x 2-y 2(A)-(B)-3= 19 1313 93[根源 学&科&网 ]8. 【 2014 年一般高等学校招生全国一致考试湖北卷8】设 a 、b 是对于 t 的方程 t 2 cost sin 0 的两个不等实根,则过( , a 2 )2) 两点的直线与双曲线x 2y 21 的公共点的个数为()A a, B(b, b22cossinA. 0B. 1C. 2D.39.【 2015 高考湖北, 文 9】将离心率为 e 1 的双曲线 C 1 的实半轴长 a 和虚半轴长 b ( a b) 同时增添 m (m 0) 个单位长度,获得离心率为e 2 的双曲线 C 2 ,则()A .对随意的 a, b , e 1 e 2B .当 a b 时, e 1 e 2 ;当 a b 时, e 1 e 2C .对随意的 a, b , e 1 e 2D .当 a b 时, e 1e 2 ;当 ab 时, e 1 e 210.【 2015 四川文 7】过双曲线 x2y 2 1 的右焦点且与 x 轴垂直的直线交该双曲线的两条渐近线于A 、 B3两点,则 |AB |= ( )43(B)2 3( C)6(D)4 3(A)311.【 2015 高考重庆,文 9】设双曲线 x 2 - y 2= 1(a > 0,b > 0) 的右焦点是 F ,左、右极点分别是A 1,A 2,过a 2b 2F 做 A 1A 2 的垂线与双曲线交于 B , C 两点,若 A 1B A 2 C ,则双曲线的渐近线的斜率为()(A) ±1(B)±2(C)±1(D)± 22212.【 2015 高考四川,文 7】过双曲线 x2y 21的右焦点且与 x 轴垂直的直线交该双曲线的两条渐近线于3A 、B 两点,则 |AB|=( )[根源:]43(B)23 (C)6(D)4 3(A)313.【 201 7 山东,文 15】在平面直角坐标系xOy 中 ,双曲线x2 y21(a 0, b 0) 的右支与焦点为 F 的a2 b2抛物线 x2 2 py( p 0) 交于A,B两点,若|AF|+|BF|=4|OF|,则该双曲线的渐近线方程为.[根源:Z&xx&]14.【 2017 课标 3,文 14】双曲线x2y2 1(a>0)的一条渐近线方程为y3x ,则a= . a2 9 515【. 2017 江苏,8】在平面直角坐标系xOy 中 ,双曲线x2y2 1 的右准线与它的两条渐近线分别交于点P,Q, 3其焦点是 F1, F2 ,则四边形 F1PF2 Q 的面积是.16. 【 2015 新课标 2 文 15】已知双曲线过点4, 3 ,且渐近线方程为y 1x ,则该双曲线的标准方程2为.17. 【 2016 高考山东文数】已知双曲线x2 y2E 上, AB,E: 2 –2 =1 ( a>0 ,b>0 ).矩形 ABCD 的四个极点在a bCD 的中点为 E 的两个焦点,且 2|AB|=3|BC |,则 E 的离心率是 _______.18.【 2016 高考浙江文数】设双曲线x2–y2 =1 的左、右焦点分别为 F 1, F 2.若点 P 在双曲线上,且△F1 PF23为锐角三角形,则|PF 1|+|PF2|的取值范围是 _______ .19.【 2016 高考北京文数】已知双曲线x2 y21 ( a 0 , b 0 )的一条渐近线为2x y 0 ,一个焦a2 b2点为 ( 5,0) ,则a _______;b _____________.20.【 2014 山东 .文 15】已知双曲线x2 y 21(a b 0 )的焦距为2c ,右极点为 A ,抛物线a2 b 2x2 2 py( p 0) ,2c ,且PA c,则双曲线的渐近线的焦点为 F 若双曲线截抛物线的准线所得线段长为方程为 ___________.21.x2 y21 的右焦点作一条与其渐近线平行的直【 2015 高考山东,文 15】过双曲线C:0, ba2 a2 ( a 0)线,交 C 于点 P .若点 P 的横坐标为2a ,则C的离心率为.。
三年高考2015_2017高考数学试题分项版解析专题8双曲线理

专题18 双曲线1.【2017课标II,理9】若双曲线C:22 221x ya b-=(0a>,0b>)的一条渐近线被圆()2224x y-+=所截得的弦长为2,则C的离心率为()A.2 B.3 C.2 D.23【答案】A【解析】即:()22243c ac-=,整理可得:224c a=,双曲线的离心率2242cea===。
故选A。
【考点】双曲线的离心率;直线与圆的位置关系,点到直线的距离公式【名师点睛】双曲线的离心率是双曲线最重要的几何性质,求双曲线的离心率(或离心率的取值范围),常见有两种方法:①求出a,c,代入公式cea=;②只需要根据一个条件得到关于a,b,c的齐次式,结合b2=c2-a2转化为a,c的齐次式,然后等式(不等式)两边分别除以a或a2转化为关于e的方程(不等式),解方程(不等式)即可得e(e 的取值范围)。
2.【2017课标3,理5】已知双曲线C:22221x ya b-= (a>0,b>0)的一条渐近线方程为52y x=,且与椭圆221123x y+=有公共焦点,则C的方程为A.221810x y-=B.22145x y-=C.22154x y-=D.22143x y-=【答案】B 【解析】试题分析:双曲线C:22221 xya b-= (a>0,b>0)的渐近线方程为by xa=±,椭圆中:2222212,3,9,c3a b c a b==∴=-==,椭圆,即双曲线的焦点为()3,0±,据此可得双曲线中的方程组:222523bac a bc⎧=⎪⎪⎪=-⎨⎪=⎪⎪⎩,解得:224,5a b==,则双曲线C的方程为2145x y2-= .故选B.3.【2017天津,理5】已知双曲线22221(0,0)x ya ba b-=>>的左焦点为F2.若经过F和(0,4)P两点的直线平行于双曲线的一条渐近线,则双曲线的方程为(A)22144x y-=(B)22188x y-=(C)22148x y-=(D)22184x y-=【答案】B【解析】由题意得224,14,22188x ya b c a bc==-⇒===⇒-=-,选B.【考点】双曲线的标准方程【名师点睛】利用待定系数法求圆锥曲线方程是高考常见题型,求双曲线方程最基础的方法就是依据题目的条件列出关于,,a b c的方程,解方程组求出,a b,另外求双曲线方程要注意巧设双曲线(1)双曲线过两点可设为221(0)mx ny mn-=>,(2)与22221x ya b-=共渐近线的双曲线可设为2222(0) x ya bλλ-=≠,(3)等轴双曲线可设为22(0)x yλλ-=≠等,均为待定系数法求标准方程.4.【2016高考新课标1卷】已知方程222213x ym n m n-=+-表示双曲线,且该双曲线两焦点间的距离为4,则n的取值范围是( )(A)()1,3-(B)()1,3-(C)()0,3(D)()0,3【答案】A【解析】试题分析:222213x ym n m n-=+-表示双曲线,则()()2230m n m n+->∴223m n m-<<,由双曲线性质知:()()222234c m n m n m=++-=,其中是半焦距∴焦距2224c m=⋅=,解得1m=,∴13n-<<,故选A.考点:双曲线的性质5.【2016高考新课标2理数】已知12,F F是双曲线2222:1x yEa b-=的左,右焦点,点M在E上,1MF与轴垂直,211sin3MF F∠=,则E的离心率为()(A2(B)32(C3(D)2【答案】A【解析】试题分析:因为1MF垂直于x轴,所以2212,2b bMF MF aa a==+,因为211sin3MF F∠=,即2122132bMF abMFaa==+,化简得b a=,故双曲线离心率12bea=+=.选A.考点:双曲线的性质.离心率.【名师点睛】区分双曲线中a,b,c的关系与椭圆中a,b,c的关系,在椭圆中a2=b2+c2,而在双曲线中c2=a2+b2.双曲线的离心率e∈(1,+∞),而椭圆的离心率e∈(0,1).6.【2015高考新课标2,理11】已知A ,B 为双曲线E 的左,右顶点,点M 在E 上,∆ABM 为等腰三角形,且顶角为120°,则E 的离心率为() A .5 B . C .3 D .2 【答案】D【考点定位】双曲线的标准方程和简单几何性质.【名师点睛】本题考查双曲线的标准方程和简单几何性质、解直角三角形知识,正确表示点M 的坐标,利用“点在双曲线上”列方程是解题关键,属于中档题.7.【2015高考四川,理5】过双曲线2213y x -=的右焦点且与x 轴垂直的直线,交该双曲线的两条渐近线于A ,B 两点,则AB =() (A)433(B)23 (C)6 (D )43 【答案】D 【解析】双曲线的右焦点为(2,0)F ,过F 与x 轴垂直的直线为2x =,渐近线方程为2203y x -=,将2x =代入2203y x -=得:212,23,||43y y AB ==±∴=.选dreamsummit.8.【2016高考天津理数】已知双曲线2224=1x y b -(b >0),以原点为圆心,双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于A 、B 、C 、D 四点,四边形的ABCD 的面积为2b ,则双曲线的方程为()(A )22443=1y x -(B )22344=1y x -(C )2224=1x y b -(D )2224=11x y -【答案】D 【解析】试题分析:根据对称性,不妨设A 在第一象限,(,)A x y ,∴22422x x y bb y x y ⎧=⎧+=⎪⎪⎪⇒⎨⎨=⎪⎪=⎩⎪⎩, ∴221612422b b xy b b =⋅=⇒=+,故双曲线的方程为221412x y -=,故选D. 考点:双曲线渐近线【名师点睛】求双曲线的标准方程关注点:(1)确定双曲线的标准方程也需要一个“定位”条件,两个“定量”条件,“定位”是指确定焦点在哪条坐标轴上,“定量”是指确定a ,b 的值,常用待定系数法.(2)利用待定系数法求双曲线的标准方程时应注意选择恰当的方程形式,以避免讨论. ①若双曲线的焦点不能确定时,可设其方程为Ax 2+By 2=1(AB <0). ②若已知渐近线方程为mx +ny =0,则双曲线方程可设为m 2x 2-n 2y 2=λ(λ≠0).9.【2015高考新课标1,理5】已知M (00,x y )是双曲线C :2212x y -=上的一点,12,F F 是C 上的两个焦点,若120MF MF •<u u u u r u u u u r,则0y 的取值范围是( )(A )(-3,3) (B )(-6,6) (C )(3-,3)(D )() 【答案】A【解析】由题知12(F F ,220012x y -=,所以12MF MF •u u u u r u u u u r= 0000(,),)x y x y -•- =2220003310x y y +-=-<,解得0y << A.10.【2015高考重庆,理10】设双曲线22221x y a b-=(a >0,b >0)的右焦点为1,过F 作AF 的垂线与双曲线交于B ,C 两点,过B ,C 分别作AC ,AB 的垂线交于点D .若D 到直线BC 的距离小于22a a b + ( )A 、(1,0)(0,1)-UB 、(,1)(1,)-∞-+∞UC 、(2,0)2)UD 、(,2)(2,)-∞+∞U 【答案】A【解析】由题意22(,0),(,),(,)b b A a B c C c a a-,由双曲线的对称性知D 在轴上,设(,0)D x ,由BD AC⊥得2201b b a a c x a c-⋅=---,解得42()b c x a c a -=-,所以4222()b c x a a b a c a c a -=<++=+-,所以42222b c a b a <-=221b a ⇒<01b a⇒<<,因此渐近线的斜率取值范围是(1,0)(0,1)-U ,选A . 【考点定位】双曲线的性质.【名师点晴】求双曲线的渐近线的斜率取舍范围的基本思想是建立关于,,a b c 的不等式,根据已知条件和双曲线中,,a b c 的关系,要据题中提供的条件列出所求双曲线中关于,a b 的不等关系,解不等式可得所求范围.解题中要注意椭圆与双曲线中,,a b c 关系的不同.11.【2015高考安徽,理4】下列双曲线中,焦点在y 轴上且渐近线方程为2y x =±的是()(A )2214y x -=(B )2214x y -=(C )2214y x -=(D )2214x y -= 【答案】C12.【2015高考湖北,理8】将离心率为的双曲线1C 的实半轴长和虚半轴长()b a b ≠同时增加(0)m m >个单位长度,得到离心率为2e 的双曲线2C ,则()A .对任意的,a b ,12e e >B .当a b >时,12e e >;当a b <时,12e e <C .对任意的,a b ,12e e <D .当a b >时,12e e <;当a b <时,12e e > 【答案】D【解析】依题意,2221)(1a b a b a e +=+=,2222)(1)()(m a m b m a m b m a e +++=++++=, 因为)()()(m a a a b m m a a am ab bm ab m a m b a b +-=+--+=++-,由于0>m ,0>a ,0>b ,所以当b a >时,10<<a b ,10<++<m a m b ,m a m b a b ++<,22)()(ma mb a b ++<,所以12e e <; 当b a <时,1>a b ,1>++m a m b ,而m a m b a b ++>,所以22)()(ma mb a b ++>,所以12e e >.所以当a b >时,12e e <;当a b <时,12e e >. 【考点定位】双曲线的性质,离心率.【名师点睛】分类讨论思想是一种重要的数学思想方法.分类讨论的时应做到:分类不重不漏;标准要统一,层次要分明;能不分类的要尽量避免或尽量推迟,决不无原则地讨论.13.【2015高考福建,理3】若双曲线22:1916x y E -= 的左、右焦点分别为12,F F ,点P 在双曲线E 上,且13PF =,则2PF 等于( )A .11B .9C .5D .3 【答案】B14.【2017课标1,理】已知双曲线C :22221x y a b-=(a >0,b >0)的右顶点为A ,以A 为圆心,b为半径作圆A ,圆A 与双曲线C 的一条渐近线交于M 、N 两点.若∠MAN =60°,则C 的离心率为________.【答案】23【解析】试题分析:如图所示,作AP MN ⊥,因为圆A 与双曲线C 的一条渐近线交于M 、N 两点,则MN 为双曲线的渐近线by x a=上的点,且(,0)A a ,AM AN b == 而AP MN ⊥,所以30PAN ∠=o , 点(,0)A a 到直线by x a=的距离221AP b a =+在Rt PAN ∆中,cos PA PAN NA=代入计算得223a b =,即3a b =由222c a b =+得2c b =所以2333c e a b ===.【考点】双曲线的简单性质.15.【2017山东,理14】在平面直角坐标系xOy 中,双曲线()222210,0x y a b a b-=>>的右支与焦点为F 的抛物线()220x px p =>交于,A B 两点,若4AF BF OF +=,则该双曲线的渐近线方程为. 【答案】22y x =±【解析】试题分析:||||=4222A B A B p p pAF BF y y y y p ++++=⨯⇒+=, 因为22222222221202x y a y pb y a b a bx py⎧-=⎪⇒-+=⇒⎨⎪=⎩,所以2222A B pb y y p a b a +==⇒=⇒渐近线方程为2y x =±. 【考点】1.双曲线的几何性质.2.抛物线的定义及其几何性质.【名师点睛】1.在双曲线的几何性质中,渐近线是其独特的一种性质,也是考查的重点内容.对渐近线:(1)掌握方程;(2)掌握其倾斜角、斜率的求法;(3)会利用渐近线方程求双曲线方程的待定系数.求双曲线方程的方法以及双曲线定义和双曲线标准方程的应用都和与椭圆有关的问题相类似.因此,双曲线与椭圆的标准方程可统一为122=+By Ax 的形式,当0>A ,0>B ,B A ≠时为椭圆,当0<AB 时为双曲线.2.凡涉及抛物线上的点到焦点距离时,一般运用定义转化为到准线距离处理.16.【2017北京,理9】若双曲线221y x m-=3m =_________.【答案】217.【2015高考北京,理10】已知双曲线()22210x y a a-=>30x y +=,则a =.【答案】33【解析】双曲线()22210x y a a -=>的渐近线方程为1y x a=±,303x y y x +=⇒=, 0a >Q ,则133,3a a-=-=【考点定位】本题考点为双曲线的几何性质,正确利用双曲线的标准方程,求出渐近线方程,利用已给渐近线方程求参数.【名师点睛】本题考查双曲线的几何性质,重点考查双曲线的渐近线方程,本题属于基础题,正确利用双曲线的标准方程,求出渐近线方程,求渐近线方程的简单方法就是把标准方程中的“1”改“0”,利用已知渐近线方程,求出参数a 的值.18.【2016高考山东理数】已知双曲线E :22221x y a b-=(a >0,b >0),若矩形ABCD 的四个顶点在E 上,AB ,CD 的中点为E 的两个焦点,且2|AB |=3|BC |,则E 的离心率是_______. 【答案】2 【解析】试题分析:假设点A 在第一象限,点B 在第二象限,则2b A(c,)a ,2b B(c,)a -,所以22b |AB |a =,|BC |2c =,由2AB 3BC =,222c a b =+得离心率e 2=或1e 2=-(舍去),所以E 的离心率为2.考点:双曲线的几何性质【名师点睛】本题主要考查双曲线的几何性质.本题解答,利用特殊化思想,通过对特殊情况的讨论,转化得到一般结论,降低了解题的难度.本题能较好的考查考生转化与化归思想、一般与特殊思想及基本运算能力等.19.【2015江苏高考,12】在平面直角坐标系xOy 中,P 为双曲线122=-y x 右支上的一个动点。
专题18双曲线—三年高考(2015-2017)数学(理)真题分项版解析(原卷版)

()2224x y -+=所截得的弦长为2,则C 的离心率为()若经过F 和(0,4)P 两点的直线平行于双曲线的一条渐近线,则双曲线的方程为的距离为4,则n 的取值范围是( )6.【2015高考新课标2,理11】已知A ,B 为双曲线E 的左,右顶点,点M 在E 上,∆ABM 为等腰三角形,且顶角为120°,则E 的离心率为()长为半径长的圆与双曲线的两条渐近线相交于A 、B 、C 、D 四点,四边形的ABCD 的面积为2b ,则双曲线的方程为()0是C 上的两个焦点,若120MF MF •<,则0y 的取值范围是( )垂线与双曲线交于B ,C 两点,过B ,C 分别作AC ,AB 的垂线交于点D 若D 到直线BC 的距A 、(1,0)(0,1)-B 、(,1)(1,)-∞-+∞2,0)(0,2) 2)(2,)+∞11.【2015高考安徽,理4】下列双曲线中,焦点在y 轴上且渐近线方程为2y x =±的是()12.【2015高考湖北,理8】将离心率为1e 的双曲线1C 的实半轴长a 和虚半轴长()b a b ≠同时增加(0)m m >个单位长度,得到离心率为2e 的双曲线2C ,则() A .对任意的,a b ,12e e >B .当a b >时,12e e >;当a b <时,12e e <C .对任意的,a b ,12e e <D .当a b >时,12e e <;当a b <时,12e e >A .11B .9C .5D .3心,b 为半径作圆A ,圆A 与双曲线C 的一条渐近线交于M 、N 两点.若∠MAN =60°,则C 的离心率为________渐近线方程为.a =.个顶点在E 上,AB ,CD 的中点为E 的两个焦点,且2|AB |=3|BC |,则E 的离心率是_______19.【2015江苏高考,12】在平面直角坐标系xOy 中,P 为双曲线122=-y x 右支上的一个动点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题15 双曲线
与x 轴垂直,点A 的坐标是(1,3),则△APF 的面积为
的渐近线上,OAF △是边长为2的等边三角形(O 为原点),则双曲线的方程为
的离心率为( )
5.【2015高考安徽,文6】下列双曲线中,渐近线方程为2y x =±的是( )
,102:+=x y l 双曲线的一个焦点在直线l 上,则双曲线的方程为( )
曲线的渐近线与圆()
2
22
y 3x -+=相切,则双曲线的方程为( )
8. 【2014年普通高等学校招生全国统一考试湖北卷8】设a 、b 是关于t 的方程
0sin c o s 2=+θθt t 的两个不等实根,则过),(2a a A ,),(2b b B 两点的直线与双曲线
A. 0
B. 1
C. 2
D. 3
9.【2015高考湖北,文9】将离心率为1e 的双曲线1C 的实半轴长a 和虚半轴长()b a b ≠同时增加(0)m m >个单位长度,得到离心率为2e 的双曲线2C ,则( ) A .对任意的,a b ,12e e > B .当a b >时,12e e >;当a b <时,12e e < C .对任意的,a b ,12e e <
D .当a b >时,12e e <;当a b <时,
12e e >
渐近线于A 、B 两点,则|AB |=( )
别是12A ,A ,过F 做12A A 的垂线与双曲线交于B ,C 两点,若12A B A C ⊥,则双曲线的渐近线的斜率为( )
的两条渐近线于A 、B 两点,则|AB |=( )
支与焦点为F 的抛物线22(0)x py
p =>交于A ,B 两点,若|AF |+|BF
|=4|OF |,则该双曲线的渐近
点在E 上,AB ,CD 的中点为E 的两个焦点,且2|AB |=3|BC |,则E 的离心率是_______.
线上,且△F 1PF 2为锐角三角形,则|PF
1|+|PF 2|的取值范围是_______.
抛物线)0(22>=p py x 的焦点为F ,若双曲线截抛物线的准线所得线段长为c 2,且。
