高三数学第三次模拟试题文新人教A版
2021-2022年高三数学第三次模拟考试 理 新人教A版

2021年高三数学第三次模拟考试理新人教A版第Ⅰ卷(选择题,共60分)一、选择题(本大题包括12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项填涂在答题卡上).1.已知集合,若,则()A.2.等差数列的前 n项和为,若,则( )A. -2B.0C.2D.43.设随机变量ξ服从正态分布N(2,σ2),若P(ξ>c)=, 则P(ξ>4-c)等于A. B.2 C. 1- D. 1-24.如图,网格纸上的正方形的边长为1,粗线画出的是某几何体的三视图,则这个几何体的体积为()(A) 30 (B) 50 (C) 75 (D) 1505.一个棱柱的底面是正六边形,侧面都是正方形,用至少过该棱柱三个顶点(不在同一侧面或同一底面内)的平面去截这个棱柱,所得截面的形状不可以是()等腰三角形 (B)等腰梯形(C)五边形 (D)正六边形6.函数在区间的最大值为()(A)1 (B) (C) (D)27.设f(x)是定义在R上的奇函数,其f(x)=f(x-2),若f(x)在区间单调递减,则()(A) f(x)在区间单调递增 (B) f(x)在区间单调递增(C) f(x)在区间单调递减 (D) f(x)在区间单调递减8.双曲线的左、右焦点分别是,过作倾斜角为的直线交双曲线右支于点,若垂直于轴,则双曲线的离心率为( )(A) (B) (C) (D)9.已知外接圆的半径为,且.,从圆内随机取一个点,若点取自内的概率恰为,则的形状为( )(A)直角三角形 (B)等边三角形 (C)钝角三角形 (D)等腰直角三角形10.已知数列满足,,则A. 143B. 156C. 168D. 19511.用1,2,3,4,5,6组成数字不重复的六位数,满足1不在左右两端,2,4,6三个偶数中有且只有两个偶数相邻,则这样的六位数的个数为()A.432 B.288 C.216 D.14412.函数在区间上单调递增,则的取值范围是 ( ) A . B. C . D . 第Ⅱ卷(非选择题 共90分)二、填空题:把答案填在相应题号后的横线上(本大题共4小题,每小题5分,共20分) 13.甲、乙、丙、丁四人商量去看电影. 甲说:乙去我才去; 乙说:丙去我才去; 丙说:甲不去我就不去; 丁说:乙不去我就不去。
高三数学第三次模拟考试试题文新人教A版

普通高等学校招生全国统一考试文 科 数 学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部份,其中第Ⅱ卷第22~24题为选考题,其它题为必考题。
考生作答时,将答案答在答题卡上,在本试卷上答题无效。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上,认真查对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上。
2.选择题答案利用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案的标号;非选择题答案利用毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
3.请依照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
4.维持卡面清洁,不折叠,不破损。
5.做选考题时,考生依照题目要求作答,并用2B 铅笔在答题卡上把所选题目对应的题号涂黑。
参考公式:样本数据n x x x ,,21的标准差 锥体体积公式(n s x x =++- 13V Sh =其中x 为样本平均数 其中S 为底面面积,h 为高 柱体体积公式 球的表面积,体积公式V Sh = 24S R π= 343V R π=其中S 为底面面积,h 为高 其中R 为球的半径第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知全集U=R ,设函数y=lg(x-1)的概念域为集合A ,函数y=522++x x 的值域为集合B ,则A∩(C U B)=( )A .[1,2]B .[1,2)C .(1,2]D .(1,2)文科数学试卷 第1页(共5页)2.已知sinθ=54,且sinθ-cosθ>1,则sin2θ=( ) A . -2524 B .-2512 C .-54 D .2524 3.已知等差数列}{n a 知足,0101321=++++a a a a 则有( ) A .01011>+a a B .01002<+a aC .0993=+a aD .5151=a4.已知011<<ba ,则下列结论不正确的是( )A .a 2<b 2B .ab<b 2C .2>+abb a D .|a|+|b|>|a+b|5. 下图给出了下一个算法流程图,该算法 流程图的功能是( )A .求a,b,c 三数的最大数B .求a,b,c 三数的最小数C .将a,b,c 按从小到大排列D .将a,b,c 按从大到小排列6. 已知函数)5(,)0)(3()0(2)(f x x f x x f x则⎪⎩⎪⎨⎧>-≤==( ) A .32 B .16C .21D .3217. 若命题“p ∧q”为假,且“⌝p”为假,则( )A .p 或q 为假B .q 假C .q 真D .不能判断q 的真假8.已知正四棱锥的各棱棱长都为23,则正四棱锥的外接球的表面积为( )A .π12B .π36C .π72D .π1089.函数y=sinxcosx+3cos 32-x 的图象的一个对称中心是( )A )23,32(-π B )23,65(-π C )23,32(π- D )3,3(-π10.甲、乙两棉农,统计持续五年的面积产量(千克∕亩)如下表:棉农甲 68 72 70 69 71 棉农乙6971686869则平均产量较高与产量较稳定的别离是( )??A .棉农甲,棉农甲B .棉农甲,棉农乙C .棉农乙,棉农甲D .棉农乙,棉农乙11. 已知函数34)(2+-=x x x f ,集合(){}0)()(,≤+=y f x f y x M , 集合(){}0)()(,≥-=y f x f y x N ,则集合N M 的面积是( )A .4π B .2πC .πD .π212.设f (x ),g (x )别离是概念在R 上的奇函数和偶函数,当x <0时,0)(')()()('>+x g x f x g x f ,且0)3(=-f ,则不等式0)()(<x g x f 的解集是( )A .(-3,0)∪(3,+∞)B .(-3,0)∪(0,3)C .(-∞,-3)∪(3,+∞)D .(-∞,-3)∪(0,3)第Ⅱ卷本卷包括必考题和选考题两部份.第13题~第21题为必考题,每一个试题考生都必需做答.第22题~第24题为选考题,考生按照要求做答. 二、填空题(本大题共4个小题,每小题5分,共20分.)13 椭圆19822=++y k x 的离心率为21,则k 的值为________.14. 已知函数),(1222)(R x a a x f xx ∈+-+⋅=是奇函数,则实数a 的值________.15. 已知边长别离为a 、b 、c 的三角形ABC 面积为S ,内切圆O 半径为r ,连接OA 、OB 、OC ,则三角形OAB 、OBC 、OAC 的面积别离为21cr 、21ar 、21br ,由S=21cr+21ar+21br 得r=cb a S++2,类比得若四面体的体积为V,四个面的面积别离为A 、B 、C 、D ,则内切球的半径R=_____________.16.若数列}{n a 知足}*1112()1nn n na a a n N a ++==∈-数列满足,,则该数列的前2013项的乘积______.三、解答题:本大题共5小题,共计70分。
三中高三数学模拟试题文新人教A版

福州三中 高三高考模拟考数学(文科)试卷本试卷共150分,考试时间120分钟 注意事项:(1) 答卷前,考生务必用0.5mm 黑色签字笔将自己的班级、姓名、座号填写在试卷和答 卷的密封线外。
请考生认真审题,将试题的答案正确书写在答卷上的指定位置,并认真检查以防止漏答、错答。
考试中不得使用计算器。
参考公式:球的表面积公式24S R π= 棱柱的体积公式 V Sh = 球的体积公式343V R π= 棱锥的体积公式13V Sh= 棱台的体积公式11221()3V h S S S S =++其中12,S S 分别表示棱台的上、下底面积,h表示棱台的高其中R 表示球的半径,其中S 表示棱柱(锥)的底面积,h 表示棱柱(锥)的高 如果事件,A B 互斥,那么()()()P A B P A P B +=+选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合(1,2),A =- 集合2{|230}B x x x =--+>,则A B =( ) A .(1,1)- B .(3,2)- C .(1,3)- D . (1,2)-2.设i 是虚数单位,则复数20131()1i z i +=-=( )A .-1B .1C .i -D . i3. 命题“x ∀∈R ,都有ln(x2+1)>0”的否定为( )(A)x ∀∈R,都有ln(x2 +1)≤0 (B)0x ∃∈R ,使得ln(x02+1)>0(C) x ∀∈R ,都有ln(x2+l)<0 (D) 0x ∃∈R,使得ln(x02+1)≤04.已知,l m 是直线,α是平面,且m a ⊂,则“l m ⊥”是“l α⊥” 的( ) A .必要不充分条件 B .充分不必要条件 C .充要条件 D .既不充分也不必要条件5.阅读程序框图(如右图),如果输出的函数值在区间[14,1]上,则输入的实数x 的取值范围是( )A.(,2]-∞-B.[-2,0]C.[0,2]D.[2,)+∞ 6.在等差数列{}n a 中,+=4722a a ,则数列{}n a 的前9项和等于( )A .3B . 9C .6D .127.设1122(,),(,),...,(,)n n x y x y x y ,是变量x 和y 的n 个 样本点,直线l 是由这些样本点通过最小二乘法得到 的线性回归方程(如图),以下结论中正确的是( )A .x 和y 正相关B .x 和y 的相关系数为直线l 的斜率C .x 和y 的相关系数在-1到0之间D .当n 为偶数时,分布在l 两侧的样本点的个数一定相同8. 已知函数y=2sin2(,2cos )4x x -+π则函数的最小正周期T 和它的图象的一条对称轴方程是( ) A .T=2π,一条对称轴方程为8π=x B .T=2π,一条对称轴方程为83π=xC .T=π,一条对称轴方程为8π=x D .T=π,一条对称轴方程为83π=x 9.函数log 1(0,1)m y x m m =+>≠的图像恒过定点M ,若点M在直线1(0,0)ax by a b +=>>上,则14a b +的最小值为( ) A .8 B .9 C .10 D .1210.若某几何体的三视图如图所示,则这个几何体的体积是( ) A .5 B .6 C .7 D .811.函数sin x xy e -=的图象大致为( )12. 已知i 是虚数单位,记cos sin ie i θθθ=+,其中 2.718...,e θ=∈R ,给出以下结论:①10ie π+= ②1ii eeθθ-= ③1212()i i i e e e θθθθ+⋅=,则其中正确结论的个数是( )A .0B .1C .2D .3二、填空题:本大题共4小题,每小题4分,共16分,把答案填在相应横线上.13. 已知向量(,1),xa e =-向量(1,1)b x =+,设函数(),f x a b =⋅则函数()f x 的零点个数为 .14.若圆22240(3)x y x y m m ++-+=<的一条弦AB 的中点为P (O ,1),则垂直于AB 的直径所在直线的方程为 .15.若x,y 满足y ax z y x y x y x 2,22,1,1+=⎪⎩⎪⎨⎧≤--≥-≥+且仅在点(1,0)处取得最小值,则实数a 的取值范围是 .16.已知命题:在平面直角坐标系xoy 中,ABC ∆的顶点)0,(p A -和)0,(p C ,顶点B在椭圆),0(1222222n m p n m n y m x -=>>=+上,则B C A sin sin sin +e 1=(其中e 为椭圆的离心率).试将该命题类比到双曲线中,给出一个真命题是 .三、解答题:(本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤.)17.(本题12分)已知函数211()22f x x x =+,数列{}n a 的前n 项和为n S ,点*(,)()n n S n N ∈均在函数()y f x =的图象上.(I) 求数列{}n a 的通项公式na ;(II)若2nn n a b =,求数列{}n b 的前n 项和n T .18.(本题12分)某市为了配合宣传新《道路交通法》举办有奖征答活动,随机对该市15~65岁的人群抽样了n 人,回答问题统计结果如图表所示.(左图是样本频率分布直方图,右表是对样本中回答正确人数的分析统计表).(Ⅰ)分别求出,,,,n a b x y 的值;(Ⅱ)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,有奖征答活动组委会决定在所抽取的6人中随机抽取2人颁发幸运奖,求获得幸运奖的2人来自不同年龄组的概率.19.(本题12分)如图三棱柱111ABC A B C -中, 侧棱与底面垂直,ABC ∆是等边三角形, 点D 是BC 的中点.(Ⅰ)证明:1//A B 平面1C AD;(Ⅱ)若在三棱柱111ABC A B C -内部(含表面)随机投放一个点P ,求点P 落在三棱锥11C A AD -内部(含表面)的概率.20. (本题12分)如图所示扇形AOB ,半径为2,3AOB π∠=,过半径OA 上一点C 作OB 的平行线,交圆弧AB 于点P . (Ⅰ)若C 是OA 的中点,求PC 的长;(Ⅱ)设θ=∠COP ,求△POC 面积的最大值及此时θ的值.21. (本题12分)已知椭圆E 的中心在坐标原点O ,焦点在x 轴上,离心率3e =且经过点(2,1)M .(Ⅰ)求椭圆E 的方程;(Ⅱ) 设平行于OM 的直线l 交椭圆E 于两个不同点A B 、,直线MA 与MB 的斜率分别为12k k 、;① 若直线l 过椭圆的左顶点,求12k k 、的值;② 试猜测12k k 、的关系;并给出你的证明.22. (本题14分)已知函数2()ln 23f x x x x =-+. (I )求函数()f x 的极值;(Ⅱ)证明:存在(1,)m ∈+∞,使得1()()2f m f =;(Ⅲ)记函数y=()f x 的图象为曲线Γ.设点11(,)A x y ,22(,)B x y 是曲线Γ上的不同两点.如果在曲线Γ上存在点00(,)M x y ,使得:①1202x x x +=;②曲线Γ在点M 处的切线平行于直线AB ,则称函数()f x 存在“中值伴随切线”,试问:函数()f x 是否存在“中值伴随切线”,请说明理由.福州三中 高三高考模拟考 数学(文史类)参考答案 选择题: ,,BDDAB CCDBC BD填空题:13.1 14.10x y +-= 15.(4,2)a ∈-16.在平面直角坐标系xoy 中,ABC ∆的顶点)0,(p A -和)0,(p C ,顶点B 在双曲线),0(1222222n m p n m n y m x +=>>=-上,则e B C A 1sin sin sin =-(其中e 为双曲线的离心率).三.解答题: 17.(I)点*(,)()n n S n N ∈在函数()y f x =的图象上,211,22n S n n ∴=+即22n S n n =+,1n =时11;a =2n ≥时212(1)(1)n S n n -=-+-,故12()2,n n S S n --=即n a n =.(II)1()2nn b n =, 2123111112()...(1)()()222211111()2()......(1)()()22222n nn n n n T n n T n n -+∴=+++-+∴=++++-+211111[1()]1111111122()...()()()1()()1222222221212(2)()2n n n n n n n nn T n n n T n +++-∴=+++-=-=---∴=-+18.(Ⅰ)由第1组数据知该组人数为5100.5=,因为第1组的频率是0.01100.1⨯=,故101000.1n ==;因为第2组人数为0.021010020⨯⨯=,故200.918a =⨯=;因为第3组人数为0.031010030⨯⨯=,故270.930x ==;因为第4组人数为0.025*******⨯⨯=,故250.369b =⨯=;因为第5组人数为0.0151010015⨯⨯=,故30.215y ==.(Ⅱ)第2,3,4组回答正确的人的比为18:27:92:3:1=,故这3组分别抽取2人,3人,1人.设第2组为12,A A ,第3组为123,,B B B ,第4组为1C ;则随机抽取2人可能是12111213(,),(,),(,),(,),A A A B A B A B 1121(,),(,),A C A B 222321(,),(,),(,),A B A B A C12(,),B B1311232131(,),(,),(,),(,),(,)B B BC B B B C B C ,共15种.其中来自不同年龄组的有111213(,),(,),(,),A B A B A B 1121(,),(,),A C A B 222321(,),(,),(,),A B A B A C11(,),B C 2131(,),(,)B C B C 共11种,故获得幸运奖的2人来自不同年龄组的概率是1115.19.(Ⅰ)连接1A C ,交1AC 于点E ,连接DE,在1A BC 中DE 是中位线,故 1//DE A B,111,DE C AD A B C AD ⊆⊄∴面面1//A B 平面1C AD.(Ⅱ)设底面边长为a ,侧棱长为h,则11124ABC A B C V a h -=,因为点D 是BC 的中点,过D 作AC 的垂线交AC 于F ,有DF=,故11111132C A AD D A AC V V ah --==⋅,所以点P 落在三棱锥11C A AD-内部(含表面)的概率16.20.(Ⅰ)//,CP OB3AOB π∠=,23OCP π∴∠=,若C 是OA 的中点,则在OPC ∆中,2222cos ,OP OC CP OC CP OCP =+-⋅⋅∠即241CP CP =++,解得12CP =.(Ⅱ) 由正弦定理2sin()sin33OC OPππθ=-,sin(),3OC πθ=-所以1sin 2OCP S OP OC θ∆=⋅⋅112sin()sin sin )sin 232πθθθθθ=⋅-⋅=-⋅212cos sin sin 2cos 2)(2cos 2)333223θθθθθθθ=-=--=+-)(0,)3633ππθθ=+-∈,52(,)(0,6663OPC S πππθ∆+∈∴∈. .33max ,6==S 时当πθ21. (Ⅰ)设椭圆方程为22221x y a b +=,依题意有:22222222211a b e a a b ⎧-==⎪⎪⎨⎪+=⎪⎩,解得228,2a b ==,所以椭圆E 的方程为22182x y +=.(Ⅱ) ①若直线l 过椭圆的左顶点且直线l 平行于OM ,则直线的方程是1:2l y x =联立方程组2212182y x x y ⎧=+⎪⎪⎨⎪+=⎪⎩,解得121200x x y y =⎧⎧=-⎪⎪⎨⎨==⎪⎪⎩⎩,故1211,22k k =-=. ②因为直线l 平行于OM ,设在y 轴上的截距为b ,又12OM k =,所以直线l 的方程为12y x b =+.由2212182y x b x y ⎧=+⎪⎪⎨⎪+=⎪⎩ 得222240x bx b ++-= .设11(,)A x y 、22(,)B x y ,则212122,24x x b x x b +=-=-. 又1111,2y k x -=-2221,2y k x -=-故1212121122y y k k x x --+=+--122112(1)(2)(1)(2)(2)(2)y x y x x x --+--=--.又112211,22y x b y x b =+=+,所以上式分子122111(1)(2)(1)(2)22x b x x b x =+--++--21212(2)()4(1)24(2)(2)4(1)0x x b x x b b b b b =+-+--=-+----= ,故120k k +=.所以直线MA 与直线MB 的倾斜角互补.22.(I )21431(1)(41)'()43(0)x x x x f x x x x x x -++--+=-+==>,'()01f x x =⇒=,(0,1)x ∈时'()0,f x >(1,)x ∈+∞时'()0,f x <故1x =时()f x 有极大值1,无极小值.(Ⅱ)构造函数:22113()()()ln 23(ln 2)ln 23ln 21222F x f x f x x x x x x =-=-+---+=-++-, 由(I )知1(1)()2f f >,故(1)0F >,又2()23ln 2(32)ln 20F e e e e e =-++=-+<,所以函数()F x 在区间(1,)e 上存在零点.即存在(1,)m ∈+∞,使得1()()2f m f =. (Ⅲ)22121212121212121212()()ln ln 2()3()ln ln 2()3AB f x f x x x x x x x x x k x x x x x x x x ----+--===-++--- 120001212'()43432x x f x x x x x +=-+=-++,假设存在“中值伴随切线”,则有0'()AB k f x =,可得1121121211212212221ln ln 2ln 2ln 21x x x x x x x x x x x x x x x x x x ---=⇒=⋅⇒=⋅-+++,令12x t x =,则1ln 21t t t -=⋅+,构造1()ln 2,1t g t t t -=-⋅+ 有22214(1)'()0(1)(1)t g t t t t t -=-=≥++恒成立,故函数()g t 单调递增,无零点,所以函数()f x 不存在“中值伴随切线” .。
广东省广州市广雅中学2014届高三数学第三次模拟试题 文 新人教A版

广东省广州市广雅中学2014届高三第三次模拟数学文试题 试本试卷分选择题和非选择题两部分,共4页,满分150分,考试用时120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的校名、姓名、考号填写在答题卡的密封线内。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案;不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在另发的答题卷各题目指定区域内的相应位置上;如需改动,先划掉原的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁,考试结束后,将答题卷和答题卡一并收回。
参考公式:柱体的体积公式sh V =,其中s 为柱体的底面积,h 为柱体的高。
锥体的体积公式sh V 31=,其中s 为锥体的底面积,h 为锥体的高。
一组数据n x x x ⋯⋯,,21的方差])()()[(12_2_22_12x x x x x x ns n -+⋯⋯+-+-=,其中_x 表示这组数据的平均数。
第一部分选择题(共50分)一.选择题(本大题共10道小题,每小题5分,满分50分。
在每小题给出的四个选项中有且只有一个是符合题目要求的)1.函数y )A. )3,(-∞B. ]1,0(C. ]3,0(D.]3,(-∞2.下列函数中周期为π且图象关于直线3x π=对称的函数是( )2sin()23x y π=+ B.2sin(2)6y x π=- C.2sin(2)6y x π=+D.2sin()23x y π=- 3.已知i 是虚数单位,若31ii z+=-,则z 的共轭复数为( )A.12i -B.24i - D.12i + 4.阅读右面的程序框图,运行相应的程序,输出的结果为( )A.2-B.12 C.1- D.25.已知等比数列{}n a 的前n 项和为n S ,且1S ,22S a +,3S 成等差数列,则数列{}n a 的公比为( )A .1B .2C .12 D .36.下列说法错误的是( ) A.在统计学中,独立性检验是检验两个分类变量是否有关系的一种统计方法.B.线性回归方程对应的直线a x b yˆˆˆ+=至少经过其样本数据),,(11y x ),,(22y x ),(,33y x …),(n n y x 中的一个点.C.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高.D.在回归分析中,相关指数2R 为98.0的模型比相关指数2R 为80.0的模型拟合的效果好. 7.一个空间几何体的三视图如图所示,则这个几何体的表面积为( ) A .61 B .23+ C .23 D .218.已知x 、y 满足231143x y x y +≥⎧⎪≤⎨⎪≤⎩,则12y z x -=+的取值范围为( )A .]32,0[ B .]1,0[ C .]32,(-∞ D .),32[+∞9.已知定义域为)1,1(-的奇函数)(x f y =又是减函数,且0)9()3(2<-+-a f a f ,则a 的取值范围是( )A .(22,3)B .(3,10)C .(22,4)D .(-2,3)10.若集合A 具有以下性质:①0A ∈,1A ∈;②若,x y A ∈,则x y A -∈,且0x ≠时,1A x∈.则称集合A 是“好集”. (1)集合{}1,0,1B =-是好集; (2)有理数集Q 是“好集”; (3)设集合A 是“好集”,若,x y A ∈,则x y A +∈; (4)设集合A 是“好集”,若,x y A ∈,则必有xy A ∈; (5)对任意的一个“好集”A ,若,x y A ∈,且0x ≠,则必有yA x∈. 则上述命题正确的个数是( )A.2个B.3个C.4个D.5个第二部分非选择题(100分)二、填空题:本大题共四小题,每小题5分,满分20分。
高三数学第三次模拟考试试题文扫描版新人教A版

河南省郑州市高三数学第三次模拟考试试题文(扫描版)高中毕业年级第三次质量预测数学(文科) 参考答案一、选择题CBDBB CCDAA DC二、填空题13.44π- 14. 2013 15. 52 16. -2 三、解答题18. 解:(Ⅰ)这120天中抽取30天,应采取分层抽样,第一组抽取81203032=⨯天;第二组抽取161203064=⨯天; 第三组抽取41203016=⨯天;第四组抽取2120308=⨯天. ……………………4分 (Ⅱ)设PM2.5的平均浓度在(75,115]内的4天记为4321,,,A A A A ,PM2.5的平均浓度在115以上的两天记为21,B B .所以6天任取2天的情况有:,21A A ,31A A ,41A A ,11B A ,21B A ,32A A ,42A A ,12B A ,22B A,43A A ,13B A ,23B A ,14B A ,24B A 21B B 共15种. ……………………8分记“恰好有一天平均浓度超过115(微克/立方米)”为事件A ,其中符合条件的有:,11B A ,21B A ,12B A ,22B A ,13B A ,23B A ,14B A 24B A 共8种. ……………………10分所求事件A 的概率().158=A P ……………………12分 19.(Ⅰ)证明:连结PC ,交DE 于N ,连结MN ,在PAC ∆中,N M ,分别为两腰PC PA ,的中点,∴.//AC MN ………………3分因为,面MDE MN ⊂,面MDE AC ⊄所以//AC 平面MDE . ………………6分(Ⅱ)由四边形PDCE 为矩形,知,DC PD ⊥又平面⊥PDCE 平面ABCD ,,ABD PD 平面⊥∴三棱锥ABD P -的体积为6221161213131=⨯⨯⨯=⨯⨯⨯=⨯=∆-PD AD AB PD S V ABD D AB P . …………8分 由已知,DC AD ⊥又平面⊥PDCE 平面ABCD ,,PDCE AD 平面⊥∴,//CD AB Θ四棱锥的体积为322122313131=⨯⨯⨯=⨯⨯=⨯==--AD PD CD AD S V V PDCE PDCE A PDCE B 矩形.………10分 ,4132262==--PDCE B DAB P V V Θ 所以原几何体被平面PBD 所分成的两部分的体积比41. ……… ………………12分0122)3(2222=-+-+k x k x k ,设),(),,(2211y x N y x M ,则343)3(2)12)(3(442222222422,1++±=+-+-±=k k k k k k k k x 312,3222212221+-=+=+k k x x k k x x . 022011x x y x x y k k NQ MQ -+-=+121020(1)(1)k x k x x x x x --=+--1202101020(1)()(1)()()()k x x x k x x x x x x x --+--=--, ………………………9分21.解: (Ⅰ) /1()21,g x ax x =++Q (),21ln 2)(ax x x a x ++-=ϕ其定义域为()+∞,0.…………1分当0=a 时,x x x 1ln 2)(+=ϕ,/222121()x x x x xφ-=-=. ……………………2分 令解得,0)('=x ϕ.21=x 当210<<x 时, ;0)('<x ϕ当21>x 时, .0)('>x ϕ 所以)(x ϕ的单调递减区间为,21,0⎪⎭⎫ ⎝⎛单调递增区间为;,21⎪⎭⎫ ⎝⎛+∞ 所以当21=x 时, )(x ϕ有极小值,2ln 2221-=⎪⎭⎫⎝⎛ϕ无极大值. ……………………4分(Ⅱ) (),21ln 2)(ax xx a x ++-=ϕΘ ()().0)1)(12(122212)(2222'>+-=--+=+--=∴x xa x x a x x a ax a x x a x ϕ …………5分当2-<a 时,211<-a .令0)('<x ϕ,得a x 10-<<,或21>x . 令0)('>x ϕ,得211<<-x a . 当2-<a 时,)(x ϕ的单调递减区间为,1,0⎪⎭⎫ ⎝⎛-a ;,21⎪⎭⎫ ⎝⎛+∞单调递增区间为.21,1⎪⎭⎫ ⎝⎛-a …………8分 (Ⅲ)由(Ⅱ)可知,当23-<<-a 时,)(x ϕ在[]3,1上单调递减,所以(),121)(max +==a x ϕϕ()().6313ln 23)(min a a x ++-==ϕϕ 所以()()()()().3ln 24326313ln 21231)()(max 21-+-=⎥⎦⎤⎢⎣⎡++--+=-=-a a a a a ϕϕλϕλϕ 因为对[]3,1,21∈∀λλ,12()()(ln 2)2ln3m a φλφλ-<+-恒成立,所以()()242ln 3ln 22ln 33a a m a -+-<+-, ……………………………………10分整理得234ln ,32ma a a >-+ 又0<a ,所以32ln 4,23m a<+- 又23-<<-a ,得,923231-<<-a ,928432313-<-<-a 所以133ln .32m ≤-+ 故实数m 的取值范围是133,ln .32⎛⎤-∞-+ ⎥⎝⎦……………………………………12分 22.解:(Ⅰ)因为AB 为切线,AE 为割线,CED CFG CDE CGF ∠=∠∠=∠∴,.CGF ∆∴∽CDE ∆.CGCD GF DE =∴.又Θ4,1==CD CG ,∴GF DE=4. ………………………………10分23.解:(Ⅰ)直线l 的直角坐标方程,01323=--+y x ………………………………2分曲线C 的直角坐标方程422=+y x . ………………………………4分(Ⅱ)曲线C 经过伸缩变换⎩⎨⎧='='y y x x 2,得到曲线C '的方程为4422=+y x ,则点M 参数方程为)(sin 4,cos 2参数θθθ⎩⎨⎧==y x ,代入y x 213+得,y x 213+==⋅+⋅θθsin 421cos 23)3sin(4cos 32sin 2πθθθ+=+, ∴y x 213+的取值范围为[]4,4-. ………………………………10分24.解:(Ⅰ)由题意得)4212(log )(2-++-=x x x f ,04212>-++-x x . 04)2()12(2>-+----<x x x 时,当, 35-<∴x ,即2-<x .1,04)2()12(212-<∴>-++--≤≤-x x x x 时,当,即12-<≤-x ,1,04)2()12(21>∴>-++->x x x x 时,当.即1>x .综上所述,函数()f x 的定义域为{}1,1>-<x x x 或. ………………………………5分 (Ⅱ)由题意得4log 2)212(log 22=≥-++-a x x 恒成立, 即4212>-++-a x x ,∴a x x >-++-4212恒成立,令=)(x g ,,21,33212,1,2,534212⎪⎪⎪⎩⎪⎪⎪⎨⎧>-≤≤----<--=-++-x x x x x x x x 显然21=x 时,)(x g 取得最小值23-,23-<∴a . ………………………………10分。
广东省紫金县中山高级中学高三数学上学期第三次段考试题 文 新人教A版

阶段测试(文科数学)本试卷共4页,21题,满分150分,测试用时120分钟. 参考公式:锥体的体积公式Sh V 31=,其中S 是锥体的底面积,h 是锥体的高. 一、选择题(本大题共10小题,每小题5分,共50分) 1、已知{}{}|10,2,1,0,1A x x B =+>=--,则()R C A B ⋂=( )A .{}2,1--B .{}2-C .{}1,0,1-D .{}0,12、已知复数z 的实部是1-,虚部是2,其中i 为虚数单位,则z1在复平面对应的点在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 3、函数)1lg()(+=x x f 的定义域是 ( )A .),1(+∞-B .),1[+∞-C .),0(+∞D .),0[+∞4.等差数列}{n a 中,,26,2491321=-=++a a a a 则此数列}{n a 前20项和等于( ). A.220 B. 200 C. 180 D. 160 5、在ABC ∆中,若A ∠=60°, ∠B=45°,BC=23 则AC= ( ) A .222 D.226、执行如图所示的程序框图,若输入8,n S ==则输出的( ) A .49 B .67 C .89 D .10117.已知向量()2,1=→a ,()1,0=→b ,()2,-=→k c ,若(2+→a →b )⊥→c ,则k =( )A.2B. 2-C.8D.8-8、若双曲线22221x y a b-=3,则其渐近线方程为 ( )A.y =±2xB.y =2xC.12y x =±D.22y x =± 9、若α、β是不重合的平面,a 、b 、c 是互不相同的空间直线,则下列命题中为真命题的是 ( )① 若α//a ,α//b ,则b a // ; ② 若α//c ,α⊥b ,则b c ⊥ ; ③ 若α⊥c ,β//c ,则βα⊥ ;④ 若α⊂b ,α⊂c 且b a ⊥,c a ⊥,则α⊥aA.③④B. ①②C. ①④D. ②③10、设()f x 与()g x 是定义在同一区间[,]a b 上的两个函数,若函()()y f x g x =-在[,]x a b ∈上有两个不同的零点,则称()f x 和()g x 在[,]a b 上是“关联函数”,区间[,]a b 称为“关联区间”.若2()34f x x x =-+与()2g x x m =+在[0,3]上是“关联函数”,则m 的取值范围为 ( )A. 9(,2]4--B.[1,0]-C.(,2]-∞-D.9(,)4-+∞二、填空题(本大题共5小题,考生作答4小题,每小题5分,满分20分) (一)必做题(11~13题)11、某几何体的三视图如图所示,则该几何体的体积是 .12、曲线y=x (3ln x +1)在点)1,1(处的切线方程为_____________.13、若x ,y 满足约束条件⎪⎩⎪⎨⎧≤+≥+≥43430y x y x x ,则yx z -=的最大值是 .(二)选做题(14、15题,考生只能从中选做一题) 14、(坐标系与参数方程选做题)若直线1223x ty t=-⎧⎨=+⎩(t 为参数)与直线41x ky +=垂直,则常数k = .15、(几何证明选讲选做题).如图,AB 为圆O 的直径,PA 为圆O 的切线,PB 与圆O 相交于D ,PA=3,916PD DB =,则AB= . 三、解答题:(本大题共6小题,共80分,解答须写出文字说明、证明过程或演算步骤.) 16、(本小题满分12分) 已知函数(1)求5()4f π的值; (2)设,求的值。
广东省揭阳一中、金山中学2014届高三数学三模联考试卷 文 新人教A版

2013—2014学年度两校三模联考数学科试题(文科)本试卷共4页,21题,满分150分.考试时间为l20分钟. 注意事项:1.答卷前,考生务必将自己的姓名、班级、座号写在答题卷密封线内. 2.非选择题必须用黑色字迹钢笔或签字笔作答.3. 答案一律写在答题区域内,不准使用铅笔和涂改液,不按以上要求作答的答案无效. 一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 若复数2(32)(1)a a a i -++-是纯虚数,则实数a 的值为( ) A. 1 B. 2 C. 1或2 D. -12.设集合{|A x y ==,{|2}x B y y ==,则AB =( )A .02)(,B .[02],C .(1,2]D .02](, 3. 某校高三一班有学生54人,二班有学生42人,现在要用分层抽样的方法从两个班抽出16人参加军训表演,则一班和二班分别被抽取的人数是( ) A. 8,8 B. 10,6 C. 9,7D. 12,44.已知()1,2=→a ,52=→b ,且→a ∥→b ,则b →为( ) A.()2,4-B.()2,4C.()2,4-或()2,4-D.()2,4--或()2,45.“1k =”是“直线0x y k -+=与圆221x y +=相交”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分又不必要条件6.一个算法的程序框图如图所示,该程序输出的结果为( ) A .89 B .910 C .1011 D .11127.已知3x ≥,则11y x x=--的最小值为( )A.2B. 72C. 38.数列{}n a 的前n 项和为n S ,首项为a ,且21()n n n S a a n N +=-+∈.若实数x y ,满足正视图 侧视图100x y x y x a ⎧-+⎪+⎨⎪⎩,,,≥≥≤则2z x y =+的最小值是( )A .-1B .12C .5D .19.已知函数()f x 是定义在R 上的奇函数,且当(],0x ∈-∞时,2()x f x e ex a -=-+,则函数()f x 在1x =处的切线方程为( )A .0x y +=B .10ex y e -+-=C .10ex y e +--=D .0x y -=10.对于函数(),y f x x D =∈,若存在常数C ,对任意1x D ∈,存在唯一的2x D ∈,使得C =,则称函数()f x 在D 上的几何平均数为 C.已知(),[2,f x x D ==,则函数()f x 在D 上的几何平均数为( )A ..3 C .2D二.填空题:本大题共6小题,每小题5分,共30分,把答案填在答题卡相应横线上. (一)必做题(第11至13题为必做题,每道题目考生都必须作答.) 11.在ABC ∆中,a 、b 、c 分别是角A 、B 、C 所对的边,,13A a c π===,则ABC∆的面积S= ______.12.椭圆2221(1)x y a a+=>上存在一点P ,使得它对两个焦点1F ,2F 张角122F PF π∠=,则该椭圆的离心率的取值范围是13.已知某几何体的三视图如图所示,则该几何体的全面积为 . (二)选做题(14~15题,考生只能从中选做一题) 14.(坐标系与参数方程)在极坐标中,已知点P 为方程()cos sin 1ρθθ+=所表示的曲线上一动点⎪⎭⎫⎝⎛3,2πQ ,则PQ 的最小值为____________.15.(几何证明选讲)如图,以4AB =为直径的圆与△ABC 的两边CEF分别交于,E F 两点,60ACB ∠=,则EF = .三、解答题:本大题共6小题,共80分. 解答应写出必要的文字说明、证明过程或演算步骤.16.(本小题满分12分)已知函数()sin()(0,0)f x x ωϕωϕπ=+><<的最小正周期为π,且函数()f x 的图象过点,12π⎛⎫-⎪⎝⎭. (1)求ω和ϕ的值; (2)设()()()4g x f x f x π=+-,求函数()g x 的单调递增区间.17.(本小题满分12分)某校从参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[)50,40,[)60,50…[]100,90后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:(1)求分数在[)70,80内的频率,并补全这个频率分布直方图; (2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;(3)用分层抽样的方法在分数段为[)80,60的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[)80,70的概率.18.(本小题满分14分)如图,在三棱柱111ABC A B C -中,AB AC ⊥,顶点1A 在底面ABC 上的射影恰为点B , 且12AB AC A B ===.第17题(1)求证:11AC ⊥平面11AA B B ;(2)若P 为线段11B C 的中点,求四棱锥11P AA B B -的体积. 19.(本小题满分14分)在等比数列{a n }中,)(0*N n a n ∈>,公比)1,0(∈q ,且252825351=++a a a a a a ,又a 3与a 5的等比中项为2.(1)求数列{a n }的通项公式;(2)设n n a b 2log =,求数列{b n }的前n 项和S n. (3)是否存在*,k N ∈使得1212nS S S k n+++<对任意*n N ∈恒成立,若存在,求出k 的最小值,若不存在,请说明理由. 20.(本小题满分14分)如图,抛物线21:8C y x =与双曲线22222:1(0,0)x y C a b a b-=>>有公共焦点2F ,点A是曲线12,C C 在第一象限的交点,且25AF =. (1)求双曲线2C 的方程;(2)以1F 为圆心的圆M 与双曲线的一条渐近线相切,圆N :22(2)1x y -+=.已知点(1P ,过点P 作互相垂 直且分别与圆M 、圆N 相交的直线1l 和2l ,设1l 被圆M 截 得的弦长为s ,2l 被圆N 截得的弦长为t . st是否为定值? 请说明理由.21.(本小题满分14分)已知函数x x a x x f --+=2)ln()(在点0=x 处取得极值.(1)求实数a 的值; (2)若关于x 的方程b x x f +-=25)(在区间[0,2]上有两个不等实根,求b 的取值范围;(3)证明:对于任意的正整数n ,不等式211ln nn n n +<+.2013—2014学年度两校三模联考数学科 (文科)参考答案及评分说明一.选择题:BDCDA BBABA二.填空题:,12. ,13.,14.三.解答题:16.解:(1)由图可知222T ππωπ===, ………………………………………………2分又由()12f π=-得,sin(2)12πϕ⋅+=-,得sin 1ϕ=0ϕπ<<2πϕ∴=, …………4分(2)由(1)知:()sin(2)cos 22f x x x π=+= ………………………………6分因为()cos 2cos(2)cos 2sin 22g x x x x x π=+-=+)4x π=+ …………9分 所以,222242k x k πππππ-≤+≤+,即3 (Z)88k x k k ππππ-≤≤+∈.………11分 故函数()g x 的单调增区间为3, (Z)88k k k ππππ⎡⎤-+∈⎢⎥⎣⎦.…12分 17. 解:(1)分数在[)70,80内的频率为:1(0.0100.0150.0150.0250.005)10-++++⨯10.70.3=-=,故0.30.0310=,……2分如图所示: ----4分(求频率2分,作图2分) (2)平均分为:450.1550.15650.15750.3850.25950.0571x =⨯+⨯+⨯+⨯+⨯+⨯=.------------6分(3)由题意,[)60,70分数段的人数为:0.15609⨯=人; ----------------7分[)70,80分数段的人数为:0.36018⨯=人; ----------------8分∵在[)80,60的学生中抽取一个容量为6的样本,∴[)60,70分数段抽取2人,分别记为,m n ;[)70,80分数段抽取4人,分别记为,,,a b c d ; 设从样本中任取2人,至多有1人在分数段[)80,70为事件A ,则基本事件空间包含的基本事件有:(,)m n 、(,)m a 、(,)m b 、(,)m c 、(,)m d 、……、(,)c d 共15种, 则事件A 包含的基本事件有:(,)m n 、(,)m a 、(,)m b 、(,)m c 、(,)m d 、(,)n a 、(,)n b 、(,)n c 、(,)n d 共9种,-11分∴93()155P A ==. --------------------------------12分18.(1) 证明:1A B ⊥平面ABC , …………………1分AC ⊂平面ABC ,1AC A B ∴⊥ …………………2分又AC AB ⊥, ………………3分 AB ⊂平面11AA B B , 1A B ⊂平面11AA B B ,1A BAB B = AC ∴⊥平面11AA B B …………5分又在三棱柱111ABC A B C -中,11AC AC // 11AC ∴⊥平面11AA B B …………6分(2)解:111224AA B B S AB AB =⨯=⨯=平行四边形………………8分取11A B 的中点R ,连结PR , 则11PR AC //,111PR A C 1==2………………10分又11AC ⊥平面11AA B B ,PR ∴⊥平面11AA B B………………12分 故点P 到平面11AA B B的距离1d =,11111433P AA B B AA B B V S d -∴=⨯⨯=平行四边形…………………14分19. 解:(1)252,252255323825151=++∴=++a a a a a a a a a a ,又5,053=+∴>a a a n , …………………………………………2分 又53a a 与的等比中项为2,453=∴a a , 而1,4,),1,0(5353==∴>∴∈a a a a q ,………3分n n n a a q --=⨯=∴==∴5112)21(16,16,21 , ……………………………5分 (2)n a b n n -==5log 2, 11-=-∴+n n b b ,4}{1=∴b b n 是以为首项,-1为公差的等差数列. …………… 7分(9)2n n n S -∴=, ……………9分 (3)由(2)知(9)9,22n n S n n n S n --=∴= 0,8>≤∴n S n n 时当;当0,9==n S n n 时;当0,9<>nSn n 时,.……………11分 31289,18123n S S S S n n∴=++++=当或时最大.…………………………13分 故存在*,k N ∈使得1212n S S S k n+++<对任意*n N ∈恒成立,k 的最小值为19.…14分20. 解:(1)∵抛物线21:8C y x =的焦点为2(2,0)F , ……………………………… 1分∴双曲线2C 的焦点为1(2,0)F -、2(2,0)F , …………………………… 2分 设00(,)A x y 在抛物线21:8C y x =上,且25AF =,由抛物线的定义得,025x +=,∴03x =, …………………………3分∴2083y =⨯,∴0y =±, ……………………… 4分∴1||7AF ==, ………………………… 5分又∵点A 在双曲线上,由双曲线定义得,2|75|2a =-=,∴1a =, ……… 6分∴双曲线的方程为:2213y x -=. ……………………………………… 7分 (2)st为定值.下面给出说明. …………………… 8分设圆M 的方程为:222(2)x y r ++=,双曲线的渐近线方程为:y =,∵圆M 与渐近线y =相切,∴圆M 的半径为2r == (9)分故圆M :22(2)3x y ++=, ………………………… 10分设1l 的方程为(1)y k x =-,即0kx y k -=,设2l 的方程为1(1)y x k=--,即10x ky +-=,∴点M 到直线1l 的距离为1d =N 到直线2l 的距离为2d =11分∴直线1l 被圆M 截得的弦长s == ……… 12分直线2l 被圆N 截得的弦长t == ………… 13分∴s t ==s t …………… 14分21. 解:(1)()()()12x x a x a f x x a-+-+'=+由题意, ()00f '= 解得1a = ………………………………2分(2)构造函数()[]()25()ln 10,22h x x x x x b x ⎛⎫=+----+∈ ⎪⎝⎭,则 ()()224545()2121x x x x h x x x --++-'==-++()()()45121x x x +-=+ 令 ()0h x '= 得 5114x x x =-=-=或或 又知[]0,2x ∈ ∴ 当01x ≤<时,函数()h x 单调递增,当12x <≤函数()h x 单调递减 方程5()2f x x b =-+在区间[]02,上有两个不同的实根,等价于函数()h x 在[]02,上有两个不同的零点,则只需()()()0031ln 21022ln 3430h b h b h b =-≤⎧⎪⎪=-+->⎨⎪⎪=-+-≤⎩ 即 01ln 22ln 31b b b ≥⎧⎪⎪<+⎨⎪≥-⎪⎩ ∴ 所求实数b 的取值范围是1ln 31ln 22b -≤<+…………………6分 (3)构造函数()2()ln 1g x x x x =+--,则 ()23()1x x g x x -+'=+ 令 ()0g x '= 解得 302x x ==-或 …………8分 当 10x -<< 时 ()0g x '>,()g x 是增函数当 0x > 时 ()0g x '<,()g x 是减函数 ……………………………10分 ∴ []()max ()00g x g == ∴ ()2ln 10x x x +--≤ 当0x ≠时,有 ()2ln 10x x x +--<取 1x n =,得 2111ln 10n n n⎛⎫⎛⎫+--< ⎪ ⎪⎝⎭⎝⎭ 即 211lnn n n n ++<.。
高三数学下学期第三次模拟考试试题理新人教A版
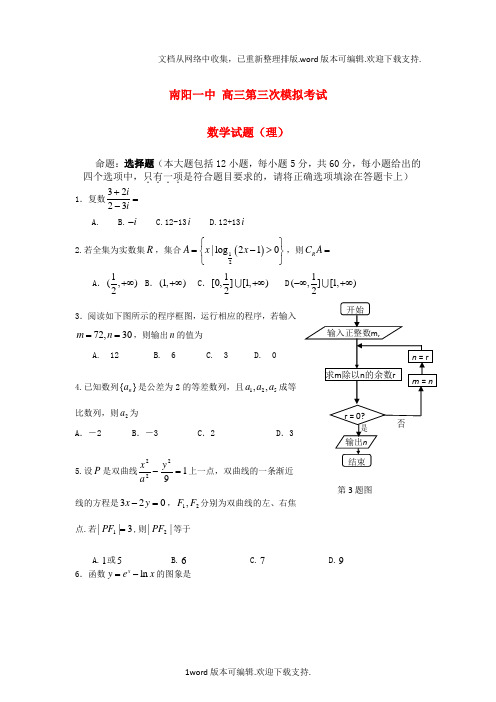
南阳一中 高三第三次模拟考试数学试题(理)命题:选择题(本大题包括12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项....是符合题目要求的,请将正确选项填涂在答题卡上) 1.复数3223ii+=- A. B.i - C.12-13i D.12+13i2.若全集为实数集R ,集合()12|log 210A x x ⎧⎫=->⎨⎬⎩⎭,则R C A =A .1(,)2+∞ B .(1,)+∞ C .1[0,][1,)2+∞ D 1(,][1,)2-∞+∞3.阅读如下图所示的程序框图,运行相应的程序,若输入72,30m n ==,则输出n 的值为A. 12B. 6C. 3D. 04.已知数列{}n a 是公差为2的等差数列,且125,,a a a 成等比数列,则2a 为A .-2B .-3C .2D .35.设P 是双曲线19222=-y ax 上一点,双曲线的一条渐近线的方程是023=-y x ,21,F F 分别为双曲线的左、右焦点.若3||1=PF ,则||2PF 等于A.1或5B.6C.7D.96.函数ln xy e x =-的图象是第3题图7.下列有关命题说法正确的是A .命题p :“∃x ∈R ,sinx+cosx=2”,则⌝p 是真命题B .“x=-1”是“x 2-5x -6=0”的必要不充分条件C .命题“∃x ∈R ,使得x 2 +x+1<0“的否定是:“∀x ∈R ,x 2+x+1<0” D .“a>l ”是“y=log a x (a >0且a ≠1)在(0,+∞)上为增函数”的充要条件8.2名男生和3名女生站成一排照相,若男生甲不站两端,3名女生中有且只有两名相邻,则不同的排法种数是A.36B.42C.48D.60 9. 若1sin 34πα⎛⎫-= ⎪⎝⎭,则cos 23πα⎛⎫+ ⎪⎝⎭=( )A .78-B .14-C .14D .7810.已知三棱锥的三视图如图所示,则它的外接球表面积为( ) A .16π B .4π C .8π D .2π11.双曲线2222:1(0,0)x y C a b a b-=>>与抛物线22()y px p =>0相交于A,B 两点,公共弦AB 恰好过它们的公共焦点F ,则双曲线C 的离心率为(A )2 (B )12+ (C )22 (D )22+12.已知定义在R 上的函数()y f x =对任意的x 都满足(1)()f x f x +=-,当11x -≤< 时,3()f x x =,若函数()()log a g x f x x =-至少6个零点,则a 取值范围是(A )10,5,5+∞(]()(B )10,[5,5+∞())(C )11,]5,775(()(D )11,[5,775())βαDCBdEA第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分13.在样本频率分布直方图中,共有11个小长方形,若中间一个小长方形的面积等于其它10个长方形的面积和的14,且样本容量为160,则中间一组的频数为14.设函数)2()(-=x nx f ,其中⎰=20cos 6πxdx n ,则)(x f 展开式中x4的系数为__________.15.设实数,x y 满足2025020x y x y y --≤⎧⎪+-≥⎨⎪-≤⎩,则1x y u x +=+的取值范围是16.如右图,它满足:(1)第n 行首尾两数均为n ;(2)表中的递推关系类似杨辉三角,则第n 行()2n ≥第2个数是三、解答题:解答应写出文字说明,证明过程和演算步骤17.(本小题满分12分)某兴趣小组要测量电视塔AE 的高度H (单位m ),如示意图,垂直放置的标杆BC 高度4=h m ,仰角βα=∠=∠ADE ABE ,.(Ⅰ) 该小组已测得一组βα,的值,20.1tan ,24.1tan ==βα,请据此算出H 的值; (Ⅱ)该小组分析若干测得的数据后,认为适当调整标杆BC 到电视塔的距离d (单位m ),使α与β之差较大,可以提高测量精确度,若电视塔实际高度为125m ,问d 为多少时,)tan(βα-最大?12 234 3 4 7 7 45 11 14 11 56 16 25 25 16 618.(本小题满分12分)现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了50人,他们月收入的频数分布及对 “楼市限购令”赞成人数如下表.(Ⅰ)由以上统计数据填下面2乘2列联表,并问是否有99%的把握认为“月收入以5500为分界点对“楼市限购令” 的态度有差异;月收入不低于55百元的人数月收入低于55百元的人数合计赞 成 a = c =不赞成 b =d =合 计(Ⅱ)若对月收入在[15,25) ,[25,35)的被调查人中各随机选取两人进行追踪调查,记选中的4人中不赞成“楼市限购令”人数为 ξ,求随机变量ξ的分布列及数学期望.参考数据:)(k ≥2K P0.050 0.010 0.001 k3.8416.63510.82819.(本小题满分12分) 在三棱柱111ABC ABC -中,侧棱1CC ⊥底面ABC ,∠ACB = 90°,且AC = BC =1CC ,O 为1AB 中点。
2021年高三数学上学期第三次模拟考试题 文 新人教A版

2021年高三数学上学期第三次模拟考试题文新人教A版时量:120分钟,总分:150分一、选择题(每小题5分,共50分)1、若全集U={-1,0,1,2},P={ },则集合关于全集U的补集是A {2}B {0,2}C {-1,2}D {-1,0,2}2、“”是“函数为偶函数”的A 充分而不必要条件B 必要而不充分条件C 充分必要条件D 既不充分也不必要条件3、已知且,则等于()A.5 B.10 C. D.154、函数,图象的对称轴方程可以为()A. B. C. D.5、已知等比数列中,,则等于()A.36 B.216 C. D.6、在中,内角的对边分别为,若,且,则()A. B. C. D.7、设函数是上的单调递减函数,则实数的取值范围为( )A. B. C. D.8、若函数有3个不同零点,则实数的取值范围是()A. B. C. D.9、等差数列的前项和为,已知,则的最小值为()A. B. C. D.10、函数的定义域为,数列是公差为的等差数列,且,记.关于实数,下列说法正确的是A 恒为负数B 恒为正数C 当时,恒为正数;当时,恒为负数D 当时,恒为负数;当时,恒为正数二、填空题(每小题5分,共25分)11、已知复数为实数,为虚数单位,则实数的值为.12、已知等比数列是递增数列,是的前项和,若是方程的两个根,则。
13、已知则等于14、已知均为单位向量,且它们的夹角为,当取得最小值时,。
15、若函数在上是减函数,则实数的取值范围是。
三、解答题:(共75分)16、(12分)已知命题}0|{)1,0(,1:<≠>>xxaaaxp x的解集是的不等式关于,命题的定义域为R,若,求实数的取值范围。
17、(12分)在中,。
(1)求的值;(2)求的值。
18、(12分)设向量(3sin,sin),(cos,sin),[0,]2a x xb x x xπ==∈。
(1)若,求的值;(2)设函数,求的最大值。
2021年高三数学上学期第三次模拟考试试题 文(含解析)新人教A版

2021年高三数学上学期第三次模拟考试试题 文(含解析)新人教A 版辨性、灵活性,基础性充分体现了考素质,考基础,考方法,考潜能的检测功能.一、 选择题:(共60分,每小题5分)【题文】1.已知集合A={-1,0,1},B={x|-1<x ≤1},则A ∩B=A {0}B {-1,,0}C {0,1}D {1}【知识点】集合运算. A1【答案解析】C 解析:因为集合A={-1,0,1},B={x|-1<x ≤1},所以A ∩B={0,1}, 故选C.【思路点拨】由交集的意义求结果.【题文】2. 对于非零向量a ,b ,“a ∥b ”是“a +b =0”的( ).A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【知识点】充分条件;必要条件. A2【答案解析】B 解析:因为:若“a ∥b ”则“a +b =0”是假命题;若“a +b =0”则“a ∥b ”是真命题.所以“a ∥b ”是“a +b =0”的必要不充分条件.故选B. 【思路点拨】根据原命题、逆命题的真假判定充分性与必要性. 【题文】3.已知正项等比数列{}中 ,则 ( )A .5B .6C .7 D.8 【知识点】等比数列. D3【答案解析】C 解析:因为正项等比数列{}中 ,所以, 所以,所求= ()()()212721726354log ()log a a a a a a a a a a =⎡⎤⎣⎦= ,故选C.【思路点拨】利用等比数列的性质及对数的运算性质求解.【题文】4.下列函数中,既是偶函数又在区间(-∞,0)上单调递增的是( )A .f(x)=1x2 B .f(x)=x 2+1 C .f(x)=x3 D .f(x)=2-x【知识点】函数的奇偶性与单调性. B3 B4【答案解析】A 解析:由偶函数排除选项C,D ,由单调性排除选项B ,故选A. 【思路点拨】根据函数奇偶性、单调性的意义确定结论.【题文】5.已知扇形的周长是6 cm ,面积是2 cm 2,则扇形的圆心角的弧度数是( )A .1或4B .1C .4D .8【知识点】扇形面积公式;弧度的意义. C1 【答案解析】A 解析:设扇形弧长,半径r ,则,所以 扇形的圆心角的弧度数==4或1.故选A.【思路点拨】根据题意得关于弧长与半径的方程组,确定弧长和半径,再利用弧长与半径的比为弧度数得结论.【题文】6.对于任意的直线l 与平面α,在平面α内必有直线m ,使m 与l ( )A .平行B .相交C .垂直D .互为异面直线 【知识点】空间直线位置关系情况分析. G3【答案解析】C 解析:当直线l 与平面α相交时A 不成立;当直线l 与平面α平行时B 不成立;当直线l 在平面α内时D 不成立.故选D. 【思路点拨】采用排除法确定结论.【题文】7. 某几何体的三视图如右图所示,则其体积为 ( )A . B. C . D . 【知识点】几何体的三视图. G2【答案解析】B 解析:由三视图可知此几何体是底面半径1,高2的半圆锥,所以其体积为,故选B.【思路点拨】由几何体的三视图,分析此几何体的结构,从而求得此几何体的体积. 【题文】8.若sin =35,则cos =( ).A. B. C. D. 【知识点】诱导公式. C2【答案解析】D 解析:因为sin =35,所以cos =sin,故选D.【思路点拨】利用诱导公式求解.【题文】9.设a>0,b>0.若4a+b=ab,则a+b的最小值是 ( ).A. 1B.5C. 7D. 9 【知识点】基本不等式求最值. E6【答案解析】D 解析:由4a+b=ab得,又a>0,b>0,所以a>1,所以a+b=()()4144415111aaa a aa a a-++=+=-++---,当且仅当a=3时等号成立.故选D.【思路点拨】将已知等式化为用b表示a,并求得a范围,代入a+b得,a+b=,再用基本不等式求解.【题文】10.若不等式组表示的平面区域是一个三角形,则a的取值范围是( ) A. B. C. D.【知识点】简单的线性规划. E5【答案解析】C 解析:画出图形如下,可得a的取值范围是.【思路点拨】画出描述性图形,易得a范围.【题文】11.设函数f(x)在R上可导,其导函数是f′(x),且函数f(x)在x=-2处取得极小值,则函数y=xf′(x)的图像可能是( )【知识点】函数的极值点与该点两边导函数值的符号的关系. B12【答案解析】C 解析:因为函数f (x )在x =-2处取得极小值,所以时, 时,所以时>0,时 <0, 时>0,故选C.【思路点拨】由已知分析的取值符号,进一步分析的取值符号.【题文】12. 已知是定义在R 上且周期为3的函数,当x∈[0,3)时, .若函数y =-a 在区间[-3,4]上有10个零点(互不相同),则实数a 的取值范围是( )A . B. C . D . 【知识点】函数的零点. B9【答案解析】A 解析:画出函数在[-3,4]上 的图像,分析它与直线y=a 有10个不同交点的条件为.故选 A.【思路点拨】画出图像分析结果. 二、 填空题:(共20分,每个小题5分)【题文】13. 已知函数f (x )=⎩⎪⎨⎪⎧log 2x ,x >0,3x,x ≤0,则f ⎝ ⎛⎭⎪⎫f ⎝ ⎛⎭⎪⎫14的值是_________.【知识点】分段函数的函数值. B1 【答案解析】 解析:因为,所以【思路点拨】先求,再求f ⎝ ⎛⎭⎪⎫f ⎝ ⎛⎭⎪⎫14的值. 【题文】14. 函数(A ,ω,φ为常数,A >0,ω>0)的部分图像如右图所示,则 ________. 【知识点】由所给图像求函数的解析式. C4 【答案解析】 解析:, A= ,由73222,1223k k k Z πππωπωπ⨯+=+⇒=+∈, 取,则,所以.【思路点拨】由所给图像求得A ,,得,所以.【题文】15. 设数列{a n }的通项公式为a n =2n -11(n ∈N *),则|a 1|+|a 2|+…+|a n |=______.【知识点】等差数列前n 项绝对值的和. D4 【答案解析】 解析:由得数列{a n }的前5项是负数,第6项以后都是正数,所以 【思路点拨】先求出此等差数列的正负转换项,进而得结论.【题文】16. 已知P,A,B,C,D 是球O 表面上的点,PA⊥平面ABCD ,四边形ABCD 是边长为的正方形,若PA=,则三棱锥B-AOP 的体积________. 【知识点】几何体的结构;锥体体积. G1【答案解析】 解析:如图,易知O 为线段PC 中点,O 到平面PAB 的距离为, 所以114722272323B AOP O PAB V V --==⨯⨯⨯⨯=.【思路点拨】利用等体积转化法求解.三、解答题:【题文】17 (本题满分12分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若向量m =(2 b - c, a),n =(cosA ,-cosC) 且 m ⊥n (1)求角A 的大小;(2)若a =3,S △ABC =334,试判断△ABC 的形状,并说明理由.【知识点】正弦定理;余弦定理的应用. C8 【答案解析】(1) ;(2)等边三角形,理由:见解析.解析:(1) 向量m =(2 b - c, a ),n =(cosA ,-cosC) 且 m ⊥n , ,由正弦定理得: , , , .(本小题还可以用余弦定理求解) (2)△ABC 为等边三角形. 即①2222cos ,3,3a b c bc A a A π=+-==, ②由①②得,△ABC 为等边三角形.【思路点拨】(1)由已知得,再把正弦定理或余弦定理代入此等式求得∠A ;(2)由面积公式得bc=3,由余弦定理得,解得,又∠A =,所以△ABC 为等边三角形.【题文】18.(本题满分12分)已知数列{a n }的前n 项和为S n ,且S n =2a n -2.(1)求数列{a n }的通项公式;(2)记S n =a 1+3a 2+…+(2n -1)a n ,求S n .【知识点】已知递推公式求通项;数列前n 项和求法. D1 D4 【答案解析】(1) 2n;(2)(2n -3)·2n +1+6. 解析:(1)∵S n =2a n -2,∴当n ≥2时,a n =S n -S n -1=2a n -2-(2a n -1-2),即a n =2a n -2a n -1,∵a n ≠0,∴a n a n -1=2(n ≥2,n ∈N *). ∵a 1=S 1,∴a 1=2a 1-2,即a 1=2.数列{a n }是以2为首项,2为公比的等比数列. ∴a n =2n.(2)S n =a 1+3a 2+…+(2n -1)a n=1×2+3×22+5×23+…+(2n -1)2n, ① ∴2S n =1×22+3×23+…+(2n -3)2n +(2n -1)2n +1, ②①-②得-S n =1×2+(2×22+2×23+…+2×2n)-(2n -1)2n +1,即-S n =1×2+(23+24+…+2n +1)-(2n -1)2n +1∴S n =(2n -3)·2n +1+6.【思路点拨】(1) 利用公式变形已知递推公式,从而求得数列的通项公式;(2)由(1)求得,则S n 是一个等差数列通项,与一个等比数列通项的积,构成的新数列的前n 项和,所以用错位相减法求S n .【题文】19.(本题满分12分)如图,在正三棱柱中,点D 在边BC 上,AD ⊥C 1D . (1)求证:平面ADC 1⊥平面BCC 1B 1; (2)设E 是B 1C 1上的一点,当B 1EEC 1的值为多少时,A 1E ∥平面ADC 1? 请给出证明.【知识点】面面垂直的判定;线面平行的条件. G4 G5 【答案解析】(1)证明:见解析;(2)当B 1EEC 1的值为1时,A 1E ∥平面ADC 1, 证明:见解析.解析:(1)证明:在正三棱柱中,平面ABC,AD 平面ABC , ADC,又AD,,平面,平面,平面. 又平面, 平面平面.(2)由(1)得,,在正三角形ABC中,D是BC的中点,当,即E为得中点时,平面.证明如下:(如图)四边形是矩形,且D,E分别是BC, 的中点,所以又,,四边形为平行四边形,而平面,平面, 故平面.【思路点拨】(1)根据面面垂直的判定定理,只需在平面ADC1 找到直线与平面BCC1B1垂直即可,此直线为AD;(2)由(1)得D是线段BC的中点,所以E为得中点时,有,进而得A1E∥平面ADC1.【题文】20.(本题满分12分)函数f(x)=m+log a x(a>0且a≠1)的图象过点(16,3)和(1,-1).(1)求函数f(x)的解析式;(2)令g(x)=2f(x)-f(x-1),求g(x)的最小值及取得最小值时x的值.【知识点】待定系数法求函数解析式;基本不等式法求最值. B1 E6【答案解析】(1) f(x)=-1+log2x;(2)当x=2时,函数g(x)取得最小值1.解析:(1)由得解得m=-1,a=2,故函数解析式为f(x)=-1+log2x.(2)g(x)=2f(x)-f(x-1)=2(-1+log2x)-[-1+log2(x-1)]=log2x2x-1-1(x>1).∵x2x-1==(x-1)+1x-1+2≥2 x-1·1x-1+2=4.当且仅当x-1=1x-1,即x=2时,等号成立.而函数y=log2x在(0,+∞)上单调递增,则log2x2x-1-1≥log24-1=1,故当x =2时,函数g (x )取得最小值1.【思路点拨】(1)把已知两点的坐标,代入函数解析式,得关于a,m 的方程组,解得a,m 值即可;(2)由(1)得函数,因为 x 2x -1=(x -1)+1x -1+2 ≥2x -1·1x -1+2=4,所以,当且仅当x=2时等号成立.【题文】21. (本题满分12分)已知函数f (x )=ax 2-e x(a ∈R ,e 为自然对数的底数),f ′(x )是f (x )的导函数.(1)解关于x 的不等式:f (x )>f ′(x );(2)若f (x )有两个极值点x 1,x 2,求实数a 的取值范围. 【知识点】导数运算;导数应用. B11 B12【答案解析】(1) 当a =0时,无解; 当a >0时,解集为{x |x <0或x >2};当a <0时,解集为{x |0<x <2}.(2) a >e2.解析:(1)f ′(x )=2ax -e x,f (x )-f ′(x )=ax (x -2)>0. 当a =0时,无解;当a >0时,解集为{x |x <0或x >2}; 当a <0时,解集为{x |0<x <2}.(2)设g (x )=f ′(x )=2ax -e x,则x 1,x 2是方程g (x )=0的两个根.g ′(x )=2a -e x, 当a ≤0时,g ′(x )<0恒成立,g (x )单调递减,方程g (x )=0不可能有两个根; 当a >0时,由g ′(x )=0,得x =ln 2a ,当x ∈(-∞,ln 2a )时,g ′(x )>0,g (x )单调递增, 当x ∈(ln 2a ,+∞)时,g ′(x )<0,g (x )单调递减.∴当g (x )max >0时,方程g (x )=0才有两个根,∴g (x )max =g (ln 2a )=2a ln 2a -2a >0,得a >e2.【思路点拨】(1)求得函数的导函数后,代入不等式f (x )>f ′(x ),整理得ax (x -2)>0. 再由a 的取值条件得不等式的解;(2)若f (x )有两个极值点x 1,x 2,则有两个不等实根x 1,x 2,然后利用导数确定此方程有两个不等实根的条件.四、选做题(从22~24题中任选一题,在答题卡相应的位置涂上标志,多涂、少涂以22题计分)【题文】22、选修41:几何证明选讲如图,EP 交圆于E ,C 两点,PD 切圆于D ,G 为CE 上一点且PG =PD ,连接DG 并延长交圆于点A ,作弦AB 垂直EP ,垂足为F . (1)求证:AB 为圆的直径; (2)若AC =BD ,求证:AB =ED .【知识点】直径所对圆周角是直角;全等三角形的判定与性质. N1 【答案解析】 解析:(1)证明:因为PD=PG,所以. 由于PD 为切线,故. 又由于,故, 所以,从而 因为,所以,所以,故AB 为圆的直径.(2)连接BC 、DC. 由于AB 是直径,故在与中,AB=BA, AC=BD,所以≌, 所以. 又因为,所以, 故.因为,所以,为直角. 所以ED 为直径.又由(1)知AB 为圆的直径,所以ED=AB.【思路点拨】(1)证明∠BDA 是直角,或者用垂径定理证明结论;(2)利用证明三角形全等证明结论.【题文】23.选修4-4:坐标系与参数方程已知曲线C :x 24+y 29=1,直线l :⎩⎪⎨⎪⎧x =2+t ,y =2-2t (t 为参数).(1)写出曲线C 的参数方程、直线l 的普通方程;(2)过曲线C 上任意一点P 作与l 夹角为30°的直线,交l 于点A ,求|PA |的最大值与最小值.【知识点】参数方程与普通方程的互化;点到直线的距离;三角函数式的最值. N3 【答案解析】(1)见解析;(2)最大值为2255,最小值为255.解析:(1)曲线C 的参数方程为⎩⎪⎨⎪⎧x =2cos θ,y =3sin θ(θ为参数),直线l 的普通方程为2x +y -6=0.(2)曲线C 上任意一点P (2cos θ,3sin θ)到直线l 的距离d =55|4cos θ+3sin θ-6|,则|PA |=d sin 30°=2 55|5sin(θ+α)-6|,其中α为锐角,且tan α=43.当sin(θ+α)=-1时,|PA |取得最大值, 最大值为2255.当sin(θ+α)=1时,|PA |取得最小值, 最小值为255.【思路点拨】(1)由椭圆参数方程公式写出椭圆参数方程,把直线参数方程中的参数消去得其普通方程;(2)设出)曲线C 上任意一点P (2cos θ,3sin θ),利用点到直线的距离公式,Rt 三角形的边角关系得|PA |关于的三角函数式,再用三角函数的最值求结论. 【题文】24、选修45:不等式选讲设函数f (x )=⎪⎪⎪⎪⎪⎪x +1a +|x -a |(a >0).(1)证明:f (x )≥2;(2)若f (3)<5,求a 的取值范围.【知识点】绝对值不等式的性质;基本不等式;绝对值不等式的解法. N4 【答案解析】(1)证明:见解析;(2). 解析:(1)证明:因为a>0, 所以111()()2f x x x a x x a a a a a=++-≥+--=+≥, 所以. (2) 。
2021年高三数学上学期第三次模拟考试试题 理(含解析)新人教A版

2021年高三数学上学期第三次模拟考试试题 理(含解析)新人教A 版【试卷综述】全面覆盖了中学数学教材中的知识模块,试卷突出了学科的主干内容,集合与函数、不等式、数列、概率统计、立体几何、解析几何、导数的应用等重点内容在试卷中占有较高的比例,也达到了必要的考查深度.注重了能力的考查,特别是运算能力,逻辑思维能力和空间想象能力的强调比较突出.至于实践能力和创新意识方面也在努力体现.一.选择题(本题共十二小题,每题5分,共60分)【题文】1.集合则等于( )【知识点】集合.A1【答案】【解析】B 解析:因为{}{}0,1,4,3,2,1,0,1,2,3,4,P M ==----所在正确选项为B.【思路点拨】根据集合的概念可知两个集合的交集,注意自变量的取值.【典例剖析】集合问题关键要注意代表元素的取值范围.【题文】2.若,其中则( )A. B. C. D.【知识点】复数的概念.L4【答案】【解析】C 解析:根据复数的概念,可知实部与实部相等,虚部与虚部相等所以()112121,12ai i bi a i bi a b +⋅=-∴-+=-∴=-=-,所以【思路点拨】根据复数的概念求出实部与虚部,再求出复数的模.【题文】3.若,则有( )A. B. C. D.【知识点】指数对数的概念.B6,B7【答案】【解析】 A 解析:由函数的性质可知0.502211221,0log 3log 1,log 1222a b c πππ=>=<=<===-=-,A 为正确选项.【思路点拨】比较大小问题主要根据函数的性质进行比较,找出中间介量也是关键.【题文】4.双曲线的顶点到其渐近线的距离等于( )A. B. C. D.【知识点】双曲线的概念.H6【答案】【解析】C 解析:由题意可知双曲线的顶点为,渐近线方程为,利用点到直线的距离公式.【思路点拨】由双曲线的概念可知渐近线方程,再根据点到直线的距离公式可求出结果.【题文】5.若某程序框图如图所示,则该程序运行后输出的B 等于( )A .B .C . D. 63【知识点】程序框图.L1【答案】【解析】D 解析:程序在运行过程中各变量的值如下表示:A B 是否继续循环循环前 1 1/第一圈 2 3 是第二圈 3 7 是第三圈 4 15 是第四圈 5 31 是第三圈 6 63 否则输出的结果为63.故答案为:63.【思路点拨】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算B 值并输出,模拟程序的运行过程,即可得到答案.【题文】6.已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能等于( )A.1B.C.D.【知识点】三视图.G2【答案】【解析】C 解析:水平放置的正方体,当正视图为正方形时,其面积最小为1;当正视图为对角面时,其面积最大为因此满足棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积的范围为因此可知:A ,B ,D 皆有可能,而,故C 不可能.故选C .【思路点拨】由三视图可知原图的数据,再根据面积的取值找出正确结果.【题文】7. 60,,,,=∠∆A C B A c b a ABC 的对边且分别为角中,已知,,则的周长等于( )B.14C.D.18【知识点】正弦定理,余弦定理.C8【答案】【解析】A 解析:在△ABC 中,角A=60°,∵5sinB=3sinC,故由正弦定理可得 5b=3c , 再由可得 bc=15,∴b=3,c=5.再由余弦定理可得 a2=b2+c2-2bc•cosA=19,故三角形的周长a+b+c=,故答案为:.【思路点拨】由条件利用正弦定理可得5b=3c ,再由,求得bc ,从而求得b 和c 的值.再由余弦定理求得a ,从而得到三角形的周长..【题文】8.从6名学生中选3名分别担任数学、物理、化学科代表,若甲、乙2人至少有一人入选,则不同的选法有( )A.40种B.60种C.96种D.120种【知识点】排列组合.J2【答案】【解析】C 解析:从6名学生中选3名分别担任数学、物理、化学科代表,没有限制条件是由=120种,甲、乙都没入选相当于从4人中选3人,有=24,故甲、乙2人至少有一人入选,则不同的方法有120-24=96.故选:C .【思路点拨】根据排列组合的方法分别求出种数,注意排列数的计算.【题文】9.设函数)2,0)(cos()sin()(πϕωϕωϕω<>+++=x x x f 的最小正周期为,且则( )B.D.【知识点】三角函数的图像.C3【答案】【解析】D 解析:由题意可知函数可化为()()4f x x x πϖϕϖ⎛⎫=++= ⎪⎝⎭又因为函数为偶函数,所以,所以,所以D 为正确选项.【思路点拨】由三角函数的性质可知正确选项.【题文】10.已知直线,且(其中O 为坐标原点),则实数的值为( )A.2B.C.2或-2D.【知识点】向量的运算.F2【答案】【解析】C 解析:以,为邻边作平行四边形,则所以平行四边形为距形,又,所以四边形为正方形,∵a>0,∴直线x+y=a经过点(0,2),∴a=2.故答案为:2【思路点拨】以OA、OB为邻边作,由已知得为正方形,由此能求出a=2.【题文】11.已知数列满足,2sin)2cos1(,2,122221ππnanaaann++===+则该数列的前18项和为()A.2101B.1067C.1012D.xx【知识点】数列的求和.D4【答案】【解析】B解析:∵数列{an}满足a1=1,a2=2,an+2=(1+cos2)an+sin2,∴∴a3=(1+cos2)a1+sin2=a1+1=2,a4=(1+cos2π)a2+sin2π=2a2=4.一般地,当n=2k﹣1(k∈N*)时,a2k+1=[1+cos2]a2k﹣1+sin2=a2k﹣1+1,即a2k+1﹣a2k﹣1=1.∴数列{a2k﹣1}是首项为1、公差为1的等差数列,∴a2k﹣1=k.当n=2k(k∈N*)时,a2k+2=(1+cos2)a2k+sin2=2a2k.∴数列{a2k}是首项为2、公比为2的等比数列,∴a2k=2k.∴数列的前18项的和为1+2+2+4+3+8+4+16+5+32+6+64+7+128+8+256+9+512=1067.故选:D.【思路点拨】由已知条件推导出数列{a2k﹣1}是首项为1、公差为1的等差数列,数列{a2k}是首项为2、公比为2的等比数列,由此能求出数列的前18项的和..【题文】12.已知函数的定义域[]的导函数,为且,)()(,2)6(3-xfxff'=∞+的图象如图所示,若正数则的取值范围是()A. B.C. D.【知识点】线性规划.E5【答案】【解析】A 解析:如图所示:f′(x)≥0在[-3,+∞)上恒成立∴函数f(x)在[-3,0)是减函数,(0,+∞)上是增函数,又∵f(2a+b)<2=f(6)∴画出平面区域令表示过定点(2,-3)的直线的斜率如图所示:故选A【思路点拨】由题意可利用数形结合的方法求出范围,再根据所求值的几何意义求出结果.【典例剖析】线性规划问题要注意数形结合的运用,同时要注意几何意义.【题文】二.填空题(本小题共四小题,每题5分,共20分)【题文】13.在等差数列{}==-=-+134111073,4,8S a a a a a a n 则中,_________.【知识点】等差数列.D2 【答案】【解析】156 解析:由题意可知()()11371041137104773212a a a a a a a a a a a a ++--=++-+=-=,又因为【思路点拨】本题由等差数列的性质可求出数列的各项和.【题文】14.若的展开式中项的系数为20,则的最小值为__________.【知识点】二项式定理.J3【答案】【解析】2 解析:的展开式中x3项的系数为20,所以,令12-3r=3,∴r=3,∴ab=1,a2+b2≥2ab=2,当且仅当a=b=1时取等号.a2+b2的最小值为:2.故答案为:2.【思路点拨】根据特定项的求法可求出a,b 的值,再由基本不等式求出结果.【题文】15.正四面体ABCD 的外接球的体积为,则正四面体ABCD 的体积是_____.【知识点】几何体的体积.G2【答案】【解析】 解析:设正四面体的棱长为x ,则底面三角形的高为,即有,棱锥的高为,由于外接球的体积为,在直角三角形得,则正四面体的体积为所以答案为【思路点拨】由几何体的体积公式可求出其体积.【题文】16.定义域是一切实数的函数,其图像是连续不断的,且存在常数使得对任意实数x 都成立,则称是一个“的相关函数”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
泗县二中 高三第三次模拟数学(文)试题本试卷分第I 卷(选择题)和第II 卷(非选择题)两部份,共150分,考试时间120分钟。
第Ⅰ卷(选择题,共50分)一、选择题:本大题共10小题,每小题5分,满分50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若曲线4y x =的一条切线l 与直线480x y +-=垂直,则l 的方程为 ( )A .430x y --=B .450x y +-=C .430x y -+=D .430x y ++= 2.下列命题正确的是( )A .函数cos()3y x π=+的图像是关于点(,0)6π成中心对称的图形 B .函数44cos sin y x x =-的最小正周期为2π C .函数sin(2)(,)336y x πππ=+-在区间内单调递增D .函数tan()3y x π=+的图像是关于直线6x π=成轴对称的图形3.若双曲线221x ky +=的离心率是2,则实数k 的值是 ( )A .—3B .13C .3D .—134.如图几何体的主(正)视图和左(侧)视图都正确的是 ( )5.已知集合I={1,2,3,4},A={1},B={2,4},则()I AC B =( )A .{1}B .{3}C .{1,3}D .{1,2,3}6.从某班学生中任意找出一人,若是该同窗的身高小于160cm 的概率为,该同窗的身高在[160,175]cm 的概率为,那么该同窗的身高超过175cm 的概率为 ( ) A . B .0.7 C . D . 7.若[()]63,()21,()f g x x g x x f x =+=+且则的解析式为 ( )A .3B .3xC .3(21)x +D .61x +8.复数212ii+=-=( )A .i -B .iC .22i -D .22i -+9.在空间四边形ABCD 中,在AB 、BC 、DC 、DA 上别离取E 、F 、G 、H 四点,若是GH 、EF 交于一点P ,则 ( ) A .P 必然在直线BD 上 B .P 必然在直线AC 上 C .P 在直线AC 或BD 上 D .P 既不在直线BD 上,也不在AC 上10.某企业生产甲、乙两种产品,已知生产每吨甲产品要用A 原料3吨,B 原料2吨;生产每吨乙产品要用A 原料1吨,B 原料3吨,销售每吨甲产品可取得利润5万元,每吨乙产品可取得利润3万元。
该企业在一个生产周期内消耗A 原料不超过13吨,B 原料不超过18吨,那么该企业可取得最大利润是 ( ) A .12万元 B . 20万元 C .25万元 D .27万元第Ⅱ卷(非选择题,共100分)二、填空题:本大题共5小题,每小题5分,共25分。
11.已知向量(,),(1,2),(1,3),||a x y b a b a ==-+=且则等于 。
12.在空间直角坐标系中,已知点A (1,0,2),B (1,—3,1),点M 在y 轴上,且M 到A 与到B 的距离相等,则M 的坐标是 。
13.若a 、b 、c 、d 均为实数,使不等式0a cad bc c d>><和都成立的一组值(a 、b 、c 、d )是 。
(只要写出适合条件的一组值即可)14.记等差数列{}n n a n S 的前项和为,利用倒序相加法的求和办法,可将n S 表示成首项1a ,末项n a 与项数的一个关系式,即1()2n n a a nS +=;类似地,记等比数列{}n b n 的前项积为*,0()n n T b n N >∈且,类比等差数列的求和方式,可将n T 表示为首项1,nb b 末项与项数的一个关系式,即公式n T = 。
15.下列说法:①从匀速传递的产品生产流水线上,质检员第10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样②某地气象局预报:5月9日本地降水概率为90%,结果此日没下雨,这表明天气预报并非科学③在回归分析模型中,残差平方和越小,说明模型的拟合效果越好④在回归直线方程0.110y x =+中,当解释变量x 每增加一个单位时,预报变量平均增加个单位其中正确的是 (填上你以为正确的序号)三、解答题:本大题共6小题,共75分,解答须写出说明、证明进程和演算步骤。
16.(本小题满分12分)对400(I )在下图中补齐频率散布直方图;(II )估量元件寿命在500800h 之内的概率。
17.(本题满分13分)已知函数()23sin 2cos .f x x x =- (I )若[0,],()x f x π∈求的最大值和最小值;(II )若22cos sin 12()0,2sin()4xx f x x π--=+求的值。
18.(本题满分12分) AB 为圆O 的直径,点E 、F 在圆上,AB1ln (),.m xf x m x-+=∈R 1m =(1,)e 22(1)1x y -+= (I )求过点P 且核心在x 轴上抛物线的标准方程;(II )过点(1,0)作直线l 与(I )中的抛物线相交于M 、N 两点,问是不是存在定点R ,使RM RN ⋅为常数?若存在,求出点R 的坐标与常数;若不存在,请说明理由。
21.(本题满分13分)如图所示,流程图给出了无穷等差整数列{}n a 满足的条件,1,5a N k +∈=且当时,输出的5,109S k =-=当时,输出的10.99S =-(其中d 为公差) (I )求数列{}n a 的通项公式;(II )是不是存在最小的正数m ,使得,n N T m +∀∈≤都有成立?若存在,求出m 的值,若不存在,请说明理由。
参考答案(II )估量元件寿命在500800h 之内的概率为++= ………………12分 17.(本题满分13分)解:(I )31()232cos 4(cos )2f x x x x x =-=- 4sin().6x π=- ………………3分又5[0,],666x x ππππ∈∴-≤-≤24sin()46x π∴-≤-≤, max min ()4,() 2.f x f x ∴==- ……………………6分(II )由于()0,232cos f x x x ==所以解得tan 3x =………………8分22cos sin12)4xxxπ--=+cos sin1tan2cos sin1tan1x x xx x x--====-+++………………13分18.(本题满分12分)解:(I)证明:因为平面ABCD⊥平面ABEF,AD⊥AB,∴AD⊥平面ABEF,∴AD⊥BF;又∵AB为圆O的直径,∴AF⊥BF,AF∩AD=A,∴BF⊥平面DAF;………………6分(II)作,,,,,,,FA AB EB AB FD CD EC CD A B C D''''''''⊥⊥⊥⊥为垂足,则1112112122322 ABCDFE FA D EB C F AA D DV V V'''''--=+=⨯⨯⨯+⨯⨯⨯⨯=(进程略)…………………………12分19.(本题满分12分)解:(I)显然函数概念域为(0,+∞)若m=1,由导数运算法则知21ln().xf xx-'=令()0,f x'=得x=e.………………2分当(0,),()0,()x e f x f x'∈>时单调递增;当(,),()0,()x e f x f x'∈+∞<时单调递减。
………………6分(II)由导数运算法则知,2ln().m xf xx-'=令()0,.mf x x e'==得………………8分当(0,),()0,()mx e f x f x'∈>时单调递增;当(,),()0,()mx e f x f x'∈+∞<时单调递减。
………………6分故当,()mx e f x=时有极大值,按照题意1,01me e m<<<<即………………12分20.(本题满分13分)解:(I )设直线PC 的方程为:3y kx =-,由241,31k k ==+得所以PC 的方程为4 3.3y x =- …………3分由1433y y x =⎧⎪⎨=-⎪⎩得P 点的坐标为(3,1)。
可求得抛物线的标准方程为21.3y x =………………6分 (II )设直线l 的方程为1x my =+,代入抛物线方程并整理得211033y my --= 1122121200101020201020102022212012012012011(,),(,),33(,),(,)()(1)(1)()()(1)()(1)()M x y N x y y y m y y R x y RM RN x x y y x x y y my x my x y y y y m y y m x y y x y y y y y y +==-⋅=--⋅-⋅-=+-+=+--=+-++-+-++设则设则2220000111(1)333x m y m x y =--+-+- ………………11分当000x y ==时上式是一个与m 无关的常数所以存在定点R (0,0),相应的常数是2.3………………13分11max5279214,,22227227(),.1616k k k k kk k kT T T T T m +---=+-====从而得即………………13分(以上答案仅供参考,其它解法酌情赋分)。
