2009年北京市海淀区初三年级一模考试
北京市海淀区2009-2010学年度九年级数学第一学期期中测评试卷全国通用

海淀区九年级第一学期期中测评数 学 试 卷(分数:120分 时间:120分钟)班级某某学号 成绩一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.一元二次方程23470x x -+=的二次项系数、一次项系数、常数项分别是( )A. 3,4,7--B. 3,4,7-C. 3,4,7D. 3,4,7-2y x =-中自变量x 的取值X 围是( )A. 2x ≤B. 2x ≠-C. 2x ≠D. 2x ≥ 3.一元二次方程2350x x ++=的根的情况是( )A.有两个不相等的实数根B. 有两个相等的实数根C. 没有实数根D. 无法判断4.右图是国庆庆祝活动标志,它以数字“60”为主体,代表着中华人民某某国60左侧小圆和右侧优弧所在的大圆之间的位置关系是( )A. 外离B. 相交C. 相切D. 内含5.用配方法解方程2420x x -+=,下列配方正确的是( )A .2(2)2x += B .2(2)2x -= C .2(2)2x -=- D .2(2)6x -= 6. 圆锥的母线长为5,底面半径为3,则它的侧面积为( )A .π30B .π15C .π20D .π107.如图,C 、D 是以AB 为直径的⊙O 上的两个点,CB BD =,∠CAB =24º,则∠ABD 的度数为( )A.24ºB.60ºC.66ºD.76ºCO AB8.如图,以(3,0)A 为圆心作⊙A ,⊙A 与y 轴交于点(0,2)B ,与x 轴交于C 、D .P 为⊙A 上不同于C 、D 的任意一点.连接PC 、PD ,过点A 分别作AE PC ⊥于E ,AF PD ⊥于F .设点P 的横坐标为x ,22AE AF y +=.当点P 在⊙A 上顺时针从点C 运动到点D 的过程中,下列图象中,能表示y 与x 的函数关系的图象是( )A .B .C .D .二、填空题(本题共16分,每小题4分)9.若实数m 、n 满足210m n ++-=,则2m n +的值为______ .10.点P (3,4)关于原点的对称点的坐标是.11.如图,PB 、PC 切⊙O 于B 、C 两点,点A 在⊙O 上,若65A ∠=︒,则∠P = °.计算正整数的乘法,请根据以下四个算图所示规律在右图中画出232312⨯的算图(标出相应的数字和曲线) .OyxF ED C B APOBC A三、解答题(本题共30分,每小题5分) 13.解方程:2280x x --=. 解:14.计算:10112()31(2)3π-++---.解:15.计算:(223)(21)-+. 解:16. 如图,点B 在⊙O 外,以点B 为圆心,OB 长为半径画弧与⊙O 相交于C 、D 两点,与直线OB 相交于A AC =5时,求AD 的长. 解:17.已知m 是方程2250x x +-=的一个根,求32259m m m +--的值. 解:18. 已知:如图,网格中每个小正方形的边长为1,△ABC是格点三角形.AB C;(1)画出△ABC绕点A逆时针旋转90º后的图形△''(2)旋转过程中,点C所经过的路线长为.解:四、解答题(本题共20分,每小题5分)贵的问题,决定下调药品的价格,某种药品经过连续两次降价后,由每盒200元下调至128元,求这种药品平均每次降价的百分率是多少?解:20.已知:⊙O的半径为5,AB为直径,CD为弦,CD⊥AB于E,若CD=6,求AE. 解:21.若关于x 的一元二次方程2420kx x -+=有实数根. (1)求k 的取值X 围;(2)若△ABC 中,2AB AC ==,AB 、BC 的长是方程2420kx x -+=的两根,求BC 的长. 解:22.已知:如图,BC 为⊙O 的弦,OA ⊥BC 于E 交⊙O 于A ,AD ⊥AC 于A ,260D B ∠=∠=.(1)求证:CD 为⊙O 的切线;(2)当BC =6时,求阴影部分的面积. 解:五、解答题(本题共22分,第23题7分,第24题8分,第25题7分) 23、如图四边形ACDE 是证明勾股定理时用到的一个图形,a 、b 、c 是Rt △ABC 和Rt △BDE 的三边长,易知c AE 2=.这时我们把形如022=++b cx ax 的方程称为关于x 的 “勾系一元二次方程”. 请解决下列问题:(1)构造一个“勾系一元二次方程”: .(2)证明:关于x 的“勾系一元二次方程”022=++b cx ax 必有实数根;(3)若1-=x 是“勾系一元二次方程”022=++b cx ax 的一个根,且四边形ACDE 的周长是62,求△ABC 的面积. 解:24.将矩形纸片ABCD 分别沿两条不同的直线剪两刀,使剪得的三块纸片恰能拼成一个三角形(不能有重叠和缝隙).图1中提供了一种剪拼成等腰三角形的示意图.图1图2(1) 请提供另一种剪拼成等腰三角形的方式,并在图2中画出示意图;图3 备用图(2)以点B 为原点,BC 所在直线为x 轴建立平面直角坐标系(如图),点D 的坐标为(8,5).若剪拼后得到等腰三角形MNP ,使点M 、N 在y 轴上(M 在N 上方),点P 在边CD 上(不与C 、D 重合).设直线PM 的解析式为y kx b =+(0k ≠),则k 的值为,b 的取值X 围是 .(不要求写解题过程).25.如图1,梯形ABCD 中,AD ∥BC ,2AB CD AD ===cm ,∠B =60°. (1)可得梯形ABCD 的周长L =cm ,面积S =cm 2;(2)如图2,E 、F 分别为AB 、BC 边上的动点,连接EF.设BF x =cm ,△BEF 的面积为y cm 2,Lk BE BF=+( k 是常数).①试用含x 的代数式表示y ;②如果L SBE BF y=+,且k 为整数,求BF 的长.图1图2海淀区九年级第一学期期中练习数学试卷答案及评分参考一、选择题(本题共32分,每小题4分) 题 号 1 2 3 4 5 6 7 8 答 案BDCABBCA二、填空题(本题共16分,每小题4分)题号 9 1011 12答案(3,4)--50三、解答题(本题共30分,每小题5分) 13.解方程:2280x x --=. 解法一:1,2,8a b c ==-=-,2(2)41(8)360∆=--⨯⨯-=>.…………………………………………2分(2)3621x --=⨯.…………………………………………3分∴124,2x x ==-.…………………………………………5分 解法二:(4)(2)0x x -+=,…………………………………………3分∴124,2x x ==-.…………………………………………5分解法三:228x x -=,22181x x -+=+.…………………………………………2分 2(1)9x -=.…………………………………………3分13x -=±.∴124,2x x ==-.…………………………………………5分14.计算:10112()31(2)3π-++---.解:原式=233311++--…………………………………………4分 =331+.…………………………………………5分 15.计算:(223)(21)-+.解:原式=422323+--…………………………………………4分=12-.…………………………………………5分16.解法一:连接OC ,OD .…………………………………………1分∵AO 是⊙B 的直径,C 、D 两点在⊙B 上,∴90,ACO ∠=︒90.ADO ∠=︒…………………………………………2分 ∴AC 、AD 是⊙O 的切线.…………………………………3分 ∴AC =AD . …………………………………4分 ∵AC =5,∴AD =5. …………………………………………5分 解法二:连接OC ,OD .……………………………1分∵AO 是⊙B 的直径,C 、D 两点在⊙B 上, ∴90,ACO ∠=︒90.ADO ∠=︒…………………2分 在Rt △ACO 和Rt △ADO 中,,,OC OD AO AO =⎧⎨=⎩ ∴Rt △ACO ≌Rt △ADO .…………………………………………3分 ∴AC =AD . …………………………………4分 ∵AC =5,∴AD =5. …………………………………………5分 17.解: ∵m 是方程2250x x +-=的一个根,∴2250m m +-=.…………………………2分 ∴32259m m m +--= 2(25)9m m m +--…………………………………………3分= 9-. …………………………………………5分18.解: (1)△''AB C 即为所求.(不写结论的不扣分) …………………………………………3分(2)2π.…………………………………………5分四、解答题(本题共20分,每小题5分)19.解:设这种药品平均每次降价的百分率是x.…………………………………1分依题意,得 2200(1)128x -=,…………………………………………3分解得 10.2x =,2 1.8x =(不合题意,舍去).…………………………………………4分 答:这种药品平均每次降价的百分率是20%.…………………………5分20. 解:如图,当弦CD 与半径OA 相交时, 连接OC .…………………………1分 ,6CD AB CD ⊥=,32CD CE ∴==. …………………………2分 5OC =又,∴224OE OC CE =-=. ……………………3分∴1AE OA OE =-=.………………………………4分当弦CD 与半径OB 相交时,同理可得549AE OA OE =+=+=.………5分21. 解:(1)根据题意,可得()20,4420,k k ≠⎧⎪⎨∆=--⨯⨯≥⎪⎩………………………………2分 ∴k 的取值X 围是2k ≤且0k ≠.…………………………………………3分(2)∵2AB =是方程2420kx x -+=的一个根,∴224220k ⨯-⨯+=.∴32k =.…………………………………………4分 ∴234202x x -+=. 解得1222,3x x ==. 经检验:BC =23符合题意. ∴BC 的长为23.…………………………………………5分 (没写检验过程的不扣分)22.(1)证明:连接OC .…………………………………………1分∵AD ⊥AC 于A ,260D B ∠=∠=,∴30ACD B ∠=∠=︒.∴260AOC B ∠=∠=︒.∵OC OA =,∴△OAC 是等边三角形.∴60ACO OAC ∠=∠=︒.∴90OCD ACD ACO ∠=∠+∠=︒. ………………………………………2分∵OC 是半径,∴CD 为⊙O 的切线.…………………………………………3分(2)∵OA ⊥BC 于E ,6BC =,∴3CE =,AB AC =.∴AB AC =.∵ 在Rt △ACE 中,60OAC ∠=︒,∴30ACE ∠=︒,2222,.AC AE AE CE AC =+=∴23AC =. …………………………………………4分 ∵ 在Rt △ACD 中,30ACD ∠=︒,∴2222,.CD AD AD AC CD =+=∴2AD =.∴S 阴影=ACD S ∆=23. …………………………………………5分五、解答题(本题共22分,第23题7分,第24题8分,第25题7分)23.解:(1)例如:2340x ++= ,只要 a 、b 、c 满足222a b c +=即可.… 2分(2)ab c 4)2(2-=∆22(2)c ab =-222(2)a b ab =+-……………………………… 3分2)(2b a -= .∵0)(2≥-b a ,∴0≥∆ .∴“勾系一元二次方程”必有实数根. ……………………………… 4分(3)∵1-=x 是“勾系一元二次方程”022=++b cx ax 的一个根, ∴02=-+c b a .∴a b += . ……………………………… 5分又∵四边形ACDE 的周长是,∴2()a b ++=∴2c =.…………………………………………6分∴224a b +=.解法一:∵222())28a b c +===, ∴2228a b ab ++=.∴2ab =.∴ABC S ∆=112ab =.…………………………………………7分 解法二:∴ABC S ∆=1(2S 四边形)ACDE ABE S ∆-=22111()222a b c ⎡⎤+-⎢⎥⎣⎦=1(84)14⨯-=. …………………………………………7分 24.解:(1)答案不唯一,例如:.………………………2分(2)k 的值为 58-,34-,12-.(答对一个给2分,答对两个给3分)……………6分 b 的取值X 围是510b <<.…………………………………………8分25. 解:(1)10,332分(2)①∵BF x =,L k BE BF=+(k 是常数), ∴10BE x k=-.………………3分 过E 作EK ⊥BF 于K . 由勾股定理易得32EK BE =. ∴213310353()24442y BF EK BF BE x x x x k k=⋅=⋅=-=-+.…………4分 ②∵L S BE BF y=+(k 为整数), ∴S ky = . 由①中结论可知,此时有2353x y x =+. ∴2353()33x k x +=整理,得210120kx x -+=.………………………………………5分∵该方程有实根,∴100480k ∆=-≥.∴2512k ≤. 由题意,得1L k BE BF =>+. ∵k 为整数, K F E A B∴2k =. ………………………………………6分将2k =代入210120kx x -+=,化简,得2560x x -+=.解得 12x =,23x =.∵BE AB ≤,即52x -≤,∴3x ≥.∴12x =(舍去),23x =.∴3BF =cm.………………………………………7分(注:本卷中许多问题解法不唯一,请老师根据评分标准酌情给分)。
海淀区英语一模试题09年

海淀区九年级第二学期期中练习英语2009.5第I 卷(选择题共70分)听力理解(共18分)一、听对话,选择与对话内容相符的图片。
(每段对话读两遍)(共4分,每小题1分)1.A B C2.A B C3.A B C4.A B C二、听对话和短文,选择正确答案。
每段对话或短文读两遍。
(共14分,每小题1分)听下面一段对话,回答第5-6小题。
5. What does the man want to buy?A. A cap.B. A sweater.C. A shirt.6. Where is the man?A. At home.B. In a shop.C. In a hospital.听下面一段对话,回答第7-8小题。
7. What is the man‟s name?A. Bob.B. Mike.C. Peter.8. Where is the woman from?A. America.B. China.C. Australia.听下面一段对话,回答第9-11小题。
9. What‟s wrong with the woman?A. She has a fever.B. She has a headache.C. She has a clod.10. Why can‟t the woman sleep well?A. She studies math too hard.B. She spends more time on TV.C. She has too much for dinner.11. What does the doctor tell her to do?A. To go to bed early.B. To eat more fruit.C. To relax herself.听下面一段对话,回答第12-14小题。
12. How many days does Tom have for his holiday?A. Five days.B. Five weeksC. Five months.13. What‟s Lily going to do on holiday?A. Go camping.B. Visit her cousin.C. Do her homework.14. Who is Tom going out with?A. His parents.B. His cousin.C. His aunt.听下面一段短文,回答第15-18小题。
2009-2010年北京市海淀区第一次抽样测试试题(试卷版)
海 淀 区 九 年 级 第 二 学 期 期 中 测 评 数 学 2010.5一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.12-的倒数是( )A. 2B.2-C.12 D.12- 2.2010年2月12日至28日,温哥华冬奥会官方网站的浏览量为275 000 000人次. 将275 000 000用科学记数法表示为( )A. 72.7510⨯B.727.510⨯ C. 82.7510⨯ D.90.27510⨯ 3.下图是某几何体的三视图,则这个几何体是( )俯视图左视图主视图A. 圆柱B. 正方体C. 球D. 圆锥4.一个多边形的内角和是外角和的2倍,则这个多边形的边数为( )A. 5B.6C. 7D. 85.一个布袋中有4个除颜色外其余都相同的小球,其中3个白球,1个红球.从袋中任意摸出1个球是白球的概率是( ) A .43 B .41 C .32 D .316. 四名运动员参加了射击预选赛,他们成绩的平均环数x 及其方差2s 如表所示.如果选出一个成绩较好且状态稳定的人去参赛,那么应选( )1.81.2117887丁丙乙甲s 2xA .甲B .乙C .丙D .丁7.把代数式 322363x x y xy -+分解因式,结果正确的是( )A .(3)(3)x x y x y +-B .223(2)x x xy y -+C .2(3)x x y +D .23()x x y -8. 如图,点E 、F 是以线段BC 为公共弦的两条圆弧的中点,6BC =. 点A 、D 分别为线段EF 、BC 上的动点.连接AB 、AD ,设BD x =, 22AB AD y -=,下列图象中,能表示y 与x 的函数关系的图象是( )E FDCBA A.B.C.D.二、填空题(本题共16分,每小题4分)9.函数y =的自变量x 的取值范围是 . 10.如图, O 的半径为2,点A 为O 上一点,OD ⊥弦BC 于点D ,1OD =,则BAC ∠=________︒.DCBA O11.若代数式26x x b -+可化为2()1x a --,则b a -的值是 .12. 如图,n +1个边长为2的等边三角形有一条边在同一直线上,设211B D C ∆的面积为1S ,322B D C ∆的面积为2S ,…,1n n n B D C +∆的面积为n S ,则2S = ;n S =____(用含n 的式子表示).C 5C 4C 3C 2C 1B A三、解答题(本题共30分,每小题5分)130112cos301)()2-︒+- .14.解方程:23233x x x +=-+. 15. 如图, △OAB 和△COD 均为等腰直角三角形,90AOB COD ∠=∠=︒, 连接AC 、BD .求证: AC BD =. DOCBA16. 已知:2310x x +=,求代数式2(2)(10)5x x x -++-的值. 17.已知:如图,一次函数y m =+与反比例函数y =的图象在第一象限的交点为(1)A n ,.(1)求m 与n 的值;(2)设一次函数的图像与x 轴交于点B ,连接OA ,求BAO ∠的度数.18. 列方程(组)解应用题:2009年12月联合国气候会议在哥本哈根召开.从某地到哥本哈根,若乘飞机需要3小时,若乘汽车需要9小时.这两种交通工具平均每小时二氧化碳的排放量之和为70千克,飞机全程二氧化碳的排放总量比汽车的多54千克,分别求飞机和汽车平均每小时二氧化碳的排放量.四、解答题(本题共20分,第19题5分,第20题5分,第21题6分,第22题4分)19.已知:如图,在直角梯形ABCD中,AD∥BC,90DCB∠=︒,AC BD⊥于点O,2,4DC BC==,求AD的长.ODCBA20.已知:如图,O为ABC∆的外接圆,BC为O的直径,作射线BF,使得BA平分CBF∠,过点A作AD BF⊥于点D.(1)求证:DA为O的切线;(2)若1BD=,1tan2BAD∠=,求O的半径.FC21. 2009年秋季以来,我国西南地区遭受了严重的旱情,某校学生会自发组织了“保护水资源从我做起”的活动. 同学们采取问卷调查的方式,随机调查了本校150名同学家庭月人均用水量和节水措施情况.以下是根据调查结果做出的统计图的一部分.图1家庭月人均用水量统计图人均月用水量(吨)人数(人)家庭节水措施调查统计图请根据以上信息解答问题:(1)补全图1和图2;(2)如果全校学生家庭总人数约为3000人,根据这150名同学家庭月人均用水量,估计全校学生家庭月用水总量.22.阅读:如图1,在ABC ∆和DEF ∆中,90ABC DEF ∠=∠=︒,,AB DE a ==BC EF b ==()a b <,B 、C 、D 、E 四点都在直线m 上,点B 与点D 重合.连接AE 、FC ,我们可以借助于ACE S ∆和FCE S ∆的大小关系证明不等式:222a b ab +>(0b a >>).证明过程如下:∵.BC b BE a EC b a ===-,,图1E D 图2mFE C BA∴11(),22ACE S EC AB b a a ∆=⋅=-11().22FCE S EC FE b a b ∆=⋅=-∵0b a >>, ∴FCE S ACE S ∆∆>.即11()()22b a b b a a ->-. ∴22b ab ab a ->-. ∴222a b ab +>. 解决下列问题:(1)现将△DEF 沿直线m 向右平移,设()BD k b a =-,且01k ≤≤.如图2,当BD EC =时, k = .利用此图,仿照上述方法,证明不等式:222a b ab +>(0b a >>).(2)用四个与ABC ∆全等的直角三角形纸板进行拼接,也能够借助图形证明上述不等式.请你画出一个..示意图,并简要说明理由.五、解答题(本题共22分,第23题7分,第24题8分,第25题7分)23.关于x的一元二次方程240-+=有实数根,且c为正整数.x x c(1)求c的值;(2)若此方程的两根均为整数,在平面直角坐标系xOy中,抛物线24=-+与x轴交于y x x cA、B两点(A在B左侧),与y轴交于点C. 点P为对称轴上一点,且四边形OBPC为直角梯形,求PC的长;(3)将(2)中得到的抛物线沿水平方向平移,设顶点D的坐标为(),m n,当抛物线与(2)中的直角梯形OBPC只有两个交点,且一个交点在PC边上时,直接写出m的取值范围.24. 点P为抛物线22m>)上任一点,将抛物线绕顶点G逆时针=-+(m为常数,0y x mx m2旋转90︒后得到的新图象与y轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.(1)当2m=,点P横坐标为4时,求Q点的坐标;(2)设点(,)Q a b,用含m、b的代数式表示a;(3) 如图,点Q在第一象限内, 点D在x轴的正半轴上,点C为OD的中点,QO平分.=,当QD m=时,求m的值AQ QC∠,2AQC25.已知:AOB △中,2AB OB ==,COD △中,3CD OC ==,ABO DCO =∠∠. 连接AD 、BC ,点M 、N 、P 分别为OA 、OD 、BC 的中点.图1NMPODCBA图2NMPODCBA(1) 如图1,若A 、O 、C 三点在同一直线上,且60ABO =∠,则PMN △的形状是________________,此时ADBC =________;(2) 如图2,若A 、O 、C 三点在同一直线上,且2ABO α=∠,证明PMN BAO △∽△,并计算ADBC的值(用含α的式子表示); (3) 在图2中,固定AOB △,将COD △绕点O 旋转,直接写出PM 的最大值.海淀区九年级第二学期期中测评数学试卷答案及评分参考一、选择题(本题共32分,每小题4分) 1.答案:B12-的倒数是2- 2.答案:C8275 000 000 2.7510=⨯3.答案:D圆锥的主视图和左视图相同,都是等腰三角形,俯视图是圆。
2009年海淀区中考一模英语试卷

2009年海淀区中考一模英语试卷二、单选19.--- would you like to go for a walk with _______?----- sure. I‟d love to.A : I B: me C: my D: my答案:B解析:考察代词宾格。
20 Li Lei often goes to school ______ 7:30 in the morning.A: at B: for C: on D: of答案:A解析:考察介词在时间前面的用法21.I usually have an egg and two _____ of milk for breakfast.A: bottle B: a bottle C: bottles D: the bottles答案:C解析:考察不可数名词前量词的用法22.--- I‟m looking for a jacket for my son. --- What color do you like _______, the blue one or the red one? A: the best B: good C: best D: better答案:D解析:考察比较级的用法,两者比较用比较级23. James hasn‟t got Jay‟s CDs,_____ his sister has.A: so B: but C: and D: ot答案:B解析:考察连词的用法,前后两句是转折关系因此用B24 ---_______?----He is a computer engineer.A, What does your father do B: How old is your fatherC: What does your father look like D: How does your father go to work答案:A解析:考察对职业进行提问。
2009年学业考试最新第一次模拟考试试卷(你值得拥有)-1.doc

北京路中学北京市2009届九年级“一摸”考试试题数学一、选择题(本大题共lO 小题.每小题3分,共30分.下列各题的四个选项中,只有一个是符合题意的) 1. 在2-、0、1、3这四个数中比0小的数是 ( )A.2- B.0 C.1 D .3 2.国家游泳中心——“水立方”,是北京2008年奥运会场馆之一,它的外层膜的展开面积约为26万m 2,将26万m 2用科学记数法表示应为 ( )A .620.2610m ⨯B .422610m ⨯C .622.610m ⨯D .522.610m ⨯3.若2x <,则2|2|x x --的值是 ( )A .1-B .0C .1D .24.(2008·福州)如图,已知直线AB CD ,相交于点O ,OA 平分EOC ∠,100EOC ∠=,则BOD ∠的度数是 ( ) A .20 B .40 C .50D .805.如图,是某工件的三视图,其中圆的半径为10cm ,等腰三角形的高为30cm ,则此工件的侧面积是( )A .π1502cmB .π3002cmC .2cmD .2cm6.(2008·台湾)19的值介于下列哪两数之间? ( ) A. 4.2,4.3 B. 4.3,4.4 C. 4.4,4.5 D.4.5,4.67.若0a >且2x a =,3y a =,则x ya -的值为 ( )A .1-B .1C .23D .32AE DO CB(第4题)(第5题)正 视 图左 视 图俯视 图8.图中所示几何体的俯视图是 ( )9.在2008年的世界无烟日(5月31日),小华学习小组为了解本地区大约有多少成年人吸烟,随机调查了100个成年人,结果其中有15个成年人吸烟.对于这个关于数据收集与处理的问题,下列说法正确的是 ( )A .调查的方式是普查B .本地区只有85个成年人不吸烟C .样本是15个吸烟的成年人D .本地区约有15%的成年人吸烟 10.如图,直线24y x =-+与x 轴,y 轴分别相交于A B ,两点,C 为OB 上一点,且12∠=∠,则ABC S =△ ( ) A .1 B .2C .3D .4(第10题) 二、填空题(本大题共6小题.每小题3分,共18分.把正确答案直接填在题中的横线上) 11.写出含有字母x 、y 的四次单项式___________(只要写出一个).12.如图,在矩形空地上铺4块扇形草地.若扇形的半径均为r 米,圆心角均为90,则铺上的草地共有 平方米.13.如图所示,请写出能判定CE ∥AB 的一个条件 .14.(2008·乌鲁木齐)乌鲁木齐农牧区校舍改造工程初见成效,农牧区最漂亮的房子是学校.2005年市政府对农牧区校舍改造的投入资金是5786万元,2007年校舍改造的投入资金是8058.9万元,若设这两年投入农牧区校舍改造资金的年平均增长率为x ,则根据题意可列方程为 .15.某市6月2日至8日的每日最高温度如图所示,则这组数据的中位数是 ,众数是 .(第12题)A(第15题)16. 将正整数按如图5所示的规律排列下去,若有序实数对(n ,m )表示第n 排,从左到右第m 个数,如(4,2)表示实数9,则表示实数17的有序实数对是 .三、解答题(本大题共12小题,共102分.解答应写出必要的计算过程、推演步骤或文字说明) 17.(本小题6分)计算:(-2-2+31)×86-20080÷sin 45°.18.(本小题6分)(2008·三明)先化简,再求值:(2a+b )(2a-b)+b(2a+b)-4a 2b ÷b ,其中a=-21,b=2.19.(本小题6分)(2008·自贡)解不等式组⎪⎩⎪⎨⎧+≥+<+4134)2(3x x x x20.(本小题8分)有五张除字不同其余都相同的卡片分别放在甲、乙两盒子中,已知甲盒子有三张,分别写有“北”、“京”、“奥”字样,乙盒子有两张,分别写有“运”、“会”字样,若依次从甲乙两盒子中各取一张卡片,求能拼成“奥运”两字的概率.21.(本小题8分)今年3月5日,花溪中学组织全体学生参加了“走出校门,服务社会”的活动.九年级一班高伟同学统计了该天本班学生打扫街道,去敬老院服务和到社区文艺演出的人数,并做了如下直方图和扇形统计图。
2009年北京市海淀区中考物理一模试卷

2 2009年北京市海淀区中考物理一模试卷第Ⅰ卷(共36分)一、下列各小题均有四个选项,其中只有一个选项符合题意.(共24分,每小题2分) 1.在国际单位制中,电压的单位是( )A.欧姆B.伏特C.安培D.瓦特2.在图1所示的现象中,能用光的折射规律解释的是( )A.经凸透镜成放大的像B.山峦在水中的倒影C.在墙上投出的手影D.烛焰通过小孔成像图13.通常情况下,下列物质中最容易导电的是( )A.塑料B.玻璃C.橡胶D.金属4.在下列物态变化过程中,放热的是( )A.熔化B.汽化C.液化D.升华5.如图2所示的措施中,为了减小压强的是( )A.切蛋器装有很细的钢丝B.冰刀磨得很锋利C.坦克上安装有履带D.图钉的钉尖做得很尖图26.下列事例中,其目的是增大摩擦的是( )A.给笨重的旅行箱装上轮子B.给自行车的车轴加润滑油C.给机器的转轴加装滚珠D.给鞋底的表面做出凹凸不平的花纹7.下列现象中,属于扩散现象的是( )A.春天,柳絮飞扬B.夏天,荷花飘香C.秋天,树叶飘落D.冬天,雪花纷飞8.在图3所示的四种情境中,人对物体做功的是( )A.举着杠铃原地不动B.沿水平地面推动小车C.抱着书不动D.推石头没有推动图39.如图4所示为一种声光报警器的电路图,闭合开关S1和S2后,会出现的现象是( ) A.灯亮,铃不响B.灯不亮,铃不响C.灯亮,铃响D.灯不亮,铃响图410.如图5所示为跳水运动员跳板跳水时的情景,运动员腾空跳起脱离跳板向上运动,然后再向下运动落入水中,若不计空气阻力,则( )图5A.运动员向上运动过程中,动能保持不变B.运动员向上运动过程中,重力势能转化为动能C.运动员向上运动过程中,动能转化为重力势能D.运动员向下运动至入水前的过程中,动能转化为重力势能11.如图6所示,电源两端的电压保持不变.将滑动变阻器的滑片P置于中点,闭合开关S后,各电表的示数和灯泡的发光情况均正常.现将滑动变阻器的滑片P由中点向右移动,则( )A.灯泡L变亮B.电流表A1示数变小C.电流表A2示数变大D.电压表V示数变小图612.如图7所示装置中,杠杆和滑轮的重力及滑轮的摩擦均可忽略不计,杠杆AB可以绕O 点在竖直平面内自由转动,A端通过竖直方向的轻绳与滑轮组相连,在B端用一轻绳沿竖直方向将杠杆拉住,使其始终保持水平平衡.在滑轮组的下方,悬挂一圆柱形的物体,此物体被浸在圆柱形容器内的液体中.已知杠杆O点两侧的长度关系为AO=2OB,圆柱形物体的底面积为10 cm2、高为12 cm,圆柱形容器的底面积为50 cm2.若容器中的液体为水,在水深为20 cm时物体的上表面恰与水面相平,此时杠杆B端绳上的拉力为F1;打开圆柱形容器下方的阀门K,将水向外释放,直到物体露出水面的体积为其总体积的2/3时,将阀门K关闭,此时杠杆B端绳上的拉力为F2,且F1∶F2=3∶4.若容器中液体为某种未知液体,其质量与最初容器中的水的质量相等,此时未知液体的深度为18 cm,杠杆B端绳上的拉力为F3.取g=10 N/kg,则( )A.圆柱形物体的密度为2g/cm3B.作用在B端的拉力F3大小为1.52 NC.未知液体的密度为1.2g/cm3D.未知液体对圆柱形容器底部的压强为1 980 Pa图7二、下列各小题均有四个选项,其中符合题意的选项均多于一个.(共12分,每小题3分,全选对的得3分,选对但不全的得2分,有错选的不得分)13.下列说法中正确的是( )A.同名磁极相互排斥,异名磁极相互吸引B.发电机是根据电磁感应现象制成的C.电动机工作时将机械能转化为电能D.发现有人触电时应立即切断电源14.关于力、运动和力的关系,下列说法中正确的是( )A.施力物体同时一定要受到力的作用B.两个不接触的物体之间一定没有力的作用C.物体不受力,运动状态一定不改变D.物体运动状态不变,一定没有受到力的作用15.小明根据表一、表二所提供的几种物质的比热容和熔点,得出以下几个结论,其中正确的是( )表一:几种常见物质的比热容表二:几种常见物质在1.01×105A .固体物质的比热容越大,其熔点一定越高B .在1.01×105Pa 大气压下,20℃时水银是液态的C .质量相同的水和冰吸收相同的热量,它们升高的温度相同D .用水作为汽车发动机散热器的冷却剂,其重要原因之一是水的比热容较大16.如图8所示,电源两端的电压保持不变,R 0为定值电阻.将滑动变阻器的滑片P 置于最右端,闭合开关S .移动滑动变阻器的滑片P 到某一位置,此时滑动变阻器接入电路中的电阻为R 1,电压表的示数为U 0,电流表的示数为I 0.继续移动滑动变阻器的滑片P ,使滑动变阻器接入电路中的电阻值减小为R 1/3,此时电压表的示数增大到2U 0,电流表的示数变为I 1.则下列说法中正确的是( )A .I 1=2I 0B .R 0∶R 1=1∶3C .当滑动变阻器的滑片P 滑到最右端时,R 两端的电压为3U 0D .当滑动变阻器的滑片P 滑到R 的最左端时,电压表的示数为4U 0图8第Ⅱ卷 (共64分)三、填空题(共14分,每空2分)17.光是一种电磁波,它在真空中的传播速度是______m/s .18.宁静、清澈的湖面是天然的平面镜,树木在水中的倒影(如图9)是湖边树木的______像.(选填“实”或“虚”)19.拉萨与北京相比,海拔要高出数千米,所以通常拉萨地区的大气压强______北京地区的大气压强.(选填“高于”、“等于”或“低于”)20.将一根粗细均匀、阻值为12 Ω的电阻丝接在输出电压恒为6 V 的电源两端,正常工作10 s,产生的热量为_________J.图921.一辆小汽车以20 m/s的速度经过杭州湾跨海大桥,从桥头驶到桥尾共用了1 800 s.由此可知,这座桥的长度为______m.22.三个定值电阻串联后接在电压恒定的电路两端,其阻值R1=5 Ω,R2=10 Ω,R3=15 Ω.某同学将一只电流表接在R2的两端,如图10所示,发现其示数为1.5 A.若将电流表的位置改接一只电压表,则电压表的示数为______V.图1023.如图11所示,底面积为S1的圆柱形容器中装有未知密度的液体.将一密度为ρ的正方体金属块放入底面积为S2的长方体塑料盒中(塑料盒的厚度可忽略不计),塑料盒漂浮在液面上(液体不会溢出容器),其浸入液体的深度为h1.若把金属块从塑料盒中取出,用细线系在塑料盒的下方,放入液体中,金属块不接触容器,塑料盒浸入液体的深度为h2.剪断细线,金属块会沉到容器的底部,塑料盒漂浮在液面上,其浸入液体的深度为h3.若塑料盒始终处于如图所示的直立状态而未发生倾斜,则细线剪断前后液体对圆柱形容器底部的压强减小了________.图11四、作图、实验与探究题(共34分,24至28题、32、33、35题各2分,30、31、34题各3分,29题4分,36题5分)24.在图12中,O是杠杆的支点,画出力F的力臂并用字母L标明.图12 图13 图1425.如图13所示,AO为入射光线,ON为法线.请画出入射光线的反射光线.26.在图14中铅笔长度的测量值是______cm.27.小明做探究影响液体蒸发快慢因素的实验过程中,他在两块相同的玻璃片上分别滴上质量相同的一滴水,水滴的表面积相同,用酒精灯给其中的一块玻璃片加热,如图15所示.观察图中情景可知,小明的上述操作主要是在研究液体蒸发快慢与液体的______是否有关.图1528.在探究杠杆平衡条件的实验中,先把杠杆装在支架上,通过调节平衡螺母,使杠杆在水平位置平衡.当左侧钩码处于如图16所示的A 位置时,应将右侧的钩码向______移动(选填“左”或“右”)______格(每格长度相同),可使杠杆在水平位置平衡.29.小华想知道金属块A 是什么物质构成的,他先用天平和量筒测出金属块A 的密度,再根据密度表确定金属块A 是什么物质.测定结果如图17所示.请你将测量数据填入表一中,并根据实验结果,结合表二进行分析判断,将表一中的其他项目填写完整.图16表一:数据表表二:几种常见金属的密度甲 乙 丙图1730.在研究串、并联电路的电流特点时,小明同学分别做了如下两组实验.实验一:小明通过比较电路中不同位置的电流表的示数来研究串联电路的电流特点,所利用的电路如图18所示.闭合开关后,两电流表指针偏转情况如图19所示.图18 图19(1)小明发现电流表A2的指针偏转角度比A1的小,所以他认为“串联电路中电流每流经一个用电器都会减弱一些”.请你指出造成他判断错误的原因是______.(2)电流表A1的示数是______A.实验二:小明在只利用图....18..中的实验器材......研究并联电路中电流的特点时,若连接好电路后不再进行拆改,则根据电流表的示数只能归纳得出如下结论:在并联电路中,干路电流大于某一支路电流.请你设计出小明得出此结论的实验电路图,并画在虚线框内.图2031.小红用焦距为15 cm的凸透镜做实验,探究凸透镜成像的规律.她首先在长为100 cm 的光具座上按图20所示完成仪器装配,然后将蜡烛置于A点,在光屏上可得到清晰的像(图中未画出);当她再把蜡烛移到B点时,光屏上的像变得很模糊,为了得到清晰的像,应把光屏向______(选填“左”或“右”)移动,这次成的是倒立、______(选填“放大”或“缩小”)的实像.若要通过此凸透镜观察到蜡烛正立、放大的虚像,则应将蜡烛置于透镜左侧A、B、C、D四点中的______点处.32.小刚同学在研究杠杆的平衡条件过程中,发现:在阻力和阻力臂保持不变的条件下,当杠杆平衡时动力跟动力臂之间有一定的关系.为研究此关系,他进行了一系列的实验,并记录了如下表所示的实验数据.请你对表格中的数据进行分析,归纳出实验结论:33.图21是一辆小车做匀速直线运动过程中的路程与时间之间的关系图象,由图象可知小车运动8 s所通过的路程为______.34.通过实验同学们已经知道影响浮力大小的因素,但小欣同学仍然认为浸没在液体中的物体所受浮力的大小似乎跟它在液体中的深度有关.请你帮她完成验证此猜想是否正确的实验.(1)现已提供的器材有:石块、细线、烧杯、适量的水.为完成此实验,还必须提供的一种器材是:______.(2)请将下面不完整的实验步骤补充完整:①用细线系牢石块,挂在弹簧测力计挂钩下,记录弹簧测力计的示数为F;图21②将石块浸没在水中某一深度,且不与烧杯接触,记录弹簧测力计的示数为F1;③_____________记录弹簧测力计的示数为F2.(3)分析与论证:若F-F1≠F-F2,则说明浸没在液体中的物体,所受浮力与它浸没的深度有关;若F-F1=F-F2,则________________________________________________.35.小明想利用实验室所提供的器材测量未知电阻R x的阻值(约为500Ω).实验室所提供的器材有:电源(两端输出电压约为14 V,且保持不变)、滑动变阻器R(标有“100 Ω 2 A”的字样)、电流表(量程为0~0.6 A)、电压表(量程为0~15 V)各一块,开关S1、S2两只,导线若干.图22是小明进行实验时电路连接的一部分情况,主要实验步骤如下:图22①将滑动变阻器的滑片P置于某一位置,使其接入电路的电阻值较大;②闭合开关S1、S2,观察并记录电压表和电流表的示数分别为U1和I1;③保持滑动变阻器接入电路中的电阻值不变,断开S2,观察并记录电压表此时的示数U2(U2<U1),此时的电流表示数几乎为零(因而无法准确读出此时电路中的电流值).(1)请你在图22中将小明所做实验的电路连接完整.(2)写出R x测量结果的表达式:R x=______.(要求用测得的物理量表示)36.实验桌上有如下器材:细长平底试管一支(已知底面积为S)、小汤匙一个、刻度尺一把、大水槽一个(水槽的高度大于小试管的高度)、足量的水、足量的细沙子、天平及配套砝码.要求从实验桌上选择适当的器材,设计一个实验证明:当液体的密度保持不变时,液体内部的压强与液体的深度成正比.要求:写出主要的实验步骤.五、计算题(共16分,37题3分,38题6分,39题7分)计算题要求:(1)写出必要的文字说明和依据的主要公式;(2)代入数据;(3)凡有数字运算的题目,运算过程和结果都要写明单位.37.一个热水袋内装有质量为1kg的水,在水温从90 ℃降到40 ℃的过程中,水放出的热量是多少?[水的比热容为4.2×103J/(kg·℃)]38.在如图23所示的电路中,电源两端的电压保持不变.当只闭合开关S和S1时,灯L1正常发光,电压表V1的示数U1与电压表V2的示数U2之比U1∶U2=2∶3,电阻R3消耗的电功率P3=2 W;当只闭合开关S和S2时,电压表V1的示数为U1′,且U1∶U1′=2∶1,电阻R4消耗的电功率P4=2.5 W.不计灯丝电阻随温度的变化,求:图23(1)在上述变化中,电流表前、后两次示数之比;(2)灯L1的额定电功率;(3)当所有开关全部闭合时,电路消耗的总功率.39.如图24所示,质量为70kg的工人站在岸边通过一滑轮组打捞一块沉没在水池底部的右材,该滑轮组中动滑轮质量为5kg.当工人用120 N的力拉滑轮组的绳端时,石材仍沉在水底不动.工人继续增大拉力将石材拉起,在整个提升过程中,石材始终以0.2 m/s 的速度匀速上升.在石材还没有露出水面之前滑轮组的机械效率为η1,当石材完全露出水面之后滑轮组的机械效率为η2.在石材脱离水池底部至完全露出水面的过程中,地面对人的支持力的最大值与最小值之比为29∶21.绳重及滑轮的摩擦均可忽略不计,石材的密度ρ石=2.5×103kg/m3,取g=10 N/kg,求:(1)与打捞前相比,当人用120 N的力拉绳端时,水池底部对石材的支持力变化了多少?(2)η1与η2的比值;(3)当石材完全露出水面以后,人拉绳子的功率.图24答案2.2009年北京市海淀区中考物理一模试卷1.B 2.A 3.D 4.C 5.C 6.D 7.B 8.B 9.A 10.C 11.B 12.D 13.ABD 14.AC 15.BD 16.ABD17.3×10818.虚19.低于20.30 21.3.6×10422.1023.)())( (3113 2212hhS hhhhgS---ρ24.24题图25.25题图26.6.65(±0.02) 27.温度28.右 1 29.27 70 2.7 铝30.实验一:(1)没有考虑电流表A1和A2选用的量程不同(2)0.5 实验二:如图所示(说明:两只电流表分别串联接在干路和支路上即为正确)30题图31.右放大D32.在杠杆平衡时,阻力和阻力臂保持不变,动力跟动力臂成反比.(或在杠杆平衡时,阻力和阻力臂保持不变,动力跟动力臂的乘积不变;在杠杆平衡时,阻力和阻力臂保持不变,动力臂越大,动力越小)33.5.4(±0.2)m(不写单位的只得1分)34.(1)(弹簧)测力计(2)改变石块浸没在水中的深度(或将石块浸没在水中另一深度),且不与烧杯接触(3)说明浸没在液体中的物体,所受浮力与它浸没的深度无关35.(1)35题图(2).)(12121I U U U U -36.(1)在试管中装入适量的沙子,用天平测出试管和沙子的总质量m 1;(2)将试管放入装有水的大水槽中,使其直立漂浮在水面上,测出浸入水中的深度h 1; (3)再增加试管中的沙子,测出试管和沙子的总质量m 2;重复步骤(2),测出浸入水中的深度h 2;(4)重复实验步骤3,再测出4组数据m 3、h 3;m 4、h 4;m 5、h 5;m 6、h 6;(5)用Smg S F p ==,依次算出水对试管底部的压强p 1、p 2、p 3、p 4、p 5、p 6. 说明:(1)上述只给出了主要步骤,如每次测质量需擦干试管等步骤不作为得分点.(2)其他设计方案,如测试管露出水面的高度、测每次减少沙子的质量等,只要正确的均得分.37.解:Q 放=cm (t 0-t )=4.2×103J/(kg ·℃)×1kg ×(90 ℃-40℃) =2.1×105J .38.解:(1)设电源两端的电压为U ,灯L 1和L 2的电阻分别为R 1和R 2.当只闭合开关S 、S 1时,电路如图甲所示,此时电路中的电流为I 1;当只闭合开关S 、S 2时,电路如图乙所示,此时电路中的电流为I 2.38题图比较图甲和图乙,因R 2的电阻不变,根据欧姆定律有 U 1=I 1R 2,U 1′=I 2R 2, 所以电流表前、后两次示数之比⋅='=121121U U I I(2)依题意,对于图甲所示的电路,根据串联电路的分压关系则有,3221221=+=R R R U U ,解得2121=R R . 因为,W 5.2,W 242243213====R I P R I P 所以54)(4322143==R R I I P P ,解得5143=R R比较图甲和图乙,因电源两端电压不变,所以根据欧姆定律有,1232142121=++++=R R R R R R I I ,解得R 3=R 1. 因为R 3=R 1,所以在图甲所示的串联电路中,P 1=P 3=2W ,又因此时灯L 1正常发光,所以灯L 1的额定功率为2W .(3)当所有开关全部闭合时,电路如图丙所示.此时的总电阻=+=4343R R R R R 总⋅165R由图甲可知,W 216)(12323213==++=R U R R R R U P ,解得.W 3212=R U所以此时电路消耗的总功率.W 4.38.56122===R U R U P 总总说明:其他解法正确的同样得分.39.解:(1)池底部对石材的支持力的变化等于滑轮组下端绳子拉石材的拉力变化:∆F =∆T =3F -G 动=3×120N -50N =310N . (2)石材浸没在水中被拉起时,人拉绳端的力,31浮动石拉F G G F -+=其中石材所受浮力F 浮=ρ 水gV 排=G 石ρ 水/ρ 石 石材在空气中时,人拉绳端的力⋅+=32动石拉G G F 设石材在水中被拉起时地面对人的最大支持力为N 1,石材在空气中时地面对人的最小支持力为N 2,所以对于石材在水中和在空气中分别有G 人=N 1+F 拉1′,G 人=N 2+ F 拉2′,因为F 拉1′与F 拉1大小相等,F 拉2′与F 拉2大小相等, 又因N 1∶N 2=29∶21,代入数据解得G 石=1 000 N ,F 浮=400 N . 石材浸没在水中被拉起时滑轮组的机械效率,1浮动石浮石F G G F G -+-=η石材完全露出水面之后滑轮组的机械效率,2动石石G G G +=η所以石动石浮动石浮石G G G F G G F G +⨯-+-=21ηη⋅=+⨯-+-=65631000N 50N 00N 01400N 50N 1000N 400N 1000N(3)人拉绳的功率石动石石拉v G G nv F P 3)(312⨯+=⋅==(1000 N +50 N)×0.2 m/s =210W . 说明:其他解法正确的同样得分.。
09年北京海淀区初三一模英语试题答案

第一部分听力(共两节20小题,每小题1.5分,满分30分)第一节 (共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What is the man?A. A lawyer.B. A teacher.C. A doctor.2. What will the woman have to do?A. Return the tape to the man.B. Keep the tape for another week.C. Borrow a tape recorder tomorrow.3. What does the man mean?A. Judy is a good photographer.B. Judy is very poor in her lessons.C. Judy should focus on her study.4. What does the thief look like?A. Very tall, with long yellow hair.B. Quite short, with long black hair.C. Medium height, with a yellow T-shirt.5. Where does the conversation probably take place?A. In a meeting room.B. In a restaurant.C. In a library.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
2009年北京市海淀区第一次模拟试题(英语)

2009年北京市海淀区第一次模拟试题英语从下列各题所给的A、B、C、D四个选项中,选择可以填入空白处的最佳选项。
19.—Would you like to go for a walk with ________?—Sure, I'd love to.A.IB.m eC.myD.min e20.Li Lei often goes to school ________ 7:30 in the morn ing.A.atB.fo rC.onD.o f21.I usually have an egg and two ________ of milk fo r breakfast.A.bottleB.a bottl eC.bottlesD.the bottle s22.—I'm looking for a jacket for my son.—What color do you like ________, the blue one or th ered one?A.the bestB.goo dC.bestD.bette r23.James hasn't got Jay's CDs, ________ his sister has.A.soB.bu tC.andD.o r24.— ________?—He is a computer engineer.A.What does your father d oB.How old is your fathe rC.What does your father look like?D.How does your father go to wor k25.— ________ did you put my glasses just now, Bill?—On the table.A.WhatB.Wh yC.WhenD.Wher e26.My mother will take me to the movie if she ________ free this weekend. A.isB.will b eC.wasD.would b e27.—Where's Susan, Mike?—She ________ in the kitchen.A.cooksB.cooke dC.is cookingD.has cooke d28.— ________ you play the piano?—No. But I can play the guitar.A.CanB.Ma yC.MustD.Shoul d29.— Do you know ________ the MP3 player last week?—Sorry, I have no idea.A.how much did she pay fo rB.how much will she pay fo rC.how much she paid fo rD.how much she will pay fo r30.—I didn't see you at the meeting.—I had a bad cold. The doctor asked me ________ i n bed.A.stayingB.to sta yC.stayedD.to stayin g31.—What's the best food you have had in Beijing, Alex?—Roast duck! I ________ to a famous restaurant t o have it last week. A.have goneB.g oC.will goD.wen t32.There is ________ water in the glass. Let's go and ge t some.A.fewB.muc hC.manyD .littl e33.It is reported that China's largest museum of moder n art ________ at the end of 2010.A .is builtB .will be buil tC .buildsD .will buil d34.It is known to all that ________ you exercise regularly, you won't stay in good health.A .unlessB .i fC .untilD .a s四、完形填空 (共12分,每小题1分)阅读下面的短文,掌握其大意,然后从短文后各题所给的A 、B 、C 、D 四个选项中,选择最佳选项。
2009年北京各区中考一模、二模试题分类汇编 较难填空选择

选择、填空较难题1.(07北京)8.右图所示是一个三棱柱纸盒,在下面四个图中,只有一个是 这个纸盒的展开图,那么这个展开图是( )2.(08北京)8.已知O 为圆锥的顶点,M 为圆锥底面上一点,点P 在OM 上.一只蜗牛从P 点出发,绕圆锥侧面爬行,回到P 点时所爬过的最短路线的痕迹如右图所示.若沿OM 将圆锥侧面剪开并展开,所得侧面展开图是( )3.(平谷二)8.将圆柱形纸筒沿母线AB 剪开铺平,得到一个矩形(如图).如果将这个纸筒沿线路B M A →→剪开铺平,得到的图形是 A .矩形 B . 半圆 C .三角形 D . 平行四边形4.(崇文一)8.右图是一块带有圆形空洞和矩形空洞的小木板,则下列物体中最有可能既可以堵住圆形空洞,又可以堵住矩形空洞的是A. B. C. D.O P M O M ' M P A .O M 'M P B . OM ' M PC . O M ' M PD . ()A )B5.(海淀一)8.右图是画有一条对角线的平行四边形 纸片ABCD ,用此纸片可以围成一个 无上下底面的三棱柱纸筒, 则所围成 的三棱柱纸筒可能是A B C D6.(西城一)8.若m 、n (m<n )是关于x 的方程1()()0x a x b ---=的两根,且a < b , 则a 、b 、m 、n 的大小关系是A . m < a < b< nB . a < m < n < bC . a < m < b< nD . m < a < n < b7.(西城一)7.如图,在边长为1的等边三角形ABC 中,若将两条含120︒圆心角的AOB 、BOC 及边A C 所围成的阴影部分的面积记为S ,则S 与△A BC面积的比等于8.(07北京)12.右图是对称中心为点O 的正六边形.如果用一个含30°角的直角三角板的角,借助点O (使角的顶点落在点O 处),把这个正六边形的面积 n 等分,那么n 的所有可能的值是 . 9.(海淀二)8. 如图,已知八边形ABCDEFGH , 对角线AE 、BF 、CG 、DH交于点O , △OAB 、△OCD 、△OEF 和△OGH 是四个全等的 等边三角形,用这四个三角形围成一个四棱锥的侧面,用其 余的四个三角形拼割出这个四棱锥的底面,则下面图形(实线为拼割后的图形)中恰为此四棱锥底面的是10.(朝阳一)8. 如图,在直角梯形ABCD 中,AD ∥BC ,90C ∠=6cm CD =,AD =2cm,动点P 、Q 同时从点B 出发,点P沿BA 、AD 、DC 运动到点C 停止,点Q 沿BC 运动到C 点停止,两点运动时的速度都是1cm/s,而当点P 到达点A 时,点Q(第8题)正好到达点C .设P 点运动的时间为(s)t ,BPQ △的面积为 y 2(cm ).下图中能正确表示整个运动中y 关于t 的函数关系的大致图象是HGF EDC BAOB (C )A (D )A (D )B (C )A (D )B (C )A (D )B (C )EACD A.B.C.D.11.(北京09)8. 如图,C为⊙O直径AB上一动点,过点C的直线交⊙O于D、E两点,且∠ACD=45°,DF⊥AB于点F,EG⊥AB于点G,当点C在AB上运动时,设AF=x,DE=y,下列中图象中,能表示y与x的函数关系式的图象大致是12.(丰台二)8.如图,在矩形ABCD中,AB=3,BC=4,点P在BC边上运动,联结DP,过点A作AE⊥DP,垂足为E,设DP=x,AE=y,则能反映y与x之间函数关系的大致图象是A.B.C.D.13.(西城二)8.已知关于x的一次函数11()y k xk k=-+,其中实数k满足0 < k <1,当自变量x在1≤x≤2的范围内变化时,此函数的最大值为A. 1B. 2C.kD. 12kk-14.(昌平二)8.当10122x-≤≤时,二次函数223y x x=--的最小值为A.4-B.154-C.12-D.1215.参考下面福娃们的讨论,请你解该题,你选择的答案是( )贝贝:我注意到当x=0时,y=m >0.晶晶:我发现图象的对称轴为x=21. 欢欢:我判断出x 1<a <x 2.迎迎:我认为关键要判断a -1的符号. 妮妮:m 可以取一个特殊的值.16.(朝阳一)12. 已知抛物线22)1(2m x m x y ++-=与x 轴的两个交点的 横坐标均为整数,且m <5,则整数m 的值为 .17.(朝阳二)8.如图,在ABC △中,AB=15,AC=12,BC=9,经过点C 且与 边AB 相切的动圆与CB 、CA 分别相交于点E 、F ,则线段EF 长度的最小值是A .512 B .536C .215D .8 18.(密云二)8.如图3,已知EF 是O 的直径,把A ∠为60的直角三角板ABC 的一条直角边BC 放在直线EF 上,斜边AB 与 O 交于点P ,点B 与点O 重合.将三角板ABC 沿OE 方 向平移,使得点B 与点E 重合为止.设POF x ∠=,则x 的取值范围是( ) A .3060x ≤≤ B .3090x ≤≤ C .30120x ≤≤D .60120x ≤≤19.(宣武二)8.如图,在Rt △ABC 中,AB AC =,D 、E 是斜边BC 上两点,且∠DAE =45°,将△ADC绕点A 顺时针旋转90︒后,得到△AFB ,连接EF ,下列结论: ①△AED ≌△AEF ; ②△ABE ∽△ACD ;③BE DC DE +=; ④222BE DC DE +=其中一定正确的是A .②④B .①③C .②③D .①④(第8题)(第8题图)A B CD E F A 图3A 4A 2A 3A 120.(东城一)12.按一定规律排列的一列数依次为:1111112310152635,,,,,……,按此规律排列下去,这列数中的第9个数是 .21.(昌平一)12.一组按规律排列的式子:3579234,,,,x x x x y y y y--(0≠xy ), 其中第6个式子是 ,第n 个式子是 (n 为正整数).22.(08北京)12.一组按规律排列的式子:2b a -,53b a ,83b a -,114b a,…(0ab ≠),其中第7个式子是 ,第n 个式子是 (n 为正整数).23.(崇文一)12.一组按规律排列的数:2,0,4,0,6,0,…,其中第7个数是 , 第n 个数是 (n 为正整数).24.(房山二)12.填在下面三个田字格内的数有相同的规律,根据此规律,请填出图4中的数字.5675320531108975图1 图2 图3 图4 25.(海淀二)12.如图,将边长为),,,( 32121=+n n的正方形纸片从左到右顺次摆放,其对应的正方形的中心依次为A 1, A 2, A 3, ….①若摆放前6 个正方形纸片,则图中被遮盖的线段(虚线部分) 之和为 ;②若摆放前n (n 为大于1的正整数)个正方形纸片,则图中被遮盖的线段(虚线部分)之和为 .26.(海淀一)12.如图,在平面直角坐标系xoy 中, A (-3,0),B (0,1),形状相同的抛物线C n (n =1, 2, 3, 4, …) 的顶点在直线AB 上,其对称轴与 x 轴的交点的横坐标依次为2,3,5,8,13, …,根据上述规律,抛物线C 2的顶点坐标为 ; 抛物线C 8的顶点坐标为 .27.(西城二)12. 如图,在平面直角坐标系xOy 中,1B (0,1),2B (0,3),3B (0,6),4B (0,10),…,以12B B 为对角线作第一个正方形1112A B C B ,以 23B B 为对角线作第二个正方形2223A B C B ,以34B B 为对角线作第三个正方形3334A B C B ,…,如果所作正方形的对角线1n n B B +都在 y 轴上,且1n n B B +的长度依次增加1个单位,顶点n A 都在第一象 限内(n ≥1,且n 为整数).那么1A 的纵坐标为 ;用n 的代数式表示n A 的纵坐标: .28.(朝阳二)12.如图,在平面直角坐标系中,一颗棋子从点P 处开始跳动,第一次跳到点P 关于x 轴的对称点1P 处,接着跳到点1P 关于y 轴 的对称点 2P 处,第三次再跳到点2P 关于原点的对称点处,…, 如此循环下去.当跳动第2009次时,棋子落点处的坐标是 .29.(顺义二)12. 如图,△ABC 中,∠A=96°,作BC 的延长线CD,∠ABC 与∠ACD 的平分线相交于1A 点, 1A BC ∠与1ACD ∠的平分线相交于2A 点,依次类推,3A BC ∠与3A CD ∠的平分线相交于4A 点,则4A ∠的度数是 .30.(崇文二)12.观察下列图形的排列规律(其中☆,□,●分别表示五角星、正方形、圆).●□☆●●□☆●□☆●●□☆●若第一个图形是圆,则第2009图形 是 (填名称).31.(北京09)12. 如图,正方形纸片ABCD 的边长为1,M 、N 分别是AD 、BC 边上的点,将纸片的一角沿过点B 的直线折叠,使A 落在MN 上,落点记为A ′,折痕交AD 于点E,若M 、N 分别是AD 、BC 边的中点,则A ′N= ; 若M 、N 分别是AD 、BC 边的上距DC 最近的n 等分点(2n ≥,且n 为整数),则A ′N= (用含有n 的式子表示) A .12B .13 C . 14 D . 16(第12题)A 2A 1DCB A(第11题)(第12题) D32.(东城二)8.如图a 是长方形纸带,∠DEF=20°,将纸带沿EF 折叠成图b ,再沿BF 折叠成图c ,则图c 中的∠CFE 的度数是A .110°B .120°C .140°D .150°33.(东城二)11.如图,宽为2 cm 的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则该圆的半径为 cm.34.(东城二)12. 如图,矩形ABCD 中,由8个面积均为1的小正方形组成的L 型模板如图放置,则矩形ABCD 的周长为 _.35.(西城一)12. 在Rt △ABC 中,∠ACB=90°,BC <AC ,若214BC AC AB ⋅=, 则∠A = °.36.(昌平二)12.如图,正方形ABCD 的面积为1,M 是AB 的中点,连接AC 、DM ,则图中阴影部分的面积是 . 37.(怀柔二)12.如图5,将直角边长为5cm 的等腰直角ABC △绕点A 逆时针旋转15后得到AB C ''△,则图中阴影部分的面积是 2cm .38.(宣武二)12. 如图,OA=OB ,A 点坐标是(,OB 与x 轴正方向夹角为45︒,则B 点坐标是 .AB 与y 轴交于点C ,若以OC 为轴,将OBC ∆沿OC 翻折,B 点落在第二象限内B '处,则BB '的长度为 .图a A D A C B A E A F A AC A C B 图c B '(图5)。
2009年北京各区中考一模、二模试题分类汇编 概率与统计
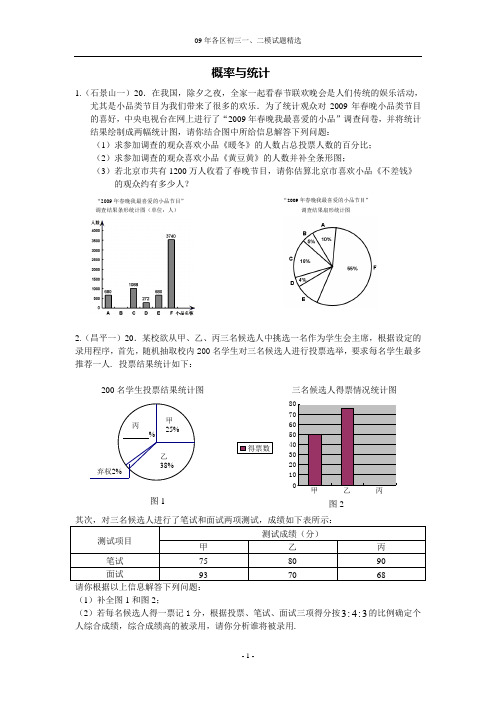
“2009年春晚我最喜爱的小品节目” 调查结果条形统计图(单位:人)“2009年春晚我最喜爱的小品节目” 调查结果扇形统计图概率与统计1.(石景山一)20.在我国,除夕之夜,全家一起看春节联欢晚会是人们传统的娱乐活动,尤其是小品类节目为我们带来了很多的欢乐.为了统计观众对2009年春晚小品类节目的喜好,中央电视台在网上进行了“2009年春晚我最喜爱的小品”调查问卷,并将统计结果绘制成两幅统计图,请你结合图中所给信息解答下列问题:(1)求参加调查的观众喜欢小品《暖冬》的人数占总投票人数的百分比; (2)求参加调查的观众喜欢小品《黄豆黄》的人数并补全条形图; (3)若北京市共有1200万人收看了春晚节目,请你估算北京市喜欢小品《不差钱》 的观众约有多少人?2.(昌平一)20.某校欲从甲、乙、丙三名候选人中挑选一名作为学生会主席,根据设定的录用程序,首先,随机抽取校内200名学生对三名候选人进行投票选举,要求每名学生最多推荐一人. 投票结果统计如下:200名学生投票结果统计图 三名候选人得票情况统计图请你根据以上信息解答下列问题: (1)补全图1和图2;(2)若每名候选人得一票记1分,根据投票、笔试、面试三项得分按3:4:3的比例确定个人综合成绩,综合成绩高的被录用,请你分析谁将被录用.弃权2%乙38% 丙%甲25% 图1 图2 乙%图中的各部分都只含最低分不含最高分3.(朝阳一)19. 通常情况居民一周时间可以分为常规工作日(周一至周五)和常规休息日(周六和周日). 居民一天的时间可以划分为工作时间、个人生活 必须时间、家务劳动时间和可以自由支配时间等 四部分. 2008年5月,北京市统计局在全市居民 家庭中开展了时间利用调查,并绘制了统计图: 图②(1)由图①,调查表明,我市居民人均常规工作日工作时间占一天时间的百分比为 ;(2)调查显示,看电视、上网、健身游戏、读书看报是居民在可自由支配时间中的主要活动方式,其中平均每天上网占可自由支配时间的12%,比读书看报的时间多8分钟. 请根据以上信息补全图②;(3)由图②,调查表明,我市居民在可自由支配时间中看电视的时间最长. 根据这一信息,请你在可自由支配时间的利用方面提出一条建议:___ ____________.4.(崇文一)20. 九年级一班的两位学生对本班的一次数学成绩(分数取整数,满分为100分)进行了一次初步统计,80分以上(含80分)有17人,但没有满分,也没有低于30分的.为更清楚了解本班的考试情况,他们分别用两种方式进行了统计分析,如图1和图2所示.请根据图中提供的信息回答下列问题:(I )该班60分以下(不含60分)的有 人;图①北京市居民每天可自由支配时间利用情况北京市居民人均常规工作日时间利用情况5.(房山一)20.今年4月,国民体质监测中心等机构开展了青少年形体测评.专家组随机抽查了某市若干名初中学生坐姿、站姿、走姿的好坏情况.我们对专家的测评数据作了适当处理(如果一个学生有一种以上不良姿势,我们以他最突出的一种作记载),并将统计结果绘制了如下两幅不完整的统计图,请你根据图中所给信息解答下列问题: (1)请将两幅统计图补充完整;(2)在这次形体测评中,一共抽查了 名学生,如果全市有10万名初中生,那么全市初中生中,三姿良好的学生约有 人; (3)根据统计结果,请你简单谈谈自己的看法.16.(密云一)21. 国家教委规定“中小学生每天在校体育活动时间不低于1小时”.为此,某地区今年初中毕业生学业考试体育学科分值提高到40分,成绩记入考试总分.某中学为了了解学生体育活动情况,随机调查了720名毕业班学生,调查内容是:“每天锻炼是否超过1小时及未超过1小时的原因”,所得的数据制成了的扇形统计图和频数分布直方图.根据图示,解答下列问题:(1)若在被调查的学生中随机选出一名学生测试其体育成绩,选出的恰好是“每天锻炼 超过1小时”的学生的概率是多少?(2)“没时间”的人数是多少?并补全频数分布直方图;(3)2008年这个地区初中毕业生约为4.3万人,按此调查,可以估计2008年这个地区初中毕业生中每天锻炼未超过1小时的学生约有多少万人? (4)请根据以上结论谈谈你的看法.25 50 75 锻炼未超过1小时人数频数分布直方图原因人数不喜欢没时间其它步行44%其他 7.(门头沟一)20.阅读对人成长的影响是巨大的,联合国教科文组织把每年的4月23日确定为“世界读书日” .某校为了了解该校学生一个学期阅读课外书籍的情况,在全校范围内随机对100名学生进行了问卷调查,根据调查的结果,绘制了统计图表的一部分:一个学期平均一天阅读课外书籍所用时间统计表24515314312010080604020人数(名)时间(分钟)图2一个学期阅读课外书籍种类人数分布统计图其他 6%动漫类 25%传记类 %科普类 35%图1/本人数/一个学期阅读课外书籍数量统计图请你根据以上信息解答下列问题: (1)补全图1、图2 ;(2)这100名学生一个学期平均每人阅读课外书籍多少本?若该校共有3000名学生,请你估计这个学校学生一个学期阅读课外书籍共多少本?(3)根据统计图和统计表,请你对该校学生阅读课外书籍的情况,谈谈你的看法.8.(平谷一)20.清明节到来之前,某中学准备组织学生去烈士陵园扫墓,就该校学生如何到烈士陵园问题进行了一次调查,并将调查结果制成了表格、条形统计图和扇形统计图,请你根据图表信息完成下列各题: (1)此次共调查了多少位学生? (2)请将表格填充完整; (3)请将条形统计图补充完整.9.(顺义一)20. 在学校组织的“我的家乡知多少?”知识竞赛中,每班参加比赛的人数相同,成绩分为A B C D ,,,四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:请你根据以上提供的信息解答下列问题:(1)此次竞赛中二班成绩在C 级以上(包括C 级)的人数为 ; (2)请你将表格补充完整:(3)请从下列不同角度对这次竞赛成绩的结果进行分析: ①从平均数和中位数的角度来比较一班和二班的成绩; ②从平均数和众数的角度来比较一班和二班的成绩;③从B 级以上(包括B 级)的人数的角度来比较一班和二班的成绩.10.(通州一)20.在“六一”儿童节来临之际,初中某校开展了向山区“希望小学”捐赠图书活动,全校1000名学生每人都捐赠了一定数量的图 书.已知各年级人数分布的扇形统计图如 图(1)所示.学校为了了解各年级捐赠图 书情况,从各年级中随机抽查了200名学 生,进行捐赠图书情况的统计,绘制成如 图(2)的频数分布直方图.根据以上信息解答下列问题: (1) (2) (1)本次调查的样本是 ;(2)从图(2)中,我们可以看出人均捐赠图书最多的是; (3)随机抽查的200名学生中初三年级学生共捐赠图书多少册? (4)估计全校共捐赠图书多少册?等级一班竞赛成绩统计图 二班竞赛成绩统计图11.(延庆一)20.为了降低能源消耗,减少环境污染,国务院办公厅下发了“关于限制生产销售使用塑料购物袋的通知”(简称“限塑令”),并从2008年6月1日起正式实施.小宇同学为了了解“限塑令”后使用购物袋的情况,6月8日到某集贸市场对部分购物者进行了调查,据了解该市场按塑料购物袋的承重能力提供了0.1元,0.2元,0.3元三种质量不同的塑料袋.下面两幅图是这次调查得到的不完整的统计图(若每人每次只使用一个购物袋),请你根据图中的信息,回答下列问题: (1)这次调查的购物者总人数是 ;(2)请补全条形统计图,并说明扇形统计图中0.2元部分所对应的圆心角是 度0.3元部分所对应的圆心角是 度;(3)若6月8日到该市场购物的人数有3000人次,则该市场需销售塑料购物袋多少个?并根据调查情况,谈谈你的看法.12.(海淀一)20. 某种子培育基地用A 、B 、C 、D 四种型号的小麦种子共2 000粒进行发芽实验,从中选出发芽率高的种子进行推广.通过实验得知,C 型号种子的发芽率为94%. 根 据实验数据绘制了图1和图2两幅尚不完整的统计图.请你根据所给信息,解答下列问题: (1)D 型号种子数是 粒;(2)请你将图2的统计图补充完整;(3)通过计算说明,应选哪一个型号的种子进行推广;如果所选型号进行推广的种子共有200 000粒,估计能有多少粒种子会发芽.类别(第20题)号各种型号种子数的百分比35 %D C BA 25 %20 %13.(东城一)19.阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.每年的4月23日被联合国教科文组织确定为“世界读书日”.如图是某校全校三个年级学生人数分布扇形统计图,其中八年级人数为350人,表(1)是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题:(1)求该校九年级的人数占全校总人数的百分率.(2)求出表(1)中A B,的值.(3)该校学生平均每人读多少本课外书?表(1)14.(大兴一)20、某中学团委为汶川地震灾区组织献爱心捐献活动,小明对本班同学的捐款情况进行了统计,其中捐10元的人数占全班总人数的%40.小明还绘制了频数分布直方图.(1)请求出小明所在班级同学的人数;(2)本次捐款的中位数是____元;(3)请补齐频数分布直方图.15.(崇文二)20.端午节吃粽子是中华民族的传统习俗.五月初五早晨,妈妈为洋洋准备了四只粽子:一只香肠馅,一只红枣馅,两只什锦馅,四只粽子除内部馅料不同外,其他一切均相同.洋洋喜欢吃什锦馅的粽子.(1)请你用树状图或列表法为洋洋预测一下吃两只粽子刚好都是什锦馅的概率;(2)在吃粽子之前,洋洋准备用如图所示的转盘进行吃粽子的模拟试验(此转盘被等分成四个扇形区域,指针的位置是固定的,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置.若指针指向两个扇形的交线时,重新转动转盘),规定:连续转动两次转盘表示随机吃两只粽子,从而估计吃两只粽子刚好都是什锦馅的概率.你认为这样模拟正确吗?试说明理由.(第19题)100元10516.(西城二)19.某地一商场贴出“五一”期间的促销海报,内容如图所示.某校一个课外实践活动小组的同学在商场促销活动期间,在该商场门口随机调查了参与促销活动的部分顾客抽奖的情况,以下是根据其中200人次的抽奖情况画出的统计图的一部分:(1)补全获奖情况频数统计图;(2)求所调查的200人次抽奖的中奖率;(3)如果促销活动期间商场每天约有2 000人次抽奖,请根据调查情况估计,该商场一天送出的购物券的总金额是多少元?17.(大兴二)20、某校为组建篮球队,对甲、乙两名备选同学进行定位投篮测试,每次投10个球共投10次,甲、乙两名同学测试情况如图所示。
2009年北京各区中考一模、二模试题分类汇编 基础填空选择

BA 基础选择、填空题1.(07北京)1.3-的倒数是( )A .13-B .13C .3-D .32.(08北京)1.6-的绝对值等于( )A .6B .16C .16-D .6-3.(北京09)1. 7的相反数是A.17B.7C.17-D.7-4.(西城二)2. 27的平方根等于 A . 3B .C . 3± D. ±5.(东城一)1.计算|2009|-的结果是A.-2009 B. 12009- C. 2009 D. 120096.(海淀一) 1.-12的相反数是 A .-2 B .2 C . -12 D .127.(西城二)1. -5的绝对值等于 A . 5B . -5C . 15D . 15-8.(07北京)2.国家游泳中心-- “水立方”是北京2008年奥运会场馆之一,它的外层膜的展开面积约为260 000平方米,将260 000用科学记数法表示应为( )A .60.2610⨯B .42610⨯C .62.610⨯D .52.610⨯9.(08北京)2.截止到2008年5月19日,已有21 600名中外记者成为北京奥运会的注册记者,创历届奥运会之最.将21 600用科学记数法表示应为( )A .50.21610⨯B .321.610⨯C .32.1610⨯D .42.1610⨯10.(北京09)2. 改革开放以来,我国国内生产总值由1978年的3645亿元增长到2008年的300670亿元。
将300670用科学记数法表示应为A.60.3006710⨯ B.53.006710⨯ C.43.006710⨯ D.430.06710⨯11.(东城一)3.我国2008年国内生产总值超过300000亿元,比上一年增长9%.将数据300000亿元用科学记数法表示为A.5310⨯亿元 B.43010⨯亿元 C.60.310⨯亿BA元 D.4310⨯亿元12.(海淀一)2.2009年北京启动了历史上规模最大的轨道交通投资建设,预计北京市轨道交通投资将达到51 800 000 000元人民币. 将51 800 000 000用科学记数法表示正确的是A .51.8×109B .5.18×1010C .0.518×1011D .518×10813.(07北京)3.如图,Rt ABC △中,90ACB ∠=°,DE 过点C 且平行于AB ,若35BCE ∠=°,则A ∠的度数为( )A .35°B .45°C .55°D .65°14.(海淀一)3.如图,已知AB ∥CD ,点E 在CD 上,BC 平分∠ABE ,若∠C =25°,则∠ABE 的度数是A .12.5°B .25°C .50°D .60°15.(08北京)3.若两圆的半径分别是1cm 和5cm ,圆心距为6cm ,则这两圆的位置关系是( )A .内切B .相交C .外切D .外离16.(东城一)6.如图,点O 在⊙A 外,点P 在线段OA 为半 径的⊙O 与⊙A 的位置关系不可能...是下列中的 A.外离. B.相交. C.外切. D.内含.17.(海淀一) 5.若两圆的半径分别为4和3,圆心距为1,则这两圆的位置关系是A .内含B .内切C .相交D .外切18.(西城二)3. 若两圆的半径分别为1cm 和5cm ,圆心距为4cm ,则这两圆的位置关系是 A . 内切B . 相交C . 外切D . 外离19.(08北京)5.若一个多边形的内角和等于720,则这个多边形的边数是( ) A .5 B .6 C .7 D .820.(西城二)5. 若圆锥的底面半径为3cm ,母线为6cm ,则圆锥的侧面积等于 A .236π cm B .227π cm C .218π cm D .29π cm 21.(西城二)7.如图,菱形ABCD 中 ,∠A=30°,AD=2,若菱形FBCE 与 菱形ABCD 关于BC 所在直线对称,则平行线AD 与FE 间的距离等于AB C . 2 D . 422.(北京09)3. 若右图是某几何体的三视图,则这个几何体是E ABC DBA A.圆柱 B.正方体C.球D.圆锥主视图 左视图 俯视图 23.(东城一)8. 在正方体的表面上画有如图⑴中所示的粗线,图⑵ 是其展开图的示意图,但只在A 面上画有粗线,那么 将图⑴中剩余两个面中的粗线画入图⑵中,画法正确的是24.(北京09)4. 若一个正多边形的一个外角是40°,则这个正多边形的边数是。
2009中考各区一模试题

二类卷(51—44) 46—39
三类卷(43—36) 38—31
四类卷(35—0) 30—0
书写(5 分)
总分
阅卷人
六、作文
题目:
100
200
300
宣武区 2008—2009 学年度第一次质量检测 初三语文试卷(第Ⅱ卷) 第 1 页 (共 2 页)
400 500
600 700
宣武区 2008—2009 学年度第一次质量检测 初三语文试卷(第Ⅱ卷) 第 2 页 (共 2 页)
北京市宣武区 2008—2009 学年度第一次质量检测
初三语文试卷答题卡(第Ⅱ卷)
2009.5
注意 1.答题前务必将学校、班级、姓名、考试编号等信息填写在密封线内的规定位置。 事项 2.在对应答题区域内作答,未在对应的答题区域内作答或超出答题区域均不给分。
项目 等级
内容、表达(55 分)
2008—2009 学年度第一次质量检测 初三语文试卷(第Ⅱ卷) 第 3 页 (共 2 页)
2009年海淀区九年级语文一模试卷及答案

2009 年海淀区九年级语文一模试卷及答案一、选择。
下面各题均有四个选项,此中只有一个切合题意,选出答案后在答题纸上用铅笔把对应题目的选项字母涂黑涂满。
(共 12 分。
每题 2 分)1.以下词语中加点字的读音完整正确的一项为哪一项A.狭小( ài )模样(mó拗( niù )庸人自扰(qǐ))执B.顿然( cù然无恙( yàn )ɡ)振作( sǒu)刊载(zǎi)安C.自夸(x ǔ)褴褛(lán)倔强(jué)锐不行当( dǎng)D.俯视((pì kàn )单薄(bó))惩恶扬善( chénɡ)怪癖2.对横线处选填汉字判断有误的一项为哪一项A.索 (检,捡 )判断:“检”有“查”的意思,而“捡”有“拾取”的意思,所以横线处应填“检” 。
B.赏 (鉴,签 )判断:“鉴”有“认真看,审查”的意思,而“签”有“写姓名或画上记号”的意思,所以横线处应填“鉴”。
C.不屑置(辩,辨 )判断:“辩”有“辩白,争辩”的意思,而“辨”有“鉴别,分辨”的意思,所以横线处应填“辨” 。
D.专心志(至,致)判断:“至”有“到”的意思,而“致”有“集中(力量、意志等)于某一方面”的意思,所以横线处应填“致”。
3.联合语境,在以下句子中的横线处填写词语正确的一项是①丰富的地区文化孕育了这个地区人民的道德品性。
他们推行“百善孝为先”的信条 ,珍惜生命,友善乡里,秉着忠君爱国的传统 ,讲究义气。
,中华民族的儒家文化思想中的“孝、爱、忠、义”已经内化到他们的精神世界中间了。
②经过艰辛的高强度新兵训练,这些被冠上“骄娇”标签的 90 后新兵们,不但炼就了一副钢筋铁骨,并且磨砺了意志,堪称。
90 后新兵为我们显现了新一代子弟兵优秀的风采。
北京市海淀区20092010年九年级第一学期期末

北京市海淀区2009-2010年九年级第一学期期末练习语文试卷2010.1第I卷(共60分)1.第I卷共五道大题,23道小题,包括选择、填空、综合性学习、文言文阅读和现代文阅读。
2.请审清题干要求,仔细作答。
一、选择。
下面各题均有四个选项。
其中只有一个符合题意。
(共10分。
每小题2分)1.下列词语中加点字的读音完全正确的一项是A.字帖(tiâ)怪癖(pì)颠簸(bǒ)安然无恙(yàng)B.沟壑(hâ)联袂(mâi)祈祷(qǐ)迥然不同(jiǒng)C.褴褛(lǚ)瞥见(piē)勋章(xūn)牵强附会(qiáng)D.氛围(fēn)拮据(jū)恣睢(suī)断壁残垣(yuán)2.下列词语书写完全正确的一项是A.奔驰待遇追溯明察秋豪B.和谐秘决闲暇焕然一新C.干燥蔓延书籍无精打采D.婉约吟诵尊命鸦雀无声3.下列句子中加点词语使用有误的一项是A.作为中国进入二十一世纪第一项重大考古发现,金沙遗址成为中华文明源远流长的又一见证。
B.今年冬季,我国在部分高校开始进行征集新兵的试点工作,地方政府各行其是,制订了许多富有特色的征兵方案。
C.马房区街道办事处为空巢老人举办联谊活动,小区里锣鼓喧天,大家载歌载舞,老人们感到无比的快乐。
D.因为“尺有所短,寸有所长”,所以大凡聪明的人总是善于学习别人的长处,以弥补自身的不足。
4.下列作家作品表述有误的一项是A.《关雎》选自《诗经》。
《诗经》是我国最早的一部诗歌总集,收入周代诗歌305篇。
B.《游山西村》《惠崇(春江晚景)》《江城子密州出猎》的作者均为北宋文学家苏轼。
C.《我的叔叔于勒》这篇小说的主人公是菲利普夫妇,作者是法国作家莫泊桑。
D.《故乡》选自《呐喊》,作者是鲁迅。
我们还学过他的小说《社戏》《孔乙己》。
5.结合语境,填入横线处最恰当的一项是十一届全运会会徽构思巧妙,设计新颖,以11个“竞技人形”为主要构成元素。
2009北京海淀区一模试卷

盐城市明达中学2011-2012学年度第二学期期中考试九年级物理试题(总分:100分 考试时间:100分钟)命题人: 审核人:注意事项:1.本试卷第一部分为选择题,共24分,第二部分为非选择题,共76分.全卷满分100分,考试时间100分钟.考生答题全部答在答题卡上,答在本试卷上无效.2.答题前,考生务必将自己的姓名、学校、考号用0.5毫米黑色墨水签字笔填写在答题卡相对应的位置上,并认真填涂考号下方的涂点.3.答选择题必须用2B 铅笔将答题卡上对应的答案标号涂黑.如需改动,请用橡皮擦干净后,再选涂其他答案.答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡的指定位置,在其他位置答题一律无效.4.作图题必须用2B 铅笔作答,并请加黑、加粗.第一部分 选择题(共24分)一、选择题(本题共12小题,每小题2分,共24分。
每小题给出的四个选项中只有一个....选项正确)1.太阳是人类的“能源之母”,以下能源来自于太阳能的是A .核能B .地热能C .潮汐能D .水能2.新年联欢会上,一位同学手持一面小鼓,置于点燃的蜡烛附近,鼓面面对烛火,敲响小鼓,周围同学看到烛火随着鼓声舞动。
对这一现象解释不正确的是A .鼓声是由鼓面振动产生的B .烛火舞动说明声音可以传递能量C .鼓面振动产生的是超声波D .周围同学听到的鼓声是由空气传来的3.如图1所示的四种情景中,属于光的直线传播的是4.两盆水里面都有没熔化的冰块,一盆放在阳光下,一盆放在阴凉处,在盆内冰块均未熔化完前,两盆水的水温相比A .在阴凉处的那盆水的温度高B .两盆水温度一样高C .在阳光下的那盆水的温度高D .无法确定5.下列数据最接近生活实际的是A .一个苹果的重约0.15NB .物理课本长约0.27mC .教室内日光灯正常工作时的电流大约2AD .一个中学生的体积5m 36.关于温度、内能和热量,下列说法中正确的是A. 物体的温度升高,它含有的热量越多B. 物体吸收热量,它的内能就增加图1A .镜中花 D .用放大镜看物体B .钢笔错位C .手影 玻璃砖L 12 3 C. 物体的内能越多,放热一定越多 D. 物体的内能增加,它的温度一定升高7.通电导线周围存在磁场,但磁场看不见、摸不着,奥斯特通过放在直导线下方的小磁针在导线通电时发生偏转,得出通电导线的周围存在磁场的结论,这种研究方法叫做“转换法”。
2009年北京市海淀区初三年级一模考试

海淀区九年级一模考试数 学 2009.5一、选择题(本题共32分,每小题4分)在下列各题的四个备选答案中,只有一个是正确的. 1.-12的相反数是 A .-2 B .2 C . -12 D .122.2009年北京启动了历史上规模最大的轨道交通投资建设,预计北京市轨道交通投资将达到51 800 000 000元人民币. 将51 800 000 000用科学记数法表示正确的是 A .51.8×109 B .5.18×1010 C .0.518×1011 D .518×1083.如图,已知AB ∥CD ,点E 在CD 上,BC 平分∠ABE , 若∠C =25°,则∠ABE 的度数是A .12.5°B .25°C .50°D .60°4. 在樱桃采摘园,五位游客每人各采摘了一袋樱桃,质量分别为(单位:千克):5,2,3,5,5,则这组数据的平均数和中位数分别为A .4,3B .3,5C .4,5D .5,55.若两圆的半径分别为4和3,圆心距为1,则这两圆的位置关系是A .内含B .内切C .相交D .外切6.袋子中有5个红球,3个蓝球,它们只有颜色上的区别. 从袋子中随机取出一个球, 取出蓝球的概率是A .53 B .83 C .85 D .81 7.把代数式a a a 4423+-分解因式,下列结果中正确的是A .22)(-a aB .)(42-a aC .22)(+a aD .))((22-+a a a 8.右图是画有一条对角线的平行四边形 纸片ABCD ,用此纸片可以围成一个 无上下底面的三棱柱纸筒, 则所围成 的三棱柱纸筒可能是E ABC D ADCBA B C D二、填空题(本题共16分, 每小题4分)9.若实数x , y 满足0322=-+-)(y x ,则代数式xy -x 2的值为 . 10.已知反比例函数y =xk的图象经过点(2,3), 则k = . 11.如图,在正方形网格中,每个小正方形的边长均为1,△ABC 的三个顶点均在格点上,则BC 边上的高为 . 12.如图,在平面直角坐标系xoy 中, A (-3,0),B (0,1),形状相同的抛物线C n (n =1, 2, 3,4, …) 的顶点在直线AB 上,其对称轴与 x 轴的交点的横坐标依次为2,3,5,8,13…,根据上述规律,抛物线C 2的顶点坐标 为 ; 抛物线C 8的顶点坐标为 .三、解答题(本题共30分, 每小题5分) 13.计算:05)-π(sin )(+︒-+-60212211.14.解不等式组:⎪⎩⎪⎨⎧<>-.,)(13112x x x15.已知:如图,点B 、E 、F 、C 在同一条直线上,AB =DE ,BE =CF ,∠B =∠CED . 求证: AF =DC .16. 计算:22111x x x ---.17.已知直线l 与直线y =-2x +m 交于点(2,0), 且与直线y =3x 平行,求m 的值及直线l的解析式.18. 如图,在梯形ABCD 中, AB //DC , ∠D =90︒, ∠ACD =30︒ ,① ② E DCB AF A B CDA BC B (C )A (D )A (D )B (C )A (D )B (C )A (D )B (C )C BA AB =12, BC =10, 求AD 的长.四、解答题(本题共20分, 第19题5分,第20题6分,第21题5分,第22题4分) 19.如图,已知AB 为⊙O 的弦,C 为⊙O 上一点,∠C =∠BAD ,且BD ⊥AB 于B .(1)求证:AD 是⊙O 的切线;(2)若⊙O 的半径为3,AB =4,求AD 的长.20. 某种子培育基地用A 、B 、C 、D 四种型号的小麦种子共2 000粒进行发芽实验,从 中选出发芽率高的种子进行推广.通过实验得知,C 型号种子的发芽率为94%. 根 据实验数据绘制了图1和图2两幅尚不完整的统计图.请你根据所给信息,解答下 列问题:(1)D 型号种子数是 粒; (2)请你将图2的统计图补充完整;(3)通过计算说明,应选哪一个型号的种子进行推广;如果所选型号进行推广的种子共有200 000粒,估计能有多少粒种子会发芽.图1 图221. 甲、乙同学帮助学校图书馆清点一批图书,已知甲同学清点200本图书与乙同学清 点300本图书所用的时间相同,且甲同学平均每分钟比乙同学少清点10本,求甲同 学平均每分钟清点图书的数量.22.我们给出如下定义:如果四边形中一对顶点到另一对顶点所连对角线的距离相等,则把这对顶点叫做这个四边形的一对等高点.例如:如图1,平行四边形ABCD 中,可证点A 、C 到BD 的距离相等,所以点A 、C 是平行四边形ABCD 的一对等高点,同理可知点B 、D也是平行四边形ABCD 的一对等高点. 图1(1)如图2,已知平行四边形ABCD , 请你在图2中画出一个只有一对等高点的四边形ABCE (要求:画出必要的辅助线);(2)已知P 是四边形ABCD 对角线BD 上任意一点(不与B 、D 点重合),请分别探究图3、图4中S 1, S 2, S 3, S 4四者之间的等量关系(S 1, S 2, S 3, S 4分别表示△ABP , △CBP , △CDP , △ADP 的面积):① 如图3,当四边形ABCD 只有一对等高点A 、C 时,你得到的一个结论是 ;号7000各种型号种子数的百分比35 %D C B A25 %20 %② 如图4,当四边形ABCD 没有等高点时,你得到的一个结论是 .图2 图3 图4五、解答题(本题共22分, 第23题7分,第24题7分,第25题8分)23.已知: 关于x 的一元一次方程kx =x +2 ①的根为正实数,二次函数y =ax 2-bx +kc (c ≠0)的图象与x 轴一个交点的横坐标为1. (1)若方程①的根为正整数,求整数k 的值;(2)求代数式akcabb kc +-22)(的值;(3)求证: 关于x 的一元二次方程ax 2-bx +c =0 ②必有两个不相等的实数根.24.在课外小组活动时,小慧拿来一道题(原问题)和小东、小明交流.原问题:如图1,已知△ABC , ∠ACB =90︒ , ∠ABC =45︒,分别以AB 、BC 为边向外作△ABD 与△BCE , 且DA =DB , EB =EC ,∠ADB =∠BEC =90︒,连接DE 交AB 于点F . 探究线段DF 与EF 的数量关系.小慧同学的思路是:过点D 作DG ⊥AB 于G ,构造全等三角形,通过推理使问 题得解.小东同学说:我做过一道类似的题目,不同的是∠ABC =30︒,∠ADB =∠BEC =60︒. 小明同学经过合情推理,提出一个猜想,我们可以把问题推广到一般情况. 请你参考小慧同学的思路,探究并解决这三位同学提出的问题: (1)写出原问题中DF 与EF 的数量关系;(2)如图2,若∠ABC =30︒,∠ADB =∠BEC =60︒,原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明;(3)如图3,若∠ADB =∠BEC =2∠ABC , 原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明.图1 图2 图325.已知抛物线经过点 A (0, 4)、B (1, 4)、C (3, 2),与x 轴正半轴交于点D .B A D F DAC E F B E F B AD A BC D S 2S 1S 4S 3S 4S 3S 2AB C P DA B C P D S 1(1)求此抛物线的解析式及点D的坐标;(2)在x轴上求一点E, 使得△BCE是以BC为底边的等腰三角形;(3)在(2)的条件下,过线段ED上动点P作直线PF//BC, 与BE、CE分别交于点F、G,将△EFG沿FG翻折得到△E'FG. 设P(x, 0), △E'FG与四边形FGCB 重叠部分的面积为S,求S与x的函数关系式及自变量x的取值范围.数学参考答案及评分标准 2009.5一、选择题(本题共32分,每小题4分)1.D 2.B 3. C 4. C 5.B 6.B 7. A 8. C 二、填空题(本题共16分, 每小题4分)9. 2 10.6 11.225 12. (3,2);(55,358) 三、解答题(本题共30分, 每小题5分).5)-π(sin )(.03312323226021221131+=+⨯-+=+︒-+-解: 14. 解:解不等式①,得 x >2; ……………………………………………………2分解不等式②,得x <3. ……………………………………………………4分所以原不等式组的解集为 2<x <3. ………………………………………………5分15.证明:∵ BE =CF ,∴ BE +EF = CF + EF .∴ BF =EC . …………………1分 在△ABF 和△DEC 中, ⎪⎩⎪⎨⎧=∠=∠=,,,EC BF DEC B DE AB …………………3分 ∴ △ABF ≌△DEC . …………………………………………………………4分 ∴ AF =DC . …………………………………………………………5分16. 解: 22111x x x ---21(1)(1)1x x x x =-+-- …………………………………………1分 2(1)(1)(1)x x x x -+=+- …………………………………………………………3分1(1)(1)x x x -=+- …………………………………………………………4分 11x =+. …………………………………………………………5分 17.解:依题意,点(2,0)在直线y =-2x +m 上,∴ 0=-2×2+m . …………………………………………………………………1分 ∴ m =4. …………………………………………………………………………2分 由直线l 与直线y =3x 平行,可设直线l 的解析式为y =3x +n . ………………3分 ∵ 点(2,0)在直线l 上,E DCB A F ………………………………………………………5分………………………………………………………4分∴ 0=3×2+n .∴ n =-6. …………………………………………………………………4分 故直线l 的解析式为 y =3x -6. …………………………………………………5分 18. 解: 过点B 作BE ⊥AC 于E , 则∠AEB =∠BEC = 90︒. …………………………1分∵ AB //DC ,∴ ∠BAE=∠ACD =30︒ .又∵ AB =12,∴ EB =AB 21=6, AE =3630=︒⋅cos AB . ………………………………………2分 在Rt △BEC 中, ∠BEC =90︒ ,∴ EC =.86102222=-=-BE BC …………………………………………3分 ∴ AC =AE +EC =36+8. ……………………………………………………4分 在Rt △ADC 中,∠D =90︒, ∠ACD =30︒ ,∴ AD =.43321+=AC ……………………………………………………5分 四、解答题(本题共20分, 第19题5分,第20题6分,第21题5分,第22题4分) 19.(1)证明: 如图, 连接AO 并延长交⊙O 于点E , 连接BE , 则∠ABE =90°.∴ ∠EAB +∠E =90°. ……………………1分 ∵ ∠E =∠C , ∠C =∠BAD , ∴ ∠EAB +∠BAD =90°.∴ AD 是⊙O 的切线. ……………………2分(2)解:由(1)可知∠ABE =90°.∵ AE =2AO =6, AB =4, ∴ 5222=-=AB AE BE . …………………………………………………3分∵ ∠E=∠C =∠BAD , BD ⊥AB ,∴ .cos cos E BAD ∠=∠ …………………………………………………4分 ∴ .AEBEAD AB = .6524=AD 即∴ 5512=AD . …………………………………………………5分 20.解:(1)400. ………………………………………………………1分 (2)C 型号种子的发芽数为470粒. 图略. ……………………………………3分 (3)A 型号种子的发芽率为%%90352000630=⨯,B 型号种子的发芽率为%.%592202000370=⨯,D 型号种子的发芽率为%%95202000380=⨯,C 型号发芽率为94%.∴ 应选D 型号的种子进行推广. …………………………………………5分D CB A E200 000×95%=190 000(粒).估计能有190 000粒种子会发芽. …………………………………………6分 21. 解:设甲同学平均每分钟清点图书x 本,则乙同学平均每分钟清点图书(x+10)本,依题意,得10300200+=x x . ………………………………………………2分 解得x =20. ……………………………………………………………………3分 经检验x =20是原方程的解,且符合题意. ………………………………………4分 答:甲同学平均每分钟清点图书205分22.解:(1)比如: 或 1分(2)①S 1 +S 4 = S 2 +S 3, S 1 +S 3 = S 2 +S 4或S 1⋅S 3 = S 2⋅S 4或3241S S S S =等. ……………2分 ②S 1⋅S 3 = S 2⋅S 4或3421S S S S =等. ……………………………………………4分 五、解答题(本题共22分, 第23题7分,第24题7分,第25题8分) 23.(1)解:由 kx =x +2,得(k -1) x =2.依题意 k -1≠0.∴ 12-=k x . ……………………………………………………………1分 ∵ 方程的根为正整数,k 为整数, ∴ k -1=1或k -1=2.∴ k 1= 2, k 2=3. ……………………………………………………………2分(2)解:依题意,二次函数y =ax 2-bx +kc 的图象经过点(1,0), ∴ 0 =a -b +kc , kc = b -a .∴222222222aab abb a ab b a b a ab b a b akc ab b kc -+-+-=-+--=+-)()()( =.122-=--a ab aba …………………………3分 (3)证明:方程②的判别式为 Δ=(-b )2-4ac = b 2-4ac . 由a ≠0, c ≠0, 得ac ≠0.( i ) 若ac <0, 则-4ac >0. 故Δ=b 2-4ac >0. 此时方程②有两个不相等的实数根. ………………………………………………………………4分 ( ii ) 证法一: 若ac >0, 由(2)知a -b +kc =0, 故 b =a +kc .Δ=b 2-4ac = (a +kc )2-4ac =a 2+2kac +(kc )2-4ac = a 2-2kac +(kc )2+4kac -4ac=(a -kc )2+4ac (k -1). …………………………………………………5分 ∵ 方程kx =x +2的根为正实数, ∴ 方程(k -1) x =2的根为正实数.EA BCD由 x >0, 2>0, 得 k -1>0. …………………………………………………6分 ∴ 4ac (k -1)>0. ∵ (a -kc )2≥0,∴Δ=(a -kc )2+4ac (k -1)>0. 此时方程②有两个不相等的实数根. …………7分 证法二: 若ac >0,∵ 抛物线y =ax 2-bx +kc 与x 轴有交点, ∴ Δ1=(-b )2-4akc =b 2-4akc ≥0. (b 2-4ac )-( b 2-4akc )=4ac (k -1).由证法一知 k -1>0,∴ b 2-4ac > b 2-4akc ≥0.∴ Δ= b 2-4ac >0. 此时方程②有两个不相等的实数根. …………………7分 综上, 方程②有两个不相等的实数根.24. 解: (1)DF= EF . ………………………………………………………………1分(2)猜想:DF= FE .证明:过点D 作DG ⊥AB 于G , 则∠DGB =90︒. ∵ DA =DB , ∠ADB =60︒. ∴ AG =BG , △DBA 是等边三角形.∴ DB =BA .∵ ∠ACB =90︒ , ∠ABC =30︒,∴ AC =21AB =BG . …………………………………………………………2分 ∴ △DBG ≌△BAC .∴ DG =BC . ……………………………………………………3分 ∵ BE=EC , ∠BEC =60︒ , ∴ △EBC 是等边三角形. ∴ BC =BE , ∠CBE =60︒.∴ DG = BE , ∠ABE =∠ABC +∠CBE =90︒ . ∵ ∠DFG =∠EFB , ∠DGF =∠EBF , ∴ △DFG ≌△EFB .∴ DF= EF . ……………………………………………………4分(3)猜想:DF= FE .证法一:过点D 作DH ⊥AB 于H , 连接HC , HE , HE 交CB 于K , 则∠DHB =90︒. ∵ DA =DB ,∴ AH =BH , ∠1=∠HDB .∵ ∠ACB =90︒, ∴ HC =HB .∵ EB =EC , HE =HE ,∴ △HBE ≌△HCE . ……………………………5分 ∴ ∠2=∠3, ∠4=∠BEH .∴ HK ⊥BC . ∴ ∠BKE =90︒. ……………………………6分 ∵ ∠ADB =∠BEC =2∠ABC , ∴ ∠HDB =∠BEH =∠ABC .∴ ∠DBC =∠DBH +∠ABC =∠DBH +∠HDB =90︒,GDABCFE K H BF E CA D 2431∠EBH =∠EBK +∠ABC =∠EBK +∠BEK =90︒. ∴ DB //HE , DH //BE .∴ 四边形DHEB 是平行四边形.∴ DF =EF . ………………………………………………………………………7分 证法二:分别过点D 、E 作DH ⊥AB 于H , EK ⊥BC 于K , 连接HK , 则∠DHB =∠EKB =90︒.∵ ∠ACB =90︒,∴ EK //AC .∵ DA =DB , EB =EC ,∴ AH =BH , ∠1=∠HDB ,CK =BK , ∠2=∠BEK .∴ HK //AC . ∴ 点H 、K 、E 在同一条直线上. …………………5分 下同证法一.25.解:(1)依题意, 设所求抛物线的解析式为42++=bx ax y , 则⎩⎨⎧++=++=.,439244b a b a ………………1分 ⎪⎪⎩⎪⎪⎨⎧=-=.,3131b a 解得 ∴ 所求抛物线的解析式为 431312++-=x x y . ……………………………………2分 由0431312=++-x x , 解得x 1=4, x 2= -3. ∴ D (4, 0).(2)如图, 过点C 作CN ⊥x 轴于N , 过点E 作x 轴、y 轴的垂线,两线交于点M .∴ ∠M =∠CNE =90°.设E (a , 0), EB=EC .∴ BM 2+EM 2= CN 2+EN 2.∴ 2222302041)()()()(a a -+-=-+-.解得 a =-1.∴ E ( -1, 0). ……………………………4(3)可求得直线BC 的解析式为y =-x +5. 从而直线BC 与x 轴的交点为H (5, 0). 如图,根据轴对称性可知S △E 'FG =S △EFG , 当点E '在BC 上时,点F 是BE 的中点. ∵ FG //BC ,∴ △EFP ∽△EBH .D A CE F B H K 12可证 EP =PH .∵ E (-1,0), H (5, 0),∴ P (2, 0). (5)( i ) 如图, 分别过点B 、C 作BK ⊥ED 于K ,CJ ⊥ED 于J , 则621=-⋅=-=∆∆∆)(CJ BK EH S S S CEHBEH BCE . 当-1< x ≤2时, ∵ PF //BC ,∴ △EGP ∽△ECH ,△EFG ∽△EBC .∴ EH EP ECEG =, .2222EH EP EC EG S S EBC EFG ==∆∆ ∵ P (x , 0), E (-1, 0), H (5,0), ∴ EP =x +1, EH =6.∴ )()('216131616122≤<-++=+===∆∆x x x x S S S EFG FG E . …………………6分 ( ii ) 如图,当2< x ≤4时, 在x 轴上截取一点Q , 使得PQ =HP , 过点Q 作 QM //FG , 分别交EB 、EC 于M 、N .可证S =S 四边形MNGF , △ENQ ∽△ECH ,△EMN ∽△EBC .∴EH EQ EC EN =, .2222EH EQ EC ENS S EBCEFG ==∆∆ ∵ P (x , 0), E (-1, 0), H (5,0),∴ EH =6,PQ =PH =5-x , EP =x +1, EQ =6-2(5-x )=2x -4. ∴.)(6422-=∆x S EMN……………7分同(i )可得 612)(+=∆x S EFG, ∴ )()()(422532164261222≤<-+-=--+=-=∆∆x x x x x S S S EMNEFG .…………8分综上,⎪⎪⎩⎪⎪⎨⎧≤<-+-≤<-++=).(),(42253212161316122x x x x x x S。
海淀区九年级第一学期期末测评2009.1

海淀区九年级第一学期期末练习数 学2009.1班级 姓名 成绩一、选择题(本题共32分,每小题4分)在下列各题的四个备选答案中,只有一个是正确的,请你把正确答案前的字母填写在相应的括号中.1.一元二次方程2x 2-3x =4的一次项系数是( )A. 2B. -3C. 4D. -42. 在下列各图中, 既是轴对称图形又是中心对称图形的是( )A B C D 3.将抛物线y =x 2向上平移2个单位, 所得抛物线的解析式为( )A. y =x 2-2B. y =x 2 +2C. y =(x+2)2D. y =(x -2)24.如图,已知点E 在⊙O 上,B 、C 分别是的三等分点,∠AED =60°, 则∠BOC 的度数为 ( )A .40°B .60°C .80°D .120° 5. 在下列事件中,不可能事件为( )A .通常加热到100℃时,水沸腾B .度量三角形内角和,结果是180°C .抛掷两枚硬币,两枚硬币全部正面朝上D .在布袋中装有两个质地相同的红球,摸出一个白球6.二次函数y = ax 2+ bx + c 的图象如图所示,则点(a , c ) 在( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限7. 已知关于x 的一元二次方程01)12()1(22=+++-x k x k 有两个不相等的实数根,则k 的取 值范围为( )A. 41>kB. 41<kC. 141≠>k k 且 D. 141-≠<k k 且ADFAB CE D8.如图,正方形ABCD 的边长为10,四个等圆的圆心分别在正方形 ABCD 的顶点上.若圆的半径为x ,且0< x ≤5,图中四个阴影部分 面积的和为y ,则能反映y 与x 之间函数关系的大致图象是( )A B C D二、填空题(本题共16分, 每小题4分)9. 若x =1是方程x 2+2kx -5=0的一个根,则k = . 10. 如图,在正方形ABCD 中,E 为DC 边上的点,连接BE , 将△BCE 绕点C 顺时针方向旋转90°得到△DCF ,连接 EF ,则∠CEF = 度.11. 如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成 一个圆锥模型.若扇形的半径为4,圆心角为90°,则圆的半径 为__________.12. 为确保信息安全,信息需要加密传输,发送方由“ ”接收方由 “ ”.已知加密规则为:当明文a ≥1时,a 对应的密文为a 2-2a +1;当明文a <1时,a 对应的密文为-a 2+2a -1. 例如:明文2对应的密文是 22-2×2+1=1; 明文-1对应的密文是 -(-1)2+2×(-1)-1=-4. 如果接收方收到的密文为4和-16, 则对应的明文分别是 和 .三、解答题(本题共30分, 第13题~第15题各5分, 第16题4分,第17题6分,第18题5分) 13.解方程:x (x -3) = x +12. 解:加密密文明文明文密文解密14. 计算:62)23(28⋅--+. 解:15. 已知:如图,点B 、C 、E 在同一条直线上,AC //DE ,AC =CE , BC =DE .求证:AB =CD . 证明:16.如图,在8×8正方形网格中,每个小正方形的边长均为1个单位长度.将格点△ABC 向下平移4个单位长度,得到△A 'B 'C ',再把△A 'B 'C ' 绕点O 顺时针旋 转90°,得到△A "B "C ",请你画出△A 'B 'C ' 和△A "B "C ". 解:17.已知抛物线经过点(0,2)、(1,-1)、(-1,7),求此抛物线的解析式、对称轴和顶点坐标. 解:AB ED18.掷一个质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,观察向上的一面的点数,求下列事件的概率: (1)点数为偶数; (2)点数大于1且小于4. 解:四、解答题(本题共20分,第19题4分,第20题、第21题各5分,第22题6分) 19.已知抛物线132+-=x x y 经过点(m , 0), 求代数式10214+-m m 的值.解:20. 如图,在△OAB 中,OA =OB =2, ∠OA E =30°, ⊙O 切AB 于E ,且分别交 OA 、OB 于C 、D , 求图中阴影部分的面积. 解:21.如图, 某小区在宽20m ,长32m 的矩形地面上修筑同样宽的人行道(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m 2,求道路的宽. 解:22.如图,在△ABC 中,∠C =90°, AD 是∠BAC 的平分线,O 是AB 上一点, 以OA 为半径的⊙O 经过点D .(1)求证: BC 是⊙O 切线; (2)若BD =5, DC =3, 求AC 的长. 解:20五、解答题(本题共22分,第23题7分,第24题8分,第25题7分) 23.已知:关于x 的一元二次方程01)2(2=+++-m x m x . (1)求证:方程有两个实数根;(2)设m <0,且方程的两个实数根分别为1x ,2x (其中1x <2x ),若y 是关于m的函数,且1214x x y -=,求这个函数的解析式; (3)在(2)的条件下,利用函数图象求关于m 的方程03=-+m y 的解. 解:24.已知:在△ABC 中,∠ABC =90 , 点E 在直线AB 上, ED 与直线AC 垂直, 垂足为D ,且点M 为EC 中点, 连接BM , DM . (1)如图1,若点E 在线段AB 上,探究线段BM 与DM 及∠BMD 与∠BCD 所满足的数量关系, 并直接写出你得到的结论;(2)如图2,若点E 在BA 延长线上,你在(1)中得到的结论是否发生变化?写出 你的猜想并加以证明;(3)若点E 在AB 延长线上,请你根据条件画出相应的图形,并直接写出线段BM与DM 及∠BMD 与∠BCD 所满足的数量关系. 解:(1)BM 与DM 的数量关系是: ;∠BMD 与∠BCD 所满足的等量关系是:. (2)图1图2(3)BED AMCEBACM25. 如图,在平面直角坐标系xOy中,经过点A,C,B的抛物线的一部分与经过点A,E,B的抛物线的一部分组合成一条封闭曲线,我们把这条封闭曲线称为“双抛物线”.已知P为AB中点, 且P(-1,0), C(2-1, 1), E(0,-3), S△CP A=1.(1)试求“双抛物线”中经过点A,E,B的抛物线的解析式;(2)若点F在“双抛物线”上,且S△F AP=S△CAP, 请你直接写出点F的坐标;(3)如果一条直线与“双抛物线”只有一个交点,那么这条直线叫做“双抛物线”的切线.若过点E与x轴平行的直线与“双抛物线”交于点G,求经过点G的“双抛物线”切线的解析式.解:海淀区九年级第一学期期末练习数学参考答案与评分标准 2009.1一、选择题1. B 2. C 3. B 4. A 5. D 6.B 7. C 8.C 二、填空题9. 2 10. 45 11. 1 12. 3, -3 说明:解答题不同于参考答案的正确解法,相应给分.三、解答题(本题共30分, 第13题~第15题各5分, 第16题4分,第17题6分,第18题5分)13.解:x 2-3 x = x +12. ………………………………………………………………1分 x 2-4x +4=16. ………………………………………………………………2分 (x -2)2=16. ………………………………………………………………3分x 1=-2, x 2=6. ………………………………………………………………5分.03222322262)23(28解:.14=--+=⋅--+ ……………………………………………4分 15.证明: ∵ AC //DE ,∴∠ACB =∠CED . …………………………………………………………1分 在△ABC 和△CDE 中,⎪⎩⎪⎨⎧=∠=∠=,,,DE BC CED ACB CE AC ……………………………………………………3分 ∴ △ABC ≌△CDE . …………………………………………………………4分 ∴ AB =CD . …………………………………………………………5分 16.说明: 正确画图并标出字母,每个图给2分; 如果字母标错累计扣1分; 图略. 17.解: 设所求抛物线的解析式为22++=bx ax y , ………………………………1分⎩⎨⎧+-=++=-.27,21b a b a 则 ………………………………………………………………2分 ⎩⎨⎧-==.4,1b a 解得 ………………………………………………………………3分……………………………………………………………… 5分∴ 所求抛物线的解析式为: y =x 2-4x +2. ……………………………………4分 ∵ y =x 2-4x +2=(x -2)2-2.∴ 抛物线y =x 2-4x +2的对称轴为x =2, 顶点坐标为(2, -2). …………………6分 18.解:掷一个质地均匀的正方体骰子时, 向上的一面的点数可能为1,2,3,4,5,6,共6种. 这些点数出现的可能性相等. …………………………………1分(1)点数为偶数有3种可能, 即点数为2,4,6. …………………………2分所以P (点数为偶数)=.2163= ……………………………………………3分(2)点数大于1且小于4有2种可能,即点数为2,3. ……………………4分 所以P (点数大于1且小于4)=.3162= ………………………………………5分四、解答题(本题共20分,第19题4分,第20题、第21题各5分,第22题6分) 19. 解:∵ 抛物线y =x 2-3x +1经过点(m , 0),∴ m 2-3m +1=0. ………………………………………………………1分∴ m 2=3m -1, m 2-3m =-1. m 4-21m +10=( m 2)2 -21m +10 …………………………………………………………2分 =(3m -1)2-21m +10= 9(m 2-3m )+11 …………………………………………………………3分 =-9+11=2. …………………………………………………………4分 20. 解: 连接OE .∵ ⊙O 切AB 于E ,∴ OE ⊥AB .∴∠OEA =90°. ……………1分 在Rt △OEA 中, ∠OAE =30°, OA =2, ∴ OE=21OA =1, ∠AOE =60°. ……………2分 ∴ AE =.322=-OE OA ……………………………………………………3分 ∵ OE ⊥AB ,OB = OA ,∴ BE = 2AE =23,∠AOB =2∠OBE =120°. ………………………………4分∴ S 阴影=S △OAB - S 扇形OCD =.3331212ππ-=⋅-⋅OE OE AB ………………5分 21.解法一:原图经过平移转化为图1. 设道路宽为x 米, 根据题意, 得(20-x )(32-x )=540. …………………………2分 整理得x 2-52x+100=0.20解得x 1=50(不合题意, 舍去), x 2=2. ………………4分答:道路宽为2米. …………………………5分 图1 解法二: 原图经过平移转化为图2. 设道路宽为x 米,根据题意, 得.540)3220(32202=++-⨯x x …………………2分整理得x 2-52x +100=0.解得x 1=50(不合题意, 舍去), x 2=2. ………………4分答:道路宽为2米. …………………………5分 图2 说明: 没画出图形不扣分.22.(1)证明: 如图1,连接OD .∵ OA =OD , AD 平分∠BAC ,∴ ∠ODA =∠OAD , ∠OAD =∠CAD . ………………1分 ∴ ∠ODA =∠CAD .∴ OD //AC . …………………………………2分∴ ∠ODB =∠C =90︒. ∴ BC 是⊙O 的切线. ……………………………3分 图1(2)解法一: 如图2,过D 作DE ⊥AB 于E .∴ ∠AED =∠C =90︒.又∵ AD =AD , ∠EAD =∠CAD , ∴ △AED ≌△ACD .∴ AE =AC , DE =DC =3. ………………………………4分在Rt △BED 中,∠BED =90︒,由勾股定理,得 图2BE =422=-DE BD . ………………………………………………………5分 设AC =x (x >0), 则AE =x .在Rt △ABC 中,∠C =90︒, BC =BD +DC =8, AB =x +4, 由勾股定理,得 x 2 +82= (x +4) 2. 解得x =6.即 AC =6. …………………………………………………………6分 解法二: 如图3,延长AC 到E ,使得AE =AB .∵ AD =AD , ∠EAD =∠BAD , ∴ △AED ≌△ABD .∴ ED =BD=5. ……………………………………4分 在Rt △DCE 中,∠DCE =90︒, 由勾股定理,得CE =422=-DC DE . ………… ……………5分在Rt △ABC 中,∠ACB =90︒, BC =BD +DC =8, 由勾股定理,得 AC 2 +BC 2= AB 2. 即 AC 2 +82=(AC +4) 2.解得 AC =6. …………………………………………………………6分 五、解答题(本题共22分,第23题7分,第24题8分,第25题7分) 23.(1)证明:∵01)2(2=+++-m x m x 是关于x 的一元二次方程,.)1(4)]2([22m m m =+-+-=∆∴ ………………………………… 1分∵ m 2≥0,∴ 原方程有实数根. ………………………………………………… 2分(2)解: 由求根公式,得.22mm x ±+=∴ x =m +1或1x =. …………………………………………… 3分 ∵ m <0, ∴ m +1<1. ∵ 1x <2x ,∴ x 1=m +1, x 2= 1. ……………………………………………………4分 ∴ mx x y 41412-=-=. 即my 4-=(m <0)为所求. …………………………………………… 5分 (3)解法一:如图1, 在同一平面直角坐标系中分别画出my 4-=(m <0)与y =-m +3(m <0)的图象. …………………………………………6分 由图象可得当m <0时,方程03=-+m y 的解为m =-1.…………………7分解法二:如图2, 在同一平面直角坐标系中分别画出my 4=(m <0) 与y =m -3(m <0)的图象. ………………………………………………6分 03=分图1 图2说明:若第(1)问直接求出两根,累计得3分;第(2)问没写m <0不扣分;第(3)问所画出函数图象没有限制取值范围m <0不扣分.24.解:(1) 结论:BM =DM ,∠BMD =2∠BCD . …………………………………2分 (2)在(1)中得到的结论仍然成立. 即BM =DM ,∠BMD =2∠BCD .证法一:∵ 点M 是Rt △BEC 的斜边EC 的中点,∴ BM =21EC=MC .又 点M 是Rt △DEC 的斜边EC 的中点,∴ DM =21EC =MC .∴ BM =DM . ……………………………………………………………3分 ∵ BM= MC , DM =MC ,∴ ∠CBM =∠BCM , ∠DCM =∠CDM . …………………………………4分 ∴ ∠BMD =∠EMB -∠EMD =2∠BCM -2∠DCM=2(∠BCM -∠DCM )= 2∠BCD . ……………………………………5分即 ∠BMD =2∠BCD .证法二:∵ 点M 是Rt △BEC 的斜边EC 的中点,∴ BM =21EC=ME .又 点M 是Rt △DEC 的斜边EC 的中点, ∴ DM =21EC =MC . ∴ BM =DM . ……………………………………………………………3分 ∵ BM =ME , DM =MC ,∴ ∠BEC =∠EBM , ∠MCD =∠MDC . …………………………………4分 ∴ ∠BEM +∠MCD =∠BAC =90︒-∠BCD . ∴ ∠BMD =180︒-(∠BMC +∠DME )= 180︒-2(∠BEM +∠MCD )=180︒ -2(90︒-∠BCD )=2∠BCD . ……………5分 即 ∠BMD =2∠BCD . (3)所画图形如图所示:BED AMCBED AMCEBMBEMEMB图1 图2 图3图1中有BM =DM ,∠BMD =2∠BCD ; 图2中∠BCD 不存在,有BM =DM ;图3中有BM =DM ,∠BMD =360︒-2∠BCD .……………………………………………………………8分 说明:每种情况图形及结论正确各1分.25.解:(1)过点C 作 CD ⊥AB 于D .∵ C (2-1, 1),∴ CD =1.又 S △CP A =CD AP ⋅21=1,∴ AP =2. ……………………………………………∵ P (-1, 0),∴ A (-3, 0), B (1, 0).设经过点A ,E ,B 抛物线的解析式为)1)(3(-+=x x a y , 则 )10)(30(3-+=-a . 解得a =1.故“双抛物线中”经过点A ,E ,B 抛物线的解析式为 y =x 2+2x -3.(-3≤x ≤1)……………… 2分(2)在“双抛物线”上,使得S △F AP =S △CAP 的点F 的坐标为:F 1(-2-1, 1), F 2 (31+-, -1), F 3 (31--, -1). ……………………4分 (3)∵ 过点E 与x 轴平行的直线与“双抛物线”交于点G ,E (0,-3),∴ G (x , -3).∵ 点G 在抛物线上, ∴ x 2+2x -3=-3. 解得 x 1=0, x 2=-2.∴ G (-2, -3). …………………………………………………………5分 设经过点G 的“双抛物线”切线的解析式为y =kx +b , 则-3=-2k +b . b =2k -3. ∴ y =kx +2k -3.∵ G 点在抛物线上,且在切线上,∴ x 2+2x -3=kx +2k -3. ……………………………………………………6分 x 2+(2-k )x -2k =0.∵ 经过点G 的“双抛物线”切线与“双抛物线”只有一个交点,∴Δ=b2-4ac=(2-k)2+8k=(2+k)2=0.解得k=-2. 故b=-7.∴经过点G的“双抛物线”切线的解析式为y=-2x-7. …………………7分说明:第(1)问不写自变量取值范围不扣分; 第(2)问F1正确给1分.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
海淀区九年级一模考试数 学 2009.5一、选择题(本题共32分,每小题4分)在下列各题的四个备选答案中,只有一个是正确的. 1.-12的相反数是 A .-2 B .2 C . -12 D .122.2009年北京启动了历史上规模最大的轨道交通投资建设,预计北京市轨道交通投资将达到51 800 000 000元人民币. 将51 800 000 000用科学记数法表示正确的是 A .51.8×109 B .5.18×1010 C .0.518×1011 D .518×1083.如图,已知AB ∥CD ,点E 在CD 上,BC 平分∠ABE , 若∠C =25°,则∠ABE 的度数是A .12.5°B .25°C .50°D .60°4. 在樱桃采摘园,五位游客每人各采摘了一袋樱桃,质量分别为(单位:千克):5,2,3,5,5,则这组数据的平均数和中位数分别为A .4,3B .3,5C .4,5D .5,55.若两圆的半径分别为4和3,圆心距为1,则这两圆的位置关系是A .内含B .内切C .相交D .外切6.袋子中有5个红球,3个蓝球,它们只有颜色上的区别. 从袋子中随机取出一个球, 取出蓝球的概率是A .53 B .83 C .85 D .81 7.把代数式a a a 4423+-分解因式,下列结果中正确的是A .22)(-a aB .)(42-a aC .22)(+a aD .))((22-+a a a 8.右图是画有一条对角线的平行四边形 纸片ABCD ,用此纸片可以围成一个 无上下底面的三棱柱纸筒, 则所围成 的三棱柱纸筒可能是E ABC D ADCBA B C D二、填空题(本题共16分, 每小题4分)9.若实数x , y 满足0322=-+-)(y x ,则代数式xy -x 2的值为 . 10.已知反比例函数y =xk的图象经过点(2,3), 则k = . 11.如图,在正方形网格中,每个小正方形的边长均为1,△ABC 的三个顶点均在格点上,则BC 边上的高为 . 12.如图,在平面直角坐标系xoy 中, A (-3,0),B (0,1),形状相同的抛物线C n (n =1, 2, 3,4, …) 的顶点在直线AB 上,其对称轴与 x 轴的交点的横坐标依次为2,3,5,8,13…,根据上述规律,抛物线C 2的顶点坐标 为 ; 抛物线C 8的顶点坐标为 .三、解答题(本题共30分, 每小题5分) 13.计算:05)-π(sin )(+︒-+-60212211.14.解不等式组:⎪⎩⎪⎨⎧<>-.,)(13112x x x15.已知:如图,点B 、E 、F 、C 在同一条直线上,AB =DE ,BE =CF ,∠B =∠CED . 求证: AF =DC .16. 计算:22111x x x ---.17.已知直线l 与直线y =-2x +m 交于点(2,0), 且与直线y =3x 平行,求m 的值及直线l的解析式.18. 如图,在梯形ABCD 中, AB //DC , ∠D =90︒, ∠ACD =30︒ ,① ② E D C B A F A B CDA BC B (C )A (D )A (D )B (C )A (D )B (C )A (D )B (C )C BA AB =12, BC =10, 求AD 的长.四、解答题(本题共20分, 第19题5分,第20题6分,第21题5分,第22题4分) 19.如图,已知AB 为⊙O 的弦,C 为⊙O 上一点,∠C =∠BAD ,且BD ⊥AB 于B .(1)求证:AD 是⊙O 的切线;(2)若⊙O 的半径为3,AB =4,求AD 的长.20. 某种子培育基地用A 、B 、C 、D 四种型号的小麦种子共2 000粒进行发芽实验,从 中选出发芽率高的种子进行推广.通过实验得知,C 型号种子的发芽率为94%. 根 据实验数据绘制了图1和图2两幅尚不完整的统计图.请你根据所给信息,解答下 列问题:(1)D 型号种子数是 粒; (2)请你将图2的统计图补充完整;(3)通过计算说明,应选哪一个型号的种子进行推广;如果所选型号进行推广的种子共有200 000粒,估计能有多少粒种子会发芽.图1 图221. 甲、乙同学帮助学校图书馆清点一批图书,已知甲同学清点200本图书与乙同学清 点300本图书所用的时间相同,且甲同学平均每分钟比乙同学少清点10本,求甲同 学平均每分钟清点图书的数量.22.我们给出如下定义:如果四边形中一对顶点到另一对顶点所连对角线的距离相等,则把这对顶点叫做这个四边形的一对等高点.例如:如图1,平行四边形ABCD 中,可证点A 、C 到BD 的距离相等,所以点A 、C 是平行四边形ABCD 的一对等高点,同理可知点B 、D也是平行四边形ABCD 的一对等高点. 图1(1)如图2,已知平行四边形ABCD , 请你在图2中画出一个只有一对等高点的四边形ABCE (要求:画出必要的辅助线);(2)已知P 是四边形ABCD 对角线BD 上任意一点(不与B 、D 点重合),请分别探究图3、图4中S 1, S 2, S 3, S 4四者之间的等量关系(S 1, S 2, S 3, S 4分别表示△ABP , △CBP , △CDP , △ADP 的面积):① 如图3,当四边形ABCD 只有一对等高点A 、C 时,你得到的一个结论是 ;号7000各种型号种子数的百分比35 %D C B A25 %20 %② 如图4,当四边形ABCD 没有等高点时,你得到的一个结论是 .图2 图3 图4五、解答题(本题共22分, 第23题7分,第24题7分,第25题8分)23.已知: 关于x 的一元一次方程kx =x +2 ①的根为正实数,二次函数y =ax 2-bx +kc (c ≠0)的图象与x 轴一个交点的横坐标为1. (1)若方程①的根为正整数,求整数k 的值;(2)求代数式akcabb kc +-22)(的值;(3)求证: 关于x 的一元二次方程ax 2-bx +c =0 ②必有两个不相等的实数根.24.在课外小组活动时,小慧拿来一道题(原问题)和小东、小明交流.原问题:如图1,已知△ABC , ∠ACB =90︒ , ∠ABC =45︒,分别以AB 、BC 为边向外作△ABD 与△BCE , 且DA =DB , EB =EC ,∠ADB =∠BEC =90︒,连接DE 交AB 于点F . 探究线段DF 与EF 的数量关系.小慧同学的思路是:过点D 作DG ⊥AB 于G ,构造全等三角形,通过推理使问 题得解.小东同学说:我做过一道类似的题目,不同的是∠ABC =30︒,∠ADB =∠BEC =60︒. 小明同学经过合情推理,提出一个猜想,我们可以把问题推广到一般情况. 请你参考小慧同学的思路,探究并解决这三位同学提出的问题: (1)写出原问题中DF 与EF 的数量关系;(2)如图2,若∠ABC =30︒,∠ADB =∠BEC =60︒,原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明;(3)如图3,若∠ADB =∠BEC =2∠ABC , 原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明.图1 图2 图325.已知抛物线经过点 A (0, 4)、B (1, 4)、C (3, 2),与x 轴正半轴交于点D .B A D F DAC E F B E F B AD A BC D S 2S 1S 4S 3S 4S 3S 2AB C P DA B C P D S 1(1)求此抛物线的解析式及点D的坐标;(2)在x轴上求一点E, 使得△BCE是以BC为底边的等腰三角形;(3)在(2)的条件下,过线段ED上动点P作直线PF//BC, 与BE、CE分别交于点F、G,将△EFG沿FG翻折得到△E'FG. 设P(x, 0), △E'FG与四边形FGCB 重叠部分的面积为S,求S与x的函数关系式及自变量x的取值范围.数学参考答案及评分标准 2009.5一、选择题(本题共32分,每小题4分)1.D 2.B 3. C 4. C 5.B 6.B 7. A 8. C 二、填空题(本题共16分, 每小题4分)9. 2 10.6 11.225 12. (3,2);(55,358) 三、解答题(本题共30分, 每小题5分).5)-π(sin )(.03312323226021221131+=+⨯-+=+︒-+-解: 14. 解:解不等式①,得 x >2; ……………………………………………………2分解不等式②,得x <3. ……………………………………………………4分所以原不等式组的解集为 2<x <3. ………………………………………………5分15.证明:∵ BE =CF ,∴ BE +EF = CF + EF .∴ BF =EC . …………………1分 在△ABF 和△DEC 中, ⎪⎩⎪⎨⎧=∠=∠=,,,EC BF DEC B DE AB …………………3分 ∴ △ABF ≌△DEC . …………………………………………………………4分 ∴ AF =DC . …………………………………………………………5分16. 解: 22111x x x ---21(1)(1)1x x x x =-+-- …………………………………………1分 2(1)(1)(1)x x x x -+=+- …………………………………………………………3分1(1)(1)x x x -=+- …………………………………………………………4分 11x =+. …………………………………………………………5分 17.解:依题意,点(2,0)在直线y =-2x +m 上,∴ 0=-2×2+m . …………………………………………………………………1分 ∴ m =4. …………………………………………………………………………2分 由直线l 与直线y =3x 平行,可设直线l 的解析式为y =3x +n . ………………3分 ∵ 点(2,0)在直线l 上,E DCB A F ………………………………………………………5分………………………………………………………4分∴ 0=3×2+n .∴ n =-6. …………………………………………………………………4分 故直线l 的解析式为 y =3x -6. …………………………………………………5分 18. 解: 过点B 作BE ⊥AC 于E , 则∠AEB =∠BEC = 90︒. …………………………1分∵ AB //DC ,∴ ∠BAE=∠ACD =30︒ .又∵ AB =12,∴ EB =AB 21=6, AE =3630=︒⋅cos AB . ………………………………………2分 在Rt △BEC 中, ∠BEC =90︒ ,∴ EC =.86102222=-=-BE BC …………………………………………3分 ∴ AC =AE +EC =36+8. ……………………………………………………4分 在Rt △ADC 中,∠D =90︒, ∠ACD =30︒ , ∴ AD =.43321+=AC ……………………………………………………5分 四、解答题(本题共20分, 第19题5分,第20题6分,第21题5分,第22题4分) 19.(1)证明: 如图, 连接AO 并延长交⊙O 于点E , 连接BE , 则∠ABE =90°.∴ ∠EAB +∠E =90°. ……………………1分 ∵ ∠E =∠C , ∠C =∠BAD , ∴ ∠EAB +∠BAD =90°.∴ AD 是⊙O 的切线. ……………………2分(2)解:由(1)可知∠ABE =90°.∵ AE =2AO =6, AB =4, ∴ 5222=-=AB AE BE . …………………………………………………3分 ∵ ∠E=∠C =∠BAD , BD ⊥AB ,∴ .cos cos E BAD ∠=∠ …………………………………………………4分∴ .AEBE AD AB =.6524=AD 即∴ 5512=AD . …………………………………………………5分 20.解:(1)400. ………………………………………………………1分 (2)C 型号种子的发芽数为470粒. 图略. ……………………………………3分 (3)A 型号种子的发芽率为%%90352000630=⨯,B 型号种子的发芽率为%.%592202000370=⨯,D 型号种子的发芽率为%%95202000380=⨯,C 型号发芽率为94%.∴ 应选D 型号的种子进行推广. …………………………………………5分D CB A E200 000×95%=190 000(粒).估计能有190 000粒种子会发芽. …………………………………………6分 21. 解:设甲同学平均每分钟清点图书x 本,则乙同学平均每分钟清点图书(x+10)本, 依题意,得10300200+=x x . ………………………………………………2分 解得x =20. ……………………………………………………………………3分经检验x =20是原方程的解,且符合题意. ………………………………………4分 答:甲同学平均每分钟清点图书205分22.解:(1)比如: 或 1分(2)①S 1 +S 4 = S 2 +S 3, S 1 +S 3 = S 2 +S 4或S 1⋅S 3 = S 2⋅S 4或3241S S S S =等. ……………2分 ②S 1⋅S 3 = S 2⋅S 4或3421S S S S =等. ……………………………………………4分 五、解答题(本题共22分, 第23题7分,第24题7分,第25题8分) 23.(1)解:由 kx =x +2,得(k -1) x =2.依题意 k -1≠0.∴ 12-=k x . ……………………………………………………………1分 ∵ 方程的根为正整数,k 为整数, ∴ k -1=1或k -1=2.∴ k 1= 2, k 2=3. ……………………………………………………………2分(2)解:依题意,二次函数y =ax 2-bx +kc 的图象经过点(1,0), ∴ 0 =a -b +kc , kc = b -a .∴222222222aab abb a ab b a b a ab b a b akc ab b kc -+-+-=-+--=+-)()()( =.122-=--a ab aba …………………………3分 (3)证明:方程②的判别式为 Δ=(-b )2-4ac = b 2-4ac . 由a ≠0, c ≠0, 得ac ≠0.( i ) 若ac <0, 则-4ac >0. 故Δ=b 2-4ac >0. 此时方程②有两个不相等的实数根. ………………………………………………………………4分 ( ii ) 证法一: 若ac >0, 由(2)知a -b +kc =0, 故 b =a +kc .Δ=b 2-4ac = (a +kc )2-4ac =a 2+2kac +(kc )2-4ac = a 2-2kac +(kc )2+4kac -4ac=(a -kc )2+4ac (k -1). …………………………………………………5分 ∵ 方程kx =x +2的根为正实数, ∴ 方程(k -1) x =2的根为正实数.EA BCD由 x >0, 2>0, 得 k -1>0. …………………………………………………6分 ∴ 4ac (k -1)>0. ∵ (a -kc )2≥0,∴Δ=(a -kc )2+4ac (k -1)>0. 此时方程②有两个不相等的实数根. …………7分 证法二: 若ac >0,∵ 抛物线y =ax 2-bx +kc 与x 轴有交点, ∴ Δ1=(-b )2-4akc =b 2-4akc ≥0. (b 2-4ac )-( b 2-4akc )=4ac (k -1).由证法一知 k -1>0,∴ b 2-4ac > b 2-4akc ≥0.∴ Δ= b 2-4ac >0. 此时方程②有两个不相等的实数根. …………………7分 综上, 方程②有两个不相等的实数根.24. 解: (1)DF= EF . ………………………………………………………………1分(2)猜想:DF= FE .证明:过点D 作DG ⊥AB 于G , 则∠DGB =90︒. ∵ DA =DB , ∠ADB =60︒. ∴ AG =BG , △DBA 是等边三角形.∴ DB =BA .∵ ∠ACB =90︒ , ∠ABC =30︒,∴ AC =21AB =BG . …………………………………………………………2分 ∴ △DBG ≌△BAC .∴ DG =BC . ……………………………………………………3分 ∵ BE=EC , ∠BEC =60︒ , ∴ △EBC 是等边三角形. ∴ BC =BE , ∠CBE =60︒.∴ DG = BE , ∠ABE =∠ABC +∠CBE =90︒ . ∵ ∠DFG =∠EFB , ∠DGF =∠EBF , ∴ △DFG ≌△EFB .∴ DF= EF . ……………………………………………………4分(3)猜想:DF= FE .证法一:过点D 作DH ⊥AB 于H , 连接HC , HE , HE 交CB 于K , 则∠DHB =90︒. ∵ DA =DB ,∴ AH =BH , ∠1=∠HDB .∵ ∠ACB =90︒, ∴ HC =HB .∵ EB =EC , HE =HE ,∴ △HBE ≌△HCE . ……………………………5分 ∴ ∠2=∠3, ∠4=∠BEH .∴ HK ⊥BC . ∴ ∠BKE =90︒. ……………………………6分 ∵ ∠ADB =∠BEC =2∠ABC , ∴ ∠HDB =∠BEH =∠ABC .∴ ∠DBC =∠DBH +∠ABC =∠DBH +∠HDB =90︒,GDABCFE K H BF E CA D 2431∠EBH =∠EBK +∠ABC =∠EBK +∠BEK =90︒. ∴ DB //HE , DH //BE .∴ 四边形DHEB 是平行四边形.∴ DF =EF . ………………………………………………………………………7分 证法二:分别过点D 、E 作DH ⊥AB 于H , EK ⊥BC 于K , 连接HK , 则∠DHB =∠EKB =90︒.∵ ∠ACB =90︒,∴ EK //AC .∵ DA =DB , EB =EC ,∴ AH =BH , ∠1=∠HDB ,CK =BK , ∠2=∠BEK .∴ HK //AC . ∴ 点H 、K 、E 在同一条直线上. …………………5分 下同证法一.25.解:(1)依题意, 设所求抛物线的解析式为42++=bx ax y , 则⎩⎨⎧++=++=.,439244b a b a ………………1分 ⎪⎪⎩⎪⎪⎨⎧=-=.,3131b a 解得 ∴ 所求抛物线的解析式为 431312++-=x x y . ……………………………………2分 由0431312=++-x x , 解得x 1=4, x 2= -3. ∴ D (4, 0).(2)如图, 过点C 作CN ⊥x 轴于N , 过点E 作x 轴、y 轴的垂线,两线交于点M .∴ ∠M =∠CNE =90°.设E (a , 0), EB=EC .∴ BM 2+EM 2= CN 2+EN 2. ∴ 2222302041)()()()(a a -+-=-+-.解得 a =-1.∴ E ( -1, 0). ……………………………4(3)可求得直线BC 的解析式为y =-x +5. 从而直线BC 与x 轴的交点为H (5, 0). 如图,根据轴对称性可知S △E 'FG =S △EFG , 当点E '在BC 上时,点F 是BE 的中点. ∵ FG //BC ,∴ △EFP ∽△EBH .D A CE F B H K 12可证 EP =PH .∵ E (-1,0), H (5, 0),∴ P (2, 0). (5)( i ) 如图, 分别过点B 、C 作BK ⊥ED 于K ,CJ ⊥ED 于J ,则621=-⋅=-=∆∆∆)(CJ BK EH S S S CEH BEH BCE .当-1< x ≤2时, ∵ PF //BC , ∴ △EGP ∽△ECH ,△EFG ∽△EBC .∴ EHEP EC EG =, .2222EH EP EC EG S S EBC EFG ==∆∆ ∵ P (x , 0), E (-1, 0), H (5,0), ∴ EP =x +1, EH =6.∴ )()('216131616122≤<-++=+===∆∆x x x x S S S EFG FG E . …………………6分( ii ) 如图,当2< x ≤4时, 在x 轴上截取一点Q , 使得PQ =HP , 过点Q 作QM //FG , 分别交EB 、EC 于M 、N .可证S =S 四边形MNGF , △ENQ ∽△ECH ,△EMN ∽△EBC . ∴EH EQ EC EN =, .2222EHEQ EC ENS S EBC EFG ==∆∆ ∵ P (x , 0), E (-1, 0), H (5,0),∴ EH =6,PQ =PH =5-x , EP =x +1, EQ =6-2(5-x )=2x -4. ∴.)(6422-=∆x S EMN……………7分同(i )可得 612)(+=∆x S EFG, ∴ )()()(422532164261222≤<-+-=--+=-=∆∆x x x x x S S S EMNEFG .…………8分综上,⎪⎪⎩⎪⎪⎨⎧≤<-+-≤<-++=).(),(42253212161316122x x x x x x S。
