基于MATLAB的GUI设计在高等数学中的应用
matlab程序设计在数学中的应用

matlab程序设计在数学中的应用Matlab程序设计在数学中的应用引言:Matlab是一种强大的数学软件,广泛应用于各个领域,尤其是在数学中具有重要的应用价值。
本文将介绍Matlab程序设计在数学中的应用,并探讨其在数学研究、教学和实践中的重要作用。
一、数学建模与分析数学建模是将实际问题转化为数学模型,并通过数学方法进行分析和求解的过程。
Matlab具有丰富的数学函数库和强大的数值计算能力,能够快速、准确地求解各类数学问题。
例如,利用Matlab可以进行线性规划、非线性规划、最优化问题等的建模和求解;可以进行微分方程的数值解法求解,如欧拉法、四阶龙格-库塔法等;可以进行概率统计分析,如概率密度函数、累积分布函数、正态分布、随机数生成等。
二、数据可视化与图像处理在数学研究和教学中,数据可视化和图像处理是非常重要的环节。
Matlab提供了丰富的绘图函数和图像处理工具箱,可以实现各种图形的绘制和处理。
例如,可以通过Matlab绘制二维和三维图形,如曲线图、散点图、柱状图、等高线图等,以直观地展示数学模型的结果;可以进行图像处理和图像分析,如图像增强、滤波、边缘检测、形态学操作等,以提取和分析图像中的数学信息。
三、符号计算与代数运算符号计算是数学中一项重要的技术,可以进行符号表达式的推导、化简、求导、积分、求解方程等。
Matlab通过Symbolic Math Toolbox提供了强大的符号计算功能,可以高效地进行符号计算和代数运算。
例如,可以通过Matlab进行多项式的因式分解、方程的求解、微积分的符号运算等,以得到精确的数学结果。
四、数值实验与数学验证数值实验和数学验证是数学研究和教学中的重要环节。
Matlab提供了丰富的数值实验工具和数学验证函数,可以帮助研究人员和教师进行数学问题的验证和实验。
例如,可以通过Matlab进行数值积分的收敛性分析和误差估计;可以进行数值解法的稳定性分析和收敛性分析;可以进行数值模拟和仿真实验,如蒙特卡罗模拟、随机过程模拟等。
matlab软件在高等数学教学课堂上的应用

matlab软件在高等数学教学课堂上的应用摘要:本文介绍了matlab软件在高等数学教学课堂上的应用。
首先,我们介绍了matlab软件的基本特点和优点,主要包括matlab 软件的易用性、高效性和多功能性。
然后,我们结合高等数学教学的实际情况,分析了matlab软件在高等数学教学课堂上的应用,主要包括matlab软件在微积分、线性代数、概率论与数理统计等方面的应用。
最后,我们总结了matlab软件在高等数学教学中的优点和不足之处,并提出了进一步完善matlab软件在高等数学教学中的应用的建议。
关键词:matlab软件;高等数学教学;微积分;线性代数;概率论与数理统计一、matlab软件的基本特点和优点matlab软件是一种数学软件,主要用于进行数学计算、数据分析和可视化等方面的工作。
matlab软件具有以下几个基本特点和优点:1.易用性:matlab软件的界面简洁明了,操作简单易学,适合各种不同层次的用户使用。
2.高效性:matlab软件的计算速度非常快,可以快速处理大量的数学计算和数据分析工作。
3.多功能性:matlab软件具有多种不同的功能模块,包括数学计算、数据分析、可视化、编程等方面的工作,可以满足不同用户的不同需求。
二、matlab软件在高等数学教学中的应用matlab软件在高等数学教学中有着广泛的应用,主要包括以下几个方面:1.微积分:matlab软件可以用于微积分的计算和可视化,可以帮助学生更好地理解微积分的概念和原理。
例如,可以使用matlab 软件计算函数的导数和积分,绘制函数的图像和曲线,进行微积分的应用实例分析等。
2.线性代数:matlab软件可以用于线性代数的计算和可视化,可以帮助学生更好地理解线性代数的概念和原理。
例如,可以使用matlab软件计算矩阵的行列式、逆矩阵、特征值和特征向量等,绘制矩阵的图像和曲线,进行线性代数的应用实例分析等。
3.概率论与数理统计:matlab软件可以用于概率论与数理统计的计算和可视化,可以帮助学生更好地理解概率论与数理统计的概念和原理。
基于matlab gui的计算方法课程在数学建模中的实践与应用

基于matlab gui的计算方法课程在数学建模中的实践与应用
基于matlab gui的计算方法课程在数学建模中的实践与应用
随着科学技术的发展,数学建模已经成为现代科学研究的重要组成部分。
基于matlab gui的计算方法课程在数学建模中发挥着重要的作用。
首先,基于matlab gui的计算方法课程可以帮助学生更好地理解数学
建模的基本原理。
matlab gui可以帮助学生更好地理解数学建模的基
本原理,从而更好地掌握数学建模的基本技能。
其次,基于matlab gui的计算方法课程可以帮助学生更好地掌握数学
建模的实践技能。
matlab gui可以帮助学生更好地掌握数学建模的实
践技能,从而更好地应用数学建模的实践技能。
最后,基于matlab gui的计算方法课程可以帮助学生更好地应用数学
建模的实践技能。
matlab gui可以帮助学生更好地应用数学建模的实
践技能,从而更好地解决实际问题。
综上所述,基于matlab gui的计算方法课程在数学建模中发挥着重要
的作用,可以帮助学生更好地理解数学建模的基本原理,掌握数学建
模的实践技能,以及应用数学建模的实践技能解决实际问题。
因此,
基于matlab gui的计算方法课程在数学建模中的实践与应用具有重要
的意义。
matlab软件在高等数学课程教学中的应用

matlab软件在高等数学课程教学中的应用
Matlab是强大的高级计算机语言,它可以用于编写程序和数
学函数,能够准确快速地求解各种复杂问题。
由于这种特性,Matlab不仅可以应用于科学计算,而且在教学领域也有着广
泛的应用。
在高等数学课程的教学中,Matlab的出色表现也
是显而易见的。
首先,Matlab可以帮助教师快速正确地求解各种复杂的数学
问题,这在数学课程的教学当中具有重要意义。
使用Matlab,教师可以轻松地实现复杂的数学计算和求解,并将完成的结果展示给学生,这有利于学生更好地理解课程内容,更加便捷地完成学习任务。
其次,Matlab也具有出色的可视化功能,可以将复杂的抽象
数学概念可视化、可视化,这对于深入理解抽象数学概念具有极大的帮助。
此外,Matlab还可以用于进一步分析结果,如
数据分析和可视化,以便更深入地了解问题背后的含义,这对学习数学有很大的帮助。
因此,Matlab在高等数学课程的教学中有着广泛的应用,它
不仅能够快速准确地完成复杂的数学计算,而且可以提供出色的可视化功能,可以帮助教师更好地完成数学课程的教学,以及让学生更好地理解课程内容。
MATLAB在高等数学教学中的应用

MATLAB在高等数学教学中的应用【摘要】本文主要探讨了MATLAB在高等数学教学中的应用。
通过对微积分、线性代数、概率论与数理统计、常微分方程和多元函数微积分等领域的具体案例分析,展示了MATLAB在教学中的重要作用。
MATLAB提供了丰富的数学函数库和可视化工具,可帮助学生更好地理解和应用数学知识。
MATLAB还能够帮助教师更加生动地展示数学概念与原理,提高教学效果。
在对MATLAB在高等数学教学中的作用进行了总结,并展望了未来MATLAB在教学中的发展前景。
MATLAB 在高等数学教学中的应用将会持续发展,并对学生的数学学习和理解起到积极的促进作用。
【关键词】MATLAB, 高等数学教学, 应用, 微积分, 线性代数, 概率论, 数理统计, 常微分方程, 多元函数微积分, 总结, 展望1. 引言1.1 MATLAB在高等数学教学中的应用概述通过MATLAB,教师可以更加生动地展示数学概念、解决实际问题,并且可以进行直观的可视化展示,帮助学生更好地理解和掌握数学知识。
对于学生来说,他们可以通过MATLAB进行实践操作,加深对数学知识的理解,提高解决问题的能力。
MATLAB还可以帮助教师和学生们快速验证和验证数学模型,加快数学计算的速度,提高教学效率。
MATLAB在高等数学教学中的应用不仅可以丰富教学内容,提高教学效果,还可以激发学生学习数学的兴趣,促进他们对数学的深入探讨和研究。
在数字化时代,MATLAB的应用将为高等数学教学带来新的发展机遇和可能性。
2. 正文2.1 MATLAB在微积分教学中的应用微积分是高等数学中的重要学科,也是许多学生感到困惑的学科之一。
利用MATLAB软件可以帮助学生更好地理解微积分的概念和原理,并提升他们的数学建模和问题解决能力。
MATLAB可以用来绘制函数图像。
学生可以通过输入函数表达式和指定变量的取值范围,快速绘制出函数的图像。
这样可以直观地展示函数的性质,帮助学生理解函数在不同区间的变化规律。
MATLAB在高等数学教学中的应用

MATLAB在高等数学教学中的应用1. 引言1.1 MATLAB在高等数学教学中的应用概述在微积分教学中,MATLAB可以用来绘制曲线和图形,解决数值积分和微分方程等数学问题,帮助学生更深入地理解微积分的概念和应用。
在线性代数教学中,MATLAB可以用来求解线性方程组、计算矩阵的特征值和特征向量,加深学生对向量空间和线性变换的理解。
MATLAB在高等数学教学中的应用不仅帮助教师更好地传授知识,也提升了学生的学习效果和兴趣。
随着技术的不断发展和完善,MATLAB在高等数学教学中的应用前景将更加广阔,为数学教育带来更多的可能性和创新。
2. 正文2.1 MATLAB在微积分教学中的应用MATLAB可以用来绘制函数的图像,帮助学生直观地理解数学概念。
通过输入函数表达式,学生可以立即看到函数的图像,从而更好地理解函数的性质和特点。
MATLAB可以进行数值计算,帮助学生解决一些复杂的积分和微分问题。
对于一些无法通过解析方法求解的问题,可以利用MATLAB进行数值积分和数值微分,提高学生的问题求解能力。
MATLAB还可以用来进行符号计算,帮助学生简化复杂的数学表达式,进行代数化简和方程求解,加深学生对微积分概念的理解。
MATLAB在微积分教学中的应用可以帮助学生更好地理解和掌握微积分知识,提高他们的问题求解能力和数学建模能力。
通过结合理论知识和实际计算,MATLAB可以使微积分课程变得更加生动和有趣,激发学生对数学学习的兴趣。
2.2 MATLAB在线性代数教学中的应用1. 矩阵运算:在线性代数课程中,学生需要进行大量的矩阵运算,包括矩阵相加、相乘、求逆等操作。
利用MATLAB可以快速进行这些运算,并且可以帮助学生更好地理解线性代数的概念。
2. 线性方程组求解:线性代数中最基本的问题之一就是求解线性方程组。
MATLAB提供了很多线性代数相关的函数,可以帮助学生查找线性方程组的解,包括使用高斯消元法、LU分解等方法。
MATLAB在高等数学教学中的应用

MATLAB在高等数学教学中的应用【摘要】本文主要介绍了MATLAB在高等数学教学中的应用。
通过对微积分、线性代数、概率论与数理统计、常微分方程和数学建模等领域的具体应用展开讨论,分析了MATLAB在教学中的优势和作用。
在微积分教学中,MATLAB可以帮助学生更直观地理解数学概念,提高问题求解的效率;在线性代数教学中,可以进行矩阵运算、线性方程组求解等;在概率论与数理统计教学中,可以进行统计分析和模拟实验等;在常微分方程教学中,可以进行数值解法验证和实例演示等;在数学建模教学中,可以帮助学生将数学知识应用到实际问题中。
MATLAB在高等数学教学中的应用是多方面的丰富多彩的,对学生的学习和理解提供了更广阔的空间和机会。
【关键词】MATLAB, 高等数学, 教学, 应用, 微积分, 线性代数, 概率论, 数理统计, 常微分方程, 数学建模, 多方面, 丰富, 多彩1. 引言1.1 MATLAB在高等数学教学中的应用MATLAB在高等数学教学中的应用是非常广泛和多样化的。
通过使用MATLAB软件,教师能够更好地展示数学知识,帮助学生更好地理解和掌握数学概念。
在微积分教学中,MATLAB可以用来绘制函数图像、计算极限、导数和积分,帮助学生直观地理解微积分的概念和应用;在线性代数教学中,MATLAB可以用来求解线性方程组、计算矩阵的特征值和特征向量,帮助学生更好地理解线性代数的基本概念和方法;在概率论与数理统计教学中,MATLAB可以用来进行概率分布的可视化、参数估计和假设检验,帮助学生更好地理解和应用概率统计知识;在常微分方程教学中,MATLAB可以用来求解常微分方程的初值问题和边值问题,帮助学生更好地理解微分方程的基本概念和解法;在数学建模教学中,MATLAB可以用来建立数学模型、进行数值模拟和优化求解,帮助学生更好地运用数学知识解决实际问题。
MATLAB在高等数学教学中的应用是多方面的丰富多彩的,可以极大地丰富教学内容,提高教学效率,激发学生学习兴趣,促进数学素养的提升。
MATLAB在《高等数学》 教学中的应用探讨

86510 数学论文MATLAB在《高等数学》教学中的应用探讨高等数学在我国高校的课程教学中一直都发挥着重要作用。
这门课程严谨的逻辑性和理论性及抽象性,对于学生的思维和能力的培养起到非常重要的作用,而且对于学生学习其他课程也有一定的帮助。
但是,由于高等数学这门课程的逻辑性太强,而且抽象性较高,学生在平时上课的时候难以听懂,课下做作业的时候不会,导致相当一部分高校学生对于高等数学产生抵触甚至是反感情绪。
同学们普遍反映高等数学摸不着、看不见,而且比较乏味无聊,所以学习兴趣也提不起来,导致高等数学不及格的人越来越多。
将MATLAB计算软件引入高等数学中,可以有效解决这一问题。
下面我们就此作探讨。
一、MATLAB的概念何谓“MATLAB”呢?MATLAB是一种计算的软件,具体来讲,它是由美国的mathworks公司研发的一种主要是针对数学计算的商业软件。
它主要适用于数学算法的开发、数据的分析处理、数据的可视化及数据计算的一种高级的计算语言。
MATLAB是matrix和laboratouy两个单词的组合,可以翻译为矩阵实验室,也就是矩阵工厂。
它可以将大量的数据的分析、非线性的动态系统及矩阵的计算等等建模和仿真这些功能集中到一个容易使用的可视窗的环境中,从而可以为科学的研究和一些工程的设计提供比较全面的解决方案,这在一定程度上这一软件代表了当今世界上计算软件的较高水平[1]。
二、MATLAB的优势特点MATLAB这一计算软件可以进行矩阵计算,可以绘制一些函数的图像,实现一些数学算法及创建用户的界面等,主要适用于工程计算、控制软件的设计、信号,以及图像的处理、金融设计等领域,而且具有其他语言不具备的优势特点。
(一)MATLAB具有较高效率的数据计算和符号的计算功能,而且处理能力较强,采用机算的方式可以适当减少用户的计算量,使得用户的计算效率得到一定的提高。
MATLAB包含了许多的计算算法,而且许多都可以应用到数学函数计算中,从而极大地为用户提供方便。
matlab软件在高等数学教学课堂上的应用

matlab软件在高等数学教学课堂上的应用随着信息技术的发展和普及,计算机在教育领域中的应用也越来越广泛。
在高等数学教学中,Matlab软件作为一款强大的数学计算工具,可以帮助学生更好地理解和掌握数学知识,提高数学学习效率。
本文将从Matlab软件在高等数学教学中的应用入手,探讨其在高等数学教学中的作用和优势。
一、Matlab软件简介Matlab是一款数学计算软件,它可以进行数值分析、数据处理、图像处理、信号处理等多种计算。
Matlab具有强大的数学计算能力和灵活的编程语言,可以帮助用户快速解决各种数学问题。
Matlab软件具有以下优势:1. 界面友好,易于操作:Matlab软件的界面简洁明了,操作简单易学,不需要过多的编程知识,即可快速上手。
2. 功能强大,适用范围广:Matlab软件不仅可以进行数学计算,还可以进行图像处理、信号处理等多种计算,适用范围非常广泛。
3. 支持多种编程语言:Matlab软件支持多种编程语言,包括C++、Java、Python等,用户可以根据自己的需求选择适合自己的编程语言。
二、Matlab软件在高等数学教学中的应用1. 数学模型建立和求解Matlab软件可以帮助学生建立数学模型,并进行求解。
例如,在微积分教学中,学生可以使用Matlab软件绘制函数图像、求导、求极值、求面积等,通过实际计算和图像展示,帮助学生深入理解微积分的概念和应用。
2. 数据分析和处理Matlab软件可以帮助学生进行数据分析和处理,例如,在统计学教学中,学生可以使用Matlab软件进行数据的统计分析、描述性统计、假设检验等,通过实际数据的处理和分析,帮助学生更好地理解统计学的概念和应用。
3. 图像处理和分析Matlab软件可以帮助学生进行图像处理和分析,例如,在线性代数教学中,学生可以使用Matlab软件进行图像的线性变换、旋转、平移等操作,通过实际图像的处理和分析,帮助学生更好地理解线性代数的概念和应用。
MATLAB在高等数学教学中的应用

MATLAB在高等数学教学中的应用
MATLAB是一种强大的数学计算软件,它能够帮助教师在高等数学教学中更好地展示概念和解决问题,并为学生提供更好的学习体验。
下面是MATLAB在高等数学教学中的应用。
1. 数据绘图
MATLAB可以通过绘制图表来展示高等数学概念,例如函数、导数、曲线等等。
这些图表可以让学生更直观地理解概念,并且可以将计算结果更好地呈现给学生。
2. 数据分析
MATLAB还可以用于高等数学研究过程中的数据分析。
它具有强大的分析工具,可以帮助教师分析多元函数、偏微分方程和其他高等数学问题。
3. 交互式模拟
MATLAB中的模拟工具可以在高等数学教学中提供交互式的体验。
通过演示动态模拟,学生可以更好地理解数学概念,并且可以更好地掌握解决问题的技能。
4. 数值计算
MATLAB还是一个强大的数值计算工具,对于高等数学问题的解决提供了很多技巧和方法。
学生可以使用平凡的MATLAB来验证和探究复杂的高等数学概念和理论。
5. 编程
MATLAB中的编程语言可以帮助高等数学教师更好地定制教学内容和试验,例如使用MATLAB中的正则化功能提高数据精度并减少误差。
MATLAB在高等数学实验中的应用

MATLAB在高等数学实验中的应用在高等数学实验中,MATLAB是一种广泛应用的计算软件,它具有强大的数学计算能力和可视化处理功能。
本文将探讨MATLAB在高等数学实验中的应用,并展示其在解决实际问题和学习数学概念中的优势。
一、MATLAB在函数绘图中的应用函数绘图是高等数学实验中常见的任务之一。
MATLAB提供了丰富的绘图函数和图形工具箱,可以方便地绘制各种函数的图像,并进行定量分析。
使用MATLAB绘制函数图像的基本步骤如下:1. 定义函数表达式:通过MATLAB的符号计算工具箱或直接使用符号表达式来定义函数。
2. 创建绘图窗口:使用MATLAB的绘图函数,如plot、scatter等来创建绘图窗口,并设置绘图参数。
3. 绘制函数图像:将定义好的函数表达式作为参数传递给绘图函数,即可绘制函数图像。
4. 添加坐标轴、标题和图例:通过MATLAB的绘图函数设置坐标轴、标题和图例等信息,以增强图像的可读性。
除了基本的函数绘图,MATLAB还可以绘制等高线图、三维曲面等复杂的图形,帮助学生更直观地理解数学概念和解决实际问题。
二、MATLAB在求解微分方程中的应用微分方程是高等数学中的重要内容,解微分方程需要进行数值计算。
MATLAB具有强大的数值计算能力和求解微分方程的工具箱,可以高效地求解各种类型的微分方程。
MATLAB中求解微分方程的基本步骤如下:1. 定义微分方程:使用MATLAB的符号计算工具箱来定义微分方程。
可以采用符号表达式或匿名函数的形式定义微分方程。
2. 设置初值条件:对于常微分方程,需要给出初值条件。
通过定义符号变量或直接赋值的方式,设置初值条件。
3. 调用求解函数:使用MATLAB的求解微分方程工具箱中的函数,如ode45、ode23等,传入定义好的微分方程和初值条件,即可求解微分方程。
4. 绘制解曲线:将求解得到的数值解通过MATLAB的绘图功能进行可视化展示,以增加对解的理解和分析。
利用MATLAB作图在高数中的应用

利用MATLAB作图在高数中的应用高等数学是大学教育中重要的基础理论课之一,在教学的过程中要教给学生基本的理论、学习方法、分析问题和解决问题的能力,高等数学又是一门比较抽象的课程,尤其对于非数学专业的学生,在教学的过程中,很难通过简单的语言将复杂的问题表述清楚,因此图形是高等数学学习过程中离不开的重要手段之一。
图形所能传达的信息远远大于文字,因此,将MATLAB的图形处理应用在高等数学的教学过程中,可起到事半功倍的作用.1 在泰勒公式中的应用泰勒公式是一个用函数在某点的信息描述其附近取值的公式。
如果函数足够光滑的话,在已知函数在某一点的各阶导数值的情况之下,可以用这些导数值做系数构建一个泰勒多项式来近似函数在这一点的邻域中的值。
泰勒公式还给出了这个多项式和实际的函数值之间的偏差。
但是在实际的教学过程中,学生对泰勒公式的理解一直不够深入,常常对泰勒公式打着一个大大的问号,大多数学生只能停留在如何展开方面,对于它的实际意义理解不透彻。
例1函数y=sinx的麦克劳林展开式为:下面,我们将绘制出原函数与它的一阶、三阶、五阶和七阶展开式的图形。
在MATLAB 的命令窗口输入如下命令:>> x=0:0.01:10;>> y=sin(x);>> y1=x;>> y2=x-x.^3/factorial(3);>> y3=x-x.^3/factorial(3)+x.^5/factorial(5);>> y4=x-x.^3/factorial(3)+x.^5/factorial(5)-x.^7/factorial(7);>> plot(x,y,x,y1,x,y2,x,y3,x,y4);>> axis([0,10,-5,5]);>>legend('y=sinx','y=x','y=x-x^3/3!','y=x-x^3/3!+x^5/5!','y=x-x^3/3!+ x^5/5!-x^7/7!');显示图形如图1所示。
GUI在高等数学中的应用

附录2:北京联合大学毕业设计(论文)任务书题目: MATLAB GUI在高等数学中的应用专业:指导教师:学院:学号:班级:姓名:一、主要内容和基本要求作为具有科学计算、符号运算和图形处理等多种功能的强有力实现工具,近年来MATLAB这一软件已得到了业界的普遍认可,应用领域已拓展到数值计算、数据处理、统计分析、工程等各个方面,从当前软件发展趋势来看,友好的图形用户界面(Graphical User Interface,GUI)已成为应用程序的基本交互入口,MATLAB这一功能强大的计算软件也应具备功能强大的GUI功能。
为此,MATLAB提供了对GUI的支持,使MATLAB开发的程序可为越来越多的用户所接受。
在高等数学的学习中,经常面临一些过于抽象,甚至难以解决的有关图形和计算的问题,使用MATLAB GUI设计可以很好地解决这些问题,以使数据的特征或性能能够清晰、直观地以GUI方式展现,利用MATLAB的强大数值计算功能对相关函数进行进一步分析,还可执行一些动作或变化来满足用户要求。
本设计要求如下:1)查阅相关文献,了解MATLAB GUI在高等数学中的研究及应用现状,了解各种数据可视化方法。
2)掌握在MATLAB中二维图形绘制的流程、函数、工具,二维图形修饰的方法,以及特殊坐标轴的绘制和多种特殊绘图函数。
3)掌握MATLAB提供的基本三维绘图命令及其使用方法,以及三维折线及曲线的绘制、三维曲面的绘制和图形基本的视图调控方式。
4) 研究MATLAB中的数据可视化方法:颜色、阴影和透明,包括各种着色技术和颜色设置。
研究MATLAB中图形用户界面编程的技术,包括界面设计、设计工具、对话框技术等。
5)编写一个数学软件,要求有良好易用的用户界面,实现矩阵分析,多项式运算,数据分析与统计,曲线拟合,数值积分,求导、微分方程等功能,并能利用MATLAB 的数据可视化方法将结果予以呈现。
二、主要参考资料[1] 陆垚光等编著. 精通MATLAB GUI设计[M]. 电子工业出版社. 2008.2[2] 徐士良等编著. 数值方法与计算机实现[M]. 清华大学出版社. 2006[3] 薛定宇, 陈阳泉编著. 高等应用数学问题的MATLAB求解[M]. 清华大学出版社.2004[4] 彭芳麟编著. 数学物理方程的MATLAB解法与可视化[M]. 清华大学出版社. 2003[5] Cleve B. Moler. Numerical computing with MATLAB[M]. Cambridge University Press. 2004三、进度要求2011.1月初——2011.1月末:研究毕设所要解决的问题,查阅资料。
MATLABGUI在数学模型中的应用课程设计

MATLABGUI在数学模型中的应用课程设计导言:MATLAB是一种常用的科学计算软件,广泛应用于工程、物理、统计等领域。
它提供了许多功能强大的工具,用于构建、模拟和分析数学模型。
为了更好地利用MATLAB在数学模型中的应用,我们设计了一个课程,介绍如何使用MATLABGUI构建数学模型,以及分析和优化模型。
一、课程目标1.熟悉MATLABGUI工具的界面和功能。
2.学习使用MATLAB编写数学模型的代码。
3.利用GUI实现模型的可视化和交互操作。
4.掌握分析和优化数学模型的方法。
二、课程内容1.MATLABGUI基础a.GUI工具箱的介绍b.GUI界面的设计和布局c.GUI的回调函数和事件处理2.数学模型的构建a.数学模型的基本概念和表示方法b.在MATLAB中实现数学模型的代码c.输入和输出的处理3.可视化和交互操作a.绘制数学模型的图形表示b.添加控件和用户界面的操作c.交互操作的实现4.数学模型的分析与优化a.参数对模型的影响分析b.模型的灵敏度分析c.优化算法在模型中的应用三、教学方法1.理论讲解:介绍MATLABGUI工具的基本概念和使用方法,以及数学模型的构建和分析方法。
2.实践操作:通过指导学生完成实例操作,锻炼学生独立完成任务的能力。
3.课堂讨论:提供学生自主提问和讨论的机会,加深对课程内容的理解和应用。
4.课程项目:学生设计和实现一个具体的数学模型,应用所学内容进行分析和优化。
四、教学评估1.平时作业:设计和完成一些小型的MATLABGUI应用程序。
2.实验报告:学生根据课堂项目,撰写实验报告,包括模型的构建和分析过程、结果分析和优化算法的应用。
3.期末考试:进行理论和实践的综合考核,检验学生对MATLABGUI在数学模型中应用的掌握程度。
五、课程成果通过本课程的学习,学生将能够:1.熟练掌握MATLABGUI的使用,能够快速构建和调试数学模型。
2.理解数学模型的构建和分析原理,能够运用优化算法解决实际问题。
MATLAB数学软件在高等数学中绘图与数值计算的实例研究

MATLAB数学软件在高等数学中绘图与数值计算的实例研究MATLAB是一种广泛应用于科学和工程领域的数学软件,具有强大的绘图和数值计算功能。
在高等数学中,MATLAB的应用可以帮助学生更好地理解和应用数学知识。
本文将通过实例研究,探讨MATLAB在高等数学中绘图与数值计算中的应用。
首先,MATLAB在高等数学中的绘图方面有着突出的性能。
它提供了丰富的绘图函数和工具,可以绘制各种图形,包括函数曲线、散点图、三维图形等。
以函数曲线为例,我们可以通过MATLAB绘制二维函数图像,观察函数的变化规律。
例如,我们可以使用MATLAB绘制函数y = sin(x)在给定区间内的图像,通过改变区间范围和坐标轴设置,可以更好地观察函数的周期、幅值和相位等特征。
此外,MATLAB还提供了灵活的函数参数调整功能,可以通过改变参数的值,观察函数图像的变化情况,从而更深入地理解函数的性质。
其次,MATLAB在高等数学中的数值计算方面也具有强大的能力。
它支持各种数值计算方法,如求解方程、数值积分、差分方程等。
以求解方程为例,我们可以使用MATLAB的数值求解函数,如fsolve和solve等,来求解高等数学中的各种方程。
例如,我们可以使用MATLAB求解非线性方程,如x^2- 2x - 1 = 0的根,只需要输入方程的表达式即可得到方程的解。
此外,MATLAB还提供了丰富的数值积分函数,可以用来计算曲线下的面积,从而实现高等数学中的定积分计算。
这些数值计算工具的使用,不仅可以节省计算时间,还可以减少计算误差,提高计算的准确度。
综上所述,MATLAB作为一种强大的数学软件,在高等数学中的绘图和数值计算中发挥了重要作用。
通过MATLAB的绘图功能,学生可以更直观地观察数学函数的特征和规律,从而更好地理解数学知识。
同时,MATLAB的数值计算功能也能够帮助学生进行复杂的数学计算,实现高等数学的各种数值解析。
因此,我们鼓励学生在学习高等数学的过程中,多加利用MATLAB软件进行绘图与数值计算的实践,以提高数学学习的效果和兴趣。
MATLAB GUI仿真软件在导数中的应用研究

1引言
高 等数 学 不 但 是理 工 科 的基 础课 程 , 同时 也 是 专 业课 的工 具 课 程, 其 应 用 十分 广 泛 [ 1 ] 。 MAT L A B G UI 将计算机 、 可视化 、 程序 设 计 融 合 到 了 一个 交互 式 工 作环 境 中 , 实 现数 值 计 算 、 建模和仿真、 可 视 化及绘图功能口 ] 。 鉴于导数理论复杂抽象 , 图形难以绘 制。 在教学时 可采用G UI 进行仿真教学 , 将导数理论与实验演示相结合 , 充分利用 MAT L AB 的可视化功能 , 通过程序编写实现导数 图像可视化、 复杂 问题 简 单化 、 抽 象 内容 形象 化 , 并 把导 数计 算 结果 和 图像 使 用 MAT L AB GU I 模 拟 出来 , 以此达 到 事 半 功倍 的效 果 。 这 样 不 仅 能让 高等数学 的授课方式更能适应学生形象思维 的特点 , 也能激发学生 学 习 的 求 知欲 , 提升学会、 学 好 高 等数 学 的信 心 , 体验 解 决 问题 的快 乐, 使学生真正学有所获 。
。
… 2 " p ; l
毒
■
≥ 。 = ; =谲妊 == = = =
姆
醚 整 : 业0 . 黛 …. 蠢 : 0 箍:
£ 壤鬻篙_ 磐臻瓣 !
≯ 鼎脚 一 _ ? t
“=
|
:= = = =
I 萤数一盼求 导
= = = = = =
参数二鼢求导 ¨
毒; = = 两 琴 ;
清辣 } 保存鼠并 }
制其参变量 函数及其导 函数在某一 区间上 的图像 , 使 图像可视化 。
3 . 1 G UI 仿 真主 要 功 能及 其设 计 意 图
基于MATLAB的GUI在高等数学教学中的应用

基于MATLAB的GUI在高等数学教学中的应用
沈静;黄登斌
【期刊名称】《高等继续教育学报》
【年(卷),期】2012(000)003
【摘要】MATLAB是一套功能强大的数学软件。
MATLAB的图形用户界面技术为高等数学的教学提供了一个交互环境,寓理论教学、实验演示于一体,有利于增强教学的直观性、互动性,丰富了教学手段,提高了教学效果,调动了学生学习的积极性。
【总页数】2页(P45-46)
【作者】沈静;黄登斌
【作者单位】海军工程大学理学院,武汉430033;海军工程大学理学院,武汉430033
【正文语种】中文
【中图分类】G642
【相关文献】
1.基于MATLAB的GUI设计在高等数学中的应用 [J], 魏娟;宋福庆
2.基于MATLAB GUI的高等数学计算机辅助教学演示系统的开发 [J], 刘兵
3.基于matlab的图形和动画技术在高等数学教学中的应用 [J], 刘广会;曹修文;齐化富
4.信息与计算科学专业教学中基于MatLAB的GUI应用 [J], 刘杰
5.基于matlab-gui的高等数学课件设计 [J], 毛建生;
因版权原因,仅展示原文概要,查看原文内容请购买。
基于matlab-gui的高等数学课件设计

基于matlab-gui的高等数学课件设计
毛建生
【期刊名称】《泸州职业技术学院学报》
【年(卷),期】2012(000)002
【摘要】课件ppt的引入,确实给我们的教学带来了极大的方面,也解决了很多教学的难点问题,但是在高等数学教学中,需要大量的计算、分析、证明、逻辑推理,课件ppt就无法胜任了,所以许多数学教师还是偏爱传统的黑板-粉笔式的教学,随着matlab软件的逐步普及,教学观念的转变,高等数学教学逐步引入数学实
验,matlab-gui课件的设计可以解决理工类教学中的证明、分析、计算等问题。
本文谈谈如何设计matlab-gui课件进行高等数学教学。
【总页数】3页(P20-22)
【作者】毛建生
【作者单位】泸州职业技术学院
【正文语种】中文
【中图分类】O13-4
【相关文献】
1.基于Matlab-GUI的数值积分界面设计 [J], 张建斌;赵静;许晓晴
2.基于MATLAB-GUI的信号采集与分析系统设计 [J], 张世弘;刘振兴
3.基于Authorware的高等数学课件的研究与实现 [J], 吴海军
4.在高等数学课件设计中注重学生创新能力的培养 [J], 李雅瑞
5.基于MATLAB-GUI的生产车间调度系统设计 [J], 王辉;张嘉薇;罗萌萌;何浩浩;吐列克·杰恩斯别克;戴敏
因版权原因,仅展示原文概要,查看原文内容请购买。
浅谈matlab的绘图功能在高等数学教学中的应用_于丽妮
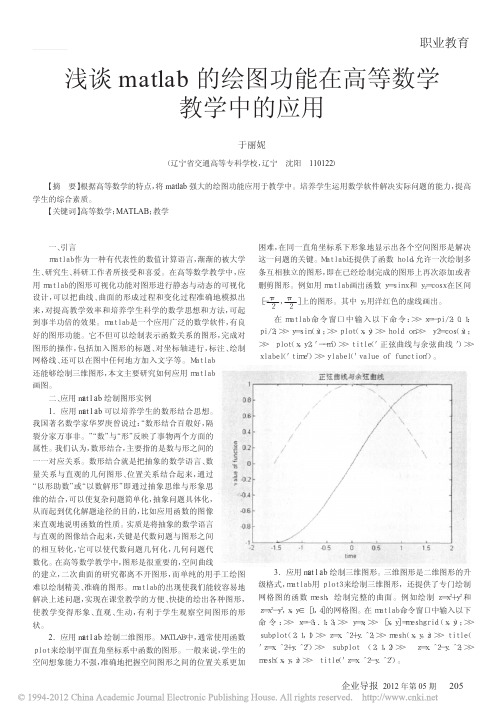
三、结论 利用 matlab 的绘图功能辅助高等数学教学,静态与动态 的三维演示,将抽象问题具体化,提高教学质量,激发学生的学 习热情,使教学方式由传统的板书式教学向多样化发展。 本文所有源代码在 matlab6.1 中调试通过。
参考文献
函数
y=sinx
和
y2=cosx
在区间[-
π 2
,π 2
]上的图形。在
[4] 牛秀敏等. 几种常规综合评价方法的比较 [J]. 统计与决策. 2006,21(3):142~143 [5]Editiorial.In search of European model for the Information Society[J]. Telematics andInformatics.2000,11(17):1~7 [6]Anders Henten,Thomas Myrup rmation society visions in the Nordiccountries [J].Telematics and Informatics.2000,14(17): 77~103 [7] 王其荣等. 综合评价方法之评价 [J]. 统计与决策,2006,4(6): 137~138 [8]王少卫等.数字化车间布局模糊层次评价研究[J].计算机仿真. 2009,22(7):290~293 [9]徐绪堪.基于模糊理论的毕业设计质量评估模型的构建[J].实验 室技术与管理.2007,24(6):117~ 119 [10]马莉,孙延明等.企业信息化评价指标体系及其评价方法的研究 [J].现代制造工程.2005,22(3):41~44 [11]朱海荣,傅铅生.企业信息化水平模糊评价模型的研究[J].科技 情报开发与经济.2005,15(15):110~ 111 项目基金:本文系甘肃省教育厅科研项目(1102- 05)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[参考文献]
1-13同济大学数学系.高等数学(第六版)EM].北京:高等 教育出版社,2007.
[2,2008.
[3]罗华飞.MATLAB GUI设计学习手记[M].北京:北 京航空航天大学出版社.2009.
The Applications of GUI Design to Higher Mathmatics Based on MATLAB
0.24≤y≤1.1下的曲线。并观察和推断当x一一
OO,p+。。,x。∞,x_O一,x·0+,x—O时,函数
的变换趋势,说明单、双侧极限的关系。 通过绘制函数的动态曲线(彗星轨迹)和静态
曲线极限图,来推断当自变量变化时函数的变化 趋势。
首先,结构设计。在布局编辑器中布置控件, 使用几何位置排列工具对控件的位置进行调整。
万方数据
130
安阳师范学院学报
20lO年
ton,用于绘制函数的动态彗星轨迹图形;设置第 二个按钮的标识为limit—pushbutton,用于绘制 函数的极限图形;设置第三个按钮的标识为close 一pushbutton,用于结束程序。界面设计如图1。
建立一级菜单file,用来执行绘制图形和关 闭图形功能(in图2)。在其下设置三个子菜单项 comet,limit和close。菜单项comet的Tag设置 为“comet—menu”。调用绘制函数的动态彗星轨迹 图形功能;菜单项limit的Tag设置为“limit— menu”,调用绘制函数的极限图形功能;菜单项 close的Tag设置为“close—menu”,执行关闭图形 功能。
其次,功能设计。编写代码完成程序中因变 量的赋值、输入/输出及绘图等工作,系统会自动 生成M文件程序代码。
function comet—pushbutton—Callback(hOb一 ject,eventdata,handles)
axes(handles.axesl); x=一700:0.1:700; box on; hold on;
万方数据
基于MATLAB的GUI设计在高等数学中的应用
作者: 作者单位: 刊名:
英文刊名: 年,卷(期): 被引用次数:
魏娟, 宋福庆, WEI Juan, SONG Fu-qing 安阳师范学院,数学与统计学院,河南,安阳,455002
安阳师范学院学报 JOURNAL OF ANYANG TEACHERS COLLEGE 2010(5) 2次
在高等数学的学习中,经常面临一些过于抽 象、甚至难以解决的有关图形和计算的问题,使用 MATLAB GUI设计可以很好地解决这些问题, 并且能对相关函数利用MATLAB的强大数值计 算功能进行进一步分析,还可执行一些动作或变 化来满足用户要求。
2 设计原理
一个完整的GUI设计分为两个阶段完成。 第一个阶段:图形界面的结构设计。利用设 计向导构造整个图形界面的布局,合理安排控件, 没计菜单,进行必要的属性设计。
[关键词]MATLAB应用;GUI设计;高等数学;函数极限
[中图分类号]0171
[文献标i.qra-g]A
[文章编号]1671—5330(2010)05一0129一03
1 引言
MATLAB作为具有科学计算、符号运算和 图形处理等多种功能的强有力实现工具,应用领 域已拓展到数值计算、数据处理、统计分析、工程 等各个方面,在各大公司、科研机构和高校得到广 泛应用。在科学研究和工程应用中,人们希望将 数据、设计或计算结果用交互式图形表示,以使数 据的特征或性能能够清晰、直观地以GUI方式展 现。MATLAB在提供强大计算功能的同时,近 年来还大力发展了面向对象的图形技术和GUI 技术,使用户可以轻松实现数据的交互式显示。
axis([--700 700--0.24 1.13); comet(x,sin(x)/x); 调用limit—pushbutton—Callback绘制函数y
—sln x:芒E一1004x4100,一0.244y41.1下的 X
静态极限图形,代码如下: function limit—pushbutton—Callback(hOb—
x+c。X
x‘++∞X
x·一X
当自变量趋近于0时,函数的变化趋势都是
无限地趋近于l,即
lim业坚; lim—sln—x== lim坐坚=I
p0一 X
x_-O+X
x一.0
X
这也从函数的图像变化上证明了极限存在的
万方数据
充要条件是两个单侧极限存在且相等。
4小结
MATLAB GUI设计在高等数学中的应用还 有很多,比如函数图形绘制、空间解析几何应用、 曲线拟合、数值积分、求导、微分方程等等。利用 GUI设计可以使抽象的数学问题直观化,有助于 进一步理解相关概念。
2010矩
安阳师范学院学报
129
基于MATI。AB的GUI设计在高等数学中的应用
魏娟,宋福庆
(安阳师范学院数学与统计学院.河南安阳455002)
【摘要]高等数学学习中经常会面临一些过于抽象、甚至难以解决的有关图形和计算的问题。本文利用MATLAB
GUI设计有效解决了这类问题,并使这些抽象的数学问题变得简单、直观。
ject,eventdata,handles) axes(handles.axes2); fplot(’sin(x)./x",[一100 100一o.24 1.13); text(30,0.5,’sin(x)/<); 运行程序后,单击“Comet”按钮或菜单项
comet后,绘制动态曲线图形,单击“Limit”按钮 或菜单项limit后绘制静态极限图形,如图3所 不。
WEI Juan,SONG Fu—qing
(School of Mathematics and Statistics,Anyang Normal University,Anyang 45 5002,China) Abstract:Leaners often face some graph and calculation Problems which are too abstract and difficuIt to solve.This paper applies the MATLAB GUI design to effectively solve the problem.It also makes the abstract problem become more simple and intuitive. Key words:Matlab application;GUI design;Higher Mathematics:Limit of function
第二个阶段:功能设计。为控件、菜单编写相 应的回调函数(Callback),具体实现界面的各种 功能。
3 应用举例
通过极限的可视化显示求函数极限的过程, 可以随着自变量取值的变化来显示函数值也随之 不断变化的动态可视化图像。观察函数和数列的 变化趋势,体会极限概念的内涵和外延。
例绘制函数y=鼍竽在一100≤x≤100,一
引证文献(2条)
1.张小凤.金永幸.马珊.田甜.刘晨鸽.刘杭州 基于Matlab的信号与系统综合实验系统研发[期刊论文]-现代电子技
术 2011(20)
2.刘演龙 基于Matlab GUI的目标跟踪算法仿真演示系统[期刊论文]-重庆理工大学学报(自然科学版) 2013(7)
本文链接:/Periodical_anysfxyxb201005033.aspx
参考文献(3条) 1.同济大学数学系 高等数学 2007 2.陈垚光;王正林 精通MATLAB GUI设计 2008 3.罗华飞 MATLAB GUI设计学习手记 2009
本文读者也读过(9条) 1. 徐德华.钱真.何秋茹.陶渝辉.张文杰 基于MATLAB GUI的数据分析软件包设计[期刊论文]-测控技术2004,23(z1) 2. 杨志明 MATLAB动画在函数极限教学中的应用[期刊论文]-数学教学研究2010,29(7) 3. 王甲春.郑伟伟.WANG Jia-chun.ZHENG Wei-wei MATLAB GUI技术在梁的内力分析可视化中的应用[期刊论文]-厦 门理工学院学报2009,17(4) 4. 王刚.查艳萍.Wang Gang.Zha Yanping 微积分MATLAB数学实验[期刊论文]-保山学院学报2010,29(5) 5. 李京秀.陈白生 基于MATLAB图形用户界面GUI的电路仿真实验的制作[期刊论文]-电气电子教学学报2004,26(4) 6. 赵军.ZHAO Jun 基于MATLAB田地面积计算的GUI设计[期刊论文]-农业网络信息2006(11) 7. 李彤.项四通.李吉宗.LI Tong.XIANG Si-tong.LI Ji-zong 基于Matlab的材料力学图形用户界面系统开发[期刊 论文]-实验室研究与探索2010,29(8) 8. 沈飞.Shen Fei 卷积在MATLAB GUI中的仿真实现[期刊论文]-工业控制计算机2010,23(12) 9. 郭良辉.孟小红.石磊.冯思慕 MATLAB在"应用重力学"课程教学中的应用[期刊论文]-科技信息2010(3)
(1)建立两个坐标轴对象.用于显示函数的动 态彗星轨迹和函数的极限图形。
(2)建立三个按钮,用于绘制图形和结束程 序。
设置第一个按钮的标识为comet—pushbut一
[收稿日期]2010-06—26 [作者简介]魏娟(1980一),女,安阳师范学院数学与统计学院教师.硕士,主要从事混沌控制与复杂网络研究。
佣。
1
O.B D.5
O.●
0.2
D
.o.2
-S00
0
啪
图2 调用comet—pushbutton—Callback绘制函数
y5坠笋在一700≤x4700下的动态曲线图形,代
码如下:
图3 从图3可以观察动态曲线图和静态曲线图,
