一个处在真空中的弓形平面载流线圈.
大学物理复习第四章知识点总结

大学物理复习第四章知识点总结大学物理复习第四章知识点总结一.静电场:1.真空中的静电场库仑定律→电场强度→电场线→电通量→真空中的高斯定理qq⑴库仑定律公式:Fk122err适用范围:真空中静止的两个点电荷F⑵电场强度定义式:Eqo⑶电场线:是引入描述电场强度分布的曲线。
曲线上任一点的切线方向表示该点的场强方向,曲线疏密表示场强的大小。
静电场电场线性质:电场线起于正电荷或无穷远,止于负电荷或无穷远,不闭合,在没有电荷的地方不中断,任意两条电场线不相交。
⑷电通量:通过任一闭合曲面S的电通量为eSdS方向为外法线方向1EdS⑸真空中的高斯定理:eSoEdSqi1int只能适用于高度对称性的问题:球对称、轴对称、面对称应用举例:球对称:0均匀带电的球面EQ4r20(rR)(rR)均匀带电的球体Qr40R3EQ240r(rR)(rR)轴对称:无限长均匀带电线E2or0(rR)无限长均匀带电圆柱面E(rR)20r面对称:无限大均匀带电平面EE⑹安培环路定理:dl0l2o★重点:电场强度、电势的计算电场强度的计算方法:①点电荷场强公式+场强叠加原理②高斯定理电势的计算方法:①电势的定义式②点电荷电势公式+电势叠加原理电势的定义式:UAAPEdl(UP0)B电势差的定义式:UABUAUBA电势能:WpqoPP0EdlEdl(WP00)2.有导体存在时的静电场导体静电平衡条件→导体静电平衡时电荷分布→空腔导体静电平衡时电荷分布⑴导体静电平衡条件:Ⅰ.导体内部处处场强为零,即为等势体。
Ⅱ.导体表面紧邻处的电场强度垂直于导体表面,即导体表面是等势面⑵导体静电平衡时电荷分布:在导体的表面⑶空腔导体静电平衡时电荷分布:Ⅰ.空腔无电荷时的分布:只分布在导体外表面上。
Ⅱ.空腔有电荷时的分布(空腔本身不带电,内部放一个带电量为q的点电荷):静电平衡时,空腔内表面带-q电荷,空腔外表面带+q。
3.有电介质存在时的静电场⑴电场中放入相对介电常量为r电介质,电介质中的场强为:E⑵有电介质存在时的高斯定理:SDdSq0,intE0r各项同性的均匀介质D0rE⑶电容器内充满相对介电常量为r的电介质后,电容为CrC0★重点:静电场的能量计算①电容:②孤立导体的电容C4R电容器的电容公式C0QQUUU举例:平行板电容器C圆柱形电容器C4oR1R2os球形电容器CR2R1d2oLR2ln()R1Q211QUC(U)2③电容器储能公式We2C22④静电场的能量公式WewedVE2dVVV12二.静磁场:1.真空中的静磁场磁感应强度→磁感应线→磁通量→磁场的高斯定理⑴磁感应强度:大小BF方向:小磁针的N极指向的方向qvsin⑵磁感应线:是引入描述磁感应强度分布的曲线。
大学物理第五章 静电场部分的习题及答案

第五章 静电场一、简答题1、为什么在无电荷的空间里电场线不能相交?答案:由实验和理论知道,静电场中任一给定点上,场强是唯一确定的,即其大小和方向都是确定的.用电场线形象描述静电场的空间分布时,电场线上任一点的切线方向表示该点的场强方向.如果在无电荷的空间里某一点上有几条电场线相交的话,则过此交点对应于每一条电场线都可作出一条切线,这意味着交点处的场强有好几个方向,这与静电场中任一给定点场强具有唯一确定方向相矛盾,故无电荷的空间里电场线不能相交.2、简述静电场中高斯定理的文字内容和数学表达式。
答案:在真空中的静电场内,通过任意封闭曲面的电通量等于该封闭曲面所包围的所有电荷电量的代数和的01ε倍。
0ε∑⎰=⋅内S Sq S d E3、写出静电场的环路定理,并分别说明其物理意义。
答案:静电场中,电场强度的环流总是等于零(或0l=⋅⎰l d E ),静电场是保守场。
4、感生电场与静电场有哪些区别和联系?二、选择题1、如图所示,两个同心均匀带电球面,内球面半径为1R 、带有电荷1Q ,外球面半径为2R 、带有电荷2Q ,则在外球面外面、距离球心为r 处的P 点的场强大小E 为 ( A ) A.20214r Q Q επ+ B.()()2202210144R r Q R r Q -π+-πεε C.()2120214R R Q Q -+επ D.2024r Q επ 2、半径为R 的均匀带电球体的静电场中各点的电场强度的大小E 与距球心的距离r 的关系曲线为:( B )3、图示一均匀带电球体,总电荷为Q +,其外部同心地罩一内、外半径分别为1r 、2r 的金属球壳.设无穷远处为电势零点,则在球壳内半径为r 的P 点处的场强和电势为: ( D )A.204r QE επ=,r Q U 04επ= B.0=E ,104r Q U επ= C. 0=E ,r Q U 04επ=D.0=E ,204r Q U επ= 4、图中实线为某电场中的电场线,虚线表示等势(位)面,由图可看出:( D )A.C B A E E E >>,C B A U U U >>B.C B A E E E <<,C B A U U U <<C.C B A E E E >>,C B A U U U <<D.C B A E E E <<,C B A U U U >>5、面积为S 的空气平行板电容器,极板上分别带电量q ±,若不考虑边缘效应,则两极板间的相互作用力为 ( B )A.S q 02εB.S q 022εC.2022S q εD.202Sq ε 6、一均匀带电球面在球面内各处产生的场强 ( A )A.处处为零B.不一定为零C.一定不为零D.是常数7、已知一高斯面所包围的体积内电量代数和0=∑i q ,则可肯定:( C )A.高斯面上各点场强均为零B.穿过高斯面上每一面元的电通量均为零C.穿过整个高斯面的电通量为零D.以上说法都不对8、下列说法中正确的是 ( D )A.电场强度为0的点,电势也一定为0.B.电场强度不为0的点,电势也一定不为0.C.电势为0的点,则电场强度也一定为0.D.电势在某一区域为常数,则电场强度在该区域也必定为0.9、如图所示,一个带电量为q 的点电荷位于正立方体的中心上,则通过其中一侧面的电场强度通量等于 ( B ):A.04εqB.06εqC.06πεqD.04πεq 三、计算题1、两无限长同轴圆柱面,半径分别为1R 和2R (21R R < ),带有等量异号电荷,单位长度的电量为λ和λ-,求:(1) 1R r <;(2)21R r R <<;(3)r R <2处各点的场强。
湖南大学物理(2)第14,15章课后习题参考答案

第14章 稳恒电流的磁场 一、选择题1(B).2(D).3(D).4(B).5(B).6(D).7(B).8(C).9(D).10(A) 二、填空题(1). 最大磁力矩.磁矩 ; (2). R 2c ;(3).)4/(0a I μ; (4).RIπ40μ ;(5).i .沿轴线方向朝右. ; (6). )2/(210R rI πμ. 0 ;(7). 4 ; (8). )/(lB mg ; (9). aIB ; (10). 正.负.三 计算题1.一无限长圆柱形铜导体(磁导率0).半径为R .通有均匀分布的电流I .今取一矩形平面S (长为1 m.宽为2 R ).位置如右图中画斜线部分所示.求通过该矩形平面的磁通量.解:在圆柱体内部与导体中心轴线相距为r 处的磁感强度的大小.由安培环路定律可得: )(220R r rRIB ≤π=μ因而.穿过导体内画斜线部分平面的磁通1为⎰⎰⋅==S B S B d d 1 Φr r RI Rd 2020⎰π=μπ=40Iμ在圆形导体外.与导体中心轴线相距r 处的磁感强度大小为 )(20R r rIB >π=μ因而.穿过导体外画斜线部分平面的磁通2为⎰⋅=S B d 2Φr r I R Rd 220⎰π=μ2ln 20π=Iμ穿过整个矩形平面的磁通量 21ΦΦΦ+=π=40I μ2ln 20π+Iμ1 m2. 横截面为矩形的环形螺线管.圆环内外半径分别为R 1和R 2.芯子材料的磁导率为.导线总匝数为N .绕得很密.若线圈通电流I .求. (1) 芯子中的B 值和芯子截面的磁通量. (2) 在r < R 1和r > R 2处的B 值.解:(1) 在环内作半径为r 的圆形回路, 由安培环路定理得NI r B μ=π⋅2. )2/(r NI B π=μ 在r 处取微小截面d S = b d r , 通过此小截面的磁通量r b rNIS B d 2d d π==μΦ穿过截面的磁通量⎰=SS B d Φr b rNId 2π=μ12ln2R R NIbπ=μ (2) 同样在环外( r < R 1 和r > R 2 )作圆形回路, 由于0=∑iI02=π⋅r B ∴ B = 03. 一根很长的圆柱形铜导线均匀载有10 A 电流.在导线内部作一平面S .S 的一个边是导线的中心轴线.另一边是S 平面与导线表面的交线.如图所示.试计算通过沿导线长度方向长为1m 的一段S 平面的磁通量.(真空的磁导率0 =4×10-7T ·m/A.铜的相对磁导率r ≈1)解:在距离导线中心轴线为x 与x x d +处.作一个单位长窄条. 其面积为 x S d 1d ⋅=.窄条处的磁感强度 202RIxB r π=μμ所以通过d S 的磁通量为 x RIxS B r d 2d d 20π==μμΦ通过1m 长的一段S 平面的磁通量为⎰π=Rr x R Ix20d 2μμΦ60104-=π=Ir μμ Wb4. 计算如图所示的平面载流线圈在P 点产生的磁感强度.设线圈中的电流强度为I .解:如图.CD 、AF 在P 点产生的 B = 0x2EF DE BC AB B B B B B+++=)sin (sin 4120ββμ-π=aIB AB . 方向其中 2/1)2/(sin 2==a a β.0sin 1=β ∴ a I B AB π=240μ. 同理, aI B BC π=240μ.方向.同样 )28/(0a I B B EF DE π==μ.方向⊙.∴ aI B π=2420μaIπ-240μaIπ=820μ 方向.5. 如图所示线框.铜线横截面积S = 2.0 mm 2.其中OA 和DO '两段保持水平不动.ABCD 段是边长为a 的正方形的三边.它可绕OO '轴无摩擦转动.整个导线放在匀强磁场B 中.B 的方向竖直向上.已知铜的密度 = 8.9×103 kg/m 3.当铜线中的电流I =10 A 时.导线处于平衡状态.AB 段和CD 段与竖直方向的夹角 =15°.求磁感强度B 的大小.解:在平衡的情况下.必须满足线框的重力矩与线框所受的磁力矩平衡(对OO '轴而言).重力矩 αραρsin sin 2121gSa a a gS a M +⋅= αρsin 22g Sa =磁力矩 ααcos )21sin(222B Ia BIa M =-π=平衡时 21M M =所以 αρsin 22g Sa αcos 2B Ia =31035.9/tg 2-⨯≈=I g S B αρ T6. 如图两共轴线圈.半径分别为R 1、R 2.电流为I 1、I 2.电流的方向相反.求轴线上相距中点O 为x 处的P 点的磁感强度. 解:取x 轴向右.那么有 2/322112101])([2x b R I R B ++=μ 沿x 轴正方向 2/322222202])([2x b R I R B -+=μ 沿x 轴负方向21B B B -=[2μ=2/32211210])([x b R I R ++μ]])([2/32222220x b R I R -+-μ若B > 0.则B 方向为沿x 轴正方向.若B < 0.则B的方向为沿x 轴负方向.P7. 如图所示.一块半导体样品的体积为a ×b ×c .沿c 方向有电流I .沿厚度a 边方向加有均匀外磁场B (B的方向和样品中电流密度方向垂直).实验得出的数据为 a =0.10 cm 、b =0.35 cm 、c=1.0 cm 、I =1.0 mA 、B =3.0×10-1T.沿b 边两侧的电势差U =6.65 mV.上表面电势高.(1) 问这半导体是p 型(正电荷导电)还是n 型(负电荷导电)?(2) 求载流子浓度n 0 (即单位体积内参加导电的带电粒子数). 解:(1) 根椐洛伦兹力公式:若为正电荷导电.则正电荷堆积在上表面.霍耳电场的方向由上指向下.故上表面电势高.可知是p 型半导体。
大物上海交大课后答案第七章

大物上海交大课后答案第七章第一篇:大物上海交大课后答案第七章习题7 7-1.如图所示的弓形线框中通有电流I,求圆心O处的磁感应强度B。
解:圆弧在O点的磁感应强度:B1=ϖμ0Iθμ0I,方向:ε;=4πR6Rμ0I[sin60-sin(-60)]=00B2=直导线在O点的磁感应强度:3μ0I2πR4πRcos600,方向:⊗;∴总场强:B=μ0I2R(1-),方向⊗。
π337-2.如图所示,两个半径均为R的线圈平行共轴放置,其圆心O1、O2相距为a,在两线圈中通以电流强度均为I的同方向电流。
(1)以O1O2连线的中点O为原点,求轴线上坐标为x的任意点的磁感应强度大小;(2)试证明:当a=R时,O点处的磁场最为均匀。
解:见书中载流圆线圈轴线上的磁场,有公式:B=(1)左线圈在x处P点产生的磁感应强度:BP1=μ0IR22(R+z)2232。
μ0IR2右线圈在x处P点产生的磁感应强度:BP2ϖϖBP1和BP2方向一致,均沿轴线水平向右,∴P点磁感应强度:BP=BP1+BP2=(2)因为BP随x变化,变化率为3a2222[R+(+x)]2μ0IR2,=3a2[R2+(-x)2]22,μ0IR2⎧23-⎫a2-3a22⎨[R+(x+)]2+[R+(x-)]2⎬;22⎩⎭2dB,若此变化率在x=0处的变化最缓慢,则O点处的dx磁场最为均匀,下面讨论O点附近磁感应强度随x变化情况,即对BP的各阶导数进行讨论。
对B求一阶导数:3μ0IR2⎧⎫aa2-5aa2-5dB2222=-(x+)[R+(x+)]+(x-)[R+(x-)]⎨⎬22222dx⎩⎭dB当x=0时,=0,可见在O点,磁感应强度B有极值。
dx对B求二阶导数:ddBd2B()== 2dxdxdx⎧a2a2⎫5(x+)5(x-)⎪3μ0IR⎪11⎪⎪22--+-⎨5757⎬2aaaa⎪[R2+(x+)2]2[R2+(x+)2]2[R2+(x-)2]2[R2+(x-)2]2⎪⎪⎪⎩2222⎭2a2-R2,x=0=3μ0IR7a[R2+()2]22d2B>0,O点的磁感应强度B有极小值,可见,当a>R时,2x=0dxd2B当x=0时,dx22d2B当a<R时,dx2d2B当a=R时,dx2x=0<0,O点的磁感应强度B有极大值,=0,说明磁感应强度B在O点附近的磁场是相当均匀的,可看成匀x=0强磁场。
第7章 稳恒磁场习题解答

第7章 稳恒磁场7-1 如图,一个处在真空中的弓形平面载流线圈acba ,acb 为半径cm 2=R 的圆弧,ab 为圆弧对应的弦,圆心角090aob ∠=,A 40=I ,试求圆心O 点的磁感应强度的大小和方向。
解 由例7-1 线段ba 的磁感应强度 o o 40140(cos45-cos135) =410T4π0.02cos45B μ-=⨯⨯︒方向垂直纸面向外。
由例7-2 圆弧acb 的磁感应强度4002π1402 3.1410T 2π2420.02I μB R μ-==⨯=⨯方向垂直纸面向内。
4120.8610TB B B -=-=⨯方向垂直纸面向外。
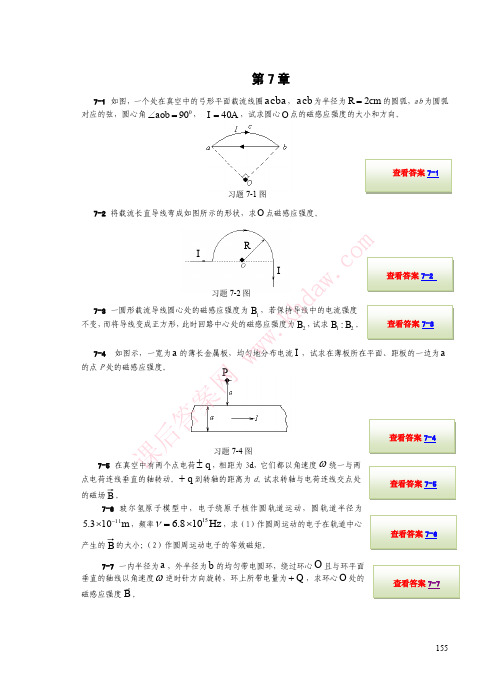
7-2 将载流长直导线弯成如图所示的形状,求圆心O 点处磁感应强度。
解 如图,将导线分成1(左侧导线)、2(半圆导线)、3(右侧导线)三部分,设各部分在O 点处产生的磁感应强度分别为1B 、2B 、3B 。
根据叠加原理可知,O 点处磁感应强度321B B B B++=。
01=B024I B Rμ=,方向垂直于纸面向里034πI B Rμ=,方向垂直于纸面向里O 点处磁感应强度大小为习题7-1图0O 23(1π)4πIB B B Rμ=+=+ ,方向垂直于纸面向里。
7-3 一圆形载流导线圆心处的磁感应强度为1B ,若保持导线中的电流强度不变,而将导线变成正方形,此时回路中心处的磁感应强度为2B ,试求21:B B解 设导线长度为l ,为圆环时, 2πl R = 001π2I I B R l μμ==为正方形时,边长为4l,由例7-100024(cos 45cos135)4π8IB lμ=⨯-=⨯212 :πB B =7-4 如图所示,一宽为a 的薄长金属板,均匀地分布电流I ,试求在薄板所在平面、距板的一边为a 的点P 处的磁感应强度。
解 取解用图示电流元,其宽度为d r ,距板下边缘距离为r ,其在P 点处激发的磁感应强度大小为00d d d 2π22π(2)II r B (a r)a r aμμ==--,方向垂直于纸面向外。
大学物理学 上册 (孙厚谦 著) 清华大学出版社 课后答案 第7章
R
7-8 半径为 R 的薄圆盘均匀带电,总电量为 q 。令此盘绕通过圆盘中心 且垂直盘面的轴线匀速转动,角速度 ,求圆盘中心 O 处的磁感应强度。
查看答案 7-8
7-9 如图所示是一根很长的长直圆管形导体的横截面,内外半径分别为 a 和 b ,导体内载有沿轴线 方向的电流 I ,且电流 I 均匀分布在管的横截面上。试求导体内部( a r
第7章
7-1 如图,一个处在真空中的弓形平面载流线圈 acba , acb 为半径为 R 2cm 的圆弧,ab 为圆弧 对应的弦,圆心角 aob 900 ,
I 40A ,试求圆心 O 点的磁感应强度的大小和方向。
查看答案 7-1 习题 7-1 图 7-2 将载流长直导线弯成如图所示的形状,求 O 点磁感应强度。
B B1 B2 0.86 104 T
方向垂直纸面向外。 7-2
m
返回 7-1
解 如图,将导线分成 1(左侧导线) 、2(半圆导线) 、3(右侧导线)三部分,设各部分在 O 点处产 生的磁感应强度分别为 B1 、 B2 、 B3 。 根据叠加原理可知, O 点处磁感应强度 B
B2
网
利用叠加原理求 P2 点场强
ww
w.
a2 a2 π j πa I 2r 2 a 2 B Bo ( B1 B2 ) 0 ( 4 4 ) 0 a a 2π r π r (4r 2 a 2 ) r r 2 2
kh
2
π
da
r
r r2 a2 4
2πr
2π
r
w. 案
网
答
案
w.
F
co
B 的分布。
(完整)传热复习题(一)参考答案

《传热技术》复习题(一)参考答案一、填空题1、写出三种间壁式换热器的名称:套管式换热器、管壳式换热器和板式换热器。
2、换热器在使用一段时间后,传热速率会下降很多,这往往是由于传热管表面有污垢积存的缘故。
3、用套管换热器加热内管的空气,蒸气在管间冷凝。
现欲通过实验方法测定蒸气和空气的给热系数,需要的主要仪器有温度计、流量计 .4、用饱和水蒸汽加热空气,总传热系数K接近于空气侧的对流传热系数,而壁温接近于饱和蒸汽侧流体的温度值。
5、蒸气冷凝分滴状冷凝和膜状冷凝.6、冷、热气体在间壁换热器中换热,热气体进口温度T1=400℃,出口温度T2为200℃,冷气体进口温度t1=50℃,两股气体的质量流量相同,物性数据可视为相同,若不计热损失时,冷气体出口温度为 250 ℃;若热损失为5%时,冷气体出口温度为 240 ℃7、应用准数关联式求取对流传热系数时,应注意:(1) 应用范围;(2)特征尺寸 ;(3)定性温度 .8、列管换热器中,用饱和水蒸汽加热空气。
空气走管内,蒸汽走管间,则管壁温度接近水蒸汽的温度,总传热系数接近空气的对流传热系数。
9、列管换热器,在壳程设置折流挡板的目的是强化传热和支撑管束。
10、如图所示为间壁式换热器中冷流体B与热流体A的稳态传热过程的温度分布曲线,该传热过程是由对流传热、热传导和对流传热三个串联的热传递环节组成,由图分析可知:α1〈α2,因此若强化该传热过程,应从 A 侧着手。
11、强化传热的方法之一是提高K值。
而要提高K值,则应提高对流传热系数较小一侧的对流传热系数.12、有两种不同的固体材料,它们的导热系数第一种为λ>第二种为λ,若作为换热器材料,应选用第一种;当作为保温材料时,应选用第二种。
13、某大型化工容器的外层包上隔热层,以减少热损失,若容器外表温度为150℃,而环境温度为20℃,要求每平方米热损失不大于500w,采用某隔热材料,其导热系数λ=0.35W/m2.K,则其厚度不低于 91mm 。
大学物理习题集答案解析-第七章-磁力
解:( 俯视逆时针旋转. )
h 2mv//
eB
eB h
v//
m
2
R
mv eB
eB v m R
B F
v
v2 v/2/
eB m
R2 h 2
2
由洛伦兹力 F ev B 可判断出 B沿螺旋轴竖直向上( 如图示 ).
7-4 如图示,一条任意形状的载流导线位于均匀磁场 中,试证明它所受到的安培力等于载流直导线ab所 受到的安培力。
为I2且AB与ab在同一平面上,ABab,如图8-2所示,a端距离 AB为ra,b端距离AB为rb,求导线ab受到的作用力。
解的:磁感在应ab上强任度取方一向线: 元B dr,d由rAB产生
A
大小: B 0 I1 2r
I1 r ab
d F I2dr sB i9n 0 I2Bd 同向r叠加
I2 dr
Fe12
q1q2
4 0a2
rˆ1(2 向上)
F12Fe12
v1 q 1
v2
qrˆ12 2
8-5 电流由长直导线1沿平行bc边方向经过a点流入一电阻均匀分布
的正三角形线框,再由b点沿cb方向流出,经长直导线2返回电源,
如图8-5所示,已知导线上的电流为I,三角框的每一边长为L,求三
角框中心O点的磁感应强度的大小。
第七章 磁力
7-1 7-5 7-9 7-2 7-6 7-3 7-7 7-4 7-8
7-1 .有一质量为m的倒U形导线,两端浸没在水银槽中,导
线的上段长l 处在均匀磁场B中,如果使一个电流脉冲,即
t
电冲量持续q时间与0导id线t跳通起过时导间线相,这比导非线常就小会,跳试起由来导,线假所定达电高脉度
大学物理练习题及答案

∙ -q OABCD关于点电荷以下说法正确的是 D(A) 点电荷是电量极小的电荷; (B) 点电荷是体积极小的电荷;(C) 点电荷是体积和电量都极小的电荷;(D) 带电体的线度与其它有关长度相比可忽略不计。
关于点电荷电场强度的计算公式E = q r / (4 π ε 0 r 3),以下说法正确的是 B(A) r →0时, E →∞;(B) r →0时, q 不能作为点电荷,公式不适用; (C) r →0时, q 仍是点电荷,但公式无意义;(D) r →0时, q 已成为球形电荷, 应用球对称电荷分布来计算电场. 如果对某一闭合曲面的电通量为S E d ⋅⎰S=0,以下说法正确的是 A(A) S 面内电荷的代数和为零; (B) S 面内的电荷必定为零; (C) 空间电荷的代数和为零; (D) S 面上的E 必定为零。
已知一高斯面所包围的空间内电荷代数和 ∑q =0 ,则可肯定: C(A). 高斯面上各点场强均为零. (B). 穿过高斯面上每一面元的电场强度通量均为零.(C). 穿过整个高斯面的电场强度通量为零. (D). 以上说法都不对.如图,在点电荷+q 的电场中,若取图中P 点处为 电势零点,则M 点的电势为 D(A) q /(4πε0a ) (B) −q /(4πε0a ) (C) q /(8πε0a ) (D) −q /(8πε0a )对于某一回路l ,积分l B d ⋅⎰l 等于零,则可以断定 D(A) 回路l 内一定有电流; (B) 回路l 内一定无电流;(C) 回路l 内可能有电流; (D) 回路l 内可能有电流,但代数和为零。
如图,一电量为-q 的点电荷位于圆心O 处,A 、B 、C 、D 为同一圆周上的四点,现将一试验电荷从A 点分别移动到B 、C 、D 各点,则 A(A) 从A 到各点,电场力做功相等; (B) 从A 到B ,电场力做功最大; (C) 从A 到D ,电场力做功最大;+q(D) 从A 到C ,电场力做功最大。
大学物理课后习题答案第六章-大学物理第六章

第6章 真空中的静电场 习题及答案1. 电荷为q +和q 2-的两个点电荷分别置于1=x m 和1-=x m 处。
一试验电荷置于x 轴上何处,它受到的合力等于零?解:根据两个点电荷对试验电荷的库仑力的大小及方向可以断定,只有试验电荷0q 位于点电荷q +的右侧,它受到的合力才可能为0,所以200200)1(π4)1(π42-=+x qq x qq εε故 223+=x2. 电量都是q 的三个点电荷,分别放在正三角形的三个顶点。
试问:(1)在这三角形的中心放一个什么样的电荷,就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系?解:(1) 以A 处点电荷为研究对象,由力平衡知,q '为负电荷,所以2220)33(π4130cos π412a q q a q '=︒εε故 q q 33-=' (2)与三角形边长无关。
3. 如图所示,半径为R 、电荷线密度为1λ的一个均匀带电圆环,在其轴线上放一长为l 、电荷线密度为2λ的均匀带电直线段,该线段的一端处于圆环中心处。
求该直线段受到的电场力。
解:先求均匀带电圆环在其轴线上产生的场强。
在带电圆环上取dl dq 1λ=,dq 在带电圆环轴线上x 处产生的场强大小为)(4220R x dqdE +=πε根据电荷分布的对称性知,0==z y E E23220)(41cos R x xdqdE dE x +==πεθR Oλ1λ2lxy z式中:θ为dq 到场点的连线与x 轴负向的夹角。
⎰+=23220)(4dq R x xE x πε232210)(24R x Rx+⋅=πλπε232201)(2R x xR +=ελ下面求直线段受到的电场力。
在直线段上取dx dq 2λ=,dq 受到的电场力大小为dq E dF x =dx R x xR 2322021)(2+=ελλ 方向沿x 轴正方向。
大学物理电子教案之稳恒磁场

第7章稳恒磁场前面我们研究了相对于观察者静止的电荷所激发的电场的性质与作用规律。
从本章起我们看到,在运动电荷周围,不仅存在着电场而且还存在着磁场。
磁场和电场一样也是物质的一种形态。
1820年,丹麦的奥斯特发现了电流的磁效应,当电流通过导线时,引起导线近旁的小磁针偏转,开拓了电磁学研究的新纪元,打开了电应用的新领域。
1837年惠斯通、莫尔斯发明了电动机,1876年美国的贝尔发明了电话。
……迄今,无论科学技术、工程应用、人类生活都与电磁学有着密切关系。
电磁学给人们开辟了一条广阔的认识自然、征服自然的道路。
7.1磁场磁感强度Fe O)能吸引铁。
十一磁现象的发现要比电现象早得多。
早在公元前人们知道磁石(34世纪我国发明了指南针。
但是,直到十九世纪,发现了电流的磁场和磁场对电流的作用以后,人们才逐渐认识到磁现象和电现象的本质以及它们之间的联系,并扩大了磁现象的应用范围。
到二十世纪初,由于科学技术的进步和原子结构理论的建立和发展,人们进一步认识到磁现象起源于运动电荷,磁场也是物质的一种形式,磁力是运动电荷之间除静电力以外的相互作用力。
7.1.1 基本磁现象磁场无论是天然磁石或是人工磁铁都有吸引铁、钴、镍等物质的性质,这种性质叫做磁性。
条形磁铁及其它任何形状的磁铁都有两个磁性最强的区域,叫做磁极。
将一条形磁铁悬挂起来,其中指北的一极是北极(用N表示),指南的一极是南极(用S表示)。
实验指出,极性相同的磁极相互排斥,极性相反的磁极相互吸引。
在相当长的一段时间内,人们一直把磁现象和电现象看成彼此独立无关的两类现象。
直到1820年,奥斯特首先发现了电流的磁效应。
后来安培发现放在磁铁附近的载流导线或载流线圈,也要受到力的作用而发生运动。
进一步的实验还发现,磁铁与磁铁之间,电流与磁铁之间,以及电流与电流之间都有磁相互作用。
上述实验现象导致了人们对“磁性本源”的研究,使人们进一步认识到磁现象起源于电荷的运动,磁现象和电现象之间有着密切的联系。
【刑侦课堂】痕迹概述手印的基础知识

【刑侦课堂】痕迹概述手印的基础知识【刑侦课堂】痕迹概述&手印的基础知识00痕迹,是一个在诸多领域被广泛使用的概念,它是一切事物运动所遗留下来的印象或形象。
是指曾经存在于某一时空中的事物或现象的客观反映,人们可以通过分析、研究这些“痕迹”来了解过去在某一时空中曾经存在过的事物或现象的本质与特性。
如“旧社会的痕迹”,化石,粒子运动痕迹等。
刑事侦查部门所研究的痕迹是专指与犯罪有关的各种犯罪痕迹,是指所遗留下来的各种映象和信息,它包括广义犯罪痕迹和狭义犯罪痕迹。
1.广义犯罪痕迹是指犯罪行为所引发的一切变化而遗留下来的各种映象或信息。
例如伤害人身形成的伤痕、血迹等。
依据这种变化的事实和客观物质内在的因果联系,可以分析和再现犯罪活动当时的情景和过程,重建犯罪现场,为分析和证实犯罪提供依据。
(图1~3)2.狭义犯罪痕迹,是指案犯在实施犯罪活动过程中,当一客体在力的作用下接触另一客体时形成并保留下来的反映形象。
前者叫做造痕体,后者叫做承痕体。
承痕体上的痕迹反映出造痕体接触部位的外表形态结构特征和作用力的性质,因此又称为“形象痕迹”,如手印中反映的乳突纹线特征,穿鞋足迹中反映出的鞋底花纹结构特征,铁锤在桌面上留下的打击特征等。
(图4、5)(一)客观反映性。
(二)相对稳定性。
(三)特定性。
(四)关联性。
现场痕迹同犯罪行为有着直接的因果关系,犯罪痕迹是犯罪行为直接引起的结果,这种内在的因果关系使痕迹成为揭露与证实犯罪事实的重要物证。
三(一)痕迹的形成机理造痕体与承痕体在力的作用下相互接触,使承痕体的组织结构或表面形态发生相应变化,从而反映并保留了造痕体接触部位的形象特征,即形成了痕迹。
造痕体与承痕体的接触方式,因力的大小、方向和作用点的不同而不同;承痕体则会因外力的作用产生形变而形成印痕或分离成若干部分(二)痕迹的形成因素痕迹的形成有三个主要因素,即造痕体,承痕体和作用力。
有些痕迹的形成还需要介质的参与。
1.造痕体。
高中语文必修五《中国建筑的特征》课文解读

高中语文必修五《中国建筑的特征》课文解读《中国建筑的特征》是一篇科学小论文,属于实用类文本。
下面是店铺给大家带来的高中语文必修五《中国建筑的特征》课文解读,希望对你有帮助。
高中语文《中国建筑的特征》课文解读中国的建筑体系是在世界各民族数千年文化史中一个独特的建筑体系。
它是中华民族数千年来世代经验的累积所创造的。
这个体系分布到很广大的地区:西起葱岭①,东至日本、朝鲜,南至越南、缅甸,北至黑龙江,包括蒙古人民共和国的区域在内。
(①葱岭:古山脉名,传说以山多青葱而得名。
包括天山、帕米尔高原、昆仑山等。
)这些地区的建筑和中国中心地区的建筑,或是同属于一个体系,或是大同小异,如弟兄之间属于一家的关系。
考古学家所发掘的殷代遗址证明,至迟在公元前15世纪,这个独特的体系已经基本上形成了,它的基本特征一直保留到了近代。
3500年来,中国世世代代的劳动人民发展了这个体系的特长,不断地在技术上和艺术上把它提高,达到了高度水平,取得了辉煌成就。
第一部分(第1、2段),作者首先指出中国建筑体系是个独特的体系,点出本文说明的中心,接着从地域和历史,即空间和时间两方面作了简要的说明。
地域分布是广阔的,不独局限于中国境内,几乎涵盖了整个东亚大陆:西起葱岭,东到日本,南至越南,北至蒙古;历史则源远流长,公元前1500年时,这个体系就“已经基本形成了”,并“一直保留到了近代”,在3500年的历史中不断完善。
这样,作者便从世界和历史的高度,突出了中国建筑体系在世界文化史中的独特地位。
中国建筑的基本特征可以概括为下列几点。
(一)个别的建筑物①,一般地由三个主要部分构成:下部的台基、中间的房屋本身和上部翼状伸展的屋顶。
(①个别的建筑物:指相对独立的一座房屋。
个别,在这里是单独的意思。
)(二)在平面布置上,中国所称为一“所”房子是由若干座这种建筑物①以及一些联系性的建筑物,如回廊、抱厦②、厢③、耳④、过厅等等,围绕着一个或若干个庭院或天井建造而成的。
大学物理磁场考试练习题含解析

大学物理磁场考试练习题一、选择题1.空间某点的磁感应强度的方向,一般可以用下列几种办法来判断,其中哪个是错误的?() (A )小磁针北(N )极在该点的指向;(B )运动正电荷在该点所受最大的力与其速度的矢积的方向;(C )电流元在该点不受力的方向;(D )载流线圈稳定平衡时,磁矩在该点的指向。
2.下列关于磁感应线的描述,哪个是正确的?() (A )条形磁铁的磁感应线是从N 极到S 极的; (B )条形磁铁的磁感应线是从S 极到N 极的; (C )磁感应线是从N 极出发终止于S 极的曲线; (D )磁感应线是无头无尾的闭合曲线。
3.磁场的高斯定理说明了下面的哪些叙述是正确的?()a 穿入闭合曲面的磁感应线条数必然等于穿出的磁感应线条数;B⎰⎰=⋅0S d Bb 穿入闭合曲面的磁感应线条数不等于穿出的磁感应线条数;c 一根磁感应线可以终止在闭合曲面内;d 一根磁感应线可以完全处于闭合曲面内。
(A )ad ;(B )ac ;(C )cd ;(D )ab 。
4.如图所示,在无限长载流直导线附近作一球形闭合曲面S ,当曲面S 向长直导线靠近时,穿过曲面S 的磁通量和面上各点的磁感应强度B 将如何变化?() (A )增大,B 也增大; (B )不变,B 也不变; (C )增大,B 不变; (D )不变,B 增大。
5.两个载有相等电流I 的半径为R 的圆线圈一个处于水平位置,一个处于竖直位置,两个线圈的圆心重合,则在圆心o 处的磁感应强度大小为多少?() (A )0;(B ); (C );(D )。
ΦΦΦΦΦR I 2/0μR I 2/20μR I /0μISIIo二、填空题1.如图所示,均匀磁场的磁感应强度为B =0.2T ,方向沿x 轴正方向,则通过abod 面的磁通量为_________,通过befo 面的磁通量为__________,通过aefd 面的磁通量为_______。
2.真空中一载有电流I 的长直螺线管,单位长度的线圈匝数为n ,管内中段部分的磁感应强度为________,端点部分的磁感应强度为__________。
普通物理习题册下答案

第9 单元 静电场(一)一 选择题[ C ]1 .一带电体可作为点电荷处理的条件是 (A)电荷必须呈球形分布。
(B)带电体的线度很小。
(C)带电体的线度与其它有关长度相比可忽略不计。
(D)电量很小。
[ C ]2.已知一高斯面所包围的体积内电量代数和∑i q =0,则可肯定:(A)高斯面上各点场强均为零。
(B)穿过高斯面上每一面元的电通量均为零。
(C)穿过整个高斯面的电通量为零。
(D)以上说法都不对。
[ D ]3.两个同心均匀带电球面,半径分别为R a 和R b ( R a <R b ) ,所带电量分别为Q a 和Q b ,设某点与球心相距r , 当R a < r < R b 时, 该点的电场强度的大小为: ( A )241r Q Q ba +⋅πε ( B )241rQ Q ba -⋅πε( C ))(4122bb a R Q rQ +⋅πε ( D )241rQ a ⋅πε[ D ]4. 如图所示,两个“无限长”的、半径分别为R 1和R 2的共轴圆柱面均匀带电,轴线方向单位长度上的带电量分别为λ1 和λ2 , 则在内圆柱面里面、距离轴线为r 处的P 点的电场强度大小 ( A )r 0212πελλ+( B )20210122R R πελπελ+( C ) 1014R πελ( D ) 0[ D ]5.图示为一具有球对称性分布的静电场的E ~r 关系曲线,请指出该静电场是由下列哪种带电体产生的。
(A)半径为R 的均匀带电球面。
(B)半径为R 的均匀带电球体。
(C)半径为R 、电荷体密度ρ=Ar(A 为常数)的非均匀带电球体。
(D)半径为R 、电荷体密度ρ=A/r(A 为常数)的非均匀带电球体。
二 填空题1. 在点电荷系的电场中,任一点的电场强度等于__各点电荷在该占单独产生的电场强度的矢量和__,这称为场强叠加原理。
2.静电场中某点的电场强度,其数值和方向等于 单位正电荷在该点受到的电场力___。
大学航空航天专业《大学物理(一)》期中考试试卷 附答案

大学航空航天专业《大学物理(一)》期中考试试卷附答案姓名:______ 班级:______ 学号:______考试须知:1、考试时间:120分钟,本卷满分为100分。
2、请首先按要求在试卷的指定位置填写您的姓名、班级、学号。
一、填空题(共10小题,每题2分,共20分)1、一条无限长直导线载有10A的电流.在离它 0.5m远的地方它产生的磁感强度B为____________。
一条长直载流导线,在离它1cm处产生的磁感强度是T,它所载的电流为____________。
2、气体分子的最可几速率的物理意义是__________________。
3、花样滑冰运动员绕通过自身的竖直轴转动,开始时两臂伸开,转动惯量为,角速度为;然后将两手臂合拢,使其转动惯量变为,则转动角速度变为_______。
4、三个容器中装有同种理想气体,分子数密度相同,方均根速率之比为,则压强之比_____________。
5、图示曲线为处于同一温度T时氦(原子量4)、氖(原子量20)和氩(原子量40)三种气体分子的速率分布曲线。
其中曲线(a)是________气分子的速率分布曲线;曲线(c)是________气分子的速率分布曲线。
6、均匀细棒质量为,长度为,则对于通过棒的一端与棒垂直的轴的转动惯量为_____,对于通过棒的中点与棒垂直的轴的转动惯量_____。
7、两列简谐波发生干涉的条件是_______________,_______________,_______________。
8、长为的匀质细杆,可绕过其端点的水平轴在竖直平面内自由转动。
如果将细杆置与水平位置,然后让其由静止开始自由下摆,则开始转动的瞬间,细杆的角加速度为_____,细杆转动到竖直位置时角加速度为_____。
9、两个相同的刚性容器,一个盛有氧气,一个盛氦气(均视为刚性分子理想气体)。
开始他们的压强和温度都相同,现将3J的热量传给氦气,使之升高一定的温度。
若使氧气也升高同样的温度,则应向氧气传递的热量为_________J。
一个处在真空中的弓形平面载流线圈.
156
7-13 一个动能为 2000eV 的正电子,射入磁感应强度 B=0.1T 的均匀磁场
中,正电子的速度与 B 成 890 角,试求正电子螺旋运动的周期、螺距和半径。
查看答案 7-13
7-14 在霍耳效应实验中,宽 1.0cm、长 4.0cm、厚 1.0×10-3cm 的导体,沿长度方向载有 3.0A 的电 流,当磁感应强度 B=1.5T 的磁场垂直地通过该薄导体时,产生 1.0×10-5V 的横向霍耳电压(在宽度两端), 试求 (1)载流子的漂移速度;(2)每立方厘米的载流子数目;(3)假设载流子是电子,试就一给定的电流 和磁场方向在图上画出霍耳电压的极性。
解
由例 7-1
线段 ba 的磁感应强度
B1
0 4π
40 0.02cos45
(cos45o
-cos135o
)
=4 104
T
方向垂直纸面向外。
由例 7-2 圆弧 acb 的磁感应强度
π
B2
2 2π
0 I 2R
1 4
μ0 2
40 0.02
3.14104 T
方向垂直纸面向内。
S πr2 8.82 1021 m2
m IS 1.09103 8.821021 9.611024 Am2
160
方向与电子转动方向成由左螺旋关系。 7-7
返回 7-6
解 均匀带电圆环在转动过程中将形成一系列圆电流,转动均匀带电圆环在环心 O 处的磁感应强度 是这些圆电流在环心 O 处的磁感应强度的矢量和。
B1
0 4π
q sin d2
π 2
0q 4πd
第10章习题答案

第10章 稳恒磁场10.1 基本要求1 掌握磁感应强度的概念。
理解毕奥—萨伐尔定律。
能计算一些简单问题中的磁感 应强度。
掌握磁通量的计算方法.2 理解反映稳恒磁场性质的高斯定理和安培环路定理,理解用安培环路定理计算磁 感应强度的条件和方法。
3 理解安培力和洛仑兹力公式。
了解霍尔效应。
了解磁矩的概念。
能计算简单几何形状载流导体和载流平面线圈在均匀磁场中或在无限长直载流导线产生的非均匀磁场中所受的磁力和磁力矩。
能分析点电荷在均匀磁场中的受力和运动。
4 了解磁介质对磁场的影响.了解铁磁质的特性。
了解各向同性介质中H和B之间的关系。
了解磁介质中的安培环路定理。
10.2 基本概念1 磁感应强度B :表征磁场性质的矢量。
磁场中某点处的磁感应强度的方向与该点处 小磁针平衡时N 极所指的方向相同,磁感应强度的大小maxF B qv=。
2 磁通量m Φ:m sd Φ=⎰ B S3 磁矩m : n IS =m e (线圈平面的正法线方向与电流成右手螺旋关系) 4 磁力矩M : =⨯M m B5 霍耳效应:将一载流导体薄片置于均匀磁场中,当电流与磁场方向垂直时,则可在垂 直于磁场和电流的方向上(即薄片的上、下两底面间)产生电势差。
6 磁场强度H :磁场强度是一个描述磁场性质的辅助量。
在各向同性均匀磁介质 中,它与磁感应强度成正比,即0r μμμ==B H H 。
10.3 基本规律1 毕奥—萨伐尔定律:024rId d rμπ⨯=l e B 2 洛仑兹力:q =⨯F v B 3 安培力:d Id =⨯F l B 4 磁场的高斯定理:0sd =⎰ B S 。
高斯定理说明,磁场是无源场。
5 安培环路定理:在真空中的磁场中,01nili d Iμ==∑⎰ B l 。
当有介质存在时, cld I=∑⎰ H l .安培环路定理表明,磁场是涡旋场。
10.4 学习指导在学习时要注意认真理解磁感应强度B的概念,切实弄懂磁场的性质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B 0I 2r
dB 0Q rdr π(b2 a2 ) 2r
积分得
磁场方向与 相同。
b
B
0Q
dr 0Q
a π(b2 a2 ) 2 2π(b a)
返回 7-7
7-8 解 解题过程同习题 7-7
B 0q 2πR
磁场方向,若 q 0 ,与 相同,若 q 0 ,与 相反。
查看答案 7-8
7-9 如图所示是一根很长的长直圆管形导体的横截面,内外半径分别为 a 和 b ,导体内载有沿轴线 方向的电流 I ,且电流 I 均匀分布在管的横截ቤተ መጻሕፍቲ ባይዱ上。试求导体内部( a r b )的磁感应强度分布。
a b
O
习题 7-9 图
查看答案 7-9
7-10 半径为 a 的长导体圆柱,内部有两个直径为 a 的圆柱形空腔,如图所示。电流 I 从纸面流出并
,
B2
0 I2 2π(r a)
0 2π
π a2 j 4
ra
,
2
2
2
2
B0
0 I0 2πr
0 2π
πa2 j r
B
Bo
(B1
B2 )
0 j 2π
πa2 (
r
π a2 4
ra
π a2 4)
r a
0 I π
2r2 a2 r(4r2 a2 )
22
方向垂直于 O1P1 向左。
查看答案 7-12
156
7-13 一个动能为 2000eV 的正电子,射入磁感应强度 B=0.1T 的均匀磁场
中,正电子的速度与 B 成 890 角,试求正电子螺旋运动的周期、螺距和半径。
查看答案 7-13
7-14 在霍耳效应实验中,宽 1.0cm、长 4.0cm、厚 1.0×10-3cm 的导体,沿长度方向载有 3.0A 的电 流,当磁感应强度 B=1.5T 的磁场垂直地通过该薄导体时,产生 1.0×10-5V 的横向霍耳电压(在宽度两端), 试求 (1)载流子的漂移速度;(2)每立方厘米的载流子数目;(3)假设载流子是电子,试就一给定的电流 和磁场方向在图上画出霍耳电压的极性。
B1
0 4π
q sin d2
π 2
0q 4πd
,方向与转动方向成由右螺旋关系。
同理,-q 在 O 处产生的磁感应强度为
B2
0 4π
q sin π 2
(2d )2
0q 8πd
,方向与转动方向成由左螺旋关系。
则由场叠加原理,得在 O 点的总磁感应强度
B
B1
B2
0 q πd
B B1 B2 0.86104 T
方向垂直纸面向外。
返回 7-1
7-2
解 如图,将导线分成 1(左侧导线)、2(半圆导线)、3(右侧导线)三部分,设各部分在 O 点处产
生的磁感应强度分别为 B1 、 B2 、 B3 。
根据叠加原理可知, O 点处磁感应强度 B B1 B2 B3。
2π r
2π
jπ a2 4
r2 a2 4
r 0I 2r2 a2
r2 a2 π 4r2 a2 r 4
7-11
解 由安培环路定理可知,导体内外的磁感应强度分布为:
B 0 Ir 2πR2
(0r R)
B 0 I 2πr
(r R)
对于题图情况,方向均为垂直于纸面向里。
返回 7-8
7-9
解 电流 I 均匀分布在内半径为 a 、外半径为 b 的导体圆管上,在圆管横截面的电流密度为
j
I π(b2
a2 )
取半径为 r ( a r b )的圆形积分回路,应用安培环路定理
可得
l
B dl B2πr
0
π(b2
I
a2
)
π(r
2
a2)
解得 B 0 I (r2 a2 ) , 方向与电流方向成右手螺旋关系。 2πr(b2 a2 )
板可分为无数个类似电流元,每个电流元在 P 点处激发的磁感应强度方向 均垂直于纸面向外,总磁感应强度大小为
I
Bp
dB 0
a
dr a
μ0 I ln2 ,方向垂直于纸面向外。
2π 0 2a - r 2πa
p
r dr
习题 7-4 解用图
返回 7-4 7-5
解 设转轴与电荷连线交点为 O。根据运动电荷产生磁场公式,可知+q 在 O 处产生的磁感应强度为
通以电流 I 2 ,与直导线共面,AB 边与直导线平行,若线 AB 与长直导线相距为 d (如图),求 ABCD
四条边所受的力的大小和方向。
习题 7-16 图
查看答案 7-16
7-17 如图所示,在长直导线旁有一矩形线圈与导线共面。导线中通有电流 I1=20A,线圈中通有电流 I2= 10A。求矩形线圈受到的合力。已知 a=1cm,b=9cm,l=20cm。
习题 7-17 图
查看答案 7-17 157
7-18 如图,一半径 R 0.1m 的半圆形闭合线圈(匝数 N 1000)载有电流 I 10A ,放在匀强 磁场中,磁场方向与线圈平行,已知 B 3.0102 T ,求(1)线圈磁矩的大小和方向;(2)线圈所受
到磁力矩的大小和方向(以直径为转轴)。
产生的 B 的大小;(2)作圆周运动电子的等效磁矩。
7-7 一内半径为 a ,外半径为 b 的均匀带电圆环,绕过环心 O 且与环平面
垂直的轴线以角速度
逆时针方向旋转,环上所带电量为
Q
,求环心
O
处的
磁感应强度 B 。
查看答案 7-4 查看答案 7-5 查看答案 7-6 查看答案 7-7
155
7-8 半径为 R 的薄圆盘均匀带电,总电量为 q 。令此盘绕通过圆盘中心 且垂直盘面的轴线匀速转动,角速度 ,求圆盘中心 O 处的磁感应强度。
均匀分布在导体截面上,试求 P1 点和 P2 点的磁感应强度 B 的大小。
习题 7-10 图
查看答案 7-10
7-11 如图所示,—根很长的直载流圆柱导体,半径为 R,电流 I 均匀分布在其截面上.求阴影部分 的磁通量。
查看答案 7-11 习题 7-11 图
7-12 质子、氘核与 α 粒子通过相同的电势差而进入均匀磁场作匀速圆周运动。(1)比较这些粒子 动能的大小;(2)已知质子圆轨道的半径为 10cm,求氘核和 α 粒子的轨道半径。
7-20 一半径为 R 的无限长圆柱形导体,其相对磁导率(μr>1)。沿圆柱的轴线方向均匀地通有电流,
其电流密度为 j(单位截面积上的电流)。试求磁场强度 H 和磁感应强度 B 的分布。
查看答案 7-20
7-21 螺绕环中心周长 L 10cm ,环上线圈匝数 N 200 匝,线圈中通有电流。 (1)当管内
(1 4
1) 8
0 q 8πd
,方向与转动方向成由右螺旋关系。
返回 7-5
7-6 解(1)
(2)
B
0 e 4π r2
0er 2π 4πr 2
0e 2r
4π 107 1.6021019 6.81015
2 5.31011
T 12.9T
I e 1.6021019 6.81015 A 1.09103A
解
由例 7-1
线段 ba 的磁感应强度
B1
0 4π
40 0.02cos45
(cos45o
-cos135o
)
=4 104
T
方向垂直纸面向外。
由例 7-2 圆弧 acb 的磁感应强度
π
B2
2 2π
0 I 2R
1 4
μ0 2
40 0.02
3.14104 T
方向垂直纸面向内。
在图中到轴线距离为 r 处作一面积元 dS hdr ,于是有 dM Bds Bhdr
则通过阴影面积的磁通量为
M
R 0 I 0 2πR2
rhdr 2R 0 I hdr R 2πr
查看答案 7-14
7-15 如图所示,一长直导线 AB 载有电流 I1=20A ,其旁放一段导线 cd 通有电流 I2=10A ,且 AB 与 cd 在同一平面上且互相垂直,如图示,试求导线 cd 所受的磁场力。
1cm
10cm
习题 7-15 图
查看答案 7-15
7-16 无限长载流直导线通有电流 I1 ,一长为 a ,宽为 b 的矩形线框 ABCD
利用叠加原理求 P2 点场强
B1
B2
0 2π
jπ a2 4
r2 a2 4
方向如图所示。
B 的大小为
B0
0 I0 2πr
0 2π
πa2 r
j
B B0 B1 cos B2 cos
习题 7-10 解用图
返回 7-10 162
方向与 B0' 相同。
0 πa2 j 2 0
的点 P 处的磁感应强度。
P
习题 7-4 图
7-5 在真空中有两个点电荷 q ,相距为 3d,它们都以角速度 绕一与两 点电荷连线垂直的轴转动。 q 到转轴的距离为 d。试求转轴与电荷连线交点处
的磁场 B 。
7-6 玻尔氢原子模型中,电子绕原子核作圆轨道运动,圆轨道半径为
