高考数学大一轮复习第三章导数及其应用3.2导数与函数的单调性、极值、最值课件文新人教A版
合集下载
北师大版高考数学一轮复习统考第3章导数及其应用第3讲导数与函数的极值最值课件

最新 PPT 欢迎下载 可修改
解析 8答案
3.(2019·岳阳模拟)函数 f(x)=ln x-x 在区间(0,e]上的最大值为( )
A.1-e
B.-1
C.-e
D.0
解析 因为 f′(x)=1x-1=1-x x,当 x∈(0,1)时,f′(x)>0;当 x∈(1, e]时,f′(x)<0,所以当 x=1 时,f(x)取得最大值 ln 1-1=-1.故选 B.
最新 PPT 欢迎下载 可修改
5
1.对于可导函数 f(x),f′(x0)=0 是函数 f(x)在 x=x0 处有极值的必要 不充分条件.
2.若函数 f(x)在开区间(a,b)内只有一个极值点,则相应的极值点一 定是函数的最值点.
3.极值有可能是最值,但最值只要不在区间端点处取得,其必定是极 值.
最新 PPT 欢迎下载 可修改
12解析
2
PART TWO
核心考向突破
最新 PPT 欢迎下载 可修改
13
精准设计考向,多角度探究突破
考向一 导数与函数的极值
角度 1 知图判断函数极值情况
例 1 (2019·浙江杭州二中 6 月热身考)如图,可知导函数 y=f(x)在点
P(x0,f(x0))处的切线为 l:y=g(x),设 h(x)=f(x)-g(x),则下列说法正确的 是( )
的极小值;
最新 PPT 欢迎下载 可修改
3
(2)函数的极大值与极大值点 若函数 f(x)在点 x=b 处的函数值 f(b)比它在点 x=b 附近其他点的函数
值□04 ___都__大___,且 f′(b)=0,而且在 x=b 附近的左侧□05 ____f_′(_x_)>__0_____, 右侧□06 ___f′_(x_)_<__0____,则点 b 叫做函数的极大值点,f(b)叫做函数的极大
高考数学一轮复习-《导数及应用》第3课时-导数的应用(二)—极值与最值课件
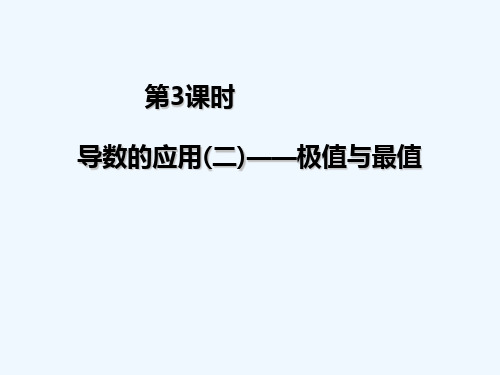
x>2
f′(x)>0
x<2
,解得c=6
授人以渔
题型一 利用导数研究函数极值
例1
已
知函数
f(x)=
ax3-
3x2+
3 1-a(a∈
R且
a≠
0),
求函数f(x)的极大值与极小值.
2 【解析】 由题设知a≠0,f′(x)=3ax2-6x=3ax(x-a).
2 令f′(x)=0得x=0或x=a.
• 当a>0时,随x的变化,f′(x)与f(x)的变化情况如下:
(2)若函数f(x)=x3-3x+a有3 个不同的零点,则实数a
的取值范围是(
)
A. (- 2,2)
B. [- 2,2]
C. (- ∞,- 1)
ቤተ መጻሕፍቲ ባይዱ
D.(1,+∞)
【解析】 f′(x)=3x2-3,令f′(x)=0,∴x=±1.三
次 函数 f(x)= 0有 3个根
⇔f(x)极大值>0且f(x)极小值<0 ∴x=-1为极大值点, x=1为极小值点.
2
43
f(x)极小值=f(a)=-a2-a+1.
• 探究1 掌握可导函数极值的步骤: • (1)确定函数的定义域. • (2)求方程f′(x)=0的根. • (3)用方程f′(x)=0的根和不可导点的x的值顺次将函数的定义域分成若干
个小开区间,并形成表格. • (4)由f′(x)=0的根左右的符号以及f′(x)在不可导点左右的符号来判断f′(x)
• 解析 y′=ex+m,则ex+m=0必有根,∴m=-ex<0.
• 4.已知f(x)=2x3-6x2+m(m为常数)在[-2,2]上有最大值3,那么此函 数在[-2,2]上的最小值是( )
高考数学一轮复习 第三章 导数及其应用 第三节 导数与函数的极值、最值课件 理

-
0
+
f(x)
↘
极小值
↗
所以当a>e时, f(x)在(0,1)内有极值且唯一.当a≤e时, f '(x)≥0在(0,1) 上恒成立,则f(x)在(0,1)上单调递增,不符合题意. 综上,a的取值范围为(e,+∞).
12/11/2021
方法技巧 1.利用导数研究函数极值问题的一般流程
12/11/2021
(2)若f(x)在区间
0
,
13上 单调递增,求b的取值范围.
12/11/2021
解析 (1)当b=4时,f(x)=(x+2)2· 1,定 2义x 域为
,
,
1 2
f '(x)=2(x+2) 1+(x2+x2)2· · 1 ·(-21)= .
2 1 2x
令f '(x)=0,解得x1=-2,x2=0.
.
2
规律总结 求函数f(x)在[a,b]上的最大值和最小值的步骤 (1)求函数在(a,b)内的极值; (2)求函数在区间端点的函数值f(a), f(b); (3)将函数f(x)的极值与f(a), f(b)比较,其中最大的一个为最大值,最小的 一个为最小值.
12/11/2021
2-1 已知函数f(x)=ln x+ 1 -1,g(x)=x 1 .
(ex)2
= ax,2(2ab)xbc
ex
令g(x)=-ax2+(2a-b)x+b-c, 因为ex>0,所以y=f '(x)的零点就是g(x)=-ax2+(2a-b)x+b-c的零点,且f '(x)与 g(x)符号相同. 因为a>0,所以由题意知:当-3<x<0时,g(x)>0,即f '(x)>0; 当x<-3或x>0时,g(x)<0, 即f '(x)<0, 所以f(x)的单调增区间是(-3,0),单调减区间是(-∞,-3),(0,+∞).
高考数学复习第三章导数及其应用3.2.2导数与函数的极值最值文ppt市赛课公开课一等奖省名师优质课获

30/43
②若 0<a<e,当 x∈(0,a)时,f′(x)<0,函数 f(x)在区间(0, a)上单调递减,当 x∈(a,e]时,f′(x)>0,函数 f(x)在区间(a,e] 上单调递增,
所以当 x=a 时,函数 f(x)取得最小值 ln a.
31/43
③若 a≥e,则当 x∈(0,e]时,f′(x)≤0,函数 f(x)在区间(0, e]上单调递减,
3/43
考点 1 用导数解决函数极值问题
4/43
函数的极值 (1)函数的极小值: 函数 y=f(x)在点 x=a 的函数值 f(a)比它在点 x=a 附近其他 点的函数值都小,f′(a)=0;而且在点 x=a 附近的左侧__f′__(_x_)<_0_, 右侧_f_′__(_x_)>_0_,则点 a 叫做函数 y=f(x)的极小值点,f(a)叫做函 数 y=f(x)的极小值.
18/43
当 x∈12,3时,f′(x)=x2-ax+1≤0, 即 a≥x+1x恒成立,a≥130. 因此要使函数 f(x)在12,3上有极值点, 实数 a 的取值范围是2,130.
19/43
(2)已知 f(x)=x3+3ax2+bx+a2 在 x=-1 时有极值 0,则 a
-b=__-__7____.
33/43
已知 y=f(x)是奇函数,当 x∈(0,2)时,f(x)=ln x-axa>12,
当 x∈(-2,0)时,f(x)的最小值为 1,则 a=( D )
1
1
A.4
B.3
1 C.2
D.1
34/43
解析:由题意知,当 x∈(0,2)时,f(x)的最大值为-1. 令 f′(x)=1x-a=0,得 x=1a, 当 0<x<1a时,f′(x)>0; 当 x>1a时,f′(x)<0. ∴f(x)max=f1a=-ln a-1=-1, 解得 a=1.
②若 0<a<e,当 x∈(0,a)时,f′(x)<0,函数 f(x)在区间(0, a)上单调递减,当 x∈(a,e]时,f′(x)>0,函数 f(x)在区间(a,e] 上单调递增,
所以当 x=a 时,函数 f(x)取得最小值 ln a.
31/43
③若 a≥e,则当 x∈(0,e]时,f′(x)≤0,函数 f(x)在区间(0, e]上单调递减,
3/43
考点 1 用导数解决函数极值问题
4/43
函数的极值 (1)函数的极小值: 函数 y=f(x)在点 x=a 的函数值 f(a)比它在点 x=a 附近其他 点的函数值都小,f′(a)=0;而且在点 x=a 附近的左侧__f′__(_x_)<_0_, 右侧_f_′__(_x_)>_0_,则点 a 叫做函数 y=f(x)的极小值点,f(a)叫做函 数 y=f(x)的极小值.
18/43
当 x∈12,3时,f′(x)=x2-ax+1≤0, 即 a≥x+1x恒成立,a≥130. 因此要使函数 f(x)在12,3上有极值点, 实数 a 的取值范围是2,130.
19/43
(2)已知 f(x)=x3+3ax2+bx+a2 在 x=-1 时有极值 0,则 a
-b=__-__7____.
33/43
已知 y=f(x)是奇函数,当 x∈(0,2)时,f(x)=ln x-axa>12,
当 x∈(-2,0)时,f(x)的最小值为 1,则 a=( D )
1
1
A.4
B.3
1 C.2
D.1
34/43
解析:由题意知,当 x∈(0,2)时,f(x)的最大值为-1. 令 f′(x)=1x-a=0,得 x=1a, 当 0<x<1a时,f′(x)>0; 当 x>1a时,f′(x)<0. ∴f(x)max=f1a=-ln a-1=-1, 解得 a=1.
高考数学一轮复习 第三章 导数及其应用 第3讲 导数与函数的极值、最值课件 文

12/11/2021
一、思考辨析 判断正误(正确的打“√”,错误的打“×”)
(1)函数在某区间上或定义域内的极大值是唯一的.( × ) (2)导数为零的点不一定是极值点.( √ ) (3)函数的极大值不一定比极小值大.( √ ) (4)函数的极大值一定是函数的最大值.( × ) (5)开区间上的单调连续函数无最值.( √ )
12/11/2021
[提醒] (1)函数的极值点一定出现在区间的内部,区间的端点不能称为极值点. (2)在函数的整个定义域内,极值不一定是唯一的,有可能有多个极大值或极小值. (3)极大值与极小值之间无确定的大小关系.
12/11/2021
2.函数的最值 (1)在闭区间[a,b]上连续的函数 f(x)在[a,b]上必有最大值与最小值. (2)若函数 f(x)在[a,b]上单调递增,则__f_(_a_) __为函数的最小值,__f_(b_)___为函数的最大值; 若函数 f(x)在[a,b]上单调递减,则__f_(a_)___为函数的最大值,___f(_b_)__为函数的最小值. [提醒] 极值只能在定义域内部取得,而最值却可以在区间的端点处取得,有极值的未必 有最值,有最值的未必有极值;极值有可能成为最值,最值只要不在端点处必定是极值.
12/11/2021
2.函数 g(x)=-x2 的极值点是_______,函数 f(x)=(x-1)3 的极值点_______ (填“存在” 或“不存在”). 解析:结合函数图象可知 g(x)=-x2 的极值点是 x=0.因为 f′(x)=3(x-1)2≥0,所以 f′(x) =0 无变号零点,故函数 f(x)=(x-1)3 不存在极值点. 答案:0 不存在
12/11/2021
(2)由(1)得 f(x)在1e,1上单调递增,在(1,e]上单调递减, 所以 f(x)在1e,e上的极大值为 f(1)=1-11-ln 1=0. 又 f1e=1-e-ln 1e=2-e,f(e)=1-1e-ln e=-1e,且 f1e<f(e). 所以 f(x)在1e,e上的最大值为 0,最小值为 2-e.
高考数学一轮复习第三章导数及其应用3.2导数与函数的单调性、极值、最值课件文北师大版

3 2
������2
+
2������
ex+
1 2
������3
+
������2
ex
=
1 2
������3
-5-
知识梳理 双基自测 自测点评
1234
3.实际问题中导数的意义 中学物理中,速度是路程 关于时间的导数,线密度是质量关于 长度 的导数,功率是功关于时间 的导数.
-6-
知识梳理 双基自测 自测点评
1234
4.函数的最值与导数 (1)最大值点:函数y=f(x)在区间[a,b]上的最大值点x0指的是:函数 在这个区间上所有点的函数值都不超过f(x0).函数的最小值点也有 类似的意义. (2)函数的最大值:最大值或者在极大值点 取得,或者在区间的 端点取得. (3)最值:函数的最大值 和最小值 统称为最值. (4)求f(x)在[a,b]上的最大值和最小值的步骤
-9-
)
f'(x)=3x2-12=3(x+2)(x-2),令f'(x)=0,得x=-2或x=2. 易得f(x)在(-2,2)上是减少的,在(-∞,-2),(2,+∞)上是增加的, 故f(x)极小值为f(2),由已知得a=2,故选D. D
解析
关闭
关闭
答案
-10-
知识梳理 双基自测 自测点评
12345
-3-
知识梳理 双基自测 自测点评
1234
2.函数的极值与导数
(1)函数的极大值点和极大值:在包含x0的一个区间(a,b)内,函数 y=f(x)在任何一点的函数值都小于x0点的函数值,称点x0为函数 y=f(x)的极大值点 ,其函数值f(x0)为函数的极大值 .
高考数学一轮复习第三章导数及其应用第二节导数与函数的单调性、极值、最值课件理

∴g′(x)≤0,即 x2-ax+2≤0 在(-2,-1)内恒成立, ∴gg′′--12≤≤00,, 即41++2aa++22≤≤00,, 解得 a≤-3,即实数 a 的取值范围为(-∞,-3].
第十三页,共36页。
[探究 1] 在本例(3)中,若 g(x)的单调减区间为(-2,-1), 如何求解?
第十一页,共36页。
[听前试做] (1)f′(x)=x2-ax+b, 由题意得ff′0=01=,0, 即cb==10,. (2)由(1)得,f′(x)=x2-ax=x(x-a). ①当 a=0 时,f′(x)=x2≥0 恒成立,即函数 f(x) 在(-∞,+∞)内为单调增函数. ②当 a>0 时,由 f′(x)>0 得,x>a 或 x<0;由 f′(x)<0 得 0<x<a. 即函数 f(x)的单调递增区间为(-∞,0),(a,+∞), 单调递减区间为(0,a).
第二十九页,共36页。
[解题模板] 利用导数求函数最值的步骤
第三十页,共36页。
已知函数 f(x)=(x-k)ex. (1)求 f(x)的单调区间; (2)求 f(x)在区间[0,1]上的最小值.
第三十一页,共36页。
第二十六页,共36页。
[典题 4] (2015·新课标全国卷Ⅱ)已知函数 f(x)=ln x+a(1 -x).
(1)讨论 f(x)的单调性; (2)当 f(x)有最大值,且最大值大于 2a-2 时,求 a 的取值 范围.
第二十七页,共36页。
[听前试做] (1)f(x)的定义域为(0,+∞),f′(x)=1x-a. 若 a≤0,则 f′(x)>0,所以 f(x)在(0,+∞)上单调递增. 若 a>0,则当 x∈0,1a时,f′(x)>0; 当 x∈1a,+∞时,f′(x)<0. 所以 f(x)在0,1a上单调递增,在1a,+∞上单调递减.
第十三页,共36页。
[探究 1] 在本例(3)中,若 g(x)的单调减区间为(-2,-1), 如何求解?
第十一页,共36页。
[听前试做] (1)f′(x)=x2-ax+b, 由题意得ff′0=01=,0, 即cb==10,. (2)由(1)得,f′(x)=x2-ax=x(x-a). ①当 a=0 时,f′(x)=x2≥0 恒成立,即函数 f(x) 在(-∞,+∞)内为单调增函数. ②当 a>0 时,由 f′(x)>0 得,x>a 或 x<0;由 f′(x)<0 得 0<x<a. 即函数 f(x)的单调递增区间为(-∞,0),(a,+∞), 单调递减区间为(0,a).
第二十九页,共36页。
[解题模板] 利用导数求函数最值的步骤
第三十页,共36页。
已知函数 f(x)=(x-k)ex. (1)求 f(x)的单调区间; (2)求 f(x)在区间[0,1]上的最小值.
第三十一页,共36页。
第二十六页,共36页。
[典题 4] (2015·新课标全国卷Ⅱ)已知函数 f(x)=ln x+a(1 -x).
(1)讨论 f(x)的单调性; (2)当 f(x)有最大值,且最大值大于 2a-2 时,求 a 的取值 范围.
第二十七页,共36页。
[听前试做] (1)f(x)的定义域为(0,+∞),f′(x)=1x-a. 若 a≤0,则 f′(x)>0,所以 f(x)在(0,+∞)上单调递增. 若 a>0,则当 x∈0,1a时,f′(x)>0; 当 x∈1a,+∞时,f′(x)<0. 所以 f(x)在0,1a上单调递增,在1a,+∞上单调递减.
高考数学一轮复习 第三章 导数及其应用 31 导数与函数的极值、最值课件 文

(2)(3) 先化简解析式 → 再求导
12/11/2021
第二十一页,共四十六页。
[解] (1)y=(x2+3x+2)(x+3)=x3+6x2+11x+6, ∴y′=3x2+12x+11.
(2)由题可得:y=sin2x-cos2x=-12sinx,
∴y′=-12sinx′=-12(sinx)′=-12cosx.
[温馨提示] (1)三个注意点:
①瞬时变化率与导数是同一个概念的两个名称;
②并不是所有的函数在其定义域上的每一点处都有导数,
如:函数 y=|x|在 x=0 处就没有导数,但在定义域上的其他点处
都有导数;
③导函数定义中的区间一般指开区间,因为开区间端点处不
一定有改变量(右端点无增量,左端点无减量).
12/11/2021
第十八页,共四十六页。
5.已知函数 f(x)=1xcosx,则 f(π)+f′π2=(
)
A.-π32
B.-π12
C.-3π
D.-1π
[解析] ∵f′(x)=-x12cosx+1x(-sinx),∴f(π)+f′π2=-1π
+2π·(-1)=-3π.
[答案] C
12/11/2021
第十九页,共四十六页。
12/11/2021
第七页,共四十六页。
[温馨提示] (1)三个应用:求切线方程,求切点坐标,求参
数的值(或范围). 如:①若曲线 y=x4 的一条切线与直线 x+4y-8=0 垂直,则
切点坐标为____(_1_,1_)_.__ ②直线 y=kx+1 与曲线 y=x3+ax+b 相切于点 A(1,3),则
第六页,共四十六页。
(2)一个易错点:f′(x0)是一个常数. ①求 f′(x0)时,应先求导再代入求值.如:已知 f(x)=x+lnx, 则 f′(1)=___2__ ②在有关计算时,f′(x0)作为常数.如:已知函数 f(x)的导函 数为 f′(x),且满足 f(x)=3x2+2x·f′(2),则 f′(2)=___-__1_2____. 2.导数的几何意义 函数 y=f(x)在 x=x0 处的导数的几何意义,就是曲线 y=f(x) 在点 P(x0,y0)处的切线的____斜__率____,过点 P 的切线方程为 ___y_-__y_0=__f_′__(_x0_)_(x_-__x_0_).___
12/11/2021
第二十一页,共四十六页。
[解] (1)y=(x2+3x+2)(x+3)=x3+6x2+11x+6, ∴y′=3x2+12x+11.
(2)由题可得:y=sin2x-cos2x=-12sinx,
∴y′=-12sinx′=-12(sinx)′=-12cosx.
[温馨提示] (1)三个注意点:
①瞬时变化率与导数是同一个概念的两个名称;
②并不是所有的函数在其定义域上的每一点处都有导数,
如:函数 y=|x|在 x=0 处就没有导数,但在定义域上的其他点处
都有导数;
③导函数定义中的区间一般指开区间,因为开区间端点处不
一定有改变量(右端点无增量,左端点无减量).
12/11/2021
第十八页,共四十六页。
5.已知函数 f(x)=1xcosx,则 f(π)+f′π2=(
)
A.-π32
B.-π12
C.-3π
D.-1π
[解析] ∵f′(x)=-x12cosx+1x(-sinx),∴f(π)+f′π2=-1π
+2π·(-1)=-3π.
[答案] C
12/11/2021
第十九页,共四十六页。
12/11/2021
第七页,共四十六页。
[温馨提示] (1)三个应用:求切线方程,求切点坐标,求参
数的值(或范围). 如:①若曲线 y=x4 的一条切线与直线 x+4y-8=0 垂直,则
切点坐标为____(_1_,1_)_.__ ②直线 y=kx+1 与曲线 y=x3+ax+b 相切于点 A(1,3),则
第六页,共四十六页。
(2)一个易错点:f′(x0)是一个常数. ①求 f′(x0)时,应先求导再代入求值.如:已知 f(x)=x+lnx, 则 f′(1)=___2__ ②在有关计算时,f′(x0)作为常数.如:已知函数 f(x)的导函 数为 f′(x),且满足 f(x)=3x2+2x·f′(2),则 f′(2)=___-__1_2____. 2.导数的几何意义 函数 y=f(x)在 x=x0 处的导数的几何意义,就是曲线 y=f(x) 在点 P(x0,y0)处的切线的____斜__率____,过点 P 的切线方程为 ___y_-__y_0=__f_′__(_x0_)_(x_-__x_0_).___
高考数学一轮复习第三章导数及其应用函数的极值与最值课件

11 撬点·基础点 重难点
撬法·命题法 解题法
撬题·对点题 必刷题
学霸团 ·撬分法 ·高考数学·理
[解] (1)当 a=1 时,f(x)=x2e1-x-(x-1), 则 f′(x)=(2x-x2)e1-x-1=2x-exx2--1 ex-1, 令 h(x)=(2x-x2)-ex-1,则 h′(x)=2-2x-ex-1,
学霸团 ·撬分法 ·高考数学·理
第三章 导数及其应用
1 撬点·基础点 重难点
撬法·命题法 解题法
撬题·对点题 必刷题
学霸团 ·撬分法 ·高考数学·理
第2讲 导数的应用
2 撬点·基础点 重难点
撬法·命题法 解题法
撬题·对点题 必刷题
学霸团 ·撬分法 ·高考数学·理
考点二 函数的极值与最值
3 撬点·基础点 重难点
8 撬点·基础点 重难点
撬法·命题法 解题法
撬题·对点题 必刷题
学霸团 ·撬分法 ·高考数学·理
3.函数 f(x)=ax3+bx 在 x=1 处有极值-2,则 a,b 的值分别为( )
A.1,-3
B.1,3
C.-1,3
D.-1,-3
解析 ∵f′(x)=3ax2+b,∴f′(1)=3a+b=0.① 又当 x=1 时有极值-2,∴a+b=-2.②
(2)由题可知 g(x)=(x2-a)e1-x, 则 g′(x)=(2x-x2+a)e1-x=(-x2+2x+a)e1-x. 根据题意,方程-x2+2x+a=0 有两个不同的实根 x1,x2(x1<x2), 所以 Δ=4+4a>0,即 a>-1,且 x1+x2=2,
12 撬点·基础点 重难点
显然 h′(x)在34,2内是减函数,又 h′43=12-41 <0,故 x∈34,2时,总有 h′(x)<0,所以 h(x)在34,2 e
高考数学一轮复习第3章一元函数的导数及其应用2利用导数研究函数的单调性课件新人教版

π
π
-π,, 0,
____________.
2
2
由题意可知 f'(x)=sin x+xcos x-sin x=xcos x.
令 f'(x)=xcos x>0,解得其在区间(-π,π)内的解集为
即 f(x)的单调递增区间为
π
-π,- 2
,
π
0, 2
.
π
-π,2
∪
π
0,
2
,
解题心得利用导数讨论函数单调性或求单调区间的方法
等,都需要考虑函数的单调性,所以也是高考必考知识.应用时,要注意函数
的定义域优先,准确求导变形,转化为导函数在某区间上的符号问题.常用
到分类讨论和数形结合的思想,对数学运算核心素养有一定的要求.
内
容
索
引
01
第一环节
必备知识落实
02
第二环节
关键能力形成
03
第三环节
学科素养提升
第一环节
必备知识落实
【知识筛查】
(2)若函数f(x)在区间[1,2]上为单调函数,求a的取值范围.
解 (1)若a=1,则f(x)=3x-2x2+ln x的定义域为(0,+∞),
1
-42 +3+1
故 f'(x)= -4x+3=
=
-(4+1)(-1)
(x>0).
当x∈(0,1)时,f'(x)>0,即函数f(x)=3x-2x2+ln x单调递增;
1
2
7
7
即 g(x)在区间[1,4]上单调递增,g(x)max=g(4)= − =- ,即 a≥- .
