13-11刚体1班
第十三章动量矩定理_理论力学

式中
分别为作用于质点上的内力和外力。求 n 个方程的矢量和有
式中
,
于 点的主矩。交换左端求和及求导的次序,有
为作用于系统上的外力系对
令 (13-3)
为质系中各质点的动量对 点之矩的矢量和,或质系动量对于 点的主矩,称为质系对 点的动量矩。由此得
(13-4) 式(13-4)为质系动量矩定理,即:质系对固定点 的动量矩对于时间的一阶导数等于外力 系对同一点的主矩。
设 Q 为体积流量, 为密度, 和 分别为水流进口处和出口处的绝对速度, 和 分别为涡轮外圆和内圆的半径, 为 与涡轮外圆切线的夹角, 为 与涡轮内圆切线的
夹角,则
由动量矩定理 得
为叶片作用于水流上的力矩。若水涡轮共有 个叶片,则水流作用于涡轮的转动力矩为
方向与图示方向相反。 §13-2 刚体绕定轴转动微分方程
解:取两叶片间的水流为研究对象(图 13-4 中的兰色部分)。作用于质系上的的外力有 重力和叶片的约束力,重力平行于 z 轴,对转动轴之矩为零。所以外力主矩为叶片对水流
的约束力对 z 轴之矩 。
计算 时间间隔内动量矩的增量 。设 t 瞬时占据 ABCD 的水流,经过 时间间隔
后,运动至占据
,设流动是稳定的,则
有
式中
得
(13-8)
或
(13-9)
此式称为刚体绕定轴转动的微分方程。
为刚体绕定轴转动的角加速度,所以上式
可写为
(13-10)
1.由于约束力对 z 轴的力矩为零,所以方程中只需考虑主动力的矩。 2.比较刚体绕定轴转动微分方程与刚体平动微分方程,即
与
形式相似,求解问题的方法和步骤也相似。 转动惯量与质量都是刚体惯性的度量,转动惯量在刚体转动时起作用,质量在刚体平动
理论力学:第13章 虚位移原理及分析力学基础
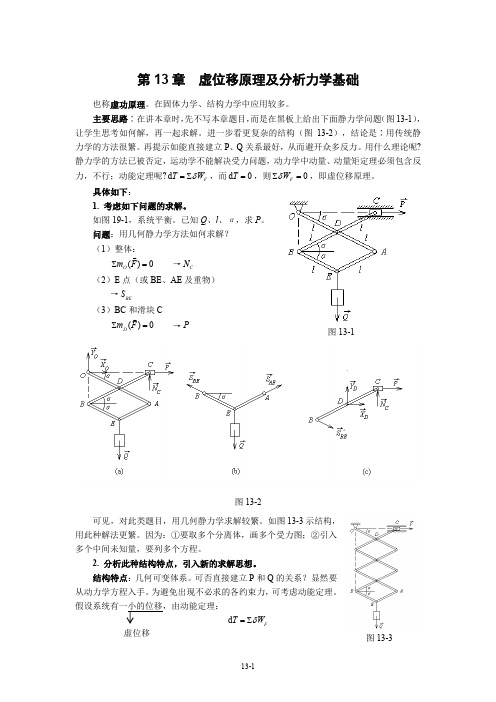
第13章 虚位移原理及分析力学基础也称虚功原理。
在固体力学、结构力学中应用较多。
主要思路∶在讲本章时,先不写本章题目,而是在黑板上给出下面静力学问题(图13-1),让学生思考如何解,再一起求解。
进一步看更复杂的结构(图13-2),结论是∶用传统静力学的方法很繁。
再提示如能直接建立P 、Q 关系最好,从而避开众多反力。
用什么理论呢?静力学的方法已被否定,运动学不能解决受力问题,动力学中动量、动量矩定理必须包含反力,不行;动能定理呢?d F T W δ=∑,而d 0T =,则0F W δ∑=,即虚位移原理。
具体如下:1. 考虑如下问题的求解。
如图19-1,系统平衡。
已知Q 、l 、α,求P 。
问题:用几何静力学方法如何求解? (1)整体:()0O m F ∑=→C N (2)E 点(或BE 、AE 及重物)→BE S(3)BC 和滑块C()0D m F ∑=→P图13-2可见,对此类题目,用几何静力学求解较繁。
如图13-3示结构,用此种解法更繁。
因为:①要取多个分离体,画多个受力图;②引入多个中间未知量,要列多个方程。
2. 分析此种结构特点,引入新的求解思想。
结构特点:几何可变体系。
可否直接建立P 和Q 的关系?显然要从动力学方程入手。
为避免出现不必求的各约束力,可考虑动能定理。
假设系统有一小的位移,由动能定理:d F T W δ=∑图13-1图13-3虚位移由于系统平衡,动能无变化,d 0T =,则0F W δ∑= → 虚功方程此方程中只包含P 和Q ,故建立了简单的方程,可求P 。
此便是虚位移原理的思想。
严格建立虚位移原理,需有诸多基本概念。
13.1 约束 约束的运动学分类静力学中讲的约束——约束的力的性质(约束的力的方面),用约束力表示,常指物体; 此处讲的约束——约束的运动的性质(约束的运动的方面),用约束方程表示,指限制条件。
一、 约束和约束方程自由质点系:运动不受任何限制。
非自由质点系:运动受到限制——约束。
刚体转动惯量测量实验

刚体转动惯量测量实验实验介绍本实验旨在通过实验测量刚体的转动惯量,进一步加深学生对刚体力学的理解。
刚体的转动惯量是描述刚体抵抗转动运动的性质的一个重要物理量,对于刚体的旋转运动具有重要意义。
实验原理在本实验中,我们将采用实验仪器,通过测量刚体在不同转动半径下的转动时间,然后根据实验数据计算刚体的转动惯量。
刚体的转动惯量和质量以及转动半径有关,可以通过以下公式进行计算:\[I = mr^2\]其中,\[I\]是刚体的转动惯量,\[m\]是刚体的质量,\[r\]是刚体的转动半径。
实验装置1.刚体转动实验仪器2.计时器3.直尺4.实验记录表实验步骤1.根据实验要求选择合适的刚体,并测量其质量\[m\]。
2.调整刚体转动实验仪器,设置好转动轴,保证转动无阻力。
3.定标:利用直尺测量刚体旋转半径\[r\],并记录。
4.手动将刚体推动,在计时器开始计时时释放刚体,记录刚体转动的时间\[t\]。
5.重复以上步骤,分别在不同的转动半径下进行实验。
实验数据处理1.根据实验记录表整理实验数据,计算不同转动半径下的刚体转动惯量。
2.利用实验数据绘制转动半径与转动惯量的关系曲线,分析数据的规律性。
实验注意事项1.操作实验仪器时要小心谨慎,避免损坏实验装置。
2.实验数据应尽量准确,避免实验误差的出现。
实验结论通过本实验的实验操作和数据处理,我们可以得出刚体的转动惯量与质量和转动半径的关系。
实验结果表明,刚体的转动惯量与其质量和转动半径的平方成正比关系。
这一实验结果验证了刚体转动惯量的计算公式,并且加深了我们对刚体力学的理解。
实验展望在今后的学习中,我们可以进一步深入研究刚体的转动运动性质,探讨更多与刚体力学相关的问题,提高的我们对物理学科的理解和应用能力。
以上是关于刚体转动惯量测量实验的实验报告,希望对大家有所帮助。
13第十三章-达朗贝尔原理(动静法)解析

13
一、刚体作平动
刚体内各点的加速度都与质心C的加速度 aC相等,任一
质点的惯性力 FIi mi aC ,组成一同向的平行力系。
这个惯性力系简化为通过质心C的合力:
FIR FIi miaC ( mi )aC FIR mac
FI1 aC
FI2
附加动约束力); 2 推出消除附加动约束力的条件。
定轴转动刚体,角速度 ,角加速度 。
坐标系oxyz如图示,o点为转轴上的一点。
取简化中心:转轴上一点O。
z
所有主动力向O点简化的结果: 主矢:FR 主矩:M O
A FAx
惯性力系向O点简化的结果:
主矢:FIR
主矩:M IO
MO O
惯性力没有Z方向的分量(Z方向无加
第九章 质点动力学的基本方程 第十章 动量定理 第十一章 动量矩定理 第十二章 动能定理 ★ 第十三章 达朗贝尔原理 第十四章 虚位移原理
本章介绍动力学的一个重要原理——达朗贝尔原 理。应用这一原理,就将动力学问题从形式上转化 为静力学问题,从而根据关于平衡的理论来求解。 这种用静力学解答动力学问题的方法,也称为动静 法。
FOx
(m1 m2 )g (m1 m2 )a
FIB
B
a 在本题中不计滑轮的质量,如果要
考虑滑轮的质量,则如何计算?
A
a
m2g
m1g
加上滑轮的惯性力和重力。
FIA
§13-3 刚体惯性力系的简化
应用达朗贝尔原理求解质点系动力学问题必须给各质点虚 加上它的惯性力。对于运动的刚体每个质点加上它的惯性力, 这些惯性力组成一惯性力系。因为刚体有无限个质点,在每个 质点上加惯性力是不可能的,为了应用方便,按照静力学中力 系的简化方法将刚体的惯性力系加以简化,这样在解题时就可 以直接施加其简化结果,使动静法切实可行。
理论力学(机械工业出版社)第十三章达朗伯原理习题解答

习 题13-1 如图13-16所示,一飞机以匀加速度a 沿与水平线成仰角b 的方向作直线运动。
已知装在飞机上的单摆的悬线与铅垂线所成的偏角为f ,摆锤的质量为m 。
试求此时飞机的加速度a 和悬线中的张力F T 。
图13-16ma F =I 0cos sin 0I T =-=∑βϕF F F xϕβsin cos IT F F =0sin cos 0I T =--=∑mg F F F y βϕ0sin cos sin cos I I =--mg F F βϕϕβ0sin )cos(I=-+mg F ϕβϕ mgma=+ϕβϕsin )cos()cos(sin βϕϕ+=g amgma F F )cos(cos sin cos sin cos I T βϕβϕβϕβ+===13-2 球磨机的简图如图13-17所示,滚筒作匀速转动,内装钢球及被粉碎的原料,当钢球随滚筒转到某一角度f 时,将脱离筒壁作抛射运动,由于钢球的撞击,从而破碎与研磨原料。
已知钢球脱离筒壁的最佳位置'4054︒=ϕ,滚筒半径R =0.6m 。
试求使钢球在'4054︒=ϕ处脱离滚筒的滚筒转速。
图13-172n I ωmR ma F == 0cos 0I N n =-+=∑F mg F F ϕ)cos (cos cos 22I N ϕωϕωϕg R m mg mR mg F F -=-=-=令0N =F0cos 2=-ϕωg RR g ϕωcos =min r/35.296.00454cos 8.9π30cos π30π30='︒⨯===R g n ϕω13-3 一质量为m 的物块A 放在匀速转动的水平转台上,如图13-18所示。
已知物块的重心距转轴的距离为r ,物块与台面之间的静摩擦因数为s μ。
试求物块不致因转台旋转而滑出时水平转台的最大转速。
图13-182n I ωmr ma F ==00N =-=∑mg F F ymg F =N00I =-=∑F F F x0N s 2=-F mr μω 0s 2=-mg mr μωrgs μω=rgn s max π30π30μω==13-4 离心调速器的主轴以匀角速度w 转动,如图13-19所示。
理论力学10动量矩定理

J11 (J 22 m2v2 R2 ) m3v3R2
v3
v2
R2 2
1 2
R11
LO
(
J1 R2 2
J2 R2 2
m2
m3 )R2v3
轮B滚而不滑,有瞬心
17
对于一个定轴转动刚体 Lz J z
代入质点系动量矩定理,有
d dt
(J
z)
M
(e) z
Jz
M
( e) z
或
Jz
d 2
dt 2
M
(e) z
—刚体定轴转动微分方程
解决两类问题: 已知作用在刚体的外力矩,求刚体的转动规律。 已知刚体的转动规律,求作用于刚体的外力(矩)。
但不能求出轴承处的约束反力,需用质心运动定理求解。
18
特殊情况:
n
若M z(e) M z (Fi(e) ) 0 ,则 0, 恒量,刚体作匀速转动或 i1 保持静止。
mT
mT ymdm 0
mT
刚体对z轴的转动惯量
JZ
r2dm
mT
(x2 y2 )dm
mT
mT [( xC xm )2 ( yC ym )2 ]dm
mT (xm2 ym2 )dm
mT (xC2 yC2 )dm 2xC
mT
xmdm
2 yC
mT
ymdm
J Z JC mT d 2
0
0 24
复杂形状刚体的转动惯量 按定义,有:
JZ
分析力学答案

K FV
m 448浒 421122 - Ík 4- 4 行mg crank
代入⻮ 器 器 - 0中 可得
mki zmisinzeuttkicq 4.1 mg2Sin4 0 mEsin244 0 4 0 运动微分方程 miii miisiuqcose mg2siuqtkRi9-线 0
C2
0 时零解渐近稳定
1.8 试利用李雅普诺夫直接方法讨论系数在取不同值时判断
系统的零解稳定性
X X2
X十 a 3 加
解 选择正定李雅诺夫函数 比吅 二 水 水
计算 治 方程解曲线的全导数 V 荪义 器加二 zxixztzxzEXitlaih I
E 2 G 37 X22
则当 以 3时 V为负定 零解渐近稳定 a 3 时 V为零 零解稳定 a 3时 V为正定 零解不稳定
讨论是否存在初积分
i
䚡 取摇杆0A的转⻆为0 则系统的动能
T 士 加 以 04 Ìmi 旰士 Ìmhyo
二 Gmt Ém EG
取系统平衡位置为零势能 则运动时系统势能为
V kid 4 Ütmlglsin0
6 -sins
则L T V
且出售了一
是
tmtimtEG 二日 mini
zkdkcitmlgl sino tkdtimsglll cme
则 fm2以g外3tmlzmxitomtmiiiomy
f 去㗊㗊 a
i riiig 二his
3 8 质量为 m的均质摇杆0A 铰接 质量为 以的匀质圆盘A 在13 处联结刚度系数为人的弹簧 当系统平衡时 以处于水平位置 弹
簧处于铝垂位置如图所示 已知 非1.013 a 若圆盘沿固定圆弧形
理论力学第七版答案_哈工大编_高等教育出版社出版
哈工大理论力学(I)第7版部分习题答案1-2两个老师都有布置的题目2-3 2-6 2-14 2- 20 2-30 6-2 6-4 7-9 7-10 7-17 7-21 8-5 8-8 8-16 8-24 10-4 10-6 11-5 11-15 10-3以下题为老师布置必做题目1-1(i,j), 1-2(e,k)2-3, 2-6, 2-14,2-20, 2-306-2, 6-47-9, 7-10, 7-17, 7-21, 7-268-5, 8-8(瞬心后留), 8-16, 8-2410-3, 10-4 10-611-5, 11-1512-10, 12-15, 综4,15,16,1813-11,13-15,13-166-2 图6-2示为把工件送入干燥炉内的机构,叉杆OA=1.5 m在铅垂面内转动,杆AB=0.8 m,A端为铰链,B端有放置工件的框架。
在机构运动时,工件的速度恒为0.05 m/s,杆AB始终铅垂。
设运动开始时,角0=?。
求运动过程中角?与时间的关系,以及点B的轨迹方程。
10-3 如图所示水平面上放 1 均质三棱柱 A ,在其斜面上又放 1 均质三棱柱 B 。
两三棱柱的横截面均为直角三角形。
三棱柱 A 的质量为 mA 三棱柱 B 质量 mB 的 3 倍,其尺寸如图所示。
设各处摩擦不计,初始时系统静止。
求当三棱柱 B 沿三棱柱 A 滑下接触到水平面时,三棱柱 A 移动的距离。
11-4解取A、B 两三棱柱组成 1 质点系为研究对象,把坐标轴Ox 固连于水平面上,O 在棱柱A 左下角的初始位置。
由于在水平方向无外力作用,且开始时系统处于静止,故系统质心位置在水平方向守恒。
设A、B 两棱柱质心初始位置(如图b 所示)在x 方向坐标分别为当棱柱B 接触水平面时,如图c所示。
两棱柱质心坐标分别为系统初始时质心坐标棱柱B 接触水平面时系统质心坐标因并注意到得10-4 如图所示,均质杆AB,长l,直立在光滑的水平面上。
刚体的定轴转动(带答案)

刚体的定轴转动一、选择题1、(本题3分)0289关于刚体对轴的转动惯量,下列说法中正确的是 [ C ] (A)只取决于刚体的质量,与质量的空间分布和轴的位置无关。
(B)取决于刚体的质量和质量的空间分布,与轴的位置无关。
(C)取决于刚体的质量、质量的空间分布和轴的位置。
(D)只取决于转轴的位置,与刚体的质量和质量的空间分布无关。
2、(本题3分)0165均匀细棒OA可绕通过某一端O而与棒垂直的水平固定光滑轴转动,如图所示,今使棒从水平位置由静止开始自由下降,在棒摆到竖直位置的过程中,下述说法哪一种是正确的?(A)角速度从小到大,角加速度从大到小。
(B)角速度从小到大,角加速度从小到大。
(C)角速度从大到小,角加速度从大到小。
(D)角速度从大到小,角加速度从小到大。
3. (本题3分)5640..一个物体正在绕固定的光滑轴自由转动,则 [ D ] (A ) 它受热或遇冷伸缩时,角速度不变. (B ) 它受热时角速度变大,遇冷时角速度变小. (C ) 它受热或遇冷伸缩时,角速度均变大. (D ) 它受热时角速度变小,遇冷时角速度变大. 4、(本题3分)0292一轻绳绕在有水平轴的定滑轮上,滑轮质量为m ,绳下端挂一物体,物体所受重力为P ,滑轮的角加速度为β,若将物体去掉而以与P 相等的力直接向下拉绳子,滑轮的角加速度β将 [ C ] (A )不变 (B )变小 (C )变大 (D )无法判断 5、(本题3分)5028如图所示,A 、B 为两个相同的绕着 轻绳的定滑轮,A 滑轮挂一质量为M 的物体,B 滑轮受拉力F ,而且F=Mg ,设A 、B 两滑轮的角加速度分别为βA 和βB ,不计滑轮轴的摩擦, 则有 [ C ] (A )βA =βB (B )βA >βB.(C )βA <βB (D )开始时βA =βB ,以后βA <βB 6、(本题3分)0294刚体角动量守恒的充分而必要的条件是[ B ] (A )刚体不受外力矩的作用。
哈工大理论力学(I)第七版答案、高等教育出版社出版

哈工大理论力学(I)第7版部分习题答案1-2两个老师都有布置的题目2-3 2-6 2-14 2- 20 2-30 6-2 6-4 7-9 7-10 7-17 7-21 8-5 8-8 8-16 8-24 10-4 10-6 11-5 11-15 10-3以下题为老师布置必做题目1-1(i,j), 1-2(e,k)2-3, 2-6, 2-14,2-20, 2-30 6-2, 6-47-9, 7-10, 7-17, 7-21, 7-268-5, 8-8(瞬心后留), 8-16, 8-24 10-3, 10-4 10-611-5, 11-1512-10, 12-15, 综4,15,16,18 13-11,13-15,13-166-2 图6-2示为把工件送入干燥炉内的机构,叉杆OA=1.5 m在铅垂面内转动,杆AB=0.8 m,A端为铰链,B端有放置工件的框架。
在机构运动时,工件的速度恒为0.05 m/s,杆AB始终铅垂。
设运动开始时,角0=?。
求运动过程中角?与时间的关系,以及点B的轨迹方程。
10-3 如图所示水平面上放1 均质三棱柱A,在其斜面上又放1 均质三棱柱B。
两三棱柱的横截面均为直角三角形。
三棱柱A 的质量为mA三棱柱B 质量mB的 3 倍,其尺寸如图所示。
设各处摩擦不计,初始时系统静止。
求当三棱柱B 沿三棱柱A 滑下接触到水平面时,三棱柱A 移动的距离。
11-4解取A、B 两三棱柱组成1 质点系为研究对象,把坐标轴Ox 固连于水平面上,O 在棱柱A 左下角的初始位置。
由于在水平方向无外力作用,且开始时系统处于静止,故系统质心位置在水平方向守恒。
设A、B 两棱柱质心初始位置(如图b 所示)在x 方向坐标分别为当棱柱B 接触水平面时,如图c所示。
两棱柱质心坐标分别为系统初始时质心坐标棱柱B 接触水平面时系统质心坐标因并注意到得10-4 如图所示,均质杆AB,长l,直立在光滑的水平面上。
求它从铅直位无初速地倒下时,端点A相对图b所示坐标系的轨迹。
大学物理学-刚体的转动定律

ω
v ri
vi
∆mi
v
Ek =
∑
i =1
n
1 1 n 1 2 2 2 2 ∆ m i ri ω = ( ∑ ∆ m i ri )ω = J ω 2 2 2 i =1 2
刚体绕定轴转动时的转动动能等于刚体的转动惯量 与角速度平方乘积的一半. 与角速度平方乘积的一半.
第2章 运动定律与力学中的守恒定律
支架S 支架S
外环 陀螺G 陀螺G 内环
2–6 刚体的定轴转动 6 直升机螺旋桨的设置
尾桨的设置: 尾桨的设置:直升机发动后机身要在旋翼旋转相反方向旋 产生一个向下的角动量。 转,产生一个向下的角动量。为了不让机身作这样的反向 旋转,在机身尾部安装一个尾桨, 旋转,在机身尾部安装一个尾桨,尾桨的旋转在水平面内 产生了一个推力,以平衡单旋翼所产生的机身扭转作用。 产生了一个推力,以平衡单旋翼所产生的机身扭转作用。 对转螺旋桨的设置:双旋翼直升机则无需尾桨, 对转螺旋桨的设置:双旋翼直升机则无需尾桨,它在直立 轴上安装了一对对转螺旋桨, 轴上安装了一对对转螺旋桨,即在同轴心的内外两轴上安 装了一对转向相反的螺旋桨。工作时它们转向相反, 装了一对转向相反的螺旋桨。工作时它们转向相反,保持 系统的总角动量仍然为零。 系统的总角动量仍然为零。
力矩的功
A=
∫θ
θ2
1
M dθ
力矩的功率 力矩的功率
dA dθ P= =M = Mω dt dt
第2章 运动定律与力学中的守恒定律
2–6 刚体的定轴转动 6
9
3、刚体定轴转动的动能定理 、
理论力学第13章-动能定理

k C
G
W1 G h 9.8 5 49N c m (a)
(b)
弹性力的功:1 0, 2 AC BC AB 2 202 52 40 1.23c m
W2
k 2
2 1
2 2
40 2
0 1.232
30.3N c m
所有力的功 W W1 W2 49 30.3 18.7N c m 0.187J
13 动能定理
13.1 力的功、功率 13.1.1 功的表达式 力的功( Work )是力在一段路程上对物体作用的累
积效果,其结果将导致物体能量的变化。
设质量为 m 的质点 M,受力 F 作用,质点在惯
性参考系中运动的元位移为 d r。
力的元功 :力F 在元位移上 累积效果
dW F dr
(13-1)
与其角速度平方的乘积之半。
根据平行轴定理
JP JC M d2
M 为刚体的质量,d = P C ,J C 为对于质心的转动惯量。
T 1 2
JC M d2
2
1 2
JC
2
1 2
M
d
2
因为 d vC
T
1 2
M
v
2 C
1 2
JC
2
(13-21)
即作平面运动的刚体的动能,等于随质心平动的动能与
绕质心转动的动能的和。
P
M
z
dj
dt
M
z
(13-15)
即力矩的功率,等于力矩与刚体转动角速度的乘积。
功率计量单位为焦耳/秒 ( J / s ),瓦 ( W ):
1W 1J/s 1N m/s
(2)机械效率。P输入、P输出、P损耗 分别表示输入功
13运动学刚体平面运动知识课件知识讲稿

即平面图形内任一点的加速度等于基点的加速度与该点随 图形绕基点转动的切向加速度和法向加速度的矢量和。
这种求解加速度的方法称为基点法,也称为合成法。是求 解平面图形内一点加速度的基本方法。
上述公式是一平面矢量方程。需知其中六个要素,方能求 出其余两个。由于 aB A,aBnA方位总是已知,所以在使用该公 式中,只要再知道四个要素,即可解出问题的待求量。
取B为动点, 则B点的运动可视为牵连运动为平动和相对
运动为圆周运动的合成 va vB; ve vA; vr vBA
指向与 转向一致。 大 小 AB ,方向 AB ,
根据速度合成定理 va ve vr, 则B点速度为:
vBvAvBA
14
即平面图形上任一点的速度等于基点的速度与该点随图形绕基点 转动的速度的矢量和。这种求解速度的方法称为基点法,也称为 合成法。它是求解平面图形内一点速度的基本方法。
25
[例2] 半径为R的车轮沿直线作纯滚动,已知轮心O点的速度 v O 及加速度 a O ,求车轮与轨道接触点P的加速度。
分析: aPaOaPO aPO n 大小 ? √ R R 2
方向 ? √ √ √
故应先求出 .
解:轮O作平面运动,P为速度瞬心,
vO/R ( )
由于此式在任何瞬时都成立,且O点作直线运动,故而
③ 速度瞬心法
研究AB,已知 vA , vB的方向,因此
可确定出P点为速度瞬心。
vAl,APl ABvA/APl/l( )
vB BPAB 2l()
试比较上述三种方法的特点。
23
§13.3 平面图形内各点的加速度计算
第十三章 静定结构的位移

F 1
A
3
2
A' R
F2
F3 W ( F1 cos 1 F2 cos 2 F3 cos 3 ) AA '
WR R cos AA '
W
WR
在任意给定或假设的位移过程中,若力的大小及方 向不变,则各个力所做功之和等于其合力所做的功。
第十三章 静定结构的位移
实功:力在自身所产生的位移上所作的功。
Fi iF M i d N i du V i ds
令Fi 1 ,得 虚功原理:状态 1的外力在状态2的位移上所作的虚功,等 于状态1各微段的内力在状态 iF M i d 2相应微段变形上所作的虚功 N i du V i ds 之和。
(b)
FAH
A
C
P= 1
B FBH
l
l
FAy
FBy
沿水平方向作用单位
力,虚力状态如图(c)所 F
AH
C P i= 1
示。 求C点的水平位移。
A
B FBH
FAy
FBy
第十三章 静定结构的位移
2.求角位移
1)求构件某截面角位移,可在该截面虚加一个单
位力偶。 2)求某铰左右截面的相对转角,可在该铰两侧虚 加一对反向的单位力偶。 3)求长为l 杆件的角位移,可在其两端虚加上垂 直杆轴的、形成的力偶的两个集中力,两力大小
第十三章 静定结构的位移
第十三章 静定结构的位移计算
教学内容:虚功原理,变形体虚功原理,静定结构在荷 载、支座移动作用下引起的位移计算,互等定理。 教学要求: 1、了解结构线位移、角位移、实功与虚功,广义力与广 义位移;变形体虚功原理的两种形式(虚力原理、虚位 移原理);互等定理; 2、理解静定结构在荷载作用下的位移计算的积分法;静 定结构因支座移动时的位移计算原理和方法;静定结构 的一般特征; 3、掌握用图乘法计算静定结构的位移 重点:用图乘法计算静定结构的位移。 难点:变形体虚功原理,图乘法。
第十三讲刚体的运动和动力学问题 (1)

第十三讲 刚体的运动学与动力学问题一 竞赛内容提要 1、刚体;2、刚体的平动和转动;3、刚体的角速度和角加速度;4、刚体的转动惯量和转动动能;5、质点、质点系和刚体的角动量;6、转动定理和角动量定理;7、角动量守恒定律。
二 竞赛扩充的内容1、刚体:在外力的作用下不计形变的物体叫刚体。
刚体的基本运动包括刚体的平动和刚体绕定轴的转动,刚体的任何复杂运动均可由这两种基本运动组合而成。
2、刚体的平动;刚体的平动指刚体内任一直线在运动中始终保持平行,刚体上任意两点运动的位移、速度和加速度始终相同。
3、刚体绕定轴的转动;刚体绕定轴的转动指刚体绕某一固定轴的转动,刚体上各点都在与转轴垂直的平面内做圆周运动,各点做圆周运动的角位移Φ、角速度ω和角加速度β相同(可与运动学的s 、v 、a 进行类比)。
且有:ω=t t ∆∆Φ→∆lim 0;β=t t ∆∆→∆ωlim0。
当β为常量时,刚体做匀加速转动,类似于匀加速运动,此时有:ω=ω0+βt ; Φ=Φ0+ω0t+βt 2/2;ω2-ω02=2β(Φ-Φ0)。
式中,Φ0、ω0分别是初始时刻的角位移和角速度。
对于绕定轴运动的刚体上某点的运动情况,有:v=ωR , a τ=βR , a n =ω2R=v 2/R, 式中,R 是该点到轴的距离,a τ、a n 分别是切向加速度和法向加速度。
例1 有一车轮绕轮心以角速度ω匀速转动,轮上有一小虫自轮心沿一根辐条向外以初速度v 0、加速度a 作匀加速爬行,求小虫运动的轨迹方程。
例2 一飞轮作定轴转动,其转过的角度θ和时间t 的关系式为:θ=at+bt 2-ct 3,式中,a 、b 、c 都是恒量,试求飞轮角加速度的表示式及距转轴r 处的切向加速度和法向加速度。
例3 如图所示,顶杆AB 可在竖直槽K 内滑动,其下端由凸轮K 推动,凸轮绕O 轴以匀角速度ω转动,在图示瞬间,OA=r ,凸轮轮缘与A 接触处,法线n 与OA 之间的夹角为α,试求此瞬时顶杆OA 的速度。
刚体惯性力系的简化

代入式(a)得 再解式(b)、式(c)有
a g 3
Ff
P 2
P g
g 3
P 6
FN P cos
3P 2
P
f Ff 6 3 0.192
FN
3P 9
2
(b) (c)
例13-7 均质杆 AB 重 P,B 点放在地面上,A 点与轮铰接,轮在平面上纯
滚动,轮心做匀速直线运动,速度为 v,如图 13-11(a)所示。试 求在图示位置(A 位于最高点)时,AB 杆在 A,B 两点的受力情况 (B 与地面无摩擦)。
在工程实际中,刚体绕定轴转动有几种特殊情况。
(1)转轴过质心。此时 aC 0 ,FI 0 ,在 0 的情况下,惯性力系简 化为一个力偶。
(2)刚体做匀速转动,此时 0 ,在转轴不过质心的情况下,惯性力 系简化为一个合力。
(3)转轴过质心,刚体做匀速转动,aC 0 , 0 ,则 FI 0 ,MIO 0 。
(a)
(b) 图13-11
(c)
解 (1)取AB杆为研究对象。
(2)受力分析。AB 杆上作用的主动力为重力 P,A 点有两个约束力 FAx 和 FAy , B 点有法向约束力 FBN ,如图 13-11(b)所示。
(3)运动分析,加惯性力。由已知条件,AB 杆为瞬时平动,即 AB 0 ,对 AB
FI FIi (miai ) aC mi 设刚体质量为 M mi ,则
FI MaC (13-8)
于是得结论:平动刚体的惯性力系可以简化为通过质心 的合力,其大小等于刚体的质量与加速度的乘积,合力的 方向与加速度方向相反。
图13-5
刚体绕定轴转动
如果刚体有对称平面S,并且该平面与转轴z垂直,则惯性力系简化 为在对称平面内的平面力系。再将此平面力系向转轴与对称平面的交 点O简化,如图13-6所示。
常见刚体的转动惯量
习题答案
第一章
F (h − 3r ), M y = 3 F (r + h ), M z = − Fr . 1-3 4 4 2 2 bc ab ca a ab M ξ = −513.36 N ⋅ m . 1-4 M x = M − F ,My = M + F ,Mz = M, k1 k1 k1 2k 2 2k 2 abc 2 2 2 2 2 2 F. 其中: k1 = (ab ) + (bc ) + (ca ) , k2 = a + b / 4 + c . 1-5 M τ = rAB b 2 + c 2
ρz =
3 r 10 3 (4r 2 + l 2 ) 80
ρx = ρy
=
圆环
3 J z = m( R 2 + r 2 ) 4
ρ z = R2 + r2
3 4
Jz =
椭圆形 薄 板
m 2 (a + b2 ) 4 m J y = a2 4 m J y = b2 4
1 2 a + b2 2 a ρx = 2 b ρy = 2
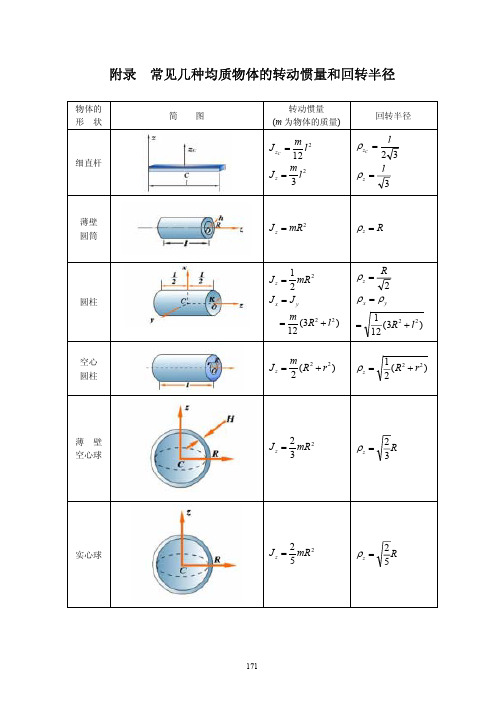
附录常见几种均质物体的转动惯量和回转半径物体的转动惯量简图回转半径形状m为物体的质量m2ljlzzcc1223细直杆m2ljzlz33薄壁2jmrr圆筒zz12rjmrzz22jj圆柱xyxym221223rl3rl1212空心m22122jzrrzrr圆柱22薄壁222jzmrzr空心球33222实心球jzmrzr55171323jzmrzr1010jj圆锥体xyxy322322m4rl4rl8080232232圆环jzmrrzrr44m22122jzabzab42椭圆形m2ajyax薄板42m2bjyby42m22122jzabzab1212m22122长方体jyacxac1212m22122jy12bcy12bcm22jz12ab122zab矩形m212ja薄板y120289axm20289bjbyy12172参考书目1朱照宣周起钊殷金生编
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
r mv0 D mvd
2
M
B
D d 2 M v0 2Gd
2
12
7. 在实验室内观察到相距很远的一个质子P (质量为mp) 和一个α粒子(质量为mα= 4mp ),沿一直线相向运动, 速率都是v0,为求得两者能达到的最近距离R,有人的 解法如下:以质子、α粒子为系统,因仅有保守力(库 仑力)做功,故系统的机械能(其中势能为电势能) 守恒。则有 p11-7
1. 转动惯量是转动惯性大小的量度 (kg· m2) 2. 转动惯量决定于刚体总质量及对轴的质量分布. 标量叠加特性 3. 同一刚体对不同的轴的转动惯量一般是不相同的.
例:质量为m,长为L的均匀细棒对某轴的转动惯量.
1.
2
x O x
2
m dx 解: dJ x dm x dx x L L 1 2 m 2 (或 J 2 J L x dx mL2 L 12 2
18
2
例:半径为R的光滑圆环铅直放臵,质量为m的小球穿在
圆环上,开始小球静止于A点并下滑. 求:小球滑至B点时( )对 O 点的角动量和角速度 . 解:分析力 N G N 对O点力矩为零 方法1: 重力矩: M r G 方向:
M mgR sin mgR cos dL d L 由: M mgR cos dt dt
6. 3 “守恒”应是整个力学过程每一状态都守恒
选择题:关于机械能守恒定律有下列表述
1.无外力与非保守内力的系统,机械能守恒。 2.外力的合功为零的系统,机械能守恒。 3.外力做功为零、非保守内力做功为零的系统, 机 械 能守恒。 4.外力做功与非保守内力做功之和为零的系统, 机 械 能守恒。 其中 最正确的是 A. (1),(2),(3) B. (1),(2),(4) C. (1),(3) D. (1),(3),(4) [ D ]
M
C
v12
4
解:由公式
v绝对 v相对 v牵连 vm地 v12 v2
v2
M m
(1)该时刻物体A相对于桌面的速度的水平分量与竖直分量 ;
vm地y v12 cos
vm地x v12 sin v2
0 R
(2)写出A相对于桌面的动能的表达式
1 1 2 2 2 mv地 m[vm地x vm地y ] 2 2
核
b
.
s
17
解: 作用力是有心力,所以角动量守恒, S…
在碰撞过程中,能量守恒 核
b 1 kZe 1 2 2 M pv s M p v0 2 S 2
2
M pv0b M pvS S v0 b vS S
v0 质子的轨道
s
vs
kZe 1 b 2 2 M pv0 1 ( ) S 2 S
2g 2 1/ 2 L mR ( sin ) R
例:一质量为 m的质点沿一条二维曲线运动 其中a,b, 为常数 r a cos t i b sin t j
试求:该质点对原点的角动量矢量 . dr 解: v a sint i b cost j dt L mr v m(a costi b sintj )
2 1 1 2 e 2 2 (mα m p )v0 (mα m p )v 2 2 40 R
5e R 2 160 m pv0
2
14
11. 质量 m=0.2kg 的小球 A,用弹性绳在光滑水平面上 与固定点 O相连,弹性绳的劲度系数为 k=8N/m,其自 由伸展长度为 l0=0.6m。最初小球的位臵及速度 v0如图 所示。当小球的速率变为 v时,它与O点的距离最大且 等于0.8m。求此时小球的速率v及初速率v0。
7
9 .如图,质量为M半径为R的圆弧形槽D臵于光滑水平面 上.开始时质量为m的物体C与弧形槽D均静止,物体C由圆 弧顶点 a 处下滑到底端 b 处的过程中判断下列说法是否正 确?并说明理由.p6-6 N C C O N a a a C R C v D D D b mg b
b
(1)以地面为参考系,槽 D 对物体 C 的支持力不 做功. (2)以槽D为参考系,槽D对物体C 的支持力不 做功. (3)以地面为参考系,物体C在b点相对于地面的速率v1满足. 1 1 1 2 2 2 mv1 mgR 应是: mv1 MV mgR 2 2 2
v r
d dt
6-1-4 定轴转动 定点转动
p
转轴
§6-2 刚体动力学
6-2-1 刚体对定轴的角动量
研究方法:质点力学的规律应用到组成刚体的质点系 L
z
Li Ri (mi vi ) | Li | mi Ri vi
对转轴 z Lz Li cos
0
m
dr
R r
例:圆环(R1, R2, m),对垂直盘面的中心轴的转动惯量.
m 解: 2 2 π( R2 R1 )
R2
2
J
R1
1 2 2π r dr m( R12 R2 ) 2
P12-11
v
v0
O
A
0.4m
30
。
15
解:以小球与绳为系统,只有保守力做功,
且对O点角动量守恒: 机械能守恒,
1 1 2 2 1 m v0 m v k ( l l0 )2 2 2 2
v0
A
0.4m
30
。
k (lmax
v2 l0 ) m 2 lmax
O
mr0v0 sin30 mlv
Lz J
( p mv )
1. L , J , 均对同一转轴 . z 注意: 2. Lz 与 同方向,即同号.
6-2-2 转动惯量及其计算
定义式:J
dV 质量连续分布: J r 2dm 其中: dm dS dl 说明:
dJ r dm
2
2 2 r m ( J r i i i i mi )
k 1 . 31 (m/s) v0 l ( l l 0 ) m( l 2 r02 sin2 300 )
v0 r0 si n30 v 0.327(m /s) l
16
13 质子被重核散射 一个质子接近一个电荷为Ze的很重 的核。当它们距离很远时,质子的能量为 1/2· Mpv02. 把 质子在远距离处的轨道直线延长到近距离,这条延长线 离重核最小的距离为 b。这个距离叫作碰撞参量。对于 实际的轨道,请列出最接近的距离 S所满足的方程。(设 重核的质量为无限大) v0 .质子的轨道 P12-13
刚体是一种特殊的 质点系统
刚体是一个理想模型.固体材料及形变.
刚体的构成
真正的刚体不存在
6-1-2 刚体平动与转动
一 刚体的平动
B
B
B
A
A
特点: AB//AB//AB
p
A
二 刚体的转动和转轴
转轴
三 刚体的一般运动 .v
平动与转动叠加
o
c
6-1-3 角速度 角加速度
d dt
mab k dL M 0! dt
( a sinti b costj ) 2 2 m(ab cos tk ab sin tk )
(恒矢量)
或由 M r F
判断下列情况角动量是否守恒:
圆锥摆运动中,做水平匀速 圆周运动的小球m. (1)对C点的角动量 (2)对O点的角动量 (3)对竖直轴CC'的角动量
今天收作业!
序号杨甦I A
练习薄
期中考试 第9周周日 19:00-21:00
守恒定律 习题课
3
7 .如图 为弧形槽B的1/4光滑圆弧,臵于光滑桌面C 上. 当质量为m的物体A沿 下滑过程中B将向左运动.若 A滑到d点时相对于B的速度为v12,此时B相对于桌面的速 度为v2,方向水平向左,试求:p6-7 (1)该时刻物体A相对于桌面的速度的水平分量与竖直分量; (2)写出A相对于桌面的动能的表达式; m 0 (3)写出A相对于桌面的动量的表达式. v 解: 2 R
O
N
R
A B
dL mgR cosdt (1) L=L( ) v 2 2 d L m r v L mR mR
mR dt d L
2
r
G
dt
(2)
(2)代入(1) : dL mgR cos dt 得 LdL m 2 gR 3 cos d
(3)写出A相对于桌面的水平动量的表达式.
C
ቤተ መጻሕፍቲ ባይዱ
v12
PAx mvm地x m(v12 sin v2 )
5
8 . 判断下列表述的正误, 并说明理由.p6-8 (1)所受合外力为零的系统机械能一定守恒; 不一定 (2)不受外力的系统,必同时满足动量守恒和机械能守恒; 不一定 (3)合外力为零,内力只有保守力的系统机械能一定守恒; 不一定 (4)只有保守力内力作用的系统,动量和机械能一定守恒; 是的 (5)一质点在某一过程中,所受合外力的冲量为零,则质点 不一定 的动量一定守恒; (6)合外力为零的系统,对某一点的角动量一定守恒。 不一定 关键 :1 清楚明确守恒条件; 2 外力合力为零,不一定不做功;
10
求碰撞后轻杆的角速度
o.
1 v0 2
2m
2 l 3
v0 m
m
11
6. 质量为m的粒子A受到另一粒子B的引力作用,B 保持 在原 点 不动。开始时A离B很远(r→∞),且具有沿水平 方向的速度v0,此速度方向与粒子B的垂直距离为D。粒 子A由于B 的引力作用偏离原来的运动方向,沿如图所 示的轨道运动,已知轨道与粒子B 之间的最短距离为d。 试求粒子B 的质量M。 A v0 解: P10-6 Mm 1 Mm 1 2 2m G m v 0 G mv D r 2 d 2 d .v
