育苗杯练习资料(2.整除和有余数的除法)
广东五年级育苗杯试卷【含答案】

广东五年级育苗杯试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 下列哪种植物适合在广东地区进行春季育苗?A. 水稻B. 玉米C. 棉花D. 花生2. 育苗时,以下哪种土壤条件最为适宜?A. 酸性土壤B. 碱性土壤C. 沙质土壤D. 黏土土壤3. 育苗期间,哪种天气状况最有利于植物生长?A. 持续高温B. 阴雨连绵C. 温暖湿润D. 寒冷干燥4. 育苗过程中,哪种措施可以有效预防病虫害?A. 增加施肥量B. 喷洒农药C. 适时灌溉D. 种植抗病虫害品种5. 在广东地区,以下哪种作物不适合进行秋季育苗?A. 小麦B. 大豆C. 番茄D. 胡萝卜二、判断题(每题1分,共5分)1. 广东地区的气候条件适合全年进行育苗。
()2. 育苗时,土壤的排水性能越好,越有利于植物生长。
()3. 育苗期间,光照时间越长,植物生长越快。
()4. 育苗时,可以使用任何类型的肥料来促进植物生长。
()5. 在广东地区,冬季不适合进行任何作物的育苗。
()三、填空题(每题1分,共5分)1. 在广东地区,最适合进行春季育苗的作物是______。
2. 育苗时,土壤的______性能对植物生长至关重要。
3. 育苗期间,保持土壤的______和______是关键。
4. 为了预防病虫害,可以在育苗期间喷洒______。
5. 在广东地区,秋季育苗的最佳时间是______。
四、简答题(每题2分,共10分)1. 简述广东地区春季育苗的注意事项。
2. 描述育苗期间土壤管理的要点。
3. 解释为什么保持适宜的土壤湿度对育苗很重要。
4. 列举三种育苗期间常用的肥料类型。
5. 简述广东地区秋季育苗的优势。
五、应用题(每题2分,共10分)1. 假设你要在广东地区进行春季育苗,你会选择哪种作物?为什么?2. 如果你发现育苗土壤排水性能不佳,你会采取哪些措施?3. 在育苗期间,如何判断土壤湿度是否适宜?4. 如果在育苗期间发现病虫害,你会如何处理?5. 假设你要在广东地区进行秋季育苗,你会选择哪种作物?为什么?六、分析题(每题5分,共10分)1. 分析广东地区春季和秋季育苗的差异,并说明原因。
育苗杯训练练习(二)

育苗杯训练练习(二)
班级姓名成绩
1、如果25×□÷3×15+5=2005,那么□=()
2、已知A÷B=22……8,而且A+B=836,那么A=()。
3、某班有40名学生,期中数学考试有2名同学因故请假未考试,这时的平均分为89分,未考试的两位同学补考后都得99分,那么这个班期中数学考试的平均分是( )分。
4、三个连续自然数的和为21,这三个连续自然数的积()。
5、一座大桥长2800米,一列火车通过大桥时每分钟行800米,从
车头开上桥到车尾离开桥共用4分。
这列火车长()米。
6、今年爸爸和女儿的年龄和是44岁,10年后,爸爸的年龄是女儿的3
倍,今年女儿是()岁。
7、小红有不同的上衣5件,裤子4件,鞋子3双,算一算,小明能有( )种
不同的穿戴装束。
.
8、2÷7的商是一个循环小数,这个循环数的小数点后第2012位上
的数是()。
9、一个数减去15后,再除以4,然后再减去6,最后扩大10倍得100,
原来的数是()。
10、现有三筐水果,已知梨子和苹果共重60千克,苹果和桃子共重
65千克,梨子和桃子共重55千克,那么苹果有()千克。
五年级育苗杯竞赛试题精选

五年级育苗杯竞赛试题1.在算式□×5÷3×9+11=1991中,□里应填入的数字是()。
2、一个自然数与它本身相加、相减、相除所得的和、差、商再相加,结果是1991,那么原来的自然数是()。
3、下面算式中只有一个算式的得数是1991,那么第()个算式的得数是1991。
①768×38-171×102 ②675×54-198×173③724×44-165×181 ④695×53-189×1944、某同学在计算一道除法题时,误将除数32写成23,所得的商是32余数是11,正确的商与余数的和是()。
5、亮亮从家步行去学校,每小时走5千米。
回家时骑自行车,每小时走13千米。
骑自行车比步行的时间少4小时,亮亮家到学校的距离是()千米。
6、一个两位数,个位数字是十位数字的3倍,如果这个数加上60,则两个数字相等,这个两位数是()。
7、两个自然数的和是286,其中一个数的末位数是0,如果把这个零去掉,所得的数与另一个数相同,那么原来两位数的积是()。
8、下图中,三角形ABC的面积是30平方厘米,D是BC的中点,AE的长是ED的长的2倍,那么三角形CDE的面积是()平方厘米。
9、甲乙丙丁四个人共卖了10个面包平均分着吃,甲拿出6个面包的钱,乙和丙都只拿出2个面包的钱,丁没带钱。
吃完后一算,丁应该拿出1.25元,甲应收回()元。
10、在200位学生中,至少有()人在同一个月过生日。
11、两个自然数的和与差的积是41,那么这两个自然数的积是()。
12、暑假小明去游园,遇到了甲、乙、丙、丁四位同学,小明和四位同学都握了手,甲和3个人握了手,乙和2个人握了手,丙和1个人握了手,那么丁和()个人握了手。
14、有一个长方形,它的长和宽各增加8厘米,这个长方形的面积就增加了208平方厘米,原来长方形的周长是()厘米。
15、甲乙二人环绕周长是400米的跑道跑步,如果两人从同一地点出发背向而行,那么经过2分钟两人相遇;如果两人从同一地点出发同向而行,那么经过20分钟两人相遇,已知甲的速度比乙的速度快,甲每分钟跑()米。
广东五年级育苗杯试卷【含答案】

广东五年级育苗杯试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 下列哪种植物适合在广东地区进行春季育苗?A. 水稻B. 玉米C. 棉花D. 花生2. 育苗时,以下哪种土壤条件最为适宜?A. 酸性土壤B. 碱性土壤C. 中性土壤D. 沙质土壤3. 广东五年级育苗杯主要培养的是哪种能力?A. 观察能力B. 动手能力C. 思维能力D. 创新能力4. 在育苗过程中,以下哪种做法是错误的?A. 经常浇水B. 施肥过多C. 保持土壤湿润D. 定期除草5. 广东五年级育苗杯的目的是什么?A. 培养学生的兴趣爱好B. 提高学生的专业技能C. 增强学生的团队协作能力D. 提升学生的综合素质二、判断题(每题1分,共5分)1. 广东地区春季育苗的最佳时间是3月份。
()2. 育苗过程中,土壤的排水性非常重要。
()3. 广东五年级育苗杯只针对五年级学生开放。
()4. 在育苗过程中,可以使用任何类型的肥料。
()5. 广东五年级育苗杯是一个省级比赛。
()三、填空题(每题1分,共5分)1. 广东地区春季育苗的最佳时间是______月份。
2. 育苗过程中,土壤的排水性非常重要,因为排水性好的土壤可以避免______。
3. 广东五年级育苗杯主要培养的是学生的______能力。
4. 在育苗过程中,施肥过多会导致______。
5. 广东五年级育苗杯是一个______比赛。
四、简答题(每题2分,共10分)1. 请简述广东地区春季育苗的最佳时间及原因。
2. 请简述育苗过程中土壤排水性的重要性。
3. 请简述广东五年级育苗杯的主要目的。
4. 请简述在育苗过程中施肥过多的危害。
5. 请简述广东五年级育苗杯的参赛对象。
五、应用题(每题2分,共10分)1. 假设你是一名五年级学生,请制定一份适合广东地区春季育苗的计划。
2. 请列举三种适合广东地区春季育苗的植物,并说明原因。
3. 请列举三种育苗过程中需要注意的事项。
4. 请说明广东五年级育苗杯的比赛形式。
育苗杯综合训练题答案

育苗杯综合训练题 (02)(满分120卷面) 姓名 分数填空题:(每题8分)1、 某铁路局从A站到F站共有6个火车站(包括A 站和F 站)铁路局要为在A 站到F 站之间运行的火车准备_30_种不同的车票,其中票价不相同的火车票有___15__种。
2、 在一根长 80厘米的木棍上,自左至右每隔5厘米染上一个红点,同时自右至左每隔4厘米染上一个红点,然后沿红点处将木棍逐段锯开,那么,长度是1厘米的短木棍有8 根3、计算(44332-443.32)÷(88664-886.64)= 0.54、 甲、乙两个养鸡专业户,一共养鸡3000只。
乙养鸡专业户卖掉800只鸡后,甲养鸡专业户养鸡的只数正好是乙养鸡专业户剩下的3倍。
甲、乙两个养鸡专业户原来各养鸡1650 只和 1350 只。
5、小军期终考试,语文、外语、自然三门的平均成绩是78分,数学成绩公布以后,四门的平均成绩提高了5分。
小军数学考了 98 分。
6、如图,长方形的长是8,宽是6,A 和B 是宽的中点,则长方形内阴影部分的面积为 12 。
7、如右图,正方形ABCD 的边长是8厘米,三角形ADF 的面积比三角形CEF 的面积小6平方厘米。
则CE 的长为 9.5厘米 。
FE DC B A8、.A、B两地相距20千米,甲、乙两人同时从A地出发去B地。
甲骑车每小时行10千米,乙步行每小时行5千米。
甲在途中停了一段时间修车。
乙到达B地时,甲比乙落后2千米。
甲修车用了 2.2小时时间。
9、一个人站在铁道旁,听见远处传来的火车汽笛声后,再过57秒火车经过他前面。
已知火车拉笛时离他1360米(轨道是直的),声音每秒可传340米远。
则火车的速度是22千米/时。
(得数保留整数。
)10、上右图是五圆连环图,相互交割成九个部分。
将1—9这九个自然数分别填入九个部分内,使每个圆圈里数的和都相等。
11、.右图是一个棱长3厘米的正方体木块,一只蚂蚁从A点沿表面爬向B点。
育苗杯训练
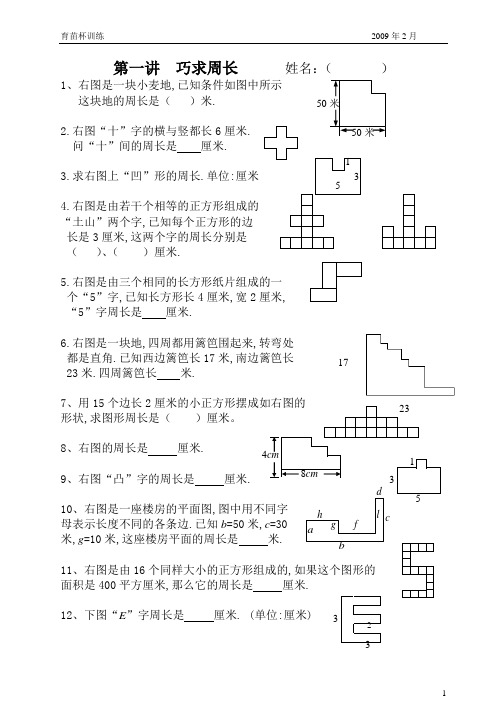
第一讲 巧求周长 姓名:( )1、右图是一块小麦地,这块地的周长是( )米.2.右图“十”字的横与竖都长6厘米. 问“十”间的周长是 厘米.3.求右图上“凹”形的周长.单位:厘米4.右图是由若干个相等的正方形组成的“土山”两个字,已知每个正方形的边长是3厘米,这两个字的周长分别是( )、( )厘米.5.右图是由三个相同的长方形纸片组成的一个“5”字,已知长方形长4厘米,宽2厘米,“5”字周长是 厘米.6.右图是一块地,四周都用篱笆围起来,转弯处都是直角.已知西边篱笆长17米,南边篱笆长 23米.四周篱笆长 米.7、用15个边长2形状,求图形周长是( )厘米。
8、右图的周长是 厘米. 9、右图“凸”字的周长是 厘米. 10、右图是一座楼房的平面图,图中用不同字 母表示长度不同的各条边.已知b =50米,c =30 米,g =10米,这座楼房平面的周长是 米.11、右图是由16个同样大小的正方形组成的,如果这个图形的面积是400平方厘米,那么它的周长是 厘米.12、下图“E ”字周长是 厘米. (单位:厘米)17 430 13、下图由5个边长8厘米的小正方形拼成的“T”字形,它的周长是厘米.14、把一块长20厘米,宽12厘米的长方形纸按右下图所示方法一层、二层、三层的摆下去,共要摆十层,摆好后图形周长是厘米.15、下图是一个零件的平面图,图中每一条最短线段均长5厘米.零件长35厘米,高30厘米,这个零件周长是()厘米?16、一个正方形被分成了5个相等的长方形.每个长方形的周长都是40厘米,求正方形的周长是()厘米?如图所示.17、如图正方形ABCD的边长为4cm,每边被四等分.求图中所有正方形周长的和是()厘米。
18、把边长分别是5厘米、4厘米、3厘米和2厘米的4个正方形按从大到小的顺序排成一行(如图),排成的图形周长是()厘米。
19、将一张边长为12厘米的正方形纸对折,再将对折后的纸沿它的竖直中线(右图虚纸)剪开,得到三个矩形纸片,其中两个较小的矩形的周长之和是()厘米。
五年级育苗杯模拟试题2及答案

五年级育苗杯模拟试题2及答案模拟试题21、19.38×39+193.8×1.7+1.938×440=19.38×(39+17+44)=19.38×100=193.82、123×456?789?456×789?123=123×〖(456?456)×(789?789)〗?123=123×(1×1)?123=123×1?123=123?123=13、1.6时= (96 )分钟1时=60分钟0.6×60=36分钟 36+60=96分钟4、如果3X-1.5X=2.7,那么X= 0.182.7=1.5X 2.7?1.5=0.185、找规律填数:(1)1,3,5,7,( 9 ),11,13……(2)2,3,5,8,( 12),17,23……6、2000年1月1日是星期六,同年6月1日是星期 5 闰年31+29+31+30+31+1=153天153?7=21 (6)7、有一种数学运算符号?,使下列等式成立:2?4=8, 5?3=13, 9?7=25,那么6?4= 规律:(8-4)?2=2 (13-3)?2=5 (25-7)?2=9 那么:12?2=6 12+4=16 所以6?4=168、有50个数的平均数是38,若去掉其中两个数,这两个数之和为124,余下的数的平均数是(37) 50×38=1900 (1900-124)?(50-2)=379、有40块糖,把它分成4份,且后一份比前一份依次多2块,那么最少一份有( 7)块。
7 9 11 1310、在12人中,爱唱歌的有8人,爱打乒乓球的有6人,既爱唱歌又爱打乒乓球的有3人,那么不爱唱歌且不爱打乒乓球的有 1 。
12-(8+6-3)=111、把一根粗细均匀的木料,锯成9小段,要3小时20分;如果锯成都是0.7米长的小段,共用去1小时40分,这根木料长( 4 )米。
育苗指引-整数和有余数的除法

育苗杯辅导资料(整数和有余数的除法)整数除法有两种情况:1.甲数除以乙数,商是整数,没有余数,叫做甲数能被乙数整除;2.甲数除以乙数得到整数的商后,还余下一个比乙数小的整数,叫做有余数的除法。
整除也可以看做是余数为0的有余数的除法。
围绕整除和有余数的除法,可以提出和解答许多有趣的问题。
例1 在四位数中,能同时被3、5、7整除的数一共有多少个?解:能同时被3、5、7整除的最小的数是3、5、7的最小公倍数104,1000除105=9……55,10000除105=95……25,那么105的10~95倍的数都是四位数中能同时被3、5、7整除的数,共有95-10+1=86(个)。
例2 一个四位数是它去掉首位数字得到的三位数的9倍,有哪几个这样的四位数?解:四位数的首位数字的值是这个数字的1000倍,例如首位数字是5,它就表示5000,四位数是去掉首位数字得到的三位数的9倍,就是把所得到的三位数作为1份,原来的四位数是这样的9倍,那么首位数字表示的这个整千数是这样的8份,整千数都能被8整除,当整千数除以8所得的商是三位数时,这个整千数与它除以8所得的商的和是符合提意的一个四位数。
1000除8=125,1125符合题意;2000除8=250,2250符合题意;3000除8=375,3375符合题意;4000除8=500,4500符合题意;5000除8=625,5625符合题意;6000除8=750,6750符合题意;7000除8=875,7875符合题意。
共有7个这样的四位数。
答:这样的四位数有1125,2250,3375,4500,5625,6750,7875共7个。
例3 一个自然数恰好有8个因数,把这8个因数按从小到大的顺序排列,第1个因数与第2个因数的和是4,第4个因数与第5个因数的和是28,这个自然数是几?解:自然数最小的因数是1,所求的自然数的第2个以因数是4-1=3,这个自然数没有因数2,它的第4个因数和第5个因数也不会是偶数。
育苗杯决赛模拟试题(十二)

育苗杯121、 8.8+8.98+8.998+8.9998+ ……… +8.9999999998的整数部分是________2、某数减去6后乘以10,加上10,除以12,结果为10,这个数是________3、两数相除,商3余10,被除数、除数、商及余数的和是143,被除数是____,除数是____4、小明和小红拿出同样多的钱合买作业本,结果小明拿了8本,小红拿了12本,这样,小红就给小明1.1元。
每本作业本的单价是_______元。
5、如图,在等腰直角三角形ABC中,已知AB的长是7厘米,那么这个直角三角形的面积为_______平方厘米。
6、、小张每工作7天后休息一天,小王每工作5天后休息一天。
如果小张今天休息,小王明天休息,那么他们有可能在同一天休息吗?答:7、从1到100的自然数中,完全吧含数字“9”的数有______。
8、ABCD四个排球队进行循环赛,到现在为止,A队赛了3场,B队赛了2场,D队赛了1场,C队赛了_______场。
9、有一个长方体把它的长和宽都增加5厘米,则它的面积比原来面积增加125平方厘米,这个长方形原来的周长是_______厘米.10、有36个桃,大猴和小猴两人争着去拿,大猴先拿了桃子若干个,小猴看到大猴拿了太多,就抢了10个,大猴不肯,又从小猴那里抢走6个,这时大猴拿的个数是小猴的2倍,大猴最初拿了_______个。
11、七只鱼缸了所放金鱼的条数分别为9、11、10、12、21、22、40条。
同一缸里的鱼同色,只有一缸是黑色的,其余都是红色和白色,且红色是白色的5倍,黑色金鱼有______ 条。
12、桌上有36粒糖,小明和小刚轮流拿走一些糖,每次拿走1颗或2颗或3颗,小明先拿,那么,为了确保小刚拿到最后一颗糖,小明第一次应该拿走颗糖13、用60个棱长是1的小立方体粘合成一个大长方体后,将大长方体的6个面涂上红色,当大长方体的三条棱分别是时,6个面都没有被涂上红色的小立方体的个数最多。
五年级育苗杯竞赛分类练习题试题集(15类问题)

五年级育苗杯竞赛分类练习题和倍问题1、甲和乙共60,甲是乙的3倍,甲是多少?2、甲乙丙共108,甲是乙的3倍,丙是乙的2倍,甲乙丙各多少?3、甲乙丙共11520,甲是乙的6倍,乙是丙的5倍,甲比丙多多少?4、甲管每小时的排水量是乙管的3倍。
水池里有水16吨,同时打开两管5小时能把水排完,甲管每小时排水多少吨?5、甲和乙共1570,乙比甲的3倍多34.甲是多少?6、长方形周长150cm,长是宽的1.5倍,求它的面积。
7、东西村相距24千米,甲从东到西,乙从西到东,甲的速度是乙的3倍,两人同时相向而行,1.5小时相遇。
甲的速度是多少?8、甲乙丙共864,乙是甲的2倍,丙是乙的3倍,乙是多少?9、甲有510吨米,乙有1170吨,每天从乙调30吨到甲,多少天后甲的大米是乙的6倍?10、甲乙丙共236,如果甲增加10就是乙的2倍,乙减少12就是丙的一半,甲是多少?11、甲乙共30,甲的8倍和乙的3倍共160,甲乙各多少?12、甲乙两站相距299千米,客车从甲开往乙,1.5小时后小轿车从乙开往甲,行的速度是客车的3倍,小轿车行驶2.5小时遇见客车,小轿车的速度是多少?13、甲134个,乙109个,甲给乙多少个,乙的个数是甲的2倍?14、甲89个,乙46个,甲每天给乙23个,乙每天给甲12个,多少天后乙的个数是甲的2倍?15、运来92棵茉莉、玫瑰和桂花,种了一半的茉莉,2棵玫瑰,又运来6棵桂花,这时还未种的棵数同样多,原来运了多少棵茉莉?16、长方形地,甲的周长是90米,乙的长是甲的3倍,乙的宽是甲的4倍,乙的周长是304米。
甲的长、宽各多少?17、甲乙合挖一条长639米的水渠,甲先挖3天,甲乙再合挖13天,乙每天挖的是甲的1.5倍。
甲乙各挖了多少米?1、甲是乙的4倍,甲比乙多138,甲是多少?2、甲是乙的3倍,从甲拿43给乙,两人就相等,甲乙共多少?3、甲是乙的2倍,乙是丙的1.5倍,丙比甲少88,甲乙丙共多少?4、黑棋是白棋的3倍,每次取走相同个数的黑棋和白棋,取了几次,白棋还有8个,黑棋还有94个,原来有多少个黑棋?5、客车和货车同时从同一个车站往同一个方向开出,客车的速度是货车的1.5倍,2.5小时后,货车行在客车后面45千米处,客车的速度多少?6、客车货车同时分别从甲乙两城开出,相向而行,两车在距甲、乙两城路程中点21千米处相遇,已知客车的速度是货车的1.5倍,甲乙两城相距多少千米?7、甲乙钱相同,甲给乙12元,乙的钱就是甲的4倍,甲原有多少钱?8、甲乙钱相同,甲每月加250元,乙每月加120元,18个月后甲的钱是乙的2倍,甲原来有多少钱?9、丙是乙的2倍,乙是甲的1.5倍,丙比甲多64,甲乙丙共多少?10、两根同样长的绳子,甲剪去10米,乙剪去28米,甲剩下的是乙的4倍,甲原来多长?11、甲有168吨水,乙有92吨水,两个池每小时都排出2吨水,多少小时后,甲剩下的是乙的3倍?12、甲减乙得6,乙除甲得6,甲乙各多少?13、甲拿28元给乙,两人钱相等,乙拿28 元给甲,甲的钱是乙的3倍,甲乙原来各多少钱?14、男67人,女31人,男女减少同样多的人,剩下的男是女的4倍,一共减少多少人?15、甲乙钱一样,甲用了28元,乙用了64元,剩下的甲是乙的5倍,甲剩多少?16、甲1110,乙510,两人每天都减少24,多少天后甲剩下的是乙的5倍?17、甲比乙大5,甲的3倍比乙的5倍大9,甲是多少?1、甲是乙的3倍,甲乙各减去80,剩下的甲是乙的5倍,剩下的甲乙各多少?2、甲乙合买一本20元的书,如果由甲付钱,付钱后乙的钱是甲的1.5倍,如果由乙付钱,付钱后甲的钱是乙的2倍,甲乙原来各多少钱?3、甲用了10元,乙的钱就是甲的2倍,乙再用45元,甲的钱就是乙的2倍,甲乙原来各多少钱?4、荔枝树去年未结果的棵树是结果的3倍,今年结果的荔枝树增加15棵,今年不结果的棵数比结果的2倍少21 棵,这个果园有多少棵荔枝树?5、甲是乙的5倍,各加8后,甲是乙的3倍,甲乙各多少?6、甲地6.7公顷,用大拖拉机每小时耕0.8公顷,乙地1.7公顷,用小拖拉机每小时耕0.2公顷,两拖拉机同时耕,几小时后,甲剩下的是乙的3倍?7、甲28,乙6,每小时向甲加1.9,向乙加0.6,多少小时后甲是乙的4倍?8、班里女生离开4人后,男生人数是女生的1.5倍,又有24个男生离开,这时女生人数是男生的2倍,原来班里多少人?9、一本书,看了2天,未看的页数是已看页数的3倍,又看了24页,未看的页数是已看的1.4倍,这书几页?10、甲原有画片张数是乙的2倍,甲给别人20张,乙又买8张,这时乙的张数比甲的2倍少9张,原来甲乙各几张?环形路上的行程问题1、甲乙在环形路练习跑步,甲每分钟210米,乙每分钟180米,两人同时同地出发,背向而跑,4分钟相遇。
育苗杯培训试题一

1.等差数列求和姓名_________例1 等差数列7、10、13、16、……、97、100,这些数的和是多少?例2 有一数列:29、36、43、50……这个数列共有25个数,这个数列所有的数的和是多少?例3 有30个连续自然数从小到大排成一列,前15个数的和是750,后15个数的和是多少?例4 小建家的所在的街的门牌号码是1、2、3……连续的自然数,除小建家的门牌号码外,其余各家的门牌号码相加的和减去小建家的门牌号码,刚好等于160。
小建家的门牌号码是几号?这条街的门牌号码共有多少个?练习一1、计算。
①176+177+178+179+180 ②549+547+545+543+541+539③83+88+93+…+2082、求所有被6除余数是1的三位数的和。
3、下面的算式按一定的规律排列,这些算式中第20个算式的得数是多少?3+8,4+11,5+14,6+17,…4、下表中各数的和是多少?1 2 3 4 5 62 3 4 5 6 73 4 5 6 7 84 5 6 7 8 95、一个电影院有18排座位,第1排的座位有24个,从第2排起,每排座位比前1排多1个,这个电影院共有多少个座位?6、一本书的页码是从1到96,但里面缺了一张(即少了2个页码数),小华算得这本书现有页码数的和是4567。
他们算得对不对?为什么?2.整除和有余数的除法例1 在四位数中,能同时被3、5、7整除的数一共有多少个?例2 一个四位数是它去掉首位数字得到的三位数的9倍,有哪几个这样的四位数?例3 一个自然数恰好有8个因数,把这8个因数按从小到大的顺序排列,第1个因数与第2个因数的和是4,第4个因数与第5个因数的和是28,这个自然数是几?例4 一个三位数既是3个连续自然数的和,又是4个连续自然数的和,也是五个连续自然数的和,这样的三位数最小是几?例5 一个数除107、221和183所得的余数都相同,这个数最大是几?练习二1、从1、3、5、7、9这5个数字中选三个不同的数字组成能同时被5和7整除的三位数,一共能组成多少个这样的三位数?2、从1~9这9个数字中选4个不同的数字组成能同时被7、8、9整除的四位数,一共能组成多少个这样的四位数?3、被6、7、8、9除余数都是4的四位数一共有多少个?4、一个四位数是它去掉首位数字得到的三位数的6倍,这样的四位数有哪几个?5、把一个数的所有因数每两个数相加,得到的所有不同的数中,最小的是4,最大的是420,求这个数。
五年级育苗杯辅导资料(余数规律、植树)

实验学校五年级育苗杯辅导资料(二)
(余数规律、植树)
班级姓名成绩
1、有一列数:4,5,7,4,5,7,4,5,7……,第83个数是(),这83
个数的和是()。
2、有一堆围棋,按照“二白三黑”排列起来,如下图,想一想,第53个是()子,第91个是(
3、老师把1-64号卡片,依次发给小红、小林、小兰和小敏四个人,第47张发
给()。
4、2001年5月1日是星期二,2001年5月31日是星期()。
5、2004年1月5日是星期三,同年3月25日是星期()。
6、一条河堤长540米,从头到尾每隔6米栽一棵树,要栽()棵树。
7、在一段长2000米的马路两旁安装路灯,每40米安一盏,两端都要安,一共
要安()盏。
8、在一段路的一边每隔40米安一盏路灯,两端都有安,一共有101盏,这条路
长()米。
9、一个圆形鱼池的周边长350米,在池边每隔7米种一棵树,一共能种树()棵。
10、一根钢材,如果锯成3段要6分钟,如果锯成12段要()分钟。
11、小敏要到高层建筑的11层,她走到5层用了100秒,照此速度,她还需要
走()秒。
12、在一个正方形操场四周放盆花,四个顶点都有一盆,这样每边都放22盆,
四周一共有()盆花。
13、把2002年这样的年份称为“对称年”(年份的个数与千位数字相同,十位
与百位数字相同),从2000年到2999年间共有()个对称年。
14、长方形
这种长方形铺满。
(1)
15、计算34×3535-35×3434 275×380+38×2750
……。
五年育苗杯辅导资料(历年计算题)

1、45.7-29.25-0.75=()。
2、2.25×2.25×32=()。
3、9+99+999+9999=()。
4、379000÷125÷8=()。
5、1.25×0.25×0.05×64=()6、297×1.7+97×1.7-97×1.7+3×1.7=()7、360×72+36×280=()。
8、0.25×0.125×0.5×64=()。
9、计算1997×370+63×19970=( ).10、计算:1907.3-63.0625+29.6+60.1-36.9375=()11、计算:28.67×67+3.2×286.7+573.4×0.05=()。
12、19.38×39+193.8×1.7+1.938×440=()13、123×456÷789÷456×789÷123=()14、计算:1.999×370-19.99×6+1999×0.69=()。
15、3.45×6.8+65.5×0.68=()16、2.8÷0.8÷0.5=()。
17、9999.6+999.6+99.6+9.6+0.6=()。
18、2222+3333+4444+5555+6666=()19、0.l+0.06+0.006+0.0006+0.00006 ……=()20、599999+59999+5999+599+59=()21、888×333+444×334=()22、5679+9999+8889+4321=( )23、2-0.2-0.02-0.002-……-0.0000000002=( )24、937×125×25×64×5=( )25、0.9+0.99+0.999+0.9999+0.99999=( )26、1.8018018÷3.003003=( )27、282-83.5=()28、2007×2006—2006×2005+2005×2004—2004×2003+2003×2002—2002×2001=()29、796.75—4.72—96.75—5.28=()30、计算5+10+15+24+…+90+95+100 =()31、计算1-0.6-0.06-0.006-0.0006 =()32、3006+300.6+30.06+3.006=()33、1996+1995-1994-1993+1992+1991-1990-1989+……-1结果是()。
人教版五年级育苗杯试题

五年级育苗杯竞赛试题1、5×19.99+16×1.999+0.34×199.9=( )2、7.5×46.7+17.9×2.5=( )3、7个连续自然数的和是105,其中最小的数是( ),最大的4、二月份有5个星期日,这一年的“十一”儿童节是星期( )。
5、甲组学生人数是乙组的3倍,而乙组学生人数比甲组的3倍少40人,求参加义务劳动的学生共有( )人。
6、某8个数的平均数为50,若将其中一个数改为90,则平均数变成60,求被改动的数原来是( )。
7、一个两位数除以一个一位数,商仍是两位数,余数是8。
被除数、除数、商及余数之和是( )。
8、甲乙两数之和加上甲数是220,如果加上乙数是170,甲乙两数之和是( )。
9、25名同学一起去游园,每人只买一瓶饮料。
如果3个空瓶可以换回1瓶饮料,他们最多可以喝到( )瓶饮料。
10、甲、乙、丙三位老师分别上语文、数学、外语课。
⑴甲上课会用汉语。
⑵外语老师是一个学生的哥哥。
⑶丙是“三八红旗手”,比数学老师年轻。
则甲、乙、丙老师分别上______、_______、_______课。
11、两辆汽车分别从A、B两地同时相向而行,甲车从A地出发,乙车从B地出发,相遇后还继续前进,乙车到达A地后立即返回,又在距B地140千米追上甲车,甲车每小时行20千米,乙车每小时行50千米。
问:A、B两地相距( )千米。
12、△、○、□分别代表三个不同的数,并且△ +△+△=○+○○+○+○+○=□+□+□△ +○+○+□=60 那么△+○+□=( )。
13、小朋友分饼干,如果每人分5块,剩余22块,如果每人分7块,还少18块。
中班有( )个小朋友,一共有( )块饼干。
14、某小学有学生402人去春游,排成两种纵队,前后两排之间相距0.5米,队伍每分钟前进56米,路上要通过一座长572米的桥,队伍从第一排上桥到最后一排离开桥共( )分钟。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
育苗杯练习资料(2.整除和有余数的除法)
例1 在四位数中,能同时被3、5、7整除的数一共有多少个?
例2 一个四位数是它去掉首位数字得到的三位数的9倍,有哪几个这样的四位数?
例3 一个自然数恰好有8个因数,把这8个因数按从小到大的顺序排列,第1个因数与第2个因数的和是4,第4个因数与第5个因数的和是28,这个自然数是几?
例4 一个三位数既是3个连续自然数的和,又是4个连续自然数的和,也是五个连续自然数的和,这样的三位数最小是几?
例5 一个数除107、221和183所得的余数都相同,这个数最大是几?
练习二
1、从1、3、5、7、9这5个数字中选三个不同的数字组成能同时被5和7整除的三位数,一共能组成多少个这样的三位数?
2、从1~9这9个数字中选4个不同的数字组成能同时被7、8、9整除的四位数,一共能组成多少个这样的四位数?
3、被6、7、8、9除余数都是4的四位数一共有多少个?
4、一个四位数是它去掉首位数字得到的三位数的6倍,这样的四位数有哪几个?
5、把一个数的所有因数每两个数相加,得到的所有不同的数中,最小的是4,最大的是420,
求这个数。
6、被15除商和余数相同的所有三位数的和是多少?
7、能同时表示成5个连续自然数的和、6个连续自然数的和、7个连续自然数的和的最小的数是多少?所有这样的三位数的和是多少?
8、有三个连续的自然数:最小的一个能被5整除,中间的一个能被7整除,最大的一个能被9整除,求符合条件的最小的一组三位数。
9、一个数除310、400和670的余数都相同,这个数最大是几?
10、一个数被55或56除,余数都是41,这个数被35除,余数是几?。
