玻璃杯问题
逻辑思维训练题

逻辑思维训练题(共75道)2008-07-30 17:03【2】你看这6只做化验用的玻璃杯,前面3只盛满了水,后面3只是空的。
你能只移动1只玻璃杯,就把盛满水的杯子和空杯子间隔起来吗?”爱动脑筋的周雯是学校里有名的“小机灵”,她只想了一会儿就做到了。
请你想想看,“小机灵”是怎样做的?【3】三个小伙子同时爱上了一个姑娘,为了决定他们谁能娶这个姑娘,他们决定用手枪进行一次决斗。
小李的命中率是30%,小黄比他好些,命中率是50%,最出色的枪手是小林,他从不失误,命中率是100%。
由于这个显而易见的事实,为公平起见,他们决定按这样的顺序:小李先开枪,小黄第二,小林最后。
然后这样循环,直到他们只剩下一个人。
那么这三个人中谁活下来的机会最大呢?他们都应该采取什么样的策略?【5】在一张长方形的桌面上放了n个一样大小的圆形硬币。
这些硬币中可能有一些不完全在桌面内,也可能有一些彼此重叠;当再多放一个硬币而它的圆心在桌面内时,新放的硬币便必定与原先某些硬币重叠。
请证明整个桌面可以用4n 个硬币完全覆盖。
【8】猜牌问题S先生、P先生、Q先生他们知道桌子的抽屉里有16张扑克牌:红桃A、Q、4,黑桃J、8、4、2、7、3,草花K、Q、5、4、6,方块A、5。
约翰教授从这16张牌中挑出一张牌来,并把这张牌的点数告诉P先生,把这张牌的花色告诉Q先生。
这时,约翰教授问P先生和Q先生:你们能从已知的点数或花色中推知这张牌是什么牌吗?于是,S先生听到如下的对话:P先生:我不知道这张牌。
Q先生:我知道你不知道这张牌。
P先生:现在我知道这张牌了。
Q先生:我也知道了。
听罢以上的对话,S先生想了一想之后,就正确地推出这张牌是什么牌。
请问:这张牌是什么牌?【9】一个教授逻辑学的教授,有三个学生,而且三个学生均非常聪明!一天教授给他们出了一个题,教授在每个人脑门上贴了一张纸条并告诉他们,每个人的纸条上都写了一个正整数,且某两个数的和等于第三个!(每个人可以看见另两个数,但看不见自己的)教授问第一个学生:你能猜出自己的数吗?回答:不能,问第二个,不能,第三个,不能,再问第一个,不能,第二个,不能,第三个:我猜出来了,是144!教授很满意的笑了。
玻璃器皿使用的注意事项

玻璃器皿使用的注意事项我们生活中常用的玻璃器皿,例如玻璃杯、玻璃碗、玻璃盘等等。
它们看似简单,使用起来也很容易,但是却有很多使用的注意事项,今天我们就来一起了解一下。
一、选择在购买玻璃器皿时,一定要选择质量好的产品。
不合格的玻璃器皿可能存在很多问题,例如玻璃杯底部厚薄不一,可能会导致容易碎裂;玻璃杯的口沿可能存在棱角,使用时可能会刮伤手指等等。
因此,我们在购买时一定要注意是否选择质量好的玻璃器皿。
二、清洁玻璃器皿的清洁是很重要的。
首先,在使用前应该清洗干净,以确保没有灰尘等杂物,避免影响后续的使用。
另外,玻璃器皿的清洁也要注意一些技巧。
例如,使用洗涤剂进行清洗时,要用流动的水冲洗干净,避免残留在器皿中对人体健康产生影响。
此外,应该用柔软的布或海绵进行清洁,避免使用硬度过高的清洁工具导致破损,影响器皿的使用寿命。
三、温度玻璃器皿的使用过程中,应当注意控制温度。
例如,从冰箱里取出冷饮之后,不应该立即倒入热水或热饮中,避免造成玻璃器皿的破裂。
此外,在煮水或者烧开饭菜时,也要遵循一定的步骤和温度,避免器皿破裂影响安全。
四、使用在平日的使用中,我们也要遵守一些规范。
例如,玻璃杯的使用时,应该控制用力,避免碰撞导致破损;玻璃碗的使用时,应该小心清理食物残渣,避免碎片混入食物,引起危险。
另外,在使用时,可以考虑使用隔热垫等器具进行保护,避免器皿与硬物直接接触。
五、储存在器皿的储存中,我们也需要一些小技巧。
例如,玻璃杯的储存应该放在平坦的物品上,避免其倾斜导致破损;玻璃碗的储存可以考虑使用密封盒进行保护,避免灰尘等杂物污染器皿。
此外,我们也应该注意不要超过其容量储存东西,避免压力过大导致器皿破损。
总之,在使用玻璃器皿时,我们需要注意质量、清洁、温度、使用和储存等方面,从而避免出现危险和影响使用寿命。
希望以上的介绍能够对大家在日常生活中有所帮助。
玻璃杯行业存在的问题与建议

玻璃杯行业存在的问题与建议玻璃杯作为日常生活中常见的容器,对于人们的生活有着重要的影响和作用。
然而,近年来,玻璃杯行业也面临着一些问题。
本文将通过对玻璃杯行业的全面评估,深入探讨存在的问题,并提出一些建议,以期能够改进和发展这个行业。
一、玻璃杯行业存在的问题1. 材质选择有限:目前市场上的玻璃杯多数采用传统的硼硅玻璃材质,虽然这种材质具有优秀的耐热性和抗腐蚀性,但在强度和透明度方面仍有待提高。
对于一些特殊需求,如保温、防摔等,市场上的选择相对较少,无法满足消费者的多样化需求。
2. 制造工艺不完善:玻璃杯制造过程中存在一些制造缺陷,如气泡、模具痕迹、不平整等问题。
这些制造缺陷不仅影响了玻璃杯的美观度,也可能影响到杯子的使用寿命和安全性。
3. 鲜有创新设计:市场上的玻璃杯设计多数都比较传统,缺乏新颖、独特的设计理念。
这导致了玻璃杯在形态和功能上的单一化,无法满足消费者对于个性和时尚的需求。
4. 不环保的包装:在销售环节,很多玻璃杯产品采用的包装材料并不环保,如塑料泡沫、胶带等。
这不仅对环境造成了一定的压力,还与玻璃杯作为一种环保产品的理念相违背。
二、玻璃杯行业改进的建议1. 多元化材质选择:玻璃杯行业可以考虑引入更多的材质选择,如钛酸盐玻璃、陶瓷复合材料等。
这些材质具有更好的透明度、强度和保温性能,能够满足消费者的多样化需求。
2. 提升制造工艺:玻璃杯生产企业应加强对制造工艺的研究和改进,优化生产过程,尽量减少制造缺陷的产生。
加强质量控制,确保产品的质量符合标准和要求。
3. 创新设计理念:玻璃杯企业应该加强对设计方向的研究和探索,引入更多新颖、独特的设计理念。
可以与设计师合作,进行合作创作,打造有个性、有创意的玻璃杯产品。
4. 环保包装材料:玻璃杯企业应该选择环保的包装材料,减少一次性包装的使用。
可以考虑使用纸盒、纸袋等可回收和可降解的材料,以减少对环境的影响。
对于玻璃杯行业的改进和发展,仅仅依靠企业一方的努力是不够的,政府、消费者等也应该积极参与其中。
小学数学数学故事玻璃杯问题

玻璃杯问题巴尼在汽水柜台工作,他用10只玻璃杯给两名顾客出了个难题.巴尼:"这一排有10只玻璃杯,左边5只内有汽水,右边5只空着,请你使这排杯子变成满杯与空杯相互交错,条件是只允许移动4只杯子."两位顾客看了看巴尼,又看了看杯子,摇了摇头,不知道怎么办.巴尼:"好吧,我来告诉你们,只要分别把第二只杯子和第七只杯子,第四只杯子和第九只杯子交换一下位置就成了."这时,奎贝尔教授正好来到柜台前,看到了他们的把戏,并且来了点小花招.奎贝尔教授:"何需移动四只杯子,我只要移动两只就行了,你行不行?"巴尼纳闷地瞧着奎贝尔教授,不明就里.奎贝尔教授:"很简单,只要拿起第二只杯子,把里面的汽水倒进第七只杯子,再拿起第四只杯子,把里面的汽水倒入第九只杯子就行了."1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10■■■■■□□□□□--->■□■□■□■□■□虽然奎贝尔教授抓住话语间的模棱两可之处解决了这个问题,但这个问题并不像乍看上去那么简单.例如,还是这么个问题,但改成100只满杯挨着100只空杯排成一排,请考虑一下,若要使其变成满杯和空杯交错排列,需将多少对杯子互换位置?显然,一般地,如果有2n只杯子,n只满杯,n只空杯,需要将[n/2]对杯子互换位置,方法是2k号杯子与2k+n号杯子互换位置即可(k=1,2,3,...)若n=100,则需互换50次.有一个与上面分析的问题类似但困难的多的古典难题.咱们这回用两种不同颜色的杯子作为道具,但是移动方法却大相径庭:每次只能一块儿移动一对相邻的杯子,使结果成交错排列,以n=3为例,解题过程如下图所示:1 2 3 4 5 6■■■□□□■□□□■■■□□■□■□■□■□■普遍的解是什么呢?当n=1时,没有意义,n=2时你会发现,无解,当n>2时,解此问题至少需要移动n次.n=4时,求解很不容易,你不妨试试,煞是有趣,或许你能够把当n>=3时的解题过程公式化.不像上两道题比较容易,这个问题我还没有仔细研究过,先把这道题上载,大家也可以发表意见.根据这一难题还可以产生许多奇异的变相问题,用来测验你的智力.这里试着举几例:(1).仍然是同时移动两只相邻的杯子,但是如果颜色不同,则要在移动过程中交换位置,这样一对黑白的杯子就变成一对白黑排列了.解8只杯子需要移动5次.对于10只杯子,5次移动也够了.我还尚不知道他的普遍解,也许你能找出来.(2).某种颜色的杯子少一个,即某种颜色的杯子有n只,另一种杯子有n+1只,其余规则不变,已经证明(不好意思,不是我证的,我还没有仔细研究过),对于任意n只杯子,其解须作n次移动,而且这是最少的移动次数.(3).使用三种不同颜色的杯子.按照通常的方法移动一对相邻的杯子,使得所有这三种颜色交相辉映.当n=3(共有9个杯子),其解需要作5次移动.在这些变相问题中,假设在最终形成的排列中,不允许留有任何空距.如果允许留有空距,则问题的解法就令人惊奇地变为移动4次了.看来,尚有许多其他的变化形式,例如,假设一次可以同时移动3只或更多的杯子,在上述各变相问题中改用这种移动方式,结果会如何呢?假如是第一次移动1只杯子,第二次移动2只杯子,第三次移动3只杯子,依次下去,那又会怎样?给定某种颜色的杯子n个,另一种颜色的杯子也为n个,这个问题的解是否总是作n次移动?这种种问题都有待于人们去解决,我还没有时间来考虑这些问题,这是非常有趣非常值得人们思考的趣题.。
用水晶玻璃杯喝水易铅中毒!

用水晶玻璃杯喝水易铅中毒!
铅中毒患者——大多用了水晶玻璃杯
用水晶餐具装盛食物、饮品,看上去华美绚丽,令人爱不释手。
但很多人想像不到,若用含铅的人造水晶制成的杯子盛放蜂蜜等酸性饮料,会造成铅污染,严重危害健康。
因此,有人说———
铅中毒患者——大多用了水晶玻璃杯
据四川大学华西第四医院中毒科主任朱启上教授介绍,该院中毒科收治的铅中毒患者中,许多都是使用水晶玻璃容器饮用了酸性饮料。
”
水晶制品——颇具威胁的铅污染源
有关专家说,水晶制品是一种颇具威胁的铅污染源。
其中的氧化铅含量往往高达20%-30%,用它来盛水,一般还不至于引起铅中毒,但若用来盛酒或酸性饮料,水晶制品中的铅就会被析出并溶于酒或酸性饮料之中。
实验表明,盛酒的时间越长,酒中的含铅量就越高。
另有国外的实验证明:把1升白兰地酒置于水晶器皿中,5年后,酒中的含铅量可高达2万微克/升,远远超过环保部门关于饮品中含铅量要低于50微克/升的规定。
铅中毒——对儿童的危害更大
世界卫生组织规定,如果一个人的血铅水平大于100微克/升就属于铅中毒。
血液中的铅蓄积到一定程度后,会使人记忆力、智力下降,出现精神障碍、噩梦、失眠等问题。
铅中毒对儿童的危害更大,容易引起儿童智力发育障碍。
因此,要尽量避免用水晶制品长期储存酒类、果汁或酸性饮料,以免铅蓄积引起。
假设法解应用题(含问题详解)

1、小红有1角、5角的硬币共35枚,一共是9元5角,问两种硬币各多少枚?2、某玻璃杯厂要为商店运送1000个玻璃杯,双方商定每个运费为1元,如果打碎一个,这一个不但不给运费,而且要赔偿4元。
结果运到目的地结算时,玻璃杯厂共得运费895元,求打碎了几个玻璃杯?3、小X、小李两进展射击比赛,约定每中一发记20分,脱靶一发如此扣12分,两人各打了10发,共得208分,其中小X比小李多得64分,问小X、小李两人各中几发?4、一个化肥厂原计划14天完成一项任务,由于每天多生产15吨,结果9天就完成任务。
原计划每天生产化肥多少吨?5、买来2角邮票和5角邮票共100X,总值41元。
求2角邮票、5角邮票各多少X?6、甲、乙两车间共加工同样零件393个,包装时,把甲车间加工的16个零件并入乙车间的零件中,这时甲车间加工的零件仍比乙车间多5个,问两个车间各加工零件多少个?7、某校举行的数学竞赛共15道题,规定每做对一题得10分,每做错一题倒扣4分,小明在这次竞赛中共得66分,问他错、对了几道题?8、甲、乙、丙、丁四人上山摘桃子,他们共摘了80个桃子,甲比乙少摘8个,丙比甲少摘14个,丁和丙摘的一样多,问他们每人摘了多少个桃子?9、某厂工人,白班补助4元,夜班另加6元,某工人工作24天,共得补助费144元,问他上了几天夜班?【试题答案】1、分析与解:9元5角=95角假设这35枚都是1角的,那么总钱数就应该是()135⨯=35角,比实际95角少了()9535-=60角,这是因为把其中5角的硬币都当成1角了,有一枚5角硬币,少算了()51-=4角,少算的60角中有几个这样的4角,就有几个5角硬币。
953560-=〔角〕 605115÷-=()〔枚〕 351520-=〔枚〕 答:5角硬币有15枚,1角硬币有20枚。
如果假设都是5角硬币,该怎样解呢?同学们试一试。
2、分析与解:假设1000个玻璃杯全部运到并完好无损,应得运费:110001000⨯=〔元〕实际上少得运费:1000895105-=〔元〕这说明在运输过程中打碎了玻璃杯,每打碎1个,不但不给1元的运费,还要赔偿4元,即打碎一个玻璃杯要从总钱数1000元中扣除()14+=5元,一共扣除105元,所以打碎的玻璃杯数为:105521÷=〔个〕综合算式:()()110008954121⨯-÷+=〔个〕 答:打碎了21个玻璃杯。
玻璃杯行业存在的问题与建议

玻璃杯行业存在的问题与建议【原创实用版】目录一、玻璃杯行业存在的问题1.产能过剩2.技术水平较低3.环保问题4.产品同质化严重5.行业标准不完善二、针对玻璃杯行业问题的建议1.提高行业技术水平2.绿色生产和环保3.打造差异化产品4.完善行业标准和监管正文玻璃杯是我们日常生活中常用的一种器皿,然而这个行业在发展的过程中也出现了一些问题,影响了行业的健康发展。
本文将对这些问题进行分析,并提出相应的解决建议。
一、玻璃杯行业存在的问题1.产能过剩:随着玻璃杯生产技术的不断提高,我国玻璃杯行业的产能大幅度提升,但是市场需求并没有同步增长,导致产能过剩,严重影响了行业的健康发展。
2.技术水平较低:虽然我国玻璃杯行业的产能较大,但是技术水平相对较低,很多企业还在使用传统的生产工艺,这使得产品的质量和性能无法得到有效提升。
3.环保问题:玻璃杯生产过程中会产生大量的废水和废气,如果处理不当,会对环境造成严重污染。
然而,目前很多玻璃杯生产企业并没有足够的环保设施和技术,这使得环保问题成为了行业发展的一个瓶颈。
4.产品同质化严重:在玻璃杯市场上,大量产品缺乏差异化,同质化竞争严重,这使得企业之间的价格战成为了一种常态,严重影响了行业的利润水平。
5.行业标准不完善:虽然我国已经制定了一系列的玻璃杯行业标准,但是在实际执行过程中,很多企业并不能严格按照标准进行生产,这使得产品的质量和安全性无法得到有效保障。
二、针对玻璃杯行业问题的建议1.提高行业技术水平:政府和企业应该加大对玻璃杯生产技术的研发投入,引进和培养高端技术人才,提高行业的技术水平,提升产品的质量和性能。
2.绿色生产和环保:企业应该加大对环保设施和技术的投入,实现生产过程的绿色化和环保化,减少对环境的污染。
3.打造差异化产品:企业应该注重产品的设计和创新,打造具有差异化的产品,满足消费者的个性化需求,避免同质化竞争。
4.完善行业标准和监管:政府应该加大对玻璃杯行业标准的完善和执行力度,加强对企业的监管,确保产品的质量和安全性。
玻璃杯行业存在的问题与建议

玻璃杯行业存在的问题与建议
玻璃杯行业存在的问题主要包括:
1. 资源消耗过大:玻璃杯的生产过程需要大量能源和原材料,对环境造成一定负担。
2. 生产污染:玻璃杯生产过程中产生的废水、废气和废渣对环境造成污染。
3. 使用不便:玻璃杯相对较重,使用时不方便携带,容易破损。
4. 回收利用率低:一些地区对废玻璃杯的回收利用率较低,导致大量废弃玻璃杯进入垃圾填埋场或焚烧,浪费资源和增加环境负担。
建议改进的方向包括:
1. 节约资源:研发新型的玻璃材料,减少生产过程中的能源和原材料消耗,提高资源利用效率。
2. 提高生产技术和环保标准:加强玻璃杯企业的环保管理,推动生产过程的清洁化、节能化和减排措施,减少对环境的污染。
3. 促进回收利用:加大玻璃杯回收的力度,提高回收利用率,推动玻璃杯的再生利用,减少废弃玻璃杯对环境的影响。
4. 创新设计和材料:通过创新设计和材料选择,开发出更轻便、
耐用的玻璃杯,提高使用便利性和耐久性,延长玻璃杯的使用寿命。
5. 宣传教育:加强对消费者的宣传教育,提高他们对环保玻璃杯的认知度和使用意识,鼓励消费者减少对一次性饮品容器的使用。
为什么玻璃杯子会碎

为什么玻璃杯子会碎玻璃杯子是我们生活中常见的日常用品,然而在使用过程中却常常会遇到碎裂的情况。
那么为什么玻璃杯子会碎呢?常见的碎裂原因1.温度差异:温度差异是造成玻璃杯子碎裂的常见原因。
当玻璃杯受到热胀冷缩的影响时,若温度变化过大,容易导致玻璃杯发生变形、张力不均等问题,使得其无法承受外界的力,从而裂开或破碎。
2.强烈的机械撞击:当玻璃杯受到强烈的机械碰撞时,也容易导致其碎裂。
这是因为玻璃是一种脆性材料,一旦受到外力作用,就会出现裂缝或破损,最终导致玻璃杯的破碎。
3.玻璃材料品质问题:玻璃作为一种材料,其内部往往存在着微小的缺陷或结构不一致的问题。
当存在缺陷的玻璃杯受到温度变化或机械撞击等因素影响时,容易因缺陷处的张力过大而裂开或破碎。
科学原理解析玻璃杯子产生碎裂的原因涉及到材料学、物理学等学科的知识,其中最基本的原理是玻璃杯子的韧性和强度问题。
韧性是指材料在受到外力作用时所具有的抵抗断裂的特性,是材料的重要弹塑性能指标之一,而强度则是材料抵抗集中载荷的能力大小,是材料抵御变形和破坏的重要机械性能指标之一。
玻璃是一种非晶态固体,其本身不具备韧性,也就是说,玻璃杯子受到外力作用时很难发生塑性变形,更容易产生断裂。
同时,玻璃杯子的强度也比较低,其会议由于材料内部的结构不均匀导致内部产生局部的应力集中。
当这些局部应力受到外部因素的作用,比如温度变化、机械碰撞等,就会发生破裂或断裂现象。
因此,玻璃杯子的韧性和强度是碎裂问题的主要原因之一。
对策和注意事项既然知道了玻璃杯子会碎裂的原因,我们也可以采取一些措施来避免这种情况的发生。
以下是一些注意事项和对策。
1.谨慎使用:在日常使用中,要避免将玻璃杯子受到强烈的机械碰撞或其他外力的作用。
2.注意温度差异:要注意避免太大的温度差异,特别是在温度对玻璃杯子形状的影响较大的情况下。
3.选购正规的产品:购买玻璃杯子时一定要选择正规品牌的产品,在保证质量的同时,也可以提高玻璃杯子的韧性和强度。
钠钙玻璃杯能倒100℃开水吗

钠钙玻璃杯能倒100℃开水吗钠钙玻璃杯能倒100℃开水吗?这是一个问题,许多人想要知道答案。
在下面的文章中,我们将讨论这个问题,帮助你更好地理解问题所涉及的细节。
1. 什么是钠钙玻璃杯?钠钙玻璃杯是一种耐热性能优越的玻璃制品,它由钠钙玻璃(NaC)制成。
它有很强的表面硬度,耐热性比普通玻璃高出3-4倍,可耐受温度达到400℃以上。
此外,钠钙玻璃杯还具有电绝缘性、耐腐蚀性和低指数差等优点。
2. 钠钙玻璃杯能倒100℃开水吗?答案是肯定的,钠钙玻璃杯可以倒100℃开水。
具体来说,由于钠钙玻璃杯的耐热性高达400℃以上,即使是高温的开水也不会造成玻璃杯损坏,或者对人体造成伤害。
3. 钠钙玻璃杯比普通玻璃杯有什么优势?钠钙玻璃杯拥有优异的使用寿命,使用寿命是普通玻璃的5倍以上,它可以耐受极端的环境,例如普通玻璃杯不能耐受的温度,它可以承受高于10000℃的高温,不会变形或裂缝、破碎,很适合用来做高温容器、耐热仪器仪表,甚至可以用来做装饰品或灯具。
4. 钠钙玻璃杯使用时有哪些安全措施?a.使用前最好检查玻璃杯,检查是否存在裂缝、破损等故障;b.注意远离高温,如用于加热容器上的浓酒,最好使用金属勺子等避免热量的直接传递;c.不要随意加热钠钙玻璃杯,即使是100℃开水,也要注意杯壁温度不能过高,为了安全,最好用一把厨房勺子慢慢倒入;d.不要与易燃物一起使用,也不要在光照下使用。
综上所述,钠钙玻璃杯可以安全地倒入100℃的开水,但要特别注意上述使用安全措施,以便保护玻璃杯的性能,使其可以得到有效的利用。
总之,使用钠钙玻璃杯是一个很好的选择,只要按照正确的使用方式,它一定能够持久、安全的为您服务。
两个玻璃杯里声音不同的原理

两个玻璃杯里声音不同的原理
首先,玻璃杯的形状和材质会影响声音的产生和传播。
每个玻
璃杯都有其独特的共振频率,这取决于玻璃的厚度、形状和材质。
当你敲击玻璃杯时,它会以特定的频率振动,产生特定的声音。
如
果两个玻璃杯的形状、大小或材质不同,它们的共振频率就会不同,因此产生的声音也会不同。
其次,玻璃杯内的空气也会影响声音的产生。
当你敲击玻璃杯时,玻璃杯内的空气会被震动,产生声音。
两个玻璃杯内的空气压力、湿度等因素可能会不同,这也会导致它们产生不同的声音。
此外,玻璃杯的摩擦力和表面特性也会对声音产生影响。
玻璃
杯表面的光滑程度和材质会影响敲击时的摩擦力,从而影响声音的
音色和音质。
总的来说,两个玻璃杯里声音不同的原理涉及到玻璃杯的共振
频率、空气的特性以及玻璃杯表面的摩擦力等多个因素。
这些因素
共同作用导致了两个玻璃杯产生不同的声音。
希望这些解释能够帮
助你更好地理解这个问题。
双层水晶玻璃杯 玻璃杯子使用时注意哪些问题

双层水晶玻璃杯玻璃杯子使用时注意哪些问题
文/诗如意双层水晶玻璃杯定制
双层水晶玻璃杯双层玻璃杯玻璃杯因为它无铅无毒,安全健康地特性,越来越多的收到人们的喜爱,那么,使用双层水晶玻璃杯,双层玻璃杯玻璃杯时该注意什么问题呢?诗如意双层水晶玻璃杯定制小编就和亲们唠唠吧!
1:使用玻璃杯前请用柔软的布用盐水或牙膏类仔细擦拭如果不方便,用清水亦可。
2:为了避免把杯体弄上那个划痕,请勿用清洁球之类的清洁工具洗刷。
3:请勿将玻璃杯带盖子在如微波炉,等高温工具上加温消毒,那样容易让杯盖变形。
4:在泡茶时,不要把水倒的太满,容易溢出茶水。
5:泡茶水时最好用80度至90度的热水,15分钟左右开始饮用,那样泡出的茶水更入味,茶叶更舒张。
6:以前用过的玻璃杯,日久不用的玻璃杯可用热水烫几遍消毒,然后用牙膏擦拭便可洁净如新,放入茶叶可去异味。
7:拧杯盖时要顺时针拧开,防止使用不当烫伤自己。
8:儿童在成人监护下使用,以免摔坏扎伤或热水烫伤。
物理杯型问题
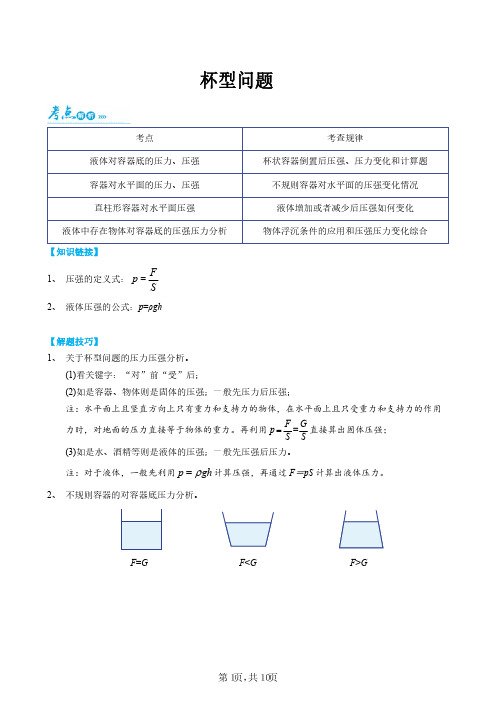
杯型问题考点考查规律液体对容器底的压力、压强 杯状容器倒置后压强、压力变化和计算题 容器对水平面的压力、压强 不规则容器对水平面的压强变化情况 直柱形容器对水平面压强液体增加或者减少后压强如何变化 液体中存在物体对容器底的压强压力分析 物体浮沉条件的应用和压强压力变化综合【知识链接】1、 压强的定义式:F p S=2、 液体压强的公式:p =ρgh【解题技巧】1、 关于杯型问题的压力压强分析。
(1)看关键字:“对”前“受”后;(2)如是容器、物体则是固体的压强;一般先压力后压强;注:水平面上且竖直方向上只有重力和支持力的物体,在水平面上且只受重力和支持力的作用力时,对地面的压力直接等于物体的重力。
再利用=F GpS S=直接算出固体压强; (3)如是水、酒精等则是液体的压强;一般先压强后压力。
注:对于液体,一般先利用p gh ρ=计算压强,再通过F=pS 计算出液体压力。
2、 不规则容器的对容器底压力分析。
F =GF <GF >G【例1】如图所示,盛有一定质量水的封闭容器放在水平面上,液体对容器底部的压力和压强分别为F1和p1,如果将容器倒过来放在水平面上,液体对容器底部的压力和压强分别为F2和p2,比较F1,F2和p1,p2,下列说法中正确的是()A.F1>F2,p1<p2B.F1<F2,p1>p2C.F1>F2,p1>p2D.F1<F2,p1<p2【例2】如图所示,密封的“凸”字形容器中装满水,放在水平桌面中央,若把它倒置,则水对容器底部的压强p1和容器对桌面的压强p2的变化情况是()A.p1增大,p2增大B.p1增大,p2不变C.p1不变,p2不变D.p1不变,p2增大【例3】如图所示,水平桌面上放有底面积和质量都相同的甲、乙两平底容器,分别装有深度相同、质量相等的不同液体.下列说法正确的是()①容器对桌面的压力:F甲>F乙②液体的密度:ρ甲=ρ乙③液体对容器底部的压强:p甲>p乙④容器对桌面的压强:p甲′=p乙′A.只有①和③B.只有①和④C.只有②和③D.只有③和④【例4】水平桌面上两个底面积相同的容器中,分别盛有甲、乙两种液体。
装热水时玻璃杯会爆炸吗

装热水时玻璃杯会爆炸吗
在日常生活中,我们经常会用玻璃杯来装热水,但是近些年一直有新闻报道玻璃杯装热水之后发生了爆炸。
接下来
2、区别玻璃杯是否属于而耐热材质,是非常简单的:耐高温玻璃杯装热水表面是不热的,不耐高温玻璃杯装热水表面是热的。
3、普通玻璃杯
普通材质的玻璃是热的不良导体,当玻璃杯内壁的一部分突然遇热(或遇冷)时,杯子的内层受热明显膨胀但外层受热不够而膨胀得少,由此使得玻璃杯各部分间温差较大,又由于物体的热胀冷缩的原因,由此而使得玻璃的各部分热膨胀不均匀,这种不均匀的差别太大时,则可能使玻璃杯碎裂。
同时,玻璃是刚性很强的物质,传热速度慢,玻璃越厚,由于受温差的影响,温度升得快的时候就越容易炸裂。
也就是说开水与玻璃杯的温差太大致使玻璃杯炸裂。
所以较厚的玻璃杯使用温度一般
“-5至70摄氏度”,或者在倒开水前先加点凉水,再加点热水,等杯子暖了以后把水倒掉,再加开水就没问题了。
4、耐高温玻璃杯高硼硅玻璃最大的特点在于具有非常低的热膨胀系数,约是普通玻璃的三分之一,也就是对温度不敏感,没有一般物体常见的热胀冷缩,因而具有耐高温、高热稳定性。
可以用来装热水。
不过,不要将市面上的钢化玻璃当作不耐高温杯子使用,钢化玻璃杯与普通玻璃杯的使用温度是一样的,一般在70度以下,需要谨慎使用。
而且有专家表示,目前国内市场上尚不存在所谓耐热钢化玻璃产品或者是钢化耐热玻璃产品,在选购时不要被误导。
如果是耐热玻璃杯,杯子上一般都会贴有相应标示,注明使用温度(比如说耐高温150°等等,当然沸水为100°)、使用范围等;在选购时最好能养成看标示的习惯,发现标称耐热玻璃但是价格却很低,要考虑其真实性。
今天。
玻璃杯移动问题的数学模型

玻璃杯移动问题的数学模型方创彬1,郑碧珍2,潘龙飞31 韶关学院2001级电脑系本〔4〕班, 广东 韶关5120052 韶关学院2001级数学与应用数学〔1〕班,广东 韶关5120053 韶关学院2002级信息技术教育〔3〕班,广东 韶关512005[摘要]:本文通过对各种玻璃杯移动问题进行了分析,找出了如何简单的解决这一类的模型.我们对“每次只能一块儿移动一对相邻的杯子”、“杯子的颜色为黑白两种,要是相邻的杯子是这两种颜色,则移动它们时,要交换位置.”、“某种颜色的杯子有n 只,另一种杯子有1+n 只”以及三种颜色的杯子是如何移动的,一一给出解答,得出了对于n 只杯子有n 大于一定数值下的移动次数,并得到定理1、定理2等. 由本文的定理2可以把各类玻璃杯的移动进行解答,轻松的找到移动的方法,解答了多种不同的移动方法的可解性.虽然这一模型所得的不一定是最少的移动次数,但给出了解决这一大类型问题的一般解法.关键词:玻璃杯;移动方法;交错排列;1 问题的提出对于杯子的移动问题,自古以来都有着许许多多的不同移动方法,简单的如将10只玻璃杯,左边5只内有汽水,右边5只空着,你如何以最少的移动次数将这排杯子变成满杯与空杯相互交错.还有困难的多的古典难题:每次只能一块儿移动一对相邻的杯子,使结果成交错排列.它们的普遍解是什么呢?能否将3>=n 时的解题过程公式化.由这一难题还可以产生许多奇异的变相问题,如下面的几个问:(1) 仍然是同时移动两只相邻的杯子,但是如果颜色不同则要在移动过程中交换位置,这样一对黑白的杯子就变成了一对白黑排列,请找出它的普遍解.(2)某种颜色的杯子少一只,即某种颜色的杯子有n 只,又有何不同.(3) 使用三种不同颜色的杯子,按照通常的方法移动一对相邻的杯子,使得所有这三种颜色交相辉映,有何普遍解?2 模型的假设(1) 在移动过程中,不能交换相邻的杯子.(2) 一对杯子一次的移动后,原来的两个位置应该是空的.(3) 一种颜色的杯子数为n 只,另一种颜色的杯子即为1+n 只3 问题的分析题目给出了几种移动方案,我们要对这几种(特别是前面的情况)进行分析,求出它们的相同点,加以归纳.如一般的模型我们有定理1,对“每次只能一块儿移动一对相邻的杯子”我们得到了定理2,即当n 对杯子时〔5≥n 〕,可以在)4(36-+n 次内把这一模型移完等等.这些都是通过我们对多种移动方案所总结出来的,对问题的解答有着一定的作用. 4 模型的建立与求解下面我们来逐步的对问题进行求解,对于简单的“一排有10只玻璃杯,左边5只内有汽水,右边5只空着”问题,我们可以将其扩展为这样的模型:有n 2只杯子,n 只满杯挨着n 只空杯,假设要使其变成满杯和空杯交错排列,需如何移动.对于这个简单的问题我们有:定理1:一般地,如果有n 2只杯子,n 只满杯,n 只空杯,需要:(1) 如果n 为奇数,则将21-n 对杯子互换位置,方法是k 2号杯子与)2(n k +号杯子互换位置即可;(2) 如果n 为偶数,则将2n 对杯子互换位置,方法是k 2号杯子与)12(-+n k 号杯子互换位置即可.就可以将它们变成交错排列,(其中 ,3,2,1=k )证明: 对于n 为奇数.如图可知,当将k 2与)2(n k +号杯子)3,2,1( =k 互换,总共21-n 对,可使结果成交错排列.同样的,对于n 为偶数可知将k 2与)12(-+n k 号杯子),3,2,1( =k 互换,总共2n 对,可使结果成交错排列. 证毕.下面我们来看看对于:“每次只能一块儿移动一对相邻的杯子.”这一问题.以3=n 为例,解题过程如下列图所示:只要移动3次即可完成要求.而对1=n 时,没有意义,2=n 时,无解.当4=n 时,可得到如下移动.由以下分析,为了更容易的求出杯子的移动次数,我们有这样的定理:定理2: 对于n 对两种颜色的杯子,如果从左右各有n 只同样颜色的杯子,移动到交错排列有m 次,则反过来,从交错排列到左右同色的移动也要m 次.n 1-nnnn123456这一定理是很明显的,我们用上一个例子来说明,见下列图即可知是成立的,无需证明.由定理2,以后在求解各类移动问题时,都可以将其步骤相反过来解答.现在我们只要在4=n 的基础上再加上4次移动就可以得到5=n 的移法,即只要将多出的一对杯子先放到一边〔先完成4=n 的移动〕,再将靠近中间的同一种颜色的两只杯子〔不管是哪一种颜色的杯子〕放到同一种颜色的最边上,将多出的一对杯子代换它的位置,就可以得到了5=n 的移法,总的要多加3次移动.所以对5≥n 的模型都可以在1-n 的基础上再移动3次来做到.于是:当n 对杯子时〔5≥n 〕,可以在)4(36-+n 次内把这一模型移完.通过以上问题的分析和定理,我们开始解决提出的几个变相问题:(1) 假设杯子的颜色为黑白两种,要是相邻的杯子是这两种颜色,则移动它们时,要交换位置.当有一对杯子时,无意义;当有两对杯子时,要移动三次当有三对杯子时, 要移动五次,且只需在两对杯子的基础上加上两步.当有四对杯子时,可以移动五次,但如果用两次两对杯子的称动方法,是需要移动六次. 由此我们可以总结出这一类的模型是可以解的,每一个移动方式都可以用42 =n 的移动来完成5≥n 后面的模型.用前面所推导的方法,同样可以解决这一问题.当5≥n 时,也只需在1-n 的基础上再移动3次,就能得到所解决方法.于是:当有n 对杯子时)5(≥n ,可以在)4(35-+n 次内把这一模型移完.(2) “某种颜色的杯子有n 只,另一种杯子有1+n 只”的移动方法.当1=n 时,须移动1次.当2=n 时,须移动3次.我们用1=n 时的结果再进行推导,有这样的移动:当3=n 时,须移动4次.但当我们用到2n的模型来推导时就要移动5次,对于4≥n的移法,可以通过以上的方法从n 的模型推导到1+n的模型,所以这一类移法是可以解的. 推理过程还是以上面两个总结相同.于是:当4≥n时,可以在)3(33-+n次内把它移完. (3)对两种不同颜色的杯子我们已经有了一定的解法,接下来就是关于三种颜色的杯子是如何移动的?1=n时没有意义,2=n时,求不到它的移动方法,现在来看看当3=n时是怎么移动的.同样的运用定理2,有如下的反推过程.我们用用了六次移动来完成这一问题.在这个的基础上来解4的模型,因为这一模型每次都要增加三个杯子,所以如果用〔1〕的方法来推导4≥n 的情况是行不通的,我们要用新的推导才能知道它到底有什么相同点. 让看下面的图形变化:上面的1步是由3n的原图前面加上三个不同的杯子,然后将其移动相对里面的两只杯子向外移,等待3=n的移动完成后再将它移回原位,就有了1这一步,这一过程要用两次移动.从2步是可以进行推导的,如果把杯子扩大到n(n 为偶数),则移动次数为)1222(+++n n ,总的移动可以为n +5(n 为偶数)次.当n 为奇数,有下面这样的移动: 12345678得到的移动次数为178)4)(422(15-=-+++n n (5≥n ,且n 为奇数),这就是说这一类的模型也是可以找到普遍解的.与用两种不同颜色的杯子来移动的模型,此种三色移动问题更有它的实际意义,从三种推到四种不同颜色的杯子,或是更多的颜色来移动,这是达得我们进一步分析了解的.但是随着颜色的增多,相对的模型的求解也会有一定程度的增加.通过我们对多个这类问题的移动和试验,最后都可以得出所要的结果.这种交错排列的要求,只要总结出它的规律,一步步的移动下出是可以实现排列的.5 模型的推广与评价在上述各变相问题中改用一次同时移动3只或更多的杯子,我们同样可以通过以上的移动方法来求得所需的次数,又假设是第一次移动1只杯子,第二次移动2只杯子,第三次移动3只杯子,依次下去,等等;给定某种颜色的杯子n 个,另一种颜色的杯子也为n 个,用上面的移动方法我们也可以求出移动次数.由本文所得出的定理,可以让各类不同移动要求的问题得到较为方便的解答,特别是一些较为难的移动过程.由于存在着各种各样的移动方案,所以不可能一一给以解答,本文所求的几个模型的普遍解并不一定是它的最少移动次数解,只是给出了它有可能的移动次数,把一类一类的模型加以归纳, 得出多种模型的移动公式.这有利于对不同的情况进行统一.6 参考文献:[1] 叶其孝,大学生数学建模竞赛辅导教材,湖南教育出版社,2001[2] 谭永基,数学模型,复旦大学出版社,1997[3] 王朝阳,离散数学,中国矿业大学出版社,2001[4] 贾希辉,概率论与应用统计,科学出版社,2002The Math model of glass move problem1Chuangbin Fang 2Bizhen Zheng 3LongfeiPan ( 1.Department of computer, 2001grade , Class 4, Shaoguan 512005, Guangdong,;2.Department of mathematics, 2001 grade, Class 1, Shaoguan 512005, Guangdong;3.Department of mathematics, 2002 grade, Class 3, Shaoguan 512005, Guangdong; )Abstract: this text construe all sorts of glass move problem, and fine out how solve this sort of model. There are some problem like:“You can move one pair of border upon glasses one time ”and “There are black and white glass, if the border upon glasses’ color is different. They must change for their place when move.”,“If there are n glasses in a sort of glass, other one is n+1 glasses ”. Along with how to move three sort of glasses. we solve they one by one. And educe theorem one and theorem two, etc. From the theorem two, we can solve many glass move model. Maybe it is not all the least move times, but it give us a way of commonly solve for this model.。
钠钙玻璃杯安全吗

钠钙玻璃杯安全吗
钠钙玻璃杯是一种新型的玻璃材料,它具有优良的耐热性和耐冷性,不易破碎,因此受到了广泛的关注。
但是,对于钠钙玻璃杯的安全性问题,人们普遍存在一定的疑虑。
那么,钠钙玻璃杯到底安全吗?接下来,我们将从几个方面来探讨这个问题。
首先,钠钙玻璃杯的原材料是天然矿物质,不含重金属和其他有害物质,因此
在生产过程中不会对环境造成污染。
这一点从根本上保证了钠钙玻璃杯的安全性。
其次,钠钙玻璃杯的耐热性和耐冷性非常好,可以耐受急剧的温度变化,不易破裂。
这就意味着,在日常使用中,即使是倒入沸水或者冰水,也不会对钠钙玻璃杯造成损坏,从而避免了因破裂而导致的安全隐患。
此外,钠钙玻璃杯的化学稳定性也非常高,不易被酸碱物质侵蚀,因此在使用
过程中也不会释放出有害物质。
相比之下,普通玻璃杯在长时间接触酸性或碱性饮料时,会释放出微量的铅和其他重金属,对人体健康造成一定的危害。
而钠钙玻璃杯则避免了这一问题,更加安全可靠。
此外,钠钙玻璃杯的表面光滑平整,不易滋生细菌,易于清洁,因此在日常使
用中也不易滋生细菌,从而保证了饮用水的卫生安全。
这一点对于人们的健康至关重要。
综上所述,钠钙玻璃杯在安全性方面表现出色。
它不含有害物质,耐热耐冷,
化学稳定,易清洁等优点,使得其成为一种安全可靠的饮用容器。
因此,我们可以放心地选择钠钙玻璃杯来使用,享受健康的生活。
玻璃杯售后维修服务

玻璃杯售后维修服务玻璃杯是我们日常生活中常见的物品之一,在使用过程中难免会遇到一些问题,比如破损、磨损等。
为了保障消费者的权益,许多品牌都提供了售后维修服务,以解决消费者在使用过程中遇到的问题。
本文将介绍玻璃杯售后维修服务的相关内容,以帮助消费者更好地了解和利用这一服务。
一、售后维修服务的介绍玻璃杯售后维修服务是指消费者在购买玻璃杯后,出现质量问题或需要维修时,可以联系品牌或相关售后服务中心进行维修。
这项服务通常在购买玻璃杯时就会被明确告知,并附带相关的售后保修政策。
不同品牌的售后维修服务政策可能会有所不同,所以在使用玻璃杯之前,消费者应该了解品牌的售后维修政策。
二、售后维修服务的流程1. 联系售后服务中心当玻璃杯出现问题或需要维修时,消费者可以联系品牌的售后服务中心。
联系方式通常可以在产品包装盒、说明书和品牌官方网站上找到。
消费者可以通过电话、电子邮件或在线客服与售后服务中心进行联系,并详细说明问题或需求。
2. 提供购买凭证和问题描述售后服务中心通常要求消费者提供购买凭证作为维修的凭证,以确认产品的购买信息和保修期限。
此外,消费者还需要详细描述玻璃杯的问题,以便售后服务人员能够更好地了解维修需求。
3. 售后服务评估在收到消费者的咨询后,售后服务中心会对问题进行评估。
根据玻璃杯的问题性质和保修政策,售后服务人员将判断是否提供免费维修或更换服务,或者消费者需要支付一定的费用来进行维修。
4. 维修或更换如果玻璃杯可以维修,售后服务中心将安排专业的技术人员进行维修,并保证维修质量。
如果玻璃杯无法维修或维修费用过高,售后服务中心可能会提供更换的选项,让消费者选择新的玻璃杯。
5. 维修反馈和售后评价维修完成后,售后服务中心通常会向消费者提供维修反馈,告知维修情况和解决方案。
消费者也可以在维修完成后对售后服务进行评价,以帮助品牌改进服务质量。
三、注意事项1. 保持购买凭证为了能够享受玻璃杯的售后维修服务,消费者应妥善保管好购买凭证。
玻璃杯遇到什么气体会起雾

玻璃杯遇到什么气体会起雾
引言:当我们用玻璃杯倒入冰冷的饮料时,不难发现杯子表面
出现了水珠和一层雾气,这是什么原因呢?
正文:玻璃杯内部空气和杯子外部空气产生温度差异,当我们
倒入冰冷的液体时,玻璃杯内部空气变得比外部空气更冷,而玻
璃的导热性非常好,从而导致玻璃表面产生了冷凝现象。
因此,
只要是相对湿度大于杯内空气相对湿度的气体接触到玻璃杯,都
会让玻璃杯起雾。
其中,相对湿度是空气中所含水蒸气的压力与该温度下水饱和
蒸气压力的比值。
当相对湿度大于100%时,就会产生湿气凝结,
形成露水或雾气。
那么,到底哪些气体的相对湿度比较高,容易让玻璃杯起雾呢?以下是几种容易让玻璃杯起雾的气体:
1. 空气中水分含量大的地区,比如本来潮湿的沿海城市,相对
湿度较高,容易让玻璃杯起雾。
2. 含有很少水分的气体,比如纯净的氧气、氮气等,它们的相对湿度很低,容易让玻璃杯起雾。
3. 富氧、富二氧化碳的气体,比如饮料瓶中的二氧化碳气体,这些气体吸附水分的能力较强,相对湿度较高,容易让玻璃杯起雾。
结论:由此可知,只要是相对湿度大于玻璃杯内部空气相对湿度的气体接触到玻璃杯,都会让玻璃杯起雾。
因此,在夏季潮湿的气候中,我们应该定期清洗玻璃杯,并在注水时等水温升高后再加入冰块,避免让玻璃杯起雾影响美观度。
【五年级上册数学】应用题解答问题试题(含答案)
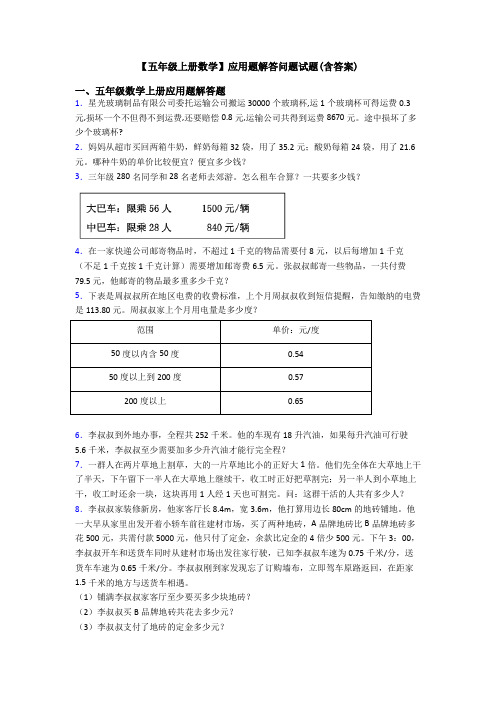
【五年级上册数学】应用题解答问题试题(含答案)一、五年级数学上册应用题解答题1.星光玻璃制品有限公司委托运输公司搬运30000个玻璃杯,运1个玻璃杯可得运费0.3元,损坏一个不但得不到运费,还要赔偿0.8元,运输公司共得到运费8670元。
途中损坏了多少个玻璃杯?2.妈妈从超市买回两箱牛奶,鲜奶每箱32袋,用了35.2元;酸奶每箱24袋,用了21.6元。
哪种牛奶的单价比较便宜?便宜多少钱?3.三年级280名同学和28名老师去郊游。
怎么租车合算?一共要多少钱?4.在一家快递公司邮寄物品时,不超过1千克的物品需要付8元,以后每增加1千克(不足1千克按1千克计算)需要增加邮寄费6.5元。
张叔叔邮寄一些物品,一共付费79.5 元,他邮寄的物品最多重多少千克?5.下表是周叔叔所在地区电费的收费标准,上个月周叔叔收到短信提醒,告知缴纳的电费是113.80元。
周叔叔家上个月用电量是多少度?范围单价:元/度50度以内含50度0.5450度以上到200度0.57200度以上0.656.李叔叔到外地办事,全程共252千米。
他的车现有18升汽油,如果每升汽油可行驶5.6千米,李叔叔至少需要加多少升汽油才能行完全程?7.一群人在两片草地上割草,大的一片草地比小的正好大1倍。
他们先全体在大草地上干了半天,下午留下一半人在大草地上继续干,收工时正好把草割完;另一半人到小草地上干,收工时还余一块,这块再用1人经1天也可割完。
问:这群干活的人共有多少人?8.李叔叔家装修新房,他家客厅长8.4m,宽3.6m,他打算用边长80cm的地砖铺地。
他一大早从家里出发开着小轿车前往建材市场,买了两种地砖,A品牌地砖比B品牌地砖多花500元,共需付款5000元,他只付了定金,余款比定金的4倍少500元。
下午3:00,李叔叔开车和送货车同时从建材市场出发往家行驶,已知李叔叔车速为0.75千米/分,送货车车速为0.65千米/分。
李叔叔刚到家发现忘了订购墙布,立即驾车原路返回,在距家1.5千米的地方与送货车相遇。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
标题:玻璃杯问题
内容:某商店的玻璃杯成箱出售,每箱20只,每箱有0、1、2只残次品的概率分别为0.8、0.1和0.1. 某顾客欲在该店购一箱玻璃杯,售货员随机地取出一箱,而顾客开箱随机抽查4只杯子.若4只杯子中没有残次品,就买下该箱玻璃杯.试求
(1)顾客买下该箱玻璃杯的概率P1;
(2)在顾客买下的一箱玻璃杯中,确实没有残次品的概率P2.
应用背景:
根据概率知识,研究顾客在商店购买成箱玻璃杯时,按一定操作规程,能买下一箱玻璃杯的概率以及若顾客买下了一箱玻璃杯中,则其中确实没有残次品的概率.
涉及知识点:
知识点一:条件概率
知识点二:全概率公式
知识点三:贝叶斯公式
解题方法:
用条件概率的概念及其相关公式,可以计算出题目要求的结果.
解题过程:
第一步:
设A ={顾客买下所察看的一箱玻璃杯},
B j ={箱中恰有j 个残次品}, j =0,1,2.
依题意有
012()0.8, ()0.1, ()0.1P B P B P B ===
441918012442020C C 412(|)1, (|), (|)C 5C 19
P A B P A B P A B =====.
第二步:
(1)由全概率公式
2
10()(|)
412 0.810.10.10.943,519j j P P A P A B ====⨯+⨯+⨯=∑
即顾客买下由售货员随机地取出的一箱玻璃杯的概率为0.943.
第三步:
(2)由贝叶斯公式
0020()(|)0.8(|)0.848()0.943
P B P A B P P B A P A ====, 即在顾客买下的一箱玻璃杯中,确实没有残次品的概率是0.848.
进一步问题:
若每箱玻璃杯有0、1、2只残次品的概率分别为0.6、0.3和0.1. 则上述概率P 1和P 2是多少?。
