海岸线长度问题
基岩海岸线长度的因素

基岩海岸线长度的因素
基岩海岸线的长度受多种因素影响,其中包括以下几个主要因素:
1. 地质构造:基岩海岸线的形成与地质构造有关。
例如,在地壳的板块运动中,如果发生断层活动或抬升作用,会导致海岸线的延伸或缩短。
2. 海洋动力学:海洋动力学是指海洋对海岸线的冲刷和侵蚀作用。
海洋动力学因素包括海浪、潮汐、海流等,它们会冲刷和剥蚀岩石,从而改变海岸线的长度。
3. 沉积作用:河流和河口的沉积作用也会影响基岩海岸线的长度。
河流带来的悬浮物质和沉积物在海岸线附近沉积,形成滩涂和沙洲,从而改变海岸线的形态和长度。
4. 气候变化:气候变化也会对基岩海岸线的长度产生影响。
例如,全球气候变暖导致海平面上升,海岸线后退;另外,气候变化也会引发极端天气事件,如飓风和暴雨,进一步影响海岸线的形成和改变。
5. 人类活动:人类活动也是影响基岩海岸线长度的重要因素。
沿海地区的人类活动,如土地开发、滥挖沙土、建设海堤和码头等,都会改变海岸线的形态和长度。
综上所述,基岩海岸线长度的因素是多样化的,包括地质构造、海洋动力学、沉
积作用、气候变化和人类活动等。
这些因素相互作用并综合影响着海岸线的长度和形态。
我国海岸线(文档3篇)

我国海岸线(文档3篇)以下是网友分享的关于我国海岸线的资料3篇,希望对您有所帮助,就爱阅读感谢您的支持。
第一篇1.我国海岸线长度?沿海开放城市发展现状?我国海岸线长度为1.8万公里,居世界第四位;大陆架面积位居世界第五,200 海里专属经济区面积为世界第十。
初步核算,2004年15个首批沿海开放城市实现地区生产总值达到29244亿元,全国国内生产总值为136515亿元,首批沿海开放城市地区生产总值占全国的1/5多。
比重比上年进一步提升,由20.9%上升到21.4%。
大大高出了人口占全国比重(7.4%)。
2004年,首批沿海开放城市经济呈现出量与质并举,速度与效益共进的良好局面。
继2003年突破3000美元大关后,2004年首批沿海开放城市人均地区生产总值又超过了30000元人民币。
达到30729元(按户籍人口计算,下同),比上年增加4626元。
15个城市人均地区生产总值全部超过1000美元,广州、上海在6000美元以上,威海、宁波、大连均为4000多美元,天津、青岛、福州、烟台超过3000美元,温州、秦皇岛达到2000多美元,南通、北海、连云港、湛江为1000多美元。
最高的广州达到56271元,最低的湛江8506元,相差不小。
2.我国南海、东海海洋资源储备特点?1、海岸线漫长、海域辽阔我国大陆位于西北太平洋沿岸,大陆海岸线长达18000多千米,海洋渔场面积200多万平方千米,大陆架面积130多万平方千米,拥有丰富的滩涂资源、海洋渔业资源、海洋矿产资源、港湾资源、海洋旅游资源、海洋能源等海洋自然资源。
我国的内水和领海面积约38万平方千米,专属经济区和大陆架因划界工作尚未完成,确切面积还难于确定,估计为200万平方千米左右。
这些管辖海域是中华民族长期生存繁衍的重要基础。
我国还可以方便的进入世界大洋,开发利用公海和国际海底区域的海洋资源。
2、拥有具战略价值的优势海洋资源油气资源和海水资源是海洋行业性战略资源。
海岸线及其划定方法探讨

海岸线是一条划分海域与陆域的自然地理 界线, 是纯自然的环境界线, 不具任何社会属 性。一些沿海地区的管理部门, 从管理方便的角 度 划 分 岸 线 是 不 可 取 的 。当 然 世 间 任 何 事 物 的 定 义 、法 律 条 文 都 存 有 难 以 涵 盖 的“ 角 落 ”, 海 岸 线 划定也一样。这样的难题, 我们只有取最接近其 原义的选择和处理。
对于海岸线还有一点应当说明, 不同比例尺 的图, 同一海岸线的长度量计是不一样的, 这是
34 海洋开发与管理
海洋管理
一 个 并 不 难 理 解 的 混 沌 现 象 。我 国 海 岸 线 长 度 统 一以 1∶5 万比例尺图量计。
图 1 海岸线位置示意图
二、海岸线划定方法探讨
海岸线虽然有明确的定义, 但也有一些岸线 的具体位置仍然不容易确定, 造成不同人或部门 对 岸 线 具 体 位 置 的 理 解 或 确 定 存 在 意 见 分 歧 。本 文重点在分歧方面依据对海岸线定义的理解, 提 出划分意见。
但作为海面尤其是高潮位时的海面很难有平静的状态在风浪和涌浪的作用下海水上冲流会比大潮高潮面向岸冲向更高更远的陆地在坡度大的海给出的海岸线定义在测绘部门称海岸线为沙质海岸上冲流可向陆更加伸入数米至数十米在低平的淤泥质潮滩可能伸入陆地更远的距离达几十米甚至百米以上
海岸线及其划定方法探讨
杨玉娣 边淑华
人 所 共 知 , 海 岸 线 在 词 典 中 的 定 义 是“ 海 洋 与 陆 地 的 分 界 线 ”。 这 个 定 义 通 俗 而 明 确 。 在 一 般课本、文艺著作和新闻报道中是常用的概念, 且完全够用了。
参考文献
1 夏东兴.海岸带与海岸线.海岸工程, 2006(25):13 ̄20
昌江黎族自治县海岸线修测和问题探讨

昌江黎族自治县海岸线修测和问题探讨巩健 何春娇自然资源部第四航测遥感院 海南 海口 570203摘 要 海岸线是海洋综合管理的重要的基础数据之一,也是海陆管理分界的法定界线,针对2019年海岸线修测工作,对昌江黎族自治县海岸线修测的技术流程及各个不同类型海岸线的位置界定方法进行介绍,对本次海岸线修测的结果与2008年和2016年的海岸线修测结果进行对比,发现昌江黎族自治县海岸线变化幅度较小,少量的变化原因主要在于不同年代的技术标准有差异,同时对海岸线修测的一些问题进行探讨并提出建议。
关键词 海岸线;测绘;技术方法引言 海岸线修测是确定海陆分界线、加强海岸线资源保护利用管理的重要基础工作。
海岸线为多年大潮平均高潮位时海陆分界痕迹线[1]。
海岸线的位置、类型和长度等是我国海洋综合管理的重要基础数据之一。
随着经济的发展,特别是沿岸的开发和利用,海岸线的变迁,2008年公布的海岸线已经难以支撑各种工作的需要。
为进一步明确海陆分界线,加强海岸线保护与利用管理,自然资源部于2019年启动全国新一轮的海岸线修测工作。
明确海岸线空间位置和属性信息,有利于各涉海部门分清管理范围和责任,促进相关涉海法律法规的有效实施,有利于海洋资源、土地资源及水资源的保护和可持续利用,对于客观准确反映当前海岸线开发、利用和保护现状和划定海岸带陆地一侧管理界线作用巨大,对于现在和未来制定各类涉海开发、利用和保护规划、实施科学管控和有效监管意义重大。
1 修测区域概况昌江黎族自治县地处海南岛西部,总面积约1600km²,成长条形,由中部山区伸向海滨,东与白沙县毗邻,东北部隔珠碧江同白沙县、儋州市相望,南与乐东县接壤,西南与东方市以昌化江为河界,西北濒临北部湾,南北分别由昌化江,珠碧江环抱,并在此入海。
地貌为西北平原,中部台地,东南山区,背山面海。
有昌化、海尾、沙渔塘、新港4个天然渔港。
昌化港是昌江主要通商港口,昌化渔场是天然渔场,也是华南四大渔场之一。
海岸线究竟有多长

海岸线究竟有多长?PB08207006 王婷一节微积分课上,宣老师简单的说了一句话,“海岸线的长度是无穷大的”。
说者无心,听者有意,百度一下,终于明白了个中究竟。
海岸线长度依赖于测量单位,若以1km为单位测量海岸线,得到的近似长度将短于1km的曲折都忽略掉了,若以1m为单位测量,则能测出被忽略掉的曲折,长度将变大,测量单位进一步变小,测得的长度将愈来愈大,这些愈来愈大的长度将趋近于一个确定值,这个极限值就是海岸线的长度。
但仔细一想:当测量单位变小时,所得的长度是无限增大的。
海岸线的长度是不确定的,或者说,在一定意义上海岸线是无限长的。
为什么?答案也许在于海岸线的极不规则和极不光滑。
实际测量中,我们将海岸线折线化,得出一个有意义的长度,这就是我们通常所说的海岸线的长度了。
下面我们来看一下经典的科赫曲线(科赫雪花):科赫曲线是一种外形像雪花的几何曲线,所以又称为雪花曲线,它是分形曲线中的一种,具体画法如下:1、任意画一个正三角形,并把每一边三等分;2、取三等分后的一边中间一段为边向外作正三角形,并把这“中间一段”擦掉;3、重复上述两步,画出更小的三角形。
4、一直重复,直到无穷,所画出的曲线叫做科赫曲线。
科赫曲线有以下几个特点:1、曲线任何处不可导,即任何地点都是不平滑的2、总长度趋向无穷大3、曲线上任意两点距离无穷大4、面积是有限的雪花曲线的面积是原来生成它的三角形的面积的8/5;面积计算方法如下Ⅰ.假定等边△ABC的面积是k。
Ⅱ.分△ABC为九个全等等边三角形,各具有面积a,如图所示。
因此k=9a。
现在确定雪花曲线六个初始尖角中每一个面积的极限。
我们知道大尖角的面积是a,因为它是九个三角形之一向外翻转而形成的。
在由它生成的下一批尖角中,每一尖角具有面积a/9,因为和原来的三角形一样,它也被分为九个全等三角形后再把其中一个向外翻转而形成下一批的一个尖角。
事实上,每一个相继的尖角都被分为九个全等三角形,同时在两边生出两个三角形。
从海岸线长度谈起

海岸线最长的国家是俄罗斯,其海 岸线长度超过10万公里,其次是加 拿大、美国、澳大利亚等国。
世界海岸线的特点
曲折程度
全球海岸线曲折程度不一,其中欧洲 和南美洲的海岸线较为曲折,而非洲 和亚洲的海岸线较为平直。
生态多样性
海岸线是生态多样性最为丰富的地区之一, 包括湿地、红树林、珊瑚礁等生态系统,这 些生态系统为众多物种提供了栖息地。
生态修复工程
实施海岸线生态修复工程,包括植被恢复、湿地 保护、沙滩治理等,提高海岸线的生态功能和环 境质量。
监测与评估
建立海岸线生态监测与评估体系,定期对海岸线 生态状况进行评估,及时发现和解决生态问题。
促进海岸线资源的合理利用与开发
科学规划
制定科学的海岸线资源利用规划,明确不同区域的功能定位和发 展方向,避免盲目开发和无序竞争。
01
02
03
港口运输
海岸线长度为港口发展提 供了有利条件,便于货物 进出口和国际贸易。
海洋资源开发
海岸线附近蕴藏着丰富的 海洋资源,如渔业、石油、 天然气等,为地区经济发 展提供资源保障。
旅游业
海岸线优美的自然景观和 丰富的文化资源吸引游客, 促进地区旅游业发展。
海岸线长度对城市发展的影响
城市扩张
资源整合
整合海岸线资源,实现资源共享和优势互补,推动产业集聚和产 业链延伸。
创新发展模式
鼓励企业加大科技投入,创新发展模式,提高海岸线资源利用效 率和经济效益。
06
结论
总结海岸线的重要性
01
生态平衡
海岸线是海洋与陆地的交汇地带,对于维持生态平衡起着重要作用。它
们为众多生物提供繁殖、觅食和栖息的场所,是生物多样性的重要保障。
海岸地貌地理题
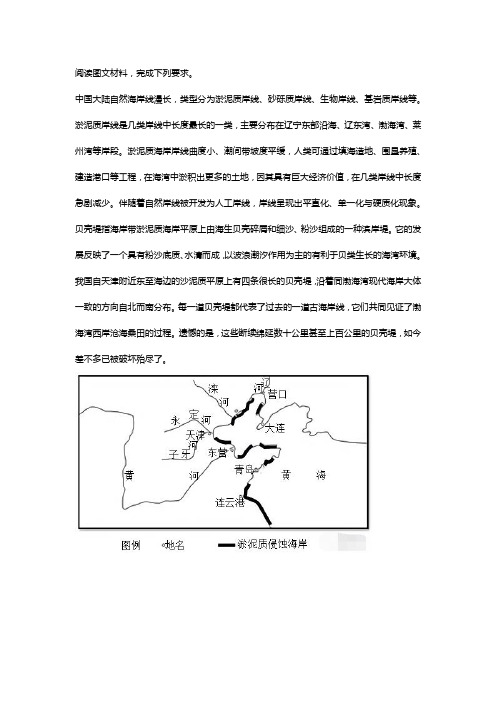
阅读图文材料,完成下列要求。
中国大陆自然海岸线漫长,类型分为淤泥质岸线、砂砾质岸线、生物岸线、基岩质岸线等。
淤泥质岸线是几类岸线中长度最长的一类,主要分布在辽宁东部沿海、辽东湾、渤海湾、莱州湾等岸段。
淤泥质海岸岸线曲度小、潮间带坡度平缓,人类可通过填海造地、围垦养殖、建造港口等工程,在海湾中淤积出更多的土地,因其具有巨大经济价值,在几类岸线中长度急剧减少。
伴随着自然岸线被开发为人工岸线,岸线呈现出平直化、单一化与硬质化现象。
贝壳堤指海岸带淤泥质海岸平原上由海生贝壳碎屑和细沙、粉沙组成的一种滨岸堤。
它的发展反映了一个具有粉沙底质、水清而成,以波浪潮汐作用为主的有利于贝类生长的海湾环境。
我国自天津附近东至海边的沙泥质平原上有四条很长的贝壳堤,沿着同渤海湾现代海岸大体一致的方向自北而南分布。
每一道贝壳堤都代表了过去的一道古海岸线,它们共同见证了渤海湾西岸沧海桑田的过程。
遗憾的是,这些断续绵延数十公里甚至上百公里的贝壳堤,如今差不多已被破坏殆尽了。
(1)淤泥质海岸和基岩质海岸在地貌上是不同的。
说出基岩质海岸的两种地貌类型。
(2)贝壳堤的形成是哪种地质作用造成的。
该地区5000年来海岸线位置的变迁,海岸线发生了哪些变化。
(3)指出淤泥质海岸线急剧缩减对地理环境产生的影响,并提出保护淤泥质海岸线的合理建议。
(4)请指出保护好、利用好贝壳堤的意义。
答案:(1)海蚀崖海蚀柱等。
(2)堆积作用;海岸线发生了海退(海岸线后退)。
(3)迁徙的候鸟无法在潮间带觅食,破坏海岸生物栖息地,生物多样性减少;加剧了海岸生态的脆弱性,净化能力降低(污染加剧);自然资源供给能力减弱;内海面积缩小。
设立保护区;在保护区内严禁围垦和填海;加强政府监管,建立健全相关法律法规;加强统筹计划,提前制定合理开发方案。
(4)是极为珍贵的地质景观;它具有独特的科学价值;见证了我们祖先的活动范围数千年来从山区向海洋扩张的发展历程。
(贝壳堤是珍贵的海洋自然遗迹,真实地记录了沧海变桑田的过程;对研究古地理、古气候、海洋生态、海陆变迁等多学科具有重要价值;是中国罕见的不可再生性资源。
海岸线测绘的常见问题与解决方案

海岸线测绘的常见问题与解决方案海岸线测绘是地理学与海洋科学领域中重要的研究方向之一,它可以帮助我们更好地了解海岸线的变化情况以及其对自然环境和人类社会的影响。
然而,海岸线测绘工作中常常会遇到一些问题,如何解决这些问题成为了研究人员和工程师们面临的挑战。
本文将讨论海岸线测绘中的常见问题,并提供一些解决方案。
首先,一个常见的问题是如何提高海岸线测绘的精度。
海岸线是一个动态的界线,其位置在不同的时间和空间上都会发生变化。
因此,测绘精度的提高对于准确评估海岸线的变化趋势至关重要。
要解决这个问题,研究人员可以采用多种方法,如使用激光雷达、卫星遥感和浮标观测等技术。
这些技术可以提供更精确的测量数据,从而减小因测量误差而引入的不确定性。
其次,海岸线测绘中另一个常见的问题是如何应对复杂的地理环境。
海岸线往往受到沙丘、悬崖、河口等地理特征的影响,这些特征会导致测绘过程中出现困难。
解决这个问题的途径之一是借助先进的遥感技术。
通过使用高分辨率的卫星图像和3D激光雷达数据,研究人员可以更好地识别和量化这些地理特征,从而提高测图的准确性和可靠性。
另外,测绘人员还需要解决海岸线测绘中的数据处理问题。
海岸线的数据通常是大数据,涉及的信息复杂而庞杂。
对这些数据进行处理和分析需要高效的算法和软件工具。
在现代技术的支持下,如人工智能、机器学习和数据挖掘等方法的应用,可以帮助测绘人员更好地处理数据,并从中提取有用的信息。
此外,海岸线测绘中还存在着资源有限的问题。
测绘一片海岸线需要大量人力、物力和财力投入。
然而,实际情况是,资源分配并不均衡,往往只有一部分海岸线得到测绘。
针对这个问题,可以采取一些策略来解决。
例如,通过制定合理的优先级和计划,确保资源的有效利用;开展跨学科和国际合作,共享资源和技术;以及开展普及教育活动,提高公众对海岸线保护的重视程度。
最后,海岸线测绘中一个重要但常常被忽视的问题是数据的准确性和可靠性。
海岸线测绘需要长时间的观测和测量,然而往往会遇到不可抗力的情况,如天气条件、测绘设备的故障等。
(修改)第七讲从海岸线长度谈起——分形几何

分形几何进入中学数学课程
▪ 1.分形几何进入中学数学课程的必要性 ▪ 1)分形几何的创立是数学发展历史上的又一次进
步 ▪ 2)分形理论是描述现实世界的有力工具 ▪ 3)分形几何是培养创新思维的极好材料 ▪ 4)有利于学生掌握数学思想方法,发展辩证思维,
提高审美情趣的思想方法。 ▪ 5)课程现代化的需要
数学文化:一般到特殊,特殊到一般, 归纳总结找规律的猜想, 证明规律的猜想得结论
▪ 雪花曲线的特点——自相似性。任何一个局 部放大后都与整体非常相似。(欧几里得中 的圆就没有这个性质)
邮票上的雪花曲线(保加利亚)有什 么奥秘?
雪花边 界线的 长度? 面积?
隆冬雪花
你细瞧海岸 线,就有类 似的形状
B.B.Mandelbrot(蒙德尔布罗)在《科学》 杂志上发表文章 “英国的海岸线有多长?” 。 他发现这个差距源于海岸线形状的不规则性及用 来测量的尺子长短不一。
这看似极其简单,但Mandelbrot发现:
当测量单位变小时, 所得的长度是无限增大的。
但是,在欧几里得几何中, 当尺的长度趋于零的时候, 测量出的长度趋于圆周长!
“首先,它们处处无规则可言。其次 ,它们 在各种尺度上都有同样程度的不规则性。不论从远 处观察,还是从近处观察,分形看起来一个模样— —它是自相似的。
“整体中的小块,从远处看是不成形的 小点,近处看则发现它变得轮廓分明,其外 形大致和以前观察的整体形状相似。 ”
“自然界提供了许多分形实例。例如, 羊齿植物、菜花和硬花甘兰,以及许多其他 植物,它们的每一分支和嫩枝都与其整体非 常相似。其生成规则保证了小尺度上的特征 成长后就变成大尺度上的特征。”
蝴蝶效应
1963年,美国气象学家洛伦茨发现的“蝴蝶效应”便是其中 典型一例。洛伦茨在一个由三维一阶微分方程组描述的气象 预报模型中,发现该确定的数学模型产生的结果不是趋于稳 定平衡的,也不是趋于某种周期性变化,而是貌似随机的。 近似的初始条件并不能获得近似的结果,更甚者,两者的差 异随时间增大而越大。但这种现象并不是由于计算机的精度 或可靠性等原因造成的。之后,这种类似现象被大量发现, 引起众多学者的关注。1975年,美国数学家约克和华人学者 李天岩将“蝴蝶效应”之类的现象称之为“混沌”。对混沌 现象的研究加深了人们对非线性现象的理解,深化了对混沌 现象本质的认识。
最新十万个为什么解释怎样测量海岸线的长度用100个字介绍

最新十万个为什么解释怎样测量海岸线的长度用100
个字介绍
1.至于地图上的海岸线的长度测量则要简单一些:用一根弹性不是很好的棉线沿着地图上的海岸线放置,在放置时注意在棉线放置的起始点和放置的终点做好标记,然后再用直尺测量棉线的放置的起点与终点间的距离,得出的长度就是地图上的海岸线的长度。
2.一般认为海岸线长度可按如下不同方法和标准来测量按海岸线自然长度测量,即测量海岸曲线的自然长度,在河流入海口处划出封口线,只计算封口线长度。
3.按海岸线的一般走向测量。
测量方法:沿海岸划出一系列同海岸线一般走向相一致的直线,测量这些直线的长度,并依此作为海岸线的长度。
4. 按海岸线的一般走向测量。
测量方法:按照一定的标准,沿海岸划出一系列直线线段的连线,例如以海岸弯曲不超过一定的公里数为限,在弯曲两端划出一条直线作为封口线,直线线段的连线长度即海岸线的长度。
趣味数学海岸线长度问题

n 1
x b
n
各小区间的长度依次为 n 个小区间, 把区间[a , b]分成
x i x i x i 1 ,( i 1,2,) , 在各小区间上任取 一点 i ( i xi ), 作乘积 f ( i )x i ( i 1,2,)
并作和 S f ( i )x i ,
n i 1
记 max{x1 , x 2 , , x n },
•
也不论在小区间[ x i 1 , x i ] 上 如果不论对[a , b] 怎样的分法, 点 i 怎样的取法,只要当 0 时,和 S 总趋于
在区间[a , b] 上的定积分, 记为
积分上限
积分和
f ( i )x i a f ( x )dx I lim 0 i 1
计算柯克曲线的长度
测量规则:第一次用长度为1的尺子测量;第二次用长度 为1/3的尺子测量,第三次用长度为1/9的尺子测量。 小组讨论:第n+1次测量时,量得的周长是多少?
计算柯克曲线的长度
1 3 3
1 12 4 3 1 16 48 9 3
后一个图的周长是前一个图的4/3倍
4 n 3 ( ) 3
尺子无限小的情况
• 大半岛外有小半岛,大海湾内有小海湾, 大石头旁有小石头,当尺子无限小时,海
岸线的长度会
无限大!!!
蝴蝶效应
• 巴西的蝴蝶扇一下翅膀,可能会引起几周 之后在美国德克萨斯州有一场风暴。 • ——洛伦兹
其原因就是蝴蝶扇动翅膀的运动,导致其身边的空 气系统发生变化,并产生微弱的气流,而微弱的气流 的产生又会引起四周空气或其他系统产生相应的变化, 由此引起一个连锁反应,最终导致其他系统的极大变 化。
从海岸线长度看维数问题

从海岸线长度看维数问题从海岸线长度看维数问题在人们的意识中海岸线总存在一个长度,例如说某国家的海岸线有多长等. 1967年, 曼德布罗特在美国《科学》杂志上发表了题为"英国的海岸线有多长?"的论文. 他认证说,任何海岸线在一定意义上都是无限长的,而在另一种意义上, 结果依赖于测量海岸线所用的尺子的长度.他对海岸线的本质所作的独特分析震惊学术界,分形(fractal)一词最初就是出现在这篇文章中.对于“大不列颠的海岸线有多长”这一问题的深入思考和分析实际上是曼德布罗特思想的转折点, 下面我们介绍海岸线长度问题.首先我们从圆周长的测量谈起,按图3―1(a)所示,用多边形的周长去近似圆的周长,不难看出它是一个逼近过程,这个过程满足下面两点:1.测量值依赖多边形的边长,边长越小,测量值越大.2.用多边形的边去近似其所对应的圆弧,当边长越来越小时,近似效果越来越好,因而在极限情况时,多边形的周长就是圆的周长.如果用类似的方法考虑图3―1(b)(英国海岸线缩影图), 设想有人用一定的步长绕海岸线走一圈,上面的第①点是满足的, 但第②点就不一样了. 从图3―1(b)可看出, 当用较大的步子时,每一步与对应的海岸线差异是明显的.但组成海岸线的沙滩、石块、海湾、断层、峡谷、江河出口、……等使得海岸线的结构十分复杂, 而在测量时尺子总有一个确定的长度(标度), 无论长度多么小, 总要忽略一些更小的精细结构.亦即对无论多么小的标度, 标度与对应的海岸线总有明显差异, 因为随着标度变小, 海湾与半岛将显露出越来越小的子海湾与子半岛. 用曼德布罗特的话说, 任何小尺度上的复杂程度与大尺度上的复杂程度有相似性. 因而, 当选定一标度对海岸线进行测量时, 你会得到一确定值,尺子长度越小,测得的值越大,在这种意义上海岸线长度依赖尺子的标度. 当标度趋于零时, 长度并不趋于一固定值,而是趋于无穷大,在这种意义上海岸线是无穷长的. 描述光滑曲线长度的数学模型无法用来描述英国海岸线,而数学家科赫(Koch Helge.Von)早在1904年构造的“妖魔”曲线却能恰如其分地描述海岸线.对海岸线的测量结果如何合理地给出解释呢?我们知道, 用一维“尺”去测量点, 点的长度为0, 用二维的面积去测量一维的线段, 线段的面积为0,用三维的体积去测量二维的区域, 区域体积为0. 反之,用点去测量线段, 用一维“尺”去测量二维区域,用二维面积去测量立体,其“度量”为∞,即对任何一个有确定维数的几何体,,若用与它维数相应的“尺”去量度, 可得一确定值, 若用低于维数的“尺”去量它,结果为无穷大, 若用高于它的维数的“尺”去量它,其结果为0. 如果把海岸线看成维数大于1的曲线,用小于它维数的一维欧氏“尺”去量度,长度为无穷大就一点也不奇怪了,这就要求我们对传统维数进行推广,下面我们来看看图形的维数问题.。
中国海岸线标准

中国海岸线标准中国海洋和领海的线型、位置,早在新石器时代就有迹可循了。
历清,这一线型基本上维持不变,虽有部分微调。
经过20世纪70年代以来对海域进行的划分和调整,在1982年改革开放以后,中国海岸线体系得到了衔接和完善。
一、中国海岸线的概念中国的海岸线是指中国的海洋、南海和领海的边界线,它包括中国的陆地沿海和内海,以及与此相邻的南海、东海和西海等海域。
它穿越多个省市,其长度为13370公里,沿着全国海岸线划分为18个海区,即东、西、北、南四大海区,其中东海区有8个、西海区有3个、北海区有2个、南海区有5个。
二、中国海岸线标准1.洋和领海的边界线由于中国的陆地边界形状特殊,各项实物线也不尽相同,有些需要在两侧设定一定的距离作为海洋和领海的边界线。
根据《1982年中国海岸线拆分和衔接条例》,中国海岸线的划定标准是:(1)陆上边界:以中国的行政区域边界线作为海洋和领海的边界线;(2)海上自然边界:以自然边界线(海床地貌线、岩礁、海岸线等)作为海洋和领海的边界线;(3)实物线:以由政府划定的实物线(仓库、港口、渔港、灯塔等)作为海洋和领海的边界线;(4)陆上正弦线:以两侧50海里正弦线作为海洋和领海的边界线。
2.域划分标准根据1983年《中国海域衔接标准》的规定:中国的陆地沿海,自然边界和实物线分别划定为内港、中港和外港,其中:(1)内港:指全国沿海内湾和河口港口;(2)中港:指全国沿海海湾,以及自然边界线两侧的海域;(3)外港:指全国沿海的实物线,以及实物线两侧的海域,其中的“外港”表示港口,“外湾”表示小湾,“外海”表示海湾。
三、中国海岸线的作用中国海岸线的作用主要有以下几个方面:1. 保障中国的海洋权利和海洋安全,划定中国的海洋和领海的边界线,以便使中国共同管理海洋资源;2. 促进中国沿海对岸国家友好互助,在海上共同维护海洋安全和空间安全;3.强海洋科学研究,以改善沿海的水质环境,保护海洋生物多样性;4.制和防护海洋污染,努力建设绿色海洋社会;5. 为海上建设和海洋经济活动提供支持,保障沿海地区安全发展。
趣味数学海岸线长度问题

柯克曲线—分形世界
• 自相似性:柯克曲线自身的任何一个局部, 放大后都与整体非常相似。因为柯克曲线 的形成就是由其中的一部分反复做同样的 事情得到的。
• 具有自相似性的曲线或图形,叫分形。
“整体中的小块,从远处看是不成形的 小点,近处看则发现它变得轮廓分明,其外 形大致和以前观察的整体形状相似。 ” “自然界提供了许多分形实例。例如, 羊齿植物、菜花和硬花甘兰,以及许多其他 植物,它们的每一分支和嫩枝都与其整体非 常相似。其生成规则保证了小尺度上的特征 成长后就变成大尺度上的特征。” ---- B.B.Mandelbrot
失之毫厘,谬之千里!
分形世界—雪花
柯克曲线
取一个边长为1的正三角形,在每个边上以中间的1/3为一 边,向外侧凸出作一个正三角形,再把原来边上中间的 1/3部分擦掉,就成了一个很像雪花的六角形。
这样不断地做下去,做出的图形边缘越来越不容易画出, 但边缘上越来越小的许许多多的三角形是真实存在的,这 样无限地做下去,得到的图形叫做柯克曲线。
0 1 2
n 1
x b
n
各小区间的长度依次为 n 个小区间, 把区间[a , b]分成
x i x i x i 1 ,( i 1,2,) , 在各小区间上任取 一点 i ( i xi ), 作乘积 f ( i )x i ( i 1,2,)
并作和 S f ( i )x i ,
第四讲 海岸线的长度问题
想过如何计算海岸线的长度吗?
英国科学家理查逊 查询了欧洲很多百科全书, 发现很多很多国家对与其相 邻国的边界测量的不完全相 同,有时候误差会达到百分 之二十以上。
为什么会出现这种问题呢?
误差产生的原因?
法国数学家蒙德尔布罗 1967年对这个 问题做出解释: 用来测量的尺子如果长短不一的话,会 产生很大的误差 故用小尺子测量海岸线结果更精准
海岸线长度问题

客观世界中更多的是“分形”
平面分形图形:海岸线、柯克曲线、下雨区域 的边界、指纹和掌纹、河流的水系图、蜗牛 爬过的路线等;
空间分形图形:天空中的云、地面上的山、河 流的河道、树皮、DNA螺旋线、人的血管分叉、 闪电的线路、人的经络等等。
山
星云
星云
天空中的云朵
植物的叶子
河流分布图
“整体中的小块,从远处看是不成形的 小点,近处看则发现它变得轮廓分明,其外 形大致和以前观察的整体形状相似。 ”
如果尺子小到无限,测得的长度也是无限。
刘徽——割圆术
2.柯克曲线
1904年,瑞典数学家柯克(Koch,1870~1924) 构造了一种雪花形状的曲线,我们习惯上称为柯克雪 花曲线.这一曲线巧妙地解释了蒙德尔布罗的分形几 何思想,其构造方法如下:
(1)取一个边长为1的正三角形,在每个边上以中间的1/3为 一边,向外侧凸出作一个正三角形. (2)将原来边上中间的1/3部分擦掉,就构成了一个很像雪 花形状的有12条边的六角星. (3)再以上图中每边上中间的1/3为一边,向外凸出作一个 正三角形,然后把原来边上中间的1/3部分擦掉,就构成了一 个更像雪花的六角星,这个六角星有48条边. (4)重复以上步骤,不断做下去,得到的图形就是柯克雪花 曲线.
(2)Cantor三分集——最简单的分形
(3)谢尔宾斯基“垫片”
(3)谢尔宾斯基“地毯”
(4)门格尔海绵
(4)门格尔海绵
谢尔宾斯基金字塔
3.分形维数的定义
用迭代函数算法画的树
三、混沌
1.洛仑兹的天气预报
美国气象学家E.N.Lorenz在天气预报中的发现是混沌认识 过程中的一个里程碑。
三、混沌
1.洛仑兹的天气预报
读图涨知识2:认识下我国的海岸线有多长
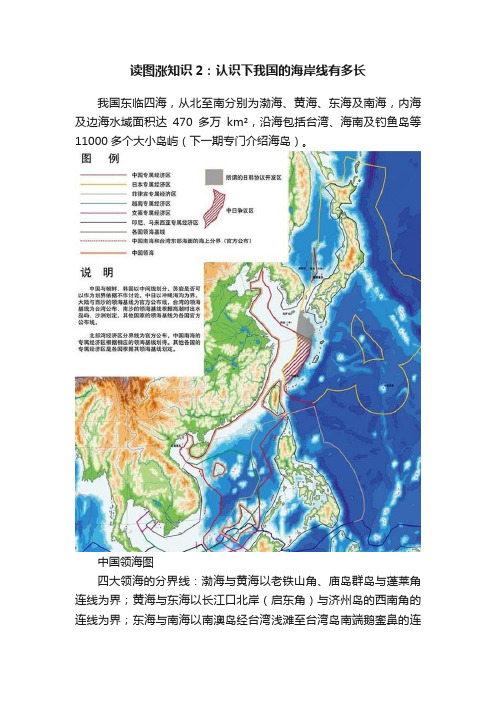
读图涨知识2:认识下我国的海岸线有多长我国东临四海,从北至南分别为渤海、黄海、东海及南海,内海及边海水域面积达470多万km²,沿海包括台湾、海南及钓鱼岛等11000多个大小岛屿(下一期专门介绍海岛)。
中国领海图四大领海的分界线:渤海与黄海以老铁山角、庙岛群岛与蓬莱角连线为界;黄海与东海以长江口北岸(启东角)与济州岛的西南角的连线为界;东海与南海以南澳岛经台湾浅滩至台湾岛南端鹅銮鼻的连线为界。
领海分界线现有我国大陆海岸线北起辽宁丹东的鸭绿江口(属于黄海)向南至广西防城港的北仑河口(属于南海北部湾),全长约1.94万千米(因为部分海岛连陆地增加1400多千米),岛屿海岸线累加长度约1.31万千米,陆地与岛屿海岸线之和约为3.24万千米。
按照最新各省级政府测绘公布的数字,从北到南沿海14个省级行政区海岸线介绍如下(包括大陆岸线岛屿岸线,单位为千米):(一)渤海沿岸1、辽宁省:大陆和岛屿海岸线总长度2797km。
陆地海岸线东起丹东市鸭绿江口西至绥中县老龙头,长度2110km。
包括濒临黄海的丹东(125km)、西临渤海东濒黄海的大连(1371km)、濒临渤海的营口(122km)、盘锦(107km)、锦州(124km)和葫芦岛(261km)6个沿海地级市。
岛屿海岸线长687公里,分属丹东、大连、葫芦岛和锦州,长海县是辽宁唯一海岛建制的县级行政区。
2、河北省:大陆和岛屿海岸线总长度613.4km。
陆地海岸线分两段,北段从秦皇岛市山海关区老龙头至唐山市涧河口,南段从黄骅市歧口至海兴县漳卫新河河口,长度487.7km。
包括秦皇岛(162.7km)、唐山(229.7km)和沧州(95.3km)3个沿海地级市。
岛屿海岸线125.7km,均属于唐山。
3、天津市:陆地海岸线位于渤海西部海域,南起歧口,北至涧河口,长153.2km;岛屿海岸线0.47km,合计总长度153.67km。
4、山东省:大陆和岛屿海岸线总长度3790.63km。
各国海岸线长度列表
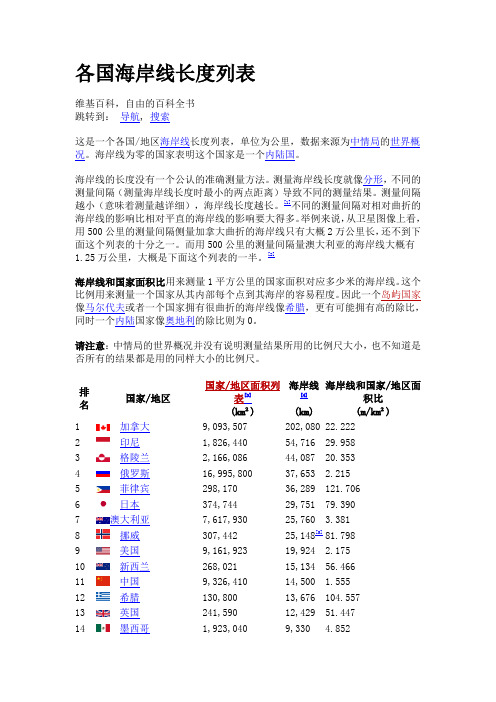
各国海岸线长度列表维基百科,自由的百科全书 跳转到: 导航, 搜索这是一个各国/地区海岸线长度列表,单位为公里,数据来源为中情局的世界概 况。
海岸线为零的国家表明这个国家是一个内陆国。
海岸线的长度没有一个公认的准确测量方法。
测量海岸线长度就像分形,不同的 测量间隔(测量海岸线长度时最小的两点距离)导致不同的测量结果。
测量间隔 越小(意味着测量越详细),海岸线长度越长。
[1]不同的测量间隔对相对曲折的 海岸线的影响比相对平直的海岸线的影响要大得多。
举例来说,从卫星图像上看, 用 500 公里的测量间隔侧量加拿大曲折的海岸线只有大概 2 万公里长,还不到下 面这个列表的十分之一。
而用 500 公里的测量间隔量澳大利亚的海岸线大概有 1.25 万公里,大概是下面这个列表的一半。
[2]海岸线和国家面积比用来测量 1 平方公里的国家面积对应多少米的海岸线。
这个 比例用来测量一个国家从其内部每个点到其海岸的容易程度。
因此一个岛屿国家 像马尔代夫或者一个国家拥有很曲折的海岸线像希腊,更有可能拥有高的除比, 同时一个内陆国家像奥地利的除比则为 0。
请注意:中情局的世界概况并没有说明测量结果所用的比例尺大小,也不知道是 否所有的结果都是用的同样大小的比例尺。
排 名国家/地区1加拿大2印尼3格陵兰4俄罗斯5菲律宾6日本7澳大利亚8挪威9美国10新西兰11中国12希腊13英国14墨西哥国家/地区面积列 海岸线 海岸线和国家/地区面表[3][4]积比(km²)(km)(m/km²)9,093,507202,080 22.2221,826,44054,716 29.9582,166,08644,087 20.35316,995,80037,653 2.215298,17036,289 121.706374,74429,751 79.3907,617,93025,760 3.381307,44225,148[5] 81.7989,161,92319,924 2.175268,02115,134 56.4669,326,41014,500 1.555130,80013,676 104.557241,59012,429 51.4471,923,0409,330 4.852排 名国家/地区国家/地区面积列 海岸线 海岸线和国家/地区面表[3][4]积比(km²)(km)(m/km²)15意大利294,0207,600 25.84916巴西8,456,5107,491 0.88617丹麦42,3947,314 172.25418土耳其770,76019印度2,973,19020智利748,80021密克罗尼西亚联邦 70222克罗地亚56,41423所罗门群岛27,5407,200 9.341 7,000 2.354 6,435 8.594 6,112 8,706.553 5,835[6] 103.432 5,313 192.91924巴布亚新几内亚 452,8605,152 11.37725阿根廷2,736,69026冰岛100,25027西班牙499,54228马达加斯加581,54029马来西亚328,55030爱沙尼亚43,21131古巴110,86032斯瓦尔巴特群岛 61,02033巴哈马10,07034越南325,36035法国545,63036泰国511,77037瑞典410,93438哥伦比亚1,038,70039索马里627,33740委内瑞拉882,05041南非1,219,91242乌克兰603,70043沙特阿拉伯2,149,69044瓦努阿图12,20045法属玻利尼西亚 3,66046 朝鲜120,41047巴拿马75,9904,989 1.823 4,988 49.756 4,964 9.937 4,828 8.302 4,675 14.229 3,794 87.802 3,735 33.691 3,587 58.784 3,542 351.738 3,444[7] 10.585 3,427[8] 6.281 3,219 6.290 3,218 7.831 3,208 3.088 3,025 4.822 2,800 3.174 2,798 2.294 2,782 4.608 2,640 1.228 2,528 207.213 2,525 689.891 2,495 20.721 2,490 32.767排 名国家/地区国家/地区面积列 海岸线 海岸线和国家/地区面表[3][4]积比(km²)(km)(m/km²)48莫桑比克784,0902,470 3.15049埃及995,4502,450 2.46150伊朗1,636,0002,440[9] 1.49151秘鲁1,280,0002,414 1.88652韩国98,1902,413 24.57553德国349,2232,389 6.84154新喀里多尼亚 18,5752,254 121.34655厄瓜多尔276,8402,237 8.08056厄立特里亚121,3202,234[6] 18.41457阿曼212,4602,092 9.84758缅甸657,7401,930 2.93459也门527,9701,906 3.61060摩洛哥446,3001,835 4.11261葡萄牙91,9511,793 19.50062海地27,5601,771 64.26063利比亚1,759,5401,770 1.00664安哥拉1,246,7001,600 1.28365纳米比亚825,4181,572 1.90466 台湾32,2601,566 48.54367帕劳4581,519 3,316.59468北马里亚纳群岛 4771,482 3,106.91869爱尔兰共和国 68,8901,448 21.01970坦桑尼亚886,0371,424 1.60771斯里兰卡64,7401,340 20.69872阿拉伯联合酋长国 83,6001,318 15.76673哥斯达黎加50,6601,290 25.46474多米尼加共和国 48,3801,288 26.62375福克兰群岛12,1731,288 105.80876芬兰304,4731,250 4.10577突尼斯155,3601,148 7.38978基里巴斯8111,143 1,409.37179斐济18,2701,129 61.79580法罗群岛1,3991,117 798.42781撒拉威阿拉伯民主 266,0001,110 4.173排 名国家/地区共和国82巴基斯坦83牙买加84阿尔及利亚85佛得角86尼加拉瓜87加蓬88尼日利亚89苏丹90洪都拉斯91毛里塔尼亚92香港93东帝汶94乌拉圭95塞浦路斯96马尔代夫97孟加拉国98利比里亚99卡塔尔100加纳101肯尼亚102拉脱维亚103塞内加尔104科特迪瓦105波多黎各106科威特107波兰108塞舌尔109圭亚那110荷兰111柬埔寨112汤加113萨摩亚国家/地区面积列 海岸线 海岸线和国家/地区面表[3][4]积比(km²)(km)(m/km²)778,720 10,831 2,381,740 4,033 120,254257,667910,768 2,376,000 111,890 1,030,400 1,042 15,007[10] 173,620 9,240 300 133,910 96,320 11,437 230,940 569,250 63,589 192,000 318,000 8,870 17,820 304,459 455 196,850 33,883 176,520 718 2,9341,046 1,022 998 965 9101.343 94.359 0.419 239.276 7.567885 3.435853 0.937 853 0.359 820 7.329 754 0.732 733 703.455 706 47.045 660 3.801 648 70.130 644 2,146.667 580 4.331 579 6.011 563 49.226 539 2.334 536 0.942 531 8.351 531 2.766 515 1.619 501 56.483 499 28.002 491 1.613 491 1,079.121 459 2.332 451 13.311 443 2.510 419 583.565 403 137.355排 名114 115 116117 岛 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146国家/地区国家/地区面积列 海岸线 海岸线和国家/地区面表[3][4]积比(km²)(km)(m/km²)喀麦隆469,440402 0.856塞拉利昂71,620402 5.613危地马拉108,430400 3.689特克斯和凯科斯群 430389 904.651伯利兹22,806苏里南161,470法属圭亚那90,000[10]马绍尔群岛181荷属安地列斯 960特立尼达和多巴哥 5,128阿尔巴尼亚27,398保加利亚110,550几内亚比绍28,000马提尼克1,102[10]科摩罗[11]2,170几内亚245,857吉布提22,980格鲁吉亚69,700萨尔瓦多20,720瓜德罗普1,628赤道几内亚28,051以色列20,330黎巴嫩10,230罗马尼亚230,340圣多美和普林西比 1,001留尼汪2,510[10]黑山13,812马耳他316叙利亚184,050新加坡683美属维尔京群岛 346马约特岛374毛里求斯2,030386 386 378 370 364 362 362 354 350 350 340 320 314 310 307 306 296 273 225 225 209 207 199 197[12] 196 196 188 185 17716.925 2.391 4.200 2,044.199 379.167 70.593 13.213 3.202 12.500 317.604 156.682 1.302 13.664 4.448 14.817 187.961 10.552 13.428 21.994 0.977 208.791 82.470 14.408 623.418 1.065 286.969 543.353 494.652 87.192排 名国家/地区国家/地区面积列 海岸线 海岸线和国家/地区面表[3][4]积比(km²)(km)(m/km²)147刚果共和国341,500169 0.495148巴林665161 242.105149文莱5,270161 30.550150马恩岛572160 279.720151开曼群岛262160 610.687152圣卢西亚606158 260.726153安提瓜和巴布达 443153 345.372154多米尼克754148 196.286155圣诞岛135139 1,029.630156圣基茨和尼维斯 261135 517.241157 岛 瓦利斯和富图纳群 274129 470.803158关岛541126 232.902159格林纳达344121 351.744160贝宁110,620121 1.094161库克群岛237120 506.329162 群岛 圣皮埃尔和密克隆 242120 495.868163美属萨摩亚199116 582.915164百慕大53103 1,943.396165托克劳10101 10,100.000166巴巴多斯43197225.058167立陶宛65,300[10]991.516168 丁斯 圣文森特和格林纳 38984215.938169冈比亚10,000808.000170英属维尔京群岛 15380522.876171泽西岛11670603.448172阿鲁巴19369357.513173比利时30,278662.180174纽埃26064246.154175安圭拉10261598.039176圣赫勒拿岛[13]12260491.803177圣马丁岛54591,092.593178伊拉克432,162580.134排 名国家/地区国家/地区面积列 海岸线 海岸线和国家/地区面表[3][4]积比(km²)(km)(m/km²)179多哥54,385561.030180皮特凯恩群岛 47511,085.106181根西岛7850641.026182斯洛文尼亚20,151472.332183澳门28411,464.286184巴勒斯坦国6,000406.667185蒙特塞拉特岛 10240392.157186特里斯坦-达库尼 亚群岛20140199.005187刚果民主共和国 2,267,600370.016188诺福克岛35189瑙鲁21190约旦91,971191 岛 科科斯(基林)群 14192图瓦卢26193 维那 波斯尼亚和黑塞哥 51,197194直布罗陀6.532914.286301,428.571260.283261,857.14324923.077200.391121,846.154195摩纳哥1.9542,051.282196哈萨克196土库曼196阿塞拜疆196乌兹别克196阿富汗196安道尔196亚美尼亚196奥地利196布隆迪196布基纳法索196不丹196白俄罗斯196玻利维亚2,669,800 488,100 86,100 425,400 647,500 468 28,454 82,444 25,650 273,800 47,000 207,600 1,084,3900[14]00[15]00[16]00[17]0000000000000000000排 名国家/地区国家/地区面积列 海岸线 海岸线和国家/地区面表[3][4]积比(km²)(km)(m/km²)196博茨瓦纳585,37000196中非共和国622,98400196乍得1,259,20000196捷克77,27600196埃塞俄比亚1,119,68300196匈牙利92,34000196科索沃10,88700196吉尔吉斯斯坦 191,30000196老挝230,80000196莱索托30,35500196列支敦士登16000196卢森堡2,58600196马拉维94,08000196摩尔多瓦33,37100196蒙古国1,554,73100196马其顿共和国 24,85600196马利1,220,00000196尼泊尔143,18100196尼日尔196巴拉圭196卢旺达196塞尔维亚196圣马利诺1,266,700397,300 24,948 77,474610000000000196瑞士196斯洛伐克196斯威士兰196塔吉克196乌干达196梵蒂冈196赞比亚39,77048,800 17,203 142,700 199,7100.44740,72400000000000000排 名国家/地区196津巴布韦国家/地区面积列 海岸线 海岸线和国家/地区面表[3][4]积比(km²)(km)(m/km²)386,67000[编辑] 备注和参考1. ^ 参见比例尺 2. ^ 谷歌地球使用 path measuring tool 测量 3. ^ 中情局世界概况:国家/地区面积 4. ^ 中情局世界概况:海岸线 5. ^ 包括长的峡湾和小的凹凸海岸。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
当你用一把固定长度的直尺(没有刻度)来测量时, 对海岸线上两点间的小于尺子尺寸的曲线,只能用直 线来近似。因此,测得的长度是不精确的。 如果你用更小的尺子来刻画这些细小之处,就会 发现,这些细小之处同样也是无数的曲线近似而成的。 随着你不停地缩短你的尺子,你发现的细小曲线就越 多,你测得的曲线长度也就越大。 如果尺子小到无限,测得的长度也是无限。
4 n 3 ( ) 3
“自相似”的特点
柯克曲线自身的任何一个局部,放大后都与整体非 常相似。
柯克曲线是通过无限的步骤创造的。这无限步骤中
的每一步,都是在上一部图形的每个边上,以中间的 1/3为一边,向外侧突出作一个正三角形,再把原来边 上中间的1/3部分擦掉。这样,柯克曲线自身的任何一 个局部,如此不断地做下去,与整体是非常相似的。
(2)海岸线在各种尺度上都有同样程度的不规则性; (3)海岸线的部分和整体是很相似的,无论从远处观察还是 从近处观察都一样复杂,有自相似性。
B.B.Mandelbrot: “我从拉丁文形容词 fractus(分裂的)造出 了 fractal(分形)这个词.相应的拉丁文动词 fragere 的意义是“使碎裂”、造成不规则的碎 片.……多么符合我们的需要啊!这样,除了“分 裂的”(像在“分数”或“折射”中那样), fracus 还应该有“不规则的”之意,这两个意义都 继承保留了下来”.
输了一场战斗,亡了一个帝国 。
三、混沌
《礼记·经解》 “君子慎始,差若毫厘,谬以千里”
《魏书·乐志 》 “但气有盈虚,黍有巨细,差之毫厘,失之千里 ”
《致我们终将逝去的青春》 陈孝正:大概是我太小题大做了,不过郑微,我跟你不一样,
我的人生是一栋只能建造一次的楼房,我必须让它精确无比,不 能有一厘米差池——所以,我太紧张,害怕行差步错。
一个美国人抽烟和中国的通货膨胀的关系
假设美国此时有一个人抽烟,不小心把没熄灭的烟头 扔在了床边,然后出门上班了,大约20分钟后,烟头慢慢 引燃床单,火越来越大,逐渐蔓延到左邻右舍,引起煤气 罐的连环爆炸。这时的美国人已经对“恐怖袭击”胆战心 惊,而这个肇事者(扔烟头的人)却忘了自己曾扔过烟头, 于是在一时无法查明原因的情况下,暂时被定为“恐怖袭 击”。这样,惊恐万状的人们纷纷抛售股票,引起股市大 跌。人们下降的消费信心影响了整个美国经济,最后造成 美元贬值,由于美元的持续贬值,使得以美元标价的基础 性原材料价格上扬,盯住美元的人民币价格也相应上扬。 从而导致以原材料为基础的商品价格上涨,引发中国的成 本拉动型通货膨胀。
三、混沌
1.洛仑兹的天气预报
1963年,他在麻省理工学院操作着一台当时比 较的先进工具——计算机进行天气模拟,试图进行 长期天气预报。 Lorenz发现,天气运动的规律不同于人们 通 常研究的物质运动规律。人们通常研究的物质运动, 小的初值改变只会导致结果的小改变。而天气运动 不然,天气运动是“混沌”运动。 Lorenz发现混沌运动的两个重要特点: (1)对初值极端敏感;(2)解并不是完全随机的。 Lorenz之后,混沌学的研究开始蓬勃发展。
海岸线长度问题
《数学文化》课程组
经典的欧氏几何学研究的对象是那些光滑和规则的空间形 体,它们一般都具有整数的维数.比如,零维的点、一维的线 (直线与曲线)、二维的面(平面和曲面)、三维的立体(多 面体和球体等)、四维的时空等.然而,自然界是很复杂的, 还普遍存在不光滑和不规则的空间构形.如弯弯曲曲的海岸线、 起伏不平的山脉,粗糙不堪的断面,变幻无常的浮云,九曲回 肠的河流,纵横交错的血管,令人眼花撩乱的满天繁星等 等.所有这些对象很难、也不可能用欧氏几何来描述,因为它 们的维数不一定是整数,而是存在一个分数维数.正因为如此 这些形体一直被视为“病态”的“数学怪物”,而被排除在传 统数学之外.近几十年,随着科学技术的迅猛发展以及人们对 物质世界和人类社会看法的改变,数学家们开始了对这个“数 学怪物”的探索,产生了几何学的新兴分支——分形几何学.
2.分形图形欣赏
(1)蒙德尔布罗集—— 分形的标志
M集的局部放大
M集的多局部放大
(2)Cantor三分集——最简单的分形
(3)谢尔宾斯基“垫片”
(3)谢尔宾斯基“地毯”
(4)门格尔海绵
(4)门格尔海绵
谢尔宾斯基金字塔
3.分形维数的定义
用迭代函数算法画的树
三、混沌
1.洛仑兹的天气预报
2. 对于气象学研究方面,似乎 混沌动力学的发展排除了长期预报 的可能性。 但是另一方面我们现在对于预 报问题有了更符合实际的态度。其 实对短期预报和长期预报的要求从 来不同。
只有对于短期预报,我们才关 心变化的细节。对于长期预报,人 们更注意各种平均量的发展趋势, 例如今后20年内华北年降水量的多 少。 混沌动力学的进步,恰恰在这 方面提高了人类的预报本领。
三、混沌
洛仑兹:巴西的蝴蝶扇一下翅膀,可能会引起几周后美国 德克萨斯州有一场风暴。(蝴蝶效应——butterfly effect)
蝴蝶效应是指在一个动力系统中,初始条件下微小的变化 能带动整个系统的长期的巨大的连锁反应。这是一种混沌 现象。 蝴蝶效应的原因就是蝴蝶扇动翅膀的运动,导致其身边 的空气系统发生变化,并产生微弱的气流,而微弱的气 流的产生又会引起四周空气或其他系统产生相应的变化, 由此引起一个连锁反应,最终导致其他系统的极大变化。
刘徽——割圆术
2.柯克曲线
1904年,瑞典数学家柯克(Koch,1870~1924) 构造了一种雪花形状的曲线,我们习惯上称为柯克雪 花曲线.这一曲线巧妙地解释了蒙德尔布罗的分形几 何思想,其构造方法如下:
(1)取一个边长为1的正三角形,在每个边上以中间的1/3为 一边,向外侧凸出作一个正三角形. (2)将原来边上中间的1/3部分擦掉,就构成了一个很像雪 花形状的有12条边的六角星. (3)再以上图中每边上中间的1/3为一边,向外凸出作一个 正三角形,然后把原来边上中间的1/3部分擦掉,就构成了一 个更像雪花的六角星,这个六角星有48条边. (4)重复以上步骤,不断做下去,得到的图形就是柯克雪花 曲线.
三、混沌
蝴蝶效应之所以令人着迷、令人激动、发人深省,不但在 于其大胆的想象力和迷人的美学色彩,更在于其深刻的科 学内涵和内在的哲学魅力。 西方民谣: 钉子缺,蹄铁卸;蹄铁卸,战马蹶;战马蹶, 骑士绝;骑士绝,战事折;战事折,国家灭。
丢失一个钉子,坏了一只蹄铁;坏了一只蹄铁,折了一匹战马 ;
折了一匹战马,伤了一位骑士 ;伤了一位骑士,输了一场战斗 ;
五、混沌学的应用
1.通过对生命现象进行的考察,发现各 种各样的生物节律既非完全周期,又不可能 属于纯粹随机,它们既有与自然界周期(季 节,昼夜等)协调的一面,又有着内在的复 杂性质。 20世纪20年代后期已经有人用非线性电 路模拟过心脏搏动。近几年更发现了心律不 齐等病症与混 沌运动的联系。
如果考察人类脑电波,对比就更为尖锐。 癫痫患者发病时的脑电波呈明显的周期性, 而正常人的脑电波近乎随机讯号。 进 一步测量表明它们不是随机的,而是接近于 混沌系统。 虽然距离最终认清它们还很远,但现在 已有人进行利用混沌过程预测和控制癫痫, 心律不齐等等病症。
美国气象学家E.N.Lorenz在天气预报中的发现是混沌认识 过程中的一个里程碑。 天气预报是怎么做出来的?
(1)分析、研究和总结天气的规律; (2)将这些规律表示成微分方程的形式; (3)编程输入计算机作为一个固定的模式; (4)采样(当地今天各个时间的气温、空气湿度、气压、风向、风力 等数据) (5)将所得的数据输入计算机,通过程序得到明天各个时间的数据; (6)计算机自动将明天各个时间的数据输入,得到后天的数据; (7)重复(6),得到近几天的天气预报。
Koch曲线
雪花曲线令惊异的性质是:它具有有限的面积,但却 有着无限的周长! 雪花曲线的周长持续增加而没有界限,但整条曲线却 可以画在一张很小的纸上,所以它的面积是有限的,实际 上其面积等于原三角形面积的8/5倍。
二、分形
1.客观世界的“分形”
蒙德尔布罗认为: 海岸线更接近于柯克曲线的形式。
(1)海岸线是没有规则的,不能用函数表达出来;
2.
混沌的意义 1) 混沌的发现与数学史上的数学危机是不同的。 数学危机是人们对于数学根基的质疑,而混沌则 是人们在看似简单的问题中发现了复杂的现象。 2) 混沌绝不单单是有趣的数学现象,混沌是比有 序更为普遍的现象,它使我们对物质世界有了更 深一层的认识,为我们研究自然的复杂性开辟了 一条道路,同时也引出了关于物质世界认识论上 的一些哲学思考。
三、混沌
三、混沌
蝴蝶效应被应用在天气、股票市场等在一定时段难以预测的 比较复杂的系统中。在社会学、心理学领域均有应用。
心理学中的蝴蝶效应是指一件表 面上看来毫无关系、非常微小的 事情,可能带来巨大的改变。此 效应说明,事物发展的结果,对 初始条件具有极为敏感的依赖性, 初始条件的极小偏差,将会引起 结果的极大差异。当一个人小时 候受到微小的心理刺激,长大后 这个刺激会被放大
当增大到3.56,周期又加倍到8;到 3.567,周期达到16,此后便是更快速 的32,64,128…周期倍增数列。 这种倍周期分岔速度如此之快,以 至到3.5699…就结束了,倍周期分岔现 象突然中断: 周期性让位于混沌。
四、关于混沌的思考
1. 混沌的特点 1) 混沌是决定论系统的内在随机性,这种 随机性与我们过去所了解的随机性现象,比 如抛硬币等有很大的区别。 2) 混沌对初值的敏感依赖性。在线性系统 中,小扰动只产生结果的小偏差,但对混沌 系统,则是“失之毫厘,谬以千里”。 3) 混沌不是简单的无序,更不是通常意义 下的有序。
客观世界中更多的是“分形”
平面分形图形:海岸线、柯克曲线、下雨区域 的边界、指纹和掌纹、河流的水系图、蜗牛 爬过的路线等;
空间分形图形:天空中的云、地面上的山、河 流的河道、树皮、DNA螺旋线、人的血管分叉、 闪电的线路、人的经络等等。
