2016高考总复习课件(人教A版)高中数学_第五章_数列_第5讲_数列的综合应用
合集下载
高三数学(理)一轮总复习(人教通用)课件第5章 第5节 数列的综合应用ppt版本

“课后·三维演练”见“课时跟踪检测(三十四)” (单击进入电子文档)
“板块命题点专练(八Βιβλιοθήκη ” (单击进入电子文档)再见
解析
[由题悟法] 等差数列、等比数列综合问题的 2 大解题策略 (1)设置中间问题:分析已知条件和求解目标,为最终解 决问题设置中间问题,例如求和需要先求出通项、求通项需 要先求出首项和公差(公比)等,确定解题的顺序. (2)注意解题细节:在等差数列与等比数列综合问题中, 如果等比数列的公比不能确定,则要看其是否有等于 1 的可 能,在数列的通项问题中第一项和后面的项能否用同一个公 式表示等,这些细节对解题的影响也是巨大的. [提醒] 在不能使用同一公式进行计算的情况下要注意 分类讨论,分类解决问题后还要注意结论的整合.
解析
考点二 等差数列与等比数列的实际应用 重点保分型考点——师生共研
[典例引领]
某企业的资金每一年都比上一年分红后的资金增加一倍,并且 每年年底固定给股东们分红 500 万元.该企业 2010 年年底分 红后的资金为 1 000 万元. (1)求该企业 2014 年年底分红后的资金; (2)求该企业从哪一年开始年底分红后的资金超过 32 500 万元.
解析
考点三 数列与其他知识的交汇 常考常新型考点——多角探明
[命题分析] 数列在高考中多与函数、不等式、解析几何、向量交汇命 题,虽然近几年高考对数列的考查难度有所降低,但为做到有 备无患,在备考中仍应引起高度重视. 常见的命题角度有: (1)数列与函数的交汇; (2)数列与不等式的交汇.
第五节
数列的综合应用
考点一 等差数列与等比数列的综合问题
重点保分型考点——师生共研
[典例引领]
在等差数列{an}中,a10=30,a20=50.
2016届高三数学人教A版文科一轮复习课件 第五章 数列 5-3
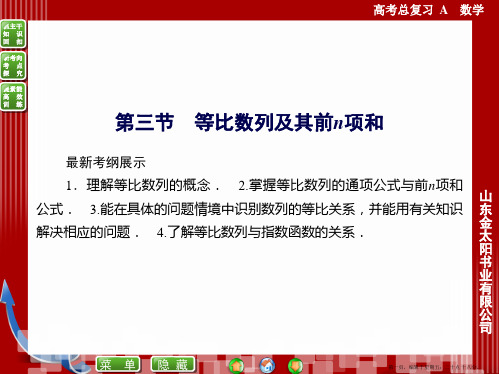
(1)等比数列的前n项和Sn是用错位相减法求得的,注意这种思想方法
在数列求和中的运用.
(2)等比数列的通项公式 an=a1qn-1 及前 n 项和公式 Sn=a111--qqn= 山
东
a11--aqnq(q≠1)共涉及五个量 a1,an,q,n,Sn,知三求二,体现了方程思
金 太
阳
想的应用.
书
业
(3)在使用等比数列的前n项和公式时,如果不确定q与1的关系,一般要
规律方法 (1)等比数列{an}中有两个基本量a1和q,在解决等比数列
山 东
的有关计算问题时,可以将条件转化为有关两者的方程(组)求解,这是解 金 太
决等比数列问题的基本方法,这也是方程思想在数列问题中的体现.
阳
书 (2)应用前n项和公式时,应根据公比q的情况分类讨论,切不可忽视 业
q的取值盲目使用求和公式.
此时 a1+a10=a1+a1q9=1+(-2)3=-7.
由aa47==-4,2,
a1=-8, 解得q3=-12,
山 东 金 太
阳
此时 a1+a10=a1+a1q9=a1(1+q9)=-81-81=-7,综上 a1+a10=
书 业 有
-7.故选 D.
限 公
司
菜 单 隐藏
第十三页,编辑于星期五:二十点 十八分。
山
7.若数列{an}的项数为 2n,则SS偶奇= q
;若项数为 2n+1,则S奇S-偶a1
东 金 太
阳
= q.
书
业
有
限
公
司
菜 单 隐藏
第四页,编辑于星期五:二十点 十八分。
高考总复习 A 数学
抓主干 知识 回扣
2016届高考数学理新课标A版一轮总复习课件 第5章 数列-1

课前学案 基础诊断
夯基固本 基础自测
第4页
返回导航
第五章 第一节 第四页,编辑于星期五:二十一点 二十分。
高考进行时 一轮总复习 ·数学(新课标通用A版 ·理)
1.数列的定义
按照 □1 __________排列的一列数称为数列,数列中的每一
个数叫做这个数列的项.
第5页
返回导航
第五章 第一节 第五页,编辑于星期五:二十一点 二十分。
第21页
返回导航
第五章 第一节 第二十一页,编辑于星期五:二十一点 二十分。
高考进行时 一轮总复习 ·数学(新课标通用A版 ·理)
(3)各项的分母分别为 21,22,23,24,…,易看出第 2,3,4 项的分子 分别比分母小 3.
因此把第 1 项变为-2-2 3, 原数列化为-212-1 3,222-2 3,-232-3 3,242-4 3,…, 故 an=(-1)n2n2-n 3.
高考进行时 一轮总复习 ·数学(新课标通用A版 ·理)
第五章
数列
第1页
返回导航
第五章
第一页,编辑于星期五:二十一点 二十分。
高考进行时 一轮总复习 ·数学(新课标通用A版 ·理)
第一节 数列的概念与简单表示法
课前学案 基础诊断
课堂学案 考点通关
自主园地 备考套餐
开卷速查
第2页
返回导航
第五章 第一节 第二页,编辑于星期五:二十一点 二十分。
返回导航
第五章 第一节 第八页,编辑于星期五:二十一点 二十分。
高考进行时 一轮总复习 ·数学(新课标通用A版 ·理)
答案: □1 一定顺序 □2 有限 □3 无限 □4 > □5 < □ □ □ □ □ □ 6 序号n 7 an=f(n) 8 S1 9 Sn-Sn-1 10 an-1 11 an+1 □ □ 12 an-1 13 an+1
夯基固本 基础自测
第4页
返回导航
第五章 第一节 第四页,编辑于星期五:二十一点 二十分。
高考进行时 一轮总复习 ·数学(新课标通用A版 ·理)
1.数列的定义
按照 □1 __________排列的一列数称为数列,数列中的每一
个数叫做这个数列的项.
第5页
返回导航
第五章 第一节 第五页,编辑于星期五:二十一点 二十分。
第21页
返回导航
第五章 第一节 第二十一页,编辑于星期五:二十一点 二十分。
高考进行时 一轮总复习 ·数学(新课标通用A版 ·理)
(3)各项的分母分别为 21,22,23,24,…,易看出第 2,3,4 项的分子 分别比分母小 3.
因此把第 1 项变为-2-2 3, 原数列化为-212-1 3,222-2 3,-232-3 3,242-4 3,…, 故 an=(-1)n2n2-n 3.
高考进行时 一轮总复习 ·数学(新课标通用A版 ·理)
第五章
数列
第1页
返回导航
第五章
第一页,编辑于星期五:二十一点 二十分。
高考进行时 一轮总复习 ·数学(新课标通用A版 ·理)
第一节 数列的概念与简单表示法
课前学案 基础诊断
课堂学案 考点通关
自主园地 备考套餐
开卷速查
第2页
返回导航
第五章 第一节 第二页,编辑于星期五:二十一点 二十分。
返回导航
第五章 第一节 第八页,编辑于星期五:二十一点 二十分。
高考进行时 一轮总复习 ·数学(新课标通用A版 ·理)
答案: □1 一定顺序 □2 有限 □3 无限 □4 > □5 < □ □ □ □ □ □ 6 序号n 7 an=f(n) 8 S1 9 Sn-Sn-1 10 an-1 11 an+1 □ □ 12 an-1 13 an+1
2016届高考数学(人教理)总复习课件:第5章-第5节 数列的综合应用

切 脉 搏 核 心 突 破
演 实 战 沙 场 点 兵
课 时 提 升 练
菜
单
高三总复习· 数学(理)
提 素 养 满 分 指 导
研 动 向 考 纲 考 向
【解析】
因为等差数列{an}的前 n 项和为 Sn=na1+
nn-1 2 d,所以 S1,S2,S4 分别为 a1,2a1-1,4a1-6. 因为 S1, S2, S4 成等比数列, 所以(2a1-1)2=a1· (4a1-6). 解 1 得 a1=-2.
nn-1 所以 Sn=na1+ 2 d=-2n+n(n-1)=n2-3n.
课 时 提 升 练
菜
单
高三总复习· 数学(理)
(2)函数 f(x)=2 在(a2, b2)处的切线方程为 y-2a2=(2a2ln
研 动 向 考 纲 考 向
x
2)(x-a2), 1 它在 x 轴上的截距为 a2-ln 2. 1 1 由题意知,a2-ln 2=2-ln 2,解得 a2=2. 所以 d=a2-a1=1,从而 an=n,bn=2n. n-1 n 1 2 3 所以 Tn=2+22+23+„+ n-1 +2n, 2 1 2 3 n 2Tn=1+2+22+„+ n-1. 2
菜 单
切 脉 搏 核 心 突 破
演 实 战 沙 场 点 兵
课 时 提 升 练
高三总复习· 数学(理)
提 素 养 满 分 指 导
研 动 向 考 纲 考 向
【思路点拨】 (1)设等差数列{an}的公差为 d, 利用等比 数列的性质得到 a2 a5,并用 2=a1· a1,d 表示 a2,a5 来求解公
提 素 养 满 分 指 导
切 脉 搏 核 心 突 破
预测 2016 年高考仍会以数列与其他知识的综 考向 合应用为重点考查对象,尤其借助等差或等比 预测 数列的有关知识解决不等式的问题将会以更新 的面貌在高考试卷中呈现.
高考数学(理)一轮复习课件:5-5数列的综合应用(人教A版)

■ ·考点自测· ■
1. [2012·蚌埠二中质检]已知数列{an}的通项公式为 an=6n-4,数列{bn}的通项公式为bn=2n,则在数列{an}
的前100项中与数列{bn}中相同的项有( )
A. 50项
B. 34项
C. 6项
D. 5项
答案:D
解析:a1=2=b1,a2=8=b3,a3=14,a4=20,a5= 26,a6=32=b5,又b10=210=1024>a100,b9=512 ==令=== 6n -4,则n=86,∴a86=b9,b8=256 ==令=== 6n-4无解,b7 =128 ==令=== 6n-4,则n=22,∴a22=b7,b6=64=6n-4 无解,综上知,数列{an}的前100项中与{bn}相同的项有5 项.
∴Tn=π2 [1·2+3·22+…+(2n-3)·2n-1+(2n-1)·2n], 2Tn=π2 [1·22+3·23+…+(2n-3)·2n+(2n-1)·2n+1],
两式相减,得
π
-Tn= 2 [1·2+2·22+2·23+…+2·2n-(2n-1)·
2n+1],∴Tn=π[(2n-3)·2n+3].
[规律总结] 本题把数列、导数、解析几何等知识巧 妙地融合在一起,具有较强的综合性,在解决数列知识 与其他章节知识的综合题时,要注意思维角度与解题途 径的选择,提高数字变形转换、推理等综合能力.
3. 数列知识的综合问题 (1)数列本身的综合 数列知识内部综合主要是指以等差数列和等比数列 为中心的综合问题,通常涉及到等差、等比数列的证 明,基本计算、求和等.
(2)数列与其他章节知识的综合 与数列常联系在一起命题的知识主要有函数、不等 式和解析几何,以及三角、复数等.有时带有探索性, 涉及到的方法有转化与化归、放缩、数学归纳法、反证 法、函数思想等.
2016高考总复习课件(人教A版)高中数学_第五章_数列_第1讲_数列的概念与简单表示法

栏目 导引
项与项间的 大小关系
递减数列 常数列
其中 n∈N*
第五章 数列
(3)数列的通项公式:
序号n 如果数列{an}的第 n 项与__________ 之间的关系可以用一
个式子来表示,那么这个公式叫做这个数列的通项公式.
2.数列的递推公式
任一项an 与它的 如果已知数列{an}的首项(或前几项),且__________ 前一项 an-1 n≥2)( 或前几项 ) 间的关系可用一个公式来表 __________(
数列
等差 数列
第五章 数列
知识点
考纲下载 1.理解等比数列的概念. 2.掌握等比数列的通项公式与前n项和公式. 3.能在具体的问题情境中识别数列的等比关 系,并能用有关知识解决相应的问题. 4.了解等比数列与指数函数的关系.
等比 数列
数列 求和
掌握等差、等比数列的前n项和公式.
第五章 数列
第1讲 数列的概念与简单表示法
也可写为 a = 3 n,n为偶数.
n
1 - ,n为奇数, n
栏目 导引
第五章 数列
[规律方法] 用观察法求数列的通项公式的技巧 (1)根据数列的前几项求它的一个通项公式,要注意观察每 一项的特点,观察出项与 n 之间的关系、规律,可使用添 项、通分、分割等办法,转化为一些常见数列的通项公式 来求.对于正负符号变化,可用(-1)n 或(-1)n
解析:当 n=1 时,a1=S1=-1; 当 n≥2 时,an=Sn-Sn-1=(2 -3)-(2 =2n 1,a1 不适合此等式.
-
n
n-1
-3)=2 -2
n
n-1
-1,n=1 ∴an= n-1 . 2 ,n≥2
项与项间的 大小关系
递减数列 常数列
其中 n∈N*
第五章 数列
(3)数列的通项公式:
序号n 如果数列{an}的第 n 项与__________ 之间的关系可以用一
个式子来表示,那么这个公式叫做这个数列的通项公式.
2.数列的递推公式
任一项an 与它的 如果已知数列{an}的首项(或前几项),且__________ 前一项 an-1 n≥2)( 或前几项 ) 间的关系可用一个公式来表 __________(
数列
等差 数列
第五章 数列
知识点
考纲下载 1.理解等比数列的概念. 2.掌握等比数列的通项公式与前n项和公式. 3.能在具体的问题情境中识别数列的等比关 系,并能用有关知识解决相应的问题. 4.了解等比数列与指数函数的关系.
等比 数列
数列 求和
掌握等差、等比数列的前n项和公式.
第五章 数列
第1讲 数列的概念与简单表示法
也可写为 a = 3 n,n为偶数.
n
1 - ,n为奇数, n
栏目 导引
第五章 数列
[规律方法] 用观察法求数列的通项公式的技巧 (1)根据数列的前几项求它的一个通项公式,要注意观察每 一项的特点,观察出项与 n 之间的关系、规律,可使用添 项、通分、分割等办法,转化为一些常见数列的通项公式 来求.对于正负符号变化,可用(-1)n 或(-1)n
解析:当 n=1 时,a1=S1=-1; 当 n≥2 时,an=Sn-Sn-1=(2 -3)-(2 =2n 1,a1 不适合此等式.
-
n
n-1
-3)=2 -2
n
n-1
-1,n=1 ∴an= n-1 . 2 ,n≥2
高考数学总复习 第5章 第5讲 数列的综合应用课件 理 新人教A版

(1)求{an}的通项公式; (2)记{an}的前n项和为Sn,若a1,ak,Sk+2成等比数列,求 正整数k的值.
第二十三页,共60页。
解:(1)设数列{an}的公差为 d,由题意知
2a1+2d=8, 2a1+4d=12.
解得 a1=2,d=2.
所以 an=a1+(n-1)d=2+2(n-1)=2n. (2)由(1)可得 Sn=na12+an=n2+2 2n=n(n+1).
[审题视点] (1)在数列中,利用an与Sn的关系求通项公式, 这是最基本的思路;(2)数列是特殊的函数,所以可用函数的思想 解决(jiějué)数列的最值问题.
[解] (1)取 n=1,得 λa21=2S1=2a1,a1(λa1-2)=0. 若 a1=0,则 Sn=0. 当 n≥2 时,an=Sn-Sn-1=0-0=0, 所以 an=0(n≥1). 若 a1≠0,则 a1=2λ.
第5讲 数列的综合应用
第一页,共60页。
不同寻常的一本书,不可不读哟iè)的等差关系或等比关 系,并能用相关知识解决相应的问题.
第三页,共60页。
1个必知应用 生活中涉及到银行利率、产品利润、人口增长、工作效率、 图形面积、曲线长度等实际问题时,常考虑用数列知识(zhī shi)求 解.
第二十一页,共60页。
对等差、等比数列的综合问题的分析,应重点分析等差、等 比数列的通项及前n项和;分析等差、等比数列项之间的关系 (guān xì).往往用到转化与化归的思想方法.
第二十二页,共60页。
[变式探究] [2012·重庆(zhònɡ qìnɡ)高考]已知{an}为等差数 列,且a1+a3=8,a2+a4=12.
第四页,共60页。
2个必会综合 1. 数列知识内部综合问题,通常涉及(shèjí)到等差、等比数 列的证明、基本计算、求和等. 2. 数列知识与其它章节知识的综合问题;有时带有探索性, 涉及(shèjí)到的方法有转化与化归、放缩、函数思想等.
第二十三页,共60页。
解:(1)设数列{an}的公差为 d,由题意知
2a1+2d=8, 2a1+4d=12.
解得 a1=2,d=2.
所以 an=a1+(n-1)d=2+2(n-1)=2n. (2)由(1)可得 Sn=na12+an=n2+2 2n=n(n+1).
[审题视点] (1)在数列中,利用an与Sn的关系求通项公式, 这是最基本的思路;(2)数列是特殊的函数,所以可用函数的思想 解决(jiějué)数列的最值问题.
[解] (1)取 n=1,得 λa21=2S1=2a1,a1(λa1-2)=0. 若 a1=0,则 Sn=0. 当 n≥2 时,an=Sn-Sn-1=0-0=0, 所以 an=0(n≥1). 若 a1≠0,则 a1=2λ.
第5讲 数列的综合应用
第一页,共60页。
不同寻常的一本书,不可不读哟iè)的等差关系或等比关 系,并能用相关知识解决相应的问题.
第三页,共60页。
1个必知应用 生活中涉及到银行利率、产品利润、人口增长、工作效率、 图形面积、曲线长度等实际问题时,常考虑用数列知识(zhī shi)求 解.
第二十一页,共60页。
对等差、等比数列的综合问题的分析,应重点分析等差、等 比数列的通项及前n项和;分析等差、等比数列项之间的关系 (guān xì).往往用到转化与化归的思想方法.
第二十二页,共60页。
[变式探究] [2012·重庆(zhònɡ qìnɡ)高考]已知{an}为等差数 列,且a1+a3=8,a2+a4=12.
第四页,共60页。
2个必会综合 1. 数列知识内部综合问题,通常涉及(shèjí)到等差、等比数 列的证明、基本计算、求和等. 2. 数列知识与其它章节知识的综合问题;有时带有探索性, 涉及(shèjí)到的方法有转化与化归、放缩、函数思想等.
高考数学总复习 第五章第5课时 数列的综合应用课件 新人教版

an=a(1+r)n,属于等比模型.
(3)递推数列模型:如果题目中给出的 前后两项之间的关系不固定,随项的变 化而变化时,应考虑是an与an+1之间的
递推关系,还是前n项和Sn与前n+1项和
Sn+1之间的递推关系.
课前热身
1.(2012· 盘锦调研 ) 已知 {an},{bn} 均为
等差数列 , 且 a2 = 8,a6 = 16,b2 = 4,b6 = a6, 则由 {an},{bn}的公共项组成的新数 列{cn}的通项公式cn=( A.3n+4 ) B.6n+2
低题目的难度,解题时有时还需利用条
件联立方程求解.
例1
已知等差数列 {an}的前四项的和
A4=60,第二项与第四项的和为 34,等比
数列{bn}的前四项的和 B4=120,第二项
与第四项的和为90. (1)求数列{an},{bn}的通项公式; (2) 设 cn = an· bn, 且 {cn} 的前 n 项和为 Sn, 求Sn.
+
① -②得:
- 2Sn = 9· 3 + 4· 32 + 4· 33 +…+ 4· 3n - (4n+ + 5)· 3n 1 3 1-3 = 27+4· 1-3 = 27+2· 3
n+ 1 2 n-1
- (4n+5)· 3n
n+ 1
+1
- 18-(4n+5)· 3
,
1 n+ 1 ∴ Sn= [(4n+ 3)· 3 - 9]. 2
答案:B
4.某种产品三次调价,单价由原来的每克
512 元降到 216 元 , 则这种产品平均每次
降价的百分率为________. 答案:25%
5.(2012· 威海调研 )已知函数 f(x)=a· bx 的图 1 象过点 A(2, ),B(3,1),若记 an= log2f(n)(n∈ 2 N*),Sn 是数列 {an}的前 n 项和 ,则 Sn 的最小 值是________.
人教A版高中数学必修5 数列专题复习ppt下载

三、求前n项和的方法
设数列{a n
}为等差数列,数列{bn
}为等比数列
1.通项c n
=a n
b n
,
利用分组求和
2.通项c n
=a
n
b n
,
利用错位相减
3.通项c = p n aa
, 利用裂项相消
n n1
常见的裂项相消
(1) 1 1 1 n(n 1) n n 1
人教A版高中数学必修5 数列专题复习ppt下载【PPT教研课 件】
人教A版高中数学必修5 数列专题复习ppt下载【PPT教研课 件】
人教A版高中数学必修5 数列专题复习ppt下载【PPT教研课 件】
常见的裂项相消 (2) 1 1 (1 1 )
n(n 2) 2 n n 2
(3)
1
(2n+1)(2n
1)
1 2
(
1 2n 1
1) 2n+1
(4)
1
1 ( nk n)
nk n k
人教A版高中数学必修5 数列专题复习ppt下载【PPT教研课 件】
若a,b, c成等差
2b a c
an =a1 (n 1)d an am (n m)d
若m+n=p+q,则 am an a p aq 特别地,若m+n=2t, 则am an 2at
an1 q或 an (q n 2)
an
an-1
若a,b, c成等比
b2 ac b ac an =a1qn1 an amqnm
数列
复习课
人教A版高中数学必修5 数列专题复习ppt下载【PPT教研课 件】
教学目标
➢ 牢记等差数列等比数列的定义、中项、通项、 下标和性质、前n项和
2016版高考数学大一轮复习课件:第5章-第5节数列的综合应用
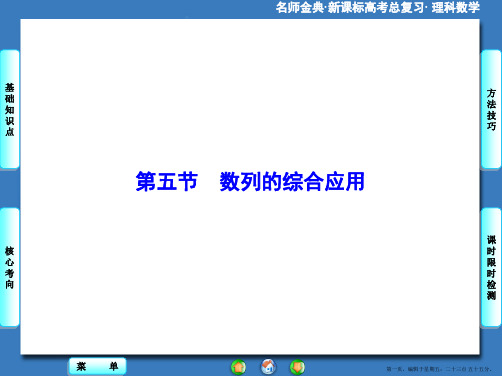
2.等比模型:如果后一个量与前一个量的比是一个固定
的数时,该模型是等比模型,这个固定的数就是公比.
3.递推数列模型:如果题目中给出的前后两项之间的关 课
核
时
心 考 向
系不固定,随项的变化而变化时,应考虑是 an 与 an+1 的递推
限 时 检
关系,还是前 n 项和 Sn 与 Sn+1 之间的递推关系.
核
时
心 思想方法求解,在问题的求解过程中往往会遇到递推数列, 限
考
时
向
检
因此掌握递推数列的常见解法有助于该类问题的解决.
测
菜单
第二十二页,编辑于星期五:二十三点 五十五 分。
名师金典·新课标高考总复习·理科数学
对点训练 已知等比数列{an}的公比 q=3,前 3 项和 S3
基 础 知
=133.
识
点
100 64 >lg
1=0,
核 心
当 n≥7 时,bn≤b7=lg
12070=lg
100 128<lg
1=0.
课 时 限
考
时
向
故数列lg
a1n的前 6 项的和最大.
检 测
菜单
第十三页,编辑于星期五:二十三点 五十五分。
名师金典·新课标高考总复习·理科数学
规律方法 1 1.(1)本题的切入点是求 a1,从而得 an 与 Sn
且 λa1an=S1+Sn 对一切正整数 n 都成立.
(1)求数列{an}的通项公式;
核
(2)设 λ=100,当 n 为何值时,数列lg
a1n的前 n 项和最
课 时
心
限
考 大?
时
向
检
2016届高三数学人教A版文科一轮复习课件 第五章 数列 5-1

类比已知数列、转化成特殊数列(等差、等比)等方法.
书 业
有
限
公
司
菜 单 隐藏
第七页,编辑于星期五:二十点 十八分。
抓主干 知识 回扣
研考向 考点 探究
提素能 高效 训练
高考总复习 A 数学
3.很多数列试题是以 an=SS1n, -nS=n-11,,n≥2. 为出发点设计的,求解
时要考虑两个方面,一个是根据 Sn-Sn-1=an 把数列中的和转化为数列 山
解析:∵an+1=an+2n,∴an+1-an=2n.
∴a2-a1=2×1;
a3-a2=2×2;
…… 山
an-an-1=2×(n-1)(n≥2).
东 金
以上各式相加,得:
太
an-a1=2[1+2+3+…+(n-1)]=n2-n.
阳 书
∴an=n2-n+a1=n2-n+2(n≥2),a1=2也适合.
业 有
山 东
=a1=2.
金 太
阳
答案:C
书
业
有
限
公
司
菜 单 隐藏
第十页,编辑于星期五:二十点 十八分。
抓主干 知识 回扣
研考向 考点 探究
提素能 高效 训练
高考总复习 A 数学
3.已知数列{an}的前n项和Sn满足:Sn+Sm=Sn+m,且a1=1,那么
a10=( )
A.1
B.9
C.10
D.55
山
解析:a10=S10-S9=(S1+S9)-S9=S1=a1=1,故选A.
高效
训练
当 n=1 时,a1=2 也符合上式,
∴an=23n2+n2.
规律方法 由数列递推式求通项公式常用方法有:累加法、累积法、
高三数学 一轮复习 第5知识块第5讲 数列的综合应用课件 文 新人教A版

同时又以一个固定的具体量增加(或减少)时,我们称该模型为生长
模型.如分期付款问题,树木的生长与砍伐问题等. (5)递推模型:如果容易找到该数列任意一项an与它的前一项an-1(或前
几项)间的递推关系式,那么我们可以用递推关系的知识求解问题.
2.数列与其他分支的知识的综合应用 (1)主要为数列与函数、方程、不等式、三角、解析几何、极限等知识的 综合. (2)解此类综合题,首先要认真审题,弄清题意,分析出涉及哪些数学分支 内容,在每个分支中各是什么问题;其次,要精心分解,把整个大题分 解成若干个小题或“步骤”,使它们成为在各自分支中的基本问题;最 后,分别求解这些小题或步骤,从而得到整个问题的结论.
答案:B
2.(2009· 江西卷)公差不为零的等差数列{an}的前n项和为Sn.若a4是a3与a7的等比
中项,S8=32,则S10等于( A.18 解析:由题意可知 B.24 ) C.60 D.90
S10=10×(-3)+ 答案:C
×2=60.
3.黑白两种颜色的正六边形地面砖按如下图的规律拼成若干个图案,则 第n个图案中有白色地面砖的块数是( )
第5讲
【考纲下载】
数列差关系或等比关系,
并能用相关知识解决相应的问题.
1.数列应用问题的常见模型 (1)等差模型:一般地,如果增加(或减少)的量有一个固定的具体量时,该模 型是等差模型,增加(或减少)的量就是公差,其一般形式是:an+1-an=d(常数). (2)等比模型:一般地,如果增加(或减少)的百分比是一个固定的数时,该模型是 等比模型. (3)混合模型:在一个问题中,同时涉及到等差数列和等比数列的模型. (4)生长模型:如果某一个量,每一期以一个固定的百分数增加(或减少),
(2)该人打算连续在一家公司工作10年,仅从工资收入总量较多作为应
高考数学 总复习 5-1数列课件 新人教A版

第四模块 平面向量、数系的扩充与复数的引入
数学
高考总复习人教A版 · (理)
1.数列是一种特殊的函数,学习时要善于利用函数 的思想来解决.如通项公式、前n项和公式等.
2.运用方程的思想解等差(比)数列是常见题型,解决 此类问题需要抓住基本量a1、d(或q),掌握好设未知数、 列出方程、解方程三个环节,常通过“设而不求,整体代 入”来简化运算.
数学
高考总复习人教A版 · (理)
高考资讯
第四模块 平面向量、数系的扩充与复数的引入
数学
高考总复习人教A版 · (理)
数列是高中数学的重要内容,在历年的高考题中占有 较大比重,数列与函数、方程、不等式、几何等知识的联 系十分密切.数列中的递推思想、函数思想、分类讨论思 想以及数列求和、求通项公式中的各种方法与技巧,在中 学数学中都有十分重要地位,涉及数列的应用问题及探索 性问题都可成为命题的方向.这一部分主要考查学生的运 算能力、逻辑思维能力及分析解决问题能力.
5.深刻理解等差(比)数列的定义,能正确使用定义和 等差(比)数列的性质是学好本章的关键.
第四模块 平面向量、数系的扩充与复数的引入
数学
高考总复习人教A版 · (理)
6.解题要善于总结基本数学方法.如类比法、错位 相减法、待定系数法、归纳法、数列结合法,养成良好的 学习习惯,定能达到事半功倍的效果.
解析:由an+1-an=n+1,可得 当n≥2时,a2-a1=2,a3-a2=3,…,an-an-1=n. 以上n-1个式子左右两边分别相加,得
第四模块 平面向量、数系的扩充与复数的引入
数学
高考总复习人教A版 · (理)
an-a1=2+3+…+n=n+22n-1, ∴an=nn+ 2 1+1.
2016届高考数学理科一轮复习课件 第五章 数列5-5

a≤1.( )
东
(4)数列{an}是正项等比数列,bn=logaan(a>0且a≠1),则数列{bn}是
金 太
等差数列.( )
阳 书
答案:(1)√ (2)√ (3)× (4)√
业
有
限
公
司
菜 单 隐藏
第五页,编辑于星期五:二十一点 四十一分。
高考总复习 A 数学
抓主干 知识 回扣
研考向
考点 探究
2.数列{an}是各项均为正数的等比数列,{bn}是等差数列,且a6=
有 限
结论.
公 司
菜 单 隐藏
第十七页,编辑于星期五:二十一点 四十一分。
高考总复习 A 数学
抓主干 知识 回扣
研考向 考点 探究
提素能 高效 训练
2.(2013年高考安徽卷)如图,互不相同的点A1,A2,…,An,…和
B1,B2,…,Bn,…分别在角O的两条边上,所有AnBn相互平行,且所有
梯形AnBnBn+1An+1的面积均相等,设OAn=an.若a1=1,a2=2,则数列{an}
书
业
(2)至少经过几年旅游业的总收入才能超过总投入?
有 限
公
司
菜 单 隐藏
第十四页,编辑于星期五:二十一点 四十一分。
抓主干 知识 回扣
高考总复习 A 数学
研考向 考点
解析 (1)第一年投入为 800 万元,
探究
提素能 高效 训练
第二年投入为 8001-15万元,
第 n 年内的总投入为 8001-15n-1 万元,所以,n 年的投入为:
太 阳
答案:6
书 业
有
限
公
司
菜 单 隐藏
2016届高考数学理新课标A版一轮总复习课件 第5章 数列-5
第15页
返回导航
第五章 第五节 第十五页,编辑于星期五:二十一点 二十一分。
高考进行时 一轮总复习 ·数学(新课标通用A版 ·理)
解析:a3+a9≥2 a3a9=2 a62=2a6=2b7=b4+b10,当且仅当 a3 =a9 时,不等式取等号.
答案:B
第16页
返回导航
第五章 第五节 第十六页,编辑
返回导航
第五第章二十七第页,五编辑节于星期五:二十一点 二十一
分。
高考进行时 一轮总复习 ·数学(新课标通用A版 ·理)
(2)该城市为响应“十八大”提出的建设“美丽中国”的号召, 决定加大减排力度.在 2012 年刚好按原计划完成减排任务的条件 下,自 2013 年起,SO2 的年排放量每年比上一年减少的百分率为 p, 为使 2020 年这一年 SO2 的年排放量控制在 6 万吨以内,求 p 的取值 范围.
考点一
等差、等比数列的综合问题
【例 1】 已知等差数列{an}的公差不为零,a1=25,且 a1,a11, a13 成等比数列.
(1)求{an}的通项公式; (2)求 a1+a4+a7+…+a3n-2.
第21页
返回导航
第五第章二十一第页,五编辑节于星期五:二十一点 二十一
分。
高考进行时 一轮总复习 ·数学(新课标通用A版 ·理)
解析:(1)设{an}的公差为 d.由题意,得 a121=a1a13, 即(a1+10d)2=a1(a1+12d). 于是 d(2a1+25d)=0. 又 a1=25,所以 d=-2 或 0(舍去). 故 an=-2n+27. (2)令 Sn=a1+a4+a7+…+a3n-2. 由(1)知 a3n-2=-6n+31,故{a3n-2}是首项为 25,公差为-6 的 等差数列.
人教版高中总复习一轮数学精品课件 第5章 数列 5.5 数学归纳法

增加了一项.( × )
(5)用数学归纳法证明等式“1+2+22+…+2n+2=2n+3-1”,验证当n=1结论成立
时,左边式子应为1+2+22+23.( √ )
2.用数学归纳法证明:首项是 a1,公差是 d 的等差数列{an}的前 n 项和公式是
(-1)
Sn=na1+
d 时,假设当 n=k 时,公式成立,则 Sk 等于( C )
2
(1 + )
A.a1+(k-1)d
B.
2
(-1)
(+1)
C.ka1+
d
D.(k+1)a1+
d
2
2
假设当 n=k 时,公式成立,只需把公式中的 n 换成 k 即可,即
3.已知数列{an}满足an+1=2 -nan+1,n∈N*,且a1=2,则a2=a3=源自4,a4=5
,猜想an=
n+1
当n=k+1时,待证等式左边=1+2+3+…+(2k+1)+(2k+2)+(2k+3),
所以从n=k到n=k+1,左边需增添的代数式是(2k+2)+(2k+3).
第二环节
关键能力形成
能力形成点1
例1
用数学归纳法证明等式
1
1
1
1
用数学归纳法证明:
+
+
+…+
=
(n∈N*).
2×4 4×6 6×8
2(2+2) 4(+1)
(5)用数学归纳法证明等式“1+2+22+…+2n+2=2n+3-1”,验证当n=1结论成立
时,左边式子应为1+2+22+23.( √ )
2.用数学归纳法证明:首项是 a1,公差是 d 的等差数列{an}的前 n 项和公式是
(-1)
Sn=na1+
d 时,假设当 n=k 时,公式成立,则 Sk 等于( C )
2
(1 + )
A.a1+(k-1)d
B.
2
(-1)
(+1)
C.ka1+
d
D.(k+1)a1+
d
2
2
假设当 n=k 时,公式成立,只需把公式中的 n 换成 k 即可,即
3.已知数列{an}满足an+1=2 -nan+1,n∈N*,且a1=2,则a2=a3=源自4,a4=5
,猜想an=
n+1
当n=k+1时,待证等式左边=1+2+3+…+(2k+1)+(2k+2)+(2k+3),
所以从n=k到n=k+1,左边需增添的代数式是(2k+2)+(2k+3).
第二环节
关键能力形成
能力形成点1
例1
用数学归纳法证明等式
1
1
1
1
用数学归纳法证明:
+
+
+…+
=
(n∈N*).
2×4 4×6 6×8
2(2+2) 4(+1)
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数列 基本特征 模型 等差 均匀增加或者减少 数列 等比 指数增长,常见的是增产率问题、存款复利问题 数列 指数增长的同时又均匀减少.如年收入增长率为 简单递 20%,每年年底要拿出a(常数)作为下年度的开销, 推数列 即数列{a }满足a =1.2a -a n n+ 1 n
栏目 导引
第五章 数列
栏目 导引
第五章 数列
(2)由等差及等比数列的求和公式得 当 n≥7 时,由于 S6=570, 故 Sn=S6+(a7+a8+…+an)
n- 6 3 3 =570+70× ×4×1- 4 4 n-6 3 . =780-210× 4
栏目 导引
第五章 数列
[规律方法] 解答数列实际应用问题的步骤: (1)确定模型类型:理解题意,看是哪类数列模型,一般有 等差数列模型、等比数列模型、简单的递推数列模型.基 本特征见下表:
[解] (1)设等差数列{an}的公差为 d,由题意得 a4-a1 12-3 d= = =3, 3 3 所以 an=a1+(n-1)d=3n(n=1,2,…).
栏目 导引
第五章 数列
设等比数列{bn-an}的公比为 q,由题意得 b4-a4 20-12 3 q= = =8,解得 q=2. b1-a1 4-3 所以 bn-an=(b1-a1)qn 1=2n 1. - 从而 bn=3n+2n 1(n=1,2,…). - (2)由(1)知 bn=3n+2n 1(n=1,2,…). 3 - 数列{3n}的前 n 项和为 n(n+1),数列{2n 1}的前 n 项和为 2 1-2n =2n-1. 1-2 3 所以,数列{bn}的前 n 项和为 n(n+1)+2n-1. 2
(2)准确解决模型:解模就是根据数列的知识,求数列的通 项、数列的和、解方程(组)或者不等式(组)等,在解模时要 注意运算准确; (3)给出问题的答案:实际应用问题最后要把求解的数学结 果化为对实际问题的答案,在解题中不要忽视了这点.
栏目 导引
第五章 数列
2.现有流量均为 300 m3
s 的两条河 A,B 汇 m3
栏目 导引
第五章 数列
(2)令 Sn=a1+a4+a7+…+a3n-2. 由(1)知 a3n-2=-6n+31, 故{a3n-2}是首项为 25,公差为-6 的等差数列. n n 从而 Sn= (a1+a3n-2)= (-6n+56)=-3n2+28n. 2 2
栏目 导引
第五章 数列
考点二 数列的实际应用问题
栏目 导引
第五章 数列
1.(2013· 高考课标全国卷Ⅱ)已知等差数列 {an}的 公差不为零,a1=25 ,且 a1,a11,a13 成等比数列. (1)求{an}的通项公式; (2)求 a1+a4+a7+…+a3n-2.
解:(1)设{an}的公差为 d,由题意得 a2 11=a1a13, 即(a1+10d)2=a1(a1+12d). 于是 d(2a1+25d)=0. 又 a1=25,所以 d=0(舍去),d=-2. 故 an=-2n+27.
合于某处后,不断混合,它们的含沙量分别为 2 kg 和 0.2 kg
m3, 假设从汇合处开始, 沿岸设有若干观测点,
两股水流在流经相邻两个观测点的过程中,其混合效果相 当于两股水流在 1 s 内交换 100 m3 的水量,即从 A 股流入 B 股 100 m3 水,经混合后,又从 B 股流入 A 股 100 m3 水 并混合,问从第几个观测点开始,两股河水的含沙量之差 小于 0.01 kg m3(不考虑沙沉淀).
某企业在第 1 年初购买一台价值为 120 万元的设备 M,M 的价值在使用过程中逐年减少.从第 2 年到第 6 年, 每年初 M 的价值比上年初减少 10 万元;从第 7 年开始, 每年初 M 的价值为上年初的 75%. (1)求第 n 年初 M 的价值 an 的表达式; (2)设 Sn 表示数列{an}的前 n 项和,求 Sn(n≥7).
栏目 导引
Байду номын сангаас
第五章 数列
解:设第 n 个观测点处 A 股水流含沙量为 an kg 股水流含沙量为 bn kg a1=2,b1=0.2, 1 1 bn= (300bn-1+100an-1)= (3bn-1+an-1), 400 4 1 1 an= (300an-1+100bn-1)= (3an-1+bn-1), 400 4 1 an-bn= (an-1-bn-1), 2 m3,则
m3,B
栏目 导引
第五章 数列
1 ∴{an-bn}是以(a1-b1)为首项, 为公比的等比数列. 2 9 1n-1 ∴an-bn= ×2 . 5 9 1n-1 - - 解不等式 ×2 <10 2,得 2n 1>180, 5 ∴n≥9. 因此,从第 9 个观测点开始,两股水流的含沙量之差小于 0.01 kg/m3.
第五章 数列
第5讲
数列的综合应用
第五章 数列
考点一 考点二 考点三
等差数列与等比数列的综合问题 数列的实际应用问题 数列与不等式的综合问题(高频考点)
栏目 导引
第五章 数列
考点一 等差数列与等比数列的综合问题
(2014· 高考北京卷)已知{an}是等差数列,满足 a1 =3,a4=12,数列{bn}满足 b1=4,b4=20,且{bn-an}为 等比数列. (1)求数列{an}和{bn}的通项公式; (2)求数列{bn}的前 n 项和.
栏目 导引
第五章 数列
[解]
(1)当 n≤6 时,数列{an}是首项为 120,公差为-10
的等差数列,an=120-10(n-1)=130-10n; 3 当 n≥6 时,数列{an}是以 a6 为首项, 为公比的等比数列. 4
n-6 3 . 又 a6=70,所以 an=70× 4
因此,第 n 年初,M 的价值 an 的表达式为 130-10n,n≤6, n-6 an= 3 ,n≥7. 70 × 4
- -
栏目 导引
第五章 数列
[规律方法] 解决等差数列与等比数列的综合问题, 关键是 理清两个数列的关系. 如果同一数列中部分项成等差数列, 部分项成等比数列,要把成等差数列或等比数列的项抽出 来单独研究;如果两个数列通过运算综合在一起,要从分 析运算入手, 把两个数列分割开弄清两个数列各自的特征, 再进行求解.
