最新中考数学专题复习--与轴对称有关的最短路径问题及解析
中考专题复习——最短路径问题(有答案)

B CD AL 中考专题复习——路径最短问题一、具体内容包括:蚂蚁沿正方体、长方体、圆柱、圆锥外侧面吃食问题; 线段(之和)最短问题;二、原理:两点之间,线段最短;垂线段最短。
(构建“对称模型”实现转化) 三、例题:例1、①如右图是一个棱长为4的正方体木块,一只蚂蚁要从木块的点A 沿木块侧面爬到点B 处,则它爬行的最短路径是 。
②如右图是一个长方体木块,已知AB=3,BC=4,CD=2,假设一只蚂蚁在点A 处,它要沿着木块侧面爬到点D 处,则蚂蚁爬行的最短路径是 。
例2、①如图,要在河边修建一个水泵站,分别向张村、李庄送水,水泵站修在河边什么地方可使所用的水管最短。
②如图,直线L 同侧有两点A 、B ,已知A 、B 到直线L 的垂直距离分别为1和3,两点的水平距离为3,要在直线L 上找一个点P ,使PA+PB 的和最小。
请在图中找出点P 的位置,并计算PA+PB 的最小值。
③要在河边修建一个水泵站,向张村、李庄铺设管道送水,若张村、李庄到河边的垂直距离分别为1Km 和3Km ,张村与李庄的水平距离为3Km ,则所用水管最短长度为 。
四、练习题(巩固提高)张村李庄ABCD 图(2)EBDACP图(3)D OP(一)1、如图是一个长方体木块,已知AB=5,BC=3,CD=4,假设一只蚂蚁在点A 处,它要沿着木块侧面爬到点D 处,则蚂蚁爬行的最短路径是 。
2、现要在如图所示的圆柱体侧面A 点与B 点之间缠一条金丝带(金丝带的宽度忽略不计),圆柱体高为6cm ,底面圆周长为16cm ,则所缠金丝带长度的最小值为 。
3、如图是一个圆柱体木块,一只蚂蚁要沿圆柱体的表面从A 点爬到点B 处吃到食物,知圆柱体的高为5 cm ,底面圆的周长为24cm ,则蚂蚁爬行的最短路径为 。
4、正方形ABCD 的边长为8,M 在DC 上,且DM =2,N 是AC 上的一动点,DN +MN的最小值为 。
第4题 第5题 第6题 第7题5、在菱形ABCD 中,AB=2, ∠BAD=60°,点E 是AB 的中点,P 是对角线AC 上的一个动点,则PE+PB 的最小值为 。
最新中考数学专题复习--与轴对称有关的最短路径问题及解析
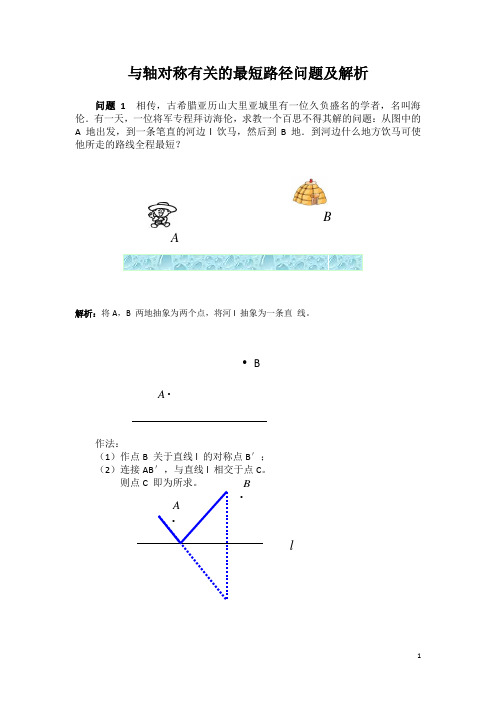
与轴对称有关的最短路径问题及解析问题1 相传,古希腊亚历山大里亚城里有一位久负盛名的学者,名叫海伦.有一天,一位将军专程拜访海伦,求教一个百思不得其解的问题:从图中的A 地出发,到一条笔直的河边l 饮马,然后到B 地.到河边什么地方饮马可使他所走的路线全程最短?解析:将A ,B 两地抽象为两个点,将河l 抽象为一条直 线。
作法:(1)作点B 关于直线l 的对称点B ′;(2)连接AB ′,与直线l 相交于点C 。
则点C 即为所求。
BAlB• ·A l B·lA ·BC证明:如图,在直线l 上任取一点C ′(与点C 不重合),连接AC ′,BC ′,B ′C ′。
由轴对称的性质知, BC =B ′C ,BC ′=B ′C ′. ∴ AC +BC = AC +B ′C = AB ′,AC ′+BC ′= AC ′+B ′C ′. 在△AB ′C ′中, AB ′<AC ′+B ′C ′,∴ AC +BC <AC ′+BC ′. 即 AC +BC 最短. 若直线l 上任意一点(与点C 不重合)与A ,B两点的距离和都大于AC +BC ,就说明AC + BC 最小.问题2 如图,一个旅游船从大桥AB 的P 处前往山脚下的Q 处接游客,然后将游客送往河岸BC 上,再返回P 处,请画出旅游船的最短路径。
解析:考点:作图—应用与设计作图,轴对称-最短路线问题专题:分析:根据“两点之间线段最短”,和轴对称最短路径问题解答.解答: 解:(1)两点之间,线段最短,连接PQ ;(2)作P 关于BC 的对称点P1,连接QP1,交BC 于M ,再连接MP .最短路线P--Q--M--P .点评:本题考查了作图--应用与设计作图,熟悉轴对称最短路径问题是解题的关键.问题3 如图,A.B 两地在一条河的两岸,现要在河上建一座桥MN ,桥造在 B · lA ·BC C何处才能使从A到B的路径AMNB最短?(假设河的两岸是平行的直线,桥要与河垂直)解析:如图,作BB'垂直于河岸GH,使BB′等于河宽,连接AB′,与河岸EF相交于M,作MN⊥GH,则MN∥BB′且MN=BB′,于是MNBB′为平行四边形,故NB=MB′.根据“两点之间线段最短”,AB′最短,即AM+BN最短.问题4已知△ABC中,D、E是边AB、AC边上的点,在边BC上找一点M,使△DEM的周长最小。
轴对称最短路径问题7种类型

轴对称最短路径问题7种类型
轴对称最短路径问题是一种经典的计算几何问题,其目标是在给定图形中找到从起点到终点的最短路径。
根据不同的条件和限制,轴对称最短路径问题可以分为以下七种类型:
1. 简单轴对称最短路径问题:给定一个轴对称图形,起点和终点分别位于对称轴的两侧,求最短路径。
2. 带有障碍物的轴对称最短路径问题:在轴对称图形中存在一些障碍物,起点和终点在障碍物两侧,求最短路径。
3. 多个起点和终点的轴对称最短路径问题:给定多个起点和终点,每个起点和终点都在对称轴的两侧,求所有起点到所有终点的最短路径。
4. 带有权值的轴对称最短路径问题:在轴对称图形中,不同的点或边具有不同的权值,求起点到终点的最短路径。
5. 动态规划解决轴对称最短路径问题:使用动态规划算法解决轴对称最短路径问题,将问题分解为子问题,逐步求解。
6. A*搜索算法解决轴对称最短路径问题:使用A*搜索算法,通过估价函数指导搜索方向,加速求解速度。
7. 双向搜索解决轴对称最短路径问题:从起点和终点同时进行搜索,通过比较两个方向的搜索结果得到最短路径。
以上七种类型是轴对称最短路径问题的常见分类,每种类型都有其特定的解决方法,需要根据具体问题的特点选择合适的方法进行求解。
初中数学专题复习(轴对称-最短距离问题)

初中数学专题复习(轴对称-最短距离问题)一.轴对称-最短路线问题1.(2020•荆门)在平面直角坐标系中,长为2的线段CD(点D在点C右侧)在x轴上移动,A(0,2),B(0,4),连接AC,BD,则AC+BD的最小值为()A.2B.2C.6D.3解:设C(m,0),∵CD=2,∴D(m+2,0),∵A(0,2),B(0,4),∴AC+BD=+,∴要求AC+BD的最小值,相当于在x轴上找一点P(n,0),使得点P到M(0,2)和N(﹣2,4)的距离和最小,如图1中,作点M关于x轴的对称点Q,连接NQ交x轴于P′,连接MP′,此时P′M+P′N的值最小,∵N(﹣2,4),Q(0,﹣2)P ′M+P′N的最小值=P′N+P′Q=NQ==2,∴AC+BD的最小值为2.故选:B.2.(2020•贵港)如图,动点M在边长为2的正方形ABCD内,且AM⊥BM,P是CD边上的一个动点,E是AD边的中点,则线段PE+PM的最小值为()A.﹣1B.+1C.D.+1解:作点E关于DC的对称点E',设AB的中点为点O,连接OE',交DC于点P,连接PE,如图:∵动点M在边长为2的正方形ABCD内,且AM⊥BM,∴点M在以AB为直径的圆上,OM=AB=1,∵正方形ABCD的边长为2,∴AD=AB=2,∠DAB=90°,∵E是AD的中点,∴DE=AD=×2=1,∵点E与点E'关于DC对称,∴DE'=DE=1,PE=PE',∴AE'=AD+DE'=2+1=3,在Rt△AOE'中,OE'===,∴线段PE+PM的最小值为:PE+PM=PE'+PM=ME'=OE'﹣OM=﹣1.故选:A.3.(2020•恩施州)如图,正方形ABCD的边长为4,点E在AB上且BE=1,F为对角线AC上一动点,则△BFE周长的最小值为()A.5B.6C.7D.8解:如图,连接ED交AC于一点F,连接BF,∵四边形ABCD是正方形,∴点B与点D关于AC对称,∴BF=DF,∴△BFE的周长=BF+EF+BE=DE+BE,此时△BEF的周长最小,∵正方形ABCD的边长为4,∴AD=AB=4,∠DAB=90°,∵点E在AB上且BE=1,∴AE=3,∴DE=,∴△BFE的周长=5+1=6,故选:B.4.(2020•潍坊)如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=4,以点O为圆心,2为半径的圆与OB 交于点C,过点C作CD⊥OB交AB于点D,点P是边OA上的动点.当PC+PD最小时,OP的长为()A.B.C.1D.解:如图,延长CO交⊙O于点E,连接ED,交AO于点P,此时PC+PD的值最小.∵CD⊥OB,∴∠DCB=90°,又∠AOB=90°,∴∠DCB=∠AOB,∴CD∥AO∴∵OC=2,OB=4,∴BC=2,∴,解得,CD=;∵CD∥AO,∴=,即=,解得,PO=故选:B.5.(2020•西宁)如图,等腰△ABC的底边BC=20,面积为120,点D在BC边上,且CD=5,直线EF是腰AC 的垂直平分线,若点M在EF上运动,则△CDM周长的最小值为18.解:如图,作AH⊥BC于H,连接AM,∵EF垂直平分线段AC,∴MA=MC,∴DM+MC=AM+MD,∴当A、D、M共线时,DM+MC的值最小,∵等腰△ABC的底边BC=20,面积为120,AH⊥BC,∴BH=CH=10,AH==12,∴DH=CH﹣CD=5,∴AD===13,∴DM+MC的最小值为13,∴△CDM周长的最小值=13+5=18,故答案为18.6.(2020•内江)如图,在矩形ABCD中,BC=10,∠ABD=30°,若点M、N分别是线段DB、AB上的两个动点,则AM+MN的最小值为15.解:作点A关于BD的对称点A′,连接MA′,BA′,过点A′作A′H⊥AB于H.∵BA=BA′,∠ABD=∠DBA′=30°,∴∠ABA′=60°,∴△ABA′是等边三角形,∵四边形ABCD是矩形,∴AD=BC=10,在Rt△ABD中,AB==10,∵A′H⊥AB,∴AH=HB=5,∴A′H=AH=15,∵AM+MN=A′M+MN≥A′H,∴AM+MN≥15,∴AM+MN的最小值为15.故答案为15.7.(2020•毕节市)如图,已知正方形ABCD的边长为4,点E是边AB的中点,点P是对角线BD上的动点,则AP+PE的最小值是.解:如图,连接CE交BD于点P,连接AP,∵四边形ABCD是正方形,∴点A与点C关于BD对称,∴AP=CP,∴AP+EP=CP+EP=CE,此时AP+PE的最小值等于CE的长,∵正方形ABCD的边长为4,点E是边AB的中点,∴BC=4,BE=2,∠ABC=90°,∴CE==,∴AP+PE的最小值是,故答案为:.8.(2020•黑龙江)如图,在边长为1的菱形ABCD中,∠ABC=60°,将△ABD沿射线BD方向平移,得到△EFG,连接EC、GC.求EC+GC的最小值为.解:∵在边长为1的菱形ABCD中,∠ABC=60°,∴AB=CD=1,∠ABD=30°,∵将△ABD沿射线BD的方向平移得到△EGF,∴EG=AB=1,EG∥AB,∵四边形ABCD是菱形,∴AB=CD,AB∥CD,∴∠BAD=120°,∴EG=CD,EG∥CD,连接ED∴四边形EGCD是平行四边形,∴ED=GC,∴EC+GC的最小值=EC+ED的最小值,∵点E在过点A且平行于BD的定直线上,∴作点D关于定直线的对称点M,连接CM交定直线于E,则CM的长度即为EC+DE的最小值,∵∠EAD=∠ADB=30°,AD=1,∴∠ADM=60°,DH=MH=AD=,∴DM=1,∴DM=CD,∵∠CDM=∠MDG+∠CDB=90°+30°=120°,∴∠M=∠DCM=30°,∴CM=2×CD=.故答案为:.9.(2020•日照)如图,Rt△ABC中,∠C=90°,以AB为边在AB上方作正方形ABDE,过点D作DF⊥CB,交CB的延长线于点F,连接BE.(1)求证:△ABC≌△BDF;(2)P,N分别为AC,BE上的动点,连接AN,PN,若DF=5,AC=9,求AN+PN的最小值.(1)证明:∵Rt△ABC中,∠C=90°,DF⊥CB,∴∠C=∠DFB=90°.∵四边形ABDE是正方形,∴BD=AB,∠DBA=90°,∵∠DBF+∠ABC=90°,∠CAB+∠ABC=90°,∴∠DBF=∠CAB,∴△ABC≌△BDF(AAS);(2)解:∵△ABC≌△BDF,∴DF=BC=5,BF=AC=9,∴FC=BF+BC=9+5=14.如图,连接DN,∵BE是正方形顶点A与顶点D的对称轴,∴AN=DN.如使得AN+PN最小,只需D、N、P在一条直线上,由于点P、N分别是AC和BE上的动点,作DP1⊥AC,交BE于点N1,垂足为P1,所以,AN+PN的最小值等于DP1=FC=14.10.(2019•西藏)如图,在矩形ABCD中,AB=6,AD=3,动点P满足S△P AB=S矩形ABCD,则点P到A、B 两点距离之和PA+PB的最小值为()A.2B.2C.3D.解:设△ABP中AB边上的高是h.∵S△P AB=S矩形ABCD,∴AB•h=AB•AD,∴h=AD=2,∴动点P在与AB平行且与AB的距离是2的直线l上,如图,作A关于直线l的对称点E,连接AE,BE,则BE的长就是所求的最短距离.在Rt△ABE中,∵AB=6,AE=2+2=4,∴BE===2,即PA+PB的最小值为2.故选:A.11.(2019•聊城)如图,在Rt△ABO中,∠OBA=90°,A(4,4),点C在边AB上,且=,点D为OB 的中点,点P为边OA上的动点,当点P在OA上移动时,使四边形PDBC周长最小的点P的坐标为()A.(2,2)B.(,)C.(,)D.(3,3)解:∵在Rt△ABO中,∠OBA=90°,A(4,4),∴AB=OB=4,∠AOB=45°,∵=,点D为OB的中点,∴BC=3,OD=BD=2,∴D(2,0),C(4,3),作D关于直线OA的对称点E,连接EC交OA于P,则此时,四边形PDBC周长最小,E(0,2),∵直线OA的解析式为y=x,设直线EC的解析式为y=kx+b,∴,解得:,∴直线EC的解析式为y=x+2,解得,,∴P(,),故选:C.12.(2019•黑龙江)如图,矩形ABCD中,AB=4,BC=6,点P是矩形ABCD内一动点,且S△P AB=S△PCD,则PC+PD的最小值为4.解:如图,作PM⊥AD于M,作点D关于直线PM的对称点E,连接PE,EC.设AM=x.∵四边形ABC都是矩形,∴AB∥CD,AB=CD=4,BC=AD=6,∵S△P AB=S△PCD,∴×4×x=××4×(6﹣x),∴x=2,∴AM=2,DM=EM=4,在Rt△ECD中,EC==4,∵PM垂直平分线段DE,∴PD=PE,∴PC+PD=PC+PE≥EC,∴PD+PC≥4,∴PD+PC的最小值为4.13.(2019•陕西)如图,在正方形ABCD中,AB=8,AC与BD交于点O,N是AO的中点,点M在BC边上,且BM=6.P为对角线BD上一点,则PM﹣PN的最大值为2.解:如图所示,以BD为对称轴作N的对称点N',连接PN',延长PN′交BC于M,根据轴对称性质可知,PN=PN',∴PM﹣PN=PM﹣PN'≤MN',当P,M,N'三点共线时,取“=”,∵正方形边长为8,∴AC=AB=,∵O为AC中点,∴AO=OC=,∵N为OA中点,∴ON=,∴ON'=CN'=,∴AN'=,∵BM=6,∴CM=AB﹣BM=8﹣6=2,∴==,∴PM∥AB∥CD,∠CMN'=90°,∵∠N'CM=45°,∴△N'CM为等腰直角三角形,∴CM=MN'=2,即PM﹣PN的最大值为2,故答案为:2.14.(2019•成都)如图,在边长为1的菱形ABCD中,∠ABC=60°,将△ABD沿射线BD的方向平移得到△A'B'D',分别连接A'C,A'D,B'C,则A'C+B'C的最小值为.解:∵在边长为1的菱形ABCD中,∠ABC=60°,∴AB=CD=1,∠ABD=30°,∵将△ABD沿射线BD的方向平移得到△A'B'D',∴A′B′=AB=1,A′B′∥AB,∵四边形ABCD是菱形,∴AB=CD,AB∥CD,∴∠BAD=120°,∴A′B′=CD,A′B′∥CD,∴四边形A′B′CD是平行四边形,∴A′D=B′C,∴A'C+B'C的最小值=A′C+A′D的最小值,∵点A′在过点A且平行于BD的定直线上,∴作点D关于定直线的对称点E,连接CE交定直线于A′,则CE的长度即为A'C+B'C的最小值,∵∠A′AD=∠ADB=30°,AD=1,∴∠ADE=60°,DH=EH=AD=,∴DE=1,∴DE=CD,∵∠CDE=∠EDB′+∠CDB=90°+30°=120°,∴∠E=∠DCE=30°,∴CE=2×CD=.故答案为:.15.(2019•德阳)如图,在四边形ABCD中,BC∥AD,BC=AD,点E为AD的中点,点F为AE的中点,AC⊥CD,连接BE、CE、CF.(1)判断四边形ABCE的形状,并说明理由;(2)如果AB=4,∠D=30°,点P为BE上的动点,求△PAF的周长的最小值.解:(1)四边形ABCE是菱形,理由如下:∵点E是AD的中点,∴AE=AD.∵BC=AD,∴AE=BC.∵BC∥AD,即BC∥AE.∴四边形ABCE是平行四边形∵AC⊥CD,点E是AD的中点,∴CE=AE=DE,∴四边形ABCE是菱形(2)由(I)得,四边形ABCE是菱形.∴AE=EC=AB=4,且点A、C关于BE对称∵点F是AE的中点,AF=AE=2∴当PA+PF最小时,△PAF的周长最小即点P为CF与BE的交点时,△PAF的周长最小,此时△PAF的周长=PA+PF+AF=CF+AF,在Rt△ACD中,点E是AD的中点,则CE=DE,∠ECD=∠D=30°,∠ACE=90°﹣30°=60°.∴△ACE是等边三角形.∴AC=AE=CE=4.∵AF=EF,CF⊥AE∴CF==2△PAF的周长最小=CF+AF=2.。
轴对称与最短路径问题

ND E
所以桥的位置建在CD处,AB两地的路程最短。
B
2. 如图,A、B是两个蓄水池,都在河流a的同侧,为了 方便灌溉作物, 要在河边建一个抽水站,将河水送到A、 B两地,问该站建在河边什么地方, 可使所修的渠道最短 ,试在图中确定该点。
作法:作点B关于直线 a 的对称点点C,连接AC交直线a于点D ,则点D为建抽水站的位置。
所以A.B两地的距:AM+MN+BN=AM+MN+EM=AE+MN,
若桥的位置建在CD处,连接AC.CD.DB.CE, 则AB两地的距离为:
A·
MC
AC+CD+DB=AC+CD+CE=AC+CE+MN,
在△ACE中,∵AC+CE>AE, ∴AC+CE+MN>AE+MN, 即AC+CD+DB >AM+MN+BN
根据:两点之间线段最短.
如图,要在燃气管道L上修建一个泵站,分别向A、B两镇 供气,泵站修在管道的什么地方,可使所用的输气管线 最短?
所以泵站建在点P可使输气管线最短
应用
P
(Ⅱ) 两点在一条直线同侧
已知:如图,A、B在直线L的同一侧,在L上 求一点,使得PA+PB最小.
作法:① 作点B关于直线l的对称点B/.
如图所示,从A地到B地有三条路可供选
择,你会选走哪条路最近?你的理由是
什么?
C ①D E
A
②
B
两点之间,线段最短
③
F
(Ⅰ)两点在一条直线异侧
已知:如图,A,B在直线L的两侧,在L上求一 点P,使得PA+PB最小。
初中数学轴对称最短路径问题

在直线 l1 、 l2 上分别求 点 M 、N ,使四边形 PQMN 的周⻓长最小小。
分别作点 Q 、P 关于直线 l1 、l2 的 对称点 Q'和 P' 连 Q'P',与两直 线交点即为 M,N.
两点之间线段最短 四边形 PQMN 周⻓长的 最小小值为线段 Q'P'的 ⻓长。
【问题 5】“造桥选址” 作法
使 AM+MN+NB 的值最
小小.
【问题 9】
作法
作图
连 AB,作 AB 的 中垂线与直线 l 在直线 l 上求一一点 P,使 的交点即为 P.
的值最小小 .
【问题 10】
作法
作图
2
两点之间线段最短. AM+MN+BN 的最小小值 为 A'B+MN.
原理理
两点之间线段最短. AM+MN+BN 的最小小值 为 A''B+MN.
4.如图,在锐⻆角△ABC 中,AB=4 ,∠ BAC=45°,∠ BAC=45°,∠ BAC 的平分线交 BC 于 点 D,M、N 分别是 AD 和 AB 上的动点,则 BM+MN 的最小小值是__________。
5.如图,Rt△ABC 中,∠ C=90°,∠ B=30°,AB=6,点 E 在 AB 边上,点 D 在 BC 边 上(不不与点 B、C 重合),且 ED=AE,则线段 AE 的取值范围是__________。 6.如图,∠ AOB=30°,点 M、N 分别在边 OA、OB 上,且 OM=1,ON=3,点 P、Q 分 别在边 OB、OA 上,则 MP+PQ+QN 的最小小值是_________.(注“勾股定理理”:直⻆角三⻆角 形中两直⻆角边的平方方和等于斜边的平方方,即 Rt△ABC 中,∠ C=90°,则有 AC 2 + BC 2 = AB 2) 7.如图,三⻆角形△ABC 中,∠ OAB=∠ AOB=15°,点 B 在 x 轴的正半轴,坐标为 B( 6 , 0).OC 平分∠ AOB,点 M 在 OC 的延⻓长线上,点 N 为边 OA 上的点,则 MA+MN 的最 小小值__________。 8.已知 A(2,4)、B(4,2).C 在 y 轴上,D 在 x 轴上,则四边形 ABCD 的周⻓长最小小值 为__________。
初中数学_中考专题复习——最短路径问题教学设计学情分析教材分析课后反思

中考专题复习教学目标知识与技能1.建立数学模型,能利用轴对称变换找对称点,并用两点之间线段最短的方法来求最短路径。
2.借助特殊四边形、一次函数、反比例函数以及二次函数的图像等这些基本图形,运用对称变换的方法,能清晰的抓住求最短路径问题的本质。
3.在探索最短路径的过程中,体会轴对称、“桥梁”作用,感悟转化思想,一题多解,一题多变的思想。
过程与方法经历探索最短路径过程,在操作、观察、分析过程中发展学生思维意识,培养学生的解题技能技巧。
情感态度与价值观体验数学活动来源于生活又服务于生活,体会异侧直接连,同侧找对称点,提高学生的学习兴趣。
重点利用轴对称数学知识,将最短路径问题转化为“两点之间线段最短”问题,增强解决实际问题的能力。
掌握解决问题的方法和技巧。
难点综合运用轴对称数学知识,将同侧的两定点通过轴对称变换转化到已侧,从而借助两点之间线段最短解决线段和(周长)最小值问题。
活动一:旧知回顾师生行为设计意图问题1 A,B是路边两个新建小区,要在路边增设一个公共汽车站C。
使两个小区到车站的路程最短,该公共汽车站应建在什么地方?问题2相传,古希腊亚历山大城里有一位久负盛名的学者,名叫海伦.有一天,一位将军专程拜访海伦,求教一个百思不得其解的问题:从图中的A 地出发,到一条笔直的河边l 饮马,然后到B 地.到河边什么地方饮马可使他所走的路线全程最短?师生集体宣誓师:提出问题。
生:讨论交流,板书作图过程师:提出问题导入课题。
师:请思考问题1和问题2的相同点是解决的那类问题?不同点是什么?解决问题的方法和技巧是什么?1、活跃课堂气氛,使学生在轻松愉快的环境中学习。
2、复习两点之间线段最短,从而引出课题3、渗透转化思想,了解解题方法和解题技巧。
4、建立数学模型:将军饮马问题5、探究解题方法:异侧直接连,同侧找对称点6、发现解题技巧活动二:典题赏析类型一:四边形中的最短路径问题培养学生善于思考、善于观察的良好习惯例1 生:一生读题一生解答师:配合学生完成审题过程师:提出新问题若本题其它条件不变。
2023年中考数学重难点复习:轴对称之最短路径(附答案解析)

第1页共7页2023年中考数学重难点复习:《轴对称之最短路径》破解策略
用轴对称思想解决线段最值问题是常用的方法,本质是利用三角形三边关系解决问题.常见的题型有:
1.已知:在直线l 同恻有A.B 两点,在l 上找一点P ,使得AP +PB 最小.
作法:如图.作点A 关于直线l 的对称点A ’,连结A 'B ,与直线,的交点就是点P
2.已知:在直线l 同侧有A ,B 两点,在l 上找一点P ,使得|AP -PB |最小作法:如图,连结AB ,作线段AB 的垂甫平分线.与直线l 的交点就是点P
3.已知:在直线l 同侧有A ,B 两点,在l 上找一点P .使得|AP -PB |最大
作法:如图,连结BA 并延长,与直线,的交点就是点P
A B
l
B A
P
l
A '
A
B
l A B
l P
A B
l
l A B
P。
轴对称解决实际问题(最短路程)(超经典、超全)

轴对称解决实际问题(最短路程问题)(1)利用轴对称解决几何极值问题仅仅是轴对称应用的一个方面,比较典型的是平面镜成像、光的反射等问题也经常用到轴对称。
(2)解决实际问题的关键是把这个实际问题抽象或转化为一个数学模型,然后通过对这个数学模型的研究来解决这个实际问题。
(3)在证明最大、最小这类问题时,常常采用任意另选一个,通过与要求证的那个“最大”或“最小”的量进行比较来证明。
问题1(分析1)如何用数学的方法解决这个问题?把这条河抽象为一条直线,而把将军的出发地(山脚)和宿营地分别看作直线同侧的两个点,建立几何模型,(如图①)把实际问题转换成“在已知直线上找一点,使它到直线同侧的两点的距离之和最小”的数学问题。
(分析2)连结AB ,作AB 的垂直平分线交直线a 于P 点,根据线段的垂直平分线的性质定理有PA =PB ,此时PA +PB 是否最短?(如图②) (用几何画板的度量及计算功能否定这种作法)(分析3)作A 点关于直线a 的对称点A ′连结P A ′,由轴对称的性质知PA =PA ′,那么PA +PB =PA ′+PB ,P 点在何处PA ′+PB 最短?(如图③)由一名学生上讲台拖动P 点,显然当B 、P 、A ′三点共线时PA ′+PB 最短。
探索得出作法:(如图④)(1)作A 点关于直线a 的对称点A ′. (2)连结BA ′,交直线a 于P 点. P 点即为所求。
如何证明? (分析4)在直线a 上另取一点P ′,连结PA 、A P ′、B P ′、 P ′A ′,(如图⑤)要证PA +PB 最小,由任意性, 只要证 :PA +PB <A P ′+B P ′, 由对称性可知:PA =PA ′, P ′A =P ′A ′只要证:PA ′+PB <P ′A ′+B P ′只要证: A ′B <P ′A ′+B P ′而△BA ′P ′中,有三角形两边之和大于第三边,问题得证。
a · · B A 图① a · · B A 图② P a · · B A 图③ A ′ · · P a · · B A 图④ A ′ · P a · ·B A 图⑤A ′ · P P ′问题2、如图,已知牧马营地在P 处,牧童每天要赶着马群先到河边饮水,再到草地吃草,然后回到营地,试设计出最短的放牧路线。
中考数学 轴对称及路径最短问题

轴对称及最短路径问题一、知识讲解1.轴对称、轴对称图形(1)轴对称图形:如果一个图形沿某条直线对折,对折的两部分是完全重合的,那么就称这样的图形为轴对称图形,这条直线称为对称轴。
对称轴一定为直线。
(2)轴对称:把一个图形沿着某一条直线翻折过去,如果它能与另一个图形重合,那么称这两个图形成轴对称。
两个图形中的对应点(即两个图形重合时互相重合的点)叫对称点。
2.轴对称图像的性质(1)对应线段相等,对应角相等;对称点的连线被对称轴垂直平分。
轴对称图形变换的特征是不改变图形的形状和大小,只改变图形的位置。
新旧图像具有对称性。
(2)轴对称的两个图形,它们对应线段或延长线相交,交点在对称轴上。
3.等腰三角形(1)性质:①两底角相等。
②顶角的角平分线、底边上的中线、底边上的高互相重合。
(2)判定:①有两条边相等的三角形是等腰三角形(定义);②有两个角相等的三角形是等腰三角形。
4.等边三角形(1)性质:①等边三角形各边都相等;②等边三角形各角都相等,并且都等于60°。
(2)判定:①三条边都相等的三角形是等边三角形。
②三个角都相等的三角形是等边三角形。
③有一个角是60°的等腰三角形是等边三角形。
5.特殊直角三角形(补充)(1)含30°的直角三角形中,30°角所对的边等于斜边一半,且三边长度比为1:2;(2)等腰直角三角形各边长比为1:1。
二、要点补充轴对称是关于某一直线对称的图形,要注意图形中隐藏的条件,要将分散的条件集中起来达到解题的目的。
本讲的学习要特别注意分类讨论思想及转化思想的运用。
要点1在平面直角坐标系中,若已知A、B两点的坐标(或位置)要求第三个点C,使得A、B、C三点构成等腰三角形的方法如下:①连接AB,以点A(或点B)为圆心,线段AB的长度为半径作圆,圆周上除点B(或点A)的所有的点,都可以与点A、点B构成等腰三角形。
②连接AB,作线段AB的垂直平分线l,该垂直平分线l上除该线与线段AB交点外的所有的点都能与点A、点B构成等腰三角形。
(完整版)利用轴对称求最短距离
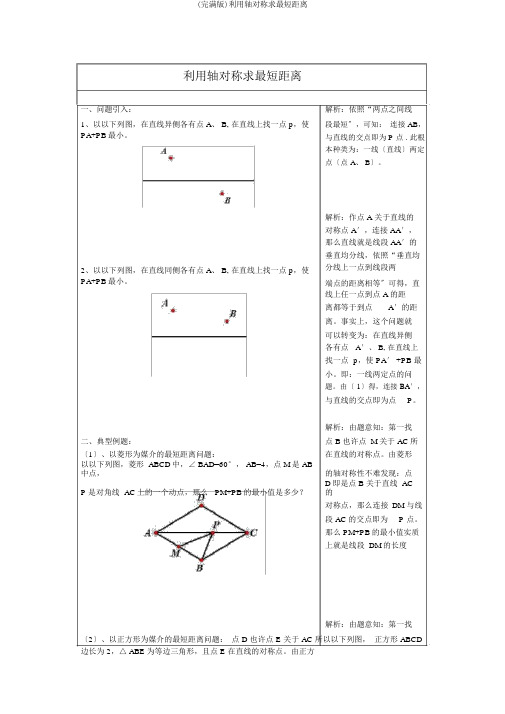
利用轴对称求最短距离一、问题引入:1、以以下列图,在直线异侧各有点 A、 B, 在直线上找一点 p,使PA+PB最小。
2、以以下列图,在直线同侧各有点 A、 B, 在直线上找一点 p,使PA+PB最小。
解析:依照“两点之间线段最短〞,可知:连接 AB,与直线的交点即为 P 点 . 此根本种类为:一线〔直线〕两定点〔点 A、 B〕。
解析:作点 A 关于直线的对称点 A′,连接 AA′,那么直线就是线段 AA′的垂直均分线,依照“垂直均分线上一点到线段两端点的距离相等〞可得,直线上任一点到点 A 的距离都等于到点A′的距离。
事实上,这个问题就可以转变为:在直线异侧各有点A′、 B, 在直线上找一点 p,使 PA′ +PB 最小。
即:一线两定点的问题。
由〔 1〕得,连接 BA′,与直线的交点即为点P。
解析:由题意知:第一找二、典型例题:点 B 也许点 M关于 AC所〔1〕、以菱形为媒介的最短距离问题:在直线的对称点。
由菱形以以下列图,菱形 ABCD中,∠ BAD=60°, AB=4,点 M是 AB中点,的轴对称性不难发现:点P 是对角线 AC上的一个动点,那么 PM+PB的最小值是多少?D即是点 B 关于直线 AC的对称点,那么连接DM 与线段 AC 的交点即为P 点。
那么 PM+PB的最小值实质上就是线段 DM的长度解析:由题意知:第一找〔2〕、以正方形为媒介的最短距离问题:点 D 也许点 E 关于 AC 所以以下列图,正方形 ABCD 边长为 2,△ ABE为等边三角形,且点 E 在直线的对称点。
由正方在正方形ABCD内部,在对角线 AC上找一点 P,使 PD+PE最小,形的轴对称性不难发现:那么这个最小值为多少?点 B 即是点 D关于直线 AC的对称点,那么连接BE 与线段 AC的交点即为P 点。
那么 PD+PE的最小值实质上就是线段BE 的长度,BE=2。
〔3〕、以圆为媒介的最短距离问题:以以下列图,⊙ O的半径为2,点 A、 B、 C 在⊙ O上,OA⊥ OB,∠AOB=60°, P 是 OB上一动点,求PA+PC的最小值解析:由题意知:第一找点 A也许点 C关于 OB所在直线的对称点。
轴对称--最短路径

轴对称--最短路径问题
解题思路:(1)作两点任意一点的对称点
(2)将对称点与另一点进行连线,连线与原直线的交点为动点的位置
(3)对称点与另一点连线的线段长度是所求线段之和的最小值(依据是“两点间线段最短”和“垂直平分线上的点到线段两端点的距离相等”)
一、两点在直线同侧模型
例题1..如图,A为马棚,B为帐篷,牧马人某一天要从马棚牵出马,到河边给马喝水,然后回到帐篷请你帮助他确定这一天的最短路线。
变式1.(2008•深圳)要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短?小聪根据实际情况,以街道旁为x轴,建立了如图所示的平面直角坐标系,测得A点的坐标为(0,3),B点的坐标为(6,5),则从A、B两点到奶站距离之和的最小值是.
变式2..如图,在正方形ABCD中,AD=8,DM=2,N是AC上一动点,求DN+MN的最小值
变式3.如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为.
变式4.(2009•陕西)如图,在锐角△ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是.。
考点13 轴对称-最短路径问题(解析版)

考点13 轴对称——最短路径问题一.选择题(共12小题)1.(2020·四川成都)如图,30AOB ∠=︒,M ,N 分别是边,OA OB 上的定点,P ,Q 分别是边,OB OA 上的动点,记,OPM OQN αβ∠=∠=,当MP PQ QN ++的值最小时,关于α,β的数量关系正确的是( )A .60βα-=︒B .210βα+=︒C .230βα-=︒D .2240βα+=︒【答案】B【解析】 如图,作M 关于OB 的对称点M ',N 关于OA 的对称点N ',连接M N ''交OA 于Q ,交OB 于P ,则此时MP PQ QN ++的值最小.易知'∠=∠=∠OPM OPM NPQ ,'∠=∠=∠OQP AQN AQN .∵18030∠=︒-︒-∠OQN ONQ ,30∠=∠=︒+∠OPM NPQ OQP30∠=∠=︒+∠OQP AQN ONQ ,∵303018030210+=︒+︒+∠+︒-︒-∠=︒ONQ ONQ αβ.故选:B.【点睛】本题考查轴对称-最短问题、三角形的内角和定理.三角形的外角的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.2.(2020·银川)如图,直线m 表示一条河,M ,N 表示两个村庄,欲在m 上的某处修建一个给水站,向两个村庄供水,现有如图所示的四种铺设管道的方案,图中实线表示铺设的管道,则所需管道最短的方案是( )A .B .C .D .【答案】D【解析】作点M 关于直线m 的对称点M ',连接NM '交直线m 于P ,则P 处即为给水站位置.根据“两点之间,线段最短”可排除A 、B 、C 选项,可知D 选项管道最短.故选:D .3.(2020·河北武安期末)如图,∵ABC 中,AB=AC=10,BC=16,AD 是BC 边上的中线且AD=6,F 是AD 上的动点,E 是AC 边上的动点,则CF EF +的最小值是( ).A .485B .16C .6D .10【答案】A【解析】解:如下图所示,作BG∵AM 于M ,交AD 于F ,∵∵ABC 中,AB=AC=10,AD 是BC 边上的中线,∵∵ABC 是等腰三角形,AD BC ⊥,BD=DC ,∵ AD 是BC 的垂直平分线,∵ BF=CF .则BF EF +有最小值时,CF EF +有相同的最小值.根据垂线段最短可得出CF EF +=BF EF +≥=BF FM BM +,则CF EF +取最小值时,=CF EF BM +.根据三角形的面积公式,可得:11==22ABC S AD BC AC BM ⨯⨯△,解得:48=5BM , 即CF EF +的最小值为485. 故答案选:A .4.(2020·河南永城)如图,在Rt ABC △中,90C ∠=︒,30B ∠=︒,点D 、E 分别在边AC 、AB 上,14AD =,点P 是边BC 上一动点,当PD PE +的值最小时,15AE =,则BE 为( )A .30B .29C .28D .27【答案】B【解析】 如图,延长AC 至点M ,使CM CD =,过点M 作ME AB ⊥于点E ,交BC 于点P ,则此时PD PE +的值最小.在Rt ABC △中,30B ∠=︒,60A ∴∠=︒.ME AB ⊥,90AEM ∴∠=︒,90A M ∴∠+∠=︒,90M ∴∠=︒.15AE =,230AM AE ∴==.AM AD DM =+,14AD =,16DM ∴=.CM CD =,8CD CM ∴==,22AC AD CD ∴=+=.在Rt ABC △中,30B ∠=︒,244AB AC ∴==.AB AE BE =+,15AE =,29BE ∴=.故选B.5.(2020·山西孝义)如图,等腰ABC ∆中,=⊥AB AC AD BC ,EF 垂直平分AB ,交AB 于点E ,交BC 于点F ,点G 是线段EF 上的一动点,若ABC ∆的面积是26cm ,6BC cm =,则ADG ∆的周长最小值是( )A .4.5cmB .5cmC .5.5cmD .6cm【答案】B【解析】解:如图,连接BG .∵AB=AC ,AD∵BC ,6BC cm∵BD=DC=3cm ,∵S ∵ABC =12•BC•AD=6, ∵AD=2,∵EF 垂直平分AB ,∵BG=AG ,∵AG+DG=BG+GD ,∵BG+GD≥BD ,,∵GA+GD≥3,∵GA+GD 的最小值为3,∵∵ADG 的最小值为2+3=5,故选:B .【点睛】本题考查轴对称-最短问题,线段的垂直平分线的性质,等腰三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.6.(2020·安徽利辛月考)已知点M(-4,2),若点N 是y 轴上一动点,则M ,N 两点之间的距离最小值为( )A .-4B .2C .4D .-2【答案】C【解析】解:过直线外一点,到直线上的所有点的连线中,垂线段最短∵点N在y轴上的纵坐标为2,此时二者之间的距离最小值为0-(-4)=4故选C7.(2020·安徽安庆期末)如图,∵MON=45°,P为∵MON内一点,A为OM上一点,B为ON上一点,当PAB的周长取最小值时,∵APB的度数为( )A.80°B.90°C.110°D.120°【答案】B【解析】作出P点关于OM、ON的对称点A′、B′,然后连接A′B′∵点A′与点P关于直线OM对称,点B′与点P关于ON对称∵A′P∵OM,B′P∵ON,A′A=AP,B′B=BP∵∵A′=∵APA′,∵B′=∵BPB′∵A′P∵OM,B′P∵ON,∵∵MON+∵A′P B′=180°∵∵A′P B′=180°-45°=135°在∵A′B′P中,由三角形的内角和定理可知:∵A′+∵B′=180°-135°=45°∵∵A′PA+∵BP B′=45°∵∵APB=135°-45°=90°故答案选择:B=,AD、BE分别是底边BC和8.(2020·山西文水期末)如图,在∵ABC中,AB AC+的最小值等于()腰AC上的中线,点P为AD上一动点,则PE PCA.线段AB的长B.线段BC的长C.线段AD的长D.线段BE的长【答案】D【解析】解:如图,连接BP,则PE+PC=PE+BP,所以BE就是PE+PC的最小值,故选D.9.(2020·辽宁连山期中)如图,等腰∵ABC的底边BC长为6,面积是36,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则∵CDM周长的最小值为()A.6B.10C.15D.16【答案】C【解析】如图:连接AD交EF于点M,∵等腰∵ABC的底边BC长为6,点D为BC边的中点,∵AD∵BC,BD=CD=3,∵EF是腰AC的垂直平分线,连接CM,∵AM=CM,此时∵CDM的周长为:CM+DM+CD=AM+DM+CD=AD+CD CD的长为3固定,∵根据两点之间线段最短,∵CDM的周长最小.∵S∵ABC=12 BC•AD,∵12×6•AD=36,∵AD=12,∵AD+CD=12+3=15.故选:C.10.(2020·山西平遥月考)如图,等腰ABC∆的面积为9,底边BC的长为3,腰AC的垂直平分线EF分别交AC、AB边于点E、F,点D为BC边的中点,点M为直线EF上一动点,则DM CM+的最小值为()A.12B.9C.6D.3【答案】C【解析】∵∵ABC是等腰三角形,点D是BC的中点∵AD∵BC∵AD=6∵EF是线段AC的垂直平分线∵点C关于直线EF的对称点为A∵AD的长为CM+MD的最小值∵CM+MD的最小值为6故答案选择:C.11.(2020·山东武城期中)如图,∵AOB=30°,∵AOB内有一定点P,且OP=10.在OA上有一点Q,OB上有一点R.若∵PQR周长最小,则最小周长是()A.10B.15C.20D.30【答案】A【解析】设∵POA=θ,则∵POB=30°﹣θ,作PM∵OA与OA相交于M,并将PM延长一倍到E,即ME=PM.作PN∵OB与OB相交于N,并将PN延长一倍到F,即NF=PN.连接EF与OA相交于Q,与OB相交于R,再连接PQ,PR,则∵PQR即为周长最短的三角形.∵OA是PE的垂直平分线,∵EQ=QP;同理,OB是PF的垂直平分线,∵FR=RP,∵∵PQR的周长=EF.∵OE=OF=OP=10,且∵EOF=∵EOP+∵POF=2θ+2(30°﹣θ)=60°,∵∵EOF是正三角形,∵EF=10,即在保持OP=10的条件下∵PQR的最小周长为10.故选A.12.(2020·广东期中)如图,在∵ABC中,AB=AC,BC=4,∵ABC的面积是16,AC边的垂直平分线EF分别交AC,AB边于点E,F,若点D为BC边的中点,点M为线段EF上一动点,则∵CDM周长的最小值为()A.4B.5C.10D.8【答案】C【解析】连接AD,AM.∵∵ABC是等腰三角形,点D是BC边的中点,∵AD∵BC,∵S∵ABC=12BC•AD=12×4×AD=16,解得AD=8,∵EF是线段AC的垂直平分线,∵点C关于直线EF的对称点为点A,∵MA=MC,∵AD≤AM+MD,∵AD的长为CM+MD的最小值,∵∵CDM的周长最短=(CM+MD)+CD=AD+12BC=8+12×4=8+2=10.故选C.二.填空题(共6小题)13.(2020·南京师范大学附属中学月考)如图,已知∵MON=40°,P为∵MON内一定点,OM上有一点A,ON上有一点B,当∵P AB的周长取最小值时,∵APB的度数是_____°.【答案】100【解析】分别作点P关于OM、ON的对称点P′、P″,连接OP′、OP″、P′P″,P′P″交OM、ON于点A、B,连接P A、PB,此时∵P AB周长的最小值等于P′P″.由轴对称性质可得,OP′=OP″=OP,∵P′OA=∵POA,∵P″OB=∵POB,∵∵P′OP″=2∵MON=2×40°=80°,∵∵OP′P″=∵OP″P′=(180°﹣80°)÷2=50°,又∵∵BPO=∵OP″B=50°,∵APO=∵AP′O=50°,∵∵APB=∵APO+∵BPO=100°.故答案为100.14.(2020·江苏省靖江市月考)如图,∵ABC中,AB=AC=5,BC=6,AD是BC边上的中线且AD=4,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为_____.【答案】24 5【解析】解:作BM∵AC于M,交AD于F,∵AB=AC=5,BC=6,AD是BC边上的中线,∵BD=DC=3,AD∵BC,AD平分∵BAC,∵B、C关于AD对称,∵BF=CF,根据垂线段最短得出:CF+EF=BF+EF≥BF+FM=BM,即CF+EF≥BM,∵S∵ABC=12×BC×AD=12×AC×BM,∵BM=BC ADAC⨯=645⨯=245,即CF+EF的最小值是245,故答案为:245.15.(2020·南通市月考)如图,在∵ABC中,AD平分∵BAC交BC于点D,点M,N分别是AD和AB上的动点,当S∵ABC=12,AC=8时,BM+MN的最小值等于_____.【答案】3【解析】解:如图,作点B关于AD的对称点B′∵AD是∵BAC的平分线,∵点B关于AD的对称点B′在AC上,过点B′作B′N∵AB于N交AD于M,由轴对称确定最短路线问题,点M即为使BM+MN最小的点,B′N=BM+MN,过点B作BE∵AC于E,∵AC=8,S∵ABC=20,∵12×8•BE=12,解得BE=3,∵AD是∵BAC的平分线,B′与B关于AD对称,∵AB=AB′,∵∵ABB′是等腰三角形,∵B′N=BE=3,即BM+MN的最小值是3.故答案为:3.16.(2020·江苏省锡山高级中学)如图,已知∵AOB的大小为α,P是∵AOB内部的一个定点,且OP=4,点E、F分别是OA、OB上的动点,若∵PEF周长的最小值等于4,则α=_____.【答案】30°【解析】解:如图,作点P关于OA的对称点C,关于OB的对称点D,连接CD,交OA于E,OB 于F.此时,∵PEF的周长最小.连接OC,OD,PE,PF.∵点P与点C关于OA对称,∵OA垂直平分PC,∵∵COA=∵AOP,PE=CE,OC=OP,同理,可得∵DOB=∵BOP,PF=DF,OD=OP.∵∵COA+∵DOB=∵AOP+∵BOP=∵AOB=α,OC=OD=4,∵∵COD=2α.又∵∵PEF的周长=PE+EF+FP=CE+EF+FD=CD=4,∵OC=OD=CD=4,∵∵COD是等边三角形,∵2α=60°,∵α=30°.故答案为30°17.(2020·广东肇庆期中)如图,四边形ABCD中,∵BAD=130°,∵B=∵D=90°,在BC、CD上分别找一点M、N,使∵AMN周长最小时,则∵AMN+∵ANM的度数为.【答案】100°【解析】作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为∵AMN 的周长最小值.作DA延长线AH,∵∵DAB=120°,∵∵HAA′=60°,∵∵AA′M+∵A″=∵HAA′=60°,∵∵MA′A=∵MAA′,∵NAD=∵A″,且∵MA′A+∵MAA′=∵AMN,∵NAD+∵A″=∵ANM,∵∵AMN+∵ANM=∵MA′A+∵MAA′+∵NAD+∵A''=2(∵AA′M+∵A'')=2×60°=120°.故答案为120°.18.(2020·广西青秀期中)如图,等腰∵ABC中,AB=AC=4,BC=6,∵ABD是等边三角形,点P是∵BAC的角平分线上一动点,连PC、PD,则PD+PC的最小值为_____.【答案】4【解析】如图,连接BP,∵点P是∵BAC的角平分线上一动点,AB=AC,∵AP垂直平分BC,∵CP=BP,∵PD+PC=PD+PB,∵当B,P,D在在同一直线上时,BP+PD的最小值为线段BD长,又∵∵ABD是等边三角形,AB=BD=4,∵PD+PC的最小值为4,故答案为4.三.解析题(共6小题)19.(2020·江苏东台月考)如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.(1)在图中画出与∵ABC关于直线l成轴对称的∵A′B′C′;(2)在直线l上找一点P,使PB+PC的长最短.【解析】解:(1)如图所示:∵A′B′C′,即为所求;(2)如图所示:点P即为所求.20.(2020·华东师范大学青岛实验中学期中)如图,在∵ABC中,AB=10,BC=12,BC 边上的中线AD=8.(1)证明:∵ABC为等腰三角形;(2)点H在线段AC上,试求AH+BH+CH的最小值.【答案】(1)证明见解析;(2)19.6【解析】(1)证明:∵AD是BC边上的中线,∵BD=DC=6,∵AB=10,BD=6,AD=8,∵BD 2+AD 2=62+82=102,∵∵ABD 是直角三角形,∵AD∵BC ,∵AD∵BC ,BD=DC ,∵AB=AC ,∵∵ABC 是等腰三角形.(2)解:∵AH+BH+CH=BH+AC=BH+10,∵当BH 最小时,AH+BH+HC 有最小值,由垂线段的性质可知:当BH∵AC 时,BH 有最小值, ∵1122BH AC BC AD ⨯⨯=⨯⨯, ∵111012822BH ⨯⨯=⨯⨯, ∵BH=9.6,∵AH+BH+HC 的最小值为:10+9.6=19.6.21.(2020·山东高唐期中)如图,在锐角ABC 中,7AC cm =,221ABC S cm =,AD 平分BAC ∠,M N 、分别是AD 和AB 上的动点,求BM MN +的最小值并说明理由.【答案】6cm【解析】解:如图,作N 关于AD 对称点为R ,作AC 边上的高BE (E 在AC 上), AD 平分CAB ∠,ABC 为锐角三角形,R ∴必在AC 上, N 关于AD 的对称点为R ,MR MN ∴=,BM MN BM MR ∴+=+,即BM MN BR BE +=≥(垂线段最短), ABC 的面积是221cm ,7AC =,17212BE ∴⨯⨯=, 6BE ∴=,即BM MN +的最小值为6cm .22.(2020·辽宁连山期中)如图,四边形ABCD 中,∵BAD =110°,∵B =∵D =90°,在BC ,CD 上分别找一点M ,N ,使∵AMN 周长最小,请在图中画出∵AMN ,写出画图过程并直接写出∵MAN 的度数.【答案】作图见解析,∵MAN的度数为40°.【解析】解:如图所示:作点A关于BC和DC的对称点E和F,连接EF,与BC和DC相交于点M和N,连接AM和AN,根据对称性得:AM=EM,AN=FN,AM+AN+MN=EM+FN+MN=EF,根据两点之间线段最短,此时∵AMN的周长最小,∵∵BAD=110°,∵∵E+∵F=180°﹣110°=70°,∵∵EAM+∵F AN=70°,∵∵MAN=∵EAF-(∵EAM+∵F AN)=40°.答:∵MAN的度数为40°.23.(2020·浙江萧山月考)已知点C为线段AB上一点,分别以AC、BC为边在线段AB同侧作∵ACD和∵BCE,且CA=CD,CB=CE,∵ACD=∵BCE,直线AE与BD交于点F,(1)如图1,若∵ACD=60°,则∵AFB=;如图2,若∵ACD=90°,则∵AFB=;如图3,若∵ACD=120°,则∵AFB=;(2)如图4,若∵ACD=α,则∵AFB=(用含α的式子表示);(3)将图4中的∵ACD绕点C顺时针旋转任意角度(交点F至少在BD、AE中的一条线段上),变成如图5所示的情形,若∵ACD=α,则∵AFB与α的有何数量关系?并给予证明.【答案】(1)120°,90°,60°;(2)180°﹣α;(3)∵AFB=180°﹣α,证明详见解析.【解析】解:(1)如图1,CA=CD,∵ACD=60°,所以∵ACD是等边三角形.∵CB=CE,∵ACD=∵BCE=60°,所以∵ECB是等边三角形.∵AC=DC,∵ACE=∵ACD+∵DCE,∵BCD=∵BCE+∵DCE,又∵∵ACD=∵BCE,∵∵ACE=∵BCD.∵AC=DC,CE=BC,∵∵ACE∵∵DCB.∵∵EAC=∵BDC.∵AFB是∵ADF的外角.∵∵AFB=∵ADF+∵FAD=∵ADC+∵CDB+∵FAD=∵ADC+∵EAC+∵FAD=∵ADC+∵DAC=120°.如图2,∵AC=CD,∵ACE=∵DCB=90°,EC=CB,∵∵ACE∵∵DCB.∵∵AEC=∵DBC,又∵∵FDE=∵CDB,∵DCB=90°,∵∵EFD=90°.∵∵AFB=90°.如图3,∵∵ACD=∵BCE,∵∵ACD﹣∵DCE=∵BCE﹣∵DCE.∵∵ACE=∵DCB.又∵CA=CD,CE=CB,∵∵ACE∵∵DCB.∵∵EAC=∵BDC.∵∵BDC+∵FBA=180°﹣∵DCB=180°﹣(180﹣∵ACD)=120°,∵∵FAB+∵FBA=120°.∵∵AFB=60°.故填120°,90°,60°.(2)∵∵ACD=∵BCE,∵∵ACD+∵DCE=∵BCE+∵DCE.∵∵ACE=∵DCB.∵∵CAE=∵CDB.∵∵DFA=∵ACD.∵∵AFB=180°﹣∵DFA=180°﹣∵ACD=180°﹣α.(3)∵AFB=180°﹣α;证明:∵∵ACD=∵BCE=α,则∵ACD+∵DCE=∵BCE+∵DCE,即∵ACE=∵DCB.在∵ACE和∵DCB中,则∵ACE∵∵DCB(SAS).则∵CBD=∵CEA,由三角形内角和知∵EFB=∵ECB=α.∵AFB=180°﹣∵EFB=180°﹣α.24.(2020·上海同济大学附属实验中学月考)已知:在ABC中,AB=AC,点E在AB上,以BE为底边作等腰DBE,取CE的中点为G,连接AG、DG.(1)如图1,若BE=AE,∵BDE=120°,∵BAC=60°,求证:AG∵DG;(2)如图2,若BE≠AE ,∵BDE +∵BAC=180°,则(1)中结论仍然成立吗?说明理由.【答案】(1)证明见解析;(2)(1)中结论AG DG ⊥仍然成立,理由见解析.【解析】解:(1)如图,延长DG 至H ,使,DG GH = 连接,,AD AH G 为CE 的中点,,EG CG ∴=,EGD CGH ∠=∠,EGD CGH ∴≌,,ED CH DEG GCH ∴=∠=∠等腰DBE ,BE 为底边,120,BDE ∠=︒,BD DE ∴= 30,DBE DEB ∠=∠=︒ BD CH ∴=,,60,AB AC BAC =∠=︒ABC ∴为等边三角形,,BE AE =,30,CE AB ACE BCE ∴⊥∠=∠=︒ 60,DEG HCG ∴∠=∠=︒30,ACH ∴∠=︒在ABD △与ACH 中,,30AB AC ABD ACH BD CH =⎧⎪∠=∠=︒⎨⎪=⎩,ABD ACH ∴≌,AD AH ∴=,DG GH =.AG DG ∴⊥(2)(1)中结论AG DG ⊥成立,理由如下: 如图,延长DG 至H ,使,DG GH = 连接,,AD AH G 为CE 的中点,,EG CG ∴=,EGD CGH ∠=∠,EGD CGH ∴≌,,ED CH DEG GCH ∴=∠=∠等腰DBE ,BE 为底边,设,BDE α∠=1,90,2BD DE DBE DEB α∴=∠=∠=︒- 180,BDE BAC ∠+=︒180,BAC α∴∠=︒-,AB AC =1,2ABC ACB α∴∠=∠=119090,22DBC ααα⎛⎫∴∠=-︒-=-︒ ⎪⎝⎭ 180,BEC EBC C ∠+∠+∠=︒ 1190180,22DEG BCE αα∴+︒-+∠+∠=︒ 90,DEG BCE ∴∠+∠=︒90,HCG BCE ∴∠+∠=︒190,2ACH ABD α∴∠=︒-=∠ 同(1)可得:,ABD ACH ≌ ,AD AH ∴=,DG GH =.AG DG ∴⊥。
中考专题复习——最短路径问题(有答案)

--B CD AL 中考专题复习——路径最短问题一、具体内容包括:蚂蚁沿正方体、长方体、圆柱、圆锥外侧面吃食问题; 线段(之和)最短问题;二、原理:两点之间,线段最短;垂线段最短。
(构建“对称模型”实现转化) 三、例题:例1、①如右图是一个棱长为4的正方体木块,一只蚂蚁要从木块的点A沿木块侧面爬到点B 处,则它爬行的最短路径是 。
②如右图是一个长方体木块,已知AB=3,BC=4,CD=2,假设一只蚂蚁在点A 处,它要沿着木块侧面爬到点D 处,则蚂蚁爬行的最短路径是 。
例2、①如图,要在河边修建一个水泵站,分别向张村、李庄送水,水泵站修在河边什么地方可使所用的水管最短。
②如图,直线L 同侧有两点A 、B,已知A 、B 到直线L的垂直距离分别为1和3,两点的水平距离为3,要在直线L 上找一个点P ,使P A+PB 的和最小。
请在图中找出点P的位置,并计算PA+PB 的最小值。
③要在河边修建一个水泵站,向张村、李庄铺设管道送水,若张村、李庄到河边的垂直距离分别为1Km 和3Km,张村与李庄的水平距离为3Km ,则所用水管最短长度为 。
张村李庄ABCD 图(2)ED ACP图(3)D OP四、练习题(巩固提高)(一)1、如图是一个长方体木块,已知AB=5,B C=3,CD=4,假设一只蚂蚁在点A处,它要沿着木块侧面爬到点D 处,则蚂蚁爬行的最短路径是 。
2、现要在如图所示的圆柱体侧面A 点与B 点之间缠一条金丝带(金丝带的宽度忽略不计),圆柱体高为6cm,底面圆周长为16cm ,则所缠金丝带长度的最小值为 。
3、如图是一个圆柱体木块,一只蚂蚁要沿圆柱体的表面从A 点爬到点B处吃到食物,知圆柱体的高为5 c m,底面圆的周长为24c m,则蚂蚁爬行的最短路径为 。
4、正方形AB CD 的边长为8,M 在D C上,且DM=2,N是AC 上的一动点,D N+MN 的最小值为 。
第4题 第5题 第6题 第7题 5、在菱形A BCD 中,AB=2, ∠BAD=60°,点E 是AB 的中点,P 是对角线AC 上的一个动点,则PE+PB 的最小值为 。
中考数学高频考点突破——轴对称的应用——最短距离问题

中考数学高频考点突破——轴对称的应用——最短距离问题一、综合题1.已知二次函数y =﹣x 2+bx+c 的图象经过点A (2,0),B (5,0),过点D (0, 54)作y 轴的垂线DP 交图象于E 、F .(1)求b 、c 的值和抛物线的顶点M 的坐标;(2)求证:四边形OAFE 是平行四边形;(3)将抛物线向左平移的过程中,抛物线的顶点记为M′,直线DP 与抛物线的左交点为E′,连接OM′,OE′,当OE′+OM′的值最小时求直线OE′的解析式. 2.(1)问题提出:如图①在 ABC 中, AD 是 ABC 边 BC 的高,点E 是 BC 上任意一点,若 3,AD = 则 AE 的最小值为_ ;(2)如图②,在等腰 ABC 中, ,120,AB AC BAC DE =∠=︒ 是 AC 的垂直平分线,分别交 BC AC 、 于点 D E 、 , 1DE cm = ,求 ABD 的周长;(3)问题解决:如图③,某公园管理员拟在园内规划一个 ABC 区域种植花卉,且为方便游客游览,欲在各顶点之间规划道路 AB BC 、 和 AC ,满足 90,BAC ∠=︒ 点 A 到 BC 的距离为 2km .为了节约成本,要使得 ,,AB BC AC 之和最短,试求AB BC AC ++ 的最小值(路宽忽略不计).3.(1)【问题提出】如图1,在矩形ABCD 中, 10AD = , 12AB = ,点E 为AD 的中点,点P 为矩形ABCD 内以BC 为直径的半圆上一点,则PE 的最小值为 ;(2)【问题探究】如图2,在ABC 中,AD 为BC 边上的高,且 4AD BC == ,点P 为 ABC 内一点,当 12PBC ABC S S = 时,求 PB PC + 的最小值;(3)【问题解决】李伯伯家有一块直角三角形菜园ABC ,如图3, 2003BC = 米,90C ∠=︒ , 60ABC ∠=︒ ,李伯伯准备在该三角形菜园内取一点P ,使得120APB ∠=︒ ,并在 ABP 内种植当季蔬菜,边BC 的中点D 为菜园出入口,为了种植方便,李伯伯打算在AC 边上取点E ,并沿PE 、DE 修两条人行走道,为了节省时间,要求人行走道的总长度( PE DE + )尽可能小,问 PE DE + 的长度是否存在最小值?若存在,求出其最小值;若不存在,请说明理由.4.如图1,已知直线l 的同侧有两个点A ,B ,在直线l 上找一点P ,使P 点到A ,B 两点的距离之和最短的问题,可以通过轴对称来确定,即作出其中一点关于直线l 的对称点,对称点与另一点的连线与直线l 的交点就是所要找的点,通过这种方法可以求解很多问题(1)如图2,在平面直角坐标系内,点A 的坐标为(1,1),点B 的坐标为(5,4),动点P 在x 轴上,求PA+PB 的最小值;(2)如图3,在锐角三角形ABC 中,AB=8,∠BAC=45°,∠BAC 的角平分线交BC 于点D ,M 、N 分别是AD 和AB 上的动点,则BM+MN 的最小值为(3)如图4,∠AOB=30°,OC=4,OD=10,点E ,F 分别是射线OA ,OB 上的动点,则CF+EF+DE 的最小值为 。
第十三章 轴对称知识 课题学习 最短路径问题

的和最小.(画出图形,不写作法,保留作图痕迹)
图13-4-4
图13-4-3
解:如图13-4-4,以直线 l1 为对称轴作点A的对称点M, 以直线 l 2 为对称轴作点A的对称点N,连接MN,分别
A2 即为所求. 交 l1 , l 2 于点 A1 , A2 ,则 A1 ,
过两条直线内侧一点,分别作关于两条直线的对称点, 即可得三点所组成的三角形的周长最小.
例1 如图13-4-1,A,B两村合伙在河MN建一座扬水站,要
使所用管道最少,请你帮助他们确定扬水站的位置.(画出图
形,不写作法,保留作图痕迹)
图13-4-1 解:如图13-4-2,点O即为所求.
图13-4-2
例2 如图13-4-3,点A是总邮局,想在公路 l1 上建一分 局 A1 ,在公路 l 2 上建一分局 A2 ,使 AA1 A1 A2 AA2
△PMN的 分别交 l 和 l 2 1 周长最小 于点M,N, 点M,N即为 所求
P′P″,依据是两点
之间,线段最短
问题
类别
问题
作法
图例
思路与依据
在直线
l1 和
分别作点P,
Q关于 l1 和
l 2 上分别找
两线
间两 点 点 M, N, 使四边形 PQNM的周 长最小
通过轴对称把周长最 小问题转化为两点间
A.BM垂直于a
B.AM与BN不平行
C.AN垂直于b
D.AM平行于BN
解析:图13-4-5根据垂线段最短,得出MN是河的宽时最短,
即MN⊥直线a(或直线b),只要AM+BN最短即可.如图13-4-5, 过点A作河的垂线AH,垂足为H,在AH所在直线上取点I, 使AI等于河宽,连接IB交河的b岸于点N,作MN垂直于河岸, 交a岸于点M,连接AM,所得MN即为所求.故选D.
初中数学最短路径问题

初中数学最短路径问题在初中数学中,最短路径问题是经常出现的一类问题,它涉及到轴对称、坐标轴、一次函数、三角函数以及两点之间的距离公式等多个方面。
下面将分别对这些问题进行介绍和解析。
1.轴对称与最短路径轴对称是最基本的一种对称形式,是指在平面内,将一个图形沿一条直线折叠,使得直线两旁的部分能够完全重合。
在最短路径问题中,轴对称可以用来寻找两点之间的最短路径。
例如,在一条直线上有两个点A和B,要求找到A到B的最短路径,可以通过作A关于直线对称的点A',然后连接A'和B,得到的线段A'B就是最短路径。
2.坐标轴上的最短路径在坐标轴上,最短路径问题通常涉及到两点之间的距离。
在x轴和y轴上分别有点A(x1,0)和B(0,y1),那么A到B的最短路径就是在x轴和y轴上分别截取两个点C(x2,0)和D(0,y2),使得AC=BD,那么线段AB就是最短路径。
3.一次函数与最短路径在一次函数中,最短路径问题通常涉及到函数的单调性和最值。
例如,在一条直线上有点A(x1,y1),有点B(x2,y2),要求找到A到B的最短路径,可以通过作A关于直线对称的点A',然后连接A'和B,得到的线段A'B就是最短路径。
在这个过程中,可以运用一次函数的单调性和最值来计算最短路径的长度。
4.三角函数与最短路径在三角函数中,最短路径问题通常涉及到角度和长度之间的关系。
例如,在一张三角形ABC中,有点A(x1,y1),有点C(x2,y2),要求找到A到C的最短路径,可以通过作AB边上的一点D,使得AD=CD,那么线段AD就是最短路径。
在这个过程中,可以运用三角函数的性质和定理来计算最短路径的长度。
5.两点之间距离公式在解决最短路径问题时,常常需要使用两点之间距离公式。
这个公式可以用来计算两点之间的直线距离,也可以用来计算两点之间的曲线距离。
例如,在一张三角形ABC中,有点A(x1,y1),有点C(x2,y2),要求找到A到C的最短路径,可以先运用两点之间距离公式计算出AC的距离,然后根据三角函数的性质和定理来计算出最短路径的长度。
8.3 轴对称之最短路径问题

8.3 轴对称之最短路径问题破解策略最短路径问题通常会转化为“两点之间,线段最短”来解决,而轴对称是实现这一转化的有效方法之一.常见的题型如下.1.两点在一条直线异侧如图,点A ,B 在直线l 的两侧.(1)在直线l 上找一点P ,使得P A +PB 最小.作法:如图,连接AB ,与直线l 的交点即为所求点P .(2)在直线l 上找一点P ,使得PA PB -最小.作法:如图,连接AB ,作AB 的垂直平分线,与直线l 的交点即为所求点P .2.两点在一条直线同侧如图,点A ,B 在直线l 的同侧.(1)在直线l 上找一点P ,使P A +PB 最小.作法:如图,作点B 关于直线l 的对称点B ,连接AB 1,与直线l 的交点即为所求点P .(2)在直线l 上找一点P ,使得PA PB -最小.作法:如图,连接AB ,作AB 的垂直平分线,与直线l 的交点即为所求点P .llll(3)在直线l 上找一点P ,使得PA PB 最大.作法:如图,作:直线AB ,与直线l 的交点即为所求点P .(4)在直线l 上找两点P 、Q (PQ 的长度等于已知线段a 的长度),使得AP +PQ +QB 是最小.作法:如图,先将点B 向若平移a 个单位长度到点B 1,再作B 1关于直线l 的对称点B 2,连接AB 2,与直线l 的交点即为所求点P ,然后将点P 向右平移a 个单位长度,所得点即为点Q .3.一点在角的内部如图,点P 在∠AOB 的内部.(1)分别在边OA ,OB 上确定点M ,N 使得PM +MN +NP 最小.作法,如图,分别作点P 关于OA ,OB 的对称点P 1,P 2,连接P 1P 2,与OA ,OB 的交点即为所求的点M 、N .(2)分别在边OA ,OB 上确定点M ,N ,使得PM +MN 最小.作法:如图,作点P 关于OA 的对称点P 1,过点P 1作OB 的垂线,与OA ,OB 的交点即为所求的点M ,N .ll P al例题讲解例1 如图,A ,B 两点在直线MN 的同侧,AC ∠MN 于点C ,BD ∠MN 于点D ,点P 在直线MN 上运动,若AC =16,BD =10,CD =8,则PA PB -的最大值等于____.分析 显然PA PB -的最大值即为线段AB 的长,只需过点B 作AC 的垂线,构成直角三角形求AB 的长即可.解答例2 如图,等边∠ABC 的面积为P 、Q 、R 分别为边AB ,BC ,AC 上的动点,则PR +QR 的最小值是____.分析 点R 在AC 上,而点P 、Q 在AC 的同侧,故作点P 关于AC 的对称点P ',当点P ',R ,Q 三点共线且P Q '⊥BC 时,PR +QR 取最小值.解答例3 如图,AB ∠BD 于点B ,DE ⊥BD 于点D ,C 为线段BD 上一动点,连接AC ,CE ,已知AB =5,DE =2,BD =12,设CD =x .(1)用含x 的代数式表示AC +CE 的长;(2)求AC +CE 的最小值;ABP C D M NAB CPRQ(3)解答例4 如图,在四边形ABCD 中,∠BAD =120°,∠B =∠D =90°,在BC ,CD 上各找一点,分别为点M ,N ,使得∠AMN 的周长最小,则此时∠AMN +∠ANM 的度数为____.分析 点A 在∠BCD 内部,作点A 关于∠BCD 两边的对称点A 1,A 2,连接A 1A 2,则A 1A 2即为∠AMN 周长的最小值.解答例5 如图,长为1的线段AB 在x 轴上移动,点C (0,1),D (0,2)在y 轴上,则AC +BD 的最小值是____.分析 AB 为x 轴上的定线段,点C ,D 在x 轴同侧,故作点C 关于x 轴的对称点C ',将点D 沿x 轴负方向平移AB 长至点D ',则C D ''的长即为AC +BD 的最小值.解答:例6 如图,∠MON =30°,点A ,D 分别在OM ,ON 上,且OA =2,OD =4,C ,B 分别为OM ,ON 上任意一点,则折线AB -BC -CD 的最短长度为____.分析 线段和差的最值问题通常都转化为“两点之间线段最短”的问题,可利用轴对称将分散的线段变成两定点间的折线,然后再化“折”为“直”即可.解答例7 如图,在△ABC 中,AC ⊥BC ,∠B =30°,E ,F 是线段AB 的三等分点,P ,Q 分别是线段BC ,AC 上的动点,若AC =3,则四边形EPQF 周长的最小值是解答例8 如图,在边长为1的正方形ABCD 中,点E ,F ,G ,H 分别是边AB ,BC ,CD ,DA 上的点,且3AE = EB ,有一只蚂蚁从点E 出发,经过点F ,G ,H ,最后回到点E ,则蚂蚁所走的最短路程是解答进阶训练1.如图1,在Rt △ABC 中,∠ACB =90°,AC =BC =4,D ,E 分别是AB ,AC 的中点,在CD 上找一点P ,使P A +PE 最小,则这个最小值是2.如图2,P 为∠AOB 内部的一点,且OP =2,E ,F 分别是OA ,OB 上的动点,若△PEF 周长的最小值等于2,则∠AOB =3.已知y =y 的最小值是4.如图3,在平面直角坐标系中有四个点A (-6,3),B (-2,5),C (0,m ),D (n ,0),当四边形ABCD 的周长最短时,m +n =5.如图4,在Rt△ABC中,∠ACB=90°,AC=BC=4,∠BAC的平分线交BC于点D,若P,Q分别是AC,AD 上的动点,求CQ+PQ的最小值.6.已知三点A(a,1),B(3,1),C(6,0),且点A在正比例函数12y x的图象上,P为x轴上的动点,当△OAP与△CBP周长之和取最小值时,求点P的坐标.7.如图5,等边△ABC的边长为2,D是边AB的中点,P,Q分别是边BC,AC上的动点,当P,Q的位置在何处时,才能使△DPQ的周长最小?并求出这个最值.8.如图6,正方形ABCD的边长为4,E为边CD的中点,点F在边BC上,且满足BF=3CF,M,N均为对角线BD上的动点,且MN求四边形EMNF周长的最小值.9.如图7,在矩形ABCD中,点E在对角线AC上,满足CE=3AE,P,Q分别为AB,AC上任意的点,若AC=2,BC=1,求折线EP+PQ+QB长的最小值.10.如图8,在平面直角坐标系xOy中,分别以点A(2,3),B(3,4)为圆心,以1,3为半径作⊙A,⊙B ,M,N分别是⊙A,⊙B上的动点,P为x轴上的动点,求PM+PN的最小值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
与轴对称有关的最短路径问题及解析
问题1 相传,古希腊亚历山大里亚城里有一位久负盛名的学者,名叫海伦.有一天,一位将军专程拜访海伦,求教一个百思不得其解的问题:从图中的A 地出发,到一条笔直的河边l 饮马,然后到B 地.到河边什么地方饮马可使他所走的路线全程最短?
解析:将A ,B 两地抽象为两个点,将河l 抽象为一条直 线。
作法:
(1)作点B 关于直线l 的对称点B ′; (2)连接AB ′,与直线l 相交于点C 。
则点C 即为所求。
B
A
l
B • ·
A l
B ·
l
A ·
B C
证明:如图,在直线l 上任取一点C ′(与点C 不重合),连接AC ′,BC ′,B ′C ′。
由轴对称的性质知, BC =B ′C ,BC ′=B ′C ′.
∴ AC +BC = AC +B ′C = AB ′,
AC ′+BC ′= AC ′+B ′C ′. 在△AB ′C ′中,
AB ′<AC ′+B ′C ′,
∴ AC +BC <AC ′+BC ′. 即 AC +BC 最短.
若直线l 上任意一点(与点C 不重合)与A ,B 两点的距离 和都大于AC +BC ,就说明AC + BC 最小.
问题2 如图,一个旅游船从大桥AB 的P 处前往山脚下的Q 处接游客,然后将游客送往河岸BC 上,再返回P 处,请画出旅游船的最短路径。
解析:考点:作图—应用与设计作图,轴对称-最短路线问题 专题:
分析:根据“两点之间线段最短”,和轴对称最短路径问题解答.
B ·
l
A ·
B C
C
解答:解:(1)两点之间,线段最短,连接PQ;
(2)作P关于BC的对称点P1,连接QP1,交BC于M,再连接MP.
最短路线P--Q--M--P.
点评:本题考查了作图--应用与设计作图,熟悉轴对称最短路径问题是解题的关键.
问题3 如图,A.B两地在一条河的两岸,现要在河上建一座桥MN,桥造在何处才能使从A到B的路径AMNB最短?(假设河的两岸是平行的直线,桥要与河垂直)
解析:如图,作BB'垂直于河岸GH,使BB′等于河宽,
连接AB′,与河岸EF相交于M,作MN⊥GH,
则MN∥BB′且MN=BB′,
于是MNBB′为平行四边形,故NB=MB′.
根据“两点之间线段最短”,AB′最短,即AM+BN最短.
问题4已知△ABC中,D、E是边AB、AC边上的点,在边BC上找一点M,使△DEM的周长最小。
解答:如图作D点的对称点D′,连接D′E,角BC与P,
△PDE的周长最小.
问题5 如图,如果我们把台球桌做成等边三角形的形状,那么从AC的中点D处发出的球,能否依次经BC,AB两边反射后回到D处?如果认为不能,请说明理由;如果认为能,请作出球的运动路线。
解析:能,如上图。
E,F分别为AB,BC中点
证明:因为等边△ABC,D,E,F为三边中点
所以,△DEF也是等边△(中位线)。
又因为CE⊥AB,DF∥AB,
所以,CE⊥DF
所以EC平分∠DEF(三线合一)
所以,球沿DE方向入射至AB,出射方向一定是EF,即图中的两个α角。
同理可证沿着EF方向入射至BC,出射方向一定是FD,所以最终回到了D点。
问题6 如图,A为马厩,B为帐篷,牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边饮水,然后回到帐篷,请你帮他确定这一天的最短路线。
问题7 已知,如图,在直线l的同侧有两点A,B.
(1)在图1的直线上找一点P,使PA+PB最短;
(2)在图2的直线上找一点P,使PA-PB最长.
解:(1)作点B关于直线l的对称点C,连接AC交直线l于点P,连接BP.点P即为所求.图略.
(2)连接AB并延长,交直线l于点P.图略.
问题8 如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN周长最小,求∠AMN+∠ANM的度数.
解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,连接AM,AN,则A′A″即为△AMN的周长最小值.作DA延长线AH.
∵∠DAB=120°,
∴∠HAA′=60°.
∴∠A′+∠A″=∠HAA′=60°.
∵∠A′=∠MAA′,∠NAD=∠A″,且∠A′+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠A′+∠MAA′+∠NAD+∠A″=2(∠A′+∠A″)=2×60°=120°.。
